licenses
sequencelengths 1
3
| version
stringclasses 677
values | tree_hash
stringlengths 40
40
| path
stringclasses 1
value | type
stringclasses 2
values | size
stringlengths 2
8
| text
stringlengths 25
67.1M
| package_name
stringlengths 2
41
| repo
stringlengths 33
86
|
|---|---|---|---|---|---|---|---|---|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 21389 | export AffineConstantFlow, AffineHalfFlow, SlowMAF, MAF, IAF, ActNorm,
Invertible1x1Conv, NormalizingFlow, NormalizingFlowModel, NeuralCouplingFlow,
autoregressive_network, FlowOp, LinearFlow, TanhFlow, AffineScalarFlow,
InvertFlow, AffineFlow
abstract type FlowOp end
#------------------------------------------------------------------------------------------
# Users can define their own FlowOp in the Main
forward(fo::T, x::Union{Array{<:Real}, PyObject}) where T<:FlowOp = Main.forward(fo, x)
backward(fo::T, z::Union{Array{<:Real}, PyObject}) where T<:FlowOp = Main.backward(fo, z)
#------------------------------------------------------------------------------------------
mutable struct LinearFlow <: FlowOp
dim::Int64
indim::Int64
outdim::Int64
A::PyObject
b::PyObject
end
@doc raw"""
LinearFlow(indim::Int64, outdim::Int64, A::Union{PyObject, Array{<:Real,2}, Missing}=missing,
b::Union{PyObject, Array{<:Real,1}, Missing}=missing, name::Union{String, Missing}=missing)
LinearFlow(A::Union{PyObject, Array{<:Real,2}},
b::Union{PyObject, Array{<:Real,1}, Missing} = missing; name::Union{String, Missing}=missing)
Creates a linear flow operator,
$$x = Az + b$$
The operator is not necessarily invertible. $A$ has the size `outdim×indim`, $b$ is a length `outdim` vector.
# Example 1: Reconstructing a Gaussian random variable using invertible A
```julia
using ADCME
using Distributions
d = MvNormal([2.0;3.0],[2.0 1.0;1.0 2.0])
flows = [LinearFlow(2, 2)]
prior = ADCME.MultivariateNormalDiag(loc = zeros(2))
model = NormalizingFlowModel(prior, flows)
x = rand(d, 10000)'|>Array
zs, prior_logpdf, logdet = model(x)
log_pdf = prior_logpdf + logdet
loss = -sum(log_pdf)
sess = Session(); init(sess)
BFGS!(sess, loss)
run(sess, flows[1].b) # approximately [2.0 3.0]
run(sess, flows[1].A * flows[1].A') # approximate [2.0 1.0;1.0 2.0]
```
# Example 2: Reconstructing a Gaussian random variable using non-invertible A
```julia
using ADCME
using Distributions
d = Normal()
A = reshape([2. 1.], 2, 1)
b = Variable(ones(2))
flows = [LinearFlow(A, b)]
prior = ADCME.MultivariateNormalDiag(loc = zeros(1))
model = NormalizingFlowModel(prior, flows)
x = rand(d, 10000, 1)
x = x * [2.0 1.0] .+ [1.0 3.0]
x = [2.0 2.0]
zs, prior_logpdf, logdet = model(x)
log_pdf = prior_logpdf + logdet
loss = -sum(log_pdf)
sess = Session(); init(sess)
BFGS!(sess, loss)
run(sess, b[1]*2 + b[2]) # approximate 6.0
```
"""
function LinearFlow(indim::Int64, outdim::Int64, A::Union{PyObject, Array{<:Real,2}, Missing}=missing,
b::Union{PyObject, Array{<:Real,1}, Missing}=missing; name::Union{String, Missing}=missing)
if ismissing(name)
name = randstring(10)
end
if ismissing(A)
if indim==outdim
A = diagm(0=>ones(indim))
A = get_variable(A, name=name*"_A")
else
A = get_variable(Float64, shape=[outdim,indim], name=name*"_A")
end
end
if ismissing(b)
b = get_variable(zeros(1,outdim), name=name*"_b")
end
A = constant(A)
b = constant(b)
b = reshape(b, (1,-1))
if size(A)!=(outdim,indim)
error("Expected A shape: $((outdim,indim)), but got $(size(A))")
end
if size(b)!=(1,outdim)
error("Expected b shape: $((1,outdim)), but got $(size(b))")
end
LinearFlow(outdim, indim, outdim, A, b)
end
function LinearFlow(dim::Int64)
LinearFlow(dim,dim)
end
function LinearFlow(A::Union{PyObject, Array{<:Real,2}},
b::Union{PyObject, Array{<:Real}, Missing} = missing; name::Union{String, Missing}=missing)
outdim, indim = size(A)
if ismissing(b)
b = zeros(outdim)
end
A = constant(A)
b = constant(b)
LinearFlow(outdim, indim, outdim, A, b)
end
function forward(fo::LinearFlow, x::Union{Array{<:Real}, PyObject})
if fo.indim==fo.outdim
return solve_batch(fo.A, x - fo.b), -log(abs(det(fo.A))) * ones(size(x, 1))
else
return solve_batch(fo.A, x - fo.b), -1/2*log(abs(det(fo.A'*fo.A))) * ones(size(x, 1))
end
end
function backward(fo::LinearFlow, z::Union{Array{<:Real}, PyObject})
d = nothing
if fo.indim==fo.outdim
d = log(abs(det(fo.A)))
end
z * fo.A' + fo.b, d
end
#------------------------------------------------------------------------------------------
mutable struct AffineConstantFlow <: FlowOp
dim::Int64
s::Union{Missing,PyObject}
t::Union{Missing,PyObject}
end
function AffineConstantFlow(dim::Int64, name::Union{String, Missing}=missing; scale::Bool=true, shift::Bool=true)
if ismissing(name)
name = randstring(10)
end
s = missing
t = missing
if scale
s = get_variable(Float64, shape=[1,dim], name=name*"_s")
end
if shift
t = get_variable(Float64, shape=[1,dim], name=name*"_t")
end
AffineConstantFlow(dim, s, t)
end
function forward(fo::AffineConstantFlow, x::Union{Array{<:Real}, PyObject})
s = ismissing(fo.s) ? zeros_like(x) : fo.s
t = ismissing(fo.t) ? zeros_like(x) : fo.t
z = x .* exp(s) + t
log_det = sum(s, dims=2)
return z, log_det
end
function backward(fo::AffineConstantFlow, z::Union{Array{<:Real}, PyObject})
s = ismissing(fo.s) ? zeros_like(z) : fo.s
t = ismissing(fo.t) ? zeros_like(z) : fo.t
x = (z-t) .* exp(-s)
log_det = sum(-s, dims=2)
return x, log_det
end
#------------------------------------------------------------------------------------------
mutable struct ActNorm <: FlowOp
dim::Int64
fo::AffineConstantFlow
initialized::PyObject
end
function ActNorm(dim::Int64, name::Union{String, Missing}=missing)
if ismissing(name)
name = "ActNorm_"*randstring(10)
end
initialized = get_variable(1, name = name)
ActNorm(dim, AffineConstantFlow(dim), initialized)
end
function forward(actnorm::ActNorm, x::Union{Array{<:Real}, PyObject})
x = constant(x)
actnorm.fo.s, actnorm.fo.t = tf.cond(tf.equal(actnorm.initialized,constant(0)),
()->(actnorm.fo.s, actnorm.fo.t), #actnorm.fo.s, actnorm.fo.t),
()->begin
setzero = assign(actnorm.initialized, 0)
x0 = copy(x)
s0 = reshape(-log(std(x0, dims=1)), 1, :)
t0 = reshape(mean(-x0 .* exp(s0), dims=1), 1, :)
op = assign([actnorm.fo.s, actnorm.fo.t], [s0, t0])
p = tf.print("ActNorm: initializing s and t...")
op[1] = bind(op[1], setzero)
op[1] = bind(op[1], p)
op[1], op[2]
end)
forward(actnorm.fo, x)
end
function backward(actnorm::ActNorm, z::Union{Array{<:Real}, PyObject})
backward(actnorm.fo, z)
end
#------------------------------------------------------------------------------------------
mutable struct SlowMAF <: FlowOp
dim::Int64
layers::Array{Function}
order::Array{Int64}
p::PyObject
end
function SlowMAF(dim::Int64, parity::Bool, nns::Array)
local order
@assert length(nns)==dim - 1
if parity
order = Array(1:dim)
else
order = reverse(Array(1:dim))
end
p = Variable(zeros(2))
SlowMAF(dim, nns, order, p)
end
function forward(fo::SlowMAF, x::Union{Array{<:Real}, PyObject})
z = tf.zeros_like(x)
log_det = zeros(size(x,1))
for i = 1:fo.dim
if i==1
st = repeat(fo.p', size(x,1), 1)
else
st = fo.layers[i-1](x[:,1:i-1])
@assert size(st, 2)==2
end
s, t = st[:,1], st[:,2]
z = scatter_update(z, :, fo.order[i], x[:, i]*exp(s) + t)
log_det += s
end
return z, log_det
end
function backward(fo::SlowMAF, z::Union{Array{<:Real}, PyObject})
x = tf.zeros_like(z)
log_det = zeros(size(z,1))
for i = 1:fo.dim
if i==1
st = repeat(fo.p', size(x,1), 1)
else
st = fo.layers[i-1](x[:,1:i-1])
end
s, t = st[:,1], st[:,2]
x = scatter_update(x, :, i, (z[:, fo.order[i]] - t) * exp(-s))
log_det += -s
end
return x, log_det
end
#------------------------------------------------------------------------------------------
mutable struct MAF <: FlowOp
dim::Int64
net::Function
parity::Bool
end
function MAF(dim::Int64, parity::Bool, config::Array{Int64}; name::Union{String, Missing} = missing,
activation::Union{Nothing,String} = "relu", kwargs...)
push!(config, 2)
kwargs = jlargs(kwargs)
if ismissing(name)
name = "MAF_"*randstring(10)
end
net = x->autoregressive_network(x, config, name; activation = activation)
MAF(dim, net, parity)
end
function forward(fo::MAF, x::Union{Array{<:Real}, PyObject})
st = fo.net(x)
# @info st, split(st, 1, dims=2)
s, t = squeeze.(split(st, 2, dims=3))
z = x .* exp(s) + t
if fo.parity
z = reverse(z, dims=2)
end
log_det = sum(s, dims=2)
return z, log_det
end
function backward(fo::MAF, z::Union{Array{<:Real}, PyObject})
x = zeros_like(z)
log_det = zeros(size(z, 1))
if fo.parity
z = reverse(z, dims=2)
end
for i = 1:fo.dim
st = fo.net(copy(x))
s, t = squeeze.(split(st, 2, dims=3))
x = scatter_update(x, :, i, (z[:, i] - t[:, i]) * exp(-s[:, i]))
log_det += -s[:,i]
end
return x, log_det
end
"""
autoregressive_network(x::Union{Array{Float64}, PyObject}, config::Array{<:Integer},
scope::String="default"; activation::String=nothing, kwargs...)
Creates an masked autoencoder for distribution estimation.
"""
function autoregressive_network(x::Union{Array{Float64}, PyObject}, config::Array{<:Integer},
scope::String="default"; activation::Union{Nothing,String}="tanh", kwargs...)
local y
x = constant(x)
params = config[end]
hidden_units = PyVector(config[1:end-1])
event_shape = [size(x, 2)]
if haskey(STORAGE, scope*"/autoregressive_network/")
made = STORAGE[scope*"/autoregressive_network/"]
y = made(x)
else
made = ADCME.tfp.bijectors.AutoregressiveNetwork(params=params, hidden_units = hidden_units,
event_shape = event_shape, activation = activation, kwargs...)
STORAGE[scope*"/autoregressive_network/"] = made
y = made(x)
end
return y
end
#------------------------------------------------------------------------------------------
mutable struct IAF <: FlowOp
maf::MAF
end
function IAF(dim::Int64, parity::Bool, config::Array{Int64}; name::Union{String, Missing} = missing,
activation::Union{Nothing,String} = "relu", kwargs...)
MAF(dim, parity, config; name=name, activation=activation, kwargs...)
end
function forward(fo::IAF, x::Union{Array{<:Real}, PyObject})
backward(fo.maf, x)
end
function backward(fo::IAF, z::Union{Array{<:Real}, PyObject})
forward(fo.maf, z)
end
#------------------------------------------------------------------------------------------
mutable struct Invertible1x1Conv <: FlowOp
dim::Int64
P::Array{Float64}
L::PyObject
S::PyObject
U::PyObject
end
function Invertible1x1Conv(dim::Int64, name::Union{Missing,String}=missing)
if ismissing(name)
name = randstring(10)
end
Q = lu(randn(dim,dim))
P, L, U = Q.P, Q.L, Q.U
L = get_variable(L, name=name*"_L")
S = get_variable(diag(U), name=name*"_S")
U = get_variable(triu(U, 1), name=name*"_U")
Invertible1x1Conv(dim, P, L, S, U)
end
function _assemble_W(fo::Invertible1x1Conv)
L = tril(fo.L, -1) + diagm(0=>ones(fo.dim))
U = triu(fo.U, 1)
W = fo.P * L * (U + diagm(fo.S))
return W
end
function forward(fo::Invertible1x1Conv, x::Union{Array{<:Real}, PyObject})
W = _assemble_W(fo)
z = x*W
log_det = sum(log(abs(fo.S)))
return z, log_det
end
function backward(fo::Invertible1x1Conv, z::Union{Array{<:Real}, PyObject})
W = _assemble_W(fo)
Winv = inv(W)
x = z*Winv
log_det = -sum(log(abs(fo.S)))
return x, log_det
end
#------------------------------------------------------------------------------------------
mutable struct AffineHalfFlow <: FlowOp
dim::Int64
parity::Bool
s_cond::Function
t_cond::Function
end
"""
AffineHalfFlow(dim::Int64, parity::Bool, s_cond::Union{Function, Missing} = missing, t_cond::Union{Function, Missing} = missing)
Creates an `AffineHalfFlow` operator.
"""
function AffineHalfFlow(dim::Int64, parity::Bool, s_cond::Union{Function, Missing} = missing, t_cond::Union{Function, Missing} = missing)
if ismissing(s_cond)
s_cond = x->constant(zeros(size(x,1), (dim+1)÷2))
end
if ismissing(t_cond)
t_cond = x->constant(zeros(size(x,1), dim÷2))
end
AffineHalfFlow(dim, parity, s_cond, t_cond)
end
function forward(fo::AffineHalfFlow, x::Union{Array{<:Real}, PyObject})
x = constant(x)
x0 = x[:,1:2:end]
x1 = x[:,2:2:end]
if fo.parity
x0, x1 = x1, x0
end
s = fo.s_cond(x0)
t = fo.t_cond(x0)
z0 = x0
z1 = exp(s) .* x1 + t
if fo.parity
z0, z1 = z1, z0
end
z = [z0 z1]
log_det = sum(s, dims=2)
return z, log_det
end
function backward(fo::AffineHalfFlow, z::Union{Array{<:Real}, PyObject})
z = constant(z)
z0 = z[:,1:2:end]
z1 = z[:,2:2:end]
if fo.parity
z0, z1 = z1, z0
end
s = fo.s_cond(z0)
t = fo.t_cond(z0)
x0 = z0
x1 = (z1-t).*exp(-s)
if fo.parity
x0, x1 = x1, x0
end
x = [x0 x1]
log_det = sum(-s, dims=2)
return x, log_det
end
#------------------------------------------------------------------------------------------
mutable struct NeuralCouplingFlow <: FlowOp
dim::Int64
K::Int64
B::Int64
f1::Function
f2::Function
end
function NeuralCouplingFlow(dim::Int64, f1::Function, f2::Function, K::Int64=8, B::Int64=3)
@assert mod(dim,2)==0
NeuralCouplingFlow(dim, K, B, f1, f2)
end
function forward(fo::NeuralCouplingFlow, x::Union{Array{<:Real}, PyObject})
x = constant(x)
dim, K, B, f1, f2 = fo.dim, fo.K, fo.B, fo.f1, fo.f2
RQS = tfp.bijectors.RationalQuadraticSpline
log_det = constant(zeros(size(x,1)))
lower, upper = x[:,1:dim÷2], x[:,dim÷2+1:end]
f1_out = f1(lower)
@assert size(f1_out,2)==(3K-1)*size(lower,2)
out = reshape(f1_out, (-1, size(lower,2), 3K-1))
W, H, D = split(out, [K, K, K-1], dims=3)
W, H = softmax(W, dims=3), softmax(H, dims=3)
W, H = 2B*W, 2B*H
D = softplus(D)
rqs = RQS(W, H, D, range_min=-B)
upper, ld = rqs.forward(upper), rqs.forward_log_det_jacobian(upper, 1)
log_det += ld
f2_out = f2(upper)
@assert size(f2_out,2)==(3K-1)*size(upper,2)
out = reshape(f2_out, (-1, size(upper,2), 3K -1))
W, H, D = split(out, [K, K, K-1], dims=3)
W, H = softmax(W, dims=3), softmax(H, dims=3)
W, H = 2B*W, 2B*H
D = softplus(D)
rqs = RQS(W, H, D, range_min=-B)
lower, ld = rqs.forward(lower), rqs.forward_log_det_jacobian(lower, 1)
log_det += ld
return [lower upper], log_det
end
function backward(fo::NeuralCouplingFlow, x::Union{Array{<:Real}, PyObject})
x = constant(x)
dim, K, B, f1, f2 = fo.dim, fo.K, fo.B, fo.f1, fo.f2
RQS = tfp.bijectors.RationalQuadraticSpline
log_det = constant(zeros(size(x,1)))
lower, upper = x[:,1:dim÷2], x[:,dim÷2+1:end]
f2_out = f2(upper)
@assert size(f2_out,2)==(3K-1)*size(upper,2)
out = reshape(f2_out, (-1, size(upper,2), 3K-1))
W, H, D = split(out, [K, K, K-1], dims=3)
W, H = softmax(W, dims=3), softmax(H, dims=3)
W, H = 2B*W, 2B*H
D = softplus(D)
rqs = RQS(W, H, D, range_min=-B)
lower, ld = rqs.inverse(lower), rqs.inverse_log_det_jacobian(lower, 1)
log_det += ld
f1_out = f1(lower)
@assert size(f1_out,2)==(3K-1)*size(lower,2)
out = reshape(f1_out, (-1, size(lower,2), 3K -1))
W, H, D = split(out, [K, K, K-1], dims=3)
W, H = softmax(W, dims=3), softmax(H, dims=3)
W, H = 2B*W, 2B*H
D = softplus(D)
rqs = RQS(W, H, D, range_min=-B)
upper, ld = rqs.inverse(upper), rqs.inverse_log_det_jacobian(upper, 1)
log_det += ld
return [lower upper], log_det
end
#------------------------------------------------------------------------------------------
mutable struct TanhFlow <: FlowOp
dim::Int64
o::PyObject
end
function TanhFlow(dim::Int64)
TanhFlow(dim, tfp.bijectors.Tanh())
end
function forward(fo::TanhFlow, x::Union{Array{<:Real}, PyObject})
fo.o.forward(x), fo.o.forward_log_det_jacobian(x, 1)
end
function backward(fo::TanhFlow, z::Union{Array{<:Real}, PyObject})
fo.o.inverse(z), fo.o.inverse_log_det_jacobian(z, 1)
end
#------------------------------------------------------------------------------------------
mutable struct AffineScalarFlow <: FlowOp
dim::Int64
o::PyObject
end
function AffineScalarFlow(dim::Int64, shift::Float64 = 0.0, scale::Float64 = 1.0)
AffineScalarFlow(dim, tfp.bijectors.AffineScalar(shift=shift, scale=constant(scale)))
end
function forward(fo::AffineScalarFlow, x::Union{Array{<:Real}, PyObject})
fo.o.forward(x), fo.o.forward_log_det_jacobian(x, 1)
end
function backward(fo::AffineScalarFlow, z::Union{Array{<:Real}, PyObject})
fo.o.inverse(z), fo.o.inverse_log_det_jacobian(z, 1)
end
#------------------------------------------------------------------------------------------
mutable struct InvertFlow <: FlowOp
dim::Int64
o::FlowOp
end
"""
InvertFlow(fo::FlowOp)
Creates a flow operator that is the invert of `fo`.
# Example
```julia
inv_tanh_flow = InvertFlow(TanhFlow(2))
```
"""
function InvertFlow(fo::FlowOp)
InvertFlow(fo.dim, fo)
end
forward(fo::InvertFlow, x::Union{Array{<:Real}, PyObject}) = backward(fo.o, x)
backward(fo::InvertFlow, z::Union{Array{<:Real}, PyObject}) = forward(fo.o, z)
#------------------------------------------------------------------------------------------
@doc raw"""
AffineFlow(args...;kwargs...)
Creates a linear flow operator,
$$z = Ax + b$$
See [`LinearFlow`](@ref)
"""
AffineFlow(args...;kwargs...) = InvertFlow(LinearFlow(args...;kwargs...))
#------------------------------------------------------------------------------------------
mutable struct NormalizingFlow
flows::Array
NormalizingFlow(flows::Array) = new(flows)
end
function forward(fo::NormalizingFlow, x::Union{PyObject, Array{<:Real,2}})
x = constant(x)
m = size(x,1)
log_det = constant(zeros(m))
zs = PyObject[x]
for flow in fo.flows
x, ld = forward(flow, x)
log_det += ld
push!(zs, x)
end
return zs, log_det
end
function backward(fo::NormalizingFlow, z::Union{PyObject, Array{<:Real,2}})
z = constant(z)
m = size(z,1)
log_det = constant(zeros(m))
xs = [z]
for flow in reverse(fo.flows)
z, ld = backward(flow, z)
if isnothing(ld) || isnothing(log_det)
log_det = nothing
else
log_det += ld
end
push!(xs, z)
end
return xs, log_det
end
#------------------------------------------------------------------------------------------
mutable struct NormalizingFlowModel
prior::ADCMEDistribution
flow::NormalizingFlow
end
function Base.:show(io::IO, model::NormalizingFlowModel)
typevec = typeof.(model.flow.flows)
println("( $(string(typeof(model.prior))[7:end]) )")
println("\t↓")
for i = length(typevec):-1:1
println("$(typevec[i]) (dim = $(model.flow.flows[i].dim))")
println("\t↓")
end
println("( Data )")
end
function NormalizingFlowModel(prior::T, flows::Array{<:FlowOp}) where T<:ADCMEDistribution
NormalizingFlowModel(prior, NormalizingFlow(flows))
end
function forward(nf::NormalizingFlowModel, x::Union{PyObject, Array{<:Real,2}})
x = constant(x)
zs, log_det = forward(nf.flow, x)
prior_logprob = logpdf(nf.prior, zs[end])
return zs, prior_logprob, log_det
end
function backward(nf::NormalizingFlowModel, z::Union{PyObject, Array{<:Real,2}})
z = constant(z)
xs, log_det = backward(nf.flow, z)
return xs, log_det
end
function Base.:rand(nf::NormalizingFlowModel, num_samples::Int64)
z = rand(nf.prior, num_samples)
xs, _ = backward(nf.flow, z)
return xs
end
#------------------------------------------------------------------------------------------
(o::NormalizingFlowModel)(x::Union{PyObject, Array{<:Real,2}}) = forward(o, x)
#------------------------------------------------------------------------------------------
# From TensorFlow Probability
for (op1, op2) in [(:Abs, :AbsoluteValue), (:Exp, :Exp), (:Log, :Log),
(:MaskedAutoregressiveFlow, :MaskedAutoregressiveFlow), (:Permute,:Permute),
(:PowerTransform, :PowerTransform), (:Sigmoid,:Sigmoid), (:Softplus,:Softplus),
(:Square, :Square)]
@eval begin
export $op1
mutable struct $op1 <: FlowOp
dim::Int64
fo::PyObject
end
function $op1(dim::Int64, args...;kwargs...)
fo = tfp.bijectors.$op2(args...;kwargs...)
$op1(dim, fo)
end
forward(o::$op1, x::Union{PyObject, Array{<:Real,2}}) = (o.fo.forward(x), o.fo.forward_log_det_jacobian(x, 1))
backward(o::$op1, z::Union{PyObject, Array{<:Real,2}}) = (o.fo.inverse(z), o.fo.inverse_log_det_jacobian(z, 1))
end
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 11989 | export GAN,
jsgan,
klgan,
wgan,
rklgan,
lsgan,
sample,
predict,
dcgan_generator,
dcgan_discriminator,
wgan_stable
mutable struct GAN
latent_dim::Int64
batch_size::Int64
dim::Int64
dat::PyObject
generator::Union{Missing, Function}
discriminator::Union{Missing, Function}
loss::Function
d_vars::Union{Missing,Array{PyObject}}
g_vars::Union{Missing,Array{PyObject}}
d_loss::Union{Missing,PyObject}
g_loss::Union{Missing,PyObject}
is_training::Union{Missing,PyObject, Bool}
update::Union{Missing,Array{PyObject}}
fake_data::Union{Missing,PyObject}
true_data::Union{Missing,PyObject}
ganid::String
noise::Union{Missing,PyObject}
ids::Union{Missing,PyObject}
STORAGE::Dict{String, Any}
end
"""
build!(gan::GAN)
Builds the GAN instances. This function returns `gan` for convenience.
"""
function build!(gan::GAN)
gan.noise = placeholder(get_dtype(gan.dat), shape=(gan.batch_size, gan.latent_dim))
gan.ids = placeholder(Int32, shape=(gan.batch_size,))
variable_scope("generator_$(gan.ganid)") do
gan.fake_data = gan.generator(gan.noise, gan)
end
gan.true_data = tf.gather(gan.dat,gan.ids-1)
variable_scope("discriminator_$(gan.ganid)") do
gan.d_loss, gan.g_loss = gan.loss(gan)
end
gan.d_vars = Array{PyObject}(get_collection("discriminator_$(gan.ganid)"))
gan.d_vars = length(gan.d_vars)>0 ? gan.d_vars : missing
gan.g_vars = Array{PyObject}(get_collection("generator_$(gan.ganid)"))
gan.g_vars = length(gan.g_vars)>0 ? gan.g_vars : missing
gan.update = Array{PyCall.PyObject}(get_collection(UPDATE_OPS))
gan.update = length(gan.update)>0 ? gan.update : missing
# gan.STORAGE["d_grad_magnitude"] = gradient_magnitude(gan.d_loss, gan.d_vars)
# gan.STORAGE["g_grad_magnitude"] = gradient_magnitude(gan.g_loss, gan.g_vars)
gan
end
@doc raw"""
GAN(dat::Union{Array,PyObject}, generator::Function, discriminator::Function,
loss::Union{Missing, Function}=missing; latent_dim::Union{Missing, Int64}=missing,
batch_size::Int64=32)
Creates a GAN instance.
- `dat` ``\in \mathbb{R}^{n\times d}`` is the training data for the GAN, where ``n`` is the number of training data, and ``d`` is the dimension per training data.
- `generator```:\mathbb{R}^{d'} \rightarrow \mathbb{R}^d`` is the generator function, ``d'`` is the hidden dimension.
- `discriminator```:\mathbb{R}^{d} \rightarrow \mathbb{R}`` is the discriminator function.
- `loss` is the loss function. See [`klgan`](@ref), [`rklgan`](@ref), [`wgan`](@ref), [`lsgan`](@ref) for examples.
- `latent_dim` (default=``d``, the same as output dimension) is the latent dimension.
- `batch_size` (default=32) is the batch size in training.
# Example: Constructing a GAN
```julia
dat = rand(10000,10)
generator = (z, gan)->10*z
discriminator = (x, gan)->sum(x)
gan = GAN(dat, generator, discriminator, "wgan_stable")
```
# Example: Learning a Gaussian random variable
```julia
using ADCME
using PyPlot
using Distributions
dat = randn(10000, 1) * 0.5 .+ 3.0
function gen(z, gan)
ae(z, [20,20,20,1], "generator_$(gan.ganid)", activation = "relu")
end
function disc(x, gan)
squeeze(ae(x, [20,20,20,1], "discriminator_$(gan.ganid)", activation = "relu"))
end
gan = GAN(dat, gen, disc, g->wgan_stable(g, 0.001); latent_dim = 10)
dopt = AdamOptimizer(0.0002, beta1=0.5, beta2=0.9).minimize(gan.d_loss, var_list=gan.d_vars)
gopt = AdamOptimizer(0.0002, beta1=0.5, beta2=0.9).minimize(gan.g_loss, var_list=gan.g_vars)
sess = Session(); init(sess)
for i = 1:5000
batch_x = rand(1:10000, 32)
batch_z = randn(32, 10)
for n_critic = 1:1
global _, dl = run(sess, [dopt, gan.d_loss],
feed_dict=Dict(gan.ids=>batch_x, gan.noise=>batch_z))
end
_, gl, gm, dm, gp = run(sess, [gopt, gan.g_loss,
gan.STORAGE["g_grad_magnitude"], gan.STORAGE["d_grad_magnitude"],
gan.STORAGE["gradient_penalty"]],
feed_dict=Dict(gan.ids=>batch_x, gan.noise=>batch_z))
mod(i, 100)==0 && (@info i, dl, gl, gm, dm, gp)
end
hist(run(sess, squeeze(rand(gan,10000))), bins=50, density = true)
nm = Normal(3.0,0.5)
x0 = 1.0:0.01:5.0
y0 = pdf.(nm, x0)
plot(x0, y0, "g")
```
"""
function GAN(dat::Union{Array,PyObject}, generator::Function, discriminator::Function,
loss::Union{Missing, Function, String}=missing; latent_dim::Union{Missing, Int64}=missing,
batch_size::Int64=32)
dim = size(dat, 2)
dat = convert_to_tensor(dat)
if ismissing(latent_dim)
latent_dim=dim
end
if ismissing(loss)
loss = "jsgan"
end
if isa(loss, String)
if loss=="jsgan"
loss = jsgan
elseif loss=="klgan"
loss = klgan
elseif loss=="wgan"
loss = wgan
elseif loss=="wgan_stable"
loss = wgan_stable
elseif loss=="rklgan"
loss = rklgan
elseif loss=="lsgan"
loss = lsgan
else
error("loss function $loss not found!")
end
end
gan = GAN(latent_dim, batch_size, dim, dat, generator, discriminator, loss, missing, missing, missing,
missing, ADCME.options.training.training, missing, missing, missing, randstring(), missing, missing, Dict())
build!(gan)
gan
end
GAN(dat::Array{T}) where T<:Real = GAN(constant(dat))
function Base.:show(io::IO, gan::GAN)
yes_or_no = x->ismissing(x) ? "✘" : "✔️"
print(
"""
( Generative Adversarial Network -- $(gan.ganid) )
==================================================
$(gan.latent_dim) D $(gan.dim) D
(Latent Space)---->(Data Space)
batch_size = $(gan.batch_size)
loss function: $(gan.loss)
generator: $(gan.generator)
discriminator: $(gan.discriminator)
d_vars ... $(yes_or_no(gan.d_vars))
g_vars ... $(yes_or_no(gan.g_vars))
d_loss ... $(yes_or_no(gan.d_loss))
g_loss ... $(yes_or_no(gan.g_loss))
update ... $(yes_or_no(gan.update))
true_data ... $(size(gan.true_data))
fake_data ... $(size(gan.fake_data))
is_training... Placeholder (Bool), $(gan.is_training)
noise ... Placeholder (Float64) of size $(size(gan.noise))
ids ... Placeholder (Int32) of size $(size(gan.ids))
"""
)
end
##################### GAN Library #####################
"""
klgan(gan::GAN)
Computes the KL-divergence GAN loss function.
"""
function klgan(gan::GAN)
P, Q = gan.true_data, gan.fake_data
D_real = gan.discriminator(P, gan)
D_fake = gan.discriminator(Q, gan)
D_loss = -mean(log(D_real) + log(1-D_fake))
G_loss = mean(log((1-D_fake)/D_fake))
D_loss, G_loss
end
"""
jsgan(gan::GAN)
Computes the vanilla GAN loss function.
"""
function jsgan(gan::GAN)
P, Q = gan.true_data, gan.fake_data
D_real = gan.discriminator(P, gan)
D_fake = gan.discriminator(Q, gan)
D_loss = -mean(log(D_real) + log(1-D_fake))
G_loss = -mean(log(D_fake))
D_loss, G_loss
end
"""
wgan(gan::GAN)
Computes the Wasserstein GAN loss function.
"""
function wgan(gan::GAN)
P, Q = gan.true_data, gan.fake_data
D_real = gan.discriminator(P, gan)
D_fake = gan.discriminator(Q, gan)
D_loss = mean(D_fake)-mean(D_real)
G_loss = -mean(D_fake)
D_loss, G_loss
end
@doc raw"""
wgan_stable(gan::GAN, λ::Float64)
Returns the discriminator and generator loss for the Wasserstein GAN loss with penalty parameter $\lambda$
The objective function is
```math
L = E_{\tilde x\sim P_g} [D(\tilde x)] - E_{x\sim P_r} [D(x)] + \lambda E_{\hat x\sim P_{\hat x}}[(||\nabla_{\hat x}D(\hat x)||^2-1)^2]
```
"""
function wgan_stable(gan::GAN, λ::Float64=1.0)
real_data, fake_data = gan.true_data, gan.fake_data
@assert length(size(real_data))==2
@assert length(size(fake_data))==2
D_logits = gan.discriminator(real_data, gan)
D_logits_ = gan.discriminator(fake_data, gan)
g_loss = -mean(D_logits_)
d_loss_real = -mean(D_logits)
d_loss_fake = tf.reduce_mean(D_logits_)
α = tf.random_uniform(
shape=(gan.batch_size, 1),
minval=0.,
maxval=1.,
dtype=tf.float64
)
differences = fake_data - real_data
interpolates = real_data + α .* differences # nb x dim
d_inter = gan.discriminator(interpolates, gan)
@assert length(size(d_inter))==1
gradients = tf.gradients(d_inter, interpolates)[1] # ∇D(xt), nb x dim
slopes = sqrt(sum(gradients^2, dims=2)) # ||∇D(xt)||, (nb,)
gradient_penalty = mean((slopes-1.)^2)
d_loss = d_loss_fake + d_loss_real + λ * gradient_penalty
gan.STORAGE["gradient_penalty"] = mean(slopes)
return d_loss, g_loss
end
"""
rklgan(gan::GAN)
Computes the reverse KL-divergence GAN loss function.
"""
function rklgan(gan::GAN)
P, Q = gan.true_data, gan.fake_data
D_real = gan.discriminator(P, gan)
D_fake = gan.discriminator(Q, gan)
G_loss = mean(log((1-D_fake)/D_fake))
D_loss = -mean(log(D_fake)+log(1-D_real))
D_loss, G_loss
end
"""
lsgan(gan::GAN)
Computes the least square GAN loss function.
"""
function lsgan(gan::GAN)
P, Q = gan.true_data, gan.fake_data
D_real = gan.discriminator(P, gan)
D_fake = gan.discriminator(Q, gan)
D_loss = mean((D_real-1)^2+D_fake^2)
G_loss = mean((D_fake-1)^2)
D_loss, G_loss
end
#######################################################
"""
sample(gan::GAN, n::Int64)
rand(gan::GAN, n::Int64)
Samples `n` instances from `gan`.
"""
function sample(gan::GAN, n::Int64)
local out
@info "Using a normal latent vector"
noise = constant(randn(n, gan.latent_dim))
variable_scope("generator_$(gan.ganid)") do
out = gan.generator(noise, gan)
end
out
end
Base.:rand(gan::GAN) = squeeze(sample(gan, 1), dims=1)
Base.:rand(gan::GAN, n::Int64) = sample(gan, n)
"""
predict(gan::GAN, input::Union{PyObject, Array})
Predicts the GAN `gan` output given input `input`.
"""
function predict(gan::GAN, input::Union{PyObject, Array})
local out
flag = false
if length(size(input))==1
flag = true
input = reshape(input, 1, length(input))
end
input = convert_to_tensor(input)
variable_scope("generator_$(gan.ganid)", initializer=random_uniform_initializer(0.0,1e-3)) do
out = gan.generator(input, gan)
end
if flag; out = squeeze(out); end
out
end
# adapted from https://github.com/aymericdamien/TensorFlow-Examples/blob/master/examples/3_NeuralNetworks/dcgan.py
function dcgan_generator(x::PyObject, n::Int64=1)
if length(size(x))!=2
error("ADCME: input must have rank 2, rank $(length(size(x))) received")
end
variable_scope("generator", reuse=AUTO_REUSE) do
# TensorFlow Layers automatically create variables and calculate their
# shape, based on the input.
x = tf.layers.dense(x, units=6n * 6n * 128)
x = tf.nn.tanh(x)
# Reshape to a 4-D array of images: (batch, height, width, channels)
# New shape: (batch, 6, 6, 128)
x = tf.reshape(x, shape=[-1, 6n, 6n, 128])
# Deconvolution, image shape: (batch, 14, 14, 64)
x = tf.layers.conv2d_transpose(x, 64, 4, strides=2)
# Deconvolution, image shape: (batch, 28, 28, 1)
x = tf.layers.conv2d_transpose(x, 1, 2, strides=2)
# Apply sigmoid to clip values between 0 and 1
x = tf.nn.sigmoid(x)
end
return squeeze(x)
end
function dcgan_discriminator(x)
variable_scope("Discriminator", reuse=AUTO_REUSE) do
# Typical convolutional neural network to classify images.
x = tf.layers.conv2d(x, 64, 5)
x = tf.nn.tanh(x)
x = tf.layers.average_pooling2d(x, 2, 2)
x = tf.layers.conv2d(x, 128, 5)
x = tf.nn.tanh(x)
x = tf.layers.average_pooling2d(x, 2, 2)
x = tf.contrib.layers.flatten(x)
x = tf.layers.dense(x, 1024)
x = tf.nn.tanh(x)
# Output 2 classes: Real and Fake images
x = tf.layers.dense(x, 2)
end
return x
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 3783 | export gpu_info, get_gpu, has_gpu
"""
gpu_info()
Returns the CUDA and GPU information. An examplary output is
```
- NVCC: /usr/local/cuda/bin/nvcc
- CUDA library directories: /usr/local/cuda/lib64
- Latest supported version of CUDA: 11000
- CUDA runtime version: 10010
- CUDA include_directories: /usr/local/cuda/include
- CUDA toolkit directories: /home/kailaix/.julia/adcme/pkgs/cudatoolkit-10.0.130-0/lib:/home/kailaix/.julia/adcme/pkgs/cudnn-7.6.5-cuda10.0_0/lib
- Number of GPUs: 7
```
"""
function gpu_info()
NVCC = "missing"
CUDALIB = "missing"
v = "missing"
u = "missing"
dcount = 0
try
NVCC = strip(String(read(`which nvcc`)))
CUDALIB = abspath(joinpath(NVCC, "../../lib64"))
v = zeros(Int32,1)
@eval ccall((:cudaRuntimeGetVersion, $(joinpath(CUDALIB, "libcudart.so"))), Cvoid, (Ref{Cint},), $v)
u = zeros(Int32,1)
@eval ccall((:cudaDriverGetVersion, $(joinpath(CUDALIB, "libcudart.so"))), Cvoid, (Ref{Cint},), $u)
dcount = zeros(Int32, 1)
@eval ccall((:cudaGetDeviceCount, $(joinpath(CUDALIB, "libcudart.so"))), Cvoid, (Ref{Cint},), $dcount)
v = v[1]
if v==0
v = "missing"
end
u = u[1]
dcount = dcount[1]
catch
end
println("- NVCC: ", NVCC)
println("- CUDA library directories: ", CUDALIB)
println("- Latest supported version of CUDA: ", u)
println("- CUDA runtime version: ", v)
println("- CUDA include_directories: ", length(ADCME.CUDA_INC)==0 ? "missing" : ADCME.CUDA_INC)
println("- CUDA toolkit directories: ", length(ADCME.LIBCUDA)==0 ? "missing" : ADCME.LIBCUDA)
println("- Number of GPUs: ", dcount)
if NVCC == "missing"
println("\nTips: nvcc is not found in the path. Please add nvcc to your environment path if you intend to use GPUs.")
end
if length(ADCME.CUDA_INC)==0
println("\nTips: ADCME is not configured to use GPUs. See https://kailaix.github.io/ADCME.jl/latest/tu_customop/#Install-GPU-enabled-TensorFlow-(Linux-and-Windows) for instructions.")
end
if dcount==0
println("\nTips: No GPU resources found. Do you have access to GPUs?")
end
end
"""
get_gpu()
Returns the compiler information for GPUs. An examplary output is
> (NVCC = "/usr/local/cuda/bin/nvcc", LIB = "/usr/local/cuda/lib64", INC = "/usr/local/cuda/include", TOOLKIT = "/home/kailaix/.julia/adcme/pkgs/cudatoolkit-10.0.130-0/lib", CUDNN = "/home/kailaix/.julia/adcme/pkgs/cudnn-7.6.5-cuda10.0_0/lib")
"""
function get_gpu()
NVCC = missing
CUDALIB = missing
CUDAINC = missing
CUDATOOLKIT = missing
CUDNN = missing
try
NVCC = strip(String(read(`which nvcc`)))
CUDALIB = abspath(joinpath(NVCC, "../../lib64"))
CUDAINC = abspath(joinpath(NVCC, "../../include"))
if length(ADCME.CUDA_INC)>0 && CUDAINC!=ADCME.CUDA_INC
@warn """
Inconsistency detected:
ADCME CUDAINC: $(ADCME.CUDA_INC)
Implied CUDAINC: $CUDAINC
"""
end
catch
end
if length(ADCME.LIBCUDA)>0
CUDATOOLKIT = split(ADCME.LIBCUDA, ":")[1]
CUDNN = split(ADCME.LIBCUDA, ":")[2]
else
end
return (NVCC=NVCC, LIB=CUDALIB, INC=CUDAINC, TOOLKIT=CUDATOOLKIT, CUDNN=CUDNN)
end
"""
has_gpu()
Check if the TensorFlow backend is using CUDA GPUs. Operators that have GPU implementations will be executed on GPU devices.
See also [`get_gpu`](@ref)
!!! note
ADCME will use GPU automatically if GPU is available. To disable GPU, set the environment variable `ENV["CUDA_VISIBLE_DEVICES"]=""` before importing ADCME
"""
function has_gpu()
s = tf.test.gpu_device_name()
if length(s)==0
return false
else
return true
end
end
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 4465 | # install.jl collects scripts to install many third party libraries
export install_adept, install_blas, install_openmpi, install_hypre, install_had, install_mfem, install_matplotlib
function install_blas(blas_binary::Bool = true)
if Sys.iswindows()
if isfile(joinpath(ADCME.LIBDIR, "openblas.lib"))
@info "openblas.lib exists"
return
end
if blas_binary
http_file("https://github.com/kailaix/tensorflow-1.15-include/releases/download/v0.1.0/openblas.lib", joinpath(ADCME.LIBDIR, "openblas.lib"))
return
end
@info "You are building openblas from source on Windows, and this process may take a long time.
Alternatively, you can place your precompiled binary to $(joinpath(ADCME.LIBDIR, "openblas.lib"))"
PWD = pwd()
change_directory()
http_file("https://github.com/xianyi/OpenBLAS/archive/v0.3.9.zip", "OpenBlas.zip")
uncompress("OpenBLAS.zip", "OpenBlas-0.3.9")
change_directory("OpenBlas-0.3.9/build")
require_cmakecache() do
ADCME.cmake(CMAKE_ARGS="-DCMAKE_Fortran_COMPILER=flang -DBUILD_WITHOUT_LAPACK=no -DNOFORTRAN=0 -DDYNAMIC_ARCH=ON")
end
require_library("lib/Release/openblas") do
ADCME.make()
end
change_directory("lib/Release")
copy_file("openblas.lib", joinpath(ADCME.LIBDIR, "openblas.lib"))
cd(PWD)
else
required_file = get_library(joinpath(ADCME.LIBDIR, "openblas"))
if !isfile(required_file)
files = readdir(ADCME.LIBDIR)
files = filter(x->!isnothing(x), match.(r"(libopenblas\S*.dylib)", files))[1]
target = joinpath(ADCME.LIBDIR, files[1])
symlink(target, required_file)
@info "Symlink $(required_file) --> $(files[1])"
end
end
end
"""
install_adept()
Install adept-2 library: https://github.com/rjhogan/Adept-2
"""
function install_adept(; blas_binary::Bool = true)
change_directory()
git_repository("https://github.com/ADCMEMarket/Adept-2", "Adept-2")
cd("Adept-2/adept")
install_blas(blas_binary)
cp("$(@__DIR__)/../deps/AdeptCMakeLists.txt", "./CMakeLists.txt", force=true)
change_directory("build")
require_cmakecache() do
ADCME.cmake()
end
if Sys.iswindows()
require_file("$(ADCME.LIBDIR)/adept.lib") do
ADCME.make()
end
else
require_library("$(ADCME.LIBDIR)/adept") do
ADCME.make()
end
end
end
function install_openmpi()
filepath = joinpath(@__DIR__, "..", "deps", "install_openmpi.jl")
include(filepath)
end
function install_hypre()
filepath = joinpath(@__DIR__, "..", "deps", "install_hypre.jl")
include(filepath)
end
function install_mfem()
PWD = pwd()
change_directory()
http_file("https://github.com/kailaix/mfem/archive/shared-msvc-dev.zip", "mfem.zip")
uncompress("mfem.zip", "mfem-shared-msvc-dev")
change_directory("mfem-shared-msvc-dev/build")
require_file("CMakeCache.txt") do
ADCME.cmake(CMAKE_ARGS = ["-DCMAKE_INSTALL_PREFIX=$(joinpath(ADCME.LIBDIR, ".."))", "-SHARED=YES", "-STATIC=NO"])
end
require_library("mfem") do
ADCME.make()
end
require_file(joinpath(ADCME.LIBDIR, get_library_name("mfem"))) do
if Sys.iswindows()
run_with_env(`cmd /c $(ADCME.CMAKE) --install .`)
else
run_with_env(`$(ADCME.NINJA) install`)
end
end
if Sys.iswindows()
mfem_h = """
// Auto-generated file.
#undef NO_ERROR
#undef READ_ERROR
#undef WRITE_ERROR
#undef ALIAS
#undef REGISTERED
#include "mfem/mfem.hpp"
"""
open(joinpath(ADCME.LIBDIR, "..", "include", "mfem.hpp"), "w") do io
write(io, mfem_h)
@info "Fixed mfem.hpp definitions"
end
end
cd(PWD)
end
function install_had()
change_directory()
git_repository("https://github.com/kailaix/had", "had")
end
function install_matplotlib()
PIP = get_pip()
run(`$PIP install matplotlib`)
if Sys.isapple()
CONDA = get_conda()
pkgs = run(`$CONDA list`)
if occursin("pyqt", pkgs)
return
end
if !isdefined(Main, :Pkg)
error("Package Pkg must be imported in the main module using `import Pkg` or `using Pkg`")
end
run(`$CONDA install -y pyqt`)
Main.Pkg.build("PyPlot")
end
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 6921 | using MAT
export
save,
load,
Diary,
scalar,
writepb,
psave,
pload,
activate,
logging,
print_tensor
pybytes(b) = PyObject(
ccall(PyCall.@pysym(PyCall.PyString_FromStringAndSize),
PyPtr, (Ptr{UInt8}, Int),
b, sizeof(b)))
"""
psave(o::PyObject, file::String)
Saves a Python objection `o` to `file`.
See also [`pload`](@ref)
"""
function psave(o::PyObject, file::String)
pickle = pyimport("pickle")
f = open(file, "w")
pickle.dump(o, f)
close(f)
end
"""
pload(file::String)
Loads a Python objection from `file`.
See also [`psave`](@ref)
"""
function pload(file::String)
r = nothing
pickle = pyimport("pickle")
@pywith pybuiltin("open")(file,"rb") as f begin
r = pickle.load(f)
end
return r
end
"""
save(sess::PyObject, file::String, vars::Union{PyObject, Nothing, Array{PyObject}}=nothing, args...; kwargs...)
Saves the values of `vars` in the session `sess`. The result is written into `file` as a dictionary. If `vars` is nothing, it saves all the trainable variables.
See also [`save`](@ref), [`load`](@ref)
"""
function save(sess::PyObject, file::String, vars::Union{PyObject, Nothing, Array{PyObject}, Array{Any}}=nothing, args...; kwargs...)
if vars==nothing
vars = get_collection(TRAINABLE_VARIABLES)
elseif isa(vars, PyObject)
vars = [vars]
elseif isa(vars, Array{Any})
vars = Array{PyObject}(vars)
end
d = Dict{String, Any}()
vals = run(sess, vars, args...;kwargs...)
for i = 1:length(vars)
name = replace(vars[i].name, ":"=>"colon")
name = replace(name, "/"=>"backslash")
d[name] = vals[i]
end
matwrite(file, d)
d
end
function save(sess::PyObject, vars::Union{PyObject, Nothing, Array{PyObject}}=nothing, args...; kwargs...)
if vars==nothing
vars = get_collection(TRAINABLE_VARIABLES)
elseif isa(vars, PyObject)
vars = [vars]
end
d = Dict{String, Any}()
vals = run(sess, vars, args...;kwargs...)
for i = 1:length(vars)
name = replace(vars[i].name, ":"=>"colon")
name = replace(name, "/"=>"backslash")
d[name] = vals[i]
end
d
end
"""
load(sess::PyObject, file::String, vars::Union{PyObject, Nothing, Array{PyObject}}=nothing, args...; kwargs...)
Loads the values of variables to the session `sess` from the file `file`. If `vars` is nothing, it loads values to all the trainable variables.
See also [`save`](@ref), [`load`](@ref)
"""
function load(sess::PyObject, file::String, vars::Union{PyObject, Nothing, Array{PyObject}}=nothing, args...; kwargs...)
if vars==nothing
vars = get_collection(TRAINABLE_VARIABLES)
elseif isa(vars, PyObject)
vars = [vars]
end
d = matread(file)
ops = PyObject[]
for i = 1:length(vars)
name = replace(vars[i].name, ":"=>"colon")
name = replace(name, "/"=>"backslash")
if !(name in keys(d))
@warn "$(vars[i].name) not found in the file, skipped"
else
if occursin("bias", name) && isa(d[name], Number)
d[name] = [d[name]]
end
push!(ops, assign(vars[i], d[name]))
end
end
run(sess, ops, args...; kwargs...)
end
function load(sess::PyObject, d::Dict, vars::Union{PyObject, Nothing, Array{PyObject}}=nothing, args...; kwargs...)
if vars==nothing
vars = get_collection(TRAINABLE_VARIABLES)
elseif isa(vars, PyObject)
vars = [vars]
end
ops = PyObject[]
for i = 1:length(vars)
name = replace(vars[i].name, ":"=>"colon")
name = replace(name, "/"=>"backslash")
if !(name in keys(d))
@warn "$(vars[i].name) not found in the file, skipped"
else
push!(ops, assign(vars[i], d[name]))
end
end
run(sess, ops, args...; kwargs...)
end
mutable struct Diary
writer::PyObject
tdir::String
end
"""
Diary(suffix::Union{String, Nothing}=nothing)
Creates a diary at a temporary directory path. It returns a writer and the corresponding directory path
"""
function Diary(suffix::Union{String, Nothing}=nothing)
tdir = mktempdir()
printstyled("tensorboard --logdir=\"$(tdir)\" --port 0\n", color=:blue)
Diary(tf.summary.FileWriter(tdir, tf.get_default_graph(),filename_suffix=suffix), tdir)
end
"""
save(sw::Diary, dirp::String)
Saves [`Diary`](@ref) to `dirp`.
"""
function save(sw::Diary, dirp::String)
cp(sw.tdir, dirp, force=true)
end
"""
load(sw::Diary, dirp::String)
Loads [`Diary`](@ref) from `dirp`.
"""
function load(sw::Diary,dirp::String)
sw.writer = tf.summary.FileWriter(dirp, tf.get_default_graph())
sw.tdir = dirp
end
"""
activate(sw::Diary, port::Int64=6006)
Running [`Diary`](@ref) at http://localhost:port.
"""
function activate(sw::Diary, port::Int64=0)
printstyled("tensorboard --logdir=\"$(sw.tdir)\" --port $port\n", color=:blue)
run(`tensorboard --logdir="$(sw.tdir)" --port $port '&'`)
end
"""
scalar(o::PyObject, name::String)
Returns a scalar summary object.
"""
function scalar(o::PyObject, name::Union{String,Missing}=missing)
if ismissing(name)
name = tensorname(o)
end
tf.summary.scalar(name, o)
end
"""
write(sw::Diary, step::Int64, cnt::Union{String, Array{String}})
Writes to [`Diary`](@ref).
"""
function Base.:write(sw::Diary, step::Int64, cnt::Union{String, Array{String}})
if isa(cnt, String)
sw.writer.add_summary(pybytes(cnt), step)
else
for c in cnt
sw.writer.add_summary(pybytes(c), step)
end
end
end
function writepb(writer::PyObject, sess::PyObject)
output_path = writer.get_logdir()
tf.io.write_graph(sess.graph_def, output_path, "model.pb")
return
end
"""
logging(file::Union{Nothing,String}, o::PyObject...; summarize::Int64 = 3, sep::String = " ")
Logging `o` to `file`. This operator must be used with [`bind`](@ref).
"""
function logging(file::Union{Nothing,String}, o::PyObject...; summarize::Int64 = 3, sep::String = " ")
if isnothing(file)
tf.print(o..., summarize=summarize, sep=sep)
else
filepath = "file://$(abspath(file))"
tf.print(o..., output_stream=filepath, summarize=summarize, sep=sep)
end
end
logging(o::PyObject...; summarize::Int64 = 3, sep::String = " ") = logging(nothing, summarize=summarize, sep=sep)
"""
print_tensor(in::Union{PyObject, Array{Float64,2}})
Prints the tensor `in`
"""
function print_tensor(in::Union{PyObject, Array{Float64,2}}, info::AbstractString = "")
@assert length(size(in))==2
print_tensor_ = load_system_op("print_tensor")
in = convert_to_tensor(Any[in], [Float64]); in = in[1]
info = tf.constant(info)
out = print_tensor_(in, info)
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 12965 | export test_jacobian, test_gradients, linedata, lineview, meshdata,
meshview, gradview, jacview, PCLview, pcolormeshview,
animate, saveanim, test_hessian
function require_pyplot()
if !isdefined(Main, :PyPlot)
error("You must load PyPlot to use this function, e.g., `using PyPlot` or `import PyPlot`")
end
Main.PyPlot
end
"""
test_gradients(f::Function, x0::Array{Float64, 1}; scale::Float64 = 1.0, showfig::Bool = true)
Testing the gradients of a vector function `f`:
`y, J = f(x)` where `y` is a scalar output and `J` is the vector gradient.
"""
function test_gradients(f::Function, x0::Array{Float64, 1};
scale::Float64 = 1.0, showfig::Bool = true, mpi::Bool = false)
v0 = rand(Float64,length(x0))
γs = scale ./10 .^(1:5)
err2 = Float64[]
err1 = Float64[]
f0, J = f(x0)
for i = 1:5
f1, _ = f(x0+γs[i]*v0)
push!(err1, abs(f1-f0))
push!(err2, abs(f1-f0-γs[i]*sum(J.*v0)))
end
if showfig
if mpi && mpi_rank()>0
return
end
mp = require_pyplot()
mp.close("all")
mp.loglog(γs, err1, label="Finite Difference")
mp.loglog(γs, err2, label="Automatic Differentiation")
mp.loglog(γs, γs * 0.5*abs(err1[1])/γs[1], "--",label="\$\\mathcal{O}(\\gamma)\$")
mp.loglog(γs, γs.^2 * 0.5*abs(err2[1])/γs[1]^2, "--",label="\$\\mathcal{O}(\\gamma^2)\$")
mp.plt.gca().invert_xaxis()
mp.legend()
mp.savefig("test.png")
@info "Results saved to test.png"
println("Finite difference: $err1")
println("Automatic differentiation: $err2")
end
return err1, err2
end
"""
test_jacobian(f::Function, x0::Array{Float64, 1}; scale::Float64 = 1.0, showfig::Bool = true)
Testing the gradients of a vector function `f`:
`y, J = f(x)` where `y` is a vector output and `J` is the Jacobian.
"""
function test_jacobian(f::Function, x0::Array{Float64, 1}; scale::Float64 = 1.0, showfig::Bool = true)
v0 = rand(Float64,size(x0))
γs = scale ./10 .^(1:5)
err2 = Float64[]
err1 = Float64[]
f0, J = f(x0)
for i = 1:5
f1, _ = f(x0+γs[i]*v0)
push!(err1, norm(f1-f0))
push!(err2, norm(f1-f0-γs[i]*J*v0))
end
if showfig
mp = require_pyplot()
mp.close("all")
mp.loglog(γs, err1, label="Finite Difference")
mp.loglog(γs, err2, label="Automatic Differentiation")
mp.loglog(γs, γs * 0.5*abs(err1[1])/γs[1], "--",label="\$\\mathcal{O}(\\gamma)\$")
mp.loglog(γs, γs.^2 * 0.5*abs(err2[1])/γs[1]^2, "--",label="\$\\mathcal{O}(\\gamma^2)\$")
mp.plt.gca().invert_xaxis()
mp.legend()
mp.savefig("test.png")
@info "Results saved to test.png"
println("Finite difference: $err1")
println("Automatic differentiation: $err2")
end
return err1, err2
end
"""
test_hessian(f::Function, x0::Array{Float64, 1}; scale::Float64 = 1.0)
Testing the Hessian of a scalar function `f`:
`g, H = f(x)` where `y` is a scalar output, `g` is a vector gradient output, and `H` is the Hessian.
"""
test_hessian(f::Function, x0::Array{Float64, 1}; kwargs...) = test_jacobian(f, x0; kwargs...)
function linedata(θ1, θ2=nothing; n::Integer = 10)
if θ2 === nothing
θ2 = θ1 .* (1 .+ randn(size(θ1)...))
end
T = []
for x in LinRange(0.0,1.0,n)
push!(T, θ1*(1-x)+θ2*x)
end
T
end
function lineview(losses::Array{Float64})
mp = require_pyplot()
n = length(losses)
v = collect(LinRange(0.0,1.0,n))
mp.close("all")
mp.plot(v, losses)
mp.xlabel("\$\\alpha\$")
mp.ylabel("loss")
mp.grid("on")
end
@doc raw"""
lineview(sess::PyObject, pl::PyObject, loss::PyObject, θ1, θ2=nothing; n::Integer = 10)
Plots the function
$$h(α) = f((1-α)θ_1 + αθ_2)$$
# Example
```julia
pl = placeholder(Float64, shape=[2])
l = sum(pl^2-pl*0.1)
sess = Session(); init(sess)
lineview(sess, pl, l, rand(2))
```
"""
function lineview(sess::PyObject, pl::PyObject, loss::PyObject, θ1, θ2=nothing; n::Integer = 10)
mp = require_pyplot()
dat = linedata(θ1, θ2, n=n)
V = zeros(length(dat))
for i = 1:length(dat)
@info i, n
V[i] = run(sess, loss, pl=>dat[i])
end
lineview(V)
end
function meshdata(θ;
a::Real=1, b::Real=1, m::Integer=10, n::Integer=10 ,direction::Union{Array{<:Real}, Missing}=missing)
local δ, γ
as = LinRange(-a, a, m)
bs = LinRange(-b, b, n)
α = zeros(m, n)
β = zeros(m, n)
θs = Array{Any}(undef, m, n)
if !ismissing(direction)
δ = direction - θ
γ = randn(size(θ)...)
γ = γ/norm(γ)*norm(δ)
else
δ = randn(size(θ)...)
γ = randn(size(θ)...)
end
for i = 1:m
for j = 1:n
α[i,j] = as[i]
β[i,j] = bs[j]
θs[i,j] = θ + δ*as[i] + γ*bs[j]
end
end
return θs
end
function meshview(losses::Array{Float64}, a::Real=1, b::Real=1)
mp = require_pyplot()
m, n = size(losses)
α = zeros(m, n)
β = zeros(m, n)
as = LinRange(-a, a, m)
bs = LinRange(-b, b, n)
for i = 1:m
for j = 1:n
α[i,j] = as[i]
β[i,j] = bs[j]
end
end
mp.close("all")
mp.mesh(α, β, losses)
mp.xlabel("\$\\alpha\$")
mp.ylabel("\$\\beta\$")
mp.zlabel("loss")
mp.scatter3D(α[(m+1)÷2, (n+1)÷2], β[(m+1)÷2, (n+1)÷2], losses[(m+1)÷2, (n+1)÷2], color="red", s=100)
return α, β, losses
end
function pcolormeshview(losses::Array{Float64}, a::Real=1, b::Real=1)
mp = require_pyplot()
m, n = size(losses)
α = zeros(m, n)
β = zeros(m, n)
as = LinRange(-a, a, m)
bs = LinRange(-b, b, n)
for i = 1:m
for j = 1:n
α[i,j] = as[i]
β[i,j] = bs[j]
end
end
mp.close("all")
mp.pcolormesh(α, β, losses)
mp.xlabel("\$\\alpha\$")
mp.ylabel("\$\\beta\$")
mp.scatter(0.0,0.0, marker="*", s=100)
mp.colorbar()
return α, β, losses
end
function meshview(sess::PyObject, pl::PyObject, loss::PyObject, θ;
a::Real=1, b::Real=1, m::Integer=9, n::Integer=9,
direction::Union{Array{<:Real}, Missing}=missing)
dat = meshdata(θ; a=a, b=b, m=m, n=n, direction=direction)
m, n = size(dat)
V = zeros(m, n)
for i = 1:m
@info i, m
for j = 1:n
V[i,j] = run(sess, loss, pl=>dat[i,j])
end
end
meshview(V, a, b)
end
function pcolormeshview(sess::PyObject, pl::PyObject, loss::PyObject, θ;
a::Real=1, b::Real=1, m::Integer=9, n::Integer=9,
direction::Union{Array{<:Real}, Missing}=missing)
dat = meshdata(θ; a=a, b=b, m=m, n=n, direction=direction)
m, n = size(dat)
V = zeros(m, n)
for i = 1:m
@info i, m
for j = 1:n
V[i,j] = run(sess, loss, pl=>dat[i,j])
end
end
pcolormeshview(V, a, b)
end
function gradview(sess::PyObject, pl::PyObject, loss::PyObject, u0, grad::PyObject;
scale::Float64 = 1.0, mpi::Bool = false)
mp = require_pyplot()
local v
if length(size(u0))==0
v = rand()
else
v = rand(length(u0))
end
γs = scale ./ 10 .^ (1:5)
v1 = Float64[]
v2 = Float64[]
L_ = run(sess, loss, pl=>u0)
J_ = run(sess, grad, pl=>u0)
for i = 1:5
@info i
L__ = run(sess, loss, pl=>u0+v*γs[i])
push!(v1, norm(L__-L_))
if size(J_)==size(v)
if length(size(J_))==0
push!(v2, norm(L__-L_-γs[i]*sum(J_*v)))
else
push!(v2, norm(L__-L_-γs[i]*sum(J_.*v)))
end
else
push!(v2, norm(L__-L_-γs[i]*J_*v))
end
end
if !(mpi) || (mpi && mpi_rank()==0)
mp.close("all")
mp.loglog(γs, abs.(v1), "*-", label="finite difference")
mp.loglog(γs, abs.(v2), "+-", label="automatic linearization")
mp.loglog(γs, γs.^2 * 0.5*abs(v2[1])/γs[1]^2, "--",label="\$\\mathcal{O}(\\gamma^2)\$")
mp.loglog(γs, γs * 0.5*abs(v1[1])/γs[1], "--",label="\$\\mathcal{O}(\\gamma)\$")
mp.plt.gca().invert_xaxis()
mp.legend()
mp.xlabel("\$\\gamma\$")
mp.ylabel("Error")
if mpi
mp.savefig("mpi_gradview.png")
end
end
return v1, v2
end
"""
gradview(sess::PyObject, pl::PyObject, loss::PyObject, u0; scale::Float64 = 1.0)
Visualizes the automatic differentiation and finite difference convergence converge. For correctly implemented
differentiable codes, the convergence rate for AD should be 2 and for FD should be 1 (if not evaluated at stationary point).
- `scale`: you can control the step size for perturbation.
"""
function gradview(sess::PyObject, pl::PyObject, loss::PyObject, u0; scale::Float64 = 1.0, mpi::Bool = false)
grad = tf.convert_to_tensor(gradients(loss, pl))
gradview(sess, pl, loss, u0, grad, scale = scale, mpi = mpi)
end
@doc raw"""
jacview(sess::PyObject, f::Function, θ::Union{Array{Float64}, PyObject, Missing},
u0::Array{Float64}, args...)
Performs gradient test for a vector function. `f` has the signature
```
f(θ, u) -> r, J
```
Here `θ` is a nuisance parameter, `u` is the state variables (w.r.t. which the Jacobian is computed),
`r` is the residual vector, and `J` is the Jacobian matrix (a dense matrix or a [`SparseTensor`](@ref)).
# Example 1
```julia
u0 = rand(10)
function verify_jacobian_f(θ, u)
r = u^3+u - u0
r, spdiag(3u^2+1.0)
end
jacview(sess, verify_jacobian_f, missing, u0)
```
# Example 2
```
u0 = rand(10)
rs = rand(10)
function verify_jacobian_f(θ, u)
r = [u^2;u] - [rs;rs]
r, [spdiag(2*u); spdiag(10)]
end
jacview(sess, verify_jacobian_f, missing, u0); close("all")
```
"""
function jacview(sess::PyObject, f::Function, θ::Union{Array{Float64}, PyObject, Missing},
u0::Array{Float64}, args...)
mp = require_pyplot()
u = placeholder(Float64, shape=[length(u0)])
L, J = f(θ, u)
init(sess)
L_ = run(sess, L, u=>u0, args...)
J_ = run(sess, J, u=>u0, args...)
v = rand(length(u0))
γs = 1.0 ./ 10 .^ (1:5)
v1 = Float64[]
v2 = Float64[]
for i = 1:5
L__ = run(sess, L, u=>u0+v*γs[i], args...)
push!(v1, norm(L__-L_))
push!(v2, norm(L__-L_-γs[i]*J_*v))
end
mp.close("all")
mp.loglog(γs, abs.(v1), "*-", label="finite difference")
mp.loglog(γs, abs.(v2), "+-", label="automatic linearization")
mp.loglog(γs, γs.^2 * 0.5*abs(v2[1])/γs[1]^2, "--",label="\$\\mathcal{O}(\\gamma^2)\$")
mp.loglog(γs, γs * 0.5*abs(v1[1])/γs[1], "--",label="\$\\mathcal{O}(\\gamma)\$")
mp.plt.gca().invert_xaxis()
mp.legend()
mp.xlabel("\$\\gamma\$")
mp.ylabel("Error")
end
function PCLview(sess::PyObject, f::Function, L::Function, θ::Union{PyObject,Array{Float64,1}, Float64},
u0::Union{PyObject, Array{Float64}}, args...; options::Union{Dict{String, T}, Missing}=missing) where T<:Real
mp = require_pyplot()
if isa(θ, PyObject)
θ = run(sess, θ, args...)
end
x = placeholder(Float64, shape=[length(θ)])
l, u, g = NonlinearConstrainedProblem(f, L, x, u0; options=options)
init(sess)
L_ = run(sess, l, x=>θ, args...)
J_ = run(sess, g, x=>θ, args...)
v = rand(length(x))
γs = 1.0 ./ 10 .^ (1:5)
v1 = Float64[]
v2 = Float64[]
for i = 1:5
@info i
L__ = run(sess, l, x=>θ+v*γs[i], args...)
# @show L__,L_,J_, v
push!(v1, L__-L_)
push!(v2, L__-L_-γs[i]*sum(J_.*v))
end
mp.close("all")
mp.loglog(γs, abs.(v1), "*-", label="finite difference")
mp.loglog(γs, abs.(v2), "+-", label="automatic linearization")
mp.loglog(γs, γs.^2 * 0.5*abs(v2[1])/γs[1]^2, "--",label="\$\\mathcal{O}(\\gamma^2)\$")
mp.loglog(γs, γs * 0.5*abs(v1[1])/γs[1], "--",label="\$\\mathcal{O}(\\gamma)\$")
mp.plt.gca().invert_xaxis()
mp.legend()
mp.xlabel("\$\\gamma\$")
mp.ylabel("Error")
end
@doc raw"""
animate(update::Function, frames; kwargs...)
Creates an animation using update function `update`.
# Example
```julia
θ = LinRange(0, 2π, 100)
x = cos.(θ)
y = sin.(θ)
pl, = plot([], [], "o-")
t = title("0")
xlim(-1.2,1.2)
ylim(-1.2,1.2)
function update(i)
t.set_text("$i")
pl.set_data([x[1:i] y[1:i]]'|>Array)
end
animate(update, 1:100)
```
"""
function animate(update::Function, frames; kwargs...)
mp = require_pyplot()
animation_ = pyimport("matplotlib.animation")
if !isa(frames, Integer)
frames = Array(frames)
end
animation_.FuncAnimation(mp.gcf(), update, frames=frames; kwargs...)
end
"""
saveanim(anim::PyObject, filename::String; kwargs...)
Saves the animation produced by [`animate`](@ref)
"""
function saveanim(anim::PyObject, filename::String; kwargs...)
if Sys.iswindows()
anim.save(filename, "ffmpeg"; kwargs...)
else
anim.save(filename, "imagemagick"; kwargs...)
end
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 25343 | export
dense,
flatten,
ae,
ae_num,
ae_init,
fc,
fc_num,
fc_init,
fc_to_code,
ae_to_code,
fcx,
bn,
sparse_softmax_cross_entropy_with_logits,
Resnet1D
#----------------------------------------------------
# activation functions
_string2fn = Dict(
"relu" => relu,
"tanh" => tanh,
"sigmoid" => sigmoid,
"leakyrelu" => leaky_relu,
"leaky_relu" => leaky_relu,
"relu6" => relu6,
"softmax" => softmax,
"softplus" => softplus,
"selu" => selu,
"elu" => elu,
"concat_elu"=>concat_elu,
"concat_relu"=>concat_relu,
"hard_sigmoid"=>hard_sigmoid,
"swish"=>swish,
"hard_swish"=>hard_swish,
"concat_hard_swish"=>concat_hard_swish,
"sin"=>sin,
"fourier"=>fourier
)
function get_activation_function(a::Union{Function, String, Nothing})
if isnothing(a)
return x->x
end
if isa(a, String)
if haskey(_string2fn, lowercase(a))
return _string2fn[lowercase(a)]
else
error("Activation function $a is not supported, available activation functions:\n$(collect(keys(_string2fn))).")
end
else
return a
end
end
@doc raw"""
fcx(x::Union{Array{Float64,2},PyObject}, output_dims::Array{Int64,1},
θ::Union{Array{Float64,1}, PyObject};
activation::String = "tanh")
Creates a fully connected neural network with output dimension `o` and inputs $x\in \mathbb{R}^{m\times n}$.
$$x \rightarrow o_1 \rightarrow o_2 \rightarrow \ldots \rightarrow o_k$$
`θ` is the weights and biases of the neural network, e.g., `θ = ae_init(output_dims)`.
`fcx` outputs two tensors:
- the output of the neural network: $u\in \mathbb{R}^{m\times o_k}$.
- the sensitivity of the neural network per sample: $\frac{\partial u}{\partial x}\in \mathbb{R}^{m \times o_k \times n}$
"""
function fcx(x::Union{Array{Float64,2},PyObject}, output_dims::Array{Int64,1},
θ::Union{Array{Float64,1}, PyObject};
activation::String = "tanh")
pth = joinpath(@__DIR__, "../deps/Plugin/ExtendedNN/build/ExtendedNn")
pth = get_library(pth)
require_file(pth) do
install_adept()
change_directory(splitdir(pth)[1])
require_cmakecache() do
cmake()
end
make()
end
extended_nn_ = load_op_and_grad(pth, "extended_nn"; multiple=true)
config = [size(x,2);output_dims]
x_,config_,θ_ = convert_to_tensor([x,config,θ], [Float64,Int64,Float64])
x_ = reshape(x_, (-1,))
u, du = extended_nn_(x_,config_,θ_,activation)
reshape(u, (size(x,1), config[end])), reshape(du, (size(x,1), config[end], size(x,2)))
end
"""
ae(x::PyObject, output_dims::Array{Int64}, scope::String = "default";
activation::Union{Function,String} = "tanh")
Alias: `fc`, `ae`
Creates a neural network with intermediate numbers of neurons `output_dims`.
"""
function ae(x::Union{Array{Float64},PyObject}, output_dims::Array{Int64}, scope::String = "default";
activation::Union{Function,String} = "tanh")
if isa(x, Array)
x = constant(x)
end
flag = false
if length(size(x))==1
x = reshape(x, length(x), 1)
flag = true
end
net = x
variable_scope(scope, reuse=AUTO_REUSE) do
for i = 1:length(output_dims)-1
net = dense(net, output_dims[i], activation=activation)
end
net = dense(net, output_dims[end])
end
if flag && (size(net,2)==1)
net = squeeze(net)
end
return net
end
"""
ae(x::Union{Array{Float64}, PyObject}, output_dims::Array{Int64}, θ::Union{Array{Float64}, PyObject};
activation::Union{Function,String, Nothing} = "tanh")
Alias: `fc`, `ae`
Creates a neural network with intermediate numbers of neurons `output_dims`. The weights are given by `θ`
# Example 1: Explicitly construct weights and biases
```julia
x = constant(rand(10,2))
n = ae_num([2,20,20,20,2])
θ = Variable(randn(n)*0.001)
y = ae(x, [20,20,20,2], θ)
```
# Example 2: Implicitly construct weights and biases
```julia
θ = ae_init([10,20,20,20,2])
x = constant(rand(10,10))
y = ae(x, [20,20,20,2], θ)
```
See also [`ae_num`](@ref), [`ae_init`](@ref).
"""
function ae(x::Union{Array{Float64}, PyObject}, output_dims::Array{Int64}, θ::Union{Array{Float64}, PyObject};
activation::Union{Function,String, Nothing} = "tanh")
activation = get_activation_function(activation)
x = convert_to_tensor(x)
θ = convert_to_tensor(θ)
flag = false
if length(size(x))==1
x = reshape(x, length(x), 1)
flag = true
end
offset = 0
net = x
output_dims = [size(x,2); output_dims]
for i = 1:length(output_dims)-2
m = output_dims[i]
n = output_dims[i+1]
net = net * reshape(θ[offset+1:offset+m*n], (m, n)) + θ[offset+m*n+1:offset+m*n+n]
net = activation(net)
offset += m*n+n
end
m = output_dims[end-1]
n = output_dims[end]
net = net * reshape(θ[offset+1:offset+m*n], (m, n)) + θ[offset+m*n+1:offset+m*n+n]
offset += m*n+n
if offset!=length(θ)
error("ADCME: the weights and configuration does not match. Required $offset but given $(length(θ)).")
end
if flag && (size(net,2)==1)
net = squeeze(net)
end
return net
end
"""
ae(x::Union{Array{Float64}, PyObject},
output_dims::Array{Int64},
θ::Union{Array{Array{Float64}}, Array{PyObject}};
activation::Union{Function,String} = "tanh")
Alias: `fc`, `ae`
Constructs a neural network with given weights and biases `θ`
# Example
```julia
x = constant(rand(10,30))
θ = ae_init([30, 20, 20, 5])
y = ae(x, [20, 20, 5], θ) # 10×5
```
"""
function ae(x::Union{Array{Float64}, PyObject},
output_dims::Array{Int64},
θ::Union{Array{Array{Float64}}, Array{PyObject}};
activation::Union{Function,String} = "tanh")
if isa(θ, Array{Array{Float64}})
val = []
for t in θ
push!(val, θ'[:])
end
val = vcat(val...)
else
val = []
for t in θ
push!(val, reshape(θ, (-1,)))
end
vcat(val...)
end
ae(x, output_dims, θ, activation=activation)
end
@doc raw"""
ae_init(output_dims::Array{Int64}; T::Type=Float64, method::String="xavier")
fc_init(output_dims::Array{Int64})
Return the initial weights and bias values by TensorFlow as a vector. The neural network architecture is
```math
o_1 (\text{Input layer}) \rightarrow o_2 \rightarrow \ldots \rightarrow o_n (\text{Output layer})
```
Three types of
random initializers are provided
- `xavier` (default). It is useful for `tanh` fully connected neural network.
```
W^l_i \sim \mathcal{N}\left(0, \sqrt{\frac{1}{n_{l-1}}}\right)
```
- `xavier_avg`. A variant of `xavier`
```math
W^l_i \sim \mathcal{N}\left(0, \sqrt{\frac{2}{n_l + n_{l-1}}}\right)
```
- `he`. This is the activation aware initialization of weights and helps mitigate the problem
of vanishing/exploding gradients.
$$W^l_i \sim \mathcal{N}\left(0, \sqrt{\frac{2}{n_{l-1}}}\right)$$
# Example
```julia
x = constant(rand(10,30))
θ = fc_init([30, 20, 20, 5])
y = fc(x, [20, 20, 5], θ) # 10×5
```
"""
function ae_init(output_dims::Array{Int64}; T::Type=Float64, method::String="xavier")
N = ae_num(output_dims)
W = zeros(T, N)
offset = 0
for i = 1:length(output_dims)-1
m = output_dims[i]
n = output_dims[i+1]
if method=="xavier"
W[offset+1:offset+m*n] = randn(T, m*n) * T(sqrt(1/m))
elseif method=="xavier_normal"
W[offset+1:offset+m*n] = randn(T, m*n) * T(sqrt(2/(n+m)))
elseif method=="xavier_uniform"
W[offset+1:offset+m*n] = rand(T, m*n) * T(sqrt(6/(n+m)))
elseif method=="he"
W[offset+1:offset+m*n] = randn(T, m*n) * T(sqrt(2/(m)))
else
error("Method $method not understood")
end
offset += m*n+n
end
W
end
"""
ae_num(output_dims::Array{Int64})
fc_num(output_dims::Array{Int64})
Estimates the number of weights and biases for the neural network. Note the first dimension
should be the feature dimension (this is different from [`ae`](@ref) since in `ae` the feature
dimension can be inferred), and the last dimension should be the output dimension.
# Example
```julia
x = constant(rand(10,30))
θ = ae_init([30, 20, 20, 5])
@assert ae_num([30, 20, 20, 5])==length(θ)
y = ae(x, [20, 20, 5], θ)
```
"""
function ae_num(output_dims::Array{Int64})
offset = 0
for i = 1:length(output_dims)-2
m = output_dims[i]
n = output_dims[i+1]
offset += m*n+n
end
m = output_dims[end-1]
n = output_dims[end]
offset += m*n+n
return offset
end
function _ae_to_code(d::Dict, scope::String; activation::String)
i = 0
nn_code = ""
while true
si = i==0 ? "" : "_$i"
Wkey = "$(scope)backslashfully_connected$(si)backslashweightscolon0"
bkey = "$(scope)backslashfully_connected$(si)backslashbiasescolon0"
if haskey(d, Wkey)
if i!=0
nn_code *= " isa(net, Array) ? (net = $activation.(net)) : (net=$activation(net))\n"
nn_code *= " #-------------------------------------------------------------------\n"
end
nn_code *= " W$i = aedict$scope[\"$Wkey\"]\n b$i = aedict$scope[\"$bkey\"];\n"
nn_code *= " isa(net, Array) ? (net = net * W$i .+ b$i') : (net = net *W$i + b$i)\n"
i += 1
else
break
end
end
nn_code = """ global nn$scope\n function nn$scope(net)
$(nn_code) return net\n end """
nn_code
end
"""
ae_to_code(file::String, scope::String; activation::String = "tanh")
Return the code string from the feed-forward neural network data in `file`. Usually we can immediately evaluate
the code string into Julia session by
```julia
eval(Meta.parse(s))
```
If `activation` is not specified, `tanh` is the default.
"""
function ae_to_code(file::String, scope::String = "default"; activation::String = "tanh")
d = matread(file)
s = "let aedict$scope = matread(\"$file\")\n"*_ae_to_code(d, scope; activation = activation)*"\nend\n"
return s
end
fc_to_code = ae_to_code
# tensorflow layers from contrib
for (op, tfop) in [(:avg_pool2d, :avg_pool2d), (:avg_pool3d, :avg_pool3d),
(:flatten, :flatten), (:max_pool2d, :max_pool2d), (:max_pool3d, :max_pool3d)]
@eval begin
export $op
$op(args...; kwargs...) = tf.contrib.layers.$tfop(args...; kwargs...)
end
end
for (op, tfop) in [(:conv1d, :conv1d), (:conv2d, :conv2d), (:conv2d_in_plane, :conv2d_in_plane),
(:conv2d_transpose, :conv2d_transpose), (:conv3d, :conv3d), (:conv3d_transpose, :conv3d_transpose)]
@eval begin
export $op
function $op(args...;activation = nothing, bias=false, kwargs...)
activation = get_activation_function(activation)
if bias
biases_initializer = tf.zeros_initializer()
else
biases_initializer = nothing
end
tf.contrib.layers.$tfop(args...; activation_fn = activation, biases_initializer=biases_initializer, kwargs...)
end
end
end
"""
dense(inputs::Union{PyObject, Array{<:Real}}, units::Int64, args...;
activation::Union{String, Function} = nothing, kwargs...)
Creates a fully connected layer with the activation function specified by `activation`
"""
function dense(inputs::Union{PyObject, Array{<:Real}}, units::Int64, args...; activation::Union{String, Function, Nothing} = nothing, kwargs...)
inputs = constant(inputs)
activation = get_activation_function(activation)
tf.contrib.layers.fully_connected(inputs, units, args...; activation_fn=activation, kwargs...)
end
"""
bn(args...;center = true, scale=true, kwargs...)
`bn` accepts a keyword parameter `is_training`.
# Example
```julia
bn(inputs, name="batch_norm", is_training=true)
```
!!! note
`bn` should be used with `control_dependency`
```julia
update_ops = get_collection(UPDATE_OPS)
control_dependencies(update_ops) do
global train_step = AdamOptimizer().minimize(loss)
end
```
"""
function bn(args...;center = true, scale=true, kwargs...)
@warn """
`bn` should be used with `control_dependency`
```julia
update_ops = get_collection(UPDATE_OPS)
control_dependencies(update_ops) do
global train_step = AdamOptimizer().minimize(loss)
end
```
""" maxlog=1
kwargs = Dict{Any, Any}(kwargs)
if :is_training in keys(kwargs)
kwargs[:training] = kwargs[:is_training]
delete!(kwargs, :is_training)
end
if :scope in keys(kwargs)
kwargs[:name] = kwargs[:scope]
delete!(kwargs, :scope)
end
tf.layers.batch_normalization(args...;center = center, scale=scale, kwargs...)
end
sparse_softmax_cross_entropy_with_logits(args...;kwargs...) = tf.nn.sparse_softmax_cross_entropy_with_logits(args...;kwargs...)
export group_conv2d
function group_conv2d(inputs::PyObject, filters::Int64, args...; groups = 1, scope=scope, kwargs...)
if groups==1
return conv2d(inputs, filters, args...;scope=scope, kwargs...)
else
dims = size(inputs)
if mod(dims[end], groups)!=0 || mod(filters, groups)!=0
error("channels and outputs must be the multiples of `groups`")
end
n = div(filters, groups)
in_ = Array{PyObject}(undef, groups)
out_ = Array{PyObject}(undef, groups)
for i = 1:groups
py"""
temp = $inputs[:,:,:,$((i-1)*n):$(i*n)]
"""
in_[i] = py"temp"
out_[i] = conv2d(in_[i], n, args...;scope=scope*"_group$i", kwargs...)
end
out = concat(out_, dims=4)
return out
end
end
export separable_conv2d
function separable_conv2d(inputs, num_outputs, args...; activation=nothing, bias=false, kwargs...)
activation = get_activation_function(activation)
if bias
biases_initializer = tf.zeros_initializer()
else
biases_initializer = nothing
end
tf.contrib.layers.separable_conv2d(inputs, num_outputs, args...;activation_fn = activation,
biases_initializer=biases_initializer, kwargs...)
end
export depthwise_conv2d
function depthwise_conv2d(input, num_outputs, args...;
kernel_size = 3, channel_multiplier = 1, stride = 1, padding="SAME", bias=false, scope="default", reuse=AUTO_REUSE, kwargs...)
local res, strides
if isa(kernel_size, Int64)
kernel_size = (3,3)
end
if isa(stride, Int64)
strides = (1, stride, stride, 1)
end
variable_scope(scope, reuse=reuse) do
filter = get_variable("dconv2d",
shape=[kernel_size[1], kernel_size[2], size(input,4), channel_multiplier],
initializer=tf.contrib.layers.xavier_initializer())
res = tf.nn.depthwise_conv2d(input, filter, strides, padding, args...; kwargs...)
if bias
res = tf.contrib.layers.bias_add(res, scope=scope, reuse=AUTO_REUSE)
end
end
return res
end
"""
$(@doc ae)
"""
fc = ae
"""
$(@doc ae_num)
"""
fc_num = ae_num
"""
$(@doc ae_init)
"""
fc_init = ae_init
#------------------------------------------------------------------------------------------
export dropout
"""
dropout(x::Union{PyObject, Real, Array{<:Real}},
rate::Union{Real, PyObject}, training::Union{PyObject,Bool} = true; kwargs...)
Randomly drops out entries in `x` with a rate of `rate`.
"""
function dropout(x::Union{PyObject, Real, Array{<:Real}},
rate::Union{Real, PyObject}, training::Union{PyObject,Bool, Nothing} = nothing ; kwargs...)
x = constant(x)
if isnothing(training)
training = options.training.training
else
training = constant(training)
end
tf.keras.layers.Dropout(rate, kwargs...)(x, training)
end
export BatchNormalization
mutable struct BatchNormalization
dims::Int64
o::PyObject
end
"""
BatchNormalization(dims::Int64=2; kwargs...)
Creates a batch normalization layer.
# Example
```julia
b = BatchNormalization(2)
x = rand(10,2)
training = placeholder(true)
y = b(x, training)
run(sess, y)
```
"""
function BatchNormalization(dims::Int64=-1; kwargs...)
local o
if dims>=1
o = tf.keras.layers.BatchNormalization(dims-1, kwargs...)
else
o = tf.keras.layers.BatchNormalization(dims, kwargs...)
end
BatchNormalization(dims, o)
end
function Base.:show(io::IO, b::BatchNormalization)
print("<BatchNormalization normalization_dim=$(b.dims)>")
end
function (o::BatchNormalization)(x, training=ADCME.options.training.training)
flag = false
if get_dtype(x)==Float64
x = cast(x, Float32)
flag = true
end
out = o.o(x, training)
if flag
out = cast(Float64, out)
end
return out
end
export Dense, Conv1D, Conv2D, Conv3D, Conv2DTranspose
mutable struct Dense
hidden_dim::Int64
activation::Union{String, Function}
o::PyObject
end
"""
Dense(units::Int64, activation::Union{String, Function, Nothing} = nothing,
args...;kwargs...)
Creates a callable dense neural network.
"""
function Dense(units::Int64, activation::Union{String, Function, Nothing} = nothing,
args...;kwargs...)
activation = get_activation_function(activation)
o = tf.keras.layers.Dense(units, activation, args...;kwargs...)
Dense(units, activation, o)
end
function Base.:show(io::IO, o::Dense)
print("<Fully connected neural network with $(o.hidden_dim) hidden units and activation function \"$(o.activation)\">")
end
(o::Dense)(x) = o.o(x)
mutable struct Conv1D
filters
kernel_size
strides
activation
o::PyObject
end
"""
Conv1D(filters, kernel_size, strides, activation, args...;kwargs...)
```julia
c = Conv1D(32, 3, 1, "relu")
x = rand(100, 6, 128) # 128-length vectors with 6 timesteps ("channels")
y = c(x) # shape=(100, 4, 32)
```
"""
function Conv1D(filters, kernel_size, strides=1, activation=nothing, args...;kwargs...)
activation = get_activation_function(activation)
o = tf.keras.layers.Conv1D(filters, kernel_size, strides,args...; activation = activation, kwargs...)
Conv1D(filters, kernel_size, strides, activation, o)
end
function Base.:show(io::IO, o::Conv1D)
print("<Conv1D filters=$(o.filters) kernel_size=$(o.kernel_size) strides=$(o.strides) activation=$(o.activation)>")
end
function (o::Conv1D)(x::Union{PyObject, Array{<:Real,3}})
x = constant(x)
@assert length(size(x))==3
o.o(x)
end
mutable struct Conv2D
filters
kernel_size
strides
activation
o::PyObject
end
"""
Conv2D(filters, kernel_size, strides, activation, args...;kwargs...)
The arrangement is (samples, rows, cols, channels) (data_format='channels_last')
```julia
Conv2D(32, 3, 1, "relu")
```
"""
function Conv2D(filters, kernel_size, strides=1, activation=nothing, args...;kwargs...)
activation = get_activation_function(activation)
o = tf.keras.layers.Conv2D(filters, kernel_size, strides,args...; activation = activation, kwargs...)
Conv2D(filters, kernel_size, strides, activation, o)
end
function Base.:show(io::IO, o::Conv2D)
print("<Conv2D filters=$(o.filters) kernel_size=$(o.kernel_size) strides=$(o.strides) activation=$(o.activation)>")
end
function (o::Conv2D)(x::Union{PyObject, Array{<:Real,4}})
x = constant(x)
@assert length(size(x))==4
o.o(x)
end
mutable struct Conv2DTranspose
filters
kernel_size
strides
activation
o::PyObject
end
function Conv2DTranspose(filters, kernel_size, strides=1, activation=nothing, args...;kwargs...)
activation = get_activation_function(activation)
o = tf.keras.layers.Conv2DTranspose(
filters, kernel_size, strides=strides; activation = activation, kwargs...
)
Conv2DTranspose(filters, kernel_size, strides, activation, o)
end
function (o::Conv2DTranspose)(x::Union{PyObject, Array{<:Real,4}})
x = constant(x)
@assert length(size(x))==4
o.o(x)
end
mutable struct Conv3D
filters
kernel_size
strides
activation
o::PyObject
end
"""
Conv3D(filters, kernel_size, strides, activation, args...;kwargs...)
The arrangement is (samples, rows, cols, channels) (data_format='channels_last')
```julia
c = Conv3D(32, 3, 1, "relu")
x = constant(rand(100, 10, 10, 10, 16))
y = c(x)
# shape=(100, 8, 8, 8, 32)
```
"""
function Conv3D(filters, kernel_size, strides=1, activation=nothing, args...;kwargs...)
activation = get_activation_function(activation)
o = tf.keras.layers.Conv3D(filters, kernel_size, strides,args...; activation = activation, kwargs...)
Conv3D(filters, kernel_size, strides, activation, o)
end
function Base.:show(io::IO, o::Conv3D)
print("<Conv3D filters=$(o.filters) kernel_size=$(o.kernel_size) strides=$(o.strides) activation=$(o.activation)>")
end
function (o::Conv3D)(x::Union{PyObject, Array{<:Real,5}})
x = constant(x)
@assert length(size(x))==5
o.o(x)
end
#------------------------------------------------------------------------------------------
# resnet, adapted from https://github.com/bayesiains/nsf/blob/master/nn/resnet.py
mutable struct ResnetBlock
use_batch_norm::Bool
activation::Union{String,Function}
linear_layers::Array{Dense}
bn_layers::Array{BatchNormalization}
dropout_probability::Float64
end
function ResnetBlock(features::Int64; dropout_probability::Float64=0., use_batch_norm::Bool,
activation::String="relu")
activation = get_activation_function(activation)
bn_layers = []
if use_batch_norm
bn_layers = [
BatchNormalization(),
BatchNormalization()
]
end
linear_layers = [
Dense(features, nothing)
Dense(features, nothing)
]
ResnetBlock(use_batch_norm, activation, linear_layers, bn_layers, dropout_probability)
end
function (res::ResnetBlock)(input)
x = input
if res.use_batch_norm
x = res.bn_layers[1](x)
end
x = res.activation(x)
x = res.linear_layers[1](x)
if res.use_batch_norm
x = res.bn_layers[2](x)
end
x = res.activation(x)
x = dropout(x, res.dropout_probability, options.training.training)
x = res.linear_layers[2](x)
return x + input
end
mutable struct Resnet1D
initial_layer::Dense
blocks::Array{ResnetBlock}
final_layer::Dense
end
"""
Resnet1D(out_features::Int64, hidden_features::Int64;
num_blocks::Int64=2, activation::Union{String, Function, Nothing} = "relu",
dropout_probability::Float64 = 0.0, use_batch_norm::Bool = false, name::Union{String, Missing} = missing)
Creates a 1D residual network. If `name` is not missing, `Resnet1D` does not create a new entity.
# Example
```julia
resnet = Resnet1D(20)
x = rand(1000,10)
y = resnet(x)
```
# Example: Digit recognition
```
using MLDatasets
using ADCME
# load data
train_x, train_y = MNIST.traindata()
train_x = reshape(Float64.(train_x), :, size(train_x,3))'|>Array
test_x, test_y = MNIST.testdata()
test_x = reshape(Float64.(test_x), :, size(test_x,3))'|>Array
# construct loss function
ADCME.options.training.training = placeholder(true)
x = placeholder(rand(64, 784))
l = placeholder(rand(Int64, 64))
resnet = Resnet1D(10, num_blocks=10)
y = resnet(x)
loss = mean(sparse_softmax_cross_entropy_with_logits(labels=l, logits=y))
# train the neural network
opt = AdamOptimizer().minimize(loss)
sess = Session(); init(sess)
for i = 1:10000
idx = rand(1:60000, 64)
_, loss_ = run(sess, [opt, loss], feed_dict=Dict(l=>train_y[idx], x=>train_x[idx,:]))
@info i, loss_
end
# test
for i = 1:10
idx = rand(1:10000,100)
y0 = resnet(test_x[idx,:])
y0 = run(sess, y0, ADCME.options.training.training=>false)
pred = [x[2]-1 for x in argmax(y0, dims=2)]
@info "Accuracy = ", sum(pred .== test_y[idx])/100
end
```

"""
function Resnet1D(out_features::Int64, hidden_features::Int64 = 20;
num_blocks::Int64=2, activation::Union{String, Function, Nothing} = "relu",
dropout_probability::Float64 = 0.0, use_batch_norm::Bool = false,
name::Union{String, Missing} = missing)
if haskey(ADCME.STORAGE, name)
@info "Reusing $name..."
return ADCME.STORAGE[name]
end
initial_layer = Dense(hidden_features)
blocks = ResnetBlock[]
for i = 1:num_blocks
push!(blocks, ResnetBlock(
hidden_features,
dropout_probability = dropout_probability,
use_batch_norm = use_batch_norm
))
end
final_layer = Dense(out_features)
if ismissing(name)
name = "Resnet1D_"*randstring(10)
end
res = Resnet1D(initial_layer, blocks, final_layer)
ADCME.STORAGE[name] = res
return res
end
function (res::Resnet1D)(x)
x = res.initial_layer(x)
for b in res.blocks
x = b(x)
end
x = res.final_layer(x)
x
end
function Base.:show(io::IO, res::Resnet1D)
println("( Input )")
println("\t↓")
show(io, res.initial_layer)
println("\n")
for i = 1:length(res.blocks)
show(io, res.blocks[i])
println("\n")
println("\t↓")
end
show(io, res.final_layer)
println("\n( Output )")
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 18484 | export mpi_bcast, mpi_init, mpi_recv, mpi_send,
mpi_sendrecv, mpi_sum, mpi_finalize, mpi_initialized, mpi_halo_exchange, mpi_halo_exchange2,
mpi_finalized, mpi_rank, mpi_size, mpi_sync!, mpi_gather, mpi_SparseTensor, require_mpi
"""
mpi_init()
Initialized the MPI session. `mpi_init` must be called before any `run(sess, ...)`.
"""
function mpi_init()
if mpi_initialized()
@warn "MPI has already been initialized"
return
end
@eval ccall((:mpi_init, $LIBADCME), Cvoid, ())
end
"""
mpi_finalize()
Finalize the MPI call.
"""
function mpi_finalize()
mpi_check()
@eval ccall((:mpi_finalize, $LIBADCME), Cvoid, ())
end
"""
mpi_rank()
Returns the rank of current MPI process (rank 0 based).
"""
function mpi_rank()
mpi_check()
out = @eval ccall((:mpi_rank, $LIBADCME), Cint, ())
Int64(out)
end
"""
mpi_size()
Returns the size of MPI world.
"""
function mpi_size()
mpi_check()
@eval ccall((:mpi_size, $LIBADCME), Cint, ())
end
"""
require_mpi()
Throws an error if `mpi_init()` has not been called.
"""
function require_mpi()
if !mpi_initialized()
error("MPI has not been initialized. Run `mpi_init()` to initialize MPI first.")
end
end
"""
mpi_finalized()
Returns a boolean indicating whether the current MPI session is finalized.
"""
function mpi_finalized()
require_mpi()
Bool(@eval ccall((:mpi_finalized, $LIBADCME), Cuchar, ()))
end
"""
mpi_initialized()
Returns a boolean indicating whether the current MPI session is initialized.
"""
function mpi_initialized()
Bool(@eval ccall((:mpi_initialized, $LIBADCME), Cuchar, ()))
end
"""
mpi_sync!(message::Array{Int64,1}, root::Int64 = 0)
mpi_sync!(message::Array{Float64,1}, root::Int64 = 0)
Sync `message` across all MPI processors.
"""
function mpi_sync!(message::Array{Int64,1}, root::Int64 = 0)
mpi_check()
@eval ccall((:mpi_sync, $LIBADCME), Cvoid, (Ptr{Clonglong}, Cint, Cint), $message, Int32(length($message)), Int32($root))
end
function mpi_sync!(message::Array{Float64,1}, root::Int64 = 0)
mpi_check()
@eval ccall((:mpi_sync_double, $LIBADCME), Cvoid, (Ptr{Cdouble}, Cint, Cint), $message, Int32(length($message)), Int32($root))
end
function mpi_check()
require_mpi()
if mpi_finalized()
error("MPI has been finalized.")
end
end
function _mpi_sum(a,root::Int64=0)
mpi_check()
mpisum_ = load_system_op("mpisum")
a,root = convert_to_tensor(Any[a,root], [Float64,Int64])
out = mpisum_(a,root)
if !isnothing(length(a))
return set_shape(out, (length(a),))
else
return out
end
end
"""
mpi_sum(a::Union{Array{Float64}, Float64, PyObject}, root::Int64 = 0)
Sum `a` on the MPI processor `root`.
"""
function mpi_sum(a::Union{Array{Float64}, Float64, PyObject}, root::Int64 = 0)
a = convert_to_tensor(a, dtype = Float64)
if length(size(a))==0
a = reshape(a, (1,))
out = _mpi_sum(a, root)
return squeeze(out)
elseif length(size(a))==1
return _mpi_sum(a, root)
elseif nothing in size(a)
error("The shape of 1st input $(size(a)) contains nothing. mpi_sum is not able to determine
the output shape.")
else
s = size(a)
a = reshape(a, (-1,))
out = _mpi_sum(a, root)
return reshape(out, s)
end
end
function _mpi_bcast(a,root::Int64=0)
mpi_check()
mpibcast_ = load_system_op("mpibcast")
a,root = convert_to_tensor(Any[a,root], [Float64,Int64])
out = mpibcast_(a,root)
if !isnothing(length(a))
return set_shape(out, (length(a),))
else
return out
end
end
"""
mpi_bcast(a::Union{Array{Float64}, Float64, PyObject}, root::Int64 = 0)
Broadcast `a` from processor `root` to all other processors.
"""
function mpi_bcast(a::Union{Array{Float64}, Float64, PyObject}, root::Int64 = 0)
a = convert_to_tensor(a, dtype = Float64)
if length(size(a))==0
a = reshape(a, (1,))
out = _mpi_bcast(a, root)
return squeeze(out)
elseif length(size(a))==1
return _mpi_bcast(a, root)
elseif nothing in size(a)
error("The shape of 1st input $(size(a)) contains nothing. mpi_bcast is not able to determine
the output shape.")
else
s = size(a)
a = reshape(a, (-1,))
out = _mpi_bcast(a, root)
return reshape(out, s)
end
end
function _mpi_send(a,dest::Int64,tag::Int64=0)
mpisend_ = load_system_op("mpisend")
a,dest,tag = convert_to_tensor(Any[a,dest,tag], [Float64,Int64,Int64])
out = mpisend_(a,dest,tag)
if !isnothing(length(a))
return set_shape(out, (length(a),))
else
return out
end
end
"""
mpi_send(a::Union{Array{Float64}, Float64, PyObject}, dest::Int64,root::Int64 = 0)
Sends `a` to processor `dest`. `a` itself is returned so that the send action can be added to the computational graph.
"""
function mpi_send(a::Union{Array{Float64}, Float64, PyObject}, dest::Int64,root::Int64 = 0)
a = convert_to_tensor(a, dtype = Float64)
if length(size(a))==0
a = reshape(a, (1,))
out = _mpi_send(a,dest, root)
return squeeze(out)
elseif length(size(a))==1
return _mpi_send(a, dest, root)
elseif nothing in size(a)
error("The shape of 1st input $(size(a)) contains nothing. mpi_send is not able to determine
the output shape.")
else
s = size(a)
a = reshape(a, (-1,))
out = _mpi_send(a, dest, root)
return reshape(out, s)
end
end
function _mpi_recv(a,src::Int64,tag::Int64=0)
mpirecv_ = load_system_op("mpirecv")
a,src,tag = convert_to_tensor(Any[a,src,tag], [Float64,Int64,Int64])
mpirecv_(a,src,tag)
end
"""
mpi_recv(a::Union{Array{Float64}, Float64, PyObject}, src::Int64, tag::Int64 = 0)
Receives an array from processor `src`. `mpi_recv` requires an input for gradient backpropagation.
Typically we can write
```julia
r = mpi_rank()
a = constant(Float64(r))
if r==1
a = mpi_send(a, 0)
end
if r==0
a = mpi_recv(a, 1)
end
```
Then `a=1` on both processor 0 and processor 1.
"""
function mpi_recv(a::Union{Array{Float64}, Float64, PyObject}, src::Int64, tag::Int64 = 0)
a = convert_to_tensor(a, dtype = Float64)
if length(size(a))==0
a = reshape(a, (1,))
out = _mpi_recv(a, src, tag)
return squeeze(out)
elseif length(size(a))==1
return _mpi_recv(a, src, tag)
elseif nothing in size(a)
error("The shape of 1st input $(size(a)) contains nothing. mpi_recv is not able to determine
the output shape.")
else
s = size(a)
a = reshape(a, (-1,))
out = _mpi_recv(a, src, tag)
return reshape(out, s)
end
end
"""
mpi_sendrecv(a::Union{Array{Float64}, Float64, PyObject}, dest::Int64, src::Int64, tag::Int64=0)
A convenient wrapper for `mpi_send` followed by `mpi_recv`.
"""
function mpi_sendrecv(a::Union{Array{Float64}, Float64, PyObject}, dest::Int64, src::Int64, tag::Int64=0)
r = mpi_rank()
@assert src != dest
if r==src
a = mpi_send(a, dest, tag)
elseif r==dest
a = mpi_recv(a, src, tag)
end
a
end
"""
mpi_gather(u::Union{Array{Float64, 1}, PyObject}, deps::Union{Missing, PyObject} = missing)
Gathers all the vectors from different processes to the root process. The function returns
a long vector which concatenates of local vectors in the order of process IDs.
"""
function mpi_gather(u::Union{Array{Float64, 1}, PyObject}, deps::Union{Missing, PyObject} = missing)
mpigather_ = load_system_op("mpigather")
u = convert_to_tensor(Any[u], [Float64]); u = u[1]
out = mpigather_(u)
set_shape(out, (mpi_size()*length(u)))
end
function load_plugin_MPITensor()
if !isfile("$(ADCME.LIBDIR)/libHYPRE.so")
scriptpath = joinpath(@__DIR__, "..", "deps", "install_hypre.jl")
include(scriptpath)
end
if Sys.isapple()
oplibpath = joinpath(@__DIR__, "..", "deps", "Plugin", "MPITensor", "build", "libMPITensor.dylib")
elseif Sys.iswindows()
oplibpath = joinpath(@__DIR__, "..", "deps", "Plugin", "MPITensor", "build", "MPITensor.dll")
else
oplibpath = joinpath(@__DIR__, "..", "deps", "Plugin", "MPITensor", "build", "libMPITensor.so")
end
if !isfile(oplibpath)
PWD = pwd()
cd(joinpath(@__DIR__, "..", "deps", "Plugin", "MPITensor"))
if !isdir("build")
mkdir("build")
end
cd("build")
cmake()
make()
cd(PWD)
end
oplibpath
end
function load_plugin_MPIHaloExchange(reach::Int64=1)
if reach==1
DIR = joinpath(@__DIR__, "..", "deps", "Plugin", "MPIHaloExchange")
LIB = "HaloExchangeTwoD"
elseif reach==2
DIR = joinpath(@__DIR__, "..", "deps", "Plugin", "MPIHaloExchange2")
LIB = "HaloExchangeNeighborTwo"
end
if Sys.isapple()
oplibpath = joinpath(DIR, "build", "lib$LIB.dylib")
elseif Sys.iswindows()
oplibpath = joinpath(DIR, "build", "$LIB.dll")
else
oplibpath = joinpath(DIR, "build", "lib$LIB.so")
end
if !isfile(oplibpath)
PWD = pwd()
cd(DIR)
if !isdir("build")
mkdir("build")
end
cd("build")
cmake()
make()
cd(PWD)
end
oplibpath
end
function mpi_halo_exchange_(oplibpath, u,fill_value,m,n, tag, deps)
halo_exchange_two_d_ = load_op_and_grad(oplibpath,"halo_exchange_two_d")
u,fill_value,m,n,tag = convert_to_tensor(Any[u,fill_value,m,n,tag], [Float64,Float64,Int64,Int64,Int64])
deps = coalesce(deps, u[1,1])
out = halo_exchange_two_d_(u,fill_value,m,n,tag, deps)
set_shape(out, (size(u,1)+2, size(u,2)+2))
end
function mpi_halo_exchange2_(oplibpath, u,fill_value,m,n,tag,w)
halo_exchange_neighbor_two_ = load_op_and_grad(oplibpath,"halo_exchange_neighbor_two")
w = coalesce(w, u[1,1])
u,fill_value,m,n,tag,w = convert_to_tensor(Any[u,fill_value,m,n,tag,w], [Float64,Float64,Int64,Int64,Int64,Float64])
out = halo_exchange_neighbor_two_(u,fill_value,m,n,tag,w)
set_shape(out, (size(u,1)+4, size(u,2)+4))
end
function mpi_create_matrix(oplibpath, indices,values,ilower,iupper)
mpi_create_matrix_ = load_op_and_grad(oplibpath,"mpi_create_matrix", multiple=true)
indices,values,ilower,iupper = convert_to_tensor(Any[indices,values,ilower,iupper], [Int64,Float64,Int64,Int64])
mpi_create_matrix_(indices,values,ilower,iupper)
end
function mpi_get_matrix(oplibpath, rows,ncols,cols,ilower,iupper,values, N)
mpi_get_matrix_ = load_op_and_grad(oplibpath,"mpi_get_matrix", multiple=true)
rows,ncols,cols,ilower_,iupper_,values = convert_to_tensor(Any[rows,ncols,cols,ilower,iupper,values], [Int32,Int32,Int32,Int64,Int64,Float64])
indices, vals = mpi_get_matrix_(rows,ncols,cols,ilower_,iupper_,values)
SparseTensor(tf.SparseTensor(indices, vals, (iupper-ilower+1, N)), false)
end
function mpi_tensor_solve(oplibpath, rows,ncols,cols,values,rhs,ilower,iupper,solver,printlevel)
mpi_tensor_solve_ = load_op_and_grad(oplibpath,"mpi_tensor_solve")
rows,ncols,cols,values,rhs,ilower,iupper,printlevel = convert_to_tensor(Any[rows,ncols,cols,values,rhs,ilower,iupper,printlevel], [Int32,Int32,Int32,Float64,Float64,Int64,Int64,Int64])
mpi_tensor_solve_(rows,ncols,cols,values,rhs,ilower,iupper,solver,printlevel)
end
@doc raw"""
mutable struct mpi_SparseTensor
rows::PyObject
ncols::PyObject
cols::PyObject
values::PyObject
ilower::Int64
iupper::Int64
N::Int64
oplibpath::String
end
A structure to hold local data of a sparse matrix. The global matrix is assumed to be a $M\times N$ square matrix.
The current processor owns rows from `ilower` to `iupper` (inclusive). The data is specified by
- `rows`: an array indicating the rows that contain nonzero values. Note `rows ≥ ilower`.
- `ncols`: an array indicating the number of nonzero values for each row in `rows`.
- `cols`: the column indices for nonzero values. Its length is $\sum_{i=1}^{\mathrm{ncols}} \mathrm{ncols}_i$
- `vals`: the nonzero values corresponding to each column index in `cols`
- `oplibpath`: the backend library (returned by `ADCME.load_plugin_MPITensor`)
All data structure are 0-based. Note if we work with a linear solver, $M=N$.
For example, consider the sparse matrix
```
[ 1 0 0 1 ]
[ 0 1 2 1 ]
```
We have
```julia
rows = Int32[0;1]
ncols = Int32[2;3]
cols = Int32[0;3;1,2,3]
values = [1.;1.;1.;2.;1.]
iupper = ilower + 2
```
"""
mutable struct mpi_SparseTensor
rows::PyObject
ncols::PyObject
cols::PyObject
values::PyObject
ilower::Int64
iupper::Int64
N::Int64
oplibpath::String
end
function Base.:show(io::IO, sp::mpi_SparseTensor)
if isnothing(length(sp.values))
len = "?"
else
len = length(sp.values)
end
print("mpi_SparseTensor($(sp.iupper - sp.ilower + 1), $(sp.N)), range = [$(sp.ilower), $(sp.iupper)], nnz = $(len)")
end
function mpi_SparseTensor(indices::PyObject, values::PyObject, ilower::Int64, iupper::Int64, N::Int64)
@assert ilower >=0
@assert ilower <= iupper
@assert iupper <= N
oplibpath = load_plugin_MPITensor()
rows, ncols, cols, out = mpi_create_matrix(oplibpath, indices,values,ilower,iupper)
mpi_SparseTensor(rows, ncols, cols, out, ilower, iupper, N, oplibpath)
end
@doc raw"""
mpi_SparseTensor(rows::Union{Array{Int32,1}, PyObject}, ncols::Union{Array{Int32,1}, PyObject}, cols::Union{Array{Int32,1}, PyObject},
vals::Union{Array{Float64,1}, PyObject}, ilower::Int64, iupper::Int64, N::Int64)
Create a $N\times N$ distributed sparse tensor `A` for the current MPI processor. The current MPI processor owns rows with indices `[ilower, iupper]`.
The submatrix is specified using the CSR format.
- `rows`: an array indicating the rows that contain nonzero values. Note `rows ≥ ilower`.
- `ncols`: an array indicating the number of nonzero values for each row in `rows`.
- `cols`: the column indices for nonzero values. Its length is $\sum_{i=1}^{\mathrm{ncols}} \mathrm{ncols}_i$
- `vals`: the nonzero values corresponding to each column index in `cols`
Note that by default the indices are zero-based.
"""
function mpi_SparseTensor(rows::Union{Array{Int32,1}, PyObject}, ncols::Union{Array{Int32,1}, PyObject}, cols::Union{Array{Int32,1}, PyObject},
vals::Union{Array{Float64,1}, PyObject}, ilower::Int64, iupper::Int64, N::Int64)
@assert ilower >=0
@assert ilower <= iupper
@assert iupper <= N
oplibpath = load_plugin_MPITensor()
rows, ncols, cols, vals = convert_to_tensor(
[rows, ncols, cols, vals],
[Int32, Int32, Int32, Float64]
)
mpi_SparseTensor(rows, ncols, cols, vals, ilower, iupper, N, oplibpath)
end
"""
mpi_SparseTensor(sp::Union{SparseTensor, SparseMatrixCSC{Float64,Int64}},
ilower::Union{Int64, Missing} = missing,
iupper::Union{Int64, Missing} = missing)
Constructing `mpi_SparseTensor` from a `SparseTensor` or a sparse Array.
"""
function mpi_SparseTensor(sp::Union{SparseTensor, SparseMatrixCSC{Float64,Int64}},
ilower::Union{Int64, Missing} = missing,
iupper::Union{Int64, Missing} = missing)
sp = constant(sp)
ilower = coalesce(ilower, 0)
iupper = coalesce(iupper, size(sp, 1)-1)
N = size(sp, 2)
mpi_SparseTensor(sp.o.indices, sp.o.values, ilower, iupper, N)
end
function LinearAlgebra.:\(sp::mpi_SparseTensor, b::Union{Array{Float64, 1}, PyObject})
b = constant(b)
@assert length(b)==sp.iupper - sp.ilower + 1
out = mpi_tensor_solve(sp.oplibpath, sp.rows,sp.ncols,
sp.cols,sp.values,b,
sp.ilower,sp.iupper,options.mpi.solver, options.mpi.printlevel)
set_shape(out, (sp.iupper-sp.ilower+1,))
end
function SparseTensor(sp::mpi_SparseTensor)
mpi_get_matrix(sp.oplibpath, sp.rows,sp.ncols,sp.cols,sp.ilower,sp.iupper,sp.values, sp.N)
end
function Base.:run(sess::PyObject, sp::mpi_SparseTensor)
run(sess, SparseTensor(sp))
end
@doc raw"""
mpi_halo_exchange(u::Union{Array{Float64, 2}, PyObject},m::Int64,n::Int64; deps::Union{Missing, PyObject} = missing,
fill_value::Float64 = 0.0, tag::Union{PyObject, Int64} = 0)
Perform Halo exchnage on `u` (a $k \times k$ matrix). The output has a shape $(k+2)\times (k+2)$
- `fill_value`: value used for the boundaries
- `tag`: message tag
- `deps`: a **scalar** tensor; it can be used to serialize the MPI calls
"""
function mpi_halo_exchange(u::Union{Array{Float64, 2}, PyObject},m::Int64,n::Int64; deps::Union{Missing, PyObject} = missing,
fill_value::Float64 = 0.0, tag::Union{PyObject, Int64} = 0)
@assert size(u,1)==size(u,2)
oplibpath = load_plugin_MPIHaloExchange()
mpi_halo_exchange_(oplibpath, u, fill_value, m, n, tag, deps)
end
@doc raw"""
mpi_halo_exchange2(u::Union{Array{Float64, 2}, PyObject},m::Int64,n::Int64; deps::Union{Missing, PyObject} = missing,
fill_value::Float64 = 0.0, tag::Union{PyObject, Int64} = 0)
Similar to [`mpi_halo_exchange`](@ref), but the reach is 2, i.e., for a $N\times N$ matrix $u$, the output will be a
$(N+4)\times (N+4)$ matrix.
"""
function mpi_halo_exchange2(u::Union{Array{Float64, 2}, PyObject},m::Int64,n::Int64; deps::Union{Missing, PyObject} = missing,
fill_value::Float64 = 0.0, tag::Union{PyObject, Int64} = 0)
@assert size(u,1)==size(u,2)
oplibpath = load_plugin_MPIHaloExchange(2)
mpi_halo_exchange2_(oplibpath, u, fill_value, m, n, tag, deps)
end
function mpi_tensor_transpose(oplibpath, row,col,ncol,val,n,rank,nt)
require_mpi()
mpi_tensor_transpose_ = load_op_and_grad(oplibpath,"mpi_tensor_transpose", multiple=true)
row,col,ncol,val,n,rank,nt = convert_to_tensor(Any[row,col,ncol,val,n,rank,nt], [Int32,Int32,Int32,Float64,Int64,Int64,Int64])
indices, vals = mpi_tensor_transpose_(row,col,ncol,val,n,rank,nt)
end
"""
adjoint(A::mpi_SparseTensor)
Returns the adjoint of `A`, i.e., `A'`. Each MPI rank owns the same number of rows.
"""
function Base.:adjoint(A::mpi_SparseTensor)
oplibpath = load_plugin_MPITensor()
n = A.iupper - A.ilower + 1
indices, vals = mpi_tensor_transpose(oplibpath, A.rows, A.cols, A.ncols, A.values, n, mpi_rank(), A.N)
sp = RawSparseTensor(indices, vals, n, A.N)
mpi_SparseTensor(sp, A.ilower, A.iupper)
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 15215 | export ode45, rk4, αscheme, αscheme_time,
αscheme_atime, TR_BDF2, ExplicitNewmark
function runge_kutta_one_step(f::Function, t::PyObject, y::PyObject, Δt::PyObject, θ::Union{PyObject, Missing})
k1 = Δt*f(t, y, θ)
k2 = Δt*f(t+Δt/2, y+k1/2, θ)
k3 = Δt*f(t+Δt/2, y+k2/2, θ)
k4 = Δt*f(t+Δt, y+k3, θ)
y = y + k1/6 + k2/3 + k3/3 + k4/6
end
function ode45_one_step(f::Function, t::PyObject, y::PyObject, h::PyObject, θ::Union{PyObject, Missing})
k1 = h * f(t, y, θ);
k2 = h * f(t + (1/5)*h, y + (1/5)*k1, θ);
k3 = h * f(t + (3/10)*h, y + (3/40)*k1 + (9/40)*k2, θ);
k4 = h * f(t + (4/5)*h, y + (44/45)*k1 + (-56/15)*k2 + (32/9)*k3, θ);
k5 = h * f(t + (8/9)*h, y + (19372/6561)*k1 + (-25360/2187)*k2 + (64448/6561)*k3 + (-212/729)*k4, θ);
k6 = h * f(t + h, y + (9017/3168)*k1 + (-355/33)*k2 + (46732/5247 )*k3 + (49/176)*k4 + (-5103/18656)*k5, θ);
k7 = h * f(t + h, y + (35/384)*k1 + (500/1113)*k3 + (125/192)*k4 + (-2187/6784)*k5 + (11/84)*k6, θ);
y_new = y + (35/384)*k1 + (500/1113)*k3 + (125/192)*k4 + (-2187/6784)*k5 + (11/84)*k6;
end
@doc raw"""
runge_kutta(f::Function, T::Union{PyObject, Float64},
NT::Union{PyObject,Int64}, y::Union{PyObject, Float64, Array{Float64}}, θ::Union{PyObject, Missing}=missing; method::String="rk4")
Solves
```math
\frac{dy}{dt} = f(y, t, \theta)
```
with Runge-Kutta method.
For example, the default solver, `RK4`, has the following numerical scheme per time step
```math
\begin{aligned}
k_1 &= \Delta t f(t_n, y_n, \theta)\\
k_2 &= \Delta t f(t_n+\Delta t/2, y_n + k_1/2, \theta)\\
k_3 &= \Delta t f(t_n+\Delta t/2, y_n + k_2/2, \theta)\\
k_4 &= \Delta t f(t_n+\Delta t, y_n + k_3, \theta)\\
y_{n+1} &= y_n + \frac{k_1}{6} +\frac{k_2}{3} +\frac{k_3}{3} +\frac{k_4}{6}
\end{aligned}
```
"""
function runge_kutta(f::Function, T::Union{PyObject, Float64},
NT::Union{PyObject,Int64}, y::Union{PyObject, Float64, Array{Float64}}, θ::Union{PyObject, Missing}=missing; method::String="rk4")
local one_step
if lowercase(method)=="rk4"
one_step = runge_kutta_one_step
elseif lowercase(method)=="rk45"
one_step = ode45_one_step
else
error("Method $method not implemented yet")
end
y = convert_to_tensor(y)
Δt = convert_to_tensor(T/NT)
ta = TensorArray(NT+1) # storing y
function condition(i, ta)
i <= NT+1
end
function body(i, ta)
y = read(ta, i-1)
y_ = one_step(f, (cast(eltype(Δt), i)-1)*Δt, y, Δt, θ)
ta = write(ta, i, y_)
i+1, ta
end
ta = write(ta, 1, y)
i = constant(2, dtype=Int32)
_, out = while_loop(condition, body, [i, ta])
res = stack(out)
end
@doc raw"""
rk4(y::Union{PyObject, Float64, Array{Float64}}, T::Union{PyObject, Float64},
NT::Union{PyObject,Int64}, f::Function, θ::Union{PyObject, Missing}=missing)
Solves
```math
\frac{dy}{dt} = f(y, t, \theta)
```
with Runge-Kutta (order 4) method.
"""
rk4(args...;kwargs...) = runge_kutta(args...;method="rk4", kwargs...)
@doc raw"""
ode45(y::Union{PyObject, Float64, Array{Float64}}, T::Union{PyObject, Float64},
NT::Union{PyObject,Int64}, f::Function, θ::Union{PyObject, Missing}=missing)
Solves
```math
\frac{dy}{dt} = f(y, t, \theta)
```
with six-stage, fifth-order, Runge-Kutta method.
"""
ode45(args...;kwargs...) = runge_kutta(args...;method="rk45", kwargs...)
@doc raw"""
αscheme(M::Union{SparseTensor, SparseMatrixCSC},
C::Union{SparseTensor, SparseMatrixCSC},
K::Union{SparseTensor, SparseMatrixCSC},
Force::Union{Array{Float64}, PyObject},
d0::Union{Array{Float64, 1}, PyObject},
v0::Union{Array{Float64, 1}, PyObject},
a0::Union{Array{Float64, 1}, PyObject},
Δt::Array{Float64};
solve::Union{Missing, Function} = missing,
extsolve::Union{Missing, Function} = missing,
ρ::Float64 = 1.0)
Generalized α-scheme.
$$M u_{tt} + C u_{t} + K u = F$$
`Force` must be an array of size `n`×`p`, where `d0`, `v0`, and `a0` have a size `p`
`Δt` is an array (variable time step).
The generalized α scheme solves the equation by the time stepping
```math
\begin{aligned}
\bf d_{n+1} &= \bf d_n + h\bf v_n + h^2 \left(\left(\frac{1}{2}-\beta_2 \right)\bf a_n + \beta_2 \bf a_{n+1} \right)\\
\bf v_{n+1} &= \bf v_n + h((1-\gamma_2)\bf a_n + \gamma_2 \bf a_{n+1})\\
\bf F(t_{n+1-\alpha_{f_2}}) &= M \bf a _{n+1-\alpha_{m_2}} + C \bf v_{n+1-\alpha_{f_2}} + K \bf{d}_{n+1-\alpha_{f_2}}
\end{aligned}
```
where
```math
\begin{aligned}
\bf d_{n+1-\alpha_{f_2}} &= (1-\alpha_{f_2})\bf d_{n+1} + \alpha_{f_2} \bf d_n\\
\bf v_{n+1-\alpha_{f_2}} &= (1-\alpha_{f_2}) \bf v_{n+1} + \alpha_{f_2} \bf v_n \\
\bf a_{n+1-\alpha_{m_2} } &= (1-\alpha_{m_2}) \bf a_{n+1} + \alpha_{m_2} \bf a_n\\
t_{n+1-\alpha_{f_2}} & = (1-\alpha_{f_2}) t_{n+1 + \alpha_{f_2}} + \alpha_{f_2}t_n
\end{aligned}
```
Here the parameters are computed using
```math
\begin{aligned}
\gamma_2 &= \frac{1}{2} - \alpha_{m_2} + \alpha_{f_2}\\
\beta_2 &= \frac{1}{4} (1-\alpha_{m_2}+\alpha_{f_2})^2 \\
\alpha_{m_2} &= \frac{2\rho_\infty-1}{\rho_\infty+1}\\
\alpha_{f_2} &= \frac{\rho_\infty}{\rho_\infty+1}
\end{aligned}
```
∘ `solve`: users can provide a solver function, `solve(A, rhs)` for solving `Ax = rhs`
∘ `extsolve`: similar to `solve`, but the signature has the form
```julia
extsolve(A, rhs, i)
```
This provides the users with more control, e.g., (time-dependent) Dirichlet boundary conditions.
See [Generalized α Scheme](https://kailaix.github.io/ADCME.jl/dev/alphascheme/) for details.
!!! note
In the case $u$ has a nonzero essential boundary condition $u_b$, we let $\tilde u=u-u_b$, then
$$M \tilde u_{tt} + C \tilde u_t + K u = F - K u_b - C \dot u_b$$
"""
function αscheme(M::Union{SparseTensor, SparseMatrixCSC},
C::Union{SparseTensor, SparseMatrixCSC},
K::Union{SparseTensor, SparseMatrixCSC},
Force::Union{Array{Float64, 2}, PyObject},
d0::Union{Array{Float64, 1}, PyObject},
v0::Union{Array{Float64, 1}, PyObject},
a0::Union{Array{Float64, 1}, PyObject},
Δt::Array{Float64, 1};
solve::Union{Missing, Function} = missing,
extsolve::Union{Missing, Function} = missing,
ρ::Float64 = 1.0)
if !ismissing(solve) && !ismissing(extsolve)
error("You cannot provide `solve` and `extsolve` at the same time.")
end
nt = length(Δt)
αm = (2ρ-1)/(ρ+1)
αf = ρ/(1+ρ)
γ = 1/2-αm+αf
β = 0.25*(1-αm+αf)^2
d = length(d0)
M = isa(M, SparseMatrixCSC) ? constant(M) : M
C = isa(C, SparseMatrixCSC) ? constant(C) : C
K = isa(K, SparseMatrixCSC) ? constant(K) : K
Force, d0, v0, a0, Δt = convert_to_tensor([Force, d0, v0, a0, Δt], [Float64, Float64, Float64, Float64, Float64])
function equ(dc, vc, ac, dt, Force, i)
dn = dc + dt*vc + dt^2/2*(1-2β)*ac
vn = vc + dt*((1-γ)*ac)
df = (1-αf)*dn + αf*dc
vf = (1-αf)*vn + αf*vc
am = αm*ac
rhs = Force - (M*am + C*vf + K*df)
A = (1-αm)*M + (1-αf)*C*dt*γ + (1-αf)*K*β*dt^2
if !ismissing(solve)
return solve(A, rhs)
elseif !ismissing(extsolve)
return extsolve(A, rhs, i)
else
return A\rhs
end
end
function condition(i, tas...)
return i<=nt
end
function body(i, tas...)
dc_arr, vc_arr, ac_arr = tas
dc = read(dc_arr, i)
vc = read(vc_arr, i)
ac = read(ac_arr, i)
y = equ(dc, vc, ac, Δt[i], Force[i], i)
dn = dc + Δt[i]*vc + Δt[i]^2/2*((1-2β)*ac+2β*y)
vn = vc + Δt[i]*((1-γ)*ac+γ*y)
i+1, write(dc_arr, i+1, dn), write(vc_arr, i+1, vn), write(ac_arr, i+1, y)
end
dM = TensorArray(nt+1); vM = TensorArray(nt+1); aM = TensorArray(nt+1)
dM = write(dM, 1, d0)
vM = write(vM, 1, v0)
aM = write(aM, 1, a0)
i = constant(1, dtype=Int32)
_, d, v, a = while_loop(condition, body, [i,dM, vM, aM])
set_shape(stack(d), (nt+1, length(d0))), set_shape(stack(v), (nt+1, length(v0))), set_shape(stack(a), (nt+1, length(a0)))
end
@doc raw"""
αscheme_time(Δt::Array{Float64}; ρ::Float64 = 1.0)
Returns the integration time $t_{i+1-\alpha_{f_2}}$ between $[t_i, t_{i+1}]$ using the alpha scheme.
If $\Delta t$ has length $n$, the output will also have length $n$.
"""
function αscheme_time(Δt::Array{Float64}; ρ::Float64 = 1.0)
n = length(Δt)
αm = (2ρ-1)/(ρ+1)
αf = ρ/(1+ρ)
γ = 1/2-αm+αf
β = 0.25*(1-αm+αf)^2
function equ(tc, dt)
tf1 = (1-αf)*(tc+dt) + αf*tc
return tf1
end
tcf = Float64[]
tc = 0.0
for i = 1:n
t1 = equ(tc, Δt[i])
push!(tcf, t1)
tc += Δt[i]
end
return tcf
end
@doc raw"""
TR_BDF2(D0::Union{SparseTensor, SparseMatrixCSC},
D1::Union{SparseTensor, SparseMatrixCSC},
Δt::Float64)
Constructs a TR-BDF2 (the Trapezoidal Rule with Second Order Backward Difference Formula) handler for
the DAE
$$D_1 \dot y + D_0 y = f$$
The struct is a functor, which performs one step simulation
```
(tr::TR_BDF2)(y::Union{PyObject, Array{Float64, 1}},
f1::Union{PyObject, Array{Float64, 1}},
f2::Union{PyObject, Array{Float64, 1}},
f3::Union{PyObject, Array{Float64, 1}})
```
Here `f1`, `f2`, and `f3` correspond to the right hand side at time step $n$, $n+\frac12$, and $n+1$.
Or we can pass a batched `F` defined as a `(2NT+1) × DOF` array
```
(tr::TR_BDF2)(y0::Union{PyObject, Array{Float64, 1}},
F::Union{PyObject, Array{Float64, 2}})
```
The output will be the entire solution of size `(NT+1) × DOF`.
!!! info
The scheme takes the following form for n = 0, 1, ...
$$\begin{aligned} D_1(y^{n+\frac12}-y^n) = \frac12\frac{\Delta t}{2}\left(f^{n+\frac12} + f^n - D_0 \left(y^{n+\frac12} + y^n\right)\right)\\ \left(\frac{\Delta t}{2}\right)^{-1} D_1 \left(\frac32y^{n+1} - 2y^{n+\frac12} + \frac12 y^n\right) + D_0 y^{n+1} = f^{n+1}\end{aligned}$$
"""
mutable struct TR_BDF2
D0::Union{SparseTensor, SparseMatrixCSC}
D1::Union{SparseTensor, SparseMatrixCSC}
Δt::Float64
_D0::Union{SparseTensor, SparseMatrixCSC}
_D1::Union{SparseTensor, SparseMatrixCSC}
symbolic::Bool
function TR_BDF2(D0::Union{SparseTensor, SparseMatrixCSC},
D1::Union{SparseTensor, SparseMatrixCSC},
Δt::Float64)
if isa(D0, SparseTensor) || isa(D1, SparseTensor)
symbolic = true
D0 = constant(D0)
D1 = constant(D1)
else
symbolic = false
end
@assert size(D0, 1)==size(D0,2)==size(D1,1)==size(D1,2)
_D0 = D1 + Δt/4 * D0
_D1 = 1/(Δt/2) * 3/2 * D1 + D0
new(D0, D1, Δt, _D0, _D1, symbolic)
end
end
"""
constant(tr::TR_BDF2)
Converts `tr` to a symbolic solver.
"""
function constant(tr::TR_BDF2)
TR_BDF2(constant(tr.D0), constant(tr.D1), tr.Δt)
end
function Base.:show(io::IO, tr::TR_BDF2)
print("""TR_BDF2 (DOF = $(size(tr.D0, 1)), Δt = $(tr.Δt)$(tr.symbolic ? ", symbolic" : ""))""")
end
function (tr::TR_BDF2)(y::Union{PyObject, Array{Float64, 1}},
f1::Union{PyObject, Array{Float64, 1}},
f2::Union{PyObject, Array{Float64, 1}},
f3::Union{PyObject, Array{Float64, 1}})
y, f1, f2, f3 = convert_to_tensor([y, f1, f2, f3], [Float64, Float64, Float64, Float64])
r1 = tr.Δt/4 * (f2 + f1) - tr.Δt/4 * (tr.D0 * y) + tr.D1 * y
yn = tr._D0\r1
r2 = f3 + 1/(tr.Δt/2)*(tr.D1* (2*yn - 0.5*y))
tr._D1\r2
end
function (tr::TR_BDF2)(y0::Union{PyObject, Array{Float64, 1}},
F::Union{PyObject, Array{Float64, 2}})
@assert size(F, 2)==size(tr.D0, 1) && mod(size(F, 1), 2)==1
y0, F = convert_to_tensor([y0, F], [Float64, Float64])
NT = size(F, 1)÷2
y_arr = TensorArray(NT+1)
y_arr = write(y_arr, 1, y0)
function condition(i, y_arr)
i<=NT
end
function body(i, y_arr)
y = read(y_arr, i)
f1, f2, f3 = F[2*i-1], F[2*i], F[2*i+1]
yn = tr(y, f1, f2, f3)
i+1, write(y_arr, i+1, yn)
end
i = constant(1, dtype = Int32)
_, ya = while_loop(condition, body, [i, y_arr])
set_shape(stack(ya), (NT+1, length(y0)))
end
function (tr::TR_BDF2)(y::Array{Float64, 1},
f1::Array{Float64, 1},
f2::Array{Float64, 1},
f3::Array{Float64, 1})
if tr.symbolic
return tr(constant(y), f1, f2, f3)
end
r1 = tr.Δt/4 * (f2 + f1) - tr.Δt/4 * (tr.D0 * y) + tr.D1 * y
yn = tr._D0\r1
r2 = f3 + 1/(tr.Δt/2)*(tr.D1* (2*yn - 0.5*y))
tr._D1\r2
end
function (tr::TR_BDF2)(y0::Array{Float64,1}, F::Array{Float64, 2})
if tr.symbolic
return tr(constant(y0), F)
end
@assert size(F, 2)==size(tr.D0, 1) && mod(size(F, 1), 2)==1
y = zeros(size(F, 1)÷2+1, 2)
y[1,:] = y0
for i = 1:size(F, 1)÷2
y[i+1,:] = tr(y[i,:], F[2*i-1,:], F[2*i,:], F[2*i+1,:])
end
y
end
# design principle: proceed one step
# (states) u0, u1, ..., (coefficients) M0, M1, ..., (step size) Δt
@doc raw"""
ExplicitNewmark(M::Union{SparseTensor, SparseMatrixCSC}, Z1::Union{Missing, SparseTensor, SparseMatrixCSC}, Z2::Union{Missing, SparseTensor, SparseMatrixCSC}, Δt::Float64)
An explicit Newmark integrator for
$$M \ddot{\mathbf{d}} + Z_1 \dot{\mathbf{d}} + Z_2 \mathbf{d} + f = 0$$
The numerical scheme is
$$\left(\frac{1}{\Delta t^2} M + \frac{1}{2\Delta t}Z_1\right)d^{n+1} = \left(\frac{2}{\Delta t^2} M - \frac{1}{2\Delta t}Z_2\right)d^n - \left(\frac{1}{\Delta t^2} M - \frac{1}{2\Delta t}Z_1\right) d^{n-1} - f$$
To use this integrator,
```julia
en = ExplicitNewmark(M, Z1, Z2, Δt)
d2 = step(en, d0, d1, f)
```
"""
struct ExplicitNewmark
A::Union{PyObject, Tuple{SparseTensor, PyObject}}
B::Union{PyObject, SparseTensor}
C::Union{PyObject, SparseTensor}
function ExplicitNewmark(M::Union{SparseTensor, PyObject, Array{Float64, 2}, SparseMatrixCSC},
Z1::Union{Missing, PyObject, Array{Float64, 2}, SparseTensor, SparseMatrixCSC},
Z2::Union{Missing, PyObject, Array{Float64, 2}, SparseTensor, SparseMatrixCSC}, Δt::Float64)
M = constant(M)
if ismissing(Z1)
A = 1/Δt^2 * M
C = -1/Δt^2 * M
else
Z1 = constant(Z1)
A = (1/Δt^2 * M + 1/(2Δt) * Z1)
C = -(1/Δt^2 * M - 1/(2Δt) * Z1)
end
if isa(A, SparseTensor)
A = factorize(A)
end
if ismissing(Z2)
B = 2/Δt^2 * M
else
Z2 = constant(Z2)
B = (2/Δt^2 * M - Z2)
end
new(A, B, C)
end
end
function Base.:show(io::IO, en::ExplicitNewmark)
print("ExplicitNewmark(DOF=$(size(en.B, 1)))")
end
function Base.:step(en::ExplicitNewmark, d0::Union{Array{Float64, 1}, PyObject}, d1::Union{Array{Float64, 1}, PyObject}, f::Union{Array{Float64, 1}, PyObject})
d0, d1, f = convert_to_tensor([d0, d1, f], [Float64, Float64, Float64])
en.A \ (en.B * d1 + en.C * d0 - f)
end
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 38630 | import Base:*, broadcast, reshape, exp, log, tanh, sum,
adjoint, inv, argmax, argmin, ^, max, maximum, min, minimum,
vec, \, cos, sin, sign, map, prod, reverse
import LinearAlgebra: tr, diag, det, norm, diagm, dot, I, svd, tril, triu
import Statistics: mean, std
import FFTW: fft, ifft
export
*,
^,
einsum,
sigmoid,
tanh,
mean,
log,
exp,
softplus,
softmax,
softsign,
sum,
relu,
relu6,
squeeze,
adjoint,
diag,
diagm,
det,
inv,
triangular_solve,
argmin,
argmax,
max,
min,
group_assign,
assign,
maximum,
minimum,
cast,
group,
clip,
scatter_add,
scatter_sub,
scatter_update,
stack,
concat,
unstack,
norm,
cvec,
rvec,
vec,
sqrt,
mean,
pad,
leaky_relu,
fft,
ifft,
I,
svd,
vector,
pmap,
std,
lgamma,
topk,
argsort,
batch_matmul,
dot,
set_shape,
selu,
elu,
tr,
tril,
triu,
solve_batch,
swish, hard_sigmoid, hard_swish, concat_elu, concat_hard_swish, concat_relu, fourier,
rollmean, rollsum, rollvar, rollstd,
softmax_cross_entropy_with_logits
@doc raw"""
batch_matmul(o1::PyObject, o2::PyObject)
Computes `o1[i,:,:] * o2[i, :]` or `o1[i,:,:] * o2[i, :, :]` for each index `i`.
"""
function batch_matmul(o1::PyObject, o2::PyObject)
flag = false
if length(size(o2))==2
flag = true
o2 = tf.expand_dims(o2, 2)
end
if length(size(o1))!=3 || length(size(o2))!=3
error("The size of o1 or o2 is not valid.")
end
out = tf.matmul(o1, o2)
if flag
squeeze(out)
else
out
end
end
batch_matmul(o1::Array{<:Real}, o2::PyObject) = batch_matmul(constant(o1), o2)
batch_matmul(o1::PyObject, o2::Array{<:Real}) = batch_matmul(o1, constant(o2))
batch_matmul(o1::Array{<:Real}, o2::Array{<:Real}) = batch_matmul(constant(o1), constant(o2))
function PyCall.:*(o1::PyObject, o2::PyObject)
s1 = size(o1)
s2 = size(o2)
if s1==nothing || s2==nothing
error("o1 and o2 should be tensors of rank 0, 1, 2")
end
if length(s1) == 0 || length(s2)==0
return tf.multiply(o1, o2)
end
if length(s1)==2 && length(s2)==2
return tf.matmul(o1, o2)
elseif length(s1)==2 && length(s2)==1
return tf.einsum("nm,m->n", o1, o2)
elseif length(s1)==2 && length(s2)==0
return tf.multiply(o1, o2)
elseif length(s1)==1 && length(s2)==2
error("[rand 1] x [rank 2] not defined")
elseif length(s1)==1 && length(s2)==1
return tf.multiply(o1, o2)
else
@warn("Unusual usage of multiplication. Check carefully")
tf.matmul(o1,o2)
end
end
Base.:*(o1::PyObject, o2::AbstractArray{<:Real}) = *(o1, constant(Array(o2), dtype=get_dtype(o1)))
Base.:*(o1::AbstractArray{<:Real}, o2::PyObject) = *(constant(Array(o1), dtype=get_dtype(o2)), o2)
Base.:*(o1::Number, o2::PyObject) = *(constant(o1, dtype=get_dtype(o2)), o2)
Base.:*(o1::PyObject, o2::Number) = *(o1, constant(o2, dtype=get_dtype(o1)))
Base.Broadcast.broadcasted(::typeof(*), o1::PyObject, o2::AbstractArray{<:Real}) = tf.multiply(o1, Array(o2))
Base.Broadcast.broadcasted(::typeof(*), o1::AbstractArray{<:Real}, o2::PyObject) = tf.multiply(Array(o1), o2)
Base.Broadcast.broadcasted(::typeof(*), o1::PyObject, o2::PyObject) = tf.multiply(o1, o2)
Base.Broadcast.broadcasted(::typeof(*), o1::PyObject, o2::Number) = tf.multiply(o1, o2)
Base.Broadcast.broadcasted(::typeof(*), o1::Number, o2::PyObject) = tf.multiply(o1, o2)
Base.Broadcast.broadcasted(::typeof(/), o1::PyObject, o2::AbstractArray{<:Real}) = tf.divide(o1, Array(o2))
Base.Broadcast.broadcasted(::typeof(/), o1::AbstractArray{<:Real}, o2::PyObject) = tf.divide(Array(o1), o2)
Base.Broadcast.broadcasted(::typeof(/), o1::PyObject, o2::PyObject) = tf.divide(o1, o2)
Base.Broadcast.broadcasted(::typeof(/), o1::PyObject, o2::Number) = tf.divide(o1, o2)
Base.Broadcast.broadcasted(::typeof(/), o1::Number, o2::PyObject) = tf.divide(o1, o2)
Base.Broadcast.broadcasted(::typeof(+), o1::PyObject, o2::AbstractArray{<:Real}) = o1 + Array(o2)
Base.Broadcast.broadcasted(::typeof(+), o1::AbstractArray{<:Real}, o2::PyObject) = Array(o1) + o2
Base.Broadcast.broadcasted(::typeof(+), o1::PyObject, o2::PyObject) = o1 + o2
Base.Broadcast.broadcasted(::typeof(+), o1::PyObject, o2::Number) = o1 + o2
Base.Broadcast.broadcasted(::typeof(+), o1::Number, o2::PyObject) = o1 + o2
Base.Broadcast.broadcasted(::typeof(-), o1::PyObject, o2::AbstractArray{<:Real}) = o1 - Array(o2)
Base.Broadcast.broadcasted(::typeof(-), o1::AbstractArray{<:Real}, o2::PyObject) = Array(o1) - o2
Base.Broadcast.broadcasted(::typeof(-), o1::PyObject, o2::PyObject) = o1 - o2
Base.Broadcast.broadcasted(::typeof(-), o1::PyObject, o2::Number) = o1 - o2
Base.Broadcast.broadcasted(::typeof(-), o1::Number, o2::PyObject) = o1 - o2
warn_broadcast_pow() = error(".^ is disabled due to eager evaluation. Use ^ instead.")
Base.Broadcast.broadcasted(::typeof(^), o1::PyObject, o2::Union{AbstractArray{<:Real},Number}) = warn_broadcast_pow()
Base.Broadcast.broadcasted(::typeof(^), o1::PyObject, o2::PyObject) = warn_broadcast_pow()
Base.Broadcast.broadcasted(::typeof(^), o1::Union{AbstractArray{<:Real},Number}, o2::PyObject) = warn_broadcast_pow()
function einsum(equation, args...; kwargs...)
tf.einsum(equation, args...; kwargs...)
end
"""
reshape(o::PyObject, s::Union{Array{<:Integer}, Tuple{Vararg{<:Integer, N}}}) where N
reshape(o::PyObject, s::Integer; kwargs...)
reshape(o::PyObject, m::Integer, n::Integer; kwargs...)
reshape(o::PyObject, ::Colon, n::Integer)
reshape(o::PyObject, n::Integer, ::Colon)
Reshapes the tensor according to row major if the "TensorFlow style" syntax is used; otherwise
reshaping according to column major is assumed.
# Example
```julia
reshape(a, [10,5]) # row major
reshape(a, 10, 5) # column major
```
"""
function reshape(o::PyObject, s::Union{Array{<:Integer}, Tuple{Vararg{<:Integer, N}}}) where N
tf.reshape(o, s)
end
function reshape(o::PyObject, s::Integer; kwargs...)
if length(size(o))>=2
return tf.reshape(o', [s]; kwargs...)
end
tf.reshape(o, [s]; kwargs...)
end
function reshape(o::PyObject, m::Integer, n::Integer; kwargs...)
if length(size(o))==1
return tf.reshape(o, [n,m]; kwargs...)'
elseif length(size(o))==2
return tf.reshape(o', [n,m]; kwargs...)'
end
tf.reshape(o, [m, n]; kwargs...)
end
reshape(o::PyObject, ::Colon, n::Integer) = reshape(o, -1, n)
reshape(o::PyObject, n::Integer, ::Colon) = reshape(o, n, -1)
"""
rvec(o::PyObject; kwargs...)
Vectorizes the tensor `o` to a row vector, assuming column major.
"""
function rvec(o::PyObject; kwargs...)
s = size(o)
if length(s)==0
return reshape(o, 1, 1, kwargs...)
elseif length(s)==1
return reshape(o, 1, s[1], kwargs...)
elseif length(s)==2
return reshape(o, 1, s[1]*s[2], kwargs...)
else
error("Invalid argument")
end
end
"""
rvec(o::PyObject; kwargs...)
Vectorizes the tensor `o` to a column vector, assuming column major.
"""
function cvec(o::PyObject;kwargs...)
s = size(o)
if length(s)==0
return reshape(o, 1, 1,kwargs...)
elseif length(s)==1
return reshape(o, s[1], 1,kwargs...)
elseif length(s)==2
return reshape(o, s[1]*s[2], 1,kwargs...)
else
error("Invalid argument")
end
end
"""
vec(o::PyObject;kwargs...)
Vectorizes the tensor `o` assuming column major.
"""
function vec(o::PyObject;kwargs...)
s = size(o)
if length(s)==0
return reshape(o, 1, kwargs...)
elseif length(s)==1
return o
elseif length(s)>=2
return reshape(o, s[1]*s[2])
end
end
"""
set_shape(o::PyObject, s::Union{Array{<:Integer}, Tuple{Vararg{<:Integer, N}}}) where N
set_shape(o::PyObject, s::Integer...)
Sets the shape of `o` to `s`. `s` must be the actual shape of `o`. This function is used to convert a
tensor with unknown dimensions to a tensor with concrete dimensions.
# Example
```julia
a = placeholder(Float64, shape=[nothing, 10])
b = set_shape(a, 3, 10)
run(sess, b, a=>rand(3,10)) # OK
run(sess, b, a=>rand(5,10)) # Error
run(sess, b, a=>rand(10,3)) # Error
```
"""
function set_shape(o::PyObject, s::Union{Array{<:Integer}, Tuple{Vararg{<:Integer, N}}}) where N
o.set_shape(s)
return o
end
set_shape(o::PyObject, s::Integer...) = set_shape(o, s)
function sigmoid(x::Real)
return 1/(1+exp(-x))
end
function sigmoid(o::PyObject; kwargs...)
tf.math.sigmoid(o; kwargs...)
end
relu(x::Real) = max(zero(x), x)
function relu(o::PyObject; kwargs...)
tf.nn.relu(o; kwargs...)
end
relu6(x::Real) = min(relu(x), one(x)*oftype(x, 6))
relu6(o::PyObject; kwargs...) = tf.nn.relu6(o; kwargs...)
function tan(o::PyObject; kwargs...)
tf.math.tan(o; kwargs...)
end
function leaky_relu(x::Real, a = oftype(x / 1, 0.2))
max(a * x, x / one(x))
end
function leaky_relu(o::PyObject; kwargs...)
tf.nn.leaky_relu(o; kwargs...)
end
function tanh(o::PyObject; kwargs...)
tf.tanh(o; kwargs...)
end
function selu(x::Real)
λ = oftype(x / 1, 1.0507009873554804934193349852946)
α = oftype(x / 1, 1.6732632423543772848170429916717)
λ * ifelse(x > 0, x / one(x), α * (exp(x) - one(x)))
end
selu(o::PyObject; kwargs...) = tf.nn.selu(o; kwargs...)
elu(x, α = one(x)) = ifelse(x ≥ 0, x / one(x), α * (exp(x) - one(x)))
elu(o::PyObject; kwargs...) = tf.nn.elu(o; kwargs...)
softsign(x::Real) = x / (one(x) + abs(x))
softsign(o::PyObject; kwargs...) = tf.nn.softsign(o; kwargs...)
function argmax(o::PyObject; kwargs...)
kwargs = jlargs(kwargs)
tf.argmax(o; kwargs...) + 1
end
function Base.:sqrt(o::PyObject; kwargs...)
kwargs = jlargs(kwargs)
tf.sqrt(o)
end
function argmin(o::PyObject; kwargs...)
kwargs = jlargs(kwargs)
tf.argmin(o; kwargs...) + 1
end
function max(o1::PyObject, o2::PyObject; kwargs...)
tf.maximum(o1, o2; kwargs...)
end
function min(o1::PyObject, o2::PyObject; kwargs...)
tf.minimum(o1, o2; kwargs...)
end
function maximum(o::PyObject; kwargs...)
kwargs = jlargs(kwargs)
tf.reduce_max(o; kwargs...)
end
function minimum(o::PyObject; kwargs...)
kwargs = jlargs(kwargs)
tf.reduce_min(o; kwargs...)
end
function std(o::PyObject; kwargs...)
kwargs = jlargs(kwargs)
tf.math.reduce_std(o; kwargs...)
end
function cast(x::PyObject, dtype::Type;kwargs...)
dtype = DTYPE[dtype]
tf.cast(x, dtype; kwargs...)
end
function cast(dtype::Type, x::PyObject;kwargs...)
dtype = DTYPE[dtype]
tf.cast(x, dtype; kwargs...)
end
softplus(x::Real) = ifelse(x > 0, x + log1p(exp(-x)), log1p(exp(x)))
function softplus(x;kwargs...)
tf.math.softplus(x; kwargs...)
end
function log(o::PyObject; kwargs...)
tf.math.log(o; kwargs...)
end
function exp(o::PyObject; kwargs...)
tf.exp(o; kwargs...)
end
function cos(o::PyObject; kwargs...)
tf.cos(o; kwargs...)
end
function sin(o::PyObject; kwargs...)
tf.sin(o; kwargs...)
end
function sign(o::PyObject; kwargs...)
tf.sign(o; kwargs...)
end
function softmax(o::PyObject; kwargs...)
kwargs = jlargs(kwargs)
tf.math.softmax(o; kwargs...)
end
function sum(o::PyObject; kwargs...)
kwargs = jlargs(kwargs)
tf.reduce_sum(o; kwargs...)
end
function mean(o::PyObject; kwargs...)
kwargs = jlargs(kwargs)
tf.reduce_mean(o; kwargs...)
end
function prod(o::PyObject; kwargs...)
kwargs = jlargs(kwargs)
tf.reduce_prod(o; kwargs...)
end
function squeeze(o::PyObject; kwargs...)
kwargs = jlargs(kwargs)
tf.squeeze(o;kwargs...)
end
"""
pad(o::PyObject, paddings::Array{Int64, 2}, args...; kwargs...)
Pads `o` with values on the boundary.
# Example
```julia
o = rand(3,3)
o = pad(o, [1 4 # first dimension
2 3]) # second dimension
run(sess, o)
```
Expected:
```
8×8 Array{Float64,2}:
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.250457 0.666905 0.823611 0.0 0.0 0.0
0.0 0.0 0.23456 0.625145 0.646713 0.0 0.0 0.0
0.0 0.0 0.552415 0.226417 0.67802 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0
```
"""
function pad(o::Union{Array{<:Real}, PyObject}, paddings::Array{Int64, 2}, args...; kwargs...)
o = constant(o)
tf.pad(o, paddings, args...; kwargs...)
end
function assign(o::PyObject,value, args...; kwargs...)
tf.compat.v1.assign(o, value, args...;kwargs...)
end
function group(args...; kwargs...)
tf.group(args...; kwargs...)
end
assign(o::Array{PyObject}, value::Array, args...;kwargs...) = group_assign(o, value, args...; kwargs...)
@deprecate group_assign assign
function group_assign(os::Array{PyObject}, values, args...; kwargs...)
ops = Array{PyObject}(undef, length(os))
for i = 1:length(os)
ops[i] = tf.compat.v1.assign(os[i], values[i], args...; kwargs...)
end
ops
end
"""
adjoint(o::PyObject; kwargs...)
Returns the conjugate adjoint of `o`.
When the dimension of `o` is greater than 2, only the last two dimensions are permuted, i.e., `permutedims(o, [1,2,...,n,n-1])`
"""
function adjoint(o::PyObject; kwargs...)
if length(size(o))==0
return o
elseif length(size(o))==1
return rvec(o)
else
return tf.linalg.adjoint(o; kwargs...)
end
end
diagm(o::PyObject; kwargs...) = tf.linalg.diag(o; kwargs...)
diag(o::PyObject; kwargs...) = tf.linalg.diag_part(o; kwargs...)
det(o::PyObject; kwargs...) = tf.linalg.det(o; kwargs...)
inv(o::PyObject; kwargs...) = tf.linalg.inv(o; kwargs...)
@doc raw"""
solve_batch(A::Union{PyObject, Array{<:Real, 2}}, rhs::Union{PyObject, Array{<:Real,2}})
Solves $$Ax = b$$ for a batch of right hand sides.
- `A`: a $m\times n$ matrix, where $m\geq n$
- `rhs`: a $n_b\times m$ matrix. Each row is a new right hand side to solve.
The returned value is a $n_b\times n$ matrix.
# Example
```julia
a = rand(10,5)
b = rand(100, 10)
sol = solve_batch(a, b)
@assert run(sess, sol) ≈ (a\b')'
```
!!! note
Internally, the matrix $A$ is factorized first and then the factorization is used to solve multiple right hand side.
"""
function solve_batch(A::Union{PyObject, Array{<:Real, 2}}, rhs::Union{PyObject, Array{<:Real,2}})
solve_batched_rhs_ = load_system_op("solve_batched_rhs"; multiple=false)
a,rhs = convert_to_tensor([A,rhs], [Float64,Float64])
sol = solve_batched_rhs_(a,rhs)
if size(a, 2)!=nothing && size(rhs,1) != nothing
sol = set_shape(sol, (size(rhs,1), size(a,2)))
end
return sol
end
function solve(matrix, rhs; kwargs...)
rhs = constant(rhs)
matrix = constant(matrix)
flag = false
if length(size(rhs))==1
flag = true
rhs = reshape(rhs, size(rhs, 1), 1)
end
if size(matrix,1)==size(matrix,2)
ret = tf.linalg.solve(matrix, rhs; kwargs...)
else
# @show matrix, rhs
ret = tf.linalg.lstsq(matrix, rhs;kwargs...)
end
if flag
ret = squeeze(ret, dims=2)
end
return ret
end
Base.:\(o1::PyObject, o2::PyObject) = solve(o1, o2)
Base.:\(o1::PyObject, o2::Array) = solve(o1, o2)
Base.:\(o1::Array, o2::PyObject) = solve(o1, o2)
function triangular_solve(matrix, rhs; kwargs...)
flag = false
if length(size(rhs))==1
flag = true
rhs = reshape(rhs, size(rhs, 1), 1)
end
ret = tf.linalg.triangular_solve(matrix, rhs; kwargs...)
if flag
ret = squeeze(ret, dims=2)
end
return ret
end
# reference: https://blog.csdn.net/LoseInVain/article/details/79638183
function concat(o::Union{PyObject,Array{PyObject}}, args...;kwargs...)
if isa(o, PyObject)
@warn "Only one input is consumed by concat" maxlog=1
return o
end
kwargs = jlargs(kwargs)
if length(size(o[1]))==0
return tf.stack(o)
end
tf.concat(o, args...; kwargs...)
end
function stack(o::Array{PyObject}, args...;kwargs...)
kwargs = jlargs(kwargs)
tf.stack(o, args...; kwargs...)
end
Base.:vcat(args::PyObject...) = concat([args...],0)
function Base.:hcat(args::PyObject...)
if length(size(args[1]))>=2
concat([args...],1)
elseif length(size(args[1]))==1
stack([args...],dims=2)
else
vcat(args...)'
end
end
"""
stack(o::PyObject)
Convert a `TensorArray` `o` to a normal tensor. The leading dimension is the size of the tensor array.
"""
function stack(o::PyObject)
o.stack()
end
function unstack(o::PyObject, args...;kwargs...)
kwargs = jlargs(kwargs)
tf.unstack(o, args...; kwargs...)
end
function _jlindex2indices(len::Int64,
indices::Union{PyObject, Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}})
if isa(indices, BitArray{1}) || isa(indices, Array{Bool,1})
indices = findall(indices)
elseif isa(indices, UnitRange{Int64}) || isa(indices, StepRange{Int64, Int64})
indices = collect(indices)
elseif isa(indices, Colon)
indices = Array(1:len)
elseif isa(indices, Int64)
indices = [indices]
end
if isa(indices, PyObject)
return indices - 1
else
return constant(indices .- 1)
end
end
for (op1, op2) = [(:_scatter_add, :tensor_scatter_nd_add), (:_scatter_sub, :tensor_scatter_nd_sub),
(:_scatter_update,:tensor_scatter_nd_update)]
@eval begin
function $op1(ref::PyObject,
indices::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
updates::Union{Array{<:Real}, Real, PyObject})
updates = convert_to_tensor(updates, dtype=get_dtype(ref))
@assert length(size(updates)) <= 1
@assert length(size(ref))==1
if length(size(updates))==0
updates = reshape(updates, (-1,))
end
indices = _jlindex2indices(length(ref),indices)
indices = reshape(indices, (-1,1))
# @info ref, indices, updates
tf.$op2(ref, indices, updates)
end
end
end
"""
scatter_update(a::PyObject,
indices::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
updates::Union{Array{<:Real}, Real, PyObject})
Updates array `a`
```
a[indices] = updates
```
# Example
Julia:
```julia
A[[1;2;3]] = rand(3)
A[2] = 1.0
```
ADCME:
```
A = scatter_update(A, [1;2;3], rand(3))
A = scatter_update(A, 2, 1.0)
```
"""
scatter_update(a::PyObject,
indices::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
updates::Union{Array{<:Real}, Real, PyObject}) = _scatter_update(a, indices, updates)
"""
scatter_sub(a::PyObject,
indices::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
updates::Union{Array{<:Real}, Real, PyObject})
Updates array `a`
```
a[indices] -= updates
```
# Example
Julia:
```julia
A[[1;2;3]] -= rand(3)
A[2] -= 1.0
```
ADCME:
```
A = scatter_sub(A, [1;2;3], rand(3))
A = scatter_sub(A, 2, 1.0)
```
"""
scatter_sub(a::PyObject,
indices::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
updates::Union{Array{<:Real}, Real, PyObject}) = _scatter_sub(a, indices, updates)
"""
scatter_add(a::PyObject,
indices::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
updates::Union{Array{<:Real}, Real, PyObject})
Updates array `add`
```
a[indices] += updates
```
# Example
Julia:
```julia
A[[1;2;3]] += rand(3)
A[2] += 1.0
```
ADCME:
```
A = scatter_add(A, [1;2;3], rand(3))
A = scatter_add(A, 2, 1.0)
```
"""
scatter_add(a::PyObject,
indices::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
updates::Union{Array{<:Real}, Real, PyObject}) = _scatter_add(a, indices, updates)
for (op1, op2) = [(:scatter_update2, :scatter_update), (:scatter_add2, :scatter_add),
(:scatter_sub2,:scatter_sub)]
@eval begin
function $op1(A::PyObject,
xind::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
yind::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
updates::Union{Array{<:Real}, Real, PyObject})
m, n = size(A)
updates = convert_to_tensor(updates, dtype=get_dtype(A))
@assert length(size(A))==2
xind = _jlindex2indices(m,xind)
yind = _jlindex2indices(n,yind)
if length(size(updates))==0
updates = reshape(updates, (1,1))
end
indices = reshape(repeat(xind, 1, length(yind)), (-1,)) * n + repeat(yind, length(xind))
out = $op2(reshape(A, (-1,)), indices + 1, reshape(updates, (-1,)))
reshape(out, (m, n))
end
end
end
"""
scatter_update(A::PyObject,
xind::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
yind::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
updates::Union{Array{<:Real}, Real, PyObject})
```julia
A[xind, yind] = updates
```
"""
scatter_update(A::PyObject,
xind::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
yind::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
updates::Union{Array{<:Real}, Real, PyObject}) = scatter_update2(A, xind, yind, updates)
"""
scatter_add(A::PyObject,
xind::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
yind::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
updates::Union{Array{<:Real}, Real, PyObject})
```julia
A[xind, yind] += updates
```
"""
scatter_add(A::PyObject,
xind::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
yind::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
updates::Union{Array{<:Real}, Real, PyObject}) = scatter_add2(A, xind, yind, updates)
"""
scatter_add(A::PyObject,
xind::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
yind::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
updates::Union{Array{<:Real}, Real, PyObject})
```julia
A[xind, yind] -= updates
```
"""
scatter_sub(A::PyObject,
xind::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
yind::Union{Colon, Int64, Array{Int64}, BitArray{1}, Array{Bool,1}, UnitRange{Int64}, StepRange{Int64, Int64}, PyObject},
updates::Union{Array{<:Real}, Real, PyObject}) = scatter_sub2(A, xind, yind, updates)
function norm(o::PyObject, args...;kwargs...)
kwargs = jlargs(kwargs)
tf.norm(o, args...;kwargs...)
end
function Base.:diff(o::PyObject; dims::Union{Int64,Nothing}=nothing)
if dims==nothing
if length(size(o))!=1
error("expect rank=1")
end
return o[2:end]-o[1:end-1]
elseif length(size(o))==2
if dims==1
return o[2:end,:]-o[1:end-1,:]
elseif dims==2
return o[:,2:end]-o[:,1:end-1]
end
else
error("Arguments not understood")
end
end
clip(o::PyObject, vmin, vmax, args...;kwargs...) = tf.clip_by_value(o, vmin, vmax, args...;kwargs...)
@doc raw"""
clip(o::Union{Array{Any}, Array{PyObject}}, vmin, vmax, args...;kwargs...)
Clips the values of `o` to the range [`vmin`, `vmax`]
# Example
```julia
a = constant(3.0)
a = clip(a, 1.0, 2.0)
b = constant(rand(3))
b = clip(b, 0.5, 1.0)
```
"""
function clip(o::Union{Array{Any}, Array{PyObject}}, vmin, vmax, args...;kwargs...)
out = Array{PyObject}(undef, length(o))
for i = 1:length(o)
out[i] = clip(o[i], vmin, vmax, args...;kwargs...)
end
out
end
function fft(o::PyObject, args...; kwargs...)
if length(size(o))==1
tf.fft(o, args...; kwargs...)
elseif length(size(o))==2
tf.fft2d(o, args...; kwargs...)
elseif length(size(o))==3
tf.fft3d(o, args...; kwargs...)
else
error("FFT for d>=4 not supported")
end
end
# mimic the Julia SVD
struct TFSVD
S::PyObject
U::PyObject
V::PyObject
Vt::PyObject
end
"""
svd(o::PyObject, args...; kwargs...)
Returns a `TFSVD` structure which holds the following data structures
```julia
S::PyObject
U::PyObject
V::PyObject
Vt::PyObject
```
We have the equality
``o = USV'``
# Example
```julia
A = rand(10,20)
r = svd(constant(A))
A2 = r.U*diagm(r.S)*r.Vt # The value of `A2` should be equal to `A`
```
"""
function svd(o::PyObject, args...; kwargs...)
s,u,v = tf.linalg.svd(o)
TFSVD(s, u, v, v')
end
function ifft(o::PyObject, args...; kwargs...)
if length(size(o))==1
tf.ifft(o, args...; kwargs...)
elseif length(size(o))==2
tf.ifft2d(o, args...; kwargs...)
elseif length(size(o))==3
tf.ifft3d(o, args...; kwargs...)
else
error("IFFT for d>=4 not supported")
end
end
function Base.:real(o::PyObject, args...; kwargs...)
tf.real(o, args...; kwargs...)
end
function Base.:imag(o::PyObject, args...; kwargs...)
tf.imag(o, args...; kwargs...)
end
@doc raw"""
map(fn::Function, o::Union{Array{PyObject},PyObject};
kwargs...)
Applies `fn` to each element of `o`.
- `o`∈`Array{PyObject}` : returns `[fn(x) for x in o]`
- `o`∈PyObject : splits `o` according to the first dimension and then applies `fn`.
# Example
```julia
a = constant(rand(10,5))
b = map(x->sum(x), a) # equivalent to `sum(a, dims=2)`
```
!!! note
If `fn` is a multivariate function, we need to specify the output type using `dtype` keyword. For example,
```julia
a = constant(ones(10))
b = constant(ones(10))
fn = x->x[1]+x[2]
c = map(fn, [a, b], dtype=Float64)
```
"""
function map(fn::Function, o::Union{Array{PyObject},PyObject};
kwargs...)
# if `o` is not a tensorflow tensor, roll back to normal `map`
if (isa(o, Array) && !hasproperty(o[1], :graph)) ||
(isa(o, PyObject) && !hasproperty(o, :graph))
return fn.(o)
end
kwargs = jlargs(kwargs)
tf.map_fn(fn, o;kwargs...)
end
"""
pmap(fn::Function, o::Union{Array{PyObject}, PyObject})
Parallel for loop. There should be no data dependency between different iterations.
# Example
```julia
x = constant(ones(10))
y1 = pmap(x->2.0*x, x)
y2 = pmap(x->x[1]+x[2], [x,x])
y3 = pmap(1:10, x) do z
i = z[1]
xi = z[2]
xi + cast(Float64, i)
end
run(sess, y1)
run(sess, y2)
run(sess, y3)
```
"""
function pmap(fn::Function, o::Union{Array{PyObject}, PyObject})
tf.compat.v1.vectorized_map(fn, o)
end
function pmap(fn::Function, range_::Union{Array{Int64},UnitRange{Int64},StepRange{Int64}, PyObject},
o::Union{Array{PyObject}, PyObject})
ipt = convert_to_tensor(collect(range_))
if isa(o, PyObject)
return tf.compat.v1.vectorized_map(fn, [ipt,o])
end
if length(o)==0
return tf.compat.v1.vectorized_map(fn, ipt)
end
if length(o)>0
tf.compat.v1.vectorized_map(fn, [ipt, o...])
end
end
dot(x::PyObject, y::PyObject) = sum(x.*y)
dot(x::PyObject, y::AbstractArray{<:Real}{<:Real}) = sum(x.*constant(y))
dot(x::AbstractArray{<:Real}{<:Real}, y::PyObject) = sum(constant(x).*y)
import PyCall: +, -
function +(o::PyObject, I::UniformScaling{Bool})
@assert size(o,1)==size(o,2)
o + diagm(0=>ones(size(o,1)))
end
function -(o::PyObject, I::UniformScaling{Bool})
@assert size(o,1)==size(o,2)
o - diagm(0=>ones(size(o,1)))
end
Base.:+(I::UniformScaling{Bool}, o::PyObject) = o+I
Base.:-(I::UniformScaling{Bool}, o::PyObject) = -(o-I)
function Base.:findall(o::PyObject)
if !(length(size(o)) in [1,2])
error("ADCME: input tensor must have rank 1 or 2")
end
if !(eltype(o) <: Bool)
error("ADCME: input tensor must have boolean types")
end
if length(size(o))==2
tf.compat.v2.where(o) + 1
else
o = reshape(o, :, 1)
res = findall(o)
res'[1,:]
end
end
"""
vector(i::Union{Array{T}, PyObject, UnitRange, StepRange}, v::Union{Array{Float64},PyObject},s::Union{Int64,PyObject})
Returns a vector `V` with length `s` such that
```
V[i] = v
```
"""
function vector(i::Union{Array{T}, PyObject, UnitRange, StepRange}, v::Union{Array{Float64},PyObject},
s::Union{Int64,PyObject}) where T<:Integer
if isa(i, UnitRange) || isa(i, StepRange)
i = collect(i)
end
i = convert_to_tensor(i)
s = convert_to_tensor(s)
i = reshape(i - 1,:,1)
s = reshape(s, 1)
tf.scatter_nd(i, v, s)
end
function Base.:repeat(o::PyObject, i::Int64, j::Int64)
if length(size(o))==0
return o*ones(eltype(o), i, j)
end
if length(size(o))==1
o = reshape(o, :, 1)
end
if length(size(o))!=2
error("ADCME: size of `o` must be 0, 1, 2")
end
tf.tile(o, (i,j))
end
function Base.:repeat(o::PyObject, i::Int64)
if length(size(o))==0
o * ones(eltype(o),i)
elseif length(size(o))==1
squeeze(repeat(o, i, 1))
elseif length(size(o))==2
repeat(o, i, 1)
else
error("ADCME: rank of `o` must be 0, 1, 2")
end
end
function lgamma(o::Union{T, PyObject}, args...;kwargs...) where T<:Real
tf.math.lgamma(convert_to_tensor(o), args...;kwargs...)
end
@doc raw"""
Base.:sort(o::PyObject;
rev::Bool=false, dims::Integer=-1, name::Union{Nothing,String}=nothing)
Sort a multidimensional array `o` along the given dimension.
- `rev`: `true` for DESCENDING and `false` (default) for ASCENDING
- `dims`: `-1` for last dimension.
"""
function Base.:sort(o::PyObject;
rev::Bool=false, dims::Integer=-1, name::Union{Nothing,String}=nothing)
direction = rev == false ? "ASCENDING" : "DESCENDING"
axis = -1
if dims!=-1
axis = dims - 1
end
tf.compat.v1.sort(o, axis=axis, direction=direction, name = name)
end
"""
topk(o::PyObject, k::Union{PyObject,Integer}=1;
sorted::Bool=true, name::Union{Nothing,String}=nothing)
Finds values and indices of the `k` largest entries for the last dimension.
If `sorted=true` the resulting k elements will be sorted by the values in descending order.
"""
function topk(o::PyObject, k::Union{PyObject,Integer}=1;
sorted::Bool=true, name::Union{Nothing,String}=nothing)
k = convert_to_tensor(k, dtype=Int32)
tf.compat.v1.math.top_k(o, k, sorted=sorted, name = name)
end
"""
argsort(o::PyObject;
stable::Bool = false, rev::Bool=false, dims::Integer=-1, name::Union{Nothing,String}=nothing)
Returns the indices of a tensor that give its sorted order along an axis.
"""
function argsort(o::PyObject;
stable::Bool = false, rev::Bool=false, dims::Integer=-1, name::Union{Nothing,String}=nothing)
direction = rev == false ? "ASCENDING" : "DESCENDING"
axis = -1
if dims!=-1
axis = dims + 1
end
tf.compat.v1.argsort(
o,
axis=axis,
direction=direction,
stable=stable,
name=name
) + 1
end
function tr(o::PyObject)
tf.linalg.trace(o)
end
function tril(o::PyObject, num::Int64 = 0)
flag = false
if length(size(o))==2
flag = true
o = tf.expand_dims(o, 0)
end
tri_lu_ = load_system_op("tri_lu"; multiple=false)
u,num,lu = convert_to_tensor([o,num,1], [Float64,Int64,Int64])
out = tri_lu_(u,num,lu)
if flag
return out[1]
else
return out
end
end
function triu(o::PyObject, num::Int64 = 0)
flag = false
if length(size(o))==2
flag = true
o = tf.expand_dims(o, 0)
end
tri_lu_ = load_system_op("tri_lu"; multiple=false)
u,num,lu = convert_to_tensor([o,num,0], [Float64,Int64,Int64])
out = tri_lu_(u,num,lu)
if flag
return out[1]
else
return out
end
end
"""
split(o::PyObject,
num_or_size_splits::Union{Integer, Array{<:Integer}, PyObject}; kwargs...)
Splits `o` according to `num_or_size_splits`
# Example 1
```julia
a = constant(rand(10,8,6))
split(a, 5)
```
Expected output:
```
5-element Array{PyCall.PyObject,1}:
PyObject <tf.Tensor 'split_5:0' shape=(2, 8, 6) dtype=float64>
PyObject <tf.Tensor 'split_5:1' shape=(2, 8, 6) dtype=float64>
PyObject <tf.Tensor 'split_5:2' shape=(2, 8, 6) dtype=float64>
PyObject <tf.Tensor 'split_5:3' shape=(2, 8, 6) dtype=float64>
PyObject <tf.Tensor 'split_5:4' shape=(2, 8, 6) dtype=float64>
```
# Example 2
```julia
a = constant(rand(10,8,6))
split(a, [4,3,1], dims=2)
```
Expected output:
```
3-element Array{PyCall.PyObject,1}:
PyObject <tf.Tensor 'split_6:0' shape=(10, 4, 6) dtype=float64>
PyObject <tf.Tensor 'split_6:1' shape=(10, 3, 6) dtype=float64>
PyObject <tf.Tensor 'split_6:2' shape=(10, 1, 6) dtype=float64>
```
# Example 3
```julia
a = constant(rand(10,8,6))
split(a, 3, dims=3)
```
Expected output:
```
3-element Array{PyCall.PyObject,1}:
PyObject <tf.Tensor 'split_7:0' shape=(10, 8, 2) dtype=float64>
PyObject <tf.Tensor 'split_7:1' shape=(10, 8, 2) dtype=float64>
PyObject <tf.Tensor 'split_7:2' shape=(10, 8, 2) dtype=float64>
```
"""
function Base.:split(o::PyObject,
num_or_size_splits::Union{Integer, Array{<:Integer}, PyObject}; kwargs...)
kwargs = jlargs(kwargs)
tf.split(o, num_or_size_splits; kwargs...)
end
"""
reverse(o::PyObject, kwargs...)
Given a tensor `o`, and an index `dims` representing the set of dimensions of tensor to reverse.
# Example
```julia
a = rand(10,2)
A = constant(a)
@assert run(sess, reverse(A, dims=1)) == reverse(a, dims=1)
@assert run(sess, reverse(A, dims=2)) == reverse(a, dims=2)
@assert run(sess, reverse(A, dims=-1)) == reverse(a, dims=2)
```
"""
function reverse(o::PyObject; dims::Integer = -1)
if dims==-1
dims = length(size(o))
end
dims = convert_to_tensor([dims-1], dtype=Int32)
tf.reverse(o, dims)
end
function swish(x)
return x*sigmoid(x)
end
function hard_swish(x)
return x*sigmoid(100*x)
end
function hard_sigmoid(x)
return min(1.0, maximum(0, x+0.5))
end
function concat_relu(x)
relu([x -x])
end
function concat_elu(x)
elu([x -x])
end
function concat_hard_swish(x)
hard_swish([x -x])
end
function fourier(x, terms::Int64=10)
list = []
for i = 1:terms
push!(list, sin(x))
push!(list, cos(x))
end
hcat(list...)
end
function __rollfunction(u, window::Int64, op)
rolling_functions_ = load_op_and_grad(libadcme,"rolling_functions")
u,window_ = convert_to_tensor(Any[u,window], [Float64,Int64])
@assert isnothing(size(u)) || length(size(u))==1
@assert length(u)>=window
@assert window>1
out = rolling_functions_(u,window_,op)
if !isnothing(length(u))
set_shape(out, (length(u) - window + 1,))
else
out
end
end
@doc raw"""
rollmean(u, window::Int64)
Returns the rolling mean given a window size `m`
$$o_k = \frac{\sum_{i=k}^{k+m-1} u_i}{m}$$
## Rolling functions in ADCME:
- [`rollmean`](@ref): rolling mean
- [`rollsum`](@ref): rolling sum
- [`rollvar`](@ref): rolling variance
- [`rollstd`](@ref): rolling standard deviation
"""
function rollmean(u, window::Int64)
__rollfunction(u, window, "mean")
end
@doc raw"""
rollsum(u, window::Int64)
Returns the rolling sum given a window size `m`
$$o_k = \sum_{i=k}^{k+m-1} u_i$$
## Rolling functions in ADCME:
- [`rollmean`](@ref): rolling mean
- [`rollsum`](@ref): rolling sum
- [`rollvar`](@ref): rolling variance
- [`rollstd`](@ref): rolling standard deviation
"""
function rollsum(u, window::Int64)
__rollfunction(u, window, "sum")
end
@doc raw"""
rollvar(u, window::Int64)
Returns the rolling variance given a window size `m`
$$o_k = \frac{\sum_{i=k}^{k+m-1} (u_i - m_i)^2}{m-1}$$
Here $m_i$ is the rolling mean computed using [`rollmean`](@ref)
## Rolling functions in ADCME:
- [`rollmean`](@ref): rolling mean
- [`rollsum`](@ref): rolling sum
- [`rollvar`](@ref): rolling variance
- [`rollstd`](@ref): rolling standard deviation
"""
function rollvar(u, window::Int64)
__rollfunction(u, window, "var")
end
@doc raw"""
rollstd(u, window::Int64)
Returns the rolling standard deviation given a window size `m`
$$o_k = \sqrt{\frac{\sum_{i=k}^{k+m-1} (u_i - m_i)^2}{m-1}}$$
Here $m_i$ is the rolling mean computed using [`rollmean`](@ref)
## Rolling functions in ADCME:
- [`rollmean`](@ref): rolling mean
- [`rollsum`](@ref): rolling sum
- [`rollvar`](@ref): rolling variance
- [`rollstd`](@ref): rolling standard deviation
"""
function rollstd(u, window::Int64)
__rollfunction(u, window, "std")
end
"""
softmax_cross_entropy_with_logits(logits::Union{Array, PyObject}, labels::Union{Array, PyObject})
Computes softmax cross entropy between `logits` and `labels`
`logits` is typically the output of a linear layer. For example,
```
logits = [
0.124575 0.511463 0.945934
0.538054 0.0749339 0.187802
0.355604 0.052569 0.177009
0.896386 0.546113 0.456832
]
labels = [2;1;2;3]
```
!!! info
The values of `labels` are from {1,2,...,`num_classes`}. Here `num_classes` is the number of columns in `logits`.
The predicted labels associated with `logits` is
```
argmax(softmax(logits), dims = 2)
```
Labels can also be one hot vectors
```
labels = [0 1
1 0
0 1
0 1]
```
"""
function softmax_cross_entropy_with_logits(logits::Union{Array, PyObject}, labels::Union{Array, PyObject})
logits = convert_to_tensor(logits, dtype = Float64)
labels = convert_to_tensor(labels, dtype = Int64)
if ndims(labels)==1
tf.nn.sparse_softmax_cross_entropy_with_logits(logits = logits, labels = labels - 1)
else
tf.nn.softmax_cross_entropy_with_logits(logits = logits, labels = labels)
end
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 29658 | export
AdadeltaOptimizer,
AdagradDAOptimizer,
AdagradOptimizer,
AdamOptimizer,
GradientDescentOptimizer,
RMSPropOptimizer,
minimize,
ScipyOptimizerInterface,
ScipyOptimizerMinimize,
BFGS!,
CustomOptimizer,
newton_raphson,
newton_raphson_with_grad,
NonlinearConstrainedProblem,
Optimize!,
optimize
#### Section 1: TensorFlow Optimizers ####
@doc raw"""
AdamOptimizer(learning_rate=1e-3;kwargs...)
Constructs an ADAM optimizer.
# Example
```julia
learning_rate = 1e-3
opt = AdamOptimizer(learning_rate).minimize(loss)
sess = Session(); init(sess)
for i = 1:1000
_, l = run(sess, [opt, loss])
@info "Iteration $i, loss = $l")
end
```
# Dynamical Learning Rate
We can also use dynamical learning rate. For example, if we want to use a learning rate
$l_t = \frac{1}{1+t}$, we have
```julia
learning_rate = placeholder(1.0)
opt = AdamOptimizer(learning_rate).minimize(loss)
sess = Session(); init(sess)
for i = 1:1000
_, l = run(sess, [opt, loss], lr = 1/(1+i))
@info "Iteration $i, loss = $l")
end
```
The usage of other optimizers such as [`GradientDescentOptimizer`](@ref), [`AdadeltaOptimizer`](@ref), and so on
is similar: we can just replace `AdamOptimizer` with the corresponding ones.
"""
function AdamOptimizer(learning_rate=1e-3;kwargs...)
return tf.train.AdamOptimizer(;learning_rate=learning_rate,kwargs...)
end
"""
AdadeltaOptimizer(learning_rate=1e-3;kwargs...)
See [`AdamOptimizer`](@ref) for descriptions.
"""
function AdadeltaOptimizer(learning_rate=1e-3;kwargs...)
return tf.train.AdadeltaOptimizer(;learning_rate=learning_rate,kwargs...)
end
"""
AdagradDAOptimizer(learning_rate=1e-3; global_step, kwargs...)
See [`AdamOptimizer`](@ref) for descriptions.
"""
function AdagradDAOptimizer(learning_rate=1e-3; global_step, kwargs...)
return tf.train.AdagradDAOptimizer(learning_rate, global_step;kwargs...)
end
"""
AdagradOptimizer(learning_rate=1e-3;kwargs...)
See [`AdamOptimizer`](@ref) for descriptions.
"""
function AdagradOptimizer(learning_rate=1e-3;kwargs...)
return tf.train.AdagradOptimizer(learning_rate;kwargs...)
end
"""
GradientDescentOptimizer(learning_rate=1e-3;kwargs...)
See [`AdamOptimizer`](@ref) for descriptions.
"""
function GradientDescentOptimizer(learning_rate=1e-3;kwargs...)
return tf.train.GradientDescentOptimizer(learning_rate;kwargs...)
end
"""
RMSPropOptimizer(learning_rate=1e-3;kwargs...)
See [`AdamOptimizer`](@ref) for descriptions.
"""
function RMSPropOptimizer(learning_rate=1e-3;kwargs...)
return tf.train.RMSPropOptimizer(learning_rate;kwargs...)
end
function minimize(o::PyObject, loss::PyObject; kwargs...)
o.minimize(loss;kwargs...)
end
"""
ScipyOptimizerInterface(loss; method="L-BFGS-B", options=Dict("maxiter"=> 15000, "ftol"=>1e-12, "gtol"=>1e-12), kwargs...)
A simple interface for Scipy Optimizer. See also [`ScipyOptimizerMinimize`](@ref) and [`BFGS!`](@ref).
"""
ScipyOptimizerInterface(loss; method="L-BFGS-B", options=Dict("maxiter"=> 15000, "ftol"=>1e-12, "gtol"=>1e-12), kwargs...) =
tf.contrib.opt.ScipyOptimizerInterface(loss; method = method, options=options, kwargs...)
"""
ScipyOptimizerMinimize(sess::PyObject, opt::PyObject; kwargs...)
Minimizes a scalar Tensor. Variables subject to optimization are updated in-place at the end of optimization.
Note that this method does not just return a minimization Op, unlike `minimize`; instead it actually performs minimization by executing commands to control a Session
https://www.tensorflow.org/api_docs/python/tf/contrib/opt/ScipyOptimizerInterface. See also [`ScipyOptimizerInterface`](@ref) and [`BFGS!`](@ref).
- feed_dict: A feed dict to be passed to calls to session.run.
- fetches: A list of Tensors to fetch and supply to loss_callback as positional arguments.
- step_callback: A function to be called at each optimization step; arguments are the current values of all optimization variables packed into a single vector.
- loss_callback: A function to be called every time the loss and gradients are computed, with evaluated fetches supplied as positional arguments.
- run_kwargs: kwargs to pass to session.run.
"""
function ScipyOptimizerMinimize(sess::PyObject, opt::PyObject; kwargs...)
opt.minimize(sess;kwargs...)
end
@doc raw"""
CustomOptimizer(opt::Function, name::String)
creates a custom optimizer with struct name `name`. For example, we can integrate `Optim.jl` with `ADCME` by
constructing a new optimizer
```julia
CustomOptimizer("Con") do f, df, c, dc, x0, x_L, x_U
opt = Opt(:LD_MMA, length(x0))
bd = zeros(length(x0)); bd[end-1:end] = [-Inf, 0.0]
opt.lower_bounds = bd
opt.xtol_rel = 1e-4
opt.min_objective = (x,g)->(g[:]= df(x); return f(x)[1])
inequality_constraint!(opt, (x,g)->( g[:]= dc(x);c(x)[1]), 1e-8)
(minf,minx,ret) = NLopt.optimize(opt, x0)
minx
end
```
Here
∘ `f`: a function that returns $f(x)$
∘ `df`: a function that returns $\nabla f(x)$
∘ `c`: a function that returns the constraints $c(x)$
∘ `dc`: a function that returns $\nabla c(x)$
∘ `x0`: initial guess
∘ `nineq`: number of inequality constraints
∘ `neq`: number of equality constraints
∘ `x_L`: lower bounds of optimizable variables
∘ `x_U`: upper bounds of optimizable variables
Then we can create an optimizer with
```
opt = Con(loss, inequalities=[c1], equalities=[c2])
```
To trigger the optimization, use
```
minimize(opt, sess)
```
Note thanks to the global variable scope of Julia, `step_callback`, `optimizer_kwargs` can actually
be passed from Julia environment directly.
"""
function CustomOptimizer(opt::Function)
name = "CustomOptimizer_"*randstring(16)
name = Symbol(name)
@eval begin
@pydef mutable struct $name <: tf.contrib.opt.ExternalOptimizerInterface
function _minimize(self; initial_val, loss_grad_func, equality_funcs,
equality_grad_funcs, inequality_funcs, inequality_grad_funcs,
packed_bounds, step_callback, optimizer_kwargs)
local x_L, x_U
x0 = initial_val # rename
nineq, neq = length(inequality_funcs), length(equality_funcs)
printstyled("[CustomOptimizer] Number of inequalities constraints = $nineq, Number of equality constraints = $neq\n", color=:blue)
nvar = Int64(sum([prod(self._vars[i].get_shape().as_list()) for i = 1:length(self._vars)]))
printstyled("[CustomOptimizer] Total number of variables = $nvar\n", color=:blue)
if isnothing(packed_bounds)
printstyled("[CustomOptimizer] No bounds provided, use (-∞, +∞) as default; or you need to provide bounds in the function CustomOptimizer\n", color=:blue)
x_L = -Inf*ones(nvar); x_U = Inf*ones(nvar)
else
x_L = vcat([x[1] for x in packed_bounds]...)
x_U = vcat([x[2] for x in packed_bounds]...)
end
ncon = nineq + neq
f(x) = loss_grad_func(x)[1]
df(x) = loss_grad_func(x)[2]
function c(x)
inequalities = vcat([inequality_funcs[i](x) for i = 1:nineq]...)
equalities = vcat([equality_funcs[i](x) for i=1:neq]...)
return Array{eltype(initial_val)}([inequalities;equalities])
end
function dc(x)
inequalities = [inequality_grad_funcs[i](x) for i = 1:nineq]
equalities = [equality_grad_funcs[i](x) for i=1:neq]
values = zeros(eltype(initial_val),nvar, ncon)
for idc = 1:nineq
values[:,idc] = inequalities[idc][1]
end
for idc = 1:neq
values[:,idc+nineq] = equalities[idc][1]
end
return values[:]
end
$opt(f, df, c, dc, x0, x_L, x_U)
end
end
return $name
end
end
@doc raw"""
BFGS!(sess::PyObject, loss::PyObject, max_iter::Int64=15000;
vars::Array{PyObject}=PyObject[], callback::Union{Function, Nothing}=nothing, method::String = "L-BFGS-B", kwargs...)
`BFGS!` is a simplified interface for **L-BFGS-B** optimizer. See also [`ScipyOptimizerInterface`](@ref).
`callback` is a callback function with signature
```julia
callback(vs::Array, iter::Int64, loss::Float64)
```
`vars` is an array consisting of tensors and its values will be the input to `vs`.
# Example 1
```julia
a = Variable(1.0)
loss = (a - 10.0)^2
sess = Session(); init(sess)
BFGS!(sess, loss)
```
# Example 2
```julia
θ1 = Variable(1.0)
θ2 = Variable(1.0)
loss = (θ1-1)^2 + (θ2-2)^2
cb = (vs, iter, loss)->begin
printstyled("[#iter $iter] θ1=$(vs[1]), θ2=$(vs[2]), loss=$loss\n", color=:green)
end
sess = Session(); init(sess)
cb(run(sess, [θ1, θ2]), 0, run(sess, loss))
BFGS!(sess, loss, 100; vars=[θ1, θ2], callback=cb)
```
# Example 3
Use `bounds` to specify upper and lower bound of a variable.
```julia
x = Variable(2.0)
loss = x^2
sess = Session(); init(sess)
BFGS!(sess, loss, bounds=Dict(x=>[1.0,3.0]))
```
!!! note
Users can also use other scipy optimization algorithm by providing `method` keyword arguments. For example, you can use the BFGS optimizer
```julia
BFGS!(sess, loss, method = "BFGS")
```
"""->
function BFGS!(sess::PyObject, loss::PyObject, max_iter::Int64=15000;
vars::Array{PyObject}=PyObject[], callback::Union{Function, Nothing}=nothing,
method::String = "L-BFGS-B", kwargs...)
__cnt = 0
__loss = 0
__var = nothing
out = []
function print_loss(l, vs...)
if !isnothing(callback); __var = vs; end
if mod(__cnt,1)==0
println("iter $__cnt, current loss=",l)
end
__loss = l
__cnt += 1
end
__iter = 0
function step_callback(rk)
if mod(__iter,1)==0
println("================ STEP $__iter ===============")
end
if !isnothing(callback)
callback(__var, __iter, __loss)
end
push!(out, __loss)
__iter += 1
end
kwargs = Dict(kwargs)
if haskey(kwargs, :bounds)
kwargs[:var_to_bounds] = kwargs[:bounds]
delete!(kwargs, :bounds)
end
feed_dict = nothing
if haskey(kwargs, :feed_dict)
feed_dict = kwargs[:feed_dict]
delete!(kwargs, :feed_dict)
end
if haskey(kwargs, :var_to_bounds)
desc = "`bounds` or `var_to_bounds` keywords of `BFGS!` only accepts dictionaries whose keys are Variables"
for (k,v) in kwargs[:var_to_bounds]
if !(hasproperty(k, "trainable"))
error("The tensor $k does not have property `trainable`, indicating it is not a `Variable`. $desc\n")
end
if !k.trainable
@warn("The variable $k is not trainable, ignoring the bounds")
end
end
end
opt = ScipyOptimizerInterface(loss, method=method,options=Dict("maxiter"=> max_iter, "ftol"=>1e-12, "gtol"=>1e-12); kwargs...)
@info "Optimization starts..."
ScipyOptimizerMinimize(sess, opt,
loss_callback=print_loss, step_callback=step_callback,
fetches=[loss, vars...],
feed_dict = feed_dict)
out
end
"""
BFGS!(value_and_gradients_function::Function, initial_position::Union{PyObject, Array{Float64}}, max_iter::Int64=50, args...;kwargs...)
Applies the BFGS optimizer to `value_and_gradients_function`
"""
function BFGS!(value_and_gradients_function::Function,
initial_position::Union{PyObject, Array{Float64}}, max_iter::Int64=50, args...;kwargs...)
tfp.optimizer.bfgs_minimize(value_and_gradients_function,
initial_position=initial_position, args...;max_iterations=max_iter, kwargs...)[5]
end
struct NRResult
x::Union{PyObject, Array{Float64}} # final solution
res::Union{PyObject, Array{Float64, 1}} # residual
u::Union{PyObject, Array{Float64, 2}} # solution history
converged::Union{PyObject, Bool} # whether it converges
iter::Union{PyObject, Int64} # number of iterations
end
function Base.:run(sess::PyObject, nr::NRResult)
NRResult(run(sess, [nr.x, nr.res, nr.u, nr.converged, nr.iter])...)
end
function backtracking(compute_gradient::Function , u::PyObject)
f0, r0, _, δ0 = compute_gradient(u)
df0 = -sum(r0.*δ0)
c1 = options.newton_raphson.linesearch_options.c1
ρ_hi = options.newton_raphson.linesearch_options.ρ_hi
ρ_lo = options.newton_raphson.linesearch_options.ρ_lo
iterations = options.newton_raphson.linesearch_options.iterations
maxstep = options.newton_raphson.linesearch_options.maxstep
αinitial = options.newton_raphson.linesearch_options.αinitial
@assert !isnothing(f0)
@assert ρ_lo < ρ_hi
@assert iterations > 0
function condition(i, ta_α, ta_f)
f = read(ta_f, i)
α = read(ta_α, i)
tf.logical_and(f > f0 + c1 * α * df0, i<=iterations)
end
function body(i, ta_α, ta_f)
α_1 = read(ta_α, i-1)
α_2 = read(ta_α, i)
d = 1/(α_1^2*α_2^2*(α_2-α_1))
f = read(ta_f, i)
a = (α_1^2*(f - f0 - df0*α_2) - α_2^2*(df0 - f0 - df0*α_1))*d
b = (-α_1^3*(f - f0 - df0*α_2) + α_2^3*(df0 - f0 - df0*α_1))*d
α_tmp = tf.cond(abs(a)<1e-10,
()->df0/(2b),
()->begin
d = max(b^2-3a*df0, constant(0.0))
(-b + sqrt(d))/(3a)
end)
α_2 = tf.cond(tf.math.is_nan(α_tmp),
()->α_2*ρ_hi,
()->begin
α_tmp = min(α_tmp, α_2*ρ_hi)
α_2 = max(α_tmp, α_2*ρ_lo)
end)
fnew, _, _, _ = compute_gradient(u - α_2*δ0)
ta_f = write(ta_f, i+1, fnew)
ta_α = write(ta_α, i+1, α_2)
i+1, ta_α, ta_f
end
ta_α = TensorArray(iterations)
ta_α = write(ta_α, 1, constant(αinitial))
ta_α = write(ta_α, 2, constant(αinitial))
ta_f = TensorArray(iterations)
ta_f = write(ta_f, 1, constant(0.0))
ta_f = write(ta_f, 2, f0)
i = constant(2, dtype=Int32)
iter, out_α, out_f = while_loop(condition, body, [i, ta_α, ta_f]; back_prop=false)
α = read(out_α, iter)
return α
end
"""
newton_raphson(func::Function,
u0::Union{Array,PyObject},
θ::Union{Missing,PyObject, Array{<:Real}}=missing,
args::PyObject...) where T<:Real
Newton Raphson solver for solving a nonlinear equation.
∘ `func` has the signature
- `func(θ::Union{Missing,PyObject}, u::PyObject)->(r::PyObject, A::Union{PyObject,SparseTensor})` (if `linesearch` is off)
- `func(θ::Union{Missing,PyObject}, u::PyObject)->(fval::PyObject, r::PyObject, A::Union{PyObject,SparseTensor})` (if `linesearch` is on)
where `r` is the residual and `A` is the Jacobian matrix; in the case where `linesearch` is on, the function value `fval` must also be supplied.
∘ `θ` are external parameters.
∘ `u0` is the initial guess for `u`
∘ `args`: additional inputs to the func function
∘ `kwargs`: keyword arguments to `func`
The solution can be configured via `ADCME.options.newton_raphson`
- `max_iter`: maximum number of iterations (default=100)
- `rtol`: relative tolerance for termination (default=1e-12)
- `tol`: absolute tolerance for termination (default=1e-12)
- `LM`: a float number, Levenberg-Marquardt modification ``x^{k+1} = x^k - (J^k + \\mu^k)^{-1}g^k`` (default=0.0)
- `linesearch`: whether linesearch is used (default=false)
Currently, the backtracing algorithm is implemented.
The parameters for `linesearch` are supplied via `options.newton_raphson.linesearch_options`
- `c1`: stop criterion, ``f(x^k) < f(0) + \\alpha c_1 f'(0)``
- `ρ_hi`: the new step size ``\\alpha_1\\leq \\rho_{hi}\\alpha_0``
- `ρ_lo`: the new step size ``\\alpha_1\\geq \\rho_{lo}\\alpha_0``
- `iterations`: maximum number of iterations for linesearch
- `maxstep`: maximum allowable steps
- `αinitial`: initial guess for the step size ``\\alpha``
"""
function newton_raphson(func::Function,
u0::Union{Array,PyObject},
θ::Union{Missing,PyObject, Array{<:Real}}=missing,
args::PyObject...; kwargs...) where T<:Real
f = (θ, u)->func(θ, u, args...; kwargs...)
if length(size(u0))!=1
error("ADCME: Initial guess must be a vector")
end
if length(u0)===nothing
error("ADCME: The length of the initial guess must be determined at compilation.")
end
u = convert_to_tensor(u0)
max_iter = options.newton_raphson.max_iter
verbose = options.newton_raphson.verbose
oprtol = options.newton_raphson.rtol
optol = options.newton_raphson.tol
LM = options.newton_raphson.LM
linesearch = options.newton_raphson.linesearch
function condition(i, ta_r, ta_u)
if verbose; @info "(2/4)Parsing Condition..."; end
if_else(tf.math.logical_and(tf.equal(i,2), tf.less(i, max_iter+1)),
constant(true),
()->begin
tol = read(ta_r, i-1)
rel_tol = read(ta_r, i-2)
if verbose
op = tf.print("Newton iteration ", i-2, ": r (abs) =", tol, " r (rel) =", rel_tol, summarize=-1)
tol = bind(tol, op)
end
return tf.math.logical_and(
tf.math.logical_and(tol>=optol, rel_tol>=oprtol),
i<=max_iter
)
end
)
end
function body(i, ta_r, ta_u)
local δ, val, r_
if verbose; @info "(3/4)Parsing Main Loop..."; end
u_ = read(ta_u, i-1)
function compute_gradients(x)
val = nothing
out = f(θ, x)
if length(out)==2
r_, J = out
else
val, r_, J = out
end
if LM>0.0 # Levenberg-Marquardt
μ = LM
μ = convert_to_tensor(μ)
δ = (J + μ*spdiag(size(J,1)))\r_
else
δ = J\r_
end
return val, r_, J, δ
end
if linesearch
if verbose; @info "Perform Linesearch..."; end
step_size = backtracking(compute_gradients, u_)
else
step_size = 1.0
end
val, r_, _, δ = compute_gradients(u_)
ta_r = write(ta_r, i, norm(r_))
δ = step_size * δ
new_u = u_ - δ
if verbose && linesearch
op = tf.print("Current Step Size = ", step_size)
new_u = bind(new_u, op)
end
ta_u = write(ta_u, i, new_u)
i+1, ta_r, ta_u
end
if verbose; @info "(1/4)Intializing TensorArray..."; end
out = f(θ, u)
r0 = length(out)==2 ? out[1] : out[2]
tol0 = norm(r0)
if verbose
op = tf.print("Newton-Raphson with absolute tolerance = $optol and relative tolerance = $oprtol")
tol0 = bind(tol0, op)
end
ta_r = TensorArray(max_iter)
ta_u = TensorArray(max_iter)
ta_u = write(ta_u, 1, u)
ta_r = write(ta_r, 1, tol0)
i = constant(2, dtype=Int32)
i_, ta_r_, ta_u_ = while_loop(condition, body, [i, ta_r, ta_u], back_prop=false)
r_out, u_out = stack(ta_r_), stack(ta_u_)
if verbose; @info "(4/4)Postprocessing Results..."; end
sol = if_else(
tf.less(tol0,optol),
u,
u_out[i_-1]
)
res = if_else(
tf.less(tol0,optol),
reshape(tol0, 1),
tf.slice(r_out, [1],[i_-2])
)
u_his = if_else(
tf.less(tol0,optol),
reshape(u, 1, length(u)),
tf.slice(u_out, [0; 0], [i_-2; length(u)])
)
iter = if_else(
tf.less(tol0,optol),
constant(1),
cast(Int64,i_)-2
)
converged = if_else(
tf.less(i_, max_iter),
constant(true),
constant(false)
)
# it makes no sense to take the gradients
sol = stop_gradient(sol)
res = stop_gradient(res)
NRResult(sol, res, u_his', converged, iter)
end
"""
newton_raphson_with_grad(f::Function,
u0::Union{Array,PyObject},
θ::Union{Missing,PyObject, Array{<:Real}}=missing,
args::PyObject...) where T<:Real
Differentiable Newton-Raphson algorithm. See [`newton_raphson`](@ref).
Use `ADCME.options.newton_raphson` to supply options.
# Example
```julia
function f(θ, x)
x^3 - θ, 3spdiag(x^2)
end
θ = constant([2. .^3;3. ^3; 4. ^3])
x = newton_raphson_with_grad(f, constant(ones(3)), θ)
run(sess, x)≈[2.;3.;4.]
run(sess, gradients(sum(x), θ))
```
"""
function newton_raphson_with_grad(func::Function,
u0::Union{Array,PyObject},
θ::Union{Missing,PyObject, Array{<:Real}}=missing,
args::PyObject...; kwargs...) where T<:Real
f = ( θ, u, args...) -> func(θ, u, args...; kwargs...)
function forward(θ, args...)
nr = newton_raphson(f, u0, θ, args...)
return nr.x
end
function backward(dy, x, θ, xargs...)
θ = copy(θ)
args = [copy(z) for z in xargs]
r, A = f(θ, x, args...)
dy = tf.convert_to_tensor(dy)
g = independent(A'\dy)
s = sum(r*g)
gs = [-gradients(s, z) for z in args]
if length(args)==0
-gradients(s, θ)
else
-gradients(s, θ), gs...
end
end
if !isa(θ, PyObject)
@warn("θ is not a PyObject, no gradients is available")
return forward(θ, args...)
end
fn = register(forward, backward)
return fn(θ, args...)
end
@doc raw"""
NonlinearConstrainedProblem(f::Function, L::Function, θ::PyObject, u0::Union{PyObject, Array{Float64}}; options::Union{Dict{String, T}, Missing}=missing) where T<:Integer
Computes the gradients ``\frac{\partial L}{\partial \theta}``
```math
\min \ L(u) \quad \mathrm{s.t.} \ F(\theta, u) = 0
```
`u0` is the initial guess for the numerical solution `u`, see [`newton_raphson`](@ref).
Caveats:
Assume `r, A = f(θ, u)` and `θ` are the unknown parameters,
`gradients(r, θ)` must be defined (backprop works properly)
Returns:
It returns a tuple (`L`: loss, `C`: constraints, and `Graidents`)
```math
\left(L(u), u, \frac{\partial L}{\partial θ}\right)
```
# Example
We want to solve the following constrained optimization problem
$$\begin{aligned}\min_\theta &\; L(u) = (u-1)^3\\ \text{s.t.} &\; u^3 + u = \theta\end{aligned}$$
The solution is $\theta = 2$. The Julia code is
```julia
function f(θ, u)
u^3 + u - θ, spdiag(3u^2+1)
end
function L(u)
sum((u-1)^2)
end
pl = Variable(ones(1))
l, θ, dldθ = NonlinearConstrainedProblem(f, L, pl, ones(1))
```
We can coupled it with a mathematical optimizer
```julia
using Optim
sess = Session(); init(sess)
BFGS!(sess, l, dldθ, pl)
```
"""
function NonlinearConstrainedProblem(f::Function, L::Function, θ::Union{Array{Float64,1},PyObject},
u0::Union{PyObject, Array{Float64}}) where T<:Real
θ = convert_to_tensor(θ)
nr = newton_raphson(f, u0, θ)
r, A = f(θ, nr.x)
l = L(nr.x)
top_grad = tf.convert_to_tensor(gradients(l, nr.x))
A = A'
g = A\top_grad
g = independent(g) # preventing gradients backprop
l, nr.x, tf.convert_to_tensor(-gradients(sum(r*g), θ))
end
@doc raw"""
BFGS!(sess::PyObject, loss::PyObject, grads::Union{Array{T},Nothing,PyObject},
vars::Union{Array{PyObject},PyObject}; kwargs...) where T<:Union{Nothing, PyObject}
Running BFGS algorithm
``\min_{\texttt{vars}} \texttt{loss}(\texttt{vars})``
The gradients `grads` must be provided. Typically, `grads[i] = gradients(loss, vars[i])`.
`grads[i]` can exist on different devices (GPU or CPU).
# Example 1
```julia
import Optim # required
a = Variable(0.0)
loss = (a-1)^2
g = gradients(loss, a)
sess = Session(); init(sess)
BFGS!(sess, loss, g, a)
```
# Example 2
```julia
import Optim # required
a = Variable(0.0)
loss = (a^2+a-1)^2
g = gradients(loss, a)
sess = Session(); init(sess)
cb = (vs, iter, loss)->begin
printstyled("[#iter $iter] a = $vs, loss=$loss\n", color=:green)
end
BFGS!(sess, loss, g, a; callback = cb)
```
"""
function BFGS!(sess::PyObject, loss::PyObject, grads::Union{Array{T},Nothing,PyObject},
vars::Union{Array{PyObject},PyObject}; kwargs...) where T<:Union{Nothing, PyObject}
Optimize!(sess, loss; vars=vars, grads = grads, kwargs...)
end
"""
Optimize!(sess::PyObject, loss::PyObject, max_iter::Int64 = 15000;
vars::Union{Array{PyObject},PyObject, Missing} = missing,
grads::Union{Array{T},Nothing,PyObject, Missing} = missing,
optimizer = missing,
callback::Union{Function, Missing}=missing,
x_tol::Union{Missing, Float64} = missing,
f_tol::Union{Missing, Float64} = missing,
g_tol::Union{Missing, Float64} = missing, kwargs...) where T<:Union{Nothing, PyObject}
An interface for using optimizers in the Optim package or custom optimizers.
- `sess`: a session;
- `loss`: a loss function;
- `max_iter`: maximum number of max_iterations;
- `vars`, `grads`: optimizable variables and gradients
- `optimizer`: Optim optimizers (default: LBFGS)
- `callback`: callback after each linesearch completion (NOT one step in the linesearch)
Other arguments are passed to Options in Optim optimizers.
We can also construct a custom optimizer. For example, to construct an optimizer out of Ipopt:
```julia
import Ipopt
x = Variable(rand(2))
loss = (1-x[1])^2 + 100(x[2]-x[1]^2)^2
function opt(f, g, fg, x0, kwargs...)
prob = createProblem(2, -100ones(2), 100ones(2), 0, Float64[], Float64[], 0, 0,
f, (x,g)->nothing, (x,G)->g(G, x), (x, mode, rows, cols, values)->nothing, nothing)
prob.x = x0
Ipopt.addOption(prob, "hessian_approximation", "limited-memory")
status = Ipopt.solveProblem(prob)
println(Ipopt.ApplicationReturnStatus[status])
println(prob.x)
Ipopt.freeProblem(prob)
nothing
end
sess = Session(); init(sess)
Optimize!(sess, loss, optimizer = opt)
```
"""
function Optimize!(sess::PyObject, loss::PyObject, max_iter::Int64 = 15000;
vars::Union{Array{PyObject},PyObject, Missing} = missing,
grads::Union{Array{T},Nothing,PyObject, Missing} = missing,
optimizer = missing,
callback::Union{Function, Missing}=missing,
x_tol::Union{Missing, Float64} = missing,
f_tol::Union{Missing, Float64} = missing,
g_tol::Union{Missing, Float64} = missing,
return_feval_loss::Bool = false, kwargs...) where T<:Union{Nothing, PyObject}
vars = coalesce(vars, get_collection())
grads = coalesce(grads, gradients(loss, vars))
if isa(vars, PyObject); vars = [vars]; end
if isa(grads, PyObject); grads = [grads]; end
if length(grads)!=length(vars); error("ADCME: length of grads and vars do not match"); end
if !all(is_variable.(vars))
error("ADCME: the input `vars` should be trainable variables")
end
idx = ones(Bool, length(grads))
pynothing = pytypeof(PyObject(nothing))
for i = 1:length(grads)
if isnothing(grads[i]) || pytypeof(grads[i])==pynothing
idx[i] = false
end
end
grads = grads[idx]
vars = vars[idx]
sizes = []
for v in vars
push!(sizes, size(v))
end
grds = vcat([tf.reshape(g, (-1,)) for g in grads]...)
vs = vcat([tf.reshape(v, (-1,)) for v in vars]...); x0 = run(sess, vs)
pl = placeholder(x0)
n = 0
assign_ops = PyObject[]
for (k,v) in enumerate(vars)
push!(assign_ops, assign(v, tf.reshape(pl[n+1:n+prod(sizes[k])], sizes[k])))
n += prod(sizes[k])
end
__loss = 0.0
__losses = Float64[]
__feval_loss = Float64[]
__iter = 0
__value = nothing
__ls_iter = 0
function f(x)
run(sess, assign_ops, pl=>x)
__loss = run(sess, loss)
__ls_iter += 1
push!(__feval_loss, __loss)
options.training.verbose && (println("iter $__ls_iter, current loss = $__loss"))
return __loss
end
function g!(G, x)
run(sess, assign_ops, pl=>x)
G[:] = run(sess, grds)
__value = x
end
function fg(G, x)
run(sess, assign_ops, pl=>x)
__loss, G[:] = run(sess, [loss, grds])
__ls_iter += 1
__value = x
return __loss
end
if isa(optimizer, Function)
if length(kwargs)>0
kwargs_ = copy(kwargs)
else
kwargs_ = Dict{Symbol, Any}()
end
kwargs_[:max_iter] = max_iter
__losses = optimizer(f, g!, fg, x0; kwargs_...)
if return_feval_loss
__losses = (__losses, __feval_loss)
end
return __losses
end
if !isdefined(Main, :Optim)
error("Package Optim.jl must be imported in the main module using `import Optim` or `using Optim`")
end
function callback1(x)
@info x.iteration, x.value
__iter = x.iteration
__loss = x.value
push!(__losses, __loss)
if options.training.verbose
println("================== STEP $__iter ==================")
end
if !ismissing(callback)
callback(__value, __iter, __loss)
end
false
end
method = coalesce(optimizer, Main.Optim.LBFGS())
@info "Optimization starts..."
res = Main.Optim.optimize(f, g!, x0, method, Main.Optim.Options(
; store_trace = false,
show_trace = false,
callback=callback1,
iterations = max_iter,
x_tol = coalesce(x_tol, 1e-12),
f_tol = coalesce(f_tol, 1e-12),
g_tol = coalesce(g_tol, 1e-12),
kwargs...))
if return_feval_loss
__losses = (__losses, __feval_loss)
end
return __losses
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 2004 | export reset_default_options
########################### OptionsSparse ###########################
"""
OptionsSparse
Options for sparse linear algebra.
"""
mutable struct OptionsSparse
auto_reorder::Bool
solver::String
OptionsSparse() = new(true, "SparseLU")
end
########################### OptionsNewtonRaphson ###########################
"""
OptionsNewtonRaphson_LineSearch
Options for the line search in the Newton Raphson algorithm.
"""
mutable struct OptionsNewtonRaphson_LineSearch
c1::Float64
ρ_hi::Float64
ρ_lo::Float64
iterations::Int64
maxstep::Int64
αinitial::Float64
OptionsNewtonRaphson_LineSearch() = new(1e-4, 0.5, 0.1, 1000, 9999999, 1.0)
end
"""
OptionsNewtonRaphson
Options for Newton Raphson related algorithms.
"""
mutable struct OptionsNewtonRaphson
max_iter::Int64
verbose::Bool
rtol::Float64
tol::Float64
LM::Float64
linesearch::Bool
linesearch_options::OptionsNewtonRaphson_LineSearch
OptionsNewtonRaphson() = new(100, false, 1e-12, 1e-12, 0.0, false, OptionsNewtonRaphson_LineSearch())
end
mutable struct OptionsTraining
training::PyObject
verbose::Bool
OptionsTraining() = new(placeholder(false), true)
end
mutable struct OptionsMPI
solver::String
printlevel::Int64
OptionsMPI() = new("BoomerAMG", 2)
end
mutable struct OptionsCustomOp
verbose::Bool
OptionsCustomOp() = new(true)
end
######################################################
"""
Options
The container of all options in ADCME.
"""
mutable struct Options
sparse::OptionsSparse
newton_raphson::OptionsNewtonRaphson
training::OptionsTraining
mpi::OptionsMPI
customop::OptionsCustomOp
Options() = new(OptionsSparse(), OptionsNewtonRaphson(), OptionsTraining(), OptionsMPI(), OptionsCustomOp())
end
"""
reset_default_options()
Results the ADCME options to default.
"""
function reset_default_options()
global options
options = Options()
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 8303 | export sinkhorn, ot_dist, empirical_sinkhorn, dtw, emd, ot_plot1D, empirical_emd
# roadmap: implement all related functions from https://github.com/rflamary/POT/blob/master/ot/bregman.py
@doc raw"""
sinkhorn(a::Union{PyObject, Array{Float64}}, b::Union{PyObject, Array{Float64}}, M::Union{PyObject, Array{Float64}};
reg::Float64 = 1.0, iter::Int64 = 1000, tol::Float64 = 1e-9, method::String="sinkhorn")
Computes the optimal transport with Sinkhorn algorithm. The mathematical formulation is
```math
\begin{aligned}
\arg\min_P &\ \left(P, M\right) + \lambda \Omega(\Gamma)\\
\text{s.t.} &\ \Gamma 1 = a\\
&\ \Gamma^T 1 = b\\
& \Gamma \geq 0
\end{aligned}
```
Here $\Omega$ is the entropic regularization. Note if $\lambda$ is very small, the algorithm may encounter numerical instabilities.
The implementation are adapted from https://github.com/rflamary/POT.
"""
function sinkhorn(a::Union{PyObject, Array{Float64}}, b::Union{PyObject, Array{Float64}}, M::Union{PyObject, Array{Float64, 2}};
reg::Union{PyObject,Float64} = 1.0, iter::Int64 = 1000, tol::Float64 = 1e-9, method::String="sinkhorn", returnall::Bool=false)
if isa(a, Array)
@assert sum(a)≈1.0
@assert all(a .>= 0)
end
if isa(b, Array)
@assert sum(b)≈1.0
@assert all(b .>= 0)
end
a = convert_to_tensor(a)
b = convert_to_tensor(b)
M = convert_to_tensor(M)
reg = convert_to_tensor(reg)
iter = convert_to_tensor(iter)
tol = convert_to_tensor(tol)
if method=="lp"
pth = install("OTNetwork")
lp = load_op_and_grad(pth, "ot_network"; multiple=true)
if returnall
P, loss = lp(a, b, M, iter)
P = set_shape(P, (length(a), length(b)))
P, loss
end
return lp(a, b, M, iter)[2]
else
METHODIDS = Dict(
"sinkhorn"=>0,
"greenkhorn"=>1
)
if !haskey(METHODIDS, method)
error("$method not implemented")
end
METHODID = METHODIDS[method]
sk = load_system_op("sinkhorn_knopp"; multiple=true)
if returnall
return sk(a,b,M,reg,iter,tol, constant(METHODID))
end
return sk(a,b,M,reg,iter,tol, constant(METHODID))[2]
end
end
@doc raw"""
emd(a::Union{PyObject, Array{Float64}}, b::Union{PyObject, Array{Float64}}, M::Union{PyObject, Array{Float64}};
iter::Int64 = 1000, tol::Float64 = 1e-9, returnall::Bool=false)
Computes the Earth Mover's Distance, which is defined as
$$D(M) = \sum_{i=1}^m \sum_{j=1}^n M_{ij} d_{ij}$$
Here $M \in \mathbb{R}^{m\times n}$ is the ground distance matrix. The algorithm solves the following optimization problem
$$\begin{aligned}\min_{M} &\ D(M)\\\text{s.t.} & \ \sum_{i=1}^m M_{ij} = b_j\\ &\ \sum_{j=1}^n M_{ij} = a_i \end{aligned}$$
The internal solver for the optimization problem is a netflow solver. The algorithm requires $\sum_i a_i = \sum_j b_j = 1$.
"""
function emd(a::Union{PyObject, Array{Float64}}, b::Union{PyObject, Array{Float64}}, M::Union{PyObject, Array{Float64}};
iter::Int64 = 1000, tol::Float64 = 1e-9, returnall::Bool=false)
return sinkhorn(a, b, M, reg = 0.0, iter = iter, tol = tol, method = "lp",
returnall = returnall)
end
"""
ot_plot1D(a::Array{Float64, 1}, b::Array{Float64, 1}, M::Array{Float64, 2})
Plots the optimal transport matrix for 1D distributions.
"""
function ot_plot1D(a::Array{Float64, 1}, b::Array{Float64, 1}, M::Array{Float64, 2})
@assert length(a) == size(M, 1)
@assert length(b) == size(M, 2)
pl = require_import(:PyPlot)
pl.figure(4, figsize = (5, 5))
xa = 0:size(M, 1)-1
xb = 0:size(M, 2)-1
ax1 = pl.subplot(222)
pl.plot(xb, b, "r")
pl.yticks(())
pl.title("Target")
ax2 = pl.subplot(223)
pl.plot(a, xa, "b")
pl.gca().invert_xaxis()
pl.gca().invert_yaxis()
pl.xticks(())
pl.title("Source")
pl.subplot(224, sharex=ax1, sharey=ax2)
pl.imshow(M, interpolation="nearest")
pl.axis("off")
pl.xlim((0, size(M, 2)-1))
pl.tight_layout()
pl.subplots_adjust(wspace=0., hspace=0.2)
end
@doc raw"""
empirical_sinkhorn(x::Union{PyObject, Array{Float64}}, y::Union{PyObject, Array{Float64}};
reg::Union{PyObject,Float64} = 1.0, iter::Int64 = 1000, tol::Float64 = 1e-9, method::String="sinkhorn", dist::Function=dist, returnall::Bool=false)
Computes the empirical Sinkhorn distance with sinkhorn algorithm. Here $x$ and $y$ are samples from two distributions.
- `reg` (default = 1.0): entropy regularization parameter
- `tol` (default = 1e-9), `iter` (default = 1000): tolerance and max iterations for the Sinkhorn algorithm
- `dist` (default = 2): Integer or Function, the distance function between two samples; if `dist` is integer, $L-dist$ norm is used.
- `returnall`: returns (`TransportMatrix`, `Loss`) if true; otherwise, only `Loss` is returned.
The implementation are adapted from https://github.com/rflamary/POT.
"""
function empirical_sinkhorn(x::Union{PyObject, Array{Float64}}, y::Union{PyObject, Array{Float64}};
reg::Union{PyObject,Float64} = 1.0, iter::Int64 = 1000, tol::Float64 = 1e-9,
method::String="sinkhorn", dist::Union{Integer,Function}=2, returnall::Bool=false, normalized::Bool = false)
x, y = convert_to_tensor([x,y], [Float64, Float64])
length(size(x))==1 && (x = reshape(x, :, 1))
length(size(y))==1 && (y = reshape(y, :, 1))
if isa(dist, Integer)
d = copy(dist)
dist = (x,y) -> ot_dist(x, y, d)
end
M = dist(x, y)
if normalized
M = M/maximum(M)
end
a = tf.ones(tf.shape(x)[1], dtype=tf.float64)/cast(Float64, tf.shape(x)[1])
b = tf.ones(tf.shape(y)[1], dtype=tf.float64)/cast(Float64, tf.shape(y)[1])
sinkhorn(a, b, M; reg=reg, iter=iter, tol=tol, method=method, returnall=returnall)
end
"""
empirical_emd(x::Union{PyObject, Array{Float64}}, y::Union{PyObject, Array{Float64}};
iter::Int64 = 1000, tol::Float64 = 1e-9, dist::Union{Integer,Function}=2, returnall::Bool=false)
Same as [`empirical_sinkhorn`](@ref), except that the Earth Mover Distance is computed.
"""
function empirical_emd(x::Union{PyObject, Array{Float64}}, y::Union{PyObject, Array{Float64}};
iter::Int64 = 1000, tol::Float64 = 1e-9, dist::Union{Integer,Function}=2, returnall::Bool=false, normalized::Bool = false)
empirical_sinkhorn(x, y; iter = iter, tol = tol, method = "lp", returnall = returnall)
end
"""
ot_dist(x::Union{PyObject, Array{Float64}}, y::Union{PyObject, Array{Float64}}, order::Union{Int64, PyObject}=2)
Computes the distance function with norm `order`. `dist` returns a ``n\\times m`` matrix, where ``x\\in \\mathbb{R}^{n\\times d}`` and
``y\\in \\mathbb{R}^{m\\times d}``, and the return ``M\\in \\mathbb{R}^{n\\times m}``
```math
M_{ij} = ||x_i - y_j||_{o}
```
"""
function ot_dist(x::Union{PyObject, Array{Float64}}, y::Union{PyObject, Array{Float64}}, order::Union{Int64, PyObject}=2)
if !(isa(x, PyObject) || isa(y, PyObject) || isa(order, PyObject))
x = reshape(x, size(x, 1), :)
y = reshape(y, size(y, 1), :)
M = zeros(size(x, 1), size(y, 1))
for i = 1:size(x, 1)
for j = 1:size(y, 1)
M[i, j] = norm(x[i,:]-y[j,:], order)
end
end
return M
end
x = convert_to_tensor(x)
y = convert_to_tensor(y)
order = convert_to_tensor(order, dtype=Float64)
x = tf.expand_dims(x, axis=1)
y = tf.expand_dims(y, axis=0)
sum(abs(x-y)^order, dims=3)^(1.0/order)
end
"""
dtw(s::Union{PyObject, Array{Float64}}, t::Union{PyObject, Array{Float64}},
use_fast::Bool = false)
Computes the dynamic time wrapping (DTW) distance between two time series `s` and `t`.
Returns the distance and path. `use_fast` specifies whether fast algorithm is used. Note
fast algorithm may not be accurate.
"""
function dtw(s::Union{PyObject, Array{Float64}}, t::Union{PyObject, Array{Float64}},
use_fast::Bool = false)
use_fast = Int32(use_fast)
pth = install("FastDTW")
dtw_ = load_op_and_grad(pth, "dtw"; multiple=true)
s,t, use_fast = convert_to_tensor([s,t,use_fast], [Float64,Float64, Int32])
cost, path = dtw_(s,t,use_fast)
return cost, path + 1
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 3329 | # This is an implementation of second order physics constrained learning
export pcl_sparse_solve, pcl_square_sum, pcl_hessian, pcl_linear_op, pcl_compress
@doc raw"""
pcl_sparse_solve(indices::Array{Int64, 2},
vals::Array{Float64, 1},
u::Array{Float64, 1},
hessian_u::Array{Float64, 2}, grad_u::Array{Float64, 1})
Hessian backpropagation for
$$Au = f$$
`A` is given by a sparse matrix (the nonzero entries are a vector $a$). This function
back-propagates the Hessian w.r.t. $u$ to the Hessian w.r.t. $A$.
"""
function pcl_sparse_solve(indices::Array{Int64, 2},
vals::Array{Float64, 1},
u::Array{Float64, 1},
hessian_u::Array{Float64, 2}, grad_u::Array{Float64, 1})
A = sparse(indices[:,1], indices[:,2], vals)
indof = length(vals)
outdof = length(u)
invA = inv(Array(A))
J = zeros(indof, outdof)
for k = 1:indof
i = indices[k,1]
j = indices[k,2]
J[k,:] = -invA[:,i] * u[j]
end
H = zeros(indof, indof)
x = A'\grad_u
for l = 1:indof
for r = 1:indof
li, lj = indices[l, :]
ri, rj = indices[r, :]
H[l, r] = -(x[li] * J[r, lj] + x[ri] * J[l, rj])
end
end
return J*hessian_u*J' + H
end
@doc raw"""
pcl_square_sum(scaling::Float64 = 1.0)
Returns the Hessian matrix for
$$\text{scaling} * \|u - u_o\|_2^2$$
`pcl_square_sum` is a reduction op, which can provides the highest level Hessian matrix.
"""
pcl_square_sum(n::Int64; scaling::Float64 = 1.0) = 2Array(I(n)) * scaling
@doc raw"""
pcl_linear_op(J::Array{Float64, 2}, W::Array{Float64,2})
For a linear operator
$$y = J^Tx + b$$
The PCL backpropagation is given by
$$H = JWJ^T$$
"""
function pcl_linear_op(J::Array{Float64, 2}, W::Array{Float64,2})
J * W * J'
end
@doc raw"""
pcl_hessian(y::PyObject, x::PyObject)
Returns the Hessian tensor for the operator
$$y = F(x)$$
$x\in \mathbb{R}^m$ and $y\in \mathbb{R}^n$ are 1D vectors. The function returns a tuple
- `H`: $m\times m$ Hessian matrix
- `W`: $n\times n$ Hessian matrix from downstream of the computational graph
- `dy`: length $n$ tensor; gradient from downstream of the computational graph
"""
function pcl_hessian(y::PyObject, x::PyObject, loss::PyObject)
@assert length(size(x))==length(size(y))==1
J = jacobian(y, x)
if isnothing(J)
error("`jacobian(y, x) = nothing. Please check the dependency of `y` on `x`")
end
W = placeholder(Float64, shape = (length(y), length(y)))
dy = independent(gradients(loss, y))
H = J' * W * J + hessian(dot(dy, y), x)
return H, W
end
@doc raw"""
pcl_compress(indices::Array{Int64, 2})
Computes the Jacobian matrix for `compress`. Assume that `compress` does the following transformation:
```
indices, values (v) --> new_indices, new_values (u)
```
This function computes
$$J_{ij} = \frac{\partial u_j}{\partial v_i}$$
"""
function pcl_compress(indices::Array{Int64, 2})
N = size(indices,1)
v = zeros(N)
nout = zeros(Int32,1)
indices = indices'[:] .- 1
out = @eval ccall((:pcl_SparseCompressor, $(ADCME.LIBADCME)), Ptr{Cdouble},
(Ptr{Clonglong}, Ptr{Cdouble}, Cint, Ptr{Cint}),
$indices, $v, Int32($N), $nout)
J = unsafe_wrap(Array, out, (N,Int64(nout[1])); own = true)
return J
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 2127 | for o in [:Scatter, :Bar, :Scattergl, :Pie, :Heatmap, :Image, :Contour, :Table, :Box, :Violin,
:Histogram, :Histogram2dContour, :Ohlc, :Candlestick, :Waterfall, :Funnel, :Funnelarea,
:Indicator, :Scatter3d, :Surface, :Mesh3d, :Cone, :Volume, :Isosurface, :Scattergeo,
:Choropleth, :Scattermapbox, :Choroplethmapbox, :Densitymapbox,
:Scatterpolar, :Scatterpolargl, :Barpolar, :Scatterternary, :Sunburst, :Treemap, :Sankey,
:Splom, :Parcats, :Parcoords, :Carpet, :Scattercarpet, :Contourcarpet, :Layout]
@eval begin
export $o
function $o(args...;kwargs...)
plotly.graph_objects.$o(args...;kwargs...)
end
end
end
export Plot
"""
Plot(rows::Int64 = 1, cols::Int64 = 1, args...; kwargs...)
Makes a figure consists of `rows × cols` subplots.
# Example
```julia
fig = Plot(3,1)
x = LinRange(0,1,100)
y1 = sin.(x)
y2 = sin.(2*x)
y3 = sin.(3*x)
fig.add_trace(Scatter(x=x, y=y1, name = "Line 1"), row = 1, col = 1)
fig.add_trace(Scatter(x=x, y=y2, name = "Line 2"), row = 2, col = 1)
fig.add_trace(Scatter(x=x, y=y3, name = "Line 3"), row = 3, col = 1)
fig.show()
```
"""
function Plot(rows::Int64 = 1, cols::Int64 = 1, args...; kwargs...)
pkgs = read(`$PIP list`, String)
if !occursin("plotly", pkgs)
run(`$PIP install plotly==4.14.3`)
end
copy!(plotly, "plotly")
spt = pyimport("plotly.subplots")
spt.make_subplots(rows = rows, cols = cols, args...;kwargs...)
end
export to_html
"""
to_html(fig::PyObject, filename::String, args...;
include_plotlyjs = "cnd",
include_mathjax = "cnd",
full_html = true,
kwargs...)
Exports the figure `fig` to an HTML file.
"""
function to_html(fig::PyObject, filename::String, args...;
include_plotlyjs = "cdn",
include_mathjax = "cdn",
full_html = true,
kwargs...)
open(filename, "w") do io
cnt = fig.to_html(
include_plotlyjs = include_plotlyjs,
include_mathjax = include_mathjax,
full_html = full_html
)
write(io, cnt)
end
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 4257 | export seed!, categorical, choice, logpdf
# random variables
for op in [:uniform, :normal]
@eval begin
export $op
function $op(shape...;kwargs...)
kwargs = jlargs(kwargs)
if !haskey(kwargs, :dtype); kwargs[:dtype] = tf.float64; end
tf.random.$op(shape;kwargs...)
end
$op() = squeeze($op(1, dtype=Float64))
# Docs.getdoc(::typeof($op)) = Docs.getdoc(tf.random.$op)
end
end
"""
categorical(n::Union{PyObject, Integer}; kwargs...)
`kwargs` has a keyword argument `logits`, a 2-D Tensor with shape `[batch_size, num_classes]`.
Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
"""
function categorical(n::Union{PyObject, Integer}; kwargs...)
flag = false
kwargs = jlargs(kwargs)
if !haskey(kwargs, :dtype); kwargs[:dtype] = tf.float64; end
if !haskey(kwargs, :logits)
kwargs[:logits] = tf.ones(n, dtype=kwargs[:dtype])
end
logits = kwargs[:logits]; delete!(kwargs, :logits)
if length(size(logits))==1
flag = true
logits = convert_to_tensor(reshape(logits, 1, length(logits)))
end
out = tf.random.categorical(logits, n)
if flag
out = squeeze(out)
end
return out+1
end
"""
choice(inputs::Union{PyObject, Array}, n_samples::Union{PyObject, Integer};replace::Bool=false)
Choose `n_samples` samples from `inputs` with/without replacement.
"""
function choice(inputs::Union{PyObject, Array}, n_samples::Union{PyObject, Integer};
replace::Bool=false)
inputs = convert_to_tensor(inputs)
if replace
Idx = categorical(n_samples, logits=ones(size(inputs,1)))
tf.gather(inputs, Idx-1)
else
dist = uniform(size(inputs,1))
_, indices_to_keep = tf.nn.top_k(dist, n_samples)
indices_to_keep_sorted = tf.sort(indices_to_keep)
tf.gather(inputs,indices_to_keep)
end
end
for op in [:Beta, :Bernoulli,:Gamma, :TruncatedNormal, :Binomial, :Cauchy,
:Chi, :Chi2, :Exponential, :Gumbel,
:HalfCauchy, :HalfNormal, :Horseshoe, :InverseGamma,
:InverseGaussian, :Kumaraswamy, :Pareto, :SinhArcsinh,
:StudentT, :VonMises,
:Poisson]
opname = Symbol(lowercase(string(op)))
@eval begin
export $opname
function $opname(shape...;kwargs...)
if !haskey(kwargs, :dtype); T = Float64;
else T=kwargs[:dtype]; end
kwargs = jlargs(kwargs)
if haskey(kwargs, :dtype); delete!(kwargs, :dtype); end
out = tfp.distributions.$op(;kwargs...).sample(shape...)
cast(out, T)
end
$opname(;kwargs...) = squeeze($opname(1; dtype =Float64, kwargs...))
# Docs.getdoc(::typeof($opname)) = Docs.getdoc(tfp.distributions.$op)
end
end
function seed!(k::Int64)
tf.random.set_random_seed(k)
end
abstract type ADCMEDistribution end
for op in [:Beta, :Bernoulli,:Gamma, :TruncatedNormal, :Binomial, :Cauchy,
:Chi, :Chi2, :Exponential, :Gumbel,
:HalfCauchy, :HalfNormal, :Horseshoe, :InverseGamma,
:InverseGaussian, :Kumaraswamy, :Pareto, :SinhArcsinh,
:StudentT, :VonMises, :Normal, :Uniform,
:Poisson, :MultivariateNormalDiag, :MultivariateNormalFullCovariance,
:Empirical]
@eval begin
mutable struct $op <: ADCMEDistribution
o::PyObject
$op(args...;kwargs...) = new(tfp.distributions.$op(args...;kwargs...))
end
end
# @eval Docs.getdoc($op) = Docs.getdoc($op.o)
end
Base.:rand(dist::T) where T<:ADCMEDistribution = dist.o.sample()
Base.:rand(dist::T, shape::Integer) where T<:ADCMEDistribution = dist.o.sample(shape)
Base.:rand(dist::T, shape::Tuple{Vararg{Int64,N}} where N) where T<:ADCMEDistribution = dist.o.sample(shape)
Base.:rand(dist::T, shape::Array{Int64}) where T<:ADCMEDistribution = dist.o.sample(shape)
Base.:rand(dist::T, shape::PyObject) where T<:ADCMEDistribution = dist.o.sample(shape)
Base.:rand(dist::T, d::Integer, dims::Integer...) where T<:ADCMEDistribution = dist.o.sample([d;dims])
"""
logpdf(dist::T, x) where T<:ADCMEDistribution
Returns the log(prob) for a distribution `dist`.
"""
function logpdf(dist::T, x) where T<:ADCMEDistribution
dist.o.log_prob(x)
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 6403 | export RBF2D, interp1, RBF3D
@doc raw"""
function RBF2D(xc::Union{PyObject, Array{Float64, 1}}, yc::Union{PyObject, Array{Float64, 1}};
c::Union{PyObject, Array{Float64, 1}, Missing} = missing,
eps::Union{PyObject, Array{Float64, 1}, Real, Missing} = missing,
d::Union{PyObject, Array{Float64, 1}} = zeros(0),
kind::Int64 = 0)
Constructs a radial basis function representation on a 2D domain
$$f(x, y) = \sum_{i=1}^N c_i \phi(r; \epsilon_i) + d_0 + d_1 x + d_2 y$$
Here `d` can be either 0, 1 (only $d_0$ is present), or 3 ($d_0$, $d_1$, and $d_2$ are all present).
`kind` determines the type of radial basis functions
* 0:Gaussian
$$\phi(r; \epsilon) = e^{-(\epsilon r)^2}$$
* 1:Multiquadric
$$\phi(r; \epsilon) = \sqrt{1+(\epsilon r)^2}$$
* 2:Inverse quadratic
$$\phi(r; \epsilon) = \frac{1}{1+(\epsilon r)^2}$$
* 3:Inverse multiquadric
$$\phi(r; \epsilon) = \frac{1}{\sqrt{1+(\epsilon r)^2}}$$
Returns a callable struct, i.e. to evaluates the function at locations $(x, y)$ (`x` and `y` are both vectors), run
```julia
rbf(x, y)
```
"""
mutable struct RBF2D
xc::PyObject
yc::PyObject
eps::PyObject
c::PyObject
d::PyObject
kind::Int64
function RBF2D(xc::Union{PyObject, Array{Float64, 1}}, yc::Union{PyObject, Array{Float64, 1}};
c::Union{PyObject, Array{Float64, 1}, Missing} = missing,
eps::Union{PyObject, Array{Float64, 1}, Real, Missing} = missing,
d::Union{PyObject, Array{Float64, 1}} = zeros(0),
kind::Int64 = 0)
if isa(eps, Real)
eps = eps * ones(length(xc))
end
c = coalesce(c, Variable(zeros(length(xc))))
eps = coalesce(eps, ones(length(xc)))
@assert length(xc)==length(yc)==length(c)==length(eps)
@assert length(d) in [0,1,3]
new(constant(xc), constant(yc), constant(eps), constant(c), constant(d), kind)
end
end
function (o::RBF2D)(x,y)
radial_basis_function_ = load_op_and_grad(libadcme,"radial_basis_function")
x,y,xc,yc,eps,c,d,kind = convert_to_tensor(Any[x,y,o.xc,o.yc,o.eps,o.c,o.d,o.kind], [Float64,Float64,Float64,Float64,Float64,Float64,Float64,Int64])
out = radial_basis_function_(x,y,xc,yc,eps,c,d,kind)
set_shape(out, (length(x,)))
end
function Base.:show(io::IO, o::RBF2D)
ct = hasproperty(o.c, :trainable) && o.c.trainable
et = hasproperty(o.eps, :trainable) && o.eps.trainable
dt = hasproperty(o.d, :trainable) && o.d.trainable
print("RadialBasisFunction(NumOfCenters=$(length(o.xc)),NumOfAdditionalTerm=$(length(o.d)),CoeffIsVariable=$(ct),ShapeIsVariable=$(et),AdditionalTermIsVariable=$dt)")
end
"""
interp1(x::Union{Array{Float64, 1}, PyObject},v::Union{Array{Float64, 1}, PyObject},xq::Union{Array{Float64, 1}, PyObject})
returns interpolated values of a 1-D function at specific query points using linear interpolation.
Vector x contains the sample points, and v contains the corresponding values, v(x).
Vector xq contains the coordinates of the query points.
!!! info
`x` should be sorted in ascending order.
# Example
```julia
x = sort(rand(10))
y = constant(@. x^2 + 1.0)
z = [x[1]; x[2]; rand(5) * (x[end]-x[1]) .+ x[1]; x[end]]
u = interp1(x,y,z)
```
"""
function interp1(x::Union{Array{Float64, 1}, PyObject},v::Union{Array{Float64, 1}, PyObject},xq::Union{Array{Float64, 1}, PyObject})
interp_dim_one_ = load_system_op("interp_dim_one")
x,v,xq = convert_to_tensor(Any[x,v,xq], [Float64,Float64,Float64])
out = interp_dim_one_(x,v,xq)
end
@doc raw"""
RBF3D(xc::Union{PyObject, Array{Float64, 1}}, yc::Union{PyObject, Array{Float64, 1}},
zc::Union{PyObject, Array{Float64, 1}};
c::Union{PyObject, Array{Float64, 1}, Missing} = missing,
eps::Union{PyObject, Array{Float64, 1}, Real, Missing} = missing,
d::Union{PyObject, Array{Float64, 1}} = zeros(0),
kind::Int64 = 0)
Constructs a radial basis function representation on a 3D domain
$$f(x, y, z) = \sum_{i=1}^N c_i \phi(r; \epsilon_i) + d_0 + d_1 x + d_2 y + d_3 z$$
Here `d` can be either 0, 1 (only $d_0$ is present), or 4 ($d_0$, $d_1$, $d_2$, and $d_3$ are all present).
`kind` determines the type of radial basis functions
* 0:Gaussian
$$\phi(r; \epsilon) = e^{-(\epsilon r)^2}$$
* 1:Multiquadric
$$\phi(r; \epsilon) = \sqrt{1+(\epsilon r)^2}$$
* 2:Inverse quadratic
$$\phi(r; \epsilon) = \frac{1}{1+(\epsilon r)^2}$$
* 3:Inverse multiquadric
$$\phi(r; \epsilon) = \frac{1}{\sqrt{1+(\epsilon r)^2}}$$
Returns a callable struct, i.e. to evaluates the function at locations $(x, y, z)$ (`x`, `y`, and `z` are all vectors), run
```julia
rbf(x, y, z)
```
"""
mutable struct RBF3D
xc::PyObject
yc::PyObject
zc::PyObject
eps::PyObject
c::PyObject
d::PyObject
kind::Int64
function RBF3D(xc::Union{PyObject, Array{Float64, 1}}, yc::Union{PyObject, Array{Float64, 1}},
zc::Union{PyObject, Array{Float64, 1}};
c::Union{PyObject, Array{Float64, 1}, Missing} = missing,
eps::Union{PyObject, Array{Float64, 1}, Real, Missing} = missing,
d::Union{PyObject, Array{Float64, 1}} = zeros(0),
kind::Int64 = 0)
if isa(eps, Real)
eps = eps * ones(length(xc))
end
c = coalesce(c, Variable(zeros(length(xc))))
eps = coalesce(eps, ones(length(xc)))
@assert length(xc)==length(yc)==length(zc)==length(c)==length(eps)
@assert length(d) in [0,1,4]
new(constant(xc), constant(yc), constant(zc), constant(eps), constant(c), constant(d), kind)
end
end
function (o::RBF3D)(x,y,z)
radial_basis_function_ = load_op_and_grad(libadcme,"radial_basis_function_three_d")
x,y,z,xc,yc,zc,eps,c,d,kind = convert_to_tensor(Any[x,y,z,o.xc,o.yc,o.zc, o.eps,o.c,o.d,o.kind], [Float64,Float64,Float64,Float64,Float64,Float64,Float64,Float64,Float64,Int64])
out = radial_basis_function_(x,y,z,xc,yc,zc,eps,c,d,kind)
set_shape(out, (length(x,)))
end
function Base.:show(io::IO, o::RBF3D)
ct = hasproperty(o.c, :trainable) && o.c.trainable
et = hasproperty(o.eps, :trainable) && o.eps.trainable
dt = hasproperty(o.d, :trainable) && o.d.trainable
print("RadialBasisFunction(NumOfCenters=$(length(o.xc)),NumOfAdditionalTerm=$(length(o.d)),CoeffIsVariable=$(ct),ShapeIsVariable=$(et),AdditionalTermIsVariable=$dt)")
end
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 3453 | import Base:run
export
run,
Session,
init,
run_profile,
save_profile
"""
Session(args...; kwargs...)
Create an ADCME session. By default, ADCME will take up all the GPU resources at the start. If you want the GPU usage to grow on a need basis,
before starting ADCME, you need to set the environment variable via
```julia
ENV["TF_FORCE_GPU_ALLOW_GROWTH"] = "true"
```
# Configuration
Session accepts some runtime optimization configurations
- `intra`: Number of threads used within an individual op for parallelism
- `inter`: Number of threads used for parallelism between independent operations.
- `CPU`: Maximum number of CPUs to use.
- `GPU`: Maximum number of GPU devices to use
- `soft`: Set to True/enabled to facilitate operations to be placed on CPU instead of GPU
!!! note
`CPU` limits the number of CPUs being used, not the number of cores or threads.
"""
function Session(args...; kwargs...)
kwargs_ = Dict{Symbol, Any}()
if haskey(kwargs, :intra)
kwargs_[:intra_op_parallelism_threads] = kwargs[:intra]
end
if haskey(kwargs, :inter)
kwargs_[:inter_op_parallelism_threads] = kwargs[:intra]
end
if haskey(kwargs, :soft)
kwargs_[:allow_soft_placement] = kwargs[:soft]
end
if haskey(kwargs, :CPU) || haskey(kwargs, :GPU)
cnt = Dict{String, Int64}()
if haskey(kwargs, :CPU)
cnt["CPU"] = kwargs[:CPU]
end
if haskey(kwargs, :GPU)
cnt["GPU"] = kwargs[:GPU]
end
kwargs_[:device_count] = cnt
end
if haskey(kwargs, :config)
sess = tf.compat.v1.Session(args...;kwargs...)
else
config = tf.ConfigProto(;kwargs_...)
sess = tf.compat.v1.Session(config = config)
end
STORAGE["session"] = sess
return sess
end
function Base.:run(sess::PyObject, fetches::Union{PyObject, Array{PyObject}, Array{Any}, Tuple}, args::Pair{PyObject, <:Any}...; kwargs...)
local ret
if length(args)>0
ret = sess.run(fetches, feed_dict = Dict(args))
else
ret = sess.run(fetches; kwargs...)
end
if isnothing(ret)
return nothing
elseif isa(ret, Array) && size(ret)==()
return ret[1]
else
return ret
end
end
function global_variables_initializer()
tf.compat.v1.global_variables_initializer()
end
function init(o::PyObject)
run(o, global_variables_initializer())
end
"""
run_profile(args...;kwargs...)
Runs the session with tracing information.
"""
function run_profile(args...;kwargs...)
global run_metadata
options = tf.compat.v1.RunOptions(trace_level=tf.compat.v1.RunOptions.FULL_TRACE)
run_metadata = tf.compat.v1.RunMetadata()
run(args...;options=options, run_metadata=run_metadata, kwargs...)
end
"""
save_profile(filename::String="default_timeline.json")
Save the timeline information to file `filename`.
- Open Chrome and navigate to chrome://tracing
- Load the timeline file
"""
function save_profile(filename::String="default_timeline.json"; kwargs...)
timeline = pyimport("tensorflow.python.client.timeline")
fetched_timeline = timeline.Timeline(run_metadata.step_stats)
chrome_trace = fetched_timeline.generate_chrome_trace_format(;kwargs...)
open(filename,"w") do io
write(io, chrome_trace)
end
@info "Timeline information saved in $filename
- Open Chrome and navigate to chrome://tracing
- Load the timeline file"
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 25995 | using SparseArrays
import Base: accumulate
import LinearAlgebra: factorize
export SparseTensor, SparseAssembler,
spdiag, find, spzero, dense_to_sparse, accumulate, assemble, rows, cols,
factorize, solve, trisolve, RawSparseTensor, compress
"""
SparseTensor
A sparse matrix object. It has two fields
- `o`: internal data structure
- `_diag`: `true` if the sparse matrix is marked as "diagonal".
"""
mutable struct SparseTensor
o::PyObject
_diag::Bool
function SparseTensor(o::PyObject, _diag::Bool=false)
new(o, _diag)
end
end
promote_(x::SparseMatrixCSC, y::SparseTensor) =
(constant(x), y)
promote_(y::SparseTensor, x::SparseMatrixCSC) =
(y, constant(x))
+(x::SparseMatrixCSC, y::SparseTensor) = +(promote_(x,y)...)
-(x::SparseMatrixCSC, y::SparseTensor) = -(promote_(x,y)...)
*(x::SparseMatrixCSC, y::SparseTensor) = *(promote_(x,y)...)
+(x::SparseTensor, y::SparseMatrixCSC) = +(promote_(x,y)...)
-(x::SparseTensor, y::SparseMatrixCSC) = -(promote_(x,y)...)
*(x::SparseTensor, y::SparseMatrixCSC) = *(promote_(x,y)...)
function Base.:values(o::SparseTensor)
o.o.values
end
function rows(o::SparseTensor)
get(o.o.indices',0)+1
end
function cols(o::SparseTensor)
get(o.o.indices',1)+1
end
"""
SparseTensor(I::Union{PyObject,Array{T,1}}, J::Union{PyObject,Array{T,1}}, V::Union{Array{Float64,1}, PyObject}, m::Union{S, PyObject, Nothing}=nothing, n::Union{S, PyObject, Nothing}=nothing) where {T<:Integer, S<:Integer}
Constructs a sparse tensor.
Examples:
```
ii = [1;2;3;4]
jj = [1;2;3;4]
vv = [1.0;1.0;1.0;1.0]
s = SparseTensor(ii, jj, vv, 4, 4)
s = SparseTensor(sprand(10,10,0.3))
```
"""
function SparseTensor(I::Union{PyObject,Array{T,1}}, J::Union{PyObject,Array{T,1}},
V::Union{Array{Float64,1}, PyObject},
m::Union{S, PyObject, Nothing}=nothing, n::Union{S, PyObject, Nothing}=nothing; is_diag::Bool=false) where {T<:Integer, S<:Integer}
if isa(I, PyObject) && size(I,2)==2
return SparseTensor_(I, J, V)
end
I, J, V = convert_to_tensor(I, dtype=Int64), convert_to_tensor(J, dtype=Int64), convert_to_tensor(V)
m, n = convert_to_tensor(m, dtype=Int64), convert_to_tensor(n, dtype=Int64)
indices = [I J] .- 1
value = V
shape = [m;n]
sp = tf.SparseTensor(indices, value, shape)
options.sparse.auto_reorder && (sp = tf.sparse.reorder(sp))
SparseTensor(sp, is_diag)
end
function dense_to_sparse(o::Union{Array, PyObject})
if isa(o, Array)
return SparseTensor(sparse(o))
else
idx = tf.where(tf.not_equal(o, 0))
indices, value = convert_to_tensor([idx, tf.gather_nd(o, idx)], [Int64, Float64])
return SparseTensor(tf.SparseTensor(indices, value, o.get_shape()), false)
end
end
"""
find(s::SparseTensor)
Returns the row, column and values for sparse tensor `s`.
"""
function find(s::SparseTensor)
ind = s.o.indices
val = s.o.values
ii = ind'[1,:]
jj = ind'[2,:]
ii+1, jj+1, val
end
function Base.:copy(s::SparseTensor)
t = SparseTensor(tf.SparseTensor(copy(s.o.indices), copy(s.o.values), s.o.dense_shape), copy(s.is_diag))
end
function Base.:eltype(o::SparseTensor)
return (eltype(o.o.indices), eltype(o.o.values))
end
function SparseTensor_(indices::Union{PyObject,Array{T,2}}, value::Union{PyObject,Array{Float64,1}},
shape::Union{PyObject,Array{T,1}}; is_diag::Bool=false) where T<:Integer
indices = convert_to_tensor(indices, dtype=Int64)
value = convert_to_tensor(value, dtype=Float64)
shape = convert_to_tensor(shape, dtype=Int64)
sp = tf.SparseTensor(indices-1, value, shape)
options.sparse.auto_reorder && (sp = tf.sparse.reorder(sp))
SparseTensor(sp, is_diag)
end
"""
RawSparseTensor(indices::Union{PyObject,Array{T,2}}, value::Union{PyObject,Array{Float64,1}},
m::Union{PyObject,Int64}, n::Union{PyObject,Int64}; is_diag::Bool=false) where T<:Integer
A convenient wrapper for making custom operators. Here `indices` is 0-based.
"""
function RawSparseTensor(indices::Union{PyObject,Array{T,2}}, value::Union{PyObject,Array{Float64,1}},
m::Union{PyObject,Int64}, n::Union{PyObject,Int64}; is_diag::Bool=false) where T<:Integer
indices = convert_to_tensor(indices, dtype=Int64)
value = convert_to_tensor(value, dtype=Float64)
m = convert_to_tensor(m, dtype = Int64)
n = convert_to_tensor(n, dtype = Int64)
shape = [m;n]
sp = tf.SparseTensor(indices, value, shape)
options.sparse.auto_reorder && (sp = tf.sparse.reorder(sp))
SparseTensor(sp, is_diag)
end
"""
SparseTensor(A::SparseMatrixCSC)
SparseTensor(A::Array{Float64, 2})
Creates a `SparseTensor` from numerical arrays.
"""
function SparseTensor(A::SparseMatrixCSC)
rows = rowvals(A)
vals = nonzeros(A)
cols = zeros(eltype(rows), length(rows))
m, n = size(A)
k = 1
for i = 1:n
for j in nzrange(A, i)
cols[k] = i
k += 1
end
end
SparseTensor(rows, cols, vals, m, n; is_diag=isdiag(A))
end
constant(o::SparseMatrixCSC) = SparseTensor(o)
constant(o::SparseTensor) = o
SparseTensor(o::SparseTensor) = o
function SparseTensor(A::Array{Float64, 2})
SparseTensor(sparse(A))
end
function Base.:show(io::IO, s::SparseTensor)
shape = size(s)
s1 = shape[1]===nothing ? "?" : shape[1]
s2 = shape[2]===nothing ? "?" : shape[2]
print(io, "SparseTensor($s1, $s2)")
end
function Base.:run(o::PyObject, S::SparseTensor, args...; kwargs...)
indices, value, shape = run(o, S.o, args...; kwargs...)
sparse(indices[:,1].+1, indices[:,2].+1, value, shape...)
end
"""
Array(A::SparseTensor)
Converts a sparse tensor `A` to dense matrix.
"""
function Base.:Array(A::SparseTensor)
ij = A.o.indices
vv = values(A)
m, n = size(A)
sparse_to_dense_ = load_system_op("sparse_to_dense_ad",multiple=false)
m_, n_ = convert_to_tensor(Any[m,n], [Int64,Int64])
out = sparse_to_dense_(ij, vv, m_,n_)
set_shape(out, (m, n))
end
function Base.:size(s::SparseTensor)
(get(s.o.shape,0).value,get(s.o.shape,1).value)
end
function Base.:size(s::SparseTensor, i::T) where T<:Integer
get(s.o.shape, i-1).value
end
function PyCall.:+(s::SparseTensor, o::PyObject)
if size(s)!=size(o)
error("size $(size(s)) and $(size(o)) does not match")
end
out = tf.sparse_add(s.o, o)
out
end
PyCall.:+(o::PyObject, s::SparseTensor) = s+o
function Base.:-(s::SparseTensor)
SparseTensor(s.o.indices+1, -s.o.values, s.o.dense_shape, is_diag=s._diag)
end
PyCall.:-(o::PyObject, s::SparseTensor) = o + (-s)
PyCall.:-(s::SparseTensor, o::PyObject) = s + (-o)
Base.:+(s1::SparseTensor, s2::SparseTensor) = SparseTensor(tf.sparse.add(s1.o,s2.o), s1._diag&&s2._diag)
Base.:-(s1::SparseTensor, s2::SparseTensor) = s1 + (-s2)
function Base.:adjoint(s::SparseTensor)
indices = [s.o.indices'[2,:] s.o.indices'[1,:]]
sp = tf.SparseTensor(indices, s.o.values, (size(s,2), size(s,1)))
options.sparse.auto_reorder && (sp = tf.sparse.reorder(sp))
SparseTensor(sp, s._diag)
end
function PyCall.:*(s::SparseTensor, o::PyObject)
flag = false
if length(size(o))==0
return o * s
end
if length(size(o))==1
flag = true
o = reshape(o, length(o), 1)
end
out = tf.sparse.sparse_dense_matmul(s.o, o)
if flag
out = squeeze(out)
end
out
end
function Base.:*(s::SparseTensor, o::Array{Float64})
s*convert_to_tensor(o)
end
function PyCall.:*(o::PyObject, s::SparseTensor)
if length(size(o))==0
SparseTensor(tf.SparseTensor(copy(s.o.indices), o*tf.identity(s.o.values), s.o.dense_shape), s._diag)
else
tf.sparse.sparse_dense_matmul(s.o, o, adjoint_a=true, adjoint_b=true)'
end
end
function Base.:*(o::Array{Float64}, s::SparseTensor)
convert_to_tensor(o)*s
end
function Base.:*(o::Real, s::SparseTensor)
o = Float64(o)
SparseTensor(tf.SparseTensor(copy(s.o.indices), o*tf.identity(s.o.values), s.o.dense_shape), s._diag)
end
Base.:*(s::SparseTensor, o::Real) = o*s
Base.:/(s::SparseTensor, o::Real) = (1/o)*s
function _sparse_concate(A1::SparseTensor, A2::SparseTensor, hcat_::Bool)
m1,n1 = size(A1)
m2,n2 = size(A2)
ii1,jj1,vv1 = find(A1)
ii2,jj2,vv2 = find(A2)
sparse_concate_ = load_system_op("sparse_concate"; multiple=true)
ii1,jj1,vv1,m1_,n1_,ii2,jj2,vv2,m2_,n2_ = convert_to_tensor([ii1,jj1,vv1,m1,n1,ii2,jj2,vv2,m2,n2], [Int64,Int64,Float64,Int32,Int32,Int64,Int64,Float64,Int32,Int32])
ii,jj,vv = sparse_concate_(ii1,jj1,vv1,m1_,n1_,ii2,jj2,vv2,m2_,n2_,constant(hcat_))
if hcat_
SparseTensor(ii,jj,vv, m1, n1+n2)
else
SparseTensor(ii,jj,vv,m1+m2,n1)
end
end
function sparse_concate(args::SparseTensor...; hcat_::Bool)
reduce((x,y)->_sparse_concate(x,y,hcat_), args)
end
Base.:vcat(args::SparseTensor...) = sparse_concate(args...;hcat_=false)
Base.:hcat(args::SparseTensor...) = sparse_concate(args...;hcat_=true)
function Base.:hvcat(rows::Tuple{Vararg{Int}}, values::SparseTensor...)
r = Array{SparseTensor}(undef, length(rows))
k = 1
for i = 1:length(rows)
r[i] = hcat(values[k:k+rows[i]-1]...)
k += rows[i]
end
vcat(r...)
end
function Base.:lastindex(o::SparseTensor, i::Int64)
return size(o,i)
end
function Base.:getindex(s::SparseTensor, i1::Union{Integer, Colon, UnitRange{S}, PyObject,Array{S,1}},
i2::Union{Integer, Colon, UnitRange{T}, PyObject,Array{T,1}}) where {S<:Real,T<:Real}
squeeze_dims = Int64[]
if isa(i1, Integer); i1 = [i1]; push!(squeeze_dims, 1); end
if isa(i2, Integer); i2 = [i2]; push!(squeeze_dims, 2); end
if isa(i1, UnitRange) || isa(i1, StepRange); i1 = collect(i1); end
if isa(i2, UnitRange) || isa(i2, StepRange); i2 = collect(i2); end
if isa(i1, Colon); i1 = collect(1:lastindex(s,1)); end
if isa(i2, Colon); i2 = collect(1:lastindex(s,2)); end
if isa(i1, Array{Bool,1}); i1 = findall(i1); end
if isa(i2, Array{Bool,1}); i2 = findall(i2); end
m_, n_ = length(i1), length(i2)
i1 = convert_to_tensor(i1, dtype=Int64)
i2 = convert_to_tensor(i2, dtype=Int64)
ii1, jj1, vv1 = find(s)
m = tf.convert_to_tensor(get(s.o.shape,0),dtype=tf.int64)
n = tf.convert_to_tensor(get(s.o.shape,1),dtype=tf.int64)
ss = load_system_op("sparse_indexing"; multiple=true)
ii2, jj2, vv2 = ss(ii1,jj1,vv1,m,n,i1,i2)
ret = SparseTensor(ii2, jj2, vv2, m_, n_)
if length(squeeze_dims)>0
ret = squeeze(Array(ret), dims=squeeze_dims)
end
ret
end
@doc raw"""
scatter_update(A::Union{SparseTensor, SparseMatrixCSC{Float64,Int64}},
i1::Union{Integer, Colon, UnitRange{T}, PyObject,Array{S,1}},
i2::Union{Integer, Colon, UnitRange{T}, PyObject,Array{T,1}},
B::Union{SparseTensor, SparseMatrixCSC{Float64,Int64}}) where {S<:Real,T<:Real}
Updates a subblock of a sparse matrix by `B`. Equivalently,
```
A[i1, i2] = B
```
"""
function scatter_update(A::Union{SparseTensor, SparseMatrixCSC{Float64,Int64}},
i1::Union{Integer, Colon, UnitRange{S}, PyObject,Array{S,1}},
i2::Union{Integer, Colon, UnitRange{T}, PyObject,Array{T,1}},
B::Union{SparseTensor, SparseMatrixCSC{Float64,Int64}}) where {S<:Real,T<:Real}
if isa(i1, Integer); i1 = [i1]; push!(squeeze_dims, 1); end
if isa(i2, Integer); i2 = [i2]; push!(squeeze_dims, 2); end
if isa(i1, UnitRange) || isa(i1, StepRange); i1 = collect(i1); end
if isa(i2, UnitRange) || isa(i2, StepRange); i2 = collect(i2); end
if isa(i1, Colon); i1 = collect(1:lastindex(A,1)); end
if isa(i2, Colon); i2 = collect(1:lastindex(A,2)); end
if isa(i1, Array{Bool,1}); i1 = findall(i1); end
if isa(i2, Array{Bool,1}); i2 = findall(i2); end
ii = convert_to_tensor(i1, dtype=Int64)
jj = convert_to_tensor(i2, dtype=Int64)
!isa(A, SparseTensor) && (A=SparseTensor(A))
!isa(B, SparseTensor) && (B=SparseTensor(B))
ii1, jj1, vv1 = find(A)
m1_, n1_ = size(A)
ii2, jj2, vv2 = find(B)
sparse_scatter_update_ = load_system_op("sparse_scatter_update"; multiple=true)
ii1,jj1,vv1,m1,n1,ii2,jj2,vv2,ii,jj = convert_to_tensor([ii1,jj1,vv1,m1_,n1_,ii2,jj2,vv2,ii,jj], [Int64,Int64,Float64,Int64,Int64,Int64,Int64,Float64,Int64,Int64])
ii, jj, vv = sparse_scatter_update_(ii1,jj1,vv1,m1,n1,ii2,jj2,vv2,ii,jj)
SparseTensor(ii, jj, vv, m1_, n1_)
end
@doc raw"""
scatter_update(A::Union{SparseTensor, SparseMatrixCSC{Float64,Int64}},
i1::Union{Integer, Colon, UnitRange{T}, PyObject,Array{S,1}},
i2::Union{Integer, Colon, UnitRange{T}, PyObject,Array{T,1}},
B::Union{SparseTensor, SparseMatrixCSC{Float64,Int64}}) where {S<:Real,T<:Real}
Adds `B` to a subblock of a sparse matrix `A`. Equivalently,
```
A[i1, i2] += B
```
"""
function scatter_add(A::Union{SparseTensor, SparseMatrixCSC{Float64,Int64}},
i1::Union{Integer, Colon, UnitRange{T}, PyObject,Array{S,1}},
i2::Union{Integer, Colon, UnitRange{T}, PyObject,Array{T,1}},
B::Union{SparseTensor, SparseMatrixCSC{Float64,Int64}}) where {S<:Real,T<:Real}
!(isa(A, SparseTensor)) && (A = SparseTensor(A))
!(isa(B, SparseTensor)) && (B = SparseTensor(B))
C = A[i1,i2]
D = B + C
scatter_update(A, i1, i2, D)
end
function Base.:reshape(s::SparseTensor, shape::T...) where T<:Integer
SparseTensor(tf.sparse.reshape(s, shape), false)
end
@doc raw"""
\(A::SparseTensor, o::PyObject, method::String="SparseLU")
Solves the linear equation
$$A x = o$$
# Method
For square matrices $A$, one of the following methods is available
- `auto`: using the solver specified by `ADCME.options.sparse.solver`
- `SparseLU`
- `SparseQR`
- `SimplicialLDLT`
- `SimplicialLLT`
!!! note
In the case `o` is 2 dimensional, `\` is understood as "batched solve". `o` must have size $n_{b} \times m$, and
$A$ has a size $m\times n$. It returns the solution matrix of size $n_b \times n$
$$s_{i,:} = A^{-1} o_{i,:}$$
"""
function PyCall.:\(s::SparseTensor, o::PyObject, method::String="auto")
local u
if method=="auto"
method = options.sparse.solver
end
if size(s,1)!=size(s,2)
_cfun = load_system_op("sparse_least_square")
ii, jj, vv = find(s)
ii, jj, vv, o = convert_to_tensor([ii, jj, vv, o], [Int32, Int32, Float64, Float64])
if length(size(o))==1
@assert size(s,1)==length(o)
o = reshape(o, (1, -1))
u = _cfun(ii, jj, vv, o, constant(size(s, 2), dtype=Int32))
return u[1]
end
@assert size(o,2)==size(s,1)
u = _cfun(ii, jj, vv, o, constant(size(s, 2), dtype=Int32))
if size(s,2)!=nothing && size(o,1)!=nothing
u.set_shape((size(o,1), size(s,2)))
end
else
ss = load_system_op("sparse_solver")
# in case `indices` has dynamical shape
ii, jj, vv = find(s)
ii,jj,vv,o = convert_to_tensor([ii,jj,vv,o], [Int64,Int64,Float64,Float64])
u = ss(ii,jj,vv,o,method)
if size(s,2)!=nothing
u.set_shape((size(s,2),))
end
end
u
end
Base.:\(s::SparseTensor, o::Array{Float64}) = s\constant(o)
"""
SparseAssembler(handle::Union{PyObject, <:Integer}, n::Union{PyObject, <:Integer}, tol::Union{PyObject, <:Real}=0.0)
Creates a SparseAssembler for accumulating `row`, `col`, `val` for sparse matrices.
- `handle`: an integer handle for creating a sparse matrix. If the handle already exists, `SparseAssembler` return the existing sparse matrix handle. If you are creating different sparse matrices, the handles should be different.
- `n`: Number of rows of the sparse matrix.
- `tol` (optional): Tolerance. `SparseAssembler` will treats any values less than `tol` as zero.
# Example 1
```julia
handle = SparseAssembler(100, 5, 1e-8)
op1 = accumulate(handle, 1, [1;2;3], [1.0;2.0;3.0])
op2 = accumulate(handle, 2, [1;2;3], [1.0;2.0;3.0])
J = assemble(5, 5, [op1;op2])
```
`J` will be a [`SparseTensor`](@ref) object.
# Example 2
```julia
handle = SparseAssembler(0, 5)
op1 = accumulate(handle, 1, [1;2;3], ones(3))
op2 = accumulate(handle, 1, [3], [1.])
op3 = accumulate(handle, 2, [1;3], ones(2))
J = assemble(5, 5, [op1;op2;op3]) # op1, op2, op3 are parallel
Array(run(sess, J))≈[1.0 1.0 2.0 0.0 0.0
1.0 0.0 1.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0]
```
"""
function SparseAssembler(handle::Union{PyObject, <:Integer}, n::Union{PyObject, <:Integer}, tol::Union{PyObject, <:Real}=0.0)
sparse_accumulator = load_system_op("sparse_accumulator", false)
n = convert_to_tensor(n, dtype=Int32)
tol = convert_to_tensor(tol, dtype=Float64)
handle = convert_to_tensor(handle, dtype=Int32)
sparse_accumulator(tol, n, handle)
end
"""
accumulate(handle::PyObject, row::Union{PyObject, <:Integer}, cols::Union{PyObject, Array{<:Integer}}, vals::Union{PyObject, Array{<:Real}})
Accumulates `row`-th row. It adds the value to the sparse matrix
```julia
for k = 1:length(cols)
A[row, cols[k]] += vals[k]
end
```
`handle` is the handle created by [`SparseAssembler`](@ref).
See [`SparseAssembler`](@ref) for an example.
!!! note
The function `accumulate` returns a `op::PyObject`. Only when `op` is executed, the nonzero values are populated into the sparse matrix.
"""
function accumulate(handle::PyObject, row::Union{PyObject, <:Integer}, cols::Union{PyObject, Array{<:Integer}},
vals::Union{PyObject, Array{<:Real}})
sparse_accumulator_add = load_system_op("sparse_accumulator_add", false)
row = convert_to_tensor(row, dtype=Int32)
cols = convert_to_tensor(cols, dtype=Int32)
vals = convert_to_tensor(vals, dtype=Float64)
return sparse_accumulator_add(handle, row, cols, vals)
end
"""
assemble(m::Union{PyObject, <:Integer}, n::Union{PyObject, <:Integer}, ops::PyObject)
Assembles the sparse matrix from the `ops` created by [`accumulate`](@ref). `ops` is either a single output from `accumulate`, or concated from several `ops`
```julia
op1 = accumulate(handle, 1, [1;2;3], [1.0;2.0;3.0])
op2 = accumulate(handle, 2, [1;2;3], [1.0;2.0;3.0])
op = [op1;op2] # equivalent to `vcat([op1, op2]...)`
```
`m` and `n` are rows and columns of the sparse matrix.
See [`SparseAssembler`](@ref) for an example.
"""
function assemble(m::Union{PyObject, <:Integer}, n::Union{PyObject, <:Integer}, ops::PyObject)
sparse_accumulator_copy = load_system_op("sparse_accumulator_copy", false)
if length(size(ops))==0
ops = reshape(ops, 1)
end
ii, jj, vv = sparse_accumulator_copy(ops)
return SparseTensor(ii, jj, vv, m, n)
end
"""
spdiag(n::Int64)
Constructs a sparse identity matrix of size ``n\\times n``, which is equivalent to `spdiag(n, 0=>ones(n))`
"""
function spdiag(n::Int64)
SparseTensor(sparse(1:n, 1:n, ones(Float64, n)))
end
"""
spdiag(o::PyObject)
Constructs a sparse diagonal matrix where the diagonal entries are `o`, which is equivalent to `spdiag(length(o), 0=>o)`
"""
function spdiag(o::PyObject)
if length(size(o))!=1
error("ADCME: input `o` must be a vector")
end
ii = collect(1:length(o))
SparseTensor(ii, ii, o, length(o), length(o), is_diag=true)
end
spdiag(o::Array{Float64, 1}) = spdiag(constant(o))
"""
spzero(m::Int64, n::Union{Missing, Int64}=missing)
Constructs a empty sparse matrix of size ``m\\times n``. `n=m` if `n` is `missing`
"""
function spzero(m::Int64, n::Union{Missing, Int64}=missing)
if ismissing(n)
n = m
end
ii = Int64[]
jj = Int64[]
vv = Float64[]
SparseTensor(ii, jj, vv, m, n, is_diag=true)
end
function Base.:*(s1::SparseTensor, s2::SparseTensor)
ii1, jj1, vv1 = find(s1)
ii2, jj2, vv2 = find(s2)
m, n = size(s1)
n_, k = size(s2)
if n!=n_
error("IGACS: matrix size mismatch: ($m, $n) vs ($n_, $k)")
end
mat_mul_fn = load_system_op("sparse_sparse_mat_mul")
if s1._diag
mat_mul_fn = load_system_op("diag_sparse_mat_mul")
elseif s2._diag
mat_mul_fn = load_system_op("sparse_diag_mat_mul")
end
ii3, jj3, vv3 = mat_mul_fn(ii1-1,jj1-1,vv1,ii2-1,jj2-1,vv2, constant(m), constant(n), constant(k))
SparseTensor(ii3, jj3, vv3, m, k, is_diag=s1._diag&&s2._diag)
end
# missing is treated as zeros
Base.:+(s1::SparseTensor, s2::Missing) = s1
Base.:-(s1::SparseTensor, s2::Missing) = s1
Base.:*(s1::SparseTensor, s2::Missing) = missing
Base.:/(s1::SparseTensor, s2::Missing) = missing
Base.:-(s1::Missing, s2::SparseTensor) = -s2
Base.:+(s1::Missing, s2::SparseTensor) = s2
Base.:*(s1::Missing, s2::SparseTensor) = missing
Base.:/(s1::Missing, s2::SparseTensor) = missing
function Base.:sum(s::SparseTensor; dims::Union{Integer, Missing}=missing)
if ismissing(dims)
tf.sparse.reduce_sum(s.o)
else
tf.sparse.reduce_sum(s.o, axis=dims-1)
end
end
@doc raw"""
spdiag(m::Integer, pair::Pair...)
Constructs a square $m\times m$ [`SparseTensor`](@ref) from pairs of the form
```
offset => array
```
# Example
Suppose we want to construct a $10\times 10$ tridiagonal matrix, where the lower off-diagonals are all -2,
the diagonals are all 2, and the upper off-diagonals are all 3, the corresponding Julia code is
```julia
spdiag(10, -1=>-2*ones(9), 0=>2*ones(10), 1=>3ones(9))
```
"""
function spdiag(n::Integer, pair::Pair...)
ii = Array{Int64}[]
jj = Array{Int64}[]
vv = PyObject[]
for (k, v) in pair
@assert -(n-1)<=k<=n-1
v = convert_to_tensor(v, dtype=Float64)
if k>=0
push!(ii, collect(1:n-k))
push!(jj, collect(k+1:n))
push!(vv, v)
else
push!(ii, collect(-k+1:n))
push!(jj, collect(1:n+k))
push!(vv, v)
end
end
ii = vcat(ii...)
jj = vcat(jj...)
vv = vcat(vv...)
indices = [ii jj] .- 1
sp = tf.SparseTensor(indices, vv, (n, n))
options.sparse.auto_reorder && (sp = tf.sparse.reorder(sp))
SparseTensor(sp)
end
@doc raw"""
factorize(A::Union{SparseTensor, SparseMatrixCSC}, max_cache_size::Int64 = 999999)
Factorizes $A$ for sparse matrix solutions. `max_cache_size` specifies the maximum cache sizes in the C++ kernels,
which determines the maximum number of factorized matrices.
The function returns the factorized matrix, which is basically `Tuple{SparseTensor, PyObject}`.
# Example
```julia
A = sprand(10,10,0.7)
Afac = factorize(A) # factorizing the matrix
run(sess, Afac\rand(10)) # no factorization, solving the equation
run(sess, Afac\rand(10)) # no factorization, solving the equation
```
"""
function factorize(A::Union{SparseTensor, SparseMatrixCSC}, max_cache_size::Int64 = 999999)
sparse_factorization_ = load_system_op("sparse_factorization"; multiple=false)
A = constant(A)
ii, jj, vv = find(A)
d = size(A, 1)
ii,jj,vv,d,max_cache_size = convert_to_tensor([ii,jj,vv,d,max_cache_size], [Int64,Int64,Float64,Int64,Int64])
o = stop_gradient(sparse_factorization_(ii,jj,vv,d,max_cache_size))
return (A, o)
end
@doc raw"""
solve(A_factorized::Tuple{SparseTensor, PyObject}, rhs::Union{Array{Float64,1}, PyObject})
Solves the equation `A_factorized * x = rhs` using the factorized sparse matrix. See [`factorize`](@ref).
"""
function solve(A_factorized::Tuple{SparseTensor, PyObject}, rhs::Union{Array{Float64,1}, PyObject})
A, o = A_factorized
solve_ = load_system_op("solve"; multiple=false)
ii, jj, vv = find(constant(A))
rhs,ii, jj, vv,o = convert_to_tensor([rhs,ii, jj, vv,o], [Float64,Int64, Int64, Float64,Int64])
out = solve_(rhs,ii, jj, vv,o)
end
@doc raw"""
Base.:\(A_factorized::Tuple{SparseTensor, PyObject}, rhs::Union{Array{Float64,1}, PyObject})
A convenient overload for [`solve`](@ref). See [`factorize`](@ref).
"""
Base.:\(A_factorized::Tuple{SparseTensor, PyObject}, rhs::Union{Array{Float64,1}, PyObject}) = solve(A_factorized, rhs)
@doc raw"""
trisolve(a::Union{PyObject, Array{Float64,1}},b::Union{PyObject, Array{Float64,1}},
c::Union{PyObject, Array{Float64,1}},d::Union{PyObject, Array{Float64,1}})
Solves a tridiagonal matrix linear system. The equation is as follows
$$a_i x_{i-1} + b_i x_i + c_i x_{i+1} = d_i$$
In the matrix format,
```math
\begin{bmatrix}
b_1 & c_1 & &0 \\
a_2 & b_2 & c_2 & \\
& a_3 & b_3 & &\\
& & & & c_{n-1}\\
0 & & &a_n & b_n
\end{bmatrix}\begin{bmatrix}
x_1\\
x_2\\
\vdots \\
x_n
\end{bmatrix} = \begin{bmatrix}
d_1\\
d_2\\
\vdots\\
d_n\end{bmatrix}
```
"""
function trisolve(a::Union{PyObject, Array{Float64,1}},b::Union{PyObject, Array{Float64,1}},
c::Union{PyObject, Array{Float64,1}},d::Union{PyObject, Array{Float64,1}})
n = length(b)
@assert length(b) == length(d) == length(a)+1 == length(c)+1
tri_solve_ = load_system_op("tri_solve"; multiple=false)
a,b,c,d = convert_to_tensor(Any[a,b,c,d], [Float64,Float64,Float64,Float64])
out = tri_solve_(a,b,c,d)
set_shape(out, (n,))
end
function Base.:bind(op::SparseTensor, ops...)
bind(op.o.values, ops...)
end
"""
compress(A::SparseTensor)
Compresses the duplicated index in `A`.
# Example
```julia
using ADCME
indices = [
1 1
1 1
2 2
3 3
]
v = [1.0;1.0;1.0;1.0]
A = SparseTensor(indices[:,1], indices[:,2], v, 3, 3)
Ac = compress(A)
sess = Session(); init(sess)
run(sess, A.o.indices) # expected: [0 0;0 0;1 1;2 2]
run(sess, A.o.values) # expected: [1.0;1.0;1.0;1.0]
run(sess, Ac.o.indices) # expected: [0 0;1 1;2 2]
run(sess, Ac.o.values) # expected: [2.0;1.0;1.0]
```
!!! note
The indices of `A` should be sorted. `compress` does not check the validity of the input arguments.
"""
function compress(A::SparseTensor)
indices, v = A.o.indices, A.o.values
sparse_compress_ = load_op_and_grad(libadcme,"sparse_compress", multiple=true)
ind, vv = sparse_compress_(indices,v)
RawSparseTensor(ind, vv, size(A)...)
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 3841 | export Database, execute, commit
mutable struct Database
conn::PyObject
c::PyObject
sqlite3::PyObject
commit_after_execute::Bool
filename::String
end
"""
Database(filename::Union{Missing, String} = missing;
commit_after_execute::Bool = true)
Creates a database from `filename`. If `filename` is not provided, an in-memory database is created.
If `commit_after_execute` is false, no commit operation is performed after each [`execute`](@ref).
- do block syntax:
```julia
Database() do db
execute(db, "create table mytable (a real, b real)")
end
```
The database is automatically closed after execution. Therefore, if execute is a query operation,
users need to store the results in a global variable.
- Query meta information
```julia
keys(db) # all tables
keys(db, "mytable") # all column names in `db.mytable`
```
"""
function Database(filename::Union{Missing, String} = missing;
commit_after_execute::Bool = true)
filename = coalesce(filename, ":memory:")
sqlite3 = pyimport("sqlite3")
db = Database(PyNULL(), PyNULL(), sqlite3, commit_after_execute, filename)
db
end
function connect(db::Database)
sqlite3 = pyimport("sqlite3")
db.conn = sqlite3.connect(db.filename)
db.c = db.conn.cursor()
end
function Database(f::Function, args...; kwargs...)
db = Database(args...;kwargs...)
out = f(db)
close(db)
out
end
"""
execute(db::Database, sql::String, args...)
Executes the SQL statement `sql` in `db`. Users can also use the do block syntax.
```julia
execute(db) do
"create table mytable (a real, b real)"
end
```
`execute` can also be used to insert a batch of records
```julia
t1 = rand(10)
t2 = rand(10)
param = collect(zip(t1, t2))
execute(db, "INSERT TO mytable VALUES (?,?)", param)
```
or
```julia
execute(db, "INSERT TO mytable VALUES (?,?)", t1, t2)
```
"""
function execute(db::Database, sql::String, args...)
connect(db)
if length(args)>=1
if length(args)>1
param = collect(zip(args...))
else
param = args[1]
end
db.c.executemany(sql, param)
else
db.c.execute(sql)
end
if db.commit_after_execute
commit(db)
end
db.c
end
function execute(f::Function, db::Database; kwargs...)
sql = f()
execute(db, sql; kwargs...)
end
"""
commit(db::Database)
Commits changes to `db`.
"""
function commit(db::Database)
db.conn.commit()
end
function Base.:close(db::Database)
if !(db.conn==PyNULL())
commit(db)
db.c.close()
db.conn.close()
db.c = PyNULL()
db.conn = PyNULL()
end
nothing
end
function Base.:keys(db::Database)
ret = execute(db, "select name from sqlite_master")|>collect
close(db)
tables = String[]
for k = 1:length(ret)
push!(tables, ret[k][1])
end
tables
end
function Base.:keys(db::Database, table::String)
execute(db, "select * from $table limit 1")
ret = db.c.description
close(db)
columns = String[]
for r in ret
push!(columns, r[1])
end
columns
end
function Base.:push!(db::Database, table::String, nts::NamedTuple...)
v1 = []
v2 = []
for nt in nts
cols = propertynames(nt)
push!(v1, join(["\"$c\"" for c in cols], ","))
push!(v2, join([isnothing(nt[i]) ? "NULL" : "\"$(nt[i])\"" for i = 1:length(nt)], ","))
end
v1 = join(v1, ",")
v2 = join(v2, ",")
execute(db,
"""
INSERT OR REPLACE INTO $table ($v1) VALUES ($v2)
"""
)
close(db)
end
function Base.:delete!(db::Database, table::String)
execute(db, "drop table $table")
close(db)
end
function Base.:getindex(db::Database, table::String)
c = execute(db, "select * from $table")
out = collect(c)
close(db)
out
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 9338 | #=
toolchain.jl implements a build system
Compilers
=========
CC
CXX
GFORTRAN
Tools
=====
CMAKE
MAKE
NINJA
Directories
===========
BINDIR
LIBDIR
PREFIXDIR
=#
export http_file, uncompress, git_repository, require_file,
link_file, make_directory, change_directory, require_library, get_library,
run_with_env, get_conda, read_with_env, get_library_name, get_pip,
copy_file, require_cmakecache, require_import, get_xml
GFORTRAN = nothing
CONDA = nothing
"""
http_file(url::AbstractString, file::AbstractString)
Download a file from `url` and rename it to `file`.
"""
function http_file(url::AbstractString, file::AbstractString)
require_file(file) do
@info "Downloading $url -> $file"
download(url, file)
@info "Downloaded $file from $url."
end
end
"""
uncompress(zipfile::AbstractString, file::AbstractString)
Uncompress a zip file `zipfile` to `file` (a directory). Note this function does not check that the
uncompressed content has the name `file`. It is used as a hint to skip `uncompress` action.
Users may use `mv uncompress_file file` to enforce the consistency.
"""
function uncompress(zipfile::AbstractString, file::Union{Missing, AbstractString}=missing)
zipfile = abspath(zipfile)
if ismissing(file)
d = "."
else
file = abspath(file)
d = splitdir(file)[1]
end
uncompress_ = ()->begin
if length(zipfile)>4 && zipfile[end-3:end]==".zip"
if Sys.iswindows()
run(`unzip $zipfile -d $d`)
else
UNZIP = joinpath(BINDIR, "unzip")
run(`$UNZIP $zipfile -d $d`)
end
elseif length(zipfile)>4 && zipfile[end-3:end]==".tar"
run(`tar -xvf $zipfile -C $d`)
elseif length(zipfile)>7 && (zipfile[end-6:end]==".tar.gz" || zipfile[end-3:end]==".tgz")
run(`tar -xvzf $zipfile -C $d`)
else
error("ADCME doesn't know how to uncompress $zipfile")
end
end
if ismissing(file)
uncompress_()
else
require_file(file) do
uncompress_()
end
end
end
"""
git_repository(url::AbstractString, file::AbstractString)
Clone a repository `url` and rename it to `file`.
"""
function git_repository(url::AbstractString, file::AbstractString)
@info "Cloning from $url to $file..."
require_file(file) do
LibGit2.clone(url, file)
@info "Cloned $url to $file"
end
end
"""
require_file(f::Function, file::Union{String, Array{String}})
If any of the files/links/directories in `file` does not exist, execute `f`.
"""
function require_file(f::Function, file::Union{String, Array{String}})
if isa(file, String)
file = [file]
end
if !all([isfile(x)||islink(x)||isdir(x) for x in file])
f()
else
if length(file)==1
@info "File $(file[1]) exists"
else
@info "Files exist: $(file)"
end
end
end
"""
get_gfortran()
Install a gfortran compiler if it does not exist.
"""
function get_gfortran()
global GFORTRAN
try
GFORTRAN = split(String(read(`which gfortran`)))[1]
catch
error("gfortran is not in the path.")
end
GFORTRAN
end
"""
link_file(target::AbstractString, link::AbstractString)
Make a symbolic link `link` -> `target`
"""
function link_file(target::AbstractString, link::AbstractString)
if isfile(link) || islink(link)
return
else
symlink(target, link)
@info "Made symbolic link $link -> $target"
end
end
"""
make_directory(directory::AbstractString)
Make a directory if it does not exist.
"""
function make_directory(directory::AbstractString)
require_file(directory) do
mkpath(directory)
@info "Made directory directory"
end
end
"""
change_directory(directory::Union{Missing, AbstractString})
Change the current working directory to `directory`. If `directory` does not exist, it is made.
If `directory` is missing, the default is `ADCME.PREFIXDIR`.
"""
function change_directory(directory::Union{Missing, AbstractString}=missing)
directory = coalesce(directory, ADCME.PREFIXDIR)
if !isdir(directory)
make_directory(directory)
end
cd(directory)
@info "Changed to directory $directory"
end
"""
get_library(filename::AbstractString)
Returns a valid library file. For example, for `filename = "adcme"`, we have
- On MacOS, the function returns `libadcme.dylib`
- On Linux, the function returns `libadcme.so`
- On Windows, the function returns `adcme.dll`
"""
function get_library(filename::AbstractString)
filename = abspath(filename)
dir, file = splitdir(filename)
if Sys.islinux() || Sys.isapple()
if length(file)<3 || file[1:3]!="lib"
file = "lib" * file
end
f, _ = splitext(file)
ext = Sys.islinux() ? "so" : "dylib"
file = f * "." * ext
else
f, _ = splitext(file)
file = f * ".dll"
end
filename = joinpath(dir, file)
end
"""
get_conda()
Returns the conda executable location.
"""
function get_conda()
global CONDA = joinpath(ADCME.BINDIR, "conda")
CONDA
end
"""
require_library(func::Function, filename::AbstractString)
If the library file `filename` does not exist, `func` is executed.
"""
function require_library(func::Function, filename::AbstractString)
filename = get_library(filename)
if !(isfile(filename) || islink(filename))
func()
else
@info "Library $filename exists"
end
end
"""
get_library_name(filename::AbstractString)
Returns the OS-dependent library name
# Example
```
get_library_name("mylibrary")
```
- Windows: `mylibrary.dll`
- MacOS: `libmylibrary.dylib`
- Linux: `libmylibrary.so`
"""
function get_library_name(filename::AbstractString)
if length(filename)>3 && filename[1:3]=="lib"
@warn "No prefix `lib` is need. Removed."
filename = filename[4:end]
end
if Sys.iswindows()
filename = filename * ".dll"
elseif Sys.isapple()
filename = "lib" * filename * ".dylib"
else
filename = "lib" * filename * ".so"
end
filename
end
"""
run_with_env(cmd::Cmd, env::Union{Missing, Dict} = missing)
Running the command with the default environment and an extra environment variables `env`
"""
function run_with_env(cmd::Cmd, env::Union{Missing, Dict} = missing)
ENV_ = copy(ENV)
LD_PATH = Sys.iswindows() ? "PATH" : "LD_LIBRARY_PATH"
if haskey(ENV_, LD_PATH)
ENV_[LD_PATH] = ENV[LD_PATH]*":$LIBDIR"
else
ENV_[LD_PATH] = LIBDIR
end
if !ismissing(env)
ENV_ = merge(env, ENV_)
end
run(setenv(cmd, ENV_))
end
"""
read_with_env(cmd::Cmd, env::Union{Missing, Dict} = missing)
Similar to [`run_with_env`](@ref), but returns a string containing the output.
"""
function read_with_env(cmd::Cmd, env::Union{Missing, Dict} = missing)
ENV_ = copy(ENV)
LD_PATH = Sys.iswindows() ? "PATH" : "LD_LIBRARY_PATH"
if haskey(ENV_, LD_PATH)
ENV_[LD_PATH] = ENV[LD_PATH]*":$LIBDIR"
else
ENV_[LD_PATH] = LIBDIR
end
if !ismissing(env)
ENV_ = merge(env, ENV_)
end
String(read(setenv(cmd, ENV_)))
end
"""
get_pip()
Returns the location for `pip`
"""
function get_pip()
PIP = ""
if Sys.iswindows()
PIP = joinpath(BINDIR, "pip.exe")
else
PIP = joinpath(BINDIR, "pip")
end
return PIP
end
"""
copy_file(src::String, dest::String)
Copy file `src` to `dest`
"""
function copy_file(src::String, dest::String)
if !isfile(src) && !isdir(src)
error("$src is neither a file nor a directory")
end
require_file(dest) do
cp(src, dest)
@info "Move file $src to $dest"
end
end
"""
require_cmakecache(func::Function, DIR::String = ".")
Check if `cmake` has output something. If not, `func` is executed.
"""
function require_cmakecache(func::Function, DIR::String = ".")
DIR = abspath(DIR)
if !isdir(DIR)
error("$DIR is not a valid directory")
end
if Sys.iswindows()
files = readdir(DIR)
if length(files)==0
func()
return
end
x = [splitext(x)[2] for x in files]
if ".sln" in x
return
else
func()
end
else
file = joinpath(DIR, "build.ninja")
if isfile(file)
return
else
func()
end
end
end
@doc raw"""
require_import(s::Symbol)
Checks whether the package `s` is imported in the Main namespace. Returns the package handle.
"""
function require_import(s::Symbol)
if !isdefined(Main, s)
error("Package $s.jl must be imported in the main module using `import $s` or `using $s`")
end
@eval Main.$s
end
raw"""
get_xml()
Returns the xml file for `conda install`. In case conda dependencies need to be reinstalled, run
```
run(`$(get_conda()) env update -n base --file $(get_xml())`)
```
"""
function get_xml()
os = ""
if Sys.iswindows()
os = "windows"
elseif Sys.isapple()
os = "osx"
else
os = "linux"
end
return abspath(joinpath(@__DIR__, "..", "deps", "$(os).yml"))
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 25077 | import Base:lastindex, getindex
export
constant,
Variable,
cell,
set_shape,
get_dtype,
get_variable,
placeholder,
variable_scope,
gradients,
gradient_magnitude,
hessian,
constant_initializer,
glorot_normal_initializer,
random_normal_initializer,
random_uniform_initializer,
truncated_normal_initializer,
uniform_unit_scaling_initializer,
variance_scaling_initializer,
sym,
spd,
tensor,
convert_to_tensor,
hessian_vector,
TensorArray,
gradient_checkpointing,
zeros_like,
ones_like,
gradients_colocate,
is_variable,
jacobian
"""
constant(value; kwargs...)
Constructs a non-trainable tensor from `value`.
"""
function constant(value; kwargs...)
if isa(value, PyObject)
return value
end
if isa(value, Char)
value = string(value)
end
kwargs = jlargs(kwargs)
if !(:dtype in keys(kwargs))
kwargs[:dtype] = DTYPE[eltype(value)]
end
tf.constant(value; kwargs...)
end
"""
Variable(initial_value;kwargs...)
Constructs a trainable tensor from `value`.
"""
function Variable(initial_value;kwargs...)
kwargs = jlargs(kwargs)
if !(:dtype in keys(kwargs))
kwargs[:dtype] = DTYPE[eltype(initial_value)]
end
tf.Variable(initial_value; kwargs...)
end
"""
cell(arr::Array, args...;kwargs...)
Construct a cell tensor.
# Example
```julia-REPL
julia> r = cell([[1.],[2.,3.]])
julia> run(sess, r[1])
1-element Array{Float32,1}:
1.0
julia> run(sess, r[2])
2-element Array{Float32,1}:
2.0
3.0
```
"""
function cell(arr::Array, args...;kwargs...)
kwargs = jlargs(kwargs)
if !(:dtype in keys(kwargs))
kwargs[:dtype] = DTYPE[eltype(arr[1])]
end
tf.ragged.constant(arr, args...;kwargs...)
end
"""
copy(o::PyObject)
Creates a tensor that has the same value that is currently stored in a variable.
!!! note
The output is a graph node that will have that value when evaluated. Any time you evaluate it, it will grab the current value of `o`.
"""
function Base.:copy(o::PyObject)
return tf.identity(o)
end
function get_variable(name::String; kwargs...)
kwargs = jlargs(kwargs)
tf.compat.v1.get_variable(name;kwargs...)
end
"""
get_variable(o::Union{PyObject, Bool, Array{<:Number}};
name::Union{String, Missing} = missing,
scope::String = "")
Creates a new variable with initial value `o`. If `name` exists, `get_variable` returns the variable instead of create a new one.
"""
function get_variable(o::Union{PyObject, Bool, Number, Array{<:Number}};
name::Union{String, Missing} = missing,
scope::String = "")
local v
o = constant(o)
if ismissing(name)
name = "unnamed_"*randstring(10)
end
variable_scope(scope) do
v = tf.compat.v1.get_variable(name = name, initializer=o, dtype=DTYPE[get_dtype(o)])
end
return v
end
"""
get_variable(dtype::Type;
shape::Union{Array{<:Integer}, NTuple{N, <:Integer}},
name::Union{Missing,String} = missing
scope::String = "")
Creates a new variable with initial value `o`. If `name` exists, `get_variable` returns the variable instead of create a new one.
"""
function get_variable(dtype::Type;
shape::Union{Array{<:Integer}, NTuple{N, <:Integer}},
name::Union{Missing,String} = missing,
scope::String = "") where N
local v
dtype = DTYPE[dtype]
if ismissing(name)
name = "unnamed_"*randstring(10)
end
variable_scope(scope) do
v = tf.compat.v1.get_variable(name = name, shape=shape, dtype = dtype)
end
return v
end
get_variable(dtype::Type,
shape::Union{Array{<:Integer}, NTuple{N, <:Integer}},
name::Union{Missing,String} = missing,
scope::String = "") where N = get_variable(dtype, shape=shape, name=name, scope = scope)
"""
placeholder(dtype::Type; kwargs...)
Creates a placeholder of the type `dtype`.
# Example
```julia
a = placeholder(Float64, shape=[20,10])
b = placeholder(Float64, shape=[]) # a scalar
c = placeholder(Float64, shape=[nothing]) # a vector
```
"""
function placeholder(dtype::Type; kwargs...)
dtype = DTYPE[dtype]
kwargs = Dict{Any,Any}(kwargs)
if !(:shape in keys(kwargs))
kwargs[:shape] = []
end
tf.compat.v1.placeholder(dtype;kwargs...)
end
"""
placeholder(o::Union{Number, Array, PyObject}; kwargs...)
Creates a placeholder of the same type and size as `o`. `o` is the default value.
"""
function placeholder(o::Union{Number, Array, PyObject}; kwargs...)
o = convert_to_tensor(o; kwargs...)
tf.compat.v1.placeholder_with_default(o, shape=size(o))
end
function variable_scope(f, name_or_scope; reuse=AUTO_REUSE, kwargs...)
@pywith tf.variable_scope(name_or_scope;reuse = reuse, kwargs...) begin
f()
end
end
function set_shape(o::PyObject, shape)
o.set_shape(shape)
o
end
function get_dtype(o::PyObject)
for (k,v) in DTYPE
if occursin(string(v),string(o.dtype))
return k
end
end
return nothing
end
Base.:eltype(o::PyObject) = get_dtype(o)
@deprecate get_shape size
get_shape(o::PyObject, i::Union{Int64,Nothing}) = size(o,i)
# compatible with Julia size
function PyCall.:size(o::PyObject, i::Union{Int64, Nothing}=nothing)
d = o.shape.dims
if d===nothing
return nothing
end
if length(d)==0
if i!=nothing
return 1
else
return ()
end
else
s = o.get_shape().as_list()
s = [isnothing(x) ? x : Int64(x) for x in s]
if i==nothing
return Tuple(s)
elseif 0<i<=length(s)
return s[i]
else
return 1
end
end
end
function PyCall.:length(o::PyObject)
# If `o.shape.dims` is invalid, it is not a TensorFlow object.
if !hasproperty(o, :graph)
return PyCall.@pycheckz ccall((PyCall.@pysym :PySequence_Size), Int, (PyCall.PyPtr,), o)
end
if any(isnothing.(size(o)))
return nothing
else
return prod(size(o))
end
end
function Base.:ndims(o::PyObject)
return length(size(o))
end
@doc raw"""
gradients(ys::PyObject, xs::PyObject; kwargs...)
Computes the gradients of `ys` w.r.t `xs`.
- If `ys` is a scalar, `gradients` returns the gradients with the same shape as `xs`.
- If `ys` is a vector, `gradients` returns the Jacobian $\frac{\partial y}{\partial x}$
!!! note
The second usage is not suggested since `ADCME` adopts reverse mode automatic differentiation.
Although in the case `ys` is a vector and `xs` is a scalar, `gradients` cleverly uses forward mode automatic differentiation,
it requires that the second order gradients are implemented for relevant operators.
"""
function gradients(ys::PyObject, xs::PyObject; kwargs...)
s1 = size(ys)
s2 = size(xs)
kwargs = jlargs(kwargs)
if isnothing(s1) && isnothing(s2)
error("s1, s2 should be rank 0, 1, 2")
end
if length(s1)==0
ret = tf.gradients(ys, xs; kwargs...)
if !isnothing(ret) && !isnothing(ret[1])
return tf.convert_to_tensor(ret[1])
else
return nothing
end
elseif length(s1)==1 && length(s2)==0
return gradients10(ys, xs; kwargs...)
elseif length(s1)==1 && length(s2)==1
return gradients11(ys, xs)
elseif length(s1)==2 && length(s2)==0
grad = gradients(vec(ys), xs; kwargs...)
reshape(grad, s1...)
else
error("gradients: Invalid argument")
end
end
function gradients(ys::PyObject, xs::Array{T}; kwargs...) where T <: Union{Any, PyObject}
zs = Array{PyObject}(undef, length(xs))
for i = 1:length(zs)
zs[i] = gradients(ys, xs[i]; kwargs...)
end
zs
end
function gradients(ys::Array{T}, xs::PyObject; kwargs...) where T <: Union{Any, PyObject}
zs = Array{PyObject}(undef, length(ys))
for i = 1:length(ys)
zs[i] = gradients(ys[i], xs; kwargs...)
end
zs
end
function gradients10(ys::PyObject, xs::PyObject; kwargs...)
kwargs = jlargs(kwargs)
try
u = Variable(rand(length(ys)), trainable=false)
g = tf.gradients(ys, xs, grad_ys=u; kwargs...)
g==nothing && (return nothing)
r = tf.gradients(g[1], u; unconnected_gradients="zero", kwargs...)[1]
catch
gradients_v(ys, xs; kwargs...)
end
end
function gradients_v(ys::PyObject, xs::PyObject;kwargs...)
kwargs = jlargs(kwargs)
if length(size(ys))!=1
error("ys should be a n dimensional vector function")
end
if length(size(xs))!=0
error("xs should be a scalar")
end
n = length(ys)
function condition(i, ta)
i<=n
end
function body(i,ta)
ta = write(ta, i, tf.gradients(ys[i], xs, unconnected_gradients="zero", kwargs...)[1])
i+1, ta
end
ta = TensorArray(n)
i = constant(1, dtype=Int32)
_, ta = while_loop(condition, body, [i,ta], parallel_iterations=10)
out = stack(ta)
end
# https://stackoverflow.com/questions/50244270/computing-jacobian-matrix-in-tensorflow
function gradients11(ys::PyObject, xs::PyObject; kwargs...)
n = size(ys,1)
function condition(i, ta)
i <= n
end
function body(i, ta)
ta = write(ta, i, tf.convert_to_tensor(gradients(ys[i], xs; unconnected_gradients="zero")))
i+1, ta
end
ta = TensorArray(n)
i = constant(1, dtype=Int32)
_, ta = while_loop(condition, body, [i,ta],parallel_iterations=10)
stack(ta)
end
"""
gradients_colocate(loss::PyObject, xs::Union{PyObject, Array{PyObject}}, args...;use_locking::Bool = true, kwargs...)
Computes the gradients of a **scalar** loss function `loss` with respect to `xs`. The gradients are colocated with respect to the forward pass.
This function is usually in distributed computing.
"""
function gradients_colocate(loss::PyObject, xs::Union{PyObject, Array{PyObject}}, args...;use_locking::Bool = true, kwargs...)
flag = false
if isa(xs, PyObject)
xs = [xs]
flag = true
end
opt = tf.train.Optimizer(use_locking, "default_optimizer_"*randstring(8))
grads_and_vars = opt.compute_gradients(
loss, var_list=xs,
colocate_gradients_with_ops=true)
grads = [x[1] for x in grads_and_vars]
flag && (grads = grads[1])
return grads
end
@doc raw"""
jacobian(y::PyObject, x::PyObject)
Computes the Jacobian matrix
$$J_{ij} = \frac{\partial y_i}{\partial x_j}$$
"""
function jacobian(y::PyObject, x::PyObject)
@assert length(size(y))==1
@assert length(size(x))==1
tfj = pyimport("tensorflow.python.ops.parallel_for.gradients")
tfj.jacobian(y, x)
end
function hessian_vector(f, xs, v; kwargs...)
kwargs = jlargs(kwargs)
gradients_impl = pyimport("tensorflow.python.ops.gradients_impl")
gradients_impl._hessian_vector_product(f, [xs], [v]; kwargs...)[1]
end
@doc raw"""
hessian(ys::PyObject, xs::PyObject; kwargs...)
`hessian` computes the hessian of a scalar function f with respect to vector inputs xs.
# Example
```julia
x = constant(rand(10))
y = 0.5 * sum(x^2)
o = hessian(y, x)
sess = Session(); init(sess)
run(sess, o) # should be an identity matrix
```
"""
function hessian(ys::PyObject, xs::PyObject; kwargs...)
if length(size(ys))==0 && length(size(xs))==1
return tf.hessians(ys, xs)[1]
end
kwargs = jlargs(kwargs)
s1 = size(ys)
s2 = size(xs)
if s1==nothing || s2 == nothing || (length(s1)!=0 && length(s2)!=1)
error("Invalid input arguments")
end
h = tf.gradients(ys, xs; kwargs...)
if h==nothing
return nothing
else
h = h[1]
end
vs = Array{PyObject}(undef, s2[1])
for i = 1:s2[1]
# verbose && (@info "_hessian... $i/$(s2[1])")
vs[i] = gradients(get(h,i-1), xs)
if isnothing(vs[i])
vs[i] = constant(zeros(get_dtype(ys), s2[1]))
end
end
stack(vs, dims=1)
end
# initializers
constant_initializer(args...;kwargs...) = tf.constant_initializer(args...;kwargs...)
glorot_normal_initializer(args...;kwargs...) = tf.glorot_normal_initializer(args...;kwargs...)
glorot_uniform_initializer(args...;kwargs...) = tf.glorot_uniform_initializer(args...;kwargs...)
random_normal_initializer(args...;kwargs...) = tf.random_normal_initializer(args...;kwargs...)
random_uniform_initializer(args...;kwargs...) = tf.random_uniform_initializer(args...;kwargs...)
truncated_normal_initializer(args...;kwargs...) = tf.truncated_normal_initializer(args...;kwargs...)
uniform_unit_scaling_initializer(args...;kwargs...) = tf.uniform_unit_scaling_initializer(args...;kwargs...)
variance_scaling_initializer(args...;kwargs...) = tf.uniform_unit_scaling_initializer(args...;kwargs...)
#--------------------------------------------------------------------------------------------------------
# Indexing
function PyCall.:lastindex(o::PyObject)
return size(o,1)
end
function PyCall.:lastindex(o::PyObject, i::Int64)
return size(o,i)
end
# rank 1 tensor
function getindex(o::PyObject, r::Union{Colon, Array{Bool,1}, BitArray{1}, Array{Int64,1},UnitRange{Int64}, StepRange{Int64, Int64}})
if typeof(r)==Colon
return vec(o)
elseif typeof(r)==Array{Bool,1} || typeof(r)==BitArray{1}
return getindex(o, findall(r))
elseif typeof(r)==UnitRange{Int64} || typeof(r)==StepRange{Int64, Int64}
return getindex(o, collect(r))
elseif typeof(r)==Array{Int64,1}
return tf.gather(o, r.-1)
end
end
function getindex(o::PyObject, i::PyObject)
return tf.gather(o, i-1)
end
# rank 2 tensor
# drawback: only access the 1st dimension of a tensor
function getindex(o::PyObject, i1::Union{Int64, Colon, Array{Bool,1},BitArray{1}, Array{Int64,1},UnitRange{Int64}, StepRange{Int64, Int64}}, c::Colon)
if typeof(i1)==Colon
return o
elseif typeof(i1)==Array{Bool,1}|| typeof(i1)==BitArray{1}
return getindex(o, findall(i1), c)
elseif typeof(i1)==UnitRange{Int64} || typeof(i1)==StepRange{Int64, Int64}
i1 = (i1|>collect)
end
tf.gather(o, i1.-1)
end
# less efficient
function _to_range_array(o::PyObject,
i::Union{Int64, Colon, Array{Bool,1},BitArray{1}, UnitRange{Int64}, Array{Int64,1}, StepRange{Int64, Int64}},
d::Int64)
if typeof(i)==Int64
return [i]
elseif typeof(i)==Colon
if isnothing(size(o,d))
error(ArgumentError("Dimension $d of `o` is `nothing`. You need to set a concrete dimension, e.g., using `set_shape`"))
end
return collect(1:size(o,d))
elseif typeof(i)<:StepRange || typeof(i)<:UnitRange
return collect(i)
elseif typeof(i)==Array{Bool,1}|| typeof(i)==BitArray{1}
return findall(i)
else
return i
end
end
function getindex(o::PyObject, i1::Union{Int64, Colon, Array{Bool,1},BitArray{1}, Array{Int64,1},UnitRange{Int64}, StepRange{Int64, Int64}},
i2::Union{Int64, Array{Bool,1},Array{Int64,1},UnitRange{Int64}, StepRange{Int64, Int64}})
sdim1 = typeof(i1)==Int64
sdim2 = typeof(i2)==Int64
if typeof(i1)==Int64 && typeof(i2)==Int64
return squeeze(tf.strided_slice(o, (i1[1]-1,i2[1]-1),(i1[1],i2[1]),(1,1)), dims=(1,2))
end
i1 = _to_range_array(o, i1, 1)
i2 = _to_range_array(o, i2, 2)
temp = Base.Iterators.product(i2,i1)|>collect
indices = [vec([x[2] for x in temp]) vec([x[1] for x in temp])] .- 1
p = tf.gather_nd(o, indices)
p = tf.reshape(p', (length(i1), length(i2)))
if sdim1
return squeeze(p, dims=1)
elseif sdim2
return squeeze(p, dims=2)
else
return p
end
end
function getindex(o::PyObject, i1, i2, i3)
sdims = Int64[]
if isa(i1, Int64)
push!(sdims, 1)
i1 = i1:i1
end
if isa(i2, Int64)
push!(sdims, 2)
i2 = i2:i2
end
if isa(i3, Int64)
push!(sdims, 3)
i3 = i3:i3
end
res = getindex(o, i1, i2, i3)
squeeze(res, dims=sdims)
end
function getindex(o::PyObject,
i1::Union{Colon, Array{Bool,1},BitArray{1}, Array{Int64,1},UnitRange{Int64}, StepRange{Int64, Int64}},
i2::Union{Colon, Array{Bool,1},BitArray{1}, Array{Int64,1},UnitRange{Int64}, StepRange{Int64, Int64}},
i3::Union{Colon, Array{Bool,1},BitArray{1}, Array{Int64,1},UnitRange{Int64}, StepRange{Int64, Int64}})
if length(size(o))!=3
error(DimensionMismatch("input tensor is $(length(size(o))) dimensional, but expected 3"))
end
i1 = _to_range_array(o, i1, 1)
i2 = _to_range_array(o, i2, 2)
i3 = _to_range_array(o, i3, 3)
idx = Int64[]
for i = 1:length(i1)
for j = 1:length(i2)
for k = 1:length(i3)
ii = i3[k] + (i2[j]-1)*size(o,3) + (i1[i]-1)*size(o,2)*size(o,3)
push!(idx, ii)
end
end
end
p = reshape(o, (-1,))[idx]
reshape(p, (length(i1), length(i2), length(i3)))
end
function Base.:getindex(o::PyObject, i::PyObject, j::Union{Int64, Colon, Array{Bool,1},BitArray{1}, Array{Int64,1},UnitRange{Int64}, StepRange{Int64, Int64}})
flag = false
if isa(j, Colon)
return o[i]
end
if length(size(i))!=0 || !(get_dtype(i)<:Integer)
error(ArgumentError("Only integer `i` is supported"))
end
if isnothing(size(o,2))
error(ArgumentError("Dimension 2 of `o` is `nothing`. You need to set a concrete dimension, e.g., using `set_shape`"))
end
if isa(j, Integer)
flag = true
end
j = _to_range_array(o, j, 2)
idx = (i-1)*size(o,2) + j
ret = tf.reshape(o, (-1,))[idx]
if flag
return get(ret, 0)
else
return ret
end
end
function Base.:getindex(o::PyObject, i::Union{Int64, Colon, Array{Bool,1},BitArray{1}, Array{Int64,1},UnitRange{Int64}, StepRange{Int64, Int64}}, j::PyObject)
flag = false
if length(size(j))!=0 || !(get_dtype(j)<:Integer)
error(ArgumentError("Only integer `j` is supported"))
end
if isnothing(size(o,2))
error(ArgumentError("Dimension 2 of `o` is `nothing`. You need to set a concrete dimension, e.g., using `set_shape`"))
end
if isa(i, Integer)
flag = true
end
i = _to_range_array(o, i, 1)
idx = (i .- 1)*size(o,2) + j
ret = tf.reshape(o, (-1,))[idx]
if flag
return get(ret, 0)
else
return ret
end
end
#-------------------------------------------------------------------------------------------------------
# https://stackoverflow.com/questions/46718356/tensorflow-symmetric-matrix
function sym(o::Union{Array{<:Real}, PyObject})
convert_to_tensor(1/2 * (o + o'))
end
function spd(o::Union{Array{<:Real}, PyObject})
if length(size(o))!=2 || size(o,1)!=size(o,2)
error("Input `o` must be a square matrix")
end
convert_to_tensor(o * o')
end
"""
tensor(v::Array{T,2}; dtype=Float64, sparse=false) where T
"""
function tensor(v::Array{T,1}; dtype=Float64, sparse=false) where T
local ret
N = length(v)
ret = Variable(zeros(dtype, N), trainable=false)
for i = 1:N
if sparse && isa(v[i], Number) && v[i]≈0
continue
end
if isa(v[i], Number)
v[i] = dtype(v[i])
end
ret = scatter_add(ret, i, v[i])
end
ret
end
"""
tensor(v::Array{T,2}; dtype=Float64, sparse=false) where T
Convert a generic array `v` to a tensor. For example,
```julia
v = [0.0 constant(1.0) 2.0
constant(2.0) 0.0 1.0]
u = tensor(v)
```
`u` will be a ``2\\times 3`` tensor.
!!! note
This function is expensive. Use with caution.
"""
function tensor(v::Array{T,2}; dtype=Float64, sparse=false) where T
local ret
M, N = size(v)
ret = Variable(zeros(dtype, M, N), trainable=false)
for i = 1:M
for j = 1:N
if sparse && isa(v[i,j], Number) && v[i,j]≈0
continue
end
if isa(v[i,j], Number)
v[i,j] = dtype(v[i,j])
end
ret = scatter_add(ret, i, j, v[i, j])
end
end
ret
end
"""
TensorArray(size_::Int64=0, args...;kwargs...)
Constructs a tensor array for [`while_loop`](@ref).
"""
function TensorArray(size_::Int64=0, args...;kwargs...)
kwargs = jlargs(kwargs)
if !(haskey(kwargs, :dtype))
kwargs[:dtype] = tf.float64
end
if !haskey(kwargs, :dynamic_size)
kwargs[:dynamic_size] = false
end
if !haskey(kwargs, :clear_after_read)
kwargs[:clear_after_read] = false
end
kwargs[:size] = size_
tf.TensorArray(args...;kwargs...)
end
"""
read(ta::PyObject, i::Union{PyObject,Integer})
Reads data from [`TensorArray`](@ref) at index `i`.
"""
function Base.:read(ta::PyObject, i::Union{PyObject,Integer})
ta.read(i-1)
end
"""
write(ta::PyObject, i::Union{PyObject,Integer}, obj)
Writes data `obj` to [`TensorArray`](@ref) at index `i`.
"""
function Base.:write(ta::PyObject, i::Union{PyObject,Integer}, obj::PyObject)
ta.write(i-1, obj)
end
Base.:write(ta::PyObject, i::Union{PyObject,Integer}, obj::Union{Array{<:Real}, Real}) = write(ta, i, constant(obj))
"""
convert_to_tensor(o::Union{PyObject, Number, Array{T}, Missing, Nothing}; dtype::Union{Type, Missing}=missing) where T<:Number
convert_to_tensor(os::Array, dtypes::Array)
Converts the input `o` to tensor. If `o` is already a tensor and `dtype` (if provided) is the same as that of `o`, the operator does nothing.
Otherwise, `convert_to_tensor` converts the numerical array to a constant tensor or casts the data type.
`convert_to_tensor` also accepts multiple tensors.
# Example
```julia
convert_to_tensor([1.0, constant(rand(2)), rand(10)], [Float32, Float64, Float32])
```
"""
function convert_to_tensor(o::Union{PyObject, Number, Array{T}, Missing, Nothing};
dtype::Union{Type, Missing}=missing) where T<:Number
if ismissing(o) || isnothing(o)
return o
end
if isa(o, PyObject)
if ismissing(dtype) || dtype==eltype(o)
return o
else
return cast(o, dtype)
end
else
if !ismissing(dtype)
return constant(o, dtype=dtype)
else
return constant(o)
end
end
end
function convert_to_tensor(os::Array, dtypes::Array)
[convert_to_tensor(o, dtype=d) for (o, d) in zip(os, dtypes)]
end
"""
gradient_checkpointing(type::String="speed")
Uses checkpointing scheme for gradients.
- 'speed': checkpoint all outputs of convolutions and matmuls. these ops are usually the most expensive,
so checkpointing them maximizes the running speed
(this is a good option if nonlinearities, concats, batchnorms, etc are taking up a lot of memory)
- 'memory': try to minimize the memory usage
(currently using a very simple strategy that identifies a number of bottleneck tensors in the graph to checkpoint)
- 'collection': look for a tensorflow collection named 'checkpoints', which holds the tensors to checkpoint
"""
function gradient_checkpointing(type::String="speed")
pyfile = "$(ADCME.LIBDIR)/memory_saving_gradients.py"
if !isfile(pyfile)
@info "Downloading memory_saving_gradients.py..."
download("https://raw.githubusercontent.com/cybertronai/gradient-checkpointing/master/memory_saving_gradients.py",
pyfile)
end
py"""exec(open($pyfile).read())"""
gradients_speed = py"gradients_speed"
gradients_memory = py"gradients_memory"
gradients_collection = py"gradients_collection"
if type=="speed"
tf.__dict__["gradients"] = gradients_speed
elseif type=="memory"
tf.__dict__["gradients"] = gradients_memory
elseif type=="collection"
tf.__dict__["gradients"] = gradients_collection
else
error("ADCME: $type not defined")
end
@info "Loaded: $type"
end
@doc raw"""
gradient_magnitude(l::PyObject, o::Union{Array, PyObject})
Returns the gradient sum
$$\sqrt{\sum_{i=1}^n \|\frac{\partial l}{\partial o_i}\|^2}$$
This function is useful for debugging the training
"""
function gradient_magnitude(l::PyObject, o::Union{Array, PyObject})
if isa(o, PyObject)
o = [o]
end
tf.global_norm(gradients(l, o))
end
"""
zeros_like(o::Union{PyObject,Real, Array{<:Real}}, args...; kwargs...)
Returns a all-zero tensor, which has the same size as `o`.
# Example
```julia
a = rand(100,10)
b = zeros_like(a)
@assert run(sess, b)≈zeros(100,10)
```
"""
function zeros_like(o::Union{PyObject,Real, Array{<:Real}}, args...; kwargs...)
kwargs = jlargs(kwargs)
tf.zeros_like(o, args...;kwargs...)
end
"""
ones_like(o::Union{PyObject,Real, Array{<:Real}}, args...; kwargs...)
Returns a all-one tensor, which has the same size as `o`.
# Example
```julia
a = rand(100,10)
b = ones_like(a)
@assert run(sess, b)≈ones(100,10)
```
"""
function ones_like(o::Union{PyObject,Real, Array{<:Real}}, args...; kwargs...)
kwargs = jlargs(kwargs)
tf.ones_like(o, args...;kwargs...)
end
"""
is_variable(o::PyObject)
Determines whether `o` is a trainable variable.
"""
function is_variable(o::PyObject)
hasproperty(o, :trainable) && o.trainable
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 4201 | reset_default_graph(); sess = Session()
# not testable
# # this must be the test
# @testset "Eager evaluation" begin
# reset_default_graph()
# sess = Session()
# enable_eager_execution()
# g = rand(10,10)
# o = Variable(g)
# @test value(o) ≈ g
# end
@testset "control_dependency" begin
a = Variable(ones(10))
b = Variable(ones(10))
for i = 1:10
control_dependencies(a) do
a = scatter_add(a, i, b[i])
end
end
a_ = constant(0.0)
b_ = Variable(0.0)
op = assign(b_, 2.0)
a_ = a_ + 1.0
a_ = bind(a_, op)
init(sess)
run(sess, a_)
@test run(sess, a)≈ones(10)*2
@test run(sess, b_)≈2.0
a = Variable(ones(10))
b = Variable(ones(10))
for i = 1:10
control_dependencies(a) do
a = scatter_add(a, i, b[i])
end
end
a_ = spdiag(ones(10))
b_ = Variable(0.0)
op = assign(b_, 2.0)
a_ = a_*2
a_ = bind(a_, op)
init(sess)
run(sess, a_)
@test run(sess, a)≈ones(10)*2
@test run(sess, b_)≈2.0
end
@testset "while loop" begin
a = constant(rand(10))
condition = (i, var)->tf.less(i,11)
function body(i, var)
var = tf.cond(tf.equal(i, 1),
()->write(var, i, a),
()->write(var, i, 2*read(var, i-1))
)
i+1, var
end
i = constant(1, dtype=Int32)
ta = TensorArray(10)
out_i, out_ta = tf.while_loop(condition, body, [i,ta])
ts = read(out_ta, 10)
sum_ts = sum(ts)
grd = gradients(sum_ts, a)
@test run(sess, grd)≈512*ones(10)
ta = TensorArray(10)
a = constant(1.0)
ta = write(ta, 1, a)
ta = write(ta, 2, read(ta,1)+a) # 2a
ta = write(ta, 3, read(ta,2)+a) # 3a
ta = write(ta, 4, read(ta,2)+read(ta,3)+a) # 6a
g = gradients(read(ta, 4), a)
@test run(sess, g)≈6
ta = TensorArray(9)
function condition(i, ta)
tf.less(i, 10)
end
ta = write(ta, 1, constant(1.0))
ta = write(ta, 2, constant(1.0))
function body(i, ta)
ta = write(ta, i, 2*read(ta,i-1)+read(ta,i-2)+a)
i+1, ta
end
i = constant(3, dtype=Int32)
_, ta_out = while_loop(condition, body, [i,ta])
g = gradients(read(ta_out,9),a)
@test run(sess, g)≈288
end
@testset "if_clause" begin
a = constant(2.0)
b = constant(1.0)
c = constant(0.0)
bb = b*2
cc = c + 3.0
res = if_else(a>1.0, bb, cc)
@test run(sess, res)≈2.0
end
@testset "if_else: tf.where" begin
condition = [true true false false
true true true true]
a = [1 1 1 1
1 1 1 1]
b = [2 2 2 2
2 2 2 2]
res = if_else(condition, a, b)
@test run(sess, res)≈[1 1 2 2
1 1 1 1]
res1 = if_else(condition[1,:], a[1,:], b[1,:])
@test run(sess, res1)≈[1;1;2;2]
end
@testset "get and add collection" begin
a = Variable(ones(10), name="my_collect1")
b = 2a
@test get_collection("my_collect")==[a]
end
@testset "has_gpu" begin
@test has_gpu() in [true, false]
@test isnothing(gpu_info())
@test isa(get_gpu(), NamedTuple)
end
@testset "timeline" begin
a = normal(2000, 5000)
b = normal(5000, 1000)
res = a*b
run_profile(sess, res)
save_profile("test.json")
rm("test.json")
end
@testset "independent" begin
x = constant(rand(10))
y = 2*x
z = sum(independent(y))
@test isnothing(gradients(z, x))
end
@testset "run corner cases" begin
pl = placeholder(0.1)
@test run(sess, pl, pl=>4.0) ≈ 4.0
end
@testset "@cpu @gpu" begin
@cpu 2 begin
global a = constant(rand(10,10))
end
@gpu 2 begin
global b = constant(rand(10,10))
end
@test a.device == "/device:CPU:2"
@test b.device == "/device:GPU:2"
@cpu begin
global a = constant(rand(10,10))
end
@gpu begin
global b = constant(rand(10,10))
end
@test a.device == "/device:CPU:0"
@test b.device == "/device:GPU:0"
end
@testset "mpi utils" begin
@test_nowarn has_mpi()
try
get_mpi()
catch
@test true
end
try
get_mpirun()
catch
@test true
end
end
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 685 | reset_default_graph(); sess = Session()
@testset "customop" begin
if isdir("temp")
rm("temp", force=true, recursive=true)
end
mkdir("temp")
cd("temp")
customop()
customop()
customop(;julia=true)
cp("$(@__DIR__)/../examples/while_loop/DirichletBD/DirichletBD.cpp", "DirichletBD.cpp", force=true)
cp("$(@__DIR__)/../examples/while_loop/DirichletBD/DirichletBD.h", "DirichletBD.h", force=true)
cp("$(@__DIR__)/../examples/while_loop/DirichletBD/CMakeLists.txt", "CMakeLists.txt", force=true)
mkdir("build")
cd("build")
ADCME.cmake()
ADCME.make()
cd("..")
rm("temp", force=true, recursive=true)
@test true
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 1705 | reset_default_graph(); sess = Session()
@testset "xavier_init" begin
@test_nowarn a = xavier_init([100,10], Float32)
end
@testset "load_op" begin
@test_nowarn load_op(ADCME.LIBADCME, "sparse_solver")
@test_nowarn load_op_and_grad(ADCME.LIBADCME, "sparse_solver")
end
@testset "ae" begin
n = ae_num([2,20,20,20,3])
@test n==length(ae_init([2,20,20,20,3]))
end
@testset "register" begin
forward = x->log(1+exp(x))
backward = (dy, y, x)->dy*(1-1/(1+y))
f = register(forward, backward)
x_ = rand(10)
x = constant(x_)
@test run(sess, f(x)) ≈ @. log(1+exp(x_))
@test_nowarn run(sess,gradients(sum(f(x)), x))
ADCME.options.newton_raphson.verbose = true
function forward2(x, θ)
f = (θ, y)->(y^3+1.0-θ -x, spdiag(3y^2))
nr = newton_raphson(f, constant(ones(length(x))), θ)
y = nr.x
return y
end
function backward2(dy, y, x, θ)
e = 1/3*(θ+x-1)^(-2/3)
e, e
end
f2 = register(forward2, backward2)
θ = constant(ones(5))
x = constant(8ones(5))
y = f2(x, θ)
@test run(sess, y)≈ones(5)*2
@test run(sess, gradients(sum(y), θ))≈0.08333333333333333*ones(5)
end
@testset "list_physical_devices" begin
devices = list_physical_devices()
@test length(devices)>0
end
@testset "timestamp" begin
@test begin
a = constant(1.0)
t0 = timestamp(a)
sleep_time = sleep_for(a)
t1 = timestamp(sleep_time)
sess = Session(); init(sess)
t0_, t1_ = run(sess, [t0, t1])
time = t1_ - t0_
true
end
end
@testset "get_library_symbols" begin
@test length(get_library_symbols(ADCME.libadcme))>0
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 3061 | reset_default_graph(); sess = Session()
function test_flow(sess, flows, dim)
prior = ADCME.MultivariateNormalDiag(loc=zeros(dim))
model = NormalizingFlowModel(prior, flows)
x = rand(3, dim)
z, _, J = model(x)
xs, iJ = ADCME.backward(model, z[end])
init(sess)
x_, J_, iJ_ = run(sess, [xs[end], J, iJ])
x, x_, J_, iJ_
end
@testset "LinearFlow" begin
dim = 3
flows = [LinearFlow(dim)]
x1, x2, j1, j2 = test_flow(sess, flows, dim)
@test x1≈x2
@test j1≈-j2
end
@testset "AffineConstantFlow" begin
dim = 3
flows = [AffineConstantFlow(dim)]
x1, x2, j1, j2 = test_flow(sess, flows, dim)
@test x1≈x2
@test j1≈-j2
end
@testset "ActNorm" begin
dim = 3
flows = [ActNorm(dim)]
x1, x2, j1, j2 = test_flow(sess, flows, dim)
@test x1≈x2
@test j1≈-j2
end
@testset "SlowMAF" begin
dim = 3
flows = [SlowMAF(dim, false, [x->fc(x, [20,20,2], "fc1"); x->fc(x,[20,20,2],"fc2")])]
x1, x2, j1, j2 = test_flow(sess, flows, dim)
@test x1≈x2
@test j1≈-j2
end
@testset "MAF" begin
dim = 3
flows = [MAF(dim, false, [20,20,20])]
x1, x2, j1, j2 = test_flow(sess, flows, dim)
@test x1≈x2
@test j1≈-j2
end
@testset "IAF" begin
dim = 3
flows = [IAF(dim, false, [20,20,20])]
x1, x2, j1, j2 = test_flow(sess, flows, dim)
@test x1≈x2
@test j1≈-j2
end
@testset "Invertible1x1Conv" begin
dim = 3
flows = [Invertible1x1Conv(dim)]
x1, x2, j1, j2 = test_flow(sess, flows, dim)
@test x1≈x2
@test j1≈-j2
end
@testset "AffineHalfFlow" begin
dim = 3
flows = [AffineHalfFlow(dim, true)]
x1, x2, j1, j2 = test_flow(sess, flows, dim)
@test x1≈x2
@test j1≈-j2
end
@testset "NeuralCouplingFlow" begin
@test_skip begin
dim = 6
K = 8
n = dim÷2
flows = [NeuralCouplingFlow(dim, x->fc(x, [20,20,n*(3K-1)], "ncf1"), x->fc(x,[20,20,n*(3K-1)],"ncf2"), K)]
x1, x2, j1, j2 = test_flow(sess, flows, dim)
@test x1≈x2
@test j1≈-j2
end
end
@testset "Permute" begin
dim = 6
flows = [Permute(dim, randperm(6) .- 1)]
x1, x2, j1, j2 = test_flow(sess, flows, dim)
@test x1≈x2
@test j1≈-j2
end
@testset "composite" begin
function create_linear_transform(dim)
permutation = randperm(dim) .- 1
flow = [Permute(dim, permutation);LinearFlow(dim)]
end
dim = 5
flows = create_linear_transform(dim)
x1, x2, j1, j2 = test_flow(sess, flows, dim)
@test x1≈x2
@test j1≈-j2
end
# @testset "composite 2" begin
# function create_base_transform(dim, K=8)
# n1 = dim÷2
# n2 = dim - n1
# r1 = x->Resnet1D(n1 * (3K-1), 256, dropout_probability=0.0, use_batch_norm=false)(x)
# r2 = x->Resnet1D(n2 * (3K-1), 256, dropout_probability=0.0, use_batch_norm=false)(x)
# NeuralCouplingFlow(dim, r1, r2)
# end
# dim = 6
# flows = [create_base_transform(dim)]
# x1, x2, j1, j2 = test_flow(sess, flows, dim)
# @test x1≈x2
# @test j1≈-j2
# end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 881 | @testset "save and load" begin
a = Variable(1.0)
b = Variable(2.0)
init(sess)
save(sess, "temp.mat", [a,b])
op1 = assign(a, 3.0)
op2 = assign(b, 3.0)
run(sess, op1)
run(sess, op2)
sess1 = Session()
load(sess1, "temp.mat", [a,b])
@test run(sess1, [a,b])≈[1.0;2.0]
rm("temp.mat", force=true)
end
@testset "psave and pload" begin
py"""
def psave_test_function(x):
return x+1
"""
a = py"psave_test_function"
psave(a, "temp.pkl")
b = pload("temp.pkl")
@test b(2)==3
rm("temp.pkl", force=true)
end
@testset "diary" begin
d = Diary("test")
b = constant(1.0)
a = scalar(b)
for i = 1:100
write(d, i, run(sess, a))
end
# activate(d)
save(d, "mydiary")
e = Diary("test2")
load(e, "mydiary")
# activate(e)
try;rm("mydiary", recursive=true, force=true);catch;end
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 1841 | reset_default_graph(); sess = Session()
@testset "test_jacobian" begin
function f(x)
x.^3, 3*diagm(0=>x.^2)
end
err1, err2 = test_jacobian(f, rand(10))
@test err2[end] < err1[end]
end
@testset "lineview" begin
@test begin
a = placeholder(rand(10))
loss = sum((a+1)^2)
close("all")
lineview(sess, a, loss, -ones(10))
savefig("lineview.png")
true
end
end
@testset "meshview" begin
@test begin
a = placeholder(rand(10))
loss = sum((a+1)^2)
close("all")
meshview(sess, a, loss, -ones(10))
savefig("meshview.png")
true
end
@test begin
a = placeholder(rand(10))
loss = sum((a+1)^2)
close("all")
pcolormeshview(sess, a, loss, -ones(10))
savefig("pcolormeshview.png")
true
end
end
@testset "gradview" begin
@test begin
a = placeholder(rand(10))
loss = sum((a+1.0)^2)
close("all")
gradview(sess, a, loss, rand(10))
true
end
end
@testset "jacview" begin
@test begin
u0 = rand(10)
function verify_jacobian_f(θ, u)
r = u^3+u - u0
r, spdiag(3u^2+1.0)
end
close("all")
jacview(sess, verify_jacobian_f, missing, u0)
savefig("jacview.png")
true
end
end
@testset "PCLview" begin
end
@testset "animate" begin
@test begin
θ = LinRange(0, 2π, 100)
x = cos.(θ)
y = sin.(θ)
pl, = plot([], [], "o-")
t = title("0")
xlim(-1.2,1.2)
ylim(-1.2,1.2)
function update(i)
t.set_text("$i")
pl.set_data([x[1:i] y[1:i]]'|>Array)
end
p = animate(update, 1:100)
saveanim(p, "anim.gif")
true
end
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 928 | reset_default_graph(); sess = Session()
@testset "indexing for rank 3 tensors" begin
a = rand(100,10,20)
i1 = 3:8
i2 = [1;3;4]
V = a[i1,i2,:]
P = constant(a)[i1,i2,:]
@test run(sess, P)≈V
P = constant(a)[2,i2,:]
@test run(sess, P)≈a[2,i2,:]
P = constant(a)[2,i2,5]
@test run(sess, P)≈a[2,i2,5]
end
@testset "fcx" begin
config = [2, 20,20,20,3]
x = constant(rand(10,2))
θ = ae_init(config)
u, du = fcx(x, config[2:end], θ)
y = ae(x, config[2:end], θ)
@test run(sess, u) ≈ run(sess, y)
DU = run(sess, du)
@test run(sess, tf.gradients(y[:,1], x)[1]) ≈ DU[:,1,:]
@test run(sess, tf.gradients(y[:,2], x)[1]) ≈ DU[:,2,:]
@test run(sess, tf.gradients(y[:,3], x)[1]) ≈ DU[:,3,:]
end
@testset "dropout" begin
a = rand(10,2)
@test sum(run(sess, dropout(a, 0.999, true)).==0)/20>0.9
@test sum(run(sess, dropout(a, 0.999, false)).==0)==0
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 1179 | @testset "poisson" begin
n = 20
h = 1/n
node = zeros((n+1)^2, 2)
node_mid = zeros(2n^2,2)
elem = zeros(Int32, 2n^2, 3)
k = 1
for i = 1:n
for j = 1:n
node[i+(j-1)*(n+1), :] = [(i-1)*h;(j-1)*h]
node[i+1+(j-1)*(n+1), :] = [i*h;(j-1)*h]
node[i+(j)*(n+1), :] = [(i-1)*h;(j)*h]
node[i+1+(j)*(n+1), :] = [(i)*h;(j)*h]
elem[k,:] = [i+(j-1)*(n+1) i+1+(j-1)*(n+1) i+(j)*(n+1)];
elem[k+1,:] = [i+1+(j)*(n+1) i+1+(j-1)*(n+1) i+(j)*(n+1)];
node_mid[k, :] = mean(node[elem[k,:], :], dims=1)
node_mid[k+1, :] = mean(node[elem[k+1,:], :], dims=1)
k += 2
end
end
bdnode = Int32[]
for i = 1:n+1
for j = 1:n+1
if i==1 || j == 1 || i==n+1 || j==n+1
push!(bdnode, i+(j-1)*(n+1))
end
end
end
x, y = node_mid[:,1], node_mid[:,2]
f = constant(@. 2y*(1-y)+2x*(1-x))
a = constant(ones(2n^2))
u = pde_poisson(node,elem,bdnode,f,a)
uval = run(sess, u)
x, y = node[:,1], node[:,2]
uexact = @. x*(1-x)*y*(1-y)
@test maximum(abs.(uval - uexact))<1e-3
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 321 | # if Sys.islinux()
# @testset "mpi_SparseTensor" begin
# A = sprand(10,10,0.3)
# B = mpi_SparseTensor(A)
# @test run(sess, B) ≈ A
# B = mpi_SparseTensor(A+5I)
# ADCME.options.mpi.solver = "GMRES"
# g = rand(10)
# @test run(sess, B\g) ≈ (A+5I)\g
# end
# end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 1784 | @testset "newton raphson with linesearch" begin
function f1(θ, u)
return u^2 - 1, 2*spdiag(u)
end
function f2(θ, u)
return u^3-2u-5, spdiag(3u^2-2)
end
function f3(θ, u)
return exp(2u)-u-6, spdiag(2*exp(2u)-1)
end
function f4(θ, u)
return (cos(u)-u)^2, spdiag((-u + cos(u))*(-2*sin(u) - 2))
end
function f5(θ, u)
return sum(1/3*(u-1)^3), (u - 1)^2, 2*spdiag(u-1)
end
function f6(θ, u)
return sum((u-1.3)^2), 2(u-1.3), 2spdiag(length(u))
end
function f7(θ, u)
return sum((0.988 * u^5 - 4.96 * u^4 + 4.978 * u^3 + 5.015 * u^2 - 6.043 * u - 1)),
4.94 * u^4 - 19.84 * u^3 + 14.934 * u^2 + 10.03 * u - 6.043,
spdiag(4.94*3*u^3 - 19.84*3*u^2 + 14.934*2*u + 10.03)
end
function f8(θ, u)
return sum((u-1.3)^2), 2(u-1.3), 2spdiag(length(u))
end
res = [1.0, 2.0946, 0.97085, 0.73989]
nr = Array{Any}(undef, 8)
fs = [f1,f2,f3,f4,f5,f6,f7,f8]
ADCME.options.newton_raphson.linesearch = true
ADCME.options.newton_raphson.verbose = false
ADCME.options.newton_raphson.rtol = 1e-12
ADCME.options.newton_raphson.linesearch_options.αinitial = 1.0
for i = 5:7
nr[i] = newton_raphson(fs[i], constant(rand(1)), missing)
end
reset_default_options()
ADCME.options.newton_raphson.verbose = false
for i = 1:4
nr[i] = newton_raphson(fs[i], constant(rand(1)), missing)
end
sess = Session(); init(sess)
nrr = [run(sess, nr[i]) for i = 1:7]
for i = 1:4
@show nrr[i].x, nrr[i].iter, nrr[i].converged
@test nrr[i].converged
end
for i = 5:7
@show nrr[i].x, nrr[i].iter, nrr[i].converged
@test nrr[i].converged
end
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 1925 | @testset "runge_kutta" begin
function f(t, y, θ)
return y
end
x0 = 1.0
out = rk4(f, 1.0, 100, x0)
@test abs(run(sess, out)[end]-exp(1))<1e-5
out = ode45(f, 1.0, 100, x0)
@test abs(run(sess, out)[end]-exp(1))<1e-5
function f(t, y, θ)
return y
end
x0 = [1.0;1.0]
out = rk4(f, 1.0, 100, x0)
@test norm(run(sess, out)[end,:] .- exp(1))<1e-5
out = ode45(f, 1.0, 100, x0)
@test norm(run(sess, out)[end,:] .- exp(1))<1e-5
x0 = [1.0 1.0
1.0 1.0]
out = rk4(f, 1.0, 100, x0)
@test norm(run(sess, out)[end,:,:] .- exp(1))<1e-5
out = ode45(f, 1.0, 100, x0)
@test norm(run(sess, out)[end,:,:] .- exp(1))<1e-5
end
@testset "alpha scheme" begin
d0 = zeros(2)
v0 = [2.;3.]
a0 = zeros(2)
Δt = 1e-3
n = 9001
Δt = Δt * ones(n)
M = sparse([1.0 0.0;0.0 1.0])
C = sparse(zeros(2,2))
K = sparse([4.0 0.0;0.0 9.0])
F = zeros(n, 2)
d, v, a = αscheme(M, C, K, F, d0, v0, a0, Δt)
d_, v_, a_ = run(sess, [d, v, a])
tspan = 0:1e-3:(n-1)*1e-3
@test norm(d_[1:end-1,1] - sin.(2tspan))<1e-3
@test norm(d_[1:end-1,2] - sin.(3tspan))<1e-3
end
@testset "tr_bdf2" begin
D0 = sparse([1.0 0.0;1.0 1.0])
D1 = sparse([2.0 0.0; 0.0 1.0])
ts = collect(LinRange(0, 1, 100))
Δt = ts[2]-ts[1]
F = zeros(199, 2)
for i = 1:100
t = ts[i]
F[2*i-1, :] = [
t^2 + 5t + 2
t^2 + 2t + 1
]
if i<100
t = t + Δt/2
F[2*i, :] = [
t^2 + 5t + 2
t^2 + 2t + 1
]
end
end
td = TR_BDF2(D0, D1, Δt)
@test td.symbolic == false
u = td(zeros(2), F)
@test abs(u[end, 1]-2.0)<1e-5
@test abs(u[end, 2]-1.0)<1e-5
td = constant(td)
ua = td(zeros(2), F)
@test run(sess, ua)≈u
end
@testset "ExplicitNewmark" begin
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 13380 | @testset "*" begin
# reset graph here.
reset_default_graph()
global sess = Session()
A = Array{Any}(undef, 6)
A[1] = rand(Float32,10,10)
A[2] = rand(Float32,10)
A[3] = rand(Float32)
A[4] = Variable(A[1])
A[5] = Variable(A[2])
A[6] = Variable(A[3])
init(sess)
for i = 1:6
for j = 1:6
if i<=3 && j<=3 || (i in [2,5] && j in [1,4]) ||
(i in [2,5] && j in [2,5])
continue
end
ret1 = A[i]*A[j]
ret1 = run(sess, ret1)
ret2 = A[i>3 ? i-3 : i] * A[j>3 ? j-3 : j]
@test ret1 ≈ ret2
end
end
@test A[1].*A[1] ≈ run(sess, A[4].*A[4])
@test A[1].*A[1] ≈ run(sess, A[4].*A[1])
@test A[1].*A[1] ≈ run(sess, A[1].*A[4])
@test A[2].*A[2] ≈ run(sess, A[2].*A[5])
@test A[2].*A[2] ≈ run(sess, A[5].*A[5])
@test A[2].*A[2] ≈ run(sess, A[5].*A[2])
end
@testset "reshape" begin
a = constant([1 2 3;4 5 6.])
@test run(sess, reshape(a, 6))≈[ 1.0
4.0
2.0
5.0
3.0
6.0]
@test run(sess, reshape(a, 3, 2))≈[1.0 5.0
4.0 3.0
2.0 6.0]
b = constant([1;2;3;4;5;6])
@test run(sess, reshape(b, 2, 3))≈[1 3 5
2 4 6]
@test run(sess, reshape(constant(2.),1 )) ≈[2.0]
a = constant([0.136944 0.364238
0.250264 0.202175
0.712224 0.388285
0.163095 0.797934
0.740991 0.382738])
@test run(sess, reshape(a, :, 1))≈reshape([0.136944 0.364238
0.250264 0.202175
0.712224 0.388285
0.163095 0.797934
0.740991 0.382738], :, 1)
@test run(sess, reshape(a, 1,:))≈reshape([0.136944 0.364238
0.250264 0.202175
0.712224 0.388285
0.163095 0.797934
0.740991 0.382738], 1,:)
end
@testset "scatter_update" begin
A = Variable(ones(3))
A = scatter_add(A, 3, 2.)
B = [1.;1.;3.]
C = Variable(ones(3,3))
D = scatter_add(C, [2], [1], 1.)
E = [1. 1. 1; 2. 1. 1.; 1. 1. 1.]
init(sess)
@test run(sess, A)≈B
@test run(sess, D)≈E
F = scatter_update(C, 1:2, :, 2ones(2, 3))
@test run(sess, F)≈[ 2.0 2.0 2.0
2.0 2.0 2.0
1.0 1.0 1.0]
F = scatter_update(C, 1, :, 2ones(1, 3))
@test run(sess, F)≈[2.0 2.0 2.0
1.0 1.0 1.0
1.0 1.0 1.0]
F = scatter_update(C, 1, 2, 2.0)
@test run(sess, F)≈[1.0 2.0 1.0
1.0 1.0 1.0
1.0 1.0 1.0]
A = Variable(rand(10))
B = Variable(rand(5))
C = scatter_add(A, [1;4;5;6;7], 2B)
D = gradients(sum(C), B)
E = gradients(sum(C), A)
init(sess)
@test run(sess, D)≈2ones(5)
@test run(sess, E)≈ones(10)
A = Variable(ones(10,10))
B = Variable(ones(3,4))
C = scatter_add(A, [1;2;3],[3;4;5;6], B)
init(sess)
@test run(sess, C)≈[1.0 1.0 2.0 2.0 2.0 2.0 1.0 1.0 1.0 1.0
1.0 1.0 2.0 2.0 2.0 2.0 1.0 1.0 1.0 1.0
1.0 1.0 2.0 2.0 2.0 2.0 1.0 1.0 1.0 1.0
1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0
1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0]
a = rand(10)
A = constant(a)
A = scatter_add(A, 3:4, -A[3:4])
a[3:4] .= 0.0
@test run(sess, A) ≈ a
end
@testset "adjoint" begin
a = 1.0
@test run(sess, constant(a)')≈a'
a = rand(10)
@test run(sess, constant(a)')≈a'
a = rand(10,10)
@test run(sess, constant(a)')≈a'
a = rand(2,3,4,5)
@test run(sess, constant(a)')≈permutedims(a, [1,2,4,3])
end
@testset "scatter_update_pyobject" begin
A = constant(ones(10))
B = constant(ones(3))
ind = constant([2;4;6], dtype=Int32)
C = scatter_add(A, ind, B)
@test run(sess, C)≈[1.0, 2.0, 1.0, 2.0, 1.0, 2.0, 1.0, 1.0, 1.0, 1.0]
@test run(sess, gradients(sum(C),B))≈ones(3)
@test run(sess, gradients(sum(C),A))≈ones(10)
C = scatter_sub(A, ind, B)
@test run(sess, C)≈[1.0, 0.0, 1.0, 0.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0]
@test run(sess, gradients(sum(C),B))≈-ones(3)
@test run(sess, gradients(sum(C),A))≈ones(10)
B = constant(3*ones(3))
C = scatter_update(A, ind, B)
@test run(sess, C)≈[1.0, 3.0, 1.0, 3.0, 1.0, 3.0, 1.0, 1.0, 1.0, 1.0]
@test run(sess, gradients(sum(C),B))≈ones(3)
@test run(sess, gradients(sum(C),A))≈[1.0, 0.0, 1.0, 0.0, 1.0, 0.0, 1.0, 1.0, 1.0, 1.0]
end
@testset "Operators" begin
A = rand(10,2)
TA = Variable(A)
a = Variable(1.0)
b = Variable(0.5)
maxA = argmax(A, dims=2)
maxA = [maxA[i][2] for i = 1:10]
maxTA = argmax(TA, dims=2)
minA = argmin(A, dims=2)
minA = [minA[i][2] for i = 1:10]
minTA = argmin(TA, dims=2)
B = rand(Float32, 10)
TB = Variable(B)
TBc = constant(B)
gop = group_assign([a,b], [2.0,2.0])
init(sess)
@test maxA ≈ run(sess, maxTA)
@test minA ≈ run(sess, minTA)
@test get_dtype(cast(maxTA, Float64))==Float64
@test B.^2 ≈ run(sess, TB^2)
@test B.^2 ≈ run(sess, TBc^2)
@test 1.0 ≈ run(sess, max(a, b))
@test 0.5 ≈ run(sess, min(a, b))
@test maximum(A) ≈ run(sess, maximum(TA))
@test minimum(A) ≈ run(sess, minimum(TA))
@test reshape(maximum(A, dims=1), 2) ≈ run(sess, maximum(TA, dims=1))
@test reshape(minimum(A, dims=1),2) ≈ run(sess, minimum(TA, dims=1))
@test reshape(maximum(A, dims=2),10) ≈ run(sess, maximum(TA, dims=2))
@test reshape(minimum(A, dims=2),10) ≈ run(sess, minimum(TA, dims=2))
run(sess, gop)
@test run(sess, a)≈2.0 && run(sess,b) ≈ 2.0
end
@testset "Other Operators" begin
A = Variable(rand(10,10))
@test_nowarn group(assign(A, rand(10,10)), A+A, 2*A)
end
@testset "Concat and stack" begin
A = Variable(rand(10))
B = Variable(rand(10,3))
@test size(stack([A, A]))==(2,10)
@test size(concat([A, A], dims=0))==(20,)
@test size([A;A])==(20,)
@test size([A A])==(10,2)
@test size([B;B])==(20,3)
@test size([B B])==(10,6)
end
@testset "Vectorize" begin
A = rand(10)
B = reshape(A, 2, 5)
tA = constant(A)
tB = constant(B)
rA = rvec(tA)
cB = vec(tB)
init(sess)
a, b = run(sess, [rA, cB])
@test a≈reshape(A, 1, 10)
@test run(sess, rvec(constant(B)))≈reshape(B[:], 1, :)
@test run(sess, cvec(constant(B)))≈B[:] && size(cvec(constant(B)))==(10,1)
@test run(sess, vec(constant(B)))≈B[:]
@test b≈A
end
@testset "Solve" begin
A = rand(10,10)
x = rand(10)
y = A*x
tA = constant(A)
ty = constant(y)
@test run(sess, tA\ty)≈x
@test run(sess, A\ty)≈x
@test run(sess, tA\y)≈x
end
@testset "diff" begin
A = rand(10,10)
a = rand(10)
tfA = constant(A)
tfa = constant(a)
@test run(sess, diff(tfA, dims=1))≈diff(A, dims=1)
@test run(sess, diff(tfA, dims=2))≈diff(A, dims=2)
@test run(sess, diff(tfa))≈diff(a)
end
@testset "clip" begin
a = constant(3.0)
a = clip(a, 1.0, 2.0)
@test run(sess,a)≈2.0
end
@testset "map" begin
a = constant([1.0,2.0,3.0])
b = map(x->x^2, a)
@test run(sess, b)≈[1.0;4.0;9.0]
end
@testset "diag" begin
C = rand(3,3)
D = rand(3)
@test run(sess, diag(constant(C))) ≈ diag(C)
@test run(sess, diagm(constant(D))) ≈ diagm(0=>D)
end
@testset "dot" begin
A = rand(10)
B = rand(10)
tA = constant(A); tB = constant(B)
u = sum(A.*B)
@test run(sess, dot(tA, tB))≈u
@test run(sess, dot(A, tB))≈u
@test run(sess, dot(tA, B))≈u
end
@testset "prod" begin
A = rand(10)
@test run(sess, prod(constant(A)))≈prod(A)
end
@testset "findall" begin
a = constant([0.849268 0.888376 0.0928501 0.119263 0.614649
0.768562 0.978984 0.0802774 0.764186 0.491608
0.00877878 0.751463 0.99539 0.613257 0.070678])
b = a>0.5
bi = findall(b)
@test run(sess, bi)==[1 1
1 2
1 5
2 1
2 2
2 4
3 2
3 3
3 4]
ci = findall(b[1,:])
@test run(sess, ci)==[1;2;5]
end
@testset "svd" begin
A = rand(10,20)
r = svd(constant(A))
A2 = r.U*diagm(r.S)*r.Vt
@test run(sess, A2)≈A
end
@testset "vector" begin
m = zeros(20)
m[2:11] = rand(10)
v = vector(2:11, m[2:11], 20)
@test run(sess, v)≈m
end
@testset "repeat" begin
A = constant(2.0)
@test run(sess, repeat(A, 2)) ≈ ones(2)*2.0
@test run(sess, repeat(A, 1, 2)) ≈ ones(1, 2)*2.0
a = rand(2)
A = constant(a)
@test run(sess, repeat(A, 2)) ≈ repeat(a, 2)
@test run(sess, repeat(A, 3, 2)) ≈ repeat(a, 3, 2)
a = rand(2, 4)
A = constant(a)
@test run(sess, repeat(A, 2)) ≈ repeat(a, 2)
@test run(sess, repeat(A, 3, 2)) ≈ repeat(a, 3, 2)
end
@testset "pmap" begin
x = constant(ones(10))
y1 = pmap(x->2.0*x, x)
y2 = pmap(x->x[1]+x[2], [x,x])
y3 = pmap(1:10, x) do z
i = z[1]
xi = z[2]
xi + cast(Float64, i)
end
@test run(sess, y1)≈[ 2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0]
@test run(sess, y2)≈[ 2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0
2.0]
@test run(sess, y3)≈[ 2.0
3.0
4.0
5.0
6.0
7.0
8.0
9.0
10.0
11.0]
end
@testset "reshape" begin
o = constant(rand(100,10,10))
A = reshape(o, (100,2,50))
B = tf.reshape(o, (100,2,50))
@test run(sess, A)≈run(sess, B)
end
@testset "batch mul" begin
A = rand(100, 10, 10)
B = rand(100, 10, 3)
C = zeros(100, 10, 3)
for i = 1:100
C[i,:,:] = A[i,:,:] * B[i,:,:]
end
C_ = batch_matmul(A, B)
@test run(sess, C_) ≈ C
end
@testset "sort" begin
A = rand(10,5)
B = constant(A)
@test run(sess, sort(B, dims=1))≈sort(A, dims=1)
@test run(sess, sort(B, rev=true, dims=2))≈sort(A, dims=2, rev=true)
end
@testset "set_shape" begin
a = placeholder(Float64, shape=[nothing, 10])
b = set_shape(a, 3, 10)
@test_nowarn run(sess, b, a=>rand(3,10)) # OK
@test_throws PyCall.PyError run(sess, b, a=>rand(5,10)) # Error
@test_throws PyCall.PyError run(sess, b, a=>rand(10,3)) # Error
end
@testset "activation" begin
x = 1.0
x_ = constant(1.0)
for fn in [sigmoid, leaky_relu, selu, elu, softsign, softplus, relu, relu6]
@test run(sess, fn(x_))≈fn(x)
end
end
@testset "trace" begin
A = rand(10,10)
@test tr(A) ≈ run(sess, tr(constant(A)))
end
@testset "trilu" begin
for num = -5:5
lu = 1
m = 10
n = 5
u = rand(1, m, n)
ref = zeros(size(u,1), m, n)
for i = 1:size(u,1)
ref[i,:,:] = tril(u[i,:,:], num)
end
out = tril(constant(u),num)
sess = Session(); init(sess)
@test norm(run(sess, out)- ref)≈0
end
for num = -5:5
lu = 0
m = 5
n = 10
u = rand(1,m, n)
ref = zeros(size(u,1), m, n)
for i = 1:size(u,1)
if lu==0
ref[i,:,:] = triu(u[i,:,:], num)
else
ref[i,:,:] = tril(u[i,:,:], num)
end
end
out = triu(constant(u),num)
sess = Session(); init(sess)
@test norm(run(sess, out)- ref)≈0
end
end
@testset "reverse" begin
a = rand(10,2)
A = constant(a)
@test run(sess, reverse(A, dims=1)) == reverse(a, dims=1)
@test run(sess, reverse(A, dims=2)) == reverse(a, dims=2)
@test run(sess, reverse(A, dims=-1)) == reverse(a, dims=2)
end
@testset "solve batch" begin
a = rand(10,5)
b = rand(100, 10)
sol = solve_batch(a, b)
@test run(sess, sol) ≈ (a\b')'
a = rand(10,10)
b = rand(100, 10)
sol = solve_batch(a, b)
@test run(sess, sol) ≈ (a\b')'
end
@testset "rolling functions" begin
n = 10
window = 9
# TODO: specify your input parameters
inu = rand(n)
for ops in [(rollsum, sum), (rollmean, mean), (rollstd, std), (rollvar, var)]
@info ops
u = ops[1](inu,window)
out = zeros(n-window+1)
for i = window:n
out[i-window+1] = ops[2](inu[i-window+1:i])
end
@test maximum(abs.(run(sess, u)-out )) < 1e-8
end
end
@testset "logits" begin
logits = [
0.124575 0.511463 0.945934
0.538054 0.0749339 0.187802
0.355604 0.052569 0.177009
0.896386 0.546113 0.456832
]
labels = [2;1;2;3]
out = softmax_cross_entropy_with_logits(logits, labels)
o1 = run(sess, out)
labels = [0 1 0
1 0 0
0 1 0
0 0 1]
out = softmax_cross_entropy_with_logits(logits, labels)
o2 = run(sess, out)
@test o1≈o2
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 7264 |
@testset "NLopt" begin
######################### integration with NLopt.jl #########################
# ================ standard NLopt ================
function myfunc(x::Vector, grad::Vector)
if length(grad) > 0
grad[1] = 0
grad[2] = 2x[2]
end
return x[2]^2
end
function myconstraint(x::Vector, grad::Vector, a, b)
if length(grad) > 0
grad[1] = 2*(x[1]-1)
grad[2] = -1
end
(x[1]-1)^2 - x[2]
end
opt = Opt(:LD_MMA, 2)
opt.lower_bounds = [-Inf, 0.0]
opt.xtol_rel = 1e-4
opt.min_objective = myfunc
inequality_constraint!(opt, (x,g) -> myconstraint(x,g,2,0), 1e-8)
(minf,minx,ret) = NLopt.optimize(opt, [1.234, 5.678])
# ================ END NLopt ================
p = ones(10)
Con = CustomOptimizer() do f, df, c, dc, x0, args...
opt = Opt(:LD_MMA, length(x0))
bd = zeros(length(x0)); bd[end-1:end] = [-Inf, 0.0]
opt.lower_bounds = bd
opt.xtol_rel = 1e-4
opt.min_objective = (x,g)->(g[:]= df(x); return f(x)[1])
inequality_constraint!(opt, (x,g)->( g[:]= dc(x);c(x)[1]), 1e-8)
(minf,minx,ret) = NLopt.optimize(opt, x0)
minx
end
# unfortunately, we must ensure only minimization variables are in the current tensorflow graph
# for NLopt to work properly
reset_default_graph()
x = Variable([1.234; 5.678])
y = Variable([1.0;2.0])
loss = x[2]^2 + sum(y^2)
c1 = (x[1]-1)^2 - x[2]
opt = Con(loss, inequalities=[c1],var_to_bounds=Dict(x=>[-1.,1.]))
sess = Session(); init(sess)
opt.minimize(sess)
xmin = run(sess, x)
@test true
end
@testset "Optim" begin
######################### integration with Optim.jl #########################
NonCon = CustomOptimizer() do f, df, c, dc, x0, args...
@show f, df, c, dc, x0
res = Optim.optimize(f, df, x0; inplace = false)
res.minimizer
end
reset_default_graph()
x = Variable(rand(2))
f = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2
f1(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2
res = Optim.optimize(f1, rand(2))
opt = NonCon(f)
sess = Session(); init(sess)
opt.minimize(sess)
xmin = run(sess, x)
@test norm(xmin-res.minimizer)<1e-2
end
@testset "newton raphson" begin
@test_skip begin
A = rand(10,10)
A = A'*A + I
rhs = rand(10)
function newton_raphson_f(θ, u)
r = A*u - rhs
r, constant(A)
end
ADCME.options.newton_raphson.verbose = true
nr = newton_raphson(newton_raphson_f, zeros(10), missing)
nr = run(sess, nr)
@test nr.x≈A\rhs
u0 = rand(10)
function newton_raphson_f2(θ, u)
r = u^3+u - u0
r, spdiag(3u^2+1.0)
end
ADCME.options.newton_raphson.verbose = true
ADCME.options.newton_raphson.tol = 1e-5
nr = newton_raphson(newton_raphson_f2, rand(10), missing)
nr = run(sess, nr)
uval = nr.x
@test norm(uval.^3+uval-u0)<1e-3
# least square
u0 = rand(10)
rs = rand(10)
function newton_raphson_f3(θ, u)
r = [u^2;u] - [rs.^2;rs]
r, [spdiag(2*u); spdiag(10)]
end
nr = newton_raphson(newton_raphson_f3, rand(10), missing)
nr = run(sess, nr)
uval = nr.x
@test norm(uval-rs)<1e-3
end
end
@testset "NonlinearConstrainedProblem" begin
@test_skip begin
θ = Variable(1.8*ones(3))
u0 = ones(3)
function f1(θ, u)
r = u+u^3-θ
A = spdiag(3u^2+1.0)
r, A
end
function L1(u)
return sum((u-u0)^2)
end
l, u, g = NonlinearConstrainedProblem(f1,L1,θ,zeros(3))
# the negative gradients and vars are (-g, θ)
opt_ = AdamOptimizer(1e-1).apply_gradients([(g, θ)])
init(sess)
for i = 1:500
run(sess, opt_)
end
@test norm(run(sess, θ)-2.0*ones(3))<1e-8
θ = constant(ones(1))
u0 = ones(3)
Random.seed!(233)
A = round.(rand(3, 3), digits=1)
t = zeros(3); t[1:2].=1.0
function f1(θ, u)
# r = u-sum(θ)^2-t*sum(θ)
# A = spdiag(length(u))
# r, A
# -t*sum(θ)
A*u-[sum(θ);sum(θ);constant(0.0)], constant(A)
end
function L1(u)
return sum(u)
end
close("all")
function value_and_gradients_function(θ)
l, u, g = NonlinearConstrainedProblem(f1,L1,θ,zeros(3))
l, g
end
results = BFGS!(value_and_gradients_function, zeros(3))
u = run(sess, results)
@test u≈[2.;2.;2.]
end
end
@testset "Custom BFGS!" begin
reset_default_graph()
x = Variable(2ones(10))
z = Variable(1.0)
w = Variable(ones(20,30,10))
loss = sum((x-1.0)^2+z^2+w^2)
grads = [gradients(loss, x), gradients(loss, z), gradients(loss, w)]
vars = [x,z, w]
global sess = Session(); init(sess)
l = BFGS!(sess, loss, grads, vars)
@test l[end]<1e-5
end
@testset "var_to_bounds" begin
x = Variable(2.0)
loss = x^2
init(sess)
BFGS!(sess, loss, bounds=Dict(x=>[1.0,3.0]))
@test run(sess, x)≈1.0
end
#=
@testset "Ipopt" begin
######################### integration with Ipopt.jl #########################
# https://github.com/jainachin/tf-ipopt/blob/master/examples/hs071.py
IPOPT = CustomOptimizer() do f, df, c, dc, x0, x_L, x_U
n = length(x0)
nz = length(dc(x0))
g_L, g_U = [-2e19;0.0], [0.0;0.0]
function eval_jac_g(x, mode, rows, cols, values)
if mode == :Structure
rows[1] = 1; cols[1] = 1
rows[2] = 1; cols[2] = 1
rows[3] = 2; cols[3] = 1
rows[4] = 2; cols[4] = 1
else
values[:]=dc(x)
end
end
prob = Ipopt.createProblem(n, x_L, x_U, 2, g_L, g_U, nz, 0,
f, (x,g)->(g[:]=c(x)), (x,g)->(g[:]=df(x)), eval_jac_g, nothing)
addOption(prob, "hessian_approximation", "limited-memory")
addOption(prob, "max_iter", 100)
prob.x = x0
status = Ipopt.solveProblem(prob)
println(Ipopt.ApplicationReturnStatus[status])
println(prob.x)
prob.x
end
reset_default_graph()
x = Variable([1.0;1.0])
x1 = x[1]; x2 = x[2];
loss = x2
g = x1
h = x1*x1 + x2*x2 - 1
opt = IPOPT(loss, inequalities=[g], equalities=[h], var_to_bounds=Dict(x=>(-1.0,1.0)))
sess = Session(); init(sess)
minimize(opt, sess)
=#
@testset "newton_raphson_with_grad" begin
function f(θ, x)
x^3 - θ, 3spdiag(x^2)
end
θ = [2. .^3;3. ^3; 4. ^3]
x = newton_raphson_with_grad(f, constant(ones(3)), θ)
@test run(sess, x)≈[2.;3.;4.]
θ = constant([2. .^3;3. ^3; 4. ^3])
x = newton_raphson_with_grad(f, constant(ones(3)), θ)
@test run(sess, x)≈[2.;3.;4.]
@test run(sess, gradients(sum(x), θ))≈1/3*[2. .^3;3. ^3; 4. ^3] .^(-2/3)
end
# @testset "Constrained Optimizer" begin
# reset_default_graph() # this is very important. UnconstrainedOptimizer only works with a fresh session
# x = Variable(2*ones(10))
# y = constant(ones(10))
# loss = sum((y-x)^4)
# init(sess)
# uo = UnconstrainedOptimizer(sess, loss)
# @test getInit(uo) ≈ 2ones(10)
# @test getLoss(uo, 3*ones(10))≈ 160.0
# @test getLossAndGrad(uo, 3*ones(10))[2] ≈ [32.0, 32.0, 32.0, 32.0, 32.0, 32.0, 32.0, 32.0, 32.0, 32.0]
# @test getLossAndGrad(uo, 3*ones(10))[1] ≈ 160.0
# end
# @testset "optimzers" begin
# ad = AndersonAcceleration()
# @test_nowarn begin
# apply!(ad, rand(10), rand(10))
# end
# end
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 800 | # test functions for developing optimizers
# see https://en.wikipedia.org/wiki/Test_functions_for_optimization
# optimal = (0, 0, 0, ...)
function sphere(x)
return sum(x^2)
end
# optimal = (1,1,1,...)
function rosenbrock(x)
x1 = x[1:end-1]
x2 = x[2:end]
return sum(100 * (x2-x1^2)^2 + (1-x1)^2)
end
# optimal = (3, 0.5)
function beale(p)
x, y = p[1], p[2]
return (1.5 - x + x*y)^2 + (2.25 - x + x*y^2)^2 +
(2.625 - x + x*y^3)
end
# optimal = (1, 3)
function booth(p)
x, y = p[1], p[2]
return (x + 2y - 7)^2 + (2x+y-5)^2
end
#optimal = (-0.2903, ...)
function stybliski_tang(x)
return sum(x^4 - 16x^2 + 5x)/2
end
# optimal = (1,1)
function levi(p)
x, y = p[1], p[2]
sin(3π*x)^2 + (x-1)^2 * (1+sin(3π*y)^2) + (y-1)^2 * (1+sin(2π*y)^2)
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 926 | @testset "sinkhorn" begin
a = Float64.(1:5)/sum(1:5)
b = Float64.(1:10)/sum(1:10)
m = zeros(5, 10)
for i = 1:5
for j = 1:10
m[i,j] = 1/(i+j)
end
end
reg = 1.0
iter = 100
tol = 1e-10
loss = sinkhorn(a, b, m)
@test run(sess, loss) ≈ 0.10269121
# @test_nowarn loss = sinkhorn(a, b, m, method = "lp")
end
@testset "dist" begin
a = rand(10,3)
b = rand(20,3)
for order in [1,2,3,4,5]
M = zeros(10, 20)
for i = 1:10
for j = 1:20
M[i,j] = norm(a[i,:] - b[j,:], order)
end
end
m = ot_dist(a, b, order)
@test m≈M
m = ot_dist(a, constant(b), order)
@test run(sess, m)≈M
end
end
# @testset "fastdtw" begin
# Sample = Float64[1,2,3,5,5,5,6]
# Test = Float64[1,1,2,2,3,5]
# u, p = dtw(Sample, Test, true)
# @test run(sess, u)≈1.0
# end
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 2879 | @testset "pcl_square_sum" begin
using Random; Random.seed!(233)
y = placeholder(rand(10))
loss = sum((y-rand(10))^2)
g = tf.convert_to_tensor(gradients(loss, y))
function test_f(x0)
run(sess, g, y=>x0), pcl_square_sum(length(y))
end
err1, err2 = test_jacobian(test_f, rand(10); showfig=false)
@test all(err1.>err2)
end
@testset "pl_hessian" begin
using Random; Random.seed!(233)
x = placeholder(rand(10))
z = (x[1:5]^2 + x[6:end]^3) * sum(x)
y = [reshape(sum(z[1:3]), (-1,));z]
loss = sum((y-rand(6))^2)
H, dW = pcl_hessian(y, x, loss)
g = gradients(loss, x)
function test_f(x0)
y0, H0 = run(sess, [g, H], feed_dict = Dict(
x=>x0,
dW => pcl_square_sum(length(y))
))
end
err1, err2 = test_hessian(test_f, rand(length(x)); showfig = false)
@test all(err1.>err2)
end
@testset "pcl_linear_op" begin
using Random; Random.seed!(233)
x = placeholder(rand(10))
A = rand(6, 10)
y = A * x + rand(6)
loss = sum((y-rand(6))^2)
J = jacobian(y, x)
g = gradients(loss, x)
function test_f(x0)
gval, Jval = run(sess, [g, J], x=>x0)
H = pcl_linear_op(Array(Jval'), pcl_square_sum(6))
return gval, H
end
err1, err2 = test_hessian(test_f, rand(length(x)); showfig = false)
@test all(err1.>err2)
end
@testset "pcl_sparse_solve" begin
using Random; Random.seed!(233)
A = sprand(10,10,0.6)
II, JJ, VV = findnz(A)
x = placeholder(rand(length(VV)))
temp = SparseTensor(II,JJ,x,10,10)
indices = run(sess, temp.o.indices)
B = RawSparseTensor(constant(indices), x, 10, 10)
rhs = rand(10)
sol = B\rhs
loss = sum(sol^2)
g = gradients(loss, sol)
G = gradients(loss, x)
indices = run(sess, B.o.indices) .+ 1
function test_f(x0)
s, gval, Gval = run(sess, [sol, g, G], x=>x0)
H = pcl_sparse_solve(indices, x0,
s,
pcl_square_sum(length(sol)), gval)
return Gval, H
end
err1, err2 = test_hessian(test_f, rand(length(x)); showfig = false)
@test all(err1.>err2)
end
@testset "pcl_compress" begin
using Random; Random.seed!(233)
if !Sys.iswindows()
indices = [
1 1
1 1
1 1
2 2
3 3
]
pl = placeholder(rand(5))
A = RawSparseTensor(constant(indices)-1, pl, 3, 3)
B = compress(A)
loss = sum(B.o.values^2)
g = gradients(loss, pl)
function test_f(x0)
G = run(sess, g, pl=>x0)
W = pcl_square_sum(3)
J = pcl_compress(indices)
H = pcl_linear_op(J, W)
G, H
end
x0 = rand(length(pl))
err1, err2 = test_hessian(test_f, x0; showfig = false)
@test all(err1.>err2)
end
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 1677 | @testset "random" begin
@test_skip run(sess, categorical(10))
for shape in [[10], [10,5]]
@test_skip run(sess, uniform(shape...))
@test_skip run(sess, normal(shape...))
@test_skip run(sess, choice(rand(10,2), 4))
@test_skip run(sess, choice(rand(10,2), 4, replace=true))
@test_skip run(sess, beta(shape...;concentration1=1.0, concentration0=1.0))
@test_skip run(sess, bernoulli(shape...; probs=0.2))
@test_skip run(sess, gamma(shape...;concentration=3.0, rate=2.0))
@test_skip run(sess, truncatednormal(shape...;loc=0.0, scale=1.0, low=-1., high=1.))
@test_skip run(sess, chi(shape...;df=5))
@test_skip run(sess, chi2(shape...;df=5))
@test_skip run(sess, exponential(shape...;rate=1.))
@test_skip run(sess, gumbel(shape...;loc=0, scale=1))
@test_skip run(sess, poisson(shape...;rate=1.0))
@test_skip run(sess, halfcauchy(shape...;loc=0, scale=1))
@test_skip run(sess, halfnormal(shape...;scale=1))
@test_skip run(sess, horseshoe(shape...;scale=1.0))
@test_skip run(sess, inversegamma(shape...;concentration=1.0, scale=1.0))
@test_skip run(sess, inversegaussian(shape...;loc=1.0, concentration=1.0))
@test_skip run(sess, kumaraswamy(shape...;concentration1=1.0, concentration0=1.0))
@test_skip run(sess, pareto(shape...;scale=1.0, concentration=1.0))
@test_skip run(sess, sinharcsinh(shape...;skewness=1.0, tailweight=1.0, loc=0.0, scale=1.0))
@test_skip run(sess, studentt(shape...;loc=0, scale=1, df=10))
@test_skip run(sess, vonmises(shape...;concentration=1.0, loc=1.0))
end
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 2662 | @testset "radial basis function" begin
xc = rand(10)
yc = rand(10)
e = rand(10)
c = rand(10)
d = rand(3)
r = RBF2D(xc, yc; c=c, eps=e, d=d, kind = 0)
x = rand(5)
y = rand(5)
o = r(x, y)
O = zeros(5)
for i = 1:5
for j = 1:10
dist = sqrt((x[i]-xc[j])^2 + (y[i]-yc[j])^2)
O[i] += c[j] * exp(-(e[j]*dist)^2)
end
O[i] += d[1] + d[2] * x[i] + d[3] * y[i]
end
init(sess)
@test norm(run(sess, o)-O)<1e-5
end
@testset "interp1" begin
Random.seed!(233)
x = sort(rand(10))
y = @. x^2 + 1.0
z = [x[1]; x[2]; rand(5) * (x[end]-x[1]) .+ x[1]; x[end]]
u = interp1(x,y,z)
@test norm(run(sess, u)-[1.026422850882909
1.044414684090653
1.312604319732756
1.810845361128137
1.280789421523103
1.600084940795178
1.930560200260898
1.972130181835701]) < 1e-10
end
@testset "rbf3d" begin
function f0(r, e)
return exp(-(e*r)^2)
end
function f1(r, e)
return sqrt((1+(e*r)^2))
end
function f2(r, e)
return 1/(1+(e*r)^2)
end
function f3(r, e)
return 1/sqrt(1+(e*r)^2)
end
fs = [f0, f1, f2, f3]
nc = 100
n = 10
xc = rand(nc)
yc = rand(nc)
zc = rand(nc)
x = rand(n)
y = rand(n)
z = rand(n)
c = rand(nc)
d = rand(4)
e = rand(nc)
for kind = 1:4
out = zeros(n)
for i = 1:n
r = @. sqrt((x[i] - xc)^2 + (y[i] - yc)^2 + (z[i] - zc)^2)
out[i] = sum(c .* fs[kind].(r, e)) + d[1] + d[2] * x[i] + d[3] * y[i] + d[4] * z[i]
end
rbf = RBF3D(xc, yc, zc, c = c, eps = e, d = d, kind = kind - 1)
o = rbf(x,y,z)
o_ = run(sess, o)
@test maximum(abs.(out .- o_)) < 1e-8
end
for kind = 1:4
out = zeros(n)
for i = 1:n
r = @. sqrt((x[i] - xc)^2 + (y[i] - yc)^2 + (z[i] - zc)^2)
out[i] = sum(c .* fs[kind].(r, e)) + d[1]
end
rbf = RBF3D(xc, yc, zc, c = c, eps = e, d = d[1:1], kind = kind - 1)
o = rbf(x,y,z)
o_ = run(sess, o)
@test maximum(abs.(out .- o_)) < 1e-8
end
for kind = 1:4
out = zeros(n)
for i = 1:n
r = @. sqrt((x[i] - xc)^2 + (y[i] - yc)^2 + (z[i] - zc)^2)
out[i] = sum(c .* fs[kind].(r, e))
end
rbf = RBF3D(xc, yc, zc, c = c, eps = e, kind = kind - 1)
o = rbf(x,y,z)
o_ = run(sess, o)
@test maximum(abs.(out .- o_)) < 1e-8
end
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 695 | using NLopt
using Optim
using ADCME
using Statistics
using LinearAlgebra
using PyCall
using SparseArrays
using Test
using Random
PIP = get_pip()
run_with_env(`$PIP install matplotlib`)
using PyPlot
if has_gpu()
use_gpu(0)
end
doctor()
sess = Session()
include("layers.jl")
include("sparse.jl")
include("random.jl")
include("io.jl")
include("variable.jl")
include("ops.jl")
include("core.jl")
include("extra.jl")
include("newton.jl")
include("optim.jl")
include("ot.jl")
include("ode.jl")
include("flow.jl")
include("mpi.jl")
include("toolchain.jl")
include("rbf.jl")
include("pcl.jl")
# The default matplotlib backend does not work for MacOSX
if !Sys.isapple()
include("kit.jl")
end
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 8047 | @testset "sparse_constructor" begin
A = sprand(10,10,0.1)
s = SparseTensor(A)
@test run(sess, s)≈A
I = [1;2;4;2;3;5]
J = [1;3;2;2;2;1]
V = rand(6)
A = sparse(I,J,V,6,5)
s = SparseTensor(I,J,V,6,5)
@test run(sess, s)≈A
indices = [I J]
s = SparseTensor(I,J,V,6,5)
@test run(sess, s)≈A
S = Array(s)
@test run(sess, S)≈Array(A)
@test size(s)==(6,5)
@test size(s,1)==6
@test size(s,2)==5
end
@testset "sparse_arithmetic" begin
A1 = rand(10,5); B1 = sprand(10,5,0.3)
A = constant(A1)
B = SparseTensor(B1)
@test run(sess, -B)≈-B1
for op in [+,-]
C = op(A, B)
C1 = op(A1, B1)
@test run(sess, C)≈C1
end
@test run(sess, B-A)≈B1-A1
end
@testset "sparse_adjoint" begin
A = sprand(10,5,0.3)
A1 = SparseTensor(A)
@test run(sess, A1')≈sparse(A')
end
@testset "sparse_mul" begin
A1 = rand(10,10); B1 = sprand(10,10,0.3)
C1 = rand(10)
A = constant(A1)
B = SparseTensor(B1)
C = constant(C1)
@test run(sess, B*A) ≈ B1*A1
@test run(sess, A*B) ≈ A1*B1
@test run(sess, B*A1) ≈ B1*A1
@test run(sess, A1*B) ≈ A1*B1
@test run(sess, B*C) ≈ B1*C1
@test run(sess, B*C1) ≈ B1*C1
end
@testset "sparse_vcat_hcat" begin
B1 = sprand(10,3,0.3)
B = SparseTensor(B1)
@test run(sess, [B;B])≈[B1;B1]
@test run(sess, [B B])≈[B1 B1]
end
@testset "sparse_indexing" begin
B1 = sprand(10,10,0.3)
B = SparseTensor(B1)
@test run(sess, B[2:3,2:3])≈B1[2:3,2:3]
@test run(sess, B[2:3,:])≈B1[2:3,:]
@test run(sess, B[:,2:3])≈B1[:,2:3]
end
@testset "sparse_solve" begin
A = sparse(I, 10,10) + sprand(10,10,0.1)
b = rand(10)
A1 = SparseTensor(A)
b1 = constant(b)
u = A1\b1
@test run(sess, u) ≈ A\b
end
@testset "sparse_assembler" begin
m = 20
n = 100
handle = SparseAssembler(100, m, 0.0)
op = PyObject[]
A = zeros(m, n)
for i = 1:1
ncol = rand(1:n, 10)
row = rand(1:m)
v = rand(10)
for (k,val) in enumerate(v)
@show k
A[row, ncol[k]] += val
end
@show v
push!(op, accumulate(handle, row, ncol, v))
end
op = vcat(op...)
J = assemble(m, n, op)
B = run(sess, J)
@test norm(A-B)<1e-8
handle = SparseAssembler(100, 5, 1.0)
op1 = accumulate(handle, 1, [1;2;3], [2.0;0.5;0.5])
J = assemble(5, 5, op1)
B = run(sess, J)
@test norm(B-[2.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0])<1e-8
handle = SparseAssembler(100, 5, 0.0)
op1 = accumulate(handle, 1, [1;1], [1.0;1.0])
op2 = accumulate(handle, 1, [1;2], [1.0;1.0])
J = assemble(5, 5, [op1;op2])
B = run(sess, J)
@test norm(B-[3.0 1.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0
0.0 0.0 0.0 0.0 0.0])<1e-8
end
@testset "sparse_least_square" begin
ii = Int32[1;1;2;2;3;3]
jj = Int32[1;2;1;2;1;2]
vv = Float64[1;2;3;4;5;6]
ff = Float64[1;1;1]
A = SparseTensor(ii, jj, vv, 3, 2)
o = A\ff
@test norm(run(sess, o)-[-1;1])<1e-6
end
@testset "sparse mat mul" begin
A = sprand(10,5,0.3)
B = sprand(5,20,0.3)
C = A*B
CC = SparseTensor(A)*SparseTensor(B)
C_ = run(sess, CC)
@test C_≈C
A = spdiagm(0=>[1.;2.;3;4;5])
B = sprand(5,20,0.3)
C = A*B
CC = SparseTensor(A)*SparseTensor(B)
C_ = run(sess, CC)
@test C_≈C
A = sprand(10,5,0.5)
B = spdiagm(0=>[1.;2.;3;4;5])
C = A*B
CC = SparseTensor(A)*SparseTensor(B)
C_ = run(sess, CC)
@test C_≈C
end
@testset "spdiag" begin
p = rand(10)
A = spdiagm(0=>p)
B = spdiag(constant(p))
C = spdiag(10)
@test run(sess, B)≈A
@test B._diag
@test run(sess, C)≈spdiagm(0=>ones(10))
end
@testset "spzero" begin
q = spzero(10)
@test run(sess, q)≈sparse(zeros(10,10))
q = spzero(10,20)
@test run(sess, q)≈sparse(zeros(10,20))
end
@testset "sparse indexing" begin
i1 = unique(rand(1:20,3))
j1 = unique(rand(1:30,3))
A = sprand(20,30,0.3)
Ad = Array(A[i1, j1])
B = SparseTensor(A)
Bd = Array(B[i1, j1])
Bd_ = run(sess, Bd)
@test Ad≈Bd_
end
@testset "sum" begin
s = sprand(10,20,0.2)
S = SparseTensor(s)
@test run(sess, sum(S)) ≈ sum(s)
@test run(sess, sum(S,dims=1)) ≈ sum(Array(s),dims=1)[:]
@test run(sess, sum(S,dims=2)) ≈ sum(Array(s),dims=2)[:]
end
@testset "dense_to_sparse" begin
A = sprand(10,20,0.3)
B = Array(A)
@test run(sess, dense_to_sparse((B))) ≈ A
@test run(sess, dense_to_sparse(constant(B))) ≈ A
end
@testset "spdiagm" begin
a = rand(10)
b = rand(9)
A = spdiag(
10,
0=>a,
-1=>b
)
B = diagm(
0=>a,
-1=>b
)
@test Array(run(sess, A)) ≈ B
b = rand(7)
A = spdiag(
10,
0=>a,
-3=>b
)
B = diagm(
0=>a,
-3=>b
)
@test Array(run(sess, A)) ≈ B
b = rand(7)
A = spdiag(
10,
0=>a,
-3=>b,
3=>4b
)
B = diagm(
0=>a,
-3=>b,
3=>4b
)
@test Array(run(sess, A)) ≈ B
b = rand(7)
A = spdiag(
10,
0=>a,
-3=>b
)
B = diagm(
0=>a,
-3=>b
)
@test Array(run(sess, A)) ≈ B
end
@testset "hvcat" begin
A = sprand(10,5,0.3)
B = sprand(10,5,0.2)
C = sprand(5,10,0.4)
D = [A B;C]
D_ = [SparseTensor(A) SparseTensor(B); SparseTensor(C)]
@test run(sess, D_)≈D
end
@testset "find" begin
A = sprand(10,10, 0.3)
ii = Int64[]
jj = Int64[]
vv = Float64[]
for i = 1:10
for j = 1:10
if A[i,j]!=0
push!(ii, i)
push!(jj, j)
push!(vv, A[i,j])
end
end
end
a = SparseTensor(A)
i, j, v = find(a)
@test run(sess, i)≈ii
@test run(sess, j)≈jj
@test run(sess, v)≈vv
@test run(sess, rows(a))≈ii
@test run(sess, cols(a))≈jj
@test run(sess, values(a))≈vv
end
@testset "sparse scatter update add" begin
A = sprand(10,10,0.3)
B = sprand(3,3,0.6)
ii = [1;4;5]
jj = [2;4;6]
u = scatter_update(A, ii, jj, B)
C = copy(A)
C[ii,jj] = B
@test run(sess, u)≈C
u = scatter_add(A, ii, jj, B)
C = copy(A)
C[ii,jj] += B
@test run(sess, u)≈C
end
@testset "constant sparse" begin
A = sprand(10,10,0.3)
B = constant(A)
@test run(sess, B)≈A
end
@testset "get index" begin
idof = [false;true]
M = spdiag(constant(ones(2)))
Md = M[idof, idof]
@test run(sess, Md) ≈ sparse(reshape([1.0],1,1))
end
@testset "sparse_factorization_and_solve" begin
A = sprand(10,10,0.7)
rhs1 = rand(10)
rhs2 = rand(10)
Afac = factorize(constant(A))
v1 = Afac\rhs1
v2 = Afac\rhs2
@test norm(run(sess, v1) - A\rhs1)<1e-8
@test norm(run(sess, v2) - A\rhs2)<1e-8
end
@testset "sparse solver warning" begin
A = SparseTensor(zeros(10,10))
b = A\rand(10)
@test_throws PyCall.PyError run(sess, b)
end
@testset "sparse promote" begin
a = sprand(10,10,0.3)
b = spdiag(constant(rand(10)))
@test_nowarn a+b
@test_nowarn a*b
@test_nowarn a-b
@test_nowarn b+a
@test_nowarn b-a
@test_nowarn b*a
end
@testset "trisolve" begin
n = 10
a = rand(n-1)
b = rand(n).+10
c = rand(n-1)
d = rand(n)
A = diagm(0=>b, -1=>a, 1=>c)
x = A\d
u = trisolve(a,b,c,d)
@test norm(run(sess, u)-x)<1e-3
end
@testset "compress" begin
indices = [
1 1
1 1
2 2
3 3
]
v = [1.0;1.0;1.0;1.0]
A = SparseTensor(indices[:,1], indices[:,2], v, 3, 3)
Ac = compress(A)
sess = Session(); init(sess)
@test run(sess, Ac.o.indices) == [0 0;1 1;2 2]
@test run(sess, Ac.o.values) ≈ [2.0;1.0;1.0]
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 2138 | @testset "sqlite" begin
db = Database()
execute(db, """
CREATE TABLE simulation_parameters (
desc text,
rho real,
gamma real,
dt real,
h real
)
""")
execute(db, """
INSERT INTO simulation_parameters VALUES
('baseline', 1.0, 2.0, 0.01, 0.02)
""")
params = [
("compare1", 1.0, 2.0, 0.01),
("compare2", 2.0, 3.0, 4.0)
]
execute(db, """
INSERT INTO simulation_parameters VALUES
(?, ?, ?, ?, 0.1)
""", params)
res = execute(db, "SELECT * FROM simulation_parameters")|>collect
@test keys(db)==["simulation_parameters"]
@test keys(db, "simulation_parameters")==[ "desc"
"rho"
"gamma"
"dt"
"h"]
@test length(res)==3
commit(db)
close(db)
end
@testset "execute many" begin
db = Database()
execute(db,
"""
CREATE TABLE temp (
t1 real,
t2 real
)
""")
execute(db, "INSERT INTO temp VALUES (?,?)", rand(10), rand(10))
@test length(db["temp"])==10
end
@testset "sqlite do syntax" begin
db = Database("temp.db")
execute(db) do
"""
CREATE TABLE simulation_parameters (
desc text,
rho real,
gamma real,
dt real,
h real
)
"""
end
@test "simulation_parameters" in keys(db)
close(db)
rm("temp.db", force=true)
Database("temp.db") do db
execute(db) do
"""
CREATE TABLE simulation_parameters (
desc text,
rho real,
gamma real,
dt real,
h real
)
"""
end
end
@test length(db["simulation_parameters"])==0
delete!(db, "simulation_parameters")
@test_throws PyCall.PyError keys(db, "simulation_parameters")
db = Database("temp.db")
@test "simulation_parameters" in keys(db)
close(db)
rm("temp.db", force=true)
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | code | 4953 | using LinearAlgebra
@testset "indexing" begin
A1 = rand(10)
A2 = rand(10,10)
B1 = Variable(A1)
B2 = Variable(A2)
ind = Array{Any}(undef, 4)
ind[1] = 3
ind[2] = 2:4
ind[3] = zeros(Bool,10)
ind[3][3:4] .= true
ind[4] = [3;4;5]
init(sess)
for i = 1:4
@test A1[ind[i]] ≈ run(sess, B1[ind[i]])
@test A2[ind[i], :] ≈ run(sess, B2[ind[i], :])
@test A2[:, ind[i]] ≈ run(sess, B2[:, ind[i]])
end
for i = 1:4
for j = 1:4
@test A2[ind[i], ind[j]] ≈ run(sess, B2[ind[i], ind[j]])
end
end
end
@testset "Variables" begin
# @test_nowarn placeholder(Float64, shape=[nothing,20], name="myvar")
# @test_nowarn Variable(rand(10,10), dtype=Float64, name="myvar")
# @test_nowarn constant(rand(10,10), dtype=Float64, name="myvar")
# @test_nowarn get_variable("W", shape=[10,20], dtype=Float64)
# @test_nowarn placeholder(Float64, shape=[nothing,20])
# @test_nowarn Variable(rand(10,10), dtype=Float64)
# @test_nowarn constant(rand(10,10), dtype=Float64)
@test get_dtype(constant(rand(10,10))) == Float64
@test get_dtype(Variable(rand(Int64,10,10))) == Int64
v = get_variable(rand(10,10), name="test_get_variable")
u = get_variable(rand(10,10), name="test_get_variable")
@test u==v
w = get_variable(Float64, shape=[10,20])
@test size(w)==(10,20)
end
@testset "tensor" begin
v = Variable(0.5)
g = [1;v;0]
G = [1 v 0; v 1 0; 0 0 (1-v)/2]
gv = tensor(g;sparse=true)
g_gv = gradients(2sum(gv), v)
Gv = tensor(G;sparse=true)
G_gv = gradients(sum(Gv), v)
init(sess)
@test run(sess, g_gv) ≈ 2.0
@test run(sess, G_gv) ≈ 1.5
end
@testset "Hessian" begin
x = Variable(randn(), dtype = Float32)
y = Variable(randn(), dtype = Float32)
g = stack([x,y])
f = g[1]^2 + 2*g[1]*g[2] + 3*g[2]^2 + 4*g[1] + 5*g[2] + 6
hess = hessian(f, g)
gv = rand(Float32,2)
hess_v = hessian_vector(f, g, gv)
val = [[2.;2.] [2.;6.]] * gv
init(sess)
@test run(sess, hess) ≈ [[2.;2.] [2.;6.]]
@test run(sess, hess_v)≈val
end
@testset "Jacobian" begin
xs = constant(rand(10))
A = rand(20,10)
ys = A*xs
jac = gradients(ys, xs)
@test run(sess, jac)≈A
end
@testset "gradients_v" begin
xs = constant(1.0)
ys = stack([xs,xs,xs,xs])
gv = gradients(ys, xs)
@test run(sess, gv)≈[1.0;1.0;1.0;1.0]
end
@testset "size and length" begin
a = Variable(1.0)
b = Variable(rand(10))
c = Variable(rand(10,20))
@test size(a)==()
@test size(b)==(10,)
@test size(b,1)==10
@test size(c) == (10,20)
@test size(c,1)==10
@test size(c,2)==20
@test length(a)==1
@test length(b)==10
@test length(c)==200
end
@testset "copy" begin
o = constant(rand(10,10))
v = copy(o)
init(sess)
@test run(sess, v)≈run(sess, o)
end
@testset "getindex" begin
i = constant(2)
a = constant([1.;2.;3.;4.])
@test run(sess, a[i])≈2.0
end
@testset "convert_to_tensor" begin
a = rand(10)
@test run(sess, convert_to_tensor(a))≈a
a = 5.0
@test run(sess, convert_to_tensor(a))≈a
a = constant(rand(10))
@test run(sess, convert_to_tensor(a))≈run(sess, a)
@test ismissing(convert_to_tensor(missing))
@test isnothing(convert_to_tensor(nothing))
end
@testset "cell" begin
r = cell([[1.],[2.,3.]])
@test run(sess, r[1])≈[1.0]
@test run(sess, r[2])≈[2.,3.]
end
@testset "special matrices" begin
A = rand(10,10)
@test run(sess, sym(A)) ≈ 0.5 * (A + A')
@test all(eigvals(run(sess, spd(A))) .> 0.0)
end
@testset "ones/zeros like" begin
a = rand(100,10)
b = ones_like(a)
@test run(sess, b)≈ones(100,10)
b = zeros_like(a)
@test run(sess, b)≈zeros(100,10)
end
@testset "gradient_magnitude" begin
x = constant(rand(10))
y = constant(rand(20))
l = sum(x) + sum(y)
gx, gy = gradients(l, [x,y])
n = gradient_magnitude(l, [x, y])
@test run(sess, n)≈sqrt(norm(run(sess, gx))^2 + norm(run(sess,gy))^2)
end
@testset "indexing with tensor" begin
a = rand(10,3)
i = constant(2)
A = constant(a)
@test run(sess, A[i,:])≈a[2,:]
@test run(sess, A[i,3])≈a[2,3]
@test run(sess, A[i,[1;2]])≈a[2,[1;2]]
@test run(sess, A[:, i])≈a[:, 2]
@test run(sess, A[3, i])≈a[3, 2]
@test run(sess, A[[1;2], i])≈a[[1;2], 2]
end
@testset "ndims" begin
@test ndims(constant(0.0))==0
@test ndims(constant(rand(2)))==1
@test ndims(constant(rand(3,3)))==2
@test ndims(constant(rand(4,4,4)))==3
end
@testset "gradients_colocate" begin
@cpu 1 begin
global a = constant(rand(10,10))
global b = 2a
end
loss = sum(b)
g = gradients_colocate(loss, a)
@test g.device == "/device:CPU:1"
end
@testset "is_variable" begin
a = Variable(rand(10))
b = constant(rand(10))
@test is_variable(a)==true
@test is_variable(b)==false
end | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 17407 | <p align="center">
<img src="https://github.com/ADCMEMarket/ADCMEImages/blob/master/ADCME/ADCME.gif?raw=true" alt="ADCME"/>
</p>



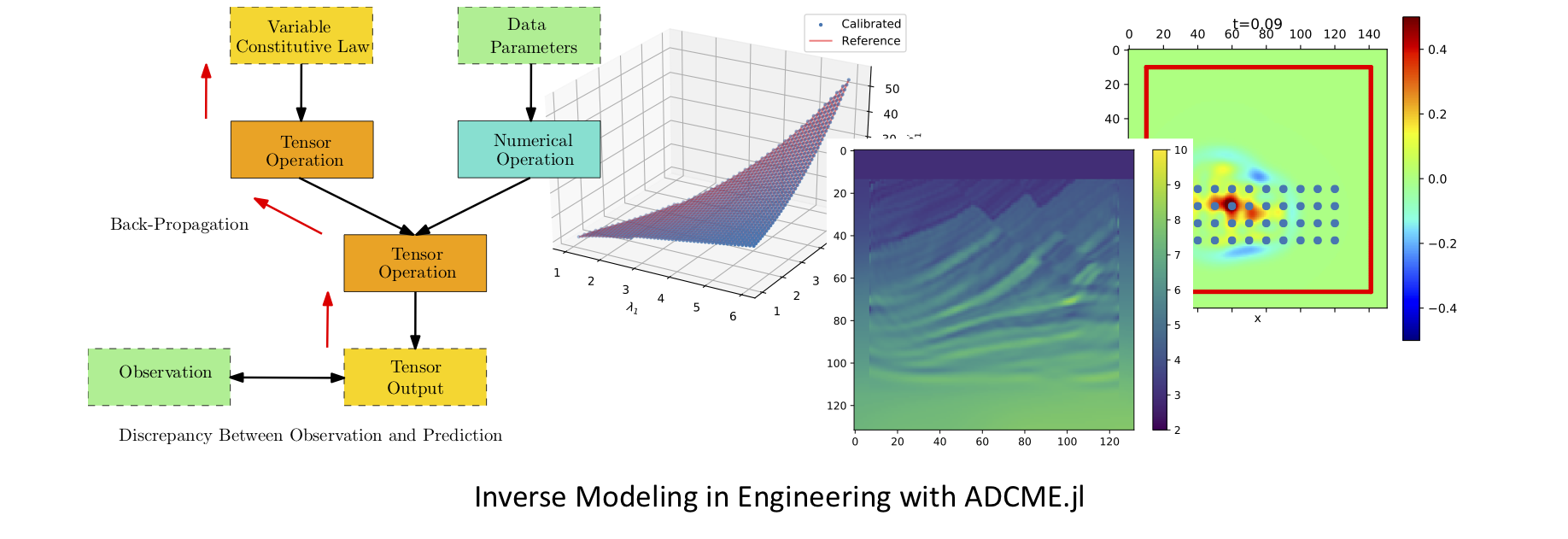
The ADCME library (**A**utomatic **D**ifferentiation Library for **C**omputational and **M**athematical **E**ngineering) aims at general and scalable inverse modeling in scientific computing with gradient-based optimization techniques. It is built on the deep learning framework, **graph-mode [TensorFlow](https://www.tensorflow.org/)**, which provides the automatic differentiation and parallel computing backend. The dataflow model adopted by the framework makes it suitable for high performance computing and inverse modeling in scientific computing. The design principles and methodologies are summarized in the [slides](https://kailaix.github.io/ADCMESlides/ADCME.pdf).
Check out more about [slides and videos on ADCME](https://kailaix.github.io/ADCME.jl/dev/videos_and_slides/)!
| [Install ADCME and Get Started (Windows, Mac, and Linux)](https://www.youtube.com/playlist?list=PLKBz8ohiA3IlrCI0VO4cRYZp2S6SYG1Ww) | [Scientific Machine Learning for Inverse Modeling](https://www.youtube.com/playlist?list=PLKBz8ohiA3In-ZlvBKbvj_TIQEaboGC9_) | [Solving Inverse Modeling Problems with ADCME](https://www.youtube.com/playlist?list=PLKBz8ohiA3ImaNykOv56ONnCofEQMg3B8) | ...**more** on [ADCME Youtube Channel](https://www.youtube.com/channel/UCeaZFluNatYpkIYcq2TTklw/playlists)! |
| ------------------------------------------------------------ | ------------------------------------------------------------ | ------------------------------------------------------------ | ------------------------------------------------------------ |
| [](https://www.youtube.com/playlist?list=PLKBz8ohiA3IlrCI0VO4cRYZp2S6SYG1Ww) | [](https://www.youtube.com/playlist?list=PLKBz8ohiA3In-ZlvBKbvj_TIQEaboGC9_) | [](https://www.youtube.com/playlist?list=PLKBz8ohiA3ImaNykOv56ONnCofEQMg3B8) | [](https://www.youtube.com/channel/UCeaZFluNatYpkIYcq2TTklw/playlists) |
Several features of the library are
* **MATLAB-style Syntax**. Write `A*B` for matrix production instead of `tf.matmul(A,B)`.
* **Custom Operators**. Implement operators in C/C++ for performance critical parts; incorporate legacy code or specially designed C/C++ code in `ADCME`; automatic differentiation through implicit schemes and iterative solvers.
* **Numerical Scheme**. Easy to implement numerical schemes for solving PDEs.
* **Physics Constrained Learning**. Embed neural network into PDEs and solve with any numerical schemes, including implicit and iterative schemes.
* **Static Graphs**. Compilation time computational graph optimization; automatic parallelism for your simulation codes.
* **Parallel Computing**. [Concurrent execution](https://kailaix.github.io/ADCME.jl/dev/multithreading/) and model/data parallel [distributed optimization](https://kailaix.github.io/ADCME.jl/dev/mpi/).
* **Custom Optimizers**. Large scale constrained optimization? Use `CustomOptimizer` to integrate your favorite optimizer. Try out prebuilt [Ipopt and NLopt](https://kailaix.github.io/ADCME.jl/dev/customopt/#Dropin-substitute-of-BFGS!-1) optimizers.
* **Sparse Linear Algebra**. Sparse linear algebra library tailored for scientific computing.
* **Inverse Modeling**. Many inverse modeling algorithms have been developed and implemented in ADCME, with wide applications in solid mechanics, fluid dynamics, geophysics, and stochastic processes.
* [](https://github.com/kailaix/AdFem.jl)**Finite Element Method**. Get [AdFem.jl](https://github.com/kailaix/AdFem.jl) today for finite element simulation and inverse modeling!
Start building your forward and inverse modeling using ADCME today!
| Documentation | Tutorial | Applications |
| ------------------------------------------------------------ | ------------------------------------------------------------ | ------------------------------------------------------------ |
| [](https://kailaix.github.io/ADCME.jl/latest/) | [](https://kailaix.github.io/ADCME.jl/dev/tutorial/) | [](https://kailaix.github.io/ADCME.jl/dev/apps) |
## Graph-mode TensorFlow for High Performance Scientific Computing
Static computational graph (graph-mode AD) enables compilation time optimization. Below is a benchmark of common AD software from [here](https://github.com/microsoft/ADBench). In inverse modeling, we usually have a scalar-valued objective function, so the left panel is most relevant for ADCME.
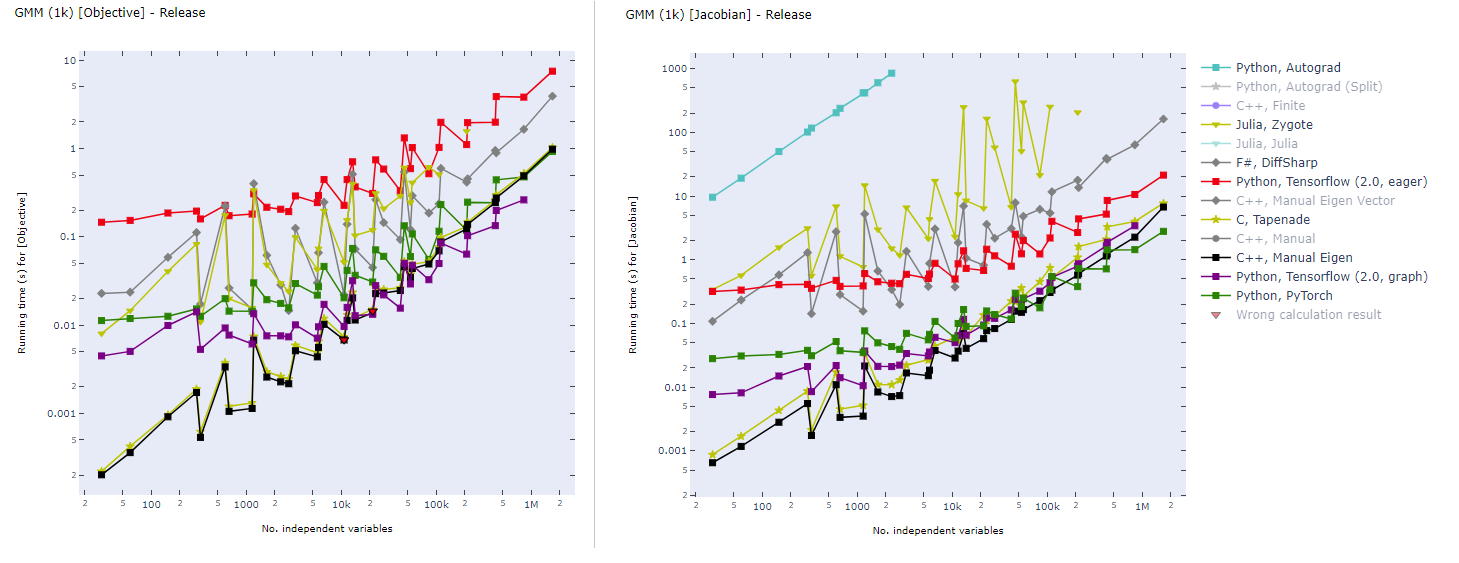
# Installation
1. Install [Julia](https://julialang.org/).
🎉 Support Matrix
| | Julia≧1.3 | GPU | Custom Operator |
|---------| ----- |-----|-----------------|
| Linux |✔ | ✔ | ✔ |
| MacOS |✔ | ✕ | ✔ |
| Windows | ✔ | ✔ | ✔ |
1. Install `ADCME`
```
using Pkg
Pkg.add("ADCME")
```
❗ FOR WINDOWS USERS: See [the instruction](https://kailaix.github.io/ADCME.jl/dev/windows_installation/) or [the video](https://www.youtube.com/playlist?list=PLKBz8ohiA3IlrCI0VO4cRYZp2S6SYG1Ww) for installation details.
❗ FOR MACOS USERS: See this [troubleshooting list](https://kailaix.github.io/ADCME.jl/dev/#Troubleshooting-for-MacOS) for potential installation and compilation problems on Mac.
2. (Optional) Test `ADCME.jl`
```julia
using Pkg
Pkg.test("ADCME")
```
See [Troubleshooting](https://kailaix.github.io/ADCME.jl/dev/tu_customop/#Troubleshooting-1) if you encounter any compilation problems.
3. (Optional) To enable GPU support, make sure `nvcc` is available from your environment (e.g., type `nvcc` in your shell and you should get the location of the executable binary file), and then type
```julia
ENV["GPU"] = 1
Pkg.build("ADCME")
```
You can check the status with `using ADCME; gpu_info()`.
4. (Optional) Check the health of your installed ADCME and install missing dependencies or fixing incorrect paths.
```julia
using ADCME
doctor()
```
For manual installation without access to the internet, see [here](https://kailaix.github.io/ADCME.jl/dev/).
## Install via Docker
If you have Docker installed on your system, you can try the no-hassle way to install ADCME (you don't even have to install Julia!):
```bash
docker run -ti kailaix/adcme
```
See [this guide](https://kailaix.github.io/ADCME.jl/latest/docker/) for details.
# Tutorial
Here we present three inverse problem examples. The first one is a parameter estimation problem, the second one is a function inverse problem where the unknown function does not depend on the state variables, and the third one is also a function inverse problem, but the unknown function depends on the state variables.
### Parameter Inverse Problem
Consider solving the following problem

where

Assume that we have observed `u(0.5)=1`, we want to estimate `b`. In this case, he true value should be `b=1`.
```julia
using LinearAlgebra
using ADCME
n = 101 # number of grid nodes in [0,1]
h = 1/(n-1)
x = LinRange(0,1,n)[2:end-1]
b = Variable(10.0) # we use Variable keyword to mark the unknowns
A = diagm(0=>2/h^2*ones(n-2), -1=>-1/h^2*ones(n-3), 1=>-1/h^2*ones(n-3))
B = b*A + I # I stands for the identity matrix
f = @. 4*(2 + x - x^2)
u = B\f # solve the equation using built-in linear solver
ue = u[div(n+1,2)] # extract values at x=0.5
loss = (ue-1.0)^2
# Optimization
sess = Session(); init(sess)
BFGS!(sess, loss)
println("Estimated b = ", run(sess, b))
```
Expected output
```
Estimated b = 0.9995582304494237
```
The gradients can be obtained very easily. For example, if we want the gradients of `loss` with respect to `b`, the following code will create a Tensor for the gradient
```
julia> gradients(loss, b)
PyObject <tf.Tensor 'gradients_1/Mul_grad/Reshape:0' shape=() dtype=float64>
```
### Function Inverse Problem: Full Field Data
Consider a nonlinear PDE,

where

Here `f(x)` can be computed from an analytical solution

In this problem, we are given the full field data of `u(x)` (the discrete value of `u(x)` is given on a very fine grid) and want to estimate the nonparametric function `b(u)`. We approximate `b(u)` using a neural network and use the [residual minimization method](https://kailaix.github.io/ADCME.jl/dev/tu_nn/) to find the optimal weights and biases of the neural network. The minimization problem is given by

```julia
using LinearAlgebra
using ADCME
using PyPlot
n = 101
h = 1/(n-1)
x = LinRange(0,1,n)|>collect
u = sin.(π*x)
f = @. (1+u^2)/(1+2u^2) * π^2 * u + u
# `fc` is short for fully connected neural network.
# Here we create a neural network with 2 hidden layers, and 20 neuron per layer.
# The default activation function is tanh.
b = squeeze(fc(u[2:end-1], [20,20,1]))
residual = -b.*(u[3:end]+u[1:end-2]-2u[2:end-1])/h^2 + u[2:end-1] - f[2:end-1]
loss = sum(residual^2)
sess = Session(); init(sess)
BFGS!(sess, loss)
plot(x, (@. (1+x^2)/(1+2*x^2)), label="Reference")
plot(u[2:end-1], run(sess, b), "o", markersize=5., label="Estimated")
legend(); xlabel("\$u\$"); ylabel("\$b(u)\$"); grid("on")
```
Here we show the estimated coefficient function and the reference one:
<p align="center">
<img src="https://github.com/ADCMEMarket/ADCMEImages/blob/master/ADCME/readmenn.png?raw=true" style="zoom:50%;" />
</p>
### Function Inverse Problem: Sparse Data
Now we consider the same problem as above, but only consider we have access to sparse observations. We assume that on the grid only the values of `u(x)` on every other 5th grid point are observable. We use the [physics constrained learning](https://arxiv.org/pdf/2002.10521.pdf) technique and train a neural network surrogate for `b(u)` by minimizing

Here `uᶿ` is the solution to the PDE with

We add 1 to the neural network to ensure the initial guess does not result in a singular Jacobian matrix in the Newton Raphson solver.
```julia
using LinearAlgebra
using ADCME
using PyPlot
n = 101
h = 1/(n-1)
x = LinRange(0,1,n)|>collect
u = sin.(π*x)
f = @. (1+u^2)/(1+2u^2) * π^2 * u + u
# we use a Newton Raphson solver to solve the nonlinear PDE problem
function residual_and_jac(θ, x)
nn = squeeze(fc(reshape(x,:,1), [20,20,1], θ)) + 1.0
u_full = vector(2:n-1, x, n)
res = -nn.*(u_full[3:end]+u_full[1:end-2]-2u_full[2:end-1])/h^2 + u_full[2:end-1] - f[2:end-1]
J = gradients(res, x)
res, J
end
θ = Variable(fc_init([1,20,20,1]))
ADCME.options.newton_raphson.rtol = 1e-4 # relative tolerance
ADCME.options.newton_raphson.tol = 1e-4 # absolute tolerance
ADCME.options.newton_raphson.verbose = true # print details in newton_raphson
u_est = newton_raphson_with_grad(residual_and_jac, constant(zeros(n-2)),θ)
residual = u_est[1:5:end] - u[2:end-1][1:5:end]
loss = sum(residual^2)
b = squeeze(fc(reshape(x,:,1), [20,20,1], θ)) + 1.0
sess = Session(); init(sess)
BFGS!(sess, loss)
figure(figsize=(10,4))
subplot(121)
plot(x, (@. (1+x^2)/(1+2*x^2)), label="Reference")
plot(x, run(sess, b), "o", markersize=5., label="Estimated")
legend(); xlabel("\$u\$"); ylabel("\$b(u)\$"); grid("on")
subplot(122)
plot(x, (@. sin(π*x)), label="Reference")
plot(x[2:end-1], run(sess, u_est), "--", label="Estimated")
plot(x[2:end-1][1:5:end], run(sess, u_est)[1:5:end], "x", markersize=5., label="Data")
legend(); xlabel("\$x\$"); ylabel("\$u\$"); grid("on")
```
We show the reconstructed `b(u)` and the solution `u` computed from `b(u)`. We see that even though the neural network model fits the data very well, `b(u)` is not the same as the true one. This problem is ubiquitous in inverse modeling, where the unknown may not be unique.

See [Applications](https://kailaix.github.io/ADCME.jl/dev/tutorial/) for more inverse modeling techniques and examples.
### Under the Hood: Computational Graph
A static computational graph is automatic constructed for your implementation. The computational graph guides the runtime execution, saves intermediate results, and records data flows dependencies for automatic differentiation. Here we show the computational graph in the parameter inverse problem:

See a detailed [tutorial](https://kailaix.github.io/ADCME.jl/dev/tutorial/), or a full [documentation](https://kailaix.github.io/ADCME.jl/dev).
# Featured Applications
| [Constitutive Modeling](https://kailaix.github.io/ADCME.jl/dev/apps_constitutive_law/) | [Seismic Inversion](https://kailaix.github.io/ADCME.jl/dev/apps_adseismic) | [Coupled Two-Phase Flow and Time-lapse FWI](https://kailaix.github.io/ADCME.jl/dev/apps_ad/) | [Calibrating Jump Diffusion](https://kailaix.github.io/ADCME.jl/dev/apps_levy/) |
| ------------------------------------------------------------ | ------------------------------------------------------------ | ------------------------------------------------------------ | ------------------------------------------------------------ |
|  | 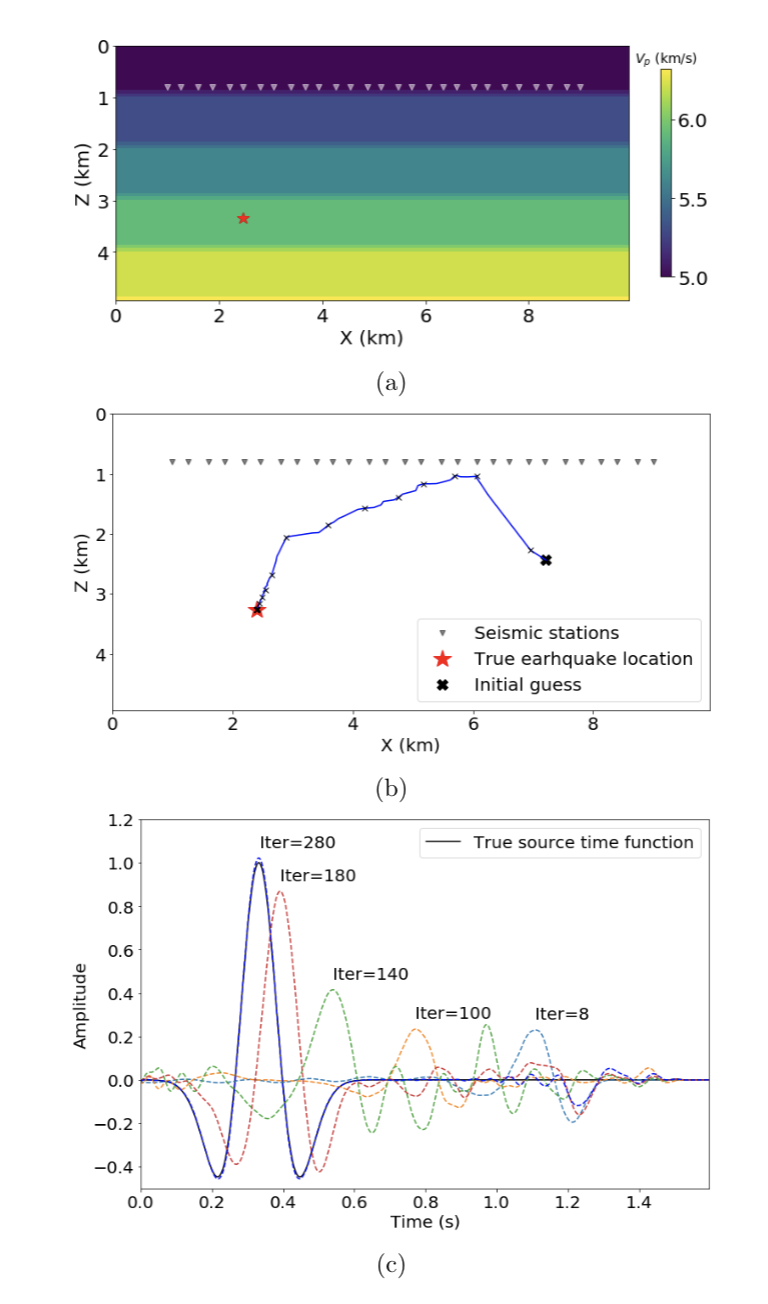 | 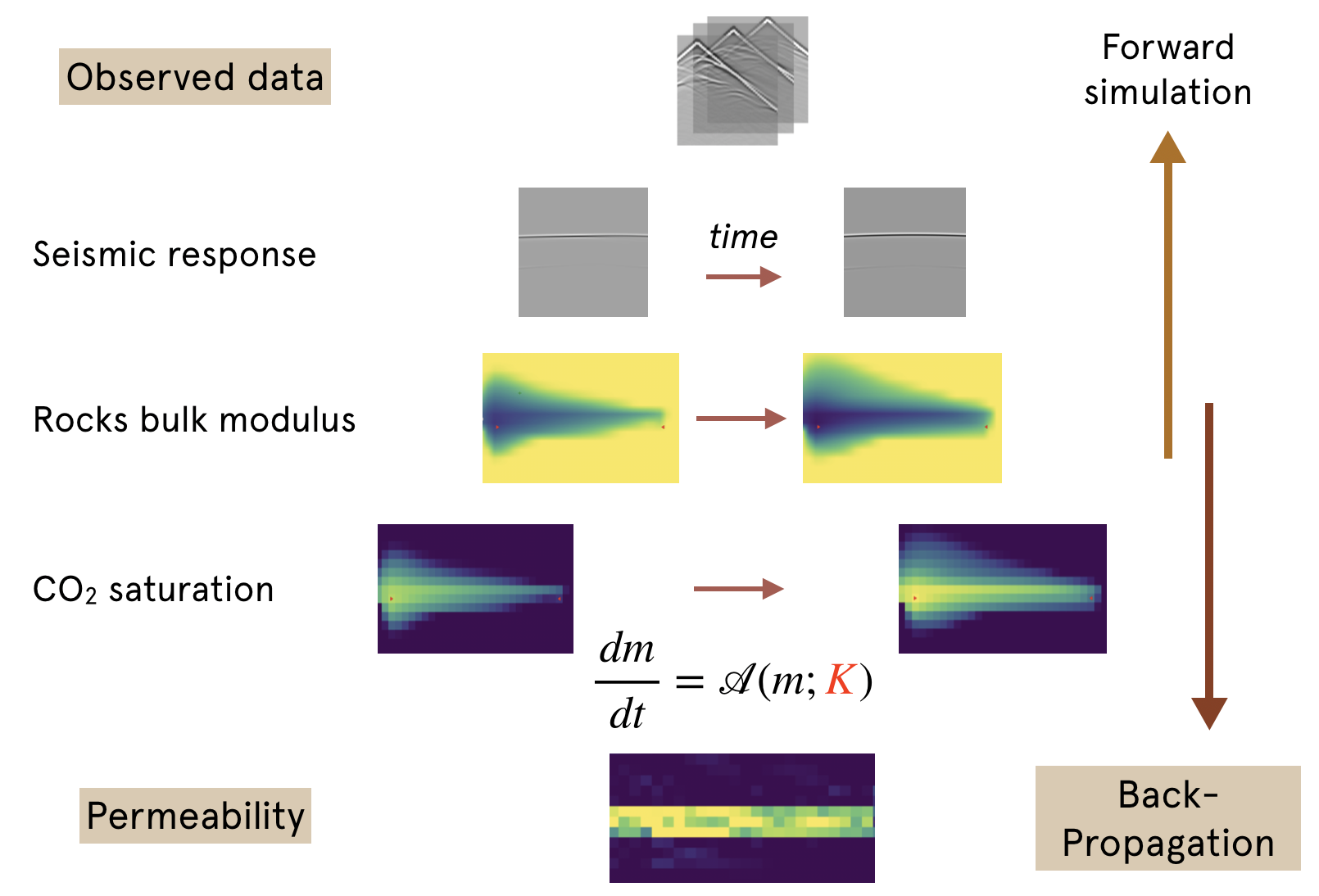 |  |
Here are some research papers using ADCME:
1. Li, Dongzhuo, Kailai Xu, Jerry M. Harris, and Eric Darve. "Coupled Time‐Lapse Full‐Waveform Inversion for Subsurface Flow Problems Using Intrusive Automatic Differentiation." Water Resources Research 56, no. 8 (2020): e2019WR027032.
2. Xu, Kailai, Alexandre M. Tartakovsky, Jeff Burghardt, and Eric Darve. "Inverse Modeling of Viscoelasticity Materials using Physics Constrained Learning." arXiv preprint arXiv:2005.04384 (2020).
3. Zhu, Weiqiang, Kailai Xu, Eric Darve, and Gregory C. Beroza. "A General Approach to Seismic Inversion with Automatic Differentiation." arXiv preprint arXiv:2003.06027 (2020).
4. Xu, K. and Darve, E., 2019. Adversarial Numerical Analysis for Inverse Problems. arXiv preprint arXiv:1910.06936.
5. Xu, Kailai, Weiqiang Zhu, and Eric Darve. "Distributed Machine Learning for Computational Engineering using MPI." arXiv preprint arXiv:2011.01349 (2020).
6. Xu, Kailai, and Eric Darve. "Physics constrained learning for data-driven inverse modeling from sparse observations." arXiv preprint arXiv:2002.10521 (2020).
7. Xu, Kailai, Daniel Z. Huang, and Eric Darve. "Learning constitutive relations using symmetric positive definite neural networks." arXiv preprint arXiv:2004.00265 (2020).
8. Xu, Kailai, and Eric Darve. "The neural network approach to inverse problems in differential equations." arXiv preprint arXiv:1901.07758 (2019).
9. Huang, D.Z., Xu, K., Farhat, C. and Darve, E., 2019. Predictive modeling with learned constitutive laws from indirect observations. arXiv preprint arXiv:1905.12530.
**Domain specific software based on ADCME**
[ADSeismic.jl](https://github.com/kailaix/ADSeismic.jl): Inverse Problems in Earthquake Location/Source-Time Function, FWI, Rupture Process
[FwiFlow.jl](https://github.com/lidongzh/FwiFlow.jl): Seismic Inversion, Two-phase Flow, Coupled seismic and flow equations
[AdFem.jl](https://github.com/kailaix/AdFem.jl/): Inverse Modeling with the Finite Element Method
# LICENSE
ADCME.jl is released under MIT License. See [License](https://github.com/kailaix/ADCME.jl/tree/master/LICENSE) for details.
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 104 | [ ] S*v
[ ] S*D
[ ] D*S
[ ] S\v
[ ] S\D
[ ] S+s
[ ] -S
[ ] S-->D
[ ] D-->S
[ ] S'
[ ] α*S*S+βS
[ ] S+D | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 14903 | # Generalized α Scheme
## Generalized $\alpha$ Scheme
The generalized $\alpha$ scheme is used to solve the second order linear differential equation of the form
$$m\ddot{ \mathbf{u}} + \gamma\dot{\mathbf{u}} + k\mathbf{u} = \mathbf{f}$$
whose discretization form is
$$M\mathbf{a} + C\mathbf v + K \mathbf d = \mathbf F$$
Here $M$, $C$ and $K$ are the generalized mass, damping, and stiffness matrices, $\mathbf a$, $\mathbf v$, and $\mathbf d$ are the generalized acceleration, velocity, and displacement, and $\mathbf F$ is the generalized force vector.
There are two types of boundary conditions
* Dirichlet (essential) boundary condition. In this case, the displacement $\mathbf{u}$ is specified at a point $\mathbf{x}_0$
$$\mathbf{u}(\mathbf{x}_0, t) = \mathbf{h}(t)$$
This boundary condition usually requires updating matrices $M$, $C$ and $K$ at each time step.
* Essential boundry condition. In this case the external force is specified
$${\sigma}(\mathbf{x})\mathbf{n}(\mathbf{x}) = \mathbf{t}(\mathbf{x})$$
This term goes directly into $\mathbf{F}$.
The generalized $\alpha$ scheme solves for a discrete time step
$$\begin{aligned}
\mathbf d_{n+1} &= \mathbf d_n + h\mathbf v_n + h^2 \left(\left(\frac{1}{2}-\beta_2 \right)\mathbf a_n + \beta_2 \mathbf a_{n+1} \right)\\
\mathbf v_{n+1} &= \mathbf v_n + h((1-\gamma_2)\mathbf a_n + \gamma_2 \mathbf a_{n+1})\\
\mathbf F(t_{n+1-\alpha_{f_2}}) &= M \mathbf a _{n+1-\alpha_{m_2}} + C \mathbf v_{n+1-\alpha_{f_2}} + K \mathbf{d}_{n+1-\alpha_{f_2}}
\end{aligned}$$
Here $h$ is the time step and
$$\begin{aligned}
\mathbf d_{n+1-\alpha_{f_2}} &= (1-\alpha_{f_2})\mathbf d_{n+1} + \alpha_{f_2} \mathbf d_n\\
\mathbf v_{n+1-\alpha_{f_2}} &= (1-\alpha_{f_2}) \mathbf v_{n+1} + \alpha_{f_2} \mathbf v_n \\
\mathbf a_{n+1-\alpha_{m_2} } &= (1-\alpha_{m_2}) \mathbf a_{n+1} + \alpha_{m_2} \mathbf a_n\\
t_{n+1-\alpha_{f_2}} & = (1-\alpha_{f_2}) t_{n+1 + \alpha_{f_2}} + \alpha_{f_2}t_n
\end{aligned}$$
The parameters $\alpha_{f_2}$, $\alpha_{m_2}$, $\gamma_2$, and $\beta_2$ are used to control the amplification of high frequency numerical modes. High frequency modes normally describe motions with no physical sense (also contains very large phase error). Therefore, it is desirable to damp those high frequency modes. By properly choosing the parameters, we can recover HHT, Newmark, or WBZ methods.
We can design new algorithms by taking $\rho_\infty\in [0,1]$ as a design variable to control the numerical dissipation above the normal frequency $\frac{h}{T}$, where $T$ is the period associated with the highest frequency of interest. The following relationships are used to obtain a good algorithm that are accurate and preserve low-frequency modes
$$\begin{aligned}
\gamma_2 &= \frac{1}{2} - \alpha_{m_2} + \alpha_{f_2}\\
\beta_2 &= \frac{1}{4} (1-\alpha_{m_2}+\alpha_{f_2})^2 \\
\alpha_{m_2} &= \frac{2\rho_\infty-1}{\rho_\infty+1}\\
\alpha_{f_2} &= \frac{\rho_\infty}{\rho_\infty+1}
\end{aligned}$$
The following figure provides a plot of spectral radii versus $\frac hT$[^radii]

[^radii]: http://www.dymoresolutions.com/AnalysisControls/CreateFEModel.html
In ADCME, we provide an API to the generalized $\alpha$ scheme, [`αscheme`](@ref), and [`αscheme_time`](@ref), which computes $t_{n+1-\alpha_{f_2}}$.
## Rayleigh Damping
Rayleigh damping is widely used to model internal structural damping. It is viscous damping that is proportional to a linear combination of mass and stiffness
$$C = \alpha M + \beta K$$
The relation between the damping value $\xi$ and the naturual frequency $\omega$ is given by
$$\xi =\frac12\left( \frac{\alpha}{\omega} + \beta\omega \right)$$
In practice, we can measure two real frequencies $\xi_1$ and $\xi_2$, corresponding to $\omega_1$ and $\omega_2$ and find the coefficients via
$$\begin{bmatrix}
\frac{1}{2\omega_1} & \frac{\omega_1}{2}\\
\frac{1}{2\omega_2} & \frac{\omega_2}{2}
\end{bmatrix}\begin{bmatrix}\alpha\\\beta\end{bmatrix} = \begin{bmatrix}\xi_1\\\xi_2\end{bmatrix}$$
This approach will produce a curve that matches the two natural frequency points. In the case where the structure has one or two very dominant frequencies, Raleigh damping can closely approximate the behavior of a prescribed modal damping.
## Example: Elasticity
In this example, we consider a plane stress elasticity deformation of a plate. The governing equation is given by
$$\begin{aligned}
\sigma_{ij,j} + f_i = \ddot u_i \\
\sigma_{ij} = \mathsf{C} \epsilon_{ij}
\end{aligned}$$
The elasticity tensor $\mathsf{C}$ is calculated using a Young's modulus $E=1$ and a Poisson's ratio $\nu=0.35$. We consider a computational domain $[0,2]\times[0,1]$ and time horizon $t\in (0,1)$, the exact solution is given by
$$u_1(x,y,t) = e^{-t}x(2-x)y(1-y)\qquad u_2(x,y,t) = e^{-t}x^2(2-x)^2y^2(1-y)^2$$
The other terms can be computed analytically based on the exact solutions.
```julia
using ADCME
using AdFem
using PyPlot
n = 20
m = 2n
NT = 200
ρ = 1.0
Δt = 1/NT
h = 1/n
x = zeros((m+1)*(n+1))
y = zeros((m+1)*(n+1))
for i = 1:m+1
for j = 1:n+1
idx = (j-1)*(m+1)+i
x[idx] = (i-1)*h
y[idx] = (j-1)*h
end
end
bd = bcnode("all", m, n, h)
u1 = (x,y,t)->exp(-t)*x*(2-x)*y*(1-y)
u2 = (x,y,t)->exp(-t)*x^2*(2-x)^2*y^2*(1-y)^2
ts = Δt * ones(NT)
dt = αscheme_time(ts, ρ = ρ )
F = zeros(NT, 2(m+1)*(n+1))
for i = 1:NT
t = dt[i]
f1 = (x,y)->(-4.93827160493827*x^2*y^2*(x - 2)*(y - 1) - 4.93827160493827*x^2*y*(x - 2)*(y - 1)^2 - 4.93827160493827*x*y^2*(x - 2)^2*(y - 1) - 4.93827160493827*x*y*(x - 2)^2*(y - 1)^2 + x*y*(x - 2)*(y - 1) - 0.740740740740741*x*(x - 2) - 3.20987654320988*y*(y - 1))*exp(-t)
f2 = (x,y)->(x^2*y^2*(x - 2)^2*(y - 1)^2 - 3.20987654320988*x^2*y^2*(x - 2)^2 - 0.740740740740741*x^2*y^2*(y - 1)^2 - 12.8395061728395*x^2*y*(x - 2)^2*(y - 1) - 3.20987654320988*x^2*(x - 2)^2*(y - 1)^2 - 2.96296296296296*x*y^2*(x - 2)*(y - 1)^2 - 1.23456790123457*x*y - 1.23456790123457*x*(y - 1) - 0.740740740740741*y^2*(x - 2)^2*(y - 1)^2 - 1.23456790123457*y*(x - 2) - 1.23456790123457*(x - 2)*(y - 1))*exp(-t)
fval1 = eval_f_on_gauss_pts(f1, m, n, h)
fval2 = eval_f_on_gauss_pts(f2, m, n, h)
F[i,:] = compute_fem_source_term(fval1, fval2, m, n, h)
end
E = 1.0
ν = 0.35
H = E/(1+ν)/(1-2ν)*[
1-ν ν 0
ν 1-ν 0
0 0 (1-2ν)/2
]
M = constant(compute_fem_mass_matrix(m, n, h))
K = constant(compute_fem_stiffness_matrix(H, m, n, h))
a0 = [(@. u1(x, y, 0.0)); (@. u2(x, y, 0.0))]
u0 = -[(@. u1(x, y, 0.0)); (@. u2(x, y, 0.0))]
d0 = [(@. u1(x, y, 0.0)); (@. u2(x, y, 0.0))]
function solver(A, rhs)
A, _ = fem_impose_Dirichlet_boundary_condition_experimental(A, bd, m, n, h)
rhs = scatter_update(rhs, [bd; bd .+ (m+1)*(n+1)], zeros(2*length(bd)))
return A\rhs
end
d, u, a = αscheme(M, spzero(2(m+1)*(n+1)), K, F, d0, u0, a0, ts; solve=solver, ρ = ρ )
sess = Session()
d_, u_, a_ = run(sess, [d, u, a])
function plot_traj(idx)
figure(figsize=(12,3))
subplot(131)
plot((0:NT)*Δt, u1.(x[idx], y[idx],(0:NT)*Δt), "b-", label="x-Acceleration")
plot((0:NT)*Δt, a_[:,idx], "y--", markersize=2)
plot((0:NT)*Δt, u2.(x[idx], y[idx],(0:NT)*Δt), "r-", label="y-Acceleration")
plot((0:NT)*Δt, a_[:,idx+(m+1)*(n+1)], "c--", markersize=2)
legend()
xlabel("Time")
ylabel("Value")
subplot(133)
plot((0:NT)*Δt, u1.(x[idx], y[idx],(0:NT)*Δt), "b-", label="x-Displacement")
plot((0:NT)*Δt, d_[:,idx], "y--", markersize=2)
plot((0:NT)*Δt, u2.(x[idx], y[idx],(0:NT)*Δt), "r-", label="y-Displacement")
plot((0:NT)*Δt, d_[:,idx+(m+1)*(n+1)], "c--", markersize=2)
legend()
xlabel("Time")
ylabel("Value")
subplot(132)
plot((0:NT)*Δt, -u1.(x[idx], y[idx],(0:NT)*Δt), "b-", label="x-Velocity")
plot((0:NT)*Δt, u_[:,idx], "y--", markersize=2)
plot((0:NT)*Δt, -u2.(x[idx], y[idx],(0:NT)*Δt), "r-", label="y-Velocity")
plot((0:NT)*Δt, u_[:,idx+(m+1)*(n+1)], "c--", markersize=2)
legend()
xlabel("Time")
ylabel("Value")
tight_layout()
end
idx2 = (n÷3)*(m+1) + m÷3
plot_traj(idx2)
```
Using the above code, we plot the trajectories of $\mathbf{a}$, $\mathbf{v}$, and $\mathbf{d}$ at $(0.64,0.32)$, and obtain the following plot
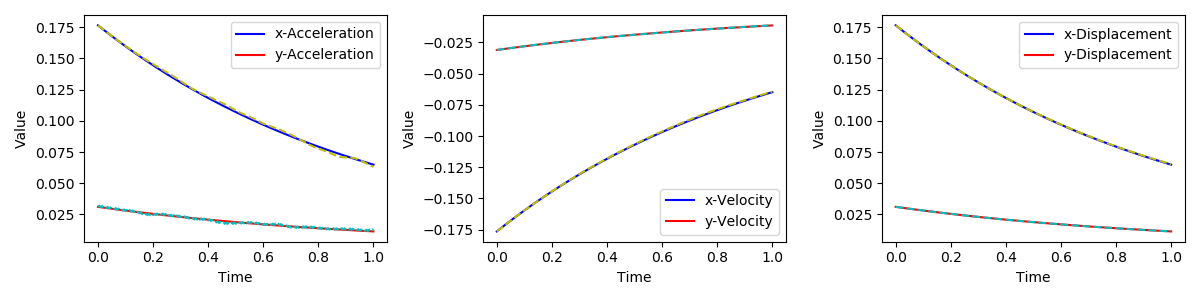
!!! info
When we have (time-dependent) Dirichlet boundary conditions, we need to impose the boundary acceleration in each time step. This can be achieved using `extsolve` in [`αscheme`](@ref).
```julia
function solver(A, rhs, i)
A, Abd = fem_impose_Dirichlet_boundary_condition(A, bd, m, n, h)
rhs = rhs - Abd * abd[i]
rhs = scatter_update(rhs, [bd; bd .+ (m+1)*(n+1)], abd[i])
return A\rhs
end
d, u, a = αscheme(M, spzero(2(m+1)*(n+1)), K, F, d0, u0, a0, ts; extsolve=solver, ρ = ρ )
```
Basically, we have
$$A_{II} a_I + A_{IB} a_B = f \Rightarrow A_{II} a_I = f-A_{IB}a_B$$
and $a_B$(`abd`) is the acceleration from the Dirichlet boundary condition.
Here is a script for demonstrating how to impose the Dirichlet boundary condition
```julia
using Revise
using ADCME
using AdFem
using PyPlot
n = 20
m = 2n
NT = 200
ρ = 0.5
Δt = 1/NT
h = 1/n
x = zeros((m+1)*(n+1))
y = zeros((m+1)*(n+1))
for i = 1:m+1
for j = 1:n+1
idx = (j-1)*(m+1)+i
x[idx] = (i-1)*h
y[idx] = (j-1)*h
end
end
bd = bcnode("all", m, n, h)
u1 = (x,y,t)->exp(-t)*(0.5-x)^2*(2-y)^2
u2 = (x,y,t)->exp(-t)*(0.5-x)*(0.5-y)
ts = Δt * ones(NT)
dt = αscheme_time(ts, ρ = ρ )
F = zeros(NT, 2(m+1)*(n+1))
for i = 1:NT
t = dt[i]
f1 = (x,y)->((x - 0.5)^2*(y - 2)^2 - 0.740740740740741*(x - 0.5)^2 - 3.20987654320988*(y - 2)^2 - 1.23456790123457)*exp(-t)
f2 = (x,y)->(-3.93827160493827*x*y + 9.37654320987654*x + 1.96913580246914*y - 4.68827160493827)*exp(-t)
fval1 = eval_f_on_gauss_pts(f1, m, n, h)
fval2 = eval_f_on_gauss_pts(f2, m, n, h)
F[i,:] = compute_fem_source_term(fval1, fval2, m, n, h)
end
abd = zeros(NT, (m+1)*(n+1)*2)
dt = αscheme_time(ts, ρ = ρ )
for i = 1:NT
t = dt[i]
abd[i,:] = [(@. u1(x, y, t)); (@. u2(x, y, t))]
end
abd = constant(abd[:, [bd; bd .+ (m+1)*(n+1)]])
E = 1.0
ν = 0.35
H = E/(1+ν)/(1-2ν)*[
1-ν ν 0
ν 1-ν 0
0 0 (1-2ν)/2
]
M = constant(compute_fem_mass_matrix(m, n, h))
K = constant(compute_fem_stiffness_matrix(H, m, n, h))
a0 = [(@. u1(x, y, 0.0)); (@. u2(x, y, 0.0))]
u0 = -[(@. u1(x, y, 0.0)); (@. u2(x, y, 0.0))]
d0 = [(@. u1(x, y, 0.0)); (@. u2(x, y, 0.0))]
function solver(A, rhs, i)
A, Abd = fem_impose_Dirichlet_boundary_condition(A, bd, m, n, h)
rhs = rhs - Abd * abd[i]
rhs = scatter_update(rhs, [bd; bd .+ (m+1)*(n+1)], abd[i])
return A\rhs
end
d, u, a = αscheme(M, spzero(2(m+1)*(n+1)), K, F, d0, u0, a0, ts; extsolve=solver, ρ = ρ )
sess = Session()
d_, u_, a_ = run(sess, [d, u, a])
function plot_traj(idx)
figure(figsize=(12,3))
subplot(131)
plot((0:NT)*Δt, u1.(x[idx], y[idx],(0:NT)*Δt), "b-", label="x-Acceleration")
plot((0:NT)*Δt, a_[:,idx], "y--", markersize=2)
plot((0:NT)*Δt, u2.(x[idx], y[idx],(0:NT)*Δt), "r-", label="y-Acceleration")
plot((0:NT)*Δt, a_[:,idx+(m+1)*(n+1)], "c--", markersize=2)
legend()
xlabel("Time")
ylabel("Value")
subplot(133)
plot((0:NT)*Δt, u1.(x[idx], y[idx],(0:NT)*Δt), "b-", label="x-Displacement")
plot((0:NT)*Δt, d_[:,idx], "y--", markersize=2)
plot((0:NT)*Δt, u2.(x[idx], y[idx],(0:NT)*Δt), "r-", label="y-Displacement")
plot((0:NT)*Δt, d_[:,idx+(m+1)*(n+1)], "c--", markersize=2)
legend()
xlabel("Time")
ylabel("Value")
subplot(132)
plot((0:NT)*Δt, -u1.(x[idx], y[idx],(0:NT)*Δt), "b-", label="x-Velocity")
plot((0:NT)*Δt, u_[:,idx], "y--", markersize=2)
plot((0:NT)*Δt, -u2.(x[idx], y[idx],(0:NT)*Δt), "r-", label="y-Velocity")
plot((0:NT)*Δt, u_[:,idx+(m+1)*(n+1)], "c--", markersize=2)
legend()
xlabel("Time")
ylabel("Value")
tight_layout()
end
idx2 = (n÷3)*(m+1) + m÷2
plot_traj(idx2)
```
## Example: Viscosity
In this section, we show how to use the generalized $\alpha$ scheme to solve the viscosity problem. The governing equation is given by
$$\begin{aligned}
\sigma_{3j,j} + f &= \ddot u \\
\sigma_{3j} &= \dot \epsilon_{3j}
\end{aligned}$$
where $u(x,y,t)$ is the displacement in the $z$-direction. We assume zero Dirichlet boundary condition, the computational domain is $[0,2]\times [0,1]$, and the exact solution is
$$u(x, y, t) = e^{-t} x(2-x)y(1-y)$$
The weak form of the equation is
$$\int_\Omega \ddot u\delta u + \int_\Omega \dot \epsilon\delta \epsilon = \int_\Omega f \delta u$$
In the discretization form we have
$$M\mathbf{a} + K \mathbf{v} = \mathbf{F}$$
```julia
using ADCME
using AdFem
n = 50
m = 2n
NT = 200
ρ = 0.1
Δt = 1/NT
h = 1/n
x = zeros((m+1)*(n+1))
y = zeros((m+1)*(n+1))
for i = 1:m+1
for j = 1:n+1
idx = (j-1)*(m+1)+i
x[idx] = (i-1)*h
y[idx] = (j-1)*h
end
end
bd = bcnode("all", m, n, h)
uexact = (x,y,t)->exp(-t)*x*(2-x)*y*(1-y)
ts = Δt * ones(NT)
dt = αscheme_time(ts, ρ = ρ )
F = zeros(NT, (m+1)*(n+1))
for i = 1:NT
t = dt[i]
f = (x,y)->uexact(x, y, t) -2*(y-y^2+2x-x^2)*exp(-t)
fval = eval_f_on_gauss_pts(f, m, n, h)
F[i,:] = compute_fem_source_term1(fval, m, n, h)
end
M = constant(compute_fem_mass_matrix1(m, n, h))
K = constant(compute_fem_stiffness_matrix1(diagm(0=>ones(2)), m, n, h))
a0 = @. x*(2-x)*y*(1-y)
u0 = @. -x*(2-x)*y*(1-y)
d0 = @. x*(2-x)*y*(1-y)
function solver(A, rhs)
A, _ = fem_impose_Dirichlet_boundary_condition1(A, bd, m, n, h)
rhs = scatter_update(rhs, bd, zeros(length(bd)))
return A\rhs
end
d, u, a = αscheme(M, K, spzero((m+1)*(n+1)), F, d0, u0, a0, ts; solve=solver, ρ = ρ )
sess = Session()
d_, u_, a_ = run(sess, [d, u, a])
function plot_traj(idx)
figure(figsize=(12,3))
subplot(131)
plot((0:NT)*Δt, uexact.(x[idx], y[idx],(0:NT)*Δt), "-", label="Acceleration")
plot((0:NT)*Δt, a_[:,idx], "--", markersize=2)
legend()
xlabel("Time")
ylabel("Value")
subplot(133)
plot((0:NT)*Δt, uexact.(x[idx], y[idx],(0:NT)*Δt), "-", label="Displacement")
plot((0:NT)*Δt, d_[:,idx], "--", markersize=2)
legend()
xlabel("Time")
ylabel("Value")
subplot(132)
plot((0:NT)*Δt, -uexact.(x[idx], y[idx],(0:NT)*Δt), "-", label="Velocity")
plot((0:NT)*Δt, u_[:,idx], "--", markersize=2)
legend()
xlabel("Time")
ylabel("Value")
tight_layout()
end
idx = (n÷2)*(m+1) + m÷2
idx2 = (n÷3)*(m+1) + m÷3
plot_traj(idx2)
```
Using the above code, we plot the trajectories of $\mathbf{a}$, $\mathbf{v}$, and $\mathbf{d}$ at $(0.64,0.32)$, and obtain the following plot
 | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 1243 | # API Reference
## Core Functions
```@autodocs
Modules = [ADCME]
Pages = ["ADCME.jl", "core.jl", "run.jl"]
```
## Variables
```@autodocs
Modules = [ADCME]
Pages = ["variable.jl"]
```
## Random Variables
```@autodocs
Modules = [ADCME]
Pages = ["random.jl"]
```
## Sparse Matrix
```@autodocs
Modules = [ADCME]
Pages = ["sparse.jl"]
```
## Operations
```@autodocs
Modules = [ADCME]
Pages = ["ops.jl"]
```
## IO
```@autodocs
Modules = [ADCME]
Pages = ["io.jl"]
```
## Optimization
```@autodocs
Modules = [ADCME]
Pages = ["optim.jl"]
```
## Neural Networks
```@autodocs
Modules = [ADCME]
Pages = ["layers.jl"]
```
## Generative Neural Nets
```@autodocs
Modules = [ADCME]
Pages = ["gan.jl"]
```
## Tools
```@autodocs
Modules = [ADCME]
Pages = ["extra.jl", "kit.jl", "sqlite.jl"]
```
## ODE
```@autodocs
Modules = [ADCME]
Pages = ["ode.jl"]
```
## Function Approximators
```@docs
RBF2D
RBF3D
interp1
```
## Optimal Transport
```@autodocs
Modules = [ADCME]
Pages = ["ot.jl"]
```
## MPI
```@autodocs
Modules = [ADCME]
Pages = ["mpi.jl"]
```
## Toolchain
```@autodocs
Modules = [ADCME]
Pages = ["toolchain.jl", "gpu.jl"]
```
## Misc
```@autodocs
Modules = [ADCME]
Pages = ["misc.jl"]
```
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 1408 | # Overview
In this section, we present some applications of ADCME to physics based machine learning.
We design data-driven algorithms for estimating unknown parameters, functions, functionals, and stochastic processes to physical or statistical models. One highlight of the applications is using neural networks to approximate the unknowns, and at the same time preserving the physical constraints such as conservation laws. We believe that as deep learning technology continues to grow, building an AD tool based on the deep learning framework will benefit scientific computing and helps solve long standing challenging inverse problems. Meanwhile, we can leverage the knowledge of physical laws to reduce the amount of data required for training deep neural networks.
This goal is achieved by the insights into the connection between deep learning algorithms and inverse modeling algorithm via automatic differentiation.
**Sample Applications**
[Adversarial Numerical Analysis](./apps_ana.md)
[Intelligent Automatic Differentiation ](./apps_ad.md)
[Learning Constitutive Relations from Indirect Observations Using Deep Neural Networks](./apps_constitutive_law.md)
[Calibrating Multivariate Lévy Processes with Neural Networks](./apps_levy.md)
[General Seismic Inversion using Automatic Differentiation](./apps_adseismic.md)
[Symmetric Positive Definite Neural Networks (SPD-NN)](./apps_nnfem.md) | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 2385 | # Intelligent Automatic Differentiation
---
Kailai Xu, Dongzhuo Li, Eric Darve, and Jerry M. Harris. "[Learning Hidden Dynamics using Intelligent Automatic Differentiation](https://arxiv.org/abs/1912.07547)"
Dongzhuo Li, Kailai Xu, Jerry M. Harris, and Eric Darve. "[Time-lapse Full Waveform Inversion for Subsurface Flow Problems with Intelligent Automatic Differentiation](https://arxiv.org/abs/1912.07552)"
[Project Website](https://github.com/lidongzh/FwiFlow.jl)
---
We treat physical simulations as a chain of multiple differentiable operators, such as discrete Laplacian evaluation, a Poisson solver and a single implicit time stepping for nonlinear PDEs. They are like building blocks that can be assembled to make simulation tools for new physical models.
Those operators are differentiable and integrated in a computational graph so that the gradients can be computed automatically and efficiently via analyzing the dependency in the graph. Independent operators are parallelized executed. With the gradients we can perform gradient-based PDE-constrained optimization for inverse problems.

This view of numerical simulation enables us to develope very sophisticated tools for inverse modeling: we decouple the individual operators and implement a forward/backward for each of them; they are consolidated using ADCME to create a computational graph. The computational dependency is then parsed and gradients are automatically computed based on the dependency. For example, in this work, we coupled multiphysics and obtain the gradients of the objective function with respect to the hidden dynamics parameters (i.e., permeability). This can be quite time-consuming and error-prone if we are going to derive the gradients by hand, implement and debug. With ADCME, we "chain" all the operators and the gradients are obtained automatically.
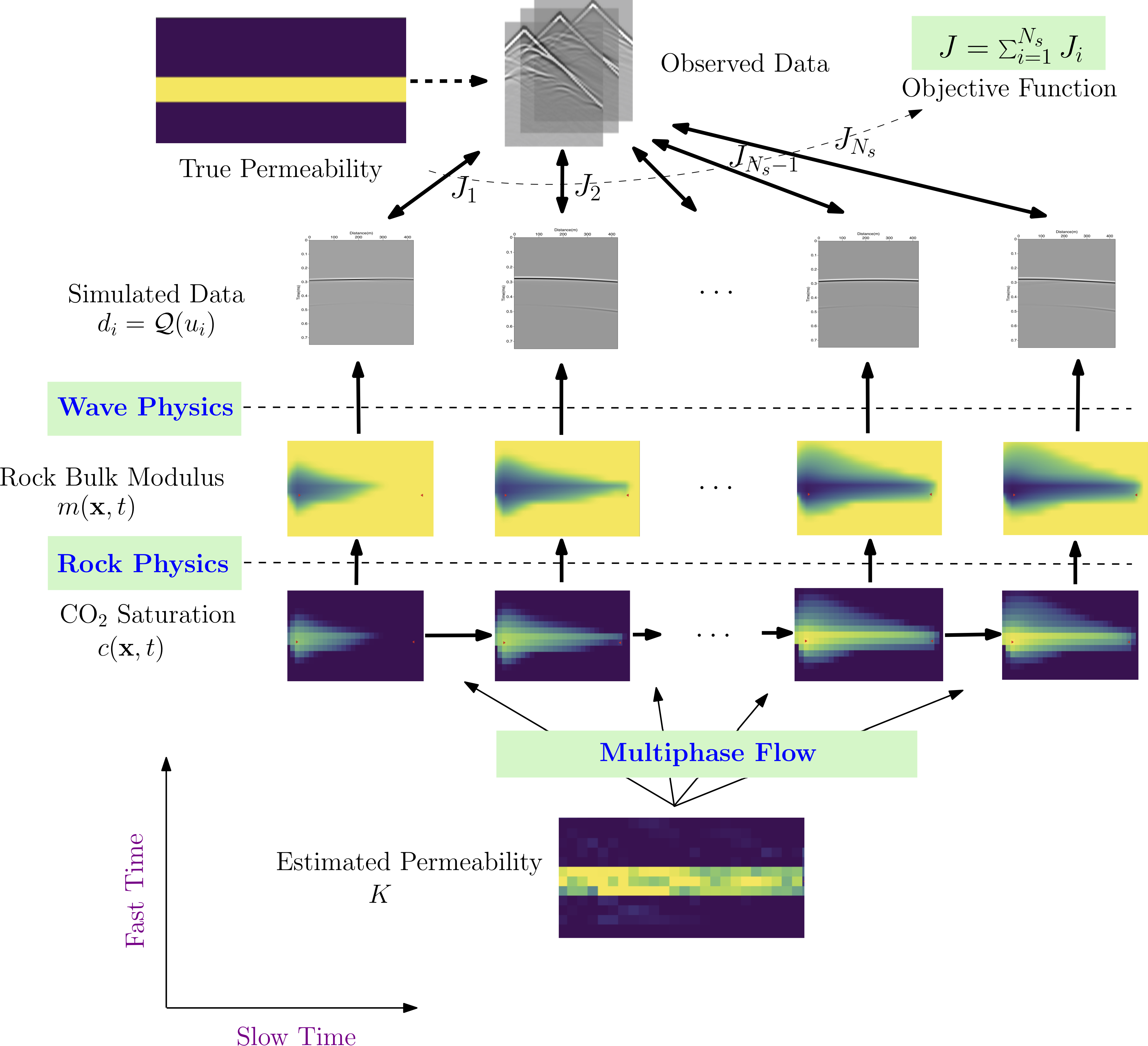
We call this technique **intelligent automatic differentiation**, since we can design our own operators for performance and those operators are submodules that can be flexibly replaced and reused. For more details, see [FwiFlow.jl](https://github.com/lidongzh/FwiFlow.jl), a package focused on elastic full waveform inversion for subsurface flow problems.
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 2054 | # General Seismic Inversion using Automatic Differentiation
---
Weiqiang Zhu (**co-first author**), Kailai Xu (**co-first author**), Eric Darve, and Gregory C. Beroza
[Project Website](https://github.com/kailaix/ADSeismic.jl)
---
Imaging Earth structure or seismic sources from seismic data involves minimizing a target misfit function, and is commonly solved through gradient-based optimization. The adjoint-state method has been developed to compute the gradient efficiently; however, its implementation can be time-consuming and difficult. We develop a general seismic inversion framework to calculate gradients using reverse-mode automatic differentiation. The central idea is that adjoint-state methods and reverse-mode automatic differentiation are mathematically equivalent. The mapping between numerical PDE simulation and deep learning allows us to build a seismic inverse modeling library, ADSeismic, based on deep learning frameworks, which supports high performance reverse-mode automatic differentiation on CPUs and GPUs. We demonstrate the performance of ADSeismic on inverse problems related to velocity model estimation, rupture imaging, earthquake location, and source time function retrieval. ADSeismic has the potential to solve a wide variety of inverse modeling applications within a unified framework.
| Connection Between the Adjoint-State Method and Automatic Differentiation | Remarkable Multi-GPU Acceleration | Earthquake Location and Source-Time Function Inversion |
| ------------------------------------------------------------ | ----------------------------------------------- | ------------------------------------------------------------ |
|  | 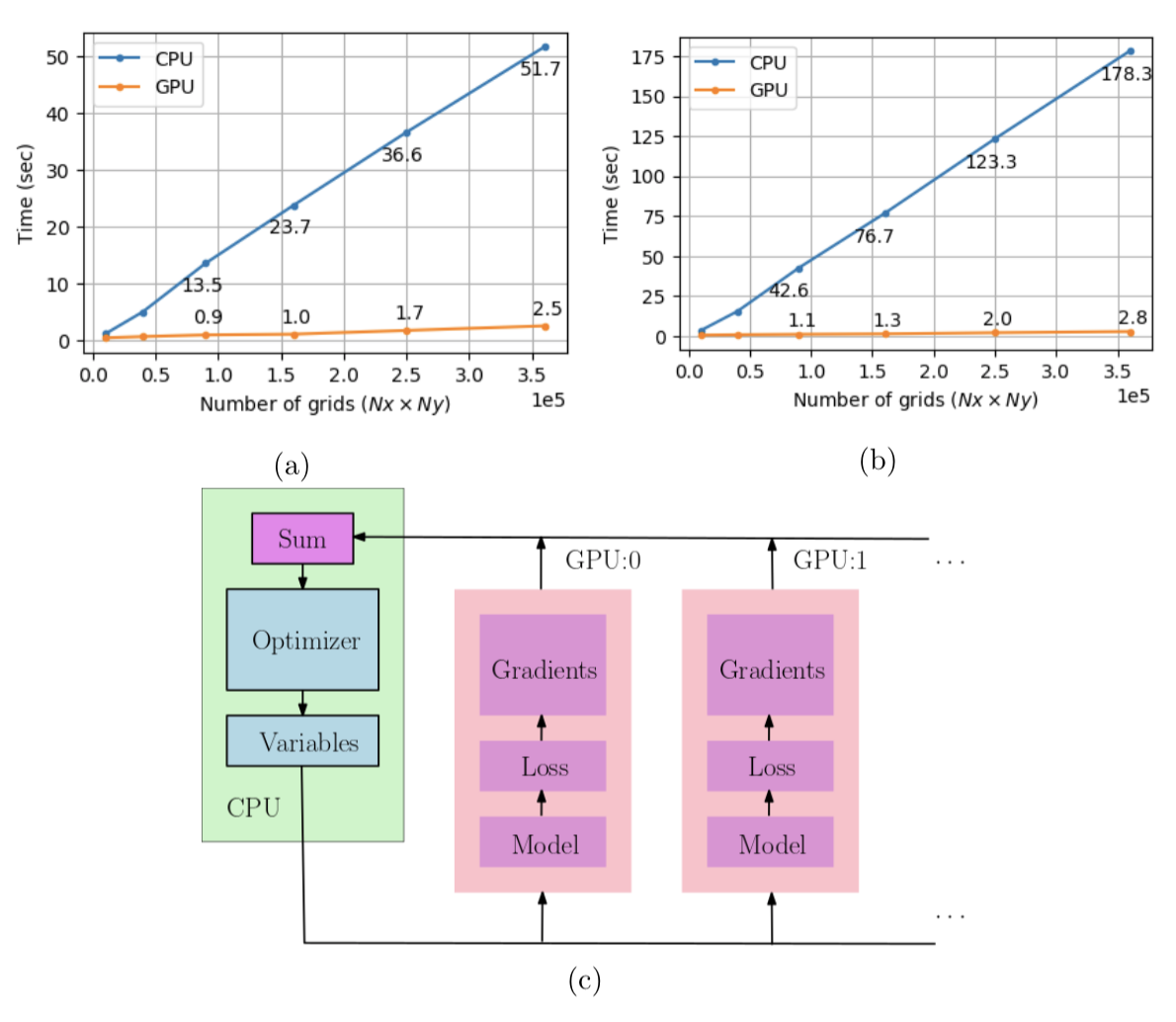 |  |
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 2404 | # Adversarial Numerical Analysis
---
Kailai Xu, and Eric Darve. "[Adversarial Numerical Analysis for Inverse Problems](https://arxiv.org/abs/1910.06936)"
[Project Website](https://github.com/kailaix/GAN)
---
Many scientific and engineering applications are formulated as inverse problems associated with stochastic models. In such cases the unknown quantities are distributions. The applicability of traditional methods is limited because of their demanding assumptions or prohibitive computational consumptions; for example, maximum likelihood methods require closed-form density functions, and Markov Chain Monte Carlo needs a large number of simulations.
Consider the forward model
```math
x = F(w, \theta)
```
Here $w$ is a known stochastic process such as Gaussian processes, $\theta$ is an unknown parameter, distribution or stochastic processes. Consequently, the output of the model $x$ is also a stochastic process. $F$ can be a very complicated model such as a system of partial differential equations. Many models fall into this category; here we solve an inverse modeling problem of boundary value Poisson equations
$$\begin{cases}
-\nabla \cdot (a(x)\nabla u(x)) = 1 & x\in(0,1)\\\\
u(0) = u(1) = 0 & \text{otherwise}
\end{cases}$$
```math
a(x) = 1-0.9\exp\left( -\frac{(x-\mu)^2}{2\sigma^2} \right)
```
Here ($\mu$, $\sigma$) is subject to unknown distribution ($\theta$ in the forward model). $w=\emptyset$ and $x$ is the solution to the equation, $u$. Assume we have observed a set of solutions $u_i$, and we want to estimate the distribution of ($\mu$, $\sigma$). Adversarial numerical analysis works as follows
1. The distribution ($\mu$, $\sigma$) is parametrized by a deep neural network $G_{\eta}$.
2. For each instance of ($\mu$, $\sigma$) sampled from the neural network parametrized distribution, we can compute a solution $u_{\mu, \sigma}$ using the finite difference method.
3. We compute a metric between the *distribution* $u_{\mu, \sigma}$ and $u_i$ with a discriminative neural network $D_{\xi}$.
4. Minimize the metric by adjusting the weights of $G_{\eta}$ and $D_{\xi}$.
The distribution of ($\mu$, $\sigma$) is given by $G_{\eta}$. The following plots show the workflow of adversarial numerical analysis and a sample result for the Dirichlet distribution.

| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 2662 | # Learning Constitutive Relations from Indirect Observations Using Deep Neural Networks
---
Huang, Daniel Z. (**co-first author**), Kailai Xu (**co-first author**), Charbel Farhat, and Eric Darve. "[Learning Constitutive Relations from Indirect Observations Using Deep Neural Networks](https://arxiv.org/abs/1905.12530)"
[Project Website](https://github.com/kailaix/UQ)
---
We present a new approach for predictive modeling and its uncertainty quantification for mechanical systems, where coarse-grained models such as constitutive relations are derived directly from observation data. We explore the use of neural networks to represent the unknowns functions (e.g., constitutive relations). Its counterparts, like piecewise linear functions and radial basis functions, are compared, and the strength of neural networks is explored. The training and predictive processes in this framework seamlessly combine the finite element method, automatic differentiation, and neural networks (or its counterparts). Under mild assumptions, we establish convergence guarantees. This framework also allows uncertainty quantification analysis in the form of intervals of confidence. Numerical examples on a multiscale fiber-reinforced plate problem and a nonlinear rubbery membrane problem from solid mechanics demonstrate the effectiveness of the framework.
The solid mechanics equation can be formulated as
```math
\mathcal{P}(u(\mathbf{x}), \mathcal{M}(u(\mathbf{x}),\dot u(\mathbf{x}), \mathbf{x})) = \mathcal{F}(u(\mathbf{x}), \mathbf{x}, p)
```
where $u$ is the displacement, $\mathbf{x}$ is the location, $p$ is the external pressure, $\mathcal{F}$ is the external force, $\mathcal{M}(u(\mathbf{x}),\dot u(\mathbf{x}), \mathbf{x})$ is the stress ($\mathcal{M}$ is also called the constitutive law), $\mathcal{P}(u(\mathbf{x}), \mathcal{M}(u(\mathbf{x}),\dot u(\mathbf{x}), \mathbf{x}))$ is the internal force. For a new material or nonhomogeneous material, the constitutive relation $\mathcal{M}$ is not known and we want to estimate it. In laboratory, usually only $u(\mathbf{x})$ can be measured but the stress cannot. The idea is to substitute the constitutive law relation--in this work, we assume $\mathcal{M}$ only depends on $u(\mathbf{x})$ and the neural network is $\mathcal{M}_{\theta}(u(\mathbf{x}))$, where $\theta$ is the unknown parameter.
We train the neural network by solving the optimization problem
```math
\min_{\theta}\|\mathcal{P}(\mathbf{u}, \mathcal{M}_{\theta}(\mathbf{u})) - \mathcal{F}(\mathbf{u}, \mathbf{x}, p) \|^2_2
```

| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 3671 | # Calibrating Multivariate Lévy Processes with Neural Networks
---
Kailai Xu and Eric Darve. "[Calibrating Multivariate Lévy Processes with Neural Networks](https://arxiv.org/abs/1812.08883)"
[Project Website](https://github.com/kailaix/LevyNN.jl)
---
Calibrating a Lévy process usually requires characterizing its jump distribution. Traditionally this problem can be solved with nonparametric estimation using the empirical characteristic functions (ECF), assuming certain regularity, and results to date are mostly in 1D. For multivariate Lévy processes and less smooth Lévy densities, the problem becomes challenging as ECFs decay slowly and have large uncertainty because of limited observations. We solve this problem by approximating the Lévy density with a parametrized functional form; the characteristic function is then estimated using numerical integration. In our benchmarks, we used deep neural networks and found that they are robust and can capture sharp transitions in the Lévy density. They perform favorably compared to piecewise linear functions and radial basis functions. The methods and techniques developed here apply to many other problems that involve nonparametric estimation of functions embedded in a system model.
The Lévy process can be described by the Lévy-Khintchine formula
``\phi({\xi}) = \mathbb{E}[e^{\mathrm{i} \langle {\xi}, \mathbf{X}_t \rangle}] =\exp\left[t\left( \mathrm{i} \langle \mathbf{b}, {\xi} \rangle - \frac{1}{2}\langle {\xi}, \mathbf{A}{\xi}\rangle +\int_{\mathbb{R}^d} \left( e^{\mathrm{i} \langle {\xi}, \mathbf{x}\rangle} - 1 - \mathrm{i} \langle {\xi}, \mathbf{x}\rangle \mathbf{1}_{\|\mathbf{x}\|\leq 1}\right)\nu(d\mathbf{x})\right) \right]``
Here the multivariate Lévy process is described by three parameters: a positive semi-definite matrix $\mathbf{A} = {\Sigma}{\Sigma}^T \in \mathbb{R}^{d\times d}$, where ${\Sigma}\in \mathbb{R}^{d\times d}$; a vector $\mathbf{b}\in \mathbb{R}^d$; and a measure $\nu\in \mathbb{R}^d\backslash\{\mathbf{0}\}$.
Given a sample path $\mathbf{X}_{i\Delta t}$, $i=1,2,3,\ldots$, we focus on estimating $\mathbf{b}$, $\mathbf{A}$ and $\nu$. In this work, we focus on the functional inverse problem--estimate $\nu$--and assume $\mathbf{b}=0,\mathbf{A}=0$. The idea is
* The Lévy density is approximated by a parametric functional form---such as piecewise linear functions---with parameters $\theta$,
```math
\nu(\mathbf{x}) \approx \nu_{\theta}(\mathbf{x})
```
* The characteristic function is approximated by numerical integration
```math
\phi({\xi})\approx \phi_{\theta}({\xi}) := \exp\left[ \Delta t \sum_{i=1}^{n_q} \left(e^{\mathrm{i} \langle{\xi}, \mathbf{x}_i \rangle}-1-\mathrm{i}\langle{\xi}, \mathbf{x}_i \rangle\mathbf{1}_{\|\mathbf{x}_i\|\leq 1} \right)\nu_{\theta}(\mathbf{x}_i) w_i \right]
```
where $\{(\mathbf{x}_i, w_i)\}_{i=1}^{n_q}$ are quadrature nodes and weights.
* The empirical characteristic functions are computed given observations $\{\mathbf{X}_{i\Delta t}\}_{i=0}^n$
```math
\hat\phi_n({\xi}) := \frac{1}{n}\sum_{i=1}^n \exp(\mathrm{i}\langle {\xi}, \mathbf{X}_{i\Delta t}-\mathbf{X}_{(i-1)\Delta t}\rangle ),\ {\xi} \in \mathbb{R}^d
```
* Solve the following optimization problem with a gradient based method. Here $\{{\xi}_i \}_{i=1}^m$ are collocation points depending on the data.
```math
\min_{\theta}\frac{1}{m} \sum_{i=1}^m \|\hat\phi_n({\xi}_i)-\phi_{\theta}({\xi}_i) \|^2
```
We show the schematic description of the method and some results on calibrating a discontinuous Lévy density function $\nu$.
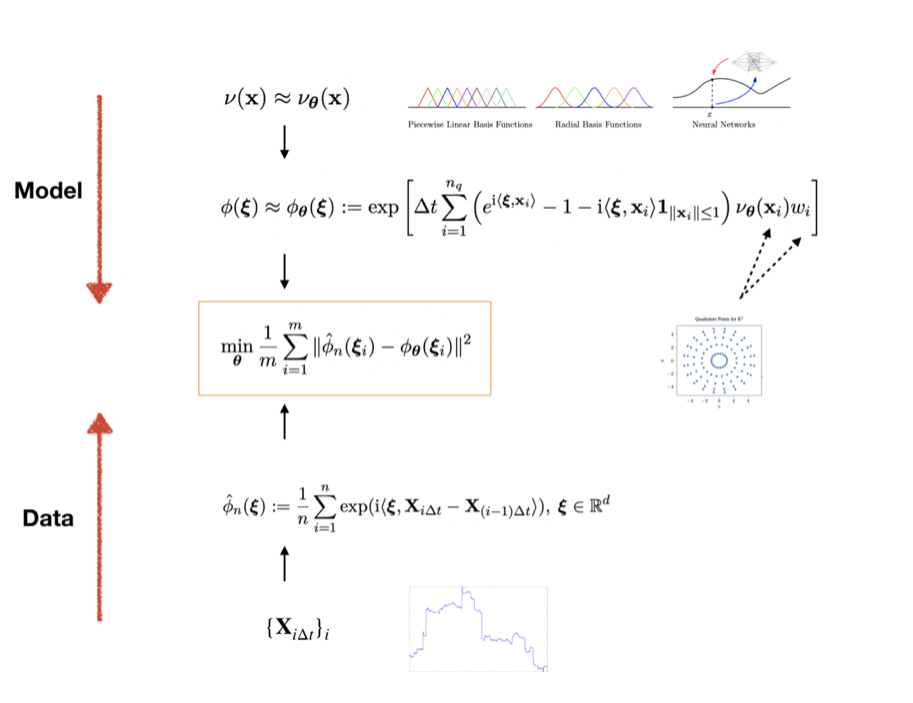
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 4174 | # Symmetric Positive Definite Neural Networks (SPD-NN)
---
Kailai Xu (**co-first author**), Huang, Daniel Z. (**co-first author**), and Eric Darve. "Learning Constitutive Relations using Symmetric Positive Definite Neural Networks"
[Project Website](https://github.com/kailaix/NNFEM.jl)
---
Material modeling aims to construct constitutive models to describe the relationship between strain and stress, in which the relationship may be hysteresis. The constitutive relations can be derived from microscopic interactions between multiscale structures or between atoms. However, the first-principles simulations, which resolve all these interactions, remain prohibitively expensive. This motivates to learn a data-driven constitutive relation that expresses the mapping from strain tensors (possibly with historic information) to stress tensors.
In a [previous application](https://kailaix.github.io/ADCME.jl/dev/apps_constitutive_law/), we showed how to learn a constitutive relation, which is a (nonlinear) map from strain tensors to stress tensors, from state variables in a static equation. However, many constitutive relations also depend on the historic information, such as (elasto-)plasticity and viscosity. The constitutive relation is much more complex since they have the form
$${\sigma}(t) = \mathcal{M}({\epsilon}(t), \mathcal{I}(t))$$
where $t$ is the time, $\sigma$, $\epsilon$ are strain and stress tensors, $\mathcal{I}$ contains the historic information in $[0,t)$, and $\mathcal{M}$ is an unknown function. This is a high dimensional mapping and traditional methods, such as piecewise linear functions, suffer from the curse of dimensionality problem. This issue motivates us to use neural network as surrogate models.
However, typically we cannot measure the stress directly and therefore a strain-stress pair training data set is not available. The idea is to plug the neural network based constitutive relation into physical laws, i.e., the kinematic and kinetic equations of motion, and obtain a hypothetical displacement $u$. $u$ is a quantity which we can measure. We can find the optimal weights and biases of the neural network by minimizing the discrepancy between $u$ and observed displacement. This procedure is done using automatic differentiation, where the gradients are back-propagated through both the numerical solver and the neural network.
The challenge here is that **the numerical solver is unstable if we plug in a random neural network based constitutive relation**. Indeed, numerical solvers are developed based on certain physical assumptions, and a neural network from random choices may go wild and can be quite ill-behaved. The idea is to **add physical constraints** to the neural network. The solution we proposed is the symmetric positive definite neural network (SPD-NN): instead of modeling the constitutive relation directly, we model the tangent stiffness matrix. To be more specific,
$$\Delta {\sigma} =\mathsf{L}_{\theta}\mathsf{L}_{\theta}^T \Delta {\epsilon}$$
where $\mathsf L_\theta$ is a Cholesky factor and therefore $\mathsf{L}_{\theta}\mathsf{L}_{\theta}^T$ is SPD. The formulation preserves both time consistency and weak convexity of the strain energy. In specific applications, the formulation is further customized. For example,
$${\sigma}^{n+1} = \mathsf{M}_{\theta}({\epsilon}^{n+1}, {\epsilon}^{n}, {\sigma}^{n}) := \left\{\begin{matrix}
& \mathsf{C}_{\theta}{\epsilon}^{n+1} & \text{Linear Elasticity}\\
&\mathsf{L}_{\theta}({\epsilon}^{n+1} )\mathsf{L}_{\theta}({\epsilon}^{n+1})^T({\epsilon}^{n+1} - {\epsilon}^{n}) + {\sigma}^{n} & \text{Nonlinear Elasticity}\\
& (1 - D(\sigma^{n}, \tilde{\sigma}_Y)) \sigma_{\mathrm{elasticity}}^{n+1} + D(\sigma^{n}, \tilde{\sigma}_Y) \sigma_{\mathrm{plasticity}}^{n+1} & \text{Elasto-Plasticity}
\end{matrix}\right.$$
As a final remark, the challenge in learning plasticity behavior is that we have to capture the loading and unloading transitions. In this case, the tangent stiffness matrix exhibits a discontinuity. To alleviate the problem, we adjust the neural network by using a transition function $D$ in the elasto-plasticity case. | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 12969 | # Bayesian Neural Networks
## Uncertainty Quantification
We want to quantify uncertainty. But what is uncertainty? In the literature, there are usually two types of uncertainty: **aleatoric**, the irreducible part of the uncertainty, and **epidemic**, the reducible part of the uncertainty. For example, when we flip a coin, the outcome of one experiment is intrinsically stochastic, and we cannot reduce the uncertainty by conducting more experiments. However, if we want to estimate the probability of heads, we can reduce the uncertainty of estimation by observing more experiments. In finance, the words for these two types of uncertainty is **systematic** and **non-systematic** uncertainty. The total uncertainty is composed of these two types of uncertainty.
| Statistics | Finance | Reducibility |
|------------|----------------|--------------|
| aleatoric | systematic | irreducible |
| epidemic | non-systematic | reducible |
## Bayesian Thinking
One popular approach for uncertainty quantification is the Bayesian method. One distinct characteristic of the Bayesian method is that we have a prior. The prior can be subjective: it is up to the researcher to pick and justify one. Even for the so-called non-informative prior, it introduces some bias if the posterior is quite different from the prior.
However, this should be the most exciting part of the Bayesian philosophy: as human beings, we do have prior knowledge on stochastic events. The prior knowledge can be domain specific knowledge, experience, or even opinions. As long as we can justify the prior well, it is fine.
## Bayesian Neural Network
The so-called Bayesian neural network is the application of the Bayesian thinking on neural networks. Instead of treating the weights and biases as deterministic numbers, we consider them as probability distributions with certain priors. As we collect more and more data, we can calculate the posteriors.
But why do we bother with the Bayesian approach? For example, if we just want to quantify the uncertainty in the prediction, suppose we have a point estimation $w$ for the neural network, we can perturb $w$ a little and run the forward inference. This process will give us many candidate values of the prediction, which serve as our uncertainty estimation.
If we think about it, it is actually an extreme case in the Bayesian approach: we actually use the **prior** to do uncertainty quantification. The perturbation is our prior, and we have not taken into account of the observed data for constructing the distribution except for that we get our point estimation $w$. The Bayesian approach goes a bit further: instead of just using a prior, we use data to calibrate our distribution, and this leads to the **posterior**.
The following figure shows training of a Bayesian network. The figure with the title "Prior" is obtained by using a prior distribution. From 1 to 3, the weight for the data (compared to the prior) is larger and larger. We can see the key idea of Bayesian methods is a trade-off game between how strongly we believe in our point estimation, and how eagerly we want to take the uncertainty exposed in the data into consideration.
| Point Estimation | Prior | 1 | 2 | 3 |
|------------------|------------|-------------|---|---|
|  |  |  |  |  |
```julia
using ADCME
using PyPlot
x0 = rand(100)
x0 = @. x0*0.4 + 0.3
x1 = collect(LinRange(0, 1, 100))
y0 = sin.(2π*x0)
w = Variable(fc_init([1, 20, 20, 20, 1]))
y = squeeze(fc(x0, [20, 20, 20, 1], w))
loss = sum((y - y0)^2)
sess = Session(); init(sess)
BFGS!(sess, loss)
y1 = run(sess, y)
plot(x0, y0, ".", label="Data")
x_dnn = run(sess, squeeze(fc(x1, [20, 20, 20, 1], w)))
plot(x1, x_dnn, "--", label="DNN Estimation")
legend()
w1 = run(sess, w)
##############################
μ = Variable(w1)
ρ = Variable(zeros(length(μ)))
σ = log(1+exp(ρ))
function likelihood(z)
w = μ + σ * z
y = squeeze(fc(x0, [20, 20, 20, 1], w))
sum((y - y0)^2) - sum((w-μ)^2/(2σ^2)) + sum((w-w1)^2)
end
function inference(x)
z = tf.random_normal((length(σ),), dtype=tf.float64)
w = μ + σ * z
y = squeeze(fc(x, [20, 20, 20, 1], w))|>squeeze
end
W = tf.random_normal((10, length(w)), dtype=tf.float64)
L = constant(0.0)
for i = 1:10
global L += likelihood(W[i])
end
y2 = inference(x1)
opt = AdamOptimizer(0.01).minimize(L)
init(sess)
# run(sess, L)
losses = []
for i = 1:2000
_, l = run(sess, [opt, L])
push!(losses, l)
@info i, l
end
Y = zeros(100, 1000)
for i = 1:1000
Y[:,i] = run(sess, y2)
end
for i = 1:1000
plot(x1, Y[:,i], "--", color="gray", alpha=0.5)
end
plot(x1, x_dnn, label="DNN Estimation")
plot(x0, y1, ".", label="Data")
legend()
##############################
# Naive Uncertainty Quantification
function inference_naive(x)
z = tf.random_normal((length(w1),), dtype=tf.float64)
w = w1 + log(2)*z
y = squeeze(fc(x, [20, 20, 20, 1], w))|>squeeze
end
y3 = inference(x1)
Y = zeros(100, 1000)
for i = 1:1000
Y[:,i] = run(sess, y3)
end
for i = 1:1000
plot(x1, Y[:,i], "--", color="gray", alpha=0.5)
end
plot(x1, x_dnn, label="DNN Estimation")
plot(x0, y1, ".", label="Data")
legend()
```
## Training the Neural Network
One caveat here is that deep neural networks may be hard to train, and we may get stuck at a local minimum. But even in this case, we can get an uncertainty quantification. But is it valid? No. The Bayesian approach assumes that your prior is reasonable. If we get stuck at a bad local minimum $w$, and use a prior $\mathcal{N}(w, \sigma I)$, then the results are not reliable at all. Therefore, to obtain a reasonable uncertainty quantification estimation, we need to make sure that our point estimation is valid.
## Mathematical Formulation
Now let us do the math.
Bayesian neural networks are different from plain neural networks in that weights and biases in Bayesian neural networks are interpreted in a probabilistic manner. Instead of finding a point estimation of weights and biases, in Bayesian neural networks, a prior distribution is assigned to the weights and biases, and a posterior distribution is obtained from the data. It relies on the Bayes formula
$$p(w|\mathcal{D}) = \frac{p(\mathcal{D}|w)p(w)}{p(\mathcal{D})}$$
Here $\mathcal{D}$ is the data, e.g., the input-output pairs of the neural network $\{(x_i, y_i)\}$, $w$ is the weights and biases of the neural network, and $p(w)$ is the prior distribution.
If we have a full posterior distribution $p(w|\mathcal{D})$, we can conduct predictive modeling using
$$p(y|x, \mathcal{D}) = \int p(y|x, w) p(w|\mathcal{D})d w$$
However, computing $p(w|\mathcal{D})$ is usually intractable since we need to compute the normalized factor $p(\mathcal{D}) = \int p(\mathcal{D}|w)p(w) dw$, which requires us to integrate over all possible $w$. Traditionally, Markov chain Monte Carlo (MCMC) has been used to sample from $p(w|\mathcal{D})$ without evaluating $p(\mathcal{D})$. However, MCMC can converge very slowly and requires a voluminous number of sampling, which can be quite expensive.
## Variational Inference
In Bayesian neural networks, the idea is to approximate $p(w|\mathcal{D})$ using a parametrized family $p(w|\theta)$, where $\theta$ is the parameters. This method is called **variational inference**. We minimize the KL divergeence between the true posterior and the approximate posterial to find the optimal $\theta$
$$\text{KL}(p(w|\theta)||p(w|\mathcal{D})) = \text{KL}(p(w|\theta)||p(W)) - \mathbb{E}_{p(w|\theta)}\log p(\mathcal{D}|w) + \log p(\mathcal{D})$$
Evaluating $p(\mathcal{D})\geq 0$ is intractable, so we seek to minimize a lower bound of the KL divergence, which is known as **variational free energy**
$$F(\mathcal{D}, \theta) = \text{KL}(p(w|\theta)||p(w)) - \mathbb{E}_{p(w|\theta)}\log p(\mathcal{D}|w)$$
In practice, thee variational free energy is approximated by the discrete samples
$$F(\mathcal{D}, \theta) \approx \frac{1}{N}\sum_{i=1}^N \left[\log p(w_i|\theta)) - \log p(w_i) - \log p(\mathcal{D}|w_i)\right]$$
## Parametric Family
In Baysian neural networks, the parametric family is usually chosen to be the Gaussian distribution. For the sake of automatic differentiation, we usually parametrize $w$ using
$$w = \mu + \sigma \otimes z\qquad z \sim \mathcal{N}(0, I) \tag{1}$$
Here $\theta = (\mu, \sigma)$. The prior distributions for $\mu$ and $\sigma$ are given as hyperparameters. For example, we can use a mixture of Gaussians as prior
$$\pi_1 \mathcal{N}(0, \sigma_1) + \pi_2 \mathcal{N}(0, \sigma_2)$$
The advantage of Equation 1 is that we can easily obtain the log probability $\log p(w|\theta)$.
Because $\sigma$ should always be positive, we can instead parametrize another parameter $\rho$ and transform $\rho$ to $\sigma$ using a softplus function
$$\sigma = \log (1+\exp(\rho))$$
## Example
Now let us consider a concrete example. The following example is adapted from [this post](http://krasserm.github.io/2019/03/14/bayesian-neural-networks/).
### Generating Training Data
We first generate some 1D training data
```julia
using ADCME
using PyPlot
using ProgressMeter
using Statistics
function f(x, σ)
ε = randn(size(x)...) * σ
return 10 * sin.(2π*x) + ε
end
batch_size = 32
noise = 1.0
X = reshape(LinRange(-0.5, 0.5, batch_size)|>Array, :, 1)
y = f(X, noise)
y_true = f(X, 0.0)
close("all")
scatter(X, y, marker="+", label="Training Data")
plot(X, y_true, label="Truth")
legend()
```
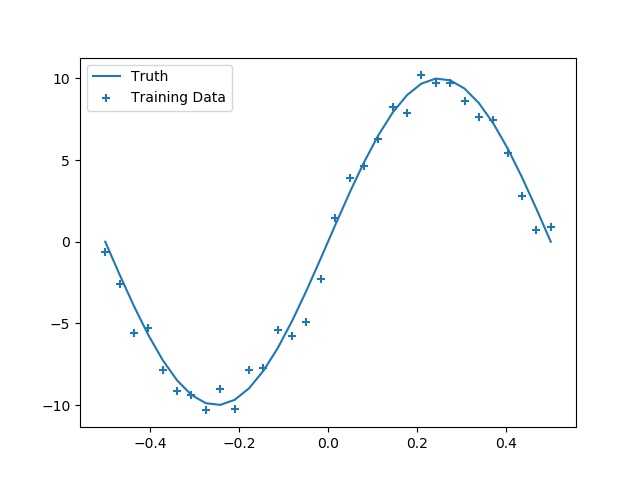
### Construct Bayesian Neural Network
```julia
mutable struct VariationalLayer
units
activation
prior_σ1
prior_σ2
prior_π1
prior_π2
Wμ
bμ
Wρ
bρ
init_σ
end
function VariationalLayer(units; activation=relu, prior_σ1=1.5, prior_σ2=0.1,
prior_π1=0.5)
init_σ = sqrt(
prior_π1 * prior_σ1^2 + (1-prior_π1)*prior_σ2^2
)
VariationalLayer(units, activation, prior_σ1, prior_σ2, prior_π1, 1-prior_π1,
missing, missing, missing, missing, init_σ)
end
function kl_loss(vl, w, μ, σ)
dist = ADCME.Normal(μ,σ)
return sum(logpdf(dist, w)-logprior(vl, w))
end
function logprior(vl, w)
dist1 = ADCME.Normal(constant(0.0), vl.prior_σ1)
dist2 = ADCME.Normal(constant(0.0), vl.prior_σ2)
log(vl.prior_π1*exp(logpdf(dist1, w)) + vl.prior_π2*exp(logpdf(dist2, w)))
end
function (vl::VariationalLayer)(x)
x = constant(x)
if ismissing(vl.bμ)
vl.Wμ = get_variable(vl.init_σ*randn(size(x,2), vl.units))
vl.Wρ = get_variable(zeros(size(x,2), vl.units))
vl.bμ = get_variable(vl.init_σ*randn(1, vl.units))
vl.bρ = get_variable(zeros(1, vl.units))
end
Wσ = softplus(vl.Wρ)
W = vl.Wμ + Wσ.*normal(size(vl.Wμ)...)
bσ = softplus(vl.bρ)
b = vl.bμ + bσ.*normal(size(vl.bμ)...)
loss = kl_loss(vl, W, vl.Wμ, Wσ) + kl_loss(vl, b, vl.bμ, bσ)
out = vl.activation(x * W + b)
return out, loss
end
function neg_log_likelihood(y_obs, y_pred, σ)
y_obs = constant(y_obs)
dist = ADCME.Normal(y_pred, σ)
sum(-logpdf(dist, y_obs))
end
ipt = placeholder(X)
x, loss1 = VariationalLayer(20, activation=relu)(ipt)
x, loss2 = VariationalLayer(20, activation=relu)(x)
x, loss3 = VariationalLayer(1, activation=x->x)(x)
loss_lf = neg_log_likelihood(y, x, noise)
loss = loss1 + loss2 + loss3 + loss_lf
```
### Optimization
We use an ADAM optimizer to optimize the loss function. In this case, quasi-Newton methods that are typically used for deterministic function optimization are not appropriate because the loss function essentially involves stochasticity.
Another caveat is that because the neural network may have many local minimum, we need to run the optimizer multiple times in order to obtain a good local minimum.
```julia
opt = AdamOptimizer(0.08).minimize(loss)
sess = Session(); init(sess)
@showprogress for i = 1:5000
run(sess, opt)
end
X_test = reshape(LinRange(-1.5,1.5,32)|>Array, :, 1)
y_pred_list = []
@showprogress for i = 1:10000
y_pred = run(sess, x, ipt=>X_test)
push!(y_pred_list, y_pred)
end
y_preds = hcat(y_pred_list...)
y_mean = mean(y_preds, dims=2)[:]
y_std = std(y_preds, dims=2)[:]
close("all")
plot(X_test, y_mean)
scatter(X[:], y[:], marker="+")
fill_between(X_test[:], y_mean-2y_std, y_mean+2y_std, alpha=0.5)
```

| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 4757 | # Convolutional Neural Network
The convolutional neural network (CNN) is one of the key building blocks for deep learning. Mathematically, it is a linear operator whose actions are "local", in the sense that each output only depends on a small number of inputs. These actions share the same kernel functions, and the sharing reduces the number of parameters significantly.
One remarkable feature of CNNs is that they are massively parallelizable. The parallesim makes CNNs very efficient on GPUs, which are good at doing a large number of simple tasks at the same time.
In the practical use of CNNs, we can stick to images, which have four dimensions: batch number, height, width, and channel. A CNN transforms the images to another images with the same four dimensions, but possibly with different heights, widths, and channels. In the following script, we use CNNs instead of fully connected neural networks to train a variational autoencoder. Readers can compare the results with [this article](./vae.md).
You are also encouraged to run the same script on CPUs and GPUs. You might get surprised at the huge performance gap for training CNNs on these two different computing environment. We also observe some CNN artifacts (the dots in the images).

```julia
using ADCME
using PyPlot
using MLDatasets
using ProgressMeter
using Images
mutable struct Generator
dim_z::Int64
layers::Array
end
function Generator( dim_z::Int64 = 100, ngf::Int64 = 8)
layers = [
Conv2DTranspose(ngf*32, 4, 1, use_bias=false)
BatchNormalization()
relu
Conv2DTranspose(ngf*16, 4, 1, padding="same", use_bias=false)
BatchNormalization()
relu
Conv2DTranspose(ngf*8, 4, 1, use_bias=false)
x -> pad(x, [
0 0
0 1
0 1
0 0
])
BatchNormalization()
relu
Conv2DTranspose(1, 4, 4, use_bias = false)
BatchNormalization()
sigmoid
]
Generator(dim_z, layers)
end
function (g::Generator)(z)
z = constant(z)
z = reshape(z, (-1, 1, 1, g.dim_z))
@info size(z)
for l in g.layers
z = l(z)
@info size(z)
end
return z
end
function encoder(x, n_hidden, n_output, rate)
local μ, σ
variable_scope("encoder") do
y = dense(x, n_hidden, activation = "elu")
y = dropout(y, rate, ADCME.options.training.training)
y = dense(y, n_hidden, activation = "tanh")
y = dropout(y, rate, ADCME.options.training.training)
y = dense(y, 2n_output)
μ = y[:, 1:n_output]
σ = 1e-6 + softplus(y[:,n_output+1:end])
end
return μ, σ
end
function decoder(z, n_hidden, n_output, rate)
Generator(dim_z)(z)
end
function autoencoder(xh, x, dim_img, dim_z, n_hidden, rate)
μ, σ = encoder(xh, n_hidden, dim_z, rate)
z = μ + σ .* tf.random_normal(size(μ), 0, 1, dtype=tf.float64)
y = decoder(z, n_hidden, dim_img, rate)
y = clip(y, 1e-8, 1-1e-8)
y = tf.reshape(y, (-1,32^2))
marginal_likelihood = sum(x .* log(y) + (1-x).*log(1-y), dims=2)
KL_divergence = 0.5 * sum(μ^2 + σ^2 - log(1e-8 + σ^2) - 1, dims=2)
marginal_likelihood = mean(marginal_likelihood)
KL_divergence = mean(KL_divergence)
ELBO = marginal_likelihood - KL_divergence
loss = -ELBO
return y, loss, -marginal_likelihood, KL_divergence
end
function step(epoch)
tx = train_x[1:batch_size,:]
@showprogress for i = 1:div(60000, batch_size)
idx = Array((i-1)*batch_size+1:i*batch_size)
run(sess, opt, x=>train_x[idx,:])
end
y_, loss_, ml_, kl_ = run(sess, [y, loss, ml, KL_divergence],
feed_dict = Dict(
ADCME.options.training.training=>false,
x => tx
))
println("epoch $epoch: L_tot = $(loss_), L_likelihood = $(ml_), L_KL = $(kl_)")
close("all")
for i = 1:3
for j = 1:3
k = (i-1)*3 + j
img = reshape(y_[k,:], 32, 32)'|>Array
img = imresize(img, 28, 28)
subplot(3,3,k)
imshow(img)
end
end
savefig("result$epoch.png")
end
n_hidden = 500
rate = 0.1
dim_z = 100
dim_img = 32^2
batch_size = 32
ADCME.options.training.training = placeholder(true)
x = placeholder(Float64, shape = [32, 32^2])
xh = x
y, loss, ml, KL_divergence = autoencoder(xh, x, dim_img, dim_z, n_hidden, rate)
opt = AdamOptimizer(1e-3).minimize(loss)
train_x_ = MNIST.traintensor(Float64);
train_x = zeros(60000, 32^2)
for i = 1:60000
train_x[i,:] = imresize(train_x_[:, :, i], 32, 32)[:]
end
sess = Session(); init(sess)
for i = 1:100
@info i
step(i)
end
``` | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 9546 | # Custom Optimizer
In this article, we describe how to make your custom optimizer
```@docs
CustomOptimizer
```
We will show here a few examples of custom optimizer. These examples can be cast to your specific applications.
## Ipopt Custom Optimizer
For a concrete example, let us consider using [Ipopt](https://github.com/JuliaOpt/Ipopt.jl) as a constrained optimization optimizer.
```julia
using Ipopt
using ADCME
IPOPT = CustomOptimizer() do f, df, c, dc, x0, x_L, x_U
n_variables = length(x0)
nz = length(dc(x0))
m = div(nz, n_variables) # Number of constraints
g_L, g_U = [-Inf;-Inf], [0.0;0.0]
function eval_jac_g(x, mode, rows, cols, values)
if mode == :Structure
rows[1] = 1; cols[1] = 1
rows[2] = 1; cols[2] = 1
rows[3] = 2; cols[3] = 1
rows[4] = 2; cols[4] = 1
else
values[:]=dc(x)
end
end
nele_jac = 0 # Number of non-zeros in Jacobian
prob = Ipopt.createProblem(n_variables, x_L, x_U, m, g_L, g_U, nz, nele_jac,
f, (x,g)->(g[:]=c(x)), (x,g)->(g[:]=df(x)), eval_jac_g, nothing)
addOption(prob, "hessian_approximation", "limited-memory")
addOption(prob, "max_iter", 100)
addOption(prob, "print_level", 2) # 0 -- 15, the larger the number, the more detailed the information
prob.x = x0
status = Ipopt.solveProblem(prob)
println(Ipopt.ApplicationReturnStatus[status])
println(prob.x)
prob.x
end
reset_default_graph() # be sure to reset graph before any optimization
x = Variable([1.0;1.0])
x1 = x[1]; x2 = x[2];
loss = x2
g = x1
h = x1*x1 + x2*x2 - 1
opt = IPOPT(loss, inequalities=[g], equalities=[h], var_to_bounds=Dict(x=>(-1.0,1.0)))
sess = Session(); init(sess)
minimize(opt, sess)
```
Here is a detailed description of the code
* `Ipopt.createProblem` has signature
```julia
function createProblem(
n::Int, # Number of variables
x_L::Vector{Float64}, # Variable lower bounds
x_U::Vector{Float64}, # Variable upper bounds
m::Int, # Number of constraints
g_L::Vector{Float64}, # Constraint lower bounds
g_U::Vector{Float64}, # Constraint upper bounds
nele_jac::Int, # Number of non-zeros in Jacobian
nele_hess::Int, # Number of non-zeros in Hessian
eval_f, # Callback: objective function
eval_g, # Callback: constraint evaluation
eval_grad_f, # Callback: objective function gradient
eval_jac_g, # Callback: Jacobian evaluation
eval_h = nothing) # Callback: Hessian evaluation
```
* Typically $\nabla c(x)$ is a $m\times n$ sparse matrix, where $m$ is the number of constraints, $n$ is the number of variables. `nz = length(dc(x0))` computes the number of nonzeros in the Jacobian matrix.
* `g_L`, `g_U` specify the constraint lower and upper bounds: $g_L \leq c(x) \leq g_U$. If $g_L=g_U=0$, the constraint is reduced to equality constraint. Each of the parameters should have the same length as the number of variables, i.e., $n$
* `eval_jac_g` has two modes. In the `Structure` mode, as we mentioned, the constraint $\nabla c(x)$ is a sparse matrix, and therefore we should specify the nonzero pattern of the sparse matrix in `row` and `col`. However, in our application, we usually assume a dense Jacobian matrix, and therefore, we can always use the following code for `Structure`
```julia
k = 1
for i = 1:div(nz, n_variables)
for j = 1:n_variables
rows[k] = i
cols[k] = j
k += 1
end
end
```
For the other mode, `eval_jac_g` simply assign values to the array.
* We can add optimions to the Ipopt optimizer via `addOptions`. See [here](https://coin-or.github.io/Ipopt/OPTIONS.html) for a full list of available options.
* To add callbacks, you can simply refactor your functions `f`, `df`, `c`, or `dc`.
## NLopt Custom Optimizer
Here is an example of using [NLopt](https://github.com/JuliaOpt/NLopt.jl) for optimization.
```julia
using ADCME
using NLopt
p = ones(10)
Con = CustomOptimizer() do f, df, c, dc, x0, x_L, x_U
opt = Opt(:LD_MMA, length(x0))
opt.upper_bounds = 10ones(length(x0))
opt.lower_bounds = zeros(length(x0))
opt.lower_bounds[end-1:end] = [-Inf, 0.0]
opt.xtol_rel = 1e-4
opt.min_objective = (x,g)->(g[:]= df(x); return f(x)[1])
inequality_constraint!(opt, (x,g)->( g[:]= dc(x);c(x)[1]), 1e-8)
(minf,minx,ret) = NLopt.optimize(opt, x0)
minx
end
reset_default_graph() # be sure to reset the graph before any operation
x = Variable([1.234; 5.678])
y = Variable([1.0;2.0])
loss = x[2]^2 + sum(y^2)
c1 = (x[1]-1)^2 - x[2]
opt = Con(loss, inequalities=[c1])
sess = Session(); init(sess)
opt.minimize(sess)
xmin = run(sess, x) # expected: (1., 0.)
```
Here is the detailed explanation
* NLopt solver takes the following parameters
```
algorithm
stopval # stop minimizing when an objective value ≤ stopval is found
ftol_rel
ftol_abs
xtol_rel
xtol_abs
constrtol_abs
maxeval
maxtime
initial_step # a vector, initial step size
population
seed
vector_storage # number of "remembered gradients" in algorithms such as "quasi-Newton"
lower_bounds
upper_bounds
```
For a full list of optimization algorithms, see [NLopt algorithms](https://nlopt.readthedocs.io/en/latest/NLopt_Algorithms/).
* You can provide upper and lower bounds either via `var_to_bounds` or inside `CustomOptimizer`.
## Drop-in Substitutes of `BFGS!`
### IPOPT
The following codes are for unconstrained optimizattion of `BFGS!` optimizer. Copy and execute the following code to have access to `IPOPT!` function.
```julia
using PyCall
using Ipopt
using ADCME
function IPOPT!(sess::PyObject, loss::PyObject, max_iter::Int64=15000;
verbose::Int64=0, vars::Array{PyObject}=PyObject[],
callback::Union{Function, Nothing}=nothing, kwargs...)
losses = Float64[]
loss_ = 0
cnt_ = -1
iter_ = 0
IPOPT = CustomOptimizer() do f, df, c, dc, x0, x_L, x_U
n_variables = length(x0)
nz = length(dc(x0))
m = div(nz, n_variables) # Number of constraints
# g_L, g_U = [-Inf;-Inf], [0.0;0.0]
g_L = Float64[]
g_U = Float64[]
function eval_jac_g(x, mode, rows, cols, values); end
function eval_f(x)
loss_ = f(x)
iter_ += 1
if iter_==1
push!(losses, loss_)
if !isnothing(callback)
callback(run(sess, vars), cnt_, loss_)
end
end
println("iter $iter_, current loss= $loss_")
return loss_
end
function eval_g(x, g)
if cnt_>=1
push!(losses, loss_)
if !isnothing(callback)
callback(run(sess, vars), cnt_, loss_)
end
end
cnt_ += 1
if cnt_>=1
println("================ ITER $cnt_ ===============")
end
g[:]=df(x)
end
nele_jac = 0 # Number of non-zeros in Jacobian
prob = Ipopt.createProblem(n_variables, x_L, x_U, m, g_L, g_U, nz, nele_jac,
eval_f, (x,g)->(), eval_g, eval_jac_g, nothing)
addOption(prob, "hessian_approximation", "limited-memory")
addOption(prob, "max_iter", max_iter)
addOption(prob, "print_level", verbose) # 0 -- 15, the larger the number, the more detailed the information
prob.x = x0
status = Ipopt.solveProblem(prob)
if status == 0
printstyled(Ipopt.ApplicationReturnStatus[status],"\n", color=:green)
else
printstyled(Ipopt.ApplicationReturnStatus[status],"\n", color=:red)
end
prob.x
end
opt = IPOPT(loss; kwargs...)
minimize(opt, sess)
return losses
end
```
The usage is exactly the same as [`BFGS!`](@ref). Therefore, you can simply replace `BFGS!` to `Ipopt`. For example
```julia
x = Variable(rand(10))
loss = sum((x-0.6)^2 + (x^2-2x+0.8)^4)
cb = (vs, i, l)->println("$i, $l")
sess = Session(); init(sess)
IPOPT!(sess, loss, vars=[x], callback = cb)
```
### NLOPT
Likewise, `NLOPT!` also has the dropin substitute of `BFGS!`
```julia
using ADCME
using NLopt
using PyCall
function NLOPT!(sess::PyObject, loss::PyObject, max_iter::Int64=15000;
algorithm::Union{Symbol, Enum} = :LD_LBFGS, vars::Array{PyObject}=PyObject[],
callback::Union{Function, Nothing}=nothing, kwargs...)
losses = Float64[]
iter_ = 0
NLOPT = CustomOptimizer() do f, df, c, dc, x0, x_L, x_U
opt = Opt(algorithm, length(x0))
opt.upper_bounds = x_U
opt.lower_bounds = x_L
opt.maxeval = max_iter
opt.min_objective = (x,g)->begin
g[:]= df(x);
iter_ += 1
l = f(x)[1]
println("================ ITER $iter_ ===============")
println("current loss= $l")
push!(losses, l)
if !isnothing(callback)
callback(run(sess, vars), iter_, l)
end
return f(x)[1]
end
(minf,minx,ret) = NLopt.optimize(opt, x0)
minx
end
opt = NLOPT(loss; kwargs...)
minimize(opt, sess)
return losses
end
```
For example
```julia
x = Variable(rand(10))
loss = sum((x-0.6)^2 + (x^2-2x+0.8)^4)
cb = (vs, i, l)->println("$i, $l")
sess = Session(); init(sess)
NLOPT!(sess, loss, vars=[x], callback = cb, algorithm = :LD_TNEWTON)
```
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 491 | # Custom Optimizers
ADCME provides a function [`UnconstrainedOptimizer`](@ref) that allows users to craft their own optimizers for unconstrained optimization problems.
```julia
using Optim
x = Variable(rand(2))
loss = (1-x[1])^2 + 100(x[2]-x[1]^2)^2
sess = Session(); init(sess)
uo = UnconstrainedOptimizer(sess, loss)
function f(x)
return getLoss(uo, x)
end
function g!(G, x)
_, g = getLossAndGrad(uo, x)
G[:] = g
end
x0 = getInit(uo)
optimize(f, g!, x0, LBFGS())
``` | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 8209 | # Design Pattern
Design patterns aim at providing reusable solutions for solving the challenges in the process of software development. The ultimate goal of design patterns is to avoid reinventing the wheels and making software flexible and resilient to change. Design patterns are neither concrete algorithms, nor programming templates, but ways of thinking. They are not always necessary if you can come up with very simple designs, which are actually more preferable in practice. Rather, they are "rules of thumb" that facilitates you when you have a hard time how to design the structure of your codes.
We strive to make ADCME easily maintainable and extendable by using well-established design patterns for some design decisions. In this section, we describe some design patterns that are useful for programming ADCME.
## Strategy Pattern
The strategy pattern defines a family of algorithms, encapsulates each one, and makes them interchangeable. The strategy pattern makes programmers wrap algorithms that are subject to frequent changes (e.g., extending) as **interfaces** instead of concrete implementations. For example, in ADCME, [`FlowOp`](@ref) is implemented using the strategy pattern.
When you want to create a flow-based model, the structure [`NormalizingFlow`](@ref) has a method that performs a sequence of forward operations. The forward operations might have different combinations, which results in a large number of different normalizing flows. If we define a different normalizing flow structure for a different combination, there will be exponentially many such structures. Instead of defining a separate `forward` method for each different normalizing flow, we define an interface [`FlowOp`](@ref), which has a `forward` method.
The interface is **implemented** with many concrete structures, which are called **algorithms** in the strategy pattern. These concrete `FlowOp`s, such as `SlowMAF` and `MAF`, have their specific `forward` implementations. Therefore, the system become easily extendable. When we have a new algorithm, we only need to add a new `FlowOp` instead of modifying `NormalizingFlow`.
## Adaptor Pattern
The adapter pattern converts the interface of a structure into another interface users expect. It is very useful to unify the APIs and reuses the existing functions, and thus reliefs users from memorizing many new functions. The typical structure of an adaptor has the form
```julia
struct Adaptor <: AbstractNewComponent
o::LegacyComponent
function new_do_this(adaptor, x)
old_do_this(adaptor.o, x)
end
...
end
```
Here users work with `AbstractNewComponent`, whose concrete types implement a function `new_do_this`. However, we have a structure of type `LegacyComponent`, which has a function `old_do_this`. An adaptor pattern is used to match an old function call `old_do_this` to `new_do_this` in the new system.
An example of adaptor pattern is [`SparseTensor`](@ref), which wraps a `PyObject`. The operations on the `SparseTensor` is propagated to the `PyObject`, and therefore users can think in terms of the new `SparseTensor` data type.
## Observer Pattern
The observer pattern define a one-to-many dependency between objects so that when one object changes state, all its dependents are notified and updated automatically. The basic pattern is
**Subject**
```julia
struct Subject
o # Observer
state
function update(s)
# some operations on `s.state`
end
function notify(s)
# some operations on `s.o`
end
end
```
**Observer**
```julia
struct Observer
subjects::Array{Subject}
function update(o)
for s in o.subjects
update(s)
end
end
end
```
For example, the `commitHistory` function in [NNFEM.jl](https://github.com/kailaix/NNFEM.jl) uses the observer pattern to update states from `Domain`, to `Element`, and finally to `Material`.
## Decorator Pattern
The decorator pattern attaches additional responsibilities to an object dynamically. Decorator patterns are very similar to adaptor patterns. The difference is that the input and output types of the decorator pattern are the same. For example, if the input is a `SparseTensor`, the output should also be a `SparseTensor`. The adaptor pattern converts `PyObject` to `SparseTensor`. Another difference is that the decorator pattern usually does not change the methods and fields of the structure. For example,
```julia
struct Juice
cost::Float64
end
function add_one_dollar(j::Juice)
Juice(j.cost+1)
end
```
Then `add_one_dollar(j)` is still a `Juice` structure but the cost is increased by 1. You can also compose multiple `add_one_dollar`:
```julia
add_one_dollar(add_one_dollar(j))
```
In Julia, this can be done elegantly using macros. We do not discuss macros in this section but leave it to another section on macros.
## Iterator Pattern
Iterator patterns provide a way to access the elements of an aggregate object sequentially without exposing its underlying representation. Julia has built-in iterator support. The `in` keyword loops through iterations and `collect` collects all the entries in the iterator. In Julia, to understand iteration, remember that the following code
```julia
for i in x
# stuff
end
```
is a shorthand for writing
```julia
it = iterate(x)
while it !== nothing
i, state = it
# stuff
it = iterate(x, state)
end
```
Therefore, we only need to implement `iterate`
```julia
iterate(iter [, state]) -> Union{Nothing, Tuple{Any, Any}}
```
## Factory Pattern
The factory pattern defines an interface for creating an object, but lets subclasses decide which class to instantiate. Simply put, we define a function that returns a specific structure
```julia
function factory(s::String)
if s=="StructA"
return StructA()
elseif s=="StructB"
return StructB()
elseif s=="StructC"
return StructC()
else
error(ArgumentError("$s is not understood"))
end
end
```
For example, `FiniteStrainContinuum` in `NNFEM.jl` has a constructor
```julia
function FiniteStrainContinuum(coords::Array{Float64}, elnodes::Array{Int64}, props::Dict{String, Any}, ngp::Int64=2)
eledim = 2
dhdx, weights, hs = get2DElemShapeData( coords, ngp )
nGauss = length(weights)
name = props["name"]
if name=="PlaneStrain"
mat = [PlaneStrain(props) for i = 1:nGauss]
elseif name=="Scalar1D"
mat = [Scalar1D(props) for i = 1:nGauss]
elseif name=="PlaneStress"
mat = [PlaneStress(props) for i = 1:nGauss]
elseif name=="PlaneStressPlasticity"
mat = [PlaneStressPlasticity(props) for i = 1:nGauss]
elseif name=="PlaneStrainViscoelasticityProny"
mat = [PlaneStrainViscoelasticityProny(props) for i = 1:nGauss]
elseif name=="PlaneStressViscoelasticityProny"
mat = [PlaneStressViscoelasticityProny(props) for i = 1:nGauss]
elseif name=="PlaneStressIncompressibleRivlinSaunders"
mat = [PlaneStressIncompressibleRivlinSaunders(props) for i = 1:nGauss]
elseif name=="NeuralNetwork2D"
mat = [NeuralNetwork2D(props) for i = 1:nGauss]
else
error("Not implemented yet: $name")
end
strain = Array{Array{Float64}}(undef, length(weights))
FiniteStrainContinuum(eledim, mat, elnodes, props, coords, dhdx, weights, hs, strain)
end
```
Every time we add a new material, we need to modify this structure. This is not very desirable. Instead, we can have a function
```julia
function get_element(s)
if name=="PlaneStrain"
PlaneStrain
elseif name=="Scalar1D"
Scalar1D
...
end
```
This can also be achieved via Julia macros, thanks to the powerful meta-programming feature in ADCME.
## Summary
We have introduced some important design patterns that facilitate design maintainable and extendable software. Design patterns should not be viewed as rules to abide by, but they are useful principles in face of design difficulties. As mentioned, Julia provides powerful meta-programming features. These features can be used in the design patterns to simplify implementations. Meta-programming will be discussed in a future section.
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 2000 | # Install ADCME Docker Image
For users who do not want to deal with installing and debugging dependencies, we also provide a [Docker](https://docs.docker.com/get-docker/) image for ADCME. Docker creates a virtual environment that isolates ADCME and its dependencies from the rest of the system. To install ADCME through docker, the user system must
1. have Docker installed;
2. have sufficient space (at least 5G).
After docker has been installed, ADCME can be installed and launched via the following line (users do not have to install Julia separately because the Docker container is shipped with a compatible Julia binary)
```julia
docker run -ti kailaix/adcme
```
This will fire a Julia prompt, which already includes precompiled ADCME.

For users who want to open a terminal, run
```julia
docker run -ti kailaix/adcme bash
```
This will launch a terminal where users can type `julia` to open a Julia prompt.
## Tips
* To detach from the docker environment without suspending the process, press `Ctrl-p Ctrl-q`. To re-attach the process, first find the corresponding container ID
```bash
docker ps -a
```
Then
```bash
docker container attach <container_id>
```
Or start a new bash from the same container
```
docker exec -ti <container_id> bash
```
* To share a folder with the host file system (e.g., share persistent data), use `-v` to attach a volume:
```bash
docker run -ti -v "/path/to/host/folder:/path/to/docker/folder" kailaix/adcme bash
```
* Create a new docker image containing all changes:
```bash
docker commit <container_id> <tag>
```
* Build and upload (change `kailaix/adcme` to your own repository)
```bash
docker build -t kailaix/adcme .
docker run -ti kailaix/adcme
docker push kailaix/adcme
```
The current directory should have a Dockerfile:
```
FROM adcme:<tag>
CMD ["/julia-1.6.1/bin/julia"]
```
* Clean up docker containers
```bash
docker system prune
``` | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 12360 | # Exercise: Inverse Modeling with ADCME
The starter code can be downloaded [here](https://github.com/kailaix/ADCME.jl/releases/download/ex_v1.0/Exercise.zip).
## Background
The **thermal diffusivity** is the measure of the ease with which heat can diffuse through a material. Let $u$ be the temperature, and $\kappa$ be the thermal diffusivity. The heat transfer process is described by the Fourier law
$$\frac{\partial u(\mathbf{x}, t)}{\partial t} = \kappa\Delta u(\mathbf{x}, t) + f(\mathbf{x}, t), \quad t\in (0,T), x\in \Omega \tag{1}$$
Here $f$ is the heat source and $\Omega$ is the domain.
To make use of the heat equation, we need additional information.
- **Initial Condition**: the initial temperature distribution is given by $u(\mathbf{x}, 0) = u_0(\mathbf{x})$.
- **Boundary Conditions**: the temperature of the material is affected by what happens on the boundary. There are several possible boundary conditions. In this exercise we consider two of them:
(1) Temperature fixed at a boundary,
$$u(\mathbf{x}, t) = 0, \quad \mathbf{x}\in \Gamma_D \tag{2}$$
(2) Insulated boundary. The heat flow can be prescribed (known as the _no flow_ boundary condition)
$$-\kappa\frac{\partial u(\mathbf{x},t)}{\partial n} = 0, \quad \mathbf{x}\in \Gamma_N \tag{3}$$
Here $n$ is the outward normal vector.
The boundaries $\Gamma_D$ and $\Gamma_N$ satisfy $\partial \Omega = \Gamma_D \cup \Gamma_N, \Gamma_D\cap \Gamma_N = \emptyset$.
Assume that we want to experiment with a piece of new material. The thermal diffusivity coefficient of the material is an unknown function of the space. Our goal of the experiment is to find out the thermal diffusivity coefficient. To this end, we place some sensors in the domain or on the boundary. The measurements are sparse in the sense that only the temperature from those sensors---but nowhere else---are collected. Namely, let the sensors be located at $\{\mathbf{x}_i\}_{i=1}^M$, then we can observe $\{\hat u(\mathbf{x}_i, t)\}_{i=1}^M$, i.e., the measurements of $\{ u(\mathbf{x}_i, t) \}_{i=1}^M$. We also assume that the boundary conditions, initial conditions and the source terms are known.

## Problem 1: Parameter Inverse Problem in 1D
We first consider the 1D case. In this problem, the material is a rod $\Omega=[0,1]$. We consider a homogeneous (zero) fixed boundary condition on the right side, and an insulated boundary on the left side. The initial temperature is zero everywhere, i.e., $u(x, 0)=0$, $x\in [0,1]$. The source term is $f(x, t) = \exp(-10(x-0.5)^2)$, and $\kappa(x)$ is a function of space
$$\kappa(x) = a + bx$$
Our task is to estimate the coefficient $a$ and $b$ in $\kappa(x)$. To this end, we place a sensor at $x=0,$ and the sensor records the temperature as a time series $u_0(t)$, $t\in (0,1)$.
Recall that in lecture slide [35](https://ericdarve.github.io/cme216-spring-2020/Slides/AD/AD.pdf#page=39)/47 of AD.pdf, we formulate the inverse modeling problem as a PDE-constrained optimization problem
$$\begin{aligned}
\min_{a, b}\ & \int_{0}^t ( u(0, t)- u_0(t))^2 dt\\
\mathrm{s.t.}\ & \frac{\partial u(x, t)}{\partial t} = \kappa(x)\Delta u(x, t) + f(x, t), \quad t\in (0,T), x\in (0,1) \\
& -\kappa(0)\frac{\partial u(0,t)}{\partial x} = 0, t>0\\
& u(1, t) = 0, t>0\\
& u(x, 0) = 0, x\in [0,1]\\
& \kappa(x) = a x + b
\end{aligned}$$
We consider the discretization of the above forward problem. We divide the domain $[0,1]$ into $n$ equispaced intervals. We consider the time horizon $T = 1$, and divide the time horizon $[0,T]$ into $m$ equispaced intervals. We use a finite difference scheme to solve the 1D heat equation Equations (1)--(3). Specifically, we use an implicit scheme for stability:
$$\frac{u^{k+1}_i-u^k_i}{\Delta t} = \kappa_i \frac{u^{k+1}_{i+1}+u^{k+1}_{i-1}-2u^{k+1}_i}{\Delta x^2} + f_i^{k+1},$$
$$k=1,2,\ldots,m, i=1,2,\ldots, n \tag{4}$$
where $\Delta t$ is the time interval, $\Delta x$ is the space interval, $u_i^k$ is the numerical approximation to $u((i-1)\Delta x, (k-1)\Delta t)$, $\kappa_i$ is the numerical approximation to $\kappa((i-1)\Delta x) = a + b(i-1)\Delta x$, and $f_i^{k} = f((i-1)\Delta x, (k-1)\Delta t)$.
For the insulated boundary, we introduce the ghost node $u_0^k$ at location $x=-\Delta x$, and the insulated boundary condition can be numerically discretized by
$$-\kappa_1 \frac{u_2^{k}-u_0^k}{2\Delta x} = 0\tag{5}$$
Let
$$U^k = \begin{bmatrix}u_1^k\\ u_2^k\\ \vdots\\ \\u_n^k\end{bmatrix}$$
The index starts from 1 and ends with $n$. Using the finite difference scheme, together with eliminating the boundary values $u_0^k$, $u_{n+1}^k$, we have the following formula
$$AU^{k+1} = U^k + F^{k+1}$$
1. Express the matrix $A\in \mathbb{R}^{n\times n}$ in terms of $\Delta t$, $\Delta x$ and $\{\kappa_i\}_{i=1}^{n}$. What is $F^{k+1}\in \mathbb{R}^n$ ?
Hint: Can you eliminate $u_0^k$ and $u_{n+1}^k$ in Eq. (4) using Eq. (5) and $u_{n+1}^k=0$ ?
The starter code `Case1D/starter1.jl` precomputes the force vector $F^k$ and packs it into a matrix $F\in \mathbb{R}^{(m+1)\times n}$.
1. Use `spdiag`[^spdiag] to construct `A` as a `SparseTensor` (see the starter code for details). `spdiag` is an ADCME function. See the documentation[^spdiag] for the syntax. Here $\kappa$ is given by
$$\kappa(x) = 2+1.5x$$
[^spdiag]: [API Reference](https://kailaix.github.io/ADCME.jl/dev/api/#ADCME.spdiag-Tuple{Integer,Vararg{Pair,N}%20where%20N})
For debugging, check that your $A_{ij}$ is tridiagonal. You can use `run(sess, A)` to evaluate the `SparseTensor` `A`. You should get the following values:
| Entry | Value |
| ---- | ---- |
| $A_{11}$ | $201$ |
| $A_{12}$ | $-200$ |
| $A_{21}$ | $-101.5$ |
| $A_{33}$ | $207$ |
| $A_{10,10}$ | $228$ |
The computational graph of the dynamical system can be efficiently constructed using `while_loop`.
* Implement the forward computation using `while_loop`. Turn in your code.
For debugging, you can plot the temperature on the left side, i.e., $u(0,t)$. You should have something similar to the following plot

Now we are ready to perform inverse modeling.
* Read the starter code `Case1D/starter2.jl` carefully and complete the missing implementations. Turn in your code. What is your estimate `a` and `b`?
## Problem 2: Function Inverse Problem
Let us consider the function inverse problem, where we do not know the form of $\kappa(x)$. To this end, we substitute $\kappa(x)$ using a neural network. We will use physics constrained learning (PCL) to train $\kappa(x)$ from the temperature data $u_0(x, t)$, where $x$ is the location of a sensor.
Since we do not know the form of $\kappa(x)$, we need more data to solve the inverse problem. Therefore, we assume that we place sensors at the first 25 locations in the discretized grid. The observation data `data_pcl.txt` is a $(m+1)\times 25$ matrix; each column corresponds to the observation at one sensor.
In this problem, let us parametrize $\kappa(x)$ with a fully connected neural network with 3 hidden layers, 20 neurons per layer, and $\tanh$ activation functions. In ADCME, such a neural network can be constructed using
```julia
y = fc(x, [20,20,20,1])
```
Here x is a $n \times 1$ input, y is a $n \times 1$ output, $[20,20,20,1]$ is the number of neurons per layer (last output layer only has 1 neuron), and fc stands for "fully-connected".
Assume that the neural network is written as $\kappa_\theta(x)$, where $\theta$ is the weights and biases.
* Write down the mathematical optimization problem for the inverse modeling. What variables are we optimizing for this problem?
* Complete the starter code `Case1D/starter3.jl` for conducting physics constrained learning. The observation data is provided as `data_pcl.txt`. Run the program several times to ensure you do not terminate early at a bad local minimum. Turn in your code.
* Plot your estimated $\kappa_\theta$ curve.
Hint: Your curve should look like the following

* Add 1% and 10% Gaussian noise to the dataset and redo (7). Plot the estimated $\kappa_\theta$ curve. Comment on your observations.
Hint: You can add noise using
```julia
uc = @. uc * (1 + 0.01*randn(length(uc)))
uc = @. uc * (1 + 0.1*randn(length(uc)))
```
Here `@.` is for elementwise operations.
## Problem 3: Parameter Inverse Problem in 2D
In this problem, we will explore more deeply how ADCME works with numerical solvers. We will use an important technique, custom operators, for incorporating C++ codes. This will be useful when you want to accelerate a performance-critical part, or you want to reuse existing codes. To make the problem simple, the `C++` kernel has been prepared for you. For this exercise, you will be working with `Case2D/starter.jl`.
We consider the 2D case and $T=1 $. We assume that $\Omega=[0,1]^2$. We impose zero boundary conditions on the entire boundary $\Gamma_D=\partial\Omega$. Additionally, we assume that the initial condition is zero everywhere. Two sensors are located at $(0.2,0.2)$ and $(0.8,0.8)$ and these sensors record time series of the temperature $u_1(t)$ and $u_2(t)$. The thermal diffusivity coefficient is a linear function of the space coordinates
$$\kappa(x, y) = a + bx + cy$$
where $a, b$ and $c$ are three coefficients we want to find out from the data $u_1(t)$ and $u_2(t)$.
* Write down the mathematical optimization problem for the inverse modeling. As before, explain what variables we are optimizing for this problem.
We use the finite difference method to discretize the PDE. Consider $\Omega=[0,1]\times [0,1]$, we use a uniform grid and divide the domain into $m\times n$ squares, with length $\Delta x$. We also divide $[0,T]$ into $N_T$ intervals of equal length. The implicit scheme for the equation is
$$\frac{u_{ij}^{k+1}-u_{ij}^k}{\Delta t} = \kappa_{ij}\frac{u_{i+1,j}^{k+1}+u_{i,j+1}^{k+1}+u_{i-1,j}^{k+1}+u_{i,j-1}^{k+1}-4u_{ij}^{k+1}}{\Delta x^2} + f_{ij}^{k+1}$$
where $i=2,3,\ldots, m, j=2,3,\ldots, n, k=1,2,\ldots, N_T$.
Here $u_{ij}^k$ is an approximation to $u((i-1)h, (j-1)h, (k-1)\Delta t)$, and $f_{ij}^k = f((i-1)h, (j-1)h, (k-1)\Delta t)$.
We flatten $\{u_{ij}^k\}$ to a 1D vector $U^k$, using $i$ as the leading dimension, i.e., the ordering of the vector is $u_{11}^k, u_{12}^k, \ldots$; We also flatten $f_{ij}^{k+1}$ and $\kappa_{ij}$ as well.
In this problem, we extend the AD framework using custom operators (also known as _external function support_ in the AD community). In the starter code `Case2D/starter.jl`, we provide a function, `heat_equation`, a differentiable heat equation solver, which is already implemented for you using C++. By using custom operators, we replace the PDE solver node in the computational graph with our own, more efficient, implementation.
Read the [instructions](./ADCME_setup.md) on how to compile the custom operator, and answer the following two questions.
* Similar to Problem 1, implement the forward computation using `while_loop` with the starter code `Case2D/starter.jl`. Plot the curve of the temperature at $(0.5,0.5)$.
Hint: you should obtain something similar to

The parameters used in this problem are: $m=50$, $n=50$, $T=1$, $N_T=50$, $f(\mathbf{x},t) = e^{-t}\exp(-50((x-0.5)^2+(y-0.5)^2))$, $a = 1.5$, $b=1.0$, $c=2.0$.
The data file `data.txt` is a $(N_T+1)\times 2$ matrix, where the first and the second columns are $u_1(t)$ and $u_2(t)$ respectively.
* Use these data to do inverse modeling and report the values $a, b$ and $c$. We do not provide a starter code intentionally, but the forward computation codes in `Case2D/starter.jl` and neural-network-based inverse modeling codes in `Case1D/starter3.jl` will be helpful.
Hint:
- For checking your program, you can save your own `data.txt` from Question 10, try to estimate $a$, $b$, and $c$, and check if you can recover the true values.
- If the optimization stops too early, you can multiply your loss function by a large number (e.g., $10^{10}$) and run your `BFGS!` optimizer again. An alternative approach is to use a smaller tolerance. See the `BFGS!` function documentation for details. | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 2412 | # Direct Methods for Sparse Matrices
## Usage
The direct methods for sparse matrix solutions feature a matrix factorization for solving a set of equations. This procedure is call **factorization** or **decomposition**. We can also support factorization or decomposition via [shared memory across kernels](https://kailaix.github.io/ADCME.jl/dev/global/). The design is to store the factorized matrix in the C++ memory and pass an identifying code (an integer) to the solution operators. Here is how you solve $Ax_i = b_i$ for a list of $(x_i, b_i)$
**Step 1:** Factorization
```julia
A_factorized = factorize(A)
```
**Step2:** Solve
```julia
x1 = A_factorized\b1
x2 = A_factorized\b2
......
```
Compared to `A\b`, the factorize-then-solve approach is more efficient, especially when you have to solve a lot of equations.
## Control Flow Safety
The factorize-then-solve method is also control flow safe. That is, we can safely use it in the control flow and gradient backpropagation is correct. For example, if the matrix $A$ keeps unchanged throught the loop, we might want to factorize $A$ first and then use the factorized $A$ to solve equations repeatly. To verify the control flow safety, consider the following code, where in the loop we have
$$u_{i+1} = A^{-1}(u_i + r), i=1,2,\ldots$$
```julia
using ADCME
using SparseArrays
using ADCMEKit
function while_loop_simulation(vv, rhs, ns = 10)
A = SparseTensor(ii, jj, vv, 10, 10) + spdiag(10)*100.
Afac = factorize(A)
ta = TensorArray(ns)
i = constant(2, dtype=Int32)
ta = write(ta, 1, ones(10))
function condition(i, ta)
i<= ns
end
function body(i, ta)
u = read(ta, i-1)
res = Afac\(u + rhs)
# res = u
ta = write(ta, i, res)
i+1, ta
end
_, out = while_loop(condition, body, [i, ta])
sum(stack(out)^2)
end
sess = Session(); init(sess)
A = sprand(10, 10, 0.8)
ii, jj, vv = find(constant(A))
k = length(vv)
# Test 1: autodiff through A
pl = placeholder(rand(k))
res = while_loop_simulation(pl, rhs , 100)
gradview(sess, pl, res, rand(k))
# Test 2: autodiff through rhs
pl = placeholder(rand(10))
res = while_loop_simulation(vv, pl , 100)
gradview(sess, pl, res, rand(10))
```
We have the following convergence plot
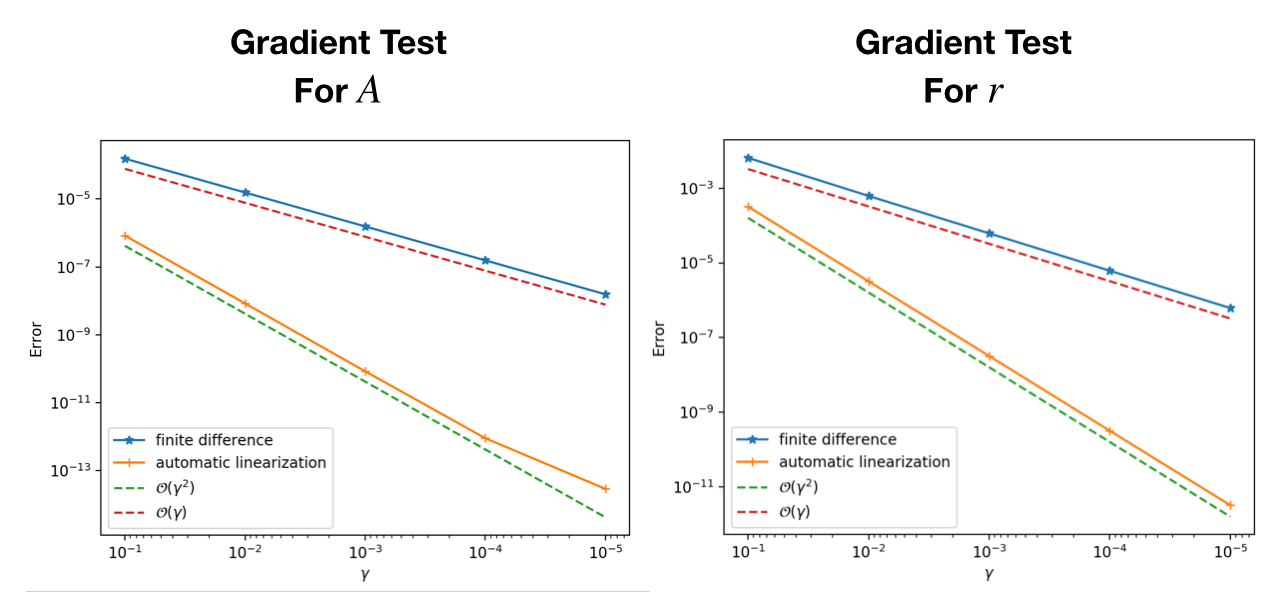 | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 11126 | # Finite-difference Time-domain for Electromagnetics and Seismic Inversion
The finite-difference time-domain (FDTD) is a very conceptually and technically simple technique for full-wave simulation. It has been widely adopted in electromagnetics and geophysics. For example, the full-waveform inversion (FWI), which is arguably the most famous seismic inversion technique, is typically implemented with FDTD. It is also known as Yee scheme. Given its significance, in this section, we show how to implement FDTD in one-dimension using ADCME, and use the forward computation code to do inverse problems.
## FDTD
To make the discussion clear and consistent throughout the session, we use notations from electromagnetics, $E$, the electric field, and $H$, the magnetic flux. In 1D, the Faraday's law and Ampere's law are simplified to
$$\begin{aligned}
\mu \frac{\partial H}{\partial t} &= \frac{\partial E}{\partial x}\\
\epsilon \frac{\partial E}{\partial t} &= \frac{\partial H}{\partial x}
\end{aligned}$$
We use the staggered grid shown in the following figure
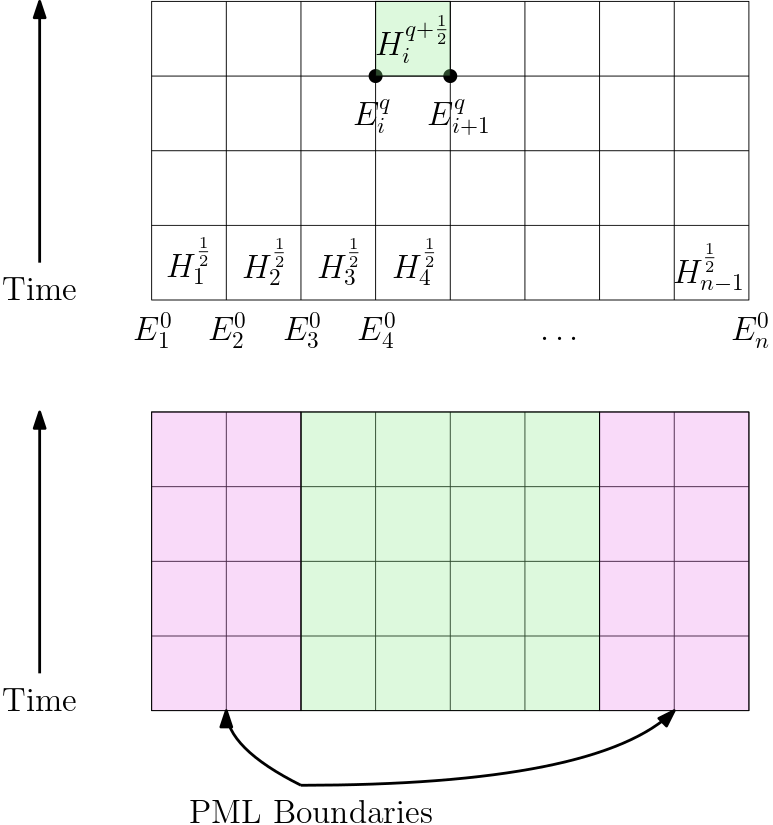
The superscript denotes time step, while the subscript denotes location index. The electric field $E_i^q$ is defined on the grid point, while the magnetic flux is defined in the cell center. The Yee algorithm alternatively updates $H$ and $E$ with
$$\begin{aligned}
H_i^{q+\frac12} & = H_i^{q-\frac12} + \frac{\Delta t}{\mu\Delta x} (E^q_{i+1} - E^q_i)\\
E_i^{q+1} &= E_i^{q} + \frac{\Delta t}{\epsilon \Delta x}(H^{q+\frac12}_{i} - H^{q+\frac12}_{i-1})
\end{aligned}$$
When we simulate within a finite computational domain, we usually need to design a boundary condition that "absorbs" reflecting waves. This can be done with the so-called perfectly matched layer (PML) boundaries. In practice, we can pad the computational domain with extra grids (the magenta region in the figure above). See the next section for a detailed discussion.
In the case we want to add some source functions, there are typically two ways:
* Hardwiring source functions by setting $E_k^q=s_k^q$ for all $q$ and certain index $k$.
* Additive source functions. This is achieved by replacing the second equation with
$$E_i^{q+1} = E_i^{q} + \frac{\Delta t}{\epsilon \Delta x}(H^{q+\frac12}_{i} - H^{q+\frac12}_{i-1}) + \frac{\Delta t}{\epsilon} J_i^{q+\frac12}$$
## Perfectly Matched Layer (PML)
Let us consider the plane wave $e^{i kx}$. In the infinite space, the plane wave will pass through the domain of interest and never get reflected back. However, in practice, computational domains are finite. If we impose a reflection boundary condition, the plane wave will get reflected. Even if we impose Dirichlet boundary conditions, some portions of reflection is still present. These reflections are not desirable for relevant applications. Therefore, we want to find a way for damping reflected waves away.
Let us consider the plane waves $e^{ikx}$. It's complex but we can always think of it as an analytical continuous of $sin(kx)$ in the complex space. Instead of looking at real $x$, we consider a complex $x$, and we have
$$e^{ik(\Re x + i\Im x)} = e^{ik\Re x - k\Im x}$$
Here is an important observation: if $\Im x = f(\Re x) >0$ for some increasing function $f(x)$, the magnitude of the wave $e^{ikx}$ along the line $\Re x + i f(\Re x)$ will decay exponentially. Thus, within a finite computational domain $[0,1]$, we can extend the governing equation beyond $[0,1]$ in the complex domain, with the path given by
$$\{ x + i f(x): x\in \mathbb{R}\}$$
Here $f(x) = 0$, $x\in (0,1)$, and
$$f'(x) = \frac{\sigma(x)}{k}, x>1$$
The case for $f(x)<0$ is similar.
The fundamental idea is that instead of looking at the governing equation in $[0,1]$, we extend it analytically into the complex space. For example, the transport equation
$$\frac{\partial u(x, t)}{\partial t} = \frac{\partial u(x, t)}{\partial x}$$
becomes
$$\frac{\partial \tilde u(z, t)}{\partial t} = \frac{\partial \tilde u(z, t)}{\partial z}, z\in \mathbb{C}$$
Then the question is: what is the governing equation for $\bar u(x, t) = \tilde u(x+i f(x), t)$?
To simplify our notation, we omit $t$ here because it is unrelated to the complex domain. We denote $z = x + i f(x)$ and
$$\Re \tilde u = u_1, \Im \tilde u = u_2$$
Then we have
$$\begin{aligned}
\frac{\partial \bar u(x)}{\partial x} &= \frac{\partial \tilde u(x+i f(x))}{\partial x}\\
&= \frac{\partial (u_1(x+i f(x)) + i u_2(x+i f(x)))}{\partial x}\\
&= \frac{\partial (u_1(x+i f(x))}{\partial x} + i \frac{\partial u_2(x+i f(x)))}{\partial x} \\
&= \frac{\partial u_1}{\partial x} + i \frac{\partial u_2}{\partial x} + i \frac{\partial u_1}{\partial x} \frac{\partial f}{\partial x} - \frac{\partial u_2}{\partial x}\frac{\partial f}{\partial x}
\end{aligned}$$
Note from complex analysis,
$$\frac{\partial \tilde u(z)}{\partial z} = \frac{\partial u_1}{\partial x} + i \frac{\partial u_2}{\partial x}$$
We have
$$\frac{\partial \bar u(x)}{\partial x} =\left(1 + i\frac{\partial f}{\partial x} \right) \frac{\partial \tilde u}{\partial z}\tag{1}$$
Now let us consider the Faraday's law
$$\mu \frac{\partial H}{\partial t} = \frac{\partial E}{\partial x}\tag{2}$$
We consider the plane wave $H = e^{-ikx}$, which we want to damp outside the computational domain. First we extend Equation 2 to the complex domain and plug $H$ to the equation (note $\frac{\partial H}{\partial t} = \frac{\partial \bar H}{\partial t}$)
$$-i\mu k \bar H = \frac{\partial \tilde E}{\partial z}$$
Using Equation 1, we have
$$-i \mu k \bar H+ \mu \sigma_x(x) \bar H= \frac{\partial \bar E}{\partial x}$$
Converting back to the time domain, we have
$$\mu\frac{\partial \bar H}{\partial t} = \frac{\partial \bar E}{\partial x} - \mu \sigma_x(x) \bar H$$
Likewise, we have
$$\epsilon\frac{\partial \bar H}{\partial t} = \frac{\partial \bar E}{\partial x} - \epsilon \sigma_x(x) \bar H$$
Note that the two above equations are exactly the original equations within the domain $[0,1]$.
## Numerical Experiment: Forward Computation
Let us consider a 1D wave equation
$$\frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2}$$
which is equivalent to
$$\begin{aligned}
\frac{\partial u}{\partial t} &= c \frac{\partial v}{\partial x}\\
\frac{\partial v}{\partial t} &= c \frac{\partial u}{\partial x}
\end{aligned}$$
This set of equations is related to Faraday's law and Ampere's law via
$$E = v, H = u, \epsilon = \frac1c, \mu = \frac1c$$
We use a hardwiring source at the center of the computational domain $[0,1]$. The source function is shown in the left panel. The evolution of $u$ is shown in the right panel.
|Source Function|Evolution of $u$|
|--|--|
||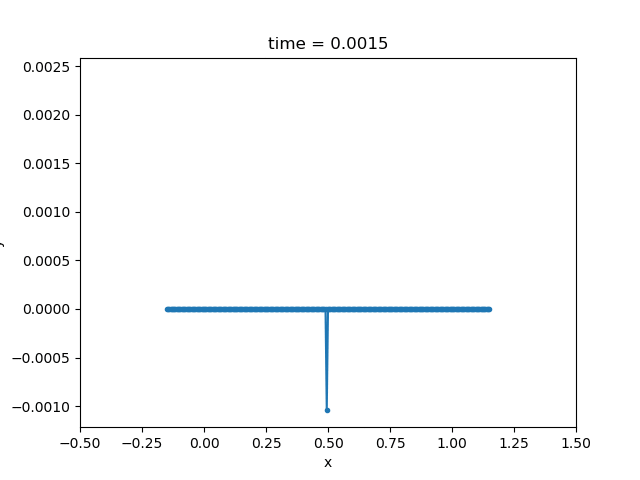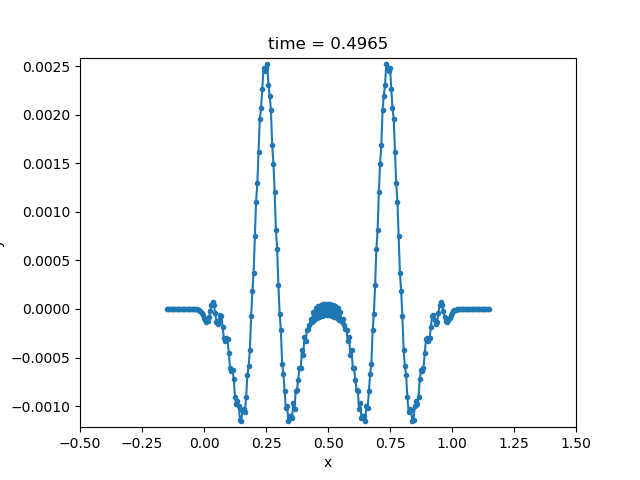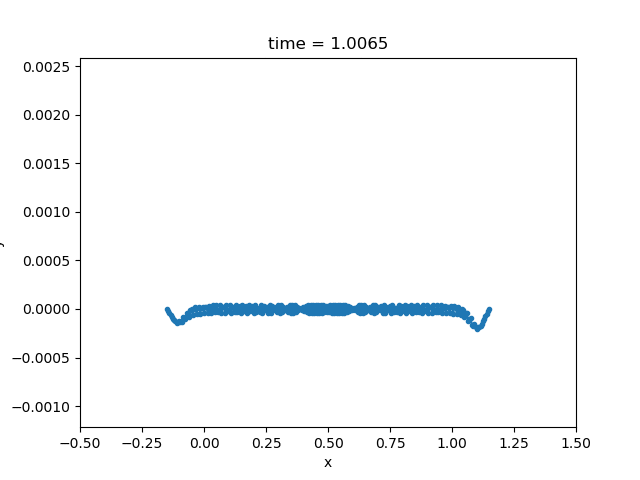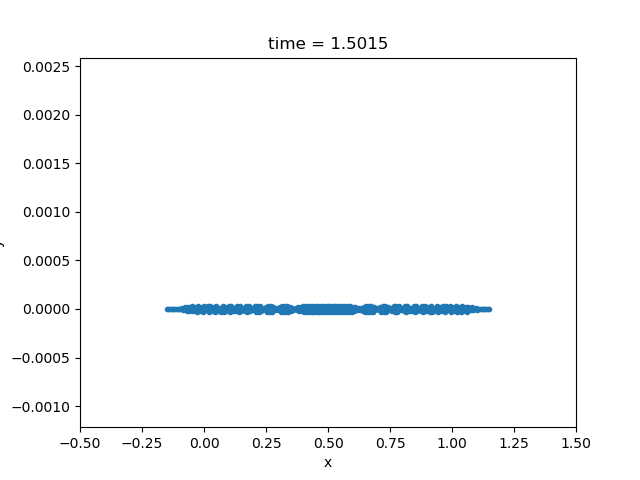|
```julia
using ADCME
using PyPlot
using ADCMEKit
n = 200
pml = 30
C = 100.0
NT = 1000
Δt = 1.5/NT
x0 = LinRange(0, 1, n+1)
h = 1/n
xE = Array((0:n+2pml)*h .- pml*h)
xH = (xE[2:end]+xE[1:end-1])/2
N = n + 2pml + 1
σE = zeros(N)
for i = 1:pml
d = i*h
σE[pml + n + 1 + i] = C* (d/(pml*h))^3
σE[pml+1-i] = C* (d/(pml*h))^3
end
σH = zeros(N-1)
for i = 1:pml
d = (i-1/2)*h
σH[pml + n + i] = C* (d/(pml*h))^3
σH[pml+1-i] = C* (d/(pml*h))^3
end
function ricker(dt = 0.002, f0 = 3.0)
nw = 2/(f0*dt)
nc = floor(Int, nw/2)
t = dt*collect(-nc:1:nc)
b = (π*f0*t).^2
w = @. (1 - 2b)*exp(-b)
end
R = ricker()
if length(R)<NT+1
R = [R;zeros(NT+1-length(R))]
end
R_ = constant(R)
# cH = constant(ones(N-1))
cH = ones(length(xH)) * 1.5
cE = (cH[1:end-1]+cH[2:end])/2
Z = zeros(N)
Z[N÷2] = 1.0
Z = Z[2:end-1]
function condition(i, E_arr, H_arr)
i<=NT+1
end
function body(i, E_arr, H_arr)
E = read(E_arr, i-1)
H = read(H_arr, i-1)
ΔH = cH * (E[2:end]-E[1:end-1])/h - σH*H
H += ΔH * Δt
ΔE = cE * (H[2:end]-H[1:end-1])/h - σE[2:end-1]*E[2:end-1] #+ R_[i] * Z
E = scatter_add(E, 2:N-1, ΔE * Δt)
E = scatter_update(E, N÷2, R_[i])
i+1, write(E_arr, i, E), write(H_arr, i, H)
end
E_arr = TensorArray(NT+1)
H_arr = TensorArray(NT+1)
E0 = zeros(N)
E0[N÷2] = R[1]
E_arr = write(E_arr, 1, E0)
H_arr = write(H_arr, 1, zeros(N-1))
i = constant(2, dtype = Int32)
_, E, H = while_loop(condition, body, [i, E_arr, H_arr])
E = stack(E)
H = stack(H)
sess = Session(); init(sess)
E_, H_ = run(sess, [E, H])
pl, = plot([], [], ".-")
xlim(-0.5,1.5)
ylim(minimum(E_), maximum(E_))
xlabel("x")
ylabel("y")
t = title("time = 0.0000")
function update(i)
t.set_text("time = $(round(i*Δt, digits=4))")
pl.set_data([xE E_[i,:]]'|>Array)
end
p = animate(update, 1:10:NT+1)
# saveanim(p, "fdtd.gif")
```
### Numerical Experiment
Let us consider inverting for a constant $c_H$. The following code is mainly a copy and paste from the above code. The optimization converges within a few iterations.
```julia
using ADCME
using PyPlot
using ADCMEKit
n = 200
pml = 30
C = 100.0
NT = 1000
Δt = 1.5/NT
x0 = LinRange(0, 1, n+1)
h = 1/n
xE = Array((0:n+2pml)*h .- pml*h)
xH = (xE[2:end]+xE[1:end-1])/2
N = n + 2pml + 1
σE = zeros(N)
for i = 1:pml
d = i*h
σE[pml + n + 1 + i] = C* (d/(pml*h))^3
σE[pml+1-i] = C* (d/(pml*h))^3
end
σH = zeros(N-1)
for i = 1:pml
d = (i-1/2)*h
σH[pml + n + i] = C* (d/(pml*h))^3
σH[pml+1-i] = C* (d/(pml*h))^3
end
function ricker(dt = 0.002, f0 = 3.0)
nw = 2/(f0*dt)
nc = floor(Int, nw/2)
t = dt*collect(-nc:1:nc)
b = (π*f0*t).^2
w = @. (1 - 2b)*exp(-b)
end
R = ricker()
if length(R)<NT+1
R = [R;zeros(NT+1-length(R))]
end
R_ = constant(R)
# cH = constant(ones(N-1))
# cH = Variable(ones(length(cH)))
b = softplus(Variable(1.0))
cH = ones(length(xH)) * b
cE = (cH[1:end-1]+cH[2:end])/2
Z = zeros(N)
Z[N÷2] = 1.0
Z = Z[2:end-1]
function condition(i, E_arr, H_arr)
i<=NT+1
end
function body(i, E_arr, H_arr)
E = read(E_arr, i-1)
H = read(H_arr, i-1)
ΔH = cH * (E[2:end]-E[1:end-1])/h - σH*H
H += ΔH * Δt
ΔE = cE * (H[2:end]-H[1:end-1])/h - σE[2:end-1]*E[2:end-1] #+ R_[i] * Z
E = scatter_add(E, 2:N-1, ΔE * Δt)
E = scatter_update(E, N÷2, R_[i])
i+1, write(E_arr, i, E), write(H_arr, i, H)
end
E_arr = TensorArray(NT+1)
H_arr = TensorArray(NT+1)
E0 = zeros(N)
E0[N÷2] = R[1]
# v0[N÷2] = 1.0
E_arr = write(E_arr, 1, E0)
H_arr = write(H_arr, 1, zeros(N-1))
i = constant(2, dtype = Int32)
_, E, H = while_loop(condition, body, [i, E_arr, H_arr])
E = stack(E); E = set_shape(E, (NT+1, N))
H = stack(H)
receivers = [pml+1:pml+10; N-pml-9:N-pml]
loss = sum((E[:,receivers] - E_[:,receivers])^2)
sess = Session(); init(sess)
BFGS!(sess, loss)
``` | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 12042 | # Normalizing Flows
In this article we introduce the ADCME module for flow-based generative models. The flow-based generative models can be used to model the joint distribution of high-dimensional random variables. It constructs a sequence of invertible transformation of distributions
$$x = f(u) \quad u \sim \pi(u)$$
based on the change of variable equation
$$p(x) = \pi(f^{-1}(x)) \left|\det\left(\frac{\partial f^{-1}(x)}{\partial x}\right)\right|$$
!!! example
Consider the transformation $f: \mathbb{R}\rightarrow [0,1]$, s.t. $f(x) = \mathrm{sigmoid}(x) = \frac{1}{1+e^{-x}}$. Consider the random variable
$$u \sim \mathcal{N}(0,1)$$
We want to find out the probability density function of $p(x)$, where $x=f(u)$. To this end, we have
$$f^{-1}(x)=\log(x) - \log(1-x) \Rightarrow \frac{\partial f^{-1}(x)}{\partial x} = \frac{1}{x} + \frac{1}{1-x}$$
Therefore, we have
$$\begin{aligned}
p(x) &= \pi(f^{-1}(x))\left( \frac{1}{x} + \frac{1}{1-x}\right) \\
&= \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{(\log(x)-\log(1-x))^2}{2}\right)\left( \frac{1}{x} + \frac{1}{1-x}\right)
\end{aligned}$$
Compared to other generative models such as variational autoencoder (VAE) and generative neural networks (GAN), the flow-based generative models give us explicit formuas of density functions. For model training, we can directly minimizes the posterier log likelihood in the flow-based generative models, while use approximate likelihood functions in VAE and adversarial training in GAN. In general, the flow-based generative model is easier to train than VAE and GAN. In the following, we give some examples of using flow-based generatives models in ADCME.
## Type Hierarchy
The flow-based generative model is organized as follows, from botton level to top level:
* `FlowOp`. This consists of unit invertible transformations, such as [`AffineConstantFlow`](@ref) and [`Invertible1x1Conv`](@ref).
* `NormalizingFlow`. This is basically a sequence of `FlowOp`. It is not exposed to users.
* `NormalizingFlowModel`. This is a container of the sequence of `FlowOp`s and a prior distribution. `NormalizingFlowModel` is callable and can "normalize" the data distribution. We can also sample from `NormalizingFlowModel`, where the prior distribution is transformed to data distribution.
## A Simple Example
Let's consider a simple example for transforming the two moons dataset to a univariate Gaussian distribution. First, we adapt a function from [here](https://github.com/wildart/nmoons) and use it to generate the dataset
```julia
using Revise
using ADCME
using PyCall
using PyPlot
using Random
# `nmoons` is adapted from https://github.com/wildart/nmoons
function nmoons(::Type{T}, n::Int=100, c::Int=2;
shuffle::Bool=false, ε::Real=0.1, d::Int = 2,
translation::Vector{T}=zeros(T, d),
rotations::Dict{Pair{Int,Int},T} = Dict{Pair{Int,Int},T}(),
seed::Union{Int,Nothing}=nothing) where {T <: Real}
rng = seed === nothing ? Random.GLOBAL_RNG : MersenneTwister(Int(seed))
ssize = floor(Int, n/c)
ssizes = fill(ssize, c)
ssizes[end] += n - ssize*c
@assert sum(ssizes) == n "Incorrect partitioning"
pi = convert(T, π)
R(θ) = [cos(θ) -sin(θ); sin(θ) cos(θ)]
X = zeros(d,0)
for (i, s) in enumerate(ssizes)
circ_x = cos.(range(zero(T), pi, length=s)).-1.0
circ_y = sin.(range(zero(T), pi, length=s))
C = R(-(i-1)*(2*pi/c)) * hcat(circ_x, circ_y)'
C = vcat(C, zeros(d-2, s))
dir = zeros(d)-C[:,end] # translation direction
X = hcat(X, C .+ dir.*translation)
end
y = vcat([fill(i,s) for (i,s) in enumerate(ssizes)]...)
if shuffle
idx = randperm(rng, n)
X, y = X[:, idx], y[idx]
end
# Add noise to the dataset
if ε > 0.0
X += randn(rng, size(X)).*convert(T,ε/d)
end
# Rotate dataset
for ((i,j),θ) in rotations
X[[i,j],:] .= R(θ)*view(X,[i,j],:)
end
return X, y
end
function sample_moons(n)
X, _ = nmoons(Float64, n, 2, ε=0.05, d=2, translation=[0.25, -0.25])
return Array(X')
end
```

Next we construct a flow-based generative model, as follows:
```julia
prior = ADCME.MultivariateNormalDiag(loc=zeros(2))
model = NormalizingFlowModel(prior, flows)
```
We can print the model by just type `model` in REPL:
```
( MultivariateNormalDiag )
↓
AffineHalfFlow
↓
AffineHalfFlow
↓
AffineHalfFlow
↓
AffineHalfFlow
↓
AffineHalfFlow
↓
AffineHalfFlow
↓
AffineHalfFlow
↓
AffineHalfFlow
↓
AffineHalfFlow
```
Finally, we maximize the log llikelihood function using [`AdamOptimizer`](@ref)
```julia
x = placeholder(rand(128,2))
zs, prior_logpdf, logdet = model(x)
log_pdf = prior_logpdf + logdet
loss = -sum(log_pdf)
model_samples = rand(model, 128*8)
sess = Session(); init(sess)
opt = AdamOptimizer(1e-4).minimize(loss)
sess = Session(); init(sess)
for i = 1:10000
_, l = run(sess, [opt, loss], x=>sample_moons(128))
if mod(i,100)==0
@info i, l
end
end
```
## Models
ADCME has implemeted some popular flow-based generative models. For example, [`AffineConstantFlow`](@ref), [`AffineHalfFlow`](@ref), [`SlowMAF`](@ref), [`MAF`](@ref), [`IAF`](@ref), [`ActNorm`](@ref), [`Invertible1x1Conv`](@ref), [`NormalizingFlow`](@ref), [`NormalizingFlowModel`](@ref), and [`NeuralCouplingFlow`](@ref).
The following script shows how to usee those functions:
```julia
# Adapted from https://github.com/karpathy/pytorch-normalizing-flows
using Revise
using ADCME
using PyCall
using PyPlot
using Random
# `nmoons` is adapted from https://github.com/wildart/nmoons
function nmoons(::Type{T}, n::Int=100, c::Int=2;
shuffle::Bool=false, ε::Real=0.1, d::Int = 2,
translation::Vector{T}=zeros(T, d),
rotations::Dict{Pair{Int,Int},T} = Dict{Pair{Int,Int},T}(),
seed::Union{Int,Nothing}=nothing) where {T <: Real}
rng = seed === nothing ? Random.GLOBAL_RNG : MersenneTwister(Int(seed))
ssize = floor(Int, n/c)
ssizes = fill(ssize, c)
ssizes[end] += n - ssize*c
@assert sum(ssizes) == n "Incorrect partitioning"
pi = convert(T, π)
R(θ) = [cos(θ) -sin(θ); sin(θ) cos(θ)]
X = zeros(d,0)
for (i, s) in enumerate(ssizes)
circ_x = cos.(range(zero(T), pi, length=s)).-1.0
circ_y = sin.(range(zero(T), pi, length=s))
C = R(-(i-1)*(2*pi/c)) * hcat(circ_x, circ_y)'
C = vcat(C, zeros(d-2, s))
dir = zeros(d)-C[:,end] # translation direction
X = hcat(X, C .+ dir.*translation)
end
y = vcat([fill(i,s) for (i,s) in enumerate(ssizes)]...)
if shuffle
idx = randperm(rng, n)
X, y = X[:, idx], y[idx]
end
# Add noise to the dataset
if ε > 0.0
X += randn(rng, size(X)).*convert(T,ε/d)
end
# Rotate dataset
for ((i,j),θ) in rotations
X[[i,j],:] .= R(θ)*view(X,[i,j],:)
end
return X, y
end
function sample_moons(n)
X, _ = nmoons(Float64, n, 2, ε=0.05, d=2, translation=[0.25, -0.25])
return Array(X')
end
#------------------------------------------------------------------------------------------
# RealNVP
function mlp(x, k, id)
x = constant(x)
variable_scope("layer$k$id") do
x = dense(x, 24, activation="leaky_relu")
x = dense(x, 24, activation="leaky_relu")
x = dense(x, 24, activation="leaky_relu")
x = dense(x, 1)
end
return x
end
flows = [AffineHalfFlow(2, mod(i,2)==1, x->mlp(x, i, 0), x->mlp(x, i, 1)) for i = 0:8]
#------------------------------------------------------------------------------------------
# RealNVP
function mlp(x, k, id)
x = constant(x)
variable_scope("layer$k$id") do
x = dense(x, 24, activation="leaky_relu")
x = dense(x, 24, activation="leaky_relu")
x = dense(x, 24, activation="leaky_relu")
x = dense(x, 1)
end
return x
end
flows = [AffineHalfFlow(2, mod(i,2)==1, x->mlp(x, i, 0), x->mlp(x, i, 1)) for i = 0:8]
#------------------------------------------------------------------------------------------
# NICE
# function mlp(x, k, id)
# x = constant(x)
# variable_scope("layer$k$id") do
# x = dense(x, 24, activation="leaky_relu")
# x = dense(x, 24, activation="leaky_relu")
# x = dense(x, 24, activation="leaky_relu")
# x = dense(x, 1)
# end
# return x
# end
# flow1 = [AffineHalfFlow(2, mod(i,2)==1, missing, x->mlp(x, i, 1)) for i = 0:4]
# flow2 = [AffineConstantFlow(2, shift=false)]
# flows = [flow1;flow2]
# SlowMAF
#------------------------------------------------------------------------------------------
# function mlp(x, k, id)
# x = constant(x)
# variable_scope("layer$k$id") do
# x = dense(x, 24, activation="leaky_relu")
# x = dense(x, 24, activation="leaky_relu")
# x = dense(x, 24, activation="leaky_relu")
# x = dense(x, 2)
# end
# return x
# end
# flows = [SlowMAF(2, mod(i,2)==1, [x->mlp(x, i, 0)]) for i = 0:3]
# MAF
#------------------------------------------------------------------------------------------
# flows = [MAF(2, mod(i,2)==1, [24, 24, 24], name="layer$i") for i = 0:3]
# IAF
#------------------------------------------------------------------------------------------
# flows = [IAF(2, mod(i,2)==1, [24, 24, 24], name="layer$i") for i = 0:3]
# prior = ADCME.MultivariateNormalDiag(loc=zeros(2))
# model = NormalizingFlowModel(prior, flows)
# Insert ActNorm to any of the flows
#------------------------------------------------------------------------------------------
# flow2 = [ActNorm(2, "ActNorm$i") for i = 1:length(flows)]
# flows = permutedims(hcat(flow2, flows))[:]
# # error()
# # msample = rand(model,1)
# # zs, prior_logprob, log_det = model([0.0040 0.4426])
# # sess = Session(); init(sess)
# # run(sess, msample)
# # run(sess,zs)
# GLOW
#------------------------------------------------------------------------------------------
# function mlp(x, k, id)
# x = constant(x)
# variable_scope("layer$k$id") do
# x = dense(x, 24, activation="leaky_relu")
# x = dense(x, 24, activation="leaky_relu")
# x = dense(x, 24, activation="leaky_relu")
# x = dense(x, 1)
# end
# return x
# end
# flows = [Invertible1x1Conv(2, "conv$i") for i = 0:2]
# norms = [ActNorm(2, "ActNorm$i") for i = 0:2]
# couplings = [AffineHalfFlow(2, mod(i, 2)==1, x->mlp(x, i, 0), x->mlp(x, i, 1)) for i = 0:length(flows)-1]
# flows = permutedims(hcat(norms, flows, couplings))[:]
#------------------------------------------------------------------------------------------
# Neural Splines Coupling
# function mlp(x, k, id)
# x = constant(x)
# variable_scope("fc$k$id") do
# x = dense(x, 16, activation="leaky_relu")
# x = dense(x, 16, activation="leaky_relu")
# x = dense(x, 16, activation="leaky_relu")
# x = dense(x, 3K-1)
# end
# return x
# end
# K = 8
# flows = [NeuralCouplingFlow(2, x->mlp(x, i, 0), x->mlp(x, i, 1), K) for i = 0:2]
# convs = [Invertible1x1Conv(2, "conv$i") for i = 0:2]
# norms = [ActNorm(2, "ActNorm$i") for i = 0:2]
# flows = permutedims(hcat(norms, convs, flows))[:]
#------------------------------------------------------------------------------------------
prior = ADCME.MultivariateNormalDiag(loc=zeros(2))
model = NormalizingFlowModel(prior, flows)
x = placeholder(rand(128,2))
zs, prior_logpdf, logdet = model(x)
log_pdf = prior_logpdf + logdet
loss = -sum(log_pdf)
model_samples = rand(model, 128*8)
sess = Session(); init(sess)
opt = AdamOptimizer(1e-4).minimize(loss)
sess = Session(); init(sess)
for i = 1:10000
_, l = run(sess, [opt, loss], x=>sample_moons(128))
if mod(i,100)==0
@info i, l
end
end
z = run(sess, model_samples[end])
x = sample_moons(128*8)
scatter(x[:,1], x[:,2], c="b", s=5, label="data")
scatter(z[:,1], z[:,2], c="r", s=5, label="prior --> posterior")
axis("scaled"); xlabel("x"); ylabel("y")#
``` | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 13680 | # Shared Memory Across Kernels
## Introuction
In many use cases, we want to share data across multiple kernels. For example, if we want to design several custom operators for finite element analysis (e.g., one for assembling, one for solving the linear system and one for performing Newton's iteration), we might want to share the geometric data such as nodes and element connectivity matrices. This can be done by the share memory mechanism of dynamical shared libraries.
The technique introduced here is very useful. For example, in the ADCME standard library, [`factorize`](@ref) is implemented using this technique. `factorize` factorizes a nonsingular matrix and store the factorized form in the shared library so you can amortize the computational cost for factorization by efficiently solving many linear systems.
## Solutions for *nix
Dynamical shared libraries have the following property: in Unix-like environments, shared libries export all `extern` global variables. That is, multiple shared libraries can change the same variable as long as the variable is marked as `extern`. However, `extern` variable itself is not a definition but only a declaration. The variable should be defined in one and only one shared library.
Therefore, when we design custom operators and want to have global variables that will be reused by multiple custom kernels (each constitutes a separate dynamical shared library), we can link each of them to a "data storage" shared library. The "data storage" shared library should contain the definition of the global variable to be shared among those kernels.

As an example, consider we want to share `Float64` vectors (with `String` keys). The data structure of the storage is given in `Saver.h`
```c++
#include <map>
#include <string>
#include <vector>
struct DataStore
{
std::map<std::string, std::vector<double>> vdata;
};
extern DataStore ds;
```
Note we include `extern DataStore ds;` for convenience: we can include `Saver.h` for our custom operator kernels so that we have access to `ds`.
Additionally, in `Saver.cpp`, we define `ds`
```c++
#include "Saver.h"
DataStore ds;
```
Now we can compile a dynamical shared library `Saver.so` (or `Saver.dylib`) with `Saver.h` and `Saver.cpp`. For all the other kernel implementation, we can include the header file `Saver.h` and link to `Saver.so` (or `Saver.dylib`) during compilation.
### Code Examples
We show an example for storing, querying and deleting $10\times 1$ `Float64` vectors with this technique. The main files are (the codes can be accessed [here](https://github.com/kailaix/ADCME.jl/tree/master/docs/src/assets/Codes/SharedMemory))
* `SaverTensor.cpp`
```c++
#include "Saver.h"
#include "tensorflow/core/framework/op_kernel.h"
#include "tensorflow/core/framework/tensor_shape.h"
#include "tensorflow/core/platform/default/logging.h"
#include "tensorflow/core/framework/shape_inference.h"
#include<cmath>
#include<string>
#include<eigen3/Eigen/Core>
using std::string;
using namespace tensorflow;
REGISTER_OP("SaveTensor")
.Input("handle : string")
.Input("val : double")
.Output("out : string")
.SetShapeFn([](::tensorflow::shape_inference::InferenceContext* c) {
shape_inference::ShapeHandle handle_shape;
TF_RETURN_IF_ERROR(c->WithRank(c->input(0), 0, &handle_shape));
shape_inference::ShapeHandle val_shape;
TF_RETURN_IF_ERROR(c->WithRank(c->input(1), 1, &val_shape));
c->set_output(0, c->Scalar());
return Status::OK();
});
class SaveTensorOp : public OpKernel {
private:
public:
explicit SaveTensorOp(OpKernelConstruction* context) : OpKernel(context) {
}
void Compute(OpKernelContext* context) override {
DCHECK_EQ(2, context->num_inputs());
const Tensor& handle = context->input(0);
const Tensor& val = context->input(1);
const TensorShape& val_shape = val.shape();
DCHECK_EQ(val_shape.dims(), 1);
// extra check
// create output shape
TensorShape out_shape({});
// create output tensor
Tensor* out = NULL;
OP_REQUIRES_OK(context, context->allocate_output(0, out_shape, &out));
// get the corresponding Eigen tensors for data access
auto handle_tensor = handle.flat<string>().data();
auto val_tensor = val.flat<double>().data();
auto out_tensor = out->flat<string>().data();
// implement your forward function here
// context->tensors_[string(*handle_tensor)] = val;
ds.vdata[string(*handle_tensor)] = std::vector<double>(val_tensor, val_tensor+10);
*out_tensor = *handle_tensor;
printf("[Add] %s to collections.\n", string(*handle_tensor).c_str());
printf("========Existing Keys========\n");
for(auto & kv: ds.vdata){
printf("Key %s\n", kv.first.c_str());
}
printf("\n");
}
};
REGISTER_KERNEL_BUILDER(Name("SaveTensor").Device(DEVICE_CPU), SaveTensorOp);
```
* `GetTensor.cpp`
```c++
#include "Saver.h"
#include "tensorflow/core/framework/op_kernel.h"
#include "tensorflow/core/framework/tensor_shape.h"
#include "tensorflow/core/platform/default/logging.h"
#include "tensorflow/core/framework/shape_inference.h"
#include<cmath>
#include<string>
#include<map>
#include<eigen3/Eigen/Core>
using std::string;
using namespace tensorflow;
REGISTER_OP("GetTensor")
.Input("handle : string")
.Output("val : double")
.SetShapeFn([](::tensorflow::shape_inference::InferenceContext* c) {
shape_inference::ShapeHandle handle_shape;
TF_RETURN_IF_ERROR(c->WithRank(c->input(0), 0, &handle_shape));
c->set_output(0, c->Vector(-1));
return Status::OK();
});
class GetTensorOp : public OpKernel {
private:
public:
explicit GetTensorOp(OpKernelConstruction* context) : OpKernel(context) {
}
void Compute(OpKernelContext* context) override {
DCHECK_EQ(1, context->num_inputs());
const Tensor& handle = context->input(0);
auto handle_tensor = handle.flat<string>().data();
auto val_shape = TensorShape({10});
Tensor *val = nullptr;
OP_REQUIRES_OK(context, context->allocate_output(0, val_shape, &val));
if (!ds.vdata.count(string(*handle_tensor))){
printf("[Get] Key %s does not exist.\n", string(*handle_tensor).c_str());
}
else{
printf("[Get] Key %s exists.\n", string(*handle_tensor).c_str());
auto v = ds.vdata[string(*handle_tensor)];
for(int i=0;i<10;i++){
val->flat<double>().data()[i] = v[i];
}
}
printf("========Existing Keys========\n");
for(auto & kv: ds.vdata){
printf("Key %s\n", kv.first.c_str());
}
printf("\n");
}
};
REGISTER_KERNEL_BUILDER(Name("GetTensor").Device(DEVICE_CPU), GetTensorOp);
```
* `DeleteTensor.cpp`
```c++
#include "Saver.h"
#include "tensorflow/core/framework/op_kernel.h"
#include "tensorflow/core/framework/tensor_shape.h"
#include "tensorflow/core/platform/default/logging.h"
#include "tensorflow/core/framework/shape_inference.h"
#include<cmath>
#include<string>
#include<map>
#include<eigen3/Eigen/Core>
using std::string;
using namespace tensorflow;
REGISTER_OP("DeleteTensor")
.Input("handle : string")
.Output("val : bool")
.SetShapeFn([](::tensorflow::shape_inference::InferenceContext* c) {
shape_inference::ShapeHandle handle_shape;
TF_RETURN_IF_ERROR(c->WithRank(c->input(0), 0, &handle_shape));
c->set_output(0, c->Scalar());
return Status::OK();
});
class DeleteTensorOp : public OpKernel {
private:
public:
explicit DeleteTensorOp(OpKernelConstruction* context) : OpKernel(context) {
}
void Compute(OpKernelContext* context) override {
DCHECK_EQ(1, context->num_inputs());
const Tensor& handle = context->input(0);
auto handle_tensor = handle.flat<string>().data();
auto val_shape = TensorShape({});
Tensor *val = nullptr;
OP_REQUIRES_OK(context, context->allocate_output(0, val_shape, &val));
if (ds.vdata.count(string(*handle_tensor))){
ds.vdata.erase(string(*handle_tensor));
printf("[Delete] Erase key %s.\n", string(*handle_tensor).c_str());
*(val->flat<bool>().data()) = true;
}
else{
printf("[Delete] Key %s does not exist.\n", string(*handle_tensor).c_str());
*(val->flat<bool>().data()) = false;
}
printf("========Existing Keys========\n");
for(auto & kv: ds.vdata){
printf("Key %s\n", kv.first.c_str());
}
printf("\n");
}
};
REGISTER_KERNEL_BUILDER(Name("DeleteTensor").Device(DEVICE_CPU), DeleteTensorOp);
```
Here is part of the [`CMakeLists.txt`](https://github.com/kailaix/ADCME.jl/tree/master/docs/src/assets/Codes/SharedMemory/CMakeLists.txt) used for compilation, where we link `XXTensor.cpp` with `Saver`
```cmake
cmake_minimum_required(VERSION 3.5)
project(TF_CUSTOM_OP)
set (CMAKE_CXX_STANDARD 11)
message("JULIA=${JULIA}")
execute_process(COMMAND ${JULIA} -e "import ADCME; print(ADCME.__STR__)" OUTPUT_VARIABLE JL_OUT)
list(GET JL_OUT 0 BINDIR)
list(GET JL_OUT 1 LIBDIR)
list(GET JL_OUT 2 TF_INC)
list(GET JL_OUT 3 TF_ABI)
list(GET JL_OUT 4 PREFIXDIR)
list(GET JL_OUT 5 CC)
list(GET JL_OUT 6 CXX)
list(GET JL_OUT 7 CMAKE)
list(GET JL_OUT 8 MAKE)
list(GET JL_OUT 9 GIT)
list(GET JL_OUT 10 PYTHON)
list(GET JL_OUT 11 TF_LIB_FILE)
message("BINDIR=${BINDIR}")
message("LIBDIR=${LIBDIR}")
message("TF_INC=${TF_INC}")
message("TF_ABI=${TF_ABI}")
message("PREFIXDIR=${PREFIXDIR}")
message("Python path=${PYTHON}")
message("TF_LIB_FILE=${TF_LIB_FILE}")
if (CMAKE_CXX_COMPILER_VERSION VERSION_GREATER 5.0 OR CMAKE_CXX_COMPILER_VERSION VERSION_EQUAL 5.0)
set(CMAKE_CXX_FLAGS "-D_GLIBCXX_USE_CXX11_ABI=${TF_ABI} ${CMAKE_CXX_FLAGS}")
endif()
set(CMAKE_BUILD_TYPE Release)
if(MSVC)
set(CMAKE_CXX_FLAGS_RELEASE "-DNDEBUG")
else()
set(CMAKE_CXX_FLAGS_RELEASE "-O3 -DNDEBUG")
endif()
include_directories(${TF_INC} ${PREFIXDIR})
link_directories(${TF_LIB})
if(MSVC)
if(CMAKE_CXX_FLAGS MATCHES "/W[0-4]")
string(REGEX REPLACE "/W[0-4]" "/W0" CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS}")
else()
set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} /W0")
endif()
add_library(Saver SHARED Saver.cpp SaveTensor.cpp GetTensor.cpp DeleteTensor.cpp)
set_property(TARGET Saver PROPERTY POSITION_INDEPENDENT_CODE ON)
target_link_libraries(Saver ${TF_LIB_FILE})
add_definitions(-DNOMINMAX)
else()
add_library(Saver SHARED Saver.cpp)
set_property(TARGET Saver PROPERTY POSITION_INDEPENDENT_CODE ON)
add_library(SaveTensor SHARED SaveTensor.cpp)
set_property(TARGET SaveTensor PROPERTY POSITION_INDEPENDENT_CODE ON)
target_link_libraries(SaveTensor ${TF_LIB_FILE} Saver)
add_library(GetTensor SHARED GetTensor.cpp)
set_property(TARGET GetTensor PROPERTY POSITION_INDEPENDENT_CODE ON)
target_link_libraries(GetTensor ${TF_LIB_FILE} Saver)
add_library(DeleteTensor SHARED DeleteTensor.cpp)
set_property(TARGET DeleteTensor PROPERTY POSITION_INDEPENDENT_CODE ON)
target_link_libraries(DeleteTensor ${TF_LIB_FILE} Saver)
endif()
```
Here we have separate procedure for Windows and *nix systems.
We can test our implementation with
```julia
using ADCME
if Sys.iswindows()
global save_tensor = load_op_and_grad("./build/Release/libSaver","save_tensor")
global get_tensor = load_op_and_grad("./build/Release/libSaver","get_tensor")
global delete_tensor = load_op_and_grad("./build/Release/libSaver","delete_tensor")
else
global save_tensor = load_op_and_grad("./build/libSaveTensor","save_tensor")
global get_tensor = load_op_and_grad("./build/libGetTensor","get_tensor")
global delete_tensor = load_op_and_grad("./build/libDeleteTensor","delete_tensor")
end
val = constant(rand(10))
t1 = constant("tensor1")
t2 = constant("tensor2")
t3 = constant("tensor3")
u1 = save_tensor(t1,val)
u2 = save_tensor(t2,2*val)
u3 = save_tensor(t3,3*val)
z1 = get_tensor(t1);
z2 = get_tensor(t2);
z3 = get_tensor(t3);
d1 = delete_tensor(t1);
d2 = delete_tensor(t2);
d3 = delete_tensor(t3);
sess = Session();
run(sess, [u1,u2,u3]) # add all the keys
# get the keys one by one
run(sess, z1)
run(sess, z2)
run(sess, z3)
# delete 2nd key
run(sess, d2)
```
The expected output is
```txt
[Add] tensor3 to collections.
========Existing Keys========
Key tensor3
[Add] tensor2 to collections.
========Existing Keys========
Key tensor2
Key tensor3
[Add] tensor1 to collections.
========Existing Keys========
Key tensor1
Key tensor2
Key tensor3
[Get] Key tensor1 exists.
========Existing Keys========
Key tensor1
Key tensor2
Key tensor3
[Get] Key tensor2 exists.
========Existing Keys========
Key tensor1
Key tensor2
Key tensor3
[Get] Key tensor3 exists.
========Existing Keys========
Key tensor1
Key tensor2
Key tensor3
[Delete] Erase key tensor2.
========Existing Keys========
Key tensor1
Key tensor3
```
For example, in [this article](./factorization.md) we use the technique introduced here to design a custom operator for direct methods for sparse matrix solutions.
## Solutions for Windows
Windows systems have special rules for creating and linking dynamic libraries. Basically you need to export symbols in the dynamic libraries so that they are visiable to application programs. To avoid many troubles that you may encounter getting the macros and configurations correct, you can instead compile all the source into a single dynamic library. The model is as follows
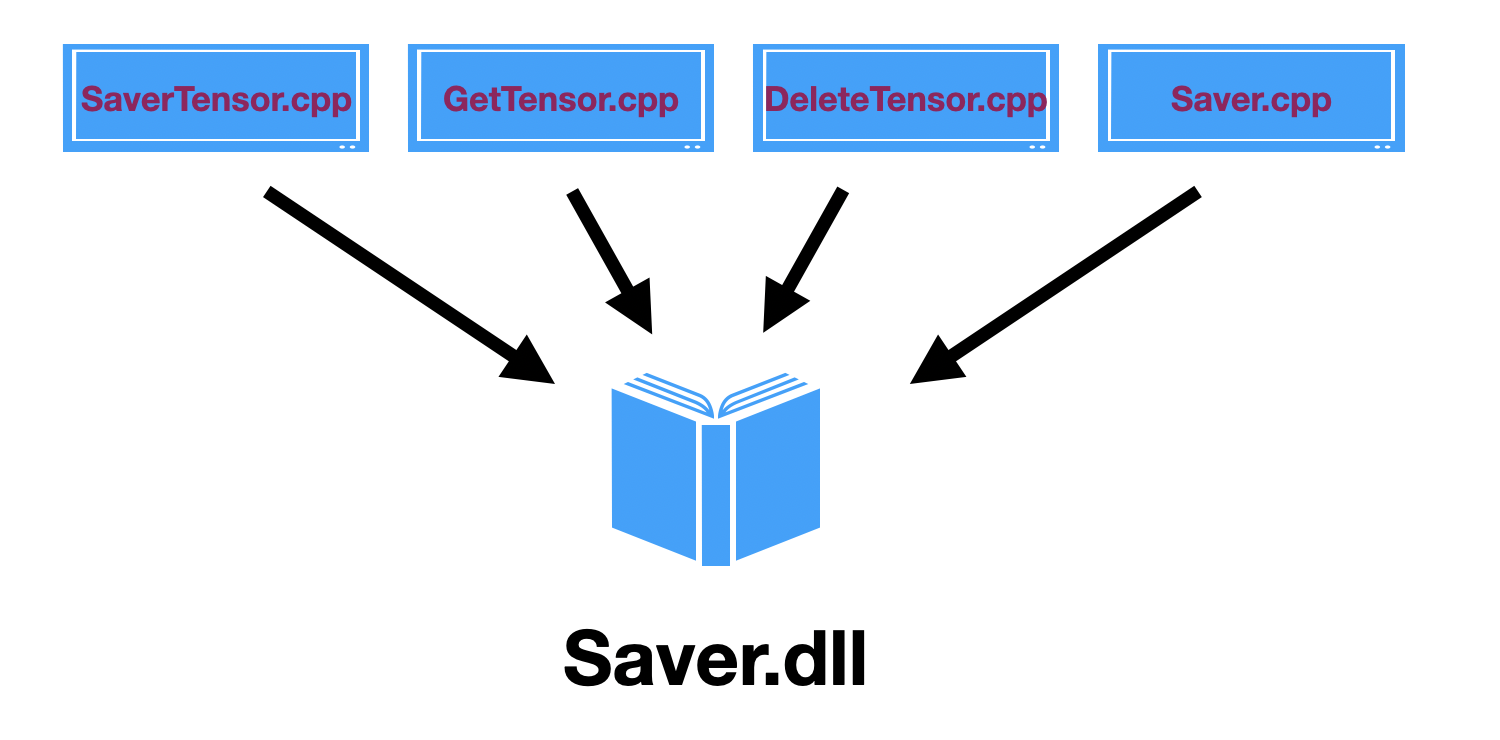
The source codes and CMakeLists.txt in the above section can be reused without any modification.
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 3144 | # The Mathematical Structure of DNN Hessians
It has been observed empirically that the converged weights and biases of DNNs are close to a proper initial guess. This indicates that DNNs are well approximated with its first order Taylor expansion.
Let us consider a scalar-valued DNN $f(x, \theta)$, where $x$ is a $d$-dimensional input and $\theta$ is the weights and biases. The initial guess is $\theta_0$. Then we have
$$f(x, \theta) \approx f(x, \theta_0) + \nabla_\theta f(x, \theta_0)^T (\theta - \theta_0)\tag{1}$$
Consider a quadratic loss function
$$L(\theta) = \sum_{i=1}^m (f(x_i, \theta) - y_i)^2$$
Using the Taylor expansion Eq. 1, we have
$$L(\theta) \approx \sum_{i=1}^m (f(x_i, \theta_0) + \nabla_\theta f(x_i, \theta_0)^T (\theta - \theta_0) - y_i)^2 \tag{2}$$
Eq. 2 is a quadratic function of $\theta$, and the Hessian matrix is given by
$$H = \sum_{i=1}^m \nabla_\theta f(x_i, \theta_0) \nabla_\theta f(x_i, \theta_0)^T$$
Let us consider $\nabla_\theta f(x_i, \theta_0) \nabla_\theta f(x_i, \theta_0)^T$, which is a rank-one matrix. Therefore, one straight-forward corollary is
$$\text{rank}(H) \leq m$$
That is, for small data, the rank of $H$ is small, and the rank of $H$ is always no greater than the size of samples. The implication is significant for applications in computational engineering: unlike many machine learning problems, where plenty of training data are available, data are usually scarce in computational engineering (e.g., expensive to collect in experiments). Thus a low rank Hessian is predominate in engineering applications.
We can also write $H$ as follows:
$$H = X^TX, \quad X = \begin{bmatrix}\nabla_\theta f(x_1, \theta_0)^T \\ \nabla_\theta f(x_2, \theta_0)^T \\ \ldots \\ \nabla_\theta f(x_m, \theta_0)^T\end{bmatrix}$$
We have $\text{rank}(H) = \text{rank}(X^TX) \leq \text{rank}(X)$, that is, the rank of $H$ is upper bounded by the rank of $X$. The rank of $X$ determines on the information provided by $\{x_i\}_{i=1}^m$. For example, if most of $x_i$ are the same or similar, we expect $X$ to have a low rank.
We demonstrate the rank of Hessians using the following examples: let $x_i = \frac{i-1}{99}$, $i = 1, 2, \ldots, 100$, and $y_i = \sin(\pi x_i)$. We train a scalar-valued deep neural network $f(x, \theta)$ with 3 hidden neurals, 20 neurons per layer, and tanh activation functions. The loss function is
$$L(\theta) = \sum_{i\in\mathcal{I}} (y_i - f(x_i, \theta))^2$$
Here $\mathcal{I}$ is a subset of $\{1,2,\ldots, 100\}$ and linearly spaced between 1 and 100. We train the deep neural network using L-BFGS-B optimizer, and calculate the Hessian matrix $H = \frac{\partial^2 L}{\partial \theta \partial \theta^T}$. We report the number of positive eigenvalues, which is defined as
$$\lambda > 10^{-6} \lambda_{\max}$$
Here $\lambda_{\max}$ is the maximum eigenvalue.

We can see when the dataset size is small, the Hessian rank is the same as the dataset size. The rank reaches plateau when the datasize increases to 6. | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 8743 | # Overview
ADCME is suitable for conducting inverse modeling in scientific computing; specifically, ADCME targets **physics informed machine learning**, which leverages machine learning techniques to solve challenging scientific computing problems. The purpose of the package is to: (1) provide differentiable programming framework for scientific computing based on TensorFlow automatic differentiation (AD) backend; (2) adapt syntax to facilitate implementing scientific computing, particularly for numerical PDE discretization schemes; (3) supply missing functionalities in the backend (TensorFlow) that are important for engineering, such as sparse linear algebra, constrained optimization, etc. Applications include
- physics informed machine learning (a.k.a., scientific machine learning, physics informed learning, etc.)
- coupled hydrological and full waveform inversion
- constitutive modeling in solid mechanics
- learning hidden geophysical dynamics
- parameter estimation in stochastic processes
The package inherits the scalability and efficiency from the well-optimized backend TensorFlow. Meanwhile, it provides access to incorporate existing C/C++ codes via the custom operators. For example, some functionalities for sparse matrices are implemented in this way and serve as extendable "plugins" for ADCME.

ADCME is open-sourced with an MIT license. You can find the source codes at
[https://github.com/kailaix/ADCME.jl](https://github.com/kailaix/ADCME.jl)
Read more about methodology, philosophy, and insights about ADCME: [slides](https://github.com/ADCMEMarket/ADCMEImages/blob/master/ADCME/Slide/ADCME.pdf?raw=true). Start with [tutorial](./tutorial.md) to solve your own inverse modeling problems!
## Installation
It is recommended to install ADCME via
```julia
using Pkg
Pkg.add("ADCME")
```
❗ For windows users, please follow the instructions [here](./windows_installation.md).
!!! info
In some cases, you may want to install the package and configure the environment manually.
Step 1: Install `ADCME` on a computer with Internet access and zip all files from the following paths
```julia
julia> using Pkg
julia> Pkg.depots()
```
The files will contain all the dependencies.
Step 2:
Copy the `deps.jl` file from your built ADCME and modify it for your local repository.
```julia
using ADCME;
print(joinpath(splitdir(pathof(ADCME))[1], "deps/deps.jl"))
```
## Docker
If you have Docker installed on your system, you can try the no-hassle way to install ADCME (you don't even have to install Julia!):
```bash
docker run -ti kailaix/adcme
```
See [this guide](./docker.md) for details.
## Troubleshooting for MacOS
Here are some common problems you may encounter on a Mac computer:
- You may get stuck at building ADCME. It is a [known issue](https://github.com/kailaix/ADCME.jl/issues/64) for some combinations of specific MacOS and Julia versions. You can verify this by checking whether the following step gets stuck:
```julia
using PyCall
pyimport("tensorflow")
```
One workaround is to use another Julia version; for example, we tested Julia 1.3 on several MacOS versions and it works fine.
- You may encounter the following warning when you run `using PyPlot`.
> PyPlot is using `tkagg` backend, which is known to cause crashes on macOS (#410); use the MPLBACKEND environment variable to request a different backend.
To fix this problem, add the following line immediately after `using PyPlot`
```julia
using PyPlot
matplotlib.use("agg")
```
The images may not show up but you can save the figure (`savefig("filename.png")`).
- Your Julia program may crash when you run `BFGS!` and show the following error message.
> Error #15: Initializing libiomp5.dylib, but found libiomp5.dylib already initialized OMP: Hint: This means that multiple copies of the OpenMP runtime have been linked into the program. That is dangerous, since it can degrade performance or cause incorrect results. The best thing to do is to ensure that only a single OpenMP runtime is linked into the process, e.g. by avoiding static linking of the OpenMP runtime in any library. As an unsafe, unsupported, undocumented workaround you can set the environment variable KMP_DUPLICATE_LIB_OK=TRUE to allow the program to continue to execute, but that may cause crashes or silently produce incorrect results. For more information, please see http://www.intel.com/software/products/support/.
This is because `matplotlib` (called by `PyPlot`) and `scipy` (called by `BFGS!`) simultaneously access OpenMP libraries in an unsafe way. To fix this problem, add the following line in the **very beginning** of your script (or run the command right after you enter a Julia prompt)
```julia
ENV["KMP_DUPLICATE_LIB_OK"] = true
```
- You may see the following error message when you run `ADCME.precompile()`:
> The C compiler
>
> "/Users/<YourUsername>/.julia/adcme/bin/clang"
>
> is not able to compile a simple test program.
>
> It fails with the following output: ...
This is because your developer tools are not the one required by `ADCME`. To solve this problem, run the following commands in your terminal:
```
rm /Users/<YourUsername>/.julia/adcme/bin/clang
rm /Users/<YourUsername>/.julia/adcme/bin/clang++
ln -s /usr/bin/clang /Users/<YourUsername>/.julia/adcme/bin/clang
ln -s /usr/bin/clang++ /Users/<YourUsername>/.julia/adcme/bin/clang++
```
Here `<YourUsername>` is your user name.
## Optimization
ADCME is an all-in-one solver for gradient-based optimization problems. It leverages highly optimized and concurrent/parallel kernels that are implemented in C++ for both the forward computation and gradient computation. Additionally, it provides a friendly user interface to specify the mathematical optimization problem: constructing a computational graph.
Let's consider a simple problem: we want to solve the unconstrained optimization problem
$$f(\mathbf{x}) = \sum_{i=1}^{n-1}\left[ 100(x_{i+1}-x_i^2) + (1-x_i)^2 \right]$$
where $x_i\in [-10,10]$ and $n=100$.
We solve the problem using the L-BFGS-B method.
```julia
using ADCME
n = 100
x = Variable(rand(n)) # Use `Variable` to mark the quantity that gets updated in optimization
f = sum(100((x[2:end]-x[1:end-1])^2 + (1-x[1:end-1])^2)) # Use typical Julia syntax
sess = Session(); init(sess) # Create and initialize a session is mandatory for activating the computational graph
BFGS!(sess, f, var_to_bounds = Dict(x=>[-10.,10.]))
```
To get the value of $\mathbf{x}$, we use [`run`](@ref) to extract the values
```julia
run(sess, x)
```
The above code will return a value close to the optimal values $\mathbf{x} = [1\ 1\ \ldots\ 1]$.
!!! info
You can also use [`Optimize!`](@ref) to use other optimizers. For example, if you want to use an optimizer, such as `ConjugateGraidient` from the `Optim` package, simply replace `BFGS!` with `Optimize!` and specify the corresponding optimizer
```julia
using Optim
Optimize!(sess, loss, optimizer = ConjugateGradient())
```
## Machine Learning
You can also use ADCME to do typical machine learning tasks and leverage the Julia machine learning ecosystem! Here is an example of training a ResNet for digital number recognition.
```julia
using MLDatasets
using ADCME
# load data
train_x, train_y = MNIST.traindata()
train_x = reshape(Float64.(train_x), :, size(train_x,3))'|>Array
test_x, test_y = MNIST.testdata()
test_x = reshape(Float64.(test_x), :, size(test_x,3))'|>Array
# construct loss function
ADCME.options.training.training = placeholder(true)
x = placeholder(rand(64, 784))
l = placeholder(rand(Int64, 64))
resnet = Resnet1D(10, num_blocks=10)
y = resnet(x)
loss = mean(sparse_softmax_cross_entropy_with_logits(labels=l, logits=y))
# train the neural network
opt = AdamOptimizer().minimize(loss)
sess = Session(); init(sess)
for i = 1:10000
idx = rand(1:60000, 64)
_, loss_ = run(sess, [opt, loss], feed_dict=Dict(l=>train_y[idx], x=>train_x[idx,:]))
@info i, loss_
end
# test
for i = 1:10
idx = rand(1:10000,100)
y0 = resnet(test_x[idx,:])
y0 = run(sess, y0, ADCME.options.training.training=>false)
pred = [x[2]-1 for x in argmax(y0, dims=2)]
@info "Accuracy = ", sum(pred .== test_y[idx])/100
end
```
## Contributing
Contribution and suggestions are always welcome. In addition, we are also looking for research collaborations. You can submit issues for suggestions, questions, bugs, and feature requests, or submit pull requests to contribute directly. You can also contact the authors for research collaboration.
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 3355 | # Configure MPI for Distributed Computing
This section will cover how to configure ADCME for MPI functionalities.
## Configure the MPI backend
The first step is to configure your MPI backend. There are many choices depending on your operation system. For example, Windows have Microsoft MPI. There are also OpenMPI and Intel MPI available on most Linux distributions. If you want to use your own MPI backend, you need to locate the MPI libraries, header files, and executable (e.g., `mpirun`). You need to build ADCME with the following environment variable:
* `MPI_C_LIBRARIES`: the MPI shared library, for example, on Windows, it may be
```
C:\\Program Files (x86)\\Microsoft SDKs\\MPI\\Lib\\x64\\msmpi.lib
```
On Unix systems, it may be
```/opt/ohpc/pub/compiler/intel-18/compilers_and_libraries_2018.2.199/linux/mpi/intel64/lib/release/libmpi.so```
Note that you must include **the shared library** in the variable.
* `MPI_INCLUDE_PATH`: the directory where `mpi.h` is located, for example,
```C:\\Program Files (x86)\\Microsoft SDKs\\MPI\\Include```
Or in a Unix system, we have
```/opt/ohpc/pub/compiler/intel-18/compilers_and_libraries_2018.2.199/linux/mpi/intel64/include/```
The simplest way is to add these variables in the environment variables. For example, in Linux, we can add the following lines in the `~/.bashrc` file.
```bash
export MPI_C_LIBRARIES=/opt/ohpc/pub/compiler/intel-18/compilers_and_libraries_2018.2.199/linux/mpi/intel64/lib/libmpi.so
export MPI_INCLUDE_PATH=/opt/ohpc/pub/compiler/intel-18/compilers_and_libraries_2018.2.199/linux/mpi/intel64/include/
alias mpirun=/opt/ohpc/pub/compiler/intel-18/compilers_and_libraries_2018.2.199/linux/mpi/intel64/bin/mpirun
```
In the case you do not have an MPI backend, ADCME provides you a convenient way to install MPI by compiling from source. Just run
```julia
using ADCME
install_openmpi()
```
This should install an OpenMPI library for you. Note this functionality does not work on Windows and is only tested on Linux.
## Build MPI Libraries
The MPI functionality of ADCME is not fulfilled at this point. To enable the MPI support, you need to recompile the built-in custom operators.
```julia
using ADCME
ADCME.precompile(true)
```
At this point, you will be able to use MPI features.
## Build MPI Custom Operators
You can also build MPI-enabled custom operators by calling
```julia
using ADCME
customop(with_mpi=true)
```
In this case, there will be extra lines in `CMakeLists.txt` to setup MPI dependencies.
```julia
IF(DEFINED ENV{MPI_C_LIBRARIES})
set(MPI_INCLUDE_PATH $ENV{MPI_INCLUDE_PATH})
set(MPI_C_LIBRARIES $ENV{MPI_C_LIBRARIES})
message("MPI_INCLUDE_PATH = ${MPI_INCLUDE_PATH}")
message("MPI_C_LIBRARIES = ${MPI_C_LIBRARIES}")
include_directories(${MPI_INCLUDE_PATH})
ELSE()
message("MPI_INCLUDE_PATH and/or MPI_C_LIBRARIES is not set. MPI operators are not compiled.")
ENDIF()
```
## Running MPI Applications with Slurm
To run MPI applications with slurm, the following commands are useful
```bash
sbatch -n 4 -c 8 mpirun -n 4 julia app.jl
```
This specifies 4 tasks and each task uses 8 cores. You can also replace `sbatch` with `salloc`.
To diagonose the application, you can also let `mpirun` print out the rank information, e.g., in OpenMPI we have
```bash
sbatch -n 4 -c 8 mpirun --report-bindings -n 4 julia app.jl
```
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 8320 | # Julia Custom Operators
!!! warning
Currently, embedding Julia suffers from multithreading issues: calling Julia from a non-Julia thread is not supported in ADCME. When TensorFlow kernel codes are executed concurrently, it is difficult to invoke the Julia functions. See [issue](https://github.com/kailaix/ADCME.jl/issues/8).
In scientific and engineering applications, the operators provided by `TensorFlow` are not sufficient for high performance computing. In addition, constraining oneself to `TensorFlow` environment sacrifices the powerful scientific computing ecosystems provided by other languages such as `Julia` and `Python`. For example, one might want to code a finite volume method for a sophisticated fluid dynamics problem; it is hard to have the flexible syntax to achieve this goal, obtain performance boost from existing fast solvers such as AMG, and benefit from many other third-party packages within `TensorFlow`. This motivates us to find a way to "plugin" custom operators to `TensorFlow`.
We have already introduced how to incooperate `C++` custom operators. For many researchers, they usually prototype the solvers in a high level language such as MATLAB, Julia or Python. To enjoy the parallelism and automatic differentiation feature of `TensorFlow`, they need to port them into `C/C++`. However, this is also cumbersome sometimes, espeically the original solvers depend on many packages in the high-level language.
We solve this problem by incorporating `Julia` functions directly into `TensorFlow`. That is, for any `Julia` functions, we can immediately convert it to a `TensorFlow` operator. At runtime, when this operator is executed, the corresponding `Julia` function is executed. That implies we have the `Julia` speed. Most importantly, the function is perfectly compitable with the native `Julia` environment; third-party packages, global variables, nested functions, etc. all work smoothly. Since `Julia` has the ability to call other languages in a quite elegant and simple manner, such as `C/C++`, `Python`, `R`, `Java`, this means it is possible to incoporate packages/codes from any supported languages into `TensorFlow` ecosystem. We need to point out that in `TensorFlow`, `tf.numpy_function` can be used to convert a `Python` function to a `TensorFlow` operator. However, in the runtime, the speed for this operator falls back to `Python` (or `numpy` operation for related parts). This is a drawback.
The key for implementing the mechanism is embedding `Julia` in `C++`. Still we need to create a `C++` dynamic library for `TensorFlow`. However, the library is only an interface for invoking `Julia` code. At runtime, `jl_get_function` is called to search for the related function in the main module. `C++` arrays, which include all the relavant data, are passed to this function through `jl_call`. It requires routine convertion from `C++` arrays to `Julia` array interfaces `jl_array_t*`. However, those bookkeeping tasks are programatic and possibly will be automated in the future. Afterwards,`Julia` returns the result to `C++` and thereafter the data are passed to the next operator.
There are two caveats in the implementation. The first is that due to GIL of Python, we must take care of the thread lock while interfacing with `Julia`. This was done by putting a guard around th e`Julia` interface
```c
PyGILState_STATE py_threadstate;
py_threadstate = PyGILState_Ensure();
// code here
PyGILState_Release(py_threadstate);
```
The second is the memory mangement of `Julia` arrays. This was done by defining gabage collection markers explicitly
```julia
jl_value_t **args;
JL_GC_PUSHARGS(args, 6); // args can now hold 2 `jl_value_t*` objects
args[0] = ...
args[1] = ...
# do something
JL_GC_POP();
```
This technique is remarkable and puts together one of the best langages in scientific computing and that in machine learning. The work that can be built on `ADCME` is enormous and significantly reduce the development time.
## Example
Here we present a simple example. Suppose we want to compute the Jacobian of a two layer neural network $\frac{\partial y}{\partial x}$
$$y = W_2\tanh(W_1x+b_1)+b_2$$
where $x, b_1, b_2, y\in \mathbb{R}^{10}$, $W_1, W_2\in \mathbb{R}^{100}$. In `TensorFlow`, this can be done by computing the gradients $\frac{\partial y_i}{\partial x}$ for each $i$. In `Julia`, we can use `ForwardDiff` to do it automatically.
```julia
function twolayer(J, x, w1, w2, b1, b2)
f = x -> begin
w1 = reshape(w1, 10, 10)
w2 = reshape(w2, 10, 10)
z = w2*tanh.(w1*x+b1)+b2
end
J[:] = ForwardDiff.jacobian(f, x)[:]
end
```
To make a custom operator, we first generate a wrapper
```julia
using ADCME
mkdir("TwoLayer")
cd("TwoLayer")
customop()
```
We modify `custom_op.txt`
```
TwoLayer
double x(?)
double w1(?)
double b1(?)
double w2(?)
double b2(?)
double y(?) -> output
```
and run
```julia
customop()
```
Three files are generated`CMakeLists.txt`, `TwoLayer.cpp` and `gradtest.jl`. Now create a new file `TwoLayer.h`
```c++
#include "julia.h"
#include "Python.h"
void forward(double *y, const double *x, const double *w1, const double *w2, const double *b1, const double *b2, int n){
PyGILState_STATE py_threadstate;
py_threadstate = PyGILState_Ensure();
jl_value_t* array_type = jl_apply_array_type((jl_value_t*)jl_float64_type, 1);
jl_value_t **args;
JL_GC_PUSHARGS(args, 6); // args can now hold 2 `jl_value_t*` objects
args[0] = (jl_value_t*)jl_ptr_to_array_1d(array_type, y, n*n, 0);
args[1] = (jl_value_t*)jl_ptr_to_array_1d(array_type, const_cast<double*>(x), n, 0);
args[2] = (jl_value_t*)jl_ptr_to_array_1d(array_type, const_cast<double*>(w1), n*n, 0);
args[3] = (jl_value_t*)jl_ptr_to_array_1d(array_type, const_cast<double*>(w2), n*n, 0);
args[4] = (jl_value_t*)jl_ptr_to_array_1d(array_type, const_cast<double*>(b1), n, 0);
args[5] = (jl_value_t*)jl_ptr_to_array_1d(array_type, const_cast<double*>(b2), n, 0);
auto fun = jl_get_function(jl_main_module, "twolayer");
if (fun==NULL) jl_errorf("Function not found in Main module.");
else jl_call(fun, args, 6);
JL_GC_POP();
if (jl_exception_occurred())
printf("%s \n", jl_typeof_str(jl_exception_occurred()));
PyGILState_Release(py_threadstate);
}
```
Most of the codes have been explanined except `jl_ptr_to_array_1d`. This function generates a `Julia` array wrapper from `C++` arrays. The last argument `0` indicates that `Julia` is not responsible for gabage collection. `TwoLayer.cpp` should also be modified according to [https://github.com/kailaix/ADCME.jl/blob/master/examples/twolayer_jacobian/TwoLayer.cpp](https://github.com/kailaix/ADCME.jl/blob/master/examples/twolayer_jacobian/TwoLayer.cpp).
Finally, we can test in `gradtest.jl`
```julia
two_layer = load_op("build/libTwoLayer", "two_layer")
w1 = rand(100)
w2 = rand(100)
b1 = rand(10)
b2 = rand(10)
x = rand(10)
J = rand(100)
twolayer(J, x, w1, w2, b1, b2)
y = two_layer(constant(x), constant(w1), constant(b1), constant(w2), constant(b2))
sess = Session(); init(sess)
J0 = run(sess, y)
@show norm(J-J0)
```
## Embedded in Modules
If the custom operator is intended to be used in a precompiled module, we can load the dynamic library at initialization
```julia
global my_op
function __init__()
global my_op = load_op("$(@__DIR__)/path/to/libMyOp", "my_op")
end
```
The corresponding `Julia` function called by `my_op` must be exported in the module (such that it is in the Main module when invoked). One such example is given in [MyModule](https://github.com/kailaix/ADCME.jl/blob/master/examples/JuliaOpModule.jl)
## Quick Reference for Implementing C++ Custom Operators in ADCME
1. Set output shape
```
c->set_output(0, c->Vector(n));
c->set_output(0, c->Matrix(m, n));
c->set_output(0, c->Scalar());
```
2. Names
`.Input` and `.Ouput` : names must be in lower case, no `_`, only letters.
3. TensorFlow Input/Output to TensorFlow Tensors
```
grad.vec<double>();
grad.scalar<double>();
grad.matrix<double>();
grad.flat<double>();
```
Obtain flat arrays
```
grad.flat<double>().data()
```
4. Scalars
Allocate scalars using TensorShape()
5. Allocate Shapes
Although you can use -1 for shape reference, you must allocate exact shapes in `Compute` | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 7143 | # Uncertainty Quantification of Neural Networks in Physics Informed Learning using MCMC
In this section, we consider uncertainty quantification of a neural network prediction using Markov Chain Monte Carlo.
The idea is that we use MCMC to sample from the posterior distribution of the **neural network weights and biases**.
We consider an inverse problem, where the governing equation is a heat equation in an 1D interval $[0,1]$.
The simulation is conducted over a time horizon $[0,1]$. We record the temperature $u(0,t)$ on the left of the interval.
The diffusivity coefficient $\kappa(x)$ is assumed unknown and will be estimated from the temperature record. $\kappa(x)$
is approximated by a neural network
$$\kappa(x) = \mathcal{NN}_{w}(x)$$
Here $w$ is the neural network weights and biases.
First of all, we define a function `simulate` that takes in the diffusivity coefficient, and returns the solution of the PDE.
File `heateq.jl`:
```julia
using ADCME
using PyPlot
using ADCME
using PyCall
using ProgressMeter
using Statistics
using MAT
using DelimitedFiles
mpl = pyimport("tikzplotlib")
function simulate(κ)
κ = constant(κ)
m = 50
n = 50
dt = 1 / m
dx = 1 / n
F = zeros(m + 1, n)
xi = LinRange(0, 1, n + 1)[1:end - 1]
f = (x, t)->exp(-50(x - 0.5)^2)
for k = 1:m + 1
t = (k - 1) * dt
F[k,:] = dt * f.(xi, t)
end
λ = κ*dt/dx^2
mask = ones(n-1)
mask[1] = 2.0
A = spdiag(n, -1=>-λ[2:end], 0=>1+2λ, 1=>-λ[1:end-1].*mask)
function condition(i, u_arr)
i <= m + 1
end
function body(i, u_arr)
u = read(u_arr, i - 1)
rhs = u + F[i]
u_next = A \ rhs
u_arr = write(u_arr, i, u_next)
i + 1, u_arr
end
F = constant(F)
u_arr = TensorArray(m + 1)
u_arr = write(u_arr, 1, zeros(n))
i = constant(2, dtype = Int32)
_, u = while_loop(condition, body, [i, u_arr])
u = set_shape(stack(u), (m + 1, n))
end
```
We set up the geometry as follows
```julia
n = 50
xi = LinRange(0, 1, n + 1)[1:end - 1]
x = Array(LinRange(0, 1, n+1)[1:end-1])
```
# Forward Computation
The forward computation is run with an analytical $\kappa(x)$, given by
$$\kappa(x) = 5x^2 + \exp(x) + 1.0$$
We can generate the code using the following code:
```julia
include("heateq.jl")
κ = @. 5x^2 + exp(x) + 1.0
out = simulate(κ)
obs = out[:,1]
sess = Session(); init(sess)
obs_ = run(sess, obs)
writedlm("obs.txt", run(sess, out))
o = run(sess, out)
pcolormesh( (0:49)*1/50, (0:50)*1/50, o, rasterized=true)
xlabel("\$x\$")
ylabel("\$t\$")
savefig("solution.png")
figure()
plot((0:50)*1/50, obs_)
xlabel("\$t\$")
ylabel("\$u(0,t)\$")
savefig("obs.png")
figure()
plot(x, κ)
xlabel("\$x\$")
ylabel("\$\\kappa\$")
savefig("kappa.png")
```
| Solution | Observation | $\kappa(x)$ |
| ------------------- | -------------- | ---------------- |
|  |  |  |
# Inverse Modeling
Although it is possible to use MCMC to solve the inverse problem, the convergence can be very slow if our initial guess is
far away from the solution.
Therefore, we first solve the inverse problem by solving a PDE-constrained optimization problem.
We use the [`BFGS!`](@ref) optimizer. Note we do not need to solve the inverse problem very accurately because in Bayesian approaches,
the solution is interpreted as a probability, instead of a point estimation.
```julia
include("heateq.jl")
using PyCall
using Distributions
using Optim
using LineSearches
reset_default_graph()
using Random; Random.seed!(2333)
w = Variable(ae_init([1,20,20,20,1]), name="nn")
κ = fc(x, [20,20,20,1], w, activation="tanh") + 1.0
u = simulate(κ)
obs = readdlm("obs.txt")
loss = sum((u[:,1]-obs[:,1])^2)
loss = loss*1e10
sess = Session(); init(sess)
BFGS!(sess, loss)
κ1 = @. 5x^2 + exp(x) + 1.0
plot(x, run(sess, κ), "+--", label="Estimation")
plot(x, κ1, label="Reference")
legend()
savefig("inversekappa.png")
```

We also save the solution for MCMC
```julia
matwrite("nn.mat", Dict("w"=>run(sess, w)))
```
# Uncertainty Quantification
Finally, we are ready to conduct uncertainty quantification using MCMC.
We will use the `Mamba` package, which provides MCMC utilities. We will use the random walk MCMC because of its simplicity.
```julia
include("heateq.jl")
using PyCall
using Mamba
using ProgressMeter
using PyPlot
```
The neural network weights and biases are conveniently expressed as a `placeholder`.
This allows us to `sample` from a distribution of weights and biases easily.
```julia
w = placeholder(ae_init([1,20,20,20,1]))
κ = fc(x, [20,20,20,1], w, activation="tanh") + 1.0
u = simulate(κ)
obs = readdlm("obs.txt")
sess = Session(); init(sess)
w0 = matread("nn.mat")["w"]
```
The log likelihood function (up to an additive constant) is given by
$$-{{{{\left\| {{u_{{\rm{est}}}}(w) - {u_{{\rm{obs}}}}} \right\|}^2}} \over {2{\sigma ^2}}} - {{{{\left\| w \right\|}^2}} \over {2\sigma _w^2}}$$
The absolute value of $\sigma$ and $\sigma_w$ does not really matter. Only their ratios matter. Let's fix $\sigma = 1$. What is the interpretation of $\sigma_w$?
A large $\sigma_w$ means very wide prior, and a small $\sigma_w$ means a very narrow prior.
The relative value $\sigma/\sigma_w$ implies **the strength of prior influence**.
Typically, we can choose a very large $\sigma_w$ so that the prior does not influence the posterior too much.
```julia
σ = 1.0
σx = 1000000.0
function logf(x)
y = run(sess, u, w=>x)
-sum((y[:,1] - obs[:,1]).^2)/2σ^2 - sum(x.^2)/2σx^2
end
n = 5000
burnin = 1000
sim = Chains(n, length(w0))
```
A second important parameter is the scale (0.002 in the following code). It controls **the uncertainty bound width** via the way we generate the random numbers.
```julia
θ = RWMVariate(copy(w0), 0.001ones(length(w0)), logf, proposal = SymUniform)
```
An immediate consequence is that the smaller the scale factor we use, the narrower the uncertainty band will be.
In sum, we have two important parameters--relative standard deviation and the scaling factor--to control our uncertainty bound.
```julia
@showprogress for i = 1:n
sample!(θ)
sim[i,:,1] = θ
end
v = sim.value
K = zeros(length(κ), n-burnin)
@showprogress for i = 1:n-burnin
ws = v[i+burnin,:,1]
K[:,i] = run(sess, κ, w=>ws)
end
kappa = mean(K, dims=2)[:]
k_std = std(K, dims=2)[:]
figure()
κ1 = @. 5x^2 + exp(x) + 1.0
PyPlot.plot(x, kappa, "--", label="Posterior Mean")
PyPlot.plot(x, κ1, "r", label="True")
PyPlot.plot(x, run(sess, κ, w=>w0), label="Point Estimation")
fill_between(x, kappa-3k_std, kappa+3k_std, alpha=0.5)
legend()
xlabel("x")
ylabel("\$\\kappa(x)\$")
savefig("kappa_mcmc.png")
```
 | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 12010 | # Distributed Scientific Machine Learning using MPI
Many large-scale scientific computing involves parallel computing. Among many parallel computing models, the MPI is one of the most popular models. In this section, we describe how ADCME can work with MPI for solving inverse modeling. Specifically, we describe how gradients can be back-propagated via MPI function calls.
!!! info
Message Passing Interface (MPI) is an interface for parallel computing based on message passing models. In the message passing model, a master process assigns work to workers by passing them a message that describes the work. The message may be data or meta information (e.g., operations to perform). A consensus was reached around 1992 and the MPI standard was born. MPI is a definition of interface, and the implementations are left to hardware venders.
## MPI Support in ADCME
The ADCME solution to distributed computing for scientific machine learning is to provide a set of "data communication" nodes in the computational graph. Each machine (MPI processor) runs an identical computational graph. The computational nodes are executed independently on each processor, and the data communication nodes need to synchronize among different processors.
These data communication nodes are implemented using MPI APIs. They are not necessarily blocking operations, but because ADCME respects the data dependency of computation, they act like blocking operations and the child operators are executed only when data communication is finished. For example, in the following example,
```julia
b = mpi_op(a)
c = custom_op(b)
```
even though `mpi_op` and `custom_op` can overlap, ADCME still sequentially execute these two operations.
This blocking behavior simplifies the synchronization logic as well as the implementation of gradient back-propagation while harming little performance.
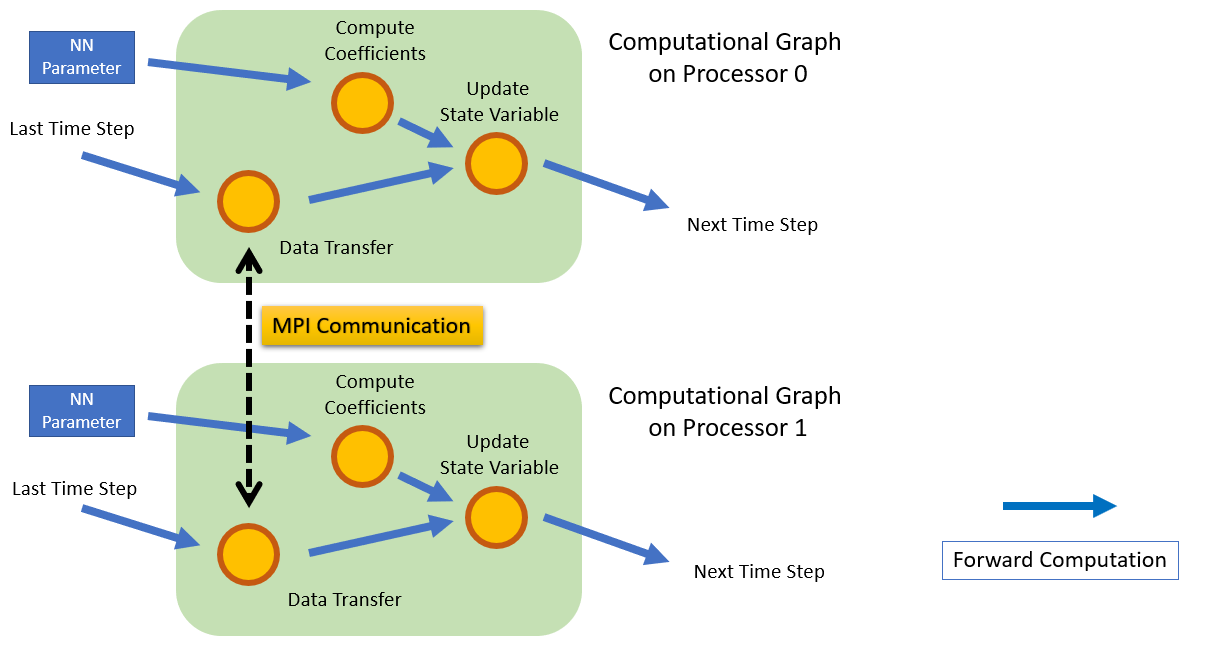

ADCME provides a set of commonly used MPI operators. See [MPI Operators](https://kailaix.github.io/ADCME.jl/dev/api/#MPI). Basically, they are
* [`mpi_init`](@ref), [`mpi_finalize`](@ref): Initialize and finalize MPI session.
* [`mpi_rank`](@ref), [`mpi_size`](@ref): Get the MPI rank and size.
* [`mpi_sum`](@ref), [`mpi_bcast`](@ref): Sum and broadcast tensors in different processors.
* [`mpi_send`](@ref), [`mpi_recv`](@ref): Send and receive operators.
The above two set of operators support automatic differentiation. They were implemented with MPI adjoint methods, which have existed in academia for decades.
[This section](./installmpi.md) shows how to configure MPI for distributed computing in ADCME.
## Limitations
Despite that the provided `mpi_*` operations meet most needs, some sophisticated data communication operations may not be easily expressed using these APIs. For example, when solving the Poisson's equation on a uniform grid, we may decompose the domain into many squares, and two adjacent squares exchange data in each iteration. A sequence of `mpi_send`, `mpi_recv` will likely cause deadlock.
Just like when it is difficult to use automatic differentiation to implement a forward computation and its gradient back-propagation, we resort to custom operators, it is the same case for MPI. We can design a specialized custom operator for data communication. To resolve the deadlock problem, we found the asynchronous sending, followed by asynchronous receiving, and then followed by waiting, a very general and convenient way to implement custom operators.

## Implementing Custom Operators using MPI
We can also make custom operators with MPI. Let us consider computing
$$f(\theta) = \sum_{i=1}^n f_i(\theta)$$
Each $f_i$ is a very expensive function so it makes sense to use MPI to split the jobs on different processors. To simplify the problem, we consider
$$f(\theta) = f_1(\theta) + f_2(\theta) + f_3(\theta) + f_4(\theta)$$
where $f_i(\theta) = \theta^{i-1}$.

Using the ADCME MPI API, we have the following code (`test_simple.jl`)
```julia
using ADCME
mpi_init()
θ = placeholder(ones(1))
fθ = mpi_bcast(θ)
l = fθ^mpi_rank()
L = sum(mpi_sum(l))
g = gradients(L, θ)
sess = Session(); init(sess)
L_ = run(sess, L, θ=>ones(1)*2.0)
g_ = run(sess, g, θ=>ones(1)*2.0)
if mpi_rank()==0
@info L_, g_
end
mpi_finalize()
```
We run the program with 4 processors
```bash
mpirun -n 4 julia test_simple.jl
```
We have the results:
```bash
[ Info: (15.0, [17.0])
```
## Hybrid Programming
Each MPI processor can communicate data between processes, which do not share memory. Within each process, ADCME also allows for multi-threaded parallelism with a shared-memory model. For example, we can use OpenMP to accelerate matrix vector production. We can also use a threadpool per process to manage more complex and dynamic parallel tasks. However, the hybrid model brings challenges to communicate data using MPI. When we post MPI calls from different threads within the same process, we need to prevent data races and match the corresponding broadcast and collective operators. For example, without any guarantee on the ordering of concurrent MPI calls, we might incorrectly matched a send operator with a gather operator.
In ADCME, we adopt the dependency injection technique: we explicitly serialize the MPI calls by adding ghost dependencies. For example, in the following computational graph, originally, Operator 2 and Operator 3 are independent. In a concurrent computing environment, Rank 0 may execute Operator 2 first and then Operator 3, while Rank 1 executes Operator 3 first and then Operator 2. Then there is a mismatch of the MPI call (race condition): Operator 2 in Rank 0 coacts with Operator 3 in Rank 1, and Operator 3 in Rank 0 coacts with Operator 2 in Rank 1.
To resolve the data race issue, we can explicitly make Operator 3 depend on Operator 2. In this way, we can ensure that **the MPI calls** Operator 1, 2, and 3 are executed in order. Note this technique sacrifices some concurrency (Operator 2 and Operator 3 cannot be executed concurrently), but the concurrency of most non-MPI operators is still preserved.

## Optimization
For solving inverse problems using distributed computing, an MPI-capable optimizer is required. The ADCME solution to distributed optimization is that the master machine holds, distributes and updates the optimizable variables. The gradients are calculated in the same device where the corresponding forward computation is done. Therefore, for a given serial optimizer, we can refactor it to a distributed one by letting worker nodes wait for instructions from the master node to compute either the objective function or the gradient.
This idea is implemented in the [`ADOPT.jl`](https://github.com/kailaix/ADOPT.jl) package, a customized version of [`Optim.jl`](https://github.com/JuliaNLSolvers/Optim.jl).

In the following, we try to solve
$$1+\theta +\theta^2+\theta^3 = 2$$
using MPI-enabled LBFGS optimizer.
```julia
using ADCME
using ADOPT
mpi_init()
θ = placeholder(ones(1))
fθ = mpi_bcast(θ)
l = fθ^mpi_rank()
L = (sum(mpi_sum(l)) - 2.0)^2
sess = Session(); init(sess)
f = x->run(sess, L, θ=>x)
g! = (G, x)->(G[:] = run(sess, g, θ=>x))
options = Options()
if mpi_rank()==0
options.show_trace = true
end
mpi_optimize(f, g!, ones(1), ADOPT.LBFGS(), options)
if mpi_rank()==0
@info result.minimizer, result.minimum
end
mpi_finalize()
```
The expected output is
```
Iter Function value Gradient norm
0 4.000000e+00 2.400000e+01
* time: 0.00012421607971191406
1 6.660012e-01 7.040518e+00
* time: 1.128843069076538
2 7.050686e-02 1.322515e+00
* time: 1.210536003112793
3 2.254820e-03 2.744374e-01
* time: 1.2910940647125244
4 4.319834e-07 3.908046e-03
* time: 1.3442070484161377
5 2.894433e-16 1.011994e-07
* time: 1.3975300788879395
6 0.000000e+00 0.000000e+00
* time: 1.4507441520690918
[ Info: ([0.5436890126920764], 0.0)
```
### Reduce Sum
```julia
using ADCME
mpi_init()
r = mpi_rank()
a = constant(Float64.(Array(1:10) * r))
b = mpi_sum(a)
L = sum(b)
g = gradients(L, a)
sess = Session(); init(sess)
v, G = run(sess, [b,g])
mpi_finalize()
```
### Broadcast
```julia
using ADCME
mpi_init()
r = mpi_rank()
a = constant(ones(10) * r)
b = mpi_bcast(a, 3)
L = sum(b^2)
L = mpi_sum(L)
g = gradients(L, a)
sess = Session(); init(sess)
v, G = run(sess, [b, G])
mpi_finalize()
```
### Send and Receive
```julia
# mpiexec.exe -n 4 julia .\mpisum.jl
using ADCME
mpi_init()
r = mpi_rank()
a = constant(ones(10) * r)
a = mpi_sendrecv(a, 0, 2)
L = sum(a^2)
g = gradients(L, a)
sess = Session(); init(sess)
v, G = run(sess, [a,g])
mpi_finalize()
```
[`mpi_sendrecv`](@ref) is a lightweight wrapper for [`mpi_send`](@ref) followed by [`mpi_recv`](@ref). Equivalently, we have
```julia
if r==2
global a
a = mpi_send(a, 0)
end
if r==0
global a
a = mpi_recv(a,2)
end
```
## Solving the Heat Equation
In this section, we consider solving the Poisson equation
$$\frac{\partial u(x,y)}{\partial t} =\kappa(x,y) \Delta u(x,y) \quad (x,y) \in [0,1]^2$$
We discretize the above PDE with an explicit finite difference scheme
$$\frac{u_{ij}^{n+1} - u^n_{ij}}{\Delta t} = \kappa_{ij} \frac{u_{i+1,j}^n + u_{i,j+1}^n + u_{i,j-1}^n + u_{i-1,j}^n - 4u_{ij}^n}{h^2} \tag{1}$$
To mitigate the computational and memory requirement, we use MPI APIs to implement a domain decomposition solver for the heat equation. The mesh is divided into $N\times M$ rectangle patches. We implemented two operation:
1. `heat_op`, which updates $u_{ij}^{n+1}$ using Equation 1 for a specific patch, with state variables $u_{ij}^n$ in the current rectangle patch and on the boundary (from adjacent patches).
2. `data_exchange`, which is a data communication operator that sends the boundary data to adjacent patches and receives boundary data from other patches.

Then the time marching scheme can be implemented with the following code:
```julia
function heat_update_u(u, kv, f)
r = mpi_rank()
I = div(r, M)
J = r%M
up_ = constant(zeros(m))
down_ = constant(zeros(m))
left_ = constant(zeros(n))
right_ = constant(zeros(n))
up = constant(zeros(m))
down = constant(zeros(m))
left = constant(zeros(n))
right = constant(zeros(n))
(I>0) && (up = u[1,:])
(I<N-1) && (down = u[end,:])
(J>0) && (left = u[:,1])
(J<M-1) && (right = u[:,end])
left_, right_, up_, down_ = data_exchange(left, right, up, down)
u = heat(u, kv, up_, down_, left_, right_, f, h, Δt)
end
```
An MPI-capable heat equation time integrator can be implemented with
```julia
function heat_solver(u0, kv, f, NT=10)
f = constant(f)
function condition(i, u_arr)
i<=NT
end
function body(i, u_arr)
u = read(u_arr, i)
u_new = heat_update_u(u, kv, f[i])
# op = tf.print(r, i)
# u_new = bind(u_new, op)
i+1, write(u_arr, i+1, u_new)
end
i = constant(1, dtype =Int32)
u_arr = TensorArray(NT+1)
u_arr = write(u_arr, 1, u0)
_, u = while_loop(condition, body, [i, u_arr])
reshape(stack(u), (NT+1, n, m))
end
```
For example, we can implement the heat solver with diffusivity coefficient $K_0$ and initial condition $u_0$ with the following code:
```julia
K = placeholder(K0)
a_ = mpi_bcast(K)
sol = heat_solver(u0, K_, F, NT)
```
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 13242 | # MPI Benchmarks
The purpose of this section is to present the distributed computing capability of ADCME via MPI. With the MPI operators, ADCME is well suited to parallel implementations on clusters with very large numbers of cores. We benchmark individual operators as well as the gradient calculation as a whole. Particularly, we use two metrics for measuring the scaling of the implementation:
1. **weak scaling**, i.e., how the solution time varies with the number of processors for a fixed problem size per processor.
2. **strong scaling**, i.e., the speedup for a fixed problem size with respect to the number of processors, and is governed by Amdahl's law.
For most operators, ADCME is just a wrapper of existing third-party parallel computing software (e.g., Hypre). However, for gradient back-propagation, some functions may be missing and are implemented at our own discretion. For example, in Hypre, distributed sparse matrices split into multiple stripes, where each MPI rank owns a stripe with continuous row indices. In gradient back-propagation, the transpose of the original matrix is usually needed and such functionalities are missing in Hypre as of September 2020.
The MPI programs are verified with serial programs. Note that ADCME uses hybrid parallel computing models, i.e., a mixture of multithreading programs and MPI communication; therefore, one MPI processor may be allocated multiple cores.
## Transposition
Matrix transposition is an operator that are common in gradient back-propagation. For example, assume the forward computation is ($x$ is the input, $y$ is the output, and $A$ is a matrix)
$$y(\theta) = Ax(\theta) \tag{1}$$
Given a loss function $L(y)$, we have
$$\frac{\partial L(y(x))}{\partial x} = \frac{\partial L(y)}{\partial y}\frac{\partial y(x)}{\partial x} = \frac{\partial L(y)}{\partial y} A$$
Note that $\frac{\partial L(y)}{\partial y}$ is a row vector, and therefore,
$$\left(\frac{\partial L(y(x))}{\partial x}\right)^T = A^T \left(\frac{\partial L(y)}{\partial y} \right)^T$$
requires a matrix vector multiplication, where the matrix is $A^T$.
Given that Equation 1 is ubiquitous in numerical PDE schemes, a distributed implementation of parallel transposition is very important.
ADCME uses the same distributed sparse matrix representation as Hypre. In Hypre, each MPI processor own a set of rows of the whole sparse matrix. The rows have continuous indices. To transpose the sparse matrix in a parallel environment, we first split the matrices in each MPI processor into blocks and then use `MPI_Isend`/`MPI_Irecv` to exchange data. Finally, we transpose the matrices in place for each block. Using this method, we obtained a CSR representation of the transposed matrix.

The following results shows the scalability of the transposition operator of [`mpi_SparseTensor`](@ref). In the plots, we show the strong scaling for a fixed matrix size of $25\text{M} \times 25\text{M}$ as well as the weak scaling, where each MPI processor owns $300^2=90000$ rows.
| Strong Scaling | Weak Scaling |
|----------------|--------------|
| 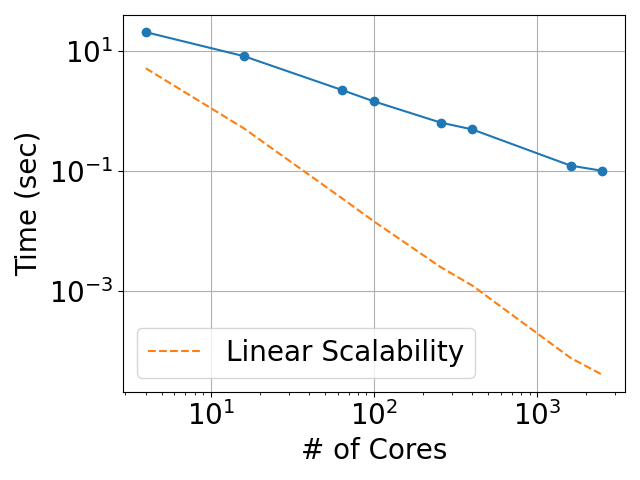 | 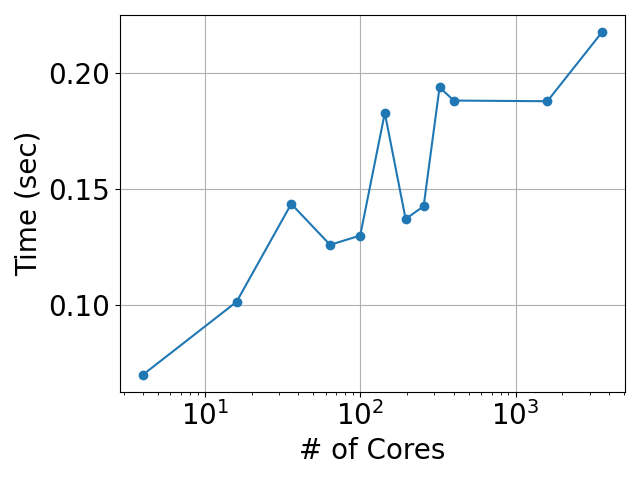 |
## Poisson's Equation
This example presents the overhead of ADCME MPI operators when the main computation is carried out through a third-party library (Hypre). We solve the Poisson's equation
$$\nabla \cdot (\kappa(x, y) \nabla u(x,y)) = f(x, y), (x,y) \in \Omega \quad u(x,y) = 0, (x,y) \in \partial \Omega$$
Here $\kappa(x, y)$ is approximated by a neural network $\kappa_\theta(x,y) = \mathcal{NN}_\theta(x,y)$, and the weights and biases $\theta$ are broadcasted from the root processor. We express the numerical scheme as a computational graph is:
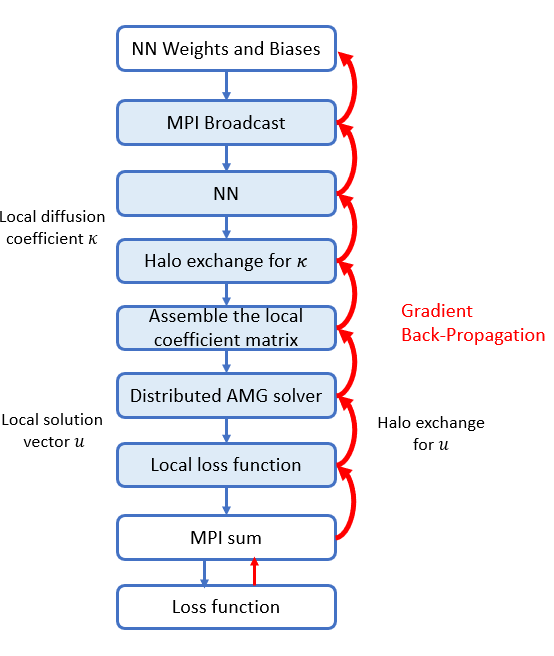
The domain decomposition is as follows:

The domain $[0,1]^2$ is divided into $N\times N$ blocks, and each block contains $n\times n$ degrees of freedom. The domain is padded with boundary nodes, which are eliminated from the discretized equation. The grid size is
$$h = \frac{1}{Nn+1}$$
We use a finite difference method for discretizing the Poisson's equation, which has the following form
$$\begin{aligned}(\kappa_{i+1, j}+\kappa_{ij})u_{i+1,j} + (\kappa_{i-1, j}+\kappa_{ij})u_{i-1,j} &\\
+ (\kappa_{i,j+1}+\kappa_{ij})u_{i,j+1} + (\kappa_{i, j-1}+\kappa_{ij})u_{i,j-1} &\\
-(\kappa_{i+1, j}+\kappa_{i-1, j}+\kappa_{i,j+1}+\kappa_{i, j-1}+4\kappa_{ij})u_{ij} &\\
= 2h^2f_{ij}
\end{aligned}$$
We show the strong scaling with a fixed problem size $1800 \times 1800$ (mesh size, which implies the matrix size is around 32 million). We also show the weak scaling where each MPI processor owns a $300\times 300$ block. For example, a problem with 3600 processors has the problem size $90000\times 3600 \approx 0.3$ billion.
### Weak Scaling
We first consider the weak scaling. The following plots shows the runtime for forward computation as well as gradient back-propagation.
| Speedup | Efficiency |
|----------------|--------------|
|  | 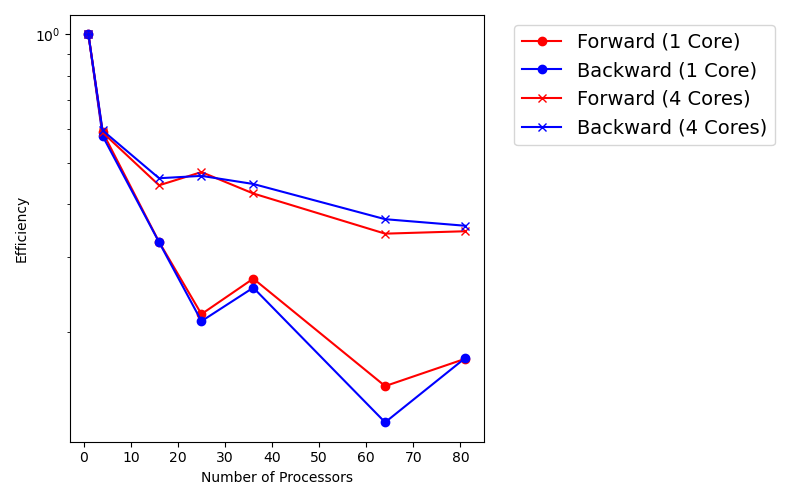 |
There are several important observations:
1. By using more cores per processor, the runtime is reduced significantly. For example, the runtime for the backward is reduced to around 10 seconds from 30 seconds by switching from 1 core to 4 cores per processor.
2. The runtime for the backward is typically less than twice the forward computation. Although the backward requires solve two linear systems (one of them is in the forward computation), the AMG linear solver in the back-propagation may converge faster, and therefore costs less than the forward.
Additionally, we show the overhead, which is defined as the difference between total runtime and Hypre linear solver time, of both the forward and backward calculation.
| 1 Core | 4 Cores |
|----------------|--------------|
|  | 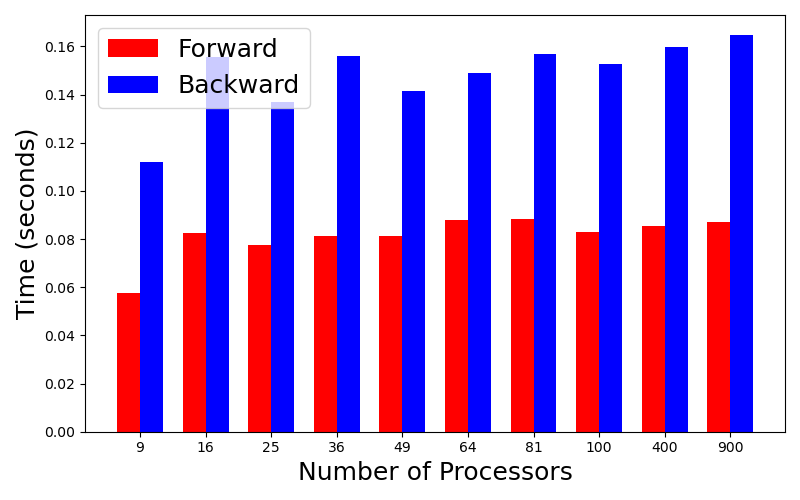 |
We see that the overhead is quite small compared to the total time, especially when the problem size is large. This indicates that the ADCME MPI implementation is very effective.
### Strong Scaling
Now we consider the strong scaling. In this case, we fixed the whole problem size and split the mesh onto different MPI processors. The following plots show the runtime for the forward computation and the gradient back-propagation
| Forward | Bckward |
|----------------|--------------|
| 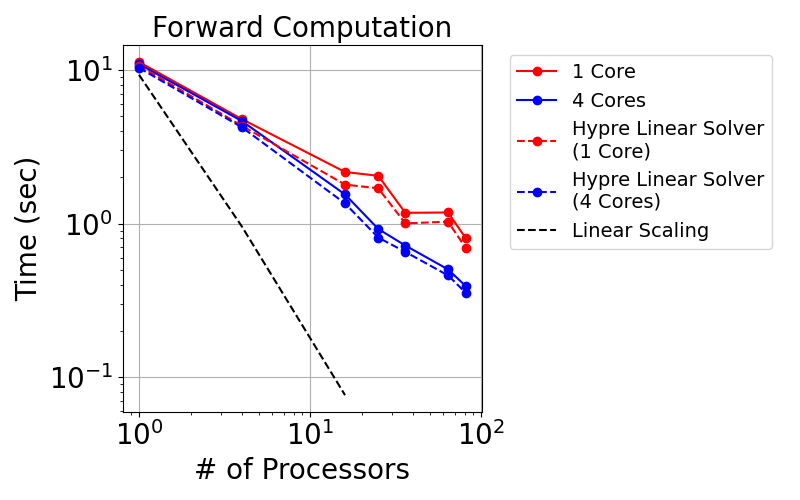 |  |
The following plots show the speedup and efficiency
| 1 Core | 4 Cores |
|----------------|--------------|
|  | 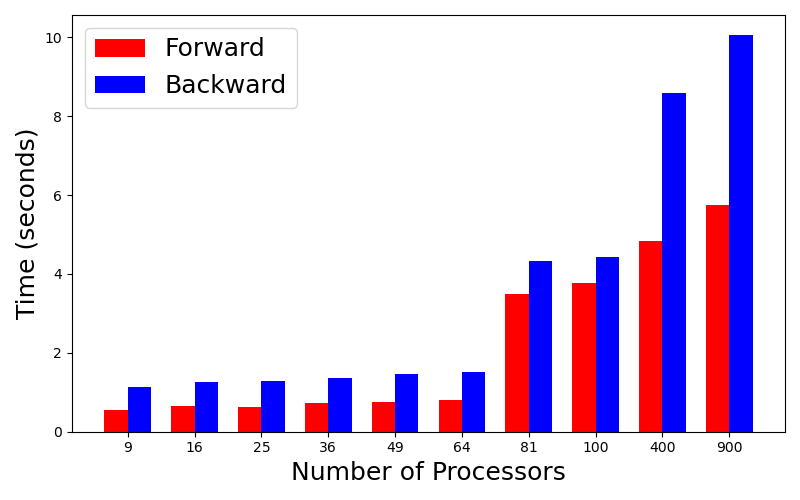 |
We can see that the 4 cores have smaller runtime compared to 1 core.
Interested readers can go to [here](https://github.com/kailaix/ADCME.jl/tree/master/docs/src/assets/Codes/MPI) for implementations. To compile the codes, make sure that MPI and Hypre is available (see [`install_openmpi`](@ref) and [`install_hypre`](@ref)) and run the following script:
```julia
using ADCME
change_directory("ccode/build")
ADCME.cmake()
ADCME.make()
```
## Acoustic Seismic Inversion
In this example, we consider the acoustic wave equation with perfectly matched layer (PML). The governing equation for the acoustic equation is
$$\frac{\partial^2 u}{\partial t^2} = \nabla \cdot (c^2 \nabla u)$$
where $u$ is the displacement, $f$ is the source term, and $c$ is the spatially varying acoustic velocity.
In the inverse problem, only the wavefield $u$ on the surface is observable, and we want to use this information to estimate $c$. The problem is usually ill-posed, so regularization techniques are usually used to constrain $c$. One approach is to represent $c$ by a deep neural network
$$c(x,y) = \mathcal{NN}_\theta(x,y)$$
where $\theta$ is the neural network weights and biases. The loss function is formulated by the square loss for the wavefield on the surface.
| Model $c$ | Wavefield |
|----------------|--------------|
|  |  |
To implement an MPI version of the acoustic wave equation propagator, we use [`mpi_halo_exchange`](@ref), which is implemented using MPI and performs the halo exchange mentioned in the last example for both wavefields and axilliary fields. This function communicates the boundary information for each block of the mesh. The following plot shows the computational graph for the numerical simulation of the acoustic wave equation

The following plot shows the strong scaling and weak scaling of our implementation. Each processor consists of 32 processors, which are used at the discretion of ADCME's backend, i.e., TensorFlow. The strong scaling result is obtained by using a $1000\times 1000$ grid and 100 times steps. For the weak scaling result, each MPI processor owns a $100\times 100$ grid, and the total number of steps is 2000.
It is remarkable that even though we increase the number of processors from 1 to 100, the total time only increases 2 times in the weak scaling.
| Strong Scaling | Weak Scaling |
|----------------|--------------|
| 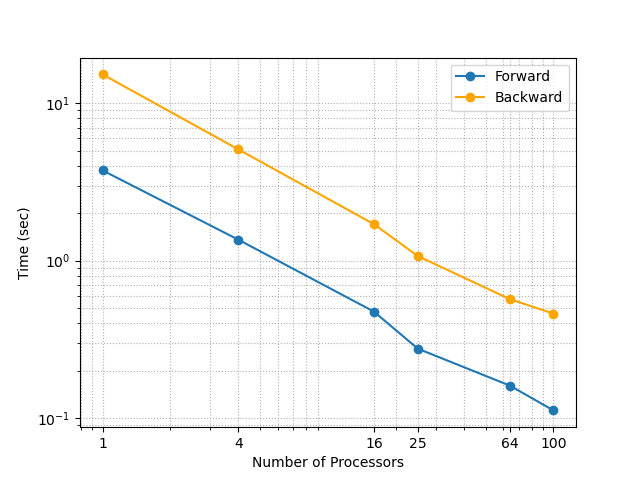 |  |
We also show the speedup and efficiency for the strong scaling case. We can achieve more than 20 times acceleration by using 100 processors (3200 cores in total) and the trend is not slowing down at this scale.

## Elastic Seismic Inversion
In the last example, we consider the elastic wave equation
$$\begin{aligned}
\rho \frac{\partial v_i}{\partial t} &= \sigma_{ij,j} + \rho f_i \\
\frac{\partial \sigma_{ij}}{\partial t} &= \lambda v_{k, k} + \mu (v_{i,j}+v_{j,i})
\end{aligned}\tag{2}$$
where $v$ is the velocity, $\sigma$ is the stress tensor, $\rho$ is the density, and $\lambda$ and $\mu$ are the Lamé constants. Similar to the acoustic equation, we use the PML boundary conditions and have observations on the surface. However, the inversion parameters are now spatially varying $\rho$, $\lambda$ and $\mu$.

As an example, we approximate $\lambda$ by a deep neural network
$$\lambda(x,y) = \mathcal{NN}_\theta(x,y)$$
and the other two parameters are kept fixed.
We use the same geometry settings as the acoustic wave equation case. Note that elastic wave equation has more state variables as well as auxilliary fields, and thus is more memory demanding. The huge memory cost calls for a distributed framework, especially for large-scale problems.
Additionally, we use fourth-order finite difference scheme for discretizing Equation 2. This scheme requires us to exchange two layers on the boundaries for each block in the mesh. This data communication is implemented using MPI, i.e., [`mpi_halo_exchange2`](@ref).
The following plots show the strong and weak scaling. Again, we see that the weak scaling of the implementation is quite effective because the runtime increases mildly even if we increase the number of processors from 1 to 100.
| Strong Scaling | Weak Scaling |
|----------------|--------------|
|  |  |
The following plots show the speedup and efficiency for the strong scaling. We can achieve more than 20 times speedup when using 100 processors.

| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 7668 | # Understand the Multi-threading Model
Multi-threading is a very important technique for accelerating simulations in ADCME. Through this section, we look into the multi-threading models of ADCME's backend, TensorFlow. Let us start with some basic concepts related to CPUs.
## Processes, Threads, and Cores
We often hear about processes and threads when talking about multi-threading. In a word, a process is a program in execution. A process may invoke multiple threads. A thread can be viewed as a scheduler for executing each line of codes in order. It tells the CPU to perform an instruction.
The biggest difference is that different processes do not share memory with each other. But different threads **within the same process** has the same memory space.
Up till now, processes and threads are **logical** concepts, which are not bound to the physical devices. Cores are physical concepts. Nowadays, each CPU contains multiple cores. Cores contain workers that actually perform computation, and these workers are called ALUs (arithmetic logic units). To use these ALUs, we need some schedulers that tell the CPU/cores to perform certain tasks. This is done by **hardware threads**. Typically when we want to do some computation, we need to load data first and then perform calculations on ALUs. The data loading process is also taken care by the hardware threads. Therefore, it is possible that the ALUs are waiting for input data. One clever idea in computer science is to use pipelining: overlapping data loading of the current instruction and computation of the last instruction. This means we need more schedulers, i.e., hardware threads, to take care of data loading and computing simultaneously. Therefore, modern CPUs usually have multiple hardware threads for one core. For example, Intel CPUs have the so-called **hyperthreading technology**, i.e., each core has two physical threads.
Now we understand four concepts: processes, (logical) threads, cores, hardware threads. So what is the relationship between threads and hardware threads? Actually this is straight-forward: logical threads are mapped to hardware threads. For example, if there are 4 logical threads and 4 hardware threads, the OS may map each logical thread to one distinct hardware thread. If there are more than 4 logical threads, some logical threads may be mapped to one. That says, these logical threads will not enjoy truly parallelism.
Now let's consider how ADCME works: for one CPU, ADCME always runs only one process. But to gain maximum efficiency, ADCME will create multiple threads to leverage any parallelism we have in hardware resources and computational models.
## Inter and Intra Parallelism
There are two types of parallelism in ADCME execution: **inter** and **intra**.
Consider a computational graph, there may be multiple independent operators and therefore we can execute them in parallel. This type of parallelism is called inter-parallelism. For example,
```julia
using ADCME
a1 = constant(rand(10))
a2 = constant(rand(10))
a3 = a1 * a2
a4 = a1 + a2
a5 = a3 + a4
```
In the above code, `a3 = a1 * a2` and `a4 = a1 + a2` are independent and can be executed in parallel.
Another type of parallelism is intra-parallel, that is, the computation within each operator can be computed in parallel. For example, in the example above, we can compute the first 5 entries and last 5 entries in `a4 = a1 + a2` in parallel.
These types of parallelism can be achieved using multi-threading. In the next section, we explain how this is implemented in TensorFlow.
## ThreadPools
The backend of ADCME, TensorFlow, uses two threadpools for multithreading. One thread pool is for inter-parallelism, and the other is for intra-parallelism. They can be set by the users.
One common mistake is that users think in terms of hardware threads instead of logical threads. For example, if we have 8 hardware threads in total, one might want to allocate 4 threads for inter-parallelism and 4 threads for intra-parallelism. That's not true. When we talk about allocating threads for intra and inter thread pools, we are always talking about logical threads. So we can have a threadpool containing 100 threads for both inter and intra thread pools even if we only have 8 hardware threads in total. And in the runtime, inter and intra thread pools may use the same hardware threads for scheduling tasks.
The following figure is an illustration of the two thread pools of ADCME.

## How to Use the Intra Thread Pool
In practice, when we implement custom operators, we may want to use the intra thread pool. [Here](https://github.com/kailaix/ADCME.jl/tree/master/docs/src/assets/Codes/ThreadPools) gives an example how to use thread pools.
```c++
#include <thread>
#include <chrono>
#include <condition_variable>
#include <atomic>
void print_thread(std::atomic_int &cnt, std::condition_variable &cv){
std::this_thread::sleep_for(std::chrono::milliseconds(1000));
printf("My thread ID is %d\n", std::this_thread::get_id());
cnt++;
if (cnt==7) cv.notify_one();
}
void threadpool_print(OpKernelContext* context){
thread::ThreadPool * const tp = context->device()->tensorflow_cpu_worker_threads()->workers;
std::atomic_int cnt = 0;
std::condition_variable cv;
std::mutex mu;
printf("Number of intra-parallel thread = %d\n", tp->NumThreads());
printf("Maximum Parallelism = %d\n", port::MaxParallelism());
for (int i = 0; i < 7; i++)
tp->Schedule([&cnt, &cv](){print_thread(cnt, cv);});
{
std::unique_lock<std::mutex> lck(mu);
cv.wait(lck, [&cnt](){return cnt==7;});
}
printf("Op finished\n");
}
```
Basically, we can asynchronously launch jobs using the thread pools. Additionally, we are responsible for synchronization. Here we have used condition variables for synchronization.
Typically our CPU operators are synchronous and do not need the thread pools. But it does not hard to have an intra thread pool.
## Runtime Optimizations
If you are using Intel CPUs, we may have some runtime optimization configurations. See this [link](https://software.intel.com/content/www/us/en/develop/articles/guide-to-tensorflow-runtime-optimizations-for-cpu.html) for details. Here, we show the effects of some optimizations.
We already understand `intra_op_parallelism_threads` and `inter_op_parallelism_threads`; now let us consider some other options. We consider computing $\sin$ function using the following formula
$$\sin x \approx x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!}$$
The implementation can be found [here]().
### Configure OpenMP
To set the number of OMP threads, we can configure the `OMP_NUM_THREADS` environment variable. One caveat is that the variable must be set before loading ADCME. For example
```julia
ENV["OMP_NUM_THREADS"] = 5
using ADCME
```
Running the `omp_thread.jl`, we have the following output
```
There are 5 OpenMP threads
4 is computing...
0 is computing...
4 is computing...
1 is computing...
1 is computing...
0 is computing...
3 is computing...
3 is computing...
2 is computing...
2 is computing...
```
We see that there are 5 threads running.
### Configure Number of Devices
[`Session`](@ref) accepts keywords `CPU`, which limits the number of CPUs we can use. Note, `CPU` corresponds to the number of CPU devices, not cores or threads. For example, if we run `num_device.jl` with (default is using all CPUs)
```julia
sess = Session(CPU=1); init(sess)
```
We will see
```
There are 144 OpenMP threads
```
This is because we have 144 cores in our machine.
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 2987 | # Newton Raphson
Newton-Raphson algorithm is widely used in scientific computing. In ADCME, the function for the algorithm is [`newton_raphson`](@ref). And the signature is
```@docs
newton_raphson
```
As an example, assume we want to solve
```math
u_i^2 - 1 = 0, i=1,2,\ldots, 10
```
We first need to construct a function
```julia
function f(θ, u)
return u^2 - 1, 2*spdiag(u)
end
```
Here $2\texttt{spdiag}(u)$ is the Jacobian matrix for the equation. Then we construct a Newton Raphson solver via
```julia
nr = newton_raphson(f, constant(rand(10)))
```
`nr` is a `NRResult` struct which is runnable and can be materialized by
```julia
nr = run(sess, nr)
```
The signature for `NRResult` is
```julia
struct NRResult
x::Union{PyObject, Array{Float64}} # final solution
res::Union{PyObject, Array{Float64, 1}} # residual
u::Union{PyObject, Array{Float64, 2}} # solution history
converged::Union{PyObject, Bool} # whether it converges
iter::Union{PyObject, Int64} # number of iterations
end
```
`u`$\in \mathbb{R}^{p\times n}$ where `p` is the solution dimension and `n` is the number of iterations.
!!! note
Sometimes we want to construct `f` via some external variables $\theta$, e.g., when $\theta$ is a trainable variable and embeded in the Newton-Raphson solver, we can pass this parameter to `newton_raphson` via the third parameter
```julia
nr = newton_raphson(f, constant(rand(10)),θ)
```
!!! note
We can provide options to `newton_raphson` using `ADCME.options.newton_raphson`. For example
```julia
ADCME.options.newton_raphson.verbose = true
ADCME.options.newton_raphson.tol = 1e-6
nr = newton_raphson(f, constant(rand(10)), missing)
```
This might be useful for debugging.
In the case we want to apply a linesearch step in our Newton-Raphson solver, we can turn on the `linesearch` option in `options`. However, in this case, we must provide the function value for `f` (assuming we are solving a minimization problem).
```julia
function f(θ, u)
return sum(1/3*u^3-u), u^2 - 1, 2*spdiag(u)
end
```
The corresponding driver code is
```julia
ADCME.options.newton_raphson.verbose = false
ADCME.options.newton_raphson.linesearch = true
ADCME.options.newton_raphson.tol = 1e-12
ADCME.options.newton_raphson.linesearch_options.αinitial = 1.0
nr = newton_raphson(f, constant(rand(10)), missing
```
Finally we consider the differentiable Newton-Raphson algorithm. Consider we want to construct a map $f:x\mapsto y$, which satisfies
```math
y^3-x=0
```
In a later stage, we also want to evaluate $\frac{dy}{dx}$. To this end, we can use [`newton_raphson_with_grad`](@ref), which provides a differentiable implementation of the Newton-Raphson's algorithm.
```julia
function f(θ, x)
x^3 - θ, 3spdiag(x^2)
end
θ = constant([2. .^3;3. ^3; 4. ^3])
x = newton_raphson_with_grad(f, constant(ones(3)), θ)
run(sess, x)≈[2.;3.;4.]
run(sess, gradients(sum(x), θ))≈1/3*[2. .^3;3. ^3; 4. ^3] .^(-2/3)
```
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 6164 | # Neural Networks
A neural network can be viewed as a computational graph where each operator in the computational graph is composed of linear transformation or simple explicit nonlinear mapping (called _activation functions_). There are essential components of the neural network
1. Input: the input to the neural network, which is a real or complex valued vector; the input is often called _features_ in machine learning. To leverage dense linear algebra, features are usually aggregated into a matrix and fed to the neural network.
2. Output: the output of the neural network is also a real or complex valued vectors. The vector can be tranformed to categorical values (labels) based on the specific application.
The common activations functions include ReLU (Rectified linear unit), tanh, leaky ReLU, SELU, ELU, etc. In general, for inverse modeling in scientific computing, tanh usually outperms the others due to its smoothness and boundedness, and forms a solid choice at the first try.
A common limitation of the neural network is overfitting. The neural network contains plenty of free parameters, which makes the neural network "memorize" the training data easily. Therefore, you may see very a small training error, but have large test errors. Regularization methods have been proposed to alleviate this problem; to name a few, restricting network sizes, imposing weight regulization (Lasso or Ridge), using Dropout and batch normalization, etc.
## Constructing a Neural Network
ADCME provides a very simple way to specify a fully connected neural network, [`fc`](@ref) (short for _autoencoder_)
```julia
x = constant(rand(10,2)) # input
config = [20,20,20,3] # hidden layers
θ = fc_init([2;config]) # getting an initial weight-and-biases vector.
y1 = fc(x, config)
y2 = fc(x, config, θ)
```
!!! note
When you construct a neural network using `fc(x, config)` syntax, ADCME will construct the weights and biases automatically for you and label the parameters (the default is `default`). In some cases, you may have multiple neural networks, and you can label the neural network manually using
```julia
fc(x1, config1, "label1")
fc(x2, config2, "label2")
...
```
In scientific computing, sometimes we not only want to evaluate the neural network output, but also the sensitivity. Specifically, if
$$y = NN_{\theta}(x)$$
We also want to compute $\nabla_x NN_{\theta}(x)$. ADCME provides a function [`fcx`](@ref) (short for _fully-connected_)
```julia
y3, dy3 = fcx(x, config, θ)
```
Here `dy3` will be a $10\times 3 \times 2$ tensor, where `dy3[i,:,:]` is the Jacobian matrix of the $i$-th output with respect to the $i$-th input (Note the $i$-th output is independent of $j$-th input, whenever $i\neq j$).
## Prediction
After training a neural network, we can use the trained neural network for prediction. Here is an example
```julia
using ADCME
x_train = rand(10,2)
x_test = rand(20,2)
y = fc(x_train, [20,20,10])
y_obs = rand(10,10)
loss = sum((y-y_obs)^2)
sess = Session(); init(sess)
BFGS!(sess, loss)
# prediction
run(sess, fc(x_test, [20,20,10]))
```
Note that the second `fc` does not create a new neural network, but instead searches for a neural network with the label `default` because the default label is `default`. If you constructed a neural network with label `mylabel`: `fc(x_train, [20,20,10], "mylabel")`, you can predict using
```julia
run(sess, fc(x_test, [20,20,10], "mylabel"))
```
## Save the Neural Network
To save the trained neural network in the Session `sess`, we can use
```julia
ADCME.save(sess, "filename.mat")
```
This will create a `.mat` file that contains all the **labeled** weights and biases. If there are other variables besides neural network parameters, these variables will also be saved.
To load the weights and biases to the current session, create a neural network with the same label and run
```julia
ADCME.load(sess, "filename.mat")
```
## Convert Neural Network to Codes
Sometimes we may also want to convert a fully-connected neural network to pure Julia codes. This can be done via [`fc_to_code`](@ref).
After saving the neural network to a mat file via `ADCME.save`, we can call
```julia
ae_to_code("filename.mat", "mylabel")
```
If the second argument is missing, the default is `default`. For example,
```
julia> ae_to_code("filename.mat", "default")|>println
let aedictdefault = matread("filename.mat")
global nndefault
function nndefault(net)
W0 = aedictdefault["defaultbackslashfully_connectedbackslashweightscolon0"]
b0 = aedictdefault["defaultbackslashfully_connectedbackslashbiasescolon0"];
isa(net, Array) ? (net = net * W0 .+ b0') : (net = net *W0 + b0)
isa(net, Array) ? (net = tanh.(net)) : (net=tanh(net))
#-------------------------------------------------------------------
W1 = aedictdefault["defaultbackslashfully_connected_1backslashweightscolon0"]
b1 = aedictdefault["defaultbackslashfully_connected_1backslashbiasescolon0"];
isa(net, Array) ? (net = net * W1 .+ b1') : (net = net *W1 + b1)
isa(net, Array) ? (net = tanh.(net)) : (net=tanh(net))
#-------------------------------------------------------------------
W2 = aedictdefault["defaultbackslashfully_connected_2backslashweightscolon0"]
b2 = aedictdefault["defaultbackslashfully_connected_2backslashbiasescolon0"];
isa(net, Array) ? (net = net * W2 .+ b2') : (net = net *W2 + b2)
return net
end
end
```
## Advance: Use Neural Network Implementations from Python Script/Modules
If you have a Python implementation of a neural network architecture and want to use that architecture, we do not need to reimplement it in ADCME. Instead, we can use the `PyCall.jl` package and import the functionalities. For example, if you have a Python package `nnpy` and it has a function `magic_neural_network`. We can use the following code to call `magic_neural_network`
```julia
using PyCall
using ADCME
nnpy = pyimport("nnpy")
x = constant(rand(100,2))
y = nnpy.magic_neural_network(x)
```
Because all the runtime computation are conducted in C++, there is no harm to performance using this mechanism. | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 7732 | # PDE/ODE Solvers
## Runge Kutta Method
The Runge Kutta method is one of the workhorses for solving ODEs. The method is a higher order interpolation to the derivatives. The system of ODE has the form
```math
\frac{dy}{dt} = f(y, t, \theta)
```
where $t$ denotes time, $y$ denotes states and $\theta$ denotes parameters.
The Runge-Kutta method is defined as
$\begin{aligned}
k_1 &= \Delta t f(t_n, y_n, \theta)\\
k_2 &= \Delta t f(t_n+\Delta t/2, y_n + k_1/2, \theta)\\
k_3 &= \Delta t f(t_n+\Delta t/2, y_n + k_2/2, \theta)\\
k_4 &= \Delta t f(t_n+\Delta t, y_n + k_3, \theta)\\
y_{n+1} &= y_n + \frac{k_1}{6} +\frac{k_2}{3} +\frac{k_3}{3} +\frac{k_4}{6}
\end{aligned}$
ADCME provides a built-in Runge Kutta solver [`rk4`](@ref) and [`ode45`](@ref). Consider an example: the Lorentz equation
$\begin{aligned}
\frac{dx}{dt} &= 10(y-x)\\
\frac{dy}{dt} &= x(27-z)-y\\
\frac{dz}{dt} &= xy -\frac{8}{3}z
\end{aligned}$
Let the initial condition be $x_0 = [1,0,0]$, the following code snippets solves the Lorentz equation with ADCME
```julia
function f(t, y, θ)
[10*(y[2]-y[1]);y[1]*(27-y[3])-y[2];y[1]*y[2]-8/3*y[3]]
end
x0 = [1.;0.;0.]
rk4(f, 30.0, 10000, x0)
```
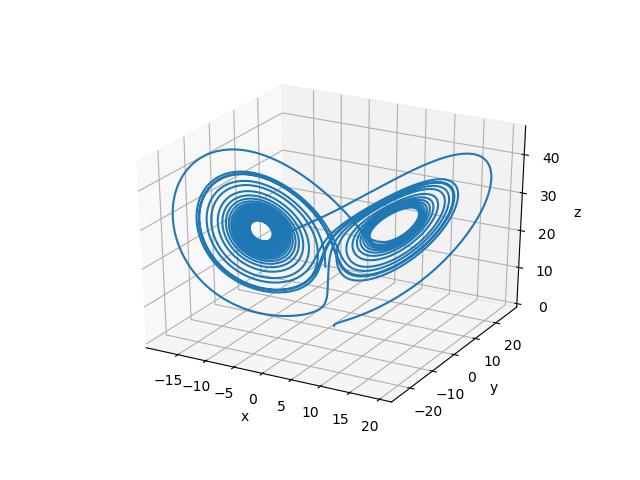
We can also solve three body problem with the Runge-Kutta method. The full script is
```julia
#
# adapted from
# https://github.com/pjpmarques/Julia-Modeling-the-World/
#
using Revise
using ADCME
using PyPlot
using Printf
function f(t, y, θ)
# Extract the position and velocity vectors from the g array
r0, v0 = y[1:2], y[3:4]
r1, v1 = y[5:6], y[7:8]
r2, v2 = y[9:10], y[11:12]
# The derivatives of the position are simply the velocities
dr0 = v0
dr1 = v1
dr2 = v2
# Now calculate the the derivatives of the velocities, which are the accelarations
# Start by calculating the distance vectors between the bodies (assumes m0, m1 and m2 are global variables)
# Slightly rewriten the expressions dv0, dv1 and dv2 comprared to the normal equations so we can reuse d0, d1 and d2
d0 = (r2 - r1) / ( norm(r2 - r1)^3.0 )
d1 = (r0 - r2) / ( norm(r0 - r2)^3.0 )
d2 = (r1 - r0) / ( norm(r1 - r0)^3.0 )
dv0 = m1*d2 - m2*d1
dv1 = m2*d0 - m0*d2
dv2 = m0*d1 - m1*d0
# Reconstruct the derivative vector
[dr0; dv0; dr1; dv1; dr2; dv2]
end
function plot_trajectory(t1, t2)
t1i = round(Int,NT * t1/T) + 1
t2i = round(Int,NT * t2/T) + 1
# Plot the initial and final positions
# In these vectors, the first coordinate will be X and the second Y
X = 1
Y = 2
# figure(figsize=(6,6))
plot(r0[t1i,X], r0[t1i,Y], "ro")
plot(r0[t2i,X], r0[t2i,Y], "rs")
plot(r1[t1i,X], r1[t1i,Y], "go")
plot(r1[t2i,X], r1[t2i,Y], "gs")
plot(r2[t1i,X], r2[t1i,Y], "bo")
plot(r2[t2i,X], r2[t2i,Y], "bs")
# Plot the trajectories
plot(r0[t1i:t2i,X], r0[t1i:t2i,Y], "r-")
plot(r1[t1i:t2i,X], r1[t1i:t2i,Y], "g-")
plot(r2[t1i:t2i,X], r2[t1i:t2i,Y], "b-")
# Plot cente of mass
# plot(cx[t1i:t2i], cy[t1i:t2i], "kx")
# Setup the axis and titles
xmin = minimum([r0[t1i:t2i,X]; r1[t1i:t2i,X]; r2[t1i:t2i,X]]) * 1.10
xmax = maximum([r0[t1i:t2i,X]; r1[t1i:t2i,X]; r2[t1i:t2i,X]]) * 1.10
ymin = minimum([r0[t1i:t2i,Y]; r1[t1i:t2i,Y]; r2[t1i:t2i,Y]]) * 1.10
ymax = maximum([r0[t1i:t2i,Y]; r1[t1i:t2i,Y]; r2[t1i:t2i,Y]]) * 1.10
axis([xmin, xmax, ymin, ymax])
title(@sprintf "3-body simulation for t=[%.1f .. %.1f]" t1 t2)
end;
m0 = 5.0
m1 = 4.0
m2 = 3.0
# Initial positions and velocities of each body (x0, y0, vx0, vy0)
gi0 = [ 1.0; -1.0; 0.0; 0.0]
gi1 = [ 1.0; 3.0; 0.0; 0.0]
gi2 = [-2.0; -1.0; 0.0; 0.0]
T = 30.0
NT = 500*300
g0 = [gi0; gi1; gi2]
res_ = ode45(f, T, NT, g0)
sess = Session(); init(sess)
res = run(sess, res_)
r0, v0, r1, v1, r2, v2 = res[:,1:2], res[:,3:4], res[:,5:6], res[:,7:8], res[:,9:10], res[:,11:12]
figure(figsize=[4,1])
subplot(131); plot_trajectory(0.0,10.0)
subplot(132); plot_trajectory(10.0,20.0)
subplot(133); plot_trajectory(20.0,30.0)
```
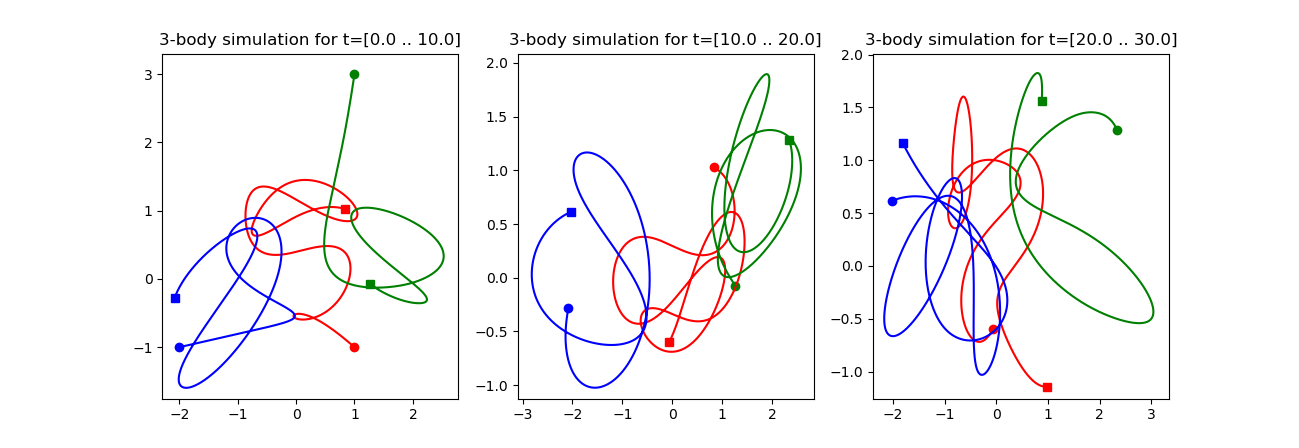
## Explicit Newmark Scheme
[`ExplicitNewmark`](@ref) provides an explicit Newmark integrator for
$$M \ddot{\mathbf{d}} + Z_1 \dot{\mathbf{d}} + Z_2 \mathbf{d} + f = 0$$
The numerical scheme is given by
$$\left(\frac{1}{\Delta t^2} M + \frac{1}{2\Delta t}Z_1\right)d^{n+1} = \left(\frac{2}{\Delta t^2} M - \frac{1}{2\Delta t}Z_2\right)d^n - \left(\frac{1}{\Delta t^2} M - \frac{1}{2\Delta t}Z_1\right) d^{n-1} - f^n$$
We consider an example:
$$\mathbf{d} = \begin{bmatrix}e^{-t}\\ e^{-2t}\end{bmatrix}$$
and
$$M = \begin{bmatrix}1 & 2\\3 &4 \end{bmatrix}\qquad Z_1 = \begin{bmatrix}5 & 6\\7 &8 \end{bmatrix}\qquad Z_2 =\begin{bmatrix}9 & 10\\11 &12 \end{bmatrix} $$
The function $f$ is given by
$$f(t) = -\begin{bmatrix}5e^{-t} + 6e^{-2t}\\ 7 e^{-t} + 12 e^{-2t}\end{bmatrix}$$
We can carry out the simulation using the following codes:
```julia
using ADCME
using PyPlot
M = Float64[1 2;3 4]
Z1 = Float64[5 6;7 8]
Z2 = Float64[9 10;11 12]
NT = 200
Δt = 1/NT
F = zeros(NT+1, 2)
for i = 1:NT+1
t = (i-1)*Δt
F[i,1] = -(5exp(-t) + 6exp(-2t))
F[i,2] = -(7exp(-t) + 12exp(-2t))
end
F = constant(F)
en = ExplicitNewmark(M, Z1, Z2, Δt)
function condition(i, d)
i<=NT
end
function body(i, d)
d0 = read(d, i-1)
d1 = read(d, i)
d2 = step(en, d0, d1, F[i-1])
i+1, write(d, i+1, d2)
end
d = TensorArray(NT+1)
d = write(d, 1, [1.0;1.0])
d = write(d, 2, [exp(-Δt);exp(-2Δt)])
i = constant(2, dtype = Int32)
_, d = while_loop(condition, body, [i, d])
d = stack(d)
sess = Session(); init(sess)
D = run(sess, d)
ts = (0:NT)*Δt
close("all")
plot(ts, D[:, 1], "b.")
plot(ts, D[:,2], "g.")
plot(ts, exp.(-ts), "r--")
plot(ts, exp.(-2ts), "r--")
xlabel("t"); ylabel("y")
savefig("ode_solution.png")
```

## Build Your Own Solvers
Sometimes it is helpful to build your own ODE/PDE solvers. The basic routine is
1. Implement the one step state transition function;
2. Use [`while_loop`](@ref) to build the time integrator.
As an example, we build a second-order Runge-Kutta scheme for
$$\dot{\mathbf{d}} + \beta \mathbf{d} = \mathbf{t}$$
The numerical scheme is
$$\begin{aligned}h_1 &= -\beta \mathbf{d}^n + \mathbf{t}^n\\ h_2 &= -\beta(\mathbf{d}^n + \Delta t h_1) + \mathbf{t}^n\\ \mathbf{d}^{n+1} &= \mathbf{d}^n + \frac{\Delta t}{2}(h_1 + h_2)\end{aligned}$$
The state transition function has the following form
```julia
function rk_one_step(d2, t)
h1 = -β*d2 + t
h2 = -β*(d2+Δt*h1)+t
d2 + Δt/2*(h1+h2)
end
```
Now consider an analytical solution
$$\mathbf{d} = \begin{bmatrix}e^{-t}\\e^{-2t}\end{bmatrix}, \quad \beta = 2$$
Then we have
$$\mathbf{t} = \begin{bmatrix}e^{-t}\\0\end{bmatrix}$$
The main code is as follows
```julia
using ADCME
using PyPlot
NT = 100
Δt = 1/NT
ts = Array((0:NT)*Δt)
t = constant([exp.(-ts) zeros(NT+1)])
β = 2.0
function condition(i, d)
i<=NT
end
function body(i, d)
d0 = read(d, i)
d1 = rk_one_step(d0, t[i])
i+1, write(d, i+1, d1)
end
d = TensorArray(NT+1)
d = write(d, 1, ones(2))
i = constant(1, dtype = Int32)
_, d = while_loop(condition, body, [i, d])
d = stack(d)
sess = Session(); init(sess)
D = run(sess, d)
close("all")
plot(ts, D[:,1], "y.")
plot(ts, D[:,2], "g.")
plot(ts, exp.(-ts), "r--")
plot(ts, exp.(-2ts), "r--")
xlabel("t"); ylabel("y")
savefig("ode_solution2.png")
```
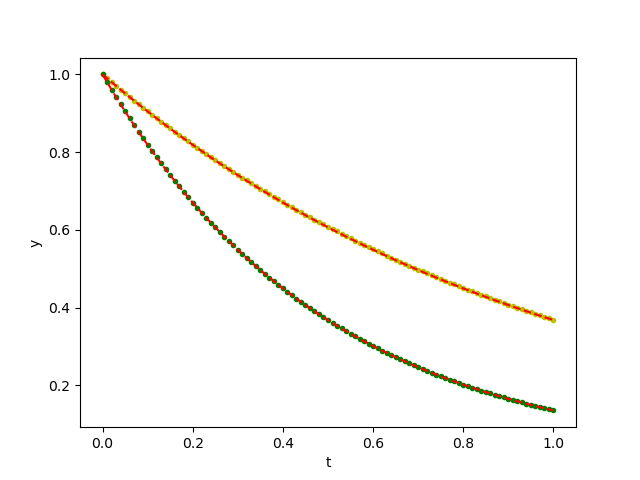 | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 8776 | # Study on Optimizers
When working with BFGS/LBFGS, there are some important aspects of the algorithm, which affect the convergence of the optimizer.
- BFGS approximates the Hessian or the inverse Hessian matrix. LBFGS, instead, stores a limited set of **vectors** and does not explicitly formulate the Hessian matrices. The Hessian matrix solve is approximated using recursions on vector vector production.
- Both BFGS and LBFGS deploy a certain kind of line search strategies. For example, the Hager-Zhang and More-Thuente are two commonly used strategies. These linesearch algorithms require evaluating gradients in each line search step. This means we need to frequently do gradient back-propagation, which may be quite expensive. We instead employ a backtracking strategy, which requires evaluating forward computation only.
- Initial guess of the line search algorithm. We found that the following initial guess is quite effective for our problems:
$$\alpha=\min\{100\alpha_0, 10\}$$
Here $\alpha_0$ is the line search step size for the last step (for the first step, $\alpha=1$ is used). Using this choice, we found that in a typical line search step, only 1~3 evaluations of the loss function is needed.
- Stopping criterion in line search algorithms. The algorithm backtracks until a certain set of condition is met. Typically the Wolfe condition, the Armijo curvature rule, or the strong Wolfe conditions are used. Note that these criterion require gradient information, and we want to avoid calculating extra gradients during linesearch. Therefore, we use the following sufficient decrease condition
$$\phi(\alpha) \leq \phi(0) + c_1 \alpha \phi'(0)$$
Here $c_1=10^{-4}$.
One interesting observation is that if we apply BFGS/LBFGS directly, we usually cannot make any progress. There are many reasons for this phenomenon:
- The initial guess for the neural network is far away from optimal, and quasi-Newton methods usually do not work well in this regime.
- The approximate Hessian is quite different from the true one. The estimated search direction may deviate from the optimal one too much.
First-order methods, such as Adam optimizer, usually does not suffer from these difficulties. Therefore, one solution to this problem is via "warm start" by running a first order optimizer (Adam) for a few iterations. Additionally, for BFGS, we can build Hessian approximations while we are running the Adam optimizer. In this way, we can use the historic information as much as possible.
Our algorithm is as follows (BFGS+Adam+Hessian):
1. Run the Adam optimizer for the first few iterations, and **build the approximate Hessian matrix at the same time**. That is, in each iteration, we update an approximate Hessian $B$ using
$$B_{k+1} = \left(I - \frac{s_k y_k^T}{y_k^Ts_k}\right)B_k\left(I - \frac{ y_ks_k^T}{y_k^Ts_k}\right) + \frac{s_ks_k^T}{y_k^Ts_k}$$
Here $y_k = \nabla f(x_{k+1}) - \nabla f(x_{k}), s_k = x_{k+1}-x_k, B_0 = I$. Note $B_k$ is not used in the Adam optimizer.
2. Run the BFGS optimizer and use the last Hessian matrix $B_k$ built in Step 1 as the initial guess.
We compare our algorithm with those without approximated Hessian (BFGS+Adam) or warm start (BFGS). Additionally, we also compare our algorithm with LBFGS counterparts.
In the test case II and III, a physical field, $f$, is approximated using deep neural networks, $f_\theta$, where $\theta$ is the weights and biases. The neural network maps coordinates to a scalar value. $f_\theta$ is coupled with a DAE:
$$F(u', u, Du, D^2u, \ldots ;f_\theta) = 0 \tag{1}$$
Here $u'$ represents the time derivative of $u$, and $Du$, $D^2u$, $\ldots$ are first-, second-, $\ldots$ order spatial gradients. Typically we can observe $u$ on some discrete points $\{\mathbf{x}_k\}_{k\in \mathcal{I}}$. To train the neural network, we consider the following optimization problem
$$\min_\theta \sum_{k\in \mathcal{I}} (u(\mathbf{x}_i) - u_\theta(\mathbf{x}_i))$$
Here $u_\theta$ is the solution from Eq. 1.
## Test Case I
In the first case, we train a 4 layer network with 20 neurons per layer, and tanh activation functions. The data set is $\{x_i, sin(x_i)\}_{i=1}^{100}$, where $x_i$ are randomly generated from $\mathcal{U}(0,1)$. The neural network $f_\theta$ is trained by solving the following optimization problem:
$$\min_\theta \sum_{i=1}^{100} (\sin(x_i) - f_\theta(x_i))^2$$
The neural network is small, and thus we can use BFGS/LBFGS to train. In fact, the following plot shows that BFGS/LBFGS is much more accurate and effective than the commonly used Adam optimizer. Considering the wide range of computational engineering applications, where a small neural network is sufficient, this result implies that BFGS/LBFGS for training neural networks should receive far more attention than what it does nowadays.
Also, in many applications, the major runtime is doing physical simulations instead of updating neural network parameters or approximate Hessian matrices, these "expensive" BFGS/LBFGS optimization algorithms should be considered a good way to leverage as much history information as possible, so as to reduce the total number of iterations (simulations).
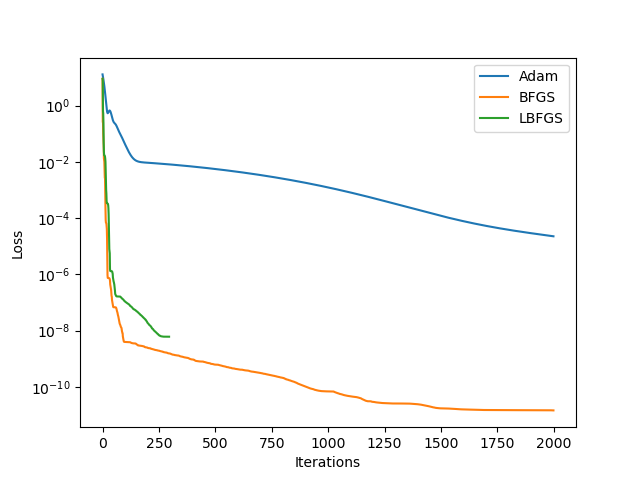
## Test Case II
In this test case, we consider solving a Poisson's equation in [this post](https://kailaix.github.io/ADCME.jl/dev/optimizers/).
The exact $\kappa$ and the corresponding solution $u$ is shown below

We run different optimization algorithms and obtain the following loss function profiles. We see that BFGS/LBFGS without Adam warm start terminates early. BFGS in general has much better accuracy than LBFGS. An extra benefit of BFGS+Adam+Hessian compared to BFGS+Adam is that we can achieve much better accuracy.
| Loss Function | Zoom-in View |
|---------------|--------------|
|  |  |
We also show the mean squared error for $\kappa$, which confirms that BFGS+Adam+Hessian achieves the best test error. The error is calculated using the formula
$$\frac{1}{n} (\kappa_{\text{true}}(\textbf{x}_i) - \kappa_\theta(\textbf{x}_i))^2$$
Here $\textbf{x}_i$ is defined on Gauss points.
| Algorithm | Adam | BFGS+Adam+Hessian | BFGS+Adam | BFGS | LBFGS+Adam | LBFGS |
|-----------|-------|-------------------|-----------|----------|------------|-------|
| MSE | 0.013 | 1.00E-11 | 1.70E-10 | 1.10E+04 | 0.00023 | 97000 |
## Test Case III
In the last example, we consider the linear elasticity. The problem description can be found [here](https://kailaix.github.io/AdFem.jl/dev/staticelasticity/).
We fix the random seed for neural network initialization and run different optimization algorithms. The initial guess for the Young's modulus and the reference one are shown in the following plot

The corresponding velocity and stress fields are

We perform the optimization using different algorithms. In the case where Adam is used as warm start, we run Adam optimization for 50 iterations. We run the optimization for at most 500 iterations (so there is at most 500 evaluations of gradients) The loss function is shown below

We see that BFGS+Adam+Hessian achieves the smallest loss functions among all algorithms. We also show the MSE for $E$, i.e., $\frac{1}{n} (E_{\text{true}}(\textbf{x}_i) - E_\theta(\textbf{x}_i))^2$, where $\textbf{x}_i$ is defined on Gauss points.
| Algorithm | Adam | BFGS+Adam+Hessian | BFGS+Adam | BFGS | LBFGS+Adam | LBFGS |
|-----------|--------|-------------------|-----------|----------|------------|--------|
| MSE | 0.0033 | 1.90E-07 | 4.00E-06 | 6.20E-06 | 0.0031 | 0.0013 |
This confirms that BFGS+Adam+Hessian indeed generates a much more accurate result.
We also compare the results for the BFGS+Adam+Hessian and Adam algorithms:

We see the Adam optimizer achieves reasonable result but is challenging to deliver high accurate estimation within 500 iterations. | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 5432 | # Optimizers
ADCME provides a rich class of optimizers and acceleration techniques for conducting inverse modeling. The programming model also allows for easily extending ADCME with customer optimizers. In this section, we show how to take advantage of the built-in optimization library by showing how to solve an inverse problem--estimating the diffusivity coefficient of a Poisson equation from sparse observations--using different kinds of optimization techniques.
## Solving an Inverse Problem using L-BFGS optimizer
Consider the Poisson equation in 2D:
$$\begin{aligned}
\nabla \cdot (\kappa (x,y)\nabla u(x,y)) &= f(x) & (x,y) \in \Omega\\
u(x,y) &=0 & (x,y)\in \partial \Omega
\end{aligned}\tag{1}$$
Here $\Omega$ is a L-shaped domain, which can be loaded using `meshread`.
$$f(x,y) = -\sin\left(20\pi y+\frac{\pi}{8}\right)$$
and the diffusivity coefficient $\kappa(x,y)$ is given by
$$\kappa(x,y) = 2+e^{10x} - (10y)^2$$
We can solve Equation 1 using a standard finite element method. Here, we use [AdFem.jl](https://github.com/kailaix/AdFem.jl) to solve the PDE.
```julia
using AdFem
using ADCME
using PyPlot
function kappa(x, y)
return 2 + exp(10x) - (10y)^2
end
function f(x, y)
return sin(2π*10y+π/8)
end
mmesh = Mesh(joinpath(PDATA, "twoholes_large.stl"))
Kappa = eval_f_on_gauss_pts(kappa, mmesh)
F = eval_f_on_gauss_pts(f, mmesh)
L = compute_fem_laplace_matrix1(Kappa, mmesh)
RHS = compute_fem_source_term1(F, mmesh)
bd = bcnode(mmesh)
L, RHS = impose_Dirichlet_boundary_conditions(L, RHS, bd, zeros(length(bd)))
SOL = L\RHS
close("all")
figure(figsize = (10, 4))
subplot(121)
visualize_scalar_on_gauss_points(Kappa, mmesh)
title("\$\\kappa\$")
subplot(122)
visualize_scalar_on_fem_points(SOL, mmesh)
title("Solution")
savefig("optimizers_poisson.png")
```
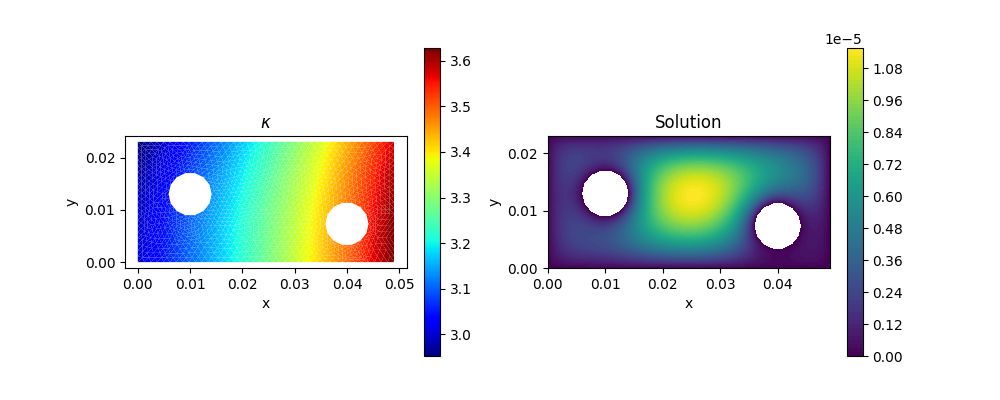
Now we approximate $\kappa(x,y)$ using a deep neural network ([`fc`](@ref) in ADCME). The script is nearly the same as the forward computation
```julia
using AdFem
using ADCME
using PyPlot
function f(x, y)
return sin(2π*10y+π/8)
end
mmesh = Mesh(joinpath(PDATA, "twoholes_large.stl"))
xy = gauss_nodes(mmesh)
Kappa = squeeze(fc(xy, [20, 20, 20, 1])) + 1.0
F = eval_f_on_gauss_pts(f, mmesh)
L = compute_fem_laplace_matrix1(Kappa, mmesh)
RHS = compute_fem_source_term1(F, mmesh)
bd = bcnode(mmesh)
L, RHS = impose_Dirichlet_boundary_conditions(L, RHS, bd, zeros(length(bd)))
sol = L\RHS
```
We want to find a deep neural network such that `sol` and `SOL` match. We can train the neural network by minimizing a loss function.
```julia
loss = sum((sol - SOL)^2)*1e10
```
Here we multiply the loss function by `1e10` because the scale of `SOL` is $10^{-5}$. We want the initial value of `loss` to have a scale of $O(1)$.
We can minimize the loss function by
```julia
sess = Session(); init(sess)
losses = BFGS!(sess, loss)
```
We can visualize the result:
```julia
figure(figsize = (10, 4))
subplot(121)
semilogy(losses)
xlabel("Iterations"); ylabel("Loss")
subplot(122)
visualize_scalar_on_gauss_points(run(sess, Kappa), mmesh)
savefig("optimizer_bfgs.png")
```

We see that the estimated $\kappa(x,y)$ is quite similar to the reference one.
## Use the optimizer from Optim.jl
We have used the built-in optimizer L-BFGS. What if we want to try out other options? [`Optimize!`](@ref) is an API that allows you to try out custom optimizers. For convenience, it also supports optimizers from the [Optim.jl](https://github.com/JuliaNLSolvers/Optim.jl) package.
Let's consider using BFGS to solve the above problem:
```julia
import Optim
sess = Session(); init(sess)
losses = Optimize!(sess, loss, optimizer = Optim.BFGS())
figure(figsize = (10, 4))
subplot(121)
semilogy(losses)
xlabel("Iterations"); ylabel("Loss")
subplot(122)
visualize_scalar_on_gauss_points(run(sess, Kappa), mmesh)
savefig("optimizer_bfgs2.png")
```

Unfortunately, it got stuck after several iterations.
## Build Your Own Optimizer
Sometimes we might want to build our own optimizer. This can be done using [`Optimize!`](@ref). To this end, we want to supply the function with the following arguments:
- `sess`: Session
- `loss`: Loss function to minimize
- `optimizer`: a **keyword argument** that specifies the optimizer function. The function takes `f`, `fprime`, and `f_fprime` (outputs both loss and gradients), initial value `x0` as input. The output is redirected to the output of `Optimize!`.
Let us consider minimizing the Rosenbrock function using an optimizer from Ipopt
```julia
import Ipopt
x = Variable(rand(2))
loss = (1-x[1])^2 + 100(x[2]-x[1]^2)^2
function opt(f, g, fg, x0)
prob = createProblem(2, -100ones(2), 100ones(2), 0, Float64[], Float64[], 0, 0,
f, (x,g)->nothing, (x,G)->g(G, x), (x, mode, rows, cols, values)->nothing, nothing)
prob.x = x0
Ipopt.addOption(prob, "hessian_approximation", "limited-memory")
status = Ipopt.solveProblem(prob)
println(Ipopt.ApplicationReturnStatus[status])
println(prob.x)
Ipopt.freeProblem(prob)
nothing
end
sess = Session(); init(sess)
Optimize!(sess, loss, optimizer = opt)
``` | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 784 | # Global Options
ADCME manages certain algorithm hyperparameters using a global option `ADCME.option`.
```@docs
Options
OptionsSparse
OptionsNewtonRaphson
OptionsNewtonRaphson_LineSearch
reset_default_options
```
The current options and their default values are
```julia
using PrettyPrint
using ADCME
pprint(ADCME.options)
```
```text
ADCME.Options(
sparse=ADCME.OptionsSparse(
auto_reorder=true,
solver="SparseLU",
),
newton_raphson=ADCME.OptionsNewtonRaphson(
max_iter=100,
verbose=false,
rtol=1.0e-12,
tol=1.0e-12,
LM=0.0,
linesearch=false,
linesearch_options=ADCME.OptionsNewtonRaphson_LineSearch(
c1=0.0001,
ρ_hi=0.5,
ρ_lo=0.1,
iterations=1000,
maxstep=9999999,
αinitial=1.0,
),
),
)
```
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 3496 | # Optimal Transport
Optimal transport (OT) can be used to measure the "distance" between two probability distribution.
## Discrete Wasserstein Distance
In this section, we introduce a novel approach for training a general model: SinkHorn Generative Networks (SGN). In this approach, a neural network is used to transform a sample from uniform distributions to a sample of targeted distribution. We train the neural network by minimizing the discrepancy between the targeted distribution and the desired distribution, which is described by optimal transport distance. Different from generative adversarial nets (GAN), we do not use a discriminator neural network to construct the discrepancy; instead, it is computed directly with efficient SinkHorn algorithm or net-flow solver. The minimization is conducted via a gradient-based optimizer, where the gradients are computed with reverse mode automatic differentiation.
To begin with, we first construct the sample `x` of the targeted distribution and the sample `s` from the desired distribution and compute the loss function with [`sinkhorn`](@ref)
```julia
using Revise
using ADCME
using PyPlot
reset_default_graph()
K = 64
z = placeholder(Float64, shape=[K, 10])
x = squeeze(ae(z, [20,20,20,1]))
s = placeholder(Float64, shape=[K])
M = abs(reshape(x, -1, 1) - reshape(s, 1, -1))
loss = sinkhorn(ones(K)/K, ones(K)/K, M, reg=0.1)
```
**Example 1**
In the first example, we assume the desired distribution is the standard Gaussian. We minimize the loss function with the Adam optimizer
```julia
opt = AdamOptimizer().minimize(loss)
sess = Session(); init(sess)
for i = 1:10000
_, l = run(sess, [opt, loss], z=>rand(K, 10), s=>randn(K))
@show i, l
end
```
The result is shown below
```julia
V = []
for k = 1:100
push!(V,run(sess, x, z=>rand(K,10)))
end
V = vcat(V...)
hist(V, bins=50, density=true)
x0 = LinRange(-3.,3.,100)
plot(x0, (@. 1/sqrt(2π)*exp(-x0^2/2)), label="Reference")
xlabel("x")
ylabel("f(x)")
legend()
```

**Example 2**
In the first example, we assume the desired distribution is the positive part of the the standard Gaussian.
```julia
opt = AdamOptimizer().minimize(loss)
sess = Session(); init(sess)
for i = 1:10000
_, l = run(sess, [opt, loss], z=>rand(K, 10), s=>abs.(randn(K)))
@show i, l
end
```
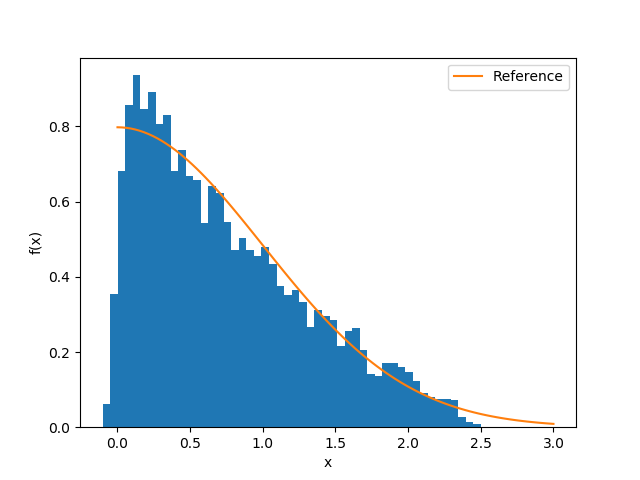
## Dynamic Time Wrapping
Dynamic time wrapping is suitable for computing the distance of two time series. The idea is that we can shift the time series to obtain the "best" match while retaining the causality in time. This is best illustrated in the following figure

In ADCME, the distance is computed using [`dtw`](@ref). As an example, given two time series
```julia
Sample = Float64[1,2,3,5,5,5,6]
Test = Float64[1,1,2,2,3,5]
```
The distance can be computed by
```julia
c, p = dtw(Sample, Test, true)
```
`c` is the distance and `p` is the path.
If we have 2000 time series `A` and 2000 time series `B` and we want to compute the total distance of the corresponding time series, we can use `map` function
```julia
A = constant(rand(2000,1000))
B = constant(rand(2000,1000))
distance = map(x->dtw(x[1],x[2],false)[1],[A,B], dtype=Float64)
```
`distances` is a 2000 length vector and gives us the pairwise distance for all time series. | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 3656 | # Parallel Computing
The ADCME backend, TensorFlow, treats each operator as the smallest computation unit. Users are allowed to manually assign each operator to a specific device (GPU, CPU, or TPU). This is usually done with the `@cpu device_id expr` or `@gpu device_id expr` syntax, where `device_id` is the index of devices you want to place all operators and variables in `expr`. For example, if we want to create a variable `a` and compute $\sin(a)$ on `GPU:0` we can write
```julia
@cpu 0 begin
global a = Variable(1.0)
global b = sin(a)
end
```
If the `device_id` is missing, 0 is treated as default.
```julia
@cpu begin
global a = Variable(1.0)
global b = sin(a)
end
```
**Custom Device Placement Functions**
The above placement function is useful and simple for placing operators on certain GPU devices without changing original codes. However, sometimes we want to place certain operators on certain devices. This can be done by implementing a custom `assign_to_device` function. As an example, we want to place all `Variables` on CPU:0 while placing all other operators on GPU:0, the code has the following form
```julia
PS_OPS = ["Variable", "VariableV2", "AutoReloadVariable"]
function assign_to_device(device, ps_device="/device:CPU:0")
function _assign(op)
node_def = pybuiltin("isinstance")(op, tf.NodeDef) ? op : op.node_def
if node_def.op in PS_OPS
return ps_device
else
return device
end
end
return _assign
end
```
Then we can write something like
```julia
@pywith tf.device(assign_to_device("/device:GPU:0")) begin
global a = Variable(1.0)
global b = sin(a)
end
```
We can check the location of `a` and `b` by inspecting their `device` attributes
```julia-repl
julia> a.device
"/device:CPU:0"
julia> b.device
"/device:GPU:0"
```
**Collocate Gradient Operators**
When we call `gradients`, TensorFlow actually creates a set of new operators, one for each operator in the forward computation. By default, those operators are placed on the default device (`GPU:0` if GPU is available; otherwise it's `CPU:0`). Sometimes we want to place the operators created by gradients on the same devices as the corresponding forward computation operators. For example, if the operator `b` (`sin`) in the last example is on `GPU:0`, we hope the corresponding gradient computation (`cos`) is also on `GPU:0`. This can be done by specifying `colocate` [^colocate] keyword arguments in `gradients`:
```julia
@pywith tf.device(assign_to_device("/device:GPU:0")) begin
global a = Variable(1.0)
global b = sin(a)
end
@pywith tf.device("/CPU:0") begin
global c = cos(b)
end
g = gradients(c, a, colocate=true)
```
In the following figure, we show the effects of `colocate` of the above codes. The test code snippet is
```julia
g = gradients(c, a, colocate=true)
sess = Session(); init(sess)
run_profile(sess, g+c)
save_profile("true.json")
g = gradients(c, a, colocate=false)
sess = Session(); init(sess)
run_profile(sess, g+c)
save_profile("false.json")
```

!!! note
If you use `bn` (batch normalization) on multi-GPUs, you must be careful to update the parameters in batch normalization on CPUs. This can be done by explicitly specify
```julia
@pywith tf.device("/cpu:0") begin
global update_ops = get_collection(tf.GraphKeys.UPDATE_OPS)
end
```
and bind `update_ops` to an active operator (or explictly execute it in `run(sess,...)`).
[^colocate]: Unfortunately, in the TensorFlow APIs, "collocate" is spelt as "colocate".
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 1490 | # Visualization with Plotly
Starting from v0.7.2, [`Plotly`](https://github.com/plotly/plotly.py) plotting backend is included in ADCME. Plotly.py is an open source software for visualizing **interactive** plots based on web technologies. ADCME exposes several APIs of Plotly: [`Plotly`](@ref), [`Layout`](@ref), and common graph objects, such as [`Scatter`](@ref).
In Plotly, each figure consists of `data`---a collection of traces---and `layout`, whcih is constructed using [`Layout`](@ref). The basic workflow for creating plotly plots is
- Create a figure object. For example:
```julia
fig = Plot()
```
In the case of subplots within a single figure, use
```julia
fig = Plot(3, 1) # 3 x 1 subplots
```
- Create traces using `add_trace` methods of `fig`. For example
```julia
x = LinRange(0, 2π, 100)
y1 = sin.(x)
y2 = sin.(2*x)
y3 = sin.(3*x)
fig.add_trace(Scatter(x=x, y=y1, name = "Line 1"), row = 1, col = 1)
fig.add_trace(Scatter(x=x, y=y2, name = "Line 2"), row = 2, col = 1)
fig.add_trace(Scatter(x=x, y=y3, name = "Line 3"), row = 3, col = 1)
```
- Update layout or properties
```julia
fig.layout.yaxis.update(title = "Y Axis")
fig.layout.update(hovermode="x unified", showlegend = false)
fig.data[1].update(hovertemplate = """<b>%{y:.2f}</b>""")
```
- Visualize or save to files
```julia
data = fig.to_dict()
fig.write_html("figure.html", full_html = false) # save to HTML
fig.show()
```
We can create a figure from dictionary as well.
```julia
fig = Plot(data)
``` | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 3542 | # Numerical Integration
This section describes how to do numerical integration in ADCME. In fact, the numerical integration functionality is independent of automatic differentiation. We can use a third-party library, such as [FastGaussQuadrature](https://github.com/JuliaApproximation/FastGaussQuadrature.jl) for extracts the quadrature weights and points. Then the quadrature weights and points can be used to calculate the integral.
The general rule for numerical integral is
$$\int_a^b w(x) f(x) dx = \sum_{i=1}^n w_i f(x_i)$$
The method works best when $f(x)$ can be approximated by a polynomial on the interval $(a, b)$.
## Examples
Let us consider some examples.
### Example 1
$$\int_0^1\frac{\sin(a*x)}{\sqrt{1-x^2}}dx$$
Here $a$ is a tensor (e.g., `a = Variable(1.0)`). We can use the Gauss-Chebyshev quadrature rule of the 1st kind. The corresponding weight function is $\frac{1}{\sqrt{1-x^2}}$
```julia
using FastGaussQuadrature, ADCME
x, w = gausschebyshev(100) # 100 is the number of quadrature nodes
a = Variable(1.0)
integral = sum(cos(a * x) * w)
```
We can verify the result with the exact value
```julia
sess = Session(); init(sess)
@show sum(cos.(x) .* w), run(sess, integral)
```
The output is
```
(sum(cos.(x) .* w), run(sess, integral)) = (2.4039394306344133, 2.4039394306344137)
```
### Example 2
$$\int_0^\infty (x-1)^β x^\alpha \exp(-x) dx$$
Here we consider the Gauss-Laguerre quadrature rule. The weight function is $w(x) = x^\alpha \exp(-x)$ and $f(x) = (x-1)^2$.
```julia
using FastGaussQuadrature, ADCME
α = 2.0
x, w = gausslaguerre(100, α)
β = Variable(2.0)
integrand = constant(x .- 1)^β
integral = sum(integrand .* w)
```
We can verify the result with the exact value
```julia
sess = Session(); init(sess)
@show sum((x .- 1).^2 .* w), run(sess, integral)
```
The output is
```
(sum((x .- 1) .^ 2 .* w), run(sess, integral)) = (14.000000000000039, 14.000000000000037)
```
The integral rule is also differentiable, for example, we can calculate the gradient of the integral with respect to $\beta$
```julia
run(sess, gradients(integral, β))
```
For convenience, here is a list of supported quadrature rules (run `using FastGaussQuadrature` first)
| Interval | ω(x) | Orthogonal polynomials | Function |
|---------------------|-----------------------------|-------------------------------------|----------|
| $[−1, 1]$ | 1 | Legendre polynomials | `gausslegendre(n)` |
| $(−1, 1)$ | $(1-x)^\alpha (1+x)^\beta$ | Jacobi polynomials | `gaussjacobi(n, a, b)` |
| $(−1, 1)$ | $\frac{1}{sqrt{1-x^2}}$ | Chebyshev polynomials (first kind) | `gausschebyshev(n, 1)` |
| $[−1, 1]$ | $\sqrt{1-x^2}$ | Chebyshev polynomials (second kind) | `gausschebyshev(n, 2)` |
| $[−1, 1]$ | $\sqrt{(1+x)/(1-x)}$ | Chebyshev polynomials (third kind) | `gausschebyshev(n, 3)` |
| $[−1, 1]$ | $\sqrt{(1-x)/(1+x)}$ | Chebyshev polynomials (fourth kind) | `gausschebyshev(n, 4)` |
| $[0, \infty)$ | $e^{-x}$ | Laguerre polynomials | `gausslaguerre(n)` |
| $[0, \infty)$ | $x^\alpha e^{-x}, \alpha>1$ | Generalized Laguerre polynomials | `gausslaguerre(n, α)` |
| $(-\infty, \infty)$ | $e^{-x^2}$ | Hermite polynomials | `gausshermite(n)` |
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 5529 | # Radial Basis Functions
The principle of radial basis functions (RBF) is to use linear combination of radial basis functions to approximate a function. The radial basis functions are usually global functions in the sense that its support spans over the entire domain. This property lends adaptivity and regularization to the RBF function form: unlike local basis functions such as piecewise linear functions, RBF usually does not suffer from local anomalies and produces a smoother approximation.
The mathematical formulation of RBFs on a 2D domain is as follows
$$f(x, y) = \sum_{i=1}^N c_i \phi(r; \epsilon_i) + d_0 + d_1 x + d_2 y$$
Here $r = \sqrt{|x-x_i|^2 + |y-y_i|^2}$. $\{x_i, y_i\}_{i=1}^N$ are called centers of the RBF, $c_i$ is the coefficient, $d_0+d_1x+d_2y$ is an additional affine term, and $\phi$ is a radial basis function parametrized by $\epsilon_i$. Four common radial basis functions are as follows (all are supported by ADCME)
* Gaussian
$$\phi(r; \epsilon) = e^{-(\epsilon r)^2}$$
* Multiquadric
$$\phi(r; \epsilon) = \sqrt{1+(\epsilon r)^2}$$
* Inverse quadratic
$$\phi(r; \epsilon) = \frac{1}{1+(\epsilon r)^2}$$
* Inverse multiquadric
$$\phi(r; \epsilon) = \frac{1}{\sqrt{1+(\epsilon r)^2}}$$
In ADCME, we allow $(x_i, y_i)$, $\epsilon_i$, $d_i$ and $c_i$ to be trainable (of course, users can allow only a subset to be trainable). This is done via [`RBF2D`](@ref) function. As an example, we consider using radial basis function to approximate
$$y = 1 + \frac{y^2}{1+x^2}$$
on the domain $[0,1]^2$. We use the following function to visualize the result
```julia
using PyPlot
n = 20
h = 1/n
x = Float64[]; y = Float64[]
for i = 1:n+1
for j = 1:n+1
push!(x, (i-1)*h)
push!(y, (j-1)*h)
end
end
close("all")
f = run(sess, rbf(x, y))
g = (@. 1+y^2/(1+x^2))
figure()
scatter3D(x, y, f, color="r")
scatter3D(x, y, g, color="g")
xlabel("x")
ylabel("y")
savefig("compare.png")
figure()
scatter3D(x, y, abs.(f-g))
xlabel("x")
ylabel("y")
savefig("diff.png")
```
We consider several cases:
* Only $c_i$ is trainable
```julia
using ADCME
# use centers on a uniform grid
n = 5
h = 1/n
xc = Float64[]; yc = Float64[]
for i = 1:n+1
for j = 1:n+1
push!(xc, (i-1)*h)
push!(yc, (j-1)*h)
end
end
# by default, c is initialized to Variable(ones(...))
# eps is initialized to ones(...) and no linear terms are used
rbf = RBF2D(xc, yc)
x = rand(100); y = rand(100)
f = @. 1+y^2/(1+x^2)
fv = rbf(x, y)
loss = sum((f-fv)^2)
sess = Session(); init(sess)
BFGS!(sess, loss)
```
| Approximation | Difference |
| ------------- |:-------------:|
|  |  |
* Only $c_i$ is trainable + Additional Linear Term
Here we need to specify `d=Variable(zeros(3))` to tell ADCME we want both the constant and linear terms. If `d=Variable(zeros(1))`, only the constant term will be present.
```julia
using ADCME
# use centers on a uniform grid
n = 5
h = 1/n
xc = Float64[]; yc = Float64[]
for i = 1:n+1
for j = 1:n+1
push!(xc, (i-1)*h)
push!(yc, (j-1)*h)
end
end
# by default, c is initialized to Variable(ones(...))
# eps is initialized to ones(...) and no linear terms are used
rbf = RBF2D(xc, yc; d = Variable(zeros(3)))
x = rand(100); y = rand(100)
f = @. 1+y^2/(1+x^2)
fv = rbf(x, y)
loss = sum((f-fv)^2)
sess = Session(); init(sess)
BFGS!(sess, loss)
```
| Approximation | Difference |
| ------------- |:-------------:|
|  |  |
* Free every trainable variables
```julia
xc = Variable(rand(25))
yc = Variable(rand(25))
d = Variable(zeros(3))
e = Variable(ones(25))
# by default, c is initialized to Variable(ones(...))
# eps is initialized to ones(...) and no linear terms are used
rbf = RBF2D(xc, yc; eps = e, d = d)
x = rand(100); y = rand(100)
f = @. 1+y^2/(1+x^2)
fv = rbf(x, y)
loss = sum((f-fv)^2)
sess = Session(); init(sess)
BFGS!(sess, loss)
```
We see we get much better result by freeing up all variables.
| Approximation | Difference |
| ------------- |:-------------:|
|  |  |
## 3D Radial Basis Function
ADCME also provides RBFs on a 3D domain. The usage of [`RBF3D`](@ref) is similar to [`RBF2D`](@ref).
```julia
xc, yc, zc, c = rand(50), rand(50), rand(50), rand(50)
d = rand(4)
e = rand(50)
rbf = RBF3D(xc, yc, zc; c = c, d = d, eps = e)
x, y, z = rand(10), rand(10), rand(10)
v = rbf(x,y,z)
sess = Session()
run(sess, v)
```
Here `xc`, `yc`, and `zc` are the centers; `e` and `d` are hyper-parameters for radial basis functions (see API documentation for [`RBF3D`](@ref)). These parameter are trainable, e.g., we elect to train `xc`, `yc`, `zc` and `e`, and set $d=0$ (no linear affine term)
```julia
xc, yc, zc, c = Variable(rand(50)), Variable(rand(50)), Variable(rand(50)), Variable(rand(50))
e = Variable(rand(50))
rbf = RBF3D(xc, yc, zc; c = c, eps = e)
# ... (details ommited)
v = rbf(x, y, z)
loss = sum((v-vobs)^2)
sess = Session(); init(sess)
BFGS!(sess, loss)
```
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 3924 | # Reinforcement Learning Basics: Q-learning and SARSA
This note gives a short introduction to Q-learning and SARSA in reinforcement learning.
## Reinforcement Learning
Reinforcement learning aims at making optimal decisions using experiences. In reinforcement learning, an **agent** interacts with an **environment**. There are three important concepts in reinforcement learning: **states**, **actions**, and **rewards**. An agent in a certain state takes an action, which results in a reward from the environment and a change of states. In this note, we assume that the states and actions are discrete, and let $\mathcal{S}$ and $\mathcal{A}$ denotes the set of states and actions, respectively.
We first define some important concepts in reinforcement learning:
- Policy. A policy is a function $\pi: \mathcal{S}\rightarrow \mathcal{A}$ that defines the agent's action at a given state.
- Reward. A reward is a function $R: \mathcal{S} \times \mathcal{A} \rightarrow \mathbb{R}$ whose value is rewarded to an agent for performing certain actions at a given state. Particularly, the goal of an agent is to maximum the discounted reward
$$\min_\pi\ R = \sum_{t=0}^\infty \gamma^t R(s_{t+1}, a_{t+1}) \tag{1}$$
where $\gamma\in (0,1)$ is a discounted factor, and $(s_t, a_t)$ are a sequence of states and actions following a policy $\pi$.
Specifically, in this note we assume that both the policy and the reward function are time-independent and deterministic.
We can now define the quality function (Q-function) for a given policy
$$Q^\pi(s_t, a_t) = \mathbf{E}(R(s_t, a_t) + \gamma R(s_{t+1}, a_{t+1}) + \gamma^2 R(s_{t+2}, a_{t+2}) + \ldots | s_t, a_t)$$
here $\pi$ is a given policy
It can be shown that the solution to Equation 1 is given by the policy $\pi$ that satisfies
$$\pi(s) = \max_a\ Q^\pi(s, a)$$
## Q-learning and SARSA
Both Q-learning and SARSA learn the Q-function iteratively. We denote the everchanging Q-function in the iterative process as $Q(s,a)$ (no superscript referring to any policy). When $|\mathcal{S}|<\infty, |\mathcal{A}|<\infty$, $Q(s,a)$ can be tabulated as a $|\mathcal{S}|\times |\mathcal{A}|$ table.
A powerful technique in reinforcment learning is the epsilon-greedy algorithm, which strikes a balance between exploration and exploitation of the state space. To describe the espilon-greedy algorithm, we introduce the **stochastic policy** $\pi_\epsilon$ given a Q-function:
$$\pi_\epsilon(s) = \begin{cases}a' & \text{w.p.}\ \epsilon \\ \arg\max_a Q(s, a) &\text{w.p.}\ 1-\epsilon\end{cases}$$
Here $a'$ is a random variable whose values are in $\mathcal{A}$ (e.g., a uniform random variable over $\mathcal{A}$).
Then the Q-learning update formula can be expressed as
$$Q(s,a) = (1-\alpha)Q(s,a) + \alpha \left(R(s,a) + \gamma\max_{a'} Q(s', a')\right)$$
The SARSA update formula can be expressed as
$$Q(s,a) \gets (1-\alpha)Q(s,a) + \alpha \left(R(s,a) + \gamma Q
(s', a')\right),\ a' = \pi_\epsilon(s')$$
In both cases, $s'$ is the subsequent state given the last action $a$ at state $s$, and $a = \pi_\epsilon(s)$.
The subtle difference between Q-learning and SARSA is **how you select your next best action**, either max or mean.
To extract the optimal deterministic policy $\pi$ from $\pi_\epsilon$, we only need to define
$$\pi(s) := \arg\max_a Q(s,a)$$
## Examples
We use OpenAI gym to perform numerical experiments. We reimplemented the Q-learning algorithm from [this post](https://www.learndatasci.com/tutorials/reinforcement-q-learning-scratch-python-openai-gym/) in Julia.
- Q-learning: [code](https://github.com/kailaix/ADCME.jl/blob/master/docs/src/assets/Codes/ML/qlearning.jl)
- SARSA: [code](https://github.com/kailaix/ADCME.jl/blob/master/docs/src/assets/Codes/ML/salsa.jl)
To run the scripts, you need to install the dependencies via
```julia
using ADCME
PIP = get_pip()
run(`$PIP install cmake 'gym[atari]'`)
```
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 1903 | # Resource Manager
Sometimes we want to store data for different operations to share, or maintain a stateful kernel (data are shared across different invocations). One way to achieve this goal in the concurrency environment is to use `ResourceMgr` in C++ custom operators.
A typical usage of `ResourceMgr` is as follows
1. Define your own resource, which should inherent from `ResourceBase` and `DebugString` must be defined (it is an abstract method in `ResourceBase`).
```c++
#include "tensorflow/core/framework/resource_mgr.h"
struct MyVar: public ResourceBase{
string DebugString() const { return "MyVar"; };
mutex mu;
int32 val;
};
```
2. Access the system `ResourceMgr` through
```c++
auto rm = context->resource_manager();
```
3. Define your resource creation and manipulation method (make sure at any time there is only one single instance given the same container name and resource name).
```c++
MyVar* my_var;
Status s = rm->LookupOrCreate<MyVar>("my_container", "my_name", &my_var, [&](MyVar** ret){
printf("Create a new container\n");
*ret = new MyVar;
(*ret)->val = *u_tensor;
return Status::OK();
});
DCHECK_EQ(s, Status::OK());
my_var->val += 1;
my_var->Unref();
```
When using the `ResourceMgr`, keep in mind that whenever you execute a new path in the computational graph, the system will create a new `ResourceMgr`. Therefore, to run operators that manipulate `ResourceMgr` in parallel, the trigger operator (which is fed to `run(sess, ...)`) must be attached those manipulation dependencies.
See the following scripts for an example
[CMakeLists.txt](https://kailaix.github.io/ADCME.jl/dev/assets/Codes/ResourceManager/CMakeLists.txt), [TestResourceManager.cpp](https://kailaix.github.io/ADCME.jl/dev/assets/Codes/ResourceManager/TestResourceManager.cpp), [gradtest.jl](https://kailaix.github.io/ADCME.jl/dev/assets/Codes/ResourceManager/gradtest.jl)
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 26436 | # Training Deep Neural Networks with Trust-Region Methods
Trust-region methods are a class of global optimization methods. The basic idea is to successively solve an approximated optimization problem in a small neighborhood of the current state. For example, we can approximate the local landscape of the objective function using a quadratic function, and thus can solve efficiently and accurately. The biggest advantage of trust-region methods in the context of deep neural network is that they can escape saddle points, which are demonstrated to be the dominant causes for slow convergence, with proper algorithm design.
However, the most challenging problem with trust-region methods is that we need to calculate the Hessian (curvature information) to leverage the local curvature information. Computing the Hessian can be quite expensive and challenging, especially if the forward computation involves complex procedures and has a large number of optimizable variables. Fortunately, for many deep neural network based inverse problems, the DNNs do not need to be huge for good accuracy. Therefore, calculating the Hessian is plausible. This does not mean that efficient computation is easy, and we introduce the technique is another post. In this post, we compare the trust-region method with other competing methods (L-BFGS-B, BFGS, and ADAM optimizer) for training deep neural networks that are coupled with a numerical solver. We also shed lights on why the other optimizers slow down.
## Trust-region Methods
We consider an unconstrained optimization problem
$$\min_x f(x) \tag{1}$$
The trust-region method solves the optimization problem Eq. 1 by iteratively solving many simpler subproblems, which are good approximation to $f(x_k)$ at the neighborhood of $x_k$. We model $f(x_k+s)$ using a quadratic model
$$m(s) = f_k + s^T g_k + \frac{1}{2}s^T H_k s \tag{2}$$
Here $f_k = f(x_k)$, $g_k = \nabla f(x_k)$, $H_k = \nabla^2 f(x_k)$.
Eq. 2 is essentially the Taylor expansion of $f(x)$ at $x_k$. This approximation is only accurate within the neighborhood of $x_k$. Therefore, we constrain our subproblem to a **trust region**
$$||s||\leq \Delta_k$$
The subproblem has the following form
$$\begin{aligned}\min_{s} & \; m(s) \\ \text{s.t.} & \; \|s\|\leq \Delta_k\end{aligned} \tag{3}$$
In this work, we use the method proposed in [^trust-region] to solve Eq. 3 nearly exactly.
[^trust-region]: A.R. Conn, N.I. Gould, and P.L. Toint, "Trust region methods", Siam, pp. 169-200, 2000.
## Example: Static Poisson's Equation
In this example, we consider the Poisson's equation
$$\nabla \cdot (\kappa_\theta(u) \nabla u)) = f(x), \;x\in \Omega, \; x\in \partial\Omega$$
Here $\kappa_\theta(u)$ is a deep neural network and $\theta$ is the weights and biases. We discretize $\Omega$ using a uniform grid. Assume we can observe the full field data $u_{obs}$ on the grid points. We can then train the deep neural network using the residual minimization method [^residual-minimization]
$$\min_\theta \sum_{i,j} (F_{i,j}(\theta) - f_{i,j})^2 \tag{4}$$
Here $F_{i,j}(\theta)$ is the finite difference discretization of $\nabla \cdot (\kappa_\theta(u_{obs}) \nabla u_{obs}))$ at the grid points. In our benchmark, we add 10% uniform random noise to $f$ and $u_{obs}$ to make the problem more challenging.
[^residual-minimization]: Huang, Daniel Z., et al. "Learning constitutive relations from indirect observations using deep neural networks." Journal of Computational Physics (2020): 109491.
We apply 4 optimizers to solve Eq. 4. Because the optimization results depend on the initialization of the deep neural network, we use 5 different initial guess for DNNs. The result is shown below
| Case | Convergence Plots |
|-------------|---|
|1 | |
|2 | |
|3 | |
|4 | |
|5 | |
We can see for all cases, the trust-region method provides a much more accurate result, and in general converges faster. The ADAM optimizer is the least competent, partially because it's a first-order optimizer and is not able to fully leverage the curvature information. The BFGS optimizers constructs an approximate Hessian that is SPD. The L-BFGS-B optimizer is an approximation to BFGS, where it uses only a limited number of previous iterates to construct the Hessian matrix. As mentioned, in the optimization problem involving deep neural networks, the slow down is mainly due to the saddle point, where the descent direction corresponds to the negative eigenvalues of the Hessian matrix. Because BFGS and L-BFGS-B ensure that the Hessian matrix is SPD, they cannot provide approximate guidance to escape the saddle point. This hypothesis is demonstrated in the following plot, where we show the distribution of Hessian eigenvalues at the last step for Case 2
| Optimizer | L-BFGS-B | BFGS | Trust Region |
|-------------|---|---|---|
| Eigenvalue Distribution | |||
In the following, we show the eigenvalue distribution of the Hessian matrix for
$$l(\theta) = \sum_{i=1}^n (\kappa_\theta(u_i) - \kappa_i)^2$$
We can see that the Hessian possesses some negative eigenvalues. This implies that the DNN and DNN-FEM loss functions indeed have different curvature structures at the local minimum. The structure is altered by the PDE constraint.
| Optimizer | L-BFGS-B | BFGS | Trust Region |
|-------------|---|---|---|
| Eigenvalue Distribution | |||
We also show the number of **negative** eigenvalues for the BFGS and trust region optimizer. Here we use a threshold $\epsilon=10^{-6}$: for a given eigenvalue $\lambda$, it is treated as "positive" if $\lambda>\epsilon \lambda_{\max}$, and "negative" if $\lambda < - \epsilon \lambda_{\max}$, otherwise zero. Here $\lambda_{\max}$ is the maximum eigenvalue.
| BFGS | Trust Region |
|-------------|---|
|||
We can see that the number of positive eigenvalues stays at around 18 and 30 for BFGS and trust region methods after a sufficient number of iterations. The number of negative eigenvalues is nearly zero. This means that both optimizers converge to points with positive semidefinite Hessian matrices. Stationary points are true local minima, instead of saddle points.
We also analyze the direction of the search direction $p_k$ in the BFGS optimizer. We consider two values
$$\begin{aligned}\cos(\theta_1) &= \frac{-p_k^T g_k}{\|p_k\|\|g_k\|} \\ \cos(\theta_2) &= \frac{p_k^T q_k}{\|p_k\|\|q_k\|}\end{aligned}$$
Here $q_k$ is the direction for the **Newton's point**
$$q_k = -H_k^{-1}g_k$$
The two quantities are shown in the following plots (since the trust-region method converges in around 270 iterations, $\cos(\theta2)$ only has limited data points)
| $\cos(\theta_1)$ | $\cos(\theta_2)$ |
|-------------|---|
|  | |
There are two conclusions to draw from the plots
1. The search direction of the BFGS optimizer deviates from the gradient descent method.
2. The search direction of the BFGS optimizer is not very correlated with the Newton's point direction; this indicates the search direction poorly recognizes the negative curvature directions.
## Example: Heat Equation
We consider a time-dependent PDE problem: the heat equation
$$\frac{\partial u}{\partial t} = \nabla \cdot (\kappa_\theta(x) \nabla u)) + f(x), \;x\in \Omega, \; x\in \partial\Omega$$
We assume that we can observe the full field data of $u$ as snapshots. We again apply the residual minimization method to train the deep neural network. The following shows the convergence plots for different initial guesses of the DNNs.
| Case | Convergence Plots |
|-------------|---|
|1 | |
|2 | |
|3 | |
|4 | |
|5 | |
We see that the trust-region is more competitive than the other methods.
We also show the eigenvalue distribution of the Hessian matrices for Case 3.
| ADAM | BFGS | LBFGS| Trust Region |
|---|---|---|---|
||  | | |
|50|31|22|35|
The eigenvalues of Hessian matrices are nonnegative except for the ADAM case, where the optimizer does not converge to a satisfactory local minimum after 5000 iterations. Hence, in what follows, we omit the discussion of ADAM optimizers.
The third row show the number of positive eigenvalues using the criterion mentioned before. We again see that among all three methods---BFGS, LBFGS, and trust region---the smaller loss function at the last step is associated with a larger number of positive eigenvalues.
We can interpret the eigenvalues associated with zero eigenvalues as "inactive directions", in the sense that given the gradient norm is small, perturbation in the direction of zero eigenvalues almost does not change the loss function values. In other words, the local minimum found by trust region methods has more active directions than BFGS and LBFGS. The active directions can also be viewed as "effective degrees of freedoms (DOFs)", and thus we conclude trust region methods find a local minimum with smaller loss function due to more effective DOFs.
The readers may wonder why different local minimums have different effective DOFs. To answer this question, we show the cumulative distribution of the maginitude of weights and biases in the following plot

The plot shows that BFGS and LBFGS outweight trust region methods in terms of large weights and biases (in terms of maginitudes). Because we use $\tanh$ as activation values, for fixed intermediate activation values, large weights and biases are more likely to cause saturation of activation values, i.e., the inputs to $\tanh$ is large or small and thus the outputs are close to 1. To illustrate the idea, consider a simple function
$$y = w_1 \tanh(w_2 x + b_2) + b_1$$
Given a reasonable $x$ (e.g., $x\approx 0.1$), if $|w_2|$ or $|b_2|$ is large, $y \approx b_1 \pm w_1$, and thus the effective DOF is 2; if $w_2$ and $b_2$ is close to 0, $y\approx w_1 w_2 x + w_1 b_2 + b_1$, perturbation of all four parameters $w_1$, $w_2$, $b_1$, $b_2$ may contribute to the change of $y$, and thus the effective DOF is 4. In sum, trust region methods yield weights and biases with smaller magnitudes compared to BFGS/LBFGS in general, and thus achieve more effective DOFs.
This conjecture is confirmed by the following plot, which shows the histogram of the intermediate activation values. We fixed the input $x = (0.5,0.5)$ (the midpoint of the computational domain), and collected all the outputs of the $\tanh$ function within the DNN. The figure shows that compared to the trust region method, the activation values of ADAM, BFGS and LBFGS are more concentrated near the extreme values $-1$ and $1$.

How can trust region methods manage the magnitudes of the weights and biases? The benefit is intrinsic to how the trust region method works: it only searches for "optimal solution" with a small neighborhood of the current state. However, BFGS and LBFGS searches for "optimal solution" along a direction aggressively. Given so many local minima, it is very likely that BFGS and LBFGS get trapped in a local minimum with smaller effective DOFs. In this perspective, trust region methods are useful methods for avoiding (instead of "escaping") bad local minima.
| ADAM | BFGS | LBFGS| Trust Region |
|---|---|---|---|
||  | | |
|132|34|41|38|
In the above plot, we show the eigenvalue distribution of the Hessian matrix for
$$l(\theta) = \sum_{i=1}^n (\kappa_\theta(x_i) - \kappa_i)^2$$
Here $\kappa_i$ is the true $\kappa$ value at location $x_i$ ($x_i$ is the Gauss quadrature point), and $\kappa_\theta(x_i)$ is the DNN estimate. We get rid of the PDE out of the loss function. The pattern of the eigenvalue distribution---a few positive eigenvalues accompanied by zero eigenvalues---still persists. The difference is that the number of positive eigenvalues are slightly larger than the loss function that couples DNNs and PDEs.This implies that PDEs restricts effective DOFs. We attribute the diminished effective DOFs to the physical constraints imposed by PDEs.
## Example: FEM for Static Poisson's Equation
Consider the Poisson's equation again. This time, the loss function is formulated as
$$L(\theta) = \sum_i (u_{obs}(x_i) - u_\theta(x_i))^2$$
Here $u_\theta$ is the numerical solution to the Poisson's equation. The evaluation of $\nabla^2_\theta L(\theta)$ requires back-propagating the Hessian matrix through various operators including the sparse solver (see [this post](https://kailaix.github.io/ADCME.jl/dev/second_order_pcl/#Example:-Developing-Second-Order-PCL-for-a-Sparse-Linear-Solver) for how the back-propagation rule is implemented).
The following shows an example of the implementation, which is annotated for convenience.
```julia
using AdFem
using PyPlot
using LinearAlgebra
using JLD2
# disable auth reordering so that the Hessian back-propagation works properly
ADCME.options.sparse.auto_reorder = false
using Random; Random.seed!(233)
sess = Session()
function simulate(θ)
# The first part is a standard piece of codes for doing numerical simulation in ADCME
global mmesh = Mesh(10,10,0.1)
x = gauss_nodes(mmesh)
Fsrc = eval_f_on_gauss_pts((x,y)->1.0, mmesh)
global kappa = squeeze(fc(x, [20,20,20,1], θ)) + 0.5
A_orig = compute_fem_laplace_matrix1(kappa, mmesh)
F = compute_fem_source_term1(Fsrc, mmesh)
global bdnode = bcnode(mmesh)
global A, F = impose_Dirichlet_boundary_conditions(A_orig, F, bdnode, zeros(length(bdnode)))
@load "Data/fwd_data.jld2" sol
SOL = sol
global sol = A\F
global loss = sum((sol-SOL)^2)
# We now calculate some extra tensors for use in Hessian back-propagation
# We use the TensorFlow tf.hessians (hessian in ADCME) to calculate the Hessian of DNNs. Note this algorithm is different from second order PCL
global H_dnn_pl, W_dnn_pl = pcl_hessian(kappa, θ, loss)
global dsol = gradients(loss, sol)
global dθ = gradients(loss, θ)
# We need the indices for sparse matrices in the Hessian back-propagation
init(sess)
global indices_orig = run(sess, A_orig.o.indices) .+ 1
global indices = run(sess, A.o.indices) .+ 1
end
function calculate_hessian(θ0)
# Retrieve intermediate values. Note in an optimized implementation, these values should already be available in the "tape". However, because second order PCL is currently in development, we recalculate these values for simplicity
A_vals, sol_vals, dsol_vals = run(sess, [A.o.values, sol, dsol], θ=>θ0)
# SoPCL for `loss = sum((sol-SOL)^2)`
W = pcl_square_sum(length(sol))
# SoPCL for `sol = A\F`
W = pcl_sparse_solve(indices,
A_vals,
sol_vals,
W,
dsol_vals)
# SoPCL for `A, F = impose_Dirichlet_boundary_conditions(...)`
J = pcl_impose_Dirichlet_boundary_conditions(indices_orig, bdnode, size(indices,1))
W = pcl_linear_op(J, W)
# SoPCL for `A_orig = compute_fem_laplace_matrix1(kappa, mmesh)`
J = pcl_compute_fem_laplace_matrix1(mmesh)
W = pcl_linear_op(J, W)
# SoPCL for DNN
run(sess, H_dnn_pl, feed_dict=Dict(W_dnn_pl=>W, θ=>θ0))
end
function calculate_gradient(θ0)
run(sess, dθ, θ=>θ0)
end
function calculate_loss(θ0)
L = run(sess, loss, θ=>θ0)
@info "Loss = $L"
L
end
# The optimization step
θ = placeholder(fc_init([2,20,20,20,1]))
simulate(θ)
res = opt.minimize(
calculate_loss,
θ0,
method = "trust-exact",
jac = calculate_gradient,
hess = calculate_hessian,
tol = 1e-12,
options = Dict(
"maxiter"=> 5000,
"gtol"=>0.0 # force the optimizer not to stop
)
)
```
It is very important that before we perform the optimization, we carry out the Hessian test using the [`test_hessian`](@ref) function.
```julia
function test_f(θ0)
calculate_gradient(θ0), calculate_hessian(θ0)
end
θ0 = run(sess, θ)
test_jacobian(test_f, θ0, scale=1e-3)
```
This should give us a plot as follows:

Now let us consider the inverse problem. First we generate the observation using
$$\kappa(x) = \frac{1}{1+\|x\|_2^2}+1$$
The observation is shown as below

We use the full field data for simplicity, although our method also applies to sparse observations. The following plots shows results where the trust region method performs significantly better than the BFGS and LBFGS method.
**Case 1**
| Description | Result |
|--------------|---|
| Loss |  |
| LBFGS |  |
| BFGS |  |
| Trust Region |  |
**Case 2**
| Description | Result |
|--------------|---|
| Loss |  |
| LBFGS |  |
| BFGS |  |
| Trust Region |  |
**Case 3**
| Description | Result |
|--------------|---|
| Loss |  |
| LBFGS |  |
| BFGS |  |
| Trust Region |  |
In the following plots, we show the absolute eigenvalue distributions of Hessians at the terminal point for Case 2. The red dashed line represents the level $10^{-6}\lambda_{\max}$, where $\lambda_{\max}$ is the maximum eigenvalue.
| LBFGS | BFGS | Trust Region|
|--------------|---|---|
||||
Eigenvalues that lie below the red dashed line can be treated as zero. This means that for BFGS and the trust region method, the optimizers find local minima. In fact, we show
$$F(\alpha) = L(x^* + \alpha v)$$
in the following plots, where $x^*$ is the converged point for LBFGS, $v$ is the eigenvector corresponding to either the minimum or maximum eigenvalues of the Hessian. The profile for the former case is quite flat, indicating that small perturbation along the eigenvector direction makes little change to the loss function. Thus, for LBFGS, we can also assume that a local minimum is found.
Interestingly, even though all optimizers find local minima. The final loss functions and errors are quite different. Trust methods perform much better in these cases compared to BFGS and LBFGS (in some other cases, BFGS may perform better).
| $\lambda_{\min}$ | $\lambda_{\max}$ |
|--------------|---|
|||
The problem itself is nonconvex and has many local minima---different from the common belief that in deep learning, stationary points are usually saddle points if they are not the global minimum. Trust region methods do not guarantee that we can find a global minimum, or even a "good" local minimum. However, because trust region methods shows faster convergence and superior accuracy in many cases, it never harms to add trust region methods into the optimization tool box. Additionally, the Hessian calculated using the second order PCL is a powerful weapon for diagnosing the convergence and provides curvature information for more sophisticated optimizers.
## Limitations
Despite many promising features of the trust region method, it is not without limitations, which we want to discuss here. The current trust-region method requires calculating the Hessian matrix. Firstly, computing the Hessian matrix can be technically difficult, especially when DNNs are coupled with a sophisticated numerical PDE solver. There are many existing techniques for computing the Hessian. The TensorFlow backend supports Hessian computation concurrently, but it requires users to implement rules for calculating "gradients of gradients". Additionally, TensorFlow uses reverse-mode automatic differentiation to evaluate the Hessian. This means that TensorFlow loops over each gradient component and calculating a row of Hessian at a time. This does not leverage the symmetry of Hessians and can be quite inefficient if the number of unknowns is large. Another approach, the edge pushing algorithm, uses one backward pass to evaluate the Hessian. This approach takes advantage of the symmetry of Hessians. However, the implementation can be quite convolved and computations can be expensive in some scenarios. We will cover this topic in more details in [another post](https://kailaix.github.io/ADCME.jl/dev/second_order_pcl/#Second-Order-Physics-Constrained-Learning).
## Conclusion
Trust-region methods are a class of global optimization techniques. They are less popular in the deep learning approach because the DNNs tend to be huge and the computation of Hessians is expensive. However, they are very suitable for many computational engineering problems, where DNNs are typically small, and convergence as well as accuracy is a critical concern. Our point of view is that although the Hessian computations are expensive, they are quite rewarding. Future researches will focus on efficient computation and automation of Hessian computations.
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 7068 | # Second Order Physics Constrained Learning
In this note, we describe the second order physics constrained learning (PCL) for efficient calculating Hessians using computational graphs. To begin with, let $x\in\mathbb{R}^d$ be the coordinates and consider a chain of operations
$$l(x) = F_n\circ F_{n-1}\circ \cdots \circ F_1(x) \tag{1}$$
Here $l$ is a scalar function, which means $F_n$ is a scalar function. It is not hard to see that we can express any computational graph with a scalar output using Eq. 1. For convenience, given a fixed $k\in\{1,2,\ldots, n\}$, we define $\Phi$, $F$ as follows
$$l(x) = \underbrace{F_n\circ F_{n-1}\circ \cdots \circ F_k}_{\Phi} \circ \underbrace{F_{k-1}\cdots \circ F_1}_{F}(x)$$
We omit $k$ in $\Phi$, $F$ for clarity.
## Calculating the Hessian in TensorFlow
TensorFlow provides [`tf.hessians`](https://www.tensorflow.org/api_docs/python/tf/hessians) to calculate hessian functions. ADCME exposes this function via [`hessians`](@ref). The idea is to first construct a computational graph for the gradients $\nabla_x l(x)$, then for **each component** of $\nabla_x l(x)$, $\nabla_{x_i} l(x)$, we construct a gradient back-propagation computational graph
$$\nabla_x \nabla_{x_i} l(x)$$
This gives us a row/column in the Hessian matrix. The following shows the main code from TensorFlow:
```python
_, hessian = control_flow_ops.while_loop(
lambda j, _: j < n,
lambda j, result: (j + 1,
result.write(j, gradients(gradient[j], x)[0])),
loop_vars
)
```
We see it's essentially a loop over each component in `gradient`
Albeit straight-forward, this approach suffers from three drawbacks:
1. The algorithm does not leverage the symmetry of the Hessian matrix. The Hessian structure can be exploited for efficient computations.
2. The algorithm can be quite expensive. Firstly, it requires a gradient back-propagation over each component of $\nabla_x l(x)$. Although TensorFlow can concurrently evaluates these Hessian rows/columns concurrently, the dimension of $x$ can be very large and therefore the computations cannot be fully parallelized. Secondly, each back-propagation of $\nabla_{x_i} l(x)$ requires both forward computation $l(x)$ and gradient back-propagation for $\nabla_{x} l(x)$, we need to carefully arrange the computations and storages so that these intermediate results can be reused. Otherwise, redundant computations lead to extra costs.
3. The most demanding requirements of the algorithm is that we need to implement---for every operator---the "gradients of gradients". Although simple for some operators (there are already existing implementations for some operators in TensorFlow!), this can be very hard for sophisticated operators, e.g., implicit operators.
## Second Order Physics Constrained Learning
Here we consider the second order physics constrained learning. The main idea is to apply the implicit function theorem to
$$l = \Phi(F(x)) \tag{2}$$
twice. First, we introduce some notation:
$$\Phi_k(y) = \frac{\partial \Phi(y)}{\partial y_k}, \quad \Phi_{kl}(y) = \frac{\partial^2 \Phi(y)}{\partial y_k \partial y_l}$$
$$F_{k,l}(x) = \frac{\partial F_k(x)}{\partial x_l}, \quad F_{k,lr}(x) = \frac{\partial^2 F_k(x)}{\partial x_l\partial x_r}$$
We take the derivative with respect to $x_i$ on both sides of Eq. 2, and get
$$\frac{\partial l}{\partial x_i} = \Phi_k F_{k,i} \tag{3}$$
We take the derivative with respect to $x_j$ on both sides of Eq. 3, and get
$$\frac{\partial^2 l}{\partial x_i\partial x_j} = \Phi_{kr} F_{k,i}F_{r,j} + \Phi_k F_{k, ij} \tag{4}$$
Here we have used the Einstein notation. Let $\bar\Phi = \nabla \Phi$ but we treat $x$ as a independent variable of $\bar\Phi$, then we can rewrite Eq. 4 to
$$\nabla_x^2 l = (\nabla_x F) \nabla^2_x\Phi (\nabla_x F)^T + \nabla_x^2 (\bar\Phi^T F)\tag{5}$$
Note the values of $\bar\Phi$ is already available in the gradient back-propagation.
## Algorithm
Based on Eq. 5, we have the following algorithm for calculating the Hessian
1. Initialize $H = 0$
2. for $k = n-1, n-2,\ldots, 1$
* Calculate $J = \nabla F_k$ and extract $\bar \Phi_{k+1}$ from the gradient back-propagation tape.
* Calculate $Z = \nabla^2 (\bar\Phi_{k+1}^T F_k)$
* $H \gets JHJ^T + Z$
This algorithm only requires one backward pass and constructs the Hessian iteratively. Additionally, we can leverage the symmetry of the Hessian when we do the calculations in the second step. This algorithm also doesn't require looping over each components of the gradient.
However, the challenge here is that we need to calculate $\nabla F_k$ and $Z = \nabla^2 (\bar\Phi_{k+1}^T F_k)$. Developing a complete support of such calculations for all operators can be a time-consuming task. But due to the benefit brought by the trust region method, we deem it to be a rewarding investment.
## Example: Developing Second Order PCL for a Sparse Linear Solver
Here we consider an application of second order PCL for a sparse solver. We focus on the operator that takes the sparse entries of a matrix $A\in\mathbb{R}^{n\times n}$ as input, and outputs $u$
$Au = f$
Let $A = [a_{ij}]$, and some of $a_{ij}$ are zero. According to 2nd order PCL, we need to calculate $\frac{\partial u_k}{\partial a_{ij}}$ and $\frac{\partial^2 (y^T u)}{\partial a_{ij} \partial a_{rs}}$.
We consider a multi-index $l$ and $r$. We take the gradient with respect to $a_l$ on both sides of
$$a_{i1}u_1 + a_{i2}u_2 + \ldots + a_{in}u_n = f_i$$
which leads to
$$a_{i1}^lu_1 + a_{i2}^lu_2 + \ldots + a_{in}^lu_n + a_{i1}u^l_1 + a_{i2}u^l_2 + \ldots + a_{in}u^l_n = 0\tag{6}$$
Here the superscript indicates the derivative.
Eq. 6 leads to
$$u^l = -A^{-1}A^l u \tag{7}$$
Note at most one entry in $A^l$ is nonzero, and therefore at most one entry in $A^l u$ is nonzero. Thus to calculate Eq. 7, we can calculate the inverse $A^{-1}$ first, and then $u^l$ can be obtained cheaply by taking a column from $A^{-1}$. The complexity will be $\mathcal{O}(n^3)$---the cost of inverting $A^{-1}$.
Now take the derivative with respect to $a_r$ on both sides of Eq. 6, we have
$$\begin{aligned}
a_{i1}^lu_1^r + a_{i2}^lu_2^r + \ldots + a_{in}^lu_n^r + \\ a_{i1}^ru^l_1 + a_{i2}^ru^l_2 + \ldots + a_{in}^ru^l_n +\\ a_{i1}u^{rl}_1 + a_{i2}u^{rl}_2 + \ldots + a_{in}u^{rl}_n = 0
\end{aligned}$$
which leads to
$$Au^{rl} = -A^l u^r - A^r u^l$$
Therefore,
$$(y^Tu)^{rl} = - y^TA^{-1}(A^l u^r + A^r u^l)$$
We can calculate $z^T = y^TA^{-1}$ first with a cost $\mathcal{O}(n^2)$. Because $u^r$, $u^l$ has already been calculated and $A^l$, $A^r$ has at most one nonzero entry, $A^l u^r + A^r u^l$ has at most two nonzero entries. The calculation $z^T(A^l u^r + A^r u^l)$ can be done in $\mathcal{O}(1)$ and therefore the total cost is $\mathcal{O}(d^2)$, where $d$ is the number of nonzero entries.
Upon obtaining $\frac{\partial u_k}{\partial a_{ij}}$ and $\frac{\partial^2 (y^T u)}{\partial a_{ij} \partial a_{rs}}$, we can apply the recursive the formula to "back-propagate" the Hessian matrix. | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 5423 | # Introducing ADCME Database and SQL Integration: an Efficient Approach to Simulation Data Management
## Introduction
If you have a massive number of simulations and results from different simulation parameters, to facilitate the data analysis and improve reproducibility, database and Structured Query Language (SQL) are convenient and powerful ways for data management.
Database allows simulation parameters and results to be stored in a permanent storage, and records can be inserted, queried, updated, and deleted as we proceed in our research. Specifically, databases are usually designed in a way that we can concurrently read and write in a transactional manner, which ensures that the reads are writes are done correctly even in the case of data conflicts. This characteristic is very useful for parallel simulations. Another important feature of databases is "indexing". By indexing tables, we can manipute tables in a more efficient way.

SQL is a standad language for accessing and manipulating databases. The four main operations in SQLs are: create, insert, update, and delete. More advanced commands include `where`, `groupby`, `join`, etc. In ADCME, we implemented an interface to SQLite, a relational database management system contained in a C library. SQLite provides basic SQL engines, which is compliant to the SQL standard. One particular feature of SQLite is that the database is a single file or in-memory. This simplifies the client and server SQL logic, but bears the limitation of scalability. Nevertheless, SQLite is more than sufficient to store and manipulate our simulation parameters and results (typically a link to the data folder).
The introduction primarily focuses on some commonly used features of database management in ADCME.
## Database Structure
In ADCME, a database is created using [`Database`](@ref). There are two types of database:
```julia
db1 = Database() # in-memory
db2 = Database("simulation.db") # file
```
If you created a file-based database, whenever you finished operation, you need to [`commit`](@ref) to the database or [`close`](@ref) the database to make the changes effective.
```julia
commit(db2)
close(db2)
```
To execute a SQL command in the database, we can use [`execute`](@ref) command. In the next section, we list some commonly used operations. By default, `commit` is called after `execute`. Users can disable this by using
```julia
db1 = Database(commit_after_execute=false) # in-memory
db2 = Database("simulation.db", commit_after_execute=false) # file
```
## Commonly Used Operations
### Create a Database
```julia
execute(db2, """
CREATE TABLE simulation_parameters (
name real primary key,
dt real,
h real,
result text
)
""")
```
### Insert an Record
```julia
execute(db2, """
INSERT INTO simulation_parameters VALUES
("sim1", 0.1, 0.01, "file1.png")
""")
```
### Insert Many Records
```julia
params = [
("sim2", 0.3, "file2.png"),
("sim3", 0.5, "file3.png"),
("sim4", 0.9, "file4.png")
]
execute(db2, """
INSERT INTO simulation_parameters VALUES
(?, ?, 0.01, ?)
""", params)
```
### Look Up Records
```julia
c = execute(db2, """
SELECT * from simulation_parameters
""")
collect(c)
```
Expected output:
```
("sim1", 0.1, 0.01, "file1.png")
("sim2", 0.3, 0.01, "file2.png")
("sim3", 0.5, 0.01, "file3.png")
("sim4", 0.9, 0.01, "file4.png")
```
### Delete a Record
```julia
execute(db2, """
DELETE from simulation_parameters WHERE name LIKE "%3"
""")
```
Now the records are
```
("sim1", 0.1, 0.01, "file1.png")
("sim2", 0.3, 0.01, "file2.png")
("sim4", 0.9, 0.01, "file4.png")
```
### Update a Record
```julia
execute(db2, """
UPDATE simulation_parameters
SET h = 0.2
WHERE name = "sim4"
""")
```
Now the records are
```
("sim1", 0.1, 0.01, "file1.png")
("sim2", 0.3, 0.01, "file2.png")
("sim4", 0.9, 0.2, "file4.png")
```
### Insert a Conflict Record
Becase we set `name` as primary key, we cannot insert a record with the same name
```julia
execute(db2, """
INSERT INTO simulation_parameters VALUES
("sim1", 0.1, 0.1, "file1_2.png")
""")
```
We have an error
```
IntegrityError('UNIQUE constraint failed: simulation_parameters.name')
```
Alternatively, we can do
```julia
execute(db2, """
INSERT OR IGNORE INTO simulation_parameters VALUES
("sim1", 0.1, 0.1, "file1_2.png")
""")
```
### Querying Meta Data
- Get all tables in the database
```julia
keys(db2)
```
Output:
```
"simulation_parameters"
"sqlite_autoindex_simulation_parameters_1"
```
We can see a table that SQLites adds indexes to some fields: `sqlite_autoindex_simulation_parameters_1`.
- Get column names in the database
```julia
keys(db2, "simulation_parameters")
```
Output:
```
"name"
"dt"
"h"
"result"
```
### Drop a Table
```julia
execute(db2, """
DROP TABLE simulation_parameters
""")
```
## Next Steps
We introduced some basic usage of ADCME database and SQL integration for simulation data management. We used one common and lightweight database management system, SQLite, for managing data of moderate sizes. Due to SQL's wide adoption, it is possible to scale the data management system by adopting a full-fledged database, such as MySQL. In this case, developers can overload ADCME functions such as `execute`, `commit`, `close`, `keys`, etc., so that the top level codes requires little changes. | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 4091 | # Built-in Toolchain for Third-party Libraries
Using third-party libraries, especially binaries with operation system and runtime dependencies, is troublesome and painful. ADCME has a built-in set of tools for downloading, uncompressing, and compiling third-party libraries. Therefore, we can compile external libraries from source and ensure that the products are compatible within the ADCME ecosystem.
The toolchain uses the same set of C/C++ compilers that were used to compile the tensorflow dynamic library. Additionally, the toolchain provide essential building tools such as `cmake` and `ninja`. This section will be a short introduction to the toolchain.
The best way to introduce the toolchain is through an example. Let us consider compiling a C++ library for use in ADCME. The library [LibHelloWorld](https://github.com/kailaix/LibHelloWorld) is hosted on GitHub and the repository contains a `CMakeLists.txt` and `HelloWorld.cpp`. Our goal is to download the repository into ADCME private workspace (`ADCME.PREFIXDIR`) and compile the library to the library path (`ADCME.LIBDIR`). The following code will do the job:
```julia
using ADCME
PWD = pwd()
change_directory(ADCME.PREFIXDIR)
git_repository("https://github.com/kailaix/LibHelloWorld", "LibHelloWorld")
change_directory("LibHelloWorld")
make_directory("build")
change_directory("build")
lib = get_library("hello_world")
require_file(lib) do
ADCME.cmake()
ADCME.make()
end
_, libname = splitdir(lib)
mv(lib, joinpath(ADCME.LIBDIR, libname), force=true)
change_directory(PWD)
```
Here [`change_directory`](@ref), [`git_repository`](@ref), and others are ADCME toolchain functions. Note we have used `ADCME.cmake()` and `ADCME.make()` to ensure that the codes are compiled with a compatible compiler. The toolchain will cache all the intermediate files and therefore will not recompile as long as the files exist. To force recompiling, users need to delete the local repository, i.e., `LibHelloWorld` in `ADCME.PREFIXDIR`. The following is an exemplary output of the program:
```bash
[ Info: Changed to directory /home/darve/kailaix/.julia/adcme/lib/Libraries
[ Info: Cloning from https://github.com/kailaix/LibHelloWorld to LibHelloWorld...
[ Info: Cloned https://github.com/kailaix/LibHelloWorld to LibHelloWorld
[ Info: Changed to directory LibHelloWorld
[ Info: Made directory directory
[ Info: Changed to directory build
-- The C compiler identification is GNU 5.4.0
-- The CXX compiler identification is GNU 5.4.0
-- Detecting C compiler ABI info
-- Detecting C compiler ABI info - done
-- Check for working C compiler: /home/darve/kailaix/.julia/adcme/bin/x86_64-conda_cos6-linux-gnu-gcc - skipped
-- Detecting C compile features
-- Detecting C compile features - done
-- Detecting CXX compiler ABI info
-- Detecting CXX compiler ABI info - done
-- Check for working CXX compiler: /home/darve/kailaix/.julia/adcme/bin/x86_64-conda_cos6-linux-gnu-g++ - skipped
-- Detecting CXX compile features
-- Detecting CXX compile features - done
JULIA=/home/darve/kailaix/julia-1.3.1/bin/julia
...
Python path=/home/darve/kailaix/.julia/adcme/bin/python
PREFIXDIR=/home/darve/kailaix/.julia/adcme/lib/Libraries
TF_INC=/home/darve/kailaix/.julia/adcme/lib/python3.7/site-packages/tensorflow_core/include
TF_ABI=1
TF_LIB_FILE=/home/darve/kailaix/.julia/adcme/lib/python3.7/site-packages/tensorflow_core/libtensorflow_framework.so.1
-- Configuring done
-- Generating done
-- Build files have been written to: /home/darve/kailaix/.julia/adcme/lib/Libraries/LibHelloWorld/build
[2/2] Linking CXX shared library libhello_world.so
[ Info: Changed to directory /home/darve/kailaix/project/MPI_Project/LibHelloWorld
```
To use the compiled library, we can write
```julia
using ADCME
libdir = joinpath(ADCME.LIBDIR, "libhello_world.so")
@eval ccall((:helloworld, $libdir), Cvoid, ())
```
Then we get the expected output:
```bash
Hello World!
```
The design idea for ADCME toolchains is that users can write an install script. Then ADCME will guarantee that the runtime and compilation eco-system are compatible. | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 2999 | # Topological Optimization
In this section, we present the ADCME implementation of a structural topology optimization problem. The optimization problem can be mathematically described as
$$\begin{aligned}\min_x &\; l(x, u) \\ \text{s.t.} &\; V(x) = fV_0(x) \\ &\; F(x, u) = 0 \\ &\; 0<x_{\min} < x \leq 1 \end{aligned}$$
Here $x$ is a design variable, such as density in each element. $u$ is the state variable, such as the displacement vector. $F(x, u) = 0$ is the governing equation. $V(x)$ is the total volumn and $f$ is the prescribed volumn fraction. $x_{\min}$ is the lower bound for the design variable.
Specifically, we consider a static linear elasticity load problem, where the governing equation is discretized to a linear system
$$K(x) U - F = 0$$
Here $U$ is the discretized solution for $u$, $F$ is the load vector, $K(x)$ is the stiffness matrix. The discretized loss function $L$ is the strain energy, which has the form
$$L(x, U) = U^T K(x) U = F^T K(x)^{-1} F$$
The original optimization problem becomes a constrained optimization problem. The following code is used for forward computation
```julia
using AdFem
m = 32
n = 20
h = 1.0
fracvol = 0.4
p = 3.0
x = Variable(fracvol*ones(m*n))
ρ = reshape(repeat(x^p, 1, 4), (-1,1))
ke = compute_plane_stress_matrix(1.0,0.3)
ρ = reshape(ρ * reshape(ke, 1, 9), (-1,3,3))
K = compute_fem_stiffness_matrix(ρ, m, n, h)
bdedge = bcedge("right", m, n, h)
t1 = zeros(size(bdedge,1))
t2 = zeros(size(bdedge, 1))
t2[end] = 0.0001
F = compute_fem_traction_term([t1 t2],bdedge, m, n, h)
bdnode = bcnode("left", m, n, h)
K_, F_ = impose_Dirichlet_boundary_conditions(K, F, [bdnode; bdnode .+ (m+1)*(n+1)], zeros(2length(bdnode)))
sol = K_\F_
```
Here shows the initial guess for $x$:
```julia
using PyPlot
sess = Session(); init(sess)
SOL = run(sess, sol)
visualize_displacement(reshape(SOL, 1, :), m, n, h)
savefig("init_opt.png")
```
We will use the Ipopt optimizer to solve the constraint optimization problem. The following code
```julia
import Ipopt
loss = sum(sol'*K*sol)
function eval_g(x, g)
g[1] = sum(x) - fracvol*m*n
end
function eval_jac_g(x, mode, rows, cols, values)
if mode == :Structure
for i = 1:length(x)
rows[i] = 1; cols[i] = i
end
else
for i = 1:length(x)
values[i] = 1.0
end
end
end
function opt(f, g, fg, x0, kwargs...)
prob = Ipopt.createProblem(m*n, 1e-6*ones(m*n), ones(m*n), 1, zeros(1), zeros(1), m*n, 0,
f, eval_g, (x,G)->g(G, x), eval_jac_g, nothing)
prob.x = x0
Ipopt.addOption(prob, "hessian_approximation", "limited-memory")
status = Ipopt.solveProblem(prob)
println(Ipopt.ApplicationReturnStatus[status])
Ipopt.freeProblem(prob)
nothing
end
sess = Session(); init(sess)
losses = Optimize!(sess, loss, optimizer = opt)
visualize_scalar_on_fvm_points(run(sess, x).^p, m, n, h, vmin = 0, vmax = 1)
```
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 9474 |
# ADCME Basics: Tensor, Type, Operator, Session & Kernel
## Tensors and Operators
`Tensor` is a data structure for storing structured data, such as a scalar, a vector, a matrix or a high dimensional tensor. The name of the ADCME backend, `TensorFlow`, is also derived from its core framework, `Tensor`. Tensors can be viewed as symbolic versions of Julia's `Array`.
A tensor is a collection of $n$-dimensional arrays. ADCME represents tensors using a `PyObject` handle to the TensorFlow `Tensor` data structure. A tensor has three important properties
- `name`: Each Tensor admits a unique name.
- `shape`: For scalars, the shape is always an empty tuple `()`; for $n$-dimensional vectors, the shape is `(n,)`; for matrices or higher order tensors, the shape has the form `(n1, n2, ...)`
- `dtype`: The type of the tensors. There is a one-to-one correspondence between most TensorFlow types and Julia types (e.g., `Int64`, `Int32`, `Float64`, `Float32`, `String`, and `Bool`). Therefore, we have overloaded the type name so users have a unified interface.

An important difference is that `tensor` object stores data in the row-major while Julia's default for `Array` is column major. The difference may affect performance if not carefully dealt with, but more often than not, the difference is not relevant if you do not convert data between Julia and Python often. Here is a representation of ADCME `tensor`
There are 4 ways to create tensors.
- [`constant`](@ref). As the name suggests, `constant` creates an immutable tensor from Julia Arrays.
```julia
constant(1.0)
constant(rand(10))
constant(rand(10,10))
```
- [`Variable`](@ref). In contrast to `constant`, `Variable` creates tensors that are mutable. The mutability allows us to update the tensor values, e.g., in an optimization procedure. It is very important to understand the difference between `constant` and `Variable`: simply put, in inverse modeling, tensors that are defined as `Variable` should be the quantity you want to invert, while `constant` is a way to provide known data.
```julia
Variable(1.0)
Variable(rand(10))
Variable(rand(10,10))
```
- [`placeholder`](@ref). `placeholder` is a convenient way to specify a tensor whose values are to be provided in the runtime. One use case is that you want to try out different values for this tensor and scrutinize the simulation result.
```julia
placeholder(Float64, shape=[10,10])
placeholder(rand(10)) # default value is `rand(10)`
```
- [`SparseTensor`](@ref). `SparseTensor` is a special data structure to store a sparse matrix. Although it is not very emphasized in machine learning, sparse linear algebra is one of the cores to scientific computing. Thus possessing a strong sparse linear algebra support is the key to success inverse modeling with physics based machine learning.
```julia
using SparseArrays
SparseTensor(sprand(10,10,0.3))
SparseTensor([1,2,3],[2,2,2],[0.1,0.3,0.5],3,3) # specify row, col, value, number of rows, number of columns
```
Now we know how to create tensors, the next step is to perform mathematical operations on those tensors.
`Operator` can be viewed as a function that takes multiple tensors and outputs multiple tensors. In the computational graph, operators are represented by nodes while tensors are represented by edges. Most mathematical operators, such as `+`, `-`, `*` and `/`, and matrix operators, such as matrix-matrix multiplication, indexing and linear system solve, also work on tensors.
```julia
a = constant(rand(10,10))
b = constant(rand(10))
a + 1.0 # add 1 to every entry in `a`
a * b # matrix vector production
a * a # matrix matrix production
a .* a # element wise production
inv(a) # matrix inversion
```
## Session
With the aforementioned syntax to create and transform tensors, we have created a computational graph. However, at this point, all the operations are symbolic, i.e., the operators have not been executed yet.
To trigger the actual computing, the TensorFlow mechanism is to create a session, which drives the graph based optimization (like detecting dependencies) and executes all the operations.
```julia
a = constant(rand(10,10))
b = constant(rand(10))
c = a * b
sess = Session()
run(sess, c) # syntax for triggering the execution of the graph
```
If your computational graph contains `Variables`, which can be listed via [`get_collection`](@ref), then you must initialize your graph before any `run` command, in which the Variables are populated with initial values
```julia
init(sess)
```
## Kernel
The kernels provide the low level C++ implementation for the operators. ADCME augments users with missing features in TensorFlow that are crucial for scientific computing and tailors the syntax for numerical schemes. Those kernels, depending on their implementation, can be used in CPU, GPU, TPU or heterogenious computing environments.
All the intensive computations are done either in Julia or C++, and therefore we can achieve very high performance if the logic is done appropriately. For performance critical part, users may resort to custom kernels using [`customop`](@ref), which allows you to incooperate custom designed C++ codes.

## Summary
ADCME performances operations on tensors. The actual computations are pushed back to low level C++ kernels via operators. A session is need to drive the executation of the computation. It will be easier for you to analyze computational cost and optimize your codes with this computation model in mind.
## Tensor Operations
Here we show a list of commonly used operators in ADCME.
| Description | API |
| --------------------------------- | ------------------------------------------------ |
| Constant creation | `constant(rand(10))` |
| Variable creation | `Variable(rand(10))` |
| Get size | `size(x)` |
| Get size of dimension | `size(x,i)` |
| Get length | `length(x)` |
| Resize | `reshape(x,5,3)` |
| Vector indexing | `v[1:3]`,`v[[1;3;4]]`,`v[3:end]`,`v[:]` |
| Matrix indexing | `m[3,:]`, `m[:,3]`, `m[1,3]`,`m[[1;2;5],[2;3]]` |
| 3D Tensor indexing | `m[1,:,:]`, `m[[1;2;3],:,3]`, `m[1:3:end, 1, 4]` |
| Index relative to end | `v[end]`, `m[1,end]` |
| Extract row (most efficient) | `m[2]`, `m[2,:]` |
| Extract column | `m[:,3]` |
| Convert to dense diagonal matrix | `diagm(v)` |
| Convert to sparse diagonal matrix | `spdiag(v)` |
| Extract diagonals as vector | `diag(m)` |
| Elementwise multiplication | `a.*b` |
| Matrix (vector) multiplication | `a*b` |
| Matrix transpose | `m'` |
| Dot product | `sum(a*b)` |
| Solve | `A\b` |
| Inversion | `inv(m)` |
| Average all elements | `mean(x)` |
| Average along dimension | `mean(x, dims=1)` |
| Maximum/Minimum of all elements | `maximum(x)`, `minimum(x)` |
| Squeeze all single dimensions | `squeeze(x)` |
| Squeeze along dimension | `squeeze(x, dims=1)`, `squeeze(x, dims=[1;2])` |
| Reduction (along dimension) | `norm(a)`, `sum(a, dims=1)` |
| Elementwise Multiplication | `a.*b` |
| Elementwise Power | `a^2` |
| SVD | `svd(a)` |
| `A[indices] = updates` | `A = scatter_update(A, indices, updates)` |
| `A[indices] += updates` | `A = scatter_add(A, indices, updates)` |
| `A[indices] -= updates` | `A = scatter_sub(A, indices, updates)` |
| `A[idx, idy] = updates` | `A = scatter_update(A, idx, idy, updates)` |
| `A[idx, idy] += updates` | `A = scatter_add(A, idx, idy, updates)` |
| `A[idx, idy] -= updates` | `A = scatter_sub(A, idx, idy, updates)` |
!!! tip
In some cases you might find some features missing in ADCME but present in TensorFlow. You can always use `tf.<function_name>`. It's compatible. | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 23584 | # Advanced: Custom Operators
!!! note
As a reminder, there are many built-in custom operators in `deps/CustomOps` and they are good resources for understanding custom operators. The following is a step-by-step instruction on how custom operators are implemented.
## The Need for Custom Operators
Custom operators are ways to add missing features or improve performance critical components in ADCME. Typically users do not have to worry about custom operators. However, in the following situation custom opreators might be very useful
- Direct implementation in ADCME is inefficient, e.g., vectorizing some codes is difficult.
- There are legacy codes users want to reuse, such as Fortran libraries or adjoint-state method solvers.
- Special acceleration techniques, such as checkpointing scheme, MPI-enabled linear solvers, and FPGA/GPU-accelerated codes.
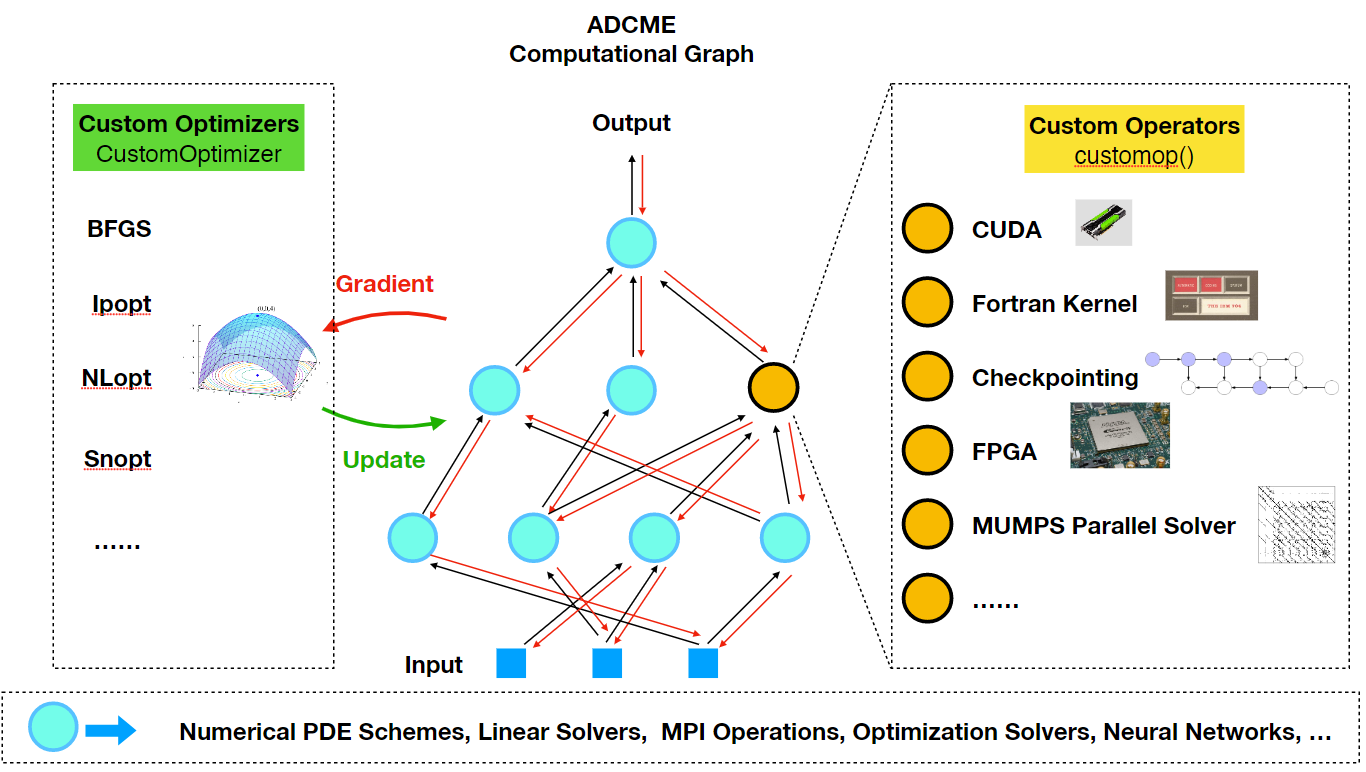
## The Philosophy of Implementing Custom Operators
Usually the motivation for implementing custom operators is to enable gradient backpropagation for some performance critical operators. However, not all performance critical operators participate the automatic differentiation. Using terminologies from programming, these computations are "constant expressions", which can be evaluated at compilation time (constant folding). Therefore, before we devote ourselves to implementating custom operators, we need to identify which operators need to be implemented as custom operators.
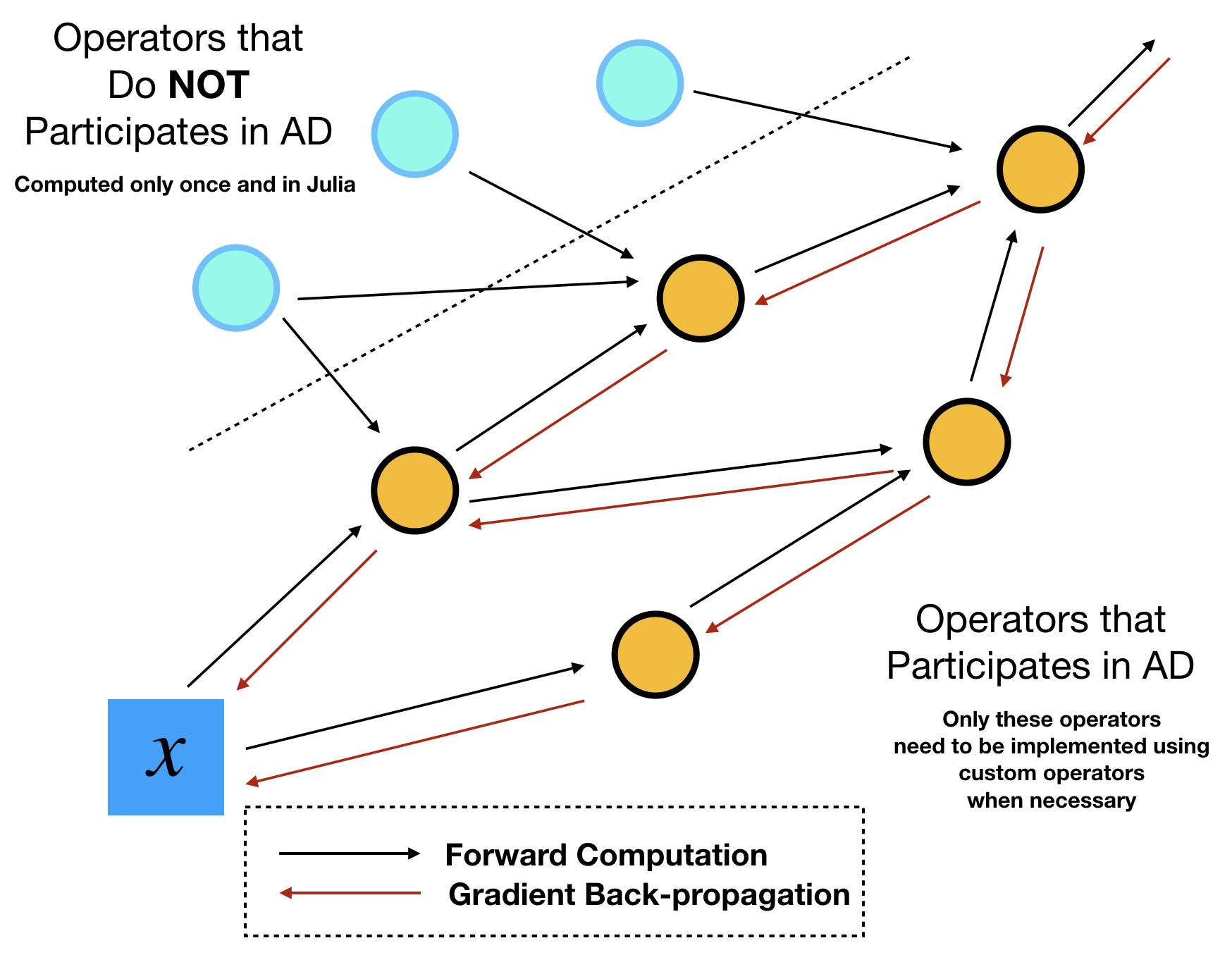
This identification task can be done by sketching out the computational graph of your program. Assume your optimization outer loops update $x$ repeatly, then we can track all downstream the operators that depend on this parameter $x$. We call the dependent operators "tensor operations", because they are essentially TensorFlow operators that consume and output tensors. The dependent variables are called "tensors". The counterpart of tensors and tensor operations are "numerical arrays" and "numerical operations", respectively. The names seem a bit vague here but the essence is that numerical operations/arrays do no participate automatic differentiation during the optimization, so the values can be precomputed only once during the entire optimization process.
In ADCME, we can precompute all numerical quantities of numerical arrays using Julia. No TensorFlow operators or custom operators are needed. This procedure combines the best of the two worlds: the simple syntax and high performance computing environment provided by Julia, and the efficient AD capability provided by TensorFlow. The high performance computing for precomputing cannot be provided by Python, the main scripting language that TensorFlow or PyTorch supports. Readers migh suspect that such precomputing may not be significant in many tasks. Actually, the precomputing constitutes a large portion in scientific computing. For example, researchers assemble matrices, prepare geometries and construct preconditioners in a finite element program. These tasks are by no means trivial and cheap. The consideration for performance in scientific computing actually forms the major motivation behind adopting Julia for the major language for ADCME.
## Build Custom Operators
In the following, we present an example of implementing a sparse solver for $Au=b$ as a custom operator.
**Input**: row vector `ii`, column vector`jj` and value vector `vv` for the sparse coefficient matrix $A$; row vector `kk` and value vector `ff` for the right hand side $b$; the coefficient matrix dimension is $d\times d$
**Output**: solution vector $u\in \mathbb{R}^d$
**Step 1: Create and modify the template file**
The following command helps create the wrapper
```julia
customop()
```
There will be a `custom_op.txt` in the current directory. Modify the template file
```txt
MySparseSolver
int32 ii(?)
int32 jj(?)
double vv(?)
int32 kk(?)
double ff(?)
int32 d()
double u(?) -> output
```
The first line is the name of the operator. It should always be in the camel case.
The 2nd to the 7th lines specify the input arguments, the signature is `type`+`variable name`+`shape`. For the shape, `()` corresponds to a scalar, `(?)` to a vector and `(?,?)` to a matrix. The variable names must be in *lower cases*. Additionally, the supported types are: `int32`, `int64`, `float`, `double`, `bool` and `string`.
The last line is the output, denoted by ` -> output` (do not forget the whitespace before and after `->`).
!!! note
If there are non-real type outputs, the corresponding top gradients input to the gradient kernel should be removed.
**Step 2: Implement the kernels**
Run `customop()` again and there will be `CMakeLists.txt`, `gradtest.jl`, `MySparseSolver.cpp` appearing in the current directory. `MySparseSolver.cpp` is the main wrapper for the codes and `gradtest.jl` is used for testing the operator and its gradients. `CMakeLists.txt` is the file for compilation. In the gradient back-propagation (`backward` below), we want to back-propagate the gradients from the output to the inputs, and the associated rule can be derived using adjoint-state methods.
Create a new file `MySparseSolver.h` and implement both the forward simulation and backward simulation (gradients)
```cpp
#include <eigen3/Eigen/Sparse>
#include <eigen3/Eigen/SparseLU>
#include <vector>
#include <iostream>
using namespace std;
typedef Eigen::SparseMatrix<double> SpMat; // declares a column-major sparse matrix type of double
typedef Eigen::Triplet<double> T;
SpMat A;
void forward(double *u, const int *ii, const int *jj, const double *vv, int nv, const int *kk, const double *ff,int nf, int d){
vector<T> triplets;
Eigen::VectorXd rhs(d); rhs.setZero();
for(int i=0;i<nv;i++){
triplets.push_back(T(ii[i]-1,jj[i]-1,vv[i]));
}
for(int i=0;i<nf;i++){
rhs[kk[i]-1] += ff[i];
}
A.resize(d, d);
A.setFromTriplets(triplets.begin(), triplets.end());
auto C = Eigen::MatrixXd(A);
Eigen::SparseLU<SpMat> solver;
solver.analyzePattern(A);
solver.factorize(A);
auto x = solver.solve(rhs);
for(int i=0;i<d;i++) u[i] = x[i];
}
void backward(double *grad_vv, const double *grad_u, const int *ii, const int *jj, const double *u, int nv, int d){
Eigen::VectorXd g(d);
for(int i=0;i<d;i++) g[i] = grad_u[i];
auto B = A.transpose();
Eigen::SparseLU<SpMat> solver;
solver.analyzePattern(B);
solver.factorize(B);
auto x = solver.solve(g);
// cout << x << endl;
for(int i=0;i<nv;i++) grad_vv[i] = 0.0;
for(int i=0;i<nv;i++){
grad_vv[i] -= x[ii[i]-1]*u[jj[i]-1];
}
}
```
!!! note
In this implementation we have used `Eigen` library for solving sparse matrix. Other choices are also possible, such as algebraic multigrid methods. Note here for convenience we have created a global variable `SpMat A;`. This is not recommend if you want to run the code concurrently, since the variable `A` must be overwritten by another concurrent thread.
**Step 3: Compile**
You should always compile your custom operator using the [built-in toolchain](https://kailaix.github.io/ADCME.jl/dev/toolchain/) `ADCME.make` and `ADCME.cmake` to ensure compatibility such as ABIs. The built-in toolchain uses exactly the same compiler that has been used to compile your tensorflow shared library. For example, some of the toolchain variables are:
| Variable | Description |
| ------------- | ------------------------------------- |
| `ADCME.CXX` | C++ Compiler |
| `ADCME.CC` | C Compiler |
| `ADCME.TF_LIB_FILE` | `libtensorflow_framework.so` location |
| `ADCME.CMAKE` | Cmake binary location |
| `ADCME.MAKE` | Make (Ninja for Unix systems) binary location |
ADCME will properly handle the environment variable for you. So we always recommend you to compile custom operators using ADCME functions:
First `cd` into your custom operator director (where `CMakeLists.txt` is located), create a directory `build` if it doesn't exist, `cd` into `build`, and do
```julia-repl
julia> using ADCME
julia> ADCME.cmake()
julia> ADCME.make()
```
Based on your operation system, you will create `libMySparseSolver.{so,dylib,dll}`. This will be the dynamic library to link in `TensorFlow`.
**Step 4: Test**
Finally, you could use `gradtest.jl` to test the operator and its gradients (specify appropriate data in `gradtest.jl` first). If you implement the gradients correctly, you will be able to obtain first order convergence for finite difference and second order convergence for automatic differentiation. Note you need to modify this file first, e.g., creating data and modifying the function `scalar_function`.
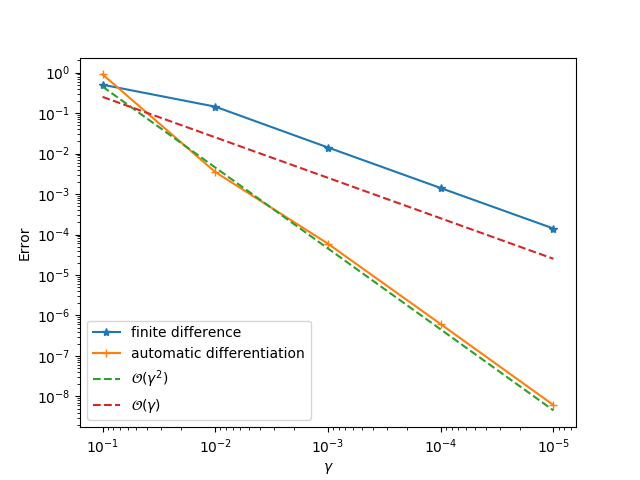
!!! info
If the process fails, it is most probable the GCC compiler is not compatible with which was used to compile `libtensorflow_framework.{so,dylib}`. ADCME downloads a GCC compiler via Conda for you. However, if you follow the above steps but encounter some problems, we are happy to resolve the compatibility issue and improve the robustness of ADCME. Submitting an issue is welcome.
Please see [this repository](https://github.com/kailaix/ADCME-CustomOp-Example) for an extra example.
## Build GPU Custom Operators
### Install GPU-enabled TensorFlow (Linux and Windows)
To use CUDA in ADCME, we need to install a GPU-enabled version of TensorFlow. In ADCME, this is achieved by simply rebuilding ADCME with `GPU` environment variabe.
```julia
using Pkg
ENV["GPU"] = 1
Pkg.build("ADCME")
```
This will install all GPU dependencies.
### Building a GPU custom operator
We consider a toy example where the custom operator is a function $f: x\rightarrow 2x$. To begin with, we create a `custom_op.txt` via [`customop`](@ref)
```text
GpuTest
double a(?)
double b(?) -> output
```
Next, by running `customop()` again several template files are generated. We can then do the implementation in those files
**GpuTest.cpp**
```c++
#include "tensorflow/core/framework/op_kernel.h"
#include "tensorflow/core/framework/tensor_shape.h"
#include "tensorflow/core/platform/default/logging.h"
#include "tensorflow/core/framework/shape_inference.h"
#include<cmath>
// Signatures for GPU kernels here
void return_double(int n, double *b, const double*a);
using namespace tensorflow;
REGISTER_OP("GpuTest")
.Input("a : double")
.Output("b : double")
.SetShapeFn([](::tensorflow::shape_inference::InferenceContext* c) {
shape_inference::ShapeHandle a_shape;
TF_RETURN_IF_ERROR(c->WithRank(c->input(0), 1, &a_shape));
c->set_output(0, c->input(0));
return Status::OK();
});
REGISTER_OP("GpuTestGrad")
.Input("grad_b : double")
.Input("b : double")
.Input("a : double")
.Output("grad_a : double");
class GpuTestOpGPU : public OpKernel {
private:
public:
explicit GpuTestOpGPU(OpKernelConstruction* context) : OpKernel(context) {
}
void Compute(OpKernelContext* context) override {
DCHECK_EQ(1, context->num_inputs());
const Tensor& a = context->input(0);
const TensorShape& a_shape = a.shape();
DCHECK_EQ(a_shape.dims(), 1);
// extra check
// create output shape
int n = a_shape.dim_size(0);
TensorShape b_shape({n});
// create output tensor
Tensor* b = NULL;
OP_REQUIRES_OK(context, context->allocate_output(0, b_shape, &b));
// get the corresponding Eigen tensors for data access
auto a_tensor = a.flat<double>().data();
auto b_tensor = b->flat<double>().data();
// implement your forward function here
// TODO:
return_double(n, b_tensor, a_tensor);
}
};
REGISTER_KERNEL_BUILDER(Name("GpuTest").Device(DEVICE_GPU), GpuTestOpGPU);
```
**GpuTest.cu**
```c++
#include "cuda.h"
__global__ void return_double_(int n, double *b, const double*a){
int i = blockIdx.x * blockDim.x + threadIdx.x;
if (i<n) b[i] = 2*a[i];
}
void return_double(int n, double *b, const double*a){
return_double_<<<(n+255)/256, 256>>>(n, b, a);
}
```
**CMakeLists.txt**
```cmake
cmake_minimum_required(VERSION 3.5)
project(TF_CUSTOM_OP)
set (CMAKE_CXX_STANDARD 11)
message("JULIA=${JULIA}")
execute_process(COMMAND ${JULIA} -e "import ADCME; print(ADCME.__STR__)" OUTPUT_VARIABLE JL_OUT)
list(GET JL_OUT 0 BINDIR)
list(GET JL_OUT 1 LIBDIR)
list(GET JL_OUT 2 TF_INC)
list(GET JL_OUT 3 TF_ABI)
list(GET JL_OUT 4 PREFIXDIR)
list(GET JL_OUT 5 CC)
list(GET JL_OUT 6 CXX)
list(GET JL_OUT 7 CMAKE)
list(GET JL_OUT 8 MAKE)
list(GET JL_OUT 9 GIT)
list(GET JL_OUT 10 PYTHON)
list(GET JL_OUT 11 TF_LIB_FILE)
list(GET JL_OUT 12 LIBCUDA)
list(GET JL_OUT 13 CUDA_INC)
message("Python path=${PYTHON}")
message("PREFIXDIR=${PREFIXDIR}")
message("TF_INC=${TF_INC}")
message("TF_ABI=${TF_ABI}")
message("TF_LIB_FILE=${TF_LIB_FILE}")
if (CMAKE_CXX_COMPILER_VERSION VERSION_GREATER 5.0 OR CMAKE_CXX_COMPILER_VERSION VERSION_EQUAL 5.0)
set(CMAKE_CXX_FLAGS "-D_GLIBCXX_USE_CXX11_ABI=${TF_ABI} ${CMAKE_CXX_FLAGS}")
endif()
set(CMAKE_BUILD_TYPE Release)
if(MSVC)
set(CMAKE_CXX_FLAGS_RELEASE "-DNDEBUG")
else()
set(CMAKE_CXX_FLAGS_RELEASE "-O3 -DNDEBUG")
endif()
include_directories(${TF_INC} ${PREFIXDIR} ${CUDA_INC})
find_package(CUDA QUIET REQUIRED)
set(CMAKE_CXX_FLAGS "-std=c++11 ${CMAKE_CXX_FLAGS}")
set(CMAKE_CXX_FLAGS "-O3 ${CMAKE_CXX_FLAGS}")
set(CMAKE_CXX_FLAGS "-shared ${CMAKE_CXX_FLAGS}")
set(CMAKE_CXX_FLAGS "-fPIC ${CMAKE_CXX_FLAGS}")
set(CUDA_NVCC_FLAGS ${CUDA_NVCC_FLAGS};--expt-relaxed-constexpr)
SET(CUDA_PROPAGATE_HOST_FLAGS ON)
add_definitions(-DGOOGLE_CUDA)
message("Compiling GPU-compatible custom operator!")
cuda_add_library(GpuTest SHARED GpuTest.cpp GpuTest.cu)
set_property(TARGET GpuTest PROPERTY POSITION_INDEPENDENT_CODE ON)
target_link_libraries(GpuTest ${TF_LIB_FILE})
file(MAKE_DIRECTORY ${CMAKE_CURRENT_SOURCE_DIR}/build)
set_target_properties(GpuTest PROPERTIES LIBRARY_OUTPUT_DIRECTORY ${CMAKE_CURRENT_SOURCE_DIR}/build RUNTIME_OUTPUT_DIRECTORY_RELEASE ${CMAKE_CURRENT_SOURCE_DIR}/build)
```
We can then compile the operator on a system where `nvcc` is available:
```julia
change_directory("build")
ADCME.cmake()
ADCME.make()
```
### Running a GPU custom operator
We can now run a GPU operator by loading the shared library
```julia
using ADCME
function gpu_test(a)
gpu_test_ = load_op_and_grad("$(@__DIR__)/build/libGpuTest","gpu_test")
a = convert_to_tensor([a], [Float64]); a = a[1]
gpu_test_(a)
end
# TODO: specify your input parameters
a = [1.0;3.0;-1.0]
u = gpu_test(a)
sess = Session(); init(sess)
run(sess, u)
```
If we run the file on a system without GPU resources, we will get the following error
```text
<class 'tensorflow.python.framework.errors_impl.InvalidArgumentError'>
```
If we have GPU resources, the kernel will run correctly with the output
```julia
2.0
6.0
-2.0
```
## Batch Build
At some point, you might have a lot of custom operators. Building one-by-one will take up too much time. To reduce the building time, you might want to build all the operators all at once concurrently. To this end, you can consider batch build by using a common CMakeLists.txt. The commands in the CMakeLists.txt are the same as a typical custom operator, except that the designated libraries are different
```cmake
# ... The same as a typical CMake script ...
# Specify all the library paths and library names.
set(LIBDIR_NAME VolumetricStrain ComputeVel DirichletBd
FemStiffness FemStiffness1 SpatialFemStiffness
SpatialVaryingTangentElastic Strain Strain1
StrainEnergy StrainEnergy1)
set(LIB_NAME VolumetricStrain ComputeVel DirichletBd
FemStiffness UnivariateFemStiffness SpatialFemStiffness
SpatialVaryingTangentElastic StrainOp StrainOpUnivariate
StrainEnergy StrainEnergyUnivariate)
# Copy and paste the following lines (no modification is required)
list(LENGTH "LIBDIR_NAME" LIBLENGTH)
message("Total number of libraries to make: ${LIBLENGTH}")
MATH(EXPR LIBLENGTH "${LIBLENGTH}-1")
foreach(IDX RANGE 0 ${LIBLENGTH})
list(GET LIBDIR_NAME ${IDX} _LIB_DIR)
list(GET LIB_NAME ${IDX} _LIB_NAME)
message("Compiling ${IDX}th library: ${_LIB_DIR}==>${_LIB_NAME}")
file(MAKE_DIRECTORY ${_LIB_DIR}/build)
add_library(${_LIB_NAME} SHARED ${_LIB_DIR}/${_LIB_NAME}.cpp)
set_property(TARGET ${_LIB_NAME} PROPERTY POSITION_INDEPENDENT_CODE ON)
set_target_properties(${_LIB_NAME} PROPERTIES LIBRARY_OUTPUT_DIRECTORY ${CMAKE_SOURCE_DIR}/${_LIB_DIR}/build)
target_link_libraries(${_LIB_NAME} ${TF_LIB_FILE})
endforeach(IDX)
```
## Loading Order
To ensure that TensorFlow can find all the registered symbols, it is recommended that you should always load the shared libraries first if you also run `ccall` on the shared library. This can be done using [`load_library`](@ref) to obtain a handle to the shared library. Then you can use the handle in [`load_op_and_grad`](@ref) or [`load_op`](@ref). For example
```julia
lib = load_library("path/to/my/library")
my_custom_op = load_op_and_grad(lib, "my_custom_op")
```
## Error Handling
Sometimes we might encounter error in C++ kernels and we want to propagate the error to the Julia interface. This is done by `OP_REQUIRES_OK`. Its syntax is
```c++
OP_REQUIRES_OK(context, status)
```
where `context` is either a `OpKernelConstruction` or a `OpKernelContext`, and `status` can be created using
```c++
Status(error::Code::ERROR_CODE, message)
```
Here `ERROR_CODE` is one of the following:
```c++
OK = 0,
CANCELLED = 1,
UNKNOWN = 2,
INVALID_ARGUMENT = 3,
DEADLINE_EXCEEDED = 4,
NOT_FOUND = 5,
ALREADY_EXISTS = 6,
PERMISSION_DENIED = 7,
UNAUTHENTICATED = 16,
RESOURCE_EXHAUSTED = 8,
FAILED_PRECONDITION = 9,
ABORTED = 10,
OUT_OF_RANGE = 11,
UNIMPLEMENTED = 12,
INTERNAL = 13,
UNAVAILABLE = 14,
DATA_LOSS = 15,
DO_NOT_USE_RESERVED_FOR_FUTURE_EXPANSION_USE_DEFAULT_IN_SWITCH_INSTEAD_ = 20,
Code_INT_MIN_SENTINEL_DO_NOT_USE_ = std::numeric_limits<::PROTOBUF_NAMESPACE_ID::int32>::min(),
Code_INT_MAX_SENTINEL_DO_NOT_USE_ = std::numeric_limits<::PROTOBUF_NAMESPACE_ID::int32>::max()
```
`message` is a string.
For example,
```c++
OP_REQUIRES_OK(context,
Status(error::Code::UNAVAILABLE, "Sparse solver type not supported."));
```
## Logging
TensorFlow has a C++ level logging system. We can conveniently log messages to specific streams using the folloing syntax
```c++
VLOG(INFO) << message;
VLOG(WARNING) << message;
VLOG(ERROR) << message;
VLOG(FATAL) << message;
VLOG(NUM_SEVERITIES) << message;
```
## Windows: Load Shared Library
Sometimes you might encounter `NotFoundError()` when using `tf.load_op_library` on Windows system, despite that the library you referred does exist. You can then check using `Libdl`
```julia
using Libdl
dlopen(<MySharedLibrary.dll>)
```
and you still get an error
```
ERROR: could not load library "MySharedLibrary.dll"
The specified module could not be found.
```
This is annoying. The reason is that when you load this shared library on windows, the system looks for all its dependencies. If at least one of the dependent library is not in the path, then the error occurs. To solve this problem, you need a dependency walker, such as [die.exe](https://gamejolt.com/games/die-exe/36157).
For example, in the following right panel we see a lot of dynamic libraries. They must be in the system path so that we can load the current dynamic library (`dlopen(...)`).
| Main Window | Import Window |
| ---- | ---- |
|  |  |
## Miscellany
### Mutable Inputs
Sometimes we want to modify tensors in place. In this case we can use mutable inputs. Mutable inputs must be [`Variable`](@ref) and it must be forwarded to one of the output. We consider implement a `my_assign` operator, with signature
```
my_assign(u::PyObject, v::PyObject)::PyObject
```
Here `u` is a `Variable` and we copy the data from `v` to `u`. In the `MyAssign.cpp` file, we modify the input and output specifications to
```c++
.Input("u : Ref(double)")
.Input("v : double")
.Output("w : Ref(double)")
```
In addition, the input tensor is obtained through
```c++
Tensor u = context->mutable_input(0, true);
```
The second argument `lock_held` specifies whether the input mutex is acquired (false) before the operation. Note the output must be a `Tensor` instead of a reference.
To forward the input, use
```c++
context->forward_ref_input_to_ref_output(0,0);
```
We use the following code snippet to test the program
```julia
my_assign = load_op("./build/libMyAssign","my_assign")
u = Variable([0.1,0.2,0.3])
v = constant(Array{Float64}(1:3))
u2 = u^2
w = my_assign(u,v)
sess = tf.Session()
init(sess)
@show run(sess, u)
@show run(sess, u2)
@show run(sess, w)
@show run(sess, u2)
```
The output is
```
[0.1,0.2,0.3]
[0.1,0.04,0.09]
[1.0,2.0,3.0]
[1.0,4.0,9.0]
```
We can see that the tensors depending on `u` are also aware of the assign operator. The complete programs can be downloaded here: [CMakeLists.txt](https://kailaix.github.io/ADCME.jl/dev/assets/Codes/Mutables/CMakeLists.txt), [MyAssign.cpp](https://kailaix.github.io/ADCME.jl/dev/assets/Codes/Mutables/MyAssign.cpp), [gradtest.jl](https://kailaix.github.io/ADCME.jl/dev/assets/Codes/Mutables/gradtest.jl).
### Third-party Plugins
ADCME also allows third-party custom operators hosted on Github. To build your own custom operators, implement your own custom operators in a Github repository.
Users are free to arrange other source files or other third-party libraries.
Upon using those libraries in ADCME, users first download those libraries to `deps` directory via
```julia
pth = install("OTNetwork")
```
`pth` is the dynamic library product generated with source codes in `OTNetwork`. The official plugins are hosted on `https://github.com/ADCMEMarket`. To get access to the custom operators in ADCME, use
```julia
op = load_op_and_grad(pth, "ot_network"; multiple=true)
```
1. https://on-demand.gputechconf.com/ai-conference-2019/T1-3_Minseok%20Lee_Adding%20custom%20CUDA%20C++%20Operations%20in%20Tensorflow%20for%20boosting%20BERT%20Inference.pdf)
## Troubleshooting
Here are some common errors you might encounter during custom operator compilation:
**Q: The cmake output for the Julia path is empty.**
```text
Julia=
```
**A:** Check whether `which julia` outputs the Julia location you are using.
**Q: The cmake output for Python path, Eigen path, etc., is empty.**
```text
Python path=
PREFIXDIR=
TF_INC=
TF_ABI=
TF_LIB_FILE=
```
**A:** Update ADCME to the latest version and check whether or not the ADCME compiler string is empty
```julia
using ADCME
ADCME.__STR__
```
**Q: Julia package precompilation errors that seem not linked to ADCME.**
**A:** Remove the corresponding packages using `using Pkg; Pkg.rm(XXX)` and reinstall those packages.
**Q: Precompilation error linked to ADCME**
```text
ERROR: LoadError: ADCME is not properly built; run `Pkg.build("ADCME")` to fix the problem.
```
**A:** Build ADCME using `Pkg.build("ADCME")`. Exit Julia and open Julia again. Check whether `deps.jl` exists in the `deps` directory of your Julia package (optional).
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 3063 | # Advanced: Debugging and Profiling
There are many handy tools implemented in `ADCME` for analysis, benchmarking, input/output, etc.
## Debugging and Printing
Add the following line before `Session` and change `tf.Session` to see verbose printing (such as GPU/CPU information)
```julia
tf.debugging.set_log_device_placement(true)
```
`tf.print` can be used for printing tensor values. It must be binded with an executive operator.
```julia
# a, b are tensors, and b is executive
op = tf.print(a)
b = bind(b, op)
```
## Debugging Python Codes
If the error comes from Python (through PyCall), we can print out the Python trace with the following commands
```julia
debug(sess, o)
```
where `o` is a tensor.
The [`debug`](@ref) function traces back the Python function call. The above code is equivalent to
```python
import traceback
try:
# Your codes here
except Exception:
print(traceback.format_exc())
```
This Python script can be inserted to Julia and use interpolation to invoke Julia functions (in the comment line).
This technique can also be applied to other TensorFlow codes. For example, we can use this trick to debug "NotFoundError" for custom operators
```julia
using ADCME, PyCall
py"""
import tensorflow as tf
import traceback
try:
tf.load_op_library("../libMyOp.so")
except Exception:
print(traceback.format_exc())
"""
```
## Profiling
Profiling can be done with the help of [`run_profile`](@ref) and [`save_profile`](@ref)
```julia
a = normal(2000, 5000)
b = normal(5000, 1000)
res = a*b
run_profile(sess, res)
save_profile("test.json")
```
- Open Chrome and navigate to chrome://tracing
- Load the timeline file
Below shows an example of profiling results.

## Suppress Debugging Messages
If you want to suppress annoying debugging messages, you can suppress them using the following command
- Messages originated from Python
By default, ADCME sets the warning level to ERROR only. To set other evels of messages, choose one from the following:
```julia
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.DEBUG)
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.INFO)
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.WARNING)
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.ERROR)
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.FATAL)
```
- Messages originated from C++
In this case, we can set `TF_CPP_MIN_LOG_LEVEL` in the environment variable. Set `TF_CPP_MIN_LOG_LEVEL` to 1 to filter out INFO logs, 2 to additionally filter out WARNING, 3 to additionally filter out ERROR (all messages).
For example,
```julia
ENV["TF_CPP_MIN_LOG_LEVEL"] = "3"
using ADCME # must be called after the above line
```
## Save and Load Diary
We can use TensorBoard to track a scalar value easily
```julia
d = Diary("test")
p = placeholder(1.0, dtype=Float64)
b = constant(1.0)+p
s = scalar(b, "variable")
for i = 1:100
write(d, i, run(sess, s, Dict(p=>Float64(i))))
end
activate(d)
```
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 7218 |
# Numerical Scheme in ADCME: Finite Difference Example
ADCME provides convenient tools to implement numerical schemes. In this tutorial, we will implement a finite difference program and conduct inverse modeling. In the first part, we consider a toy example of estimating parameters in a partial differential equation. In the second part, we showcase a real world application of ADCME to geophysical inversion.
## Estimating a scalar unknown in the PDE
Consider the following partial differential equation
```math
-bu''(x)+u(x)=f(x)\quad x\in[0,1], u(0)=u(1)=0
```
where
```math
f(x) = 8 + 4x - 4x^2
```
Assume that we have observed $u(0.5)=1$, we want to estimate $b$. The true value in this case should be $b=1$. We can discretize the system using finite difference method, and the resultant linear system will be
```math
(bA+I)\mathbf{u} = \mathbf{f}
```
where
```math
A = \begin{bmatrix}
\frac{2}{h^2} & -\frac{1}{h^2} & \dots & 0\\
-\frac{1}{h^2} & \frac{2}{h^2} & \dots & 0\\
\dots \\
0 & 0 & \dots & \frac{2}{h^2}
\end{bmatrix}, \quad \mathbf{u} = \begin{bmatrix}
u_2\\
u_3\\
\vdots\\
u_{n}
\end{bmatrix}, \quad \mathbf{f} = \begin{bmatrix}
f(x_2)\\
f(x_3)\\
\vdots\\
f(x_{n})
\end{bmatrix}
```
The idea for implementing the inverse modeling method in ADCME is that we make the unknown $b$ a `Variable` and then solve the forward problem pretending $b$ is known. The following code snippet shows the implementation
```julia
using LinearAlgebra
using ADCME # (1)
n = 101 # number of grid nodes in [0,1]
h = 1/(n-1)
x = LinRange(0,1,n)[2:end-1] # (2)
b = Variable(10.0) # we use Variable keyword to mark the unknowns # (3)
A = diagm(0=>2/h^2*ones(n-2), -1=>-1/h^2*ones(n-3), 1=>-1/h^2*ones(n-3))
B = b*A + I # I stands for the identity matrix
f = @. 4*(2 + x - x^2)
u = B\f # solve the equation using built-in linear solver
ue = u[div(n+1,2)] # extract values at x=0.5 # (4)
loss = (ue-1.0)^2 # (5)
# Optimization
sess = Session(); init(sess) # (6)
BFGS!(sess, loss) # (7)
println("Estimated b = ", run(sess, b))
```
The expected output is
```
Estimated b = 0.9995582304494237
```
The detailed explaination is as follow: (1) The first two lines load necessary packages; (2) We split the interval $[0,1]$ into $100$ equal length subintervals; (3) Since $b$ is unknown and needs to be updated during optimization, we mark it as trainable using the `Variable` keyword; (4) Solve the linear system and extract the value at $x=0.5$. here `I` stands for the identity matrix and `@.` denotes element-wise operation. They are `Julia`-style syntax but are also compatible with tensors by overloading; (5) Formulate the loss function; (6) Create and initialize a `TensorFlow` session, which analyzes the computational graph and initializes the tensor values; (7) Finally, we trigger the optimization by invoking `BFGS!`, which wraps the `L-BFGS-B` algorithm.
## ADSeismic.jl: A General Approach to Seismic Inversion
ADSeismic is a software package for solving seismic inversion problems, such as velocity model estimation, rupture imaging, earthquake location, and source time function retrieval. The governing equation for the acoustic wave equation is
$$ \frac{\partial^2 u}{\partial t^2} = \nabla\cdot(c^2 \nabla u) + f$$
where $u$ is displacement, $f$ is the source term, and $c$ is the spatially varying acoustic velocity. The inversion parameters of interest are $c$ or $f$.
The governing equation for the elastic wave equation is
$$\begin{aligned}
\rho \frac{\partial v_i}{\partial t} &= \sigma_{ij, j} + \rho f_i \\
\frac{\partial \sigma_{ij}}{\partial t} &= \lambda v_{k,k} + \mu(v_{i,j} + v_{j,i})
\end{aligned}$$
where $v$ is velocity, $\sigma$ is stress tensor, $\rho$ is density, and $\lambda$ and $\mu$ are the Lam\'e's constants. The inversion parameters in the elastic wave equation case are $\lambda$, $\mu$, $\rho$ or $f$.
The idea is to substitute the unknowns such as the $c$ and $f$ using mutable tensors (with the `Variable` keyword) and implement the finite difference method. The implementation detail is beyond the scope of this tutorial. Basically, when explicit schemes are used, the finite difference scheme can be expressed by a computational graph as follows, where $U$ is the discretization of $u$, $A(\theta)$ is the fintie difference coefficient matrix and $\theta$ is the unknown (in this case, the entries in the coefficient matrix depends on $\theta$ ). The loss function is formulated by matching the predicted wavefield $U_i$ and the observed wavefield $U_i^{\mathrm{obs}}$.
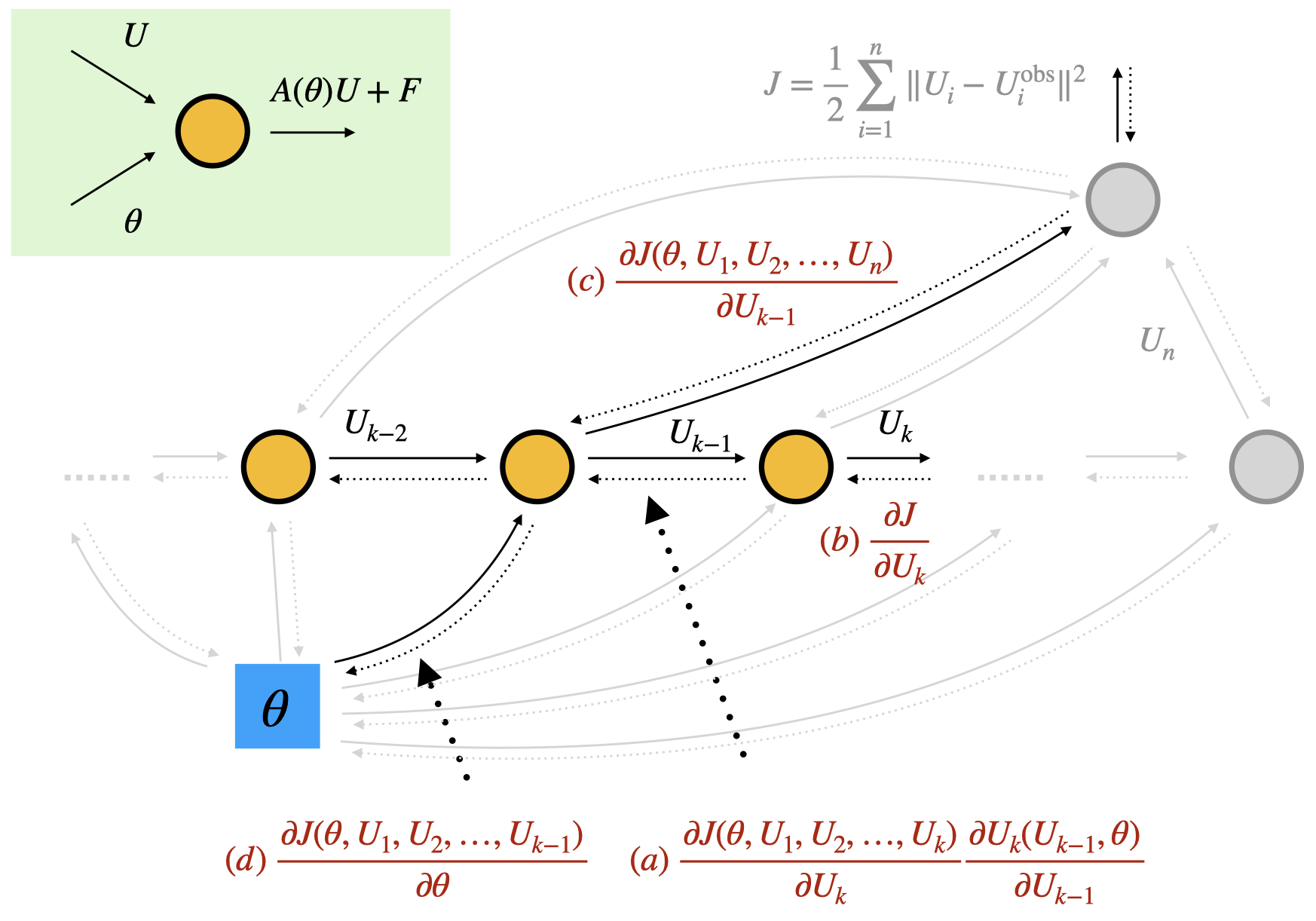
The unknown $\theta$ is sought by solving a minimization problem using L-BFGS-B, using gradients computed in AD. Besides the simplification of implementation, a direct benefit of implementing the numerical in ADCME is that we can leverage multi-GPU computing resources. We distribute the loss function for each scenario (in practice, we can collect many $\{U_i^{\mathbf{obs}}\}$ corresponding to different source functions $f$) onto different GPUs and compute the gradients separately. Using this strategy, we can achieve more than 20 times and 60 times acceleration for acoustic and elastic wave equations respectively.
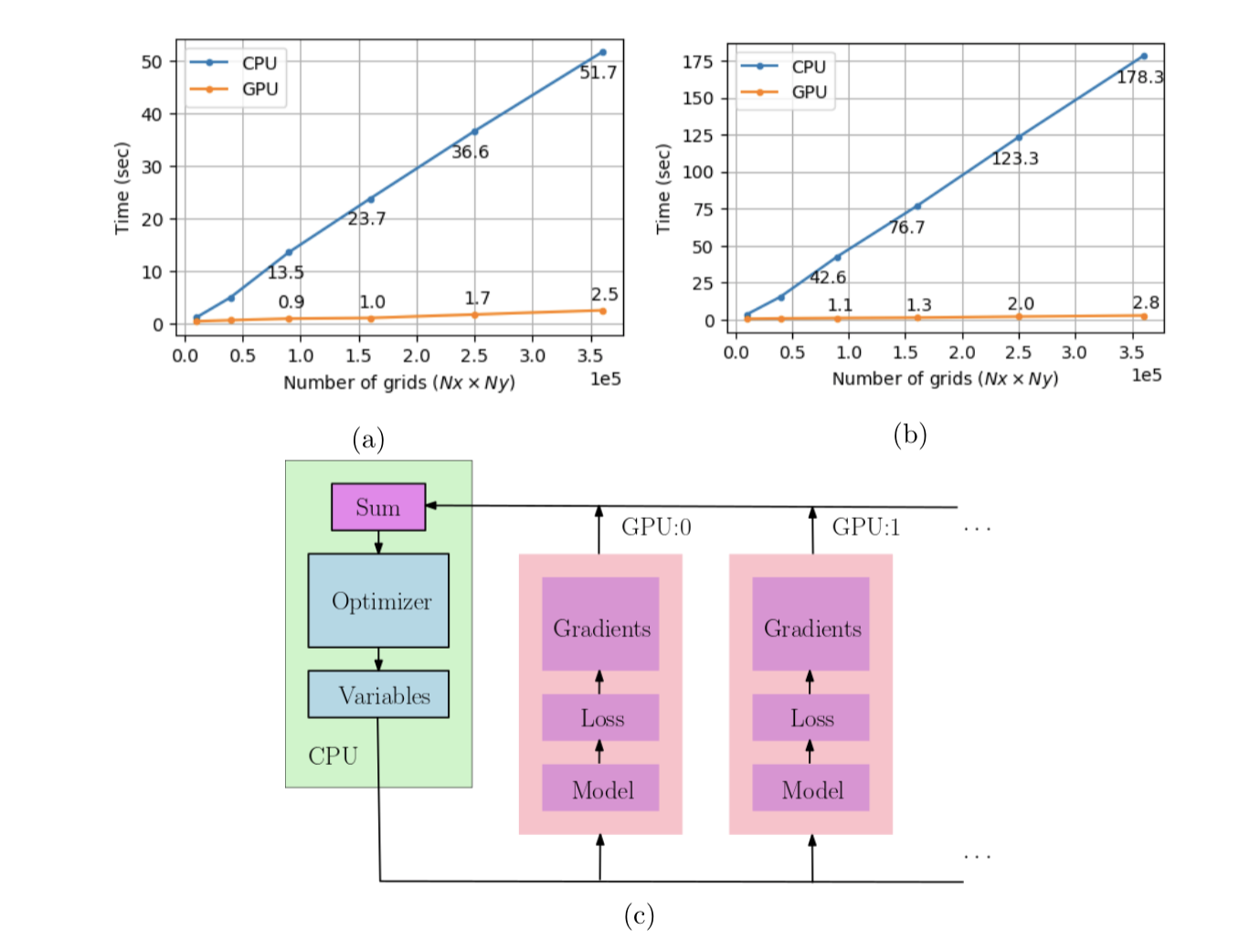
Here we show a case in locating the centroid of an earthquake. The red star denotes the location where the earthquake happens and the triangles denote the seismic stations. The subsurface constitutes layers of different properties (the values of $c$ are different), affecting the propagation of the seismic waves.
| Source/Receiver Location | Forward Simulation |
| ------------------------------------------------------------ | ------------------------------------------------------------ |
| |  |
By running the optimization problem by specifying the earthquake location as `Variable` [^delta], we can locate the centroid of an earthquake. The result is amazingly good. It is worth noting that it requires substantial effort to implement the traditional adjoint-state solver for this problem (e.g., it takes time to manually deriving and implementing the gradients). However, in view of ADCME, the inversion functionality is merely a by-product of the forward simulation codes, which can be reused in many other inversion problems.
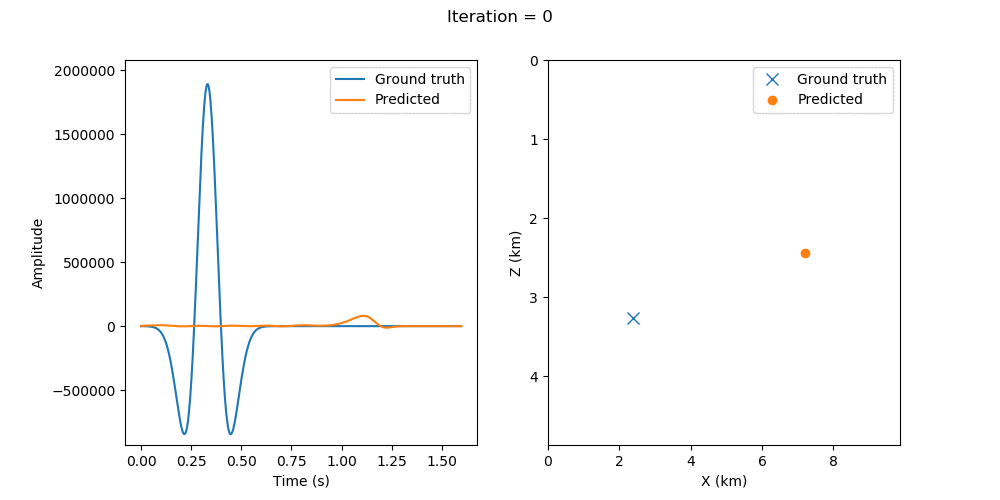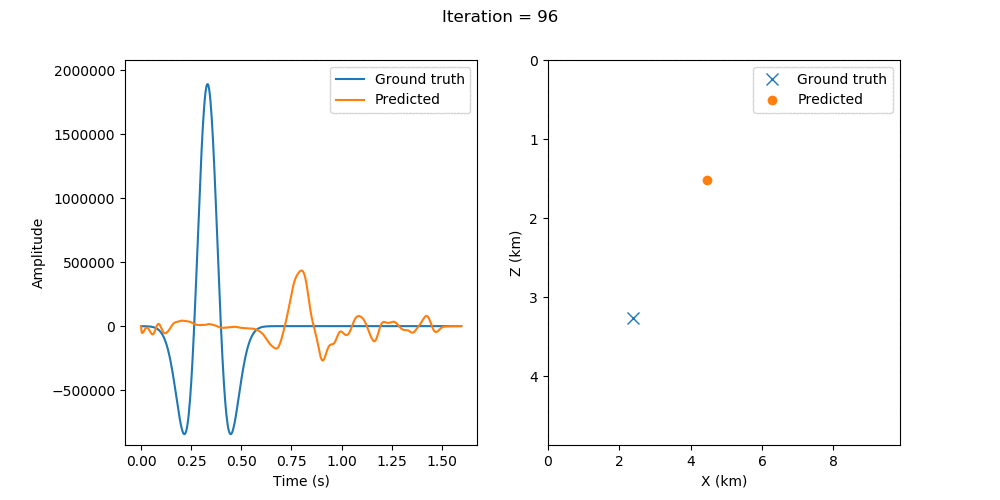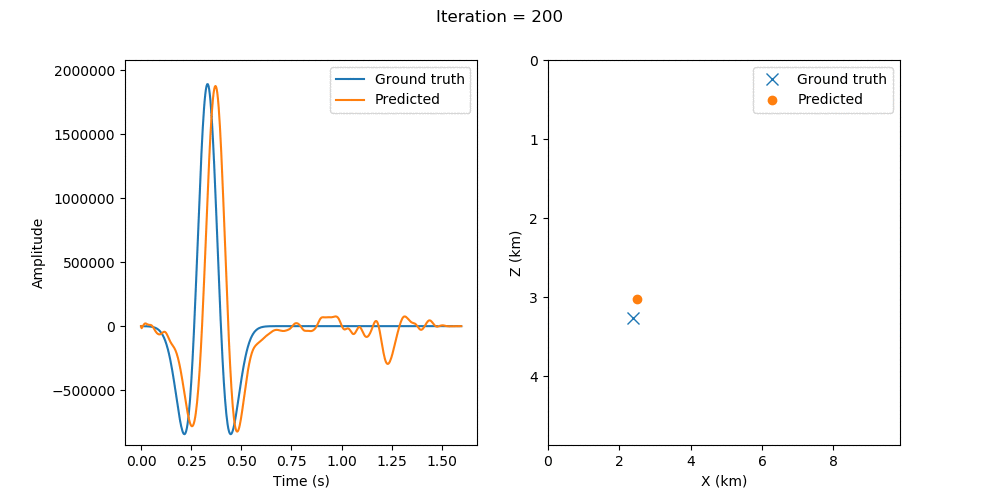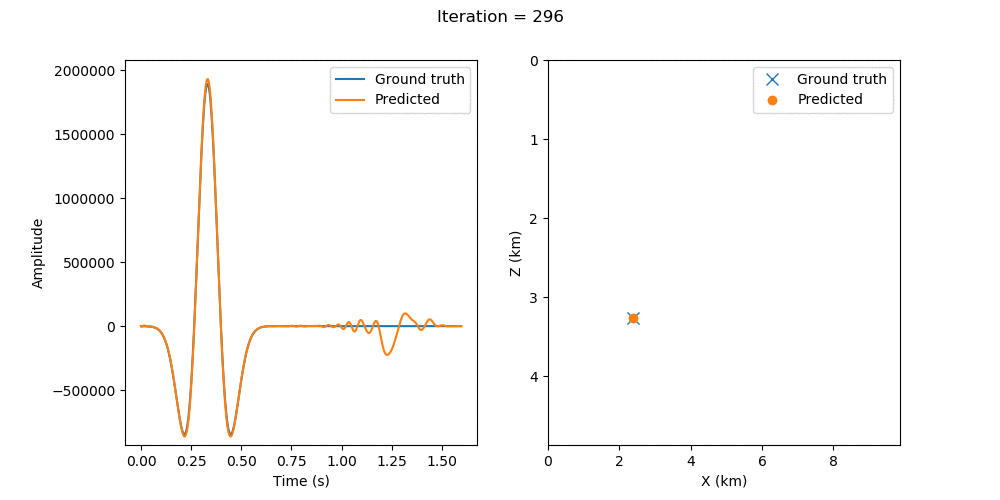
[^delta]: Mathematically, $f(t, \mathbf{x})$ is a Delta function in $\mathbf{x}$; to make the inversion problem continuous, we use $f_{\theta}(t, \mathbf{x}) = g(t) \frac{1}{2\pi\sigma^2}\exp(-\frac{\|\mathbf{x}-\theta\|^2}{2\sigma^2})$ to approximate $f(t, \mathbf{x})$; here $\theta\in\mathbb{R}^2$ and $g(t)$ are unknown.
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 7663 |
# Numerical Scheme in ADCME: Finite Element Example
The purpose of this tutorial is to show how to work with the finite element method (FEM) in ADCME. The tutorial is divided into two part:
* In the first part, we implement a finite element code for a time independent Poisson's equation in 1D and 2D. We present two styles of implementing a finite element code: using vectorized expression and low level C++ implementation using custom operators. The first approach is elegant and only uses ADCME syntax. The second approach is more flexible and allows for efficient optimization. However, the limitation is that you are responsible to calculate the sensititity of your finite element sensitivity matrix.
* The second part is about solving a time dependent problem. Here we use finite element methods for the spatial discretization and a backward Euler for time integration. The custom operator approach is used. In this example, you will understand how [`while_loop`](@ref) can help avoid creating a computational graph for each time step. This is important because for many applications the number of time steps can be enormous.
## Poisson's Problem: Vectorized Implementation
Let us consider the following Poisson's equation in $(0,1)$:
$$(\kappa(x) u'(x))' = f(x)\qquad u(0) = u(1) = 0\tag{1}$$
To make the problem more interesting, we make $\kappa$ parameterized by `a`, which is constructed using [`constant`](@ref) so we can keep track of the dependencies of intermediate values on `a`.
$$\kappa(x) = \frac{1}{1+x^2}, \ u(x) = x(1-x)$$
and $f(x)$ can be calculated according to Equation 1. We use the finite element method with a linear basis to solve Equation 1: find $u\in H_0^1((0,1))$, such that
$$\int_0^1 \kappa(x) u'(x) v'(x) dx = \int_0^1 f(x) v(x) dx \quad \forall v\in H_0^1((0,1))$$
We consider a uniform grid with $n$ intervals of equal lengths. The common approach for assembling the finite element matrix $A$ is to iterate over elements and compute the contribution $\int_E \kappa(x) \phi'_i(x)\phi'_j(x) dx$ and add it to the entry $A_{ij}$; here $\phi_i(x)$ is the basis function associated with node $i$.
The integration is usually done with numerical integration. Here we consider the Gauss quadrature. Consider the $i$-th element, the local stiffness matrix is
$$L_i = \sum_{k=1}^G h\begin{bmatrix} \frac{w_k\kappa(x_k)}{h^2} & -\frac{w_k\kappa(x_k)}{h^2} \\ -\frac{w_k\kappa(x_k)}{h^2} & \frac{w_k\kappa(x_k)}{h^2} \end{bmatrix} = \begin{bmatrix} 1 & -1\\ -1 & 1 \end{bmatrix}\frac{\sum_{k=1}^G w_k\kappa(x_k)}{h} $$
Here $(\xi_k, w_k)$ are Gauss quadrature points and weights on $[0,1]$, and
$$x_k = (1-\xi_k) (i-1)h + \xi_k ih$$
The corresponding DOF (degrees of freedom) matrix, i.e., the mapping of local index to global index, is
$$D_i = \begin{bmatrix}(i,i) & (i,i+1) \\ (i+1, i) & (i+1, i+1)\end{bmatrix}$$
```julia
xk = zeros(n, length(ξ))
for i = 1:length(ξ)
xk[:,i] = x[1:end-1] * (1-ξ[i]) + x[2:end] * ξ[i]
end
xk = constant(xk) # convert xk from Julia array to tensor
s = kappa(xk) * w / h
i0 = Array(1:n)
i1 = Array(2:n+1)
II = [i0;i0;i1;i1]
JJ = [i0;i1;i0;i1]
VV = [s;-s;-s;s]
A = SparseTensor(II, JJ, VV, n+1, n+1)
```
The right hand side $\int_\Omega f(x) v(x) dx$ can be computed in a similar fashion: the local contribution $l_i$ and DOF $d_i$ are
$$l_i = \sum_{k=1}^G h\begin{bmatrix}
w_k f(x_k) (1-\xi_k)\\
w_k f(x_k) \xi_k\\
\end{bmatrix}\qquad d_i = \begin{bmatrix}
i\\
i+1
\end{bmatrix}$$
This is done with
```julia
rhs = zeros(n+1)
s = [f(xk) * (w .* (1 .-ξ)); f(xk) * (w .* ξ)] * h
rhs = -vector([i0;i1], s, n+1)
```
### Full Code Listing
```julia
using ADCME
function kappa(x)
return 1/(1+a*x^2)
end
function f(x)
return -2*a*x .* (1 - 2*x) ./(a*x^2 + 1)^2 - 2/(a*x^2 + 1)
end
function uexact(x)
return x*(1-x)
end
n = 100
h = 1/n
x = Array(LinRange(0, 1, n+1))
a = constant(1.0)
ξ = [0.1127016653792583; 0.5;0.8872983346207417]
w = [5/18; 4/9; 5/18]
xk = zeros(n, length(ξ))
for i = 1:length(ξ)
xk[:,i] = x[1:end-1] * (1-ξ[i]) + x[2:end] * ξ[i]
end
xk = constant(xk) # convert xk from Julia array to tensor
# Assemble left hand side
s = kappa(xk) * w / h
i0 = Array(1:n)
i1 = Array(2:n+1)
II = [i0;i0;i1;i1]
JJ = [i0;i1;i0;i1]
VV = [s;-s;-s;s]
A = SparseTensor(II, JJ, VV, n+1, n+1)
# Assemble right hand side
rhs = zeros(n+1)
s = [f(xk) * (w .* (1 .-ξ)); f(xk) * (w .* ξ)] * h
rhs = -vector([i0;i1], s, n+1)
# Impose boundary condition using static condensation
A = A[2:end-1, 2:end-1]
rhs = rhs[2:end-1]
# Solve
sol = A\rhs
sess = Session(); init(sess)
solution = run(sess, sol)
```
The result for $a=1$ is shown below
```@raw html
<center><img src="https://github.com/ADCMEMarket/ADCMEImages/blob/master/ADCME/poisson.png?raw=true" width="50%"></center>
```
## Poisson's Problem: Custom Operators
Vectorized implementation is great and elegant when we can easily figure out the mathematical formula. However, for more complicated problems and modular development, it is awkward to reason about vectorization each time. A preferred approach is to loop over elements and focus on calculating local contribution. However, a direct for loop will create a large computational graph and will not be able to take advantage of efficient implementation (e.g., parallel computing).
In what follows, we consider another approach: custom operator. To motivate our method, we consider a 2D Poisson's equation in a domain $\Omega$
$$\nabla \cdot (\kappa(x) \nabla u) = f(x)\qquad u(x) = 0, x\in \partial\Omega$$
The weak formulation is given by
$$\int_\Omega \kappa(x) \nabla u \cdot \nabla v dx = - \int_\Omega f(x) v(x) dx\quad \forall v \in H_0^1(\Omega)$$
The strategy is to implement two custom operators, one for computing the stiffness matrix, and the other for computing the right hand side. We suggest readers to use our [AdFem](https://github.com/kailaix/AdFem.jl) library instead of their own. the AdFem library is built on ADCME and contains a rich set of custom operators that allow users to implement FEM fairly easily.
```julia
using AdFem
using PyPlot
mmesh = Mesh(50, 50, 1/50)
function kappa(x, y)
return 1/(1+a*(x^2+y^2))
end
function ffun(x, y)
return -2*x*(1 - x)/(x^2 + y^2 + 1) - 2*x*(-x*y*(1 - y) + y*(1 - x)*(1 - y))/(x^2 + y^2 + 1)^2 - 2*y*(1 - y)/ (x^2 + y^2 + 1) - 2*y*(-x*y*(1 - x) + x*(1 - x)*(1 - y))/(x^2 + y^2 + 1)^2
end
a = constant(1.0)
κ = eval_f_on_gauss_pts(kappa, mmesh, tensor_input = true)
fv = eval_f_on_gauss_pts(ffun, mmesh, tensor_input = true)
A = compute_fem_laplace_matrix1(κ, mmesh)
rhs = -compute_fem_source_term1(fv, mmesh)
bd = bcnode(mmesh)
A, rhs = impose_Dirichlet_boundary_conditions(A, rhs, bd, zeros(length(bd)))
sol = A\rhs
sess = Session(); init(sess)
U = run(sess, sol)
close("all")
figure(figsize = (15, 5))
subplot(131)
visualize_scalar_on_fem_points(U, mmesh)
subplot(132)
xy = fem_nodes(mmesh)
x, y = xy[:,1], xy[:,2]
visualize_scalar_on_fem_points((@. x*(1-x)*y*(1-y)), mmesh)
subplot(133)
visualize_scalar_on_fem_points(abs.(U - (@. x*(1-x)*y*(1-y))), mmesh)
savefig("poisson2d.png")
```
```@raw html
<center><img src="https://github.com/ADCMEMarket/ADCMEImages/blob/master/ADCME/poisson2d.png?raw=true" width="50%"></center>
```
## Summary
Finite element analysis is a powerful tool in numerical PDEs. However, it is more conceptually sophisticated than the finite difference method and requires more implementation efforts. The important lesson we learned from this tutorial is how to separate the computation into pure Julia and ADCME C++ kernels, and how complex numerical schemes can be implemented in ADCME.
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 6065 | # Advanced: Automatic Differentiation for Implicit Operators
An explicit operator is an operator directly supplied by the AD library while an implicit operator is an operator whose outputs must be computed using compositions of functions that may not be differentiable, or involving iterative algorithms. For example, $y = \texttt{sigmoid}(x)$ is an implicit operator while $x = \texttt{sigmoid}(y)$ is an implicit operator if the library does not provide $\texttt{sigmoid}^{-1}$, where $x$ is the input and $y$ is the output.
Implicit operators are everywhere in scientific computing, from implicit numerical schemes to iterative algorithms. How to incooperate implicit operators into a differentiable programming framework is the true challenge in AD. AD is not the panacea to all inverse modeling problems; it must be augmented with abilities to tackle implicit operators to be real useful for a large variety of real-world applications.
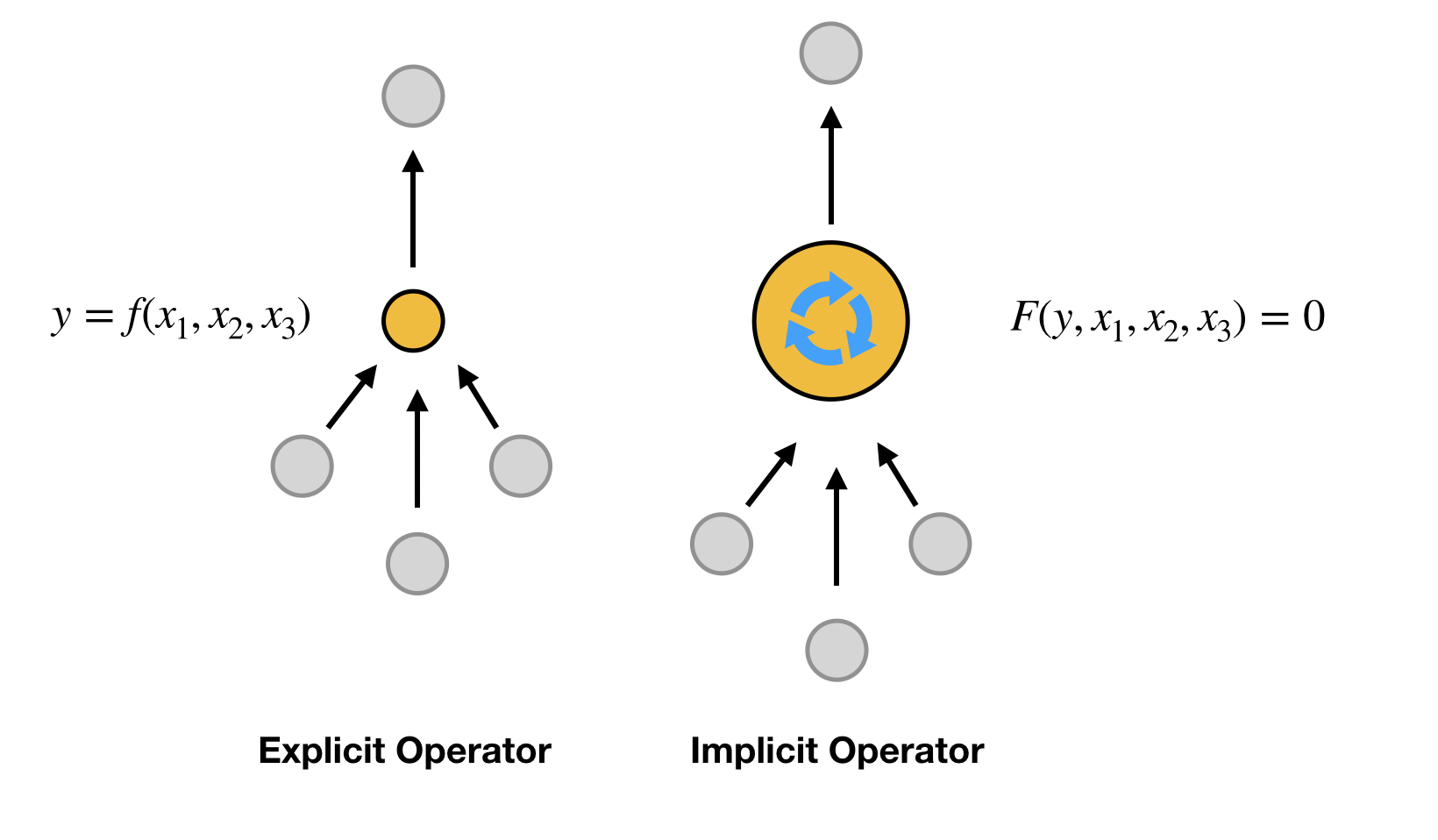
Roughly speaking, there are four types of operators in the computational graph, depending on whether it is linear or nonlinear and whether it is explicit or implicit. Let $A$ be a matrix, $f$ be a nonlinear function, $F$ be a bivariate nonlinear function, and it is hard to express $y$ analytically as a function of $x$ in $F(x,y)=0$.
| Operator | Linear | Nonlinear |
| -------- | -------- | ----------- |
| Explicit | $y = Ax$ | $y = f(x)$ |
| Implicit | $Ay = x$ | $F(x, y)=0$ |
It is straightforward to apply AD to explicit operators, provided that the AD library supports the corresponding operators $A$ and $f$ (which usually do). In this tutorial, we focus on the implicit operators.
## Implicit Function Theorem
We change our notation for clarity in this section. Let $L_h$ be a error functional, $F_h$ be the corresponding nonlinear implicit operator, $\theta$ is all the input to this operator and $u_h$ is all the output of this node.
$$\begin{aligned}
\min_{\theta}&\; L_h(u_h) \\
\mathrm{s.t.}&\;\; F_h(\theta, u_h) = 0
\end{aligned}$$
Assume in the forward computation, we solve for $u_h=G_h(\theta)$ in $F_h(\theta, u_h)=0$, and then
$$\tilde L_h(\theta) = L_h(G_h(\theta))$$
Applying the implicit function theorem
$$\begin{aligned}
& \frac{{\partial {F_h(\theta, u_h)}}}{{\partial \theta }} + {\frac{{\partial {F_h(\theta, u_h)}}}{{\partial {u_h}}}} \frac{\partial G_h(\theta)}{\partial \theta} = 0 \qquad \Rightarrow \\[4pt]
& \frac{\partial G_h(\theta)}{\partial \theta} = -\Big( \frac{{\partial {F_h(\theta, u_h)}}}{{\partial {u_h}}} \Big)^{ - 1} \frac{{\partial {F_h(\theta, u_h)}}}{{\partial \theta }}
\end{aligned}$$
therefore we have
$$\begin{aligned}
\frac{{\partial {{\tilde L}_h}(\theta )}}{{\partial \theta }}
&= \frac{\partial {{ L}_h}(u_h )}{\partial u_h}\frac{\partial G_h(\theta)}{\partial \theta} \\
&= - \frac{{\partial {L_h}({u_h})}}{{\partial {u_h}}} \;
\Big( {\frac{{\partial {F_h(\theta, u_h)}}}{{\partial {u_h}}}\Big|_{u_h = {G_h}(\theta )}} \Big)^{ - 1} \;
\frac{{\partial {F_h(\theta, u_h)}}}{{\partial \theta }}\Big|_{u_h = {G_h}(\theta )}
\end{aligned}$$
This is the desired gradient. For efficiency, the computation strategy is crucial. We can either evaluate from left to right or from right to left. The correct approach is to compute from left to right. A detailed justification of this computational order is beyond the scope of this tutorial. Instead, we simply list the steps for calculating the gradients
Step 1: Calculate $w$ by solving a linear system (never invert the matrix!)
$$w^T = \underbrace{\frac{{\partial {L_h}({u_h})}}{{\partial {u_h}}\rule[-9pt]{1pt}{0pt}}}_{1\times N}
\;\;
\underbrace{\Big( {\frac{{\partial {F_h}}}{{\partial {u_h}}}\Big|_{u_h = {G_h}(\theta )}} \Big)^{ - 1}}_{N\times N}$$
Step 2: Calculate the gradient by automatic differentiation
$$w^T\;\underbrace{\frac{{\partial {F_h}}}{{\partial \theta }}\Big|_{u_h = {G_h}(\theta )}}_{N\times p} = \frac{\partial (w^T\; {F_h}(\theta, u_h))}{\partial \theta }\Bigg|_{u_h = {G_h}(\theta )}$$
This step can be done using [`independent`](@ref), which stops back-propagating the gradients for its argument.
```julia
l = L(u)
r = F(theta, u)
g = gradients(l, u)
x = dF'\g
x = independent(x)
dL = -gradients(sum(r*x), theta)
```
Despite the complex nature of this approach, it is quite powerful and efficient in treating implicit operators. To make it more clear, we consider a simpler special case below: the linear implicit operator.
## Special Case: Linear Implicit Operator
The linear implicit operator can be viewed as a special case of the nonlinear explicit operator. In this case
$$F(x,y) = x - Ay$$
and therefore
$$\frac{\partial J}{\partial x} = \frac{\partial J}{\partial y}A^{-1}$$
This requires us to solve a linear system with the adjoint of $A$, i.e.,
$$A^T g = \left(\frac{\partial J}{\partial y}\right)^T$$
## Implementation in ADCME
Let's see in action how to implement an implicit operator in ADCME. First of all, we can use the [`NonlinearConstrainedProblem`](@ref) used in [Functional Inverse Problem](https://kailaix.github.io/ADCME.jl/dev/tutorial/#Functional-Inverse-Problem-1). The API is suitable when the residual and the Jacobian matrix can be expressed using ADCME operators (or through custom operators) and a general Newton-Raphson algorithm is satisfactory. However, if the forward solver is performance critical and requires special accleration (such as preconditioning), then building custom operator is a preferable approach.
This approach is named **physics constrained learning** and has been used to develop [`FwiFlow.jl`](https://github.com/lidongzh/FwiFlow.jl), a package for elastic full waveform inversion for subsurface flow problems. The physical equation is nonlinear, the discretization is implicit, and thus it must be solved using the Newton-Raphson method.
 | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 13626 |
# Inverse Modeling with ADCME
Roughly speaking, there are four types of inverse modeling in partial differential equations. We have developed numerical methods that takes advantage of deep neural networks and automatic differentiation. To be more concrete, let the forward model be a 1D Poisson equation
$$\begin{aligned}-\nabla (X\nabla u(x)) &= \varphi(x) & x\in (0,1)\\ u(0)=u(1) &= 0\end{aligned}$$
Here $X$ is the unknown which may be one of the four forms: parameter, function, functional or random variable.
| **Inverse problem** | **Problem type** | **ADCME Approach** | **Reference** |
| ---------------------------------------- | -------------------- | ------------------------------- | :-----------------------------------: |
| $\nabla\cdot(c\nabla u) = \varphi(x)$ | Parameter | Adjoint-State Method | [1](http://arxiv.org/abs/1912.07552) [2](http://arxiv.org/abs/1912.07547) |
| $\nabla\cdot(f(x)\nabla u) = \varphi(x)$ | Function | DNN as a Function Approximator | [3](https://arxiv.org/abs/1901.07758) |
| $\nabla\cdot(f(u)\nabla u) = \varphi(x)$ | Functional | Residual Learning or Physics Constrained Learning | [4](https://arxiv.org/abs/1905.12530) |
| $\nabla\cdot(\varpi\nabla u) = \varphi(x)$ | Stochastic Inversion | Generative Neural Networks | [5](https://arxiv.org/abs/1910.06936) |
## Parameter Inverse Problem
When $X$ is just a scalar/vector, we call this type of problem **parameter inverse problem**. We consider a manufactured solution: the exact $X=1$ and $u(x)=x(1-x)$, so we have
```math
\varphi(x) = 2
```
Assume we can observe $u(0.5)=0.25$ and the initial guess for $X_0=10$. We use finite difference method to discretize the PDE and the interval $[0,1]$ is divided uniformly to $0=x_0<x_1<\ldots<x_n=1$, with $n=100$, $x_{i+1}-x_i = h=\frac{1}{n}$.
we can solve the problem with the following code snippet
```julia
using ADCME
n = 100
h = 1/n
X0 = Variable(10.0)
A = X0 * diagm(0=>2/h^2*ones(n-1), 1=>-1/h^2*ones(n-2), -1=>-1/h^2*ones(n-2)) # coefficient matrix for the finite difference
φ = 2.0*ones(n-1) # right hand side
u = A\φ
loss = (u[50] - 0.25)^2
sess = Session(); init(sess)
BFGS!(sess, loss)
```
After around 7 iterations, the estimated $X_0$ converges to 1.0000000016917243.
## Function Inverse Problem
When $X$ is a function that does not depend on $u$, i.e., a function of location $x$, we call this type of problem **function inverse problem**. A common approach to this type of problem is to approximate the unknown function $X$ with a parametrized form, such as piecewise linear functions, radial basis functions or Chebyshev polynomials; sometimes we can also discretize $X$ and substitute $X$ by a vector of its values at the discrete grid nodes.
This tutorial is not aimed at the comparison of different methods. Instead, we show how we can use neural networks to represent $X$ and train the neural network by coupling it with numerical schemes. The gradient calculation can be laborious with the traditional adjoint state methods but is trivial with automatic differentiation.
Let's assume the true $X$ has the following form
```math
X(x) = \frac{1}{1+x^2}
```
The exact $\varphi$ is given by
```math
\varphi(x) = \frac{2 \left(x^{2} - x \left(2 x - 1\right) + 1\right)}{\left(x^{2} + 1\right)^{2}}
```
The idea is to use a neural network $\mathcal{N}(x;w)$ with weights and biases $w$ that maps the location $x\in \mathbb{R}$ to a scalar value such that
```math
\mathcal{N}(x; w)\approx X(x)
```
To find the optional $w$, we solve the Poisson equation with $X(x)=\mathcal{N}(x;w)$, where the numerical scheme is
```math
\left( -\frac{X_i+X_{i+1}}{2} \right) u_{i+1} + \frac{X_{i-1}+2X_i+X_{i+1}}{2} u_i + \left( -\frac{X_i+X_{i-1}}{2} \right) = \varphi(x_i) h^2
```
Here $X_i = \mathcal{N}(x_i; w)$.
Assume we can observe the full solution $u(x)$, we can compare it with the solution $u(x;w)$, and minimize the loss function
```math
L(w) = \sum_{i=2}^{n-1} (u(x_i;w)-u(x_i))^2
```
```julia
using ADCME
n = 100
h = 1/n
x = collect(LinRange(0, 1.0, n+1))
X = ae(x, [20,20,20,1])^2 # to ensure that X is positive, we use NN^2 instead of NN
A = spdiag(
n-1,
1=>-(X[2:end-2] + X[3:end-1])/2,
-1=>-(X[3:end-1] + X[2:end-2])/2,
0=>(2*X[2:end-1]+X[3:end]+X[1:end-2])/2
)/h^2
φ = @. 2*x*(1 - 2*x)/(x^2 + 1)^2 + 2 /(x^2 + 1)
u = A\φ[2:end-1] # for efficiency, we can use A\φ[2:end-1] (sparse solver)
u_obs = (@. x * (1-x))[2:end-1]
loss = sum((u - u_obs)^2)
sess = Session(); init(sess)
BFGS!(sess, loss)
```
We show the exact $X(x)$ and the pointwise error in the following plots
```math
\left|\mathcal{N}(x_i;w)-X(x_i)\right|
```
| 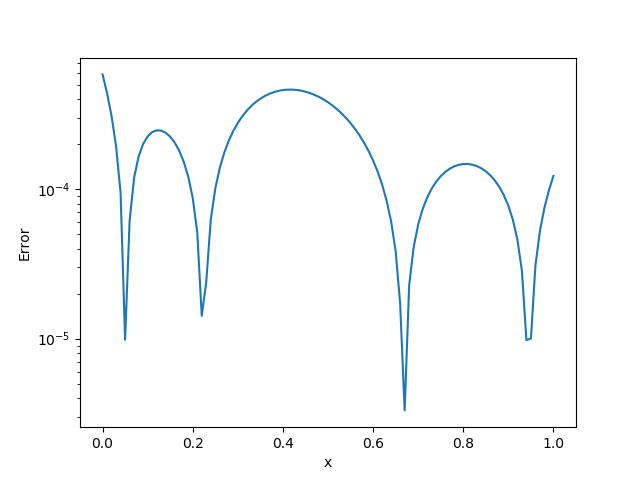 | 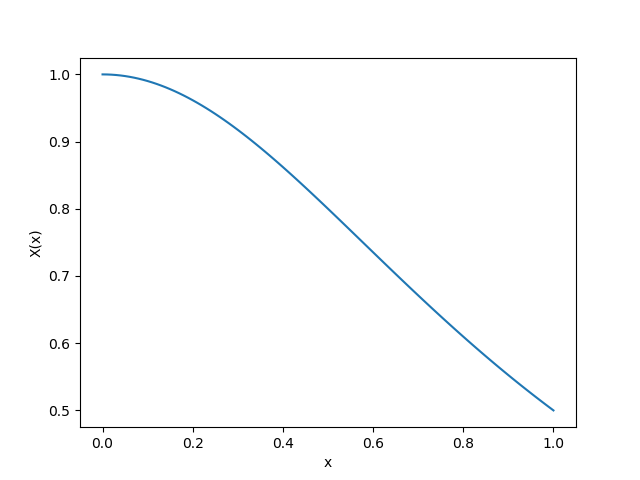 |
| ---------------------------- | ---------------------------- |
| Pointwise Absolute Error | Exact $X(u)$ |
## Functional Inverse Problem
In the **functional inverse problem**, $X$ is a function that _depends_ on $u$ (or both $x$ and $u$); it must not be confused with the functional inverse problem and it is much harder to solve (since the equation is nonlinear).
As an example, assume
$$\begin{aligned}\nabla (X(u)\nabla u(x)) &= \varphi(x) & x\in (0,1)\\ u(0)=u(1) &= 0\end{aligned}$$
where the quantity of interest is
```math
X(u) = \frac{1}{1+100u^2}
```
The corresponding $\varphi$ can be analytically evaluated (e.g., using SymPy).
To solve the Poisson equation, we use the standard Newton-Raphson scheme, in which case, we need to compute the residual
$$R_i = X'(u_i)\left(\frac{u_{i+1}-u_{i-1}}{2h}\right)^2 + X(u_i)\frac{u_{i+1}+u_{i-1}-2u_i}{h^2} - \varphi(x_i)$$
and the corresponing Jacobian
$$\frac{\partial R_i}{\partial u_j} = \left\{ \begin{matrix} -\frac{X'(u_i)}{h}\frac{u_{i+1}-u_{i-1}}{2h} + \frac{X(u_i)}{h^2} & j=i-1\\ X''(u_i)\frac{u_{i+1}-u_{i-1}}{2h} + X'(u_i)\frac{u_{i+1}+u_{i-1}-2u_i}{h^2} - \frac{2}{h^2}X(u_i) & j=i \\ \frac{X'(u_i)}{2h}\frac{u_{i+1}-u_{i-1}}{2h} + \frac{X(u_i)}{h^2} & j=i+1\\ 0 & |j-i|>1 \end{matrix} \right.$$
Just like the function inverse problem, we also use a neural network to approximate $X(u)$; the difference is that the input of the neural network is $u$ instead of $x$. It is convenient to compute $X'(u)$ with automatic differentiation.
Solving the forward problem (given $X(u)$, solve for $u$) requires conducting Newton-Raphson iterations. One challenge here is that the Newton-Raphson operator is a nonlinear implicit operator that does not fall into the types of operators where automatic differentiation applies. The relevant technique is **physics constrained learning**. The basic idea is to extract the gradients by the implicit function theorem. The limitation is that we need to provide the Jacobian matrix for the residual term in the Newton-Raphson algorithm. In ADCME, the complex algorithm is wrapped in the API [`NonlinearConstrainedProblem`](@ref) and users only need to focus on constructing the residual and the gradient term
```julia
using ADCME
using PyPlot
function residual_and_jacobian(θ, u)
X = ae(u, config, θ) + 1.0 # (1)
Xp = tf.gradients(X, u)[1]
Xpp = tf.gradients(Xp, u)[1]
up = [u[2:end];constant(zeros(1))]
un = [constant(zeros(1)); u[1:end-1]]
R = Xp .* ((up-un)/2h)^2 + X .* (up+un-2u)/h^2 - φ
dRdu = Xpp .* ((up-un)/2h)^2 + Xp.*(up+un-2u)/h^2 - 2/h^2*X
dRdun = -Xp[2:end]/h .* (up-un)[2:end]/2h + X[2:end]/h^2
dRdup = Xp[1:end-1]/h .* (up-un)[1:end-1]/2h + X[1:end-1]/h^2
J = spdiag(n-1,
-1=>dRdun,
0=>dRdu,
1=>dRdup) # (2)
return R, J
end
config = [20,20,20,1]
n = 100
h = 1/n
x = collect(LinRange(0, 1.0, n+1))
φ = @. (1 - 2*x)*(-100*x^2*(2*x - 2) - 200*x*(1 - x)^2)/(100*x^2*(1 - x)^2 + 1)^2 - 2 - 2/(100*x^2*(1 - x)^2 + 1)
φ = φ[2:end-1]
θ = Variable(ae_init([1,config...]))
u0 = constant(zeros(n-1))
function L(u) # (3)
u_obs = (@. x * (1-x))[2:end-1]
loss = mean((u - u_obs)^2)
end
loss, solution, grad = NonlinearConstrainedProblem(residual_and_jacobian, L, θ, u0)
X_pred = ae(collect(LinRange(0.0,0.25,100)), config, θ) + 1.0
sess = Session(); init(sess)
BFGS!(sess, loss, grad, θ)
x_pred, sol = run(sess, [X_pred, solution])
figure(figsize=(10,4))
subplot(121)
s = LinRange(0.0,0.25,100)
x_exact = @. 1/(1+100*s^2) + 1
plot(s, x_exact, "-", linewidth=3, label="Exact")
plot(s, x_pred, "o", markersize=2, label="Estimated")
legend()
xlabel("u")
ylabel("X(u)")
subplot(122)
s = LinRange(0.0,1.0,101)[2:end-1]
plot(s, (@. s * (1-s)), "-", linewidth=3, label="Exact")
plot(s, sol, "o", markersize=2, label="Estimated")
legend()
xlabel("x")
ylabel("u")
savefig("nn.png")
```
Detailed explaination: (1) This is the neural network we constructed. Note that with default initialization, the neural network output values are close to 0, and thus poses numerical stability issue for the solver. We can shift the neural network value by $+1$ (equivalently, we use 1 for the initial guess of the last bias term); (2) The jacobian matrix is sparse, and thus we use [`spdiag`](@ref) to create a sparse matrix; (3) A loss function is formulated and minimized in the physics constrained learning.
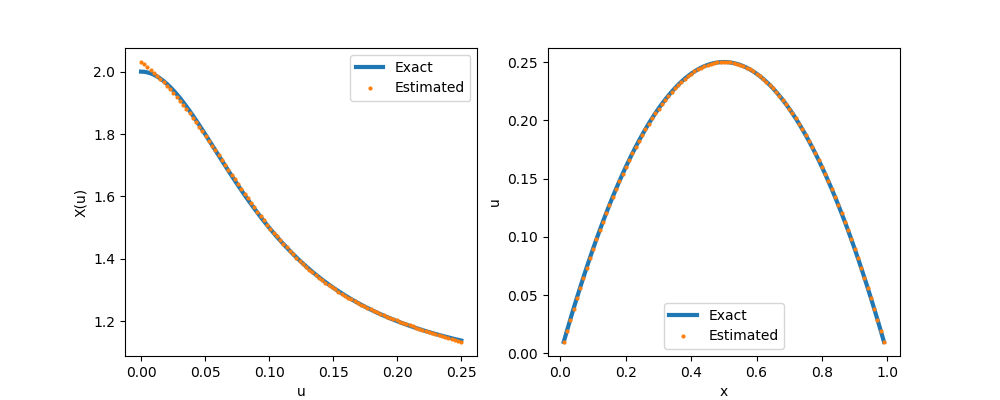
## Stochastic Inverse Problem
The final type of inverse problem is called **stochastic inverse problem**. In this problem, $X$ is a random variable with unknown distribution. Consequently, the solution $u$ will also be a random variable. For example, we may have the following settings in practice
- The measurement of $u(0.5)$ may not be accurate. We might assume that $u(0.5) \sim \mathcal{N}(\hat u(0.5), \sigma^2)$ where $\hat u(0.5)$ is one observation and $\sigma$ is the prescribed standard deviation of the measurement. Thus, we want to estimate the distribution of $X$ which will produce the same distribution for $u(0.5)$. This type of problem falls under the umbrella of **uncertainty quantification**.
- The quantity $X$ itself is subject to randomness in nature, but its distribution may be positively/negatively skewed (e.g., the stock price returns). We can measure several samples of $u(0.5)$ and want to estimate the distribution of $X$ based on the samples. This problem is also called the **probabilistic inverse problem**.
We cannot simply minimize the distance between $u(0.5)$ and `u` (which are random variables) as usual; instead, we need a metric to measure the discrepancy between two distributions--`u` and $u(0.5)$. The observables $u(0.5)$ may be given in multiple forms
- The probability density function.
- The unnormalized log-likelihood function.
- Discrete samples.
We consider the third type in this tutorial. The idea is to construct a sampler for $X$ with a neural network and find the optimal weights and biases by minimizing the discrepancy between actually observed samples and produced ones. Here is how we train the neural network:
We first propose a candidate neural network that transforms a sample from $\mathcal{N}(0, I_d)$ to a sample from $X$. Then we randomly generate $K$ samples $\{z_i\}_{i=1}^K$ from $\mathcal{N}(0, I_d)$ and transform them to $\{X_i; w\}_{i=1}^K$. We solve the Poisson equation $K$ times to obtain $\{u(0.5;z_i, w)\}_{i=1}^K$. Meanwhile, we sample $K$ items from the observations (e.g., with the bootstrap method) $\{u_i(0.5)\}_{i=1}^K$. We can use a probability metric $D$ to measure the discrepancy between $\{u(0.5;z_i, w)\}_{i=1}^K$ and $\{u_i(0.5)\}_{i=1}^K$. There are many choices for $D$, such as (they are not necessarily non-overlapped)
- Wasserstein distance (from optimal transport)
- KL-divergence, JS-divergence, etc.
- Discriminator neural networks (from generative adversarial nets)
For example, we can consider the first approach, and invoke [`sinkhorn`](@ref) provided by ADCME
```julia
using ADCME
using Distributions
# we add a mixture Gaussian noise to the observation
m = MixtureModel(Normal[
Normal(0.3, 0.1),
Normal(0.0, 0.1)], [0.5, 0.5])
function solver(a)
n = 100
h = 1/n
A = a[1] * diagm(0=>2/h^2*ones(n-1), 1=>-1/h^2*ones(n-2), -1=>-1/h^2*ones(n-2))
φ = 2.0*ones(n-1) # right hand side
u = A\φ
u[50]
end
batch_size = 64
x = placeholder(Float64, shape=[batch_size,10])
z = placeholder(Float64, shape=[batch_size,1])
dat = z + 0.25
fdat = reshape(map(solver, ae(x, [20,20,20,1])+1.0), batch_size, 1)
loss = empirical_sinkhorn(fdat, dat, dist=(x,y)->dist(x,y,2), method="lp")
opt = AdamOptimizer(0.01, beta1=0.5).minimize(loss)
sess = Session(); init(sess)
for i = 1:100000
run(sess, opt, feed_dict=Dict(
x=>randn(batch_size, 10),
z=>rand(m, batch_size,1)
))
end
```
| Loss Function | Iteration 5000 | Iteration 15000 | Iteration 25000 |
| ------------------------ | -------------------------------- | ---------------------------------- | ---------------------------------- |
| 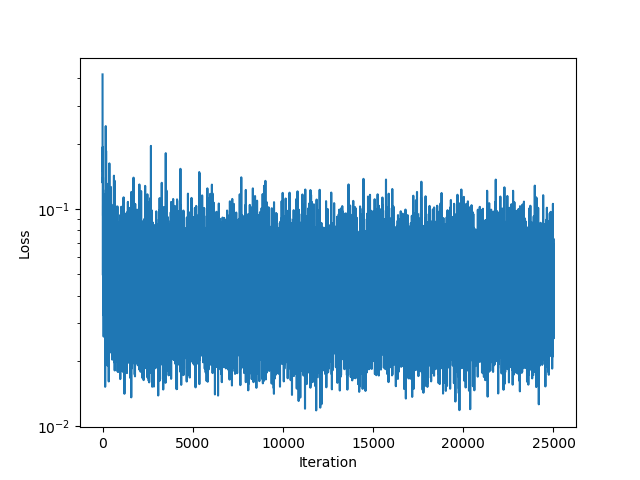 | 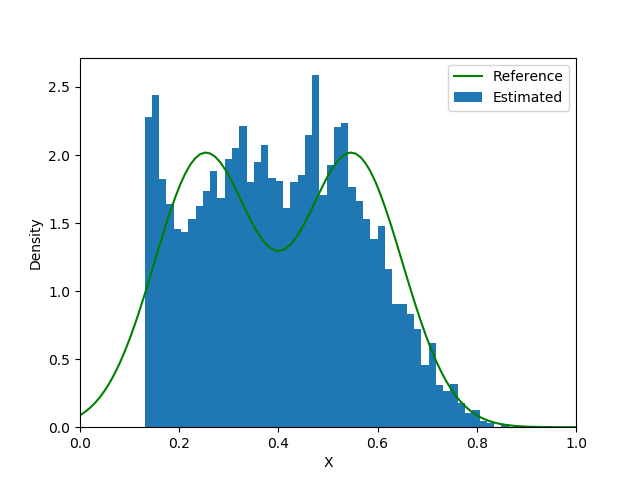 | 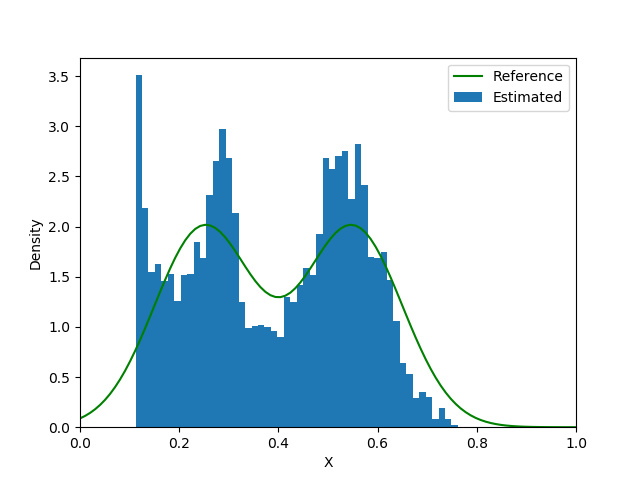 | 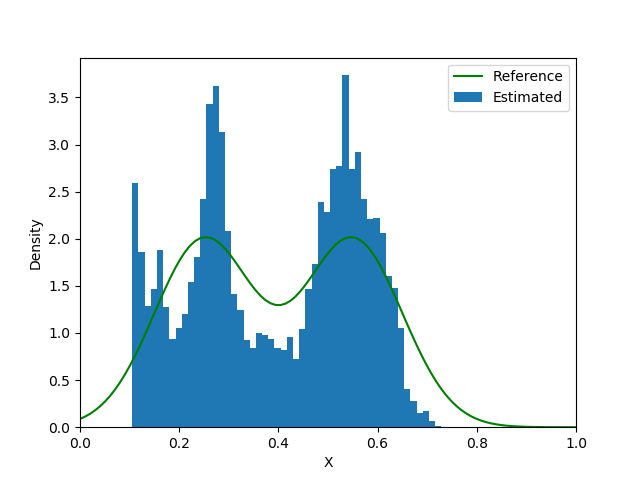 |
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 8294 | # Combining Neural Networks with Numerical Schemes
Modeling unknown componenets in a physical models using a neural networks is an important method for function inverse problem. This approach includes a wide variety of applications, including
* Koopman operator in dynamical systems
* Constitutive relations in solid mechanics.
* Turbulent closure relations in fluid mechanics.
* ......
To use the known physics to the largest extent, we couple the neural networks and numerical schemes (e.g., finite difference, finite element, or finite volumn method) for partial differential equations. Based on the nature of the observation data, we present three methods to train the neural networks using gradient-based optimization method: the residual minimization method, the penalty method, and the physics constrained learning. We discuss the pros and cons for each method and show how the gradients can be computed using automatic differentiation in ADCME.
## Introduction
Many science and engineering problems use models to describe the physical processes. These physical processes are usually derived from first principles or based on empirical relations. Neural networks have shown to be effective to model complex and high dimensional functions, and can be used to model the unknown mapping within a physical model. The known part of the model, such as conservation laws and boundary conditions, are preserved to obey the physics. Basically, we substutite unknown part of the model using neural networks in a physical system. As an example, consider a simple 1D heat equation
$$\begin{aligned}
\frac{\partial}{\partial x}\left(\kappa(u)\frac{\partial u}{\partial x}\right) &= f(x)& x\in \Omega\\
u(0) = u(1) &= 0
\end{aligned}$$
The diffusivity coefficient $\kappa(u)$ is a function of the temperature $u$, and is an unknown function to be calibrated. We consider a data-driven approach to discover $\kappa(u)$ using only the temperature data set $\mathcal{T}$. In the case where we do not know the constitutive relation, it can be modeled using a neural network $\kappa_\theta (u)$, where $\theta$ is the weights and biases of the neural network.
In the following, we will discuss three methods based on the nature of the observation data set $\mathcal{T}$ to train the neural network.
## Residual Minimization for Full Field Data
In the case $\mathcal{T}$ consist of full-field data, i.e., the values of $u(x)$ on a very fine grid, we can use the **residual minimization** to learn the neural network. Specifically, we can discretize the PDE using a numerical scheme, such as finite element method (FEM), and obtain the residual term
$$R_j(\theta) =\sum_i u(x_i)\int_0^1 \kappa_\theta(\sum_i c_i \phi_i) \phi_i'(x) \phi_j'(x) dx - \int_0^1 f(x)\phi_j(x)dx$$
where $\phi_i$ are the basis functions in FEM. To find the optimal values for $\theta$, we can perform a residual minimization
$$\min_\theta \sum_j R_j(\theta)^2$$
The residual minimization method avoids solving the PDE system, which can be expensive. The implication is straightforward using ADCME: all we need is to evaluate $R_j(\theta)$ and $\frac{\partial R_j(\theta)}{\partial \theta}$ (using automatic differention). However, the limitation is that this method is only applicable when full-field data are available.
In the following two references, we explore the applications of the residual minimization method to constitutive modeling
DZ Huang, K Xu, C Farhat, E Darve. [Learning Constitutive Relations from Indirect Observations Using Deep Neural Networks](https://arxiv.org/pdf/1905.12530.pdf)
K Xu, DZ Huang, E Darve. [Learning Constitutive Relations using Symmetric Positive Definite Neural Networks](https://arxiv.org/pdf/2004.00265.pdf)
## Penalty Method for Sparse Observations
In the case where $\mathcal{T}$ only consists of sparse observations, i.e., $u_o(x_i)$ (observation of $u(x_i)$) at only a few locations $\{x_i\}$, we can formulate the problem as a PDE-constrained optimization problem
$$\begin{aligned}
\min_\theta& \;\sum_i (u(x_i) - u_o(x_i))^2\\
\text{s.t.} &\; \frac{\partial}{\partial x}\left(\kappa_\theta(u)\frac{\partial u}{\partial x}\right) = f(x)& x\in \Omega\\
& u(0) = u(1) = 0
\end{aligned}\tag{1}$$
As pointed in [this article](https://kailaix.github.io/ADCME.jl/dev/tu_optimization/), we can apply the **penalty method** to solve the contrained optimization problem,
$$\min_{\theta,u} \;\sum_i (u(x_i) - u_o(x_i))^2 + \rho \|F(u, \theta)\|^2_2$$
Here $\rho$ is the penalty parameter and $F(u, \theta)$ is the discretized form of the PDE. For example, $F(u,\theta)_i$ can be $R_i(\theta)$ in the residual minimization problem.
The penalty method is conceptually simple and easy to implement. Like the residual minimization method, the penalty method requires limited insights into the numerical simulator to evaluate the gradients with respect to $u$ and $\theta$. The method does not require solving the PDE.
However, the penalty method treats $u$ as optimization variable and therefore typically has much more degrees of freedom than the original constrained optimization problem. Mathematically, the penalty method suffers from worse conditioning than the constrained one, making it unfavorable in many scenarios.
## Physics Constrained Learning
An alternative approach to the penalty method in the context of sparse observations is the **physics constrained learning** (PCL). The physics constrained learning reduces Equation 1 to an unconstrained optimization problem by two steps:
1. Solve for $u$ from the PDE constraint, given a candidate neural network;
2. Plug the solution $u(\theta)$ into the objective function and obtain a reduced loss function
The reduced loss function only depends on $\theta$ and therefore we can perform the unconstrained optimization, in which case a wide variety of off-the-shelf optimizers are available. The advantage of this approach is that PCL enforces the physics constraints, which can be crucial for some applications and are essential for numerical solvers. Additionally, PCL typically exhibits high efficiency and fast convergence compared to the other two methods. However, PCL requires deep insights into the numerical simulator since an analytical form of $u(\theta)$ is not always tractable. It requires automatic differentiation through implict numerical solvers as well as iterative algorithms, which are usually not supported in AD frameworks. In the references below, we provide the key techniques for solving these problems. A final limitation of PCL is that it consumes much more memory and runtime per iteration than the other two methods.
For more details on PCL, and comparison between the penalty method and PCL, see the following reference
K Xu, E Darve. [Physics Constrained Learning for Data-driven Inverse Modeling from Sparse Observations](https://arxiv.org/pdf/2002.10521.pdf)
## Summary
Using physics based machine learning to solve inverse problems requires techniques from different areas, deep learning, automatic differentiation, numerical PDEs, and physical modeling. By a combination of the best from all worlds, we can leverage the power of modern high performance computing environments to solve long standing inverse problems in physical modeling. Specially, in this article we review three methods for training a neural network in a physical model using automatic differentiation. These methods can be readily implemented in ADCME. We conclude this article by a direct comparison of the three methods
| Method | Residual Minimization | Penalty Method | Physics Constrained Learning |
| ------------------------------ | --------------------- | -------------- | ---------------------------- |
| Sparse Observations | ❌ | ✔️ | ✔️ |
| Easy-to-implement | ✔️ | ✔️ | ❌ |
| Enforcing Physical Constraints | ❌ | ❌ | ✔️ |
| Fast Convergence | ❌ | ❌ | ✔️ |
| Minimal Optimization Variables | ✔️ | ❌ | ✔️ |
| ADCME | https://github.com/kailaix/ADCME.jl.git |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.