licenses
sequencelengths 1
3
| version
stringclasses 677
values | tree_hash
stringlengths 40
40
| path
stringclasses 1
value | type
stringclasses 2
values | size
stringlengths 2
8
| text
stringlengths 25
67.1M
| package_name
stringlengths 2
41
| repo
stringlengths 33
86
|
|---|---|---|---|---|---|---|---|---|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 16885 | # PDE Constrained Optimization
In the broad context, the physics based machine learning can be formulated as a PDE-constrained optimization problem. The PDE-constrained optimization problem aims at finding the optimal design variables such that the objective function is minimized and the constraints---usually described by PDEs---are satisfied. PDE-contrained optimization has a large variety of applications, such as optimal control and inverse problem. The topic is at the intersection of numerical PDE discretization, mathematical optimization, software design, and physics modeling.
Mathematically, a PDE-constrained optimization can be formulated as
$$\begin{aligned}
\min_{y\in \mathcal{Y}, u\in \mathcal{U}}&\; J(y, u)\\
\text{s.t.}&\; F(y, u)=0 & \text{the governing PDEs}\\
&\; c(y,u)=0&\text{additional equality constraints}\\
&\; h(y, u)\geq 0&\text{additional inequality constraints}
\end{aligned}$$
Here $J$ is the objective function, $y$ is the **design variable**, $u$ is the **state variable**.
In this section, we will focus on the PDE-constrained optimization with only the governing PDE constraints, and we consider a discretize-then-optimize and gradient-based optimization approach. Specifically, the objective function and the PDEs are first discretized numerically, leading to a constrained optimization problem with a finite dimensional optimization variable. We use gradient-based optimization because it provides fast convergence and an efficient way to integrate optimization and simulation. However, this approach requires insight into the simulator and can be quite all-consuming to obtain the gradients.
## Example
We consider an exemplary PDE-constrained optimization problem: assume we want to have a specific temperature distribution on a metal bar $\bar u(x)$ by imposing a heat source $y(x)$ on the bar
$$\begin{aligned}
\min_{y\in \mathcal{Y}, u\in \mathcal{U}}&\; L(y, u) = \frac{1}{2}\int_0^1 \|u(x) - \bar u(x)\|^2 dx + \frac{\rho}{2}\int_0^1 y(x)^2 dx \\
\text{s.t.}&\; f(y, u)=0
\end{aligned}$$
Here $f(y,u)=0$ is the static heat equation with the boundary conditions.
$$c(x)u_{xx}(x) = y(x),\quad x\in (0,1), \quad u(0)=u_0, u(1)=u_1$$
where $c(x)$ is the diffusivity coefficient, $u_0$ and $u_1$ are fixed boundaries.
After discretization, the optimization problem becomes
$$\begin{aligned}
\min_{y, u}&\; J(y, u) = \frac{1}{2}\|u-\bar u\|_2 + \frac{\rho}{2}\|y\|^2\\
\text{s.t.}&\; F(y, u)= Ku - y = 0
\end{aligned}\tag{1}$$
where $K$ is the stiffness matrix, taking into account of the boundary conditions, $u$, $\bar u$, and $y$ are vectors.
In what follows, we basically apply common optimization method to the constrained optimization problem Equation 1.
## Method 1: Penalty Method
The simplest method for solving the unconstrained optimization problem Equation 1 is via the penalty method. Specifically, instead of solving the original constrained optimization problem, we solve
$$\min_{y, u} \frac{1}{2}\|u-\bar u\|_2 + \frac{\rho}{2}\|y\|^2 + \lambda \|f(y, u)\|^2_2$$
where $\lambda$ is the penalty parameter.
The penalty method is **conceptually simple** and is also **easy-to-implement**. Additionally, it does not require solving the PDE constraint $f(y,u)=0$ and thus the comptuational cost for each iteration can be small. However, avoid solving the PDE constraint is also a disadvantage since it means the penalty method **does not eventually enforce the physical constraint**. The solution from the penalty method only converges to the the true solution when $\lambda\rightarrow \infty$, which is **not computationally feasible**. Additionally, despite less cost per iteration, the total number of iterations can be huge when the PDE constraint is "stiff". To gain some intuition, consider the following problem
$$\begin{aligned}
\min_{u}&\; 0\\
\text{s.t.}&\; Ku - y = 0
\end{aligned}$$
The optimal value is $u = K^{-1}y$ and the cost by solving the linear system is usually propertional to $\mathrm{cond}(K)$. However, if we were to solve the problem using the penalty method
$$\min_{u} \|Ku-y\|^2_2$$
The condition number for solving the least square problem (e.g., by solving the normal equation $K^TK u = K^Ty$) is usually propertional to $\mathrm{cond}(K)^2$. When the problem is stiff, i.e., $\mathrm{cond}(K)$ is large, the penaty formulation can be much more **ill-conditioned** than the original problem.
## Method 2: Primal and Primal-Dual Method
A classical theory regarding constrained optimization is the Karush-Kuhn-Tucker (KKT) Theorm. It states a necessary and sufficient condition for a value to be optimal under certain assumptions. To formulate the KKT condition, consider the **Lagrangian function**
$$L(u, y, \lambda) = \frac{1}{2}\|u-\bar u\|_2 + \frac{\rho}{2}\|y\|^2 + \lambda^T(Ku - y)$$
where $\lambda$ is the **adjoint variable**. The corresponding KKT condition is
$$\begin{aligned}
\frac{\partial L}{\partial u} &= u - \bar u + K^T\lambda = 0 \\
\frac{\partial L}{\partial y} &= \rho y - \lambda = 0 \\
\frac{\partial L}{\partial \lambda} &= Ku - y = 0
\end{aligned}$$
The **primal-dual method** solves for $(u, y, \lambda)$ simultaneously from the linear system
$$\begin{bmatrix} 1 & 0 & K^T\\ 0 & \rho & -1\\K & -1 & 0 \end{bmatrix}\begin{bmatrix}u\\ y\\ \lambda\end{bmatrix} = \begin{bmatrix}\bar u\\ 0 \\ 0\end{bmatrix}$$
In contrast, the **dual method** eliminates the state variables $u$ and $y$ and solves for $\lambda$
$$(1+\rho KK^T)\lambda = \rho K\bar u$$
The primal-dual and dual method have some advantages. For example, we reduce finding the minimum of a constrained optimization method to solving a nonlinear equation, where certain tools are available. For the primal-dual method, the limitation is that the system of equations can be very large and difficult to solve. The dual method requires analytical derivation and is not always obvious in practice, especially for nonlinear problems.
## Method 3: Primal Method
The primal method reduces the constrained optimization problem to an unconstrained optimization problem by "solving" the numerical PDE first. In the previous example, we have $u(y) = K^{-1}y$ and therefore we have
$$\min_y \frac{1}{2}\|K^{-1}y-\bar u\|_2 + \frac{\rho}{2}\|y\|^2$$
The advantage is three-folds
* Dimension reduction. The optimization variables are reduced from $(u,y)$ to the design variables $y$ only.
* Enforced physical constraints. The physical constraints are enforced numerically.
* Unconstrained optimization. The reduced problem is a constrained optimization problem and many off-the-shelf optimizers (gradient descent, BFGS, CG, etc.) are available.
However, to compute the gradients, the primal method requires deep insights into the numerical solver, which may be highly nonlinear and implicit. The usual automatic differentiation (AD) framework are in general not applicable to this type of operators (nodes in the computational graph) and we need special algorithms.
### Link to Adjoint-State Method
The adjoint state method is a standard method for computing the gradients of the objective function with respect to design variables in PDE-constrained optimization. Consider
$$\begin{aligned}
\min_{y, u}&\; J(y, u)\\
\text{s.t.}&\; F(y, u)=0
\end{aligned}$$
Let $u$ be the state variable and $y$ be the design variable. Assume we solve for $u=u(y)$ from the PDE constraint, then we have the reduced objective function
$$\hat J(y) = J(y, u(y))$$
To conduct gradient-based optimization, we need to compute the gradient
$$\frac{d \hat J(y)}{d y} =\nabla_y J(y, u(y)) +\nabla_u J(y, u(y))\frac{du(y)}{dy} \tag{2}$$
To compute the $\frac{du(y)}{dy}$ we have
$$F(y, u(y))=0 \Rightarrow \nabla_y F + \nabla_u F \frac{du}{dy} = 0 \tag{3}$$
Therefore we can use Equations 2 and 3 to evaluate the gradient of the objective function
$$\frac{d \hat J(y)}{d y} = \nabla_y J(y, u(y)) - \nabla_u J(y, u(y)) (\nabla_u F(y,u(y)))^{-1} \nabla_y F(y, u(y))\tag{4}$$
### Link to the Lagrange Function
There is a nice interpretation of Equations 2 and 3 using the Lagrange function. Consider the langrange function
$$L(y, u, \lambda) = J(y, u) + \lambda^T F(y, u) \tag{5}$$
The KKT condition says
$$\begin{aligned}
\frac{\partial L}{\partial \lambda} &= F(y, u) = 0\\
\frac{\partial L}{\partial u} &= \nabla_u J + \lambda^T \nabla_u F(y, u) = 0\\
\frac{\partial L}{\partial y} &= \nabla_y J + \lambda^T \nabla_y F(y, u) = 0\\
\end{aligned}$$
Now we relax the third equation: given a fixed $y$ (not necessarily optimal), we can solve for $(u,\lambda)$ from the first two equations. We plug the solutions into the third equation and obtain (note $u$ satisfies $F(y, u)=0$)
$$\frac{\partial L}{\partial y} = \nabla_y J(y, u) - \nabla_u J(y, u) (\nabla_u F(y,u))^{-1} \nabla_y F(y, u)$$
which is the same expression as Equation 4. When $y$ is optimal, this expression is equal to zero, i.e., all the KKT conditions are satisfied. The gradient of the unconstrained optimization problem is also zero. Both the primal system and the primal-dual system confirm the optimality. This relation also explains why we call the method above as "adjoint" state method. In summary, the adjoint-state method involves a three-step process
* **Step 1.** Create the Lagrangian Equation 5.
* **Step 2**. Conduct forward computation and solve for $u$ from
$$F(y, u) = 0$$
* **Step 3.** Compute the adjoint variable $\lambda$ from
$$\nabla_u J + \lambda^T \nabla_u F(y, u) = 0$$
* **Step 4.** Compute the sensitivity
$$\frac{\partial \hat J}{\partial y} = \nabla_y J + \lambda^T \nabla_y F(y, u)$$
### Link to Automatic Differentiation
#### Computational Graph
The adjoint-state method is also closely related to the reverse-mode automatic differentiation. Consider a concrete PDE-constrained optimization problem
$$\begin{aligned}
\min_{\mathbf{u}_1, {\theta}} &\ J = f_4(\mathbf{u}_1, \mathbf{u}_2, \mathbf{u}_3, \mathbf{u}_4), \\
\mathrm{s.t.} & \ \mathbf{u}_2 = f_1(\mathbf{u}_1, {\theta}), \\
& \ \mathbf{u}_3 = f_2(\mathbf{u}_2, {\theta}),\\
& \ \mathbf{u}_4 = f_3(\mathbf{u}_3, {\theta}).
\end{aligned}$$
where $f_1$, $f_2$, $f_3$ are PDE constraints, $f_4$ is the loss function, $\mathbf{u}_1$ is the initial condition, and $\theta$ is the model parameter.
#### Adjoint-State Method
The Lagrangian function is
$$\mathcal{L}= f_4(\mathbf{u}_1, \mathbf{u}_2, \mathbf{u}_3, \mathbf{u}_4) + {\lambda}^{T}_{2}(f_1(\mathbf{u}_1, {\theta}) - \mathbf{u}_2) + {\lambda}^T_{3}(f_2(\mathbf{u}_2, {\theta}) - \mathbf{u}_3) + {\lambda}^T_{4}(f_3(\mathbf{u}_3, {\theta}) - \mathbf{u}_4)$$
Upon conducting the foward computation we have all $\mathbf{u}_i$ available. To compute the adjoint variable $\lambda_i$, we have
$$\begin{aligned}
{\lambda}_4^T &= \frac{\partial f_4}{\partial \mathbf{u}_4} \\
{\lambda}_3^T &= \frac{\partial f_4}{\partial \mathbf{u}_3} + {\lambda}_4^T\frac{\partial f_3}{\partial \mathbf{u}_3} \\
{\lambda}_2^T &= \frac{\partial f_4}{\partial \mathbf{u}_2} + {\lambda}_3^T\frac{\partial f_2}{\partial \mathbf{u}_2}
\end{aligned}$$
The gradient of the objective function in the constrained optimization problem is given by
$$\frac{\partial \mathcal{L}}{\partial {\theta}} = {\lambda}_2^T\frac{\partial f_1}{\partial {\theta}} + {\lambda}_3^T\frac{\partial f_2}{\partial {\theta}} + {\lambda}_4^T\frac{\partial f_3}{\partial {\theta}}$$

#### Automatic Differentiation
Now let's see how the computation is linked to automatic differentiation. As explained in the previous tutorials, when we implement the automatic differentiation operator, we need to backpropagate the "top" gradients to its upstreams in the computational graph. Consider the operator $f_2$, we need to implement two operators
$$\begin{aligned}
\text{Forward:}&\; \mathbf{u}_3 = f_2(\mathbf{u}_2, \theta)\\
\text{Backward:}&\; \frac{\partial J}{\partial \mathbf{u}_2}, \frac{\partial J}{\partial \theta} = b_2\left(\frac{\partial J^{\mathrm{tot}}}{\partial \mathbf{u}_3}, \mathbf{u}_2, \theta\right)
\end{aligned}$$
Here $\frac{\partial J^{\mathrm{tot}}}{\partial \mathbf{u}_3}$ is the "total" gradient $\mathbf{u}_3$ received from the downstream in the computational graph.
#### Relation between AD and Adjoint-State Method
The backward operator is implemented using the chain rule
$$\begin{aligned}
\frac{\partial J}{\partial \mathbf{u}_2} = \frac{\partial J^{\mathrm{tot}}}{\partial \mathbf{u}_3} \frac{\partial f_2}{\partial \mathbf{u}_2}\qquad
\frac{\partial J}{\partial \theta} = \frac{\partial J^{\mathrm{tot}}}{\partial \mathbf{u}_3} \frac{\partial f_2}{\partial \theta}
\end{aligned}$$
The total gradient $\mathbf{u}_2$ received is
$$\frac{\partial J^{\mathrm{tot}}}{\partial \mathbf{u}_2} = \frac{\partial f_4}{\partial \mathbf{u}_2} + \frac{\partial J}{\partial \mathbf{u}_2} = \frac{\partial f_4}{\partial \mathbf{u}_2} + \frac{\partial J^{\mathrm{tot}}}{\partial \mathbf{u}_3} \frac{\partial f_2}{\partial \mathbf{u}_2}$$
The dual constraint in the KKT condition
$${\lambda}_2^T = \frac{\partial f_4}{\partial \mathbf{u}_2} + {\lambda}_3^T\frac{\partial f_2}{\partial \mathbf{u}_2}$$
Now we see the important relation
$$\boxed{{\lambda}_i^T = \frac{\partial J^{\mathrm{tot}}}{\partial \mathbf{u}_i}}$$
That means, in general, **the reverse-mode AD is back-propagating the Lagrange multiplier (adjoint variables)**.
#### Dicussion and Physics based Machine Learning
However, although the link between AD and adjoint state methods enables us to use AD tools for PDE-constrained optimization, many standard numerical schemes, such as implicit ones, involve an iterative process (e.g., Newton-Raphson) in nature. AD is usually designed for explicit operators. To this end, we can borrow the idea from the adjoint-state methods and enhance the current AD framework to differentiate through iterative solvers or implicit schemes. This is known as **physics constrained learning**. For more details, see [the paper](https://arxiv.org/pdf/2002.10521.pdf) here.
Another ongoing research is the combination of neural networks and physical modeling. One idea is to model the unknown relations in the physical system using neural networks. Those includes
* Koopman operator in dynamical systems
* Constitutive relations in solid mechanics.
* Turbulent closure relations in fluid mechanics.
* ......
In the context of PDE-constrained optimization, there is no essential difference between learning a neural network and finding the optimal physical parameters, except that the design variables become the weights and biases of neural networks. However, the neural networks raise some questions, for example: does one optimization technique preferable than the others? How to stabilize the numerical solvers when neural networks are present? How to add physical constraints to the neural network? How to scale the algorithm? How is the well-posedness and conditioning of the optimization problem? How much data do we need? How to stabilize the training (e.g., regularization, projected gradients)? Indeed, the application of neural networks in the physics machine learning leave more problems than what have been answered here.
## Other Optimization Techniques
Besides the formulation and optimization techniques introduced here, there are many other topics, which we have not covered here, on PDE-constrained optimization. It is worthwhile mentioning that we consider the optimize-then-discretize approach. The alternative approach, discretize-then-optimize, derives the optimal condition (KKT condition) on the continuous level and then discretize the dual PDE. In this formulation, we can use the same discretization method for both the primal and dual system, and therefore we may preserve some essential physical properties. However, the gradients derived in this way may deviate from the true gradients of the constrained optimization problem.
Another noteworthy ongoing research is to formulate the optimization as an action functional. Just like every PDE can be viewed as a minimization of an energy function, a PDE-constrained optimization problem can also be formulated as a problem of minimizing a functional. These discussions are beyond the scope of the tutorial.
## Summary
PDE-constrained optimization has a wide variety of applications. Specifically, formulating the physics based machine learning as a PDE-constrained optimization problem lends us a rich toolbox for optimization, discretization, and algorithm design. The combination of neural networks and physics modeling poses a lot of opportunities as well as challenges for solving long standing problems. The gradient based optimization with automatic differentiation has the potential to consolidate the techniques in a single framework. | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 6726 | # Inverse Modeling Recipe
Here is a tip for inverse modeling using ADCME.
## Forward Modeling
The first step is to implement your forward computation in ADCME. Let's consider a simple example. Assume that we want to compute a transformation from $\{x_1,x_2, \ldots, x_n\}$ to $\{f_\theta(x_1), f_\theta(x_2), \ldots, f_\theta(x_n)\}$, where
$$f_\theta(x) = a_2\sigma(a_1x+b_1)+b_2\quad \theta=(a_1,b_2,a_2,b_2)$$
The value $\theta=(1,2,3,4)$. We can code the forward computation as follows
```julia
using ADCME
θ = constant([1.;2.;3.;4.])
x = collect(LinRange(0.0,1.0,10))
f = θ[3]*sigmoid(θ[1]*x+θ[2])+θ[4]
sess = Session(); init(sess)
f0 = run(sess, f)
```
We obtained
```text
10-element Array{Float64,1}:
6.6423912339336475
6.675935315969742
6.706682200447601
6.734800968378825
6.7604627001561575
6.783837569144308
6.805092492614008
6.824389291376896
6.841883301751329
6.8577223804673
```
## Inverse Modeling
Assume that we want to estimate the target variable $\theta$ from observations $\{f_\theta(x_1), f_\theta(x_2), \ldots, f_\theta(x_n)\}$. The inverse modeling is split into 6 steps. Follow the steps one by one
* **Step 1: Mark the target variable as `placeholder`**. That is, we replace `θ = constant([1.;2.;3.;4.])` by `θ = placeholder([1.;2.;3.;4.])`.
* **Step 2: Check that the loss is zero given true values.** The loss function is usually formulated so that it equals zero when we plug the true value to the target variable.
You should expect `0.0` using the following codes.
```julia
using ADCME
θ = placeholder([1.;2.;3.;4.])
x = collect(LinRange(0.0,1.0,10))
f = θ[3]*sigmoid(θ[1]*x+θ[2])+θ[4]
loss = sum((f - f0)^2)
sess = Session(); init(sess)
@show run(sess, loss)
```
* **Step 3: Use `lineview` to visualize the landscape**. Assume the initial guess is $\theta_0$, we can use the `lineview` function from [`ADCMEKit.jl`](https://github.com/kailaix/ADCMEKit.jl) package to visualize the landscape from $\theta_0=[0,0,0,0]$ to $\theta^*$ (true value). This gives us early confidence on the correctness of the implementation as well as the difficulty of the optimization problem. You can also use `meshview`, which shows a 2D landscape but is more expensive to evaluate.
```julia
using ADCME
using ADCMEKit
θ = placeholder([1.;2.;3.;4.])
x = collect(LinRange(0.0,1.0,10))
f = θ[3]*sigmoid(θ[1]*x+θ[2])+θ[4]
loss = sum((f - f0)^2)
sess = Session(); init(sess)
@show run(sess, loss)
lineview(sess, θ, loss, [1.;2.;3.;4.], zeros(4)) # or meshview(sess, θ, loss, [1.;2.;3.;4.])
```
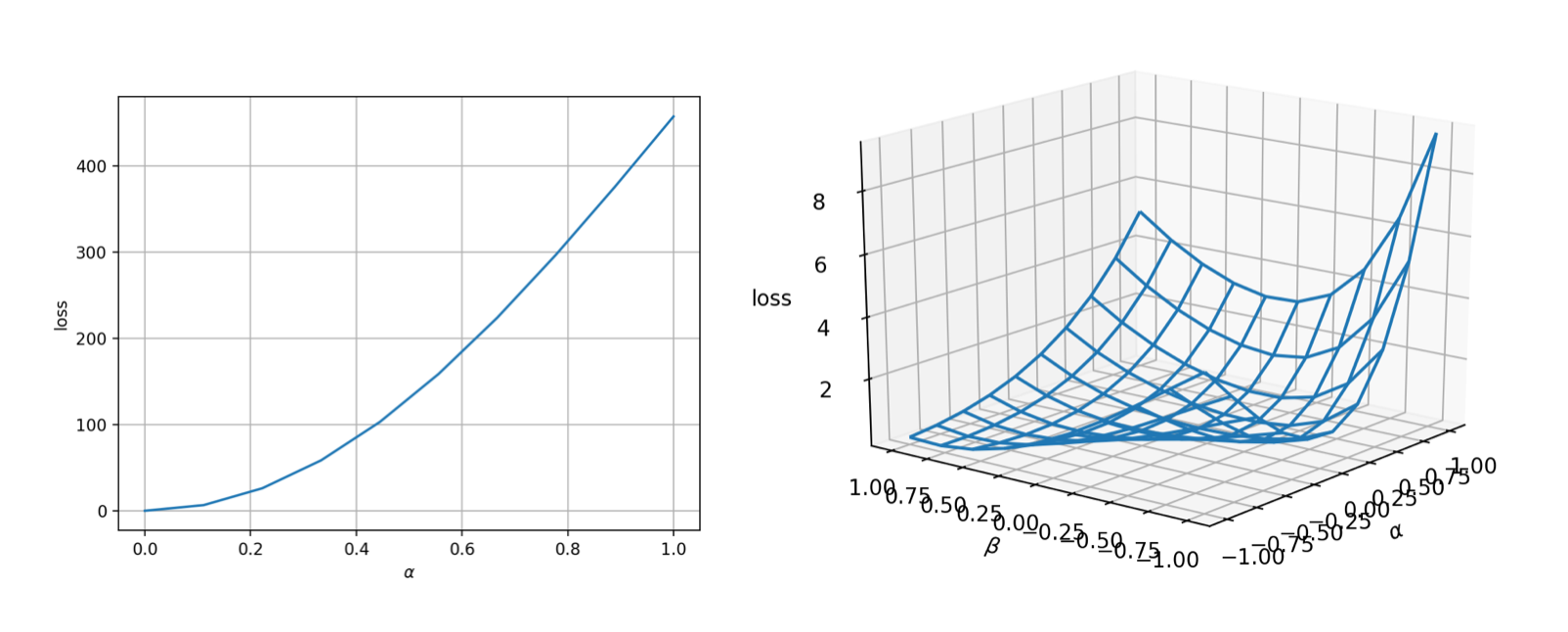
The landscape is very nice (convex and smooth)! That means the optimization should be very easy.
* **Step 4: Use `gradview` to check the gradients.** `ADCMEKit.jl` also provides `gradview` which visualizes the gradients at arbitrary points. This helps us to check whether the gradient is implemented correctly.
```julia
using ADCME
using ADCMEKit
θ = placeholder([1.;2.;3.;4.])
x = collect(LinRange(0.0,1.0,10))
f = θ[3]*sigmoid(θ[1]*x+θ[2])+θ[4]
loss = sum((f - f0)^2)
sess = Session(); init(sess)
@show run(sess, loss)
lineview(sess, θ, loss, [1.;2.;3.;4.], zeros(4)) # or meshview(sess, θ, loss, [1.;2.;3.;4.])
gradview(sess, θ, loss, zeros(4))
```
You should get something like this:
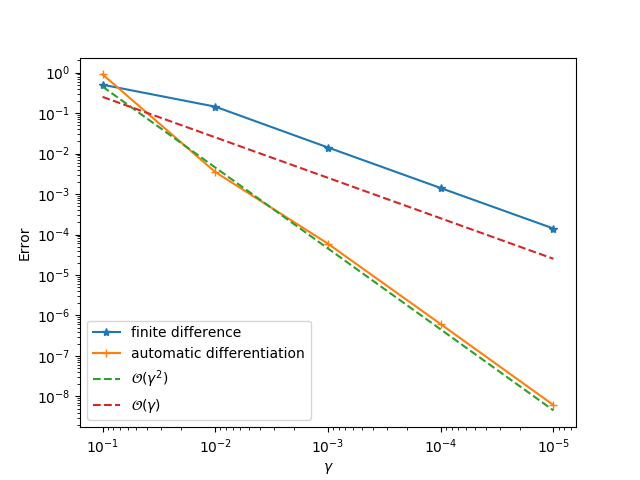
* **Step 5: Change `placeholder` to `Variable` and perform optimization!** We use L-BFGS-B optimizer to solve the minimization problem. A useful trick is to multiply the loss function by a large scalar so that the optimizer does not stop early (or reduce the tolerance).
```julia
using ADCME
using ADCMEKit
θ = Variable(zeros(4))
x = collect(LinRange(0.0,1.0,10))
f = θ[3]*sigmoid(θ[1]*x+θ[2])+θ[4]
loss = 1e10*sum((f - f0)^2)
sess = Session(); init(sess)
BFGS!(sess, loss)
run(sess, θ)
```
You should get
```bash
4-element Array{Float64,1}:
1.0000000000008975
2.0000000000028235
3.0000000000056493
3.999999999994123
```
That's exact what we want.
* **Step 6: Last but not least, repeat step 3 and step 4 if you get stuck in a local minimum.** Scrutinizing the landscape at the local minimum will give you useful information so you can make educated next step!
## Debugging
### Sensitivity Analysis
When the gradient test fails, we can perform _unit sensitivity analysis_. The idea is that given a function $y = f(x_1, x_2, \ldots, x_n)$, if we want to confirm that the gradients $\frac{\partial f}{\partial x_i}$ is correctly implemented, we can perform 1D gradient test with respect to a small perturbation $\varepsilon_i$:
$$y(\varepsilon_i) = f(x_1, x_2, \ldots, x_i + \varepsilon_i, \ldots, x_n)$$
or in the case you are not sure about the scale of $x_i$,
$$y(\varepsilon_i) = f(x_1, x_2, \ldots, x_i (1 + \varepsilon_i), \ldots, x_n)$$
As an example, if we want to check whether the gradients for `sigmoid` is correctly backpropagated in the above code, we have
```julia
using ADCME
using ADCMEKit
ε = placeholder(1.0)
θ = constant([1.;2.;3.;4.])
x = collect(LinRange(0.0,1.0,10))
f = θ[3]*sigmoid(θ[1]*x+θ[2] + ε)+θ[4]
loss = sum((f - f0)^2)
sess = Session(); init(sess)
gradview(sess, ε, loss, 0.01)
```
We will see a second order convergence for the automatic differentiation method while a first order convergence for the finite difference method. The principle for identifying problematic operator is to go from downstream operators to top stream operators in the computational graph. For example, given the computational graph
$$f_1\rightarrow f_2 \rightarrow \cdots \rightarrow f_i \rightarrow f_{i+1} \rightarrow \ldots \rightarrow f_n$$
If we conduct sensitivity analysis for $f_i:o_i \mapsto o_{i+1}$, and find that the gradient is wrong, then we can infer that at least one of the operators in the downstream $f_i \rightarrow f_{i+1} \rightarrow \ldots \rightarrow f_n$ has problematic gradients.
### Check Your Training Data
Sometimes it is also useful to check your training data. For example, if you are working with numerical schemes, check whether your training data are generated from reasonable physical parameters, and whether or not the numerical schemes are stable.
### Local Minimum
To check whether or not the optimization converged to a local minimum, you can either check `meshview` or `lineview`. However, these functions only give you some hints and you should only rely solely on their results. A more reliable check is to consider `gradview`. In principle, if you have a local minimum, the gradient at the local minimum should be zero, and therefore the finite difference curve should also have second order convergence. | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 2831 | # Sparse Linear Algebra
ADCME augments TensorFlow APIs by adding sparse linear algebra support. In ADCME, sparse matrices are represented by [`SparseTensor`](@ref). This data structure stores `indices`, `rows` and `cols` of the sparse matrices and keep track of relevant information such as whether it is diagonal for performance consideration. The default is row major (due to TensorFlow backend).
When evaluating `SparseTensor`, the output will be `SparseMatrixCSC`, the native Julia representation of sparse matrices
```julia
A = run(sess, s) # A has type SparseMatrixCSC{Float64,Int64}
```
## Sparse Matrix Construction
* By passing columns (`Int64`), rows (`Int64`) and values (`Float64`) arrays
```julia
ii = [1;2;3;4]
jj = [1;2;3;4]
vv = [1.0;1.0;1.0;1.0]
s = SparseTensor(ii, jj, vv, 4, 4)
```
* By passing a `SparseMatrixCSC`
```julia
using SparseArrays
s = SparseTensor(sprand(10,10,0.3))
```
* By passing a dense array (tensor or numerical array)
```julia
D = Array(sprand(10,10,0.3)) # a dense array
d = constant(D)
s = dense_to_sparse(d)
```
There are also special constructors.
| Description | Code |
| --------------------------------- | -------------- |
| Diagonal matrix with diagonal `v` | `spdiag(v)` |
| Empty matrix with size `m`, `n` | `spzero(m, n)` |
| Identity matrix with size `m` | `spdiag(m)` |
## Matrix Traits
1. Size of the matrices
```julia
size(s) # (10,20)
size(s,1) # 10
```
2. Return `row`, `col`, `val` arrays (also known as COO arrays)
```julia
ii,jj,vv = find(s)
```
## Arithmetic Operations
1. Add Subtract
```julia
s = s1 + s2
s = s1 - s2
```
2. Scalar Product
```julia
s = 2.0 * s1
s = s1 / 2.0
```
3. Sparse Product
```julia
s = s1 * s2
```
4. Transposition
```julia
s = s1'
```
## Sparse Solvers
1. Solve a linear system (`s` is a square matrix)
```julia
sol = s\rhs
```
2. Solve a least square system (`s` is a tall matrix)
```julia
sol = s\rhs
```
!!! note
The least square solvers are implemented using Eigen sparse linear packages, and the gradients are also implemented. Thus, the following codes will work as expected (the gradients functions will correctly compute the gradients):
```julia
ii = [1;2;3;4]
jj = [1;2;3;4]
vv = constant([1.0;1.0;1.0;1.0])
rhs = constant(rand(4))
s = SparseTensor(ii, jj, vv, 4, 4)
sol = s\rhs
run(sess, sol)
run(sess, gradients(sum(sol), rhs))
run(sess, gradients(sum(sol), vv))
```
## Assembling Sparse Matrix
In many applications, we want to accumulate `row`, `col` and `val` to assemble a sparse matrix in iterations. For this purpose, we provide the `SparseAssembler` utilities.
```@docs
SparseAssembler
accumulate
assemble
```
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 14057 | # What is ADCME? Computational Graph, Automatic Differentiation & TensorFlow
## Computational Graph
A computational graph is a functional description of the required computation. In the computationall graph, an edge represents a value, such as a scalar, a vector, a matrix or a tensor. A node represents a function whose input arguments are the the incoming edges and output values are are the outcoming edges. Based on the number of input arguments, a function can be nullary, unary, binary, ..., and n-ary; based on the number of output arguments, a function can be single-valued or multiple-valued.
Computational graphs are directed and acyclic. The acyclicity implies the forward propagation computation is well-defined: we loop over edges in topological order and evaluates the outcoming edges for each node. To make the discussion more concrete, we illustrate the computational graph for
$$z = \sin(x_1+x_2) + x_2^2 x_3$$

There are in general two programmatic ways to construct computational graphs: static and dynamic declaration. In the static declaration, the computational graph is first constructed symbolically, i.e., no actual numerical arithmetic are executed. Then a bunch of data is fed to the graph for the actual computation. An advantage of static declarations is that they allow for graph optimization such as removing unused branches. Additionally, the dependencies can be analyzed for parallel execution of independent components. Another approach is the dynamic declaration, where the computational graph is constructed on-the-fly as the forward computation is executed. The dynamic declaration interleaves construction and evaluation of the graph, making software development more intuitive.
## Automatic Differentiation
An important application of computational graphs is automatic differentiation (AD). In general, there are three modes of AD: reverse-mode, forward-mode, and mixed mode. In this tutorial, we focus on the forward-mode and reverse-mode.
Basically, the forward mode and the reverse mode automatic differenation both use the. chain rule for computing the gradients. They evaluate the gradients of "small" functions analytically (symbolically) and chain all the computed **numerical** gradients via the chain rule
$$\frac{\partial f\circ g (x)}{\partial x} = \frac{\partial f'\circ g(x)}{\partial g} {\frac{\partial g'(x)}{\partial x}}$$
### Forward Mode
In the forward mode, the gradients are computed in the same order as function evaluation, i.e., ${\frac{\partial g'(x)}{\partial x}}$ is computed first, and then $\frac{\partial f'\circ g(x)}{\partial g} {\frac{\partial g'(x)}{\partial x}}$ as a whole. The idea is the same for a computational graph, except that we need to **aggregate** all the gradients from up-streams first, and then **forward** the gradients to down-stream nodes. Here we show how the gradient
$$f(x) = \begin{bmatrix}
x^4\\
x^2 + \sin(x) \\
-\sin(x)\end{bmatrix}$$
is computed.
| Forward-mode AD in the Computational Graph | Example |
| ------------------------------------------ | ----------------------------- |
|  |  |
### Reverse Mode
In contrast, the reverse-mode AD computes the gradient in the reverse order of forward computation, i.e., $\frac{\partial f'\circ g(x)}{\partial g}$ is first evaluated and then $\frac{\partial f'\circ g(x)}{\partial g} {\frac{\partial g'(x)}{\partial x}}$ as a whole. In the computational graph, each node first aggregate all the gradients from down-streams and then back-propagates the gradient to upstream nodes.
We show how the gradients of $z = \sin(x_1+x_2) + x_2^2 x_3$ is evaluated.
| Reverse-mode AD in the Computational Graph | Step 1 | Step 2 | Step 3 | Step 4 |
| ------------------------------------------ | ---------------------- | ---------------------- | ---------------------- | ---------------------- |
|  | 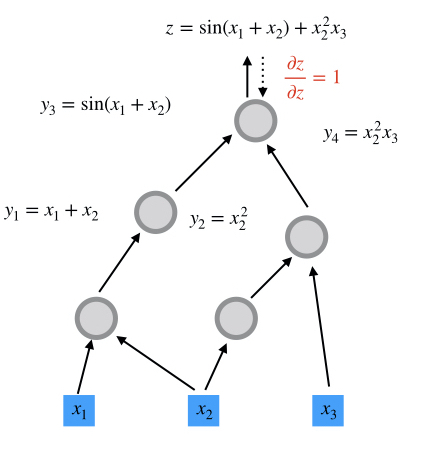 |  |  |  |
## Comparison
Reverse-mode AD reuses gradients from down-streams. Therefore, this mode is useful for many-to-few mappings. In contrast, forward-mode AD reuses gradients from upstreams. This mechanism makes forward-mode AD suitable for few-to-many mappings. Therefore, for inverse modeling problems where the objective function is usually a scalar, reverse-mode AD is most relevant. For uncertainty quantification or sensitivity analysis, the forward-mode AD is most useful. We summarize the two modes in the following table:
For a function $f:\mathbf{R}^n \rightarrow \mathbf{R}^m$
| Mode | Suitable for... | Complexity[^OPS] | Application |
| ------- | --------------- | ------------------------------ | ---------------- |
| Forward | $m\gg n$ | $\leq 2.5\;\mathrm{OPS}(f(x))$ | UQ |
| Reverse | $m\ll n$ | $\leq 4\;\mathrm{OPS}(f(x))$ | Inverse Modeling |
[^OPS]: See "Margossian CC. A review of automatic differentiation and its efficient implementation. Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery. 2019 Jul;9(4):e1305.".
## A Mathematical Description of Reverse-mode Automatic Differentiation
Because the reverse-mode automatic differentiation is very important for inverse modeling, we devote this section to a rigorious mathematical description of the reverse-mode automatic differentiation.
To explain how reverse-mode AD works, let's consider constructing a computational graph with independent variables
$$\{x_1, x_2, \ldots, x_n\}$$
and the forward propagation produces a single output $x_N$, $N>n$. The gradients $\frac{\partial x_N(x_1, x_2, \ldots, x_n)}{\partial x_i}$
$i=1$, $2$, $\ldots$, $n$ are queried.
The idea is that this algorithm can be decomposed into a sequence of functions $f_i$ ($i=n+1, n+2, \ldots, N$) that can be easily differentiated analytically, such as addition, multiplication, or basic functions like exponential, logarithm and trigonometric functions. Mathematically, we can formulate it as
$$\begin{aligned}
x_{n+1} &= f_{n+1}(\mathbf{x}_{\pi({n+1})})\\
x_{n+2} &= f_{n+2}(\mathbf{x}_{\pi({n+2})})\\
\ldots\\
x_{N} &= f_{N}(\mathbf{x}_{\pi({N})})\\
\end{aligned}$$
where $\mathbf{x} = \{x_i\}_{i=1}^N$ and $\pi(i)$ are the parents of $x_i$, s.t., $\pi(i) \in \{1,2,\ldots,i-1\}$.

The idea to compute $\partial x_N / \partial x_i$ is to start from $i = N$, and establish recurrences to calculate derivatives with respect to $x_i$ in terms of derivatives with respect to $x_j$, $j >i$. To define these recurrences rigorously, we need to define different functions that differ by the choice of independent variables.
The starting point is to define $x_i$ considering all previous $x_j$, $j < i$, as independent variables. Then:
$$x_i(x_1, x_2, \ldots, x_{i-1}) = f_i(\mathbf{x}_{\pi(i)})$$
Next, we observe that $x_{i-1}$ is a function of previous $x_j$, $j < i-1$, and so on; so that we can recursively define $x_i$ in terms of fewer independent variables, say in terms of $x_1$, ..., $x_k$, with $k < i-1$. This is done recursively using the following definition:
$$x_i(x_1, x_2, \ldots, x_j) = x_i(x_1, x_2, \ldots, x_j, f_{j+1}(\mathbf{x}_{\pi(j+1)})), \quad n < j+1 < i$$
Observe that the function of the left-hand side has $j$ arguments, while the function on the right has $j+1$ arguments. This equation is used to "reduce" the number of arguments in $x_i$.
With these definitions, we can define recurrences for our partial derivatives which form the basis of the back-propagation algorithm. The partial derivatives for
$$x_N(x_1, x_2, \ldots, x_{N-1})$$
are readily available since we can differentiate
$$f_N(\mathbf{x}_{\pi(N)})$$
directly. The problem is therefore to calculate partial derivatives for functions of the type $x_N(x_1, x_2, \ldots, x_i)$ with $i<N-1$. This is done using the following recurrence:
$$\frac{\partial x_N(x_1, x_2, \ldots, x_{i})}{\partial x_i} = \sum_{j\,:\,i\in \pi(j)}
\frac{\partial x_N(x_1, x_2, \ldots, x_j)}{\partial x_j}
\frac{\partial x_j(x_1, x_2, \ldots, x_{j-1})}{\partial x_i}$$
with $n < i< N-1$. Since $i \in \pi(j)$, we have $i < j$. So we are defining derivatives with respect to $x_i$ in terms of derivatives with respect to $x_j$ with $j > i$. The last term
$$\frac{\partial x_j(x_1, x_2, \ldots, x_{j-1})}{\partial x_k}$$
is readily available since:
$$x_j(x_1, x_2, \ldots, x_{j-1}) = f_j(\mathbf{x}_{\pi(j)})$$

The computational cost of this recurrence is proportional to the number of edges in the computational graph (excluding the nodes $1$ through $n$), assuming that the cost of differentiating $f_k$ is $O(1)$. The last step is defining
$$\frac{\partial x_N(x_1, x_2, \ldots, x_n)}{\partial x_i} = \sum_{j\,:\,i\in \pi(j)}
\frac{\partial x_N(x_1, x_2, \ldots, x_j)}{\partial x_j}
\frac{\partial x_j(x_1, x_2, \ldots, x_{j-1})}{\partial x_i}$$
with $1 \le i \le n$. Since $n < j$, the first term
$$\frac{\partial x_N(x_1, x_2, \ldots, x_j)}{\partial x_j}$$
has already been computed in earlier steps of the algorithm. The computational cost is equal to the number of edges connected to one of the nodes in $\{1, \dots, n\}$.
We can see that the complexity of the back-propagation is bounded by that of the forward step, up to a constant factor. Reverse mode differentiation is very useful in the penalty method, where the loss function is a scalar, and no other constraints are present.
As a concrete example, we consider the example of evaluating $\frac{dz(x_1,x_2,x_3)}{dx_i}$, where $z = \sin(x_1+x_2) + x_2^2x_3$. The gradients are backward propagated exactly in the reverse order of the forward propagation.
| Step 1 | Step 2 | Step 3 | Step 4 |
| ---------------------- | ---------------------- | ---------------------- | ---------------------- |
|  |  |  |  |
## TensorFlow
Google's TensorFlow provides a convenient way to specify the computational graph statically. TensorFlow has automatic differentiation features and its performance is optimized for large-scale computing. ADCME is built on TensorFlow by overloading numerical operators and augmenting TensorFlow with essential scientific computing functionalities. We contrast the TensorFlow implementation with the ADCME implementation of computing the objective function and its gradient in the following example.
$$y(x) = \|(AA^T+xI)^{-1}b-c\|^2, \; z = y'(x)$$
where $A\in \mathbb{R}^{n\times n}$ is a random matrix, $x,b,c$ are scalars, and $n=10$.
**TensorFlow Implementation**
```python
import tensorflow as tf
import numpy as np
A = tf.constant(np.random.rand(10,10), dtype=tf.float64)
x = tf.constant(1.0, dtype=tf.float64)
b = tf.constant(np.random.rand(10), dtype=tf.float64)
c = tf.constant(np.random.rand(10), dtype=tf.float64)
B = tf.matmul(A, tf.transpose(A)) + x * tf.constant(np.identity(10))
y = tf.reduce_sum((tf.squeeze(tf.matrix_solve(B, tf.reshape(b, (-1,1))))-c)**2)
z = tf.gradients(y, x)[0]
sess = tf.Session()
sess.run([y, z])
```
**Julia Implementation**
```julia
using ADCME, LinearAlgebra
A = constant(rand(10,10))
x = constant(1.0)
b = rand(10)
c = rand(10)
y = sum(((A*A'+x*diagm(0=>ones(10)))\b - c)^2)
z = gradients(y, x)
sess = Session()
run(sess, [y,z])
```
## Summary
The computational graph and automatic differentiation are the core concepts underlying ADCME. TensorFlow works as the workhorse for optimion and execution of the computational graph in a high performance environment.
To construct a computational graph for a Julia program, ADCME overloads most numerical operators like `+`, `-`, `*`, `/` and matrix multiplication in Julia by the corresponding TensorFlow operators. Therefore, you will find many similar workflows and concepts as TensorFlow, such as `constant`, `Variable`, `session`, etc. However, not all operators relevant to scientific computing in Julia have its counterparts in TensorFlow. To that end, custom kernels are implemented to supplement TensorFlow, such as sparse linear algebra related functions.
ADCME aims at providing a easy-to-use, flexible, and high performance interface to do data processing, implement numerical schemes, and conduct mathematical optimization. It is built not only for academic interest but also for real-life large-scale simulations.
Like TensorFlow, ADCME works in sessions, in which each session consumes a computational graph. Usually the workflow is split into three steps:
1. Define independent variables. `constant` for tensors that do not require gradients and `Variable` for those requiring gradients.
```julia
a = constant(0.0)
```
2. Construct the computational graph by defining the computation
```julia
L = (a-1)^2
```
3. Create a session and run the computational graph
```julia
sess = Session()
run(sess, L)
```
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 1813 |
# Overview
> ADCME: Your Gateway to Inverse Modeling with Physics Based Machine Learning
ADCME is an open-source Julia package for inverse modeling in scientific computing using automatic differentiation. The backend of ADCME is the high performance deep learning framework, TensorFlow, which provides parallel computing and automatic differentiation features based on computational graph, but ADCME augments TensorFlow by functionalities---like sparse linear algebra---essential for scientific computing. ADCME leverages the Julia environment for maximum efficiency of computing. Additionally, the syntax of ADCME is designed from the beginning to be compatible with the Julia syntax, which is friendly for scientific computing.
**Prerequisites**
The tutorial does not assume readers with experience in deep learning. However, basic knowledge of scientific computing in Julia is required.
**Tutorial Series**
[What is ADCME? Computational Graph, Automatic Differentiation & TensorFlow](./tu_whatis.md)
[ADCME Basics: Tensor, Type, Operator, Session & Kernel](./tu_basic.md)
[PDE Constrained Optimization](./tu_optimization.md)
[Sparse Linear Algebra in ADCME](./tu_sparse.md)
[Numerical Scheme in ADCME: Finite Difference Example](./tu_fd.md)
[Numerical Scheme in ADCME: Finite Element Example](./tu_fem.md)
[Inverse Modeling in ADCME](./tu_inv.md)
[Inverse Modeling Recipe](./tu_recipe.md)
[Combining NN with Numerical Schemes](./tu_nn.md)
[Advanced: Automatic Differentiation for Implicit Operations](./tu_implicit.md)
[Advanced: Custom Operators](./tu_customop.md)
[Advanced: Debugging and Profiling](./tu_debug.md)
[Exercise](./exercise.md)[^exercise]
[^exercise]: If you want to discuss or check your exercise solutions, you are welcome to send an email to [email protected].
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 14503 | # Uncertainty Quantification
<!-- qunatifying uncertainty of neural networks in inverse problems using linearized Gaussian modeels -->
## Theory
### Basic Model
We consider a physical model
$$\begin{aligned}
y &= h(s) + \delta \\
s &= g(z) + \epsilon
\end{aligned}\tag{1}$$
Here $\delta$ and $\epsilon$ are independent Gaussian noises. $s\in \mathbb{R}^m$ is the physical quantities we are interested in predicting, and $y\in \mathbb{R}^n$ is the measurement. $g$ is a function approximator, which we learn from observations in our inverse problem. $z$ is considered fixed for quantifying the uncertainty for a specific observation under small perturbation, although $z$ and $s$ may have complex dependency.
$\delta$ can be interpreted as the measurement error
$$\mathbb{E}(\delta\delta^T) = R$$
$\epsilon$ is interpreted as our prior for $s$
$$\mathbb{E}(\epsilon\epsilon^T) = Q$$
### Linear Gaussian Model
When the standard deviation of $\epsilon$ is small, we can safely approximate $h(s)$ using its linearized form
$$h(s)\approx \nabla h(s_0) (s-s_0) + h(s_0) := \mu + H s$$
Here
$$\mu = h(s_0) - \nabla h(s_0) s_0\quad H = \nabla h(x_0)$$
Therefore, we have an approximate governing equation for Equation 1:
$$\begin{aligned}
y &= H s + \mu + \delta\\
s &= g(z) + \epsilon
\end{aligned}\tag{2}$$
Using Equation 2, we have
$$\begin{aligned}
\mathbb{E}(y) & = H g(z) + \mu \\
\text{cov}(y) & = \mathbb{E}\left[(H (x-g(z)) + \delta )(H (x-g(z)) + \delta )^T \right] = H QH^T + R
\end{aligned}$$
### Bayesian Inversion
#### Derivation
From the model Equation 2 we can derive the joint distribution of $s$ and $y$, which is a multivariate Gaussian distribution
$$\begin{bmatrix}
x_1\\
x_2
\end{bmatrix}\sim \mathcal{N}\left(
\begin{bmatrix}
g(z)\\
Hg(z) + \mu
\end{bmatrix} \Bigg| \begin{bmatrix}
Q & QH^T \\
HQ & HQH^T + R
\end{bmatrix}
\right)$$
Here the covariance matrix $\text{cov}(s, y)$ is obtained via
$$\text{cov}(s, y) = \mathbb{E}(s, Hs + \mu+\delta) = \mathbb{E}(s-g(z), H(s-g(z))) = \mathbb{E}((s-g(z))(s-g(z))^T) H^T = QH^T$$
Recall the formulas for conditional Gaussian distributions:
Given
$$\begin{bmatrix}
s\\
y
\end{bmatrix}\sim \mathcal{N}\left(
\begin{bmatrix}
\mu_1\\
\mu_2
\end{bmatrix} \Bigg| \begin{bmatrix}
\Sigma_{11} & \Sigma_{12} \\
\Sigma_{21} & \Sigma_{22}
\end{bmatrix}
\right)$$
We have
$$x_1 | x_2 \sim \mathcal{N}(\mu_{1|2}, V_{1|2})$$
where
$$\begin{aligned}
\mu_{1|2} &= \mu_1 + \Sigma_{12}\Sigma_{22}^{-1} (x_2-\mu_2)\\
V_{1|2} &= \Sigma_{11} - \Sigma_{12} \Sigma_{22}^{-1}\Sigma_{21}
\end{aligned}$$
Let $x_1 = s$, $x_2 = y$, we have the following formula for Baysian inversion:
$$\begin{aligned}
\mu_{s|y} &= g(z) + QH^{T}(HQH^T + R)^{-1} (y - Hg(z) - \mu)\\
V_{s|y} &= Q - QH^T(HQH^T + R)^{-1} HQ
\end{aligned}\tag{3}$$
#### Analysis
Now we consider how to compute Equation 3. In practice, we should avoid direct inverting the matrix $HQH^T + R$ since the cost is cubic in the size of dimensions of the matrix. Instead, the following theorem gives us a convenient way to solve the problem
!!! info "Theorem"
Let $\begin{bmatrix}L \\ x^T\end{bmatrix}$ be the solution to
$$\begin{bmatrix}
HQH^T + R & H g(z) \\
g(z)^T H^T & 0
\end{bmatrix}\begin{bmatrix}
L \\
x^T
\end{bmatrix} = \begin{bmatrix}
HQ \\
g(z)^T
\end{bmatrix}\tag{4}$$
Then we have
$$\begin{aligned}
\mu_{s|y} = g(z) + L^T (y-\mu) \\
V_{s|y} = Q - gx^T - QH^TL
\end{aligned}\tag{5}$$
The linear system in Equation 5 is symmetric but may not be SPD and therefore we may encounter numerical difficulty when solving the linear system Equation 4. In this case, we can add perturbation $\varepsilon g^T g$ to the zero entry.
!!! info "Theorem"
If $\varepsilon> \frac{1}{4\lambda_{\min}}$, where $\lambda_{\min}$ is the minimum eigenvalue of $Q$, then the linear system in Equation 4 is SPD.
The above theorem has a nice interpretation: typically we can choosee our prior for the physical quantity $s$ to be a scalar matrix $Q = \sigma_{{s}}^2 I$, where $\sigma_{s}$ is the standard deviation, then $\lambda_{\min} = \sigma_s^2$. This indicates that if we use a very concentrated prior, the linear system can be far away from SPD and requires us to use a large perturbation for numerical stability. Therefore, in the numerical example below, we choose a moderate $\sigma_s$. The alternative approach is to add the perturbation.
In ADCME, we provide the implementation [`uq`](@ref)
```julia
s, Σ = uqlin(y-μ, H, R, gz, Q)
```
## Benchmark
To show how the proposed method work compared to MCMC, we consider a model problem: estimating Young's modulus and Poisson's ratio from sparse observations.
$$\begin{aligned}
\mathrm{div}\; \sigma &= f & \text{ in } \Omega \\
\sigma n &= 0 & \text{ on }\Gamma_N \\
u &= 0 & \text{ on }\Gamma_D \\
\sigma & = H\epsilon
\end{aligned}$$
Here the computational domain $\Omega=[0,1]\times [0,1.5]$. We fixed the left side ($\Gamma_D$) and impose an upward pressure on the right side. The other side is considered fixed. We consider the plane stress linear elasticity, where the constitutive relation determined by
$$H = \frac{E}{(1+\nu)(1-2\nu)}\begin{bmatrix}
1-\nu & \nu & 0 \\
\nu & 1-\nu & 0 \\
0 & 0 & \frac{1-2\nu}{2}
\end{bmatrix}$$
Here the true parameters
$$E = 200\;\text{GPa} \quad \nu = 0.35$$
They are the parameters to be calibrated in the inverse modeling. The observation is given by the displacement vectors of 20 random points on the plate.
We consider a uniform prior for the random walk MCMC simuation, so the log likelihood up to a constant is given by
$$l(y') = -\frac{(y-y')^2}{2\sigma_0^2}$$
where $y'$ is the current proposal, $y$ is the measurement, and $\sigma_0$ is the standard deviation. We simulate 100000 times, and the first 20% samples are used as "burn-in" and thus discarded.
For the linearized Gaussian model, we use $Q=I$ and $R=\sigma_0^2I$ to account for a unit Gaussian prior and measurement error, respectively.
The following plots show the results
| $\sigma_0=0.01$ | $\sigma_0=0.05$ | $\sigma_0=0.1$ |
| ------------------------------------------------------------ | ------------------------------------------------------------ | ------------------------------------------------------------ |
|  |  |  |
| $\sigma_0=0.2$ | $\sigma_0=0.5$ | |
|  |  | |
We see that when $\sigma_0$ is small, the approximation is quite consistent with MCMC results. When $\sigma_0$ is large, due to the assumption that the uncertainty is Gaussian, the linearized Gaussian model does not fit well with the uncertainty shape obtained with MCMC; however, the result is still consistent since the linearized Gaussian model yields a larger standard deviation.
## Example 1: UQ for Parameter Inverse Problems
We consider a simple example for 2D Poisson problem.
$$\begin{aligned}
\nabla (K(x, y) \nabla u(x, y)) &= 1 & \text{ in } \Omega\\
u(x,y) &= 0 & \text{ on } \partial \Omega
\end{aligned}$$
where $K(x,y) = e^{c_1 + c_2 x + c_3 y}$.
Here $c_1$, $c_2$, $c_3$ are parameter to be estimated. We first generate data using $c_1=1,c_2=2,c_3=3$ and add Gaussian noise $\mathcal{N}(0, 10^{-3})$ to 64 observation in the center of the domain $[0,1]^2$. We run the inverse modeling and obtain an estimation of $c_i$'s. Finally, we use [`uq`](@ref) to conduct the uncertainty quantification. We assume $\text{error}_{\text{model}}=0$.
The following plot shows the estimated mean together with 2 standard deviations.

```julia
using ADCME
using PyPlot
using AdFem
Random.seed!(233)
idx = fem_randidx(100, m, n, h)
function poisson1d(c)
m = 40
n = 40
h = 0.1
bdnode = bcnode("all", m, n, h)
c = constant(c)
xy = gauss_nodes(m, n, h)
κ = exp(c[1] + c[2] * xy[:,1] + c[3]*xy[:,2])
κ = compute_space_varying_tangent_elasticity_matrix(κ, m, n, h)
K = compute_fem_stiffness_matrix1(κ, m, n, h)
K, _ = fem_impose_Dirichlet_boundary_condition1(K, bdnode, m, n, h)
rhs = compute_fem_source_term1(ones(4m*n), m, n, h)
rhs[bdnode] .= 0.0
sol = K\rhs
sol[idx]
end
c = Variable(rand(3))
y = poisson1d(c)
Γ = gradients(y, c)
Γ = reshape(Γ, (100, 3))
# generate data
sess = Session(); init(sess)
run(sess, assign(c, [1.0;2.0;3.0]))
obs = run(sess, y) + 1e-3 * randn(100)
# Inverse modeling
loss = sum((y - obs)^2)
init(sess)
BFGS!(sess, loss)
y = obs
H = run(sess, Γ)
R = (2e-3)^2 * diagm(0=>ones(100))
X = run(sess, c)
Q = diagm(0=>ones(3))
m, V = uqlin(y, H, R, X, Q)
plot([1;2;3], [1.;2.;3.], "o", label="Reference")
errorbar([1;2;3],m + run(sess, c), yerr=2diag(V), label="Estimated")
legend()
```
!!! info "The choice of $R$"
The standard deviation $2\times 10^{-3}$ consists of the model error ($10^{-3}$) and the measurement error $10^{-3}$.
## Example 2: UQ for Function Inverse Problems
In this example, let us consider uncertainty quantification for function inverse problems. We consider the same problem as Example 1, except that $K(x,y)$ is represented by a neural network (the weights and biases are represented by $\theta$)
$$\mathcal{NN}_\theta:\mathbb{R}^2 \rightarrow \mathbb{R}$$
We consider a highly nonlinear $K(x,y)$
$$K(x,y) = 0.1 + \sin x+ x(y-1)^2 + \log (1+y)$$

The left panel above shows the exact $K(x,y)$ and the learned $K(x,y)$. We see we have a good approximation but with some error.

The left panel above shows the exact solution while the right panel shows the reconstructed solution after learning.
We apply the UQ method and obtain the standard deviation plot on the left, together with absolute error on the right. We see that our UQ estimation predicts that the right side has larger uncertainty, which is true in consideration of the absolute error.

```julia
using Revise
using ADCME
using PyPlot
using AdFem
m = 40
n = 40
h = 1/n
bdnode = bcnode("all", m, n, h)
xy = gauss_nodes(m, n, h)
xy_fem = fem_nodes(m, n, h)
function poisson1d(κ)
κ = compute_space_varying_tangent_elasticity_matrix(κ, m, n, h)
K = compute_fem_stiffness_matrix1(κ, m, n, h)
K, _ = fem_impose_Dirichlet_boundary_condition1(K, bdnode, m, n, h)
rhs = compute_fem_source_term1(ones(4m*n), m, n, h)
rhs[bdnode] .= 0.0
sol = K\rhs
end
κ = @. 0.1 + sin(xy[:,1]) + (xy[:,2]-1)^2 * xy[:,1] + log(1+xy[:,2])
y = poisson1d(κ)
sess = Session(); init(sess)
SOL = run(sess, y)
# inverse modeling
κnn = squeeze(abs(ae(xy, [20,20,20,1])))
y = poisson1d(κnn)
using Random; Random.seed!(233)
idx = fem_randidx(100, m, n, h)
obs = y[idx]
OBS = SOL[idx]
loss = sum((obs-OBS)^2)
init(sess)
BFGS!(sess, loss, 200)
figure(figsize=(10,4))
subplot(121)
visualize_scalar_on_fem_points(SOL, m, n, h)
subplot(122)
visualize_scalar_on_fem_points(run(sess, y), m, n, h)
plot(xy_fem[idx,1], xy_fem[idx,2], "o", c="red", label="Observation")
legend()
figure(figsize=(10,4))
subplot(121)
visualize_scalar_on_gauss_points(κ, m, n, h)
title("Exact \$K(x, y)\$")
subplot(122)
visualize_scalar_on_gauss_points(run(sess, κnn), m, n, h)
title("Estimated \$K(x, y)\$")
H = gradients(obs, κnn)
H = run(sess, H)
y = OBS
hs = run(sess, obs)
R = (1e-1)^2*diagm(0=>ones(length(obs)))
s = run(sess, κnn)
Q = (1e-2)^2*diagm(0=>ones(length(κnn)))
μ, Σ = uqnlin(y, hs, H, R, s, Q)
σ = diag(Σ)
figure(figsize=(10,4))
subplot(121)
visualize_scalar_on_gauss_points(σ, m, n, h)
title("Standard Deviation")
subplot(122)
visualize_scalar_on_gauss_points(abs.(run(sess, κnn)-κ), m, n, h)
title("Absolute Error")
```
## Example 3: UQ for Function Inverse Problem
In this case, we consider a more challenging case, where $K$ is a function of the state variable, i.e., $K(u)$. $K$ is approximated by a neural network, but we need an iterative solver that involves the neural network to solve the problem
$$\begin{aligned}
\nabla\cdot (K(u) \nabla u(x, y)) &= 1 & \text{ in } \Omega\\
u(x,y) &= 0 & \text{ on } \partial \Omega
\end{aligned}$$
We tested two cases: in the first case, we use the synthetic observation $u_{\text{obs}}\in\mathbb{R}$ without adding any noise, while in the second case, we add 1% Gaussian noise to the observation data
$$u'_{\text{obs}} = u_{\text{obs}} (1+0.01 z)\quad z\sim \mathcal{N}(0, I_n)$$
The prior for $K(u)$ is $\mathcal{N}(0, 10^{-2})$, where one standard deviation is around 10%~20% of the actual $K(u)$ value. The measurement prior is given by
$$\mathcal{N}(0, \sigma_{\text{model}}^2 + \sigma_{\text{noise}}^2)$$
The total error is modeled by $\sigma_{\text{model}}^2 + \sigma_{\text{noise}}^2\approx 10^{-4}$.
| Description | Uncertainty Bound (two standard deviation) | Standard Deviation at Grid Points |
| --------------------------- | ---- | ---- |
| $\sigma_{\text{noise}}=0$ |  |  |
| $\sigma_{\text{noise}}=0.01$ |  |  |
We see that in general when $u$ is larger, the uncertainty bound is larger. For small $u$, we can estimate the map $K(u)$ quite accurately using a neural network. | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 6155 | # Variational Autoencoder
Let's see how to implement an autoencoder for generating MNIST images in ADCME. The mathematics underlying autoencoder is the Bayes formula
$$p(z|x) = \frac{p(x|z)p(z)}{p(x)}$$
where $x$ a sample from the data distribution and $z$ is latent variables. To model the data distribution given the latent variable, $p(x|z)$, we use a deep generative neural network $g_\phi$ that takees $z$ as the input and outputs $x$. This gives us the approximate $p_\phi(x|z) \approx p(x|z)$.
However, computing $p(z|x)$ directly can be intractable. To this end, we approximate the posterior using $z\sim \mathcal{N}(\mu_x, \sigma_x^2I)$, where $\mu_x$ and $\sigma_x$ are both encoded using neural networks, where $x$ is the input to the neural network. In this way, we obtain an approximate posterior
$$p_w(z|x) = \frac{1}{(\sqrt{2\pi \sigma_x^2})^d}\exp\left( -\frac{\|z-\mu_x)\|^2}{2\sigma_x^2} \right) \tag{1}$$
How can we choose the correct weights and biases $\phi$ and $w$? The idea is to minimize the discrepancy between the true posterior and the approximate posterior Equation (1). We can use the KL divergence, which is a metric for measuring the discrepancy between two distributions
$$\mathrm{KL}(p_w(z|x)|| p(z|x)) = \mathbb{E}_{p_w}(\log p_w(z|x) - \log p(z|x)) \tag{2}$$
However, computing Equation 2 is still intractable since we do not know $\log p(z|x)$. Instead, we seek to minimize a maximize bound of the KL divergence
$$\begin{aligned}
\mathrm{ELBO} &= \log p(x) - \mathrm{KL}(p_w(z|x)|| p(z|x))\\
& = \mathbb{E}_{p_w}( \log p(z,x) - \log p_w(z|x)) \\
& = \mathbb{E}_{p_w(z|x)}[\log p_\phi(x|z)] - \mathrm{KL}(p_w(z|x) || p(z))
\end{aligned}$$
Note that we assumed that the generative neural network $g_\phi$ is sufficiently expressive so $p_\phi(y|z)\approx p(y|z)$. Additionally, because KL divergence is always positive
$$\mathrm{ELBO} \leq \log p(x)\tag{3}$$
Equation (3) justifies the name "evidence lower bound".
Let's consider how to compute ELBO for our autoencoder. For the marginal likelihood term $\mathbb{E}_{p_w(z|x)}[\log p_\phi(x|z)]$, for each given sample $y$, we can calculate the mean and covariance of $z$, namely $\mu_x$ and $\sigma_x^2I$. We sample $z_i\sim \mathcal{N}(\mu_x, \sigma_x^2I)$ and plug them into $g_\phi$ and obtain the outputs $x_i = g_\phi(z_i)$. If we assume that the decoder model is subject to Bernoulli distribution $x \sim Ber(g_\phi(z))$ (in this case we have $g_\phi(z)\in [0,1]$), we have the approximation
$$\mathbb{E}_{p_w(z|x)}[\log p_\phi(x|z)] \approx \frac{1}{n}\sum_{i=1}^n \left[x_i\log (g_\phi(z_i)) + (1-x_i) \log(1-g_\phi(z_i))\right]\tag{4}$$
Now let us consider the second term $\mathrm{KL}(p_w(z|x) || p(z))$. If we assign a unit Gaussian prior on $z$, we have
$$\begin{aligned}
\mathrm{KL}(p_w(z|x) || p(z)) &= \mathbb{E}_{p_w}[\log(p_w(z|x)) - \log(p(z)) ]\\
& = \mathbb{E}_{p_w}\left[-\frac{\|z-\mu_x\|^2}{2\sigma_x^2} - d\log(\sigma_x) + \frac{\|z\|^2}{2} \right]\\
& = -d - d\log(\sigma_x) +\frac{1}{2} \|\mu_x\|^2 + \frac{d}{2}\sigma_x^2
\end{aligned} \tag{5}$$
Using Equation 4 and 5 we can formulate a loss function, which we can use a stochastic gradient descent method to minimize.
The following code is an example of applying the autoencoder to learn a data distribution from MNIST dataset. Here is the result using this script:

```julia
using ADCME
using PyPlot
using MLDatasets
using ProgressMeter
function encoder(x, n_hidden, n_output, rate)
local μ, σ
variable_scope("encoder") do
y = dense(x, n_hidden, activation = "elu")
y = dropout(y, rate, ADCME.options.training.training)
y = dense(y, n_hidden, activation = "tanh")
y = dropout(y, rate, ADCME.options.training.training)
y = dense(y, 2n_output)
μ = y[:, 1:n_output]
σ = 1e-6 + softplus(y[:,n_output+1:end])
end
return μ, σ
end
function decoder(z, n_hidden, n_output, rate)
local y
variable_scope("decoder") do
y = dense(z, n_hidden, activation="tanh")
y = dropout(y, rate, ADCME.options.training.training)
y = dense(y, n_hidden, activation="elu")
y = dropout(y, rate, ADCME.options.training.training)
y = dense(y, n_output, activation="sigmoid")
end
return y
end
function autoencoder(xh, x, dim_img, dim_z, n_hidden, rate)
μ, σ = encoder(xh, n_hidden, dim_z, rate)
z = μ + σ .* tf.random_normal(size(μ), 0, 1, dtype=tf.float64)
y = decoder(z, n_hidden, dim_img, rate)
y = clip(y, 1e-8, 1-1e-8)
marginal_likelihood = sum(x .* log(y) + (1-x).*log(1-y), dims=2)
KL_divergence = 0.5 * sum(μ^2 + σ^2 - log(1e-8 + σ^2) - 1, dims=2)
marginal_likelihood = mean(marginal_likelihood)
KL_divergence = mean(KL_divergence)
ELBO = marginal_likelihood - KL_divergence
loss = -ELBO
return y, loss, -marginal_likelihood, KL_divergence
end
function step(epoch)
tx = train_x[1:batch_size,:]
@showprogress for i = 1:div(60000, batch_size)
idx = Array((i-1)*batch_size+1:i*batch_size)
run(sess, opt, x=>train_x[idx,:])
end
y_, loss_, ml_, kl_ = run(sess, [y, loss, ml, KL_divergence],
feed_dict = Dict(
ADCME.options.training.training=>false,
x => tx
))
println("epoch $epoch: L_tot = $(loss_), L_likelihood = $(ml_), L_KL = $(kl_)")
close("all")
for i = 1:3
for j = 1:3
k = (i-1)*3 + j
img = reshape(y_[k,:], 28, 28)'|>Array
subplot(3,3,k)
imshow(img)
end
end
savefig("result$epoch.png")
end
n_hidden = 500
rate = 0.1
dim_z = 20
dim_img = 28^2
batch_size = 128
ADCME.options.training.training = placeholder(true)
x = placeholder(Float64, shape = [128, 28^2])
xh = x
y, loss, ml, KL_divergence = autoencoder(xh, x, dim_img, dim_z, n_hidden, rate)
opt = AdamOptimizer(1e-3).minimize(loss)
train_x = MNIST.traintensor(Float64);
train_x = Array(reshape(train_x, :, 60000)');
sess = Session(); init(sess)
for i = 1:100
step(i)
end
```
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 2881 | # Video Lectures and Slides
---
Do you know...
**ADCME has its own YouTube channel [ADCME](https://www.youtube.com/channel/UCeaZFluNatYpkIYcq2TTklw)!**
---
## Slides
* [Physics Based Machine Learning for Inverse Problems (60 Pages)](https://kailaix.github.io/ADCMESlides/ADCME.pdf)
* [Automatic Differentiation for Scientific Computing (51 Pages)](https://kailaix.github.io/ADCMESlides/AD.pdf)
* [Deep Neural Networks and Inverse Modeling (50 Pages)](https://kailaix.github.io/ADCMESlides/Inverse.pdf)
* [Subsurface Inverse Modeling with Physics Based Machine Learning (35 Pages)](https://kailaix.github.io/ADCMESlides/Subsurface.pdf)
* [Calibrating Multivariate Lévy Processes with Neural Networks](https://kailaix.github.io/ADCMESlides/MSML2020.pdf)
* [ADCME.jl -- Physics Based Machine Learning for Inverse Problems (JuliaCN 2020, 40 Pages)](https://kailaix.github.io/ADCMESlides/JuliaConference2020_08_21.pdf)
* [ADCME -- Machine Learning for Computational Engineering (Berkeley/Stanford CompFest)](https://kailaix.github.io/ADCMESlides/CompFest2020.pdf)
* [Presentation on 09/23/2020 (29 Pages)](https://kailaix.github.io/ADCMESlides/InversePoreFlow2020_09_23.pdf)
* [Presentation on 10/01/2020 (40 Pages)](https://kailaix.github.io/ADCMESlides/2020_10_01.pdf)
* [Presentation on 10/06/2020 (37 Pages)](https://kailaix.github.io/ADCMESlides/2020_10_06.pdf)
* [Presentation in SMS, Peking University 10/22/2020 (35 Pages)](https://kailaix.github.io/ADCMESlides/2020_10_22.pdf)
* [Presentation in Berkeley, 11/17/2020 (60 Pages)](https://kailaix.github.io/ADCMESlides/2020_11_17.pdf); a relative comprehensive slide, see [here (31 Pages)](https://kailaix.github.io/ADCMESlides/2020_12_3.pdf) for a short version.
* [WCCM 2020 (23 Pages)](https://kailaix.github.io/ADCMESlides/2020_11_27.pdf)
* [SIAM CSE21 (21 Pages)](https://kailaix.github.io/ADCMESlides/2020_2_19.pdf)
* [AAAI MLPS 2021 (22 Pages)](https://kailaix.github.io/ADCMESlides/2021_3_9.pdf)
* [Ph.D. Oral Defense (~50 Pages)](https://kailaix.github.io/ADCMESlides/oral_defense.pdf)
## Instruction on Installing ADCME
1. [Installing ADCME (Windows)](https://www.youtube.com/watch?v=Vsc_dpyOD6k)
2. [Installing ADCME (MacOS)](https://youtu.be/nz1g-f-1s9Y)
3. [Installing ADCME (Linux)](https://youtu.be/fH0QrqgzUeo)
4. [Getting Started with ADCME](https://youtu.be/ZQyczBYZjQw)
## Posters
* [SPD-NN Poster](https://kailaix.github.io/ADCMESlides/NNFEM_poster.pdf)
## Videos
* [ADCME.jl -- Physics Based Machine Learning for Inverse Problems (中文)](https://www.bilibili.com/video/BV1va4y177fe)
* [Data-Driven Inverse Modeling with Incomplete Observations](https://www.youtube.com/watch?v=0r9qekmZGqk&t=480s)
* [AAAI Conference](https://studio.slideslive.com/web_recorder/share/20201126T052150Z__WCCM-ECCOMAS20__1328__data-driven-inverse-modeling-a?s=8f06e214-939f-467e-8899-bc66c2d64027) | ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.7.3 | 4ecfc24dbdf551f92b5de7ea2d99da3f7fde73c9 | docs | 2964 | # Install ADCME on Windows
The following sections provide instructions on installing ADCME on Windows computers.
## Install Julia
Windows users can install ADCME following these [instructions](https://julialang.org/downloads/). Choose your version of Windows (32-bit or 64-bit).
[Detailed instructions to install Julia on Windows](https://julialang.org/downloads/platform/#windows)
For Windows users, you can press the Windows button or click the Windows icon (usually located in the lower left of your screen) and type `julia`. Open the Desktop App `Julia` and you will see a Julia prompt.

## Install C/C++ Compilers
To use and build custom operators, you need a C/C++ compiler that is compatible with the TensorFlow backend. The prebuilt TensorFlow shipped with ADCME was built using Microsoft Visual Studio 2017 15. Therefore, you need to install this specific version.
1. Download and install from [here](https://visualstudio.microsoft.com/vs/older-downloads/)

Note that this is an older version of Visual Studio. It's not the one from 2019 but the previous version from 2017.
2. Double click the installer that you just downloaded. You will see the following image:

A free community version is available (**Visual Studio Community 2017**). Click **install** and a window will pop up.
3. Make sure the following two checkboxes are checked:
- In the **Workloads** tab, **Desktop development with C++** is checked.

- In the **Indivisual components** tab, **MSBuild** is checked.

4. Click **install** on the lower right corner. You will see the following window.
5. The installation may take some time. Once the installation is finished, you can safely close the installer.

## Configure Paths
In order to locate shared libraries and executable files provided by ADCME, you also need to set an extra set of PATH environment variables. Please add the following environment variables to your system path (my user name is `kaila`; please replace it with yours!)
```
C:\Users\kaila\.julia\adcme\Scripts
C:\Users\kaila\.julia\adcme\Library\bin
C:\Users\kaila\.julia\adcme\
```
Here is how you can add these environment paths:

## Install ADCME
Now you can install ADCME via
```julia
using Pkg
Pkg.add("ADCME")
```
| ADCME | https://github.com/kailaix/ADCME.jl.git |
|
[
"MIT"
] | 0.3.3 | d34a07459e1ebdc6b551ecb28e3c19993f544d91 | code | 662 | using Documenter, Noise
using Images, TestImages, ImageIO, Random
# set seed fixed for documentation
Random.seed!(42)
DocMeta.setdocmeta!(Noise, :DocTestSetup, :(using Noise, Images, TestImages, ImageIO); recursive=true)
makedocs(modules = [Noise],
sitename = "Noise.jl",
pages = ["index.md",
"man/additive_white_gaussian.md",
"man/mult_gauss.md",
"man/salt_pepper.md",
"man/poisson.md",
"man/quantization.md",
"man/function_references.md",
]
)
deploydocs(repo = "github.com/roflmaostc/Noise.jl.git")
| Noise | https://github.com/roflmaostc/Noise.jl.git |
|
[
"MIT"
] | 0.3.3 | d34a07459e1ebdc6b551ecb28e3c19993f544d91 | code | 2761 | module Noise
using PoissonRandom
using Random
using ImageCore
"""
complex_copy(x)
If `x` is real, it returns `x + im * x`
If `x` is complex, it returns `x`,
"""
complex_copy(a::T) where T = (a + 1im * a)::Complex{T}
complex_copy(a::Complex{T}) where T= a::Complex{T}
# clipping a single value
function clip_v(x)
return max(0, min(1, x))
end
function clip_v(x, minv, maxv)
return max(minv, min(maxv, x))
end
# get the maximum single value of a RGB image
function max_rgb(X::AbstractArray{RGB{T}}) where T
max_v = -Inf
for i in eachindex(X)
max_v = max(red(X[i]), max_v)
max_v = max(green(X[i]), max_v)
max_v = max(blue(X[i]), max_v)
end
return max_v
end
function apply_noise!(pixel_f, noise_f, X::Union{AbstractArray{Gray{T}}, AbstractArray{RGB{T}},
AbstractArray{T}}, clip) where T
f(x) = pixel_f(x, noise_f(x))
# defining the core functions inside here, gives 6x speed improvement
# core functions non clipping
function core_f(x::RGB)
return RGB(f(red(x)),
f(green(x)),
f(blue(x)))
end
function core_f(x::Gray)
return Gray(f(gray(x)))
end
function core_f(x)
return f(x)
end
function core_f_clip(x::RGB)
return RGB(clip_v(f(red(x))),
clip_v(f(green(x))),
clip_v(f(blue(x))))
end
function core_f_clip(x::Gray)
return Gray(clip_v(f(gray(x))))
end
function core_f_clip(x)
return clip_v(f(x))
end
# if normed clip the values to be in [0, 1]
if T <: Normed || clip
@inbounds for i in eachindex(X)
X[i] = core_f_clip(X[i])
end
else
@inbounds for i in eachindex(X)
X[i] = core_f(X[i])
end
end
return X
end
# function which use exactly the same noise for each color channel of a pixel
function apply_noise_chn!(pixel_f, noise_f, X::AbstractArray{RGB{T}}, clip) where T
if T <: Normed || clip
@inbounds for i in eachindex(X)
a = X[i]
n = noise_f(red(a)*0)
X[i] = RGB(clip_v(pixel_f(red(a), n)),
clip_v(pixel_f(green(a), n)),
clip_v(pixel_f(blue(a), n)))
end
else
@inbounds for i in eachindex(X)
a = X[i]
n = noise_f(red(a)*0)
X[i] = RGB(pixel_f(red(a), n),
pixel_f(green(a), n),
pixel_f(blue(a), n))
end
end
return X
end
include("poisson.jl")
include("salt_pepper.jl")
include("white_noise_additive.jl")
include("quantization.jl")
include("multiplicative_noise.jl")
end
| Noise | https://github.com/roflmaostc/Noise.jl.git |
|
[
"MIT"
] | 0.3.3 | d34a07459e1ebdc6b551ecb28e3c19993f544d91 | code | 1974 | export mult_gauss, mult_gauss!, mult_gauss_chn, mult_gauss_chn!
@inline function comb_mult_gauss(x, n)
return x * n
end
mult_gauss!(X, σ=0.1, μ=1; clip=false) = apply_noise!(comb_mult_gauss, f_awg(σ, μ, complex_copy(σ), complex_copy(μ)), X, clip)
mult_gauss(X, σ=0.1, μ=1; clip=false) = mult_gauss!(copy(X), σ, μ, clip=clip)
"""
mult_gauss(X; clip=false[, σ=0.1, μ=1])
Returns the array `X` with the array value multiplied with a gauss distribution (standard deviation `σ` and mean `μ`) .
`σ` and `μ` are optional arguments representing standard deviation and mean of gauss.
If keyword argument `clip` is provided the values are clipped to be in [0, 1].
If `X` is a RGB{Normed} or Gray{Normed} image, then the values will be automatically clipped and the keyword
`clip` is meaningless.
If `X<:Complex`, `μ` and `σ` are applied to the imaginary in the same way as for the real part.
If you want to have different behaviour for real and imaginary part, simply
choose `μ` or `σ` complex.
"""
mult_gauss
mult_gauss_chn(X, σ=0.1, μ=1; clip=false) = mult_gauss_chn!(copy(X), σ, μ, clip=clip)
mult_gauss_chn!(X, σ=0.1, μ=1; clip=false) = apply_noise_chn!(comb_mult_gauss, f_awg(σ, μ, complex_copy(σ), complex_copy(μ)), X, clip)
"""
mult_gauss_chn(X; clip=false[, σ=0.1, μ=0.0])
Returns the RGB image `X` with the values of the pixel multiplied with a
gauss distribution (standard deviation `σ` and mean `μ`) pixelwise.
However, every channel of one pixel receives the same amount of noise.
The noise therefore acts roughly as intensity - but not color - changing noise.
If keyword argument `clip` is provided the values are clipped to be in [0, 1].
`σ` and `μ` are optional arguments representing standard deviation and mean of gauss.
If `X<:Complex`, `μ` and `σ` are applied to the imaginary in the same way as for the real part.
If you want to have different behaviour for real and imaginary part, simply
choose `μ` or `σ` complex.
"""
mult_gauss_chn
| Noise | https://github.com/roflmaostc/Noise.jl.git |
|
[
"MIT"
] | 0.3.3 | d34a07459e1ebdc6b551ecb28e3c19993f544d91 | code | 1571 | export poisson, poisson!
# get the maximum intensity of an image
mymax(X::AbstractArray{<:RGB}) = max_rgb(X)
mymax(X::AbstractArray{<:Gray}) = gray(maximum(X))
mymax(X::AbstractArray) = maximum(X)
# noise function for poisson
function noise_f(x, scaling, max_intens)
# scale image to max_intensity and apply poisson noise
# after Poisson noise scale it back
return pois_rand(x * scaling / max_intens) * max_intens / scaling
end
f_pois(scaling, max_intens) = x -> scaling == nothing ? pois_rand(x) : noise_f(x, scaling, max_intens)
comb_pois(x, n) = n
poisson(X::AbstractArray, scaling=nothing; clip=false) = poisson!(copy(X), scaling, clip=clip)
function poisson!(X::AbstractArray, scaling=nothing; clip=false)
max_intens = convert(Float64, mymax(X))
return apply_noise!(comb_pois, f_pois(scaling, max_intens), X, clip)
end
"""
poisson(X; scaling=nothing, clip=false)
Returns the array `X` affected by Poisson noise.
At every position the Poisson noise affects the intensity individually
and the values at the positions represent the expected value of the Poisson
Distribution.
Since Poisson Noise due to discrete events you should
provide the optional argument `scaling`. This `scaling` connects
the highest value of the array with the discrete number of events.
The highest value will be then scaled and the poisson noise is applied
Afterwards we scale the whole array back so that the initial intensity
is preserved but with applied Poisson noise.
`clip` is a keyword argument. If given, it clips the values to [0, 1]
"""
poisson
| Noise | https://github.com/roflmaostc/Noise.jl.git |
|
[
"MIT"
] | 0.3.3 | d34a07459e1ebdc6b551ecb28e3c19993f544d91 | code | 958 | export quantization!, quantization
# apply quantization and clipping
function quant(x, levels, minv, maxv)
return clip_v(round((x - minv)/(maxv-minv) * levels) / levels * (maxv-minv) + minv, minv, maxv)
end
f_quant(levels, minv, maxv) = x -> quant(x, levels, minv, maxv)
comb_quant(x, n) = n
quantization(X::AbstractArray, levels; minv=0, maxv=1) =
quantization!(copy(X), levels, minv=minv, maxv=maxv)
quantization!(X::AbstractArray, levels; minv=0, maxv=1) =
apply_noise!(comb_quant, f_quant(levels-1, minv, maxv), X, false)
"""
quantization(X, levels; minv=0, maxv=1)
Returns array `X` discretized to `levels` different values.
Therefore the array is discretized.
`levels` describes how many different value steps the resulting image has.
`minv=0` and `maxv` indicate the minimum and maximum possible values of the images.
In RGB and Gray images this is usually 0 and 1.
There is also `quantization!` available.
"""
quantization
| Noise | https://github.com/roflmaostc/Noise.jl.git |
|
[
"MIT"
] | 0.3.3 | d34a07459e1ebdc6b551ecb28e3c19993f544d91 | code | 2390 | export salt_pepper, salt_pepper_chn
salt_or_pepper(salt_prob, salt, pepper) = rand() < salt_prob ? salt : pepper
# function for a raw value
function f_sp(prob, salt_prob, salt, pepper)
return x -> rand() < prob ? salt_or_pepper(salt_prob, salt, pepper) : x
end
@inline function comb_sp(x, n)
return n
end
function salt_pepper(X, prob=0.1; salt_prob=0.5, salt=1, pepper=0)
return salt_pepper!(copy(X), prob, salt_prob=salt_prob, salt=salt, pepper=pepper)
end
# for arbitrary array, RGB and Gray images
function salt_pepper!(X, prob=0.1; salt_prob=0.5, salt=1, pepper=0)
# type conversion of salt & pepper makes it faster
a = X[1]
salt = convert(eltype(a), salt)
pepper = convert(eltype(a), pepper)
return apply_noise!(comb_sp, f_sp(prob, salt_prob, salt, pepper), X, false)
end
"""
salt_pepper(X; salt_prob=0.5, salt=1.0, pepper=0.0[, prob=0.1])
Returns array `X` affected by salt and pepper noise.
`X` can be an array or an RGB or Gray image
`prob` is a optional argument for the probability that a pixel will be affected by the noise.
`salt_prob` is a keyword argument representing the probability for salt noise.
The probability for pepper noise is therefore 1-`salt_prob`.
`salt` is a keyword argument for specifying the value of salt noise.
`pepper` is a keyword argument for specifying the value of pepper noise.
"""
salt_pepper
function salt_pepper_chn(X, prob=0.1; salt_prob=0.5, salt=1.0, pepper=0.0)
return salt_pepper_chn!(copy(X), prob, salt_prob=salt_prob, salt=salt, pepper=pepper)
end
function salt_pepper_chn!(X, prob=0.1; salt_prob=0.5, salt=1.0, pepper=0.0)
return apply_noise_chn!(comb_sp, f_sp(prob, salt_prob, salt, pepper), X, false)
end
"""
salt_pepper_chn(X; salt_prob=0.5, salt=1.0, pepper=0.0[, prob=0.1])
Returns a RGB Image `X` affected by salt and pepper noise.
When a salt or pepper occurs, it is applied to all channels of the RGB making a real salt
and pepper on the whole image.
`prob` is a optional argument for the probability that a pixel will be affected by the noise.
`salt_prob` is a keyword argument representing the probability for salt noise.
The probability for pepper noise is therefore 1-`salt_prob`.
`salt` is a keyword argument for specifying the value of salt noise.
`pepper` is a keyword argument for specifying the value of pepper noise.
"""
salt_pepper_chn
| Noise | https://github.com/roflmaostc/Noise.jl.git |
|
[
"MIT"
] | 0.3.3 | d34a07459e1ebdc6b551ecb28e3c19993f544d91 | code | 2151 | export add_gauss, add_gauss!, add_gauss_chn, add_gauss_chn!
# function for a raw value
function f_awg(σ, μ, σ_c, μ_c)
f(x::Real) = randn() * σ + μ
function f(x::Complex{T}) where T
return ((randn() * real(σ_c) + real(μ_c)
+ randn() * 1im * imag(σ_c) + 1im * imag(μ_c)))
end
return f
end
@inline function comb_add_gauss(x, n)
return x + n
end
add_gauss(X, σ=0.1, μ=0; clip=false) = add_gauss!(copy(X), σ, μ, clip=clip)
add_gauss!(X, σ=0.1, μ=0; clip=false) = apply_noise!(comb_add_gauss, f_awg(σ, μ, complex_copy(σ), complex_copy(μ)), X, clip)
"""
add_gauss(X; clip=false[, σ=0.1, μ=0.0])
Returns the array `X` with gauss noise (standard deviation `σ` and mean `μ`)
added.
`σ` and `μ` are optional arguments representing standard deviation and mean of gauss.
If keyword argument `clip` is provided the values are clipped to be in [0, 1].
If `X` is a RGB{Normed} or Gray{Normed} image, then the values will be automatically clipped and the keyword
`clip` is meaningless.
If `X<:Complex`, `μ` and `σ` are applied to the imaginary in the same way as for the real part.
If you want to have different behaviour for real and imaginary part, simply
choose `μ` or `σ` complex.
"""
add_gauss
add_gauss_chn(X, σ=0.1, μ=0; clip=false) = add_gauss_chn!(copy(X), σ, μ, clip=clip)
add_gauss_chn!(X, σ=0.1, μ=0; clip=false) = apply_noise_chn!(comb_add_gauss, f_awg(σ, μ, complex_copy(σ), complex_copy(μ)), X, clip)
"""
add_gauss_chn(X; clip=false[, σ=0.1, μ=0.0])
Returns the RGB image `X` with gauss noise (standard deviation `σ` and mean `μ`)
added pixelwise. However, every channel of one pixel receives the same amount of noise.
The noise therefore acts roughly as intensity - but not color - changing noise.
If keyword argument `clip` is provided the values are clipped to be in [0, 1].
`σ` and `μ` are optional arguments representing standard deviation and mean of gauss.
If `X<:Complex`, `μ` and `σ` are applied to the imaginary in the same way as for the real part.
If you want to have different behaviour for real and imaginary part, simply
choose `μ` or `σ` complex.
"""
add_gauss_chn
| Noise | https://github.com/roflmaostc/Noise.jl.git |
|
[
"MIT"
] | 0.3.3 | d34a07459e1ebdc6b551ecb28e3c19993f544d91 | code | 13103 | using Noise
using Test
using Statistics
using Random
using ImageCore
using ColorVectorSpace
@testset "Util functions" begin
x = 1f0
@test 1f0 + 1f0im == Noise.complex_copy(x)
x = 12f0 + 13f0im
@test 12f0 + 13f0im == Noise.complex_copy(x)
end
Random.seed!(42)
tpl = (1000, 1000)
arr = rand(Float64, tpl)
arr_ones = ones(tpl)
arr_rand_int = convert(Array{Int64}, map(x -> round(1000*x), arr))
arr_zeros = zeros(tpl)
img_zeros = colorview(RGB, zeros(Normed{UInt8, 8}, 3, 1000, 1000))
img_zeros_gray = colorview(Gray, zeros(Normed{UInt8, 8}, 1000, 1000))
img_rand = colorview(RGB, rand(Normed{UInt8, 8}, 3, 1000, 1000))
img_rand_gray = colorview(Gray, rand(Normed{UInt8, 8}, 1000, 1000))
img_12 = colorview(RGB, 0.5 .* ones(Normed{UInt8, 8}, 3, 1000, 1000))
img_12_gray= colorview(Gray, 0.5 .* ones(Normed{UInt8, 8}, 1000, 1000))
img = colorview(RGB, ones(Normed{UInt8, 8}, 3, 1000, 1000))
img_gray= colorview(Gray, ones(Normed{UInt8, 8}, 1000, 1000))
img_zeros_float = colorview(RGB, zeros(Float64, 3, 1000, 1000))
img_zeros_gray_float = colorview(Gray, zeros(Float64, 1000, 1000))
img_rand_float = colorview(RGB, rand(Float64, 3, 1000, 1000))
img_rand_gray_float = colorview(Gray, rand(Float64, 1000, 1000))
img_12_float = colorview(RGB, 0.5 .* ones(Float64, 3, 1000, 1000))
img_12_gray_float = colorview(Gray, 0.5 .* ones(Float64, 1000, 1000))
img_float = colorview(RGB, ones(Float64, 3, 1000, 1000))
img_gray_float = colorview(Gray, ones(Float64, 1000, 1000))
@testset "Clip functions" begin
@test mean(Noise.clip_v(1.1)) ≈ 1.0
@test mean(Noise.clip_v(1.0)) ≈ 1.0
@test mean(Noise.clip_v(10.0)) ≈ 1.0
@test mean(Noise.clip_v(0.1)) ≈ 0.1
@test mean(Noise.clip_v(-1.0)) ≈ 0.0
@test mean(Noise.clip_v(0.0)) ≈ 0.0
end
@testset "Salt and Pepper noise" begin
#check 100% salt
@test salt_pepper(arr, 1.0, salt_prob=1.0) == ones(tpl)
#check 100% pepper
@test salt_pepper(arr, 1.0, salt_prob=0.0) == zeros(tpl)
#check 100% salt with custom value
@test salt_pepper(arr, 1.0, salt_prob=1.0, salt=0.23) == 0.23 .* ones(tpl)
#check 100% pepper with custom value
@test salt_pepper(arr, 1.0, salt_prob=0.0, pepper=0.63) == 0.63 .* ones(tpl)
#check average salt and pepper roughly
@test abs(mean(salt_pepper(arr, 1.0) .-0.5)) < 0.1
#check that average salt and pepper are roughly 0.5
@test abs(mean(salt_pepper(arr, 0.1) .-0.5)) < 0.05
@test abs(mean(salt_pepper(arr, 0.1, salt_prob=1.0) .-0.5)) > 0.001
@test abs(mean(salt_pepper(arr, 0.1, salt_prob=0.0) .-0.5)) > 0.001
#check that average is different to 0.5 if salt or pepper are not 1.0 or 0.0
@test abs(mean(salt_pepper(arr, 0.1, pepper=1.0) .-0.5)) > 0.001
@test abs(mean(salt_pepper(arr, 0.1, salt=0.0) .-0.5)) > 0.001
# check images chn
@test abs(mean(channelview(salt_pepper_chn(img_zeros, 1.0))) - 0.5)< 0.001
#check that average is different to 0.5 if salt or pepper are not 1.0 or 0.0
@test abs(sum(channelview(salt_pepper_chn(img_zeros, 0.1, pepper=1.0)) .-0.5)/100/100) > 0.001
@test abs(sum(channelview(salt_pepper_chn(img_rand, 0.1, salt=0.0)) .-0.5)/100/100) > 0.001
# check RGB images
@test abs(mean(channelview(salt_pepper(img_zeros, 1.0))) - 0.5)< 0.001
#check that average is different to 0.5 if salt or pepper are not 1.0 or 0.0
@test abs(mean(channelview(salt_pepper(img_zeros, 0.1, pepper=1.0)) .-0.5)) > 0.001
@test abs(mean(channelview(salt_pepper(img_rand, 0.1, salt=0.0)) .-0.5)) > 0.001
# check std
@test abs(std(channelview(salt_pepper(img_rand, 1.0, salt=0.0, pepper=0.5))) -0.25) < 0.001
@test abs(std(channelview(salt_pepper(img_rand, 1.0, salt=0.4, pepper=0.5))) -0.05) < 0.001
# check gray images
@test abs(mean(channelview(salt_pepper(img_zeros_gray, 1.0))) - 0.5)< 0.001
#check that average is different to 0.5 if salt or pepper are not 1.0 or 0.0
@test abs(mean(channelview(salt_pepper(img_zeros_gray, 0.1, pepper=1.0)) .-0.5)) > 0.001
@test abs(mean(channelview(salt_pepper(img_rand_gray, 0.1, salt=0.0)) .-0.5)) > 0.001
# check std
@test abs(std(channelview(salt_pepper(img_rand_gray, 1.0, salt=0.0, pepper=0.5))) -0.25) < 0.001
@test abs(std(channelview(salt_pepper(img_rand_gray, 1.0, salt=0.4, pepper=0.5))) -0.05) < 0.001
# check images but with float
@test abs(mean(channelview(salt_pepper_chn(img_zeros_float, 1.0))) - 0.5)< 0.001
#check that average is different to 0.5 if salt or pepper are not 1.0 or 0.0
@test abs(sum(channelview(salt_pepper_chn(img_zeros_float, 0.1, pepper=1.0)) .-0.5)/100/100) > 0.001
@test abs(sum(channelview(salt_pepper_chn(img_rand_float, 0.1, salt=0.0)) .-0.5)/100/100) > 0.001
# check RGB images
@test abs(mean(channelview(salt_pepper(img_zeros_float, 1.0))) - 0.5)< 0.001
#check that average is different to 0.5 if salt or pepper are not 1.0 or 0.0
@test abs(mean(channelview(salt_pepper(img_zeros_float, 0.1, pepper=1.0)) .-0.5)) > 0.001
@test abs(mean(channelview(salt_pepper(img_rand_float, 0.1, salt=0.0)) .-0.5)) > 0.001
# check std
@test abs(std(channelview(salt_pepper(img_rand_float, 1.0, salt=0.0, pepper=0.5))) -0.25) < 0.001
@test abs(std(channelview(salt_pepper(img_rand_float, 1.0, salt=0.4, pepper=0.5))) -0.05) < 0.001
# check gray images
@test abs(mean(channelview(salt_pepper(img_zeros_gray_float, 1.0))) - 0.5)< 0.001
#check that average is different to 0.5 if salt or pepper are not 1.0 or 0.0
@test abs(mean(channelview(salt_pepper(img_zeros_gray_float, 0.1, pepper=1.0)) .-0.5)) > 0.001
@test abs(mean(channelview(salt_pepper(img_rand_gray_float, 0.1, salt=0.0)) .-0.5)) > 0.001
# check std
@test abs(std(channelview(salt_pepper(img_rand_gray_float, 1.0, salt=0.0, pepper=0.5))) -0.25) < 0.001
@test abs(std(channelview(salt_pepper(img_rand_gray_float, 1.0, salt=0.4, pepper=0.5))) -0.05) < 0.001
end
@testset "Additive white Gaussian" begin
@test (std(imag(add_gauss(Complex.(arr_zeros), 13im))) -13) < 0.1
@test (std(real(add_gauss(Complex.(arr_zeros), 13im)))) == 0
@test (std(imag(add_gauss(Complex.(arr_zeros), 13))) -13) < 0.1
@test (std(real(add_gauss(Complex.(arr_zeros), 13))) -13) < 0.1
# check array with white gaussian noise
@test abs(std(add_gauss(arr_zeros, 13.0)) - 13.0) < 0.1
@test abs(mean(add_gauss(arr_zeros, 1.0))) < 0.05
@test abs(mean(add_gauss(arr_zeros, 1.0, 10.0)) - 10) < 0.05
@test mean(add_gauss(arr_zeros, 0.5, -1.0, clip=false)) < 0
@test mean(add_gauss(arr_zeros, 0.5, -1.0, clip=true)) >= 0
@test mean(add_gauss(arr_zeros, 0.5, 2.0, clip=false)) > 1
@test mean(add_gauss(arr_zeros, 0.5, 2.0, clip=true)) <= 1
# check images for gaussian white noise
# check mean offset channelwise
@test abs(mean(channelview(add_gauss_chn(img_zeros, 0.1, 0.5))) - 0.5) < 0.05
@test abs(mean(channelview(add_gauss_chn(img_zeros, 0.2, 0.3))) - 0.3) < 0.05
# check mean offset with clip
@test abs(mean(channelview(add_gauss(img_zeros, 0.1, 0.5))) - 0.5) < 0.05
@test abs(mean(channelview(add_gauss(img_zeros, 0.2, 0.3))) - 0.3) < 0.05
@test abs(mean(channelview(add_gauss(img_zeros, 0.0, 10))) - 1.0) < 0.005
# check mean offet with gray
@test abs(mean(channelview(add_gauss(img_zeros_gray, 0.1, 0.5))) - 0.5) < 0.05
@test abs(mean(channelview(add_gauss(img_zeros_gray, 0.2, 0.3))) - 0.3) < 0.05
@test abs(mean(channelview(add_gauss(img_zeros_gray, 0.0, 10))) - 1.0) < 0.005
# check the same but with float images
# check images for gaussian white noise
# check mean offset channelwise
@test abs(mean(channelview(add_gauss_chn(img_zeros_float, 0.1, 0.5))) - 0.5) < 0.05
@test abs(mean(channelview(add_gauss_chn(img_zeros_float, 0.2, 0.3))) - 0.3) < 0.05
# check mean offset, now it's not clipped
@test abs(mean(channelview(add_gauss(img_zeros_float, 0.1, 0.5))) - 0.5) < 0.05
@test abs(mean(channelview(add_gauss(img_zeros_float, 0.2, 0.3))) - 0.3) < 0.05
@test abs(mean(channelview(add_gauss(img_zeros_float, 0.0, 10))) - 10.0) < 0.005
# check mean offet with gray
@test abs(mean(channelview(add_gauss(img_zeros_gray_float, 0.1, 0.5))) - 0.5) < 0.05
@test abs(mean(channelview(add_gauss(img_zeros_gray_float, 0.2, 0.3))) - 0.3) < 0.05
@test abs(mean(channelview(add_gauss(img_zeros_gray_float, 0.0, 10))) - 10.0) < 0.005
end
@testset "Poisson Noise" begin
#test std of poisson with clip and no clip
@test abs(std(poisson(arr_ones .* 13.0)) - sqrt(13)) < 0.01
@test abs(std(poisson(arr_ones .* 13.0, clip=true))) < 0.01
#test mean with clip and no clip
@test abs(mean(poisson(arr_ones .* 13.0)) - 13) < 0.05
@test abs(mean(poisson(arr_ones .* 13.0, clip=true)) - 1) < 0.001
#test mean with scaling
@test abs(mean(poisson(arr, 1000.0))-0.5) < 0.005
#test mean int
@test abs(mean(poisson(arr_rand_int)))-500<1
@test abs(std(channelview(poisson(img_12_gray, 100.0))) - 0.5 .* sqrt(100.0)./100.0) < 0.005
@test abs(std(channelview(poisson(img_12, 100.0))) - 0.5 .* sqrt(100.0)./100.0) < 0.005
@test abs(std(channelview(poisson(img_12_gray, 4200.0))) - 0.3 .* sqrt(4200.0)./4200.0) < 0.005
@test abs(std(channelview(poisson(img_12, 4200.0))) - 0.3 .* sqrt(4200.0)./4200.0) < 0.005
@test abs(std(channelview(poisson(img_gray, 10000.0, clip=true))))< 0.02
@test abs(std(channelview(poisson(img, 10000.0, clip=true)))) < 0.02
@test abs(mean(channelview(poisson(img_gray, 10000.0, clip=true)))-1.0)< 0.02
@test abs(mean(channelview(poisson(img, 10000.0, clip=true))) -1.0) < 0.02
@test abs(std(channelview(poisson(img_12_gray_float, 100.0))) - 0.5 .* sqrt(100.0)./100.0) < 0.005
@test abs(std(channelview(poisson(img_12_float, 100.0))) - 0.5 .* sqrt(100.0)./100.0) < 0.005
@test abs(std(channelview(poisson(img_12_gray_float, 4200.0))) - 0.3 .* sqrt(4200.0)./4200.0) < 0.005
@test abs(std(channelview(poisson(img_12_float, 4200.0))) - 0.3 .* sqrt(4200.0)./4200.0) < 0.005
@test abs(std(channelview(poisson(img_gray_float, 10000.0, clip=true))))< 0.02
@test abs(std(channelview(poisson(img_float, 10000.0, clip=true)))) < 0.02
@test abs(mean(channelview(poisson(img_gray_float, 10000.0, clip=true)))-1.0)< 0.02
@test abs(mean(channelview(poisson(img_float, 10000.0, clip=true))) -1.0) < 0.02
end
@testset "Quantization" begin
@test quantization(img_gray, 10000) ≈ img_gray
@test quantization(img_gray, 255) ≈ img_gray
@test abs(sum(quantization(img_gray, 255)) - sum(img_gray)) < 0.01 * sum(img_gray)
@test quantization(img, 10000) ≈ img
@test quantization(img, 255) ≈ img
@test quantization(img_float, 1000) ≈ img_float
@test quantization(img_float, 255) ≈ img_float
@test abs((quantization(img_12_gray_float, 100) |> channelview |> mean) - 0.5) < 0.01
@test abs((quantization(img_12_gray_float, 50) |> channelview |> mean) - 0.5) < 0.05
@test abs(sum(quantization(img_12_gray_float, 255)) - sum(img_12_gray_float)) < 0.01 * sum(img_12_gray_float)
@test abs((quantization(arr , 100) |> mean) - 0.5) < 0.01
@test abs((quantization(arr, 50) |> mean) - 0.5) < 0.05
@test abs(sum(quantization(arr, 255)) - sum(arr)) < 0.01 * sum(arr)
@test minimum(quantization(img_rand_gray_float, 2, minv=0.32, maxv=0.98)) ≈ 0.32
@test maximum(quantization(img_rand_gray_float, 2, minv=0.32, maxv=0.98)) ≈ 0.98
@test minimum(quantization(img_rand_gray, 5, minv=0.1, maxv=0.96)) ≈ Gray{N0f8}(0.1)
@test maximum(quantization(img_rand_gray, 2, minv=0.32, maxv=0.98)) ≈ Gray{N0f8}(0.98)
end
@testset "Multiplicative gauss Noise" begin
@test (std(imag(mult_gauss(Complex.(arr_ones), 13im))) -13) < 0.1
@test (std(real(mult_gauss(Complex.(arr_ones), 13im)))) == 0
@test (std(imag(mult_gauss(Complex.(arr_ones), 13))) -13) < 0.1
@test (std(real(mult_gauss(Complex.(arr_ones), 13))) -13) < 0.1
# check array with white gauss noise
@test abs(std(mult_gauss(arr_zeros, 13.0)) - 0) < 0.1
@test mean(mult_gauss(arr_zeros, 0.5, -1.0, clip=false)) ≈ 0
@test mean(mult_gauss(arr_zeros, 0.5, -1.0, clip=true)) ≈ 0
# check images for gauss white noise
# check mean offset channelwise
@test abs(mean(channelview(mult_gauss_chn(img_zeros, 0.1, 0.5)))) ≈ 0
@test abs(mean(channelview(mult_gauss_chn(img_zeros, 0.2, 0.3)))) ≈ 0
# check mean offset with clip
@test abs(mean(channelview(mult_gauss(img_zeros, 0.1, 0.5)))) ≈ 0
@test abs(mean(channelview(mult_gauss(img_zeros, 0.2, 0.3)))) ≈ 0
@test abs(mean(channelview(mult_gauss(img_zeros, 0.0, 10)))) ≈ 0
# check mean offset with clip
@test abs(mean(channelview(mult_gauss(img, 0.1, 0.5))) - 0.5) < 0.05
@test abs(std(channelview(mult_gauss(img, 0.2, 0.3))) - 0.2) < 0.05
@test abs(mean(channelview(mult_gauss(img, 0.01, 0.2))) - 0.2) < 0.05
@test abs(std(channelview(mult_gauss(img, 0.1, 0.5))) - 0.1) < 0.05
end
| Noise | https://github.com/roflmaostc/Noise.jl.git |
|
[
"MIT"
] | 0.3.3 | d34a07459e1ebdc6b551ecb28e3c19993f544d91 | docs | 385 | # History of Noise.jl
## v0.2.0 (2020-04-22)
* Major Refactoring of code giving little speed improvements
* Renaming of `additive_white_gaussian` to `add_gauss`
* new methods: `mult_gauss` and `quantization`
## v0.1.0 (2020-04-16)
Initial release.
* `additive_white_gaussian` for Gaussian white noise
* `salt_pepper` for Salt and Pepper noise
* `poisson` for Poisson shot noise
| Noise | https://github.com/roflmaostc/Noise.jl.git |
|
[
"MIT"
] | 0.3.3 | d34a07459e1ebdc6b551ecb28e3c19993f544d91 | docs | 4400 | # Noise.jl
Noise.jl is a Julia package to add different kinds of noise to a digital signal like a array or images.
| **Documentation** | **Build Status** | **Code Coverage** | **DOI** |
|:---------------------------------------:|:-----------------------------------------:|:-------------------------------:|:----:|
| [![][docs-stable-img]][docs-stable-url] [![][docs-dev-img]][docs-dev-url] | [![][CI-img]][CI-url] | [![][codecov-img]][codecov-url] | [](https://zenodo.org/badge/latestdoi/254694216) |
## Documentation
The complete manual of Noise.jl is available at [the documentation page][docs-stable-url].
It has more detailed explanations of the methods and contains examples for data arrays and images.
## Installation
`Noise.jl` is available for all version equal or above Julia 1.3.
It can be installed with the following command
```julia
julia> ] add Noise
```
## Usage
Currently, all methods are provided with a trailing `!` (like `poisson!`), so there is a in-place method available.
In general, if images like `Array{RGB{<:Normed}` or `Array{Gray{<:Normed}}` are given to a method, an image with same type will be returned.
The methods also work for normal Arrays like `Array{<:Number}`.
At the moment five different types of noise are possible: Additive and multiplicative Gaussian, Salt-Pepper, Poisson and Quantization noise.
```julia
using Noise, TestImages, Images, Plots
img = testimage("fabio_gray_256")
img_color = testimage("fabio_color_256")
img_gray_gauss = add_gauss(img, 0.1)
img_color_gauss = add_gauss(img_color, 0.1)
img_gray_sp = salt_pepper(img, 0.1)
# 1D array
x = LinRange(0.0, 10.0, 300)
y = sin.(x)
# small noise
y_noise = add_gauss(y, 0.1)
plot(x,y) # hide
plot!(x, y_noise) # hide
savefig("images/series_index.png") # hide
save("images/img_gray_gauss_index.png", img_gray_gauss) # hide
save("images/img_color_gauss_index.png", img_color_gauss) # hide
save("images/img_gray_sp_index.png", img_gray_sp) # hide
nothing # hide
```
The left gray image is affected by Gaussian noise with a standard deviation of .
In the image in the middle, we added Gaussian noise with the same standard deviation but to each individual color channel. Therefore the image has a fluctuating color look.
The image on the right is affected by salt and pepper noise by a probability of 10%.
| Gray image with noise | RGB image with noise | Gray image with salt and pepper noise |
|:------------------------------------|:------------------------------------- |:--------------------------------------|
| |  |  |
This 1D array is affected by a additive gaussian white noise ().

## Cite
If you use this package in an academic work, please cite us!
See on the right side the *Cite this repository*:
```
@misc{Wechsler_Noise.jl__Adding,
author = {Wechsler, Felix},
title = {Noise.jl - Adding Noise in Julia},
url = {https://github.com/roflmaostc/Noise.jl}
}
```
## Development
The package is developed at [GitHub](https://www.github.com/roflmaostc/Noise.jl). There
you can submit bug reports, propose new types of noise with pull
requests, and make suggestions. We are very happy about new types of noise, which can be also very
specific for some applications. The aim is to provide via `Noise.jl` a central package which can
be used by many different types of application from Biology to Astronomy and Electrical Engineering.
[docs-dev-img]: https://img.shields.io/badge/docs-dev-pink.svg
[docs-dev-url]: https://roflmaostc.github.io/Noise.jl/dev/
[docs-stable-img]: https://img.shields.io/badge/docs-stable-darkgreen.svg
[docs-stable-url]: https://roflmaostc.github.io/Noise.jl/stable/
[CI-img]: https://github.com/roflmaostc/Noise.jl/workflows/CI/badge.svg
[CI-url]: https://github.com/roflmaostc/Noise.jl/actions?query=workflow%3ACI
[codecov-img]: https://codecov.io/gh/roflmaostc/Noise.jl/branch/master/graph/badge.svg
[codecov-url]: https://codecov.io/gh/roflmaostc/Noise.jl
| Noise | https://github.com/roflmaostc/Noise.jl.git |
|
[
"MIT"
] | 0.3.3 | d34a07459e1ebdc6b551ecb28e3c19993f544d91 | docs | 3046 | # Noise.jl
## Introduction
The purpose of this package is to provide several methods to add different kinds of noise to images or arrays.
## Installation
`Noise.jl` is available for all version equal or above Julia 1.0. It is mainly tested under Linux but should also work on Windows.
It and can be installed with the following command
```julia
julia> Pkt.update()
julia> Pkg.add("Noise")
```
## Usage
Currently, all methods are not working in place and return always a new array.
In general, if images like `Array{RGB{<:Normed}` `Array{Gray{<:Normed}}` are given to a method, a new image with same type will be returned.
The methods also work for normal Arrays like `Array{<:Number}`.
At the moment three different types of noise are possible: Additive white Gaussian, Salt and Pepper and Poisson noise.
```@example
using Noise, TestImages, Images, Plots
img = testimage("fabio_gray_256")
img_color = testimage("fabio_color_256")
img_gray_gauss = add_gauss(img, 0.1)
img_color_gauss = add_gauss(img_color, 0.1)
img_gray_sp = salt_pepper(img, 0.1)
# 1D array
x = LinRange(0.0, 10.0, 300)
y = sin.(x)
# small noise
y_noise = add_gauss(y, 0.1)
plot(x,y); # hide
plot!(x, y_noise); # hide
savefig("images/series_index.png") # hide
save("images/img_gray_gauss_index.png", img_gray_gauss) # hide
save("images/img_color_gauss_index.png", img_color_gauss) # hide
save("images/img_gray_sp_index.png", img_gray_sp) # hide
nothing # hide
```
The left gray image is affected by Gaussian noise with a standard deviation of $\sigma = 0.1$.
In the image in the middle, we added Gaussian noise with the same standard deviation but to each individual color pixel giving the fluctuating color look.
The image on the right is affected by salt and pepper noise by a probability of $10\%$
| Gray image with noise | RGB image with noise | Gray image with salt and pepper noise |
|:------------------------------------|:------------------------------------- |:--------------------------------------|
| |  |  |
This 1D array is affected by a additive gaussian white noise ($\sigma=0.1, \mu=0$).

## Overview
Look here for more details and arguments of each function.
```@contents
Pages = ["man/additive_white_gaussian.md",
"man/mult_gauss.md",
"man/salt_pepper.md",
"man/poisson.md",
"man/quantization.md",
"man/function_references.md"
]
Depth = 2
```
## Development
The package is developed at [GitHub](https://www.github.com/roflmaostc/Noise.jl). There
you can submit bug reports, propose new types of noise with pull
requests, and make suggestions. We are very happy about new types of noise, which can be also very
specific for some applications. The aim is to provide via `Noise.jl` a central package which can
be used by many different types of application from Biology to Astronomy and Electrical Engineering.
| Noise | https://github.com/roflmaostc/Noise.jl.git |
|
[
"MIT"
] | 0.3.3 | d34a07459e1ebdc6b551ecb28e3c19993f544d91 | docs | 4621 | # Additive White Gaussian
Additive white Gaussian noise is one of the most common types of noise.
We simply add a random number to each pixel.
The random number has a mean $\mu$ of zero and a certain standard deviation $\sigma$.
## Usage
### Arrays, Grayscale Images and RGB Images
For arrays, grayscale images (`Array{<:Gray}`) and RGB images (`Array{<:RGB}`) we provide the following method:
```julia
add_gauss(X; clip=false[, σ=0.1, μ=0.0])
```
This methods adds a random Gaussian value to each individual element of the array.
In the case of RGB images, this means that every colorchannel of one pixel receives a different amount of noise.
The array `X` must be provided, `clip` is a keyword argument. If `clip=true`
the values will be clipped to the interval [0,1]. $\sigma$ and $\mu$ represent the standard deviation
and the mean of the gaussian noise respectively. If $\mu$ is unequal to 0, we increase the overall intensity
of an image. $\sigma$ represents how strong the noise is, alreay a value of $\sigma=0.5$ introduces a lot of noise.
If the stored numbers of the array are somehow a subtype of `Normed` we automatically clip them. This is quite common
if you use the `Images` library which uses by default a type `Array{Gray{Normed{UInt8, 8}}}`.
For Float arrays we don't clip any values, this should be preferably used for any use case outside of images.
### RGB images each Channel the same
For RGB images (`Array{<:RGB}`) we also provide the following:
```julia
add_gauss_chn(X; clip=false[, σ=0.1, μ=0.0])
```
This method, in contradiction to the previous one, adds the same noise value to all color channels of one pixel.
## Examples
### Images
Here some examples with images.
```@example; output=False
using Noise, TestImages, Images
img_gray = testimage("fabio_gray_256")
img_color = testimage("fabio_color_256")
img_float = convert(Array{Gray{Float64}}, img_gray)
img_gray_noise = add_gauss(img_gray)
# the following call sets the standard deviation and the mean manually
img_color_noise = add_gauss(img_color, 0.1, 0.0)
# since mean is by default 0.0 we can leave it out
img_color_channel_noise = add_gauss_chn(img_color, 0.1)
img_gray_noise_heavy = add_gauss(img_gray, 0.5)
img_gray_noise_intensity = add_gauss(img_gray, 0.1, 0.3)
# without clip the intensity can be above 1.0 as well
# however, we can only save (see below) a image with intensities [0, 1]
img_float_noise = add_gauss(img_float, 0.3, -0.6, clip=true)
save("../images/awg_img_gray_noise.png", img_gray_noise) # hide
save("../images/awg_img_color_noise.png", img_color_noise) # hide
save("../images/awg_img_color_channel_noise.png", img_color_channel_noise) # hide
save("../images/awg_img_gray_noise_heavy.png", img_gray_noise_heavy) # hide
save("../images/awg_img_gray_noise_intensity.png", img_gray_noise_intensity) #hide
save("../images/awg_float_noise.png", img_float_noise) #hide
nothing # hide
```
The images are in the same order as the commands are.
The middle image has applied noise to each color channel individually, in the right the same noise is added to all channels of a pixel.
Therefore the midle image has a color noise, the noise in the image in the right corresponds to some intensity noise.
Grayscale image noise| All channels of a pixel have different noise| All channels of a pixel have the same noise
|:---------------------------------------------- |:----------------------------------------------- |:------------------------------------------------------- |
|  |  |  |
|Gray image with heavy noise | Gray image intensity gain noise | Float Image with intensity reducing noise
|:---------------------------------------------------- |:-------------------------------------------------------- |:--------------------------------------------|
|  |  |  |
### 1D Arrays
Some examples with 1D arrays.
```@example
using Noise, Plots
x = LinRange(0.0, 10.0, 300)
y = sin.(x)
# small noise
y_noise = add_gauss(y, 0.05)
# heavy noise and mean shift
y_noise_2 = add_gauss(y, 0.2, -0.4)
plot(x,y);
plot!(x, y_noise);
plot!(x, y_noise_2);
savefig("../images/awg_series.png") # hide
nothing # hide
```
As you can see we are able to introduce white gaussian noise the same way to 1D arrays. The green curved is shifted downwards because of the negative $\mu$.

| Noise | https://github.com/roflmaostc/Noise.jl.git |
|
[
"MIT"
] | 0.3.3 | d34a07459e1ebdc6b551ecb28e3c19993f544d91 | docs | 293 | # Function References
## Additive White
```@docs
add_gauss
add_gauss_chn
```
## Salt and Pepper
```@docs
salt_pepper
salt_pepper_chn
```
## Poisson
```@docs
poisson
```
## Quantization
```@docs
quantization
```
## Multiplicative Gaussian Noise
```@docs
mult_gauss
mult_gauss_chn
```
| Noise | https://github.com/roflmaostc/Noise.jl.git |
|
[
"MIT"
] | 0.3.3 | d34a07459e1ebdc6b551ecb28e3c19993f544d91 | docs | 4733 | # Multiplicative White Gaussian
Multiplicative white Gaussian noise is common for image sensor where the pixels have different gain.
We simply multiply a random number with a Gaussian distribution.
The random number has usually a mean $\mu$ of 1 and a certain standard deviation $\sigma$.
## Usage
### Arrays, Grayscale Images and RGB Images
For arrays, grayscale images (`Array{<:Gray}`) and RGB images (`Array{<:RGB}`) we provide the following method:
```julia
mult_gauss(X; clip=false[, σ=0.1, μ=1])
```
This methods multiplieds a random Gaussian value with each individual element of the array.
In the case of RGB images, this means that every colorchannel of one pixel receives a different amount of noise.
The array `X` must be provided, `clip` is a keyword argument. If `clip=true`
the values will be clipped to the interval [0,1]. $\sigma$ and $\mu$ represent the standard deviation
and the mean of the gaussian noise respectively. If $\mu$ is unequal to 1, we change the overall intensity
of an image. $\sigma$ represents how strong the noise is, alreay a value of $\sigma=0.5$ introduces a lot of noise.
If the stored numbers of the array are somehow a subtype of `Normed` we automatically clip them. This is quite common
if you use the `Images` library which uses by default a type `Array{Gray{Normed{UInt8, 8}}}`.
For Float arrays we don't clip any values, this should be preferably used for any use case outside of images.
### RGB images each Channel the same
For RGB images (`Array{<:RGB}`) we also provide the following:
```julia
mult_gauss_chn(X; clip=false[, σ=0.1, μ=1])
```
This method, in contradiction to the previous one, multiplies the same noise value to all color channels of one pixel.
## Examples
### Images
Here some examples with images.
```@example; output=False
using Noise, TestImages, Images
img_gray = testimage("fabio_gray_256")
img_color = testimage("fabio_color_256")
img_float = convert(Array{Gray{Float64}}, img_gray)
img_gray_noise = mult_gauss(img_gray)
# the following call sets the standard deviation and the mean manually
img_color_noise = mult_gauss(img_color, 0.1, 1.0)
# since mean is by default 0.0 we can leave it out
img_color_channel_noise = mult_gauss_chn(img_color, 0.1)
img_gray_noise_heavy = mult_gauss(img_gray, 0.5)
img_gray_noise_intensity = mult_gauss(img_gray, 0.1, 1.2)
# without clip the intensity can be above 1.0 as well
# however, we can only save (see below) a image with intensities [0, 1]
img_float_noise = mult_gauss(img_float, 0.3, 0.5, clip=true)
save("../images/mg_img_gray_noise.png", img_gray_noise) # hide
save("../images/mg_img_color_noise.png", img_color_noise) # hide
save("../images/mg_img_color_channel_noise.png", img_color_channel_noise) # hide
save("../images/mg_img_gray_noise_heavy.png", img_gray_noise_heavy) # hide
save("../images/mg_img_gray_noise_intensity.png", img_gray_noise_intensity) #hide
save("../images/mg_float_noise.png", img_float_noise) #hide
nothing # hide
```
The images are in the same order as the commands are.
The middle image has applied noise to each color channel individually, in the right the same noise is added to all channels of a pixel.
Therefore the midle image has a color noise, the noise in the image in the right corresponds to some intensity noise.
Grayscale image noise| All channels of a pixel have different noise| All channels of a pixel have the same noise
|:---------------------------------------------- |:----------------------------------------------- |:------------------------------------------------------- |
|  |  |  |
|Gray image with heavy noise | Gray image intensity gain noise | Float Image with intensity reducing noise
|:---------------------------------------------------- |:-------------------------------------------------------- |:--------------------------------------------|
|  |  |  |
### 1D Arrays
Some examples with 1D arrays.
```@example
using Noise, Plots
x = LinRange(0.0, 10.0, 300)
y = sin.(x)
# small noise
y_noise = mult_gauss(y, 0.05)
# heavy noise and mean shift
y_noise_2 = mult_gauss(y, 0.2, 0.4)
plot(x,y);
plot!(x, y_noise);
plot!(x, y_noise_2);
savefig("../images/mg_series.png") # hide
nothing # hide
```
The amplitude of the green curve is roughly halved because $\mu=0.4$. Furthermore we can see that the noise amplitude is higher for higher values.
This is reasonable since we multiplied it with the value.

| Noise | https://github.com/roflmaostc/Noise.jl.git |
|
[
"MIT"
] | 0.3.3 | d34a07459e1ebdc6b551ecb28e3c19993f544d91 | docs | 3092 | # Poisson
Poisson noise originates from the discrete nature of events.
For example the dataset could be a microscopy image with
very limited intensity (like a flourescent specimen).
In this case the probability that one measures a specific number of photons is:
$$P(k) = \frac{\lambda^k \exp(-\lambda)}{k!}$$
where $\lambda$ being the expected value and $k$ the measured one.
Our Poisson noise randomly picks values out of this distribution.
## Usage
We provide the following method for arrays, Gray images and RGB images.
```julia
poisson(X; scaling=1, clip=false)
```
`X` is the array.
Poisson noise is applied to each array element individually where $\lambda$ is determined by the value itself.
However, for example sensors do not measure the number of photons directly but instead some intensity.
`scaling` is a optional argument to connect the intensity to a number of discrete events.
For example, usually one can estimate that the highest pixel in the measured data corresponds to 100 photons, in that case you provide `scaling=100` to the method.
Usually one wants to provide this parameter. If you provide an array which already contains integer numbers which corresponds to the measured discrete events,
you can ommit `scaling`.
## Examples
Here some examples with images.
```@example; output=False
using Noise, TestImages, Images
img_gray = testimage("fabio_gray_256")
img_color = testimage("fabio_color_256")
# the highest intensity corresponds to 10 photons
img_gray_noise = poisson(img_gray, 10.0)
# the highest intensity corresponds to 1000 photons
img_gray_noise_heavy = poisson(img_gray, 1000.0)
img_color_noise = poisson(img_color, 100.0)
save("../images/pois_img_gray_noise.png", img_gray_noise) # hide
save("../images/pois_img_gray_noise_heavy.png", img_gray_noise_heavy) # hide
save("../images/pois_img_color_noise.png", img_color_noise) # hide
nothing # hide
```
As it can be seen clearly, the image with more measured photons, is less affected by noise.
| Grayscale with 10 photons at the brightest value | Grayscale image 1000 photons at the brightest value | RGB image with 100 photons at the brightest value |
|:------------------------------------------------ |:----------------------------------------------------- |:------------------------------------------------------- |
|  |  |  |
### 1D Arrays
Poisson noise cannot handle negative occurences by design, therefore the 1D array is a y-shifted sinus curve.
```@example
using Noise, Plots
x = LinRange(0.0, 10.0, 1000)
y = 1 .* sin.(x) .+ 1
# small noise
y_noise = poisson(y, 100)
# heavy noise and mean shift
plot(x,y);
plot!(x, y_noise);
savefig("../images/pois_series.png") # hide
nothing # hide
```
We notice that amount of noise is, in contradiction to additive noise, higher for higher intensity values.
However, the signal-to-noise ratio is better for higher intensity values. This was visible in the fabio image.

| Noise | https://github.com/roflmaostc/Noise.jl.git |
|
[
"MIT"
] | 0.3.3 | d34a07459e1ebdc6b551ecb28e3c19993f544d91 | docs | 2190 | # Quantization
Quantizes the image into discrete intensities levels.
## Usage
### Arrays, Grayscale Images and RGB Images
For arrays, grayscale images (`Array{<:Gray}`) and RGB images (`Array{<:RGB}`) we provide the following method:
```julia
quantization(X, levels; minv=0, maxv=1)
```
We round the intensities of the array values to `levels` different value levels.
`minv` and `maxv` indicate the minimum and maximum value of the discretization interval.
For `Normed` datatypes like `Normed{UInt8, 8}` you can't choose values above 1 and below 0.
## Examples
### Images
Some examples with images.
```@example; output=False
using Noise, TestImages, Images
img_gray = testimage("fabio_gray_256")
img_color = testimage("fabio_color_256")
img_gray_noise = quantization(img_gray, 20)
img_gray_noise_heavy= quantization(img_gray, 5)
img_color_noise = quantization(img_color, 10)
save("../images/q_img_gray_noise.png", img_gray_noise) # hide
save("../images/q_img_gray_noise_heavy.png", img_gray_noise_heavy) # hide
save("../images/q_img_color_noise.png", img_color_noise) # hide
nothing # hide
```
The images are in the same order as the commands are.
The left image has 20 different value levels. The middle image only 5. The right image has 20 different value levels for each color channel.
Gray image with 20 levels | Gray image with 5 levels | RGB image with 20 color levels each
|:---------------------------------------------- |:----------------------------------------------- |:------------------------------------------------------- |
|  |  |  |
### 1D Arrays
Some examples with 1D arrays.
```@example
using Noise, Plots
x = LinRange(0.0, 10.0, 300)
y = sin.(x)
y_noise = quantization(y, 20, minv=-1, maxv=1)
y_noise_2 = quantization(y, 5, minv=-1, maxv=1)
plot(x,y);
plot!(x, y_noise);
plot!(x, y_noise_2);
savefig("../images/q_series.png") # hide
nothing # hide
```
The green curve consists of 5 different levels, the orange one of 20. As it can be seen, already 20 different value sample the original signal quite good.

| Noise | https://github.com/roflmaostc/Noise.jl.git |
|
[
"MIT"
] | 0.3.3 | d34a07459e1ebdc6b551ecb28e3c19993f544d91 | docs | 4445 | # Salt and Pepper
Salt and Pepper noise in general is a noise which modifies a pixel with two different values of noise.
Usually it sets randomly black and white spots on the image.
## Usage
### Arrays, Grayscale Images and RGB Images
For arrays, grayscale images (`Array{<:Gray}`) and RGB images (`Array{<:RGB}`) we provide the following method:
```julia
salt_pepper(X; salt_prob=0.5, salt=1.0, pepper=0.0[, prob])
```
This methods sets the salt or pepper noise to each pixel and channel individually.
In the case of RGB images, this means that every colorchannel of a pixel receives its own salt or pepper.
The array `X` must be provided.
`prob` is a optional argument following `X`. This value is the probability that a individual pixel is affected by noise.
In the case a pixel receives a noise, we either choose salt or pepper. `salt_prob` is a keyword argument describes
the probability that a choosen pixel will be affected by salt. `1-salt_prob` describes therefore the probabilty for pepper.
Additionally we can also choose the numerical value for salt and pepper using the keyword argument `salt` and `pepper` respectively.
For RGB images the effect is more a color effect since we affect each channel individually and not only the pixel.
### RGB images each Channel the same
For RGB images (`Array{<:RGB}`) we also provide the following:
```julia
salt_pepper_chn(X; salt_prob=0.5, salt=1.0, pepper=0.0[, prob])
```
This method, in contradiction to the previous one, doesn't add the noise to each colorchannel of a element independently but rather
sets the noise value for each channel of a pixel.
For RGB this introduces real black and white spots.
## Examples
### Images
Some examples with images.
```@example; output=False
using Noise, TestImages, Images
img_gray = testimage("fabio_gray_256")
img_color = testimage("fabio_color_256")
img_gray_noise = salt_pepper(img_gray)
img_color_noise = salt_pepper(img_color)
img_color_channel_noise = salt_pepper_chn(img_color)
# 30% of pixels are black or white
img_gray_noise_heavy = salt_pepper(img_gray, 0.3)
# 10% of pixels are white
img_gray_noise_white = salt_pepper(img_gray, 0.1, salt_prob=1)
# 10% of pixels are gray
img_gray_noise_gray = salt_pepper(img_gray, 0.1, salt_prob=0, pepper=0.7)
save("../images/sp_img_gray_noise.png", img_gray_noise) # hide
save("../images/sp_img_color_noise.png", img_color_noise) # hide
save("../images/sp_img_color_channel_noise.png", img_color_channel_noise) # hide
save("../images/sp_img_gray_noise_heavy.png", img_gray_noise_heavy) # hide
save("../images/sp_img_gray_noise_white.png", img_gray_noise_white) #hide
save("../images/sp_gray_noise_gray.png", img_gray_noise_gray) #hide
nothing # hide
```
The images are in the same order as the commands are.
The middle image has applied noise to each color channel individually, in the right the same noise is added to all channels of a pixel.
Therefore the midle image has a color noise, the noise in the image in the right corresponds to some intensity noise.
10% noise means that only 10% of all pixels are noisy, by default this means roughly 5% white pixels and 5% black pixels.
Gray image with 10% noise| RGB image with channelwise noise| RGB image with pixelwise noise
|:---------------------------------------------- |:----------------------------------------------- |:------------------------------------------------------- |
|  |  |  |
|Gray image with 30% salt or pepper | Gray image with 10% salt | Gray image with 10% gray |
|:---------------------------------------------------- |:--------------------------------------------------- |:---------------------------------------------- |
|  |  |  |
### 1D Arrays
Some examples with 1D arrays.
```@example
using Noise, Plots
x = LinRange(0.0, 10.0, 300)
y = sin.(x)
y_noise = salt_pepper(y, 0.05, pepper=-1.0)
y_noise_2 = salt_pepper(y, 0.2, pepper=-0.5, salt=0.5)
plot(x,y);
plot!(x, y_noise);
plot!(x, y_noise_2);
savefig("../images/sp_series.png") # hide
nothing # hide
```
As you can see we are able to introduce salt and pepper noise the same way to 1D arrays.

| Noise | https://github.com/roflmaostc/Noise.jl.git |
|
[
"MIT"
] | 0.2.1 | 110d6267f395cdf474822a3e5a1974ac1a9bfe33 | code | 3412 | using Pkg
Pkg.activate(@__DIR__)
Pkg.develop(; path = joinpath(@__DIR__, ".."))
Pkg.update()
using Ignite
using BenchmarkTools
function sleep_expensive(dt)
t = time_ns()
while time_ns() - t < 1e9 * dt
# More accurate than `sleep(dt)` and is blocking, simulating a workload
end
return nothing
end
function dummy_process_function(dt)
process_function(engine, batch) = Ignite.@timeit engine.timer "sleep_expensive" sleep_expensive(dt)
return process_function
end
function dummy_event_handlers!(engine)
add_event_handler!(engine, STARTED()) do engine
@assert engine.state.iteration == 0
@assert engine.state.epoch == 0
end
add_event_handler!(engine, EPOCH_STARTED()) do engine
@assert mod(engine.state.iteration, engine.state.epoch_length) == 0
end
add_event_handler!(engine, ITERATION_STARTED()) do engine
Ignite.@timeit engine.timer "dummy timing" 1 + 1
end
add_event_handler!(engine, ITERATION_COMPLETED()) do engine
Ignite.@timeit engine.timer "dummy timing" 1 + 1
end
add_event_handler!(engine, EPOCH_COMPLETED()) do engine
@assert mod1(engine.state.iteration, engine.state.epoch_length) == engine.state.epoch_length
end
add_event_handler!(engine, COMPLETED()) do engine
@assert engine.state.epoch == engine.state.max_epochs
@assert engine.state.iteration == engine.state.max_epochs * engine.state.epoch_length
end
return engine
end
function run_trainer(;
dt = 1e-3,
max_epochs = 5,
epoch_length = round(Int, 1 / dt),
add_event_handlers = true,
)
dl = [rand(1) for _ in 1:100]
trainer = Engine(dummy_process_function(dt))
add_event_handlers && dummy_event_handlers!(trainer)
@time Ignite.run!(trainer, dl; max_epochs, epoch_length)
end
trainer = run_trainer(; max_epochs = 1, dt = 1e-3, add_event_handlers = false);
trainer = run_trainer(; max_epochs = 5, dt = 1e-3, add_event_handlers = false);
Ignite.print_timer(trainer.timer);
trainer = run_trainer(; max_epochs = 1, dt = 1e-3, add_event_handlers = true);
trainer = run_trainer(; max_epochs = 5, dt = 1e-3, add_event_handlers = true);
Ignite.print_timer(trainer.timer);
function fire_all_events!(engine)
fire_event!(engine, STARTED())
fire_event!(engine, EPOCH_STARTED())
fire_event!(engine, ITERATION_STARTED())
fire_event!(engine, ITERATION_COMPLETED())
fire_event!(engine, EPOCH_COMPLETED())
fire_event!(engine, COMPLETED())
return nothing
end
function set_event_handlers!(engine, num_handlers::Int)
events = [STARTED(), EPOCH_STARTED(), ITERATION_STARTED(), ITERATION_COMPLETED(), EPOCH_COMPLETED(), COMPLETED()]
empty!(engine.event_handlers)
while length(engine.event_handlers) < num_handlers
for event in events
add_event_handler!(engine, event) do engine
return sqrt(time()) # dummy work
end
length(engine.event_handlers) >= num_handlers && break
end
end
return engine
end
function bench_fire_events!(engine)
for num_handlers in [0, 16, 64, 256, 257]
set_event_handlers!(engine, num_handlers)
@info "num. handlers: $(length(trainer.event_handlers))"
@info "fire_all_events!:"
@time fire_all_events!(engine)
@btime fire_all_events!($engine)
end
return engine
end
bench_fire_events!(trainer);
| Ignite | https://github.com/jondeuce/Ignite.jl.git |
|
[
"MIT"
] | 0.2.1 | 110d6267f395cdf474822a3e5a1974ac1a9bfe33 | code | 704 | using Ignite
using Documenter
DocMeta.setdocmeta!(Ignite, :DocTestSetup, :(using Ignite); recursive = true)
makedocs(;
modules = [Ignite],
authors = "Jonathan Doucette <[email protected], Christian Kames <[email protected]>",
repo = "https://github.com/jondeuce/Ignite.jl/blob/{commit}{path}#{line}",
sitename = "Ignite.jl",
format = Documenter.HTML(;
prettyurls = get(ENV, "CI", "false") == "true",
canonical = "https://jondeuce.github.io/Ignite.jl",
edit_link = "master",
assets = String[],
),
pages = [
"Home" => "index.md",
],
)
deploydocs(;
repo = "github.com/jondeuce/Ignite.jl",
devbranch = "master",
)
| Ignite | https://github.com/jondeuce/Ignite.jl.git |
|
[
"MIT"
] | 0.2.1 | 110d6267f395cdf474822a3e5a1974ac1a9bfe33 | code | 10516 | # # Ignite.jl
# [](https://jondeuce.github.io/Ignite.jl/dev/)
# [](https://github.com/jondeuce/Ignite.jl/actions/workflows/CI.yml?query=branch%3Amaster)
# [](https://codecov.io/gh/jondeuce/Ignite.jl)
# [](https://github.com/JuliaTesting/Aqua.jl)
# Welcome to `Ignite.jl`, a Julia port of the Python library [`ignite`](https://github.com/pytorch/ignite) for simplifying neural network training and validation loops using events and handlers.
# `Ignite.jl` provides a simple yet flexible engine and event system, allowing for the easy composition of training pipelines with various events such as artifact saving, metric logging, and model validation. Event-based training abstracts away the training loop, replacing it with:
# 1. An *engine* which wraps a *process function* that consumes a single batch of data,
# 2. An iterable data loader which produces said batches of data, and
# 3. Events and corresponding event handlers which are attached to the engine, configured to fire at specific points during training.
# Event handlers are much more flexibile compared to other approaches like callbacks: handlers can be any callable; multiple handlers can be attached to a single event; multiple events can trigger the same handler; and custom events can be defined to fire at user-specified points during training. This makes adding functionality to your training pipeline easy, minimizing the need to modify existing code.
# ## Quick Start
# The example below demonstrates how to use `Ignite.jl` to train a simple neural network. Key features to note:
# * The training step is factored out of the training loop: the `train_step` process function takes a batch of training data and computes the training loss, gradients, and updates the model parameters.
# * Data loaders can be any iterable collection. Here, we use a [`DataLoader`](https://juliaml.github.io/MLUtils.jl/stable/api/#MLUtils.DataLoader) from [`MLUtils.jl`](https://github.com/JuliaML/MLUtils.jl)
using Ignite
using Flux, Zygote, Optimisers, MLUtils # for training a neural network
## Build simple neural network and initialize Adam optimizer
model = Chain(Dense(1 => 32, tanh), Dense(32 => 1))
optim = Flux.setup(Optimisers.Adam(1.0f-3), model)
## Create mock data and data loaders
f(x) = 2x - x^3
xtrain, xtest = 2 * rand(Float32, 1, 10_000) .- 1, collect(reshape(range(-1.0f0, 1.0f0; length = 100), 1, :))
ytrain, ytest = f.(xtrain), f.(xtest)
train_data_loader = DataLoader((; x = xtrain, y = ytrain); batchsize = 64, shuffle = true, partial = false)
eval_data_loader = DataLoader((; x = xtest, y = ytest); batchsize = 10, shuffle = false)
## Create training engine:
## - `engine` is a reference to the parent `trainer` engine, created below
## - `batch` is a batch of training data, retrieved by iterating `train_data_loader`
## - (optional) return value is stored in `trainer.state.output`
function train_step(engine, batch)
x, y = batch
l, gs = Zygote.withgradient(m -> sum(abs2, m(x) .- y), model)
Optimisers.update!(optim, model, gs[1])
return Dict("loss" => l)
end
trainer = Engine(train_step)
## Start the training
Ignite.run!(trainer, train_data_loader; max_epochs = 25, epoch_length = 100)
# ### Periodically evaluate model
# The real power of `Ignite.jl` comes when adding *event handlers* to our training engine.
# Let's evaluate our model after every 5th training epoch. This can be easily incorporated without needing to modify any of the above training code:
# 1. Create an `evaluator` engine which consumes batches of evaluation data
# 2. Add *event handlers* to the `evaluator` engine which accumulate a running average of evaluation metrics over batches of evaluation data; we use [`OnlineStats.jl`](https://github.com/joshday/OnlineStats.jl) to make this easy.
# 3. Add an event handler to the `trainer` which runs the `evaluator` on the evaluation data loader every 5 training epochs.
using OnlineStats: Mean, fit!, value # for tracking evaluation metrics
## Create an evaluation engine using `do` syntax:
evaluator = Engine() do engine, batch
x, y = batch
ypred = model(x) # evaluate model on a single batch of validation data
return Dict("ytrue" => y, "ypred" => ypred) # result is stored in `evaluator.state.output`
end
## Add event handlers to the evaluation engine to track metrics:
add_event_handler!(evaluator, STARTED()) do engine
## When `evaluator` starts, initialize the running mean
engine.state.metrics = Dict("abs_err" => Mean()) # new fields can be added to `engine.state` dynamically
end
add_event_handler!(evaluator, ITERATION_COMPLETED()) do engine
## Each iteration, compute eval metrics from predictions
o = engine.state.output
m = engine.state.metrics["abs_err"]
fit!(m, abs.(o["ytrue"] .- o["ypred"]) |> vec)
end
## Add an event handler to `trainer` which runs `evaluator` every 5 epochs:
add_event_handler!(trainer, EPOCH_COMPLETED(; every = 5)) do engine
Ignite.run!(evaluator, eval_data_loader)
@info "Evaluation metrics: abs_err = $(evaluator.state.metrics["abs_err"])"
end
## Run the trainer with periodic evaluation
Ignite.run!(trainer, train_data_loader; max_epochs = 25, epoch_length = 100)
# ### Terminating a run
# There are several ways to stop a training run before it has completed:
# 1. Throw an exception as usual. This will immediately stop training. An `EXCEPTION_RAISED()` event will be subsequently be fired.
# 2. Use a keyboard interrupt, i.e. throw an `InterruptException` via `Ctrl+C` or `Cmd+C`. Training will halt, and an `INTERRUPT()` event will be fired.
# 3. Gracefully terminate via [`Ignite.terminate!(trainer)`](https://jondeuce.github.io/Ignite.jl/dev/#Ignite.terminate!-Tuple{Engine}), or equivalently, `trainer.should_terminate = true`. This will allow the current iteration to finish but no further iterations will begin. Then, a `TERMINATE()` event will be fired followed by a `COMPLETED()` event.
# ### Early stopping
# To implement early stopping, we can add an event handler to `trainer` which checks the evaluation metrics and gracefully terminates `trainer` if the metrics fail to improve. To do so, we first define a training termination trigger using [`Flux.early_stopping`](http://fluxml.ai/Flux.jl/stable/training/callbacks/#Flux.early_stopping):
## Callback which returns `true` if the eval loss fails to decrease by
## at least `min_dist` for two consecutive evaluations
early_stop_trigger = Flux.early_stopping(2; init_score = Inf32, min_dist = 5.0f-3) do
return value(evaluator.state.metrics["abs_err"])
end
# Then, we add an event handler to `trainer` which checks the early stopping trigger and terminates training if the trigger returns `true`:
## This handler must fire every 5th epoch, the same as the evaluation event handler,
## to ensure new evaluation metrics are available
add_event_handler!(trainer, EPOCH_COMPLETED(; every = 5)) do engine
if early_stop_trigger()
@info "Stopping early"
Ignite.terminate!(trainer)
end
end
## Run the trainer with periodic evaluation and early stopping
Ignite.run!(trainer, train_data_loader; max_epochs = 25, epoch_length = 100)
# Note: instead of adding a new event, the evaluation event handler from the previous section could have been modified to check `early_stop_trigger()` immediately after `evaluator` is run.
# ### Artifact saving
# Logging artifacts can be easily added to the trainer, again without modifying the above code. For example, save the current model and optimizer state to disk every 10 epochs using [`JLD2.jl`](https://github.com/JuliaIO/JLD2.jl):
using JLD2
## Save model and optimizer state every 10 epochs
add_event_handler!(trainer, EPOCH_COMPLETED(; every = 10)) do engine
model_state = Flux.state(model)
jldsave("model_and_optim.jld2"; model_state, optim)
@info "Saved model and optimizer state to disk"
end
# ### Trigger multiple functions per event
# Multiple event handlers can be added to the same event:
add_event_handler!(trainer, COMPLETED()) do engine
## Runs after training has completed
end
add_event_handler!(trainer, COMPLETED()) do engine
## Also runs after training has completed, after the above function runs
end
# ### Attach the same handler to multiple events
# The boolean operators `|` and `&` can be used to combine events together:
add_event_handler!(trainer, EPOCH_COMPLETED(; every = 10) | COMPLETED()) do engine
## Runs at the end of every 10th epoch, or when training is completed
end
throttled_event = EPOCH_COMPLETED(; every = 3) & EPOCH_COMPLETED(; event_filter = throttle_filter(30.0))
add_event_handler!(trainer, throttled_event) do engine
## Runs at the end of every 3rd epoch if at least 30s has passed since the last firing
end
# ### Define custom events
# Custom events can be created and fired at user-defined stages in the training process.
# For example, suppose we want to define events that fire at the start and finish of both the backward pass and the optimizer step. All we need to do is define new event types that subtype `AbstractLoopEvent`, and then fire them at appropriate points in the `train_step` process function using `fire_event!`:
struct BACKWARD_STARTED <: AbstractLoopEvent end
struct BACKWARD_COMPLETED <: AbstractLoopEvent end
struct OPTIM_STEP_STARTED <: AbstractLoopEvent end
struct OPTIM_STEP_COMPLETED <: AbstractLoopEvent end
function train_step(engine, batch)
x, y = batch
## Compute the gradients of the loss with respect to the model
fire_event!(engine, BACKWARD_STARTED())
l, gs = Zygote.withgradient(m -> sum(abs2, m(x) .- y), model)
engine.state.gradients = gs # the engine state can be accessed by event handlers
fire_event!(engine, BACKWARD_COMPLETED())
## Update the model's parameters
fire_event!(engine, OPTIM_STEP_STARTED())
Optimisers.update!(optim, model, gs[1])
fire_event!(engine, OPTIM_STEP_COMPLETED())
return Dict("loss" => l)
end
trainer = Engine(train_step)
# Then, add event handlers for these custom events as usual:
add_event_handler!(trainer, BACKWARD_COMPLETED(; every = 10)) do engine
## This code runs after every 10th backward pass is completed
end
| Ignite | https://github.com/jondeuce/Ignite.jl.git |
|
[
"MIT"
] | 0.2.1 | 110d6267f395cdf474822a3e5a1974ac1a9bfe33 | code | 297 | using Pkg
ignite_dir = realpath(joinpath(@__DIR__, "../.."))
Pkg.activate(@__DIR__)
Pkg.develop(; path = ignite_dir)
Pkg.update()
using Literate
readme_src = joinpath(@__DIR__, "README.jl")
readme_dst = ignite_dir
Literate.markdown(readme_src, readme_dst; flavor = Literate.CommonMarkFlavor())
| Ignite | https://github.com/jondeuce/Ignite.jl.git |
|
[
"MIT"
] | 0.2.1 | 110d6267f395cdf474822a3e5a1974ac1a9bfe33 | code | 23142 | """
$(README)
"""
module Ignite
using Logging: AbstractLogger, NullLogger, current_logger, global_logger, with_logger
using DataStructures: DefaultOrderedDict, OrderedDict
using DocStringExtensions: README, TYPEDEF, TYPEDFIELDS, TYPEDSIGNATURES
using TimerOutputs: TimerOutput, @timeit, print_timer, reset_timer!
export AbstractEvent, AbstractFiringEvent, AbstractLoopEvent
export STARTED, EPOCH_STARTED, ITERATION_STARTED, GET_BATCH_STARTED, GET_BATCH_COMPLETED, ITERATION_COMPLETED, EPOCH_COMPLETED, COMPLETED
export INTERRUPT, EXCEPTION_RAISED, DATALOADER_STOP_ITERATION, TERMINATE
export State, Engine, EventHandler, FilteredEvent, OrEvent, AndEvent
export filter_event, every_filter, once_filter, throttle_filter, timeout_filter
export add_event_handler!, fire_event!
"""
$(TYPEDEF)
Abstract supertype for all events.
"""
abstract type AbstractEvent end
"""
$(TYPEDEF)
Abstract supertype for all events which can trigger event handlers via [`fire_event!`](@ref).
"""
abstract type AbstractFiringEvent <: AbstractEvent end
"""
$(TYPEDEF)
Abstract supertype for events fired during the normal execution of [`Ignite.run!`](@ref).
A default convenience constructor `(EVENT::Type{<:AbstractLoopEvent})(; kwargs...)` is provided to allow for easy filtering of `AbstractLoopEvent`s.
For example, `EPOCH_COMPLETED(every = 3)` will build a [`FilteredEvent`](@ref) which is triggered every third epoch.
See [`filter_event`](@ref) for allowed keywords.
By inheriting from `AbstractLoopEvent`, custom events will inherit these convenience constructors, too.
If this is undesired, one can instead inherit from the supertype `AbstractFiringEvent`.
"""
abstract type AbstractLoopEvent <: AbstractFiringEvent end
(EVENT::Type{<:AbstractLoopEvent})(; kwargs...) = filter_event(EVENT(); kwargs...)
struct EPOCH_STARTED <: AbstractLoopEvent end
struct ITERATION_STARTED <: AbstractLoopEvent end
struct GET_BATCH_STARTED <: AbstractLoopEvent end
struct GET_BATCH_COMPLETED <: AbstractLoopEvent end
struct ITERATION_COMPLETED <: AbstractLoopEvent end
struct EPOCH_COMPLETED <: AbstractLoopEvent end
struct STARTED <: AbstractFiringEvent end
struct TERMINATE <: AbstractFiringEvent end
struct COMPLETED <: AbstractFiringEvent end
struct INTERRUPT <: AbstractFiringEvent end
struct EXCEPTION_RAISED <: AbstractFiringEvent end
struct DATALOADER_STOP_ITERATION <: AbstractFiringEvent end
struct DataLoaderEmptyException <: Exception end
struct DataLoaderUnknownLengthException <: Exception end
"""
$(TYPEDEF)
`EventHandler`s wrap an `event` and a corresponding `handler!`.
The `handler!` is executed when `event` is triggered by a call to [`fire_event!`](@ref).
The output from `handler!` is ignored.
Additional `args` for `handler!` may be stored in `EventHandler` at construction; see [`add_event_handler!`](@ref).
When `h::EventHandler` is triggered, the event handler is called as `h.handler!(engine::Engine, h.args...)`.
Fields: $(TYPEDFIELDS)
"""
Base.@kwdef struct EventHandler{E <: AbstractEvent, H, A <: Tuple}
"Event which triggers handler"
event::E
"Event handler which executes when triggered by `event`"
handler!::H
"Additional arguments passed to the event handler"
args::A
end
"""
$(TYPEDEF)
Current state of the engine.
`State` is a light wrapper around a `DefaultOrderedDict{Symbol, Any, Nothing}` with the following keys:
* `:iteration`: the current iteration, beginning with 1.
* `:epoch`: the current epoch, beginning with 1.
* `:max_epochs`: The number of epochs to run.
* `:epoch_length`: The number of batches processed per epoch.
* `:output`: The output of `process_function` after a single iteration.
* `:last_event`: The last event fired.
* `:counters`: A `DefaultOrderedDict{AbstractFiringEvent, Int, Int}(0)` with firing event firing counters.
* `:times`: An `OrderedDict{AbstractFiringEvent, Float64}()` with total and per-epoch times fetched on firing event keys.
Fields can be accessed and modified using `getproperty` and `setproperty!`.
For example, `engine.state.iteration` can be used to access the current iteration, and `engine.state.new_field = value` can be used to store `value` for later use e.g. by an event handler.
"""
Base.@kwdef struct State <: AbstractDict{Symbol, Any}
state::DefaultOrderedDict{Symbol, Any, Nothing} = DefaultOrderedDict{Symbol, Any, Nothing}(
nothing,
OrderedDict{Symbol, Any}(
:iteration => nothing, # 1-based, the first iteration is 1
:epoch => nothing, # 1-based, the first epoch is 1
:max_epochs => nothing, # number of epochs to run
:epoch_length => nothing, # number of batches processed per epoch
:output => nothing, # most recent output of `process_function`
:last_event => nothing, # most recent event fired
:counters => DefaultOrderedDict{AbstractFiringEvent, Int, Int}(0), # firing event counters
:times => OrderedDict{AbstractFiringEvent, Float64}(), # firing event times
# :seed => nothing, # seed to set at each epoch
# :metrics => nothing, # dictionary with defined metrics
),
)
end
state(s::State) = getfield(s, :state)
Base.getindex(s::State, k::Symbol) = getindex(state(s), k)
Base.setindex!(s::State, v, k::Symbol) = setindex!(state(s), v, k)
Base.getproperty(s::State, k::Symbol) = s[k]
Base.setproperty!(s::State, k::Symbol, v) = (s[k] = v)
Base.propertynames(s::State) = collect(keys(state(s)))
Base.get(s::State, k::Symbol, v) = get(state(s), k, v)
Base.get!(s::State, k::Symbol, v) = get!(state(s), k, v)
Base.iterate(s::State, args...) = iterate(state(s), args...)
Base.length(s::State) = length(state(s))
"""
$(TYPEDEF)
An `Engine` struct to be run using [`Ignite.run!`](@ref).
Can be constructed via `engine = Engine(process_function; kwargs...)`, where the process function takes two arguments: the parent `engine`, and a batch of data.
Fields: $(TYPEDFIELDS)
"""
Base.@kwdef mutable struct Engine{P}
"A function that processes a single batch of data and returns an output."
process_function::P
"An object that holds the current state of the engine."
state::State = State()
"A list of event handlers that are called at specific points when the engine is running."
event_handlers::Vector{EventHandler} = EventHandler[]
"An optional logger; if `nothing`, then `current_logger()` will be used."
logger::Union{Nothing, AbstractLogger} = nothing
"Internal timer. Can be used with `TimerOutputs` to record event timings"
timer::TimerOutput = TimerOutput()
"A flag that indicates whether the engine should stop running."
should_terminate::Bool = false
"Exception thrown during training"
exception::Union{Nothing, Exception} = nothing
# should_terminate_single_epoch::Bool = false
# should_interrupt::Bool = false
end
Engine(process_function; kwargs...) = Engine(; process_function, kwargs...)
# Copied from Parameters.jl: https://github.com/mauro3/Parameters.jl/blob/e55b025b96275142ba52b2a725aedf460f26ff6f/src/Parameters.jl#L581
Base.show(io::IO, engine::Engine) = dump(IOContext(io, :limit => true), engine; maxdepth = 1)
#### Internal data loader cycler
struct DataCycler{D}
iter::D
end
function Base.iterate(dl::DataCycler, ::Nothing)
batch_and_state = iterate(dl.iter)
(batch_and_state === nothing) && throw(DataLoaderEmptyException()) # empty iterator
return batch_and_state
end
Base.iterate(dl::DataCycler) = iterate(dl, nothing)
function Base.iterate(dl::DataCycler, iter_state)
batch_and_state = iterate(dl.iter, iter_state)
(batch_and_state === nothing) && return iterate(dl) # restart iterator
return batch_and_state
end
Base.IteratorSize(::DataCycler) = Base.IsInfinite()
Base.IteratorEltype(dl::DataCycler) = Base.IteratorEltype(dl.iter)
Base.eltype(dl::DataCycler) = Base.eltype(dl.iter)
default_epoch_length(dl::DataCycler) = default_epoch_length(dl, Base.IteratorSize(dl.iter))
default_epoch_length(dl::DataCycler, ::Union{Base.HasLength, Base.HasShape}) = length(dl.iter)
default_epoch_length(::DataCycler, ::Base.IteratorSize) = throw(DataLoaderUnknownLengthException())
#### Engine methods
function initialize!(engine::Engine; max_epochs::Int, epoch_length::Int)
engine.should_terminate = false
engine.exception = nothing
engine.state.iteration = 0
engine.state.epoch = 0
engine.state.max_epochs = max_epochs
engine.state.epoch_length = epoch_length
engine.state.last_event = nothing
empty!(engine.state.counters)
empty!(engine.state.times)
return engine
end
function isdone(engine::Engine)
iteration = engine.state.iteration
epoch = engine.state.epoch
max_epochs = engine.state.max_epochs
epoch_length = engine.state.epoch_length
return !any(isnothing, (iteration, epoch, max_epochs, epoch_length)) && ( # counters are initialized
engine.should_terminate || ( # early termination
epoch == max_epochs &&
iteration == epoch_length * max_epochs # regular termination
)
)
end
"""
$(TYPEDSIGNATURES)
Reset the engine state.
"""
function reset!(engine::Engine)
engine.state = State()
return engine
end
"""
$(TYPEDSIGNATURES)
Terminate the engine by setting `engine.should_terminate = true`.
"""
function terminate!(engine::Engine)
engine.should_terminate = true
return engine
end
"""
$(TYPEDSIGNATURES)
Add an event handler to an engine which is fired when `event` is triggered.
When fired, the event handler is called as `handler!(engine::Engine, handler_args...)`.
"""
function add_event_handler!(handler!, engine::Engine, event::AbstractEvent, handler_args...)
push!(engine.event_handlers, EventHandler(event, handler!, handler_args))
return engine
end
#### Run engine
function load_batch!(engine::Engine, dl::DataCycler, iter_state)
to = engine.timer
engine.state.times[GET_BATCH_STARTED()] = time()
@timeit to "Event: GET_BATCH_STARTED" fire_event!(engine, GET_BATCH_STARTED())
@timeit to "Iterate data loader" batch, iter_state = iterate(dl, iter_state)
@timeit to "Event: GET_BATCH_COMPLETED" fire_event!(engine, GET_BATCH_COMPLETED())
engine.state.times[GET_BATCH_COMPLETED()] = time() - engine.state.times[GET_BATCH_STARTED()]
return batch, iter_state
end
function process_function!(engine::Engine, batch)
to = engine.timer
engine.state.times[ITERATION_STARTED()] = time()
@timeit to "Event: ITERATION_STARTED" fire_event!(engine, ITERATION_STARTED())
@timeit to "Process function" output = engine.state.output = engine.process_function(engine, batch)
@timeit to "Event: ITERATION_COMPLETED" fire_event!(engine, ITERATION_COMPLETED())
engine.state.times[ITERATION_COMPLETED()] = time() - engine.state.times[ITERATION_STARTED()]
return output
end
"""
$(TYPEDSIGNATURES)
Run the `engine`.
Data batches are retrieved by iterating `dataloader`.
The data loader may be infinite; by default, it is restarted if it empties.
Inputs:
* `engine::Engine`: An instance of the `Engine` struct containing the `process_function` to run each iteration.
* `dataloader`: A data loader to iterate over.
* `max_epochs::Int`: the number of epochs to run. Defaults to 1.
* `epoch_length::Int`: the length of an epoch. If `nothing`, falls back to `length(dataloader)`.
Conceptually, running the engine is roughly equivalent to the following:
1. The engine state is initialized.
2. The engine begins running for `max_epochs` epochs, or until `engine.should_terminate == true`.
3. At the start of each epoch, `EPOCH_STARTED()` event is fired.
4. An iteration loop is performed for `epoch_length` number of iterations, or until `engine.should_terminate == true`.
5. At the start of each iteration, `ITERATION_STARTED()` event is fired, and a batch of data is loaded.
6. The `process_function` is called on the loaded data batch.
7. At the end of each iteration, `ITERATION_COMPLETED()` event is fired.
8. At the end of each epoch, `EPOCH_COMPLETED()` event is fired.
9. At the end of all the epochs, `COMPLETED()` event is fired.
If `engine.should_terminate` is set to `true` while running the engine, the engine will be terminated gracefully after the next completed iteration.
This will subsequently trigger a `TERMINATE()` event to be fired followed by a `COMPLETED()` event.
"""
function run!(
engine::Engine,
dataloader;
max_epochs::Int = 1,
epoch_length::Union{Int, Nothing} = nothing,
)
logger = something(engine.logger, current_logger())
to = engine.timer
reset_timer!(to)
@timeit to "Ignite.run!" with_logger(logger) do
try
dl = DataCycler(dataloader)
iter_state = nothing
(epoch_length === nothing) && (epoch_length = default_epoch_length(dl))
initialize!(engine; max_epochs, epoch_length)
engine.state.times[STARTED()] = time()
@timeit to "Event: STARTED" fire_event!(engine, STARTED())
@timeit to "Epoch loop" while engine.state.epoch < max_epochs && !engine.should_terminate
engine.state.epoch += 1
engine.state.times[EPOCH_STARTED()] = time()
@timeit to "Event: EPOCH_STARTED" fire_event!(engine, EPOCH_STARTED())
epoch_iteration = 0
@timeit to "Iteration loop" while epoch_iteration < epoch_length && !engine.should_terminate
batch, iter_state = load_batch!(engine, dl, iter_state)
epoch_iteration += 1
engine.state.iteration += 1
process_function!(engine, batch)
end
engine.should_terminate && break
@timeit to "Event: EPOCH_COMPLETED" fire_event!(engine, EPOCH_COMPLETED())
engine.state.times[EPOCH_COMPLETED()] = time() - engine.state.times[EPOCH_STARTED()]
hours, mins, secs = to_hours_mins_secs(engine.state.times[EPOCH_COMPLETED()])
@info "Epoch[$(engine.state.epoch)] Complete. Time taken: $(hours):$(mins):$(secs)"
end
if engine.should_terminate
@info "Terminating run"
@timeit to "Event: TERMINATE" fire_event!(engine, TERMINATE())
end
@timeit to "Event: COMPLETED" fire_event!(engine, COMPLETED())
engine.state.times[COMPLETED()] = time() - engine.state.times[STARTED()]
hours, mins, secs = to_hours_mins_secs(engine.state.times[COMPLETED()])
@info "Engine run complete. Time taken: $(hours):$(mins):$(secs)"
catch e
engine.exception = e
if e isa InterruptException
@info "User interrupt"
@timeit to "Event: INTERRUPT" fire_event!(engine, INTERRUPT())
elseif e isa DataLoaderEmptyException
@error "Restarting data loader failed: `iterate(dataloader)` returned `nothing`"
@timeit to "Event: DATALOADER_STOP_ITERATION" fire_event!(engine, DATALOADER_STOP_ITERATION())
elseif e isa DataLoaderUnknownLengthException
@error "Length of data loader iterator is not known; must set `epoch_length` explicitly"
else
@error "Exception raised during training"
@timeit to "Event: EXCEPTION_RAISED" fire_event!(engine, EXCEPTION_RAISED())
end
@error sprint(showerror, e, catch_backtrace())
finally
return engine
end
end
end
#### Event firing
"""
$(TYPEDSIGNATURES)
Execute all event handlers triggered by the firing event `e`.
"""
function fire_event!(engine::Engine, e::AbstractFiringEvent)
engine.state.last_event = e
engine.state.counters[e] += 1
fire_event_handlers!(engine, e)
return engine
end
function fire_event_handlers!(engine::Engine, e::AbstractFiringEvent)
if length(engine.event_handlers) <= 256
# Make the common case fast via loop unrolling
fire_event_handlers_generated!(engine, (engine.event_handlers...,), e)
else
# Fallback to a dynamic loop for large numbers of handlers
fire_event_handlers_loop!(engine, engine.event_handlers, e)
end
end
@generated function fire_event_handlers_generated!(engine::Engine, handlers::H, e::AbstractFiringEvent) where {N, H <: Tuple{Vararg{EventHandler, N}}}
quote
Base.Cartesian.@nexprs $N i -> fire_event_handler!(engine, handlers[i], e)
end
end
function fire_event_handlers_loop!(engine::Engine, handlers::AbstractVector{EventHandler}, e::AbstractFiringEvent)
for handler in handlers
fire_event_handler!(engine, handler, e)
end
end
"""
$(TYPEDSIGNATURES)
Execute `event_handler!` if it is triggered by the firing event `e`.
"""
function fire_event_handler!(engine::Engine, event_handler!::EventHandler, e::AbstractFiringEvent)
if is_triggered_by(engine, event_handler!, e)
fire_event_handler!(engine, event_handler!)
end
return engine
end
is_triggered_by(engine::Engine, h::EventHandler, e) = is_triggered_by(engine, h.event, e)
fire_event_handler!(engine::Engine, h::EventHandler) = h.handler!(engine, h.args...)
#### Helpers
Base.@kwdef struct EveryFilter{T}
every::T
end
function (f::EveryFilter)(engine::Engine, e::AbstractFiringEvent)
count = engine.state.counters[e]
return count > 0 && any(mod1.(count, f.every) .== f.every)
end
Base.@kwdef struct OnceFilter{T}
once::T
end
function (f::OnceFilter)(engine::Engine, e::AbstractFiringEvent)
count = engine.state.counters[e]
return count > 0 && any(count .== f.once)
end
Base.@kwdef struct ThrottleFilter
throttle::Float64
last_fire::Base.RefValue{Float64}
end
function (f::ThrottleFilter)(engine::Engine, e::AbstractFiringEvent)
t = time()
return t - f.last_fire[] >= f.throttle ? (f.last_fire[] = t; true) : false
end
Base.@kwdef struct TimeoutFilter
timeout::Float64
start_time::Float64
end
function (f::TimeoutFilter)(engine::Engine, e::AbstractFiringEvent)
return time() - f.start_time >= f.timeout
end
"""
$(TYPEDSIGNATURES)
Creates an event filter function for use in a `FilteredEvent` that returns `true` periodically depending on `every`:
* If `every = n::Int`, the filter will trigger every `n`th firing of the event.
* If `every = Int[n₁, n₂, ...]`, the filter will trigger every `n₁`th firing, every `n₂`th firing, and so on.
"""
every_filter(every::Union{Int, <:AbstractVector{Int}}) = EveryFilter(every)
"""
$(TYPEDSIGNATURES)
Creates an event filter function for use in a `FilteredEvent` that returns `true` at specific points depending on `once`:
* If `once = n::Int`, the filter will trigger only on the `n`th firing of the event.
* If `once = Int[n₁, n₂, ...]`, the filter will trigger only on the `n₁`th firing, the `n₂`th firing, and so on.
"""
once_filter(once::Union{Int, <:AbstractVector{Int}}) = OnceFilter(once)
"""
$(TYPEDSIGNATURES)
Creates an event filter function for use in a `FilteredEvent` that returns `true` if at least `throttle` seconds has passed since it was last fired.
"""
throttle_filter(throttle::Real, last_fire::Real = -Inf) = ThrottleFilter(throttle, Ref(last_fire))
"""
$(TYPEDSIGNATURES)
Creates an event filter function for use in a `FilteredEvent` that returns `true` if at least `timeout` seconds has passed since the filter function was created.
"""
timeout_filter(timeout::Real, start_time::Real = time()) = TimeoutFilter(timeout, start_time)
function to_hours_mins_secs(time_taken)
mins, secs = divrem(time_taken, 60.0)
hours, mins = divrem(mins, 60.0)
return map(x -> lpad(x, 2, '0'), (round(Int, hours), round(Int, mins), floor(Int, secs)))
end
#### Custom events
is_triggered_by(::Engine, e1::AbstractEvent, e2::AbstractFiringEvent) = e1 == e2
"""
$(TYPEDEF)
`FilteredEvent(event::E, event_filter::F)` wraps an `event` and a `event_filter` function.
When a firing event `e` is fired, if `event_filter(engine, e)` returns `true` then the filtered event will be fired too.
Fields: $(TYPEDFIELDS)
"""
Base.@kwdef struct FilteredEvent{E <: AbstractEvent, F} <: AbstractEvent
"The wrapped event that will be fired if the filter function returns true when applied to a firing event."
event::E
"The filter function `(::Engine, ::AbstractFiringEvent) -> Bool` returns `true` if the filtered event should be fired."
event_filter::F
end
"""
$(TYPEDEF)
Filter the input `event` to fire conditionally:
Inputs:
* `event::AbstractFiringEvent`: event to be filtered.
* `event_filter::Any`: A event_filter function `(::Engine, ::AbstractFiringEvent) -> Bool` returning `true` if the filtered event should be fired.
* `every::Union{Int, <:AbstractVector{Int}}`: the period(s) in which the filtered event should be fired; see [`every_filter`](@ref).
* `once::Union{Int, <:AbstractVector{Int}}`: the point(s) at which the filtered event should be fired; see [`once_filter`](@ref).
"""
function filter_event(event::AbstractFiringEvent; event_filter = nothing, every = nothing, once = nothing)
@assert sum(!isnothing, (event_filter, every, once)) == 1 "Exactly one of `event_filter`, `every`, or `once` must be supplied."
if event_filter === nothing
event_filter = every !== nothing ? every_filter(every) : once_filter(once)
end
return FilteredEvent(event, event_filter)
end
is_triggered_by(engine::Engine, e1::FilteredEvent, e2::AbstractFiringEvent) = is_triggered_by(engine, e1.event, e2) && e1.event_filter(engine, e2)
"""
$(TYPEDEF)
`OrEvent(event1, event2)` wraps two events and triggers if either of the wrapped events are triggered by a firing event firing.
`OrEvent`s can be constructed via the `|` operator: `event1 | event2`.
Fields: $(TYPEDFIELDS)
"""
Base.@kwdef struct OrEvent{E1 <: AbstractEvent, E2 <: AbstractEvent} <: AbstractEvent
"The first wrapped event that will be checked if it should be fired."
event1::E1
"The second wrapped event that will be checked if it should be fired."
event2::E2
end
Base.:|(event1::AbstractEvent, event2::AbstractEvent) = OrEvent(event1, event2)
is_triggered_by(engine::Engine, e1::OrEvent, e2::AbstractFiringEvent) = is_triggered_by(engine, e1.event1, e2) || is_triggered_by(engine, e1.event2, e2)
"""
$(TYPEDEF)
`AndEvent(event1, event2)` wraps two events and triggers if and only if both wrapped events are triggered by the same firing event firing.
`AndEvent`s can be constructed via the `&` operator: `event1 & event2`.
Fields: $(TYPEDFIELDS)
"""
Base.@kwdef struct AndEvent{E1 <: AbstractEvent, E2 <: AbstractEvent} <: AbstractEvent
"The first wrapped event that will be considered for triggering."
event1::E1
"The second wrapped event that will be considered for triggering."
event2::E2
end
Base.:&(event1::AbstractEvent, event2::AbstractEvent) = AndEvent(event1, event2)
is_triggered_by(engine::Engine, e1::AndEvent, e2::AbstractFiringEvent) = is_triggered_by(engine, e1.event1, e2) && is_triggered_by(engine, e1.event2, e2)
end # module Ignite
| Ignite | https://github.com/jondeuce/Ignite.jl.git |
|
[
"MIT"
] | 0.2.1 | 110d6267f395cdf474822a3e5a1974ac1a9bfe33 | code | 16009 | using Ignite
using Test
using Aqua: test_all
using DataStructures: OrderedDict
using Logging: NullLogger
@testset "Ignite.jl" begin
function dummy_process_function(engine, batch)
engine.state.batch = batch
return Dict("loss" => sum(map(sum, batch)))
end
function dummy_engine(f = dummy_process_function; logger = NullLogger(), kwargs...)
return Engine(f; kwargs..., logger)
end
function dummy_trainer_and_loader(args...; max_epochs = 10, epoch_length = 10, kwargs...)
engine = dummy_engine(args...; kwargs...)
dataloader = (rand(3) for _ in 1:max_epochs*epoch_length)
return engine, dataloader
end
function fire_and_check_triggered(engine, event, prim_event)
fire_event!(engine, prim_event)
return Ignite.is_triggered_by(engine, event, prim_event)
end
@testset "EPOCH_STARTED" begin
@testset "every <Int>" begin
trainer = dummy_engine()
event = EPOCH_STARTED(; every = 2)
for i in 1:5
@test !fire_and_check_triggered(trainer, event, EPOCH_COMPLETED())
@test !fire_and_check_triggered(trainer, event, ITERATION_COMPLETED())
t = fire_and_check_triggered(trainer, event, EPOCH_STARTED())
@test !t || (t && mod1(i, 2) == 2)
end
end
@testset "every <Int list>" begin
trainer = dummy_engine()
every = [2, 5, 7]
event = EPOCH_STARTED(; every = every)
for i in 1:25
@test !fire_and_check_triggered(trainer, event, EPOCH_COMPLETED())
@test !fire_and_check_triggered(trainer, event, ITERATION_COMPLETED())
t = fire_and_check_triggered(trainer, event, EPOCH_STARTED())
@test !t || (t && any(mod1.(i, every) .== every))
end
end
@testset "once <Int list>" begin
trainer = dummy_engine()
once = [2, 5, 7]
event = EPOCH_STARTED(; once = once)
for i in 1:25
@test !fire_and_check_triggered(trainer, event, EPOCH_COMPLETED())
@test !fire_and_check_triggered(trainer, event, ITERATION_COMPLETED())
t = fire_and_check_triggered(trainer, event, EPOCH_STARTED())
@test !t || (t && any(i .== once))
end
end
end
@testset "ITERATION_COMPLETED" begin
@testset "once <Int>" begin
trainer = dummy_engine()
event = ITERATION_COMPLETED(; once = 4)
for i in 1:7
@test !fire_and_check_triggered(trainer, event, EPOCH_STARTED())
@test !fire_and_check_triggered(trainer, event, EPOCH_COMPLETED())
t = fire_and_check_triggered(trainer, event, ITERATION_COMPLETED())
@test !t || (t && i == 4)
end
end
end
@testset "throttle filter" begin
engine, event = dummy_engine(), EPOCH_COMPLETED() # dummy arguments
event_filter = throttle_filter(1.0)
@test event_filter(engine, event) # first call is unthrottled
sleep(0.6)
@test !event_filter(engine, event)
sleep(0.6)
@test event_filter(engine, event) # throttle resets
sleep(0.3)
@test !event_filter(engine, event)
sleep(0.3)
@test !event_filter(engine, event)
sleep(0.6)
@test event_filter(engine, event) # throttle resets
end
@testset "timeout filter" begin
engine, event = dummy_engine(), EPOCH_COMPLETED() # dummy arguments
event_filter = timeout_filter(0.8)
t₀ = event_filter.start_time[]
while (Δt = time() - t₀) < 1.5
@test event_filter(engine, event) === (Δt >= 0.8)
sleep(0.25)
end
end
@testset "OrEvent" begin
trainer = dummy_engine()
event_filter = (_engine, _event) -> _engine.state.new_field !== nothing
event = EPOCH_COMPLETED(; every = 3) | EPOCH_COMPLETED(; event_filter)
@test !fire_and_check_triggered(trainer, event, EPOCH_COMPLETED())
@test !fire_and_check_triggered(trainer, event, EPOCH_COMPLETED())
@test fire_and_check_triggered(trainer, event, EPOCH_COMPLETED())
Ignite.reset!(trainer)
@test !fire_and_check_triggered(trainer, event, EPOCH_COMPLETED())
trainer.state.new_field = 1
@test fire_and_check_triggered(trainer, event, EPOCH_COMPLETED())
@test fire_and_check_triggered(trainer, event, EPOCH_COMPLETED())
end
@testset "AndEvent" begin
trainer = dummy_engine()
event_filter = (_engine, _event) -> _engine.state.new_field !== nothing
event = EPOCH_COMPLETED(; every = 3) & EPOCH_COMPLETED(; event_filter)
@test !fire_and_check_triggered(trainer, event, EPOCH_COMPLETED())
@test !fire_and_check_triggered(trainer, event, EPOCH_COMPLETED())
@test !fire_and_check_triggered(trainer, event, EPOCH_COMPLETED())
trainer.state.new_field = 1
@test !fire_and_check_triggered(trainer, event, EPOCH_COMPLETED())
@test !fire_and_check_triggered(trainer, event, EPOCH_COMPLETED())
@test fire_and_check_triggered(trainer, event, EPOCH_COMPLETED())
end
@testset "custom show methods" begin
@test startswith(sprint(show, dummy_engine()), "Engine")
end
@testset "State methods" begin
s = State()
s[:iteration] = 0
s.epoch = 0
s[:new_field_1] = :one
s.new_field_2 = "two"
@test s[:iteration] == s.iteration == 0
@test s[:epoch] == s.epoch == 0
@test s[:new_field_1] == s.new_field_1 == :one
@test s[:new_field_2] == s.new_field_2 == "two"
@test get!(s, :new_field_3, 3) == 3
@test s[:new_field_3] == s.new_field_3 == 3
@test get(s, :new_field_4, 4.0) == 4.0
@test !haskey(s, :new_field_4)
@test length(s) == length(State()) + 3 == 11
@test all(k ∈ propertynames(s) for k in [:iteration, :epoch, :new_field_1, :new_field_2, :new_field_3])
@test propertynames(s) == collect(keys(Ignite.state(s)))
@test OrderedDict(k => v for (k, v) in s) == Ignite.state(s)
end
@testset "DataCycler" begin
dl = Ignite.DataCycler(1:5)
@test_throws MethodError length(dl)
@test Ignite.default_epoch_length(dl) == 5
@test Base.IteratorSize(dl) == Base.IsInfinite()
@test Base.IteratorEltype(dl) == Base.HasEltype()
@test Base.eltype(dl) == Int
dl = Ignite.DataCycler(Iterators.cycle(1.0:5.0))
@test_throws MethodError length(dl)
@test_throws Ignite.DataLoaderUnknownLengthException Ignite.default_epoch_length(dl)
@test Base.IteratorSize(dl) == Base.IsInfinite()
@test Base.IteratorEltype(dl) == Base.HasEltype()
@test Base.eltype(dl) == Float64
end
@testset "run!" begin
@testset "early termination" begin
max_epochs, epoch_length = 3, 5
trainer, dl = dummy_trainer_and_loader(; max_epochs, epoch_length)
add_event_handler!(trainer, EPOCH_COMPLETED()) do engine
@test engine.state.output isa Dict
@test engine.state.output["loss"] isa Float64
Ignite.terminate!(engine)
end
add_event_handler!(trainer, TERMINATE()) do engine
engine.state.terminate_event_fired = true
end
Ignite.run!(trainer, dl; max_epochs, epoch_length)
@test Ignite.isdone(trainer) === true
@test trainer.exception === nothing
@test trainer.should_terminate === true
@test trainer.state.iteration == epoch_length
@test trainer.state.epoch == 1
@test trainer.state.terminate_event_fired === true
end
@testset "all default events" begin
max_epochs, epoch_length = 3, 5
trainer, dl = dummy_trainer_and_loader(; max_epochs, epoch_length)
add_event_handler!(trainer, STARTED()) do engine
@test engine.state.iteration == 0
@test engine.state.epoch == 0
end
add_event_handler!(trainer, EPOCH_STARTED()) do engine
@test mod(engine.state.iteration, epoch_length) == 0
end
add_event_handler!(trainer, ITERATION_STARTED()) do engine
#TODO
end
add_event_handler!(trainer, ITERATION_COMPLETED()) do engine
#TODO
end
add_event_handler!(trainer, EPOCH_COMPLETED()) do engine
@test mod1(engine.state.iteration, epoch_length) == epoch_length
end
add_event_handler!(trainer, COMPLETED()) do engine
@test engine.state.epoch == max_epochs
@test engine.state.iteration == max_epochs * epoch_length
end
Ignite.run!(trainer, dl; max_epochs, epoch_length)
@test Ignite.isdone(trainer) === true
end
@testset "event ordering" begin
for early_exit_mode in [:interrupt, :terminate, :exception]
max_epochs, epoch_length = 7, 3
final_iter = epoch_length * (max_epochs - 1) + 1
trainer, dl = dummy_trainer_and_loader(; max_epochs, epoch_length)
event_list = Any[]
event_to_log = EPOCH_COMPLETED(; every = 3) | INTERRUPT() | EXCEPTION_RAISED() | TERMINATE() | COMPLETED()
add_event_handler!(trainer, event_to_log) do engine
push!(event_list, engine.state.last_event)
end
if early_exit_mode === :interrupt
add_event_handler!(trainer, ITERATION_COMPLETED(; once = final_iter)) do engine
@test engine.state.iteration == final_iter
throw(InterruptException())
end
Ignite.run!(trainer, dl; max_epochs, epoch_length)
@test Ignite.isdone(trainer) === false
@test trainer.exception isa InterruptException
@test event_list == Any[EPOCH_COMPLETED(), EPOCH_COMPLETED(), INTERRUPT()]
elseif early_exit_mode === :terminate
add_event_handler!(trainer, ITERATION_COMPLETED(; once = final_iter)) do engine
@test engine.state.iteration == final_iter
Ignite.terminate!(engine)
end
Ignite.run!(trainer, dl; max_epochs, epoch_length)
@test Ignite.isdone(trainer) === true
@test trainer.exception === nothing
@test event_list == Any[EPOCH_COMPLETED(), EPOCH_COMPLETED(), TERMINATE(), COMPLETED()]
elseif early_exit_mode === :exception
add_event_handler!(trainer, ITERATION_COMPLETED(; once = final_iter)) do engine
@test engine.state.iteration == final_iter
return 1 + nothing # trigger MethodError
end
Ignite.run!(trainer, dl; max_epochs, epoch_length)
@test Ignite.isdone(trainer) === false
@test trainer.exception isa MethodError
@test event_list == Any[EPOCH_COMPLETED(), EPOCH_COMPLETED(), EXCEPTION_RAISED()]
else
error("Unknown early exit mode: :$(early_exit_mode)")
end
end
end
@testset "default epoch length" begin
max_epochs, epoch_length = 7, 3
trainer = dummy_engine()
dl = 1:5
# test that `length` fails for infinite data loader
Ignite.run!(trainer, Iterators.cycle(dl))
@test Ignite.isdone(trainer) === false
@test trainer.exception isa Ignite.DataLoaderUnknownLengthException
dl = collect(dl)
add_event_handler!(trainer, ITERATION_COMPLETED()) do engine
@test engine.state.batch == dl[mod1(engine.state.iteration, length(dl))]
end
Ignite.run!(trainer, dl)
@test Ignite.isdone(trainer) === true
end
@testset "empty data loader" begin
max_epochs, epoch_length = 7, 3
trainer = dummy_engine()
dl = []
add_event_handler!(trainer, DATALOADER_STOP_ITERATION()) do engine
engine.state.dataloader_stop_event_fired = true
end
Ignite.run!(trainer, dl; max_epochs, epoch_length)
@test Ignite.isdone(trainer) === false
@test trainer.exception isa Ignite.DataLoaderEmptyException
@test trainer.state.dataloader_stop_event_fired === true
end
@testset "exception raised" begin
max_epochs, epoch_length = 7, 3
trainer, dl = dummy_trainer_and_loader(; max_epochs, epoch_length) do engine, batch
return engine.state.iteration >= 10 ? x : nothing # x is undefined
end
add_event_handler!(trainer, EXCEPTION_RAISED()) do engine
engine.state.exception_raised_event_fired = true
end
Ignite.run!(trainer, dl; max_epochs, epoch_length)
@test Ignite.isdone(trainer) === false
@test trainer.exception isa UndefVarError
@test trainer.state.exception_raised_event_fired === true
end
@testset "many handlers" begin
max_epochs, epoch_length = 7, 3
trainer, dl = dummy_trainer_and_loader(; max_epochs, epoch_length)
num_handlers = 1000
events = [STARTED(), EPOCH_STARTED(), ITERATION_STARTED(), ITERATION_COMPLETED(), EPOCH_COMPLETED(), COMPLETED()]
buffer = zeros(Int, num_handlers)
for (i, event) in zip(1:num_handlers, Iterators.cycle(events))
add_event_handler!(trainer, event) do engine
return buffer[i] = i
end
end
Ignite.run!(trainer, dl)
@test Ignite.isdone(trainer) === true
@test buffer == 1:num_handlers
end
@testset "additional handler args" begin
max_epochs, epoch_length = 7, 3
trainer, dl = dummy_trainer_and_loader(; max_epochs, epoch_length)
data = Ref(0)
add_event_handler!(trainer, ITERATION_COMPLETED(), data) do engine, _data
_data[] += engine.state.iteration
end
@test trainer.event_handlers[1].args[1] === data
Ignite.run!(trainer, dl)
@test Ignite.isdone(trainer) === true
@test data[] == sum(1:max_epochs*epoch_length)
end
@testset "custom events" begin
struct NEW_LOOP_EVENT <: AbstractLoopEvent end
struct NEW_FIRING_EVENT <: AbstractFiringEvent end
@test NEW_LOOP_EVENT(; every = 3) isa FilteredEvent
@test_throws MethodError NEW_FIRING_EVENT(every = 3)
trainer = dummy_engine() do engine, batch
fire_event!(engine, NEW_LOOP_EVENT())
fire_event!(engine, NEW_FIRING_EVENT())
return nothing
end
loop_event_counter, firing_event_counter = Ref(0), Ref(0)
add_event_handler!(_ -> loop_event_counter[] += 1, trainer, NEW_LOOP_EVENT(; every = 3))
add_event_handler!(_ -> firing_event_counter[] += 1, trainer, NEW_FIRING_EVENT())
Ignite.run!(trainer, [1]; epoch_length = 12)
@test Ignite.isdone(trainer) === true
@test loop_event_counter[] == 4
@test firing_event_counter[] == 12
end
end
end
# (A)uto (QU)ality (A)ssurance tests
@testset "Aqua.jl" begin
test_all(Ignite)
end
| Ignite | https://github.com/jondeuce/Ignite.jl.git |
|
[
"MIT"
] | 0.2.1 | 110d6267f395cdf474822a3e5a1974ac1a9bfe33 | docs | 10643 | # Ignite.jl
[](https://jondeuce.github.io/Ignite.jl/dev/)
[](https://github.com/jondeuce/Ignite.jl/actions/workflows/CI.yml?query=branch%3Amaster)
[](https://codecov.io/gh/jondeuce/Ignite.jl)
[](https://github.com/JuliaTesting/Aqua.jl)
Welcome to `Ignite.jl`, a Julia port of the Python library [`ignite`](https://github.com/pytorch/ignite) for simplifying neural network training and validation loops using events and handlers.
`Ignite.jl` provides a simple yet flexible engine and event system, allowing for the easy composition of training pipelines with various events such as artifact saving, metric logging, and model validation. Event-based training abstracts away the training loop, replacing it with:
1. An *engine* which wraps a *process function* that consumes a single batch of data,
2. An iterable data loader which produces said batches of data, and
3. Events and corresponding event handlers which are attached to the engine, configured to fire at specific points during training.
Event handlers are much more flexibile compared to other approaches like callbacks: handlers can be any callable; multiple handlers can be attached to a single event; multiple events can trigger the same handler; and custom events can be defined to fire at user-specified points during training. This makes adding functionality to your training pipeline easy, minimizing the need to modify existing code.
## Quick Start
The example below demonstrates how to use `Ignite.jl` to train a simple neural network. Key features to note:
* The training step is factored out of the training loop: the `train_step` process function takes a batch of training data and computes the training loss, gradients, and updates the model parameters.
* Data loaders can be any iterable collection. Here, we use a [`DataLoader`](https://juliaml.github.io/MLUtils.jl/stable/api/#MLUtils.DataLoader) from [`MLUtils.jl`](https://github.com/JuliaML/MLUtils.jl)
````julia
using Ignite
using Flux, Zygote, Optimisers, MLUtils # for training a neural network
# Build simple neural network and initialize Adam optimizer
model = Chain(Dense(1 => 32, tanh), Dense(32 => 1))
optim = Flux.setup(Optimisers.Adam(1.0f-3), model)
# Create mock data and data loaders
f(x) = 2x - x^3
xtrain, xtest = 2 * rand(Float32, 1, 10_000) .- 1, collect(reshape(range(-1.0f0, 1.0f0; length = 100), 1, :))
ytrain, ytest = f.(xtrain), f.(xtest)
train_data_loader = DataLoader((; x = xtrain, y = ytrain); batchsize = 64, shuffle = true, partial = false)
eval_data_loader = DataLoader((; x = xtest, y = ytest); batchsize = 10, shuffle = false)
# Create training engine:
# - `engine` is a reference to the parent `trainer` engine, created below
# - `batch` is a batch of training data, retrieved by iterating `train_data_loader`
# - (optional) return value is stored in `trainer.state.output`
function train_step(engine, batch)
x, y = batch
l, gs = Zygote.withgradient(m -> sum(abs2, m(x) .- y), model)
Optimisers.update!(optim, model, gs[1])
return Dict("loss" => l)
end
trainer = Engine(train_step)
# Start the training
Ignite.run!(trainer, train_data_loader; max_epochs = 25, epoch_length = 100)
````
### Periodically evaluate model
The real power of `Ignite.jl` comes when adding *event handlers* to our training engine.
Let's evaluate our model after every 5th training epoch. This can be easily incorporated without needing to modify any of the above training code:
1. Create an `evaluator` engine which consumes batches of evaluation data
2. Add *event handlers* to the `evaluator` engine which accumulate a running average of evaluation metrics over batches of evaluation data; we use [`OnlineStats.jl`](https://github.com/joshday/OnlineStats.jl) to make this easy.
3. Add an event handler to the `trainer` which runs the `evaluator` on the evaluation data loader every 5 training epochs.
````julia
using OnlineStats: Mean, fit!, value # for tracking evaluation metrics
# Create an evaluation engine using `do` syntax:
evaluator = Engine() do engine, batch
x, y = batch
ypred = model(x) # evaluate model on a single batch of validation data
return Dict("ytrue" => y, "ypred" => ypred) # result is stored in `evaluator.state.output`
end
# Add event handlers to the evaluation engine to track metrics:
add_event_handler!(evaluator, STARTED()) do engine
# When `evaluator` starts, initialize the running mean
engine.state.metrics = Dict("abs_err" => Mean()) # new fields can be added to `engine.state` dynamically
end
add_event_handler!(evaluator, ITERATION_COMPLETED()) do engine
# Each iteration, compute eval metrics from predictions
o = engine.state.output
m = engine.state.metrics["abs_err"]
fit!(m, abs.(o["ytrue"] .- o["ypred"]) |> vec)
end
# Add an event handler to `trainer` which runs `evaluator` every 5 epochs:
add_event_handler!(trainer, EPOCH_COMPLETED(; every = 5)) do engine
Ignite.run!(evaluator, eval_data_loader)
@info "Evaluation metrics: abs_err = $(evaluator.state.metrics["abs_err"])"
end
# Run the trainer with periodic evaluation
Ignite.run!(trainer, train_data_loader; max_epochs = 25, epoch_length = 100)
````
### Terminating a run
There are several ways to stop a training run before it has completed:
1. Throw an exception as usual. This will immediately stop training. An `EXCEPTION_RAISED()` event will be subsequently be fired.
2. Use a keyboard interrupt, i.e. throw an `InterruptException` via `Ctrl+C` or `Cmd+C`. Training will halt, and an `INTERRUPT()` event will be fired.
3. Gracefully terminate via [`Ignite.terminate!(trainer)`](https://jondeuce.github.io/Ignite.jl/dev/#Ignite.terminate!-Tuple{Engine}), or equivalently, `trainer.should_terminate = true`. This will allow the current iteration to finish but no further iterations will begin. Then, a `TERMINATE()` event will be fired followed by a `COMPLETED()` event.
### Early stopping
To implement early stopping, we can add an event handler to `trainer` which checks the evaluation metrics and gracefully terminates `trainer` if the metrics fail to improve. To do so, we first define a training termination trigger using [`Flux.early_stopping`](http://fluxml.ai/Flux.jl/stable/training/callbacks/#Flux.early_stopping):
````julia
# Callback which returns `true` if the eval loss fails to decrease by
# at least `min_dist` for two consecutive evaluations
early_stop_trigger = Flux.early_stopping(2; init_score = Inf32, min_dist = 5.0f-3) do
return value(evaluator.state.metrics["abs_err"])
end
````
Then, we add an event handler to `trainer` which checks the early stopping trigger and terminates training if the trigger returns `true`:
````julia
# This handler must fire every 5th epoch, the same as the evaluation event handler,
# to ensure new evaluation metrics are available
add_event_handler!(trainer, EPOCH_COMPLETED(; every = 5)) do engine
if early_stop_trigger()
@info "Stopping early"
Ignite.terminate!(trainer)
end
end
# Run the trainer with periodic evaluation and early stopping
Ignite.run!(trainer, train_data_loader; max_epochs = 25, epoch_length = 100)
````
Note: instead of adding a new event, the evaluation event handler from the previous section could have been modified to check `early_stop_trigger()` immediately after `evaluator` is run.
### Artifact saving
Logging artifacts can be easily added to the trainer, again without modifying the above code. For example, save the current model and optimizer state to disk every 10 epochs using [`JLD2.jl`](https://github.com/JuliaIO/JLD2.jl):
````julia
using JLD2
# Save model and optimizer state every 10 epochs
add_event_handler!(trainer, EPOCH_COMPLETED(; every = 10)) do engine
model_state = Flux.state(model)
jldsave("model_and_optim.jld2"; model_state, optim)
@info "Saved model and optimizer state to disk"
end
````
### Trigger multiple functions per event
Multiple event handlers can be added to the same event:
````julia
add_event_handler!(trainer, COMPLETED()) do engine
# Runs after training has completed
end
add_event_handler!(trainer, COMPLETED()) do engine
# Also runs after training has completed, after the above function runs
end
````
### Attach the same handler to multiple events
The boolean operators `|` and `&` can be used to combine events together:
````julia
add_event_handler!(trainer, EPOCH_COMPLETED(; every = 10) | COMPLETED()) do engine
# Runs at the end of every 10th epoch, or when training is completed
end
throttled_event = EPOCH_COMPLETED(; every = 3) & EPOCH_COMPLETED(; event_filter = throttle_filter(30.0))
add_event_handler!(trainer, throttled_event) do engine
# Runs at the end of every 3rd epoch if at least 30s has passed since the last firing
end
````
### Define custom events
Custom events can be created and fired at user-defined stages in the training process.
For example, suppose we want to define events that fire at the start and finish of both the backward pass and the optimizer step. All we need to do is define new event types that subtype `AbstractLoopEvent`, and then fire them at appropriate points in the `train_step` process function using `fire_event!`:
````julia
struct BACKWARD_STARTED <: AbstractLoopEvent end
struct BACKWARD_COMPLETED <: AbstractLoopEvent end
struct OPTIM_STEP_STARTED <: AbstractLoopEvent end
struct OPTIM_STEP_COMPLETED <: AbstractLoopEvent end
function train_step(engine, batch)
x, y = batch
# Compute the gradients of the loss with respect to the model
fire_event!(engine, BACKWARD_STARTED())
l, gs = Zygote.withgradient(m -> sum(abs2, m(x) .- y), model)
engine.state.gradients = gs # the engine state can be accessed by event handlers
fire_event!(engine, BACKWARD_COMPLETED())
# Update the model's parameters
fire_event!(engine, OPTIM_STEP_STARTED())
Optimisers.update!(optim, model, gs[1])
fire_event!(engine, OPTIM_STEP_COMPLETED())
return Dict("loss" => l)
end
trainer = Engine(train_step)
````
Then, add event handlers for these custom events as usual:
````julia
add_event_handler!(trainer, BACKWARD_COMPLETED(; every = 10)) do engine
# This code runs after every 10th backward pass is completed
end
````
---
*This page was generated using [Literate.jl](https://github.com/fredrikekre/Literate.jl).*
| Ignite | https://github.com/jondeuce/Ignite.jl.git |
|
[
"MIT"
] | 0.2.1 | 110d6267f395cdf474822a3e5a1974ac1a9bfe33 | docs | 224 | ```@meta
CurrentModule = Ignite
```
# Ignite.jl
Documentation for [Ignite.jl](https://github.com/jondeuce/Ignite.jl).
## [Docstrings](@id docstrings)
```@index
Modules = [Ignite]
```
```@autodocs
Modules = [Ignite]
```
| Ignite | https://github.com/jondeuce/Ignite.jl.git |
|
[
"MIT"
] | 0.1.25 | 577951abc2adc6f961a9e60141eca8bfbb30f841 | code | 106 | using PyCall: python
run(`$python -m pip install --upgrade pip`)
run(`$python -m pip install jqdatasdk`)
| Backtester | https://github.com/AStupidBear/Backtester.jl.git |
|
[
"MIT"
] | 0.1.25 | 577951abc2adc6f961a9e60141eca8bfbb30f841 | code | 477 | __precompile__(true)
module Backtester
using Distributed, Statistics, Printf, Dates, DelimitedFiles, Random
using Glob, DataStructures, Parameters, ProgressMeter
using PyCall, StandardMarketData, MLSuiteBase
using Iconv, HDF5Utils, PandasLite, PyCallUtils
using StatsBase: corspearman
export Strategy, backtest, combine
export eglob, rglob
export @NT, @redirect, @indir, @gc, @roll
include("util.jl")
include("strategy.jl")
include("backtest.jl")
include("output.jl")
end
| Backtester | https://github.com/AStupidBear/Backtester.jl.git |
|
[
"MIT"
] | 0.1.25 | 577951abc2adc6f961a9e60141eca8bfbb30f841 | code | 8724 | function backtest(strat, data; mode = "train")
记忆仓位 = @staticvar zeros(Float32, 100000)
F, N, T = size(data.特征)
T < 1 && return 0f0
@unpack sim, 最大持仓, 持仓天数, 最多交易次数, 禁止平今,
夜盘最早开仓时间, 夜盘最晚开仓时间, 夜盘最晚平仓时间,
早盘最早开仓时间, 早盘最晚开仓时间,早盘最晚平仓时间 = strat
最大持仓 = iszero(最大持仓) ? ncodes(data) : clamp(最大持仓, 1, ncodes(data))
虚拟信号, 综合评分 = simulate(sim, data)
持仓天数′ = size(虚拟信号, 1) ÷ N
if 持仓天数′ == 1
虚拟信号 = lockphase(虚拟信号, 持仓天数)
综合评分 = lockphase(综合评分, 持仓天数)
else
持仓天数 = 持仓天数′
end
data = repeat(data, 持仓天数)
@unpack 涨幅, 时间戳, 代码, 最新价, 买1价, 卖1价, 手续费率, 涨停, 跌停, 交易池 = data
map!(fillnan, 时间戳, 时间戳)
if size(记忆仓位, 1) != size(虚拟信号, 1)
fill!(resize!(记忆仓位, size(虚拟信号, 1)), 0f0)
end
转移函数 = transition(sim)
# TODO: merge select
if select(sim)
是否为ST = repeat(getfeat(data, r"is_st", errors = "ignore"), 持仓天数)
实际仓位 = select_stocks(时间戳, 代码, 买1价, 卖1价, 涨停, 跌停, 交易池, 是否为ST, 虚拟信号, 综合评分,
记忆仓位, 最大持仓, 持仓天数, 最多交易次数, 转移函数, 禁止平今, 夜盘最早开仓时间, 夜盘最晚开仓时间,
夜盘最晚平仓时间, 早盘最早开仓时间, 早盘最晚开仓时间, 早盘最晚平仓时间)
else
实际仓位 = constraint(时间戳, 代码, 买1价, 卖1价, 涨停, 跌停, 虚拟信号, 记忆仓位, 转移函数, 最多交易次数, 禁止平今,
夜盘最早开仓时间, 夜盘最晚开仓时间, 夜盘最晚平仓时间, 早盘最早开仓时间, 早盘最晚开仓时间, 早盘最晚平仓时间)
end
if size(实际仓位, 2) == 1 && !any(isnan, 实际仓位)
记忆仓位 .= 实际仓位[:, end]
end
if T > 1 && parseenv("CLOSE_LAST_POS", true)
实际仓位[:, end] .= 0
end
pnl = if mode == "train"
summarize_train(涨幅, 时间戳, 代码, 最新价, 买1价, 卖1价, 手续费率, 交易池, 记忆仓位, 实际仓位, 综合评分, 最大持仓)
else
summarize_test(涨幅, 时间戳, 代码, 最新价, 买1价, 卖1价, 手续费率, 交易池, 记忆仓位, 实际仓位, 综合评分, 虚拟信号, 最大持仓 * 持仓天数)
end
return pnl
end
function constraint(时间戳, 代码, 买1价, 卖1价, 涨停, 跌停, 虚拟信号, 记忆仓位, 转移函数, 最多交易次数, 禁止平今, 夜盘最早开仓时间, 夜盘最晚开仓时间, 夜盘最晚平仓时间, 早盘最早开仓时间, 早盘最晚开仓时间, 早盘最晚平仓时间)
实际仓位 = zero(虚拟信号)
N, T = size(实际仓位)
交易次数 = zeros(Float32, N)
@inbounds for t in 1:T, n in 1:N
小时 = to_trade_hour(时间戳[n, t])
之前仓位 = t > 1 ? 实际仓位[n, t - 1] : 记忆仓位[n]
是否平仓 = 夜盘最晚平仓时间 <= 小时 <= 8 || 早盘最晚平仓时间 <= 小时 <= 16
当前仓位 = 是否平仓 ? 0f0 : 转移函数(之前仓位, 虚拟信号[n, t])
if (涨停[n, t] == 1 || isnan(卖1价[n, t])) && 当前仓位 > 之前仓位 ||
(跌停[n, t] == 1 || isnan(买1价[n, t])) && 当前仓位 < 之前仓位 ||
abs(当前仓位) > abs(之前仓位) && (交易次数[n] >= 最多交易次数 ||
!(夜盘最早开仓时间 <= 小时 <= 夜盘最晚开仓时间) ||
!(早盘最早开仓时间 <= 小时 <= 早盘最晚开仓时间)) ||
abs(当前仓位) < abs(之前仓位) && 交易次数[n] >= 1 && 禁止平今 && !是否平仓
当前仓位 = 之前仓位
end
时间差 = 时间戳[n, t] - 时间戳[n, max(1, t - 1)]
if 小时 > 8 && 时间差 > 3600 * 5
交易次数[n] = 0
else
交易次数[n] += abs(当前仓位 - 之前仓位)
end
if 代码[n, t] != 代码[n, min(t + 1, end)] # || 时间戳[n, t] == 0
当前仓位 = 0f0
交易次数[n] = 0
end
实际仓位[n, t] = 当前仓位
end
return 实际仓位
end
function select_stocks(时间戳, 代码, 买1价, 卖1价, 涨停, 跌停, 交易池, 是否为ST, 虚拟信号, 综合评分,
记忆仓位, 最大持仓, 持仓天数, 最多交易次数, 转移函数, 禁止平今, 夜盘最早开仓时间,
夜盘最晚开仓时间, 夜盘最晚平仓时间, 早盘最早开仓时间, 早盘最晚开仓时间, 早盘最晚平仓时间)
实际仓位 = zero(虚拟信号)
N, T = size(虚拟信号)
交易次数 = zeros(Int, N)
选股池 = zeros(Bool, N)
for t in 1:T
fill!(选股池, 0)
选股数 = 最大持仓 * 持仓天数
for n in 1:N
小时 = to_trade_hour(时间戳[n, t])
之前仓位 = t > 1 ? 实际仓位[n, t - 1] : 记忆仓位[n]
是否平仓 = 夜盘最晚平仓时间 <= 小时 <= 8 || 早盘最晚平仓时间 <= 小时 <= 16
当前仓位 = 是否平仓 ? 0f0 : 转移函数(之前仓位, 虚拟信号[n, t])
if (涨停[n, t] == 1 || isnan(卖1价[n, t])) && 当前仓位 > 之前仓位 ||
(跌停[n, t] == 1 || isnan(买1价[n, t])) && 当前仓位 < 之前仓位 ||
abs(当前仓位) > abs(之前仓位) && (交易次数[n] >= 最多交易次数 ||
!(夜盘最早开仓时间 <= 小时 <= 夜盘最晚开仓时间) ||
!(早盘最早开仓时间 <= 小时 <= 早盘最晚开仓时间)) ||
abs(当前仓位) < abs(之前仓位) && 交易次数[n] >= 1 && 禁止平今 && !是否平仓
当前仓位 = 之前仓位
end
时间差 = 时间戳[n, t] - 时间戳[n, max(1, t - 1)]
if 小时 > 8 && 时间差 > 3600 * 5
交易次数[n] = 0
else
交易次数[n] += 当前仓位 != 之前仓位
end
if 代码[n, t] != 代码[n, min(t + 1, end)] || 时间戳[n, t] == 0
当前仓位 = 0f0
交易次数[n] = 0
end
if isnan(虚拟信号[n, t]) || 当前仓位 > 之前仓位
选股池[n] = 1
实际仓位[n, t] = 0
else
实际仓位[n, t] = 当前仓位
end
if 代码[n, t] != 代码[n, min(t + 1, end)] || 时间戳[n, t] == 0
实际仓位[n, t] = 0
选股池[n] = 0
交易次数[n] = 0
elseif 交易池[n, t] == 0 || 是否为ST[n, t] == 1
实际仓位[n, t] = 0
选股池[n] = 0
elseif 涨停[n, t] == 1 || 跌停[n, t] == 1
实际仓位[n, t] = 之前仓位
选股池[n] = 0
end
选股数 -= 实际仓位[n, t] == 1
end
选股数 = min(选股数, 最大持仓)
选股列表 = findall(选股池)
if length(选股列表) <= 选股数
实际仓位[选股列表, t] .= 1
else
选股列表索引 = partialsortperm(综合评分[选股列表, t], 1:选股数, rev = true)
实际仓位[选股列表[选股列表索引], t] .= 1
end
end
return 实际仓位
end
function summarize_core(涨幅, 时间戳, 代码, 最新价, 买1价, 卖1价, 手续费率, 交易池, 记忆仓位, 实际仓位, 综合评分, 最大持仓)
记忆收益率 = @staticvar Dict{UInt64, Array{Float32}}()
N, T = size(实际仓位)
天数 = 1
for n in 1:size(时间戳, 1)
时间戳一行 = filter(!iszero, 时间戳[n, :])
if !isempty(时间戳一行)
天数 = sortednunique(unix2date, 时间戳一行)
break
end
end
复利 = get(ENV, "USE_COMPLEX", "0") == "1"
收益率 = zero(实际仓位)
之前仓位 = copy(记忆仓位)
之前盈亏 = zeros(Float32, N)
@inbounds for t in 1:T
当前平均涨幅 = @views mean(涨幅[:, t])
for n in 1:N
当前仓位 = 实际仓位[n, t]
仓位变化 = 当前仓位 - 之前仓位[n]
买滑点 = fillnan((卖1价[n, t] - 最新价[n, t]) ⧶ 最新价[n, t])
卖滑点 = fillnan((最新价[n, t] - 买1价[n, t]) ⧶ 最新价[n, t])
交易成本 = fillnan(手续费率[n, t]) * abs(仓位变化)
滑点 = ifelse(仓位变化 > 0, 买滑点, -卖滑点) * 仓位变化
收益率[n, t] = 之前盈亏[n] - 交易成本 - 滑点
之前仓位[n] = 当前仓位
end
t < T && for n in 1:N
当前仓位 = 实际仓位[n, t]
未来涨幅 = fillnan(涨幅[n, t + 1])
之前盈亏[n] = 当前仓位 * 未来涨幅
end
end
倍数 = 年化收益率 = 1f0
资金曲线 = ones(Float32, T)
if 复利
@inbounds for t in 1:size(实际仓位, 2)
Δ = @views sum(收益率[:, t]) ⧶ 最大持仓
资金曲线[t] = 倍数 = (1 + Δ) * 倍数
end
年化收益率 = 倍数^(240f0 / 天数) - 1
else
@inbounds for t in 1:T
Δ = @views sum(收益率[:, t]) ⧶ 最大持仓
资金曲线[t] = 倍数 = 倍数 + Δ
end
年化收益率 = 240f0 * (倍数 - 1f0) / 天数
end
最大回撤, 最大回撤期 = drawdown(资金曲线)
夏普率 = sharperatio(资金曲线, 240T / 天数)
length(记忆收益率) > 10 && empty!(记忆收益率)
记忆收益率[objectid(时间戳)] = 收益率
return 收益率, 资金曲线, 年化收益率, 最大回撤, 夏普率
end
function summarize_train(涨幅, 时间戳, 代码, 最新价, 买1价, 卖1价, 手续费率, 交易池, 记忆仓位, 实际仓位, 综合评分, 最大持仓)
收益率, 资金曲线, 年化收益率, 最大回撤, 夏普率 =
summarize_core(涨幅, 时间戳, 代码, 最新价, 买1价, 卖1价, 手续费率, 交易池, 记忆仓位, 实际仓位, 综合评分, 最大持仓)
评分模式 = parseenv("SCORE", "R")
if 评分模式 == "R" # Return
分数 = 年化收益率
elseif 评分模式 == "SHARPE"
分数 = 夏普率
elseif 评分模式 == "RoMaD" # Return Over Maximum Drawdown
分数 = 年化收益率 ⧶ abs(最大回撤)
elseif occursin("LAR", 评分模式) # Loss Amplified Return
λ = Meta.parse(split(评分模式, '_')[2])
分数 = sum(x -> amploss(x, λ), 年化收益率)
elseif occursin("IR", 评分模式) # Information Rank
nonan(x) = ifelse(isnan(x), zero(x), x)
分数 = mean(nonan(corspearman(综合评分[:, t], 涨幅[:, t])) for t in 1:size(实际仓位, 2))
elseif occursin("WR", 评分模式) # Average Winning Ratio
分数 = mean(mean(涨幅[实际仓位[:, t] .> 0, t]) >
mean(涨幅[交易池[:, t] .> 0, t])
for t in 1:(size(实际仓位, 2) - 1))
elseif occursin("ACC", 评分模式) # Accuracy
分数 = mean(mean(涨幅[实际仓位[:, t] .> 0, t] .>
mean(涨幅[交易池[:, t] .> 0, t]))
for t in 1:(size(实际仓位, 2) - 1))
end
@assert !isnan(分数)
return 分数
end
function summarize_test(涨幅, 时间戳, 代码, 最新价, 买1价, 卖1价, 手续费率, 交易池, 记忆仓位, 实际仓位, 综合评分, 虚拟信号, 最大持仓)
收益率, 资金曲线, 年化收益率, 最大回撤, 夏普率 = summarize_core(涨幅, 时间戳, 代码, 最新价, 买1价, 卖1价, 手续费率, 交易池, 记忆仓位, 实际仓位, 综合评分, 最大持仓)
目录名 = mkpath(产生目录(时间戳, 代码, 年化收益率, 最大回撤, 夏普率))
@indir 目录名 begin
输出每日持股明细(代码, 时间戳, 实际仓位)
输出资金和仓位曲线(时间戳, 实际仓位, 资金曲线)
输出个股交易记录(时间戳, 代码, 最新价, 买1价, 卖1价, 手续费率, 收益率, 实际仓位)
新目录名 = 输出资金曲线(时间戳, 代码, 实际仓位, 收益率, 最大持仓)
报告后处理()
parseenv("OUTPUT_POS", false) && 输出仓位评分信号(代码, 时间戳, 实际仓位, 综合评分, 虚拟信号)
parseenv("OUTPUT_MINPOS", false) && 输出分钟仓位(代码, 时间戳, 最新价, 实际仓位, 收益率)
end
return 年化收益率
end | Backtester | https://github.com/AStupidBear/Backtester.jl.git |
|
[
"MIT"
] | 0.1.25 | 577951abc2adc6f961a9e60141eca8bfbb30f841 | code | 17330 | function 产生目录(时间戳, 代码, 年化收益率, 最大回撤, 夏普率)
结果名 = @sprintf("%.2f倍%d%%%.1f", 1 + 年化收益率, -100最大回撤, 夏普率)
结束时间戳 = maximum(时间戳)
开始时间戳 = minimum(t -> ifelse(iszero(t), 结束时间戳, t), 时间戳)
测试区间 = unix2str6(开始时间戳) * "-" * unix2str6(结束时间戳)
目录名 = join([结果名, 测试区间, getpid()], '_')
rm(目录名, force = true, recursive = true)
return 目录名
end
function 输出每日持股明细(代码, 时间戳, 实际仓位)
median(diff(时间戳[1, :])) < 3600 * 12 && return
fid = open("每日持股明细.csv", "w")
for t in 1:size(实际仓位, 2)
print(fid, unix2date(时间戳[1, t]), ',')
for n in 1:size(实际仓位, 1)
实际仓位[n, t] == 1 && print(fid, 代码[n, t], ',')
end
println(fid)
end
close(fid)
end
function 输出资金和仓位曲线(时间戳, 实际仓位, 资金曲线)
fid = open("资金和仓位曲线.csv", "w")
之前日期 = unix2date(时间戳[1, 1]) - Day(1)
之前实际仓位 = zeros(Float32, size(实际仓位, 1))
write(fid, g"日期,资金曲线,持仓份额,多空份额,开仓份额,平仓份额,买入份额,卖出份额", '\n')
for t in 1:size(实际仓位, 2)
iszero(时间戳[1, t]) && continue
持仓份额 = 多空份额 = 开仓份额 = 平仓份额 = 买入份额 = 卖出份额 = 0f0
for n in 1:size(实际仓位, 1)
当前仓位, 之前仓位 = 实际仓位[n, t], 之前实际仓位[n]
当前仓位绝对值, 之前仓位绝对值 = abs(当前仓位), abs(之前仓位)
仓位变化, 仓位绝对值变化 = 当前仓位 - 之前仓位, 当前仓位绝对值 - 之前仓位绝对值
持仓份额 += 当前仓位
多空份额 += 当前仓位绝对值
开仓份额 += max(0f0, 仓位绝对值变化)
平仓份额 += max(0f0, -仓位绝对值变化)
买入份额 += max(0f0, 仓位变化)
卖出份额 += max(0f0, -仓位变化)
之前实际仓位[n] = 当前仓位
end
当前日期 = unix2date(时间戳[1, t])
if 当前日期 != 之前日期
for x in (当前日期, 资金曲线[t], 持仓份额, 多空份额, 开仓份额, 平仓份额, 买入份额, 卖出份额)
print(fid, x, ',')
end
skip(fid, -1)
println(fid)
end
之前日期 = 当前日期
end
close(fid)
end
function 输出资金曲线(时间戳, 代码, 实际仓位, 收益率, 最大持仓)
复利 = get(ENV, "USE_COMPLEX", "0") == "1"
N, T = size(收益率)
nttype = NamedTuple{(:时间戳, :代码, :收益率, :仓位, :行数),
Tuple{Float64, String, Float32, Float32, Int64}}
nts = nttype[]
dict = DefaultDict{Int, Int}(() -> 0)
@showprogress 10 "pnl..." for n in 1:N
pnl, date = 0f0, 0.0
for t in 1:T
if date == 0 && 时间戳[n, t] > 0
date = 时间戳[n, t] ÷ 86400 * 86400
end
pos = 实际仓位[n, t]
pnl += 收益率[n, t]
date′ = 时间戳[n, min(end, t + 1)] ÷ 86400 * 86400
if date > 0 && (date′ > 0 && date′ != date || t == T)
code = replace(代码[n, t], r"(?<=[a-zA-Z])\d+" => "")
nt = nttype((date, code, pnl, pos, n))
pnl != 0 && push!(nts, nt)
dict[date] += 1
pnl = 0f0
date = date′
end
end
end
df = DataFrame(nts)
df["时间戳"] = df["时间戳"].mul(1e9).astype("datetime64[ns]")
每行每股每日收益率 = df.groupby(["时间戳", "行数", "代码"])["收益率"].sum()
最大持仓 = min(最大持仓, df.groupby("时间戳")["代码"].nunique().max())
每日收益率 = 每行每股每日收益率.groupby("时间戳").sum().div(最大持仓).to_frame()
资金曲线 = (复利 ? (1 + 每日收益率).cumprod() : 1 + 每日收益率.cumsum()).rename(columns = Dict("收益率" => "资金曲线"))
资金曲线["持仓份额"] = df.groupby("时间戳")["仓位"].sum()
资金曲线["持仓份额"] = df["仓位"].groupby(df["时间戳"]).sum()
资金曲线["多空份额"] = df["仓位"].abs().groupby(df["时间戳"]).sum()
if df["代码"].nunique() < 50 && df["时间戳"].nunique() > 1
分品种每日收益率 = 每行每股每日收益率.groupby(["时间戳", "代码"]).mean()
分品种每日收益率 = 分品种每日收益率.to_frame().pivot_table(columns = "代码", index = "时间戳", values = "收益率").fillna(0)
分品种资金曲线 = 复利 ? (1 + 分品种每日收益率).cumprod() : 1 + 分品种每日收益率.cumsum()
资金曲线 = pd.concat([资金曲线, 分品种资金曲线], axis = 1, sort = true)
end
资金曲线 = 添加指数(资金曲线)
资金曲线.index.name = "日期"
to_csv(资金曲线.reset_index(), "资金曲线.csv", encoding = "gbk", index = false)
资金曲线 = 资金曲线["资金曲线"].values
最大回撤, 最大回撤期 = drawdown(资金曲线)
夏普率 = sharperatio(资金曲线)
年化收益率 = 240f0 * (资金曲线[end] - 1f0) / length(资金曲线)
产生目录(时间戳, 代码, 年化收益率, 最大回撤, 夏普率)
end
function 输出个股交易记录(时间戳, 代码, 最新价, 买1价, 卖1价, 手续费率, 收益率, 实际仓位)
复利 = get(ENV, "USE_COMPLEX", "0") == "1"
# fid = open("个股交易记录.csv", "w")
fid′ = open("交易记录表.csv", "w")
# io = IOBuffer()
# # 写表头
# write(fid, g"代码,总交易次数,总收益率,平均收益率,")
# write(fid, g"总开多次数,总开多收益,平均开多收益,")
# write(fid, g"总开空次数,总开空收益,平均开空收益,")
# for i in 1:20, h in [g"持仓", g"开仓天", g"开仓时间", g"平仓天", g"平仓时间", g"开仓价格", g"平仓价格", g"收益率"]
# write(fid, h)
# print(fid, i, ',')
# end
# println(fid)
write(fid′, g"代码,持仓,开仓时间,平仓时间,开仓价格,平仓价格,开仓手续费率,平仓手续费率,开仓滑点,平仓滑点,收益率,复利收益率", '\n')
# 逐行写表体
N, T = size(实际仓位)
for n in 1:N
总收益率 = 总开多收益 = 总开空收益 = zeroel(收益率)
开仓索引 = 总交易次数 = 总开多次数 = 总开空次数 = 0
持仓 = 开仓价格 = 之前仓位 = 开仓手续费率 = 开仓滑点 = zeroel(实际仓位)
for t in 1:T
当前仓位 = ifelse(t == T, 0f0, 实际仓位[n, t])
买滑点 = (卖1价[n, t] - 最新价[n, t]) / 最新价[n, t]
卖滑点 = (最新价[n, t] - 买1价[n, t]) / 最新价[n, t]
之前仓位 == 当前仓位 && continue
if 之前仓位 != 0 # 平仓或反手
平仓天 = unix2date(时间戳[n, t])
平仓时间 = unix2time(时间戳[n, t])
平仓价格 = ifelse(之前仓位 > 0, 买1价[n, t], 卖1价[n, t])
平仓滑点 = ifelse(之前仓位 > 0, 卖滑点, 买滑点)
平仓手续费率 = 手续费率[n, t]
if 复利
单笔收益率 = 1f0
for t′ in (开仓索引 + 1):t
单笔收益率 *= 1 + 收益率[n, t′]
end
单笔收益率 -= 1
else
单笔收益率 = 0f0
for t′ in (开仓索引 + 1):t
单笔收益率 += 收益率[n, t′]
end
end
总收益率 += 单笔收益率
总交易次数 += 1
if 持仓 > 0
总开多收益 += 单笔收益率
总开多次数 += 1
elseif 持仓 < 0
总开空收益 += 单笔收益率
总开空次数 += 1
end
# print(io, 平仓天, ',', 平仓时间, ',')
# print(io, 开仓价格, ',', 平仓价格, ',', 单笔收益率, ',')
print(fid′, 平仓天, ' ', 平仓时间, ',')
print(fid′, 开仓价格, ',', 平仓价格, ',')
复利收益率 = (之前仓位 * (平仓价格 - 开仓价格) - 开仓价格 * 开仓手续费率 - 开仓价格 * 平仓手续费率) / 开仓价格
print(fid′, 开仓手续费率, ',', 平仓手续费率, ',')
print(fid′, 开仓滑点, ',', 平仓滑点, ',')
println(fid′, 单笔收益率, ',', 复利收益率)
end
if 当前仓位 != 0 # 开仓或反手
持仓 = 当前仓位
开仓价格 = ifelse(当前仓位 > 0, 卖1价[n, t], 买1价[n, t])
开仓滑点 = ifelse(当前仓位 > 0, 买滑点, 卖滑点)
开仓手续费率 = 手续费率[n, t]
开仓天 = unix2date(时间戳[n, t])
开仓时间 = unix2time(时间戳[n, t])
开仓索引 = max(1, ifelse(之前仓位 == 0, t - 1, t))
# print(io, 持仓, ',', 开仓天, ',', 开仓时间, ',')
print(fid′, 代码[n, t], ',')
print(fid′, 持仓, ',', 开仓天, ' ', 开仓时间, ',')
end
之前仓位 = 当前仓位
end
平均收益率 = 总收益率 ⧶ 总交易次数
平均开多收益 = 总开多收益 ⧶ 总开多次数
平均开空收益 = 总开空收益 ⧶ 总开空次数
# print(fid, 代码[n, 1], ',')
# print(fid, 总交易次数, ',', 总收益率, ',', 平均收益率, ',')
# print(fid, 总开多次数, ',', 总开多收益, ',', 平均开多收益, ',')
# print(fid, 总开空次数, ',', 总开空收益, ',', 平均开空收益, ',')
# write(fid, take!(io), '\n')
end
# close(fid)
close(fid′)
end
function 输出仓位评分信号(代码, 时间戳, 实际仓位, 综合评分, 虚拟信号)
@from warnings imports filterwarnings
@from tables imports NaturalNameWarning
filterwarnings("ignore", category=NaturalNameWarning)
codes, dates = 代码[:, 1], 时间戳[1, :]
for (key, x) in pairs(@NT(实际仓位, 综合评分, 虚拟信号))
df = DataFrame(trunc.(x, digits = 4), columns = dates, index = codes)
to_hdf(df, "仓位评分信号.h5", key, complib = "lzo", complevel = 9)
end
end
function 输出分钟仓位(代码, 时间戳, 最新价, 实际仓位, 收益率)
资金曲线 = cumsum(收益率, dims = 2)
Δt = 时间戳[1, 2] - 时间戳[1, 1]
间隔 = round(Int, max(1, 600 / Δt))
切片 = 1:间隔:size(实际仓位, 2)
df = DataFrame()
for n in 1:size(实际仓位, 1)
code = 代码[n, 1]
df["时间戳:$code"] = pd.to_datetime(1e9 * 时间戳[n, 切片])
df["最新价:$code"] = 最新价[n, 切片]
df["仓位:$code"] = 实际仓位[n, 切片]
df["资金曲线:$code"] = 资金曲线[n, 切片]
end
to_csv(df, "分钟仓位.csv", index = false, encoding = "gbk")
end
function combine(dir; remove = false)
isdir(dir) || return
dirs = filter(glob("*%*", dir)) do dir
!occursin("NaN", dir)
end
cdir = 合并汇总(dirs)
isnothing(cdir) && return
remove && rm(dir, force = true, recursive = true)
mv(cdir, dir * "_" * cdir, force = true)
end
function 合并汇总(目录列表)
length(目录列表) < 1 && return
日期模式 = r"(\d{6})-(\d{6})"
日期 = map(目录列表) do 目录
m = match(日期模式, basename(目录))
String.(m.captures)
end
multisort!(日期, 目录列表, by = first)
ti, tf = minimum(first, 日期), maximum(last, 日期)
合并目录名 = replace(basename(目录列表[1]), 日期模式 => ti * "-" * tf)
资金和仓位曲线文件 = @. abspath(目录列表 * "/资金和仓位曲线.csv")
资金曲线文件 = @. abspath(目录列表 * "/资金曲线.csv")
个股交易记录文件 = @. abspath(目录列表 * "/个股交易记录.csv")
交易记录表文件 = @. abspath(目录列表 * "/交易记录表.csv")
每日持股明细文件 = @. abspath(目录列表 * "/每日持股明细.csv")
仓位评分信号文件 = @. abspath(目录列表 * "/仓位评分信号.h5")
分钟仓位文件 = @. abspath(目录列表 * "/分钟仓位.csv")
结果名 = @indir 合并目录名 begin
# 合并个股交易记录(个股交易记录文件)
合并交易记录表(交易记录表文件)
合并每日持股明细(每日持股明细文件)
合并仓位评分信号(仓位评分信号文件)
合并分钟仓位(分钟仓位文件)
合并资金和仓位曲线(资金和仓位曲线文件)
合并资金曲线(资金曲线文件)
end
@indir 合并目录名 报告后处理()
目录模式 = r"-?\d+\.\d+倍\d+%\-?\d+\.\d+"
最终目录名 = "合并汇总" * replace(合并目录名, 目录模式 => 结果名)
mv(合并目录名, 最终目录名, force = true)
end
function 合并资金和仓位曲线(csvs)
复利 = get(ENV, "USE_COMPLEX", "0") == "1"
all(isfile, csvs) || return ""
df = (dfs = filter(!isempty, pd.read_csv.(csvs, encoding = "gbk"))) |> first
所有列 = reduce(union, map(x -> x.columns.to_list(), dfs))
资金有关列 = filter(c -> !occursin(r"日期|份额", c), 所有列)
for df′ in dfs[2:end]
for c in 资金有关列
c ∉ df′.columns && (df′[c] = 1)
c ∉ df.columns && (df[c] = 1)
df′[c] = 复利 ? df′[c] * df[c].iloc[end] : df′[c] + (df[c].iloc[end] - 1)
end
df = pd.concat([df, df′], ignore_index = true, sort = true)
end
to_csv(df, "资金和仓位曲线.csv", index = false, encoding = "gbk")
资金曲线 = Array(df["资金曲线"])
倍数, 天数 = 资金曲线[end], length(资金曲线)
年化收益率 = 复利 ? 倍数^(240f0 / 天数) - 1 : 240f0 * (倍数 - 1f0) / 天数
最大回撤, 最大回撤期 = drawdown(资金曲线)
夏普率 = sharperatio(资金曲线)
结果名 = @sprintf("%.2f倍%d%%%.1f", 1 + 年化收益率, -100最大回撤, 夏普率)
return 结果名
end
function 合并资金曲线(csvs)
复利 = get(ENV, "USE_COMPLEX", "0") == "1"
all(isfile, csvs) || return ""
df = (dfs = filter(!isempty, pd.read_csv.(csvs, encoding = "gbk"))) |> first
所有列 = reduce(union, map(x -> x.columns.to_list(), dfs))
资金有关列 = filter(c -> !occursin(r"日期|份额", c), 所有列)
for df′ in dfs[2:end]
for c in 资金有关列
c ∉ df′.columns && (df′[c] = 1)
c ∉ df.columns && (df[c] = 1)
df′[c] = 复利 ? df′[c] * df[c].iloc[end] : df′[c] + (df[c].iloc[end] - 1)
end
df = pd.concat([df, df′], ignore_index = true, sort = true)
end
df = df.drop(columns = filter(c -> occursin(r"SZ|HS|ZZ", c), 所有列))
df = 添加指数(df.groupby("日期").last()).reset_index()
to_csv(df[所有列], "资金曲线.csv", index = false, encoding = "gbk")
资金曲线 = Array(df["资金曲线"])
倍数, 天数 = 资金曲线[end], length(资金曲线)
年化收益率 = 复利 ? 倍数^(240f0 / 天数) - 1 : 240f0 * (倍数 - 1f0) / 天数
最大回撤, 最大回撤期 = drawdown(资金曲线)
夏普率 = sharperatio(资金曲线)
结果名 = @sprintf("%.2f倍%d%%%.1f", 1 + 年化收益率, -100最大回撤, 夏普率)
end
function 合并个股交易记录(csvs)
all(isfile, csvs) || return
nstock = countlines(first(csvs)) - 1
buffs = [IOBuffer() for n in 1:nstock]
buff = IOBuffer()
codes = ["" for n in 1:nstock]
stats = zeros(nstock, 9)
header = ""
for csv in csvs
fid = open(csv, "r")
header = readline(fid, keep = true)
for n in 1:nstock
codes[n] = readuntil(fid, ',', keep = true)
for i in 1:9
write(buff, readuntil(fid, ',', keep = true))
end
skip(buff, -1); write(buff, '\n')
seek(buff, 0)
stats[n:n, :] .+= readdlm(buff, ',', Float64)
truncate(buff, 0)
write(buffs[n], readline(fid))
end
close(fid)
end
stats[:, 3:3:9] .= stats[:, 2:3:8] .⧶ stats[:, 1:3:7]
fid = open("个股交易记录.csv", "w")
write(fid, header)
for n in 1:nstock
write(fid, codes[n])
writedlm(fid, stats[n:n, :], ',')
skip(fid, -1)
write(fid, ',', take!(buffs[n]), '\n')
end
close(fid)
end
function 合并每日持股明细(csvs)
all(isfile, csvs) || return
SMD.concat_txts("每日持股明细.csv", csvs)
end
function 合并仓位评分信号(h5s)
all(isfile, h5s) || return
for key in ["实际仓位", "综合评分", "虚拟信号"]
df = pd.concat(pd.read_hdf.(h5s, key), axis = 1, sort = true)
to_hdf(df, "仓位评分信号.h5", key, complib = "lzo", complevel = 9)
end
end
function 合并分钟仓位(csvs)
all(isfile, csvs) || return
SMD.concat_txts("每日持股明细.csv", csvs)
end
function 合并交易记录表(csvs)
all(isfile, csvs) || return
SMD.concat_txts("交易记录表.csv", csvs)
end
function 报告后处理()
汇总交易记录表()
输出盈亏报告()
end
function 输出盈亏报告()
df = pd.read_csv("资金曲线.csv", encoding = "gbk", parse_dates = ["日期"], index_col = "日期")
df["收益率"] = df["资金曲线"].pct_change()
df′ = pd.read_csv("交易记录表.csv", encoding = "gbk", parse_dates = ["开仓时间", "平仓时间"])
isempty(df′) && return
for freq in ["A"]
srs = map(df.groupby(pd.Grouper(freq = freq))) do (t, dft)
isempty(dft) && return Series()
topen = df′["开仓时间"].dt.to_period(freq)
dft′ = df′.loc[topen.eq(pd.Period(t, freq))]
if isempty(dft′)
sr = Series()
else
sr = 单周期盈亏报告(dft, dft′)
p = freq == "A" ? Year : Month
sr.name = Date(round(t, p))
end
return sr
end
pushfirst!(srs, Series(单周期盈亏报告(df, df′), name = "ALL"))
filter!(!isempty, srs)
dfc = pd.concat(srs, axis = 1, sort = true)
dfc = freq == "A" ? dfc : dfc.T
cn = freq == "A" ? "年" : "月"
to_csv(dfc, cn * "盈亏报告.csv", encoding = "gbk")
end
end
function 汇总交易记录表()
df = pd.read_csv("交易记录表.csv", encoding = "gbk", parse_dates = ["开仓时间", "平仓时间"])
if isempty(df)
df["开仓时刻"] = df["平仓时刻"] = 0
else
df["开仓时刻"] = df["开仓时间"].dt.time
df["平仓时刻"] = df["平仓时间"].dt.time
end
to_csv(df, "交易记录表.csv", encoding = "gbk", index = false)
if !isempty(df)
df["日期"] = pd.to_datetime(df["开仓时间"]).dt.date
df.set_index("日期", inplace = true)
df′ = DataFrame()
df′["交易次数"] = df["代码"].groupby("日期").count()
df′["最大仓位"] = df["代码"].groupby("日期").nunique().max()
df′["平均开仓滑点"] = df["开仓滑点"].groupby("日期").mean()
df′["平均平仓滑点"] = df["平仓滑点"].groupby("日期").mean()
df′["平均收益率"] = df["收益率"].groupby("日期").sum() / df′["最大仓位"]
df′["平均开仓时间"] = df["开仓时间"].view("int64").groupby("日期").mean().astype("datetime64[ns]")
df′["平均平仓时间"] = df["平仓时间"].view("int64").groupby("日期").mean().astype("datetime64[ns]")
to_csv(df′.reset_index(), "交易记录表汇总.csv", encoding = "gbk", index = false)
end
return nothing
end
function 单周期盈亏报告(df, df′)
资金曲线 = Array(df["资金曲线"])
收益 = 资金曲线[end] - 资金曲线[1]
最大回撤, 最大回撤期 = drawdown(资金曲线)
收益回撤比 = 收益 / abs(最大回撤)
夏普率 = sharperatio(资金曲线)
交易天数 = length(df)
盈利天数 = (df["收益率"] > 0).sum()
亏损天数 = (df["收益率"] < 0).sum()
最长连续盈利天数 = SMD.lngstconsec(df["收益率"] > 0)
最长连续亏损天数 = SMD.lngstconsec(df["收益率"] < 0)
平均日盈利率 = df["收益率"].mean()
平均盈利日盈利率 = df["收益率"].loc[df["收益率"] > 0].mean()
平均亏损日亏损率 = df["收益率"].loc[df["收益率"] < 0].mean()
日盈亏比 = 平均盈利日盈利率 / abs(平均亏损日亏损率)
最大日盈利率 = df["收益率"].max()
最大日亏损率 = df["收益率"].min()
交易次数 = length(df′)
做多次数 = (df′["持仓"] > 0).sum()
做空次数 = 交易次数 - 做多次数
做多收益率 = df′.loc[df′["持仓"] > 0, "收益率"].sum()
做空收益率 = df′.loc[df′["持仓"] < 0, "收益率"].sum()
盈利次数 = (df′["收益率"] > 0).sum()
亏损次数 = (df′["收益率"] < 0).sum()
平均每次交易盈利率 = df′["收益率"].mean()
平均盈利交易盈利率 = df′["收益率"].loc[df′["收益率"] > 0].mean()
平均亏损交易亏损率 = df′["收益率"].loc[df′["收益率"] < 0].mean()
次盈亏比 = 平均盈利交易盈利率 / abs(平均亏损交易亏损率)
最大单次盈利率 = df′["收益率"].max()
最大单次亏损率 = df′["收益率"].min()
最长连续盈利次数 = SMD.lngstconsec(df′["收益率"] > 0)
最长连续亏损次数 = SMD.lngstconsec(df′["收益率"] < 0)
平均持仓时间 = round((df′["平仓时间"] - df′["开仓时间"]).mean(), Second)
nt = @NT(收益, 夏普率, 最大回撤, 最大回撤期, 收益回撤比, 平均持仓时间, 交易天数,
盈利天数, 亏损天数, 最长连续盈利天数, 最长连续亏损天数, 平均日盈利率,
平均盈利日盈利率, 平均亏损日亏损率, 日盈亏比, 最大日盈利率, 最大日亏损率,
交易次数, 做多次数, 做空次数, 做多收益率, 做空收益率, 盈利次数, 亏损次数,
平均每次交易盈利率, 平均盈利交易盈利率, 平均亏损交易亏损率, 次盈亏比,
最大单次盈利率,最大单次亏损率, 最长连续盈利次数, 最长连续亏损次数)
sr = Series(OrderedDict(pairs(nt)))
对冲 = df.filter(regex = "对冲")
对冲 = 对冲.iloc[end] - 对冲.iloc[1]
sr = pd.concat([sr, 对冲])
return sr
end
function 添加指数(df)
df_index = get_index_price()
isnothing(df_index) && return df
df = df.merge(df_index, how = "left", left_index = true, right_index = true)
for pool in df_index.columns
Δ = df["资金曲线"].diff() - df[pool].pct_change()
df["对冲" * pool] = Δ.fillna(0).cumsum()
df[pool] = df[pool] / df[pool].iloc[1]
end
return df
end | Backtester | https://github.com/AStupidBear/Backtester.jl.git |
|
[
"MIT"
] | 0.1.25 | 577951abc2adc6f961a9e60141eca8bfbb30f841 | code | 399 | @with_kw mutable struct Strategy{S}
sim::S
最大持仓::Int = 0
持仓天数::Int = 1
最多交易次数::Int = 1000
禁止平今::Bool = false
夜盘最早开仓时间::Float32 = -Inf
夜盘最晚开仓时间::Float32 = Inf
夜盘最晚平仓时间::Float32 = Inf
早盘最早开仓时间::Float32 = -Inf
早盘最晚开仓时间::Float32 = Inf
早盘最晚平仓时间::Float32 = Inf
end
function simulate end
function transition end
function threshgrid end
select(::Any) = false
| Backtester | https://github.com/AStupidBear/Backtester.jl.git |
|
[
"MIT"
] | 0.1.25 | 577951abc2adc6f961a9e60141eca8bfbb30f841 | code | 7364 | function update_param!(o, param)
for s in fieldnames(typeof(o))
x = getfield(o, s)
if fieldcount(typeof(x)) > 0
update_param!(x, param)
else
x′ = get(param, string(s), x)
x !== x′ && setproperty!(o, s, x′)
end
end
end
function update_param!(o::PyObject, param)
for (k, v) in param
s = Symbol(k)
PyCall.hasproperty(o, s) &&
setproperty!(o, s, v)
end
end
function gridsearch(f, bounds)
xs = collect(Iterators.product(bounds...))
ys = pmap(f ∘ collect, xs)
yᵒ, i = findmin(ys)
x = xs[i]
return x, y, xs, ys
end
amploss(x, λ = zero(x)) = ifelse(x < zero(x), λ, one(x)) * x
entropy(p, ϵ = 1f-9) = -sum(p .* log.(p .+ ϵ)) / log(length(p))
mae(x, ϵ = 1f-2) = sum(z -> max(abs(z) - ϵ , zero(x)), x) / length(x)
eglob(pattern::String, prefix = pwd()) = eglob(Regex(pattern), prefix)
eglob(pattern::Regex, prefix = pwd()) = glob([pattern], prefix)
rglob(pattern, prefix = pwd()) = Iterators.flatten(map(rdf -> glob(pattern, rdf[1]), walkdir(prefix)))
function lcp(strs)
io = IOBuffer()
if !isempty(strs)
i = 1
while all(i ≤ length(s) for s in strs) &&
all(s == strs[1][i] for s in getindex.(strs, i))
print(io, strs[1][i])
i += 1
end
end
return String(take!(io))
end
function findtoroot(file)
dir = pwd()
while !isfile(file)
dir = joinpath(dir, "..")
file = joinpath(dir, file)
end
return realpath(file)
end
macro everydir(dir, ex)
cwd = gensym()
dir_quot, cwd_quot = Expr(:$, dir), Expr(:$, cwd)
quote
mkpath($dir); $cwd = pwd(); @everywhere cd($dir_quot)
try $ex finally @everywhere cd($cwd_quot) end
end |> esc
end
macro indir(dir, ex)
cwd = gensym()
quote
mkpath($dir); $cwd = pwd(); cd($dir)
try $ex finally cd($cwd) end
end |> esc
end
macro roll(ex)
quote
if isdir("roll")
date = Dates.format(today(), dateformat"yymmdd")
mv("roll", "roll-" * date, force = true)
end
$(esc(ex))
combine("roll")
end
end
macro NT(xs...)
@static if VERSION >= v"0.7.0"
xs = [:($x = $x) for x in xs]
esc(:(($(xs...),)))
else
esc(:(@NT($(xs...))($(xs...))))
end
end
macro redirect(src, ex)
src = src == :devnull ? "/dev/null" : src
quote
io = open($(esc(src)), "a")
o, e = stdout, stderr
redirect_stdout(io)
redirect_stderr(io)
res = nothing
try
res = $(esc(ex))
sleep(0.01)
finally
flush(io)
close(io)
redirect_stdout(o)
redirect_stderr(e)
end
res
end
end
zeroel(x) = zero(eltype(x))
oneel(x) = one(eltype(x))
lvcha(资金曲线) = 10000 * mean(amploss.(diff(资金曲线), 2f0))
function cumsum_reset(x, r)
z = zero(x)
s = zero(eltype(x))
for i in 1:length(x)
s = ifelse(r[i], zero(s), s + x[i])
z[i] = s
end
return z
end
function drawdown(资金曲线)
最大值 = 当前回撤 = 最大回撤 = zeroel(资金曲线)
回撤期 = 最大回撤期 = 0
for i in eachindex(资金曲线)
回撤期 = ifelse(资金曲线[i] > 最大值, 0, 回撤期 + 1)
最大值 = max(最大值, 资金曲线[i])
当前回撤 = 资金曲线[i] - 最大值
最大回撤 = min(当前回撤, 最大回撤)
最大回撤期 = max(最大回撤期, 回撤期)
end
return 最大回撤, 最大回撤期
end
function pct_change(x, T)
ϵ = eps(eltype(x))
z = zero(x)
for t in 1:length(x)
t′ = clamp(t - T, 1, length(x))
t1, t2 = minmax(t, t′)
z[t] = (x[t2] - x[t1]) / (x[t1] + ϵ)
end
return z
end
@noinline function sharperatio(资金曲线, 一年天数 = 240)
日收益率 = pct_change(资金曲线, 1)
年化夏普率 = eltype(资金曲线)(mean(日收益率) ⧶ std(日收益率) * √一年天数)
end
@noinline function sortinoratio(资金曲线, 一年天数 = 240)
日收益率 = pct_change(资金曲线, 1)
eltype(r)(mean(日收益率) ⧶ std(min.(日收益率, 0)) * √一年天数)
end
function moving_max(A, k)
B = similar(A)
Q = Int[1]
sizehint!(Q, length(A))
for t = 1 : k
if A[t] >= A[Q[1]]
Q[1] = t
end
B[t] = A[Q[1]]
end
for t = (k + 1):length(A)
while !isempty(Q) && A[t] >= A[Q[end]]
pop!(Q)
end
while !isempty(Q) && Q[1] <= t - k
popfirst!(Q)
end
push!(Q, t)
B[t] = A[Q[1]]
end
return B
end
function moving_min(A, k)
B = similar(A)
Q = Int[1]
sizehint!(Q, length(A))
for t = 1 : k
if A[t] <= A[Q[1]]
Q[1] = t
end
B[t] = A[Q[1]]
end
for t = (k + 1):length(A)
while !isempty(Q) && A[t] <= A[Q[end]]
pop!(Q)
end
while !isempty(Q) && Q[1] <= t - k
popfirst!(Q)
end
push!(Q, t)
B[t] = A[Q[1]]
end
return B
end
parseenv(key, default::String) = get(ENV, string(key), string(default))
function parseenv(key, default::T) where T
str = get(ENV, string(key), string(default))
if hasmethod(parse, (Type{T}, String))
parse(T, str)
else
include_string(Main, str)
end
end
macro gc(exs...)
Expr(:block, [:($ex = 0) for ex in exs]..., :(@eval GC.gc())) |> esc
end
function lockphase(x, P)
P == 1 && return x
N, T = size(x)
x′ = zeros(Float32, N * P, T)
for ph in 1:P, t in ph:P:T, n in 1:N
n′ = n + N * (ph - 1)
x′[n′, t] = x[n, t]
end
return x′
end
function get_index_price(;update = false, delay = 30)
pkl = joinpath(DEPOT_PATH[1], "index.pkl")
if isfile(pkl) && !update
df = pd.read_pickle(pkl)
if now() - df.index[end] < Day(delay)
return df
end
end
haskey(ENV, "JQDATA_USERNAME") || return nothing
jqdata = pyimport("jqdatasdk")
dfs = DataFrame[]
for (pool, code) in zip(["SZ50", "HS300", "ZZ500", "ZZ1000"],
["000016.XSHG", "000300.XSHG", "000905.XSHG", "000852.XSHG"])
df = jqdata.get_price(code, start_date = "2010-01-01", end_date = string(Date(now())), fields = "close")
df.rename(columns = Dict("close" => pool), inplace = true)
push!(dfs, df)
end
df = pdhcat(dfs...)
df = df.ffill().bfill()
df.to_pickle(pkl)
return df
end
function multisort(xs::AbstractArray...; ka...)
p = sortperm(first(xs); ka...)
map(x -> x[p], xs)
end
function multisort!(xs::AbstractArray...; ka...)
p = sortperm(first(xs); ka...)
for x in xs
permute!(x, p)
end
return xs
end
unsqueeze(xs, dim) = reshape(xs, (size(xs)[1:dim-1]..., 1, size(xs)[dim:end]...))
function read_csv(csv, a...; ka...)
tmp = randstring() * ".csv"
cp(csv, tmp, force = true)
df = pd.read_csv(tmp, a...; ka...)
rm(tmp, force = true)
return df
end
function to_csv(df, csv, a...; ka...)
tmp = randstring() * ".csv"
df.to_csv(tmp, a...; ka...)
mv(tmp, csv, force = true)
return csv
end
function read_hdf(h5, a...; ka...)
tmp = randstring() * ".h5"
cp(h5, tmp, force = true)
df = pd.read_hdf(tmp, a...; ka...)
rm(tmp, force = true)
return df
end
function to_hdf(df, h5, a...; ka...)
tmp = randstring() * ".h5"
df.to_hdf(tmp, a...; ka...)
mv(tmp, h5, force = true)
return h5
end
function to_trade_hour(timestamp)
hour = unix2hour(timestamp)
ifelse(hour > 16, hour - 24, hour)
end
| Backtester | https://github.com/AStupidBear/Backtester.jl.git |
|
[
"MIT"
] | 0.1.25 | 577951abc2adc6f961a9e60141eca8bfbb30f841 | code | 1759 | using Backtester
using StandardMarketData
using HDF5Utils
using Statistics
using Dates
using Random
using Test
import Backtester: simulate, transition
mutable struct SignalSimulator{S}
sgnl::S
end
simulate(sim::SignalSimulator, data) = (sim.sgnl, sim.sgnl)
transition(sim::SignalSimulator) = (s, a) -> a
cd(mktempdir())
F, N, T = 2, 5, 100
Random.seed!(1234)
特征名 = idxmap(string.("f", 1:F))
特征 = randn(Float32, F, N, T)
涨幅 = reshape(mean(特征, dims = 1) / 100, N, T)
涨幅 = circshift(涨幅, (0, 1))
ti, Δt = DateTime(2019, 1, 1), Hour(1)
时间戳 = reshape(range(ti, step = Δt, length = T), 1, :)
时间戳 = datetime2unix.(repeat(时间戳, N, 1))
代码 = MLString{8}[string(n) for n in 1:N, t in 1:T]
买1价 = 卖1价 = 最新价 = 1 .+ cumsum(涨幅, dims = 2)
手续费率 = fill(0f0, N, T)
涨停 = 跌停 = zeros(Float32, N, T)
交易池 = ones(Float32, N, T)
data = Data(特征名, 特征, 涨幅, 时间戳, 代码, 最新价, 买1价, 卖1价, 手续费率, 涨停, 跌停, 交易池)
sgnl = reshape(sum(特征, dims = 1), N, T)
sgnl = @. ifelse(sgnl > 0, 1f0, -1f0)
pnl′ = sum(mean(abs, 涨幅[:, 2:end] , dims = 1)) / ndays(data) * 240
strat = Strategy(sim = SignalSimulator(sgnl))
pnl = backtest(strat, data, mode = "train")
@test pnl ≈ pnl′
时间戳 = range(ti, step = Δt, length = T ÷ 2)
时间戳 = datetime2unix.(repeat(reshape(时间戳, 1, :), N, 2))
代码 = MLString{8}[string(2t <= T ? n : N + n) for n in 1:N, t in 1:T]
时间戳[:, end - 10:end] .= 0
代码[:, end - 10:end] .= MLString{8}("")
买1价 = 最新价 .- 0.001
卖1价 = 最新价 .+ 0.001
data.手续费率 = fill(1f-4, N, T)
data = Data(特征名, 特征, 涨幅, 时间戳, 代码, 最新价, 买1价, 卖1价, 手续费率, 涨停, 跌停, 交易池)
sgnl = @. ifelse(rand() > 0.05, sgnl, -sgnl)
strat = Strategy(sim = SignalSimulator(sgnl))
pnl = backtest(strat, data, mode = "train")
pnl′ = sum(mean(abs, 涨幅[:, 2:end] , dims = 1)) / ndays(data) * 240
@test pnl > pnl′ * 0.6
backtest(strat, data, mode = "test")
| Backtester | https://github.com/AStupidBear/Backtester.jl.git |
|
[
"MIT"
] | 0.1.25 | 577951abc2adc6f961a9e60141eca8bfbb30f841 | docs | 283 | [](https://github.com/AStupidBear/Backtester.jl/actions)
[](https://codecov.io/gh/AStupidBear/Backtester.jl)
| Backtester | https://github.com/AStupidBear/Backtester.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1270 | using TwinCopulas
using Documenter
DocMeta.setdocmeta!(TwinCopulas, :DocTestSetup, :(using TwinCopulas); recursive=true)
makedocs(;
modules=[TwinCopulas],
authors="Santiago Jimenez Ramos",
sitename="TwinCopulas.jl",
format=Documenter.HTML(;
canonical="https://Santymax98.github.io/TwinCopulas.jl",
edit_link="master",
assets=String[],
),
pages=[
"Home" => ["index.md",
"starting.md"]
"Guide" => [
"Getting starting" => "Copula_Sklar.md",
"Archimedean Copulas" => "Archimedean/Archimedean_theory.md",
"Elliptical Copulas" => "Elliptical/Elliptical_theory.md",
"Extreme Value Copulas"=>"Extreme/Extreme_Value_theory.md",
#"Empirical Copula" => "Empirical.md",
#"Dependence Measure" => "Dependence.md"
]
"Avaliable Models" => [
"Archimedean Copulas" => "Archimedean/Avaliable_Archimedean_models.md",
"Elliptical Copulas" => "Elliptical/Avaliable_Elliptical_models.md",
"Extreme Value Copulas"=>"Extreme/Avaliable_Extreme_models.md",
]
],
)
deploydocs(;
repo="github.com/Santymax98/TwinCopulas.jl",
devbranch="master",
)
| TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1413 | struct ArchimaxCopula{A<:ArchimedeanCopula, E<:ExtremeValueCopula} <: bicopula
Archimedean::A
Extreme::E
function ArchimaxCopula(Archimedean::A, Extreme::E) where {A<:ArchimedeanCopula, E<:ExtremeValueCopula}
new{A, E}(Archimedean, Extreme)
end
end
function Distributions.cdf(C::ArchimaxCopula, x::AbstractVector)
Archimedean = C.Archimedean
Extreme = C.Extreme
term1 = ϕ⁻¹(Archimedean, x[1]) + ϕ⁻¹(Archimedean, x[2])
term2 = (ϕ⁻¹(Archimedean, x[2]))/term1
term3 = 𝘈(Extreme, term2)
return ϕ(Archimedean, term1*term3)
end
function Distributions.pdf(C::ArchimaxCopula, x::AbstractVector)
# Definimos una función que toma un vector y devuelve el cdf
cdf_func = y -> Distributions.cdf(C, y)
# Calculamos la derivada parcial mixta
pdf_value = ForwardDiff.hessian(cdf_func, x)[1, 2]
return pdf_value
end
function τ(C::ArchimaxCopula)
Archimedean = C.Archimedean
Extreme = C.Extreme
tA = τ(Extreme)
tphi = τ(Archimedean)
return tA + (1 - tA)*tphi
end
function Distributions._rand!(rng::Distributions.AbstractRNG, C::ArchimaxCopula, x::AbstractVector{T}) where {T<:Real}
Archimedean = C.Archimedean
Extreme = C.Extreme
v1, v2 = Distributions.rand(rng, Extreme, 2)
M = rand(rng, 𝘙(Archimedean))
x[1] = ϕ(Archimedean, -log(v1)/M)
x[2] = ϕ(Archimedean, -log(v2)/M)
return x
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 2102 | abstract type ArchimedeanCopula{P} <: bicopula end
𝘙(C::ArchimedeanCopula) = 𝘙(C.θ)
ϕ(C::ArchimedeanCopula, x) = throw(ArgumentError("Function ϕ must be defined for specific copula"))
dϕ(C::ArchimedeanCopula, x) = throw(ArgumentError("Function dϕ must be defined for specific copula"))
d²ϕ(C::ArchimedeanCopula, x) = throw(ArgumentError("Function d²ϕ must be defined for specific copula"))
ϕ⁻¹(C::ArchimedeanCopula, x) = throw(ArgumentError("Function ϕ⁻¹ must be defined for specific copula"))
dϕ⁻¹(C::ArchimedeanCopula, x) = throw(ArgumentError("Function dϕ⁻¹ must be defined for specific copula"))
function Distributions.cdf(C::ArchimedeanCopula, u::Vector)
inner_term = ϕ⁻¹(C, u[1]) + ϕ⁻¹(C, u[2])
return ϕ(C, inner_term)
end
function Distributions.pdf(C::ArchimedeanCopula, u::Vector)
u1, u2 = u
inner_term = ϕ⁻¹(C, u1) + ϕ⁻¹(C, u2)
product = dϕ⁻¹(C, u1) * dϕ⁻¹(C, u2)
return d²ϕ(C, inner_term) * product
end
function Distributions._rand!(rng::Distributions.AbstractRNG, C::ArchimedeanCopula, x::AbstractVector{T}) where {T<:Real}
if 𝘙(C) == 1
u2, v = rand(rng, Distributions.Uniform(0, 1), 2)
func(u) = (u - ϕ⁻¹(C, u)/dϕ⁻¹(C, u)) - v
if func(eps()) > 0.0
u1 = 0.0
else
u1 = Roots.find_zero(func, (eps(), 1-eps()), Roots.Brent())
end
x[1] = ϕ(C, u2 * ϕ⁻¹(C, u1))
x[2] = ϕ(C, (1 - u2) * ϕ⁻¹(C, u1))
return x
elseif 𝘙(C) == RadialDist(C)
Y = rand(rng, Distributions.Exponential(), 2)
S = Y/sum(Y)
R = rand(rng, 𝘙(C))
x[1] = ϕ(C, R*S[1])
x[2] = ϕ(C, R*S[2])
return x
else
W = Distributions.rand(rng, 𝘙(C))
Z = rand(rng, Distributions.Erlang(2))
R = Z / W
E = rand(rng, Distributions.Exponential(), 2)
S = sum(E)
x[1] = ϕ(C, R * E[1] / S)
x[2] = ϕ(C, R * E[2] / S)
return x
end
end
function τ(C::ArchimedeanCopula)
integrand(x) = ϕ⁻¹(C, x) / dϕ⁻¹(C, x)
result, _ = QuadGK.quadgk(integrand, 0, 1)
return 1 + 4 * result
end
| TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 931 | abstract type EllipticalCopula{P} <: bicopula end
function Distributions._rand!(rng::Distributions.AbstractRNG, C::EllipticalCopula, x::AbstractVector{T}) where {T<:Real}
Σ = [1.0 C.θ; C.θ 1.0]
A = LinearAlgebra.cholesky(Σ).L
y = rand(rng, Distributions.Normal(), 2)
if C isa GaussianCopula
z = A*y
x[1] = Distributions.cdf(Distributions.Normal(), z[1])
x[2] = Distributions.cdf(Distributions.Normal(), z[2])
elseif C isa tCopula
w = rand(rng, Distributions.InverseGamma(C.ν/2.0, C.ν/2.0))
z = sqrt(w)*A*y
x[1] = Distributions.cdf(Distributions.TDist(C.ν), z[1])
x[2] = Distributions.cdf(Distributions.TDist(C.ν), z[2])
else
throw(ArgumentError("Unsupported copula type"))
end
return x
end
τ(C::EllipticalCopula) = (2/π)*asin(C.θ)
ρₛ(C::EllipticalCopula) = (6/π)*asin(C.θ/2)
β(C::EllipticalCopula) = (2/π)*asin(C.θ)
| TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 2753 | abstract type ExtremeValueCopula{P} <: bicopula end
# Función genérica para A
function 𝘈(C::ExtremeValueCopula, t::Real)
throw(ArgumentError("Function A must be defined for specific copula"))
end
function d𝘈(C::ExtremeValueCopula, t::Real)
ForwardDiff.derivative(t -> 𝘈(C, t), t)
end
function d²𝘈(C::ExtremeValueCopula, t::Real)
ForwardDiff.derivative(t -> d𝘈(C, t), t)
end
function ℓ(C::ExtremeValueCopula, t::Vector)
sumu = sum(t)
vectw = t[1] / sumu
return sumu * 𝘈(C, vectw)
end
# Función CDF para ExtremeValueCopula
function Distributions.cdf(C::ExtremeValueCopula, u::AbstractArray)
t = -log.(u)
return exp(-ℓ(C, t))
end
# Función genérica para calcular derivadas parciales de ℓ
function D_B_ℓ(C::ExtremeValueCopula, t::Vector{Float64}, B::Vector{Int})
f = x -> ℓ(C, x)
if length(B) == 1
return ForwardDiff.gradient(f, t)[B[1]]
elseif length(B) == 2
return ForwardDiff.hessian(f, t)[B[1], B[2]]
else
throw(ArgumentError("Higher order partial derivatives are not required for bivariate case"))
end
end
# Función PDF para ExtremeValueCopula usando ℓ
function Distributions.pdf(C::ExtremeValueCopula, u::AbstractArray{<:Real})
t = -log.(u)
c = exp(-ℓ(C, t))
D1 = D_B_ℓ(C, t, [1])
D2 = D_B_ℓ(C, t, [2])
D12 = D_B_ℓ(C, t, [1, 2])
return c * (-D12 + D1 * D2) / (u[1] * u[2])
end
# Definir la función para calcular τ
function τ(C::ExtremeValueCopula)
integrand(x) = begin
A = 𝜜(C, x)
dA = d𝘈(C, x)
return (x * (1 - x) / A) * dA
end
integrate, _ = QuadGK.quadgk(integrand, 0.0, 1.0)
return integrate
end
function ρₛ(C::ExtremeValueCopula)
integrand(x) = 1 / (1 + 𝜜(C, x))^2
integral, _ = QuadGK.quadgk(integrand, 0, 1)
ρs = 12 * integral - 3
return ρs
end
# Función para calcular el coeficiente de dependencia en el límite superior
function λᵤ(C::ExtremeValueCopula)
return 2(1 - 𝜜(C, 0.5))
end
function λₗ(C::ExtremeValueCopula)
if 𝜜(C, 0.5) > 0.5
return 0
else
return 1
end
end
function probability_z(C::ExtremeValueCopula, z)
num = z*(1 - z)*d²𝘈(C, z)
dem = 𝘈(C, z)*_pdf(ExtremeDist(C), z)
p = num / dem
return clamp(p, 0.0, 1.0)
end
function Distributions._rand!(rng::Distributions.AbstractRNG, C::ExtremeValueCopula, x::AbstractVector{T}) where {T<:Real}
u1, u2 = rand(rng, Distributions.Uniform(0,1), 2)
z = rand(rng, ExtremeDist(C))
p = probability_z(C, z)
if p < -eps() || p > eps()
p = 0
end
c = rand(rng, Distributions.Bernoulli(p))
w = 0
if c == 1
w = u1
else
w = u1*u2
end
A = 𝘈(C, z)
x[1] = w^(z/A)
x[2] = w^((1-z)/A)
return x
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1622 | struct SklarDist{C<:bicopula, M<:Tuple{<:Distributions.UnivariateDistribution, <:Distributions.UnivariateDistribution}} <: Distributions.ContinuousMultivariateDistribution
copula::C
margins::M
function SklarDist(copula::C, margins::Vector{<:Distributions.UnivariateDistribution}) where {C<:bicopula}
@assert length(margins) == 2 "Marginal distributions must be of length 2 for bivariate case"
@assert all(margin -> margin isa Distributions.UnivariateDistribution, margins) "All margins must be univariate distributions"
return new{C, Tuple{typeof(margins[1]), typeof(margins[2])}}(copula, (margins[1], margins[2]))
end
end
# Definir la función length para SklarDist
Base.length(d::SklarDist) = 2
function Distributions.cdf(d::SklarDist, x::AbstractVector)
u1 = Distributions.cdf(d.margins[1], x[1])
u2 = Distributions.cdf(d.margins[2], x[2])
return Distributions.cdf(d.copula, [u1, u2])
end
# Función para calcular la PDF conjunta
function Distributions.pdf(d::SklarDist, x::AbstractVector)
u1 = Distributions.cdf(d.margins[1], x[1])
u2 = Distributions.cdf(d.margins[2], x[2])
du1 = Distributions.pdf(d.margins[1], x[1])
du2 = Distributions.pdf(d.margins[2], x[2])
copula_density = Distributions.pdf(d.copula, [u1, u2])
return copula_density * du1 * du2
end
function Distributions._rand!(rng::Distributions.AbstractRNG, d::SklarDist, x::AbstractVector{T}) where {T<:Real}
u1, u2 = Distributions.rand(rng, d.copula, 2)
x[1] = Distributions.quantile(d.margins[1], u1)
x[2] = Distributions.quantile(d.margins[2], u2)
return x
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 3680 | module TwinCopulas
import Base
import Random
import SpecialFunctions
import Roots
import Distributions
import StatsBase
import StatsFuns
import ForwardDiff
import Cubature
import WilliamsonTransforms
import LinearAlgebra
import QuadGK
import PolyLog
import LogExpFunctions
import Statistics
#principal module
include("bicopula.jl")
include("Archimedean.jl")
include("ExtremeValue.jl")
include("Elliptical.jl")
include("SklarDist.jl")
export
ArchimedeanCopula,
ExtremeValueCopula,
EllipticalCopula,
SklarDist
#Utils
include("Distributions/ExtremeDist.jl")
include("Distributions/Logarithmic.jl")
include("Distributions/PStable.jl")
include("Distributions/RadialDist.jl") #To test API Radial Distributions
include("Distributions/Sibuya.jl")
include("Distributions/Stable.jl")
#Elliptical Copulas
include("EllipticalCopulas/GaussianCopula.jl")
include("EllipticalCopulas/tCopula.jl")
export
GaussianCopula,
tCopula
#Archimedean Copulas
include("ArchimedeanCopulas/AMHCopula.jl")
include("ArchimedeanCopulas/ClaytonCopula.jl")
include("ArchimedeanCopulas/FrankCopula.jl")
include("ArchimedeanCopulas/GumbelCopula.jl")
include("ArchimedeanCopulas/GumbelBarnettCopula.jl")
include("ArchimedeanCopulas/InvGaussianCopula.jl")
include("ArchimedeanCopulas/JoeCopula.jl")
include("ArchimedeanCopulas/Nelsen2Copula.jl") #To test API Radial Distributions
include("ArchimedeanCopulas/UtilCopula.jl")
export
AMHCopula,
ClaytonCopula,
GumbelCopula,
GumbelBarnettCopula,
FrankCopula,
InvGaussianCopula,
JoeCopula,
Nelsen2Copula, #To test API Radial Distributions
UtilCopula #Special case of some copulas
# Extreme value Copulas
include("ExtremeValueCopulas/AsymGalambosCopula.jl")
include("ExtremeValueCopulas/AsymLogCopula.jl")
include("ExtremeValueCopulas/AsymMixedCopula.jl")
include("ExtremeValueCopulas/BC2Copula.jl")
include("ExtremeValueCopulas/CuadrasAugeCopula.jl")
include("ExtremeValueCopulas/GalambosCopula.jl")
include("ExtremeValueCopulas/HuslerReissCopula.jl")
include("ExtremeValueCopulas/LogCopula.jl")
include("ExtremeValueCopulas/MixedCopula.jl")
include("ExtremeValueCopulas/MOCopula.jl")
include("ExtremeValueCopulas/tEVCopula.jl")
export
AsymGalambosCopula,
AsymLogCopula,
AsymMixedCopula,
BC2Copula,
CuadrasAugeCopula,
GalambosCopula,
HuslerReissCopula,
LogCopula,
MixedCopula,
MOCopula,
tEVCopula
#important Copulas
include("SeveralCopulas/ArchimaxCopula.jl")
include("SeveralCopulas/EmpiricalCopula.jl")
include("SeveralCopulas/IndependentCopula.jl")
include("SeveralCopulas/MCopula.jl")
include("SeveralCopulas/SurvivalCopula.jl")
include("SeveralCopulas/WCopula.jl")
export
ArchimaxCopula,
EmpiricalCopula,
IndependentCopula,
MCopula,
SurvivalCopula,
WCopula
#Other practical Copulas
include("Others/B11Copula.jl")
include("Others/FrechetCopula.jl")
include("Others/MardiaCopula.jl")
include("Others/MaresiasCopula.jl")
include("Others/MorgensternCopula.jl")
include("Others/PlackettCopula.jl")
include("Others/RafteryCopula.jl")
export
B11Copula,
FrechetCopula,
MardiaCopula,
MaresiasCopula,
MorgensternCopula,
PlackettCopula,
RafteryCopula
end
| TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 2284 | abstract type bicopula <: Distributions.ContinuousMultivariateDistribution end
# Función de longitud específica para bicopula
Base.length(::bicopula) = 2
function ρₛ(C::bicopula)
F(x) = Distributions.cdf(C, x)
z = zeros(2)
i = ones(2)
result, _ = Cubature.hcubature(F, z, i, reltol=sqrt(eps()))
return 12 * result - 3
end
# Función para el tau de Kendall τ
function τ(C::bicopula)
F(x) = Distributions.cdf(C, x)
z = zeros(2)
i = ones(2)
result, _ = Cubature.hcubature(F, z, i, reltol=sqrt(eps()))
return 4 * result - 1
end
function γ(C::bicopula)
integrand1(u) = Distributions.cdf(C, [u, 1-u])
integrand2(u) = u - Distributions.cdf(C, [u, u])
integral1, _ = QuadGK.quadgk(integrand1, 0.0, 1.0)
integral2, _ = QuadGK.quadgk(integrand2, 0.0, 1.0)
return 4 * (integral1 - integral2)
end
# Función para calcular la medida de Blomqvist β
function β(C::bicopula)
return 4 * Distributions.cdf(C, [0.5, 0.5]) - 1
end
# Función para calcular λ_u
function λᵤ(C::bicopula)
u_vals = 0.999:0.00001:1.0
λu_vals = [(Distributions.cdf(C, [u, u]) - 2u + 1) / (1 - u) for u in u_vals]
return λu_vals[end] # Aproximar el límite cuando u tiende a 1 desde la izquierda
end
# Función para calcular λ_l
function λₗ(C::bicopula)
u_vals = 0.0:0.00001:0.001
λl_vals = [Distributions.cdf(C, [u, u]) / u for u in u_vals if u != 0]
return λl_vals[end] # Aproximar el límite cuando u tiende a 0 desde la derecha
end
function dot_C(C::bicopula, x::AbstractVector)
u1, u2 = x
# Definimos una función que toma solo u2 como argumento
cdf_wrt_u2(u2) = Distributions.cdf(C, [u1, u2])
# Usamos ForwardDiff para calcular la derivada
ForwardDiff.derivative(cdf_wrt_u2, u2)
end
function Distributions._rand!(rng::Distributions.AbstractRNG, C::bicopula, x::AbstractVector{T}) where {T<:Real}
# Simular U2 y V uniformemente distribuidos
u2, v = rand(rng, Distributions.Uniform(0, 1), 2)
# Definir la función condicional
function func(u)
vectu = [u, u2]
return dot_C(C, vectu) - v
end
u1 = Roots.find_zero(func, (eps(), 1 - eps()), Roots.Brent())
# Asignar los valores calculados a x
x[1] = u1
x[2] = u2
return x
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1600 | """
AMHCopula{P}
Fields:
- θ::Real - parameter
Constructor
AMHCopula(θ)
The bivariate [AMH](https://en.wikipedia.org/wiki/Copula_(probability_theory)#Most_important_Archimedean_copulas) copula is parameterized by ``\\theta \\in [-1,1)``. It is an Archimedean copula with generator :
```math
\\phi(t) = 1 - \\frac{1-\\theta}{e^{-t}-\\theta}
```
It has a few special cases:
- When θ = 0, it is the IndependentCopula
- When θ = 1, it is the UtilCopula
References:
* [nelsen2006](@cite) Nelsen, Roger B. An introduction to copulas. Springer, 2006.
"""
struct AMHCopula{P} <: ArchimedeanCopula{P}
θ::P
function AMHCopula(θ)
if !(-1 <= θ <= 1)
throw(ArgumentError("El parámetro θ debe estar en [-1, 1]"))
elseif θ == 0
return IndependentCopula()
elseif θ == 1
return UtilCopula()
else
return new{typeof(θ)}(θ)
end
end
end
𝘙(C::AMHCopula) = C.θ >= 0 ? 1 + Distributions.Geometric(1 - C.θ) : 1
ϕ(C::AMHCopula, x) = (1 - C.θ) / (exp(x) - C.θ)
ϕ⁻¹(C::AMHCopula, x) = log((1 - C.θ) / x + C.θ)
dϕ(C::AMHCopula, x) = -((1 - C.θ) * exp(x)) / (exp(x) - C.θ)^2
dϕ⁻¹(C::AMHCopula, x) = -(1 - C.θ) / (x * (C.θ * x + 1 - C.θ))
d²ϕ(C::AMHCopula, x) = ((1 - C.θ) * exp(x) * (exp(2 * x) - C.θ^2)) / (exp(x) - C.θ)^4
τ(C::AMHCopula) = (3 * C.θ - 2) / (3 * C.θ) - (2 * (1 - C.θ)^2 / (3 * C.θ^2)) * log(1 - C.θ)
ρₛ(C::AMHCopula) = (12 * (1 + C.θ) / C.θ^2) * PolyLog.reli2(1 - C.θ) - (24 * (1 - C.θ) / C.θ^2) * log(1 - C.θ) - (3 * (C.θ + 12) / C.θ)
λᵤ(C::AMHCopula) = 0.0
λₗ(C::AMHCopula) = 0.0 | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1031 | struct AMHCopula{P} <: ArchimedeanCopula{P}
θ::P
function AMHCopula(θ)
if !(-1 <= θ <= 1)
throw(ArgumentError("El parámetro θ debe estar en [-1, 1]"))
elseif θ == 0
return IndependentCopula()
elseif θ == 1
return UtilCopula()
else
return new{typeof(θ)}(θ)
end
end
end
𝘙(C::AMHCopula) = C.θ >= 0 ? 1 + Distributions.Geometric(1 - C.θ) : 1
ϕ(C::AMHCopula, x) = (1 - C.θ) / (exp(x) - C.θ)
ϕ⁻¹(C::AMHCopula, x) = log((1 - C.θ) / x + C.θ)
dϕ(C::AMHCopula, x) = -((1 - C.θ) * exp(x)) / (exp(x) - C.θ)^2
dϕ⁻¹(C::AMHCopula, x) = -(1 - C.θ) / (x * (C.θ * x + 1 - C.θ))
d²ϕ(C::AMHCopula, x) = ((1 - C.θ) * exp(x) * (exp(2 * x) - C.θ^2)) / (exp(x) - C.θ)^4
τ(C::AMHCopula) = (3 * C.θ - 2) / (3 * C.θ) - (2 * (1 - C.θ)^2 / (3 * C.θ^2)) * log(1 - C.θ)
ρₛ(C::AMHCopula) = (12 * (1 + C.θ) / C.θ^2) * PolyLog.reli2(1 - C.θ) - (24 * (1 - C.θ) / C.θ^2) * log(1 - C.θ) - (3 * (C.θ + 12) / C.θ)
λᵤ(C::AMHCopula) = 0.0
λₗ(C::AMHCopula) = 0.0 | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1700 | """
ClaytonCopula{P}
Fields:
- θ::Real - parameter
Constructor
ClaytonCopula(d,θ)
The bivariate [Clayton](https://en.wikipedia.org/wiki/Copula_(probability_theory)#Most_important_Archimedean_copulas) copula is parameterized by ``\\theta \\in [-1,\\infty)``. It is an Archimedean copula with generator :
```math
\\phi(t) = \\left(1+\\mathrm{sign}(\\theta)*t\\right)^{-1\\frac{1}{\\theta}}
```
It has a few special cases:
- When θ = -1, it is the WCopula (Lower Frechet-Hoeffding bound)
- When θ = 0, it is the IndependentCopula
- When θ = 1, it is the UtilCopula
- When θ = ∞, is is the MCopula (Upper Frechet-Hoeffding bound)
References:
* [nelsen2006](@cite) Nelsen, Roger B. An introduction to copulas. Springer, 2006.
"""
struct ClaytonCopula{P} <: ArchimedeanCopula{P}
θ::P
function ClaytonCopula(θ)
if !(-1 <= θ)
throw(ArgumentError("El parámetro θ debe estar en [-1, ∞)"))
elseif θ == -1
return WCopula()
elseif θ == 0
return IndependentCopula()
elseif θ == 1
return UtilCopula()
elseif θ == Inf
return MCopula()
else
return new{typeof(θ)}(θ)
end
end
end
ϕ(C::ClaytonCopula, x) = max(1 + C.θ * x, zero(x))^(-1 / C.θ)
dϕ(C::ClaytonCopula, x) = (-1 / C.θ) * (1 + x)^(-1 / C.θ - 1)
d²ϕ(C::ClaytonCopula, x) = (1 / C.θ) * (1 / C.θ + 1) * (1 + x)^(-1 / C.θ - 2)
ϕ⁻¹(C::ClaytonCopula, x) = (x^(-C.θ) - 1) / C.θ
dϕ⁻¹(C::ClaytonCopula, x) = -x^(-C.θ - 1)
τ(C::ClaytonCopula) = C.θ / (C.θ + 2)
λᵤ(C::ClaytonCopula) = 0.0
λₗ(C::ClaytonCopula) = 2^(-1 / C.θ)
𝘙(C::ClaytonCopula) = C.θ > 0 ? Distributions.Gamma(1/C.θ) : 1
| TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1927 | """
FrankCopula{P}
Fields:
- θ::Real - parameter
Constructor
FrankCopula(θ)
The bivariate [Frank](https://en.wikipedia.org/wiki/Copula_(probability_theory)#Most_important_Archimedean_copulas) copula is parameterized by ``\\theta \\in (-\\infty,\\infty)``. It is an Archimedean copula with generator :
```math
\\phi(t) = -\\frac{\\log\\left(1+e^{-t}(e^{-\\theta-1})\\right)}{\theta}
```
It has a few special cases:
- When θ = -∞, it is the WCopula (Lower Frechet-Hoeffding bound)
- When θ = 1, it is the IndependentCopula
- When θ = ∞, is is the MCopula (Upper Frechet-Hoeffding bound)
References:
* [nelsen2006](@cite) Nelsen, Roger B. An introduction to copulas. Springer, 2006.
"""
struct FrankCopula{P} <: ArchimedeanCopula{P}
θ::P
function FrankCopula(θ)
if θ == -Inf
return WCopula()
elseif θ == 0
return IndependentCopula()
elseif θ == Inf
return MCopula()
else
return new{typeof(θ)}(θ)
end
end
end
𝘙(C::FrankCopula) = C.θ > 0 ? Logarithmic(1 - exp(-C.θ)) : 1
ϕ(C::FrankCopula, x) = C.θ > 0 ? -LogExpFunctions.log1mexp(LogExpFunctions.log1mexp(-C.θ) - x) / C.θ : -log1p(exp(-x) * expm1(-C.θ)) / C.θ
dϕ(C::FrankCopula, x) = (exp(-x) * expm1(-C.θ)) / (C.θ * (exp(-x) * expm1(-C.θ)) + 1)
d²ϕ(C::FrankCopula, x) = -(exp(-x) * expm1(-C.θ)) / (C.θ * (exp(-x) * expm1(-C.θ) + 1)^2)
ϕ⁻¹(C::FrankCopula, x) = -log((exp(-C.θ * x) - 1) / (exp(-C.θ) - 1))
dϕ⁻¹(C::FrankCopula, x) = (C.θ * exp(-C.θ * x)) / (exp(-C.θ * x) - 1)
τ(C::FrankCopula) = (1 + 4 * (𝘋(1, C.θ) - 1) / C.θ)
ρₛ(C::FrankCopula) = (1 + 12 * (𝘋(2, C.θ) - 𝘋(1, C.θ)) / C.θ)
λᵤ(C::FrankCopula) = 0.0
λₗ(C::FrankCopula) = 0.0
function 𝘋(n, x)
if x == 0
return 1.0
else
integrand(t) = (t^n) / (exp(t) - 1)
integral, _ = QuadGK.quadgk(integrand, 0, x)
return (n / x^n) * integral
end
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1360 | """
GumbelBarnettCopula{P}
Fields:
- θ::Real - parameter
Constructor
GumbelBarnettCopula(θ)
The bivariate Gumbel-Barnett copula is parameterized by ``\\theta \\in (0,1]``. It is an Archimedean copula with generator :
```math
\\phi(t) = \\exp{θ^{-1}(1-e^{t})}, 0 \\leq \\theta \\leq 1.
```
It has a few special cases:
- When θ = 0, it is the IndependentCopula
References:
* [joe2014](@cite) Joe, H. (2014). Dependence modeling with copulas. CRC press, Page.437
* [nelsen2006](@cite) Nelsen, Roger B. An introduction to copulas. Springer, 2006.
"""
struct GumbelBarnettCopula{T} <: ArchimedeanCopula{T}
θ::T
function GumbelBarnettCopula(θ)
if !(0 <= θ <= 1)
throw(ArgumentError("Theta must be in [0,1]"))
elseif θ == 0
return IndependentCopula()
else
return new{typeof(θ)}(θ)
end
end
end
𝘙(C::GumbelBarnettCopula) = 1 # ϕ is not completely monotone so we cannot use the Williamsons transform
ϕ(C::GumbelBarnettCopula, x) = exp((1 - exp(x)) / C.θ)
ϕ⁻¹(C::GumbelBarnettCopula, x) = log1p(-C.θ * log(x))
dϕ(C::GumbelBarnettCopula, x) = -exp(x) / C.θ * exp((1 - exp(x)) / C.θ)
dϕ⁻¹(C::GumbelBarnettCopula, x) = -C.θ / (x * (1 - C.θ * log(x)))
d²ϕ(C::GumbelBarnettCopula, x) = -exp(x) / C.θ * exp((1 - exp(x)) / C.θ) + exp(2x) / C.θ^2 * exp((1 - exp(x)) / C.θ)
| TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1483 | """
GumbelCopula{P}
Fields:
- θ::Real - parameter
Constructor
GumbelCopula(d,θ)
The bivariate [Gumbel](https://en.wikipedia.org/wiki/Copula_(probability_theory)#Most_important_Archimedean_copulas) copula is parameterized by ``\\theta \\in [1,\\infty)``. It is an Archimedean copula with generator :
```math
\\phi(t) = \\exp{-t^{\\frac{1}{θ}}}
```
It has a few special cases:
- When θ = 1, it is the IndependentCopula
- When θ = ∞, is is the MCopula (Upper Frechet-Hoeffding bound)
References:
* [nelsen2006](@cite) Nelsen, Roger B. An introduction to copulas. Springer, 2006.
"""
struct GumbelCopula{P} <: ArchimedeanCopula{P}
θ::P
function GumbelCopula(θ)
if !(1 <= θ)
throw(ArgumentError("El parámetro θ debe estar en [1, ∞)"))
elseif θ == 1
return IndependentCopula()
elseif θ == Inf
return MCopula()
else
return new{typeof(θ)}(θ)
end
end
end
𝘙(C::GumbelCopula) = Stable(1 / C.θ)
ϕ(C::GumbelCopula, x) = exp(-x^(1 / C.θ))
dϕ(C::GumbelCopula, x) = - (1 / C.θ) * x^(1 / C.θ - 1) * exp(-x^(1 / C.θ))
d²ϕ(C::GumbelCopula, x) = -(1 / C.θ) * (1 / C.θ - 1) * x^(1 / C.θ - 2) * exp(-x^(1 / C.θ)) + (1 / C.θ^2) * x^(2 / C.θ - 2) * exp(-x^(1 / C.θ))
ϕ⁻¹(C::GumbelCopula, x) = (-log(x))^C.θ
dϕ⁻¹(C::GumbelCopula, x) = -(C.θ / x) * (-log(x))^(C.θ - 1)
τ(C::GumbelCopula) = (C.θ - 1) / C.θ
λᵤ(C::GumbelCopula) = 2 - 2^(1 / C.θ)
λₗ(C::GumbelCopula) = 0.0
| TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1638 | """
InvGaussianCopula{P}
Fields:
- θ::Real - parameter
Constructor
InvGaussianCopula(θ)
The bivariate Inverse Gaussian copula is parameterized by ``\\theta \\in [0,\\infty)``. It is an Archimedean copula with generator :
```math
\\phi(t) = \\exp{\\frac{1-\\sqrt{1+2θ^{2}t}}{θ}}.
```
More details about Inverse Gaussian Archimedean copula are found in :
Mai, Jan-Frederik, and Matthias Scherer. Simulating copulas: stochastic models, sampling algorithms, and applications. Vol. 6. # N/A, 2017. Page 74.
It has a few special cases:
- When θ = 0, it is the IndependentCopula
References:
* [nelsen2006](@cite) Nelsen, Roger B. An introduction to copulas. Springer, 2006.
"""
struct InvGaussianCopula{P} <: ArchimedeanCopula{P}
θ::P
function InvGaussianCopula(θ)
if !(0 <= θ) throw(ArgumentError("El parámetro θ debe estar en (0, ∞)"))
elseif θ == 0
return IndependentCopula()
else
return new{typeof(θ)}(θ)
end
end
end
𝘙(C::InvGaussianCopula) = Distributions.InverseGaussian(C.θ, 1)
ϕ(C::InvGaussianCopula, x) = exp((1 - sqrt(1 + 2 * C.θ^2 * x)) / C.θ)
dϕ(C::InvGaussianCopula, x) = -C.θ / sqrt(1 + 2 * C.θ^2 * x) * exp((1 - sqrt(1 + 2 * C.θ^2 * x)) / C.θ)
d²ϕ(C::InvGaussianCopula, x) = C.θ^3 / (1 + 2 * C.θ^2 * x)^(3/2) * exp((1 - sqrt(1 + 2 * C.θ^2 * x)) / C.θ) + C.θ^2 / (1 + 2 * C.θ^2 * x) * exp((1 - sqrt(1 + 2 * C.θ^2 * x)) / C.θ)
ϕ⁻¹(C::InvGaussianCopula, x) = ((1 - C.θ * log(x))^2 - 1) / (2 * C.θ^2)
dϕ⁻¹(C::InvGaussianCopula, x) = - (1 - C.θ * log(x)) / (x * C.θ)
λᵤ(C::InvGaussianCopula) = 0.0
λₗ(C::InvGaussianCopula) = 0.0
| TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1536 | """
JoeCopula{P}
Fields:
- θ::Real - parameter
Constructor
JoeCopula(θ)
The bivariate [Joe](https://en.wikipedia.org/wiki/Copula_(probability_theory)#Most_important_Archimedean_copulas) copula is parameterized by ``\\theta \\in [1,\\infty)``. It is an Archimedean copula with generator :
```math
\\phi(t) = 1 - \\left(1 - e^{-t}\\right)^{\\frac{1}{\\theta}}
```
It has a few special cases:
- When θ = 1, it is the IndependentCopula
- When θ = ∞, is is the MCopula (Upper Frechet-Hoeffding bound)
References:
* [nelsen2006](@cite) Nelsen, Roger B. An introduction to copulas. Springer, 2006.
"""
struct JoeCopula{P} <: ArchimedeanCopula{P}
θ::P
function JoeCopula(θ)
if !(1 <= θ)
throw(ArgumentError("El parámetro θ debe estar en [1, ∞)"))
elseif θ == 1
return IndependentCopula()
elseif θ == Inf
return MCopula()
else
return new{typeof(θ)}(θ)
end
end
end
𝘙(C::JoeCopula) = Sibuya(1 / C.θ)
ϕ(C::JoeCopula, x) = 1 - (-expm1(-x))^(1 / C.θ)
dϕ(C::JoeCopula, x) = -(1 / C.θ) * (-expm1(-x))^(1 / C.θ - 1) * exp(-x)
d²ϕ(C::JoeCopula, x) = -(1 / C.θ) * ((1 / C.θ - 1) * exp(-2 * x) * (-expm1(-x))^(1 / C.θ - 2) - exp(-x) * (-expm1(-x))^(1 / C.θ - 1))
ϕ⁻¹(C::JoeCopula, x) = -log1p(-(1 - x)^C.θ)
dϕ⁻¹(C::JoeCopula, x) = (C.θ * (1 - x)^(C.θ - 1)) / (1 - (1 - x)^C.θ)
τ(C::JoeCopula) = 1 - 4 * sum(1 / (k * (2 + k * C.θ) * (C.θ * (k - 1) + 2)) for k in 1:1000)
λᵤ(C::JoeCopula) = 2 - 2^(1 / C.θ)
λₗ(C::JoeCopula) = 0.0 | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1467 | """
Nelsen2Copula{P}
Fields:
- θ::Real - parameter
Constructor
Nelsen2Copula(θ)
The bivariate Nelsen2Copula copula is parameterized by ``\\theta \\in [1,\\infty)``. It is an Archimedean copula with generator :
```math
\\phi(t) = 1 - t^{\\frac{1}{\\theta}}
```
It has a few special cases:
- When θ = 1, it is the IndependentCopula
- When θ = ∞, is is the MCopula (Upper Frechet-Hoeffding bound)
References:
* [nelsen2006](@cite) Nelsen, Roger B. An introduction to copulas. Springer, 2006.
"""
struct Nelsen2Copula{P} <: ArchimedeanCopula{P}
θ::P
function Nelsen2Copula(θ)
if !(1 <= θ)
throw(ArgumentError("El parámetro θ debe estar en [1, ∞]"))
elseif θ == 1
return WCopula()
elseif θ == Inf
return MCopula()
else
return new{typeof(θ)}(θ)
end
end
end
𝘙(C::Nelsen2Copula) = C.θ <= 4.5 ? RadialDist(C) : 1
ϕ(C::Nelsen2Copula, x) = 1 - x^(1/C.θ)
ϕ⁻¹(C::Nelsen2Copula, x) = (1 - x)^C.θ
dϕ(C::Nelsen2Copula, x) = -(1 / C.θ) * x^(1/C.θ - 1)
dϕ⁻¹(C::Nelsen2Copula, x) = C.θ * (1 - x)^(C.θ - 1)
d²ϕ(C::Nelsen2Copula, x) = -(1 / C.θ)*(1/C.θ - 1)*(x^(1/C.θ - 2))
τ(C::Nelsen2Copula) = (3 * C.θ - 2) / (3 * C.θ) - (2 * (1 - C.θ)^2 / (3 * C.θ^2)) * log(1 - C.θ)
ρₛ(C::Nelsen2Copula) = (12 * (1 + C.θ) / C.θ^2) * PolyLog.reli2(1 - C.θ) - (24 * (1 - C.θ) / C.θ^2) * log(1 - C.θ) - (3 * (C.θ + 12) / C.θ)
λᵤ(C::Nelsen2Copula) = 0.0
λₗ(C::Nelsen2Copula) = 0.0 | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 683 | """
UtilCopula{}
Constructor
UtilCopula()
The bivariate UtilCopula is a simple copula that appears as a special case of several copulas, that has the form :
```math
C(u_1, u_2) = \\frac{u_1u_2}{u_1+u_2 - u_1u_2}
```
It happends to be an Archimedean Copula, with generator :
```math
\\phi(t) = 1 / (t + 1)
```
References:
* [nelsen2006](@cite) Nelsen, Roger B. An introduction to copulas. Springer, 2006.
"""
struct UtilCopula <: ArchimedeanCopula{Nothing} end
𝘙(C::UtilCopula) = 1
ϕ(C::UtilCopula, x) = 1 / (x + 1)
dϕ(C::UtilCopula, x) = -1 / (x + 1)^2
d²ϕ(C::UtilCopula, x) = 2 / (x + 1)^3
ϕ⁻¹(C::UtilCopula, x) = 1 / x - 1
dϕ⁻¹(C::UtilCopula, x) = -1 / x^2
| TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 940 | struct ExtremeDist{C<:ExtremeValueCopula} <: Distributions.ContinuousUnivariateDistribution
G::C
end
function Distributions.cdf(d::ExtremeDist, z)
copula = d.G
return z + z*(1 - z)*(d𝘈(copula, z)/𝘈(copula, z))
end
using Distributions
function _pdf(d::ExtremeDist, z)
copula = d.G
A = 𝘈(copula, z)
A_prime = d𝘈(copula, z)
A_double_prime = d²𝘈(copula, z)
return 1 + (1 - 2z) * A_prime / A + z * (1 - z) * (A_double_prime * A - A_prime^2) / A^2
end
function Distributions.quantile(d::ExtremeDist, p)
cdf_func(x) = Distributions.cdf(d, x) - p
return Roots.find_zero(cdf_func, (eps(), 1-eps()), Roots.Brent())
end
# Generar muestras aleatorias de la distribución radial usando la función cuantil
function Distributions.rand(rng::Distributions.AbstractRNG, d::ExtremeDist)
u = rand(rng, Distributions.Uniform(0,1)) # Muestra de una distribución uniforme
return Distributions.quantile(d, u)
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1195 | struct Logarithmic{T<:Real} <: Distributions.DiscreteUnivariateDistribution
θ::T
function Logarithmic(θ::Real)
if !(0 < θ < 1)
throw(ArgumentError("Parameter θ must be in (0, 1)"))
else
return new{typeof(θ)}(θ)
end
end
end
Statistics.mean(d::Logarithmic) = -d.θ / ((1 - d.θ) * log(1 - d.θ))
Statistics.var(d::Logarithmic) = -d.θ * (d.θ + log(1 - d.θ)) / ((1 - d.θ)^2 * (log(1 - d.θ))^2)
function Distributions.pdf(d::Logarithmic, x::Int)
x > 0 ? -d.θ^x / (x * log(1 - d.θ)) : 0.0
end
function Distributions.cdf(d::Logarithmic, x::Int)
θ = d.θ
ks = 1:x
s = sum(θ .^ ks ./ ks)
return -s / log(1 - θ)
end
function Distributions.rand(rng::Distributions.AbstractRNG, d::Logarithmic{T}) where T
θ = d.θ
h = log(1 - θ)
u2 = rand(rng, Distributions.Uniform(0, 1))
x = 1
if u2 > θ
return x
else
u1 = rand(rng, Distributions.Uniform(0, 1))
q = 1 - exp(u1*h)
if u2 < q^2
return Int(trunc(1 + log(u2) / log(q)))
else
if u2 > q
return 1
else
return 2
end
end
end
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 620 | struct PStable{T<:Real} <: Distributions.ContinuousUnivariateDistribution
α::T
end
function PStable(α)
if α <= 0 || α > 2
throw(ArgumentError("Parameter α must be in (0, 2]"))
end
return PStable{typeof(α)}(α)
end
function Distributions.rand(rng::Distributions.AbstractRNG, d::PStable{T}) where T
α = d.α
if α == 1
return 0.0
else
tα = 1 - α
u = rand(rng, Distributions.Uniform(0,π))
w = rand(rng, Distributions.Exponential())
term1 = log((sin(tα*u)/w)^(tα/α))
term2 = log(sin(α*u)/(sin(u)^(1/α)))
return term1*term2
end
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1284 | struct RadialDist{C<:ArchimedeanCopula} <: Distributions.ContinuousUnivariateDistribution
G::C
end
# Transformada de Williamson W_2
function 𝔚(G::ArchimedeanCopula, x)
integrand(t) = (1 - x / t) * ϕ(G, t) * (t > x ? 1 : 0)
integral, _ = QuadGK.quadgk(integrand, x, Inf)
return integral
end
# Inversa de la transformada de Williamson para d = 2
function 𝔚⁻¹(G::ArchimedeanCopula, x)
if x < 0.0
return 0.0
elseif x >= 1.0
return 1.0
else
return 1 - ϕ(G, x) + x*dϕ(G, x)
end
end
# CDF de la distribución radial
function Distributions.cdf(d::RadialDist, x)
G = d.G
if x <= 0
return 0.0
else
return 𝔚⁻¹(G, x)
end
end
# PDF de la distribución radial
function Distributions.pdf(d::RadialDist, x)
G = d.G
return (x * d²ϕ(G, x))
end
function Distributions.quantile(d::RadialDist, p)
cdf_func(x) = Distributions.cdf(d, x) - p
return Roots.find_zero(cdf_func, (eps(), 1000.0), Roots.Brent())
end
# Generar muestras aleatorias de la distribución radial usando la función cuantil
function Distributions.rand(rng::Distributions.AbstractRNG, d::RadialDist)
u = rand(rng, Distributions.Uniform(0,1)) # Muestra de una distribución uniforme
return Distributions.quantile(d, u)
end
| TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1079 | struct Sibuya{T<:Real} <: Distributions.DiscreteUnivariateDistribution
θ::T
function Sibuya(θ::Real)
if !(0 < θ <=1)
throw(ArgumentError("Parameter θ must be in (0, 1]"))
else
new{typeof(θ)}(θ)
end
end
end
#Statistics.mean(d::Sibuya) = 0.0
#Statistics.var(d::Sibuya) = 0.0
function Distributions.pdf(d::Sibuya, x::Int)
x > 0 ? (-1)^(x+1)*(1/(x*SpecialFunctions.beta(x, d.θ-x+1))) : 0.0
end
function Distributions.cdf(d::Sibuya, x::Int)
θ = d.θ
if x < 0
throw(ArgumentError("x must be a positive integer"))
else
return 1-(1/(x*SpecialFunctions.beta(x,1-θ)))
end
end
function Distributions.rand(rng::Distributions.AbstractRNG, d::Sibuya{T}) where T
θ = d.θ
Z1 = rand(rng, Distributions.Exponential())
Z2 = rand(rng, Distributions.Gamma(1 - θ))
Z3 = rand(rng, Distributions.Gamma(θ))
λ = (Z1 * Z2) / Z3
# Limitar λ utilizando eps
xMax = 1 / eps(T)
if λ > xMax
λ = xMax
end
return 1 + rand(rng, Distributions.Poisson(λ))
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 760 | # Definición de la estructura Stable
struct Stable{T<:Real} <: Distributions.ContinuousUnivariateDistribution
α::T
end
# Constructor de la distribución estable
function Stable(α, β, γ, δ)
if 0 < α <= 2 && -1 <= β <= 1 && γ > 0
return Stable{typeof(α)}(α, β, γ, δ)
else
throw(ArgumentError("Parameters α must be in (0, 2], β must be in [-1, 1], and γ must be greater than 0"))
end
end
function Distributions.rand(rng::Distributions.AbstractRNG, d::Stable{T}) where T
θ = d.α
U = rand(Distributions.Uniform(0,1))
E = rand(Distributions.Exponential())
U = π*(U - 0.5)
term1 = sin(θ*(π/2 + U))
term2 = cos(U)^(1/θ)
term3 = (cos(U - θ*(π/2 + U))/E)^((1-θ)/θ)
X = (term1/term2)*term3
return X
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 2156 | """
GaussianCopula{P}
Fields:
- θ::Real - Parameter
Constructor
GaussianCopula(θ)
The bivariate [Gaussian](https://en.wikipedia.org/wiki/Copula_(probability_theory)#Gaussian_copula) copula. It is constructed as:
```math
C(u_1, u_2; \\theta) = \\Phi_{\\theta}(\\Phi^{-1}(u_1),\\Phi^{-1}(u_2))
```
where ``\\Phi_{\\theta}`` is the cumulative distribution function (CDF) of a standard bivariate normal distribution with correlation coefficient ``\\theta \\in
[-1, 1]`` and ``\\Phi^{-1}``is the quantile function of the standard normal distribution.
It has a few special cases:
- When θ = -1, it is the WCopula (Lower Frechet-Hoeffding bound)
- When θ = 0, it is the IndependentCopula
- When θ = 1, is is the MCopula (Upper Frechet-Hoeffding bound)
References:
* [nelsen2006](@cite) Nelsen, Roger B. An introduction to copulas. Springer, 2006.
"""
struct GaussianCopula{P} <: EllipticalCopula{P}
θ::P # Copula parameter
function GaussianCopula(θ)
if !(-1 <= θ <= 1)
throw(ArgumentError("Theta must be in (-1, 1)"))
elseif θ == 0
return IndependentCopula()
elseif θ == -1
return WCopula()
elseif θ == 1
return MCopula()
else
return new{typeof(θ)}(θ)
end
end
end
function Distributions.cdf(C::GaussianCopula, x::AbstractVector)
θ = C.θ
u1 = Distributions.quantile(Distributions.Normal(), x[1])
u2 = Distributions.quantile(Distributions.Normal(), x[2])
mvn_density = Distributions.MvNormal([0.0, 0.0], [1.0 θ; θ 1.0])
integrand(v) = Distributions.pdf(mvn_density, v)
lower_bounds = [-1000.0, -1000.0]
upper_bounds = [u1, u2]
result, _ = Cubature.hcubature(integrand, lower_bounds, upper_bounds)
return result
end
function Distributions.pdf(C::GaussianCopula, x::AbstractVector)
θ = C.θ
u1 = Distributions.quantile(Distributions.Normal(), x[1])
u2 = Distributions.quantile(Distributions.Normal(), x[2])
factor1 = 1 / sqrt(1 - θ^2)
exponent = (2θ * u1 * u2 - θ^2 * (u1^2 + u2^2)) / (2 * (1 - θ^2))
density = factor1 * exp(exponent)
return density
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 2783 | """
tCopula{P}
Fields:
- ν::Real - paremeter
- θ::Real - Parameter
Constructor
tCopula(ν, θ)
The bivariate t copula. It is constructed as:
```math
C(u_1, u_2; \\nu, \\theta) = t_{\\nu, \\theta}(t_{\\nu}^{-1}(u_1),t_{\\nu}^{-1}(u_2))
```
where ``t_{\\nu, \\theta}`` is the cumulative distribution function (CDF) of a bivariate t-distribution with ``\\nu \\in \\mathbb{R}^{+}`` degrees of freedom, zero means, and correlation ``\\theta \\in [-1, 1]``, and ``t_{\\nu}^{-1}`` is the quantile function of the standard t-distribution with ``\\nu`` degrees of freedom.
It has a few special cases:
- When θ = -1, it is the WCopula (Lower Frechet-Hoeffding bound)
- When θ = 0, it is the IndependentCopula
- When θ = 1, is is the MCopula (Upper Frechet-Hoeffding bound)
References:
* [joe2014](@cite) Joe, Harry. Dependence modeling with Copulas. Chapman & Hall, 2014.
"""
struct tCopula{df, P} <: EllipticalCopula{P}
θ::P # Parámetro de correlación
ν::df # Grados de libertad
function tCopula(ν::df, θ::P) where {df<:Real, P<:Real}
if ν <= 0
throw(ArgumentError("Los grados de libertad ν deben ser reales positivos"))
end
if !(-1 <= θ <= 1)
throw(ArgumentError("El parámetro de correlación ρ debe estar entre -1 y 1"))
elseif θ == 0
return IndependentCopula()
elseif θ == 1
return MCopula()
elseif θ == -1
return WCopula()
else
return new{df, typeof(θ)}(θ, ν)
end
end
end
function Distributions.cdf(C::tCopula, x::AbstractVector)
θ = C.θ
ν = C.ν
u1 = Distributions.quantile(Distributions.TDist(ν), x[1])
u2 = Distributions.quantile(Distributions.TDist(ν), x[2])
mvt_density = Distributions.MvTDist(ν, [0.0, 0.0], [1.0 θ; θ 1.0])
integrand(v) = Distributions.pdf(mvt_density, v)
lower_bounds = [-1000.0, -1000.0]
upper_bounds = [u1, u2]
result, _ = Cubature.hcubature(integrand, lower_bounds, upper_bounds)
return result
end
function Distributions.pdf(C::tCopula, x::AbstractVector)
θ = C.θ
ν = C.ν
u1 = Distributions.quantile(Distributions.TDist(ν), x[1])
u2 = Distributions.quantile(Distributions.TDist(ν), x[2])
num = (ν/2)*(SpecialFunctions.gamma(ν/2)^2)*(1 + (u1^2 + u2^2 -2*θ*u1*u2)/(ν*(1-θ^2)))^(-(ν+2)/2)
dem = sqrt(1-θ^2)*(SpecialFunctions.gamma((ν+1)/2)^2)*((1+ (u1^2)/ν)*(1+(u2^2)/ν))^(-(ν+1)/2)
return num/dem
end
function λᵤ(C::tCopula)
θ = C.θ
ν = C.ν
term = -sqrt(((ν+1)*(1-θ))/(1+θ))
return 2*Distributions.cdf(Distributions.TDist(ν+1), term)
end
function λₗ(C::tCopula)
θ = C.θ
ν = C.ν
term = -sqrt(((ν+1)*(1-θ))/(1+θ))
return 2*Distributions.cdf(Distributions.TDist(ν+1), term)
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1949 | """
AsymGalambosCopula{P}
Fields:
- α::Real - Dependency parameter
- θ::Vector - Asymmetry parameters (size 2)
Constructor
AsymGalambosCopula(α, θ)
The Asymmetric bivariate Galambos copula is parameterized by one dependence parameter ``\\alpha \\in [0, \\infty]`` and two asymmetry parameters ``\\theta_{i} \\in [0,1], i=1,2``. It is an Extreme value copula with Pickands function:
```math
\\A(t) = 1 - ((\\theta_1t)^{-\\alpha}+(\\theta_2(1-t))^{-\\alpha})^{-\\frac{1}{\\alpha}}
```
It has a few special cases:
- When α = 0, it is the Independent Copula
- When θ₁ = θ₂ = 0, it is the Independent Copula
- When θ₁ = θ₂ = 1, it is the Galambos Copula
References:
* [Joe1990](@cite) Families of min-stable multivariate exponential and multivariate extreme value distributions. Statist. Probab, 1990.
"""
# Definición de la estructura AsymGalambosCopula
struct AsymGalambosCopula{P} <: ExtremeValueCopula{P}
α::P # Parámetro de dependencia
θ::Vector{P} # Parámetros de asimetría (de tamaño 2 para el caso bivariado)
function AsymGalambosCopula(α::P, θ::Vector{P}) where {P}
if length(θ) != 2
throw(ArgumentError("El vector θ debe tener 2 elementos para el caso bivariado"))
elseif !(0 <= α)
throw(ArgumentError("El parámetro α debe estar ser mayor o igual que 0"))
elseif !(0 <= θ[1] <= 1) || !(0 <= θ[2] <= 1)
throw(ArgumentError("Todos los parámetros θ deben estar en el intervalo [0, 1]"))
elseif α == 0 || (θ[1] == 0 && θ[2] == 0)
return IndependentCopula()
elseif θ[1] == 1 && θ[2] == 1
return GalambosCopula(α)
else
return new{P}(α, θ)
end
end
end
function 𝘈(C::AsymGalambosCopula, t::Real)
α = C.α
θ = C.θ
term1 = (θ[1] * t)^(-α)
term2 = (θ[2] * (1 - t))^(-α)
inner_term = term1 + term2
result = 1 - inner_term^(-1 / α)
return result
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1582 | """
AsymLogCopula{P}
Fields:
- α::Real - Dependency parameter
- θ::Vector - Asymmetry parameters (size 2)
Constructor
AsymLogCopula(α, θ)
The Asymmetric bivariate Logistic copula is parameterized by one dependence parameter ``\\alpha \\in [1, \\infty]`` and two asymmetry parameters ``\\theta_{i} \\in [0,1], i=1,2``. It is an Extreme value copula with Pickands dependence function:
```math
A(t) = (\\theta_1^{\\alpha}(1-t)^{\\alpha} + \\theta_2^{\\alpha}t^{\\alpha})^{\\frac{1}{\\alpha}} + (\\theta_1 - \\theta_2)t + 1 - \\theta_1
```
References:
* [Tawn1988](@cite) Bivariate extreme value theory: models and estimation. Biometrika, 1988.
"""
struct AsymLogCopula{P} <: ExtremeValueCopula{P}
α::P # Parámetro de dependencia
θ::Vector{P} # Parámetros de asimetría (de tamaño 2 para el caso bivariado)
function AsymLogCopula(α::P, θ::Vector{P}) where {P}
if length(θ) != 2
throw(ArgumentError("El vector θ debe tener 2 elementos para el caso bivariado"))
elseif !(1 <= α)
throw(ArgumentError("El parámetro α debe estar ser mayor o igual que 1"))
elseif !(0 <= θ[1] <= 1) || !(0 <= θ[2] <= 1)
throw(ArgumentError("Todos los parámetros θ deben estar en el intervalo [0, 1]"))
else
return new{P}(α, θ)
end
end
end
# Definir la función A específica para la copula logística asimétrica bivariada
function 𝘈(C::AsymLogCopula, t::Real)
α = C.α
θ = C.θ
A = ((θ[1]^α)*(1-t)^α + (θ[2]^α)*(t^α))^(1/α)+(θ[1]- θ[2])*t + 1 -θ[1]
return A
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1706 | """
AsymMixedCopula{P}
Fields:
- θ::Vector - parameters (size 2)
Constructor
AsymMixedCopula(θ)
The Asymmetric bivariate Mixed copula is parameterized by two parameters ``\\theta_{i}, i=1,2`` that must meet the following conditions:
* θ₁ ≥ 0
* θ₁+θ₂ ≤ 1
* θ₁+2θ₂ ≤ 1
* θ₁+3θ₂ ≥ 0
It is an Extreme value copula with Pickands dependence function:
```math
A(t) = \\theta_{2}t^3 + \\theta_{1}t^2-(\\theta_1+\\theta_2)t+1
```
It has a few special cases:
- When θ₁ = θ₂ = 0, it is the Independent Copula
- When θ₂ = 0, it is the Mixed Copula
References:
* [Tawn1988](@cite) Bivariate extreme value theory: models and estimation. Biometrika, 1988.
"""
struct AsymMixedCopula{P} <: ExtremeValueCopula{P}
θ::Vector{P} # Parámetros de asimetría (de tamaño 2 para el caso bivariado)
function AsymMixedCopula(θ::Vector{P}) where {P}
if length(θ) != 2
throw(ArgumentError("El vector θ debe tener 2 elementos para el caso bivariado"))
elseif !(0 <= θ[1])
throw(ArgumentError("El parámetro θ₁ debe estar ser mayor o igual que 0"))
elseif !(θ[1]+θ[2] <= 1)
throw(ArgumentError("la suma de θ₁+θ₂ ≤ 1"))
elseif !(θ[1]+2*θ[2] <= 1)
throw(ArgumentError("la suma de θ₁+2θ₂ ≤ 1"))
elseif !(0 <= θ[1]+3*θ[2])
throw(ArgumentError("la suma de 0 ≤ θ₁+3θ₂"))
elseif θ[1] == 0 && θ[2] == 0
return IndependentCopula()
else
return new{P}(θ)
end
end
end
# Definir la función A específica para la copula logística asimétrica bivariada
function 𝘈(C::AsymMixedCopula, t::Real)
θ = C.θ
A = θ[2]*t^3 + θ[1]*t^2-(θ[1]+θ[2])*t+1
return A
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 2096 | """
BC2Copula{P}
Fields:
- θ1::Real - parameter
- θ1::Real - parameter
Constructor
BC2Copula(θ1, θ2)
The bivariate BC₂ copula is parameterized by two parameters ``\\theta_{i} \\in [0,1], i=1,2``. It is an Extreme value copula with Pickands dependence function:
```math
A(t) = \\max\\{\\theta_1 t, \\theta_2(1-t) \\} + \\max\\{(1-\\theta_1)t, (1-\\theta_2)(1-t)\\}
```
References:
* [Mai2011](@cite) Bivariate extreme-value copulas with discrete Pickands dependence measure. Springer, 2011.
"""
struct BC2Copula{P} <: ExtremeValueCopula{P}
θ1::P
θ2::P
function BC2Copula(θ::Vararg{Real})
if length(θ) !== 2
throw(ArgumentError("BC2Copula requires only 2 arguments."))
end
# Promover todos los parámetros al mismo tipo
T = promote_type(typeof(θ[1]), typeof(θ[2]))
θ1, θ2 = T(θ[1]), T(θ[2])
# Validar que los parámetros sean no negativos
if !(0 <= θ1 <= 1) || !(0 <= θ2 <= 1)
throw(ArgumentError("All θ parameters must be in [0,1]"))
end
return new{T}(θ1, θ2)
end
end
function ℓ(C::BC2Copula, t::Vector)
θ1, θ2 = C.θ1, C.θ2
t₁, t₂ = t
return max(θ1*t₁, θ2*t₂) + max((1-θ1)*t₁, (1-θ2)*t₂)
end
function 𝜜(C::BC2Copula, t::Real)
θ1, θ2 = C.θ1, C.θ2
return max(θ1*t, θ2*(1-t)) + max((1-θ1)*t, (1-θ2)*(1-t))
end
function d𝘈(C::BC2Copula, t::Float64)
θ1, θ2 = C.θ1, C.θ2
# Conditions for the derivative of the first part
if θ1*t >= θ2*(1-t)
f1_derivative = θ1
else
f1_derivative = -θ2
end
# Conditions for the derivative of the second part
if (1-θ1)*t >= (1-θ2)*(1-t)
f2_derivative = 1-θ1
else
f2_derivative = -(1-θ2)
end
return f1_derivative + f2_derivative
end
function Distributions._rand!(rng::Distributions.AbstractRNG, C::BC2Copula, u::AbstractVector{T}) where {T<:Real}
θ1, θ2 = C.θ1, C.θ2
v1, v2 = rand(rng, Distributions.Uniform(0,1), 2)
u[1] = max(v1^(1/θ1),v2^(1/(1-θ1)))
u[2] = max(v1^(1/θ2),v2^(1/(1-θ2)))
return u
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1561 | """
CuadrasAugeCopula{P}
Fields:
- α::Real - parameter
Constructor
CuadrasAugeCopula(α)
The bivariate Cuadras Auge copula is parameterized by ``\\alpha \\in [0,1]``. It is an Extreme value copula with Pickands dependence function:
```math
A(t) = \\max\\{t, 1-t \\} + (1-\\theta)\\max\\{t, 1-t\\}
```
References:
* [Mai2017](@cite) Simulating copulas: stochastic models, sampling algorithms, and applications. 2017.
"""
struct CuadrasAugeCopula{P} <: ExtremeValueCopula{P}
θ::P # Copula parameter
function CuadrasAugeCopula(θ)
if !(0 <= θ <= 1)
throw(ArgumentError("Theta must be in [0,1]"))
elseif θ == 0
return IndependentCopula()
elseif θ == 1
return MCopula()
else
return new{typeof(θ)}(θ)
end
end
end
𝘈(C::CuadrasAugeCopula, t::Real) = max(t, 1-t) + (1-C.θ) * min(t, 1-t)
d𝘈(C::CuadrasAugeCopula, t::Real) = t <= 0.5 ? -C.θ : C.θ
τ(C::CuadrasAugeCopula) = C.θ/(2-C.θ)
ρₛ(C::CuadrasAugeCopula) = (3*C.θ)/(4-C.θ)
# Definir la función ℓ específica para la copula de Cuadras-Auge
function ℓ(C::CuadrasAugeCopula, t::Vector)
θ = C.θ
t₁, t₂ = t
return max(t₁, t₂) + (1-θ) * min(t₁, t₂)
end
function Distributions._rand!(rng::Distributions.AbstractRNG, C::CuadrasAugeCopula, x::AbstractVector{T}) where {T<:Real}
θ = C.θ
E₁, E₂ = rand(rng, Distributions.Exponential(θ/(1-θ)),2)
E₁₂ = rand(rng, Distributions.Exponential())
x[1] = exp(-(1/θ)*min(E₁,E₁₂))
x[2] = exp(-(1/θ)*min(E₂,E₁₂))
return x
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1040 | """
GalambosCopula{P}
Fields:
- θ::Real - parameter
Constructor
GalambosCopula(θ)
The bivariate Galambos copula is parameterized by ``\\alpha \\in [0,\\infty)``. It is an Extreme value copula with Pickands dependence function:
```math
A(t) = 1 - (t^{-\\theta}+(1-t)^{-\\theta})^{-\\frac{1}{\\theta}}
```
It has a few special cases:
- When θ = 0, it is the Independent Copula
- When θ = ∞, it is the M Copula (Upper Frechet-Hoeffding bound)
References:
* [Galambos1975](@cite) Order statistics of samples from multivariate distributions. J. Amer. Statist Assoc. 1975.
"""
struct GalambosCopula{P} <: ExtremeValueCopula{P}
θ::P # Copula parameter
function GalambosCopula(θ)
if θ < 0
throw(ArgumentError("Theta must be >= 0"))
elseif θ == 0
return IndependentCopula()
elseif θ == Inf
return MCopula()
else
return new{typeof(θ)}(θ)
end
end
end
𝘈(C::GalambosCopula, t::Real) = 1 - (t^(-C.θ) + (1 - t)^(-C.θ))^(-1/C.θ) | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 2369 | """
HuslerReissCopula{P}
Fields:
- θ::Real - parameter
Constructor
HuslerReissCopula(θ)
The bivariate Husler-Reiss copula is parameterized by ``\\theta \\in [0,\\infty)``. It is an Extreme value copula with Pickands dependence function:
```math
A(t) = t\\Phi(\\theta^{-1}+\\frac{1}{2}\\theta\\log(\\frac{t}{1-t})) +(1-t)\\Phi(\\theta^{-1}+\\frac{1}{2}\\theta\\log(\\frac{1-t}{t}))
```
Where ``\\Phi``is the cumulative distribution function (CDF) of the standard normal distribution.
It has a few special cases:
- When θ = 0, it is the Independent Copula
- When θ = ∞, it is the M Copula (Upper Frechet-Hoeffding bound)
References:
* [Husler1989](@cite) Maxima of normal random vectors: between independence and complete dependence. Statist. Probab. 1989.
"""
struct HuslerReissCopula{P} <: ExtremeValueCopula{P}
θ::P # Copula parameter
function HuslerReissCopula(θ)
if θ < 0
throw(ArgumentError("Theta must be ≥ 0"))
elseif θ == 0
return IndependentCopula()
elseif θ == Inf
return MCopula()
else
return new{typeof(θ)}(θ)
end
end
end
# Definir la función ℓ específica para la copula de Galambos
function ℓ(H::HuslerReissCopula, t::Vector)
θ = H.θ
t₁, t₂ = t
return t₁*Distributions.cdf(Distributions.Normal(),θ^(-1)+0.5*θ*log(t₁/t₂))+t₂*Distributions.cdf(Distributions.Normal(),θ^(-1)+0.5*θ*log(t₂/t₁))
end
# Definir la función A específica para la copula de Galambos
function 𝘈(H::HuslerReissCopula, t::Real)
θ = H.θ
term1 = t * Distributions.cdf(Normal(), θ^(-1) + 0.5 * θ * log(t / (1 - t)))
term2 = (1 - t) * Distributions.cdf(Normal(), θ^(-1) + 0.5 * θ * log((1 - t) / t))
A = term1 + term2
return A
end
function d𝘈(H::HuslerReissCopula, t::Real)
θ = H.θ
# Derivada de A(x) respecto a t
dA_term1 = Distributions.cdf(Normal(), θ^(-1) + 0.5 * θ * log(t / (1 - t))) +
t * Distributions.pdf(Normal(), θ^(-1) + 0.5 * θ * log(t / (1 - t))) * (0.5 * θ * (1 / t + 1 / (1 - t)))
dA_term2 = -Distributions.cdf(Normal(), θ^(-1) + 0.5 * θ * log((1 - t) / t)) +
(1 - t) * Distributions.pdf(Normal(), θ^(-1) + 0.5 * θ * log((1 - t) / t)) * (0.5 * θ * (-1 / t - 1 / (1 - t)))
dA = dA_term1 + dA_term2
return dA
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1375 | """
LogCopula{P}
Fields:
- θ::Real - parameter
Constructor
LogCopula(θ)
The bivariate Logistic copula (or Gumbel Copula) is parameterized by ``\\theta \\in [1,\\infty)``. It is an Extreme value copula with Pickands dependence function:
```math
A(t) = (t^{\\theta}+(1-t)^{\\theta})^{\\frac{1}{\\theta}}
```
It has a few special cases:
- When θ = 1, it is the IndependentCopula
- When θ = ∞, is is the MCopula (Upper Frechet-Hoeffding bound)
References:
* [Tawn1988](@cite) Bivariate extreme value theory: models and estimation. Biometrika, 1988.
"""
struct LogCopula{P} <: ExtremeValueCopula{P}
θ::P # Copula parameter
function LogCopula(θ)
if !(1 <= θ)
throw(ArgumentError("El parámetro θ debe estar en [1, ∞)"))
elseif θ == 1
return IndependentCopula()
elseif θ == Inf
return MCopula()
else
return new{typeof(θ)}(θ)
end
end
end
# Definir la función ℓ específica para la copula de Galambos
function ℓ(G::LogCopula, t::Vector)
θ = G.θ
t₁, t₂ = t
return (t₁^θ + t₂^θ)^(1/θ)
end
# Definir la función A específica para la copula de Galambos
function 𝘈(C::LogCopula, t::Real)
θ = C.θ
return (t^θ + (1 - t)^θ)^(1/θ)
end
function d𝘈(C::LogCopula, t::Real)
θ = C.θ
return ((t^θ + (1 - t)^θ)^((1/θ)-1))*(t^(θ-1)- (1-t)^(θ-1))
end
| TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 2053 | """
MOCopula{P}
Fields:
- λ1::Real - parameter
- λ2::Real - parameter
- λ12::Real - parameter
Constructor
MOCopula(θ)
The bivariate Marshall-Olkin copula is parameterized by ``\\lambda_i \\in [0,\\infty), i = 1, 2, \\{1,2\\}``. It is an Extreme value copula with Pickands dependence function:
```math
A(t) = \\frac{\\lambda_1 (1-t)}{\\lambda_1 + \\lambda_{1,2}} + \\frac{\\lambda_2 t}{\\lambda_2 + \\lambda_{1,2}} + \\lambda_{1,2}\\max\\left \\{\\frac{1-t}{\\lambda_1 + \\lambda_{1,2}}, \\frac{t}{\\lambda_2 + \\lambda_{1,2}} \\right \\}
```
References:
* [Mai2017](@cite) Simulating copulas: stochastic models, sampling algorithms, and applications. 2017.
"""
struct MOCopula{P} <: ExtremeValueCopula{P}
λ1::P
λ2::P
λ12::P
function MOCopula(λ::Vararg{Real})
if length(λ) !== 3
throw(ArgumentError("MOCopula requires only 3 arguments."))
end
# Promover todos los parámetros al mismo tipo
T = promote_type(typeof(λ[1]), typeof(λ[2]), typeof(λ[3]))
λ1, λ2, λ12 = T(λ[1]), T(λ[2]), T(λ[3])
# Validar que los parámetros sean no negativos
if λ1 < 0 || λ2 < 0 || λ12 < 0
throw(ArgumentError("All λ parameters must be >= 0"))
end
return new{T}(λ1, λ2, λ12)
end
end
function ℓ(C::MOCopula, t::Vector)
λ1, λ2, λ12 = C.λ1, C.λ2, C.λ12
t₁, t₂ = t
return (λ1*t₂)/(λ1+λ12) + (λ1*t₁)/(λ2+λ12) + λ12*max(t₂/(λ1+λ12),t₁/(λ2+λ12))
end
function 𝜜(C::MOCopula, t::Real)
λ1, λ2, λ12 = C.λ1, C.λ2, C.λ12
A = (λ1 * (1 - t)) / (λ1 + λ12) + (λ2 * t) / (λ2 + λ12) + λ12 * max((1 - t) / (λ1 + λ12), t / (λ2 + λ12))
return A
end
function Distributions._rand!(rng::Distributions.AbstractRNG, C::MOCopula, u::AbstractVector{T}) where {T<:Real}
λ1, λ2, λ12 = C.λ1, C.λ2, C.λ12
r, s, t = rand(Distributions.Uniform(0,1),3)
x = min(-log(r)/λ1, -log(t)/λ12)
y = min(-log(s)/λ2, -log(t)/λ12)
u[1] = exp(-(λ1+λ12)*x)
u[2] = exp(-(λ2+λ12)*y)
return u
end
| TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 869 | """
MixedCopula{P}
Fields:
- θ::Real - parameter
Constructor
MixedCopula(θ)
The bivariate Mixed copula is parameterized by ``\\alpha \\in [0,1]``. It is an Extreme value copula with Pickands dependence function:
```math
A(t) = \\theta t^2 - \\theta t + 1
```
It has a few special cases:
- When θ = 0, it is the IndependentCopula
References:
* [Tawn1988](@cite) Bivariate extreme value theory: models and estimation. Biometrika, 1988.
"""
struct MixedCopula{P} <: ExtremeValueCopula{P}
θ::P # Parámetro de la copula
function MixedCopula(θ)
if !(0 <= θ <= 1)
throw(ArgumentError("El parámetro θ debe estar en el intervalo [0, 1]"))
elseif θ == 0
return IndependentCopula()
else
return new{typeof(θ)}(θ)
end
end
end
𝘈(C::MixedCopula, t::Real) = C.θ*t^2 - C.θ*t + 1 | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 4716 | """
tEVCopula{P}
Fields:
- ν::Real - paremeter
- θ::Real - Parameter
Constructor
tEVCopula(ν, θ)
The bivariate extreme t copula is parameterized by ``\\nu \\in [0,\\infty)`` and \\theta \\in (-1,1]. It is an Extreme value copula with Pickands dependence function:
```math
A(x) = xt_{\\nu+1}(Z_x) +(1-x)t_{\\nu+1}(Z_{1-x})
```
Where ``t_{\\nu + 1}``is the cumulative distribution function (CDF) of the standard t distribution with \\nu + 1 degrees of freedom and
```math
Z_x = \\frac{(1+\\nu)^{1/2}{\\sqrt{1-\\theta^2}}\\left [ \\left (\\frac{x}{1-x} \\right )^{1/\\nu} - \\theta \\right ]
```
It has a few special cases:
- When θ = 0, it is the Independent Copula
- When θ = ∞, it is the M Copula (Upper Frechet-Hoeffding bound)
References:
* [Nikolopoulos2008](@cite) Extreme value properties of multivariate t copulas. Springer. 2008.
"""
struct tEVCopula{df, P} <: ExtremeValueCopula{P}
ρ::P # Parámetro de correlación
ν::df # Grados de libertad
function tEVCopula(ν::df, ρ::P) where {df<:Real, P<:Real}
if ν <= 0
throw(ArgumentError("Los grados de libertad ν deben ser reales positivos"))
end
if !(-1 < ρ <= 1)
throw(ArgumentError("El parámetro de correlación ρ debe estar entre -1 y 1"))
elseif ρ == 0
return IndependentCopula()
elseif ρ == 1
return MCopula()
end
return new{df, typeof(ρ)}(ρ, ν)
end
end
# Definir la función ℓ específica para la copula de Galambos
function ℓ(T::tEVCopula{P}, t::Vector) where P
ρ = T.ρ
ν = T.ν
t₁, t₂ = t
b = sqrt(ν + 1) / sqrt(1 - ρ^2)
term1 = t₁ * StatsFuns.tdistcdf(ν + 1, b * ((t₁ / t₂)^(1 / ν) - ρ))
term2 = t₂ * StatsFuns.tdistcdf(ν + 1, b * ((t₂ / t₁)^(1 / ν) - ρ))
return term1 + term2
end
function z(T::tEVCopula, t)
ρ = T.ρ
ν = T.ν
return ((1+ν)^(1/2))*((t/(1-t))^(1/ν) - ρ)*(1-ρ^2)^(-1/2)
end
# Definir la función A específica para la copula de Galambos
function 𝘈(T::tEVCopula, t::Real)
ρ = T.ρ
ν = T.ν
t = clamp(t, 0, 1)
zt = z(T,t)
tt_minus = z(T,1-t)
term1 = t * StatsFuns.tdistcdf(ν + 1, zt)
term2 = (1-t) * StatsFuns.tdistcdf(ν + 1, tt_minus)
return term1 + term2
end
function d𝘈(C::tEVCopula, t::Real)
h = 1e-5
t_h_clamped = clamp(t - h, 0, 1)
t_h_clamped_plus = clamp(t + h, 0, 1)
dA_minus = 𝘈(C, t_h_clamped)
dA_plus = 𝘈(C, t_h_clamped_plus)
dA = (dA_plus - dA_minus) / (2 * h)
return dA
end
# Aproximación de la segunda derivada de A
function d²𝘈(C::tEVCopula, t::Real)
h = 1e-5
t_h_clamped = clamp(t - h, 0, 1)
t_h_clamped_plus = clamp(t + h, 0, 1)
dA_minus = d𝘈(C, t_h_clamped)
dA_plus = d𝘈(C, t_h_clamped_plus)
d2A = (dA_plus - dA_minus) / (2 * h)
return d2A
end
# Función PDF para ExtremeValueCopula usando ℓ
function Distributions.pdf(C::tEVCopula, u::AbstractArray{<:Real})
t = -log.(u)
c = exp(-ℓ(C, t))
D1 = D_B_ℓ(C, t, [1])
D2 = D_B_ℓ(C, t, [2])
D12 = D_B_ℓ(C, t, [1, 2])
return c * (-D12 + D1 * D2) / (u[1] * u[2])
end
function D_B_ℓ(C::tEVCopula, t::Vector{Float64}, B::Vector{Int})
h = 1e-5
if length(B) == 1
# Primera derivada parcial
return partial_derivative_1(C, t, B[1], h)
elseif length(B) == 2
# Segunda derivada parcial o derivada mixta
return partial_derivative_2(C, t, B[1], B[2], h)
else
throw(ArgumentError("Higher order partial derivatives are not required for bivariate case"))
end
end
function partial_derivative_1(C::tEVCopula, t::Vector{Float64}, i::Int, h::Float64)
t_plus = copy(t)
t_minus = copy(t)
t_plus[i] += h
t_minus[i] -= h
return (ℓ(C, t_plus) - ℓ(C, t_minus)) / (2 * h)
end
function partial_derivative_2(C::tEVCopula, t::Vector{Float64}, i::Int, j::Int, h::Float64)
if i == j
# Segunda derivada parcial
t_plus = copy(t)
t_minus = copy(t)
t_plus[i] += h
t_minus[i] -= h
d_plus = partial_derivative_1(C, t_plus, i, h)
d_minus = partial_derivative_1(C, t_minus, i, h)
return (d_plus - d_minus) / (2 * h)
else
# Derivada mixta
t_plus_plus = copy(t)
t_plus_minus = copy(t)
t_minus_plus = copy(t)
t_minus_minus = copy(t)
t_plus_plus[i] += h
t_plus_plus[j] += h
t_plus_minus[i] += h
t_plus_minus[j] -= h
t_minus_plus[i] -= h
t_minus_plus[j] += h
t_minus_minus[i] -= h
t_minus_minus[j] -= h
return (ℓ(C, t_plus_plus) - ℓ(C, t_plus_minus) - ℓ(C, t_minus_plus) + ℓ(C, t_minus_minus)) / (4 * h^2)
end
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1476 | """
B11Copula{P}
Fields:
- θ::Real - parameter
Constructor
B11Copula(θ)
The bivariate B11 copula is parameterized by ``\\theta \\in [0,1]``. It is constructed as:
```math
C(u_1, u_2) = \\theta \\min\\{u_1,u_2\\} + (1-\\theta)u_1u_2
```
It has a few special cases:
- When θ = 0, it is the IndependentCopula
- When θ = 1, is is the MCopula (Upper Frechet-Hoeffding bound)
References:
* [Joe1997](@cite) Joe, Harry, Multivariate Models and Multivariate Dependence Concepts, Chapman & Hall. 1997.
"""
struct B11Copula{P} <: bicopula
θ::P # Copula parameter
function B11Copula(θ)
if !(0 <= θ <= 1)
throw(ArgumentError("Theta must be in [0,1]"))
elseif θ == 0
return IndependentCopula()
elseif θ == 1
return MCopula()
else
return new{typeof(θ)}(θ)
end
end
end
τ(C::B11Copula) = C.θ
function Distributions.cdf(C::B11Copula, x::AbstractVector)
θ = C.θ
u1, u2 = x
return θ*(min(u1,u2)) + (1-θ)*u1*u2
end
function Distributions.pdf(C::B11Copula, x::AbstractVector)
return (1 - C.θ)
end
function Distributions._rand!(rng::Distributions.AbstractRNG, C::B11Copula, x::AbstractVector{T}) where {T<:Real}
θ = C.θ
v, w = rand(rng, Distributions.Uniform(0,1),2)
b = rand(rng, Distributions.Bernoulli(θ))
if b == 0
x[1] = v
x[2] = w
else
x[1] = min(v, w)
x[2] = min(v, w)
end
return x
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 2552 | """
FrechetCopula{P}
Fields:
- θ1::Real - parameter
- θ2::Real - parameter
Constructor
FrechetCopula(θ1, θ2)
The bivariate Fréchet copula is parameterized by ``\\theta_{i} \\in [0,1], i = 1,2``, such that ``\\theta_1 + \\theta_2 \\leq 1 \\``. It is constructed as:
```math
C(u_1, u_2) = \\theta_1 \\min\\{u_1, u_2\\} + (1- \\theta_1 - \\theta_2)u_1u_2 + \\theta_2 \\max\\{u_1 + u_2 - 1, 0\\}
```
It has a few special cases:
- When θ1 = θ2 = 0, it is the Independent Copula
- When θ1 = 1, it is the MCopula (Upper Frechet-Hoeffding bound)
- When θ2 = 1, is is the WCopula (Lower Frechet-Hoeffding bound)
References:
* [nelsen2006](@cite) Nelsen, Roger B. An introduction to copulas. Springer, 2006.
"""
struct FrechetCopula{P} <: bicopula
θ1::P
θ2::P
function FrechetCopula(θ::Vararg{Real})
if length(θ) !== 2
throw(ArgumentError("FrechetCopula requires only 2 arguments."))
end
# Promover todos los parámetros al mismo tipo
T = promote_type(typeof(θ[1]), typeof(θ[2]))
θ1, θ2 = T(θ[1]), T(θ[2])
# Validar que los parámetros sean no negativos
if !(0 <= θ1 <= 1) || !(0 <= θ2 <= 1)
throw(ArgumentError("All θ parameters must be in [0,1]"))
elseif !(θ1 + θ2 <= 1)
throw(ArgumentError("θ1 + θ2 must be in [0,1]"))
elseif θ1 == 1
return MCopula()
elseif θ2 == 1
return WCopula()
elseif θ1 == 0 && θ2 == 0
return IndependentCopula()
else
return new{T}(θ1, θ2)
end
end
end
function Distributions.cdf(C::FrechetCopula, u::AbstractVector)
θ1, θ2 = C.θ1, C.θ2
u1, u2 = u
return θ1*min(u1, u2) + (1 - θ1 - θ2)*u1*u2 + θ2*max(u1 + u2 - 1, 0)
end
function Distributions.pdf(C::FrechetCopula, u::AbstractVector)
throw(ArgumentError("There is no density for the Frechet Copula."))
end
function Distributions._rand!(rng::Distributions.AbstractRNG, C::FrechetCopula, x::AbstractVector{T}) where {T<:Real}
p = [C.θ1, 1-C.θ1-C.θ2, C.θ2]
u1, u2 = rand(rng, Distributions.Uniform(0,1), 2)
z = rand(rng, Distributions.Categorical(p))
if z == 1
u1 = min(u1,u2)
x[1] = u1
x[2] = u1
elseif z == 2
x[1] = u1
x[2] = u2
else
u1 = max(u1 + u2 - 1, 0)
x[1] = u1
x[2] = 1-u1
end
return x
end
function τ(C::FrechetCopula)
θ1, θ2 = C.θ1, C.θ2
term = (θ1 - θ2)(θ1 + θ2 + 2)
return term/3
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 2004 | """
MardiaCopula{P}
Fields:
- θ::Real - parameter
Constructor
MardiaCopula(θ)
The bivariate Mardia copula is parameterized by ``\\theta \\in [-1,1]``. It is constructed as:
```math
C(u_1, u_2) = \\frac{\\theta^2(1+\\theta)}{2}\\min\\{u_1,u_2\\} + (1-\\theta^2)u_1u_2 + \\frac{\\theta^2(1-\\theta)}{2}\\max\\{u_1+u_2-1,0\\}
```
It has a few special cases:
- When θ = 0, it is the Independent Copula
- When θ = 1, it is the MCopula (Upper Frechet-Hoeffding bound)
- When θ = -1, is is the WCopula (Lower Frechet-Hoeffding bound)
References:
* [nelsen2006](@cite) Nelsen, Roger B. An introduction to copulas. Springer, 2006.
"""
struct MardiaCopula{P} <: bicopula
θ::P # Copula parameter
function MardiaCopula(θ)
if !(-1 <= θ <= 1)
throw(ArgumentError("Theta must be in [-1,1]"))
elseif θ == 0
return IndependentCopula()
elseif θ == 1
return MCopula()
elseif θ == -1
return WCopula()
else
return new{typeof(θ)}(θ)
end
end
end
function Distributions.cdf(C::MardiaCopula, u::AbstractVector)
θ = C.θ
u1, u2 = u
term1 = (θ^2 * (1 + θ) / 2) * min(u1, u2)
term2 = (1 - θ^2) * u1 * u2
term3 = (θ^2 * (1 - θ) / 2) * max(u1 + u2 - 1, 0)
return term1 + term2 + term3
end
function Distributions.pdf(C::MardiaCopula, u::AbstractVector)
throw(ArgumentError("There is no density for the Frechet Copula."))
end
function Distributions._rand!(rng::Distributions.AbstractRNG, C::MardiaCopula, x::AbstractVector{T}) where {T<:Real}
θ = C.θ
u1, u2 = rand(rng, Distributions.Uniform(0,1), 2)
p = [θ^2 * (1 + θ) / 2, 1 - θ^2, θ^2 * (1 - θ) / 2]
z = rand(rng, Distributions.Categorical(p))
if z == 1
u1 = min(u1, u2)
x[1] = u1
x[2] = u1
elseif z == 2
x[1] = u1
x[2] = u2
else
u1 = max(u1 + u2 - 1, 0)
x[1] = u1
x[2] = 1 - u1
end
return x
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1497 | """
MaresiasCopula{P}
Fields:
- G::Function
Constructor
MaresiasCopula(G)
The bivariate Maresias copula is parameterized by functions ``G, H: [0,1] \\to [0,1]``, such that ``G(u) = 2u - H(u), u \\in [0,1]``. It is constructed as:
```math
C(u_1, u_2) = \\frac{1}{2}\\left ( G(u_1)G(u_2) + H(u_1)H(u_2) \\right )
```
References:
* [Mai2017](@cite) Simulating copulas: stochastic models, sampling algorithms, and applications. 2017.
"""
struct MaresiasCopula{G} <: bicopula
G::G # debe ser una función
function MaresiasCopula(G)
if !is_valid_function(G)
error("La función G debe ser creciente y estar entre 0 y 1")
else
return new{typeof(G)}(G)
end
end
end
function is_valid_function(G)
u_values = range(0, stop=1, length=100)
for u in u_values
value = G(u)
if value < 0 || value > 1
return false
end
end
return true
end
function Distributions.cdf(C::MaresiasCopula, x::AbstractVector)
u1, u2 = x # solamente caso bivariado
G = C.G
H(u) = 2u - G(u)
prod_G = G(u1) * G(u2)
prod_H = H(u1) * H(u2)
return 0.5 * (prod_G + prod_H)
end
function Distributions.pdf(C::MaresiasCopula, x::AbstractVector)
# Definimos una función que toma un vector y devuelve el cdf
cdf_func = y -> Distributions.cdf(C, y)
# Calculamos la derivada parcial mixta
pdf_value = ForwardDiff.hessian(cdf_func, x)[1, 2]
return pdf_value
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1453 | """
MorgensternCopula{P}
Fields:
- θ::Real - parameter
Constructor
MorgensternCopula(θ)
The bivariate Morgenstern copula or FGM Copula is parameterized by ``\\theta \\in [-1,1]``. It is constructed as:
```math
C(u_1, u_2) = u_1u_2(1+\\theta(1-u_1)(1-u_2))
```
It has a few special cases:
- When θ = 0, it is the Independent Copula
References:
* [Joe1997](@cite) Joe, Harry, Multivariate Models and Multivariate Dependence Concepts, Chapman & Hall. 1997.
"""
struct MorgensternCopula{P} <: bicopula
θ::P # Copula parameter
function MorgensternCopula(θ)
if !(-1 <= θ <= 1)
throw(ArgumentError("Theta must be in [-1,1]"))
elseif θ == 0
return IndependentCopula()
else
return new{typeof(θ)}(θ)
end
end
end
τ(C::MorgensternCopula) = 2*C.θ/9
function Distributions.cdf(C::MorgensternCopula, x::AbstractVector)
θ = C.θ
u1, u2 = x
return u1*u2*(1+θ*(1-u1)*(1-u2))
end
function Distributions.pdf(C::MorgensternCopula, x::AbstractVector)
θ = C.θ
u1, u2 = x
return 1+θ*(1-2*u1)*(1-2*u2)
end
function Distributions._rand!(rng::Distributions.AbstractRNG, C::MorgensternCopula, x::AbstractVector{T}) where {T<:Real}
θ = C.θ
u1, v2 = rand(rng, Distributions.Uniform(0,1),2)
A = θ*(2*u1-1)-1
B = (1-2*θ*(2*u1-1)+(θ^2)*(2*u1-1)^2 + 4*θ*v2*(2*u1-1))^(1/2)
u2 = (2*v2)/(B-A)
x[1] = u1
x[2] = u2
return x
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 2677 | """
PlackettCopula{P}
Fields:
- θ::Real - parameter
Constructor
PlackettCopula(θ)
The bivariate Plackett Copula parameterized by ``\\theta > 0`` The [Plackett](https://www.cambridge.org/core/books/abs/copulas-and-their-applications-in-water-resources-engineering/plackett-copula/2D407DAB691623AB52CF74044B42C61F). It is constructed as:
```math
C(u_1,u_2) = \\frac{1}{2}\\eta^{-1}(1+\\eta(u_1+u_2)-((1+\\eta(u_1+u_2))^2 - 4\\theta \\eta u_1 u_2)^{1/2})
```
where ``\\eta)=\\theta-1.``
It has a few special cases:
- When θ = ∞, is is the MCopula (Upper Frechet-Hoeffding bound)
- When θ = 1, it is the IndependentCopula
- When θ = 0, is is the WCopula (Lower Frechet-Hoeffding bound)
References:
* [joe2014](@cite) Joe, H. (2014). Dependence modeling with copulas. CRC press, Page.164
* [johnson1987multivariate](@cite) Johnson, Mark E. Multivariate statistical simulation: A guide to selecting and generating continuous multivariate distributions. Vol. 192. John Wiley & Sons, 1987. Page 193.
* [nelsen2006](@cite) Nelsen, Roger B. An introduction to copulas. Springer, 2006. Exercise 3.38.
"""
struct PlackettCopula{P} <: bicopula
θ::P # Copula parameter
function PlackettCopula(θ)
if θ < 0
throw(ArgumentError("Theta must be non-negative"))
elseif θ == 0
return MCopula()
elseif θ == 1
return IndependentCopula()
elseif θ == Inf
return WCopula()
else
return new{typeof(θ)}(θ)
end
end
end
# CDF calculation for bivariate Plackett Copula
function Distributions.cdf(C::PlackettCopula, x::AbstractVector)
u1, u2 = x
θ = C.θ
η = θ - 1
term1 = 1 + η * (u1 + u2)
term2 = sqrt(term1^2 - 4 * θ * η * u1 * u2)
return 0.5 * η^(-1) * (term1 - term2)
end
# PDF calculation for bivariate Plackett Copula
function Distributions.pdf(C::PlackettCopula, x::AbstractVector)
u1, u2 = x
θ = C.θ
η = θ - 1
term1 = θ * (1 + η * (u1 + u2 - 2 * u1 * u2))
term2 = (1+η*(u1+u2))^2-4*(θ)*η*u1*u2
return (term1)*(term2)^(-3/2)
end
function Distributions._rand!(rng::Distributions.AbstractRNG, C::PlackettCopula, x::AbstractVector{T}) where {T<:Real}
θ = C.θ
u1, t = rand(rng, Distributions.Uniform(0,1),2)
a = t * (1 - t)
b = θ + a * (θ - 1)^2
cc = 2*a * (u1 * θ^2 + 1 - u1) + θ * (1 - 2a)
d = sqrt(θ) * sqrt(θ + 4a * u1 * (1 - u1) * (1 - θ)^2)
u2 = (cc - (1 - 2t) * d) / (2b)
x[1] = u1
x[2] = u2
return x
end
# Calculate Spearman's rho based on the PlackettCopula parameters
function ρ(C::PlackettCopula)
θ = C.θ
return (θ+1)/(θ-1)-(2*θ*log(θ)/(θ-1)^2)
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1965 | """
RafteryCopula{P}
Fields:
- θ::Real - parameter
Constructor
RafteryCopula(θ)
The bivariate Raftery Copula is parameterized by ``\\theta \\in [0,1]``. It is constructed as:
```math
C(u_1, u_2) = \\min\\{u_1,u_2\\} +\\frac{1-\\theta}{1+\\theta}(u_1u_2)^{1/(1-\\theta)}\\left \\{1-(\\max\\{u_1,u_2\\})^{-(1+\\theta)/(1-\\theta)} \\right \\}
```
It has a few special cases:
- When θ = 0, it is the Independent Copula
- When θ = 1, it is the MCopula (Upper Frechet-Hoeffding bound)
References:
* [Joe1997](@cite) Joe, Harry, Multivariate Models and Multivariate Dependence Concepts, Chapman & Hall. 1997.
"""
struct RafteryCopula{P} <: bicopula
θ::P # Copula parameter
function RafteryCopula(θ)
if !(0 <= θ <= 1)
throw(ArgumentError("Theta must be in [0,1]"))
elseif θ == 0
return IndependentCopula()
elseif θ == 1
return MCopula()
else
return new{typeof(θ)}(θ)
end
end
end
# CDF calculation for bivariate Plackett Copula
function Distributions.cdf(C::RafteryCopula, x::AbstractVector)
u1, u2 = x
θ = C.θ
term1 = ((1-θ)/(1+θ))*(u1*u2)^(1/(1-θ))
term2 = 1-(max(u1,u2))^(-(1+θ)/(1-θ))
return min(u1,u2)+(term1*term2)
end
# PDF calculation for bivariate Plackett Copula
function Distributions.pdf(C::RafteryCopula, x::AbstractVector)
θ = C.θ
u1, u2 = sort(x)
term1 = 1/(θ^2 - 1)
term2 = -1-θ*(u2)^((-θ-1)/(1-θ))
term3 = (u1*u2)^(θ/(1-θ))
return term1*term2*term3
end
function Distributions._rand!(rng::Distributions.AbstractRNG, C::RafteryCopula, x::AbstractVector{T}) where {T<:Real}
θ = C.θ
u, u1, u2 = rand(rng, Distributions.Uniform(0,1),3)
j = rand(rng, Distributions.Bernoulli(θ))
x[1] = (u1^(1 - θ)) * (u)^j
x[2] = (u2^(1 - θ)) * (u)^j
return x
end
# CCorregir este rho
function ρ(C::RafteryCopula)
θ = C.θ
return (θ+1)/(θ-1)-(2*θ*log(θ)/(θ-1)^2)
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 2149 | """
ArchimaxCopula{A, E}
Fields:
-Archimedean::A - Archimedean Copula
-Extreme::E - Extreme Value Copula
Constructor
ArchimaxCopula(Archimedean, Extreme)
The bivariate Archimax Copula is parameterized by an Archimedean Copula and Extreme Value Copula. It is constructed as follows:
```math
C_{\\ell, \\varphi}(u_1, u_2) = \\varphi(\\ell(\\varphi^{-1}(u_1),\\varphi^{-1}(u_2)))
```
where ``\\varphi`` is the generator of the Archimedean Copula and ``\\varphi^{-1}`` is the inverse and ``\\ell`` is the stable tail dependece function of Extreme value Copula
For more details see
References:
* [Charpentier2014](@cite) Charpentier et al, Multivariate Archimax Copulas, Journal of Multivariate analysis. 2014.
"""
struct ArchimaxCopula{A<:ArchimedeanCopula, E<:ExtremeValueCopula} <: bicopula
Archimedean::A
Extreme::E
function ArchimaxCopula(Archimedean::A, Extreme::E) where {A<:ArchimedeanCopula, E<:ExtremeValueCopula}
new{A, E}(Archimedean, Extreme)
end
end
function Distributions.cdf(C::ArchimaxCopula, x::AbstractVector)
Archimedean = C.Archimedean
Extreme = C.Extreme
term1 = ϕ⁻¹(Archimedean, x[1]) + ϕ⁻¹(Archimedean, x[2])
term2 = (ϕ⁻¹(Archimedean, x[2]))/term1
term3 = 𝘈(Extreme, term2)
return ϕ(Archimedean, term1*term3)
end
function Distributions.pdf(C::ArchimaxCopula, x::AbstractVector)
# Definimos una función que toma un vector y devuelve el cdf
cdf_func = y -> Distributions.cdf(C, y)
# Calculamos la derivada parcial mixta
pdf_value = ForwardDiff.hessian(cdf_func, x)[1, 2]
return pdf_value
end
function τ(C::ArchimaxCopula)
Archimedean = C.Archimedean
Extreme = C.Extreme
tA = τ(Extreme)
tphi = τ(Archimedean)
return tA + (1 - tA)*tphi
end
function Distributions._rand!(rng::Distributions.AbstractRNG, C::ArchimaxCopula, x::AbstractVector{T}) where {T<:Real}
Archimedean = C.Archimedean
Extreme = C.Extreme
v1, v2 = Distributions.rand(rng, Extreme, 2)
M = rand(rng, 𝘙(Archimedean))
x[1] = ϕ(Archimedean, -log(v1)/M)
x[2] = ϕ(Archimedean, -log(v2)/M)
return x
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 3022 | """
EmpiricalCopula{M}
Fields:
-data::M - 2xn matrix observations
Constructor
EmpiricalCopula(data)
Let ``(x_k, y_k), k = 1,2, \\ldots, n`` denote a sample of size ``n`` from continuous bivariate distribution. The Empirical Copula is the function
```math
C_n(\\frac{i}{n},\\frac{j}{n}) = \\frac{\\text{number of pairs (x,y) in the sample with} x \\leq x_{(i)}, y \\leq y_{(j)}}{n}
```
For more details see
References:
* [nelsen2006](@cite) Nelsen, Roger B. An introduction to copulas. Springer, 2006.
"""
struct EmpiricalCopula{M} <: bicopula
data::M
pseudos::M
function EmpiricalCopula(data)
@assert size(data, 1) == 2 "Data must have two dimensions for bivariate case"
pseudo_obs = pseudos(data)
new{typeof(data)}(data, pseudo_obs)
end
end
# Función para calcular la CDF empírica
function Distributions.cdf(C::EmpiricalCopula, x::AbstractVector)
u1, u2 = clamp.(x, 0, 1)
n = size(C.data, 2)
count = sum((C.pseudos[1, :] .<= u1) .& (C.pseudos[2, :] .<= u2))
return count / n
end
function Distributions.pdf(C::EmpiricalCopula, x::AbstractVector)
n = size(C.data, 2)
u1, u2 = clamp.(x, 0, 1)
h = 1 / sqrt(n) # Ancho de banda adaptativo
kernel_vals = epanechnikov_kernel.((C.pseudos[1, :] .- u1) / h) .* epanechnikov_kernel.((C.pseudos[2, :] .- u2) / h)
return sum(kernel_vals) / (n * h^2)
end
function frequency(C::EmpiricalCopula, x::AbstractVector)
n = size(C.data, 2)
i = round(Int, x[1] * n)
j = round(Int, x[2] * n)
return sum((C.pseudos[1, :] .== i/n) .& (C.pseudos[2, :] .== j/n)) / n
end
# Función para generar muestras
function Distributions._rand!(rng::Distributions.AbstractRNG, C::EmpiricalCopula, x::AbstractVector{T}) where {T<:Real}
n = size(C.data, 2)
# Generar U(0,1) aleatorios
u1, u2 = rand(rng), rand(rng)
# Encontrar los índices más cercanos
i1 = searchsortedfirst(C.pseudos[1, :], u1)
i2 = searchsortedfirst(C.pseudos[2, :], u2)
# Interpolación lineal simple para u1
if i1 == 1
x[1] = C.pseudos[1, 1]
elseif i1 > n
x[1] = C.pseudos[1, n]
else
x[1] = C.pseudos[1, i1-1] + (u1 - C.pseudos[1, i1-1]) * (C.pseudos[1, i1] - C.pseudos[1, i1-1]) / (C.pseudos[1, i1] - C.pseudos[1, i1-1])
end
# Interpolación lineal simple para u2
if i2 == 1
x[2] = C.pseudos[2, 1]
elseif i2 > n
x[2] = C.pseudos[2, n]
else
x[2] = C.pseudos[2, i2-1] + (u2 - C.pseudos[2, i2-1]) * (C.pseudos[2, i2] - C.pseudos[2, i2-1]) / (C.pseudos[2, i2] - C.pseudos[2, i2-1])
end
return x
end
function pseudos(sample::AbstractArray)
d, n = size(sample)
@assert d == 2 "Sample must have exactly two dimensions for bivariate case"
ranks = zeros(eltype(sample), d, n)
for i in 1:d
ranks[i, :] = (StatsBase.ordinalrank(sample[i, :]) .- 0.5) ./ n
end
return ranks
end
function epanechnikov_kernel(u)
return abs(u) <= 1 ? 0.75 * (1 - u^2) : 0.0
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 898 | """
IndependentCopula
Constructor
IndependentCopula()
The bivariate [Independent Copula](https://en.wikipedia.org/wiki/Copula_(probability_theory)#Most_important_Archimedean_copulas) is
the simplest copula, that has the form :
```math
C(u_1,u_2) = u_1u_2
```
References:
* [nelsen2006](@cite) Nelsen, Roger B. An introduction to copulas. Springer, 2006.
"""
struct IndependentCopula <: bicopula end
# Función CDF para la Copula Independiente
function Distributions.cdf(C::IndependentCopula, u::AbstractArray)
return prod(u)
end
# Función PDF para la Copula Independiente
function Distributions.pdf(C::IndependentCopula, u::AbstractVector)
return 1.0
end
function Distributions._rand!(rng::Distributions.AbstractRNG, C::IndependentCopula, x::AbstractVector{T}) where {T<:Real}
u1, u2 = rand(rng, Distributions.Uniform(0,1),2)
x[1] = u1
x[2] = u2
return x
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 883 | """
MCopula
Constructor
MCopula()
The [Upper Frechet-Hoeffding bound](https://en.wikipedia.org/wiki/Copula_(probability_theory)#Fr%C3%A9chet%E2%80%93Hoeffding_copula_bounds) is defined as
```math
M(u_1,u_2) = \\min\\{u_1,u_2\\}
```
References:
* [nelsen2006](@cite) Nelsen, Roger B. An introduction to copulas. Springer, 2006.
"""
struct MCopula <: bicopula end
# Función CDF para la W Copula
function Distributions.cdf(C::MCopula, u::AbstractVector)
u1, u2 = u
return min(u1,u2)
end
# Función PDF para la W Copula
function Distributions.pdf(C::MCopula, u::AbstractVector)
throw(ArgumentError("There is no density for the Frechet-Hoeffding bounds."))
end
function Distributions._rand!(rng::Distributions.AbstractRNG, C::MCopula, x::AbstractVector{T}) where {T<:Real}
U = rand(rng, Distributions.Uniform(0,1))
x[1] = U
x[2] = U
return x
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 1044 | """
SurvivalCopula{P}
Fields:
- C::bicopula
Constructor
SurvivalCopula(C)
The bivariate Survival copula is defined as
```math
\\overbar{C}(u_1,u_2) = C(u_1, u_2) + u_1 + u_2 - 1
```
Where ``C(u_1, u_2)`` is a copula as we know them.
References:
* [nelsen2006](@cite) Nelsen, Roger B. An introduction to copulas. Springer, 2006.
"""
struct SurvivalCopula{P<:bicopula} <: bicopula
C::P
function SurvivalCopula(C::P) where {P<:bicopula}
new{P}(C)
end
end
function Distributions.cdf(Cop::SurvivalCopula, x::AbstractVector)
u1, u2 = x
copula = Distributions.cdf(Cop.C, [1-u1, 1-u2])
return copula + u1 + u2 - 1
end
function Distributions.pdf(Cop::SurvivalCopula, x::AbstractVector)
u1, u2 = x
return Distributions.pdf(Cop.C, [1-u1, 1-u2])
end
function Distributions._rand!(rng::Distributions.AbstractRNG, Cop::SurvivalCopula, x::AbstractVector{T}) where {T<:Real}
sample1, sample2 = Distributions.rand(rng, Cop.C, 2)
x[1] = 1 - sample1
x[2] = 1 - sample2
return x
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 888 | """
WCopula
Constructor
WCopula()
The [Lower Frechet-Hoeffding bound](https://en.wikipedia.org/wiki/Copula_(probability_theory)#Fr%C3%A9chet%E2%80%93Hoeffding_copula_bounds) is defined as
```math
W(u_1,u_2) = \\max\\{u_1 + u_2 - 1, 0\\}
```
References:
* [nelsen2006](@cite) Nelsen, Roger B. An introduction to copulas. Springer, 2006.
"""
struct WCopula <: bicopula end
# Función CDF para la W Copula
function Distributions.cdf(C::WCopula, u::AbstractVector)
return max(sum(u) - 1, 0)
end
# Función PDF para la W Copula
function Distributions.pdf(C::WCopula, u::AbstractVector)
throw(ArgumentError("There is no density for the Frechet-Hoeffding bounds."))
end
function Distributions._rand!(rng::Distributions.AbstractRNG, C::WCopula, x::AbstractVector{T}) where {T<:Real}
U = rand(rng, Distributions.Uniform(0,1))
x[1] = U
x[2] = 1-U
return x
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 6174 | using Test
using TwinCopulas
using Distributions
using Random
@testset "Archimedean Copulas Tests" begin
rng = MersenneTwister(2024)
d = 100
@testset "AMHCopula - sampling, pdf, cdf" begin
for θ in [-1.0, -rand(rng), 0.0, rand(rng)]
C = AMHCopula(θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
@test 0.0 <= cdf(C, u) <= 1.0
@test pdf(C, u) >= 0.0
end
end
end
@testset "ClaytonCopula - sampling, pdf, cdf" begin
for θ in [-1.0, -rand(rng), 0.0, rand(rng, Uniform(10, 20)), Inf]
C = ClaytonCopula(θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
if isinf(θ) || (θ == -1)
# En el caso especial de θ = Inf, se espera que PDF no esté definido
@test_throws ArgumentError pdf(C, u)
else
@test 0.0 <= cdf(C, u) <= 1.0
@test pdf(C, u) >= 0.0
end
end
end
end
@testset "FrankCopula - sampling, pdf, cdf" begin
for θ in [-Inf, -rand(rng, Uniform(10, 20)), 0.0, rand(rng, Uniform(10, 20)), Inf]
C = FrankCopula(θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
if isinf(θ)
# En el caso especial de θ = Inf, se espera que PDF no esté definido
@test_throws ArgumentError pdf(C, u)
else
@test 0.0 <= cdf(C, u) <= 1.0
@test pdf(C, u) >= 0.0
end
end
end
end
@testset "GumbelBarnettCopula - sampling, pdf, cdf" begin
for θ in [0.0, rand(rng), rand(rng), 1.0]
C = GumbelBarnettCopula(θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
@test 0.0 <= cdf(C, u) <= 1.0
@test pdf(C, u) >= 0.0
end
end
end
@testset "GumbelCopula- sampling, pdf, cdf" begin
for θ in [1.0, rand(rng, Uniform(1, 10)), rand(rng, Uniform(10, 20)), Inf]
C = GumbelCopula(θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
if isinf(θ)
@test_throws ArgumentError pdf(C, u)
else
@test 0.0 <= cdf(C, u) <= 1.0
@test pdf(C, u) >= 0.0
end
end
end
end
@testset "InvGaussianCopula - sampling, pdf, cdf" begin
for θ in [0.01, rand(rng, Uniform(5, 10)), rand(rng, Uniform(10, 15))]
C = InvGaussianCopula(θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
@test 0.0 <= cdf(C, u) <= 1.0
@test pdf(C, u) >= 0.0
end
end
end
@testset "JoeCopula - sampling, pdf, cdf" begin
for θ in [1.0, rand(rng, Uniform(1, 10)), rand(rng, Uniform(10, 20)), Inf]
C = JoeCopula(θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
if isinf(θ)
# En el caso especial de θ = Inf, se espera que PDF no esté definido
@test_throws ArgumentError pdf(C, u)
else
@test 0.0 <= cdf(C, u) <= 1.0
@test pdf(C, u) >= 0.0
end
end
end
end
@testset "Nelsen2Copula - sampling, pdf, cdf" begin
for θ in [1.0, rand(rng, Uniform(5.0, 10.0)), rand(rng, Uniform(15.0, 20.0)), Inf]
C = Nelsen2Copula(θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
if isinf(θ) || θ == 1
# En el caso especial de θ = Inf, se espera que PDF no esté definido
@test_throws ArgumentError pdf(C, u)
else
cdf_value = cdf(C, u)
if !(0.0 <= cdf_value <= 1.0)
error("Fallo en la CDF: θ=$θ, u=$u, cdf_value=$cdf_value")
end
@test 0.0 <= cdf_value <= 1.0
@test pdf(C, u) >= 0.0
end
end
end
end
end
| TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 2727 | using Test
using TwinCopulas
using Distributions
using Random
@testset "Elliptical Copulas Tests" begin
rng = MersenneTwister(2024)
d = 100
@testset "GaussianCopula - sampling, pdf, cdf" begin
for θ in [-1.0, -rand(rng), 0.0, rand(rng), 1.0]
C = GaussianCopula(θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
if θ == -1 || θ == 1
@test_throws ArgumentError pdf(C, u)
else
@test 0.0 <= cdf(C, u) <= 1.0
@test pdf(C, u) >= 0.0
end
end
end
end
@testset "tCopula - sampling, pdf, cdf" begin
# Lista de ejemplos de parámetros para probar
param_sets = [
(2.0, 0.5), # ν > 0 y -1 < ρ <= 1
(5.0, -0.5), # ν > 0 y -1 < ρ <= 1
(10.0, 1.0), # ν > 0 y ρ == 1, debería crear MCopula
(3.0, 0.0), # ν > 0 y ρ == 0, debería crear IndependentCopula
(-2.0, 0.5), # Caso inválido: ν <= 0
(3.0, 1.1), # Caso inválido: ρ fuera de rango
(3.0, -1.1), # Caso inválido: ρ fuera de rango
(rand(rng, Uniform(4.0, 10.0)), rand(rng, Uniform(-0.9, 1.0))) # Parámetros aleatorios dentro de rango
]
for (ν, ρ) in param_sets
try
C = tCopula(ν, ρ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
cdf_value = cdf(C, u)
if ρ == 1
# En los casos especiales de θ = 1
@test_throws ArgumentError pdf(C, u)
else
pdf_value = pdf(C, u)
# Añadir mensaje de error detallado si el test falla
@test 0.0 <= cdf_value <= 1.0 || error("Fallo en la CDF: θ=$θ, u=$u, cdf_value=$cdf_value")
@test pdf_value >= 0.0 || error("Fallo en la PDF: θ=$θ, u=$u, pdf_value=$pdf_value")
end
end
catch e
@test e isa ArgumentError
println("No se pudo construir copula t con θ=$ν, ρ=$ρ: ", e)
end
end
end
end
| TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 14939 | using Test
using TwinCopulas
using Distributions
using Random
@testset "Extreme Value Copulas Tests" begin
rng = MersenneTwister(2024)
d = 100
@testset "AsymGalambosCopula - sampling, pdf, cdf" begin
for α in [0.0, rand(rng, Uniform()), rand(rng, Uniform(5.0, 9.0)), rand(rng, Uniform(10.0, 15.0))]
for θ in [[rand(rng, Uniform(0, 1)), rand(rng, Uniform(0, 1))], [0.0, 0.0], [1.0, 1.0]]
C = AsymGalambosCopula(α, θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
cdf_value = cdf(C, u)
pdf_value = pdf(C, u)
@test 0.0 <= cdf_value <= 1.0
@test pdf_value >= 0.0
end
end
end
end
@testset "AsymLogCopula - sampling, pdf, cdf" begin
for α in [1.0, rand(rng, Uniform(1.0, 5.0)), rand(rng, Uniform(10.0, 15.0))]
for θ in [[rand(rng, Uniform(0, 1)), rand(rng, Uniform(0, 1))], [0.0, 0.0], [1.0, 1.0]]
C = AsymLogCopula(α, θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
cdf_value = cdf(C, u)
pdf_value = pdf(C, u)
@test 0.0 <= cdf_value <= 1.0
@test pdf_value >= 0.0
end
end
end
end
@testset "AsymMixedCopula - sampling, pdf, cdf" begin
for θ in [[0.1, 0.2], [0.0, 0.0], [0.3, 0.4], [0.2, 0.4]]
try
C = AsymMixedCopula(θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
cdf_value = cdf(C, u)
pdf_value = pdf(C, u)
# Añadir mensaje de error detallado si el test falla
@test 0.0 <= cdf_value <= 1.0 || error("Fallo en la CDF: θ=$θ, u=$u, cdf_value=$cdf_value")
@test pdf_value >= 0.0 || error("Fallo en la PDF: θ=$θ, u=$u, pdf_value=$pdf_value")
end
catch e
@test e isa ArgumentError
println("No se pudo construir AsymMixedCopula con θ=$θ: ", e)
end
end
end
@testset "BC2Copula - sampling, pdf, cdf" begin
for θ in [[rand(rng), rand(rng)], [1.0, 0.0], [0.5, 0.5], [-0.1, 0.2], [1.1, 0.5], [0.5, -0.2]]
try
C = BC2Copula(θ...)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
cdf_value = cdf(C, u)
pdf_value = pdf(C, u)
# Añadir mensaje de error detallado si el test falla
@test 0.0 <= cdf_value <= 1.0 || error("Fallo en la CDF: θ=$θ, u=$u, cdf_value=$cdf_value")
@test pdf_value >= 0.0 || error("Fallo en la PDF: θ=$θ, u=$u, pdf_value=$pdf_value")
end
catch e
@test e isa ArgumentError
println("No se pudo construir BC2Copula con θ=$θ: ", e)
end
end
end
@testset "CuadrasAugeCopula - sampling, pdf, cdf" begin
for θ in [rand(rng), 0.0, 1.0, -0.1, 1.1, rand(rng)]
try
C = CuadrasAugeCopula(θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
cdf_value = cdf(C, u)
if θ == 1.0
# En el caso especial de θ = 1, se espera que PDF no esté definido
@test_throws ArgumentError pdf(C, u)
else
pdf_value = pdf(C, u)
# Añadir mensaje de error detallado si el test falla
@test 0.0 <= cdf_value <= 1.0 || error("Fallo en la CDF: θ=$θ, u=$u, cdf_value=$cdf_value")
@test pdf_value >= 0.0 || error("Fallo en la PDF: θ=$θ, u=$u, pdf_value=$pdf_value")
end
end
catch e
@test e isa ArgumentError
println("No se pudo construir CuadrasAugeCopula con θ=$θ: ", e)
end
end
end
@testset "GalambosCopula - sampling, pdf, cdf" begin
for θ in [rand(rng), 0.0, Inf, -1.0, rand(rng, Uniform(1.0, 5.0)), rand(rng, Uniform(5.0, 10.0))]
try
C = GalambosCopula(θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
cdf_value = cdf(C, u)
if θ == Inf
# En los casos especiales de θ = 0 o θ = Inf, se espera que PDF no esté definido
@test_throws ArgumentError pdf(C, u)
else
pdf_value = pdf(C, u)
# Añadir mensaje de error detallado si el test falla
@test 0.0 <= cdf_value <= 1.0 || error("Fallo en la CDF: θ=$θ, u=$u, cdf_value=$cdf_value")
@test pdf_value >= 0.0 || error("Fallo en la PDF: θ=$θ, u=$u, pdf_value=$pdf_value")
end
end
catch e
@test e isa ArgumentError
println("No se pudo construir GalambosCopula con θ=$θ: ", e)
end
end
end
@testset "HuslerReissCopula - sampling, pdf, cdf" begin
for θ in [rand(rng), 0.0, Inf, -1.0, rand(rng, Uniform(1.0, 5.0)), rand(rng, Uniform(5.0, 10.0))]
try
C = HuslerReissCopula(θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
cdf_value = cdf(C, u)
if θ == Inf
# En los casos especiales de θ = 0 o θ = Inf, se espera que PDF no esté definido
@test_throws ArgumentError pdf(C, u)
else
pdf_value = pdf(C, u)
# Añadir mensaje de error detallado si el test falla
@test 0.0 <= cdf_value <= 1.0 || error("Fallo en la CDF: θ=$θ, u=$u, cdf_value=$cdf_value")
@test pdf_value >= 0.0 || error("Fallo en la PDF: θ=$θ, u=$u, pdf_value=$pdf_value")
end
end
catch e
@test e isa ArgumentError
println("No se pudo construir HuslerReissCopula con θ=$θ: ", e)
end
end
end
@testset "LogCopula - sampling, pdf, cdf" begin
for θ in [1.0, Inf, 0.5, rand(rng, Uniform(1.0, 10.0))]
try
C1 = LogCopula(θ)
C2 = GumbelCopula(θ)
data = rand(rng, C1, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
cdf_value_C1 = cdf(C1, u)
cdf_value_C2 = cdf(C2, u)
if θ == Inf
# En los casos especiales de θ = Inf, se espera que PDF no esté definido
@test_throws ArgumentError pdf(C1, u)
@test_throws ArgumentError pdf(C2, u)
else
pdf_value_C1 = pdf(C1, u)
pdf_value_C2 = pdf(C2, u)
# Añadir mensaje de error detallado si el test falla
@test 0.0 <= cdf_value_C1 <= 1.0 || error("Fallo en la CDF de LogCopula: θ=$θ, u=$u, cdf_value_C1=$cdf_value_C1")
@test 0.0 <= cdf_value_C2 <= 1.0 || error("Fallo en la CDF de GumbelCopula: θ=$θ, u=$u, cdf_value_C2=$cdf_value_C2")
@test pdf_value_C1 >= 0.0 || error("Fallo en la PDF de LogCopula: θ=$θ, u=$u, pdf_value_C1=$pdf_value_C1")
@test pdf_value_C2 >= 0.0 || error("Fallo en la PDF de GumbelCopula: θ=$θ, u=$u, pdf_value_C2=$pdf_value_C2")
# Comparar los valores de CDF y PDF entre LogCopula y GumbelCopula
@test isapprox(cdf_value_C1, cdf_value_C2, atol=1e-6) || error("CDF de LogCopula y GumbelCopula no coinciden: θ=$θ, u=$u, cdf_value_C1=$cdf_value_C1, cdf_value_C2=$cdf_value_C2")
@test isapprox(pdf_value_C1, pdf_value_C2, atol=1e-6) || error("PDF de LogCopula y GumbelCopula no coinciden: θ=$θ, u=$u, pdf_value_C1=$pdf_value_C1, pdf_value_C2=$pdf_value_C2")
end
end
catch e
@test e isa ArgumentError
println("No se pudo construir LogCopula con θ=$θ: ", e)
end
end
end
@testset "MixedCopula - sampling, pdf, cdf" begin
for θ in [0.0, 1.0, 0.2, -rand(rng), 0.5]
try
C = MixedCopula(θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
cdf_value = cdf(C, u)
pdf_value = pdf(C, u)
# Añadir mensaje de error detallado si el test falla
@test 0.0 <= cdf_value <= 1.0 || error("Fallo en la CDF: θ=$θ, u=$u, cdf_value=$cdf_value")
@test pdf_value >= 0.0 || error("Fallo en la PDF: θ=$θ, u=$u, pdf_value=$pdf_value")
end
catch e
@test e isa ArgumentError
println("No se pudo construir HuslerReissCopula con θ=$θ: ", e)
end
end
end
@testset "MOCopula - sampling, pdf, cdf" begin
# Lista de ejemplos de parámetros para probar
param_sets = [
(0.1, 0.2, 0.3),
(1.0, 1.0, 1.0),
(0.5, 0.5, 0.5),
(-0.1, 0.2, 0.3), # Caso inválido: parámetro negativo
(0.1, -0.2, 0.3), # Caso inválido: parámetro negativo
(0.1, 0.2, -0.3), # Caso inválido: parámetro negativo
(rand(rng), rand(rng), rand(rng)) # Parámetros aleatorios
]
for λ in param_sets
try
C = MOCopula(λ...)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
cdf_value = cdf(C, u)
pdf_value = pdf(C, u)
# Añadir mensaje de error detallado si el test falla
@test 0.0 <= cdf_value <= 1.0 || error("Fallo en la CDF: λ=$λ, u=$u, cdf_value=$cdf_value")
@test pdf_value >= 0.0 || error("Fallo en la PDF: λ=$λ, u=$u, pdf_value=$pdf_value")
end
catch e
@test e isa ArgumentError
println("No se pudo construir MOCopula con λ=$λ: ", e)
end
end
end
@testset "tEVCopula - sampling, pdf, cdf" begin
# Lista de ejemplos de parámetros para probar
param_sets = [
(2.0, 0.5), # ν > 0 y -1 < ρ <= 1
(5.0, -0.5), # ν > 0 y -1 < ρ <= 1
(10.0, 1.0), # ν > 0 y ρ == 1, debería crear MCopula
(3.0, 0.0), # ν > 0 y ρ == 0, debería crear IndependentCopula
(-2.0, 0.5), # Caso inválido: ν <= 0
(3.0, 1.1), # Caso inválido: ρ fuera de rango
(3.0, -1.1), # Caso inválido: ρ fuera de rango
(rand(rng, Uniform(4.0, 10.0)), rand(rng, Uniform(-0.9, 1.0))) # Parámetros aleatorios dentro de rango
]
for (ν, ρ) in param_sets
try
C = tEVCopula(ν, ρ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
cdf_value = cdf(C, u)
if ρ == 1
# En los casos especiales de θ = 0
@test_throws ArgumentError pdf(C, u)
else
pdf_value = pdf(C, u)
# Añadir mensaje de error detallado si el test falla
@test 0.0 <= cdf_value <= 1.0 || error("Fallo en la CDF: ν=$ν, ρ=$ρ, u=$u, cdf_value=$cdf_value")
@test pdf_value >= 0.0 || error("Fallo en la PDF: ν=$ν, ρ=$ρ, u=$u, pdf_value=$pdf_value")
end
end
catch e
@test e isa ArgumentError
println("No se pudo construir tEVCopula con ν=$ν, ρ=$ρ: ", e)
end
end
end
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 7818 | using Test
using TwinCopulas
using Distributions
using Random
@testset "Others Copulas Tests" begin
rng = MersenneTwister(2024)
d = 100
@testset "B11Copula - sampling, pdf, cdf" begin
for θ in [0.0, rand(rng), rand(rng), 1.0]
C = B11Copula(θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
if θ == 1
@test_throws ArgumentError pdf(C, u)
else
@test 0.0 <= cdf(C, u) <= 1.0
@test pdf(C, u) >= 0.0
end
end
end
end
@testset "FrechetCopula - sampling, pdf, cdf" begin
# Lista de ejemplos de parámetros para probar
param_sets = [
(0.1, 0.2), # θ1 + θ2 <= 1
(0.5, 0.5), # θ1 + θ2 <= 1
(0.7, 0.3), # θ1 + θ2 <= 1
(-0.1, 0.2), # Caso inválido: θ1 < 0
(0.1, -0.2), # Caso inválido: θ2 < 0
(0.5, 0.6), # Caso inválido: θ1 + θ2 > 1
(1.1, 0.1), # Caso inválido: θ1 > 1
(0.1, 1.1), # Caso inválido: θ2 > 1
(rand(rng), rand(rng) * (1 - rand(rng))) # Parámetros aleatorios dentro de rango
]
for (θ1, θ2) in param_sets
try
C = FrechetCopula(θ1, θ2)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
cdf_value = cdf(C, u)
pdf_value = pdf(C, u)
# Añadir mensaje de error detallado si el test falla
@test 0.0 <= cdf_value <= 1.0 || error("Fallo en la CDF: θ1=$θ1, θ2=$θ2, u=$u, cdf_value=$cdf_value")
@test pdf_value >= 0.0 || error("Fallo en la PDF: θ1=$θ1, θ2=$θ2, u=$u, pdf_value=$pdf_value")
end
catch e
@test e isa ArgumentError
println("No se pudo construir FrechetCopula con θ1=$θ1, θ2=$θ2: ", e)
end
end
end
@testset "MardiaCopula - sampling, pdf, cdf" begin
# Lista de ejemplos de parámetros para probar
param_sets = [
-1.0, # θ = -1, debería crear WCopula
-0.5, # -1 < θ < 0
0.0, # θ = 0, debería crear IndependentCopula
0.5, # 0 < θ < 1
1.0, # θ = 1, debería crear MCopula
-1.1, # Caso inválido: θ < -1
1.1, # Caso inválido: θ > 1
rand(rng, Uniform(-1.0, 1.0)) # Parámetro aleatorio dentro de rango
]
for θ in param_sets
try
C = MardiaCopula(θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
cdf_value = cdf(C, u)
pdf_value = pdf(C, u)
# Añadir mensaje de error detallado si el test falla
@test 0.0 <= cdf_value <= 1.0 || error("Fallo en la CDF: θ=$θ, u=$u, cdf_value=$cdf_value")
@test pdf_value >= 0.0 || error("Fallo en la PDF: θ=$θ, u=$u, pdf_value=$pdf_value")
end
catch e
@test e isa ArgumentError
println("No se pudo construir MardiaCopula con θ=$θ: ", e)
end
end
end
@testset "MaresiasCopula - sampling, cdf" begin
# Definición de funciones G válidas
function G1(u)
return u > 0.5 ? 2u - 1 : 0
end
function G2(u)
α = rand(rng, Uniform(1.0, 2.0))
return u^α
end
function G3(u)
α = 5.5 # α ≥ 1
return u < 0.5 ? u / α : (2 - 1/α) * u - (1 - 1/α) * u
end
valid_functions = [G1, G2, G3]
for G in valid_functions
try
C = MaresiasCopula(G)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
cdf_value = cdf(C, u)
# Añadir mensaje de error detallado si el test falla
@test 0.0 <= cdf_value <= 1.0 || error("Fallo en la CDF: G=$G, u=$u, cdf_value=$cdf_value")
@test pdf(C, u) >= 0.0
end
catch e
@test e isa ArgumentError
println("No se pudo construir MaresiasCopula con G=$G: ", e)
end
end
end
@testset "MorgensternCopula - sampling, pdf, cdf" begin
for θ in [-1.0, -rand(rng), 0.0, rand(rng), 1.0]
C = MorgensternCopula(θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
@test 0.0 <= cdf(C, u) <= 1.0
@test pdf(C, u) >= 0.0
end
end
end
@testset "PlackettCopula - sampling, pdf, cdf" begin
for θ in [0.0, 1.0, rand(rng), rand(rng, Uniform(1.5, 5.5)), rand(rng, Uniform(6.0, 10.0)), Inf]
C = PlackettCopula(θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
cdf_value = cdf(C, u)
if θ == Inf || θ == 0
# En los casos especiales de θ = 0
@test_throws ArgumentError pdf(C, u)
else
pdf_value = pdf(C, u)
# Añadir mensaje de error detallado si el test falla
@test 0.0 <= cdf_value <= 1.0
@test pdf_value >= 0.0
end
end
end
end
@testset "RafteryCopula - sampling, pdf, cdf" begin
for θ in [0.0, 1.0, rand(rng), rand(rng)]
C = RafteryCopula(θ)
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
cdf_value = cdf(C, u)
if θ == 1
# En los casos especiales de θ = 0
@test_throws ArgumentError pdf(C, u)
else
pdf_value = pdf(C, u)
# Añadir mensaje de error detallado si el test falla
@test 0.0 <= cdf_value <= 1.0
@test pdf_value >= 0.0
end
end
end
end
end
| TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 8625 | using Test
using TwinCopulas
using Distributions
using Random
@testset "Several Copulas Tests" begin
rng = MersenneTwister(2024)
d = 100
@testset "EmpiricalCopula - creation, cdf, pdf, and sampling" begin
# Generar datos de prueba válidos bivariados
data_valid = rand(2, 100)
# Generar datos de prueba inválidos (unidimensional)
data_invalid = rand(rng, 100)
@testset "Valid Data" begin
try
C = EmpiricalCopula(data_valid)
# Verificar que la creación de la copula empírica tiene la estructura correcta
@test size(C.data) == (2, 100)
@test size(C.pseudos) == (2, 100)
# Verificar que las pseudo-observaciones están en el rango [0, 1]
@test all(0 .<= C.pseudos .<= 1)
# Evaluar CDF y PDF en algunos puntos
u_points = [[0.5, 0.5], [0.1, 0.9], [0.7, 0.3]]
for u in u_points
cdf_value = cdf(C, u)
pdf_value = pdf(C, u)
@test 0.0 <= cdf_value <= 1.0 || error("Fallo en la CDF: u=$u, cdf_value=$cdf_value")
@test pdf_value >= 0.0 || error("Fallo en la PDF: u=$u, pdf_value=$pdf_value")
end
# Verificar la generación de muestras
samples = rand(rng, C, 100)
@test size(samples) == (2, 100)
catch e
@test e isa ErrorException
println("Error inesperado al construir EmpiricalCopula con datos válidos: ", e)
end
end
@testset "Invalid Data" begin
try
C = EmpiricalCopula(data_invalid)
catch e
@test e isa AssertionError
println("Correctamente no se pudo construir EmpiricalCopula con datos inválidos: ", e)
end
end
end
@testset "IndependentCopula - sampling, pdf, cdf" begin
C = IndependentCopula()
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
@test 0.0 <= cdf(C, u) <= 1.0
@test pdf(C, u) >= 0.0
end
end
@testset "MCopula - sampling, pdf, cdf" begin
C = MCopula()
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
@test 0.0 <= cdf(C, u) <= 1.0
@test_throws ArgumentError pdf(C, u)
end
end
@testset "WCopula - sampling, pdf, cdf" begin
C = WCopula()
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
@test 0.0 <= cdf(C, u) <= 1.0
@test_throws ArgumentError pdf(C, u)
end
end
@testset "SurvivalCopula - creation, cdf, pdf, and sampling" begin
# Lista de copulas base para pruebas
copula_bases = [
GaussianCopula(0.5),
ClaytonCopula(2.0),
GumbelCopula(3.0),
FrankCopula(4.0),
JoeCopula(5.0),
]
for base_copula in copula_bases
# Crear la SurvivalCopula a partir de la copula base
survival_copula = SurvivalCopula(base_copula)
samples = rand(survival_copula, 100)
@test size(samples) == (2, 100)
@test all(0 .<= s .<= 1 for s in samples)
# Verificar que la creación de la copula de supervivencia tiene la estructura correcta
@test survival_copula.C == base_copula
for i in 1:d
u = samples[:,i]
cdf_value = cdf(survival_copula, u)
pdf_value = pdf(survival_copula, u)
@test 0.0 <= cdf_value <= 1.0 || error("Fallo en la CDF: base_copula=$base_copula, u=$u, cdf_value=$cdf_value")
@test pdf_value >= 0.0 || error("Fallo en la PDF: base_copula=$base_copula, u=$u, pdf_value=$pdf_value")
end
end
end
@testset "UtilCopula - sampling, pdf, cdf" begin
C = UtilCopula()
data = rand(rng, C, 100)
# Verificar que la generación de números aleatorios tiene la forma correcta
@test size(data) == (2, 100)
# Evaluar CDF y PDF en cada columna de los datos generados
for i in 1:d
u = data[:,i]
@test 0.0 <= cdf(C, u) <= 1.0
@test pdf(C, u) >= 0.0
end
end
@testset "ArchimaxCopula - creation, cdf, pdf, and sampling" begin
# Lista de copulas Archimedean y ExtremeValue para pruebas
archimedean_copulas = [
ClaytonCopula(2.0),
GumbelCopula(2.5)
]
extreme_value_copulas = [
LogCopula(3.5),
GalambosCopula(4.5)
]
for archimedean in archimedean_copulas
for extreme in extreme_value_copulas
# Crear la ArchimaxCopula a partir de las copulas base
archimax_copula = ArchimaxCopula(archimedean, extreme)
# Verificar que la creación de la copula tiene la estructura correcta
@test archimax_copula.Archimedean == archimedean
@test archimax_copula.Extreme == extreme
# Generar muestras
samples = rand(rng, archimax_copula, 150)
@test size(samples) == (2, 150)
@test all(0 .<= s .<= 1 for s in samples)
# Evaluar CDF y PDF en algunos puntos
for i in 1:150
u = samples[:,i]
cdf_value = cdf(archimax_copula, u)
pdf_value = pdf(archimax_copula, u)
@test 0.0 <= cdf_value <= 1.0 || error("Fallo en la CDF: archimedean=$archimedean, extreme=$extreme, u=$u, cdf_value=$cdf_value")
@test (pdf_value >= 0.0 || isnan(pdf_value)) || error("Fallo en la PDF: archimedean=$archimedean, extreme=$extreme, u=$u, pdf_value=$pdf_value")
end
end
end
end
@testset "SklarDist - creation, cdf, pdf, and sampling" begin
# Lista de copulas base para pruebas
copula_bases = [
GaussianCopula(0.5),
ClaytonCopula(2.0),
GalambosCopula(3.5)
]
# Lista de distribuciones marginales para pruebas
margins_list = [
(Normal(), Normal()),
(Exponential(1.0), Exponential(1.0)),
(Beta(2.0, 5.0), Beta(2.0, 5.0)),
(Beta(3.2, 2.3), Normal(4.0, 1.0))
]
for copula in copula_bases
for margins in margins_list
# Crear la SklarDist a partir de la copula base y las distribuciones marginales
sklar_dist = SklarDist(copula, [margins[1], margins[2]])
# Verificar que la creación de la distribución de Sklar tiene la estructura correcta
@test sklar_dist.copula == copula
@test sklar_dist.margins == margins
# Generar muestras
samples = rand(rng, sklar_dist, 100)
@test size(samples) == (2, 100)
# Evaluar CDF y PDF en algunos puntos
for i in 1:d
u = samples[:,i]
cdf_value = cdf(sklar_dist, u)
pdf_value = pdf(sklar_dist, u)
@test 0.0 <= cdf_value <= 1.0 || error("Fallo en la CDF: copula=$copula, margins=$margins, u=$u, cdf_value=$cdf_value")
@test pdf_value >= 0.0 || error("Fallo en la PDF: copula=$copula, margins=$margins, u=$u, pdf_value=$pdf_value")
end
end
end
end
end | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | code | 159 | println("Testing...")
include("ArchimedeanTest.jl")
include("ExtremeValueTest.jl")
include("EllipticalTest.jl")
include("OthersTest.jl")
include("Several.jl") | TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | docs | 2469 | # TwinCopulas
[](https://Santymax98.github.io/TwinCopulas.jl/stable/)
[](https://Santymax98.github.io/TwinCopulas.jl/dev/)
[](https://github.com/Santymax98/TwinCopulas.jl/actions/workflows/CI.yml?query=branch%3Amaster)
[](https://cirrus-ci.com/github/Santymax98/TwinCopulas.jl)
[](https://codecov.io/gh/Santymax98/TwinCopulas.jl)
[](https://coveralls.io/github/Santymax98/TwinCopulas.jl?branch=master)
*TwinCopulas* is a Julia package for probability distributions and associated functions, focusing on the implementation of copulas. This package includes:
* Probability density/mass functions (pdf).
* Sampling from a population or from a distribution.
## Installation
You can install *TwinCopulas* using Julia's package manager:
```julia
using Pkg
Pkg.add("TwinCopulas")
```
## Usage
Here is a basic example of how to use *TwinCopulas*:
```julia
Julia> using TwinCopulas
Julia> G = GaussianCopula(0.8)
```
## Roadmap
### Upcoming Features and Improvements
1. **Revised Calculation of Dependency Measures:**
- Enhance the accuracy and efficiency of dependency measure calculations.
2. **Additional Copulas:**
- Implement more copulas, potentially including dynamic copulas to capture time-varying dependencies.
3. **Copula Fitting (Parameter Estimation):**
- Develop robust methods for parameter estimation of copulas to better fit data.
4. **Model Selection:**
- Introduce model selection techniques to choose the best copula model for given data.
5. **Graphical Representations:**
- Add functions to create informative plots and visualizations of copulas and their properties.
## Contributing
Contributions are welcome! Please open an issue if you have any questions, feature requests, or bug reports. Feel free to submit pull requests to improve the package.
## License
This project is licensed under the MIT License.
## Acknowledgements
We would like to thank all contributors and the Julia community for their support and contributions.
| TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
|
[
"MIT"
] | 0.1.0 | 160f2150f988cc7532e7a70e4c19355f0cd0a67b | docs | 9991 | # Copulas
The law of 2-dimensional random vector $X = (X_1, X_2)$ defined on a probability space $(\Omega, \mathcal{F}, \mathbb{P}),$ is usually studied from its *distribution function*
$$F(x_1,x_2)= \mathbb{P}(X_1 \leq x_2, X_2 \leq x_2), \hspace{0.5cm} x_1, x_2 \in \mathbb{R}.$$
For $i = 1,2$ the distribution function $F_i$ of $X_i$ is called the (univariate) *marginal law* or *margin* and be retrieved from $F$ via
$$F_i(x_i) = \mathbb{P}(X_i \leq x_i)=F(x_i,\infty), \hspace{0.5cm} x_i \in \mathbb{R}.$$
It is important to note that knowing the marginal distributions $F_1, F_2$ is not sufficient to determine the joint distribution $F.$ Additionally, it is required to understand how the marginal distributions are coupled. This is achieved by means of a *copula* of $(X_1, X_2).$ Generally speaking, knowing the margins and a copula is equivalent to knowing the joint distribution. It is now appropriate to provide the definition of a copula.
> **Definition (Copula):**
>
> *(1)* A function $C: [0, 1]^2 \to [0, 1]$ is called a *bivariate copula*, if there is a probability space $(\Omega, \mathcal{F}, \mathbb{P})$ supporting a random vector $(U_1, U_2)$ such that $U_k \sim \mathcal{U}[0,1]$ for all $k=1,2$ and $$ C(u_1,u_2)=\mathbb{P}(U_1 \leq u_1, U_2 \leq u_2), \hspace{0.5 cm} u_1, u_2 \in [0, 1].$$
*(2)* On a probability space $(\Omega, \mathcal{F}, \mathbb{P})$ let $(U_1, U_2)$ be a random vector on $[0,1]^2$ whose joint distribution function is a copula $C: [0,1]^2 \to [0,1].$
```@example 1
using TwinCopulas
θ = 0.5 # Parameter
G = GaussianCopula(θ) # A 2-dimensional Gaussian Copula with parameter θ = 0.5.
```
This object is a random vector, and behaves exactly as you would expect a random vector from Distributions.jl to behave: you may sample it with rand(C,100), compute its pdf or cdf with pdf(C,x) and cdf(C,x), etc:
```@example 1
u = rand(G,10)
```
```@example 1
cdf(C,u)
```
> **Example (Independent Copula)**
>
> The function $\Pi: [0,1]^2 \to [0,1],$ given by $$\Pi(u_1, u_2)=u_1u_2, \hspace{0.5 cm} u_1,u_2 \in [0,1],$$ is called the *Independence Copula.*
> **Example (Fréchet-Hoeffding bounds)**
>
>The Fréchet-Hoeffding bounds represent the extreme cases of dependence for a copula. These bounds are given by the following functions:
>
>- **Lower Fréchet-Hoeffding bound**:$$
W(u_1, u_2) = \max\{u_1 + u_2 - 1, 0\}$$
>
>- **Upper Fréchet-Hoeffding bound**:$$M(u_1, u_2) = \min\{u_1, u_2\}$$
>
These limits can be viewed as the extreme cases of dependence in a copula:
- The **lower bound** $W(u_1, u_2)$ corresponds to the case of the most negative dependence, where the variables are perfectly anti-monotonic. This means that if one variable increases, the other decreases in a perfectly predictable manner.
- The **upper bound** $M(u_1, u_2)$ corresponds to the case of the most positive dependence, where the variables are perfectly monotonic. This means that if one variable increases, the other also increases in a perfectly predictable manner.
These bounds provide a way to understand the range of possible dependence structures that can be modeled by a copula, from complete negative dependence to complete positive dependence.
The syntax to use these copulas in TwinCopulas is the following:
```@example 2
using TwinCopulas
I = IndependentCopula() # A 2-dimensional Independent Copula.
M = MCopula() # A 2-dimensional upper bound.
W = WCopula() # A 2-dimensional lower bound.
```
# Sklar's Theorem
In probability theory and statistics, Sklar's Theorem is a fundamental result that connects multivariate distribution functions to their marginal distributions through a copula. This theorem provides a powerful framework for modeling and analyzing the dependence structure between random variables.
**Sklar's Theorem:**
Let $F$ a 2-dimensional distribution function with margins $F_1,F_2$. Then there exist a 2-dimensional copula $C$ such that for all $(x_1,x_2) \in \mathbb{R}^2$ it holds that
$$F(x_1, x_2)=C(F_1(x_1),F_2(x_2)).$$
If $F_1, F_2$ are continuous, then $C$ is unique. Conversely, if $C$ is a 2-dimensional copula and $F_1, F_2$ are univariate distribution functions, then he function $F$ is a 2-dimensional distribution function [`sklar1959`](@cite).
Sklar's Theorem is significant because it allows us to separate the marginal behavior of each variable from their dependence structure. The marginal distributions $F_1$ and $F_2$ describe the individual behavior of the random variables, while the copula $C$ captures how these variables are related to each other.
This separation is particularly useful in various applications:
1. **Modeling Flexibility**: By using copulas, we can model complex dependencies between variables while maintaining flexibility in choosing different marginal distributions. This is especially valuable in fields like finance, insurance, and risk management, where understanding dependencies between risks is crucial.
2. **Dependence Structure**: Copulas provide a way to quantify and visualize the dependence structure between variables, which is not possible by looking at marginals alone. This helps in understanding the nature and strength of the relationships between variables.
3. **Simulation and Sampling**: Sklar's Theorem facilitates the generation of multivariate data with specified marginals and dependence structures. This is useful for simulations and scenarios where realistic modeling of dependencies is required.
In summary, Sklar's Theorem is a cornerstone in the field of copula theory, enabling the decoupling of marginal distributions and dependence structures, and providing a versatile tool for statistical modeling and analysis of multivariate data.
The syntax for generating bivariate distributions with Sklar's theorem is as follows:
```@example 3
using TwinCopulas, Distributions
margins = [Normal(), Beta(3.5, 2.3)]
copula = ClaytonCopula(3.5)
F = SklarDist(copula, margins)
```
# Survival Copulas
In some cases, it is more convenient to describe the distribution of a random vector $(X_1, X_2)$ using its survival function instead of its distribution function, especially when the components $X_1$ and $X_2$ are interpreted as lifetimes. The survival function provides a more intuitive description in such contexts.
## Definition of the Bivariate Survival Function
For a bivariate random vector $(X_1, X_2)$ defined on a probability space $(\Omega, \mathcal{F}, \mathbb{P})$, the survival function $\overline{F}$ is defined as:
$$\overline{F}(x_1, x_2) := \mathbb{P}(X_1 > x_1, X_2 > x_2), \quad x_1, x_2 \in \mathbb{R}.$$
## Marginal Survival Functions
For $i = 1, 2$, the univariate marginal survival function $\overline{F}_i$ of $X_i$ can be retrieved from the bivariate survival function $\overline{F}$ as follows:
$$\overline{F}_i(x_i) = \mathbb{P}(X_i > x_i) = \overline{F}(x_i, -\infty) \quad \text{for} \; i = 1, \; \text{and} \; \overline{F}_i(x_i) = \overline{F}(-\infty, x_i) \quad \text{for} \; i = 2, \quad x_i \in \mathbb{R}.$$
## Relationship to Sklar's Theorem
Analogous to Sklar's Theorem for distribution functions, the survival function of a bivariate random vector can be decomposed into a copula and its marginal survival functions. This decomposition allows for a more nuanced understanding of the dependence structure between the variables.
## Survival Analog of Sklar's Theorem
Let $\overline{F}$ be a bivariate survival function with marginal survival functions $\overline{F}_1$ and $\overline{F}_2$. Then there exists a bivariate copula $\overline{C}$ such that for all $(x_1, x_2) \in \mathbb{R}^2$, the following holds:
$$\overline{F}(x_1, x_2) = \overline{C}(\overline{F}_1(x_1), \overline{F}_2(x_2)).$$
If the marginal survival functions $\overline{F}_1$ and $\overline{F}_2$ are continuous, then the copula $\overline{C}$ is unique. Conversely, if $\overline{C}$ is a bivariate copula and $\overline{F}_1$ and $\overline{F}_2$ are univariate survival functions, then the function $\overline{F}$ is a bivariate survival function.
The survival copula approach is particularly useful in reliability theory and survival analysis, where it is common to deal with the lifetimes of components or systems. The survival function provides a direct way to model the joint survival probabilities, and the survival copula captures the dependence structure between these lifetimes. This method allows for a clearer interpretation and more effective modeling of the joint behavior of the variables involved.
By utilizing survival copulas, one can effectively separate the marginal survival characteristics of each variable from their dependence structure, leading to a more flexible and comprehensive approach to multivariate survival analysis.
The syntax to use the survival copula in TwinCopulas is the following:
```@example 4
using TwinCopulas
cop = GumbelCopula(5.5)
S = SurvivalCopula(cop)
```
# Conditional Sampling for Bivariate Copulas
As the main sampling method, TwinCopulas implements conditional sampling based on a bivariate probability space, supporting two iid random variables. This algorithm is not restricted to any specific class of copulas, making it versatile for sampling arbitrary bivariate copulas. The only challenging step is calculating the partial derivative and its generalized inverse, which usually requires a well-defined analytical form of the copula and is not easy to obtain.
The imput for the algorithm is a bivariate copula $C: [0,1]^2 \to [0,1].$
> **Algotithm 1**
>
> *(1)* Simulate $U_2 \sim \mathcal{U}[0,1]$
>
> *(2)* Compute (the right continuous version of) the function $$F_{U_1|U_2}(u_1)=\frac{\partial}{\partial u_2}C(u_1,u_2)|_{u_2=U_2}, \quad u_2 \in [0,1].$$
> *(3)* Compute de generalized inverse of $F_{U_1|U_2},$ i.e $$F^{-1}_{U_1|U_2}(v)=\inf\{u_1 > 0: F_{U_1|U_2}(u_1)\geq v\}, \quad v \in [0,1].$$
> *(4)* Simulate $V \sim \mathcal{U}[0,1],$ independent of $U_2.$
>
> *(5)* Set $U_1 = F^{-1}_{U_1|U_2}(V)$ and return $(U_1, U_2).$
| TwinCopulas | https://github.com/Santymax98/TwinCopulas.jl.git |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.