licenses
sequencelengths 1
3
| version
stringclasses 677
values | tree_hash
stringlengths 40
40
| path
stringclasses 1
value | type
stringclasses 2
values | size
stringlengths 2
8
| text
stringlengths 25
67.1M
| package_name
stringlengths 2
41
| repo
stringlengths 33
86
|
|---|---|---|---|---|---|---|---|---|
[
"MIT"
] | 0.1.0 | d064f853e5eca1d684a85b943723dacc9e0f6d7c | code | 2386 | struct ReparametrizableBSLDP{F,W} <: AbstractWrappedDistribution
lib_path::AbstractString
proxy::StanModel
model_function::F
wrapped::W
end
ReparametrizableBSLDP(lib_path::AbstractString, model_function, data::AbstractDict) = ReparametrizableBSLDP(
lib_path,
StanModel(String(lib_path), JSON.json(data)),
model_function,
model_function(data)
)
# LogDensityProblems.dimension(source::ReparametrizableBSLDP) = Int64(BridgeStan.param_unc_num(source.proxy))
LogDensityProblems.capabilities(::Type{<:ReparametrizableBSLDP}) = LogDensityProblems.LogDensityOrder{2}()
LogDensityProblems.logdensity(source::ReparametrizableBSLDP, draw::AbstractVector) = try
BridgeStan.log_density(source.proxy, collect(draw))
catch e
@warn """
Failed to evaluate log density:
$source
$draw
$(WarmupHMC.exception_to_string(e))
"""
-Inf
end
LogDensityProblems.logdensity_and_gradient(source::ReparametrizableBSLDP, draw::AbstractVector) = try
BridgeStan.log_density_gradient(source.proxy, collect(draw))
catch e
@warn """
Failed to evaluate log density gradient:
$source
$draw
$(WarmupHMC.exception_to_string(e))
"""
-Inf, -Inf .* draw
end
LogDensityProblems.logdensity_gradient_and_hessian(source::ReparametrizableBSLDP, draw::AbstractVector) = try
BridgeStan.log_density_hessian(source.proxy, collect(draw))
catch e
@warn """
Failed to evaluate log density gradient:
$source
$draw
$(WarmupHMC.exception_to_string(e))
"""
-Inf, -Inf .* draw, -Inf .* draw .* draw'
end
# IMPLEMENT THIS
update_nt(::Any, ::Any) = error("unimplemented")
update_dict(model_function, reparent) = Dict([
(String(key), value) for (key, value) in pairs(update_nt(model_function, reparent))
])
recombine(source::ReparametrizableBSLDP, reparent) = ReparametrizableBSLDP(
source.lib_path,
source.model_function,
merge(JSON.parse(source.proxy.data), update_dict(source.model_function, reparent))
)
verify(source::ReparametrizableBSLDP, draws::AbstractMatrix) = begin
@assert BridgeStan.param_unc_num(source.proxy) == length(source.wrapped)
proxy_lpdfs = LogDensityProblems.logdensity.(source, eachcol(draws))
wrapped_lpdfs = [lpdf_and_invariants(source, draw).lpdf for draw in eachcol(draws)]
@assert WarmupHMC.nanstd(proxy_lpdfs - wrapped_lpdfs) < 1e-8 """
Failed lpdf check: $(hcat(proxy_lpdfs, wrapped_lpdfs))
"""
end | ReparametrizableDistributions | https://github.com/nsiccha/ReparametrizableDistributions.jl.git |
|
[
"MIT"
] | 0.1.0 | d064f853e5eca1d684a85b943723dacc9e0f6d7c | code | 869 | struct ReparametrizablePosterior{L,P} <: AbstractCompositeReparametrizableDistribution
likelihood::L
prior::P
end
parts(source::ReparametrizablePosterior) = source.prior
recombine(source::ReparametrizablePosterior, prior) = ReparametrizablePosterior(
source.likelihood, prior
)
divide(source::ReparametrizablePosterior, draws::AbstractMatrix) = parts(source), to_nt(source, draws)
lpdf_update(source::ReparametrizablePosterior, draw::NamedTuple, lpdf=0.) = begin
prior_invariants = kmap(lpdf_and_invariants, source.prior, draw, lpdf)
if isa(lpdf, Ignore)
(;lpdf, prior_invariants...)
else
likelihood_invariants = source.likelihood(prior_invariants)
lpdf += likelihood_invariants.lpdf + sum(getproperty.(values(prior_invariants), :lpdf))
(;lpdf, likelihood=likelihood_invariants, prior_invariants...)
end
end | ReparametrizableDistributions | https://github.com/nsiccha/ReparametrizableDistributions.jl.git |
|
[
"MIT"
] | 0.1.0 | d064f853e5eca1d684a85b943723dacc9e0f6d7c | code | 7179 | struct ScaleHierarchy{I} <: AbstractReparametrizableDistribution
info::I
end
ScaleHierarchy(log_scale, centeredness) = ScaleHierarchy((;log_scale, centeredness))
parts(source::ScaleHierarchy) = (;source.log_scale, weights=source.centeredness)
reparametrization_parameters(source::ScaleHierarchy) = (;source.centeredness)
optimization_parameters_fn(::ScaleHierarchy) = finite_logit
reparametrize(source::ScaleHierarchy, parameters::NamedTuple) = ScaleHierarchy(source.log_scale, parameters.centeredness)
lpdf_update(source::ScaleHierarchy, draw::NamedTuple, lpdf=0.) = lpdf_update(
LocScaleHierarchy((), source.log_scale, source.centeredness), (;location=0., draw...), lpdf
)
lja_update(source::ScaleHierarchy, target::ScaleHierarchy, draw::NamedTuple, lpdf=0.) = lja_update(
LocScaleHierarchy((), source.log_scale, source.centeredness),
LocScaleHierarchy((), target.log_scale, target.centeredness),
(;location=0., draw...), lpdf
)
slice_if_possible(x::Real, ::Any) = x
slice_if_possible(x::AbstractVector, i) = length(x) >= i ? x[i:i] : x[1:1]
divide(source::ScaleHierarchy, draws::AbstractVector{<:NamedTuple}) = begin
subsources = [
ScaleHierarchy(source.log_scale, [centeredness])
for centeredness in source.centeredness
]
subdraws = [
kmap.(slice_if_possible, draws, i)
# [
# (;log_scale=slice_if_possible(draw.log_scale, i), weights=draw.weights[i:i])
# for draw in draws
# ]
for i in eachindex(source.centeredness)
]
subsources, subdraws
end
recombine(source::ScaleHierarchy, resources) = begin
ScaleHierarchy(
source.log_scale,
vcat(getproperty.(resources, :centeredness)...)
)
end
struct LocScaleHierarchy{I} <: AbstractReparametrizableDistribution
info::I
end
LocScaleHierarchy(location, log_scale, c1, c2=c1) = LocScaleHierarchy((;location, log_scale, c1, c2))
parts(source::LocScaleHierarchy) = (;source.location, source.log_scale, weights=source.c1)
reparametrization_parameters(source::LocScaleHierarchy) = (;source.c1, source.c2)
optimization_parameters_fn(::LocScaleHierarchy) = finite_logit
# reparametrize(source::LocScaleHierarchy, parameters::NamedTuple) = LocScaleHierarchy(merge(source.info, parameters))
lpdf_update(source::LocScaleHierarchy, draw::NamedTuple, lpdf=0.) = begin
# Mirroring https://num.pyro.ai/en/stable/_modules/numpyro/infer/reparam.html#LocScaleReparam
# delta = decentered_value - centered * fn.loc
# value = fn.loc + jnp.power(fn.scale, 1 - centered) * delta
weights = draw.location .+ xexpy.(
draw.weights - source.c1 .* draw.location,
draw.log_scale .* (1 .- source.c2)
)
# Mirroring https://num.pyro.ai/en/stable/_modules/numpyro/infer/reparam.html#LocScaleReparam
# params["loc"] = fn.loc * centered
# params["scale"] = fn.scale**centered
prior_weights = Normal.(draw.location .* source.c1, exp.(draw.log_scale .* source.c2))
if length(source.location) > 0
lpdf += sum_logpdf(source.location, draw.location)
end
if length(source.log_scale) > 0
lpdf += sum_logpdf(source.log_scale, draw.log_scale)
end
lpdf += sum_logpdf(prior_weights, draw.weights)
(;lpdf, weights)
end
lja_update(::LocScaleHierarchy, target::LocScaleHierarchy, invariants::NamedTuple, lja=0.) = begin
weights = xexpy.(
invariants.weights .- invariants.location,
invariants.log_scale .* (target.c2 .- 1)
) .+ target.c1 .* invariants.location
# tdraw = vcat(invariants.location, invariants.log_scale, tweights)
prior_weights = Normal.(invariants.location .* target.c1, exp.(invariants.log_scale .* target.c2))
lja += sum_logpdf(prior_weights, weights)
(;lja, weights)
end
divide(source::LocScaleHierarchy, draws::AbstractVector{<:NamedTuple}) = begin
subsources = [
LocScaleHierarchy(source.location, source.log_scale, [c1], [c2])
for (c1, c2) in zip(source.c1, source.c2)
]
subdraws = [
kmap.(slice_if_possible, draws, i)
# [
# (;draw.location, draw.log_scale, weights=draw.weights[i:i])
# for draw in draws
# ]
for i in eachindex(source.c1)
]
subsources, subdraws
end
recombine(source::LocScaleHierarchy, resources) = begin
LocScaleHierarchy(
source.location, source.log_scale,
vcat(getproperty.(resources, :c1)...), vcat(getproperty.(resources, :c2)...)
)
end
struct TScaleHierarchy{I} <: AbstractReparametrizableDistribution
info::I
end
TScaleHierarchy(log_nu, log_scale, centeredness) = TScaleHierarchy((;log_nu, log_scale, centeredness))
parts(source::TScaleHierarchy) = (;source.log_nu, source.log_scale, weights=source.centeredness)
reparametrization_parameters(source::TScaleHierarchy) = (;source.centeredness)
optimization_parameters_fn(::TScaleHierarchy) = finite_logit
lpdf_update(source::TScaleHierarchy, draw::NamedTuple, lpdf=0.) = begin
draw = merge(draw, (;location=0.))
# Mirroring https://num.pyro.ai/en/stable/_modules/numpyro/infer/reparam.html#LocScaleReparam
# delta = decentered_value - centered * fn.loc
# value = fn.loc + jnp.power(fn.scale, 1 - centered) * delta
weights = draw.location .+ xexpy.(
draw.weights - source.centeredness .* draw.location,
draw.log_scale .* (1 .- source.centeredness)
)
# Mirroring https://num.pyro.ai/en/stable/_modules/numpyro/infer/reparam.html#LocScaleReparam
# params["loc"] = fn.loc * centered
# params["scale"] = fn.scale**centered
prior_weights = draw.location .* source.centeredness .+ exp.(draw.log_scale .* source.centeredness) .* TDist.(exp.(draw.log_nu))
if length(source.log_nu) > 0
lpdf += sum_logpdf(source.log_nu, draw.log_nu)
end
if length(source.log_scale) > 0
lpdf += sum_logpdf(source.log_scale, draw.log_scale)
end
lpdf += sum_logpdf(prior_weights, draw.weights)
(;lpdf, weights)
end
lja_update(::TScaleHierarchy, target::TScaleHierarchy, invariants::NamedTuple, lja=0.) = begin
invariants = merge(invariants, (;location=0.))
weights = xexpy.(
invariants.weights .- invariants.location,
invariants.log_scale .* (target.centeredness .- 1)
) .+ target.centeredness .* invariants.location
prior_weights = invariants.location .* target.centeredness .+ exp.(invariants.log_scale .* target.centeredness) .* TDist.(exp.(invariants.log_nu))
lja += sum_logpdf(prior_weights, weights)
(;lja, weights)
end
divide(source::TScaleHierarchy, draws::AbstractVector{<:NamedTuple}) = begin
subsources = [reparametrize(source, (;centeredness=[centeredness])) for centeredness in source.centeredness]
subdraws = [
# [
kmap.(slice_if_possible, draws, i)
# merge(draw, (log_scale=slice_if_possible(draw.log_scale, i), weights=draw.weights[i:i],))
# for draw in draws
# ]
for i in eachindex(source.centeredness)
]
subsources, subdraws
end
recombine(source::TScaleHierarchy, resources) = begin
reparametrize(source, map(vcat, reparametrization_parameters.(resources)...))
end | ReparametrizableDistributions | https://github.com/nsiccha/ReparametrizableDistributions.jl.git |
|
[
"MIT"
] | 0.1.0 | d064f853e5eca1d684a85b943723dacc9e0f6d7c | code | 2772 | struct StackedArray{T,N,B,V<:AbstractArray{T,N}} <: AbstractArray{T,N}
boundaries::B
data::V
end
StackedVector{T,B,V} = StackedArray{T,1,B,V}
StackedMatrix{T,B,V} = StackedArray{T,2,B,V}
struct Length{C} size::C end
total_length(what) = sum(length.(values(what)))
total_length(what::Length) = sum(values(what.size))
Base.eltype(::Type{StackedArray{T}}) where {T} = T
# Base.eltype(what::StackedVector) = eltype(what.data)
Base.size(what::StackedArray) = size(what.data)
Base.IndexStyle(::Type{StackedArray{T,N,B,V}}) where {T,N,B,V} = IndexStyle(V)
Base.getindex(what::StackedArray, i::Int) = getindex(what.data, i)
Base.setindex!(what::StackedArray, v, i::Int) = setindex!(what.data, v, i)
Base.iterate(what::StackedArray) = Base.iterate(what.data)
Base.similar(what::StackedArray) = StackedArray(what.boundaries, similar(what.data))
Base.similar(what::StackedArray, type::Type{S}) where {S} = StackedArray(what.boundaries, similar(what.data, type))
Base.copy(what::StackedArray) = StackedArray(what.boundaries, copy(what.data))
Base.oftype(proto::StackedArray, y::AbstractArray) = StackedArray(proto.boundaries, oftype(proto.data, y))
TupleNamedTuple(::Any, values) = tuple(values...)
TupleNamedTuple(proto::NamedTuple, values) = (;zip(keys(proto), values)...)
stack_array(proto::Length, data::AbstractArray) = StackedArray(
TupleNamedTuple(proto.size, cumsum(values(proto.size))),
data
)
stack_array(proto, data::AbstractArray) = stack_array(Length(map(length, proto)), data)
stack_array(proto::StackedArray, data::AbstractArray) = StackedArray(proto.boundaries, data)
# TupleNamedTuple(proto, cumsum(length.(values(proto)))),
# data
# )
StackedArray(what) = stack_array(what, vcat(values(what)...))
general_slice(what::StackedArray, f, args...) = TupleNamedTuple(
what.boundaries,
(
f(what.data, range(1, what.boundaries[1]), args...),
f.(
[what.data],
range.(1 .+ values(what.boundaries)[1:end-1], values(what.boundaries)[2:end]),
args...
)...
)
)
arrays(what::StackedVector) = general_slice(what, getindex)
arrays(what::StackedMatrix) = general_slice(what, getindex, :)
arrays(proto, data::AbstractArray) = arrays(stack_array(proto, data))
views(what::StackedVector) = general_slice(what, view)
views(what::StackedMatrix) = general_slice(what, view, :)
views(proto, data::AbstractArray) = views(stack_array(proto, data))
# views_sized(proto, data::AbstractArray) = views(stack_vector_sized(proto, data))
# Base.getproperty(what::StackedVector, key::Symbol) = hasfield(StackedVector, key) ? getfield(what, key) : getproperty(views(what), key)
# Base.map(f::Function, first::StackedVector, args...; kwargs...) = StackedVector(map(f, views(first), args...; kwargs...)) | ReparametrizableDistributions | https://github.com/nsiccha/ReparametrizableDistributions.jl.git |
|
[
"MIT"
] | 0.1.0 | d064f853e5eca1d684a85b943723dacc9e0f6d7c | code | 499 | find_centeredness(log_scales::AbstractMatrix, x::AbstractMatrix, centeredness::AbstractVector) = begin
@assert size(log_scales, 2) == size(x, 2)
@assert size(log_scales, 1) == size(x, 1) || size(log_scales, 1) == 1
@assert size(x, 1) == length(centeredness)
scale_hierarchy = ScaleHierarchy([], centeredness)
find_reparametrization(scale_hierarchy, [
(;log_scale, weights)
for (log_scale, weights) in zip(eachcol(log_scales), eachcol(x))
]).centeredness
end | ReparametrizableDistributions | https://github.com/nsiccha/ReparametrizableDistributions.jl.git |
|
[
"MIT"
] | 0.1.0 | d064f853e5eca1d684a85b943723dacc9e0f6d7c | code | 227 |
finite_logit(x, reg=1e-4) = logit.(.5 .+ (x .- .5) .* (1 .- reg))
finite_log(x, reg=1e-16) = log.(x .+ reg)
inverse(::typeof(finite_logit)) = logistic
inverse(::typeof(finite_log)) = exp
inverse(::typeof(identity)) = identity | ReparametrizableDistributions | https://github.com/nsiccha/ReparametrizableDistributions.jl.git |
|
[
"MIT"
] | 0.1.0 | d064f853e5eca1d684a85b943723dacc9e0f6d7c | code | 3235 | sum_logpdf(dists, xs) = length(dists) > 0 ? sum(logpdf.(dists, xs)) : 0.
_logpdf(distribution, x) = logpdf(distribution, x)
_cdf(distribution, x) = cdf(distribution, x)
_quantile(distribution, x) = quantile(distribution, x)
_logcdf(distribution, x) = logcdf(distribution, x)
_invlogcdf(distribution, x) = invlogcdf(distribution, x)
quantile_cdf(target, source, x) = _invlogcdf(target, _logcdf(source, x))
# https://github.com/stan-dev/math/blob/9b2e93ba58fa00521275b22a190468ab22f744a3/stan/math/prim/fun/log_modified_bessel_first_kind.hpp#L191-L213
logbesseli(k, z) = begin
log_half_z = log(.5 * z)
lgam = loggamma(k + 1.)
lcons = (2. + k) * log_half_z
out = logsumexp([k * log_half_z - lgam, lcons - loggamma(k + 2.)])
lgam += log1p(k)
m = 2
lfac = 0
while true
old_out = out
lfac += log(m)
lgam += log(k+m)
lcons += 2 * log_half_z
out = logsumexp([out, lcons - lfac - lgam])
m += 1
(out > old_out || out < old_out) || break
end
return out
end
_logpdf(distribution::NoncentralChisq, x::Real) = begin
k, lambda = distribution.ν, distribution.λ
if lambda > 0
try (
log(2)
- (x+lambda)/2
+ (k/4-.5) * log(x/lambda)
# + log(besseli(k/2-1, sqrt(lambda*x)))
+ logbesseli(k/2-1, sqrt(lambda*x))
)
catch e
println(e)
-Inf
end
else
logpdf(Chisq(k), x)
end
end
function ChainRulesCore.rrule(::typeof(_logcdf), d, x::Real)
lq = _logcdf(d, x)
function _logcdf_pullback(a)
q = exp(lq)
la = a / q
pullback(grad) = la * grad
da = @thunk(Tangent{typeof(d)}(;map(pullback, grad_d_cdf(d, x, q))...))
# da = @thunk(la * Tangent{typeof(d)}(;grad_d_cdf(d, x, q)...))
xa = pullback(pdf(d, x))
ChainRulesCore.NoTangent(), da, xa
end
lq, _logcdf_pullback
end
grad_d_cdf(d::Gamma, x, q) = begin
a, b = params(d)
xi = x / b
# https://discourse.julialang.org/t/gamma-inc-derivatives/93148
g = gamma(a)
dg = digamma(a)
lx = log(xi)
r = pFq([a,a],[a+1,a+1],-xi)
grad_a = a^(-2) * xi^a * r/g + q*(dg - lx)
# # https://www.wolframalpha.com/input?i=D%5BGammaRegularized%5Ba%2C+0%2C+x%2Fb%5D%2C+b%5D
grad_b = -exp(-xi) * xi^a / (b * gamma(a))
(α=-grad_a::Float64, θ=grad_b::Float64)
end
grad_d_cdf(d::NoncentralChisq, x, q) = begin
# https://en.wikipedia.org/wiki/Noncentral_chi-squared_distribution
k, lambda = params(d)
nu, a, b = k/2, sqrt(lambda), sqrt(x)
# https://en.wikipedia.org/wiki/Marcum_Q-function#Differentiation
grad_a = a * (b/a)^nu*exp(-(a^2+b^2)/2)*besseli(nu,a*b)
grad_k = 0.
grad_lambda = -grad_a/(2a)
(ν=grad_k::Float64, λ=grad_lambda::Float64)
end
function ChainRulesCore.rrule(::typeof(_invlogcdf), d, lq::Real)
x = _invlogcdf(d, lq)
function _invlogcdf_pullback(a)
q = exp(lq)
difdx = q/pdf(d,x)
pullback(grad) = a*grad/pdf(d,x)
da = @thunk(-Tangent{typeof(d)}(;map(pullback, grad_d_cdf(d, x, q))...))
lqa = a * difdx
ChainRulesCore.NoTangent(), da, lqa
end
x, _invlogcdf_pullback
end | ReparametrizableDistributions | https://github.com/nsiccha/ReparametrizableDistributions.jl.git |
|
[
"MIT"
] | 0.1.0 | d064f853e5eca1d684a85b943723dacc9e0f6d7c | code | 218 | struct LogTransformed{D} <: ContinuousUnivariateDistribution
distribution::D
end
log_transform(d) = LogTransformed(d)
Distributions.logpdf(source::LogTransformed, x::Real) = x + logpdf(source.distribution, exp(x)) | ReparametrizableDistributions | https://github.com/nsiccha/ReparametrizableDistributions.jl.git |
|
[
"MIT"
] | 0.1.0 | d064f853e5eca1d684a85b943723dacc9e0f6d7c | code | 10546 | using TestEnv; TestEnv.activate("ReparametrizableDistributions");
using WarmupHMC, ReparametrizableDistributions, ReverseDiff, Distributions, Random, Test, Optim, ChainRulesTestUtils, NaNStatistics, Plots, LinearAlgebra, DynamicPlots
using DynamicHMC, LogDensityProblemsAD
import ReparametrizableDistributions: _logcdf, _invlogcdf
rmse(x,y; m=nanmean) = sqrt(m((x.-y).^2))
pairwise(f, arg, args...; kwargs...) = [
f(lhs, rhs, args...; kwargs...) for lhs in arg, rhs in arg
]
transformation_tests(parametrizations, args...; kwargs...) = begin
@testset "reparametrization" pairwise(reparametrization_test, parametrizations)
@testset "nan" pairwise(nan_test, parametrizations, args...)
@testset "rmse" pairwise(rmse_test, parametrizations, args...)
@testset "loss" pairwise(loss_test, parametrizations, args...)
@testset "easy_convergence" pairwise(easy_convergence_test, parametrizations, args...)
@testset "hard_convergence" pairwise(hard_convergence_test, parametrizations, args...; kwargs...)
end
test_draws(lhs; seed=0, rng=Xoshiro(seed), n_draws=100) = randn(rng, (length(lhs), n_draws))
reparametrization_test(lhs, rhs, tol=1e-4) = begin
parameters = WarmupHMC.reparametrization_parameters.([lhs, rhs])
rlhs = WarmupHMC.reparametrize(lhs, parameters[2])
lrlhs = WarmupHMC.reparametrize(rlhs, parameters[1])
@test rmse(parameters[2], WarmupHMC.reparametrization_parameters(rlhs)) <= tol
@test rmse(parameters[1], WarmupHMC.reparametrization_parameters(lrlhs)) <= tol
end
count_nan(x) = sum(map(count_nan, x))
count_nan(x::Real) = isnan(x) ? 1 : 0
nan_test(lhs, rhs, draws=test_draws(lhs), tol=1e-4) = begin
rdraws = WarmupHMC.reparametrize(lhs, rhs, draws)
@test count_nan(WarmupHMC.lpdf_and_invariants.([lhs], eachcol(draws))) == 0
@test count_nan(rdraws) == 0
end
rmse_test(lhs, rhs, draws=test_draws(lhs), tol=1e-4) = begin
rdraws = WarmupHMC.reparametrize(lhs, rhs, draws)
lrdraws = WarmupHMC.reparametrize(rhs, lhs, rdraws)
@test rmse(draws, lrdraws) < tol
end
loss_test(lhs, rhs, draws=test_draws(lhs)) = begin
parameters = WarmupHMC.reparametrization_parameters.([lhs, rhs])
loss = WarmupHMC.reparametrization_loss_function(lhs, draws)
lloss, rloss = loss.(parameters)
@test lloss <= rloss
end
easy_convergence_test(lhs, rhs, draws=test_draws(lhs)) = begin
flhs = WarmupHMC.find_reparametrization(:ReverseDiff, lhs, draws)
lp, rp, fp = WarmupHMC.reparametrization_parameters.([lhs, rhs, flhs])
@test rmse(lp, fp) <= rmse(rp, fp)
end
hard_convergence_test(lhs, rhs, draws=test_draws(lhs); kwargs...) = begin
rdraws = WarmupHMC.reparametrize(lhs, rhs, draws)
flhs = WarmupHMC.find_reparametrization(:ReverseDiff, rhs, rdraws; kwargs...)
lp, rp, fp = WarmupHMC.reparametrization_parameters.([lhs, rhs, flhs])
@test rmse(lp, fp) <= rmse(rp, fp)
end
ChainRulesTestUtils.test_approx(actual::Distribution, expected::Distribution, args...; kwargs...) = test_approx(params(actual), params(expected), args...; kwargs...)
sensitivity_tests(dists, draws) = begin
broadcast(dists, draws) do dist, q
# for dist in dists, q in draws
lq = log(q)
x = _invlogcdf(dist, lq)
re_lq = _logcdf(dist, x)
re_q = exp(re_lq)
@test q ≈ re_q
test_rrule(_logcdf, dist, x)
test_rrule(_invlogcdf, dist, lq)
end
end
rng = Xoshiro(0)
n_parametrizations = 12
n_parameters = 4
n_draws = 100
# xi = randn(rng, (n_parameters, n_draws))
cs = exp.(randn(rng, n_parametrizations))
scales = exp.(randn(rng, n_parametrizations))
concentrations = [
c .* exp.(scale .* randn(rng, n_parameters))
for (c, scale) in zip(cs, scales)
]
hierarchies = [
ScaleHierarchy(Normal(), rand(rng, n_parameters))
for concentration in concentrations
]
mean_shifts = [
MeanShift(Normal(), randn(rng, n_parameters))
for concentration in concentrations
]
simplices = [
GammaSimplex(Dirichlet(ones(length(concentration))), Dirichlet(concentration))
for concentration in concentrations
]
r2d2s = [
R2D2(Normal(), Normal(), rand(rng, simplices), ScaleHierarchy([], rand(rng, n_parameters)))
for concentration in concentrations
]
n_functions = 3
hsgps = [
HSGP(
MeanShift(Normal(), randn(rng, n_functions)),
Normal(),
Normal(),
# ScaleHierarchy([], 1e-3.+zeros(n_functions))
ScaleHierarchy([], rand(rng, n_functions))
)
for concentration in concentrations
]
# Directional = ReparametrizableDistributions.Directional
test_draws(lhs::Directional; seed=0, rng=Xoshiro(seed), n_draws=100) = begin
# return randn(rng, (length(lhs), n_draws))
location = randn(rng, length(lhs))
# location .*= (median(lhs.info.radius)) / norm(location)
location .*= sqrt(median(lhs.info.radius_squared)) / norm(location)
location .+ randn(rng, (length(lhs), n_draws))
end
directionals2 = [
Directional(2, exp(4 + 4 * randn(rng)))
for _ in 1:8
]
# directionals2 = Directional.(2, exp.(3 .+ 2 .* randn(rng, 8)))
# directionals4 = Directional.(4, exp.(randn(rng, length(concentrations))))
# plots = broadcast(directionals2, reshape(directionals2, (1,:))) do lhs, rhs
# println("====================")
# d0 = Directional(2, 0)
# @time draws = test_draws(lhs, rng=rng)
# @time parameters = WarmupHMC.reparametrization_parameters.([lhs, rhs])
# @time loss = WarmupHMC.reparametrization_loss_function(lhs, draws)
# @time lloss, rloss = loss.(parameters)
# @time rdraws = WarmupHMC.reparametrize(lhs, rhs, draws)
# @time zdraws = WarmupHMC.reparametrize(lhs, d0, draws)
# # rdraws = test_draws(rhs, rng=rng)
# @time Scatter(eachrow(draws)..., label=lloss) + Scatter(eachrow(rdraws)..., label=rloss) + Scatter(eachrow(zdraws)..., label=loss([-Inf])) + Scatter([0], [0], color=:black)
# # println("====================")
# # scatter!(p, eachrow(tdraws)...)
# end
# Figure(plots)
# WarmupHMC.reparametrize(source::ADGradientWrapper, )
# using WarmupHMC, Optim, ReverseDiff
# WarmupHMC.find_reparametrization(::Val{:ReverseDiff}, source, draws::AbstractMatrix; iterations=5, method=LBFGS(), verbose=false) = begin
# loss = WarmupHMC.reparametrization_loss_function(source, draws)
# init_arg = WarmupHMC.reparametrization_parameters(source)
# # loss_tape = ReverseDiff.compile(ReverseDiff.GradientTape(loss, init_arg))
# loss_g!(g, arg) = ReverseDiff.gradient!(g, loss, arg)
# optimization_result = optimize(
# loss, loss_g!, init_arg, method,
# Optim.Options(iterations=iterations)
# )
# verbose && display(optimization_result)
# WarmupHMC.reparametrize(source, Optim.minimizer(optimization_result))
# end
@testset "All Tests" begin
n_sensitivity_tests = 10
gammas = Gamma.(exp.(randn(rng, n_sensitivity_tests)), exp.(randn(rng, n_sensitivity_tests)))
ncss = NoncentralChisq.(exp.(randn(rng, n_sensitivity_tests)), exp.(randn(rng, n_sensitivity_tests)))
qs = rand(rng, n_sensitivity_tests)
@testset "Sensitivities" begin
# @testset "Gamma" sensitivity_tests(gammas, qs)
@testset "NoncentralChisq" sensitivity_tests(ncss, qs)
end
@testset "Transformation tests" begin
# @testset "ScaleHierarchy" transformation_tests(hierarchies)
# @testset "MeanShift" transformation_tests(mean_shifts)
# @testset "GammaSimplex" transformation_tests(simplices)
# @testset "R2D2" transformation_tests(r2d2s)
# @testset "HSGP" transformation_tests(hsgps, (test_draws(hsgps[1])); iterations=50)
# @testset "Directionals2" transformation_tests(directionals2)
# @testset "Directionals4" transformation_tests(directionals4)
end
@testset "DynamicHMC" begin
# mcmc_with_warmup(rng, ADgradient(:ReverseDiff, directionals2[1]), 1000)
end
end
mcmc_with_reparametrization(rng, ADgradient(:ReverseDiff, directionals2[6]), 1000).final_reparametrization_state.reparametrization |> parent |> WarmupHMC.reparametrization_parameters
WarmupHMC.mcmc_keep_reparametrization(
rng, ADgradient(:ReverseDiff, directionals2[6]), 1000
)
mcmc_with_reparametrization(rng, ADgradient(:ReverseDiff, hierarchies[1]), 1000).final_reparametrization_state.reparametrization |> parent |> WarmupHMC.reparametrization_parameters
mcmc_with_reparametrization(rng, ADgradient(:ReverseDiff, simplices[1]), 1000).final_reparametrization_state.reparametrization |> parent |> WarmupHMC.reparametrization_parameters
mcmc_with_reparametrization(rng, ADgradient(:ReverseDiff, hsgps[1]), 1000)
WarmupHMC.reparametrization_parameters(::Any) = Float64[]
mcmc_with_reparametrization(rng, ADgradient(:ReverseDiff, r2d2s[1]), 1000)
loss_matrix(parametrizations) = begin
draws = (test_draws(parametrizations[1]))
rv = pairwise(parametrizations) do lhs, rhs
parameters = WarmupHMC.reparametrization_parameters(rhs)
loss = WarmupHMC.reparametrization_loss_function(lhs, draws)
loss(parameters)
end
rv .-= diag(rv)
rv
end
diff_matrix(parametrizations) = pairwise(parametrizations) do lhs, rhs
rmse(WarmupHMC.reparametrization_parameters.((lhs, rhs))...)
end
scatter_matrix(parametrizations) = begin
draws = test_draws(parametrizations[1], n_draws=1000)
pairwise(parametrizations) do lhs, rhs
rdraws = WarmupHMC.reparametrize(lhs, rhs, draws)
scatter(rdraws[1,:], rdraws[2,:])
end
end
# plot(scatter_matrix(mean_shifts[1:4])..., size=(1600, 1600))
# loss_matrix(mean_shifts)
LocScaleHierarchy = ReparametrizableDistributions.LocScaleHierarchy
WarmupHMC.lpdf_and_invariants(source::UnivariateDistribution, draw::AbstractVector, lpdf=0.) = begin
lpdf += sum(logpdf.(source, draw))
(;lpdf, draw)
end
WarmupHMC.lja_reparametrize(source::UnivariateDistribution, target::UnivariateDistribution, invariants::NamedTuple, lja=0.) = begin
lja, invariants.draw
end
using Logging, LogDensityProblems
debug_logger = ConsoleLogger(stderr, Logging.Debug)
with_logger(debug_logger) do
n = 16
post = heteroskedastic_gp(
rand(Uniform(-1,1), 10), missing,
1.5, randn(n), zeros(n), randn(n), zeros(n)
)
xi = randn(length(post))
xi |> display
WarmupHMC.lpdf_and_invariants(post, xi) |> display
WarmupHMC.lja_reparametrize(post, post, xi) |> display
rv = mcmc_with_reparametrization(rng, ADgradient(:ReverseDiff, post), 1000)
rv |> display
WarmupHMC.lpdf_and_invariants(post, rv.posterior_matrix[:, 1]) |> display
end
| ReparametrizableDistributions | https://github.com/nsiccha/ReparametrizableDistributions.jl.git |
|
[
"MIT"
] | 0.1.0 | d064f853e5eca1d684a85b943723dacc9e0f6d7c | docs | 886 | # ReparametrizableDistributions.jl
Implements functionality to reparametrize distributions/posteriors to make them easier to sample from using MCMC methods.
## Installation
Initialize julia project if not done yet, see e.g. [https://pkgdocs.julialang.org/v1/environments/](https://pkgdocs.julialang.org/v1/environments/).
In short, something like:
```{.bash}
# Start julia REPL with project defined in current directory
julia --project=.
```
From that REPL, run:
```{.julia}
# Enter julia package manager
]
# Add registered external packages
add Optim ReverseDiff Random Distributions
# Add reparametrization package
add https://github.com/nsiccha/ReparametrizableDistributions.jl
```
After doing that, you should be able to run one of the examples at [https://nsiccha.github.io/ReparametrizableDistributions.jl/](https://nsiccha.github.io/ReparametrizableDistributions.jl/). | ReparametrizableDistributions | https://github.com/nsiccha/ReparametrizableDistributions.jl.git |
|
[
"MIT"
] | 0.1.0 | d064f853e5eca1d684a85b943723dacc9e0f6d7c | docs | 83 | ---
listing:
contents: examples
---
{{< include ../README.md >}}
## Examples
| ReparametrizableDistributions | https://github.com/nsiccha/ReparametrizableDistributions.jl.git |
|
[
"MIT"
] | 0.1.0 | d064f853e5eca1d684a85b943723dacc9e0f6d7c | docs | 1447 | ---
title: "Scale hierarchy reparametrization using `CmdStanR` and `JuliaCall`"
date: 2023/11/14
execute:
cache: false
---
Using `ReparametrizableDistributions.jl` from R to reparametrize a Stan model using `CmdStanR` and `JuliaCall`.
## Initializing, fitting, reparametrizing and refitting
```{r}
#| output: false
library(pacman)
p_load(cmdstanr, posterior, JuliaCall)
julia_library("Pkg")
julia_command("Pkg.activate(\"..\")")
julia_library("ReparametrizableDistributions")
julia_library("Optim")
julia_library("ReverseDiff")
mod_grp <- cmdstan_model("stan/dynamic.stan")
ng <- 10
n_obs = 100
data_grp <- list(
N = n_obs * ng,
K = ng,
x = rep(1:ng, n_obs)
)
data_grp$y <- rnorm(ng*n_obs,mean=data_grp$x)
data_grp$centeredness <- rep(0, ng)
fit <- mod_grp$sample(data = data_grp)
d <- fit$draws(c("mu", "log_sigma0"))
log_sigma0 <- t(matrix(extract_variable(d, "log_sigma0")))
mu <- t(matrix(subset_draws(d, "mu"), ncol = ng))
data_grp$centeredness <- julia_call("ReparametrizableDistributions.find_centeredness", log_sigma0, mu, rep(0, ng))
afit <- mod_grp$sample(data = data_grp, chains = 4)
```
## Initial fit diagnostics and summary
```{r}
fit$diagnostic_summary()
fit$summary(c("sigma0", "sigma", "mu"))
```
## Refit diagnostics and summary
```{r}
data_grp$centeredness
afit$diagnostic_summary()
afit$summary(c("sigma0", "sigma", "mu"))
```
# Appendix
## stan/dynamic.stan
```{.stan include="stan/dynamic.stan"}
``` | ReparametrizableDistributions | https://github.com/nsiccha/ReparametrizableDistributions.jl.git |
|
[
"MIT"
] | 0.1.0 | d064f853e5eca1d684a85b943723dacc9e0f6d7c | docs | 1282 | ---
title: "Scale hierarchy reparametrization"
date: 2023/11/13
---
Finding the best centeredness for a scale hierarchy using independent draws from a funnel.
## Independently sampling from the funnel
```{julia}
using Random, Distributions, DynamicPlots
rng = Xoshiro(0)
n_parameters = 999
n_draws = 1000
log_scales = rand(rng, Normal(), (n_parameters, n_draws))
xi = rand(rng, Normal(), (n_parameters, n_draws))
x = exp.(log_scales) .* xi
Figure([
Scatter(x[1, :], log_scales[1, :], xlabel="x1", ylabel="log scale", title="\ncentered"),
Scatter(xi[1, :], log_scales[1, :], xlabel="xi1", ylabel="log scale", title="\nnon-centered"),
], plot_title="Centered vs non-centered parametrization")'
```
## Reparametrizing the funnel
```{julia}
# Currently, the three below "imports" are needed
using Optim, ReverseDiff, ReparametrizableDistributions
@time centeredness = ReparametrizableDistributions.find_centeredness(
log_scales, x, ones(n_parameters)
)
```
## Visualizing the found parametrization parameters
```{julia}
using DynamicPlots
ECDFPlot(centeredness, xlabel="centeredness", label="estimated") + Vline([0], label="ideal")
```
(The above visualizations uses the `DynamicPlots` package, but any other plotting packages works as well or better.) | ReparametrizableDistributions | https://github.com/nsiccha/ReparametrizableDistributions.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | code | 1991 | using SparseArrays, MatrixNetworks, Graphs, SimpleWeightedGraphs
using SimpleValueGraphs
# using IndexedGraphs
include("../src/IndexedGraphs.jl")
using .IndexedGraphs
using Random
using LinearAlgebra
# build directed graph
N = 10_000
W = sprand(N, N, 5/N)
# remove self loops
for i in 1:size(W,2); W[i,i] = 0; end
dropzeros!(W)
W = W + W'
w = sparse(UpperTriangular(W)).nzval # unique wights for Graph
wD = nonzeros(permutedims(W)) # duplicate weights for DiGraph
# pick source at random
rng = MersenneTwister(0)
s = rand(rng, 1:size(W,2))
g = IndexedGraph(W)
gD = IndexedDiGraph(W)
g_MN = MatrixNetwork(W)
g_Graphs = SimpleGraph(W)
g_SWG = SimpleWeightedGraph(W)
g_SVG = ValGraph(g_Graphs,
edgeval_types=(Float64,), edgeval_init=(s, d) -> (W[s,d],))
ds_IG = dijkstra_shortest_paths(g, s, w)
d_IG = ds_IG.dists; p_IG = ds_IG.parents
ds_IDG = dijkstra_shortest_paths(gD, s, wD)
d_IDG = ds_IDG.dists; p_IDG = ds_IDG.parents
d_MN, p_MN = MatrixNetworks.dijkstra(g_MN, s)
ds_Graphs = dijkstra_shortest_paths(g_Graphs, s, W)
d_Graphs = ds_Graphs.dists; p_Graphs = ds_Graphs.parents
ds_SWG = dijkstra_shortest_paths(g_SWG, s)
d_SWG = ds_SWG.dists; p_SWG = ds_SWG.parents
ds_SVG = SimpleValueGraphs.Experimental.dijkstra_shortest_paths(g_SVG, s)
d_SVG = ds_SVG.dists; p_SVG = ds_SVG.parents
# check that results are correct
@assert d_IG == d_MN == d_Graphs == d_SWG == d_SVG == d_IDG
@assert p_IG == p_MN == p_Graphs == p_SWG == p_SVG == p_IDG
### BENCHMARK
using BenchmarkTools
println("IndexedDiGraph:")
@btime dijkstra_shortest_paths($gD, $s, $wD)
println("IndexedGraph:")
@btime dijkstra_shortest_paths($g, $s, $w)
println("MatrixNetwork:")
@btime MatrixNetworks.dijkstra($g_MN, $s)
println("SimpleGraph")
@btime dijkstra_shortest_paths($g_Graphs, $s, $W)
println("SimpleWeightedGraph:")
@btime dijkstra_shortest_paths($g_SWG, $s);
println("ValGraph (SimpleValueGraphs.Experimental):")
@btime SimpleValueGraphs.Experimental.dijkstra_shortest_paths($g_SVG, $s); | IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | code | 494 | using Documenter, IndexedGraphs, Graphs, Random
makedocs(sitename="IndexedGraphs Documentation",
# format = Documenter.HTML(prettyurls = false),
pages = [
"Home" => "index.md",
"Graph types" => [
"graph.md",
"bidigraph.md",
"digraph.md",
"bipartite.md"
],
"Reference" => "reference.md"
]
)
deploydocs(
repo = "github.com/stecrotti/IndexedGraphs.jl.git",
push_preview = true,
) | IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | code | 2690 | module IndexedGraphs
using SparseArrays: sparse, SparseMatrixCSC, nnz, nzrange, rowvals, nonzeros, spzeros
using Graphs: Graphs, AbstractGraph, SimpleGraph, AbstractSimpleGraph, AbstractEdge,
src, dst, edgetype, has_vertex, has_edge, ne, nv,
edges, vertices, neighbors, inneighbors, outneighbors, is_directed, is_bipartite,
bipartite_map, DijkstraState, dijkstra_shortest_paths,
prufer_decode
import Graphs: degree
using Graphs.LinAlg
using LinearAlgebra: LinearAlgebra, issymmetric
using Random: AbstractRNG, default_rng
using StatsBase: sample
using TrackingHeaps: TrackingHeap, pop!, NoTrainingWheels, MinHeapOrder
export
# Graphs.jl
src, dst, edgetype, has_vertex, has_edge, ne, nv, adjacency_matrix, degree,
edges, vertices, neighbors, inneighbors, outneighbors, is_directed, is_bipartite,
# Base
==, iterate,
# IndexedGraphs
AbstractIndexedGraph, inedges, outedges, idx,
# undirected graphs
IndexedGraph, get_edge,
# directed graphs
AbstractIndexedDiGraph, IndexedDiGraph, IndexedBiDiGraph,
# bipartite graphs
BipartiteIndexedGraph, Left, Right, LeftorRight, BipartiteGraphVertex,
nv_left, nv_right, vertex, linearindex, vertices_left, vertices_right,
vertex_left, vertex_right,
is_directed, issymmetric,
bidirected_with_mappings,
rand_bipartite_graph, rand_regular_bipartite_graph, rand_bipartite_tree
"""
AbstractIndexedEdge{T<:Integer} <: AbstractEdge{T}
Abstract type for indexed edge.
`AbstractIndexedEdge{T}`s must have the following elements:
- `idx::T` integer positive index
"""
abstract type AbstractIndexedEdge{T<:Integer} <: AbstractEdge{T}; end
"""
IndexedEdge{T<:Integer} <: AbstractIndexedEdge{T}
Edge type for `IndexedGraph`s. Edge indices can be used to access edge
properties stored in separate containers.
"""
struct IndexedEdge{T<:Integer} <: AbstractIndexedEdge{T}
src::T
dst::T
idx::T
end
Graphs.src(e::IndexedEdge) = e.src
Graphs.dst(e::IndexedEdge) = e.dst
idx(e::AbstractIndexedEdge) = e.idx
function Base.:(==)(e1::T, e2::T) where {T<:AbstractIndexedEdge}
fns = fieldnames(T)
all( getproperty(e1, fn) == getproperty(e2, fn) for fn in fns )
end
function Base.show(io::IO, e::AbstractIndexedEdge)
print(io, "Indexed Edge $(src(e)) => $(dst(e)) with index $(idx(e))")
end
Base.iterate(e::IndexedEdge, args...) = iterate((e.src, e.dst, e.idx), args...)
include("utils.jl")
include("abstractindexedgraph.jl")
include("indexedgraph.jl")
include("abstractindexeddigraph.jl")
include("indexeddigraph.jl")
include("indexedbidigraph.jl")
include("bipartiteindexedgraph.jl")
include("algorithms/dijkstra.jl")
end # end module
| IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | code | 1612 | """
AbstractIndexedDiGraph{T} <: AbstractIndexedGraph{T}
Abstract type for representing directed graphs.
"""
abstract type AbstractIndexedDiGraph{T} <: AbstractIndexedGraph{T}; end
Graphs.edges(g::AbstractIndexedDiGraph) = @inbounds (IndexedEdge{Int}(i, g.A.rowval[k], k) for i=1:size(g.A,2) for k=nzrange(g.A,i))
Graphs.ne(g::AbstractIndexedDiGraph) = nnz(g.A)
Graphs.is_directed(g::AbstractIndexedDiGraph) = true
Graphs.is_directed(::Type{<:AbstractIndexedDiGraph}) = true
"""
outedges(g::AbstractIndexedDiGraph, i::Integer)
Return a lazy iterator to the edges outgoing from node `i` in `g`.
"""
outedges(g::AbstractIndexedDiGraph, i::Integer) = @inbounds (IndexedEdge{Int}(i, g.A.rowval[k], k) for k in nzrange(g.A, i))
edge_idx(g::AbstractIndexedDiGraph, src::Integer, dst::Integer) = nzindex(g.A, dst, src)
edge_src_dst(g::AbstractIndexedDiGraph, id::Integer) = reverse(nzindex(g.A, id))
"""
get_edge(g::AbstractIndexedDiGraph, src::Integer, dst::Integer)
get_edge(g::AbstractIndexedDiGraph, id::Integer)
Get edge given source and destination or given edge index.
"""
function get_edge(g::AbstractIndexedDiGraph, src::Integer, dst::Integer)
id = edge_idx(g, src, dst)
IndexedEdge(src, dst, id)
end
function get_edge(g::AbstractIndexedDiGraph, id::Integer)
i, j = edge_src_dst(g, id)
IndexedEdge(i, j, id)
end
# Returns sparse adj matrix. Elements default to Int (to match Graphs)
function Graphs.LinAlg.adjacency_matrix(g::AbstractIndexedDiGraph, T::DataType=Int)
M = sparse(transpose(g.A))
SparseMatrixCSC(M.m, M.n, M.colptr, M.rowval, ones(T, nnz(M)))
end | IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | code | 1183 | """
AbstractIndexedGraph{T} <: AbstractGraph{T}
An abstract type representing an indexed graph.
`AbstractIndexedGraph`s must have the following elements:
- `A::SparseMatrixCSC` adjacency matrix
"""
abstract type AbstractIndexedGraph{T} <: AbstractGraph{T} end
function Base.show(io::IO, g::AbstractIndexedGraph{T}) where T
s = is_directed(g) ? "directed" : "undirected"
println(io, "{$(nv(g)), $(ne(g))} ", s, " AbstractIndexedGraph{$T}")
end
Base.eltype(::AbstractIndexedGraph{T}) where T = T
Graphs.edgetype(::AbstractIndexedGraph{T}) where T = IndexedEdge{T}
Graphs.has_vertex(g::AbstractIndexedGraph, i::Integer) = i ≤ size(g.A, 2)
Graphs.has_edge(g::AbstractIndexedGraph, i::Integer, j::Integer) = g.A[i,j] != 0
Graphs.nv(g::AbstractIndexedGraph) = size(g.A, 2)
Graphs.vertices(g::AbstractIndexedGraph) = 1:size(g.A, 2)
Graphs.outneighbors(g::AbstractIndexedGraph, i::Integer) = @inbounds @view g.A.rowval[nzrange(g.A,i)]
# Returns sparse adj matrix. Elements default to Int (to match Graphs)
function Graphs.LinAlg.adjacency_matrix(g::AbstractIndexedGraph, T::DataType=Int)
SparseMatrixCSC(g.A.m, g.A.n, g.A.colptr, g.A.rowval, ones(T, nnz(g.A)))
end | IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | code | 14136 | """
BipartiteIndexedGraph{T<:Integer} <: AbstractIndexedGraph{T}
A type representing a sparse, undirected bipartite graph.
### FIELDS
- `A` -- adjacency matrix filled with `NullNumber`s. Rows are vertices belonging to the left block, columns to the right block
- `X` -- square matrix for efficient access by row. `X[j,i]` points to the index of element `A[i,j]` in `A.nzval`.
"""
struct BipartiteIndexedGraph{T<:Integer} <: AbstractIndexedGraph{T}
A :: SparseMatrixCSC{NullNumber, T}
X :: SparseMatrixCSC{T, T}
end
function BipartiteIndexedGraph(A::AbstractMatrix{NullNumber})
A = sparse(A)
X = sparse(SparseMatrixCSC(A.m, A.n, A.colptr, A.rowval, collect(1:nnz(A)))')
BipartiteIndexedGraph(A, X)
end
"""
BipartiteIndexedGraph(A::AbstractMatrix)
Construct a `BipartiteIndexedGraph` from adjacency matrix `A` with the convention that
rows are vertices belonging to the left block, columns to the right block
"""
function BipartiteIndexedGraph(A::AbstractMatrix)
A = sparse(A)
BipartiteIndexedGraph(SparseMatrixCSC(A.m, A.n, A.colptr, A.rowval, fill(NullNumber(), length(A.nzval))))
end
"""
BipartiteIndexedGraph(g::AbstractGraph)
Build a `BipartiteIndexedGraph` from any undirected, bipartite graph.
"""
function BipartiteIndexedGraph(g::AbstractGraph)
is_directed(g) && throw(ArgumentError("Only an undirected graph can be converted into a `BipartiteIndexedGraph`"))
is_bipartite(g) || throw(ArgumentError("Graph must be bipartite"))
bm = bipartite_map(g)
p = vcat([i for i in eachindex(bm) if bm[i]==1], [i for i in eachindex(bm) if bm[i]==2])
pl = [i for i in eachindex(bm) if bm[i]==1]
pr = [i for i in eachindex(bm) if bm[i]==2]
nl = sum(isequal(1), bm)
A = adjacency_matrix(g)[p,p][nl+1:end, 1:nl]
A = adjacency_matrix(g)[pl, pr]
return BipartiteIndexedGraph(A)
end
function Base.show(io::IO, g::BipartiteIndexedGraph{T}) where T
nl = nv_left(g)
nr = nv_right(g)
ned = ne(g)
println(io, "BipartiteIndexedGraph{$T} with $nl + $nr vertices and $ned edges")
end
"""
nv_left(g::BipartiteIndexedGraph)
Return the number of vertices in the left block
"""
nv_left(g::BipartiteIndexedGraph) = size(g.A, 1)
"""
nv_right(g::BipartiteIndexedGraph)
Return the number of vertices in the right block
"""
nv_right(g::BipartiteIndexedGraph) = size(g.A, 2)
Graphs.ne(g::BipartiteIndexedGraph) = nnz(g.A)
Graphs.nv(g::BipartiteIndexedGraph) = nv_left(g) + nv_right(g)
Graphs.is_directed(g::BipartiteIndexedGraph) = false
Graphs.is_directed(::Type{BipartiteIndexedGraph{T}}) where T = false
Graphs.is_bipartite(g::BipartiteIndexedGraph) = true
"""
Left
Singleton type used to represent a vertex belonging to the left block in a [`BipartiteGraphVertex`](@ref)
"""
struct Left end
"""
Right
Singleton type used to represent a vertex belonging to the ` Right` block in a [`BipartiteGraphVertex`](@ref)
"""
struct Right end
"""
LeftorRight
`LeftorRight = Union{Left, Right}`
"""
LeftorRight = Union{Left, Right}
"""
BipartiteGraphVertex
A `BipartiteGraphVertex{LR<:LeftorRight,T<:Integer}` represents a vertex in a bipartite graph.
### PARAMETERS
- `LR` -- Either [`Left`](@ref) or [`Right`](@ref)
### FIELDS
- `i` -- The index of the vertex within its block.
"""
struct BipartiteGraphVertex{LR<:LeftorRight,T<:Integer}
i :: T
function BipartiteGraphVertex{LR}(i::T) where {LR<:LeftorRight,T<:Integer}
i > 0 || throw(ArgumentError("Vertex index must be positive, got $i"))
new{LR,T}(i)
end
end
"""
vertex(i::Integer, ::Type{<:LeftorRight})
Build a [`BipartiteGraphVertex`](@ref)
"""
vertex(i::Integer, ::Type{LR}) where LR<:LeftorRight = BipartiteGraphVertex{LR}(i)
"""
vertex(g::BipartiteIndexedGraph, i::Integer)
Build the [`BipartiteGraphVertex`](@ref) corresponding to linear index `i`.
Throws an error if `i` is not in the range of vertices of `g`
"""
function vertex(g::BipartiteIndexedGraph, i::Integer)
has_vertex(g, i) || throw(ArgumentError("Index $i not in range of vertices."))
nl = nv_left(g)
if 1 ≤ i ≤ nl
return vertex(i, Left)
else
return vertex(i - nl, Right)
end
end
"""
linearindex(g::BipartiteIndexedGraph, v::BipartiteGraphVertex{LR}) where {LR<:LeftorRight}
linearindex(g::BipartiteIndexedGraph, i::Integer, ::Type{LR}) where LR<:LeftorRight
Return the linear index of a vertex, specified either by a [`BipartiteGraphVertex`](@ref) or by its index and block.
"""
linearindex(g::BipartiteIndexedGraph, r::BipartiteGraphVertex{Right}) = r.i + nv_left(g)
linearindex(::BipartiteIndexedGraph, l::BipartiteGraphVertex{Left}) = l.i
function linearindex(g::BipartiteIndexedGraph, i::Integer, ::Type{LR}) where LR<:LeftorRight
return linearindex(g, vertex(i, LR))
end
Graphs.edgetype(::BipartiteIndexedGraph{T}) where T = IndexedEdge{T}
function Graphs.edges(g::BipartiteIndexedGraph{T}) where T
(IndexedEdge(linearindex(g, g.A.rowval[k], Left), linearindex(g, j, Right), k)
for j=1:size(g.A,2) for k=nzrange(g.A,j))
end
Graphs.vertices(g::BipartiteIndexedGraph) = 1:nv(g)
Graphs.has_vertex(g::BipartiteIndexedGraph, i::Integer) = i ∈ vertices(g)
"""
vertices_left(g::BipartiteIndexedGraph)
Return a lazy iterator to the vertices in the left block
"""
vertices_left(g::BipartiteIndexedGraph) = 1:nv_left(g)
"""
vertices_right(g::BipartiteIndexedGraph)
Return a lazy iterator to the vertices in the right block
"""
vertices_right(g::BipartiteIndexedGraph) = nv_left(g)+1:nv(g)
_checkrightindex(g::BipartiteIndexedGraph, i::Integer) = nv_left(g) + 1 ≤ i ≤ nv(g)
Graphs.has_edge(g::BipartiteIndexedGraph, e::IndexedEdge) = e ∈ edges(g)
function Graphs.has_edge(g::BipartiteIndexedGraph, s::Integer, d::Integer)
(has_vertex(g, s) && has_vertex(g, d)) || return false
l, rlin = extrema((s, d))
_checkrightindex(g, rlin) || return false
r = vertex(g, rlin).i
return !iszero(g.A[l, r])
end
_ordered_edge(e::IndexedEdge) = extrema((src(e), dst(e)))
"""
vertex_left(g::BipartiteIndexedGraph, e::IndexedEdge)
Return the (in-block) index of the left-block vertex in `e`.
"""
function vertex_left(g::BipartiteIndexedGraph, e::IndexedEdge)
l, rlin = _ordered_edge(e)
return vertex(g, l).i
end
"""
vertex_right(g::BipartiteIndexedGraph, e::IndexedEdge)
Return the (in-block) index of the right-block vertex in `e`.
"""
function vertex_right(g::BipartiteIndexedGraph, e::IndexedEdge)
l, rlin = _ordered_edge(e)
return vertex(g, rlin).i
end
"""
inneighbors(g::BipartiteIndexedGraph, v::BipartiteGraphVertex{<:LeftorRight})
Return a lazy iterator to the neighbors of variable `v` specified by a [`BipartiteGraphVertex`](@ref).
"""
function Graphs.inneighbors(g::BipartiteIndexedGraph, l::BipartiteGraphVertex{Left})
return (linearindex(g, r, Right) for r in @view g.X.rowval[nzrange(g.X, l.i)])
end
function Graphs.inneighbors(g::BipartiteIndexedGraph, r::BipartiteGraphVertex{Right})
return @view g.A.rowval[nzrange(g.A, r.i)]
end
"""
inneighbors(g::BipartiteIndexedGraph, i::Integer)
Return a lazy iterator to the neighbors of variable `i` specified by its linear index.
"""
Graphs.inneighbors(g::BipartiteIndexedGraph, i::Integer) = inneighbors(g, vertex(g, i))
"""
outneighbors(g::BipartiteIndexedGraph, v::BipartiteGraphVertex{<:LeftorRight})
Return a lazy iterator to the neighbors of variable `v` specified by a [`BipartiteGraphVertex`](@ref).
"""
Graphs.outneighbors(g::BipartiteIndexedGraph, v::BipartiteGraphVertex) = inneighbors(g, v)
"""
outneighbors(g::BipartiteIndexedGraph, i::Integer)
Return a lazy iterator to the neighbors of variable `i` specified by its linear index.
"""
Graphs.outneighbors(g::BipartiteIndexedGraph, i::Integer) = inneighbors(g, i)
"""
degree(g::BipartiteIndexedGraph, v::BipartiteGraphVertex)
Return the degree of variable `v` specified by a [`BipartiteGraphVertex`](@ref).
"""
Graphs.degree(g::BipartiteIndexedGraph, v::BipartiteGraphVertex) = length(inneighbors(g, v))
"""
inedges(g::BipartiteIndexedGraph, v::BipartiteGraphVertex{<:LeftorRight})
Return a lazy iterator to the edges incident on a variable `v` specified by a [`BipartiteGraphVertex`](@ref), with `v` as the destination.
"""
function inedges(g::BipartiteIndexedGraph, l::BipartiteGraphVertex{Left})
return (
IndexedEdge(linearindex(g, g.X.rowval[k], Right), linearindex(g, l), g.X.nzval[k])
for k in nzrange(g.X, l.i)
)
end
function inedges(g::BipartiteIndexedGraph, r::BipartiteGraphVertex{Right})
return (
IndexedEdge(linearindex(g, g.A.rowval[k], Left), linearindex(g, r), k)
for k in nzrange(g.A, r.i)
)
end
"""
inedges(g::BipartiteIndexedGraph, i::Integer)
Return a lazy iterator to the edges incident on a variable `i` specified by its linear index, with `i` as the destination.
"""
inedges(g::BipartiteIndexedGraph, i::Integer) = inedges(g, vertex(g, i))
"""
outedges(g::BipartiteIndexedGraph, v::BipartiteGraphVertex{<:LeftorRight})
Return a lazy iterator to the edges incident on a variable `v` specified by a [`BipartiteGraphVertex`](@ref), with `v` as the source.
"""
function outedges(g::BipartiteIndexedGraph, l::BipartiteGraphVertex{Left})
return (
IndexedEdge(linearindex(g, l), linearindex(g, g.X.rowval[k], Right), g.X.nzval[k])
for k in nzrange(g.X, l.i)
)
end
function outedges(g::BipartiteIndexedGraph, r::BipartiteGraphVertex{Right})
return (
IndexedEdge(linearindex(g, r), linearindex(g, g.A.rowval[k], Left), k)
for k in nzrange(g.A, r.i)
)
end
"""
outedges(g::BipartiteIndexedGraph, i::Integer)
Return a lazy iterator to the edges incident on a variable `i` specified by its linear index, with `i` as the source.
"""
outedges(g::BipartiteIndexedGraph, i::Integer) = outedges(g, vertex(g, i))
"""
adjacency_matrix(g::BipartiteIndexedGraph, T::DataType=Int)
Return the symmetric adjacency matrix of size `nv(g) = nv_left(g) + nv_right(g)`
where no distinction is made between left and right nodes.
"""
function Graphs.adjacency_matrix(g::BipartiteIndexedGraph, T::DataType=Int)
m, n = nv_left(g), nv_right(g)
A = SparseMatrixCSC(g.A.m, g.A.n, g.A.colptr, g.A.rowval, ones(T, nnz(g.A)))
return [ spzeros(T, m, m) A ;
A' spzeros(T, n, n) ]
end
##### GENERATORS
"""
rand_bipartite_graph([rng=default_rng()], nleft, nright, ned)
Create a bipartite graph with `nleft` nodes in the left block, `nright` nodes in the right block and `ned` edges taken uniformly at random.
"""
function rand_bipartite_graph(rng::AbstractRNG, nleft::Integer, nright::Integer, ned::Integer)
nleft > 0 || throw(ArgumentError("Number of variable nodes must be positive, got $nleft"))
nright > 0 || throw(ArgumentError("Number of left nodes must be positive, got $nright"))
ned > 0 || throw(ArgumentError("Number of edges must be positive, got $ned"))
nedmax = nleft * nright
ned ≤ nedmax || throw(ArgumentError("Maximum number of edges is $nleft*$nright=$nedmax, got $ned"))
I = zeros(Int, ned)
J = zeros(Int, ned)
K = ones(Int, ned)
n = 1
while n ≤ ned
I[n] = rand(rng, 1:nleft)
J[n] = rand(rng, 1:nright)
if !any((i,j) == (I[n], J[n]) for (i,j) in Iterators.take(zip(I,J), n-1))
n += 1
end
end
A = sparse(I, J, K, nleft, nright)
return BipartiteIndexedGraph(A)
end
function rand_bipartite_graph(nleft::Integer, nright::Integer, ned::Integer)
rand_bipartite_graph(default_rng(), nleft, nright, ned)
end
"""
rand_bipartite_graph([rng=default_rng()], nleft, nright, p)
Create a bipartite graph with `nleft` nodes in the left block, `nright` nodes in the right block and edges taken independently with probability `p`.
"""
function rand_bipartite_graph(rng::AbstractRNG, nleft::Integer, nright::Integer, p::Real)
nright > 0 || throw(ArgumentError("Number of right nodes must be positive, got $nright"))
nleft > 0 || throw(ArgumentError("Number of left nodes must be positive, got $nleft"))
0 ≤ p ≤ 1 || throw(ArgumentError("Probability must be in [0,1], got $ned"))
I = zeros(Int, 0)
J = zeros(Int, 0)
for (a, i) in Iterators.product(1:nleft, 1:nright)
if rand(rng) < p
push!(I, a)
push!(J, i)
end
end
K = ones(Int, length(I))
A = sparse(I, J, K, nleft, nright)
return BipartiteIndexedGraph(A)
end
function rand_bipartite_graph(nleft::Integer, nright::Integer, p::Real)
rand_bipartite_graph(default_rng(), nleft, nright, p)
end
"""
rand_regular_bipartite_graph([rng=default_rng()], nleft, nright, k)
Create a bipartite graph with `nleft` nodes in the left block, `nright` nodes in the right block, where all left nodes have degree `k`.
"""
function rand_regular_bipartite_graph(rng::AbstractRNG, nleft::Integer, nright::Integer,
k::Integer)
nright > 0 || throw(ArgumentError("Number of right nodes must be positive, got $nright"))
nleft > 0 || throw(ArgumentError("Number of left nodes must be positive, got $nleft"))
k > 0 || throw(ArgumentError("Degree `k` must be positive, got $k"))
k ≤ nright || throw(ArgumentError("Degree `k` must be smaller or equal than number of rights, got $k"))
I = reduce(vcat, fill(a, k) for a in 1:nleft)
J = reduce(vcat, sample(rng, 1:nright, k; replace=false) for _ in 1:nleft)
K = ones(Int, length(I))
A = sparse(I, J, K, nleft, nright)
return BipartiteIndexedGraph(A)
end
function rand_regular_bipartite_graph(nleft::Integer, nright::Integer, k::Integer)
rand_regular_bipartite_graph(default_rng(), nleft, nright, k)
end
"""
rand_bipartite_tree([rng=default_rng()], n)
Create a tree bipartite graph with `n` vertices in total. The proportion of left/right nodes is random.
"""
function rand_bipartite_tree(rng::AbstractRNG, n::Integer)
gg = prufer_decode(rand(rng, 1:n, n-2))
return BipartiteIndexedGraph(gg)
end
rand_bipartite_tree(n::Integer) = rand_bipartite_tree(default_rng(), n) | IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | code | 3771 | """
IndexedBiDiGraph{T<:Integer} <: AbstractIndexedDiGraph{T}
A type representing a sparse directed graph with access to both outedges and inedges.
### FIELDS
- `A` -- square matrix filled with `NullNumber`s. `A[i,j]` corresponds to edge `j=>i`.
- `X` -- square matrix for efficient access by row. `X[j,i]` points to the index of element `A[i,j]` in `A.nzval`.
"""
struct IndexedBiDiGraph{T<:Integer} <: AbstractIndexedDiGraph{T}
A :: SparseMatrixCSC{NullNumber, T}
X :: SparseMatrixCSC{T, T}
end
"""
IndexedBiDiGraph(A::AbstractMatrix)
Construct an `IndexedBiDiGraph` from the adjacency matrix `A`.
`IndexedBiDiGraph` internally stores the transpose of `A`. To avoid overhead due
to the transposition, use `IndexedBiDiGraph(transpose(At))` where `At` is the
transpose of `A`.
"""
function IndexedBiDiGraph(A::AbstractMatrix)
_checksquare(A)
_check_selfloops(A)
B = convert(SparseMatrixCSC, transpose(A))
X = permutedims( SparseMatrixCSC(B.m, B.n, B.colptr, B.rowval, collect(1:nnz(B))) )
At = SparseMatrixCSC(B.m, B.n, B.colptr, B.rowval, fill(NullNumber(), nnz(B)))
IndexedBiDiGraph(At, X)
end
"""
IndexedBiDiGraph(A::AbstractSimpleGraph)
Construct an `IndexedBiDiGraph` from any `AbstractSimpleGraph` (Graphs.jl),
directed or otherwise.
"""
IndexedBiDiGraph(sg::AbstractSimpleGraph) = IndexedBiDiGraph(adjacency_matrix(sg))
function Base.show(io::IO, g::IndexedBiDiGraph{T}) where T
println(io, "{$(nv(g)), $(ne(g))} IndexedBiDiGraph{$T}")
end
Graphs.inneighbors(g::IndexedBiDiGraph, i::Integer) = @inbounds @view g.X.rowval[nzrange(g.X,i)]
Base.zero(g::IndexedBiDiGraph) = IndexedBiDiGraph(zero(g.A))
"""
inedges(g::AbstractIndexedBiDiGraph, i::Integer)
Return a lazy iterator to the edges ingoing to node `i` in `g`.
"""
inedges(g::IndexedBiDiGraph, i::Integer) = @inbounds (IndexedEdge{Int}(g.X.rowval[k], i, g.X.nzval[k]) for k in nzrange(g.X, i))
# Return a copy of the adjacency matrix with elements of type `T`
function Graphs.LinAlg.adjacency_matrix(g::IndexedBiDiGraph, T::DataType=Int)
SparseMatrixCSC(g.X.m, g.X.n, g.X.colptr, g.X.rowval, ones(T, nnz(g.X)))
end
"""
issymmetric(g::IndexedBiDiGraph) -> Bool
Test whether a directed graph is symmetric, i.e. for each directed edge `i=>j` there also exists the edge `j=>i`
"""
function LinearAlgebra.issymmetric(g::IndexedBiDiGraph)
for i in vertices(g)
ein = inedges(g, i)
eout = outedges(g, i)
length(ein) == length(eout) || return false
for (ei, eo) in zip(ein, eout)
src(ei) == dst(eo) || return false
end
end
return true
end
"""
bidirected_with_mappings(g::IndexedGraph) -> (gdir, dir2undir, undir2dir)
Construct an `IndexedBiDiGraph` `gdir` from an `IndexedGraph` `g` by building two directed edges per every undirected edge in `g`.
In addition, return two vectors containing mappings from the undirected edges of `g` to the corresponding directed edges of `gdir`.
### OUTPUT
- `gdir` -- The directed graph
- `dir2undir` -- A vector of integers mapping the indices of the directed edges of `gdir` to the corresponding undirected edges of `g`
- `undir2dir` -- A vector of vectors with two integers each mapping the indices of the undirected edges of `g` to the two corresponding directed edges of `gdir`
"""
function bidirected_with_mappings(g::IndexedGraph{T}) where {T<:Integer}
gdir = IndexedBiDiGraph(g.A)
dir2undir = zeros(T, ne(gdir))
undir2dir = [zeros(T, 0) for _ in edges(g)]
for i in vertices(gdir)
for (dir, undir) in zip(inedges(gdir, i), inedges(g,i))
dir2undir[idx(dir)] = idx(undir)
push!(undir2dir[idx(undir)], idx(dir))
end
end
return gdir, dir2undir, undir2dir
end | IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | code | 1717 | """
IndexedDiGraph{T<:Integer} <: AbstractIndexedDiGraph{T}
A type representing a sparse directed graph with access only to outedges.
### FIELDS
- `A` -- square matrix filled with `NullNumber`s. `A[i,j]` corresponds to an edge `j=>i`
"""
struct IndexedDiGraph{T<:Integer} <: AbstractIndexedDiGraph{T}
A :: SparseMatrixCSC{NullNumber, T}
function IndexedDiGraph(A::SparseMatrixCSC{NullNumber, T}) where {T<:Integer}
_checksquare(A)
_check_selfloops(A)
new{T}(A)
end
end
"""
IndexedDiGraph(A::AbstractMatrix)
Constructs a IndexedDiGraph from the adjacency matrix A.
`IndexedDiGraph` internally stores the transpose of `A`. To avoid overhead due
to the transposition, use `IndexedDiGraph(transpose(At))` where `At` is the
transpose of `A`.
"""
function IndexedDiGraph(A::AbstractMatrix)
B = convert(SparseMatrixCSC, transpose(A))
At = SparseMatrixCSC(B.m, B.n, B.colptr, B.rowval, fill(NullNumber(), nnz(B)))
IndexedDiGraph(At)
end
"""
IndexedDiGraph(A::AbstractSimpleGraph)
Construct an `IndexedDiGraph` from any `AbstractSimpleGraph` (Graphs.jl),
directed or otherwise.
"""
IndexedDiGraph(sg::AbstractSimpleGraph) = IndexedDiGraph(adjacency_matrix(sg))
# WARNING: very slow! Not recommended, if you need inneighbors, check out `IndexedBiDiGraph`
# here only to comply with the requirements for subtyping `AbstractGraph` from Graphs.jl
function Graphs.inneighbors(g::IndexedDiGraph, i::Integer)
X = sparse(transpose(g.A))
@view X.rowval[nzrange(X,i)]
end
Base.zero(g::IndexedDiGraph) = IndexedDiGraph(zero(g.A))
function Base.show(io::IO, g::IndexedDiGraph{T}) where T
println(io, "{$(nv(g)), $(ne(g))} IndexedDiGraph{$T}")
end
| IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | code | 4028 | """
IndexedGraph{T<:Integer} <: AbstractIndexedGraph{T}
A type representing a sparse undirected graph.
### FIELDS
- `A` -- square adjacency matrix. `A[i,j] == A[j,i]` contains the unique index associated to unidrected edge `(i,j)`
"""
struct IndexedGraph{T<:Integer} <: AbstractIndexedGraph{T}
A :: SparseMatrixCSC{T, T} # Adjacency matrix. Values are unique edge id's
function IndexedGraph(A::SparseMatrixCSC{T}) where T
_checksquare(A)
_check_selfloops(A)
M = SparseMatrixCSC(A.m, A.n, A.colptr, A.rowval, ones(Int, nnz(A)))
idx_map = inverse_edge_idx(M)
cnt = 1
# give increasing indices to upper triangular elements
for j in 1:size(M, 2)
for k in nzrange(M, j)
i = M.rowval[k]
if i < j
M.nzval[k] = cnt; cnt += 1
else
break
end
end
end
@assert cnt - 1 == (nnz(M) / 2) # sanity check
# give (i=>j) the same idx as (j=>i)
for j in 1:size(M, 2)
for k in nzrange(M, j)
i = M.rowval[k]
if i > j
M.nzval[k] = M.nzval[idx_map[k]]
end
end
end
new{Int}(M)
end
end
"""
IndexedGraph(A::AbstractMatrix)
Construct an `IndexedGraph` from symmetric adjacency matrix A.
"""
IndexedGraph(A::AbstractMatrix) = IndexedGraph(convert(SparseMatrixCSC, A))
"""
IndexedGraph(A::SimpleGraph)
Construct an `IndexedGraph` from undirected `SimpleGraph` (Graphs.jl).
"""
IndexedGraph(sg::SimpleGraph) = IndexedGraph(adjacency_matrix(sg))
function Graphs.edges(g::IndexedGraph)
(IndexedEdge{Int}(extrema((i, g.A.rowval[k]))..., g.A.nzval[k])
for i=1:size(g.A,2) for k=nzrange(g.A,i) if i > g.A.rowval[k])
end
function Base.show(io::IO, g::IndexedGraph{T}) where T
println(io, "{$(nv(g)), $(ne(g))} undirected IndexedGraph{$T}")
end
Graphs.ne(g::IndexedGraph) = Int( nnz(g.A) / 2 )
Graphs.neighbors(g::IndexedGraph, i::Integer) = outneighbors(g, i)
Graphs.inneighbors(g::IndexedGraph, i::Integer) = outneighbors(g, i)
Graphs.is_directed(g::IndexedGraph) = false
Graphs.is_directed(::Type{IndexedGraph{T}}) where T = false
Base.zero(g::IndexedGraph) = IndexedGraph(zero(g.A))
"""
edges(g::IndexedGraph, i::Integer)
Return a lazy iterators to the edges incident to `i`.
By default unordered edges sort source and destination nodes in increasing order.
See [`outedges`](@ref outedges(g::IndexedGraph, i::Integer)) and [`inedges`](@ref inedges(g::IndexedGraph, i::Integer)) if you need otherwise.
"""
function Graphs.edges(g::IndexedGraph, i::Integer)
(IndexedEdge(extrema((i, g.A.rowval[k]))..., g.A.nzval[k])
for k in nzrange(g.A, i))
end
"""
outedges(g::IndexedGraph, i::Integer)
Return a lazy iterators to the edges incident to `i` with `i` as the source.
"""
function outedges(g::IndexedGraph, i::Integer)
(IndexedEdge(i, g.A.rowval[k], g.A.nzval[k]) for k in nzrange(g.A, i))
end
"""
inedges(g::IndexedGraph, i::Integer)
Return a lazy iterators to the edges incident to `i` with `i` as the destination.
"""
function inedges(g::IndexedGraph, i::Integer)
(IndexedEdge(g.A.rowval[k], i, g.A.nzval[k]) for k in nzrange(g.A, i))
end
function edge_idx(g::IndexedGraph, src::Integer, dst::Integer)
k = nzindex(g.A, src, dst)
g.A.nzval[k]
end
function edge_src_dst(g::IndexedGraph, id::Integer)
k = findfirst(isequal(id), g.A.nzval)
i, j = nzindex(g.A, k)
return extrema((i,j)) # return sorted
end
"""
get_edge(g::IndexedGraph, src::Integer, dst::Integer)
get_edge(g::IndexedGraph, id::Integer)
Get edge given source and destination or given edge index.
"""
function get_edge(g::IndexedGraph, src::Integer, dst::Integer)
id = edge_idx(g, src, dst)
IndexedEdge(src, dst, id)
end
function get_edge(g::IndexedGraph, id::Integer)
i, j = edge_src_dst(g, id)
IndexedEdge(i, j, id)
end | IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | code | 2059 | function _checksquare(A::AbstractMatrix)
size(A,1) != size(A,2) && throw(ArgumentError("Matrix should be square"))
end
function _check_selfloops(A::AbstractMatrix)
s = min(size(A)...)
any(!iszero, A[i,i] for i=1:s) && throw(ArgumentError("Self loops are not allowed"))
end
# vector that maps edge i->j to edge j->i in A.nzval
function inverse_edge_idx(A::SparseMatrixCSC)
issymmetric(A) || throw(ArgumentError("Matrix should be symmetric"))
n = size(A, 2)
X = zeros(Int, nnz(A))
rowcnt = zeros(Int, n)
for j in 1:n
for k in nzrange(A, j)
r = A.rowval[k]
rowcnt[r] += 1
if r > j
z = nzrange(A, r)[rowcnt[r]]
X[k], X[z] = z, k
end
end
end
X
end
# return the index in `A.nzval` of element (`i`,`j`) if it's nonzero,
# otherwise raise an error
#
# copied from julia/stdlib/v1.7/SparseArrays/src/sparsematrix.jl:2158
function nzindex(A::SparseMatrixCSC, i::Integer, j::Integer)
if !(1 <= i <= size(A, 1) && 1 <= j <= size(A, 2)); throw(BoundsError()); end
k1 = Int(A.colptr[j])
k2 = Int(A.colptr[j+1]-1)
(k1 > k2) && throw(ArgumentError("Matrix element ($i,$j) is zero"))
k = searchsortedfirst(rowvals(A), i, k1, k2, Base.Order.Forward)
if k > k2 || A.rowval[k] != i
throw(ArgumentError("Matrix element ($i,$j) is zero"))
end
return k
# ???? Propagate errors to higher-level functions? E.g. do not throw errors
# here but return some Int, then from `edge_idx` print something like
# "Graph does not contain edge (i,j)" ?????
end
# return the indices `(i,j)` of the `k`th element in `A.nzval`
function nzindex(A::SparseMatrixCSC, k::Integer)
j = searchsortedfirst(A.colptr, k+1) - 1
i = rowvals(A)[k]
i, j
end
# Void type used to fill sparse arrays w/o using memory for the nonzero values,
# only for their positions
struct NullNumber <: Number; end
Base.zero(::NullNumber) = false
Base.zero(::Type{NullNumber}) = false
Base.iszero(::NullNumber) = false | IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | code | 3627 | ### Override for Graphs' version, copied from https://github.com/JuliaGraphs/Graphs.jl/blob/master/src/shortestpaths/dijkstra.jl with some adjustments
function Graphs.dijkstra_shortest_paths(g::AbstractIndexedGraph,
srcs::Vector{U},
distvec::AbstractVector{T}=ones(Int, ne(g));
allpaths=false,
trackvertices=false
) where T <: Real where U <: Integer
issubset(1:ne(g), eachindex(distvec)) || throw(ArgumentError("Bad indices in distvec"))
nvg = nv(g)
dists = fill(typemax(T), nvg)
parents = zeros(U, nvg)
pathcounts = zeros(nvg)
preds = fill(Vector{U}(), nvg)
H::TrackingHeap{Int64, T, 2, MinHeapOrder, NoTrainingWheels} = TrackingHeap(T; S=NoTrainingWheels)
sizehint!(H, nvg)
for src in srcs
dists[src] = zero(T)
pathcounts[src] = one(Float64)
H[src] = zero(T)
end
closest_vertices = Vector{U}() # Maintains vertices in order of distances from source
trackvertices && sizehint!(closest_vertices, nvg)
@inbounds while !isempty(H)
u, d = pop!(H)
if trackvertices
push!(closest_vertices, u)
end
for e in outedges(g, u)
alt = d + distvec[idx(e)]
v = dst(e)
visited = dists[v] != typemax(T)
if !visited
dists[v] = alt
parents[v] = u
pathcounts[v] += pathcounts[u]
if allpaths
preds[v] = [u;]
end
H[v] = alt
elseif alt < dists[v]
dists[v] = alt
parents[v] = u
#615
pathcounts[v] = pathcounts[u]
if allpaths
resize!(preds[v], 1)
preds[v][1] = u
end
H[v] = alt
elseif alt == dists[v]
pathcounts[v] += pathcounts[u]
if allpaths
push!(preds[v], u)
end
end
end
end
if trackvertices
for s in vertices(g)
visited = dists[s] != typemax(T)
if !visited
push!(closest_vertices, s)
end
end
end
for src in srcs
pathcounts[src] = one(Float64)
parents[src] = 0
empty!(preds[src])
end
return DijkstraState{T,U}(parents, dists, preds, pathcounts, closest_vertices)
end
function Graphs.dijkstra_shortest_paths(g::AbstractIndexedGraph, src::Integer,
distvec::AbstractVector=ones(Int, ne(g)); kw...)
dijkstra_shortest_paths(g, [src;], distvec; kw...)
end
function Graphs.dijkstra_shortest_paths(g::AbstractIndexedGraph, src,
distmx::AbstractMatrix; kw...)
Wt = convert(SparseMatrixCSC, transpose(distmx))
distvec = nonzeros(Wt)
dijkstra_shortest_paths(g, src, distvec; kw...)
end
### Homemade minimal version
function dijkstra(g::AbstractIndexedGraph{T}, s::Integer,
w::AbstractVector{U}=ones(Int, ne(g))) where {T<:Integer, U<:Real}
n = nv(g)
inf = typemax(U)
D = fill(inf, n); D[s] = 0
parents = fill(0, n); parents[s] = 0
Q::TrackingHeap{Int64, U, 2, MinHeapOrder, NoTrainingWheels} = TrackingHeaps.TrackingHeap(U; S=TrackingHeaps.NoTrainingWheels)
sizehint!(Q, n)
Q[s] = zero(U)
while !isempty(Q)
v, d = TrackingHeaps.pop!(Q)
for e in outedges(g, v)
i = dst(e)
dd = d + w[idx(e)]
if dd < D[i]
Q[i] = D[i] = dd
parents[i] = v
end
end
end
return D, parents
end
| IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | code | 3860 | using Graphs, IndexedGraphs, SparseArrays
@testset "bipartite graph" begin
nl = 15
nr = 27
n = nl + nr
g = complete_bipartite_graph(nl, nr) |> IndexedGraph
gb = BipartiteIndexedGraph(g)
@testset "static properties" begin
@test !is_directed(gb)
@test !is_directed(typeof(gb))
@test is_bipartite(gb)
end
@testset "basics" begin
@test vertices(g) == vertices(gb)
@test collect(edges(g)) == collect(edges(gb))
@test nv(g) == nv(gb)
@test ne(g) == ne(gb)
@test all(collect(neighbors(g,i)) == collect(neighbors(gb, i)) for i in vertices(g))
@test all(collect(inedges(g,i)) == collect(inedges(gb, i)) for i in vertices(g))
@test all(collect(outedges(g,i)) == collect(outedges(gb, i)) for i in vertices(g))
@test all(has_edge(gb, s, d) for (s, d) in edges(gb))
@test all(degree(g, i) == length(collect(neighbors(g, i))) for i in vertices(g))
@test all(degree(g, i) == length(collect(inedges(g, i))) for i in vertices(g))
@test adjacency_matrix(gb) == adjacency_matrix(g)
end
@testset "degree" begin
@test all(1:nv_left(gb)) do iL
v = vertex(iL, Left)
i = linearindex(gb, v)
degree(gb, v) == degree(g, i)
end
@test all(1:nv_right(gb)) do iR
v = vertex(iR, Right)
i = linearindex(gb, v)
degree(gb, v) == degree(g, i)
end
end
@testset "left and right" begin
vl = [linearindex(gb, i, Left) for i in 1:nv_left(gb)]
vr = [linearindex(gb, i, Right) for i in 1:nv_right(gb)]
@test vl == vertices_left(gb)
@test vr == vertices_right(gb)
@test all(all(vertex_left(gb, e)==l for e in outedges(gb, vertex(l, Left)))
for l in 1:nv_left(gb))
@test all(all(vertex_left(gb, e)==l for e in inedges(gb, vertex(l, Left)))
for l in 1:nv_left(gb))
@test all(all(vertex_right(gb, e)==r for e in outedges(gb, vertex(r, Right)))
for r in 1:nv_right(gb))
@test all(all(vertex_right(gb, e)==r for e in inedges(gb, vertex(r, Right)))
for r in 1:nv_right(gb))
end
@testset "dijkstra" begin
distmx = adjacency_matrix(g) .* rand(n,n)
distvec = nonzeros(permutedims(distmx))
sources = rand(1:n, 10)
d = dijkstra_shortest_paths(g, sources, distvec)
db = dijkstra_shortest_paths(gb, sources, distvec)
@test all(getproperty(d, p) == getproperty(db, p) for p in fieldnames(typeof(d)))
end
@testset "bipartite generators" begin
ngraphs = 20
nrights = rand(5:50, ngraphs)
nlefts = rand(5:50, ngraphs)
es = [rand(1:n*m) for (n, m) in zip(nrights, nlefts)]
@testset "Random bipartite graph - fixed # edges" begin
@test all(zip(nrights, nlefts, es)) do (n, m, e)
g = rand_bipartite_graph(m, n, e)
nv_right(g) == n && nv_left(g) == m && ne(g) == e
end
end
@testset "Random bipartite graph - prob of edges" begin
p = 0.1
@test all(zip(nrights, nlefts)) do (n, m)
g = rand_bipartite_graph(m, n, p)
nv_right(g) == n && nv_left(g) == m
end
end
@testset "Random regular bipartite graph" begin
k = 4
@test all(zip(nrights, nlefts)) do (n, m)
g = rand_regular_bipartite_graph(m, n, k)
nv_right(g) == n && nv_left(g) == m && ne(g) == m * k
end
end
@testset "Random bipartite tree" begin
@test all(nrights) do n
g = rand_bipartite_tree(n)
nv(g) == n && !is_cyclic(g)
end
end
end
end | IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | code | 2213 | using SparseArrays, Graphs, IndexedGraphs, LinearAlgebra
function dotest(ds_IG, ds_Graphs)
# check that results are correct
@test ds_IG.dists == ds_Graphs.dists
@test ds_IG.parents == ds_Graphs.parents
@test ds_IG.predecessors == ds_Graphs.predecessors
@test ds_IG.pathcounts == ds_Graphs.pathcounts
@test ds_IG.closest_vertices == ds_Graphs.closest_vertices
end
@testset "dijkstra " begin
@testset "directed" begin
for allpaths = (true,false)
for trackvertices = (true, false)
for N=(10,20,30)
# build directed graph
W = sprand(N, N, 0.5)
# remove self loops
for i in 1:size(W,2); W[i,i] = 0; end
dropzeros!(W)
# pick sources at random
s = rand(1:N, 2)
g_Graphs = SimpleDiGraph(W)
ds_Graphs = dijkstra_shortest_paths(g_Graphs, s, W; allpaths=allpaths, trackvertices=trackvertices)
for G in (IndexedDiGraph, IndexedBiDiGraph)
g = G(W)
w = nonzeros(permutedims(W))
ds_IG = dijkstra_shortest_paths(g, s, w; allpaths=allpaths, trackvertices=trackvertices)
dotest(ds_IG, ds_Graphs)
end
end
end
end
end
@testset "undirected" begin
for allpaths = (true,false)
for trackvertices = (true, )
for N = (10,20,30)
W = sprand(N, N, 0.5)
W[diagind(W)] .= 0
Wl = triu(W)
dropzeros!(Wl)
W = Wl .+ Wl'
g = IndexedGraph(W)
g_Graphs = SimpleDiGraph(W)
s = rand(1:N, 2)
ds_Graphs = dijkstra_shortest_paths(g_Graphs, s, W; allpaths=allpaths, trackvertices=trackvertices)
ds_IG = dijkstra_shortest_paths(g, s, Wl.nzval; allpaths=allpaths, trackvertices=trackvertices)
dotest(ds_IG, ds_Graphs)
end
end
end
end
end
| IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | code | 2349 | using SparseArrays, Graphs
A = sprand(Bool, 20, 20, 0.5)
for i in 1:20; A[i,i] = 0; end
dropzeros!(A)
g = IndexedBiDiGraph(A)
@testset "BiDirected graph" begin
@testset "issymmetric" begin
@test issymmetric(g) == issymmetric(adjacency_matrix(g))
end
@testset "show" begin
buf = IOBuffer()
show(buf, g)
@test String(take!(buf)) == "{20, $(ne(g))} IndexedBiDiGraph{$(Int)}\n"
end
@testset "transpose constructor" begin
At = sparse(A')
gg = IndexedBiDiGraph( transpose(At) )
@test gg.A.rowval === At.rowval
@test gg.A.rowval == g.A.rowval
end
@testset "basics" begin
@test is_directed(typeof(g))
@test is_directed(g)
@test length(collect(edges(g))) == ne(g)
i = 3
ine = inedges(g, i)
inn = inneighbors(g, i)
@test all(src(e) == j for (e,j) in zip(ine, inn))
@test all(dst(e) == i for e in ine)
end
@testset "edge indexing" begin
@test all( e == get_edge(g, src(e), dst(e)) for e in edges(g) )
@test all( e == get_edge(g, idx(e)) for e in edges(g) )
passed = falses(ne(g))
for (i,e) in enumerate(edges(g))
id = idx(get_edge(g, src(e), dst(e)))
ee = get_edge(g, id)
passed[i] = ee == e
end
@test all(passed)
end
@testset "construct from SimpleGraph" begin
sg = SimpleDiGraph(A)
ig = IndexedBiDiGraph(sg)
@test adjacency_matrix(sg) == adjacency_matrix(ig)
S = A + A'
sg = SimpleDiGraph(S)
ig = IndexedBiDiGraph(sg)
@test adjacency_matrix(sg) == adjacency_matrix(ig)
end
@testset "construct from IndexedGraph" begin
B = A + A'
dropzeros!(B)
g = IndexedGraph(B)
gd, dir2undir, undir2dir = bidirected_with_mappings(g)
@test issymmetric(gd)
eu = edges(g) |> collect # undirected edges
ed = edges(gd) |> collect # directed edges
@test all( let
e = eu[dir2undir[idd]]
src(e) == min(i,j) && dst(e) == max(i,j)
end for (i,j,idd) in ed
)
@test all( let
es = ed[undir2dir[idu]]
src(es[1]) == dst(es[2]) && src(es[2]) == dst(es[1])
end for (i,j,idu) in eu
)
end
end
| IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | code | 1543 | using SparseArrays, Graphs
A = sprand(Bool, 20, 20, 0.5)
for i in 1:20; A[i,i] = 0; end
dropzeros!(A)
g = IndexedDiGraph(A)
@testset "directed graph" begin
@testset "show" begin
buf = IOBuffer()
show(buf, g)
@test String(take!(buf)) == "{20, $(ne(g))} IndexedDiGraph{$(Int)}\n"
end
@testset "transpose constructor" begin
At = sparse(A')
gg = IndexedDiGraph( transpose(At) )
@test gg.A.rowval === At.rowval
@test gg.A.rowval == g.A.rowval
end
@testset "basics" begin
@test is_directed(g)
@test length(collect(edges(g))) == ne(g)
i = 3
oute = outedges(g, i)
outn = outneighbors(g, i)
@test all(dst(e) == j for (e,j) in zip(oute, outn))
@test all(src(e) == i for e in oute)
end
@testset "edge indexing" begin
@test all( e == get_edge(g, src(e), dst(e)) for e in edges(g) )
@test all( e == get_edge(g, idx(e)) for e in edges(g) )
passed = falses(ne(g))
for (i,e) in enumerate(edges(g))
id = idx(get_edge(g, src(e), dst(e)))
ee = get_edge(g, id)
passed[i] = ee == e
end
@test all(passed)
end
@testset "construct from SimpleGraph" begin
sg = SimpleDiGraph(A)
ig = IndexedDiGraph(sg)
@test adjacency_matrix(sg) == adjacency_matrix(ig)
S = A + A'
sg = SimpleDiGraph(S)
ig = IndexedDiGraph(sg)
@test adjacency_matrix(sg) == adjacency_matrix(ig)
end
end | IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | code | 1197 | using SparseArrays, Graphs
A = sprand(Bool, 20, 20, 0.5)
for i in 1:20; A[i,i] = 0; end
A = A + A'
dropzeros!(A)
g = IndexedGraph(A)
@testset "undirected graph" begin
@testset "show" begin
buf = IOBuffer()
show(buf, g)
@test String(take!(buf)) == "{20, $(ne(g))} undirected IndexedGraph{$(Int)}\n"
end
@testset "basics" begin
@test !is_directed(g)
@test length(collect(edges(g))) == ne(g)
i = 3
es = inedges(g, i)
neigs = neighbors(g, i)
@test all(
((src(e), dst(e)) == (i, j)) || ((src(e), dst(e)) == (j, i))
for (e, j) in zip(es, neigs)
)
end
@testset "edge indexing" begin
@test all( e == get_edge(g, src(e), dst(e)) for e in edges(g) )
@test all( e == get_edge(g, idx(e)) for e in edges(g) )
end
@testset "construct from SimpleGraph" begin
sg = SimpleGraph(A)
ig = IndexedGraph(sg)
@test adjacency_matrix(sg) == adjacency_matrix(ig)
end
end
@testset "iterator within edge" begin
es = map(edges(g)) do e
i, j, ij = e
i==src(e) && j == dst(e) && ij == idx(e)
end
@test all(es)
end | IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | code | 174 | using IndexedGraphs
using Test
include("indexeddigraph.jl")
include("indexedbidigraph.jl")
include("indexedgraph.jl")
include("bipartite.jl")
include("dijkstra.jl")
nothing | IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | docs | 3892 | # IndexedGraphs.jl
_Not all edges come with an index. These do_
[](https://github.com/stecrotti/IndexedGraphs.jl/actions/workflows/ci.yml)
[](https://codecov.io/gh/stecrotti/IndexedGraphs.jl)
[](https://stecrotti.github.io/IndexedGraphs.jl/stable)
[](https://stecrotti.github.io/IndexedGraphs.jl/dev)
## Overview
A **Graphs.jl**-compatible implementation of [SparseMatrixCSC](https://github.com/JuliaLang/SparseArrays.jl)-based graphs, allowing fast access to arbitrary edge properties
* The code implements the **Graphs.jl** interface for directed and undirected graphs.
* Edge properties live separate from the graph, so different sets of properties can be associated to the same graph.
* In addition, it implements `inedges` and `outedges` for O(1) access to neighborhood
* Edges are indexed, and the index can be used to access edge properties very efficiently.
* `IndexedBiDirectedGraphs` store both the direct and the transposed adjancency matrix for efficient access
A number of other packages implement graph based on CSC matrix representation or similar, namely **StaticGraphs**, **SimpleWeightedGraphs** and **MatrixNetworks**
* [StaticGraphs](https://github.com/JuliaGraphs/StaticGraphs.jl): No edge properties
* [SimpleWeightedGraphs](https://github.com/JuliaGraphs/SimpleWeightedGraphs.jl): Also based on `SparseMatrixCSC`, allows for numerical edge properties. However, no edge weight can be 0 (or otherwise the edge is sometimes removed), and does not allow arbitrary edge properties
* [MatrixNetworks](https://github.com/JuliaGraphs/MatrixNetworks.jl): Also based on `SparseMatrixCSC`, allows for numerical edge properties. However, no edge weight can be 0 (or otherwise the edge is sometimes removed), and does not allow arbitrary edge properties. Does not implement the Graphs interface.
## Navigating graphs
The most natural and efficient way to iterate over an `IndexedGraph` is to iterate over neighboring nodes or edges
```julia
A = [0 0 1;
1 0 0;
1 1 0]
g = IndexedDiGraph(A)
i = 3
out_i = outedges(g, i)
collect(out_i)
```
outputs:
```julia
2-element Vector{IndexedGraphs.IndexedEdge{Int64}}:
Indexed Edge 3 => 1 with index 4
Indexed Edge 3 => 2 with index 5
```
Edge indices, 4 and 5 in this case, can be extracted with `idx` and used to access properties stored in a separate container
```julia
e = first(out_i)
src(e), dst(e), idx(e)
```
outputs:
```julia
(3, 1, 4)
```
## Benchmark
Performance on [Dijkstra's algorithm](https://en.wikipedia.org/wiki/Dijkstra%27s_algorithm) compared with the packages listed above, as computed [here](https://github.com/stecrotti/IndexedGraphs.jl/blob/main/benchmark/dijkstra_benchmark.jl) for a random symmetric weight matrix with 10^4 nodes and ~10^5 edges.
```julia
IndexedDiGraph:
2.840 ms (22 allocations: 547.91 KiB)
IndexedGraph:
3.131 ms (22 allocations: 547.91 KiB)
MatrixNetwork:
3.031 ms (13 allocations: 407.45 KiB)
SimpleGraph
11.935 ms (45 allocations: 1008.58 KiB)
SimpleWeightedGraph:
10.610 ms (45 allocations: 1008.58 KiB)
ValGraph (SimpleValueGraphs.Experimental):
6.620 ms (48 allocations: 1000.06 KiB)
```
**Note**: For an undirected graph, `IndexedGraph` gives one unique index to each undirected edge (`i=>j` and `j=>i` have the same index). This makes the memory layout less efficient when traversing the graph (although it is very efficient to modify the properties compared with the alternatives).
If no property modification is needed, as is the case with Dijkstra, it is more convenient to just employ an `IndexedDiGraph` with symmetric edges and weights.
| IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | docs | 541 | # IndexedBiDiGraph
A type representing directed graphs.
Use this when you need to access both inedges and outedges (or inneighbors and outneighbors).
For a lighter data structure check out [IndexedDiGraph](@ref).
```@docs
IndexedBiDiGraph
```
```@docs
IndexedBiDiGraph(A::AbstractMatrix)
```
Example:
```@example
using SparseArrays, IndexedGraphs
At = sprand(100, 100, 0.1) # At[i,j] corresponds to edge j=>i
for i in 1:100; At[i,i] = 0; end
dropzeros!(At)
g = IndexedBiDiGraph(transpose(At))
g.A.rowval === At.rowval
```
| IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | docs | 2634 | # BipartiteIndexedGraph
A graph is [bipartite](https://en.wikipedia.org/wiki/Bipartite_graph) if the set of vertices
can be partitioned into two blocks such that there is no edge between vertices of different blocks.
Here we adopt the notation of referring to these as the "left" and "right" block.
A `BipartiteIndexedGraph` behaves just like a bipartite, undirected `IndexedGraph`, with two differences:
- Vertices can be indexed as usual via their integer index (which is called here a [`linearindex`](@ref)), or via a [`BipartiteGraphVertex`](@ref), i.e. by specifying `Left` or `Right` and the integer index of that vertex within its block. The typical use case is that where one has two vectors storing vertex properties of the two blocks, possibly with different `eltype`s, and each with indices starting at one.
- The adjacency matrix of a bipartite graph (possibly after permutation of the vertex indices) is made of two specular rectangular submatrices `A`. Only one of these is stored, leading to a slight improvement in efficiency.
`BipartiteIndexedGraph`s use the same edge type `IndexedEdge` as the other `AbstractIndexedGraph`s, which stores source and destination as linear indices. To retrieve the in-block indices of the two vertices incident on an edge, use [`vertex_left`](@ref), [`vertex_right`](@ref).
```@docs
BipartiteIndexedGraph
```
```@docs
BipartiteIndexedGraph(A::AbstractMatrix)
BipartiteIndexedGraph(g::AbstractGraph)
nv_left
nv_right
Left
Right
LeftorRight
BipartiteGraphVertex
vertex(i::Integer, ::Type{<:LeftorRight})
vertex(g::BipartiteIndexedGraph, i::Integer)
linearindex
vertices_left
vertices_right
vertex_left
vertex_right
inedges(g::BipartiteIndexedGraph, i::Integer)
inedges(g::BipartiteIndexedGraph, l::BipartiteGraphVertex{Left})
outedges(g::BipartiteIndexedGraph, i::Integer)
outedges(g::BipartiteIndexedGraph, l::BipartiteGraphVertex{Left})
```
## Overrides from Graphs.jl
```@docs
degree(g::BipartiteIndexedGraph, v::BipartiteGraphVertex)
inneighbors(g::BipartiteIndexedGraph, i::Integer)
inneighbors(g::BipartiteIndexedGraph, l::BipartiteGraphVertex{Left})
outneighbors(g::BipartiteIndexedGraph, i::Integer)
outneighbors(g::BipartiteIndexedGraph, v::BipartiteGraphVertex)
adjacency_matrix(g::BipartiteIndexedGraph, T::DataType=Int)
```
## Generators
```@docs
rand_bipartite_graph([rng::AbstractRNG], nleft::Integer, nright::Integer, ned::Integer)
rand_bipartite_graph([rng::AbstractRNG], nleft::Integer, nright::Integer, p::Real)
rand_regular_bipartite_graph([rng::AbstractRNG], nleft::Integer, nright::Integer, k::Integer)
rand_bipartite_tree([rng::AbstractRNG], n::Integer)
``` | IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | docs | 290 | # IndexedDiGraph
A type representing directed graphs.
Use this when you need to access only outedges and outneighbors.
If you also need access to inedges and inneighbors, check out [IndexedBiDiGraph](@ref).
```@docs
IndexedDiGraph
```
```@docs
IndexedDiGraph(A::AbstractMatrix)
```
| IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | docs | 348 | # IndexedGraph
A type representing undirected graphs.
```@docs
IndexedGraph
```
```@docs
IndexedGraph(A::AbstractMatrix)
```
```@docs
inedges(g::IndexedGraph, i::Integer)
outedges(g::IndexedGraph, i::Integer)
get_edge(g::IndexedGraph, src::Integer, dst::Integer)
```
## Overrides from Graphs.jl
```@docs
edges(g::IndexedGraph, i::Integer)
``` | IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | docs | 374 | IndexedGraphs.jl
====
This package defines three basic types of Graphs:
- [IndexedGraph](@ref)
- [IndexedDiGraph](@ref)
- [IndexedBiDiGraph](@ref)
In addition, it provides a [BipartiteIndexedGraph](@ref) type.
They all comply with the [Developing Alternate Graph Types](https://juliagraphs.org/Graphs.jl/dev/developing/) rules for subtyping from `Graphs.AbstractGraph`.
| IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"Apache-2.0"
] | 0.6.1 | 1dd5a1d97080714db9160afd6a2e40150302b1eb | docs | 72 | # Reference
```@autodocs; canonical=false
Modules = [IndexedGraphs]
``` | IndexedGraphs | https://github.com/stecrotti/IndexedGraphs.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 672 | using Documenter, ReservoirComputing
cp("./docs/Manifest.toml", "./docs/src/assets/Manifest.toml", force = true)
cp("./docs/Project.toml", "./docs/src/assets/Project.toml", force = true)
ENV["PLOTS_TEST"] = "true"
ENV["GKSwstype"] = "100"
include("pages.jl")
makedocs(modules = [ReservoirComputing],
sitename = "ReservoirComputing.jl",
clean = true, doctest = false, linkcheck = true,
warnonly = [:missing_docs],
format = Documenter.HTML(assets = ["assets/favicon.ico"],
canonical = "https://docs.sciml.ai/ReservoirComputing/stable/"),
pages = pages)
deploydocs(repo = "github.com/SciML/ReservoirComputing.jl.git";
push_preview = true)
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 1295 | pages = [
"ReservoirComputing.jl" => "index.md",
"General Settings" => Any[
"Changing Training Algorithms" => "general/different_training.md",
"Altering States" => "general/states_variation.md",
"Generative vs Predictive" => "general/predictive_generative.md"],
"Echo State Network Tutorials" => Any[
"Lorenz System Forecasting" => "esn_tutorials/lorenz_basic.md",
#"Mackey-Glass Forecasting on GPU" => "esn_tutorials/mackeyglass_basic.md",
"Using Different Layers" => "esn_tutorials/change_layers.md",
"Using Different Reservoir Drivers" => "esn_tutorials/different_drivers.md",
#"Using Different Training Methods" => "esn_tutorials/different_training.md",
"Deep Echo State Networks" => "esn_tutorials/deep_esn.md",
"Hybrid Echo State Networks" => "esn_tutorials/hybrid.md"],
"Reservoir Computing with Cellular Automata" => "reca_tutorials/reca.md",
"API Documentation" => Any["Training Algorithms" => "api/training.md",
"States Modifications" => "api/states.md",
"Prediction Types" => "api/predict.md",
"Echo State Networks" => "api/esn.md",
"ESN Layers" => "api/esn_layers.md",
"ESN Drivers" => "api/esn_drivers.md",
"ReCA" => "api/reca.md"]
]
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 818 | module RCLIBSVMExt
using ReservoirComputing
using LIBSVM
function ReservoirComputing.train(svr::LIBSVM.AbstractSVR, states, target)
out_size = size(target, 1)
output_matrix = []
if out_size == 1
output_matrix = LIBSVM.fit!(svr, states', vec(target))
else
for i in 1:out_size
push!(output_matrix, LIBSVM.fit!(svr, states', target[i, :]))
end
end
return OutputLayer(svr, output_matrix, out_size, target[:, end])
end
function ReservoirComputing.get_prediction(
training_method::LIBSVM.AbstractSVR, output_layer, x)
out = zeros(output_layer.out_size)
for i in 1:(output_layer.out_size)
x_new = reshape(x, 1, length(x))
out[i] = LIBSVM.predict(output_layer.output_matrix[i], x_new)[1]
end
return out
end
end #module
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 786 | module RCMLJLinearModelsExt
using ReservoirComputing
using MLJLinearModels
function ReservoirComputing.train(regressor::MLJLinearModels.GeneralizedLinearRegression,
states::AbstractArray{T},
target::AbstractArray{T};
kwargs...) where {T <: Number}
out_size = size(target, 1)
output_layer = similar(target, size(target, 1), size(states, 1))
if regressor.fit_intercept
throw(ArgumentError("fit_intercept=true is not yet supported.
Please add fit_intercept=false to the MLJ regressor"))
end
for i in axes(target, 1)
output_layer[i, :] = MLJLinearModels.fit(regressor, states',
target[i, :]; kwargs...)
end
return OutputLayer(regressor, output_layer, out_size, target[:, end])
end
end #module
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 3692 | module ReservoirComputing
using Adapt
using CellularAutomata
using Distances
using Distributions
using LinearAlgebra
using NNlib
using Optim
using PartialFunctions
using Random
using Statistics
using WeightInitializers
export NLADefault, NLAT1, NLAT2, NLAT3
export StandardStates, ExtendedStates, PaddedStates, PaddedExtendedStates
export StandardRidge
export scaled_rand, weighted_init, informed_init, minimal_init
export rand_sparse, delay_line, delay_line_backward, cycle_jumps, simple_cycle, pseudo_svd
export RNN, MRNN, GRU, GRUParams, FullyGated, Minimal
export ESN, train
export HybridESN, KnowledgeModel
export DeepESN
export RECA, train
export RandomMapping, RandomMaps
export Generative, Predictive, OutputLayer
#define global types
abstract type AbstractReservoirComputer end
abstract type AbstractOutputLayer end
abstract type AbstractPrediction end
#should probably move some of these
abstract type AbstractGRUVariant end
#general output layer struct
struct OutputLayer{T, I, S, L} <: AbstractOutputLayer
training_method::T
output_matrix::I
out_size::S
last_value::L
end
#prediction types
"""
Generative(prediction_len)
This prediction methodology allows the models to produce an autonomous prediction, feeding the prediction into itself to generate the next step.
The only parameter needed is the number of steps for the prediction.
"""
struct Generative{T} <: AbstractPrediction
prediction_len::T
end
struct Predictive{I, T} <: AbstractPrediction
prediction_data::I
prediction_len::T
end
"""
Predictive(prediction_data)
Given a set of labels as `prediction_data`, this method of prediction will return the corresponding labels in a standard Machine Learning fashion.
"""
function Predictive(prediction_data)
prediction_len = size(prediction_data, 2)
Predictive(prediction_data, prediction_len)
end
#fallbacks for initializers
for initializer in (:rand_sparse, :delay_line, :delay_line_backward, :cycle_jumps,
:simple_cycle, :pseudo_svd,
:scaled_rand, :weighted_init, :informed_init, :minimal_init)
NType = ifelse(initializer === :rand_sparse, Real, Number)
@eval function ($initializer)(dims::Integer...; kwargs...)
return $initializer(WeightInitializers._default_rng(), Float32, dims...; kwargs...)
end
@eval function ($initializer)(rng::AbstractRNG, dims::Integer...; kwargs...)
return $initializer(rng, Float32, dims...; kwargs...)
end
@eval function ($initializer)(::Type{T},
dims::Integer...; kwargs...) where {T <: $NType}
return $initializer(WeightInitializers._default_rng(), T, dims...; kwargs...)
end
@eval function ($initializer)(rng::AbstractRNG; kwargs...)
return WeightInitializers.__partial_apply($initializer, (rng, (; kwargs...)))
end
@eval function ($initializer)(rng::AbstractRNG,
::Type{T}; kwargs...) where {T <: $NType}
return WeightInitializers.__partial_apply($initializer, ((rng, T), (; kwargs...)))
end
@eval ($initializer)(; kwargs...) = WeightInitializers.__partial_apply(
$initializer, (; kwargs...))
end
#general
include("states.jl")
include("predict.jl")
#general training
include("train/linear_regression.jl")
#esn
include("esn/esn_input_layers.jl")
include("esn/esn_reservoirs.jl")
include("esn/esn_reservoir_drivers.jl")
include("esn/esn.jl")
include("esn/deepesn.jl")
include("esn/hybridesn.jl")
include("esn/esn_predict.jl")
#reca
include("reca/reca.jl")
include("reca/reca_input_encodings.jl")
# Julia < 1.9 support
if !isdefined(Base, :get_extension)
include("../ext/RCMLJLinearModelsExt.jl")
include("../ext/RCLIBSVMExt.jl")
end
end #module
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 1876 | function obtain_prediction(rc::AbstractReservoirComputer,
prediction::Generative,
x,
output_layer,
args...;
initial_conditions = output_layer.last_value)
#x = last_state
prediction_len = prediction.prediction_len
train_method = output_layer.training_method
out_size = output_layer.out_size
output = output_storing(train_method, out_size, prediction_len, typeof(rc.states))
out = initial_conditions
for i in 1:prediction_len
x, x_new = next_state_prediction!(rc, x, out, i, args...)
out_tmp = get_prediction(train_method, output_layer, x_new)
out = store_results!(train_method, out_tmp, output, i)
end
return output
end
function obtain_prediction(rc::AbstractReservoirComputer,
prediction::Predictive,
x,
output_layer,
args...;
kwargs...)
prediction_len = prediction.prediction_len
train_method = output_layer.training_method
out_size = output_layer.out_size
output = output_storing(train_method, out_size, prediction_len, typeof(rc.states))
for i in 1:prediction_len
y = @view prediction.prediction_data[:, i]
x, x_new = next_state_prediction!(rc, x, y, i, args...)
out_tmp = get_prediction(train_method, output_layer, x_new)
out = store_results!(output_layer.training_method, out_tmp, output, i)
end
return output
end
#linear models
function get_prediction(training_method, output_layer, x)
return output_layer.output_matrix * x
end
#single matrix for other training methods
function output_storing(training_method, out_size, prediction_len, storing_type)
return Adapt.adapt(storing_type, zeros(out_size, prediction_len))
end
#general storing -> single matrix
function store_results!(training_method, out, output, i)
output[:, i] = out
return out
end
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 7435 | abstract type AbstractStates end
abstract type AbstractPaddedStates <: AbstractStates end
abstract type NonLinearAlgorithm end
function pad_state!(states_type::AbstractPaddedStates, x_pad, x)
x_pad = vcat(fill(states_type.padding, (1, size(x, 2))), x)
return x_pad
end
function pad_state!(states_type, x_pad, x)
x_pad = x
return x_pad
end
#states types
"""
StandardStates()
When this struct is employed, the states of the reservoir are not modified. It represents the default behavior
in scenarios where no specific state modification is required. This approach is ideal for applications
where the inherent dynamics of the reservoir are sufficient, and no external manipulation of the states
is necessary. It maintains the original state representation, ensuring that the reservoir's natural properties
are preserved and utilized in computations.
"""
struct StandardStates <: AbstractStates end
"""
ExtendedStates()
The `ExtendedStates` struct is used to extend the reservoir states by
vertically concatenating the input data (during training) and the prediction data (during the prediction phase).
This method enriches the state representation by integrating external data, enhancing the model's capability
to capture and utilize complex patterns in both training and prediction stages.
"""
struct ExtendedStates <: AbstractStates end
struct PaddedStates{T} <: AbstractPaddedStates
padding::T
end
struct PaddedExtendedStates{T} <: AbstractPaddedStates
padding::T
end
"""
PaddedStates(padding)
PaddedStates(;padding=1.0)
Creates an instance of the `PaddedStates` struct with specified padding value.
This padding is typically set to 1.0 by default but can be customized.
The states of the reservoir are padded by vertically concatenating this padding value,
enhancing the dimensionality and potentially improving the performance of the reservoir computing model.
This function is particularly useful in scenarios where adding a constant baseline to the states is necessary
for the desired computational task.
"""
function PaddedStates(; padding = 1.0)
return PaddedStates(padding)
end
"""
PaddedExtendedStates(padding)
PaddedExtendedStates(;padding=1.0)
Constructs a `PaddedExtendedStates` struct, which first extends the reservoir states with training or prediction data,
then pads them with a specified value (defaulting to 1.0). This process is achieved through vertical concatenation,
combining the padding value, data, and states.
This function is particularly useful for enhancing the reservoir's state representation in more complex scenarios,
where both extended contextual information and consistent baseline padding are crucial for the computational
effectiveness of the reservoir computing model.
"""
function PaddedExtendedStates(; padding = 1.0)
return PaddedExtendedStates(padding)
end
#functions of the states to apply modifications
function (::StandardStates)(nla_type, x, y)
return nla(nla_type, x)
end
function (::ExtendedStates)(nla_type, x, y)
x_tmp = vcat(y, x)
return nla(nla_type, x_tmp)
end
#check matrix/vector
function (states_type::PaddedStates)(nla_type, x, y)
tt = typeof(first(x))
x_tmp = vcat(fill(tt(states_type.padding), (1, size(x, 2))), x)
#x_tmp = reduce(vcat, x_tmp)
return nla(nla_type, x_tmp)
end
#check matrix/vector
function (states_type::PaddedExtendedStates)(nla_type, x, y)
tt = typeof(first(x))
x_tmp = vcat(y, x)
x_tmp = vcat(fill(tt(states_type.padding), (1, size(x, 2))), x_tmp)
#x_tmp = reduce(vcat, x_tmp)
return nla(nla_type, x_tmp)
end
#non linear algorithms
"""
NLADefault()
`NLADefault` represents the default non-linear algorithm option.
When used, it leaves the input array unchanged.
This option is suitable in cases where no non-linear transformation of the data is required,
maintaining the original state of the input array for further processing.
It's the go-to choice for preserving the raw data integrity within the computational pipeline
of the reservoir computing model.
"""
struct NLADefault <: NonLinearAlgorithm end
function nla(::NLADefault, x)
return x
end
"""
NLAT1()
`NLAT1` implements the T₁ transformation algorithm introduced in [^Chattopadhyay] and [^Pathak].
The T₁ algorithm selectively squares elements of the input array,
specifically targeting every second row. This non-linear transformation enhances certain data characteristics,
making it a valuable tool in analyzing chaotic systems and improving the performance of reservoir computing models.
The T₁ transformation's uniqueness lies in its selective approach, allowing for a more nuanced manipulation of the input data.
References:
[^Chattopadhyay]: Chattopadhyay, Ashesh, et al.
"Data-driven prediction of a multi-scale Lorenz 96 chaotic system using a
hierarchy of deep learning methods: Reservoir computing, ANN, and RNN-LSTM." (2019).
[^Pathak]: Pathak, Jaideep, et al.
"Model-free prediction of large spatiotemporally chaotic systems from data:
A reservoir computing approach."
Physical review letters 120.2 (2018): 024102.
"""
struct NLAT1 <: NonLinearAlgorithm end
function nla(::NLAT1, x_old)
x_new = copy(x_old)
for i in 1:size(x_new, 1)
if mod(i, 2) != 0
x_new[i, :] = copy(x_old[i, :] .* x_old[i, :])
end
end
return x_new
end
"""
NLAT2()
`NLAT2` implements the T₂ transformation algorithm as defined in [^Chattopadhyay].
This transformation algorithm modifies the reservoir states by multiplying each odd-indexed
row (starting from the second row) with the product of its two preceding rows.
This specific approach to non-linear transformation is useful for capturing and
enhancing complex patterns in the data, particularly beneficial in the analysis of chaotic
systems and in improving the dynamics within reservoir computing models.
Reference:
[^Chattopadhyay]: Chattopadhyay, Ashesh, et al.
"Data-driven prediction of a multi-scale Lorenz 96 chaotic system using a
hierarchy of deep learning methods: Reservoir computing, ANN, and RNN-LSTM." (2019).
"""
struct NLAT2 <: NonLinearAlgorithm end
function nla(::NLAT2, x_old)
x_new = copy(x_old)
for i in 2:(size(x_new, 1) - 1)
if mod(i, 2) != 0
x_new[i, :] = copy(x_old[i - 1, :] .* x_old[i - 2, :])
end
end
return x_new
end
"""
NLAT3()
The `NLAT3` struct implements the T₃ transformation algorithm as detailed in [^Chattopadhyay].
This algorithm modifies the reservoir's states by multiplying each odd-indexed row
(beginning from the second row) with the product of the immediately preceding and the
immediately following rows. T₃'s unique approach to data transformation makes it particularly
useful for enhancing complex data patterns, thereby improving the modeling and analysis
capabilities within reservoir computing, especially for chaotic and dynamic systems.
Reference:
[^Chattopadhyay]: Chattopadhyay, Ashesh, et al.
"Data-driven prediction of a multi-scale Lorenz 96 chaotic system using a hierarchy of deep learning methods:
Reservoir computing, ANN, and RNN-LSTM." (2019).
"""
struct NLAT3 <: NonLinearAlgorithm end
function nla(::NLAT3, x_old)
x_new = copy(x_old)
for i in 2:(size(x_new, 1) - 1)
if mod(i, 2) != 0
x_new[i, :] = copy(x_old[i - 1, :] .* x_old[i + 1, :])
end
end
return x_new
end
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 1650 | struct DeepESN{I, S, N, T, O, M, B, ST, W, IS} <: AbstractEchoStateNetwork
res_size::I
train_data::S
nla_type::N
input_matrix::T
reservoir_driver::O
reservoir_matrix::M
bias_vector::B
states_type::ST
washout::W
states::IS
end
function DeepESN(train_data,
in_size::Int,
res_size::Int;
depth::Int = 2,
input_layer = fill(scaled_rand, depth),
bias = fill(zeros64, depth),
reservoir = fill(rand_sparse, depth),
reservoir_driver = RNN(),
nla_type = NLADefault(),
states_type = StandardStates(),
washout::Int = 0,
rng = WeightInitializers._default_rng(),
T = Float64,
matrix_type = typeof(train_data))
if states_type isa AbstractPaddedStates
in_size = size(train_data, 1) + 1
train_data = vcat(Adapt.adapt(matrix_type, ones(1, size(train_data, 2))),
train_data)
end
reservoir_matrix = [reservoir[i](rng, T, res_size, res_size) for i in 1:depth]
input_matrix = [i == 1 ? input_layer[i](rng, T, res_size, in_size) :
input_layer[i](rng, T, res_size, res_size) for i in 1:depth]
bias_vector = [bias[i](rng, res_size) for i in 1:depth]
inner_res_driver = reservoir_driver_params(reservoir_driver, res_size, in_size)
states = create_states(inner_res_driver, train_data, washout, reservoir_matrix,
input_matrix, bias_vector)
train_data = train_data[:, (washout + 1):end]
DeepESN(res_size, train_data, nla_type, input_matrix,
inner_res_driver, reservoir_matrix, bias_vector, states_type, washout,
states)
end
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 4737 | abstract type AbstractEchoStateNetwork <: AbstractReservoirComputer end
struct ESN{I, S, N, T, O, M, B, ST, W, IS} <: AbstractEchoStateNetwork
res_size::I
train_data::S
nla_type::N
input_matrix::T
reservoir_driver::O
reservoir_matrix::M
bias_vector::B
states_type::ST
washout::W
states::IS
end
"""
ESN(train_data; kwargs...) -> ESN
Creates an Echo State Network (ESN) using specified parameters and training data, suitable for various machine learning tasks.
# Parameters
- `train_data`: Matrix of training data (columns as time steps, rows as features).
- `variation`: Variation of ESN (default: `Default()`).
- `input_layer`: Input layer of ESN (default: `DenseLayer()`).
- `reservoir`: Reservoir of the ESN (default: `RandSparseReservoir(100)`).
- `bias`: Bias vector for each time step (default: `NullLayer()`).
- `reservoir_driver`: Mechanism for evolving reservoir states (default: `RNN()`).
- `nla_type`: Non-linear activation type (default: `NLADefault()`).
- `states_type`: Format for storing states (default: `StandardStates()`).
- `washout`: Initial time steps to discard (default: `0`).
- `matrix_type`: Type of matrices used internally (default: type of `train_data`).
# Returns
- An initialized ESN instance with specified parameters.
# Examples
```julia
using ReservoirComputing
train_data = rand(10, 100) # 10 features, 100 time steps
esn = ESN(train_data, reservoir = RandSparseReservoir(200), washout = 10)
```
"""
function ESN(train_data,
in_size::Int,
res_size::Int;
input_layer = scaled_rand,
reservoir = rand_sparse,
bias = zeros64,
reservoir_driver = RNN(),
nla_type = NLADefault(),
states_type = StandardStates(),
washout = 0,
rng = WeightInitializers._default_rng(),
T = Float32,
matrix_type = typeof(train_data))
if states_type isa AbstractPaddedStates
in_size = size(train_data, 1) + 1
train_data = vcat(Adapt.adapt(matrix_type, ones(1, size(train_data, 2))),
train_data)
end
reservoir_matrix = reservoir(rng, T, res_size, res_size)
input_matrix = input_layer(rng, T, res_size, in_size)
bias_vector = bias(rng, res_size)
inner_res_driver = reservoir_driver_params(reservoir_driver, res_size, in_size)
states = create_states(inner_res_driver, train_data, washout, reservoir_matrix,
input_matrix, bias_vector)
train_data = train_data[:, (washout + 1):end]
ESN(res_size, train_data, nla_type, input_matrix,
inner_res_driver, reservoir_matrix, bias_vector, states_type, washout,
states)
end
function (esn::AbstractEchoStateNetwork)(prediction::AbstractPrediction,
output_layer::AbstractOutputLayer;
last_state = esn.states[:, [end]],
kwargs...)
pred_len = prediction.prediction_len
return obtain_esn_prediction(esn, prediction, last_state, output_layer;
kwargs...)
end
#training dispatch on esn
"""
train(esn::AbstractEchoStateNetwork, target_data, training_method = StandardRidge(0.0))
Trains an Echo State Network (ESN) using the provided target data and a specified training method.
# Parameters
- `esn::AbstractEchoStateNetwork`: The ESN instance to be trained.
- `target_data`: Supervised training data for the ESN.
- `training_method`: The method for training the ESN (default: `StandardRidge(0.0)`).
# Returns
- The trained ESN model. Its type and structure depend on `training_method` and the ESN's implementation.
# Returns
The trained ESN model. The exact type and structure of the return value depends on the
`training_method` and the specific ESN implementation.
```julia
using ReservoirComputing
# Initialize an ESN instance and target data
esn = ESN(train_data, reservoir = RandSparseReservoir(200), washout = 10)
target_data = rand(size(train_data, 2))
# Train the ESN using the default training method
trained_esn = train(esn, target_data)
# Train the ESN using a custom training method
trained_esn = train(esn, target_data, training_method = StandardRidge(1.0))
```
"""
function train(esn::AbstractEchoStateNetwork,
target_data,
training_method = StandardRidge();
kwargs...)
states_new = esn.states_type(esn.nla_type, esn.states, esn.train_data[:, 1:end])
return train(training_method, states_new, target_data; kwargs...)
end
#function pad_esnstate(variation::Hybrid, states_type, x_pad, x, model_prediction_data)
# x_tmp = vcat(x, model_prediction_data)
# x_pad = pad_state!(states_type, x_pad, x_tmp)
#end
#function pad_esnstate!(variation, states_type, x_pad, x, args...)
# x_pad = pad_state!(states_type, x_pad, x)
#end
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 8094 | """
scaled_rand(rng::AbstractRNG, ::Type{T}, dims::Integer...; scaling=T(0.1)) where {T <: Number}
Create and return a matrix with random values, uniformly distributed within a range defined by `scaling`. This function is useful for initializing matrices, such as the layers of a neural network, with scaled random values.
# Arguments
- `rng`: An instance of `AbstractRNG` for random number generation.
- `T`: The data type for the elements of the matrix.
- `dims`: Dimensions of the matrix. It must be a 2-element tuple specifying the number of rows and columns (e.g., `(res_size, in_size)`).
- `scaling`: A scaling factor to define the range of the uniform distribution. The matrix elements will be randomly chosen from the range `[-scaling, scaling]`. Defaults to `T(0.1)`.
# Returns
A matrix of type with dimensions specified by `dims`. Each element of the matrix is a random number uniformly distributed between `-scaling` and `scaling`.
# Example
```julia
rng = Random.default_rng()
matrix = scaled_rand(rng, Float64, (100, 50); scaling = 0.2)
```
"""
function scaled_rand(rng::AbstractRNG,
::Type{T},
dims::Integer...;
scaling = T(0.1)) where {T <: Number}
res_size, in_size = dims
layer_matrix = T.(rand(rng, Uniform(-scaling, scaling), res_size, in_size))
return layer_matrix
end
"""
weighted_init(rng::AbstractRNG, ::Type{T}, dims::Integer...; scaling=T(0.1)) where {T <: Number}
Create and return a matrix representing a weighted input layer for Echo State Networks (ESNs). This initializer generates a weighted input matrix with random non-zero elements distributed uniformly within the range [-`scaling`, `scaling`], inspired by the approach in [^Lu].
# Arguments
- `rng`: An instance of `AbstractRNG` for random number generation.
- `T`: The data type for the elements of the matrix.
- `dims`: A 2-element tuple specifying the approximate reservoir size and input size (e.g., `(approx_res_size, in_size)`).
- `scaling`: The scaling factor for the weight distribution. Defaults to `T(0.1)`.
# Returns
A matrix representing the weighted input layer as defined in [^Lu2017]. The matrix dimensions will be adjusted to ensure each input unit connects to an equal number of reservoir units.
# Example
```julia
rng = Random.default_rng()
input_layer = weighted_init(rng, Float64, (3, 300); scaling = 0.2)
```
# References
[^Lu2017]: Lu, Zhixin, et al.
"Reservoir observers: Model-free inference of unmeasured variables in chaotic systems."
Chaos: An Interdisciplinary Journal of Nonlinear Science 27.4 (2017): 041102.
"""
function weighted_init(rng::AbstractRNG,
::Type{T},
dims::Integer...;
scaling = T(0.1)) where {T <: Number}
approx_res_size, in_size = dims
res_size = Int(floor(approx_res_size / in_size) * in_size)
layer_matrix = zeros(T, res_size, in_size)
q = floor(Int, res_size / in_size)
for i in 1:in_size
layer_matrix[((i - 1) * q + 1):((i) * q), i] = rand(rng,
Uniform(-scaling, scaling),
q)
end
return layer_matrix
end
"""
informed_init(rng::AbstractRNG, ::Type{T}, dims::Integer...; scaling=T(0.1), model_in_size, gamma=T(0.5)) where {T <: Number}
Create a layer of a neural network.
# Arguments
- `rng::AbstractRNG`: The random number generator.
- `T::Type`: The data type.
- `dims::Integer...`: The dimensions of the layer.
- `scaling::T = T(0.1)`: The scaling factor for the input matrix.
- `model_in_size`: The size of the input model.
- `gamma::T = T(0.5)`: The gamma value.
# Returns
- `input_matrix`: The created input matrix for the layer.
# Example
```julia
rng = Random.default_rng()
dims = (100, 200)
model_in_size = 50
input_matrix = informed_init(rng, Float64, dims; model_in_size = model_in_size)
```
"""
function informed_init(rng::AbstractRNG, ::Type{T}, dims::Integer...;
scaling = T(0.1), model_in_size, gamma = T(0.5)) where {T <: Number}
res_size, in_size = dims
state_size = in_size - model_in_size
if state_size <= 0
throw(DimensionMismatch("in_size must be greater than model_in_size"))
end
input_matrix = zeros(res_size, in_size)
zero_connections = zeros(in_size)
num_for_state = floor(Int, res_size * gamma)
num_for_model = floor(Int, res_size * (1 - gamma))
for i in 1:num_for_state
idxs = findall(Bool[zero_connections .== input_matrix[i, :]
for i in 1:size(input_matrix, 1)])
random_row_idx = idxs[rand(rng, 1:end)]
random_clm_idx = range(1, state_size, step = 1)[rand(rng, 1:end)]
input_matrix[random_row_idx, random_clm_idx] = rand(rng, Uniform(-scaling, scaling))
end
for i in 1:num_for_model
idxs = findall(Bool[zero_connections .== input_matrix[i, :]
for i in 1:size(input_matrix, 1)])
random_row_idx = idxs[rand(rng, 1:end)]
random_clm_idx = range(state_size + 1, in_size, step = 1)[rand(rng, 1:end)]
input_matrix[random_row_idx, random_clm_idx] = rand(rng, Uniform(-scaling, scaling))
end
return input_matrix
end
"""
irrational_sample_init(rng::AbstractRNG, ::Type{T}, dims::Integer...;
weight = 0.1,
sampling = IrrationalSample(; irrational = pi, start = 1)
) where {T <: Number}
Create a layer matrix using the provided random number generator and sampling parameters.
# Arguments
- `rng::AbstractRNG`: The random number generator used to generate random numbers.
- `dims::Integer...`: The dimensions of the layer matrix.
- `weight`: The weight used to fill the layer matrix. Default is 0.1.
- `sampling`: The sampling parameters used to generate the input matrix. Default is IrrationalSample(irrational = pi, start = 1).
# Returns
The layer matrix generated using the provided random number generator and sampling parameters.
# Example
```julia
using Random
rng = Random.default_rng()
dims = (3, 2)
weight = 0.5
layer_matrix = irrational_sample_init(rng, Float64, dims; weight = weight,
sampling = IrrationalSample(irrational = sqrt(2), start = 1))
```
"""
function minimal_init(rng::AbstractRNG, ::Type{T}, dims::Integer...;
sampling_type::Symbol = :bernoulli,
weight::Number = T(0.1),
irrational::Real = pi,
start::Int = 1,
p::Number = T(0.5)) where {T <: Number}
res_size, in_size = dims
if sampling_type == :bernoulli
layer_matrix = _create_bernoulli(p, res_size, in_size, weight, rng, T)
elseif sampling_type == :irrational
layer_matrix = _create_irrational(irrational,
start,
res_size,
in_size,
weight,
rng,
T)
else
error("Sampling type not allowed. Please use one of :bernoulli or :irrational")
end
return layer_matrix
end
function _create_bernoulli(p::T,
res_size::Int,
in_size::Int,
weight::T,
rng::AbstractRNG,
::Type{T}) where {T <: Number}
input_matrix = zeros(T, res_size, in_size)
for i in 1:res_size
for j in 1:in_size
rand(rng, Bernoulli(p)) ? (input_matrix[i, j] = weight) :
(input_matrix[i, j] = -weight)
end
end
return input_matrix
end
function _create_irrational(irrational::Irrational,
start::Int,
res_size::Int,
in_size::Int,
weight::T,
rng::AbstractRNG,
::Type{T}) where {T <: Number}
setprecision(BigFloat, Int(ceil(log2(10) * (res_size * in_size + start + 1))))
ir_string = string(BigFloat(irrational)) |> collect
deleteat!(ir_string, findall(x -> x == '.', ir_string))
ir_array = zeros(length(ir_string))
input_matrix = zeros(T, res_size, in_size)
for i in 1:length(ir_string)
ir_array[i] = parse(Int, ir_string[i])
end
for i in 1:res_size
for j in 1:in_size
random_number = rand(rng, T)
input_matrix[i, j] = random_number < 0.5 ? -weight : weight
end
end
return T.(input_matrix)
end
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 3980 | function obtain_esn_prediction(esn,
prediction::Generative,
x,
output_layer,
args...;
initial_conditions = output_layer.last_value,
save_states = false)
out_size = output_layer.out_size
training_method = output_layer.training_method
prediction_len = prediction.prediction_len
output = output_storing(training_method, out_size, prediction_len, typeof(esn.states))
out = initial_conditions
states = similar(esn.states, size(esn.states, 1), prediction_len)
out_pad = allocate_outpad(esn, esn.states_type, out)
tmp_array = allocate_tmp(esn.reservoir_driver, typeof(esn.states), esn.res_size)
x_new = esn.states_type(esn.nla_type, x, out_pad)
for i in 1:prediction_len
x, x_new = next_state_prediction!(esn, x, x_new, out, out_pad, i, tmp_array,
args...)
out_tmp = get_prediction(output_layer.training_method, output_layer, x_new)
out = store_results!(output_layer.training_method, out_tmp, output, i)
states[:, i] = x
end
save_states ? (output, states) : output
end
function obtain_esn_prediction(esn,
prediction::Predictive,
x,
output_layer,
args...;
initial_conditions = output_layer.last_value,
save_states = false)
out_size = output_layer.out_size
training_method = output_layer.training_method
prediction_len = prediction.prediction_len
output = output_storing(training_method, out_size, prediction_len, typeof(esn.states))
out = initial_conditions
states = similar(esn.states, size(esn.states, 1), prediction_len)
out_pad = allocate_outpad(esn, esn.states_type, out)
tmp_array = allocate_tmp(esn.reservoir_driver, typeof(esn.states), esn.res_size)
x_new = esn.states_type(esn.nla_type, x, out_pad)
for i in 1:prediction_len
x, x_new = next_state_prediction!(esn, x, x_new, prediction.prediction_data[:, i],
out_pad, i, tmp_array, args...)
out_tmp = get_prediction(training_method, output_layer, x_new)
out = store_results!(training_method, out_tmp, output, i)
states[:, i] = x
end
save_states ? (output, states) : output
end
#prediction dispatch on esn
function next_state_prediction!(
esn::AbstractEchoStateNetwork, x, x_new, out, out_pad, i, tmp_array, args...)
out_pad = pad_state!(esn.states_type, out_pad, out)
xv = @view x[1:(esn.res_size)]
x = next_state!(x, esn.reservoir_driver, x, out_pad,
esn.reservoir_matrix, esn.input_matrix, esn.bias_vector, tmp_array)
x_new = esn.states_type(esn.nla_type, x, out_pad)
return x, x_new
end
#TODO fixme @MatrinuzziFra
function next_state_prediction!(hesn::HybridESN,
x,
x_new,
out,
out_pad,
i,
tmp_array,
model_prediction_data)
out_tmp = vcat(out, model_prediction_data[:, i])
out_pad = pad_state!(hesn.states_type, out_pad, out_tmp)
x = next_state!(x, hesn.reservoir_driver, x[1:(hesn.res_size)], out_pad,
hesn.reservoir_matrix, hesn.input_matrix, hesn.bias_vector, tmp_array)
x_tmp = vcat(x, model_prediction_data[:, i])
x_new = hesn.states_type(hesn.nla_type, x_tmp, out_pad)
return x, x_new
end
function allocate_outpad(ens::AbstractEchoStateNetwork, states_type, out)
return allocate_singlepadding(states_type, out)
end
function allocate_outpad(hesn::HybridESN, states_type, out)
pad_length = length(out) + size(hesn.model.model_data[:, 1], 1)
out_tmp = Adapt.adapt(typeof(out), zeros(pad_length))
return allocate_singlepadding(states_type, out_tmp)
end
function allocate_singlepadding(::AbstractPaddedStates, out)
Adapt.adapt(typeof(out), zeros(size(out, 1) + 1))
end
function allocate_singlepadding(::StandardStates, out)
Adapt.adapt(typeof(out), zeros(size(out, 1)))
end
function allocate_singlepadding(::ExtendedStates, out)
Adapt.adapt(typeof(out), zeros(size(out, 1)))
end
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 14121 | abstract type AbstractReservoirDriver end
"""
create_states(
reservoir_driver::AbstractReservoirDriver,
train_data,
washout,
reservoir_matrix,
input_matrix,
bias_vector
)
Create and return the trained Echo State Network (ESN) states according to the specified reservoir driver.
# Arguments
- `reservoir_driver::AbstractReservoirDriver`: The reservoir driver that determines how the ESN states evolve over time.
- `train_data`: The training data used to train the ESN.
- `washout::Int`: The number of initial time steps to discard during training to allow the reservoir dynamics to wash out the initial conditions.
- `reservoir_matrix`: The reservoir matrix representing the dynamic, recurrent part of the ESN.
- `input_matrix`: The input matrix that defines the connections between input features and reservoir nodes.
- `bias_vector`: The bias vector to be added at each time step during the reservoir update.
# Returns
- A matrix of trained ESN states, where each column represents the state at a specific time step.
This function is responsible for creating and returning the states of the ESN during training based on the provided training data and parameters.
"""
function create_states(reservoir_driver::AbstractReservoirDriver,
train_data,
washout,
reservoir_matrix,
input_matrix,
bias_vector)
train_len = size(train_data, 2) - washout
res_size = size(reservoir_matrix, 1)
states = Adapt.adapt(typeof(train_data), zeros(res_size, train_len))
tmp_array = allocate_tmp(reservoir_driver, typeof(train_data), res_size)
_state = Adapt.adapt(typeof(train_data), zeros(res_size, 1))
for i in 1:washout
yv = @view train_data[:, i]
_state = next_state!(_state, reservoir_driver, _state, yv, reservoir_matrix,
input_matrix, bias_vector, tmp_array)
end
for j in 1:train_len
yv = @view train_data[:, washout + j]
_state = next_state!(_state, reservoir_driver, _state, yv,
reservoir_matrix, input_matrix, bias_vector, tmp_array)
states[:, j] = _state
end
return states
end
function create_states(reservoir_driver::AbstractReservoirDriver,
train_data,
washout,
reservoir_matrix::Vector,
input_matrix,
bias_vector)
train_len = size(train_data, 2) - washout
res_size = sum([size(reservoir_matrix[i], 1) for i in 1:length(reservoir_matrix)])
states = Adapt.adapt(typeof(train_data), zeros(res_size, train_len))
tmp_array = allocate_tmp(reservoir_driver, typeof(train_data), res_size)
_state = Adapt.adapt(typeof(train_data), zeros(res_size))
for i in 1:washout
for j in 1:length(reservoir_matrix)
_inter_state = next_state!(_inter_state, reservoir_driver, _inter_state,
train_data[:, i],
reservoir_matrix, input_matrix, bias_vector,
tmp_array)
end
_state = next_state!(_state, reservoir_driver, _state, train_data[:, i],
reservoir_matrix, input_matrix, bias_vector, tmp_array)
end
for j in 1:train_len
_state = next_state!(_state, reservoir_driver, _state, train_data[:, washout + j],
reservoir_matrix, input_matrix, bias_vector, tmp_array)
states[:, j] = _state
end
return states
end
#standard RNN driver
struct RNN{F, T} <: AbstractReservoirDriver
activation_function::F
leaky_coefficient::T
end
"""
RNN(activation_function, leaky_coefficient)
RNN(;activation_function=tanh, leaky_coefficient=1.0)
Returns a Recurrent Neural Network (RNN) initializer for the Echo State Network (ESN).
# Arguments
- `activation_function`: The activation function used in the RNN.
- `leaky_coefficient`: The leaky coefficient used in the RNN.
# Keyword Arguments
- `activation_function`: The activation function used in the RNN. Defaults to `tanh`.
- `leaky_coefficient`: The leaky coefficient used in the RNN. Defaults to 1.0.
This function creates an RNN object with the specified activation function and leaky coefficient,
which can be used as a reservoir driver in the ESN.
"""
function RNN(; activation_function = NNlib.fast_act(tanh), leaky_coefficient = 1.0)
RNN(activation_function, leaky_coefficient)
end
function reservoir_driver_params(rnn::RNN, args...)
rnn
end
function next_state!(out, rnn::RNN, x, y, W, W_in, b, tmp_array)
mul!(tmp_array[1], W, x)
mul!(tmp_array[2], W_in, y)
@. tmp_array[1] = rnn.activation_function(tmp_array[1] + tmp_array[2] + b) *
rnn.leaky_coefficient
@. out = (1 - rnn.leaky_coefficient) * x + tmp_array[1]
end
function next_state!(out, rnn::RNN, x, y, W::Vector, W_in, b, tmp_array)
esn_depth = length(W)
res_sizes = vcat(0, [size(W[i], 1) for i in 1:esn_depth])
inner_states = [x[(1 + sum(res_sizes[1:i])):sum(res_sizes[1:(i + 1)])]
for i in 1:esn_depth]
inner_inputs = vcat([y], inner_states[1:(end - 1)])
for i in 1:esn_depth
inner_states[i] = (1 - rnn.leaky_coefficient) .* inner_states[i] +
rnn.leaky_coefficient *
rnn.activation_function.((W[i] * inner_states[i]) .+
(W_in[i] * inner_inputs[i]) .+
reduce(vcat, b[i]))
end
return reduce(vcat, inner_states)
end
function allocate_tmp(::RNN, tmp_type, res_size)
return [Adapt.adapt(tmp_type, zeros(res_size, 1)) for i in 1:2]
end
#multiple RNN driver
struct MRNN{F, T, R} <: AbstractReservoirDriver
activation_function::F
leaky_coefficient::T
scaling_factor::R
end
"""
MRNN(activation_function, leaky_coefficient, scaling_factor)
MRNN(;activation_function=[tanh, sigmoid], leaky_coefficient=1.0,
scaling_factor=fill(leaky_coefficient, length(activation_function)))
Returns a Multiple RNN (MRNN) initializer for the Echo State Network (ESN), introduced in [^lun].
# Arguments
- `activation_function`: A vector of activation functions used in the MRNN.
- `leaky_coefficient`: The leaky coefficient used in the MRNN.
- `scaling_factor`: A vector of scaling factors for combining activation functions.
# Keyword Arguments
- `activation_function`: A vector of activation functions used in the MRNN. Defaults to `[tanh, sigmoid]`.
- `leaky_coefficient`: The leaky coefficient used in the MRNN. Defaults to 1.0.
- `scaling_factor`: A vector of scaling factors for combining activation functions. Defaults to an array of the same size as `activation_function` with all elements set to `leaky_coefficient`.
This function creates an MRNN object with the specified activation functions, leaky coefficient, and scaling factors, which can be used as a reservoir driver in the ESN.
# Reference:
[^lun]: Lun, Shu-Xian, et al.
"_A novel model of leaky integrator echo state network for
time-series prediction._" Neurocomputing 159 (2015): 58-66.
"""
function MRNN(; activation_function = [tanh, sigmoid],
leaky_coefficient = 1.0,
scaling_factor = fill(leaky_coefficient, length(activation_function)))
@assert length(activation_function) == length(scaling_factor)
return MRNN(activation_function, leaky_coefficient, scaling_factor)
end
function reservoir_driver_params(mrnn::MRNN, args...)
return mrnn
end
function next_state!(out, mrnn::MRNN, x, y, W, W_in, b, tmp_array)
@. out = (1 - mrnn.leaky_coefficient) * x
for i in 1:length(mrnn.scaling_factor)
mul!(tmp_array[1], W, x)
mul!(tmp_array[2], W_in, y)
@. out += mrnn.activation_function[i](tmp_array[1] + tmp_array[2] + b) *
mrnn.scaling_factor[i]
end
return out
end
#=
function next_state!(out, mrnn::MRNN, x, y, W, W_in, b, tmp_array)
rnn_next_state = (1-mrnn.leaky_coefficient).*x
for i=1:length(mrnn.scaling_factor)
rnn_next_state += mrnn.scaling_factor[i]*mrnn.activation_function[i].((W*x).+(W_in*y).+b)
end
rnn_next_state
end
=#
function allocate_tmp(::MRNN, tmp_type, res_size)
return [Adapt.adapt(tmp_type, zeros(res_size, 1)) for i in 1:2]
end
#GRU-based driver
struct GRU{F, L, R, V, B} #not an abstractreservoirdriver
activation_function::F
inner_layer::L
reservoir::R
bias::B
variant::V
end
#https://arxiv.org/abs/1701.05923# variations of gru
"""
FullyGated()
Returns a Fully Gated Recurrent Unit (FullyGated) initializer for the Echo State Network (ESN).
This function creates a FullyGated object, which can be used as a reservoir driver in the ESN.
The FullyGated variant is described in the literature reference [^cho].
# Returns
- `FullyGated`: A FullyGated reservoir driver.
# Reference
[^cho]: Cho, Kyunghyun, et al.
"_Learning phrase representations using RNN encoder-decoder for statistical machine translation._"
arXiv preprint arXiv:1406.1078 (2014).
"""
struct FullyGated <: AbstractGRUVariant end
"""
Minimal()
Returns a minimal GRU ESN initializer as described in [^Zhou].
[^Zhou]: Zhou, Guo-Bing, et al. "_Minimal gated unit for recurrent neural networks._"
International Journal of Automation and Computing 13.3 (2016): 226-234.
"""
struct Minimal <: AbstractGRUVariant end
#layer_init and activation_function must be vectors
"""
GRU(;activation_function=[NNlib.sigmoid, NNlib.sigmoid, tanh],
inner_layer = fill(DenseLayer(), 2),
reservoir = fill(RandSparseReservoir(), 2),
bias = fill(DenseLayer(), 2),
variant = FullyGated())
Returns a Gated Recurrent Unit (GRU) reservoir driver for Echo State Networks (ESNs). This driver is based on the GRU architecture [^Cho], which is designed to capture temporal dependencies in data and is commonly used in various machine learning applications.
# Arguments
- `activation_function`: An array of activation functions for the GRU layers. By default, it uses sigmoid activation functions for the update gate, reset gate, and tanh for the hidden state.
- `inner_layer`: An array of inner layers used in the GRU architecture. By default, it uses two dense layers.
- `reservoir`: An array of reservoir layers. By default, it uses two random sparse reservoirs.
- `bias`: An array of bias layers for the GRU. By default, it uses two dense layers.
- `variant`: The GRU variant to use. By default, it uses the "FullyGated" variant.
# Returns
A GRUParams object containing the parameters needed for the GRU-based reservoir driver.
# References
[^Cho]: Cho, Kyunghyun, et al.
"_Learning phrase representations using RNN encoder-decoder for statistical machine translation._"
arXiv preprint arXiv:1406.1078 (2014).
"""
function GRU(; activation_function = [NNlib.sigmoid, NNlib.sigmoid, tanh],
inner_layer = fill(scaled_rand, 2),
reservoir = fill(rand_sparse, 2),
bias = fill(scaled_rand, 2),
variant = FullyGated())
return GRU(activation_function, inner_layer, reservoir, bias, variant)
end
#the actual params are only available inside ESN(), so a different driver is needed
struct GRUParams{F, V, S, I, N, SF, IF, NF} <: AbstractReservoirDriver
activation_function::F
variant::V
Wz_in::S
Wz::I
bz::N
Wr_in::SF
Wr::IF
br::NF
end
#vreation of the actual driver
function reservoir_driver_params(gru::GRU, res_size, in_size)
gru_params = create_gru_layers(gru, gru.variant, res_size, in_size)
return gru_params
end
#dispatch on the different gru variations
function create_gru_layers(gru, variant::FullyGated, res_size, in_size)
Wz_in = gru.inner_layer[1](res_size, in_size)
Wz = gru.reservoir[1](res_size, res_size)
bz = gru.bias[1](res_size, 1)
Wr_in = gru.inner_layer[2](res_size, in_size)
Wr = gru.reservoir[2](res_size, res_size)
br = gru.bias[2](res_size, 1)
return GRUParams(gru.activation_function, variant, Wz_in, Wz, bz, Wr_in, Wr, br)
end
#check this one, not sure
function create_gru_layers(gru, variant::Minimal, res_size, in_size)
Wz_in = gru.inner_layer(res_size, in_size)
Wz = gru.reservoir(res_size, res_size)
bz = gru.bias(res_size, 1)
Wr_in = nothing
Wr = nothing
br = nothing
return GRUParams(gru.activation_function, variant, Wz_in, Wz, bz, Wr_in, Wr, br)
end
#in case the user wants to use this driver
function reservoir_driver_params(gru::GRUParams, args...)
return gru
end
#dispatch on the important function: next_state
function next_state!(out, gru::GRUParams, x, y, W, W_in, b, tmp_array)
gru_next_state = obtain_gru_state!(out, gru.variant, gru, x, y, W, W_in, b, tmp_array)
return gru_next_state
end
function allocate_tmp(::GRUParams, tmp_type, res_size)
return [Adapt.adapt(tmp_type, zeros(res_size, 1)) for i in 1:9]
end
#W=U, W_in=W in papers. x=h, and y=x. I know, it's confusing. ( on the left our notation)
#fully gated gru
function obtain_gru_state!(out, variant::FullyGated, gru, x, y, W, W_in, b, tmp_array)
mul!(tmp_array[1], gru.Wz_in, y)
mul!(tmp_array[2], gru.Wz, x)
@. tmp_array[3] = gru.activation_function[1](tmp_array[1] + tmp_array[2] + gru.bz)
mul!(tmp_array[4], gru.Wr_in, y)
mul!(tmp_array[5], gru.Wr, x)
@. tmp_array[6] = gru.activation_function[2](tmp_array[4] + tmp_array[5] + gru.br)
mul!(tmp_array[7], W_in, y)
mul!(tmp_array[8], W, tmp_array[6] .* x)
@. tmp_array[9] = gru.activation_function[3](tmp_array[7] + tmp_array[8] + b)
@. out = (1 - tmp_array[3]) * x + tmp_array[3] * tmp_array[9]
end
#minimal
function obtain_gru_state!(out, variant::Minimal, gru, x, y, W, W_in, b, tmp_array)
mul!(tmp_array[1], gru.Wz_in, y)
mul!(tmp_array[2], gru.Wz, x)
@. tmp_array[3] = gru.activation_function[1](tmp_array[1] + tmp_array[2] + gru.bz)
mul!(tmp_array[4], W_in, y)
mul!(tmp_array[5], W, tmp_array[3] .* x)
@. tmp_array[6] = gru.activation_function[2](tmp_array[4] + tmp_array[5] + b)
@. out = (1 - tmp_array[3]) * x + tmp_array[3] * tmp_array[6]
end
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 10838 | """
rand_sparse(rng::AbstractRNG, ::Type{T}, dims::Integer...; radius=1.0, sparsity=0.1)
Create and return a random sparse reservoir matrix for use in Echo State Networks (ESNs). The matrix will be of size specified by `dims`, with specified `sparsity` and scaled spectral radius according to `radius`.
# Arguments
- `rng`: An instance of `AbstractRNG` for random number generation.
- `T`: The data type for the elements of the matrix.
- `dims`: Dimensions of the reservoir matrix.
- `radius`: The desired spectral radius of the reservoir. Defaults to 1.0.
- `sparsity`: The sparsity level of the reservoir matrix, controlling the fraction of zero elements. Defaults to 0.1.
# Returns
A matrix representing the random sparse reservoir.
# References
This type of reservoir initialization is commonly used in ESNs for capturing temporal dependencies in data.
"""
function rand_sparse(rng::AbstractRNG,
::Type{T},
dims::Integer...;
radius = T(1.0),
sparsity = T(0.1),
std = T(1.0)) where {T <: Number}
lcl_sparsity = T(1) - sparsity #consistency with current implementations
reservoir_matrix = sparse_init(rng, T, dims...; sparsity = lcl_sparsity, std = std)
rho_w = maximum(abs.(eigvals(reservoir_matrix)))
reservoir_matrix .*= radius / rho_w
if Inf in unique(reservoir_matrix) || -Inf in unique(reservoir_matrix)
error("Sparsity too low for size of the matrix. Increase res_size or increase sparsity")
end
return reservoir_matrix
end
"""
delay_line(rng::AbstractRNG, ::Type{T}, dims::Integer...; weight=0.1) where {T <: Number}
Create and return a delay line reservoir matrix for use in Echo State Networks (ESNs). A delay line reservoir is a deterministic structure where each unit is connected only to its immediate predecessor with a specified weight. This method is particularly useful for tasks that require specific temporal processing.
# Arguments
- `rng`: An instance of `AbstractRNG` for random number generation. This argument is not used in the current implementation but is included for consistency with other initialization functions.
- `T`: The data type for the elements of the matrix.
- `dims`: Dimensions of the reservoir matrix. Typically, this should be a tuple of two equal integers representing a square matrix.
- `weight`: The weight determines the absolute value of all connections in the reservoir. Defaults to 0.1.
# Returns
A delay line reservoir matrix with dimensions specified by `dims`. The matrix is initialized such that each element in the `i+1`th row and `i`th column is set to `weight`, and all other elements are zeros.
# Example
```julia
reservoir = delay_line(Float64, 100, 100; weight = 0.2)
```
# References
This type of reservoir initialization is described in:
Rodan, Ali, and Peter Tino. "Minimum complexity echo state network." IEEE Transactions on Neural Networks 22.1 (2010): 131-144.
"""
function delay_line(rng::AbstractRNG,
::Type{T},
dims::Integer...;
weight = T(0.1)) where {T <: Number}
reservoir_matrix = zeros(T, dims...)
@assert length(dims) == 2&&dims[1] == dims[2] "The dimensions must define a square matrix (e.g., (100, 100))"
for i in 1:(dims[1] - 1)
reservoir_matrix[i + 1, i] = weight
end
return reservoir_matrix
end
"""
delay_line_backward(rng::AbstractRNG, ::Type{T}, dims::Integer...;
weight = T(0.1), fb_weight = T(0.2)) where {T <: Number}
Create a delay line backward reservoir with the specified by `dims` and weights. Creates a matrix with backward connections
as described in [^Rodan2010]. The `weight` and `fb_weight` can be passed as either arguments or
keyword arguments, and they determine the absolute values of the connections in the reservoir.
# Arguments
- `rng::AbstractRNG`: Random number generator.
- `T::Type`: Type of the elements in the reservoir matrix.
- `dims::Integer...`: Dimensions of the reservoir matrix.
- `weight::T`: The weight determines the absolute value of forward connections in the reservoir, and is set to 0.1 by default.
- `fb_weight::T`: The `fb_weight` determines the absolute value of backward connections in the reservoir, and is set to 0.2 by default.
# Returns
Reservoir matrix with the dimensions specified by `dims` and weights.
# References
[^Rodan2010]: Rodan, Ali, and Peter Tino. "Minimum complexity echo state network."
IEEE transactions on neural networks 22.1 (2010): 131-144.
"""
function delay_line_backward(rng::AbstractRNG,
::Type{T},
dims::Integer...;
weight = T(0.1),
fb_weight = T(0.2)) where {T <: Number}
res_size = first(dims)
reservoir_matrix = zeros(T, dims...)
for i in 1:(res_size - 1)
reservoir_matrix[i + 1, i] = weight
reservoir_matrix[i, i + 1] = fb_weight
end
return reservoir_matrix
end
"""
cycle_jumps(rng::AbstractRNG, ::Type{T}, dims::Integer...;
cycle_weight = T(0.1), jump_weight = T(0.1), jump_size = 3) where {T <: Number}
Create a cycle jumps reservoir with the specified dimensions, cycle weight, jump weight, and jump size.
# Arguments
- `rng::AbstractRNG`: Random number generator.
- `T::Type`: Type of the elements in the reservoir matrix.
- `dims::Integer...`: Dimensions of the reservoir matrix.
- `cycle_weight::T = T(0.1)`: The weight of cycle connections.
- `jump_weight::T = T(0.1)`: The weight of jump connections.
- `jump_size::Int = 3`: The number of steps between jump connections.
# Returns
Reservoir matrix with the specified dimensions, cycle weight, jump weight, and jump size.
# References
[^Rodan2012]: Rodan, Ali, and Peter Tiňo. "Simple deterministically constructed cycle reservoirs
with regular jumps." Neural computation 24.7 (2012): 1822-1852.
"""
function cycle_jumps(rng::AbstractRNG,
::Type{T},
dims::Integer...;
cycle_weight::Number = T(0.1),
jump_weight::Number = T(0.1),
jump_size::Int = 3) where {T <: Number}
res_size = first(dims)
reservoir_matrix = zeros(T, dims...)
for i in 1:(res_size - 1)
reservoir_matrix[i + 1, i] = cycle_weight
end
reservoir_matrix[1, res_size] = cycle_weight
for i in 1:jump_size:(res_size - jump_size)
tmp = (i + jump_size) % res_size
if tmp == 0
tmp = res_size
end
reservoir_matrix[i, tmp] = jump_weight
reservoir_matrix[tmp, i] = jump_weight
end
return reservoir_matrix
end
"""
simple_cycle(rng::AbstractRNG, ::Type{T}, dims::Integer...;
weight = T(0.1)) where {T <: Number}
Create a simple cycle reservoir with the specified dimensions and weight.
# Arguments
- `rng::AbstractRNG`: Random number generator.
- `T::Type`: Type of the elements in the reservoir matrix.
- `dims::Integer...`: Dimensions of the reservoir matrix.
- `weight::T = T(0.1)`: Weight of the connections in the reservoir matrix.
# Returns
Reservoir matrix with the dimensions specified by `dims` and weights.
# References
[^Rodan2010]: Rodan, Ali, and Peter Tino. "Minimum complexity echo state network."
IEEE transactions on neural networks 22.1 (2010): 131-144.
"""
function simple_cycle(rng::AbstractRNG,
::Type{T},
dims::Integer...;
weight = T(0.1)) where {T <: Number}
reservoir_matrix = zeros(T, dims...)
for i in 1:(dims[1] - 1)
reservoir_matrix[i + 1, i] = weight
end
reservoir_matrix[1, dims[1]] = weight
return reservoir_matrix
end
"""
pseudo_svd(rng::AbstractRNG, ::Type{T}, dims::Integer...;
max_value, sparsity, sorted = true, reverse_sort = false) where {T <: Number}
Returns an initializer to build a sparse reservoir matrix with the given `sparsity` by using a pseudo-SVD approach as described in [^yang].
# Arguments
- `rng::AbstractRNG`: Random number generator.
- `T::Type`: Type of the elements in the reservoir matrix.
- `dims::Integer...`: Dimensions of the reservoir matrix.
- `max_value`: The maximum absolute value of elements in the matrix.
- `sparsity`: The desired sparsity level of the reservoir matrix.
- `sorted`: A boolean indicating whether to sort the singular values before creating the diagonal matrix. By default, it is set to `true`.
- `reverse_sort`: A boolean indicating whether to reverse the sorted singular values. By default, it is set to `false`.
# Returns
Reservoir matrix with the specified dimensions, max value, and sparsity.
# References
This reservoir initialization method, based on a pseudo-SVD approach, is inspired by the work in [^yang], which focuses on designing polynomial echo state networks for time series prediction.
[^yang]: Yang, Cuili, et al. "_Design of polynomial echo state networks for time series prediction._" Neurocomputing 290 (2018): 148-160.
"""
function pseudo_svd(rng::AbstractRNG,
::Type{T},
dims::Integer...;
max_value::Number = T(1.0),
sparsity::Number = 0.1,
sorted::Bool = true,
reverse_sort::Bool = false) where {T <: Number}
reservoir_matrix = create_diag(dims[1],
max_value,
T;
sorted = sorted,
reverse_sort = reverse_sort)
tmp_sparsity = get_sparsity(reservoir_matrix, dims[1])
while tmp_sparsity <= sparsity
reservoir_matrix *= create_qmatrix(dims[1],
rand(1:dims[1]),
rand(1:dims[1]),
rand(T) * T(2) - T(1),
T)
tmp_sparsity = get_sparsity(reservoir_matrix, dims[1])
end
return reservoir_matrix
end
function create_diag(dim::Number, max_value::Number, ::Type{T};
sorted::Bool = true, reverse_sort::Bool = false) where {T <: Number}
diagonal_matrix = zeros(T, dim, dim)
if sorted == true
if reverse_sort == true
diagonal_values = sort(rand(T, dim) .* max_value, rev = true)
diagonal_values[1] = max_value
else
diagonal_values = sort(rand(T, dim) .* max_value)
diagonal_values[end] = max_value
end
else
diagonal_values = rand(T, dim) .* max_value
end
for i in 1:dim
diagonal_matrix[i, i] = diagonal_values[i]
end
return diagonal_matrix
end
function create_qmatrix(dim::Number,
coord_i::Number,
coord_j::Number,
theta::Number,
::Type{T}) where {T <: Number}
qmatrix = zeros(T, dim, dim)
for i in 1:dim
qmatrix[i, i] = 1.0
end
qmatrix[coord_i, coord_i] = cos(theta)
qmatrix[coord_j, coord_j] = cos(theta)
qmatrix[coord_i, coord_j] = -sin(theta)
qmatrix[coord_j, coord_i] = sin(theta)
return qmatrix
end
function get_sparsity(M, dim)
return size(M[M .!= 0], 1) / (dim * dim - size(M[M .!= 0], 1)) #nonzero/zero elements
end
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 3996 | struct HybridESN{I, S, V, N, T, O, M, B, ST, W, IS} <: AbstractEchoStateNetwork
res_size::I
train_data::S
model::V
nla_type::N
input_matrix::T
reservoir_driver::O
reservoir_matrix::M
bias_vector::B
states_type::ST
washout::W
states::IS
end
struct KnowledgeModel{T, K, O, I, S, D}
prior_model::T
u0::K
tspan::O
dt::I
datasize::S
model_data::D
end
"""
Hybrid(prior_model, u0, tspan, datasize)
Constructs a `Hybrid` variation of Echo State Networks (ESNs) integrating a knowledge-based model
(`prior_model`) with ESNs for advanced training and prediction in chaotic systems.
# Parameters
- `prior_model`: A knowledge-based model function for integration with ESNs.
- `u0`: Initial conditions for the model.
- `tspan`: Time span as a tuple, indicating the duration for model operation.
- `datasize`: The size of the data to be processed.
# Returns
- A `Hybrid` struct instance representing the combined ESN and knowledge-based model.
This method is effective for chaotic processes as highlighted in [^Pathak].
Reference:
[^Pathak]: Jaideep Pathak et al.
"Hybrid Forecasting of Chaotic Processes:
Using Machine Learning in Conjunction with a Knowledge-Based Model" (2018).
"""
function KnowledgeModel(prior_model, u0, tspan, datasize)
trange = collect(range(tspan[1], tspan[2], length = datasize))
dt = trange[2] - trange[1]
tsteps = push!(trange, dt + trange[end])
tspan_new = (tspan[1], dt + tspan[2])
model_data = prior_model(u0, tspan_new, tsteps)
return KnowledgeModel(prior_model, u0, tspan, dt, datasize, model_data)
end
function HybridESN(model,
train_data,
in_size::Int,
res_size::Int;
input_layer = scaled_rand,
reservoir = rand_sparse,
bias = zeros64,
reservoir_driver = RNN(),
nla_type = NLADefault(),
states_type = StandardStates(),
washout = 0,
rng = WeightInitializers._default_rng(),
T = Float32,
matrix_type = typeof(train_data))
train_data = vcat(train_data, model.model_data[:, 1:(end - 1)])
if states_type isa AbstractPaddedStates
in_size = size(train_data, 1) + 1
train_data = vcat(Adapt.adapt(matrix_type, ones(1, size(train_data, 2))),
train_data)
else
in_size = size(train_data, 1)
end
reservoir_matrix = reservoir(rng, T, res_size, res_size)
#different from ESN, why?
input_matrix = input_layer(rng, T, res_size, in_size)
bias_vector = bias(rng, res_size)
inner_res_driver = reservoir_driver_params(reservoir_driver, res_size, in_size)
states = create_states(inner_res_driver, train_data, washout, reservoir_matrix,
input_matrix, bias_vector)
train_data = train_data[:, (washout + 1):end]
HybridESN(res_size, train_data, model, nla_type, input_matrix,
inner_res_driver, reservoir_matrix, bias_vector, states_type, washout,
states)
end
function (hesn::HybridESN)(prediction::AbstractPrediction,
output_layer::AbstractOutputLayer;
last_state = hesn.states[:, [end]],
kwargs...)
km = hesn.model
pred_len = prediction.prediction_len
model = km.prior_model
predict_tsteps = [km.tspan[2] + km.dt]
[append!(predict_tsteps, predict_tsteps[end] + km.dt) for i in 1:pred_len]
tspan_new = (km.tspan[2] + km.dt, predict_tsteps[end])
u0 = km.model_data[:, end]
model_pred_data = model(u0, tspan_new, predict_tsteps)[:, 2:end]
return obtain_esn_prediction(hesn, prediction, last_state, output_layer,
model_pred_data;
kwargs...)
end
function train(hesn::HybridESN,
target_data,
training_method = StandardRidge();
kwargs...)
states = vcat(hesn.states, hesn.model.model_data[:, 2:end])
states_new = hesn.states_type(hesn.nla_type, states, hesn.train_data[:, 1:end])
return train(training_method, states_new, target_data; kwargs...)
end
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 2150 | abstract type AbstractReca <: AbstractReservoirComputer end
struct RECA{S, R, E, T, Q} <: AbstractReca
#res_size::I
train_data::S
automata::R
input_encoding::E
nla_type::ReservoirComputing.NonLinearAlgorithm
states::T
states_type::Q
end
"""
RECA(train_data,
automata;
generations = 8,
input_encoding=RandomMapping(),
nla_type = NLADefault(),
states_type = StandardStates())
[1] Yilmaz, Ozgur. “_Reservoir computing using cellular automata._”
arXiv preprint arXiv:1410.0162 (2014).
[2] Nichele, Stefano, and Andreas Molund. “_Deep reservoir computing using cellular
automata._” arXiv preprint arXiv:1703.02806 (2017).
"""
function RECA(train_data,
automata;
generations = 8,
input_encoding = RandomMapping(),
nla_type = NLADefault(),
states_type = StandardStates())
in_size = size(train_data, 1)
#res_size = obtain_res_size(input_encoding, generations)
state_encoding = create_encoding(input_encoding, train_data, generations)
states = reca_create_states(state_encoding, automata, train_data)
return RECA(train_data, automata, state_encoding, nla_type, states, states_type)
end
#training dispatch
function train(reca::AbstractReca, target_data, training_method = StandardRidge; kwargs...)
states_new = reca.states_type(reca.nla_type, reca.states, reca.train_data)
return train(training_method, states_new, target_data; kwargs...)
end
#predict dispatch
function (reca::RECA)(prediction,
output_layer::AbstractOutputLayer,
initial_conditions = output_layer.last_value,
last_state = zeros(reca.input_encoding.ca_size))
return obtain_prediction(reca, prediction, last_state, output_layer;
initial_conditions = initial_conditions)
end
function next_state_prediction!(reca::RECA, x, out, i, args...)
rm = reca.input_encoding
x = encoding(rm, out, x)
ca = CellularAutomaton(reca.automata, x, rm.generations + 1)
ca_states = ca.evolution[2:end, :]
x_new = reshape(transpose(ca_states), rm.states_size)
x = ca.evolution[end, :]
return x, x_new
end
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 3395 | abstract type AbstractInputEncoding end
abstract type AbstractEncodingData end
struct RandomMapping{I, T} <: AbstractInputEncoding
permutations::I
expansion_size::T
end
"""
RandomMapping(permutations, expansion_size)
RandomMapping(permutations; expansion_size=40)
RandomMapping(;permutations=8, expansion_size=40)
Random mapping of the input data directly in the reservoir. The `expansion_size`
determines the dimension of the single reservoir, and `permutations` determines the
number of total reservoirs that will be connected, each with a different mapping.
The detail of this implementation can be found in [1].
[1] Nichele, Stefano, and Andreas Molund. “Deep reservoir computing using cellular
automata.” arXiv preprint arXiv:1703.02806 (2017).
"""
function RandomMapping(; permutations = 8, expansion_size = 40)
RandomMapping(permutations, expansion_size)
end
function RandomMapping(permutations; expansion_size = 40)
RandomMapping(permutations, expansion_size)
end
struct RandomMaps{T, E, G, M, S} <: AbstractEncodingData
permutations::T
expansion_size::E
generations::G
maps::M
states_size::S
ca_size::S
end
function create_encoding(rm::RandomMapping, input_data, generations)
maps = init_maps(size(input_data, 1), rm.permutations, rm.expansion_size)
states_size = generations * rm.expansion_size * rm.permutations
ca_size = rm.expansion_size * rm.permutations
return RandomMaps(rm.permutations, rm.expansion_size, generations, maps, states_size,
ca_size)
end
function reca_create_states(rm::RandomMaps, automata, input_data)
train_time = size(input_data, 2)
states = zeros(rm.states_size, train_time)
init_ca = zeros(rm.expansion_size * rm.permutations)
for i in 1:train_time
init_ca = encoding(rm, input_data[:, i], init_ca)
ca = CellularAutomaton(automata, init_ca, rm.generations + 1)
ca_states = ca.evolution[2:end, :]
states[:, i] = reshape(transpose(ca_states), rm.states_size)
init_ca = ca.evolution[end, :]
end
return states
end
function encoding(rm::RandomMaps, input_vector, tot_encoded_vector)
input_size = size(input_vector, 1)
#single_encoded_size = Int(size(tot_encoded_vector, 1)/permutations)
new_tot_enc_vec = copy(tot_encoded_vector)
for i in 1:(rm.permutations)
new_tot_enc_vec[((i - 1) * rm.expansion_size + 1):(i * rm.expansion_size)] = single_encoding(
input_vector,
new_tot_enc_vec[((i - 1) * rm.expansion_size + 1):(i * rm.expansion_size)],
rm.maps[i,
:])
end
return new_tot_enc_vec
end
#function obtain_res_size(rm::RandomMapping, generations)
# generations*rm.expansion_size*rm.permutations
#end
function single_encoding(input_vector, encoded_vector, map)
new_enc_vec = copy(encoded_vector)
for i in 1:size(input_vector, 1)
new_enc_vec[map[i]] = input_vector[i]
end
return new_enc_vec
end
function init_maps(input_size, permutations, mapped_vector_size)
maps = Array{Int}(undef, permutations, input_size)
#tot_size = input_size*permutations
for i in 1:permutations
maps[i, :] = mapping(input_size, mapped_vector_size)
end
return maps
end
function mapping(input_size, mapped_vector_size)
return sample(1:mapped_vector_size, input_size, replace = false)
end
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 628 | struct StandardRidge
reg::Number
end
function StandardRidge(::Type{T}, reg) where {T <: Number}
return StandardRidge(T.(reg))
end
function StandardRidge()
return StandardRidge(0.0)
end
function train(sr::StandardRidge,
states::AbstractArray{T},
target_data::AbstractArray{T}) where {T <: Number}
#A = states * states' + sr.reg * I
#b = states * target_data
#output_layer = (A \ b)'
output_layer = Matrix(((states * states' + sr.reg * I) \
(states * target_data'))')
return OutputLayer(sr, output_layer, size(target_data, 1), target_data[:, end])
end
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 460 | using ReservoirComputing, Aqua
@testset "Aqua" begin
Aqua.find_persistent_tasks_deps(ReservoirComputing)
Aqua.test_ambiguities(ReservoirComputing, recursive = false)
Aqua.test_deps_compat(ReservoirComputing)
Aqua.test_piracies(ReservoirComputing)
Aqua.test_project_extras(ReservoirComputing)
Aqua.test_stale_deps(ReservoirComputing)
Aqua.test_unbound_args(ReservoirComputing)
Aqua.test_undefined_exports(ReservoirComputing)
end
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 629 | using SafeTestsets
using Test
@testset "Common Utilities" begin
@safetestset "Quality Assurance" include("qa.jl")
@safetestset "States" include("test_states.jl")
end
@testset "Echo State Networks" begin
@safetestset "ESN Input Layers" include("esn/test_inits.jl")
@safetestset "ESN Train and Predict" include("esn/test_train.jl")
@safetestset "ESN Drivers" include("esn/test_drivers.jl")
@safetestset "Hybrid ESN" include("esn/test_hybrid.jl")
@safetestset "Deep ESN" include("esn/deepesn.jl")
end
@testset "CA based Reservoirs" begin
@safetestset "RECA" include("reca/test_predictive.jl")
end
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 1254 | using ReservoirComputing
test_array = [1, 2, 3, 4, 5, 6, 7, 8, 9]
extension = [0, 0, 0]
padding = 10.0
test_types = [Float64, Float32, Float16]
nlas = [(NLADefault(), test_array),
(NLAT1(), [1, 2, 9, 4, 25, 6, 49, 8, 81]),
(NLAT2(), [1, 2, 2, 4, 12, 6, 30, 8, 9]),
(NLAT3(), [1, 2, 8, 4, 24, 6, 48, 8, 9])]
pes = [(StandardStates(), test_array),
(PaddedStates(padding = padding),
reshape(vcat(padding, test_array), length(test_array) + 1, 1)),
(PaddedExtendedStates(padding = padding),
reshape(vcat(padding, extension, test_array),
length(test_array) + length(extension) + 1,
1)),
(ExtendedStates(), vcat(extension, test_array))]
@testset "States Testing" for T in test_types
@testset "Nonlinear Algorithms Testing: $algo $T" for (algo, expected_output) in nlas
nla_array = ReservoirComputing.nla(algo, T.(test_array))
@test nla_array == expected_output
@test eltype(nla_array) == T
end
@testset "States Testing: $state_type $T" for (state_type, expected_output) in pes
states_output = state_type(NLADefault(), T.(test_array), T.(extension))
@test states_output == expected_output
@test eltype(states_output) == T
end
end
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 662 | using ReservoirComputing, Random, Statistics
const res_size = 20
const ts = 0.0:0.1:50.0
const data = sin.(ts)
const train_len = 400
const predict_len = 100
const input_data = reduce(hcat, data[1:(train_len - 1)])
const target_data = reduce(hcat, data[2:train_len])
const test = reduce(hcat, data[(train_len + 1):(train_len + predict_len)])
const reg = 10e-6
#test_types = [Float64, Float32, Float16]
Random.seed!(77)
res = rand_sparse(; radius = 1.2, sparsity = 0.1)
esn = DeepESN(input_data, 1, res_size)
output_layer = train(esn, target_data)
output = esn(Generative(length(test)), output_layer)
@test mean(abs.(test .- output)) ./ mean(abs.(test)) < 0.22
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 1613 | using ReservoirComputing, Random, Statistics, NNlib
const res_size = 50
const ts = 0.0:0.1:50.0
const data = sin.(ts)
const train_len = 400
const input_data = reduce(hcat, data[1:(train_len - 1)])
const target_data = reduce(hcat, data[2:train_len])
const predict_len = 100
const test_data = reduce(hcat, data[(train_len + 1):(train_len + predict_len)])
const training_method = StandardRidge(10e-6)
Random.seed!(77)
function test_esn(input_data, target_data, training_method, esn_config)
esn = ESN(input_data, 1, res_size; esn_config...)
output_layer = train(esn, target_data, training_method)
output = esn(Predictive(target_data), output_layer, initial_conditions = target_data[1])
@test mean(abs.(target_data .- output)) ./ mean(abs.(target_data)) < 0.15
end
esn_configs = [
Dict(:reservoir => rand_sparse(; radius = 1.2),
:reservoir_driver => GRU(variant = FullyGated(),
reservoir = [
rand_sparse(; radius = 1.0, sparsity = 0.5),
rand_sparse(; radius = 1.2, sparsity = 0.1)
])),
Dict(:reservoir => rand_sparse(; radius = 1.2),
:reservoir_driver => GRU(variant = Minimal(),
reservoir = rand_sparse(; radius = 1.0, sparsity = 0.5),
inner_layer = scaled_rand,
bias = scaled_rand)),
Dict(:reservoir => rand_sparse(; radius = 1.2),
:reservoir_driver => MRNN(activation_function = (tanh, sigmoid),
scaling_factor = (0.8, 0.1)))
]
@testset "Test Drivers: $config" for config in esn_configs
test_esn(input_data, target_data, training_method, config)
end
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 1269 | using ReservoirComputing, DifferentialEquations, Statistics, Random
u0 = [1.0, 0.0, 0.0]
tspan = (0.0, 1000.0)
datasize = 100000
tsteps = range(tspan[1], tspan[2], length = datasize)
function lorenz(du, u, p, t)
p = [10.0, 28.0, 8 / 3]
du[1] = p[1] * (u[2] - u[1])
du[2] = u[1] * (p[2] - u[3]) - u[2]
du[3] = u[1] * u[2] - p[3] * u[3]
end
function prior_model_data_generator(u0, tspan, tsteps, model = lorenz)
prob = ODEProblem(lorenz, u0, tspan)
sol = Array(solve(prob, saveat = tsteps))
return sol
end
train_len = 10000
ode_prob = ODEProblem(lorenz, u0, tspan)
ode_sol = solve(ode_prob, saveat = tsteps)
ode_data = Array(ode_sol)
input_data = ode_data[:, 1:train_len]
target_data = ode_data[:, 2:(train_len + 1)]
test_data = ode_data[:, (train_len + 1):end][:, 1:1000]
predict_len = size(test_data, 2)
tspan_train = (tspan[1], ode_sol.t[train_len])
km = KnowledgeModel(prior_model_data_generator, u0, tspan_train, train_len)
Random.seed!(77)
hesn = HybridESN(km,
input_data,
3,
300;
reservoir = rand_sparse)
output_layer = train(hesn, target_data, StandardRidge(0.3))
output = hesn(Generative(predict_len), output_layer)
@test mean(abs.(test_data[1:100] .- output[1:100])) ./ mean(abs.(test_data[1:100])) < 0.11
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 2532 | using ReservoirComputing
using LinearAlgebra
using Random
const res_size = 30
const in_size = 3
const radius = 1.0
const sparsity = 0.1
const weight = 0.2
const jump_size = 3
const rng = Random.default_rng()
function check_radius(matrix, target_radius; tolerance = 1e-5)
eigenvalues = eigvals(matrix)
spectral_radius = maximum(abs.(eigenvalues))
return isapprox(spectral_radius, target_radius, atol = tolerance)
end
ft = [Float16, Float32, Float64]
reservoir_inits = [
rand_sparse,
delay_line,
delay_line_backward,
cycle_jumps,
simple_cycle,
pseudo_svd
]
input_inits = [
scaled_rand,
weighted_init,
minimal_init,
minimal_init(; sampling_type = :irrational)
]
@testset "Reservoir Initializers" begin
@testset "Sizes and types: $init $T" for init in reservoir_inits, T in ft
#sizes
@test size(init(res_size, res_size)) == (res_size, res_size)
@test size(init(rng, res_size, res_size)) == (res_size, res_size)
#types
@test eltype(init(T, res_size, res_size)) == T
@test eltype(init(rng, T, res_size, res_size)) == T
#closure
cl = init(rng)
@test eltype(cl(T, res_size, res_size)) == T
end
@testset "Check spectral radius" begin
sp = rand_sparse(res_size, res_size)
@test check_radius(sp, radius)
end
@testset "Minimum complexity: $init" for init in [
delay_line,
delay_line_backward,
cycle_jumps,
simple_cycle
]
dl = init(res_size, res_size)
if init === delay_line_backward
@test unique(dl) == Float32.([0.0, 0.1, 0.2])
else
@test unique(dl) == Float32.([0.0, 0.1])
end
end
end
# TODO: @MartinuzziFrancesco Missing tests for informed_init
@testset "Input Initializers" begin
@testset "Sizes and types: $init $T" for init in input_inits, T in ft
#sizes
@test size(init(res_size, in_size)) == (res_size, in_size)
@test size(init(rng, res_size, in_size)) == (res_size, in_size)
#types
@test eltype(init(T, res_size, in_size)) == T
@test eltype(init(rng, T, res_size, in_size)) == T
#closure
cl = init(rng)
@test eltype(cl(T, res_size, in_size)) == T
end
@testset "Minimum complexity: $init" for init in [
minimal_init,
minimal_init(; sampling_type = :irrational)
]
dl = init(res_size, in_size)
@test sort(unique(dl)) == Float32.([-0.1, 0.1])
end
end
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 1437 | using ReservoirComputing, MLJLinearModels, Random, Statistics, LIBSVM
const res_size = 20
const ts = 0.0:0.1:50.0
const data = sin.(ts)
const train_len = 400
const predict_len = 100
const input_data = reduce(hcat, data[1:(train_len - 1)])
const target_data = reduce(hcat, data[2:train_len])
const test = reduce(hcat, data[(train_len + 1):(train_len + predict_len)])
const reg = 10e-6
#test_types = [Float64, Float32, Float16]
Random.seed!(77)
res = rand_sparse(; radius = 1.2, sparsity = 0.1)
esn = ESN(input_data, 1, res_size;
reservoir = res)
# different models that implement a train dispatch
# TODO add classification
linear_training = [StandardRidge(0.0), LinearRegression(; fit_intercept = false),
RidgeRegression(; fit_intercept = false), LassoRegression(; fit_intercept = false),
ElasticNetRegression(; fit_intercept = false), HuberRegression(; fit_intercept = false),
QuantileRegression(; fit_intercept = false), LADRegression(; fit_intercept = false)]
svm_training = [EpsilonSVR(), NuSVR()]
# TODO check types
@testset "Linear training: $lt" for lt in linear_training
output_layer = train(esn, target_data, lt)
@test output_layer isa OutputLayer
@test output_layer.output_matrix isa AbstractArray
end
@testset "SVM training: $st" for st in svm_training
output_layer = train(esn, target_data, st)
@test output_layer isa OutputLayer
@test output_layer.output_matrix isa typeof(st)
end
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | code | 572 | using ReservoirComputing, CellularAutomata
const input = ones(2, 10)
const output = zeros(2, 10)
const g = 6
const rule = 90
reca = RECA(input, DCA(rule);
generations = g,
input_encoding = RandomMapping(6, 10))
output_layer = train(reca, output, StandardRidge(0.001))
prediction = reca(Predictive(input), output_layer)
final_pred = convert(AbstractArray{Int}, prediction .> 0.5)
@test final_pred == output
rm1 = RandomMapping(6, 10)
rm2 = RandomMapping(6, expansion_size = 10)
rm3 = RandomMapping(permutations = 6, expansion_size = 10)
@test rm1 == rm2 == rm3
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | docs | 5403 | # ReservoirComputing.jl
[](https://julialang.zulipchat.com/#narrow/stream/279055-sciml-bridged)
[](https://docs.sciml.ai/ReservoirComputing/stable/)
[](https://arxiv.org/abs/2204.05117)
[](https://codecov.io/gh/SciML/ReservoirComputing.jl)
[](https://github.com/SciML/ReservoirComputing.jl/actions?query=workflow%3ACI)
[](https://buildkite.com/julialang/reservoircomputing-dot-jl)
[](https://github.com/SciML/ColPrac)
[](https://github.com/SciML/SciMLStyle)

ReservoirComputing.jl provides an efficient, modular and easy to use implementation of Reservoir Computing models such as Echo State Networks (ESNs). For information on using this package please refer to the [stable documentation](https://docs.sciml.ai/ReservoirComputing/stable/). Use the [in-development documentation](https://docs.sciml.ai/ReservoirComputing/dev/) to take a look at at not yet released features.
## Quick Example
To illustrate the workflow of this library we will showcase how it is possible to train an ESN to learn the dynamics of the Lorenz system. As a first step we will need to gather the data. For the `Generative` prediction we need the target data to be one step ahead of the training data:
```julia
using ReservoirComputing, OrdinaryDiffEq
#lorenz system parameters
u0 = [1.0, 0.0, 0.0]
tspan = (0.0, 200.0)
p = [10.0, 28.0, 8 / 3]
#define lorenz system
function lorenz(du, u, p, t)
du[1] = p[1] * (u[2] - u[1])
du[2] = u[1] * (p[2] - u[3]) - u[2]
du[3] = u[1] * u[2] - p[3] * u[3]
end
#solve and take data
prob = ODEProblem(lorenz, u0, tspan, p)
data = solve(prob, ABM54(), dt = 0.02)
shift = 300
train_len = 5000
predict_len = 1250
#one step ahead for generative prediction
input_data = data[:, shift:(shift + train_len - 1)]
target_data = data[:, (shift + 1):(shift + train_len)]
test = data[:, (shift + train_len):(shift + train_len + predict_len - 1)]
```
Now that we have the data we can initialize the ESN with the chosen parameters. Given that this is a quick example we are going to change the least amount of possible parameters. For more detailed examples and explanations of the functions please refer to the documentation.
```julia
input_size = 3
res_size = 300
esn = ESN(input_data, input_size, res_size;
reservoir = rand_sparse(; radius = 1.2, sparsity = 6 / res_size),
input_layer = weighted_init,
nla_type = NLAT2())
```
The echo state network can now be trained and tested. If not specified, the training will always be ordinary least squares regression. The full range of training methods is detailed in the documentation.
```julia
output_layer = train(esn, target_data)
output = esn(Generative(predict_len), output_layer)
```
The data is returned as a matrix, `output` in the code above, that contains the predicted trajectories. The results can now be easily plotted (for the actual script used to obtain this plot please refer to the documentation):
```julia
using Plots
plot(transpose(output), layout = (3, 1), label = "predicted")
plot!(transpose(test), layout = (3, 1), label = "actual")
```
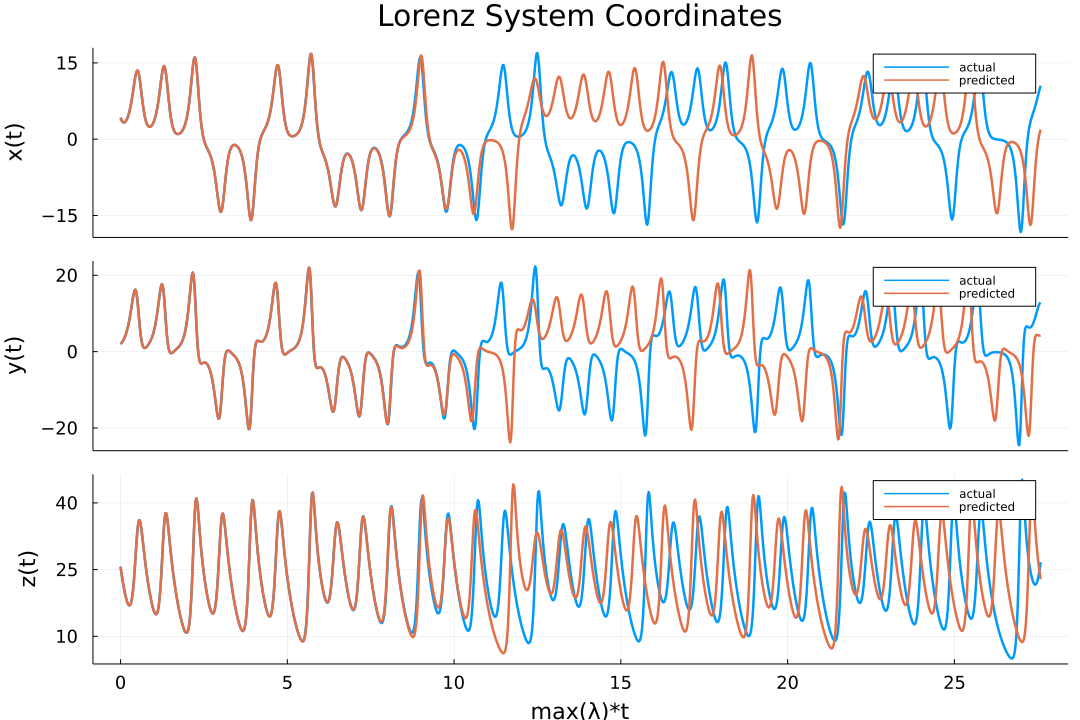
One can also visualize the phase space of the attractor and the comparison with the actual one:
```julia
plot(transpose(output)[:, 1],
transpose(output)[:, 2],
transpose(output)[:, 3],
label = "predicted")
plot!(transpose(test)[:, 1], transpose(test)[:, 2], transpose(test)[:, 3], label = "actual")
```
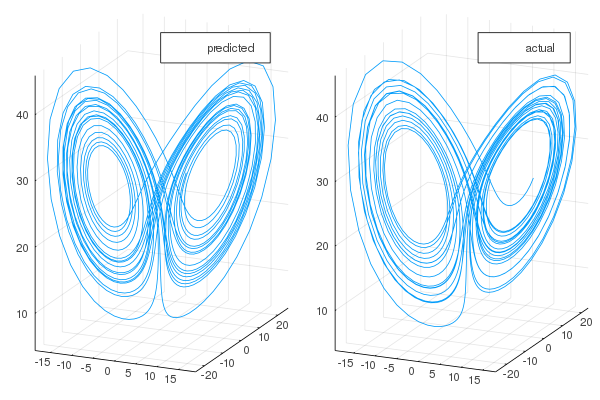
## Citing
If you use this library in your work, please cite:
```bibtex
@article{JMLR:v23:22-0611,
author = {Francesco Martinuzzi and Chris Rackauckas and Anas Abdelrehim and Miguel D. Mahecha and Karin Mora},
title = {ReservoirComputing.jl: An Efficient and Modular Library for Reservoir Computing Models},
journal = {Journal of Machine Learning Research},
year = {2022},
volume = {23},
number = {288},
pages = {1--8},
url = {http://jmlr.org/papers/v23/22-0611.html}
}
```
## Acknowledgements
This project was possible thanks to initial funding through the [Google summer of code](https://summerofcode.withgoogle.com/) 2020 program. Francesco M. further acknowledges [ScaDS.AI](https://scads.ai/) and [RSC4Earth](https://rsc4earth.de/) for supporting the current progress on the library.
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | docs | 5513 | # ReservoirComputing.jl
ReservoirComputing.jl is a versatile and user-friendly Julia package designed for the implementation of advanced Reservoir Computing models, such as Echo State Networks (ESNs). Central to Reservoir Computing is the expansion of input data into a higher-dimensional space, leveraging regression techniques for effective model training. This approach bears resemblance to kernel methods, offering a unique perspective in machine learning. ReservoirComputing.jl offers a modular design, ensuring both ease of use for newcomers and flexibility for advanced users, establishing it as a key tool for innovative computing solutions.
!!! info "Introductory material"
This library assumes some basic knowledge of Reservoir Computing. For a good introduction, we suggest the following papers: the first two are the seminal papers about ESN and LSM, the others are in-depth review papers that should cover all the needed information. For the majority of the algorithms implemented in this library we cited in the documentation the original work introducing them. If you ever are in doubt about a method or a function just type `? function` in the Julia REPL to read the relevant notes.
- Jaeger, Herbert: The “echo state” approach to analyzing and training recurrent neural networks-with an erratum note.
- Maass W, Natschläger T, Markram H: Real-time computing without stable states: a new framework for neural computation based on perturbations.
- Lukoševičius, Mantas: A practical guide to applying echo state networks." Neural networks: Tricks of the trade.
- Lukoševičius, Mantas, and Herbert Jaeger: Reservoir computing approaches to recurrent neural network training.
!!! info "Performance tip"
For faster computations on the CPU it is suggested to add `using MKL` to the script. For clarity's sake this library will not be indicated under every example in the documentation.
## Installation
To install ReservoirComputing.jl, ensure you have Julia version 1.6 or higher. Follow these steps:
1. Open the Julia command line.
2. Enter the Pkg REPL mode by pressing ].
3. Type add ReservoirComputing and press Enter.
For a more customized installation or to contribute to the package, consider cloning the repository:
```julia
using Pkg
Pkg.clone("https://github.com/SciML/ReservoirComputing.jl.git")
```
or `dev` the package.
## Features Overview
- **Multiple Training Algorithms**: Supports Ridge Regression, Linear Models, and LIBSVM regression methods for Reservoir Computing models.
- **Diverse Prediction Methods**: Offers both generative and predictive methods for Reservoir Computing predictions.
- **Modifiable Training and Prediction**: Allows modifications in Reservoir Computing states, such as state extension, padding, and combination methods.
- **Non-linear Algorithm Options**: Includes options for non-linear modifications in algorithms.
- **Echo State Networks (ESNs)**: Features various input layers, reservoirs, and methods for driving ESN reservoir states.
- **Cellular Automata-Based Reservoir Computing**: Introduces models based on one-dimensional Cellular Automata for Reservoir Computing.
## Contributing
Contributions to ReservoirComputing.jl are highly encouraged and appreciated. Whether it's through implementing new RC model variations, enhancing documentation, adding examples, or any improvement, your contribution is valuable. We welcome posts of relevant papers or ideas in the issues section. For deeper insights into the library's functionality, the API section in the documentation is a great resource. For any queries not suited for issues, please reach out to the lead developers via Slack or email.
## Citing
If you use ReservoirComputing.jl in your work, we kindly ask you to cite it. Here is the BibTeX entry for your convenience:
```bibtex
@article{JMLR:v23:22-0611,
author = {Francesco Martinuzzi and Chris Rackauckas and Anas Abdelrehim and Miguel D. Mahecha and Karin Mora},
title = {ReservoirComputing.jl: An Efficient and Modular Library for Reservoir Computing Models},
journal = {Journal of Machine Learning Research},
year = {2022},
volume = {23},
number = {288},
pages = {1--8},
url = {http://jmlr.org/papers/v23/22-0611.html}
}
```
## Reproducibility
```@raw html
<details><summary>The documentation of this SciML package was built using these direct dependencies,</summary>
```
```@example
using Pkg # hide
Pkg.status() # hide
```
```@raw html
</details>
```
```@raw html
<details><summary>and using this machine and Julia version.</summary>
```
```@example
using InteractiveUtils # hide
versioninfo() # hide
```
```@raw html
</details>
```
```@raw html
<details><summary>A more complete overview of all dependencies and their versions is also provided.</summary>
```
```@example
using Pkg # hide
Pkg.status(; mode = PKGMODE_MANIFEST) # hide
```
```@raw html
</details>
```
```@eval
using TOML
using Markdown
version = TOML.parse(read("../../Project.toml", String))["version"]
name = TOML.parse(read("../../Project.toml", String))["name"]
link_manifest = "https://github.com/SciML/" * name * ".jl/tree/gh-pages/v" * version *
"/assets/Manifest.toml"
link_project = "https://github.com/SciML/" * name * ".jl/tree/gh-pages/v" * version *
"/assets/Project.toml"
Markdown.parse("""You can also download the
[manifest]($link_manifest)
file and the
[project]($link_project)
file.
""")
```
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | docs | 1195 | # Echo State Networks
The core component of an ESN is the `ESN` type. It represents the entire Echo State Network and includes parameters for configuring the reservoir, input scaling, and output weights. Here's the documentation for the `ESN` type:
```@docs
ESN
```
## Variations
In addition to the standard `ESN` model, there are variations that allow for deeper customization of the underlying model. Currently, there are two available variations: `Default` and `Hybrid`. These variations provide different ways to configure the ESN. Here's the documentation for the variations:
```@docs
Default
Hybrid
```
The `Hybrid` variation is the most complex option and offers additional customization. Note that more variations may be added in the future to provide even greater flexibility.
## Training
To train an ESN model, you can use the `train` function. It takes the ESN model, training data, and other optional parameters as input and returns a trained model. Here's the documentation for the train function:
```@docs
train
```
With these components and variations, you can configure and train ESN models for various time series and sequential data prediction tasks.
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | docs | 257 | # ESN Drivers
```@docs
RNN
MRNN
GRU
```
The `GRU` driver also provides the user with the choice of the possible variants:
```@docs
FullyGated
Minimal
```
Please refer to the original papers for more detail about these architectures.
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | docs | 1990 | # ESN Layers
## Input Layers
```@docs
WeightedLayer
DenseLayer
SparseLayer
InformedLayer
MinimumLayer
NullLayer
```
The signs in the `MinimumLayer` are chosen based on the following methods:
```@docs
BernoulliSample
IrrationalSample
```
To derive the matrix one can call the following function:
```@docs
create_layer
```
To create new input layers, it suffices to define a new struct containing the needed parameters of the new input layer. This struct will need to be an `AbstractLayer`, so the `create_layer` function can be dispatched over it. The workflow should follow this snippet:
```julia
#creation of the new struct for the layer
struct MyNewLayer <: AbstractLayer
#the layer params go here
end
#dispatch over the function to actually build the layer matrix
function create_layer(input_layer::MyNewLayer, res_size, in_size)
#the new algorithm to build the input layer goes here
end
```
## Reservoirs
```@docs
RandSparseReservoir
PseudoSVDReservoir
DelayLineReservoir
DelayLineBackwardReservoir
SimpleCycleReservoir
CycleJumpsReservoir
NullReservoir
```
Like for the input layers, to actually build the matrix of the reservoir, one can call the following function:
```@docs
create_reservoir
```
To create a new reservoir, the procedure is similar to the one for the input layers. First, the definition of the new struct of type `AbstractReservoir` with the reservoir parameters is needed. Then the dispatch over the `create_reservoir` function makes the model actually build the reservoir matrix. An example of the workflow is given in the following snippet:
```julia
#creation of the new struct for the reservoir
struct MyNewReservoir <: AbstractReservoir
#the reservoir params go here
end
#dispatch over the function to build the reservoir matrix
function create_reservoir(reservoir::AbstractReservoir, res_size)
#the new algorithm to build the reservoir matrix goes here
end
```
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | docs | 63 | # Prediction Types
```@docs
Generative
Predictive
```
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | docs | 475 | # Reservoir Computing with Cellular Automata
```@docs
RECA
```
The input encodings are the equivalent of the input matrices of the ESNs. These are the available encodings:
```@docs
RandomMapping
```
The training and prediction follow the same workflow as the ESN. It is important to note that currently we were unable to find any papers using these models with a `Generative` approach for the prediction, so full support is given only to the `Predictive` method.
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | docs | 233 | # States Modifications
## Padding and Estension
```@docs
StandardStates
ExtendedStates
PaddedStates
PaddedExtendedStates
```
## Non Linear Transformations
```@docs
NLADefault
NLAT1
NLAT2
NLAT3
```
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | docs | 399 | # Training Algorithms
## Linear Models
```@docs
StandardRidge
LinearModel
```
## Gaussian Regression
Currently, v0.9 is unavailable.
## Support Vector Regression
Support Vector Regression is possible using a direct call to [LIBSVM](https://github.com/JuliaML/LIBSVM.jl) regression methods. Instead of a wrapper, please refer to the use of `LIBSVM.AbstractSVR` in the original library.
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | docs | 4557 | # Using Different Layers
A great deal of effort in the ESNs field is devoted to finding the ideal construction for the reservoir matrices. With a simple interface using ReservoirComputing.jl it is possible to leverage the currently implemented matrix construction methods for both the reservoir and the input layer. On this page, it is showcased how it is possible to change both of these layers.
The `input_init` keyword argument provided with the `ESN` constructor allows for changing the input layer. The layers provided in ReservoirComputing.jl are the following:
- `WeightedLayer(scaling)`
- `DenseLayer(scaling)`
- `SparseLayer(scaling, sparsity)`
- `MinimumLayer(weight, sampling)`
- `InformedLayer(model_in_size; scaling=0.1, gamma=0.5)`
In addition, the user can define a custom layer following this workflow:
```julia
#creation of the new struct for the layer
struct MyNewLayer <: AbstractLayer
#the layer params go here
end
#dispatch over the function to actually build the layer matrix
function create_layer(input_layer::MyNewLayer, res_size, in_size)
#the new algorithm to build the input layer goes here
end
```
Similarly the `reservoir_init` keyword argument provides the possibility to change the construction for the reservoir matrix. The available reservoir are:
- `RandSparseReservoir(res_size, radius, sparsity)`
- `PseudoSVDReservoir(res_size, max_value, sparsity, sorted, reverse_sort)`
- `DelayLineReservoir(res_size, weight)`
- `DelayLineBackwardReservoir(res_size, weight, fb_weight)`
- `SimpleCycleReservoir(res_size, weight)`
- `CycleJumpsReservoir(res_size, cycle_weight, jump_weight, jump_size)`
And, like before, it is possible to build a custom reservoir by following this workflow:
```julia
#creation of the new struct for the reservoir
struct MyNewReservoir <: AbstractReservoir
#the reservoir params go here
end
#dispatch over the function to build the reservoir matrix
function create_reservoir(reservoir::AbstractReservoir, res_size)
#the new algorithm to build the reservoir matrix goes here
end
```
## Example of a minimally complex ESN
Using [^1] and [^2] as references, this section will provide an example of how to change both the input layer and the reservoir for ESNs. The full script for this example can be found [here](https://github.com/MartinuzziFrancesco/reservoir-computing-examples/blob/main/change_layers/layers.jl). This example was run on Julia v1.7.2.
The task for this example will be the one step ahead prediction of the Henon map. To obtain the data, one can leverage the package [DynamicalSystems.jl](https://juliadynamics.github.io/DynamicalSystems.jl/dev/). The data is scaled to be between -1 and 1.
```@example mesn
using PredefinedDynamicalSystems
train_len = 3000
predict_len = 2000
ds = PredefinedDynamicalSystems.henon()
traj, time = trajectory(ds, 7000)
data = Matrix(traj)'
data = (data .- 0.5) .* 2
shift = 200
training_input = data[:, shift:(shift + train_len - 1)]
training_target = data[:, (shift + 1):(shift + train_len)]
testing_input = data[:, (shift + train_len):(shift + train_len + predict_len - 1)]
testing_target = data[:, (shift + train_len + 1):(shift + train_len + predict_len)]
```
Now it is possible to define the input layers and reservoirs we want to compare and run the comparison in a simple for loop. The accuracy will be tested using the mean squared deviation `msd` from [StatsBase](https://juliastats.org/StatsBase.jl/stable/).
```@example mesn
using ReservoirComputing, StatsBase
res_size = 300
input_layer = [
MinimumLayer(0.85, IrrationalSample()),
MinimumLayer(0.95, IrrationalSample())
]
reservoirs = [SimpleCycleReservoir(res_size, 0.7),
CycleJumpsReservoir(res_size, cycle_weight = 0.7, jump_weight = 0.2, jump_size = 5)]
for i in 1:length(reservoirs)
esn = ESN(training_input;
input_layer = input_layer[i],
reservoir = reservoirs[i])
wout = train(esn, training_target, StandardRidge(0.001))
output = esn(Predictive(testing_input), wout)
println(msd(testing_target, output))
end
```
As it is possible to see, changing layers in ESN models is straightforward. Be sure to check the API documentation for a full list of reservoirs and layers.
## Bibliography
[^1]: Rodan, Ali, and Peter Tiňo. “Simple deterministically constructed cycle reservoirs with regular jumps.” Neural computation 24.7 (2012): 1822-1852.
[^2]: Rodan, Ali, and Peter Tiňo. “Minimum complexity echo state network.” IEEE transactions on neural networks 22.1 (2010): 131-144.
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | docs | 4491 | # Deep Echo State Networks
Deep Echo State Network architectures started to gain some traction recently. In this guide, we illustrate how it is possible to use ReservoirComputing.jl to build a deep ESN.
The network implemented in this library is taken from [^1]. It works by stacking reservoirs on top of each other, feeding the output from one into the next. The states are obtained by merging all the inner states of the stacked reservoirs. For a more in-depth explanation, refer to the paper linked above. The full script for this example can be found [here](https://github.com/MartinuzziFrancesco/reservoir-computing-examples/blob/main/deep-esn/deepesn.jl). This example was run on Julia v1.7.2.
## Lorenz Example
For this example, we are going to reuse the Lorenz data used in the [Lorenz System Forecasting](@ref) example.
```@example deep_lorenz
using OrdinaryDiffEq
#define lorenz system
function lorenz!(du, u, p, t)
du[1] = 10.0 * (u[2] - u[1])
du[2] = u[1] * (28.0 - u[3]) - u[2]
du[3] = u[1] * u[2] - (8 / 3) * u[3]
end
#solve and take data
prob = ODEProblem(lorenz!, [1.0, 0.0, 0.0], (0.0, 200.0))
data = solve(prob, ABM54(), dt = 0.02)
#determine shift length, training length and prediction length
shift = 300
train_len = 5000
predict_len = 1250
#split the data accordingly
input_data = data[:, shift:(shift + train_len - 1)]
target_data = data[:, (shift + 1):(shift + train_len)]
test_data = data[:, (shift + train_len + 1):(shift + train_len + predict_len)]
```
Again, it is *important* to notice that the data needs to be formatted in a matrix, with the features as rows and time steps as columns, as in this example. This is needed even if the time series consists of single values.
The construction of the ESN is also really similar. The only difference is that the reservoir can be fed as an array of reservoirs.
```@example deep_lorenz
using ReservoirComputing
reservoirs = [RandSparseReservoir(99, radius = 1.1, sparsity = 0.1),
RandSparseReservoir(100, radius = 1.2, sparsity = 0.1),
RandSparseReservoir(200, radius = 1.4, sparsity = 0.1)]
esn = ESN(input_data;
variation = Default(),
reservoir = reservoirs,
input_layer = DenseLayer(),
reservoir_driver = RNN(),
nla_type = NLADefault(),
states_type = StandardStates())
```
As it is possible to see, different sizes can be chosen for the different reservoirs. The input layer and bias can also be given as vectors, but of course, they have to be of the same size of the reservoirs vector. If they are not passed as a vector, the value passed will be used for all the layers in the deep ESN.
In addition to using the provided functions for the construction of the layers, the user can also choose to build their own matrix, or array of matrices, and feed that into the `ESN` in the same way.
The training and prediction follow the usual framework:
```@example deep_lorenz
training_method = StandardRidge(0.0)
output_layer = train(esn, target_data, training_method)
output = esn(Generative(predict_len), output_layer)
```
Plotting the results:
```@example deep_lorenz
using Plots
ts = 0.0:0.02:200.0
lorenz_maxlyap = 0.9056
predict_ts = ts[(shift + train_len + 1):(shift + train_len + predict_len)]
lyap_time = (predict_ts .- predict_ts[1]) * (1 / lorenz_maxlyap)
p1 = plot(lyap_time, [test_data[1, :] output[1, :]], label = ["actual" "predicted"],
ylabel = "x(t)", linewidth = 2.5, xticks = false, yticks = -15:15:15);
p2 = plot(lyap_time, [test_data[2, :] output[2, :]], label = ["actual" "predicted"],
ylabel = "y(t)", linewidth = 2.5, xticks = false, yticks = -20:20:20);
p3 = plot(lyap_time, [test_data[3, :] output[3, :]], label = ["actual" "predicted"],
ylabel = "z(t)", linewidth = 2.5, xlabel = "max(λ)*t", yticks = 10:15:40);
plot(p1, p2, p3, plot_title = "Lorenz System Coordinates",
layout = (3, 1), xtickfontsize = 12, ytickfontsize = 12, xguidefontsize = 15,
yguidefontsize = 15,
legendfontsize = 12, titlefontsize = 20)
```
Note that there is a known bug at the moment with using `WeightedLayer` as the input layer with the deep ESN. We are in the process of investigating and solving it. The leak coefficient for the reservoirs has to always be the same in the current implementation. This is also something we are actively looking into expanding.
## Documentation
[^1]: Gallicchio, Claudio, and Alessio Micheli. "_Deep echo state network (deepesn): A brief survey._" arXiv preprint arXiv:1712.04323 (2017).
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | docs | 13873 | # Using Different Reservoir Drivers
While the original implementation of the Echo State Network implemented the model using the equations of Recurrent Neural Networks to obtain non-linearity in the reservoir, other variations have been proposed in recent years. More specifically, the different drivers implemented in ReservoirComputing.jl are the multiple activation function RNN `MRNN()` and the Gated Recurrent Unit `GRU()`. To change them, it suffices to give the chosen method to the `ESN` keyword argument `reservoir_driver`. In this section, some examples, of their usage will be given, as well as a brief introduction to their equations.
## Multiple Activation Function RNN
Based on the double activation function ESN (DAFESN) proposed in [^1], the Multiple Activation Function ESN expands the idea and allows a custom number of activation functions to be used in the reservoir dynamics. This can be thought of as a linear combination of multiple activation functions with corresponding parameters.
```math
\mathbf{x}(t+1) = (1-\alpha)\mathbf{x}(t) + \lambda_1 f_1(\mathbf{W}\mathbf{x}(t)+\mathbf{W}_{in}\mathbf{u}(t)) + \dots + \lambda_D f_D(\mathbf{W}\mathbf{x}(t)+\mathbf{W}_{in}\mathbf{u}(t))
```
where ``D`` is the number of activation functions and respective parameters chosen.
The method to call to use the multiple activation function ESN is `MRNN(activation_function, leaky_coefficient, scaling_factor)`. The arguments can be used as both `args` and `kwargs`. `activation_function` and `scaling_factor` have to be vectors (or tuples) containing the chosen activation functions and respective scaling factors (``f_1,...,f_D`` and ``\lambda_1,...,\lambda_D`` following the nomenclature introduced above). The `leaky_coefficient` represents ``\alpha`` and it is a single value.
Starting with the example, the data used is based on the following function based on the DAFESN paper [^1]. A full script of the example is available [here](https://github.com/MartinuzziFrancesco/reservoir-computing-examples/blob/main/change_drivers/mrnn/mrnn.jl). This example was run on Julia v1.7.2.
```@example mrnn
u(t) = sin(t) + sin(0.51 * t) + sin(0.22 * t) + sin(0.1002 * t) + sin(0.05343 * t)
```
For this example, the type of prediction will be one step ahead. The metric used to assure a good prediction will be the normalized root-mean-square deviation `rmsd` from [StatsBase](https://juliastats.org/StatsBase.jl/stable/). Like in the other examples, first it is needed to gather the data:
```@example mrnn
train_len = 3000
predict_len = 2000
shift = 1
data = u.(collect(0.0:0.01:500))
training_input = reduce(hcat, data[shift:(shift + train_len - 1)])
training_target = reduce(hcat, data[(shift + 1):(shift + train_len)])
testing_input = reduce(hcat,
data[(shift + train_len):(shift + train_len + predict_len - 1)])
testing_target = reduce(hcat,
data[(shift + train_len + 1):(shift + train_len + predict_len)])
```
To follow the paper more closely, it is necessary to define a couple of activation functions. The numbering of them follows the ones in the paper. Of course, one can also use any custom-defined function, available in the base language or any activation function from [NNlib](https://fluxml.ai/Flux.jl/stable/models/nnlib/#Activation-Functions).
```@example mrnn
f2(x) = (1 - exp(-x)) / (2 * (1 + exp(-x)))
f3(x) = (2 / pi) * atan((pi / 2) * x)
f4(x) = x / sqrt(1 + x * x)
```
It is now possible to build different drivers, using the parameters suggested by the paper. Also, in this instance, the numbering follows the test cases of the paper. In the end, a simple for loop is implemented to compare the different drivers and activation functions.
```@example mrnn
using ReservoirComputing, Random, StatsBase
#fix seed for reproducibility
Random.seed!(42)
#baseline case with RNN() driver. Parameter given as args
base_case = RNN(tanh, 0.85)
#MRNN() test cases
#Parameter given as kwargs
case3 = MRNN(activation_function = [tanh, f2],
leaky_coefficient = 0.85,
scaling_factor = [0.5, 0.3])
#Parameter given as kwargs
case4 = MRNN(activation_function = [tanh, f3],
leaky_coefficient = 0.9,
scaling_factor = [0.45, 0.35])
#Parameter given as args
case5 = MRNN([tanh, f4], 0.9, [0.43, 0.13])
#tests
test_cases = [base_case, case3, case4, case5]
for case in test_cases
esn = ESN(training_input,
input_layer = WeightedLayer(scaling = 0.3),
reservoir = RandSparseReservoir(100, radius = 0.4),
reservoir_driver = case,
states_type = ExtendedStates())
wout = train(esn, training_target, StandardRidge(10e-6))
output = esn(Predictive(testing_input), wout)
println(rmsd(testing_target, output, normalize = true))
end
```
In this example, it is also possible to observe the input of parameters to the methods `RNN()` `MRNN()`, both by argument and by keyword argument.
## Gated Recurrent Unit
Gated Recurrent Units (GRUs) [^2] have been proposed in more recent years with the intent of limiting notable problems of RNNs, like the vanishing gradient. This change in the underlying equations can be easily transported into the Reservoir Computing paradigm, by switching the RNN equations in the reservoir with the GRU equations. This approach has been explored in [^3] and [^4]. Different variations of GRU have been proposed [^5][^6]; this section is subdivided into different sections that go into detail about the governing equations and the implementation of them into ReservoirComputing.jl. Like before, to access the GRU reservoir driver, it suffices to change the `reservoir_diver` keyword argument for `ESN` with `GRU()`. All the variations that will be presented can be used in this package by leveraging the keyword argument `variant` in the method `GRU()` and specifying the chosen variant: `FullyGated()` or `Minimal()`. Other variations are possible by modifying the inner layers and reservoirs. The default is set to the standard version `FullyGated()`. The first section will go into more detail about the default of the `GRU()` method, and the following ones will refer to it to minimize repetitions. This example was run on Julia v1.7.2.
### Standard GRU
The equations for the standard GRU are as follows:
```math
\mathbf{r}(t) = \sigma (\mathbf{W}^r_{\text{in}}\mathbf{u}(t)+\mathbf{W}^r\mathbf{x}(t-1)+\mathbf{b}_r) \\
\mathbf{z}(t) = \sigma (\mathbf{W}^z_{\text{in}}\mathbf{u}(t)+\mathbf{W}^z\mathbf{x}(t-1)+\mathbf{b}_z) \\
\tilde{\mathbf{x}}(t) = \text{tanh}(\mathbf{W}_{in}\mathbf{u}(t)+\mathbf{W}(\mathbf{r}(t) \odot \mathbf{x}(t-1))+\mathbf{b}) \\
\mathbf{x}(t) = \mathbf{z}(t) \odot \mathbf{x}(t-1)+(1-\mathbf{z}(t)) \odot \tilde{\mathbf{x}}(t)
```
Going over the `GRU` keyword argument, it will be explained how to feed the desired input to the model.
- `activation_function` is a vector with default values `[NNlib.sigmoid, NNlib.sigmoid, tanh]`. This argument controls the activation functions of the GRU, going from top to bottom. Changing the first element corresponds to changing the activation function for ``\mathbf{r}(t)`` and so on.
- `inner_layer` is a vector with default values `fill(DenseLayer(), 2)`. This keyword argument controls the ``\mathbf{W}_{\text{in}}``s going from top to bottom like before.
- `reservoir` is a vector with default value `fill(RandSparseReservoir(), 2)`. In a similar fashion to `inner_layer`, this keyword argument controls the reservoir matrix construction in a top to bottom order.
- `bias` is again a vector with default value `fill(DenseLayer(), 2)`. It is meant to control the ``\mathbf{b}``s, going as usual from top to bottom.
- `variant` controls the GRU variant. The default value is set to `FullyGated()`.
It is important to notice that `inner_layer` and `reservoir` control every layer except ``\mathbf{W}_{in}`` and ``\mathbf{W}`` and ``\mathbf{b}``. These arguments are given as input to the `ESN()` call as `input_layer`, `reservoir` and `bias`.
The following sections are going to illustrate the variations of the GRU architecture and how to obtain them in ReservoirComputing.jl
### Type 1
The first variation of the GRU is dependent only on the previous hidden state and the bias:
```math
\mathbf{r}(t) = \sigma (\mathbf{W}^r\mathbf{x}(t-1)+\mathbf{b}_r) \\
\mathbf{z}(t) = \sigma (\mathbf{W}^z\mathbf{x}(t-1)+\mathbf{b}_z) \\
```
To obtain this variation, it will suffice to set `inner_layer = fill(NullLayer(), 2)` and leaving the `variant = FullyGated()`.
### Type 2
The second variation only depends on the previous hidden state:
```math
\mathbf{r}(t) = \sigma (\mathbf{W}^r\mathbf{x}(t-1)) \\
\mathbf{z}(t) = \sigma (\mathbf{W}^z\mathbf{x}(t-1)) \\
```
Similarly to before, to obtain this variation, it is only required to set `inner_layer = fill(NullLayer(), 2)` and `bias = fill(NullLayer(), 2)` while keeping `variant = FullyGated()`.
### Type 3
The final variation, before the minimal one, depends only on the biases
```math
\mathbf{r}(t) = \sigma (\mathbf{b}_r) \\
\mathbf{z}(t) = \sigma (\mathbf{b}_z) \\
```
This means that it is only needed to set `inner_layer = fill(NullLayer(), 2)` and `reservoir = fill(NullReservoir(), 2)` while keeping `variant = FullyGated()`.
### Minimal
The minimal GRU variation merges two gates into one:
```math
\mathbf{f}(t) = \sigma (\mathbf{W}^f_{\text{in}}\mathbf{u}(t)+\mathbf{W}^f\mathbf{x}(t-1)+\mathbf{b}_f) \\
\tilde{\mathbf{x}}(t) = \text{tanh}(\mathbf{W}_{in}\mathbf{u}(t)+\mathbf{W}(\mathbf{f}(t) \odot \mathbf{x}(t-1))+\mathbf{b}) \\
\mathbf{x}(t) = (1-\mathbf{f}(t)) \odot \mathbf{x}(t-1) + \mathbf{f}(t) \odot \tilde{\mathbf{x}}(t)
```
This variation can be obtained by setting `variation=Minimal()`. The `inner_layer`, `reservoir` and `bias` kwargs this time are **not** vectors, but must be defined like, for example `inner_layer = DenseLayer()` or `reservoir = SparseDenseReservoir()`.
### Examples
To showcase the use of the `GRU()` method, this section will only illustrate the standard `FullyGated()` version. The full script for this example with the data can be found [here](https://github.com/MartinuzziFrancesco/reservoir-computing-examples/blob/main/change_drivers/gru/).
The data used for this example is the Santa Fe laser dataset [^7] retrieved from [here](https://web.archive.org/web/20160427182805/http://www-psych.stanford.edu/%7Eandreas/Time-Series/SantaFe.html). The data is split to account for a next step prediction.
```@example gru
using DelimitedFiles
data = reduce(hcat, readdlm("./data/santafe_laser.txt"))
train_len = 5000
predict_len = 2000
training_input = data[:, 1:train_len]
training_target = data[:, 2:(train_len + 1)]
testing_input = data[:, (train_len + 1):(train_len + predict_len)]
testing_target = data[:, (train_len + 2):(train_len + predict_len + 1)]
```
The construction of the ESN proceeds as usual.
```@example gru
using ReservoirComputing, Random
res_size = 300
res_radius = 1.4
Random.seed!(42)
esn = ESN(training_input;
reservoir = RandSparseReservoir(res_size, radius = res_radius),
reservoir_driver = GRU())
```
The default inner reservoir and input layer for the GRU are the same defaults for the `reservoir` and `input_layer` of the ESN. One can use the explicit call if they choose to.
```@example gru
gru = GRU(reservoir = [RandSparseReservoir(res_size),
RandSparseReservoir(res_size)],
inner_layer = [DenseLayer(), DenseLayer()])
esn = ESN(training_input;
reservoir = RandSparseReservoir(res_size, radius = res_radius),
reservoir_driver = gru)
```
The training and prediction can proceed as usual:
```@example gru
training_method = StandardRidge(0.0)
output_layer = train(esn, training_target, training_method)
output = esn(Predictive(testing_input), output_layer)
```
The results can be plotted using Plots.jl
```@example gru
using Plots
plot([testing_target' output'], label = ["actual" "predicted"],
plot_title = "Santa Fe Laser",
titlefontsize = 20,
legendfontsize = 12,
linewidth = 2.5,
xtickfontsize = 12,
ytickfontsize = 12,
size = (1080, 720))
```
It is interesting to see a comparison of the GRU driven ESN and the standard RNN driven ESN. Using the same parameters defined before it is possible to do the following
```@example gru
using StatsBase
esn_rnn = ESN(training_input;
reservoir = RandSparseReservoir(res_size, radius = res_radius),
reservoir_driver = RNN())
output_layer = train(esn_rnn, training_target, training_method)
output_rnn = esn_rnn(Predictive(testing_input), output_layer)
println(msd(testing_target, output))
println(msd(testing_target, output_rnn))
```
[^1]: Lun, Shu-Xian, et al. "_A novel model of leaky integrator echo state network for time-series prediction._" Neurocomputing 159 (2015): 58-66.
[^2]: Cho, Kyunghyun, et al. “_Learning phrase representations using RNN encoder-decoder for statistical machine translation._” arXiv preprint arXiv:1406.1078 (2014).
[^3]: Wang, Xinjie, Yaochu Jin, and Kuangrong Hao. "_A Gated Recurrent Unit based Echo State Network._" 2020 International Joint Conference on Neural Networks (IJCNN). IEEE, 2020.
[^4]: Di Sarli, Daniele, Claudio Gallicchio, and Alessio Micheli. "_Gated Echo State Networks: a preliminary study._" 2020 International Conference on INnovations in Intelligent SysTems and Applications (INISTA). IEEE, 2020.
[^5]: Dey, Rahul, and Fathi M. Salem. "_Gate-variants of gated recurrent unit (GRU) neural networks._" 2017 IEEE 60th international midwest symposium on circuits and systems (MWSCAS). IEEE, 2017.
[^6]: Zhou, Guo-Bing, et al. "_Minimal gated unit for recurrent neural networks._" International Journal of Automation and Computing 13.3 (2016): 226-234.
[^7]: Hübner, Uwe, Nimmi B. Abraham, and Carlos O. Weiss. "_Dimensions and entropies of chaotic intensity pulsations in a single-mode far-infrared NH 3 laser._" Physical Review A 40.11 (1989): 6354.
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | docs | 127 | # Using Different Training Methods
## Linear Methods
## Echo State Gaussian Processes
## Support Vector Echo State Machines
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | docs | 3379 | # Hybrid Echo State Networks
Following the idea of giving physical information to machine learning models, the hybrid echo state networks [^1] try to achieve this results by feeding model data into the ESN. In this example, it is explained how to create and leverage such models in ReservoirComputing.jl.
## Generating the data
For this example, we are going to forecast the Lorenz system. As usual, the data is generated leveraging `DifferentialEquations.jl`:
```@example hybrid
using DifferentialEquations
u0 = [1.0, 0.0, 0.0]
tspan = (0.0, 1000.0)
datasize = 100000
tsteps = range(tspan[1], tspan[2], length = datasize)
function lorenz(du, u, p, t)
p = [10.0, 28.0, 8 / 3]
du[1] = p[1] * (u[2] - u[1])
du[2] = u[1] * (p[2] - u[3]) - u[2]
du[3] = u[1] * u[2] - p[3] * u[3]
end
ode_prob = ODEProblem(lorenz, u0, tspan)
ode_sol = solve(ode_prob, saveat = tsteps)
ode_data = Array(ode_sol)
train_len = 10000
input_data = ode_data[:, 1:train_len]
target_data = ode_data[:, 2:(train_len + 1)]
test_data = ode_data[:, (train_len + 1):end][:, 1:1000]
predict_len = size(test_data, 2)
tspan_train = (tspan[1], ode_sol.t[train_len])
```
## Building the Hybrid Echo State Network
To feed the data to the ESN, it is necessary to create a suitable function.
```@example hybrid
function prior_model_data_generator(u0, tspan, tsteps, model = lorenz)
prob = ODEProblem(lorenz, u0, tspan)
sol = Array(solve(prob, saveat = tsteps))
return sol
end
```
Given the initial condition, time span, and time steps, this function returns the data for the chosen model. Now, using the `KnowledgeModel` method, it is possible to input all this information to `HybridESN`.
```@example hybrid
using ReservoirComputing, Random
Random.seed!(42)
km = KnowledgeModel(prior_model_data_generator, u0, tspan_train, train_len)
in_size = 3
res_size = 300
hesn = HybridESN(km,
input_data,
in_size,
res_size;
reservoir = rand_sparse)
```
## Training and Prediction
The training and prediction of the Hybrid ESN can proceed as usual:
```@example hybrid
output_layer = train(hesn, target_data, StandardRidge(0.3))
output = esn(Generative(predict_len), output_layer)
```
It is now possible to plot the results, leveraging Plots.jl:
```@example hybrid
using Plots
lorenz_maxlyap = 0.9056
predict_ts = tsteps[(train_len + 1):(train_len + predict_len)]
lyap_time = (predict_ts .- predict_ts[1]) * (1 / lorenz_maxlyap)
p1 = plot(lyap_time, [test_data[1, :] output[1, :]], label = ["actual" "predicted"],
ylabel = "x(t)", linewidth = 2.5, xticks = false, yticks = -15:15:15);
p2 = plot(lyap_time, [test_data[2, :] output[2, :]], label = ["actual" "predicted"],
ylabel = "y(t)", linewidth = 2.5, xticks = false, yticks = -20:20:20);
p3 = plot(lyap_time, [test_data[3, :] output[3, :]], label = ["actual" "predicted"],
ylabel = "z(t)", linewidth = 2.5, xlabel = "max(λ)*t", yticks = 10:15:40);
plot(p1, p2, p3, plot_title = "Lorenz System Coordinates",
layout = (3, 1), xtickfontsize = 12, ytickfontsize = 12, xguidefontsize = 15,
yguidefontsize = 15,
legendfontsize = 12, titlefontsize = 20)
```
## Bibliography
[^1]: Pathak, Jaideep, et al. "_Hybrid forecasting of chaotic processes: Using machine learning in conjunction with a knowledge-based model._" Chaos: An Interdisciplinary Journal of Nonlinear Science 28.4 (2018): 041101.
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | docs | 9336 | # Lorenz System Forecasting
This example expands on the readme Lorenz system forecasting to better showcase how to use methods and functions provided in the library for Echo State Networks. Here the prediction method used is `Generative`, for a more detailed explanation of the differences between `Generative` and `Predictive` please refer to the other examples given in the documentation.
## Generating the data
Starting off the workflow, the first step is to obtain the data. Leveraging `OrdinaryDiffEq` it is possible to derive the Lorenz system data in the following way:
```@example lorenz
using OrdinaryDiffEq
#define lorenz system
function lorenz!(du, u, p, t)
du[1] = 10.0 * (u[2] - u[1])
du[2] = u[1] * (28.0 - u[3]) - u[2]
du[3] = u[1] * u[2] - (8 / 3) * u[3]
end
#solve and take data
prob = ODEProblem(lorenz!, [1.0, 0.0, 0.0], (0.0, 200.0))
data = solve(prob, ABM54(), dt = 0.02)
```
After obtaining the data, it is necessary to determine the kind of prediction for the model. Since this example will use the `Generative` prediction type, this means that the target data will be the next step of the input data. In addition, it is important to notice that the Lorenz system just obtained presents a transient period that is not representative of the general behavior of the system. This can easily be discarded by setting a `shift` parameter.
```@example lorenz
#determine shift length, training length and prediction length
shift = 300
train_len = 5000
predict_len = 1250
#split the data accordingly
input_data = data[:, shift:(shift + train_len - 1)]
target_data = data[:, (shift + 1):(shift + train_len)]
test_data = data[:, (shift + train_len + 1):(shift + train_len + predict_len)]
```
It is *important* to notice that the data needs to be formatted in a matrix with the features as rows and time steps as columns as in this example. This is needed even if the time series consists of single values.
## Building the Echo State Network
Once the data is ready, it is possible to define the parameters for the ESN and the `ESN` struct itself. In this example, the values from [^1] are loosely followed as general guidelines.
```@example lorenz
using ReservoirComputing
#define ESN parameters
res_size = 300
in_size = 3
res_radius = 1.2
res_sparsity = 6 / 300
input_scaling = 0.1
#build ESN struct
esn = ESN(input_data, in_size, res_size;
reservoir = rand_sparse(; radius = res_radius, sparsity = res_sparsity),
input_layer = weighted_init(; scaling = input_scaling),
reservoir_driver = RNN(),
nla_type = NLADefault(),
states_type = StandardStates())
```
Most of the parameters chosen here mirror the default ones, so a direct call is not necessary. The readme example is identical to this one, except for the explicit call. Going line by line to see what is happening, starting from `res_size`: this value determines the dimensions of the reservoir matrix. In this case, a size of 300 has been chosen, so the reservoir matrix will be 300 x 300. This is not always the case, since some input layer constructions can modify the dimensions of the reservoir, but in that case, everything is taken care of internally.
The `res_radius` determines the scaling of the spectral radius of the reservoir matrix; a proper scaling is necessary to assure the Echo State Property. The default value in the `rand_sparse` method is 1.0 in accordance with the most commonly followed guidelines found in the literature (see [^2] and references therein). The `sparsity` of the reservoir matrix in this case is obtained by choosing a degree of connections and dividing that by the reservoir size. Of course, it is also possible to simply choose any value between 0.0 and 1.0 to test behaviors for different sparsity values.
The value of `input_scaling` determines the upper and lower bounds of the uniform distribution of the weights in the `weighted_init`. The value of 0.1 represents the default. The default input layer is the `scaled_rand`, a dense matrix. The details of the weighted version can be found in [^3], for this example, this version returns the best results.
The reservoir driver represents the dynamics of the reservoir. In the standard ESN definition, these dynamics are obtained through a Recurrent Neural Network (RNN), and this is reflected by calling the `RNN` driver for the `ESN` struct. This option is set as the default, and unless there is the need to change parameters, it is not needed. The full equation is the following:
```math
\textbf{x}(t+1) = (1-\alpha)\textbf{x}(t) + \alpha \cdot \text{tanh}(\textbf{W}\textbf{x}(t)+\textbf{W}_{\text{in}}\textbf{u}(t))
```
where ``α`` represents the leaky coefficient, and tanh can be any activation function. Also, ``\textbf{x}`` represents the state vector, ``\textbf{u}`` the input data, and ``\textbf{W}, \textbf{W}_{\text{in}}`` are the reservoir matrix and input matrix, respectively. The default call to the RNN in the library is the following `RNN(;activation_function=tanh, leaky_coefficient=1.0)`, where the meaning of the parameters is clear from the equation above. Instead of the hyperbolic tangent, any activation function can be used, either leveraging external libraries such as `NNlib` or creating a custom one.
The final calls are modifications to the states in training or prediction. The default calls, depicted in the example, do not make any modifications to the states. This is the safest bet if one is not sure how these work. The `nla_type` applies a non-linear algorithm to the states, while the `states_type` can expand them by concatenating them with the input data, or padding them by concatenating a constant value to all the states. More in depth descriptions of these parameters are given in other examples in the documentation.
## Training and Prediction
Now that the ESN has been created and all the parameters have been explained, it is time to proceed with the training. The full call of the readme example follows this general idea:
```@example lorenz
#define training method
training_method = StandardRidge(0.0)
#obtain output layer
output_layer = train(esn, target_data, training_method)
```
The training returns an `OutputLayer` struct containing the trained output matrix and other needed for the prediction. The necessary elements in the `train()` call are the `ESN` struct created in the previous step and the `target_data`, which in this case is the one step ahead evolution of the Lorenz system. The training method chosen in this example is the standard one, so an equivalent way of calling the `train` function here is `output_layer = train(esn, target_data)` like the readme basic version. Likewise, the default value for the ridge regression parameter is set to zero, so the actual default training is Ordinary Least Squares regression. Other training methods are available and will be explained in the following examples.
Once the `OutputLayer` has been obtained, the prediction can be done following this procedure:
```@example lorenz
output = esn(Generative(predict_len), output_layer)
```
both the training method and the output layer are needed in this call. The number of steps for the prediction must be specified in the `Generative` method. The output results are given in a matrix.
!!! info "Saving the states during prediction"
While the states are saved in the `ESN` struct for the training, for the prediction they are not saved by default. To inspect the states, it is necessary to pass the boolean keyword argument `save_states` to the prediction call, in this example using `esn(... ; save_states=true)`. This returns a tuple `(output, states)` where `size(states) = res_size, prediction_len`
To inspect the results, they can easily be plotted using an external library. In this case, `Plots` is adopted:
```@example lorenz
using Plots, Plots.PlotMeasures
ts = 0.0:0.02:200.0
lorenz_maxlyap = 0.9056
predict_ts = ts[(shift + train_len + 1):(shift + train_len + predict_len)]
lyap_time = (predict_ts .- predict_ts[1]) * (1 / lorenz_maxlyap)
p1 = plot(lyap_time, [test_data[1, :] output[1, :]], label = ["actual" "predicted"],
ylabel = "x(t)", linewidth = 2.5, xticks = false, yticks = -15:15:15);
p2 = plot(lyap_time, [test_data[2, :] output[2, :]], label = ["actual" "predicted"],
ylabel = "y(t)", linewidth = 2.5, xticks = false, yticks = -20:20:20);
p3 = plot(lyap_time, [test_data[3, :] output[3, :]], label = ["actual" "predicted"],
ylabel = "z(t)", linewidth = 2.5, xlabel = "max(λ)*t", yticks = 10:15:40);
plot(p1, p2, p3, plot_title = "Lorenz System Coordinates",
layout = (3, 1), xtickfontsize = 12, ytickfontsize = 12, xguidefontsize = 15,
yguidefontsize = 15,
legendfontsize = 12, titlefontsize = 20)
```
## Bibliography
[^1]: Pathak, Jaideep, et al. "_Using machine learning to replicate chaotic attractors and calculate Lyapunov exponents from data._" Chaos: An Interdisciplinary Journal of Nonlinear Science 27.12 (2017): 121102.
[^2]: Lukoševičius, Mantas. "_A practical guide to applying echo state networks._" Neural networks: Tricks of the trade. Springer, Berlin, Heidelberg, 2012. 659-686.
[^3]: Lu, Zhixin, et al. "_Reservoir observers: Model-free inference of unmeasured variables in chaotic systems._" Chaos: An Interdisciplinary Journal of Nonlinear Science 27.4 (2017): 041102.
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | docs | 3245 | # Changing Training Algorithms
Notably Echo State Networks have been trained with Ridge Regression algorithms, but the range of useful algorithms to use is much greater. In this section of the documentation, it is possible to explore how to use other training methods to obtain the readout layer. All the methods implemented in ReservoirComputing.jl can be used for all models in the library, not only ESNs. The general workflow illustrated in this section will be based on a dummy RC model `my_model = MyModel(...)` that needs training to obtain the readout layer. The training is done as follows:
```julia
training_algo = TrainingAlgo()
readout_layer = train(my_model, train_data, training_algo)
```
In this section, it is possible to explore how to properly build the `training_algo` and all the possible choices available. In the example section of the documentation it will be provided copy-pasteable code to better explore the training algorithms and their impact on the model.
## Linear Models
The library includes a standard implementation of ridge regression, callable using `StandardRidge(regularization_coeff)`. The default regularization coefficient is set to zero. This is also the default model called when no model is specified in `train()`. This makes the default call for training `train(my_model, train_data)` use Ordinary Least Squares (OLS) for regression.
Leveraging [MLJLinearModels](https://juliaai.github.io/MLJLinearModels.jl/stable/) you can expand your choices of linear models for training. The wrappers provided follow this structure:
```julia
struct LinearModel
regression::Any
solver::Any
regression_kwargs::Any
end
```
To call the ridge regression using the MLJLinearModels APIs, you can use `LinearModel(;regression=LinearRegression)`. You can also choose a specific solver by calling, for example, `LinearModel(regression=LinearRegression, solver=Analytical())`. For all the available solvers, please refer to the [MLJLinearModels documentation](https://juliaai.github.io/MLJLinearModels.jl/stable/models/).
To change the regularization coefficient in the ridge example, using for example `lambda = 0.1`, it is needed to pass it in the `regression_kwargs` like so `LinearModel(;regression=LinearRegression, solver=Analytical(), regression_kwargs=(lambda=lambda))`. The nomenclature of the coefficients must follow the MLJLinearModels APIs, using `lambda, gamma` for `LassoRegression` and `delta, lambda, gamma` for `HuberRegression`. Again, please check the [relevant documentation](https://juliaai.github.io/MLJLinearModels.jl/stable/api/) if in doubt. When using MLJLinearModels based regressors, do remember to specify `using MLJLinearModels`.
## Support Vector Regression
Contrary to the `LinearModel`s, no wrappers are needed for support vector regression. By using [LIBSVM.jl](https://github.com/JuliaML/LIBSVM.jl), LIBSVM wrappers in Julia, it is possible to call both `epsilonSVR()` or `nuSVR()` directly in `train()`. For the full range of kernels provided and the parameters to call, we refer the user to the official [documentation](https://www.csie.ntu.edu.tw/%7Ecjlin/libsvm/). Like before, if one intends to use LIBSVM regressors, it is necessary to specify `using LIBSVM`.
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | docs | 1996 | # Generative vs Predictive
The library provides two different methods for prediction, denoted as `Predictive()` and `Generative()`. These methods correspond to the two major applications of Reservoir Computing models found in the literature. This section aims to clarify the differences between these two methods before providing further details on their usage in the library.
## Predictive
In the first method, users can utilize Reservoir Computing models in a manner similar to standard Machine Learning models. This involves using a set of features as input and a set of labels as outputs. In this case, both the feature and label sets can consist of vectors of different dimensions. Specifically, let's denote the feature set as ``X=\{x_1,...,x_n\}`` where ``x_i \in \mathbb{R}^{N}``, and the label set as ``Y=\{y_1,...,y_n\}`` where ``y_i \in \mathbb{R}^{M}``.
To make predictions using this method, you need to provide the feature set that you want to predict the labels for. For example, you can call `Predictive(X)` using the feature set ``X`` as input. This method allows for both one-step-ahead and multi-step-ahead predictions.
## Generative
The generative method provides a different approach to forecasting with Reservoir Computing models. It enables you to extend the forecasting capabilities of the model by allowing predicted results to be fed back into the model to generate the next prediction. This autonomy allows the model to make predictions without the need for a feature dataset as input.
To use the generative method, you only need to specify the number of time steps that you intend to forecast. For instance, you can call `Generative(100)` to generate predictions for the next one hundred time steps.
The key distinction between these methods lies in how predictions are made. The predictive method relies on input feature sets to make predictions, while the generative method allows for autonomous forecasting by feeding predicted results back into the model.
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | docs | 3958 | # Altering States
In ReservoirComputing models, it's possible to perform alterations on the reservoir states during the training stage. These alterations can improve prediction results or replicate results found in the literature. Alterations are categorized into two possibilities: padding or extending the states, and applying non-linear algorithms to the states.
## Padding and Extending States
### Extending States
Extending the states involves appending the corresponding input values to the reservoir states. If \(\textbf{x}(t)\) represents the reservoir state at time \(t\) corresponding to the input \(\textbf{u}(t)\), the extended state is represented as \([\textbf{x}(t); \textbf{u}(t)]\), where \([;]\) denotes vertical concatenation. This procedure is commonly used in Echo State Networks and is described in [Jaeger's Scholarpedia](http://www.scholarpedia.org/article/Echo_state_network). You can extend the states in every ReservoirComputing.jl model by using the `states_type` keyword argument and calling the `ExtendedStates()` method. No additional arguments are needed.
### Padding States
Padding the states involves appending a constant value, such as 1.0, to each state. In the notation introduced earlier, padded states can be represented as \([\textbf{x}(t); 1.0]\). This approach is detailed in the [seminal guide](https://mantas.info/get-publication/?f=Practical_ESN.pdf) to Echo State Networks by Mantas Lukoševičius. To pad the states, you can use the `states_type` keyword argument and call the `PaddedStates(padding)` method, where `padding` represents the value to be concatenated to the states. By default, the padding value is set to 1.0, so most of the time, calling `PaddedStates()` will suffice.
Additionally, you can pad the extended states by using the `PaddedExtendedStates(padding)` method, which also has a default padding value of 1.0.
You can choose not to apply any of these changes to the states by calling `StandardStates()`, which is the default choice for the states.
## Non-Linear Algorithms
First introduced in [^1] and expanded in [^2], non-linear algorithms are nonlinear combinations of the columns of the matrix states. There are three such algorithms implemented in ReservoirComputing.jl, and you can choose which one to use with the `nla_type` keyword argument. The default value is set to `NLADefault()`, which means no non-linear algorithm is applied.
The available non-linear algorithms are:
- `NLAT1()`
- `NLAT2()`
- `NLAT3()`
These algorithms perform specific operations on the reservoir states. To provide a better understanding of what they do, let ``\textbf{x}_{i, j}`` be elements of the state matrix, with ``i=1,...,T \ j=1,...,N`` where ``T`` is the length of the training and ``N`` is the reservoir size.
**NLAT1**
```math
\tilde{\textbf{x}}_{i,j} = \textbf{x}_{i,j} \times \textbf{x}_{i,j} \ \ \text{if \textit{j} is odd} \\
\tilde{\textbf{x}}_{i,j} = \textbf{x}_{i,j} \ \ \text{if \textit{j} is even}
```
**NLAT2**
```math
\tilde{\textbf{x}}_{i,j} = \textbf{x}_{i,j-1} \times \textbf{x}_{i,j-2} \ \ \text{if \textit{j} > 1 is odd} \\
\tilde{\textbf{x}}_{i,j} = \textbf{x}_{i,j} \ \ \text{if \textit{j} is 1 or even}
```
**NLAT3**
```math
\tilde{\textbf{x}}_{i,j} = \textbf{x}_{i,j-1} \times \textbf{x}_{i,j+1} \ \ \text{if \textit{j} > 1 is odd} \\
\tilde{\textbf{x}}_{i,j} = \textbf{x}_{i,j} \ \ \text{if \textit{j} is 1 or even}
```
[^1]: Pathak, Jaideep, et al. "_Using machine learning to replicate chaotic attractors and calculate Lyapunov exponents from data._" Chaos: An Interdisciplinary Journal of Nonlinear Science 27.12 (2017): 121102.
[^2]: Chattopadhyay, Ashesh, Pedram Hassanzadeh, and Devika Subramanian. "_Data-driven predictions of a multiscale Lorenz 96 chaotic system using machine-learning methods: reservoir computing, artificial neural network, and long short-term memory network._" Nonlinear Processes in Geophysics 27.3 (2020): 373-389.
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.10.2 | cbbfba6465a40992c1a0e595b2997903ed4fe3a0 | docs | 2653 | # Reservoir Computing using Cellular Automata
Reservoir Computing based on Elementary Cellular Automata (ECA) has been recently introduced. Dubbed as ReCA [^1][^2] it proposed the advantage of storing the reservoir states as binary data. Less parameter tuning represents another advantage of this model. The architecture implemented in ReservoirComputing.jl follows [^3] which builds on top of the original implementation, improving the results. It is strongly suggested to go through the paper to get a solid understanding of the model before delving into experimentation with the code.
To showcase how to use these models, this page illustrates the performance of ReCA in the 5 bit memory task [^4]. The script for the example and companion data can be found [here](https://github.com/MartinuzziFrancesco/reservoir-computing-examples/tree/main/reca).
## 5 bit memory task
The data can be read as follows:
```@example reca
using DelimitedFiles
input = readdlm("./5bitinput.txt", ',', Float32)
output = readdlm("./5bitoutput.txt", ',', Float32)
```
To use a ReCA model, it is necessary to define the rule one intends to use. To do so, ReservoirComputing.jl leverages [CellularAutomata.jl](https://github.com/MartinuzziFrancesco/CellularAutomata.jl) that needs to be called as well to define the `RECA` struct:
```@example reca
using ReservoirComputing, CellularAutomata
ca = DCA(90)
```
To define the ReCA model, it suffices to call:
```@example reca
reca = RECA(input, ca;
generations = 16,
input_encoding = RandomMapping(16, 40))
```
After this, the training can be performed with the chosen method.
```@example reca
output_layer = train(reca, output, StandardRidge(0.00001))
```
The prediction in this case will be a `Predictive()` with the input data equal to the training data. In addition, to test the 5 bit memory task, a conversion from Float to Bool is necessary (at the moment, we are aware of a bug that doesn't allow boolean input data to the RECA models):
```@example reca
prediction = reca(Predictive(input), output_layer)
final_pred = convert(AbstractArray{Float32}, prediction .> 0.5)
final_pred == output
```
[^1]: Yilmaz, Ozgur. "Reservoir computing using cellular automata." arXiv preprint arXiv:1410.0162 (2014).
[^2]: Margem, Mrwan, and Ozgür Yilmaz. "An experimental study on cellular automata reservoir in pathological sequence learning tasks." (2017).
[^3]: Nichele, Stefano, and Andreas Molund. "Deep reservoir computing using cellular automata." arXiv preprint arXiv:1703.02806 (2017).
[^4]: Hochreiter, Sepp, and Jürgen Schmidhuber. "Long short-term memory." Neural computation 9.8 (1997): 1735-1780.
| ReservoirComputing | https://github.com/SciML/ReservoirComputing.jl.git |
|
[
"MIT"
] | 0.1.1 | 58269d14168a82ada381a5359ff6cad714e09b38 | code | 2952 | using LoRaPHY
using ProgressMeter
import DigitalComm: addNoise
using PGFPlotsX
using ColorSchemes
# Bandwidth and frequency used
# < Note that the value are not that important, this is Fs/B that matters >
Fs = 125e3
BW = Fs
""" Single realisation for N LoRa symbol for a given SNR. Returns current SNR value, number of erroneous bits and number of bits
"""
function atomic_ber(N, SF, Fs, BW, snr)
# --- LoRa Encoding
sig, bitSeq, bitEnc, bitInter = loraEncode(N, SF, BW, Fs, 0)
# --- Channel
sigNoise, _ = addNoise(sig, snr)
# --- LoRa Decoding
bitDec, bitPreFec, bitPreInterl = loraDecode(sigNoise, SF, BW, Fs, 0)
# --- Performance metrics
# BER
nbBits = length(bitSeq)
nbErr = sum(xor.(bitDec, bitSeq))
return (snr, nbErr, nbBits)
end
""" Monte Carlo BER calculation for different SNR values in `snrVect`. LoRa is parametrized by its spreading factor `SF`, the bandwidth and the sampling frqeuency
"""
function BER_AWGN(snrVect, SF, Fs, BW)
# Symbol per iteration
N = 128
# Stopping criterion
nb_err_max = 1e4
nb_bit_max = 1e6
berV = zeros(Float64, length(snrVect)) # Bit Error Rate
perV = zeros(Float64, length(snrVect)) # Packet Error Rate
@showprogress Threads.@threads for iSnr in eachindex(snrVect)
# Current SNR
snr = snrVect[iSnr]
# Counters
c_b = 0 # Bits
c_be = 0 # Bits with error
# MC run
while (c_be < nb_err_max)
# Atomic run
(snr, nbErr, nbBits) = atomic_ber(N, SF, Fs, BW, snr)
# Update counter
c_b += nbBits
c_be += nbErr
# Break if we have enough bits
(c_b > nb_bit_max) && break
end
berV[iSnr] = c_be / c_b
end
return berV
end
# --- Define SNR
snrVect = range(-30, stop=-5, length=55)
# --- Define Spreading factor
sfVect = [7; 8; 9; 10; 11; 12]
@pgf a = Axis({
height = "3in",
width = "4in",
ymode = "log",
grid,
ymin = 1e-6,
xmin = snrVect[1],
xmax = snrVect[end],
xlabel = "SNR [dB]",
ylabel = "Bit Error Rate ",
legend_style = "{at={(0,0)},anchor=south west,legend cell align=left,align=left,draw=white!15!black}"
},
)
dictColor = ColorSchemes.tableau_superfishel_stone
dictMarker = ["square*","triangle*","diamond*","*","pentagon*","o","otimes","triangle*"];
for (iSf,sf) in enumerate(sfVect)
@info "Processing SF = $sf"
# --- Calculate BER
ber = BER_AWGN(snrVect, sf, Fs, BW)
# -- Theoretical PER
per_theo = [LoRaPHY.AWGN_SEP_theo_hamming74(sf, 5, snr) for snr in snrVect]
ber_theo = (2^(sf - 1)) / (2^sf - 1) * per_theo
# Update plot
@pgf push!(a, Plot({color = dictColor[iSf], mark = dictMarker[iSf]}, Table([snrVect, ber])))
@pgf push!(a, LegendEntry("SF = $sf"))
@pgf push!(a, Plot({color = "black",forget_plot}, Table([snrVect, ber_theo])))
display(a)
end
| LoRaPHY | https://github.com/JuliaTelecom/LoRaPHY.jl.git |
|
[
"MIT"
] | 0.1.1 | 58269d14168a82ada381a5359ff6cad714e09b38 | code | 1412 | using LoRaPHY
using AbstractSDRs
# ----------------------------------------------------
# --- LoRa configuration
# ----------------------------------------------------
# Spreading factor used in LoRa
SF = 7
# Number of LoRa symbols to transmit
N = SF*4*2
bitSeq = Int.(randn(N) .> 0) # A vector of binary elements
# Bandwidth and frequency used
BW = 125e3
Fs = BW * 20 # Oversampling to have a fsampling supported by SDRs
# --- LoRa Encoding
sig, bitSeq, bitEnc, bitInter = loraEncode(bitSeq, SF, BW, Fs, 0)
# --- Normalization
sig .= sig * (1-2^-15)
# ----------------------------------------------------
# --- SDR configuration
# ----------------------------------------------------
radio = :pluto
carrierFreq = 868e6
gain = 10
samplingRate = Fs # If your radio does not support low datarate use a Fs in LoRa that is a multiple of BW and compatible with your SDR
kw = (;addr="usb:1.4.5") # Additionnal arguments such as SDR address, ...
sdr = openSDR(radio,carrierFreq,samplingRate,gain;kw...)
# ----------------------------------------------------
# --- Transmit
# ----------------------------------------------------
nbB = 0
try
@info "Type <c-c> to interrupt"
while true
send(sdr,sig)
global nbB += 1
end
catch exception
@info "Interruption"
display(exception)
end
close(sdr)
@info "Transmit $(nbB) LoRa bursts" | LoRaPHY | https://github.com/JuliaTelecom/LoRaPHY.jl.git |
|
[
"MIT"
] | 0.1.1 | 58269d14168a82ada381a5359ff6cad714e09b38 | code | 554 | using LoRaPHY
import DigitalComm: addNoise
# Number of LoRa symbols to transmit
N = 128
# Spreading factor used in LoRa
SF = 7
# Bandwidth and frequency used
# < Note that the value are not that important, this is Fs/B that matters>
BW = 125e3
Fs = BW
snr = 0 # In dB
# --- LoRa Encoding
sig,bitSeq,bitEnc,bitInter = loraEncode(N,SF,BW,Fs,0)
# --- Channel
sigNoise,_ = addNoise(sig,snr)
# --- LoRa Decoding
bitDec,bitPreFec,bitPreInterl = loraDecode(sigNoise,SF,BW,Fs,0)
# --- BER calculation
ber = sum(xor.(bitDec,bitSeq)) / length(bitSeq) | LoRaPHY | https://github.com/JuliaTelecom/LoRaPHY.jl.git |
|
[
"MIT"
] | 0.1.1 | 58269d14168a82ada381a5359ff6cad714e09b38 | code | 1396 |
""""
g = grayencode(n)\\
Convert the integer `n` as its value with Gray encoding \\
Inputs :
- n : Input integer
Outputs :
- g : Gray-coded integer
Example: grayencode(2) = 3
"""
grayencode(n::Integer) = n ⊻ (n >> 1)
"""
n = graydecode(n)
Convert the gray encoded word `n` back
Inputs :
- g : Gray-coded integer
Outputs :
- n : Input integer
"""
function graydecode(n::Integer)
r = n
while (n >>= 1) != 0
r ⊻= n
end
return r
end
"""
n = bin2dec(data)
Convert a binary vector into its integer representation. The input should be a vector with the first element the MSB and the last element the LSB. \\
Example : bin2dec([0;0;1]) = 1; bin2dec([1;0;1;0])=10 \\
If the input is a matrix, the conversion is down per line (e.g bin2dec([1 0 1 0 ; 1 1 1 0]) = [10;14]
"""
function bin2dec(data::AbstractMatrix)
pow2 = [2^(k-1) for k in (size(data,2)):-1:1]
dataout = [sum(data[k,:] .* pow2) for k ∈ 1:size(data,1)]
return dataout
end
bin2dec(data::AbstractVector) = bin2dec(data')
"""
Binary representation of Int on a given number of bits. MSB in pos 1 and LSB at end
"""
function dec2bin(input::Vector{Int},n::Int)
Output_bin = zeros(Int, length(input), n)
for i ∈ eachindex(input)
c = bitstring(input[i])
data = [Int(c[j]-48) for j ∈ length(c)-(n-1):length(c)]
Output_bin[i,:] = data
end
return Output_bin
end
| LoRaPHY | https://github.com/JuliaTelecom/LoRaPHY.jl.git |
|
[
"MIT"
] | 0.1.1 | 58269d14168a82ada381a5359ff6cad714e09b38 | code | 1591 | function hammingEncode!(y,x)
# --- Matrix encoder
nL = length(x)÷4;
# ---
@inbounds @simd for iN = 1 : 1 : nL
# --- Spacing parameters
Δx = (iN-1)*4;
Δy = (iN-1)*7;
# --- Get 4 bits
for n ∈ 1 : 4
y[ Δy + n] = x[Δx + n];
end
# --- Add parity bits
y[Δy + 5] = x[Δx + 2] ⊻ x[Δx + 3] ⊻ x[Δx + 4];
y[Δy + 6] = x[Δx + 1] ⊻ x[Δx + 3] ⊻ x[Δx + 4];
y[Δy + 7] = x[Δx + 1] ⊻ x[Δx + 2] ⊻ x[Δx + 4];
end
return y;
end
function hammingDecode!(x,y)
nL = length(y)÷7
cnt = 0
@inbounds @simd for n ∈ 1 : 1 : nL
# --- Calculate 3 equations to deduce syndrome
s0 = y[ (n-1)*7 + 4] ⊻ y[ (n-1)*7 + 5] ⊻ y[ (n-1)*7 + 6] ⊻ y[ (n-1)*7 + 7]
s1 = y[ (n-1)*7 + 2] ⊻ y[ (n-1)*7 + 3] ⊻ y[ (n-1)*7 + 6] ⊻ y[ (n-1)*7 + 7]
s2 = y[ (n-1)*7 + 1] ⊻ y[ (n-1)*7 + 3] ⊻ y[ (n-1)*7 + 5] ⊻ y[ (n-1)*7 + 7]
# --- Syndrome calculation
pos = s0 << 2 + s1 << 1 + s2
# --- Switch is syndrome is non-null
if pos > 0
bitflip!(y,(n-1)*7 +pos)
cnt += 1
end
for k ∈ 1 : 1 : 4
x[(n-1)*4 + k] = y[(n-1)*7 + k]
end
end
return cnt
end
function hammingDecode(y::Vector{T}) where T
x = zeros(T,length(y)÷7*4);
hammingDecode!(x,y);
return x;
end
function hammingEncode(x::Vector{T}) where T
y = zeros(T,length(x)÷4*7)
hammingEncode!(y,x)
return y
end
@inline function bitflip!(in,index)
in[index] == 1 ? in[index] = 0 : in[index]=1;
end
| LoRaPHY | https://github.com/JuliaTelecom/LoRaPHY.jl.git |
|
[
"MIT"
] | 0.1.1 | 58269d14168a82ada381a5359ff6cad714e09b38 | code | 869 |
function interleaver(bitSeq::AbstractVector{T},SF) where T
# reshape per symbol
nbBit = length(bitSeq)
@assert mod(nbBit,7) == 0 "Number of bits after hamming should be divisible by 7 [$(nbBit) is not]"
nbWord = nbBit ÷ 7 # Number of symbols
nbSymb = nbWord ÷ SF
matSymb = reshape(bitSeq,7,nbWord)
matInter= zeros(T,nbSymb*7,SF)
for k ∈ 1:nbSymb # interleaver
matInter[(k-1)*7 + 1 : 7*k,:] = matSymb[:,SF*(k-1) + 1 : SF*k]
end
return matInter
end
function deInterleaver(bitInter::AbstractVector{T},SF) where T
nbWord = length(bitInter) ÷ 7 # Number of symbols
nbSymb = nbWord ÷ SF
output = zeros(T, 7, nbWord)
bitInterM = reshape(bitInter,nbSymb*7,SF)
for k ∈ 1 : nbSymb #deinterleave
output[:,SF*(k-1) + 1 : SF*k] = bitInterM[(k-1)*7 + 1 : 7*k,:]
end
return output[:]
end
| LoRaPHY | https://github.com/JuliaTelecom/LoRaPHY.jl.git |
|
[
"MIT"
] | 0.1.1 | 58269d14168a82ada381a5359ff6cad714e09b38 | code | 1105 | module LoRaPHY
# using Parameters
using FFTW # for Rx
using LinearAlgebra # for Rx
using QuadGK # Theoretical expression (Metrics)
using Bessels # Theoretical expression (Metrics)
include("Binaryops.jl")
# ----------------------------------------------------
# --- Hamming 7/4 encoding
# ----------------------------------------------------
include("Hamming.jl")
# ----------------------------------------------------
# --- Interleaver
# ----------------------------------------------------
include("Interleaver.jl")
# No export here, this function is internal
# ----------------------------------------------------
# --- Transmitter
# ----------------------------------------------------
include("Transmitter.jl")
export loraEncode
# ----------------------------------------------------
# --- Receiver
# ----------------------------------------------------
include("Receiver.jl")
export loraDecode
# ----------------------------------------------------
# --- Theory
# ----------------------------------------------------
include("Theory.jl")
end # module
| LoRaPHY | https://github.com/JuliaTelecom/LoRaPHY.jl.git |
|
[
"MIT"
] | 0.1.1 | 58269d14168a82ada381a5359ff6cad714e09b38 | code | 1452 | """
"""
function demodulation(sigrecu::Vector{Complex{T}},SF,BW,Fs,num_samples,inverse) where T
# inverse = 1;
lora_total_sym = length(sigrecu) ÷ num_samples
out_reverse = modulation(0,SF,BW,Fs,1-inverse)
decoded_out = similar(sigrecu)
Symbols = zeros(Int64,lora_total_sym);
result = zeros(Complex{T},num_samples)
win = similar(result)
plan = plan_fft(result;flags=FFTW.PATIENT)
container_abs = zeros(T,num_samples)
for m = 1:1:lora_total_sym
win = sigrecu[((m-1)*num_samples) .+ (1 : num_samples)] .* out_reverse
decoded_out[ ((m-1)*num_samples) .+ (1:num_samples) ] .= win
mul!(result,plan,win) # THIS IS AN FFT
container_abs .= abs2.( result )
posindex = argmax(container_abs) - 1
Symbols[m] = posindex
end
return Symbols
end
"""
"""
function loraDecode(sigrecu::Vector{Complex{T}},SF,BW,Fs,inverse) where T
num_samples = Int64(floor(Fs*(2^SF)/BW))
data_received = demodulation(sigrecu,SF,BW,Fs,num_samples,inverse) # symbols after CSS demodulation
# Output = dec2gray(data_received); # symbols after Gray decoding
output = graydecode.(data_received)[:]
bitPreInterl = dec2bin(output,SF)[:] # zeros(Int, length(Output), SF)
N = Int(length(output)/7)
bitPreFec = deInterleaver(bitPreInterl,SF) # De-interleaving
bitDec = hammingDecode(bitPreFec) # Hamming decoding
return bitDec,bitPreFec,bitPreInterl
end
| LoRaPHY | https://github.com/JuliaTelecom/LoRaPHY.jl.git |
|
[
"MIT"
] | 0.1.1 | 58269d14168a82ada381a5359ff6cad714e09b38 | code | 1122 |
function marcumq(a,b,v) #Mercum-Q function of order v
f = x -> ((x^v) * exp(-((x^2)+(a^2))/2) * besseli((v-1),(a*x)))
Q = 1-((1/(a^(v-1))) * quadgk(f, 0, b)[1])
return Q
end
"""
Theoretical expression of Symbol Error Rate in an AWGN channel without Hamming code correction
"""
function AWGN_SEP_theo_noFEC(SF,DL,SNRdB)
#Compute the Symbole Error Probability for a LoRa transmission in an AWGN channel
SEP_theo=0;
RSB=10^(SNRdB/10);
N=2^SF;
z_c1=2*log(N-1);
tau=cbrt((N-4)*(N-5)/((N-1)*(N-2)*(N-3)^3)-sqrt(2)*(N-4)/((N-1)*((N-2)*(N-3))^(1.5)));
z_c3=-2*log(tau-(N-4)/(tau*(N-2)*(N-3)^2)+1/(N-3));
alpha0=(3*exp(-z_c1/2)-exp(-z_c3/2))/2;
alpha1=(exp(-z_c3/2)-exp(-z_c1/2))/2;
z_c=-2*log(alpha1*DL+alpha0);
for j=1:DL+1
SEP_theo = SEP_theo + (-1)^j*binomial(N,j)*exp(-N*RSB*(j-1)/j)*marcumq(sqrt(2*N*RSB/j),sqrt(j*z_c),1);
end
SEP_theo = 1+SEP_theo/N;
return SEP_theo
end
"""
"""
function AWGN_SEP_theo_hamming74(SF,DL,SNRdB)
BEP_noFEC = AWGN_SEP_theo_noFEC(SF,DL,SNRdB) ./ 2
return 1 .- (1 .- BEP_noFEC).^6 .* (1 .+ 6 .* BEP_noFEC)
end
| LoRaPHY | https://github.com/JuliaTelecom/LoRaPHY.jl.git |
|
[
"MIT"
] | 0.1.1 | 58269d14168a82ada381a5359ff6cad714e09b38 | code | 2867 | # module Tx
function loraEncode(bitSeq::AbstractVector,SF,BW,Fs,inverse=0)
# Ensure that number of symbols is divided by 4
@assert mod(length(bitSeq),4) == 0 "Bit sequence should have length with mutiple of 4 and given size is $(length(bitSeq))"
@assert mod(length(bitSeq),SF) == 0 "Bit sequence should have length with mutiple of SF ($SF) and given size is $(length(bitSeq))"
# Hamming encoding
bitEnc = hammingEncode(bitSeq)
# Interleaver
bitInter = interleaver(bitEnc,SF)
# Gray encoding
symbols = grayencode.(bin2dec(bitInter))
nbSymbols = length(symbols)
# Modulation
num_samples = Int64(floor(Fs*(2^SF)/BW)); # Number of samples
sig = zeros(ComplexF64,Int(num_samples * nbSymbols))
for k ∈ 1 : nbSymbols
_sig = modulation(symbols[k],SF,BW,Fs,inverse)
sig[ (k-1)*num_samples .+ (1:num_samples)] .= _sig
end
return sig,bitSeq,bitEnc,bitInter
end
"""
Generate LoRa symbols
sig,bitSeq,bitEnc,bitInter = loraEncode(N,SF,BW,Fs,inverse)
# Input
- N: Number of block to transmit, a block correspond to SF LoRa symbols
- SF: Spreading factor of the CSS modulation
- BW: Bandwidth used for transmission
- Fs: sampling frequency
- inverse: 0 to send upchirp, 1 for downchirp
# Output
- sig : Baseband signal emitted from the transmitter (complex form)
- bitSeq : randomly generated binary data (Payload message)
- bitEnc : Binary sequence after Hamming encoding
- bitInterl : Binary sequence after interleaving
Dispatch method :
sig,bitSeq,bitEnc,bitInter = lora_encode(bitSeq,SF,BW,Fs,inverse) \\
- Uses a payload message bitSeq (must be of size N x SF x 4)
"""
function loraEncode(nbSymb::Int,SF,BW,Fs,inverse=0)
N = SF*nbSymb;
bitSeq = Int.(randn(4*N) .> 0)
sig,bitSeq,bitEnc,bitInter = loraEncode(bitSeq::AbstractVector,SF,BW,Fs,inverse)
return sig,bitSeq,bitEnc,bitInter
end
"""
Do the CSS modulation
"""
function modulation(symbol,SF,BW,Fs,inverse)
num_samples = Int64(floor(Fs*(2^SF)/BW)); # Number of samples
#initialization
phase = 0;
Frequency_Offset = (Fs/2) - (BW/2);
shift = symbol;
out_preamble = zeros(ComplexF64,num_samples);
for k = 1:num_samples
# output the complex signal
out_preamble[k] = cos(phase) + 1im*sin(phase);
# Frequency from cyclic shift
f = BW*shift/(2^SF);
if(inverse == 1)
f = BW - f;
end
# apply Frequency offset away from DC
f = f + Frequency_Offset;
# Increase the phase according to frequency
phase = phase + 2*pi*f/Fs;
if phase > pi
phase = phase - 2*pi;
end
# update cyclic shift
shift = shift + BW/Fs;
if shift >= (2^SF)
shift = shift - 2^SF;
end
end
return out_preamble
end
| LoRaPHY | https://github.com/JuliaTelecom/LoRaPHY.jl.git |
|
[
"MIT"
] | 0.1.1 | 58269d14168a82ada381a5359ff6cad714e09b38 | code | 185 | #!/bin/bash
#=
exec julia -O3 --color=yes -qi "${BASH_SOURCE[0]}"
=#
using Pkg
cd(@__DIR__)
Pkg.activate("..")
using Retest
@retest(@__DIR__)
# Local Variables:
# mode: julia
# End:
| LoRaPHY | https://github.com/JuliaTelecom/LoRaPHY.jl.git |
|
[
"MIT"
] | 0.1.1 | 58269d14168a82ada381a5359ff6cad714e09b38 | code | 1786 | using LoRaPHY
using Test
const SFVect = [7;8;9;10;11;12]
# Test cases for Gray encoding
@testset "Gray Encoding Tests" begin
@testset "Binary to Gray Encoding/Decoding" begin
LoRaPHY.grayencode(1) == 1
LoRaPHY.grayencode(3) == 2
for n ∈ 1:1024
@test n === LoRaPHY.graydecode(LoRaPHY.grayencode(n))
end
end
end
# Test for Hamming74 encoding
@testset "Hamming FEC scheme" begin
bitSeq = [1;1;0;1]
bitEnc = LoRaPHY.hammingEncode(bitSeq)
bitDec = LoRaPHY.hammingDecode(bitEnc)
@test length(bitEnc) == 7
@test length(bitDec) == 4
@test all(bitSeq .== bitDec)
bitEncFalse = bitEnc
LoRaPHY.bitflip!(bitEncFalse,2)
bitDec = LoRaPHY.hammingDecode(bitEncFalse)
@test length(bitEncFalse) == 7
@test length(bitDec) == 4
@test all(bitSeq .== bitDec)
# --- One error, we detect and correct one error
for n ∈ 1 : 7
bitEncFalse = bitEnc
LoRaPHY.bitflip!(bitEncFalse,n)
bitDec2 = similar(bitDec)
nbErr = LoRaPHY.hammingDecode!(bitDec2,bitEncFalse)
@test nbErr == 1
@test all(bitSeq .== bitDec2)
end
end
@testset "Interleaver" begin
for SF in SFVect
N = SF*100;
bitSeq = Int.(randn(4*N) .> 0)
bitEnc = LoRaPHY.hammingEncode(bitSeq)
bitInterl = LoRaPHY.interleaver(bitEnc,SF)[:]
bitDeInterl = LoRaPHY.deInterleaver(bitInterl,SF)
@test all(bitDeInterl[:] .== bitEnc[:])
end
end
@testset "LoRa Tx//Rx" begin
for SF in SFVect
N = 100;
sig,bitSeq,bitEnc,bitInter = loraEncode(N,SF,1,1,0)
bitDec,bitPreFec,bitPreInterl = loraDecode(sig,SF,1,1,0)
@test all(bitSeq[:] .== bitDec[:])
@test all(bitEnc[:] .== bitPreFec[:])
end
end | LoRaPHY | https://github.com/JuliaTelecom/LoRaPHY.jl.git |
|
[
"MIT"
] | 0.1.1 | 58269d14168a82ada381a5359ff6cad714e09b38 | code | 363 | ####
#### Coverage summary, printed as "(percentage) covered".
####
#### Useful for CI environments that just want a summary (eg a Gitlab setup).
####
using Coverage
cd(joinpath(@__DIR__, "..", "..")) do
covered_lines, total_lines = get_summary(process_folder())
percentage = covered_lines / total_lines * 100
println("($(percentage)%) covered")
end
| LoRaPHY | https://github.com/JuliaTelecom/LoRaPHY.jl.git |
|
[
"MIT"
] | 0.1.1 | 58269d14168a82ada381a5359ff6cad714e09b38 | code | 266 | # only push coverage from one bot
get(ENV, "TRAVIS_OS_NAME", nothing) == "linux" || exit(0)
get(ENV, "TRAVIS_JULIA_VERSION", nothing) == "1.2" || exit(0)
using Coverage
cd(joinpath(@__DIR__, "..", "..")) do
Codecov.submit(Codecov.process_folder())
end
| LoRaPHY | https://github.com/JuliaTelecom/LoRaPHY.jl.git |
|
[
"MIT"
] | 0.1.1 | 58269d14168a82ada381a5359ff6cad714e09b38 | code | 955 | #!/bin/bash
#=
export __JULIA_SPAWNED__=1
exec julia --color=yes --startup-file=no "${BASH_SOURCE[0]}"
=#
if get(ENV, "__JULIA_SPAWNED__", "0") != "1"
@info "Spawning new Julia process"
let file = @__FILE__
try
ENV["__JULIA_SPAWNED__"] = "1"
run(`$(Base.julia_cmd()) $file`)
finally
ENV["__JULIA_SPAWNED__"] = "0"
end
end
else
using Pkg
Pkg.activate(@__DIR__)
Pkg.instantiate()
using Coverage
cd(joinpath(@__DIR__, "..", "..")) do
coverage = process_folder()
infofile = joinpath(@__DIR__, "coverage-lcov.info")
LCOV.writefile(infofile, coverage)
outdir = joinpath(@__DIR__, "html")
rm(outdir, recursive=true, force=true)
mkdir(outdir)
cmd = Sys.iswindows() ? "genhtml.cmd" : "genhtml"
run(`$cmd $infofile --output-directory=$outdir`)
end
end
nothing
# Local Variables:
# mode: julia
# End:
| LoRaPHY | https://github.com/JuliaTelecom/LoRaPHY.jl.git |
|
[
"MIT"
] | 0.1.1 | 58269d14168a82ada381a5359ff6cad714e09b38 | docs | 6002 | # LoRaPHY.jl: Physical Layer Package for Long Range Communication in Julia
This Julia package provides a comprehensive implementation of a LoRA (Long Range) Physical Layer (PHY) with Hamming encoding, interleaving, CSS modulation, and associated decoding algorithms. LoRA technology is known for its efficient long-range communication capabilities, making it ideal for IoT (Internet of Things) and other low-power, wide-area network applications.
## Installation
You can install this package by using the Julia package manager. From the Julia REPL (Read-Eval-Print Loop), type the following in Pgk mode
```julia
] add LoRaPHY
```
or equally
```julia
julia> using Pkg; Pkg.add("LoRaPHY")
```
## Usage
A minimal transmitter-receiver can be found in `example/tx_rx.jl`
```julia
# Number of LoRa symbols to transmit
N = 128
# Spreading factor used in LoRa
SF = 7
# Bandwidth and frequency used
# < Note that the values are not that important; this is Fs/B that matters>
BW = 125e3
Fs = BW
snr = 0 # In dB
# --- LoRa Encoding
sig, bitSeq, bitEnc, bitInter = loraEncode(N, SF, BW, Fs, 0)
# --- Channel
sigNoise, _ = addNoise(sig, snr)
# --- LoRa Decoding
bitDec, bitPreFec, bitPreInterl = loraDecode(sigNoise, SF, BW, Fs, 0)
# --- BER calculation
ber = sum(xor.(bitDec, bitSeq)) / length(bitSeq)
```
This creates a binary sequence, modulates with LoRa, and applies some additive white Gaussian noise. The Bit Error Rate can be deduced by calculating the number of differences between the emitted sequence and the received one.
The important LoRa parameters are as follows:
- `SF` is the Spreading Factor as defined in the LoRa norm: a value between 7 and 12.
- `BW` is the bandwidth: The LoRa devices can use 125, 250, or 500kHz, but the LoRaWAN standard mandates 125k for data rates 1 to 5, and 250k for DR6
- `Fs` sampling frequency: this should be a multiple of `BW` (or Fs=BW to have no oversampling)
### Modulation
If you already have a binary sequence `bitSeq` (an array of 0 and 1) and you want to modulate this binary sequence, you can do the following:
```julia
# Spreading factor used in LoRa
SF = 7
# Number of LoRa symbols to transmit
N = 128
# Number of bits to transmit
nbBits = N * SF
bitSeq = Int.(randn(nbBits) .> 0) # A vector of binary elements
# Bandwidth and frequency used
BW = 125e3
Fs = BW
# --- LoRa Encoding
sig, bitSeq, bitEnc, bitInter = loraEncode(bitSeq, SF, BW, Fs, 0)
```
The output parameters are:
- `sig`: LoRa signal as a complex vector in the time domain.
- `bitSeq`: Binary sequence (info bits) used for generation (of size `N x SF`)
- `bitEnc`: Sequence of bits after Hamming74 encoding (of size `N / 4 x 7`)
- `bitInter`: Sequence of bits after Hamming74 encoding and interleaver (of size `N / 4 x 7`)
### Demodulation
To decode a received signal, follow these steps:
```julia
# Number of LoRa symbols to transmit
# Spreading factor used in LoRa
SF = 7
# Bandwidth and frequency used
BW = 125e3
Fs = BW
bitDec, bitPreFec, bitPreInterl = loraDecode(sigNoise, SF, BW, Fs, 0)
```
The output parameters are:
- `bitDec`: Decoded binary sequence (matches `bitSeq` if no noise)
- `bitDec`: Binary sequence before Hamming74 decoder (matches `bitEnc` if no noise)
- `bitPreInterl`: Binary sequence before Deinterleaver (matches `bitInter` if no noise)
### Example for Bit Error Rate Calculation
An example of a Bit Error Rate calculation versus signal-to-noise ratio (SNR) in an additive white Gaussian noise (AWGN) process is given in `example/perf_awgn.jl`
Performance matches the theory (theoretical Symbol Error Rate (SER) formula is given in `src/Theoretical.jl`) from [1,2]. This script requires `DigitalComm.jl` for noise application and `PGFPLotsX.jl` for displaying the results.
Simulated performance matches theory as demonstrated by the following performance

[1] J. Courjault, B. Vrigneau, O. Berder and M. R. Bhatnagar, "A Computable Form for LoRa Performance Estimation: Application to Ricean and Nakagami Fading," in IEEE Access, vol. 9, pp. 81601-81611, 2021, doi: 10.1109/ACCESS.2021.3074704.
[2] J. Courjault, B. Vrigneau, M. Gautier and O. Berder, "Accurate LoRa Performance Evaluation Using Marcum Function," 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 2019, pp. 1-5, doi: 10.1109/GLOBECOM38437.2019.9014148.
### Use with Software Defined Radio
If you want to transmit a LoRa signal with a Software Defined Radio, you can use `AbstractSDRs.jl` with a compatible device
```julia
# --- Dependencies
using LoRaPHY
using AbstractSDRs
# ----------------------------------------------------
# --- LoRa configuration
# ----------------------------------------------------
# Spreading factor used in LoRa
SF = 7
# Number of LoRa symbols to transmit
N = SF*4*2
bitSeq = Int.(randn(N) .> 0) # A vector of binary elements
# Bandwidth and frequency used
BW = 125e3
Fs = BW * 20
# --- LoRa Encoding
sig, bitSeq, bitEnc, bitInter = loraEncode(bitSeq, SF, BW, Fs, 0)
# --- Normalization
sig .= sig * (1-2^-15) # With some radio signal has to be normalized but < 1. Ensure this can be a Q(16,0,15)
# ----------------------------------------------------
# --- SDR configuration
# ----------------------------------------------------
radio = :pluto
carrierFreq = 868e6
gain = 10
samplingRate = Fs # If your radio does not support low datarate use a Fs in LoRa that is a multiple of BW and compatible with your SDR
kw = (;) # Additionnal arguments such as SDR address, ...
sdr = openSDR(radio,carrierFreq,samplingRate,gain;kw...)
# ----------------------------------------------------
# --- Transmit
# ----------------------------------------------------
nbB = 0
try
@info "Type <c-c> to interrupt"
while true
send(sdr,sig)
global nbB += 1
end
catch exception
@info "Interruption"
display(exception)
end
close(sdr)
@info "Transmit $(nbB) LoRa bursts"
```
| LoRaPHY | https://github.com/JuliaTelecom/LoRaPHY.jl.git |
|
[
"MIT"
] | 0.2.1 | 177e19ca8dbce81ba0c8f1c3468b72a8f78f9412 | code | 593 | using Documenter
using GalacticPotentials
makedocs(
sitename="GalacticPotentials",
format=Documenter.HTML(),
modules=[GalacticPotentials],
pages=[
"Overview" => [
"Getting Started" => "index.md",
"Gravitational Potentials" => "potentials.md",
"Example Usage" => "examples.md",
],
"Reference" => "reference.md"
]
)
deploydocs(
target="build",
repo="github.com/cadojo/GalacticPotentials.jl.git",
branch="gh-pages",
devbranch="main",
versions=["stable" => "v^", "manual", "v#.#", "v#.#.#"],
)
| GalacticPotentials | https://github.com/cadojo/GalacticPotentials.jl.git |
|
[
"MIT"
] | 0.2.1 | 177e19ca8dbce81ba0c8f1c3468b72a8f78f9412 | code | 1365 | #
# This script bootstraps GalacticPotentials.jl through the "gala" Python package!
# An attempt is made to convert all potentials in the package to SymPy expressions,
# and then to LaTeX expressions. The results are printed to an ImmutableDict within
# GalacticPotentials.jl. Thank you Gala!
#
ENV["PYTHON"] = "/opt/homebrew/bin/python3" # must have `gala` installed!
import Pkg
Pkg.activate(@__DIR__)
Pkg.instantiate()
Pkg.build("PyCall")
using Dates
using PyCall, SymPy, LaTeXStrings
gala = pyimport("gala.potential")
expressions = Dict{String,LaTeXString}()
latex!(collection::AbstractDict, name::AbstractString) =
try
collection[name] = getproperty(gala.potential, name).to_latex()
catch
@warn "Unable to get expression for $name."
end
for potential in gala.potential.__dir__()
if occursin("Potential", potential)
latex!(expressions, potential)
end
end
open(joinpath(@__DIR__, "..", "src", "gen", "expressions.jl"), "w") do file
write(
file,
"""
#
# This is an autogenerated file! It was created on $(today()).
#
const LATEX_EXPRESSIONS = Base.ImmutableDict(
"""
)
for potential in sort(collect(keys(expressions)))
write(file, """\t"$potential" => L"\\Phi = $(expressions[potential])",\n""")
end
write(file, ")\n")
end | GalacticPotentials | https://github.com/cadojo/GalacticPotentials.jl.git |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.