licenses
sequencelengths 1
3
| version
stringclasses 677
values | tree_hash
stringlengths 40
40
| path
stringclasses 1
value | type
stringclasses 2
values | size
stringlengths 2
8
| text
stringlengths 25
67.1M
| package_name
stringlengths 2
41
| repo
stringlengths 33
86
|
|---|---|---|---|---|---|---|---|---|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | code | 380 | using Test
using Random
Random.seed!(0)
@testset "Linear" begin
for R in [Float16, Float32, Float64]
for shape in [(5,), (3, 5), (3, 4, 5)]
c = randn(R, shape)
f = Linear(c)
predicates_test(f)
x = randn(R, shape)
@test gradient_test(f, x) == (c, f(x))
call_test(f, x)
prox_test(f, x, R(0.5)+rand(R))
end
end
end
| ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | code | 843 | using LinearAlgebra
using Test
using ProximalOperators
@testset "LogisticLoss" for T in [Float32, Float64]
y = T[1.0, -1.0, 1.0, -1.0, 1.0]
mu = T(1.5)
f = LogisticLoss(y, mu)
x = T[-1.0, -2.0, 3.0, 2.0, 1.0]
f_x_1 = f(x)
@test typeof(f_x_1) == T
grad_f_x, f_x_2 = gradient_test(f, x)
f_x_ref = 5.893450123044199
grad_f_x_ref = [-1.0965878679450072, 0.17880438303317633, -0.07113880976635019, 1.3211956169668235, -0.4034121320549927]
@test f_x_1 β f_x_ref
@test f_x_2 β f_x_ref
@test all(grad_f_x .β grad_f_x_ref)
z1, f_z1 = prox(f, x)
grad_f_z1, = gradient_test(f, z1)
@test typeof(f_z1) == T
@test norm((x - z1)./1.0 - grad_f_z1, Inf)/norm(grad_f_z1, Inf) <= 1e-4
z2, f_z2 = prox(f, x, T(2.0))
grad_f_z2, = gradient_test(f, z2)
@test typeof(f_z2) == T
@test norm((x - z2)./2.0 - grad_f_z2, Inf)/norm(grad_f_z2, Inf) <= 1e-4
end | ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | code | 1466 | using Test
using LinearAlgebra
@testset "Moreau envelope" begin
@testset "Box indicator" for R in [Float32, Float64]
f = IndBox(-1, 1)
for g in [
MoreauEnvelope(f),
MoreauEnvelope(f, R(0.01))
]
predicates_test(g)
@test ProximalOperators.is_smooth(g) == true
@test ProximalOperators.is_quadratic(g) == false
@test ProximalOperators.is_set(g) == false
x = R[1.0, 2.0, 3.0, 4.0, 5.0]
grad_g_x, g_x = gradient_test(g, x)
y, g_y = prox_test(g, x, R(1/2))
grad_g_y, _ = gradient_test(g, y)
@test y + grad_g_y / 2 β x
@test g(y) β g_y
end
end
@testset "L2 norm" for R in [Float32, Float64]
for (g, h) in [
(MoreauEnvelope(NormL2()), HuberLoss()),
(MoreauEnvelope(NormL2(R(1)), R(0.1)), HuberLoss(R(0.1), R(1)/R(0.1)))
]
predicates_test(g)
@test ProximalOperators.is_smooth(g) == true
@test ProximalOperators.is_quadratic(g) == false
@test ProximalOperators.is_set(g) == false
x = R[1.0, 2.0, 3.0, 4.0, 5.0]
@test g(x) β h(x)
grad_g_x, g_x = gradient_test(g, x)
grad_h_x, h_x = gradient_test(h, x)
@test g_x β g(x)
@test h_x β h(x)
@test all(grad_g_x .β grad_h_x)
y, g_y = prox_test(g, x, R(1/2))
grad_g_y, _ = gradient_test(g, y)
@test y + grad_g_y / 2 β x
@test g(y) β g_y
end
end
end | ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | code | 931 |
using Random
using ProximalOperators
using Test
@testset "NormL1plusL2 standard case" begin
f = NormL1(1.0)
g = NormL2(2.0)
fplusg = NormL1plusL2(1.0, 2.0)
x = randn(50)
y1, f1 = prox(f, x)
y2, f2 = prox(g, y1)
y3, f3 = prox(fplusg, x)
@test f3 β f(y3)+g(y3)
@test y3 β y2
end
@testset "NormL1plusL2 norm constructor" begin
f = NormL1(1.0)
g = NormL2(2.0)
fplusg = NormL1plusL2(f, g)
x = randn(50)
y1, f1 = prox(f, x)
y2, f2 = prox(g, y1)
y3, f3 = prox(fplusg, x)
@test f3 β f(y3)+g(y3)
@test y3 β y2
end
@testset "NormL1plusL2 vector case" begin
Ξ»1 = abs.(randn(50))
f = NormL1(Ξ»1)
g = NormL2(2.0)
fplusg = NormL1plusL2(Ξ»1, 2.0)
x = randn(50)
y1, f1 = prox(f, x)
y2, f2 = prox(g, y1)
y3, f3 = prox(fplusg, x)
@test f3 β f(y3)+g(y3)
@test y3 β y2
end | ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | code | 4906 | # test whether prox satisfies necessary conditions for optimality
using LinearAlgebra
using SparseArrays
using ProximalOperators
using Test
check_optimality(f::LeastSquares, x, gamma, y) = norm(y + gamma * f.lambda * (f.A' * (f.A * y - f.b)) - x) <= 1e-10
check_optimality(f::HuberLoss, x, gamma, y) = isapprox((x - y) / gamma, (norm(y) <= f.rho ? f.mu * y : f.rho * f.mu * y / norm(y)))
check_optimality(f::SqrHingeLoss, x, gamma, y) = isapprox((x - y) / gamma, -2 .* f.mu .* f.y .* max.(0, 1 .- f.y .* y))
check_optimality(::IndSimplex, x, _, y) = begin
w = x - y
tau = dot(w, y) / sum(y)
all(w .<= tau + 10 * eps(eltype(x)))
end
check_optimality(f::IndBallL1, x, gamma, y) = begin
if norm(x, 1) <= f.r
return all(y .== x)
end
sign_is_correct = (sign.(y) .== 0) .| (sign.(x) .== sign.(y))
return all(sign_is_correct) && check_optimality(IndSimplex(f.r), abs.(x), gamma, abs.(y))
end
check_optimality(f::TotalVariation1D, x, gamma, y) = begin
N = length(x)
# compute dual solution
R = real(eltype(x))
u = zeros(R, N+1)
u[1] = 0
for k in 2:N+1
u[k] = x[k-1]-y[k-1]+u[k-1]
end
# check whether all duals in interval
c1 = all(abs.(u) .<= gamma*f.lambda + 10*eps(R))
# check whether last equals 0 (first by construction)
c2 = isapprox(u[end], 0, atol=10*eps(R))
# check whether equal +- gamma*lambda
h = sign.(y[1:end-1] - y[2:end])
c3 = all(isapprox.( u[2:end-1] .* abs.(h) , h *f.lambda*gamma))
return c1 && c2 && c3
end
test_cases = [
Dict(
"f" => LeastSquares(randn(20, 10), randn(20)),
"x" => randn(10),
"gamma" => rand(),
),
Dict(
"f" => LeastSquares(randn(15, 40), randn(15), rand()),
"x" => randn(40),
"gamma" => rand(),
),
Dict(
"f" => LeastSquares(rand(Complex{Float64}, 15, 40), rand(Complex{Float64}, 15), rand()),
"x" => rand(Complex{Float64}, 40),
"gamma" => rand(),
),
Dict(
"f" => LeastSquares(sprandn(100,1000,0.05), randn(100), rand()),
"x" => randn(1000),
"gamma" => rand(),
),
Dict(
"f" => IndSimplex(),
"x" => randn(10),
"gamma" => rand(),
),
Dict(
"f" => IndSimplex(2),
"x" => [1.5, 0.0, 0.5, 0.0, 0.0],
"gamma" => rand(),
),
Dict(
"f" => IndSimplex(5.0),
"x" => [0.5, 0.5, 1.0, 1.0, 2.0],
"gamma" => rand(),
),
Dict(
"f" => IndSimplex(5.0),
"x" => [0.5, 0.5, 1.0, 1.0, 2.0] * 3,
"gamma" => rand(),
),
Dict(
"f" => IndSimplex(rand()),
"x" => randn(10),
"gamma" => rand(),
),
Dict(
"f" => IndBallL1(),
"x" => [-0.39, 0.1, -0.2, 0.3],
"gamma" => rand(),
),
Dict(
"f" => IndBallL1(),
"x" => [0.1, -0.1, 0.2, -0.3, 0.4, 0.5],
"gamma" => rand(),
),
Dict(
"f" => IndBallL1(1.7),
"x" => [0.1, -0.1, 0.2, -0.3, 0.4, 0.5],
"gamma" => rand(),
),
Dict(
"f" => IndBallL1(1.7),
"x" => [0.4, 0.1, 0.6, 0.2, -0.1, -0.3, 0.5],
"gamma" => rand(),
),
Dict(
"f" => IndBallL1(1.7),
"x" => [0.5, 0.1, -0.1, 0.4, 0.6, -0.3, 0.2] * 10,
"gamma" => rand(),
),
Dict(
"f" => HuberLoss(),
"x" => randn(10),
"gamma" => rand(),
),
Dict(
"f" => HuberLoss(rand()),
"x" => randn(8, 10),
"gamma" => rand(),
),
Dict(
"f" => HuberLoss(rand(), rand()),
"x" => randn(20),
"gamma" => rand(),
),
Dict(
"f" => HuberLoss(rand(), rand()),
"x" => rand(Complex{Float64}, 12, 15),
"gamma" => rand(),
),
Dict(
"f" => SqrHingeLoss(randn(5)),
"x" => randn(5),
"gamma" => 0.1 + rand(),
),
Dict(
"f" => SqrHingeLoss(randn(5), 0.1+rand()),
"x" => randn(5),
"gamma" => 0.1 + rand(),
),
Dict(
"f" => SqrHingeLoss(randn(3, 5), 0.1+rand()),
"x" => randn(3, 5),
"gamma" => 0.1 + rand(),
),
Dict(
"f" => TotalVariation1D(0.01),
"x" => vcat(LinRange(1., -1., 10), -1*ones(3), LinRange(-1., 1., 10)),
"gamma" => 1.,
),
Dict(
"f" => TotalVariation1D(1.0),
"x" => [-2.0, 0.0625, 0.125, 0.1875, 0.25, 0.3125, 0.375, 0.4375, 0.5, 2.4375],
"gamma" => 1.0,
),
Dict(
"f" => TotalVariation1D(1.0),
"x" => [0.0, 0.0625, 0.125, 0.1875, 0.25, 0.3125, 0.375, 0.4375, 0.5, 2.4375],
"gamma" => 1.0,
),
]
@testset "Optimality conditions" begin
@testset "$(typeof(d["f"]))" for d in test_cases
f, x, gamma = d["f"], d["x"], d["gamma"]
y, fy = prox(f, x, gamma)
@test fy β f(y)
@test check_optimality(f, x, gamma, y)
end
end
| ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | code | 330 | using ProximalOperators
using Test
@testset "PointwiseMinimum" begin
T = Float64
f = PointwiseMinimum(IndPoint(T[-1.0]), IndPoint(T[1.0]))
x = T[0.1]
predicates_test(f)
@test ProximalOperators.is_set(f) == true
@test ProximalOperators.is_cone(f) == false
y, fy = prox_test(f, x)
@test all(y .== T[1.0])
@test fy == T(0)
end
| ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | code | 1088 | using LinearAlgebra
# Postcompose HuberLoss
f = HuberLoss(1.0, 1.0)
g = Postcompose(f, 2.5)
h = HuberLoss(1.0, 2.5)
x = randn(10)
x = 0.5*x/norm(x)
gx = call_test(g, x)
hx = call_test(h, x)
@test abs(gx-hx)/(1+abs(gx)) <= 1e-12
grad_gx, gx1 = gradient_test(g, x)
grad_hx, hx1 = gradient_test(h, x)
@test abs(gx1-gx)/(1+abs(gx)) <= 1e-12
@test abs(hx1-hx)/(1+abs(hx)) <= 1e-12
@test norm(grad_gx-grad_hx, Inf)/(1+norm(grad_gx, Inf)) <= 1e-12
yg, gyg = prox_test(g, x, 1.3)
yh, hyh = prox_test(h, x, 1.3)
@test abs(gyg-hyh)/(1+abs(gyg)) <= 1e-12
@test norm(yg-yh, Inf)/(1+norm(yg, Inf)) <= 1e-12
x = randn(10)
x = 1.2*x/norm(x)
gx = call_test(g, x)
hx = call_test(h, x)
@test abs(gx-hx)/(1+abs(gx)) <= 1e-12
grad_gx, gx1 = gradient_test(g, x)
grad_hx, hx1 = gradient_test(h, x)
@test abs(gx1-gx)/(1+abs(gx)) <= 1e-12
@test abs(hx1-hx)/(1+abs(hx)) <= 1e-12
@test norm(grad_gx-grad_hx, Inf)/(1+norm(grad_gx, Inf)) <= 1e-12
yg, gyg = prox_test(g, x, 1.3)
yh, hyh = prox_test(h, x, 1.3)
@test abs(gyg-hyh)/(1+abs(gyg)) <= 1e-12
@test norm(yg-yh, Inf)/(1+norm(yg, Inf)) <= 1e-12
| ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | code | 3922 | using LinearAlgebra
@testset "Precompose" begin
@testset "IndBallL1 w/ OM" begin
# Indicator of L1 norm ball composed with orthogonal matrix
f = IndBallL1()
A = randn(10, 10)
F = qr(A)
Q = Matrix(F.Q)
@test Q'*Q β I
@test Q*Q' β I
g = Precompose(f, Q, 1.0)
predicates_test(g)
@test ProximalOperators.is_smooth(g) == false
@test ProximalOperators.is_quadratic(g) == false
@test ProximalOperators.is_set(g) == true
x = randn(10)
call_test(g, x)
prox_test(g, x, 1.0)
end
@testset "IndBallL1 w/ OM multiple" begin
# L1 norm composed with multiple of orthogonal matrix
f = NormL1()
A = randn(10, 10)
F = qr(A)
Q = Matrix(F.Q)
@test Q'*Q β I
@test Q*Q' β I
g = Precompose(f, 3.0*Q, 9.0)
x = randn(10)
call_test(g, x)
prox_test(g, x, 1.0)
end
@testset "NormL2 w/ OM multiple" begin
# L2 norm composed with multiple of orthogonal matrix
f = NormL2()
A = randn(10, 10)
F = qr(A)
Q = Matrix(F.Q)
@test Q'*Q β I
@test Q*Q' β I
g = Precompose(f, 0.9*Q, 0.9^2)
x = randn(10)
call_test(g, x)
prox_test(g, x, 1.0)
end
@testset "NormL2 w/ OM + translation" begin
# L2 norm composed with orthogonal matrix + translation
f = NormL2()
A = randn(10, 10)
b = randn(10)
F = qr(A)
Q = Matrix(F.Q)
@test Q'*Q β I
@test Q*Q' β I
g = Precompose(f, Q, 1.0, -b)
x = randn(10)
call_test(g, x)
prox_test(g, x, 1.0)
end
@testset "NormL2 w/ DM + translation" begin
# L2 norm composed with diagonal matrix + translation
# checking that Precompose and PrecomposeDiagonal agree
f = NormL2()
A = Diagonal(3.0*ones(10))
b = randn(10)
g1 = Precompose(f, A, 9.0, -b)
g2 = PrecomposeDiagonal(f, 3.0, -b)
x = randn(10)
call_test(g1, x)
y1, gy1 = prox_test(g1, x, 1.0)
call_test(g2, x)
y2, gy2 = prox_test(g2, x, 1.0)
@test abs(gy1 - gy2) <= (1 + abs(gy1))*1e-12
@test norm(y1 - y2) <= (1 + norm(y1))*1e-12
end
@testset "SqrNormL2 w/ DM + translation" begin
# Squared L2 norm composed with diagonal matrix + translation
# checking that Precompose and PrecomposeDiagonal agree
# checking that weighted squared L2 norm + Translate agrees too
f = SqrNormL2()
diagA = [rand(5); -rand(5)]
A = Diagonal(diagA)
b = randn(10)
g1 = Precompose(f, A, diagA .* diagA, -diagA .* b)
g2 = PrecomposeDiagonal(f, diagA, -diagA .* b)
g3 = Translate(SqrNormL2(diagA .* diagA), -b)
x = randn(10)
gx = 0.5*sum((diagA .* diagA) .* (x-b).^2)
grad_gx = diagA.*diagA.*(x - b)
@test abs(g1(x) - gx)/(1+abs(gx)) <= 1e-14
@test abs(g2(x) - gx)/(1+abs(gx)) <= 1e-14
@test abs(g3(x) - gx)/(1+abs(gx)) <= 1e-14
call_test(g1, x)
grad_g1_x, g1_x = gradient_test(g1, x)
@test abs(g1_x - gx) <= (1 + abs(gx))*1e-12
@test norm(grad_gx - grad_g1_x, Inf) <= 1e-12
call_test(g2, x)
grad_g2_x, g2_x = gradient_test(g2, x)
@test abs(g2_x - gx) <= (1 + abs(gx))*1e-12
@test norm(grad_gx - grad_g2_x, Inf) <= 1e-12
call_test(g3, x)
grad_g3_x, g3_x = gradient_test(g3, x)
@test abs(g3_x - gx) <= (1 + abs(gx))*1e-12
@test norm(grad_gx - grad_g3_x, Inf) <= 1e-12
y1, gy1 = prox_test(g1, x, 1.0)
y2, gy2 = prox_test(g2, x, 1.0)
@test abs(gy1 - gy2) <= (1 + abs(gy1))*1e-12
@test norm(y1 - y2) <= (1 + norm(y1))*1e-12
y3, gy3 = prox_test(g3, x, 1.0)
@test abs(gy2 - gy3) <= (1 + abs(gy2))*1e-12
@test norm(y2 - y3) <= (1 + norm(y2))*1e-12
end
@testset "IndSOC w/ [I, I, I]" begin
# IndSOC composed with [I, I, I]
f = IndSOC()
A = [Matrix{Float64}(I, 3, 3) Matrix{Float64}(I, 3, 3) Matrix{Float64}(I, 3, 3)]
g = Precompose(f, A, 3.0)
x = [0.4, 0.2, 0.4, 0.5, 0.3, 0.3, 0.6, 0.4, 0.2]
@test g(x) == 0.0
call_test(g, x)
y, gy = prox_test(g, x, 1.0)
x = [0.1, 0.2, 0.4, 0.2, 0.3, 0.3, 0.3, 0.4, 0.2]
@test g(x) == Inf
call_test(g, x)
y, gy = prox_test(g, x, 1.0)
end
@testset "ElasticNet w/ [DM, DM, DM]" begin
# ElasticNet composed with [diag, diag, diag]
f = ElasticNet()
d = 1.0:10.0
n = length(d)
A = [Diagonal(d) Diagonal(d) Diagonal(d)]
g = Precompose(f, A, 3*(Array(d).^2))
x = randn(3*n)
call_test(g, x)
y, gy = prox_test(g, x, 1.0)
end
end
| ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | code | 1160 | using LinearAlgebra
using SparseArrays
using Test
using ProximalOperators
@testset "Quadratic" begin
# Test with full matrices
n, k = 5, 4
A = randn(n, k)
Q = A*A'
q = randn(n)
f = Quadratic(Q, q)
@test typeof(f) <: ProximalOperators.QuadraticDirect
predicates_test(f)
@test ProximalOperators.is_smooth(f) == true
@test ProximalOperators.is_quadratic(f) == true
@test ProximalOperators.is_set(f) == false
x = randn(n)
grad_fx, fx = gradient_test(f, x)
@test fx β 0.5*dot(x, Q*x) + dot(x, q)
@test all(grad_fx .β (Q*x + q))
call_test(f, x)
prox_test(f, x)
prox_test(f, x, 1.5)
f = Quadratic(Q, q, iterative=true)
@test typeof(f) <: ProximalOperators.QuadraticIterative
call_test(f, x)
prox_test(f, x)
prox_test(f, x, 2.1)
# Test with sparse matrices
Q = sparse(Q)
f = Quadratic(Q, q)
@test typeof(f) <: ProximalOperators.QuadraticDirect
grad_fx, fx = gradient_test(f, x)
@test fx β 0.5*dot(x, Q*x) + dot(x, q)
@test all(grad_fx .β (Q*x + q))
call_test(f, x)
prox_test(f, x)
prox_test(f, x, 0.8)
f = Quadratic(Q, q, iterative=true)
@test typeof(f) <: ProximalOperators.QuadraticIterative
call_test(f, x)
prox_test(f, x)
prox_test(f, x, 1.3)
end | ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | code | 863 | using ProximalOperators
using LinearAlgebra
# Nonsmooth + regularization
mu, lam = 2.0, 3.0
f = NormL1(mu)
g = Regularize(f, lam)
h = ElasticNet(mu, lam)
x = randn(10)
gx = call_test(g, x)
hx = call_test(h, x)
@test abs(gx - hx)/(1+abs(gx)) <= 1e-12
yg, gy = prox_test(g, x, 0.5)
yh, hy = prox_test(h, x, 0.5)
@test abs(gy - hy)/(1+abs(gy)) <= 1e-12
@test norm(yg - yh, Inf)/(1+norm(yg, Inf)) <= 1e-12
# Smooth + regularization (test also gradient)
m, n = 10, 20
lam = 1.5
A = randn(m, n)
b = randn(m)
f = LeastSquares(A, b)
g = Regularize(f, lam)
x = randn(n)
res = A*x-b
gx = call_test(g, x)
@test abs(0.5*norm(res)^2 + (0.5*lam)*norm(x)^2 - gx)/(1+abs(gx)) <= 1e-12
prox_test(g, x, 0.7)
grad_gx, gx1 = gradient_test(g, x)
@test abs(gx - gx1)/(1+abs(gx)) <= 1e-12
@test norm(grad_gx - A'*(A*x - b) - lam*x, Inf)/(1+norm(grad_gx, Inf)) <= 1e-12
| ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | code | 18084 | # Test the correctness of f(x) and prox(f,x,gamma) for a few hardcoded cases
using LinearAlgebra
using ProximalOperators
using Test
stuff = [
Dict( "f" => NormL2(0.5),
"x" => [-1.472658469388188,-0.2715944116787317,-0.05323943816203797,1.0714599486778327,-1.5331256392574706,0.4083764366610342,-0.9444383691511559,-0.7504607478410741,0.7438914169983039,-0.15652009656239366],
"f(x)" => 1.4092215084194275,
"gamma" => 0.3,
"y" => [-1.3942822988967276,-0.2571399197807538,-0.0504059887445427,1.0144359140099486,-1.4515313531517497,0.38664228587878424,-0.8941745339321049,-0.7105205711181053,0.7043008658028084,-0.14818996026228431],
"f(y)" => 1.3342215084194275,
),
Dict( "f" => NormL1(0.6),
"x" => [0.24488032099324117,0.6361148017053393,-0.7468003460445393,-0.39461027607226284,-0.766936244339526,0.08238242897650354,-1.4822688010626806,0.23915849610266143,-0.5124773673251194,0.14222091048851146],
"f(x)" => 3.148709995866231,
"gamma" => 0.4,
"y" => [0.004880320993241177,0.3961148017053393,-0.5068003460445393,-0.15461027607226285,-0.526936244339526,0.0,-1.2422688010626806,0.0,-0.2724773673251194,0.0],
"f(y)" => 1.8624528945256253,
),
Dict( "f" => NormL1(0.45),
"x" => Complex{Float64}[0.48383139850861223 + 0.14880666357496075im -0.476452189543104 + 0.5373862840906938im -0.47734819961688757 + 1.5821400827207137im;
0.731503968722083 + 0.16028191387997026im -0.43401778891072196 + 0.31094682923492956im -0.6171419681732582 + 1.6633154232600766im;
0.8143294700727339 + 0.9825764200556435im 0.9956758203961695 + 0.6666719567389796im 0.9364063971363472 + 0.03175404144697325im],
"f(x)" => 4.2053455230857,
"gamma" => 0.55,
"y" => Complex{Float64}[0.24726722632640047 + 0.07604924168725978im -0.3122580040459822 + 0.3521930891591931im -0.40585785798447027 + 1.3451899169615815im;
0.48973954188193203 + 0.1073082231018745im -0.23282376734737972 + 0.16680379025222528im -0.5310468296940786 + 1.4312725885716275im;
0.6563976577692634 + 0.7920146383087744im 0.7900191090320431 + 0.5289709506755073im 0.6890485776638721 + 0.02336600557303825im],
"f(y)" => 3.2029705230857,
),
Dict( "f" => NormL0(0.6),
"x" => [0.14315338571566838,0.6534693088076117,-0.35221109634545744,-1.0843092036012738,-0.21687748781464977,0.38416472626106707,0.46644748241896083,-1.7104462861427205,0.29913996761129763,1.4566599915371263],
"f(x)" => 6.0,
"gamma" => 0.4,
"y" => [0.0,0.0,-0.0,-1.0843092036012738,-0.0,0.0,0.0,-1.7104462861427205,0.0,1.4566599915371263],
"f(y)" => 1.7999999999999998,
),
Dict( "f" => NormL0(0.45),
"x" => [-0.9617311985566904 -0.518012365217699 0.4416517549177308 1.0497034474382447;
0.273994311984438 0.33356795744106194 0.24747082687586053 1.369695656039301;
-0.778053112909331 1.7320620010973118 1.6366272293068256 -0.5828690748881356;
-0.9706863561972737 1.4039270788692668 1.126542963082653 -0.06669611410738466],
"f(x)" => 7.2,
"gamma" => 0.55,
"y" => [-0.9617311985566904 -0.0 0.0 1.0497034474382447;
0.0 0.0 0.0 1.369695656039301;
-0.778053112909331 1.7320620010973118 1.6366272293068256 -0.0;
-0.9706863561972737 1.4039270788692668 1.126542963082653 -0.0],
"f(y)" => 4.05,
),
Dict( "f" => IndBallL0(5),
"x" => [-0.1553737486872724,-0.3805093036732066,-1.1359877819928568,-1.4074575535421312,-0.014354093517417054,-0.7828347886276972,0.7289354484199504,0.8077049251507309,-0.011180606660407861,-0.08252274792015224],
"f(x)" => +Inf,
"gamma" => rand(),
"y" => [0.0,0.0,-1.1359877819928568,-1.4074575535421312,0.0,-0.7828347886276972,0.7289354484199504,0.8077049251507309,0.0,0.0],
"f(y)" => 0.0,
),
Dict( "f" => IndBallL0(4),
"x" => [0.11718035918656403 0.7413899585297815 2.536889607960003;
-0.7905417065462554 -2.528853472235987 -0.21157829025742098;
0.7335959778823463 -0.842619689213128 -1.6389387126978623],
"f(x)" => +Inf,
"gamma" => rand(),
"y" => [0.0 0.0 2.536889607960003;
0.0 -2.528853472235987 0.0;
0.0 -0.842619689213128 -1.6389387126978623],
"f(y)" => 0.0,
),
Dict( "f" => IndBallL0(6),
"x" => Complex{Float64}[0.4123814653942677 + 0.5477281536949097im 0.1180210182125836 + 0.48721833026698946im 0.18165793415201192 + 0.33083070659243896im;
0.14567574789746107 + 0.9797631246910778im 0.8859137252355573 + 0.24593117579841173im 0.1119791184116512 + 0.1782455833267571im;
0.6971105660873709 + 0.4456778795521643im 0.6815819496354292 + 0.7246319393377785im 0.36348180980544 + 0.06420454004464782im],
"f(x)" => +Inf,
"gamma" => rand(),
"y" => Complex{Float64}[0.4123814653942677 + 0.5477281536949097im 0.1180210182125836 + 0.48721833026698946im 0.0 + 0.0im;
0.14567574789746107 + 0.9797631246910778im 0.8859137252355573 + 0.24593117579841173im 0.0 + 0.0im;
0.6971105660873709 + 0.4456778795521643im 0.6815819496354292 + 0.7246319393377785im 0.0 + 0.0im],
"f(y)" => 0.0,
),
Dict( "f" => IndBallRank(2),
"x" => [0.3251909299381841 0.32669352058736867 0.30878476770613905 0.16430992796261545 0.34512333306839693 0.7106693424891355 0.671658396200979;
0.6281016205611978 0.6824858855301283 0.606248150077644 0.7254139031156339 0.1170408384465551 0.4388768890760757 0.8615311184291088;
0.8463682898731775 0.41051188285054874 0.2212552529414713 0.017263014648567054 0.5688479305824816 0.5689918983334776 0.6308030513994181;
0.9844519526932385 0.05957039918524343 0.16920598873503145 0.26466787431210026 0.3273430016867569 0.4490502773732654 0.6726433619983658],
"f(x)" => +Inf,
"gamma" => rand(),
"y" => [0.5886430110085807 0.32914238645718963 0.2888520521840012 0.26968674730017794 0.27465218034535255 0.4459822389240827 0.6034776156707196;
0.5489756852899045 0.6774563889771498 0.6117937125809438 0.6957514636660374 0.1363090899378463 0.519717627394074 0.8835443097850474;
0.874187543238049 0.24314229392781217 0.20193146854590316 0.10594782088443547 0.4873420015660753 0.5935040655910679 0.6835493401730847;
0.8183028926081628 0.23998278025388683 0.2004676236930234 0.11402374950138522 0.45218188314537655 0.5590320254995675 0.6505724202640549],
"f(y)" => 0.0,
),
Dict( "f" => IndBallRank(3),
"x" => Complex{Float64}[0.2894901144233224 + 0.7901100704032158im 0.6756627927190222 + 0.17732824522289703im 0.4032334590351583 + 0.5586502215509941im 0.6765530083696047 + 0.9932602290818195im 0.6239659886851328 + 0.4722390586145797im;
0.9584404572720246 + 0.3400250643041498im 0.2817204876721717 + 0.1672398933443462im 0.12128240130180257 + 0.4551933013068352im 0.009961310207793783 + 0.7338453218632623im 0.6212643707424914 + 0.9635158606442724im;
0.24433751578157148 + 0.9730339027739963im 0.561280208357009 + 0.633283020406419im 0.7756547213943652 + 0.6363562132601082im 0.524463206504971 + 0.4679827241988874im 0.8880524015305997 + 0.7435744407640921im;
0.269826028779663 + 0.9982313659183581im 0.41546528075221145 + 0.6214520195056343im 0.8504698227465424 + 0.2768665057621147im 0.8444300571451868 + 0.03191011411950728im 0.03554939244925781 + 0.14138957996692292im;
0.2597821446989732 + 0.17685782088084867im 0.019472122622971932 + 0.06869500820139018im 0.25268066733355 + 0.9806451815396378im 0.48324598010201014 + 0.44249079773617583im 0.6889781312674093 + 0.7634231410250403im;
0.43816794443248064 + 0.6397332714961954im 0.46903438458543123 + 0.8824836781826655im 0.7497646614950952 + 0.36740503730557905im 0.3126961801169257 + 0.3291723529075903im 0.8244963378972998 + 0.008092801141097006im],
"f(x)" => +Inf,
"gamma" => rand(),
"y" => Complex{Float64}[0.3585122350782503 + 0.7204931620772194im 0.6873338530452431 + 0.2610974701292823im 0.39252783201763075 + 0.6238384834518138im 0.700958438487958 + 0.9854327001665436im 0.5535168614106272 + 0.44685210138441234im;
0.8350120893298553 + 0.3426664307287768im 0.4178136548191302 + 0.12698832094230983im 0.07358671256699245 + 0.47861707516508023im 0.002816461229650763 + 0.6363648374894336im 0.6956352575477227 + 1.0157211189866961im;
0.4135468294332672 + 0.9576574664510645im 0.4469496743511391 + 0.715289225146536im 0.7730346403491004 + 0.687733965182209im 0.5363213279663741 + 0.5318375665022115im 0.7965680634261025 + 0.6450297581065603im;
0.18649674078077969 + 1.095680382782847im 0.44917829901846035 + 0.5101097836542252im 0.824251628465519 + 0.2737731007006557im 0.7934464219269162 - 0.008707537347000721im 0.13522586261104846 + 0.137751277271351im;
0.27744885345156756 + 0.22735326748520787im -0.09129603800027204 + 0.0806859574437441im 0.23111156369091165 + 0.8472792964657452im 0.5259959290489749 + 0.5120663051072597im 0.7236832860052391 + 0.7728579942500509im;
0.3176634693027552 + 0.6443692910531424im 0.506476440217625 + 0.7834437422168772im 0.8489778225663775 + 0.2954271540742297im 0.27758349592855164 + 0.34110887017651426im 0.8565371173527224 + 0.09997874104615029im],
"f(y)" => 0.0,
),
Dict( "f" => NuclearNorm(1.0),
"x" => Float64[
1.0 2.0 3.0;
4.0 5.0 6.0;
7.0 8.0 9.0 ],
"f(x)" => 17.916472867168920,
"gamma" => 1.0,
"y" => Float64[
1.586052850795247 1.944185442781408 2.302318034767569;
3.944185442781405 4.720927213907027 5.497668985032647;
6.302318034767567 7.497668985032650 8.693019935297732 ],
"f(y)" => 15.916472867168915,
),
Dict( "f" => IndPSD(),
"x" => Symmetric(Float64[
1.0 2.0 3.0 2.0;
2.0 2.0 6.0 2.5;
3.0 6.0 3.0 1.5;
2.0 2.5 1.5 1.0 ]),
"f(x)" => +Inf,
"gamma" => 1.0,
"y" => Symmetric(Float64[
1.6410947195520720 2.3777145021117252 2.5281090002887159 1.4927448378285653;
2.3777145021117252 3.9278061374789126 4.2522683130214816 1.9740014117486595;
2.5281090002887159 4.2522683130214816 4.6140313368981438 2.0691378959547362;
1.4927448378285653 1.9740014117486600 2.0691378959547362 1.4316113417275229 ]),
"f(y)" => 0.0,
),
Dict( "f" => IndPSD(),
"x" => Float64[1.0, 2.0, 3.0, 2.0, 2.0, 6.0, 2.5, 3.0, 1.5, 1.0],
"f(x)" => +Inf,
"gamma" => 1.0,
"y" => Float64[1.6410947195520720, 2.3777145021117252, 2.5281090002887159, 1.4927448378285653,
3.9278061374789126, 4.2522683130214816, 1.9740014117486600,
4.6140313368981438, 2.0691378959547362,
1.4316113417275229],
"f(y)" => 0.0,
),
Dict( "f" => IndPSD(scaling=true),
"x" => Float64[1.0, 2.0sqrt(2), 3.0sqrt(2), 2.0sqrt(2), 2.0, 6.0sqrt(2), 2.5sqrt(2), 3.0, 1.5sqrt(2), 1.0],
"f(x)" => +Inf,
"gamma" => 1.0,
"y" => Float64[1.6410947195520720, 2.3777145021117252sqrt(2), 2.5281090002887159sqrt(2), 1.4927448378285653sqrt(2),
3.9278061374789126, 4.2522683130214816sqrt(2), 1.9740014117486600sqrt(2),
4.6140313368981438, 2.0691378959547362sqrt(2),
1.4316113417275229],
"f(y)" => 0.0,
),
Dict( "f" => IndBallL1(3.5),
"x" => [0.183227263001437, -1.029767543566621, 0.949221831131023, 0.307061919146703,
0.135174942099456, 0.515246335524849, 0.261406324055383, -0.941485770955434,
-0.162337672803828, -0.146054634331526, -0.532011376808821, 1.682103594663179,
-0.875729346160017, -0.483815050110121, -0.712004549027422, -1.174212331456816,
-0.192239517539275, -0.274070229932602, 1.530072514424096, -0.249024742513714,
-1.064213412889327, 1.603457298120044, 1.234679146890778, -0.229626450963180,
-1.506159703979719, -0.444627816446985, -0.155941035724769, 0.276068253931536,
-0.261163645776479, 0.443421912904091],
"f(x)" => +Inf,
"gamma" => 1.0,
"y" => [ 0.0000000000000000e+00, -1.0823022875891708e-01, 2.7684516323319142e-02, 0.0000000000000000e+00,
0.0000000000000000e+00, 0.0000000000000000e+00, 0.0000000000000000e+00, -1.9948456147730109e-02,
-0.0000000000000000e+00, -0.0000000000000000e+00, -0.0000000000000000e+00, 7.6056627985547520e-01,
-0.0000000000000000e+00, -0.0000000000000000e+00, -0.0000000000000000e+00, -2.5267501664911218e-01,
-0.0000000000000000e+00, -0.0000000000000000e+00, 6.0853519961639224e-01, -0.0000000000000000e+00,
-1.4267609808162318e-01, 6.8191998331234005e-01, 3.1314183208307422e-01, -0.0000000000000000e+00,
-5.8462238917201514e-01, -0.0000000000000000e+00, -0.0000000000000000e+00, 0.0000000000000000e+00,
-0.0000000000000000e+00, 0.0000000000000000e+00],
"f(y)" => 0.0,
),
Dict( "f" => IndExpPrimal(),
"x" => [0.537667139546100, 1.833885014595086, -2.258846861003648],
"f(x)" => +Inf,
"gamma" => 2*rand(),
"y" => [-2.331395211405815e-01, 2.108704992310933e-01, 6.980034791326437e-02],
"f(y)" => 0.0,
),
Dict( "f" => IndExpPrimal(),
"x" => [8.621733203681206e-01, 3.187652398589808e-01, -1.307688296305273e+00],
"f(x)" => +Inf,
"gamma" => 2*rand(),
"y" => [0.0, 0.0, 0.0],
"f(y)" => 0.0,
),
Dict( "f" => IndExpPrimal(),
"x" => [-4.335920223056836e-01, 3.426244665386499e-01, 3.578396939725760e+00],
"f(x)" => 0.0,
"gamma" => 2*rand(),
"y" => [-4.335920223056836e-01, 3.426244665386499e-01, 3.578396939725760e+00],
"f(y)" => 0.0,
),
Dict( "f" => IndExpPrimal(),
"x" => [-2.049660582997746e-01, -1.241443482163119e-01, 1.489697607785465e+00],
"f(x)" => +Inf,
"gamma" => 2*rand(),
"y" => [-2.049660582997746e-01, 0, 1.489697607785465e+00],
"f(y)" => 0.0,
),
Dict( "f" => IndExpPrimal(),
"x" => [0.7647528861899316, -0.20198832835175584, 0.9528202307304982],
"f(x)" => +Inf,
"gamma" => 2*rand(),
"y" => [0.30504984970236265,0.1688454299327435,1.0283026364773413],
"f(y)" => 0.0,
),
Dict( "f" => IndNonnegative(),
"x" => [0.7647528861899316, 0.20198832835175584, 0.0],
"f(x)" => 0.0,
"gamma" => 2*rand(),
"y" => [0.7647528861899316, 0.20198832835175584, 0.0],
"f(y)" => 0.0,
),
Dict( "f" => IndNonnegative(),
"x" => [0.7647528861899316, -0.20198832835175584, 0.0],
"f(x)" => Inf,
"gamma" => 2*rand(),
"y" => [0.7647528861899316, 0.0, 0.0],
"f(y)" => 0.0,
),
Dict( "f" => IndNonpositive(),
"x" => [-0.7647528861899316, -0.20198832835175584, 0.0],
"f(x)" => 0.0,
"gamma" => 2*rand(),
"y" => [-0.7647528861899316, -0.20198832835175584, 0.0],
"f(y)" => 0.0,
),
Dict( "f" => IndNonpositive(),
"x" => [-0.7647528861899316, 0.20198832835175584, 0.0],
"f(x)" => Inf,
"gamma" => 2*rand(),
"y" => [-0.7647528861899316, 0.0, 0.0],
"f(y)" => 0.0,
),
Dict( "f" => IndZero(),
"x" => [-0.0, 0.0],
"f(x)" => 0.0,
"gamma" => 2*rand(),
"y" => [0.0, 0.0],
"f(y)" => 0.0,
),
Dict( "f" => IndZero(),
"x" => [-0.01, 0.0],
"f(x)" => Inf,
"gamma" => 2*rand(),
"y" => [0.0, 0.0],
"f(y)" => 0.0,
),
Dict( "f" => IndSOC(),
"x" => [1., 2.],
"f(x)" => Inf,
"gamma" => 2*rand(),
"y" => [1.5, 1.5],
"f(y)" => 0.0,
),
Dict( "f" => IndSOC(),
"x" => [2., 1.],
"f(x)" => 0.0,
"gamma" => 2*rand(),
"y" => [2., 1.],
"f(y)" => 0.0,
),
Dict( "f" => IndRotatedSOC(),
"x" => [1., 1., 2.],
"f(x)" => Inf,
"gamma" => 2*rand(),
"y" => [1/2*(1+sqrt(2)), 1/2*(1+sqrt(2)), 1/2*(2+sqrt(2))],
"f(y)" => 0.0,
),
Dict( "f" => IndRotatedSOC(),
"x" => [1., 1., 1.],
"f(x)" => 0.0,
"gamma" => 2*rand(),
"y" => [1., 1., 1.],
"f(y)" => 0.0,
),
Dict( "f" => IndGraph([1. 0. 0.; 0. 1. 0.]),
"x" => [2., 3., 400., 5., 6.],
"f(x)" => +Inf,
"gamma" => 1.0,
"y" => [3.5, 4.5, 400., 3.5, 4.5],
"f(y)" => 0.0,
)
]
@testset "$(i)" for i in eachindex(stuff)
f = stuff[i]["f"]
x = stuff[i]["x"]
ref_fx = stuff[i]["f(x)"]
gamma = stuff[i]["gamma"]
ref_y = stuff[i]["y"]
ref_fy = stuff[i]["f(y)"]
fx = call_test(f, x)
if fx !== nothing
@test fx β ref_fx
end
y, fy = prox_test(f, x, gamma)
@test y β ref_y
if ProximalOperators.is_prox_accurate(f)
@test fy β ref_fy
end
end
| ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | code | 1355 | using Random
using LinearAlgebra
Random.seed!(123)
x = randn(10)
X = randn(10,10) .+ im*randn(10,10)
y0 = randn(size(x))
Y0 = randn(size(X)) .+ im*randn(size(X))
y, Y = copy(y0), copy(Y0)
lambdas = (abs.(randn(size(x))), 0.1)
prox_col = (NormL1(lambdas[1]), NormL2(lambdas[2]))
# testing constructors
f = SeparableSum(prox_col)
y, fy = prox(f, (x, X), 1.)
y1, fy1 = prox(prox_col[1], x, 1.)
y2, fy2 = prox(prox_col[2], X, 1.)
@test abs((fy1+fy2)-fy) <= 1e-12
@test norm(y[1]-y1, Inf) <= 1e-12
@test norm(y[2]-y2, Inf) <= 1e-12
y, fy = prox(f, (x, X), (0.5, 1.3))
y1, fy1 = prox(prox_col[1], x, 0.5)
y2, fy2 = prox(prox_col[2], X, 1.3)
@test abs((fy1+fy2)-fy) <= 1e-11
@test norm(y[1]-y1, Inf) <= 1e-11
@test norm(y[2]-y2, Inf) <= 1e-11
gamma1 = 0.5 .+ rand(10)
y, fy = prox(f, (x, X), (gamma1, 1.3))
y1, fy1 = prox(prox_col[1], x, gamma1)
y2, fy2 = prox(prox_col[2], X, 1.3)
@test abs((fy1+fy2)-fy) <= 1e-11
@test norm(y[1]-y1, Inf) <= 1e-11
@test norm(y[2]-y2, Inf) <= 1e-11
# Test two differentiable functions
fs = (SqrNormL2(), LeastSquares(randn(5,10), randn(5)))
f = SeparableSum(fs)
x, y = randn(10), randn(10)
grad_f_x_y, f_x_y = gradient_test(f, (x, y))
grad_f_x, f_x = gradient_test(fs[1], x)
grad_f_y, f_y = gradient_test(fs[2], y)
@test norm(grad_f_x_y .- (grad_f_x, grad_f_y), Inf) <= 1e-12
@test abs((f_x+f_y)-f_x_y) <= 1e-12
| ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | code | 2053 | using LinearAlgebra
using Random
Random.seed!(123)
# CASE 1
x = randn(10)
y0 = randn(10)
y = copy(y0)
prox_col = (NormL1(0.1),IndBallL0(1))
ind_col = ((1:5,),(6:10,))
f = SlicedSeparableSum(prox_col,ind_col)
y, fy = prox(f,x,1.)
yn,fyn = ProximalOperators.prox_naive(f,x,1.)
y1,fy1 = prox(prox_col[1],x[ind_col[1]...],1.)
y2,fy2 = prox(prox_col[2],x[ind_col[2]...],1.)
@test abs(f(y)-fy)<1e-11
@test abs(fyn-fy)<1e-11
@test norm(yn-y)<1e-11
@test abs((fy1+fy2)-fy)<1e-11
@test norm(y-[y1;y2])<1e-11
# CASE 2
X1,X2 = randn(10,10),randn(10,10)
X = [X1; X2]
f = SlicedSeparableSum((NormL1(1.), NormL21(0.1)), ((1:10,:),(11:20,:)))
y,fy = prox(f,X,1.)
yn,fyn = ProximalOperators.prox_naive(f,X,1.)
y1,fy1 = prox(NormL1(1.),X1,1.)
y2,fy2 = prox(NormL21(0.1),X2,1.)
@test abs(f(y)-fy)<1e-11
@test abs(fyn-fy)<1e-11
@test norm(yn-y)<1e-11
@test abs((fy1+fy2)-fy)<1e-11
@test norm(y-[y1; y2])<1e-11
# CASE 3
x1, x2, x3 = randn(10), randn(10), randn(10)
X = [x1 x2 x3]
f = NormL2()
F = SlicedSeparableSum(f, ((:,1),(:,2),(:,3)))
y,Fy = prox(F,X,1.)
yn,Fyn = ProximalOperators.prox_naive(F,X,1.)
y1,fy1 = prox(f,x1,1.)
y2,fy2 = prox(f,x2,1.)
y3,fy3 = prox(f,x3,1.)
@test abs(F(y)-Fy)<1e-11
@test abs(Fyn-Fy)<1e-11
@test norm(yn-y)<1e-11
@test abs((fy1+fy2+fy3)-Fy)<1e-11
@test norm(y-[y1 y2 y3])<1e-11
# CASE 4
x = randn(10)
y0 = randn(10)
y = copy(y0)
prox_col = (NormL1(0.1),IndBallL0(1))
ind_col = ((collect(1:5),),(collect(6:10),))
f = SlicedSeparableSum(prox_col,ind_col)
y, fy = prox(f,x,1.)
yn,fyn = ProximalOperators.prox_naive(f,x,1.)
y1,fy1 = prox(prox_col[1],x[ind_col[1]...],1.)
y2,fy2 = prox(prox_col[2],x[ind_col[2]...],1.)
@test abs(f(y)-fy)<1e-11
@test abs(fyn-fy)<1e-11
@test norm(yn-y)<1e-11
@test abs((fy1+fy2)-fy)<1e-11
@test norm(y-[y1;y2])<1e-11
# Test with Quadratic (iterative)
Q = randn(5,10)
Q = Q'*Q
q = randn(10)
x = randn(10)
xx = vcat(x, x)
f = Quadratic(Q, q, iterative=true)
g = SlicedSeparableSum((f, f), ((1:10,), (11:20,)))
y, fy = prox(f, x)
yy, fyy = prox(g, xx)
@test yy β vcat(y, y)
@test fyy β 2*fy
| ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | code | 998 | using Random
Random.seed!(123)
# smooth case
f1 = SqrNormL2()
f2 = Translate(SqrNormL2(2.5), randn(10))
f = Sum(f1, f2)
predicates_test(f)
@test ProximalOperators.is_quadratic(f) == true
@test ProximalOperators.is_strongly_convex(f) == true
@test ProximalOperators.is_set(f) == false
xtest = randn(10)
result = f1(xtest) + f2(xtest)
@test f(xtest) β result
grad1, val1 = gradient_test(f1, xtest)
grad2, val2 = gradient_test(f2, xtest)
gradsum, valsum = gradient_test(f, xtest)
@test gradsum β grad1 + grad2
# nonsmooth case
g1 = NormL2()
g2 = Translate(SqrNormL2(2.5), randn(10))
g = Sum(g1, g2)
predicates_test(g)
@test ProximalOperators.is_smooth(g) == false
@test ProximalOperators.is_strongly_convex(g) == true
@test ProximalOperators.is_set(g) == false
xtest = randn(10)
result = g1(xtest) + g2(xtest)
@test g(xtest) β result
grad1, val1 = gradient_test(g1, xtest)
grad2, val2 = gradient_test(g2, xtest)
gradsum, valsum = gradient_test(g, xtest)
@test gradsum β grad1 + grad2
| ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | code | 842 | ############
# dspev!
############
using LinearAlgebra
if isdefined(ProximalOperators, :dspev!) && isdefined(ProximalOperators, :dspevV!)
a = [1.0,2.0,3.0,5.0,6.0,9.0]
W_ref = [0.0,0.6992647456322766,14.300735254367698]
Z_ref = [0.9486832980505137 0.17781910596911388 -0.26149639682478454;
0.0 -0.8269242138935418 -0.5623133863572413;
-0.3162277660168381 0.5334573179073402 -0.7844891904743537]
A_ref = [1.0 2.0 3.0; 2.0 5.0 6.0; 3.0 6.0 9.0]
a_copy = copy(a); W1, Z1 = ProximalOperators.dspev!(:V,:L,a_copy)
a_copy = copy(a); W2, Z2 = ProximalOperators.dspevV!(:L,a_copy)
A1 = Z1*Diagonal(W1)*Z1'
A2 = Z2*Diagonal(W2)*Z2'
@test all((W1-W_ref)./(1 .+ abs.(W_ref)) .<= 1e-8)
@test all((A1-A_ref)./(1 .+ abs.(A_ref)) .<= 1e-8)
@test all((W2-W_ref)./(1 .+ abs.(W_ref)) .<= 1e-8)
@test all((A2-A_ref)./(1 .+ abs.(A_ref)) .<= 1e-8)
end
| ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | docs | 3783 | # ProximalOperators.jl
[](https://github.com/JuliaFirstOrder/ProximalOperators.jl/actions?query=workflow%3ATest+branch%3Amaster)
[](https://codecov.io/gh/JuliaFirstOrder/ProximalOperators.jl)
[](https://doi.org/10.5281/zenodo.4020558)
[](https://github.com/JuliaTesting/Aqua.jl)
[](https://juliafirstorder.github.io/ProximalOperators.jl/stable)
[](https://juliafirstorder.github.io/ProximalOperators.jl/latest)
Proximal operators for nonsmooth optimization in Julia.
This package can be used to easily implement proximal algorithms for convex and nonconvex optimization problems such as ADMM, the alternating direction method of multipliers.
See [ProximalAlgorithms.jl](https://github.com/JuliaFirstOrder/ProximalAlgorithms.jl) for generic implementations of algorithms based on the primitives here defined.
See the [documentation](https://juliafirstorder.github.io/ProximalOperators.jl/latest) on how to use the package.
## Installation
To install the package, hit `]` from the Julia command line to enter the package manager, then
```julia
pkg> add ProximalOperators
```
## Usage
With `using ProximalOperators` the package exports the `prox` and `prox!` methods to evaluate the proximal mapping of several functions.
A list of available function constructors is in the [documentation](https://juliafirstorder.github.io/ProximalOperators.jl/latest).
For example, you can create the L1-norm as follows.
```julia
julia> f = NormL1(3.5)
description : weighted L1 norm
type : Array{Complex} β Real
expression : x β¦ Ξ»||x||_1
parameters : Ξ» = 3.5
```
Functions created this way are, of course, callable.
```julia
julia> x = randn(10) # some random point
julia> f(x)
32.40700818735099
```
**`prox`** evaluates the proximal operator associated with a function,
given a point and (optionally) a positive stepsize parameter,
returning the proximal point `y` and the value of the function at `y`:
```julia
julia> y, fy = prox(f, x, 0.5) # last argument is 1.0 if absent
```
**`prox!`** evaluates the proximal operator *in place*,
and only returns the function value at the proximal point:
```julia
julia> fy = prox!(y, f, x, 0.5) # in-place equivalent to y, fy = prox(f, x, 0.5)
```
## Related packages
* [FirstOrderSolvers.jl](https://github.com/mfalt/FirstOrderSolvers.jl)
* [ProximalAlgorithms.jl](https://github.com/JuliaFirstOrder/ProximalAlgorithms.jl)
* [StructuredOptimization.jl](https://github.com/JuliaFirstOrder/StructuredOptimization.jl)
## References
1. N. Parikh and S. Boyd (2014), [*Proximal Algorithms*](http://dx.doi.org/10.1561/2400000003),
Foundations and Trends in Optimization, vol. 1, no. 3, pp. 127-239.
2. S. Boyd, N. Parikh, E. Chu, B. Peleato and J. Eckstein (2011), [*Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers*](http://dx.doi.org/10.1561/2200000016), Foundations and Trends in Machine Learning, vol. 3, no. 1, pp. 1-122.
## Credits
ProximalOperators.jl is developed by
[Lorenzo Stella](https://lostella.github.io)
and [NiccolΓ² Antonello](http://homes.esat.kuleuven.be/~nantonel/)
at [KU Leuven, ESAT/Stadius](https://www.esat.kuleuven.be/stadius/),
and [Mattias FΓ€lt](http://www.control.lth.se/Staff/MattiasFalt.html) at [Lunds Universitet, Department of Automatic Control](http://www.control.lth.se/).
| ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | docs | 871 | # Benchmarks
This folder contains the necessary code to define and execute benchmarks, for
example to compare the performance of two different versions (branches, commits,
tags) of the package on a predefined tasks.
Benchmarks are defined in [benchmarks.jl](./benchmarks.jl), using the tooling
provided by [BenchmarkTools](https://github.com/JuliaCI/BenchmarkTools.jl).
You can executed benchmarks by running the [runbenchmarks.jl](./runbenchmarks.jl)
script, which makes heavy use of the tooling offered by
[PkgBenchmark](https://github.com/JuliaCI/PkgBenchmark.jl) instead.
To simply run benchmarks, execute the following command from the package root directory:
```sh
julia --project=benchmark benchmark/runbenchmarks.jl
```
To know more about the available options, use the `--help` option:
```sh
julia --project=benchmark benchmark/runbenchmarks.jl --help
```
| ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | docs | 487 | # Calculus rules
The calculus rules described in the following allow to modify and combine [functions](functions.md), to obtain new ones with efficiently computable proximal mapping.
## Duality
```@docs
Conjugate
```
## Functions combination
```@docs
PointwiseMinimum
SeparableSum
SlicedSeparableSum
Sum
```
## Functions regularization
```@docs
MoreauEnvelope
Regularize
```
## Pre- and post-transformations
```@docs
Postcompose
Precompose
PrecomposeDiagonal
Tilt
Translate
```
| ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | docs | 522 | # Demos
The [demos folder](https://github.com/JuliaFirstOrder/ProximalOperators.jl/tree/master/demos/) contains examples on how to use the functions of ProximalOperators to implement optimization algorithms. **Warning:** Make sure that the version of ProximalOperators that you have installed is up-to-date with the demo script you are trying to run, as the package features may change over time and the [master branch](https://github.com/kul-forbes/ProximalOperators.jl/tree/master) be ahead of what you have installed.
| ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | docs | 2157 | # Functions
Here we list the available functions, grouped by category. Each function is documented with its exact definition and the necessary parameters for construction.
The proximal mapping (and gradient, when defined) of such functions is computed by calling the [`prox`](@ref) and [`prox!`](@ref) methods (and [`gradient`](@ref), [`gradient!`](@ref), when defined).
These functions can be modified and/or combined together to make new ones, by means of [calculus rules](calculus.md).
## Indicators of sets
When function ``f`` is the indicator function of a set ``S``, that is
```math
f(x) = Ξ΄_S(x) =
\begin{cases}
0 & \text{if}\ x \in S, \\
+β & \text{otherwise},
\end{cases}
```
then ``\mathrm{prox}_{Ξ³f} = Ξ _S`` is the projection onto ``S``.
Therefore ProximalOperators includes in particular projections onto commonly used sets, which are here listed.
```@docs
IndAffine
IndBallLinf
IndBallL0
IndBallL1
IndBallL2
IndBallRank
IndBinary
IndBox
IndGraph
IndHalfspace
IndHyperslab
IndPoint
IndPolyhedral
IndSimplex
IndSphereL2
IndStiefel
```
## Indicators of convex cones
An important class of sets in optimization is that of convex cones.
These are used in particular for formulating [cone programming problems](https://en.wikipedia.org/wiki/Conic_optimization), a family of problems which includes linear programs (LP), quadratic programs (QP), quadratically constrained quadratic programs (QCQP) and semidefinite programs (SDP).
```@docs
IndExpPrimal
IndExpDual
IndFree
IndNonnegative
IndNonpositive
IndPSD
IndSOC
IndRotatedSOC
IndZero
```
## Norms and regularization functions
```@docs
CubeNormL2
ElasticNet
NormL0
NormL1
NormL2
NormL21
NormL1plusL2
NormLinf
NuclearNorm
SqrNormL2
TotalVariation1D
```
## Penalties and other functions
```@docs
CrossEntropy
HingeLoss
HuberLoss
LeastSquares
Linear
LogBarrier
LogisticLoss
Maximum
Quadratic
SqrHingeLoss
SumPositive
```
## Distances from convex sets
When the indicator of a convex set is constructed (see [Indicators of sets](@ref)) the (squared) distance from the set can be constructed using the following:
```@docs
DistL2
SqrDistL2
```
| ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | docs | 3430 | # ProximalOperators.jl
ProximalOperators is a [Julia](https://julialang.org) package that implements first-order primitives for a variety of functions, which are commonly used for implementing optimization algorithms in several application areas, *e.g.*, statistical learning, image and signal processing, optimal control.
The package relies on the interfaces defined in [ProximalCore](https://github.com/JuliaFirstOrder/ProximalCore.jl).
Please refer to the [GitHub repository](https://github.com/JuliaFirstOrder/ProximalOperators.jl) to browse the source code, report issues and submit pull requests.
## Installation
To install the package, hit `]` from the Julia command line to enter the package manager, then
```julia
pkg> add ProximalOperators
```
To load the package simply type
```julia
using ProximalOperators
```
Remember to do `Pkg.update()` from time to time, to keep the package up to date.
## Quick introduction
For a function ``f`` and a stepsize ``\gamma > 0``, the *proximal operator* (or *proximal mapping*) is given by
```math
\mathrm{prox}_{\gamma f}(x) = \arg\min_z \left\{ f(z) + \tfrac{1}{2\gamma}\|z-x\|^2 \right\}
```
and can be efficiently computed for many functions ``f`` used in applications.
ProximalOperators allows to pick function ``f`` from a [library of commonly used functions](functions.md), and to modify and combine them using [calculus rules](calculus.md) to obtain new ones. The proximal mapping of ``f`` is then provided through the [`prox`](@ref) and [`prox!`](@ref) methods, as described [here](operators.md).
For example, one can create the L1-norm as follows.
```jldoctest quickex1
julia> using ProximalOperators
julia> f = NormL1(3.5)
NormL1{Float64}(3.5)
```
Functions created this way are, of course, callable.
```jldoctest quickex1
julia> x = [1.0, 2.0, 3.0, 4.0, 5.0]; # some point
julia> f(x)
52.5
```
Method [`prox`](@ref) evaluates the proximal operator associated with a function,
given a point and (optionally) a positive stepsize parameter,
returning the proximal point `y` and the value of the function at `y`:
```jldoctest quickex1
julia> y, fy = prox(f, x, 0.5) # last argument is 1.0 if absent
([0.0, 0.25, 1.25, 2.25, 3.25], 24.5)
```
Method [`prox!`](@ref) evaluates the proximal operator *in place*,
and only returns the function value at the proximal point (in this case `y` must be preallocated and have the same shape/size as `x`):
```jldoctest quickex1
julia> y = similar(x); # allocate y
julia> fy = prox!(y, f, x, 0.5) # in-place equivalent to y, fy = prox(f, x, 0.5)
24.5
```
## Bibliographic references
1. N. Parikh and S. Boyd (2014), [*Proximal Algorithms*](http://dx.doi.org/10.1561/2400000003), Foundations and Trends in Optimization, vol. 1, no. 3, pp. 127-239.
2. S. Boyd, N. Parikh, E. Chu, B. Peleato and J. Eckstein (2011), [*Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers*](http://dx.doi.org/10.1561/2200000016), Foundations and Trends in Machine Learning, vol. 3, no. 1, pp. 1-122.
## Credits
ProximalOperators.jl is developed by
[Lorenzo Stella](https://lostella.github.io)
and [NiccolΓ² Antonello](http://homes.esat.kuleuven.be/~nantonel/)
at [KU Leuven, ESAT/Stadius](https://www.esat.kuleuven.be/stadius/),
and [Mattias FΓ€lt](http://www.control.lth.se/Staff/MattiasFalt.html) at [Lunds Universitet, Department of Automatic Control](http://www.control.lth.se/).
| ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.16.1 | af4153db223c4b262747aaa656ed7b30b15c038c | docs | 3087 | # Prox and gradient
ProximalOperators relies on the first-order primitives defined in [ProximalCore](https://github.com/JuliaFirstOrder/ProximalCore.jl).
The following methods allow to evaluate the proximal mapping (and gradient, when defined) of mathematical functions, which are constructed according to what described in [Functions](@ref) and [Calculus rules](@ref).
```@docs
ProximalCore.prox
ProximalCore.prox!
ProximalCore.gradient
ProximalCore.gradient!
```
## Complex and matrix variables
The proximal mapping is usually discussed in the case of functions over ``\mathbb{R}^n``. However, by adapting the inner product ``\langle\cdot,\cdot\rangle`` and associated norm ``\|\cdot\|`` adopted in its definition, one can extend the concept to functions over more general spaces.
When functions of unidimensional arrays (vectors) are concerned, the standard Euclidean product and norm are used in defining [`prox`](@ref) (therefore [`prox!`](@ref), but also [`gradient`](@ref) and [`gradient!`](@ref)).
This are the inner product and norm which are computed by `dot` and `norm` in Julia.
When bidimensional, tridimensional (matrices and tensors) and higher dimensional arrays are concerned, then the definitions of proximal mapping and gradient are naturally extended by considering the appropriate inner product.
For ``k``-dimensional arrays, of size ``n_1 \times n_2 \times \ldots \times n_k``, we consider the inner product
```math
\langle A, B \rangle = \sum_{i_1,\ldots,i_k} A_{i_1,\ldots,i_k} \cdot B_{i_1,\ldots,i_k}
```
which reduces to the usual Euclidean product in case of unidimensional arrays, and to the *trace product* ``\langle A, B \rangle = \mathrm{tr}(A^\top B)`` in the case of matrices (bidimensional arrays). This inner product, and the associated norm, are again the ones computed by `dot` and `norm` in Julia.
## Multiple variable blocks
By combining functions together through [`SeparableSum`](@ref), the resulting function will have multiple inputs, *i.e.*, it will be defined over the *Cartesian product* of the domains of the individual functions.
To represent elements (points) of such product space, here we use Julia's `Tuple` objects.
**Example.** Suppose that the following function needs to be represented:
```math
f(x, Y) = \|x\|_1 + \|Y\|_*,
```
that is, the sum of the ``L_1`` norm of some vector ``x`` and the nuclear norm (the sum of the singular values) of some matrix ``Y``. This is accomplished as follows:
```example blocks
using ProximalOperators
f = SeparableSum(NormL1(), NuclearNorm());
```
Now, function `f` is defined over *pairs* of appropriate `Array` objects. Likewise, the [`prox`](@ref) method will take pairs of `Array`s as inputs, and return pairs of `Array`s as output:
```example block
x = randn(10); # some random vector
Y = randn(20, 30); # some random matrix
f_xY = f((x, Y)); # evaluates f at (x, Y)
(u, V), f_uV = prox(f, (x, Y), 1.3); # computes prox at (x, Y)
```
The same holds for the separable sum of more than two functions, in which case "pairs" are to be replaced with `Tuple`s of the appropriate length.
| ProximalOperators | https://github.com/JuliaFirstOrder/ProximalOperators.jl.git |
|
[
"MIT"
] | 0.1.3 | e15f073896b34170334ce0c48f69347ac529f534 | code | 278 | module MapMakie
using FileIO
using HTTP
using IntervalSets
using LRUCache
using Makie
using MapMaths
using TileProviders
using Unitful
export MapAxis
include("mapped_ticks.jl")
include("ticks_coordinate.jl")
include("limits.jl")
include("map_axis.jl")
end # module MapMakie
| MapMakie | https://github.com/subnero1/MapMakie.jl.git |
|
[
"MIT"
] | 0.1.3 | e15f073896b34170334ce0c48f69347ac529f534 | code | 1439 | function convert_limits(
C::Type{<:Coordinate{2}},
limits::NTuple{4, Any};
origin::Coordinate{2},
)
return convert_limits(
C,
(
(limits[1], limits[2]),
(limits[3], limits[4]),
);
origin
)
end
function convert_limits(
C::Type{<:Coordinate{2}},
limits::NTuple{2, Any};
origin::Coordinate{2},
)
return (
convert_limits(EastWestCoordinate(C), limits[1]; origin),
convert_limits(NorthSouthCoordinate(C), limits[2]; origin),
)
end
function convert_limits(
::Type{<:Coordinate{1}},
::Nothing;
origin::Coordinate{2},
)
return nothing
end
function convert_limits(
C::Type{<:Coordinate{1}},
limits::NTuple{2, Any};
origin::Coordinate{2},
)
return (
convert_limit(C, limits[1]; origin),
convert_limit(C, limits[2]; origin),
)
end
function convert_limit(
::Type{<:Coordinate{1}},
::Nothing;
origin::Coordinate{2}
)
return nothing
end
function convert_limit(
::Type{<:Coordinate{1}},
v::Number;
origin::Coordinate{2}
)
return v
end
function convert_limit(
C::Type{<:Coordinate{1}},
c::Coordinate{1};
origin::Coordinate{2}
)
(C(c, NorthSouthCoordinate(origin)) - C(origin))[]
end
function convert_limit(
C::Type{<:Coordinate{1}},
c::Union{East, North};
origin::Coordinate{2}
)
C(c, NorthSouthCoordinate(origin))[]
end
| MapMakie | https://github.com/subnero1/MapMakie.jl.git |
|
[
"MIT"
] | 0.1.3 | e15f073896b34170334ce0c48f69347ac529f534 | code | 5230 | """
MapAxis(args...; origin, kwargs...) -> axis::Makie.Axis
Create a new `Axis` showing OpenStreetMap.
The object returned by this function is a plain `Makie.Axis` and can be used to
plot additional data like any other `Axis`. The map is shown in
`MapMaths.WebMercator` coordinates shifted by `-WebMercator(origin)`.
All positional arguments and any keyword arguments other than the ones mentioned
below are forwarded to `Axis()`.
# Keyword arguments
- `origin::MapMaths.Coordinate{2}`: Map origin.
This parameter serves two purposes:
1) Avoid the loss of precision that would otherwise be incurred for locations
at high latitudes and longitudes due to Makie performing most computations
in `Float32`. See also [Loss of precision when plotting large floats in
Makie](https://github.com/MakieOrg/Makie.jl/issues/1196) and related issues
in Makie.jl.
2) Set the origin for the x- and y-ticks if `ticks_coordinate` is `EastNorth`
(see `ticks_coordinate` below).
- `ticks_coordinate = WebMercator`: The coordinate system in which to show the
x- and y-ticks.
Can be any subtype of `MapMaths.Coordinate{2}`, or `(MapMaths.EastNorth,
unit)` where `unit` is either a plain number denoting meters, a
`Unitful.LengthUnits` or a `Unitful.Length`. `EastNorth` ticks are shown
relative to `origin`, all other ticks are shown using their global values.
- `limits = ((-1,1), (-1,1))`: Axis limits.
Follows the same format as `Makie.Axis()`, except that any number can also be
a `MapMaths.EastWestCoordinate` or `MapMaths.NorthSouthCoordinate` as
appropriate. `East` and `North` limits are applied relative to `origin`, all
other limits are applied as global values. Plain numbers are interpreted as
WebMercator coordinates.
- `tile_provider = TileProviders.OpenStreetMap()`: Any tile provider from the
`TileProviders` package.
# Example
```
using GLMakie, MapMakie, MapMaths, Unitful
f = Figure()
a = MapAxis(
f[1,1];
origin = LatLon(1.286770, 103.854307), # Merlion, Singapore
ticks_coordinate = (EastNorth, u"km"),
limits = (East.(2e3.*(-1,1)), North.(2e3.*(-1,1))),
)
scatter!(
a,
Point2f[(0,0)], # WebMercator coordinates relative to `origin`
color = :red,
markersize = 15,
strokewidth = 6,
)
display(f)
```
"""
function MapAxis(
args...;
origin,
tile_provider = OpenStreetMap(),
ticks_coordinate = WebMercator,
limits = ((-1,1), (-1,1)),
kwargs...
)
origin = WebMercator(origin)
kwargs = map_ticks_coordinate(;
plot_coordinate = WebMercator,
ticks_coordinate,
origin,
kwargs...,
)
axis = Axis(
args...;
autolimitaspect = 1.0,
limits = convert_limits(WebMercator, limits; origin),
kwargs...,
)
limits = axis.finallimits[]
limits = Rect2f(origin .+ limits.origin, limits.widths)
resolution = axis.scene.camera.resolution[]
(; zoom, xmin, xmax, ymin, ymax) = tile_indices(limits, resolution; max_zoom = TileProviders.max_zoom(tile_provider))
img = image!(
ClosedInterval((map_xlimits(zoom, xmin, xmax) .- origin[1])...),
ClosedInterval((map_ylimits(zoom, ymin, ymax) .- origin[2])...),
map_image(; tile_provider, zoom, xmin, xmax, ymin, ymax)
)
onany(axis.finallimits, axis.scene.camera.resolution) do limits, resolution
limits = Rect2f(origin .+ limits.origin, limits.widths)
(; zoom, xmin, xmax, ymin, ymax) = tile_indices(limits, resolution; max_zoom = TileProviders.max_zoom(tile_provider))
img[1][] = ClosedInterval((map_xlimits(zoom, xmin, xmax) .- origin[1])...)
img[2][] = ClosedInterval((map_ylimits(zoom, ymin, ymax) .- origin[2])...)
img[3][] = map_image(; tile_provider, zoom, xmin, xmax, ymin, ymax)
end
return axis
end
const tile_cache = LRU{Tuple{Any,Int,Int,Int}, Any}(maxsize = Int(1e8), by = Base.summarysize)
function map_tile(tile_provider, zoom::Int, x::Int, y::Int)
@assert 0 <= y <= 1<<zoom-1
reduced_x = mod(x, 1<<zoom)
return get!(
() -> load(HTTP.URI(geturl(tile_provider, reduced_x, y, zoom))),
tile_cache,
(tile_provider, zoom, reduced_x, y),
)
end
function map_image(; tile_provider, zoom, xmin, xmax, ymin, ymax)
map = Matrix{RGBf}(undef, 256*(xmax-xmin+1), 256*(ymax-ymin+1))
@sync for y in ymin:ymax, x in xmin:xmax
@async map[
256*(x-xmin) .+ (1:256),
256*(ymax-y) .+ (1:256),
] .= rotr90(map_tile(tile_provider, zoom, x, y))
end
return map
end
map_xlimits(zoom, min, max) = (min, max+1) .* 2f0^(1-zoom) .- 1f0
map_ylimits(zoom, min, max) = 1f0 .- (max+1, min) .* 2f0^(1-zoom)
function tile_indices(limits, resolution; max_zoom = 19)
zoom = clamp(round(Int, log2(first(resolution ./ widths(limits)))) - 7, 0, max_zoom)
xmin = floor(Int, 2f0^(zoom-1) * (minimum(limits)[1] + 1f0))
ymin = floor(Int, 2f0^(zoom-1) * (1f0 - maximum(limits)[2]))
xmax = ceil(Int, 2f0^(zoom-1) * (maximum(limits)[1] + 1f0)) - 1
ymax = ceil(Int, 2f0^(zoom-1) * (1f0 - minimum(limits)[2])) - 1
(ymin, ymax) = clamp.((ymin, ymax), 0, 1<<zoom-1)
return (; zoom, xmin, xmax, ymin, ymax)
end
| MapMakie | https://github.com/subnero1/MapMakie.jl.git |
|
[
"MIT"
] | 0.1.3 | e15f073896b34170334ce0c48f69347ac529f534 | code | 939 | """
MappedTicks(; ticks = Makie.automatic, plot_to_ticks, ticks_to_plot)
Map `ticks` using the given functions.
`plot_to_ticks` and `ticks_to_plot` should be mutually inverse, i.e.
`plot_to_ticks β ticks_to_plot β identity`.
# Example
```
scatter(
Point2f[(0,0)];
axis = (;
# These ticks will make it look as if the point was at (0,1)
yticks = MapMakie.MappedTicks(;
plot_to_ticks = x->x+1,
ticks_to_plot = x->x-1,
),
),
)
```
"""
@kwdef struct MappedTicks{T,P2T,T2P}
ticks::T = Makie.automatic
plot_to_ticks::P2T
ticks_to_plot::T2P
end
function Makie.get_ticks(
ticks::MappedTicks,
scale,
format,
plot_min,
plot_max,
)
ticks_min, ticks_max = ticks.plot_to_ticks.((plot_min, plot_max))
(ticks_vals, labels) = Makie.get_ticks(ticks.ticks, scale, format, ticks_min, ticks_max)
return ticks.ticks_to_plot.(ticks_vals), labels
end | MapMakie | https://github.com/subnero1/MapMakie.jl.git |
|
[
"MIT"
] | 0.1.3 | e15f073896b34170334ce0c48f69347ac529f534 | code | 3715 | """
map_ticks_coordinate(;
plot_coordinate,
[ticks_coordinate | (ticks_coordinate = MapMaths.EastNorth, unit)],
origin,
xticks = Makie.automatic,
yticks = Makie.automatic,
) -> kwargs
Show axis ticks in the `ticks_coordinate` system (optionally scaled by `unit`),
assuming the plot axis are in the `plot_coordinate` system.
"""
function map_ticks_coordinate end
function map_ticks_coordinate(; plot_coordinate, ticks_coordinate, kwargs...)
map_ticks_coordinate(plot_coordinate, ticks_coordinate; kwargs...)
end
function map_ticks_coordinate(plot_coordinate, ticks_coordinate_and_unit::Tuple; kwargs...)
return map_ticks_coordinate(plot_coordinate, ticks_coordinate_and_unit...; kwargs...)
end
function map_ticks_coordinate(
plot_coordinate::Type{<:Coordinate{2}},
ticks_coordinate::Type{<:Coordinate{2}},
unit::Union{Number, Unitful.Unit};
kwargs...,
)
error("Scaling of $ticks_coordinate coordinates is not supported")
end
function map_ticks_coordinate(
plot_coordinate::Type{<:Coordinate{2}},
ticks_coordinate::Type{<:Coordinate{2}};
origin::Coordinate{2},
xticks = Makie.automatic,
yticks = Makie.automatic,
kwargs...,
)
plot_ew = EastWestCoordinate(plot_coordinate)
plot_ns = NorthSouthCoordinate(plot_coordinate)
ticks_ew = EastWestCoordinate(ticks_coordinate)
ticks_ns = NorthSouthCoordinate(ticks_coordinate)
return (;
xticks = MappedTicks(
ticks = xticks,
plot_to_ticks = x -> ticks_ew(plot_ew(x) + plot_ew(origin))[],
ticks_to_plot = x -> plot_ew(ticks_ew(x) - ticks_ew(origin))[],
),
yticks = MappedTicks(
ticks = yticks,
plot_to_ticks = x -> ticks_ns(plot_ns(x) + plot_ns(origin))[],
ticks_to_plot = x -> plot_ns(ticks_ns(x) - ticks_ns(origin))[],
),
axis_labels(ticks_coordinate)...,
kwargs...,
)
end
axis_labels(::Type{WebMercator}) = (;)
function axis_labels(::Union{Type{LatLon}, Type{LonLat}})
return (;
xlabel = "Latitude [Β°]",
ylabel = "Longitude [Β°]",
)
end
function map_ticks_coordinate(
plot_coordinate::Type{<:Coordinate{2}},
ticks_coordinate::Type{EastNorth};
kwargs...,
)
return map_ticks_coordinate(plot_coordinate, ticks_coordinate, u"m"; kwargs...)
end
function map_ticks_coordinate(
plot_coordinate::Type{<:Coordinate{2}},
ticks_coordinate::Type{EastNorth},
unit::Number;
kwargs...,
)
return map_ticks_coordinate(plot_coordinate, ticks_coordinate, unit*u"m"; kwargs...)
end
function map_ticks_coordinate(
plot_coordinate::Type{<:Coordinate{2}},
::Type{EastNorth},
unit::Union{Unitful.LengthUnits, Unitful.Length};
origin::Coordinate{2},
xticks = Makie.automatic,
yticks = Makie.automatic,
kwargs...,
)
return (;
east_north_ticks(unit, WMY(origin), xticks, yticks)...,
xlabel = "Easting [$unit]",
ylabel = "Northing [$unit]",
kwargs...,
)
end
function east_north_ticks(unit::Unitful.LengthUnits, wmy::WMY, xticks, yticks)
return east_north_ticks(1*unit, wmy, xticks, yticks)
end
function east_north_ticks(unit::Unitful.Length, wmy::WMY, xticks, yticks)
factor = ustrip(u"m", unit)
return (;
xticks = MappedTicks(
ticks = xticks,
plot_to_ticks = x -> East(WMX(x), wmy)[] / factor,
ticks_to_plot = x -> WMX(East(x * factor), wmy)[],
),
yticks = MappedTicks(
ticks = yticks,
plot_to_ticks = y -> North(WMY(y), wmy)[] / factor,
ticks_to_plot = y -> WMY(North(y * factor), wmy)[],
),
)
end
| MapMakie | https://github.com/subnero1/MapMakie.jl.git |
|
[
"MIT"
] | 0.1.3 | e15f073896b34170334ce0c48f69347ac529f534 | docs | 2722 | # MapMakie.jl
Plot on OpenStreetMap using Makie.
## Example
```julia
using GLMakie, MapMakie, MapMaths, Unitful
f = Figure()
a = MapAxis(
f[1,1];
origin = LatLon(1.286770, 103.854307), # Merlion, Singapore
ticks_coordinate = (EastNorth, u"km"),
limits = (East.(2e3.*(-1,1)), North.(2e3.*(-1,1))),
)
scatter!(
a,
Point2f[(0,0)], # WebMercator coordinates relative to `origin`
color = :red,
markersize = 15,
strokewidth = 6,
)
display(f)
save("/tmp/merlion.png", f)
```
## Documentation
#### MapAxis
```
MapAxis(args...; origin, kwargs...) -> axis::Makie.Axis
```
Create a new `Axis` showing OpenStreetMap.
The object returned by this function is a plain `Makie.Axis` and can be used to plot additional data like any other `Axis`. The map is shown in `MapMaths.WebMercator` coordinates shifted by `-WebMercator(origin)`.
All positional arguments and any keyword arguments other than the ones mentioned below are forwarded to `Axis()`.
##### Keyword arguments
- `origin::MapMaths.Coordinate{2}`: Map origin.
This parameter serves two purposes:
1) Avoid the loss of precision that would otherwise be incurred for locations at high latitudes and longitudes due to Makie performing most computations in `Float32`. See also [Loss of precision when plotting large floats in Makie](https://github.com/MakieOrg/Makie.jl/issues/1196) and related issues in Makie.jl.
2) Set the origin for the x- and y-ticks if `ticks_coordinate` is `EastNorth` (see `ticks_coordinate` below).
- `ticks_coordinate = WebMercator`: The coordinate system in which to show the x- and y-ticks.
Can be any subtype of `MapMaths.Coordinate{2}`, or `(MapMaths.EastNorth, unit)` where `unit` is either a plain number denoting meters, a `Unitful.LengthUnits` or a `Unitful.Length`. `EastNorth` ticks are shown relative to `origin`, all other ticks are shown using their global values.
- `limits = ((-1,1), (-1,1))`: Axis limits.
Follows the same format as `Makie.Axis()`, except that any number can also be a `MapMaths.EastWestCoordinate` or `MapMaths.NorthSouthCoordinate` as appropriate. `East` and `North` limits are applied relative to `origin`, all other limits are applied as global values.
- `tile_provider = TileProviders.OpenStreetMap()`: Any tile provider from the `TileProviders` package.
## Technical details
MapMakie dynamically loads the map tiles required from https://tile.openstreetmap.org/. Users of this package must therefore adhere to [OpenStreetMap's Tile Usage Policy](https://operations.osmfoundation.org/policies/tiles/). The most-recently used 100 MB of map tiles are cached in memory using [LRUCache.jl](https://github.com/JuliaCollections/LRUCache.jl). | MapMakie | https://github.com/subnero1/MapMakie.jl.git |
|
[
"MIT"
] | 5.0.0 | 8733f1a23680f235eb0aa2a64c57922f32fe9b7f | code | 965 | using Documenter, ActuaryUtilities, FinanceCore
# Setup for doctests embedded in docstrings.
DocMeta.setdocmeta!(ActuaryUtilities, :DocTestSetup, :(import Pkg; Pkg.add("DayCounts"); using ActuaryUtilities, Dates, DayCounts), recursive=true)
makedocs(;
modules=[ActuaryUtilities, FinanceCore],
format=Documenter.HTML(),
pages=[
"Overview" => "index.md",
"Financial Math" => "financial_math.md",
"Risk Measures" => "risk_measures.md",
"Other Utilities" => "utilities.md",
"API" => [
"ActuaryUtilities" => "API/ActuaryUtilities.md",
"FinanceCore (re-exported)" => "API/FinanceCore.md",
],
"Upgrade from Prior Versions" => "upgrade.md",
],
repo="https://github.com/JuliaActuary/ActuaryUtilities.jl/blob/{commit}{path}#L{line}",
sitename="ActuaryUtilities.jl",
authors="Alec Loudenback"
)
deploydocs(;
repo="github.com/JuliaActuary/ActuaryUtilities.jl"
)
| ActuaryUtilities | https://github.com/JuliaActuary/ActuaryUtilities.jl.git |
|
[
"MIT"
] | 5.0.0 | 8733f1a23680f235eb0aa2a64c57922f32fe9b7f | code | 582 | module ActuaryUtilities
using Reexport
import Dates
import FinanceCore
@reexport using FinanceCore: internal_rate_of_return, irr, present_value, pv
import ForwardDiff
import QuadGK
import FinanceModels
import StatsBase
using PrecompileTools
import Distributions
# need to define this here to extend it without conflict inside FinancialMath
function duration() end
include("financial_math.jl")
include("risk_measures.jl")
include("utilities.jl")
# include("precompile.jl")
@reexport using .FinancialMath
@reexport using .RiskMeasures
@reexport using .Utilities
end # module
| ActuaryUtilities | https://github.com/JuliaActuary/ActuaryUtilities.jl.git |
|
[
"MIT"
] | 5.0.0 | 8733f1a23680f235eb0aa2a64c57922f32fe9b7f | code | 15240 | module FinancialMath
import ..FinanceCore
import ..FinanceModels
import ..ForwardDiff
import ..ActuaryUtilities: duration
export irr, internal_rate_of_return, spread,
pv, present_value, price, present_values,
breakeven, moic,
Macaulay, Modified, DV01, KeyRatePar, KeyRateZero, KeyRate, duration, convexity
"""
present_values(interest, cashflows, timepoints)
Efficiently calculate a vector representing the present value of the given cashflows at each period prior to the given timepoint.
# Examples
```julia-repl
julia> present_values(0.00, [1,1,1])
[3,2,1]
julia> present_values(ForwardYield([0.1,0.2]), [10,20],[0,1]) # after `using FinanceModels`
2-element Vector{Float64}:
28.18181818181818
18.18181818181818
```
"""
function present_values(interest, cashflows, times=eachindex(cashflows))
present_values_accumulator(interest, cashflows, times)
end
function present_values_accumulator(interest, cashflows, times, pvs=[0.0])
from_time = length(times) == 1 ? 0.0 : times[end-1]
pv = FinanceCore.discount(interest, from_time, last(times)) * (first(pvs) + last(cashflows))
pvs = pushfirst!(pvs, pv)
if length(cashflows) > 1
new_cfs = @view cashflows[1:end-1]
new_times = @view times[1:end-1]
return present_values_accumulator(interest, new_cfs, new_times, pvs)
else
# last discount and return
return pvs[1:end-1] # end-1 get rid of trailing 0.0
end
end
"""
price(...)
The absolute value of the `present_value(...)`.
# Extended help
Using `price` can be helpful if the directionality of the value doesn't matter. For example, in the common usage, duration is more interested in the change in price than present value, so `price` is used there.
"""
price(x1, x2) = FinanceCore.present_value(x1, x2) |> abs
price(x1, x2, x3) = FinanceCore.present_value(x1, x2, x3) |> abs
"""
breakeven(yield, cashflows::Vector)
breakeven(yield, cashflows::Vector,times::Vector)
Calculate the time when the accumulated cashflows breakeven given the yield.
Assumptions:
- cashflows occur at the end of the period
- cashflows evenly spaced with the first one occuring at time zero if `times` not given
Returns `nothing` if cashflow stream never breaks even.
```julia
julia> breakeven(0.10, [-10,1,2,3,4,8])
5
julia> breakeven(0.10, [-10,15,2,3,4,8])
1
julia> breakeven(0.10, [-10,-15,2,3,4,8]) # returns the `nothing` value
```
"""
function breakeven(y, cashflows, timepoints=(eachindex(cashflows) .- 1))
accum = 0.0
last_neg = nothing
# `amount` and `timepoint` allow to generically handle `Cashflow`s and amount/time vectors
accum += FinanceCore.amount(cashflows[1])
if accum >= 0 && isnothing(last_neg)
last_neg = FinanceCore.timepoint(cashflows[1], timepoints[1])
end
for i in 2:length(cashflows)
# accumulate the flow from each timepoint to the next
a = FinanceCore.timepoint(cashflows[i-1], timepoints[i-1])
b = FinanceCore.timepoint(cashflows[i], timepoints[i])
accum *= FinanceCore.accumulation(y, a, b)
accum += FinanceCore.amount(cashflows[i])
if accum >= 0 && isnothing(last_neg)
last_neg = b
elseif accum < 0
last_neg = nothing
end
end
return last_neg
end
abstract type Duration end
struct Macaulay <: Duration end
struct Modified <: Duration end
struct DV01 <: Duration end
abstract type KeyRateDuration <: Duration end
"""
KeyRatePar(timepoint,shift=0.001) <: KeyRateDuration
Shift the par curve by the given amount at the given timepoint. Use in conjunction with `duration` to calculate the key rate duration.
Unlike other duration statistics which are computed using analytic derivatives, `KeyRateDuration`s are computed via a shift-and-compute the yield curve approach.
`KeyRatePar` is more commonly reported (than [`KeyRateZero`](@ref)) in the fixed income markets, even though the latter has more analytically attractive properties. See the discussion of KeyRateDuration in the FinanceModels.jl docs.
"""
struct KeyRatePar{T,R} <: KeyRateDuration
timepoint::T
shift::R
KeyRatePar(timepoint, shift=0.001) = new{typeof(timepoint),typeof(shift)}(timepoint, shift)
end
"""
KeyRateZero(timepoint,shift=0.001) <: KeyRateDuration
Shift the par curve by the given amount at the given timepoint. Use in conjunction with `duration` to calculate the key rate duration.
Unlike other duration statistics which are computed using analytic derivatives, `KeyRateDuration` is computed via a shift-and-compute the yield curve approach.
`KeyRateZero` is less commonly reported (than [`KeyRatePar`](@ref)) in the fixed income markets, even though the latter has more analytically attractive properties. See the discussion of KeyRateDuration in the FinanceModels.jl docs.
"""
struct KeyRateZero{T,R} <: KeyRateDuration
timepoint::T
shift::R
KeyRateZero(timepoint, shift=0.001) = new{typeof(timepoint),typeof(shift)}(timepoint, shift)
end
"""
KeyRate(timepoints,shift=0.001)
A convenience constructor for [`KeyRateZero`](@ref).
## Extended Help
[`KeyRateZero`](@ref) is chosen as the default constructor because it has more attractive properties than [`KeyRatePar`](@ref):
- rates after the key `timepoint` remain unaffected by the `shift`
- e.g. this causes a 6-year zero coupon bond would have a negative duration if the 5-year par rate was used
"""
KeyRate = KeyRateZero
"""
duration(Macaulay(),interest_rate,cfs,times)
duration(Modified(),interest_rate,cfs,times)
duration(DV01(),interest_rate,cfs,times)
duration(interest_rate,cfs,times) # Modified Duration
duration(interest_rate,valuation_function) # Modified Duration
Calculates the Macaulay, Modified, or DV01 duration. `times` may be ommitted and the valuation will assume evenly spaced cashflows starting at the end of the first period.
Note that the calculated duration will depend on the periodicity convention of the `interest_rate`: a `Periodic` yield (or yield model with that convention) will be a slightly different computed duration than a `Continous` which follows from the present value differing according to the periodicity.
When not given `Modified()` or `Macaulay()` as an argument, will default to `Modified()`.
- Modified duration: the relative change per point of yield change.
- Macaulay: the cashflow-weighted average time.
- DV01: the absolute change per basis point (hundredth of a percentage point).
# Examples
Using vectors of cashflows and times
```julia-repl
julia> times = 1:5;
julia> cfs = [0,0,0,0,100];
julia> duration(0.03,cfs,times)
4.854368932038835
julia> duration(Periodic(0.03,1),cfs,times)
4.854368932038835
julia> duration(Continuous(0.03),cfs,times)
5.0
julia> duration(Macaulay(),0.03,cfs,times)
5.0
julia> duration(Modified(),0.03,cfs,times)
4.854368932038835
julia> convexity(0.03,cfs,times)
28.277877274012614
```
Using any given value function:
```julia-repl
julia> lump_sum_value(amount,years,i) = amount / (1 + i ) ^ years
julia> my_lump_sum_value(i) = lump_sum_value(100,5,i)
julia> duration(0.03,my_lump_sum_value)
4.854368932038835
julia> convexity(0.03,my_lump_sum_value)
28.277877274012617
```
"""
function duration(::Macaulay, yield, cfs, times)
return sum(FinanceCore.timepoint.(cfs, times) .* price.(yield, cfs, times) / price(yield, cfs, times))
end
function duration(::Modified, yield, cfs, times)
D(i) = price(i, cfs, times)
return duration(yield, D)
end
function duration(yield, valuation_function::T) where {T<:Function}
D(i) = log(valuation_function(i + yield))
Ξ΄V = -ForwardDiff.derivative(D, 0.0)
end
function duration(yield, cfs, times)
return duration(Modified(), yield, vec(cfs), times)
end
# timepoints are used to make the function more generic
# with respect to allowing Cashflow objects
function duration(yield, cfs)
times = FinanceCore.timepoint.(cfs, 1:length(cfs))
return duration(Modified(), yield, cfs, times)
end
function duration(::DV01, yield, cfs, times)
return duration(DV01(), yield, i -> price(i, vec(cfs), times))
end
function duration(d::Duration, yield, cfs)
times = FinanceCore.timepoint.(cfs, 1:length(cfs))
return duration(d, yield, vec(cfs), times)
end
function duration(::DV01, yield, valuation_function::Y) where {Y<:Function}
return duration(yield, valuation_function) * valuation_function(yield) / 10000
end
"""
convexity(yield,cfs,times)
convexity(yield,valuation_function)
Calculates the convexity.
- `yield` should be a fixed effective yield (e.g. `0.05`).
- `times` may be omitted and it will assume `cfs` are evenly spaced beginning at the end of the first period.
# Examples
Using vectors of cashflows and times
```julia-repl
julia> times = 1:5
julia> cfs = [0,0,0,0,100]
julia> duration(0.03,cfs,times)
4.854368932038834
julia> duration(Macaulay(),0.03,cfs,times)
5.0
julia> duration(Modified(),0.03,cfs,times)
4.854368932038835
julia> convexity(0.03,cfs,times)
28.277877274012614
```
Using any given value function:
```julia-repl
julia> lump_sum_value(amount,years,i) = amount / (1 + i ) ^ years
julia> my_lump_sum_value(i) = lump_sum_value(100,5,i)
julia> duration(0.03,my_lump_sum_value)
4.854368932038835
julia> convexity(0.03,my_lump_sum_value)
28.277877274012617
```
"""
function convexity(yield, cfs, times)
return convexity(yield, i -> price(i, cfs, times))
end
function convexity(yield, cfs)
times = 1:length(cfs)
return convexity(yield, i -> price(i, cfs, times))
end
function convexity(yield, valuation_function::T) where {T<:Function}
v(x) = abs(valuation_function(yield + x[1]))
βΒ²P = ForwardDiff.hessian(v, [0.0])
return βΒ²P[1] / v([0.0])
end
"""
duration(keyrate::KeyRateDuration,curve,cashflows)
duration(keyrate::KeyRateDuration,curve,cashflows,timepoints)
duration(keyrate::KeyRateDuration,curve,cashflows,timepoints,krd_points)
Calculate the key rate duration by shifting the **zero** (not par) curve by the kwarg `shift` at the timepoint specified by a KeyRateDuration(time).
The approach is to carve up the curve into `krd_points` (default is the unit steps between `1` and the last timepoint of the casfhlows). The
zero rate corresponding to the timepoint within the `KeyRateDuration` is shifted by `shift` (specified by the `KeyRateZero` or `KeyRatePar` constructors. A new curve is created from the shifted rates. This means that the
"width" of the shifted section is Β± 1 time period, unless specific points are specified via `krd_points`.
The `curve` may be any FinanceModels.jl curve (e.g. does not have to be a curve constructed via `FinanceModels.Zero(...)`).
!!! Experimental: Due to the paucity of examples in the literature, this feature does not have unit tests like the rest of JuliaActuary functionality. Additionally, the API may change in a future major/minor version update.
# Examples
```julia-repl
julia> riskfree_maturities = [0.5, 1.0, 1.5, 2.0];
julia> riskfree = [0.05, 0.058, 0.064,0.068];
julia> rf_curve = FinanceModels.Zero(riskfree,riskfree_maturities);
julia> cfs = [10,10,10,10,10];
julia> duration(KeyRate(1),rf_curve,cfs)
8.932800152336995
```
# Extended Help
Key Rate Duration is not a well specified topic in the literature and in practice. The reference below suggest that shocking the par curve is more common
in practice, but that the zero curve produces more consistent results. Future versions may support shifting the par curve.
References:
- [Quant Finance Stack Exchange: To compute key rate duration, shall I use par curve or zero curve?](https://quant.stackexchange.com/questions/33891/to-compute-key-rate-duration-shall-i-use-par-curve-or-zero-curve)
- (Financial Exam Help 123](http://www.financialexamhelp123.com/key-rate-duration/)
"""
function duration(keyrate::KeyRateDuration, curve, cashflows, timepoints, krd_points)
shift = keyrate.shift
curve_up = _krd_new_curve(keyrate, curve, krd_points)
curve_down = _krd_new_curve(opposite(keyrate), curve, krd_points)
price = FinanceCore.pv(curve, cashflows, timepoints)
price_up = FinanceCore.pv(curve_up, cashflows, timepoints)
price_down = FinanceCore.pv(curve_down, cashflows, timepoints)
return (price_down - price_up) / (2 * shift * price)
end
opposite(kr::KeyRateZero) = KeyRateZero(kr.timepoint, -kr.shift)
opposite(kr::KeyRatePar) = KeyRatePar(kr.timepoint, -kr.shift)
function _krd_new_curve(keyrate::KeyRateZero, curve, krd_points)
curve_times = krd_points
shift = keyrate.shift
zeros = FinanceModels.zero.(curve, curve_times)
zero_index = findfirst(==(keyrate.timepoint), curve_times)
target_rate = zeros[zero_index]
zeros[zero_index] += FinanceModels.Rate(shift, target_rate.compounding)
new_curve = FinanceModels.fit(FinanceModels.Spline.Linear(), FinanceModels.ZCBYield.(zeros, curve_times), FinanceModels.Fit.Bootstrap())
return new_curve
end
function _krd_new_curve(keyrate::KeyRatePar, curve, krd_points)
curve_times = krd_points
shift = keyrate.shift
pars = FinanceModels.par.(curve, curve_times)
zero_index = findfirst(==(keyrate.timepoint), curve_times)
target_rate = pars[zero_index]
pars[zero_index] += FinanceModels.Rate(shift, target_rate.compounding)
new_curve = FinanceModels.fit(FinanceModels.Spline.Linear(), FinanceModels.ParYield.(pars, curve_times), FinanceModels.Fit.Bootstrap())
return new_curve
end
function duration(keyrate::KeyRateDuration, curve, cashflows, timepoints)
krd_points = 1:maximum(timepoints)
return duration(keyrate, curve, cashflows, timepoints, krd_points)
end
function duration(keyrate::KeyRateDuration, curve, cashflows)
timepoints = eachindex(cashflows)
krd_points = 1:maximum(timepoints)
return duration(keyrate, curve, cashflows, timepoints, krd_points)
end
"""
spread(curve1,curve2,cashflows)
Return the solved-for constant spread to add to `curve1` in order to equate the discounted `cashflows` with `curve2`
# Examples
```julia-repl
spread(0.04, 0.05, cfs)
Rate{Float64, Periodic}(0.010000000000000009, Periodic(1))
```
"""
function spread(curve1, curve2, cashflows, times=eachindex(cashflows))
times = FinanceCore.timepoint.(cashflows, times)
cashflows = FinanceCore.amount.(cashflows)
pv1 = FinanceCore.pv(curve1, cashflows, times)
pv2 = FinanceCore.pv(curve2, cashflows, times)
irr1 = FinanceCore.irr([-pv1; cashflows], [0.0; times])
irr2 = FinanceCore.irr([-pv2; cashflows], [0.0; times])
return irr2 - irr1
end
"""
moic(cashflows<:AbstractArray)
The multiple on invested capital ("moic") is the un-discounted sum of distributions divided by the sum of the contributions. The function assumes that negative numbers in the array represent contributions and positive numbers represent distributions.
# Examples
```julia-repl
julia> moic([-10,20,30])
5.0
```
"""
function moic(cfs::T) where {T<:AbstractArray}
returned = sum(FinanceCore.amount(cf) for cf in cfs if FinanceCore.amount(cf) > 0)
invested = -sum(FinanceCore.amount(cf) for cf in cfs if FinanceCore.amount(cf) < 0)
return returned / invested
end
end | ActuaryUtilities | https://github.com/JuliaActuary/ActuaryUtilities.jl.git |
|
[
"MIT"
] | 5.0.0 | 8733f1a23680f235eb0aa2a64c57922f32fe9b7f | code | 1311 |
# created with the help of SnoopCompile.jl
@setup_workload begin
# Putting some things in `setup` can reduce the size of the
# precompile file and potentially make loading faster.
cfs = [10 for i in 1:10]
# 2021-03-31 rates from Treasury.gov
rates = [0.01, 0.01, 0.03, 0.05, 0.07, 0.16, 0.35, 0.92, 1.40, 1.74, 2.31, 2.41] ./ 100
mats = [1 / 12, 2 / 12, 3 / 12, 6 / 12, 1, 2, 3, 5, 7, 10, 20, 30]
y = FinanceModels.fit(FinanceModels.Spline.Linear(), FinanceModels.CMTYield.(rates, mats), FinanceModels.Fit.Bootstrap())
r = 0.05
rates = [r, y]
@compile_workload begin
# all calls in this block will be precompiled, regardless of whether
# they belong to your package or not (on Julia 1.8 and higher)
moic([-80; cfs])
for v in rates
pv(v, cfs)
duration(v, cfs)
convexity(v, cfs)
duration(Macaulay(), v, cfs)
duration(DV01(), v, cfs)
duration(Modified(), v, cfs)
# duration(KeyRate(5),v,cfs)
breakeven(v, [-10, 1, 2, 3, 4, 8])
spread(v - 0.01, v, cfs)
end
spread(y, y + 0.01, cfs)
years_between(Date(2018, 9, 30), Date(2018, 9, 30))
duration(Date(2018, 9, 30), Date(2019, 9, 30))
end
end | ActuaryUtilities | https://github.com/JuliaActuary/ActuaryUtilities.jl.git |
|
[
"MIT"
] | 5.0.0 | 8733f1a23680f235eb0aa2a64c57922f32fe9b7f | code | 8580 | module RiskMeasures
import ..Distributions
import ..StatsBase
import ..QuadGK
export VaR, ValueAtRisk, CTE, ConditionalTailExpectation, WangTransform, DualPower, ProportionalHazard
abstract type RiskMeasure end
"""
g(rm::RiskMeasure,x)
The probability distortion function associated with the given risk measure.
See [Distortion Function g(u)](@ref)
"""
function g(rm::RiskMeasure, x) end
"""
Expectation()::RiskMeasure
Expectation()(risk)::T (where T is the type of values sampled in `risk`)
The expected value of the risk.
`Expectation()` returns a functor which can then be called on a risk distribution.
## Examples
```julia-repl
julia> RiskMeasures.Expectation(rand(1000))
0.4793223308812537
julia> rm = RiskMeasures.Expectation()
ActuaryUtilities.RiskMeasures.Expectation()
julia> rm(rand(1000))
0.4941708036889741
```
"""
struct Expectation <: RiskMeasure end
g(rm::Expectation, x) = x
"""
VaR(Ξ±)::RiskMeasure
VaR(Ξ±)(risk)::T (where T is the type of values sampled in `risk`)
The `Ξ±`th quantile of the `risk` distribution is the Value at Risk, or Ξ±th quantile. `risk` can be a univariate distribution or an array of outcomes.
Assumes more positive values are higher risk measures, so a higher p will return a more positive number. For a discrete risk, the VaR returned is the first value above the Ξ±th percentile.
`VaR(Ξ±)` returns a functor which can then be called on a risk distribution.
## Parameters
- Ξ±: [0,1.0)
## Examples
```julia-repl
julia> VaR(0.95)(rand(1000))
0.9561843082268024
julia> rm = VaR(0.95)
VaR{Float64}(0.95)
julia> rm(rand(1000))
0.9597070153670079
```
"""
struct VaR{T<:Real} <: RiskMeasure
Ξ±::T
function VaR(Ξ±::T) where {T}
@assert 0 <= Ξ± < 1 "Ξ± of $Ξ± is not 0 β€ Ξ± < 1"
return new{T}(Ξ±)
end
end
g(rm::VaR, x) = x < (1 - rm.Ξ±) ? 0 : 1
"""
[`VaR`](@ref)
"""
ValueAtRisk = VaR
"""
CTE(Ξ±)::RiskMeasure
CTE(Ξ±)(risk)::T (where T is the type of values sampled in risk)
The Conditional Tail Expectation (CTE) at level Ξ± is the expected value of the risk distribution above the Ξ±th quantile. `risk` can be a univariate distribution or an array of outcomes.
Assumes more positive values are higher risk measures, so a higher p will return a more positive number.
CTE(Ξ±) returns a functor which can then be called on a risk distribution.
## Parameters
- Ξ±: [0,1.0)
## Examples
```julia-repl
julia> CTE(0.95)(rand(1000))
0.9766218612020593
julia> rm = CTE(0.95)
CTE{Float64}(0.95)
julia> rm(rand(1000))
0.9739835010268733
```
"""
struct CTE{T<:Real} <: RiskMeasure
Ξ±::T
function CTE(Ξ±::T) where {T}
@assert 0 <= Ξ± < 1 "Ξ± of $Ξ± is not 0 β€ Ξ± < 1"
return new{T}(Ξ±)
end
end
g(rm::CTE, x) = x < (1 - rm.Ξ±) ? x / (1 - rm.Ξ±) : 1
"""
[`CTE`](@ref)
"""
ConditionalTailExpectation = CTE
"""
WangTransform(Ξ±)::RiskMeasure
WangTransform(Ξ±)(risk)::T (where T is the type of values sampled in risk)
The Wang Transform is a distortion risk measure that transforms the cumulative distribution function (CDF) of the risk distribution using a normal distribution with mean Ξ¦β»ΒΉ(Ξ±) and standard deviation 1. risk can be a univariate distribution or an array of outcomes.
WangTransform(Ξ±) returns a functor which can then be called on a risk distribution.
## Parameters
- Ξ±: [0,1.0]
In the literature, sometimes Ξ» is used where ``\\lambda = \\Phi^{-1}(\\alpha)``.
## Examples
```julia-repl
julia> WangTransform(0.95)(rand(1000))
0.8799465543360105
julia> rm = WangTransform(0.95)
WangTransform{Float64}(0.95)
julia> rm(rand(1000))
0.8892245759705852
```
## References
- "A Risk Measure That Goes Beyond Coherence", Shaun S. Wang, 2002
"""
struct WangTransform{T} <: RiskMeasure
Ξ±::T
function WangTransform(Ξ±::T) where {T}
@assert 0 < Ξ± < 1 "Ξ± of $Ξ± is not 0 < Ξ± < 1"
return new{T}(Ξ±)
end
end
function g(rm::WangTransform, x)
Ξ¦_inv(x) = Distributions.quantile(Distributions.Normal(), x)
Distributions.cdf(Distributions.Normal(), Ξ¦_inv(x) + Ξ¦_inv(rm.Ξ±))
end
"""
DualPower(v)::RiskMeasure
DualPower(v)(risk)::T (where T is the type of values sampled in risk)
The Dual Power distortion risk measure is defined as ``1 - (1 - x)^v``, where x is the cumulative distribution function (CDF) of the risk distribution and v is a positive parameter. risk can be a univariate distribution or an array of outcomes.
DualPower(v) returns a functor which can then be called on a risk distribution.
"""
struct DualPower{T} <: RiskMeasure
v::T
end
g(rm::DualPower, x) = 1 - (1 - x)^rm.v
"""
ProportionalHazard(y)::RiskMeasure
ProportionalHazard(y)(risk)::T (where T is the type of values sampled in risk)
The Proportional Hazard distortion risk measure is defined as ``x^(1/y)``, where x is the cumulative distribution function (CDF) of the risk distribution and y is a positive parameter. risk can be a univariate distribution or an array of outcomes.
ProportionalHazard(y) returns a functor which can then be called on a risk distribution.
## Examples
```julia-repl
julia> ProportionalHazard(2)(rand(1000))
0.6659603556774121
julia> rm = ProportionalHazard(2)
ProportionalHazard{Int64}(2)
julia> rm(rand(1000))
0.6710587338367799
```
"""
struct ProportionalHazard{T} <: RiskMeasure
y::T
end
g(rm::ProportionalHazard, x) = x^(1 / rm.y)
function (rm::RiskMeasure)(risk)
# Definition 4.2 of "A Risk Measure that Goes Beyond Coherence", Wang 2002
F(x) = cdf_func(risk)(x)
H(x) = 1 - g(rm, 1 - x)
integral1, _ = QuadGK.quadgk(x -> 1 - H(F(x)), 0, Inf)
integral2, _ = QuadGK.quadgk(x -> H(F(x)), -Inf, 0)
return integral1 - integral2
end
"""
cdf_function(risk)
Returns the appropriate cumulative distribution function depending on the type, specifically:
cdf_func(S::AbstractArray{<:Real}) = StatsBase.ecdf(S)
cdf_func(S::Distributions.UnivariateDistribution) = x -> Distributions.cdf(S, x)
"""
cdf_func(S::AbstractArray{<:Real}) = StatsBase.ecdf(S)
cdf_func(S::Distributions.UnivariateDistribution) = x -> Distributions.cdf(S, x)
######################################################################
## This section is old, work-in-progress VaR and CTE revamp applicable only for
# AbstractArrays. Keeping this around for now in case perforamnce needs dicatate a specialized
# version of the two, but the above implementation has proved more flexible and general
# than below.
# """
# VaR(v::AbstractArray,p::Real;rev::Bool=false)
# The `p`th quantile of the vector `v` is the Value at Risk. Assumes more positive values are higher risk measures, so a higher p will return a more positive number., but this can be reversed if `rev` is `true`.
# Also can be called with `ValueAtRisk(...)`.
# """
# function VaR_empirical(v::T, p; sorted=false) where {T<:AbstractArray}
# if sorted
# _VaR_sorted(v, p)
# else
# _VaR_sorted(sort(v), p)
# end
# end
# # Core VaR assumes v is sorted
# function _VaR_sorted(v, p)
# i = 1
# n = length(v)
# q_prior = 0.0
# x_prior = first(v)
# for (i, x) in enumerate(v)
# q = i / n
# if q >= p
# # return weighted between two points
# return x * (p - q_prior) / (q - q_prior) + x_prior * (q - p) / (q - q_prior)
# end
# x_prior = x
# q_prior = q
# end
# return last(v)
# end
# """
# CTE(v::AbstractArray,p::Real;rev::Bool=false)
# The average of the values β₯ the `p`th percentile of the vector `v` is the Conditiona Tail Expectation. Assumes more positive values are higher risk measures, so a higher p will return a more positive number, but this can be reversed if `rev` is `true`.
# May also be called with `ConditionalTailExpectation(...)`.
# Also known as Tail Value at Risk (TVaR), or Tail Conditional Expectation (TCE)
# """
# function CTE(v::T, p; sorted=false) where {T<:AbstractArray}
# if sorted
# _CTE_sorted(v, p)
# else
# _CTE_sorted(sort(v), p)
# end
# end
# # Core CTE assumes v is sorted
# function _CTE_sorted(v, p)
# i = 1
# n = length(v)
# q_prior = 0.0
# x_prior = first(v)
# sub_total = zero(eltype(v))
# in_range = false
# for (i, x) in enumerate(v)
# q = i / n
# if in_range || q >= p
# # return weighted between two points
# # return x * (p - q_prior) / (q - q_prior) + x_prior * (q - p) / (q - q_prior)
# in_range = true
# end
# x_prior = x
# q_prior = q
# end
# return last(v)
# end
######################
end | ActuaryUtilities | https://github.com/JuliaActuary/ActuaryUtilities.jl.git |
|
[
"MIT"
] | 5.0.0 | 8733f1a23680f235eb0aa2a64c57922f32fe9b7f | code | 3098 | module Utilities
import ..Dates
import ..ActuaryUtilities: duration
export years_between, duration,
accum_offset
"""
Years_Between(d1::Date, d2::Date)
Compute the number of integer years between two dates, with the
first date typically before the second. Will return negative number if
first date is after the second. Use third argument to indicate if calendar
anniversary should count as a full year.
# Examples
```julia
julia> d1 = Date(2018,09,30);
julia> d2 = Date(2019,09,30);
julia> d3 = Date(2019,10,01);
julia> years_between(d1,d3)
1
julia> years_between(d1,d2,false) # same month/day but `false` overlap
0
julia> years_between(d1,d2) # same month/day but `true` overlap
1
julia> years_between(d1,d2) # using default `true` overlap
1
```
"""
function years_between(d1::Dates.Date, d2::Dates.Date, overlap=true)
iy, im, id = Dates.year(d1), Dates.month(d1), Dates.day(d1)
vy, vm, vd = Dates.year(d2), Dates.month(d2), Dates.day(d2)
dur = vy - iy
if vm == im
if overlap
if vd >= id
dur += 1
end
else
if vd > id
dur += 1
end
end
elseif vm > im
dur += 1
end
return dur - 1
end
"""
duration(d1::Date, d2::Date)
Compute the duration given two dates, which is the number of years
since the first date. The interval `[0,1)` is defined as having
duration `1`. Can return negative durations if second argument is before the first.
```julia
julia> issue_date = Date(2018,9,30);
julia> duration(issue_date , Date(2019,9,30) )
2
julia> duration(issue_date , issue_date)
1
julia> duration(issue_date , Date(2018,10,1) )
1
julia> duration(issue_date , Date(2019,10,1) )
2
julia> duration(issue_date , Date(2018,6,30) )
0
julia> duration(Date(2018,9,30),Date(2017,6,30))
-1
```
"""
function duration(issue_date::Dates.Date, proj_date::Dates.Date)
return years_between(issue_date, proj_date, true) + 1
end
"""
accum_offset(x; op=*, init=1.0)
A shortcut for the common operation wherein a vector is scanned with an operation, but has an initial value and the resulting array is offset from the traditional accumulate.
This is a common pattern when calculating things like survivorship given a mortality vector and you want the first value of the resulting vector to be `1.0`, and the second value to be `1.0 * x[1]`, etc.
Two keyword arguments:
- `op` is the binary (two argument) operator you want to use, such as `*` or `+`
- `init` is the initial value in the returned array
# Examples
```julia=repl
julia> accum_offset([0.9, 0.8, 0.7])
3-element Array{Float64,1}:
1.0
0.9
0.7200000000000001
julia> accum_offset(1:5) # the product of elements 1:n, with the default `1` as the first value
5-element Array{Int64,1}:
1
1
2
6
24
julia> accum_offset(1:5,op=+)
5-element Array{Int64,1}:
1
2
4
7
11
```
"""
function accum_offset(x; op=*, init=1.0)
xnew = similar(x)
xnew[1] = init
for i in 2:length(x)
xnew[i] = op(xnew[i-1], x[i-1])
end
return xnew
end
end | ActuaryUtilities | https://github.com/JuliaActuary/ActuaryUtilities.jl.git |
|
[
"MIT"
] | 5.0.0 | 8733f1a23680f235eb0aa2a64c57922f32fe9b7f | code | 1265 | @testset "Derivatives" begin
@testset "Euro Options" begin
# tested against https://option-price.com/index.php
params = (S = 1.0, K = 1.0, Ο = 1, r = 0.05, Ο = 0.25, q = 0.0)
@test eurocall(; params...) β 0.12336 atol = 1e-5
@test europut(; params...) β 0.07459 atol = 1e-5
params = (S = 1.0, K = 1.0, Ο = 1, r = 0.05, Ο = 0.25, q = 0.03)
@test eurocall(; params...) β 0.105493 atol = 1e-5
@test europut(; params...) β 0.086277 atol = 1e-5
params = (S = 1.0, K = 0.5, Ο = 1, r = 0.05, Ο = 0.25, q = 0.03)
@test eurocall(; params...) β 0.49494 atol = 1e-5
@test europut(; params...) β 0.00011 atol = 1e-5
params = (S = 1.0, K = 0.5, Ο = 1, r = 0.05, Ο = 0.25, q = 0.03)
@test eurocall(; params...) β 0.49494 atol = 1e-5
@test europut(; params...) β 0.00011 atol = 1e-5
params = (S = 1.0, K = 0.5, Ο = 0, r = 0.05, Ο = 0.25, q = 0.03)
@test eurocall(; params...) β 0.5 atol = 1e-5
@test europut(; params...) β 0.0 atol = 1e-5
params = (S = 1.0, K = 1.5, Ο = 0, r = 0.05, Ο = 0.25, q = 0.03)
@test eurocall(; params...) β 0.0 atol = 1e-5
@test europut(; params...) β 0.5 atol = 1e-5
end
end
| ActuaryUtilities | https://github.com/JuliaActuary/ActuaryUtilities.jl.git |
|
[
"MIT"
] | 5.0.0 | 8733f1a23680f235eb0aa2a64c57922f32fe9b7f | code | 4517 | @testset "Risk Measures" begin
@test_throws AssertionError VaR(-0.5)
@test_throws AssertionError VaR(1.0)
@test_throws AssertionError VaR(1.5)
@test_throws AssertionError CTE(-0.5)
@test_throws AssertionError CTE(1.0)
@test_throws AssertionError CTE(1.5)
@test_throws AssertionError WangTransform(0.0)
@test_throws AssertionError WangTransform(1.0)
# https://utstat.utoronto.ca/sam/coorses/act466/rmn.pdf pg 17
@test RiskMeasures.g(WangTransform(cdf(Normal(), 1)), 1 - cdf(LogNormal(0, 1), 12)) β 0.06879 atol = 1e-5
@test RiskMeasures.Expectation()(LogNormal(0, 2 * 1)) β mean(LogNormal(0, 2 * 1))
@test CTE(0.9)(Uniform(-1, 0)) β -0.05 atol = 1e-8
@test RiskMeasures.Expectation()(Uniform(-1, 0)) β -0.5 atol = 1e-8
@test CTE(0.0)(Uniform(0, 1) - 0.5) β 0.0 atol = 1e-8
@test CTE(0.5)(Uniform(0, 1) - 0.5) β 0.25 atol = 1e-8
@test CTE(0.0)(Distributions.Normal(0, 1)) β 0
@test RiskMeasures.Expectation()(Distributions.Normal(3, 1)) β 3
# http://actuaries.org/events/congresses/cancun/afir_subject/afir_14_wang.pdf
A = Distributions.DiscreteNonParametric([0.0, 1.0, 5.0], [0.6, 0.375, 0.025])
B = Distributions.DiscreteNonParametric([0.0, 1.0, 11.0], [0.6, 0.390, 0.01])
@test WangTransform(0.95)(A) β 2.42 atol = 1e-2
@test WangTransform(0.95)(B) β 3.40 atol = 1e-2
@test CTE(0.95)(A) β 3
@test CTE(0.95)(B) β 3
## example 4.3
@test WangTransform(0.9)(LogNormal(3, 2)) β exp(3 + quantile(Normal(), 0.9) * 2 + 2^2 / 2) atol = 1e-3
## example 4.4
C = Distributions.Exponential(1)
Ξ± = 0.99
@test CTE(Ξ±)(C) β 5.61 atol = 1e-2
@test VaR(Ξ±)(C) β 4.61 atol = 1e-2
@test WangTransform(Ξ±)(C) β 5.02 atol = 1e-1
## example 4.5
@test WangTransform(Ξ±)(Uniform()) β 0.95 atol = 1e-2
# Sepanski & Wang, "New Classes of Distortion Risk Measures and Their Estimation, Table 6
# note the parameterization of Exp, Lomax (GP), and Weibull is different in Julia
# than in the paper
# TODO: add additional risk measures defined in the paper
dists = [
Distributions.Uniform(0, 100),
Distributions.Exponential(1 / 0.02),
Distributions.GeneralizedPareto(0, 580.40 / 12.61, 1 / 12.61),
Distributions.Weibull(0.50, 5^(1 / 0.5)),
Distributions.Weibull(1.50, 412.2^(1 / 1.5))
]
cte_targets = [
[62.6, 75.0, 87.5, 97.5, 99.5],
[64.38, 84.66, 119.31, 199.79, 280.26],
[64.54, 85.61, 123.25, 219.04, 327.87],
[66.45, 96.67, 167.36, 424.15, 810.45],
[62.01, 76.23, 97.32, 138.63, 174.22]
]
var_targets = [
[25.0, 50.0, 75.0, 95.0, 99.0],
[14.38, 34.66, 69.31, 149.79, 230.26],
[13.39, 32.80, 67.45, 155.64, 255.84],
[2.07, 12.01, 48.05, 224.36, 530.19],
[24.14, 43.38, 68.86, 115.10, 153.31]
]
alphas = [0.25, 0.5, 0.75, 0.95, 0.99]
@testset "distribution $dist" for (i, dist) in enumerate(dists)
@testset "alpha $Ξ±" for (j, Ξ±) in enumerate(alphas)
@test CTE(Ξ±)(dist) β cte_targets[i][j] rtol = 1e-2
@test VaR(Ξ±)(dist) β var_targets[i][j] rtol = 1e-2
end
end
# Hardy, "An Introduction to Risk Measures for Actuarial Applications
# note the difference for VaR where our VaR is L(NΞ±+1), as opposed to L(NΞ±)
# or the smoothed empirical estimate
# Also, confusingly the examples for VaR don't use the same Table 1 (L) as CTE
L = append!(vec([
169.1 170.4 171.3 171.9 172.3 173.3 173.8 174.3 174.9 175.9
176.4 177.2 179.1 179.7 180.2 180.5 181.9 182.6 183.0 183.1
183.3 184.4 186.9 187.7 188.2 188.5 191.8 191.9 193.1 193.8
194.2 196.3 197.6 197.8 199.1 200.5 200.5 200.5 202.8 202.9
203.0 203.7 204.4 204.8 205.1 205.8 206.7 207.5 207.9 209.2
209.5 210.6 214.7 217.0 218.2 226.2 226.3 226.9 227.5 227.7
229.0 231.4 231.6 233.2 237.5 237.9 238.1 240.3 241.0 241.3
241.6 243.8 244.0 247.2 247.8 248.8 254.1 255.6 255.9 257.4
265.0 265.0 268.9 271.2 271.6 276.5 279.2 284.1 284.3 287.8
287.9 298.7 301.6 305.0 313.0 323.8 334.5 343.5 350.3 359.4
]), zeros(900)) |> sort
@test VaR(0.950)(L) β L[951] atol = 1e-2
@test VaR(0.9505)(L) β L[951] atol = 1e-2
@test VaR(0.951)(L) β L[952] atol = 1e-2
@test VaR(0.95)(L) β L[951] atol = 1e-2
@test CTE(0.95)(L) β 260.68 atol = 1e-1
@test CTE(0.99)(L) β 321.8 atol = 1e-1
end
| ActuaryUtilities | https://github.com/JuliaActuary/ActuaryUtilities.jl.git |
|
[
"MIT"
] | 5.0.0 | 8733f1a23680f235eb0aa2a64c57922f32fe9b7f | code | 12333 | using ActuaryUtilities
using Dates
using Test
using Distributions
using StatsBase
const FM = ActuaryUtilities.FinanceModels
const FC = ActuaryUtilities.FinanceCore
include("risk_measures.jl")
@testset "Temporal functions" begin
@testset "years_between" begin
@test years_between(Date(2018, 9, 30), Date(2018, 9, 30)) == 0
@test years_between(Date(2022, 10, 30), Date(2022, 10, 30)) == 0
@test years_between(Date(2021, 10, 30), Date(2021, 10, 30)) == 0
@test years_between(Date(2021, 11, 30), Date(2021, 10, 30)) == -1
@test years_between(Date(2022, 10, 30), Date(2021, 10, 30)) == -1
@test years_between(Date(2018, 9, 30), Date(2018, 9, 30), true) == 0
@test years_between(Date(2018, 9, 30), Date(2019, 9, 30), false) == 0
@test years_between(Date(2018, 9, 30), Date(2019, 9, 30), true) == 1
@test years_between(Date(2018, 9, 30), Date(2019, 10, 1), true) == 1
@test years_between(Date(2018, 9, 30), Date(2019, 10, 1), false) == 1
end
@testset "duration tests" begin
@test duration(Date(2018, 9, 30), Date(2019, 9, 30)) == 2
@test duration(Date(2018, 9, 30), Date(2018, 9, 30)) == 1
@test duration(Date(2018, 9, 30), Date(2018, 10, 1)) == 1
@test duration(Date(2018, 9, 30), Date(2019, 10, 1)) == 2
@test duration(Date(2018, 9, 30), Date(2018, 6, 30)) == 0
@test duration(Date(2018, 9, 30), Date(2017, 6, 30)) == -1
@test duration(Date(2018, 10, 15), Date(2019, 9, 30)) == 1
@test duration(Date(2018, 10, 15), Date(2019, 10, 30)) == 2
@test duration(Date(2018, 10, 15), Date(2019, 10, 15)) == 2
@test duration(Date(2018, 10, 15), Date(2019, 10, 14)) == 1
end
end
@testset "accum_offset" begin
@test all(accum_offset([0.9, 0.8, 0.7]) .== [1.0, 0.9, 1.0 * 0.9 * 0.8])
@test all(accum_offset([0.9, 0.8, 0.7], op=+) .== [1.0, 1.9, 2.7])
@test all(accum_offset([0.9, 0.8, 0.7], op=+, init=2) .== [2.0, 2.9, 3.7])
@test all(accum_offset(1:5, op=+) .== [1, 2, 4, 7, 11])
@test all(accum_offset(1:5) .== [1, 1, 2, 6, 24])
@test all(accum_offset([1, 2, 3]) .== [1, 1, 2])
end
@testset "financial calcs" begin
@testset "price and present_value" begin
cf = [100, 100]
@test price(0.05, cf) β pv(0.05, cf)
cfs = ones(3)
@test present_values(FM.Yield.Constant(0.0), cfs) == [3, 2, 1]
pvs = present_values(FM.Yield.Constant(0.1), cfs)
@test pvs[3] β 1 / 1.1
@test pvs[2] β (1 / 1.1 + 1) / 1.1
@test all(present_values(0.00, [1, 1, 1]) .β [3, 2, 1])
@test all(present_values(0.00, [1, 1, 1], [0, 1, 2]) .β [3, 2, 1])
@test all(present_values(0.00, [1, 1, 1], [1, 2, 3]) .β [3, 2, 1])
@test all(present_values(0.00, [1, 1, 1], [1, 2, 3]) .β [3, 2, 1])
@test all(present_values(0.01, [1, 2, 3]) .β [5.862461552497766, 4.921086168022744, 2.9702970297029707])
cf = [100, 100]
ts = [0.5, 1]
@test pv(0.05, cf, ts) β 100 / 1.05^0.5 + 100 / 1.05^1
@test price(0.05, cf, ts) β pv(0.05, cf, ts)
@test price(0.05, -1 .* cf, ts) β abs(pv(0.05, cf, ts))
@test pv(0.05, FC.Cashflow.(cf, ts)) β pv(0.05, cf, ts)
@test price(0.05, FC.Cashflow.(cf, ts)) β price(0.05, cf, ts)
end
end
@testset "Breakeven time" begin
@testset "basic" begin
@test breakeven(0.10, [-10, 1, 2, 3, 4, 8]) == 5
@test breakeven(0.10, [-10, 15, 2, 3, 4, 8]) == 1
@test breakeven(0.10, [-10, 15, 2, 3, 4, 8]) == 1
@test breakeven(0.10, [10, 15, 2, 3, 4, 8]) == 0
@test isnothing(breakeven(0.10, [-10, -15, 2, 3, 4, 8]))
@test breakeven(0.10, FC.Cashflow.([-10, 1, 2, 3, 4, 8], 0:5)) == 5
end
@testset "timepoints" begin
times = [t for t in 0:5]
@test breakeven(0.10, [-10, 1, 2, 3, 4, 8], times) == 5
@test breakeven(0.10, [-10, 15, 2, 3, 4, 8], times) == 1
@test breakeven(0.10, [-10, 15, 2, 3, 4, 8], times) == 1
@test isnothing(breakeven(0.10, [-10, -15, 2, 3, 4, 8], times))
end
end
@testset "moic" begin
# https://bankingprep.com/multiple-on-invested-capital/
ex1 = [-100; [t == 200 ? 100 * 1.067^t : 0 for t in 1:200]]
@test moic(ex1) β 429421.59914697794
@test moic(FC.Cashflow.(ex1, 0:200)) β 429421.59914697794
ex2 = ex1[end] *= 0.5
@test moic(ex1) β 429421.59914697794 * 0.5
end
@testset "duration and convexity" begin
# per issue #74
@testset "generators" begin
g = (10 for t in 1:10)
v = collect(g)
i = FM.Yield.Constant(0.04)
@test duration(0.04, g) β duration(0.04, v)
@test duration(i, g) β duration(i, v)
@test convexity(0.04, g) β convexity(0.04, v)
end
@testset "wikipedia example" begin
times = [0.5, 1, 1.5, 2]
cfs = [10, 10, 10, 110]
cfo = FC.Cashflow.(cfs, times)
V = present_value(0.04, cfs, times)
@test duration(Macaulay(), 0.04, cfs, times) β 1.777570320376649
@test duration(Modified(), 0.04, cfs, times) β 1.777570320376649 / (1 + 0.04)
@test duration(0.04, cfs, times) β 1.777570320376649 / (1 + 0.04)
@test duration(Macaulay(), 0.04, cfo) β 1.777570320376649
@test duration(Modified(), 0.04, cfo) β 1.777570320376649 / (1 + 0.04)
@test duration(0.04, cfo) β 1.777570320376649 / (1 + 0.04)
# wikipedia example defines DV01 as a per point change, but industry practice is per basis point. Ref Issue #96
@test duration(DV01(), 0.04, cfs, times) β 1.777570320376649 / (1 + 0.04) * V / 10000
@test duration(DV01(), 0.04, cfo) β 1.777570320376649 / (1 + 0.04) * V / 10000
# test with a Rate
r = FC.Periodic(0.04, 1)
@test duration(Macaulay(), r, cfs, times) β 1.777570320376649
@test duration(Modified(), r, cfs, times) β 1.777570320376649 / (1 + 0.04)
@test duration(r, cfs, times) β 1.777570320376649 / (1 + 0.04)
@test duration(DV01(), r, cfs, times) β 1.777570320376649 / (1 + 0.04) * V / 10000
#test without times
r = FC.Periodic(0.04, 1)
@test duration(Macaulay(), r, cfs) β duration(Macaulay(), r, cfs, 1:4)
@test duration(Modified(), r, cfs) β duration(Modified(), r, cfs, 1:4)
@test duration(r, cfs) β duration(r, cfs, 1:4)
@test duration(DV01(), r, cfs) β duration(DV01(), r, cfs, 1:4)
@test duration(FM.Yield.Constant(0.04), cfs, times) β 1.777570320376649 / (1 + 0.04)
@test duration(FM.Yield.Constant(0.04), -1 .* cfs, times) β 1.777570320376649 / (1 + 0.04) atol = 0.00001
@test duration(FM.fit(FM.Spline.Linear(), FM.ForwardYields([0.04, 0.04]), FM.Fit.Bootstrap()), cfs, times) β 1.777570320376649 / (1 + 0.04) atol = 0.00001
# test that dispatch resolves the ambiguity between duration(FM.Yield,vec) and duration(FM.Yield, function)
@test duration(FM.Yield.Constant(0.03), cfs) > 0
@test convexity(FM.Yield.Constant(0.03), cfs) > 0
end
@testset "finpipe example" begin
# from https://www.finpipe.com/duration-macaulay-and-modified-duration-convexity/
cfs = zeros(10) .+ 3.75
cfs[10] += 100
times = 0.5:0.5:5.0
int = (1 + 0.075 / 2)^2 - 1 # convert bond yield to effective yield
@test isapprox(present_value(int, cfs, times), 100.00, atol=1e-2)
@test isapprox(duration(Macaulay(), int, cfs, times), 4.26, atol=1e-2)
end
@testset "Primer example" begin
# from https://math.illinoisstate.edu/krzysio/Primer.pdf
# the duration tests are commented out because I think the paper is wrong on the duration?
cfs = [0, 0, 0, 0, 1.0e6]
times = 1:5
cfo = FC.Cashflow.(cfs, times)
@test isapprox(present_value(0.04, cfs, times), 821927.11, atol=1e-2)
# @test isapprox(duration(0.04,cfs,times),4.76190476,atol=1e-6)
@test isapprox(convexity(0.04, cfs, times), 27.7366864, atol=1e-6)
@test isapprox(convexity(0.04, cfs), 27.7366864, atol=1e-6)
@test isapprox(convexity(0.04, cfo), 27.7366864, atol=1e-6)
# the same, but with a functional argument
value(i) = present_value(i, cfs, times)
# @test isapprox(duration(0.04,value),4.76190476,atol=1e-6)
@test isapprox(convexity(0.04, value), 27.7366864, atol=1e-6)
end
@testset "Quantlib" begin
# https://mhittesdorf.wordpress.com/2013/03/12/introduction-to-quantlib-duration-and-convexity/
cfs = [5, 5, 105]
times = 1:3
@test present_value(0.03, cfs, times) β 105.6572227097894
@test duration(Macaulay(), 0.03, cfs, times) β 2.863504670671131
@test duration(0.03, cfs, times) β 2.780101622010806
@test convexity(0.03, cfs, times) β 10.62580548268594
# test omitting the times argument
@test duration(Macaulay(), 0.03, cfs) β 2.863504670671131
@test duration(0.03, cfs) β 2.780101622010806
@test convexity(0.03, cfs) β 10.62580548268594
# test a single matrix dimension
cfs = [5 0 0
0 5 105]
@test duration(0.03, sum(cfs, dims=1), times) β 2.780101622010806
cfs = [5 0
5 0
0 105]
@test duration(0.03, sum(cfs, dims=2), times) β 2.780101622010806
end
@testset "Key Rate Durations" begin
default_shift = 0.001
@test KeyRate(5) == KeyRateZero(5)
@test KeyRate(5) == KeyRateZero(5, default_shift)
@test KeyRatePar(5) == KeyRatePar(5, default_shift)
c = FM.Yield.Constant(FC.Periodic(0.04, 2))
cp = FinancialMath._krd_new_curve(KeyRatePar(5), c, 1:10)
cz = FinancialMath._krd_new_curve(KeyRateZero(5), c, 1:10)
# test some relationships between par and zero curve
@test FM.par(cp, 5) β FM.par(c, 5) + default_shift atol = 0.0002 # 0.001 is the default shift
@test FM.par(cp, 4) β FC.Periodic(0.04, 2) atol = 0.0001
@test zero(cp, 5) > FM.par(cp, 5)
@test zero(cp, 6) < FM.par(cp, 6)
@testset "FEH123" begin
# http://www.financialexamhelp123.com/key-rate-duration/
#test some curve properties
bond = (
cfs=[0.02 for t in 1:10],
times=collect(0.5:0.5:5)
)
bond.cfs[end] += 1.0
@test duration(KeyRatePar(1), c, bond.cfs, bond.times) β 0.0 atol = 0.01
@test duration(KeyRatePar(2), c, bond.cfs, bond.times) β 0.0 atol = 0.01
@test duration(KeyRatePar(3), c, bond.cfs, bond.times) β 0.0 atol = 0.01
@test duration(KeyRatePar(4), c, bond.cfs, bond.times) β 0.0 atol = 0.01
@test duration(KeyRatePar(5), c, bond.cfs, bond.times) β 4.45 atol = 0.05
bond = (times=[1, 2, 3, 4, 5], cfs=[0, 0, 0, 0, 100])
c = FC.Continuous(0.05)
@test duration(KeyRateZero(1), c, bond.cfs, bond.times) β 0.0 atol = 1e-10
@test duration(KeyRateZero(2), c, bond.cfs, bond.times) β 0.0 atol = 1e-10
@test duration(KeyRateZero(3), c, bond.cfs, bond.times) β 0.0 atol = 1e-10
@test duration(KeyRateZero(4), c, bond.cfs, bond.times) β 0.0 atol = 1e-10
@test duration(KeyRateZero(5), c, bond.cfs, bond.times) β duration(c, bond.cfs, bond.times) atol = 0.1
cfo = FC.Cashflow.(bond.cfs, bond.times)
@test duration(KeyRateZero(5), c, cfo) β duration(c, bond.cfs, bond.times) atol = 0.1
end
end
end
@testset "spread" begin
cfs = fill(10, 10)
cfo = FC.Cashflow.(cfs, 1:10)
@test spread(0.04, 0.05, cfs) β FC.Periodic(0.01, 1)
@test spread(0.04, 0.05, cfo) β FC.Periodic(0.01, 1)
@test spread(FC.Continuous(0.04), FC.Continuous(0.05), cfs) β FC.Periodic(1)(FC.Continuous(0.05)) - FC.Periodic(1)(FC.Continuous(0.04))
# 2021-03-31 rates from Treasury.gov
rates = [0.01, 0.01, 0.03, 0.05, 0.07, 0.16, 0.35, 0.92, 1.40, 1.74, 2.31, 2.41] ./ 100
mats = [1 / 12, 2 / 12, 3 / 12, 6 / 12, 1, 2, 3, 5, 7, 10, 20, 30]
y = FM.fit(FM.Spline.Linear(), FM.CMTYield.(rates, mats), FM.Fit.Bootstrap())
y2 = y + FC.Periodic(0.01, 1)
s = spread(y, y2, cfs)
@test s β FC.Periodic(0.01, 1) atol = 0.002
end | ActuaryUtilities | https://github.com/JuliaActuary/ActuaryUtilities.jl.git |
|
[
"MIT"
] | 5.0.0 | 8733f1a23680f235eb0aa2a64c57922f32fe9b7f | docs | 4024 | # ActuaryUtilities
[](https://JuliaActuary.github.io/ActuaryUtilities.jl/stable/)
[](https://JuliaActuary.github.io/ActuaryUtilities.jl/dev/)
[](https://codecov.io/gh/JuliaActuary/ActuaryUtilities.jl)
## Quickstart
```julia
cfs = [5, 5, 105]
times = [1, 2, 3]
discount_rate = 0.03
present_value(discount_rate, cfs, times) # 105.65
duration(Macaulay(), discount_rate, cfs, times) # 2.86
duration(discount_rate, cfs, times) # 2.78
convexity(discount_rate, cfs, times) # 10.62
```
## Features
A collection of common functions/manipulations used in Actuarial Calculations.
### Financial Maths
- `duration`:
- Calculate the `Macaulay`, `Modified`, or `DV01` durations for a set of cashflows
- Calculate the `KeyRate(time)` (a.k.a. `KeyRateZero`)duration or `KeyRatePar(time)` duration
- `convexity` for price sensitivity
- Flexible interest rate models via the [`FinanceModels.jl`](https://github.com/JuliaActuary/FinanceModels.jl) package.
- `internal_rate_of_return` or `irr` to calculate the IRR given cashflows (including at timepoints like Excel's `XIRR`)
- `breakeven` to calculate the breakeven time for a set of cashflows
- `accum_offset` to calculate accumulations like survivorship from a mortality vector
- `spread` will calculate the spread needed between two yield curves to equate a set of cashflows
### Risk Measures
- Calculate risk measures for a given vector of risks:
- `CTE` for the Conditional Tail Expectation
- `VaR` for the percentile/Value at Risk
- `WangTransform` for the Wang Transformation
- `ProportionalHazard` for proportional hazards
- `DualPower` for dual power measure
### Insurance mechanics
- `duration`:
- Calculate the duration given an issue date and date (a.k.a. policy duration)
### Typed Rates
- functions which return a rate/yield will return a `FinanceCore.Rate` object. E.g. `irr(cashflows)` will return a `Rate(0.05,Periodic(1))` instead of just a `0.05` (`float64`) to convey the compounding frequency. This is compatible across the JuliaActuary ecosystem and can be used anywhere you would otherwise use a simple floating point rate.
A couple of other notes:
- `rate(...)` will return the scalar rate value from a `Rate` struct:
```julia-repl
julia> r = Rate(0.05,Periodic(1));
julia> rate(r)
0.05
```
- You can still pass a simple floating point rate to various methods. E.g. these two are the same (the default compounding convention is periodic once per period):
```julia
discount(0.05,cashflows)
r = Rate(0.05,Periodic(1));
discount(r,cashflows)
```
- convert between rates with:
```julia
r = Rate(0.05,Periodic(1));
convert(Periodic(2), r) # convert to compounded twice per timestep
convert(Continuous(2),r) # convert to compounded twice per timestep
```
For more on Rates, see [FinanceCore.jl](https://github.com/JuliaActuary/FinanceCore.jl). [FinanceModels.jl](https://github.com/JuliaActuary/FinanceModels.jl) also provides a rich and flexible set of yield models to use.
## Documentation
Full documentation is [available here](https://JuliaActuary.github.io/ActuaryUtilities.jl/stable/).
## Examples
### Interactive, basic cashflow analysis
See [JuliaActuary.org for instructions](https://juliaactuary.org/tutorials/cashflowanalysis/) on running this example.
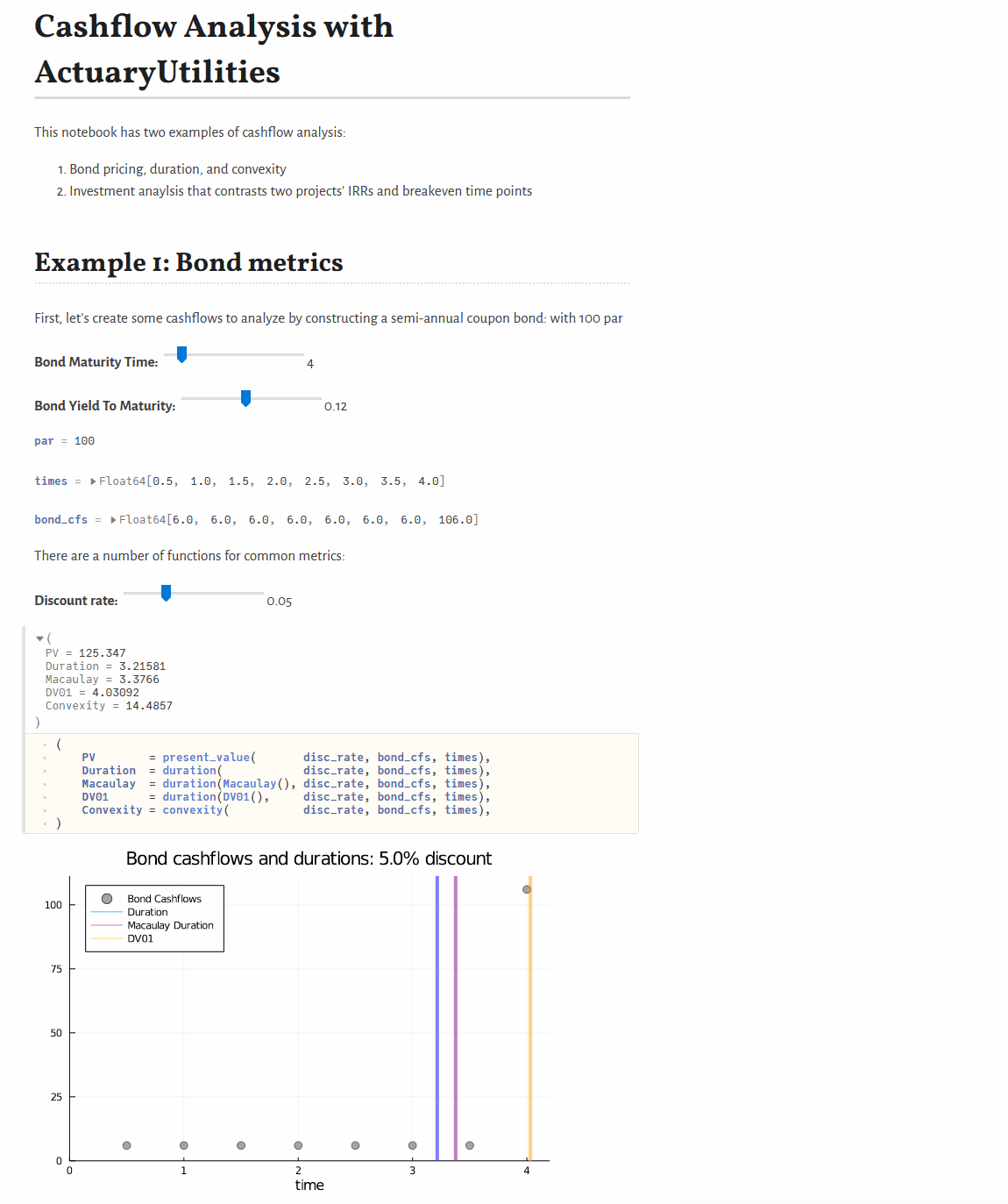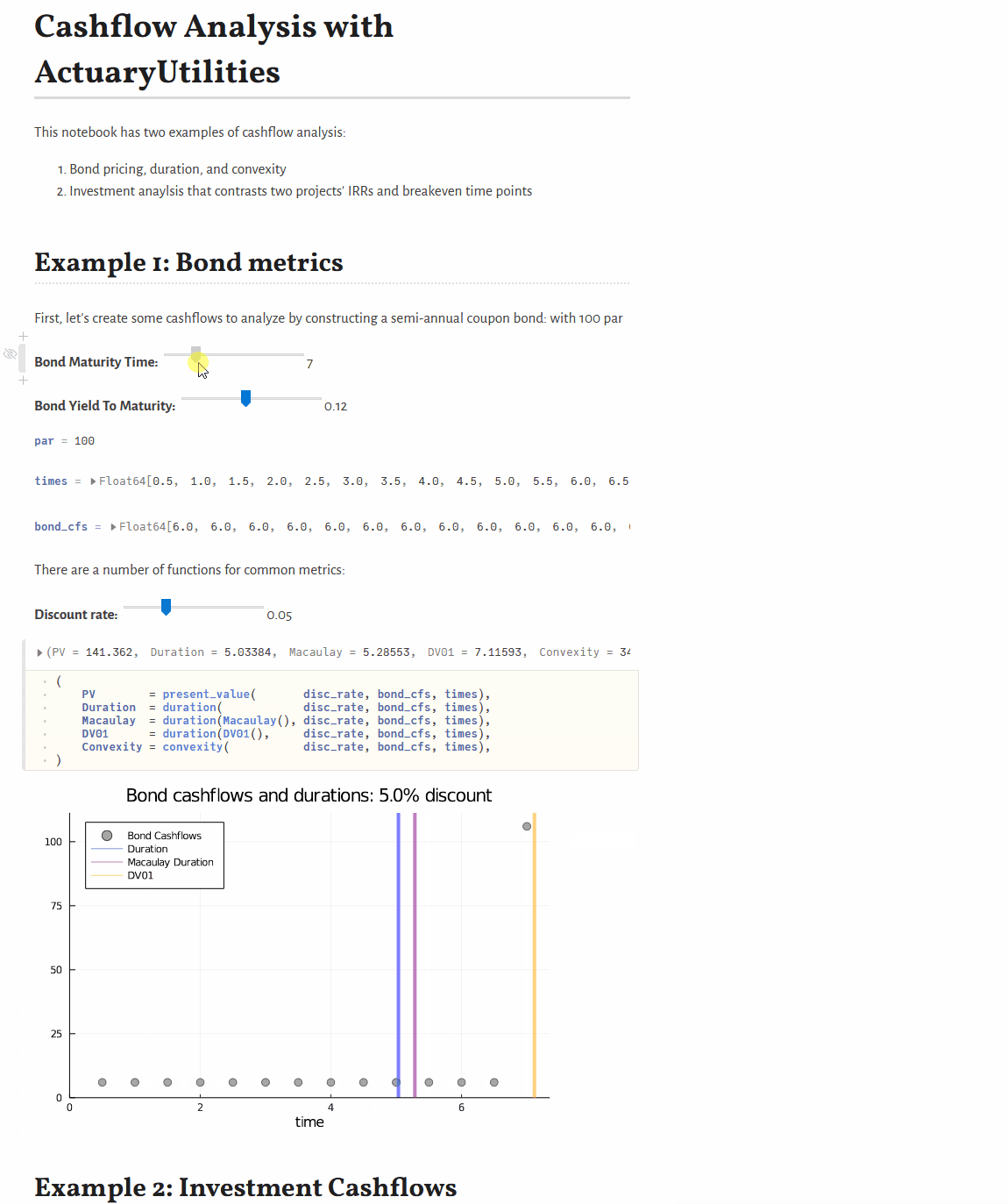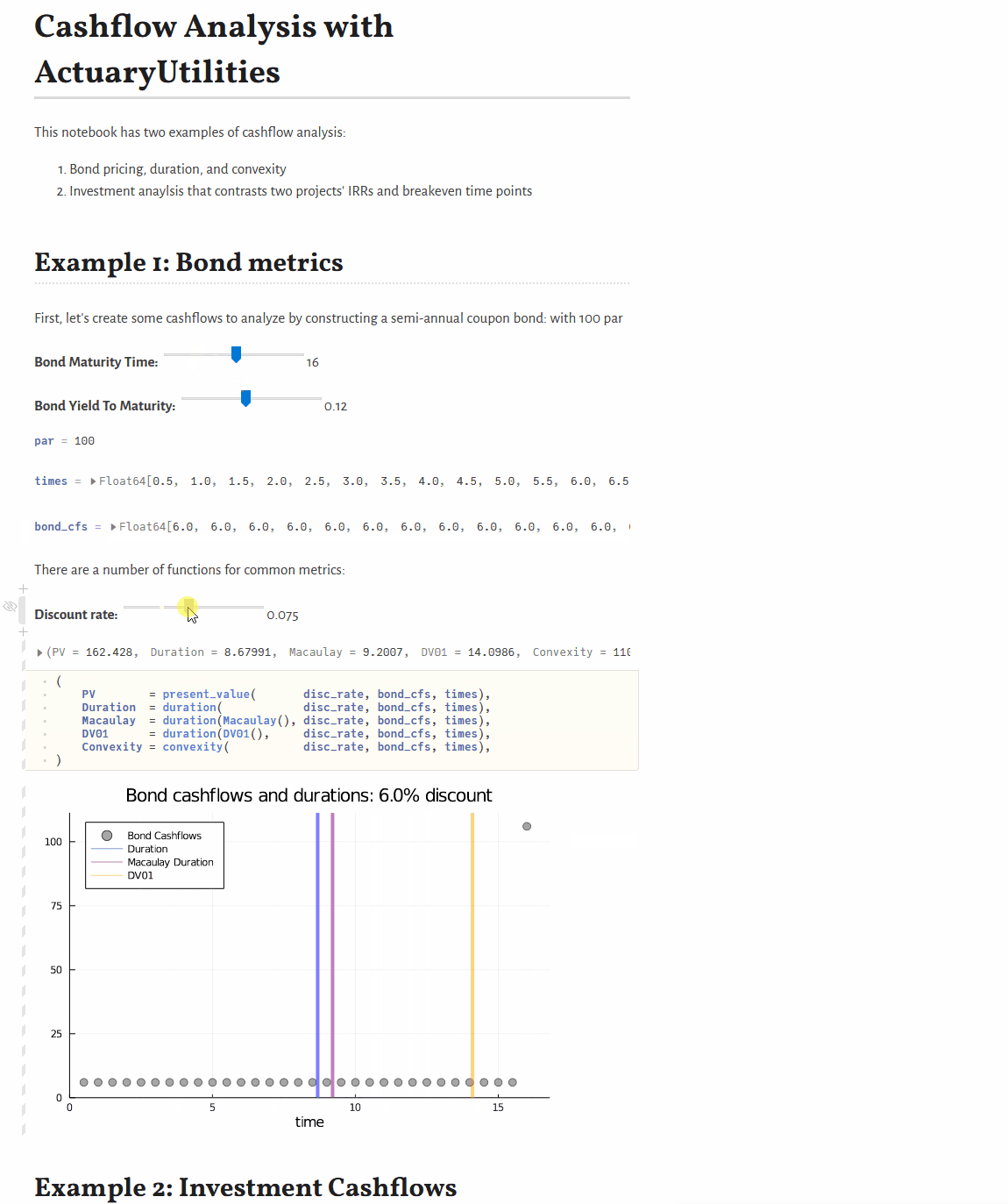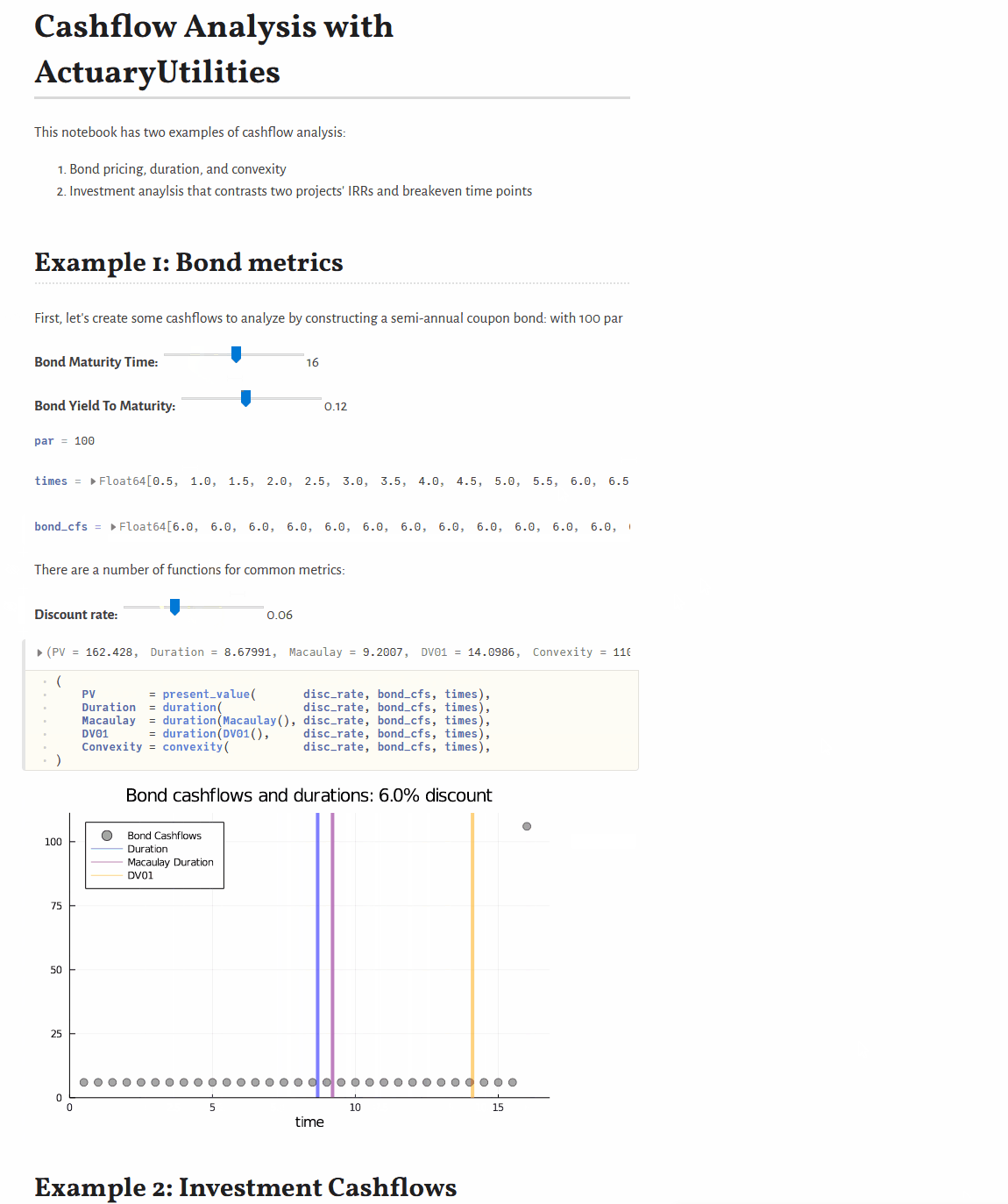[](https://juliaactuary.org/tutorials/cashflowanalysis/)
## Useful tips
Functions often use a mix of interest_rates, cashflows, and timepoints. When calling functions, the general order of the arguments is 1) interest rates, 2) cashflows, and 3) timepoints.
| ActuaryUtilities | https://github.com/JuliaActuary/ActuaryUtilities.jl.git |
|
[
"MIT"
] | 5.0.0 | 8733f1a23680f235eb0aa2a64c57922f32fe9b7f | docs | 610 | # Financial Math Submodule
Provides a set of common routines in financial maths.
## Quickstart
```julia
cfs = [5, 5, 105]
times = [1, 2, 3]
discount_rate = 0.03
present_value(discount_rate, cfs, times) # 105.65
duration(Macaulay(), discount_rate, cfs, times) # 2.86
duration(discount_rate, cfs, times) # 2.78
convexity(discount_rate, cfs, times) # 10.62
```
## API
### Exported API
```@autodocs
Modules = [ActuaryUtilities.FinancialMath]
Private = false
```
### Unexported API
```@autodocs
Modules = [ActuaryUtilities.FinancialMath]
Public = false
``` | ActuaryUtilities | https://github.com/JuliaActuary/ActuaryUtilities.jl.git |
|
[
"MIT"
] | 5.0.0 | 8733f1a23680f235eb0aa2a64c57922f32fe9b7f | docs | 3529 | ## Quickstart
```julia
cfs = [5, 5, 105]
times = [1, 2, 3]
discount_rate = 0.03
present_value(discount_rate, cfs, times) # 105.65
duration(Macaulay(), discount_rate, cfs, times) # 2.86
duration(discount_rate, cfs, times) # 2.78
convexity(discount_rate, cfs, times) # 10.62
```
## Features
A collection of common functions/manipulations used in Actuarial Calculations.
### Financial Maths
- `duration`:
- Calculate the `Macaulay`, `Modified`, or `DV01` durations for a set of cashflows
- Calculate the `KeyRate(time)` (a.k.a. `KeyRateZero`)duration or `KeyRatePar(time)` duration
- `convexity` for price sensitivity
- Flexible interest rate models via the [`FinanceModels.jl`](https://github.com/JuliaActuary/FinanceModels.jl) package.
- `internal_rate_of_return` or `irr` to calculate the IRR given cashflows (including at timepoints like Excel's `XIRR`)
- `breakeven` to calculate the breakeven time for a set of cashflows
- `accum_offset` to calculate accumulations like survivorship from a mortality vector
- `spread` will calculate the spread needed between two yield curves to equate a set of cashflows
### Risk Measures
- Calculate risk measures for a given vector of risks:
- `CTE` for the Conditional Tail Expectation
- `VaR` for the percentile/Value at Risk
- `WangTransform` for the Wang Transformation
- `ProportionalHazard` for proportional hazards
- `DualPower` for dual power measure
### Insurance mechanics
- `duration`:
- Calculate the duration given an issue date and date (a.k.a. policy duration)
### Typed Rates
- functions which return a rate/yield will return a `FinanceCore.Rate` object. E.g. `irr(cashflows)` will return a `Rate(0.05,Periodic(1))` instead of just a `0.05` (`float64`) to convey the compounding frequency. This is compatible across the JuliaActuary ecosystem and can be used anywhere you would otherwise use a simple floating point rate.
A couple of other notes:
- `rate(...)` will return the scalar rate value from a `Rate` struct:
```julia-repl
julia> r = Rate(0.05,Periodic(1));
julia> rate(r)
0.05
```
- You can still pass a simple floating point rate to various methods. E.g. these two are the same (the default compounding convention is periodic once per period):
```julia
discount(0.05,cashflows)
r = Rate(0.05,Periodic(1));
discount(r,cashflows)
```
- convert between rates with:
```julia
r = Rate(0.05,Periodic(1));
convert(Periodic(2), r) # convert to compounded twice per timestep
convert(Continuous(2),r) # convert to compounded twice per timestep
```
For more on Rates, see [FinanceCore.jl](https://github.com/JuliaActuary/FinanceCore.jl). [FinanceModels.jl](https://github.com/JuliaActuary/FinanceModels.jl) also provides a rich and flexible set of yield models to use.
## Documentation
Full documentation is [available here](https://JuliaActuary.github.io/ActuaryUtilities.jl/stable/).
## Examples
### Interactive, basic cashflow analysis
See [JuliaActuary.org for instructions](https://juliaactuary.org/tutorials/cashflowanalysis/) on running this example.
[](https://juliaactuary.org/tutorials/cashflowanalysis/)
## Useful tips
Functions often use a mix of interest_rates, cashflows, and timepoints. When calling functions, the general order of the arguments is 1) interest rates, 2) cashflows, and 3) timepoints.
| ActuaryUtilities | https://github.com/JuliaActuary/ActuaryUtilities.jl.git |
|
[
"MIT"
] | 5.0.0 | 8733f1a23680f235eb0aa2a64c57922f32fe9b7f | docs | 6958 | # Risk Measures
## Quickstart
```julia
outcomes = rand(100)
# direct usage
VaR(0.90)(outcomes) # β 0.90
CTE(0.90)(outcomes) # β 0.95
WangTransform(0.90)(outcomes) # β 0.81
# construct a reusable object (functor)
rm = VaR(0.90)
rm(outcomes) # β 0.90
```
## Introduction
Risk measures encompass the set of functions that map a set of outcomes to an output value characterizing the associated riskiness of those outcomes. As is usual when attempting to compress information (e.g. condensing information into a single value), there are multiple ways we can charactize this riskiness.
## Coherence & Other Desirable Properties
Further, it is desireable that a risk measure has certain properties, and risk measures that meet the first four criteria are called "Coherent" in the literature. From "An Introduction to Risk Measures for Actuarial Applications" (Hardy), she describes as follows:
Using $H$ as a risk measure and $X$ as the associated risk distribution:
### 1. Translation Invariance
For any non-random $c$
%$H(X + c) = H(X) + c$%
This means that adding a constant amount (positive or negative) to a risk adds the same amount to the risk measure. It also implies that the risk measure for a non-random loss, with known value c, say, is just the amount of the loss c.
### 2. Positive Homogeneity
For any non-random $Ξ» > 0$:
$$H(Ξ»X) = Ξ»H(X)$$
This axiom implies that changing the units of loss does not change the risk measure.
### 3. Subadditivity
For any two random losses $X$ and $Y$,
$$H(X + Y) β€ H(X) + H(Y)$$
It should not be possible to reduce the economic capital required (or the appropriate premium) for a risk by splitting it into constituent parts. Or, in other words, diversification (ie consolidating risks) cannot make the risk greater, but it might make the risk smaller if the risks are less than perfectly correlated.
### 4. Monotonicity
If $Pr(X β€ Y) = 1$ then $H(X) β€ H(Y)$.
If one risk is always bigger then another, the risk measures should be similarly ordered.
### Other Properties
In "Properties of Distortion Risk Measures" (BalbaΜs, Garrido, Mayoral) also note other properties of interest:
#### Complete
Completeness is the property that the distortion function associated with the risk measure produces a unique mapping between the original risk's survial function $S(x)$ and the distorted $S*(x)$ for each $x$. See [Distortion Risk Measures](@ref) for more detail on this.
In practice, this means that a non-complete risk measure ignores some part of the risk distribution (e.g. CTE and VaR don't use the full distribution and have the same)
#### Exhaustive
A risk measure is "exhaustive" if it is coherent and complete.
#### Adaptable
A risk measure is "adapted" or "adaptable" if its distortion function (ee [Distortion Risk Measures](@ref)).$g$:
1. $g$ is strictly concave, that is $g$ is strictly decreasing.
2. $lim_{u\to0+} g\prime(u) = \inf and lim_{u\to1-} g\prime(u) = 0.
Adaptive risk measures are exhaustive but the converse is not true.
### Summary of Risk Measure Properties
| Measure | Coherent | Complete | Exhaustive | Adaptable | Condition 2 |
|--------------|----------|----------|------------|-----------|-------------|
| [VaR](@ref) | No | No | No | No | No |
| [CTE](@ref) | Yes | No | No | No | No |
| [DualPower](@ref) $(y > 1)$ | Yes | Yes | Yes | No | Yes |
| [ProportionalHazard](@ref) $(Ξ³ > 1)$ | Yes | Yes | Yes | No | Yes |
| [WangTransform](@ref) | Yes | Yes | Yes | Yes | Yes |
## Distortion Risk Measures
Distortion Risk Measures ([Wikipedia Link](https://en.wikipedia.org/wiki/Distortion_risk_measure)) are a way of remapping the probabilities of a risk distribution in order to compute a risk measure $H$ on the risk distribution $X$.
Adapting Wang (2002), there are two key components:
### Distortion Function $g(u)$
This remaps values in the [0,1] range to another value in the [0,1] range, and in $H$ below, operates on the survival function $S$ and $F=1-S$.
Let $g:[0,1]\to[0,1]$ be an increasing function with $g(0)=0$ and $g(1)=1$. The transform $F^*(x)=g(F(x))$ defines a distorted probability distribution, where "$g$" is called a distortion function.
Note that $F^*$ and $F$ are equivalent probability measures if and only if $g:[0,1]\to[0,1]$ is continuous and one-to-one.
Definition 4.2. We define a family of distortion risk-measures using the mean-value under the distorted probability $F^*(x)=g(F(x))$:
### Risk Measure Integration
To calculate a risk measure $H$, we integrate the distorted $F$ across all possible values in the risk distribution (i.e. $x \in X$):
$$H(X) = E^*(X) = - \int_{-\infty}^0 g(F(x))dx + \int_0^{+\infty}[1-g(F(x))]dx$$
That is, the risk measure ($H$) is equal to the expected value of the distortion of the risk ditribution ($E^*(X)$).
## Examples
### Basic Usage
```julia
outcomes = rand(100)
# direct usage
VaR(0.90)(outcomes) # β 0.90
CTE(0.90)(outcomes) # β 0.95
WangTransform(0.90)(outcomes) # β 0.81
# construct a reusable object (functor)
rm = VaR(0.90)
rm(outcomes) # β 0.90
```
### Comparison
We will generate a random outcome and show how the risk measures behave:
```@example
using Distributions
using ActuaryUtilities
using CairoMakie
outcomes = Weibull(1,5)
# or this could be discrete outcomes as in the next line
#outcomes = rand(LogNormal(2,10)*100,2000)
Ξ±s= range(0.00,0.99;length=100)
let
f = Figure()
ax = Axis(f[1,1],
xlabel="Ξ±",
ylabel="Loss",
title = "Comparison of Risk Measures",
xgridvisible=false,
ygridvisible=false,
)
lines!(ax,
Ξ±s,
[quantile(outcomes, Ξ±) for Ξ± in Ξ±s],
label = "Quantile Ξ± of Outcome",
color = :grey10,
linewidth = 3,
)
lines!(ax,
Ξ±s,
[VaR(Ξ±)(outcomes) for Ξ± in Ξ±s],
label = "VaR(Ξ±)",
linestyle=:dash
)
lines!(ax,
Ξ±s,
[CTE(Ξ±)(outcomes) for Ξ± in Ξ±s],
label = "CTE(Ξ±)",
)
lines!(ax,
Ξ±s[2:end],
[WangTransform(Ξ±)(outcomes) for Ξ± in Ξ±s[2:end]],
label = "WangTransform(Ξ±)",
)
lines!(ax,
Ξ±s,
[ProportionalHazard(2)(outcomes) for Ξ± in Ξ±s],
label = "ProportionalHazard(2)",
)
lines!(ax,
Ξ±s,
[DualPower(2)(outcomes) for Ξ± in Ξ±s],
label = "DualPower(2)",
)
lines!(ax,
Ξ±s,
[RiskMeasures.Expectation()(outcomes) for Ξ± in Ξ±s],
label = "Expectation",
)
axislegend(ax,position=:lt)
f
end
```
## API
### Exported API
```@autodocs
Modules = [ActuaryUtilities.RiskMeasures]
Private = false
```
### Unexported API
```@autodocs
Modules = [ActuaryUtilities.RiskMeasures]
Public = false
``` | ActuaryUtilities | https://github.com/JuliaActuary/ActuaryUtilities.jl.git |
|
[
"MIT"
] | 5.0.0 | 8733f1a23680f235eb0aa2a64c57922f32fe9b7f | docs | 994 | # Version Upgrade Guide
## v3 to v4
### Overview
The shape and API of the package is mostly unchanged. The changes that have made fall into a few categores:
- Accommodating FinanceModels.jl, the next-generation version of Yields.jl.
- Simplifying the API, generally making function calls require more specific arguments to avoid ambiguity
- Accommodating the new `Cashflow` type which makes modeling heterogeneous assets and liabilities simpler.
### API Changes
- Breaking: The functions `europut` and `eurocall` have been moved to `FinanceModels`
- Breaking: Previously, the first argument to `present_value` or `present_values` would be interpreted as a set of `Periodic(1)` one-period forward rates if a vector of real values was passed. Users should explicitly create the yield model first, instead of relying on the implicit conversion:
```julia
# old
pv([0.05,0.1], cfs)
# new
using FinanceModels
y = fit(Spline.Linear(),ForwardYields([0.05,0.1]),Bootstrap())
pv(y,cfs)
```
| ActuaryUtilities | https://github.com/JuliaActuary/ActuaryUtilities.jl.git |
|
[
"MIT"
] | 5.0.0 | 8733f1a23680f235eb0aa2a64c57922f32fe9b7f | docs | 199 | # Utilities submodule
Provides miscellaneous routines common in actuarial and financial work.
## API
### Exported API
```@docs
Utilities.duration
Utilities.years_between
Utilities.accum_offset
``` | ActuaryUtilities | https://github.com/JuliaActuary/ActuaryUtilities.jl.git |
|
[
"MIT"
] | 5.0.0 | 8733f1a23680f235eb0aa2a64c57922f32fe9b7f | docs | 379 | # ActuaryUtilities API Reference
```@index
Modules = [ActuaryUtilities]
```
## Exported API
```@autodocs
Modules = [ActuaryUtilities]
Private = false
```
## Unexported API
```@autodocs
Modules = [ActuaryUtilities]
Public = false
```
Please [open an issue](https://github.com/JuliaActuary/ActuaryUtilities.jl/issues) if you encounter any issues or confusion with the package.
| ActuaryUtilities | https://github.com/JuliaActuary/ActuaryUtilities.jl.git |
|
[
"MIT"
] | 5.0.0 | 8733f1a23680f235eb0aa2a64c57922f32fe9b7f | docs | 359 | # FinanceCore API Reference
```@index
Modules = [FinanceCore]
```
## Exported API
```@autodocs
Modules = [FinanceCore]
Private = false
```
## Unexported API
```@autodocs
Modules = [FinanceCore]
Public = false
```
Please [open an issue](https://github.com/JuliaActuary/ActuaryUtilities.jl/issues) if you encounter any issues or confusion with the package.
| ActuaryUtilities | https://github.com/JuliaActuary/ActuaryUtilities.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 4850 | cd(@__DIR__)
using Pkg
CI = get(ENV, "CI", nothing) == "true" || get(ENV, "GITHUB_TOKEN", nothing) !== nothing
CI && Pkg.activate(@__DIR__)
CI && Pkg.instantiate()
CI && (ENV["GKSwstype"] = "100")
using Documenter
using DocumenterTools
using DocumenterMarkdown
using UncertainData
using Distributions
using KernelDensity
using StatsBase
using Measurements
using Interpolations
PAGES = [
"index.md",
"Uncertain values" => [
"uncertain_values/uncertainvalues_overview.md",
"uncertain_values/uncertainvalues_theoreticaldistributions.md",
"uncertain_values/uncertainvalues_kde.md",
"uncertain_values/uncertainvalues_fitted.md",
"uncertain_values/uncertainvalues_certainvalue.md",
"uncertain_values/uncertainvalues_populations.md",
"uncertain_values/uncertainvalues_Measurements.md",
"uncertain_values/merging.md",
"uncertain_values/uncertainvalues_examples.md",
],
"Uncertain datasets" => [
"uncertain_datasets/uncertain_datasets_overview.md",
"uncertain_datasets/uncertain_index_dataset.md",
"uncertain_datasets/uncertain_value_dataset.md",
"uncertain_datasets/uncertain_indexvalue_dataset.md",
"uncertain_datasets/uncertain_dataset.md",
],
"Uncertain statistics" => [
"Core statistics" => [
"uncertain_statistics/core_stats/core_statistics.md",
"uncertain_statistics/core_stats/core_statistics_point_estimates.md",
"uncertain_statistics/core_stats/core_statistics_pairwise_estimates.md",
"uncertain_statistics/core_stats/core_statistics_datasets_single_dataset_estimates.md",
"uncertain_statistics/core_stats/core_statistics_datasets_pairwise_estimates.md",
"uncertain_statistics/core_stats/core_statistics_datasets.md"
],
"Hypothesis tests" => [
"uncertain_statistics/hypothesistests/hypothesis_tests_overview.md",
"uncertain_statistics/hypothesistests/one_sample_t_test.md",
"uncertain_statistics/hypothesistests/equal_variance_t_test.md",
"uncertain_statistics/hypothesistests/unequal_variance_t_test.md",
"uncertain_statistics/hypothesistests/exact_kolmogorov_smirnov_test.md",
"uncertain_statistics/hypothesistests/approximate_twosample_kolmogorov_smirnov_test.md",
"uncertain_statistics/hypothesistests/jarque_bera_test.md",
"uncertain_statistics/hypothesistests/mann_whitney_u_test.md",
"uncertain_statistics/hypothesistests/anderson_darling_test.md"
],
],
"Sampling constraints" => [
"sampling_constraints/available_constraints.md",
"sampling_constraints/constrain_uncertain_values.md",
"sampling_constraints/sequential_constraints.md"
],
"Binning" => [
"binning/bin.md"
],
"Resampling" => [
"resampling/resampling_overview.md",
"resampling/resampling_uncertain_values.md",
"resampling/resampling_uncertain_datasets.md",
"resampling/resampling_uncertain_indexvalue_datasets.md",
"resampling/sequential/resampling_uncertaindatasets_sequential.md",
"resampling/sequential/resampling_indexvalue_sequential.md",
"resampling/sequential/strictly_increasing.md",
"resampling/sequential/strictly_decreasing.md",
"resampling/interpolation/interpolation.md",
"resampling/interpolation/gridded.md",
"resampling/resampling_schemes/resampling_schemes_uncertain_value_collections.md",
"resampling/resampling_schemes/resampling_schemes_uncertain_indexvalue_collections.md",
"resampling/resampling_schemes/resampling_with_schemes_uncertain_value_collections.md",
"resampling/resampling_schemes/resampling_with_schemes_uncertain_indexvalue_collections.md",
"resampling/resampling_inplace.md"
#"resampling/models/resampling_with_models.md"
],
"Propagation of errors" => [
"propagation_of_errors/propagation_of_errors.md"
],
"Mathematics" => [
"mathematics/elementary_operations.md",
"mathematics/trig_functions.md"
],
"Tutorials" => [
"tutorials/tutorial_overview.md",
"tutorials/tutorial_transforming_data_to_regular_grid.md"
],
"implementing_algorithms_for_uncertaindata.md",
"changelog.md",
"publications.md",
"citing.md"
]
# %% Build docs
#PyPlot.ioff()
cd(@__DIR__)
ENV["JULIA_DEBUG"] = "Documenter"
makedocs(
modules = [UncertainData],
sitename = "UncertainData.jl documentation",
format = format = Documenter.HTML(
prettyurls = CI,
),
pages = PAGES
)
if CI
deploydocs(
repo = "github.com/kahaaga/UncertainData.jl.git",
target = "build",
push_preview = true
)
end
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 1457 | module UncertainData
using Distributions
using IntervalArithmetic
using RecipesBase
using StatsBase
using StaticArrays
using Statistics
using KernelDensity
display_update = false
version = "v0.10.4"
update_name = "update_$version"
if display_update
if !isfile(joinpath(@__DIR__, update_name))
printstyled(stdout,
"""
\nUpdate message: UncertainData $version
- Fixed some minor bugs.
"""; color = :light_magenta)
touch(joinpath(@__DIR__, update_name))
end
end
include("definitions.jl")
# Uncertain values
include("uncertain_values/UncertainValues.jl")
# Uncertain datasets
include("uncertain_datasets/UncertainDatasets.jl")
# Sampling constraints
include("sampling_constraints/SamplingConstraints.jl")
# Interpolation and interpolation grids
include("interpolation_and_binning/InterpolationsAndGrids.jl")
# Resampling
include("resampling/Resampling.jl")
# Mathematics
include("mathematics/UncertainMathematics.jl")
# Uncertain statistics
include("statistics/UncertainStatistics.jl")
# Plot recipes
include("plot_recipes/UncertainDataPlotRecipes.jl")
# Operations between uncertain UncertainValues
include("uncertain_values/operations/merging.jl")
# Example datasets
include("example_datasets/example_uvals.jl")
include("example_datasets/example_constraints.jl")
include("example_datasets/example_uncertainindexvalue_dataset.jl")
export UncertainScalarBinomialDistributed
include("sensitivity_testing/SensitivityTests.jl")
end # module
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 29 | function bin end
export bin | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 2748 | """
example_constraints(X::AbstractUncertainIndexValueDataset,
d_xinds = Uniform(0.5, 1.1), d_yinds = Uniform(0.9, 1.7))
Generate a set of random sampling constraints that can be used to constrain
the indices and values of an uncertain index-value dataset `X`. These are
generated as follows:
- `constraints_inds = TruncateStd(rand(d_xinds))`
- `constraints_vals = [TruncateQuantiles(0.5 - rand(d_xvals), 0.5 + rand(d_xvals)) for i = 1:length(X)];`
Returns the tuple (constraints_inds, constraints_vals).
"""
function example_constraints(X::AbstractUncertainIndexValueDataset,
d_xinds = Uniform(0.5, 1.1), d_yinds = Uniform(0.9, 1.7))
# Truncate indices at some fraction time their standard deviation around the man
constraints_inds = TruncateStd(rand(d_xinds))
# Truncate values at some percentile range
constraints_vals = [TruncateQuantiles(0.5 - rand(d_xvals), 0.5 + rand(d_xvals)) for i = 1:length(X)];
return (constraints_x_inds, constraints_vals)
end
"""
example_constraints(X::AbstractUncertainIndexValueDataset,
Y::AbstractUncertainIndexValueDataset;
d_xinds = Uniform(0.5, 1.1), d_yinds = Uniform(0.9, 1.7),
d_xvals = Uniform(0.05, 0.15), d_yvals = Uniform(0.3, 0.4))
Generate a set of random sampling constraints that can be used to constrain
the indices and values of two uncertain index-value datasets `X` and `Y`.
The constraints are generated as follows:
- `constraints_inds_x = TruncateStd(rand(d_xinds))`
- `constraints_inds_x = TruncateStd(rand(d_yinds))`
- `constraints_vals_x = [TruncateQuantiles(0.5 - rand(d_xvals), 0.5 + rand(d_xvals)) for i = 1:length(X)]`
- `constraints_vals_x = [TruncateQuantiles(0.5 - rand(d_yvals), 0.5 + rand(d_yvals)) for i = 1:length(Y)]`
Returns the tuple of tuples `((constraints_inds_x, constraints_vals_x), (constraints_inds_y, constraints_vals_y))`
"""
function example_constraints(X::AbstractUncertainIndexValueDataset,
Y::AbstractUncertainIndexValueDataset;
d_xinds = Uniform(0.5, 1.1), d_yinds = Uniform(0.9, 1.7),
d_xvals = Uniform(0.05, 0.15), d_yvals = Uniform(0.3, 0.4))
# Truncate indices at some fraction time their standard deviation around the man
constraints_x_inds = TruncateStd(rand(d_xinds))
constraints_y_inds = TruncateStd(rand(d_yinds))
# Truncate values at some percentile range
constraints_x_vals = [TruncateQuantiles(0.5 - rand(d_xvals), 0.5 + rand(d_xvals)) for i = 1:length(X)];
constraints_y_vals = [TruncateQuantiles(0.5 - rand(d_yvals), 0.5 + rand(d_yvals)) for i = 1:length(Y)];
cs_x = (constraints_x_inds, constraints_x_vals)
cs_y = (constraints_y_inds, constraints_y_vals)
cs_x, cs_y
end
export example_constraints | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 2136 | using DynamicalSystemsBase
"""
example_uncertain_indexvalue_datasets(system::DynamicalSystems.DiscreteDynamicalSystem, n::Int, vars; Ttr = 1000,
d_xval = Uniform(0.01, 0.4), d_yval = Uniform(0.01, 0.5),
d_xind = Uniform(0.5, 1.5), d_yind = Uniform(0.5, 1.5))
Generate a pair of `UncertainIndexValueDataset`s from a discrete dynamical `system`, generated
by iterating the system `n` time after a transient run of `Ttr` steps, then gathering the
columns at positions `vars` (should be two column indices) as separate time series.
Each of the time series, call them `x` and `y`, are then converted to uncertain values.
Specifically, replace `x[i]` and `y[i]` with `UncertainValue(Normal, x[i], rand(d_xval)`
and `UncertainValue(Normal, y[i], rand(d_xval)`. Because the time series don't have
explicit time indices associated with them, we'll create some time indices as the range
`1:tstep:length(x)*tstep`, call them `x_inds` and `y_inds`. The time indices for `x` and `y`
are also normally distributed, such that `x_inds[i] = UncertainValue(Normal, i, rand(d_xind)`,
and the same for `y_inds`.
Returns a tuple of `UncertainIndexValueDataset` instances, one for `x` and one for `y`.
"""
function example_uncertain_indexvalue_datasets(system::DiscreteDynamicalSystem, n::Int, vars; Ttr = 1000,
tstep = 3,
d_xval = Uniform(0.01, 0.4), d_yval = Uniform(0.01, 0.5),
d_xind = Uniform(0.5, 1.5), d_yind = Uniform(0.5, 1.5))
orbit = trajectory(system, n - 1, Ttr = 1000);
x_vals = UncertainValueDataset([UncertainValue(Normal, x, rand(d_xval)) for x in orbit[:, vars[1]]])
y_vals = UncertainValueDataset([UncertainValue(Normal, y, rand(d_yval)) for y in orbit[:, vars[2]]])
x_inds = UncertainIndexDataset([UncertainValue(Normal, i, rand(d_xind)) for i = 1:tstep:length(x_vals)*tstep]);
y_inds = UncertainIndexDataset([UncertainValue(Normal, i, rand(d_yind)) for i = 1:tstep:length(y_vals)*tstep]);
X = UncertainIndexValueDataset(x_inds, x_vals)
Y = UncertainIndexValueDataset(y_inds, y_vals);
return X, Y
end
export example_uncertain_indexvalue_datasets | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 1980 | using StatsBase
##########################################
# Uncertain theoretical distributions
##########################################
uncertain_theoretical_distributions = [
UncertainValue(Uniform, -1, 1),
UncertainValue(Normal, 0, 1),
UncertainValue(Gamma, 1, 2),
UncertainValue(Beta, 1, 2),
UncertainValue(BetaPrime, 4, 5),
UncertainValue(Frechet, 1, 1),
UncertainValue(Binomial, 10, 0.3),
UncertainValue(BetaBinomial, 100, 2, 3)
]
##########################################
# Kernel density estimates
##########################################
n = 10
uncertain_kde_estimates = [
UncertainValue(rand(100))
]
##########################################
# Fitted theoretical distributions
##########################################
n = 10
uncertain_fitted_distributions = [
UncertainValue(Uniform, rand(Uniform(-2, 2), n)),
UncertainValue(Normal, rand(Normal(0, 1), n))
]
########################
# Uncertain populations
########################
pop1 = UncertainValue(
[3.0, UncertainValue(Normal, 0, 1),
UncertainValue(Gamma, 2, 3),
UncertainValue(Uniform, rand(1000))],
[0.5, 0.5, 0.5, 0.5]
)
pop2 = UncertainValue(1:10 |> collect, rand(10))
pop3 = UncertainValue(1.0:10.0 |> collect, Weights(rand(10)))
# Uncertain population consisting of uncertain populations and other stuff
pop4 = UncertainValue([pop1, pop2], [0.1, 0.5])
pop5 = UncertainValue([pop1, pop2, 2, UncertainValue(Normal, -2, 3)], Weights(rand(4)));
uncertain_scalar_populations = [pop1, pop2, pop3, pop4, pop5]
##########################################
# Gather all examples
##########################################
example_uvals = [
uncertain_scalar_populations;
uncertain_theoretical_distributions;
uncertain_kde_estimates;
uncertain_fitted_distributions
];
example_uidxs = [UncertainValue(Normal, i, rand()*2) for i = 1:length(example_uvals)]
export example_uvals, example_uidxs | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 299 | using Reexport
@reexport module InterpolationAndGrids
using Interpolations
include("findall_nan_chunks.jl")
include("fill_nans.jl")
include("grids/RectangularGrid.jl")
include("methods/interpolation.jl")
include("interpolate_and_bin.jl")
include("binning.jl")
end | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 8314 |
import ..bin
"""
bin(left_bin_edges::AbstractRange, xs, ys) -> Vector{Vector{T}} where T
Distribute the elements of `ys` into `N-1` different bin vectors, based on
how the values in `xs` are distributed among the bins defined by the `N` grid
points in `left_bin_edges`. If `xs[i]` falls in the `n`-th bin interval, then `ys[i]`
is assigned to the `n`-th bin vector. If `xs[i]` lie outside the grid, then the
corresponding `ys[i]` is ignored. See also [`bin!`](@ref)
Returns `N - 1` bin vectors.
## Examples
### Getting the values in each bin:
```julia
xs = [1.2, 1.7, 2.2, 3.3, 4.5, 4.6, 7.1]
ys = [4.2, 5.1, 6.5, 4.2, 3.2, 3.1, 2.5]
left_bin_edges = 0.0:1.0:6.0
bin(left_bin_edges, xs, ys)
```
```julia
# Some example data with unevenly spaced time indices
npts = 300
time, vals = sort(rand(1:1000, npts)), rand(npts)
# See which values fall in 25 time step wide time bins ranging
# from time indices 100 to 900.
left_bin_edges = 100:25:900
bin(left_bin_edges, time, vals)
```
"""
function bin(left_bin_edges::AbstractRange{T}, xs, ys) where T
if length(xs) != length(ys)
msg = "`length(xs)` not equal to `length(ys)`"
throw(ArgumentError(msg))
end
# Each bin is represented by (potentially differently sized) vectors of type `eltype(ys)`
YT = eltype(ys)
n_bins = length(left_bin_edges) - 1
bin_vals = [Array{YT}(undef, 0) for i = 1:n_bins]
# Assign values to bins. Can be done faster if `xs` is guaranteed to be ordered.
g_min = minimum(left_bin_edges)
g_step = step(left_bin_edges)
for (x, y) in zip(xs, ys)
arr_idx = ceil(Int, (x - g_min)/g_step)
# Check that the value falls inside the grid; if not, ignore it
if 0 < arr_idx <= n_bins
push!(bin_vals[arr_idx], y)
end
end
return bin_vals
end
"""
bin(f::Function, left_bin_edges::AbstractRange, xs, ys, args...; kwargs...) -> Vector{T} where T
Distribute the elements of `ys` into `N-1` different bin vectors, based on
how the values in `xs` are distributed among the bins defined by the `N` grid
points in `left_bin_edges`. If `xs[i]` falls in the `n`-th bin interval, then `ys[i]`
is assigned to the `n`-th bin vector. If `xs[i]` lie outside the grid, then the
corresponding `ys[i]` is ignored. See also [`bin!`](@ref)
Then, apply the summary function element-wise to each of the bin vectors, with `args`
and `kwargs` as arguments and keyword arguments. Then, `N-1` summary values, one for
each bin, are returned. Empty bins are assigned `NaN` values.
Returns `N-1` bin summaries.
## Examples
### Applying a summary function to each bin
Any function that accepts a vector of values can be used in conjunction with `bin`.
```julia
xs = [1.2, 1.7, 2.2, 3.3, 4.5, 4.6, 7.1]
ys = [4.2, 5.1, 6.5, 4.2, 3.2, 3.1, 2.5]
left_bin_edges = 0.0:1.0:6.0
bin(median, left_bin_edges, xs, ys)
```
Functions with additional arguments also work (arguments and keyword
arguments must be supplied last in the function call):
```julia
xs = [1.2, 1.7, 2.2, 3.3, 4.5, 4.6, 7.1]
ys = [4.2, 5.1, 6.5, 4.2, 3.2, 3.1, 2.5]
left_bin_edges = 0.0:1.0:6.0
bin(quantile, left_bin_edges, xs, ys, [0.1])
```
"""
function bin(f::Function, left_bin_edges::AbstractRange{T}, xs, ys, args...; kwargs...) where T
if length(xs) != length(ys)
msg = "`length(xs)` not equal to `length(ys)`"
throw(ArgumentError(msg))
end
# Each bin is represented by (potentially differently sized) vectors of type `eltype(ys)`
YT = eltype(ys)
n_bins = length(left_bin_edges) - 1
bin_vals = [Array{YT}(undef, 0) for i = 1:n_bins]
# Assign values to bins. Can be done faster if `xs` is guaranteed to be ordered.
g_min = minimum(left_bin_edges)
g_step = step(left_bin_edges)
for (x, y) in zip(xs, ys)
arr_idx = ceil(Int, (x - g_min)/g_step)
# Check that the value falls inside the grid; if not, ignore it
if 0 < arr_idx <= n_bins
push!(bin_vals[arr_idx], y)
end
end
# Get bin summaries by applying function to non-empty bins.
bin_summaries = fill(NaN, n_bins)
inds_nonempty_bins = findall(length.(bin_vals) .> 0)
bin_summaries[inds_nonempty_bins] = f.(bin_vals[inds_nonempty_bins], args...; kwargs...)
return bin_summaries
end
"""
bin!(bins::Vector{AbstractVector{T}}, left_bin_edges::AbstractRange{T}, xs, ys) where T
Distribute the elements of `ys` into `N-1` different pre-allocated empty
bin vectors, based on how the values in `xs` are distributed among
the bins defined by the `N` grid points in `left_bin_edges`.
`bins` must be a vector of vector-like mutable containers.
If `xs[i]` falls in the `n`-th bin interval, then `ys[i]`
is assigned to the `n`-th bin vector. If `xs[i]` lie outside the grid,
the corresponding `ys[i]` is ignored.
See also [`bin(::AbstractRange)`](@ref).
"""
function bin!(bins::Vector{AbstractVector{T}}, left_bin_edges::AbstractRange{T}, xs, ys) where T
if length(xs) != length(ys)
msg = "`length(xs)` not equal to `length(ys)`"
throw(ArgumentError(msg))
end
# Each bin is represented by (potentially differently sized) vectors of type `eltype(ys)`
n_bins = length(left_bin_edges) - 1
if length(bins) != n_bins
msg = "`The number of pre-allocated bins ($n_bins) does not match the number of bins defined by the grid in `left_bin_edges`"
throw(ArgumentError(msg))
end
ELTYPE_YS, ELTYPE_BINS = eltype(ys), eltype(eltype(bins))
if ELTYPE_BINS != ELTYPE_YS
msg = "Element type of bin vectors `bins` ($ELTYPE_BINS) is not equal to the element type of `ys` ($ELTYPE_YS)"
end
# Assign values to bins. Can be done faster if `xs` is guaranteed to be ordered.
g_min = minimum(left_bin_edges)
g_step = step(left_bin_edges)
@inbounds for (x, y) in zip(xs, ys)
arr_idx = ceil(Int, (x - g_min)/g_step)
# Check that the value falls inside the grid; if not, ignore it
if 0 < arr_idx <= n_bins
push!(bins[arr_idx], y)
end
end
return bins
end
"""
bin_mean(left_bin_edges::AbstractRange, xs, ys)
Distribute the elements of `ys` into `N - 1` different bin vectors, based on
how the values in `xs` are distributed among the bins defined by the `N` grid
points in `left_bin_edges`. Then compute the bin mean for each bin.
If `xs[i]` falls in the `n`-th bin interval, then `ys[i]` is assigned to the
`n`-th bin vector. If values fall outside the grid, they are ignored (if
`xs[i] < minimum(left_bin_edges)`, ignore `ys[i]`). After the `ys` values
have been assigned to bin vectors, apply the summary function `f` element-wise
to each of the bin vectors, with `args` and `kwargs` as arguments and keyword
arguments.
Returns `N - 1` mean values, one for each bin.
## Examples
```julia
xs = [1.2, 1.7, 2.2, 3.3, 4.5, 4.6, 7.1]
ys = [4.2, 5.1, 6.5, 4.2, 3.2, 3.2, 2.5]
left_bin_edges = 0.0:1.0:6.0
bin_mean(left_bin_edges, xs, ys)
# output
6-element Array{Float64,1}:
NaN
4.65
6.5
4.2
3.2
NaN
```
"""
function bin_mean(left_bin_edges::AbstractRange, xs, ys; nan_threshold = 0)
if length(xs) != length(ys)
msg = "`length(xs)` not equal to `length(ys)`"
throw(ArgumentError(msg))
end
# Check that the value falls inside the grid; if not, ignore it
n_bins = length(left_bin_edges) - 1
bin_sums = fill(0.0, n_bins)
bin_sums_n_entries = fill(0.0, n_bins)
# Assign values to bins. Can be done faster if `xs` is guaranteed to be ordered.
g_min = minimum(left_bin_edges)
g_step = step(left_bin_edges)
for (x, y) in zip(xs, ys)
arr_idx = ceil(Int, (x - g_min)/g_step)
if 0 < arr_idx <= n_bins
bin_sums[arr_idx] += y
bin_sums_n_entries[arr_idx] += 1.0
end
end
# Return bin averages (entries with 0s are represented as NaNs)
bin_avgs = bin_sums ./ bin_sums_n_entries
bin_avgs[isapprox.(bin_avgs, 0.0)] .= NaN
# If there aren't enough entries in a bin, set it to NaN
# and interpolate it instead.
bin_avgs[bin_sums_n_entries .< nan_threshold] .= NaN
return bin_avgs
end
export bin, bin!, bin_mean | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 2162 | """
fill_nans(x, intp::Linear)
Fill `NaN` values in `x` using linear interpolation. `NaN`s at
the left or right edges of `x` are not interpolated, but left
as they are. See also [`fill_nans!`](@ref).
## Example
```julia
x = [NaN, 1.4, 5.6, NaN, 4.3, 3.1, NaN, NaN, 5.6, NaN]
fill_nans(x, Linear())
```
"""
function fill_nans(x, intp::Linear)
if isnan(x[1]) && isnan(x[end])
nan_chunks = findall_nan_chunks(x)[2:end-1]
elseif isnan(x[1])
nan_chunks = findall_nan_chunks(x)[2:end]
elseif isnan(x[end])
nan_chunks = findall_nan_chunks(x)[1:end-1]
else
nan_chunks = findall_nan_chunks(x)
end
x_filled = copy(x)
for (start_idx, stop_idx) in nan_chunks
x1 = start_idx - 1
x2 = stop_idx + 1
y1 = x[start_idx - 1]
y2 = x[stop_idx + 1]
slope = (y2 - y1) / (x2 - x1)
intcpt = y1 - slope*x1
for (i, idx) in enumerate(start_idx:stop_idx)
x_filled[idx] = y1 + i*slope
end
end
return x_filled
end
"""
fill_nans!(x, intp::Linear)
Fill `NaN` values in `x` in-place using linear interpolation. `NaN`s at
the left or right edges of `x` are not interpolated, but left
as they are. See also [`fill_nans`](@ref).
## Example
```julia
x = [NaN, 1.4, 5.6, NaN, 4.3, 3.1, NaN, NaN, 5.6, NaN]
fill_nans!(x, Linear())
```
"""
function fill_nans!(x, intp::Linear)
if isnan(x[1]) && isnan(x[end])
nan_chunks = findall_nan_chunks(x)[2:end-1]
elseif isnan(x[1])
nan_chunks = findall_nan_chunks(x)[2:end]
elseif isnan(x[end])
nan_chunks = findall_nan_chunks(x)[1:end-1]
else
nan_chunks = findall_nan_chunks(x)
end
for (start_idx, stop_idx) in nan_chunks
x1 = start_idx - 1
x2 = stop_idx + 1
y1 = x[start_idx - 1]
y2 = x[stop_idx + 1]
slope = (y2 - y1) / (x2 - x1)
intcpt = y1 - slope*x1
for (i, idx) in enumerate(start_idx:stop_idx)
x[idx] = y1 + i*slope
end
end
return x
end
export fill_nans, fill_nans! | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 2360 | """
findall_nan_chunks(x)
Finds the `(start, stop)` indices of each `NaN` chunk in `x` and returns a vector
of index tuples for the `NaN` ranges.
See also: [`findall_nan_chunks!`](@ref)
## Examples
```julia
x = [NaN, NaN, 2.3, NaN, 5.6, NaN, NaN, NaN]
findall_nan_chunks(x)
```
"""
function findall_nan_chunks(x)
N = length(x)
x_isnans = isnan.(x)
# (start_idx, stop_idx) for each chunk of nans
nan_chunks = Vector{Tuple{Int, Int}}(undef, 0)
i = 1
@inbounds while i <= N
if x_isnans[i] == true
# Now we know that the Nan range starts at position i
j = i
# Update j until there are no more nans
while j < N && x_isnans[j + 1]
j += 1
end
# So now we know the end of the range is at position j
push!(nan_chunks, (i, j))
# Update current position based on how many NaNs we found
i = j + 1
end
i += 1
end
return nan_chunks
end
"""
findall_nan_chunks!(v, x)
Finds the (start,a stop) indices of each `NaN` chunk in `x` and returns a vector
of those index tuples, using a preallocated boolean vector `v`, where
`length(x) == length(v)`, to keep track of `NaN` positions.
See also: [`findall_nan_chunks`](@ref)
## Example
```julia
x = [NaN, NaN, 2.3, NaN, 5.6, NaN, NaN, NaN]
v = zeros(Bool, length(x))
findall_nan_chunks!(v, x)
```
"""
function findall_nan_chunks!(v::AbstractVector{Bool}, x)
v .= isnan.(x)
# (start_idx, stop_idx) for each chunk of nans
nan_chunks = Vector{Tuple{Int, Int}}(undef, 0)
i = 1
N = length(x)
@inbounds while i <= N
if v[i] == true
# Now we know that the Nan range starts at position i
j = i
# Update j until there are no more nans
while j < N && v[j + 1]
j += 1
end
# So now we know the end of the range is at position j
push!(nan_chunks, (i, j))
# Update current position based on how many NaNs we found
i = j + 1
end
i += 1
end
return nan_chunks
end
export findall_nan_chunks, findall_nan_chunks! | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 3385 | """
interpolate_and_bin(
left_bin_edges::AbstractRange{T2}, xs, ys,
intp::Linear, intp_grid::AbstractRange{T1},
extrapolation_bc::Union{<:Real, Interpolations.BoundaryCondition}
f::Function, args...; kwargs...) where {T1, T2}
Linearly interpolate the `xs` and `ys` to `intp_grid`, then bin the interpolated data
on the grid defined by the `N`-element `left_bin_edges` grid. After binning, apply
`f` with arguments `args` and keyword arguments `kwargs` element-wise to each of the bins.
Returns a vector of `N-1` bin summaries.
## Details
Binning is performed *after* interpolating `xs` and `ys` to `intp_grid`. Binning is done
by distributing the `intp_grid` values among the bins defined by `left_bin_edges`. That is,
if `intp_grid[i]` falls in the `k`-th bin, then `intp(xs)[i]` is assigned to the `k`-th bin.
If `left_bin_edges` contain `N` grid points, then there will be `N - 1` bins in total.
If `xs` contain `NaN` values, then these are filled internally by linear interpolation
*before* interpolating to the provided `intp_grid`.
"""
function interpolate_and_bin(f::Function,
left_bin_edges::AbstractRange{T2}, xs, ys,
intp::Linear, intp_grid::AbstractRange{T1}, extrapolation_bc::Union{<:Real, Interpolations.BoundaryCondition},
args...; kwargs...) where {T1, T2}
if length(xs) != length(ys)
msg = "`length(xs)` not equal to `length(ys)`"
throw(ArgumentError(msg))
end
#=
Handle `NaN` values initially present in `xs` by linear interpolation and
extrapolating using the provided boundary condition. Only internal `NaN`s are
interpolated; if there are `NaN`s present at the edges of `xs` initially, then
the corresponding `ys` are ignored.
=#
if any(isnan.(xs))
println("There were `NaN`s in `xs`. Interpolating them by introducing an internal grid in `xs`.")
xs = fill_nans(xs, Linear())
end
if any(isnan.(ys))
println("There were `NaN`s in `ys`. Interpolating them by introducing an internal grid in `ys`.")
ys = fill_nans(ys, Linear())
end
isnotnans = findall(isfinite.(xs) .& isfinite.(ys))
tmp_intp = LinearInterpolation(xs[isnotnans], ys[isnotnans],
extrapolation_bc = extrapolation_bc)
# Interpolate `ys` to `intp_grid`
intp_ys = tmp_intp(intp_grid)
# Each bin is represented by (potentially differently sized) vectors of type `eltype(ys)`
YT = eltype(intp_ys)
n_bins = length(left_bin_edges) - 1
bin_vals = [Array{YT}(undef, 0) for i = 1:n_bins]
# Assign values to bins. Can be done faster if `xs` is guaranteed to be ordered.
g_min = minimum(left_bin_edges)
g_step = step(left_bin_edges)
for (x, y) in zip(intp_grid, intp_ys)
arr_idx = ceil(Int, (x - g_min)/g_step)
# Check that the value falls inside the grid; if not, ignore it
if 0 < arr_idx <= n_bins
push!(bin_vals[arr_idx], y)
end
end
# Get bin summaries by applying function to non-empty bins.
bin_summaries = fill(NaN, n_bins)
inds_nonempty_bins = findall(length.(bin_vals) .> 0)
bin_summaries[inds_nonempty_bins] = f.(bin_vals[inds_nonempty_bins], args...; kwargs...)
return bin_summaries
end
export interpolate_and_bin | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 324 |
abstract type InterpolationGrid end
Base.minimum(g::InterpolationGrid) = g.min
Base.maximum(g::InterpolationGrid) = g.max
Base.min(g::InterpolationGrid) = g.min
Base.max(g::InterpolationGrid) = g.max
Base.range(g::InterpolationGrid) = g.min:g.step:g.max
Base.step(g::InterpolationGrid) = g.step
export InterpolationGrid
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 680 |
"""
IrregularGrid
## Fields
- **gridvals**: The values of the grid.
- **extrapolation_bc**: The extrapolation condition.
"""
struct IrregularGrid{BC <: BoundaryCondition} <: InterpolationGrid
gridvals::Vector{Float64}
extrapolation_bc::Union{BC, Float64}
end
Base.minimum(g::IrregularGrid) = minimum(g.gridvals)
Base.maximum(g::IrregularGrid) = maximum(g.gridvals)
Base.min(g::IrregularGrid) = minimum(g.gridvals)
Base.max(g::IrregularGrid) = maximum(g.gridvals)
Base.range(g::IrregularGrid) =
throw(MethodError("step is not defined for irregular grids"))
Base.step(g::IrregularGrid) =
throw(MethodError("step is not defined for irregular grids"))
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 93 | include("AbstractInterpolationGrid.jl")
include("RegularGrid.jl")
include("IrregularGrid.jl") | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 4162 |
import Interpolations:
BoundaryCondition,
Flat
import ..UncertainDatasets:
AbstractUncertainValueDataset,
UncertainIndexValueDataset
import ..SamplingConstraints:
TruncateQuantiles,
constrain
const EXTRAP_BC = Union{BoundaryCondition, Float64}
##############################################################################
# Rectangular grid composite types
##############################################################################
const BCC = Union{BoundaryCondition, Float64}
"""
RegularGrid
## Fields
- **min**: The minimum value of the grid.
- **max**: The maximum value of the grid.
- **step**: The interval size.
- **extrapolation_bc**: The extrapolation condition. Can also be NaN.
"""
struct RegularGrid <: InterpolationGrid
min::Number
max::Number
step::Number
extrapolation_bc::BCC
end
function get_edgepoints(x::RegularGrid)
x.min:x.step:x.max
end
Base.length(x::RegularGrid) = length(x.min:x.step:x.max)
##############################################################################
# Rectangular grid constructors for different types of uncertain datasets
##############################################################################
function RegularGrid(x::AbstractUncertainValueDataset, n_steps::Int;
extrapolation_bc::EXTRAP_BC = Flat(), round_digits::Int = 7,
trunc_finite::TruncateQuantiles = TruncateQuantiles(0.001, 0.999))
# Constrain to some large quantile to avoid taking the minima and
# maximuma of distributions with infinite supports
constrained_indices = constrain(x, TruncateQuantiles(0.0001, 0.9999))
min_x = floor(minimum(constrained_indices), digits = round_digits)
max_x = ceil(maximum(constrained_indices), digits = round_digits)
RegularGrid(min_x, max_x, (max_x - min_x)/n_steps, extrapolation_bc)
end
function RegularGrid(x::UncertainIndexValueDataset, n_steps::Int;
extrapolation_bc::EXTRAP_BC = Flat(), round_digits::Int = 7,
trunc_finite::TruncateQuantiles = TruncateQuantiles(0.001, 0.999))
# Constrain to some large quantile to avoid taking the minima and
# maximuma of distributions with infinite supports
constrained_indices = constrain(x.indices, TruncateQuantiles(0.0001, 0.9999))
min_x = floor(minimum(constrained_indices), digits = round_digits)
max_x = ceil(maximum(constrained_indices), digits = round_digits)
RegularGrid(min_x, max_x, (max_x - min_x)/n_steps, extrapolation_bc)
end
function RegularGrid(x::AbstractUncertainValueDataset, step::Float64;
extrapolation_bc::EXTRAP_BC = Flat(),
round_digits = 7,
trunc_finite::TruncateQuantiles = TruncateQuantiles(0.001, 0.999))
# Constrain to some large quantile to avoid taking the minima and
# maximuma of distributions with infinite supports
constrained_data = constrain(x, trunc_finite)
min_x = floor(minimum(constrained_data), digits = round_digits)
max_x = ceil(maximum(constrained_data), digits = round_digits)
RegularGrid(min_x, max_x, step, extrapolation_bc)
end
function RegularGrid(x::UncertainIndexValueDataset, step::Float64;
extrapolation_bc::EXTRAP_BC = Flat(), round_digits::Int = 7,
trunc_finite::TruncateQuantiles = TruncateQuantiles(0.001, 0.999))
# Constrain to some large quantile to avoid taking the minima and
# maximuma of distributions with infinite supports
constrained_indices = constrain(x.indices, TruncateQuantiles(0.0001, 0.9999))
min_x = floor(minimum(constrained_indices), digits = round_digits)
max_x = ceil(maximum(constrained_indices), digits = round_digits)
RegularGrid(min_x, max_x, step, extrapolation_bc)
end
RegularGrid(xmin, xmax, step; extrapolation_bc::EXTRAP_BC = Flat()) =
RegularGrid(xmin, xmax, step, extrapolation_bc)
function RegularGrid(xvals::AbstractRange; extrapolation_bc::EXTRAP_BC = Flat())
RegularGrid(minimum(xvals), maximum(xvals), step(xvals), extrapolation_bc)
end
function RegularGrid(xvals::Vector{T}; extrapolation_bc::EXTRAP_BC = Flat()) where {T}
RegularGrid(minimum(xvals), maximum(xvals), xvals[2] - xvals[1], extrapolation_bc)
end
export RegularGrid
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 322 |
import Interpolations.AbstractExtrapolation
abstract type AbstractInterpolationScheme end
struct InterpolationScheme1D <: AbstractInterpolationScheme
xgrid::InterpolationGrid
interpolation_method::AbstractInterpolation
end
export AbstractInterpolationScheme,
InterpolationScheme1D,
InterpolationGrid
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 1684 | include("interpolation_cubicspline.jl")
include("interpolation_linear.jl")
include("../grids/schemes.jl")
"""
Interpolation(x, y, gridargs...; method::Symbol = :linear, kwargs...)
Create an interpolation scheme from a set of `x` values and `y` values (to be interpolated).
`method` sets the interpolation type, and `extrapolation_bc` sets the extrapolation
boundary condition (either a valid `BoundaryCondition` or `NaN`).
"""
function create_interp_scheme(x, y, grid::InterpolationGrid; method::Symbol = :linear,
extrapolation_bc::Union{BoundaryCondition, Float64} = Flat())
if method == :linear
intp = InterpolationScheme1D(grid, linear_interpolation(x, y;
extrapolation_bc = extrapolation_bc))
end
return intp
end
"""
interpolate_nans(grid, x, intp::Linear, extr::BoundaryCondition)
Interpolate `x` (which potentially has `NaN` values) linearly over the
provided `grid`.
If there are `NaN`s at the edges of `x`, then the `extrapolation_bc`
boundary condition is applied (see `Interpolations.BoundaryCondition`
documentation for more details). The boundary condition defaults to `NaN`,
which leaves the `NaN` values at the edges of `x` non-interpolated.
Other boundary conditions, like `Flat(gt)` or `Line(gt)`, with
`gt = OnCell()` or `gt = OnGrid()` will also work.
"""
function interpolate_nans(grid, x, intp::Linear,
extrapolation_bc::Union{Interpolations.BoundaryCondition, Real} = NaN)
idxs_nonnans = findall(.!(isnan.(x)))
ext = LinearInterpolation(grid[idxs_nonnans], x[idxs_nonnans], extrapolation_bc = extrapolation_bc)
ext(grid)
end
export create_interp_scheme, interpolate_nans | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 963 | import Interpolations:
CubicSplineInterpolation,
Line, OnGrid, Throw
"""
Cubic spline interpolation of `x` and `y` on a regular grid `inpt_grid_x`. Returns the
interpolated `y` values.
"""
function cubicspline_interpolation(x::AbstractRange, y, inpt_grid_x;
bc = Line(OnGrid()),
extrapolation_bc = NaN,
sort = true)
# Knots must be sorted in ascending order.
if sort
sort_inds = sortperm(x)
# Interpolation object
itp = CubicSplineInterpolation(x[sort_inds], y[sort_inds],
bc = bc,
extrapolation_bc = extrapolation_bc)
else
itp = CubicSplineInterpolation(x, y,
bc = bc,
extrapolation_bc = extrapolation_bc)
end
# Evaluate the interpolation object at the x-axis grid we provide. These will
# be our interpolated y-axis values
itp(inpt_grid_x)
end
export cubicspline_interpolation | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 849 | import Interpolations:
LinearInterpolation,
Line
"""
linear_interpolation(x, y; extrapolation_bc = NaN, sort = true)
Create a linear interpolation object from two vectors `x` and `y` (to be interpolated).
"""
function linear_interpolation(x, y; extrapolation_bc = NaN, sort = true)
# Knots must be sorted in ascending order.
if sort
sort_inds = sortperm(x)
itp = LinearInterpolation(x[sort_inds], y[sort_inds], extrapolation_bc = extrapolation_bc)
else
itp = LinearInterpolation(x, y, extrapolation_bc = extrapolation_bc)
end
# Don't evaluate the interpolation object on an x-axis grid we provide, but return
# the interpolation object that can be interpolated at a set of x values later
# (i.e. itp(inpt_grid_x))
return itp
end
export linear_interpolation | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 541 | using Reexport
@reexport module UncertainMathematics
include("uncertainvalues/elementary_operations_uncertainvalues.jl")
include("uncertainvalues/elementary_operations_uncertainvalues_special_cases.jl")
include("uncertainvalues/trig_functions_uncertainvalues.jl")
include("uncertaindataset/elementary_operations_uncertaindatasets.jl")
include("uncertainvaluedataset/elementary_operations_uncertainvaluedatasets.jl")
include("uncertainindexdataset/elementary_operations_uncertainindexdatasets.jl")
end # module | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 3448 |
"""
Base.:+(a::UncertainDataset, b::UncertainDataset; n = 10000)
Addition operator for two uncertain value datasets.
To obtain the sum for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th added uncertain value is a kernel density estimate to those sums, i.e.
`added_val = UncertainValue(UnivariateKDE, sample_xα΅’ .+ sample_yα΅’)`.
"""
function Base.:+(a::UncertainDataset, b::UncertainDataset; n = 10000)
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainDataset([a[i] + b[i] for i = 1:N])
end
"""
Base.:+(a::Real, b::UncertainDataset;
n = 10000)
Addition operator for scalars and uncertain value datasets.
To obtain the sum for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th added uncertain value is a kernel density estimate to those sums, i.e.
`added_val = UncertainValue(UnivariateKDE, sample_xα΅’ .+ sample_yα΅’)`.
"""
function Base.:+(a::T, b::UncertainDataset; n = 10000) where {T <: Number}
N = length(a)
UncertainDataset([a + b[i] for i = 1:N])
end
"""
Base.:+(a::Vector{Real}, b::UncertainDataset; n = 10000)
Addition operator for scalars and uncertain value datasets.
To obtain the sum for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th added uncertain value is a kernel density estimate to those sums, i.e.
`added_val = UncertainValue(UnivariateKDE, sample_xα΅’ .+ sample_yα΅’)`.
"""
function Base.:+(a::Vector{T}, b::UncertainDataset; n = 10000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainDataset([a[i] + b[i] for i = 1:N])
end
"""
Base.:+(a::UncertainDataset, b::Real; n = 10000)
Addition scalars to uncertain value datasets.
To obtain the sum for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th added uncertain value is a kernel density estimate to those sums, i.e.
`added_val = UncertainValue(UnivariateKDE, sample_xα΅’ .+ sample_yα΅’)`.
"""
function Base.:+(a::UncertainDataset, b::T; n = 10000) where {T <: Number}
N = length(a)
UncertainDataset([a[i] + b for i = 1:N])
end
"""
Base.:+(a::UncertainDataset, b::Real; n = 10000)
Addition scalars to uncertain value datasets.
To obtain the sum for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th added uncertain value is a kernel density estimate to those sums, i.e.
`added_val = UncertainValue(UnivariateKDE, sample_xα΅’ .+ sample_yα΅’)`.
"""
function Base.:+(a::UncertainDataset, b::Vector{T}; n = 10000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainDataset([a[i] + b[i] for i = 1:N])
end | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 3554 |
"""
Base.:/(a::UncertainDataset, b::UncertainDataset;
n = 10000)
Division operator for two uncertain value datasets.
To obtain the quotient for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th divided uncertain value is a kernel density estimate to those quotients, i.e.
`divided_val = UncertainValue(UnivariateKDE, sample_xα΅’ ./ sample_yα΅’)`.
"""
function Base.:/(a::UncertainDataset, b::UncertainDataset; n = 10000)
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainDataset([a[i] / b[i] for i = 1:N])
end
"""
Base.:/(a::Real, b::UncertainDataset;
n = 10000)
Division operator for scalars and uncertain value datasets.
To obtain the quotient for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th divided uncertain value is a kernel density estimate to those quotients, i.e.
`divided_val = UncertainValue(UnivariateKDE, sample_xα΅’ ./ sample_yα΅’)`.
"""
function Base.:/(a::T, b::UncertainDataset; n = 10000) where {T <: Number}
N = length(a)
UncertainDataset([a / b[i] for i = 1:N])
end
"""
Base.:/(a::Vector{Real}, b::UncertainDataset;
n = 10000)
Division operator for scalars and uncertain value datasets.
To obtain the quotient for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th divided uncertain value is a kernel density estimate to those quotients, i.e.
`divided_val = UncertainValue(UnivariateKDE, sample_xα΅’ ./ sample_yα΅’)`.
"""
function Base.:/(a::Vector{T}, b::UncertainDataset; n = 10000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainDataset([a[i] / b[i] for i = 1:N])
end
"""
Base.:/(a::UncertainDataset, b::Real; n = 10000)
Division operator for scalars and uncertain value datasets.
To obtain the quotient for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th divided uncertain value is a kernel density estimate to those quotients, i.e.
`divided_val = UncertainValue(UnivariateKDE, sample_xα΅’ ./ sample_yα΅’)`.
"""
function Base.:/(a::UncertainDataset, b::T; n = 10000) where {T <: Number}
N = length(a)
UncertainDataset([a[i] / b for i = 1:N])
end
"""
Base.:/(a::UncertainDataset, b::Real; n = 10000)
Division operator for scalars and uncertain value datasets.
To obtain the quotient for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th divided uncertain value is a kernel density estimate to those quotients, i.e.
`divided_val = UncertainValue(UnivariateKDE, sample_xα΅’ ./ sample_yα΅’)`.
"""
function Base.:/(a::UncertainDataset, b::Vector{T}; n = 10000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainDataset([a[i] / b[i] for i = 1:N])
end | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 315 | import ..Resampling: resample
import ..UncertainValues: UncertainValue
import ..UncertainDatasets: UncertainDataset
include("add_uncertaindataset.jl")
include("subtract_uncertaindataset.jl")
include("multiply_uncertaindataset.jl")
include("divide_uncertaindataset.jl")
include("exponentiate_uncertaindataset.jl")
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 1152 |
function Base.:^(a::UncertainDataset, b::UncertainDataset; n = 10000)
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainDataset([a[i] ^ b[i] for i = 1:N])
end
function Base.:^(a::T, b::UncertainDataset; n = 10000) where {T <: Number}
N = length(a)
UncertainDataset([a ^ b[i] for i = 1:N])
end
function Base.:^(a::Vector{T}, b::UncertainDataset; n = 10000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainDataset([a[i] ^ b[i] for i = 1:N])
end
function Base.:^(a::UncertainDataset, b::T; n = 10000) where {T <: Number}
N = length(a)
UncertainDataset([a[i] ^ b for i = 1:N])
end
function Base.:^(a::UncertainDataset, b::Vector{T}; n = 10000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainDataset([a[i] ^ b[i] for i = 1:N])
end | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 3546 |
"""
Base.:*(a::UncertainDataset, b::UncertainDataset; n = 10000)
Multiplication operator for two uncertain value datasets.
To obtain the product for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th multiplied uncertain value is a kernel density estimate to those products, i.e.
`mult_val = UncertainValue(UnivariateKDE, sample_xα΅’ .* sample_yα΅’)`.
"""
function Base.:*(a::UncertainDataset, b::UncertainDataset; n = 10000)
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainDataset([a[i] * b[i] for i = 1:N])
end
"""
Base.:*(a::Real, b::UncertainDataset;
n = 10000)
Multiplication operator for scalars and uncertain value datasets.
To obtain the product for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th multiplied uncertain value is a kernel density estimate to those products, i.e.
`mult_val = UncertainValue(UnivariateKDE, sample_xα΅’ .* sample_yα΅’)`.
"""
function Base.:*(a::T, b::UncertainDataset; n = 10000) where {T <: Number}
N = length(a)
UncertainDataset([a * b[i] for i = 1:N])
end
"""
Base.:*(a::Vector{Real}, b::UncertainDataset;
n = 10000)
Multiplication operator for scalars and uncertain value datasets.
To obtain the product for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th multiplied uncertain value is a kernel density estimate to those products, i.e.
`mult_val = UncertainValue(UnivariateKDE, sample_xα΅’ .* sample_yα΅’)`.
"""
function Base.:*(a::Vector{T}, b::UncertainDataset; n = 10000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainDataset([a[i] * b[i] for i = 1:N])
end
"""
Base.:*(a::UncertainDataset, b::Real; n = 10000)
Multiplication scalars to uncertain value datasets.
To obtain the product for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th multiplied uncertain value is a kernel density estimate to those products, i.e.
`mult_val = UncertainValue(UnivariateKDE, sample_xα΅’ .* sample_yα΅’)`.
"""
function Base.:*(a::UncertainDataset, b::T; n = 10000) where {T <: Number}
N = length(a)
UncertainDataset([a[i] * b for i = 1:N])
end
"""
Base.:*(a::UncertainDataset, b::Real; n = 10000)
Multiplication scalars to uncertain value datasets.
To obtain the product for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th multiplied uncertain value is a kernel density estimate to those products, i.e.
`mult_val = UncertainValue(UnivariateKDE, sample_xα΅’ .* sample_yα΅’)`.
"""
function Base.:*(a::UncertainDataset, b::Vector{T}; n = 10000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainDataset([a[i] * b[i] for i = 1:N])
end | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 3798 |
"""
Base.:-(a::UncertainDataset, b::UncertainDataset;
n = 10000)
Subtraction operator for uncertain value datasets.
To obtain the difference for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th subtracted uncertain value is a kernel density estimate to those differences, i.e.
`subt_val = UncertainValue(UnivariateKDE, sample_xα΅’ .- sample_yα΅’)`.
"""
function Base.:-(a::UncertainDataset, b::UncertainDataset; n = 10000)
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
sum_dists = [resample(a[i], n) .- resample(b[i], n) for i = 1:N]
UncertainDataset([UncertainValue(sum_dists[i]) for i = 1:N])
end
"""
Base.:-(a::Real, b::UncertainDataset;
n = 10000)
Subtraction operator for scalars and uncertain value datasets.
To obtain the difference for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th subtracted uncertain value is a kernel density estimate to those differences, i.e.
`subt_val = UncertainValue(UnivariateKDE, sample_xα΅’ .- sample_yα΅’)`.
"""
function Base.:-(a::T, b::UncertainDataset; n = 10000) where {T <: Number}
N = length(a)
UncertainDataset([UncertainValue(a .- resample(b[i], n)) for i = 1:N])
end
"""
Base.:-(a::Vector{Real}, b::UncertainDataset;
n = 10000)
Subtraction operator for scalars and uncertain value datasets.
To obtain the difference for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th subtracted uncertain value is a kernel density estimate to those differences, i.e.
`subt_val = UncertainValue(UnivariateKDE, sample_xα΅’ .- sample_yα΅’)`.
"""
function Base.:-(a::Vector{T}, b::UncertainDataset; n = 10000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Lengths do not match ($N, $n_vals_b)"))
end
UncertainDataset([UncertainValue(a[i] .- resample(b[i], n)) for i = 1:N])
end
"""
Base.:-(a::UncertainDataset, b::Real;
n = 10000)
Subtraction operator for scalars and uncertain value datasets.
To obtain the difference for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th subtracted uncertain value is a kernel density estimate to those differences, i.e.
`subt_val = UncertainValue(UnivariateKDE, sample_xα΅’ .- sample_yα΅’)`.
"""
function Base.:-(a::UncertainDataset, b::T; n = 10000) where {T <: Number}
N = length(a)
UncertainDataset([UncertainValue(resample(a[i], n) .- b) for i = 1:N])
end
"""
Base.:-(a::UncertainDataset, b::Real;
n = 10000)
Subtraction operator for scalars and uncertain value datasets.
To obtain the difference for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th subtracted uncertain value is a kernel density estimate to those differences, i.e.
`subt_val = UncertainValue(UnivariateKDE, sample_xα΅’ .- sample_yα΅’)`.
"""
function Base.:-(a::UncertainDataset, b::Vector{T}; n = 10000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Lengths do not match ($N, $n_vals_b)"))
end
UncertainDataset([UncertainValue(resample(a[i], n) .- b[i]) for i = 1:N])
end
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 3533 |
"""
Base.:+(a::UncertainIndexDataset, b::UncertainIndexDataset; n = 30000)
Addition operator for two uncertain value datasets.
To obtain the sum for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th added uncertain value is a kernel density estimate to those sums, i.e.
`added_val = UncertainValue(UnivariateKDE, sample_xα΅’ .+ sample_yα΅’)`.
"""
function Base.:+(a::UncertainIndexDataset, b::UncertainIndexDataset; n = 30000)
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainIndexDataset([a[i] + b[i] for i = 1:N])
end
"""
Base.:+(a::Real, b::UncertainIndexDataset;
n = 30000)
Addition operator for scalars and uncertain value datasets.
To obtain the sum for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th added uncertain value is a kernel density estimate to those sums, i.e.
`added_val = UncertainValue(UnivariateKDE, sample_xα΅’ .+ sample_yα΅’)`.
"""
function Base.:+(a::T, b::UncertainIndexDataset; n = 30000) where {T <: Number}
N = length(a)
UncertainIndexDataset([a + b[i] for i = 1:N])
end
"""
Base.:+(a::Vector{Real}, b::UncertainIndexDataset; n = 30000)
Addition operator for scalars and uncertain value datasets.
To obtain the sum for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th added uncertain value is a kernel density estimate to those sums, i.e.
`added_val = UncertainValue(UnivariateKDE, sample_xα΅’ .+ sample_yα΅’)`.
"""
function Base.:+(a::Vector{T}, b::UncertainIndexDataset; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainIndexDataset([a[i] + b[i] for i = 1:N])
end
"""
Base.:+(a::UncertainIndexDataset, b::Real; n = 30000)
Addition scalars to uncertain value datasets.
To obtain the sum for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th added uncertain value is a kernel density estimate to those sums, i.e.
`added_val = UncertainValue(UnivariateKDE, sample_xα΅’ .+ sample_yα΅’)`.
"""
function Base.:+(a::UncertainIndexDataset, b::T; n = 30000) where {T <: Number}
N = length(a)
UncertainIndexDataset([a[i] + b for i = 1:N])
end
"""
Base.:+(a::UncertainIndexDataset, b::Real; n = 30000)
Addition scalars to uncertain value datasets.
To obtain the sum for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th added uncertain value is a kernel density estimate to those sums, i.e.
`added_val = UncertainValue(UnivariateKDE, sample_xα΅’ .+ sample_yα΅’)`.
"""
function Base.:+(a::UncertainIndexDataset, b::Vector{T}; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainIndexDataset([a[i] + b[i] for i = 1:N])
end | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 3639 |
"""
Base.:/(a::UncertainIndexDataset, b::UncertainIndexDataset;
n = 30000)
Division operator for two uncertain value datasets.
To obtain the quotient for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th divided uncertain value is a kernel density estimate to those quotients, i.e.
`divided_val = UncertainValue(UnivariateKDE, sample_xα΅’ ./ sample_yα΅’)`.
"""
function Base.:/(a::UncertainIndexDataset, b::UncertainIndexDataset; n = 30000)
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainIndexDataset([a[i] / b[i] for i = 1:N])
end
"""
Base.:/(a::Real, b::UncertainIndexDataset;
n = 30000)
Division operator for scalars and uncertain value datasets.
To obtain the quotient for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th divided uncertain value is a kernel density estimate to those quotients, i.e.
`divided_val = UncertainValue(UnivariateKDE, sample_xα΅’ ./ sample_yα΅’)`.
"""
function Base.:/(a::T, b::UncertainIndexDataset; n = 30000) where {T <: Number}
N = length(a)
UncertainIndexDataset([a / b[i] for i = 1:N])
end
"""
Base.:/(a::Vector{Real}, b::UncertainIndexDataset;
n = 30000)
Division operator for scalars and uncertain value datasets.
To obtain the quotient for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th divided uncertain value is a kernel density estimate to those quotients, i.e.
`divided_val = UncertainValue(UnivariateKDE, sample_xα΅’ ./ sample_yα΅’)`.
"""
function Base.:/(a::Vector{T}, b::UncertainIndexDataset; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainIndexDataset([a[i] / b[i] for i = 1:N])
end
"""
Base.:/(a::UncertainIndexDataset, b::Real; n = 30000)
Division operator for scalars and uncertain value datasets.
To obtain the quotient for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th divided uncertain value is a kernel density estimate to those quotients, i.e.
`divided_val = UncertainValue(UnivariateKDE, sample_xα΅’ ./ sample_yα΅’)`.
"""
function Base.:/(a::UncertainIndexDataset, b::T; n = 30000) where {T <: Number}
N = length(a)
UncertainIndexDataset([a[i] / b for i = 1:N])
end
"""
Base.:/(a::UncertainIndexDataset, b::Real; n = 30000)
Division operator for scalars and uncertain value datasets.
To obtain the quotient for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th divided uncertain value is a kernel density estimate to those quotients, i.e.
`divided_val = UncertainValue(UnivariateKDE, sample_xα΅’ ./ sample_yα΅’)`.
"""
function Base.:/(a::UncertainIndexDataset, b::Vector{T}; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainIndexDataset([a[i] / b[i] for i = 1:N])
end | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 345 | import ..Resampling: resample
import ..UncertainValues: UncertainValue
import ..UncertainDatasets: UncertainIndexDataset
include("add_uncertainindexdataset.jl")
include("subtract_uncertainindexdataset.jl")
include("multiply_uncertainindexdataset.jl")
include("divide_uncertainindexdataset.jl")
include("exponentiate_uncertainindexdataset.jl")
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 1207 |
function Base.:^(a::UncertainIndexDataset, b::UncertainIndexDataset; n = 30000)
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainIndexDataset([a[i] ^ b[i] for i = 1:N])
end
function Base.:^(a::T, b::UncertainIndexDataset; n = 30000) where {T <: Number}
N = length(a)
UncertainIndexDataset([a ^ b[i] for i = 1:N])
end
function Base.:^(a::Vector{T}, b::UncertainIndexDataset; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainIndexDataset([a[i] ^ b[i] for i = 1:N])
end
function Base.:^(a::UncertainIndexDataset, b::T; n = 30000) where {T <: Number}
N = length(a)
UncertainIndexDataset([a[i] ^ b for i = 1:N])
end
function Base.:^(a::UncertainIndexDataset, b::Vector{T}; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainIndexDataset([a[i] ^ b[i] for i = 1:N])
end | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 3631 |
"""
Base.:*(a::UncertainIndexDataset, b::UncertainIndexDataset; n = 30000)
Multiplication operator for two uncertain value datasets.
To obtain the product for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th multiplied uncertain value is a kernel density estimate to those products, i.e.
`mult_val = UncertainValue(UnivariateKDE, sample_xα΅’ .* sample_yα΅’)`.
"""
function Base.:*(a::UncertainIndexDataset, b::UncertainIndexDataset; n = 30000)
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainIndexDataset([a[i] * b[i] for i = 1:N])
end
"""
Base.:*(a::Real, b::UncertainIndexDataset;
n = 30000)
Multiplication operator for scalars and uncertain value datasets.
To obtain the product for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th multiplied uncertain value is a kernel density estimate to those products, i.e.
`mult_val = UncertainValue(UnivariateKDE, sample_xα΅’ .* sample_yα΅’)`.
"""
function Base.:*(a::T, b::UncertainIndexDataset; n = 30000) where {T <: Number}
N = length(a)
UncertainIndexDataset([a * b[i] for i = 1:N])
end
"""
Base.:*(a::Vector{Real}, b::UncertainIndexDataset;
n = 30000)
Multiplication operator for scalars and uncertain value datasets.
To obtain the product for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th multiplied uncertain value is a kernel density estimate to those products, i.e.
`mult_val = UncertainValue(UnivariateKDE, sample_xα΅’ .* sample_yα΅’)`.
"""
function Base.:*(a::Vector{T}, b::UncertainIndexDataset; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainIndexDataset([a[i] * b[i] for i = 1:N])
end
"""
Base.:*(a::UncertainIndexDataset, b::Real; n = 30000)
Multiplication scalars to uncertain value datasets.
To obtain the product for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th multiplied uncertain value is a kernel density estimate to those products, i.e.
`mult_val = UncertainValue(UnivariateKDE, sample_xα΅’ .* sample_yα΅’)`.
"""
function Base.:*(a::UncertainIndexDataset, b::T; n = 30000) where {T <: Number}
N = length(a)
UncertainIndexDataset([a[i] * b for i = 1:N])
end
"""
Base.:*(a::UncertainIndexDataset, b::Real; n = 30000)
Multiplication scalars to uncertain value datasets.
To obtain the product for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th multiplied uncertain value is a kernel density estimate to those products, i.e.
`mult_val = UncertainValue(UnivariateKDE, sample_xα΅’ .* sample_yα΅’)`.
"""
function Base.:*(a::UncertainIndexDataset, b::Vector{T}; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainIndexDataset([a[i] * b[i] for i = 1:N])
end | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 3883 |
"""
Base.:-(a::UncertainIndexDataset, b::UncertainIndexDataset;
n = 30000)
Subtraction operator for uncertain value datasets.
To obtain the difference for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th subtracted uncertain value is a kernel density estimate to those differences, i.e.
`subt_val = UncertainValue(UnivariateKDE, sample_xα΅’ .- sample_yα΅’)`.
"""
function Base.:-(a::UncertainIndexDataset, b::UncertainIndexDataset; n = 30000)
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
sum_dists = [resample(a[i], n) .- resample(b[i], n) for i = 1:N]
UncertainIndexDataset([UncertainValue(sum_dists[i]) for i = 1:N])
end
"""
Base.:-(a::Real, b::UncertainIndexDataset;
n = 30000)
Subtraction operator for scalars and uncertain value datasets.
To obtain the difference for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th subtracted uncertain value is a kernel density estimate to those differences, i.e.
`subt_val = UncertainValue(UnivariateKDE, sample_xα΅’ .- sample_yα΅’)`.
"""
function Base.:-(a::T, b::UncertainIndexDataset; n = 30000) where {T <: Number}
N = length(a)
UncertainIndexDataset([UncertainValue(a .- resample(b[i], n)) for i = 1:N])
end
"""
Base.:-(a::Vector{Real}, b::UncertainIndexDataset;
n = 30000)
Subtraction operator for scalars and uncertain value datasets.
To obtain the difference for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th subtracted uncertain value is a kernel density estimate to those differences, i.e.
`subt_val = UncertainValue(UnivariateKDE, sample_xα΅’ .- sample_yα΅’)`.
"""
function Base.:-(a::Vector{T}, b::UncertainIndexDataset; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Lengths do not match ($N, $n_vals_b)"))
end
UncertainIndexDataset([UncertainValue(a[i] .- resample(b[i], n)) for i = 1:N])
end
"""
Base.:-(a::UncertainIndexDataset, b::Real;
n = 30000)
Subtraction operator for scalars and uncertain value datasets.
To obtain the difference for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th subtracted uncertain value is a kernel density estimate to those differences, i.e.
`subt_val = UncertainValue(UnivariateKDE, sample_xα΅’ .- sample_yα΅’)`.
"""
function Base.:-(a::UncertainIndexDataset, b::T; n = 30000) where {T <: Number}
N = length(a)
UncertainIndexDataset([UncertainValue(resample(a[i], n) .- b) for i = 1:N])
end
"""
Base.:-(a::UncertainIndexDataset, b::Real;
n = 30000)
Subtraction operator for scalars and uncertain value datasets.
To obtain the difference for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th subtracted uncertain value is a kernel density estimate to those differences, i.e.
`subt_val = UncertainValue(UnivariateKDE, sample_xα΅’ .- sample_yα΅’)`.
"""
function Base.:-(a::UncertainIndexDataset, b::Vector{T}; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Lengths do not match ($N, $n_vals_b)"))
end
UncertainIndexDataset([UncertainValue(resample(a[i], n) .- b[i]) for i = 1:N])
end
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 3533 |
"""
Base.:+(a::UncertainValueDataset, b::UncertainValueDataset; n = 30000)
Addition operator for two uncertain value datasets.
To obtain the sum for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th added uncertain value is a kernel density estimate to those sums, i.e.
`added_val = UncertainValue(UnivariateKDE, sample_xα΅’ .+ sample_yα΅’)`.
"""
function Base.:+(a::UncertainValueDataset, b::UncertainValueDataset; n = 30000)
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainValueDataset([a[i] + b[i] for i = 1:N])
end
"""
Base.:+(a::Real, b::UncertainValueDataset;
n = 30000)
Addition operator for scalars and uncertain value datasets.
To obtain the sum for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th added uncertain value is a kernel density estimate to those sums, i.e.
`added_val = UncertainValue(UnivariateKDE, sample_xα΅’ .+ sample_yα΅’)`.
"""
function Base.:+(a::T, b::UncertainValueDataset; n = 30000) where {T <: Number}
N = length(a)
UncertainValueDataset([a + b[i] for i = 1:N])
end
"""
Base.:+(a::Vector{Real}, b::UncertainValueDataset; n = 30000)
Addition operator for scalars and uncertain value datasets.
To obtain the sum for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th added uncertain value is a kernel density estimate to those sums, i.e.
`added_val = UncertainValue(UnivariateKDE, sample_xα΅’ .+ sample_yα΅’)`.
"""
function Base.:+(a::Vector{T}, b::UncertainValueDataset; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainValueDataset([a[i] + b[i] for i = 1:N])
end
"""
Base.:+(a::UncertainValueDataset, b::Real; n = 30000)
Addition scalars to uncertain value datasets.
To obtain the sum for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th added uncertain value is a kernel density estimate to those sums, i.e.
`added_val = UncertainValue(UnivariateKDE, sample_xα΅’ .+ sample_yα΅’)`.
"""
function Base.:+(a::UncertainValueDataset, b::T; n = 30000) where {T <: Number}
N = length(a)
UncertainValueDataset([a[i] + b for i = 1:N])
end
"""
Base.:+(a::UncertainValueDataset, b::Real; n = 30000)
Addition scalars to uncertain value datasets.
To obtain the sum for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th added uncertain value is a kernel density estimate to those sums, i.e.
`added_val = UncertainValue(UnivariateKDE, sample_xα΅’ .+ sample_yα΅’)`.
"""
function Base.:+(a::UncertainValueDataset, b::Vector{T}; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainValueDataset([a[i] + b[i] for i = 1:N])
end | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 3639 |
"""
Base.:/(a::UncertainValueDataset, b::UncertainValueDataset;
n = 30000)
Division operator for two uncertain value datasets.
To obtain the quotient for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th divided uncertain value is a kernel density estimate to those quotients, i.e.
`divided_val = UncertainValue(UnivariateKDE, sample_xα΅’ ./ sample_yα΅’)`.
"""
function Base.:/(a::UncertainValueDataset, b::UncertainValueDataset; n = 30000)
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainValueDataset([a[i] / b[i] for i = 1:N])
end
"""
Base.:/(a::Real, b::UncertainValueDataset;
n = 30000)
Division operator for scalars and uncertain value datasets.
To obtain the quotient for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th divided uncertain value is a kernel density estimate to those quotients, i.e.
`divided_val = UncertainValue(UnivariateKDE, sample_xα΅’ ./ sample_yα΅’)`.
"""
function Base.:/(a::T, b::UncertainValueDataset; n = 30000) where {T <: Number}
N = length(a)
UncertainValueDataset([a / b[i] for i = 1:N])
end
"""
Base.:/(a::Vector{Real}, b::UncertainValueDataset;
n = 30000)
Division operator for scalars and uncertain value datasets.
To obtain the quotient for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th divided uncertain value is a kernel density estimate to those quotients, i.e.
`divided_val = UncertainValue(UnivariateKDE, sample_xα΅’ ./ sample_yα΅’)`.
"""
function Base.:/(a::Vector{T}, b::UncertainValueDataset; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainValueDataset([a[i] / b[i] for i = 1:N])
end
"""
Base.:/(a::UncertainValueDataset, b::Real; n = 30000)
Division operator for scalars and uncertain value datasets.
To obtain the quotient for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th divided uncertain value is a kernel density estimate to those quotients, i.e.
`divided_val = UncertainValue(UnivariateKDE, sample_xα΅’ ./ sample_yα΅’)`.
"""
function Base.:/(a::UncertainValueDataset, b::T; n = 30000) where {T <: Number}
N = length(a)
UncertainValueDataset([a[i] / b for i = 1:N])
end
"""
Base.:/(a::UncertainValueDataset, b::Real; n = 30000)
Division operator for scalars and uncertain value datasets.
To obtain the quotient for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th divided uncertain value is a kernel density estimate to those quotients, i.e.
`divided_val = UncertainValue(UnivariateKDE, sample_xα΅’ ./ sample_yα΅’)`.
"""
function Base.:/(a::UncertainValueDataset, b::Vector{T}; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainValueDataset([a[i] / b[i] for i = 1:N])
end | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 345 | import ..Resampling: resample
import ..UncertainValues: UncertainValue
import ..UncertainDatasets: UncertainValueDataset
include("add_uncertainvaluedataset.jl")
include("subtract_uncertainvaluedataset.jl")
include("multiply_uncertainvaluedataset.jl")
include("divide_uncertainvaluedataset.jl")
include("exponentiate_uncertainvaluedataset.jl")
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 1207 |
function Base.:^(a::UncertainValueDataset, b::UncertainValueDataset; n = 30000)
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainValueDataset([a[i] ^ b[i] for i = 1:N])
end
function Base.:^(a::T, b::UncertainValueDataset; n = 30000) where {T <: Number}
N = length(a)
UncertainValueDataset([a ^ b[i] for i = 1:N])
end
function Base.:^(a::Vector{T}, b::UncertainValueDataset; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainValueDataset([a[i] ^ b[i] for i = 1:N])
end
function Base.:^(a::UncertainValueDataset, b::T; n = 30000) where {T <: Number}
N = length(a)
UncertainValueDataset([a[i] ^ b for i = 1:N])
end
function Base.:^(a::UncertainValueDataset, b::Vector{T}; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainValueDataset([a[i] ^ b[i] for i = 1:N])
end | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 3631 |
"""
Base.:*(a::UncertainValueDataset, b::UncertainValueDataset; n = 30000)
Multiplication operator for two uncertain value datasets.
To obtain the product for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th multiplied uncertain value is a kernel density estimate to those products, i.e.
`mult_val = UncertainValue(UnivariateKDE, sample_xα΅’ .* sample_yα΅’)`.
"""
function Base.:*(a::UncertainValueDataset, b::UncertainValueDataset; n = 30000)
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainValueDataset([a[i] * b[i] for i = 1:N])
end
"""
Base.:*(a::Real, b::UncertainValueDataset;
n = 30000)
Multiplication operator for scalars and uncertain value datasets.
To obtain the product for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th multiplied uncertain value is a kernel density estimate to those products, i.e.
`mult_val = UncertainValue(UnivariateKDE, sample_xα΅’ .* sample_yα΅’)`.
"""
function Base.:*(a::T, b::UncertainValueDataset; n = 30000) where {T <: Number}
N = length(a)
UncertainValueDataset([a * b[i] for i = 1:N])
end
"""
Base.:*(a::Vector{Real}, b::UncertainValueDataset;
n = 30000)
Multiplication operator for scalars and uncertain value datasets.
To obtain the product for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th multiplied uncertain value is a kernel density estimate to those products, i.e.
`mult_val = UncertainValue(UnivariateKDE, sample_xα΅’ .* sample_yα΅’)`.
"""
function Base.:*(a::Vector{T}, b::UncertainValueDataset; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainValueDataset([a[i] * b[i] for i = 1:N])
end
"""
Base.:*(a::UncertainValueDataset, b::Real; n = 30000)
Multiplication scalars to uncertain value datasets.
To obtain the product for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th multiplied uncertain value is a kernel density estimate to those products, i.e.
`mult_val = UncertainValue(UnivariateKDE, sample_xα΅’ .* sample_yα΅’)`.
"""
function Base.:*(a::UncertainValueDataset, b::T; n = 30000) where {T <: Number}
N = length(a)
UncertainValueDataset([a[i] * b for i = 1:N])
end
"""
Base.:*(a::UncertainValueDataset, b::Real; n = 30000)
Multiplication scalars to uncertain value datasets.
To obtain the product for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th multiplied uncertain value is a kernel density estimate to those products, i.e.
`mult_val = UncertainValue(UnivariateKDE, sample_xα΅’ .* sample_yα΅’)`.
"""
function Base.:*(a::UncertainValueDataset, b::Vector{T}; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
UncertainValueDataset([a[i] * b[i] for i = 1:N])
end | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 3883 |
"""
Base.:-(a::UncertainValueDataset, b::UncertainValueDataset;
n = 30000)
Subtraction operator for uncertain value datasets.
To obtain the difference for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th subtracted uncertain value is a kernel density estimate to those differences, i.e.
`subt_val = UncertainValue(UnivariateKDE, sample_xα΅’ .- sample_yα΅’)`.
"""
function Base.:-(a::UncertainValueDataset, b::UncertainValueDataset; n = 30000)
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Dataset lengths do not match ($N, $n_vals_b)"))
end
sum_dists = [resample(a[i], n) .- resample(b[i], n) for i = 1:N]
UncertainValueDataset([UncertainValue(sum_dists[i]) for i = 1:N])
end
"""
Base.:-(a::Real, b::UncertainValueDataset;
n = 30000)
Subtraction operator for scalars and uncertain value datasets.
To obtain the difference for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th subtracted uncertain value is a kernel density estimate to those differences, i.e.
`subt_val = UncertainValue(UnivariateKDE, sample_xα΅’ .- sample_yα΅’)`.
"""
function Base.:-(a::T, b::UncertainValueDataset; n = 30000) where {T <: Number}
N = length(a)
UncertainValueDataset([UncertainValue(a .- resample(b[i], n)) for i = 1:N])
end
"""
Base.:-(a::Vector{Real}, b::UncertainValueDataset;
n = 30000)
Subtraction operator for scalars and uncertain value datasets.
To obtain the difference for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th subtracted uncertain value is a kernel density estimate to those differences, i.e.
`subt_val = UncertainValue(UnivariateKDE, sample_xα΅’ .- sample_yα΅’)`.
"""
function Base.:-(a::Vector{T}, b::UncertainValueDataset; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Lengths do not match ($N, $n_vals_b)"))
end
UncertainValueDataset([UncertainValue(a[i] .- resample(b[i], n)) for i = 1:N])
end
"""
Base.:-(a::UncertainValueDataset, b::Real;
n = 30000)
Subtraction operator for scalars and uncertain value datasets.
To obtain the difference for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th subtracted uncertain value is a kernel density estimate to those differences, i.e.
`subt_val = UncertainValue(UnivariateKDE, sample_xα΅’ .- sample_yα΅’)`.
"""
function Base.:-(a::UncertainValueDataset, b::T; n = 30000) where {T <: Number}
N = length(a)
UncertainValueDataset([UncertainValue(resample(a[i], n) .- b) for i = 1:N])
end
"""
Base.:-(a::UncertainValueDataset, b::Real;
n = 30000)
Subtraction operator for scalars and uncertain value datasets.
To obtain the difference for a pair of uncertain values `(xα΅’ β a, yα΅’ β b)`, both `uβ` and `uβ` are
resampled `n` times each, so `sample_xα΅’ = resample(x, n)` and `sample_yα΅’ = resample(y, n)`.
The i-th subtracted uncertain value is a kernel density estimate to those differences, i.e.
`subt_val = UncertainValue(UnivariateKDE, sample_xα΅’ .- sample_yα΅’)`.
"""
function Base.:-(a::UncertainValueDataset, b::Vector{T}; n = 30000) where {T <: Number}
N = length(a)
n_vals_b = length(b)
if N != n_vals_b
throw(ArgumentError("Lengths do not match ($N, $n_vals_b)"))
end
UncertainValueDataset([UncertainValue(resample(a[i], n) .- b[i]) for i = 1:N])
end
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 4933 |
##########
# Addition
##########
"""
Base.:+(a::AbstractUncertainValue, b::AbstractUncertainValue) -> UncertainValue
Addition operator for pairs of uncertain values.
Computes the element-wise sum between for a default of `n = 10000` realizations of `a` and
`b`, then returns an uncertain value based on a kernel density estimate to the distribution
of the element-wise sums.
Use the `+(a, b, n)` syntax to tune the number (`n`) of draws.
"""
function Base.:+(a::AbstractUncertainValue, b::AbstractUncertainValue; n::Int = 30000)
UncertainValue(resample(a, n) .+ resample(b, n))
end
"""
Base.:+(a::Real, b::AbstractUncertainValue) -> UncertainValue
Addition operator for between scalars and uncertain values.
Computes the element-wise sum between `a` and `b` for a default of `n = 10000` realizations
of `b`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise sums.
Use the `+(a, b, n)` syntax to tune the number (`n`) of draws.
"""
Base.:+(a::Real, b::AbstractUncertainValue; n::Int = 30000) =
UncertainValue(a .+ resample(b, n))
"""
Base.:+(a::AbstractUncertainValue, b::Real) -> UncertainValue
Addition operator for between uncertain values and scalars.
Computes the element-wise sum between `a` and `b` for a default of `n = 10000` realizations
of `a`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise sums.
Use the `+(a, b, n)` syntax to tune the number (`n`) of draws.
"""
Base.:+(a::AbstractUncertainValue, b::Real; n::Int = 30000) =
UncertainValue(resample(a, n) .+ b)
"""
Base.:+(a::AbstractUncertainValue, b::AbstractUncertainValue, n::Int) -> UncertainValue
Addition operator for pairs of uncertain values.
Computes the element-wise sum between `a` and `b` for `n` realizations
of `a` and `b`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise sums.
Call this function using the `+(a, b, n)` syntax.
"""
function Base.:+(a::AbstractUncertainValue, b::AbstractUncertainValue, n::Int)
UncertainValue(resample(a, n) .+ resample(b, n))
end
"""
Base.:+(a::Real, b::AbstractUncertainValue, n::Int) -> UncertainValue
Addition operator for scalar-uncertain value pairs.
Computes the element-wise sum between `a` and `b` for `n` realizations
of `b`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise sums.
Call this function using the `+(a, b, n)` syntax.
"""
Base.:+(a::Real, b::AbstractUncertainValue, n::Int) =
UncertainValue(a .+ resample(b, n))
"""
Base.:+(a::AbstractUncertainValue, b::Real, n::Int) -> UncertainValue
Addition operator for scalar-uncertain value pairs.
Computes the element-wise sum between `a` and `b` for `n` realizations
of `a`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise sums.
Call this function using the `+(a, b, n)` syntax.
"""
Base.:+(a::AbstractUncertainValue, b::Real, n::Int) =
UncertainValue(resample(a, n) .+ b)
#######################################
# Adding vectors of uncertain values
#######################################
function Base.:+(a::AbstractVector{AbstractUncertainValue},
b::AbstractVector{AbstractUncertainValue})
[a[i] + b[i] for i = 1:length(a)]
end
function Base.:+(a::AbstractVector{AbstractUncertainValue}, b::AbstractUncertainValue)
[a[i] + b for i = 1:length(a)]
end
function Base.:+(a::AbstractUncertainValue, b::AbstractVector{AbstractUncertainValue})
[a + b[i] for i = 1:length(b)]
end
function Base.:+(a::AbstractVector{AbstractUncertainValue},
b::AbstractVector{AbstractUncertainValue}, n::Int)
[+(a[i], b[i], n) for i = 1:length(a)]
end
function Base.:+(a::AbstractVector{AbstractUncertainValue},
b::AbstractUncertainValue, n::Int)
[+(a[i], b, n) for i = 1:length(a)]
end
function Base.:+(a::AbstractUncertainValue,
b::AbstractVector{AbstractUncertainValue}, n::Int)
[+(a, b[i], n) for i = 1:length(b)]
end
#####################################################################################
# Special cases
#####################################################################################
import ..UncertainValues: CertainValue
##################
# `CertainValue`s
#################
"""
Base.:+(a::Union{CertainValue, Real}, b::Union{CertainValue, Real})
Addition of certain values with themselves or scalars acts as regular addition, but
returns the result wrapped in a `CertainValue` instance.
"""
Base.:+(a::Union{CertainValue, Real}, b::Union{CertainValue, Real})
Base.:+(a::CertainValue, b::CertainValue) = CertainValue(a.value + b.value)
Base.:+(a::CertainValue, b::Real) = CertainValue(a.value + b)
Base.:+(a::Real, b::CertainValue) = CertainValue(a + b.value)
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 4001 | ################
# Division
################
"""
Base.:/(a::AbstractUncertainValue, b::AbstractUncertainValue) -> UncertainValue
Division operator for pairs of uncertain values.
Computes the element-wise quotients between for a default of `n = 10000` realizations of `a` and
`b`, then returns an uncertain value based on a kernel density estimate to the distribution
of the element-wise quotients.
Use the `/(a, b, n)` syntax to tune the number (`n`) of draws.
"""
function Base.:/(a::AbstractUncertainValue, b::AbstractUncertainValue; n::Int = 30000)
UncertainValue(resample(a, n) ./ resample(b, n))
end
"""
Base.:/(a::Real, b::AbstractUncertainValue) -> UncertainValue
Division operator for between scalars and uncertain values.
Computes the element-wise quotients between `a` and `b` for a default of `n = 10000` realizations
of `b`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise quotients.
Use the `/(a, b, n)` syntax to tune the number (`n`) of draws.
"""
Base.:/(a::Real, b::AbstractUncertainValue; n::Int = 30000) =
UncertainValue(a ./ resample(b, n))
"""
Base.:/(a::AbstractUncertainValue, b::Real) -> UncertainValue
Division operator for between uncertain values and scalars.
Computes the element-wise quotients between `a` and `b` for a default of `n = 10000` realizations
of `a`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise quotients.
Use the `/(a, b, n)` syntax to tune the number (`n`) of draws.
"""
Base.:/(a::AbstractUncertainValue, b::Real; n::Int = 30000) =
UncertainValue(resample(a, n) ./ b)
"""
Base.:/(a::AbstractUncertainValue, b::AbstractUncertainValue, n::Int) -> UncertainValue
Division operator for pairs of uncertain values.
Computes the element-wise quotients between `a` and `b` for `n` realizations
of `a` and `b`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise quotients.
Call this function using the `/(a, b, n)` syntax.
"""
function Base.:/(a::AbstractUncertainValue, b::AbstractUncertainValue, n::Int)
UncertainValue(resample(a, n) ./ resample(b, n))
end
"""
Base.:/(a::Real, b::AbstractUncertainValue, n::Int) -> UncertainValue
Division operator for scalar-uncertain value pairs.
Computes the element-wise quotients between `a` and `b` for `n` realizations
of `b`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise quotients.
Call this function using the `/(a, b, n)` syntax.
"""
Base.:/(a::Real, b::AbstractUncertainValue, n::Int) =
UncertainValue(a ./ resample(b, n))
"""
Base.:/(a::AbstractUncertainValue, b::Real, n::Int) -> UncertainValue
Division operator for scalar-uncertain value pairs.
Computes the element-wise quotients between `a` and `b` for `n` realizations
of `a`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise quotients.
Call this function using the `/(a, b, n)` syntax.
"""
Base.:/(a::AbstractUncertainValue, b::Real, n::Int) =
UncertainValue(resample(a, n) ./ b)
#####################################################################################
# Special cases
#####################################################################################
import ..UncertainValues: CertainValue
##################
# `CertainValue`s
#################
"""
Base.:/(a::Union{CertainValue, Real}, b::Union{CertainValue, Real})
Division of certain values with themselves or scalars acts as regular division, but
returns the result wrapped in a `CertainValue` instance.
"""
Base.:/(a::Union{CertainValue, Real}, b::Union{CertainValue, Real})
Base.:/(a::CertainValue, b::CertainValue) = CertainValue(a.value / b.value)
Base.:/(a::CertainValue, b::Real) = CertainValue(a.value / b)
Base.:/(a::Real, b::CertainValue) = CertainValue(a / b.value)
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 308 | import ..UncertainValues:
UncertainValue,
AbstractUncertainValue
import ..Resampling:
resample
include("add_uncertainvalues.jl")
include("subtract_uncertainvalues.jl")
include("multiply_uncertainvalues.jl")
include("divide_uncertainvalues.jl")
include("exponentiation_uncertainvalues.jl")
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 2202 | operators = [:(+), :(-), :(*), :(/)]
for operator in operators
f = Meta.parse("Base.:$(operator)")
elementwise_operator = Meta.parse(".$(operator)")
funcs = quote
"""
$($f)(a::CertainValue, b::AbstractUncertainValue; n::Int = 30000)
Compute `a $($operator) b`. Treats the certain value as a scalar and performs the
operation element-wise on a default of `n = 30000` realizations of `b`.
To tune the number of draws to `n`, use the `$($operator)(a, b, n::Int)` syntax.
"""
function $(f)(a::CertainValue, b::AbstractUncertainValue; n::Int = 30000)
$(elementwise_operator)(a.value, b, n)
end
"""
$($f)(a::AbstractUncertainValue, b::CertainValue; n::Int = 30000)
Compute `a $($operator) b`. Treats the certain value as a scalar and performs the
operation element-wise on a default of `n = 30000` realizations of `a`.
To tune the number of draws to `n`, use the `$($operator)(a, b, n::Int)` syntax.
"""
function $(f)(a::AbstractUncertainValue, b::CertainValue; n::Int = 30000)
$(elementwise_operator)(a, b.value, n)
end
"""
$($f)(a::AbstractUncertainValue, b::CertainValue; n::Int)
Compute `a $($operator) b`. Treats the certain value as a scalar and performs the
operation element-wise on `n` realizations of `a`.
This function is called with the `$($operator)(a, b, n::Int)` syntax.
"""
function $(f)(a::AbstractUncertainValue, b::CertainValue, n::Int)
$(elementwise_operator)(a, b.value, n)
end
"""
$($f)(a::CertainValue, b::AbstractUncertainValue, n::Int)
Compute `a $($operator) b`. Treats the certain value as a scalar and performs the
operation element-wise on `n` realizations of `b`.
This function is called with the `$($operator)(a, b, n::Int)` syntax.
"""
function $(f)(a::CertainValue, b::AbstractUncertainValue, n::Int)
$(elementwise_operator)(a.value, b, n)
end
end
eval(funcs)
end
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 5258 |
################
# Exponentiation
################
"""
Base.:^(a::AbstractUncertainValue, b::AbstractUncertainValue) -> UncertainValue
Exponentiation operator for pairs of uncertain values.
The operator first computes a default of `n = 10000` realizations of both `a` and `b`,
which gives `10000` base-exponent pairs. Then, it exponentiates element-wise over these
base-exponent pairs, and finally returns an uncertain value based on a kernel density
estimate to the distribution of numbers resulting from the exponentiation operations.
Use the `^(a, b, n)` syntax to tune the number (`n`) of draws.
"""
function Base.:^(a::AbstractUncertainValue, b::AbstractUncertainValue; n::Int = 30000)
UncertainValue(resample(a, n) .^ resample(b, n))
end
"""
Base.:^(a::Real, b::AbstractUncertainValue) -> UncertainValue
Exponentiation operator for between scalars and uncertain values.
The operator first computes a default of `n = 10000` realizations of `b`, which are used
as exponents. Then, it makes `10000` base-exponent pairs, where the base is always `a` and
the exponents are the exponents generated from `b`. Next, it exponentiates element-wise
over these base-exponent pairs, and finally returns an uncertain value based on a kernel
density estimate to the distribution of numbers resulting from the exponentiation operations.
Use the `^(a, b, n)` syntax to tune the number (`n`) of draws.
"""
Base.:^(a::Real, b::AbstractUncertainValue; n::Int = 30000) =
UncertainValue(a .^ resample(b, n))
"""
Base.:^(a::AbstractUncertainValue, b::Real) -> UncertainValue
Exponentiation operator for between uncertain values and scalars.
The operator first computes a default of `n = 10000` realizations of `a`, which are used
as exponents. Then, it makes `10000` base-exponent pairs, where the base is always `b` and
the exponents are the exponents generated from `a`. Next, it exponentiates element-wise
over these base-exponent pairs, and finally returns an uncertain value based on a kernel
density estimate to the distribution of numbers resulting from the exponentiation operations.
Use the `^(a, b, n)` syntax to tune the number (`n`) of draws.
"""
Base.:^(a::AbstractUncertainValue, b::Real; n::Int = 30000) =
UncertainValue(resample(a, n) .^ b)
"""
Base.:^(a::AbstractUncertainValue, b::AbstractUncertainValue, n::Int) -> UncertainValue
Exponentiation operator for pairs of uncertain values.
The operator first computes `n` realizations of both `a` and `b`,
which gives `n` base-exponent pairs. Then, it exponentiates element-wise over these
base-exponent pairs, and finally returns an uncertain value based on a kernel density
estimate to the distribution of numbers resulting from the exponentiation operations.
Call this function using the `^(a, b, n)` syntax.
"""
function Base.:^(a::AbstractUncertainValue, b::AbstractUncertainValue, n::Int)
UncertainValue(resample(a, n) .^ resample(b, n))
end
"""
Base.:^(a::Real, b::AbstractUncertainValue, n::Int) -> UncertainValue
Exponentiation operator for between scalars and uncertain values.
The operator first computes `n = 10000` realizations of `b`, which are used
as exponents. Then, it makes `n` base-exponent pairs, where the base is always `a` and
the exponents are the exponents generated from `b`. Next, it exponentiates element-wise
over these base-exponent pairs, and finally returns an uncertain value based on a kernel
density estimate to the distribution of numbers resulting from the exponentiation operations.
Call this function using the `^(a, b, n)` syntax.
"""
Base.:^(a::Real, b::AbstractUncertainValue, n::Int) =
UncertainValue(a .^ resample(b, n))
"""
Base.:^(a::AbstractUncertainValue, b::Real, n::Int) -> UncertainValue
Exponentiation operator for between scalars and uncertain values.
The operator first computes `n = 10000` realizations of `a`, which are used
as exponents. Then, it makes `n` base-exponent pairs, where the base is always `b` and
the exponents are the exponents generated from `a`. Next, it exponentiates element-wise
over these base-exponent pairs, and finally returns an uncertain value based on a kernel
density estimate to the distribution of numbers resulting from the exponentiation operations.
Call this function using the `^(a, b, n)` syntax.
"""
Base.:^(a::AbstractUncertainValue, b::Real, n::Int) =
UncertainValue(resample(a, n) .^ b)
#####################################################################################
# Special cases
#####################################################################################
import ..UncertainValues: CertainValue
##################
# `CertainValue`s
#################
"""
Base.:^(a::Union{CertainValue, Real}, b::Union{CertainValue, Real})
Exponentiation of certain values with themselves or scalars acts as regular exponentiation,
but returns the result wrapped in a `CertainValue` instance.
"""
Base.:^(a::Union{CertainValue, Real}, b::Union{CertainValue, Real})
Base.:^(a::CertainValue, b::CertainValue) = CertainValue(a.value ^ b.value)
Base.:^(a::CertainValue, b::Real) = CertainValue(a.value ^ b)
Base.:^(a::Real, b::CertainValue) = CertainValue(a ^ b.value)
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 4044 |
################
# Multiplication
################
"""
Base.:*(a::AbstractUncertainValue, b::AbstractUncertainValue) -> UncertainValue
Multiplication operator for pairs of uncertain values.
Computes the element-wise products between for a default of `n = 10000` realizations of `a` and
`b`, then returns an uncertain value based on a kernel density estimate to the distribution
of the element-wise products.
Use the `*(a, b, n)` syntax to tune the number (`n`) of draws.
"""
function Base.:*(a::AbstractUncertainValue, b::AbstractUncertainValue; n::Int = 30000)
UncertainValue(resample(a, n) .* resample(b, n))
end
"""
Base.:*(a::Real, b::AbstractUncertainValue) -> UncertainValue
Multiplication operator for between scalars and uncertain values.
Computes the element-wise products between `a` and `b` for a default of `n = 10000` realizations
of `b`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise products.
Use the `*(a, b, n)` syntax to tune the number (`n`) of draws.
"""
Base.:*(a::Real, b::AbstractUncertainValue; n::Int = 30000) =
UncertainValue(a .* resample(b, n))
"""
Base.:*(a::AbstractUncertainValue, b::Real) -> UncertainValue
Multiplication operator for between uncertain values and scalars.
Computes the element-wise products between `a` and `b` for a default of `n = 10000` realizations
of `a`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise products.
Use the `*(a, b, n)` syntax to tune the number (`n`) of draws.
"""
Base.:*(a::AbstractUncertainValue, b::Real; n::Int = 30000) =
UncertainValue(resample(a, n) .* b)
"""
Base.:*(a::AbstractUncertainValue, b::AbstractUncertainValue, n::Int) -> UncertainValue
Multiplication operator for pairs of uncertain values.
Computes the element-wise products between `a` and `b` for `n` realizations
of `a` and `b`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise products.
Call this function using the `*(a, b, n)` syntax.
"""
function Base.:*(a::AbstractUncertainValue, b::AbstractUncertainValue, n::Int)
UncertainValue(resample(a, n) .* resample(b, n))
end
"""
Base.:*(a::Real, b::AbstractUncertainValue, n::Int) -> UncertainValue
Multiplication operator for scalar-uncertain value pairs.
Computes the element-wise products between `a` and `b` for `n` realizations
of `b`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise products.
Call this function using the `*(a, b, n)` syntax.
"""
Base.:*(a::Real, b::AbstractUncertainValue, n::Int) =
UncertainValue(a .* resample(b, n))
"""
Base.:*(a::AbstractUncertainValue, b::Real, n::Int) -> UncertainValue
Multiplication operator for scalar-uncertain value pairs.
Computes the element-wise products between `a` and `b` for `n` realizations
of `a`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise products.
Call this function using the `*(a, b, n)` syntax.
"""
Base.:*(a::AbstractUncertainValue, b::Real, n::Int) =
UncertainValue(resample(a, n) .* b)
#####################################################################################
# Special cases
#####################################################################################
import ..UncertainValues: CertainValue
##################
# `CertainValue`s
#################
"""
Base.:*(a::Union{CertainValue, Real}, b::Union{CertainValue, Real})
Multiplication of certain values with themselves or scalars acts as regular multiplication,
but returns the result wrapped in a `CertainValue` instance.
"""
Base.:*(a::Union{CertainValue, Real}, b::Union{CertainValue, Real})
Base.:*(a::CertainValue, b::CertainValue) = CertainValue(a.value * b.value)
Base.:*(a::CertainValue, b::Real) = CertainValue(a.value * b)
Base.:*(a::Real, b::CertainValue) = CertainValue(a * b.value)
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 4135 | import ..UncertainValues:
AbstractUncertainValue
import ..Resampling:
resample
#############
# Subtraction
#############
"""
Base.:-(a::AbstractUncertainValue, b::AbstractUncertainValue) -> UncertainValue
Subtraction operator for pairs of uncertain values.
Computes the element-wise differences between for a default of `n = 30000` realizations of `a` and
`b`, then returns an uncertain value based on a kernel density estimate to the distribution
of the element-wise differences.
Use the `-(a, b, n)` syntax to tune the number (`n`) of draws.
"""
function Base.:-(a::AbstractUncertainValue, b::AbstractUncertainValue; n::Int = 30000)
UncertainValue(resample(a, n) .- resample(b, n))
end
"""
Base.:-(a::Real, b::AbstractUncertainValue) -> UncertainValue
Subtraction operator for between scalars and uncertain values.
Computes the element-wise differences between `a` and `b` for a default of `n = 30000` realizations
of `b`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise differences.
Use the `-(a, b, n)` syntax to tune the number (`n`) of draws.
"""
Base.:-(a::Real, b::AbstractUncertainValue; n::Int = 30000) =
UncertainValue(a .- resample(b, n))
"""
Base.:-(a::AbstractUncertainValue, b::Real) -> UncertainValue
Subtraction operator for between uncertain values and scalars.
Computes the element-wise differences between `a` and `b` for a default of `n = 30000` realizations
of `a`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise differences.
Use the `-(a, b, n)` syntax to tune the number (`n`) of draws.
"""
Base.:-(a::AbstractUncertainValue, b::Real; n::Int = 30000) =
UncertainValue(resample(a, n) .- b)
"""
Base.:-(a::AbstractUncertainValue, b::AbstractUncertainValue, n::Int) -> UncertainValue
Subtraction operator for pairs of uncertain values.
Computes the element-wise differences between `a` and `b` for `n` realizations
of `a` and `b`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise differences.
Call this function using the `-(a, b, n)` syntax.
"""
function Base.:-(a::AbstractUncertainValue, b::AbstractUncertainValue, n::Int)
UncertainValue(resample(a, n) .- resample(b, n))
end
"""
Base.:-(a::Real, b::AbstractUncertainValue, n::Int) -> UncertainValue
Subtraction operator for scalar-uncertain value pairs.
Computes the element-wise differences between `a` and `b` for `n` realizations
of `b`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise differences.
Call this function using the `-(a, b, n)` syntax.
"""
Base.:-(a::Real, b::AbstractUncertainValue, n::Int) =
UncertainValue(a .- resample(b, n))
"""
Base.:-(a::AbstractUncertainValue, b::Real, n::Int) -> UncertainValue
Subtraction operator for scalar-uncertain value pairs.
Computes the element-wise differences between `a` and `b` for `n` realizations
of `a`, then returns an uncertain value based on a kernel density estimate to the
distribution of the element-wise differences.
Call this function using the `-(a, b, n)` syntax.
"""
Base.:-(a::AbstractUncertainValue, b::Real, n::Int) =
UncertainValue(resample(a, n) .- b)
#####################################################################################
# Special cases
#####################################################################################
import ..UncertainValues: CertainValue
##################
# `CertainValue`s
#################
"""
Base.:-(a::Union{CertainValue, Real}, b::Union{CertainValue, Real})
Subtraction of certain values with themselves or scalars acts as regular subtraction,
but returns the result wrapped in a `CertainValue` instance.
"""
Base.:-(a::Union{CertainValue, Real}, b::Union{CertainValue, Real})
Base.:-(a::CertainValue, b::CertainValue) = CertainValue(a.value - b.value)
Base.:-(a::CertainValue, b::Real) = CertainValue(a.value - b)
Base.:-(a::Real, b::CertainValue) = CertainValue(a - b.value)
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 26519 | import ..UncertainValues:
AbstractUncertainValue
import ..Resampling:
resample
# Cosine functions
"""
Base.cos(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the cosine of the uncertain value `x`, where `x` is in radians. Computes the
element-wise cosine for `n` realizations.
"""
Base.cos(x::AbstractUncertainValue; n::Int = 10000) = cos.(resample(x, n))
"""
Base.cos(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the cosine of the uncertain value `x`, where `x` is in radians. Computes the
element-wise cosine for `n` realizations.
"""
Base.cos(x::AbstractUncertainValue, n::Int) = cos.(resample(x, n))
"""
Base.cos(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the cosine of the uncertain value `x`, where `x` is in degrees. Computes the
element-wise cosine for `n` realizations.
"""
Base.cosd(x::AbstractUncertainValue; n::Int = 10000) = cosd.(resample(x, n))
"""
Base.cos(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the cosine of the uncertain value `x`, where `x` is in degrees. Computes the
element-wise cosine for `n` realizations.
"""
Base.cosd(x::AbstractUncertainValue, n::Int) = cosd.(resample(x, n))
"""
Base.cos(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the hyperbolic cosine of the uncertain value `x`.
Computes the element-wise hyperbolic cosine for `n` realizations.
"""
Base.cosh(x::AbstractUncertainValue; n::Int = 10000) = cosh.(resample(x, n))
"""
Base.cos(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the hyperbolic cosine of the uncertain value `x`.
Computes the element-wise hyperbolic cosine for `n` realizations.
"""
Base.cosh(x::AbstractUncertainValue, n::Int) = cosh.(resample(x, n))
# Sine functions
"""
Base.sin(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the sine of the uncertain value `x`, where `x` is in radians. Computes the
element-wise sine for `n` realizations.
"""
Base.sin(x::AbstractUncertainValue; n::Int = 10000) = sin.(resample(x, n))
"""
Base.sin(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the sine of the uncertain value `x`, where `x` is in radians. Computes the
element-wise sine for `n` realizations.
"""
Base.sin(x::AbstractUncertainValue, n::Int) = sin.(resample(x, n))
"""
Base.sind(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the sine of the uncertain value `x`, where `x` is in degrees. Computes the
element-wise sine for `n` realizations.
"""
Base.sind(x::AbstractUncertainValue; n::Int = 10000) = sind.(resample(x, n))
"""
Base.sind(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the sine of the uncertain value `x`, where `x` is in degrees. Computes the
element-wise sine for `n` realizations.
"""
Base.sind(x::AbstractUncertainValue, n::Int) = sind.(resample(x, n))
"""
Base.sinh(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the hyperbolic sine of the uncertain value `x`.
Computes the element-wise hyperbolic sine for `n` realizations.
"""
Base.sinh(x::AbstractUncertainValue; n::Int = 10000) = sinh.(resample(x, n))
"""
Base.sinh(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the hyperbolic sine of the uncertain value `x`.
Computes the element-wise hyperbolic sine for `n` realizations.
"""
Base.sinh(x::AbstractUncertainValue, n::Int) = sinh.(resample(x, n))
# Tan functions
"""
Base.tan(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the tangent of the uncertain value `x`, where `x` is in radians. Computes the
element-wise tangent for `n` realizations.
"""
Base.tan(x::AbstractUncertainValue; n::Int = 10000) = tan.(resample(x, n))
"""
Base.tan(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the tangent of the uncertain value `x`, where `x` is in radians. Computes the
element-wise tangent for `n` realizations.
"""
Base.tan(x::AbstractUncertainValue, n::Int) = tan.(resample(x, n))
"""
Base.tand(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the tangent of the uncertain value `x`, where `x` is in degrees. Computes the
element-wise tangent for `n` realizations.
"""
Base.tand(x::AbstractUncertainValue; n::Int = 10000) = tand.(resample(x, n))
"""
Base.tand(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the tangent of the uncertain value `x`, where `x` is in degrees. Computes the
element-wise tangent for `n` realizations.
"""
Base.tand(x::AbstractUncertainValue, n::Int) = tand.(resample(x, n))
"""
Base.tanh(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the hyperbolic tangent of the uncertain value `x`.
Computes the element-wise hyperbolic tangent for `n` realizations.
"""
Base.tanh(x::AbstractUncertainValue; n::Int = 10000) = tanh.(resample(x, n))
"""
Base.tanh(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the hyperbolic tangent of the uncertain value `x`.
Computes the element-wise hyperbolic tangent for `n` realizations.
"""
Base.tanh(x::AbstractUncertainValue, n::Int) = tanh.(resample(x, n))
# Other
"""
Base.sincos(x::AbstractUncertainValue; n::Int = 10000)
Simultaneously compute the sine and cosine of the uncertain value `x`, where `x` is in
radians. Computes the element-wise `sincos` for `n` realizations.
"""
Base.sincos(x::AbstractUncertainValue; n::Int = 10000) = sincos.(resample(x, n))
"""
Base.sincos(x::AbstractUncertainValue, n::Int = 10000)
Simultaneously compute the sine and cosine of the uncertain value `x`, where `x` is in
radians. Computes the element-wise `sincos` for `n` realizations.
"""
Base.sincos(x::AbstractUncertainValue, n::Int) = sincos.(resample(x, n))
"""
Base.sinc(x::AbstractUncertainValue; n::Int = 10000)
In an element-wise manner for `n` realizations of the uncertain value `x`, compute
``\\sin(\\pi x) / (\\pi x)`` if ``x \\neq 0``, and ``1`` if ``x = 0``.
"""
Base.sinc(x::AbstractUncertainValue; n::Int = 10000) = sinc.(resample(x, n))
"""
Base.sinc(x::AbstractUncertainValue, n::Int = 10000)
Compute ``\\sin(\\pi x) / (\\pi x)`` if ``x \\neq 0``, and ``1`` if ``x = 0`` element-wise
over `n` realizations of the uncertain value `x`.
"""
Base.sinc(x::AbstractUncertainValue, n::Int) = sinc.(resample(x, n))
"""
Base.sinpi(x::AbstractUncertainValue; n::Int = 10000)
Compute ``\\sin(\\pi x)`` more accurately than `sin(pi*x)`, especially for large `x`,
in an element-wise over `n` realizations of the uncertain value `x`.
"""
Base.sinpi(x::AbstractUncertainValue; n::Int = 10000) = sinpi.(resample(x, n))
"""
Base.sinpi(x::AbstractUncertainValue; n::Int = 10000)
Compute ``\\sin(\\pi x)`` more accurately than `sin(pi*x)`, especially for large `x`,
in an element-wise over `n` realizations of the uncertain value `x`.
"""
Base.sinpi(x::AbstractUncertainValue, n::Int) = sinpi.(resample(x, n))
"""
Base.cosc(x::AbstractUncertainValue; n::Int = 10000)
Compute ``\\cos(\\pi x) / x - \\sin(\\pi x) / (\\pi x^2)`` if ``x \\neq 0``, and ``0`` if
``x = 0``, in an element-wise manner over `n` realizations of the uncertain value `x`.
This is the derivative of `sinc(x)`.
"""
Base.cosc(x::AbstractUncertainValue; n::Int = 10000) = cosc.(resample(x, n))
"""
Base.cosc(x::AbstractUncertainValue, n::Int = 10000)
Compute ``\\cos(\\pi x) / x - \\sin(\\pi x) / (\\pi x^2)`` if ``x \\neq 0``, and ``0`` if
``x = 0``, in an element-wise manner over `n` realizations of the uncertain value `x`.
This is the derivative of `sinc(x)`.
"""
Base.cosc(x::AbstractUncertainValue, n::Int) = cosc.(resample(x, n))
"""
Base.cospi(x::AbstractUncertainValue; n::Int = 10000)
Compute ``\\cos(\\pi x)`` more accurately than `cos(pi*x)`, especially for large `x`,
in an element-wise over `n` realizations of the uncertain value `x`.
"""
Base.cospi(x::AbstractUncertainValue; n::Int = 10000) = cospi.(resample(x, n))
"""
Base.cospi(x::AbstractUncertainValue, n::Int = 10000)
Compute ``\\cos(\\pi x)`` more accurately than `cos(pi*x)`, especially for large `x`,
in an element-wise over `n` realizations of the uncertain value `x`.
"""
Base.cospi(x::AbstractUncertainValue, n::Int) = cospi.(resample(x, n))
############################
# Inverse trig functions
############################
"""
Base.acos(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the inverse cosine of the uncertain value `x`, where `x` is in radians. Computes the
element-wise inverse cosine for `n` realizations.
"""
Base.acos(x::AbstractUncertainValue; n::Int = 10000) = acos.(resample(x, n))
"""
Base.acos(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the inverse cosine of the uncertain value `x`, where `x` is in radians. Computes the
element-wise inverse cosine for `n` realizations.
"""
Base.acos(x::AbstractUncertainValue, n::Int) = acos.(resample(x, n))
"""
Base.acosd(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the inverse cosine of the uncertain value `x`, where `x` is in degrees. Computes the
element-wise inverse cosine for `n` realizations.
"""
Base.acosd(x::AbstractUncertainValue; n::Int = 10000) = acosd.(resample(x, n))
"""
Base.acosd(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the inverse cosine of the uncertain value `x`, where `x` is in degrees. Computes the
element-wise inverse cosine for `n` realizations.
"""
Base.acosd(x::AbstractUncertainValue, n::Int) = acosd.(resample(x, n))
"""
Base.acosh(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the inverse hyperbolic cosine of the uncertain value `x`.
Computes the element-wise inverse hyperbolic cosine for `n` realizations.
"""
Base.acosh(x::AbstractUncertainValue; n::Int = 10000) = acosh.(resample(x, n))
"""
Base.acosh(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the inverse hyperbolic cosine of the uncertain value `x`.
Computes the element-wise inverse hyperbolic cosine for `n` realizations.
"""
Base.acosh(x::AbstractUncertainValue, n::Int) = acosh.(resample(x, n))
"""
Base.asin(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the inverse sine of the uncertain value `x`, where `x` is in radians. Computes the
element-wise inverse sine for `n` realizations.
"""
Base.asin(x::AbstractUncertainValue; n::Int = 10000) = asin.(resample(x, n))
"""
Base.asin(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the inverse sine of the uncertain value `x`, where `x` is in radians. Computes the
element-wise inverse sine for `n` realizations.
"""
Base.asin(x::AbstractUncertainValue, n::Int) = asin.(resample(x, n))
"""
Base.asind(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the inverse sine of the uncertain value `x`, where `x` is in degrees. Computes the
element-wise inverse sine for `n` realizations.
"""
Base.asind(x::AbstractUncertainValue; n::Int = 10000) = asind.(resample(x, n))
"""
Base.asind(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the inverse sine of the uncertain value `x`, where `x` is in degrees. Computes the
element-wise inverse sine for `n` realizations.
"""
Base.asind(x::AbstractUncertainValue, n::Int) = asind.(resample(x, n))
"""
Base.asinh(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the inverse hyperbolic sine of the uncertain value `x`.
Computes the element-wise inverse hyperbolic csine for `n` realizations.
"""
Base.asinh(x::AbstractUncertainValue; n::Int = 10000) = asinh.(resample(x, n))
"""
Base.asinh(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the inverse hyperbolic sine of the uncertain value `x`.
Computes the element-wise inverse hyperbolic csine for `n` realizations.
"""
Base.asinh(x::AbstractUncertainValue, n::Int) = asinh.(resample(x, n))
"""
Base.atan(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the inverse tangent of the uncertain value `x`, where `x` is in radians.
Computes the element-wise inverse tangent for `n` realizations.
"""
Base.atan(x::AbstractUncertainValue; n::Int = 10000) = atan.(resample(x, n))
"""
Base.atan(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the inverse tangent of the uncertain value `x`, where `x` is in radians.
Computes the element-wise inverse tangent for `n` realizations.
"""
Base.atan(x::AbstractUncertainValue, n::Int) = atan.(resample(x, n))
"""
Base.atand(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the inverse tangent of the uncertain value `x`, where `x` is in degrees.
Computes the element-wise inverse tangent for `n` realizations.
"""
Base.atand(x::AbstractUncertainValue; n::Int = 10000) = atand.(resample(x, n))
"""
Base.atand(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the inverse tangent of the uncertain value `x`, where `x` is in degrees.
Computes the element-wise inverse tangent for `n` realizations.
"""
Base.atand(x::AbstractUncertainValue, n::Int) = atand.(resample(x, n))
"""
Base.atanh(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the inverse hypoerbolic tangent of the uncertain value `x`.
Computes the element-wise inverse hypoerbolic tangent for `n` realizations.
"""
Base.atanh(x::AbstractUncertainValue; n::Int = 10000) = atanh.(resample(x, n))
"""
Base.atanh(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the inverse hypoerbolic tangent of the uncertain value `x`.
Computes the element-wise inverse hypoerbolic tangent for `n` realizations.
"""
Base.atanh(x::AbstractUncertainValue, n::Int) = atanh.(resample(x, n))
"""
Base.asec(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the inverse secant of the uncertain value `x`, where `x` is in radians.
Computes the element-wise inverse secant for `n` realizations.
"""
Base.asec(x::AbstractUncertainValue; n::Int = 10000) = asec.(resample(x, n))
"""
Base.asec(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the inverse secant of the uncertain value `x`, where `x` is in radians.
Computes the element-wise inverse secant for `n` realizations.
"""
Base.asec(x::AbstractUncertainValue, n::Int) = asec.(resample(x, n))
"""
Base.asecd(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the inverse secant of the uncertain value `x`, where `x` is in degrees.
Computes the element-wise inverse secant for `n` realizations.
"""
Base.asecd(x::AbstractUncertainValue; n::Int = 10000) = asec.(resample(x, n))
"""
Base.asecd(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the inverse secant of the uncertain value `x`, where `x` is in degrees.
Computes the element-wise inverse secant for `n` realizations.
"""
Base.asecd(x::AbstractUncertainValue, n::Int) = asec.(resample(x, n))
"""
Base.asech(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the inverse hyperbolic secant of the uncertain value `x`.
Computes the element-wise inverse hyperbolic secant for `n` realizations.
"""
Base.asech(x::AbstractUncertainValue; n::Int = 10000) = asec.(resample(x, n))
"""
Base.asech(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the inverse hyperbolic secant of the uncertain value `x`.
Computes the element-wise inverse hyperbolic secant for `n` realizations.
"""
Base.asech(x::AbstractUncertainValue, n::Int) = asec.(resample(x, n))
"""
Base.acsc(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the inverse cosecant of the uncertain value `x`, where `x` is in radians.
Computes the element-wise inverse cosecant for `n` realizations.
"""
Base.acsc(x::AbstractUncertainValue; n::Int = 10000) = acsc.(resample(x, n))
"""
Base.acsc(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the inverse cosecant of the uncertain value `x`, where `x` is in radians.
Computes the element-wise inverse cosecant for `n` realizations.
"""
Base.acsc(x::AbstractUncertainValue, n::Int) = acsc.(resample(x, n))
"""
Base.acscd(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the inverse cosecant of the uncertain value `x`, where `x` is in degrees.
Computes the element-wise inverse cosecant for `n` realizations.
"""
Base.acscd(x::AbstractUncertainValue; n::Int = 10000) = acsc.(resample(x, n))
"""
Base.acscd(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the inverse cosecant of the uncertain value `x`, where `x` is in degrees.
Computes the element-wise inverse cosecant for `n` realizations.
"""
Base.acscd(x::AbstractUncertainValue, n::Int) = acsc.(resample(x, n))
"""
Base.acscd(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the inverse hyperbolic cosecant of the uncertain value `x`.
Computes the element-wise inverse hypoerbolic cosecant for `n` realizations.
"""
Base.acsch(x::AbstractUncertainValue; n::Int = 10000) = acsc.(resample(x, n))
"""
Base.acscd(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the inverse hyperbolic cosecant of the uncertain value `x`.
Computes the element-wise inverse hypoerbolic cosecant for `n` realizations.
"""
Base.acsch(x::AbstractUncertainValue, n::Int) = acsc.(resample(x, n))
"""
Base.acot(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the inverse cotangent of the uncertain value `x`, where `x` is in radians.
Computes the element-wise inverse secant for `n` realizations.
"""
Base.acot(x::AbstractUncertainValue; n::Int = 10000) = acot.(resample(x, n))
"""
Base.acot(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the inverse cotangent of the uncertain value `x`, where `x` is in radians.
Computes the element-wise inverse secant for `n` realizations.
"""
Base.acot(x::AbstractUncertainValue, n::Int) = acot.(resample(x, n))
"""
Base.acotd(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the inverse cotangent of the uncertain value `x`, where `x` is in degrees.
Computes the element-wise inverse secant for `n` realizations.
"""
Base.acotd(x::AbstractUncertainValue; n::Int = 10000) = acot.(resample(x, n))
"""
Base.acotd(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the inverse cotangent of the uncertain value `x`, where `x` is in degrees.
Computes the element-wise inverse secant for `n` realizations.
"""
Base.acotd(x::AbstractUncertainValue, n::Int) = acot.(resample(x, n))
"""
Base.acoth(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the inverse hyperbolic cotangent of the uncertain value `x`.
Computes the element-wise inverse hyperbolic secant for `n` realizations.
"""
Base.acoth(x::AbstractUncertainValue; n::Int = 10000) = acot.(resample(x, n))
"""
Base.acoth(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the inverse hyperbolic cotangent of the uncertain value `x`.
Computes the element-wise inverse hyperbolic secant for `n` realizations.
"""
Base.acoth(x::AbstractUncertainValue, n::Int) = acot.(resample(x, n))
############################
# Reciprocal trig functions
############################
"""
Base.csc(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the cosecant of the uncertain value `x`, where `x` is in radians. Computes the
element-wise cosecant for `n` realizations.
"""
Base.csc(x::AbstractUncertainValue; n::Int = 10000) = csc.(resample(x, n))
"""
Base.csc(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the cosecant of the uncertain value `x`, where `x` is in radians. Computes the
element-wise cosecant for `n` realizations.
"""
Base.csc(x::AbstractUncertainValue, n::Int) = csc.(resample(x, n))
"""
Base.cscd(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the cosecant of the uncertain value `x`, where `x` is in degrees. Computes the
element-wise cosecant for `n` realizations.
"""
Base.cscd(x::AbstractUncertainValue; n::Int = 10000) = cscd.(resample(x, n))
"""
Base.cscd(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the cosecant of the uncertain value `x`, where `x` is in degrees. Computes the
element-wise cosecant for `n` realizations.
"""
Base.cscd(x::AbstractUncertainValue, n::Int) = cscd.(resample(x, n))
"""
Base.cscd(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the hyperbolic cosecant of the uncertain value `x`, where `x` is in degrees.
Computes the element-wise hyperbolic cosecant for `n` realizations.
"""
Base.csch(x::AbstractUncertainValue; n::Int = 10000) = csch.(resample(x, n))
"""
Base.cscd(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the hyperbolic cosecant of the uncertain value `x`, where `x` is in degrees.
Computes the element-wise hyperbolic cosecant for `n` realizations.
"""
Base.csch(x::AbstractUncertainValue, n::Int) = csch.(resample(x, n))
"""
Base.sec(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the secant of the uncertain value `x`, where `x` is in radians. Computes the
element-wise secant for `n` realizations.
"""
Base.sec(x::AbstractUncertainValue; n::Int = 10000) = sec.(resample(x, n))
"""
Base.sec(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the secant of the uncertain value `x`, where `x` is in radians. Computes the
element-wise secant for `n` realizations.
"""
Base.sec(x::AbstractUncertainValue, n::Int) = sec.(resample(x, n))
"""
Base.secd(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the secant of the uncertain value `x`, where `x` is in degrees. Computes the
element-wise cosecant for `n` realizations.
"""
Base.secd(x::AbstractUncertainValue; n::Int = 10000) = secd.(resample(x, n))
"""
Base.secd(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the secant of the uncertain value `x`, where `x` is in degrees. Computes the
element-wise cosecant for `n` realizations.
"""
Base.secd(x::AbstractUncertainValue, n::Int) = secd.(resample(x, n))
"""
Base.sech(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the hyperbolic secant of the uncertain value `x`, where `x` is in degrees.
Computes the element-wise hyperbolic secant for `n` realizations.
"""
Base.sech(x::AbstractUncertainValue; n::Int = 10000) = sech.(resample(x, n))
"""
Base.sech(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the hyperbolic secant of the uncertain value `x`, where `x` is in degrees.
Computes the element-wise hyperbolic secant for `n` realizations.
"""
Base.sech(x::AbstractUncertainValue, n::Int) = sech.(resample(x, n))
"""
Base.cot(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the cotangent of the uncertain value `x`, where `x` is in radians. Computes the
element-wise cotangent for `n` realizations.
"""
Base.cot(x::AbstractUncertainValue; n::Int = 10000) = cot.(resample(x, n))
"""
Base.cot(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the cotangent of the uncertain value `x`, where `x` is in radians. Computes the
element-wise cotangent for `n` realizations.
"""
Base.cot(x::AbstractUncertainValue, n::Int) = cot.(resample(x, n))
"""
Base.cotd(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the cotangent of the uncertain value `x`, where `x` is in degrees. Computes the
element-wise cotangent for `n` realizations.
"""
Base.cotd(x::AbstractUncertainValue; n::Int = 10000) = cotd.(resample(x, n))
"""
Base.cotd(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the cotangent of the uncertain value `x`, where `x` is in degrees. Computes the
element-wise cotangent for `n` realizations.
"""
Base.cotd(x::AbstractUncertainValue, n::Int) = cotd.(resample(x, n))
"""
Base.coth(x::AbstractUncertainValue; n::Int = 10000) -> Vector{Float64}
Compute the hyperbolic cotangent of the uncertain value `x`, where `x` is in radians.
Computes the element-wise hyperbolic cotangent for `n` realizations.
"""
Base.coth(x::AbstractUncertainValue; n::Int = 10000) = coth.(resample(x, n))
"""
Base.coth(x::AbstractUncertainValue, n::Int = 10000) -> Vector{Float64}
Compute the hyperbolic cotangent of the uncertain value `x`, where `x` is in radians.
Computes the element-wise hyperbolic cotangent for `n` realizations.
"""
Base.coth(x::AbstractUncertainValue, n::Int) = coth.(resample(x, n))
#####################################################################################
# Special cases
#####################################################################################
trigfuncs = [:(cos), :(cosd), :(cosh), :(sin), :(sind), :(sinh), :(tan), :(tand), :(tanh),
:(sincos), :(sinc), :(sinpi), :(cosc), :(cospi), :(acos), :(acosd), :(acosh), :(asin),
:(asind), :(asinh), :(atan), :(atand), :(atanh), :(asec), :(asecd), :(asech), :(acsc),
:(acscd), :(acsch), :(acot), :(acotd), :(acoth), :(csc), :(cscd), :(csch), :(sec),
:(secd), :(sech), :(cot), :(cotd), :(coth)]
##################
# `CertainValue`s
#################
import ..UncertainValues: CertainValue
"""
Base.:-(a::Union{CertainValue, Real}, b::Union{CertainValue, Real})
Subtraction of certain values with themselves or scalars acts as regular subtraction,
but returns the result wrapped in a `CertainValue` instance.
"""
for trigfunc in trigfuncs
f = Meta.parse("Base.$(trigfunc)")
regular_func = quote
"""
$($f)(x::CertainValue)
Compute `$($trigfunc)(x)`.
"""
$(f)(x::CertainValue) = x.value
end
n_reps_func = quote
"""
$($f)(x::CertainValue, n::Int)
Compute `$($trigfunc)(x)` `n` times and return the result(s) as a vector (just
repeating the value `n` times).
"""
$(f)(x::CertainValue, n::Int) = [x.value for i = 1:n]
end
eval(regular_func)
eval(n_reps_func)
end | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 830 | using Reexport
@reexport module UncertainDataPlotRecipes
import ..Resampling.resample
using RecipesBase
# Recipes for uncertain values
include("recipes_certainvalues.jl")
include("recipes_populations.jl")
include("recipes_uncertainvalues_theoretical.jl")
include("recipes_uncertainvalues_kde.jl")
include("recipes_uncertaindatasets.jl")
# Uncertainties for values with uncertainties both in index and value
include("recipes_uncertain_index_and_value.jl")
include("recipes_uncertainindexvaluedataset.jl")
include("recipes_vectors_of_uncertainvalues.jl")
# Recipes for resampled statistics
#include("recipes_resampledstatistics.jl")
end # module
"""
UncertainDataPlotRecipes
Plot recipes for uncertain values and uncertain datasets.
"""
UncertainDataPlotRecipes | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 406 | import ..UncertainValues: CertainValue
using RecipesBase
@recipe f(::Type{CertainValue{T}}, x::CertainValue{T}) where {T} = [x.value]
@recipe function f(certainvals::Vector{CertainValue})
@series begin
[val.value for val in certainvals]
end
end
@recipe function f(certainvals::Vararg{CertainValue,N}) where {N}
@series begin
[val.value for val in certainvals]
end
end
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 474 | import ..UncertainValues: UncertainScalarPopulation
using RecipesBase
#@recipe f(::Type{UncertainScalarPopulation{T}}, x::UncertainScalarPopulation{T}) where {T} =
# rand(x, 10000)
@recipe function f(p::UncertainScalarPopulation{T}) where T
@series begin
rand(p, 10000)
end
end
@recipe function f(populations::Vector{UncertainScalarPopulation{T}}) where {T}
for p in populations
@series begin
p
end
end
end | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 201 | using RecipesBase
import ..Resampling: ResampledDatasetStatistic
@recipe function f(::Type{ResampledDatasetStatistic{T,B}},
x::ResampledDatasetStatistic{T,B}) where {T, B}
x.estimates
end | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 1720 | import ..UncertainStatistics: quantile
@recipe function f(uval::Tuple{AbstractUncertainValue, AbstractUncertainValue},
quants_index::Vector{Float64} = [0.33, 0.67],
quants_values::Vector{Float64} = [0.33, 0.67])
legend --> false
idx, val = uval[1], uval[2]
med_idx = median(idx, 10000)
lower_idx = quantile(idx, minimum(quants_index), 10000)
upper_idx = quantile(idx, maximum(quants_index), 10000)
med_val = median(val, 10000)
lower_val = quantile(val, minimum(quants_values), 10000)
upper_val = quantile(val, maximum(quants_values), 10000)
@series begin
seriescolor --> :black
xerror --> ([med_idx - lower_idx], [upper_idx - med_idx])
yerror --> ([med_val - lower_val], [upper_val - med_val])
[med_idx], [med_val]
end
end
@recipe function f(uvals::Vector{Tuple{AbstractUncertainValue, AbstractUncertainValue}},
quants_index::Vector{Float64} = [0.33, 0.67],
quants_values::Vector{Float64} = [0.33, 0.67])
n_vals = length(uvals)
for i = 1:n_vals
idx, val = uvals[i]
med_idx = median(idx, 10000)
lower_idx = quantile(idx, minimum(quants_index), 10000)
upper_idx = quantile(idx, maximum(quants_index), 10000)
med_val = median(val, 10000)
lower_val = quantile(val, minimum(quants_values), 10000)
upper_val = quantile(val, maximum(quants_values), 10000)
@series begin
#seriescolor --> :black
label --> ""
xerror --> ([med_idx - lower_idx], [upper_idx - med_idx])
yerror --> ([med_val - lower_val], [upper_val - med_val])
[med_idx], [med_val]
end
end
end | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 629 | import ..UncertainDatasets:
AbstractUncertainValueDataset
import ..UncertainStatistics: mean, std, median, quantile
@recipe function f(udata::AbstractUncertainValueDataset, quants::Vector{Float64} = [0.33, 0.67])
n_points = length(udata)
for i = 1:n_points
med = median(udata[i], 10000)
lower = quantile(udata[i], minimum(quants), 10000)
upper = quantile(udata[i], maximum(quants), 10000)
@series begin
seriescolor --> :black
label --> ""
yerror --> ([med - lower], [upper - med])
[i], [med]
end
end
end | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 1028 | import ..UncertainValues: AbstractUncertainValue
import ..UncertainDatasets: AbstractUncertainIndexValueDataset
import ..UncertainStatistics: quantile, median
@recipe function f(uvals::AbstractUncertainIndexValueDataset,
quants_index::Vector{Float64} = [0.33, 0.67],
quants_values::Vector{Float64} = [0.33, 0.67])
n_vals = length(uvals)
for i = 1:n_vals
idx, val = uvals[i]
med_idx = median(idx, 10000)
lower_idx = quantile(idx, minimum(quants_index), 10000)
upper_idx = quantile(idx, maximum(quants_index), 10000)
med_val = median(val, 10000)
lower_val = quantile(val, minimum(quants_values), 10000)
upper_val = quantile(val, maximum(quants_values), 10000)
@series begin
#seriescolor --> :black
label --> ""
xerror --> ([med_idx - lower_idx], [upper_idx - med_idx])
yerror --> ([med_val - lower_val], [upper_val - med_val])
[med_idx], [med_val]
end
end
end | UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 871 | import ..UncertainValues.AbstractUncertainScalarKDE
import ..SamplingConstraints:
SamplingConstraint,
constrain
@recipe function plot_uncertainvalueKDE(uv::AbstractUncertainScalarKDE)
@series begin
seriestype := :path
fΞ± --> 0.5
fc --> :green
xlabel --> "Value"
ylabel --> "Density"
label --> ""
uv.distribution.x, uv.distribution.density ./ sum(uv.distribution.density)
end
end
@recipe function plot_uncertainvalueKDE(uv::AbstractUncertainScalarKDE,
constraint::SamplingConstraint)
cuv = constrain(uv, constraint)
@series begin
seriestype := :path
fΞ± --> 0.5
fc --> :green
xlabel --> "Value"
ylabel --> "Density"
label --> ""
cuv.distribution.x, cuv.distribution.density ./ sum(cuv.distribution.density)
end
end
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
|
[
"MIT"
] | 0.16.0 | df107bbf91afba419309adb9daa486b0457c693c | code | 949 |
@recipe function fmultiple(o1::AbstractUncertainValue,
o2::AbstractUncertainValue;
mix = false,
n_samples = 10000, nbins = 50)
size --> (300, 400)
d1 = o1.distribution
d2 = o1.distribution
@series begin
label --> "P1, $d1"
seriestype := :bar
fΞ± --> 0.4
fc --> :green
fit(Histogram, resample(d1, n_samples), nbins = nbins)
end
@series begin
label --> "P2, $d2"
seriestype := :bar
fc --> :blue
fΞ± --> 0.4
fit(Histogram, resample(d2, n_samples), nbins = nbins)
end
if mix
M = MixtureModel([d1, d2])
@series begin
label --> "MixtureModel with uniform priors"
seriestype := :bar
fΞ± --> 0.6
fc --> :black
fit(Histogram, rand(M, n_samples), nbins = nbins)
end
end
end
| UncertainData | https://github.com/kahaaga/UncertainData.jl.git |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.