code
stringlengths 2.5k
150k
| kind
stringclasses 1
value |
|---|---|
```
import torch
from torch.autograd import grad
import torch.nn as nn
from numpy import genfromtxt
import torch.optim as optim
import matplotlib.pyplot as plt
import torch.nn.functional as F
import math
tuberculosis_data = genfromtxt('tuberculosis.csv', delimiter=',') #in the form of [t, S,L,I,T]
torch.manual_seed(1234)
%%time
PATH = 'tuberculosis'
class DINN(nn.Module):
def __init__(self, t, S_data, L_data, I_data, T_data):
super(DINN, self).__init__()
self.t = torch.tensor(t, requires_grad=True)
self.t_float = self.t.float()
self.t_batch = torch.reshape(self.t_float, (len(self.t),1)) #reshape for batch
self.S = torch.tensor(S_data)
self.L = torch.tensor(L_data)
self.I = torch.tensor(I_data)
self.T = torch.tensor(T_data)
self.N = torch.tensor(1001)
self.losses = [] #keep the losses
self.save = 2 #which file to save to
#learnable parameters
self.delta_tilda = torch.nn.Parameter(torch.rand(1, requires_grad=True)) #torch.tensor(500)
self.beta_tilda = torch.nn.Parameter(torch.rand(1, requires_grad=True)) #torch.tensor(13)
self.c_tilda = torch.nn.Parameter(torch.rand(1, requires_grad=True)) #torch.tensor(1)
self.mu_tilda = torch.nn.Parameter(torch.rand(1, requires_grad=True)) #torch.tensor(0.143)
self.k_tilda = torch.nn.Parameter(torch.rand(1, requires_grad=True)) #torch.tensor(0.5)
self.r_1_tilda = torch.nn.Parameter(torch.rand(1, requires_grad=True)) #torch.tensor(2)
self.r_2_tilda = torch.nn.Parameter(torch.rand(1, requires_grad=True)) #torch.tensor(1)
self.beta_prime_tilda = torch.nn.Parameter(torch.rand(1, requires_grad=True)) #torch.tensor(13)
self.d_tilda = torch.nn.Parameter(torch.rand(1, requires_grad=True)) #torch.tensor(0)
#matrices (x4 for S, L, I, T) for the gradients
self.m1 = torch.zeros((len(self.t), 4)); self.m1[:, 0] = 1
self.m2 = torch.zeros((len(self.t), 4)); self.m2[:, 1] = 1
self.m3 = torch.zeros((len(self.t), 4)); self.m3[:, 2] = 1
self.m4 = torch.zeros((len(self.t), 4)); self.m4[:, 3] = 1
#values for norm
self.S_max = max(self.S)
self.S_min = min(self.S)
self.L_max = max(self.L)
self.L_min = min(self.L)
self.I_max = max(self.I)
self.I_min = min(self.I)
self.T_max = max(self.T)
self.T_min = min(self.T)
#normalize
self.S_hat = (self.S - self.S_min) / (self.S_max - self.S_min)
self.L_hat = (self.L - self.L_min) / (self.L_max - self.L_min)
self.I_hat = (self.I - self.I_min) / (self.I_max - self.I_min)
self.T_hat = (self.T - self.T_min) / (self.T_max - self.T_min)
#NN
self.net_tuberculosis = self.Net_tuberculosis()
self.params = list(self.net_tuberculosis.parameters())
self.params.extend(list([self.delta_tilda ,self.beta_tilda ,self.c_tilda ,self.mu_tilda ,self.k_tilda ,self.r_1_tilda ,self.r_2_tilda ,self.beta_prime_tilda ,self.d_tilda]))
#force parameters to be in a range
@property
def delta(self):
return torch.tanh(self.delta_tilda) * 20 + 500 #self.delta_tilda
@property
def beta(self):
return torch.tanh(self.beta_tilda) * 3 + 12 #self.beta_tilda
@property
def c(self):
return torch.tanh(self.c_tilda) * 2 + 1 #self.c_tilda
@property
def mu(self):
return torch.tanh(self.mu_tilda) * 0.1 + 0.2 #self.mu_tilda
@property
def k(self):
return torch.tanh(self.k_tilda) * 0.5 + 0.5 #self.k_tilda
@property
def r_1(self):
return torch.tanh(self.r_1_tilda) + 2 #self.r_1_tilda
@property
def r_2(self):
return torch.tanh(self.r_2_tilda) * 2 + 1 #self.r_2_tilda
@property
def beta_prime(self):
return torch.tanh(self.beta_prime_tilda) * 3 + 12 #self.beta_prime_tilda
@property
def d(self):
return torch.tanh(self.d_tilda) * 0.4 #self.d_tilda
#nets
class Net_tuberculosis(nn.Module): # input = [t]
def __init__(self):
super(DINN.Net_tuberculosis, self).__init__()
self.fc1=nn.Linear(1, 20) #takes 100 t's
self.fc2=nn.Linear(20, 20)
self.fc3=nn.Linear(20, 20)
self.fc4=nn.Linear(20, 20)
self.fc5=nn.Linear(20, 20)
self.fc6=nn.Linear(20, 20)
self.fc7=nn.Linear(20, 20)
self.fc8=nn.Linear(20, 20)
self.out=nn.Linear(20, 4) #outputs S, L, I, T
def forward(self, t):
tuberculosis=F.relu(self.fc1(t))
tuberculosis=F.relu(self.fc2(tuberculosis))
tuberculosis=F.relu(self.fc3(tuberculosis))
tuberculosis=F.relu(self.fc4(tuberculosis))
tuberculosis=F.relu(self.fc5(tuberculosis))
tuberculosis=F.relu(self.fc6(tuberculosis))
tuberculosis=F.relu(self.fc7(tuberculosis))
tuberculosis=F.relu(self.fc8(tuberculosis))
tuberculosis=self.out(tuberculosis)
return tuberculosis
def net_f(self, t_batch):
tuberculosis_hat = self.net_tuberculosis(t_batch)
S_hat, L_hat, I_hat, T_hat = tuberculosis_hat[:,0], tuberculosis_hat[:,1], tuberculosis_hat[:,2], tuberculosis_hat[:,3]
#S_hat
tuberculosis_hat.backward(self.m1, retain_graph=True)
S_hat_t = self.t.grad.clone()
self.t.grad.zero_()
#L_hat
tuberculosis_hat.backward(self.m2, retain_graph=True)
L_hat_t = self.t.grad.clone()
self.t.grad.zero_()
#I_hat
tuberculosis_hat.backward(self.m3, retain_graph=True)
I_hat_t = self.t.grad.clone()
self.t.grad.zero_()
#T_hat
tuberculosis_hat.backward(self.m4, retain_graph=True)
T_hat_t = self.t.grad.clone()
self.t.grad.zero_()
#unnormalize
S = self.S_min + (self.S_max - self.S_min) * S_hat
L = self.L_min + (self.L_max - self.L_min) * L_hat
I = self.I_min + (self.I_max - self.I_min) * I_hat
T = self.T_min + (self.T_max - self.T_min) * T_hat
#equations
f1_hat = S_hat_t - (self.delta - self.beta * self.c * S * I / self.N - self.mu * S) / (self.S_max - self.S_min)
f2_hat = L_hat_t - (self.beta * self.c * S * I / self.N - (self.mu + self.k + self.r_1) * L + self.beta_prime * self.c * T * 1/self.N) / (self.L_max - self.L_min)
f3_hat = I_hat_t - (self.k*L - (self.mu + self.d) * I - self.r_2 * I) / (self.I_max - self.I_min)
f4_hat = T_hat_t - (self.r_1 * L + self.r_2 * I - self.beta_prime * self.c * T * 1/self.N - self.mu*T) / (self.T_max - self.T_min)
return f1_hat, f2_hat, f3_hat, f4_hat, S_hat, L_hat, I_hat, T_hat
def load(self):
# Load checkpoint
try:
checkpoint = torch.load(PATH + str(self.save)+'.pt')
print('\nloading pre-trained model...')
self.load_state_dict(checkpoint['model'])
self.optimizer.load_state_dict(checkpoint['optimizer_state_dict'])
self.scheduler.load_state_dict(checkpoint['scheduler'])
epoch = checkpoint['epoch']
loss = checkpoint['loss']
self.losses = checkpoint['losses']
print('loaded previous loss: ', loss)
except RuntimeError :
print('changed the architecture, ignore')
pass
except FileNotFoundError:
pass
def train(self, n_epochs):
#try loading
self.load()
#train
print('\nstarting training...\n')
for epoch in range(n_epochs):
#lists to hold the output (maintain only the final epoch)
S_pred_list = []
L_pred_list = []
I_pred_list = []
T_pred_list = []
f1_hat, f2_hat, f3_hat, f4_hat, S_hat_pred, L_hat_pred, I_hat_pred, T_hat_pred = self.net_f(self.t_batch)
self.optimizer.zero_grad()
S_pred_list.append(self.S_min + (self.S_max - self.S_min) * S_hat_pred)
L_pred_list.append(self.L_min + (self.L_max - self.L_min) * L_hat_pred)
I_pred_list.append(self.I_min + (self.I_max - self.I_min) * I_hat_pred)
T_pred_list.append(self.T_min + (self.T_max - self.T_min) * T_hat_pred)
loss = (
torch.mean(torch.square(self.S_hat - S_hat_pred)) + torch.mean(torch.square(self.L_hat - L_hat_pred)) +
torch.mean(torch.square(self.I_hat - I_hat_pred)) + torch.mean(torch.square(self.T_hat - T_hat_pred))+
torch.mean(torch.square(f1_hat)) + torch.mean(torch.square(f2_hat)) +
torch.mean(torch.square(f3_hat)) + torch.mean(torch.square(f4_hat))
)
loss.backward()
self.optimizer.step()
self.scheduler.step()
# self.scheduler.step(loss)
self.losses.append(loss.item())
if epoch % 1000 == 0:
print('\nEpoch ', epoch)
#loss + model parameters update
if epoch % 4000 == 9999:
#checkpoint save
print('\nSaving model... Loss is: ', loss)
torch.save({
'epoch': epoch,
'model': self.state_dict(),
'optimizer_state_dict': self.optimizer.state_dict(),
'scheduler': self.scheduler.state_dict(),
'loss': loss,
'losses': self.losses,
}, PATH + str(self.save)+'.pt')
if self.save % 2 > 0: #its on 3
self.save = 2 #change to 2
else: #its on 2
self.save = 3 #change to 3
print('epoch: ', epoch)
print('#################################')
#plot
plt.plot(self.losses, color = 'teal')
plt.xlabel('Epochs')
plt.ylabel('Loss')
return S_pred_list, L_pred_list, I_pred_list, T_pred_list
%%time
dinn = DINN(tuberculosis_data[0], tuberculosis_data[1], tuberculosis_data[2], tuberculosis_data[3], tuberculosis_data[4])
learning_rate = 1e-3
optimizer = optim.Adam(dinn.params, lr = learning_rate)
dinn.optimizer = optimizer
scheduler = torch.optim.lr_scheduler.CyclicLR(dinn.optimizer, base_lr=1e-7, max_lr=1e-3, step_size_up=1000, mode="exp_range", gamma=0.85, cycle_momentum=False)
dinn.scheduler = scheduler
try:
S_pred_list, L_pred_list, I_pred_list, T_pred_list = dinn.train(1) #train
except EOFError:
if dinn.save == 2:
dinn.save = 3
S_pred_list, L_pred_list, I_pred_list, T_pred_list = dinn.train(1) #train
elif dinn.save == 3:
dinn.save = 2
S_pred_list, L_pred_list, I_pred_list, T_pred_list = dinn.train(1) #train
plt.plot(dinn.losses[3000000:], color = 'teal')
plt.xlabel('Epochs')
plt.ylabel('Loss')
fig = plt.figure(figsize=(12,12))
ax = fig.add_subplot(111, facecolor='#dddddd', axisbelow=True)
ax.set_facecolor('xkcd:white')
ax.scatter(tuberculosis_data[0], tuberculosis_data[1], color = 'pink', alpha=0.5, lw=2, label='S Data', s=20)
ax.plot(tuberculosis_data[0], S_pred_list[0].detach().numpy(), 'navy', alpha=0.9, lw=2, label='S Prediction', linestyle='dashed')
ax.scatter(tuberculosis_data[0], tuberculosis_data[2], color = 'violet', alpha=0.5, lw=2, label='L Data', s=20)
ax.plot(tuberculosis_data[0], L_pred_list[0].detach().numpy(), 'dodgerblue', alpha=0.9, lw=2, label='L Prediction', linestyle='dashed')
ax.scatter(tuberculosis_data[0], tuberculosis_data[3], color = 'darkgreen', alpha=0.5, lw=2, label='I Data', s=20)
ax.plot(tuberculosis_data[0], I_pred_list[0].detach().numpy(), 'gold', alpha=0.9, lw=2, label='I Prediction', linestyle='dashed')
ax.scatter(tuberculosis_data[0], tuberculosis_data[4], color = 'red', alpha=0.5, lw=2, label='T Data', s=20)
ax.plot(tuberculosis_data[0], T_pred_list[0].detach().numpy(), 'blue', alpha=0.9, lw=2, label='T Prediction', linestyle='dashed')
ax.set_xlabel('Time /days',size = 20)
ax.set_ylabel('Number',size = 20)
#ax.set_ylim([-1,50])
ax.yaxis.set_tick_params(length=0)
ax.xaxis.set_tick_params(length=0)
plt.xticks(size = 20)
plt.yticks(size = 20)
# ax.grid(b=True, which='major', c='black', lw=0.2, ls='-')
legend = ax.legend(prop={'size':20})
legend.get_frame().set_alpha(0.5)
for spine in ('top', 'right', 'bottom', 'left'):
ax.spines[spine].set_visible(False)
plt.savefig('tuberculosis.pdf')
plt.show()
#vaccination!
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
# Initial conditions
S0 = 1000
L0 = 0
I0 = 1
T0 = 0
N = 1001 #S0 + L0 + I0 + T0
# A grid of time points (in days)
t = np.linspace(0, 40, 50)
#parameters
delta = dinn.delta
print(delta)
beta = dinn.beta
print(beta)
c = dinn.c
print(c)
mu = dinn.mu
print(mu)
k = dinn.k
print(k)
r_1 = dinn.r_1
print(r_1)
r_2 = dinn.r_2
print(r_2)
beta_prime = dinn.beta_prime
print(beta_prime)
d = dinn.d
print(d)
# The SIR model differential equations.
def deriv(y, t, N, delta ,beta ,c ,mu ,k ,r_1 ,r_2 ,beta_prime,d ):
S, L, I, T= y
dSdt = delta - beta * c * S * I / N - mu * S
dLdt = beta * c * S * I / N - (mu + k + r_1) * L + beta_prime * c * T * 1/N
dIdt = k*L - (mu + d) * I - r_2 * I
dTdt = r_1 * L + r_2 * I - beta_prime * c * T * 1/N - mu*T
return dSdt, dLdt, dIdt, dTdt
# Initial conditions vector
y0 = S0, L0, I0, T0
# Integrate the SIR equations over the time grid, t.
ret = odeint(deriv, y0, t, args=(N, delta ,beta ,c ,mu ,k ,r_1 ,r_2 ,beta_prime,d ))
S, L, I, T = ret.T
# Plot the data on two separate curves for S(t), I(t)
fig = plt.figure(figsize=(12,12))
ax = fig.add_subplot(111, facecolor='#dddddd', axisbelow=True)
ax.set_facecolor('xkcd:white')
ax.plot(t, S, 'violet', alpha=0.5, lw=2, label='S_pred', linestyle='dashed')
ax.plot(tuberculosis_data[0], tuberculosis_data[1], 'grey', alpha=0.5, lw=2, label='S')
ax.plot(t, L, 'darkgreen', alpha=0.5, lw=2, label='L_pred', linestyle='dashed')
ax.plot(tuberculosis_data[0], tuberculosis_data[2], 'purple', alpha=0.5, lw=2, label='L')
ax.plot(t, I, 'blue', alpha=0.5, lw=2, label='I_pred', linestyle='dashed')
ax.plot(tuberculosis_data[0], tuberculosis_data[3], 'teal', alpha=0.5, lw=2, label='I')
ax.plot(t, T, 'black', alpha=0.5, lw=2, label='T_pred', linestyle='dashed')
ax.plot(tuberculosis_data[0], tuberculosis_data[4], 'red', alpha=0.5, lw=2, label='T')
ax.set_xlabel('Time /days',size = 20)
ax.set_ylabel('Number',size = 20)
#ax.set_ylim([-1,50])
ax.yaxis.set_tick_params(length=0)
ax.xaxis.set_tick_params(length=0)
plt.xticks(size = 20)
plt.yticks(size = 20)
ax.grid(b=True, which='major', c='black', lw=0.2, ls='-')
legend = ax.legend(prop={'size':20})
legend.get_frame().set_alpha(0.5)
for spine in ('top', 'right', 'bottom', 'left'):
ax.spines[spine].set_visible(False)
plt.show()
#calculate relative MSE loss
import math
S_total_loss = 0
S_den = 0
L_total_loss = 0
L_den = 0
I_total_loss = 0
I_den = 0
T_total_loss = 0
T_den = 0
for timestep in range(len(t)):
S_value = tuberculosis_data[1][timestep] - S[timestep]
S_total_loss += S_value**2
S_den += (tuberculosis_data[1][timestep])**2
L_value = tuberculosis_data[2][timestep] - L[timestep]
L_total_loss += L_value**2
L_den += (tuberculosis_data[2][timestep])**2
I_value = tuberculosis_data[3][timestep] - I[timestep]
I_total_loss += I_value**2
I_den += (tuberculosis_data[3][timestep])**2
T_value = tuberculosis_data[4][timestep] - T[timestep]
T_total_loss += T_value**2
T_den += (tuberculosis_data[4][timestep])**2
S_total_loss = math.sqrt(S_total_loss/S_den)
L_total_loss = math.sqrt(L_total_loss/L_den)
I_total_loss = math.sqrt(I_total_loss/I_den)
T_total_loss = math.sqrt(T_total_loss/T_den)
print('S_total_loss: ', S_total_loss)
print('I_total_loss: ', L_total_loss)
print('S_total_loss: ', I_total_loss)
print('I_total_loss: ', T_total_loss)
```
| github_jupyter |
```
#IMPORT SEMUA LIBARARY
#IMPORT LIBRARY PANDAS
import pandas as pd
#IMPORT LIBRARY UNTUK POSTGRE
from sqlalchemy import create_engine
import psycopg2
#IMPORT LIBRARY CHART
from matplotlib import pyplot as plt
from matplotlib import style
#IMPORT LIBRARY BASE PATH
import os
import io
#IMPORT LIBARARY PDF
from fpdf import FPDF
#IMPORT LIBARARY CHART KE BASE64
import base64
#IMPORT LIBARARY EXCEL
import xlsxwriter
#FUNGSI UNTUK MENGUPLOAD DATA DARI CSV KE POSTGRESQL
def uploadToPSQL(columns, table, filePath, engine):
#FUNGSI UNTUK MEMBACA CSV
df = pd.read_csv(
os.path.abspath(filePath),
names=columns,
keep_default_na=False
)
#APABILA ADA FIELD KOSONG DISINI DIFILTER
df.fillna('')
#MENGHAPUS COLUMN YANG TIDAK DIGUNAKAN
del df['kategori']
del df['jenis']
del df['pengiriman']
del df['satuan']
#MEMINDAHKAN DATA DARI CSV KE POSTGRESQL
df.to_sql(
table,
engine,
if_exists='replace'
)
#DIHITUNG APABILA DATA YANG DIUPLOAD BERHASIL, MAKA AKAN MENGEMBALIKAN KELUARAN TRUE(BENAR) DAN SEBALIKNYA
if len(df) == 0:
return False
else:
return True
#FUNGSI UNTUK MEMBUAT CHART, DATA YANG DIAMBIL DARI DATABASE DENGAN MENGGUNAKAN ORDER DARI TANGGAL DAN JUGA LIMIT
#DISINI JUGA MEMANGGIL FUNGSI MAKEEXCEL DAN MAKEPDF
def makeChart(host, username, password, db, port, table, judul, columns, filePath, name, subjudul, limit, negara, basePath):
#TEST KONEKSI DATABASE
try:
#KONEKSI KE DATABASE
connection = psycopg2.connect(user=username,password=password,host=host,port=port,database=db)
cursor = connection.cursor()
#MENGAMBL DATA DARI TABLE YANG DIDEFINISIKAN DIBAWAH, DAN DIORDER DARI TANGGAL TERAKHIR
#BISA DITAMBAHKAN LIMIT SUPAYA DATA YANG DIAMBIL TIDAK TERLALU BANYAK DAN BERAT
postgreSQL_select_Query = "SELECT * FROM "+table+" ORDER BY tanggal ASC LIMIT " + str(limit)
cursor.execute(postgreSQL_select_Query)
mobile_records = cursor.fetchall()
uid = []
lengthx = []
lengthy = []
#MELAKUKAN LOOPING ATAU PERULANGAN DARI DATA YANG SUDAH DIAMBIL
#KEMUDIAN DATA TERSEBUT DITEMPELKAN KE VARIABLE DIATAS INI
for row in mobile_records:
uid.append(row[0])
lengthx.append(row[1])
if row[2] == "":
lengthy.append(float(0))
else:
lengthy.append(float(row[2]))
#FUNGSI UNTUK MEMBUAT CHART
#bar
style.use('ggplot')
fig, ax = plt.subplots()
#MASUKAN DATA ID DARI DATABASE, DAN JUGA DATA TANGGAL
ax.bar(uid, lengthy, align='center')
#UNTUK JUDUL CHARTNYA
ax.set_title(judul)
ax.set_ylabel('Total')
ax.set_xlabel('Tanggal')
ax.set_xticks(uid)
#TOTAL DATA YANG DIAMBIL DARI DATABASE, DIMASUKAN DISINI
ax.set_xticklabels((lengthx))
b = io.BytesIO()
#CHART DISIMPAN KE FORMAT PNG
plt.savefig(b, format='png', bbox_inches="tight")
#CHART YANG SUDAH DIJADIKAN PNG, DISINI DICONVERT KE BASE64
barChart = base64.b64encode(b.getvalue()).decode("utf-8").replace("\n", "")
#CHART DITAMPILKAN
plt.show()
#line
#MASUKAN DATA DARI DATABASE
plt.plot(lengthx, lengthy)
plt.xlabel('Tanggal')
plt.ylabel('Total')
#UNTUK JUDUL CHARTNYA
plt.title(judul)
plt.grid(True)
l = io.BytesIO()
#CHART DISIMPAN KE FORMAT PNG
plt.savefig(l, format='png', bbox_inches="tight")
#CHART YANG SUDAH DIJADIKAN PNG, DISINI DICONVERT KE BASE64
lineChart = base64.b64encode(l.getvalue()).decode("utf-8").replace("\n", "")
#CHART DITAMPILKAN
plt.show()
#pie
#UNTUK JUDUL CHARTNYA
plt.title(judul)
#MASUKAN DATA DARI DATABASE
plt.pie(lengthy, labels=lengthx, autopct='%1.1f%%',
shadow=True, startangle=180)
plt.axis('equal')
p = io.BytesIO()
#CHART DISIMPAN KE FORMAT PNG
plt.savefig(p, format='png', bbox_inches="tight")
#CHART YANG SUDAH DIJADIKAN PNG, DISINI DICONVERT KE BASE64
pieChart = base64.b64encode(p.getvalue()).decode("utf-8").replace("\n", "")
#CHART DITAMPILKAN
plt.show()
#MENGAMBIL DATA DARI CSV YANG DIGUNAKAN SEBAGAI HEADER DARI TABLE UNTUK EXCEL DAN JUGA PDF
header = pd.read_csv(
os.path.abspath(filePath),
names=columns,
keep_default_na=False
)
#MENGHAPUS COLUMN YANG TIDAK DIGUNAKAN
header.fillna('')
del header['tanggal']
del header['total']
#MEMANGGIL FUNGSI EXCEL
makeExcel(mobile_records, header, name, limit, basePath)
#MEMANGGIL FUNGSI PDF
makePDF(mobile_records, header, judul, barChart, lineChart, pieChart, name, subjudul, limit, basePath)
#JIKA GAGAL KONEKSI KE DATABASE, MASUK KESINI UNTUK MENAMPILKAN ERRORNYA
except (Exception, psycopg2.Error) as error :
print (error)
#KONEKSI DITUTUP
finally:
if(connection):
cursor.close()
connection.close()
#FUNGSI MAKEEXCEL GUNANYA UNTUK MEMBUAT DATA YANG BERASAL DARI DATABASE DIJADIKAN FORMAT EXCEL TABLE F2
#PLUGIN YANG DIGUNAKAN ADALAH XLSXWRITER
def makeExcel(datarow, dataheader, name, limit, basePath):
#MEMBUAT FILE EXCEL
workbook = xlsxwriter.Workbook(basePath+'jupyter/BLOOMBERG/SektorHargaInflasi/excel/'+name+'.xlsx')
#MENAMBAHKAN WORKSHEET PADA FILE EXCEL TERSEBUT
worksheet = workbook.add_worksheet('sheet1')
#SETINGAN AGAR DIBERIKAN BORDER DAN FONT MENJADI BOLD
row1 = workbook.add_format({'border': 2, 'bold': 1})
row2 = workbook.add_format({'border': 2})
#MENJADIKAN DATA MENJADI ARRAY
data=list(datarow)
isihead=list(dataheader.values)
header = []
body = []
#LOOPING ATAU PERULANGAN, KEMUDIAN DATA DITAMPUNG PADA VARIABLE DIATAS
for rowhead in dataheader:
header.append(str(rowhead))
for rowhead2 in datarow:
header.append(str(rowhead2[1]))
for rowbody in isihead[1]:
body.append(str(rowbody))
for rowbody2 in data:
body.append(str(rowbody2[2]))
#MEMASUKAN DATA DARI VARIABLE DIATAS KE DALAM COLUMN DAN ROW EXCEL
for col_num, data in enumerate(header):
worksheet.write(0, col_num, data, row1)
for col_num, data in enumerate(body):
worksheet.write(1, col_num, data, row2)
#FILE EXCEL DITUTUP
workbook.close()
#FUNGSI UNTUK MEMBUAT PDF YANG DATANYA BERASAL DARI DATABASE DIJADIKAN FORMAT EXCEL TABLE F2
#PLUGIN YANG DIGUNAKAN ADALAH FPDF
def makePDF(datarow, dataheader, judul, bar, line, pie, name, subjudul, lengthPDF, basePath):
#FUNGSI UNTUK MENGATUR UKURAN KERTAS, DISINI MENGGUNAKAN UKURAN A4 DENGAN POSISI LANDSCAPE
pdf = FPDF('L', 'mm', [210,297])
#MENAMBAHKAN HALAMAN PADA PDF
pdf.add_page()
#PENGATURAN UNTUK JARAK PADDING DAN JUGA UKURAN FONT
pdf.set_font('helvetica', 'B', 20.0)
pdf.set_xy(145.0, 15.0)
#MEMASUKAN JUDUL KE DALAM PDF
pdf.cell(ln=0, h=2.0, align='C', w=10.0, txt=judul, border=0)
#PENGATURAN UNTUK UKURAN FONT DAN JUGA JARAK PADDING
pdf.set_font('arial', '', 14.0)
pdf.set_xy(145.0, 25.0)
#MEMASUKAN SUB JUDUL KE PDF
pdf.cell(ln=0, h=2.0, align='C', w=10.0, txt=subjudul, border=0)
#MEMBUAT GARIS DI BAWAH SUB JUDUL
pdf.line(10.0, 30.0, 287.0, 30.0)
pdf.set_font('times', '', 10.0)
pdf.set_xy(17.0, 37.0)
#PENGATURAN UNTUK UKURAN FONT DAN JUGA JARAK PADDING
pdf.set_font('Times','',10.0)
#MENGAMBIL DATA HEADER PDF YANG SEBELUMNYA SUDAH DIDEFINISIKAN DIATAS
datahead=list(dataheader.values)
pdf.set_font('Times','B',12.0)
pdf.ln(0.5)
th1 = pdf.font_size
#MEMBUAT TABLE PADA PDF, DAN MENAMPILKAN DATA DARI VARIABLE YANG SUDAH DIKIRIM
pdf.cell(100, 2*th1, "Kategori", border=1, align='C')
pdf.cell(177, 2*th1, datahead[0][0], border=1, align='C')
pdf.ln(2*th1)
pdf.cell(100, 2*th1, "Jenis", border=1, align='C')
pdf.cell(177, 2*th1, datahead[0][1], border=1, align='C')
pdf.ln(2*th1)
pdf.cell(100, 2*th1, "Pengiriman", border=1, align='C')
pdf.cell(177, 2*th1, datahead[0][2], border=1, align='C')
pdf.ln(2*th1)
pdf.cell(100, 2*th1, "Satuan", border=1, align='C')
pdf.cell(177, 2*th1, datahead[0][3], border=1, align='C')
pdf.ln(2*th1)
#PENGATURAN PADDING
pdf.set_xy(17.0, 75.0)
#PENGATURAN UNTUK UKURAN FONT DAN JUGA JARAK PADDING
pdf.set_font('Times','B',11.0)
data=list(datarow)
epw = pdf.w - 2*pdf.l_margin
col_width = epw/(lengthPDF+1)
#PENGATURAN UNTUK JARAK PADDING
pdf.ln(0.5)
th = pdf.font_size
#MEMASUKAN DATA HEADER YANG DIKIRIM DARI VARIABLE DIATAS KE DALAM PDF
pdf.cell(50, 2*th, str("Negara"), border=1, align='C')
for row in data:
pdf.cell(40, 2*th, str(row[1]), border=1, align='C')
pdf.ln(2*th)
#MEMASUKAN DATA ISI YANG DIKIRIM DARI VARIABLE DIATAS KE DALAM PDF
pdf.set_font('Times','B',10.0)
pdf.set_font('Arial','',9)
pdf.cell(50, 2*th, negara, border=1, align='C')
for row in data:
pdf.cell(40, 2*th, str(row[2]), border=1, align='C')
pdf.ln(2*th)
#MENGAMBIL DATA CHART, KEMUDIAN CHART TERSEBUT DIJADIKAN PNG DAN DISIMPAN PADA DIRECTORY DIBAWAH INI
#BAR CHART
bardata = base64.b64decode(bar)
barname = basePath+'jupyter/BLOOMBERG/SektorHargaInflasi/img/'+name+'-bar.png'
with open(barname, 'wb') as f:
f.write(bardata)
#LINE CHART
linedata = base64.b64decode(line)
linename = basePath+'jupyter/BLOOMBERG/SektorHargaInflasi/img/'+name+'-line.png'
with open(linename, 'wb') as f:
f.write(linedata)
#PIE CHART
piedata = base64.b64decode(pie)
piename = basePath+'jupyter/BLOOMBERG/SektorHargaInflasi/img/'+name+'-pie.png'
with open(piename, 'wb') as f:
f.write(piedata)
#PENGATURAN UNTUK UKURAN FONT DAN JUGA JARAK PADDING
pdf.set_xy(17.0, 75.0)
col = pdf.w - 2*pdf.l_margin
widthcol = col/3
#MEMANGGIL DATA GAMBAR DARI DIREKTORY DIATAS
pdf.image(barname, link='', type='',x=8, y=100, w=widthcol)
pdf.set_xy(17.0, 75.0)
col = pdf.w - 2*pdf.l_margin
pdf.image(linename, link='', type='',x=103, y=100, w=widthcol)
pdf.set_xy(17.0, 75.0)
col = pdf.w - 2*pdf.l_margin
pdf.image(piename, link='', type='',x=195, y=100, w=widthcol)
pdf.ln(2*th)
#MEMBUAT FILE PDF
pdf.output(basePath+'jupyter/BLOOMBERG/SektorHargaInflasi/pdf/'+name+'.pdf', 'F')
#DISINI TEMPAT AWAL UNTUK MENDEFINISIKAN VARIABEL VARIABEL SEBELUM NANTINYA DIKIRIM KE FUNGSI
#PERTAMA MANGGIL FUNGSI UPLOADTOPSQL DULU, KALAU SUKSES BARU MANGGIL FUNGSI MAKECHART
#DAN DI MAKECHART MANGGIL FUNGSI MAKEEXCEL DAN MAKEPDF
#DEFINISIKAN COLUMN BERDASARKAN FIELD CSV
columns = [
"kategori",
"jenis",
"tanggal",
"total",
"pengiriman",
"satuan",
]
#UNTUK NAMA FILE
name = "SektorHargaInflasi3_6"
#VARIABLE UNTUK KONEKSI KE DATABASE
host = "localhost"
username = "postgres"
password = "1234567890"
port = "5432"
database = "bloomberg_SektorHargaInflasi"
table = name.lower()
#JUDUL PADA PDF DAN EXCEL
judul = "Data Sektor Harga Inflasi"
subjudul = "Badan Perencanaan Pembangunan Nasional"
#LIMIT DATA UNTUK SELECT DI DATABASE
limitdata = int(8)
#NAMA NEGARA UNTUK DITAMPILKAN DI EXCEL DAN PDF
negara = "Indonesia"
#BASE PATH DIRECTORY
basePath = 'C:/Users/ASUS/Documents/bappenas/'
#FILE CSV
filePath = basePath+ 'data mentah/BLOOMBERG/SektorHargaInflasi/' +name+'.csv';
#KONEKSI KE DATABASE
engine = create_engine('postgresql://'+username+':'+password+'@'+host+':'+port+'/'+database)
#MEMANGGIL FUNGSI UPLOAD TO PSQL
checkUpload = uploadToPSQL(columns, table, filePath, engine)
#MENGECEK FUNGSI DARI UPLOAD PSQL, JIKA BERHASIL LANJUT MEMBUAT FUNGSI CHART, JIKA GAGAL AKAN MENAMPILKAN PESAN ERROR
if checkUpload == True:
makeChart(host, username, password, database, port, table, judul, columns, filePath, name, subjudul, limitdata, negara, basePath)
else:
print("Error When Upload CSV")
```
| github_jupyter |
```
import pytest
from scipy.stats import zscore
from mne.preprocessing import create_ecg_epochs
from sklearn.model_selection import train_test_split
%run parameters.py
%run Utility_Functions.ipynb
%matplotlib qt5
data = np.load('All_Subject_IR_Index_'+str(epoch_length)+'.npy')
print(data.shape)
sb.set()
def ir_plot(data):
for i, subject in enumerate(subjects):
temp = []
for j, trial in enumerate(trials):
temp.append(data[i][j][:])
plt.subplot(3,6,i+1)
plt.boxplot(temp, showfliers=False)
plt.tight_layout()
ir_plot(data)
data = np.load('All_Subject_IR_Index_'+str(epoch_length)+'.npy')
print(data.shape)
plt.figure()
def ir_plot(data):
for i, subject in enumerate(subjects):
temp = []
for j, trial in enumerate(trials):
if trial=='HighFine' or trial=='LowFine':
temp.append(data[i][j][:])
plt.subplot(3,6,i+1)
for element in temp:
plt.plot(element)
plt.tight_layout()
def min_max(data):
data -= data.min()
# data /= data.ptp()
return data
plt.figure()
def ir_plot(data):
for i, subject in enumerate(subjects):
temp = []
for j, trial in enumerate(trials):
if trial=='HighFine' or trial=='LowFine':
temp.append(data[i][j][:])
temp_z = zscore(np.vstack((np.expand_dims(temp[0], axis=1),np.expand_dims(temp[1], axis=1))))
plt.plot(temp_z[0:len(temp[0])], 'r')
plt.plot(temp_z[len(temp[0]):], 'b')
plt.tight_layout()
def test_epoch_length(subjects, trials):
s = []
for subject in subjects:
for trial in trials:
read_eeg_path = '../Cleaned Data/' + subject + '/EEG/'
read_force_path = '../Cleaned Data/' + subject + '/Force/'
cleaned_eeg = mne.read_epochs(read_eeg_path + subject + '_' + trial + '_' + str(epoch_length)
+ '_cleaned_epo.fif', verbose=False)
cleaned_force = mne.read_epochs(read_force_path + subject + '_' + trial + '_' + str(epoch_length)
+ '_cleaned_epo.fif', verbose=False)
eeg = cleaned_eeg.get_data()
force = cleaned_force.get_data()
# Check whether eeg and force data are same
assert eeg.shape[0]==force.shape[0]
s.append(subject)
# Check whether all subjects were tested
assert len(s)==len(subjects), 'Huston! We have got a problem!'
return 'Reached moon!'
def test_data():
x = np.load('PSD_X_Data_' + str(epoch_length) + '.npy')
y = np.load('IR_Y_Data_' + str(epoch_length) + '.npy')
assert x.shape[0]==y.shape[0], "Houston we've got a problem!"
def test_psd_image():
x = np.load('PSD_X_Data_' + str(epoch_length) +'.npy')
plt.imshow(x[5,:,0].reshape(image_size, image_size))
def test_x_y_length():
x = np.load('X.npy')
y = np.load('Y.npy')
assert x.shape[0]==y.shape[0], 'Huston! We have got a problem!'
return 'Reached moon!'
def test_x_y_length():
x = np.load('X.npy')
y = np.load('Y.npy')
print(sum(y)/len(y))
assert x.shape[0]==y.shape[0], 'Huston! We have got a problem!'
return 'Reached moon!'
test_x_y_length()
x = np.load('X.npy')
y = np.load('Y.npy')
print(x.shape)
x_normal = x[np.argmax(y, axis=1)==1,:,:]
y_normal = y[np.argmax(y, axis=1)==1]
print(np.argmax(y, axis=1)==0)
x_low = x[np.argmax(y, axis=1)==0,:,:]
y_low = y[np.argmax(y, axis=1)==0]
print(x_low.shape)
x_high = x[np.argmax(y, axis=1)==2,:,:]
y_high = y[np.argmax(y, axis=1)==2]
x_normal, x_test, y_normal, y_test = train_test_split(x_normal, y_normal, test_size = 0.50)
x_balanced = np.vstack((x_low, x_normal, x_high))
```
| github_jupyter |
# Produit matriciel avec une matrice creuse
Les dictionnaires sont une façon assez de représenter les matrices creuses en ne conservant que les coefficients non nuls. Comment écrire alors le produit matriciel ?
```
from jyquickhelper import add_notebook_menu
add_notebook_menu()
```
## Matrice creuse et dictionnaire
Une [matrice creuse](https://fr.wikipedia.org/wiki/Matrice_creuse) ou [sparse matrix](https://en.wikipedia.org/wiki/Sparse_matrix) est constituée majoritairement de 0. On utilise un dictionnaire avec les coefficients non nuls. La fonction suivante pour créer une matrice aléatoire.
```
import random
def random_matrix(n, m, ratio=0.1):
mat = {}
nb = min(n * m, int(ratio * n * m + 0.5))
while len(mat) < nb:
i = random.randint(0, n-1)
j = random.randint(0, m-1)
mat[i, j] = 1
return mat
mat = random_matrix(3, 3, ratio=0.5)
mat
```
## Calcul de la dimension
Pour obtenir la dimension de la matrice, il faut parcourir toutes les clés du dictionnaire.
```
def dimension(mat):
maxi, maxj = 0, 0
for k in mat:
maxi = max(maxi, k[0])
maxj = max(maxj, k[1])
return maxi + 1, maxj + 1
dimension(mat)
```
Cette fonction possède l'inconvénient de retourner une valeur fausse si la matrice ne possède aucun coefficient non nul sur la dernière ligne ou la dernière colonne. Cela peut être embarrassant, tout dépend de l'usage.
## Produit matriciel classique
On implémente le produit matriciel classique, à trois boucles.
```
def produit_classique(m1, m2):
dim1 = dimension(m1)
dim2 = dimension(m2)
if dim1[1] != dim2[0]:
raise Exception("Impossible de multiplier {0}, {1}".format(
dim1, dim2))
res = {}
for i in range(dim1[0]):
for j in range(dim2[1]):
s = 0
for k in range(dim1[1]):
s += m1.get((i, k), 0) * m2.get((k, j), 0)
if s != 0: # Pour éviter de garder les coefficients non nuls.
res[i, j] = s
return res
simple = {(0, 1): 1, (1, 0): 1}
produit_classique(simple, simple)
```
Sur la matrice aléatoire...
```
produit_classique(mat, mat)
```
## Produit matriciel plus élégant
A-t-on vraiment besoin de s'enquérir des dimensions de la matrice pour faire le produit matriciel ? Ne peut-on pas tout simplement faire une boucle sur les coefficients non nul ?
```
def produit_elegant(m1, m2):
res = {}
for (i, k1), v1 in m1.items():
if v1 == 0:
continue
for (k2, j), v2 in m2.items():
if v2 == 0:
continue
if k1 == k2:
if (i, j) in res:
res[i, j] += v1 * v2
else :
res[i, j] = v1 * v2
return res
produit_elegant(simple, simple)
produit_elegant(mat, mat)
```
## Mesure du temps
A priori, la seconde méthode est plus rapide puisque son coût est proportionnel au produit du nombre de coefficients non nuls dans les deux matrices. Vérifions.
```
bigmat = random_matrix(100, 100)
%timeit produit_classique(bigmat, bigmat)
%timeit produit_elegant(bigmat, bigmat)
```
C'est beaucoup mieux. Mais peut-on encore faire mieux ?
## Dictionnaires de dictionnaires
Ca sonne un peu comme [mille millions de mille sabords](https://fr.wikipedia.org/wiki/Vocabulaire_du_capitaine_Haddock) mais le dictionnaire que nous avons créé a pour clé un couple de coordonnées et valeur des coefficients. La fonction ``produit_elegant`` fait plein d'itérations inutiles en quelque sorte puisque les coefficients sont nuls. Peut-on éviter ça ?
Et si on utilisait des dictionnaires de dictionnaires : ``{ ligne : { colonne : valeur } }``.
```
def matrice_dicodico(mat):
res = {}
for (i, j), v in mat.items():
if i not in res:
res[i] = {j: v}
else:
res[i][j] = v
return res
matrice_dicodico(simple)
```
Peut-on adapter le calcul matriciel élégant ? Il reste à associer les indices de colonnes de la première avec les indices de lignes de la seconde. Cela pose problème en l'état quand les indices de colonnes sont inaccessibles sans connaître les indices de lignes d'abord à moins d'échanger l'ordre pour la seconde matrice.
```
def matrice_dicodico_lc(mat, ligne=True):
res = {}
if ligne:
for (i, j), v in mat.items():
if i not in res:
res[i] = {j: v}
else:
res[i][j] = v
else:
for (j, i), v in mat.items():
if i not in res:
res[i] = {j: v}
else:
res[i][j] = v
return res
matrice_dicodico_lc(simple, ligne=False)
```
Maintenant qu'on a fait ça, on peut songer au produit matriciel.
```
def produit_elegant_rapide(m1, m2):
res = {}
for k, vs in m1.items():
if k in m2:
for i, v1 in vs.items():
for j, v2 in m2[k].items():
if (i, j) in res:
res[i, j] += v1 * v2
else :
res[i, j] = v1 * v2
return res
m1 = matrice_dicodico_lc(simple, ligne=False)
m2 = matrice_dicodico_lc(simple)
produit_elegant_rapide(m1, m2)
m1 = matrice_dicodico_lc(mat, ligne=False)
m2 = matrice_dicodico_lc(mat)
produit_elegant_rapide(m1, m2)
```
On mesure le temps avec une grande matrice.
```
m1 = matrice_dicodico_lc(bigmat, ligne=False)
m2 = matrice_dicodico_lc(bigmat)
%timeit produit_elegant_rapide(m1, m2)
```
Beaucoup plus rapide, il n'y a plus besoin de tester les coefficients non nuls. La comparaison n'est pas très juste néanmoins car il faut transformer les deux matrices avant de faire le calcul. Et si on l'incluait ?
```
def produit_elegant_rapide_transformation(mat1, mat2):
m1 = matrice_dicodico_lc(mat1, ligne=False)
m2 = matrice_dicodico_lc(mat2)
return produit_elegant_rapide(m1, m2)
produit_elegant_rapide_transformation(simple, simple)
%timeit produit_elegant_rapide_transformation(bigmat, bigmat)
```
Finalement ça vaut le coup... mais est-ce le cas pour toutes les matrices.
```
%matplotlib inline
import time
mesures = []
for ratio in [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.99]:
big = random_matrix(100, 100, ratio=ratio)
t1 = time.perf_counter()
produit_elegant_rapide_transformation(big, big)
t2 = time.perf_counter()
dt = (t2 - t1)
obs = {"dicodico": dt, "ratio": ratio}
if ratio <= 0.3:
# après c'est trop lent
t1 = time.perf_counter()
produit_elegant(big, big)
t2 = time.perf_counter()
dt = (t2 - t1)
obs["dico"] = dt
t1 = time.perf_counter()
produit_classique(big, big)
t2 = time.perf_counter()
dt = (t2 - t1)
obs["classique"] = dt
mesures.append(obs)
print(obs)
from pandas import DataFrame
df = DataFrame(mesures)
ax = df.plot(x="ratio", y="dicodico", label="dico dico")
df.plot(x="ratio", y="dico", label="dico", ax=ax)
df.plot(x="ratio", y="classique", label="classique", ax=ax)
ax.legend();
```
Cette dernière version est efficace.
| github_jupyter |
<a href="https://colab.research.google.com/github/mohd-faizy/03_TensorFlow_In-Practice/blob/master/03_callbacks.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# __Callbacks API__
A __callback__ is an object that can perform actions at various stages of training (e.g. at the start or end of an epoch, before or after a single batch, etc).
_You can use callbacks to:_
- Write TensorBoard logs after every batch of training to monitor your metrics.
- Periodically save your model to disk.
- Do early stopping.
- Get a view on internal states and statistics of a model during training...and more
## __Usage of callbacks via the built-in `fit()` loop__
You can pass a list of callbacks (as the keyword argument callbacks) to the `.fit()` method of a model:
```
my_callbacks = [
tf.keras.callbacks.EarlyStopping(patience=2),
tf.keras.callbacks.ModelCheckpoint(filepath='model.{epoch:02d}-{val_loss:.2f}.h5'),
tf.keras.callbacks.TensorBoard(log_dir='./logs'),
]
model.fit(dataset, epochs=10, callbacks=my_callbacks)
```
The relevant methods of the callbacks will then be called at each stage of the training.
__Using custom callbacks__
Creating new callbacks is a simple and powerful way to customize a training loop. Learn more about creating new callbacks in the guide [__Writing your own Callbacks__](https://keras.io/guides/writing_your_own_callbacks/), and refer to the documentation for the [__base Callback class__](https://keras.io/api/callbacks/base_callback/).
__Available callbacks__
```
- Base Callback class
- ModelCheckpoint
- TensorBoard
- EarlyStopping
- LearningRateScheduler
- ReduceLROnPlateau
- RemoteMonitor
- LambdaCallback
- TerminateOnNaN
- CSVLogger
- ProgbarLogger
```
> [__Writing your own callbacks__](https://www.tensorflow.org/guide/keras/custom_callback)
```
import tensorflow as tf
# Defining the callback class
class myCallback(tf.keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs={}):
if(logs.get('accuracy')>0.6):
print("\nReached 60% accuracy so cancelling training!")
self.model.stop_training = True
mnist = tf.keras.datasets.fashion_mnist
(x_train, y_train),(x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
callbacks = myCallback()
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(input_shape=(28, 28)),
tf.keras.layers.Dense(512, activation=tf.nn.relu),
tf.keras.layers.Dense(10, activation=tf.nn.softmax)
])
model.compile(optimizer=tf.optimizers.Adam(),
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model.fit(x_train, y_train, epochs=10, callbacks=[callbacks])
```
| github_jupyter |
```
from PIL import Image
import numpy as np
import os
import cv2
import keras
from keras.utils import np_utils
from keras.models import Sequential
from keras.layers import Conv2D,MaxPooling2D,Dense,Flatten,Dropout
import pandas as pd
import sys
import tensorflow as tf
%matplotlib inline
import matplotlib.pyplot as plt
import plotly.express as px
def readData(filepath, label):
cells = []
labels = []
file = os.listdir(filepath)
for img in file:
try:
image = cv2.imread(filepath + img)
image_from_array = Image.fromarray(image, 'RGB')
size_image = image_from_array.resize((50, 50))
cells.append(np.array(size_image))
labels.append(label)
except AttributeError as e:
print('Skipping file: ', img, e)
print(len(cells), ' Data Points Read!')
return np.array(cells), np.array(labels)
def genesis_train(file):
print('Reading Training Data')
ParasitizedCells, ParasitizedLabels = readData(file + '/Parasitized/', 1)
UninfectedCells, UninfectedLabels = readData(file + '/Uninfected/', 0)
Cells = np.concatenate((ParasitizedCells, UninfectedCells))
Labels = np.concatenate((ParasitizedLabels, UninfectedLabels))
print('Reading Testing Data')
TestParasitizedCells, TestParasitizedLabels = readData('./input/fed/test/Parasitized/', 1)
TestUninfectedCells, TestUninfectedLabels = readData('./input/fed/test/Uninfected/', 0)
TestCells = np.concatenate((TestParasitizedCells, TestUninfectedCells))
TestLabels = np.concatenate((TestParasitizedLabels, TestUninfectedLabels))
s = np.arange(Cells.shape[0])
np.random.shuffle(s)
Cells = Cells[s]
Labels = Labels[s]
sTest = np.arange(TestCells.shape[0])
np.random.shuffle(sTest)
TestCells = TestCells[sTest]
TestLabels = TestLabels[sTest]
num_classes=len(np.unique(Labels))
len_data=len(Cells)
print(len_data, ' Data Points')
(x_train,x_test)=Cells, TestCells
(y_train,y_test)=Labels, TestLabels
# Since we're working on image data, we normalize data by divinding 255.
x_train = x_train.astype('float32')/255
x_test = x_test.astype('float32')/255
train_len=len(x_train)
test_len=len(x_test)
#Doing One hot encoding as classifier has multiple classes
y_train=keras.utils.to_categorical(y_train,num_classes)
y_test=keras.utils.to_categorical(y_test,num_classes)
#creating sequential model
model=Sequential()
model.add(Conv2D(filters=16,kernel_size=2,padding="same",activation="relu",input_shape=(50,50,3)))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=32,kernel_size=2,padding="same",activation="relu"))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=64,kernel_size=2,padding="same",activation="relu"))
model.add(MaxPooling2D(pool_size=2))
model.add(Dropout(0.2))
model.add(Flatten())
model.add(Dense(500,activation="relu"))
model.add(Dropout(0.2))
model.add(Dense(2,activation="softmax"))#2 represent output layer neurons
# model.summary()
# compile the model with loss as categorical_crossentropy and using adam optimizer
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
#Fit the model with min batch size as 50[can tune batch size to some factor of 2^power ]
model.fit(x_train, y_train, batch_size=100, epochs=5, verbose=1)
scores = model.evaluate(x_test, y_test)
print("Loss: ", scores[0]) #Loss
print("Accuracy: ", scores[1]) #Accuracy
#Saving Model
model.save("./output.h5")
return len_data, scores[1]
def update_train(file, d):
print('Reading Training Data')
ParasitizedCells, ParasitizedLabels = readData(file + '/Parasitized/', 1)
UninfectedCells, UninfectedLabels = readData(file + '/Uninfected/', 0)
Cells = np.concatenate((ParasitizedCells, UninfectedCells))
Labels = np.concatenate((ParasitizedLabels, UninfectedLabels))
print('Reading Testing Data')
TestParasitizedCells, TestParasitizedLabels = readData('./input/fed/test/Parasitized/', 1)
TestUninfectedCells, TestUninfectedLabels = readData('./input/fed/test/Uninfected/', 0)
TestCells = np.concatenate((TestParasitizedCells, TestUninfectedCells))
TestLabels = np.concatenate((TestParasitizedLabels, TestUninfectedLabels))
s = np.arange(Cells.shape[0])
np.random.shuffle(s)
Cells = Cells[s]
Labels = Labels[s]
sTest = np.arange(TestCells.shape[0])
np.random.shuffle(sTest)
TestCells = TestCells[sTest]
TestLabels = TestLabels[sTest]
num_classes=len(np.unique(Labels))
len_data=len(Cells)
print(len_data, ' Data Points')
(x_train,x_test)=Cells, TestCells
(y_train,y_test)=Labels, TestLabels
# Since we're working on image data, we normalize data by divinding 255.
x_train = x_train.astype('float32')/255
x_test = x_test.astype('float32')/255
train_len=len(x_train)
test_len=len(x_test)
#Doing One hot encoding as classifier has multiple classes
y_train=keras.utils.to_categorical(y_train,num_classes)
y_test=keras.utils.to_categorical(y_test,num_classes)
#creating sequential model
model=Sequential()
model.add(Conv2D(filters=16,kernel_size=2,padding="same",activation="relu",input_shape=(50,50,3)))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=32,kernel_size=2,padding="same",activation="relu"))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=64,kernel_size=2,padding="same",activation="relu"))
model.add(MaxPooling2D(pool_size=2))
model.add(Dropout(0.2))
model.add(Flatten())
model.add(Dense(500,activation="relu"))
model.add(Dropout(0.2))
model.add(Dense(2,activation="softmax"))#2 represent output layer neurons
# model.summary()
model.load_weights("./output.h5")
# compile the model with loss as categorical_crossentropy and using adam optimizer
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
#Fit the model with min batch size as 50[can tune batch size to some factor of 2^power ]
model.fit(x_train, y_train, batch_size=100, epochs=5, verbose=1)
scores = model.evaluate(x_test, y_test)
print("Loss: ", scores[0]) #Loss
print("Accuracy: ", scores[1]) #Accuracy
#Saving Model
model.save("./weights/" + str(d) + ".h5")
return len_data, scores[1]
FLAccuracy = {}
# FLAccuracy['Complete Dataset'] = genesis_train('./input/cell_images')
FLAccuracy['Genesis'] = genesis_train('./input/fed/genesis')
FLAccuracy['d1'] = update_train('./input/fed/d1', 'd1')
FLAccuracy['d2'] = update_train('./input/fed/d2', 'd2')
FLAccuracy['d3'] = update_train('./input/fed/d3', 'd3')
FLAccuracy['d4'] = update_train('./input/fed/d4', 'd4')
FLAccuracy['d5'] = update_train('./input/fed/d5', 'd5')
FLAccuracy['d6'] = update_train('./input/fed/d6', 'd6')
FLAccuracy['d7'] = update_train('./input/fed/d7', 'd7')
FLAccuracy['d8'] = update_train('./input/fed/d8', 'd8')
FLAccuracy['d9'] = update_train('./input/fed/d9', 'd9')
FLAccuracy['d10'] = update_train('./input/fed/d10', 'd10')
FLAccuracy['d11'] = update_train('./input/fed/d11', 'd11')
FLAccuracy['d12'] = update_train('./input/fed/d12', 'd12')
FLAccuracy['d13'] = update_train('./input/fed/d13', 'd13')
FLAccuracy['d14'] = update_train('./input/fed/d14', 'd14')
FLAccuracy['d15'] = update_train('./input/fed/d15', 'd15')
FLAccuracy['d16'] = update_train('./input/fed/d16', 'd16')
FLAccuracy['d17'] = update_train('./input/fed/d17', 'd17')
FLAccuracy['d18'] = update_train('./input/fed/d18', 'd18')
FLAccuracy['d19'] = update_train('./input/fed/d19', 'd19')
FLAccuracy['d20'] = update_train('./input/fed/d20', 'd20')
FLAccuracy
FLAccuracyDF = pd.DataFrame.from_dict(FLAccuracy, orient='index', columns=['DataSize', 'Accuracy'])
FLAccuracyDF
FLAccuracyDF.index
n = 0
for w in FLAccuracy:
if 'Complete' in w:
continue
n += FLAccuracy[w][0]
print('Total number of data points in this round: ', n)
FLAccuracyDF['Weightage'] = FLAccuracyDF['DataSize'].apply(lambda x: x/n)
FLAccuracyDF
def scale(weight, scaler):
scaledWeights = []
for i in range(len(weight)):
scaledWeights.append(scaler * weight[i])
return scaledWeights
def getScaledWeight(d, scaler):
#creating sequential model
model=Sequential()
model.add(Conv2D(filters=16,kernel_size=2,padding="same",activation="relu",input_shape=(50,50,3)))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=32,kernel_size=2,padding="same",activation="relu"))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=64,kernel_size=2,padding="same",activation="relu"))
model.add(MaxPooling2D(pool_size=2))
model.add(Dropout(0.2))
model.add(Flatten())
model.add(Dense(500,activation="relu"))
model.add(Dropout(0.2))
model.add(Dense(2,activation="softmax"))#2 represent output layer neurons
fpath = "./weights/"+d+".h5"
model.load_weights(fpath)
weight = model.get_weights()
scaledWeight = scale(weight, scaler)
return scaledWeight
def avgWeights(scaledWeights):
avg = list()
for weight_list_tuple in zip(*scaledWeights):
layer_mean = tf.math.reduce_sum(weight_list_tuple, axis=0)
avg.append(layer_mean)
return avg
def FedAvg(models):
scaledWeights = []
for m in models:
scaledWeights.append(getScaledWeight(m, FLAccuracyDF.loc[m]['Weightage']))
avgWeight = avgWeights(scaledWeights)
return avgWeight
models = ['d1', 'd2', 'd3', 'd4', 'd5', 'd6', 'd7', 'd8', 'd9', 'd10', 'd11', 'd12', 'd13', 'd14', 'd15', 'd16', 'd17', 'd18', 'd19', 'd20']
avgWeight = FedAvg(models)
print(avgWeight)
def testNewGlobal(weight):
print('Reading Testing Data')
TestParasitizedCells, TestParasitizedLabels = readData('./input/fed/test/Parasitized/', 1)
TestUninfectedCells, TestUninfectedLabels = readData('./input/fed/test/Uninfected/', 0)
TestCells = np.concatenate((TestParasitizedCells, TestUninfectedCells))
TestLabels = np.concatenate((TestParasitizedLabels, TestUninfectedLabels))
sTest = np.arange(TestCells.shape[0])
np.random.shuffle(sTest)
TestCells = TestCells[sTest]
TestLabels = TestLabels[sTest]
num_classes=len(np.unique(TestLabels))
(x_test) = TestCells
(y_test) = TestLabels
# Since we're working on image data, we normalize data by divinding 255.
x_test = x_test.astype('float32')/255
test_len=len(x_test)
#Doing One hot encoding as classifier has multiple classes
y_test=keras.utils.to_categorical(y_test,num_classes)
#creating sequential model
model=Sequential()
model.add(Conv2D(filters=16,kernel_size=2,padding="same",activation="relu",input_shape=(50,50,3)))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=32,kernel_size=2,padding="same",activation="relu"))
model.add(MaxPooling2D(pool_size=2))
model.add(Conv2D(filters=64,kernel_size=2,padding="same",activation="relu"))
model.add(MaxPooling2D(pool_size=2))
model.add(Dropout(0.2))
model.add(Flatten())
model.add(Dense(500,activation="relu"))
model.add(Dropout(0.2))
model.add(Dense(2,activation="softmax"))#2 represent output layer neurons
# model.summary()
model.set_weights(weight)
# compile the model with loss as categorical_crossentropy and using adam optimizer
model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy'])
scores = model.evaluate(x_test, y_test)
print("Loss: ", scores[0]) #Loss
print("Accuracy: ", scores[1]) #Accuracy
#Saving Model
model.save("./output.h5")
return scores[1]
testNewGlobal(avgWeight)
FLAccuracyDF
```
| github_jupyter |
# Loan predictions
## Problem Statement
We want to automate the loan eligibility process based on customer details that are provided as online application forms are being filled. You can find the dataset [here](https://drive.google.com/file/d/1h_jl9xqqqHflI5PsuiQd_soNYxzFfjKw/view?usp=sharing). These details concern the customer's Gender, Marital Status, Education, Number of Dependents, Income, Loan Amount, Credit History and other things as well.
|Variable| Description|
|: ------------- |:-------------|
|Loan_ID| Unique Loan ID|
|Gender| Male/ Female|
|Married| Applicant married (Y/N)|
|Dependents| Number of dependents|
|Education| Applicant Education (Graduate/ Under Graduate)|
|Self_Employed| Self employed (Y/N)|
|ApplicantIncome| Applicant income|
|CoapplicantIncome| Coapplicant income|
|LoanAmount| Loan amount in thousands|
|Loan_Amount_Term| Term of loan in months|
|Credit_History| credit history meets guidelines|
|Property_Area| Urban/ Semi Urban/ Rural|
|Loan_Status| Loan approved (Y/N)
### Explore the problem in following stages:
1. Hypothesis Generation – understanding the problem better by brainstorming possible factors that can impact the outcome
2. Data Exploration – looking at categorical and continuous feature summaries and making inferences about the data.
3. Data Cleaning – imputing missing values in the data and checking for outliers
4. Feature Engineering – modifying existing variables and creating new ones for analysis
5. Model Building – making predictive models on the data
## 1. Hypothesis Generation
Generating a hypothesis is a major step in the process of analyzing data. This involves understanding the problem and formulating a meaningful hypothesis about what could potentially have a good impact on the outcome. This is done BEFORE looking at the data, and we end up creating a laundry list of the different analyses which we can potentially perform if data is available.
#### Possible hypotheses
Which applicants are more likely to get a loan
1. Applicants having a credit history
2. Applicants with higher applicant and co-applicant incomes
3. Applicants with higher education level
4. Properties in urban areas with high growth perspectives
Do more brainstorming and create some hypotheses of your own. Remember that the data might not be sufficient to test all of these, but forming these enables a better understanding of the problem.
```
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
df = pd.read_csv('data.csv')
df.head(10)
df.shape
```
## 2. Data Exploration
Let's do some basic data exploration here and come up with some inferences about the data. Go ahead and try to figure out some irregularities and address them in the next section.
One of the key challenges in any data set are missing values. Lets start by checking which columns contain missing values.
```
df.isnull().sum()
```
Look at some basic statistics for numerical variables.
```
df.dtypes
df.nunique()
```
1. How many applicants have a `Credit_History`? (`Credit_History` has value 1 for those who have a credit history and 0 otherwise)
2. Is the `ApplicantIncome` distribution in line with your expectation? Similarly, what about `CoapplicantIncome`?
3. Tip: Can you see a possible skewness in the data by comparing the mean to the median, i.e. the 50% figure of a feature.
Let's discuss nominal (categorical) variable. Look at the number of unique values in each of them.
Explore further using the frequency of different categories in each nominal variable. Exclude the ID obvious reasons.
### Distribution analysis
Study distribution of various variables. Plot the histogram of ApplicantIncome, try different number of bins.
Look at box plots to understand the distributions.
Look at the distribution of income segregated by `Education`
Look at the histogram and boxplot of LoanAmount
There might be some extreme values. Both `ApplicantIncome` and `LoanAmount` require some amount of data munging. `LoanAmount` has missing and well as extreme values values, while `ApplicantIncome` has a few extreme values, which demand deeper understanding.
### Categorical variable analysis
Try to understand categorical variables in more details using `pandas.DataFrame.pivot_table` and some visualizations.
## 3. Data Cleaning
This step typically involves imputing missing values and treating outliers.
### Imputing Missing Values
Missing values may not always be NaNs. For instance, the `Loan_Amount_Term` might be 0, which does not make sense.
Impute missing values for all columns. Use the values which you find most meaningful (mean, mode, median, zero.... maybe different mean values for different groups)
```
from sklearn.impute import SimpleImputer
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import FunctionTransformer
from sklearn.metrics import accuracy_score
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder
from sklearn.model_selection import GridSearchCV
from sklearn.svm import SVC
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.compose import make_column_selector
import pickle
ohe=OneHotEncoder(drop='first', sparse=False)
X= df.drop(columns=['Loan_Status', 'Loan_ID'])
y=df['Loan_Status']
#y=ohe.fit_transform(df['Loan_Status'].to_numpy().reshape(-1, 1))
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,
random_state=0)
column_trans = ColumnTransformer(
[('imp_most_frequent', SimpleImputer(strategy='most_frequent'), ['Gender', 'Married',
'Dependents', 'Self_Employed',
'Property_Area',
'Education',
'Credit_History']),
('imp_median', SimpleImputer(strategy='median'), ['LoanAmount', 'Loan_Amount_Term']),
('scaling', StandardScaler(), make_column_selector(dtype_include=np.number))
]
)
column_enc = ColumnTransformer([('one_hot_enc', OneHotEncoder(handle_unknown='ignore'),
[0,
1,
2,
3,
4,
10])])
pipeline = Pipeline(steps=[('column_transf', column_trans),
('column_enc', column_enc),
('classifier', SVC(random_state = 17))])
# Find the best hyperparameters using GridSearchCV on the train set
param_grid = [
{'classifier':(SVC(random_state = 17),),
'classifier__C': [0.5, 1, 2, 4],
'classifier__kernel': ['linear', 'poly', 'rbf', 'sigmoid'],
'classifier__degree': [2, 3],
'classifier__gamma':['scale', 'auto']},
{'classifier':(LogisticRegression(random_state = 17),),
'classifier__penalty':['l1', 'l2', 'elasticnet'],
'classifier__C': [0.5, 1, 2, 4],
'classifier__solver': ['newton-cg', 'lbfgs', 'liblinear', 'sag', 'saga']
}]
grid = GridSearchCV(pipeline, param_grid=param_grid, verbose=2, n_jobs=5, scoring='accuracy')
grid.fit(X_train, y_train)
grid.best_params_
grid.best_score_
y_pred=grid.predict(X_test)
accuracy_score(y_test, y_pred)
pipeline = Pipeline(steps=[('column_transf', column_trans),
('column_enc', column_enc),
('classifier', grid.best_params_['classifier'])])
pipeline.fit(X_train, y_train)
with open('myfile.pickle', 'wb') as file_handle:
pickle.dump(pipeline, file_handle)
```
### Extreme values
Try a log transformation to get rid of the extreme values in `LoanAmount`. Plot the histogram before and after the transformation
Combine both incomes as total income and take a log transformation of the same.
## 4. Building a Predictive Model
Try paramater grid search to improve the results
## 5. Using Pipeline
If you didn't use pipelines before, transform your data prep, feat. engineering and modeling steps into Pipeline. It will be helpful for deployment.
The goal here is to create the pipeline that will take one row of our dataset and predict the probability of being granted a loan.
`pipeline.predict(x)`
## 6. Deploy your model to cloud and test it with PostMan, BASH or Python
| github_jupyter |
# Looking at the randomness (or otherwise) of mouse behaviour
### Also, the randomness (or otherwise) of trial types to know when best to start looking at 'full task' behaviour
```
# Import libraries
import matplotlib.pyplot as plt
%matplotlib inline
import pandas as pd
import seaborn as sns
import random
import copy
import numpy as np
from scipy.signal import resample
from scipy.stats import zscore
from scipy import interp
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn import metrics
from sklearn import cross_validation
# Load data
# data loading function
def data_load_and_parse(mouse_name):
tt = pd.read_csv('~/work/whiskfree/data/trialtype_' + mouse_name + '.csv',header=None)
ch = pd.read_csv('~/work/whiskfree/data/choice_' + mouse_name + '.csv',header=None)
sess = pd.read_csv('~/work/whiskfree/data/session_' + mouse_name + '.csv',header=None)
AB = pd.read_csv('~/work/whiskfree/data/AB_' + mouse_name + '.csv',header=None)
clean1 = np.nan_to_num(tt) !=0
clean2 = np.nan_to_num(ch) !=0
clean = clean1&clean2
tt_c = tt[clean].values
ch_c = ch[clean].values
s_c = sess[clean].values
ab_c = AB[clean].values
return tt_c, ch_c, clean, s_c, ab_c
mouse_name = '36_r'
tt, ch, clean, sess, AB = data_load_and_parse(mouse_name)
# work out AB/ON trials
AB_pol = np.nan_to_num(AB) !=0
ON_pol = np.nan_to_num(AB) ==0
cm_AB = confusion_matrix(tt[AB_pol],ch[AB_pol])
cm_ON = confusion_matrix(tt[ON_pol],ch[ON_pol])
print(cm_AB)
print(cm_ON)
print(accuracy_score(tt[AB_pol],ch[AB_pol]))
print(accuracy_score(tt[ON_pol],ch[ON_pol]))
# Format TT/ choice data and plot
fig, ax = plt.subplots(2,1,figsize=(20,5))
_ = ax[0].plot(tt[ON_pol][:100],label='TT ON')
_ = ax[0].plot(ch[ON_pol][:100],label='Ch ON')
ax[0].legend()
_ = ax[1].plot(tt[AB_pol][:100],label='TT AB')
_ = ax[1].plot(ch[AB_pol][:100],label='Ch AB')
ax[1].legend()
# Measure randomness and plot that
# First plot cumsum of trial types. Periods of bias (of choice 1 and 3, anyway) will be seen as deviations from the mean line
plt.plot(np.cumsum(tt[AB_pol][:100]),label='Cumsum TT AB')
plt.plot(np.cumsum(ch[AB_pol][:100]),label='Cumsum Ch AB')
plt.plot([0,99],[0,np.sum(tt[AB_pol][:100])],label='Mean cumsum')
plt.legend()
# How about looking at the distribution of individual states, pairs, triples.
# Compare to random sequence (with no conditions)
P_i = np.zeros(3)
P_i[0] = len(tt[tt[AB_pol]==1])
P_i[1] = len(tt[tt[AB_pol]==2])
P_i[2] = len(tt[tt[AB_pol]==3])
with sns.axes_style("white"):
_ = plt.imshow(np.expand_dims(P_i/sum(P_i),axis=0),interpolation='none')
for j in range(0,3):
plt.text(j, 0, P_i[j]/sum(P_i), va='center', ha='center',bbox=dict(facecolor='white',edgecolor='white', alpha=0.5))
# _ = ax[1].bar([0,1,2],P_i/sum(P_i))
# Pairs and triples (in dumb O(n) format)
P_ij = np.zeros([3,3])
P_ijk = np.zeros([3,3,3])
for i in range(len(tt[AB_pol]) - 2):
#p_i = tt[AB_pol][i]
#p_j = tt[AB_pol][i+1]
#p_k = tt[AB_pol][i+2]
p_i = ch[AB_pol][i]
p_j = ch[AB_pol][i+1]
p_k = ch[AB_pol][i+2]
P_ij[p_i-1,p_j-1] += 1
P_ijk[p_i-1,p_j-1,[p_k-1]] += 1
cmap = sns.diverging_palette(220,10, l=70, as_cmap=True, center="dark") # blue to green via black
with sns.axes_style("white"):
plt.imshow(P_ij/np.sum(P_ij),interpolation='none',cmap=cmap)
for i in range(0,3):
for j in range(0,3):
plt.text(j, i, "{0:.2f}".format(P_ij[i,j]/np.sum(P_ij)*9), va='center', ha='center',bbox=dict(facecolor='white',edgecolor='white', alpha=0.5))
#plt.savefig('figs/graphs/state_transition_matrix_AB'+ mouse_name +'.png')
plt.savefig('figs/graphs/choice_state_transition_matrix_AB'+ mouse_name +'.png')
# Plot P(state) for all 27 triple states
plt.plot(P_ijk_ON.flatten()/np.sum(P_ijk_ON))
plt.plot([0,26],[1/27,1/27],'--')
1/27
import graph_tool.all as gt
# Transition probabilities between individual states, pairs, triples
g = gt.Graph()
g.add_edge_list(np.transpose(P_ij.nonzero()))
with sns.axes_style("white"):
plt.imshow(P_ij,interpolation='none')
g = gt.Graph(directed = True)
g.add_vertex(len(P_ij))
edge_weights = g.new_edge_property('double')
edge_labels = g.new_edge_property('string')
for i in range(P_ij.shape[0]):
for j in range(P_ij.shape[1]):
e = g.add_edge(i, j)
edge_weights[e] = P_ij[i,j]
edge_labels[e] = str(P_ij[i,j])
# Fancy drawing code where node colour/size is degree. Edge colour/size is betweenness
deg = g.degree_property_map("in")
# deg.a = 4 * (np.sqrt(deg.a) * 0.5 + 0.4)
deg.a = deg.a*20
print(deg.a)
ewidth = edge_weights.a / 10
#ebet.a /= ebet.a.max() / 10.
#print(ebet.a)
pos = gt.sfdp_layout(g)
#control = g.new_edge_property("vector<double>")
#for e in g.edges():
# d = np.sqrt(sum((pos[e.source()].a - pos[e.target()].a) ** 2))
# print(d)
# control[e] = [10, d, 10,d] #[0.3, d, 0.7, d]
cmap = sns.cubehelix_palette(as_cmap=True) # cubehelix
cmap = sns.diverging_palette(220,10, l=70, as_cmap=True, center="dark") # blue to green via black
# gt.graph_draw(g, pos=pos, vertex_size=deg, vertex_fill_color=deg, vorder=deg,
# edge_color=ebet, eorder=eorder, edge_pen_width=ebet,
# edge_control_points=control) # some curvy edges
# output="graph-draw.pdf")
gt.graph_draw(g, pos=pos, vertex_size=deg, vertex_color=deg, vertex_fill_color=deg, edge_color=edge_weights, edge_text=edge_labels,
vcmap=cmap,ecmap=cmap, vertex_text=g.vertex_index, vertex_font_size=18,fit_view=0.5)
#vcmap=plt.cm.Pastel1,ecmap=plt.cm.Pastel1 )
# edge_control_points=control) # some curvy edges
# output="graph-draw.pdf")
# Same as g but normalised so total trials/9 = 1
g_n = gt.Graph(directed = True)
edge_weights_n = g_n.new_edge_property('double')
edge_labels_n = g_n.new_edge_property('string')
node_size_n = g_n.new_vertex_property('double')
g_n.add_vertex(len(P_ij))
P_ij_n = P_ij /(P_ij.sum()/9)
for i in range(P_ij.shape[0]):
#v = g_n.add_vertex()
node_size_n[i] = 3* sum(P_ij)[i] / np.sum(P_ij)
for j in range(P_ij.shape[1]):
e = g_n.add_edge(i, j)
edge_weights_n[e] = P_ij_n[i,j]
edge_labels_n[e] = "{0:.2f}".format(P_ij_n[i,j])
# Minimal drawing code, but with scaled colours/weights for network properties
# Line width changes on each loop ATM. Needs fixing..
pos = gt.sfdp_layout(g_n)
#deg_n = g_n.degree_property_map("in")
# deg.a = 4 * (np.sqrt(deg.a) * 0.5 + 0.4)
#deg_n.a = deg_n.a*20
n_size = copy.copy(node_size_n)
n_size.a = 50* n_size.a/ max(n_size.a)
edge_w = copy.copy(edge_weights_n)
edge_w.a = edge_w.a*10
cmap = sns.cubehelix_palette(as_cmap=True) # cubehelix
cmap = sns.diverging_palette(220,10, l=70, as_cmap=True, center="dark") # blue to green via black
gt.graph_draw(g_n, pos=pos, vertex_color = n_size, vertex_fill_color = n_size,
vertex_size = n_size,
edge_pen_width=edge_w, edge_color=edge_weights_n,
edge_text=edge_labels_n,
vcmap=cmap,ecmap=cmap,
vertex_text=g_n.vertex_index,
vertex_font_size=18,
output_size=(600,600), fit_view=0.4,
output="figs/graphs/choice_1st_order_transition_AB.pdf")
#vcmap=plt.cm.Pastel1,ecmap=plt.cm.Pastel1 )
# edge_control_points=control) # some curvy edges
# output="graph-draw.pdf")
current_palette = sns.color_palette("cubehelix")
current_palette = sns.diverging_palette(220,10, l=50, n=7, center="dark")
sns.palplot(current_palette)
# Now write a loop to construct a tree-type graph
# Same as g but normalised so total trials/9 = 1
t = gt.Graph(directed = False)
P_ij_n = P_ij /(P_ij.sum()/9)
P_ijk_n = P_ijk /(P_ijk.sum()/27)
edge_weights_t = t.new_edge_property('double')
edge_labels_t = t.new_edge_property('string')
node_labels_t = t.new_vertex_property('string')
node_size = t.new_vertex_property('double')
h = t.add_vertex()
node_labels_t[h] = "0"
for i in range(P_ij.shape[0]):
v = t.add_vertex()
node_labels_t[v] = str(i)
e = t.add_edge(h,v)
node_size[v] = sum(P_ij_n)[i] *10
for j in range(P_ij.shape[1]):
v2 = t.add_vertex()
node_labels_t[v2] = str(i) + "-" + str(j)
e = t.add_edge(v,v2)
edge_weights_t[e] = P_ij_n[i,j]*10
edge_labels_t[e] = "{0:.2f}".format(P_ij_n[i,j])
node_size[v2] = P_ij_n[i,j]*20
for k in range(P_ijk.shape[2]):
v3 = t.add_vertex()
node_labels_t[v3] = str(i) + "-" + str(j) + "-" + str(k)
e2 = t.add_edge(v2,v3)
edge_weights_t[e2] = P_ijk_n[i,j,k]*10
edge_labels_t[e2] = "{0:.2f}".format(P_ijk_n[i,j,k])
node_size[v3] = P_ijk_n[i,j,k]*20
#pos = gt.sfdp_layout(t)
#pos = gt.fruchterman_reingold_layout(t)
pos = gt.radial_tree_layout(t,t.vertex(0))
cmap = sns.diverging_palette(220,10, l=70, as_cmap=True, center="dark") # blue to green via black
gt.graph_draw(t,pos=pos,vertex_size=node_size,edge_pen_width=edge_weights_t,
vertex_text = node_labels_t, edge_text=edge_labels_t,
ecmap=cmap, edge_color = edge_weights_t,
vcmap=cmap, vertex_color = node_size,vertex_fill_color = node_size,
output_size=(1000, 1000), fit_view=0.8,
output="figs/graphs/choice_3_step_statespace_AB.pdf")
"{0:.2f}".format(P_ijk[1,1,1])
"{0:.2f}".format(P_ijk[1,1,1])
len(P_ij)
```
# Repeat the trick for ON policy trials
```
# P_ijk_ON
P_ij_ON = np.zeros([3,3])
P_ijk_ON = np.zeros([3,3,3])
for i in range(len(tt[AB_pol]) - 2):
# p_i = tt[ON_pol][i]
# p_j = tt[ON_pol][i+1]
# p_k = tt[ON_pol][i+2]
p_i = ch[AB_pol][i]
p_j = ch[AB_pol][i+1]
p_k = ch[AB_pol][i+2]
P_ij_ON[p_i-1,p_j-1] += 1
P_ijk_ON[p_i-1,p_j-1,[p_k-1]] += 1
# Make graph
t_ON = gt.Graph(directed = False)
P_ij_ON = P_ij_ON /(P_ij_ON.sum()/9)
P_ijk_ON = P_ijk_ON /(P_ijk_ON.sum()/27)
edge_weights_tON = t_ON.new_edge_property('double')
edge_labels_tON = t_ON.new_edge_property('string')
node_labels_tON = t_ON.new_vertex_property('string')
node_size_ON = t_ON.new_vertex_property('double')
h = t_ON.add_vertex()
node_labels_tON[h] = "0"
for i in range(P_ij_ON.shape[0]):
v = t_ON.add_vertex()
node_labels_tON[v] = str(i)
e = t_ON.add_edge(h,v)
node_size_ON[v] = sum(P_ij_ON)[i] *10
for j in range(P_ij_ON.shape[1]):
v2 = t_ON.add_vertex()
node_labels_tON[v2] = str(i) + "-" + str(j)
e = t_ON.add_edge(v,v2)
edge_weights_tON[e] = P_ij_ON[i,j]*10
edge_labels_tON[e] = "{0:.2f}".format(P_ij_ON[i,j])
node_size_ON[v2] = P_ij_ON[i,j]*20
for k in range(P_ijk_ON.shape[2]):
v3 = t_ON.add_vertex()
node_labels_tON[v3] = str(i) + "-" + str(j) + "-" + str(k)
e2 = t_ON.add_edge(v2,v3)
edge_weights_tON[e2] = P_ijk_ON[i,j,k]*10
edge_labels_tON[e2] = "{0:.2f}".format(P_ijk_ON[i,j,k])
node_size_ON[v3] = P_ijk_ON[i,j,k]*20
# Plot graph
pos = gt.radial_tree_layout(t_ON,t_ON.vertex(0))
cmap = sns.diverging_palette(220,10, l=70, as_cmap=True, center="dark") # blue to green via black
gt.graph_draw(t_ON,pos=pos,vertex_size=node_size_ON,edge_pen_width=edge_weights_tON,
vertex_text = node_labels_tON, edge_text=edge_labels_tON,
ecmap=cmap, edge_color = edge_weights_tON,
vcmap=cmap, vertex_color = node_size_ON,
vertex_fill_color = node_size_ON,
output_size=(1000, 1000), fit_view=0.8)
# output="figs/graphs/choice_3_step_statespace_AB_"+ mouse_name +".pdf")
# image of ON trials transition matrix
cmap = sns.diverging_palette(220,10, l=70, as_cmap=True, center="dark") # blue to green via black
with sns.axes_style("white"):
plt.imshow(P_ij_ON/np.sum(P_ij_ON),interpolation='none',cmap=cmap)
for i in range(0,3):
for j in range(0,3):
plt.text(j, i, "{0:.2f}".format(P_ij_ON[i,j]), va='center', ha='center',bbox=dict(facecolor='white',edgecolor='white', alpha=0.5))
ylabels = ['Anterior','Posterior','No Go']
plt.xticks([0,1,2],ylabels)
plt.yticks([0,1,2],ylabels)
# plt.set_yticks([0,1,2])
# plt.set_yticklabels(ylabels)
# plt.savefig('figs/graphs/choice_state_transition_matrix_AB_'+ mouse_name +'.png')
# Just plot P(state)
plt.figure(figsize=(16,2))
ax1 = plt.subplot2grid((1,4),(0,0))
ax1.plot(P_ij_ON.flatten()/np.sum(P_ij_ON) * 9)
ax1.plot([0,8],[1,1],'--')
state_names = np.empty([3,3],dtype=object)
for i in range(0,3):
for j in range(0,3):
state_names[i,j] = str(i) + "-" + str(j)
ax1.set_xticks(range(0,9))
ax1.set_xticklabels(state_names.flatten(),rotation=45)
ax2 = plt.subplot2grid((1,4),(0,1),colspan=3)
ax2.plot(P_ijk_ON.flatten()/np.sum(P_ijk_ON) * 27)
ax2.plot([0,26],[1,1],'--')
state_names = np.empty([3,3,3],dtype=object)
for i in range(0,3):
for j in range(0,3):
for k in range(0,3):
state_names[i,j,k] = str(i) + "-" + str(j) + "-" + str(k)
_ = ax2.set_xticks(range(0,27))
_ = ax2.set_xticklabels(state_names.flatten(),rotation=45)
plt.tight_layout()
plt.savefig('figs/graphs/CH_state_prob_AB_'+ mouse_name +'.png')
from scipy.stats import chisquare
# chisquare(P_ij_ON.flatten())
chisquare?
# First order transition graph
g_ON = gt.Graph(directed = True)
edge_weights_ON = g_ON.new_edge_property('double')
edge_labels_ON = g_ON.new_edge_property('string')
node_size_ON = g_ON.new_vertex_property('double')
g_ON.add_vertex(len(P_ij_ON))
for i in range(P_ij_ON.shape[0]):
#v = g_n.add_vertex()
node_size_ON[i] = 3* sum(P_ij_ON)[i] / np.sum(P_ij_ON)
for j in range(P_ij_ON.shape[1]):
e = g_ON.add_edge(i, j)
edge_weights_ON[e] = P_ij_ON[i,j]
edge_labels_ON[e] = "{0:.2f}".format(P_ij_ON[i,j])
# Plot graph
pos = gt.sfdp_layout(g_ON)
n_size = copy.copy(node_size_ON)
n_size.a = 50* n_size.a/ max(n_size.a)
edge_w = copy.copy(edge_weights_ON)
edge_w.a = edge_w.a*10
cmap = sns.cubehelix_palette(as_cmap=True) # cubehelix
cmap = sns.diverging_palette(220,10, l=70, as_cmap=True, center="dark") # blue to red via black
gt.graph_draw(g_ON, pos=pos, vertex_color = n_size, vertex_fill_color = n_size,
vertex_size = n_size,
edge_pen_width=edge_w, edge_color=edge_w,
edge_text=edge_labels_ON,
vcmap=cmap,ecmap=cmap,
vertex_text=g_ON.vertex_index,
vertex_font_size=18,
output_size=(800, 800), fit_view=0.45,
output="figs/graphs/choice_1st_order_transition_ON"+ mouse_name +".pdf")
```
# Finally, transition probabilities for choices - do they follow the trial types?
## (Actually, let's just re-run the code from above changing tt to ch)
# Now, let's use graphs to visualise confusion matrices
```
cm_AB = confusion_matrix(tt[AB_pol],ch[AB_pol])
cm_ON = confusion_matrix(tt[ON_pol],ch[ON_pol])
print(cm_AB)
print(cm_ON)
print(accuracy_score(tt[AB_pol],ch[AB_pol]))
print(accuracy_score(tt[ON_pol],ch[ON_pol]))
cmap = sns.diverging_palette(220,10, l=70, as_cmap=True, center="dark") # blue to red via black
with sns.axes_style("white"):
fig, ax = plt.subplots(1,2)
ax[0].imshow(cm_ON/np.sum(cm_ON),interpolation='none',cmap=cmap)
ax[1].imshow(cm_AB/np.sum(cm_AB),interpolation='none',cmap=cmap)
for i in range(0,3):
for j in range(0,3):
ax[0].text(j, i, "{0:.2f}".format(cm_ON[i,j]), va='center', ha='center',bbox=dict(facecolor='white',edgecolor='white', alpha=0.5))
ax[1].text(j, i, "{0:.2f}".format(cm_AB[i,j]), va='center', ha='center',bbox=dict(facecolor='white',edgecolor='white', alpha=0.5))
ax[0].set_title('Mouse ON')
ax[1].set_title('Mouse AB')
# plt.savefig('figs/graphs/confusion_matrix_AB_'+ mouse_name +'.png')
```
# Should also look at patterns in licking wrt correct/incorrect
```
for v in g.vertices():
print(v)
for e in g.edges():
print(e)
19.19 - 9.92
# gt.graph_draw(g,output_size=(400,400),fit_view=True,output='simple_graph.pdf')
gt.graph_draw(g2,output_size=(400,400),fit_view=True)
deg.
# Stats...
len(tt[tt[AB_pol]])
gt.graph_draw?
```
## Load and plot protraction/retraction trial data for one mouse
```
# quick load and classification of pro/ret data
tt = pd.read_csv('~/work/whiskfree/data/tt_36_subset_sorted.csv',header=None)
ch = pd.read_csv('~/work/whiskfree/data/ch_36_subset_sorted.csv',header=None)
proret = pd.read_csv('~/work/whiskfree/data/proret_36_subset_sorted.csv',header=None)
tt = tt.values.reshape(-1,1)
ch = ch.values.reshape(-1,1)
proret = proret.values.reshape(-1,1)
cm = confusion_matrix(tt,ch)
print(cm)
cm_tt_t = confusion_matrix(tt,proret)
cm_ch_t = confusion_matrix(ch,proret)
print(cm_tt_t)
print(cm_ch_t)
plt.imshow(cm_tt_t,interpolation='none')
with sns.axes_style("white"):
fig, ax = plt.subplots(1,2,figsize=(10,6))
ax[0].imshow(cm_tt_t/np.sum(cm_tt_t),interpolation='none')
ax[1].imshow(cm_ch_t/np.sum(cm_ch_t),interpolation='none')
for i in range(0,3):
for j in range(0,3):
ax[0].text(j, i, "{0:.2f}".format(cm_tt_t[i,j]), va='center', ha='center',bbox=dict(facecolor='white',edgecolor='white', alpha=0.5))
ax[1].text(j, i, "{0:.2f}".format(cm_ch_t[i,j]), va='center', ha='center',bbox=dict(facecolor='white',edgecolor='white', alpha=0.5))
xlabels = ['Retraction','Protraction','No Touch']
ylabels = ['Posterior','Anterior','No Go']
ax[0].set_title('Trialtype | touch type' + '. ' + str(int(100 * accuracy_score(tt,proret))) + '%')
ax[1].set_title('Choice | touch type' + '. ' + str(int(100 * accuracy_score(ch,proret))) + '%')
ax[0].set_ylabel('Trial type')
ax[1].set_ylabel('Choice')
for i in range(0,2):
ax[i].set_xlabel('Touch type')
ax[i].set_xticks([0,1,2])
ax[i].set_xticklabels(xlabels)
ax[i].set_yticks([0,1,2])
ax[i].set_yticklabels(ylabels)
plt.tight_layout()
# plt.savefig('../figs/classification/pro_ret/310816/touchtype_confmatrix_both_32.png')
plt.savefig('../figs/classification/pro_ret/36/touchtype_confmatrix_both_36.png')
lr_tt = LogisticRegression(solver='lbfgs',multi_class='multinomial')
lr_tt.fit(proret,tt)
c_tt = lr_tt.predict(proret)
print('TT prediction accuracy =',accuracy_score(tt,c_tt))
lr_ch = LogisticRegression(solver='lbfgs',multi_class='multinomial')
lr_ch.fit(proret,ch)
c_ch = lr_ch.predict(proret)
print('Choice prediction accuracy =',accuracy_score(ch,c_ch))
print('Mouse prediction accuracy =',accuracy_score(tt,ch))
print(confusion_matrix(ch,c_ch))
print(confusion_matrix(tt,c_tt))
print(accuracy_score(ch,proret))
print(accuracy_score(tt,proret))
plt.plot(c_ch)
# Confusion matrix predicting trial type based on protraction/retraction
cm = confusion_matrix(tt,c_tt)
cm_m = confusion_matrix(tt,ch)
# xlabels = ['Retraction','Protraction','No Touch']
ylabels = ['Posterior','Anterior','No Go']
with sns.axes_style("white"):
fig, ax = plt.subplots(1,2,figsize=(10,6))
ax[0].imshow(cm,interpolation='none')
for i in range(0,3):
for j in range(0,3):
ax[0].text(j, i, "{0:.2f}".format(cm[i,j]), va='center', ha='center',bbox=dict(facecolor='white',edgecolor='white', alpha=0.5))
ax[0].set_title('Logistic Regression - TT' + '. ' + str(int(100 * accuracy_score(tt,c_tt))) + '%')
ax[1].imshow(cm_m,interpolation='none')
for i in range(0,3):
for j in range(0,3):
ax[1].text(j, i, "{0:.2f}".format(cm_m[i,j]), va='center', ha='center',bbox=dict(facecolor='white',edgecolor='white', alpha=0.5))
ax[1].set_title('Mouse' + '. ' + str(int(100 * accuracy_score(tt,ch))) + '%')
for i in range(0,2):
ax[i].set_ylabel('True label')
ax[i].set_xlabel('Predicted label')
ax[i].set_xticks([0,1,2])
ax[i].set_xticklabels(ylabels)
ax[i].set_yticks([0,1,2])
ax[i].set_yticklabels(ylabels)
plt.tight_layout()
# plt.savefig('../figs/classification/pro_ret/310816/LR_confmatrix_TT_32.png')
plt.savefig('../figs/classification/pro_ret/36/LR_confmatrix_TT_36.png')
# Confusion matrix predicting choice based on protraction/retraction
cm_ch = confusion_matrix(ch,c_ch)
cm_m = confusion_matrix(ch,tt)
# xlabels = ['Retraction','Protraction','No Touch']
ylabels = ['Posterior','Anterior','No Go']
with sns.axes_style("white"):
fig, ax = plt.subplots(1,2,figsize=(10,6))
ax[0].imshow(cm_ch,interpolation='none')
for i in range(0,3):
for j in range(0,3):
ax[0].text(j, i, "{0:.2f}".format(cm_ch[i,j]), va='center', ha='center',bbox=dict(facecolor='white',edgecolor='white', alpha=0.5))
ax[0].set_title('Logistic Regression - Ch' + '. ' + str(int(100 * accuracy_score(ch,c_ch))) + '%')
ax[1].imshow(cm_m,interpolation='none')
for i in range(0,3):
for j in range(0,3):
ax[1].text(j, i, "{0:.2f}".format(cm_m[i,j]), va='center', ha='center',bbox=dict(facecolor='white',edgecolor='white', alpha=0.5))
ax[1].set_title('Mouse' + '. ' + str(int(100 * accuracy_score(ch,tt))) + '%')
for i in range(0,2):
ax[i].set_ylabel('True label')
ax[i].set_xlabel('Predicted label')
ax[i].set_xticks([0,1,2])
ax[i].set_xticklabels(ylabels)
ax[i].set_yticks([0,1,2])
ax[i].set_yticklabels(ylabels)
plt.tight_layout()
# plt.savefig('../figs/classification/pro_ret/310816/LR_confmatrix_Ch_32.png')
plt.savefig('../figs/classification/pro_ret/36/LR_confmatrix_Ch_36.png')
# Correct/incorrect
correct = tt==ch
errors = tt!=ch
cm_c = confusion_matrix(ch[correct],proret[correct])
cm_ic = confusion_matrix(ch[errors],proret[errors])
xlabels = ['Retraction','Protraction','No Touch']
ylabels = ['Posterior','Anterior','No Go']
with sns.axes_style("white"):
fig, ax = plt.subplots(1,2,figsize=(10,6))
ax[0].imshow(cm_c,interpolation='none')
for i in range(0,3):
for j in range(0,3):
ax[0].text(j, i, "{0:.2f}".format(cm_c[i,j]), va='center', ha='center',bbox=dict(facecolor='white',edgecolor='white', alpha=0.5))
ax[0].set_title('Correct choice | touch type')
ax[1].imshow(cm_ic,interpolation='none')
for i in range(0,3):
for j in range(0,3):
ax[1].text(j, i, "{0:.2f}".format(cm_ic[i,j]), va='center', ha='center',bbox=dict(facecolor='white',edgecolor='white', alpha=0.5))
ax[1].set_title('Incorrect choice | touch type')
for i in range(0,2):
ax[i].set_ylabel('Choice')
ax[i].set_xlabel('Touch Type')
ax[i].set_xticks([0,1,2])
ax[i].set_xticklabels(xlabels)
ax[i].set_yticks([0,1,2])
ax[i].set_yticklabels(ylabels)
plt.tight_layout()
# plt.savefig('../figs/classification/pro_ret/310816/Correct_incorrect_confmatrix_Ch_32.png')
plt.savefig('../figs/classification/pro_ret/36/Correct_incorrect_confmatrix_Ch_36.png')
# Try graph of trialtype/choice/touchtype plots
# P_ijk_ON
# import graph_tool.all as gt
cm_3 = np.zeros([3,3,3])
for i in range(len(tt) - 2):
cm_3[tt[i]-1,proret[i]-1 ,ch[i]-1] += 1
# Make graph
cm_G = gt.Graph(directed = False)
# trialtypes = ['P','A','NG']
# touchtypes = ['Ret','Pro','NT']
# choices = ['P','A','NG']
trialtypes = ['Posterior','Anterior','No Go']
touchtypes = ['Retraction','Protraction','No Touch']
choices = ['Posterior','Anterior','No Go']
edge_weights_cm_G = cm_G.new_edge_property('double')
edge_labels_cm_G = cm_G.new_edge_property('string')
node_labels_cm_G = cm_G.new_vertex_property('string')
node_size_cm_G = cm_G.new_vertex_property('double')
h = cm_G.add_vertex()
node_labels_cm_G[h] = "0"
for i in range(cm_3.shape[0]):
v = cm_G.add_vertex()
node_labels_cm_G[v] = trialtypes[i]
e = cm_G.add_edge(h,v)
node_size_cm_G[v] = np.sum(cm_3[i]) / 4
for j in range(cm_3.shape[1]):
v2 = cm_G.add_vertex()
node_labels_cm_G[v2] = touchtypes[j]
e = cm_G.add_edge(v,v2)
edge_weights_cm_G[e] = np.sum(cm_3[i,j]) /4
edge_labels_cm_G[e] = str(int(np.sum(cm_3[i,j])))
node_size_cm_G[v2] = np.sum(cm_3[i,j]) /4
for k in range(cm_3.shape[2]):
v3 = cm_G.add_vertex()
node_labels_cm_G[v3] = choices[k]
e2 = cm_G.add_edge(v2,v3)
edge_weights_cm_G[e2] = int(cm_3[i,j,k])/4
edge_labels_cm_G[e2] = str(int(cm_3[i,j,k]))
node_size_cm_G[v3] = int(cm_3[i,j,k])/2
# Plot graph
pos = gt.radial_tree_layout(cm_G,cm_G.vertex(0))
# cmap = sns.diverging_palette(220,10, l=70, as_cmap=True, center="dark") # blue to green via black
cmap =plt.get_cmap('Greys')
gt.graph_draw(cm_G,pos=pos,vertex_size=node_size_cm_G,edge_pen_width=edge_weights_cm_G,
vertex_text = node_labels_cm_G, #vertex_text_position = 'centered',
edge_text=edge_labels_cm_G,
vertex_font_size = 22, vertex_font_family = 'sansserif',
edge_font_size = 24, edge_font_family = 'sansserif',
ecmap=cmap, vcmap=cmap,
edge_color = edge_weights_cm_G,
vertex_color = node_size_cm_G,
vertex_fill_color = node_size_cm_G,
output_size=(1500, 1500), fit_view=0.8,
# output="../figs/classification/pro_ret/310816/tt_touch_ch_graph_BW_"+ mouse_name +".pdf")
output="../figs/classification/pro_ret/36/tt_touch_ch_graph_BW_"+ mouse_name +".pdf")
np.sum(cm_3)
error_matrix
choice_matrix
with sns.axes_style("white"):
cmap = sns.diverging_palette(220,10, l=70, as_cmap=True, center="dark") # blue to green via black
fig, ax = plt.subplots(1,2)
ax[0].imshow(error_matrix,interpolation='none',cmap=cmap)
for i in range(0,3):
for j in range(0,3):
ax[0].text(j, i, "{0:.2f}".format(error_matrix[i,j]), va='center', ha='center',bbox=dict(facecolor='white',edgecolor='white', alpha=0.5))
ax[0].set_title('Error matrix') # + '. ' + str(int(100 * accuracy_score(tt,c_tt))) + '%')
ax[0].set_ylabel('Trial type')
ax[0].set_xlabel('Touch type')
ax[1].imshow(choice_matrix,interpolation='none',cmap=cmap)
for i in range(0,3):
for j in range(0,3):
ax[1].text(j, i, "{0:.2f}".format(choice_matrix[i,j]), va='center', ha='center',bbox=dict(facecolor='white',edgecolor='white', alpha=0.5))
ax[1].set_title('Choice matrix') # + '. ' + str(int(100 * accuracy_score(tt,ch))) + '%')
ax[1].set_ylabel('Choice')
ax[1].set_xlabel('Touch type')
# plt.savefig('figs/graphs/pro_ret_confmatrix_TT_32_full.png')
plt.plot(c_ch)
print(confusion_matrix(ch,proret))
print(confusion_matrix(tt,proret))
```
| github_jupyter |
# ClarityViz
## Pipeline: .img -> histogram .nii -> graph represented as csv -> graph as graphml -> plotly
### To run:
### Step 1:
First, run the following. This takes the .img, generates the localeq histogram as an nii file, gets the nodes and edges as a csv and converts the csv into a graphml
```
python runclarityviz.py --token Fear199Coronal --file-type img --source-directory /cis/project/clarity/data/clarity/isoCoronal
```
### Step 2:
Then run this. This just converts the graphml into a plotly
```
python runclarityviz.py --token Fear199Coronal --plotly yes
```
## Results
```
Starting pipeline for Fear199.img
Generating Histogram...
FINISHED GENERATING HISTOGRAM
Loading: Fear199/Fear199localeq.nii
Image Loaded: Fear199/Fear199localeq.nii
FINISHED LOADING NII
Coverting to points...
token=Fear199
total=600735744
max=255.000000
threshold=0.300000
sample=0.500000
(This will take couple minutes)
Above threshold=461409948
Samples=230718301
Finished
FINISHED GETTING POINTS
~/clarityviztesting/Fear199Coronal$ ls
Fear199Coronal.csv Fear199Coronal.graphml Fear199Coronal.nodes.csv
Fear199Coronal.edges.csv Fear199Coronallocaleq.nii Fear199Coronalplotly.html
```
# Code
## runclarityviz.py:
```
from clarityviz import clarityviz
import ...
def get_args():
parser = argparse.ArgumentParser(description="Description")
parser.add_argument("--token", type=str, required=True, help="The token.")
parser.add_argument("--file-type", type=str, required=False, help="The file type.")
parser.add_argument("--source-directory", type=str, required=False,
help="Optional setting of the source directory.")
parser.add_argument("--plotly", type=str, required=False, help="Optional method to generate the plotly graphs.")
parser.add_argument("--generate-nii-from-csv", type=str, required=False, help="script to generate nii")
args = parser.parse_args()
return args
def main():
print('ayyooooo')
args = get_args()
if args.plotly == 'yes':
## Type in the path to your csv file here
thedata = np.genfromtxt(args.token + '/' + args.token + '.csv',
delimiter=',', dtype='int', usecols = (0,1,2), names=['a','b','c'])
trace1 = go.Scatter3d(
x = thedata['a'],
y = thedata['b'],
z = thedata['c'],
mode='markers',
marker=dict(
size=1.2,
color='purple', # set color to an array/list of desired values
colorscale='Viridis', # choose a colorscale
opacity=0.15
)
)
data = [trace1]
layout = go.Layout(
margin=dict(
l=0,
r=0,
b=0,
t=0
)
)
fig = go.Figure(data=data, layout=layout)
print args.token + "plotly"
plotly.offline.plot(fig, filename= args.token + "/" + args.token + "plotly.html")
else:
print('Starting pipeline for %s' % (args.token + '.' + args.file_type))
if args.source_directory == None:
c = clarityviz(args.token)
else:
c = clarityviz(args.token, args.source_directory)
if args.file_type == 'img':
#c.loadEqImg()
c.generateHistogram()
print('FINISHED GENERATING HISTOGRAM')
c.loadNiiImg()
print('FINISHED LOADING NII')
elif args.file_type == 'nii':
c.loadNiiImg()
print('FINISHED LOADING NII')
c.imgToPoints(0.3, 0.5)
print("FINISHED GETTING POINTS")
c.savePoints()
c.plot3d()
print("FINISHED PLOT3D")
c.graphmlconvert()
print("FINISHED GRAPHMLCONVERT")
if __name__ == "__main__":
main()
```
## clarityviz.py
```
def generateHistogram(self):
print('Generating Histogram...')
if self._source_directory == None:
path = self._token + '.img'
else:
path = self._source_directory + "/" + self._token + ".img"
im = nib.load(path)
im = im.get_data()
img = im[:,:,:]
shape = im.shape
#affine = im.get_affine()
x_value = shape[0]
y_value = shape[1]
z_value = shape[2]
#####################################################
imgflat = img.reshape(-1)
#img_grey = np.array(imgflat * 255, dtype = np.uint8)
#img_eq = exposure.equalize_hist(img_grey)
#new_img = img_eq.reshape(x_value, y_value, z_value)
#globaleq = nib.Nifti1Image(new_img, np.eye(4))
######################################################
#clahe = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(8,8))
clahe = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(8,8))
img_grey = np.array(imgflat * 255, dtype = np.uint8)
#threshed = cv2.adaptiveThreshold(img_grey, 255, cv2.ADAPTIVE_THRESH_MEAN_C, cv2.THRESH_BINARY, 3, 0)
cl1 = clahe.apply(img_grey)
#cv2.imwrite('clahe_2.jpg',cl1)
#cv2.startWindowThread()
#cv2.namedWindow("adaptive")
#cv2.imshow("adaptive", cl1)
#cv2.imshow("adaptive", threshed)
#plt.imshow(threshed)
localimgflat = cl1 #cl1.reshape(-1)
newer_img = localimgflat.reshape(x_value, y_value, z_value)
localeq = nib.Nifti1Image(newer_img, np.eye(4))
nib.save(localeq, self._token + '/' + self._token + 'localeq.nii')
def loadGeneratedNii(self, path=None, info=False):
path = self._token + '/' + self._token + 'localeq.nii'
print("Loading: %s"%(path))
#pathname = path+self._token+".nii"
img = nib.load(path)
if info:
print(img)
#self._img = img.get_data()[:,:,:,0]
self._img = img.get_data()
self._shape = self._img.shape
self._max = np.max(self._img)
print("Image Loaded: %s"%(path))
return self
def imgToPoints(self, threshold=0.1, sample=0.5, optimize=True):
"""Method to extract points data from the img file."""
if not 0 <= threshold < 1:
raise ValueError("Threshold should be within [0,1).")
if not 0 < sample <= 1:
raise ValueError("Sample rate should be within (0,1].")
if self._img is None:
raise ValueError("Img haven't loaded, please call loadImg() first.")
total = self._shape[0]*self._shape[1]*self._shape[2]
print("Coverting to points...\ntoken=%s\ntotal=%d\nmax=%f\nthreshold=%f\nsample=%f"\
%(self._token,total,self._max,threshold,sample))
print("(This will take couple minutes)")
# threshold
filt = self._img > threshold * self._max
x, y, z = np.where(filt)
v = self._img[filt]
if optimize:
self.discardImg()
v = np.int16(255*(np.float32(v)/np.float32(self._max)))
l = v.shape
print("Above threshold=%d"%(l))
# sample
if sample < 1.0:
filt = np.random.random(size=l) < sample
x = x[filt]
y = y[filt]
z = z[filt]
v = v[filt]
self._points = np.vstack([x,y,z,v])
self._points = np.transpose(self._points)
print("Samples=%d"%(self._points.shape[0]))
print("Finished")
return self
def plot3d(self, infile = None):
"""Method for plotting the Nodes and Edges"""
filename = ""
points_file = None
if infile == None:
points_file = self._points
filename = self._token
else:
self.loadInitCsv(infile)
infile = self._infile
filename = self._filename
# points is an array of arrays
points = self._points
outpath = self._token + '/'
nodename = outpath + filename + '.nodes.csv'
edgename = outpath + filename + '.edges.csv'
with open(nodename, 'w') as nodefile:
with open(edgename, 'w') as edgefile:
for ind in range(len(points)):
#temp = points[ind].strip().split(',')
temp = points[ind]
x = temp[0]
y = temp[1]
z = temp[2]
v = temp[3]
radius = 18
nodefile.write("s" + str(ind + 1) + "," + str(x) + "," + str(y) + "," + str(z) + "\n")
for index in range(ind + 1, len(points)):
tmp = points[index]
distance = math.sqrt(math.pow(int(x) - int(tmp[0]), 2) + math.pow(int(y) - int(tmp[1]), 2) + math.pow(int(z) - int(tmp[2]), 2))
if distance < radius:
edgefile.write("s" + str(ind + 1) + "," + "s" + str(index + 1) + "\n")
self._nodefile = nodefile
self._edgefile = edgefile
def graphmlconvert(self, nodefilename = None, edgefilename = None):
"""Method for extracting the data to a graphml file, based on the node and edge files"""
nodefile = None
edgefile = None
# If no nodefilename was entered, used the Clarity object's nodefile
if nodefilename == None:
#nodefile = self._nodefile
#nodefile = open(self._nodefile, 'r')
self.loadNodeCsv(self._token + "/" + self._token + ".nodes.csv")
nodefile = self._nodefile
else:
self.loadNodeCsv(nodefilename)
nodefile = self._nodefile
# If no edgefilename was entered, used the Clarity object's edgefile
if edgefilename == None:
#edgefile = self._edgefile
#edgefile = open(self._edgefile, 'r')
self.loadEdgeCsv(self._token + "/" + self._token + ".edges.csv")
edgefile = self._edgefile
else:
self.loadEdgeCsv(edgefilename)
edgefile = self._edgefile
# Start writing to the output graphml file
path = self._token + "/" + self._token + ".graphml"
with open(path, 'w') as outfile:
outfile.write("<?xml version=\"1.0\" encoding=\"UTF-8\"?>\n")
outfile.write("<graphml xmlns=\"http://graphml.graphdrawing.org/xmlns\"\n")
outfile.write(" xmlns:xsi=\"http://www.w3.org/2001/XMLSchema-instance\"\n")
outfile.write(" xsi:schemaLocation=\"http://graphml.graphdrawing.org/xmlns\n")
outfile.write(" http://graphml.graphdrawing.org/xmlns/1.0/graphml.xsd\">\n")
outfile.write(" <key id=\"d0\" for=\"node\" attr.name=\"attr\" attr.type=\"string\"/>\n")
outfile.write(" <key id=\"e_weight\" for=\"edge\" attr.name=\"weight\" attr.type=\"double\"/>\n")
outfile.write(" <graph id=\"G\" edgedefault=\"undirected\">\n")
for line in nodefile:
if len(line) == 0:
continue
line = line.strip().split(',')
outfile.write(" <node id=\"" + line[0] + "\">\n")
outfile.write(" <data key=\"d0\">[" + line[1] + ", " + line[2] + ", " + line[3] +"]</data>\n")
outfile.write(" </node>\n")
for line in edgefile:
if len(line) == 0:
continue
line = line.strip().split(',')
outfile.write(" <edge source=\"" + line[0] + "\" target=\"" + line[1] + "\">\n")
outfile.write(" <data key=\"e_weight\">1</data>\n")
outfile.write(" </edge>\n")
outfile.write(" </graph>\n</graphml>")
def graphmlToPlotly(self, path):
## Type in the path to your csv file here
thedata = np.genfromtxt('../data/points/localeq.csv', delimiter=',', dtype='int', usecols = (0,1,2), names=['a','b','c'])
trace1 = go.Scatter3d(
x = thedata['a'],
y = thedata['b'],
z = thedata['c'],
mode='markers',
marker=dict(
size=1.2,
color='purple', # set color to an array/list of desired values
colorscale='Viridis', # choose a colorscale
opacity=0.15
)
)
data = [trace1]
layout = go.Layout(
margin=dict(
l=0,
r=0,
b=0,
t=0
)
)
fig = go.Figure(data=data, layout=layout)
print "localeq"
plotly.offline.plot(fig, filename= "localeq")
```
| github_jupyter |
```
{
"nodes": [
{
"op": "null",
"name": "data",
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_conv0_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(8L, 3L, 3L, 3L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv0_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(3, 3)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "8",
"num_group": "1",
"pad": "(1, 1)",
"stride": "(2, 2)"
},
"inputs": [[0, 0, 0], [1, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm0_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(8L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm0_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(8L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm0_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(8L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm0_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(8L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm0_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[2, 0, 0], [3, 0, 0], [4, 0, 0], [5, 0, 1], [6, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu0_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[7, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv1_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(8L, 1L, 3L, 3L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv1_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(3, 3)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "8",
"num_group": "8",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[8, 0, 0], [9, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm1_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(8L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm1_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(8L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm1_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(8L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm1_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(8L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm1_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[10, 0, 0], [11, 0, 0], [12, 0, 0], [13, 0, 1], [14, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu1_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[15, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv2_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(16L, 8L, 1L, 1L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv2_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(1, 1)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "16",
"num_group": "1",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[16, 0, 0], [17, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm2_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(16L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm2_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(16L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm2_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(16L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm2_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(16L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm2_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[18, 0, 0], [19, 0, 0], [20, 0, 0], [21, 0, 1], [22, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu2_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[23, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv3_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(16L, 1L, 3L, 3L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv3_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(3, 3)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "16",
"num_group": "16",
"pad": "(1, 1)",
"stride": "(2, 2)"
},
"inputs": [[24, 0, 0], [25, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm3_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(16L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm3_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(16L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm3_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(16L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm3_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(16L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm3_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[26, 0, 0], [27, 0, 0], [28, 0, 0], [29, 0, 1], [30, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu3_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[31, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv4_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(32L, 16L, 1L, 1L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv4_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(1, 1)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "32",
"num_group": "1",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[32, 0, 0], [33, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm4_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(32L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm4_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(32L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm4_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(32L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm4_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(32L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm4_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[34, 0, 0], [35, 0, 0], [36, 0, 0], [37, 0, 1], [38, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu4_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[39, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv5_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(32L, 1L, 3L, 3L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv5_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(3, 3)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "32",
"num_group": "32",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[40, 0, 0], [41, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm5_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(32L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm5_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(32L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm5_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(32L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm5_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(32L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm5_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[42, 0, 0], [43, 0, 0], [44, 0, 0], [45, 0, 1], [46, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu5_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[47, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv6_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(32L, 32L, 1L, 1L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv6_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(1, 1)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "32",
"num_group": "1",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[48, 0, 0], [49, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm6_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(32L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm6_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(32L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm6_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(32L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm6_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(32L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm6_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[50, 0, 0], [51, 0, 0], [52, 0, 0], [53, 0, 1], [54, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu6_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[55, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv7_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(32L, 1L, 3L, 3L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv7_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(3, 3)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "32",
"num_group": "32",
"pad": "(1, 1)",
"stride": "(2, 2)"
},
"inputs": [[56, 0, 0], [57, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm7_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(32L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm7_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(32L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm7_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(32L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm7_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(32L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm7_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[58, 0, 0], [59, 0, 0], [60, 0, 0], [61, 0, 1], [62, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu7_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[63, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv8_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(64L, 32L, 1L, 1L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv8_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(1, 1)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "64",
"num_group": "1",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[64, 0, 0], [65, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm8_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(64L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm8_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(64L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm8_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(64L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm8_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(64L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm8_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[66, 0, 0], [67, 0, 0], [68, 0, 0], [69, 0, 1], [70, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu8_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[71, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv9_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(64L, 1L, 3L, 3L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv9_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(3, 3)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "64",
"num_group": "64",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[72, 0, 0], [73, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm9_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(64L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm9_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(64L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm9_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(64L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm9_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(64L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm9_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[74, 0, 0], [75, 0, 0], [76, 0, 0], [77, 0, 1], [78, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu9_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[79, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv10_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(64L, 64L, 1L, 1L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv10_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(1, 1)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "64",
"num_group": "1",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[80, 0, 0], [81, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm10_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(64L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm10_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(64L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm10_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(64L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm10_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(64L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm10_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[82, 0, 0], [83, 0, 0], [84, 0, 0], [85, 0, 1], [86, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu10_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[87, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv11_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(64L, 1L, 3L, 3L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv11_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(3, 3)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "64",
"num_group": "64",
"pad": "(1, 1)",
"stride": "(2, 2)"
},
"inputs": [[88, 0, 0], [89, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm11_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(64L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm11_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(64L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm11_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(64L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm11_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(64L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm11_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[90, 0, 0], [91, 0, 0], [92, 0, 0], [93, 0, 1], [94, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu11_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[95, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv12_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(128L, 64L, 1L, 1L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv12_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(1, 1)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "128",
"num_group": "1",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[96, 0, 0], [97, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm12_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm12_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm12_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm12_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm12_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[98, 0, 0], [99, 0, 0], [100, 0, 0], [101, 0, 1], [102, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu12_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[103, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv13_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(128L, 1L, 3L, 3L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv13_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(3, 3)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "128",
"num_group": "128",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[104, 0, 0], [105, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm13_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm13_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm13_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm13_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm13_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[106, 0, 0], [107, 0, 0], [108, 0, 0], [109, 0, 1], [110, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu13_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[111, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv14_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(128L, 128L, 1L, 1L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv14_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(1, 1)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "128",
"num_group": "1",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[112, 0, 0], [113, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm14_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm14_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm14_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm14_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm14_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[114, 0, 0], [115, 0, 0], [116, 0, 0], [117, 0, 1], [118, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu14_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[119, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv15_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(128L, 1L, 3L, 3L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv15_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(3, 3)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "128",
"num_group": "128",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[120, 0, 0], [121, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm15_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm15_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm15_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm15_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm15_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[122, 0, 0], [123, 0, 0], [124, 0, 0], [125, 0, 1], [126, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu15_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[127, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv16_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(128L, 128L, 1L, 1L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv16_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(1, 1)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "128",
"num_group": "1",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[128, 0, 0], [129, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm16_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm16_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm16_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm16_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm16_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[130, 0, 0], [131, 0, 0], [132, 0, 0], [133, 0, 1], [134, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu16_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[135, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv17_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(128L, 1L, 3L, 3L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv17_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(3, 3)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "128",
"num_group": "128",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[136, 0, 0], [137, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm17_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm17_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm17_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm17_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm17_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[138, 0, 0], [139, 0, 0], [140, 0, 0], [141, 0, 1], [142, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu17_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[143, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv18_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(128L, 128L, 1L, 1L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv18_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(1, 1)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "128",
"num_group": "1",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[144, 0, 0], [145, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm18_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm18_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm18_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm18_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm18_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[146, 0, 0], [147, 0, 0], [148, 0, 0], [149, 0, 1], [150, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu18_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[151, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv19_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(128L, 1L, 3L, 3L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv19_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(3, 3)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "128",
"num_group": "128",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[152, 0, 0], [153, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm19_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm19_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm19_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm19_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm19_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[154, 0, 0], [155, 0, 0], [156, 0, 0], [157, 0, 1], [158, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu19_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[159, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv20_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(128L, 128L, 1L, 1L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv20_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(1, 1)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "128",
"num_group": "1",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[160, 0, 0], [161, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm20_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm20_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm20_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm20_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm20_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[162, 0, 0], [163, 0, 0], [164, 0, 0], [165, 0, 1], [166, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu20_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[167, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv21_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(128L, 1L, 3L, 3L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv21_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(3, 3)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "128",
"num_group": "128",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[168, 0, 0], [169, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm21_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm21_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm21_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm21_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm21_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[170, 0, 0], [171, 0, 0], [172, 0, 0], [173, 0, 1], [174, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu21_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[175, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv22_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(128L, 128L, 1L, 1L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv22_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(1, 1)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "128",
"num_group": "1",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[176, 0, 0], [177, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm22_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm22_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm22_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm22_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm22_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[178, 0, 0], [179, 0, 0], [180, 0, 0], [181, 0, 1], [182, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu22_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[183, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv23_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(128L, 1L, 3L, 3L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv23_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(3, 3)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "128",
"num_group": "128",
"pad": "(1, 1)",
"stride": "(2, 2)"
},
"inputs": [[184, 0, 0], [185, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm23_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm23_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm23_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm23_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(128L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm23_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[186, 0, 0], [187, 0, 0], [188, 0, 0], [189, 0, 1], [190, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu23_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[191, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv24_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(256L, 128L, 1L, 1L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv24_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(1, 1)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "256",
"num_group": "1",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[192, 0, 0], [193, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm24_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(256L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm24_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(256L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm24_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(256L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm24_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(256L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm24_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[194, 0, 0], [195, 0, 0], [196, 0, 0], [197, 0, 1], [198, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu24_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[199, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv25_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(256L, 1L, 3L, 3L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv25_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(3, 3)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "256",
"num_group": "256",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[200, 0, 0], [201, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm25_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(256L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm25_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(256L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm25_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(256L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm25_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(256L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm25_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[202, 0, 0], [203, 0, 0], [204, 0, 0], [205, 0, 1], [206, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu25_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[207, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_conv26_weight",
"attrs": {
"__dtype__": "0",
"__lr_mult__": "1.0",
"__shape__": "(256L, 256L, 1L, 1L)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "mobilenet0_conv26_fwd",
"attrs": {
"dilate": "(1, 1)",
"kernel": "(1, 1)",
"layout": "NCHW",
"no_bias": "True",
"num_filter": "256",
"num_group": "1",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[208, 0, 0], [209, 0, 0]]
},
{
"op": "null",
"name": "mobilenet0_batchnorm26_gamma",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(256L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm26_beta",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(256L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm26_running_mean",
"attrs": {
"__dtype__": "0",
"__init__": "zeros",
"__lr_mult__": "1.0",
"__shape__": "(256L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "mobilenet0_batchnorm26_running_var",
"attrs": {
"__dtype__": "0",
"__init__": "ones",
"__lr_mult__": "1.0",
"__shape__": "(256L,)",
"__storage_type__": "0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "mobilenet0_batchnorm26_fwd",
"attrs": {
"axis": "1",
"eps": "1e-05",
"fix_gamma": "False",
"momentum": "0.9",
"use_global_stats": "False"
},
"inputs": [[210, 0, 0], [211, 0, 0], [212, 0, 0], [213, 0, 1], [214, 0, 1]]
},
{
"op": "Activation",
"name": "mobilenet0_relu26_fwd",
"attrs": {"act_type": "relu"},
"inputs": [[215, 0, 0]]
},
{
"op": "null",
"name": "rf_c3_lateral_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_lateral_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c3_lateral",
"attrs": {
"kernel": "(1, 1)",
"num_filter": "64",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[216, 0, 0], [217, 0, 0], [218, 0, 0]]
},
{
"op": "null",
"name": "rf_c3_lateral_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_lateral_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_lateral_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_lateral_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c3_lateral_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[219, 0, 0], [220, 0, 0], [221, 0, 0], [222, 0, 1], [223, 0, 1]]
},
{
"op": "Activation",
"name": "rf_c3_lateral_relu",
"attrs": {"act_type": "relu"},
"inputs": [[224, 0, 0]]
},
{
"op": "null",
"name": "rf_c3_det_conv1_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_conv1_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c3_det_conv1",
"attrs": {
"kernel": "(3, 3)",
"num_filter": "32",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[225, 0, 0], [226, 0, 0], [227, 0, 0]]
},
{
"op": "null",
"name": "rf_c3_det_conv1_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_conv1_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_conv1_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_conv1_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c3_det_conv1_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[228, 0, 0], [229, 0, 0], [230, 0, 0], [231, 0, 1], [232, 0, 1]]
},
{
"op": "null",
"name": "rf_c3_det_context_conv1_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_context_conv1_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c3_det_context_conv1",
"attrs": {
"kernel": "(3, 3)",
"num_filter": "16",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[225, 0, 0], [234, 0, 0], [235, 0, 0]]
},
{
"op": "null",
"name": "rf_c3_det_context_conv1_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_context_conv1_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_context_conv1_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_context_conv1_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c3_det_context_conv1_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[236, 0, 0], [237, 0, 0], [238, 0, 0], [239, 0, 1], [240, 0, 1]]
},
{
"op": "Activation",
"name": "rf_c3_det_context_conv1_relu",
"attrs": {"act_type": "relu"},
"inputs": [[241, 0, 0]]
},
{
"op": "null",
"name": "rf_c3_det_context_conv2_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_context_conv2_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c3_det_context_conv2",
"attrs": {
"kernel": "(3, 3)",
"num_filter": "16",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[242, 0, 0], [243, 0, 0], [244, 0, 0]]
},
{
"op": "null",
"name": "rf_c3_det_context_conv2_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_context_conv2_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_context_conv2_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_context_conv2_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c3_det_context_conv2_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[245, 0, 0], [246, 0, 0], [247, 0, 0], [248, 0, 1], [249, 0, 1]]
},
{
"op": "null",
"name": "rf_c3_det_context_conv3_1_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_context_conv3_1_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c3_det_context_conv3_1",
"attrs": {
"kernel": "(3, 3)",
"num_filter": "16",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[242, 0, 0], [251, 0, 0], [252, 0, 0]]
},
{
"op": "null",
"name": "rf_c3_det_context_conv3_1_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_context_conv3_1_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_context_conv3_1_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_context_conv3_1_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c3_det_context_conv3_1_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[253, 0, 0], [254, 0, 0], [255, 0, 0], [256, 0, 1], [257, 0, 1]]
},
{
"op": "Activation",
"name": "rf_c3_det_context_conv3_1_relu",
"attrs": {"act_type": "relu"},
"inputs": [[258, 0, 0]]
},
{
"op": "null",
"name": "rf_c3_det_context_conv3_2_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_context_conv3_2_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c3_det_context_conv3_2",
"attrs": {
"kernel": "(3, 3)",
"num_filter": "16",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[259, 0, 0], [260, 0, 0], [261, 0, 0]]
},
{
"op": "null",
"name": "rf_c3_det_context_conv3_2_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_context_conv3_2_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_context_conv3_2_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c3_det_context_conv3_2_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c3_det_context_conv3_2_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[262, 0, 0], [263, 0, 0], [264, 0, 0], [265, 0, 1], [266, 0, 1]]
},
{
"op": "Concat",
"name": "rf_c3_det_concat",
"attrs": {
"dim": "1",
"num_args": "3"
},
"inputs": [[233, 0, 0], [250, 0, 0], [267, 0, 0]]
},
{
"op": "Activation",
"name": "rf_c3_det_concat_relu",
"attrs": {"act_type": "relu"},
"inputs": [[268, 0, 0]]
},
{
"op": "null",
"name": "face_rpn_cls_score_stride32_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "face_rpn_cls_score_stride32_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "face_rpn_cls_score_stride32",
"attrs": {
"kernel": "(1, 1)",
"num_filter": "4",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[269, 0, 0], [270, 0, 0], [271, 0, 0]]
},
{
"op": "Reshape",
"name": "face_rpn_cls_score_reshape_stride32",
"attrs": {"shape": "(0, 2, -1, 0)"},
"inputs": [[272, 0, 0]]
},
{
"op": "SoftmaxActivation",
"name": "face_rpn_cls_prob_stride32",
"attrs": {"mode": "channel"},
"inputs": [[273, 0, 0]]
},
{
"op": "Reshape",
"name": "face_rpn_cls_prob_reshape_stride32",
"attrs": {"shape": "(0, 4, -1, 0)"},
"inputs": [[274, 0, 0]]
},
{
"op": "null",
"name": "face_rpn_bbox_pred_stride32_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "face_rpn_bbox_pred_stride32_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "face_rpn_bbox_pred_stride32",
"attrs": {
"kernel": "(1, 1)",
"num_filter": "8",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[269, 0, 0], [276, 0, 0], [277, 0, 0]]
},
{
"op": "null",
"name": "face_rpn_landmark_pred_stride32_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "face_rpn_landmark_pred_stride32_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "face_rpn_landmark_pred_stride32",
"attrs": {
"kernel": "(1, 1)",
"num_filter": "20",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[269, 0, 0], [279, 0, 0], [280, 0, 0]]
},
{
"op": "null",
"name": "rf_c2_lateral_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_lateral_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c2_lateral",
"attrs": {
"kernel": "(1, 1)",
"num_filter": "64",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[184, 0, 0], [282, 0, 0], [283, 0, 0]]
},
{
"op": "null",
"name": "rf_c2_lateral_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_lateral_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_lateral_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_lateral_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c2_lateral_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[284, 0, 0], [285, 0, 0], [286, 0, 0], [287, 0, 1], [288, 0, 1]]
},
{
"op": "Activation",
"name": "rf_c2_lateral_relu",
"attrs": {"act_type": "relu"},
"inputs": [[289, 0, 0]]
},
{
"op": "UpSampling",
"name": "rf_c3_upsampling",
"attrs": {
"num_args": "1",
"sample_type": "nearest",
"scale": "2",
"workspace": "512"
},
"inputs": [[225, 0, 0]]
},
{
"op": "Crop",
"name": "crop0",
"attrs": {"num_args": "2"},
"inputs": [[291, 0, 0], [290, 0, 0]]
},
{
"op": "elemwise_add",
"name": "plus0",
"inputs": [[290, 0, 0], [292, 0, 0]]
},
{
"op": "null",
"name": "rf_c2_aggr_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_aggr_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c2_aggr",
"attrs": {
"kernel": "(3, 3)",
"num_filter": "64",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[293, 0, 0], [294, 0, 0], [295, 0, 0]]
},
{
"op": "null",
"name": "rf_c2_aggr_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_aggr_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_aggr_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_aggr_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c2_aggr_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[296, 0, 0], [297, 0, 0], [298, 0, 0], [299, 0, 1], [300, 0, 1]]
},
{
"op": "Activation",
"name": "rf_c2_aggr_relu",
"attrs": {"act_type": "relu"},
"inputs": [[301, 0, 0]]
},
{
"op": "null",
"name": "rf_c2_det_conv1_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_conv1_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c2_det_conv1",
"attrs": {
"kernel": "(3, 3)",
"num_filter": "32",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[302, 0, 0], [303, 0, 0], [304, 0, 0]]
},
{
"op": "null",
"name": "rf_c2_det_conv1_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_conv1_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_conv1_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_conv1_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c2_det_conv1_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[305, 0, 0], [306, 0, 0], [307, 0, 0], [308, 0, 1], [309, 0, 1]]
},
{
"op": "null",
"name": "rf_c2_det_context_conv1_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_context_conv1_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c2_det_context_conv1",
"attrs": {
"kernel": "(3, 3)",
"num_filter": "16",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[302, 0, 0], [311, 0, 0], [312, 0, 0]]
},
{
"op": "null",
"name": "rf_c2_det_context_conv1_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_context_conv1_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_context_conv1_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_context_conv1_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c2_det_context_conv1_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[313, 0, 0], [314, 0, 0], [315, 0, 0], [316, 0, 1], [317, 0, 1]]
},
{
"op": "Activation",
"name": "rf_c2_det_context_conv1_relu",
"attrs": {"act_type": "relu"},
"inputs": [[318, 0, 0]]
},
{
"op": "null",
"name": "rf_c2_det_context_conv2_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_context_conv2_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c2_det_context_conv2",
"attrs": {
"kernel": "(3, 3)",
"num_filter": "16",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[319, 0, 0], [320, 0, 0], [321, 0, 0]]
},
{
"op": "null",
"name": "rf_c2_det_context_conv2_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_context_conv2_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_context_conv2_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_context_conv2_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c2_det_context_conv2_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[322, 0, 0], [323, 0, 0], [324, 0, 0], [325, 0, 1], [326, 0, 1]]
},
{
"op": "null",
"name": "rf_c2_det_context_conv3_1_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_context_conv3_1_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c2_det_context_conv3_1",
"attrs": {
"kernel": "(3, 3)",
"num_filter": "16",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[319, 0, 0], [328, 0, 0], [329, 0, 0]]
},
{
"op": "null",
"name": "rf_c2_det_context_conv3_1_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_context_conv3_1_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_context_conv3_1_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_context_conv3_1_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c2_det_context_conv3_1_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[330, 0, 0], [331, 0, 0], [332, 0, 0], [333, 0, 1], [334, 0, 1]]
},
{
"op": "Activation",
"name": "rf_c2_det_context_conv3_1_relu",
"attrs": {"act_type": "relu"},
"inputs": [[335, 0, 0]]
},
{
"op": "null",
"name": "rf_c2_det_context_conv3_2_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_context_conv3_2_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c2_det_context_conv3_2",
"attrs": {
"kernel": "(3, 3)",
"num_filter": "16",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[336, 0, 0], [337, 0, 0], [338, 0, 0]]
},
{
"op": "null",
"name": "rf_c2_det_context_conv3_2_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_context_conv3_2_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_context_conv3_2_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c2_det_context_conv3_2_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c2_det_context_conv3_2_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[339, 0, 0], [340, 0, 0], [341, 0, 0], [342, 0, 1], [343, 0, 1]]
},
{
"op": "Concat",
"name": "rf_c2_det_concat",
"attrs": {
"dim": "1",
"num_args": "3"
},
"inputs": [[310, 0, 0], [327, 0, 0], [344, 0, 0]]
},
{
"op": "Activation",
"name": "rf_c2_det_concat_relu",
"attrs": {"act_type": "relu"},
"inputs": [[345, 0, 0]]
},
{
"op": "null",
"name": "face_rpn_cls_score_stride16_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "face_rpn_cls_score_stride16_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "face_rpn_cls_score_stride16",
"attrs": {
"kernel": "(1, 1)",
"num_filter": "4",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[346, 0, 0], [347, 0, 0], [348, 0, 0]]
},
{
"op": "Reshape",
"name": "face_rpn_cls_score_reshape_stride16",
"attrs": {"shape": "(0, 2, -1, 0)"},
"inputs": [[349, 0, 0]]
},
{
"op": "SoftmaxActivation",
"name": "face_rpn_cls_prob_stride16",
"attrs": {"mode": "channel"},
"inputs": [[350, 0, 0]]
},
{
"op": "Reshape",
"name": "face_rpn_cls_prob_reshape_stride16",
"attrs": {"shape": "(0, 4, -1, 0)"},
"inputs": [[351, 0, 0]]
},
{
"op": "null",
"name": "face_rpn_bbox_pred_stride16_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "face_rpn_bbox_pred_stride16_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "face_rpn_bbox_pred_stride16",
"attrs": {
"kernel": "(1, 1)",
"num_filter": "8",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[346, 0, 0], [353, 0, 0], [354, 0, 0]]
},
{
"op": "null",
"name": "face_rpn_landmark_pred_stride16_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "face_rpn_landmark_pred_stride16_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "face_rpn_landmark_pred_stride16",
"attrs": {
"kernel": "(1, 1)",
"num_filter": "20",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[346, 0, 0], [356, 0, 0], [357, 0, 0]]
},
{
"op": "null",
"name": "rf_c1_red_conv_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_red_conv_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c1_red_conv",
"attrs": {
"kernel": "(1, 1)",
"num_filter": "64",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[88, 0, 0], [359, 0, 0], [360, 0, 0]]
},
{
"op": "null",
"name": "rf_c1_red_conv_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_red_conv_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_red_conv_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_red_conv_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c1_red_conv_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[361, 0, 0], [362, 0, 0], [363, 0, 0], [364, 0, 1], [365, 0, 1]]
},
{
"op": "Activation",
"name": "rf_c1_red_conv_relu",
"attrs": {"act_type": "relu"},
"inputs": [[366, 0, 0]]
},
{
"op": "UpSampling",
"name": "rf_c2_upsampling",
"attrs": {
"num_args": "1",
"sample_type": "nearest",
"scale": "2",
"workspace": "512"
},
"inputs": [[302, 0, 0]]
},
{
"op": "Crop",
"name": "crop1",
"attrs": {"num_args": "2"},
"inputs": [[368, 0, 0], [367, 0, 0]]
},
{
"op": "elemwise_add",
"name": "plus1",
"inputs": [[367, 0, 0], [369, 0, 0]]
},
{
"op": "null",
"name": "rf_c1_aggr_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_aggr_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "1.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c1_aggr",
"attrs": {
"kernel": "(3, 3)",
"num_filter": "64",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[370, 0, 0], [371, 0, 0], [372, 0, 0]]
},
{
"op": "null",
"name": "rf_c1_aggr_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_aggr_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_aggr_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_aggr_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c1_aggr_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[373, 0, 0], [374, 0, 0], [375, 0, 0], [376, 0, 1], [377, 0, 1]]
},
{
"op": "Activation",
"name": "rf_c1_aggr_relu",
"attrs": {"act_type": "relu"},
"inputs": [[378, 0, 0]]
},
{
"op": "null",
"name": "rf_c1_det_conv1_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_conv1_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c1_det_conv1",
"attrs": {
"kernel": "(3, 3)",
"num_filter": "32",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[379, 0, 0], [380, 0, 0], [381, 0, 0]]
},
{
"op": "null",
"name": "rf_c1_det_conv1_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_conv1_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_conv1_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_conv1_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c1_det_conv1_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[382, 0, 0], [383, 0, 0], [384, 0, 0], [385, 0, 1], [386, 0, 1]]
},
{
"op": "null",
"name": "rf_c1_det_context_conv1_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_context_conv1_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c1_det_context_conv1",
"attrs": {
"kernel": "(3, 3)",
"num_filter": "16",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[379, 0, 0], [388, 0, 0], [389, 0, 0]]
},
{
"op": "null",
"name": "rf_c1_det_context_conv1_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_context_conv1_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_context_conv1_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_context_conv1_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c1_det_context_conv1_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[390, 0, 0], [391, 0, 0], [392, 0, 0], [393, 0, 1], [394, 0, 1]]
},
{
"op": "Activation",
"name": "rf_c1_det_context_conv1_relu",
"attrs": {"act_type": "relu"},
"inputs": [[395, 0, 0]]
},
{
"op": "null",
"name": "rf_c1_det_context_conv2_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_context_conv2_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c1_det_context_conv2",
"attrs": {
"kernel": "(3, 3)",
"num_filter": "16",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[396, 0, 0], [397, 0, 0], [398, 0, 0]]
},
{
"op": "null",
"name": "rf_c1_det_context_conv2_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_context_conv2_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_context_conv2_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_context_conv2_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c1_det_context_conv2_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[399, 0, 0], [400, 0, 0], [401, 0, 0], [402, 0, 1], [403, 0, 1]]
},
{
"op": "null",
"name": "rf_c1_det_context_conv3_1_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_context_conv3_1_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c1_det_context_conv3_1",
"attrs": {
"kernel": "(3, 3)",
"num_filter": "16",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[396, 0, 0], [405, 0, 0], [406, 0, 0]]
},
{
"op": "null",
"name": "rf_c1_det_context_conv3_1_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_context_conv3_1_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_context_conv3_1_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_context_conv3_1_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c1_det_context_conv3_1_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[407, 0, 0], [408, 0, 0], [409, 0, 0], [410, 0, 1], [411, 0, 1]]
},
{
"op": "Activation",
"name": "rf_c1_det_context_conv3_1_relu",
"attrs": {"act_type": "relu"},
"inputs": [[412, 0, 0]]
},
{
"op": "null",
"name": "rf_c1_det_context_conv3_2_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_context_conv3_2_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "rf_c1_det_context_conv3_2",
"attrs": {
"kernel": "(3, 3)",
"num_filter": "16",
"pad": "(1, 1)",
"stride": "(1, 1)"
},
"inputs": [[413, 0, 0], [414, 0, 0], [415, 0, 0]]
},
{
"op": "null",
"name": "rf_c1_det_context_conv3_2_bn_gamma",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_context_conv3_2_bn_beta",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_context_conv3_2_bn_moving_mean",
"attrs": {
"__init__": "[\"zero\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "null",
"name": "rf_c1_det_context_conv3_2_bn_moving_var",
"attrs": {
"__init__": "[\"one\", {}]",
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": []
},
{
"op": "BatchNorm",
"name": "rf_c1_det_context_conv3_2_bn",
"attrs": {
"eps": "2e-05",
"fix_gamma": "False",
"momentum": "0.9"
},
"inputs": [[416, 0, 0], [417, 0, 0], [418, 0, 0], [419, 0, 1], [420, 0, 1]]
},
{
"op": "Concat",
"name": "rf_c1_det_concat",
"attrs": {
"dim": "1",
"num_args": "3"
},
"inputs": [[387, 0, 0], [404, 0, 0], [421, 0, 0]]
},
{
"op": "Activation",
"name": "rf_c1_det_concat_relu",
"attrs": {"act_type": "relu"},
"inputs": [[422, 0, 0]]
},
{
"op": "null",
"name": "face_rpn_cls_score_stride8_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "face_rpn_cls_score_stride8_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "face_rpn_cls_score_stride8",
"attrs": {
"kernel": "(1, 1)",
"num_filter": "4",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[423, 0, 0], [424, 0, 0], [425, 0, 0]]
},
{
"op": "Reshape",
"name": "face_rpn_cls_score_reshape_stride8",
"attrs": {"shape": "(0, 2, -1, 0)"},
"inputs": [[426, 0, 0]]
},
{
"op": "SoftmaxActivation",
"name": "face_rpn_cls_prob_stride8",
"attrs": {"mode": "channel"},
"inputs": [[427, 0, 0]]
},
{
"op": "Reshape",
"name": "face_rpn_cls_prob_reshape_stride8",
"attrs": {"shape": "(0, 4, -1, 0)"},
"inputs": [[428, 0, 0]]
},
{
"op": "null",
"name": "face_rpn_bbox_pred_stride8_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "face_rpn_bbox_pred_stride8_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "face_rpn_bbox_pred_stride8",
"attrs": {
"kernel": "(1, 1)",
"num_filter": "8",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[423, 0, 0], [430, 0, 0], [431, 0, 0]]
},
{
"op": "null",
"name": "face_rpn_landmark_pred_stride8_weight",
"attrs": {
"__init__": "[\"normal\", {\"sigma\": 0.01}]",
"__lr_mult__": "1.0"
},
"inputs": []
},
{
"op": "null",
"name": "face_rpn_landmark_pred_stride8_bias",
"attrs": {
"__init__": "[\"constant\", {\"value\": 0.0}]",
"__lr_mult__": "2.0",
"__wd_mult__": "0.0"
},
"inputs": []
},
{
"op": "Convolution",
"name": "face_rpn_landmark_pred_stride8",
"attrs": {
"kernel": "(1, 1)",
"num_filter": "20",
"pad": "(0, 0)",
"stride": "(1, 1)"
},
"inputs": [[423, 0, 0], [433, 0, 0], [434, 0, 0]]
}
],
"arg_nodes": [
0,
1,
3,
4,
5,
6,
9,
11,
12,
13,
14,
17,
19,
20,
21,
22,
25,
27,
28,
29,
30,
33,
35,
36,
37,
38,
41,
43,
44,
45,
46,
49,
51,
52,
53,
54,
57,
59,
60,
61,
62,
65,
67,
68,
69,
70,
73,
75,
76,
77,
78,
81,
83,
84,
85,
86,
89,
91,
92,
93,
94,
97,
99,
100,
101,
102,
105,
107,
108,
109,
110,
113,
115,
116,
117,
118,
121,
123,
124,
125,
126,
129,
131,
132,
133,
134,
137,
139,
140,
141,
142,
145,
147,
148,
149,
150,
153,
155,
156,
157,
158,
161,
163,
164,
165,
166,
169,
171,
172,
173,
174,
177,
179,
180,
181,
182,
185,
187,
188,
189,
190,
193,
195,
196,
197,
198,
201,
203,
204,
205,
206,
209,
211,
212,
213,
214,
217,
218,
220,
221,
222,
223,
226,
227,
229,
230,
231,
232,
234,
235,
237,
238,
239,
240,
243,
244,
246,
247,
248,
249,
251,
252,
254,
255,
256,
257,
260,
261,
263,
264,
265,
266,
270,
271,
276,
277,
279,
280,
282,
283,
285,
286,
287,
288,
294,
295,
297,
298,
299,
300,
303,
304,
306,
307,
308,
309,
311,
312,
314,
315,
316,
317,
320,
321,
323,
324,
325,
326,
328,
329,
331,
332,
333,
334,
337,
338,
340,
341,
342,
343,
347,
348,
353,
354,
356,
357,
359,
360,
362,
363,
364,
365,
371,
372,
374,
375,
376,
377,
380,
381,
383,
384,
385,
386,
388,
389,
391,
392,
393,
394,
397,
398,
400,
401,
402,
403,
405,
406,
408,
409,
410,
411,
414,
415,
417,
418,
419,
420,
424,
425,
430,
431,
433,
434
],
"node_row_ptr": [
0,
1,
2,
3,
4,
5,
6,
7,
10,
11,
12,
13,
14,
15,
16,
17,
20,
21,
22,
23,
24,
25,
26,
27,
30,
31,
32,
33,
34,
35,
36,
37,
40,
41,
42,
43,
44,
45,
46,
47,
50,
51,
52,
53,
54,
55,
56,
57,
60,
61,
62,
63,
64,
65,
66,
67,
70,
71,
72,
73,
74,
75,
76,
77,
80,
81,
82,
83,
84,
85,
86,
87,
90,
91,
92,
93,
94,
95,
96,
97,
100,
101,
102,
103,
104,
105,
106,
107,
110,
111,
112,
113,
114,
115,
116,
117,
120,
121,
122,
123,
124,
125,
126,
127,
130,
131,
132,
133,
134,
135,
136,
137,
140,
141,
142,
143,
144,
145,
146,
147,
150,
151,
152,
153,
154,
155,
156,
157,
160,
161,
162,
163,
164,
165,
166,
167,
170,
171,
172,
173,
174,
175,
176,
177,
180,
181,
182,
183,
184,
185,
186,
187,
190,
191,
192,
193,
194,
195,
196,
197,
200,
201,
202,
203,
204,
205,
206,
207,
210,
211,
212,
213,
214,
215,
216,
217,
220,
221,
222,
223,
224,
225,
226,
227,
230,
231,
232,
233,
234,
235,
236,
237,
240,
241,
242,
243,
244,
245,
246,
247,
250,
251,
252,
253,
254,
255,
256,
257,
260,
261,
262,
263,
264,
265,
266,
267,
270,
271,
272,
273,
274,
275,
276,
277,
278,
281,
282,
283,
284,
285,
286,
287,
288,
289,
292,
293,
294,
295,
296,
297,
298,
299,
302,
303,
304,
305,
306,
307,
308,
309,
310,
313,
314,
315,
316,
317,
318,
319,
320,
323,
324,
325,
326,
327,
328,
329,
330,
331,
334,
335,
336,
337,
338,
339,
340,
341,
342,
343,
344,
345,
346,
347,
348,
349,
350,
351,
352,
353,
354,
355,
358,
359,
360,
361,
362,
363,
364,
365,
366,
367,
368,
369,
372,
373,
374,
375,
376,
377,
378,
379,
380,
383,
384,
385,
386,
387,
388,
389,
390,
393,
394,
395,
396,
397,
398,
399,
400,
401,
404,
405,
406,
407,
408,
409,
410,
411,
414,
415,
416,
417,
418,
419,
420,
421,
422,
425,
426,
427,
428,
429,
430,
431,
432,
433,
434,
435,
436,
437,
438,
439,
440,
441,
442,
443,
444,
445,
446,
449,
450,
451,
452,
453,
454,
455,
456,
457,
458,
459,
460,
463,
464,
465,
466,
467,
468,
469,
470,
471,
474,
475,
476,
477,
478,
479,
480,
481,
484,
485,
486,
487,
488,
489,
490,
491,
492,
495,
496,
497,
498,
499,
500,
501,
502,
505,
506,
507,
508,
509,
510,
511,
512,
513,
516,
517,
518,
519,
520,
521,
522,
523,
524,
525,
526,
527,
528,
529,
530
],
"heads": [[272, 0, 0], [349, 0, 0], [426, 0, 0], [269,0,0], [346,0,0], [423,0,0]],
"attrs": {"mxnet_version": ["int", 10300]}
}
```
| github_jupyter |
# Mixture Density Networks with Edward, Keras and TensorFlow
This notebook explains how to implement Mixture Density Networks (MDN) with Edward, Keras and TensorFlow.
Keep in mind that if you want to use Keras and TensorFlow, like we do in this notebook, you need to set the backend of Keras to TensorFlow, [here](http://keras.io/backend/) it is explained how to do that.
In you are not familiar with MDNs have a look at the [following blog post](http://cbonnett.github.io/MDN.html) or at orginal [paper](http://research.microsoft.com/en-us/um/people/cmbishop/downloads/Bishop-NCRG-94-004.pdf) by Bishop.
Edward implements many probability distribution functions that are TensorFlow compatible, this makes it attractive to use Edward for MDNs.
Here are all the distributions that are currently implemented in Edward, there are more to come:
1. [Bernoulli](https://github.com/blei-lab/edward/blob/master/edward/stats/distributions.py#L49)
2. [Beta](https://github.com/blei-lab/edward/blob/master/edward/stats/distributions.py#L58)
3. [Binomial](https://github.com/blei-lab/edward/blob/master/edward/stats/distributions.py#L68)
4. [Chi Squared](https://github.com/blei-lab/edward/blob/master/edward/stats/distributions.py#L79)
5. [Dirichlet](https://github.com/blei-lab/edward/blob/master/edward/stats/distributions.py#L89)
6. [Exponential](https://github.com/blei-lab/edward/blob/master/edward/stats/distributions.py#L109)
7. [Gamma](https://github.com/blei-lab/edward/blob/master/edward/stats/distributions.py#L118)
8. [Geometric](https://github.com/blei-lab/edward/blob/master/edward/stats/distributions.py#L129)
9. [Inverse Gamma](https://github.com/blei-lab/edward/blob/master/edward/stats/distributions.py#L138)
10. [log Normal](https://github.com/blei-lab/edward/blob/master/edward/stats/distributions.py#L155)
11. [Multinomial](https://github.com/blei-lab/edward/blob/master/edward/stats/distributions.py#L165)
12. [Multivariate Normal](https://github.com/blei-lab/edward/blob/master/edward/stats/distributions.py#L194)
13. [Negative Binomial](https://github.com/blei-lab/edward/blob/master/edward/stats/distributions.py#L283)
14. [Normal](https://github.com/blei-lab/edward/blob/master/edward/stats/distributions.py#L294)
15. [Poisson](https://github.com/blei-lab/edward/blob/master/edward/stats/distributions.py#L310)
16. [Student-t](https://github.com/blei-lab/edward/blob/master/edward/stats/distributions.py#L319)
17. [Truncated Normal](https://github.com/blei-lab/edward/blob/master/edward/stats/distributions.py#L333)
18. [Uniform](https://github.com/blei-lab/edward/blob/master/edward/stats/distributions.py#L352)
Let's start with the necessary imports.
```
# imports
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
import edward as ed
import numpy as np
import tensorflow as tf
from edward.stats import norm # Normal distribution from Edward.
from keras import backend as K
from keras.layers import Dense
from sklearn.cross_validation import train_test_split
```
We will need some functions to plot the results later on, these are defined in the next code block.
```
from scipy.stats import norm as normal
def plot_normal_mix(pis, mus, sigmas, ax, label='', comp=True):
"""
Plots the mixture of Normal models to axis=ax
comp=True plots all components of mixture model
"""
x = np.linspace(-10.5, 10.5, 250)
final = np.zeros_like(x)
for i, (weight_mix, mu_mix, sigma_mix) in enumerate(zip(pis, mus, sigmas)):
temp = normal.pdf(x, mu_mix, sigma_mix) * weight_mix
final = final + temp
if comp:
ax.plot(x, temp, label='Normal ' + str(i))
ax.plot(x, final, label='Mixture of Normals ' + label)
ax.legend(fontsize=13)
def sample_from_mixture(x, pred_weights, pred_means, pred_std, amount):
"""
Draws samples from mixture model.
Returns 2 d array with input X and sample from prediction of Mixture Model
"""
samples = np.zeros((amount, 2))
n_mix = len(pred_weights[0])
to_choose_from = np.arange(n_mix)
for j,(weights, means, std_devs) in enumerate(zip(pred_weights, pred_means, pred_std)):
index = np.random.choice(to_choose_from, p=weights)
samples[j,1]= normal.rvs(means[index], std_devs[index], size=1)
samples[j,0]= x[j]
if j == amount -1:
break
return samples
```
## Making some toy-data to play with.
This is the same toy-data problem set as used in the [blog post](http://blog.otoro.net/2015/11/24/mixture-density-networks-with-tensorflow/) by Otoro where he explains MDNs. This is an inverse problem as you can see, for every ```X``` there are multiple ```y``` solutions.
```
def build_toy_dataset(nsample=40000):
y_data = np.float32(np.random.uniform(-10.5, 10.5, (1, nsample))).T
r_data = np.float32(np.random.normal(size=(nsample, 1))) # random noise
x_data = np.float32(np.sin(0.75 * y_data) * 7.0 + y_data * 0.5 + r_data * 1.0)
return train_test_split(x_data, y_data, random_state=42, train_size=0.1)
X_train, X_test, y_train, y_test = build_toy_dataset()
print("Size of features in training data: {:s}".format(X_train.shape))
print("Size of output in training data: {:s}".format(y_train.shape))
print("Size of features in test data: {:s}".format(X_test.shape))
print("Size of output in test data: {:s}".format(y_test.shape))
sns.regplot(X_train, y_train, fit_reg=False)
```
### Building a MDN using Edward, Keras and TF
We will define a class that can be used to construct MDNs. In this notebook we will be using a mixture of Normal Distributions. The advantage of defining a class is that we can easily reuse this to build other MDNs with different amount of mixture components. Furthermore, this makes it play nicely with Edward.
```
class MixtureDensityNetwork:
"""
Mixture density network for outputs y on inputs x.
p((x,y), (z,theta))
= sum_{k=1}^K pi_k(x; theta) Normal(y; mu_k(x; theta), sigma_k(x; theta))
where pi, mu, sigma are the output of a neural network taking x
as input and with parameters theta. There are no latent variables
z, which are hidden variables we aim to be Bayesian about.
"""
def __init__(self, K):
self.K = K # here K is the amount of Mixtures
def mapping(self, X):
"""pi, mu, sigma = NN(x; theta)"""
hidden1 = Dense(15, activation='relu')(X) # fully-connected layer with 15 hidden units
hidden2 = Dense(15, activation='relu')(hidden1)
self.mus = Dense(self.K)(hidden2) # the means
self.sigmas = Dense(self.K, activation=K.exp)(hidden2) # the variance
self.pi = Dense(self.K, activation=K.softmax)(hidden2) # the mixture components
def log_prob(self, xs, zs=None):
"""log p((xs,ys), (z,theta)) = sum_{n=1}^N log p((xs[n,:],ys[n]), theta)"""
# Note there are no parameters we're being Bayesian about. The
# parameters are baked into how we specify the neural networks.
X, y = xs
self.mapping(X)
result = tf.exp(norm.logpdf(y, self.mus, self.sigmas))
result = tf.mul(result, self.pi)
result = tf.reduce_sum(result, 1)
result = tf.log(result)
return tf.reduce_sum(result)
```
We can set a seed in Edward so we can reproduce all the random components. The following line:
```ed.set_seed(42)```
sets the seed in Numpy and TensorFlow under the [hood](https://github.com/blei-lab/edward/blob/master/edward/util.py#L191). We use the class we defined above to initiate the MDN with 20 mixtures, this now can be used as an Edward model.
```
ed.set_seed(42)
model = MixtureDensityNetwork(20)
```
In the following code cell we define the TensorFlow placeholders that are then used to define the Edward data model.
The following line passes the ```model``` and ```data``` to ```MAP``` from Edward which is then used to initialise the TensorFlow variables.
```inference = ed.MAP(model, data)```
MAP is a Bayesian concept and stands for Maximum A Posteriori, it tries to find the set of parameters which maximizes the posterior distribution. In the example here we don't have a prior, in a Bayesian context this means we have a flat prior. For a flat prior MAP is equivalent to Maximum Likelihood Estimation. Edward is designed to be Bayesian about its statistical inference. The cool thing about MDN's with Edward is that we could easily include priors!
```
X = tf.placeholder(tf.float32, shape=(None, 1))
y = tf.placeholder(tf.float32, shape=(None, 1))
data = ed.Data([X, y]) # Make Edward Data model
inference = ed.MAP(model, data) # Make the inference model
sess = tf.Session() # Start TF session
K.set_session(sess) # Pass session info to Keras
inference.initialize(sess=sess) # Initialize all TF variables using the Edward interface
```
Having done that we can train the MDN in TensorFlow just like we normally would, and we can get out the predictions we are interested in from ```model```, in this case:
* ```model.pi``` the mixture components,
* ```model.mus``` the means,
* ```model.sigmas``` the standard deviations.
This is done in the last line of the code cell :
```
pred_weights, pred_means, pred_std = sess.run([model.pi, model.mus, model.sigmas],
feed_dict={X: X_test})
```
The default minimisation technique used is ADAM with a decaying scale factor.
This can be seen [here](https://github.com/blei-lab/edward/blob/master/edward/inferences.py#L94) in the code base of Edward. Having a decaying scale factor is not the standard way of using ADAM, this is inspired by the Automatic Differentiation Variational Inference [(ADVI)](http://arxiv.org/abs/1603.00788) work where it was used in the RMSPROP minimizer.
The loss that is minimised in the ```MAP``` model from Edward is the negative log-likelihood, this calculation uses the ```log_prob``` method in the ```MixtureDensityNetwork``` class we defined above.
The ```build_loss``` method in the ```MAP``` class can be found [here](https://github.com/blei-lab/edward/blob/master/edward/inferences.py#L396).
However the method ```inference.loss``` used below, returns the log-likelihood, so we expect this quantity to be maximized.
```
NEPOCH = 1000
train_loss = np.zeros(NEPOCH)
test_loss = np.zeros(NEPOCH)
for i in range(NEPOCH):
_, train_loss[i] = sess.run([inference.train, inference.loss],
feed_dict={X: X_train, y: y_train})
test_loss[i] = sess.run(inference.loss, feed_dict={X: X_test, y: y_test})
pred_weights, pred_means, pred_std = sess.run([model.pi, model.mus, model.sigmas],
feed_dict={X: X_test})
```
We can plot the log-likelihood of the training and test sample as function of training epoch.
Keep in mind that ```inference.loss``` returns the total log-likelihood, so not the loss per data point, so in the plotting routine we divide by the size of the train and test data respectively.
We see that it converges after 400 training steps.
```
fig, axes = plt.subplots(nrows=1, ncols=1, figsize=(16, 3.5))
plt.plot(np.arange(NEPOCH), test_loss/len(X_test), label='Test')
plt.plot(np.arange(NEPOCH), train_loss/len(X_train), label='Train')
plt.legend(fontsize=20)
plt.xlabel('Epoch', fontsize=15)
plt.ylabel('Log-likelihood', fontsize=15)
```
Next we can have a look at how some individual examples perform. Keep in mind this is an inverse problem
so we can't get the answer correct, we can hope that the truth lies in area where the model has high probability.
In the next plot the truth is the vertical grey line while the blue line is the prediction of the mixture density network. As you can see, we didn't do too bad.
```
obj = [0, 4, 6]
fig, axes = plt.subplots(nrows=3, ncols=1, figsize=(16, 6))
plot_normal_mix(pred_weights[obj][0], pred_means[obj][0], pred_std[obj][0], axes[0], comp=False)
axes[0].axvline(x=y_test[obj][0], color='black', alpha=0.5)
plot_normal_mix(pred_weights[obj][2], pred_means[obj][2], pred_std[obj][2], axes[1], comp=False)
axes[1].axvline(x=y_test[obj][2], color='black', alpha=0.5)
plot_normal_mix(pred_weights[obj][1], pred_means[obj][1], pred_std[obj][1], axes[2], comp=False)
axes[2].axvline(x=y_test[obj][1], color='black', alpha=0.5)
```
We can check the ensemble by drawing samples of the prediction and plotting the density of those.
Seems the MDN learned what it needed too.
```
a = sample_from_mixture(X_test, pred_weights, pred_means, pred_std, amount=len(X_test))
sns.jointplot(a[:,0], a[:,1], kind="hex", color="#4CB391", ylim=(-10,10), xlim=(-14,14))
```
| github_jupyter |
<H3>Importing Required Libraries
```
from pyspark.sql import SparkSession
from pyspark.sql import functions as F
```
<H3>Getting Spark Session
```
spark = SparkSession.builder.getOrCreate()
```
<H3>Reading CSV
```
df = spark.read.csv("Big_Cities_Health_Data_Inventory.csv", header=True)
df.show(10)
```
<H3>Printing Schema
```
df.printSchema()
```
<H3>Dropping Unwanted Columns
```
df = df.drop("Notes", "Methods", "Source", "BCHC Requested Methodology")
df.printSchema()
```
<H3>Counting Null Values
```
df.select([F.count(F.when(F.isnan(c) | F.col(c).isNull(), c)).alias(c) for c in df.columns]).show()
```
Since there are several null values in the columns as shown in the table above, first steps would be to remove / replace null values in each column
<H3>Working with Null Values
```
df.filter(df["Indicator"].isNull()).show(28)
```
Since all the rows that have null values in Indicator have null values for other columns like Year, Gender, Race and etc, it would be better to remove these observations
```
# Counting total number of rows in the dataset to compare with the rows after null value rows are removed.
rows_count_pre = df.count()
print("Total number of rows before deleting: ",rows_count_pre)
# deleting all the rows where there are null values in the columns mentioned below
df = df.na.drop(subset=["Indicator", "Year", "Gender", "Race/ Ethnicity", "Value", "Place"])
rows_count_post = df.count()
print("Total number of rows after deleting: ",rows_count_post)
total_rows_removed = rows_count_pre - rows_count_post
print("Total number of rows deleted: ", total_rows_removed)
#Checking the null values again to see if the dataset is clean
df.select([F.count(F.when(F.isnan(c) | F.col(c).isNull(), c)).alias(c) for c in df.columns]).show()
```
The results above show that all the rows with null values have been deleted from the dataset. This completes the step of removing all the null values from the dataset
<H3>Splitting the Place Column into City and State Columns
```
split_col = F.split(df["Place"], ',')
df = df.withColumn("City_County", split_col.getItem(0))
df = df.withColumn("State", split_col.getItem(1))
df.select("City_County", "State").show(truncate=False)
Creating a User Defined Function to take care of the City_County column to extract the city. Same can be done using
import re
def extract_city(city_str):
result = re.sub(r'\([^)]*\)', '', city_str)
return result
from pyspark.sql.types import StringType
udfExtract = F.udf(extract_city, StringType())
df = df.withColumn("City", udfExtract(df["City_County"]))
df.select("City", "State").show(truncate=False)
```
This sums up the cleaning process of data using PySpark. Below is the final state of the dataset
```
df.show()
```
| github_jupyter |
# Exploratory Data Analysis
* Dataset taken from https://github.com/Tariq60/LIAR-PLUS
## 1. Import Libraries
```
import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
TRAIN_PATH = "../data/raw/dataset/tsv/train2.tsv"
VAL_PATH = "../data/raw/dataset/tsv/val2.tsv"
TEST_PATH = "../data/raw/dataset/tsv/test2.tsv"
columns = ["id", "statement_json", "label", "statement", "subject", "speaker", "speaker_title", "state_info",
"party_affiliation", "barely_true_count", "false_count", "half_true_count", "mostly_true_count",
"pants_fire_count", "context", "justification"]
```
## 2. Read the dataset
```
train_df = pd.read_csv(TRAIN_PATH, sep="\t", names=columns)
val_df = pd.read_csv(VAL_PATH, sep="\t", names=columns)
test_df = pd.read_csv(TEST_PATH, sep="\t", names=columns)
print(f"Length of train set: {len(train_df)}")
print(f"Length of validation set: {len(val_df)}")
print(f"Length of test set: {len(test_df)}")
train_df.head()
```
## 3. Data Cleaning
* Some of the most important coloumns are "label", "statement".
* Now we should check if any of them have null values.
```
print("Do we have empty strings in `label`?")
pd.isna(train_df["label"]).value_counts()
```
* 2 entries without any label
* What exactly are those 2 entries?
```
train_df.loc[pd.isna(train_df["label"]), :].index
train_df.loc[[2143]]
train_df.loc[[9377]]
```
* All the coloumns of those 2 entries are blank
* Drop those 2 entries
```
train_df.dropna(subset=["label"], inplace=True)
len(train_df)
```
## 4. Some Feature Analysis
### 4.1 Party Affiliation
```
print(train_df["party_affiliation"].value_counts())
if not os.path.exists("./img"):
os.makedirs("./img")
fig = plt.figure(figsize=(10, 6))
party_affil_plot = train_df["party_affiliation"].value_counts().plot.bar()
plt.tight_layout(pad=1)
plt.savefig("img/party_affil_plot.png", dpi=200)
```
### 4.2 States Stats
```
print(train_df["state_info"].value_counts())
fig = plt.figure(figsize=(10, 6))
state_info_plot = train_df["state_info"].value_counts().plot.bar()
plt.tight_layout(pad=1)
plt.savefig("img/state_info_plot.png", dpi=200)
```
* Apparently, we have a state_info entry with value as "Virginia director, Coalition to Stop Gun Violence".
It should be replaced with "Virginia" only
```
train_df[train_df["state_info"]=="Virginia director, Coalition to Stop Gun Violence"]
indx = train_df[train_df["state_info"]=="Virginia director, Coalition to Stop Gun Violence"].index[0]
train_df.loc[indx, "state_info"] = "Virginia"
fig = plt.figure(figsize=(10, 6))
state_info_plot = train_df["state_info"].value_counts().plot.bar()
plt.tight_layout(pad=1)
plt.savefig("img/state_info_plot.png", dpi=200)
```
### 4.3 Label Distribution
```
print(train_df["label"].value_counts())
fig = plt.figure(figsize=(10, 6))
label_stats_plot = train_df["label"].value_counts().plot.bar()
plt.tight_layout(pad=1)
plt.savefig("img/label_stats_plot.png", dpi=100)
```
### 4.4 Speaker Distribution
```
print(train_df.speaker.value_counts())
fig = plt.figure(figsize=(10, 6))
speaker_stats_plot = train_df["speaker"].value_counts()[:10].plot.bar()
plt.tight_layout(pad=1)
plt.title("Speakers")
plt.savefig("img/speaker_stats_plot.png", dpi=100)
print(train_df.speaker_title.value_counts())
fig = plt.figure(figsize=(10, 6))
speaker_title_stats_plot = train_df["speaker_title"].value_counts()[:10].plot.bar()
plt.tight_layout(pad=1)
plt.title("Speaker Title")
plt.savefig("img/speaker_title_stats_plot.png", dpi=100)
```
### 4.5 Democrats vs Republicans
* Let's see how the 2 main parties compete with each other in terms of
truthfulness in the labels
```
fig = plt.figure(figsize=(8,4))
plt.suptitle("Party-wise Label")
ax1 = fig.add_subplot(121)
party_wise = train_df[train_df["party_affiliation"]=="democrat"]["label"].value_counts().to_frame()
ax1.pie(party_wise["label"], labels=party_wise.index, autopct='%1.1f%%',
startangle=90)
ax1.set_title("Democrat")
plt.suptitle("Party-wise Label")
ax2 = fig.add_subplot(122)
party_wise = train_df[train_df["party_affiliation"]=="republican"]["label"].value_counts().to_frame()
ax2.pie(party_wise["label"], labels=party_wise.index, autopct='%1.1f%%',
startangle=90)
ax2.set_title("Republican")
plt.tight_layout()
plt.savefig("img/dems_gop_label_plot.png", dpi=200)
```
* We can combine some labels to get a more simplified plot
```
def get_binary_label(label):
if label in ["pants-fire", "barely-true", "false"]:
return False
elif label in ["true", "half-true", "mostly-true"]:
return True
train_df["binary_label"] = train_df.label.apply(get_binary_label)
fig = plt.figure(figsize=(8,4))
plt.suptitle("Party-wise Label")
ax1 = fig.add_subplot(121)
party_wise = train_df[train_df["party_affiliation"]=="democrat"]["binary_label"].value_counts().to_frame()
ax1.pie(party_wise["binary_label"], labels=party_wise.index, autopct='%1.1f%%',
startangle=90)
ax1.set_title("Democrat")
plt.suptitle("Party-wise Label")
ax2 = fig.add_subplot(122)
party_wise = train_df[train_df["party_affiliation"]=="republican"]["binary_label"].value_counts().to_frame()
ax2.pie(party_wise["binary_label"], labels=party_wise.index, autopct='%1.1f%%',
startangle=90)
ax2.set_title("Republican")
plt.tight_layout()
plt.savefig("img/dems_gop_binary_label_plot.png", dpi=200)
```
## 5. Sentiment Analysis
```
from textblob import TextBlob
pol = lambda x: TextBlob(x).sentiment.polarity
sub = lambda x: TextBlob(x).sentiment.subjectivity
train_df['polarity_true'] = train_df[train_df["binary_label"]==True]['statement'].apply(pol)
train_df['subjectivity_true'] = train_df[train_df["binary_label"]==True]['statement'].apply(sub)
plt.rcParams['figure.figsize'] = [10, 8]
x = train_df["polarity_true"]
y = train_df["subjectivity_true"]
plt.scatter(x, y, color='blue')
plt.title('Sentiment Analysis', fontsize=20)
plt.xlabel('<-- Negative ---------------- Positive -->', fontsize=10)
plt.ylabel('<-- Facts ---------------- Opinions -->', fontsize=10)
plt.savefig("img/sa_true.png", format="png", dpi=200)
plt.show()
train_df['polarity_false'] = train_df[train_df["binary_label"]==False]['statement'].apply(pol)
train_df['subjectivity_false'] = train_df[train_df["binary_label"]==False]['statement'].apply(sub)
plt.rcParams['figure.figsize'] = [10, 8]
x = train_df["polarity_false"]
y = train_df["subjectivity_false"]
plt.scatter(x, y, color='blue')
plt.title('Sentiment Analysis', fontsize=20)
plt.xlabel('<-- Negative ---------------- Positive -->', fontsize=10)
plt.ylabel('<-- Facts ---------------- Opinions -->', fontsize=10)
plt.savefig("img/sa_false.png", format="png", dpi=200)
plt.show()
```
| github_jupyter |
```
#hide
#skip
! [[ -e /content ]] && pip install -Uqq fastai # upgrade fastai on colab
#default_exp collab
#default_class_lvl 3
#export
from fastai.tabular.all import *
#hide
from nbdev.showdoc import *
```
# Collaborative filtering
> Tools to quickly get the data and train models suitable for collaborative filtering
This module contains all the high-level functions you need in a collaborative filtering application to assemble your data, get a model and train it with a `Learner`. We will go other those in order but you can also check the [collaborative filtering tutorial](http://docs.fast.ai/tutorial.collab).
## Gather the data
```
#export
class TabularCollab(TabularPandas):
"Instance of `TabularPandas` suitable for collaborative filtering (with no continuous variable)"
with_cont=False
```
This is just to use the internal of the tabular application, don't worry about it.
```
#export
class CollabDataLoaders(DataLoaders):
"Base `DataLoaders` for collaborative filtering."
@delegates(DataLoaders.from_dblock)
@classmethod
def from_df(cls, ratings, valid_pct=0.2, user_name=None, item_name=None, rating_name=None, seed=None, path='.', **kwargs):
"Create a `DataLoaders` suitable for collaborative filtering from `ratings`."
user_name = ifnone(user_name, ratings.columns[0])
item_name = ifnone(item_name, ratings.columns[1])
rating_name = ifnone(rating_name, ratings.columns[2])
cat_names = [user_name,item_name]
splits = RandomSplitter(valid_pct=valid_pct, seed=seed)(range_of(ratings))
to = TabularCollab(ratings, [Categorify], cat_names, y_names=[rating_name], y_block=TransformBlock(), splits=splits)
return to.dataloaders(path=path, **kwargs)
@classmethod
def from_csv(cls, csv, **kwargs):
"Create a `DataLoaders` suitable for collaborative filtering from `csv`."
return cls.from_df(pd.read_csv(csv), **kwargs)
CollabDataLoaders.from_csv = delegates(to=CollabDataLoaders.from_df)(CollabDataLoaders.from_csv)
```
This class should not be used directly, one of the factory methods should be preferred instead. All those factory methods accept as arguments:
- `valid_pct`: the random percentage of the dataset to set aside for validation (with an optional `seed`)
- `user_name`: the name of the column containing the user (defaults to the first column)
- `item_name`: the name of the column containing the item (defaults to the second column)
- `rating_name`: the name of the column containing the rating (defaults to the third column)
- `path`: the folder where to work
- `bs`: the batch size
- `val_bs`: the batch size for the validation `DataLoader` (defaults to `bs`)
- `shuffle_train`: if we shuffle the training `DataLoader` or not
- `device`: the PyTorch device to use (defaults to `default_device()`)
```
show_doc(CollabDataLoaders.from_df)
```
Let's see how this works on an example:
```
path = untar_data(URLs.ML_SAMPLE)
ratings = pd.read_csv(path/'ratings.csv')
ratings.head()
dls = CollabDataLoaders.from_df(ratings, bs=64)
dls.show_batch()
show_doc(CollabDataLoaders.from_csv)
dls = CollabDataLoaders.from_csv(path/'ratings.csv', bs=64)
```
## Models
fastai provides two kinds of models for collaborative filtering: a dot-product model and a neural net.
```
#export
class EmbeddingDotBias(Module):
"Base dot model for collaborative filtering."
def __init__(self, n_factors, n_users, n_items, y_range=None):
self.y_range = y_range
(self.u_weight, self.i_weight, self.u_bias, self.i_bias) = [Embedding(*o) for o in [
(n_users, n_factors), (n_items, n_factors), (n_users,1), (n_items,1)
]]
def forward(self, x):
users,items = x[:,0],x[:,1]
dot = self.u_weight(users)* self.i_weight(items)
res = dot.sum(1) + self.u_bias(users).squeeze() + self.i_bias(items).squeeze()
if self.y_range is None: return res
return torch.sigmoid(res) * (self.y_range[1]-self.y_range[0]) + self.y_range[0]
@classmethod
def from_classes(cls, n_factors, classes, user=None, item=None, y_range=None):
"Build a model with `n_factors` by inferring `n_users` and `n_items` from `classes`"
if user is None: user = list(classes.keys())[0]
if item is None: item = list(classes.keys())[1]
res = cls(n_factors, len(classes[user]), len(classes[item]), y_range=y_range)
res.classes,res.user,res.item = classes,user,item
return res
def _get_idx(self, arr, is_item=True):
"Fetch item or user (based on `is_item`) for all in `arr`"
assert hasattr(self, 'classes'), "Build your model with `EmbeddingDotBias.from_classes` to use this functionality."
classes = self.classes[self.item] if is_item else self.classes[self.user]
c2i = {v:k for k,v in enumerate(classes)}
try: return tensor([c2i[o] for o in arr])
except Exception as e:
print(f"""You're trying to access {'an item' if is_item else 'a user'} that isn't in the training data.
If it was in your original data, it may have been split such that it's only in the validation set now.""")
def bias(self, arr, is_item=True):
"Bias for item or user (based on `is_item`) for all in `arr`"
idx = self._get_idx(arr, is_item)
layer = (self.i_bias if is_item else self.u_bias).eval().cpu()
return to_detach(layer(idx).squeeze(),gather=False)
def weight(self, arr, is_item=True):
"Weight for item or user (based on `is_item`) for all in `arr`"
idx = self._get_idx(arr, is_item)
layer = (self.i_weight if is_item else self.u_weight).eval().cpu()
return to_detach(layer(idx),gather=False)
```
The model is built with `n_factors` (the length of the internal vectors), `n_users` and `n_items`. For a given user and item, it grabs the corresponding weights and bias and returns
``` python
torch.dot(user_w, item_w) + user_b + item_b
```
Optionally, if `y_range` is passed, it applies a `SigmoidRange` to that result.
```
x,y = dls.one_batch()
model = EmbeddingDotBias(50, len(dls.classes['userId']), len(dls.classes['movieId']), y_range=(0,5)
).to(x.device)
out = model(x)
assert (0 <= out).all() and (out <= 5).all()
show_doc(EmbeddingDotBias.from_classes)
```
`y_range` is passed to the main init. `user` and `item` are the names of the keys for users and items in `classes` (default to the first and second key respectively). `classes` is expected to be a dictionary key to list of categories like the result of `dls.classes` in a `CollabDataLoaders`:
```
dls.classes
```
Let's see how it can be used in practice:
```
model = EmbeddingDotBias.from_classes(50, dls.classes, y_range=(0,5)
).to(x.device)
out = model(x)
assert (0 <= out).all() and (out <= 5).all()
```
Two convenience methods are added to easily access the weights and bias when a model is created with `EmbeddingDotBias.from_classes`:
```
show_doc(EmbeddingDotBias.weight)
```
The elements of `arr` are expected to be class names (which is why the model needs to be created with `EmbeddingDotBias.from_classes`)
```
mov = dls.classes['movieId'][42]
w = model.weight([mov])
test_eq(w, model.i_weight(tensor([42])))
show_doc(EmbeddingDotBias.bias)
```
The elements of `arr` are expected to be class names (which is why the model needs to be created with `EmbeddingDotBias.from_classes`)
```
mov = dls.classes['movieId'][42]
b = model.bias([mov])
test_eq(b, model.i_bias(tensor([42])))
#export
class EmbeddingNN(TabularModel):
"Subclass `TabularModel` to create a NN suitable for collaborative filtering."
@delegates(TabularModel.__init__)
def __init__(self, emb_szs, layers, **kwargs):
super().__init__(emb_szs=emb_szs, n_cont=0, out_sz=1, layers=layers, **kwargs)
show_doc(EmbeddingNN)
```
`emb_szs` should be a list of two tuples, one for the users, one for the items, each tuple containing the number of users/items and the corresponding embedding size (the function `get_emb_sz` can give a good default). All the other arguments are passed to `TabularModel`.
```
emb_szs = get_emb_sz(dls.train_ds, {})
model = EmbeddingNN(emb_szs, [50], y_range=(0,5)
).to(x.device)
out = model(x)
assert (0 <= out).all() and (out <= 5).all()
```
## Create a `Learner`
The following function lets us quickly create a `Learner` for collaborative filtering from the data.
```
# export
@log_args(to_return=True, but_as=Learner.__init__)
@delegates(Learner.__init__)
def collab_learner(dls, n_factors=50, use_nn=False, emb_szs=None, layers=None, config=None, y_range=None, loss_func=None, **kwargs):
"Create a Learner for collaborative filtering on `dls`."
emb_szs = get_emb_sz(dls, ifnone(emb_szs, {}))
if loss_func is None: loss_func = MSELossFlat()
if config is None: config = tabular_config()
if y_range is not None: config['y_range'] = y_range
if layers is None: layers = [n_factors]
if use_nn: model = EmbeddingNN(emb_szs=emb_szs, layers=layers, **config)
else: model = EmbeddingDotBias.from_classes(n_factors, dls.classes, y_range=y_range)
return Learner(dls, model, loss_func=loss_func, **kwargs)
```
If `use_nn=False`, the model used is an `EmbeddingDotBias` with `n_factors` and `y_range`. Otherwise, it's a `EmbeddingNN` for which you can pass `emb_szs` (will be inferred from the `dls` with `get_emb_sz` if you don't provide any), `layers` (defaults to `[n_factors]`) `y_range`, and a `config` that you can create with `tabular_config` to customize your model.
`loss_func` will default to `MSELossFlat` and all the other arguments are passed to `Learner`.
```
learn = collab_learner(dls, y_range=(0,5))
learn.fit_one_cycle(1)
```
## Export -
```
#hide
from nbdev.export import *
notebook2script()
```
| github_jupyter |
# ***Introduction to Radar Using Python and MATLAB***
## Andy Harrison - Copyright (C) 2019 Artech House
<br/>
# Pulse Train Ambiguity Function
***
Referring to Section 8.6.1, the amibguity function for a coherent pulse train is found by employing the generic waveform technique outlined in Section 8.6.3.
***
Begin by getting the library path
```
import lib_path
```
Set the pulsewidth (s), the pulse repetition interval (s) and the number of pulses
```
pulsewidth = 0.4
pri = 1.0
number_of_pulses = 6
```
Generate the time delay (s) using the `linspace` routine from `scipy`
```
from numpy import linspace
# Set the time delay
time_delay = linspace(-number_of_pulses * pri, number_of_pulses * pri, 5000)
```
Calculate the ambiguity function for the pulse train
```
from Libs.ambiguity.ambiguity_function import pulse_train
from numpy import finfo
ambiguity = pulse_train(time_delay, finfo(float).eps, pulsewidth, pri, number_of_pulses)
```
Plot the zero-Doppler cut using the `matplotlib` routines
```
from matplotlib import pyplot as plt
# Set the figure size
plt.rcParams["figure.figsize"] = (15, 10)
# Plot the ambiguity function
plt.plot(time_delay, ambiguity, '')
# Set the x and y axis labels
plt.xlabel("Time (s)", size=12)
plt.ylabel("Relative Amplitude", size=12)
# Turn on the grid
plt.grid(linestyle=':', linewidth=0.5)
# Set the plot title and labels
plt.title('Pulse Train Ambiguity Function', size=14)
# Set the tick label size
plt.tick_params(labelsize=12)
```
Set the Doppler mismatch frequencies using the `linspace` routine
```
doppler_frequency = linspace(-2.0 / pulsewidth, 2.0 / pulsewidth, 1000)
```
Calculate the ambiguity function for the pulse train
```
ambiguity = pulse_train(finfo(float).eps, doppler_frequency, pulsewidth, pri, number_of_pulses)
```
Display the zero-range cut for the pulse train
```
plt.plot(doppler_frequency, ambiguity, '')
# Set the x and y axis labels
plt.xlabel("Doppler (Hz)", size=12)
plt.ylabel("Relative Amplitude", size=12)
# Turn on the grid
plt.grid(linestyle=':', linewidth=0.5)
# Set the plot title and labels
plt.title('Pulse Train Ambiguity Function', size=14)
# Set the tick label size
plt.tick_params(labelsize=12)
```
Set the time delay and Doppler mismatch frequency and create the two-dimensional grid using the `meshgrid` routine from `scipy`
```
from numpy import meshgrid
# Set the time delay
time_delay = linspace(-number_of_pulses * pri, number_of_pulses * pri, 1000)
# Set the Doppler mismatch
doppler_frequency = linspace(-2.0 / pulsewidth, 2.0 / pulsewidth, 1000)
# Create the grid
t, f = meshgrid(time_delay, doppler_frequency)
```
Calculate the ambiguity function for the pulse train
```
ambiguity = pulse_train(t, f, pulsewidth, pri, number_of_pulses)
```
Display the two-dimensional contour plot for the pulse train ambiguity function
```
# Plot the ambiguity function
from numpy import finfo
plt.contour(t, f, ambiguity + finfo('float').eps, 20, cmap='jet', vmin=-0.2, vmax=1.0)
# Set the x and y axis labels
plt.xlabel("Time (s)", size=12)
plt.ylabel("Doppler (Hz)", size=12)
# Turn on the grid
plt.grid(linestyle=':', linewidth=0.5)
# Set the plot title and labels
plt.title('Pulse Pulse Ambiguity Function', size=14)
# Set the tick label size
plt.tick_params(labelsize=12)
```
| github_jupyter |
# 5.2 Fourier transform and Fourier series
We make use of the theory of tempered distributions (see
[@strichartz2003guide] for an introduction) and we begin by collecting
some results of independent interest, which will also be important
later.
## 5.2.1 Fourier transform
Before studying the Fourier transform, we first consider Schwartz space
which is defined below.
````{prf:definition}
The Schwartz space
$\mathcal{S}\left(\mathbb{R}^{n}\right)$ is the topological vector space
of functions $f: \mathbb{R}^{n} \rightarrow \mathbb{C}$ such that
$f \in C^{\infty}\left(\mathbb{R}^{n}\right)$ and
$$
x^{\alpha} \partial^{\beta} f(x) \rightarrow 0 \quad \text { as }|x| \rightarrow \infty
$$
for every pair of multi-indices $\alpha, \beta \in \mathbb{N}_{0}^{n} .$
For $\alpha, \beta \in \mathbb{N}_{0}^{n}$ and
$f \in \mathcal{S}\left(\mathbb{R}^{n}\right)$ let (5.10)
$$
\|f\|_{\alpha, \beta}=\sup _{\mathbb{R}^{n}}\left|x^{\alpha} \partial^{\beta} f\right|
$$
A sequence of functions $\left\{f_{k}: k \in \mathbb{N}\right\}$
converges to a function $f$ in $\mathcal{S}\left(\mathbb{R}^{n}\right)$
if
$$
\left\|f_{n}-f\right\|_{\alpha, \beta} \rightarrow 0 \quad \text { as } k \rightarrow \infty
$$
for every $\alpha, \beta \in \mathbb{N}_{0}^{n}$.
````
The Schwartz space consists of smooth functions whose derivatives and
the function itself decay at infinity faster than any power. Schwartz
functions are rapidly decreasing. When there is no ambiguity, we will
write $\mathcal{S}\left(\mathbb{R}^{n}\right)$ as $\mathcal{S}$. Roughly
speaking, tempered distributions grow no faster than a polynomial at
infinity.
````{prf:definition}
A tempered distribution $T$ on $\mathbb{R}^{n}$ is a continuous linear
functional
$T: \mathcal{S}\left(\mathbb{R}^{n}\right) \rightarrow \mathbb{C} .$ The
topological vector space of tempered distributions is denoted by
$\mathcal{S}^{\prime}\left(\mathbb{R}^{n}\right)$ or
$\mathcal{S}^{\prime} .$ If $\langle T, f\rangle$ denotes the value of
$T \in \mathcal{S}^{\prime}$ acting on $f \in \mathcal{S}$ then a
sequence $\left\{T_{k}\right\}$ converges to $T$ in
$\mathcal{S}^{\prime}$, written $T_{k} \rightarrow T$, if
$$
\left\langle T_{k}, f\right\rangle \rightarrow\langle T, f\rangle
$$
for every $f \in \mathcal{S}$.
````
Since $\mathcal{D} \subset \mathcal{S}$ is densely and continuously
imbedded, we have $\mathcal{S}^{\prime} \subset \mathcal{D}^{\prime} .$
Moreover, a distribution $T \in \mathcal{D}^{\prime}$ extends uniquely
to a tempered distribution $T \in \mathcal{S}^{\prime}$ if and only if
it is continuous on $\mathcal{D}$ with respect to the topology on
$\mathcal{S}$. Every function $f \in L_{\text {loc }}^{1}$ defines a
regular distribution $T_{f} \in \mathcal{D}^{\prime}$ by
$$
\left\langle T_{f}, \phi\right\rangle=\int f \phi d x \quad \text { for all } \phi \in \mathcal{D}.
$$
If $|f| \leq p$ is bounded by some polynomial $p,$ then $T_{f}$ extends
to a tempered distribution $T_{f} \in \mathcal{S}^{\prime}$, but this is
not the case for functions $f$ that grow too rapidly at infinity.
The Schwartz space is a natural one to use for the Fourier transform.
Differentiation and multiplication exchange roles under the Fourier
transform and therefore so do the properties of smoothness and rapid
decrease. As a result, the Fourier transform is an automorphism of the
Schwartz space. By duality, the Fourier transform is also an
automorphism of the space of tempered distributions.
````{prf:definition}
The Fourier transform of a function $f \in \mathcal{S}\left(\mathbb{R}^{n}\right)$
is the function $\hat{f}: \mathbb{R}^{n} \rightarrow \mathbb{C}$ defined
by
$$
\hat{f}(\omega)= \int f(x) e^{-2 \pi i\omega \cdot x} d x.
$$
The inverse Fourier transform of $f$ is the function
$\check{f}: \mathbb{R}^{n} \rightarrow \mathbb{C}$ defined by
$$
\check{f}(x)=\int f(\omega) e^{2 \pi i\omega \cdot x} d k.
$$
````
````{prf:definition}
The Fourier transform of a tempered distribution $f \in \mathcal{S}'$ is defined by
$$
\langle \hat{f}, \phi\rangle = \langle f, \hat \phi\rangle,\quad \forall \phi\in \mathcal{S}.
$$
````
The support of a continuous function $f$ is the closure of the set
$\{x\in \mathbb{R}: f(x)\neq 0\}$.
```{admonition} Properties
The Fourier transform has the following properties
1. If $f\in \mathcal{S}'$ and the support of $\hat f$ is $\{0\}$, then
$f$ is a polynomial.
2. If $f\in \mathcal{S}'$ and the support of $\hat f$ is a single point
$\{a\}$, then $f(x)=e^{2\pi iax}P(x)$, where $P(x)$ is a polynomial.
```
## 5.2.2 Poisson summation formula
``` {prf:theorem}
Let $f \in L^{1}(\mathbb{R})$ and $f$ is continuous. Then we have for
almost all $(x, \omega ) \in \mathbb{R} \times \hat{\mathbb{R}}$ that
$$
T \sum_{n \in \mathbb{Z}} f(x+n T) e^{-2 \pi i \omega (x+n T)}=\sum_{n \in \mathbb{Z}} \hat{f}\left(\omega +\frac{n}{T}\right) e^{2 \pi i n x / T}
$$
where both sides converge absolutely.
In addition, let $\Lambda$ be the lattice in $\mathbb{R}^{d}$ consisting
of points with integer coordinates. For a function $f$ in
$L^{1}\left(\mathbb{R}^{d}\right)$ and $f$ is continuous, we have
$$
\sum_{\omega \in \Lambda} f(x+\omega )=\sum_{\nu \in \Lambda} \hat{f}(\omega ) e^{2 \pi i x \cdot \omega }.
$$
where both series converge absolutely and uniformly on $\Lambda$.
```
```{prf;proof}
*Proof.* We just give a proof of a simple case that
$f: \mathbb{R} \rightarrow \mathbb{C}$ is a Schwarz function (see
Definition [\[def:schwarz\]](#def:schwarz){reference-type="ref"
reference="def:schwarz"}). Let: $$F(x)=\sum_{n \in \mathbb{Z}} f(x+n).$$
Then $F(x)$ is 1-periodic (because of absolute convergence), and has
Fourier coefficients: $$\begin{aligned}
\hat{F}_{\omega } &=\int_{0}^{1} \sum_{n \in \mathbb{Z}} f(x+n) e^{-2 \pi i \omega x} \mathrm{~d} x \\
&=\sum_{n \in \mathbb{Z}} \int_{0}^{1} f(x+n) e^{-2 \pi i \omega x} \mathrm{~d} x \quad \text { because } f \text { is Schwarz, so convergence is uniform}\\
&=\sum_{n \in \mathbb{Z}} \int_{n}^{n+1} f(x) e^{-2 \pi i\omega x} \mathrm{~d} x \\
&=\int_{\mathbb{R}} f(x) e^{-2 \pi i \omega x} \mathrm{~d} x\\
&=\hat{f}(k)\\
\end{aligned}$$ where $\hat{f}$ is the Fourier transform of $f$.
Therefore by the definition of the Fourier series of $f:$
$$
F(x) =\sum_{\omega \in \mathbb{Z}} \hat{f}(k) e^{2\pi i \omega x}.
$$
Choosing $x=0$ in this formula:
$$\sum_{n \in \mathbb{Z}} f(n)=\sum_{\omega \in \mathbb{Z}} \hat{f}(\omega )$$
as required. ◻
```
## 5.2.3 A special cut-off function
Let us first state the following simple result that can be obtained by
following a calculation given in Section 3 of [@johnson2015saddle].
```{prf:lemma}
Given $\alpha>1$, consider
$$
\label{alpha-g}
g(t) = \begin{cases}
e^{-(1-t^2)^{1 - \alpha}} & t\in (-1,1) \\
0 & \text{otherwise}.
\end{cases}
$$
then there is a constant $c_\alpha$ such that
$$
|\hat{g}(\omega )|\lesssim e^{-c_\alpha|\omega |^{1-\alpha^{-1}}},
$$
```
```{prf:proof}
*Proof.* Consider the asymptotic behavior of the Fourier transform
$$
F(\omega )=\int_{-\infty}^{\infty} g(t) e^{2\pi i \omega t} dt=2 \operatorname{Re} \int_{0}^{1} e^{2\pi i \omega t- (1-t^{2})^{1-\alpha}} dt
$$
for $|\operatorname{Re} \omega | \gg 1.$ (Without loss of generality, we
can restrict ourselves to real $\omega \geq 0$). With a change of
variable $x=1-t$,
$$
F(\omega )=2 \operatorname{Re} \int_{0}^{1} e^{f(x)} dx
$$
with $f(x)=2\pi i \omega - 2\pi i \omega x- (2x-x^2)^{1-\alpha}\approx \tilde f(x)+O\left(x^{2-\alpha}\right)$
and
$$
\tilde f(x) = 2\pi i \omega - 2\pi i \omega x - (2 x)^{1-\alpha}.
$$
The saddle point is the $x=x_0$ where $f'(x_0)=0$. Since
$\tilde f'(x)=-2\pi i \omega + (\alpha-1)2^{1-\alpha} x^{-\alpha},$
$$
x_{0} \approx \tilde x_0=\left (2^{-\alpha} (\alpha-1) / i \omega \pi \right )^{1 / \alpha} \sim \omega ^{-1 / \alpha}.
$$
Therefore $\tilde f(\tilde x_{0}) \sim \omega ^{(\alpha-1) / \alpha}$
asymptotically. The second derivative is
$$
\tilde f'' (\tilde x_{0} )=-2^{1-\alpha} \alpha(\alpha-1) \tilde x_{0}^{-\alpha-1}=-i^{(\alpha+1) / \alpha} 2 A \omega ^{(\alpha+1)/\alpha},
$$
where $$A=2\alpha (\alpha-1)^{-1/\alpha}\pi^{(\alpha+1)/\alpha}.$$ Now,
$$
\begin{split}
\tilde f(x)\approx &\tilde f(\tilde x_0) + {\tilde f''(\tilde x_0)\over 2} (x-\tilde x_0)^2
\\
=&2\pi i \omega - (\alpha - 1)^{1\over \alpha}(i\omega \pi )^{\alpha -1\over \alpha} - (\alpha - 1)^{1-\alpha\over \alpha} (i\omega \pi )^{\alpha -1\over \alpha}
\\
&-i^{(\alpha+1) / \alpha} A \omega ^{(\alpha+1)/\alpha}(x- 2^{-1}(\alpha - 1)^{-{1\over \alpha}}(i\omega \pi )^{-{1\over \alpha}} )^2.
\end{split}
$$
Choose a contour $x=i^{-1 / \alpha}u$, in which case
$$
\tilde f(x) \approx \tilde f(\tilde x_{0}) -i^{(\alpha-1) / \alpha} A \omega ^{(\alpha+1) / \alpha}\left(u-u_{0}\right)^{2},
$$
which is a path of descent so we can perform a Gaussian integral.
Recall that the integral of
$$
\label{gaussInt}
\int_{-\infty}^{\infty} e^{-a u^{2}} d u=\sqrt{\pi / a}
$$
as long as Re$a>0,$ which is true here. Note also that, in the limit as $\omega$
becomes large, the integrand becomes zero except close to
$u=\sqrt{1 / 2 \omega },$ so we can neglect the rest of the contour and
treat the integral over $u$ as going from $-\infty$ to $\infty$.
(Thankfully, the width of the Gaussian $\Delta u \sim \omega ^{-3 / 4}$
goes to zero faster than the location of the maximum
$u_{0} \sim \omega ^{-1 / 2},$ so we don't have to worry about the $u=0$
origin). Also note that the change of variables from $x$ to $u$ gives us
the Jacobian factor for $$dx=i^{-1 / \alpha}d u.$$ Thus, when all is
said and done, we obtain the exact asymptotic form of the Fourier
integral for $\omega \gg 1$:
$$
\begin{split}
F(\omega ) \approx &2 \operatorname{Re}\int_{0}^{1} e^{\tilde f(\tilde x_0) - i^{(\alpha-1) / \alpha} A \omega ^{(\alpha+1) / \alpha}\left(u-u_{0}\right)^{2}} dx
\\
=&2 \operatorname{Re} e^{\tilde f(\tilde x_0)} i^{-1 / \alpha} \int_{-\infty}^{\infty} e^{- i^{(\alpha-1) \over \alpha} A \omega ^{(\alpha+1) / \alpha}\left(u-u_{0}\right)^{2}} du
\\
=&2 \operatorname{Re} e^{\tilde f(\tilde x_0)} \pi^{1/2}i^{-1 / \alpha} i^{(1-\alpha) \over 2\alpha} A^{-1/2} \omega ^{-(\alpha+1) / 2\alpha}\qquad \text{ by \eqref{gaussInt}}
\\
=&2 \operatorname{Re}\left[\sqrt{\frac{\pi}{(i \omega )^{(\alpha+1) / \alpha} A}} e^{\tilde f(\tilde x_0)}\right]
\\
\approx &2 \operatorname{Re}\left[\sqrt{\frac{\pi}{(i \omega )^{(\alpha+1) / \alpha} A}} e^{ 2\pi i \omega - 2\pi i \omega \tilde x_{0}- \left[\left(2-\tilde x_{0}\right) \tilde x_{0}\right]^{1-\alpha}}\right]
\end{split}
$$
with $x_{0}$ and $A$ given above. Notice that
$\tilde x_0\sim \omega ^{-1 / \alpha}$. Thus,
$$
|F(\omega ) | \approx e^{-c_\alpha|\omega |^{1-\alpha^{-1}}}.
$$ ◻
```
## 5.2.4 Fourier transform of polynomials
We begin by noting that an activation function $\sigma$, which satisfies
a polynomial growth condition $|\sigma(x)| \leq C(1 + |x|)^n$ for some
constants $C$ and $n$, is a tempered distribution. As a result, we make
this assumption on our activation functions in the following theorems.
We briefly note that this condition is sufficient, but not necessary
(for instance an integrable function need not satisfy a pointwise
polynomial growth bound) for $\sigma$ to be represent a tempered
distribution.
We begin by studying the convolution of $\sigma$ with a Gaussian
mollifier. Let $\eta$ be a Gaussian mollifier
$$
\eta(x) = \frac{1}{\sqrt{\pi}}e^{-x^2}.
$$
Set
$\eta_\epsilon=\frac{1}{\epsilon}\eta(\frac{x}{\epsilon})$. Then
consider
$$
\sigma_{\epsilon}(x):=\sigma\ast{\eta_\epsilon}(x)=\int_{\mathbb{R}}\sigma(x-y){\eta_\epsilon}(y)dy
$$ (sigma-epsilon)
for a given activation function $\sigma$. It is clear that
$\sigma_{\epsilon}\in C^\infty(\mathbb{R})$. Moreover, by considering
the Fourier transform (as a tempered distribution) we see that
$$
\hat{\sigma}_{\epsilon} = \hat{\sigma}\hat{\eta}_{\epsilon} = \hat{\sigma}\eta_{\epsilon^{-1}}.
$$ (eq_278)
We begin by stating a lemma which characterizes the set of polynomials
in terms of their Fourier transform.
```{prf:lemma}
:label: polynomial_lemma
Given
a tempered distribution $\sigma$, the following statements are
equivalent:
1. $\sigma$ is a polynomial
2. $\sigma_\epsilon$ given by {eq}`sigma-epsilon` is a polynomial for any $\epsilon>0$.
3. $\text{supp}(\hat{\sigma})\subset \{0\}$.
```
```{prf:proof}
*Proof.* We begin by proving that (3) and (1) are equivalent. This
follows from a characterization of distributions supported at a single
point (see [@strichartz2003guide], section 6.3). In particular, a
distribution supported at $0$ must be a finite linear combination of
Dirac masses and their derivatives. In particular, if $\hat{\sigma}$ is
supported at $0$, then
$$
\hat{\sigma} = \displaystyle\sum_{i=1}^n a_i\delta^{(i)}.
$$
Taking the inverse Fourier transform and noting that the inverse Fourier transform
of $\delta^{(i)}$ is $c_ix^i$, we see that $\sigma$ is a polynomial.
This shows that (3) implies (1), for the converse we simply take the
Fourier transform of a polynomial and note that it is a finite linear
combination of Dirac masses and their derivatives.
Finally, we prove the equivalence of (2) and (3). For this it suffices
to show that $\hat{\sigma}$ is supported at $0$ iff
$\hat{\sigma}_\epsilon$ is supported at $0$. This follows from equation
{eq}`eq_278` and the
fact that $\eta_{\epsilon^{-1}}$ is nowhere vanishing. ◻
```
As an application of Lemma {prf:ref}`polynomial_lemma`, we give a simple proof of the result in
the next section.
| github_jupyter |
```
from sklearn.model_selection import train_test_split
import pandas as pd
import numpy as np
from sklearn.preprocessing import StandardScaler
from keras.utils import to_categorical
from keras.models import Sequential
from keras.layers import Dense
#df = pd.read_csv(".\\Data_USD.csv", header=None,skiprows=1)
df = pd.read_csv(".\\Data_USD.csv")
df.head().to_csv(".\\test.csv")
T=df.groupby("SEX")
T.describe()
df.tail()
# X = df.drop('Y_Value',axis =1).values
# y = df['Y_Value'].values
X = df.drop('DEFAULT_PAYMENT_NEXT_MO',axis =1).values
X[2999,0]
X.shape
y = df['DEFAULT_PAYMENT_NEXT_MO'].values
#y.reshape(-1,1)
#print(X.shape)
X.shape
#print(y.shape)
y.shape
X_train, X_test, y_train, y_test = train_test_split (X,y,test_size=0.2, random_state=42)
y_test.T
X_test.shape
from sklearn.preprocessing import StandardScaler
X_scaler = StandardScaler().fit(X_train)
X_scaler
X_train_scaled = X_scaler.transform(X_train)
X_test_scaled = X_scaler.transform(X_test)
X_train_scaled
y_train_categorical = to_categorical(y_train)
y_test_categorical = to_categorical(y_test)
from keras.models import Sequential
#instantiate
model = Sequential()
from keras.layers import Dense
number_inputs = 10
number_hidden = 30
model.add(Dense(units = number_hidden, activation ='relu', input_dim=number_inputs))
model.add(Dense(units = 35, activation ='relu')) #second hidden layer
model.add(Dense(units = 25, activation ='relu')) #second hidden layer
model.add(Dense(units = 15, activation ='relu')) #second hidden layer
model.add(Dense(units = 5, activation ='relu')) #third hidden layer
number_classes =2 ## yes or no
model.add(Dense(units = number_classes, activation = 'softmax'))
model.summary()
#compile the model
model.compile(optimizer = 'sgd' ,
loss = 'categorical_crossentropy',
metrics =['accuracy'])
#train the model
model.fit(X_train_scaled, y_train_categorical, epochs=100,shuffle = True,verbose =2)
model.save("ccneuralnetwork.h5")
#quantify the model
model_loss, model_accuracy = model.evaluate(X_test_scaled,y_test_categorical,verbose =2)
print( model_loss )
print (model_accuracy)
```
F1, Precision Recall, and Confusion Matrix
```
from sklearn.metrics import precision_recall_fscore_support
from sklearn.metrics import recall_score
from sklearn.metrics import classification_report
y_prediction = model.predict_classes(X_test)
y_prediction.reshape(-1,1)
print("Recall score:"+ str(recall_score(y_test, y_prediction)))
print(classification_report(y_test, y_prediction,
target_names=["default", "non_default"]))
import itertools
import matplotlib.pyplot as plt
from sklearn.metrics import confusion_matrix
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="red" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
# Compute confusion matrix
cnf_matrix = confusion_matrix(y_test, y_prediction)
np.set_printoptions(precision=2)
# Plot non-normalized confusion matrix
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=['Defualt', 'Non_default'],
title='Confusion matrix, without normalization')
# Plot normalized confusion matrix
plt.figure()
plot_confusion_matrix(cnf_matrix, classes=['Defualt', 'Non_default'], normalize=True,
title='Normalized confusion matrix')
plt.show()
```
| github_jupyter |
# Nonlinear recharge models
*R.A. Collenteur, University of Graz*
This notebook explains the use of the `RechargeModel` stress model to simulate the combined effect of precipitation and potential evaporation on the groundwater levels. For the computation of the groundwater recharge, three recharge models are currently available:
- `Linear` ([Berendrecht et al., 2003](#References); [von Asmuth et al., 2008](#References))
- `Berendrecht` ([Berendrecht et al., 2006](#References))
- `FlexModel` ([Collenteur et al., 2021](#References))
The first model is a simple linear function of precipitation and potential evaporation while the latter two are simulate a nonlinear response of recharge to precipitation using a soil-water balance concepts. Detailed descriptions of these models can be found in articles listed in the [References](#References) at the end of this notebook.
<div class="alert alert-info">
<b>Tip</b>
To run this notebook and the related non-linear recharge models, it is strongly recommended to install Numba (http://numba.pydata.org). This Just-In-Time (JIT) compiler compiles the computationally intensive part of the recharge calculation, making the non-linear model as fast as the Linear recharge model.
</div>
```
import pandas as pd
import pastas as ps
import matplotlib.pyplot as plt
ps.show_versions(numba=True)
ps.set_log_level("INFO")
```
## Read Input data
Input data handling is similar to other stressmodels. The only thing that is necessary to check is that the precipitation and evaporation are provided in mm/day. This is necessary because the parameters for the nonlinear recharge models are defined in mm for the length unit and days for the time unit. It is possible to use other units, but this would require manually setting the initial values and parameter boundaries for the recharge models.
```
head = pd.read_csv("../data/B32C0639001.csv", parse_dates=['date'],
index_col='date', squeeze=True)
# Make this millimeters per day
evap = ps.read_knmi("../data/etmgeg_260.txt", variables="EV24").series * 1e3
rain = ps.read_knmi("../data/etmgeg_260.txt", variables="RH").series * 1e3
fig, axes = plt.subplots(3,1, figsize=(10,6), sharex=True)
head.plot(ax=axes[0], x_compat=True, linestyle=" ", marker=".")
evap.plot(ax=axes[1], x_compat=True)
rain.plot(ax=axes[2], x_compat=True)
axes[0].set_ylabel("Head [m]")
axes[1].set_ylabel("Evap [mm/d]")
axes[2].set_ylabel("Rain [mm/d]")
plt.xlim("1985", "2005");
```
## Make a basic model
The normal workflow may be used to create and calibrate the model.
1. Create a Pastas `Model` instance
2. Choose a recharge model. All recharge models can be accessed through the recharge subpackage (`ps.rch`).
3. Create a `RechargeModel` object and add it to the model
4. Solve and visualize the model
```
ml = ps.Model(head)
# Select a recharge model
rch = ps.rch.FlexModel()
#rch = ps.rch.Berendrecht()
#rch = ps.rch.Linear()
rm = ps.RechargeModel(rain, evap, recharge=rch, rfunc=ps.Gamma, name="rch")
ml.add_stressmodel(rm)
ml.solve(noise=True, tmin="1990", report="basic")
ml.plots.results(figsize=(10,6));
```
## Analyze the estimated recharge flux
After the parameter estimation we can take a look at the recharge flux computed by the model. The flux is easy to obtain using the `get_stress` method of the model object, which automatically provides the optimal parameter values that were just estimated. After this, we can for example look at the yearly recharge flux estimated by the Pastas model.
```
recharge = ml.get_stress("rch").resample("A").sum()
ax = recharge.plot.bar(figsize=(10,3))
ax.set_xticklabels(recharge.index.year)
plt.ylabel("Recharge [mm/year]");
```
## A few things to keep in mind:
Below are a few things to keep in mind while using the (nonlinear) recharge models.
- The use of an appropriate warmup period is necessary, so make sure the precipitation and evaporation are available some time (e.g., one year) before the calibration period.
- Make sure that the units of the precipitation fluxes are in mm/day and that the DatetimeIndex matches exactly.
- It may be possible to fix or vary certain parameters, dependent on the problem. Obtaining better initial parameters may be possible by solving without a noise model first (`ml.solve(noise=False)`) and then solve it again using a noise model.
- For relatively shallow groundwater levels, it may be better to use the `Exponential` response function as the the non-linear models already cause a delayed response.
## References
- Berendrecht, W. L., Heemink, A. W., van Geer, F. C., and Gehrels, J. C. (2003) [Decoupling of modeling and measuring interval in groundwater time series analysis based on response characteristics](https://doi.org/10.1016/S0022-1694(03)00075-1), Journal of Hydrology, 278, 1–16.
- Berendrecht, W. L., Heemink, A. W., van Geer, F. C., and Gehrels, J. C. (2006) [A non-linear state space approach to model groundwater fluctuations](https://www.sciencedirect.com/science/article/abs/pii/S0309170805002113), Advances in Water Resources, 29, 959–973.
- Collenteur, R., Bakker, M., Klammler, G., and Birk, S. (2021) [Estimation of groundwater recharge from groundwater levels using nonlinear transfer function noise models and comparison to lysimeter data](https://doi.org/10.5194/hess-2020-392), Hydrol. Earth Syst. Sci., 25, 2931–2949.
- Von Asmuth, J.R., Maas, K., Bakker, M. and Petersen, J. (2008) [Modeling Time Series of Ground Water Head Fluctuations Subjected to Multiple Stresses](https://doi.org/10.1111/j.1745-6584.2007.00382.x). Groundwater, 46: 30-40.
## Data Sources
In this notebook we analysed a head time series near the town of De Bilt in the Netherlands. Data is obtained from the following resources:
- The heads (`B32C0639001.csv`) are downloaded from https://www.dinoloket.nl/
- The precipitation and potential evaporation (`etmgeg_260.txt`) are downloaded from https://knmi.nl
| github_jupyter |
# Place Stock Trades into Senator Dataframe
## 1. Understand the Senator Trading Report (STR) Dataframe
```
import pandas as pd
#https://docs.google.com/spreadsheets/d/1lH_LpTgRlfzKvpRnWYgoxlkWvJj0v1r3zN3CeWMAgqI/edit?usp=sharing
try:
sen_df = pd.read_csv("Senator Stock Trades/Senate Stock Watcher 04_16_2020 All Transactions.csv")
except:
sen_df = pd.read_csv("https://github.com/pkm29/big_data_final_project/raw/master/Senate%20Stock%20Trades/Senate%20Stock%20Watcher%2004_16_2020%20All%20Transactions.csv")
sen_df.head()
sen_df.type.unique()
```
There are 4 types of trades.
Exchanges: Exchange 1 stock for another
Sale (Full): Selling all of their stock
Purchase: Buying a stock
Sale (Partial): Selling some of that particular stock
```
n_exchanges = len(sen_df.loc[sen_df['type'] == "Exchange"])
n_trades = len(sen_df)
print("There are " +str(n_exchanges) +" exchange trades out of a total of " +str(n_trades)+ " trades.")
sen_df = sen_df.loc[sen_df['type'] != "Exchange"]
```
At this point in time, I will exclude exchange trades because they are so few and wish to build the basic structure of the project. As you can see, this would require splitting up the exchange into two rows with each company and so on. I may include this step later if time permits.
There should now be 8516 trades remaining in the dataframe. Let's make sure this is so.
```
n_trades = len(sen_df)
print("There are " +str(n_trades)+ " trades in the dataframe")
n_blank_ticker = len(sen_df.loc[sen_df['ticker'] == "--"])
print("There are " +str(n_blank_ticker) +" trades w/o a ticker out of a total of " +str(n_trades)+ " trades")
sen_df = sen_df.loc[sen_df['ticker'] != "--"]
```
For the same reasons we excluded exchange trades, we will also exclude trades without a ticker (which all public stocks have - the ticker is their identifier on the stock exchange). Eliminating trades without a ticker takes out trades of other types of securities (corporate bonds, municipal securities, non-public stock).
There should now be 6644 trades remaining in the dataframe. Let's make sure this is so.
```
n_trades = len(sen_df)
print("There are " +str(n_trades)+ " trades in the dataframe")
```
## 2. Add Data to STR Dataframe
### Import Data
In this step we will be using company information such as market cap and industry from online lists provided by the NYSE, NASDAQ, and ASXL exchange. Links can be found here:https://stackoverflow.com/questions/25338608/download-all-stock-symbol-list-of-a-market
```
ticker_list = list()
try:
NYSE_df = pd.read_csv("NYSEcompanylist.csv")
except:
NYSE_df = pd.read_csv("https://github.com/pkm29/big_data_final_project/raw/master/Stocks/NYSEcompanylist.csv")
try:
NASDAQ_df = pd.read_csv("NASDAQcompanylist.csv")
except:
NASDAQ_df = pd.read_csv("https://github.com/pkm29/big_data_final_project/raw/master/Stocks/NASDAQcompanylist.csv")
ticker_list.append(NYSE_df)
ticker_list.append(NASDAQ_df)
NYSE_df.head()
NASDAQ_df.head()
"""
Add data for Berkshire Hathaway, Lions Gate Entertainment, and Royal Dutch Shell to the NYSE company list. While
#these companies are in the company list, their fields are empty. Also, change the tickers of these companies to
#match Senate Stock Data (since dashes are used instead of periods in that dataset, we make sure the same is true
in the NYSE company list). What matters is consistent convention here.
"""
row_count = 0
replacement_count = 0
for row_tuple in NYSE_df.itertuples():
if replacement_count == 4:
break
if row_tuple.Symbol == "BRK.B":
#row_tuple.Symbol = "BRK-B"
NYSE_df.at[row_count, 'Symbol'] = "BRK-B"
#Shares outstanding reported in Q1 2020 financial reports, stock price from May 6, when this data is dated
#row_tuple.MarketCap = "$420.02B"
NYSE_df.at[row_count, 'MarketCap'] = "$420.02B"
#row_tuple.Sector = "Miscellaneous"
NYSE_df.at[row_count, 'Sector'] = "Miscellaneous"
#row_tuple.industry = "Conglomerate"
NYSE_df.at[row_count, 'industry'] = "Conglomerate"
replacement_count = replacement_count + 1
if row_tuple.Symbol == "LGF.B":
#row_tuple.Symbol = "LGF-B"
#Shares outstanding reported in Q1 2020 financial reports, stock price from May 6, when this data is dated
#row_tuple.MarketCap = "$14.62B"
#row_tuple.Sector = "Consumer Services"
#row_tuple.industry = "Movies/Entertainment"
NYSE_df.at[row_count, 'Symbol'] = "LGF-B"
NYSE_df.at[row_count, 'MarketCap'] = "$14.62B"
NYSE_df.at[row_count, 'Sector'] = "Consumer Services"
NYSE_df.at[row_count, 'industry'] = "Movies/Entertainment"
replacement_count = replacement_count + 1
if row_tuple.Symbol == "RDS.A":
#row_tuple.Symbol = "RDS-A"
#Shares outstanding reported in Q1 2020 financial reports, stock price from May 6, when this data is dated
#row_tuple.MarketCap = "$122.28B"
#row_tuple.Sector = "Energy"
#row_tuple.industry = "Oil & Gas Production"
NYSE_df.at[row_count, 'Symbol'] = "RDS-A"
NYSE_df.at[row_count, 'MarketCap'] = "$122.28B"
NYSE_df.at[row_count, 'Sector'] = "Energy"
NYSE_df.at[row_count, 'industry'] = "Oil & Gas Production"
replacement_count = replacement_count + 1
if row_tuple.Symbol == "RDS.B":
#row_tuple.Symbol = "RDS-B"
#Shares outstanding reported in Q1 2020 financial reports, stock price from May 6, when this data is dated
#row_tuple.MarketCap = "$122.09B"
#row_tuple.Sector = "Energy"
#row_tuple.industry = "Oil & Gas Production"
NYSE_df.at[row_count, 'Symbol'] = "RDS-B"
NYSE_df.at[row_count, 'MarketCap'] = "$122.09B"
NYSE_df.at[row_count, 'Sector'] = "Energy"
NYSE_df.at[row_count, 'industry'] = "Oil & Gas Production"
replacement_count = replacement_count + 1
row_count = row_count + 1
#Confirm changes have been made successfully
for row_tuple in NYSE_df.itertuples():
if row_tuple.Symbol == "BRK-B":
print (row_tuple)
if row_tuple.Symbol == "LGF-B":
print (row_tuple)
if row_tuple.Symbol == "RDS-A":
print (row_tuple)
if row_tuple.Symbol == "RDS-B":
print (row_tuple)
#There are also 2 instances where a wrong ticker for Berkshire Hathaway is found in the Senate Stock data
#(BRKB is used as opposed to BRK-B). Thus, we correct for those instances here.
#Find indices of these two trades
for row_tuple in sen_df.itertuples():
if row_tuple.ticker == "BRKB":
print (row_tuple)
#We can see that the indices are 1207 and 4611, so we will manually modify the ticker field of these trades.
sen_df.at[1207, 'ticker'] = "BRK-B"
sen_df.at[4611, 'ticker'] = "BRK-B"
len(sen_df)
#Get sector data for each stock trade
sector_data = list()
for row_tuple in sen_df.itertuples():
tic = row_tuple.ticker
count = 0
for row_tuple_tic in NYSE_df.itertuples():
sym = row_tuple_tic.Symbol
if tic == sym:
count = count+1
if row_tuple_tic.Sector == "n/a":
sector_data.append("none")
else:
sector_data.append(row_tuple_tic.Sector)
break
if count == 0:
for row_tuple_tic in NASDAQ_df.itertuples():
sym = row_tuple_tic.Symbol
if tic == sym:
count = count+1
if row_tuple_tic.Sector == "n/a":
sector_data.append("none")
else:
sector_data.append(row_tuple_tic.Sector)
break
if count == 0:
sector_data.append("none")
print(sector_data[0:9])
#make sure length matches number of rows in df
print(len(sector_data))
#counter for how many times the stock traded by senator not found in exchange data set
no_ticker_cnt = 0
for i in sector_data:
if i == "none":
no_ticker_cnt = no_ticker_cnt + 1
print(no_ticker_cnt)
#Get industry data for each stock trade
industry_data = list()
for row_tuple in sen_df.itertuples():
tic = row_tuple.ticker
count = 0
for row_tuple_tic in NYSE_df.itertuples():
sym = row_tuple_tic.Symbol
if tic == sym:
count = count+1
if row_tuple_tic.industry == "n/a":
industry_data.append("none")
else:
industry_data.append(row_tuple_tic.industry)
break
if count == 0:
for row_tuple_tic in NASDAQ_df.itertuples():
sym = row_tuple_tic.Symbol
if tic == sym:
count = count+1
if row_tuple_tic.industry == "n/a":
industry_data.append("none")
else:
industry_data.append(row_tuple_tic.industry)
break
if count == 0:
industry_data.append("none")
print(industry_data[0:9])
#make sure length matches number of rows in df
print(len(industry_data))
#counter for how many times the stock traded by senator not found in exchange data set
no_ticker_cnt = 0
for i in industry_data:
if i == "none":
no_ticker_cnt = no_ticker_cnt + 1
print(no_ticker_cnt)
#Get market cap data for each stock trade
mktcap_data = list()
for row_tuple in sen_df.itertuples():
tic = row_tuple.ticker
count = 0
for row_tuple_tic in NYSE_df.itertuples():
sym = row_tuple_tic.Symbol
if tic == sym:
count = count+1
if row_tuple_tic.MarketCap == "n/a":
mktcap_data.append("none")
else:
mktcap_data.append(row_tuple_tic.MarketCap)
break
if count == 0:
for row_tuple_tic in NASDAQ_df.itertuples():
sym = row_tuple_tic.Symbol
if tic == sym:
count = count+1
if row_tuple_tic.MarketCap == "n/a":
mktcap_data.append("none")
else:
mktcap_data.append(row_tuple_tic.MarketCap)
break
if count == 0:
mktcap_data.append("none")
print(mktcap_data[0:9])
#make sure length matches number of rows in df
print(len(mktcap_data))
#counter for how many times the stock traded by senator not found in exchange data set
no_ticker_cnt = 0
for i in mktcap_data:
if i == "none":
no_ticker_cnt = no_ticker_cnt + 1
print(no_ticker_cnt)
#add new columns to df
sen_df['mkt_cap'] = mktcap_data
sen_df['sector'] = sector_data
sen_df['industry'] = industry_data
sen_df = sen_df.fillna("none")
sen_df.head()
"""
Print out names of companies with missing data to find out why we have so many misses (~17% of our data).
There seem to be 3 reasons for this:
1. Companies merging with another or being acquired (or even acquiring and taking the acquired company's name - very rare)
2. Foreign companies (listed abroad)
3. American companies listed abroad - this applies to a very small number of trades
"""
from collections import Counter
company_missing_data = list()
for row_tuple in sen_df.itertuples():
if row_tuple.mkt_cap == "none":
company_missing_data.append(row_tuple.asset_description)
print(Counter(company_missing_data))
#Get a view of how many industries are found in our senate stock data.
industry_dict = Counter(industry_data)
industry_list = list()
for x in industry_dict:
industry_list.append(x)
print(industry_list[0:9])
n_industries = len(industry_list)
#since 'none' is included in our list
n_industries = n_industries - 1
print("There are " + str(n_industries) + " industries covered by the trades of senators.")
import string
industry_size_data = list()
for row_tuple in sen_df.itertuples():
industry_size = row_tuple.industry
if industry_size == 'none':
industry_size_data.append("none")
continue
size = row_tuple.mkt_cap
factor = 0
x = size.find("M")
if x != -1:
factor = 1000000
else:
factor = 1000000000
size = size.lstrip("$")
size = size.rstrip("MB")
size = float(size)
size = size*factor
if size < 500000000:
industry_size = industry_size + "1"
industry_size_data.append(industry_size)
continue
elif size < 1000000000:
industry_size = industry_size + "2"
industry_size_data.append(industry_size)
continue
elif size < 10000000000:
industry_size = industry_size + "3"
industry_size_data.append(industry_size)
continue
elif size < 50000000000:
industry_size = industry_size + "4"
industry_size_data.append(industry_size)
continue
elif size < 100000000000:
industry_size = industry_size + "5"
industry_size_data.append(industry_size)
continue
elif size < 500000000000:
industry_size = industry_size + "6"
industry_size_data.append(industry_size)
continue
else:
industry_size = industry_size + "7"
industry_size_data.append(industry_size)
continue
print(industry_size_data[0:9])
print(len(industry_size_data))
#add the new column to df
sen_df['classification'] = industry_size_data
sen_df.head()
#create a list of all the classifications per industry across whole dataframe, to get a view of the breakdown in
#classifications across each industry
classification_industry_breakdown = list()
for x in industry_list:
y = list()
for row_tuple in sen_df.itertuples():
if row_tuple.industry == x:
y.append(row_tuple.classification)
classification_industry_breakdown.append(y)
print(classification_industry_breakdown[0:9])
```
| github_jupyter |
# Collaborative filtering on Google Analytics data
This notebook demonstrates how to implement a WALS matrix refactorization approach to do collaborative filtering.
```
import os
PROJECT = "qwiklabs-gcp-00-34ffb0f0dc65" # REPLACE WITH YOUR PROJECT ID
BUCKET = "cloud-training-demos-ml" # REPLACE WITH YOUR BUCKET NAME
REGION = "us-central1" # REPLACE WITH YOUR BUCKET REGION e.g. us-central1
# Do not change these
os.environ["PROJECT"] = PROJECT
os.environ["BUCKET"] = BUCKET
os.environ["REGION"] = REGION
os.environ["TFVERSION"] = "1.13"
%%bash
gcloud config set project $PROJECT
gcloud config set compute/region $REGION
import tensorflow as tf
print(tf.__version__)
```
## Create raw dataset
<p>
For collaborative filtering, we don't need to know anything about either the users or the content. Essentially, all we need to know is userId, itemId, and rating that the particular user gave the particular item.
<p>
In this case, we are working with newspaper articles. The company doesn't ask their users to rate the articles. However, we can use the time-spent on the page as a proxy for rating.
<p>
Normally, we would also add a time filter to this ("latest 7 days"), but our dataset is itself limited to a few days.
```
from google.cloud import bigquery
bq = bigquery.Client(project = PROJECT)
sql = """
#standardSQL
WITH CTE_visitor_page_content AS (
SELECT
fullVisitorID,
(SELECT MAX(IF(index=10, value, NULL)) FROM UNNEST(hits.customDimensions)) AS latestContentId,
(LEAD(hits.time, 1) OVER (PARTITION BY fullVisitorId ORDER BY hits.time ASC) - hits.time) AS session_duration
FROM
`cloud-training-demos.GA360_test.ga_sessions_sample`,
UNNEST(hits) AS hits
WHERE
# only include hits on pages
hits.type = "PAGE"
GROUP BY
fullVisitorId,
latestContentId,
hits.time )
-- Aggregate web stats
SELECT
fullVisitorID as visitorId,
latestContentId as contentId,
SUM(session_duration) AS session_duration
FROM
CTE_visitor_page_content
WHERE
latestContentId IS NOT NULL
GROUP BY
fullVisitorID,
latestContentId
HAVING
session_duration > 0
ORDER BY
latestContentId
"""
df = bq.query(sql).to_dataframe()
df.head()
stats = df.describe()
stats
df[["session_duration"]].plot(kind="hist", logy=True, bins=100, figsize=[8,5])
# The rating is the session_duration scaled to be in the range 0-1. This will help with training.
median = stats.loc["50%", "session_duration"]
df["rating"] = 0.3 * df["session_duration"] / median
df.loc[df["rating"] > 1, "rating"] = 1
df[["rating"]].plot(kind="hist", logy=True, bins=100, figsize=[8,5])
del df["session_duration"]
%%bash
rm -rf data
mkdir data
df.to_csv(path_or_buf = "data/collab_raw.csv", index = False, header = False)
!head data/collab_raw.csv
```
## Create dataset for WALS
<p>
The raw dataset (above) won't work for WALS:
<ol>
<li> The userId and itemId have to be 0,1,2 ... so we need to create a mapping from visitorId (in the raw data) to userId and contentId (in the raw data) to itemId.
<li> We will need to save the above mapping to a file because at prediction time, we'll need to know how to map the contentId in the table above to the itemId.
<li> We'll need two files: a "rows" dataset where all the items for a particular user are listed; and a "columns" dataset where all the users for a particular item are listed.
</ol>
<p>
### Mapping
```
import pandas as pd
import numpy as np
def create_mapping(values, filename):
with open(filename, 'w') as ofp:
value_to_id = {value:idx for idx, value in enumerate(values.unique())}
for value, idx in value_to_id.items():
ofp.write("{},{}\n".format(value, idx))
return value_to_id
df = pd.read_csv(filepath_or_buffer = "data/collab_raw.csv",
header = None,
names = ["visitorId", "contentId", "rating"],
dtype = {"visitorId": str, "contentId": str, "rating": np.float})
df.to_csv(path_or_buf = "data/collab_raw.csv", index = False, header = False)
user_mapping = create_mapping(df["visitorId"], "data/users.csv")
item_mapping = create_mapping(df["contentId"], "data/items.csv")
!head -3 data/*.csv
df["userId"] = df["visitorId"].map(user_mapping.get)
df["itemId"] = df["contentId"].map(item_mapping.get)
mapped_df = df[["userId", "itemId", "rating"]]
mapped_df.to_csv(path_or_buf = "data/collab_mapped.csv", index = False, header = False)
mapped_df.head()
```
### Creating rows and columns datasets
```
import pandas as pd
import numpy as np
mapped_df = pd.read_csv(filepath_or_buffer = "data/collab_mapped.csv", header = None, names = ["userId", "itemId", "rating"])
mapped_df.head()
NITEMS = np.max(mapped_df["itemId"]) + 1
NUSERS = np.max(mapped_df["userId"]) + 1
mapped_df["rating"] = np.round(mapped_df["rating"].values, 2)
print("{} items, {} users, {} interactions".format( NITEMS, NUSERS, len(mapped_df) ))
grouped_by_items = mapped_df.groupby("itemId")
iter = 0
for item, grouped in grouped_by_items:
print(item, grouped["userId"].values, grouped["rating"].values)
iter = iter + 1
if iter > 5:
break
import tensorflow as tf
grouped_by_items = mapped_df.groupby("itemId")
with tf.python_io.TFRecordWriter("data/users_for_item") as ofp:
for item, grouped in grouped_by_items:
example = tf.train.Example(features = tf.train.Features(feature = {
"key": tf.train.Feature(int64_list = tf.train.Int64List(value = [item])),
"indices": tf.train.Feature(int64_list = tf.train.Int64List(value = grouped["userId"].values)),
"values": tf.train.Feature(float_list = tf.train.FloatList(value = grouped["rating"].values))
}))
ofp.write(example.SerializeToString())
grouped_by_users = mapped_df.groupby("userId")
with tf.python_io.TFRecordWriter("data/items_for_user") as ofp:
for user, grouped in grouped_by_users:
example = tf.train.Example(features = tf.train.Features(feature = {
"key": tf.train.Feature(int64_list = tf.train.Int64List(value = [user])),
"indices": tf.train.Feature(int64_list = tf.train.Int64List(value = grouped["itemId"].values)),
"values": tf.train.Feature(float_list = tf.train.FloatList(value = grouped["rating"].values))
}))
ofp.write(example.SerializeToString())
!ls -lrt data
```
To summarize, we created the following data files from collab_raw.csv:
<ol>
<li> ```collab_mapped.csv``` is essentially the same data as in ```collab_raw.csv``` except that ```visitorId``` and ```contentId``` which are business-specific have been mapped to ```userId``` and ```itemId``` which are enumerated in 0,1,2,.... The mappings themselves are stored in ```items.csv``` and ```users.csv``` so that they can be used during inference.
<li> ```users_for_item``` contains all the users/ratings for each item in TFExample format
<li> ```items_for_user``` contains all the items/ratings for each user in TFExample format
</ol>
## Train with WALS
Once you have the dataset, do matrix factorization with WALS using the [WALSMatrixFactorization](https://www.tensorflow.org/versions/master/api_docs/python/tf/contrib/factorization/WALSMatrixFactorization) in the contrib directory.
This is an estimator model, so it should be relatively familiar.
<p>
As usual, we write an input_fn to provide the data to the model, and then create the Estimator to do train_and_evaluate.
Because it is in contrib and hasn't moved over to tf.estimator yet, we use tf.contrib.learn.Experiment to handle the training loop.
```
import os
import tensorflow as tf
from tensorflow.python.lib.io import file_io
from tensorflow.contrib.factorization import WALSMatrixFactorization
def read_dataset(mode, args):
def decode_example(protos, vocab_size):
features = {
"key": tf.FixedLenFeature(shape = [1], dtype = tf.int64),
"indices": tf.VarLenFeature(dtype = tf.int64),
"values": tf.VarLenFeature(dtype = tf.float32)}
parsed_features = tf.parse_single_example(serialized = protos, features = features)
values = tf.sparse_merge(sp_ids = parsed_features["indices"], sp_values = parsed_features["values"], vocab_size = vocab_size)
# Save key to remap after batching
# This is a temporary workaround to assign correct row numbers in each batch.
# You can ignore details of this part and remap_keys().
key = parsed_features["key"]
decoded_sparse_tensor = tf.SparseTensor(indices = tf.concat(values = [values.indices, [key]], axis = 0),
values = tf.concat(values = [values.values, [0.0]], axis = 0),
dense_shape = values.dense_shape)
return decoded_sparse_tensor
def remap_keys(sparse_tensor):
# Current indices of our SparseTensor that we need to fix
bad_indices = sparse_tensor.indices # shape = (current_batch_size * (number_of_items/users[i] + 1), 2)
# Current values of our SparseTensor that we need to fix
bad_values = sparse_tensor.values # shape = (current_batch_size * (number_of_items/users[i] + 1),)
# Since batch is ordered, the last value for a batch index is the user
# Find where the batch index chages to extract the user rows
# 1 where user, else 0
user_mask = tf.concat(values = [bad_indices[1:,0] - bad_indices[:-1,0], tf.constant(value = [1], dtype = tf.int64)], axis = 0) # shape = (current_batch_size * (number_of_items/users[i] + 1), 2)
# Mask out the user rows from the values
good_values = tf.boolean_mask(tensor = bad_values, mask = tf.equal(x = user_mask, y = 0)) # shape = (current_batch_size * number_of_items/users[i],)
item_indices = tf.boolean_mask(tensor = bad_indices, mask = tf.equal(x = user_mask, y = 0)) # shape = (current_batch_size * number_of_items/users[i],)
user_indices = tf.boolean_mask(tensor = bad_indices, mask = tf.equal(x = user_mask, y = 1))[:, 1] # shape = (current_batch_size,)
good_user_indices = tf.gather(params = user_indices, indices = item_indices[:,0]) # shape = (current_batch_size * number_of_items/users[i],)
# User and item indices are rank 1, need to make rank 1 to concat
good_user_indices_expanded = tf.expand_dims(input = good_user_indices, axis = -1) # shape = (current_batch_size * number_of_items/users[i], 1)
good_item_indices_expanded = tf.expand_dims(input = item_indices[:, 1], axis = -1) # shape = (current_batch_size * number_of_items/users[i], 1)
good_indices = tf.concat(values = [good_user_indices_expanded, good_item_indices_expanded], axis = 1) # shape = (current_batch_size * number_of_items/users[i], 2)
remapped_sparse_tensor = tf.SparseTensor(indices = good_indices, values = good_values, dense_shape = sparse_tensor.dense_shape)
return remapped_sparse_tensor
def parse_tfrecords(filename, vocab_size):
if mode == tf.estimator.ModeKeys.TRAIN:
num_epochs = None # indefinitely
else:
num_epochs = 1 # end-of-input after this
files = tf.gfile.Glob(filename = os.path.join(args["input_path"], filename))
# Create dataset from file list
dataset = tf.data.TFRecordDataset(files)
dataset = dataset.map(map_func = lambda x: decode_example(x, vocab_size))
dataset = dataset.repeat(count = num_epochs)
dataset = dataset.batch(batch_size = args["batch_size"])
dataset = dataset.map(map_func = lambda x: remap_keys(x))
return dataset.make_one_shot_iterator().get_next()
def _input_fn():
features = {
WALSMatrixFactorization.INPUT_ROWS: parse_tfrecords("items_for_user", args["nitems"]),
WALSMatrixFactorization.INPUT_COLS: parse_tfrecords("users_for_item", args["nusers"]),
WALSMatrixFactorization.PROJECT_ROW: tf.constant(True)
}
return features, None
return _input_fn
```
This code is helpful in developing the input function. You don't need it in production.
```
def try_out():
with tf.Session() as sess:
fn = read_dataset(
mode = tf.estimator.ModeKeys.EVAL,
args = {"input_path": "data", "batch_size": 4, "nitems": NITEMS, "nusers": NUSERS})
feats, _ = fn()
print(feats["input_rows"].eval())
print(feats["input_rows"].eval())
try_out()
def find_top_k(user, item_factors, k):
all_items = tf.matmul(a = tf.expand_dims(input = user, axis = 0), b = tf.transpose(a = item_factors))
topk = tf.nn.top_k(input = all_items, k = k)
return tf.cast(x = topk.indices, dtype = tf.int64)
def batch_predict(args):
import numpy as np
with tf.Session() as sess:
estimator = tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"])
# This is how you would get the row factors for out-of-vocab user data
# row_factors = list(estimator.get_projections(input_fn=read_dataset(tf.estimator.ModeKeys.EVAL, args)))
# user_factors = tf.convert_to_tensor(np.array(row_factors))
# But for in-vocab data, the row factors are already in the checkpoint
user_factors = tf.convert_to_tensor(value = estimator.get_row_factors()[0]) # (nusers, nembeds)
# In either case, we have to assume catalog doesn"t change, so col_factors are read in
item_factors = tf.convert_to_tensor(value = estimator.get_col_factors()[0])# (nitems, nembeds)
# For each user, find the top K items
topk = tf.squeeze(input = tf.map_fn(fn = lambda user: find_top_k(user, item_factors, args["topk"]), elems = user_factors, dtype = tf.int64))
with file_io.FileIO(os.path.join(args["output_dir"], "batch_pred.txt"), mode = 'w') as f:
for best_items_for_user in topk.eval():
f.write(",".join(str(x) for x in best_items_for_user) + '\n')
def train_and_evaluate(args):
train_steps = int(0.5 + (1.0 * args["num_epochs"] * args["nusers"]) / args["batch_size"])
steps_in_epoch = int(0.5 + args["nusers"] / args["batch_size"])
print("Will train for {} steps, evaluating once every {} steps".format(train_steps, steps_in_epoch))
def experiment_fn(output_dir):
return tf.contrib.learn.Experiment(
tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"]),
train_input_fn = read_dataset(tf.estimator.ModeKeys.TRAIN, args),
eval_input_fn = read_dataset(tf.estimator.ModeKeys.EVAL, args),
train_steps = train_steps,
eval_steps = 1,
min_eval_frequency = steps_in_epoch
)
from tensorflow.contrib.learn.python.learn import learn_runner
learn_runner.run(experiment_fn = experiment_fn, output_dir = args["output_dir"])
batch_predict(args)
import shutil
shutil.rmtree(path = "wals_trained", ignore_errors=True)
train_and_evaluate({
"output_dir": "wals_trained",
"input_path": "data/",
"num_epochs": 0.05,
"nitems": NITEMS,
"nusers": NUSERS,
"batch_size": 512,
"n_embeds": 10,
"topk": 3
})
!ls wals_trained
!head wals_trained/batch_pred.txt
```
## Run as a Python module
Let's run it as Python module for just a few steps.
```
os.environ["NITEMS"] = str(NITEMS)
os.environ["NUSERS"] = str(NUSERS)
%%bash
rm -rf wals.tar.gz wals_trained
gcloud ml-engine local train \
--module-name=walsmodel.task \
--package-path=${PWD}/walsmodel \
-- \
--output_dir=${PWD}/wals_trained \
--input_path=${PWD}/data \
--num_epochs=0.01 --nitems=${NITEMS} --nusers=${NUSERS} \
--job-dir=./tmp
```
## Run on Cloud
```
%%bash
gsutil -m cp data/* gs://${BUCKET}/wals/data
%%bash
OUTDIR=gs://${BUCKET}/wals/model_trained
JOBNAME=wals_$(date -u +%y%m%d_%H%M%S)
echo $OUTDIR $REGION $JOBNAME
gsutil -m rm -rf $OUTDIR
gcloud ml-engine jobs submit training $JOBNAME \
--region=$REGION \
--module-name=walsmodel.task \
--package-path=${PWD}/walsmodel \
--job-dir=$OUTDIR \
--staging-bucket=gs://$BUCKET \
--scale-tier=BASIC_GPU \
--runtime-version=$TFVERSION \
-- \
--output_dir=$OUTDIR \
--input_path=gs://${BUCKET}/wals/data \
--num_epochs=10 --nitems=${NITEMS} --nusers=${NUSERS}
```
This took <b>10 minutes</b> for me.
## Get row and column factors
Once you have a trained WALS model, you can get row and column factors (user and item embeddings) from the checkpoint file. We'll look at how to use these in the section on building a recommendation system using deep neural networks.
```
def get_factors(args):
with tf.Session() as sess:
estimator = tf.contrib.factorization.WALSMatrixFactorization(
num_rows = args["nusers"],
num_cols = args["nitems"],
embedding_dimension = args["n_embeds"],
model_dir = args["output_dir"])
row_factors = estimator.get_row_factors()[0]
col_factors = estimator.get_col_factors()[0]
return row_factors, col_factors
args = {
"output_dir": "gs://{}/wals/model_trained".format(BUCKET),
"nitems": NITEMS,
"nusers": NUSERS,
"n_embeds": 10
}
user_embeddings, item_embeddings = get_factors(args)
print(user_embeddings[:3])
print(item_embeddings[:3])
```
You can visualize the embedding vectors using dimensional reduction techniques such as PCA.
```
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from sklearn.decomposition import PCA
pca = PCA(n_components = 3)
pca.fit(user_embeddings)
user_embeddings_pca = pca.transform(user_embeddings)
fig = plt.figure(figsize = (8,8))
ax = fig.add_subplot(111, projection = "3d")
xs, ys, zs = user_embeddings_pca[::150].T
ax.scatter(xs, ys, zs)
```
<pre>
# Copyright 2018 Google Inc. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# http://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
</pre>
| github_jupyter |
<script async src="https://www.googletagmanager.com/gtag/js?id=UA-59152712-8"></script>
<script>
window.dataLayer = window.dataLayer || [];
function gtag(){dataLayer.push(arguments);}
gtag('js', new Date());
gtag('config', 'UA-59152712-8');
</script>
# Computing the 4-Velocity Time-Component $u^0$, the Magnetic Field Measured by a Comoving Observer $b^{\mu}$, and the Poynting Vector $S^i$
## Authors: Zach Etienne & Patrick Nelson
[comment]: <> (Abstract: TODO)
**Notebook Status:** <font color='green'><b> Validated </b></font>
**Validation Notes:** This module has been validated against a trusted code (the hand-written smallbPoynET in WVUThorns_diagnostics, which itself is based on expressions in IllinoisGRMHD... which was validated against the original GRMHD code of the Illinois NR group)
### NRPy+ Source Code for this module: [u0_smallb_Poynting__Cartesian.py](../edit/u0_smallb_Poynting__Cartesian/u0_smallb_Poynting__Cartesian.py)
[comment]: <> (Introduction: TODO)
<a id='toc'></a>
# Table of Contents
$$\label{toc}$$
This notebook is organized as follows
1. [Step 1](#u0bu): Computing $u^0$ and $b^{\mu}$
1. [Step 1.a](#4metric): Compute the 4-metric $g_{\mu\nu}$ and its inverse $g^{\mu\nu}$ from the ADM 3+1 variables, using the [`BSSN.ADMBSSN_tofrom_4metric`](../edit/BSSN/ADMBSSN_tofrom_4metric.py) ([**tutorial**](Tutorial-ADMBSSN_tofrom_4metric.ipynb)) NRPy+ module
1. [Step 1.b](#u0): Compute $u^0$ from the Valencia 3-velocity
1. [Step 1.c](#uj): Compute $u_j$ from $u^0$, the Valencia 3-velocity, and $g_{\mu\nu}$
1. [Step 1.d](#gamma): Compute $\gamma=$ `gammaDET` from the ADM 3+1 variables
1. [Step 1.e](#beta): Compute $b^\mu$
1. [Step 2](#poynting_flux): Defining the Poynting Flux Vector $S^{i}$
1. [Step 2.a](#g): Computing $g^{i\nu}$
1. [Step 2.b](#s): Computing $S^{i}$
1. [Step 3](#code_validation): Code Validation against `u0_smallb_Poynting__Cartesian` NRPy+ module
1. [Step 4](#appendix): Appendix: Proving Eqs. 53 and 56 in [Duez *et al* (2005)](https://arxiv.org/pdf/astro-ph/0503420.pdf)
1. [Step 5](#latex_pdf_output): Output this notebook to $\LaTeX$-formatted PDF file
<a id='u0bu'></a>
# Step 1: Computing $u^0$ and $b^{\mu}$ \[Back to [top](#toc)\]
$$\label{u0bu}$$
First some definitions. The spatial components of $b^{\mu}$ are simply the magnetic field as measured by an observer comoving with the plasma $B^{\mu}_{\rm (u)}$, divided by $\sqrt{4\pi}$. In addition, in the ideal MHD limit, $B^{\mu}_{\rm (u)}$ is orthogonal to the plasma 4-velocity $u^\mu$, which sets the $\mu=0$ component.
Note also that $B^{\mu}_{\rm (u)}$ is related to the magnetic field as measured by a *normal* observer $B^i$ via a simple projection (Eq 21 in [Duez *et al* (2005)](https://arxiv.org/pdf/astro-ph/0503420.pdf)), which results in the expressions (Eqs 23 and 24 in [Duez *et al* (2005)](https://arxiv.org/pdf/astro-ph/0503420.pdf)):
\begin{align}
\sqrt{4\pi} b^0 = B^0_{\rm (u)} &= \frac{u_j B^j}{\alpha} \\
\sqrt{4\pi} b^i = B^i_{\rm (u)} &= \frac{B^i + (u_j B^j) u^i}{\alpha u^0}\\
\end{align}
$B^i$ is related to the actual magnetic field evaluated in IllinoisGRMHD, $\tilde{B}^i$ via
$$B^i = \frac{\tilde{B}^i}{\gamma},$$
where $\gamma$ is the determinant of the spatial 3-metric.
The above expressions will require that we compute
1. the 4-metric $g_{\mu\nu}$ from the ADM 3+1 variables
1. $u^0$ from the Valencia 3-velocity
1. $u_j$ from $u^0$, the Valencia 3-velocity, and $g_{\mu\nu}$
1. $\gamma$ from the ADM 3+1 variables
<a id='4metric'></a>
## Step 1.a: Compute the 4-metric $g_{\mu\nu}$ and its inverse $g^{\mu\nu}$ from the ADM 3+1 variables, using the [`BSSN.ADMBSSN_tofrom_4metric`](../edit/BSSN/ADMBSSN_tofrom_4metric.py) ([**tutorial**](Tutorial-ADMBSSN_tofrom_4metric.ipynb)) NRPy+ module \[Back to [top](#toc)\]
$$\label{4metric}$$
We are given $\gamma_{ij}$, $\alpha$, and $\beta^i$ from ADMBase, so let's first compute
$$
g_{\mu\nu} = \begin{pmatrix}
-\alpha^2 + \beta^k \beta_k & \beta_i \\
\beta_j & \gamma_{ij}
\end{pmatrix}.
$$
```
# Step 1: Initialize needed Python/NRPy+ modules
import sympy as sp # SymPy: The Python computer algebra package upon which NRPy+ depends
import NRPy_param_funcs as par # NRPy+: Parameter interface
import indexedexp as ixp # NRPy+: Symbolic indexed expression (e.g., tensors, vectors, etc.) support
import reference_metric as rfm # NRPy+: Reference metric support
from outputC import * # NRPy+: Basic C code output functionality
import BSSN.ADMBSSN_tofrom_4metric as AB4m # NRPy+: ADM/BSSN <-> 4-metric conversions
# Set spatial dimension = 3
DIM=3
thismodule = "smallbPoynET"
# Step 1.a: Compute the 4-metric $g_{\mu\nu}$ and its inverse
# $g^{\mu\nu}$ from the ADM 3+1 variables, using the
# BSSN.ADMBSSN_tofrom_4metric NRPy+ module
import BSSN.ADMBSSN_tofrom_4metric as AB4m
gammaDD,betaU,alpha = AB4m.setup_ADM_quantities("ADM")
AB4m.g4DD_ito_BSSN_or_ADM("ADM",gammaDD,betaU,alpha)
g4DD = AB4m.g4DD
AB4m.g4UU_ito_BSSN_or_ADM("ADM",gammaDD,betaU,alpha)
g4UU = AB4m.g4UU
```
<a id='u0'></a>
## Step 1.b: Compute $u^0$ from the Valencia 3-velocity \[Back to [top](#toc)\]
$$\label{u0}$$
According to Eqs. 9-11 of [the IllinoisGRMHD paper](https://arxiv.org/pdf/1501.07276.pdf), the Valencia 3-velocity $v^i_{(n)}$ is related to the 4-velocity $u^\mu$ via
\begin{align}
\alpha v^i_{(n)} &= \frac{u^i}{u^0} + \beta^i \\
\implies u^i &= u^0 \left(\alpha v^i_{(n)} - \beta^i\right)
\end{align}
Defining $v^i = \frac{u^i}{u^0}$, we get
$$v^i = \alpha v^i_{(n)} - \beta^i,$$
and in terms of this variable we get
\begin{align}
g_{00} \left(u^0\right)^2 + 2 g_{0i} u^0 u^i + g_{ij} u^i u^j &= \left(u^0\right)^2 \left(g_{00} + 2 g_{0i} v^i + g_{ij} v^i v^j\right)\\
\implies u^0 &= \pm \sqrt{\frac{-1}{g_{00} + 2 g_{0i} v^i + g_{ij} v^i v^j}} \\
&= \pm \sqrt{\frac{-1}{(-\alpha^2 + \beta^2) + 2 \beta_i v^i + \gamma_{ij} v^i v^j}} \\
&= \pm \sqrt{\frac{1}{\alpha^2 - \gamma_{ij}\left(\beta^i + v^i\right)\left(\beta^j + v^j\right)}}\\
&= \pm \sqrt{\frac{1}{\alpha^2 - \alpha^2 \gamma_{ij}v^i_{(n)}v^j_{(n)}}}\\
&= \pm \frac{1}{\alpha}\sqrt{\frac{1}{1 - \gamma_{ij}v^i_{(n)}v^j_{(n)}}}
\end{align}
Generally speaking, numerical errors will occasionally drive expressions under the radical to either negative values or potentially enormous values (corresponding to enormous Lorentz factors). Thus a reliable approach for computing $u^0$ requires that we first rewrite the above expression in terms of the Lorentz factor squared: $\Gamma^2=\left(\alpha u^0\right)^2$:
\begin{align}
u^0 &= \pm \frac{1}{\alpha}\sqrt{\frac{1}{1 - \gamma_{ij}v^i_{(n)}v^j_{(n)}}}\\
\implies \left(\alpha u^0\right)^2 &= \frac{1}{1 - \gamma_{ij}v^i_{(n)}v^j_{(n)}} \\
\implies \gamma_{ij}v^i_{(n)}v^j_{(n)} &= 1 - \frac{1}{\left(\alpha u^0\right)^2} \\
&= 1 - \frac{1}{\Gamma^2}
\end{align}
In order for the bottom expression to hold true, the left-hand side must be between 0 and 1. Again, this is not guaranteed due to the appearance of numerical errors. In fact, a robust algorithm will not allow $\Gamma^2$ to become too large (which might contribute greatly to the stress-energy of a given gridpoint), so let's define $\Gamma_{\rm max}$, the largest allowed Lorentz factor.
Then our algorithm for computing $u^0$ is as follows:
If
$$R=\gamma_{ij}v^i_{(n)}v^j_{(n)}>1 - \frac{1}{\Gamma_{\rm max}^2},$$
then adjust the 3-velocity $v^i$ as follows:
$$v^i_{(n)} = \sqrt{\frac{1 - \frac{1}{\Gamma_{\rm max}^2}}{R}}v^i_{(n)}.$$
After this rescaling, we are then guaranteed that if $R$ is recomputed, it will be set to its ceiling value $R=R_{\rm max} = 1 - \frac{1}{\Gamma_{\rm max}^2}$.
Then, regardless of whether the ceiling on $R$ was applied, $u^0$ can be safely computed via
$$
u^0 = \frac{1}{\alpha \sqrt{1-R}}.
$$
```
ValenciavU = ixp.register_gridfunctions_for_single_rank1("AUX","ValenciavU",DIM=3)
# Step 1: Compute R = 1 - 1/max(Gamma)
R = sp.sympify(0)
for i in range(DIM):
for j in range(DIM):
R += gammaDD[i][j]*ValenciavU[i]*ValenciavU[j]
GAMMA_SPEED_LIMIT = par.Cparameters("REAL",thismodule,"GAMMA_SPEED_LIMIT",10.0) # Default value based on
# IllinoisGRMHD.
# GiRaFFE default = 2000.0
Rmax = 1 - 1/(GAMMA_SPEED_LIMIT*GAMMA_SPEED_LIMIT)
rescaledValenciavU = ixp.zerorank1()
for i in range(DIM):
rescaledValenciavU[i] = ValenciavU[i]*sp.sqrt(Rmax/R)
rescaledu0 = 1/(alpha*sp.sqrt(1-Rmax))
regularu0 = 1/(alpha*sp.sqrt(1-R))
computeu0_Cfunction = """
/* Function for computing u^0 from Valencia 3-velocity. */
/* Inputs: ValenciavU[], alpha, gammaDD[][], GAMMA_SPEED_LIMIT (C parameter) */
/* Output: u0=u^0 and velocity-limited ValenciavU[] */\n\n"""
computeu0_Cfunction += outputC([R,Rmax],["const double R","const double Rmax"],"returnstring",
params="includebraces=False,CSE_varprefix=tmpR,outCverbose=False")
computeu0_Cfunction += "if(R <= Rmax) "
computeu0_Cfunction += outputC(regularu0,"u0","returnstring",
params="includebraces=True,CSE_varprefix=tmpnorescale,outCverbose=False")
computeu0_Cfunction += " else "
computeu0_Cfunction += outputC([rescaledValenciavU[0],rescaledValenciavU[1],rescaledValenciavU[2],rescaledu0],
["ValenciavU0","ValenciavU1","ValenciavU2","u0"],"returnstring",
params="includebraces=True,CSE_varprefix=tmprescale,outCverbose=False")
print(computeu0_Cfunction)
```
<a id='uj'></a>
## Step 1.c: Compute $u_j$ from $u^0$, the Valencia 3-velocity, and $g_{\mu\nu}$ \[Back to [top](#toc)\]
$$\label{uj}$$
The basic equation is
\begin{align}
u_j &= g_{\mu j} u^{\mu} \\
&= g_{0j} u^0 + g_{ij} u^i \\
&= \beta_j u^0 + \gamma_{ij} u^i \\
&= \beta_j u^0 + \gamma_{ij} u^0 \left(\alpha v^i_{(n)} - \beta^i\right) \\
&= u^0 \left(\beta_j + \gamma_{ij} \left(\alpha v^i_{(n)} - \beta^i\right) \right)\\
&= \alpha u^0 \gamma_{ij} v^i_{(n)} \\
\end{align}
```
u0 = par.Cparameters("REAL",thismodule,"u0",1e300) # Will be overwritten in C code. Set to crazy value to ensure this.
uD = ixp.zerorank1()
for i in range(DIM):
for j in range(DIM):
uD[j] += alpha*u0*gammaDD[i][j]*ValenciavU[i]
```
<a id='beta'></a>
## Step 1.d: Compute $b^\mu$ \[Back to [top](#toc)\]
$$\label{beta}$$
We compute $b^\mu$ from the above expressions:
\begin{align}
\sqrt{4\pi} b^0 = B^0_{\rm (u)} &= \frac{u_j B^j}{\alpha} \\
\sqrt{4\pi} b^i = B^i_{\rm (u)} &= \frac{B^i + (u_j B^j) u^i}{\alpha u^0}\\
\end{align}
$B^i$ is exactly equal to the $B^i$ evaluated in IllinoisGRMHD/GiRaFFE.
Pulling this together, we currently have available as input:
+ $\tilde{B}^i$
+ $u_j$
+ $u^0$,
with the goal of outputting now $b^\mu$ and $b^2$:
```
M_PI = par.Cparameters("#define",thismodule,"M_PI","")
BU = ixp.register_gridfunctions_for_single_rank1("AUX","BU",DIM=3)
# uBcontraction = u_i B^i
uBcontraction = sp.sympify(0)
for i in range(DIM):
uBcontraction += uD[i]*BU[i]
# uU = 3-vector representing u^i = u^0 \left(\alpha v^i_{(n)} - \beta^i\right)
uU = ixp.zerorank1()
for i in range(DIM):
uU[i] = u0*(alpha*ValenciavU[i] - betaU[i])
smallb4U = ixp.zerorank1(DIM=4)
smallb4U[0] = uBcontraction/(alpha*sp.sqrt(4*M_PI))
for i in range(DIM):
smallb4U[1+i] = (BU[i] + uBcontraction*uU[i])/(alpha*u0*sp.sqrt(4*M_PI))
```
<a id='poynting_flux'></a>
# Step 2: Defining the Poynting Flux Vector $S^{i}$ \[Back to [top](#toc)\]
$$\label{poynting_flux}$$
The Poynting flux is defined in Eq. 11 of [Kelly *et al.*](https://arxiv.org/pdf/1710.02132.pdf) (note that we choose the minus sign convention so that the Poynting luminosity across a spherical shell is $L_{\rm EM} = \int (-\alpha T^i_{\rm EM\ 0}) \sqrt{\gamma} d\Omega = \int S^r \sqrt{\gamma} d\Omega$, as in [Farris *et al.*](https://arxiv.org/pdf/1207.3354.pdf):
$$
S^i = -\alpha T^i_{\rm EM\ 0} = -\alpha\left(b^2 u^i u_0 + \frac{1}{2} b^2 g^i{}_0 - b^i b_0\right)
$$
<a id='s'></a>
## Step 2.a: Computing $S^{i}$ \[Back to [top](#toc)\]
$$\label{s}$$
Given $g^{\mu\nu}$ computed above, we focus first on the $g^i{}_{0}$ term by computing
$$
g^\mu{}_\delta = g^{\mu\nu} g_{\nu \delta},
$$
and then the rest of the Poynting flux vector can be immediately computed from quantities defined above:
$$
S^i = -\alpha T^i_{\rm EM\ 0} = -\alpha\left(b^2 u^i u_0 + \frac{1}{2} b^2 g^i{}_0 - b^i b_0\right)
$$
```
# Step 2.a.i: compute g^\mu_\delta:
g4UD = ixp.zerorank2(DIM=4)
for mu in range(4):
for delta in range(4):
for nu in range(4):
g4UD[mu][delta] += g4UU[mu][nu]*g4DD[nu][delta]
# Step 2.a.ii: compute b_{\mu}
smallb4D = ixp.zerorank1(DIM=4)
for mu in range(4):
for nu in range(4):
smallb4D[mu] += g4DD[mu][nu]*smallb4U[nu]
# Step 2.a.iii: compute u_0 = g_{mu 0} u^{mu} = g4DD[0][0]*u0 + g4DD[i][0]*uU[i]
u_0 = g4DD[0][0]*u0
for i in range(DIM):
u_0 += g4DD[i+1][0]*uU[i]
# Step 2.a.iv: compute b^2, setting b^2 = smallb2etk, as gridfunctions with base names ending in a digit
# are forbidden in NRPy+.
smallb2etk = sp.sympify(0)
for mu in range(4):
smallb2etk += smallb4U[mu]*smallb4D[mu]
# Step 2.a.v: compute S^i
PoynSU = ixp.zerorank1()
for i in range(DIM):
PoynSU[i] = -alpha * (smallb2etk*uU[i]*u_0 + sp.Rational(1,2)*smallb2etk*g4UD[i+1][0] - smallb4U[i+1]*smallb4D[0])
```
<a id='code_validation'></a>
# Step 3: Code Validation against `u0_smallb_Poynting__Cartesian` NRPy+ module \[Back to [top](#toc)\]
$$\label{code_validation}$$
Here, as a code validation check, we verify agreement in the SymPy expressions for u0, smallbU, smallb2etk, and PoynSU between
1. this tutorial and
2. the NRPy+ [u0_smallb_Poynting__Cartesian module](../edit/u0_smallb_Poynting__Cartesian/u0_smallb_Poynting__Cartesian.py).
```
import sys
import u0_smallb_Poynting__Cartesian.u0_smallb_Poynting__Cartesian as u0etc
u0etc.compute_u0_smallb_Poynting__Cartesian(gammaDD,betaU,alpha,ValenciavU,BU)
if u0etc.computeu0_Cfunction != computeu0_Cfunction:
print("FAILURE: u0 C code has changed!")
sys.exit(1)
else:
print("PASSED: u0 C code matches!")
for i in range(4):
print("u0etc.smallb4U["+str(i)+"] - smallb4U["+str(i)+"] = "
+ str(u0etc.smallb4U[i]-smallb4U[i]))
print("u0etc.smallb2etk - smallb2etk = " + str(u0etc.smallb2etk-smallb2etk))
for i in range(DIM):
print("u0etc.PoynSU["+str(i)+"] - PoynSU["+str(i)+"] = "
+ str(u0etc.PoynSU[i]-PoynSU[i]))
```
<a id='appendix'></a>
# Step 4: Appendix: Proving Eqs. 53 and 56 in [Duez *et al* (2005)](https://arxiv.org/pdf/astro-ph/0503420.pdf)
$$\label{appendix}$$
$u^\mu u_\mu = -1$ implies
\begin{align}
g^{\mu\nu} u_\mu u_\nu &= g^{00} \left(u_0\right)^2 + 2 g^{0i} u_0 u_i + g^{ij} u_i u_j = -1 \\
\implies &g^{00} \left(u_0\right)^2 + 2 g^{0i} u_0 u_i + g^{ij} u_i u_j + 1 = 0\\
& a x^2 + b x + c = 0
\end{align}
Thus we have a quadratic equation for $u_0$, with solution given by
\begin{align}
u_0 &= \frac{-b \pm \sqrt{b^2 - 4 a c}}{2 a} \\
&= \frac{-2 g^{0i}u_i \pm \sqrt{\left(2 g^{0i} u_i\right)^2 - 4 g^{00} (g^{ij} u_i u_j + 1)}}{2 g^{00}}\\
&= \frac{-g^{0i}u_i \pm \sqrt{\left(g^{0i} u_i\right)^2 - g^{00} (g^{ij} u_i u_j + 1)}}{g^{00}}\\
\end{align}
Notice that (Eq. 4.49 in [Gourgoulhon](https://arxiv.org/pdf/gr-qc/0703035.pdf))
$$
g^{\mu\nu} = \begin{pmatrix}
-\frac{1}{\alpha^2} & \frac{\beta^i}{\alpha^2} \\
\frac{\beta^i}{\alpha^2} & \gamma^{ij} - \frac{\beta^i\beta^j}{\alpha^2}
\end{pmatrix},
$$
so we have
\begin{align}
u_0 &= \frac{-\beta^i u_i/\alpha^2 \pm \sqrt{\left(\beta^i u_i/\alpha^2\right)^2 + 1/\alpha^2 (g^{ij} u_i u_j + 1)}}{1/\alpha^2}\\
&= -\beta^i u_i \pm \sqrt{\left(\beta^i u_i\right)^2 + \alpha^2 (g^{ij} u_i u_j + 1)}\\
&= -\beta^i u_i \pm \sqrt{\left(\beta^i u_i\right)^2 + \alpha^2 \left(\left[\gamma^{ij} - \frac{\beta^i\beta^j}{\alpha^2}\right] u_i u_j + 1\right)}\\
&= -\beta^i u_i \pm \sqrt{\left(\beta^i u_i\right)^2 + \alpha^2 \left(\gamma^{ij}u_i u_j + 1\right) - \beta^i\beta^j u_i u_j}\\
&= -\beta^i u_i \pm \sqrt{\alpha^2 \left(\gamma^{ij}u_i u_j + 1\right)}\\
\end{align}
Now, since
$$
u^0 = g^{\alpha 0} u_\alpha = -\frac{1}{\alpha^2} u_0 + \frac{\beta^i u_i}{\alpha^2},
$$
we get
\begin{align}
u^0 &= \frac{1}{\alpha^2} \left(u_0 + \beta^i u_i\right) \\
&= \pm \frac{1}{\alpha^2} \sqrt{\alpha^2 \left(\gamma^{ij}u_i u_j + 1\right)}\\
&= \pm \frac{1}{\alpha} \sqrt{\gamma^{ij}u_i u_j + 1}\\
\end{align}
By convention, the relativistic Gamma factor is positive and given by $\alpha u^0$, so we choose the positive root. Thus we have derived Eq. 53 in [Duez *et al* (2005)](https://arxiv.org/pdf/astro-ph/0503420.pdf):
$$
u^0 = \frac{1}{\alpha} \sqrt{\gamma^{ij}u_i u_j + 1}.
$$
Next we evaluate
\begin{align}
u^i &= u_\mu g^{\mu i} \\
&= u_0 g^{0 i} + u_j g^{i j}\\
&= u_0 \frac{\beta^i}{\alpha^2} + u_j \left(\gamma^{ij} - \frac{\beta^i\beta^j}{\alpha^2}\right)\\
&= \gamma^{ij} u_j + u_0 \frac{\beta^i}{\alpha^2} - u_j \frac{\beta^i\beta^j}{\alpha^2}\\
&= \gamma^{ij} u_j + \frac{\beta^i}{\alpha^2} \left(u_0 - u_j \beta^j\right)\\
&= \gamma^{ij} u_j - \beta^i u^0,\\
\implies v^i &= \frac{\gamma^{ij} u_j}{u^0} - \beta^i
\end{align}
which is equivalent to Eq. 56 in [Duez *et al* (2005)](https://arxiv.org/pdf/astro-ph/0503420.pdf). Notice in the last step, we used the above definition of $u^0$.
<a id='latex_pdf_output'></a>
# Step 5: Output this notebook to $\LaTeX$-formatted PDF file \[Back to [top](#toc)\]
$$\label{latex_pdf_output}$$
The following code cell converts this Jupyter notebook into a proper, clickable $\LaTeX$-formatted PDF file. After the cell is successfully run, the generated PDF may be found in the root NRPy+ tutorial directory, with filename
[Tutorial-u0_smallb_Poynting-Cartesian.pdf](Tutorial-u0_smallb_Poynting-Cartesian.pdf) (Note that clicking on this link may not work; you may need to open the PDF file through another means.)
```
!jupyter nbconvert --to latex --template latex_nrpy_style.tplx --log-level='WARN' Tutorial-u0_smallb_Poynting-Cartesian.ipynb
!pdflatex -interaction=batchmode Tutorial-u0_smallb_Poynting-Cartesian.tex
!pdflatex -interaction=batchmode Tutorial-u0_smallb_Poynting-Cartesian.tex
!pdflatex -interaction=batchmode Tutorial-u0_smallb_Poynting-Cartesian.tex
!rm -f Tut*.out Tut*.aux Tut*.log
```
| github_jupyter |
```
# import re
# import tensorflow as tf
# from tensorflow.keras.preprocessing.text import text_to_word_sequence
# tokens=text_to_word_sequence("manta.com/c/mmcdqky/lily-co")
# print(tokens)
# #to map the features to a dictioanary and then convert it to a csv file.
# # Feauture extraction
# class feature_extractor(object):
# def __init__(self,url):
# self.url=url
# self.length=len(url)
# #self.domain=url.split('//')[-1].split('/')[0]
# #def entropy(self):
# #.com,.org,.net,.edu
# #has www.
# #.extension-- .htm,.html,.php,.js
# # Pattern regex = Pattern.compile(".com[,/.]")
# def domain(self):
# if re.search(".com[ .,/]",self.url):
# return 1
# elif re.search(".org[.,/]",self.url):
# return 2
# elif re.search(".net[.,/]",self.url):
# return 3
# elif re.search(".edu[.,/]",self.url):
# return 4
# else:
# return 0
# #def extension(self):
# def num_digits(self):
# return sum(n.isdigit() for n in self.url)
# def num_char(self):
# return sum(n.alpha() for n in self.url)
# def has_http(self):
# if "http" in self.url:
# return 1
# else:
# return 0
# def has_https(self):
# if "https" in self.url:
# return 1
# else:
# return 0
# #def num_special_char(self):
# #
# #def num
# def clean(input):
# tokensBySlash = str(input.encode('utf-8')).split('/')
# allTokens=[]
# for i in tokensBySlash:
# tokens = str(i).split('-')
# tokensByDot = []
# for j in range(0,len(tokens)):
# tempTokens = str(tokens[j]).split('.')
# tokentsByDot = tokensByDot + tempTokens
# allTokens = allTokens + tokens + tokensByDot
# allTokens = list(set(allTokens))
# if 'com' in allTokens:
# allTokens.remove('com')
# return allTokens
from urllib.parse import urlparse
url="http://www.pn-wuppertal.de/links/2-linkseite/5-httpwwwkrebshilfede"
def getTokens(input):
tokensBySlash = str(input.encode('utf-8')).split('/')
allTokens=[]
for i in tokensBySlash:
tokens = str(i).split('-')
tokensByDot = []
for j in range(0,len(tokens)):
tempTokens = str(tokens[j]).split('.')
tokentsByDot = tokensByDot + tempTokens
allTokens = allTokens + tokens + tokensByDot
allTokens = list(set(allTokens))
if 'com' in allTokens:
allTokens.remove('com')
return allTokens
url="http://www.pn-wuppertal.de/links/2-linkseite/5-httpwwwkrebshilfede"
x=(lambda s: sum(not((i.isalpha()) and not(i.isnumeric())) for i in s))
print((url))
from urllib.parse import urlparse
url="http://www.pn-wuppertal.de/links/2-linkseite/5-httpwwwkrebshilfede"
def fd_length(url):
urlpath= urlparse(url).path
try:
return len(urlpath.split('/')[1])
except:
return 0
print(urlparse(url))
print(fd_length(urlparse(url)))
urlparse(url).scheme
s='https://www.yandex.ru'
print(urlparse(s))
s='yourbittorrent.com/?q=anthony-hamilton-soulife'
print(urlparse(s))
print(tldextract.extract(s))
from urllib.parse import urlparse
import tldextract
s='movies.yahoo.com/shop?d=hv&cf=info&id=1800340831'
print(urlparse(s))
print(tldextract.extract(s).subdomain)
len(urlparse(s).query)
def tld_length(tld):
try:
return len(tld)
except:
return -1
import tldextract
from urllib.parse import urlparse
import tldextract
s='http://peluqueriadeautor.com/index.php?option=com_virtuemart&page=shop.browse&category_id=31&Itemid=70'
def extension(s):
domains={'com':1,'edu':2,'org':3,'net':4,'onion':5}
if s in domains.keys():
return domains[s]
else:
return 0
#s=tldextract.extract(s).suffix
#print(extension(s))
print(tldextract.extract(s))
print(urlparse(s))
from urllib.parse import urlparse
import tldextract
print(tldextract.extract("http://motthegioi.com/the-gioi-cuoi/clip-dai-gia-mac-ca-voi-co-ban-banh-my-185682.html"))
print(urlparse("http://motthegioi.vn/the-gioi-cuoi/clip-dai-gia-mac-ca-voi-co-ban-banh-my-185682.html"))
```
| github_jupyter |
```
from sklearn.preprocessing import LabelBinarizer
from keras.datasets import cifar10
from keras.preprocessing.image import ImageDataGenerator
from keras.models import Sequential, model_from_json
from keras.callbacks import ModelCheckpoint, EarlyStopping, ReduceLROnPlateau
from keras.constraints import maxnorm
from keras import regularizers
from keras.layers.normalization import BatchNormalization
from keras.layers import Dense, Dropout, Activation, Flatten
from keras.layers import Conv2D, MaxPooling2D
from keras.applications import imagenet_utils
from keras.preprocessing.image import img_to_array
import numpy as np
import json
import os
import cv2
import h5py
import matplotlib.pyplot as plt
%matplotlib inline
from helpers import TrainingMonitor
from helpers import Utils
output_path = "../output/"
import tensorflow as tf
config = tf.ConfigProto()
config.gpu_options.allow_growth = True
session = tf.Session(config=config)
import os
os.environ["PATH"] += os.pathsep + 'C:/Program Files (x86)/Graphviz2.38/bin/'
(x_train, y_train), (x_test, y_test) = cifar10.load_data()
x_train = x_train.astype('float32')
x_test = x_test.astype('float32')
mean = np.mean(x_train, axis=0)
x_train -= mean
x_test -= mean
lb = LabelBinarizer()
y_train = lb.fit_transform(y_train)
y_test = lb.fit_transform(y_test)
db_train = h5py.File("../input/datasets/cifar_rgbmean_train.hdf5")
db_test = h5py.File("../input/datasets/cifar_rgbmean_test.hdf5")
x_train_rgbmean = db_train["images"][:].astype('float32')
x_test_rgbmean = db_test["images"][:].astype('float32')
mean = np.mean(x_train_rgbmean, axis=0)
x_train_rgbmean -= mean
x_test_rgbmean -= mean
y_train_rgbmean = db_train["labels"][:]
y_test_rgbmean = db_test["labels"][:]
json_file = open(output_path + 'saved/vgg_base_model_86.03.json', 'r')
model_json = json_file.read()
json_file.close()
model = model_from_json(model_json)
model.load_weights(output_path + "saved/vgg_base_weight_86.03.hdf5")
model.summary()
for (i, layer) in enumerate(model.layers):
print("{}\t{}".format(i, layer.__class__.__name__))
from keras.utils import plot_model
plot_model(model, to_file='models/baseline-vgg.png', show_shapes=True, show_layer_names=True)
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
filepath=output_path + "progress/weights-{val_acc:.4f}.hdf5"
MC = ModelCheckpoint(filepath, monitor='val_acc', verbose=0, save_best_only=True, mode='max')
figPath = os.path.sep.join([output_path, "monitor/{}.png".format(os.getpid())])
jsonPath = os.path.sep.join([output_path, "monitor/{}.json".format(os.getpid())])
TM = TrainingMonitor(figPath, jsonPath=jsonPath, startAt=0)
RLR = ReduceLROnPlateau(factor=np.sqrt(0.1), cooldown=0, patience=5, min_lr=0.5e-6)
callbacks = [MC, TM, RLR]
history = model.fit(x_train_rgbmean, y_train_rgbmean,
batch_size=64,
epochs=1,
validation_split=0.33,
shuffle="batch",
callbacks=callbacks)
scores = model.evaluate(x_test_rgbmean, y_test_rgbmean, verbose=0)
print("Train: %.2f%%; Val: %.2f%%; Test: %.2f%%" %
(np.max(history.history['acc'])*100, np.max(history.history['val_acc'])*100, scores[1]*100)
)
```
| github_jupyter |
<a href="https://colab.research.google.com/github/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_04_1_feature_encode.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# T81-558: Applications of Deep Neural Networks
**Module 4: Training for Tabular Data**
* Instructor: [Jeff Heaton](https://sites.wustl.edu/jeffheaton/), McKelvey School of Engineering, [Washington University in St. Louis](https://engineering.wustl.edu/Programs/Pages/default.aspx)
* For more information visit the [class website](https://sites.wustl.edu/jeffheaton/t81-558/).
# Module 4 Material
* **Part 4.1: Encoding a Feature Vector for Keras Deep Learning** [[Video]](https://www.youtube.com/watch?v=Vxz-gfs9nMQ&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_04_1_feature_encode.ipynb)
* Part 4.2: Keras Multiclass Classification for Deep Neural Networks with ROC and AUC [[Video]](https://www.youtube.com/watch?v=-f3bg9dLMks&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_04_2_multi_class.ipynb)
* Part 4.3: Keras Regression for Deep Neural Networks with RMSE [[Video]](https://www.youtube.com/watch?v=wNhBUC6X5-E&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_04_3_regression.ipynb)
* Part 4.4: Backpropagation, Nesterov Momentum, and ADAM Neural Network Training [[Video]](https://www.youtube.com/watch?v=VbDg8aBgpck&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_04_4_backprop.ipynb)
* Part 4.5: Neural Network RMSE and Log Loss Error Calculation from Scratch [[Video]](https://www.youtube.com/watch?v=wmQX1t2PHJc&list=PLjy4p-07OYzulelvJ5KVaT2pDlxivl_BN) [[Notebook]](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/t81_558_class_04_5_rmse_logloss.ipynb)
# Google CoLab Instructions
The following code ensures that Google CoLab is running the correct version of TensorFlow.
```
try:
%tensorflow_version 2.x
COLAB = True
print("Note: using Google CoLab")
except:
print("Note: not using Google CoLab")
COLAB = False
```
# Part 4.1: Encoding a Feature Vector for Keras Deep Learning
Neural networks can accept many types of data. We will begin with tabular data, where there are well defined rows and columns. This is the sort of data you would typically see in Microsoft Excel. An example of tabular data is shown below.
Neural networks require numeric input. This numeric form is called a feature vector. Each row of training data typically becomes one vector. The individual input neurons each receive one feature (or column) from this vector. In this section, we will see how to encode the following tabular data into a feature vector.
```
import pandas as pd
pd.set_option('display.max_columns', 7)
pd.set_option('display.max_rows', 5)
df = pd.read_csv(
"https://data.heatonresearch.com/data/t81-558/jh-simple-dataset.csv",
na_values=['NA','?'])
pd.set_option('display.max_columns', 9)
pd.set_option('display.max_rows', 5)
display(df)
```
The following observations can be made from the above data:
* The target column is the column that you seek to predict. There are several candidates here. However, we will initially use product. This field specifies what product someone bought.
* There is an ID column. This column should not be fed into the neural network as it contains no information useful for prediction.
* Many of these fields are numeric and might not require any further processing.
* The income column does have some missing values.
* There are categorical values: job, area, and product.
To begin with, we will convert the job code into dummy variables.
```
pd.set_option('display.max_columns', 7)
pd.set_option('display.max_rows', 5)
dummies = pd.get_dummies(df['job'],prefix="job")
print(dummies.shape)
pd.set_option('display.max_columns', 9)
pd.set_option('display.max_rows', 10)
display(dummies)
```
Because there are 33 different job codes, there are 33 dummy variables. We also specified a prefix, because the job codes (such as "ax") are not that meaningful by themselves. Something such as "job_ax" also tells us the origin of this field.
Next, we must merge these dummies back into the main data frame. We also drop the original "job" field, as it is now represented by the dummies.
```
pd.set_option('display.max_columns', 7)
pd.set_option('display.max_rows', 5)
df = pd.concat([df,dummies],axis=1)
df.drop('job', axis=1, inplace=True)
pd.set_option('display.max_columns', 9)
pd.set_option('display.max_rows', 10)
display(df)
```
We also introduce dummy variables for the area column.
```
pd.set_option('display.max_columns', 7)
pd.set_option('display.max_rows', 5)
df = pd.concat([df,pd.get_dummies(df['area'],prefix="area")],axis=1)
df.drop('area', axis=1, inplace=True)
pd.set_option('display.max_columns', 9)
pd.set_option('display.max_rows', 10)
display(df)
```
The last remaining transformation is to fill in missing income values.
```
med = df['income'].median()
df['income'] = df['income'].fillna(med)
```
There are more advanced ways of filling in missing values, but they require more analysis. The idea would be to see if another field might give a hint as to what the income were. For example, it might be beneficial to calculate a median income for each of the areas or job categories. This is something to keep in mind for the class Kaggle competition.
At this point, the Pandas dataframe is ready to be converted to Numpy for neural network training. We need to know a list of the columns that will make up *x* (the predictors or inputs) and *y* (the target).
The complete list of columns is:
```
print(list(df.columns))
```
This includes both the target and predictors. We need a list with the target removed. We also remove **id** because it is not useful for prediction.
```
x_columns = df.columns.drop('product').drop('id')
print(list(x_columns))
```
### Generate X and Y for a Classification Neural Network
We can now generate *x* and *y*. Note, this is how we generate y for a classification problem. Regression would not use dummies and would simply encode the numeric value of the target.
```
# Convert to numpy - Classification
x_columns = df.columns.drop('product').drop('id')
x = df[x_columns].values
dummies = pd.get_dummies(df['product']) # Classification
products = dummies.columns
y = dummies.values
```
We can display the *x* and *y* matrices.
```
print(x)
print(y)
```
The x and y values are now ready for a neural network. Make sure that you construct the neural network for a classification problem. Specifically,
* Classification neural networks have an output neuron count equal to the number of classes.
* Classification neural networks should use **categorical_crossentropy** and a **softmax** activation function on the output layer.
### Generate X and Y for a Regression Neural Network
For a regression neural network, the *x* values are generated the same. However, *y* does not use dummies. Make sure to replace **income** with your actual target.
```
y = df['income'].values
```
# Module 4 Assignment
You can find the first assignment here: [assignment 4](https://github.com/jeffheaton/t81_558_deep_learning/blob/master/assignments/assignment_yourname_class1.ipynb)
| github_jupyter |
**This notebook is an exercise in the [Intermediate Machine Learning](https://www.kaggle.com/learn/intermediate-machine-learning) course. You can reference the tutorial at [this link](https://www.kaggle.com/alexisbcook/categorical-variables).**
---
By encoding **categorical variables**, you'll obtain your best results thus far!
# Setup
The questions below will give you feedback on your work. Run the following cell to set up the feedback system.
```
# Set up code checking
import os
if not os.path.exists("../input/train.csv"):
os.symlink("../input/home-data-for-ml-course/train.csv", "../input/train.csv")
os.symlink("../input/home-data-for-ml-course/test.csv", "../input/test.csv")
from learntools.core import binder
binder.bind(globals())
from learntools.ml_intermediate.ex3 import *
print("Setup Complete")
```
In this exercise, you will work with data from the [Housing Prices Competition for Kaggle Learn Users](https://www.kaggle.com/c/home-data-for-ml-course).

Run the next code cell without changes to load the training and validation sets in `X_train`, `X_valid`, `y_train`, and `y_valid`. The test set is loaded in `X_test`.
```
import pandas as pd
from sklearn.model_selection import train_test_split
# Read the data
X = pd.read_csv('../input/train.csv', index_col='Id')
X_test = pd.read_csv('../input/test.csv', index_col='Id')
# Remove rows with missing target, separate target from predictors
X.dropna(axis=0, subset=['SalePrice'], inplace=True)
y = X.SalePrice
X.drop(['SalePrice'], axis=1, inplace=True)
# To keep things simple, we'll drop columns with missing values
cols_with_missing = [col for col in X.columns if X[col].isnull().any()]
X.drop(cols_with_missing, axis=1, inplace=True)
X_test.drop(cols_with_missing, axis=1, inplace=True)
# Break off validation set from training data
X_train, X_valid, y_train, y_valid = train_test_split(X, y,
train_size=0.8, test_size=0.2,
random_state=0)
```
Use the next code cell to print the first five rows of the data.
```
X_train.head()
```
Notice that the dataset contains both numerical and categorical variables. You'll need to encode the categorical data before training a model.
To compare different models, you'll use the same `score_dataset()` function from the tutorial. This function reports the [mean absolute error](https://en.wikipedia.org/wiki/Mean_absolute_error) (MAE) from a random forest model.
```
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import mean_absolute_error
# function for comparing different approaches
def score_dataset(X_train, X_valid, y_train, y_valid):
model = RandomForestRegressor(n_estimators=100, random_state=0)
model.fit(X_train, y_train)
preds = model.predict(X_valid)
return mean_absolute_error(y_valid, preds)
```
# Step 1: Drop columns with categorical data
You'll get started with the most straightforward approach. Use the code cell below to preprocess the data in `X_train` and `X_valid` to remove columns with categorical data. Set the preprocessed DataFrames to `drop_X_train` and `drop_X_valid`, respectively.
```
# Fill in the lines below: drop columns in training and validation data
drop_X_train = X_train.select_dtypes(exclude=['object'])
drop_X_valid = X_valid.select_dtypes(exclude=['object'])
# Check your answers
step_1.check()
# Lines below will give you a hint or solution code
#step_1.hint()
#step_1.solution()
```
Run the next code cell to get the MAE for this approach.
```
print("MAE from Approach 1 (Drop categorical variables):")
print(score_dataset(drop_X_train, drop_X_valid, y_train, y_valid))
```
Before jumping into label encoding, we'll investigate the dataset. Specifically, we'll look at the `'Condition2'` column. The code cell below prints the unique entries in both the training and validation sets.
```
print("Unique values in 'Condition2' column in training data:", X_train['Condition2'].unique())
print("\nUnique values in 'Condition2' column in validation data:", X_valid['Condition2'].unique())
```
# Step 2: Label encoding
### Part A
If you now write code to:
- fit a label encoder to the training data, and then
- use it to transform both the training and validation data,
you'll get an error. Can you see why this is the case? (_You'll need to use the above output to answer this question._)
```
# Check your answer (Run this code cell to receive credit!)
step_2.a.check()
#step_2.a.hint()
```
This is a common problem that you'll encounter with real-world data, and there are many approaches to fixing this issue. For instance, you can write a custom label encoder to deal with new categories. The simplest approach, however, is to drop the problematic categorical columns.
Run the code cell below to save the problematic columns to a Python list `bad_label_cols`. Likewise, columns that can be safely label encoded are stored in `good_label_cols`.
```
# All categorical columns
object_cols = [col for col in X_train.columns if X_train[col].dtype == "object"]
# Columns that can be safely label encoded
good_label_cols = [col for col in object_cols if
set(X_train[col]) == set(X_valid[col])]
# Problematic columns that will be dropped from the dataset
bad_label_cols = list(set(object_cols)-set(good_label_cols))
print('Categorical columns that will be label encoded:', good_label_cols)
print('\nCategorical columns that will be dropped from the dataset:', bad_label_cols)
```
### Part B
Use the next code cell to label encode the data in `X_train` and `X_valid`. Set the preprocessed DataFrames to `label_X_train` and `label_X_valid`, respectively.
- We have provided code below to drop the categorical columns in `bad_label_cols` from the dataset.
- You should label encode the categorical columns in `good_label_cols`.
```
from sklearn.preprocessing import LabelEncoder
# Drop categorical columns that will not be encoded
label_X_train = X_train.drop(bad_label_cols, axis=1)
label_X_valid = X_valid.drop(bad_label_cols, axis=1)
# Apply label encoder
label_encoder = LabelEncoder()
for col in good_label_cols:
label_X_train[col] = label_encoder.fit_transform(label_X_train[col])
label_X_valid[col] = label_encoder.transform(label_X_valid[col])
# Check your answer
step_2.b.check()
# Lines below will give you a hint or solution code
#step_2.b.hint()
#step_2.b.solution()
```
Run the next code cell to get the MAE for this approach.
```
print("MAE from Approach 2 (Label Encoding):")
print(score_dataset(label_X_train, label_X_valid, y_train, y_valid))
```
So far, you've tried two different approaches to dealing with categorical variables. And, you've seen that encoding categorical data yields better results than removing columns from the dataset.
Soon, you'll try one-hot encoding. Before then, there's one additional topic we need to cover. Begin by running the next code cell without changes.
```
# Get number of unique entries in each column with categorical data
object_nunique = list(map(lambda col: X_train[col].nunique(), object_cols))
d = dict(zip(object_cols, object_nunique))
# Print number of unique entries by column, in ascending order
sorted(d.items(), key=lambda x: x[1])
```
# Step 3: Investigating cardinality
### Part A
The output above shows, for each column with categorical data, the number of unique values in the column. For instance, the `'Street'` column in the training data has two unique values: `'Grvl'` and `'Pave'`, corresponding to a gravel road and a paved road, respectively.
We refer to the number of unique entries of a categorical variable as the **cardinality** of that categorical variable. For instance, the `'Street'` variable has cardinality 2.
Use the output above to answer the questions below.
```
# Fill in the line below: How many categorical variables in the training data
# have cardinality greater than 10?
high_cardinality_numcols = 3
# Fill in the line below: How many columns are needed to one-hot encode the
# 'Neighborhood' variable in the training data?
num_cols_neighborhood = 25
# Check your answers
step_3.a.check()
# Lines below will give you a hint or solution code
#step_3.a.hint()
#step_3.a.solution()
```
### Part B
For large datasets with many rows, one-hot encoding can greatly expand the size of the dataset. For this reason, we typically will only one-hot encode columns with relatively low cardinality. Then, high cardinality columns can either be dropped from the dataset, or we can use label encoding.
As an example, consider a dataset with 10,000 rows, and containing one categorical column with 100 unique entries.
- If this column is replaced with the corresponding one-hot encoding, how many entries are added to the dataset?
- If we instead replace the column with the label encoding, how many entries are added?
Use your answers to fill in the lines below.
```
# Fill in the line below: How many entries are added to the dataset by
# replacing the column with a one-hot encoding?
OH_entries_added = 1e4*100 - 1e4
# Fill in the line below: How many entries are added to the dataset by
# replacing the column with a label encoding?
label_entries_added = 0
# Check your answers
step_3.b.check()
# Lines below will give you a hint or solution code
#step_3.b.hint()
#step_3.b.solution()
```
Next, you'll experiment with one-hot encoding. But, instead of encoding all of the categorical variables in the dataset, you'll only create a one-hot encoding for columns with cardinality less than 10.
Run the code cell below without changes to set `low_cardinality_cols` to a Python list containing the columns that will be one-hot encoded. Likewise, `high_cardinality_cols` contains a list of categorical columns that will be dropped from the dataset.
```
# Columns that will be one-hot encoded
low_cardinality_cols = [col for col in object_cols if X_train[col].nunique() < 10]
# Columns that will be dropped from the dataset
high_cardinality_cols = list(set(object_cols)-set(low_cardinality_cols))
print('Categorical columns that will be one-hot encoded:', low_cardinality_cols)
print('\nCategorical columns that will be dropped from the dataset:', high_cardinality_cols)
```
# Step 4: One-hot encoding
Use the next code cell to one-hot encode the data in `X_train` and `X_valid`. Set the preprocessed DataFrames to `OH_X_train` and `OH_X_valid`, respectively.
- The full list of categorical columns in the dataset can be found in the Python list `object_cols`.
- You should only one-hot encode the categorical columns in `low_cardinality_cols`. All other categorical columns should be dropped from the dataset.
```
from sklearn.preprocessing import OneHotEncoder
# Use as many lines of code as you need!
OH_encoder = OneHotEncoder(handle_unknown='ignore', sparse=False)
OH_cols_train = pd.DataFrame(OH_encoder.fit_transform(X_train[low_cardinality_cols]))
OH_cols_valid = pd.DataFrame(OH_encoder.transform(X_valid[low_cardinality_cols]))
# One-hot encoding removed index; put it back
OH_cols_train.index = X_train.index
OH_cols_valid.index = X_valid.index
# Remove categorical columns (will replace with one-hot encoding)
num_X_train = X_train.drop(object_cols, axis=1)
num_X_valid = X_valid.drop(object_cols, axis=1)
# Add one-hot encoded columns to numerical features
OH_X_train = pd.concat([num_X_train, OH_cols_train], axis=1)
OH_X_valid = pd.concat([num_X_valid, OH_cols_valid], axis=1)
# Check your answer
step_4.check()
# Lines below will give you a hint or solution code
#step_4.hint()
#step_4.solution()
```
Run the next code cell to get the MAE for this approach.
```
print("MAE from Approach 3 (One-Hot Encoding):")
print(score_dataset(OH_X_train, OH_X_valid, y_train, y_valid))
```
# Generate test predictions and submit your results
After you complete Step 4, if you'd like to use what you've learned to submit your results to the leaderboard, you'll need to preprocess the test data before generating predictions.
**This step is completely optional, and you do not need to submit results to the leaderboard to successfully complete the exercise.**
Check out the previous exercise if you need help with remembering how to [join the competition](https://www.kaggle.com/c/home-data-for-ml-course) or save your results to CSV. Once you have generated a file with your results, follow the instructions below:
1. Begin by clicking on the blue **Save Version** button in the top right corner of the window. This will generate a pop-up window.
2. Ensure that the **Save and Run All** option is selected, and then click on the blue **Save** button.
3. This generates a window in the bottom left corner of the notebook. After it has finished running, click on the number to the right of the **Save Version** button. This pulls up a list of versions on the right of the screen. Click on the ellipsis **(...)** to the right of the most recent version, and select **Open in Viewer**. This brings you into view mode of the same page. You will need to scroll down to get back to these instructions.
4. Click on the **Output** tab on the right of the screen. Then, click on the file you would like to submit, and click on the blue **Submit** button to submit your results to the leaderboard.
You have now successfully submitted to the competition!
If you want to keep working to improve your performance, select the blue **Edit** button in the top right of the screen. Then you can change your code and repeat the process. There's a lot of room to improve, and you will climb up the leaderboard as you work.
```
# (Optional) Your code here
```
# Keep going
With missing value handling and categorical encoding, your modeling process is getting complex. This complexity gets worse when you want to save your model to use in the future. The key to managing this complexity is something called **pipelines**.
**[Learn to use pipelines](https://www.kaggle.com/alexisbcook/pipelines)** to preprocess datasets with categorical variables, missing values and any other messiness your data throws at you.
---
*Have questions or comments? Visit the [Learn Discussion forum](https://www.kaggle.com/learn-forum/161289) to chat with other Learners.*
| github_jupyter |
##### Copyright 2018 The TensorFlow Authors.
Licensed under the Apache License, Version 2.0 (the "License");
```
#@title Licensed under the Apache License, Version 2.0 (the "License"); { display-mode: "form" }
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
<table class="tfo-notebook-buttons" align="left">
<td>
<a target="_blank" href="https://www.tensorflow.org/beta/{PATH}">
<img src="https://www.tensorflow.org/images/tf_logo_32px.png" />
View on TensorFlow.org</a>
</td>
<td>
<a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs/blob/master/site/{PATH}.ipynb">
<img src="https://www.tensorflow.org/images/colab_logo_32px.png" />
Run in Google Colab</a>
</td>
<td>
<a target="_blank" href="https://github.com/tensorflow/docs/blob/master/site/{PATH}.ipynb">
<img src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" />
View source on GitHub</a>
</td>
</table>
# Using TPUs
Tensor Processing Units (TPUs) are Google's specialized ASICs designed to dramatically accelerate machine learning workloads. They are available on Google Colab, the TensorFlow Research Cloud and Google Compute Engine.
In this notebook, you can try training a convolutional neural network against the Fashion MNIST dataset on Cloud TPUs using tf.keras and Distribution Strategy.
## Learning Objectives
In this Colab, you will learn how to:
* Write a standard 4-layer conv-net with drop-out and batch normalization in Keras.
* Use TPUs and Distribution Strategy to train the model.
* Run a prediction to see how well the model can predict fashion categories and output the result.
## Instructions
To use TPUs in Colab:
1. On the main menu, click Runtime and select **Change runtime type**. Set "TPU" as the hardware accelerator.
1. Click Runtime again and select **Runtime > Run All**. You can also run the cells manually with Shift-ENTER.
## Data, Model, and Training
### Download the Data
Begin by downloading the fashion MNIST dataset using `tf.keras.datasets`, as shown below. We will also need to convert the data to `float32` format, as the data types supported by TPUs are limited right now.
TPUs currently do not support Eager Execution, so we disable that with `disable_eager_execution()`.
```
from __future__ import absolute_import, division, print_function, unicode_literals
import numpy as np
from __future__ import absolute_import, division, print_function
!pip install tensorflow-gpu==2.0.0-beta1
import tensorflow as tf
tf.compat.v1.disable_eager_execution()
import numpy as np
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.fashion_mnist.load_data()
# add empty color dimension
x_train = np.expand_dims(x_train, -1)
x_test = np.expand_dims(x_test, -1)
# convert types to float32
x_train = x_train.astype(np.float32)
x_test = x_test.astype(np.float32)
y_train = y_train.astype(np.float32)
y_test = y_test.astype(np.float32)
```
### Initialize TPUStrategy
We first initialize the TPUStrategy object before creating the model, so that Keras knows that we are creating a model for TPUs.
To do this, we are first creating a TPUClusterResolver using the IP address of the TPU, and then creating a TPUStrategy object from the Cluster Resolver.
```
import os
resolver = tf.distribute.cluster_resolver.TPUClusterResolver()
tf.tpu.experimental.initialize_tpu_system(resolver)
strategy = tf.distribute.experimental.TPUStrategy(resolver)
```
### Define the Model
The following example uses a standard conv-net that has 4 layers with drop-out and batch normalization between each layer. Note that we are creating the model within a `strategy.scope`.
```
with strategy.scope():
model = tf.keras.models.Sequential()
model.add(tf.keras.layers.BatchNormalization(input_shape=x_train.shape[1:]))
model.add(tf.keras.layers.Conv2D(64, (5, 5), padding='same', activation='elu'))
model.add(tf.keras.layers.MaxPooling2D(pool_size=(2, 2), strides=(2,2)))
model.add(tf.keras.layers.Dropout(0.25))
model.add(tf.keras.layers.BatchNormalization())
model.add(tf.keras.layers.Conv2D(128, (5, 5), padding='same', activation='elu'))
model.add(tf.keras.layers.MaxPooling2D(pool_size=(2, 2)))
model.add(tf.keras.layers.Dropout(0.25))
model.add(tf.keras.layers.BatchNormalization())
model.add(tf.keras.layers.Conv2D(256, (5, 5), padding='same', activation='elu'))
model.add(tf.keras.layers.MaxPooling2D(pool_size=(2, 2), strides=(2,2)))
model.add(tf.keras.layers.Dropout(0.25))
model.add(tf.keras.layers.BatchNormalization())
model.add(tf.keras.layers.Conv2D(512, (5, 5), padding='same', activation='elu'))
model.add(tf.keras.layers.MaxPooling2D(pool_size=(2, 2), strides=(2,2)))
model.add(tf.keras.layers.Dropout(0.25))
model.add(tf.keras.layers.Flatten())
model.add(tf.keras.layers.Dense(256))
model.add(tf.keras.layers.Activation('elu'))
model.add(tf.keras.layers.Dropout(0.5))
model.add(tf.keras.layers.Dense(10))
model.add(tf.keras.layers.Activation('softmax'))
model.summary()
```
### Train on the TPU
To train on the TPU, we can simply call `model.compile` under the strategy scope, and then call `model.fit` to start training. In this case, we are training for 5 epochs with 60 steps per epoch, and running evaluation at the end of 5 epochs.
It may take a while for the training to start, as the data and model has to be transferred to the TPU and compiled before training can start.
```
with strategy.scope():
model.compile(
optimizer=tf.train.AdamOptimizer(learning_rate=1e-3),
loss=tf.keras.losses.sparse_categorical_crossentropy,
metrics=['sparse_categorical_accuracy']
)
model.fit(
(x_train, y_train),
epochs=5,
steps_per_epoch=60,
validation_data=(x_test, y_test),
validation_freq=5,
)
```
### Check our results with Inference
Now that we are done training, we can see how well the model can predict fashion categories:
```
LABEL_NAMES = ['t_shirt', 'trouser', 'pullover', 'dress', 'coat', 'sandal', 'shirt', 'sneaker', 'bag', 'ankle_boots']
from matplotlib import pyplot
%matplotlib inline
def plot_predictions(images, predictions):
n = images.shape[0]
nc = int(np.ceil(n / 4))
f, axes = pyplot.subplots(nc, 4)
for i in range(nc * 4):
y = i // 4
x = i % 4
axes[x, y].axis('off')
label = LABEL_NAMES[np.argmax(predictions[i])]
confidence = np.max(predictions[i])
if i > n:
continue
axes[x, y].imshow(images[i])
axes[x, y].text(0.5, -1.5, label + ': %.3f' % confidence, fontsize=12)
pyplot.gcf().set_size_inches(8, 8)
plot_predictions(np.squeeze(x_test[:16]),
model.predict(x_test[:16]))
```
### What's next
* Learn about [Cloud TPUs](https://cloud.google.com/tpu/docs) that Google designed and optimized specifically to speed up and scale up ML workloads for training and inference and to enable ML engineers and researchers to iterate more quickly.
* Explore the range of [Cloud TPU tutorials and Colabs](https://cloud.google.com/tpu/docs/tutorials) to find other examples that can be used when implementing your ML project.
On Google Cloud Platform, in addition to GPUs and TPUs available on pre-configured [deep learning VMs](https://cloud.google.com/deep-learning-vm/), you will find [AutoML](https://cloud.google.com/automl/)*(beta)* for training custom models without writing code and [Cloud ML Engine](https://cloud.google.com/ml-engine/docs/) which will allows you to run parallel trainings and hyperparameter tuning of your custom models on powerful distributed hardware.
| github_jupyter |
<a href="https://colab.research.google.com/github/cseveriano/spatio-temporal-forecasting/blob/master/notebooks/thesis_experiments/20200924_eMVFTS_Wind_Energy_Raw.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
## Forecasting experiments for GEFCOM 2012 Wind Dataset
## Install Libs
```
!pip3 install -U git+https://github.com/PYFTS/pyFTS
!pip3 install -U git+https://github.com/cseveriano/spatio-temporal-forecasting
!pip3 install -U git+https://github.com/cseveriano/evolving_clustering
!pip3 install -U git+https://github.com/cseveriano/fts2image
!pip3 install -U hyperopt
!pip3 install -U pyts
import pandas as pd
import numpy as np
from hyperopt import hp
from spatiotemporal.util import parameter_tuning, sampling
from spatiotemporal.util import experiments as ex
from sklearn.metrics import mean_squared_error
from google.colab import files
import matplotlib.pyplot as plt
import pickle
import math
from pyFTS.benchmarks import Measures
from pyts.decomposition import SingularSpectrumAnalysis
from google.colab import files
import warnings
warnings.filterwarnings("ignore", category=DeprecationWarning)
import datetime
```
## Aux Functions
```
def normalize(df):
mindf = df.min()
maxdf = df.max()
return (df-mindf)/(maxdf-mindf)
def denormalize(norm, _min, _max):
return [(n * (_max-_min)) + _min for n in norm]
def getRollingWindow(index):
pivot = index
train_start = pivot.strftime('%Y-%m-%d')
pivot = pivot + datetime.timedelta(days=20)
train_end = pivot.strftime('%Y-%m-%d')
pivot = pivot + datetime.timedelta(days=1)
test_start = pivot.strftime('%Y-%m-%d')
pivot = pivot + datetime.timedelta(days=6)
test_end = pivot.strftime('%Y-%m-%d')
return train_start, train_end, test_start, test_end
def calculate_rolling_error(cv_name, df, forecasts, order_list):
cv_results = pd.DataFrame(columns=['Split', 'RMSE', 'SMAPE'])
limit = df.index[-1].strftime('%Y-%m-%d')
test_end = ""
index = df.index[0]
for i in np.arange(len(forecasts)):
train_start, train_end, test_start, test_end = getRollingWindow(index)
test = df[test_start : test_end]
yhat = forecasts[i]
order = order_list[i]
rmse = Measures.rmse(test.iloc[order:], yhat[:-1])
smape = Measures.smape(test.iloc[order:], yhat[:-1])
res = {'Split' : index.strftime('%Y-%m-%d') ,'RMSE' : rmse, 'SMAPE' : smape}
cv_results = cv_results.append(res, ignore_index=True)
cv_results.to_csv(cv_name+".csv")
index = index + datetime.timedelta(days=7)
return cv_results
def get_final_forecast(norm_forecasts):
forecasts_final = []
for i in np.arange(len(norm_forecasts)):
f_raw = denormalize(norm_forecasts[i], min_raw, max_raw)
forecasts_final.append(f_raw)
return forecasts_final
from spatiotemporal.test import methods_space_oahu as ms
from spatiotemporal.util import parameter_tuning, sampling
from spatiotemporal.util import experiments as ex
from sklearn.metrics import mean_squared_error
import numpy as np
from hyperopt import fmin, tpe, hp, STATUS_OK, Trials
from hyperopt import space_eval
import traceback
from . import sampling
import pickle
def calculate_error(loss_function, test_df, forecast, offset):
error = loss_function(test_df.iloc[(offset):], forecast)
print("Error : "+str(error))
return error
def method_optimize(experiment, forecast_method, train_df, test_df, space, loss_function, max_evals):
def objective(params):
print(params)
try:
_output = list(params['output'])
forecast = forecast_method(train_df, test_df, params)
_step = params.get('step', 1)
offset = params['order'] + _step - 1
error = calculate_error(loss_function, test_df[_output], forecast, offset)
except Exception:
traceback.print_exc()
error = 1000
return {'loss': error, 'status': STATUS_OK}
print("Running experiment: " + experiment)
trials = Trials()
best = fmin(objective, space, algo=tpe.suggest, max_evals=max_evals, trials=trials)
print('best parameters: ')
print(space_eval(space, best))
pickle.dump(best, open("best_" + experiment + ".pkl", "wb"))
pickle.dump(trials, open("trials_" + experiment + ".pkl", "wb"))
def run_search(methods, data, train, loss_function, max_evals=100, resample=None):
if resample:
data = sampling.resample_data(data, resample)
train_df, test_df = sampling.train_test_split(data, train)
for experiment, method, space in methods:
method_optimize(experiment, method, train_df, test_df, space, loss_function, max_evals)
```
## Load Dataset
```
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import math
from sklearn.metrics import mean_squared_error
#columns names
wind_farms = ['wp1', 'wp2', 'wp3', 'wp4', 'wp5', 'wp6', 'wp7']
# read raw dataset
import pandas as pd
df = pd.read_csv('https://query.data.world/s/3zx2jusk4z6zvlg2dafqgshqp3oao6', parse_dates=['date'], index_col=0)
df.index = pd.to_datetime(df.index, format="%Y%m%d%H")
interval = ((df.index >= '2009-07') & (df.index <= '2010-08'))
df = df.loc[interval]
#Normalize Data
# Save Min-Max for Denorm
min_raw = df.min()
max_raw = df.max()
# Perform Normalization
norm_df = normalize(df)
# Tuning split
tuning_df = norm_df["2009-07-01":"2009-07-31"]
norm_df = norm_df["2009-08-01":"2010-08-30"]
df = df["2009-08-01":"2010-08-30"]
```
## Forecasting Methods
### Persistence
```
def persistence_forecast(train, test, step):
predictions = []
for t in np.arange(0,len(test), step):
yhat = [test.iloc[t]] * step
predictions.extend(yhat)
return predictions
def rolling_cv_persistence(df, step):
forecasts = []
lags_list = []
limit = df.index[-1].strftime('%Y-%m-%d')
test_end = ""
index = df.index[0]
while test_end < limit :
print("Index: ", index.strftime('%Y-%m-%d'))
train_start, train_end, test_start, test_end = getRollingWindow(index)
index = index + datetime.timedelta(days=7)
train = df[train_start : train_end]
test = df[test_start : test_end]
yhat = persistence_forecast(train, test, step)
lags_list.append(1)
forecasts.append(yhat)
return forecasts, lags_list
forecasts_raw, order_list = rolling_cv_persistence(norm_df, 1)
forecasts_final = get_final_forecast(forecasts_raw)
calculate_rolling_error("rolling_cv_wind_raw_persistence", norm_df, forecasts_final, order_list)
files.download('rolling_cv_wind_raw_persistence.csv')
```
### VAR
```
from statsmodels.tsa.api import VAR, DynamicVAR
def evaluate_VAR_models(test_name, train, validation,target, maxlags_list):
var_results = pd.DataFrame(columns=['Order','RMSE'])
best_score, best_cfg, best_model = float("inf"), None, None
for lgs in maxlags_list:
model = VAR(train)
results = model.fit(maxlags=lgs, ic='aic')
order = results.k_ar
forecast = []
for i in range(len(validation)-order) :
forecast.extend(results.forecast(validation.values[i:i+order],1))
forecast_df = pd.DataFrame(columns=validation.columns, data=forecast)
rmse = Measures.rmse(validation[target].iloc[order:], forecast_df[target].values)
if rmse < best_score:
best_score, best_cfg, best_model = rmse, order, results
res = {'Order' : str(order) ,'RMSE' : rmse}
print('VAR (%s) RMSE=%.3f' % (str(order),rmse))
var_results = var_results.append(res, ignore_index=True)
var_results.to_csv(test_name+".csv")
print('Best VAR(%s) RMSE=%.3f' % (best_cfg, best_score))
return best_model
def var_forecast(train, test, params):
order = params['order']
step = params['step']
model = VAR(train.values)
results = model.fit(maxlags=order)
lag_order = results.k_ar
print("Lag order:" + str(lag_order))
forecast = []
for i in np.arange(0,len(test)-lag_order+1,step) :
forecast.extend(results.forecast(test.values[i:i+lag_order],step))
forecast_df = pd.DataFrame(columns=test.columns, data=forecast)
return forecast_df.values, lag_order
def rolling_cv_var(df, params):
forecasts = []
order_list = []
limit = df.index[-1].strftime('%Y-%m-%d')
test_end = ""
index = df.index[0]
while test_end < limit :
print("Index: ", index.strftime('%Y-%m-%d'))
train_start, train_end, test_start, test_end = getRollingWindow(index)
index = index + datetime.timedelta(days=7)
train = df[train_start : train_end]
test = df[test_start : test_end]
# Concat train & validation for test
yhat, lag_order = var_forecast(train, test, params)
forecasts.append(yhat)
order_list.append(lag_order)
return forecasts, order_list
params_raw = {'order': 4, 'step': 1}
forecasts_raw, order_list = rolling_cv_var(norm_df, params_raw)
forecasts_final = get_final_forecast(forecasts_raw)
calculate_rolling_error("rolling_cv_wind_raw_var", df, forecasts_final, order_list)
files.download('rolling_cv_wind_raw_var.csv')
```
### e-MVFTS
```
from spatiotemporal.models.clusteredmvfts.fts import evolvingclusterfts
def evolvingfts_forecast(train_df, test_df, params, train_model=True):
_variance_limit = params['variance_limit']
_defuzzy = params['defuzzy']
_t_norm = params['t_norm']
_membership_threshold = params['membership_threshold']
_order = params['order']
_step = params['step']
model = evolvingclusterfts.EvolvingClusterFTS(variance_limit=_variance_limit, defuzzy=_defuzzy, t_norm=_t_norm,
membership_threshold=_membership_threshold)
model.fit(train_df.values, order=_order, verbose=False)
forecast = model.predict(test_df.values, steps_ahead=_step)
forecast_df = pd.DataFrame(data=forecast, columns=test_df.columns)
return forecast_df.values
def rolling_cv_evolving(df, params):
forecasts = []
order_list = []
limit = df.index[-1].strftime('%Y-%m-%d')
test_end = ""
index = df.index[0]
first_time = True
while test_end < limit :
print("Index: ", index.strftime('%Y-%m-%d'))
train_start, train_end, test_start, test_end = getRollingWindow(index)
index = index + datetime.timedelta(days=7)
train = df[train_start : train_end]
test = df[test_start : test_end]
# Concat train & validation for test
yhat = list(evolvingfts_forecast(train, test, params, train_model=first_time))
#yhat.append(yhat[-1]) #para manter o formato do vetor de metricas
forecasts.append(yhat)
order_list.append(params['order'])
first_time = False
return forecasts, order_list
params_raw = {'variance_limit': 0.001, 'order': 2, 'defuzzy': 'weighted', 't_norm': 'threshold', 'membership_threshold': 0.6, 'step':1}
forecasts_raw, order_list = rolling_cv_evolving(norm_df, params_raw)
forecasts_final = get_final_forecast(forecasts_raw)
calculate_rolling_error("rolling_cv_wind_raw_emvfts", df, forecasts_final, order_list)
files.download('rolling_cv_wind_raw_emvfts.csv')
```
### MLP
```
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from keras.layers import Dropout
from keras.constraints import maxnorm
from keras.models import Sequential
from keras.layers.core import Dense, Dropout, Activation
from keras.layers.normalization import BatchNormalization
# convert series to supervised learning
def series_to_supervised(data, n_in=1, n_out=1, dropnan=True):
n_vars = 1 if type(data) is list else data.shape[1]
df = pd.DataFrame(data)
cols, names = list(), list()
# input sequence (t-n, ... t-1)
for i in range(n_in, 0, -1):
cols.append(df.shift(i))
names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)]
# forecast sequence (t, t+1, ... t+n)
for i in range(0, n_out):
cols.append(df.shift(-i))
if i == 0:
names += [('var%d(t)' % (j+1)) for j in range(n_vars)]
else:
names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)]
# put it all together
agg = pd.concat(cols, axis=1)
agg.columns = names
# drop rows with NaN values
if dropnan:
agg.dropna(inplace=True)
return agg
```
#### MLP Parameter Tuning
```
from spatiotemporal.util import parameter_tuning, sampling
from spatiotemporal.util import experiments as ex
from sklearn.metrics import mean_squared_error
from hyperopt import hp
import numpy as np
mlp_space = {'choice':
hp.choice('num_layers',
[
{'layers': 'two',
},
{'layers': 'three',
'units3': hp.choice('units3', [8, 16, 64, 128, 256, 512]),
'dropout3': hp.choice('dropout3', [0, 0.25, 0.5, 0.75])
}
]),
'units1': hp.choice('units1', [8, 16, 64, 128, 256, 512]),
'units2': hp.choice('units2', [8, 16, 64, 128, 256, 512]),
'dropout1': hp.choice('dropout1', [0, 0.25, 0.5, 0.75]),
'dropout2': hp.choice('dropout2', [0, 0.25, 0.5, 0.75]),
'batch_size': hp.choice('batch_size', [28, 64, 128, 256, 512]),
'order': hp.choice('order', [1, 2, 3]),
'input': hp.choice('input', [wind_farms]),
'output': hp.choice('output', [wind_farms]),
'epochs': hp.choice('epochs', [100, 200, 300])}
def mlp_tuning(train_df, test_df, params):
_input = list(params['input'])
_nlags = params['order']
_epochs = params['epochs']
_batch_size = params['batch_size']
nfeat = len(train_df.columns)
nsteps = params.get('step',1)
nobs = _nlags * nfeat
output_index = -nfeat*nsteps
train_reshaped_df = series_to_supervised(train_df[_input], n_in=_nlags, n_out=nsteps)
train_X, train_Y = train_reshaped_df.iloc[:, :nobs].values, train_reshaped_df.iloc[:, output_index:].values
test_reshaped_df = series_to_supervised(test_df[_input], n_in=_nlags, n_out=nsteps)
test_X, test_Y = test_reshaped_df.iloc[:, :nobs].values, test_reshaped_df.iloc[:, output_index:].values
# design network
model = Sequential()
model.add(Dense(params['units1'], input_dim=train_X.shape[1], activation='relu'))
model.add(Dropout(params['dropout1']))
model.add(BatchNormalization())
model.add(Dense(params['units2'], activation='relu'))
model.add(Dropout(params['dropout2']))
model.add(BatchNormalization())
if params['choice']['layers'] == 'three':
model.add(Dense(params['choice']['units3'], activation='relu'))
model.add(Dropout(params['choice']['dropout3']))
model.add(BatchNormalization())
model.add(Dense(train_Y.shape[1], activation='sigmoid'))
model.compile(loss='mse', optimizer='adam')
# includes the call back object
model.fit(train_X, train_Y, epochs=_epochs, batch_size=_batch_size, verbose=False, shuffle=False)
# predict the test set
forecast = model.predict(test_X, verbose=False)
return forecast
methods = []
methods.append(("EXP_OAHU_MLP", mlp_tuning, mlp_space))
train_split = 0.6
run_search(methods, tuning_df, train_split, Measures.rmse, max_evals=30, resample=None)
```
#### MLP Forecasting
```
def mlp_multi_forecast(train_df, test_df, params):
nfeat = len(train_df.columns)
nlags = params['order']
nsteps = params.get('step',1)
nobs = nlags * nfeat
output_index = -nfeat*nsteps
train_reshaped_df = series_to_supervised(train_df, n_in=nlags, n_out=nsteps)
train_X, train_Y = train_reshaped_df.iloc[:, :nobs].values, train_reshaped_df.iloc[:, output_index:].values
test_reshaped_df = series_to_supervised(test_df, n_in=nlags, n_out=nsteps)
test_X, test_Y = test_reshaped_df.iloc[:, :nobs].values, test_reshaped_df.iloc[:, output_index:].values
# design network
model = designMLPNetwork(train_X.shape[1], train_Y.shape[1], params)
# fit network
model.fit(train_X, train_Y, epochs=500, batch_size=1000, verbose=False, shuffle=False)
forecast = model.predict(test_X)
# fcst = [f[0] for f in forecast]
fcst = forecast
return fcst
def designMLPNetwork(input_shape, output_shape, params):
model = Sequential()
model.add(Dense(params['units1'], input_dim=input_shape, activation='relu'))
model.add(Dropout(params['dropout1']))
model.add(BatchNormalization())
model.add(Dense(params['units2'], activation='relu'))
model.add(Dropout(params['dropout2']))
model.add(BatchNormalization())
if params['choice']['layers'] == 'three':
model.add(Dense(params['choice']['units3'], activation='relu'))
model.add(Dropout(params['choice']['dropout3']))
model.add(BatchNormalization())
model.add(Dense(output_shape, activation='sigmoid'))
model.compile(loss='mse', optimizer='adam')
return model
def rolling_cv_mlp(df, params):
forecasts = []
order_list = []
limit = df.index[-1].strftime('%Y-%m-%d')
test_end = ""
index = df.index[0]
while test_end < limit :
print("Index: ", index.strftime('%Y-%m-%d'))
train_start, train_end, test_start, test_end = getRollingWindow(index)
index = index + datetime.timedelta(days=7)
train = df[train_start : train_end]
test = df[test_start : test_end]
# Perform forecast
yhat = list(mlp_multi_forecast(train, test, params))
yhat.append(yhat[-1]) #para manter o formato do vetor de metricas
forecasts.append(yhat)
order_list.append(params['order'])
return forecasts, order_list
# Enter best params
params_raw = {'batch_size': 64, 'choice': {'layers': 'two'}, 'dropout1': 0.25, 'dropout2': 0.5, 'epochs': 200, 'input': ('wp1', 'wp2', 'wp3', 'wp4', 'wp5', 'wp6', 'wp7'), 'order': 2, 'output': ('wp1', 'wp2', 'wp3', 'wp4', 'wp5', 'wp6', 'wp7'), 'units1': 128, 'units2': 128}
forecasts_raw, order_list = rolling_cv_mlp(norm_df, params_raw)
forecasts_final = get_final_forecast(forecasts_raw)
calculate_rolling_error("rolling_cv_wind_raw_mlp_multi", df, forecasts_final, order_list)
files.download('rolling_cv_wind_raw_mlp_multi.csv')
```
### Granular FTS
```
from pyFTS.models.multivariate import granular
from pyFTS.partitioners import Grid, Entropy
from pyFTS.models.multivariate import variable
from pyFTS.common import Membership
from pyFTS.partitioners import Grid, Entropy
```
#### Granular Parameter Tuning
```
granular_space = {
'npartitions': hp.choice('npartitions', [100, 150, 200]),
'order': hp.choice('order', [1, 2]),
'knn': hp.choice('knn', [1, 2, 3, 4, 5]),
'alpha_cut': hp.choice('alpha_cut', [0, 0.1, 0.2, 0.3]),
'input': hp.choice('input', [['wp1', 'wp2', 'wp3']]),
'output': hp.choice('output', [['wp1', 'wp2', 'wp3']])}
def granular_tuning(train_df, test_df, params):
_input = list(params['input'])
_output = list(params['output'])
_npartitions = params['npartitions']
_order = params['order']
_knn = params['knn']
_alpha_cut = params['alpha_cut']
_step = params.get('step',1)
## create explanatory variables
exp_variables = []
for vc in _input:
exp_variables.append(variable.Variable(vc, data_label=vc, alias=vc,
npart=_npartitions, func=Membership.trimf,
data=train_df, alpha_cut=_alpha_cut))
model = granular.GranularWMVFTS(explanatory_variables=exp_variables, target_variable=exp_variables[0], order=_order,
knn=_knn)
model.fit(train_df[_input], num_batches=1)
if _step > 1:
forecast = pd.DataFrame(columns=test_df.columns)
length = len(test_df.index)
for k in range(0,(length -(_order + _step - 1))):
fcst = model.predict(test_df[_input], type='multivariate', start_at=k, steps_ahead=_step)
forecast = forecast.append(fcst.tail(1))
else:
forecast = model.predict(test_df[_input], type='multivariate')
return forecast[_output].values
methods = []
methods.append(("EXP_WIND_GRANULAR", granular_tuning, granular_space))
train_split = 0.6
run_search(methods, tuning_df, train_split, Measures.rmse, max_evals=10, resample=None)
```
#### Granular Forecasting
```
def granular_forecast(train_df, test_df, params):
_input = list(params['input'])
_output = list(params['output'])
_npartitions = params['npartitions']
_knn = params['knn']
_alpha_cut = params['alpha_cut']
_order = params['order']
_step = params.get('step',1)
## create explanatory variables
exp_variables = []
for vc in _input:
exp_variables.append(variable.Variable(vc, data_label=vc, alias=vc,
npart=_npartitions, func=Membership.trimf,
data=train_df, alpha_cut=_alpha_cut))
model = granular.GranularWMVFTS(explanatory_variables=exp_variables, target_variable=exp_variables[0], order=_order,
knn=_knn)
model.fit(train_df[_input], num_batches=1)
if _step > 1:
forecast = pd.DataFrame(columns=test_df.columns)
length = len(test_df.index)
for k in range(0,(length -(_order + _step - 1))):
fcst = model.predict(test_df[_input], type='multivariate', start_at=k, steps_ahead=_step)
forecast = forecast.append(fcst.tail(1))
else:
forecast = model.predict(test_df[_input], type='multivariate')
return forecast[_output].values
def rolling_cv_granular(df, params):
forecasts = []
order_list = []
limit = df.index[-1].strftime('%Y-%m-%d')
test_end = ""
index = df.index[0]
while test_end < limit :
print("Index: ", index.strftime('%Y-%m-%d'))
train_start, train_end, test_start, test_end = getRollingWindow(index)
index = index + datetime.timedelta(days=7)
train = df[train_start : train_end]
test = df[test_start : test_end]
# Perform forecast
yhat = list(granular_forecast(train, test, params))
yhat.append(yhat[-1]) #para manter o formato do vetor de metricas
forecasts.append(yhat)
order_list.append(params['order'])
return forecasts, order_list
def granular_get_final_forecast(forecasts_raw, input):
forecasts_final = []
l_min = df[input].min()
l_max = df[input].max()
for i in np.arange(len(forecasts_raw)):
f_raw = denormalize(forecasts_raw[i], l_min, l_max)
forecasts_final.append(f_raw)
return forecasts_final
# Enter best params
params_raw = {'alpha_cut': 0.3, 'input': ('wp1', 'wp2', 'wp3'), 'knn': 5, 'npartitions': 200, 'order': 2, 'output': ('wp1', 'wp2', 'wp3')}
forecasts_raw, order_list = rolling_cv_granular(norm_df, params_raw)
forecasts_final = granular_get_final_forecast(forecasts_raw, list(params_raw['input']))
calculate_rolling_error("rolling_cv_wind_raw_granular", df[list(params_raw['input'])], forecasts_final, order_list)
files.download('rolling_cv_wind_raw_granular.csv')
```
## Result Analysis
```
import pandas as pd
from google.colab import files
files.upload()
def createBoxplot(filename, data, xticklabels, ylabel):
# Create a figure instance
fig = plt.figure(1, figsize=(9, 6))
# Create an axes instance
ax = fig.add_subplot(111)
# Create the boxplot
bp = ax.boxplot(data, patch_artist=True)
## change outline color, fill color and linewidth of the boxes
for box in bp['boxes']:
# change outline color
box.set( color='#7570b3', linewidth=2)
# change fill color
box.set( facecolor = '#AACCFF' )
## change color and linewidth of the whiskers
for whisker in bp['whiskers']:
whisker.set(color='#7570b3', linewidth=2)
## change color and linewidth of the caps
for cap in bp['caps']:
cap.set(color='#7570b3', linewidth=2)
## change color and linewidth of the medians
for median in bp['medians']:
median.set(color='#FFE680', linewidth=2)
## change the style of fliers and their fill
for flier in bp['fliers']:
flier.set(marker='o', color='#e7298a', alpha=0.5)
## Custom x-axis labels
ax.set_xticklabels(xticklabels)
ax.set_ylabel(ylabel)
plt.show()
fig.savefig(filename, bbox_inches='tight')
var_results = pd.read_csv("rolling_cv_wind_raw_var.csv")
evolving_results = pd.read_csv("rolling_cv_wind_raw_emvfts.csv")
mlp_results = pd.read_csv("rolling_cv_wind_raw_mlp_multi.csv")
granular_results = pd.read_csv("rolling_cv_wind_raw_granular.csv")
metric = 'RMSE'
results_data = [evolving_results[metric],var_results[metric], mlp_results[metric], granular_results[metric]]
xticks = ['e-MVFTS','VAR','MLP','FIG-FTS']
ylab = 'RMSE'
createBoxplot("e-mvfts_boxplot_rmse_solar", results_data, xticks, ylab)
pd.options.display.float_format = '{:.2f}'.format
metric = 'RMSE'
rmse_df = pd.DataFrame(columns=['e-MVFTS','VAR','MLP','FIG-FTS'])
rmse_df["e-MVFTS"] = evolving_results[metric]
rmse_df["VAR"] = var_results[metric]
rmse_df["MLP"] = mlp_results[metric]
rmse_df["FIG-FTS"] = granular_results[metric]
rmse_df.std()
metric = 'SMAPE'
results_data = [evolving_results[metric],var_results[metric], mlp_results[metric], granular_results[metric]]
xticks = ['e-MVFTS','VAR','MLP','FIG-FTS']
ylab = 'SMAPE'
createBoxplot("e-mvfts_boxplot_smape_solar", results_data, xticks, ylab)
metric = 'SMAPE'
smape_df = pd.DataFrame(columns=['e-MVFTS','VAR','MLP','FIG-FTS'])
smape_df["e-MVFTS"] = evolving_results[metric]
smape_df["VAR"] = var_results[metric]
smape_df["MLP"] = mlp_results[metric]
smape_df["FIG-FTS"] = granular_results[metric]
smape_df.std()
metric = "RMSE"
data = pd.DataFrame(columns=["VAR", "Evolving", "MLP", "Granular"])
data["VAR"] = var_results[metric]
data["Evolving"] = evolving_results[metric]
data["MLP"] = mlp_results[metric]
data["Granular"] = granular_results[metric]
ax = data.plot(figsize=(18,6))
ax.set(xlabel='Window', ylabel=metric)
fig = ax.get_figure()
#fig.savefig(path_images + exp_id + "_prequential.png")
x = np.arange(len(data.columns.values))
names = data.columns.values
values = data.mean().values
plt.figure(figsize=(5,6))
plt.bar(x, values, align='center', alpha=0.5, width=0.9)
plt.xticks(x, names)
#plt.yticks(np.arange(0, 1.1, 0.1))
plt.ylabel(metric)
#plt.savefig(path_images + exp_id + "_bars.png")
metric = "SMAPE"
data = pd.DataFrame(columns=["VAR", "Evolving", "MLP", "Granular"])
data["VAR"] = var_results[metric]
data["Evolving"] = evolving_results[metric]
data["MLP"] = mlp_results[metric]
data["Granular"] = granular_results[metric]
ax = data.plot(figsize=(18,6))
ax.set(xlabel='Window', ylabel=metric)
fig = ax.get_figure()
#fig.savefig(path_images + exp_id + "_prequential.png")
x = np.arange(len(data.columns.values))
names = data.columns.values
values = data.mean().values
plt.figure(figsize=(5,6))
plt.bar(x, values, align='center', alpha=0.5, width=0.9)
plt.xticks(x, names)
#plt.yticks(np.arange(0, 1.1, 0.1))
plt.ylabel(metric)
#plt.savefig(path_images + exp_id + "_bars.png")
```
| github_jupyter |
# Use `Lale` `AIF360` scorers to calculate and mitigate bias for credit risk AutoAI model
This notebook contains the steps and code to demonstrate support of AutoAI experiments in Watson Machine Learning service. It introduces commands for bias detecting and mitigation performed with `lale.lib.aif360` module.
Some familiarity with Python is helpful. This notebook uses Python 3.8.
## Contents
This notebook contains the following parts:
1. [Setup](#setup)
2. [Optimizer definition](#definition)
3. [Experiment Run](#run)
4. [Pipeline bias detection and mitigation](#bias)
5. [Deployment and score](#scoring)
6. [Clean up](#cleanup)
7. [Summary and next steps](#summary)
<a id="setup"></a>
## 1. Set up the environment
If you are not familiar with <a href="https://console.ng.bluemix.net/catalog/services/ibm-watson-machine-learning/" target="_blank" rel="noopener no referrer">Watson Machine Learning (WML) Service</a> and AutoAI experiments please read more about it in the sample notebook: <a href="https://github.com/IBM/watson-machine-learning-samples/blob/master/cloud/notebooks/python_sdk/experiments/autoai/Use%20AutoAI%20and%20Lale%20to%20predict%20credit%20risk.ipynb" target="_blank" rel="noopener no referrer">"Use AutoAI and Lale to predict credit risk with `ibm-watson-machine-learning`"</a>
### Install and import the `ibm-watson-machine-learning`, `lale` ,`aif360` and dependencies.
**Note:** `ibm-watson-machine-learning` documentation can be found <a href="http://ibm-wml-api-pyclient.mybluemix.net/" target="_blank" rel="noopener no referrer">here</a>.
```
!pip install -U ibm-watson-machine-learning | tail -n 1
!pip install -U scikit-learn==0.23.2 | tail -n 1
!pip install -U autoai-libs | tail -n 1
!pip install -U lale | tail -n 1
!pip install -U aif360 | tail -n 1
!pip install -U liac-arff | tail -n 1
!pip install -U cvxpy | tail -n 1
!pip install -U fairlearn | tail -n 1
```
### Connection to WML
Authenticate the Watson Machine Learning service on IBM Cloud. You need to provide Cloud `API key` and `location`.
**Tip**: Your `Cloud API key` can be generated by going to the [**Users** section of the Cloud console](https://cloud.ibm.com/iam#/users). From that page, click your name, scroll down to the **API Keys** section, and click **Create an IBM Cloud API key**. Give your key a name and click **Create**, then copy the created key and paste it below. You can also get a service specific url by going to the [**Endpoint URLs** section of the Watson Machine Learning docs](https://cloud.ibm.com/apidocs/machine-learning). You can check your instance location in your <a href="https://console.ng.bluemix.net/catalog/services/ibm-watson-machine-learning/" target="_blank" rel="noopener no referrer">Watson Machine Learning (WML) Service</a> instance details.
You can use [IBM Cloud CLI](https://cloud.ibm.com/docs/cli/index.html) to retrieve the instance `location`.
```
ibmcloud login --apikey API_KEY -a https://cloud.ibm.com
ibmcloud resource service-instance WML_INSTANCE_NAME
```
**NOTE:** You can also get a service specific apikey by going to the [**Service IDs** section of the Cloud Console](https://cloud.ibm.com/iam/serviceids). From that page, click **Create**, and then copy the created key and paste it in the following cell.
**Action**: Enter your `api_key` and `location` in the following cell.
```
api_key = 'PUT_YOUR_KEY_HERE'
location = 'us-south'
wml_credentials = {
"apikey": api_key,
"url": 'https://' + location + '.ml.cloud.ibm.com'
}
from ibm_watson_machine_learning import APIClient
client = APIClient(wml_credentials)
```
### Working with spaces
You need to create a space that will be used for your work. If you do not have a space, you can use [Deployment Spaces Dashboard](https://dataplatform.cloud.ibm.com/ml-runtime/spaces?context=cpdaas) to create one.
- Click **New Deployment Space**
- Create an empty space
- Select Cloud Object Storage
- Select Watson Machine Learning instance and press **Create**
- Copy `space_id` and paste it below
**Tip**: You can also use SDK to prepare the space for your work. More information can be found [here](https://github.com/IBM/watson-machine-learning-samples/blob/master/cloud/notebooks/python_sdk/instance-management/Space%20management.ipynb).
**Action**: assign space ID below
```
space_id = 'PASTE YOUR SPACE ID HERE'
client.spaces.list(limit=10)
client.set.default_space(space_id)
```
### Connections to COS
In next cell we read the COS credentials from the space.
```
cos_credentials = client.spaces.get_details(space_id=space_id)['entity']['storage']['properties']
```
<a id="definition"></a>
## 2. Optimizer definition
### Training data connection
Define connection information to COS bucket and training data CSV file. This example uses the [German Credit Risk dataset](https://raw.githubusercontent.com/IBM/watson-machine-learning-samples/master/cloud/data/credit_risk/credit_risk_training_light.csv).
The code in next cell uploads training data to the bucket.
```
filename = 'german_credit_data_biased_training.csv'
datasource_name = 'bluemixcloudobjectstorage'
bucketname = cos_credentials['bucket_name']
```
Download training data from git repository and split for training and test set.
```
import os, wget
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
url = 'https://raw.githubusercontent.com/IBM/watson-machine-learning-samples/master/cloud/data/credit_risk/german_credit_data_biased_training.csv'
if not os.path.isfile(filename): wget.download(url)
credit_risk_df = pd.read_csv(filename)
X = credit_risk_df.drop(['Risk'], axis=1)
y = credit_risk_df['Risk']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1)
credit_risk_df.head()
```
#### Create connection
```
conn_meta_props= {
client.connections.ConfigurationMetaNames.NAME: f"Connection to Database - {datasource_name} ",
client.connections.ConfigurationMetaNames.DATASOURCE_TYPE: client.connections.get_datasource_type_uid_by_name(datasource_name),
client.connections.ConfigurationMetaNames.DESCRIPTION: "Connection to external Database",
client.connections.ConfigurationMetaNames.PROPERTIES: {
'bucket': bucketname,
'access_key': cos_credentials['credentials']['editor']['access_key_id'],
'secret_key': cos_credentials['credentials']['editor']['secret_access_key'],
'iam_url': 'https://iam.cloud.ibm.com/identity/token',
'url': cos_credentials['endpoint_url']
}
}
conn_details = client.connections.create(meta_props=conn_meta_props)
```
**Note**: The above connection can be initialized alternatively with `api_key` and `resource_instance_id`.
The above cell can be replaced with:
```
conn_meta_props= {
client.connections.ConfigurationMetaNames.NAME: f"Connection to Database - {db_name} ",
client.connections.ConfigurationMetaNames.DATASOURCE_TYPE: client.connections.get_datasource_type_uid_by_name(db_name),
client.connections.ConfigurationMetaNames.DESCRIPTION: "Connection to external Database",
client.connections.ConfigurationMetaNames.PROPERTIES: {
'bucket': bucket_name,
'api_key': cos_credentials['apikey'],
'resource_instance_id': cos_credentials['resource_instance_id'],
'iam_url': 'https://iam.cloud.ibm.com/identity/token',
'url': 'https://s3.us.cloud-object-storage.appdomain.cloud'
}
}
conn_details = client.connections.create(meta_props=conn_meta_props)
```
```
connection_id = client.connections.get_uid(conn_details)
```
Define connection information to training data and upload train dataset to COS bucket.
```
from ibm_watson_machine_learning.helpers import DataConnection, S3Location
credit_risk_conn = DataConnection(
connection_asset_id=connection_id,
location=S3Location(bucket=bucketname,
path=filename))
credit_risk_conn._wml_client = client
training_data_reference=[credit_risk_conn]
credit_risk_conn.write(data=X_train.join(y_train), remote_name=filename)
```
### Optimizer configuration
Provide the input information for AutoAI optimizer:
- `name` - experiment name
- `prediction_type` - type of the problem
- `prediction_column` - target column name
- `scoring` - optimization metric
- `daub_include_only_estimators` - estimators which will be included during AutoAI training. More available estimators can be found in `experiment.ClassificationAlgorithms` enum
```
from ibm_watson_machine_learning.experiment import AutoAI
experiment = AutoAI(wml_credentials, space_id=space_id)
pipeline_optimizer = experiment.optimizer(
name='Credit Risk Bias detection in AutoAI',
prediction_type=AutoAI.PredictionType.BINARY,
prediction_column='Risk',
scoring=AutoAI.Metrics.ROC_AUC_SCORE,
include_only_estimators=[experiment.ClassificationAlgorithms.XGB]
)
```
<a id="run"></a>
## 3. Experiment run
Call the `fit()` method to trigger the AutoAI experiment. You can either use interactive mode (synchronous job) or background mode (asychronous job) by specifying `background_model=True`.
```
run_details = pipeline_optimizer.fit(
training_data_reference=training_data_reference,
background_mode=False)
pipeline_optimizer.get_run_status()
summary = pipeline_optimizer.summary()
summary
```
### Get selected pipeline model
Download pipeline model object from the AutoAI training job.
```
best_pipeline = pipeline_optimizer.get_pipeline()
```
<a id="bias"></a>
## 4. Bias detection and mitigation
The `fairness_info` dictionary contains some fairness-related metadata. The favorable and unfavorable label are values of the target class column that indicate whether the loan was granted or denied. A protected attribute is a feature that partitions the population into groups whose outcome should have parity. The credit-risk dataset has two protected attribute columns, sex and age. Each prottected attributes has privileged and unprivileged group.
Note that to use fairness metrics from lale with numpy arrays `protected_attributes.feature` need to be passed as index of the column in dataset, not as name.
```
fairness_info = {'favorable_labels': ['No Risk'],
'protected_attributes': [
{'feature': X.columns.get_loc('Sex'),'reference_group': ['male']},
{'feature': X.columns.get_loc('Age'), 'reference_group': [[26, 40]]}]}
fairness_info
```
### Calculate fairness metrics
We will calculate some model metrics. Accuracy describes how accurate is the model according to dataset.
Disparate impact is defined by comparing outcomes between a privileged group and an unprivileged group,
so it needs to check the protected attribute to determine group membership for the sample record at hand.
The third calculated metric takes the disparate impact into account along with accuracy. The best value of the score is 1.0.
```
import sklearn.metrics
from lale.lib.aif360 import disparate_impact, accuracy_and_disparate_impact
accuracy_scorer = sklearn.metrics.make_scorer(sklearn.metrics.accuracy_score)
print(f'accuracy {accuracy_scorer(best_pipeline, X_test.values, y_test.values):.1%}')
disparate_impact_scorer = disparate_impact(**fairness_info)
print(f'disparate impact {disparate_impact_scorer(best_pipeline, X_test.values, y_test.values):.2f}')
combined_scorer = accuracy_and_disparate_impact(**fairness_info)
print(f'accuracy and disparate impact metric {combined_scorer(best_pipeline, X_test.values, y_test.values):.2f}')
```
### Mitigation
`Hyperopt` minimizes (best_score - score_returned_by_the_scorer), where best_score is an argument to Hyperopt and score_returned_by_the_scorer is the value returned by the scorer for each evaluation point. We will use the `Hyperopt` to tune hyperparametres of the AutoAI pipeline to get new and more fair model.
```
from sklearn.linear_model import LogisticRegression as LR
from sklearn.tree import DecisionTreeClassifier as Tree
from sklearn.neighbors import KNeighborsClassifier as KNN
from lale.lib.lale import Hyperopt
from lale.lib.aif360 import FairStratifiedKFold
from lale import wrap_imported_operators
wrap_imported_operators()
prefix = best_pipeline.remove_last().freeze_trainable()
prefix.visualize()
new_pipeline = prefix >> (LR | Tree | KNN)
new_pipeline.visualize()
fair_cv = FairStratifiedKFold(**fairness_info, n_splits=3)
pipeline_fairer = new_pipeline.auto_configure(
X_train.values, y_train.values, optimizer=Hyperopt, cv=fair_cv,
max_evals=10, scoring=combined_scorer, best_score=1.0)
```
As with any trained model, we can evaluate and visualize the result.
```
print(f'accuracy {accuracy_scorer(pipeline_fairer, X_test.values, y_test.values):.1%}')
print(f'disparate impact {disparate_impact_scorer(pipeline_fairer, X_test.values, y_test.values):.2f}')
print(f'accuracy and disparate impact metric {combined_scorer(pipeline_fairer, X_test.values, y_test.values):.2f}')
pipeline_fairer.visualize()
```
As the result demonstrates, the best model found by AI Automation
has lower accuracy and much better disparate impact as the one we saw
before. Also, it has tuned the repair level and
has picked and tuned a classifier. These results may vary by dataset and search space.
You can get source code of the created pipeline. You just need to change the below cell type `Raw NBCovert` to `code`.
<a id="scoring"></a>
## 5. Deploy and Score
In this section you will learn how to deploy and score Lale pipeline model using WML instance.
#### Custom software_specification
Created model is AutoAI model refined with Lale. We will create new software specification based on default Python 3.7
environment extended by `autoai-libs` package.
```
base_sw_spec_uid = client.software_specifications.get_uid_by_name("default_py3.7")
print("Id of default Python 3.7 software specification is: ", base_sw_spec_uid)
url = 'https://raw.githubusercontent.com/IBM/watson-machine-learning-samples/master/cloud/configs/config.yaml'
if not os.path.isfile('config.yaml'): wget.download(url)
!cat config.yaml
```
`config.yaml` file describes details of package extention. Now you need to store new package extention with `APIClient`.
```
meta_prop_pkg_extn = {
client.package_extensions.ConfigurationMetaNames.NAME: "Scikt with autoai-libs",
client.package_extensions.ConfigurationMetaNames.DESCRIPTION: "Pkg extension for autoai-libs",
client.package_extensions.ConfigurationMetaNames.TYPE: "conda_yml"
}
pkg_extn_details = client.package_extensions.store(meta_props=meta_prop_pkg_extn, file_path="config.yaml")
pkg_extn_uid = client.package_extensions.get_uid(pkg_extn_details)
pkg_extn_url = client.package_extensions.get_href(pkg_extn_details)
```
Create new software specification and add created package extention to it.
```
meta_prop_sw_spec = {
client.software_specifications.ConfigurationMetaNames.NAME: "Mitigated AutoAI bases on scikit spec",
client.software_specifications.ConfigurationMetaNames.DESCRIPTION: "Software specification for scikt with autoai-libs",
client.software_specifications.ConfigurationMetaNames.BASE_SOFTWARE_SPECIFICATION: {"guid": base_sw_spec_uid}
}
sw_spec_details = client.software_specifications.store(meta_props=meta_prop_sw_spec)
sw_spec_uid = client.software_specifications.get_uid(sw_spec_details)
status = client.software_specifications.add_package_extension(sw_spec_uid, pkg_extn_uid)
```
You can get details of created software specification using `client.software_specifications.get_details(sw_spec_uid)`
### Store the model
```
model_props = {
client.repository.ModelMetaNames.NAME: "Fairer AutoAI model",
client.repository.ModelMetaNames.TYPE: 'scikit-learn_0.23',
client.repository.ModelMetaNames.SOFTWARE_SPEC_UID: sw_spec_uid
}
feature_vector = list(X.columns)
published_model = client.repository.store_model(
model=best_pipeline.export_to_sklearn_pipeline(),
meta_props=model_props,
training_data=X_train.values,
training_target=y_train.values,
feature_names=feature_vector,
label_column_names=['Risk']
)
published_model_uid = client.repository.get_model_id(published_model)
```
### Deployment creation
```
metadata = {
client.deployments.ConfigurationMetaNames.NAME: "Deployment of fairer model",
client.deployments.ConfigurationMetaNames.ONLINE: {}
}
created_deployment = client.deployments.create(published_model_uid, meta_props=metadata)
deployment_id = client.deployments.get_uid(created_deployment)
```
#### Deployment scoring
You need to pass scoring values as input data if the deployed model. Use `client.deployments.score()` method to get predictions from deployed model.
```
values = X_test.values
scoring_payload = {
"input_data": [{
'values': values[:5]
}]
}
predictions = client.deployments.score(deployment_id, scoring_payload)
predictions
```
<a id="cleanup"></a>
## 5. Clean up
If you want to clean up all created assets:
- experiments
- trainings
- pipelines
- model definitions
- models
- functions
- deployments
please follow up this sample [notebook](https://github.com/IBM/watson-machine-learning-samples/blob/master/cloud/notebooks/python_sdk/instance-management/Machine%20Learning%20artifacts%20management.ipynb).
<a id="summary"></a>
## 6. Summary and next steps
You successfully completed this notebook!.
Check out used packeges domuntations:
- `ibm-watson-machine-learning` [Online Documentation](https://www.ibm.com/cloud/watson-studio/autoai)
- `lale`: https://github.com/IBM/lale
- `aif360`: https://aif360.mybluemix.net/
### Authors
**Dorota Dydo-Rożniecka**, Intern in Watson Machine Learning at IBM
Copyright © 2020, 2021 IBM. This notebook and its source code are released under the terms of the MIT License.
| github_jupyter |
# Trade-off between classification accuracy and reconstruction error during dimensionality reduction
- Low-dimensional LSTM representations are excellent at dimensionality reduction, but are poor at reconstructing the original data
- On the other hand, PCs are excellent at reconstructing the original data but these high-variance components do not preserve class information
```
import numpy as np
import pandas as pd
import scipy as sp
import pickle
import os
import random
import sys
# visualizations
from _plotly_future_ import v4_subplots
import plotly.offline as py
py.init_notebook_mode(connected=True)
import plotly.graph_objs as go
import plotly.subplots as tls
import plotly.figure_factory as ff
import plotly.io as pio
import plotly.express as px
pio.templates.default = 'plotly_white'
pio.orca.config.executable = '/home/joyneelm/fire/bin/orca'
colors = px.colors.qualitative.Plotly
class ARGS():
roi = 300
net = 7
subnet = 'wb'
train_size = 100
batch_size = 32
num_epochs = 50
zscore = 1
#gru
k_hidden = 32
k_layers = 1
dims = [3, 4, 5, 10]
args = ARGS()
def _get_results(k_dim):
RES_DIR = 'results/clip_gru_recon'
load_path = (RES_DIR +
'/roi_%d_net_%d' %(args.roi, args.net) +
'_trainsize_%d' %(args.train_size) +
'_k_hidden_%d' %(args.k_hidden) +
'_kdim_%d' %(k_dim) +
'_k_layers_%d' %(args.k_layers) +
'_batch_size_%d' %(args.batch_size) +
'_num_epochs_45' +
'_z_%d.pkl' %(args.zscore))
with open(load_path, 'rb') as f:
results = pickle.load(f)
# print(results.keys())
return results
r = {}
for k_dim in args.dims:
r[k_dim] = _get_results(k_dim)
def _plot_fig(ss):
title_text = ss
if ss=='var':
ss = 'mse'
invert = True
else:
invert = False
subplot_titles = ['train', 'test']
fig = tls.make_subplots(rows=1,
cols=2,
subplot_titles=subplot_titles,
print_grid=False)
for ii, x in enumerate(['train', 'test']):
gru_score = {'mean':[], 'ste':[]}
pca_score = {'mean':[], 'ste':[]}
for k_dim in args.dims:
a = r[k_dim]
# gru decoder
y = np.mean(a['%s_%s'%(x, ss)])
gru_score['mean'].append(y)
# pca decoder
y = np.mean(a['%s_pca_%s'%(x, ss)])
pca_score['mean'].append(y)
x = np.arange(len(args.dims))
if invert:
y = 1 - np.array(gru_score['mean'])
else:
y = gru_score['mean']
error_y = gru_score['ste']
trace = go.Bar(x=x, y=y,
name='lstm decoder',
marker_color=colors[0])
fig.add_trace(trace, 1, ii+1)
if invert:
y = 1 - np.array(pca_score['mean'])
else:
y = pca_score['mean']
error_y = pca_score['ste']
trace = go.Bar(x=x, y=y,
name='pca recon',
marker_color=colors[1])
fig.add_trace(trace, 1, ii+1)
fig.update_xaxes(tickvals=np.arange(len(args.dims)),
ticktext=args.dims)
fig.update_layout(height=350, width=700,
title_text=title_text)
return fig
```
## Mean-squared error vs number of dimensions
```
'''
mse
'''
ss = 'mse'
fig = _plot_fig(ss)
fig.show()
```
## Variance captured vs number of dimensions
```
'''
variance
'''
ss = 'var'
fig = _plot_fig(ss)
fig.show()
```
## R-squared vs number of dimensions
```
'''
r2
'''
ss = 'r2'
fig = _plot_fig(ss)
fig.show()
results = r[10]
# variance not captured by pca recon
pca_not = 1 - np.sum(results['pca_var'])
print('percent variance captured by pca components = %0.3f' %(1 - pca_not))
# this is proportional to pca mse
pca_mse = results['test_pca_mse']
# variance not captured by lstm decoder?
lstm_mse = results['test_mse']
lstm_not = lstm_mse*(pca_not/pca_mse)
print('percent variance captured by lstm recon = %0.3f' %(1 - lstm_not))
def _plot_fig_ext(ss):
title_text = ss
if ss=='var':
ss = 'mse'
invert = True
else:
invert = False
subplot_titles = ['train', 'test']
fig = go.Figure()
x = 'test'
lstm_score = {'mean':[], 'ste':[]}
pca_score = {'mean':[], 'ste':[]}
lstm_acc = {'mean':[], 'ste':[]}
pc_acc = {'mean':[], 'ste':[]}
for k_dim in args.dims:
a = r[k_dim]
# lstm encoder
k_sub = len(a['test'])
y = np.mean(a['test'])
error_y = 3/np.sqrt(k_sub)*np.std(a['test'])
lstm_acc['mean'].append(y)
lstm_acc['ste'].append(error_y)
# lstm decoder
y = np.mean(a['%s_%s'%(x, ss)])
lstm_score['mean'].append(y)
lstm_score['ste'].append(error_y)
# pca encoder
b = r_pc[k_dim]
y = np.mean(b['test'])
error_y = 3/np.sqrt(k_sub)*np.std(b['test'])
pc_acc['mean'].append(y)
pc_acc['ste'].append(error_y)
# pca decoder
y = np.mean(a['%s_pca_%s'%(x, ss)])
pca_score['mean'].append(y)
pca_score['ste'].append(error_y)
x = np.arange(len(args.dims))
y = lstm_acc['mean']
error_y = lstm_acc['ste']
trace = go.Bar(x=x, y=y,
name='GRU Accuracy',
error_y=dict(type='data',
array=error_y),
marker_color=colors[3])
fig.add_trace(trace)
y = pc_acc['mean']
error_y = pc_acc['ste']
trace = go.Bar(x=x, y=y,
name='PCA Accuracy',
error_y=dict(type='data',
array=error_y),
marker_color=colors[4])
fig.add_trace(trace)
if invert:
y = 1 - np.array(lstm_score['mean'])
else:
y = lstm_score['mean']
error_y = lstm_score['ste']
trace = go.Bar(x=x, y=y,
name='GRU Reconstruction',
error_y=dict(type='data',
array=error_y),
marker_color=colors[5])
fig.add_trace(trace)
if invert:
y = 1 - np.array(pca_score['mean'])
else:
y = pca_score['mean']
error_y = pca_score['ste']
trace = go.Bar(x=x, y=y,
name='PCA Reconstruction',
error_y=dict(type='data',
array=error_y),
marker_color=colors[2])
fig.add_trace(trace)
fig.update_yaxes(title=dict(text='Accuracy or % variance',
font_size=20),
gridwidth=1, gridcolor='#bfbfbf',
tickfont=dict(size=20))
fig.update_xaxes(title=dict(text='Number of dimensions',
font_size=20),
tickvals=np.arange(len(args.dims)),
ticktext=args.dims,
tickfont=dict(size=20))
fig.update_layout(height=470, width=570,
font_color='black',
legend_orientation='h',
legend_font_size=20,
legend_x=-0.1,
legend_y=-0.3)
return fig
def _get_pc_results(PC_DIR, k_dim):
load_path = (PC_DIR +
'/roi_%d_net_%d' %(args.roi, args.net) +
'_nw_%s' %(args.subnet) +
'_trainsize_%d' %(args.train_size) +
'_kdim_%d_batch_size_%d' %(k_dim, args.batch_size) +
'_num_epochs_%d_z_%d.pkl' %(args.num_epochs, args.zscore))
with open(load_path, 'rb') as f:
results = pickle.load(f)
print(results.keys())
return results
```
## Comparison of LSTM and PCA: classification accuracy and variance captured
```
'''
variance
'''
r_pc = {}
PC_DIR = 'results/clip_pca'
for k_dim in args.dims:
r_pc[k_dim] = _get_pc_results(PC_DIR, k_dim)
colors = px.colors.qualitative.Set3
#colors = ["#D55E00", "#009E73", "#56B4E9", "#E69F00"]
ss = 'var'
fig = _plot_fig_ext(ss)
fig.show()
fig.write_image('figures/fig3c.png')
```
| github_jupyter |
```
imatlab_export_fig('print-png')
```
# Quadrature rules for 2.5-D resistivity modelling
We consider the evaluation of the integral
$$
\Phi(x, y, z) = \frac{2}{\pi} \int_0^\infty \tilde\Phi(k, y, z) \cos(k x)\, dk
$$
where
$$
\tilde\Phi(k, y, z) = K_0\left({k}{\sqrt{y^2 + z^2}}\right).
$$
The function $\tilde\Phi$ exhibits a different asymptotic behaviour depending on the magnitude of the argument, i.e., with $u := kr$
$$
u\to 0: K_0(u) \to -\ln(u)
$$
and
$$
u \to \infty: K_0(u) \to \frac{e^{-u}}{\sqrt{u}}.
$$
For a fixed distance $r = \sqrt{y^2 + z^2} = 1$ and $10^{-6} \le k \le 10^1$, we obtain the following figure:
```
k = logspace(-6, 4, 101);
kk = 1e-3;
u = besselk(0, k * kk);
padln = 65;
padexp = 15;
loglog(k, u, 'k', k(1:padln), -log(kk * k(1:padln)), 'r.', ...
k(end-padexp:end), exp(-kk * k(end-padexp:end))./sqrt(kk * k(end-padexp:end)), 'b.')
legend('K_0(u)', '-ln(u)', 'exp(-u)/sqrt(u)')
ylabel('\Phi(u)')
xlabel('u')
```
We split the integration at $k = k_0$, $0 < k_0 < \infty$.
We obtain
$$
\int_0^\infty \tilde\Phi(k)\,dk = \int_0^{k_0}\tilde\Phi(k)\,dk + \int_{k_0}^\infty\tilde\Phi(k)\,dk.
$$
### Gauss-Legendre quadrature
To avoid the singularity at $k \to 0$ for the first integral, we substitute $k'=\sqrt{k / k_0}$ and obtain with $dk = 2 k_0 k' dk'$
$$
\int_0^{k_0}\tilde\Phi(k)\,dk = \int_0^1 g(k')\,dk' \approx \sum_{n=1}^N w_n' g(k_n') = \sum_{n=1}^N w_n \tilde\Phi(k_n)
$$
with $w_n = 2 k_0 k_n' w_n' $ and $k_n = k_0 k_n'^2$.
### Gauss-Laguerre quadrature
For the second integral, we substitute $k' = k / k_0 - 1$, define $g(k') = k_0 \tilde\Phi(k)e^{k'}$, and obtain
$$
\int_{k_0}^\infty\tilde\Phi(k)\,dk = \int_0^\infty e^{-k'} g(k')\,dk' \approx \sum_{n=1}^N w_n' g(k_n') = \sum_{n=1}^N w_n \tilde\Phi(k_n)
$$
with $w_n = k_0 e^{k_n'}w_n'$ and $k_n = k_0 (k_n'+1)$.
### Choice of $k_0$
The actual value of $k_0$ depends on the smallest electrode spacing $r_{min}$.
More precisely, $k_0 = (2 r_{min})^{-1}$.
## Numerical test
In the case of a point electrode with current $I$ located at $\mathbf r' = (x', y', 0)^\top$ at the surface of a homogeneous halfspace with resistivity $\rho$, we obtain for the electric potential at point $\mathbf r = (x, y, z)^\top$
$$
\Phi(\mathbf r) = \dfrac{\rho I}{2 \pi |\mathbf r - \mathbf r'|}.
$$
We try to approximate the inverse Cosine transform
$$
\Phi(x, y, z) = \frac{2}{\pi} \int_0^\infty \tilde\Phi(k, y, z) \cos(k x)\, dk
$$
for the special case of $x = 0$ ($\cos(0) = 1$) by means of the Gauss quadrature rules introduced above.
For the smallest electrode spacing of, e.g., $|\mathbf r - \mathbf r'| = r_{min} = 1$ we would set $k_0 = 0.5$.
```
rmin = 1;
rp = rmin:1:100;
rp = rp(:);
k0 = 1 / (2 * rmin);
[x1, w1] = gauleg(0, 1, 17);
[x2, w2] = gaulag(7);
kn1 = k0 * x1 .* x1;
wn1 = 2 * k0 * x1 .* w1;
kn2 = k0 * (x2 + 1);
wn2 = k0 * exp(x2) .* w2;
k = [kn1(:); kn2(:)];
w = [wn1(:); wn2(:)];
```
We check the validity of the approximation by checking against the analytical solution for the homogeneous halfspace, which, in the case of $\rho = 2 \pi$ and $I = 1$, is simply
$$
\Phi_a(r) = \dfrac{1}{r}.
$$
```
k(1)
v = zeros(length(rp), 1);
for i = 1:length(rp)
v(i) = 2 / pi * sum(w .* besselk(0, k * rp(i)));
end
plot(rp, v, 'r.-', rp, 1 ./ rp, 'b')
xlabel('r in m')
ylabel('potential in V')
legend('transformed', 'analytical')
```
In the following plot, we display the relative error of the approximation
$$
e(r) := \left(1 - \dfrac{\Phi(r)}{\Phi_a(r)}\right) \cdot 100 \%
$$
with respect to the (normalized) electrode distance.
```
plot(rp / rmin, 100 * (1 - v .* rp), '.-');
grid();
xlabel('r / r_{min}');
ylabel('rel. error in %');
ylim([-0.05 0.05])
```
| github_jupyter |
# Introduction to Gym toolkit
## Gym Environments
The centerpiece of Gym is the environment, which defines the "game" in which your reinforcement algorithm will compete. An environment does not need to be a game; however, it describes the following game-like features:
* **action space**: What actions can we take on the environment, at each step/episode, to alter the environment.
* **observation space**: What is the current state of the portion of the environment that we can observe. Usually, we can see the entire environment.
Before we begin to look at Gym, it is essential to understand some of the terminology used by this library.
* **Agent** - The machine learning program or model that controls the actions.
Step - One round of issuing actions that affect the observation space.
* **Episode** - A collection of steps that terminates when the agent fails to meet the environment's objective, or the episode reaches the maximum number of allowed steps.
* **Render** - Gym can render one frame for display after each episode.
* **Reward** - A positive reinforcement that can occur at the end of each episode, after the agent acts.
* **Nondeterministic** - For some environments, randomness is a factor in deciding what effects actions have on reward and changes to the observation space.
```
import gym
def query_environment(name):
env = gym.make(name)
spec = gym.spec(name)
print(f"Action Space: {env.action_space}")
print(f"Observation Space: {env.observation_space}")
print(f"Max Episode Steps: {spec.max_episode_steps}")
print(f"Nondeterministic: {spec.nondeterministic}")
print(f"Reward Range: {env.reward_range}")
print(f"Reward Threshold: {spec.reward_threshold}")
query_environment("CartPole-v1")
```
The CartPole-v1 environment challenges the agent to move a cart while keeping a pole balanced. The environment has an observation space of 4 continuous numbers:
* Cart Position
* Cart Velocity
* Pole Angle
* Pole Velocity At Tip
To achieve this goal, the agent can take the following actions:
* Push cart to the left
* Push cart to the right
There is also a continuous variant of the mountain car. This version does not simply have the motor on or off. For the continuous car the action space is a single floating point number that specifies how much forward or backward force is being applied.
### Simple
```
import random
from typing import List
class Environment:
def __init__(self):
self.steps_left = 10
def get_observation(self) -> List[float]:
return [0.0, 0.0, 0.0]
def get_actions(self) -> List[int]:
return [0, 1]
def is_done(self) -> bool:
return self.steps_left == 0
def action(self, action: int) -> float:
if self.is_done():
raise Exception("Game is over")
self.steps_left -= 1
return random.random()
class Agent:
def __init__(self):
self.total_reward = 0.0
def step(self, env: Environment):
current_obs = env.get_observation()
actions = env.get_actions()
reward = env.action(random.choice(actions))
self.total_reward += reward
if __name__ == "__main__":
env = Environment()
agent = Agent()
while not env.is_done():
agent.step(env)
print("Total reward got: %.4f" % agent.total_reward)
```
### Frozenlake
```
import gym
env = gym.make("FrozenLake-v0")
env.render()
print(env.observation_space)
print(env.action_space)
```
| Number | Action |
| ------ | ------ |
| 0 | Left |
| 1 | Down |
| 2 | Right |
| 3 | Up |
We can obtain the transition probability and the reward function by just typing env.P[state][action]. So, to obtain the transition probability of moving from state S to the other states by performing the action right, we can type env.P[S][right]. But we cannot just type state S and action right directly since they are encoded as numbers. We learned that state S is encoded as 0 and the action right is encoded as 2, so, to obtain the transition probability of state S by performing the action right, we type env.P[0][2]
```
print(env.P[0][2])
```
Our output is in the form of [(transition probability, next state, reward, Is terminal state?)]
```
state = env.reset()
env.step(1)
(next_state, reward, done, info) = env.step(1)
```
- **next_state** represents the next state.
- **reward** represents the obtained reward.
- **done** implies whether our episode has ended. That is, if the next state is a terminal state, then our episode will end, so done will be marked as True else it will be marked as False.
- **info** — Apart from the transition probability, in some cases, we also obtain other information saved as info, which is used for debugging purposes.
```
random_action = env.action_space.sample()
next_state, reward, done, info = env.step(random_action)
```
**Generating an episode**
The episode is the agent environment interaction starting from the initial state to the terminal state. The agent interacts with the environment by performing some action in each state. An episode ends if the agent reaches the terminal state. So, in the Frozen Lake environment, the episode will end if the agent reaches the terminal state, which is either the hole state (H) or goal state (G).
```
import gym
env = gym.make("FrozenLake-v0")
state = env.reset()
print('Time Step 0 :')
env.render()
num_timesteps = 20
for t in range(num_timesteps):
random_action = env.action_space.sample()
new_state, reward, done, info = env.step(random_action)
print ('Time Step {} :'.format(t+1))
env.render()
if done:
break
```
Instead of generating one episode, we can also generate a series of episodes by taking some random action in each state
```
import gym
env = gym.make("FrozenLake-v0")
num_episodes = 10
num_timesteps = 20
for i in range(num_episodes):
state = env.reset()
print('Time Step 0 :')
env.render()
for t in range(num_timesteps):
random_action = env.action_space.sample()
new_state, reward, done, info = env.step(random_action)
print ('Time Step {} :'.format(t+1))
env.render()
if done:
break
```
### Cartpole
```
env = gym.make("CartPole-v0")
print(env.observation_space)
```
Note that all of these values are continuous, that is:
- The value of the cart position ranges from -4.8 to 4.8.
- The value of the cart velocity ranges from -Inf to Inf ( to ).
- The value of the pole angle ranges from -0.418 radians to 0.418 radians.
- The value of the pole velocity at the tip ranges from -Inf to Inf.
```
print(env.reset())
print(env.observation_space.high)
```
It implies that:
1. The maximum value of the cart position is 4.8.
2. We learned that the maximum value of the cart velocity is +Inf, and we know that infinity is not really a number, so it is represented using the largest positive real value 3.4028235e+38.
3. The maximum value of the pole angle is 0.418 radians.
4. The maximum value of the pole velocity at the tip is +Inf, so it is represented using the largest positive real value 3.4028235e+38.
```
print(env.observation_space.low)
```
It states that:
1. The minimum value of the cart position is -4.8.
2. We learned that the minimum value of the cart velocity is -Inf, and we know that infinity is not really a number, so it is represented using the largest negative real value -3.4028235e+38.
3. The minimum value of the pole angle is -0.418 radians.
4. The minimum value of the pole velocity at the tip is -Inf, so it is represented using the largest negative real value -3.4028235e+38.
```
print(env.action_space)
```
| Number | Action |
| ------ | ------ |
| 0 | Push cart to the left |
| 1 | Push cart to the right |
```
import gym
if __name__ == "__main__":
env = gym.make("CartPole-v0")
total_reward = 0.0
total_steps = 0
obs = env.reset()
while True:
action = env.action_space.sample()
obs, reward, done, _ = env.step(action)
total_reward += reward
total_steps += 1
if done:
break
print("Episode done in %d steps, total reward %.2f" % (
total_steps, total_reward))
```
## Wrappers
Very frequently, you will want to extend the environment's functionality in some generic way. For example, imagine an environment gives you some observations, but you want to accumulate them in some buffer and provide to the agent the N last observations. This is a common scenario for dynamic computer games, when one single frame is just not enough to get the full information about the game state. Another example is when you want to be able to crop or preprocess an image's pixels to make it more convenient for the agent to digest, or if you want to normalize reward scores somehow. There are many such situations that have the same structure – you want to "wrap" the existing environment and add some extra logic for doing something. Gym provides a convenient framework for these situations – the Wrapper class.
**Random action wrapper**
```
import gym
from typing import TypeVar
import random
Action = TypeVar('Action')
class RandomActionWrapper(gym.ActionWrapper):
def __init__(self, env, epsilon=0.1):
super(RandomActionWrapper, self).__init__(env)
self.epsilon = epsilon
def action(self, action: Action) -> Action:
if random.random() < self.epsilon:
print("Random!")
return self.env.action_space.sample()
return action
if __name__ == "__main__":
env = RandomActionWrapper(gym.make("CartPole-v0"))
obs = env.reset()
total_reward = 0.0
while True:
obs, reward, done, _ = env.step(0)
total_reward += reward
if done:
break
print("Reward got: %.2f" % total_reward)
```
## Atari GAN
```
! wget http://www.atarimania.com/roms/Roms.rar
! mkdir /content/ROM/
! unrar e /content/Roms.rar /content/ROM/
! python -m atari_py.import_roms /content/ROM/
```
### Normal
```
import random
import argparse
import cv2
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.tensorboard import SummaryWriter
import torchvision.utils as vutils
import gym
import gym.spaces
import numpy as np
log = gym.logger
log.set_level(gym.logger.INFO)
LATENT_VECTOR_SIZE = 100
DISCR_FILTERS = 64
GENER_FILTERS = 64
BATCH_SIZE = 16
# dimension input image will be rescaled
IMAGE_SIZE = 64
LEARNING_RATE = 0.0001
REPORT_EVERY_ITER = 100
SAVE_IMAGE_EVERY_ITER = 1000
class InputWrapper(gym.ObservationWrapper):
"""
Preprocessing of input numpy array:
1. resize image into predefined size
2. move color channel axis to a first place
"""
def __init__(self, *args):
super(InputWrapper, self).__init__(*args)
assert isinstance(self.observation_space, gym.spaces.Box)
old_space = self.observation_space
self.observation_space = gym.spaces.Box(
self.observation(old_space.low),
self.observation(old_space.high),
dtype=np.float32)
def observation(self, observation):
# resize image
new_obs = cv2.resize(
observation, (IMAGE_SIZE, IMAGE_SIZE))
# transform (210, 160, 3) -> (3, 210, 160)
new_obs = np.moveaxis(new_obs, 2, 0)
return new_obs.astype(np.float32)
class Discriminator(nn.Module):
def __init__(self, input_shape):
super(Discriminator, self).__init__()
# this pipe converges image into the single number
self.conv_pipe = nn.Sequential(
nn.Conv2d(in_channels=input_shape[0], out_channels=DISCR_FILTERS,
kernel_size=4, stride=2, padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=DISCR_FILTERS, out_channels=DISCR_FILTERS*2,
kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(DISCR_FILTERS*2),
nn.ReLU(),
nn.Conv2d(in_channels=DISCR_FILTERS * 2, out_channels=DISCR_FILTERS * 4,
kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(DISCR_FILTERS * 4),
nn.ReLU(),
nn.Conv2d(in_channels=DISCR_FILTERS * 4, out_channels=DISCR_FILTERS * 8,
kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(DISCR_FILTERS * 8),
nn.ReLU(),
nn.Conv2d(in_channels=DISCR_FILTERS * 8, out_channels=1,
kernel_size=4, stride=1, padding=0),
nn.Sigmoid()
)
def forward(self, x):
conv_out = self.conv_pipe(x)
return conv_out.view(-1, 1).squeeze(dim=1)
class Generator(nn.Module):
def __init__(self, output_shape):
super(Generator, self).__init__()
# pipe deconvolves input vector into (3, 64, 64) image
self.pipe = nn.Sequential(
nn.ConvTranspose2d(in_channels=LATENT_VECTOR_SIZE, out_channels=GENER_FILTERS * 8,
kernel_size=4, stride=1, padding=0),
nn.BatchNorm2d(GENER_FILTERS * 8),
nn.ReLU(),
nn.ConvTranspose2d(in_channels=GENER_FILTERS * 8, out_channels=GENER_FILTERS * 4,
kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(GENER_FILTERS * 4),
nn.ReLU(),
nn.ConvTranspose2d(in_channels=GENER_FILTERS * 4, out_channels=GENER_FILTERS * 2,
kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(GENER_FILTERS * 2),
nn.ReLU(),
nn.ConvTranspose2d(in_channels=GENER_FILTERS * 2, out_channels=GENER_FILTERS,
kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(GENER_FILTERS),
nn.ReLU(),
nn.ConvTranspose2d(in_channels=GENER_FILTERS, out_channels=output_shape[0],
kernel_size=4, stride=2, padding=1),
nn.Tanh()
)
def forward(self, x):
return self.pipe(x)
def iterate_batches(envs, batch_size=BATCH_SIZE):
batch = [e.reset() for e in envs]
env_gen = iter(lambda: random.choice(envs), None)
while True:
e = next(env_gen)
obs, reward, is_done, _ = e.step(e.action_space.sample())
if np.mean(obs) > 0.01:
batch.append(obs)
if len(batch) == batch_size:
# Normalising input between -1 to 1
batch_np = np.array(batch, dtype=np.float32) * 2.0 / 255.0 - 1.0
yield torch.tensor(batch_np)
batch.clear()
if is_done:
e.reset()
if __name__ == "__main__":
parser = argparse.ArgumentParser()
parser.add_argument(
"--cuda", default=False, action='store_true',
help="Enable cuda computation")
args = parser.parse_args(args={})
device = torch.device("cuda" if args.cuda else "cpu")
envs = [
InputWrapper(gym.make(name))
for name in ('Breakout-v0', 'AirRaid-v0', 'Pong-v0')
]
input_shape = envs[0].observation_space.shape
net_discr = Discriminator(input_shape=input_shape).to(device)
net_gener = Generator(output_shape=input_shape).to(device)
objective = nn.BCELoss()
gen_optimizer = optim.Adam(
params=net_gener.parameters(), lr=LEARNING_RATE,
betas=(0.5, 0.999))
dis_optimizer = optim.Adam(
params=net_discr.parameters(), lr=LEARNING_RATE,
betas=(0.5, 0.999))
writer = SummaryWriter()
gen_losses = []
dis_losses = []
iter_no = 0
true_labels_v = torch.ones(BATCH_SIZE, device=device)
fake_labels_v = torch.zeros(BATCH_SIZE, device=device)
for batch_v in iterate_batches(envs):
# fake samples, input is 4D: batch, filters, x, y
gen_input_v = torch.FloatTensor(
BATCH_SIZE, LATENT_VECTOR_SIZE, 1, 1)
gen_input_v.normal_(0, 1)
gen_input_v = gen_input_v.to(device)
batch_v = batch_v.to(device)
gen_output_v = net_gener(gen_input_v)
# train discriminator
dis_optimizer.zero_grad()
dis_output_true_v = net_discr(batch_v)
dis_output_fake_v = net_discr(gen_output_v.detach())
dis_loss = objective(dis_output_true_v, true_labels_v) + \
objective(dis_output_fake_v, fake_labels_v)
dis_loss.backward()
dis_optimizer.step()
dis_losses.append(dis_loss.item())
# train generator
gen_optimizer.zero_grad()
dis_output_v = net_discr(gen_output_v)
gen_loss_v = objective(dis_output_v, true_labels_v)
gen_loss_v.backward()
gen_optimizer.step()
gen_losses.append(gen_loss_v.item())
iter_no += 1
if iter_no % REPORT_EVERY_ITER == 0:
log.info("Iter %d: gen_loss=%.3e, dis_loss=%.3e",
iter_no, np.mean(gen_losses),
np.mean(dis_losses))
writer.add_scalar(
"gen_loss", np.mean(gen_losses), iter_no)
writer.add_scalar(
"dis_loss", np.mean(dis_losses), iter_no)
gen_losses = []
dis_losses = []
if iter_no % SAVE_IMAGE_EVERY_ITER == 0:
writer.add_image("fake", vutils.make_grid(
gen_output_v.data[:64], normalize=True), iter_no)
writer.add_image("real", vutils.make_grid(
batch_v.data[:64], normalize=True), iter_no)
```
### Ignite
```
import random
import argparse
import cv2
import torch
import torch.nn as nn
import torch.optim as optim
from ignite.engine import Engine, Events
from ignite.metrics import RunningAverage
from ignite.contrib.handlers import tensorboard_logger as tb_logger
import torchvision.utils as vutils
import gym
import gym.spaces
import numpy as np
log = gym.logger
log.set_level(gym.logger.INFO)
LATENT_VECTOR_SIZE = 100
DISCR_FILTERS = 64
GENER_FILTERS = 64
BATCH_SIZE = 16
# dimension input image will be rescaled
IMAGE_SIZE = 64
LEARNING_RATE = 0.0001
REPORT_EVERY_ITER = 100
SAVE_IMAGE_EVERY_ITER = 1000
class InputWrapper(gym.ObservationWrapper):
"""
Preprocessing of input numpy array:
1. resize image into predefined size
2. move color channel axis to a first place
"""
def __init__(self, *args):
super(InputWrapper, self).__init__(*args)
assert isinstance(self.observation_space, gym.spaces.Box)
old_space = self.observation_space
self.observation_space = gym.spaces.Box(self.observation(old_space.low), self.observation(old_space.high),
dtype=np.float32)
def observation(self, observation):
# resize image
new_obs = cv2.resize(observation, (IMAGE_SIZE, IMAGE_SIZE))
# transform (210, 160, 3) -> (3, 210, 160)
new_obs = np.moveaxis(new_obs, 2, 0)
return new_obs.astype(np.float32)
class Discriminator(nn.Module):
def __init__(self, input_shape):
super(Discriminator, self).__init__()
# this pipe converges image into the single number
self.conv_pipe = nn.Sequential(
nn.Conv2d(in_channels=input_shape[0], out_channels=DISCR_FILTERS,
kernel_size=4, stride=2, padding=1),
nn.ReLU(),
nn.Conv2d(in_channels=DISCR_FILTERS, out_channels=DISCR_FILTERS*2,
kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(DISCR_FILTERS*2),
nn.ReLU(),
nn.Conv2d(in_channels=DISCR_FILTERS * 2, out_channels=DISCR_FILTERS * 4,
kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(DISCR_FILTERS * 4),
nn.ReLU(),
nn.Conv2d(in_channels=DISCR_FILTERS * 4, out_channels=DISCR_FILTERS * 8,
kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(DISCR_FILTERS * 8),
nn.ReLU(),
nn.Conv2d(in_channels=DISCR_FILTERS * 8, out_channels=1,
kernel_size=4, stride=1, padding=0),
nn.Sigmoid()
)
def forward(self, x):
conv_out = self.conv_pipe(x)
return conv_out.view(-1, 1).squeeze(dim=1)
class Generator(nn.Module):
def __init__(self, output_shape):
super(Generator, self).__init__()
# pipe deconvolves input vector into (3, 64, 64) image
self.pipe = nn.Sequential(
nn.ConvTranspose2d(in_channels=LATENT_VECTOR_SIZE, out_channels=GENER_FILTERS * 8,
kernel_size=4, stride=1, padding=0),
nn.BatchNorm2d(GENER_FILTERS * 8),
nn.ReLU(),
nn.ConvTranspose2d(in_channels=GENER_FILTERS * 8, out_channels=GENER_FILTERS * 4,
kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(GENER_FILTERS * 4),
nn.ReLU(),
nn.ConvTranspose2d(in_channels=GENER_FILTERS * 4, out_channels=GENER_FILTERS * 2,
kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(GENER_FILTERS * 2),
nn.ReLU(),
nn.ConvTranspose2d(in_channels=GENER_FILTERS * 2, out_channels=GENER_FILTERS,
kernel_size=4, stride=2, padding=1),
nn.BatchNorm2d(GENER_FILTERS),
nn.ReLU(),
nn.ConvTranspose2d(in_channels=GENER_FILTERS, out_channels=output_shape[0],
kernel_size=4, stride=2, padding=1),
nn.Tanh()
)
def forward(self, x):
return self.pipe(x)
def iterate_batches(envs, batch_size=BATCH_SIZE):
batch = [e.reset() for e in envs]
env_gen = iter(lambda: random.choice(envs), None)
while True:
e = next(env_gen)
obs, reward, is_done, _ = e.step(e.action_space.sample())
if np.mean(obs) > 0.01:
batch.append(obs)
if len(batch) == batch_size:
# Normalising input between -1 to 1
batch_np = np.array(batch, dtype=np.float32) * 2.0 / 255.0 - 1.0
yield torch.tensor(batch_np)
batch.clear()
if is_done:
e.reset()
if __name__ == "__main__":
parser = argparse.ArgumentParser()
parser.add_argument("--cuda", default=False, action='store_true', help="Enable cuda computation")
args = parser.parse_args(args={})
device = torch.device("cuda" if args.cuda else "cpu")
# envs = [InputWrapper(gym.make(name)) for name in ('Breakout-v0', 'AirRaid-v0', 'Pong-v0')]
envs = [InputWrapper(gym.make(name)) for name in ['Breakout-v0']]
input_shape = envs[0].observation_space.shape
net_discr = Discriminator(input_shape=input_shape).to(device)
net_gener = Generator(output_shape=input_shape).to(device)
objective = nn.BCELoss()
gen_optimizer = optim.Adam(params=net_gener.parameters(), lr=LEARNING_RATE, betas=(0.5, 0.999))
dis_optimizer = optim.Adam(params=net_discr.parameters(), lr=LEARNING_RATE, betas=(0.5, 0.999))
true_labels_v = torch.ones(BATCH_SIZE, device=device)
fake_labels_v = torch.zeros(BATCH_SIZE, device=device)
def process_batch(trainer, batch):
gen_input_v = torch.FloatTensor(
BATCH_SIZE, LATENT_VECTOR_SIZE, 1, 1)
gen_input_v.normal_(0, 1)
gen_input_v = gen_input_v.to(device)
batch_v = batch.to(device)
gen_output_v = net_gener(gen_input_v)
# train discriminator
dis_optimizer.zero_grad()
dis_output_true_v = net_discr(batch_v)
dis_output_fake_v = net_discr(gen_output_v.detach())
dis_loss = objective(dis_output_true_v, true_labels_v) + \
objective(dis_output_fake_v, fake_labels_v)
dis_loss.backward()
dis_optimizer.step()
# train generator
gen_optimizer.zero_grad()
dis_output_v = net_discr(gen_output_v)
gen_loss = objective(dis_output_v, true_labels_v)
gen_loss.backward()
gen_optimizer.step()
if trainer.state.iteration % SAVE_IMAGE_EVERY_ITER == 0:
fake_img = vutils.make_grid(
gen_output_v.data[:64], normalize=True)
trainer.tb.writer.add_image(
"fake", fake_img, trainer.state.iteration)
real_img = vutils.make_grid(
batch_v.data[:64], normalize=True)
trainer.tb.writer.add_image(
"real", real_img, trainer.state.iteration)
trainer.tb.writer.flush()
return dis_loss.item(), gen_loss.item()
engine = Engine(process_batch)
tb = tb_logger.TensorboardLogger(log_dir=None)
engine.tb = tb
RunningAverage(output_transform=lambda out: out[1]).\
attach(engine, "avg_loss_gen")
RunningAverage(output_transform=lambda out: out[0]).\
attach(engine, "avg_loss_dis")
handler = tb_logger.OutputHandler(tag="train",
metric_names=['avg_loss_gen', 'avg_loss_dis'])
tb.attach(engine, log_handler=handler,
event_name=Events.ITERATION_COMPLETED)
@engine.on(Events.ITERATION_COMPLETED)
def log_losses(trainer):
if trainer.state.iteration % REPORT_EVERY_ITER == 0:
log.info("%d: gen_loss=%f, dis_loss=%f",
trainer.state.iteration,
trainer.state.metrics['avg_loss_gen'],
trainer.state.metrics['avg_loss_dis'])
engine.run(data=iterate_batches(envs))
```
## Render environments in Colab
### Alternative 1
It is possible to visualize the game your agent is playing, even on CoLab. This section provides information on how to generate a video in CoLab that shows you an episode of the game your agent is playing. This video process is based on suggestions found [here](https://colab.research.google.com/drive/1flu31ulJlgiRL1dnN2ir8wGh9p7Zij2t).
Begin by installing **pyvirtualdisplay** and **python-opengl**.
```
!pip install gym pyvirtualdisplay > /dev/null 2>&1
!apt-get install -y xvfb python-opengl ffmpeg > /dev/null 2>&1
!apt-get update > /dev/null 2>&1
!apt-get install cmake > /dev/null 2>&1
!pip install --upgrade setuptools 2>&1
!pip install ez_setup > /dev/null 2>&1
!pip install gym[atari] > /dev/null 2>&1
!wget http://www.atarimania.com/roms/Roms.rar
!mkdir /content/ROM/
!unrar e /content/Roms.rar /content/ROM/
!python -m atari_py.import_roms /content/ROM/
import gym
from gym.wrappers import Monitor
import glob
import io
import base64
from IPython.display import HTML
from pyvirtualdisplay import Display
from IPython import display as ipythondisplay
display = Display(visible=0, size=(1400, 900))
display.start()
"""
Utility functions to enable video recording of gym environment
and displaying it.
To enable video, just do "env = wrap_env(env)""
"""
def show_video():
mp4list = glob.glob('video/*.mp4')
if len(mp4list) > 0:
mp4 = mp4list[0]
video = io.open(mp4, 'r+b').read()
encoded = base64.b64encode(video)
ipythondisplay.display(HTML(data='''<video alt="test" autoplay
loop controls style="height: 400px;">
<source src="data:video/mp4;base64,{0}" type="video/mp4" />
</video>'''.format(encoded.decode('ascii'))))
else:
print("Could not find video")
def wrap_env(env):
env = Monitor(env, './video', force=True)
return env
#env = wrap_env(gym.make("MountainCar-v0"))
env = wrap_env(gym.make("Atlantis-v0"))
observation = env.reset()
while True:
env.render()
#your agent goes here
action = env.action_space.sample()
observation, reward, done, info = env.step(action)
if done:
break;
env.close()
show_video()
```
### Alternative 2
```
!apt-get install -y xvfb python-opengl ffmpeg > /dev/null 2>&1
!pip install colabgymrender
import gym
from colabgymrender.recorder import Recorder
env = gym.make("Breakout-v0")
directory = './video'
env = Recorder(env, directory)
observation = env.reset()
terminal = False
while not terminal:
action = env.action_space.sample()
observation, reward, terminal, info = env.step(action)
env.play()
```
| github_jupyter |
| Name | Description | Date
| :- |-------------: | :-:
|<font color=red>__Reza Hashemi__</font>| __Function approximation by linear model and deep network LOOP test__. | __On 10th of August 2019__
# Function approximation with linear models and neural network
* Are Linear models sufficient for approximating transcedental functions? What about polynomial functions?
* Do neural networks perform better in those cases?
* Does the depth of the neural network matter?
### Import basic libraries
```
import numpy as np
import pandas as pd
import math
import matplotlib.pyplot as plt
%matplotlib inline
```
### Global variables for the program
```
N_points = 100 # Number of points for constructing function
x_min = 1 # Min of the range of x (feature)
x_max = 25 # Max of the range of x (feature)
noise_mean = 0 # Mean of the Gaussian noise adder
noise_sd = 10 # Std.Dev of the Gaussian noise adder
test_set_fraction = 0.2
```
### Generate feature and output vector for a non-linear function with transcedental terms
The ground truth or originating function is as follows:
$$ y=f(x)= (20x+3x^2+0.1x^3).sin(x).e^{-0.1x}+\psi(x) $$
$$ {OR} $$
$$ y=f(x)= (20x+3x^2+0.1x^3)+\psi(x) $$
$${where,}\ \psi(x) : {\displaystyle f(x\;|\;\mu ,\sigma ^{2})={\frac {1}{\sqrt {2\pi \sigma ^{2}}}}\;e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}} $$
```
# Definition of the function with exponential and sinusoidal terms
def func_trans(x):
result = (20*x+3*x**2+0.1*x**3)*np.sin(x)*np.exp(-0.1*x)
return (result)
# Definition of the function without exponential and sinusoidal terms i.e. just the polynomial
def func_poly(x):
result = 20*x+3*x**2+0.1*x**3
return (result)
# Densely spaced points for generating the ideal functional curve
x_smooth = np.array(np.linspace(x_min,x_max,501))
# Use one of the following
y_smooth = func_trans(x_smooth)
#y_smooth = func_poly(x_smooth)
# Linearly spaced sample points
X=np.array(np.linspace(x_min,x_max,N_points))
# Added observational/measurement noise
noise_x = np.random.normal(loc=noise_mean,scale=noise_sd,size=N_points)
# Observed output after adding the noise
y = func_trans(X)+noise_x
# Store the values in a DataFrame
df = pd.DataFrame(data=X,columns=['X'])
df['Ideal y']=df['X'].apply(func_trans)
df['Sin_X']=df['X'].apply(math.sin)
df['y']=y
df.head()
```
### Plot the function(s), both the ideal characteristic and the observed output (with process and observation noise)
```
df.plot.scatter('X','y',title='True process and measured samples\n',
grid=True,edgecolors=(0,0,0),c='blue',s=60,figsize=(10,6))
plt.plot(x_smooth,y_smooth,'k')
```
### Import scikit-learn librares and prepare train/test splits
```
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import LassoCV
from sklearn.linear_model import RidgeCV
from sklearn.ensemble import AdaBoostRegressor
from sklearn.preprocessing import PolynomialFeatures
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
X_train, X_test, y_train, y_test = train_test_split(df[['X','Sin_X']], df['y'], test_size=test_set_fraction)
#X_train=X_train.reshape(X_train.size,1)
#y_train=y_train.reshape(y_train.size,1)
#X_test=X_test.reshape(X_test.size,1)
#y_test=y_test.reshape(y_test.size,1)
#X_train=X_train.reshape(-1,1)
#y_train=y_train.reshape(-1,1)
#X_test=X_test.reshape(-1,1)
#y_test=y_test.reshape(-1,1)
from sklearn import preprocessing
X_scaled = preprocessing.scale(X_train)
y_scaled = preprocessing.scale(y_train)
```
### Polynomial model with LASSO/Ridge regularization (pipelined) with lineary spaced samples
** This is an advanced machine learning method which prevents over-fitting by penalizing high-valued coefficients i.e. keep them bounded **
```
# Regression model parameters
ridge_alpha = tuple([10**(x) for x in range(-3,0,1) ]) # Alpha (regularization strength) of ridge regression
# Alpha (regularization strength) of LASSO regression
lasso_eps = 0.0001
lasso_nalpha=20
lasso_iter=5000
# Min and max degree of polynomials features to consider
degree_min = 2
degree_max = 8
linear_sample_score = []
poly_degree = []
rmse=[]
t_linear=[]
import time
for degree in range(degree_min,degree_max+1):
t1=time.time()
#model = make_pipeline(PolynomialFeatures(degree), RidgeCV(alphas=ridge_alpha,normalize=True,cv=5))
model = make_pipeline(PolynomialFeatures(degree), LassoCV(eps=lasso_eps,n_alphas=lasso_nalpha,
max_iter=lasso_iter,normalize=True,cv=5))
#model = make_pipeline(PolynomialFeatures(degree), LinearRegression(normalize=True))
model.fit(X_train, y_train)
t2=time.time()
t = t2-t1
t_linear.append(t)
test_pred = np.array(model.predict(X_test))
RMSE=np.sqrt(np.sum(np.square(test_pred-y_test)))
test_score = model.score(X_test,y_test)
linear_sample_score.append(test_score)
rmse.append(RMSE)
poly_degree.append(degree)
#print("Test score of model with degree {}: {}\n".format(degree,test_score))
plt.figure()
plt.title("Predicted vs. actual for polynomial of degree {}".format(degree),fontsize=15)
plt.xlabel("Actual values")
plt.ylabel("Predicted values")
plt.scatter(y_test,test_pred)
plt.plot(y_test,y_test,'r',lw=2)
linear_sample_score
plt.figure(figsize=(8,5))
plt.grid(True)
plt.plot(poly_degree,rmse,lw=3,c='red')
plt.title("Model complexity (highest polynomial degree) vs. test score\n",fontsize=20)
plt.xlabel ("\nDegree of polynomial",fontsize=20)
plt.ylabel ("Root-mean-square error on test set",fontsize=15)
df_score = pd.DataFrame(data={'degree':[d for d in range(degree_min,degree_max+1)],
'Linear sample score':linear_sample_score})
# Save the best R^2 score
r2_linear = max(linear_sample_score)
print("Best R^2 score for linear polynomial degree models:",r2_linear)
plt.figure(figsize=(8,5))
plt.grid(True)
plt.plot(poly_degree,linear_sample_score,lw=3,c='red')
plt.xlabel ("\nModel Complexity: Degree of polynomial",fontsize=20)
plt.ylabel ("R^2 score on test set",fontsize=15)
```
## 1-hidden layer (Shallow) network
```
import tensorflow as tf
learning_rate = 1e-6
training_epochs = 150000
n_input = 1 # Number of features
n_output = 1 # Regression output is a number only
n_hidden_layer = 100 # layer number of features
weights = {
'hidden_layer': tf.Variable(tf.random_normal([n_input, n_hidden_layer])),
'out': tf.Variable(tf.random_normal([n_hidden_layer, n_output]))
}
biases = {
'hidden_layer': tf.Variable(tf.random_normal([n_hidden_layer])),
'out': tf.Variable(tf.random_normal([n_output]))
}
# tf Graph input
x = tf.placeholder("float32", [None,n_input])
y = tf.placeholder("float32", [None,n_output])
# Hidden layer with RELU activation
layer_1 = tf.add(tf.matmul(x, weights['hidden_layer']),biases['hidden_layer'])
layer_1 = tf.sin(layer_1)
# Output layer with linear activation
ops = tf.add(tf.matmul(layer_1, weights['out']), biases['out'])
# Define loss and optimizer
cost = tf.reduce_mean(tf.squared_difference(ops,y))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(cost)
from tqdm import tqdm
import time
# Initializing the variables
init = tf.global_variables_initializer()
# Empty lists for book-keeping purpose
epoch=0
log_epoch = []
epoch_count=[]
acc=[]
loss_epoch=[]
X_train, X_test, y_train, y_test = train_test_split(df['X'], df['y'],
test_size=test_set_fraction)
X_train=X_train.reshape(X_train.size,1)
y_train=y_train.reshape(y_train.size,1)
X_test=X_test.reshape(X_test.size,1)
y_test=y_test.reshape(y_test.size,1)
# Launch the graph and time the session
t1=time.time()
with tf.Session() as sess:
sess.run(init)
# Loop over epochs
for epoch in tqdm(range(training_epochs)):
# Run optimization process (backprop) and cost function (to get loss value)
_,l=sess.run([optimizer,cost], feed_dict={x: X_train, y: y_train})
loss_epoch.append(l) # Save the loss for every epoch
epoch_count.append(epoch+1) #Save the epoch count
# print("Epoch {}/{} finished. Loss: {}, Accuracy: {}".format(epoch+1,training_epochs,round(l,4),round(accu,4)))
#print("Epoch {}/{} finished. Loss: {}".format(epoch+1,training_epochs,round(l,4)))
w=sess.run(weights)
b = sess.run(biases)
yhat=sess.run(ops,feed_dict={x:X_test})
t2=time.time()
time_SNN = t2-t1
plt.plot(loss_epoch)
# Total variance
SSt_SNN = np.sum(np.square(y_test-np.mean(y_test)))
# Residual sum of squares
SSr_SNN = np.sum(np.square(yhat-y_test))
# Root-mean-square error
RMSE_SNN = np.sqrt(np.sum(np.square(yhat-y_test)))
# R^2 coefficient
r2_SNN = 1-(SSr_SNN/SSt_SNN)
print("RMSE error of the shallow neural network:",RMSE_SNN)
print("R^2 value of the shallow neural network:",r2_SNN)
plt.figure(figsize=(10,6))
plt.title("Predicted vs. actual (test set) for shallow (1-hidden layer) neural network\n",fontsize=15)
plt.xlabel("Actual values (test set)")
plt.ylabel("Predicted values")
plt.scatter(y_test,yhat,edgecolors='k',s=100,c='green')
plt.grid(True)
plt.plot(y_test,y_test,'r',lw=2)
```
## Deep Neural network for regression
### Import and declaration of variables
```
import tensorflow as tf
learning_rate = 1e-6
training_epochs = 15000
n_input = 1 # Number of features
n_output = 1 # Regression output is a number only
n_hidden_layer_1 = 30 # Hidden layer 1
n_hidden_layer_2 = 30 # Hidden layer 2
```
### Weights and bias variable
```
# Store layers weight & bias as Variables classes in dictionaries
weights = {
'hidden_layer_1': tf.Variable(tf.random_normal([n_input, n_hidden_layer_1])),
'hidden_layer_2': tf.Variable(tf.random_normal([n_hidden_layer_1, n_hidden_layer_2])),
'out': tf.Variable(tf.random_normal([n_hidden_layer_2, n_output]))
}
biases = {
'hidden_layer_1': tf.Variable(tf.random_normal([n_hidden_layer_1])),
'hidden_layer_2': tf.Variable(tf.random_normal([n_hidden_layer_2])),
'out': tf.Variable(tf.random_normal([n_output]))
}
```
### Input data as placeholder
```
# tf Graph input
x = tf.placeholder("float32", [None,n_input])
y = tf.placeholder("float32", [None,n_output])
```
### Hidden and output layers definition (using TensorFlow mathematical functions)
```
# Hidden layer with activation
layer_1 = tf.add(tf.matmul(x, weights['hidden_layer_1']),biases['hidden_layer_1'])
layer_1 = tf.sin(layer_1)
layer_2 = tf.add(tf.matmul(layer_1, weights['hidden_layer_2']),biases['hidden_layer_2'])
layer_2 = tf.nn.relu(layer_2)
# Output layer with linear activation
ops = tf.add(tf.matmul(layer_2, weights['out']), biases['out'])
```
### Gradient descent optimizer for training (backpropagation):
For the training of the neural network we need to perform __backpropagation__ i.e. propagate the errors, calculated by this cost function, backwards through the layers all the way up to the input weights and bias in order to adjust them accordingly (minimize the error). This involves taking first-order derivatives of the activation functions and applying chain-rule to ___'multiply'___ the effect of various layers as the error propagates back.
You can read more on this here: [Backpropagation in Neural Network](https://en.wikipedia.org/wiki/Backpropagation)
Fortunately, TensorFlow already implicitly implements this step i.e. takes care of all the chained differentiations for us. All we need to do is to specify an Optimizer object and pass on the cost function. Here, we are using a Gradient Descent Optimizer.
Gradient descent is a first-order iterative optimization algorithm for finding the minimum of a function. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient (or of the approximate gradient) of the function at the current point.
You can read more on this: [Gradient Descent](https://en.wikipedia.org/wiki/Gradient_descent)
```
# Define loss and optimizer
cost = tf.reduce_mean(tf.squared_difference(ops,y))
optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(cost)
```
### TensorFlow Session for training and loss estimation
```
from tqdm import tqdm
import time
# Initializing the variables
init = tf.global_variables_initializer()
# Empty lists for book-keeping purpose
epoch=0
log_epoch = []
epoch_count=[]
acc=[]
loss_epoch=[]
r2_DNN = []
test_size = []
for i in range(5):
X_train, X_test, y_train, y_test = train_test_split(df['X'], df['y'],
test_size=test_set_fraction)
X_train=X_train.reshape(X_train.size,1)
y_train=y_train.reshape(y_train.size,1)
X_test=X_test.reshape(X_test.size,1)
y_test=y_test.reshape(y_test.size,1)
# Launch the graph and time the session
with tf.Session() as sess:
sess.run(init)
# Loop over epochs
for epoch in tqdm(range(training_epochs)):
# Run optimization process (backprop) and cost function (to get loss value)
#r1 = int(epoch/10000)
#learning_rate = learning_rate-r1*3e-6
#optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate).minimize(cost)
_,l=sess.run([optimizer,cost], feed_dict={x: X_train, y: y_train})
yhat=sess.run(ops,feed_dict={x:X_test})
#test_size.append(0.5-(i*0.04))
# Total variance
SSt_DNN = np.sum(np.square(y_test-np.mean(y_test)))
# Residual sum of squares
SSr_DNN = np.sum(np.square(yhat-y_test))
# Root-mean-square error
RMSE_DNN = np.sqrt(np.sum(np.square(yhat-y_test)))
# R^2 coefficient
r2 = 1-(SSr_DNN/SSt_DNN)
r2_DNN.append(r2)
print("Run: {} finished. Score: {}".format(i+1,r2))
```
### Plot R2 score corss-validation results
```
plt.figure(figsize=(10,6))
plt.title("\nR2-score for cross-validation runs of \ndeep (2-layer) neural network\n",fontsize=25)
plt.xlabel("\nCross-validation run with random test/train split #",fontsize=15)
plt.ylabel("R2 score (test set)\n",fontsize=15)
plt.scatter([i+1 for i in range(5)],r2_DNN,edgecolors='k',s=100,c='green')
plt.grid(True)
```
| github_jupyter |
# Controlling Flow with Conditional Statements
Now that you've learned how to create conditional statements, let's learn how to use them to control the flow of our programs. This is done with `if`, `elif`, and `else` statements.
## The `if` Statement
What if we wanted to check if a number was divisible by 2 and if so then print that number out. Let's diagram that out.

- Check to see if A is even
- If yes, then print our message: "A is even"
This use case can be translated into a "if" statement. I'm going to write this out in pseudocode which looks very similar to Python.
```text
if A is even:
print "A is even"
```
```
# Let's translate this into Python code
def check_evenness(A):
if A % 2 == 0:
print(f"A ({A:02}) is even!")
for i in range(1, 11):
check_evenness(i)
# You can do multiple if statements and they're executed sequentially
A = 10
if A > 0:
print('A is positive')
if A % 2 == 0:
print('A is even!')
```
## The `else` Statement
But what if we wanted to know if the number was even OR odd? Let's diagram that out:

Again, translating this to pseudocode, we're going to use the 'else' statement:
```text
if A is even:
print "A is even"
else:
print "A is odd"
```
```
# Let's translate this into Python code
def check_evenness(A):
if A % 2 == 0:
print(f"A ({A:02}) is even!")
else:
print(f'A ({A:02}) is odd!')
for i in range(1, 11):
check_evenness(i)
```
# The 'else if' or `elif` Statement
What if we wanted to check if A is divisible by 2 or 3? Let's diagram that out:

Again, translating this into psuedocode, we're going to use the 'else if' statement.
```text
if A is divisible by 2:
print "2 divides A"
else if A is divisible by 3:
print "3 divides A"
else
print "2 and 3 don't divide A"
```
```
# Let's translate this into Python code
def check_divisible_by_2_and_3(A):
if A % 2 == 0:
print(f"2 divides A ({A:02})!")
# else if in Python is elif
elif A % 3 == 0:
print(f'3 divides A ({A:02})!')
else:
print(f'A ({A:02}) is not divisible by 2 or 3)')
for i in range(1, 11):
check_divisible_by_2_and_3(i)
```
## Order Matters
When chaining conditionals, you need to be careful how you order them. For example, what if we wanted te check if a number is divisible by 2, 3, or both:

```
# Let's translate this into Python code
def check_divisible_by_2_and_3(A):
if A % 2 == 0:
print(f"2 divides A ({A:02})!")
elif A % 3 == 0:
print(f'3 divides A ({A:02})!')
elif A % 2 == 0 and A % 3 == 0:
print(f'2 and 3 divides A ({A:02})!')
else:
print(f"2 or 3 doesn't divide A ({A:02})")
for i in range(1, 11):
check_divisible_by_2_and_3(i)
```
Wait! we would expect that 6, which is divisible by both 2 and 3 to show that! Looking back at the graphic, we can see that the flow is checking for 2 first, and since that's true we follow that path first. Let's make a correction to our diagram to fix this:

```
# Let's translate this into Python code
def check_divisible_by_2_and_3(A):
if A % 2 == 0 and A % 3 == 0:
print(f'2 and 3 divides A ({A:02})!')
elif A % 3 == 0:
print(f'3 divides A ({A:02})!')
elif A % 2 == 0:
print(f"2 divides A ({A:02})!")
else:
print(f"2 or 3 doesn't divide A ({A:02})")
for i in range(1, 11):
check_divisible_by_2_and_3(i)
```
**NOTE:** Always put your most restrictive conditional at the top of your if statements and then work your way down to the least restrictive.

## In-Class Assignments
- Create a funcition that takes two inputs variables `A` and `divisor`. Check if `divisor` divides into `A`. If it does, print `"<value of A> is divided by <value of divisor>"`. Don't forget about the `in` operator that checks if a substring is in another string.
- Create a function that takes an input variable `A` which is a string. Check if `A` has the substring `apple`, `peach`, or `blueberry` in it. Print out which of these are found within the string. Note: you could do this using just if/elif/else statements, but is there a better way using lists, for loops, and if/elif/else statements?
## Solutions
```
def is_divisible(A, divisor):
if A % divisor == 0:
print(f'{A} is divided by {divisor}')
A = 37
# this is actually a crude way to find if the number is prime
for i in range(2, int(A / 2)):
is_divisible(A, i)
# notice that nothing was printed? That's because 37 is prime
B = 27
for i in range(2, int(B / 2)):
is_divisible(B, i)
# this is ONE solution. There are more out there and probably better
# one too
def check_for_fruit(A):
found_fruit = []
if 'apple' in A:
found_fruit.append('apple')
if 'peach' in A:
found_fruit.append('peach')
if 'blueberry' in A:
found_fruit.append('blueberry')
found_fruit_str = ''
for fruit in found_fruit:
found_fruit_str += fruit
found_fruit_str += ', '
if len(found_fruit) > 0:
print(found_fruit_str + ' is found within the string')
else:
print('No fruit found in the string')
check_for_fruit('there are apples and peaches in this pie')
```
| github_jupyter |
# Laboratorio 8
```
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.neighbors import KNeighborsClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import plot_confusion_matrix
%matplotlib inline
digits_X, digits_y = datasets.load_digits(return_X_y=True, as_frame=True)
digits = pd.concat([digits_X, digits_y], axis=1)
digits.head()
```
## Ejercicio 1
(1 pto.)
Utilizando todos los datos, ajusta un modelo de regresión logística a los datos de dígitos. No agregues intercepto y define un máximo de iteraciones de 400.
Obtén el _score_ y explica el tan buen resultado.
```
logistic = LogisticRegression(solver="lbfgs", max_iter=400, fit_intercept=False)
fit=logistic.fit(digits_X, digits_y)
print(f"El score del modelo de regresión logística es {fit.score(digits_X, digits_y)}")
```
__Respuesta:__ Supongo que es porque no estamos usando los datos originales, y no otros datos predecidos a partir de los originales
## Ejercicio 2
(1 pto.)
Utilizando todos los datos, ¿Cuál es la mejor elección del parámetro $k$ al ajustar un modelo kNN a los datos de dígitos? Utiliza valores $k=2, ..., 10$.
```
for k in range(2, 11):
kNN = KNeighborsClassifier(n_neighbors=k)
fit=kNN.fit(digits_X, digits_y)
print(f"El score del modelo de kNN con k={k} es {fit.score(digits_X, digits_y)}")
```
__Respuesta:__ El caso k=3, porque es el mas cercano a 1.
## Ejercicio 3
(1 pto.)
Grafica la matriz de confusión normalizada por predicción de ambos modelos (regresión logística y kNN con la mejor elección de $k$).
¿Qué conclusión puedes sacar?
Hint: Revisa el argumento `normalize` de la matriz de confusión.
```
plot_confusion_matrix(logistic, digits_X, digits_y, normalize='true');
best_knn = KNeighborsClassifier(n_neighbors=3)
B_kNN = best_knn.fit(digits_X, digits_y)
plot_confusion_matrix(B_kNN, digits_X, digits_y, normalize='true');
```
__Respuesta:__ Que la primera matriz es una mejor prediccion que la segunda, esto porque se pudo obtener una matriz diagonal con, asumo, menor cantidad de errores comparado a los valores que no se encuentran en la diagonal y que son distintos de 0 en el segundo caso.
## Ejercicio 4
(1 pto.)
Escoge algún registro donde kNN se haya equivocado, _plotea_ la imagen y comenta las razones por las que el algoritmo se pudo haber equivocado.
```
neigh_tt = KNeighborsClassifier(n_neighbors=5)
neigh_tt.fit(digits_X, digits_y)
```
El valor real del registro seleccionado es
```
i = 5
neigh_tt.predict(digits_X.iloc[[i], :])
```
Mentras que la predicción dada por kNN es
```
neigh_tt.predict_proba(digits_X.iloc[[i], :])
```
A continuación la imagen
```
plt.imshow(digits_X.loc[[i], :].to_numpy().reshape(8, 8), cmap=plt.cm.gray_r, interpolation='nearest');
```
__Respuesta:__ Se me viene a la cabeza la forma de los numeros de los relojes digitales tipo : https://i.linio.com/p/b6286f5db6ae58cdd0aef38e070a51b5-product.jpg
Donde las figuras se parecen bastante, sobre todo porque tienen un formato reducido para mostrar los numeritos (hay una base donde detras que se ilumina dependiendo del numero), entonces como la matriz es chikita, igual quedan figuras similares y con no tan buena resolucion, por lo que lleva a errores, en este caso, confundiendo un 5 con un 9.
| github_jupyter |
# **Spit some [tensor] flow**
We need to learn the intricacies of tensorflow to master deep learning
`Let's get this over with`
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import tensorflow as tf
import cv2
print(tf.__version__)
def evaluation_tf(report, y_test, y_pred, classes):
plt.plot(report.history['loss'], label = 'training_loss')
plt.plot(report.history['val_loss'], label = 'validation_loss')
plt.legend()
plt.show()
plt.plot(report.history['accuracy'], label = 'training_accuracy')
plt.plot(report.history['val_accuracy'], label = 'validation_accuracy')
plt.legend()
plt.show()
from sklearn.metrics import confusion_matrix
import itertools
cm = confusion_matrix(y_test, y_pred)
plt.figure(figsize=(10,10))
plt.imshow(cm, cmap=plt.cm.Blues)
for i,j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i,j], 'd'),
horizontalalignment = 'center',
color='black')
plt.xlabel("Predicted labels")
plt.ylabel("True labels")
plt.xticks(range(0,classes))
plt.yticks(range(0,classes))
plt.title('Confusion matrix')
plt.colorbar()
plt.show()
# Taken from https://www.cs.toronto.edu/~kriz/cifar.html
labels = "airplane,automobile,bird,cat,deer,dog,frog,horse,ship,truck".split(",")
```
## As a rule of thumb
Remember that the pooling operation decreases the size of the image, and we lose information.
However, the number of features generally increases and we get more features extracted from the images.
The choices of hyperparams bother us sometimes, because DL has a lot of trial and error involved, we can choose the
- learning rate
- number of layers
- number of neurons per layer
- feature size
- feature number
- pooling size
- stride
On a side note, if you use strided convolution layers, they will decrease the size of the image as well
If we have images with different sizes as inputs; for example; H1 x W1 x 3 and H2 x W2 x 3, then the output will be flatten-ed to different sizes, this won't work for DENSE layers as they do not have change-able input sizes, so we use global max pooling to make a vector of size 1 x 1 x (#_Of_Feature_Maps_)
```
from tensorflow.keras.layers import Input, Conv2D, Dropout, Dense, Flatten, BatchNormalization, MaxPooling2D
from tensorflow.keras.models import Model
from tensorflow.keras.datasets import cifar10
(X_train, y_train), (X_test, y_test) = cifar10.load_data()
X_train, X_test = X_train / 255.0 , X_test / 255.0
print(X_train.shape)
print(X_test.shape)
print(y_train.shape)
print(y_test.shape)
y_train, y_test = y_train.flatten(), y_test.flatten()
print(y_train.shape)
print(y_test.shape)
classes = len(set(y_train))
print(classes)
input_shape = X_train[0].shape
i_layer = Input(shape = input_shape)
h_layer = Conv2D(32, (3,3),activation='relu', padding='same')(i_layer)
h_layer = BatchNormalization()(h_layer)
h_layer = Conv2D(64, (3,3), activation='relu', padding='same')(h_layer)
h_layer = BatchNormalization()(h_layer)
h_layer = Conv2D(128, (3,3), activation='relu', padding='same')(h_layer)
h_layer = BatchNormalization()(h_layer)
h_layer = MaxPooling2D((2,2))(h_layer)
h_layer = Conv2D(128, (3,3), activation='relu', padding='same')(h_layer)
h_layer = BatchNormalization()(h_layer)
h_layer = MaxPooling2D((2,2))(h_layer)
h_layer = Flatten()(h_layer)
h_layer = Dropout(0.5)(h_layer)
h_layer = Dense(512, activation='relu')(h_layer)
h_layer = Dropout(0.5)(h_layer)
o_layer = Dense(classes, activation='softmax')(h_layer)
model = Model(i_layer, o_layer)
model.compile(optimizer='adam',
loss = 'sparse_categorical_crossentropy',
metrics = ['accuracy'])
report = model.fit(X_train, y_train, validation_data=(X_test, y_test), epochs=50)
y_pred = model.predict(X_test).argmax(axis=1)
# only for sparse categorical crossentropy
evaluation_tf(report, y_test, y_pred, classes)
misshits = np.where(y_pred!=y_test)[0]
print("total Mishits = " + str(len(misshits)))
index = np.random.choice(misshits)
plt.imshow(X_test[index])
plt.title("Predicted = " + str(labels[y_pred[index]]) + ", Real = " + str(labels[y_test[index]]))
```
## LET'S ADD SOME DATA AUGMENTATION FROM KERAS
taken from https://keras.io/api/preprocessing/image/
```
batch_size = 32
data_generator = tf.keras.preprocessing.image.ImageDataGenerator(width_shift_range = 0.1,
height_shift_range = 0.1,
horizontal_flip=True)
model_dg = Model(i_layer, o_layer)
model_dg.compile(optimizer='adam',
loss = 'sparse_categorical_crossentropy',
metrics = ['accuracy'])
train_data_generator = data_generator.flow(X_train, y_train, batch_size)
spe = X_train.shape[0] // batch_size
report = model_dg.fit_generator(train_data_generator, validation_data=(X_test, y_test), steps_per_epoch=spe, epochs=50)
y_pred = model.predict(X_test).argmax(axis=1)
# only for sparse categorical crossentropy
evaluation_tf(report, y_test, y_pred, classes)
misshits = np.where(y_pred!=y_test)[0]
print("total Mishits = " + str(len(misshits)))
index = np.random.choice(misshits)
plt.imshow(X_test[index])
plt.title("Predicted = " + str(labels[y_pred[index]]) + ", Real = " + str(labels[y_test[index]]))
```
| github_jupyter |
# Google Apps Workspace
## Imports
```
%matplotlib inline
import os
import pandas as pd
import numpy as np
import seaborn as sns
from matplotlib import pyplot as plt
```
## Load Dataset
```
apps_df = pd.read_csv('googleplaystore.csv', index_col = 0)
reviews_df = pd.read_csv('googleplaystore_user_reviews.csv', index_col = 0)
apps_df.head()
apps_df.shape
apps_df.describe()
reviews_df.head()
reviews_df.shape
reviews_df.describe()
```
**Remove empty reviews**
```
reviews_df = reviews_df.dropna(axis=0, how='all')
apps_reviews_df = pd.merge(apps_df, reviews_df, on='App', how='inner')
apps_reviews_df.head()
```
Remove 1.9 Category \
*Because it doesn't make sense*
```
apps_df = apps_df[apps_df['Category'] != '1.9']
```
Change underscores to spaces
```
apps_df['Category'] = apps_df['Category'].str.replace('_', ' ')
```
Categories
```
categories = apps_df['Category'].unique()
categories
apps_df['Reviews'] = pd.to_numeric(apps_df['Reviews'])
```
Remove dollar signs
```
apps_df['Price'] = pd.to_numeric(apps_df['Price'].str.replace('$', ''))
```
Standardize App size to MB
```
# apps_df['Size'] = pd.to_numeric(apps_df['Size'].str.replace('M', ''))
def convert_to_M(s):
if 'k' in s:
return str(float(s[:-1])/1000)
if 'M' in s:
return s[:-1]
return np.nan
apps_df['Size'] = apps_df['Size'].apply(convert_to_M)
apps_df['Size'] = pd.to_numeric(apps_df['Size'])
```
Fill varying app sizes to the average app size of all the apps
```
apps_df['Size'] = apps_df['Size'].fillna(apps_df['Size'].mean())
```
## Insights
### Top Apps per Category
Only taking into account those with reviews greater than the median
```
n = 3
temp_apps_df = apps_df.reset_index()
print("Median Ratings: %.0f" % temp_apps_df['Reviews'].median())
temp_apps_df[temp_apps_df['Reviews'] > temp_apps_df['Reviews'].median()].sort_values('Rating', ascending=False).groupby('Category').head(n).reset_index(drop=True).sort_values("Category").set_index("App")
```
### Free vs Paid
```
apps_df.groupby('Type').agg('size').plot.bar()
sns.jointplot(apps_df['Price'], apps_df['Rating'])
```
### App Size (in MB) vs Rating
```
sns.jointplot(apps_df['Size'], apps_df['Rating'])
```
### Distribution of Apps per Price
If it's not free, it's an outlier.
```
plt.figure(figsize=(18,6))
ax = sns.boxplot(x='Category', y='Price', data=apps_df, orient='v')
ax.set_xticklabels(ax.get_xticklabels(),rotation=60)
plt.show()
```
### Most Expensive Apps
Possibly implies that you can't price an app above 400$ in Google App Store
```
apps_df.sort_values('Price', ascending=False)[['Category', 'Price', 'Installs']].head(15)
```
| github_jupyter |
# Geolocalizacion de dataset de escuelas argentinas
```
#Importar librerias
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
```
### Preparacion de data
```
# Vamos a cargar un padron de escuelas de Argentina
# Estos son los nombres de columna
cols = ['Jurisdicción','CUE Anexo','Nombre','Sector','Estado','Ámbito','Domicilio','CP','Teléfono','Código Localidad','Localidad','Departamento','E-mail','Ed. Común','Ed. Especial','Ed. de Jóvenes y Adultos','Ed. Artística','Ed. Hospitalaria Domiciliaria','Ed. Intercultural Bilingüe','Ed. Contexto de Encierro','Jardín maternal','Jardín de infantes','Primaria','Secundaria','Secundaria Técnica (INET)','Superior no Universitario','Superior No Universitario (INET)']
# Leer csv, remplazar las 'X' con True y los '' (NaN) con False
escuelas = pd.read_csv('../../datos/escuelas_arg.csv', names=cols).fillna(False).replace('X', True)
# Construir la columna 'dpto_link' con los codigos indetificatorios de partidos como los que teniamos
escuelas['dpto_link'] = escuelas['C\xc3\xb3digo Localidad'].astype(str).str.zfill(8).str[:5]
# Tenemos los radios censales del AMBA, que creamos en el notebook anterior. Creemos los 'dpto_link' del AMBA.
radios_censales_AMBA = pd.read_csv('../../datos/AMBA_datos', dtype=object)
dpto_links_AMBA = (radios_censales_AMBA['prov'] + radios_censales_AMBA['depto']).unique()
# Filtramos las escuelas AMBA
escuelas_AMBA = escuelas.loc[escuelas['dpto_link'].isin(dpto_links_AMBA)]
escuelas_AMBA = pd.concat([escuelas_AMBA, escuelas.loc[escuelas['Jurisdicci\xc3\xb3n'] == 'Ciudad de Buenos Aires']])
# Filtramos secundaria estatal
escuelas_AMBA_secundaria_estatal = escuelas_AMBA.loc[escuelas_AMBA['Secundaria'] & (escuelas_AMBA[u'Sector'] == 'Estatal')]
escuelas_AMBA_secundaria_estatal.reset_index(inplace=True, drop=True)
```
### Columnas de 'Address'
```
# Creamos un campo que llamamos 'Address', uniendo domicilio, localidad, departamento, jurisdiccion, y ', Argentina'
escuelas_AMBA_secundaria_estatal['Address'] = \
escuelas_AMBA_secundaria_estatal['Domicilio'].astype(str) + ', ' + \
escuelas_AMBA_secundaria_estatal['Localidad'].astype(str) + ', ' + \
escuelas_AMBA_secundaria_estatal['Departamento'].astype(str) + ', ' + \
escuelas_AMBA_secundaria_estatal['Jurisdicci\xc3\xb3n'].astype(str) +', Argentina'
pd.set_option('display.max_colwidth', -1)
import re
def filtrar_entre_calles(string):
"""
Removes substring between 'E/' and next field (delimited by ','). Case insensitive.
example:
>>> out = filtrar_entre_calles('LASCANO E/ ROMA E ISLAS MALVINAS 6213, ISIDRO CASANOVA')
>>> print out
'LASCANO 6213, ISIDRO CASANOVA'
"""
s = string.lower()
try:
m = re.search("\d", s)
start = s.index( 'e/' )
# end = s.index( last, start )
end = m.start()
return string[:start] + string[end:]
except:
return string
def filtrar_barrio(string, n = 3):
"""
Leaves only n most aggregate fields and the address.
example:
>>> out = filtrar_entre_calles('LASCANO 6213, ISIDRO CASANOVA, LA MATANZA, Buenos Aires, Argentina')
>>> print out
'LASCANO 6213, LA MATANZA, Buenos Aires, Argentina'
"""
try:
coma_partido_jurisdiccion = [m.start() for m in re.finditer(',', string)][-n]
coma_direccion = [m.start() for m in re.finditer(',', string)][0]
s = string[:coma_direccion][::-1]
if "n/s" in s.lower():
start = s.lower().index('n/s')
cut = len(s) - len('n/s') - start
else:
m = re.search("\d", s)
cut = len(s) - m.start(0)
return string[:cut] + string[coma_partido_jurisdiccion:]
except AttributeError:
return string
escuelas_AMBA_secundaria_estatal['Address_2'] = escuelas_AMBA_secundaria_estatal['Address'].apply(filtrar_entre_calles)
escuelas_AMBA_secundaria_estatal['Address_3'] = escuelas_AMBA_secundaria_estatal['Address_2'].apply(filtrar_barrio)
escuelas_AMBA_secundaria_estatal.to_csv('../../datos/escuelas_AMBA_secundaria_estatal.csv', index = False)
```
### Geolocalizacion
```
import json
import time
import urllib
import urllib2
def geolocate(inp, API_key = None, BACKOFF_TIME = 30):
# See https://developers.google.com/maps/documentation/timezone/get-api-key
# with open('googleMapsAPIkey.txt', 'r') as myfile:
# maps_key = myfile.read().replace('\n', '')
base_url = 'https://maps.googleapis.com/maps/api/geocode/json'
# This joins the parts of the URL together into one string.
url = base_url + '?' + urllib.urlencode({
'address': "%s" % (inp),
'key': API_key,
})
try:
# Get the API response.
response = str(urllib2.urlopen(url).read())
except IOError:
pass # Fall through to the retry loop.
else:
# If we didn't get an IOError then parse the result.
result = json.loads(response.replace('\\n', ''))
if result['status'] == 'OK':
return result['results'][0]
elif result['status'] != 'UNKNOWN_ERROR':
# Many API errors cannot be fixed by a retry, e.g. INVALID_REQUEST or
# ZERO_RESULTS. There is no point retrying these requests.
# raise Exception(result['error_message'])
return None
# If we're over the API limit, backoff for a while and try again later.
elif result['status'] == 'OVER_QUERY_LIMIT':
print "Hit Query Limit! Backing off for "+str(BACKOFF_TIME)+" minutes..."
time.sleep(BACKOFF_TIME * 60) # sleep for 30 minutes
geocoded = False
def set_geolocation_values(df, loc):
df.set_value(i,'lng', loc['geometry']['location']['lng'])
df.set_value(i,'lat', loc['geometry']['location']['lat'])
df.set_value(i, 'id', loc['place_id'])
dataframe = escuelas_AMBA_secundaria_estatal
col, col_2, col_3 = 'Address', 'Address_2', 'Address_3'
API_key = 'AIzaSyDjBFMZlNTyds2Sfihu2D5LTKupKDBpf6c'
for i, row in dataframe.iterrows():
loc = geolocate(row[col], API_key)
if loc:
set_geolocation_values(dataframe, loc)
else:
loc = geolocate(row[col_2], API_key)
if loc:
set_geolocation_values(dataframe, loc)
else:
loc = geolocate(row[col_3], API_key)
if loc:
set_geolocation_values(dataframe, loc)
if i%50 == 0:
print 'processed row '+str(i)
dataframe.to_csv('../../datos/esc_sec_AMBA_geoloc.csv', index = False, encoding = 'utf8')
# esc_sec_AMBA_geoloc_1200 = pd.read_csv('../../datos/esc_sec_AMBA_geoloc_1200.csv', encoding = 'utf8')
# esc_sec_AMBA_geoloc_480_1200 = pd.read_csv('../../datos/esc_sec_AMBA_geoloc_480_1200.csv', encoding = 'utf8')
# esc_sec_AMBA_geoloc = pd.read_csv('../../datos/esc_sec_AMBA_geoloc.csv', encoding = 'utf8')
# esc_sec_AMBA_geoloc_900_1200 = pd.read_csv('../../datos/esc_sec_AMBA_geoloc_900_1200.csv', encoding = 'utf8')
# pd.concat([esc_sec_AMBA_geoloc[:480],esc_sec_AMBA_geoloc_480_1200[:420],esc_sec_AMBA_geoloc_900_1200, esc_sec_AMBA_geoloc_1200]).to_csv('../../datos/esc_sec_AMBA_geoloc_full.csv', index = False, encoding = 'utf8')
print len(pd.read_csv('../../datos/esc_sec_AMBA_geoloc_full.csv', encoding = 'utf8').dropna())
print len(pd.read_csv('../../datos/esc_sec_AMBA_geoloc_full.csv', encoding = 'utf8'))
1840/2066.
import numpy as np
df = pd.read_csv('../../datos/esc_sec_AMBA_geoloc_full.csv', encoding = 'utf8')
index = df['lat'].index[df['lat'].apply(np.isnan)]
plt.hist(index, 100)
# plt.xlim(900, 1300)
plt.show()
df.iloc[np.where(pd.isnull(df['lat']))][['Nombre','Address', 'Address_2', 'Address_3']].to_csv('../../datos/no_result_addresses.csv', index = False, encoding = 'utf8')
```
| github_jupyter |
# Combining DataFrames with pandas
In many "real world" situations, the data that we want to use come in multiple
files. We often need to combine these files into a single DataFrame to analyze
the data. The pandas package provides [various methods for combining
DataFrames](http://pandas.pydata.org/pandas-docs/stable/merging.html) including
`merge` and `concat`.
To work through the examples below, we first need to load the species and
surveys files into pandas DataFrames. In iPython:
Take note that the `read_csv` method we used can take some additional options which
we didn't use previously. Many functions in python have a set of options that
can be set by the user if needed. In this case, we have told Pandas to assign
empty values in our CSV to NaN `keep_default_na=False, na_values=[""]`.
[More about all of the read_csv options here.](http://pandas.pydata.org/pandas-docs/dev/generated/pandas.io.parsers.read_csv.html)
# Concatenating DataFrames
We can use the `concat` function in Pandas to append either columns or rows from
one DataFrame to another. Let's grab two subsets of our data to see how this
works.
```
# read in first 10 lines of surveys table
# grab the last 10 rows
# reset the index values to the second dataframe appends properly
# drop=True option avoids adding new index column with old index values
```
When we concatenate DataFrames, we need to specify the axis. `axis=0` tells
Pandas to stack the second DataFrame under the first one. It will automatically
detect whether the column names are the same and will stack accordingly.
`axis=1` will stack the columns in the second DataFrame to the RIGHT of the
first DataFrame. To stack the data vertically, we need to make sure we have the
same columns and associated column format in both datasets. When we stack
horizonally, we want to make sure what we are doing makes sense (ie the data are
related in some way).
```
# stack the DataFrames on top of each other
# place the DataFrames side by side
```
### Row Index Values and Concat
Have a look at the `vertical_stack` dataframe? Notice anything unusual?
The row indexes for the two data frames `survey_sub` and `survey_sub_last10`
have been repeated. We can reindex the new dataframe using the `reset_index()` method.
## Writing Out Data to CSV
We can use the `to_csv` command to do export a DataFrame in CSV format. Note that the code
below will by default save the data into the current working directory. We can
save it to a different folder by adding the foldername and a slash to the file
`vertical_stack.to_csv('foldername/out.csv')`. We use the 'index=False' so that
pandas doesn't include the index number for each line.
```
# Write DataFrame to CSV
```
Check out your working directory to make sure the CSV wrote out properly, and
that you can open it! If you want, try to bring it back into python to make sure
it imports properly.
```
# for kicks read our output back into python and make sure all looks good
```
> ## Challenge - Combine Data
>
> In the data folder, there are two survey data files: `survey2001.csv` and
> `survey2002.csv`. Read the data into python and combine the files to make one
> new data frame. Create a plot of average plot weight by year grouped by sex.
> Export your results as a CSV and make sure it reads back into python properly.
# Joining DataFrames
When we concatenated our DataFrames we simply added them to each other -
stacking them either vertically or side by side. Another way to combine
DataFrames is to use columns in each dataset that contain common values (a
common unique id). Combining DataFrames using a common field is called
"joining". The columns containing the common values are called "join key(s)".
Joining DataFrames in this way is often useful when one DataFrame is a "lookup
table" containing additional data that we want to include in the other.
NOTE: This process of joining tables is similar to what we do with tables in an
SQL database.
For example, the `species.csv` file that we've been working with is a lookup
table. This table contains the genus, species and taxa code for 55 species. The
species code is unique for each line. These species are identified in our survey
data as well using the unique species code. Rather than adding 3 more columns
for the genus, species and taxa to each of the 35,549 line Survey data table, we
can maintain the shorter table with the species information. When we want to
access that information, we can create a query that joins the additional columns
of information to the Survey data.
Storing data in this way has many benefits including:
1. It ensures consistency in the spelling of species attributes (genus, species
and taxa) given each species is only entered once. Imagine the possibilities
for spelling errors when entering the genus and species thousands of times!
2. It also makes it easy for us to make changes to the species information once
without having to find each instance of it in the larger survey data.
3. It optimizes the size of our data.
## Joining Two DataFrames
To better understand joins, let's grab the first 10 lines of our data as a
subset to work with. We'll use the `.head` method to do this. We'll also read
in a subset of the species table.
```
# read in first 10 lines of surveys table
# import a small subset of the species data designed for this part of the lesson.
# It is stored in the data folder.
```
In this example, `species_sub` is the lookup table containing genus, species, and
taxa names that we want to join with the data in `survey_sub` to produce a new
DataFrame that contains all of the columns from both `species_df` *and*
`survey_df`.
## Identifying join keys
To identify appropriate join keys we first need to know which field(s) are
shared between the files (DataFrames). We might inspect both DataFrames to
identify these columns. If we are lucky, both DataFrames will have columns with
the same name that also contain the same data. If we are less lucky, we need to
identify a (differently-named) column in each DataFrame that contains the same
information.
In our example, the join key is the column containing the two-letter species
identifier, which is called `species_id`.
Now that we know the fields with the common species ID attributes in each
DataFrame, we are almost ready to join our data. However, since there are
[different types of joins](http://blog.codinghorror.com/a-visual-explanation-of-sql-joins/), we
also need to decide which type of join makes sense for our analysis.
## Inner joins
The most common type of join is called an _inner join_. An inner join combines
two DataFrames based on a join key and returns a new DataFrame that contains
**only** those rows that have matching values in *both* of the original
DataFrames.
Inner joins yield a DataFrame that contains only rows where the value being
joins exists in BOTH tables. An example of an inner join, adapted from [this
page](http://blog.codinghorror.com/a-visual-explanation-of-sql-joins/) is below:

The pandas function for performing joins is called `merge` and an Inner join is
the default option:
The result of an inner join of `survey_sub` and `species_sub` is a new DataFrame
that contains the combined set of columns from `survey_sub` and `species_sub`. It
*only* contains rows that have two-letter species codes that are the same in
both the `survey_sub` and `species_sub` DataFrames. In other words, if a row in
`survey_sub` has a value of `species_id` that does *not* appear in the `species_id`
column of `species`, it will not be included in the DataFrame returned by an
inner join. Similarly, if a row in `species_sub` has a value of `species_id`
that does *not* appear in the `species_id` column of `survey_sub`, that row will not
be included in the DataFrame returned by an inner join.
The two DataFrames that we want to join are passed to the `merge` function using
the `left` and `right` argument. The `left_on='species'` argument tells `merge`
to use the `species_id` column as the join key from `survey_sub` (the `left`
DataFrame). Similarly , the `right_on='species_id'` argument tells `merge` to
use the `species_id` column as the join key from `species_sub` (the `right`
DataFrame). For inner joins, the order of the `left` and `right` arguments does
not matter.
The result `merged_inner` DataFrame contains all of the columns from `survey_sub`
(record id, month, day, etc.) as well as all the columns from `species_sub`
(species_id, genus, species, and taxa).
Notice that `merged_inner` has fewer rows than `survey_sub`. This is an
indication that there were rows in `surveys_df` with value(s) for `species_id` that
do not exist as value(s) for `species_id` in `species_df`.
## Left joins
What if we want to add information from `species_sub` to `survey_sub` without
losing any of the information from `survey_sub`? In this case, we use a different
type of join called a "left outer join", or a "left join".
Like an inner join, a left join uses join keys to combine two DataFrames. Unlike
an inner join, a left join will return *all* of the rows from the `left`
DataFrame, even those rows whose join key(s) do not have values in the `right`
DataFrame. Rows in the `left` DataFrame that are missing values for the join
key(s) in the `right` DataFrame will simply have null (i.e., NaN or None) values
for those columns in the resulting joined DataFrame.
Note: a left join will still discard rows from the `right` DataFrame that do not
have values for the join key(s) in the `left` DataFrame.

A left join is performed in pandas by calling the same `merge` function used for
inner join, but using the `how='left'` argument:
The result DataFrame from a left join (`merged_left`) looks very much like the
result DataFrame from an inner join (`merged_inner`) in terms of the columns it
contains. However, unlike `merged_inner`, `merged_left` contains the **same
number of rows** as the original `survey_sub` DataFrame. When we inspect
`merged_left`, we find there are rows where the information that should have
come from `species_sub` (i.e., `species_id`, `genus`, and `taxa`) is
missing (they contain NaN values):
These rows are the ones where the value of `species_id` from `survey_sub` (in this
case, `PF`) does not occur in `species_sub`.
## Other join types
The pandas `merge` function supports two other join types:
* Right (outer) join: Invoked by passing `how='right'` as an argument. Similar
to a left join, except *all* rows from the `right` DataFrame are kept, while
rows from the `left` DataFrame without matching join key(s) values are
discarded.
* Full (outer) join: Invoked by passing `how='outer'` as an argument. This join
type returns the all pairwise combinations of rows from both DataFrames; i.e.,
the result DataFrame will `NaN` where data is missing in one of the dataframes. This join type is
very rarely used.
# Final Challenges
> ## Challenge - Distributions
> Create a new DataFrame by joining the contents of the `surveys.csv` and
> `species.csv` tables. Then calculate and plot the distribution of:
>
> 1. taxa by plot
> 2. taxa by sex by plot
> ## Challenge - Diversity Index
>
> 1. In the data folder, there is a plot `CSV` that contains information about the
> type associated with each plot. Use that data to summarize the number of
> plots by plot type.
> 2. Calculate a diversity index of your choice for control vs rodent exclosure
> plots. The index should consider both species abundance and number of
> species. You might choose to use the simple [biodiversity index described
> here](http://www.amnh.org/explore/curriculum-collections/biodiversity-counts/plant-ecology/how-to-calculate-a-biodiversity-index)
> which calculates diversity as:
>
> the number of species in the plot / the total number of individuals in the plot = Biodiversity index.
| github_jupyter |
# Chapter 13: Analyzing sound waves with Fourier Series
Helper functions
```
import matplotlib.pyplot as plt
def plot_function(f,xmin,xmax,**kwargs):
ts = np.linspace(xmin,xmax,1000)
plt.plot(ts,[f(t) for t in ts],**kwargs)
def plot_sequence(points,max=100,line=False,**kwargs):
if line:
plt.plot(range(0,max),points[0:max],**kwargs)
else:
plt.scatter(range(0,max),points[0:max],**kwargs)
```
## 13.1 Playing sound waves in Python
### 13.1.1 Producing our first sound
```
import pygame, pygame.sndarray
pygame.mixer.init(frequency=44100, size=-16, channels=1)
import numpy as np
arr = np.random.randint(-32768, 32767, size=44100)
arr
plot_sequence(arr)
plot_sequence(arr,line=True,max=441)
```
**CAUTION: May play a loud sound!!!**
```
sound = pygame.sndarray.make_sound(arr)
sound.play()
arr = np.random.randint(-10000, 10000, size=44100)
sound = pygame.sndarray.make_sound(arr)
sound.play()
```
### 13.1.2 Playing a musical note
```
form = np.repeat([10000,-10000],50) #<1>
plot_sequence(form)
arr = np.tile(form,441)
plot_sequence(arr,line=True,max=1000)
sound = pygame.sndarray.make_sound(arr)
sound.play()
```
### 13.1.3 Exercises
**Exercise:** Our musical note “A” was a pattern that repeated 441 times in a second. Create a similar pattern that repeats 350 times in one second, which will produce the musical note “F”.
**Solution:**
```
form = np.repeat([10000,-10000],63)
arr = np.tile(form,350)
sound = pygame.sndarray.make_sound(arr)
sound.play()
```
## 13.2 Turning a sinusoidal wave into a sound
### 13.2.1 Making audio from sinusoidal functions
```
from math import sin,cos,pi
plot_function(sin,0,4*pi)
```
### 13.2.2 Changing the frequency of a sinusoid
```
def make_sinusoid(frequency,amplitude):
def f(t): #<1>
return amplitude * sin(2*pi*frequency*t) #<2>
return f
plot_function(make_sinusoid(5,4),0,1)
```
### 13.2.3 Sampling and playing the sound wave
```
sinusoid = make_sinusoid(441,8000)
np.arange(0,1,0.1)
np.arange(0,1,1/44100)
def sample(f,start,end,count): #<1>
mapf = np.vectorize(f) #<2>
ts = np.arange(start,end,(end-start)/count) #<3>
values = mapf(ts) #<4>
return values.astype(np.int16) #<5>
sinusoid = make_sinusoid(441,8000)
arr = sample(sinusoid, 0, 1, 44100)
sound = pygame.sndarray.make_sound(arr)
sound.play()
```
### 13.2.4 Exercises
**Exercise:** Plot the tangent function $\tan(t) = \sin(t)/\cos(t).$ What is its period?
**Solution:** The period is $\pi$.
```
from math import tan
plot_function(tan,0,5*pi)
plt.ylim(-10,10) #<1>
```
**Exercise:** Find the value of $k$ such that $\cos(kt)$ has a frequency of 5. Plot the resulting function $\cos(kt)$ from zero to one and show that it repeats itself 5 times.
**Solution:**
```
plot_function(lambda t: cos(10*pi*t),0,1)
```
## 13.3 Combining sound waves to make new ones
### 13.3.1 Adding sampled sound waves to build a chord
```
np.array([1,2,3]) + np.array([4,5,6])
sample1 = sample(make_sinusoid(441,8000),0,1,44100)
sample2 = sample(make_sinusoid(551,8000),0,1,44100)
sound1 = pygame.sndarray.make_sound(sample1)
sound2 = pygame.sndarray.make_sound(sample2)
sound1.play()
sound2.play()
chord = pygame.sndarray.make_sound(sample1 + sample2)
chord.play()
```
### 13.3.2 Picturing the sum of two sound waves
```
plot_sequence(sample1,max=400)
plot_sequence(sample2,max=400)
plot_sequence(sample1+sample2,max=400)
```
### 13.3.3 Building a linear combination of sinusoids
```
def const(n):
return 1
def fourier_series(a0,a,b):
def result(t):
cos_terms = [an*cos(2*pi*(n+1)*t) for (n,an) in enumerate(a)] #<1>
sin_terms = [bn*sin(2*pi*(n+1)*t) for (n,bn) in enumerate(b)] #<2>
return a0*const(t) + sum(cos_terms) + sum(sin_terms) #<3>
return result
f = fourier_series(0,[0,0,0,0,0],[0,0,0,1,1])
plot_function(f,0,1)
```
### 13.3.4 Building a familiar function with sinusoids
```
f1 = fourier_series(0,[],[4/pi])
f3 = fourier_series(0,[],[4/pi,0,4/(3*pi)])
plot_function(f1,0,1)
plot_function(f3,0,1)
b = [4/(n * pi) if n%2 != 0 else 0 for n in range(1,10)] #<1>
f = fourier_series(0,[],b)
plot_function(f,0,1)
b = [4/(n * pi) if n%2 != 0 else 0 for n in range(1,20)]
f = fourier_series(0,[],b)
plot_function(f,0,1)
b = [4/(n * pi) if n%2 != 0 else 0 for n in range(1,100)]
f = fourier_series(0,[],b)
plot_function(f,0,1)
```
### 13.3.5 Exercises
**Mini-project:** Create a manipulated version of the square wave Fourier series so that is frequency is 441 Hz, sample it, and confirm that it doesn’t just look like the square wave -- it sounds like the square wave as well.
**Solution:** Here's a quick idea of how to do this with the function `f` you just built.
```
arr = sample(lambda t: 10000* f(441*t), 0, 1, 44100)
sound = pygame.sndarray.make_sound(arr)
sound.play()
```
## 13.4 Decomposing a sound wave into its Fourier Series
### 13.4.1 Finding vector components with an inner product
### 13.4.2 Defining an inner product for periodic functions
```
def inner_product(f,g,N=1000):
dt = 1/N #<1>
return 2*sum([f(t)*g(t)*dt for t in np.arange(0,1,dt)]) #<2>
def s(n): #<1>
def f(t):
return sin(2*pi*n*t)
return f
def c(n): #<2>
def f(t):
return cos(2*pi*n*t)
return f
inner_product(s(1),c(1))
inner_product(s(1),s(2))
inner_product(c(3),s(10))
inner_product(s(1),s(1))
inner_product(c(1),c(1))
inner_product(c(3),c(3))
from math import sqrt
def const(n):
return 1 /sqrt(2)
inner_product(const,s(1))
inner_product(const,c(1))
inner_product(const,const)
```
### 13.4.3 Writing a function to find Fourier coefficients
**note** we have a new `const` function so `fourier_series` will behave differently
```
def fourier_series(a0,a,b):
def result(t):
cos_terms = [an*cos(2*pi*(n+1)*t) for (n,an) in enumerate(a)] #<1>
sin_terms = [bn*sin(2*pi*(n+1)*t) for (n,bn) in enumerate(b)] #<2>
return a0*const(t) + sum(cos_terms) + sum(sin_terms) #<3>
return result
def fourier_coefficients(f,N):
a0 = inner_product(f,const) #<1>
an = [inner_product(f,c(n)) for n in range(1,N+1)] #<2>
bn = [inner_product(f,s(n)) for n in range(1,N+1)] #<3>
return a0, an, bn
f = fourier_series(0,[2,3,4],[5,6,7])
fourier_coefficients(f,3)
```
### 13.4.4 Finding the Fourier coefficients for the square wave
```
def square(t):
return 1 if (t%1) < 0.5 else -1
a0, a, b = fourier_coefficients(square,10)
b[0], 4/pi
b[2], 4/(3*pi)
b[4], 4/(5*pi)
```
### 4.5 Fourier coefficients for other waveforms
```
def sawtooth(t):
return t%1
plot_function(sawtooth,0,5)
approx = fourier_series(*fourier_coefficients(sawtooth,10))
plot_function(sawtooth,0,5)
plot_function(approx,0,5)
def speedbumps(t):
if abs(t%1 - 0.5) > 0.25:
return 0
else:
return sqrt(0.25*0.25 - (t%1 - 0.5)**2)
approx = fourier_series(*fourier_coefficients(speedbumps,10))
plot_function(speedbumps,0,5)
plot_function(approx,0,5)
```
### 13.4.6 Exercises
**Mini project:** Play a sawtooth wave at 441 Hz and compare it with the square and sinusoidal waves you played at that frequency.
**Solution:**
```
def modified_sawtooth(t):
return 8000 * sawtooth(441*t)
arr = sample(modified_sawtooth,0,1,44100)
sound = pygame.sndarray.make_sound(arr)
sound.play()
```
| github_jupyter |
# info
##### クレンジング
1. 欠損値があった場合、基礎分析の結果に基づいて値埋めか行の削除を行なっている
1. 表記揺れがあった場合、漏れなく修正している
1. 水準数が多く、なおかつまとめられそうな質的変数があった場合に、論理的な基準に基づいて値をまとめている
##### 特徴量エンジニアリング
1. 質的変数を量的変数(加減乗除して意味のある数値)に変換している
1. 量的変数を基礎分析の結果をもとに変換している
1. 量的変数のスケーリングを行っている
1. 元データを素に、有用であると考えられるような特徴を少なくとも1は生成している
# init
```
import numpy as np
import pandas as pd
```
# load
```
path_data = "../data/"
path_raw = path_data + "raw/"
path_mid = path_data + "mid/"
path_clns = path_data + "clns/"
cats = pd.read_csv(path_mid+"cats.csv", index_col=0)
nums = pd.read_csv(path_mid+"nums.csv", index_col=0)
bools = pd.read_csv(path_mid+"bools.csv", index_col=0)
```
# clns
## fillna
##### embarked
```
cats["embarked"] = cats["embarked"].fillna("S")
cats["embarked"].isna().any()
```
##### age
```
from sklearn.linear_model import LogisticRegression, LinearRegression
from sklearn.metrics import roc_auc_score
from sklearn.preprocessing import StandardScaler
fill_mean = nums[["age", "survived"]]
fill_mean = fill_mean[~fill_mean.survived.isna()]
fill_mean["age"] = fill_mean.age.fillna(fill_mean.age.mean())
fill_median = nums[["age", "survived"]]
fill_median = fill_median[~fill_median.survived.isna()]
fill_median["age"] = fill_median.age.fillna(fill_median.age.median())
# 線形回帰で値埋め
def zscore(x):
m = x.mean()
s = x.std(ddof=1)
return (x-m)/s
X = pd.get_dummies(cats, drop_first=True)
z = zscore(nums.drop(["age", "survived"], 1))
X = X.join(z)
y = nums.age
is_na = y.isna()
y = np.log1p(y)
rgs = LinearRegression()
rgs.fit(X[~is_na], y[~is_na])
pred = rgs.predict(X[is_na])
pred = np.exp(pred)-1
base = X[~is_na]
base["age"] = np.exp(y[~is_na])-1
fill = X[is_na]
fill["age"] = pred
fill_linear = pd.concat([base, fill]).join(nums[["survived"]])
fill_linear = fill_linear[["age", "survived"]]
fill_linear = fill_linear[~fill_linear.survived.isna()]
def check_auc(data):
X, y = data[["age"]], data["survived"]
clf = LogisticRegression()
clf.fit(X, y)
proba = clf.predict_proba(X)[:,1]
auc = roc_auc_score(y_true=y, y_score=proba)
print(auc)
check_auc(fill_mean)
check_auc(fill_median)
check_auc(fill_linear)
nums["age"] = nums.fillna(nums.age.mean())
```
##### チェックポイント1: 欠損値があった場合、基礎分析の結果に基づいて値埋めか行の削除を行なっている
##### チェックポイント2: 表記揺れがあった場合、漏れなく修正している
- 表記揺れはない
## union-value
```
cats_union = cats.copy()
```
##### embarked
```
cats_union["embarked"] = cats_union.embarked.replace(["Q", "S"], "QorS")
```
##### family-size
```
family = nums.parch + nums.sibsp
parch = nums.parch.apply(lambda x: "4+" if x >= 4 else x)
sibsp = nums.sibsp.apply(lambda x: "4+" if x >= 4 else x)
```
##### チェックポイント3: 水準数が多く、なおかつまとめられそうな質的変数があった場合に、論理的な基準に基づいて値をまとめている
# feature engineering
## onehot-encoding
```
pd.get_dummies(cats_union, drop_first=True).to_csv(path_clns+"onehot_cats.csv")
pd.get_dummies(pd.concat([parch, sibsp], axis=1), drop_first=True).to_csv(path_clns+"onehot_parch_sibsp.csv")
pd.get_dummies(family, drop_first=True, prefix="family-size").to_csv(path_clns+"onehot_familysize.csv")
(bools*1).to_csv(path_clns+"onehot_bools.csv")
nums[["survived"]].to_csv(path_clns+"y.csv")
is_child = (nums.age <= 7)*1
is_child.name = "is_child"
is_child.to_frame().to_csv(path_clns+"onehot_ischild.csv")
```
##### チェックポイント4: 元データを素に、有用であると考えられるような特徴を少なくとも1は生成している
## target-encoding
```
def tgt_encoding(data, y):
data = data.copy()
idname = data.index.name
data = data.reset_index()
train = data.dropna()
for x in set(data)-set([idname, y]):
dfg = train.groupby(x)[y].mean()
dfg = dfg.to_frame()
data = data.merge(dfg, on=x, suffixes=["", "_%s_tgt"%x], how="left")
data = data.set_index(idname)
data = data.filter(regex="_tgt")
return data
y = "survived"
data = cats.join(nums[[y]])
data = tgt_encoding(data, y)
data.to_csv(path_clns+"tgt_cats.csv")
data = bools.join(nums[[y]])
data = tgt_encoding(data, y)
data.to_csv(path_clns+"tgt_bools.csv")
data = pd.concat([parch, sibsp], axis=1).join(nums[[y]])
data = tgt_encoding(data, y)
data.to_csv(path_clns+"tgt_parch_sibsp.csv")
data = family.to_frame()
data.columns = ["familysize"]
data = data.join(nums[[y]])
data = tgt_encoding(data, y)
data.to_csv(path_clns+"tgt_familysize.csv")
```
##### チェックポイント1: 質的変数を量的変数(加減乗除して意味のある数値)に変換している
## log, zscore
```
def zscore(x):
m = x.mean()
s = x.std(ddof=1)
return (x-m)/s
nums_tgt = nums[["age", "fare"]]
z = zscore(nums_tgt)
z.to_csv(path_clns+"num_z.csv")
z = zscore(np.log1p(nums_tgt))
z.to_csv(path_clns+"num_logz.csv")
```
##### チェックポイント2: 量的変数を基礎分析の結果をもとに変換している
##### チェックポイント3: 量的変数のスケーリングを行っている
| github_jupyter |
# FloPy shapefile export demo
The goal of this notebook is to demonstrate ways to export model information to shapefiles.
This example will cover:
* basic exporting of information for a model, individual package, or dataset
* custom exporting of combined data from different packages
* general exporting and importing of geographic data from other sources
```
import sys
import os
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import pandas as pd
# run installed version of flopy or add local path
try:
import flopy
except:
fpth = os.path.abspath(os.path.join('..', '..'))
sys.path.append(fpth)
import flopy
print(sys.version)
print('numpy version: {}'.format(np.__version__))
print('matplotlib version: {}'.format(mpl.__version__))
print('flopy version: {}'.format(flopy.__version__))
# set the output directory
outdir = os.path.join('temp', 'shapefile_export')
if not os.path.isdir(outdir):
os.makedirs(outdir)
# load an existing model
model_ws = "../data/freyberg"
m = flopy.modflow.Modflow.load("freyberg.nam", model_ws=model_ws, verbose=False,
check=False, exe_name="mfnwt")
m.get_package_list()
```
### set the model coordinate information
the coordinate information where the grid is located in a projected coordinate system (e.g. UTM)
```
grid = m.modelgrid
grid.set_coord_info(xoff=273170, yoff=5088657, epsg=26916)
grid.extent
```
## Declarative export using attached `.export()` methods
#### Export the whole model to a single shapefile
```
fname = '{}/model.shp'.format(outdir)
m.export(fname)
ax = plt.subplot(1, 1, 1, aspect='equal')
extents = grid.extent
pc = flopy.plot.plot_shapefile(fname, ax=ax, edgecolor='k', facecolor='none')
ax.set_xlim(extents[0], extents[1])
ax.set_ylim(extents[2], extents[3])
ax.set_title(fname);
fname = '{}/wel.shp'.format(outdir)
m.wel.export(fname)
```
### Export a package to a shapefile
### Export a FloPy list or array object
```
m.lpf.hk
fname = '{}/hk.shp'.format(outdir)
m.lpf.hk.export('{}/hk.shp'.format(outdir))
ax = plt.subplot(1, 1, 1, aspect='equal')
extents = grid.extent
a = m.lpf.hk.array.ravel()
pc = flopy.plot.plot_shapefile(fname, ax=ax, a=a)
ax.set_xlim(extents[0], extents[1])
ax.set_ylim(extents[2], extents[3])
ax.set_title(fname);
m.riv.stress_period_data
m.riv.stress_period_data.export('{}/riv_spd.shp'.format(outdir))
```
### MfList.export() exports the whole grid by default, regardless of the locations of the boundary cells
`sparse=True` only exports the boundary cells in the MfList
```
m.riv.stress_period_data.export('{}/riv_spd.shp'.format(outdir), sparse=True)
m.wel.stress_period_data.export('{}/wel_spd.shp'.format(outdir), sparse=True)
```
## Ad-hoc exporting using `recarray2shp`
* The main idea is to create a recarray with all of the attribute information, and a list of geometry features (one feature per row in the recarray)
* each geometry feature is an instance of the `Point`, `LineString` or `Polygon` classes in `flopy.utils.geometry`. The shapefile format requires all the features to be of the same type.
* We will use pandas dataframes for these examples because they are easy to work with, and then convert them to recarrays prior to exporting.
```
from flopy.export.shapefile_utils import recarray2shp
```
### combining data from different packages
write a shapefile of RIV and WEL package cells
```
wellspd = pd.DataFrame(m.wel.stress_period_data[0])
rivspd = pd.DataFrame(m.riv.stress_period_data[0])
spd = wellspd.append(rivspd)
spd.head()
```
##### create a list of Polygon features from the cell vertices stored in the SpatialReference object
```
from flopy.utils.geometry import Polygon
vertices = []
for row, col in zip(spd.i, spd.j):
vertices.append(grid.get_cell_vertices(row, col))
polygons = [Polygon(vrt) for vrt in vertices]
polygons
```
##### write the shapefile
```
fname = '{}/bcs.shp'.format(outdir)
recarray2shp(spd.to_records(), geoms=polygons,
shpname=fname,
epsg=grid.epsg)
ax = plt.subplot(1, 1, 1, aspect='equal')
extents = grid.extent
pc = flopy.plot.plot_shapefile(fname, ax=ax)
ax.set_xlim(extents[0], extents[1])
ax.set_ylim(extents[2], extents[3])
ax.set_title(fname);
```
### exporting other data
Suppose we have some well data with actual locations that we want to export to a shapefile
```
welldata = pd.DataFrame({'wellID': np.arange(0, 10),
'q': np.random.randn(10)*100 - 1000,
'x_utm': np.random.rand(10)*1000 + grid.yoffset,
'y_utm': grid.xoffset - np.random.rand(10)*3000})
welldata.head()
```
##### convert the x, y coorindates to point features and then export
```
from flopy.utils.geometry import Point
geoms = [Point(x, y) for x, y in zip(welldata.x_utm, welldata.y_utm)]
fname = '{}/wel_data.shp'.format(outdir)
recarray2shp(welldata.to_records(), geoms=geoms,
shpname=fname,
epsg=grid.epsg)
ax = plt.subplot(1, 1, 1, aspect='equal')
extents = grid.extent
pc = flopy.plot.plot_shapefile(fname, ax=ax, radius=25)
ax.set_xlim(extents[0], extents[1])
ax.set_ylim(extents[2], extents[3])
ax.set_title(fname);
```
### Adding attribute data to an existing shapefile
Suppose we have a GIS coverage representing the river in the riv package
```
from flopy.utils.geometry import LineString
### make up a linestring shapefile of the river reaches
i, j = m.riv.stress_period_data[0].i, m.riv.stress_period_data[0].j
x0 = grid.xyzcellcenters[0][i[0], j[0]]
x1 = grid.xyzcellcenters[0][i[-1], j[-1]]
y0 = grid.xyzcellcenters[1][i[0], j[0]]
y1 = grid.xyzcellcenters[1][i[-1], j[-1]]
x = np.linspace(x0, x1, m.nrow+1)
y = np.linspace(y0, y1, m.nrow+1)
l0 = zip(list(zip(x[:-1], y[:-1])), list(zip(x[1:], y[1:])))
lines = [LineString(l) for l in l0]
rivdata = pd.DataFrame(m.riv.stress_period_data[0])
rivdata['reach'] = np.arange(len(lines))
lines_shapefile = '{}/riv_reaches.shp'.format(outdir)
recarray2shp(rivdata.to_records(index=False), geoms=lines,
shpname=lines_shapefile,
epsg=grid.epsg)
ax = plt.subplot(1, 1, 1, aspect='equal')
extents = grid.extent
pc = flopy.plot.plot_shapefile(lines_shapefile, ax=ax, radius=25)
ax.set_xlim(extents[0], extents[1])
ax.set_ylim(extents[2], extents[3])
ax.set_title(lines_shapefile);
```
#### read in the GIS coverage using `shp2recarray`
`shp2recarray` reads a shapefile into a numpy record array, which can easily be converted to a DataFrame
```
from flopy.export.shapefile_utils import shp2recarray
linesdata = shp2recarray(lines_shapefile)
linesdata = pd.DataFrame(linesdata)
linesdata.head()
```
##### Suppose we have some flow information that we read in from the cell budget file
```
# make up some fluxes between the river and aquifer at each reach
q = np.random.randn(len(linesdata))+1
q
```
##### Add reachs fluxes and cumulative flow to lines DataFrame
```
linesdata['qreach'] = q
linesdata['qstream'] = np.cumsum(q)
recarray2shp(linesdata.drop('geometry', axis=1).to_records(),
geoms=linesdata.geometry,
shpname=lines_shapefile,
epsg=grid.epsg)
ax = plt.subplot(1, 1, 1, aspect='equal')
extents = grid.extent
pc = flopy.plot.plot_shapefile(lines_shapefile, ax=ax, radius=25)
ax.set_xlim(extents[0], extents[1])
ax.set_ylim(extents[2], extents[3])
ax.set_title(lines_shapefile);
```
## Overriding the model's modelgrid with a user supplied modelgrid
In some cases it may be necessary to override the model's modelgrid instance with a seperate modelgrid. An example of this is if the model discretization is in feet and the user would like it projected in meters. Exporting can be accomplished by supplying a modelgrid as a `kwarg` in any of the `export()` methods within flopy. Below is an example:
```
mg0 = m.modelgrid
# build a new modelgrid instance with discretization in meters
modelgrid = flopy.discretization.StructuredGrid(delc=mg0.delc * 0.3048, delr=mg0.delr * 0.3048,
top= mg0.top, botm=mg0.botm, idomain=mg0.idomain,
xoff=mg0.xoffset * 0.3048, yoff=mg0.yoffset * 0.3048)
# exporting an entire model
m.export('{}/freyberg.shp'.format(outdir), modelgrid=modelgrid)
```
And for a specific parameter the method is the same
```
fname = '{}/hk.shp'.format(outdir)
m.lpf.hk.export(fname, modelgrid=modelgrid)
ax = plt.subplot(1, 1, 1, aspect='equal')
extents = modelgrid.extent
a = m.lpf.hk.array.ravel()
pc = flopy.plot.plot_shapefile(fname, ax=ax, a=a)
ax.set_xlim(extents[0], extents[1])
ax.set_ylim(extents[2], extents[3])
ax.set_title(fname);
```
| github_jupyter |
# BERT finetuning on AG_news-4
## Librairy
```
# !pip install transformers==4.8.2
# !pip install datasets==1.7.0
import os
import time
import pickle
import numpy as np
import torch
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score
from transformers import BertTokenizer, BertTokenizerFast
from transformers import BertForSequenceClassification, AdamW
from transformers import Trainer, TrainingArguments
from transformers import EarlyStoppingCallback
from transformers.data.data_collator import DataCollatorWithPadding
from datasets import load_dataset, Dataset, concatenate_datasets
# print(torch.__version__)
# print(torch.cuda.device_count())
# print(torch.cuda.is_available())
# print(torch.cuda.get_device_name(0))
device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')
# if torch.cuda.is_available():
# torch.set_default_tensor_type('torch.cuda.FloatTensor')
device
```
## Global variables
```
BATCH_SIZE = 24
NB_EPOCHS = 4
RESULTS_FILE = '~/Results/BERT_finetune/ag_news-4_BERT_finetune_b'+str(BATCH_SIZE)+'_results.pkl'
RESULTS_PATH = '~/Results/BERT_finetune/ag_news-4_b'+str(BATCH_SIZE)+'/'
CACHE_DIR = '~/Data/huggignface/' # path of your folder
```
## Dataset
```
# download dataset
raw_datasets = load_dataset('ag_news', cache_dir=CACHE_DIR)
# tokenize
tokenizer = BertTokenizer.from_pretrained("bert-base-uncased")
def tokenize_function(examples):
return tokenizer(examples["text"], padding=True, truncation=True)
tokenized_datasets = raw_datasets.map(tokenize_function, batched=True)
tokenized_datasets.set_format(type='torch', columns=['input_ids', 'attention_mask', 'label'])
train_dataset = tokenized_datasets["train"].shuffle(seed=42)
train_val_datasets = train_dataset.train_test_split(train_size=0.8)
train_dataset = train_val_datasets['train'].rename_column('label', 'labels')
val_dataset = train_val_datasets['test'].rename_column('label', 'labels')
test_dataset = tokenized_datasets["test"].shuffle(seed=42).rename_column('label', 'labels')
# get number of labels
num_labels = len(set(train_dataset['labels'].tolist()))
num_labels
```
## Model
#### Model
```
model = BertForSequenceClassification.from_pretrained("bert-base-uncased", num_labels=num_labels)
model.to(device)
```
#### Training
```
training_args = TrainingArguments(
# output
output_dir=RESULTS_PATH,
# params
num_train_epochs=NB_EPOCHS, # nb of epochs
per_device_train_batch_size=BATCH_SIZE, # batch size per device during training
per_device_eval_batch_size=BATCH_SIZE, # cf. paper Sun et al.
learning_rate=2e-5, # cf. paper Sun et al.
# warmup_steps=500, # number of warmup steps for learning rate scheduler
warmup_ratio=0.1, # cf. paper Sun et al.
weight_decay=0.01, # strength of weight decay
# # eval
evaluation_strategy="steps",
eval_steps=50,
# evaluation_strategy='no', # no more evaluation, takes time
# log
logging_dir=RESULTS_PATH+'logs',
logging_strategy='steps',
logging_steps=50,
# save
# save_strategy='epoch',
# save_strategy='steps',
# load_best_model_at_end=False
load_best_model_at_end=True # cf. paper Sun et al.
)
def compute_metrics(p):
pred, labels = p
pred = np.argmax(pred, axis=1)
accuracy = accuracy_score(y_true=labels, y_pred=pred)
return {"val_accuracy": accuracy}
trainer = Trainer(
model=model,
args=training_args,
tokenizer=tokenizer,
train_dataset=train_dataset,
eval_dataset=val_dataset,
# compute_metrics=compute_metrics,
# callbacks=[EarlyStoppingCallback(early_stopping_patience=5)]
)
results = trainer.train()
training_time = results.metrics["train_runtime"]
training_time_per_epoch = training_time / training_args.num_train_epochs
training_time_per_epoch
trainer.save_model(os.path.join(RESULTS_PATH, 'best_model-0'))
```
## Results
```
results_d = {}
epoch = 1
ordered_files = sorted( [f for f in os.listdir(RESULTS_PATH)
if (not f.endswith("logs")) and (f.startswith("best")) # best model eval only
],
key=lambda x: int(x.split('-')[1]) )
for filename in ordered_files:
print(filename)
# load model
model_file = os.path.join(RESULTS_PATH, filename)
finetuned_model = BertForSequenceClassification.from_pretrained(model_file, num_labels=num_labels)
finetuned_model.to(device)
finetuned_model.eval()
# compute test acc
test_trainer = Trainer(finetuned_model, data_collator=DataCollatorWithPadding(tokenizer))
raw_preds, labels, _ = test_trainer.predict(test_dataset)
preds = np.argmax(raw_preds, axis=1)
test_acc = accuracy_score(y_true=labels, y_pred=preds)
# results_d[filename] = (test_acc, training_time_per_epoch*epoch)
results_d[filename] = test_acc # best model evaluation only
print((test_acc, training_time_per_epoch*epoch))
epoch += 1
results_d['training_time'] = training_time
# save results
with open(RESULTS_FILE, 'wb') as fh:
pickle.dump(results_d, fh)
# load results
with open(RESULTS_FILE, 'rb') as fh:
results_d = pickle.load(fh)
results_d
```
| github_jupyter |
This tutorial shows how to generate an image of handwritten digits using Deep Convolutional Generative Adversarial Network (DCGAN).
Generative Adversarial Networks (GANs) are one of the most interesting fields in machine learning. The standard GAN consists of two models, a generative and a discriminator one. Two models are trained simultaneously by an adversarial process. A generative model (`the artist`) learns to generate images that look real, while the discriminator (`the art critic`) one learns to tell real images apart from the fakes.
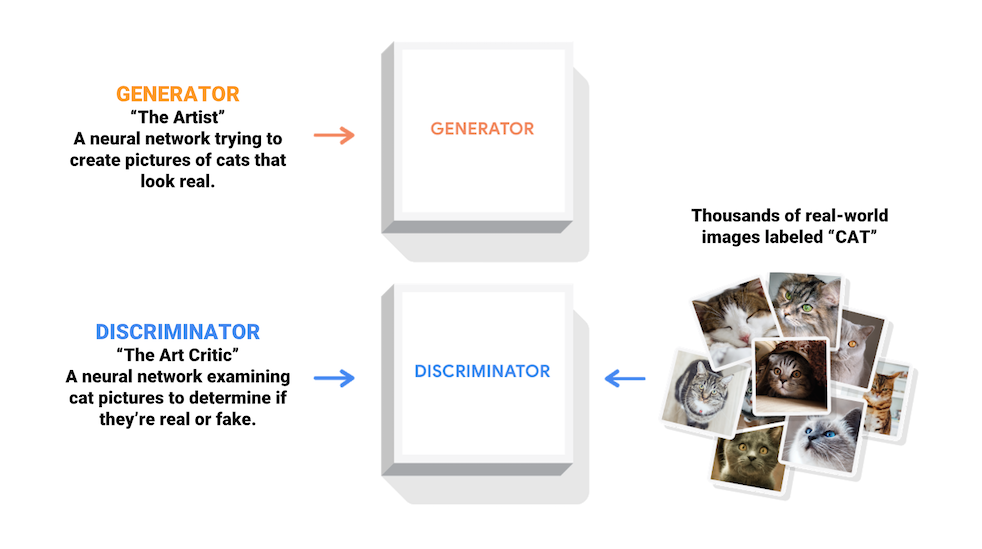
Refer to Tensorflow.org (2020).
During training, the generative model becomes progressively creating images that look real, and the discriminator model becomes progressively telling them apart. The whole process reaches equilibrium when the discriminator is no longer able to distinguish real images from fakes.
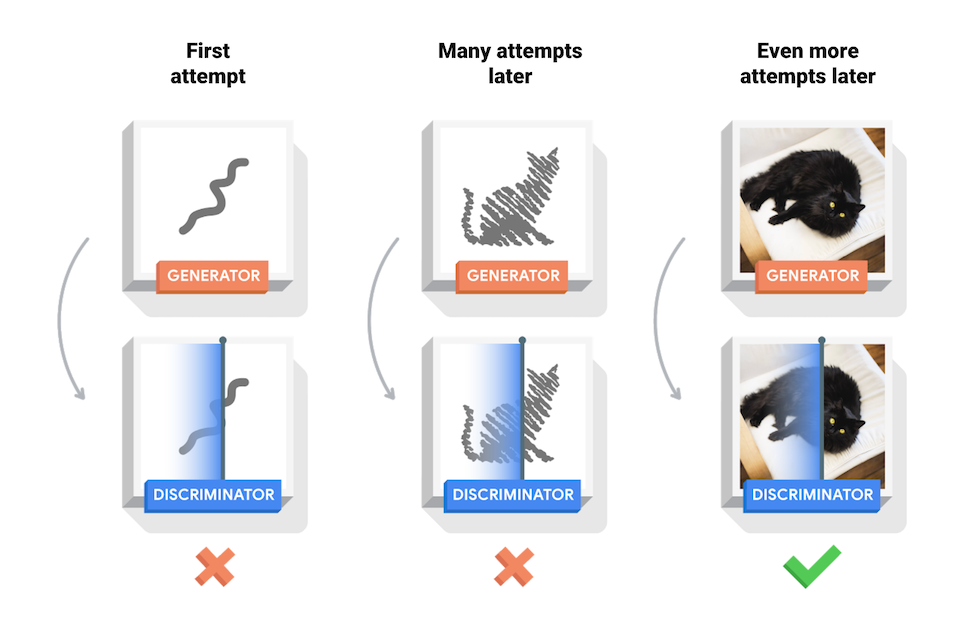
Refer to Tensorflow.org (2020).
In this demo, we show how to train a GAN model on MNIST and FASHION MNIST dataset.
```
!pip uninstall -y tensorflow
!pip install -q tf-nightly tfds-nightly
import glob
import tensorflow as tf
import tensorflow_datasets as tfds
import matplotlib.pyplot as plt
from tensorflow.keras.layers import Conv2D, Conv2DTranspose, Dense, Flatten, BatchNormalization, ELU, LeakyReLU, Reshape, Dropout
import numpy as np
import IPython.display as display
from IPython.display import clear_output
import os
import time
import imageio
tfds.disable_progress_bar()
print("Tensorflow Version: {}".format(tf.__version__))
print("GPU {} available.".format("is" if tf.config.experimental.list_physical_devices("GPU") else "not"))
```
# Data Preprocessing
```
def normalize(image):
img = image['image']
img = (tf.cast(img, tf.float32) - 127.5) / 127.5
return img
```
## MNIST Dataset
```
raw_datasets, metadata = tfds.load(name="mnist", with_info=True)
raw_train_datasets, raw_test_datasets = raw_datasets['train'], raw_datasets['test']
raw_test_datasets, metadata
BUFFER_SIZE = 10000
BATCH_SIZE = 256
train_datasets = raw_train_datasets.map(normalize).cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE)
test_datasets = raw_test_datasets.map(normalize).batch(BATCH_SIZE)
for imgs in train_datasets.take(1):
img = imgs[0]
plt.imshow(tf.keras.preprocessing.image.array_to_img(img))
plt.axis("off")
plt.show()
```
## Fashion_MNIST Dataset
```
raw_datasets, metadata = tfds.load(name="fashion_mnist", with_info=True)
raw_train_datasets, raw_test_datasets = raw_datasets['train'], raw_datasets['test']
raw_train_datasets
for image in raw_train_datasets.take(1):
plt.imshow(tf.keras.preprocessing.image.array_to_img(image['image']))
plt.axis("off")
plt.title("Label: {}".format(image['label']))
plt.show()
BUFFER_SIZE = 10000
BATCH_SIZE = 256
train_datasets = raw_train_datasets.map(normalize).cache().prefetch(BUFFER_SIZE).batch(BATCH_SIZE)
test_datasets = raw_test_datasets.map(normalize).batch(BATCH_SIZE)
for imgs in train_datasets.take(1):
img = imgs[0]
plt.imshow(tf.keras.preprocessing.image.array_to_img(img))
plt.axis("off")
plt.show()
```
# Build the GAN Model
## The Generator
The generator uses the `tf.keras.layers.Conv2DTranspose` (upsampling) layer to produce an image from a seed input (a random noise). Start from this seed input, upsample it several times to reach the desired output (28x28x1).
```
def build_generator_model():
model = tf.keras.Sequential()
model.add(Dense(units=7 * 7 * 256, use_bias=False, input_shape=(100,)))
model.add(BatchNormalization())
model.add(LeakyReLU())
model.add(Reshape(target_shape=[7,7,256]))
assert model.output_shape == (None, 7, 7, 256)
model.add(Conv2DTranspose(filters=128, kernel_size=(5,5), strides=(1,1), padding="same", use_bias=False))
model.add(BatchNormalization())
model.add(LeakyReLU())
assert model.output_shape == (None, 7, 7, 128)
model.add(Conv2DTranspose(filters=64, kernel_size=(5,5), strides=(2,2), padding='same', use_bias=False))
model.add(BatchNormalization())
model.add(LeakyReLU())
assert model.output_shape == (None, 14, 14, 64)
model.add(Conv2DTranspose(filters=1, kernel_size=(5,5), strides=(2,2), padding='same', use_bias=False,
activation="tanh"))
assert model.output_shape == (None, 28, 28, 1)
return model
generator = build_generator_model()
generator_input = tf.random.normal(shape=[1, 100])
generator_outputs = generator(generator_input, training=False)
plt.imshow(generator_outputs[0, :, :, 0], cmap='gray')
plt.show()
```
## The Discriminator
The discriminator is basically a CNN network.
```
def build_discriminator_model():
model = tf.keras.Sequential()
# [None, 28, 28, 64]
model.add(Conv2D(filters=64, kernel_size=(5,5), strides=(1,1), padding="same",
input_shape=[28,28,1]))
model.add(LeakyReLU())
model.add(Dropout(rate=0.3))
# [None, 14, 14, 128]
model.add(Conv2D(filters=128, kernel_size=(3,3), strides=(2,2), padding='same'))
model.add(LeakyReLU())
model.add(Dropout(rate=0.3))
model.add(Flatten())
model.add(Dense(units=1))
return model
```
The output of the discriminator was trained that the negative values are for the fake images and the positive values are for real ones.
```
discriminator = build_discriminator_model()
discriminator_outputs = discriminator(generator_outputs)
discriminator_outputs
```
# Define the losses and optimizers
Define the loss functions and the optimizers for both models.
```
# define the cross entropy as the helper function
cross_entropy = tf.keras.losses.BinaryCrossentropy(from_logits=True)
```
## Discriminator Loss
The discriminator's loss quantifies how well the discriminator can tell the real images from fakes. It compares the discriminator's predictions on real images to an array of 1s, and the discriminator's predictions on fake images to an array of 0s.
```
def discriminator_loss(real_output, fake_output):
real_loss = cross_entropy(tf.ones_like(real_output), real_output)
fake_loss = cross_entropy(tf.zeros_like(fake_output), fake_output)
total_loss = real_loss + fake_loss
return total_loss
```
## Generator Loss
The generator's loss quantifies how well the generator model can trick the discriminator model. If the generator performs well, the discriminator will classify the fake images as real (or 1). Here, we will compare the discriminator decisions on the generated images to an array of 1s.
```
def generator_loss(fake_output):
# the generator learns to make the discriminator predictions became real
# (or an array of 1s) on the fake images
return cross_entropy(tf.ones_like(fake_output), fake_output)
```
## Define optimizers.
```
generator_optimizer = tf.keras.optimizers.Adam(learning_rate=1e-4)
discriminator_optimizer = tf.keras.optimizers.Adam(learning_rate=1e-4)
```
## Save Checkpoints
```
ckpt_dir = "./gan_ckpt"
ckpt_prefix = os.path.join(ckpt_dir, "ckpt")
ckpt = tf.train.Checkpoint(generator_optimizer=generator_optimizer,
discriminator_optimizer=discriminator_optimizer,
generator=generator,
discriminator=discriminator)
ckpt
```
# Define the training loop
```
EPOCHS = 50
noise_dim = 100
num_generated_examples = 16
# You will reuse the seed overtime to visualize progress in the animated GIF.
seed = tf.random.normal(shape=[num_generated_examples, noise_dim])
```
In the training loop, the generator model takes the noise as the input to generate the fake images. The discriminator model takes real images and fake images to give the discriminations (or outputs) for them. Calculate the generator and discriminator losses each using the real outputs and the fake outputs. Calculate the gradients of the model trainable variables based on these losses and then apply gradients back to them.
```
@tf.function
def train_step(images):
fake_noises = tf.random.normal(shape=[BATCH_SIZE, noise_dim])
with tf.GradientTape() as disc_tape, tf.GradientTape() as gen_tape:
fake_images = generator(fake_noises, training=True)
fake_outputs = discriminator(fake_images, training=True)
real_outputs = discriminator(images, training=True)
disc_loss = discriminator_loss(real_output=real_outputs,
fake_output=fake_outputs)
gen_loss = generator_loss(fake_output=fake_outputs)
disc_gradients = disc_tape.gradient(disc_loss, discriminator.trainable_variables)
gen_gradients = gen_tape.gradient(gen_loss, generator.trainable_variables)
discriminator_optimizer.apply_gradients(zip(disc_gradients, discriminator.trainable_variables))
generator_optimizer.apply_gradients(zip(gen_gradients, generator.trainable_variables))
def generate_and_save_images(model, epoch, test_input):
"""Helps to generate the images from a fixed seed."""
predictions = model(test_input, training=False)
fig = plt.figure(figsize=(8,8))
for i in range(predictions.shape[0]):
plt.subplot(4, 4, i+1)
plt.imshow(predictions[i, :, :, 0] * 127.5 + 127.5, cmap='gray')
plt.axis("off")
plt.savefig('image_epoch_{:04d}.png'.format(epoch))
plt.show()
def train(dataset, epochs):
for epoch in range(epochs):
start = time.time()
for batch_dataset in dataset:
train_step(batch_dataset)
clear_output(wait=True)
generate_and_save_images(generator, epoch+1, seed)
if (epoch+1) % 15 == 0:
ckpt.save(file_prefix=ckpt_prefix)
print("Epoch {} in time {}.".format(epoch + 1, time.time()-start))
# after the training
clear_output(wait=True)
generate_and_save_images(generator, epoch+1, seed)
```
## Train the Model
Call the `train()` function to start the model training. Note, training GANs can be tricky. It's important that the generator and discriminator do not overpower each other (e.g. they train at a similar rate).
```
train(train_datasets, epochs=EPOCHS)
```
# Create a GIF
```
def display_image(epoch_no):
image_path = 'image_epoch_{:04d}.png'.format(epoch_no)
img = plt.imread(fname=image_path)
plt.imshow(img)
plt.margins(0)
plt.axis("off")
plt.tight_layout()
plt.show()
display_image(50)
anim_file = 'dcgan.gif'
with imageio.get_writer(anim_file, mode="I") as writer:
filenames = glob.glob('image*.png')
filenames = sorted(filenames)
for _, filename in enumerate(filenames):
image = imageio.imread(filename)
writer.append_data(image)
try:
from google.colab import files
except ImportError:
pass
else:
files.download(anim_file)
```
| github_jupyter |
## Setup
If you are running this generator locally(i.e. in a jupyter notebook in conda, just make sure you installed:
- RDKit
- DeepChem 2.5.0 & above
- Tensorflow 2.4.0 & above
Then, please skip the following part and continue from `Data Preparations`.
To increase efficiency, we recommend running this molecule generator in Colab.
Then, we'll first need to run the following lines of code, these will download conda with the deepchem environment in colab.
```
#!curl -Lo conda_installer.py https://raw.githubusercontent.com/deepchem/deepchem/master/scripts/colab_install.py
#import conda_installer
#conda_installer.install()
#!/root/miniconda/bin/conda info -e
#!pip install --pre deepchem
#import deepchem
#deepchem.__version__
```
## Data Preparations
Now we are ready to import some useful functions/packages, along with our model.
### Import Data
```
import model##our model
from rdkit import Chem
from rdkit.Chem import AllChem
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import deepchem as dc
```
Then, we are ready to import our dataset for training.
Here, for demonstration, we'll be using this dataset of in-vitro assay that detects inhibition of SARS-CoV 3CL protease via fluorescence.
The dataset is originally from [PubChem AID1706](https://pubchem.ncbi.nlm.nih.gov/bioassay/1706), previously handled by [JClinic AIcure](https://www.aicures.mit.edu/) team at MIT into this [binarized label form](https://github.com/yangkevin2/coronavirus_data/blob/master/data/AID1706_binarized_sars.csv).
```
df = pd.read_csv('AID1706_binarized_sars.csv')
```
Observe the data above, it contains a 'smiles' column, which stands for the smiles representation of the molecules. There is also an 'activity' column, in which it is the label specifying whether that molecule is considered as hit for the protein.
Here, we only need those 405 molecules considered as hits, and we'll be extracting features from them to generate new molecules that may as well be hits.
```
true = df[df['activity']==1]
```
### Set Minimum Length for molecules
Since we'll be using graphic neural network, it might be more helpful and efficient if our graph data are of the same size, thus, we'll eliminate the molecules from the training set that are shorter(i.e. lacking enough atoms) than our desired minimum size.
```
num_atoms = 6 #here the minimum length of molecules is 6
input_df = true['smiles']
df_length = []
for _ in input_df:
df_length.append(Chem.MolFromSmiles(_).GetNumAtoms() )
true['length'] = df_length #create a new column containing each molecule's length
true = true[true['length']>num_atoms] #Here we leave only the ones longer than 6
input_df = true['smiles']
input_df_smiles = input_df.apply(Chem.MolFromSmiles) #convert the smiles representations into rdkit molecules
```
Now, we are ready to apply the `featurizer` function to our molecules to convert them into graphs with nodes and edges for training.
```
#input_df = input_df.apply(Chem.MolFromSmiles)
train_set = input_df_smiles.apply( lambda x: model.featurizer(x,max_length = num_atoms))
train_set
```
We'll take one more step to make the train_set into separate nodes and edges, which fits the format later to supply to the model for training
```
nodes_train, edges_train = list(zip(*train_set) )
```
## Training
Now, we're finally ready for generating new molecules. We'll first import some necessay functions from tensorflow.
```
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
```
The network here we'll be using is Generative Adversarial Network, as mentioned in the project introduction. Here's a great [introduction](https://machinelearningmastery.com/what-are-generative-adversarial-networks-gans/).
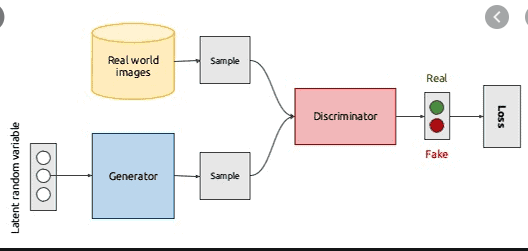
Here we'll first initiate a discriminator and a generator model with the corresponding functions in the package.
```
disc = model.make_discriminator(num_atoms)
gene = model.make_generator(num_atoms, noise_input_shape = 100)
```
Then, with the `train_batch` function, we'll supply the necessary inputs and train our network. Upon some experimentations, an epoch of around 160 would be nice for this dataset.
```
generator_trained = model.train_batch(
disc, gene,
np.array(nodes_train), np.array(edges_train),
noise_input_shape = 100, EPOCH = 160, BATCHSIZE = 2,
plot_hist = True, temp_result = False
)
```
There are two possible kind of failures regarding a GAN model: model collapse and failure of convergence. Model collapse would often mean that the generative part of the model wouldn't be able to generate diverse outcomes. Failure of convergence between the generative and the discriminative model could likely way be identified as that the loss for the discriminator has gone to zero or close to zero.
Observe the above generated plot, in the upper plot, the loss of discriminator has not gone to zero/close to zero, indicating that the model has possibily find a balance between the generator and the discriminator. In the lower plot, the accuracy is fluctuating between 1 and 0, indicating possible variability within the data generated.
Therefore, it is reasonable to conclude that within the possible range of epoch and other parameters, the model has successfully avoided the two common types of failures associated with GAN.
## Rewarding Phase
The above `train_batch` function is set to return a trained generator. Thus, we could use that function directly and observe the possible molecules we could get from that function.
```
no, ed = generator_trained(np.random.randint(0,20
, size =(1,100)))#generated nodes and edges
abs(no.numpy()).astype(int).reshape(num_atoms), abs(ed.numpy()).astype(int).reshape(num_atoms,num_atoms)
```
With the `de_featurizer`, we could convert the generated matrix into a smiles molecule and plot it out=)
```
cat, dog = model.de_featurizer(abs(no.numpy()).astype(int).reshape(num_atoms), abs(ed.numpy()).astype(int).reshape(num_atoms,num_atoms))
Chem.MolToSmiles(cat)
Chem.MolFromSmiles(Chem.MolToSmiles(cat))
```
## Brief Result Analysis
```
from rdkit import DataStructs
```
With the rdkit function of comparing similarities, here we'll demonstrate a preliminary analysis of the molecule we've generated. With "CCO" molecule as a control, we could observe that the new molecule we've generated is more similar to a random selected molecule(the fourth molecule) from the initial training set.
This may indicate that our model has indeed extracted some features from our original dataset and generated a new molecule that is relevant.
```
DataStructs.FingerprintSimilarity(Chem.RDKFingerprint(Chem.MolFromSmiles("[Li]NBBC=N")), Chem.RDKFingerprint(Chem.MolFromSmiles("CCO")))# compare with the control
#compare with one from the original data
DataStructs.FingerprintSimilarity(Chem.RDKFingerprint(Chem.MolFromSmiles("[Li]NBBC=N")), Chem.RDKFingerprint(Chem.MolFromSmiles("CCN1C2=NC(=O)N(C(=O)C2=NC(=N1)C3=CC=CC=C3)C")))
```
| github_jupyter |
```
import pandas as pd
import numpy as np
import glob
result_file = '/tmp/fuzzydatatest/20220209-150332_perf.csv'
perf_df = pd.read_csv(result_file, index_col=0)
perf_df
import numpy as np
perf_df['end_time_seconds'] = np.cumsum(perf_df.elapsed_time)
perf_df['start_time_seconds'] = end_time.shift().fillna(0)
perf_df
import matplotlib.pyplot as plt
from matplotlib.patches import Patch
# GANTT Chart function
def plot_gantt(df, title='fuzzydata', x_range=None):
# Adapted from
# https://towardsdatascience.com/gantt-charts-with-pythons-matplotlib-395b7af72d72
#### Prepare the DF ####
c_dict = {'merge':'#E64646', 'pivot':'#E69646', 'groupby':'#34D05C',
'project':'#34D0C3', 'sample':'#3475D0' , 'select': '#29335C' , 'load': '#f7ef07'}
df['end_time_seconds'] = np.cumsum(perf_df.elapsed_time)
df['start_time_seconds'] = df['end_time_seconds'].shift().fillna(0)
df['task_label'] = df.index.astype(str) +'_'+ df['op']
df['color'] = df['op'].apply(lambda x: c_dict[x])
df = df.iloc[::-1]
#### PLOT #####
fig, ax = plt.subplots(1, figsize=(16,6))
ax.barh(df.task_label, df.elapsed_time, left=df.start_time_seconds,
color=df.color)
##### LEGENDS #####
legend_elements = [Patch(facecolor=c_dict[i], label=i) for i in c_dict]
plt.legend(handles=legend_elements)
##### TICKS #####
#xticks = np.arange(0, df.end_num.max()+1, 3)
#xticks_labels = pd.date_range(proj_start, end=df.End.max()).strftime("%m/%d")
#xticks_minor = np.arange(0, df.end_num.max()+1, 1)
#ax.set_xticks(xticks)
#ax.set_xticks(xticks_minor, minor=True)
#ax.set_xticklabels(xticks_labels[::3])
ax.set_axisbelow(True)
ax.xaxis.grid(color='gray', linestyle='dashed', alpha=0.2, which='both')
if x_range:
plt.xlim(x_range)
plt.title(title)
plt.ylabel('Operation')
plt.xlabel('Seconds')
plt.show()
plot_gantt(perf_df)
# Plot all gantt charts
BASE_DIR = '/tmp/fuzzydatatest/'
frameworks = ['pandas', 'sqlite', 'modin_dask', 'modin_ray']
for f in frameworks:
result_file = glob.glob(f"{BASE_DIR}/{f}/*_perf.csv")[0]
perf_df = pd.read_csv(result_file, index_col=0)
plot_gantt(perf_df, title=f'Example Workflow Base Table (20 columns x 10,000 rows), 15 artifacts on {f}', x_range=[0.0,2.0])
BASE_DIR = '/tmp/fuzzydatatest_big/'
frameworks = ['pandas', 'sqlite', 'modin_dask', 'modin_ray']
for f in frameworks:
result_file = glob.glob(f"{BASE_DIR}/{f}/*_perf.csv")[0]
perf_df = pd.read_csv(result_file, index_col=0)
plot_gantt(perf_df, title=f'Example Workflow Base Table (20 columns x 100,000 rows), 15 artifacts on {f}', x_range=[0.0, 5.0])
BASE_DIR = '/tmp/fuzzydatatest_1m/'
frameworks = ['pandas', 'sqlite', 'modin_dask', 'modin_ray']
for f in frameworks:
result_file = glob.glob(f"{BASE_DIR}/{f}/*_perf.csv")[0]
perf_df = pd.read_csv(result_file, index_col=0)
plot_gantt(perf_df, title=f'Example Workflow Base Table (20 columns x 1,000,000 rows), 15 artifacts on {f}', x_range=[0.0, 35.0])
```
# Large DataFrame Tests - NYC CAB
```
BASE_DIR = '/mnt/roscoe/data/fuzzydata/fuzzydatatest/nyc-cab/'
frameworks = ['pandas', 'sqlite', 'modin_dask', 'modin_ray']
all_perfs = []
for f in frameworks:
result_file = glob.glob(f"{BASE_DIR}/{f}/*_perf.csv")[0]
perf_df = pd.read_csv(result_file, index_col=0)
perf_df['end_time_seconds'] = np.cumsum(perf_df.elapsed_time)
perf_df['start_time_seconds'] = perf_df['end_time_seconds'].shift().fillna(0)
perf_df['framework'] = f
all_perfs.append(perf_df)
#plot_gantt(perf_df, title=f'Example Workflow 1.18 GB CSV load/groupby on {f}', x_range=[0.0, 320])
nyc_cab_perfs = pd.concat(all_perfs, ignore_index=True)
new_op_labels = ['load', 'groupby_1', 'groupby_2', 'groupby_3']
nyc_cab_perfs['op'] = np.tile(new_op_labels,4)
pivoted = nyc_cab_perfs.pivot(index='framework', columns='op', values='elapsed_time')
pivoted = pivoted.reindex(['pandas', 'modin_dask', 'modin_ray', 'sqlite'])[new_op_labels]
ax = pivoted.plot.bar(stacked=True)
plt.xticks(rotation=0)
plt.legend()
plt.xlabel('Client')
plt.ylabel('Runtime (Seconds)')
plt.savefig('real_example.pdf', bbox_inches='tight')
```
# Combined Performance / Scaling Graph
```
BASE_DIR = '/mnt/roscoe/data/fuzzydata/fuzzydata_scaling_test_3/'
frameworks = ['pandas', 'sqlite', 'modin_dask', 'modin_ray']
sizes = ['1000', '10000', '100000', '1000000', '5000000']
all_perfs = []
for framework in frameworks:
for size in sizes:
input_dir = f"{BASE_DIR}/{framework}_{size}/"
try:
#print(f"{input_dir}/*_perf.csv")
perf_file = glob.glob(f"{input_dir}/*_perf.csv")[0]
perf_df = pd.read_csv(perf_file, index_col=0)
perf_df['end_time_seconds'] = np.cumsum(perf_df.elapsed_time)
perf_df['start_time_seconds'] = perf_df['end_time_seconds'].shift().fillna(0)
perf_df['framework'] = framework
perf_df['size'] = size
all_perfs.append(perf_df)
except (IndexError, FileNotFoundError) as e:
#raise(e)
pass
all_perfs_df = pd.concat(all_perfs, ignore_index=True)
total_wf_times = all_perfs_df.loc[all_perfs_df.dst == 'artifact_14'][['framework','size','end_time_seconds']].reset_index(drop=True).pivot(index='size', columns='framework', values='end_time_seconds')
total_wf_times = total_wf_times.rename_axis('Client')
total_wf_times = total_wf_times[['pandas', 'modin_dask', 'modin_ray', 'sqlite']]
total_wf_times
import seaborn as sns
import matplotlib
import matplotlib.pyplot as plt
font = {'family' : 'serif',
'weight' : 'normal',
'size' : 12}
matplotlib.rc('font', **font)
x_axis_replacements = ['1K', '10K', '100K', '1M', '5M']
plt.figure(figsize=(6,4))
ax = sns.lineplot(data=total_wf_times, markers=True, linewidth=2.5, markersize=10)
plt.xticks(total_wf_times.index, x_axis_replacements)
plt.grid()
plt.xlabel('Base Artifact Number of Rows (r)')
plt.ylabel('Runtime (Seconds)')
handles, labels = ax.get_legend_handles_labels()
ax.legend(handles=handles, labels=labels)
plt.savefig("scaling.pdf", bbox_inches='tight')
breakdown = all_perfs_df[['framework', 'size', 'op', 'elapsed_time']].groupby(['framework', 'size', 'op']).sum().reset_index()
pivoted_breakdown = breakdown.pivot(index=['size', 'framework'], columns=['op'], values='elapsed_time')
pivoted_breakdown
pivoted_breakdown.plot.bar(stacked=True)
plt.savefig("breakdown.pdf", bbox_inches='tight')
breakdown
# Sources: https://stackoverflow.com/questions/22787209/how-to-have-clusters-of-stacked-bars-with-python-pandas
import pandas as pd
import matplotlib.cm as cm
import numpy as np
import matplotlib.pyplot as plt
def plot_clustered_stacked(dfall, labels=None, title="multiple stacked bar plot", H="/",
x_axis_replacements=None, **kwargs):
"""Given a list of dataframes, with identical columns and index, create a clustered stacked bar plot.
labels is a list of the names of the dataframe, used for the legend
title is a string for the title of the plot
H is the hatch used for identification of the different dataframe"""
n_df = len(dfall)
n_col = len(dfall[0].columns)
n_ind = len(dfall[0].index)
fig = plt.figure(figsize=(6,4))
axe = fig.add_subplot(111)
for df in dfall : # for each data frame
axe = df.plot(kind="bar",
linewidth=0,
stacked=True,
ax=axe,
legend=False,
grid=False,
**kwargs) # make bar plots
hatches = ['', 'oo', '///', '++']
h,l = axe.get_legend_handles_labels() # get the handles we want to modify
for i in range(0, n_df * n_col, n_col): # len(h) = n_col * n_df
for j, pa in enumerate(h[i:i+n_col]):
for rect in pa.patches: # for each index
rect.set_x(rect.get_x() + 1 / float(n_df + 1) * i / float(n_col) -0.1)
rect.set_hatch(hatches[int(i / n_col)]) #edited part
rect.set_width(1 / float(n_df + 1))
axe.set_xticks((np.arange(0, 2 * n_ind, 2) + 1 / float(n_df + 1)) / 2.)
if x_axis_replacements == None:
x_axis_replacements = df.index
axe.set_xticklabels(x_axis_replacements, rotation = 0)
#axe.set_title(title)
# Add invisible data to add another legend
n=[]
for i in range(n_df):
n.append(axe.bar(0, 0, color="gray", hatch=hatches[i]))
l1 = axe.legend(h[:n_col], l[:n_col], loc=[0.38, 0.545])
if labels is not None:
l2 = plt.legend(n, labels)# , loc=[1.01, 0.1])
axe.add_artist(l1)
return axe
cols = ['groupby','load','merge','project','sample']
pbr = pivoted_breakdown.reset_index()
pbr = pbr.set_index('size')
df_splits = [pbr.loc[pbr.framework == f][cols] for f in ['pandas', 'modin_dask', 'modin_ray', 'sqlite']]
# Then, just call :
plot_clustered_stacked(df_splits,['pandas', 'modin_dask', 'modin_ray', 'sqlite'],
x_axis_replacements=x_axis_replacements,
title='Timing Breakdown Per Operation Type')
plt.xlabel('Base Artifact Number of Rows (r)')
plt.ylabel('Runtime (Seconds)')
plt.savefig("breakdown.eps")
pivoted_breakdown.reset_index().set_index('size')
```
| github_jupyter |
# DataMining TwitterAPI
Requirements:
- TwitterAccount
- TwitterApp credentials
## Imports
The following imports are requiered to mine data from Twitter
```
# http://tweepy.readthedocs.io/en/v3.5.0/index.html
import tweepy
# https://api.mongodb.com/python/current/
import pymongo
import json
import sys
```
## Access and Test the TwitterAPI
Insert your `CONSUMER_KEY`, `CONSUMER_SECRET`, `ACCESS_TOKEN` and `ACCESS_TOKEN_SECRET` and run the code snippet to test if access is granted. If everything works well 'tweepy...' will be posted to your timeline.
```
# Set the received credentials for your recently created TwitterAPI
CONSUMER_KEY = 'MmiELrtF7fSp3vptCID8jKril'
CONSUMER_SECRET = 'HqtMRk4jpt30uwDOLz30jHqZm6TPN6rj3oHFaL6xFxw2k0GkDC'
ACCESS_TOKEN = '116725830-rkT63AILxR4fpf4kUXd8xJoOcHTsGkKUOKSMpMJQ'
ACCESS_TOKEN_SECRET = 'eKzxfku4GdYu1wWcMr5iusTmhFT35cDWezMU2Olr5UD4i'
# auth with your provided
auth = tweepy.OAuthHandler(CONSUMER_KEY, CONSUMER_SECRET)
auth.set_access_token(ACCESS_TOKEN, ACCESS_TOKEN_SECRET)
# Create an instance for the TwitterApi
twitter = tweepy.API(auth)
status = twitter.update_status('tweepy ...')
print(json.dumps(status._json, indent=1))
```
## mongoDB
To gain access to the mongoDB the library `pymongo` is used.
In the first step the mongoDB URL is defined.
```
MONGO_URL = 'mongodb://twitter-mongodb:27017/'
```
Next, two functions are defined to save and load data from mongoDB.
```
def save_to_mongo(data, mongo_db, mongo_db_coll):
# Connects to the MongoDB server running on
client = pymongo.MongoClient(MONGO_URL)
# Get a reference to a particular database
db = client[mongo_db]
# Reference a particular collection in the database
coll = db[mongo_db_coll]
# Perform a bulk insert and return the IDs
return coll.insert_one(data)
def load_from_mongo(mongo_db, mongo_db_coll, return_cursor=False, criteria=None, projection=None):
# Optionally, use criteria and projection to limit the data that is
# returned - http://docs.mongodb.org/manual/reference/method/db.collection.find/
# Connects to the MongoDB server running on
client = pymongo.MongoClient(MONGO_URL)
# Reference a particular collection in the database
db = client[mongo_db]
# Perform a bulk insert and return the IDs
coll = db[mongo_db_coll]
if criteria is None:
criteria = {}
if projection is None:
cursor = coll.find(criteria)
else:
cursor = coll.find(criteria, projection)
# Returning a cursor is recommended for large amounts of data
if return_cursor:
return cursor
else:
return [ item for item in cursor ]
```
## Stream tweets to mongoDB
Now we want to stream tweets to a current trend to the mongoDB.
Therefore we ask the TwitterAPI for current Trends within different places. Places are defined with WOEID https://www.flickr.com/places/info/1
```
# WORLD
print('trends WORLD')
trends = twitter.trends_place(1)[0]['trends']
for t in trends[:5]:
print(json.dumps(t['name'],indent=1))
# US
print('\ntrends US')
trends = twitter.trends_place(23424977)[0]['trends']
for t in trends[:5]:
print(json.dumps(t['name'],indent=1))
# AT
print('\ntrends AUSTRIA')
trends = twitter.trends_place(23424750)[0]['trends']
for t in trends[:5]:
print(json.dumps(t['name'],indent=1))
```
### StreamListener
tweepy provides a StreamListener that allows to stream live tweets. All streamed tweets are stored to the mongoDB.
```
MONGO_DB = 'trends'
MONGO_COLL = 'tweets'
TREND = '#BestBoyBand'
class CustomStreamListener(tweepy.StreamListener):
def __init__(self, twitter):
self.twitter = twitter
super(tweepy.StreamListener, self).__init__()
self.db = pymongo.MongoClient(MONGO_URL)[MONGO_DB]
self.number = 1
print('Streaming tweets to mongo ...')
def on_data(self, tweet):
self.number += 1
self.db[MONGO_COLL].insert_one(json.loads(tweet))
if self.number % 100 == 0 : print('{} tweets added'.format(self.number))
def on_error(self, status_code):
return True # Don't kill the stream
def on_timeout(self):
return True # Don't kill the stream
sapi = tweepy.streaming.Stream(auth, CustomStreamListener(twitter))
sapi.filter(track=[TREND])
```
## Collect tweets from a specific user
In this use-case we mine data from a specific user.
```
MONGO_DB = 'trump'
MONGO_COLL = 'tweets'
TWITTER_USER = '@realDonaldTrump'
def get_all_tweets(screen_name):
#initialize a list to hold all the tweepy Tweets
alltweets = []
#make initial request for most recent tweets (200 is the maximum allowed count)
new_tweets = twitter.user_timeline(screen_name = screen_name,count=200)
#save most recent tweets
alltweets.extend(new_tweets)
#save the id of the oldest tweet less one
oldest = alltweets[-1].id - 1
#keep grabbing tweets until there are no tweets left to grab
while len(new_tweets) > 0:
#all subsiquent requests use the max_id param to prevent duplicates
new_tweets = twitter.user_timeline(screen_name = screen_name,count=200,max_id=oldest)
#save most recent tweets
alltweets.extend(new_tweets)
#update the id of the oldest tweet less one
oldest = alltweets[-1].id - 1
print("...{} tweets downloaded so far".format(len(alltweets)))
#write tweet objects to JSON
print("Writing tweet objects to MongoDB please wait...")
number = 1
for status in alltweets:
print(save_to_mongo(status._json, MONGO_DB, MONGO_COLL))
number += 1
print("Done - {} tweets saved!".format(number))
#pass in the username of the account you want to download
get_all_tweets(TWITTER_USER)
```
## Load tweets from mongo
```
data = load_from_mongo('trends', 'tweets')
for d in data[:5]:
print(d['text'])
```
| github_jupyter |
# Graphs from the presentation
```
import matplotlib.pyplot as plt
%matplotlib notebook
# create a new figure
plt.figure()
# create x and y coordinates via lists
x = [99, 19, 88, 12, 95, 47, 81, 64, 83, 76]
y = [43, 18, 11, 4, 78, 47, 77, 70, 21, 24]
# scatter the points onto the figure
plt.scatter(x, y)
# create a new figure
plt.figure()
# create x and y values via lists
x = [1, 2, 3, 4, 5, 6, 7, 8]
y = [1, 4, 9, 16, 25, 36, 49, 64]
# plot the line
plt.plot(x, y)
# create a new figure
plt.figure()
# create a list of observations
observations = [5.24, 3.82, 3.73, 5.3 , 3.93, 5.32, 6.43, 4.4 , 5.79, 4.05, 5.34, 5.62, 6.02, 6.08, 6.39, 5.03, 5.34, 4.98, 3.84, 4.91, 6.62, 4.66, 5.06, 2.37, 5. , 3.7 , 5.22, 5.86, 3.88, 4.68, 4.88, 5.01, 3.09, 5.38, 4.78, 6.26, 6.29, 5.77, 4.33, 5.96, 4.74, 4.54, 7.99, 5. , 4.85, 5.68, 3.73, 4.42, 4.99, 4.47, 6.06, 5.88, 4.56, 5.37, 6.39, 4.15]
# create a histogram with 15 intervals
plt.hist(observations, bins=15)
# create a new figure
plt.figure()
# plot a red line with a transparancy of 40%. Label this 'line 1'
plt.plot(x, y, color='red', alpha=0.4, label='line 1')
# make a key appear on the plot
plt.legend()
# import pandas
import pandas as pd
# read in data from a csv
data = pd.read_csv('data/weather.csv', parse_dates=['Date'])
# create a new matplotlib figure
plt.figure()
# plot the temperature over time
plt.plot(data['Date'], data['Temp (C)'])
# add a ylabel
plt.ylabel('Temperature (C)')
plt.figure()
# create inputs
x = ['UK', 'France', 'Germany', 'Spain', 'Italy']
y = [67.5, 65.1, 83.5, 46.7, 60.6]
# plot the chart
plt.bar(x, y)
plt.ylabel('Population (M)')
plt.figure()
# create inputs
x = ['UK', 'France', 'Germany', 'Spain', 'Italy']
y = [67.5, 65.1, 83.5, 46.7, 60.6]
# create a list of colours
colour = ['red', 'green', 'blue', 'orange', 'purple']
# plot the chart with the colors and transparancy
plt.bar(x, y, color=colour, alpha=0.5)
plt.ylabel('Population (M)')
plt.figure()
x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
y1 = [2, 4, 6, 8, 10, 12, 14, 16, 18]
y2 = [4, 8, 12, 16, 20, 24, 28, 32, 36]
plt.scatter(x, y1, color='cyan', s=5)
plt.scatter(x, y2, color='violet', s=15)
plt.figure()
x = [1, 2, 3, 4, 5, 6, 7, 8, 9]
y1 = [2, 4, 6, 8, 10, 12, 14, 16, 18]
y2 = [4, 8, 12, 16, 20, 24, 28, 32, 36]
size1 = [10, 20, 30, 40, 50, 60, 70, 80, 90]
size2 = [90, 80, 70, 60, 50, 40, 30, 20, 10]
plt.scatter(x, y1, color='cyan', s=size1)
plt.scatter(x, y2, color='violet', s=size2)
co2_file = '../5. Examples of Visual Analytics in Python/data/national/co2_emissions_tonnes_per_person.csv'
gdp_file = '../5. Examples of Visual Analytics in Python/data/national/gdppercapita_us_inflation_adjusted.csv'
pop_file = '../5. Examples of Visual Analytics in Python/data/national/population.csv'
co2_per_cap = pd.read_csv(co2_file, index_col=0, parse_dates=True)
gdp_per_cap = pd.read_csv(gdp_file, index_col=0, parse_dates=True)
population = pd.read_csv(pop_file, index_col=0, parse_dates=True)
plt.figure()
x = gdp_per_cap.loc['2017'] # gdp in 2017
y = co2_per_cap.loc['2017'] # co2 emmissions in 2017
# population in 2017 will give size of points (divide pop by 1M)
size = population.loc['2017'] / 1e6
# scatter points with vector size and some transparancy
plt.scatter(x, y, s=size, alpha=0.5)
# set a log-scale
plt.xscale('log')
plt.yscale('log')
plt.xlabel('GDP per capita, $US')
plt.ylabel('CO2 emissions per person per year, tonnes')
plt.figure()
# create grid of numbers
grid = [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]
# plot the grid with 'autumn' color map
plt.imshow(grid, cmap='autumn')
# add a colour key
plt.colorbar()
import pandas as pd
data = pd.read_csv("../5. Examples of Visual Analytics in Python/data/stocks/FTSE_stock_prices.csv", index_col=0)
correlation_matrix = data.pct_change().corr()
# create a new figure
plt.figure()
# imshow the grid of correlation
plt.imshow(correlation_matrix, cmap='terrain')
# add a color bar
plt.colorbar()
# remove cluttering x and y ticks
plt.xticks([])
plt.yticks([])
elevation = pd.read_csv('data/UK_elevation.csv', index_col=0)
# create figure
plt.figure()
# imshow data
plt.imshow(elevation, # grid data
vmin=-50, # minimum for colour bar
vmax=500, # maximum for colour bar
cmap='terrain', # terrain style colour map
extent=[-11, 3, 50, 60]) # [x1, x2, y1, y2] plot boundaries
# add axis labels and a title
plt.xlabel('Longitude')
plt.ylabel('Latitude')
plt.title('UK Elevation Profile')
# add a colourbar
plt.colorbar()
```
| github_jupyter |
<a href="https://colab.research.google.com/github/VxctxrTL/daa_2021_1/blob/master/28Octubre.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
### SOLUCION 1
```
h1 = 0
h2 = 0
m1 = 0
m2 = 0 # 1440 + 24 *6
contador = 0 # 5 + (1440 + ?) * 2 + 144 + 24 + 2= 3057
while [h1, h2, m1, m2] != [2,3,5,9]:
if [h1, h2] == [m2, m1]:
print(h1, h2,":", m1, m2)
m2 = m2 + 1
if m2 == 10:
m2 = 0
m1 = m1 + 1
if m1 == 6:
h2 = h2 + 1
m2 = 0
contador = contador + 1
m2 = m2 + 1
if m2 == 10:
m2 = 0
m1 = m1 + 1
if m1 == 6:
m1 = 0
h2 = h2 +1
if h2 == 10:
h2 = 0
h1 = h1 +1
print("Numero de palindromos: ",contador)
```
### Solucion 2
```
horario="0000"
contador=0
while horario!="2359":
inv=horario[::-1]
if horario==inv:
contador+=1
print(horario[0:2],":",horario[2:4])
new=int(horario)
new+=1
horario=str(new).zfill(4)
print("son ",contador,"palindromos")
# 2 + (2360 * 4 ) + 24
```
### Solucion 3
```
lista=[]
for i in range(0,24,1): # 24
for j in range(0,60,1): # 60 1440
if i<10:
if j<10:
lista.append("0"+str(i)+":"+"0"+str(j))
elif j>=10:
lista.append("0"+str(i)+":"+str(j))
else:
if i>=10:
if j<10:
lista.append(str(i)+":"+"0"+str(j))
elif j>=10:
lista.append(str(i)+":"+str(j))
# 1440 + 2 + 1440 + 16 * 2 = 2900
lista2=[]
contador=0
for i in range(len(lista)): # 1440
x=lista[i][::-1]
if x==lista[i]:
lista2.append(x)
contador=contador+1
print(contador)
for j in (lista2):
print(j)
for x in range (0,24,1):
for y in range(0,60,1): #1440 * 3 +13 = 4333
hora=str(x)+":"+str(y)
if x<10:
hora="0"+str(x)+":"+str(y)
if y<10:
hora=str(x)+"0"+":"+str(y)
p=hora[::-1]
if p==hora:
print(f"{hora} es palindromo")
total = int(0) #Contador de numero de palindromos
for hor in range(0,24): #Bucles anidados for para dar aumentar las horas y los minutos al mismo tiempo
for min in range(0,60):
hor_n = str(hor) #Variables
min_n = str(min)
if (hor<10): #USamos condiciones para que las horas y los minutos no rebasen el horario
hor_n = ("0"+hor_n)
if (min<10):
min_n = ("0"+ min_n)
if (hor_n[::-1] == min_n): #Mediante un slicing le damos el formato a las horas para que este empiece desde la derecha
print("{}:{}".format(hor_n,min_n))
total += 1
#1 + 1440 * 5 =7201
```
| github_jupyter |
## Getting ready
```
import tensorflow as tf
import tensorflow.keras as keras
import pandas as pd
import numpy as np
census_dir = 'https://archive.ics.uci.edu/ml/machine-learning-databases/adult/'
train_path = tf.keras.utils.get_file('adult.data', census_dir + 'adult.data')
test_path = tf.keras.utils.get_file('adult.test', census_dir + 'adult.test')
columns = ['age', 'workclass', 'fnlwgt', 'education', 'education_num', 'marital_status', 'occupation',
'relationship', 'race', 'gender', 'capital_gain', 'capital_loss', 'hours_per_week', 'native_country',
'income_bracket']
train_data = pd.read_csv(train_path, header=None, names=columns)
test_data = pd.read_csv(test_path, header=None, names=columns, skiprows=1)
```
## How to do it
```
predictors = ['age', 'workclass', 'education', 'education_num', 'marital_status', 'occupation', 'relationship',
'gender']
y_train = (train_data.income_bracket==' >50K').astype(int)
y_test = (test_data.income_bracket==' >50K').astype(int)
train_data = train_data[predictors]
test_data = test_data[predictors]
train_data[['age', 'education_num']] = train_data[['age', 'education_num']].fillna(train_data[['age', 'education_num']]).mean()
test_data[['age', 'education_num']] = test_data[['age', 'education_num']].fillna(test_data[['age', 'education_num']]).mean()
def define_feature_columns(data_df, numeric_cols, categorical_cols, categorical_embeds, dimension=30):
numeric_columns = []
categorical_columns = []
embeddings = []
for feature_name in numeric_cols:
numeric_columns.append(tf.feature_column.numeric_column(feature_name, dtype=tf.float32))
for feature_name in categorical_cols:
vocabulary = data_df[feature_name].unique()
categorical_columns.append(tf.feature_column.categorical_column_with_vocabulary_list(feature_name, vocabulary))
for feature_name in categorical_embeds:
vocabulary = data_df[feature_name].unique()
to_categorical = tf.feature_column.categorical_column_with_vocabulary_list(feature_name, vocabulary)
embeddings.append(tf.feature_column.embedding_column(to_categorical, dimension=dimension))
return numeric_columns, categorical_columns, embeddings
def create_interactions(interactions_list, buckets=10):
feature_columns = []
for (a, b) in interactions_list:
crossed_feature = tf.feature_column.crossed_column([a, b], hash_bucket_size=buckets)
crossed_feature_one_hot = tf.feature_column.indicator_column(crossed_feature)
feature_columns.append(crossed_feature_one_hot)
return feature_columns
numeric_columns, categorical_columns, embeddings = define_feature_columns(train_data,
numeric_cols=['age', 'education_num'],
categorical_cols=['gender'],
categorical_embeds=['workclass', 'education',
'marital_status', 'occupation',
'relationship'],
dimension=32
)
interactions = create_interactions([['education', 'occupation']], buckets=10)
estimator = tf.estimator.DNNLinearCombinedClassifier(
# wide settings
linear_feature_columns=numeric_columns+categorical_columns+interactions,
linear_optimizer=keras.optimizers.Ftrl(learning_rate=0.0002),
# deep settings
dnn_feature_columns=embeddings,
dnn_hidden_units=[1024, 256, 128, 64],
dnn_optimizer=keras.optimizers.Adam(learning_rate=0.0001))
def make_input_fn(data_df, label_df, num_epochs=10, shuffle=True, batch_size=256):
def input_function():
ds = tf.data.Dataset.from_tensor_slices((dict(data_df), label_df))
if shuffle:
ds = ds.shuffle(1000)
ds = ds.batch(batch_size).repeat(num_epochs)
return ds
return input_function
train_input_fn = make_input_fn(train_data, y_train, num_epochs=100, batch_size=256)
test_input_fn = make_input_fn(test_data, y_test, num_epochs=1, shuffle=False)
estimator.train(input_fn=train_input_fn, steps=1500)
results = estimator.evaluate(input_fn=test_input_fn)
print(results)
def predict_proba(predictor):
preds = list()
for pred in predictor:
preds.append(pred['probabilities'])
return np.array(preds)
predictions = predict_proba(estimator.predict(input_fn=test_input_fn))
print(predictions)
```
| github_jupyter |
# Automated Machine Learning
#### Forecasting away from training data
## Contents
1. [Introduction](#Introduction)
2. [Setup](#Setup)
3. [Data](#Data)
4. [Prepare remote compute and data.](#prepare_remote)
4. [Create the configuration and train a forecaster](#train)
5. [Forecasting from the trained model](#forecasting)
6. [Forecasting away from training data](#forecasting_away)
## Introduction
This notebook demonstrates the full interface to the `forecast()` function.
The best known and most frequent usage of `forecast` enables forecasting on test sets that immediately follows training data.
However, in many use cases it is necessary to continue using the model for some time before retraining it. This happens especially in **high frequency forecasting** when forecasts need to be made more frequently than the model can be retrained. Examples are in Internet of Things and predictive cloud resource scaling.
Here we show how to use the `forecast()` function when a time gap exists between training data and prediction period.
Terminology:
* forecast origin: the last period when the target value is known
* forecast periods(s): the period(s) for which the value of the target is desired.
* lookback: how many past periods (before forecast origin) the model function depends on. The larger of number of lags and length of rolling window.
* prediction context: `lookback` periods immediately preceding the forecast origin

## Setup
Please make sure you have followed the `configuration.ipynb` notebook so that your ML workspace information is saved in the config file.
```
import os
import pandas as pd
import numpy as np
import logging
import warnings
import azureml.core
from azureml.core.dataset import Dataset
from pandas.tseries.frequencies import to_offset
from azureml.core.compute import AmlCompute
from azureml.core.compute import ComputeTarget
from azureml.core.runconfig import RunConfiguration
from azureml.core.conda_dependencies import CondaDependencies
# Squash warning messages for cleaner output in the notebook
warnings.showwarning = lambda *args, **kwargs: None
np.set_printoptions(precision=4, suppress=True, linewidth=120)
```
This sample notebook may use features that are not available in previous versions of the Azure ML SDK.
```
print("This notebook was created using version 1.8.0 of the Azure ML SDK")
print("You are currently using version", azureml.core.VERSION, "of the Azure ML SDK")
from azureml.core.workspace import Workspace
from azureml.core.experiment import Experiment
from azureml.train.automl import AutoMLConfig
ws = Workspace.from_config()
# choose a name for the run history container in the workspace
experiment_name = 'automl-forecast-function-demo'
experiment = Experiment(ws, experiment_name)
output = {}
output['Subscription ID'] = ws.subscription_id
output['Workspace'] = ws.name
output['SKU'] = ws.sku
output['Resource Group'] = ws.resource_group
output['Location'] = ws.location
output['Run History Name'] = experiment_name
pd.set_option('display.max_colwidth', -1)
outputDf = pd.DataFrame(data = output, index = [''])
outputDf.T
```
## Data
For the demonstration purposes we will generate the data artificially and use them for the forecasting.
```
TIME_COLUMN_NAME = 'date'
GRAIN_COLUMN_NAME = 'grain'
TARGET_COLUMN_NAME = 'y'
def get_timeseries(train_len: int,
test_len: int,
time_column_name: str,
target_column_name: str,
grain_column_name: str,
grains: int = 1,
freq: str = 'H'):
"""
Return the time series of designed length.
:param train_len: The length of training data (one series).
:type train_len: int
:param test_len: The length of testing data (one series).
:type test_len: int
:param time_column_name: The desired name of a time column.
:type time_column_name: str
:param
:param grains: The number of grains.
:type grains: int
:param freq: The frequency string representing pandas offset.
see https://pandas.pydata.org/pandas-docs/stable/user_guide/timeseries.html
:type freq: str
:returns: the tuple of train and test data sets.
:rtype: tuple
"""
data_train = [] # type: List[pd.DataFrame]
data_test = [] # type: List[pd.DataFrame]
data_length = train_len + test_len
for i in range(grains):
X = pd.DataFrame({
time_column_name: pd.date_range(start='2000-01-01',
periods=data_length,
freq=freq),
target_column_name: np.arange(data_length).astype(float) + np.random.rand(data_length) + i*5,
'ext_predictor': np.asarray(range(42, 42 + data_length)),
grain_column_name: np.repeat('g{}'.format(i), data_length)
})
data_train.append(X[:train_len])
data_test.append(X[train_len:])
X_train = pd.concat(data_train)
y_train = X_train.pop(target_column_name).values
X_test = pd.concat(data_test)
y_test = X_test.pop(target_column_name).values
return X_train, y_train, X_test, y_test
n_test_periods = 6
n_train_periods = 30
X_train, y_train, X_test, y_test = get_timeseries(train_len=n_train_periods,
test_len=n_test_periods,
time_column_name=TIME_COLUMN_NAME,
target_column_name=TARGET_COLUMN_NAME,
grain_column_name=GRAIN_COLUMN_NAME,
grains=2)
```
Let's see what the training data looks like.
```
X_train.tail()
# plot the example time series
import matplotlib.pyplot as plt
whole_data = X_train.copy()
target_label = 'y'
whole_data[target_label] = y_train
for g in whole_data.groupby('grain'):
plt.plot(g[1]['date'].values, g[1]['y'].values, label=g[0])
plt.legend()
plt.show()
```
### Prepare remote compute and data. <a id="prepare_remote"></a>
The [Machine Learning service workspace](https://docs.microsoft.com/en-us/azure/machine-learning/service/concept-workspace), is paired with the storage account, which contains the default data store. We will use it to upload the artificial data and create [tabular dataset](https://docs.microsoft.com/en-us/python/api/azureml-core/azureml.data.tabulardataset?view=azure-ml-py) for training. A tabular dataset defines a series of lazily-evaluated, immutable operations to load data from the data source into tabular representation.
```
# We need to save thw artificial data and then upload them to default workspace datastore.
DATA_PATH = "fc_fn_data"
DATA_PATH_X = "{}/data_train.csv".format(DATA_PATH)
if not os.path.isdir('data'):
os.mkdir('data')
pd.DataFrame(whole_data).to_csv("data/data_train.csv", index=False)
# Upload saved data to the default data store.
ds = ws.get_default_datastore()
ds.upload(src_dir='./data', target_path=DATA_PATH, overwrite=True, show_progress=True)
train_data = Dataset.Tabular.from_delimited_files(path=ds.path(DATA_PATH_X))
```
You will need to create a [compute target](https://docs.microsoft.com/en-us/azure/machine-learning/service/how-to-set-up-training-targets#amlcompute) for your AutoML run. In this tutorial, you create AmlCompute as your training compute resource.
```
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
# Choose a name for your CPU cluster
amlcompute_cluster_name = "fcfn-cluster"
# Verify that cluster does not exist already
try:
compute_target = ComputeTarget(workspace=ws, name=amlcompute_cluster_name)
print('Found existing cluster, use it.')
except ComputeTargetException:
compute_config = AmlCompute.provisioning_configuration(vm_size='STANDARD_D2_V2',
max_nodes=6)
compute_target = ComputeTarget.create(ws, amlcompute_cluster_name, compute_config)
compute_target.wait_for_completion(show_output=True)
```
## Create the configuration and train a forecaster <a id="train"></a>
First generate the configuration, in which we:
* Set metadata columns: target, time column and grain column names.
* Validate our data using cross validation with rolling window method.
* Set normalized root mean squared error as a metric to select the best model.
* Set early termination to True, so the iterations through the models will stop when no improvements in accuracy score will be made.
* Set limitations on the length of experiment run to 15 minutes.
* Finally, we set the task to be forecasting.
* We apply the lag lead operator to the target value i.e. we use the previous values as a predictor for the future ones.
```
lags = [1,2,3]
max_horizon = n_test_periods
time_series_settings = {
'time_column_name': TIME_COLUMN_NAME,
'grain_column_names': [ GRAIN_COLUMN_NAME ],
'max_horizon': max_horizon,
'target_lags': lags
}
```
Run the model selection and training process.
```
from azureml.core.workspace import Workspace
from azureml.core.experiment import Experiment
from azureml.train.automl import AutoMLConfig
automl_config = AutoMLConfig(task='forecasting',
debug_log='automl_forecasting_function.log',
primary_metric='normalized_root_mean_squared_error',
experiment_timeout_hours=0.25,
enable_early_stopping=True,
training_data=train_data,
compute_target=compute_target,
n_cross_validations=3,
verbosity = logging.INFO,
max_concurrent_iterations=4,
max_cores_per_iteration=-1,
label_column_name=target_label,
**time_series_settings)
remote_run = experiment.submit(automl_config, show_output=False)
remote_run.wait_for_completion()
# Retrieve the best model to use it further.
_, fitted_model = remote_run.get_output()
```
## Forecasting from the trained model <a id="forecasting"></a>
In this section we will review the `forecast` interface for two main scenarios: forecasting right after the training data, and the more complex interface for forecasting when there is a gap (in the time sense) between training and testing data.
### X_train is directly followed by the X_test
Let's first consider the case when the prediction period immediately follows the training data. This is typical in scenarios where we have the time to retrain the model every time we wish to forecast. Forecasts that are made on daily and slower cadence typically fall into this category. Retraining the model every time benefits the accuracy because the most recent data is often the most informative.

We use `X_test` as a **forecast request** to generate the predictions.
#### Typical path: X_test is known, forecast all upcoming periods
```
# The data set contains hourly data, the training set ends at 01/02/2000 at 05:00
# These are predictions we are asking the model to make (does not contain thet target column y),
# for 6 periods beginning with 2000-01-02 06:00, which immediately follows the training data
X_test
y_pred_no_gap, xy_nogap = fitted_model.forecast(X_test)
# xy_nogap contains the predictions in the _automl_target_col column.
# Those same numbers are output in y_pred_no_gap
xy_nogap
```
#### Confidence intervals
Forecasting model may be used for the prediction of forecasting intervals by running ```forecast_quantiles()```.
This method accepts the same parameters as forecast().
```
quantiles = fitted_model.forecast_quantiles(X_test)
quantiles
```
#### Distribution forecasts
Often the figure of interest is not just the point prediction, but the prediction at some quantile of the distribution.
This arises when the forecast is used to control some kind of inventory, for example of grocery items or virtual machines for a cloud service. In such case, the control point is usually something like "we want the item to be in stock and not run out 99% of the time". This is called a "service level". Here is how you get quantile forecasts.
```
# specify which quantiles you would like
fitted_model.quantiles = [0.01, 0.5, 0.95]
# use forecast_quantiles function, not the forecast() one
y_pred_quantiles = fitted_model.forecast_quantiles(X_test)
# quantile forecasts returned in a Dataframe along with the time and grain columns
y_pred_quantiles
```
#### Destination-date forecast: "just do something"
In some scenarios, the X_test is not known. The forecast is likely to be weak, because it is missing contemporaneous predictors, which we will need to impute. If you still wish to predict forward under the assumption that the last known values will be carried forward, you can forecast out to "destination date". The destination date still needs to fit within the maximum horizon from training.
```
# We will take the destination date as a last date in the test set.
dest = max(X_test[TIME_COLUMN_NAME])
y_pred_dest, xy_dest = fitted_model.forecast(forecast_destination=dest)
# This form also shows how we imputed the predictors which were not given. (Not so well! Use with caution!)
xy_dest
```
## Forecasting away from training data <a id="forecasting_away"></a>
Suppose we trained a model, some time passed, and now we want to apply the model without re-training. If the model "looks back" -- uses previous values of the target -- then we somehow need to provide those values to the model.

The notion of forecast origin comes into play: the forecast origin is **the last period for which we have seen the target value**. This applies per grain, so each grain can have a different forecast origin.
The part of data before the forecast origin is the **prediction context**. To provide the context values the model needs when it looks back, we pass definite values in `y_test` (aligned with corresponding times in `X_test`).
```
# generate the same kind of test data we trained on,
# but now make the train set much longer, so that the test set will be in the future
X_context, y_context, X_away, y_away = get_timeseries(train_len=42, # train data was 30 steps long
test_len=4,
time_column_name=TIME_COLUMN_NAME,
target_column_name=TARGET_COLUMN_NAME,
grain_column_name=GRAIN_COLUMN_NAME,
grains=2)
# end of the data we trained on
print(X_train.groupby(GRAIN_COLUMN_NAME)[TIME_COLUMN_NAME].max())
# start of the data we want to predict on
print(X_away.groupby(GRAIN_COLUMN_NAME)[TIME_COLUMN_NAME].min())
```
There is a gap of 12 hours between end of training and beginning of `X_away`. (It looks like 13 because all timestamps point to the start of the one hour periods.) Using only `X_away` will fail without adding context data for the model to consume.
```
try:
y_pred_away, xy_away = fitted_model.forecast(X_away)
xy_away
except Exception as e:
print(e)
```
How should we read that eror message? The forecast origin is at the last time the model saw an actual value of `y` (the target). That was at the end of the training data! The model is attempting to forecast from the end of training data. But the requested forecast periods are past the maximum horizon. We need to provide a define `y` value to establish the forecast origin.
We will use this helper function to take the required amount of context from the data preceding the testing data. It's definition is intentionally simplified to keep the idea in the clear.
```
def make_forecasting_query(fulldata, time_column_name, target_column_name, forecast_origin, horizon, lookback):
"""
This function will take the full dataset, and create the query
to predict all values of the grain from the `forecast_origin`
forward for the next `horizon` horizons. Context from previous
`lookback` periods will be included.
fulldata: pandas.DataFrame a time series dataset. Needs to contain X and y.
time_column_name: string which column (must be in fulldata) is the time axis
target_column_name: string which column (must be in fulldata) is to be forecast
forecast_origin: datetime type the last time we (pretend to) have target values
horizon: timedelta how far forward, in time units (not periods)
lookback: timedelta how far back does the model look?
Example:
```
forecast_origin = pd.to_datetime('2012-09-01') + pd.DateOffset(days=5) # forecast 5 days after end of training
print(forecast_origin)
X_query, y_query = make_forecasting_query(data,
forecast_origin = forecast_origin,
horizon = pd.DateOffset(days=7), # 7 days into the future
lookback = pd.DateOffset(days=1), # model has lag 1 period (day)
)
```
"""
X_past = fulldata[ (fulldata[ time_column_name ] > forecast_origin - lookback) &
(fulldata[ time_column_name ] <= forecast_origin)
]
X_future = fulldata[ (fulldata[ time_column_name ] > forecast_origin) &
(fulldata[ time_column_name ] <= forecast_origin + horizon)
]
y_past = X_past.pop(target_column_name).values.astype(np.float)
y_future = X_future.pop(target_column_name).values.astype(np.float)
# Now take y_future and turn it into question marks
y_query = y_future.copy().astype(np.float) # because sometimes life hands you an int
y_query.fill(np.NaN)
print("X_past is " + str(X_past.shape) + " - shaped")
print("X_future is " + str(X_future.shape) + " - shaped")
print("y_past is " + str(y_past.shape) + " - shaped")
print("y_query is " + str(y_query.shape) + " - shaped")
X_pred = pd.concat([X_past, X_future])
y_pred = np.concatenate([y_past, y_query])
return X_pred, y_pred
```
Let's see where the context data ends - it ends, by construction, just before the testing data starts.
```
print(X_context.groupby(GRAIN_COLUMN_NAME)[TIME_COLUMN_NAME].agg(['min','max','count']))
print(X_away.groupby(GRAIN_COLUMN_NAME)[TIME_COLUMN_NAME].agg(['min','max','count']))
X_context.tail(5)
# Since the length of the lookback is 3,
# we need to add 3 periods from the context to the request
# so that the model has the data it needs
# Put the X and y back together for a while.
# They like each other and it makes them happy.
X_context[TARGET_COLUMN_NAME] = y_context
X_away[TARGET_COLUMN_NAME] = y_away
fulldata = pd.concat([X_context, X_away])
# forecast origin is the last point of data, which is one 1-hr period before test
forecast_origin = X_away[TIME_COLUMN_NAME].min() - pd.DateOffset(hours=1)
# it is indeed the last point of the context
assert forecast_origin == X_context[TIME_COLUMN_NAME].max()
print("Forecast origin: " + str(forecast_origin))
# the model uses lags and rolling windows to look back in time
n_lookback_periods = max(lags)
lookback = pd.DateOffset(hours=n_lookback_periods)
horizon = pd.DateOffset(hours=max_horizon)
# now make the forecast query from context (refer to figure)
X_pred, y_pred = make_forecasting_query(fulldata, TIME_COLUMN_NAME, TARGET_COLUMN_NAME,
forecast_origin, horizon, lookback)
# show the forecast request aligned
X_show = X_pred.copy()
X_show[TARGET_COLUMN_NAME] = y_pred
X_show
```
Note that the forecast origin is at 17:00 for both grains, and periods from 18:00 are to be forecast.
```
# Now everything works
y_pred_away, xy_away = fitted_model.forecast(X_pred, y_pred)
# show the forecast aligned
X_show = xy_away.reset_index()
# without the generated features
X_show[['date', 'grain', 'ext_predictor', '_automl_target_col']]
# prediction is in _automl_target_col
```
## Forecasting farther than the maximum horizon <a id="recursive forecasting"></a>
When the forecast destination, or the latest date in the prediction data frame, is farther into the future than the specified maximum horizon, the `forecast()` function will still make point predictions out to the later date using a recursive operation mode. Internally, the method recursively applies the regular forecaster to generate context so that we can forecast further into the future.
To illustrate the use-case and operation of recursive forecasting, we'll consider an example with a single time-series where the forecasting period directly follows the training period and is twice as long as the maximum horizon given at training time.

Internally, we apply the forecaster in an iterative manner and finish the forecast task in two interations. In the first iteration, we apply the forecaster and get the prediction for the first max-horizon periods (y_pred1). In the second iteraction, y_pred1 is used as the context to produce the prediction for the next max-horizon periods (y_pred2). The combination of (y_pred1 and y_pred2) gives the results for the total forecast periods.
A caveat: forecast accuracy will likely be worse the farther we predict into the future since errors are compounded with recursive application of the forecaster.


```
# generate the same kind of test data we trained on, but with a single grain/time-series and test period twice as long as the max_horizon
_, _, X_test_long, y_test_long = get_timeseries(train_len=n_train_periods,
test_len=max_horizon*2,
time_column_name=TIME_COLUMN_NAME,
target_column_name=TARGET_COLUMN_NAME,
grain_column_name=GRAIN_COLUMN_NAME,
grains=1)
print(X_test_long.groupby(GRAIN_COLUMN_NAME)[TIME_COLUMN_NAME].min())
print(X_test_long.groupby(GRAIN_COLUMN_NAME)[TIME_COLUMN_NAME].max())
# forecast() function will invoke the recursive forecast method internally.
y_pred_long, X_trans_long = fitted_model.forecast(X_test_long)
y_pred_long
# What forecast() function does in this case is equivalent to iterating it twice over the test set as the following.
y_pred1, _ = fitted_model.forecast(X_test_long[:max_horizon])
y_pred_all, _ = fitted_model.forecast(X_test_long, np.concatenate((y_pred1, np.full(max_horizon, np.nan))))
np.array_equal(y_pred_all, y_pred_long)
```
#### Confidence interval and distributional forecasts
AutoML cannot currently estimate forecast errors beyond the maximum horizon set during training, so the `forecast_quantiles()` function will return missing values for quantiles not equal to 0.5 beyond the maximum horizon.
```
fitted_model.forecast_quantiles(X_test_long)
```
Similarly with the simple senarios illustrated above, forecasting farther than the max horizon in other senarios like 'multiple grain', 'Destination-date forecast', and 'forecast away from the training data' are also automatically handled by the `forecast()` function.
| github_jupyter |
```
import pandas as pd
import seaborn as sns
import scipy
import matplotlib.pyplot as plt
df_Dodgers = pd.read_csv('dodgers.csv')
df_Dodgers.head()
# Takes binary categories and returns 0 or 1
def binning_cats(word, zero='no', one='yes'):
if word.strip().lower()==zero:
return(0)
elif word.strip().lower()==one:
return(1)
# These are the variables and their outcomes that need to be converted
bins = {'skies':['cloudy','clear'],
'day_night':['day','night'],
'cap':['no','yes'],
'shirt':['no','yes'],
'fireworks':['no','yes'],
'bobblehead':['no','yes']}
# Here we convert the above columns to binary
for column in bins.keys():
df_Dodgers[column+'_bin']=df_Dodgers[column].apply(binning_cats,args=(bins[column][0],bins[column][1]))
df_Dodgers.head()
# Here we check the correlations
df_Dodgers.corr()
# Here we draft a scatterplot to see if any relationship between attendance and temperature
sns.regplot(df_Dodgers['temp'],df_Dodgers['attend'])
slope,intercept,r_value,p_value,std_err = scipy.stats.linregress(df_Dodgers['temp'],df_Dodgers['attend'])
# Bar charts showing average attendance by day of the week
days = {'M':'Monday','T':'Tuesday','W':'Wednesday','R':'Thursday','F':'Friday','S':'Saturday','U':'Sunday'}
day_attendance = []
for day in days.keys():
day_attendance.append(df_Dodgers[df_Dodgers['day_of_week']==days[day]].attend.mean())
fig=plt.figure()
ax=fig.add_axes([0,0,1,1])
x=days.keys()
ax.bar(x,day_attendance)
ax.set_xlabel('day of week')
ax.set_ylabel('average attendance')
plt.show()
# This shows the distribution for each perk
fig, axs = plt.subplots(4,figsize=(10,30))
plot_coords = [(0,0),(0,1),(1,0),(1,1)]
perks = ['cap','shirt','fireworks','bobblehead']
count = 0
for perk in perks:
ys=[]
for day in days.keys():
df_ = df_Dodgers[df_Dodgers['day_of_week']==days[day]]
ys.append(len(df_[df_[perk]==bins[perk][1].upper()]))
axs[count].set_title(f'perk: {perk}')
axs[count].bar(days.keys(),ys)
axs[count].set_xlabel('day of week')
axs[count].set_ylabel('number of games at which perk given')
axs[count].set_ylim(0,15)
count+=1
# Checks to see if any null or duplicate values
df_Dodgers.month.unique()
# More temperature and attendance relationship research
months = ['APR','MAY','JUN','JUL','AUG','SEP','OCT']
print('Month marginal tickets/deg probability')
print('----- -------------------- -----------')
for month in months:
x = df_Dodgers[df_Dodgers['month'] == month]['temp']
y = df_Dodgers[df_Dodgers['month'] == month]['attend']
slope, intercept, r_value, p_value, std_err = scipy.stats.linregress(x, y)
print(f'{month:>4} {round(slope):16} {" "*10}{round(p_value,3)}')
# This plots the average temperature on game nights by month for the hotter months
fig = plt.figure()
ax = fig.add_axes([0,0,1,1])
x = months[4:]
temps = [df_Dodgers[df_Dodgers['month']==month].temp.mean() for month in x]
ax.bar(x,temps)
ax.set_xlabel('month')
ax.set_ylabel('average gameday temp')
# 0 isn't particularly meaningful for degrees F, so I set ymin to LA's absolute 0.
plt.ylim(50,90)
plt.show()
"""
Attendance during the summer months actually declined instead of increased which leads me to believe that the heat is more of a
factor in determining attendance than the fact that school is out for summer break. Based on all of the data, I inferred that
giving bobbleheads held the most significance and did the most to increase attendance. Also, I did a boxplot to the attendance
based on the days of the week and found that Tuesdays had the greatest means and range of attendance. Just to make sure I wasn't
missing anything else, I ran a correlation analysis on the opposing team, on the day or night game data, and on the day of the
week. Tuesday proved to show the greatest correlation.
Based on this analysis, I would recommend giving out more bobbleheads. Reserve the giving of these objects for periods when
attendance is typically lower like cooler or hotter days. Also, I would recommend installing misters, air movers, and temporary
shade structures
"""
```
| github_jupyter |
```
import torch
import torch.nn as nn
from torch.nn import functional as F
from torch.utils.data import Dataset, DataLoader
from torch.utils.tensorboard import SummaryWriter
writer = SummaryWriter()
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['figure.dpi']= 100
import seaborn as sns
sns.set(style="whitegrid")
#hyperparameters
batch_size = 64
seq_len = 31
input_size = 7
lstm_hidden_size = 84
linear_hidden_size_1 = 109
linear_hidden_size_2 = 100
linear_hidden_size_3 = 36
output_size = 6
dropout_1 = 0.444263
dropout_2 = 0.246685
dropout_3 = 0.200149
learning_rate = 0.002635
num_epochs = 500
seed = 1504062
#seed = np.random.randint(10000000, size=1).item() #random seed
####################################################
#dataset import and sequencing
####################################################
#data importing
df = pd.read_excel('ALL VAR cleaned.xlsx')
df.Date = pd.to_datetime(df.Date, format = '%m/%d/%Y')
df = df.set_index('Date')
#data scaling
df_scaled = (df - df.mean())/ df.std()
#print(df_scaled.head())
#storing mean and std
df_np_mean = df.mean().to_numpy()
df_np_std = df.std().to_numpy()
#dropping date column
df_scaled.reset_index(inplace = True)
df_scaled = df_scaled.drop('Date', 1)
#creating sequences
def split_sequences(sequences, n_steps):
X, y = list(), list()
for i in range(len(sequences)):
# find the end of this pattern
end_ix = i + n_steps
# check if we are beyond the dataset
if end_ix +1 >= len(sequences): break
# gather input and output parts of the pattern
seq_x, seq_y = sequences[i:end_ix, 0:7], sequences[end_ix + 1, 7:14]
X.append(seq_x)
y.append(seq_y)
return X, y
array = df_scaled.iloc[:, :].values
print ('shape of the datset array: {}'.format(array.shape))
X, y = split_sequences(array, seq_len)
X_array = np.array(X, dtype = np.float32)
y_array = np.array(y)
print('sequenced X array shape: {}'.format(X_array.shape))
print('y array shape: {}'.format(y_array.shape))
print('null values in dataset?: {}'.format(df_scaled.isnull().values.any()))
####################################################
#output mask preparation
####################################################
#import output masked data
df_mask = pd.read_excel('COMBINED CAMS MASK.xlsx')
#print(df_mask.head())
mask_array = df_mask.iloc[:, :].values
#print(mask_array.shape)
#sequencing
def mask_sequence(sequence, n_steps):
y = list()
for i in range(len(sequence)):
# find the end of this pattern
end_iy = i + n_steps
# check if we are beyond the dataset
if end_iy + 1 >= len(sequence): break
# gather input and output parts of the pattern
seq_y = sequence[end_iy + 1, 0:6]
y.append(seq_y)
return y
mask_list = mask_sequence(mask_array, seq_len)
mask_array = np.array(mask_list)
print('masked output array shape: {}'.format(mask_array.shape))
####################################################
#creating dataset and subsets
####################################################
#creating dataset
class AirMeteoroDataset(Dataset):
def __init__(self):
self.len = X_array.shape[0]
self.data_id = torch.arange(0,len(X_array),1)
self.X_data = torch.from_numpy(X_array)
self.y_data = torch.from_numpy(y_array)
self.y_mask = torch.from_numpy(mask_array)
def __getitem__(self, index):
return self.data_id[index], self.X_data[index], self.y_data[index], self.y_mask[index]
def __len__(self):
return self.len
dataset = AirMeteoroDataset()
#test train split
seed = 1504062
train_size = round(len(X_array) * 0.85)
test_size = len(X_array) - train_size
train_set, test_set = torch.utils.data.random_split(dataset,
[train_size, test_size],
generator = torch.Generator().manual_seed(seed))
####################################################
#making mini-batches using dataloader
####################################################
train_loader = DataLoader(dataset = train_set,
batch_size = batch_size,
drop_last = True,
shuffle = True)
test_loader = DataLoader(dataset = test_set,
batch_size = batch_size,
drop_last = True,
shuffle = True)
#for i, (X_data, y_data, y_mask) in enumerate(train_loader):
#print(X_data)
#break
####################################################
#model building
####################################################
class Model(nn.Module):
def __init__(self,
input_size,
lstm_hidden_size,
linear_hidden_size_1,
linear_hidden_size_2,
linear_hidden_size_3,
output_size,
dropout_1,
dropout_2,
dropout_3):
super(Model, self).__init__()
self.input_size = input_size
self.lstm_hidden_size = lstm_hidden_size
self.linear_hidden_size_1 = linear_hidden_size_1
self.linear_hidden_size_2 = linear_hidden_size_2
self.linear_hidden_size_3 = linear_hidden_size_3
self.output_size = output_size
self.batchnorm1 = nn.BatchNorm1d(num_features = linear_hidden_size_1)
self.batchnorm2 = nn.BatchNorm1d(num_features = linear_hidden_size_2)
self.batchnorm3 = nn.BatchNorm1d(num_features = linear_hidden_size_3)
self.relu = nn.ReLU()
self.dropout_1 = nn.Dropout(p = dropout_1)
self.dropout_2 = nn.Dropout(p = dropout_2)
self.dropout_3 = nn.Dropout(p = dropout_3)
self.lstm = nn.LSTM(
input_size = self.input_size,
hidden_size = self.lstm_hidden_size,
batch_first = True)
self.linear_1 = nn.Linear(self.lstm_hidden_size, self.linear_hidden_size_1)
self.linear_2 = nn.Linear(self.linear_hidden_size_1, self.linear_hidden_size_2)
self.linear_3 = nn.Linear(self.linear_hidden_size_2, self.output_size)
def forward(self, sequences):
lstm_out, _ = self.lstm(sequences)
z1 = self.linear_1(lstm_out[:, -1, :])
a1 = self.dropout_linear(self.relu(self.batchnorm1(z1)))
z2 = self.linear_2(a1)
a2 = self.dropout_linear(self.relu(self.batchnorm2(z2)))
y_pred = self.linear_3(a2)
return y_pred
class modsmoothl1(nn.SmoothL1Loss):
def __init__(self, size_average=None, reduce=None, reduction = 'none'):
super(modsmoothl1, self).__init__(size_average, reduce, reduction)
def forward(self, observed, predicted, mask):
predicted_masked = mask*predicted
loss = F.smooth_l1_loss(observed, predicted_masked, reduction=self.reduction)
avg_loss = torch.sum(loss)/torch.sum(mask)
return avg_loss
forecast_model = Model(input_size,
lstm_hidden_size,
linear_hidden_size_1,
linear_hidden_size_2,
linear_hidden_size_3,
output_size,
dropout_1,
dropout_2,
dropout_3,).cuda().float()
criterion = modsmoothl1()
optimizer = torch.optim.RMSprop(forecast_model.parameters(), lr = learning_rate)
####################################################
#model training and validation
####################################################
all_train_loss = []
all_val_loss = []
total_iter = 0
for epoch in range(num_epochs):
forecast_model.train()
epoch_total_loss = 0.0
for i, (data_id,X_data, y_data, y_mask) in enumerate(train_loader):
optimizer.zero_grad()
X_data = X_data.cuda().float()
y_data = y_data.cuda().float()
y_mask = y_mask.cuda().float()
y_pred = forecast_model(X_data)
loss = criterion(y_data, y_pred, y_mask)
total_iter += 1
writer.add_scalar("Loss/train", loss, total_iter)
loss.backward()
optimizer.step()
epoch_total_loss = epoch_total_loss + loss.item()
epoch_avg_loss = epoch_total_loss/len(train_loader)
if (epoch +1) % round(num_epochs/10) == 0:
print (f'Train loss after Epoch [{epoch+1}/{num_epochs}]: {epoch_avg_loss:.6f}, Val loss: {epoch_avg_val_loss:.6f}')
all_train_loss.append(epoch_avg_loss)
#validation
forecast_model.eval()
with torch.no_grad():
epoch_total_val_loss = 0.0
for i, (data_id, X_val, y_val, y_mask_val) in enumerate(val_loader):
X_val = X_val.cuda().float()
y_val = y_val.cuda().float()
y_mask_val = y_mask_val.cuda().float()
val_pred = forecast_model(X_val).cuda()
val_loss = criterion(y_val, val_pred, y_mask_val)
epoch_total_val_loss = epoch_total_val_loss + val_loss.item()
epoch_avg_val_loss = epoch_total_val_loss/len(val_loader)
all_val_loss.append(epoch_avg_val_loss)
writer.add_scalar("Loss/Validation", epoch_avg_val_loss, epoch)
import statistics
print (statistics.mean(all_val_loss[:-20:-1]))
plt.plot(list(range(1, num_epochs + 1)), all_train_loss, label = 'Train')
plt.plot(list(range(1, num_epochs + 1)), all_val_loss, label = 'Validation')
plt.legend(loc="upper right")
plt.xlabel('No. of epochs')
plt.ylabel('Loss')
writer.flush()
all_id = torch.empty(0).cuda()
all_obs = torch.empty(0, output_size).cuda()
all_pred = torch.empty(0, output_size).cuda()
with torch.no_grad():
total_test_loss = 0.0
for i, (data_id, X_test, y_test, y_mask_test) in enumerate(test_loader):
data_id = data_id.cuda()
X_test = X_test.cuda().float()
y_test = y_test.cuda().float()
y_mask_test = y_mask_test.cuda().float()
test_pred = forecast_model(X_test).cuda()
test_loss = criterion(y_test, test_pred, y_mask_test)
total_test_loss = total_test_loss + test_loss.item()
all_id = torch.cat((all_id, data_id), 0)
all_obs = torch.cat((all_obs, y_test), 0)
all_pred = torch.cat((all_pred, test_pred), 0)
avg_test_loss = total_test_loss/len(test_loader)
print(avg_test_loss)
#all_pred.shape
pred_out_np = all_pred.cpu().numpy()
obs_out_np = all_obs.cpu().numpy()
print(pred_out_np.shape)
print(obs_out_np.shape)
df_out_mean = df_np_mean[7:13]
df_out_std = df_np_std[7:13]
final_pred = pred_out_np * df_out_std + df_out_mean
final_observed = obs_out_np * df_out_std + df_out_mean
out_obs_data = pd.DataFrame({'SO2 ': final_observed[:, 0],
'NO2': final_observed[:, 1],
'CO': final_observed[:, 2],
'O3': final_observed[:, 3],
'PM2.5': final_observed[:, 4],
'PM10': final_observed[:, 5]})
filename_obs = 'plot_obs.xlsx'
out_obs_data.to_excel(filename_obs, index=True)
out_pred_data = pd.DataFrame({'SO2 ': final_pred[:, 0],
'NO2': final_pred[:, 1],
'CO': final_pred[:, 2],
'O3': final_pred[:, 3],
'PM2.5': final_pred[:, 4],
'PM10': final_pred[:, 5]})
filename_pred = 'plot_pred.xlsx'
out_pred_data.to_excel(filename_pred, index=True)
```
| github_jupyter |
# Introduction and Foundations: Titanic Survival Exploration
> Udacity Machine Learning Engineer Nanodegree: _Project 0_
>
> Author: _Ke Zhang_
>
> Submission Date: _2017-04-27_ (Revision 2)
## Abstract
In 1912, the ship RMS Titanic struck an iceberg on its maiden voyage and sank, resulting in the deaths of most of its passengers and crew. In this introductory project, we will explore a subset of the RMS Titanic passenger manifest to determine which features best predict whether someone survived or did not survive. To complete this project, you will need to implement several conditional predictions and answer the questions below. Your project submission will be evaluated based on the completion of the code and your responses to the questions.
## Content
- [Getting Started](#Getting-Started)
- [Making Predictions](#Making-Predictions)
- [Conclusion](#Conclusion)
- [References](#References)
- [Reproduction Environment](#Reproduction-Environment)
# Getting Started
To begin working with the RMS Titanic passenger data, we'll first need to `import` the functionality we need, and load our data into a `pandas` DataFrame.
```
# Import libraries necessary for this project
import numpy as np
import pandas as pd
from IPython.display import display # Allows the use of display() for DataFrames
# Import supplementary visualizations code visuals.py
import visuals as vs
# Pretty display for notebooks
%matplotlib inline
# Load the dataset
in_file = 'titanic_data.csv'
full_data = pd.read_csv(in_file)
# Print the first few entries of the RMS Titanic data
display(full_data.head())
```
From a sample of the RMS Titanic data, we can see the various features present for each passenger on the ship:
- **Survived**: Outcome of survival (0 = No; 1 = Yes)
- **Pclass**: Socio-economic class (1 = Upper class; 2 = Middle class; 3 = Lower class)
- **Name**: Name of passenger
- **Sex**: Sex of the passenger
- **Age**: Age of the passenger (Some entries contain `NaN`)
- **SibSp**: Number of siblings and spouses of the passenger aboard
- **Parch**: Number of parents and children of the passenger aboard
- **Ticket**: Ticket number of the passenger
- **Fare**: Fare paid by the passenger
- **Cabin** Cabin number of the passenger (Some entries contain `NaN`)
- **Embarked**: Port of embarkation of the passenger (C = Cherbourg; Q = Queenstown; S = Southampton)
Since we're interested in the outcome of survival for each passenger or crew member, we can remove the **Survived** feature from this dataset and store it as its own separate variable `outcomes`. We will use these outcomes as our prediction targets.
Run the code cell below to remove **Survived** as a feature of the dataset and store it in `outcomes`.
```
# Store the 'Survived' feature in a new variable and remove it from the dataset
outcomes = full_data['Survived']
data = full_data.drop('Survived', axis = 1)
# Show the new dataset with 'Survived' removed
display(data.head())
```
The very same sample of the RMS Titanic data now shows the **Survived** feature removed from the DataFrame. Note that `data` (the passenger data) and `outcomes` (the outcomes of survival) are now *paired*. That means for any passenger `data.loc[i]`, they have the survival outcome `outcomes[i]`.
To measure the performance of our predictions, we need a metric to score our predictions against the true outcomes of survival. Since we are interested in how *accurate* our predictions are, we will calculate the proportion of passengers where our prediction of their survival is correct. Run the code cell below to create our `accuracy_score` function and test a prediction on the first five passengers.
**Think:** *Out of the first five passengers, if we predict that all of them survived, what would you expect the accuracy of our predictions to be?*
```
def accuracy_score(truth, pred):
""" Returns accuracy score for input truth and predictions. """
# Ensure that the number of predictions matches number of outcomes
if len(truth) == len(pred):
# Calculate and return the accuracy as a percent
return "Predictions have an accuracy of {:.2f}%.".format((truth == pred).mean()*100)
else:
return "Number of predictions does not match number of outcomes!"
# Test the 'accuracy_score' function
predictions = pd.Series(np.ones(5, dtype = int))
print accuracy_score(outcomes[:5], predictions)
```
> **Tip:** If you save an iPython Notebook, the output from running code blocks will also be saved. However, the state of your workspace will be reset once a new session is started. Make sure that you run all of the code blocks from your previous session to reestablish variables and functions before picking up where you last left off.
# Making Predictions
If we were asked to make a prediction about any passenger aboard the RMS Titanic whom we knew nothing about, then the best prediction we could make would be that they did not survive. This is because we can assume that a majority of the passengers (more than 50%) did not survive the ship sinking.
The `predictions_0` function below will always predict that a passenger did not survive.
```
def predictions_0(data):
""" Model with no features. Always predicts a passenger did not survive. """
predictions = []
for _, passenger in data.iterrows():
# Predict the survival of 'passenger'
predictions.append(0)
# Return our predictions
return pd.Series(predictions)
# Make the predictions
predictions = predictions_0(data)
```
### Question 1
*Using the RMS Titanic data, how accurate would a prediction be that none of the passengers survived?*
**Hint:** Run the code cell below to see the accuracy of this prediction.
```
print accuracy_score(outcomes, predictions)
```
**Answer:** The prediction accuracy is **61.62%**
***
Let's take a look at whether the feature **Sex** has any indication of survival rates among passengers using the `survival_stats` function. This function is defined in the `titanic_visualizations.py` Python script included with this project. The first two parameters passed to the function are the RMS Titanic data and passenger survival outcomes, respectively. The third parameter indicates which feature we want to plot survival statistics across.
Run the code cell below to plot the survival outcomes of passengers based on their sex.
```
vs.survival_stats(data, outcomes, 'Sex')
```
Examining the survival statistics, a large majority of males did not survive the ship sinking. However, a majority of females *did* survive the ship sinking. Let's build on our previous prediction: If a passenger was female, then we will predict that they survived. Otherwise, we will predict the passenger did not survive.
Fill in the missing code below so that the function will make this prediction.
**Hint:** You can access the values of each feature for a passenger like a dictionary. For example, `passenger['Sex']` is the sex of the passenger.
```
def predictions_1(data):
""" Model with one feature:
- Predict a passenger survived if they are female. """
predictions = []
for _, passenger in data.iterrows():
predictions.append(True if passenger['Sex'] == 'female'
else False)
# Return our predictions
return pd.Series(predictions)
# Make the predictions
predictions = predictions_1(data)
```
### Question 2
*How accurate would a prediction be that all female passengers survived and the remaining passengers did not survive?*
**Hint:** Run the code cell below to see the accuracy of this prediction.
```
print accuracy_score(outcomes, predictions)
```
**Answer**: **78.68**%
***
Using just the **Sex** feature for each passenger, we are able to increase the accuracy of our predictions by a significant margin. Now, let's consider using an additional feature to see if we can further improve our predictions. For example, consider all of the male passengers aboard the RMS Titanic: Can we find a subset of those passengers that had a higher rate of survival? Let's start by looking at the **Age** of each male, by again using the `survival_stats` function. This time, we'll use a fourth parameter to filter out the data so that only passengers with the **Sex** 'male' will be included.
Run the code cell below to plot the survival outcomes of male passengers based on their age.
```
vs.survival_stats(data, outcomes, 'Age', ["Sex == 'male'"])
```
Examining the survival statistics, the majority of males younger than 10 survived the ship sinking, whereas most males age 10 or older *did not survive* the ship sinking. Let's continue to build on our previous prediction: If a passenger was female, then we will predict they survive. If a passenger was male and younger than 10, then we will also predict they survive. Otherwise, we will predict they do not survive.
Fill in the missing code below so that the function will make this prediction.
**Hint:** You can start your implementation of this function using the prediction code you wrote earlier from `predictions_1`.
```
def predictions_2(data):
""" Model with two features:
- Predict a passenger survived if they are female.
- Predict a passenger survived if they are male and younger than 10. """
predictions = []
for _, passenger in data.iterrows():
predictions.append(True if passenger['Sex'] == 'female' or
passenger['Age'] < 10 else False)
# Return our predictions
return pd.Series(predictions)
# Make the predictions
predictions = predictions_2(data)
```
### Question 3
*How accurate would a prediction be that all female passengers and all male passengers younger than 10 survived?*
**Hint:** Run the code cell below to see the accuracy of this prediction.
```
print accuracy_score(outcomes, predictions)
```
**Answer**: **79.35**
***
Adding the feature **Age** as a condition in conjunction with **Sex** improves the accuracy by a small margin more than with simply using the feature **Sex** alone. Now it's your turn: Find a series of features and conditions to split the data on to obtain an outcome prediction accuracy of at least 80%. This may require multiple features and multiple levels of conditional statements to succeed. You can use the same feature multiple times with different conditions.
**Pclass**, **Sex**, **Age**, **SibSp**, and **Parch** are some suggested features to try.
Use the `survival_stats` function below to to examine various survival statistics.
**Hint:** To use mulitple filter conditions, put each condition in the list passed as the last argument. Example: `["Sex == 'male'", "Age < 18"]`
```
# survival by Embarked
vs.survival_stats(data, outcomes, 'Embarked')
# survival by Embarked
vs.survival_stats(data, outcomes, 'SibSp')
vs.survival_stats(data, outcomes, 'Age', ["Sex == 'male'", "Age < 18"])
```
We found out earlier that female and children had better chance to survive. In the next step we'll add another criteria 'Pclass' to further distinguish the survival rates among the different groups.
```
# female passengers in the higher pclass had great chance to survive
vs.survival_stats(data, outcomes, 'Pclass', [
"Sex == 'female'"
])
# male passengers in the higher pclass had great chance to survive
vs.survival_stats(data, outcomes, 'Pclass', [
"Sex == 'male'"
])
# more female passengers survived in all age groups
vs.survival_stats(data, outcomes, 'Age', [
"Sex == 'female'",
])
# more male passengers survived only when age < 10
vs.survival_stats(data, outcomes, 'Age', [
"Sex == 'male'",
])
```
It looks like that all female passengers under 20 survived from the accident. Let's check passengers in the lower class to complete our guess.
```
# ... but not in the lower class when they're older than 20
vs.survival_stats(data, outcomes, 'Age', [
"Sex == 'female'",
"Pclass == 3"
])
# ... actually only females under 20 had more survivers in the lower class
vs.survival_stats(data, outcomes, 'Age', [
"Sex == 'male'",
"Pclass == 3"
])
```
> We conclude that in the lower class only female under 20 had better chance to survive. In the other classes all children under 10 and female passengers had more likey survived. Let's check if we have reached our 80% target.
After exploring the survival statistics visualization, fill in the missing code below so that the function will make your prediction.
Make sure to keep track of the various features and conditions you tried before arriving at your final prediction model.
**Hint:** You can start your implementation of this function using the prediction code you wrote earlier from `predictions_2`.
```
def predictions_3(data):
"""
Model with multiple features: Sex, Age and Pclass
Makes a prediction with an accuracy of at least 80%.
"""
predictions = []
for _, passenger in data.iterrows():
if passenger['Age'] < 10:
survived = True
elif passenger['Sex'] == 'female' and not (
passenger['Pclass'] == 3 and passenger['Age'] > 20
):
survived = True
else:
survived = False
predictions.append(survived)
# Return our predictions
return pd.Series(predictions)
# Make the predictions
predictions = predictions_3(data)
```
### Question 4
*Describe the steps you took to implement the final prediction model so that it got an accuracy of at least 80%. What features did you look at? Were certain features more informative than others? Which conditions did you use to split the survival outcomes in the data? How accurate are your predictions?*
**Hint:** Run the code cell below to see the accuracy of your predictions.
```
print accuracy_score(outcomes, predictions)
```
**Answer**:
Using the features *Sex*, *Pclass* and *Age* we increased the accuracy score to **80.36%**.
We tried to plot the survival statistics with different features and chose the ones under which conditions the differences were the largest.
* some features are just not relevant like *PassengerId* or *Name*
* some features have to be decoded to be helpful like *Cabin* which could be helpful if we have more information on the location of each cabin
* some features are less informative than the others: e.g. we could use *Embarked*, *SibSp* or *Parch* to group the passengers but the resulting model would be more complicated.
* Eventually we chose *Sex*, *Pclass* and *Age* as our final features.
We derived the conditions to split the survival outcomes from the survival plots. The split conditions are:
1. All children under 10 => **survived**
2. Female passengers in the upper and middle class, or less than 20 => **survived**
3. Others => **died**
The final accuracy score was **80.36%**.
# Conclusion
After several iterations of exploring and conditioning on the data, you have built a useful algorithm for predicting the survival of each passenger aboard the RMS Titanic. The technique applied in this project is a manual implementation of a simple machine learning model, the *decision tree*. A decision tree splits a set of data into smaller and smaller groups (called *nodes*), by one feature at a time. Each time a subset of the data is split, our predictions become more accurate if each of the resulting subgroups are more homogeneous (contain similar labels) than before. The advantage of having a computer do things for us is that it will be more exhaustive and more precise than our manual exploration above. [This link](http://www.r2d3.us/visual-intro-to-machine-learning-part-1/) provides another introduction into machine learning using a decision tree.
A decision tree is just one of many models that come from *supervised learning*. In supervised learning, we attempt to use features of the data to predict or model things with objective outcome labels. That is to say, each of our data points has a known outcome value, such as a categorical, discrete label like `'Survived'`, or a numerical, continuous value like predicting the price of a house.
### Question 5
*Think of a real-world scenario where supervised learning could be applied. What would be the outcome variable that you are trying to predict? Name two features about the data used in this scenario that might be helpful for making the predictions.*
**Answer**:
A real-world scenario would be that we have a buch of animal photos labeled with the animal type on them and try to recognize new photos with supervised learning model predictions.
Useful featrues could be:
* number of legs
* size of the animal
* color of the skin or fur
* surrounding environment (tropical, water, air, iceberg etc.)
Outcome variable is the animal type.
## References
- [Udacity Website](http://www.udacity.com)
- [Pandas Documentation](http://pandas.pydata.org/pandas-docs/stable/)
## Reproduction Environment
```
import IPython
print IPython.sys_info()
!pip freeze
```
| github_jupyter |
<a href="https://colab.research.google.com/github/darshanbk/100-Days-Of-ML-Code/blob/master/Getting_started_with_BigQuery.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Before you begin
1. Use the [Cloud Resource Manager](https://console.cloud.google.com/cloud-resource-manager) to Create a Cloud Platform project if you do not already have one.
2. [Enable billing](https://support.google.com/cloud/answer/6293499#enable-billing) for the project.
3. [Enable BigQuery](https://console.cloud.google.com/flows/enableapi?apiid=bigquery) APIs for the project.
### Provide your credentials to the runtime
```
from google.colab import auth
auth.authenticate_user()
print('Authenticated')
```
## Optional: Enable data table display
Colab includes the ``google.colab.data_table`` package that can be used to display large pandas dataframes as an interactive data table.
It can be enabled with:
```
%load_ext google.colab.data_table
```
If you would prefer to return to the classic Pandas dataframe display, you can disable this by running:
```python
%unload_ext google.colab.data_table
```
# Use BigQuery via magics
The `google.cloud.bigquery` library also includes a magic command which runs a query and either displays the result or saves it to a variable as a `DataFrame`.
```
# Display query output immediately
%%bigquery --project yourprojectid
SELECT
COUNT(*) as total_rows
FROM `bigquery-public-data.samples.gsod`
# Save output in a variable `df`
%%bigquery --project yourprojectid df
SELECT
COUNT(*) as total_rows
FROM `bigquery-public-data.samples.gsod`
df
```
# Use BigQuery through google-cloud-bigquery
See [BigQuery documentation](https://cloud.google.com/bigquery/docs) and [library reference documentation](https://googlecloudplatform.github.io/google-cloud-python/latest/bigquery/usage.html).
The [GSOD sample table](https://bigquery.cloud.google.com/table/bigquery-public-data:samples.gsod) contains weather information collected by NOAA, such as precipitation amounts and wind speeds from late 1929 to early 2010.
### Declare the Cloud project ID which will be used throughout this notebook
```
project_id = '[your project ID]'
```
### Sample approximately 2000 random rows
```
from google.cloud import bigquery
client = bigquery.Client(project=project_id)
sample_count = 2000
row_count = client.query('''
SELECT
COUNT(*) as total
FROM `bigquery-public-data.samples.gsod`''').to_dataframe().total[0]
df = client.query('''
SELECT
*
FROM
`bigquery-public-data.samples.gsod`
WHERE RAND() < %d/%d
''' % (sample_count, row_count)).to_dataframe()
print('Full dataset has %d rows' % row_count)
```
### Describe the sampled data
```
df.describe()
```
### View the first 10 rows
```
df.head(10)
# 10 highest total_precipitation samples
df.sort_values('total_precipitation', ascending=False).head(10)[['station_number', 'year', 'month', 'day', 'total_precipitation']]
```
# Use BigQuery through pandas-gbq
The `pandas-gbq` library is a community led project by the pandas community. It covers basic functionality, such as writing a DataFrame to BigQuery and running a query, but as a third-party library it may not handle all BigQuery features or use cases.
[Pandas GBQ Documentation](https://pandas.pydata.org/pandas-docs/stable/generated/pandas.read_gbq.html)
```
import pandas as pd
sample_count = 2000
df = pd.io.gbq.read_gbq('''
SELECT name, SUM(number) as count
FROM `bigquery-public-data.usa_names.usa_1910_2013`
WHERE state = 'TX'
GROUP BY name
ORDER BY count DESC
LIMIT 100
''', project_id=project_id, dialect='standard')
df.head()
```
# Syntax highlighting
`google.colab.syntax` can be used to add syntax highlighting to any Python string literals which are used in a query later.
```
from google.colab import syntax
query = syntax.sql('''
SELECT
COUNT(*) as total_rows
FROM
`bigquery-public-data.samples.gsod`
''')
pd.io.gbq.read_gbq(query, project_id=project_id, dialect='standard')
```
| github_jupyter |
# Solving Multi-armed Bandit Problems
We will focus on how to solve the multi-armed bandit problem using four strategies, including epsilon-greedy, softmax exploration, upper confidence bound, and Thompson sampling. We will see how they deal with the exploration-exploitation dilemma in their own unique ways. We will also work on a billion-dollar problem, online advertising, and demonstrate how to solve it using a multi-armed bandit algorithm. Finally, we will solve the contextual advertising problem using contextual bandits to make more informed decisions in ad optimization.
## Creating a multi-armed bandit environment
The multi-armed bandit problem is one of the simplest reinforcement learning problems. It is best described as a slot machine with multiple levers (arms), and each lever has a different payout and payout probability. Our goal is to discover the best lever with the maximum return so that we can keep choosing it afterward. Let’s start with a simple multi-armed bandit problem in which the payout and payout probability is fixed for each arm. After creating the environment, we will solve it using the random policy algorithm.
```
import torch
class BanditEnv():
"""
Multi-armed bandit environment
payout_list:
A list of probabilities of the likelihood that a particular bandit will pay out
reward_list:
A list of rewards of the payout that bandit has
"""
def __init__(self, payout_list, reward_list):
self.payout_list = payout_list
self.reward_list = reward_list
def step(self, action):
if torch.rand(1).item() < self.payout_list[action]:
return self.reward_list[action]
return 0
if __name__ == "__main__":
bandit_payout = [0.1, 0.15, 0.3]
bandit_reward = [4, 3, 1]
bandit_env = BanditEnv(bandit_payout, bandit_reward)
n_episode = 100000
n_action = len(bandit_payout)
action_count = [0 for _ in range(n_action)]
action_total_reward = [0 for _ in range(n_action)]
action_avg_reward = [[] for action in range(n_action)]
def random_policy():
action = torch.multinomial(torch.ones(n_action), 1).item()
return action
for episode in range(n_episode):
action = random_policy()
reward = bandit_env.step(action)
action_count[action] += 1
action_total_reward[action] += reward
for a in range(n_action):
if action_count[a]:
action_avg_reward[a].append(action_total_reward[a] / action_count[a])
else:
action_avg_reward[a].append(0)
import matplotlib.pyplot as plt
for action in range(n_action):
plt.plot(action_avg_reward[action])
plt.legend(['Arm {}'.format(action) for action in range(n_action)])
plt.xscale('log')
plt.title('Average reward over time')
plt.xlabel('Episode')
plt.ylabel('Average reward')
plt.show()
```
In the example we just worked on, there are three slot machines. Each machine has a different payout (reward) and payout probability. In each episode, we randomly chose one arm of the machine to pull (one action to execute) and get a payout at a certain probability.
Arm 1 is the best arm with the largest average reward. Also, the average rewards start to saturate round 10,000 episodes.
This solution seems very naive as we only perform an exploration of all arms. We will come up with more intelligent strategies in the upcoming sections.
## Solving multi-armed bandit problems with the epsilon-greedy policy
Instead of exploring solely with random policy, we can do better with a combination of exploration and exploitation. Here comes the well-known epsilon-greedy policy.
Epsilon-greedy for multi-armed bandits exploits the best action the majority of the time and also keeps exploring different actions from time to time. Given a parameter, ε, with a value from 0 to 1, the probabilities of performing exploration and exploitation are ε and 1 - ε, respectively.
Similar to other MDP problems, the epsilon-greedy policy selects the best arm with a probability of 1 - ε and performs random exploration with a probability of ε. Epsilon manages the trade-off between exploration and exploitation.
```
import torch
bandit_payout = [0.1, 0.15, 0.3]
bandit_reward = [4, 3, 1]
bandit_env = BanditEnv(bandit_payout, bandit_reward)
n_episode = 100000
n_action = len(bandit_payout)
action_count = [0 for _ in range(n_action)]
action_total_reward = [0 for _ in range(n_action)]
action_avg_reward = [[] for action in range(n_action)]
def gen_epsilon_greedy_policy(n_action, epsilon):
def policy_function(Q):
probs = torch.ones(n_action) * epsilon / n_action
best_action = torch.argmax(Q).item()
probs[best_action] += 1.0 - epsilon
action = torch.multinomial(probs, 1).item()
return action
return policy_function
epsilon = 0.2
epsilon_greedy_policy = gen_epsilon_greedy_policy(n_action, epsilon)
Q = torch.zeros(n_action)
for episode in range(n_episode):
action = epsilon_greedy_policy(Q)
reward = bandit_env.step(action)
action_count[action] += 1
action_total_reward[action] += reward
Q[action] = action_total_reward[action] / action_count[action]
for a in range(n_action):
if action_count[a]:
action_avg_reward[a].append(action_total_reward[a] / action_count[a])
else:
action_avg_reward[a].append(0)
import matplotlib.pyplot as plt
for action in range(n_action):
plt.plot(action_avg_reward[action])
plt.legend(['Arm {}'.format(action) for action in range(n_action)])
plt.xscale('log')
plt.title('Average reward over time')
plt.xlabel('Episode')
plt.ylabel('Average reward')
plt.show()
```
Arm 1 is the best arm, with the largest average reward at the end. Also, its average reward starts to saturate after around 1,000 episodes.
You may wonder whether the epsilon-greedy policy actually outperforms the random policy. Besides the fact that the value for the optimal arm converges earlier with the epsilon-greedy policy, we can also prove that, on average, the reward we get during the course of training is higher with the epsilon-greedy policy than the random policy.
We can simply average the reward over all episodes:
```
print(sum(action_total_reward) / n_episode)
```
Over 100,000 episodes, the average payout is 0.43718 with the epsilon-greedy policy. Repeating the same computation for the random policy solution, we get 0.37902 as the average payout.
## Solving multi-armed bandit problems with the softmax exploration
As we've seen with epsilon-greedy, when performing exploration we randomly select one of the non-best arms with a probability of ε/|A|. Each non-best arm is treated equivalently regardless of its value in the Q function. Also, the best arm is chosen with a fixed probability regardless of its value. In softmax exploration, an arm is chosen based on a probability from the softmax distribution of the Q function values.
With the softmax exploration strategy, the dilemma of exploitation and exploration is solved with a softmax function based on the Q values. Instead of using a fixed pair of probabilities for the best arm and non-best arms, it adjusts the probabilities according to the softmax distribution with the τ parameter as a temperature factor. The higher the value of τ, the more focus will be shifted to exploration.
```
import torch
bandit_payout = [0.1, 0.15, 0.3]
bandit_reward = [4, 3, 1]
bandit_env = BanditEnv(bandit_payout, bandit_reward)
n_episode = 100000
n_action = len(bandit_payout)
action_count = [0 for _ in range(n_action)]
action_total_reward = [0 for _ in range(n_action)]
action_avg_reward = [[] for action in range(n_action)]
def gen_softmax_exploration_policy(tau):
def policy_function(Q):
probs = torch.exp(Q / tau)
probs = probs / torch.sum(probs)
action = torch.multinomial(probs, 1).item()
return action
return policy_function
tau = 0.1
softmax_exploration_policy = gen_softmax_exploration_policy(tau)
Q = torch.zeros(n_action)
for episode in range(n_episode):
action = softmax_exploration_policy(Q)
reward = bandit_env.step(action)
action_count[action] += 1
action_total_reward[action] += reward
Q[action] = action_total_reward[action] / action_count[action]
for a in range(n_action):
if action_count[a]:
action_avg_reward[a].append(action_total_reward[a] / action_count[a])
else:
action_avg_reward[a].append(0)
import matplotlib.pyplot as plt
for action in range(n_action):
plt.plot(action_avg_reward[action])
plt.legend(['Arm {}'.format(action) for action in range(n_action)])
plt.xscale('log')
plt.title('Average reward over time')
plt.xlabel('Episode')
plt.ylabel('Average reward')
plt.show()
```
Arm 1 is the best arm, with the largest average reward at the end. Also, its average reward starts to saturate after around 800 episodes in this example.
## Solving multi-armed bandit problems with the upper confidence bound algorithm
In the previous two recipes, we explored random actions in the multi-armed bandit problem with probabilities that are either assigned as fixed values in the epsilon-greedy policy or computed based on the Q-function values in the softmax exploration algorithm. In either algorithm, the probabilities of taking random actions are not adjusted over time. Ideally, we want less exploration as learning progresses. In this recipe, we will use a new algorithm called upper confidence bound to achieve this goal.
The upper confidence bound (UCB) algorithm stems from the idea of the confidence interval. In general, the confidence interval is a range of values where the true value lies. In the UCB algorithm, the confidence interval for an arm is a range where the mean reward obtained with this arm lies. The interval is in the form of [lower confidence bound, upper confidence bound] and we only use the upper bound, which is the UCB, to estimate the potential of the arm. The UCB is computed as follows:
$$UCB(a) = Q(a) + \sqrt{2log(t)/N(a)}$$
Here, t is the number of episodes, and N(a) is the number of times arm a is chosen among t episodes. As learning progresses, the confidence interval shrinks and becomes more and more accurate. The arm to pull is the one with the highest UCB.
In this recipe, we solved the multi-armed bandit with the UCB algorithm. It adjusts the exploitation-exploration dilemma according to the number of episodes. For an action with a few data points, its confidence interval is relatively wide, hence, choosing this action is of relatively high uncertainty. With more episodes of the action being selected, the confidence interval becomes narrow and shrinks to its actual value. In this case, it is of high certainty to choose (or not) this action. Finally, the UCB algorithm pulls the arm with the highest UCB in each episode and gains more and more confidence over time.
```
import torch
bandit_payout = [0.1, 0.15, 0.3]
bandit_reward = [4, 3, 1]
bandit_env = BanditEnv(bandit_payout, bandit_reward)
n_episode = 100000
n_action = len(bandit_payout)
action_count = torch.tensor([0. for _ in range(n_action)])
action_total_reward = [0 for _ in range(n_action)]
action_avg_reward = [[] for action in range(n_action)]
def upper_confidence_bound(Q, action_count, t):
ucb = torch.sqrt((2 * torch.log(torch.tensor(float(t)))) / action_count) + Q
return torch.argmax(ucb)
Q = torch.empty(n_action)
for episode in range(n_episode):
action = upper_confidence_bound(Q, action_count, episode)
reward = bandit_env.step(action)
action_count[action] += 1
action_total_reward[action] += reward
Q[action] = action_total_reward[action] / action_count[action]
for a in range(n_action):
if action_count[a]:
action_avg_reward[a].append(action_total_reward[a] / action_count[a])
else:
action_avg_reward[a].append(0)
import matplotlib.pyplot as plt
for action in range(n_action):
plt.plot(action_avg_reward[action])
plt.legend(['Arm {}'.format(action) for action in range(n_action)])
plt.xscale('log')
plt.title('Average reward over time')
plt.xlabel('Episode')
plt.ylabel('Average reward')
plt.show()
```
Arm 1 is the best arm, with the largest average reward in the end.
You may wonder whether UCB actually outperforms the epsilon-greedy policy. We can compute the average reward over the entire training process, and the policy with the highest average reward learns faster.
We can simply average the reward over all episodes:
```
print(sum(action_total_reward) / n_episode)
```
Over 100,000 episodes, the average payout is 0.44605 with UCB, which is higher than 0.43718 with the epsilon-greedy policy.
## Solving internet advertising problems with a multi-armed bandit
Imagine you are an advertiser working on ad optimization on a website:
- There are three different colors of ad background – red, green, and blue. Which one will achieve the best click-through rate (CTR)?
- There are three types of wordings of the ad – learn …, free ..., and try .... Which one will achieve the best CTR?
For each visitor, we need to choose an ad in order to maximize the CTR over time. How can we solve this?
Perhaps you are thinking about A/B testing, where you randomly split the traffic into groups and assign each ad to a different group, and then choose the ad from the group with the highest CTR after a period of observation. However, this is basically a complete exploration, and we are usually unsure of how long the observation period should be and will end up losing a large portion of potential clicks. Besides, in A/B testing, the unknown CTR for an ad is assumed to not change over time. Otherwise, such A/B testing should be re-run periodically.
A multi-armed bandit can certainly do better than A/B testing. Each arm is an ad, and the reward for an arm is either 1 (click) or 0 (no click).
Let's try to solve it with the UCB algorithm.
In this recipe, we solved the ad optimization problem in a multi-armed bandit manner. It overcomes the challenges confronting the A/B testing approach. We used the UCB algorithm to solve the multi-armed (multi-ad) bandit problem; the reward for each arm is either 1 or 0. Instead of pure exploration and no interaction between action and reward, UCB (or other algorithms such as epsilon-greedy and softmax exploration) dynamically switches between exploitation and exploration where necessarly. For an ad with a few data points, the confidence interval is relatively wide, hence, choosing this action is of relatively high uncertainty. With more episodes of the ad being selected, the confidence interval becomes narrow and shrinks to its actual value.
```
import torch
bandit_payout = [0.01, 0.015, 0.03]
bandit_reward = [1, 1, 1]
bandit_env = BanditEnv(bandit_payout, bandit_reward)
n_episode = 100000
n_action = len(bandit_payout)
action_count = torch.tensor([0. for _ in range(n_action)])
action_total_reward = [0 for _ in range(n_action)]
action_avg_reward = [[] for action in range(n_action)]
def upper_confidence_bound(Q, action_count, t):
ucb = torch.sqrt((2 * torch.log(torch.tensor(float(t)))) / action_count) + Q
return torch.argmax(ucb)
Q = torch.empty(n_action)
for episode in range(n_episode):
action = upper_confidence_bound(Q, action_count, episode)
reward = bandit_env.step(action)
action_count[action] += 1
action_total_reward[action] += reward
Q[action] = action_total_reward[action] / action_count[action]
for a in range(n_action):
if action_count[a]:
action_avg_reward[a].append(action_total_reward[a] / action_count[a])
else:
action_avg_reward[a].append(0)
import matplotlib.pyplot as plt
for action in range(n_action):
plt.plot(action_avg_reward[action])
plt.legend(['Arm {}'.format(action) for action in range(n_action)])
plt.xscale('log')
plt.title('Average reward over time')
plt.xlabel('Episode')
plt.ylabel('Average reward')
plt.show()
```
Ad 2 is the best ad with the highest predicted CTR (average reward) after the model converges.
Eventually, we found that ad 2 is the optimal one to choose, which is true. Also, the sooner we figure this out the better, because we will lose fewer potential clicks. In this example, ad 2 outperformed the others after around 1000 episodes.
## Solving multi-armed bandit problems with the Thompson sampling algorithm
In this recipe, we will tackle the exploitation and exploration dilemma in the advertising bandits problem using another algorithm, Thompson sampling. We will see how it differs greatly from the previous three algorithms.
Thompson sampling (TS) is also called Bayesian bandits as it applies the Bayesian way of thinking from the following perspectives:
- It is a probabilistic algorithm.
- It computes the prior distribution for each arm and samples a value from each distribution.
- It then selects the arm with the highest value and observes the reward.
- Finally, it updates the prior distribution based on the observed reward. This process is called Bayesian updating.
As we have seen that in our ad optimization case, the reward for each arm is either 1 or 0. We can use beta distribution for our prior distribution because the value of the beta distribution is from 0 to 1. The beta distribution is parameterized by two parameters, α and β. α represents the number of times we receive the reward of 1 and β, indicates the number of times we receive the reward of 0.
To help you understand the beta distribution better, we will start by looking at several beta distributions before we implement the TS algorithm.
```
import torch
import matplotlib.pyplot as plt
beta1 = torch.distributions.beta.Beta(1, 1)
samples1 = [beta1.sample() for _ in range(100000)]
plt.hist(samples1, range=[0, 1], bins=10)
plt.title('beta(1, 1)')
plt.show()
beta2 = torch.distributions.beta.Beta(5, 1)
samples2 = [beta2.sample() for _ in range(100000)]
plt.hist(samples2, range=[0, 1], bins=10)
plt.title('beta(5, 1)')
plt.show()
beta3 = torch.distributions.beta.Beta(1, 5)
samples3= [beta3.sample() for _ in range(100000)]
plt.hist(samples3, range=[0, 1], bins=10)
plt.title('beta(1, 5)')
plt.show()
beta4 = torch.distributions.beta.Beta(5, 5)
samples4= [beta4.sample() for _ in range(100000)]
plt.hist(samples4, range=[0, 1], bins=10)
plt.title('beta(5, 5)')
plt.show()
bandit_payout = [0.01, 0.015, 0.03]
bandit_reward = [1, 1, 1]
bandit_env = BanditEnv(bandit_payout, bandit_reward)
n_episode = 100000
n_action = len(bandit_payout)
action_count = torch.tensor([0. for _ in range(n_action)])
action_total_reward = [0 for _ in range(n_action)]
action_avg_reward = [[] for action in range(n_action)]
```
In this recipe, we solved the ad bandits problem with the TS algorithm. The biggest difference between TS and the three other approaches is the adoption of Bayesian optimization. It first computes the prior distribution for each possible arm, and then randomly draws a value from each distribution. It then picks the arm with the highest value and uses the observed outcome to update the prior distribution. The TS policy is both stochastic and greedy. If an ad is more likely to receive clicks, its beta distribution shifts toward 1 and, hence, the value of a random sample tends to be closer to 1.
```
def thompson_sampling(alpha, beta):
prior_values = torch.distributions.beta.Beta(alpha, beta).sample()
return torch.argmax(prior_values)
alpha = torch.ones(n_action)
beta = torch.ones(n_action)
for episode in range(n_episode):
action = thompson_sampling(alpha, beta)
reward = bandit_env.step(action)
action_count[action] += 1
action_total_reward[action] += reward
if reward > 0:
alpha[action] += 1
else:
beta[action] += 1
for a in range(n_action):
if action_count[a]:
action_avg_reward[a].append(action_total_reward[a] / action_count[a])
else:
action_avg_reward[a].append(0)
for action in range(n_action):
plt.plot(action_avg_reward[action])
plt.legend(['Arm {}'.format(action) for action in range(n_action)])
plt.xscale('log')
plt.title('Average reward over time')
plt.xlabel('Episode')
plt.ylabel('Average reward')
plt.show()
```
Ad 2 is the best ad, with the highest predicted CTR (average reward).
## Solving internet advertising problems with contextual bandits
You may notice that in the ad optimization problem, we only care about the ad and ignore other information, such as user information and web page information, that might affect the ad being clicked on or not. In this recipe, we will talk about how we take more information into account beyond the ad itself and solve the problem with contextual bandits.
The multi-armed bandit problems we have worked with so far do not involve the concept of state, which is very different from MDPs. We only have several actions, and a reward will be generated that is associated with the action selected. Contextual bandits extend multi-armed bandits by introducing the concept of state. State provides a description of the environment, which helps the agent take more informed actions. In the advertising example, the state could be the user's gender (two states, male and female), the user’s age group (four states, for example), or page category (such as sports, finance, or news). Intuitively, users of certain demographics are more likely to click on an ad on certain pages.
It is not difficult to understand contextual bandits. A multi-armed bandit is a single machine with multiple arms, while contextual bandits are a set of such machines (bandits). Each machine in contextual bandits is a state that has multiple arms. The learning goal is to find the best arm (action) for each machine (state).
We will work with an advertising example with two states for simplicity.
In this recipe, we solved the contextual advertising problem with contextual bandits using the UCB algorithm.
```
import torch
bandit_payout_machines = [
[0.01, 0.015, 0.03],
[0.025, 0.01, 0.015]
]
bandit_reward_machines = [
[1, 1, 1],
[1, 1, 1]
]
n_machine = len(bandit_payout_machines)
bandit_env_machines = [BanditEnv(bandit_payout, bandit_reward)
for bandit_payout, bandit_reward in
zip(bandit_payout_machines, bandit_reward_machines)]
n_episode = 100000
n_action = len(bandit_payout_machines[0])
action_count = torch.zeros(n_machine, n_action)
action_total_reward = torch.zeros(n_machine, n_action)
action_avg_reward = [[[] for action in range(n_action)] for _ in range(n_machine)]
def upper_confidence_bound(Q, action_count, t):
ucb = torch.sqrt((2 * torch.log(torch.tensor(float(t)))) / action_count) + Q
return torch.argmax(ucb)
Q_machines = torch.empty(n_machine, n_action)
for episode in range(n_episode):
state = torch.randint(0, n_machine, (1,)).item()
action = upper_confidence_bound(Q_machines[state], action_count[state], episode)
reward = bandit_env_machines[state].step(action)
action_count[state][action] += 1
action_total_reward[state][action] += reward
Q_machines[state][action] = action_total_reward[state][action] / action_count[state][action]
for a in range(n_action):
if action_count[state][a]:
action_avg_reward[state][a].append(action_total_reward[state][a] / action_count[state][a])
else:
action_avg_reward[state][a].append(0)
import matplotlib.pyplot as plt
for state in range(n_machine):
for action in range(n_action):
plt.plot(action_avg_reward[state][action])
plt.legend(['Arm {}'.format(action) for action in range(n_action)])
plt.xscale('log')
plt.title('Average reward over time for state {}'.format(state))
plt.xlabel('Episode')
plt.ylabel('Average reward')
plt.show()
```
Given the first state, ad 2 is the best ad, with the highest predicted CTR. Given the second state, ad 0 is the optimal ad, with the highest average reward. And these are both true.
Contextual bandits are a set of multi-armed bandits. Each bandit represents a unique state of the environment. The state provides a description of the environment, which helps the agent take more informed actions. In our advertising example, male users might be more likely to click an ad than female users. We simply used two slot machines to incorporate two states and searched for the best arm to pull given each state.
One thing to note is that contextual bandits are still different from MDPs, although they involve the concept of state. First, the states in contextual bandits are not determined by the previous actions or states, but are simply observations of the environment. Second, there is no delayed or discounted reward in contextual bandits because a bandit episode is one step. However, compared to multi-armed bandits, contextual bandits are closer to MDP as the actions are conditional to the states in the environment. It is safe to say that contextual bandits are in between multi-armed bandits and full MDP reinforcement learning.
| github_jupyter |
##### Copyright 2018 The TensorFlow Authors.
```
#@title Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# 不规则张量
<table class="tfo-notebook-buttons" align="left">
<td> <a target="_blank" href="https://tensorflow.google.cn/guide/ragged_tensor"><img src="https://tensorflow.google.cn/images/tf_logo_32px.png">在 TensorFlow.org 上查看</a>
</td>
<td><a target="_blank" href="https://colab.research.google.com/github/tensorflow/docs-l10n/blob/master/site/zh-cn/guide/ragged_tensor.ipynb"><img src="https://tensorflow.google.cn/images/colab_logo_32px.png">在 Google Colab 中运行 </a></td>
<td><a target="_blank" href="https://github.com/tensorflow/docs-l10n/blob/master/site/zh-cn/guide/ragged_tensor.ipynb"><img src="https://tensorflow.google.cn/images/GitHub-Mark-32px.png">在 Github 上查看源代码</a></td>
<td><a href="https://storage.googleapis.com/tensorflow_docs/docs/site/en/guide/ragged_tensor.ipynb">{img}下载笔记本</a></td>
</table>
**API 文档:** [`tf.RaggedTensor`](https://tensorflow.google.cn/api_docs/python/tf/RaggedTensor) [`tf.ragged`](https://tensorflow.google.cn/api_docs/python/tf/ragged)
## 设置
```
!pip install -q tf_nightly
import math
import tensorflow as tf
```
## 概述
数据有多种形状;张量也应当有多种形状。*不规则张量*是嵌套的可变长度列表的 TensorFlow 等效项。它们使存储和处理包含非均匀形状的数据变得容易,包括:
- 可变长度特征,例如电影的演员名单。
- 成批的可变长度顺序输入,例如句子或视频剪辑。
- 分层输入,例如细分为节、段落、句子和单词的文本文档。
- 结构化输入中的各个字段,例如协议缓冲区。
### 不规则张量的功能
有一百多种 TensorFlow 运算支持不规则张量,包括数学运算(如 `tf.add` 和 `tf.reduce_mean`)、数组运算(如 `tf.concat` 和 `tf.tile`)、字符串操作运算(如 `tf.substr`)、控制流运算(如 `tf.while_loop` 和 `tf.map_fn`)等:
```
digits = tf.ragged.constant([[3, 1, 4, 1], [], [5, 9, 2], [6], []])
words = tf.ragged.constant([["So", "long"], ["thanks", "for", "all", "the", "fish"]])
print(tf.add(digits, 3))
print(tf.reduce_mean(digits, axis=1))
print(tf.concat([digits, [[5, 3]]], axis=0))
print(tf.tile(digits, [1, 2]))
print(tf.strings.substr(words, 0, 2))
print(tf.map_fn(tf.math.square, digits))
```
还有专门针对不规则张量的方法和运算,包括工厂方法、转换方法和值映射运算。有关支持的运算列表,请参阅 **`tf.ragged` 包文档**。
许多 TensorFlow API 都支持不规则张量,包括 [Keras](https://tensorflow.google.cn/guide/keras)、[Dataset](https://tensorflow.google.cn/guide/data)、[tf.function](https://tensorflow.google.cn/guide/function)、[SavedModel](https://tensorflow.google.cn/guide/saved_model) 和 [tf.Example](https://tensorflow.google.cn/tutorials/load_data/tfrecord)。有关更多信息,请参阅下面的 **TensorFlow API** 一节。
与普通张量一样,您可以使用 Python 风格的索引来访问不规则张量的特定切片。有关更多信息,请参阅下面的**索引**一节。
```
print(digits[0]) # First row
print(digits[:, :2]) # First two values in each row.
print(digits[:, -2:]) # Last two values in each row.
```
与普通张量一样,您可以使用 Python 算术和比较运算符来执行逐元素运算。有关更多信息,请参阅下面的**重载运算符**一节。
```
print(digits + 3)
print(digits + tf.ragged.constant([[1, 2, 3, 4], [], [5, 6, 7], [8], []]))
```
如果需要对 `RaggedTensor` 的值进行逐元素转换,您可以使用 `tf.ragged.map_flat_values`(它采用一个函数加上一个或多个参数的形式),并应用这个函数来转换 `RaggedTensor` 的值。
```
times_two_plus_one = lambda x: x * 2 + 1
print(tf.ragged.map_flat_values(times_two_plus_one, digits))
```
不规则张量可以转换为嵌套的 Python `list` 和 numpy `array`:
```
digits.to_list()
digits.numpy()
```
### 构造不规则张量
构造不规则张量的最简单方法是使用 `tf.ragged.constant`,它会构建与给定的嵌套 Python `list` 或 numpy `array` 相对应的 `RaggedTensor`:
```
sentences = tf.ragged.constant([
["Let's", "build", "some", "ragged", "tensors", "!"],
["We", "can", "use", "tf.ragged.constant", "."]])
print(sentences)
paragraphs = tf.ragged.constant([
[['I', 'have', 'a', 'cat'], ['His', 'name', 'is', 'Mat']],
[['Do', 'you', 'want', 'to', 'come', 'visit'], ["I'm", 'free', 'tomorrow']],
])
print(paragraphs)
```
还可以通过将扁平的*值*张量与*行分区*张量进行配对来构造不规则张量,行分区张量使用 `tf.RaggedTensor.from_value_rowids`、`tf.RaggedTensor.from_row_lengths` 和 `tf.RaggedTensor.from_row_splits` 等工厂类方法指示如何将值分成各行。
#### `tf.RaggedTensor.from_value_rowids`
如果知道每个值属于哪一行,可以使用 `value_rowids` 行分区张量构建 `RaggedTensor`:
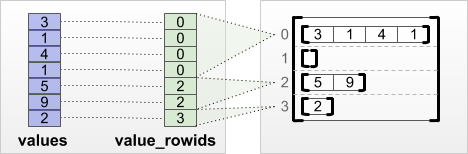
```
print(tf.RaggedTensor.from_value_rowids(
values=[3, 1, 4, 1, 5, 9, 2],
value_rowids=[0, 0, 0, 0, 2, 2, 3]))
```
#### `tf.RaggedTensor.from_row_lengths`
如果知道每行的长度,可以使用 `row_lengths` 行分区张量:
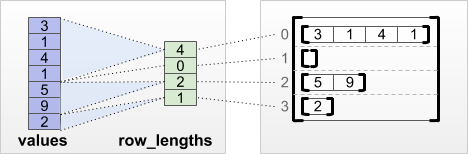
```
print(tf.RaggedTensor.from_row_lengths(
values=[3, 1, 4, 1, 5, 9, 2],
row_lengths=[4, 0, 2, 1]))
```
#### `tf.RaggedTensor.from_row_splits`
如果知道指示每行开始和结束的索引,可以使用 `row_splits` 行分区张量:
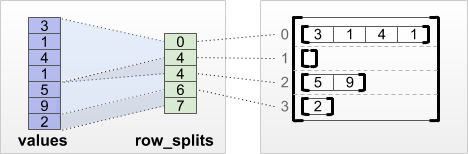
```
print(tf.RaggedTensor.from_row_splits(
values=[3, 1, 4, 1, 5, 9, 2],
row_splits=[0, 4, 4, 6, 7]))
```
有关完整的工厂方法列表,请参阅 `tf.RaggedTensor` 类文档。
注:默认情况下,这些工厂方法会添加断言,说明行分区张量结构良好且与值数量保持一致。如果您能够保证输入的结构良好且一致,可以使用 `validate=False` 参数跳过此类检查。
### 可以在不规则张量中存储什么
与普通 `Tensor` 一样,`RaggedTensor` 中的所有值必须具有相同的类型;所有值必须处于相同的嵌套深度(张量的*秩*):
```
print(tf.ragged.constant([["Hi"], ["How", "are", "you"]])) # ok: type=string, rank=2
print(tf.ragged.constant([[[1, 2], [3]], [[4, 5]]])) # ok: type=int32, rank=3
try:
tf.ragged.constant([["one", "two"], [3, 4]]) # bad: multiple types
except ValueError as exception:
print(exception)
try:
tf.ragged.constant(["A", ["B", "C"]]) # bad: multiple nesting depths
except ValueError as exception:
print(exception)
```
## 示例用例
以下示例演示了如何使用 `RaggedTensor`,通过为每个句子的开头和结尾使用特殊标记,为一批可变长度查询构造和组合一元元组与二元元组嵌入。有关本例中使用的运算的更多详细信息,请参阅 `tf.ragged` 包文档。
```
queries = tf.ragged.constant([['Who', 'is', 'Dan', 'Smith'],
['Pause'],
['Will', 'it', 'rain', 'later', 'today']])
# Create an embedding table.
num_buckets = 1024
embedding_size = 4
embedding_table = tf.Variable(
tf.random.truncated_normal([num_buckets, embedding_size],
stddev=1.0 / math.sqrt(embedding_size)))
# Look up the embedding for each word.
word_buckets = tf.strings.to_hash_bucket_fast(queries, num_buckets)
word_embeddings = tf.nn.embedding_lookup(embedding_table, word_buckets) # ①
# Add markers to the beginning and end of each sentence.
marker = tf.fill([queries.nrows(), 1], '#')
padded = tf.concat([marker, queries, marker], axis=1) # ②
# Build word bigrams & look up embeddings.
bigrams = tf.strings.join([padded[:, :-1], padded[:, 1:]], separator='+') # ③
bigram_buckets = tf.strings.to_hash_bucket_fast(bigrams, num_buckets)
bigram_embeddings = tf.nn.embedding_lookup(embedding_table, bigram_buckets) # ④
# Find the average embedding for each sentence
all_embeddings = tf.concat([word_embeddings, bigram_embeddings], axis=1) # ⑤
avg_embedding = tf.reduce_mean(all_embeddings, axis=1) # ⑥
print(avg_embedding)
```
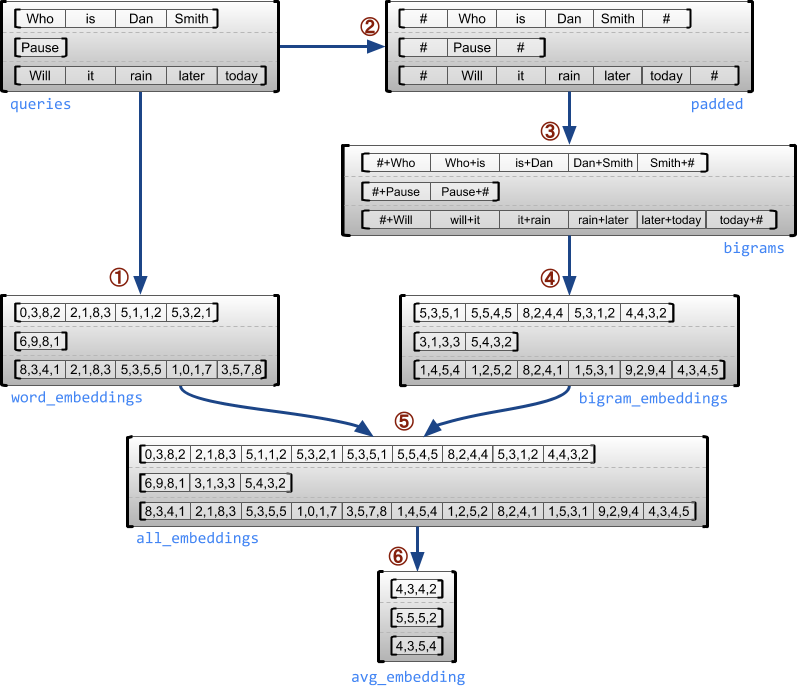
## 不规则维度和均匀维度
***不规则维度***是切片可能具有不同长度的维度。例如,`rt=[[3, 1, 4, 1], [], [5, 9, 2], [6], []]` 的内部(列)维度是不规则的,因为列切片 (`rt[0, :]`, ..., `rt[4, :]`) 具有不同的长度。切片全都具有相同长度的维度称为*均匀维度*。
不规则张量的最外层维始终是均匀维度,因为它只包含一个切片(因此不可能有不同的切片长度)。其余维度可能是不规则维度也可能是均匀维度。例如,我们可以使用形状为 `[num_sentences, (num_words), embedding_size]` 的不规则张量为一批句子中的每个单词存储单词嵌入,其中 `(num_words)` 周围的括号表示维度是不规则维度。
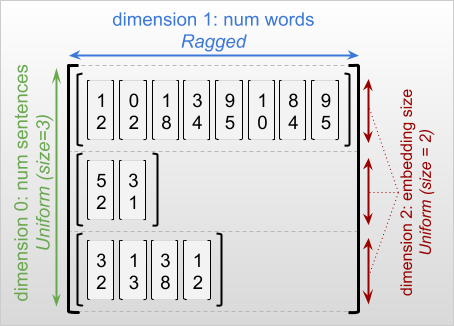
不规则张量可以有多个不规则维度。例如,我们可以使用形状为 `[num_documents, (num_paragraphs), (num_sentences), (num_words)]` 的张量存储一批结构化文本文档(其中,括号同样用于表示不规则维度)。
与 `tf.Tensor` 一样,不规则张量的***秩***是其总维数(包括不规则维度和均匀维度)。***潜在的不规则张量***是一个值,这个值可能是 `tf.Tensor` 或 `tf.RaggedTensor`。
描述 RaggedTensor 的形状时,按照惯例,不规则维度会通过括号进行指示。例如,如上面所见,存储一批句子中每个单词的单词嵌入的三维 RaggedTensor 的形状可以写为 `[num_sentences, (num_words), embedding_size]`。
`RaggedTensor.shape` 特性返回不规则张量的 `tf.TensorShape`,其中不规则维度的大小为 `None`:
```
tf.ragged.constant([["Hi"], ["How", "are", "you"]]).shape
```
可以使用方法 `tf.RaggedTensor.bounding_shape` 查找给定 `RaggedTensor` 的紧密边界形状:
```
print(tf.ragged.constant([["Hi"], ["How", "are", "you"]]).bounding_shape())
```
## 不规则张量和稀疏张量对比
不规则张量*不*应该被认为是一种稀疏张量。尤其是,稀疏张量是以紧凑的格式对相同数据建模的 *tf.Tensor 的高效编码*;而不规则张量是对扩展的数据类建模的 *tf.Tensor 的延伸*。这种区别在定义运算时至关重要:
- 对稀疏张量或密集张量应用某一运算应当始终获得相同结果。
- 对不规则张量或稀疏张量应用某一运算可能获得不同结果。
一个说明性的示例是,考虑如何为不规则张量和稀疏张量定义 `concat`、`stack` 和 `tile` 之类的数组运算。连接不规则张量时,会将每一行连在一起,形成一个具有组合长度的行:

```
ragged_x = tf.ragged.constant([["John"], ["a", "big", "dog"], ["my", "cat"]])
ragged_y = tf.ragged.constant([["fell", "asleep"], ["barked"], ["is", "fuzzy"]])
print(tf.concat([ragged_x, ragged_y], axis=1))
```
但连接稀疏张量时,相当于连接相应的密集张量,如以下示例所示(其中 Ø 表示缺失的值):
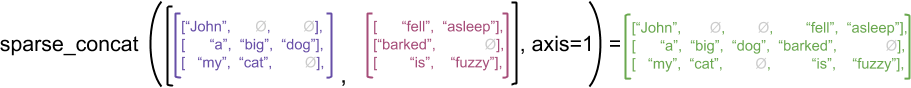
```
sparse_x = ragged_x.to_sparse()
sparse_y = ragged_y.to_sparse()
sparse_result = tf.sparse.concat(sp_inputs=[sparse_x, sparse_y], axis=1)
print(tf.sparse.to_dense(sparse_result, ''))
```
另一个说明为什么这种区别非常重要的示例是,考虑一个运算(如 `tf.reduce_mean`)的“每行平均值”的定义。对于不规则张量,一行的平均值是该行的值总和除以该行的宽度。但对于稀疏张量来说,一行的平均值是该行的值总和除以稀疏张量的总宽度(大于等于最长行的宽度)。
## TensorFlow API
### Keras
[tf.keras](https://tensorflow.google.cn/guide/keras) 是 TensorFlow 的高级 API,用于构建和训练深度学习模型。通过在 `tf.keras.Input` 或 `tf.keras.layers.InputLayer` 上设置 `ragged=True`,不规则张量可以作为输入传送到 Keras 模型。不规则张量还可以在 Keras 层之间传递,并由 Keras 模型返回。以下示例显示了一个使用不规则张量训练的小 LSTM 模型。
```
# Task: predict whether each sentence is a question or not.
sentences = tf.constant(
['What makes you think she is a witch?',
'She turned me into a newt.',
'A newt?',
'Well, I got better.'])
is_question = tf.constant([True, False, True, False])
# Preprocess the input strings.
hash_buckets = 1000
words = tf.strings.split(sentences, ' ')
hashed_words = tf.strings.to_hash_bucket_fast(words, hash_buckets)
# Build the Keras model.
keras_model = tf.keras.Sequential([
tf.keras.layers.Input(shape=[None], dtype=tf.int64, ragged=True),
tf.keras.layers.Embedding(hash_buckets, 16),
tf.keras.layers.LSTM(32, use_bias=False),
tf.keras.layers.Dense(32),
tf.keras.layers.Activation(tf.nn.relu),
tf.keras.layers.Dense(1)
])
keras_model.compile(loss='binary_crossentropy', optimizer='rmsprop')
keras_model.fit(hashed_words, is_question, epochs=5)
print(keras_model.predict(hashed_words))
```
### tf.Example
[tf.Example](https://tensorflow.google.cn/tutorials/load_data/tfrecord) 是 TensorFlow 数据的标准 [protobuf](https://developers.google.com/protocol-buffers/) 编码。使用 `tf.Example` 编码的数据往往包括可变长度特征。例如,以下代码定义了一批具有不同特征长度的四条 `tf.Example` 消息:
```
import google.protobuf.text_format as pbtext
def build_tf_example(s):
return pbtext.Merge(s, tf.train.Example()).SerializeToString()
example_batch = [
build_tf_example(r'''
features {
feature {key: "colors" value {bytes_list {value: ["red", "blue"]} } }
feature {key: "lengths" value {int64_list {value: [7]} } } }'''),
build_tf_example(r'''
features {
feature {key: "colors" value {bytes_list {value: ["orange"]} } }
feature {key: "lengths" value {int64_list {value: []} } } }'''),
build_tf_example(r'''
features {
feature {key: "colors" value {bytes_list {value: ["black", "yellow"]} } }
feature {key: "lengths" value {int64_list {value: [1, 3]} } } }'''),
build_tf_example(r'''
features {
feature {key: "colors" value {bytes_list {value: ["green"]} } }
feature {key: "lengths" value {int64_list {value: [3, 5, 2]} } } }''')]
```
我们可以使用 `tf.io.parse_example` 解析这个编码数据,它采用序列化字符串的张量和特征规范字典,并将字典映射特征名称返回给张量。要将长度可变特征读入不规则张量,我们只需在特征规范字典中使用 `tf.io.RaggedFeature` 即可:
```
feature_specification = {
'colors': tf.io.RaggedFeature(tf.string),
'lengths': tf.io.RaggedFeature(tf.int64),
}
feature_tensors = tf.io.parse_example(example_batch, feature_specification)
for name, value in feature_tensors.items():
print("{}={}".format(name, value))
```
`tf.io.RaggedFeature` 还可用于读取具有多个不规则维度的特征。有关详细信息,请参阅 [API 文档](https://tensorflow.google.cn/api_docs/python/tf/io/RaggedFeature)。
### 数据集
[tf.data](https://tensorflow.google.cn/guide/data) 是一个 API,可用于通过简单的可重用代码块构建复杂的输入流水线。它的核心数据结构是 `tf.data.Dataset`,表示一系列元素,每个元素包含一个或多个分量。
```
# Helper function used to print datasets in the examples below.
def print_dictionary_dataset(dataset):
for i, element in enumerate(dataset):
print("Element {}:".format(i))
for (feature_name, feature_value) in element.items():
print('{:>14} = {}'.format(feature_name, feature_value))
```
#### 使用不规则张量构建数据集
可以采用通过 `tf.Tensor` 或 numpy `array` 构建数据集时使用的方法,如 `Dataset.from_tensor_slices`,通过不规则张量构建数据集:
```
dataset = tf.data.Dataset.from_tensor_slices(feature_tensors)
print_dictionary_dataset(dataset)
```
注:`Dataset.from_generator` 目前还不支持不规则张量,但不久后将会支持这种张量。
#### 批处理和取消批处理具有不规则张量的数据集
可以使用 `Dataset.batch` 方法对具有不规则张量的数据集进行批处理(将 *n* 个连续元素组合成单个元素)。
```
batched_dataset = dataset.batch(2)
print_dictionary_dataset(batched_dataset)
```
相反,可以使用 `Dataset.unbatch` 将批处理后的数据集转换为扁平数据集。
```
unbatched_dataset = batched_dataset.unbatch()
print_dictionary_dataset(unbatched_dataset)
```
#### 对具有可变长度非不规则张量的数据集进行批处理
如果您有一个包含非不规则张量的数据集,而且各个元素的张量长度不同,则可以应用 `dense_to_ragged_batch` 转换,将这些非不规则张量批处理成不规则张量:
```
non_ragged_dataset = tf.data.Dataset.from_tensor_slices([1, 5, 3, 2, 8])
non_ragged_dataset = non_ragged_dataset.map(tf.range)
batched_non_ragged_dataset = non_ragged_dataset.apply(
tf.data.experimental.dense_to_ragged_batch(2))
for element in batched_non_ragged_dataset:
print(element)
```
#### 转换具有不规则张量的数据集
还可以使用 `Dataset.map` 创建或转换数据集中的不规则张量。
```
def transform_lengths(features):
return {
'mean_length': tf.math.reduce_mean(features['lengths']),
'length_ranges': tf.ragged.range(features['lengths'])}
transformed_dataset = dataset.map(transform_lengths)
print_dictionary_dataset(transformed_dataset)
```
### tf.function
[tf.function](https://tensorflow.google.cn/guide/function) 是预计算 Python 函数的 TensorFlow 计算图的装饰器,它可以大幅改善 TensorFlow 代码的性能。不规则张量能够透明地与 `@tf.function` 装饰的函数一起使用。例如,以下函数对不规则张量和非不规则张量均有效:
```
@tf.function
def make_palindrome(x, axis):
return tf.concat([x, tf.reverse(x, [axis])], axis)
make_palindrome(tf.constant([[1, 2], [3, 4], [5, 6]]), axis=1)
make_palindrome(tf.ragged.constant([[1, 2], [3], [4, 5, 6]]), axis=1)
```
如果您希望为 `tf.function` 明确指定 `input_signature`,可以使用 `tf.RaggedTensorSpec` 执行此操作。
```
@tf.function(
input_signature=[tf.RaggedTensorSpec(shape=[None, None], dtype=tf.int32)])
def max_and_min(rt):
return (tf.math.reduce_max(rt, axis=-1), tf.math.reduce_min(rt, axis=-1))
max_and_min(tf.ragged.constant([[1, 2], [3], [4, 5, 6]]))
```
#### 具体函数
[具体函数](https://tensorflow.google.cn/guide/function#obtaining_concrete_functions)封装通过 `tf.function` 构建的各个跟踪图。不规则张量可以透明地与具体函数一起使用。
```
# Preferred way to use ragged tensors with concrete functions (TF 2.3+):
try:
@tf.function
def increment(x):
return x + 1
rt = tf.ragged.constant([[1, 2], [3], [4, 5, 6]])
cf = increment.get_concrete_function(rt)
print(cf(rt))
except Exception as e:
print(f"Not supported before TF 2.3: {type(e)}: {e}")
```
### SavedModel
[SavedModel](https://tensorflow.google.cn/guide/saved_model) 是序列化 TensorFlow 程序,包括权重和计算。它可以通过 Keras 模型或自定义模型构建。在任何一种情况下,不规则张量都可以透明地与 SavedModel 定义的函数和方法一起使用。
#### 示例:保存 Keras 模型
```
import tempfile
keras_module_path = tempfile.mkdtemp()
tf.saved_model.save(keras_model, keras_module_path)
imported_model = tf.saved_model.load(keras_module_path)
imported_model(hashed_words)
```
#### 示例:保存自定义模型
```
class CustomModule(tf.Module):
def __init__(self, variable_value):
super(CustomModule, self).__init__()
self.v = tf.Variable(variable_value)
@tf.function
def grow(self, x):
return x * self.v
module = CustomModule(100.0)
# Before saving a custom model, we must ensure that concrete functions are
# built for each input signature that we will need.
module.grow.get_concrete_function(tf.RaggedTensorSpec(shape=[None, None],
dtype=tf.float32))
custom_module_path = tempfile.mkdtemp()
tf.saved_model.save(module, custom_module_path)
imported_model = tf.saved_model.load(custom_module_path)
imported_model.grow(tf.ragged.constant([[1.0, 4.0, 3.0], [2.0]]))
```
注:SavedModel [签名](https://tensorflow.google.cn/guide/saved_model#specifying_signatures_during_export)是具体函数。如上文的“具体函数”部分所述,从 TensorFlow 2.3 开始,只有具体函数才能正确处理不规则张量。如果您需要在先前版本的 TensorFlow 中使用 SavedModel 签名,建议您将不规则张量分解成其张量分量。
## 重载运算符
`RaggedTensor` 类会重载标准 Python 算术和比较运算符,使其易于执行基本的逐元素数学:
```
x = tf.ragged.constant([[1, 2], [3], [4, 5, 6]])
y = tf.ragged.constant([[1, 1], [2], [3, 3, 3]])
print(x + y)
```
由于重载运算符执行逐元素计算,因此所有二进制运算的输入必须具有相同的形状,或者可以广播至相同的形状。在最简单的广播情况下,单个标量与不规则张量中的每个值逐元素组合:
```
x = tf.ragged.constant([[1, 2], [3], [4, 5, 6]])
print(x + 3)
```
有关更高级的用例,请参阅**广播**一节。
不规则张量重载与正常 `Tensor` 相同的一组运算符:一元运算符 `-`、`~` 和 `abs()`;二元运算符 `+`、`-`、`*`、`/`、`//`、`%`、`**`、`&`、`|`、`^`、`==`、`<`、`<=`、`>` 和 `>=`。
## 索引
不规则张量支持 Python 风格的索引,包括多维索引和切片。以下示例使用二维和三维不规则张量演示了不规则张量索引。
### 索引示例:二维不规则张量
```
queries = tf.ragged.constant(
[['Who', 'is', 'George', 'Washington'],
['What', 'is', 'the', 'weather', 'tomorrow'],
['Goodnight']])
print(queries[1]) # A single query
print(queries[1, 2]) # A single word
print(queries[1:]) # Everything but the first row
print(queries[:, :3]) # The first 3 words of each query
print(queries[:, -2:]) # The last 2 words of each query
```
### 索引示例:三维不规则张量
```
rt = tf.ragged.constant([[[1, 2, 3], [4]],
[[5], [], [6]],
[[7]],
[[8, 9], [10]]])
print(rt[1]) # Second row (2-D RaggedTensor)
print(rt[3, 0]) # First element of fourth row (1-D Tensor)
print(rt[:, 1:3]) # Items 1-3 of each row (3-D RaggedTensor)
print(rt[:, -1:]) # Last item of each row (3-D RaggedTensor)
```
`RaggedTensor` 支持多维索引和切片,但有一个限制:不允许索引一个不规则维度。这种情况是有问题的,因为指示的值可能在某些行中存在,而在其他行中不存在。这种情况下,我们不知道是应该 (1) 引发 `IndexError`;(2) 使用默认值;还是 (3) 跳过该值并返回一个行数比开始时少的张量。根据 [Python 的指导原则](https://www.python.org/dev/peps/pep-0020/)(“当面对不明确的情况时,不要尝试去猜测”),我们目前不允许此运算。
## 张量类型转换
`RaggedTensor` 类定义了可用于在 `RaggedTensor` 与 `tf.Tensor` 或 `tf.SparseTensors` 之间转换的方法:
```
ragged_sentences = tf.ragged.constant([
['Hi'], ['Welcome', 'to', 'the', 'fair'], ['Have', 'fun']])
# RaggedTensor -> Tensor
print(ragged_sentences.to_tensor(default_value='', shape=[None, 10]))
# Tensor -> RaggedTensor
x = [[1, 3, -1, -1], [2, -1, -1, -1], [4, 5, 8, 9]]
print(tf.RaggedTensor.from_tensor(x, padding=-1))
#RaggedTensor -> SparseTensor
print(ragged_sentences.to_sparse())
# SparseTensor -> RaggedTensor
st = tf.SparseTensor(indices=[[0, 0], [2, 0], [2, 1]],
values=['a', 'b', 'c'],
dense_shape=[3, 3])
print(tf.RaggedTensor.from_sparse(st))
```
## 评估不规则张量
要访问不规则张量中的值,您可以:
1. 使用 `tf.RaggedTensor.to_list()` 将不规则张量转换为嵌套 Python 列表。
2. 使用 `tf.RaggedTensor.numpy()` 将不规则张量转换为 numpy 数组,数组的值是嵌套的 numpy 数组。
3. 使用 `tf.RaggedTensor.values` 和 `tf.RaggedTensor.row_splits` 属性,或 `tf.RaggedTensor.row_lengths()` 和 `tf.RaggedTensor.value_rowids()` 之类的行分区方法,将不规则张量分解成其分量。
4. 使用 Python 索引从不规则张量中选择值。
```
rt = tf.ragged.constant([[1, 2], [3, 4, 5], [6], [], [7]])
print("python list:", rt.to_list())
print("numpy array:", rt.numpy())
print("values:", rt.values.numpy())
print("splits:", rt.row_splits.numpy())
print("indexed value:", rt[1].numpy())
```
## 广播
广播是使具有不同形状的张量在进行逐元素运算时具有兼容形状的过程。有关广播的更多背景,请参阅:
- [Numpy:广播](https://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
- `tf.broadcast_dynamic_shape`
- `tf.broadcast_to`
广播两个输入 `x` 和 `y`,使其具有兼容形状的基本步骤是:
1. 如果 `x` 和 `y` 没有相同的维数,则增加外层维度(使用大小 1),直至它们具有相同的维数。
2. 对于 `x` 和 `y` 的大小不同的每一个维度:
- 如果 `x` 或 `y` 在 `d` 维中的大小为 `1`,则跨 `d` 维重复其值以匹配其他输入的大小。
- 否则,引发异常(`x` 和 `y` 非广播兼容)。
其中,均匀维度中一个张量的大小是一个数字(跨该维的切片大小);不规则维度中一个张量的大小是切片长度列表(跨该维的所有切片)。
### 广播示例
```
# x (2D ragged): 2 x (num_rows)
# y (scalar)
# result (2D ragged): 2 x (num_rows)
x = tf.ragged.constant([[1, 2], [3]])
y = 3
print(x + y)
# x (2d ragged): 3 x (num_rows)
# y (2d tensor): 3 x 1
# Result (2d ragged): 3 x (num_rows)
x = tf.ragged.constant(
[[10, 87, 12],
[19, 53],
[12, 32]])
y = [[1000], [2000], [3000]]
print(x + y)
# x (3d ragged): 2 x (r1) x 2
# y (2d ragged): 1 x 1
# Result (3d ragged): 2 x (r1) x 2
x = tf.ragged.constant(
[[[1, 2], [3, 4], [5, 6]],
[[7, 8]]],
ragged_rank=1)
y = tf.constant([[10]])
print(x + y)
# x (3d ragged): 2 x (r1) x (r2) x 1
# y (1d tensor): 3
# Result (3d ragged): 2 x (r1) x (r2) x 3
x = tf.ragged.constant(
[
[
[[1], [2]],
[],
[[3]],
[[4]],
],
[
[[5], [6]],
[[7]]
]
],
ragged_rank=2)
y = tf.constant([10, 20, 30])
print(x + y)
```
下面是一些不广播的形状示例:
```
# x (2d ragged): 3 x (r1)
# y (2d tensor): 3 x 4 # trailing dimensions do not match
x = tf.ragged.constant([[1, 2], [3, 4, 5, 6], [7]])
y = tf.constant([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
try:
x + y
except tf.errors.InvalidArgumentError as exception:
print(exception)
# x (2d ragged): 3 x (r1)
# y (2d ragged): 3 x (r2) # ragged dimensions do not match.
x = tf.ragged.constant([[1, 2, 3], [4], [5, 6]])
y = tf.ragged.constant([[10, 20], [30, 40], [50]])
try:
x + y
except tf.errors.InvalidArgumentError as exception:
print(exception)
# x (3d ragged): 3 x (r1) x 2
# y (3d ragged): 3 x (r1) x 3 # trailing dimensions do not match
x = tf.ragged.constant([[[1, 2], [3, 4], [5, 6]],
[[7, 8], [9, 10]]])
y = tf.ragged.constant([[[1, 2, 0], [3, 4, 0], [5, 6, 0]],
[[7, 8, 0], [9, 10, 0]]])
try:
x + y
except tf.errors.InvalidArgumentError as exception:
print(exception)
```
## RaggedTensor 编码
不规则张量使用 `RaggedTensor` 类进行编码。在内部,每个 `RaggedTensor` 包含:
- 一个 `values` 张量,它将可变长度行连接成扁平列表。
- 一个 `row_partition`,它指示如何将这些扁平值分成各行。
可以使用四种不同的编码存储 `row_partition`:
- `row_splits` 是一个整型向量,用于指定行之间的拆分点。
- `value_rowids` 是一个整型向量,用于指定每个值的行索引。
- `row_lengths` 是一个整型向量,用于指定每一行的长度。
- `uniform_row_length` 是一个整型标量,用于指定所有行的单个长度。
整型标量 `nrows` 还可以包含在 `row_partition` 编码中,以考虑具有 `value_rowids` 的空尾随行或具有 `uniform_row_length` 的空行。
```
rt = tf.RaggedTensor.from_row_splits(
values=[3, 1, 4, 1, 5, 9, 2],
row_splits=[0, 4, 4, 6, 7])
print(rt)
```
选择为行分区使用哪种编码由不规则张量在内部进行管理,以提高某些环境下的效率。尤其是,不同行分区方案的某些优点和缺点是:
- **高效索引**:`row_splits` 编码可以实现不规则张量的恒定时间索引和切片。
- **高效连接**:`row_lengths` 编码在连接不规则张量时更有效,因为当两个张量连接在一起时,行长度不会改变。
- **较小的编码大小**:`value_rowids` 编码在存储有大量空行的不规则张量时更有效,因为张量的大小只取决于值的总数。另一方面,`row_splits` 和 `row_lengths` 编码在存储具有较长行的不规则张量时更有效,因为它们每行只需要一个标量值。
- **兼容性**:`value_rowids` 方案与 `tf.math.segment_sum` 等运算使用的[分段](https://tensorflow.google.cn/api_docs/python/tf/math#about_segmentation)格式相匹配。`row_limits` 方案与 `tf.sequence_mask` 等运算使用的格式相匹配。
- **均匀维度**:如下文所述,`uniform_row_length` 编码用于对具有均匀维度的不规则张量进行编码。
### 多个不规则维度
具有多个不规则维度的不规则张量通过为 `values` 张量使用嵌套 `RaggedTensor` 进行编码。每个嵌套 `RaggedTensor` 都会增加一个不规则维度。
```
rt = tf.RaggedTensor.from_row_splits(
values=tf.RaggedTensor.from_row_splits(
values=[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
row_splits=[0, 3, 3, 5, 9, 10]),
row_splits=[0, 1, 1, 5])
print(rt)
print("Shape: {}".format(rt.shape))
print("Number of partitioned dimensions: {}".format(rt.ragged_rank))
```
工厂函数 `tf.RaggedTensor.from_nested_row_splits` 可用于通过提供一个 `row_splits` 张量列表,直接构造具有多个不规则维度的 RaggedTensor:
```
rt = tf.RaggedTensor.from_nested_row_splits(
flat_values=[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
nested_row_splits=([0, 1, 1, 5], [0, 3, 3, 5, 9, 10]))
print(rt)
```
### 不规则秩和扁平值
不规则张量的***不规则秩***是底层 `values` 张量的分区次数(即 `RaggedTensor` 对象的嵌套深度)。最内层的 `values` 张量称为其 ***flat_values***。在以下示例中,`conversations` 具有 ragged_rank=3,其 `flat_values` 为具有 24 个字符串的一维 `Tensor`:
```
# shape = [batch, (paragraph), (sentence), (word)]
conversations = tf.ragged.constant(
[[[["I", "like", "ragged", "tensors."]],
[["Oh", "yeah?"], ["What", "can", "you", "use", "them", "for?"]],
[["Processing", "variable", "length", "data!"]]],
[[["I", "like", "cheese."], ["Do", "you?"]],
[["Yes."], ["I", "do."]]]])
conversations.shape
assert conversations.ragged_rank == len(conversations.nested_row_splits)
conversations.ragged_rank # Number of partitioned dimensions.
conversations.flat_values.numpy()
```
### 均匀内层维度
具有均匀内层维度的不规则张量通过为 flat_values(即最内层 `values`)使用多维 `tf.Tensor` 进行编码。
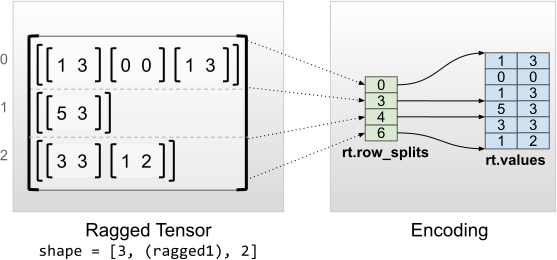
```
rt = tf.RaggedTensor.from_row_splits(
values=[[1, 3], [0, 0], [1, 3], [5, 3], [3, 3], [1, 2]],
row_splits=[0, 3, 4, 6])
print(rt)
print("Shape: {}".format(rt.shape))
print("Number of partitioned dimensions: {}".format(rt.ragged_rank))
print("Flat values shape: {}".format(rt.flat_values.shape))
print("Flat values:\n{}".format(rt.flat_values))
```
### 均匀非内层维度
具有均匀非内层维度的不规则张量通过使用 `uniform_row_length` 对行分区进行编码。
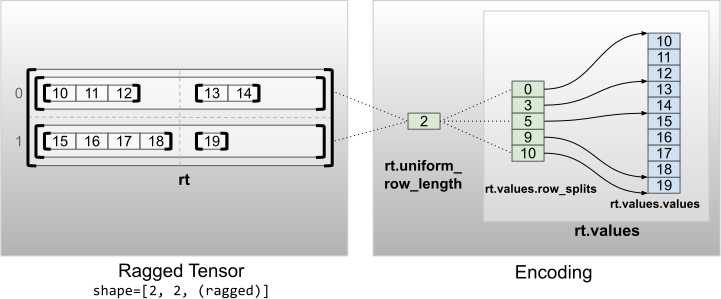
```
rt = tf.RaggedTensor.from_uniform_row_length(
values=tf.RaggedTensor.from_row_splits(
values=[10, 11, 12, 13, 14, 15, 16, 17, 18, 19],
row_splits=[0, 3, 5, 9, 10]),
uniform_row_length=2)
print(rt)
print("Shape: {}".format(rt.shape))
print("Number of partitioned dimensions: {}".format(rt.ragged_rank))
```
| github_jupyter |
# Data Space Report
<img src="images/polito_logo.png" alt="Polito Logo" style="width: 200px;"/>
## Pittsburgh Bridges Data Set
<img src="images/andy_warhol_bridge.jpg" alt="Andy Warhol Bridge" style="width: 200px;"/>
Andy Warhol Bridge - Pittsburgh.
Report created by Student Francesco Maria Chiarlo s253666, for A.A 2019/2020.
**Abstract**:The aim of this report is to evaluate the effectiveness of distinct, different statistical learning approaches, in particular focusing on their characteristics as well as on their advantages and backwards when applied onto a relatively small dataset as the one employed within this report, that is Pittsburgh Bridgesdataset.
**Key words**:Statistical Learning, Machine Learning, Bridge Design.
## TOC:
* [Imports Section](#imports-section)
* [Dataset's Attributes Description](#attributes-description)
* [Data Preparation and Investigation](#data-preparation)
* [Learning Models](#learning-models)
* [Improvements and Conclusions](#improvements-and-conclusions)
* [References](#references)
### Imports Section <a class="anchor" id="imports-section"></a>
```
# =========================================================================== #
# STANDARD IMPORTS
# =========================================================================== #
print(__doc__)
from pprint import pprint
import warnings
warnings.filterwarnings('ignore')
import copy
import os
import sys
import time
import pandas as pd
import numpy as np
%matplotlib inline
# Matplotlib pyplot provides plotting API
import matplotlib as mpl
from matplotlib import pyplot as plt
import chart_studio.plotly.plotly as py
import seaborn as sns; sns.set()
# =========================================================================== #
# UTILS IMPORTS (Done by myself)
# =========================================================================== #
from utils.display_utils import *
from utils.preprocessing_utils import *
from utils.training_utils import *
from utils.training_utils_v2 import fit_by_n_components, fit_all_by_n_components
from itertools import islice
# =========================================================================== #
# sklearn IMPORT
# =========================================================================== #
from sklearn.decomposition import PCA, KernelPCA
# Import scikit-learn classes: models (Estimators).
from sklearn.naive_bayes import GaussianNB # Non-parametric Generative Model
from sklearn.naive_bayes import MultinomialNB # Non-parametric Generative Model
from sklearn.linear_model import LinearRegression # Parametric Linear Discriminative Model
from sklearn.linear_model import LogisticRegression # Parametric Linear Discriminative Model
from sklearn.linear_model import Ridge, Lasso
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC # Parametric Linear Discriminative "Support Vector Classifier"
from sklearn.tree import DecisionTreeClassifier # Non-parametric Model
from sklearn.ensemble import BaggingClassifier # Non-parametric Model (Meta-Estimator, that is, an Ensemble Method)
from sklearn.ensemble import RandomForestClassifier # Non-parametric Model (Meta-Estimator, that is, an Ensemble Method)
```
### Dataset's Attributes Description <a class="anchor" id="attributes-description"></a>
The analyses that I aim at accomplishing while using as means the methods or approaches provided by both Statistical Learning and Machine Learning fields, concern the dataset Pittsburgh Bridges, and what follows is a overview and brief description of the main characteristics, as well as, basic information about this precise dataset.
The Pittsburgh Bridges dataset is a dataset available from the web site called mainly *"UCI Machine Learing Repository"*, which is one of the well known web site that let a large amount of different datasets, from different domains or fields, to be used for machine-learning research and which have been cited in peer-reviewed academic journals.
In particular, the dataset I'm going to treat and analyze, which is Pittsburgh Bridges dataset, has been made freely available from the Western Pennsylvania Regional Data Center (WPRDC), which is a project led by the University Center of Social and Urban Research (UCSUR) at the University of Pittsburgh ("University") in collaboration with City of Pittsburgh and The County of Allegheny in Pennsylvania. The WPRDC and the WPRDC Project is supported by a grant from the Richard King Mellon Foundation.
In order to be more precise, from the official and dedicated web page, within UCI Machine Learning cite, Pittsburgh Bridges dataset is a dataset that has been created after the works of some co-authors which are:
- Yoram Reich & Steven J. Fenves from Department of Civil Engineering and Engineering Design Research Center Carnegie Mellon University Pittsburgh, PA 15213
The Pittsburgh Bridges dataset is made of up to 108 distinct observations and each of that data sample is made of 12 attributes or features where some of them are considered to be continuous properties and other to be categorical or nominal properties. Those variables are the following:
- **RIVER**: which is a nominal type variable that can assume the subsequent possible discrete values which are: A, M, O. Where A stands for Allegheny river, while M stands for Monongahela river and lastly O stands for Ohio river.
- **LOCATION**: which represents a nominal type variable too, and assume a positive integer value from 1 up to 52 used as categorical attribute.
- **ERECTED**: which might be either a numerical or categorical variable, depending on the fact that we want to aggregate a bunch of value under a categorical quantity. What this means is that, basically such attribute is made of date starting from 1818 up to 1986, but we may imagine to aggregate somehow these data within a given category among those suggested, that are CRAFTS, EMERGENING, MATURE, MODERN.
- **PURPOSE**: which is a categorical attribute and represents the reason why a particular bridge has been built, which means that this attribute represents what kind of vehicle can cross the bridge or if the bridge has been made just for people. For this reasons the allowd values for this attributes are the following: WALK, AQUEDUCT, RR, HIGHWAY. Three out of four are self explained values, while RR value that might be tricky at first glance, it just stands for railroad.
- **LENGTH**: which represents the bridge's length, is a numerical attribute if we just look at the real number values that go from 804 up to 4558, but we can again decide to handle or arrange such values so that they can be grouped into range of values mapped into SHORT, MEDIUM, LONG so that we can refer to a bridge's length by means of these new categorical values.
- **LANES**: which is a categorical variable which is represented by numerical values, that are 1, 2, 4, 6 which indicate the number of distinct lanes that a bridge in Pittsburgh city may have. The larger the value the wider the bridge.
- **CLEAR-G**: specifies whether a vertical navigation clearance requirement was enforced in the design or not.
- **T-OR-D**: which is a nominal attribute, in other words, a categorical attribute that can assume THROUGH, DECK values. In order to be more precise, this samples attribute deals with structural elements of a bridge. In fact, a deck is the surface of a bridge and this structural element, of bridge's superstructure, may be constructed of concrete, steel, open grating, or wood. On the other hand, a through arch bridge, also known as a half-through arch bridge or a through-type arch bridge, is a bridge that is made from materials such as steel or reinforced concrete, in which the base of an arch structure is below the deck but the top rises above it.
- **MATERIAL**: which is a categorical or nominal variable and is used to describe the bridge telling which is the main or core material used to build it.
This attribute can assume one of the possible, following values which are: WOOD, IRON, STEEL. Furthermore, we expect to see somehow a bit of correlation between the values assumed by the pairs represented by T-OR-D and MATERIAL columns, when looking just to them.
- **SPAN**: which is a categorical or nominal value and has been recorded by means of three possible values for each sample, that are SHORT, MEDIUM, LONG. This attribute, within the field of Structural Engineering, is the distance between two intermediate supports for a structure, e.g. a beam or a bridge. A span can be closed by a solid beam or by a rope. The first kind is used for bridges, the second one for power lines, overhead telecommunication lines, some type of antennas or for aerial tramways.
- **REL-L**: which is a categorical or nominal variable and stands for relative length of the main span of the bridge to the total crossing length, it can assume three possible values that are S, S-F, F.
- Lastly, **TYPE** which indicates as a categorical or nominal attributes what type of bridge each record represents, among the possible 6 distinct classes or types of bridges that are: WOOD, SUSPEN, SIMPLE-T, ARCH, CANTILEV, CONT-T.
### Data Preparation and Investigation <a class="anchor" id="data-preparation"></a>
The aim of this chapter is to get in the data, that are available within Pittsburgh Bridge Dataset, in order to investigate a bit more in to detail and generally speaking deeper the main or high level statistics quantities, such as mean, median, standard deviation of each attribute, as well as displaying somehow data distribution for each attribute by means of histogram plots. This phase allows or enables us to decide which should be the best feature to be selected as the target variable, in other word the attribute that will represent the dependent variable with respect to the remaining attributes that instead will play the role of predictors and independent variables, as well.
In order to investigate and explore our data we make usage of *Pandas library*. We recall mainly that, in computer programming, Pandas is a software library written for the Python programming language* for *data manipulation and analysis*. In particular, it offers data structures and operations for manipulating numerical tables and time series. It is free software and a interesting and funny things about such tool is that the name is derived from the term "panel data", an econometrics term for data sets that include observations over multiple time periods for the same individuals.
We also note that as the analysis proceeds we will introduce other computer programming as well as programming libraries that allow or enable us to fulfill our goals.
Initially, once I have downloaded from the provided web page the dataset with the data samples about Pittsburgh Bridge we load the data by means of functions available using python library's pandas. We notice that the overall set of data points is large up to 108 records or rows, which are sorted by Erected attributes, so this means that are sorted in decreasing order from the oldest bridge which has been built in 1818 up to the most modern bridge that has been erected in 1986. Then we display the first 5 rows to get an overview and have a first idea about what is inside the overall dataset, and the result we obtain by means of head() function applied onto the fetched dataset is equals to what follows:
```
# =========================================================================== #
# READ INPUT DATASET
# =========================================================================== #
dataset_path = 'C:\\Users\\Francesco\Documents\\datasets\\pittsburgh_dataset'
dataset_name = 'bridges.data.csv'
# column_names = ['IDENTIF', 'RIVER', 'LOCATION', 'ERECTED', 'PURPOSE', 'LENGTH', 'LANES', 'CLEAR-G', 'T-OR-D', 'MATERIAL', 'SPAN', 'REL-L', 'TYPE']
column_names = ['RIVER', 'LOCATION', 'ERECTED', 'PURPOSE', 'LENGTH', 'LANES', 'CLEAR-G', 'T-OR-D', 'MATERIAL', 'SPAN', 'REL-L', 'TYPE']
dataset = pd.read_csv(os.path.join(dataset_path, dataset_name), names=column_names, index_col=0)
# SHOW SOME STANDARD DATASET INFOS
# --------------------------------------------------------------------------- #
print('Dataset shape: {}'.format(dataset.shape))
print(dataset.info())
# SHOWING FIRSTS N-ROWS AS THEY ARE STORED WITHIN DATASET
# --------------------------------------------------------------------------- #
dataset.head(5)
```
What we can notice from just the table above is that there are some attributes that are characterized by a special character that is '?' which stands for a missing value, so by chance there was not possibility to get the value for this attribute, such as for LENGTH and SPAN attributes. Analyzing in more details the dataset we discover that there are up to 6 different attributes, in the majority attributes with categorical or nominal nature such as CLEAR-G, T-OR-D, MATERIAL, SPAN, REL-L, and TYPE that contain at list one row characterized by the fact that one of its attributes is set to assuming '?' value that stands, as we already know for a missing value.
Here, we can follow different strategies that depends onto the level of complexity as well as accuracy we want to obtain or achieve for models we are going to fit to the data after having correctly pre-processed them, speaking about what we could do with missing values. In fact one can follow the simplest way and can decide to simply discard those rows that contain at least one attribute with a missing value represented by the '?' symbol. Otherwise one may alos decide to follow a different strategy that aims at keeping also those rows that have some missing values by means of some kind of technique that allows to establish a potential substituting value for the missing one.
So, in this setting, that is our analyses, we start by just leaving out those rows that at least contain one attribute that has a missing value, this choice leads us to reduce the size of our dataset from 108 records to 70 remaining samples, with a drop of 38 data examples, which may affect the final results, since we left out more or less the 46\% of the data because of missing values.
```
# INVESTIGATING DATASET IN ORDER TO DETECT NULL VALUES
# --------------------------------------------------------------------------- #
print('Before preprocessing dataset and handling null values')
result = dataset.isnull().values.any()
print('There are any null values ? Response: {}'.format(result))
result = dataset.isnull().sum()
print('Number of null values for each predictor:\n{}'.format(result))
# DISCOVERING VALUES WITHIN EACH PREDICTOR DOMAIN
# --------------------------------------------------------------------------- #
columns_2_avoid = ['ERECTED', 'LENGTH', 'LOCATION', 'LANES']
# columns_2_avoid = None
list_columns_2_fix = show_categorical_predictor_values(dataset, columns_2_avoid)
# FIXING, UPDATING NULL VALUES CODED AS '?' SYMBOL
# WITHIN EACH CATEGORICAL VARIABLE, IF DETECTED ANY
# --------------------------------------------------------------------------- #
print('"Before" removing \'?\' rows, Dataset dim:', dataset.shape)
for _, predictor in enumerate(list_columns_2_fix):
dataset = dataset[dataset[predictor] != '?']
print('"After" removing \'?\' rows, Dataset dim: ', dataset.shape)
print('-' * 50)
_ = show_categorical_predictor_values(dataset, columns_2_avoid)
# INTERMEDIATE RESULT FOUND
# --------------------------------------------------------------------------- #
preprocess_categorical_variables(dataset, columns_2_avoid)
print(dataset.info())
dataset.head(5)
```
The next step is represented by the effort of mapping categorical variables into numerical variables, so that them are comparable with the already existing numerical or continuous variables, and also by mapping the categorical variables into numerical variables we allow or enable us to perform some kind of normalization or just transformation onto the entire dataset in order to let some machine learning algorithm to work better or to take advantage of normalized data within our pre-processed dataset. Furthermore, by transforming first the categorical attributes into a continuous version we are also able to calculate the \textit{heatmap}, which is a very useful way of representing a correlation matrix calculated on the whole dataset. Moreover we have displayed data distribution for each attribute by means of histogram representation to take some useful information about the number of occurrences for each possible value, in particular for those attributes that have a categorical nature.
```
# MAP NUMERICAL VALUES TO INTEGER VALUES
# --------------------------------------------------------------------------- #
print('Before', dataset.shape)
columns_2_map = ['ERECTED', 'LANES']
for _, predictor in enumerate(columns_2_map):
dataset = dataset[dataset[predictor] != '?']
dataset[predictor] = np.array(list(map(lambda x: int(x), dataset[predictor].values)))
print('After', dataset.shape)
print(dataset.info())
# print(dataset.head(5))
# MAP NUMERICAL VALUES TO FLOAT VALUES
# --------------------------------------------------------------------------- #
# print('Before', dataset.shape)
columns_2_map = ['LOCATION', 'LANES', 'LENGTH']
for _, predictor in enumerate(columns_2_map):
dataset = dataset[dataset[predictor] != '?']
dataset[predictor] = np.array(list(map(lambda x: float(x), dataset[predictor].values)))
# print('After', dataset.shape)
# print(dataset.info())
# print(dataset.head(5))
# columns_2_avoid = None
# list_columns_2_fix = show_categorical_predictor_values(dataset, None)
result = dataset.isnull().values.any()
# print('After handling null values\nThere are any null values ? Response: {}'.format(result))
result = dataset.isnull().sum()
# print('Number of null values for each predictor:\n{}'.format(result))
dataset.head(5)
dataset.describe(include='all')
# sns.pairplot(dataset, hue='T-OR-D', size=1.5)
columns_2_avoid = ['ERECTED', 'LENGTH', 'LOCATION']
target_col = 'T-OR-D'
# show_frequency_distribution_predictors(dataset, columns_2_avoid)
# show_frequency_distribution_predictor(dataset, predictor_name='RIVER', columns_2_avoid=columns_2_avoid)
# build_boxplot(dataset, predictor_name='RIVER', columns_2_avoid=columns_2_avoid, target_col='T-OR-D')
# show_frequency_distribution_predictors(dataset, columns_2_avoid)
# show_frequency_distribution_predictor(dataset, predictor_name='T-OR-D', columns_2_avoid=columns_2_avoid)
# show_frequency_distribution_predictors(dataset, columns_2_avoid)
# show_frequency_distribution_predictor(dataset, predictor_name='CLEAR-G', columns_2_avoid=columns_2_avoid)
# build_boxplot(dataset, predictor_name='CLEAR-G', columns_2_avoid=columns_2_avoid, target_col='T-OR-D')
# show_frequency_distribution_predictors(dataset, columns_2_avoid)
# show_frequency_distribution_predictor(dataset, predictor_name='SPAN', columns_2_avoid=columns_2_avoid)
# build_boxplot(dataset, predictor_name='SPAN', columns_2_avoid=columns_2_avoid, target_col='T-OR-D')
# show_frequency_distribution_predictors(dataset, columns_2_avoid)
# show_frequency_distribution_predictor(dataset, predictor_name='MATERIAL', columns_2_avoid=columns_2_avoid)
# build_boxplot(dataset, predictor_name='MATERIAL', columns_2_avoid=columns_2_avoid, target_col='T-OR-D')
# show_frequency_distribution_predictors(dataset, columns_2_avoid)
# show_frequency_distribution_predictor(dataset, predictor_name='REL-L', columns_2_avoid=columns_2_avoid)
# show_frequency_distribution_predictors(dataset, columns_2_avoid)
# show_frequency_distribution_predictor(dataset, predictor_name='TYPE', columns_2_avoid=columns_2_avoid)
# build_boxplot(dataset, predictor_name='TYPE', columns_2_avoid=columns_2_avoid, target_col='T-OR-D')
corr_result = dataset.corr()
# corr_result.head(corr_result.shape[0])
display_heatmap(corr_result)
# show_histograms_from_heatmap_corr_matrix(corr_result, row_names=dataset.columns)
# Make distinction between Target Variable and Predictors
# --------------------------------------------------------------------------- #
columns = dataset.columns # List of all attribute names
target_col = 'T-OR-D' # Target variable name
# Get Target values and map to 0s and 1s
y = np.array(list(map(lambda x: 0 if x == 1 else 1, dataset[target_col].values)))
print('Summary about Target Variable {target_col}')
print('-' * 50)
print(dataset['T-OR-D'].value_counts())
# Get Predictors
X = dataset.loc[:, dataset.columns != target_col].values
# Standardizing the features
# --------------------------------------------------------------------------- #
scaler_methods = ['minmax', 'standard', 'norm']
scaler_method = 'standard'
rescaledX = preprocessing_data_rescaling(scaler_method, X)
```
### Pricipal Component Analysis
After having investigate the data points inside the dataset, I move one to another section of my report where I decide to explore examples that made up the entire dataset using a particular technique in the field of statistical analysis that corresponds, precisely, to so called Principal Component Analysis. In fact, the major objective of this section is understand whether it is possible to transform, by means of some kind of linear transformation given by a mathematical calculation, the original data examples into reprojected representation that allows me to retrieve most useful information to be later exploited at training time. So, lets dive a bit whitin what is and which are main concepts, pros and cons about Principal Component Analysis.
Firstly, we know that **Principal Component Analysis**, more shortly PCA, is a statistical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of linearly uncorrelated variables called *principal components*. This transformation is defined in such a way that:
- the first principal component has the largest possible variance (that is, accounts for as much of the variability in the data as possible),
- and each succeeding component in turn has the highest variance possible under the constraint that it is orthogonal to the preceding components.
The resulting vectors, each being a linear combination of the variables and containing n observations, are an uncorrelated orthogonal basis set. PCA is sensitive to the relative scaling of the original variables.
PCA is mostly used as a tool in *exploratory data analysis* and for making predictive models, for that reasons I used such a technique here, before going through the different learning technique for producing my models.
#### Several Different Implementation
From the theory and the filed of research in statistics, we know that out there, there are several different implementation and way of computing principal component analysis, and each adopted technique has different performance as well as numerical stability. The three major derivations are:
- PCA by means of an iterative based procedure of extraing pricipal components one after the other selecting each time the one that account for the most of variance along its own axis, within the remainig subspace to be derived.
- The second possible way of performing PCA is done via calculation of *Covariance Matrix* applied to attributes, that are our independent predictive variables, used to represent data points.
- Lastly, it is used the technique known as *Singular Valued Decomposition* applied to the overall data points within our dataset.
Reading scikit-learn documentation, I discovered that PCA's derivation uses the *LAPACK implementation* of the *full SVD* or a *randomized truncated SVD* by the method of *Halko et al. 2009*, depending on the shape of the input data and the number of components to extract. Therefore I will descrive mainly that way of deriving the method with respect to the others that, instead, will be described more briefly and roughly.
#### PCA's Iterative based Method
Going in order, as depicted briefly above, I start describing PCA obtained by means of iterative based procedure to extract one at a time a new principal componet explointing the data points at hand.
We begin, recalling that, PCA is defined as an orthogonal linear transformation that transforms the data to a new coordinate system such that the greatest variance by some scalar projection of the data comes to lie on the first coordinate (called the first principal component), the second greatest variance on the second coordinate, and so on.
We suppose to deal with a data matrix X, with column-wise zero empirical mean, where each of the n rows represents a different repetition of the experiment, and each of the p columns gives a particular kind of feature.
From a math poitn of view, the transformation is defined by a set of p-dimensional vectors of weights or coefficients $\mathbf {w} _{(k)}=(w_{1},\dots ,w_{p})_{(k)}$ that map each row vector $\mathbf{x}_{(i)}$ of X to a new vector of principal component scores ${\displaystyle \mathbf {t} _{(i)}=(t_{1},\dots ,t_{l})_{(i)}}$, given by: ${\displaystyle {t_{k}}_{(i)}=\mathbf {x} _{(i)}\cdot \mathbf {w} _{(k)}\qquad \mathrm {for} \qquad i=1,\dots ,n\qquad k=1,\dots ,l}$.
In this way all the individual variables ${\displaystyle t_{1},\dots ,t_{l}}$ of t considered over the data set successively inherit the maximum possible variance from X, with each coefficient vector w constrained to be a unit vector.
More precisely, the first component In order to maximize variance has to satisfy the following expression:
${\displaystyle \mathbf {w} _{(1)}={\underset {\Vert \mathbf {w} \Vert =1}{\operatorname {\arg \,max} }}\,\left\{\sum _{i}\left(t_{1}\right)_{(i)}^{2}\right\}={\underset {\Vert \mathbf {w} \Vert =1}{\operatorname {\arg \,max} }}\,\left\{\sum _{i}\left(\mathbf {x} _{(i)}\cdot \mathbf {w} \right)^{2}\right\}}$
So, with $w_{1}$ found, the first principal component of a data vector $x_{1}$ can then be given as a score $t_{1(i)} = x_{1} ⋅ w_{1}$ in the transformed co-ordinates, or as the corresponding vector in the original variables, $(x_{1} ⋅ w_{1})w_{1}$.
The others remainig components are computed as folloes. The kth component can be found by subtracting the first k − 1 principal components from X, as in the following expression:
- ${\displaystyle \mathbf {\hat {X}} _{k}=\mathbf {X} -\sum _{s=1}^{k-1}\mathbf {X} \mathbf {w} _{(s)}\mathbf {w} _{(s)}^{\rm {T}}}$
- and then finding the weight vector which extracts the maximum variance from this new data matrix ${\mathbf {w}}_{{(k)}}={\underset {\Vert {\mathbf {w}}\Vert =1}{\operatorname {arg\,max}}}\left\{\Vert {\mathbf {{\hat {X}}}}_{{k}}{\mathbf {w}}\Vert ^{2}\right\}={\operatorname {\arg \,max}}\,\left\{{\tfrac {{\mathbf {w}}^{T}{\mathbf {{\hat {X}}}}_{{k}}^{T}{\mathbf {{\hat {X}}}}_{{k}}{\mathbf {w}}}{{\mathbf {w}}^{T}{\mathbf {w}}}}\right\}$
It turns out that:
- from the formulas depicted above me get the remaining eigenvectors of $X^{T}X$, with the maximum values for the quantity in brackets given by their corresponding eigenvalues. Thus the weight vectors are eigenvectors of $X^{T}X$.
- The kth principal component of a data vector $x_(i)$ can therefore be given as a score $t_{k(i)} = x_{(i)} ⋅ w_(k)$ in the transformed co-ordinates, or as the corresponding vector in the space of the original variables, $(x_{(i)} ⋅ w_{(k)}) w_{(k)}$, where $w_{(k)}$ is the kth eigenvector of $X^{T}X$.
- The full principal components decomposition of X can therefore be given as: ${\displaystyle \mathbf {T} =\mathbf {X} \mathbf {W}}$, where W is a p-by-p matrix of weights whose columns are the eigenvectors of $X^{T}X$.
#### Covariance Matrix for PCA analysis
PCA made from covarian matrix computation requires the calculation of sample covariance matrix of the dataset as follows: $\mathbf{Q} \propto \mathbf{X}^T \mathbf{X} = \mathbf{W} \mathbf{\Lambda} \mathbf{W}^T$.
The empirical covariance matrix between the principal components becomes ${\displaystyle \mathbf {W} ^{T}\mathbf {Q} \mathbf {W} \propto \mathbf {W} ^{T}\mathbf {W} \,\mathbf {\Lambda } \,\mathbf {W} ^{T}\mathbf {W} =\mathbf {\Lambda } }$.
#### Singular Value Decomposition for PCA analysis
Finally, the principal components transformation can also be associated with another matrix factorization, the singular value decomposition (SVD) of X, ${\displaystyle \mathbf {X} =\mathbf {U} \mathbf {\Sigma } \mathbf {W} ^{T}}$, where more precisely:
- Σ is an n-by-p rectangular diagonal matrix of positive numbers $σ_{(k)}$, called the singular values of X;
- instead U is an n-by-n matrix, the columns of which are orthogonal unit vectors of length n called the left singular vectors of X;
- Then, W is a p-by-p whose columns are orthogonal unit vectors of length p and called the right singular vectors of X.
factorizingn the matrix ${X^{T}X}$, it can be written as:
${\begin{aligned}\mathbf {X} ^{T}\mathbf {X} &=\mathbf {W} \mathbf {\Sigma } ^{T}\mathbf {U} ^{T}\mathbf {U} \mathbf {\Sigma } \mathbf {W} ^{T}\\&=\mathbf {W} \mathbf {\Sigma } ^{T}\mathbf {\Sigma } \mathbf {W} ^{T}\\&=\mathbf {W} \mathbf {\hat {\Sigma }} ^{2}\mathbf {W} ^{T}\end{aligned}}$
Where we recall that ${\displaystyle \mathbf {\hat {\Sigma }} }$ is the square diagonal matrix with the singular values of X and the excess zeros chopped off that satisfies ${\displaystyle \mathbf {{\hat {\Sigma }}^{2}} =\mathbf {\Sigma } ^{T}\mathbf {\Sigma } } {\displaystyle \mathbf {{\hat {\Sigma }}^{2}} =\mathbf {\Sigma } ^{T}\mathbf {\Sigma } }$. Comparison with the eigenvector factorization of $X^{T}X$ establishes that the right singular vectors W of X are equivalent to the eigenvectors of $X^{T}X$ , while the singular values $σ_{(k)}$ of X are equal to the square-root of the eigenvalues $λ_{(k)}$ of $X^{T}X$ .
At this point we understand that using the singular value decomposition the score matrix T can be written as:
$\begin{align} \mathbf{T} & = \mathbf{X} \mathbf{W} \\ & = \mathbf{U}\mathbf{\Sigma}\mathbf{W}^T \mathbf{W} \\ & = \mathbf{U}\mathbf{\Sigma} \end{align}$
so each column of T is given by one of the left singular vectors of X multiplied by the corresponding singular value. This form is also the polar decomposition of T.
Efficient algorithms exist to calculate the SVD, as in scikit-learn package, of X without having to form the matrix $X^{T}X$, so computing the SVD is now the standard way to calculate a principal components analysis from a data matrix
```
n_components = rescaledX.shape[1]
pca = PCA(n_components=n_components)
# pca = PCA(n_components=2)
# X_pca = pca.fit_transform(X)
pca = pca.fit(rescaledX)
X_pca = pca.transform(rescaledX)
print(f"Cumulative varation explained(percentage) up to given number of pcs:")
tmp_data = []
principal_components = [pc for pc in '2,5,6,7,8,9,10'.split(',')]
for _, pc in enumerate(principal_components):
n_components = int(pc)
cum_var_exp_up_to_n_pcs = np.cumsum(pca.explained_variance_ratio_)[n_components-1]
# print(f"Cumulative varation explained up to {n_components} pcs = {cum_var_exp_up_to_n_pcs}")
# print(f"# pcs {n_components}: {cum_var_exp_up_to_n_pcs*100:.2f}%")
tmp_data.append([n_components, cum_var_exp_up_to_n_pcs * 100])
tmp_df = pd.DataFrame(data=tmp_data, columns=['# PCS', 'Cumulative Varation Explained (percentage)'])
tmp_df.head(len(tmp_data))
n_components = rescaledX.shape[1]
pca = PCA(n_components=n_components)
# pca = PCA(n_components=2)
#X_pca = pca.fit_transform(X)
pca = pca.fit(rescaledX)
X_pca = pca.transform(rescaledX)
fig = show_cum_variance_vs_components(pca, n_components)
# py.sign_in('franec94', 'QbLNKpC0EZB0kol0aL2Z')
# py.iplot(fig, filename='selecting-principal-components {}'.format(scaler_method))
```
#### Major Pros & Cons of PCA
## Learning Models <a class="anchor" id="learning-models"></a>
```
# Parameters to be tested for Cross-Validation Approach
estimators_list = [GaussianNB(), LogisticRegression(), KNeighborsClassifier(), SVC(), DecisionTreeClassifier(), RandomForestClassifier()]
estimators_names = ['GaussianNB', 'LogisticRegression', 'KNeighborsClassifier', 'SVC', 'DecisionTreeClassifier', 'RandomForestClassifier']
plots_names = list(map(lambda xi: f"{xi}_learning_curve.png", estimators_names))
pca_kernels_list = ['linear', 'poly', 'rbf', 'cosine',]
cv_list = [10, 9, 8, 7, 6, 5, 4, 3, 2]
parameters_sgd_classifier = {
'clf__loss': ('hinge', 'log', 'modified_huber', 'squared_hinge', 'perceptron'),
'clf__penalty': ('l2', 'l1', 'elasticnet'),
'clf__alpha': (1e-1, 1e-2, 1e-3, 1e-4),
'clf__max_iter': (50, 100, 150, 200, 500, 1000, 1500, 2000, 2500),
'clf__learning_rate': ('optimal',),
'clf__tol': (None, 1e-2, 1e-4, 1e-5, 1e-6)
}
kernel_type = 'svm-rbf-kernel'
parameters_svm = {
'clf__gamma': (0.003, 0.03, 0.05, 0.5, 0.7, 1.0, 1.5),
'clf__max_iter':(1e+2, 1e+3, 2 * 1e+3, 5 * 1e+3, 1e+4, 1.5 * 1e+3),
'clf__C': (1e-4, 1e-3, 1e-2, 0.1, 1.0, 10, 1e+2, 1e+3),
}
parmas_decision_tree = {
'clf__splitter': ('random', 'best'),
'clf__criterion':('gini', 'entropy'),
'clf__max_features': (None, 'auto', 'sqrt', 'log2')
}
parmas_random_forest = {
'clf__n_estimators': (3, 5, 7, 10, 30, 50, 70, 100, 150, 200),
'clf__criterion':('gini', 'entropy'),
'clf__bootstrap': (True, False)
}
model = PCA(n_components=2)
model.fit(X)
X_2D = model.transform(X)
df = pd.DataFrame()
df['PCA1'] = X_2D[:, 0]
df['PCA2'] = X_2D[:, 1]
df[target_col] = dataset[target_col].values
sns.lmplot("PCA1", "PCA2", hue=target_col, data=df, fit_reg=False)
# show_pca_1_vs_pca_2_pcaKernel(X, pca_kernels_list, target_col, dataset)
# show_scatter_plots_pcaKernel(X, pca_kernels_list, target_col, dataset, n_components=12)
```
## PCA = 2
```
plot_dest = os.path.join("figures", "n_comp_2_analysis")
N_CV, N_KERNEL = 9, 4
assert len(cv_list) >= N_CV, f"Error: N_CV={N_CV} > len(cv_list)={len(cv_list)}"
assert len(pca_kernels_list) >= N_KERNEL, f"Error: N_KERNEL={N_KERNEL} > len(pca_kernels_list)={len(pca_kernels_list)}"
X = rescaledX
n = len(estimators_list) # len(estimators_list)
dfs_list, df_strfd = fit_all_by_n_components(
estimators_list=estimators_list[:n], \
estimators_names=estimators_names[:n], \
X=X, \
y=y, \
n_components=2, \
show_plots=False, \
cv_list=cv_list[:N_CV], \
# pca_kernels_list=['linear'],
pca_kernels_list=pca_kernels_list[:N_KERNEL],
verbose=0 # 0=silent, 1=show informations
)
df_strfd.head(df_strfd.shape[0])
# GaussianNB
# -----------------------------------
dfs_list[0].head(dfs_list[0].shape[0])
pos = 0
plot_name = plots_names[pos]
show_learning_curve(dfs_list[pos], n=len(cv_list[:N_CV]), plot_dest=plot_dest, grid_size=[2, 2], plot_name=plot_name)
# LogisticRegression
# -----------------------------------
dfs_list[1].head(dfs_list[0].shape[0])
pos = pos + 1
plot_name = plots_names[pos]
show_learning_curve(dfs_list[pos], n=len(cv_list[:N_CV]), plot_dest=plot_dest, grid_size=[2, 2], plot_name=plot_name)
# SVC
# -----------------------------------
dfs_list[2].head(dfs_list[0].shape[0])
pos = pos + 1
plot_name = plots_names[pos]
show_learning_curve(dfs_list[pos], n=len(cv_list[:N_CV]), plot_dest=plot_dest, grid_size=[2, 2], plot_name=plot_name)
# DecisionTreeClassifier
# -----------------------------------
dfs_list[3].head(dfs_list[0].shape[0])
pos = pos + 1
plot_name = plots_names[pos]
show_learning_curve(dfs_list[pos], n=len(cv_list[:N_CV]), plot_dest=plot_dest, grid_size=[2, 2], plot_name=plot_name)
# RandomForestClassifier
# -----------------------------------
dfs_list[4].head(dfs_list[0].shape[0])
pos = pos + 1
plot_name = plots_names[pos]
show_learning_curve(dfs_list[pos], n=len(cv_list[:N_CV]), plot_dest=plot_dest, grid_size=[2, 2], plot_name=plot_name)
```
## PCA = 9
```
plot_dest = os.path.join("figures", "n_comp_9_analysis")
n = len(estimators_list) # len(estimators_list)
pos = 0
dfs_list, df_strfd = fit_all_by_n_components(
estimators_list=estimators_list[:n], \
estimators_names=estimators_names[:n], \
X=X, \
y=y, \
n_components=9, \
show_plots=False, \
cv_list=cv_list[:N_CV], \
# pca_kernels_list=['linear'],
pca_kernels_list=pca_kernels_list[:N_KERNEL],
verbose=0 # 0=silent, 1=show informations
)
df_strfd.head(df_strfd.shape[0])
# GaussianNB
# -----------------------------------
dfs_list[0].head(dfs_list[0].shape[0])
pos = pos + 1
plot_name = plots_names[pos]
show_learning_curve(dfs_list[pos], n=len(cv_list[:N_CV]), plot_dest=plot_dest, grid_size=[2, 2], plot_name=plot_name)
# LogisticRegression
# -----------------------------------
dfs_list[1].head(dfs_list[0].shape[0])
ppos = pos + 1
plot_name = plots_names[pos]
show_learning_curve(dfs_list[pos], n=len(cv_list[:N_CV]), plot_dest=plot_dest, grid_size=[2, 2], plot_name=plot_name)
# SVC
# -----------------------------------
dfs_list[2].head(dfs_list[0].shape[0])
pos = pos + 1
plot_name = plots_names[pos]
show_learning_curve(dfs_list[pos], n=len(cv_list[:N_CV]), plot_dest=plot_dest, grid_size=[2, 2], plot_name=plot_name)
# DecisionTreeClassifier
# -----------------------------------
dfs_list[3].head(dfs_list[0].shape[0])
pos = pos + 1
plot_name = plots_names[pos]
show_learning_curve(dfs_list[pos], n=len(cv_list[:N_CV]), plot_dest=plot_dest, grid_size=[2, 2], plot_name=plot_name)
# RandomForestClassifier
# -----------------------------------
dfs_list[4].head(dfs_list[0].shape[0])
pos = pos + 1
plot_name = plots_names[pos]
show_learning_curve(dfs_list[pos], n=len(cv_list[:N_CV]), plot_dest=plot_dest, grid_size=[2, 2], plot_name=plot_name)
```
## PCA = 12
```
plot_dest = os.path.join("figures", "n_comp_12_analysis")
n = len(estimators_list) # len(estimators_list)
pos = 0
dfs_list, df_strfd = fit_all_by_n_components(
estimators_list=estimators_list[:n], \
estimators_names=estimators_names[:n], \
X=X, \
y=y, \
n_components=12, \
show_plots=False, \
cv_list=cv_list[:N_CV], \
# pca_kernels_list=['linear'],
pca_kernels_list=pca_kernels_list[:N_KERNEL],
verbose=0 # 0=silent, 1=show informations
)
df_strfd.head(df_strfd.shape[0])
# GaussianNB
# -----------------------------------
dfs_list[0].head(dfs_list[0].shape[0])
pos = pos + 1
plot_name = plots_names[pos]
show_learning_curve(dfs_list[pos], n=len(cv_list[:N_CV]), plot_dest=plot_dest, grid_size=[2, 2], plot_name=plot_name)
# LogisticRegression
# -----------------------------------
dfs_list[1].head(dfs_list[0].shape[0])
pos = pos + 1
plot_name = plots_names[pos]
show_learning_curve(dfs_list[pos], n=len(cv_list[:N_CV]), plot_dest=plot_dest, grid_size=[2, 2], plot_name=plot_name)
# SVC
# -----------------------------------
dfs_list[2].head(dfs_list[0].shape[0])
pos = pos + 1
plot_name = plots_names[pos]
show_learning_curve(dfs_list[pos], n=len(cv_list[:N_CV]), plot_dest=plot_dest, grid_size=[2, 2], plot_name=plot_name)
# DecisionTreeClassifier
# -----------------------------------
dfs_list[3].head(dfs_list[0].shape[0])
pos = pos + 1
plot_name = plots_names[pos]
show_learning_curve(dfs_list[pos], n=len(cv_list[:N_CV]), plot_dest=plot_dest, grid_size=[2, 2], plot_name=plot_name)
# RandomForestClassifier
# -----------------------------------
dfs_list[4].head(dfs_list[0].shape[0])
pos = pos + 1
plot_name = plots_names[pos]
show_learning_curve(dfs_list[pos], n=len(cv_list[:N_CV]), plot_dest=plot_dest, grid_size=[2, 2], plot_name=plot_name)
from sklearn.metrics import f1_score
y_true = [0, 1, 2, 0, 1, 2]
y_pred = [0, 2, 1, 0, 0, 1]
f1_score(y_true, y_pred, average='macro')
```
### Naive Bayes Classification
Naive Bayes models are a group of extremely fast and simple classification algorithms that are often suitable for very high-dimensional datasets. Because they are so fast and have so few tunable parameters, they end up being very useful as a quick-and-dirty baseline for a classification problem. Here I will provide an intuitive and brief explanation of how naive Bayes classifiers work, followed by its exploitation onto my datasets.
I start saying that Naive Bayes classifiers are built on Bayesian classification methods. These rely on Bayes's theorem, which is an equation describing the relationship of conditional probabilities of statistical quantities.
n Bayesian classification, we're interested in finding the probability of a label given some observed features, which we can write as P(L | features). Bayes's theorem tells us how to express this in terms of quantities we can compute more directly:
$P(L|features)=\frac{P(features|L)}{P(L)P(features)}$
If we are trying to decide between two labels, and we call them L1 and L2, then one way to make this decision is to compute the ratio of the posterior probabilities for each label:
$\frac{P(L1 | features)}{P(L2 | features)}=\frac{P(features | L1)P(L1)}{P(features | L2)P(L2)}$
All we need now is some model by which we can compute P(features | $L_{i}$)
for each label. Such a model is called a generative model because it specifies the hypothetical random process that generates the data. Specifying this generative model for each label is the main piece of the training of such a Bayesian classifier. The general version of such a training step is a very difficult task, but we can make it simpler through the use of some simplifying assumptions about the form of this model.
This is where the "naive" in "naive Bayes" comes in: if we make very naive assumptions about the generative model for each label, we can find a rough approximation of the generative model for each class, and then proceed with the Bayesian classification. Different types of naive Bayes classifiers rest on different naive assumptions about the data, and we will examine a few of these in the following sections.
#### Gaussian Naive Bayes
Perhaps the easiest naive Bayes classifier to understand is Gaussian naive Bayes. In this classifier, the assumption is that data from each label is drawn from a simple Gaussian distribution. In fact, one extremely fast way to create a simple model is to assume that the data is described by a Gaussian distribution with no covariance between dimensions. This model can be fit by simply finding the mean and standard deviation of the points within each label, which is all you need to define such a distribution.
$P(x_i \mid y) = \frac{1}{\sqrt{2\pi\sigma^2_y}} \exp\left(-\frac{(x_i - \mu_y)^2}{2\sigma^2_y}\right)$
The parameters $\sigma_{y}$ and $\mu_{y}$ are estimated usually using maximum likelihood.
#### When to Use Naive Bayes
Because naive Bayesian classifiers make such stringent assumptions about data, they will generally not perform as well as a more complicated model. That said, they have several advantages:
- They are extremely fast for both training and prediction
- They provide straightforward probabilistic prediction
- They are often very easily interpretable
- They have very few (if any) tunable parameters
These advantages mean a naive Bayesian classifier is often a good choice as an initial baseline classification. If it performs suitably, then congratulations: you have a very fast, very interpretable classifier for your problem. If it does not perform well, then you can begin exploring more sophisticated models, with some baseline knowledge of how well they should perform.
Naive Bayes classifiers tend to perform especially well in one of the following situations:
- When the naive assumptions actually match the data (very rare in practice)
- For very well-separated categories, when model complexity is less important
- For very high-dimensional data, when model complexity is less important
The last two points seem distinct, but they actually are related: as the dimension of a dataset grows, it is much less likely for any two points to be found close together (after all, they must be close in every single dimension to be close overall). This means that clusters in high dimensions tend to be more separated, on average, than clusters in low dimensions, assuming the new dimensions actually add information. For this reason, simplistic classifiers like naive Bayes tend to work as well or better than more complicated classifiers as the dimensionality grows: once you have enough data, even a simple model can be very powerful.
### Support Vector Machines Classifier
<img src="images/SVM_margin.png" alt="SVM Margin " style="width: 200px;"/>
Here, in this section I'm going to exploit a machine learning techinique known as Support Vectors Machines in order to detect and so select the best model I can produce throughout the usage of data points contained within the dataset at hand. So let discuss a bit those kind of classifiers.
In machine learning, **support-vector machines**, shortly SVMs, are *supervised learning models* with associated learning algorithms that analyze data used for classification and regression analysis. Given a set of training examples, each marked as belonging to one or the other of two categories, an SVM training algorithm builds a model that assigns new examples to one category or the other, making it a *non-probabilistic binary linear classifier*. An SVM model is a representation of the examples as points in space, mapped so that the examples of the separate categories are divided by a clear gap that is as wide as possible. New examples are then mapped into that same space and predicted to belong to a category based on the side of the gap on which they fall.
More formally, a support-vector machine constructs a hyperplane or set of hyperplanes in a high-dimensional space, which can be used for classification, regression. Intuitively, a good separation is achieved by the hyperplane that has the largest distance to the nearest training-data point of any class, so-called *functional margin*, since in general the larger the margin, the lower the *generalization error* of the classifier.
#### Mathematical formulation of SVMs
Here, I'm going to describe the main mathematical properties and characteristics used to derive from a math point of view the algorithm derived and proven by researches when they have studied SVMs classifiers.
I start saying and recalling that A support vector machine constructs a hyper-plane or set of hyper-planes in a high or infinite dimensional space, which can be used for classification, regression or other tasks. Intuitively, a good separation is achieved by the hyper-plane that has the largest distance to the nearest training data points of any class so-called functional margin, since in general the larger the margin the lower the generalization error of the classifier.
When demonstrating SVMs classifier algorithm I suppose that We are given a training dataset of *n*n points of the form:
\begin{align}
(\vec{x_1} y_1),..,(\vec{x_n},y_n)
\end{align}
where the $y_{1}$ are either 1 or −1, each indicating the class to which the point $\vec{x}_{i}$ belongs. Each $\vec{x}_{i}$is a *p-dimensional real vector*. We want to find the "maximum-margin hyperplane" that divides the group of points $\vec{x}_{i}$ for which $y_{1}$ = 1from the group of points for which $y_{1}$ = − 1, which is defined so that the distance between the hyperplane and the nearest point $\vec{x}_{i}$ from either group is maximized.
Any hyperplane can be written as the set of points $\vec{x}_{i}$ satisfying : $\vec{w}_{i}\cdot{\vec{x}_{i}} - b = 0$; where $\vec{w}_{i}$ is the, even if not necessarily, normal vector to the hyperplane. The parameter $\tfrac {b}{\|\vec{w}\|}$ determines the offset of the hyperplane from the origin along the normal vector $\vec{x}_{i}$.
Arrived so far, I have to distiguish between two distinct cases which both depende on the nature of data points that generally made up a given dataset. Those two different cases are called *Hard-Margin* and *Soft Margin* and, respectively.
The first case, so the ***Hard-Margin*** case, happens just for really optimistics datasets. In fact it is the case when the training data is linearly separable, hence, we can select two parallel hyperplanes that separate the two classes of data, so that the distance between them is as large as possible. The region bounded by these two hyperplanes is called the "margin", and the maximum-margin hyperplane is the hyperplane that lies halfway between them. With a normalized or standardized dataset, these hyperplanes can be described by the equations:
- $\vec{w}_{i}\cdot{\vec{x}_{i}} - b = 1$, that is anything on or above this boundary is of one class, with label 1;
- and, $\vec{w}_{i}\cdot{\vec{x}_{i}} - b = -1$, that is anything on or above this boundary is of one class, with label -1.
We can notice also that the distance between these two hyperplanes is ${\displaystyle {\tfrac {2}{\|{\vec {w}}\|}}}$ so to maximize the distance between the planes we want to minimize ‖ w → ‖ {\displaystyle \|{\vec {w}}\|} \|{\vec {w}}\|. The distance is computed using the distance from a point to a plane equation. We also have to prevent data points from falling into the margin, we add the following constraint: for each *i*:
- either, ${\displaystyle {\vec {w}}\cdot {\vec {x}}_{i}-b\geq 1}$, ${\displaystyle y_{i}=1}$;
- or, ${\displaystyle {\vec {w}}\cdot {\vec {x}}_{i}-b\leq -1}$, if ${\displaystyle y_{i}=-1}$.
These constraints state that each data point must lie on the correct side of the margin.
Finally, we collect all the previous observations and define the following optimization problem:
- from $y_{i}(\vec{w}_{i}\cdot{\vec{x}_{i}} - b) \geq 1$, for all $1 \leq i \leq n$;
- to minimize ${\displaystyle y_{i}({\vec {w}}\cdot {\vec {x}}_{i}-b)\geq 1}$ ${\displaystyle i=1,\ldots ,n}$.
The classifier we obtain is made from ${\vec {w}}$ and ${\displaystyle b}$ that solve this problem, and he max-margin hyperplane is completely determined by those ${\vec {x}}_{i}$ that lie nearest to it. These $\vec{x}_{i}$ are called *support vectors*.
The other case, so the ***Soft-Margin*** case, convercely happens when the training data is not linearly separable. To deal with such situation, as well as, to extend SVM to cases in which the data are not linearly separable, we introduce the hinge loss function, that is: $max(y_{i}(\vec{w}_{i}\cdot{\vec{x}_{i}} - b))$.
Once we have provided the new loss function we go ahead with the new optimization problem that we aim at minimizing that is:
\begin{align}
{\displaystyle \left[{\frac {1}{n}}\sum _{i=1}^{n}\max \left(0,1-y_{i}({\vec {w}}\cdot {\vec {x}}_{i}-b)\right)\right]+\lambda \lVert {\vec {w}}\rVert ^{2},}
\end{align}
where the parameter \lambda determines the trade-off between increasing the margin size and ensuring that the ${\vec {x}}_{i}$ lie on the correct side of the margin. Thus, for sufficiently small values of\lambda , the second term in the loss function will become negligible, hence, it will behave similar to the hard-margin SVM, if the input data are linearly classifiable, but will still learn if a classification rule is viable or not.
What we notice from last equations written just above is that we deal with a quadratic programming problem, and its solution is provided, detailed below.
We start defining a *Primal Problem* as follow:
- For each $\{1,\,\ldots ,\,n\}$ we introduce a variable ${\displaystyle \zeta _{i}=\max \left(0,1-y_{i}(w\cdot x_{i}-b)\right)}$. Note that ${\displaystyle \zeta _{i}}$ is the smallest nonnegative number satisfying ${\displaystyle y_{i}(w\cdot x_{i}-b)\geq 1-\zeta _{i}}$;
- we can rewrite the optimization problem as follows: ${\displaystyle {\text{minimize }}{\frac {1}{n}}\sum _{i=1}^{n}\zeta _{i}+\lambda \|w\|^{2}}$, ${\displaystyle {\text{subject to }}y_{i}(w\cdot x_{i}-b)\geq 1-\zeta _{i}\,{\text{ and }}\,\zeta _{i}\geq 0,\,{\text{for all }}i.}$
However, by solving for the *Lagrangian dual* of the above problem, one obtains the simplified problem:
\begin{align}
{\displaystyle {\text{maximize}}\,\,f(c_{1}\ldots c_{n})=\sum _{i=1}^{n}c_{i}-{\frac {1}{2}}\sum _{i=1}^{n}\sum _{j=1}^{n}y_{i}c_{i}(x_{i}\cdot x_{j})y_{j}c_{j},} \\
{\displaystyle {\text{subject to }}\sum _{i=1}^{n}c_{i}y_{i}=0,\,{\text{and }}0\leq c_{i}\leq {\frac {1}{2n\lambda }}\;{\text{for all }}i.}
\end{align}
- moreover, the variables $c_i$ are defined as ${\displaystyle {\vec {w}}=\sum _{i=1}^{n}c_{i}y_{i}{\vec {x}}_{i}}$. Where, ${\displaystyle c_{i}=0}$ exactly when ${\displaystyle {\vec {x}}_{i}}$ lies on the correct side of the margin, and ${\displaystyle 0<c_{i}<(2n\lambda )^{-1}}$ when ${\vec {x}}_{i}$ lies on the margin's boundary. It follows that ${\displaystyle {\vec {w}}}$ can be written as a linear combination of the support vectors.
The offset, ${\displaystyle b}$, can be recovered by finding an ${\vec {x}}_{i}$ on the margin's boundary and solving: ${\displaystyle y_{i}({\vec {w}}\cdot {\vec {x}}_{i}-b)=1\iff b={\vec {w}}\cdot {\vec {x}}_{i}-y_{i}.}$
This is called the *dual problem*. Since the dual maximization problem is a quadratic function of the ${\displaystyle c_{i}}$ subject to linear constraints, it is efficiently solvable by quadratic programming algorithms.
Lastly, I will discuss what in the context of SVMs classifier is called as ***Kernel Trick***.
Roughly speaking, we know that a possible way of dealing with datasets that are not linearly separable but that can become linearnly separable within an higher dimensional space, or feature space, we can try to remap the original data points into a higher order feature space by means of some kind of remapping function, hence, solve the SVMs classifier optimization problem to find out a linear classifier in that new larger feature space. Then, we project back to the original feature space the solution we have found, reminding that in the hold feature space the decision boundaries founded will be non-linear, but still allow to classify new examples.
Usually, especially, dealing with large datasets or with datasets with large set of features this approach becomes computationally intensive and and unfeasible if we run out of memory. So, in other words, the procedure is constrained in time and space, and might become time consuming or even unfeasible because of the large amount of memory we have to exploit.
An reasonable alternative is represented by the usage of kernel functions that are function which satisfy ${\displaystyle k({\vec {x}}_{i},{\vec {x}}_{j})=\varphi ({\vec {x}}_{i})\cdot \varphi ({\vec {x}}_{j})}$, where we recall that classification vector ${\vec {w}}$ in the transformed space satisfies ${\displaystyle {\vec {w}}=\sum _{i=1}^{n}c_{i}y_{i}\varphi ({\vec {x}}_{i}),}$
where, the ${\displaystyle c_{i}}$ are obtained by solving the optimization problem:
${\displaystyle {\begin{aligned}{\text{maximize}}\,\,f(c_{1}\ldots c_{n})&=\sum _{i=1}^{n}c_{i}-{\frac {1}{2}}\sum _{i=1}^{n}\sum _{j=1}^{n}y_{i}c_{i}(\varphi ({\vec {x}}_{i})\cdot \varphi ({\vec {x}}_{j}))y_{j}c_{j}\\&=\sum _{i=1}^{n}c_{i}-{\frac {1}{2}}\sum _{i=1}^{n}\sum _{j=1}^{n}y_{i}c_{i}k({\vec {x}}_{i},{\vec {x}}_{j})y_{j}c_{j}\\\end{aligned}}}$
${\displaystyle {\text{subject to }}\sum _{i=1}^{n}c_{i}y_{i}=0,\,{\text{and }}0\leq c_{i}\leq {\frac {1}{2n\lambda }}\;{\text{for all }}i.}$
The coefficients ${\displaystyle c_{i}}$ can be solved for using quadratic programming, and we can find some index ${\displaystyle i}$ such that ${\displaystyle 0<c_{i}<(2n\lambda )^{-1}}$, so that ${\displaystyle \varphi ({\vec {x}}_{i})}$ lies on the boundary of the margin in the transformed space, and then solve, by substituting doto product between remapped data points with kernel function applied upon the same arguments:
${\displaystyle {\begin{aligned}b={\vec {w}}\cdot \varphi ({\vec {x}}_{i})-y_{i}&=\left[\sum _{j=1}^{n}c_{j}y_{j}\varphi ({\vec {x}}_{j})\cdot \varphi ({\vec {x}}_{i})\right]-y_{i}\\&=\left[\sum _{j=1}^{n}c_{j}y_{j}k({\vec {x}}_{j},{\vec {x}}_{i})\right]-y_{i}.\end{aligned}}}$
Finally, ${\displaystyle {\vec {z}}\mapsto \operatorname {sgn}({\vec {w}}\cdot \varphi ({\vec {z}})-b)=\operatorname {sgn} \left(\left[\sum _{i=1}^{n}c_{i}y_{i}k({\vec {x}}_{i},{\vec {z}})\right]-b\right).}$
What follows is a briefly list of the most commonly used kernel functions. They should be fine tuned, by means of a either grid search or random search approaches, identifying the best set of values to replace whitin the picked kernel function, where the choice depend on the dataset at hand:
- Polynomial (homogeneous): ${\displaystyle k({\vec {x_{i}}},{\vec {x_{j}}})=({\vec {x_{i}}}\cdot {\vec {x_{j}}})^{d}}$.
- Polynomial (inhomogeneous): ${\displaystyle k({\vec {x_{i}}},{\vec {x_{j}}})=({\vec {x_{i}}}\cdot {\vec {x_{j}}}+1)^{d}}$.
- Gaussian radial basis function: ${\displaystyle \gamma =1/(2\sigma ^{2})} {\displaystyle \gamma =1/(2\sigma ^{2})}$.
- Hyperbolic tangent: ${\displaystyle k({\vec {x_{i}}},{\vec {x_{j}}})=\tanh(\kappa {\vec {x_{i}}}\cdot {\vec {x_{j}}}+c)}$ for some (not every) ${\displaystyle \kappa >0}$ and ${\displaystyle c<0}$.
What follows is the application or use of SVMs classifier for learning a model that best fit the training data in order to be able to classify new instance in a reliable way, selecting the most promising model trained.
#### Advantages and Backwards of SVMs
Finally, I conclude this section providing a description of major advantages and backwards of such a machine learning technique, that have been noticed by researches who studied SVMs properties. The advantages of support vector machines are:
- Effective in high dimensional spaces.
- Still effective in cases where number of dimensions is greater than the number of samples.
- Uses a subset of training points in the decision function (called support vectors), so it is also memory efficient.
- Versatile: different Kernel functions can be specified for the decision function. Common kernels are provided, but it is also possible to specify custom kernels.
On the other and, the disadvantages of support vector machines include:
- If the number of features is much greater than the number of samples, avoid over-fitting in choosing Kernel functions and regularization term is crucial.
- SVMs do not directly provide probability estimates, these are calculated using an expensive five-fold cross-validation (see Scores and probabilities, below).
### Decision Tree Models
Decision Trees, for short DTs, are a *non-parametric supervised learning method* used for classification and regression. The goal is to create a model that predicts the value of a target variable by learning simple decision rules inferred from the data features.
Their mathematical formulation is generally provided as follows: Given training vectors $x_{i} \in R^{n}$, $i=1,…, l$ and a label vector $y \in R^{l}$, a decision tree recursively partitions the space such that the samples with the same labels are grouped together.
Let the data at node $m$ be represented by $Q$. For each candidate split $\theta = (j, t_{m})$
consisting of a feature $j$ and threshold $t_{m}$, partition the data into $Q_{left}(\theta)$ and $Q_{left}(\theta)$ subsets as:
\begin{align}\begin{aligned}Q_{left}(\theta) = {(x, y) | x_j <= t_m}\\Q_{right}(\theta) = Q \setminus Q_{left}(\theta)\end{aligned}\end{align}
The impurity at $m$ is computed using an impurity function $H()$, the choice of which depends on the task being solved (classification or regression) like:
\begin{align}
G(Q, \theta) = \frac{n_{left}}{N_m} H(Q_{left}(\theta)) + \frac{n_{right}}{N_m} H(Q_{right}(\theta))
\end{align}
Select the parameters that minimises the impurity: $\theta^* = \operatorname{argmin}_\theta G(Q, \theta)$.
Recurse for subsets $Q_{left}(\theta^*)$ and $Q_{right}(\theta^*)$ until the maximum allowable depth is reached,
$N_m < \min_{samples}$ or N_m = 1.
Speaking about *Classification Criteria* referred to the procedure used for learining or fit to the data a decision tree we can state what follows: If a target is a classification outcome taking on values $0,1,…,K-1$, for node $m$, representing a region $R_{m}$ with $N_{m}$ observations, let $p_{mk} = 1/ N_m \sum_{x_i \in R_m} I(y_i = k)$ be the proportion of class $k$ observations in node $m$.
So, Common measures of impurity are:
- Gini, specified as $H(X_m) = \sum_k p_{mk} (1 - p_{mk})$
- Entropy, definead as $(X_m) = - \sum_k p_{mk} \log(p_{mk})$
where, we recall that $X_{m}$ is the training data in node $m$.
#### Decision Tree's Advantages & Bacwards
Some advantages of decision trees are:
- Simple to understand and to interpret. Trees can be visualised.
- Requires little data preparation. Other techniques often require data normalisation, dummy variables need to be created and blank values to be removed. Note however that this module does not support missing values.
- The cost of using the tree (i.e., predicting data) is logarithmic in the number of data points used to train the tree.
- Able to handle both numerical and categorical data. Other techniques are usually specialised in analysing datasets that have only one type of variable. See algorithms for more information.
- Able to handle multi-output problems.
- Uses a white box model. If a given situation is observable in a model, the explanation for the condition is easily explained by boolean logic. By contrast, in a black box model (e.g., in an artificial neural network), results may be more difficult to interpret.
- Possible to validate a model using statistical tests. That makes it possible to account for the reliability of the model.
- Performs well even if its assumptions are somewhat violated by the true model from which the data were generated.
The disadvantages of decision trees include:
- Decision-tree learners can create over-complex trees that do not generalise the data well. This is called overfitting. Mechanisms such as pruning (not currently supported), setting the minimum number of samples required at a leaf node or setting the maximum depth of the tree are necessary to avoid this problem.
- Decision trees can be unstable because small variations in the data might result in a completely different tree being generated. This problem is mitigated by using decision trees within an ensemble.
- The problem of learning an optimal decision tree is known to be NP-complete under several aspects of optimality and even for simple concepts. Consequently, practical decision-tree learning algorithms are based on heuristic algorithms such as the greedy algorithm where locally optimal decisions are made at each node. Such algorithms cannot guarantee to return the globally optimal decision tree. This can be mitigated by training multiple trees in an ensemble learner, where the features and samples are randomly sampled with replacement.
- There are concepts that are hard to learn because decision trees do not express them easily, such as XOR, parity or multiplexer problems.
- Decision tree learners create biased trees if some classes dominate. It is therefore recommended to balance the dataset prior to fitting with the decision tree.
### Ensemble methods
The goal of ensemble methods is to combine the predictions of several base estimators built with a given learning algorithm in order to improve generalizability / robustness over a single estimator.
Two families of ensemble methods are usually distinguished:
- In averaging methods, the driving principle is to build several estimators independently and then to average their predictions. On average, the combined estimator is usually better than any of the single base estimator because its variance is reduced. So, some examples are: Bagging methods, Forests of randomized trees, but still exist more classifiers;
- Instead, in boosting methods, base estimators are built sequentially and one tries to reduce the bias of the combined estimator. The motivation is to combine several weak models to produce a powerful ensemble. Hence, some examples are: AdaBoost, Gradient Tree Boosting,but still exist more options.
#### Random Forests
The **sklearn.ensemble module** includes two averaging algorithms based on randomized decision trees: the RandomForest algorithm and the Extra-Trees method. Both algorithms are perturb-and-combine techniques, specifically designed for trees. This means a diverse set of classifiers is created by introducing randomness in the classifier construction. The prediction of the ensemble is given as the averaged prediction of the individual classifiers.
In random forests (see RandomForestClassifier and RandomForestRegressor classes), each tree in the ensemble is built from a sample drawn with replacement (i.e., a bootstrap sample) from the training set.
The main parameters to adjust when using these methods is *number of estimators* and *maxima features*. The former is the number of trees in the forest. The larger the better, but also the longer it will take to compute. In addition, note that results will stop getting significantly better beyond a critical number of trees. The latter is the size of the random subsets of features to consider when splitting a node. The lower the greater the reduction of variance, but also the greater the increase in bias.
Empirical good default values are maxima features equals to null, that means always considering all features instead of a random subset, for regression problems, and maxima features equals to "sqrt", using a random subset of size sqrt(number of features)) for classification tasks, where number of features is the number of features in the data. The best parameter values should always be cross-validated.
We note that the size of the model with the default parameters is $O( M * N * log (N) )$, where $M$ is the number of trees and $N$ is the number of samples.
### Improvements and Conclusions <a class="anchor" id="Improvements-and-conclusions"></a>
### References <a class="anchor" id="references"></a>
- Data Domain Information part:
- (Deck) https://en.wikipedia.org/wiki/Deck_(bridge)
- (Cantilever bridge) https://en.wikipedia.org/wiki/Cantilever_bridge
- (Arch bridge) https://en.wikipedia.org/wiki/Deck_(bridge)
- Machine Learning part:
- (Theory Book) https://jakevdp.github.io/PythonDataScienceHandbook/
- (Decsion Trees) https://scikit-learn.org/stable/modules/tree.html#tree
- (SVM) https://scikit-learn.org/stable/modules/svm.html
- (PCA) https://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html
- Chart part:
- (Seaborn Charts) https://acadgild.com/blog/data-visualization-using-matplotlib-and-seaborn
- Markdown Math part:
- https://share.cocalc.com/share/b4a30ed038ee41d868dad094193ac462ccd228e2/Homework%20/HW%201.2%20-%20Markdown%20and%20LaTeX%20Cheatsheet.ipynb?viewer=share
- https://jupyter-notebook.readthedocs.io/en/stable/examples/Notebook/Typesetting%20Equations.html
| github_jupyter |
# Setup
First, let's import a few common modules, ensure MatplotLib plots figures inline and prepare a function to save the figures. We also check that Python 3.5 or later is installed (although Python 2.x may work, it is deprecated so we strongly recommend you use Python 3 instead), as well as Scikit-Learn ≥0.20.
```
# Python ≥3.5 is required
import sys
assert sys.version_info >= (3, 5)
# Scikit-Learn ≥0.20 is required
import sklearn
assert sklearn.__version__ >= "0.20"
# Common imports
import numpy as np
import os
# to make this notebook's output stable across runs
np.random.seed(42)
# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)
N_JOBS= 3
# Where to save the figures
PROJECT_ROOT_DIR = "."
CHAPTER_ID = "svm"
IMAGES_PATH = os.path.join(PROJECT_ROOT_DIR, "images", CHAPTER_ID)
os.makedirs(IMAGES_PATH, exist_ok=True)
def save_fig(fig_id, tight_layout=True, fig_extension="png", resolution=300):
path = os.path.join(IMAGES_PATH, fig_id + "." + fig_extension)
print("Saving figure", fig_id)
if tight_layout:
plt.tight_layout()
plt.savefig(path, format=fig_extension, dpi=resolution)
```
# Linear SVM Classification
The next few code cells generate the first figures in chapter 5. The first actual code sample comes after.
**Code to generate Figure 5–1. Large margin classification**
```
from sklearn.svm import SVC
from sklearn import datasets
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)] # petal length, petal width
y = iris["target"]
setosa_or_versicolor = (y == 0) | (y == 1)
X = X[setosa_or_versicolor]
y = y[setosa_or_versicolor]
# SVM Classifier model
svm_clf = SVC(kernel="linear", C=float("inf"))
svm_clf.fit(X, y)
# Bad models
x0 = np.linspace(0, 5.5, 200)
pred_1 = 5*x0 - 20
pred_2 = x0 - 1.8
pred_3 = 0.1 * x0 + 0.5
def plot_svc_decision_boundary(svm_clf, xmin, xmax):
w = svm_clf.coef_[0]
b = svm_clf.intercept_[0]
# At the decision boundary, w0*x0 + w1*x1 + b = 0
# => x1 = -w0/w1 * x0 - b/w1
x0 = np.linspace(xmin, xmax, 200)
decision_boundary = -w[0]/w[1] * x0 - b/w[1]
margin = 1/w[1]
gutter_up = decision_boundary + margin
gutter_down = decision_boundary - margin
svs = svm_clf.support_vectors_
plt.scatter(svs[:, 0], svs[:, 1], s=180, facecolors='#FFAAAA')
plt.plot(x0, decision_boundary, "k-", linewidth=2)
plt.plot(x0, gutter_up, "k--", linewidth=2)
plt.plot(x0, gutter_down, "k--", linewidth=2)
fig, axes = plt.subplots(ncols=2, figsize=(10,2.7), sharey=True)
plt.sca(axes[0])
plt.plot(x0, pred_1, "g--", linewidth=2)
plt.plot(x0, pred_2, "m-", linewidth=2)
plt.plot(x0, pred_3, "r-", linewidth=2)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", label="Iris versicolor")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", label="Iris setosa")
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="upper left", fontsize=14)
plt.axis([0, 5.5, 0, 2])
plt.sca(axes[1])
plot_svc_decision_boundary(svm_clf, 0, 5.5)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo")
plt.xlabel("Petal length", fontsize=14)
plt.axis([0, 5.5, 0, 2])
save_fig("large_margin_classification_plot")
plt.show()
```
**Code to generate Figure 5–2. Sensitivity to feature scales**
```
Xs = np.array([[1, 50], [5, 20], [3, 80], [5, 60]]).astype(np.float64)
ys = np.array([0, 0, 1, 1])
svm_clf = SVC(kernel="linear", C=100)
svm_clf.fit(Xs, ys)
plt.figure(figsize=(9,2.7))
plt.subplot(121)
plt.plot(Xs[:, 0][ys==1], Xs[:, 1][ys==1], "bo")
plt.plot(Xs[:, 0][ys==0], Xs[:, 1][ys==0], "ms")
plot_svc_decision_boundary(svm_clf, 0, 6)
plt.xlabel("$x_0$", fontsize=20)
plt.ylabel("$x_1$ ", fontsize=20, rotation=0)
plt.title("Unscaled", fontsize=16)
plt.axis([0, 6, 0, 90])
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(Xs)
svm_clf.fit(X_scaled, ys)
plt.subplot(122)
plt.plot(X_scaled[:, 0][ys==1], X_scaled[:, 1][ys==1], "bo")
plt.plot(X_scaled[:, 0][ys==0], X_scaled[:, 1][ys==0], "ms")
plot_svc_decision_boundary(svm_clf, -2, 2)
plt.xlabel("$x'_0$", fontsize=20)
plt.ylabel("$x'_1$ ", fontsize=20, rotation=0)
plt.title("Scaled", fontsize=16)
plt.axis([-2, 2, -2, 2])
save_fig("sensitivity_to_feature_scales_plot")
```
## Soft Margin Classification
**Code to generate Figure 5–3. Hard margin sensitivity to outliers**
```
X_outliers = np.array([[3.4, 1.3], [3.2, 0.8]])
y_outliers = np.array([0, 0])
Xo1 = np.concatenate([X, X_outliers[:1]], axis=0)
yo1 = np.concatenate([y, y_outliers[:1]], axis=0)
Xo2 = np.concatenate([X, X_outliers[1:]], axis=0)
yo2 = np.concatenate([y, y_outliers[1:]], axis=0)
svm_clf2 = SVC(kernel="linear", C=10**9)
svm_clf2.fit(Xo2, yo2)
fig, axes = plt.subplots(ncols=2, figsize=(10,2.7), sharey=True)
plt.sca(axes[0])
plt.plot(Xo1[:, 0][yo1==1], Xo1[:, 1][yo1==1], "bs")
plt.plot(Xo1[:, 0][yo1==0], Xo1[:, 1][yo1==0], "yo")
plt.text(0.3, 1.0, "Impossible!", fontsize=24, color="red")
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.annotate("Outlier",
xy=(X_outliers[0][0], X_outliers[0][1]),
xytext=(2.5, 1.7),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.1),
fontsize=16,
)
plt.axis([0, 5.5, 0, 2])
plt.sca(axes[1])
plt.plot(Xo2[:, 0][yo2==1], Xo2[:, 1][yo2==1], "bs")
plt.plot(Xo2[:, 0][yo2==0], Xo2[:, 1][yo2==0], "yo")
plot_svc_decision_boundary(svm_clf2, 0, 5.5)
plt.xlabel("Petal length", fontsize=14)
plt.annotate("Outlier",
xy=(X_outliers[1][0], X_outliers[1][1]),
xytext=(3.2, 0.08),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.1),
fontsize=16,
)
plt.axis([0, 5.5, 0, 2])
save_fig("sensitivity_to_outliers_plot")
plt.show()
```
**This is the first code example in chapter 5:**
```
import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
iris = datasets.load_iris()
X = iris["data"][:, (2, 3)] # petal length, petal width
y = (iris["target"] == 2).astype(np.float64) # Iris virginica
svm_clf = Pipeline([
("scaler", StandardScaler()),
("linear_svc", LinearSVC(C=1, loss="hinge", random_state=42)),
])
svm_clf.fit(X, y)
svm_clf.predict([[5.5, 1.7]])
```
**Code to generate Figure 5–4. Large margin versus fewer margin violations**
```
scaler = StandardScaler()
svm_clf1 = LinearSVC(C=1, loss="hinge", random_state=42)
svm_clf2 = LinearSVC(C=100, loss="hinge", random_state=42)
scaled_svm_clf1 = Pipeline([
("scaler", scaler),
("linear_svc", svm_clf1),
])
scaled_svm_clf2 = Pipeline([
("scaler", scaler),
("linear_svc", svm_clf2),
])
scaled_svm_clf1.fit(X, y)
scaled_svm_clf2.fit(X, y)
# Convert to unscaled parameters
b1 = svm_clf1.decision_function([-scaler.mean_ / scaler.scale_])
b2 = svm_clf2.decision_function([-scaler.mean_ / scaler.scale_])
w1 = svm_clf1.coef_[0] / scaler.scale_
w2 = svm_clf2.coef_[0] / scaler.scale_
svm_clf1.intercept_ = np.array([b1])
svm_clf2.intercept_ = np.array([b2])
svm_clf1.coef_ = np.array([w1])
svm_clf2.coef_ = np.array([w2])
# Find support vectors (LinearSVC does not do this automatically)
t = y * 2 - 1
support_vectors_idx1 = (t * (X.dot(w1) + b1) < 1).ravel()
support_vectors_idx2 = (t * (X.dot(w2) + b2) < 1).ravel()
svm_clf1.support_vectors_ = X[support_vectors_idx1]
svm_clf2.support_vectors_ = X[support_vectors_idx2]
fig, axes = plt.subplots(ncols=2, figsize=(10,2.7), sharey=True)
plt.sca(axes[0])
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^", label="Iris virginica")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs", label="Iris versicolor")
plot_svc_decision_boundary(svm_clf1, 4, 5.9)
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
plt.legend(loc="upper left", fontsize=14)
plt.title("$C = {}$".format(svm_clf1.C), fontsize=16)
plt.axis([4, 5.9, 0.8, 2.8])
plt.sca(axes[1])
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
plot_svc_decision_boundary(svm_clf2, 4, 5.99)
plt.xlabel("Petal length", fontsize=14)
plt.title("$C = {}$".format(svm_clf2.C), fontsize=16)
plt.axis([4, 5.9, 0.8, 2.8])
save_fig("regularization_plot")
```
# Nonlinear SVM Classification
**Code to generate Figure 5–5. Adding features to make a dataset linearly separable**
```
X1D = np.linspace(-4, 4, 9).reshape(-1, 1)
X2D = np.c_[X1D, X1D**2]
y = np.array([0, 0, 1, 1, 1, 1, 1, 0, 0])
plt.figure(figsize=(10, 3))
plt.subplot(121)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.plot(X1D[:, 0][y==0], np.zeros(4), "bs")
plt.plot(X1D[:, 0][y==1], np.zeros(5), "g^")
plt.gca().get_yaxis().set_ticks([])
plt.xlabel(r"$x_1$", fontsize=20)
plt.axis([-4.5, 4.5, -0.2, 0.2])
plt.subplot(122)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.plot(X2D[:, 0][y==0], X2D[:, 1][y==0], "bs")
plt.plot(X2D[:, 0][y==1], X2D[:, 1][y==1], "g^")
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"$x_2$ ", fontsize=20, rotation=0)
plt.gca().get_yaxis().set_ticks([0, 4, 8, 12, 16])
plt.plot([-4.5, 4.5], [6.5, 6.5], "r--", linewidth=3)
plt.axis([-4.5, 4.5, -1, 17])
plt.subplots_adjust(right=1)
save_fig("higher_dimensions_plot", tight_layout=False)
plt.show()
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)
def plot_dataset(X, y, axes):
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "bs")
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "g^")
plt.axis(axes)
plt.grid(True, which='both')
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"$x_2$", fontsize=20, rotation=0)
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
plt.show()
```
**Here is second code example in the chapter:**
```
from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
polynomial_svm_clf = Pipeline([
("poly_features", PolynomialFeatures(degree=3)),
("scaler", StandardScaler()),
("svm_clf", LinearSVC(C=10, loss="hinge", random_state=42))
])
polynomial_svm_clf.fit(X, y)
```
**Code to generate Figure 5–6. Linear SVM classifier using polynomial features**
```
def plot_predictions(clf, axes):
x0s = np.linspace(axes[0], axes[1], 100)
x1s = np.linspace(axes[2], axes[3], 100)
x0, x1 = np.meshgrid(x0s, x1s)
X = np.c_[x0.ravel(), x1.ravel()]
y_pred = clf.predict(X).reshape(x0.shape)
y_decision = clf.decision_function(X).reshape(x0.shape)
plt.contourf(x0, x1, y_pred, cmap=plt.cm.brg, alpha=0.2)
plt.contourf(x0, x1, y_decision, cmap=plt.cm.brg, alpha=0.1)
plot_predictions(polynomial_svm_clf, [-1.5, 2.5, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.5, -1, 1.5])
save_fig("moons_polynomial_svc_plot")
plt.show()
```
## Polynomial Kernel
**Next code example:**
```
from sklearn.svm import SVC
poly_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=3, coef0=1, C=5))
])
poly_kernel_svm_clf.fit(X, y)
```
**Code to generate Figure 5–7. SVM classifiers with a polynomial kernel**
```
poly100_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="poly", degree=10, coef0=100, C=5))
])
poly100_kernel_svm_clf.fit(X, y)
fig, axes = plt.subplots(ncols=2, figsize=(10.5, 4), sharey=True)
plt.sca(axes[0])
plot_predictions(poly_kernel_svm_clf, [-1.5, 2.45, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.4, -1, 1.5])
plt.title(r"$d=3, r=1, C=5$", fontsize=18)
plt.sca(axes[1])
plot_predictions(poly100_kernel_svm_clf, [-1.5, 2.45, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.4, -1, 1.5])
plt.title(r"$d=10, r=100, C=5$", fontsize=18)
plt.ylabel("")
save_fig("moons_kernelized_polynomial_svc_plot")
plt.show()
```
## Similarity Features
**Code to generate Figure 5–8. Similarity features using the Gaussian RBF**
```
def gaussian_rbf(x, landmark, gamma):
return np.exp(-gamma * np.linalg.norm(x - landmark, axis=1)**2)
gamma = 0.3
x1s = np.linspace(-4.5, 4.5, 200).reshape(-1, 1)
x2s = gaussian_rbf(x1s, -2, gamma)
x3s = gaussian_rbf(x1s, 1, gamma)
XK = np.c_[gaussian_rbf(X1D, -2, gamma), gaussian_rbf(X1D, 1, gamma)]
yk = np.array([0, 0, 1, 1, 1, 1, 1, 0, 0])
plt.figure(figsize=(10.5, 4))
plt.subplot(121)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.scatter(x=[-2, 1], y=[0, 0], s=150, alpha=0.5, c="red")
plt.plot(X1D[:, 0][yk==0], np.zeros(4), "bs")
plt.plot(X1D[:, 0][yk==1], np.zeros(5), "g^")
plt.plot(x1s, x2s, "g--")
plt.plot(x1s, x3s, "b:")
plt.gca().get_yaxis().set_ticks([0, 0.25, 0.5, 0.75, 1])
plt.xlabel(r"$x_1$", fontsize=20)
plt.ylabel(r"Similarity", fontsize=14)
plt.annotate(r'$\mathbf{x}$',
xy=(X1D[3, 0], 0),
xytext=(-0.5, 0.20),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.1),
fontsize=18,
)
plt.text(-2, 0.9, "$x_2$", ha="center", fontsize=20)
plt.text(1, 0.9, "$x_3$", ha="center", fontsize=20)
plt.axis([-4.5, 4.5, -0.1, 1.1])
plt.subplot(122)
plt.grid(True, which='both')
plt.axhline(y=0, color='k')
plt.axvline(x=0, color='k')
plt.plot(XK[:, 0][yk==0], XK[:, 1][yk==0], "bs")
plt.plot(XK[:, 0][yk==1], XK[:, 1][yk==1], "g^")
plt.xlabel(r"$x_2$", fontsize=20)
plt.ylabel(r"$x_3$ ", fontsize=20, rotation=0)
plt.annotate(r'$\phi\left(\mathbf{x}\right)$',
xy=(XK[3, 0], XK[3, 1]),
xytext=(0.65, 0.50),
ha="center",
arrowprops=dict(facecolor='black', shrink=0.1),
fontsize=18,
)
plt.plot([-0.1, 1.1], [0.57, -0.1], "r--", linewidth=3)
plt.axis([-0.1, 1.1, -0.1, 1.1])
plt.subplots_adjust(right=1)
save_fig("kernel_method_plot")
plt.show()
x1_example = X1D[3, 0]
for landmark in (-2, 1):
k = gaussian_rbf(np.array([[x1_example]]), np.array([[landmark]]), gamma)
print("Phi({}, {}) = {}".format(x1_example, landmark, k))
```
## Gaussian RBF Kernel
**Next code example:**
```
rbf_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="rbf", gamma=5, C=0.001))
])
rbf_kernel_svm_clf.fit(X, y)
```
**Code to generate Figure 5–9. SVM classifiers using an RBF kernel**
```
from sklearn.svm import SVC
gamma1, gamma2 = 0.1, 5
C1, C2 = 0.001, 1000
hyperparams = (gamma1, C1), (gamma1, C2), (gamma2, C1), (gamma2, C2)
svm_clfs = []
for gamma, C in hyperparams:
rbf_kernel_svm_clf = Pipeline([
("scaler", StandardScaler()),
("svm_clf", SVC(kernel="rbf", gamma=gamma, C=C))
])
rbf_kernel_svm_clf.fit(X, y)
svm_clfs.append(rbf_kernel_svm_clf)
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(10.5, 7), sharex=True, sharey=True)
for i, svm_clf in enumerate(svm_clfs):
plt.sca(axes[i // 2, i % 2])
plot_predictions(svm_clf, [-1.5, 2.45, -1, 1.5])
plot_dataset(X, y, [-1.5, 2.45, -1, 1.5])
gamma, C = hyperparams[i]
plt.title(r"$\gamma = {}, C = {}$".format(gamma, C), fontsize=16)
if i in (0, 1):
plt.xlabel("")
if i in (1, 3):
plt.ylabel("")
save_fig("moons_rbf_svc_plot")
plt.show()
```
# SVM Regression
```
np.random.seed(42)
m = 50
X = 2 * np.random.rand(m, 1)
y = (4 + 3 * X + np.random.randn(m, 1)).ravel()
```
**Next code example:**
```
from sklearn.svm import LinearSVR
svm_reg = LinearSVR(epsilon=1.5, random_state=42)
svm_reg.fit(X, y)
```
**Code to generate Figure 5–10. SVM Regression**
```
svm_reg1 = LinearSVR(epsilon=1.5, random_state=42)
svm_reg2 = LinearSVR(epsilon=0.5, random_state=42)
svm_reg1.fit(X, y)
svm_reg2.fit(X, y)
def find_support_vectors(svm_reg, X, y):
y_pred = svm_reg.predict(X)
off_margin = (np.abs(y - y_pred) >= svm_reg.epsilon)
return np.argwhere(off_margin)
svm_reg1.support_ = find_support_vectors(svm_reg1, X, y)
svm_reg2.support_ = find_support_vectors(svm_reg2, X, y)
eps_x1 = 1
eps_y_pred = svm_reg1.predict([[eps_x1]])
def plot_svm_regression(svm_reg, X, y, axes):
x1s = np.linspace(axes[0], axes[1], 100).reshape(100, 1)
y_pred = svm_reg.predict(x1s)
plt.plot(x1s, y_pred, "k-", linewidth=2, label=r"$\hat{y}$")
plt.plot(x1s, y_pred + svm_reg.epsilon, "k--")
plt.plot(x1s, y_pred - svm_reg.epsilon, "k--")
plt.scatter(X[svm_reg.support_], y[svm_reg.support_], s=180, facecolors='#FFAAAA')
plt.plot(X, y, "bo")
plt.xlabel(r"$x_1$", fontsize=18)
plt.legend(loc="upper left", fontsize=18)
plt.axis(axes)
fig, axes = plt.subplots(ncols=2, figsize=(9, 4), sharey=True)
plt.sca(axes[0])
plot_svm_regression(svm_reg1, X, y, [0, 2, 3, 11])
plt.title(r"$\epsilon = {}$".format(svm_reg1.epsilon), fontsize=18)
plt.ylabel(r"$y$", fontsize=18, rotation=0)
#plt.plot([eps_x1, eps_x1], [eps_y_pred, eps_y_pred - svm_reg1.epsilon], "k-", linewidth=2)
plt.annotate(
'', xy=(eps_x1, eps_y_pred), xycoords='data',
xytext=(eps_x1, eps_y_pred - svm_reg1.epsilon),
textcoords='data', arrowprops={'arrowstyle': '<->', 'linewidth': 1.5}
)
plt.text(0.91, 5.6, r"$\epsilon$", fontsize=20)
plt.sca(axes[1])
plot_svm_regression(svm_reg2, X, y, [0, 2, 3, 11])
plt.title(r"$\epsilon = {}$".format(svm_reg2.epsilon), fontsize=18)
save_fig("svm_regression_plot")
plt.show()
np.random.seed(42)
m = 100
X = 2 * np.random.rand(m, 1) - 1
y = (0.2 + 0.1 * X + 0.5 * X**2 + np.random.randn(m, 1)/10).ravel()
```
**Note**: to be future-proof, we set `gamma="scale"`, as this will be the default value in Scikit-Learn 0.22.
**Next code example:**
```
from sklearn.svm import SVR
svm_poly_reg = SVR(kernel="poly", degree=2, C=100, epsilon=0.1, gamma="scale")
svm_poly_reg.fit(X, y)
```
**Code to generate Figure 5–11. SVM Regression using a second-degree polynomial kernel**
```
from sklearn.svm import SVR
svm_poly_reg1 = SVR(kernel="poly", degree=2, C=100, epsilon=0.1, gamma="scale")
svm_poly_reg2 = SVR(kernel="poly", degree=2, C=0.01, epsilon=0.1, gamma="scale")
svm_poly_reg1.fit(X, y)
svm_poly_reg2.fit(X, y)
fig, axes = plt.subplots(ncols=2, figsize=(9, 4), sharey=True)
plt.sca(axes[0])
plot_svm_regression(svm_poly_reg1, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_poly_reg1.degree, svm_poly_reg1.C, svm_poly_reg1.epsilon), fontsize=18)
plt.ylabel(r"$y$", fontsize=18, rotation=0)
plt.sca(axes[1])
plot_svm_regression(svm_poly_reg2, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_poly_reg2.degree, svm_poly_reg2.C, svm_poly_reg2.epsilon), fontsize=18)
save_fig("svm_with_polynomial_kernel_plot")
plt.show()
```
| github_jupyter |
<a href="https://colab.research.google.com/github/JamesHorrex/AI_stock_trading/blob/master/SS_AITrader_INTC.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
%matplotlib inline
import numpy as np
import tensorflow as tf
print(tf.__version__)
!pip install git+https://github.com/tensorflow/docs
import tensorflow_docs as tfdocs
import tensorflow_docs.plots
import tensorflow_docs.modeling
from google.colab import drive
drive.mount('/content/gdrive')
import pandas as pd
df=pd.read_csv('gdrive/My Drive/SS_AITrader/INTC/df_INTC_20drtn_features.csv')
df.head()
df['timestamp'] = pd.to_datetime(df['timestamp'])
from_date='2010-01-01'
to_date='2020-01-01'
df = df[pd.to_datetime(from_date) < df['timestamp'] ]
df = df[pd.to_datetime(to_date) > df['timestamp'] ]
df.head()
df.tail()
df.drop(['timestamp'], inplace=True, axis=1)
train_dataset = df.sample(frac=0.8,random_state=0)
test_dataset = df.drop(train_dataset.index)
train_dataset.head()
train_labels = train_dataset.pop('labels')
test_labels = test_dataset.pop('labels')
train_labels.head()
from sklearn.utils import compute_class_weight
def get_sample_weights(y):
y = y.astype(int) # compute_class_weight needs int labels
class_weights = compute_class_weight('balanced', np.unique(y), y)
print("real class weights are {}".format(class_weights), np.unique(y))
print("value_counts", np.unique(y, return_counts=True))
sample_weights = y.copy().astype(float)
for i in np.unique(y):
sample_weights[sample_weights == i] = class_weights[i] # if i == 2 else 0.8 * class_weights[i]
# sample_weights = np.where(sample_weights == i, class_weights[int(i)], y_)
return sample_weights
get_sample_weights(train_labels)
SAMPLE_WEIGHT=get_sample_weights(train_labels)
train_stats = train_dataset.describe()
train_stats = train_stats.transpose()
def norm(x):
return (x - train_stats['mean']) / train_stats['std']
normed_train_data = norm(train_dataset)
normed_test_data = norm(test_dataset)
from sklearn.feature_selection import SelectKBest, f_classif, mutual_info_classif
from operator import itemgetter
k=20
list_features = list(normed_train_data.columns)
select_k_best = SelectKBest(f_classif, k=k)
select_k_best.fit(normed_train_data, train_labels)
selected_features_anova = itemgetter(*select_k_best.get_support(indices=True))(list_features)
selected_features_anova
select_k_best = SelectKBest(mutual_info_classif, k=k)
select_k_best.fit(normed_train_data, train_labels)
selected_features_mic = itemgetter(*select_k_best.get_support(indices=True))(list_features)
selected_features_mic
list_features = list(normed_train_data.columns)
feat_idx = []
for c in selected_features_mic:
feat_idx.append(list_features.index(c))
feat_idx = sorted(feat_idx)
X_train_new=normed_train_data.iloc[:, feat_idx]
X_test_new=normed_test_data.iloc[:, feat_idx]
#kbest=SelectKBest(f_classif, k=10)
#X_train_new = kbest.fit_transform(normed_train_data, train_labels)
#X_test_new = kbest.transform(normed_test_data)
X_test_new.shape
X_test_new.head()
def build_model(hidden_dim,dropout=0.5):
## input layer
inputs=tf.keras.Input(shape=(X_train_new.shape[1],))
h1= tf.keras.layers.Dense(units=hidden_dim,activation='relu')(inputs)
h2= tf.keras.layers.Dropout(dropout)(h1)
h3= tf.keras.layers.Dense(units=hidden_dim*2,activation='relu')(h2)
h4= tf.keras.layers.Dropout(dropout)(h3)
h5= tf.keras.layers.Dense(units=hidden_dim*2,activation='relu')(h4)
h6= tf.keras.layers.Dropout(dropout)(h5)
h7= tf.keras.layers.Dense(units=hidden_dim,activation='relu')(h6)
##output
outputs=tf.keras.layers.Dense(units=2,activation='softmax')(h7)
return tf.keras.Model(inputs=inputs, outputs=outputs)
tf.random.set_seed(1)
criterion = tf.keras.losses.sparse_categorical_crossentropy
optimizer = tf.keras.optimizers.Adam(learning_rate=0.001)
model = build_model(hidden_dim=64)
model.compile(optimizer=optimizer,loss=criterion,metrics=['accuracy'])
example_batch = X_train_new[:10]
example_result = model.predict(example_batch)
example_result
EPOCHS=200
BATCH_SIZE=20
history = model.fit(
X_train_new, train_labels,
epochs=EPOCHS, batch_size=BATCH_SIZE ,sample_weight=SAMPLE_WEIGHT,shuffle=True,validation_split = 0.2, verbose=1,
callbacks=[tfdocs.modeling.EpochDots()])
hist = pd.DataFrame(history.history)
hist['epoch'] = history.epoch
hist.tail()
import matplotlib.pyplot as plt
hist=history.history
fig=plt.figure(figsize=(12,5))
ax=fig.add_subplot(1,2,1)
ax.plot(hist['loss'],lw=3)
ax.plot(hist['val_loss'],lw=3)
ax.set_title('Training & Validation Loss',size=15)
ax.set_xlabel('Epoch',size=15)
ax.tick_params(axis='both',which='major',labelsize=15)
ax=fig.add_subplot(1,2,2)
ax.plot(hist['accuracy'],lw=3)
ax.plot(hist['val_accuracy'],lw=3)
ax.set_title('Training & Validation accuracy',size=15)
ax.set_xlabel('Epoch',size=15)
ax.tick_params(axis='both',which='major',labelsize=15)
plt.show()
!pip install shap
import shap
explainer = shap.DeepExplainer(model, np.array(X_train_new))
shap_values = explainer.shap_values(np.array(X_test_new))
shap.summary_plot(shap_values[1], X_test_new)
pred=model.predict(X_test_new)
pred.argmax(axis=1)
from sklearn.metrics import classification_report, confusion_matrix
cm=confusion_matrix(test_labels, pred.argmax(axis=1))
print('Confusion Matrix')
fig,ax = plt.subplots(figsize=(2.5,2.5))
ax.matshow(cm,cmap=plt.cm.Blues,alpha=0.3)
for i in range(cm.shape[0]):
for j in range(cm.shape[1]):
ax.text(x=j,y=i,
s=cm[i,j],
va='center',ha='center')
plt.xlabel('Predicted Label')
plt.ylabel('True Label')
plt.show()
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score, f1_score
print('Precision: %.3f' % precision_score(y_true=test_labels,y_pred=pred.argmax(axis=1)))
print('Recall: %.3f' % recall_score(y_true=test_labels,y_pred=pred.argmax(axis=1)))
print('F1: %.3f' % f1_score(y_true=test_labels,y_pred=pred.argmax(axis=1)))
from sklearn.pipeline import Pipeline
from sklearn.feature_selection import SelectKBest, chi2
import xgboost as xgb
from sklearn.model_selection import KFold, GridSearchCV
from sklearn.metrics import accuracy_score, make_scorer
pipe = Pipeline([
('fs', SelectKBest()),
('clf', xgb.XGBClassifier(objective='binary:logistic'))
])
search_space = [
{
'clf__n_estimators': [200],
'clf__learning_rate': [0.05, 0.1],
'clf__max_depth': range(3, 10),
'clf__colsample_bytree': [i/10.0 for i in range(1, 3)],
'clf__gamma': [i/10.0 for i in range(3)],
'fs__score_func': [mutual_info_classif,f_classif],
'fs__k': [20,30,40],
}
]
kfold = KFold(n_splits=5, shuffle=True, random_state=42)
scoring = {'AUC':'roc_auc', 'Accuracy':make_scorer(accuracy_score)}
grid = GridSearchCV(
pipe,
param_grid=search_space,
cv=kfold,
scoring=scoring,
refit='AUC',
verbose=1,
n_jobs=-1
)
model = grid.fit(normed_train_data, train_labels)
import pickle
# Dictionary of best parameters
best_pars = grid.best_params_
# Best XGB model that was found based on the metric score you specify
best_model = grid.best_estimator_
# Save model
pickle.dump(grid.best_estimator_, open('gdrive/My Drive/SS_AITrader/INTC/xgb_INTC_log_reg.pickle', "wb"))
predict = model.predict(normed_test_data)
print('Best AUC Score: {}'.format(model.best_score_))
print('Accuracy: {}'.format(accuracy_score(test_labels, predict)))
cm=confusion_matrix(test_labels,predict)
print('Confusion Matrix')
fig,ax = plt.subplots(figsize=(2.5,2.5))
ax.matshow(cm,cmap=plt.cm.Blues,alpha=0.3)
for i in range(cm.shape[0]):
for j in range(cm.shape[1]):
ax.text(x=j,y=i,
s=cm[i,j],
va='center',ha='center')
plt.xlabel('Predicted Label')
plt.ylabel('True Label')
plt.show()
print(model.best_params_)
model_opt = xgb.XGBClassifier(max_depth=9,
objective='binary:logistic',
n_estimators=200,
learning_rate = 0.1,
colsample_bytree= 0.2,
gamma= 0.1)
eval_set = [(X_train_new, train_labels), (X_test_new, test_labels)]
model_opt.fit(X_train_new, train_labels, early_stopping_rounds=15, eval_metric=["error", "logloss"], eval_set=eval_set, verbose=True)
# make predictions for test data
y_pred = model_opt.predict(X_test_new)
predictions = [round(value) for value in y_pred]
# evaluate predictions
accuracy = accuracy_score(test_labels, predictions)
print("Accuracy: %.2f%%" % (accuracy * 100.0))
from matplotlib import pyplot
results = model_opt.evals_result()
epochs = len(results['validation_0']['error'])
x_axis = range(0, epochs)
# plot log loss
fig, ax = pyplot.subplots()
ax.plot(x_axis, results['validation_0']['logloss'], label='Train')
ax.plot(x_axis, results['validation_1']['logloss'], label='Test')
ax.legend()
pyplot.ylabel('Log Loss')
pyplot.title('XGBoost Log Loss')
pyplot.show()
# plot classification error
fig, ax = pyplot.subplots()
ax.plot(x_axis, results['validation_0']['error'], label='Train')
ax.plot(x_axis, results['validation_1']['error'], label='Test')
ax.legend()
pyplot.ylabel('Classification Error')
pyplot.title('XGBoost Classification Error')
pyplot.show()
shap_values = shap.TreeExplainer(model_opt).shap_values(X_test_new)
shap.summary_plot(shap_values, X_test_new)
predict = model_opt.predict(X_test_new)
cm=confusion_matrix(test_labels,predict)
print('Confusion Matrix')
fig,ax = plt.subplots(figsize=(2.5,2.5))
ax.matshow(cm,cmap=plt.cm.Blues,alpha=0.3)
for i in range(cm.shape[0]):
for j in range(cm.shape[1]):
ax.text(x=j,y=i,
s=cm[i,j],
va='center',ha='center')
plt.xlabel('Predicted Label')
plt.ylabel('True Label')
plt.show()
```
| github_jupyter |
# Deriving a Point-Spread Function in a Crowded Field
### following Appendix III of Peter Stetson's *User's Manual for DAOPHOT II*
### Using `pydaophot` form `astwro` python package
All *italic* text here have been taken from Stetson's manual.
The only input file for this procedure is a FITS file containing reference frame image. Here we use sample FITS form astwro package (NGC6871 I filter 20s frame). Below we get filepath for this image, as well as create instances of `Daophot` and `Allstar` classes - wrappers around `daophot` and `allstar` respectively.
One should also provide `daophot.opt`, `photo.opt` and `allstar.opt` in apropiriete constructors. Here default, build in, sample, `opt` files are used.
```
from astwro.sampledata import fits_image
frame = fits_image()
```
`Daophot` object creates temporary working directory (*runner directory*), which is passed to `Allstar` constructor to share.
```
from astwro.pydaophot import Daophot, Allstar
dp = Daophot(image=frame)
al = Allstar(dir=dp.dir)
```
Daophot got FITS file in construction, which will be automatically **ATTACH**ed.
#### *(1) Run FIND on your frame*
Daophot `FIND` parameters `Number of frames averaged, summed` are defaulted to `1,1`, below are provided for clarity.
```
res = dp.FInd(frames_av=1, frames_sum=1)
```
Check some results returned by `FIND`, every method for `daophot` command returns results object.
```
print ("{} pixels analysed, sky estimate {}, {} stars found.".format(res.pixels, res.sky, res.stars))
```
Also, take a look into *runner directory*
```
!ls -lt $dp.dir
```
We see symlinks to input image and `opt` files, and `i.coo` - result of `FIND`
#### *(2) Run PHOTOMETRY on your frame*
Below we run photometry, providing explicitly radius of aperture `A1` and `IS`, `OS` sky radiuses.
```
res = dp.PHotometry(apertures=[8], IS=35, OS=50)
```
List of stars generated by daophot commands, can be easily get as `astwro.starlist.Starlist` being essentially `pandas.DataFrame`:
```
stars = res.photometry_starlist
```
Let's check 10 stars with least A1 error (``mag_err`` column). ([pandas](https://pandas.pydata.org) style)
```
stars.sort_values('mag_err').iloc[:10]
```
#### *(3) SORT the output from PHOTOMETRY*
*in order of increasing apparent magnitude decreasing
stellar brightness with the renumbering feature. This step is optional but it can be more convenient than not.*
`SORT` command of `daophor` is not implemented (yet) in `pydaohot`. But we do sorting by ourself.
```
sorted_stars = stars.sort_values('mag')
sorted_stars.renumber()
```
Here we write sorted list back info photometry file at default name (overwriting existing one), because it's convenient to use default files in next commands.
```
dp.write_starlist(sorted_stars, 'i.ap')
!head -n20 $dp.PHotometry_result.photometry_file
dp.PHotometry_result.photometry_file
```
#### *(4) PICK to generate a set of likely PSF stars*
*How many stars you want to use is a function of the degree of variation you expect and the frequency with which stars are contaminated by cosmic rays or neighbor stars. [...]*
```
pick_res = dp.PIck(faintest_mag=20, number_of_stars_to_pick=40)
```
If no error reported, symlink to image file (renamed to `i.fits`), and all daophot output files (`i.*`) are in the working directory of runner:
```
ls $dp.dir
```
One may examine and improve `i.lst` list of PSF stars. Or use `astwro.tools.gapick.py` to obtain list of PSF stars optimised by genetic algorithm.
#### *(5) Run PSF *
*tell it the name of your complete (sorted renumbered) aperture photometry file, the name of the file with the list of PSF stars, and the name of the disk file you want the point spread function stored in (the default should be fine) [...]*
*If the frame is crowded it is probably worth your while to generate the first PSF with the "VARIABLE PSF" option set to -1 --- pure analytic PSF. That way, the companions will not generate ghosts in the model PSF that will come back to haunt you later. You should also have specified a reasonably generous fitting radius --- these stars have been preselected to be as isolated as possible and you want the best fits you can get. But remember to avoid letting neighbor stars intrude within one fitting radius of the center of any PSF star.*
For illustration we will set `VARIABLE PSF` option, before `PSf()`
```
dp.set_options('VARIABLE PSF', 2)
psf_res = dp.PSf()
```
#### *(6) Run GROUP and NSTAR or ALLSTAR on your NEI file*
*If your PSF stars have many neighbors this may take some minutes of real time. Please be patient or submit it as a batch job and perform steps on your next frame while you wait.*
We use `allstar`. (`GROUP` and `NSTAR` command are not implemented in current version of `pydaophot`). We use prepared above `Allstar` object: `al` operating on the same runner dir that `dp`.
As parameter we set input image (we haven't do that on constructor), and `nei` file produced by `PSf()`. We do not remember name `i.psf` so use `psf_res.nei_file` property.
Finally we order `allstar` to produce subtracted FITS .
```
alls_res = al.ALlstar(image_file=frame, stars=psf_res.nei_file, subtracted_image_file='is.fits')
```
All `result` objects, has `get_buffer()` method, useful to lookup unparsed `daophot` or `allstar` output:
```
print (alls_res.get_buffer())
```
#### *(8) EXIT from DAOPHOT and send this new picture to the image display *
*Examine each of the PSF stars and its environs. Have all of the PSF stars subtracted out more or less cleanly, or should some of them be rejected from further use as PSF stars? (If so use a text editor to delete these stars from the LST file.) Have the neighbors mostly disappeared, or have they left behind big zits? Have you uncovered any faint companions that FIND missed?[...]*
The absolute path to subtracted file (like for most output files) is available as result's property:
```
sub_img = alls_res.subtracted_image_file
```
We can also generate region file for psf stars:
```
from astwro.starlist.ds9 import write_ds9_regions
reg_file_path = dp.file_from_runner_dir('lst.reg')
write_ds9_regions(pick_res.picked_starlist, reg_file_path)
# One can run ds9 directly from notebook:
!ds9 $sub_img -regions $reg_file_path
```
#### *(9) Back in DAOPHOT II ATTACH the original picture and run SUBSTAR*
*specifying the file created in step (6) or in step (8f) as the stars to subtract, and the stars in the LST file as the stars to keep.*
Lookup into runner dir:
```
ls $al.dir
sub_res = dp.SUbstar(subtract=alls_res.profile_photometry_file, leave_in=pick_res.picked_stars_file)
```
*You have now created a new picture which has the PSF stars still in it but from which the known neighbors of these PSF stars have been mostly removed*
#### (10) ATTACH the new star subtracted frame and repeat step (5) to derive a new point spread function
#### (11+...) Run GROUP NSTAR or ALLSTAR
```
for i in range(3):
print ("Iteration {}: Allstar chi: {}".format(i, alls_res.als_stars.chi.mean()))
dp.image = 'is.fits'
respsf = dp.PSf()
print ("Iteration {}: PSF chi: {}".format(i, respsf.chi))
alls_res = al.ALlstar(image_file=frame, stars='i.nei')
dp.image = frame
dp.SUbstar(subtract='i.als', leave_in='i.lst')
print ("Final: Allstar chi: {}".format(alls_res.als_stars.chi.mean()))
alls_res.als_stars
```
Check last image with subtracted PSF stars neighbours.
```
!ds9 $dp.SUbstar_result.subtracted_image_file -regions $reg_file_path
```
*Once you have produced a frame in which the PSF stars and their neighbors all subtract out cleanly, one more time through PSF should produce a point-spread function you can be proud of.*
```
dp.image = 'is.fits'
psf_res = dp.PSf()
print ("PSF file: {}".format(psf_res.psf_file))
```
| github_jupyter |
```
# python standard library
import sys
import os
import operator
import itertools
import collections
import functools
import glob
import csv
import datetime
import bisect
import sqlite3
import subprocess
import random
import gc
import shutil
import shelve
import contextlib
import tempfile
import math
import pickle
# general purpose third party packages
import cython
%reload_ext Cython
import numpy as np
nnz = np.count_nonzero
import scipy
import scipy.stats
import scipy.spatial.distance
import numexpr
import h5py
import tables
import bcolz
import dask
import dask.array as da
import pandas
import IPython
from IPython.display import clear_output, display, HTML
import sklearn
import sklearn.decomposition
import sklearn.manifold
import petl as etl
etl.config.display_index_header = True
import humanize
from humanize import naturalsize, intcomma, intword
import zarr
import graphviz
import statsmodels.formula.api as sfa
# plotting setup
import matplotlib as mpl
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from matplotlib.gridspec import GridSpec
import matplotlib_venn as venn
import seaborn as sns
sns.set_context('paper')
sns.set_style('white')
sns.set_style('ticks')
rcParams = plt.rcParams
base_font_size = 8
rcParams['font.size'] = base_font_size
rcParams['axes.titlesize'] = base_font_size
rcParams['axes.labelsize'] = base_font_size
rcParams['xtick.labelsize'] = base_font_size
rcParams['ytick.labelsize'] = base_font_size
rcParams['legend.fontsize'] = base_font_size
rcParams['axes.linewidth'] = .5
rcParams['lines.linewidth'] = .5
rcParams['patch.linewidth'] = .5
rcParams['ytick.direction'] = 'out'
rcParams['xtick.direction'] = 'out'
rcParams['savefig.jpeg_quality'] = 100
rcParams['lines.markeredgewidth'] = .5
rcParams['figure.max_open_warning'] = 1000
rcParams['figure.dpi'] = 120
rcParams['figure.facecolor'] = 'w'
# bio third party packages
import Bio
import pyfasta
# currently broken, not compatible
# import pysam
# import pysamstats
import petlx
import petlx.bio
import vcf
import anhima
import allel
sys.path.insert(0, '../agam-report-base/src/python')
from util import *
import zcache
import veff
# import hapclust
ag1k_dir = '../ngs.sanger.ac.uk/production/ag1000g'
from ag1k import phase1_ar3
phase1_ar3.init(os.path.join(ag1k_dir, 'phase1', 'AR3'))
from ag1k import phase1_ar31
phase1_ar31.init(os.path.join(ag1k_dir, 'phase1', 'AR3.1'))
from ag1k import phase2_ar1
phase2_ar1.init(os.path.join(ag1k_dir, 'phase2', 'AR1'))
region_vgsc = SeqFeature('2L', 2358158, 2431617, label='Vgsc')
```
| github_jupyter |
# 内容
- lightGBMモデル初版
- ターゲットエンコーディング:Holdout TS
- 外部データ3つ(ステージ面積1,ステージ面積2,ブキ)を結合
- ステージ面積1:
https://probspace-stg.s3-ap-northeast-1.amazonaws.com/uploads/user/c10947bba5cde4ad3dd4a0d42a0ec35b/files/2020-09-06-0320/stagedata.csv
- ステージ面積2:https://stat.ink/api-info/stage2
- ブキ:https://stat.ink/api-info/weapon2
```
# ライブラリのインポート
import pandas as pd
import numpy as np
import re
import matplotlib.pyplot as plt
import seaborn as sns
import lightgbm as lgb
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold
from sklearn.metrics import accuracy_score
import warnings
warnings.filterwarnings('ignore')
# データの読込
train = pd.read_csv("../data/train_data.csv")
test = pd.read_csv('../data/test_data.csv')
```
# データの確認
```
def inspection_datas(df):
print('######################################')
print('①サイズ(行数、列数)の確認')
print(df.shape)
print('######################################')
print('②最初の5行の表示')
display(df.head())
print('######################################')
print('③各行のデータ型の確認(オブジェクト型の有無)')
display(df.info())
display(df.select_dtypes(include=object).columns)
print('######################################')
print('④各種統計値の確認(③で、Objectのものは統計されない)')
display(df.describe())
print('######################################')
print('➄欠損値がある列の確認')
null_df =df.isnull().sum()[df.columns[df.isnull().sum()!=0]]
display(null_df)
display(null_df.shape)
print('######################################')
print('⑥相関係数のヒートマップ')
sns.heatmap(df.corr())
inspection_datas(train)
```
# 外部データの結合
```
# 外部データの読込
# stage,stage2は若干面積が異なる、バージョンによる違いや計算方法による誤差
stage = pd.read_csv('../gaibu_data/stagedata.csv')
stage2 = pd.read_json('../gaibu_data/stage.json')
weapon = pd.read_csv('../gaibu_data/statink-weapon2.csv')
stage.head(3)
stage2.head(3)
weapon.head(3)
```
## stageを結合
```
# 表記揺れの確認
print(np.sort(train['stage'].unique()))
print(np.sort(test['stage'].unique()))
print(np.sort(stage['stage'].unique()))
# 結合のため列名変更
stage_r = stage.rename(columns = {'size':'stage_size1'})
# 結合
train_s = pd.merge(train, stage_r, on = 'stage', how = 'left')
test_s = pd.merge(test, stage_r, on = 'stage', how = 'left')
# null確認
print(train_s[['stage_size1']].isnull().sum())
print(test_s[['stage_size1']].isnull().sum())
```
## stage2を結合
```
# 表記揺れの確認
print(np.sort(train['stage'].unique()))
print(np.sort(test['stage'].unique()))
# 「mystery~」はイベント時に解放されるステージ、今回のtrain,testデータには無し
print(np.sort(stage2['key'].unique()))
stage2_r.columns
# 結合のため列名変更
stage2_r = stage2.rename(columns = {'key':'stage', 'area':'stage_size2'})
# 必要カラム
st2_col = ['stage_size2', # ステージの面積
'stage', # ステージ名
# 'name', # 外国語ステージ名
# 'release_at', #リリース日時
# 'short_name', # 省略名
# 'splatnet' # ID?
]
stage2_rc = stage2_r[st2_col]
# 結合
train_ss = pd.merge(train_s, stage2_rc, on = 'stage', how = 'left')
test_ss = pd.merge(test_s, stage2_rc, on = 'stage', how = 'left')
# null確認
print(train_ss[['stage_size2']].isnull().sum())
print(test_ss[['stage_size2']].isnull().sum())
```
## weaponを結合
```
# trainのブキ
train_weapon = sorted(list(set(train['A1-weapon'])&set(train['A2-weapon'])&set(train['A3-weapon'])&set(train['A4-weapon'])\
&set(train['B1-weapon'])&set(train['B2-weapon'])&set(train['B3-weapon'])&set(train['B4-weapon'])))
print('{}種類'.format(len(train_weapon)))
print(train_weapon)
# testのブキ
test_weapon = sorted(list(set(test['A1-weapon'])&set(test['A2-weapon'])&set(test['A3-weapon'])&set(test['A4-weapon'])\
&set(test['B1-weapon'])&set(test['B2-weapon'])&set(test['B3-weapon'])&set(test['B4-weapon'])))
print('{}種類'.format(len(test_weapon)))
print(test_weapon)
# 外部データのブキ
gaibu_weapon = train_weapon = np.sort(weapon['key'].unique())
print('{}種類'.format(len(gaibu_weapon)))
print(gaibu_weapon)
# 表記に差分ないか比較→無し
print(set(train_weapon)-set(gaibu_weapon))
print(set(gaibu_weapon)-set(train_weapon))
print(set(test_weapon)-set(gaibu_weapon))
print(set(gaibu_weapon)-set(test_weapon))
# 必要カラム
# 参照:https://stat.ink/api-info/weapon2
weapon_col = ['category1', # ブキ区分
'category2', # ブキ区分
'key', # ブキ名
'subweapon', # サブウェポン
'special', # スペシャルウェポン
'mainweapon', # メインブキ
'reskin', # 同一性能のブキ
# 'splatnet', # アプリのユーザID
# 以下外国語ブキ名
# '[de-DE]', '[en-GB]', '[en-US]', '[es-ES]','[es-MX]', '[fr-CA]',
# '[fr-FR]', '[it-IT]', '[ja-JP]', '[nl-NL]','[ru-RU]', '[zh-CN]', '[zh-TW]'
]
# 必要カラム抽出&結合キー名変更
weapon_c = weapon[weapon_col].rename(columns = {'key': 'weapon'})
weapon_c.head(3)
# 各A1~B4-weapon列に対して結合
weapon_cc = weapon_c.copy()
train_ssw = train_ss.copy()
test_ssw = test_ss.copy()
import itertools
for a,num in itertools.product(['A','B'],[1,2,3,4]):
col_list = []
# ブキのカラム名の先頭にA1~B4追加
for col in weapon_c.columns:
tmp_col = a+str(num) + '-' + col
col_list.append(tmp_col)
weapon_cc.columns = col_list
#train,testに結合
train_ssw = pd.merge(train_ssw, weapon_cc, on = a+str(num) + '-weapon', how = 'left')
test_ssw = pd.merge(test_ssw, weapon_cc, on = a+str(num) + '-weapon', how = 'left')
# 結合後nullチェック
print(train_ssw[col_list].isnull().sum())
print(test_ssw[col_list].isnull().sum())
# 元データにweapon情報がないもののみ(回線落ち)がnullなのでok
train_input = train_ssw.copy()
test_input = test_ssw.copy()
```
# 前処理
```
# 欠損値埋める
def fill_all_null(df, num):
for col_name in df.columns[df.isnull().sum()!=0]:
df[col_name] = df[col_name].fillna(num)
# 訓練データ、テストデータの欠損値を-1で補完
fill_all_null(train_input, -1)
fill_all_null(test_input, -1)
# ターゲットエンコーディングの関数定義
## Holdout TSを用いる 変更の余地あり
def change_to_target2(train_df,test_df,input_column_name,output_column_name):
from sklearn.model_selection import KFold
# nan埋め処理
## 上でやってるのでいらない
# train_df[input_column_name] = train_df[input_column_name].fillna('-1')
# test_df[input_column_name] = test_df[input_column_name].fillna('-1')
kf = KFold(n_splits=5, shuffle=True, random_state=71)
#=========================================================#
c=input_column_name
# 学習データ全体で各カテゴリにおけるyの平均を計算
data_tmp = pd.DataFrame({c: train_df[c],'target':train_df['y']})
target_mean = data_tmp.groupby(c)['target'].mean()
#テストデータのカテゴリを置換★
test_df[output_column_name] = test_df[c].map(target_mean)
# 変換後の値を格納する配列を準備
tmp = np.repeat(np.nan, train_df.shape[0])
for i, (train_index, test_index) in enumerate(kf.split(train_df)): # NFOLDS回まわる
#学習データについて、各カテゴリにおける目的変数の平均を計算
target_mean = data_tmp.iloc[train_index].groupby(c)['target'].mean()
#バリデーションデータについて、変換後の値を一時配列に格納
tmp[test_index] = train_df[c].iloc[test_index].map(target_mean)
#変換後のデータで元の変数を置換
train_df[output_column_name] = tmp
#========================================================#
# オブジェクトの列のリストを作成
object_col_list = train_input.select_dtypes(include=object).columns
# オブジェクトの列は全てターゲットエンコーディング実施
for col in object_col_list:
change_to_target2(train_input,test_input,col,"enc_"+col)
# 変換前の列を削除
train_input = train_input.drop(object_col_list,axis=1)
test_input = test_input.drop(object_col_list,axis=1)
# 'id'の列を削除
train_input = train_input.drop('id',axis=1)
test_input = test_input.drop('id',axis=1)
# 訓練データ欠損確認
train_input.isnull().sum().sum()
# テストデータ欠損確認
test_input.isnull().sum().sum()
# 欠損値はターゲットエンコーディング時に学習データが少なくなって平均値が計算できなくなってしまうため発生。0埋め。
fill_all_null(train_input, 0)
fill_all_null(test_input, 0)
```
# データの確認
```
# 訓練データとテストデータの列を確認
print(train_input.columns)
print(test_input.columns)
```
# 学習の準備
```
# 訓練データを説明変数と目的変数に分割
target = train_input['y']
train_x = train_input.drop('y',axis=1)
# LGBMのパラメータを設定
params = {
# 二値分類問題
'objective': 'binary',
# 損失関数は二値のlogloss
#'metric': 'auc',
'metric': 'binary_logloss',
# 最大イテレーション回数指定
'num_iterations' : 1000,
# early_stopping 回数指定
'early_stopping_rounds' : 100,
}
```
# 学習・予測の実行
```
# k-分割交差検証を使って学習&予測(K=10)
FOLD_NUM = 10
kf = KFold(n_splits=FOLD_NUM,
random_state=42)
#lgbmのラウンド数を定義
num_round = 10000
#検証時のスコアを初期化
scores = []
#テストデータの予測値を初期化
pred_cv = np.zeros(len(test.index))
for i, (tdx, vdx) in enumerate(kf.split(train_x, target)):
print(f'Fold : {i}')
# 訓練用データと検証用データに分割
X_train, X_valid, y_train, y_valid = train_x.iloc[tdx], train_x.iloc[vdx], target.values[tdx], target.values[vdx]
lgb_train = lgb.Dataset(X_train, y_train)
lgb_valid = lgb.Dataset(X_valid, y_valid)
# 学習の実行
model = lgb.train(params, lgb_train, num_boost_round=num_round,
valid_names=["train", "valid"], valid_sets=[lgb_train, lgb_valid],
verbose_eval=100)
# 検証データに対する予測値を求めて、勝敗(0 or 1)に変換
va_pred = np.round(model.predict(X_valid,num_iteration=model.best_iteration))
# accuracyスコアを計算
score_ = accuracy_score(y_valid, va_pred)
# フォールド毎の検証時のスコアを格納
scores.append(score_)
#テストデータに対する予測値を求める
submission = model.predict(test_input,num_iteration=model.best_iteration)
#テストデータに対する予測値をフォールド数で割って蓄積
#(フォールド毎の予測値の平均値を求めることと同じ)
pred_cv += submission/FOLD_NUM
# 最終的なテストデータに対する予測値を勝敗(0 or 1)に変換
pred_cv_int = np.round(pred_cv)
# 最終的なaccuracyスコアを平均値で出力
print('')
print('################################')
print('CV_score:'+ str(np.mean(scores)))
# 提出用ファイルを作成する
pd.DataFrame({"id": range(len(pred_cv_int)), "y": pred_cv_int.astype(np.int64) }).to_csv("../submit/submission_v0.2.csv", index=False)
```
| github_jupyter |
```
import numpy as np
from copy import deepcopy
from scipy.special import expit
from scipy.optimize import minimize
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression as skLogisticRegression
from sklearn.multiclass import OneVsRestClassifier as skOneVsRestClassifier
class OneVsRestClassifier():
def __init__(self, estimator):
self.estimator = estimator
def _encode(self, y):
classes = np.unique(y)
y_train = np.zeros((y.shape[0], len(classes)))
for i, c in enumerate(classes):
y_train[y == c, i] = 1
return classes, y_train
def fit(self, X, y):
self.classes_, y_train = self._encode(y)
self.estimators_ = []
for i in range(y_train.shape[1]):
cur_y = y_train[:, i]
clf = deepcopy(self.estimator)
clf.fit(X, cur_y)
self.estimators_.append(clf)
return self
def decision_function(self, X):
scores = np.zeros((X.shape[0], len(self.classes_)))
for i, est in enumerate(self.estimators_):
scores[:, i] = est.decision_function(X)
return scores
def predict(self, X):
scores = self.decision_function(X)
indices = np.argmax(scores, axis=1)
return self.classes_[indices]
# Simplified version of LogisticRegression, only work for binary classification
class BinaryLogisticRegression():
def __init__(self, C=1.0):
self.C = C
@staticmethod
def _cost_grad(w, X, y, alpha):
def _log_logistic(x):
if x > 0:
return -np.log(1 + np.exp(-x))
else:
return x - np.log(1 + np.exp(x))
yz = y * (np.dot(X, w[:-1]) + w[-1])
cost = -np.sum(np.vectorize(_log_logistic)(yz)) + 0.5 * alpha * np.dot(w[:-1], w[:-1])
grad = np.zeros(len(w))
t = (expit(yz) - 1) * y
grad[:-1] = np.dot(X.T, t) + alpha * w[:-1]
grad[-1] = np.sum(t)
return cost, grad
def _solve_lbfgs(self, X, y):
y_train = np.full(X.shape[0], -1)
y_train[y == 1] = 1
w0 = np.zeros(X.shape[1] + 1)
res = minimize(fun=self._cost_grad, jac=True, x0=w0,
args=(X, y_train, 1 / self.C), method='L-BFGS-B')
return res.x[:-1], res.x[-1]
def fit(self, X, y):
self.coef_, self.intercept_ = self._solve_lbfgs(X, y)
return self
def decision_function(self, X):
scores = np.dot(X, self.coef_) + self.intercept_
return scores
def predict(self, X):
scores = self.decision_function(X)
indices = (scores > 0).astype(int)
return indices
for C in [0.1, 1, 10, np.inf]:
X, y = load_iris(return_X_y=True)
clf1 = OneVsRestClassifier(BinaryLogisticRegression(C=C)).fit(X, y)
clf2 = skOneVsRestClassifier(skLogisticRegression(C=C, multi_class="ovr", solver="lbfgs",
# keep consisent with scipy default
tol=1e-5, max_iter=15000)).fit(X, y)
prob1 = clf1.decision_function(X)
prob2 = clf2.decision_function(X)
pred1 = clf1.predict(X)
pred2 = clf2.predict(X)
assert np.allclose(prob1, prob2)
assert np.array_equal(pred1, pred2)
```
| github_jupyter |
```
import tensorflow as tf
from keras.layers import Conv1D, Dense, Dropout, Concatenate, GlobalAveragePooling1D, GlobalMaxPooling1D, Input, MaxPooling1D, Flatten
from keras.optimizers import Adam
from keras.losses import sparse_categorical_crossentropy
from sklearn.model_selection import train_test_split
from keras.utils import plot_model
from keras.models import Model
import numpy as np
import pandas as pd
amazon_review = pd.read_csv('1429_1.csv')
ratings_df = amazon_review[['reviews.text','reviews.rating']]
ratings_df.dropna(inplace=True)
ratings_df['reviews.rating'].value_counts()
maxlen = 1024
alphabet_list = "abcdefghijklmnopqrstuvwxyz0123456789-,;.!?:'\"/\|_@#$%ˆ&* ̃‘+-=<>()[]{} "
alphabet_index = {v:i for i,v in enumerate(alphabet_list)}
matrix = np.eye(len(alphabet_list))
def prepare_data_for_character_cnn(documents, maxlen,alphabet_list, alphabet_index, matrix):
doc_array = []
for doc in documents:
doc_char_list = []
if len(str(doc)) <= maxlen:
try:
doc = str(doc) + "".join(['`']*(maxlen-len(doc)+1))
except:
print (type(doc),doc)
for c in str(doc).lower()[:maxlen]:
doc_char_list.append(matrix[alphabet_index[c]].T if c in alphabet_index else np.zeros(len(alphabet_list)))
doc_array.append(np.array(doc_char_list).T)
return np.array(doc_array)
train, test = train_test_split(ratings_df,test_size=0.2, random_state=42,stratify=ratings_df['reviews.rating'])
charcnn_dataset_train = prepare_data_for_character_cnn(train['reviews.text'].values.tolist(), maxlen, alphabet_list, alphabet_index, matrix)
charcnn_dataset_test = prepare_data_for_character_cnn(test['reviews.text'].values.tolist(), maxlen, alphabet_list, alphabet_index, matrix)
print(charcnn_dataset_train[0].shape)
print(charcnn_dataset_test[0].shape)
def get_char_cnn_model(kernels, maxlen, char_len):
input = Input(shape=(char_len,maxlen))
cnns = []
cnn = input
for kernel in kernels:
cnn = Conv1D(kernel_size=kernel, filters=128, padding="SAME")(cnn)
cnn = MaxPooling1D(2)(cnn)
# cnn_average = GlobalAveragePooling1D()(cnn)
# cnns.append(cnn_max)
# cnns.append(cnn_average)
# cnn_layer = Concatenate()(cnns)
cnn_flatten = Flatten()(cnn)
output = Dense(128, activation='relu')(cnn_flatten)
output = Dropout(0.2)(output)
output = Dense(64, activation='relu')(output)
output = Dropout(0.2)(output)
output = Dense(32, activation='relu')(output)
output = Dropout(0.2)(output)
output = Dense(5, activation='softmax')(output)
model = Model(input, output)
return model
char_cnn_model = get_char_cnn_model([7,6,5,4,3,2],maxlen, len(alphabet_list))
char_cnn_model.summary()
plot_model(char_cnn_model, 'char_cnn.png')
from IPython import display
display.Image('char_cnn.png')
char_cnn_model.compile(loss='sparse_categorical_crossentropy', optimizer=Adam(lr=0.001), metrics=['acc'])
train_y = train['reviews.rating'].values-1
test_y = test['reviews.rating'].values-1
char_cnn_model.fit(charcnn_dataset_train,train_y.tolist(),validation_data=(charcnn_dataset_test,test_y.tolist()),batch_size=128, epochs=10)
# for item in charcnn_dataset:
# if item.shape[0] != 71 or item.shape[1] != 1024:
# print ("PROBLEM!!!!!",item.shape, item)
from sklearn.metrics import classification_report
values = char_cnn_model.predict(charcnn_dataset_test)
prediction = np.argmax(values,axis=1)
print(classification_report(test_y,prediction))
test_1 = prepare_data_for_character_cnn(['I hate this. worst ever.'], maxlen, alphabet_list, alphabet_index, matrix)
char_cnn_model.predict(test_1)
```
| github_jupyter |
# OPTIMIZATION PHASES
### List of variables
<table>
<thead>
<tr>
<th style="width: 10%">Variable</th>
<th style="width: 45%">Description</th>
<th style="width: 30%">Comment</th>
</tr>
</thead>
<tbody>
<tr>
<td>$B$</td>
<td>Number of full blocks/pages that need the records</td>
<td>$\lceil \frac{|T|}{R} \rceil$; $B \ll |T|$</td>
</tr>
<tr>
<td>$R$</td>
<td>Number of records per block/page</td>
<td></td>
</tr>
<tr>
<td>$|T|$</td>
<td>Cardinality. Number of tuples of a table</td>
<td>Size of table</td>
</tr>
<tr>
<td>$D$</td>
<td>Time to access (read or write) a disk block</td>
<td>Approximately 0'010 seconds</td>
</tr>
<tr>
<td>$C$</td>
<td>Time for the CPU to process a record</td>
<td>Approximately 10<sup>-9</sup></td>
</tr>
<tr>
<td>$d$</td>
<td>Tree order</td>
<td>Usually greater than 100</td>
</tr>
<tr>
<td>$h$</td>
<td>Tree depth minus 1</td>
<td>$\lceil \log_u |T| \rceil - 1$</td>
</tr>
<tr>
<td>$v$</td>
<td>Number of different values in a search</td>
<td></td>
</tr>
<tr>
<td>$u$</td>
<td>$\%load \cdot 2d$</td>
<td></td>
</tr>
<tr>
<td>$k$</td>
<td>Number of repetitions of every value in the search</td>
<td></td>
</tr>
<tr>
<td>ndist(A)</td>
<td>Number of different values for attribute A</td>
<td>Obtained from DB catalog</td>
</tr>
<tr>
<td>max</td>
<td>Maximum value of an attribute</td>
<td>Obtained from DB catalog</td>
</tr>
<tr>
<td>min</td>
<td>Minimum value of an attribute</td>
<td>Obtained from DB catalog</td>
</tr>
<tr>
<td>$H$</td>
<td>Time to evaluate the hash function</td>
<td></td>
</tr>
<tr>
<td>$M$</td>
<td>Memory pages for a join/sorting algorithm</td>
<td></td>
</tr>
<tr>
<td>bits</td>
<td>Bits per index block</td>
<td></td>
</tr>
<tr>
<td></td>
<td>Domain Cardinality</td>
<td>Maximum number of different values</td>
</tr>
</tbody>
</table>
### List of variables for intermediate results
Record length. $\sum$ attribute length<sub>i</sub> (+ control information)
$$|R|$$
Number of records per block
$$R_R = \lfloor \frac{B}{|R|} \rfloor$$
Number of blocks per table
$$B_R = \lceil \frac{|R|}{R_R} \rceil$$
### Cardinalities estimation
Selectivity Factor. % of tuples in the output regarding the input. ~0: very selective ~1: not very selective
$$\mathrm{SF}$$
Output of cardinality estimation
$$|O| = \mathrm{SF} \cdot |R|$$ or $$|O| = \mathrm{SF} \cdot |R1| \cdot |R2|$$
Selection
$$|\mathrm{selection}(R)| = \mathrm{SF} \cdot |R|$$
Join
$$|\mathrm{join}(R, S)| = \mathrm{SF} \cdot |R| \cdot |S|$$
Unions with repetitions
$$|\mathrm{union}(R, S)| = |R| + |S|$$
Unions without repetitions
$$|\mathrm{union}(R, S)| = |R| + |S| - |\mathrm{union}(R, S)|$$
Difference (anti-join)
$$|\mathrm{difference}(R, S)| = |R| - |\mathrm{union}(R, S)|$$
## Optimization phases
**Asumptions**
* Materialized views
* Focus on Disk access time
* Physical address of the record
* Only consider cases
1. No index
2. Unordered B-Tree with addresses (B<sup>+</sup>)
3. Unordered Hash with addresses
4. Orderered B-Tree with addresses (Clustered)
### Unordered B-tree with addresses (B<sup>+</sup>)
**Assumptions**
* In every tree node **2d** addresses fit
* Tree load 66% (2/3)
### Orderered B-Tree with addresses (Clustered)
**Assumptions**
* Tree load 66% (2/3) (index and table blocks)
### Unordered Hash with addresses
**Assumptions**
* No blocks for excess
* The same number of entries fit in a bucket block as in a tree block
* Bucket blocks at 80% (4/5)
## Space
**No index**
$$B$$
**B<sup>+</sup>**
$$\sum_1^{h+1} \lceil \frac{|T|}{u^i} \rceil + B$$
**Clustered**
$$\sum_1^{h+1} \lceil \frac{|T|}{u^i} \rceil + \lceil 1.5B \rceil$$
**Hash**
$$1 + \lceil 1.25(\frac{|T|}{2d}) \rceil + B$$
Example:
$$\mathrm{Lvl_1} = \frac{|T|}{u}$$
$$\mathrm{Lvl_2} = \frac{|T|}{u^2}$$
$$\mathrm{Lvl_3} = \frac{|T|}{u^3}$$
## Access paths
### Table scan
The whole table
<div style="text-align: right"> $u = \frac{2}{3} \cdot 2d$ </div>
**No index**
$$B \cdot D$$
**B<sup>+</sup>**
<span style="color:orange">Only useful for sort</span>
$$\lceil \frac{|T|}{u} \rceil \cdot D + |T| \cdot D$$
**Clustered**
$$\lceil 1.5B \rceil \cdot D$$
**Hash**
<span style="color:red">Useless</span>
$$\lceil 1.25(\frac{|T|}{2d}) \rceil \cdot D + |T| \cdot D $$
### Search one tuple
Equality of unique attribute
<div style="text-align: right">
$u = \frac{2}{3} \cdot 2d$ <br>
$h = \lceil \log_u |T| \rceil - 1$
</div>
**No index**
$$0.5B \cdot D$$
**B<sup>+</sup>**
$$h \cdot D + D$$
**Clustered**
$$h \cdot D + D$$
**Hash**
$$H + D + D$$
### Search several tuples
Interval
No unique attribute
<div style="text-align: right">
$u = \frac{2}{3} \cdot 2d$ <br>
$h = \lceil \log_u |T| \rceil - 1$ <br>
$|O|$: cardinality of Output <br>
$v$: value in range <br>
$k$: repetitions per value <br>
</div>
**No index**
$$B \cdot D$$
**B<sup>+</sup>**
$$h \cdot D + \frac{|O| - 1}{u} \cdot D + |O| \cdot D$$
**Clustered**
$$h \cdot D + D + 1.5 \left( \frac{|O|-1}{R} \right) \cdot D$$
**Hash**
$$v = 1: 1 \cdot (H + D + k \cdot D) = H + D + k \cdot D$$
$$v > 1: v \cdot (H + D + k \cdot D)$$
$$v \;\mathrm{is\;unknown}: \mathrm{Useless}$$
### Statistics in Oracle
DBA is responsible for the statistics.
`ANALYZE [TABLE|INDEX|CLUSTER] <name> [COMPUTE|ESTIMATE] STATISTICS;`
```sql
ANALYZE TABLE departments COMPUTE STATISTICS;
ANALYZE TABLE employees COMPUTE STATISTICS;
```
`DBMS_STATS.GATHER_TABLE_STATS( <esquema>, <table> );`
```sql
DBMS_STATS.GATHER_TABLE_STATS("username", "departments");
DBMS_STATS.GATHER_TABLE_STATS("username", "employees");
```
Kinds of statistics
| Relations | Attributes |
|:--|:--|
| Cardinality | Length |
| Number of blocks | Domain cardinality |
| Average length of records | Number of existing different values |
| | Maximum value |
| | Minimum value |
Main hypothesis in most DBMS
* Uniform distribution of values for each attribute
* Independence of attributes
## Selectivity Factor of a Selection
Assuming equi-probability of values
`WHERE A = c`
$$\mathrm{SF}(A = c) = \frac{1}{\mathrm{ndist}(A)}$$
Assuming uniform distribution and $A \in [\min, \max]$
`WHERE A > c`
$$
\mathrm{SF}(A > c) = \frac{\max - c}{\max - \min} =
\begin{cases}
0 & \quad \text{if}\; c \geq \max \\
1 & \quad \text{if}\; c < \min
\end{cases}
$$
`WHERE A < c`
$$
\mathrm{SF}(A < c) = \frac{c - \min}{\max - \min} =
\begin{cases}
0 & \quad \text{if}\; c \leq \min \\
1 & \quad \text{if}\; c > \max
\end{cases}
$$
Assuming $\text{ndist}(A)$ is big enough
`WHERE A <= c`
$$
\mathrm{SF}(A \leq c) = \mathrm{SF}(A < c)
$$
`WHERE A >= c`
$$
\mathrm{SF}(A \geq c) = \mathrm{SF}(A > c)
$$
Assuming P and Q statistically **independent**
`WHERE P AND Q`
$$
\text{SF}(P \;\text{AND}\; Q) = \text{SF}(P) \cdot \text{SF}(Q)
$$
`WHERE P OR Q`
$$
\text{SF}(P \;\text{OR}\; Q) = \text{SF}(P) + \text{SF}(Q) - \text{SF}(P) \cdot \text{SF}(Q)
$$
`WHERE NOT P`
$$
\text{SF}(\text{NOT}\;P) = 1 - \text{SF}(P)
$$
`WHERE A IN (c1, c2, ... , cn)`
$$
\text{SF}(A \in (c_1, c_2, \dots, c_n)) = \min(1, \frac{n}{\mathrm{ndist}(A)})
$$
`WHERE A BETWEEN (c1, c2)`
$$
\text{SF}(c_1 \leq A \leq c_2) = \frac{\min(c_2, \max)-\max(c_1, \min)}{\max - \min}
$$
### Selectivity Factor of a Join
For $R[A \theta B]S$
Too difficult to approximate this general case. Usually, the required statistics are not available because it
would be too expensive to maintain them.
Results depend on operator:
$$
\text{SF}(R[A\times B]S) = 1
$$
$$
\text{SF}(R[A \neq B]S) = 1
$$
$$
\text{SF}(R[A=B]S) = \frac{1}{|R|}
\begin{cases}
S_B & \quad \text{is not null} \\
S_B & \quad \text{FK to } R_A \\
R_A & \quad \text{PK}
\end{cases}
$$
If there is no FK
$$
\text{SF}(R[A=B]S) = \frac{1}{\max(\text{ndist}(A), \text{ndist}(B))}
$$
$$
\text{SF}(R[A<B]S) = {^1/_2}
$$
$$
\text{SF}(R[A \leq B]S) = {^1/_2}
$$
## Phases of physiscal optimization
1. Alternatives generation
2. Intermediate results estimation
3. Cost estimation for each algorithm
4. Choose the best option
## Example
```sql
SELECT
DISTINCT w.strength
FROM
wines w, producers p, vintages v
WHERE
v.wineId = w.wineId
AND
p.prodId = v.prodId
AND
p.region = "Priorat"
AND
v.quantity > 100;
```

Tables have the following structures
Producers
* Clustered by `prodId`
* B<sup>+</sup> by `region`
Wines
* Clustered by `wineId`
Vintages
* Clustered by `wineId` and `prodId`
Statistics:
Tables (extra space due to being clustered needs to be added)
$$
\begin{matrix}
|P| = 10000 & |W| = 5000 & |V| = 100000 \\
R_p = 12 & R_w = 10 & R_v = 20 \\
B_p = 834 & B_w = 500 & B_v = 5000
\end{matrix}
$$
Attributes
prodId, wineId and strength: $|R_R| = 5$ bytes
$\text{ndist(region)} = 30$
$\min(\text{quantity}) = 10$ $\max(\text{quantity}) = 500$
$\text{ndist(strength)} = 10$
**System Parameters**
$B = 500$ bytes per intermediate disk block
$D = 1$
$C = 0$
$d = 75$
DBMS:
* Block Nested Loops (6 Memory pages, $M = 4$)
* Row Nested Loops
* Sort Match (with 3 memory pages for sorting, $M = 2$)
```
import math
c_P, c_W, c_V = 10000, 5000, 100000
R_p, R_w, R_v = 12, 10, 20
B_p, B_w, B_v = math.ceil(c_P / R_p), math.ceil(c_W / R_w), math.ceil(c_V / R_v)
print("Cardinality of {}: {}, Records: {}, number of Full Blocks: {}".format('P', c_P, R_p, B_p))
print("Cardinality of {}: {}, Records: {}, number of Full Blocks: {}".format('W', c_W, R_w, B_w))
print("Cardinality of {}: {}, Records: {}, number of Full Blocks: {}".format('V', c_V, R_v, B_v))
```
### Phase 1. Alternatives generation
```sql
SELECT
DISTINCT w.strength
FROM
wines w, producers p, vintages v
WHERE
v.wineId = w.wineId AND p.prodId = v.prodId
AND p.region = "Priorat"
AND v.quantity > 100;
```
Change selection and join arrangement

### Phase 2. Intermediate results estimation
```sql
SELECT
DISTINCT w.strength
FROM
wines w, producers p, vintages v
WHERE
v.wineId = w.wineId AND p.prodId = v.prodId
AND p.region = "Priorat"
AND v.quantity > 100;
```
**PT1 and PT2**
**Selection over V: V'**

Record length of prodId and wineId:
$$|R_{V'}| = 5 + 5 = 10$$
Selectivity factor of selection:
$$
\mathrm{SF}(A > c) = \frac{\max - c}{\max - \min}
$$
Where $c = 100$ and the query specifies `v.quantity > 100`, then:
$$
\text{SF}(\text{quantity} > 100) = \frac{500 - 100}{500 - 10} = 0.81632
$$
Output cardinality of V':
$$
|O| = \text{SF} \cdot |R|
$$
$$
|V'| = \text{SF}(\text{quantity} > 100) \cdot |V| = 0.81632 \cdot 100000 = 81632
$$
Number of records per block:
$$
R_{V'} = \lfloor \frac{B}{|R_{V'}|} \rfloor = \lfloor \frac{500}{10} \rfloor = 50
$$
Number of blocks needed for V':
$$
B_{V'} = \lceil \frac{|V'|}{R_{V'}} \rceil = \lceil \frac{81632}{50} \rceil = 1633
$$
```
c = 100
min_v = 10
max_v = 500
SF_v_prime = (max_v - c) / (max_v - min_v)
print("Selectivity factor of V': {} \n".format(SF_v_prime))
C_v_prime = math.floor(SF_v_prime * c_V)
print("Cardinality output of V': {} \n".format(C_v_prime))
R_v_len = 5 + 5
B = 500
R_v_prime = math.floor(B / R_v_len)
print("V' number of records per block : {} \n".format(R_v_prime))
B_v_prime = math.ceil(C_v_prime / R_v_prime)
print("Blocks needed for V': {} \n".format(B_v_prime))
```
**Selection over P: P'**

Record length of prodId:
$$|R_{P'}| = 5$$
Selectivity factor of selection:
$$
\mathrm{SF}(A = c) = \frac{1}{\text{ndist}(A)}
$$
Where $c = 'Priorat'$ and the query specifies `p.region = 'Priorat'`, then:
$$
\text{SF}(\text{region} = \text{Priorat}) = \frac{1}{30} = 0.033333
$$
Output cardinality of P':
$$
|O| = \text{SF} \cdot |R|
$$
$$
|P'| = \text{SF}(\text{region} = \text{Priorat}) \cdot |P| = 0.03333 \cdot 10000 = 333
$$
Number of records per block:
$$
R_{P'} = \lfloor \frac{B}{|R_{P'}|} \rfloor = \lfloor \frac{500}{5} \rfloor = 100
$$
Number of blocks needed for P':
$$
B_{P'} = \lceil \frac{|P'|}{R_{P'}} \rceil = \lceil \frac{333}{100} \rceil = 4
$$
```
ndist_region = 30
SF_p_prime = 1 / ndist_region
print("Selectivity factor of P': {} \n".format(SF_p_prime))
C_p_prime = math.floor(SF_p_prime * c_P)
print("Cardinality output of P': {} \n".format(C_p_prime))
R_p_len = 5
B = 500
R_p_prime = math.floor(B / R_p_len)
print("P' number of records per block : {} \n".format(R_p_prime))
B_p_prime = math.ceil(C_p_prime / R_p_prime)
print("Blocks needed for P': {} \n".format(B_p_prime))
```
**PT1**
**Join between W and V': WV'**

Record length of `strength` and `prodId`:
$$
|R_{WV'}| = 5 + 5
$$
Selectivity factor
$$
\text{SF}_{WV'} = \frac{1}{|W|} = \frac{1}{5000} = 0.0002
$$
Cardinality ouput of WV'
$$
|WV'| = SF_{WV'} \cdot |W| \cdot |V'| = \frac{1}{5000} \cdot 5000 \cdot 81632 = 81632
$$
Number of rows per block for WV':
$$
R_{WV'} = \lfloor \frac{B}{|R_{WV'}|} \rfloor = \lfloor \frac{500}{5} \rfloor = 50
$$
Number of blocks used for WV':
$$
B_{WV'} = \lceil \frac{|WV'|}{R_{WV'}} \rceil = \lceil \frac{81632}{50} \rceil = 1633
$$
```
SF_wv_prime = 1 / c_W
print("Selectivity factor of WV': {} \n".format(SF_wv_prime))
C_wv_prime = math.floor(SF_wv_prime * c_W * C_v_prime)
print("Cardinality output of WV': {} \n".format(C_wv_prime))
R_wv_prime_len = 5 + 5
B = 500
R_wv_prime = math.floor(B / R_wv_prime_len)
print("WV' number of records per block : {} \n".format(R_wv_prime))
B_wv_prime = math.ceil(C_wv_prime / R_wv_prime)
print("Blocks needed for WV': {} \n".format(B_wv_prime))
```
**Join between WV' and P': WV'P'**

Record length for `strength`:
$$
|R_{WV'P'}| = 5
$$
Selectivity Factor, assuming quantity and region independent
$$
\text{SF(WV'} \cdot \text{P')} = \frac{1}{|P'|} \cdot \frac{1}{ndist(\text{region})} = \frac{1}{333 \cdot 30} = 10^{-4}
$$
Cardinality output
$$
|WV'P'| = SF_{WV'P'} \cdot |WV'| \cdot |P'| = 10^{-4} \cdot 81632 \cdot 333 = 2721
$$
Records per block
$$
R_{WV'P'} = \lfloor \frac{B}{|R_{WV'P'}|} \rfloor = \lfloor \frac{500}{5} \rfloor = 100
$$
Blocks for WV'P'
$$
B_{WV'P'} = \lceil \frac{|WV'P'|}{R_{WV'P'}} \rceil = \lceil \frac{1234}{100} \rceil = 28
$$
```
SF_wvp_prime = (1 / C_p_prime) * (1 / ndist_region)
print("Selectivity factor of WV'P': {} \n".format(SF_wvp_prime))
C_wvp_prime = math.floor(SF_wvp_prime * C_wv_prime * C_p_prime)
print("Cardinality output of WV'P': {} \n".format(C_wvp_prime))
R_wvp_prime_len = 5
B = 500
R_wvp_prime = math.floor(B / R_wvp_prime_len)
print("WV'P' number of records per block : {} \n".format(R_wvp_prime))
B_wvp_prime = math.ceil(C_wvp_prime / R_wvp_prime)
print("Blocks needed for WV'P': {} \n".format(B_wvp_prime))
```
**PT2**

**Join V' and P': V'P'**
Assuming independence of variables
Record length for `wineId`
$$
|R_{V'P'}| = 5
$$
Selectivity factor
$$
\text{SF}_{V'P'} = \frac{1}{ndist(\text{region})} \cdot \frac{1}{|P'|} = \frac{1}{30} \cdot \frac{1}{333} = 10^{-4}
$$
Output cardinality
$$
|V'P'| = \text{SF}_{V'P'} \cdot |V'| \cdot |P'| = 10^{-4} \cdot 81632 \cdot 333 = 2721
$$
Number of records per blocks
$$
R_{V'P'} = \lfloor \frac{B}{R_{V'P'}} \rfloor = \lfloor \frac{500}{R_{5}} \rfloor = 100
$$
Blocks needed for V'P'
$$
B_{V'P'} = \lceil \frac{|V'P'|}{R_{V'P'}} \rceil = \lceil \frac{2721}{100} \rceil = 28
$$
```
ndist_region = 30
SF_vp_prime = (1 / ndist_region) * (1 / C_p_prime)
print("Selectivity factor of V'P': {} \n".format(SF_vp_prime))
C_vp_prime = math.floor(SF_vp_prime * C_v_prime * C_p_prime)
print("Cardinality output of V'P': {} \n".format(C_vp_prime))
R_vp_len = 5
B = 500
R_vp_prime = math.floor(B / R_vp_len)
print("V'P' number of records per block : {} \n".format(R_vp_prime))
B_vp_prime = math.ceil(C_vp_prime / R_vp_prime)
print("Blocks needed for V'P': {} \n".format(B_vp_prime))
```
**Join between W and V'P': WV'P'**

Record length for WV'P'
$$
|R_{WV'P'}| = 5
$$
Selectivity Factor for WV'P'
$$
\text{SF} = \frac{1}{|W|} = \frac{1}{5000} = 0.0002
$$
Cardinality Output
$$
|WV'P'| = SF \cdot |W| \cdot |V'P'| = 10^{-4} \cdot 5000 \cdot 2721 = 2721
$$
Number of records per block
$$
R_{WV'P'} = \lfloor \frac{B}{|R_{WV'P'}|} \rfloor = \lfloor \frac{500}{5} \rfloor = 100
$$
Blocks needes for WV'P'
$$
B_{WV'P'} = \lceil \frac{|WV'P'|}{R_{WV'P'}} \rceil = \lceil \frac{2721}{100} \rceil = 28
$$
```
SF_wv_pr_p_pr = 1 / c_W
print("Selectivity factor of WV'P': {} \n".format(SF_wv_pr_p_pr))
C_wv_pr_p_pr = math.floor(SF_wv_pr_p_pr * c_W * C_vp_prime)
print("Cardinality output of WV'P': {} \n".format(C_wv_pr_p_pr))
R_wv_pr_p_pr_len = 5
B = 500
R_wv_pr_p_pr = math.floor(B / R_wv_pr_p_pr_len)
print("WV'P' number of records per block : {} \n".format(R_wv_pr_p_pr))
B_wv_pr_p_pr = math.ceil(C_wv_pr_p_pr / R_wv_pr_p_pr)
print("Blocks needed for WV'P': {} \n".format(B_wv_pr_p_pr))
```
**PT1/PT2**
**Final result = O**
Record length
$$
|R_O| = 5
$$
Output cardinality
$$
|O| = \text{ndist}(\text{strength}) = 100
$$
Number of records
$$
R_O = \lfloor \frac{B}{|R_O|} \rfloor = \lfloor \frac{500}{5} \rfloor = 100
$$
Blocks needed
$$
B_O = \lceil \frac{|O|}{R_O} \rceil = \lceil \frac{100}{100} \rceil = 1
$$
```
ndist_strength = 100
C_o = ndist_strength
print("Cardinality output of O: {} \n".format(C_o))
R_o_len = 5
B = 500
R_o = math.floor(B / R_o_len)
print("O number of records per block : {} \n".format(R_o))
B_o = math.ceil(C_o / R_o)
print("Blocks needed for O: {} \n".format(B_o))
```
**Map result**

### Phase 3. Cost estimation for each algorithm
Recall:
$$
u = \frac{2}{3} \cdot 2(75) = 100
$$
**AP1/AP2**
**Selection over V: V'**
Recall that for Vintages is clustered by wineId and prodId
Available access paths: No index
$$
\text{cost}_{\text{scan}}(V') = \lceil 1.5 B_{V} \rceil \cdot D = \lceil 1.5 \cdot 5000 \rceil \cdot 1 = 7500
$$
Chosen algorithm: **Scan**
**Selection over P: P'**
Available access paths: B<sup>+</sup> and no index
For a table scan
$$
\text{cost}_{\text{scan}}(P') = \lceil 1.5 B_{P} \rceil \cdot D = \lceil 1.5 \cdot 834 \rceil \cdot 1 = 1251
$$
Tree depth of h for B<sup>+</sup> is:
$$
h = \lceil \log_u |P| \rceil - 1 = \lceil \log_u |P| \rceil - 1 = \lceil \log_{100} 10000 \rceil - 1 = 1
$$
For an index of several tuples
$$
\begin{align}
\text{cost}_{B^+}(P')
& = h \cdot D + \frac{|P'| - 1}{u} \cdot D + |P'| \cdot D \\
& = h \cdot D + \frac{SF_{\text{region = 'Priorat'}} \cdot |P| - 1}{u} \cdot D + SF_{\text{region = 'Priorat'}} \cdot |P| \cdot D \\
& = 1 \cdot 1 + \frac{{^1/_{30}} \cdot 10000 - 1}{100} \cdot D + {^1/_{30}} \cdot 10000 \cdot 1 \\
& = 1 + \frac{332}{100} + 333 \\
& = 337.33
\end{align}
$$
Chosen algorithm: **B<sup>+</sup>**
```
load = 2/3
d = 75
u = load * (2 * d)
h = math.ceil(math.log(c_P, u)) - 1
D = 1
print("load is: {}\nd is: {}\nu is: {}\nh is: {}\nD is: {}\n".format(load, d, u, h, D))
cost_scan_p = math.ceil(1.5 * B_p) * D
cost_bplus_p = (h * D) + ((C_p_prime / u) * D) + (C_p_prime * D)
print("Cost of scan is: {} \nCost of B+ is: {}".format(cost_scan_p, cost_bplus_p))
```
**PT1**
**Join over W and V': WV'**
Available algorithms: Block Nested Loops (BML), Row Nested Loops (RML) and Sort-Match (SM)
*Block Nested Loops*
Recall:
$$
M = 4
$$
$\lceil 1.5 B_{W} \rceil < B_{V'}$ we use the commutative property of joins
$$
\begin{align}
\text{cost}_{\text{BML}}(WV')
& = \lceil 1.5 B_{W} \rceil + \lceil \frac{1.5 B_{W}}{M} \rceil \cdot B_{V'} \\
& = \lceil 1.5 \cdot 500 \rceil + \lceil \frac{1.5\cdot 500}{4} \rceil \cdot 1633 \\
& = 307,754
\end{align}
$$
*Row Nested Loops*
Look for attributes of W
$V'$ does not use extra space any more for being ordered
$$
\begin{align}
\text{cost}_{\text{RML}}(WV')
& = B_{V'} + |V'| \cdot \left( \lceil \log_u |W| \rceil - 1 + 1 + (\frac{1.5(k-1)}{10} \right) \\
& = 1633 + 81,632 \cdot \left( \lceil \log_{100} 5000 \rceil - 1 + 1 \right) \\
& = 164,887
\end{align}
$$
<span style='color:red'>Note: This wasn't explained. Maybe $k = 1$ but needs confirmation.</span>
*Sort-Match*
$W$ is ordered by `wineID`, $V'$ is still ordered y `wineID` and `prodID`.
$$
\text{cost}_{\text{SM}}(WV') = \lceil 1.5 B_{W} \rceil + B_{V'} = \lceil 1.5 \cdot 500 \rceil + 1633 = 2383
$$
Chosen algorithm: **Sort-Match**
**Join between WV' and P': WV'P'**
*Block Nested Loops*
$B_{P'} < B_{WV'}$ we use the commutative property of joins
$$
\begin{align}
\text{cost}_{\text{BML}}(WV'P')
& = B_{P'} + \lceil \frac{B_{P'}}{M} \rceil \cdot B_{WV'} \\
& = 4 + \lceil \frac{4}{4} \rceil \cdot 1633 \\
& = 1637
\end{align}
$$
<span style='color:red'>Note: It isn't explained why BML is analyzed but not RML.</span>
*Sort-Match*
Neither WV’ nor P’ are ordered by `prodID`
$$
\begin{align}
\text{cost}_{\text{SM}}(WV'P')
&= 2 B_{WV'} \cdot \lceil \log_2 B_{WV'} \rceil + 2 B_{P'} \cdot \lceil \log_2 B_{P'} \rceil + B_{WV'} + B_{P'}\\
&= 2 \cdot 1633 \cdot \lceil \log_2 1633 \rceil + 2 \cdot 4 \cdot \lceil \log_2 4 \rceil + 1633 + 4 \\
&= 37,579
\end{align}
$$
Chosen algorithm: **Block Nested Loop**
```
print("B_p' is {}\nB_wv' is {}".format(B_p_prime, B_wv_prime))
(2 * B_wv_prime * math.ceil(math.log(B_wv_prime, 2))) + (2 * B_p_prime * math.ceil(math.log(B_p_prime, 2))) + B_wv_prime + B_p_prime
```
**PT2**
**Join between V' and P': V'P'
Available algorithms: BNL and SM.
*Block Nested Loops*
$B_{P'} < B_{V'}$ we use the commutative property of joins
$$
\begin{align}
\text{cost}_{\text{BML}}(V'P')
& = B_{P'} + \lceil \frac{B_{P'}}{M} \rceil \cdot B_{V'} \\
& = 4 + \lceil \frac{4}{4} \rceil \cdot 1633 \\
& = 1637
\end{align}
$$
*Sort-Match*
Neither V’ nor P’ are ordered by `prodID`
$$
\begin{align}
\text{cost}_{\text{SM}}(V'P')
&= 2 B_{V'} \cdot \lceil \log_2 B_{V'} \rceil + 2 B_{P'} \cdot \lceil \log_2 B_{P'} \rceil + B_{V'} + B_{P'}\\
&= 2 \cdot 1633 \cdot \lceil \log_2 1633 \rceil + 2 \cdot 4 \cdot \lceil \log_2 4 \rceil + 1633 + 4 \\
&= 37,579
\end{align}
$$
Chosen algorithm: **Block Nested Loop**
```
print("B_p' is {}\nB_v' is {}".format(B_p_prime, B_v_prime))
```
**Join between W and V'P': WV'P'**
Available algorithms: Block Nested Loops (BML), Row Nested Loops (RML) and Sort-Match (SM)
*Block Nested Loops*
$B_{V'P'} < \lceil 1.5 B_{W} \rceil$ we use the commutative property of joins
$$
\begin{align}
\text{cost}_{\text{BML}}(WV'P')
& = B_{V'P'} + \lceil \frac{B_{V'P'}}{M} \rceil \cdot \lceil 1.5 B_{W} \rceil \\
& = 28 + \lceil \frac{28}{4} \rceil \cdot \lceil 750 \rceil \\
& = 5278
\end{align}
$$
*Row Nested Loops*
Look for attributes of W
$$
\begin{align}
\text{cost}_{\text{RML}}(WV'P')
& = B_{V'P'} + |V'P'| \cdot \left( \lceil \log_u |W| \rceil - 1 + 1 + (\frac{1.5(k-1)}{10} \right) \\
& = 28 + 2721 \cdot \left( \lceil \log_{100} 5000 \rceil - 1 + 1 \right) \\
& = 5470
\end{align}
$$
*Sort-Match*
W is ordered by `wineID`, V'P' is not sorted by `wineID`
$$
\begin{align}
\text{cost}_{\text{SM}}(WV'P')
&= 2 B_{V'P'} \cdot \lceil \log_2 B_{V'P'} \rceil + \lceil 1.5 B_{W} \rceil + B_{V'P'} \\
&= 2 \cdot 28 \cdot \lceil \log_2 28 \rceil + \lceil 1.5 \cdot 500 \rceil + 28 \\
&= 1058
\end{align}
$$
Chosen algorithm: **Sort-Match**
```
print("B_v'p' is {}\n1.5*B_w is {}\n|V'P'| is {}".format(B_vp_prime, math.ceil(1.5*B_w), C_vp_prime))
28 + math.ceil(28/4) * 750
28+(2721*(math.ceil(math.log(5000, 100)) - 1 + 1))
Cost_v_prime = 1633 + 7500
Cost_p_prime = 4 + 337
Cost_wv = 1633 + 2383
Cost_vp = 28 + 1637
Cost_wvp_pt1 = 28 + 1637
Cost_wvp_pt2 = 28 + 1058
Cost_o = 1 + 252
Cost_pt1 = Cost_v_prime + Cost_p_prime + Cost_wv + Cost_wvp_pt1 + Cost_o
Cost_pt2 = Cost_v_prime + Cost_p_prime + Cost_vp + Cost_wvp_pt2 + Cost_o
print("Total cost of:\nPT1: {}\nPT2: {}".format(Cost_pt1, Cost_pt2))
```
**Map result**
<span style="color:red">Output algorithm is Merge Sort but it's not explained, nor its cost calculation</span>

### Phase 4. Choose the best option
**PT2**
| github_jupyter |
# BLU15 - Model CSI
## Intro:
It often happens that your data distribution changes with time.
More than that, sometimes you don't know how a model was trained and what was the original training data.
In this learning unit we're going to try to identify whether an existing model meets our expectations and redeploy it.
## Problem statement:
As an example, we're going to use the same problem that you met in the last BLU.
You're already familiar with the problem, but just as a reminder:
> The police department has received lots of complaints about its stop and search policy. Every time a car is stopped, the police officers have to decide whether or not to search the car for contraband. According to critics, these searches have a bias against people of certain backgrounds.
You got a model from your client, and **here is the model's description:**
> It's a LightGBM model (LGBMClassifier) trained on the following features:
> - Department Name
> - InterventionLocationName
> - InterventionReasonCode
> - ReportingOfficerIdentificationID
> - ResidentIndicator
> - SearchAuthorizationCode
> - StatuteReason
> - SubjectAge
> - SubjectEthnicityCode
> - SubjectRaceCode
> - SubjectSexCode
> - TownResidentIndicator
> All the categorical feature were one-hot encoded. The only numerical feature (SubjectAge) was not changed. The rows that contain rare categorical features (the ones that appear less than N times in the dataset) were removed. Check the original_model.ipynb notebook for more details.
P.S., if you never heard about lightgbm, XGboost and other gradient boosting, I highly recommend you to read this [article](https://mlcourse.ai/articles/topic10-boosting/) or watch these videos: [part1](https://www.youtube.com/watch?v=g0ZOtzZqdqk), [part2](https://www.youtube.com/watch?v=V5158Oug4W8)
It's not essential for this BLU, so you might leave this link as a desert after you go through the learning materials and solve the exercises, but these are very good models you can use later on, so I suggest reading about them.
**Here are the requirements that the police department created:**
> - A minimum 50% success rate for searches (when a car is searched, it should be at least 50% likely that contraband is found)
> - No police sub-department should have a discrepancy bigger than 5% between the search success rate between protected classes (race, ethnicity, gender)
> - The largest possible amount of contraband found, given the constraints above.
**And here is the description of how the current model succeeds with the requirements:**
- precision score = 50%
- recall = 89.3%
- roc_auc_score for the probability predictions = 82.7%
The precision and recall above are met for probability predictions with a specified threshold equal to **0.21073452797732833**
It's not said whether the second requirement is met, and as it was not met in the previous learning unit, let's ignore it for now.
## Model diagnosing:
Let's firstly try to compare these models to the ones that we created in the previous BLU:
| Model | Baseline | Second iteration | New model | Best model |
|-------------------|---------|--------|--------|--------|
| Requirement 1 - success rate | 0.53 | 0.38 | 0.5 | 1 |
| Requirement 2 - global discrimination (race) | 0.105 | 0.11 | NaN | 1 |
| Requirement 2 - global discrimination (sex) | 0.012 | 0.014 | NaN | 1 |
| Requirement 2 - global discrimination (ethnicity) | 0.114 | 0.101 | NaN | 2 |
| Requirement 2 - # department discrimination (race) | 27 | 17 | NaN | 2 |
| Requirement 2 - # department discrimination (sex) | 19 | 23 | NaN | 1 |
| Requirement 2 - # department discrimination (ethnicity) | 24 | NaN | 23 | 2 |
| Requirement 3 - contraband found (Recall) | 0.65 | 0.76 | 0.893 | 3 |
As we can see, the last model has the exact required success rate (Requirement 1) as we need, and a very good Recall (Requirement 3).
But it might be risky to have such a specific threshold, as we might end up success rate < 0.5 really quickly. It might be a better idea to have a bigger threshold (e.g. 0.25), but let's see.
Let's imagine that the model was trained long time ago.
And now you're in the future trying to evaluate the model, because things might have changed. Data distribution is not always the same, so something that used to work even a year ago could be completely wrong today.
Especially in 2020!
<img src="media/future_2020.jpg" width=400/>
First of all, let's start the server which is running this model.
Open the shell,
```sh
python protected_server.py
```
And read a csv files with new observations from 2020:
```
import joblib
import pandas as pd
import json
import joblib
import pickle
from sklearn.metrics import precision_score, recall_score, roc_auc_score
from sklearn.metrics import confusion_matrix
import requests
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
from sklearn.metrics import precision_recall_curve
%matplotlib inline
df = pd.read_csv('./data/new_observations.csv')
df.head()
```
Let's start from sending all those requests and comparing the model prediction results with the target values.
The model is already prepared to convert our observations to the format its expecting, the only thing we need to change is making department and intervention location names lowercase, and we're good to extract fields from the dataframe and put them to the post request.
```
# lowercaes departments and location names
df['Department Name'] = df['Department Name'].apply(lambda x: str(x).lower())
df['InterventionLocationName'] = df['InterventionLocationName'].apply(lambda x: str(x).lower())
url = "http://127.0.0.1:5000/predict"
headers = {'Content-Type': 'application/json'}
def send_request(index: int, obs: dict, url: str, headers: dict):
observation = {
"id": index,
"observation": {
"Department Name": obs["Department Name"],
"InterventionLocationName": obs["InterventionLocationName"],
"InterventionReasonCode": obs["InterventionReasonCode"],
"ReportingOfficerIdentificationID": obs["ReportingOfficerIdentificationID"],
"ResidentIndicator": obs["ResidentIndicator"],
"SearchAuthorizationCode": obs["SearchAuthorizationCode"],
"StatuteReason": obs["StatuteReason"],
"SubjectAge": obs["SubjectAge"],
"SubjectEthnicityCode": obs["SubjectEthnicityCode"],
"SubjectRaceCode": obs["SubjectRaceCode"],
"SubjectSexCode": obs["SubjectSexCode"],
"TownResidentIndicator": obs["TownResidentIndicator"]
}
}
r = requests.post(url, data=json.dumps(observation), headers=headers)
result = json.loads(r.text)
return result
responses = [send_request(i, obs, url, headers) for i, obs in df.iterrows()]
print(responses[0])
df['proba'] = [r['proba'] for r in responses]
threshold = 0.21073452797732833
# we're going to use the threshold we got from the client
df['prediction'] = [1 if p >= threshold else 0 for p in df['proba']]
```
**NOTE:** We could also load the model and make predictions locally (without using the api), but:
1. I wanted to show you how you might send requests in a similar situation
2. If you have a running API and some model file, you always need to understand how the API works (if it makes any kind of data preprocessing), which might sometimes be complicated, and if you're trying to analyze the model running in production, you still need to make sure that the local predictions you do are equal to the one that the production api does.
```
confusion_matrix(df['ContrabandIndicator'], df['prediction'])
```
If you're not familiar with confusion matrixes, **here is an explanation of the values:**
<img src="./media/confusion_matrix.jpg" alt="drawing" width="500"/>
These values don't seem to be good. Let's once again take a look on the client's requirements and see if we still meet them:
> A minimum 50% success rate for searches (when a car is searched, it should be at least 50% likely that contraband is found)
```
def verify_success_rate_above(y_true, y_pred, min_success_rate=0.5):
"""
Verifies the success rate on a test set is above a provided minimum
"""
precision = precision_score(y_true, y_pred, pos_label=True)
is_satisfied = (precision >= min_success_rate)
return is_satisfied, precision
verify_success_rate_above(df['ContrabandIndicator'], df['prediction'], 0.5)
```

> The largest possible amount of contraband found, given the constraints above.
As the client says, their model recall was 0.893. And what now?
```
def verify_amount_found(y_true, y_pred):
"""
Verifies the amout of contraband found in the test dataset - a.k.a the recall in our test set
"""
recall = recall_score(y_true, y_pred, pos_label=True)
return recall
verify_amount_found(df['ContrabandIndicator'], df['prediction'])
```
<img src="./media/no_please_2.jpg" alt="drawing" width="500"/>
Okay, relax, it happens. Let's start from checking different thresholds. Maybe the selected threshold was to specific and doesn't work anymore.
What about 0.25?
```
threshold = 0.25
df['prediction'] = [1 if p >= threshold else 0 for p in df['proba']]
verify_success_rate_above(df['ContrabandIndicator'], df['prediction'], 0.5)
verify_amount_found(df['ContrabandIndicator'], df['prediction'])
```
<img src="./media/poker.jpg" alt="drawing" width="200"/>
Okay, let's try the same technique to identify the best threshold as they originally did. Maybe we find something good enough.
It's not a good idea to verify such things on the test data, but we're going to use it just to confirm the model's performance, not to select the threshold.
```
precision, recall, thresholds = precision_recall_curve(df['ContrabandIndicator'], df['proba'])
precision = precision[:-1]
recall = recall[:-1]
fig=plt.figure()
ax1 = plt.subplot(211)
ax2 = plt.subplot(212)
ax1.hlines(y=0.5,xmin=0, xmax=1, colors='red')
ax1.plot(thresholds,precision)
ax2.plot(thresholds,recall)
ax1.get_shared_x_axes().join(ax1, ax2)
ax1.set_xticklabels([])
plt.xlabel('Threshold')
ax1.set_title('Precision')
ax2.set_title('Recall')
plt.show()
```
So what do we see? There is some threshold value (around 0.6) that gives us precision >= 0.5.
But the threshold is so big, that the recall at this point is really-really low.
Let's calculate the exact values:
```
min_index = [i for i, prec in enumerate(precision) if prec >= 0.5][0]
print(min_index)
thresholds[min_index]
precision[min_index]
recall[min_index]
```
<img src="./media/incredible.jpg" alt="drawing" width="400"/>
Before we move on, we need to understand why this happens, so that we can decide what kind of action to perform.
Let's try to analyze the changes in data and discuss different things we might want to do.
```
old_df = pd.read_csv('./data/train_searched.csv')
old_df.head()
```
We're going to apply the same changes to the dataset as in the original model notebook unit to understand what was the original data like and how the current dataset differs.
```
old_df = old_df[(old_df['VehicleSearchedIndicator']==True)]
# lowercaes departments and location names
old_df['Department Name'] = old_df['Department Name'].apply(lambda x: str(x).lower())
old_df['InterventionLocationName'] = old_df['InterventionLocationName'].apply(lambda x: str(x).lower())
train_features = old_df.columns.drop(['VehicleSearchedIndicator', 'ContrabandIndicator'])
categorical_features = train_features.drop(['InterventionDateTime', 'SubjectAge'])
numerical_features = ['SubjectAge']
target = 'ContrabandIndicator'
# I'm going to remove less common features.
# Let's create a dictionary with the minimum required number of appearences
min_frequency = {
"Department Name": 50,
"InterventionLocationName": 50,
"ReportingOfficerIdentificationID": 30,
"StatuteReason": 10
}
def filter_values(df: pd.DataFrame, column_name: str, threshold: int):
value_counts = df[column_name].value_counts()
to_keep = value_counts[value_counts > threshold].index
filtered = df[df[column_name].isin(to_keep)]
return filtered
for feature, threshold in min_frequency.items():
old_df = filter_values(old_df, feature, threshold)
old_df.shape
old_df.head()
old_df['ContrabandIndicator'].value_counts(normalize=True)
df['ContrabandIndicator'].value_counts(normalize=True)
```
Looks like we got a bit more contraband now, and it's already a good sign:
if the training data had a different target feature distribution than the test set, the model's predictions might have a different distribution as well. It's a good practice to have the same target feature distribution both in training and test sets.
Let's investigate further
```
new_department_names = df['Department Name'].unique()
old_department_names = old_df['Department Name'].unique()
unknown_departments = [department for department in new_department_names if department not in old_department_names]
len(unknown_departments)
df[df['Department Name'].isin(unknown_departments)].shape
```
So we have 10 departments that the original model was not trained on, but they are only 23 rows from the test set.
Let's repeat the same thing for the Intervention Location names
```
new_location_names = df['InterventionLocationName'].unique()
old_location_names = old_df['InterventionLocationName'].unique()
unknown_locations = [location for location in new_location_names if location not in old_location_names]
len(unknown_locations)
df[df['InterventionLocationName'].isin(unknown_locations)].shape[0]
print('unknown locations: ', df[df['InterventionLocationName'].isin(unknown_locations)].shape[0] * 100 / df.shape[0], '%')
```
Alright, a bit more of unknown locations.
We don't know if the feature was important for the model, so these 5.3% of unknown locations might be important or not.
But it's worth keeping it in mind.
**Here are a few ideas of what we could try to do:**
1. Reanalyze the filtered locations, e.g. filter more rare ones.
2. Create a new category for the rare locations
3. Analyze the unknown locations for containing typos
Let's go further and take a look on the relation between department names and the number of contrabands they find.
We're going to select the most common department names, and then see the percentage of contraband indicator in each one for the training and test sets
```
common_departments = df['Department Name'].value_counts().head(20).index
departments_new = df[df['Department Name'].isin(common_departments)]
departments_old = old_df[old_df['Department Name'].isin(common_departments)]
pd.crosstab(departments_new['ContrabandIndicator'], departments_new['Department Name'], normalize="columns")
pd.crosstab(departments_old['ContrabandIndicator'], departments_old['Department Name'], normalize="columns")
```
We can clearly see that some departments got a huge difference in the contraband indicator.
E.g. Bridgeport used to have 93% of False contrabands, and now has only 62%.
Similar situation with Danbury and New Haven.
Why? Hard to say. There are really a lot of variables here. Maybe the departments got instructed on how to look for contraband.
But we might need to retrain the model.
Let's just finish reviewing other columns.
```
common_location = df['InterventionLocationName'].value_counts().head(20).index
locations_new = df[df['InterventionLocationName'].isin(common_location)]
locations_old = old_df[old_df['InterventionLocationName'].isin(common_location)]
pd.crosstab(locations_new['ContrabandIndicator'], locations_new['InterventionLocationName'], normalize="columns")
pd.crosstab(locations_old['ContrabandIndicator'], locations_old['InterventionLocationName'], normalize="columns")
```
What do we see? First of all, the InterventionLocationName and the Department Name are often same.
It sounds pretty logic, as probably policeman's usually work in the area of their department. But we could try to create a feature saying whether InterventionLocationName is equal to the Department Name.
Or maybe we could just get rid of one of them, if all the values are equal.
What else?
Well, There are similar changes in the Contraband distribution as in Department Name case.
Let's move on:
```
pd.crosstab(df['ContrabandIndicator'], df['InterventionReasonCode'], normalize="columns")
pd.crosstab(old_df['ContrabandIndicator'], old_df['InterventionReasonCode'], normalize="columns")
```
There are some small changes, but they don't seem to be significant.
Especially that all the 3 values have around 33% of Contraband.
Time for officers:
```
df['ReportingOfficerIdentificationID'].value_counts()
filter_values(df, 'ReportingOfficerIdentificationID', 2)['ReportingOfficerIdentificationID'].nunique()
```
Well, looks like there are a lot of unique values for the officer id (1166 for 2000 records), and there are not so many common ones (only 206 officers have more than 2 rows in the dataset) so it doesn't make much sense to analyze it.
Let's quickly go throw the rest of the columns:
```
df.columns
rest = ['ResidentIndicator', 'SearchAuthorizationCode',
'StatuteReason', 'SubjectEthnicityCode',
'SubjectRaceCode', 'SubjectSexCode','TownResidentIndicator']
for col in rest:
display(pd.crosstab(df['ContrabandIndicator'], df[col], normalize="columns"))
display(pd.crosstab(old_df['ContrabandIndicator'], old_df[col], normalize="columns"))
```
We see that all the columns got changes, but they don't seem to be so significant as in the Departments cases.
Anyway, it seems like we need to retrain the model.
<img src="./media/retrain.jpg" alt="drawing" width="400"/>
Retraining a model is always a decision we need to think about.
Was this change in data constant, temporary or seasonal?
In other words, do we expect the data distribution to stay as it is? To change back after Covid? To change from season to season?
**Depending on that, we could retrain the model differently:**
- **If it's a seasonality**, we might want to add features like season or month and train the same model to predict differently depending on the season. We could also investigate time-series classification algorithms.
- **If it's something that is going to change back**, we might either train a new model for this particular period in case the current data distrubution changes were temporary. Otherwise, if we expect the data distribution change here and back from time to time (and we know these periods in advance), we could create a new feature that would help model understand which period it is.
> E.g. if we had a task of predicting beer consumption and had a city that has a lot of football matches, we might add a feature like **football_championship** and make the model predict differently for this occasions.
- **If the data distribution has simply changed and we know that it's never going to come back**, we can simply retrain the model.
> But in some cases we have no idea why some changes appeared (e.g. in this case of departments having more contraband).
- In this case it might be a good idea to train a new model on the new datast and create some monitoring for these features distribution, so we could react when things change.
> So, in our case we don't know what was the reason of data distribution changes, so we'd like to train a model on the new dataset.
> The only thing is the size of the dataset. Original dataset had around 50k rows, and our new set has only 2000. It's not enough to train a good model, so this time we're going to combine both the datasets and add a new feature helping model to distinguish between them. If we had more data, it would be probably better to train a completely new model.
And we're done!
<img src="./media/end.jpg" alt="drawing" width="400"/>
| github_jupyter |
# Reviewing Automated Machine Learning Explanations
As machine learning becomes more and more and more prevelant, the predictions made by models have greater influence over many aspects of our society. For example, machine learning models are an increasingly significant factor in how banks decide to grant loans or doctors prioritise treatments. The ability to interpret and explain models is increasingly important, so that the rationale for the predictions made by machine learning models can be explained and justified, and any inadvertant bias in the model can be identified.
When you use automated machine learning to train a model, you have the option to generate explanations of feature importance that quantify the extent to which each feature influences label prediction. In this lab, you'll explore the explanations generated by an automated machine learning experiment.
## Connect to Your Workspace
The first thing you need to do is to connect to your workspace using the Azure ML SDK.
> **Note**: If the authenticated session with your Azure subscription has expired since you completed the previous exercise, you'll be prompted to reauthenticate.
```
import azureml.core
from azureml.core import Workspace
# Load the workspace from the saved config file
ws = Workspace.from_config()
print('Ready to use Azure ML {} to work with {}'.format(azureml.core.VERSION, ws.name))
```
## Run an Automated Machine Learning Experiment
To reduce time in this lab, you'll run an automated machine learning experiment with only three iterations.
Note that the **model_explainability** configuration option is set to **True**.
```
import pandas as pd
from azureml.train.automl import AutoMLConfig
from azureml.core.experiment import Experiment
from azureml.widgets import RunDetails
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
from azureml.core import Dataset
cluster_name = "gmalc-aml-clust" # Change to your compute cluster name
# Prepare data for training
default_ds = ws.get_default_datastore()
if 'diabetes dataset' not in ws.datasets:
default_ds.upload_files(files=['./data/diabetes.csv', './data/diabetes2.csv'], # Upload the diabetes csv files in /data
target_path='diabetes-data/', # Put it in a folder path in the datastore
overwrite=True, # Replace existing files of the same name
show_progress=True)
#Create a tabular dataset from the path on the datastore (this may take a short while)
tab_data_set = Dataset.Tabular.from_delimited_files(path=(default_ds, 'diabetes-data/*.csv'))
# Register the tabular dataset
try:
tab_data_set = tab_data_set.register(workspace=ws,
name='diabetes dataset',
description='diabetes data',
tags = {'format':'CSV'},
create_new_version=True)
print('Dataset registered.')
except Exception as ex:
print(ex)
else:
print('Dataset already registered.')
train_data = ws.datasets.get("diabetes dataset")
# Configure Auto ML
automl_config = AutoMLConfig(name='Automated ML Experiment',
task='classification',
compute_target='local',
enable_local_managed=True,
training_data = train_data,
n_cross_validations = 2,
label_column_name='Diabetic',
iterations=3,
primary_metric = 'AUC_weighted',
max_concurrent_iterations=3,
featurization='off',
model_explainability=True # Generate feature importance!
)
# Run the Auto ML experiment
print('Submitting Auto ML experiment...')
automl_experiment = Experiment(ws, 'diabetes_automl')
automl_run = automl_experiment.submit(automl_config)
automl_run.wait_for_completion(show_output=True)
RunDetails(automl_run).show()
```
## View Feature Importance
When the experiment has completed in the widget above, click the run that produced the best result to see its details. Then scroll to the bottom of the visualizations to see the relative feature importance.
You can also view feature importance for the best model produced by the experiment by using the **ExplanationClient** class:
```
from azureml.contrib.interpret.explanation.explanation_client import ExplanationClient
from azureml.core.run import Run
# Wait for the best model explanation run to complete
model_explainability_run_id = automl_run.get_properties().get('ModelExplainRunId')
print(model_explainability_run_id)
if model_explainability_run_id is not None:
model_explainability_run = Run(experiment=automl_experiment, run_id=model_explainability_run_id)
model_explainability_run.wait_for_completion(show_output=True)
# Get the best model (2nd item in outputs)
best_run, fitted_model = automl_run.get_output()
# Get the feature explanations
client = ExplanationClient.from_run(best_run)
engineered_explanations = client.download_model_explanation()
feature_importances = engineered_explanations.get_feature_importance_dict()
# Overall feature importance
print('Feature\tImportance')
for key, value in feature_importances.items():
print(key, '\t', value)
```
## View the Model Explanation in Azure Machine Learning studio
With the experiment run completed, click the link in the widget to see the run in Azure Machine Learning studio, and view the **Explanations** tab. Then:
1. Select the explainer that was created by the automated machine learning run.
2. View the **Global Importance** chart, which shows the overall global feature importance.
3. View the **Summary Importance** chart, which shows each data point from the test data in a *swarm*, *violin*, or *box* plot.
4. Select an individual point to see the **Local Feature Importance** for the individual prediction for the selected data point.
> **More Information**: For more information Automated machine Learning, see the [Azure ML documentation](https://docs.microsoft.com/azure/machine-learning/how-to-machine-learning-interpretability-automl).
| github_jupyter |
# Classifying Fashion-MNIST
Now it's your turn to build and train a neural network. You'll be using the [Fashion-MNIST dataset](https://github.com/zalandoresearch/fashion-mnist), a drop-in replacement for the MNIST dataset. MNIST is actually quite trivial with neural networks where you can easily achieve better than 97% accuracy. Fashion-MNIST is a set of 28x28 greyscale images of clothes. It's more complex than MNIST, so it's a better representation of the actual performance of your network, and a better representation of datasets you'll use in the real world.
<img src='assets/fashion-mnist-sprite.png' width=500px>
In this notebook, you'll build your own neural network. For the most part, you could just copy and paste the code from Part 3, but you wouldn't be learning. It's important for you to write the code yourself and get it to work. Feel free to consult the previous notebooks though as you work through this.
First off, let's load the dataset through torchvision.
```
import torch
from torchvision import datasets, transforms
import helper
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))])
# Download and load the training data
trainset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
# Download and load the test data
testset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=False, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=64, shuffle=True)
```
Here we can see one of the images.
```
image, label = next(iter(trainloader))
helper.imshow(image[0,:]);
```
## Building the network
Here you should define your network. As with MNIST, each image is 28x28 which is a total of 784 pixels, and there are 10 classes. You should include at least one hidden layer. We suggest you use ReLU activations for the layers and to return the logits or log-softmax from the forward pass. It's up to you how many layers you add and the size of those layers.
```
from torch import nn, optim
import torch.nn.functional as F
# TODO: Define your network architecture here
class Classifier(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 10)
def forward(self, x):
# make sure input tensor is flattened
x = x.view(x.shape[0], -1)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
x = F.log_softmax(self.fc4(x), dim=1)
return x
```
# Train the network
Now you should create your network and train it. First you'll want to define [the criterion](http://pytorch.org/docs/master/nn.html#loss-functions) (something like `nn.CrossEntropyLoss` or `nn.NLLLoss`) and [the optimizer](http://pytorch.org/docs/master/optim.html) (typically `optim.SGD` or `optim.Adam`).
Then write the training code. Remember the training pass is a fairly straightforward process:
* Make a forward pass through the network to get the logits
* Use the logits to calculate the loss
* Perform a backward pass through the network with `loss.backward()` to calculate the gradients
* Take a step with the optimizer to update the weights
By adjusting the hyperparameters (hidden units, learning rate, etc), you should be able to get the training loss below 0.4.
```
# TODO: Create the network, define the criterion and optimizer
model = Classifier()
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
# TODO: Train the network here
epochs = 5
for e in range(epochs):
running_loss = 0
for images, labels in trainloader:
log_ps = model(images)
loss = criterion(log_ps, labels)
optimizer.zero_grad()
loss.backward()
optimizer.step()
running_loss += loss.item()
else:
print(f"Training loss: {running_loss/len(trainloader)}")
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import helper
# Test out your network!
dataiter = iter(testloader)
images, labels = dataiter.next()
img = images[1]
# TODO: Calculate the class probabilities (softmax) for img
ps = torch.exp(model(img))
# Plot the image and probabilities
helper.view_classify(img, ps, version='Fashion')
```
| github_jupyter |
```
import numpy as np
#Load the predicted 9x12 array
#1st pass
im1=np.array([[4,4,4,4,4,4,4,4,4,4,4,4],
[6,6,2,1,6,6,6,6,6,1,1,2],
[6,6,6,1,1,6,6,6,6,1,1,2],
[2,6,6,6,1,5,5,5,6,1,1,2],
[5,6,6,6,5,5,5,5,5,1,5,5],
[5,5,2,5,5,5,5,5,5,1,5,5],
[5,5,2,5,5,5,5,5,5,6,5,5],
[2,6,6,6,5,5,5,5,5,6,2,2],
[2,6,6,6,6,6,6,2,2,6,2,2]])
#zoomed into driveway
im2=np.array([[2,2,2,1,1,1,2,6,6,6,6,6],
[2,2,2,1,1,1,2,6,6,6,6,6],
[2,2,2,1,1,1,2,6,6,6,6,6],
[2,2,2,1,1,1,1,6,6,6,6,6],
[2,2,2,6,1,1,1,6,6,6,6,6],
[6,6,6,6,1,1,1,1,6,6,6,6],
[6,6,6,6,6,1,1,1,6,6,6,6],
[6,6,6,6,6,6,1,1,2,2,2,2],
[6,6,6,6,6,6,6,1,5,5,5,5]])
#%%timeit
from scipy.ndimage.measurements import label
from scipy.ndimage.measurements import center_of_mass
A=im1
#Center of the 9x12 array
img_center=np.array([4,5.5])
#Label all the driveways and roofs
driveway, num_driveway = label(A==1)
roof, num_roof = label(A==5)
#Save number of driveways into array
d=np.arange(1,num_driveway+1)
r=np.arange(1,num_roof+1)
#Find the center of the all the driveways
driveway_center=center_of_mass(A,driveway,d)
roof_center=center_of_mass(A,roof,r)
print(driveway_center)
#Function to find the closest roof/driveway
def closest(list,img_center):
closest=list[0]
for c in list:
if np.linalg.norm(c-img_center) < np.linalg.norm(closest-img_center):
closest = c
return closest
#Find the closest roof to the center of the image
closest_roof=closest(roof_center,img_center)
#Find the closest driveway to the closest roof
closest_driveway=closest(driveway_center,np.asarray(closest_roof))
print(closest_driveway)
#Look for 3x3 driveway when we have reached a certain height (maybe 5m above ground)
a=im2
#Sliding window function
def sliding_window_view(arr, shape):
n = np.array(arr.shape)
o = n - shape + 1 # output shape
strides = arr.strides
new_shape = np.concatenate((o, shape), axis=0)
new_strides = np.concatenate((strides, strides), axis=0)
return np.lib.stride_tricks.as_strided(arr ,new_shape, new_strides)
#Creates a 7x10 ndarray with all the 3x3 submatrices
sub_image=sliding_window_view(a,(3,3))
#Empty list
driveway_list=[]
#Loop through the 7x10 ndarray
for i in range(0,7):
for j in range(i,10):
#Calculate the total of the submatrices
output=sum(sum(sub_image[i,j]))
#if the output is 9, that means we have a 3x3 that is all driveway
if output==9:
#append the i(row) and j(column) to a list declared previously
#we add 1 to the i and j to find the center of the 3x3
driveway_list.append((i+1,j+1))
#Call closest function to find driveway closest to house.
closest_driveway=closest(driveway_list,np.asarray(closest_roof))
print(closest_driveway)
#Read altitude from csv & Ground Sampling
import csv
def GSD(alt):
sensor_height=4.5 #mm
sensor_width=6.17 #mm
focal_length=1.8
image_height=1080 #pixels
image_width=1920 #pixels
#GSD = (sensor height (mm) x flight height (m) x 100) / (focal lenght (mm) x image height (pixel))
GSD_x=((sensor_width*altitude*100)/(focal_length*image_width))
GSD_y=((sensor_height*altitude*100)/(focal_length*image_height))
return (GSD_x,GSD_y)
#Read alt.csv
with open('alt.csv', 'r') as csvfile:
alt_list = [line.rstrip('\n') for line in csvfile]
#chose last value in alt_list
altitude=int(alt_list[-1]) #in meters
multiplier=GSD(altitude) #cm/pixel
move_coordinates=np.asarray(closest_driveway)*np.asarray(multiplier)*40 #40 is the center of the 80x80 superpixel
print(closest_driveway)
print(multiplier)
print(move_coordinates)
# Write to CSV
import csv
with open('coordinates.csv', 'a', newline='') as csvfile:
filewriter = csv.writer(csvfile, delimiter=',')
filewriter.writerow(move_coordinates)
```
| github_jupyter |
<script async src="https://www.googletagmanager.com/gtag/js?id=UA-59152712-8"></script>
<script>
window.dataLayer = window.dataLayer || [];
function gtag(){dataLayer.push(arguments);}
gtag('js', new Date());
gtag('config', 'UA-59152712-8');
</script>
# Start-to-Finish Example: Unit Testing `GiRaFFE_NRPy`: $A_k$ to $B^i$
## Author: Patrick Nelson
## This module Validates the A-to-B routine for `GiRaFFE`.
**Notebook Status:** <font color='green'><b>Validated</b></font>
**Validation Notes:** This module will validate the routines in [Tutorial-GiRaFFE_NRPy-A2B](Tutorial-GiRaFFE_NRPy-A2B.ipynb).
### NRPy+ Source Code for this module:
* [GiRaFFE_NRPy/GiRaFFE_NRPy_A2B.py](../../edit/in_progress/GiRaFFE_NRPy/GiRaFFE_NRPy_A2B.py) [\[**tutorial**\]](Tutorial-GiRaFFE_NRPy-A2B.ipynb) Generates the driver to compute the magnetic field from the vector potential in arbitrary spactimes.
## Introduction:
This notebook validates our A-to-B solver for use in `GiRaFFE_NRPy`. Because the original `GiRaFFE` used staggered grids and we do not, we can not trivially do a direct comparison to the old code. Instead, we will compare the numerical results with the expected analytic results.
It is, in general, good coding practice to unit test functions individually to verify that they produce the expected and intended output. Here, we expect our functions to produce the correct cross product in an arbitrary spacetime. To that end, we will choose functions that are easy to differentiate, but lack the symmetries that would trivialize the finite-difference algorithm. Higher-order polynomials are one such type of function.
When this notebook is run, if `Use_Gaussian_Data` is `True`, the difference between the approximate and exact magnetic field will be output to text files that can be found in the same directory as this notebook. These will be read in in [Step 3](#convergence), and used there to confirm second order convergence of the algorithm. Otherwise, is `Use_Gaussian_Data` is `False`, polynomial data will be used and the significant digits of agreement between the approximate and exact magnetic field will be printed to the screen right after the code is run [here](#compile_run).
<a id='toc'></a>
# Table of Contents
$$\label{toc}$$
This notebook is organized as follows
1. [Step 1](#setup): Set up core functions and parameters for unit testing the A2B algorithm
1. [Step 1.a](#polynomial) Polynomial vector potential
1. [Step 1.b](#gaussian) Gaussian vector potential
1. [Step 1.c](#magnetic) The magnetic field $B^i$
1. [Step 1.d](#vector_potential) The vector potential $A_k$
1. [Step 1.e](#free_parameters) Set free parameters in the code
1. [Step 2](#mainc): `A2B_unit_test.c`: The Main C Code
1. [Step 2.a](#compile_run): Compile and run the code
1. [Step 3](#convergence): Code validation: Verify that relative error in numerical solution converges to zero at the expected order
1. [Step 4](#latex_pdf_output): Output this notebook to $\LaTeX$-formatted PDF file
<a id='setup'></a>
# Step 1: Set up core functions and parameters for unit testing the A2B algorithm \[Back to [top](#toc)\]
$$\label{setup}$$
We'll start by appending the relevant paths to `sys.path` so that we can access sympy modules in other places. Then, we'll import NRPy+ core functionality and set up a directory in which to carry out our test. We must also set the desired finite differencing order.
```
import shutil, os, sys # Standard Python modules for multiplatform OS-level functions
# First, we'll add the parent directory to the list of directories Python will check for modules.
nrpy_dir_path = os.path.join("..")
if nrpy_dir_path not in sys.path:
sys.path.append(nrpy_dir_path)
from outputC import * # NRPy+: Core C code output module
import finite_difference as fin # NRPy+: Finite difference C code generation module
import NRPy_param_funcs as par # NRPy+: Parameter interface
import grid as gri # NRPy+: Functions having to do with numerical grids
import loop as lp # NRPy+: Generate C code loops
import indexedexp as ixp # NRPy+: Symbolic indexed expression (e.g., tensors, vectors, etc.) support
import reference_metric as rfm # NRPy+: Reference metric support
import cmdline_helper as cmd # NRPy+: Multi-platform Python command-line interface
out_dir = "Validation/"
cmd.mkdir(out_dir)
thismodule = "Start_to_Finish_UnitTest-GiRaFFE_NRPy-A2B"
# Set the finite-differencing order to 2
par.set_parval_from_str("finite_difference::FD_CENTDERIVS_ORDER", 2)
Use_Gaussian_Data = True
a,b,c,d,e,f,g,h,l,m,n,o,p,q,r,s,t,u = par.Cparameters("REAL",thismodule,["a","b","c","d","e","f","g","h","l","m","n","o","p","q","r","s","t","u"],1e300)
gammaDD = ixp.register_gridfunctions_for_single_rank2("AUXEVOL","gammaDD","sym01")
AD = ixp.register_gridfunctions_for_single_rank1("EVOL","AD")
BU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","BU")
```
<a id='polynomial'></a>
## Step 1.a: Polynomial vector potential \[Back to [top](#toc)\]
$$\label{polynomial}$$
We will start with the simplest case - testing the second-order solver. In second-order finite-differencing, we use a three-point stencil that can exactly differentiate polynomials up to quadratic. So, we will use cubic functions three variables. For instance,
\begin{align}
A_x &= ax^3 + by^3 + cz^3 + dy^2 + ez^2 + f \\
A_y &= gx^3 + hy^3 + lz^3 + mx^2 + nz^2 + p \\
A_z &= px^3 + qy^3 + rz^3 + sx^2 + ty^2 + u. \\
\end{align}
It will be much simpler to let NRPy+ handle most of this work. So, we will import the core functionality of NRPy+, build the expressions, and then output them using `outputC()`.
```
if not Use_Gaussian_Data:
is_gaussian = par.Cparameters("int",thismodule,"is_gaussian",0)
par.set_parval_from_str("reference_metric::CoordSystem","Cartesian")
rfm.reference_metric()
x = rfm.xxCart[0]
y = rfm.xxCart[1]
z = rfm.xxCart[2]
AD[0] = a*x**3 + b*y**3 + c*z**3 + d*y**2 + e*z**2 + f
AD[1] = g*x**3 + h*y**3 + l*z**3 + m*x**2 + n*z**2 + o
AD[2] = p*x**3 + q*y**3 + r*z**3 + s*x**2 + t*y**2 + u
```
<a id='gaussian'></a>
## Step 1.b: Gaussian vector potential \[Back to [top](#toc)\]
$$\label{gaussian}$$
Alternatively, we might want to use different functions for the vector potential. Here, we'll give some 3D Gaussians:
\begin{align}
A_x &= a e^{-((x-b)^2+(y-c)^2+(z-d)^2)} \\
A_y &= f e^{-((x-g)^2+(y-h)^2+(z-l)^2)} \\
A_z &= m e^{-((x-n)^2+(y-o)^2+(z-p)^2)}, \\
\end{align}
where $e$ is the natural number.
```
if Use_Gaussian_Data:
is_gaussian = par.Cparameters("int",thismodule,"is_gaussian",1)
par.set_parval_from_str("reference_metric::CoordSystem","Cartesian")
rfm.reference_metric()
x = rfm.xxCart[0]
y = rfm.xxCart[1]
z = rfm.xxCart[2]
AD[0] = a * sp.exp(-((x-b)**2 + (y-c)**2 + (z-d)**2))
AD[1] = f * sp.exp(-((x-g)**2 + (y-h)**2 + (z-l)**2))
AD[2] = m * sp.exp(-((x-n)**2 + (y-o)**2 + (z-p)**2))
```
<a id='magnetic'></a>
## Step 1.c: The magnetic field $B^i$ \[Back to [top](#toc)\]
$$\label{magnetic}$$
Next, we'll let NRPy+ compute derivatives analytically according to $$B^i = \frac{[ijk]}{\sqrt{\gamma}} \partial_j A_k.$$ Then we can carry out two separate tests to verify the numerical derivatives. First, we will verify that when we let the cubic terms be zero, the two calculations of $B^i$ agree to roundoff error. Second, we will verify that when we set the cubic terms, our error is dominated by trunction error that converges to zero at the expected rate.
We will need a sample metric $\gamma_{ij}$ for $\sqrt{\gamma}$. We will thus write a function with the following arbitrary equations.
\begin{align}
\gamma_{xx} &= ax^3 + by^3 + cz^3 + dy^2 + ez^2 + 1 \\
\gamma_{yy} &= gx^3 + hy^3 + lz^3 + mx^2 + nz^2 + 1 \\
\gamma_{zz} &= px^3 + qy^3 + rz^3 + sx^2 + ty^2 + 1. \\
\gamma_{xy} &= \frac{1}{10} \exp\left(-\left((x-b)^2+(y-c)^2+(z-d)^2\right)\right) \\
\gamma_{xz} &= \frac{1}{10} \exp\left(-\left((x-g)^2+(y-h)^2+(z-l)^2\right)\right) \\
\gamma_{yz} &= \frac{1}{10} \exp\left(-\left((x-n)^2+(y-o)^2+(z-p)^2\right)\right), \\
\end{align}
```
par.set_parval_from_str("reference_metric::CoordSystem","Cartesian")
rfm.reference_metric()
x = rfm.xxCart[0]
y = rfm.xxCart[1]
z = rfm.xxCart[2]
gammaDD[0][0] = a*x**3 + b*y**3 + c*z**3 + d*y**2 + e*z**2 + sp.sympify(1)
gammaDD[1][1] = g*x**3 + h*y**3 + l*z**3 + m*x**2 + n*z**2 + sp.sympify(1)
gammaDD[2][2] = p*x**3 + q*y**3 + r*z**3 + s*x**2 + t*y**2 + sp.sympify(1)
gammaDD[0][1] = sp.Rational(1,10) * sp.exp(-((x-b)**2 + (y-c)**2 + (z-d)**2))
gammaDD[0][2] = sp.Rational(1,10) * sp.exp(-((x-g)**2 + (y-h)**2 + (z-l)**2))
gammaDD[1][2] = sp.Rational(1,10) * sp.exp(-((x-n)**2 + (y-o)**2 + (z-p)**2))
import GRHD.equations as gh
gh.compute_sqrtgammaDET(gammaDD)
import WeylScal4NRPy.WeylScalars_Cartesian as weyl
LeviCivitaDDD = weyl.define_LeviCivitaSymbol_rank3()
LeviCivitaUUU = ixp.zerorank3()
for i in range(3):
for j in range(3):
for k in range(3):
LeviCivitaUUU[i][j][k] = LeviCivitaDDD[i][j][k] / gh.sqrtgammaDET
B_analyticU = ixp.register_gridfunctions_for_single_rank1("AUXEVOL","B_analyticU")
for i in range(3):
B_analyticU[i] = 0
for j in range(3):
for k in range(3):
B_analyticU[i] += LeviCivitaUUU[i][j][k] * sp.diff(AD[k],rfm.xxCart[j])
metric_gfs_to_print = [\
lhrh(lhs=gri.gfaccess("aux_gfs","gammaDD00"),rhs=gammaDD[0][0]),\
lhrh(lhs=gri.gfaccess("aux_gfs","gammaDD01"),rhs=gammaDD[0][1]),\
lhrh(lhs=gri.gfaccess("aux_gfs","gammaDD02"),rhs=gammaDD[0][2]),\
lhrh(lhs=gri.gfaccess("aux_gfs","gammaDD11"),rhs=gammaDD[1][1]),\
lhrh(lhs=gri.gfaccess("aux_gfs","gammaDD12"),rhs=gammaDD[1][2]),\
lhrh(lhs=gri.gfaccess("aux_gfs","gammaDD22"),rhs=gammaDD[2][2]),\
]
desc = "Calculate the metric gridfunctions"
name = "calculate_metric_gfs"
outCfunction(
outfile = os.path.join(out_dir,name+".h"), desc=desc, name=name,
params ="const paramstruct *restrict params,REAL *restrict xx[3],REAL *restrict auxevol_gfs",
body = fin.FD_outputC("returnstring",metric_gfs_to_print,params="outCverbose=False").replace("IDX4","IDX4S"),
loopopts="AllPoints,Read_xxs")
```
We also should write a function that will use the analytic formulae for $B^i$.
```
B_analyticU_to_print = [\
lhrh(lhs=gri.gfaccess("out_gfs","B_analyticU0"),rhs=B_analyticU[0]),\
lhrh(lhs=gri.gfaccess("out_gfs","B_analyticU1"),rhs=B_analyticU[1]),\
lhrh(lhs=gri.gfaccess("out_gfs","B_analyticU2"),rhs=B_analyticU[2]),\
]
desc = "Calculate the exact magnetic field"
name = "calculate_exact_BU"
outCfunction(
outfile = os.path.join(out_dir,name+".h"), desc=desc, name=name,
params ="const paramstruct *restrict params,REAL *restrict xx[3],REAL *restrict auxevol_gfs",
body = fin.FD_outputC("returnstring",B_analyticU_to_print,params="outCverbose=False").replace("IDX4","IDX4S"),
loopopts="AllPoints,Read_xxs")
```
<a id='vector_potential'></a>
## Step 1.d: The vector potential $A_k$ \[Back to [top](#toc)\]
$$\label{vector_potential}$$
We'll now write a function to set the vector potential $A_k$. This simply uses NRPy+ to generate most of the code from the expressions we wrote at the beginning. Then, we'll need to call the function from the module `GiRaFFE_NRPy_A2B` to generate the code we need. Also, we will declare the parameters for the vector potential functions.
```
AD_to_print = [\
lhrh(lhs=gri.gfaccess("out_gfs","AD0"),rhs=AD[0]),\
lhrh(lhs=gri.gfaccess("out_gfs","AD1"),rhs=AD[1]),\
lhrh(lhs=gri.gfaccess("out_gfs","AD2"),rhs=AD[2]),\
]
desc = "Calculate the vector potential"
name = "calculate_AD"
outCfunction(
outfile = os.path.join(out_dir,name+".h"), desc=desc, name=name,
params ="const paramstruct *restrict params,REAL *restrict xx[3],REAL *restrict out_gfs",
body = fin.FD_outputC("returnstring",AD_to_print,params="outCverbose=False").replace("IDX4","IDX4S"),
loopopts="AllPoints,Read_xxs")
# cmd.mkdir(os.path.join(out_dir))
import GiRaFFE_NRPy.GiRaFFE_NRPy_A2B as A2B
# We'll generate these into the A2B subdirectory since that's where the functions
# we're testing expect them to be.
AD = ixp.declarerank1("AD") # Make sure these aren't analytic expressions
gammaDD = ixp.declarerank2("gammaDD","sym01")
A2B.GiRaFFE_NRPy_A2B(os.path.join(out_dir,"A2B"),gammaDD,AD,BU)
```
<a id='free_parameters'></a>
## Step 1.e: Set free parameters in the code \[Back to [top](#toc)\]
$$\label{free_parameters}$$
We also need to create the files that interact with NRPy's C parameter interface.
```
# Step 3.d.i: Generate declare_Cparameters_struct.h, set_Cparameters_default.h, and set_Cparameters[-SIMD].h
# par.generate_Cparameters_Ccodes(os.path.join(out_dir))
# Step 3.d.ii: Set free_parameters.h
with open(os.path.join(out_dir,"free_parameters.h"),"w") as file:
file.write("""
// Override parameter defaults with values based on command line arguments and NGHOSTS.
// We'll use this grid. It has one point and one ghost zone.
params.Nxx0 = atoi(argv[1]);
params.Nxx1 = atoi(argv[2]);
params.Nxx2 = atoi(argv[3]);
params.Nxx_plus_2NGHOSTS0 = params.Nxx0 + 2*NGHOSTS;
params.Nxx_plus_2NGHOSTS1 = params.Nxx1 + 2*NGHOSTS;
params.Nxx_plus_2NGHOSTS2 = params.Nxx2 + 2*NGHOSTS;
// Step 0d: Set up space and time coordinates
// Step 0d.i: Declare \Delta x^i=dxx{0,1,2} and invdxx{0,1,2}, as well as xxmin[3] and xxmax[3]:
const REAL xxmin[3] = {-0.01,-0.01,-0.01};
const REAL xxmax[3] = { 0.01, 0.01, 0.01};
params.dxx0 = (xxmax[0] - xxmin[0]) / ((REAL)params.Nxx_plus_2NGHOSTS0-1.0);
params.dxx1 = (xxmax[1] - xxmin[1]) / ((REAL)params.Nxx_plus_2NGHOSTS1-1.0);
params.dxx2 = (xxmax[2] - xxmin[2]) / ((REAL)params.Nxx_plus_2NGHOSTS2-1.0);
printf("dxx0,dxx1,dxx2 = %.5e,%.5e,%.5e\\n",params.dxx0,params.dxx1,params.dxx2);
params.invdx0 = 1.0 / params.dxx0;
params.invdx1 = 1.0 / params.dxx1;
params.invdx2 = 1.0 / params.dxx2;
\n""")
# Generates declare_Cparameters_struct.h, set_Cparameters_default.h, and set_Cparameters[-SIMD].h
par.generate_Cparameters_Ccodes(os.path.join(out_dir))
```
<a id='mainc'></a>
# Step 2: `A2B_unit_test.c`: The Main C Code \[Back to [top](#toc)\]
$$\label{mainc}$$
Now that we have our vector potential and analytic magnetic field to compare against, we will start writing our unit test. We'll also import common C functionality, define `REAL`, the number of ghost zones, and the faces, and set the standard macros for NRPy+ style memory access.
```
%%writefile $out_dir/A2B_unit_test.c
// These are common packages that we are likely to need.
#include "stdio.h"
#include "stdlib.h"
#include "math.h"
#include "string.h" // Needed for strncmp, etc.
#include "stdint.h" // Needed for Windows GCC 6.x compatibility
#include <time.h> // Needed to set a random seed.
#define REAL double
#include "declare_Cparameters_struct.h"
const int MAXFACE = -1;
const int NUL = +0;
const int MINFACE = +1;
const int NGHOSTS = 3;
const int NGHOSTS_A2B = 3;
REAL a,b,c,d,e,f,g,h,l,m,n,o,p,q,r,s,t,u;
// Standard NRPy+ memory access:
#define IDX4S(g,i,j,k) \
( (i) + Nxx_plus_2NGHOSTS0 * ( (j) + Nxx_plus_2NGHOSTS1 * ( (k) + Nxx_plus_2NGHOSTS2 * (g) ) ) )
```
We'll now define the gridfunction names.
```
%%writefile -a $out_dir/A2B_unit_test.c
// Let's also #define the NRPy+ gridfunctions
#define AD0GF 0
#define AD1GF 1
#define AD2GF 2
#define NUM_EVOL_GFS 3
#define GAMMADD00GF 0
#define GAMMADD01GF 1
#define GAMMADD02GF 2
#define GAMMADD11GF 3
#define GAMMADD12GF 4
#define GAMMADD22GF 5
#define B_ANALYTICU0GF 6
#define B_ANALYTICU1GF 7
#define B_ANALYTICU2GF 8
#define BU0GF 9
#define BU1GF 10
#define BU2GF 11
#define NUM_AUXEVOL_GFS 12
```
Now, we'll handle the different A2B codes. There are several things to do here. First, we'll add `#include`s to the C code so that we have access to the functions we want to test, as generated above. We will choose to do this in the subfolder `A2B` relative to this tutorial.
```
%%writefile -a $out_dir/A2B_unit_test.c
#include "A2B/driver_AtoB.h" // This file contains both functions we need.
#include "calculate_exact_BU.h"
#include "calculate_AD.h"
#include "calculate_metric_gfs.h"
```
Now, we'll write the main method. First, we'll set up the grid. In this test, we cannot use only one point. As we are testing a three-point stencil, we can get away with a minimal $3 \times 3 \times 3$ grid. Then, we'll write the A fields. After that, we'll calculate the magnetic field two ways.
```
%%writefile -a $out_dir/A2B_unit_test.c
int main(int argc, const char *argv[]) {
paramstruct params;
#include "set_Cparameters_default.h"
// Let the last argument be the test we're doing. 1 = coarser grid, 0 = finer grid.
int do_quadratic_test = atoi(argv[4]);
// Step 0c: Set free parameters, overwriting Cparameters defaults
// by hand or with command-line input, as desired.
#include "free_parameters.h"
#include "set_Cparameters-nopointer.h"
// We'll define our grid slightly different from how we normally would. We let our outermost
// ghostzones coincide with xxmin and xxmax instead of the interior of the grid. This means
// that the ghostzone points will have identical positions so we can do convergence tests of them. // Step 0d.ii: Set up uniform coordinate grids
REAL *xx[3];
xx[0] = (REAL *)malloc(sizeof(REAL)*Nxx_plus_2NGHOSTS0);
xx[1] = (REAL *)malloc(sizeof(REAL)*Nxx_plus_2NGHOSTS1);
xx[2] = (REAL *)malloc(sizeof(REAL)*Nxx_plus_2NGHOSTS2);
for(int j=0;j<Nxx_plus_2NGHOSTS0;j++) xx[0][j] = xxmin[0] + ((REAL)(j))*dxx0;
for(int j=0;j<Nxx_plus_2NGHOSTS1;j++) xx[1][j] = xxmin[1] + ((REAL)(j))*dxx1;
for(int j=0;j<Nxx_plus_2NGHOSTS2;j++) xx[2][j] = xxmin[2] + ((REAL)(j))*dxx2;
//for(int j=0;j<Nxx_plus_2NGHOSTS0;j++) printf("x[%d] = %.5e\n",j,xx[0][j]);
//for(int i=0;i<Nxx_plus_2NGHOSTS0;i++) printf("xx[0][%d] = %.15e\\n",i,xx[0][i]);
// This is the array to which we'll write the NRPy+ variables.
REAL *auxevol_gfs = (REAL *)malloc(sizeof(REAL) * NUM_AUXEVOL_GFS * Nxx_plus_2NGHOSTS2 * Nxx_plus_2NGHOSTS1 * Nxx_plus_2NGHOSTS0);
REAL *evol_gfs = (REAL *)malloc(sizeof(REAL) * NUM_EVOL_GFS * Nxx_plus_2NGHOSTS2 * Nxx_plus_2NGHOSTS1 * Nxx_plus_2NGHOSTS0);
for(int i=0;i<Nxx_plus_2NGHOSTS0;i++) for(int j=0;j<Nxx_plus_2NGHOSTS1;j++) for(int k=0;k<Nxx_plus_2NGHOSTS1;k++) {
auxevol_gfs[IDX4S(BU0GF,i,j,k)] = 0.0;
auxevol_gfs[IDX4S(BU1GF,i,j,k)] = 0.0;
auxevol_gfs[IDX4S(BU2GF,i,j,k)] = 0.0;
}
// We now want to set up the vector potential. First, we must set the coefficients.
if(is_gaussian) {
// Gaussian coefficients:
// Magnitudes:
a = (double)(rand()%20)/5.0;
f = (double)(rand()%20)/5.0;
m = (double)(rand()%20)/5.0;
// Offsets:
b = (double)(rand()%10-5)/1000.0;
c = (double)(rand()%10-5)/1000.0;
d = (double)(rand()%10-5)/1000.0;
g = (double)(rand()%10-5)/1000.0;
h = (double)(rand()%10-5)/1000.0;
l = (double)(rand()%10-5)/1000.0;
n = (double)(rand()%10-5)/1000.0;
o = (double)(rand()%10-5)/1000.0;
p = (double)(rand()%10-5)/1000.0;
/*printf("Offsets: b,c,d = %f,%f,%f\n",b,c,d);
printf("Offsets: g,h,l = %f,%f,%f\n",g,h,l);
printf("Offsets: n,o,p = %f,%f,%f\n",n,o,p);*/
// First, calculate the test data on our grid:
}
else {
// Polynomial coefficients
// We will use random integers between -10 and 10. For the first test, we let the
// Cubic coefficients remain zero. Those are a,b,c,g,h,l,p,q, and r.
d = (double)(rand()%20-10);
e = (double)(rand()%20-10);
f = (double)(rand()%20-10);
m = (double)(rand()%20-10);
n = (double)(rand()%20-10);
o = (double)(rand()%20-10);
s = (double)(rand()%20-10);
t = (double)(rand()%20-10);
u = (double)(rand()%20-10);
}
calculate_metric_gfs(¶ms,xx,auxevol_gfs);
if(do_quadratic_test && !is_gaussian) {
calculate_AD(¶ms,xx,evol_gfs);
// We'll also calculate the exact solution for B^i
calculate_exact_BU(¶ms,xx,auxevol_gfs);
// And now for the numerical derivatives:
driver_A_to_B(¶ms,evol_gfs,auxevol_gfs);
printf("This test uses quadratic vector potentials, so the magnetic fields should agree to roundoff error.\n");
printf("Below, each row represents one point. Each column represents a component of the magnetic field.\n");
printf("Shown is the number of Significant Digits of Agreement, at least 13 is good, higher is better:\n\n");
for(int i2=0;i2<Nxx_plus_2NGHOSTS2;i2++) for(int i1=0;i1<Nxx_plus_2NGHOSTS1;i1++) for(int i0=0;i0<Nxx_plus_2NGHOSTS0;i0++) {
printf("i0,i1,i2=%d,%d,%d; SDA: %.3f, %.3f, %.3f\n",i0,i1,i2,
1.0-log10(2.0*fabs(auxevol_gfs[IDX4S(B_ANALYTICU0GF,i0,i1,i2)]-auxevol_gfs[IDX4S(BU0GF,i0,i1,i2)])/(fabs(auxevol_gfs[IDX4S(B_ANALYTICU0GF,i0,i1,i2)])+fabs(auxevol_gfs[IDX4S(BU0GF,i0,i1,i2)])+1.e-15)),
1.0-log10(2.0*fabs(auxevol_gfs[IDX4S(B_ANALYTICU1GF,i0,i1,i2)]-auxevol_gfs[IDX4S(BU1GF,i0,i1,i2)])/(fabs(auxevol_gfs[IDX4S(B_ANALYTICU1GF,i0,i1,i2)])+fabs(auxevol_gfs[IDX4S(BU1GF,i0,i1,i2)])+1.e-15)),
1.0-log10(2.0*fabs(auxevol_gfs[IDX4S(B_ANALYTICU2GF,i0,i1,i2)]-auxevol_gfs[IDX4S(BU2GF,i0,i1,i2)])/(fabs(auxevol_gfs[IDX4S(B_ANALYTICU2GF,i0,i1,i2)])+fabs(auxevol_gfs[IDX4S(BU2GF,i0,i1,i2)])+1.e-15))
);
/*printf("%.3f, %.3f, %.3f\n",
auxevol_gfs[IDX4S(BU0GF,i0,i1,i2)],
auxevol_gfs[IDX4S(BU1GF,i0,i1,i2)],
auxevol_gfs[IDX4S(BU2GF,i0,i1,i2)]
);*/
}
}
if(!is_gaussian) {
// Now, we'll set the cubic coefficients:
a = (double)(rand()%20-10);
b = (double)(rand()%20-10);
c = (double)(rand()%20-10);
g = (double)(rand()%20-10);
h = (double)(rand()%20-10);
l = (double)(rand()%20-10);
p = (double)(rand()%20-10);
q = (double)(rand()%20-10);
r = (double)(rand()%20-10);
// First, calculate the test data on our grid:
calculate_metric_gfs(¶ms,xx,auxevol_gfs);
}
// And recalculate on our initial grid:
calculate_AD(¶ms,xx,evol_gfs);
// We'll also calculate the exact solution for B^i
calculate_exact_BU(¶ms,xx,auxevol_gfs);
// And now for the numerical derivatives:
driver_A_to_B(¶ms,evol_gfs,auxevol_gfs);
char filename[100];
sprintf(filename,"out%d-numer.txt",Nxx0);
FILE *out2D = fopen(filename, "w");
if(do_quadratic_test || is_gaussian) {
for(int i2=0;i2<Nxx_plus_2NGHOSTS2;i2++) for(int i1=0;i1<Nxx_plus_2NGHOSTS1;i1++) for(int i0=0;i0<Nxx_plus_2NGHOSTS0;i0++) {
// We print the difference between approximate and exact numbers.
fprintf(out2D,"%.16e\t%.16e\t%.16e %e %e %e\n",
auxevol_gfs[IDX4S(B_ANALYTICU0GF,i0,i1,i2)]-auxevol_gfs[IDX4S(BU0GF,i0,i1,i2)],
auxevol_gfs[IDX4S(B_ANALYTICU1GF,i0,i1,i2)]-auxevol_gfs[IDX4S(BU1GF,i0,i1,i2)],
auxevol_gfs[IDX4S(B_ANALYTICU2GF,i0,i1,i2)]-auxevol_gfs[IDX4S(BU2GF,i0,i1,i2)],
xx[0][i0],xx[1][i1],xx[2][i2]
);
}
}
else {
for(int i2=0;i2<Nxx_plus_2NGHOSTS2;i2++) for(int i1=0;i1<Nxx_plus_2NGHOSTS1;i1++) for(int i0=0;i0<Nxx_plus_2NGHOSTS0;i0++) {
if (i0%2==0 && i1%2==0 && i2%2==0) {
// We print the difference between approximate and exact numbers.
fprintf(out2D,"%.16e\t%.16e\t%.16e %e %e %e\n",
auxevol_gfs[IDX4S(B_ANALYTICU0GF,i0,i1,i2)]-auxevol_gfs[IDX4S(BU0GF,i0,i1,i2)],
auxevol_gfs[IDX4S(B_ANALYTICU1GF,i0,i1,i2)]-auxevol_gfs[IDX4S(BU1GF,i0,i1,i2)],
auxevol_gfs[IDX4S(B_ANALYTICU2GF,i0,i1,i2)]-auxevol_gfs[IDX4S(BU2GF,i0,i1,i2)],
xx[0][i0],xx[1][i1],xx[2][i2]
);
}
}
}
fclose(out2D);
}
```
<a id='compile_run'></a>
## Step 2.a: Compile and run the code \[Back to [top](#toc)\]
$$\label{compile_run}$$
Now that we have our file, we can compile it and run the executable.
```
import time
print("Now compiling, should take ~2 seconds...\n")
start = time.time()
cmd.C_compile(os.path.join(out_dir,"A2B_unit_test.c"), os.path.join(out_dir,"A2B_unit_test"))
end = time.time()
print("Finished in "+str(end-start)+" seconds.\n\n")
print("Now running...\n")
start = time.time()
!./Validation/A2B_unit_test 1 1 1 1
if Use_Gaussian_Data:
# To do a convergence test, we'll also need a second grid with twice the resolution.
!./Validation/A2B_unit_test 7 7 7 1
# !./Validation/A2B_unit_test 19 19 19 1
end = time.time()
print("Finished in "+str(end-start)+" seconds.\n\n")
```
<a id='convergence'></a>
# Step 3: Code validation: Verify that relative error in numerical solution converges to zero at the expected order \[Back to [top](#toc)\]
$$\label{convergence}$$
Now that we have shown that when we use a quadratic vector potential, we get roundoff-level agreement (which is to be expected, since the finite-differencing used approximates the underlying function with a quadratic), we will use do a convergence test to show that when we can't exactly model the function, the truncation error dominates and converges to zero at the expected rate. For this, we use cubic functions for the vector potential. In the code above, we output the difference beteween the numeric and exact magnetic fields at the overlapping, non-edge, non-vertex points of two separate grids. Here, we import that data and calculate the convergence in the usual way,
$$
k = \log_2 \left( \frac{F - F_1}{F - F_2} \right),
$$
where $k$ is the convergence order, $F$ is the exact solution, $F_1$ is the approximate solution on the coarser grid with resolution $\Delta x$, and $F_2$ is the approximate solution on the finer grid with resolution $\Delta x/2$.
Here, we will calculate the convergence of the L2 Norm over the points in each region:
$$
| B^i_{\rm approx} - B^i_{\rm exact}| = \sqrt{\frac{1}{N} \sum_{ijk} \left( B^i_{\rm approx} - B^i_{\rm exact} \right)^2}
$$
```
import numpy as np
import matplotlib.pyplot as plt
Data1 = np.loadtxt("out1-numer.txt")
Data2 = np.loadtxt("out7-numer.txt")
# print("Convergence test: All should be approximately 2\n")
# convergence = np.log(np.divide(np.abs(Data1),np.abs(Data2)))/np.log(2)
# for i in range(len(convergence[:,0])):
# print(convergence[i,:])
def IDX4(i,j,k,Nxx_plus_2NGHOSTS0,Nxx_plus_2NGHOSTS1,Nxx_plus_2NGHOSTS2):
return (i) + Nxx_plus_2NGHOSTS0 * ( (j) + Nxx_plus_2NGHOSTS1 * ( (k) + Nxx_plus_2NGHOSTS2 * (0) ) )
comp = 0 # 0->Bx, 1->By, 2->Bz
# First, let's do this over the interior
N = 7 # This is the number of total gridpoints
nface = 0 # This is the number of points we are taking the norm of.
nint = 0 # This is the number of points we are taking the norm of.
L2_1 = 0
L2_1_xm = 0 # We declare one L2 norm for each face.
L2_1_xp = 0
L2_1_ym = 0
L2_1_yp = 0
L2_1_zm = 0
L2_1_zp = 0
for k in range(N):
for j in range(N):
for i in range(N):
if i==0:
L2_1_xm += Data1[IDX4(i,j,k,N,N,N),comp]**2
nface += 1
if i==N-1:
L2_1_xp += Data1[IDX4(i,j,k,N,N,N),comp]**2
if j==0:
L2_1_ym += Data1[IDX4(i,j,k,N,N,N),comp]**2
if j==N-1:
L2_1_yp += Data1[IDX4(i,j,k,N,N,N),comp]**2
if k==0:
L2_1_zm += Data1[IDX4(i,j,k,N,N,N),comp]**2
if k==N-1:
L2_1_zp += Data1[IDX4(i,j,k,N,N,N),comp]**2
if not (i%(N-1)==0 or j%(N-1)==0 or k%(N-1)==0):
L2_1 += Data1[IDX4(i,j,k,N,N,N),comp]**2
nint += 1
L2_1 = np.sqrt(L2_1/(nint))
L2_1_xm = np.sqrt(L2_1_xm/(nface))
L2_1_xp = np.sqrt(L2_1_xp/(nface))
L2_1_ym = np.sqrt(L2_1_ym/(nface))
L2_1_yp = np.sqrt(L2_1_yp/(nface))
L2_1_zm = np.sqrt(L2_1_zm/(nface))
L2_1_zp = np.sqrt(L2_1_zp/(nface))
N = 13 # This is the number of total gridpoints
nface = 0 # This is the number of points we are taking the norm of.
nint = 0 # This is the number of points we are taking the norm of.
L2_2 = 0
L2_2_xm = 0
L2_2_xp = 0
L2_2_ym = 0
L2_2_yp = 0
L2_2_zm = 0
L2_2_zp = 0
for k in range(N):
for j in range(N):
for i in range(N):
if i==0:
L2_2_xm += Data2[IDX4(i,j,k,N,N,N),comp]**2
nface += 1
if i==N-1:
L2_2_xp += Data2[IDX4(i,j,k,N,N,N),comp]**2
if j==0:
L2_2_ym += Data2[IDX4(i,j,k,N,N,N),comp]**2
if j==N-1:
L2_2_yp += Data2[IDX4(i,j,k,N,N,N),comp]**2
if k==0:
L2_2_zm += Data2[IDX4(i,j,k,N,N,N),comp]**2
if k==N-1:
L2_2_zp += Data2[IDX4(i,j,k,N,N,N),comp]**2
if not (i%(N-1)==0 or j%(N-1)==0 or k%(N-1)==0):
L2_2 += Data2[IDX4(i,j,k,N,N,N),comp]**2
nint += 1
L2_2 = np.sqrt(L2_2/(nint))
L2_2_xm = np.sqrt(L2_2_xm/(nface))
L2_2_xp = np.sqrt(L2_2_xp/(nface))
L2_2_ym = np.sqrt(L2_2_ym/(nface))
L2_2_yp = np.sqrt(L2_2_yp/(nface))
L2_2_zm = np.sqrt(L2_2_zm/(nface))
L2_2_zp = np.sqrt(L2_2_zp/(nface))
print("Face | Res | L2 norm | Conv. Order")
print(" Int | Dx | " + "{:.7f}".format(L2_1) + " | -- ")
print(" -- | Dx/2 | " + "{:.7f}".format(L2_2) + " | " + "{:.5f}".format(np.log2(L2_1/L2_2)))
print(" -x | Dx | " + "{:.7f}".format(L2_1_xm) + " | -- ")
print(" -- | Dx/2 | " + "{:.7f}".format(L2_2_xm) + " | " + "{:.5f}".format(np.log2(L2_1_xm/L2_2_xm)))
print(" +x | Dx | " + "{:.7f}".format(L2_1_xp) + " | -- ")
print(" -- | Dx/2 | " + "{:.7f}".format(L2_2_xp) + " | " + "{:.5f}".format(np.log2(L2_1_xp/L2_2_xp)))
print(" -y | Dx | " + "{:.7f}".format(L2_1_ym) + " | -- ")
print(" -- | Dx/2 | " + "{:.7f}".format(L2_2_ym) + " | " + "{:.5f}".format(np.log2(L2_1_ym/L2_2_ym)))
print(" +y | Dx | " + "{:.7f}".format(L2_1_yp) + " | -- ")
print(" -- | Dx/2 | " + "{:.7f}".format(L2_2_yp) + " | " + "{:.5f}".format(np.log2(L2_1_yp/L2_2_yp)))
print(" -z | Dx | " + "{:.7f}".format(L2_1_zm) + " | -- ")
print(" -- | Dx/2 | " + "{:.7f}".format(L2_2_zm) + " | " + "{:.5f}".format(np.log2(L2_1_zm/L2_2_zm)))
print(" +z | Dx | " + "{:.7f}".format(L2_1_zp) + " | -- ")
print(" -- | Dx/2 | " + "{:.7f}".format(L2_2_zp) + " | " + "{:.5f}".format(np.log2(L2_1_zp/L2_2_zp)))
```
<a id='latex_pdf_output'></a>
# Step 4: Output this notebook to $\LaTeX$-formatted PDF file \[Back to [top](#toc)\]
$$\label{latex_pdf_output}$$
The following code cell converts this Jupyter notebook into a proper, clickable $\LaTeX$-formatted PDF file. After the cell is successfully run, the generated PDF may be found in the root NRPy+ tutorial directory, with filename
[Tutorial-Start_to_Finish_UnitTest-GiRaFFE_NRPy-A2B.pdf](Tutorial-Start_to_Finish_UnitTest-GiRaFFE_NRPy-A2B.pdf) (Note that clicking on this link may not work; you may need to open the PDF file through another means.)
```
!jupyter nbconvert --to latex --template latex_nrpy_style.tplx --log-level='WARN' Tutorial-Start_to_Finish_UnitTest-GiRaFFE_NRPy-A2B.ipynb
!pdflatex -interaction=batchmode Tutorial-Start_to_Finish_UnitTest-GiRaFFE_NRPy-A2B.tex
!pdflatex -interaction=batchmode Tutorial-Start_to_Finish_UnitTest-GiRaFFE_NRPy-A2B.tex
!pdflatex -interaction=batchmode Tutorial-Start_to_Finish_UnitTest-GiRaFFE_NRPy-A2B.tex
!rm -f Tut*.out Tut*.aux Tut*.log
```
| github_jupyter |
http://www.yr.no/place/Norway/Telemark/Vinje/Haukeliseter/climate.month12.html
```
import matplotlib.pyplot as plt
import matplotlib.dates as dates
import numpy as np
import csv
import pandas as pd
import datetime
from datetime import date
import calendar
%matplotlib inline
year = np.arange(2000,2017, 1)
T_av = [-4.1,\
-8.2,\
-10.7,\
-4.3,\
-4.1,\
-5.5,\
-0.5,\
-6.4,\
-6.6,\
-9.4,\
-14.8,\
-4.4,\
-10.7,\
-2.1,\
-6.0,\
-2.4,\
-2.3]
T_av = [float(i) for i in T_av]
Prec = [131.9,\
91.0,\
57.7,\
120.8,\
70.9,\
79.2,\
140.2,\
143.6,\
72.2,\
104.4,\
50.9,\
145.2,\
112.5,\
196.9,\
73.6,\
132.5,\
73.2]
T_ano = -7.5 +4.4
T_ano
prec_tick = np.arange(0,300,50)
t_tick = np.arange(-16,2,2)
fig1 = plt.figure(figsize=(11,7))
ax1 = fig1.add_subplot(1,1,1)
bar2 = ax1.bar(year,Prec, label='precipitation',color='lightblue')
ax1.axhline(y=100,c="gray",linewidth=2,zorder=1, linestyle = '--')
plt.grid(b=None, which='major', axis='y')
# add some text for labels, title and axes ticks
ax1.set_ylabel('Precipitation (%)', fontsize = '16')
ax1.set_yticklabels(prec_tick, fontsize='14')
ax1.set_title('30-yr Climate statistics December (2000 - 2016)', fontsize = '16')
ax1.set_xticks(year)
ax1.set_xticklabels(year, rotation=45,fontsize = '14') # rotate x label
ax1.set_ylim([0, 250])
def autolabel(rects):
"""
Attach a text label above each bar displaying its height
"""
for rect in rects:
height = rect.get_height()
ax1.text(rect.get_x() + rect.get_width()/2., 1.05*height,
'%d.2' % int(height),
ha='center', va='bottom',fontsize =14)
autolabel(bar2)
plt.savefig('../Observations/clim_precDec_Haukeli.png')
#plt.close(fig)
plt.show(fig1)
fig2 = plt.figure(figsize=(11,7))
ax2 = fig2.add_subplot(1,1,1)
line1 = ax2.plot(year,T_av, 'og', label = 'T_avg', markersize = 16)
ax2.axhline(y = -7.5, c ='darkgreen', linewidth = 2, zorder = 0, linestyle = '--')
plt.grid(b=None, which='major', axis='both')
ax2.set_title('30-yr Climate statistics December (2000 - 2016)', fontsize = '16')
ax2.set_xticks(year)
ax2.set_yticklabels(t_tick, fontsize='14')
ax2.set_xticklabels(year, rotation=45,fontsize = '14') # rotate x label
#ax1.legend((bar1[0], bar2[0]), ('Men', 'Women'))
# add some text for labels, title and axes ticks
ax2.set_ylabel('Temperature C$^o$', fontsize = '16')
ax2.set_ylim([-15.5, 0])
plt.savefig('../Observations/clim_tempDec_Haukeli.png')
#plt.close(fig)
plt.show(fig2)
t08 = 100/204.7 * 15.9
t09 = 100/204.7 * 6.7
t10 = 100/204.7 * 5.7
t11 = 100/204.7 * 5.9
t22 = 100/204.7 * 21.4
t23 = 100/204.7 * 23.6
t24 = 100/204.7 * 24.9
t25 = 100/204.7 * 20.8
t26 = 100/204.7 * 13.7
t27 = 100/204.7 * 20.9
t31 = 100/204.7 * 37.8
print(t08,t09,t10,t11)
print(t22,t23,t24,t25,t26,t27)
print(t31)
t22+t23+t24+t25+t26+t27
```
| github_jupyter |
# DB2 Jupyter Notebook Extensions
Version: 2021-08-23
This code is imported as a Jupyter notebook extension in any notebooks you create with DB2 code in it. Place the following line of code in any notebook that you want to use these commands with:
<pre>
%run db2.ipynb
</pre>
This code defines a Jupyter/Python magic command called `%sql` which allows you to execute DB2 specific calls to
the database. There are other packages available for manipulating databases, but this one has been specifically
designed for demonstrating a number of the SQL features available in DB2.
There are two ways of executing the `%sql` command. A single line SQL statement would use the
line format of the magic command:
<pre>
%sql SELECT * FROM EMPLOYEE
</pre>
If you have a large block of sql then you would place the %%sql command at the beginning of the block and then
place the SQL statements into the remainder of the block. Using this form of the `%%sql` statement means that the
notebook cell can only contain SQL and no other statements.
<pre>
%%sql
SELECT * FROM EMPLOYEE
ORDER BY LASTNAME
</pre>
You can have multiple lines in the SQL block (`%%sql`). The default SQL delimiter is the semi-column (`;`).
If you have scripts (triggers, procedures, functions) that use the semi-colon as part of the script, you
will need to use the `-d` option to change the delimiter to an at "`@`" sign.
<pre>
%%sql -d
SELECT * FROM EMPLOYEE
@
CREATE PROCEDURE ...
@
</pre>
The `%sql` command allows most DB2 commands to execute and has a special version of the CONNECT statement.
A CONNECT by itself will attempt to reconnect to the database using previously used settings. If it cannot
connect, it will prompt the user for additional information.
The CONNECT command has the following format:
<pre>
%sql CONNECT TO <database> USER <userid> USING <password | ?> HOST <ip address> PORT <port number>
</pre>
If you use a "`?`" for the password field, the system will prompt you for a password. This avoids typing the
password as clear text on the screen. If a connection is not successful, the system will print the error
message associated with the connect request.
If the connection is successful, the parameters are saved on your system and will be used the next time you
run a SQL statement, or when you issue the %sql CONNECT command with no parameters.
In addition to the -d option, there are a number different options that you can specify at the beginning of
the SQL:
- `-d, -delim` - Change SQL delimiter to "`@`" from "`;`"
- `-q, -quiet` - Quiet results - no messages returned from the function
- `-r, -array` - Return the result set as an array of values instead of a dataframe
- `-t, -time` - Time the following SQL statement and return the number of times it executes in 1 second
- `-j` - Format the first character column of the result set as a JSON record
- `-json` - Return result set as an array of json records
- `-a, -all` - Return all rows in answer set and do not limit display
- `-grid` - Display the results in a scrollable grid
- `-pb, -bar` - Plot the results as a bar chart
- `-pl, -line` - Plot the results as a line chart
- `-pp, -pie` - Plot the results as a pie chart
- `-e, -echo` - Any macro expansions are displayed in an output box
- `-sampledata` - Create and load the EMPLOYEE and DEPARTMENT tables
<p>
You can pass python variables to the `%sql` command by using the `{}` braces with the name of the
variable inbetween. Note that you will need to place proper punctuation around the variable in the event the
SQL command requires it. For instance, the following example will find employee '000010' in the EMPLOYEE table.
<pre>
empno = '000010'
%sql SELECT LASTNAME FROM EMPLOYEE WHERE EMPNO='{empno}'
</pre>
The other option is to use parameter markers. What you would need to do is use the name of the variable with a colon in front of it and the program will prepare the statement and then pass the variable to Db2 when the statement is executed. This allows you to create complex strings that might contain quote characters and other special characters and not have to worry about enclosing the string with the correct quotes. Note that you do not place the quotes around the variable even though it is a string.
<pre>
empno = '000020'
%sql SELECT LASTNAME FROM EMPLOYEE WHERE EMPNO=:empno
</pre>
## Development SQL
The previous set of `%sql` and `%%sql` commands deals with SQL statements and commands that are run in an interactive manner. There is a class of SQL commands that are more suited to a development environment where code is iterated or requires changing input. The commands that are associated with this form of SQL are:
- AUTOCOMMIT
- COMMIT/ROLLBACK
- PREPARE
- EXECUTE
Autocommit is the default manner in which SQL statements are executed. At the end of the successful completion of a statement, the results are commited to the database. There is no concept of a transaction where multiple DML/DDL statements are considered one transaction. The `AUTOCOMMIT` command allows you to turn autocommit `OFF` or `ON`. This means that the set of SQL commands run after the `AUTOCOMMIT OFF` command are executed are not commited to the database until a `COMMIT` or `ROLLBACK` command is issued.
`COMMIT` (`WORK`) will finalize all of the transactions (`COMMIT`) to the database and `ROLLBACK` will undo all of the changes. If you issue a `SELECT` statement during the execution of your block, the results will reflect all of your changes. If you `ROLLBACK` the transaction, the changes will be lost.
`PREPARE` is typically used in a situation where you want to repeatidly execute a SQL statement with different variables without incurring the SQL compilation overhead. For instance:
```
x = %sql PREPARE SELECT LASTNAME FROM EMPLOYEE WHERE EMPNO=?
for y in ['000010','000020','000030']:
%sql execute :x using :y
```
`EXECUTE` is used to execute a previously compiled statement.
To retrieve the error codes that might be associated with any SQL call, the following variables are updated after every call:
* SQLCODE
* SQLSTATE
* SQLERROR - Full error message retrieved from Db2
### Install Db2 Python Driver
If the ibm_db driver is not installed on your system, the subsequent Db2 commands will fail. In order to install the Db2 driver, issue the following command from a Jupyter notebook cell:
```
!pip install --user ibm_db
```
### Db2 Jupyter Extensions
This section of code has the import statements and global variables defined for the remainder of the functions.
```
#
# Set up Jupyter MAGIC commands "sql".
# %sql will return results from a DB2 select statement or execute a DB2 command
#
# IBM 2021: George Baklarz
# Version 2021-07-13
#
from __future__ import print_function
from IPython.display import HTML as pHTML, Image as pImage, display as pdisplay, Javascript as Javascript
from IPython.core.magic import (Magics, magics_class, line_magic,
cell_magic, line_cell_magic, needs_local_scope)
import ibm_db
import pandas
import ibm_db_dbi
import json
import matplotlib
import matplotlib.pyplot as plt
import getpass
import os
import pickle
import time
import sys
import re
import warnings
warnings.filterwarnings("ignore")
# Python Hack for Input between 2 and 3
try:
input = raw_input
except NameError:
pass
_settings = {
"maxrows" : 10,
"maxgrid" : 5,
"runtime" : 1,
"display" : "PANDAS",
"database" : "",
"hostname" : "localhost",
"port" : "50000",
"protocol" : "TCPIP",
"uid" : "DB2INST1",
"pwd" : "password",
"ssl" : ""
}
_environment = {
"jupyter" : True,
"qgrid" : True
}
_display = {
'fullWidthRows': True,
'syncColumnCellResize': True,
'forceFitColumns': False,
'defaultColumnWidth': 150,
'rowHeight': 28,
'enableColumnReorder': False,
'enableTextSelectionOnCells': True,
'editable': False,
'autoEdit': False,
'explicitInitialization': True,
'maxVisibleRows': 5,
'minVisibleRows': 5,
'sortable': True,
'filterable': False,
'highlightSelectedCell': False,
'highlightSelectedRow': True
}
# Connection settings for statements
_connected = False
_hdbc = None
_hdbi = None
_stmt = []
_stmtID = []
_stmtSQL = []
_vars = {}
_macros = {}
_flags = []
_debug = False
# Db2 Error Messages and Codes
sqlcode = 0
sqlstate = "0"
sqlerror = ""
sqlelapsed = 0
# Check to see if QGrid is installed
try:
import qgrid
qgrid.set_defaults(grid_options=_display)
except:
_environment['qgrid'] = False
# Check if we are running in iPython or Jupyter
try:
if (get_ipython().config == {}):
_environment['jupyter'] = False
_environment['qgrid'] = False
else:
_environment['jupyter'] = True
except:
_environment['jupyter'] = False
_environment['qgrid'] = False
```
## Options
There are four options that can be set with the **`%sql`** command. These options are shown below with the default value shown in parenthesis.
- **`MAXROWS n (10)`** - The maximum number of rows that will be displayed before summary information is shown. If the answer set is less than this number of rows, it will be completely shown on the screen. If the answer set is larger than this amount, only the first 5 rows and last 5 rows of the answer set will be displayed. If you want to display a very large answer set, you may want to consider using the grid option `-g` to display the results in a scrollable table. If you really want to show all results then setting MAXROWS to -1 will return all output.
- **`MAXGRID n (5)`** - The maximum size of a grid display. When displaying a result set in a grid `-g`, the default size of the display window is 5 rows. You can set this to a larger size so that more rows are shown on the screen. Note that the minimum size always remains at 5 which means that if the system is unable to display your maximum row size it will reduce the table display until it fits.
- **`DISPLAY PANDAS | GRID (PANDAS)`** - Display the results as a PANDAS dataframe (default) or as a scrollable GRID
- **`RUNTIME n (1)`** - When using the timer option on a SQL statement, the statement will execute for **`n`** number of seconds. The result that is returned is the number of times the SQL statement executed rather than the execution time of the statement. The default value for runtime is one second, so if the SQL is very complex you will need to increase the run time.
- **`LIST`** - Display the current settings
To set an option use the following syntax:
```
%sql option option_name value option_name value ....
```
The following example sets all options:
```
%sql option maxrows 100 runtime 2 display grid maxgrid 10
```
The values will **not** be saved between Jupyter notebooks sessions. If you need to retrieve the current options values, use the LIST command as the only argument:
```
%sql option list
```
```
def setOptions(inSQL):
global _settings, _display
cParms = inSQL.split()
cnt = 0
while cnt < len(cParms):
if cParms[cnt].upper() == 'MAXROWS':
if cnt+1 < len(cParms):
try:
_settings["maxrows"] = int(cParms[cnt+1])
except Exception as err:
errormsg("Invalid MAXROWS value provided.")
pass
cnt = cnt + 1
else:
errormsg("No maximum rows specified for the MAXROWS option.")
return
elif cParms[cnt].upper() == 'MAXGRID':
if cnt+1 < len(cParms):
try:
maxgrid = int(cParms[cnt+1])
if (maxgrid <= 5): # Minimum window size is 5
maxgrid = 5
_display["maxVisibleRows"] = int(cParms[cnt+1])
try:
import qgrid
qgrid.set_defaults(grid_options=_display)
except:
_environment['qgrid'] = False
except Exception as err:
errormsg("Invalid MAXGRID value provided.")
pass
cnt = cnt + 1
else:
errormsg("No maximum rows specified for the MAXROWS option.")
return
elif cParms[cnt].upper() == 'RUNTIME':
if cnt+1 < len(cParms):
try:
_settings["runtime"] = int(cParms[cnt+1])
except Exception as err:
errormsg("Invalid RUNTIME value provided.")
pass
cnt = cnt + 1
else:
errormsg("No value provided for the RUNTIME option.")
return
elif cParms[cnt].upper() == 'DISPLAY':
if cnt+1 < len(cParms):
if (cParms[cnt+1].upper() == 'GRID'):
_settings["display"] = 'GRID'
elif (cParms[cnt+1].upper() == 'PANDAS'):
_settings["display"] = 'PANDAS'
else:
errormsg("Invalid DISPLAY value provided.")
cnt = cnt + 1
else:
errormsg("No value provided for the DISPLAY option.")
return
elif (cParms[cnt].upper() == 'LIST'):
print("(MAXROWS) Maximum number of rows displayed: " + str(_settings["maxrows"]))
print("(MAXGRID) Maximum grid display size: " + str(_settings["maxgrid"]))
print("(RUNTIME) How many seconds to a run a statement for performance testing: " + str(_settings["runtime"]))
print("(DISPLAY) Use PANDAS or GRID display format for output: " + _settings["display"])
return
else:
cnt = cnt + 1
save_settings()
```
### SQL Help
The calling format of this routine is:
```
sqlhelp()
```
This code displays help related to the %sql magic command. This help is displayed when you issue a %sql or %%sql command by itself, or use the %sql -h flag.
```
def sqlhelp():
global _environment
if (_environment["jupyter"] == True):
sd = '<td style="text-align:left;">'
ed1 = '</td>'
ed2 = '</td>'
sh = '<th style="text-align:left;">'
eh1 = '</th>'
eh2 = '</th>'
sr = '<tr>'
er = '</tr>'
helpSQL = """
<h3>SQL Options</h3>
<p>The following options are available as part of a SQL statement. The options are always preceded with a
minus sign (i.e. -q).
<table>
{sr}
{sh}Option{eh1}{sh}Description{eh2}
{er}
{sr}
{sd}a, all{ed1}{sd}Return all rows in answer set and do not limit display{ed2}
{er}
{sr}
{sd}d{ed1}{sd}Change SQL delimiter to "@" from ";"{ed2}
{er}
{sr}
{sd}e, echo{ed1}{sd}Echo the SQL command that was generated after macro and variable substituion.{ed2}
{er}
{sr}
{sd}h, help{ed1}{sd}Display %sql help information.{ed2}
{er}
{sr}
{sd}j{ed1}{sd}Create a pretty JSON representation. Only the first column is formatted{ed2}
{er}
{sr}
{sd}json{ed1}{sd}Retrieve the result set as a JSON record{ed2}
{er}
{sr}
{sd}pb, bar{ed1}{sd}Plot the results as a bar chart{ed2}
{er}
{sr}
{sd}pl, line{ed1}{sd}Plot the results as a line chart{ed2}
{er}
{sr}
{sd}pp, pie{ed1}{sd}Plot Pie: Plot the results as a pie chart{ed2}
{er}
{sr}
{sd}q, quiet{ed1}{sd}Quiet results - no answer set or messages returned from the function{ed2}
{er}
{sr}
{sd}r, array{ed1}{sd}Return the result set as an array of values{ed2}
{er}
{sr}
{sd}sampledata{ed1}{sd}Create and load the EMPLOYEE and DEPARTMENT tables{ed2}
{er}
{sr}
{sd}t,time{ed1}{sd}Time the following SQL statement and return the number of times it executes in 1 second{ed2}
{er}
{sr}
{sd}grid{ed1}{sd}Display the results in a scrollable grid{ed2}
{er}
</table>
"""
else:
helpSQL = """
SQL Options
The following options are available as part of a SQL statement. Options are always
preceded with a minus sign (i.e. -q).
Option Description
a, all Return all rows in answer set and do not limit display
d Change SQL delimiter to "@" from ";"
e, echo Echo the SQL command that was generated after substitution
h, help Display %sql help information
j Create a pretty JSON representation. Only the first column is formatted
json Retrieve the result set as a JSON record
pb, bar Plot the results as a bar chart
pl, line Plot the results as a line chart
pp, pie Plot Pie: Plot the results as a pie chart
q, quiet Quiet results - no answer set or messages returned from the function
r, array Return the result set as an array of values
sampledata Create and load the EMPLOYEE and DEPARTMENT tables
t,time Time the SQL statement and return the execution count per second
grid Display the results in a scrollable grid
"""
helpSQL = helpSQL.format(**locals())
if (_environment["jupyter"] == True):
pdisplay(pHTML(helpSQL))
else:
print(helpSQL)
```
### Connection Help
The calling format of this routine is:
```
connected_help()
```
This code displays help related to the CONNECT command. This code is displayed when you issue a %sql CONNECT command with no arguments or you are running a SQL statement and there isn't any connection to a database yet.
```
def connected_help():
sd = '<td style="text-align:left;">'
ed = '</td>'
sh = '<th style="text-align:left;">'
eh = '</th>'
sr = '<tr>'
er = '</tr>'
if (_environment['jupyter'] == True):
helpConnect = """
<h3>Connecting to Db2</h3>
<p>The CONNECT command has the following format:
<p>
<pre>
%sql CONNECT TO <database> USER <userid> USING <password|?> HOST <ip address> PORT <port number> <SSL>
%sql CONNECT CREDENTIALS <varname>
%sql CONNECT CLOSE
%sql CONNECT RESET
%sql CONNECT PROMPT - use this to be prompted for values
</pre>
<p>
If you use a "?" for the password field, the system will prompt you for a password. This avoids typing the
password as clear text on the screen. If a connection is not successful, the system will print the error
message associated with the connect request.
<p>
The <b>CREDENTIALS</b> option allows you to use credentials that are supplied by Db2 on Cloud instances.
The credentials can be supplied as a variable and if successful, the variable will be saved to disk
for future use. If you create another notebook and use the identical syntax, if the variable
is not defined, the contents on disk will be used as the credentials. You should assign the
credentials to a variable that represents the database (or schema) that you are communicating with.
Using familiar names makes it easier to remember the credentials when connecting.
<p>
<b>CONNECT CLOSE</b> will close the current connection, but will not reset the database parameters. This means that
if you issue the CONNECT command again, the system should be able to reconnect you to the database.
<p>
<b>CONNECT RESET</b> will close the current connection and remove any information on the connection. You will need
to issue a new CONNECT statement with all of the connection information.
<p>
If the connection is successful, the parameters are saved on your system and will be used the next time you
run an SQL statement, or when you issue the %sql CONNECT command with no parameters.
<p>If you issue CONNECT RESET, all of the current values will be deleted and you will need to
issue a new CONNECT statement.
<p>A CONNECT command without any parameters will attempt to re-connect to the previous database you
were using. If the connection could not be established, the program to prompt you for
the values. To cancel the connection attempt, enter a blank value for any of the values. The connection
panel will request the following values in order to connect to Db2:
<table>
{sr}
{sh}Setting{eh}
{sh}Description{eh}
{er}
{sr}
{sd}Database{ed}{sd}Database name you want to connect to.{ed}
{er}
{sr}
{sd}Hostname{ed}
{sd}Use localhost if Db2 is running on your own machine, but this can be an IP address or host name.
{er}
{sr}
{sd}PORT{ed}
{sd}The port to use for connecting to Db2. This is usually 50000.{ed}
{er}
{sr}
{sd}SSL{ed}
{sd}If you are connecting to a secure port (50001) with SSL then you must include this keyword in the connect string.{ed}
{sr}
{sd}Userid{ed}
{sd}The userid to use when connecting (usually DB2INST1){ed}
{er}
{sr}
{sd}Password{ed}
{sd}No password is provided so you have to enter a value{ed}
{er}
</table>
"""
else:
helpConnect = """\
Connecting to Db2
The CONNECT command has the following format:
%sql CONNECT TO database USER userid USING password | ?
HOST ip address PORT port number SSL
%sql CONNECT CREDENTIALS varname
%sql CONNECT CLOSE
%sql CONNECT RESET
If you use a "?" for the password field, the system will prompt you for a password.
This avoids typing the password as clear text on the screen. If a connection is
not successful, the system will print the error message associated with the connect
request.
The CREDENTIALS option allows you to use credentials that are supplied by Db2 on
Cloud instances. The credentials can be supplied as a variable and if successful,
the variable will be saved to disk for future use. If you create another notebook
and use the identical syntax, if the variable is not defined, the contents on disk
will be used as the credentials. You should assign the credentials to a variable
that represents the database (or schema) that you are communicating with. Using
familiar names makes it easier to remember the credentials when connecting.
CONNECT CLOSE will close the current connection, but will not reset the database
parameters. This means that if you issue the CONNECT command again, the system
should be able to reconnect you to the database.
CONNECT RESET will close the current connection and remove any information on the
connection. You will need to issue a new CONNECT statement with all of the connection
information.
If the connection is successful, the parameters are saved on your system and will be
used the next time you run an SQL statement, or when you issue the %sql CONNECT
command with no parameters. If you issue CONNECT RESET, all of the current values
will be deleted and you will need to issue a new CONNECT statement.
A CONNECT command without any parameters will attempt to re-connect to the previous
database you were using. If the connection could not be established, the program to
prompt you for the values. To cancel the connection attempt, enter a blank value for
any of the values. The connection panel will request the following values in order
to connect to Db2:
Setting Description
Database Database name you want to connect to
Hostname Use localhost if Db2 is running on your own machine, but this can
be an IP address or host name.
PORT The port to use for connecting to Db2. This is usually 50000.
Userid The userid to use when connecting (usually DB2INST1)
Password No password is provided so you have to enter a value
SSL Include this keyword to indicate you are connecting via SSL (usually port 50001)
"""
helpConnect = helpConnect.format(**locals())
if (_environment['jupyter'] == True):
pdisplay(pHTML(helpConnect))
else:
print(helpConnect)
```
### Prompt for Connection Information
If you are running an SQL statement and have not yet connected to a database, the %sql command will prompt you for connection information. In order to connect to a database, you must supply:
- Database name
- Host name (IP address or name)
- Port number
- Userid
- Password
- Secure socket
The routine is called without any parameters:
```
connected_prompt()
```
```
# Prompt for Connection information
def connected_prompt():
global _settings
_database = ''
_hostname = ''
_port = ''
_uid = ''
_pwd = ''
_ssl = ''
print("Enter the database connection details (Any empty value will cancel the connection)")
_database = input("Enter the database name: ");
if (_database.strip() == ""): return False
_hostname = input("Enter the HOST IP address or symbolic name: ");
if (_hostname.strip() == ""): return False
_port = input("Enter the PORT number: ");
if (_port.strip() == ""): return False
_ssl = input("Is this a secure (SSL) port (y or n)");
if (_ssl.strip() == ""): return False
if (_ssl == "n"):
_ssl = ""
else:
_ssl = "Security=SSL;"
_uid = input("Enter Userid on the DB2 system: ").upper();
if (_uid.strip() == ""): return False
_pwd = getpass.getpass("Password [password]: ");
if (_pwd.strip() == ""): return False
_settings["database"] = _database.strip()
_settings["hostname"] = _hostname.strip()
_settings["port"] = _port.strip()
_settings["uid"] = _uid.strip()
_settings["pwd"] = _pwd.strip()
_settings["ssl"] = _ssl.strip()
_settings["maxrows"] = 10
_settings["maxgrid"] = 5
_settings["runtime"] = 1
return True
# Split port and IP addresses
def split_string(in_port,splitter=":"):
# Split input into an IP address and Port number
global _settings
checkports = in_port.split(splitter)
ip = checkports[0]
if (len(checkports) > 1):
port = checkports[1]
else:
port = None
return ip, port
```
### Connect Syntax Parser
The parseConnect routine is used to parse the CONNECT command that the user issued within the %sql command. The format of the command is:
```
parseConnect(inSQL)
```
The inSQL string contains the CONNECT keyword with some additional parameters. The format of the CONNECT command is one of:
```
CONNECT RESET
CONNECT CLOSE
CONNECT CREDENTIALS <variable>
CONNECT TO database USER userid USING password HOST hostname PORT portnumber <SSL>
```
If you have credentials available from Db2 on Cloud, place the contents of the credentials into a variable and then use the `CONNECT CREDENTIALS <var>` syntax to connect to the database.
In addition, supplying a question mark (?) for password will result in the program prompting you for the password rather than having it as clear text in your scripts.
When all of the information is checked in the command, the db2_doConnect function is called to actually do the connection to the database.
```
# Parse the CONNECT statement and execute if possible
def parseConnect(inSQL,local_ns):
global _settings, _connected
_connected = False
cParms = inSQL.split()
cnt = 0
_settings["ssl"] = ""
while cnt < len(cParms):
if cParms[cnt].upper() == 'TO':
if cnt+1 < len(cParms):
_settings["database"] = cParms[cnt+1].upper()
cnt = cnt + 1
else:
errormsg("No database specified in the CONNECT statement")
return
elif cParms[cnt].upper() == "SSL":
_settings["ssl"] = "Security=SSL;"
cnt = cnt + 1
elif cParms[cnt].upper() == 'CREDENTIALS':
if cnt+1 < len(cParms):
credentials = cParms[cnt+1]
tempid = eval(credentials,local_ns)
if (isinstance(tempid,dict) == False):
errormsg("The CREDENTIALS variable (" + credentials + ") does not contain a valid Python dictionary (JSON object)")
return
if (tempid == None):
fname = credentials + ".pickle"
try:
with open(fname,'rb') as f:
_id = pickle.load(f)
except:
errormsg("Unable to find credential variable or file.")
return
else:
_id = tempid
try:
_settings["database"] = _id["db"]
_settings["hostname"] = _id["hostname"]
_settings["port"] = _id["port"]
_settings["uid"] = _id["username"]
_settings["pwd"] = _id["password"]
try:
fname = credentials + ".pickle"
with open(fname,'wb') as f:
pickle.dump(_id,f)
except:
errormsg("Failed trying to write Db2 Credentials.")
return
except:
errormsg("Credentials file is missing information. db/hostname/port/username/password required.")
return
else:
errormsg("No Credentials name supplied")
return
cnt = cnt + 1
elif cParms[cnt].upper() == 'USER':
if cnt+1 < len(cParms):
_settings["uid"] = cParms[cnt+1].upper()
cnt = cnt + 1
else:
errormsg("No userid specified in the CONNECT statement")
return
elif cParms[cnt].upper() == 'USING':
if cnt+1 < len(cParms):
_settings["pwd"] = cParms[cnt+1]
if (_settings["pwd"] == '?'):
_settings["pwd"] = getpass.getpass("Password [password]: ") or "password"
cnt = cnt + 1
else:
errormsg("No password specified in the CONNECT statement")
return
elif cParms[cnt].upper() == 'HOST':
if cnt+1 < len(cParms):
hostport = cParms[cnt+1].upper()
ip, port = split_string(hostport)
if (port == None): _settings["port"] = "50000"
_settings["hostname"] = ip
cnt = cnt + 1
else:
errormsg("No hostname specified in the CONNECT statement")
return
elif cParms[cnt].upper() == 'PORT':
if cnt+1 < len(cParms):
_settings["port"] = cParms[cnt+1].upper()
cnt = cnt + 1
else:
errormsg("No port specified in the CONNECT statement")
return
elif cParms[cnt].upper() == 'PROMPT':
if (connected_prompt() == False):
print("Connection canceled.")
return
else:
cnt = cnt + 1
elif cParms[cnt].upper() in ('CLOSE','RESET') :
try:
result = ibm_db.close(_hdbc)
_hdbi.close()
except:
pass
success("Connection closed.")
if cParms[cnt].upper() == 'RESET':
_settings["database"] = ''
return
else:
cnt = cnt + 1
_ = db2_doConnect()
```
### Connect to Db2
The db2_doConnect routine is called when a connection needs to be established to a Db2 database. The command does not require any parameters since it relies on the settings variable which contains all of the information it needs to connect to a Db2 database.
```
db2_doConnect()
```
There are 4 additional variables that are used throughout the routines to stay connected with the Db2 database. These variables are:
- hdbc - The connection handle to the database
- hstmt - A statement handle used for executing SQL statements
- connected - A flag that tells the program whether or not we are currently connected to a database
- runtime - Used to tell %sql the length of time (default 1 second) to run a statement when timing it
The only database driver that is used in this program is the IBM DB2 ODBC DRIVER. This driver needs to be loaded on the system that is connecting to Db2. The Jupyter notebook that is built by this system installs the driver for you so you shouldn't have to do anything other than build the container.
If the connection is successful, the connected flag is set to True. Any subsequent %sql call will check to see if you are connected and initiate another prompted connection if you do not have a connection to a database.
```
def db2_doConnect():
global _hdbc, _hdbi, _connected, _runtime
global _settings
if _connected == False:
if len(_settings["database"]) == 0:
return False
dsn = (
"DRIVER={{IBM DB2 ODBC DRIVER}};"
"DATABASE={0};"
"HOSTNAME={1};"
"PORT={2};"
"PROTOCOL=TCPIP;"
"UID={3};"
"PWD={4};{5}").format(_settings["database"],
_settings["hostname"],
_settings["port"],
_settings["uid"],
_settings["pwd"],
_settings["ssl"])
# Get a database handle (hdbc) and a statement handle (hstmt) for subsequent access to DB2
try:
_hdbc = ibm_db.connect(dsn, "", "")
except Exception as err:
db2_error(False,True) # errormsg(str(err))
_connected = False
_settings["database"] = ''
return False
try:
_hdbi = ibm_db_dbi.Connection(_hdbc)
except Exception as err:
db2_error(False,True) # errormsg(str(err))
_connected = False
_settings["database"] = ''
return False
_connected = True
# Save the values for future use
save_settings()
success("Connection successful.")
return True
```
### Load/Save Settings
There are two routines that load and save settings between Jupyter notebooks. These routines are called without any parameters.
```
load_settings() save_settings()
```
There is a global structure called settings which contains the following fields:
```
_settings = {
"maxrows" : 10,
"maxgrid" : 5,
"runtime" : 1,
"display" : "TEXT",
"database" : "",
"hostname" : "localhost",
"port" : "50000",
"protocol" : "TCPIP",
"uid" : "DB2INST1",
"pwd" : "password"
}
```
The information in the settings structure is used for re-connecting to a database when you start up a Jupyter notebook. When the session is established for the first time, the load_settings() function is called to get the contents of the pickle file (db2connect.pickle, a Jupyter session file) that will be used for the first connection to the database. Whenever a new connection is made, the file is updated with the save_settings() function.
```
def load_settings():
# This routine will load the settings from the previous session if they exist
global _settings
fname = "db2connect.pickle"
try:
with open(fname,'rb') as f:
_settings = pickle.load(f)
# Reset runtime to 1 since it would be unexpected to keep the same value between connections
_settings["runtime"] = 1
_settings["maxgrid"] = 5
except:
pass
return
def save_settings():
# This routine will save the current settings if they exist
global _settings
fname = "db2connect.pickle"
try:
with open(fname,'wb') as f:
pickle.dump(_settings,f)
except:
errormsg("Failed trying to write Db2 Configuration Information.")
return
```
### Error and Message Functions
There are three types of messages that are thrown by the %db2 magic command. The first routine will print out a success message with no special formatting:
```
success(message)
```
The second message is used for displaying an error message that is not associated with a SQL error. This type of error message is surrounded with a red box to highlight the problem. Note that the success message has code that has been commented out that could also show a successful return code with a green box.
```
errormsg(message)
```
The final error message is based on an error occuring in the SQL code that was executed. This code will parse the message returned from the ibm_db interface and parse it to return only the error message portion (and not all of the wrapper code from the driver).
```
db2_error(quiet,connect=False)
```
The quiet flag is passed to the db2_error routine so that messages can be suppressed if the user wishes to ignore them with the -q flag. A good example of this is dropping a table that does not exist. We know that an error will be thrown so we can ignore it. The information that the db2_error routine gets is from the stmt_errormsg() function from within the ibm_db driver. The db2_error function should only be called after a SQL failure otherwise there will be no diagnostic information returned from stmt_errormsg().
If the connect flag is True, the routine will get the SQLSTATE and SQLCODE from the connection error message rather than a statement error message.
```
def db2_error(quiet,connect=False):
global sqlerror, sqlcode, sqlstate, _environment
try:
if (connect == False):
errmsg = ibm_db.stmt_errormsg().replace('\r',' ')
errmsg = errmsg[errmsg.rfind("]")+1:].strip()
else:
errmsg = ibm_db.conn_errormsg().replace('\r',' ')
errmsg = errmsg[errmsg.rfind("]")+1:].strip()
sqlerror = errmsg
msg_start = errmsg.find("SQLSTATE=")
if (msg_start != -1):
msg_end = errmsg.find(" ",msg_start)
if (msg_end == -1):
msg_end = len(errmsg)
sqlstate = errmsg[msg_start+9:msg_end]
else:
sqlstate = "0"
msg_start = errmsg.find("SQLCODE=")
if (msg_start != -1):
msg_end = errmsg.find(" ",msg_start)
if (msg_end == -1):
msg_end = len(errmsg)
sqlcode = errmsg[msg_start+8:msg_end]
try:
sqlcode = int(sqlcode)
except:
pass
else:
sqlcode = 0
except:
errmsg = "Unknown error."
sqlcode = -99999
sqlstate = "-99999"
sqlerror = errmsg
return
msg_start = errmsg.find("SQLSTATE=")
if (msg_start != -1):
msg_end = errmsg.find(" ",msg_start)
if (msg_end == -1):
msg_end = len(errmsg)
sqlstate = errmsg[msg_start+9:msg_end]
else:
sqlstate = "0"
msg_start = errmsg.find("SQLCODE=")
if (msg_start != -1):
msg_end = errmsg.find(" ",msg_start)
if (msg_end == -1):
msg_end = len(errmsg)
sqlcode = errmsg[msg_start+8:msg_end]
try:
sqlcode = int(sqlcode)
except:
pass
else:
sqlcode = 0
if quiet == True: return
if (errmsg == ""): return
html = '<p><p style="border:2px; border-style:solid; border-color:#FF0000; background-color:#ffe6e6; padding: 1em;">'
if (_environment["jupyter"] == True):
pdisplay(pHTML(html+errmsg+"</p>"))
else:
print(errmsg)
# Print out an error message
def errormsg(message):
global _environment
if (message != ""):
html = '<p><p style="border:2px; border-style:solid; border-color:#FF0000; background-color:#ffe6e6; padding: 1em;">'
if (_environment["jupyter"] == True):
pdisplay(pHTML(html + message + "</p>"))
else:
print(message)
def success(message):
if (message != ""):
print(message)
return
def debug(message,error=False):
global _environment
if (_environment["jupyter"] == True):
spacer = "<br>" + " "
else:
spacer = "\n "
if (message != ""):
lines = message.split('\n')
msg = ""
indent = 0
for line in lines:
delta = line.count("(") - line.count(")")
if (msg == ""):
msg = line
indent = indent + delta
else:
if (delta < 0): indent = indent + delta
msg = msg + spacer * (indent*2) + line
if (delta > 0): indent = indent + delta
if (indent < 0): indent = 0
if (error == True):
html = '<p><pre style="font-family: monospace; border:2px; border-style:solid; border-color:#FF0000; background-color:#ffe6e6; padding: 1em;">'
else:
html = '<p><pre style="font-family: monospace; border:2px; border-style:solid; border-color:#008000; background-color:#e6ffe6; padding: 1em;">'
if (_environment["jupyter"] == True):
pdisplay(pHTML(html + msg + "</pre></p>"))
else:
print(msg)
return
```
## Macro Processor
A macro is used to generate SQL to be executed by overriding or creating a new keyword. For instance, the base `%sql` command does not understand the `LIST TABLES` command which is usually used in conjunction with the `CLP` processor. Rather than specifically code this in the base `db2.ipynb` file, we can create a macro that can execute this code for us.
There are three routines that deal with macros.
- checkMacro is used to find the macro calls in a string. All macros are sent to parseMacro for checking.
- runMacro will evaluate the macro and return the string to the parse
- subvars is used to track the variables used as part of a macro call.
- setMacro is used to catalog a macro
### Set Macro
This code will catalog a macro call.
```
def setMacro(inSQL,parms):
global _macros
names = parms.split()
if (len(names) < 2):
errormsg("No command name supplied.")
return None
macroName = names[1].upper()
_macros[macroName] = inSQL
return
```
### Check Macro
This code will check to see if there is a macro command in the SQL. It will take the SQL that is supplied and strip out three values: the first and second keywords, and the remainder of the parameters.
For instance, consider the following statement:
```
CREATE DATABASE GEORGE options....
```
The name of the macro that we want to run is called `CREATE`. We know that there is a SQL command called `CREATE` but this code will call the macro first to see if needs to run any special code. For instance, `CREATE DATABASE` is not part of the `db2.ipynb` syntax, but we can add it in by using a macro.
The check macro logic will strip out the subcommand (`DATABASE`) and place the remainder of the string after `DATABASE` in options.
```
def checkMacro(in_sql):
global _macros
if (len(in_sql) == 0): return(in_sql) # Nothing to do
tokens = parseArgs(in_sql,None) # Take the string and reduce into tokens
macro_name = tokens[0].upper() # Uppercase the name of the token
if (macro_name not in _macros):
return(in_sql) # No macro by this name so just return the string
result = runMacro(_macros[macro_name],in_sql,tokens) # Execute the macro using the tokens we found
return(result) # Runmacro will either return the original SQL or the new one
```
### Split Assignment
This routine will return the name of a variable and it's value when the format is x=y. If y is enclosed in quotes, the quotes are removed.
```
def splitassign(arg):
var_name = "null"
var_value = "null"
arg = arg.strip()
eq = arg.find("=")
if (eq != -1):
var_name = arg[:eq].strip()
temp_value = arg[eq+1:].strip()
if (temp_value != ""):
ch = temp_value[0]
if (ch in ["'",'"']):
if (temp_value[-1:] == ch):
var_value = temp_value[1:-1]
else:
var_value = temp_value
else:
var_value = temp_value
else:
var_value = arg
return var_name, var_value
```
### Parse Args
The commands that are used in the macros need to be parsed into their separate tokens. The tokens are separated by blanks and strings that enclosed in quotes are kept together.
```
def parseArgs(argin,_vars):
quoteChar = ""
inQuote = False
inArg = True
args = []
arg = ''
for ch in argin.lstrip():
if (inQuote == True):
if (ch == quoteChar):
inQuote = False
arg = arg + ch #z
else:
arg = arg + ch
elif (ch == "\"" or ch == "\'"): # Do we have a quote
quoteChar = ch
arg = arg + ch #z
inQuote = True
elif (ch == " "):
if (arg != ""):
arg = subvars(arg,_vars)
args.append(arg)
else:
args.append("null")
arg = ""
else:
arg = arg + ch
if (arg != ""):
arg = subvars(arg,_vars)
args.append(arg)
return(args)
```
### Run Macro
This code will execute the body of the macro and return the results for that macro call.
```
def runMacro(script,in_sql,tokens):
result = ""
runIT = True
code = script.split("\n")
level = 0
runlevel = [True,False,False,False,False,False,False,False,False,False]
ifcount = 0
_vars = {}
for i in range(0,len(tokens)):
vstr = str(i)
_vars[vstr] = tokens[i]
if (len(tokens) == 0):
_vars["argc"] = "0"
else:
_vars["argc"] = str(len(tokens)-1)
for line in code:
line = line.strip()
if (line == "" or line == "\n"): continue
if (line[0] == "#"): continue # A comment line starts with a # in the first position of the line
args = parseArgs(line,_vars) # Get all of the arguments
if (args[0] == "if"):
ifcount = ifcount + 1
if (runlevel[level] == False): # You can't execute this statement
continue
level = level + 1
if (len(args) < 4):
print("Macro: Incorrect number of arguments for the if clause.")
return insql
arg1 = args[1]
arg2 = args[3]
if (len(arg2) > 2):
ch1 = arg2[0]
ch2 = arg2[-1:]
if (ch1 in ['"',"'"] and ch1 == ch2):
arg2 = arg2[1:-1].strip()
op = args[2]
if (op in ["=","=="]):
if (arg1 == arg2):
runlevel[level] = True
else:
runlevel[level] = False
elif (op in ["<=","=<"]):
if (arg1 <= arg2):
runlevel[level] = True
else:
runlevel[level] = False
elif (op in [">=","=>"]):
if (arg1 >= arg2):
runlevel[level] = True
else:
runlevel[level] = False
elif (op in ["<>","!="]):
if (arg1 != arg2):
runlevel[level] = True
else:
runlevel[level] = False
elif (op in ["<"]):
if (arg1 < arg2):
runlevel[level] = True
else:
runlevel[level] = False
elif (op in [">"]):
if (arg1 > arg2):
runlevel[level] = True
else:
runlevel[level] = False
else:
print("Macro: Unknown comparison operator in the if statement:" + op)
continue
elif (args[0] in ["exit","echo"] and runlevel[level] == True):
msg = ""
for msgline in args[1:]:
if (msg == ""):
msg = subvars(msgline,_vars)
else:
msg = msg + " " + subvars(msgline,_vars)
if (msg != ""):
if (args[0] == "echo"):
debug(msg,error=False)
else:
debug(msg,error=True)
if (args[0] == "exit"): return ''
elif (args[0] == "pass" and runlevel[level] == True):
pass
elif (args[0] == "var" and runlevel[level] == True):
value = ""
for val in args[2:]:
if (value == ""):
value = subvars(val,_vars)
else:
value = value + " " + subvars(val,_vars)
value.strip()
_vars[args[1]] = value
elif (args[0] == 'else'):
if (ifcount == level):
runlevel[level] = not runlevel[level]
elif (args[0] == 'return' and runlevel[level] == True):
return(result)
elif (args[0] == "endif"):
ifcount = ifcount - 1
if (ifcount < level):
level = level - 1
if (level < 0):
print("Macro: Unmatched if/endif pairs.")
return ''
else:
if (runlevel[level] == True):
if (result == ""):
result = subvars(line,_vars)
else:
result = result + "\n" + subvars(line,_vars)
return(result)
```
### Substitute Vars
This routine is used by the runMacro program to track variables that are used within Macros. These are kept separate from the rest of the code.
```
def subvars(script,_vars):
if (_vars == None): return script
remainder = script
result = ""
done = False
while done == False:
bv = remainder.find("{")
if (bv == -1):
done = True
continue
ev = remainder.find("}")
if (ev == -1):
done = True
continue
result = result + remainder[:bv]
vvar = remainder[bv+1:ev]
remainder = remainder[ev+1:]
upper = False
allvars = False
if (vvar[0] == "^"):
upper = True
vvar = vvar[1:]
elif (vvar[0] == "*"):
vvar = vvar[1:]
allvars = True
else:
pass
if (vvar in _vars):
if (upper == True):
items = _vars[vvar].upper()
elif (allvars == True):
try:
iVar = int(vvar)
except:
return(script)
items = ""
sVar = str(iVar)
while sVar in _vars:
if (items == ""):
items = _vars[sVar]
else:
items = items + " " + _vars[sVar]
iVar = iVar + 1
sVar = str(iVar)
else:
items = _vars[vvar]
else:
if (allvars == True):
items = ""
else:
items = "null"
result = result + items
if (remainder != ""):
result = result + remainder
return(result)
```
### SQL Timer
The calling format of this routine is:
```
count = sqlTimer(hdbc, runtime, inSQL)
```
This code runs the SQL string multiple times for one second (by default). The accuracy of the clock is not that great when you are running just one statement, so instead this routine will run the code multiple times for a second to give you an execution count. If you need to run the code for more than one second, the runtime value needs to be set to the number of seconds you want the code to run.
The return result is always the number of times that the code executed. Note, that the program will skip reading the data if it is a SELECT statement so it doesn't included fetch time for the answer set.
```
def sqlTimer(hdbc, runtime, inSQL):
count = 0
t_end = time.time() + runtime
while time.time() < t_end:
try:
stmt = ibm_db.exec_immediate(hdbc,inSQL)
if (stmt == False):
db2_error(flag(["-q","-quiet"]))
return(-1)
ibm_db.free_result(stmt)
except Exception as err:
db2_error(False)
return(-1)
count = count + 1
return(count)
```
### Split Args
This routine takes as an argument a string and then splits the arguments according to the following logic:
* If the string starts with a `(` character, it will check the last character in the string and see if it is a `)` and then remove those characters
* Every parameter is separated by a comma `,` and commas within quotes are ignored
* Each parameter returned will have three values returned - one for the value itself, an indicator which will be either True if it was quoted, or False if not, and True or False if it is numeric.
Example:
```
"abcdef",abcdef,456,"856"
```
Three values would be returned:
```
[abcdef,True,False],[abcdef,False,False],[456,False,True],[856,True,False]
```
Any quoted string will be False for numeric. The way that the parameters are handled are up to the calling program. However, in the case of Db2, the quoted strings must be in single quotes so any quoted parameter using the double quotes `"` must be wrapped with single quotes. There is always a possibility that a string contains single quotes (i.e. O'Connor) so any substituted text should use `''` so that Db2 can properly interpret the string. This routine does not adjust the strings with quotes, and depends on the variable subtitution routine to do that.
```
def splitargs(arguments):
import types
# String the string and remove the ( and ) characters if they at the beginning and end of the string
results = []
step1 = arguments.strip()
if (len(step1) == 0): return(results) # Not much to do here - no args found
if (step1[0] == '('):
if (step1[-1:] == ')'):
step2 = step1[1:-1]
step2 = step2.strip()
else:
step2 = step1
else:
step2 = step1
# Now we have a string without brackets. Start scanning for commas
quoteCH = ""
pos = 0
arg = ""
args = []
while pos < len(step2):
ch = step2[pos]
if (quoteCH == ""): # Are we in a quote?
if (ch in ('"',"'")): # Check to see if we are starting a quote
quoteCH = ch
arg = arg + ch
pos += 1
elif (ch == ","): # Are we at the end of a parameter?
arg = arg.strip()
args.append(arg)
arg = ""
inarg = False
pos += 1
else: # Continue collecting the string
arg = arg + ch
pos += 1
else:
if (ch == quoteCH): # Are we at the end of a quote?
arg = arg + ch # Add the quote to the string
pos += 1 # Increment past the quote
quoteCH = "" # Stop quote checking (maybe!)
else:
pos += 1
arg = arg + ch
if (quoteCH != ""): # So we didn't end our string
arg = arg.strip()
args.append(arg)
elif (arg != ""): # Something left over as an argument
arg = arg.strip()
args.append(arg)
else:
pass
results = []
for arg in args:
result = []
if (len(arg) > 0):
if (arg[0] in ('"',"'")):
value = arg[1:-1]
isString = True
isNumber = False
else:
isString = False
isNumber = False
try:
value = eval(arg)
if (type(value) == int):
isNumber = True
elif (isinstance(value,float) == True):
isNumber = True
else:
value = arg
except:
value = arg
else:
value = ""
isString = False
isNumber = False
result = [value,isString,isNumber]
results.append(result)
return results
```
### DataFrame Table Creation
When using dataframes, it is sometimes useful to use the definition of the dataframe to create a Db2 table. The format of the command is:
```
%sql using <df> create table <table> [with data | columns asis]
```
The value <df> is the name of the dataframe, not the contents (`:df`). The definition of the data types in the dataframe will be used to create the Db2 table using typical Db2 data types rather than generic CLOBs and FLOAT for numeric objects. The two options are used to handle how the conversion is done. If you supply `with data`, the contents of the df will be inserted into the table, otherwise the table is defined only. The column names will be uppercased and special characters (like blanks) will be replaced with underscores. If `columns asis` is specified, the column names will remain the same as in the dataframe, with each name using quotes to guarantee the same spelling as in the DF.
If the table already exists, the command will not run and an error message will be produced.
```
def createDF(hdbc,sqlin,local_ns):
import datetime
import ibm_db
global sqlcode
# Strip apart the command into tokens based on spaces
tokens = sqlin.split()
token_count = len(tokens)
if (token_count < 5): # Not enough parameters
errormsg("Insufficient arguments for USING command. %sql using df create table name [with data | columns asis]")
return
keyword_command = tokens[0].upper()
dfName = tokens[1]
keyword_create = tokens[2].upper()
keyword_table = tokens[3].upper()
table = tokens[4]
if (keyword_create not in ("CREATE","REPLACE") or keyword_table != "TABLE"):
errormsg("Incorrect syntax: %sql using <df> create table <name> [options]")
return
if (token_count % 2 != 1):
errormsg("Insufficient arguments for USING command. %sql using df create table name [with data | columns asis | keep float]")
return
flag_withdata = False
flag_asis = False
flag_float = False
flag_integer = False
limit = -1
if (keyword_create == "REPLACE"):
%sql -q DROP TABLE {table}
for token_idx in range(5,token_count,2):
option_key = tokens[token_idx].upper()
option_val = tokens[token_idx+1].upper()
if (option_key == "WITH" and option_val == "DATA"):
flag_withdata = True
elif (option_key == "COLUMNS" and option_val == "ASIS"):
flag_asis = True
elif (option_key == "KEEP" and option_val == "FLOAT64"):
flag_float = True
elif (option_key == "KEEP" and option_val == "INT64"):
flag_integer = True
elif (option_key == "LIMIT"):
if (option_val.isnumeric() == False):
errormsg("The LIMIT must be a valid number from -1 (unlimited) to the maximun number of rows to insert")
return
limit = int(option_val)
else:
errormsg("Invalid options. Must be either WITH DATA | COLUMNS ASIS | KEEP FLOAT64 | KEEP FLOAT INT64")
return
dfName = tokens[1]
if (dfName not in local_ns):
errormsg("The variable ({dfName}) does not exist in the local variable list.")
return
try:
df_value = eval(dfName,None,local_ns) # globals()[varName] # eval(varName)
except:
errormsg("The variable ({dfName}) does not contain a value.")
return
if (isinstance(df_value,pandas.DataFrame) == False): # Not a Pandas dataframe
errormsg("The variable ({dfName}) is not a Pandas dataframe.")
return
sql = []
columns = dict(df_value.dtypes)
sql.append(f'CREATE TABLE {table} (')
datatypes = []
comma = ""
for column in columns:
datatype = columns[column]
if (datatype == "object"):
datapoint = df_value[column][0]
if (isinstance(datapoint,datetime.datetime)):
type = "TIMESTAMP"
elif (isinstance(datapoint,datetime.time)):
type = "TIME"
elif (isinstance(datapoint,datetime.date)):
type = "DATE"
elif (isinstance(datapoint,float)):
if (flag_float == True):
type = "FLOAT"
else:
type = "DECFLOAT"
elif (isinstance(datapoint,int)):
if (flag_integer == True):
type = "BIGINT"
else:
type = "INTEGER"
elif (isinstance(datapoint,str)):
maxlength = df_value[column].apply(str).apply(len).max()
type = f"VARCHAR({maxlength})"
else:
type = "CLOB"
elif (datatype == "int64"):
if (flag_integer == True):
type = "BIGINT"
else:
type = "INTEGER"
elif (datatype == "float64"):
if (flag_float == True):
type = "FLOAT"
else:
type = "DECFLOAT"
elif (datatype == "datetime64"):
type = "TIMESTAMP"
elif (datatype == "bool"):
type = "BINARY"
else:
type = "CLOB"
datatypes.append(type)
if (flag_asis == False):
if (isinstance(column,str) == False):
column = str(column)
identifier = "ABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789_"
column_name = column.strip().upper()
new_name = ""
for ch in column_name:
if (ch not in identifier):
new_name = new_name + "_"
else:
new_name = new_name + ch
new_name = new_name.lstrip('_').rstrip('_')
if (new_name == "" or new_name[0] not in "ABCDEFGHIJKLMNOPQRSTUVWXYZ"):
new_name = f'"{column}"'
else:
new_name = f'"{column}"'
sql.append(f" {new_name} {type}")
sql.append(")")
sqlcmd = ""
for i in range(0,len(sql)):
if (i > 0 and i < len(sql)-2):
comma = ","
else:
comma = ""
sqlcmd = "{}\n{}{}".format(sqlcmd,sql[i],comma)
print(sqlcmd)
%sql {sqlcmd}
if (sqlcode != 0):
return
if (flag_withdata == True):
autocommit = ibm_db.autocommit(hdbc)
ibm_db.autocommit(hdbc,False)
row_count = 0
insert_sql = ""
rows, cols = df_value.shape
for row in range(0,rows):
insert_row = ""
for col in range(0, cols):
value = df_value.iloc[row][col]
if (datatypes[col] == "CLOB" or "VARCHAR" in datatypes[col]):
value = str(value)
value = addquotes(value,True)
elif (datatypes[col] in ("TIME","DATE","TIMESTAMP")):
value = str(value)
value = addquotes(value,True)
elif (datatypes[col] in ("INTEGER","DECFLOAT","FLOAT","BINARY")):
strvalue = str(value)
if ("NAN" in strvalue.upper()):
value = "NULL"
else:
value = str(value)
value = addquotes(value,True)
if (insert_row == ""):
insert_row = f"{value}"
else:
insert_row = f"{insert_row},{value}"
if (insert_sql == ""):
insert_sql = f"INSERT INTO {table} VALUES ({insert_row})"
else:
insert_sql = f"{insert_sql},({insert_row})"
row_count += 1
if (row_count % 1000 == 0 or row_count == limit):
result = ibm_db.exec_immediate(hdbc, insert_sql) # Run it
if (result == False): # Error executing the code
db2_error(False)
return
ibm_db.commit(hdbc)
print(f"\r{row_count} of {rows} rows inserted.",end="")
insert_sql = ""
if (row_count == limit):
break
if (insert_sql != ""):
result = ibm_db.exec_immediate(hdbc, insert_sql) # Run it
if (result == False): # Error executing the code
db2_error(False)
ibm_db.commit(hdbc)
ibm_db.autocommit(hdbc,autocommit)
print("\nInsert completed.")
return
```
### SQL Parser
The calling format of this routine is:
```
sql_cmd, encoded_sql = sqlParser(sql_input)
```
This code will look at the SQL string that has been passed to it and parse it into two values:
- sql_cmd: First command in the list (so this may not be the actual SQL command)
- encoded_sql: SQL with the parameters removed if there are any (replaced with ? markers)
```
def sqlParser(sqlin,local_ns):
sql_cmd = ""
encoded_sql = sqlin
firstCommand = "(?:^\s*)([a-zA-Z]+)(?:\s+.*|$)"
findFirst = re.match(firstCommand,sqlin)
if (findFirst == None): # We did not find a match so we just return the empty string
return sql_cmd, encoded_sql
cmd = findFirst.group(1)
sql_cmd = cmd.upper()
#
# Scan the input string looking for variables in the format :var. If no : is found just return.
# Var must be alpha+number+_ to be valid
#
if (':' not in sqlin): # A quick check to see if parameters are in here, but not fool-proof!
return sql_cmd, encoded_sql
inVar = False
inQuote = ""
varName = ""
encoded_sql = ""
STRING = 0
NUMBER = 1
LIST = 2
RAW = 3
PANDAS = 5
for ch in sqlin:
if (inVar == True): # We are collecting the name of a variable
if (ch.upper() in "@_ABCDEFGHIJKLMNOPQRSTUVWXYZ0123456789[]"):
varName = varName + ch
continue
else:
if (varName == ""):
encode_sql = encoded_sql + ":"
elif (varName[0] in ('[',']')):
encoded_sql = encoded_sql + ":" + varName
else:
if (ch == '.'): # If the variable name is stopped by a period, assume no quotes are used
flag_quotes = False
else:
flag_quotes = True
varValue, varType = getContents(varName,flag_quotes,local_ns)
if (varType != PANDAS and varValue == None):
encoded_sql = encoded_sql + ":" + varName
else:
if (varType == STRING):
encoded_sql = encoded_sql + varValue
elif (varType == NUMBER):
encoded_sql = encoded_sql + str(varValue)
elif (varType == RAW):
encoded_sql = encoded_sql + varValue
elif (varType == PANDAS):
insertsql = ""
coltypes = varValue.dtypes
rows, cols = varValue.shape
for row in range(0,rows):
insertrow = ""
for col in range(0, cols):
value = varValue.iloc[row][col]
if (coltypes[col] == "object"):
value = str(value)
value = addquotes(value,True)
else:
strvalue = str(value)
if ("NAN" in strvalue.upper()):
value = "NULL"
if (insertrow == ""):
insertrow = f"{value}"
else:
insertrow = f"{insertrow},{value}"
if (insertsql == ""):
insertsql = f"({insertrow})"
else:
insertsql = f"{insertsql},({insertrow})"
encoded_sql = encoded_sql + insertsql
elif (varType == LIST):
start = True
for v in varValue:
if (start == False):
encoded_sql = encoded_sql + ","
if (isinstance(v,int) == True): # Integer value
encoded_sql = encoded_sql + str(v)
elif (isinstance(v,float) == True):
encoded_sql = encoded_sql + str(v)
else:
flag_quotes = True
try:
if (v.find('0x') == 0): # Just guessing this is a hex value at beginning
encoded_sql = encoded_sql + v
else:
encoded_sql = encoded_sql + addquotes(v,flag_quotes) # String
except:
encoded_sql = encoded_sql + addquotes(str(v),flag_quotes)
start = False
encoded_sql = encoded_sql + ch
varName = ""
inVar = False
elif (inQuote != ""):
encoded_sql = encoded_sql + ch
if (ch == inQuote): inQuote = ""
elif (ch in ("'",'"')):
encoded_sql = encoded_sql + ch
inQuote = ch
elif (ch == ":"): # This might be a variable
varName = ""
inVar = True
else:
encoded_sql = encoded_sql + ch
if (inVar == True):
varValue, varType = getContents(varName,True,local_ns) # We assume the end of a line is quoted
if (varType != PANDAS and varValue == None):
encoded_sql = encoded_sql + ":" + varName
else:
if (varType == STRING):
encoded_sql = encoded_sql + varValue
elif (varType == NUMBER):
encoded_sql = encoded_sql + str(varValue)
elif (varType == PANDAS):
insertsql = ""
coltypes = varValue.dtypes
rows, cols = varValue.shape
for row in range(0,rows):
insertrow = ""
for col in range(0, cols):
value = varValue.iloc[row][col]
if (coltypes[col] == "object"):
value = str(value)
value = addquotes(value,True)
else:
strvalue = str(value)
if ("NAN" in strvalue.upper()):
value = "NULL"
if (insertrow == ""):
insertrow = f"{value}"
else:
insertrow = f"{insertrow},{value}"
if (insertsql == ""):
insertsql = f"({insertrow})"
else:
insertsql = f"{insertsql},({insertrow})"
encoded_sql = encoded_sql + insertsql
elif (varType == LIST):
flag_quotes = True
start = True
for v in varValue:
if (start == False):
encoded_sql = encoded_sql + ","
if (isinstance(v,int) == True): # Integer value
encoded_sql = encoded_sql + str(v)
elif (isinstance(v,float) == True):
encoded_sql = encoded_sql + str(v)
else:
try:
if (v.find('0x') == 0): # Just guessing this is a hex value
encoded_sql = encoded_sql + v
else:
encoded_sql = encoded_sql + addquotes(v,flag_quotes) # String
except:
encoded_sql = encoded_sql + addquotes(str(v),flag_quotes)
start = False
return sql_cmd, encoded_sql
```
### Variable Contents Function
The calling format of this routine is:
```
value = getContents(varName,quote,name_space)
```
This code will take the name of a variable as input and return the contents of that variable. If the variable is not found then the program will return None which is the equivalent to empty or null. Note that this function looks at the global variable pool for Python so it is possible that the wrong version of variable is returned if it is used in different functions. For this reason, any variables used in SQL statements should use a unique namimg convention if possible.
The other thing that this function does is replace single quotes with two quotes. The reason for doing this is that Db2 will convert two single quotes into one quote when dealing with strings. This avoids problems when dealing with text that contains multiple quotes within the string. Note that this substitution is done only for single quote characters since the double quote character is used by Db2 for naming columns that are case sensitive or contain special characters.
If the quote value is True, the field will have quotes around it. The name_space is the variables currently that are registered in Python.
```
def getContents(varName,flag_quotes,local_ns):
#
# Get the contents of the variable name that is passed to the routine. Only simple
# variables are checked, i.e. arrays and lists are not parsed
#
STRING = 0
NUMBER = 1
LIST = 2
RAW = 3
DICT = 4
PANDAS = 5
try:
value = eval(varName,None,local_ns) # globals()[varName] # eval(varName)
except:
return(None,STRING)
if (isinstance(value,dict) == True): # Check to see if this is JSON dictionary
return(addquotes(value,flag_quotes),STRING)
elif(isinstance(value,list) == True): # List - tricky
return(value,LIST)
elif (isinstance(value,pandas.DataFrame) == True): # Pandas dataframe
return(value,PANDAS)
elif (isinstance(value,int) == True): # Integer value
return(value,NUMBER)
elif (isinstance(value,float) == True): # Float value
return(value,NUMBER)
else:
try:
# The pattern needs to be in the first position (0 in Python terms)
if (value.find('0x') == 0): # Just guessing this is a hex value
return(value,RAW)
else:
return(addquotes(value,flag_quotes),STRING) # String
except:
return(addquotes(str(value),flag_quotes),RAW)
```
### Add Quotes
Quotes are a challenge when dealing with dictionaries and Db2. Db2 wants strings delimited with single quotes, while Dictionaries use double quotes. That wouldn't be a problems except imbedded single quotes within these dictionaries will cause things to fail. This routine attempts to double-quote the single quotes within the dicitonary.
```
def addquotes(inString,flag_quotes):
if (isinstance(inString,dict) == True): # Check to see if this is JSON dictionary
serialized = json.dumps(inString)
else:
serialized = inString
# Replace single quotes with '' (two quotes) and wrap everything in single quotes
if (flag_quotes == False):
return(serialized)
else:
return("'"+serialized.replace("'","''")+"'") # Convert single quotes to two single quotes
```
### Create the SAMPLE Database Tables
The calling format of this routine is:
```
db2_create_sample(quiet)
```
There are a lot of examples that depend on the data within the SAMPLE database. If you are running these examples and the connection is not to the SAMPLE database, then this code will create the two (EMPLOYEE, DEPARTMENT) tables that are used by most examples. If the function finds that these tables already exist, then nothing is done. If the tables are missing then they will be created with the same data as in the SAMPLE database.
The quiet flag tells the program not to print any messages when the creation of the tables is complete.
```
def db2_create_sample(quiet):
create_department = """
BEGIN
DECLARE FOUND INTEGER;
SET FOUND = (SELECT COUNT(*) FROM SYSIBM.SYSTABLES WHERE NAME='DEPARTMENT' AND CREATOR=CURRENT USER);
IF FOUND = 0 THEN
EXECUTE IMMEDIATE('CREATE TABLE DEPARTMENT(DEPTNO CHAR(3) NOT NULL, DEPTNAME VARCHAR(36) NOT NULL,
MGRNO CHAR(6),ADMRDEPT CHAR(3) NOT NULL)');
EXECUTE IMMEDIATE('INSERT INTO DEPARTMENT VALUES
(''A00'',''SPIFFY COMPUTER SERVICE DIV.'',''000010'',''A00''),
(''B01'',''PLANNING'',''000020'',''A00''),
(''C01'',''INFORMATION CENTER'',''000030'',''A00''),
(''D01'',''DEVELOPMENT CENTER'',NULL,''A00''),
(''D11'',''MANUFACTURING SYSTEMS'',''000060'',''D01''),
(''D21'',''ADMINISTRATION SYSTEMS'',''000070'',''D01''),
(''E01'',''SUPPORT SERVICES'',''000050'',''A00''),
(''E11'',''OPERATIONS'',''000090'',''E01''),
(''E21'',''SOFTWARE SUPPORT'',''000100'',''E01''),
(''F22'',''BRANCH OFFICE F2'',NULL,''E01''),
(''G22'',''BRANCH OFFICE G2'',NULL,''E01''),
(''H22'',''BRANCH OFFICE H2'',NULL,''E01''),
(''I22'',''BRANCH OFFICE I2'',NULL,''E01''),
(''J22'',''BRANCH OFFICE J2'',NULL,''E01'')');
END IF;
END"""
%sql -d -q {create_department}
create_employee = """
BEGIN
DECLARE FOUND INTEGER;
SET FOUND = (SELECT COUNT(*) FROM SYSIBM.SYSTABLES WHERE NAME='EMPLOYEE' AND CREATOR=CURRENT USER);
IF FOUND = 0 THEN
EXECUTE IMMEDIATE('CREATE TABLE EMPLOYEE(
EMPNO CHAR(6) NOT NULL,
FIRSTNME VARCHAR(12) NOT NULL,
MIDINIT CHAR(1),
LASTNAME VARCHAR(15) NOT NULL,
WORKDEPT CHAR(3),
PHONENO CHAR(4),
HIREDATE DATE,
JOB CHAR(8),
EDLEVEL SMALLINT NOT NULL,
SEX CHAR(1),
BIRTHDATE DATE,
SALARY DECIMAL(9,2),
BONUS DECIMAL(9,2),
COMM DECIMAL(9,2)
)');
EXECUTE IMMEDIATE('INSERT INTO EMPLOYEE VALUES
(''000010'',''CHRISTINE'',''I'',''HAAS'' ,''A00'',''3978'',''1995-01-01'',''PRES '',18,''F'',''1963-08-24'',152750.00,1000.00,4220.00),
(''000020'',''MICHAEL'' ,''L'',''THOMPSON'' ,''B01'',''3476'',''2003-10-10'',''MANAGER '',18,''M'',''1978-02-02'',94250.00,800.00,3300.00),
(''000030'',''SALLY'' ,''A'',''KWAN'' ,''C01'',''4738'',''2005-04-05'',''MANAGER '',20,''F'',''1971-05-11'',98250.00,800.00,3060.00),
(''000050'',''JOHN'' ,''B'',''GEYER'' ,''E01'',''6789'',''1979-08-17'',''MANAGER '',16,''M'',''1955-09-15'',80175.00,800.00,3214.00),
(''000060'',''IRVING'' ,''F'',''STERN'' ,''D11'',''6423'',''2003-09-14'',''MANAGER '',16,''M'',''1975-07-07'',72250.00,500.00,2580.00),
(''000070'',''EVA'' ,''D'',''PULASKI'' ,''D21'',''7831'',''2005-09-30'',''MANAGER '',16,''F'',''2003-05-26'',96170.00,700.00,2893.00),
(''000090'',''EILEEN'' ,''W'',''HENDERSON'' ,''E11'',''5498'',''2000-08-15'',''MANAGER '',16,''F'',''1971-05-15'',89750.00,600.00,2380.00),
(''000100'',''THEODORE'' ,''Q'',''SPENSER'' ,''E21'',''0972'',''2000-06-19'',''MANAGER '',14,''M'',''1980-12-18'',86150.00,500.00,2092.00),
(''000110'',''VINCENZO'' ,''G'',''LUCCHESSI'' ,''A00'',''3490'',''1988-05-16'',''SALESREP'',19,''M'',''1959-11-05'',66500.00,900.00,3720.00),
(''000120'',''SEAN'' ,'' '',''O`CONNELL'' ,''A00'',''2167'',''1993-12-05'',''CLERK '',14,''M'',''1972-10-18'',49250.00,600.00,2340.00),
(''000130'',''DELORES'' ,''M'',''QUINTANA'' ,''C01'',''4578'',''2001-07-28'',''ANALYST '',16,''F'',''1955-09-15'',73800.00,500.00,1904.00),
(''000140'',''HEATHER'' ,''A'',''NICHOLLS'' ,''C01'',''1793'',''2006-12-15'',''ANALYST '',18,''F'',''1976-01-19'',68420.00,600.00,2274.00),
(''000150'',''BRUCE'' ,'' '',''ADAMSON'' ,''D11'',''4510'',''2002-02-12'',''DESIGNER'',16,''M'',''1977-05-17'',55280.00,500.00,2022.00),
(''000160'',''ELIZABETH'',''R'',''PIANKA'' ,''D11'',''3782'',''2006-10-11'',''DESIGNER'',17,''F'',''1980-04-12'',62250.00,400.00,1780.00),
(''000170'',''MASATOSHI'',''J'',''YOSHIMURA'' ,''D11'',''2890'',''1999-09-15'',''DESIGNER'',16,''M'',''1981-01-05'',44680.00,500.00,1974.00),
(''000180'',''MARILYN'' ,''S'',''SCOUTTEN'' ,''D11'',''1682'',''2003-07-07'',''DESIGNER'',17,''F'',''1979-02-21'',51340.00,500.00,1707.00),
(''000190'',''JAMES'' ,''H'',''WALKER'' ,''D11'',''2986'',''2004-07-26'',''DESIGNER'',16,''M'',''1982-06-25'',50450.00,400.00,1636.00),
(''000200'',''DAVID'' ,'' '',''BROWN'' ,''D11'',''4501'',''2002-03-03'',''DESIGNER'',16,''M'',''1971-05-29'',57740.00,600.00,2217.00),
(''000210'',''WILLIAM'' ,''T'',''JONES'' ,''D11'',''0942'',''1998-04-11'',''DESIGNER'',17,''M'',''2003-02-23'',68270.00,400.00,1462.00),
(''000220'',''JENNIFER'' ,''K'',''LUTZ'' ,''D11'',''0672'',''1998-08-29'',''DESIGNER'',18,''F'',''1978-03-19'',49840.00,600.00,2387.00),
(''000230'',''JAMES'' ,''J'',''JEFFERSON'' ,''D21'',''2094'',''1996-11-21'',''CLERK '',14,''M'',''1980-05-30'',42180.00,400.00,1774.00),
(''000240'',''SALVATORE'',''M'',''MARINO'' ,''D21'',''3780'',''2004-12-05'',''CLERK '',17,''M'',''2002-03-31'',48760.00,600.00,2301.00),
(''000250'',''DANIEL'' ,''S'',''SMITH'' ,''D21'',''0961'',''1999-10-30'',''CLERK '',15,''M'',''1969-11-12'',49180.00,400.00,1534.00),
(''000260'',''SYBIL'' ,''P'',''JOHNSON'' ,''D21'',''8953'',''2005-09-11'',''CLERK '',16,''F'',''1976-10-05'',47250.00,300.00,1380.00),
(''000270'',''MARIA'' ,''L'',''PEREZ'' ,''D21'',''9001'',''2006-09-30'',''CLERK '',15,''F'',''2003-05-26'',37380.00,500.00,2190.00),
(''000280'',''ETHEL'' ,''R'',''SCHNEIDER'' ,''E11'',''8997'',''1997-03-24'',''OPERATOR'',17,''F'',''1976-03-28'',36250.00,500.00,2100.00),
(''000290'',''JOHN'' ,''R'',''PARKER'' ,''E11'',''4502'',''2006-05-30'',''OPERATOR'',12,''M'',''1985-07-09'',35340.00,300.00,1227.00),
(''000300'',''PHILIP'' ,''X'',''SMITH'' ,''E11'',''2095'',''2002-06-19'',''OPERATOR'',14,''M'',''1976-10-27'',37750.00,400.00,1420.00),
(''000310'',''MAUDE'' ,''F'',''SETRIGHT'' ,''E11'',''3332'',''1994-09-12'',''OPERATOR'',12,''F'',''1961-04-21'',35900.00,300.00,1272.00),
(''000320'',''RAMLAL'' ,''V'',''MEHTA'' ,''E21'',''9990'',''1995-07-07'',''FIELDREP'',16,''M'',''1962-08-11'',39950.00,400.00,1596.00),
(''000330'',''WING'' ,'' '',''LEE'' ,''E21'',''2103'',''2006-02-23'',''FIELDREP'',14,''M'',''1971-07-18'',45370.00,500.00,2030.00),
(''000340'',''JASON'' ,''R'',''GOUNOT'' ,''E21'',''5698'',''1977-05-05'',''FIELDREP'',16,''M'',''1956-05-17'',43840.00,500.00,1907.00),
(''200010'',''DIAN'' ,''J'',''HEMMINGER'' ,''A00'',''3978'',''1995-01-01'',''SALESREP'',18,''F'',''1973-08-14'',46500.00,1000.00,4220.00),
(''200120'',''GREG'' ,'' '',''ORLANDO'' ,''A00'',''2167'',''2002-05-05'',''CLERK '',14,''M'',''1972-10-18'',39250.00,600.00,2340.00),
(''200140'',''KIM'' ,''N'',''NATZ'' ,''C01'',''1793'',''2006-12-15'',''ANALYST '',18,''F'',''1976-01-19'',68420.00,600.00,2274.00),
(''200170'',''KIYOSHI'' ,'' '',''YAMAMOTO'' ,''D11'',''2890'',''2005-09-15'',''DESIGNER'',16,''M'',''1981-01-05'',64680.00,500.00,1974.00),
(''200220'',''REBA'' ,''K'',''JOHN'' ,''D11'',''0672'',''2005-08-29'',''DESIGNER'',18,''F'',''1978-03-19'',69840.00,600.00,2387.00),
(''200240'',''ROBERT'' ,''M'',''MONTEVERDE'',''D21'',''3780'',''2004-12-05'',''CLERK '',17,''M'',''1984-03-31'',37760.00,600.00,2301.00),
(''200280'',''EILEEN'' ,''R'',''SCHWARTZ'' ,''E11'',''8997'',''1997-03-24'',''OPERATOR'',17,''F'',''1966-03-28'',46250.00,500.00,2100.00),
(''200310'',''MICHELLE'' ,''F'',''SPRINGER'' ,''E11'',''3332'',''1994-09-12'',''OPERATOR'',12,''F'',''1961-04-21'',35900.00,300.00,1272.00),
(''200330'',''HELENA'' ,'' '',''WONG'' ,''E21'',''2103'',''2006-02-23'',''FIELDREP'',14,''F'',''1971-07-18'',35370.00,500.00,2030.00),
(''200340'',''ROY'' ,''R'',''ALONZO'' ,''E21'',''5698'',''1997-07-05'',''FIELDREP'',16,''M'',''1956-05-17'',31840.00,500.00,1907.00)');
END IF;
END"""
%sql -d -q {create_employee}
if (quiet == False): success("Sample tables [EMPLOYEE, DEPARTMENT] created.")
```
### Check option
This function will return the original string with the option removed, and a flag or true or false of the value is found.
```
args, flag = checkOption(option_string, option, false_value, true_value)
```
Options are specified with a -x where x is the character that we are searching for. It may actually be more than one character long like -pb/-pi/etc... The false and true values are optional. By default these are the boolean values of T/F but for some options it could be a character string like ';' versus '@' for delimiters.
```
def checkOption(args_in, option, vFalse=False, vTrue=True):
args_out = args_in.strip()
found = vFalse
if (args_out != ""):
if (args_out.find(option) >= 0):
args_out = args_out.replace(option," ")
args_out = args_out.strip()
found = vTrue
return args_out, found
```
### Plot Data
This function will plot the data that is returned from the answer set. The plot value determines how we display the data. 1=Bar, 2=Pie, 3=Line, 4=Interactive.
```
plotData(flag_plot, hdbi, sql, parms)
```
The hdbi is the ibm_db_sa handle that is used by pandas dataframes to run the sql. The parms contains any of the parameters required to run the query.
```
def plotData(hdbi, sql):
try:
df = pandas.read_sql(sql,hdbi)
except Exception as err:
db2_error(False)
return
if df.empty:
errormsg("No results returned")
return
col_count = len(df.columns)
if flag(["-pb","-bar"]): # Plot 1 = bar chart
if (col_count in (1,2,3)):
if (col_count == 1):
df.index = df.index + 1
_ = df.plot(kind='bar');
_ = plt.plot();
elif (col_count == 2):
xlabel = df.columns.values[0]
ylabel = df.columns.values[1]
df.plot(kind='bar',x=xlabel,y=ylabel);
_ = plt.plot();
else:
values = df.columns.values[2]
columns = df.columns.values[0]
index = df.columns.values[1]
pivoted = pandas.pivot_table(df, values=values, columns=columns, index=index)
_ = pivoted.plot.bar();
else:
errormsg("Can't determine what columns to plot")
return
elif flag(["-pp","-pie"]): # Plot 2 = pie chart
if (col_count in (1,2)):
if (col_count == 1):
df.index = df.index + 1
yname = df.columns.values[0]
_ = df.plot(kind='pie',y=yname);
else:
xlabel = df.columns.values[0]
xname = df[xlabel].tolist()
yname = df.columns.values[1]
_ = df.plot(kind='pie',y=yname,labels=xname);
plt.show();
else:
errormsg("Can't determine what columns to plot")
return
elif flag(["-pl","-line"]): # Plot 3 = line chart
if (col_count in (1,2,3)):
if (col_count == 1):
df.index = df.index + 1
_ = df.plot(kind='line');
elif (col_count == 2):
xlabel = df.columns.values[0]
ylabel = df.columns.values[1]
_ = df.plot(kind='line',x=xlabel,y=ylabel) ;
else:
values = df.columns.values[2]
columns = df.columns.values[0]
index = df.columns.values[1]
pivoted = pandas.pivot_table(df, values=values, columns=columns, index=index)
_ = pivoted.plot();
plt.show();
else:
errormsg("Can't determine what columns to plot")
return
else:
return
```
### Find a Procedure
This routine will check to see if a procedure exists with the SCHEMA/NAME (or just NAME if no schema is supplied) and returns the number of answer sets returned. Possible values are 0, 1 (or greater) or None. If None is returned then we can't find the procedure anywhere.
```
def findProc(procname):
global _hdbc, _hdbi, _connected, _runtime
# Split the procedure name into schema.procname if appropriate
upper_procname = procname.upper()
schema, proc = split_string(upper_procname,".") # Expect schema.procname
if (proc == None):
proc = schema
# Call ibm_db.procedures to see if the procedure does exist
schema = "%"
try:
stmt = ibm_db.procedures(_hdbc, None, schema, proc)
if (stmt == False): # Error executing the code
errormsg("Procedure " + procname + " not found in the system catalog.")
return None
result = ibm_db.fetch_tuple(stmt)
resultsets = result[5]
if (resultsets >= 1): resultsets = 1
return resultsets
except Exception as err:
errormsg("Procedure " + procname + " not found in the system catalog.")
return None
```
### Parse Call Arguments
This code will parse a SQL call #name(parm1,...) and return the name and the parameters in the call.
```
def parseCallArgs(macro):
quoteChar = ""
inQuote = False
inParm = False
ignore = False
name = ""
parms = []
parm = ''
sqlin = macro.replace("\n","")
sqlin.lstrip()
for ch in sqlin:
if (inParm == False):
# We hit a blank in the name, so ignore everything after the procedure name until a ( is found
if (ch == " "):
ignore == True
elif (ch == "("): # Now we have parameters to send to the stored procedure
inParm = True
else:
if (ignore == False): name = name + ch # The name of the procedure (and no blanks)
else:
if (inQuote == True):
if (ch == quoteChar):
inQuote = False
else:
parm = parm + ch
elif (ch in ("\"","\'","[")): # Do we have a quote
if (ch == "["):
quoteChar = "]"
else:
quoteChar = ch
inQuote = True
elif (ch == ")"):
if (parm != ""):
parms.append(parm)
parm = ""
break
elif (ch == ","):
if (parm != ""):
parms.append(parm)
else:
parms.append("null")
parm = ""
else:
parm = parm + ch
if (inParm == True):
if (parm != ""):
parms.append(parm_value)
return(name,parms)
```
### Get Columns
Given a statement handle, determine what the column names are or the data types.
```
def getColumns(stmt):
columns = []
types = []
colcount = 0
try:
colname = ibm_db.field_name(stmt,colcount)
coltype = ibm_db.field_type(stmt,colcount)
while (colname != False):
columns.append(colname)
types.append(coltype)
colcount += 1
colname = ibm_db.field_name(stmt,colcount)
coltype = ibm_db.field_type(stmt,colcount)
return columns,types
except Exception as err:
db2_error(False)
return None
```
### Call a Procedure
The CALL statement is used for execution of a stored procedure. The format of the CALL statement is:
```
CALL PROC_NAME(x,y,z,...)
```
Procedures allow for the return of answer sets (cursors) as well as changing the contents of the parameters being passed to the procedure. In this implementation, the CALL function is limited to returning one answer set (or nothing). If you want to use more complex stored procedures then you will have to use the native python libraries.
```
def parseCall(hdbc, inSQL, local_ns):
global _hdbc, _hdbi, _connected, _runtime, _environment
# Check to see if we are connected first
if (_connected == False): # Check if you are connected
db2_doConnect()
if _connected == False: return None
remainder = inSQL.strip()
procName, procArgs = parseCallArgs(remainder[5:]) # Assume that CALL ... is the format
resultsets = findProc(procName)
if (resultsets == None): return None
argvalues = []
if (len(procArgs) > 0): # We have arguments to consider
for arg in procArgs:
varname = arg
if (len(varname) > 0):
if (varname[0] == ":"):
checkvar = varname[1:]
varvalue = getContents(checkvar,True,local_ns)
if (varvalue == None):
errormsg("Variable " + checkvar + " is not defined.")
return None
argvalues.append(varvalue)
else:
if (varname.upper() == "NULL"):
argvalues.append(None)
else:
argvalues.append(varname)
else:
argvalues.append(None)
try:
if (len(procArgs) > 0):
argtuple = tuple(argvalues)
result = ibm_db.callproc(_hdbc,procName,argtuple)
stmt = result[0]
else:
result = ibm_db.callproc(_hdbc,procName)
stmt = result
if (resultsets != 0 and stmt != None):
columns, types = getColumns(stmt)
if (columns == None): return None
rows = []
rowlist = ibm_db.fetch_tuple(stmt)
while ( rowlist ) :
row = []
colcount = 0
for col in rowlist:
try:
if (types[colcount] in ["int","bigint"]):
row.append(int(col))
elif (types[colcount] in ["decimal","real"]):
row.append(float(col))
elif (types[colcount] in ["date","time","timestamp"]):
row.append(str(col))
else:
row.append(col)
except:
row.append(col)
colcount += 1
rows.append(row)
rowlist = ibm_db.fetch_tuple(stmt)
if flag(["-r","-array"]):
rows.insert(0,columns)
if len(procArgs) > 0:
allresults = []
allresults.append(rows)
for x in result[1:]:
allresults.append(x)
return allresults # rows,returned_results
else:
return rows
else:
df = pandas.DataFrame.from_records(rows,columns=columns)
if flag("-grid") or _settings['display'] == 'GRID':
if (_environment['qgrid'] == False):
with pandas.option_context('display.max_rows', None, 'display.max_columns', None):
pdisplay(df)
else:
try:
pdisplay(qgrid.show_grid(df))
except:
errormsg("Grid cannot be used to display data with duplicate column names. Use option -a or %sql OPTION DISPLAY PANDAS instead.")
return
else:
if flag(["-a","-all"]) or _settings["maxrows"] == -1 : # All of the rows
with pandas.option_context('display.max_rows', None, 'display.max_columns', None):
pdisplay(df)
else:
return df
else:
if len(procArgs) > 0:
allresults = []
for x in result[1:]:
allresults.append(x)
return allresults # rows,returned_results
else:
return None
except Exception as err:
db2_error(False)
return None
```
### Parse Prepare/Execute
The PREPARE statement is used for repeated execution of a SQL statement. The PREPARE statement has the format:
```
stmt = PREPARE SELECT EMPNO FROM EMPLOYEE WHERE WORKDEPT=? AND SALARY<?
```
The SQL statement that you want executed is placed after the PREPARE statement with the location of variables marked with ? (parameter) markers. The variable stmt contains the prepared statement that need to be passed to the EXECUTE statement. The EXECUTE statement has the format:
```
EXECUTE :x USING z, y, s
```
The first variable (:x) is the name of the variable that you assigned the results of the prepare statement. The values after the USING clause are substituted into the prepare statement where the ? markers are found.
If the values in USING clause are variable names (z, y, s), a **link** is created to these variables as part of the execute statement. If you use the variable subsitution form of variable name (:z, :y, :s), the **contents** of the variable are placed into the USING clause. Normally this would not make much of a difference except when you are dealing with binary strings or JSON strings where the quote characters may cause some problems when subsituted into the statement.
```
def parsePExec(hdbc, inSQL):
import ibm_db
global _stmt, _stmtID, _stmtSQL, sqlcode
cParms = inSQL.split()
parmCount = len(cParms)
if (parmCount == 0): return(None) # Nothing to do but this shouldn't happen
keyword = cParms[0].upper() # Upper case the keyword
if (keyword == "PREPARE"): # Prepare the following SQL
uSQL = inSQL.upper()
found = uSQL.find("PREPARE")
sql = inSQL[found+7:].strip()
try:
pattern = "\?\*[0-9]+"
findparm = re.search(pattern,sql)
while findparm != None:
found = findparm.group(0)
count = int(found[2:])
markers = ('?,' * count)[:-1]
sql = sql.replace(found,markers)
findparm = re.search(pattern,sql)
stmt = ibm_db.prepare(hdbc,sql) # Check error code here
if (stmt == False):
db2_error(False)
return(False)
stmttext = str(stmt).strip()
stmtID = stmttext[33:48].strip()
if (stmtID in _stmtID) == False:
_stmt.append(stmt) # Prepare and return STMT to caller
_stmtID.append(stmtID)
else:
stmtIX = _stmtID.index(stmtID)
_stmt[stmtiX] = stmt
return(stmtID)
except Exception as err:
print(err)
db2_error(False)
return(False)
if (keyword == "EXECUTE"): # Execute the prepare statement
if (parmCount < 2): return(False) # No stmtID available
stmtID = cParms[1].strip()
if (stmtID in _stmtID) == False:
errormsg("Prepared statement not found or invalid.")
return(False)
stmtIX = _stmtID.index(stmtID)
stmt = _stmt[stmtIX]
try:
if (parmCount == 2): # Only the statement handle available
result = ibm_db.execute(stmt) # Run it
elif (parmCount == 3): # Not quite enough arguments
errormsg("Missing or invalid USING clause on EXECUTE statement.")
sqlcode = -99999
return(False)
else:
using = cParms[2].upper()
if (using != "USING"): # Bad syntax again
errormsg("Missing USING clause on EXECUTE statement.")
sqlcode = -99999
return(False)
uSQL = inSQL.upper()
found = uSQL.find("USING")
parmString = inSQL[found+5:].strip()
parmset = splitargs(parmString)
if (len(parmset) == 0):
errormsg("Missing parameters after the USING clause.")
sqlcode = -99999
return(False)
parms = []
parm_count = 0
CONSTANT = 0
VARIABLE = 1
const = [0]
const_cnt = 0
for v in parmset:
parm_count = parm_count + 1
if (v[1] == True or v[2] == True): # v[1] true if string, v[2] true if num
parm_type = CONSTANT
const_cnt = const_cnt + 1
if (v[2] == True):
if (isinstance(v[0],int) == True): # Integer value
sql_type = ibm_db.SQL_INTEGER
elif (isinstance(v[0],float) == True): # Float value
sql_type = ibm_db.SQL_DOUBLE
else:
sql_type = ibm_db.SQL_INTEGER
else:
sql_type = ibm_db.SQL_CHAR
const.append(v[0])
else:
parm_type = VARIABLE
# See if the variable has a type associated with it varname@type
varset = v[0].split("@")
parm_name = varset[0]
parm_datatype = "char"
# Does the variable exist?
if (parm_name not in globals()):
errormsg("SQL Execute parameter " + parm_name + " not found")
sqlcode = -99999
return(false)
if (len(varset) > 1): # Type provided
parm_datatype = varset[1]
if (parm_datatype == "dec" or parm_datatype == "decimal"):
sql_type = ibm_db.SQL_DOUBLE
elif (parm_datatype == "bin" or parm_datatype == "binary"):
sql_type = ibm_db.SQL_BINARY
elif (parm_datatype == "int" or parm_datatype == "integer"):
sql_type = ibm_db.SQL_INTEGER
else:
sql_type = ibm_db.SQL_CHAR
try:
if (parm_type == VARIABLE):
result = ibm_db.bind_param(stmt, parm_count, globals()[parm_name], ibm_db.SQL_PARAM_INPUT, sql_type)
else:
result = ibm_db.bind_param(stmt, parm_count, const[const_cnt], ibm_db.SQL_PARAM_INPUT, sql_type)
except:
result = False
if (result == False):
errormsg("SQL Bind on variable " + parm_name + " failed.")
sqlcode = -99999
return(false)
result = ibm_db.execute(stmt) # ,tuple(parms))
if (result == False):
errormsg("SQL Execute failed.")
return(False)
if (ibm_db.num_fields(stmt) == 0): return(True) # Command successfully completed
return(fetchResults(stmt))
except Exception as err:
db2_error(False)
return(False)
return(False)
return(False)
```
### Fetch Result Set
This code will take the stmt handle and then produce a result set of rows as either an array (`-r`,`-array`) or as an array of json records (`-json`).
```
def fetchResults(stmt):
global sqlcode
rows = []
columns, types = getColumns(stmt)
# By default we assume that the data will be an array
is_array = True
# Check what type of data we want returned - array or json
if (flag(["-r","-array"]) == False):
# See if we want it in JSON format, if not it remains as an array
if (flag("-json") == True):
is_array = False
# Set column names to lowercase for JSON records
if (is_array == False):
columns = [col.lower() for col in columns] # Convert to lowercase for each of access
# First row of an array has the column names in it
if (is_array == True):
rows.append(columns)
result = ibm_db.fetch_tuple(stmt)
rowcount = 0
while (result):
rowcount += 1
if (is_array == True):
row = []
else:
row = {}
colcount = 0
for col in result:
try:
if (types[colcount] in ["int","bigint"]):
if (is_array == True):
row.append(int(col))
else:
row[columns[colcount]] = int(col)
elif (types[colcount] in ["decimal","real"]):
if (is_array == True):
row.append(float(col))
else:
row[columns[colcount]] = float(col)
elif (types[colcount] in ["date","time","timestamp"]):
if (is_array == True):
row.append(str(col))
else:
row[columns[colcount]] = str(col)
else:
if (is_array == True):
row.append(col)
else:
row[columns[colcount]] = col
except:
if (is_array == True):
row.append(col)
else:
row[columns[colcount]] = col
colcount += 1
rows.append(row)
result = ibm_db.fetch_tuple(stmt)
if (rowcount == 0):
sqlcode = 100
else:
sqlcode = 0
return rows
```
### Parse Commit
There are three possible COMMIT verbs that can bs used:
- COMMIT [WORK] - Commit the work in progress - The WORK keyword is not checked for
- ROLLBACK - Roll back the unit of work
- AUTOCOMMIT ON/OFF - Are statements committed on or off?
The statement is passed to this routine and then checked.
```
def parseCommit(sql):
global _hdbc, _hdbi, _connected, _runtime, _stmt, _stmtID, _stmtSQL
if (_connected == False): return # Nothing to do if we are not connected
cParms = sql.split()
if (len(cParms) == 0): return # Nothing to do but this shouldn't happen
keyword = cParms[0].upper() # Upper case the keyword
if (keyword == "COMMIT"): # Commit the work that was done
try:
result = ibm_db.commit (_hdbc) # Commit the connection
if (len(cParms) > 1):
keyword = cParms[1].upper()
if (keyword == "HOLD"):
return
del _stmt[:]
del _stmtID[:]
except Exception as err:
db2_error(False)
return
if (keyword == "ROLLBACK"): # Rollback the work that was done
try:
result = ibm_db.rollback(_hdbc) # Rollback the connection
del _stmt[:]
del _stmtID[:]
except Exception as err:
db2_error(False)
return
if (keyword == "AUTOCOMMIT"): # Is autocommit on or off
if (len(cParms) > 1):
op = cParms[1].upper() # Need ON or OFF value
else:
return
try:
if (op == "OFF"):
ibm_db.autocommit(_hdbc, False)
elif (op == "ON"):
ibm_db.autocommit (_hdbc, True)
return
except Exception as err:
db2_error(False)
return
return
```
### Set Flags
This code will take the input SQL block and update the global flag list. The global flag list is just a list of options that are set at the beginning of a code block. The absence of a flag means it is false. If it exists it is true.
```
def setFlags(inSQL):
global _flags
_flags = [] # Delete all of the current flag settings
pos = 0
end = len(inSQL)-1
inFlag = False
ignore = False
outSQL = ""
flag = ""
while (pos <= end):
ch = inSQL[pos]
if (ignore == True):
outSQL = outSQL + ch
else:
if (inFlag == True):
if (ch != " "):
flag = flag + ch
else:
_flags.append(flag)
inFlag = False
else:
if (ch == "-"):
flag = "-"
inFlag = True
elif (ch == ' '):
outSQL = outSQL + ch
else:
outSQL = outSQL + ch
ignore = True
pos += 1
if (inFlag == True):
_flags.append(flag)
return outSQL
```
### Check to see if flag Exists
This function determines whether or not a flag exists in the global flag array. Absence of a value means it is false. The parameter can be a single value, or an array of values.
```
def flag(inflag):
global _flags
if isinstance(inflag,list):
for x in inflag:
if (x in _flags):
return True
return False
else:
if (inflag in _flags):
return True
else:
return False
```
### Generate a list of SQL lines based on a delimiter
Note that this function will make sure that quotes are properly maintained so that delimiters inside of quoted strings do not cause errors.
```
def splitSQL(inputString, delimiter):
pos = 0
arg = ""
results = []
quoteCH = ""
inSQL = inputString.strip()
if (len(inSQL) == 0): return(results) # Not much to do here - no args found
while pos < len(inSQL):
ch = inSQL[pos]
pos += 1
if (ch in ('"',"'")): # Is this a quote characters?
arg = arg + ch # Keep appending the characters to the current arg
if (ch == quoteCH): # Is this quote character we are in
quoteCH = ""
elif (quoteCH == ""): # Create the quote
quoteCH = ch
else:
None
elif (quoteCH != ""): # Still in a quote
arg = arg + ch
elif (ch == delimiter): # Is there a delimiter?
results.append(arg)
arg = ""
else:
arg = arg + ch
if (arg != ""):
results.append(arg)
return(results)
```
### Main %sql Magic Definition
The main %sql Magic logic is found in this section of code. This code will register the Magic command and allow Jupyter notebooks to interact with Db2 by using this extension.
```
@magics_class
class DB2(Magics):
@needs_local_scope
@line_cell_magic
def sql(self, line, cell=None, local_ns=None):
# Before we event get started, check to see if you have connected yet. Without a connection we
# can't do anything. You may have a connection request in the code, so if that is true, we run those,
# otherwise we connect immediately
# If your statement is not a connect, and you haven't connected, we need to do it for you
global _settings, _environment
global _hdbc, _hdbi, _connected, _runtime, sqlstate, sqlerror, sqlcode, sqlelapsed
# If you use %sql (line) we just run the SQL. If you use %%SQL the entire cell is run.
flag_cell = False
flag_output = False
sqlstate = "0"
sqlerror = ""
sqlcode = 0
sqlelapsed = 0
start_time = time.time()
end_time = time.time()
# Macros gets expanded before anything is done
SQL1 = setFlags(line.strip())
SQL1 = checkMacro(SQL1) # Update the SQL if any macros are in there
SQL2 = cell
if flag("-sampledata"): # Check if you only want sample data loaded
if (_connected == False):
if (db2_doConnect() == False):
errormsg('A CONNECT statement must be issued before issuing SQL statements.')
return
db2_create_sample(flag(["-q","-quiet"]))
return
if SQL1 == "?" or flag(["-h","-help"]): # Are you asking for help
sqlhelp()
return
if len(SQL1) == 0 and SQL2 == None: return # Nothing to do here
# Check for help
if SQL1.upper() == "? CONNECT": # Are you asking for help on CONNECT
connected_help()
return
sqlType,remainder = sqlParser(SQL1,local_ns) # What type of command do you have?
if (sqlType == "CONNECT"): # A connect request
parseConnect(SQL1,local_ns)
return
elif (sqlType == "USING"): # You want to use a dataframe to create a table?
createDF(_hdbc,SQL1,local_ns)
return
elif (sqlType == "DEFINE"): # Create a macro from the body
result = setMacro(SQL2,remainder)
return
elif (sqlType == "OPTION"):
setOptions(SQL1)
return
elif (sqlType == 'COMMIT' or sqlType == 'ROLLBACK' or sqlType == 'AUTOCOMMIT'):
parseCommit(remainder)
return
elif (sqlType == "PREPARE"):
pstmt = parsePExec(_hdbc, remainder)
return(pstmt)
elif (sqlType == "EXECUTE"):
result = parsePExec(_hdbc, remainder)
return(result)
elif (sqlType == "CALL"):
result = parseCall(_hdbc, remainder, local_ns)
return(result)
else:
pass
sql = SQL1
if (sql == ""): sql = SQL2
if (sql == ""): return # Nothing to do here
if (_connected == False):
if (db2_doConnect() == False):
errormsg('A CONNECT statement must be issued before issuing SQL statements.')
return
if _settings["maxrows"] == -1: # Set the return result size
pandas.reset_option('display.max_rows')
else:
pandas.options.display.max_rows = _settings["maxrows"]
runSQL = re.sub('.*?--.*$',"",sql,flags=re.M)
remainder = runSQL.replace("\n"," ")
if flag(["-d","-delim"]):
sqlLines = splitSQL(remainder,"@")
else:
sqlLines = splitSQL(remainder,";")
flag_cell = True
# For each line figure out if you run it as a command (db2) or select (sql)
for sqlin in sqlLines: # Run each command
sqlin = checkMacro(sqlin) # Update based on any macros
sqlType, sql = sqlParser(sqlin,local_ns) # Parse the SQL
if (sql.strip() == ""): continue
if flag(["-e","-echo"]): debug(sql,False)
if flag("-t"):
cnt = sqlTimer(_hdbc, _settings["runtime"], sql) # Given the sql and parameters, clock the time
if (cnt >= 0): print("Total iterations in %s second(s): %s" % (_settings["runtime"],cnt))
return(cnt)
elif flag(["-pb","-bar","-pp","-pie","-pl","-line"]): # We are plotting some results
plotData(_hdbi, sql) # Plot the data and return
return
else:
try: # See if we have an answer set
stmt = ibm_db.prepare(_hdbc,sql)
if (ibm_db.num_fields(stmt) == 0): # No, so we just execute the code
result = ibm_db.execute(stmt) # Run it
if (result == False): # Error executing the code
db2_error(flag(["-q","-quiet"]))
continue
rowcount = ibm_db.num_rows(stmt)
if (rowcount == 0 and flag(["-q","-quiet"]) == False):
errormsg("No rows found.")
continue # Continue running
elif flag(["-r","-array","-j","-json"]): # raw, json, format json
row_count = 0
resultSet = []
try:
result = ibm_db.execute(stmt) # Run it
if (result == False): # Error executing the code
db2_error(flag(["-q","-quiet"]))
return
if flag("-j"): # JSON single output
row_count = 0
json_results = []
while( ibm_db.fetch_row(stmt) ):
row_count = row_count + 1
jsonVal = ibm_db.result(stmt,0)
jsonDict = json.loads(jsonVal)
json_results.append(jsonDict)
flag_output = True
if (row_count == 0): sqlcode = 100
return(json_results)
else:
return(fetchResults(stmt))
except Exception as err:
db2_error(flag(["-q","-quiet"]))
return
else:
try:
df = pandas.read_sql(sql,_hdbi)
except Exception as err:
db2_error(False)
return
if (len(df) == 0):
sqlcode = 100
if (flag(["-q","-quiet"]) == False):
errormsg("No rows found")
continue
flag_output = True
if flag("-grid") or _settings['display'] == 'GRID': # Check to see if we can display the results
if (_environment['qgrid'] == False):
with pandas.option_context('display.max_rows', None, 'display.max_columns', None):
print(df.to_string())
else:
try:
pdisplay(qgrid.show_grid(df))
except:
errormsg("Grid cannot be used to display data with duplicate column names. Use option -a or %sql OPTION DISPLAY PANDAS instead.")
return
else:
if flag(["-a","-all"]) or _settings["maxrows"] == -1 : # All of the rows
pandas.options.display.max_rows = None
pandas.options.display.max_columns = None
return df # print(df.to_string())
else:
pandas.options.display.max_rows = _settings["maxrows"]
pandas.options.display.max_columns = None
return df # pdisplay(df) # print(df.to_string())
except:
db2_error(flag(["-q","-quiet"]))
continue # return
end_time = time.time()
sqlelapsed = end_time - start_time
if (flag_output == False and flag(["-q","-quiet"]) == False): print("Command completed.")
# Register the Magic extension in Jupyter
ip = get_ipython()
ip.register_magics(DB2)
load_settings()
success("Db2 Extensions Loaded.")
```
## Pre-defined Macros
These macros are used to simulate the LIST TABLES and DESCRIBE commands that are available from within the Db2 command line.
```
%%sql define LIST
#
# The LIST macro is used to list all of the tables in the current schema or for all schemas
#
var syntax Syntax: LIST TABLES [FOR ALL | FOR SCHEMA name]
#
# Only LIST TABLES is supported by this macro
#
if {^1} <> 'TABLES'
exit {syntax}
endif
#
# This SQL is a temporary table that contains the description of the different table types
#
WITH TYPES(TYPE,DESCRIPTION) AS (
VALUES
('A','Alias'),
('G','Created temporary table'),
('H','Hierarchy table'),
('L','Detached table'),
('N','Nickname'),
('S','Materialized query table'),
('T','Table'),
('U','Typed table'),
('V','View'),
('W','Typed view')
)
SELECT TABNAME, TABSCHEMA, T.DESCRIPTION FROM SYSCAT.TABLES S, TYPES T
WHERE T.TYPE = S.TYPE
#
# Case 1: No arguments - LIST TABLES
#
if {argc} == 1
AND OWNER = CURRENT USER
ORDER BY TABNAME, TABSCHEMA
return
endif
#
# Case 2: Need 3 arguments - LIST TABLES FOR ALL
#
if {argc} == 3
if {^2}&{^3} == 'FOR&ALL'
ORDER BY TABNAME, TABSCHEMA
return
endif
exit {syntax}
endif
#
# Case 3: Need FOR SCHEMA something here
#
if {argc} == 4
if {^2}&{^3} == 'FOR&SCHEMA'
AND TABSCHEMA = '{^4}'
ORDER BY TABNAME, TABSCHEMA
return
else
exit {syntax}
endif
endif
#
# Nothing matched - Error
#
exit {syntax}
%%sql define describe
#
# The DESCRIBE command can either use the syntax DESCRIBE TABLE <name> or DESCRIBE TABLE SELECT ...
#
var syntax Syntax: DESCRIBE [TABLE name | SELECT statement]
#
# Check to see what count of variables is... Must be at least 2 items DESCRIBE TABLE x or SELECT x
#
if {argc} < 2
exit {syntax}
endif
CALL ADMIN_CMD('{*0}');
```
Set the table formatting to left align a table in a cell. By default, tables are centered in a cell. Remove this cell if you don't want to change Jupyter notebook formatting for tables. In addition, we skip this code if you are running in a shell environment rather than a Jupyter notebook
```
#%%html
#<style>
# table {margin-left: 0 !important; text-align: left;}
#</style>
```
#### Credits: IBM 2021, George Baklarz [[email protected]]
| github_jupyter |
# Profiling TensorFlow Multi GPU Multi Node Training Job with Amazon SageMaker Debugger
This notebook will walk you through creating a TensorFlow training job with the SageMaker Debugger profiling feature enabled. It will create a multi GPU multi node training using Horovod.
### (Optional) Install SageMaker and SMDebug Python SDKs
To use the new Debugger profiling features released in December 2020, ensure that you have the latest versions of SageMaker and SMDebug SDKs installed. Use the following cell to update the libraries and restarts the Jupyter kernel to apply the updates.
```
import sys
import IPython
install_needed = False # should only be True once
if install_needed:
print("installing deps and restarting kernel")
!{sys.executable} -m pip install -U sagemaker smdebug
IPython.Application.instance().kernel.do_shutdown(True)
```
## 1. Create a Training Job with Profiling Enabled<a class="anchor" id="option-1"></a>
You will use the standard [SageMaker Estimator API for Tensorflow](https://sagemaker.readthedocs.io/en/stable/frameworks/tensorflow/sagemaker.tensorflow.html#tensorflow-estimator) to create training jobs. To enable profiling, create a `ProfilerConfig` object and pass it to the `profiler_config` parameter of the `TensorFlow` estimator.
### Define parameters for distributed training
This parameter tells SageMaker how to configure and run horovod. If you want to use more than 4 GPUs per node then change the process_per_host paramter accordingly.
```
distributions = {
"mpi": {
"enabled": True,
"processes_per_host": 4,
"custom_mpi_options": "-verbose -x HOROVOD_TIMELINE=./hvd_timeline.json -x NCCL_DEBUG=INFO -x OMPI_MCA_btl_vader_single_copy_mechanism=none",
}
}
```
### Configure rules
We specify the following rules:
- loss_not_decreasing: checks if loss is decreasing and triggers if the loss has not decreased by a certain persentage in the last few iterations
- LowGPUUtilization: checks if GPU is under-utilizated
- ProfilerReport: runs the entire set of performance rules and create a final output report with further insights and recommendations.
```
from sagemaker.debugger import Rule, ProfilerRule, rule_configs
rules = [
Rule.sagemaker(rule_configs.loss_not_decreasing()),
ProfilerRule.sagemaker(rule_configs.LowGPUUtilization()),
ProfilerRule.sagemaker(rule_configs.ProfilerReport()),
]
```
### Specify a profiler configuration
The following configuration will capture system metrics at 500 milliseconds. The system metrics include utilization per CPU, GPU, memory utilization per CPU, GPU as well I/O and network.
Debugger will capture detailed profiling information from step 5 to step 15. This information includes Horovod metrics, dataloading, preprocessing, operators running on CPU and GPU.
```
from sagemaker.debugger import ProfilerConfig, FrameworkProfile
profiler_config = ProfilerConfig(
system_monitor_interval_millis=500,
framework_profile_params=FrameworkProfile(
local_path="/opt/ml/output/profiler/", start_step=5, num_steps=10
),
)
```
### Get the image URI
The image that we will is dependent on the region that you are running this notebook in.
```
import boto3
session = boto3.session.Session()
region = session.region_name
image_uri = f"763104351884.dkr.ecr.{region}.amazonaws.com/tensorflow-training:2.3.1-gpu-py37-cu110-ubuntu18.04"
```
### Define estimator
To enable profiling, you need to pass the Debugger profiling configuration (`profiler_config`), a list of Debugger rules (`rules`), and the image URI (`image_uri`) to the estimator. Debugger enables monitoring and profiling while the SageMaker estimator requests a training job.
```
import sagemaker
from sagemaker.tensorflow import TensorFlow
estimator = TensorFlow(
role=sagemaker.get_execution_role(),
image_uri=image_uri,
instance_count=2,
instance_type="ml.p3.8xlarge",
entry_point="tf-hvd-train.py",
source_dir="entry_point",
profiler_config=profiler_config,
distribution=distributions,
rules=rules,
)
```
### Start training job
The following `estimator.fit()` with `wait=False` argument initiates the training job in the background. You can proceed to run the dashboard or analysis notebooks.
```
estimator.fit(wait=False)
```
## 2. Analyze Profiling Data
Copy outputs of the following cell (`training_job_name` and `region`) to run the analysis notebooks `profiling_generic_dashboard.ipynb`, `analyze_performance_bottlenecks.ipynb`, and `profiling_interactive_analysis.ipynb`.
```
training_job_name = estimator.latest_training_job.name
print(f"Training jobname: {training_job_name}")
print(f"Region: {region}")
```
While the training is still in progress you can visualize the performance data in SageMaker Studio or in the notebook.
Debugger provides utilities to plot system metrics in form of timeline charts or heatmaps. Checkout out the notebook
[profiling_interactive_analysis.ipynb](analysis_tools/profiling_interactive_analysis.ipynb) for more details. In the following code cell we plot the total CPU and GPU utilization as timeseries charts. To visualize other metrics such as I/O, memory, network you simply need to extend the list passed to `select_dimension` and `select_events`.
### Install the SMDebug client library to use Debugger analysis tools
```
import pip
def import_or_install(package):
try:
__import__(package)
except ImportError:
pip.main(["install", package])
import_or_install("smdebug")
```
### Access the profiling data using the SMDebug `TrainingJob` utility class
```
from smdebug.profiler.analysis.notebook_utils.training_job import TrainingJob
tj = TrainingJob(training_job_name, region)
tj.wait_for_sys_profiling_data_to_be_available()
```
### Plot time line charts
The following code shows how to use the SMDebug `TrainingJob` object, refresh the object if new event files are available, and plot time line charts of CPU and GPU usage.
```
from smdebug.profiler.analysis.notebook_utils.timeline_charts import TimelineCharts
system_metrics_reader = tj.get_systems_metrics_reader()
system_metrics_reader.refresh_event_file_list()
view_timeline_charts = TimelineCharts(
system_metrics_reader,
framework_metrics_reader=None,
select_dimensions=["CPU", "GPU"],
select_events=["total"],
)
```
## 3. Download Debugger Profiling Report
The `ProfilerReport()` rule creates an html report `profiler-report.html` with a summary of builtin rules and recommenades of next steps. You can find this report in your S3 bucket.
```
rule_output_path = estimator.output_path + estimator.latest_training_job.job_name + "/rule-output"
print(f"You will find the profiler report in {rule_output_path}")
```
For more information about how to download and open the Debugger profiling report, see [SageMaker Debugger Profiling Report](https://docs.aws.amazon.com/sagemaker/latest/dg/debugger-profiling-report.html) in the SageMaker developer guide.
| github_jupyter |
## Лабораторная работа 2 - Линейная и полиномиальная регрессия.
Одна из множества задач, которой занимается современная физика это поиск материала для изготовления сверхпроводника, работающего при комнатной температуре. Кроме теоретических методов есть и подход со стороны статистики, который подразумевает анализ базы данных материалов для нахождения зависимости критической температуры от других физических характеристик. Именно этим Вы и займетесь.
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
```
В файле **data.csv** содержится весь датасет.
```
data = pd.read_csv('data.csv')
data
```
Итого имеем 21 тысячу строк и 169 колонок, из которых первые 167 - признаки, колонка **critical_temp** содержит величину, которую надо предсказать. Колонка **material** - содержит химическую формулу материала, ее можно отбросить.
Выполним предобработку данных и разобъем на тренировочную и тестовую выборки:
```
# X - last two columns cut.
# Y - pre last column.
x, y = data.values[:, :-2].astype(np.float32), data.values[:, -2:-1].astype(np.float32)
np.random.seed(1337)
is_train = np.random.uniform(size=(x.shape[0],)) < 0.95
x_train, y_train = x[is_train], y[is_train]
x_test, y_test = x[~is_train], y[~is_train]
print(f'Train samples: {len(x_train)}')
print(f'Test samples: {len(x_test)}')
```
Реализуйте методы с пометкой `#TODO` класса PolynomialRegression:
Метод `preprocess` должен выполнять следующее преобразование:
$$
\begin{array}{l}
X=\begin{bmatrix}
x_{i,j}
\end{bmatrix}_{m\times n}\\
preprocess( X) =\begin{bmatrix}
1 & x_{1,1} & \dotsc & x_{1,1} & x^{2}_{1,1} & \dotsc & x^{2}_{1,1} & \dotsc & x^{p}_{1,1} & \dotsc & x^{p}_{1,1}\\
1 & x_{2,1} & \dotsc & x_{2,n} & x^{2}_{2,1} & \dotsc & x^{2}_{2,n} & \dotsc & x^{p}_{2,1} & \dotsc & x^{p}_{2,n}\\
\vdots & & & & & & & & & & \\
1 & x_{m,1} & \dotsc & x_{m,n} & x^{2}_{m,1} & \dotsc & x^{2}_{m,n} & \dotsc & x^{p}_{m,1} & \dotsc & x^{p}_{m,n}
\end{bmatrix}_{m,N}
\end{array}
$$где p - степень полинома (`self.poly_deg` в коде).
Таким образом, preprocess добавляет полиномиальные признаки к $X$.
Метод `J` должен вычислять оценочную функцию регрессии:
$$
J( \theta ) =MSE( Y,\ h_{\theta }( X)) +\alpha _{1}\sum ^{N}_{i=1}\sum ^{k}_{j=1} |\hat{\theta }_{i,j} |+\alpha _{2}\sum ^{N}_{i=1}\sum ^{k}_{j=1}\hat{\theta }^{2}_{i,j}
$$
Метод `grad` должен вычислять градиент $\frac{\partial J}{\partial \theta }$:
$$
{\displaystyle \frac{\partial J}{\partial \theta }} =-{\displaystyle \frac{2}{m}} X^{T} (Y-X\theta )+\begin{bmatrix}
0 & & & \\
& 1 & & \\
& & \ddots & \\
& & & 1
\end{bmatrix} \times ( \alpha _{1} sign(\theta )+2\alpha _{2} \theta )
$$
Метод `moments` должен возвращать вектор-строки $\mu,\sigma$ для среднего и стандартного отклонения каждой колонки. Помните, что колонку с единицами не нужно нормализировать, так что соответствующие среднее и стандартное отколонение для нее укажите равными 0 и 1 соответственно. Можно использовать функции
[np.mean](https://numpy.org/doc/stable/reference/generated/numpy.mean.html) и [np.std](https://numpy.org/doc/stable/reference/generated/numpy.std.html).
Метод `normalize` должен выполнять нормализацию $X$ на основе статистик $\mu,\sigma$, что вернул метод **moments**. Для того чтобы избежать деления на 0, можете к $\sigma$ прибавить маленькую величину, например $10^{-8}$.
Метод `get_batch` должен возвращать матрицы $X_b, Y_b$ из произвольно выбранных $b$ элементов выборки ($b$ в коде - `self.batch_size`).
Метод `fit` выполняет оптимизацию $J(\theta)$. Для лучшей сходимости реализуйте алгоритм оптимизации **Momentum**:
$$
\begin{array}{l}
v_t = \gamma v_{t-1} + \alpha\nabla J(\theta_{t-1})\\
\theta_t = \theta_{t-1} - v_t
\end{array}
$$
где $\gamma$ установите равным $0.9$ (можете поэкспериментировать с другими величиными), $v_1=[0]_{N,k}$.
```
class PolynomialRegression:
def __init__(
self,
alpha1,
alpha2,
poly_deg,
learning_rate,
batch_size,
train_steps
):
self.alpha1 = alpha1
self.alpha2 = alpha2
self.poly_deg = poly_deg
self.learning_rate = learning_rate
self.batch_size = batch_size
self.train_steps = train_steps
def preprocess(self, x):
# Create first one column.
ones = [np.ones(shape=(x.shape[0], 1))]
# Polynomic scale.
powers = [x ** i for i in range(1, self.poly_deg + 1)]
# Unite into one.
result = np.concatenate(ones + powers, axis=1)
return result
def normalize(self, x):
return (x - self.mu) / (self.sigma + 1e-8)
def moments(self, x):
# Arttimetic average (a + b + ... + z) / n.
mu = np.mean(x, axis=0)
# Standart deviation.
sigma = np.std(x, axis=0)
mu[0] = 0
sigma[0] = 1
return mu, sigma
def J(self, x, y, theta):
# Theta is not multiply with first (ones) column.
circumcized_theta = theta[1::]
# Mean squared error.
mse = ((y - np.dot(x, theta)) ** 2).mean(axis=None)
# Module sum of theta (alpha1).
l1 = self.alpha1 * np.sum(np.abs(circumcized_theta), axis=None)
# Quadro sum of theta (alpha2).
l2 = self.alpha2 * np.sum(circumcized_theta ** 2, axis=None)
return mse + l1 + l2
def grad(self, x, y, theta):
# Create ones matrix.
diag = np.eye(x.shape[1], x.shape[1])
# Init first element as 0.
diag[0][0] = 0
# Left assign.
l1l2 = self.alpha1 * np.sign(theta) + 2 * self.alpha2 * theta
return (-2/x.shape[0]) * x.T @ (y - (x @ theta)) + (diag @ l1l2)
def get_batch(self, x, y):
# Return random values.
i = np.random.default_rng().choice(x.shape[0], self.batch_size, replace=False)
return x[i], y[i]
def fit(self, x, y):
## Trasform source data to polynom regression.
x = self.preprocess(x)
(m, N), (_, k) = x.shape, y.shape
# Calculate mu and standart deviation.
self.mu, self.sigma = self.moments(x)
# Normalize using average values.
x = self.normalize(x)
try:
assert np.allclose(x[:, 1:].mean(axis=0), 0, atol=1e-3)
assert np.all((np.abs(x[:, 1:].std(axis=0)) < 1e-2) | (np.abs(x[:, 1:].std(axis=0) - 1) < 1e-2))
except AssertionError as e:
print('Something wrong with normalization')
raise e
# Random x & y.
x_batch, y_batch = self.get_batch(x, y)
try:
assert x_batch.shape[0] == self.batch_size
assert y_batch.shape[0] == self.batch_size
except AssertionError as e:
print('Something wrong with get_batch')
raise e
theta = np.zeros(shape=(N, k))
v_1 = np.zeros(shape=(N, k))
v_t = v_1
for step in range(self.train_steps):
x_batch, y_batch = self.get_batch(x, y)
theta_grad = self.grad(x_batch, y_batch, theta)
v_t = 0.9 * v_t + self.learning_rate * theta_grad
theta = theta - v_t
self.theta = theta
return self
def predict(self, x):
x = self.preprocess(x)
x = self.normalize(x)
return x @ self.theta
def score(self, x, y):
y_pred = self.predict(x)
return np.abs(y - y_pred).mean()
reg = PolynomialRegression(0, 0, 1, 1e-3, 1024, 1000).fit(x_train, y_train)
print(f'Test MAE: {reg.score(x_test, y_test)}')
```
Полученный MAE на тестовой выборке должен быть приблизительно равен $12.5$.
Выполните поиск оптимальных параметров регуляризации $\alpha_1,\alpha_2$ по отдельности (то есть устанавливаете один параметр равным нулю и ищете второй, потом наоборот) и старшей степени полиномиальной регрессии (`poly_deg`). Обратите внимание, что поиск параметра регуляризации следует искать на логарифмической шкале. То есть, например, список кандидатов может быть задан как: `10 ** np.linspace(-5, -1, 5)`, что даст вам величины $10^{-5},10^{-4},10^{-3},10^{-2},10^{-1}$.
При надобности, можете отрегулировать оптимальный `batch_size`, `learning_rate`, `training_steps`.
Результаты представьте в виде графиков по примеру ниже.
Дополнительные баллы будут начислены за выполнение поиска оптимальных параметров $\alpha_1,\alpha_2$ вместе. В таком случае результаты представьте при помощи [plt.matshow](https://matplotlib.org/3.3.2/api/_as_gen/matplotlib.pyplot.matshow.html).
```
a1 = 10 ** np.linspace(-9, -1, 9)
a2 = 10 ** np.linspace(-9, -1, 9)
fig, (ax1, ax2) = plt.subplots(ncols=2, nrows=1, figsize=(20, 10))
fig.suptitle('Poly deg. = 5')
ax1.set_xlabel('Alpha 1')
ax1.set_ylabel('Score')
ax1.set_xscale('log')
ax1.plot([a1i for a1i in a1], [PolynomialRegression(a1i, 0, 1, 1e-3, 1024, 1000).fit(x_train, y_train).score(x_test, y_test) for a1i in a1])
ax2.set_xlabel('Alpha 2')
ax2.set_ylabel('Score')
ax2.set_xscale('log')
ax2.plot([a2i for a2i in a2], [PolynomialRegression(0, a2i, 1, 1e-3, 1024, 1000).fit(x_train, y_train).score(x_test, y_test) for a2i in a2])
plt.show()
```
Визуализируйте зависимость предсказанной критической температуры от истинной для лучшей модели:
```
reg = PolynomialRegression(1e-5, 1e-5, 5, 1e-3, 1024, 1000).fit(x_train, y_train)
y_test_pred = reg.predict(x_test)
print(f'Test MAE: {reg.score(x_test, y_test)}')
plt.figure(figsize=(10, 10))
plt.scatter(y_test[:, 0], y_test_pred[:, 0], marker='.', c='r')
plt.xlabel('True Y')
plt.ylabel('Predicted Y')
plt.show()
```
| github_jupyter |
```
import sys
import os
sys.path.append(os.path.abspath("../src/"))
import extract.data_loading as data_loading
import extract.compute_predictions as compute_predictions
import extract.compute_shap as compute_shap
import extract.compute_ism as compute_ism
import model.util as model_util
import model.profile_models as profile_models
import model.binary_models as binary_models
import plot.viz_sequence as viz_sequence
import torch
import numpy as np
import scipy.stats
import matplotlib.pyplot as plt
import matplotlib.font_manager as font_manager
import json
import tqdm
tqdm.tqdm_notebook() # It is necessary to call this before the tqdm.notebook submodule is available
font_manager.fontManager.ttflist.extend(
font_manager.createFontList(
font_manager.findSystemFonts(fontpaths="/users/amtseng/modules/fonts")
)
)
plot_params = {
"axes.titlesize": 22,
"axes.labelsize": 20,
"legend.fontsize": 18,
"xtick.labelsize": 16,
"ytick.labelsize": 16,
"font.family": "Roboto",
"font.weight": "bold"
}
plt.rcParams.update(plot_params)
```
### Define paths for the model and data of interest
```
model_type = "profile"
# Shared paths/constants
reference_fasta = "/users/amtseng/genomes/hg38.fasta"
chrom_sizes = "/users/amtseng/genomes/hg38.canon.chrom.sizes"
data_base_path = "/users/amtseng/att_priors/data/processed/"
model_base_path = "/users/amtseng/att_priors/models/trained_models/%s/" % model_type
chrom_set = ["chr1"]
input_length = 1346 if model_type == "profile" else 1000
profile_length = 1000
# SPI1
condition_name = "SPI1"
files_spec_path = os.path.join(data_base_path, "ENCODE_TFChIP/%s/config/SPI1/SPI1_training_paths.json" % model_type)
num_tasks = 4
num_strands = 2
task_index = None
controls = "matched"
if model_type == "profile":
model_class = profile_models.ProfilePredictorWithMatchedControls
else:
model_class = binary_models.BinaryPredictor
noprior_model_base_path = os.path.join(model_base_path, "SPI1/")
prior_model_base_path = os.path.join(model_base_path, "SPI1_prior/")
peak_retention = "all"
# GATA2
condition_name = "GATA2"
files_spec_path = os.path.join(data_base_path, "ENCODE_TFChIP/%s/config/GATA2/GATA2_training_paths.json" % model_type)
num_tasks = 3
num_strands = 2
task_index = None
controls = "matched"
if model_type == "profile":
model_class = profile_models.ProfilePredictorWithMatchedControls
else:
model_class = binary_models.BinaryPredictor
noprior_model_base_path = os.path.join(model_base_path, "GATA2/")
prior_model_base_path = os.path.join(model_base_path, "GATA2_prior/")
peak_retention = "all"
# K562
condition_name = "K562"
files_spec_path = os.path.join(data_base_path, "ENCODE_DNase/%s/config/K562/K562_training_paths.json" % model_type)
num_tasks = 1
num_strands = 1
task_index = None
controls = "shared"
if model_type == "profile":
model_class = profile_models.ProfilePredictorWithSharedControls
else:
model_class = binary_models.BinaryPredictor
noprior_model_base_path = os.path.join(model_base_path, "K562/")
prior_model_base_path = os.path.join(model_base_path, "K562_prior/")
peak_retention = "all"
# BPNet
condition_name = "BPNet"
reference_fasta = "/users/amtseng/genomes/mm10.fasta"
chrom_sizes = "/users/amtseng/genomes/mm10.canon.chrom.sizes"
files_spec_path = os.path.join(data_base_path, "BPNet_ChIPseq/%s/config/BPNet_training_paths.json" % model_type)
num_tasks = 3
num_strands = 2
task_index = None
controls = "shared"
if model_type == "profile":
model_class = profile_models.ProfilePredictorWithSharedControls
else:
model_class = binary_models.BinaryPredictor
noprior_model_base_path = os.path.join(model_base_path, "BPNet/")
prior_model_base_path = os.path.join(model_base_path, "BPNet_prior/")
peak_retention = "all"
```
### Get all runs/epochs with random initializations
```
def import_metrics_json(model_base_path, run_num):
"""
Looks in {model_base_path}/{run_num}/metrics.json and returns the contents as a
Python dictionary. Returns None if the path does not exist.
"""
path = os.path.join(model_base_path, str(run_num), "metrics.json")
if not os.path.exists(path):
return None
with open(path, "r") as f:
return json.load(f)
def get_model_paths(
model_base_path, metric_name="val_prof_corr_losses",
reduce_func=(lambda values: np.mean(values)), compare_func=(lambda x, y: x < y),
print_found_values=True
):
"""
Looks in `model_base_path` and for each run, returns the full path to
the best epoch. By default, the best epoch in a run is determined by
the lowest validation profile loss.
"""
# Get the metrics, ignoring empty or nonexistent metrics.json files
metrics = {run_num : import_metrics_json(model_base_path, run_num) for run_num in os.listdir(model_base_path)}
metrics = {key : val for key, val in metrics.items() if val} # Remove empties
model_paths, metric_vals = [], []
for run_num in sorted(metrics.keys(), key=lambda x: int(x)):
try:
# Find the best epoch within that run
best_epoch_in_run, best_val_in_run = None, None
for i, subarr in enumerate(metrics[run_num][metric_name]["values"]):
val = reduce_func(subarr)
if best_val_in_run is None or compare_func(val, best_val_in_run):
best_epoch_in_run, best_val_in_run = i + 1, val
model_path = os.path.join(model_base_path, run_num, "model_ckpt_epoch_%d.pt" % best_epoch_in_run)
model_paths.append(model_path)
metric_vals.append(best_val_in_run)
if print_found_values:
print("\tRun %s, epoch %d: %6.2f" % (run_num, best_epoch_in_run, best_val_in_run))
except Exception:
print("Warning: Was not able to compute values for run %s" % run_num)
continue
return model_paths, metric_vals
metric_name = "val_prof_corr_losses" if model_type == "profile" else "val_corr_losses"
noprior_model_paths, noprior_metric_vals = get_model_paths(noprior_model_base_path, metric_name=metric_name)
prior_model_paths, prior_metric_vals = get_model_paths(prior_model_base_path, metric_name=metric_name)
torch.set_grad_enabled(True)
device = torch.device("cuda") if torch.cuda.is_available() else torch.device("cpu")
def restore_model(model_path):
model = model_util.restore_model(model_class, model_path)
model.eval()
model = model.to(device)
return model
```
### Data preparation
Create an input data loader, that maps coordinates or bin indices to data needed for the model
```
if model_type == "profile":
input_func = data_loading.get_profile_input_func(
files_spec_path, input_length, profile_length, reference_fasta
)
pos_examples = data_loading.get_positive_profile_coords(
files_spec_path, chrom_set=chrom_set
)
else:
input_func = data_loading.get_binary_input_func(
files_spec_path, input_length, reference_fasta
)
pos_examples = data_loading.get_positive_binary_bins(
files_spec_path, chrom_set=chrom_set
)
```
### Compute importances
```
# Pick a sample of 100 random coordinates/bins
num_samples = 100
rng = np.random.RandomState(20200318)
sample = pos_examples[rng.choice(len(pos_examples), size=num_samples, replace=False)]
# For profile models, add a random jitter to avoid center-bias
if model_type == "profile":
jitters = np.random.randint(-128, 128 + 1, size=len(sample))
sample[:, 1] = sample[:, 1] + jitters
sample[:, 2] = sample[:, 2] + jitters
def compute_gradients(model_paths, sample):
"""
Given a list of paths to M models and a list of N coordinates or bins, computes
the input gradients over all models, returning an M x N x I x 4 array of
gradient values and an N x I x 4 array of one-hot encoded sequence.
"""
num_models, num_samples = len(model_paths), len(sample)
all_input_grads = np.empty((num_models, num_samples, input_length, 4))
all_one_hot_seqs = np.empty((num_samples, input_length, 4))
for i in tqdm.notebook.trange(num_models):
model = restore_model(model_paths[i])
if model_type == "profile":
results = compute_predictions.get_profile_model_predictions(
model, sample, num_tasks, input_func, controls=controls,
return_losses=False, return_gradients=True, show_progress=False
)
else:
results = compute_predictions.get_binary_model_predictions(
model, sample, input_func,
return_losses=False, return_gradients=True, show_progress=False
)
all_input_grads[i] = results["input_grads"]
if i == 0:
all_one_hot_seqs = results["input_seqs"]
return all_input_grads, all_one_hot_seqs
def compute_shap_scores(model_paths, sample, batch_size=128):
"""
Given a list of paths to M models and a list of N coordinates or bins, computes
the SHAP scores over all models, returning an M x N x I x 4 array of
SHAP scores and an N x I x 4 array of one-hot encoded sequence.
"""
num_models, num_samples = len(model_paths), len(sample)
num_batches = int(np.ceil(num_samples / batch_size))
all_shap_scores = np.empty((num_models, num_samples, input_length, 4))
all_one_hot_seqs = np.empty((num_samples, input_length, 4))
for i in tqdm.notebook.trange(num_models):
model = restore_model(model_paths[i])
if model_type == "profile":
shap_explainer = compute_shap.create_profile_explainer(
model, input_length, profile_length, num_tasks, num_strands, controls,
task_index=task_index
)
else:
shap_explainer = compute_shap.create_binary_explainer(
model, input_length, task_index=task_index
)
for j in range(num_batches):
batch_slice = slice(j * batch_size, (j + 1) * batch_size)
batch = sample[batch_slice]
if model_type == "profile":
input_seqs, profiles = input_func(sample)
shap_scores = shap_explainer(
input_seqs, cont_profs=profiles[:, num_tasks:], hide_shap_output=True
)
else:
input_seqs, _, _ = input_func(sample)
shap_scores = shap_explainer(
input_seqs, hide_shap_output=True
)
all_shap_scores[i, batch_slice] = shap_scores
if i == 0:
all_one_hot_seqs[batch_slice] = input_seqs
return all_shap_scores, all_one_hot_seqs
# Compute the importance scores and 1-hot seqs
imp_type = ("DeepSHAP scores", "input gradients")[0]
imp_func = compute_shap_scores if imp_type == "DeepSHAP scores" else compute_gradients
noprior_scores, _ = imp_func(noprior_model_paths, sample)
prior_scores, one_hot_seqs = imp_func(prior_model_paths, sample)
```
### Compute similarity
```
def cont_jaccard(seq_1, seq_2):
"""
Takes two gradient sequences (I x 4 arrays) and computes a similarity between
them, using a continuous Jaccard metric.
"""
# L1-normalize
norm_1 = np.sum(np.abs(seq_1), axis=1, keepdims=True)
norm_2 = np.sum(np.abs(seq_2), axis=1, keepdims=True)
norm_1[norm_1 == 0] = 1
norm_2[norm_2 == 0] = 1
seq_1 = seq_1 / norm_1
seq_2 = seq_2 / norm_2
ab_1, ab_2 = np.abs(seq_1), np.abs(seq_2)
inter = np.sum(np.minimum(ab_1, ab_2) * np.sign(seq_1) * np.sign(seq_2), axis=1)
union = np.sum(np.maximum(ab_1, ab_2), axis=1)
zero_mask = union == 0
inter[zero_mask] = 0
union[zero_mask] = 1
return np.sum(inter / union)
def cosine_sim(seq_1, seq_2):
"""
Takes two gradient sequences (I x 4 arrays) and computes a similarity between
them, using a cosine similarity.
"""
seq_1, seq_2 = np.ravel(seq_1), np.ravel(seq_2)
dot = np.sum(seq_1 * seq_2)
mag_1, mag_2 = np.sqrt(np.sum(seq_1 * seq_1)), np.sqrt(np.sum(seq_2 * seq_2))
return dot / (mag_1 * mag_2) if mag_1 * mag_2 else 0
def compute_similarity_matrix(imp_scores, sim_func=cosine_sim):
"""
Given the M x N x I x 4 importance scores returned by `compute_gradients`
or `compute_shap_scores`, computes an N x M x M similarity matrix of
similarity across models (i.e. each coordinate gets a similarity matrix
across different models). By default uses cosine similarity.
"""
num_models, num_coords = imp_scores.shape[0], imp_scores.shape[1]
sim_mats = np.empty((num_coords, num_models, num_models))
for i in tqdm.notebook.trange(num_coords):
for j in range(num_models):
sim_mats[i, j, j] = 0
for k in range(j):
sim_score = sim_func(imp_scores[j][i], imp_scores[k][i])
sim_mats[i, j, k] = sim_score
sim_mats[i, k, j] = sim_score
return sim_mats
sim_type = ("Cosine", "Continuous Jaccard")[1]
sim_func = cosine_sim if sim_type == "Cosine" else cont_jaccard
noprior_sim_matrix = compute_similarity_matrix(noprior_scores, sim_func=sim_func)
prior_sim_matrix = compute_similarity_matrix(prior_scores, sim_func=sim_func)
# Plot some examples of poor consistency, particularly ones that showed an improvement
num_to_show = 100
center_view_length = 200
plot_zoom = True
midpoint = input_length // 2
start = midpoint - (center_view_length // 2)
end = start + center_view_length
center_slice = slice(550, 800)
noprior_sim_matrix_copy = noprior_sim_matrix.copy()
for i in range(len(noprior_sim_matrix_copy)):
noprior_sim_matrix_copy[i][np.diag_indices(noprior_sim_matrix.shape[1])] = np.inf # Put infinity in diagonal
diffs = np.max(prior_sim_matrix, axis=(1, 2)) - np.min(noprior_sim_matrix_copy, axis=(1, 2))
best_example_inds = np.flip(np.argsort(diffs))[:num_to_show]
best_example_inds = [7] #, 38]
for sample_index in best_example_inds:
noprior_model_ind_1, noprior_model_ind_2 = np.unravel_index(np.argmin(np.ravel(noprior_sim_matrix_copy[sample_index])), noprior_sim_matrix[sample_index].shape)
prior_model_ind_1, prior_model_ind_2 = np.unravel_index(np.argmax(np.ravel(prior_sim_matrix[sample_index])), prior_sim_matrix[sample_index].shape)
noprior_model_ind_1, noprior_model_ind_2 = 5, 17
prior_model_ind_1, prior_model_ind_2 = 13, 17
print("Sample index: %d" % sample_index)
if model_type == "binary":
bin_index = sample[sample_index]
coord = input_func(np.array([bin_index]))[2][0]
print("Coordinate: %s (bin %d)" % (str(coord), bin_index))
else:
coord = sample[sample_index]
print("Coordinate: %s" % str(coord))
print("Model indices without prior: %d vs %d" % (noprior_model_ind_1, noprior_model_ind_2))
plt.figure(figsize=(20, 2))
plt.plot(np.sum(noprior_scores[noprior_model_ind_1, sample_index] * one_hot_seqs[sample_index], axis=1), color="coral")
plt.show()
if plot_zoom:
viz_sequence.plot_weights(noprior_scores[noprior_model_ind_1, sample_index, center_slice], subticks_frequency=1000)
viz_sequence.plot_weights(noprior_scores[noprior_model_ind_1, sample_index, center_slice] * one_hot_seqs[sample_index, center_slice], subticks_frequency=1000)
plt.figure(figsize=(20, 2))
plt.plot(np.sum(noprior_scores[noprior_model_ind_2, sample_index] * one_hot_seqs[sample_index], axis=1), color="coral")
plt.show()
if plot_zoom:
viz_sequence.plot_weights(noprior_scores[noprior_model_ind_2, sample_index, center_slice], subticks_frequency=1000)
viz_sequence.plot_weights(noprior_scores[noprior_model_ind_2, sample_index, center_slice] * one_hot_seqs[sample_index, center_slice], subticks_frequency=1000)
print("Model indices with prior: %d vs %d" % (prior_model_ind_1, prior_model_ind_2))
plt.figure(figsize=(20, 2))
plt.plot(np.sum(prior_scores[prior_model_ind_1, sample_index] * one_hot_seqs[sample_index], axis=1), color="slateblue")
plt.show()
if plot_zoom:
viz_sequence.plot_weights(prior_scores[prior_model_ind_1, sample_index, center_slice], subticks_frequency=1000)
viz_sequence.plot_weights(prior_scores[prior_model_ind_1, sample_index, center_slice] * one_hot_seqs[sample_index, center_slice], subticks_frequency=1000)
plt.figure(figsize=(20, 2))
plt.plot(np.sum(prior_scores[prior_model_ind_2, sample_index] * one_hot_seqs[sample_index], axis=1), color="slateblue")
plt.show()
if plot_zoom:
viz_sequence.plot_weights(prior_scores[prior_model_ind_2, sample_index, center_slice], subticks_frequency=1000)
viz_sequence.plot_weights(prior_scores[prior_model_ind_2, sample_index, center_slice] * one_hot_seqs[sample_index, center_slice], subticks_frequency=1000)
sample_index = 7
for i in range(30):
print(i)
plt.figure(figsize=(20, 2))
plt.plot(np.sum(noprior_scores[i, sample_index] * one_hot_seqs[sample_index], axis=1), color="coral")
plt.show()
for i in range(30):
print(i)
plt.figure(figsize=(20, 2))
plt.plot(np.sum(prior_scores[i, sample_index] * one_hot_seqs[sample_index], axis=1), color="coral")
plt.show()
noprior_avg_sims, prior_avg_sims = [], []
bin_num = 30
for i in range(num_samples):
noprior_avg_sims.append(np.mean(noprior_sim_matrix[i][np.tril_indices(len(noprior_model_paths), k=-1)]))
prior_avg_sims.append(np.mean(prior_sim_matrix[i][np.tril_indices(len(prior_model_paths), k=-1)]))
noprior_avg_sims, prior_avg_sims = np.array(noprior_avg_sims), np.array(prior_avg_sims)
all_vals = np.concatenate([noprior_avg_sims, prior_avg_sims])
bins = np.linspace(np.min(all_vals), np.max(all_vals), bin_num)
fig, ax = plt.subplots(figsize=(16, 8))
ax.hist(noprior_avg_sims, bins=bins, color="coral", label="No prior", alpha=0.7)
ax.hist(prior_avg_sims, bins=bins, color="slateblue", label="With Fourier prior", alpha=0.7)
plt.legend()
plt.title(
("Mean pairwise similarities of %s between different random initializations" % imp_type) +
("\n%s %s models" % (condition_name, model_type)) +
"\nComputed over %d/%d models without/with Fourier prior on %d randomly drawn test peaks" % (len(noprior_model_paths), len(prior_model_paths), num_samples)
)
plt.xlabel("%s similarity" % sim_type)
print("Average similarity without priors: %f" % np.nanmean(noprior_avg_sims))
print("Average similarity with priors: %f" % np.nanmean(prior_avg_sims))
print("Standard error without priors: %f" % scipy.stats.sem(noprior_avg_sims, nan_policy="omit"))
print("Standard error with priors: %f" % scipy.stats.sem(prior_avg_sims, nan_policy="omit"))
w, p = scipy.stats.wilcoxon(noprior_avg_sims, prior_avg_sims, alternative="less")
print("One-sided Wilcoxon test: w = %f, p = %f" % (w, p))
avg_sim_diffs = prior_avg_sims - noprior_avg_sims
plt.figure(figsize=(16, 8))
plt.hist(avg_sim_diffs, bins=30, color="mediumorchid")
plt.title(
("Paired difference of %s similarity between different random initializations" % imp_type) +
("\n%s %s models" % (condition_name, model_type)) +
"\nComputed over %d/%d models without/with Fourier prior on %d randomly drawn test peaks" % (len(noprior_model_paths), len(prior_model_paths), num_samples)
)
plt.xlabel("Average similarity difference: with Fourier prior - no prior")
def get_bias(sim_matrix):
num_examples, num_models, _ = sim_matrix.shape
bias_vals = []
for i in range(num_models):
avg = np.sum(sim_matrix[:, i]) / (num_examples * (num_models - 1))
bias_vals.append(avg)
print("%d: %f" % (i + 1, avg))
return bias_vals
print("Model-specific bias without priors")
noprior_bias_vals = get_bias(noprior_sim_matrix)
print("Model-specific bias with priors")
prior_bias_vals = get_bias(prior_sim_matrix)
fig, ax = plt.subplots(1, 2, figsize=(10, 5))
fig.suptitle("Model-specific average Jaccard similarity vs model performance")
ax[0].scatter(noprior_bias_vals, np.array(noprior_metric_vals)[noprior_keep_mask])
ax[0].set_title("No priors")
ax[1].scatter(prior_bias_vals, np.array(prior_metric_vals)[prior_keep_mask])
ax[1].set_title("With priors")
plt.grid(False)
fig.text(0.5, 0.04, "Average Jaccard similarity with other models over all samples", ha="center", va="center")
fig.text(0.06, 0.5, "Model profile validation loss", ha="center", va="center", rotation="vertical")
# Compute some simple bounds on the expected consistency using
# the "no-prior" scores
rng = np.random.RandomState(1234)
def shuf_none(track):
# Do nothing
return track
def shuf_bases(track):
# Shuffle the importances across each base dimension separately,
# but keep positions intact
inds = np.random.rand(*track.shape).argsort(axis=1) # Each row is 0,1,2,3 in random order
return np.take_along_axis(track, inds, axis=1)
def shuf_pos(track):
# Shuffle the importances across the positions, but keep the base
# importances at each position intact
shuf = np.copy(track)
rng.shuffle(shuf)
return shuf
def shuf_all(track):
# Shuffle the importances across positions and bases
return np.ravel(track)[rng.permutation(track.size)].reshape(track.shape)
for shuf_type, shuf_func in [
("no", shuf_none), ("base", shuf_bases), ("position", shuf_pos), ("all", shuf_all)
]:
sims = []
for i in tqdm.notebook.trange(noprior_scores.shape[0]):
for j in range(noprior_scores.shape[1]):
track = noprior_scores[i, j]
track_shuf = shuf_func(track)
sims.append(sim_func(track, track_shuf))
fig, ax = plt.subplots()
ax.hist(sims, bins=30)
ax.set_title("%s similarity with %s shuffing" % (sim_type, shuf_type))
plt.show()
print("Mean: %f" % np.mean(sims))
print("Standard deviation: %f" % np.std(sims))
```
| github_jupyter |
<h1>Table of Contents<span class="tocSkip"></span></h1>
<div class="toc"><ul class="toc-item"><li><span><a href="#init" data-toc-modified-id="init-1"><span class="toc-item-num">1 </span>init</a></span></li><li><span><a href="#モデリング" data-toc-modified-id="モデリング-2"><span class="toc-item-num">2 </span>モデリング</a></span><ul class="toc-item"><li><span><a href="#べースモデル" data-toc-modified-id="べースモデル-2.1"><span class="toc-item-num">2.1 </span>べースモデル</a></span></li><li><span><a href="#グリッドサーチ" data-toc-modified-id="グリッドサーチ-2.2"><span class="toc-item-num">2.2 </span>グリッドサーチ</a></span></li></ul></li><li><span><a href="#本番モデル" data-toc-modified-id="本番モデル-3"><span class="toc-item-num">3 </span>本番モデル</a></span></li><li><span><a href="#ランダムフォレスト" data-toc-modified-id="ランダムフォレスト-4"><span class="toc-item-num">4 </span>ランダムフォレスト</a></span></li><li><span><a href="#work" data-toc-modified-id="work-5"><span class="toc-item-num">5 </span>work</a></span></li></ul></div>
# init
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
pwd
cd ../
cd data
cd raw
pdf_train = pd.read_csv("train.tsv", sep="\t")
pdf_train.T
pdf_test = pd.read_csv("test.tsv", sep="\t")
pdf_test.T
pdf_test.describe()
for str_col in ["C%s"%i for i in range(1,7)]:
print("# "+str_col)
v_cnt = pdf_test[str_col].value_counts(dropna=None)
print(v_cnt)
print()
def get_C_dummie(df):
dct_dummie = {}
for tgt_col in lst_srt_tgt_cols:
psr_tgt_col = df[tgt_col]
dct_dummie[tgt_col] = {}
for tgt_val in dct_C_vals[tgt_col]:
dummie = psr_tgt_col.apply(lambda x: 1 if x == tgt_val else 0)
dct_dummie[tgt_col][tgt_col + "_%s"%tgt_val] = dummie
_df = df.copy()
for tgt_col in dct_dummie.keys():
dummies = pd.DataFrame(dct_dummie[tgt_col])
_df = pd.concat([_df, dummies], axis=1)
else:
lst_str_drop_tgt_str = ["C%s"%i for i in range(1,7)]
# lst_str_drop_tgt_int = ["I%s"%i for i in range(11,15)]
_df = _df.drop(lst_str_drop_tgt_str + ["id"],1)
# _df = _df.drop(lst_str_drop_tgt_str + lst_str_drop_tgt_int + ["id"],1)
return _df
pdf_clns_train = get_C_dummie(pdf_train)
pdf_clns_test = get_C_dummie(pdf_test)
pdf_clns_train.T
pdf_clns_test.T
```
# モデリング
```
from sklearn.metrics import roc_auc_score
from sklearn.model_selection import ParameterGrid, KFold, train_test_split
import lightgbm as lgb
```
## べースモデル
```
def cross_valid_lgb(X,y,param,n_splits,random_state=1234, num_boost_round=1000,early_stopping_rounds=5):
from sklearn.metrics import roc_auc_score
from sklearn.model_selection import StratifiedKFold, train_test_split
import lightgbm as lgb
kf = StratifiedKFold(n_splits=n_splits, shuffle=True,random_state=random_state)
lst_auc = []
for train_index, test_index in kf.split(X,y):
learn_X, learn_y, test_X, test_y = X.iloc[train_index], y.iloc[train_index], X.iloc[test_index], y.iloc[test_index]
train_X, valid_X, train_y, valid_y = train_test_split(learn_X, learn_y,test_size=0.3, random_state=random_state)
lgb_train = lgb.Dataset(train_X, train_y)
lgb_valid = lgb.Dataset(valid_X, valid_y)
gbm = lgb.train(
params,
lgb_train,
num_boost_round=num_boost_round,
valid_sets=lgb_valid,
early_stopping_rounds=early_stopping_rounds,
verbose_eval = False
)
pred = gbm.predict(test_X)
auc = roc_auc_score(y_true=test_y, y_score=pred)
lst_auc.append(auc)
auc_mean = np.mean(lst_auc)
return auc_mean
def cross_lgb(X,y,param,n_splits,random_state=1234, num_boost_round=1000,early_stopping_rounds=5):
from sklearn.metrics import roc_auc_score
from sklearn.model_selection import StratifiedKFold, train_test_split
import lightgbm as lgb
kf = StratifiedKFold(n_splits=n_splits, shuffle=True,random_state=random_state)
lst_model = []
for train_index, test_index in kf.split(X,y):
learn_X, learn_y, test_X, test_y = X.iloc[train_index], y.iloc[train_index], X.iloc[test_index], y.iloc[test_index]
# train_X, valid_X, train_y, valid_y = train_test_split(learn_X, learn_y,test_size=0.3, random_state=random_state)
lgb_train = lgb.Dataset(learn_X, learn_y)
lgb_valid = lgb.Dataset(test_X, test_y)
gbm = lgb.train(
params,
lgb_train,
num_boost_round=num_boost_round,
valid_sets=lgb_valid,
early_stopping_rounds=early_stopping_rounds,
verbose_eval = False
)
lst_model.append(gbm)
return lst_model
```
## グリッドサーチ
```
grid = {
'boosting_type': ['goss'],
'objective': ['binary'],
'metric': ['auc'],
# 'num_leaves':[31 + i for i in range(-10, 11)],
# 'min_data_in_leaf':[20 + i for i in range(-10, 11)],
'num_leaves':[31],
'min_data_in_leaf':[20],
'max_depth':[-1]
}
X = pdf_clns_train.drop("click",1)
y = pdf_clns_train.click
score_grid = []
best_param = {}
best_auc = 0
for param in list(ParameterGrid(grid)):
auc_mean = cross_valid_lgb(
X,
y,
param=param,n_splits=3,
random_state=1234,
num_boost_round=1000,
early_stopping_rounds=5
)
score_grid.append([param,auc_mean])
if auc_mean >= best_auc:
best_auc = auc_mean
best_param = param
print(best_auc,best_param)
```
# 本番モデル
```
lst_model = cross_lgb(X,y,param=best_param,n_splits=5,random_state=1234, num_boost_round=1000,early_stopping_rounds=5)
lst_model
lst_pred = []
for mdl in lst_model:
pred = mdl.predict(pdf_clns_test)
lst_pred.append(pred)
nparr_preds = np.array(lst_pred)
mean_pred = nparr_preds.mean(0)
mean_pred
pdf_submit = pd.DataFrame({
"id":pdf_test.id,
"score":mean_pred
})
pdf_submit.T
pdf_submit.to_csv("submit_v02_lgb5.csv", index=False, header=False)
```
# ランダムフォレスト
```
from sklearn.ensemble import RandomForestClassifier
X = X.fillna(0)
clf = RandomForestClassifier()
clf.fit(X,y)
pdf_clns_test = pdf_clns_test.fillna(0)
pred = clf.predict_proba(pdf_clns_test)
pred
pdf_submit_rf = pd.DataFrame({
"id":pdf_test.id,
"score":pred[:,1]
})
pdf_submit_rf.T
pdf_submit_rf.to_csv("submit_rf.csv", index=False, header=False)
```
# work
```
params = {
'boosting_type': 'goss',
'objective': 'binary',
'metric': 'auc',
'learning_rate': 0.1,
'num_leaves': 23,
'min_data_in_leaf': 1,
}
gbm = lgb.train(
params,
lds_train,
num_boost_round=1000,
valid_sets=lds_test,
early_stopping_rounds=5,
)
dct_C_vals
pdf_train.C1
params = {
'boosting_type': 'goss',
'objective': 'binary',
'metric': 'auc',
'verbose': 0,
'learning_rate': 0.1,
'num_leaves': 23,
'min_data_in_leaf': 1
}
kf = KFold(n_splits=3, shuffle=True,random_state=1234)
# score_grid = []
lst_auc = []
for train_index, test_index in kf.split(pdf_train):
pdf_train_kf, pdf_test_kf = pdf_clns_train.iloc[train_index], pdf_clns_train.iloc[test_index]
train, valid = train_test_split(pdf_train_kf,test_size=0.3, random_state=1234)
lgb_train = lgb.Dataset(train.drop("click",1), train["click"])
lgb_valid = lgb.Dataset(valid.drop("click",1), valid["click"])
# lgb_test = lgb.Dataset(pdf_test_kf.drop("click",1), pdf_test_kf["click"])
pdf_test_X = pdf_test_kf.drop("click",1)
pdf_test_y = pdf_test_kf["click"]
gbm = lgb.train(
params,
lgb_train,
num_boost_round=10,
valid_sets=lgb_valid,
early_stopping_rounds=5,
)
pred = gbm.predict(pdf_test_X)
auc = roc_auc_score(y_true=pdf_test_y, y_score=pred)
lst_auc.append(auc)
auc_mean = np.mean(lst_auc)
```
| github_jupyter |
<a href="https://colab.research.google.com/github/poojan-dalal/fashion-MNIST/blob/master/Course_1_Part_4_Lesson_2_Notebook.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import tensorflow as tf
print(tf.__version__)
```
The Fashion MNIST data is available directly in the tf.keras datasets API. You load it like this:
```
mnist = tf.keras.datasets.fashion_mnist
```
Calling load_data on this object will give you two sets of two lists, these will be the training and testing values for the graphics that contain the clothing items and their labels.
```
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
```
What does these values look like? Let's print a training image, and a training label to see...Experiment with different indices in the array. For example, also take a look at index 42...that's a a different boot than the one at index 0
```
import numpy as np
np.set_printoptions(linewidth=200)
import matplotlib.pyplot as plt
plt.imshow(training_images[0])
print(training_labels[0])
print(training_images[0])
```
You'll notice that all of the values in the number are between 0 and 255. If we are training a neural network, for various reasons it's easier if we treat all values as between 0 and 1, a process called '**normalizing**'...and fortunately in Python it's easy to normalize a list like this without looping. You do it like this:
```
training_images = training_images / 255.0
test_images = test_images / 255.0
```
Now you might be wondering why there are 2 sets...training and testing -- remember we spoke about this in the intro? The idea is to have 1 set of data for training, and then another set of data...that the model hasn't yet seen...to see how good it would be at classifying values. After all, when you're done, you're going to want to try it out with data that it hadn't previously seen!
Let's now design the model. There's quite a few new concepts here, but don't worry, you'll get the hang of them.
```
model = tf.keras.models.Sequential([tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation=tf.nn.relu),
tf.keras.layers.Dense(10, activation=tf.nn.softmax)])
```
**Sequential**: That defines a SEQUENCE of layers in the neural network
**Flatten**: Remember earlier where our images were a square, when you printed them out? Flatten just takes that square and turns it into a 1 dimensional set.
**Dense**: Adds a layer of neurons
Each layer of neurons need an **activation function** to tell them what to do. There's lots of options, but just use these for now.
**Relu** effectively means "If X>0 return X, else return 0" -- so what it does it it only passes values 0 or greater to the next layer in the network.
**Softmax** takes a set of values, and effectively picks the biggest one, so, for example, if the output of the last layer looks like [0.1, 0.1, 0.05, 0.1, 9.5, 0.1, 0.05, 0.05, 0.05], it saves you from fishing through it looking for the biggest value, and turns it into [0,0,0,0,1,0,0,0,0] -- The goal is to save a lot of coding!
The next thing to do, now the model is defined, is to actually build it. You do this by compiling it with an optimizer and loss function as before -- and then you train it by calling **model.fit ** asking it to fit your training data to your training labels -- i.e. have it figure out the relationship between the training data and its actual labels, so in future if you have data that looks like the training data, then it can make a prediction for what that data would look like.
```
model.compile(optimizer = tf.optimizers.Adam(),
loss = 'sparse_categorical_crossentropy',
metrics=['accuracy'])
model.fit(training_images, training_labels, epochs=5)
```
Once it's done training -- you should see an accuracy value at the end of the final epoch. It might look something like 0.9098. This tells you that your neural network is about 91% accurate in classifying the training data. I.E., it figured out a pattern match between the image and the labels that worked 91% of the time. Not great, but not bad considering it was only trained for 5 epochs and done quite quickly.
But how would it work with unseen data? That's why we have the test images. We can call model.evaluate, and pass in the two sets, and it will report back the loss for each. Let's give it a try:
```
model.evaluate(test_images, test_labels)
```
For me, that returned a accuracy of about .8838, which means it was about 88% accurate. As expected it probably would not do as well with *unseen* data as it did with data it was trained on! As you go through this course, you'll look at ways to improve this.
To explore further, try the below exercises:
###Exercise 1:
For this first exercise run the below code: It creates a set of classifications for each of the test images, and then prints the first entry in the classifications. The output, after you run it is a list of numbers. Why do you think this is, and what do those numbers represent?
```
classifications = model.predict(test_images)
print(classifications[0])
```
Hint: try running print(test_labels[0]) -- and you'll get a 9. Does that help you understand why this list looks the way it does?
```
print(test_labels[0])
```
##Exercise 2:
Let's now look at the layers in your model. Experiment with different values for the dense layer with 512 neurons. What different results do you get for loss, training time etc? Why do you think that's the case?
```
import tensorflow as tf
print(tf.__version__)
mnist = tf.keras.datasets.mnist
(training_images, training_labels) , (test_images, test_labels) = mnist.load_data()
training_images = training_images/255.0
test_images = test_images/255.0
model = tf.keras.models.Sequential([tf.keras.layers.Flatten(),
tf.keras.layers.Dense(1024, activation=tf.nn.relu),
tf.keras.layers.Dense(10, activation=tf.nn.softmax)])
model.compile(optimizer = 'adam',
loss = 'sparse_categorical_crossentropy')
model.fit(training_images, training_labels, epochs=5)
model.evaluate(test_images, test_labels)
classifications = model.predict(test_images)
print(classifications[0])
print(test_labels[0])
```
##Exercise 3:
What would happen if you remove the Flatten() layer. Why do you think that's the case?
You get an error about the shape of the data. It may seem vague right now, but it reinforces the rule of thumb that the first layer in your network should be the same shape as your data. Right now our data is 28x28 images, and 28 layers of 28 neurons would be infeasible, so it makes more sense to 'flatten' that 28,28 into a 784x1. Instead of wriitng all the code to handle that ourselves, we add the Flatten() layer at the begining, and when the arrays are loaded into the model later, they'll automatically be flattened for us.
```
import tensorflow as tf
print(tf.__version__)
mnist = tf.keras.datasets.mnist
(training_images, training_labels) , (test_images, test_labels) = mnist.load_data()
training_images = training_images/255.0
test_images = test_images/255.0
model = tf.keras.models.Sequential([#tf.keras.layers.Flatten(),
tf.keras.layers.Dense(64, activation=tf.nn.relu),
tf.keras.layers.Dense(10, activation=tf.nn.softmax)])
model.compile(optimizer = 'adam',
loss = 'sparse_categorical_crossentropy')
model.fit(training_images, training_labels, epochs=5)
model.evaluate(test_images, test_labels)
classifications = model.predict(test_images)
print(classifications[0])
print(test_labels[0])
```
##Exercise 4:
Consider the final (output) layers. Why are there 10 of them? What would happen if you had a different amount than 10? For example, try training the network with 5
You get an error as soon as it finds an unexpected value. Another rule of thumb -- the number of neurons in the last layer should match the number of classes you are classifying for. In this case it's the digits 0-9, so there are 10 of them, hence you should have 10 neurons in your final layer.
```
import tensorflow as tf
print(tf.__version__)
mnist = tf.keras.datasets.mnist
(training_images, training_labels) , (test_images, test_labels) = mnist.load_data()
training_images = training_images/255.0
test_images = test_images/255.0
model = tf.keras.models.Sequential([tf.keras.layers.Flatten(),
tf.keras.layers.Dense(64, activation=tf.nn.relu),
tf.keras.layers.Dense(5, activation=tf.nn.softmax)])
model.compile(optimizer = 'adam',
loss = 'sparse_categorical_crossentropy')
model.fit(training_images, training_labels, epochs=5)
model.evaluate(test_images, test_labels)
classifications = model.predict(test_images)
print(classifications[0])
print(test_labels[0])
```
##Exercise 5:
Consider the effects of additional layers in the network. What will happen if you add another layer between the one with 512 and the final layer with 10.
Ans: There isn't a significant impact -- because this is relatively simple data. For far more complex data (including color images to be classified as flowers that you'll see in the next lesson), extra layers are often necessary.
```
import tensorflow as tf
print(tf.__version__)
mnist = tf.keras.datasets.mnist
(training_images, training_labels) , (test_images, test_labels) = mnist.load_data()
training_images = training_images/255.0
test_images = test_images/255.0
model = tf.keras.models.Sequential([tf.keras.layers.Flatten(),
tf.keras.layers.Dense(512, activation=tf.nn.relu),
tf.keras.layers.Dense(256, activation=tf.nn.relu),
tf.keras.layers.Dense(10, activation=tf.nn.softmax)])
model.compile(optimizer = 'adam',
loss = 'sparse_categorical_crossentropy')
model.fit(training_images, training_labels, epochs=5)
model.evaluate(test_images, test_labels)
classifications = model.predict(test_images)
print(classifications[0])
print(test_labels[0])
```
#Exercise 6:
Consider the impact of training for more or less epochs. Why do you think that would be the case?
Try 15 epochs -- you'll probably get a model with a much better loss than the one with 5
Try 30 epochs -- you might see the loss value stops decreasing, and sometimes increases. This is a side effect of something called 'overfitting' which you can learn about [somewhere] and it's something you need to keep an eye out for when training neural networks. There's no point in wasting your time training if you aren't improving your loss, right! :)
```
import tensorflow as tf
print(tf.__version__)
mnist = tf.keras.datasets.mnist
(training_images, training_labels) , (test_images, test_labels) = mnist.load_data()
training_images = training_images/255.0
test_images = test_images/255.0
model = tf.keras.models.Sequential([tf.keras.layers.Flatten(),
tf.keras.layers.Dense(128, activation=tf.nn.relu),
tf.keras.layers.Dense(10, activation=tf.nn.softmax)])
model.compile(optimizer = 'adam',
loss = 'sparse_categorical_crossentropy')
model.fit(training_images, training_labels, epochs=30)
model.evaluate(test_images, test_labels)
classifications = model.predict(test_images)
print(classifications[34])
print(test_labels[34])
```
#Exercise 7:
Before you trained, you normalized the data, going from values that were 0-255 to values that were 0-1. What would be the impact of removing that? Here's the complete code to give it a try. Why do you think you get different results?
```
import tensorflow as tf
print(tf.__version__)
mnist = tf.keras.datasets.mnist
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
training_images=training_images/255.0
test_images=test_images/255.0
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(512, activation=tf.nn.relu),
tf.keras.layers.Dense(10, activation=tf.nn.softmax)
])
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy')
model.fit(training_images, training_labels, epochs=5)
model.evaluate(test_images, test_labels)
classifications = model.predict(test_images)
print(classifications[0])
print(test_labels[0])
```
#Exercise 8:
Earlier when you trained for extra epochs you had an issue where your loss might change. It might have taken a bit of time for you to wait for the training to do that, and you might have thought 'wouldn't it be nice if I could stop the training when I reach a desired value?' -- i.e. 95% accuracy might be enough for you, and if you reach that after 3 epochs, why sit around waiting for it to finish a lot more epochs....So how would you fix that? Like any other program...you have callbacks! Let's see them in action...
```
import tensorflow as tf
print(tf.__version__)
class myCallback(tf.keras.callbacks.Callback):
def on_epoch_end(self, epoch, logs={}):
if(logs.get('loss')<0.4):
print("\nReached 60% accuracy so cancelling training!")
self.model.stop_training = True
callbacks = myCallback()
mnist = tf.keras.datasets.fashion_mnist
(training_images, training_labels), (test_images, test_labels) = mnist.load_data()
training_images=training_images/255.0
test_images=test_images/255.0
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(512, activation=tf.nn.relu),
tf.keras.layers.Dense(10, activation=tf.nn.softmax)
])
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy')
model.fit(training_images, training_labels, epochs=5, callbacks=[callbacks])
```
| github_jupyter |
# [Advent of Code 2020: Day 10](https://adventofcode.com/2020/day/10)
## \-\-\- Day 10: Adapter Array \-\-\-
Patched into the aircraft's data port, you discover weather forecasts of a massive tropical storm. Before you can figure out whether it will impact your vacation plans, however, your device suddenly turns off!
Its battery is dead.
You'll need to plug it in. There's only one problem: the charging outlet near your seat produces the wrong number of **jolts**. Always prepared, you make a list of all of the joltage adapters in your bag.
Each of your joltage adapters is rated for a specific **output joltage** (your puzzle input). Any given adapter can take an input `1`, `2`, or `3` jolts **lower** than its rating and still produce its rated output joltage.
In addition, your device has a built\-in joltage adapter rated for **`3` jolts higher** than the highest\-rated adapter in your bag. (If your adapter list were `3`, `9`, and `6`, your device's built\-in adapter would be rated for `12` jolts.)
Treat the charging outlet near your seat as having an effective joltage rating of `0`.
Since you have some time to kill, you might as well test all of your adapters. Wouldn't want to get to your resort and realize you can't even charge your device!
If you *use every adapter in your bag* at once, what is the distribution of joltage differences between the charging outlet, the adapters, and your device?
For example, suppose that in your bag, you have adapters with the following joltage ratings:
```
16
10
15
5
1
11
7
19
6
12
4
```
With these adapters, your device's built\-in joltage adapter would be rated for `19 + 3 = `**`22`** jolts, 3 higher than the highest\-rated adapter.
Because adapters can only connect to a source 1\-3 jolts lower than its rating, in order to use every adapter, you'd need to choose them like this:
* The charging outlet has an effective rating of `0` jolts, so the only adapters that could connect to it directly would need to have a joltage rating of `1`, `2`, or `3` jolts. Of these, only one you have is an adapter rated `1` jolt (difference of **`1`**).
* From your `1`\-jolt rated adapter, the only choice is your `4`\-jolt rated adapter (difference of **`3`**).
* From the `4`\-jolt rated adapter, the adapters rated `5`, `6`, or `7` are valid choices. However, in order to not skip any adapters, you have to pick the adapter rated `5` jolts (difference of **`1`**).
* Similarly, the next choices would need to be the adapter rated `6` and then the adapter rated `7` (with difference of **`1`** and **`1`**).
* The only adapter that works with the `7`\-jolt rated adapter is the one rated `10` jolts (difference of **`3`**).
* From `10`, the choices are `11` or `12`; choose `11` (difference of **`1`**) and then `12` (difference of **`1`**).
* After `12`, only valid adapter has a rating of `15` (difference of **`3`**), then `16` (difference of **`1`**), then `19` (difference of **`3`**).
* Finally, your device's built\-in adapter is always 3 higher than the highest adapter, so its rating is `22` jolts (always a difference of **`3`**).
In this example, when using every adapter, there are **`7`** differences of 1 jolt and **`5`** differences of 3 jolts.
Here is a larger example:
```
28
33
18
42
31
14
46
20
48
47
24
23
49
45
19
38
39
11
1
32
25
35
8
17
7
9
4
2
34
10
3
```
In this larger example, in a chain that uses all of the adapters, there are **`22`** differences of 1 jolt and **`10`** differences of 3 jolts.
Find a chain that uses all of your adapters to connect the charging outlet to your device's built\-in adapter and count the joltage differences between the charging outlet, the adapters, and your device. **What is the number of 1\-jolt differences multiplied by the number of 3\-jolt differences?**
```
import unittest
from IPython.display import Markdown, display
from aoc_puzzle import AocPuzzle
class AdapterArray(AocPuzzle):
def parse_data(self, raw_data):
self.adapter_list = list(map(int, raw_data.split('\n')))
self.adapter_list.sort()
self.adapter_list.insert(0,0)
self.adapter_list.append(self.adapter_list[-1]+3)
def calc_jolt_diff(self, output=False):
jolt_diffs = {}
for i in range(1,len(self.adapter_list)):
adapter = self.adapter_list[i]
prev_adapter = self.adapter_list[i-1]
jdiff = adapter - prev_adapter
if jdiff not in jolt_diffs:
jolt_diffs[jdiff] = 1
else:
jolt_diffs[jdiff] += 1
jolt_diff_product = jolt_diffs[1] * jolt_diffs[3]
if output:
display(Markdown(f'### Jolt diff product: `{jolt_diff_product}`'))
return jolt_diff_product
class TestBasic(unittest.TestCase):
def test_parse_data(self):
in_data = '16\n10\n15\n5\n1\n11\n7\n19\n6\n12\n4'
exp_out = [0, 1, 4, 5, 6, 7, 10, 11, 12, 15, 16, 19, 22]
aa = AdapterArray(in_data)
self.assertEqual(aa.adapter_list, exp_out)
def test_puzzle(self):
input_data = ['16\n10\n15\n5\n1\n11\n7\n19\n6\n12\n4','28\n33\n18\n42\n31\n14\n46\n20\n48\n47\n24\n23\n49\n45\n19\n38\n39\n11\n1\n32\n25\n35\n8\n17\n7\n9\n4\n2\n34\n10\n3']
exp_output = [35,220]
for in_data, exp_out in tuple(zip(input_data, exp_output)):
aa = AdapterArray(in_data)
self.assertEqual(aa.calc_jolt_diff(), exp_out)
unittest.main(argv=[""], exit=False)
aa = AdapterArray("input/d10.txt")
aa.calc_jolt_diff(output=True)
```
## --- Part Two ---
To completely determine whether you have enough adapters, you'll need to figure out how many different ways they can be arranged. Every arrangement needs to connect the charging outlet to your device. The previous rules about when adapters can successfully connect still apply.
The first example above (the one that starts with `16`, `10`, `15`) supports the following arrangements:
```
(0), 1, 4, 5, 6, 7, 10, 11, 12, 15, 16, 19, (22)
(0), 1, 4, 5, 6, 7, 10, 12, 15, 16, 19, (22)
(0), 1, 4, 5, 7, 10, 11, 12, 15, 16, 19, (22)
(0), 1, 4, 5, 7, 10, 12, 15, 16, 19, (22)
(0), 1, 4, 6, 7, 10, 11, 12, 15, 16, 19, (22)
(0), 1, 4, 6, 7, 10, 12, 15, 16, 19, (22)
(0), 1, 4, 7, 10, 11, 12, 15, 16, 19, (22)
(0), 1, 4, 7, 10, 12, 15, 16, 19, (22)
```
(The charging outlet and your device's built-in adapter are shown in parentheses.) Given the adapters from the first example, the total number of arrangements that connect the charging outlet to your device is **`8`**.
The second example above (the one that starts with `28`, `33`, `18`) has many arrangements. Here are a few:
```
(0), 1, 2, 3, 4, 7, 8, 9, 10, 11, 14, 17, 18, 19, 20, 23, 24, 25, 28, 31,
32, 33, 34, 35, 38, 39, 42, 45, 46, 47, 48, 49, (52)
(0), 1, 2, 3, 4, 7, 8, 9, 10, 11, 14, 17, 18, 19, 20, 23, 24, 25, 28, 31,
32, 33, 34, 35, 38, 39, 42, 45, 46, 47, 49, (52)
(0), 1, 2, 3, 4, 7, 8, 9, 10, 11, 14, 17, 18, 19, 20, 23, 24, 25, 28, 31,
32, 33, 34, 35, 38, 39, 42, 45, 46, 48, 49, (52)
(0), 1, 2, 3, 4, 7, 8, 9, 10, 11, 14, 17, 18, 19, 20, 23, 24, 25, 28, 31,
32, 33, 34, 35, 38, 39, 42, 45, 46, 49, (52)
(0), 1, 2, 3, 4, 7, 8, 9, 10, 11, 14, 17, 18, 19, 20, 23, 24, 25, 28, 31,
32, 33, 34, 35, 38, 39, 42, 45, 47, 48, 49, (52)
(0), 3, 4, 7, 10, 11, 14, 17, 20, 23, 25, 28, 31, 34, 35, 38, 39, 42, 45,
46, 48, 49, (52)
(0), 3, 4, 7, 10, 11, 14, 17, 20, 23, 25, 28, 31, 34, 35, 38, 39, 42, 45,
46, 49, (52)
(0), 3, 4, 7, 10, 11, 14, 17, 20, 23, 25, 28, 31, 34, 35, 38, 39, 42, 45,
47, 48, 49, (52)
(0), 3, 4, 7, 10, 11, 14, 17, 20, 23, 25, 28, 31, 34, 35, 38, 39, 42, 45,
47, 49, (52)
(0), 3, 4, 7, 10, 11, 14, 17, 20, 23, 25, 28, 31, 34, 35, 38, 39, 42, 45,
48, 49, (52)
```
In total, this set of adapters can connect the charging outlet to your device in **`19208`** distinct arrangements.
You glance back down at your bag and try to remember why you brought so many adapters; there must be **more than a trillion** valid ways to arrange them! Surely, there must be an efficient way to count the arrangements.
**What is the total number of distinct ways you can arrange the adapters to connect the charging outlet to your device?**
```
class AdapterArray2(AdapterArray):
def count_all_arrangements(self, output=False):
arrangements_list = [1]
for a_index in range(1,len(self.adapter_list)):
adapter = self.adapter_list[a_index]
arrangements = 0
for pa_index in range(a_index):
prev_adapter = self.adapter_list[pa_index]
jdiff = adapter - prev_adapter
if jdiff <= 3:
arrangements += arrangements_list[pa_index]
arrangements_list.append(arrangements)
all_arrangements = arrangements_list[-1]
if output:
display(Markdown(f'### Total possible ways to arrange the adapters: `{all_arrangements}`'))
return all_arrangements
class TestBasic(unittest.TestCase):
def test_puzzle2(self):
input_data = ['28\n33\n18\n42\n31\n14\n46\n20\n48\n47\n24\n23\n49\n45\n19\n38\n39\n11\n1\n32\n25\n35\n8\n17\n7\n9\n4\n2\n34\n10\n3','16\n10\n15\n5\n1\n11\n7\n19\n6\n12\n4']
exp_output = [19208, 8]
for in_data, exp_out in tuple(zip(input_data, exp_output)):
aa = AdapterArray2(in_data)
self.assertEqual(aa.count_all_arrangements(), exp_out)
unittest.main(argv=[""], exit=False)
aa = AdapterArray2("input/d10.txt")
aa.count_all_arrangements(output=True)
```
| github_jupyter |
<img style="float: right;" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAOIAAAAjCAYAAACJpNbGAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAABR0RVh0Q3JlYXRpb24gVGltZQAzLzcvMTNND4u/AAAAHHRFWHRTb2Z0d2FyZQBBZG9iZSBGaXJld29ya3MgQ1M26LyyjAAACMFJREFUeJztnD1y20gWgD+6nJtzAsPhRqKL3AwqwQdYDpXDZfoEppNNTaWbmD7BUEXmI3EPMFCR2YI1UDQpdAPqBNzgvRZA/BGUZEnk9FeFIgj0z2ugX7/XP+jGer2mLv/8b6d+4Efgf/8KG0+Zn8XyXLx+bgEslqegcfzxSY3Irrx6bgEsFssBWsRGowGufwHAYtq7u+H6fUCOxTTWax4wBAbr+SRqNDKesOv3gN/133sW0yh927j1mucIaFWINl7PJ+OcvMcfW8Bol3iN44+mLIOsTCp3UJFfAETr+WRQcG8EOJpunEnTyDlYzycbeWr5xxq3jOF6PglK8ix9buv5xCsrAzBkMV1l5OwD/aJ4BXzV3+8F9z4gz/hTSbz8cxc84FuNvDc4VIsYA7+qohmGwAnycA194G22YqUYlZxv4vpN4AuwBv4oON5m8k3TVLnK4sYFcRyN86dWvCwnlCvFCeUVvwX8CkSZZ5eWs5mLJWE/VZThBMgpfirPk5J4f1SU4QsQ6LNP4+j9OkSUKdRiGlD87CWe3PcyR5PFdAhc1cz/joOziMoIeVF95GX1EGVY6bWhvsAeZQrm+kON80PDneD6PRbTi4LQpmJfsZieFaR1qXlXURh3y2BaBPyG63sspv0t6e+CKJTrf2YxHe8Qr6z8AXBdGbMoHgCTshgr4AiItfxljenPJGv5roCi+rGVw1TExTTWl99ThRsglfYHUnF7SMv+Bhjn4idxbhFLGiAu6gjXD3LuUBF5VzWi3CoAfMP1kxe7mNYZMT5DLFgf13eAXi3ZtvMOsUb3V3J5/mmqy+/66RbnTC1LFdfIu/kd8Qx2bTQeg2GBTPfiUF1TgHNE0QaIq/JDX9RKr/WBy/V8EhfEHWncWMO2EKV8S7UypYnYdE2r+o8gyj5MHXVYsZh+JnG7A+3LPQxR5g9II/UJ148ockmrybqm2+Qapo6gppwB8J7EM6jqaz8u0lhfkXgB58BKPam6rvEdh2kRARbTMa7/HXEfVqnW8hxxWwE+5+JJRTYd9CM90gxw/XFuMKMo/yTNDzUkLnbr6rCYnuH6N8igQ3CvNPJproDPuH6MKMd4Z5kMUjnrh98tn1if72/Ie729Vzq708L0YV3/HGmgB4iHsjOProhhd1lrEr4zaz/FvM4lolTnqWum/6jKmeuDmFb1jHylNg96hPQbhcU0wPVBXESvQI4W5aNshsK4jeOPhSOcOaThMVb48dhU8m2UlR+29ZHzrqyhLL0EaTROteGt67EYIsT6F1HXC/ikcvS00dl51PRwLaIwQtzCxGWRFnRMkT8v/SyAy8I+iliHJtDUsHHq7imipE42GtJanxdcB6mgQcm9MmKNs1m5F9MI13+n+cXZSEpAeV8mQgZqNkmU/HsuT7kf4PrGhXcK0h1SXv7iPKsJKCrDYvoV17+meMqhiDFlll7GEb4U3iseAf+k7mqksmU9qUoaj73E7TEtol3iZnks7Moai8WylUN3TS0WANbzyYv2rqxFtFheANYi7iGNRoPOrO2QGTQIu8vhU8vSmbWNDAHQD7vLYWfWbgFx2F3ee3FBZ9ZuIgMpTWAQdpeRXm9pPoPOrD3UMCtkQM4BRmF3ubG6ZZdxkOfCWsT9pU96CuX56KfOjeIFVC8Ar8NI0xuyOQJsVkWl8xzptQGPNY/6xFiLuL+0gIu0FVTrNESmbK7C7tLrzNpmPW0EeGF32UyFN19UnCAT4ZHGWWnYqDNrB4jViZBK/kbD9sLuMiBZSD8AVp1Z+0LD/NmZta+BIzOS3pm1xwBhd9kvkeEGUbQeqSmIdHhkXnGs5fIQRUxPV1x0Zm2zMuoq7C69rU/yBWAt4v7iAd86s/ZaDweZP+wBvwBOZ9b2SCrrmPzk+AWizA09j1QxMK4gZumcWKUWMvkdA56mfxN2l7GmHWk6V2F32Qi7yxaIsmnYHvkJ9zEQqAwBotQXwK2m0c+EN/Kk8zPTZiOkIWrp/xNTnpeOtYh7iFauN+k5W+0vXab6UsbyecAw229SxWiG3aVZ7NBCKrGHuneazy2iyBeIuxkjk9UDE1bzOtJ4IzbdwysNN0D6dnf9Rk3/iKSBWOnhUbASSWW+DbvLWM+HKreZ3O/r77gza5u842w6LxFrEfcTj+Jv3mK4q7Co63hE+fI6E94hUaT0cry+XushSuvoNZO2CdsCrlXJHDYVMUIUJso2BmhfL+wuV6rMvVR6AXnS1428XupaE7Hwnrqkg4cMGD0lr3NfpVegrUw1m2sN0+crNirEX1uTqiPbPoyI/QSKKmqA9I9aer+fcR2zxIj7GiMV+EYVIkZc3r5eH2rYI+0vnpBYIE/vGwUCdYM7s3agbqXJu58VIOwug86sfd2ZtSPNKwi7S9PHy4UnscCmXKuUZQRdsqbPwCHp2754pKYnW0akcZBO/x2df29XnvA//6iV8T3TSluBmOQlR+v5JNvaHixlDZRalRZifbZaAg3vIIrkmP6YVu6owI1M9x2r0vVIFCBGXNLS96Ph45IGY2ey6e1DY20UMaLGItUXoIhVvCv5tvDg2MWLqYNaoKBKWe6Z7gBR8OwAzZOyD4poBmtidlwt/gIxw/QHz0+oWKIoj19fRz8p3YOjoV8195F5l31ltZ5PfnluISyW+/IK6SPstRIiH/FaLHvLa2R+6F6f978AVsD7v0vf0HK4vNK9VfbVojSBceP4o/PcglgsD8GMmjaRbRCc1PEQIrbv45nlIfleIrs778XkrcWSZXMcXPZyqbvfxy7ckuyqHJPslJzH9c3We2ZRbx1O/07ziJbDI1FE2Qwp4n4DNzHJhkZF16+3bnwrCmi40U2eWoj7KZvobn7+YtKO1vPJVyyWPSZrER1kNU0TqfienpvlaWZR7oX+3tba6lxcX7MK3tNfo2RlpNc8tthsIFbAKYtpsA+TtRbLNp5/H4/EFXX0MOfbOGUxvbCKaDkEnl8Rq0jc1ayFjhFFjKwiWg6B/wNk+JCXXNBIXQAAAABJRU5ErkJggg==">
# An Jupyter notebook for running PCSE/WOFOST on a CGMS8 database
This Jupyter notebook will demonstrate how to connect and read data from a CGMS8 database for a single grid. Next the data will be used to run a PCSE/WOFOST simulation for potential and water-limited conditions, the latter is done for all soil types present in the selected grid. Results are visualized and exported to an Excel file.
Note that no attempt is made to *write* data to a CGMS8 database as writing data to a CGMS database can be tricky and slow. In our experience it is better to first dump simulation results to a CSV file and use specialized loading tools for loading data into the database such as [SQLLoader](http://www.oracle.com/technetwork/database/enterprise-edition/sql-loader-overview-095816.html) for ORACLE or [pgloader](http://pgloader.io/) for PostgreSQL databases.
A dedicated package is now available for running WOFOST simulations using a CGMS database: [pyCGMS](https://github.com/ajwdewit/pycgms). The steps demonstrated in this notebook are implemented in as well in the pyCGMS package which provides a nicer interface to run simulations using a CGMS database.
**Prerequisites for running this notebook**
Several packages need to be installed for running PCSE/WOFOST on a CGMS8 database:
1. PCSE and its dependencies. See the [PCSE user guide](http://pcse.readthedocs.io/en/stable/installing.html) for more information;
2. The database client software for the database that will be used, this depends on your database of choice. For SQLite no client software is needed as it is included with python. For Oracle you will need the [Oracle client software](http://www.oracle.com/technetwork/database/features/instant-client/index-097480.html) as well as the [python bindings for the Oracle client (cx_Oracle)](http://sourceforge.net/projects/cx-oracle/files/)). See [here](https://wiki.python.org/moin/DatabaseInterfaces) for an overview of database connectors for python;
3. The `pandas` module for processing and visualizing WOFOST output;
4. The `matplotlib` module, although we will mainly use it through pandas;
## Importing the relevant modules
First the required modules need to be imported. These include the CGMS8 data providers for PCSE as well as other relevant modules.
```
%matplotlib inline
import os, sys
data_dir = os.path.join(os.getcwd(), "data")
import matplotlib as mpl
import matplotlib.pyplot as plt
plt.style.use('ggplot')
import sqlalchemy as sa
import pandas as pd
import pcse
from pcse.db.cgms8 import GridWeatherDataProvider, AgroManagementDataProvider, SoilDataIterator, \
CropDataProvider, STU_Suitability, SiteDataProvider
from pcse.models import Wofost71_WLP_FD, Wofost71_PP
from pcse.util import DummySoilDataProvider, WOFOST71SiteDataProvider
from pcse.base_classes import ParameterProvider
print("This notebook was built with:")
print("python version: %s " % sys.version)
print("PCSE version: %s" % pcse.__version__)
```
## Building the connection to a CGMS8 database
The connection to the database will be made using SQLAlchemy. This requires a database URL to be provided, the format of this URL depends on the database of choice. See the SQLAlchemy documentation on [database URLs](http://docs.sqlalchemy.org/en/latest/core/engines.html#database-urls) for the different database URL formats.
For this example we will use a database that was created for Anhui province in China. This database can be downloaded [here](https://wageningenur4-my.sharepoint.com/:u:/g/personal/allard_dewit_wur_nl/EdwuayKW2IhOp6zCYElA0zsB3NGxcKjZc2zE_JGfVPv89Q?e=oEgI9R).
```
cgms8_db = "d:/nobackup/CGMS8_Anhui/CGMS_Anhui_complete.db"
dbURL = "sqlite:///%s" % cgms8_db
engine = sa.create_engine(dbURL)
```
## Defining what should be simulated
For the simulation to run, some IDs must be provided that refer to the location (`grid_no`), crop type (`crop_no`) and year (`campaign_year`) for which the simulation should be carried out. These IDs refer to columns in the CGMS database that are used to define the relationships.
```
grid_no = 81159
crop_no = 1 # Winter-wheat
campaign_year = 2008
# if input/output should be printed set show_results=True
show_results = True
```
## Retrieving data for the simulation from the database
### Weather data
Weather data will be derived from the GRID_WEATHER table in the database. By default, the entire time-series of weather data available for this grid cell will be fetched from the database.
```
weatherdata = GridWeatherDataProvider(engine, grid_no)
print(weatherdata)
```
### Agromanagement information
Agromanagement in CGMS mainly refers to the cropping calendar for the given crop and location.
```
agromanagement = AgroManagementDataProvider(engine, grid_no, crop_no, campaign_year)
agromanagement
```
### Soil information
A CGMS grid cell can contain multiple soils which may or may not be suitable for a particular crop. Moreover, a complicating factor is the arrangement of soils in many soil maps which consist of *Soil Mapping Units* `(SMUs)` which are soil associations whose location on the map is known. Within an SMU, the actual soil types are known as *Soil Typological Units* `(STUs)` whose spatial delination is not known, only the percentage area within the SMU is known.
Therefore, fetching soil information works in two steps:
1. First of all the `SoilDataIterator` will fetch all soil information for the given grid cell. It presents it as a list which contains all the SMUs that are present in the grid cell with their internal STU representation. The soil information is organized in such a way that the system can iterate over the different soils including information on soil physical properties as well as SMU area and STU percentage with the SMU.
2. Second, the `STU_Suitability` will contain all soils that are suitable for a given crop. The 'STU_NO' of each crop can be used to check if a particular STU is suitable for that crop.
The example grid cell used here only contains a single SMU/STU combination.
```
soil_iterator = SoilDataIterator(engine, grid_no)
soil_iterator
suitable_stu = STU_Suitability(engine, crop_no)
```
### Crop parameters
Crop parameters are needed for parameterizing the crop simulation model. The `CropDataProvider` will retrieve them from the database for the given crop_no, grid_no and campaign_year.
```
cropd = CropDataProvider(engine, grid_no, crop_no, campaign_year)
if show_results:
print(cropd)
```
### Site parameters
Site parameters are an ancillary class of parameters that are related to a given site. For example, an important parameter is the initial amount of moisture in the soil profile (WAV) and the Atmospheric CO$_2$ concentration (CO2). Site parameters will be fetched for each soil type within the soil iteration loop.
## Simulating with WOFOST
### Place holders for storing simulation results
```
daily_results = {}
summary_results = {}
```
### Potential production
```
# For potential production we can provide site data directly
sited = WOFOST71SiteDataProvider(CO2=360, WAV=25)
# We do not need soildata for potential production so we provide some dummy values here
soild = DummySoilDataProvider()
# Start WOFOST, run the simulation
parameters = ParameterProvider(sitedata=sited, soildata=soild, cropdata=cropd)
wofost = Wofost71_PP(parameters, weatherdata, agromanagement)
wofost.run_till_terminate()
# convert output to Pandas DataFrame and store it
daily_results['Potential'] = pd.DataFrame(wofost.get_output()).set_index("day")
summary_results['Potential'] = wofost.get_summary_output()
```
### Water-limited production
Water-limited simulations will be carried out for each soil type. First we will check that the soil type is suitable. Next we will retrieve the site data and run the simulation. Finally, we will collect the output and store the results.
```
for smu_no, area, stu_no, percentage, soild in soil_iterator:
# Check if this is a suitable STU
if stu_no not in suitable_stu:
continue
# retrieve the site data for this soil type
sited = SiteDataProvider(engine, grid_no, crop_no, campaign_year, stu_no)
# Start WOFOST, run the simulation
parameters = ParameterProvider(sitedata=sited, soildata=soild, cropdata=cropd)
wofost = Wofost71_WLP_FD(parameters, weatherdata, agromanagement)
wofost.run_till_terminate()
# Store simulation results
runid = "smu_%s-stu_%s" % (smu_no, stu_no)
daily_results[runid] = pd.DataFrame(wofost.get_output()).set_index("day")
summary_results[runid] = wofost.get_summary_output()
```
## Visualizing and exporting simulation results
### We can visualize the simulation results using pandas and matplotlib
```
# Generate a figure with 10 subplots
fig, axes = plt.subplots(nrows=5, ncols=2, figsize=(12, 30))
# Plot results
for runid, results in daily_results.items():
for var, ax in zip(results, axes.flatten()):
results[var].plot(ax=ax, title=var, label=runid)
ax.set_title(var)
fig.autofmt_xdate()
axes[0][0].legend(loc='upper left')
```
### Exporting the simulation results
A pandas DataFrame or panel can be easily export to a [variety of formats](http://pandas.pydata.org/pandas-docs/stable/io.html) including CSV, Excel or HDF5. First we convert the results to a Panel, next we will export to an Excel file.
```
excel_fname = os.path.join(data_dir, "output", "cgms8_wofost_results.xls")
panel = pd.Panel(daily_results)
panel.to_excel(excel_fname)
```
## Simulating with a different start date waterbalance
By default CGMS starts the simulation when the crop is planted. Particularly in dry climates this can be problematic because the results become very sensitive to the initial value of the soil water balance. In such scenarios, it is more realistic to start the water balance with a dry soil profile well before the crop is planted and let the soil 'fill up' as a result of rainfall.
To enable this option, the column `GIVEN_STARTDATE_WATBAL` in the table `INITIAL_SOIL_WATER` should be set to the right starting date for each grid_no, crop_no, year and stu_no. Moreover, the other parameters in the table should be set to the appropriate values (particularly the initial soil moisture `WAV`).
The start date of the water balance should then be used to update the agromanagement data during the simulation loop, see the example below.
```
for smu_no, area, stu_no, percentage, soild in soil_iterator:
# Check if this is a suitable STU
if stu_no not in suitable_stu:
continue
# retrieve the site data for this soil type
sited = SiteDataProvider(engine, grid_no, crop_no, campaign_year, stu_no)
# update the campaign start date in the agromanagement data
agromanagement.set_campaign_start_date(sited.start_date_waterbalance)
# Start WOFOST, run the simulation
parameters = ParameterProvider(sitedata=sited, soildata=soild, cropdata=cropd)
wofost = Wofost71_WLP_FD(parameters, weatherdata, agromanagement)
wofost.run_till_terminate()
# Store simulation results
runid = "smu_%s-stu_%s" % (smu_no, stu_no)
daily_results[runid] = pd.DataFrame(wofost.get_output()).set_index("day")
summary_results[runid] = wofost.get_summary_output()
```
## Let's show the results
As you can see, the results from the simulation are slightly different because of a different start date of the water balance.
NOTE: the dates on the x-axis are the same except for the soil moisture chart 'SM' where the water-limited simulation results start before potential results. This is a matplotlib problem.
```
# Generate a figure with 10 subplots
fig, axes = plt.subplots(nrows=5, ncols=2, figsize=(12, 30))
# Plot results
for runid, results in daily_results.items():
for var, ax in zip(results, axes.flatten()):
results[var].plot(ax=ax, title=var, label=runid)
fig.autofmt_xdate()
axes[0][0].legend(loc='upper left')
```
| github_jupyter |
# 7.6 Transformerモデル(分類タスク用)の実装
- 本ファイルでは、クラス分類のTransformerモデルを実装します。
※ 本章のファイルはすべてUbuntuでの動作を前提としています。Windowsなど文字コードが違う環境での動作にはご注意下さい。
# 7.6 学習目標
1. Transformerのモジュール構成を理解する
2. LSTMやRNNを使用せずCNNベースのTransformerで自然言語処理が可能な理由を理解する
3. Transformerを実装できるようになる
# 事前準備
書籍の指示に従い、本章で使用するデータを用意します
```
import math
import numpy as np
import random
import torch
import torch.nn as nn
import torch.nn.functional as F
import torchtext
# Setup seeds
torch.manual_seed(1234)
np.random.seed(1234)
random.seed(1234)
class Embedder(nn.Module):
'''idで示されている単語をベクトルに変換します'''
def __init__(self, text_embedding_vectors):
super(Embedder, self).__init__()
self.embeddings = nn.Embedding.from_pretrained(
embeddings=text_embedding_vectors, freeze=True)
# freeze=Trueによりバックプロパゲーションで更新されず変化しなくなります
def forward(self, x):
x_vec = self.embeddings(x)
return x_vec
# 動作確認
# 前節のDataLoaderなどを取得
from utils.dataloader import get_IMDb_DataLoaders_and_TEXT
train_dl, val_dl, test_dl, TEXT = get_IMDb_DataLoaders_and_TEXT(
max_length=256, batch_size=24)
# ミニバッチの用意
batch = next(iter(train_dl))
# モデル構築
net1 = Embedder(TEXT.vocab.vectors)
# 入出力
x = batch.Text[0]
x1 = net1(x) # 単語をベクトルに
print("入力のテンソルサイズ:", x.shape)
print("出力のテンソルサイズ:", x1.shape)
class PositionalEncoder(nn.Module):
'''入力された単語の位置を示すベクトル情報を付加する'''
def __init__(self, d_model=300, max_seq_len=256):
super().__init__()
self.d_model = d_model # 単語ベクトルの次元数
# 単語の順番(pos)と埋め込みベクトルの次元の位置(i)によって一意に定まる値の表をpeとして作成
pe = torch.zeros(max_seq_len, d_model)
# GPUが使える場合はGPUへ送る、ここでは省略。実際に学習時には使用する
# device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# pe = pe.to(device)
for pos in range(max_seq_len):
for i in range(0, d_model, 2):
pe[pos, i] = math.sin(pos / (10000 ** ((2 * i)/d_model)))
pe[pos, i + 1] = math.cos(pos /
(10000 ** ((2 * (i + 1))/d_model)))
# 表peの先頭に、ミニバッチ次元となる次元を足す
self.pe = pe.unsqueeze(0)
# 勾配を計算しないようにする
self.pe.requires_grad = False
def forward(self, x):
# 入力xとPositonal Encodingを足し算する
# xがpeよりも小さいので、大きくする
ret = math.sqrt(self.d_model)*x + self.pe
return ret
# 動作確認
# モデル構築
net1 = Embedder(TEXT.vocab.vectors)
net2 = PositionalEncoder(d_model=300, max_seq_len=256)
# 入出力
x = batch.Text[0]
x1 = net1(x) # 単語をベクトルに
x2 = net2(x1)
print("入力のテンソルサイズ:", x1.shape)
print("出力のテンソルサイズ:", x2.shape)
class Attention(nn.Module):
'''Transformerは本当はマルチヘッドAttentionですが、
分かりやすさを優先しシングルAttentionで実装します'''
def __init__(self, d_model=300):
super().__init__()
# SAGANでは1dConvを使用したが、今回は全結合層で特徴量を変換する
self.q_linear = nn.Linear(d_model, d_model)
self.v_linear = nn.Linear(d_model, d_model)
self.k_linear = nn.Linear(d_model, d_model)
# 出力時に使用する全結合層
self.out = nn.Linear(d_model, d_model)
# Attentionの大きさ調整の変数
self.d_k = d_model
def forward(self, q, k, v, mask):
# 全結合層で特徴量を変換
k = self.k_linear(k)
q = self.q_linear(q)
v = self.v_linear(v)
# Attentionの値を計算する
# 各値を足し算すると大きくなりすぎるので、root(d_k)で割って調整
weights = torch.matmul(q, k.transpose(1, 2)) / math.sqrt(self.d_k)
# ここでmaskを計算
mask = mask.unsqueeze(1)
weights = weights.masked_fill(mask == 0, -1e9)
# softmaxで規格化をする
normlized_weights = F.softmax(weights, dim=-1)
# AttentionをValueとかけ算
output = torch.matmul(normlized_weights, v)
# 全結合層で特徴量を変換
output = self.out(output)
return output, normlized_weights
class FeedForward(nn.Module):
def __init__(self, d_model, d_ff=1024, dropout=0.1):
'''Attention層から出力を単純に全結合層2つで特徴量を変換するだけのユニットです'''
super().__init__()
self.linear_1 = nn.Linear(d_model, d_ff)
self.dropout = nn.Dropout(dropout)
self.linear_2 = nn.Linear(d_ff, d_model)
def forward(self, x):
x = self.linear_1(x)
x = self.dropout(F.relu(x))
x = self.linear_2(x)
return x
class TransformerBlock(nn.Module):
def __init__(self, d_model, dropout=0.1):
super().__init__()
# LayerNormalization層
# https://pytorch.org/docs/stable/nn.html?highlight=layernorm
self.norm_1 = nn.LayerNorm(d_model)
self.norm_2 = nn.LayerNorm(d_model)
# Attention層
self.attn = Attention(d_model)
# Attentionのあとの全結合層2つ
self.ff = FeedForward(d_model)
# Dropout
self.dropout_1 = nn.Dropout(dropout)
self.dropout_2 = nn.Dropout(dropout)
def forward(self, x, mask):
# 正規化とAttention
x_normlized = self.norm_1(x)
output, normlized_weights = self.attn(
x_normlized, x_normlized, x_normlized, mask)
x2 = x + self.dropout_1(output)
# 正規化と全結合層
x_normlized2 = self.norm_2(x2)
output = x2 + self.dropout_2(self.ff(x_normlized2))
return output, normlized_weights
# 動作確認
# モデル構築
net1 = Embedder(TEXT.vocab.vectors)
net2 = PositionalEncoder(d_model=300, max_seq_len=256)
net3 = TransformerBlock(d_model=300)
# maskの作成
x = batch.Text[0]
input_pad = 1 # 単語のIDにおいて、'<pad>': 1 なので
input_mask = (x != input_pad)
print(input_mask[0])
# 入出力
x1 = net1(x) # 単語をベクトルに
x2 = net2(x1) # Positon情報を足し算
x3, normlized_weights = net3(x2, input_mask) # Self-Attentionで特徴量を変換
print("入力のテンソルサイズ:", x2.shape)
print("出力のテンソルサイズ:", x3.shape)
print("Attentionのサイズ:", normlized_weights.shape)
class ClassificationHead(nn.Module):
'''Transformer_Blockの出力を使用し、最後にクラス分類させる'''
def __init__(self, d_model=300, output_dim=2):
super().__init__()
# 全結合層
self.linear = nn.Linear(d_model, output_dim) # output_dimはポジ・ネガの2つ
# 重み初期化処理
nn.init.normal_(self.linear.weight, std=0.02)
nn.init.normal_(self.linear.bias, 0)
def forward(self, x):
x0 = x[:, 0, :] # 各ミニバッチの各文の先頭の単語の特徴量(300次元)を取り出す
out = self.linear(x0)
return out
# 動作確認
# ミニバッチの用意
batch = next(iter(train_dl))
# モデル構築
net1 = Embedder(TEXT.vocab.vectors)
net2 = PositionalEncoder(d_model=300, max_seq_len=256)
net3 = TransformerBlock(d_model=300)
net4 = ClassificationHead(output_dim=2, d_model=300)
# 入出力
x = batch.Text[0]
x1 = net1(x) # 単語をベクトルに
x2 = net2(x1) # Positon情報を足し算
x3, normlized_weights = net3(x2, input_mask) # Self-Attentionで特徴量を変換
x4 = net4(x3) # 最終出力の0単語目を使用して、分類0-1のスカラーを出力
print("入力のテンソルサイズ:", x3.shape)
print("出力のテンソルサイズ:", x4.shape)
# 最終的なTransformerモデルのクラス
class TransformerClassification(nn.Module):
'''Transformerでクラス分類させる'''
def __init__(self, text_embedding_vectors, d_model=300, max_seq_len=256, output_dim=2):
super().__init__()
# モデル構築
self.net1 = Embedder(text_embedding_vectors)
self.net2 = PositionalEncoder(d_model=d_model, max_seq_len=max_seq_len)
self.net3_1 = TransformerBlock(d_model=d_model)
self.net3_2 = TransformerBlock(d_model=d_model)
self.net4 = ClassificationHead(output_dim=output_dim, d_model=d_model)
def forward(self, x, mask):
x1 = self.net1(x) # 単語をベクトルに
x2 = self.net2(x1) # Positon情報を足し算
x3_1, normlized_weights_1 = self.net3_1(
x2, mask) # Self-Attentionで特徴量を変換
x3_2, normlized_weights_2 = self.net3_2(
x3_1, mask) # Self-Attentionで特徴量を変換
x4 = self.net4(x3_2) # 最終出力の0単語目を使用して、分類0-1のスカラーを出力
return x4, normlized_weights_1, normlized_weights_2
# 動作確認
# ミニバッチの用意
batch = next(iter(train_dl))
# モデル構築
net = TransformerClassification(
text_embedding_vectors=TEXT.vocab.vectors, d_model=300, max_seq_len=256, output_dim=2)
# 入出力
x = batch.Text[0]
input_mask = (x != input_pad)
out, normlized_weights_1, normlized_weights_2 = net(x, input_mask)
print("出力のテンソルサイズ:", out.shape)
print("出力テンソルのsigmoid:", F.softmax(out, dim=1))
```
ここまでの内容をフォルダ「utils」のtransformer.pyに別途保存しておき、次節からはこちらから読み込むようにします
以上
| github_jupyter |
# Run model module locally
```
import os
# Import os environment variables for file hyperparameters.
os.environ["TRAIN_FILE_PATTERN"] = "gs://machine-learning-1234-bucket/gan/data/cifar10/train*.tfrecord"
os.environ["EVAL_FILE_PATTERN"] = "gs://machine-learning-1234-bucket/gan/data/cifar10/test*.tfrecord"
os.environ["OUTPUT_DIR"] = "gs://machine-learning-1234-bucket/gan/cdcgan/trained_model2"
# Import os environment variables for train hyperparameters.
os.environ["TRAIN_BATCH_SIZE"] = str(100)
os.environ["TRAIN_STEPS"] = str(50000)
os.environ["SAVE_SUMMARY_STEPS"] = str(100)
os.environ["SAVE_CHECKPOINTS_STEPS"] = str(5000)
os.environ["KEEP_CHECKPOINT_MAX"] = str(10)
os.environ["INPUT_FN_AUTOTUNE"] = "False"
# Import os environment variables for eval hyperparameters.
os.environ["EVAL_BATCH_SIZE"] = str(16)
os.environ["EVAL_STEPS"] = str(10)
os.environ["START_DELAY_SECS"] = str(6000)
os.environ["THROTTLE_SECS"] = str(6000)
# Import os environment variables for image hyperparameters.
os.environ["HEIGHT"] = str(32)
os.environ["WIDTH"] = str(32)
os.environ["DEPTH"] = str(3)
# Import os environment variables for label hyperparameters.
num_classes = 10
os.environ["NUM_CLASSES"] = str(num_classes)
os.environ["LABEL_EMBEDDING_DIMENSION"] = str(10)
# Import os environment variables for generator hyperparameters.
os.environ["LATENT_SIZE"] = str(512)
os.environ["GENERATOR_PROJECTION_DIMS"] = "4,4,256"
os.environ["GENERATOR_USE_LABELS"] = "True"
os.environ["GENERATOR_EMBED_LABELS"] = "True"
os.environ["GENERATOR_CONCATENATE_LABELS"] = "True"
os.environ["GENERATOR_NUM_FILTERS"] = "128,128,128"
os.environ["GENERATOR_KERNEL_SIZES"] = "4,4,4"
os.environ["GENERATOR_STRIDES"] = "2,2,2"
os.environ["GENERATOR_FINAL_NUM_FILTERS"] = str(3)
os.environ["GENERATOR_FINAL_KERNEL_SIZE"] = str(3)
os.environ["GENERATOR_FINAL_STRIDE"] = str(1)
os.environ["GENERATOR_LEAKY_RELU_ALPHA"] = str(0.2)
os.environ["GENERATOR_FINAL_ACTIVATION"] = "tanh"
os.environ["GENERATOR_L1_REGULARIZATION_SCALE"] = str(0.)
os.environ["GENERATOR_L2_REGULARIZATION_SCALE"] = str(0.)
os.environ["GENERATOR_OPTIMIZER"] = "Adam"
os.environ["GENERATOR_LEARNING_RATE"] = str(0.0002)
os.environ["GENERATOR_ADAM_BETA1"] = str(0.5)
os.environ["GENERATOR_ADAM_BETA2"] = str(0.999)
os.environ["GENERATOR_ADAM_EPSILON"] = str(1e-8)
os.environ["GENERATOR_CLIP_GRADIENTS"] = "None"
os.environ["GENERATOR_TRAIN_STEPS"] = str(1)
# Import os environment variables for discriminator hyperparameters.
os.environ["DISCRIMINATOR_USE_LABELS"] = "True"
os.environ["DISCRIMINATOR_EMBED_LABELS"] = "True"
os.environ["DISCRIMINATOR_CONCATENATE_LABELS"] = "True"
os.environ["DISCRIMINATOR_NUM_FILTERS"] = "64,128,128,256"
os.environ["DISCRIMINATOR_KERNEL_SIZES"] = "3,3,3,3"
os.environ["DISCRIMINATOR_STRIDES"] = "1,2,2,2"
os.environ["DISCRIMINATOR_DROPOUT_RATES"] = "0.3,0.3,0.3,0.3"
os.environ["DISCRIMINATOR_LEAKY_RELU_ALPHA"] = str(0.2)
os.environ["DISCRIMINATOR_L1_REGULARIZATION_SCALE"] = str(0.)
os.environ["DISCRIMINATOR_L2_REGULARIZATION_SCALE"] = str(0.)
os.environ["DISCRIMINATOR_OPTIMIZER"] = "Adam"
os.environ["DISCRIMINATOR_LEARNING_RATE"] = str(0.0002)
os.environ["DISCRIMINATOR_ADAM_BETA1"] = str(0.5)
os.environ["DISCRIMINATOR_ADAM_BETA2"] = str(0.999)
os.environ["DISCRIMINATOR_ADAM_EPSILON"] = str(1e-8)
os.environ["DISCRIMINATOR_CLIP_GRADIENTS"] = "None"
os.environ["DISCRIMINATOR_TRAIN_STEPS"] = str(1)
os.environ["LABEL_SMOOTHING"] = str(0.9)
```
## Train cdcgan model
```
%%bash
gsutil -m rm -rf ${OUTPUT_DIR}
export PYTHONPATH=$PYTHONPATH:$PWD/cdcgan_module
python3 -m trainer.task \
--train_file_pattern=${TRAIN_FILE_PATTERN} \
--eval_file_pattern=${EVAL_FILE_PATTERN} \
--output_dir=${OUTPUT_DIR} \
--job-dir=./tmp \
\
--train_batch_size=${TRAIN_BATCH_SIZE} \
--train_steps=${TRAIN_STEPS} \
--save_summary_steps=${SAVE_SUMMARY_STEPS} \
--save_checkpoints_steps=${SAVE_CHECKPOINTS_STEPS} \
--keep_checkpoint_max=${KEEP_CHECKPOINT_MAX} \
--input_fn_autotune=${INPUT_FN_AUTOTUNE} \
\
--eval_batch_size=${EVAL_BATCH_SIZE} \
--eval_steps=${EVAL_STEPS} \
--start_delay_secs=${START_DELAY_SECS} \
--throttle_secs=${THROTTLE_SECS} \
\
--height=${HEIGHT} \
--width=${WIDTH} \
--depth=${DEPTH} \
\
--num_classes=${NUM_CLASSES} \
--label_embedding_dimension=${LABEL_EMBEDDING_DIMENSION} \
\
--latent_size=${LATENT_SIZE} \
--generator_projection_dims=${GENERATOR_PROJECTION_DIMS} \
--generator_use_labels=${GENERATOR_USE_LABELS} \
--generator_embed_labels=${GENERATOR_EMBED_LABELS} \
--generator_concatenate_labels=${GENERATOR_CONCATENATE_LABELS} \
--generator_num_filters=${GENERATOR_NUM_FILTERS} \
--generator_kernel_sizes=${GENERATOR_KERNEL_SIZES} \
--generator_strides=${GENERATOR_STRIDES} \
--generator_final_num_filters=${GENERATOR_FINAL_NUM_FILTERS} \
--generator_final_kernel_size=${GENERATOR_FINAL_KERNEL_SIZE} \
--generator_final_stride=${GENERATOR_FINAL_STRIDE} \
--generator_leaky_relu_alpha=${GENERATOR_LEAKY_RELU_ALPHA} \
--generator_final_activation=${GENERATOR_FINAL_ACTIVATION} \
--generator_l1_regularization_scale=${GENERATOR_L1_REGULARIZATION_SCALE} \
--generator_l2_regularization_scale=${GENERATOR_L2_REGULARIZATION_SCALE} \
--generator_optimizer=${GENERATOR_OPTIMIZER} \
--generator_learning_rate=${GENERATOR_LEARNING_RATE} \
--generator_adam_beta1=${GENERATOR_ADAM_BETA1} \
--generator_adam_beta2=${GENERATOR_ADAM_BETA2} \
--generator_adam_epsilon=${GENERATOR_ADAM_EPSILON} \
--generator_clip_gradients=${GENERATOR_CLIP_GRADIENTS} \
--generator_train_steps=${GENERATOR_TRAIN_STEPS} \
\
--discriminator_use_labels=${DISCRIMINATOR_USE_LABELS} \
--discriminator_embed_labels=${DISCRIMINATOR_EMBED_LABELS} \
--discriminator_concatenate_labels=${DISCRIMINATOR_CONCATENATE_LABELS} \
--discriminator_num_filters=${DISCRIMINATOR_NUM_FILTERS} \
--discriminator_kernel_sizes=${DISCRIMINATOR_KERNEL_SIZES} \
--discriminator_strides=${DISCRIMINATOR_STRIDES} \
--discriminator_dropout_rates=${DISCRIMINATOR_DROPOUT_RATES} \
--discriminator_leaky_relu_alpha=${DISCRIMINATOR_LEAKY_RELU_ALPHA} \
--discriminator_l1_regularization_scale=${DISCRIMINATOR_L1_REGULARIZATION_SCALE} \
--discriminator_l2_regularization_scale=${DISCRIMINATOR_L2_REGULARIZATION_SCALE} \
--discriminator_optimizer=${DISCRIMINATOR_OPTIMIZER} \
--discriminator_learning_rate=${DISCRIMINATOR_LEARNING_RATE} \
--discriminator_adam_beta1=${DISCRIMINATOR_ADAM_BETA1} \
--discriminator_adam_beta2=${DISCRIMINATOR_ADAM_BETA2} \
--discriminator_adam_epsilon=${DISCRIMINATOR_ADAM_EPSILON} \
--discriminator_clip_gradients=${DISCRIMINATOR_CLIP_GRADIENTS} \
--discriminator_train_steps=${DISCRIMINATOR_TRAIN_STEPS} \
--label_smoothing=${LABEL_SMOOTHING}
```
## Prediction
```
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
!gsutil ls gs://machine-learning-1234-bucket/gan/cdcgan/trained_model2/export/exporter
predict_fn = tf.contrib.predictor.from_saved_model(
"gs://machine-learning-1234-bucket/gan/cdcgan/trained_model2/export/exporter/1592859903"
)
predictions = predict_fn(
{
"Z": np.random.normal(size=(num_classes, 512)),
"label": np.arange(num_classes)
}
)
print(list(predictions.keys()))
```
Convert image back to the original scale.
```
generated_images = np.clip(
a=((predictions["generated_images"] + 1.0) * (255. / 2)).astype(np.int32),
a_min=0,
a_max=255
)
print(generated_images.shape)
def plot_images(images):
"""Plots images.
Args:
images: np.array, array of images of
[num_images, height, width, depth].
"""
num_images = len(images)
plt.figure(figsize=(20, 20))
for i in range(num_images):
image = images[i]
plt.subplot(1, num_images, i + 1)
plt.xticks([])
plt.yticks([])
plt.grid(False)
plt.imshow(
image,
cmap=plt.cm.binary
)
plt.show()
plot_images(generated_images)
```
| github_jupyter |
```
# !/usr/bin/env python
# 测试tensorflow是否安装好
import numpy as np
import tensorflow as tf
# Prepare train data
train_X = np.linspace(-1, 1, 100)
train_Y = 2 * train_X + np.random.randn(*train_X.shape) * 0.33 + 10
# Define the model
X = tf.placeholder("float")
Y = tf.placeholder("float")
w = tf.Variable(0.0, name="weight")
b = tf.Variable(0.0, name="bias")
loss = tf.square(Y - X * w - b)
train_op = tf.train.GradientDescentOptimizer(0.01).minimize(loss)
# Create session to run
with tf.Session() as sess:
sess.run(tf.initialize_all_variables())
epoch = 1
for i in range(10):
for (x, y) in zip(train_X, train_Y):
_, w_value, b_value = sess.run([train_op, w, b], feed_dict={X: x, Y: y})
print("Epoch: {}, w: {}, b: {}".format(epoch, w_value, b_value))
epoch += 1
### 窗口显示
import tkinter
import tkinter.messagebox
def main():
flag = True
# 修改标签上的文字
def change_label_text():
nonlocal flag
flag = not flag
color, msg = ('red', 'Hello, world!')\
if flag else ('blue', 'Goodbye, world!')
label.config(text=msg, fg=color)
# 确认退出
def confirm_to_quit():
if tkinter.messagebox.askokcancel('温馨提示', '确定要退出吗?'):
top.quit()
# 创建顶层窗口
top = tkinter.Tk()
# 设置窗口大小
top.geometry('240x160')
# 设置窗口标题
top.title('小游戏')
# 创建标签对象并添加到顶层窗口
label = tkinter.Label(top, text='Hello, world!', font='Arial -32', fg='red')
label.pack(expand=1)
# 创建一个装按钮的容器
panel = tkinter.Frame(top)
# 创建按钮对象 指定添加到哪个容器中 通过command参数绑定事件回调函数
button1 = tkinter.Button(panel, text='修改', command=change_label_text)
button1.pack(side='left')
button2 = tkinter.Button(panel, text='退出', command=confirm_to_quit)
button2.pack(side='right')
panel.pack(side='bottom')
# 开启主事件循环
tkinter.mainloop()
if __name__ == '__main__':
main()
### 读取并显示cifar_10图片
import numpy as np
import os
from matplotlib import pyplot as plt
import pickle
def load_batch_cifar10(filename,dtype="float 64"):
path = os.path.join(data_dir_cifar10,filename)#链接字符串,合成文件路径
fi = open(path, 'rb') # 打开文件
batch = pickle.load(fi, encoding="bytes") # 读入数据
fi.close()
#batch = np.load(path)
data = batch[b'data']/255.0
labels = batch[b'labels']#每一个数据的标签
return data,labels#返回标签矩阵
def load_cifar10():
x_train = []#存放训练数据,最终是50000*3072的矩阵
y_train = []
for i in range(5):#读取五个文件
x,t = load_batch_cifar10("data_batch_%d"%(i+1))
x_train.append(x)
y_train.append(t)
x_test ,y_test= load_batch_cifar10("test_batch")#读取测试文件
x_train = np.concatenate(x_train,axis=0)#将五个文件的矩阵合成一个
y_train = np.concatenate(y_train, axis=0)
x_train = x_train.reshape(x_train.shape[0],3,32,32)
x_test = x_test.reshape(x_test.shape[0],3,32,32)
return x_train,y_train,x_test,y_test
data_dir = "C:\\dl"
data_dir_cifar10 = os.path.join(data_dir,"cifarpy")
class_name_cifar10 = np.load(os.path.join(data_dir_cifar10,"batches.meta"))
#print(class_name_cifar10)
Xtrain,Ytrain,Xtest,Ytest = load_cifar10()
imlist = []
for i in range(24): #显示24张图片
red = Xtrain[i][0].reshape(1024,1)
green = Xtrain[i][1].reshape(1024,1)
blue = Xtrain[i][2].reshape(1024,1)
pic = np.hstack((red,green,blue))
pic_grab = pic.reshape(32,32,3)#合成一个三维矩阵,每一个点包含红绿蓝三种颜色
imlist.append(pic_grab)
fig = plt.figure()
for j in range(1,25):
ax = fig.add_subplot(4,6,j)#这三个参数是,图片行数,列数,编号
plt.title(class_name_cifar10['label_names'][Ytrain[j-1]])
plt.axis('off')#不显示坐标值
plt.imshow(imlist[j-1])#显示图片
plt.subplots_adjust(wspace=0,hspace=0)
plt.show()
#end
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
np.random.seed(42)
# 采样个数500
n_samples = 500
dim = 3
# 先生成一组3维正态分布数据,数据方向完全随机
samples = np.random.multivariate_normal(
np.zeros(dim),
np.eye(dim),
n_samples
)
# 通过把每个样本到原点距离和均匀分布吻合得到球体内均匀分布的样本
for i in range(samples.shape[0]):
r = np.power(np.random.random(), 1.0/3.0)
samples[i] *= r / np.linalg.norm(samples[i])
upper_samples = []
lower_samples = []
for x, y, z in samples:
# 3x+2y-z=1作为判别平面
if z > 3*x + 2*y - 1:
upper_samples.append((x, y, z))
else:
lower_samples.append((x, y, z))
fig = plt.figure('3D scatter plot')
ax = fig.add_subplot(111, projection='3d')
uppers = np.array(upper_samples)
lowers = np.array(lower_samples)
# 用不同颜色不同形状的图标表示平面上下的样本
# 判别平面上半部分为红色圆点,下半部分为绿色三角
ax.scatter(uppers[:, 0], uppers[:, 1], uppers[:, 2], c='r', marker='o')
ax.scatter(lowers[:, 0], lowers[:, 1], lowers[:, 2], c='g', marker='^')
plt.show()
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rcParams['axes.titlesize'] = 20
mpl.rcParams['xtick.labelsize'] = 16
mpl.rcParams['ytick.labelsize'] = 16
mpl.rcParams['axes.labelsize'] = 16
mpl.rcParams['xtick.major.size'] = 0
mpl.rcParams['ytick.major.size'] = 0
# 包含了狗,猫和猎豹的最高奔跑速度,还有对应的可视化颜色
speed_map = {
'dog': (48, '#7199cf'),
'cat': (45, '#4fc4aa'),
'cheetah': (120, '#e1a7a2')
}
# 整体图的标题
fig = plt.figure('Bar chart & Pie chart')
# 在整张图上加入一个子图,121的意思是在一个1行2列的子图中的第一张
ax = fig.add_subplot(121)
ax.set_title('Running speed - bar chart')
# 生成x轴每个元素的位置
xticks = np.arange(3)
# 定义柱状图每个柱的宽度
bar_width = 0.5
# 动物名称
animals = speed_map.keys()
# 奔跑速度
speeds = [x[0] for x in speed_map.values()]
# 对应颜色
colors = [x[1] for x in speed_map.values()]
# 画柱状图,横轴是动物标签的位置,纵轴是速度,定义柱的宽度,同时设置柱的边缘为透明
bars = ax.bar(xticks, speeds, width=bar_width, edgecolor='none')
# 设置y轴的标题
ax.set_ylabel('Speed(km/h)')
# x轴每个标签的具体位置,设置为每个柱的中央
ax.set_xticks(xticks+bar_width/2)
# 设置每个标签的名字
ax.set_xticklabels(animals)
# 设置x轴的范围
ax.set_xlim([bar_width/2-0.5, 3-bar_width/2])
# 设置y轴的范围
ax.set_ylim([0, 125])
# 给每个bar分配指定的颜色
for bar, color in zip(bars, colors):
bar.set_color(color)
# 在122位置加入新的图
ax = fig.add_subplot(122)
ax.set_title('Running speed - pie chart')
# 生成同时包含名称和速度的标签
labels = ['{}\n{} km/h'.format(animal, speed) for animal, speed in zip(animals, speeds)]
# 画饼状图,并指定标签和对应颜色
ax.pie(speeds, labels=labels, colors=colors)
plt.show()
import matplotlib.pyplot as plt
# 读取一张照片并显示
plt.figure('A Little White Dog')
little_dog_img = plt.imread('c:\\dl\\other\\t.jpg')
plt.imshow(little_dog_img)
plt.show()
import matplotlib.pyplot as plt
import numpy as np
# 3D图标必须的模块,project='3d'的定义
from mpl_toolkits.mplot3d import Axes3D
np.random.seed(42)
n_grids = 51 # x-y平面的格点数
c = n_grids // 2 # 中心位置
nf = 2 # 低频成分的个数
# 生成格点
x = np.linspace(0, 1, n_grids)
y = np.linspace(0, 1, n_grids)
# x和y是长度为n_grids的array
# meshgrid会把x和y组合成n_grids*n_grids的array,X和Y对应位置就是所有格点的坐标
X, Y = np.meshgrid(x, y)
# 生成一个0值的傅里叶谱
spectrum = np.zeros((n_grids, n_grids), dtype=np.complex)
# 生成一段噪音,长度是(2*nf+1)**2/2
noise = [np.complex(x, y) for x, y in np.random.uniform(-1,1,((2*nf+1)**2//2, 2))]
# 傅里叶频谱的每一项和其共轭关于中心对称
noisy_block = np.concatenate((noise, [0j], np.conjugate(noise[::-1])))
# 将生成的频谱作为低频成分
spectrum[c-nf:c+nf+1, c-nf:c+nf+1] = noisy_block.reshape((2*nf+1, 2*nf+1))
# 进行反傅里叶变换
Z = np.real(np.fft.ifft2(np.fft.ifftshift(spectrum)))
# 创建图表
fig = plt.figure('3D surface & wire')
# 第一个子图,surface图
ax = fig.add_subplot(1, 2, 1, projection='3d')
# alpha定义透明度,cmap是color map
# rstride和cstride是两个方向上的采样,越小越精细,lw是线宽
ax.plot_surface(X, Y, Z, alpha=0.7, cmap='jet', rstride=1, cstride=1, lw=0)
# 第二个子图,网线图
ax = fig.add_subplot(1, 2, 2, projection='3d')
ax.plot_wireframe(X, Y, Z, rstride=3, cstride=3, lw=0.5)
plt.show()
### Python+Opencv进行识别相似图片
### 来自https://blog.csdn.net/feimengjuan/article/details/51279629
### -*- coding: utf-8 -*-
### 利用python实现多种方法来实现图像识别
import cv2
import numpy as np
from matplotlib import pyplot as plt
### 最简单的以灰度直方图作为相似比较的实现
def classify_gray_hist(image1,image2,size = (256,256)):
###### 先计算直方图
##### 几个参数必须用方括号括起来
##### 这里直接用灰度图计算直方图,所以是使用第一个通道,
##### 也可以进行通道分离后,得到多个通道的直方图
##### bins 取为16
image1 = cv2.resize(image1,size)
image2 = cv2.resize(image2,size)
hist1 = cv2.calcHist([image1],[0],None,[256],[0.0,255.0])
hist2 = cv2.calcHist([image2],[0],None,[256],[0.0,255.0])
##### 可以比较下直方图
plt.plot(range(256),hist1,'r')
plt.plot(range(256),hist2,'b')
plt.show()
##### 计算直方图的重合度
degree = 0
for i in range(len(hist1)):
if hist1[i] != hist2[i]:
degree = degree + (1 - abs(hist1[i]-hist2[i])/max(hist1[i],hist2[i]))
else:
degree = degree + 1
degree = degree/len(hist1)
return degree
### 计算单通道的直方图的相似值
def calculate(image1,image2):
hist1 = cv2.calcHist([image1],[0],None,[256],[0.0,255.0])
hist2 = cv2.calcHist([image2],[0],None,[256],[0.0,255.0])
##### 计算直方图的重合度
degree = 0
for i in range(len(hist1)):
if hist1[i] != hist2[i]:
degree = degree + (1 - abs(hist1[i]-hist2[i])/max(hist1[i],hist2[i]))
else:
degree = degree + 1
degree = degree/len(hist1)
return degree
### 通过得到每个通道的直方图来计算相似度
def classify_hist_with_split(image1,image2,size = (256,256)):
##### 将图像resize后,分离为三个通道,再计算每个通道的相似值
image1 = cv2.resize(image1,size)
image2 = cv2.resize(image2,size)
sub_image1 = cv2.split(image1)
sub_image2 = cv2.split(image2)
sub_data = 0
for im1,im2 in zip(sub_image1,sub_image2):
sub_data += calculate(im1,im2)
sub_data = sub_data/3
return sub_data
### 平均哈希算法计算
def classify_aHash(image1,image2):
image1 = cv2.resize(image1,(8,8))
image2 = cv2.resize(image2,(8,8))
gray1 = cv2.cvtColor(image1,cv2.COLOR_BGR2GRAY)
gray2 = cv2.cvtColor(image2,cv2.COLOR_BGR2GRAY)
hash1 = getHash(gray1)
hash2 = getHash(gray2)
return Hamming_distance(hash1,hash2)
def classify_pHash(image1,image2):
image1 = cv2.resize(image1,(32,32))
image2 = cv2.resize(image2,(32,32))
gray1 = cv2.cvtColor(image1,cv2.COLOR_BGR2GRAY)
gray2 = cv2.cvtColor(image2,cv2.COLOR_BGR2GRAY)
##### 将灰度图转为浮点型,再进行dct变换
dct1 = cv2.dct(np.float32(gray1))
dct2 = cv2.dct(np.float32(gray2))
##### 取左上角的8*8,这些代表图片的最低频率
##### 这个操作等价于c++中利用opencv实现的掩码操作
##### 在python中进行掩码操作,可以直接这样取出图像矩阵的某一部分
dct1_roi = dct1[0:8,0:8]
dct2_roi = dct2[0:8,0:8]
hash1 = getHash(dct1_roi)
hash2 = getHash(dct2_roi)
return Hamming_distance(hash1,hash2)
### 输入灰度图,返回hash
def getHash(image):
avreage = np.mean(image)
hash = []
for i in range(image.shape[0]):
for j in range(image.shape[1]):
if image[i,j] > avreage:
hash.append(1)
else:
hash.append(0)
return hash
### 计算汉明距离
def Hamming_distance(hash1,hash2):
num = 0
for index in range(len(hash1)):
if hash1[index] != hash2[index]:
num += 1
return num
if __name__ == '__main__':
img1 = cv2.imread('train\\黑炮1.jpg')
cv2.imshow('img1',img1)
img2 = cv2.imread('train\\红炮1.jpg')
cv2.imshow('img2',img2)
degree = classify_gray_hist(img1,img2)
#degree = classify_hist_with_split(img1,img2)
#degree = classify_aHash(img1,img2)
#degree = classify_pHash(img1,img2)
print(degree)
cv2.waitKey(0)
```
| github_jupyter |
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import xarray as xr
import seaborn as sns
sns.set()
```
#### Check surface fluxes of CO$_2$
```
# check the data folder to swith to another mixing conditions
#ds = xr.open_dataset('data/results_so4_adv/5_po75-25_di10e-9/water.nc')
ds = xr.open_dataset('data/results_so4_adv/9_po75-25_di30e-9/water.nc')
#ds = xr.open_dataset('data/no_denitrification/water.nc')
dicflux_df = ds['B_C_DIC _flux'].to_dataframe()
oxyflux_df = ds['B_BIO_O2 _flux'].to_dataframe()
dicflux_surface = dicflux_df.groupby('z_faces').get_group(0)
oxyflux_surface = oxyflux_df.groupby('z_faces').get_group(0)
dicflux_surface_year = dicflux_surface.loc['2011-01-01':'2011-12-31']
oxyflux_surface_year = oxyflux_surface.loc['2011-01-01':'2011-12-31']
ox = np.arange(1,366,1)
plt.plot(ox, dicflux_surface_year); plt.gcf().set_size_inches(10, 2);
plt.title('Air-sea CO$_2$ flux, positive means upwards');
plt.xlabel('Day'); plt.ylabel('Flux, mmol m$^{-2}$ d$^{-1}$');
```
#### Advective TA exchange
These are data on how alkalinity in the Wadden Sea changes due to mixing with the North Sea. Positive means alkalinity comes from the North Sea, negative - goes to the North Sea.
```
nh4ta_df = ds['TA_due_to_NH4'].to_dataframe()
no3ta_df = ds['TA_due_to_NO3'].to_dataframe()
po4ta_df = ds['TA_due_to_PO4'].to_dataframe()
so4ta_df = ds['TA_due_to_SO4'].to_dataframe()
nh4ta_year = nh4ta_df.loc['2011-01-01':'2011-12-31']
no3ta_year = no3ta_df.loc['2011-01-01':'2011-12-31']
po4ta_year = po4ta_df.loc['2011-01-01':'2011-12-31']
so4ta_year = so4ta_df.loc['2011-01-01':'2011-12-31']
nh4ta = np.array(nh4ta_year.TA_due_to_NH4.values)
no3ta = np.array(no3ta_year.TA_due_to_NO3.values)
po4ta = np.array(po4ta_year.TA_due_to_PO4.values)
so4ta = np.array(so4ta_year.TA_due_to_SO4.values)
total = nh4ta+no3ta+po4ta+so4ta
plt.plot(ox, total); plt.gcf().set_size_inches(10, 2);
plt.title('WS - NS alkalinity flux, positive means to the WS');
plt.xlabel('Day'); plt.ylabel('Flux, mmol m$^{-2}$ d$^{-1}$');
year = (('2011-01-01','2011-01-31'), ('2011-02-01','2011-02-28'), ('2011-03-01','2011-03-31'), ('2011-04-01','2011-04-30'),
('2011-05-01','2011-05-31'), ('2011-06-01','2011-06-30'), ('2011-07-01','2011-07-31'), ('2011-08-01','2011-08-31'),
('2011-09-01','2011-09-30'), ('2011-10-01','2011-10-31'), ('2011-11-01','2011-11-30'), ('2011-12-01','2011-12-31'))
nh4ta_year = []
no3ta_year = []
po4ta_year = []
so4ta_year = []
for month in year:
nh4ta_month = nh4ta_df.loc[month[0]:month[1]]
no3ta_month = no3ta_df.loc[month[0]:month[1]]
po4ta_month = po4ta_df.loc[month[0]:month[1]]
so4ta_month = so4ta_df.loc[month[0]:month[1]]
nh4ta_year.append(nh4ta_month['TA_due_to_NH4'].sum())
no3ta_year.append(no3ta_month['TA_due_to_NO3'].sum())
po4ta_year.append(po4ta_month['TA_due_to_PO4'].sum())
so4ta_year.append(so4ta_month['TA_due_to_SO4'].sum())
nh4ta = np.array(nh4ta_year)
no3ta = np.array(no3ta_year)
po4ta = np.array(po4ta_year)
so4ta = np.array(so4ta_year)
total = nh4ta+no3ta+po4ta+so4ta
```
here and further, units: mmol m$^{-2}$
```
nh4ta
sum(nh4ta)
no3ta
sum(no3ta)
po4ta
sum(po4ta)
so4ta
sum(so4ta)
total
sum(total)
```
| github_jupyter |
# Using Ray for Highly Parallelizable Tasks
While Ray can be used for very complex parallelization tasks,
often we just want to do something simple in parallel.
For example, we may have 100,000 time series to process with exactly the same algorithm,
and each one takes a minute of processing.
Clearly running it on a single processor is prohibitive: this would take 70 days.
Even if we managed to use 8 processors on a single machine,
that would bring it down to 9 days. But if we can use 8 machines, each with 16 cores,
it can be done in about 12 hours.
How can we use Ray for these types of task?
We take the simple example of computing the digits of pi.
The algorithm is simple: generate random x and y, and if ``x^2 + y^2 < 1``, it's
inside the circle, we count as in. This actually turns out to be pi/4
(remembering your high school math).
The following code (and this notebook) assumes you have already set up your Ray cluster and that you are running on the head node. For more details on how to set up a Ray cluster please see the [Ray Cluster Quickstart Guide](https://docs.ray.io/en/master/cluster/quickstart.html).
```
import ray
import random
import time
import math
from fractions import Fraction
# Let's start Ray
ray.init(address='auto')
```
We use the ``@ray.remote`` decorator to create a Ray task.
A task is like a function, except the result is returned asynchronously.
It also may not run on the local machine, it may run elsewhere in the cluster.
This way you can run multiple tasks in parallel,
beyond the limit of the number of processors you can have in a single machine.
```
@ray.remote
def pi4_sample(sample_count):
"""pi4_sample runs sample_count experiments, and returns the
fraction of time it was inside the circle.
"""
in_count = 0
for i in range(sample_count):
x = random.random()
y = random.random()
if x*x + y*y <= 1:
in_count += 1
return Fraction(in_count, sample_count)
```
To get the result of a future, we use ray.get() which
blocks until the result is complete.
```
SAMPLE_COUNT = 1000 * 1000
start = time.time()
future = pi4_sample.remote(sample_count = SAMPLE_COUNT)
pi4 = ray.get(future)
end = time.time()
dur = end - start
print(f'Running {SAMPLE_COUNT} tests took {dur} seconds')
```
Now let's see how good our approximation is.
```
pi = pi4 * 4
float(pi)
abs(pi-math.pi)/pi
```
Meh. A little off -- that's barely 4 decimal places.
Why don't we do it a 100,000 times as much? Let's do 100 billion!
```
FULL_SAMPLE_COUNT = 100 * 1000 * 1000 * 1000 # 100 billion samples!
BATCHES = int(FULL_SAMPLE_COUNT / SAMPLE_COUNT)
print(f'Doing {BATCHES} batches')
results = []
for _ in range(BATCHES):
results.append(pi4_sample.remote())
output = ray.get(results)
```
Notice that in the above, we generated a list with 100,000 futures.
Now all we do is have to do is wait for the result.
Depending on your ray cluster's size, this might take a few minutes.
But to give you some idea, if we were to do it on a single machine,
when I ran this it took 0.4 seconds.
On a single core, that means we're looking at 0.4 * 100000 = about 11 hours.
Here's what the Dashboard looks like:

So now, rather than just a single core working on this,
I have 168 working on the task together. And its ~80% efficient.
```
pi = sum(output)*4/len(output)
float(pi)
abs(pi-math.pi)/pi
```
Not bad at all -- we're off by a millionth.
| github_jupyter |
<a href="https://colab.research.google.com/github/Collin-Campbell/DS-Unit-2-Linear-Models/blob/master/module3-ridge-regression/LS_DS_213_assignment.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
Lambda School Data Science
*Unit 2, Sprint 1, Module 3*
---
# Ridge Regression
## Assignment
We're going back to our other **New York City** real estate dataset. Instead of predicting apartment rents, you'll predict property sales prices.
But not just for condos in Tribeca...
- [ ] Use a subset of the data where `BUILDING_CLASS_CATEGORY` == `'01 ONE FAMILY DWELLINGS'` and the sale price was more than 100 thousand and less than 2 million.
- [ ] Do train/test split. Use data from January — March 2019 to train. Use data from April 2019 to test.
- [ ] Do one-hot encoding of categorical features.
- [ ] Do feature selection with `SelectKBest`.
- [ ] Fit a ridge regression model with multiple features. Use the `normalize=True` parameter (or do [feature scaling](https://scikit-learn.org/stable/modules/preprocessing.html) beforehand — use the scaler's `fit_transform` method with the train set, and the scaler's `transform` method with the test set)
- [ ] Get mean absolute error for the test set.
- [ ] As always, commit your notebook to your fork of the GitHub repo.
The [NYC Department of Finance](https://www1.nyc.gov/site/finance/taxes/property-rolling-sales-data.page) has a glossary of property sales terms and NYC Building Class Code Descriptions. The data comes from the [NYC OpenData](https://data.cityofnewyork.us/browse?q=NYC%20calendar%20sales) portal.
## Stretch Goals
Don't worry, you aren't expected to do all these stretch goals! These are just ideas to consider and choose from.
- [ ] Add your own stretch goal(s) !
- [ ] Instead of `Ridge`, try `LinearRegression`. Depending on how many features you select, your errors will probably blow up! 💥
- [ ] Instead of `Ridge`, try [`RidgeCV`](https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.RidgeCV.html).
- [ ] Learn more about feature selection:
- ["Permutation importance"](https://www.kaggle.com/dansbecker/permutation-importance)
- [scikit-learn's User Guide for Feature Selection](https://scikit-learn.org/stable/modules/feature_selection.html)
- [mlxtend](http://rasbt.github.io/mlxtend/) library
- scikit-learn-contrib libraries: [boruta_py](https://github.com/scikit-learn-contrib/boruta_py) & [stability-selection](https://github.com/scikit-learn-contrib/stability-selection)
- [_Feature Engineering and Selection_](http://www.feat.engineering/) by Kuhn & Johnson.
- [ ] Try [statsmodels](https://www.statsmodels.org/stable/index.html) if you’re interested in more inferential statistical approach to linear regression and feature selection, looking at p values and 95% confidence intervals for the coefficients.
- [ ] Read [_An Introduction to Statistical Learning_](http://faculty.marshall.usc.edu/gareth-james/ISL/ISLR%20Seventh%20Printing.pdf), Chapters 1-3, for more math & theory, but in an accessible, readable way.
- [ ] Try [scikit-learn pipelines](https://scikit-learn.org/stable/modules/compose.html).
```
import numpy as np
%%capture
import sys
# If you're on Colab:
if 'google.colab' in sys.modules:
DATA_PATH = 'https://raw.githubusercontent.com/LambdaSchool/DS-Unit-2-Applied-Modeling/master/data/'
!pip install category_encoders==2.*
# If you're working locally:
else:
DATA_PATH = '../data/'
# Ignore this Numpy warning when using Plotly Express:
# FutureWarning: Method .ptp is deprecated and will be removed in a future version. Use numpy.ptp instead.
import warnings
warnings.filterwarnings(action='ignore', category=FutureWarning, module='numpy')
import pandas as pd
import pandas_profiling
# Read New York City property sales data
df = pd.read_csv(DATA_PATH+'condos/NYC_Citywide_Rolling_Calendar_Sales.csv',
parse_dates=['SALE DATE'],
index_col=('SALE DATE'))
# Changing space to underscore in index name
df.index.name = 'SALE_DATE'
# Change column names: replace spaces with underscores
df.columns = [col.replace(' ', '_') for col in df]
# SALE_PRICE was read as strings.
# Remove symbols, convert to integer
df['SALE_PRICE'] = (
df['SALE_PRICE']
.str.replace('$','')
.str.replace('-','')
.str.replace(',','')
.astype(int)
)
# BOROUGH is a numeric column, but arguably should be a categorical feature,
# so convert it from a number to a string
df['BOROUGH'] = df['BOROUGH'].astype(str)
# Reduce cardinality for NEIGHBORHOOD feature
# Get a list of the top 10 neighborhoods
top10 = df['NEIGHBORHOOD'].value_counts()[:10].index
# At locations where the neighborhood is NOT in the top 10,
# replace the neighborhood with 'OTHER'
df.loc[~df['NEIGHBORHOOD'].isin(top10), 'NEIGHBORHOOD'] = 'OTHER'
print(df.shape)
df.head()
# Getting rid of commas from land square ft and converting all values to floats
df['LAND_SQUARE_FEET'] = df['LAND_SQUARE_FEET'].str.replace(',','')
df['LAND_SQUARE_FEET'] = df['LAND_SQUARE_FEET'].replace({'': np.NaN, '########': np.NaN})
df['LAND_SQUARE_FEET'] = df['LAND_SQUARE_FEET'].astype(float)
df['LAND_SQUARE_FEET'].value_counts()
df.info()
def wrangle(df):
# Making a copy of the dataset
df = df.copy()
# Making a subset of the data where BUILDING_CLASS_CATEGORY == '01 ONE FAMILY
# DWELLINGS' and the sale price was more than 100 thousand and less than 2 million
df = df[(df['BUILDING_CLASS_CATEGORY'] == '01 ONE FAMILY DWELLINGS') &
(df['SALE_PRICE'] > 100000) &
(df['SALE_PRICE'] < 2000000)]
# Dropping high-cardinality categorical columns
hc_cols = [col for col in df.select_dtypes('object').columns
if df[col].nunique() > 11]
df.drop(columns=hc_cols, inplace=True)
return df
df = wrangle(df)
df['TAX_CLASS_AT_TIME_OF_SALE'].value_counts()
df.info()
# Dropping NaN columns, building class column since now they are all the same,
# and tax class at time of sale column since they are also all identical
df = df.drop(['BUILDING_CLASS_CATEGORY', 'EASE-MENT', 'APARTMENT_NUMBER', 'TAX_CLASS_AT_TIME_OF_SALE'], axis=1)
print(df.shape)
df.head()
df.info()
# Splitting Data
# splitting into target and feature matrix
target = 'SALE_PRICE'
y = df[target]
X = df.drop(columns=target)
# splitting into training and test sets:
# Using data from January — March 2019 to train. Using data from April 2019 to test
cutoff = '2019-04-01'
mask = X.index < cutoff
X_train, y_train = X.loc[mask], y.loc[mask]
X_test, y_test = X.loc[~mask], y.loc[~mask]
# Establishing Baseline
y_pred = [y_train.mean()] * len(y_train)
from sklearn.metrics import mean_absolute_error
print('Baseline MAE:', mean_absolute_error(y_train, y_pred))
# Applying transformer: OneHotEncoder
# Step 1: Importing the transformer class
from category_encoders import OneHotEncoder, OrdinalEncoder
# Step 2: Instantiating the transformer
ohe = OneHotEncoder(use_cat_names=True)
# Step 3: Fitting my TRAINING data to the transfomer
ohe.fit(X_train)
# Step 4: Transforming
XT_train = ohe.transform(X_train)
print(len(XT_train.columns))
XT_train.columns
print(XT_train.shape)
XT_train.head()
# Performing feature selection with SelectKBest
# Importing the feature selector utility:
from sklearn.feature_selection import SelectKBest, f_regression
# Creating the selector object with the best k=1 features:
selector = SelectKBest(score_func=f_regression, k=1)
# Running the selector on the training data:
XT_train_selected = selector.fit_transform(XT_train, y_train)
# Finding the features that were selected:
selected_mask = selector.get_support()
all_features = XT_train.columns
selected_feature = all_features[selected_mask]
print('The selected feature: ', selected_feature[0])
# Scaling the ohe data with StandardScaler:
from sklearn.preprocessing import StandardScaler
ss = StandardScaler()
ss.fit(XT_train)
XTT_train = ss.transform(XT_train)
# Building Ridge Regression Model:
from sklearn.linear_model import Ridge
model = Ridge(alpha=150)
model.fit(XTT_train, y_train)
# Checking metrics:
XT_test = ohe.transform(X_test)
XTT_test = ss.transform(XT_test)
print('RIDGE train MAE', mean_absolute_error(y_train, model.predict(XTT_train)))
print('RIDGE test MAE', mean_absolute_error(y_test, model.predict(XTT_test)))
```
| github_jupyter |
# Zircon model training notebook; (extensively) modified from Detectron2 training tutorial
This Colab Notebook will allow users to train new models to detect and segment detrital zircon from RL images using Detectron2 and the training dataset provided in the colab_zirc_dims repo. It is set up to train a Mask RCNN model (ResNet depth=101), but could be modified for other instance segmentation models provided that they are supported by Detectron2.
The training dataset should be uploaded to the user's Google Drive before running this notebook.
## Install detectron2
```
!pip install pyyaml==5.1
import torch
TORCH_VERSION = ".".join(torch.__version__.split(".")[:2])
CUDA_VERSION = torch.__version__.split("+")[-1]
print("torch: ", TORCH_VERSION, "; cuda: ", CUDA_VERSION)
# Install detectron2 that matches the above pytorch version
# See https://detectron2.readthedocs.io/tutorials/install.html for instructions
!pip install detectron2 -f https://dl.fbaipublicfiles.com/detectron2/wheels/$CUDA_VERSION/torch$TORCH_VERSION/index.html
exit(0) # Automatically restarts runtime after installation
# Some basic setup:
# Setup detectron2 logger
import detectron2
from detectron2.utils.logger import setup_logger
setup_logger()
# import some common libraries
import numpy as np
import os, json, cv2, random
from google.colab.patches import cv2_imshow
import copy
import time
import datetime
import logging
import random
import shutil
import torch
# import some common detectron2 utilities
from detectron2.engine.hooks import HookBase
from detectron2 import model_zoo
from detectron2.evaluation import inference_context, COCOEvaluator
from detectron2.engine import DefaultPredictor
from detectron2.config import get_cfg
from detectron2.utils.visualizer import Visualizer
from detectron2.utils.logger import log_every_n_seconds
from detectron2.data import MetadataCatalog, DatasetCatalog, build_detection_train_loader, DatasetMapper, build_detection_test_loader
import detectron2.utils.comm as comm
from detectron2.data import detection_utils as utils
from detectron2.config import LazyConfig
import detectron2.data.transforms as T
```
## Define Augmentations
The cell below defines augmentations used while training to ensure that models never see the same exact image twice during training. This mitigates overfitting and allows models to achieve substantially higher accuracy in their segmentations/measurements.
```
custom_transform_list = [T.ResizeShortestEdge([800,800]), #resize shortest edge of image to 800 pixels
T.RandomCrop('relative', (0.95, 0.95)), #randomly crop an area (95% size of original) from image
T.RandomLighting(100), #minor lighting randomization
T.RandomContrast(.85, 1.15), #minor contrast randomization
T.RandomFlip(prob=.5, horizontal=False, vertical=True), #random vertical flipping
T.RandomFlip(prob=.5, horizontal=True, vertical=False), #and horizontal flipping
T.RandomApply(T.RandomRotation([-30, 30], False), prob=.8), #random (80% probability) rotation up to 30 degrees; \
# more rotation does not seem to improve results
T.ResizeShortestEdge([800,800])] # resize img again for uniformity
```
## Mount Google Drive, set paths to dataset, model saving directories
```
from google.colab import drive
drive.mount('/content/drive')
#@markdown ### Add path to training dataset directory
dataset_dir = '/content/drive/MyDrive/training_dataset' #@param {type:"string"}
#@markdown ### Add path to model saving directory (automatically created if it does not yet exist)
model_save_dir = '/content/drive/MyDrive/NAME FOR MODEL SAVING FOLDER HERE' #@param {type:"string"}
os.makedirs(model_save_dir, exist_ok=True)
```
## Define dataset mapper, training, loss eval functions
```
from detectron2.engine import DefaultTrainer
from detectron2.data import DatasetMapper
from detectron2.structures import BoxMode
# a function to convert Via image annotation .json dict format to Detectron2 \
# training input dict format
def get_zircon_dicts(img_dir):
json_file = os.path.join(img_dir, "via_region_data.json")
with open(json_file) as f:
imgs_anns = json.load(f)['_via_img_metadata']
dataset_dicts = []
for idx, v in enumerate(imgs_anns.values()):
record = {}
filename = os.path.join(img_dir, v["filename"])
height, width = cv2.imread(filename).shape[:2]
record["file_name"] = filename
record["image_id"] = idx
record["height"] = height
record["width"] = width
#annos = v["regions"]
annos = {}
for n, eachitem in enumerate(v['regions']):
annos[str(n)] = eachitem
objs = []
for _, anno in annos.items():
#assert not anno["region_attributes"]
anno = anno["shape_attributes"]
px = anno["all_points_x"]
py = anno["all_points_y"]
poly = [(x + 0.5, y + 0.5) for x, y in zip(px, py)]
poly = [p for x in poly for p in x]
obj = {
"bbox": [np.min(px), np.min(py), np.max(px), np.max(py)],
"bbox_mode": BoxMode.XYXY_ABS,
"segmentation": [poly],
"category_id": 0,
}
objs.append(obj)
record["annotations"] = objs
dataset_dicts.append(record)
return dataset_dicts
# loss eval hook for getting vaidation loss, copying to metrics.json; \
# from https://gist.github.com/ortegatron/c0dad15e49c2b74de8bb09a5615d9f6b
class LossEvalHook(HookBase):
def __init__(self, eval_period, model, data_loader):
self._model = model
self._period = eval_period
self._data_loader = data_loader
def _do_loss_eval(self):
# Copying inference_on_dataset from evaluator.py
total = len(self._data_loader)
num_warmup = min(5, total - 1)
start_time = time.perf_counter()
total_compute_time = 0
losses = []
for idx, inputs in enumerate(self._data_loader):
if idx == num_warmup:
start_time = time.perf_counter()
total_compute_time = 0
start_compute_time = time.perf_counter()
if torch.cuda.is_available():
torch.cuda.synchronize()
total_compute_time += time.perf_counter() - start_compute_time
iters_after_start = idx + 1 - num_warmup * int(idx >= num_warmup)
seconds_per_img = total_compute_time / iters_after_start
if idx >= num_warmup * 2 or seconds_per_img > 5:
total_seconds_per_img = (time.perf_counter() - start_time) / iters_after_start
eta = datetime.timedelta(seconds=int(total_seconds_per_img * (total - idx - 1)))
log_every_n_seconds(
logging.INFO,
"Loss on Validation done {}/{}. {:.4f} s / img. ETA={}".format(
idx + 1, total, seconds_per_img, str(eta)
),
n=5,
)
loss_batch = self._get_loss(inputs)
losses.append(loss_batch)
mean_loss = np.mean(losses)
self.trainer.storage.put_scalar('validation_loss', mean_loss)
comm.synchronize()
return losses
def _get_loss(self, data):
# How loss is calculated on train_loop
metrics_dict = self._model(data)
metrics_dict = {
k: v.detach().cpu().item() if isinstance(v, torch.Tensor) else float(v)
for k, v in metrics_dict.items()
}
total_losses_reduced = sum(loss for loss in metrics_dict.values())
return total_losses_reduced
def after_step(self):
next_iter = self.trainer.iter + 1
is_final = next_iter == self.trainer.max_iter
if is_final or (self._period > 0 and next_iter % self._period == 0):
self._do_loss_eval()
#trainer for zircons which incorporates augmentation, hooks for eval
class ZirconTrainer(DefaultTrainer):
@classmethod
def build_train_loader(cls, cfg):
#return a custom train loader with augmentations; recompute_boxes \
# is important given cropping, rotation augs
return build_detection_train_loader(cfg, mapper=
DatasetMapper(cfg, is_train=True, recompute_boxes = True,
augmentations = custom_transform_list
),
)
@classmethod
def build_evaluator(cls, cfg, dataset_name, output_folder=None):
if output_folder is None:
output_folder = os.path.join(cfg.OUTPUT_DIR, "inference")
return COCOEvaluator(dataset_name, cfg, True, output_folder)
#set up validation loss eval hook
def build_hooks(self):
hooks = super().build_hooks()
hooks.insert(-1,LossEvalHook(
cfg.TEST.EVAL_PERIOD,
self.model,
build_detection_test_loader(
self.cfg,
self.cfg.DATASETS.TEST[0],
DatasetMapper(self.cfg,True)
)
))
return hooks
```
## Import train, val catalogs
```
#registers training, val datasets (converts annotations using get_zircon_dicts)
for d in ["train", "val"]:
DatasetCatalog.register("zircon_" + d, lambda d=d: get_zircon_dicts(dataset_dir + "/" + d))
MetadataCatalog.get("zircon_" + d).set(thing_classes=["zircon"])
zircon_metadata = MetadataCatalog.get("zircon_train")
train_cat = DatasetCatalog.get("zircon_train")
```
## Visualize train dataset
```
# visualize random sample from training dataset
dataset_dicts = get_zircon_dicts(os.path.join(dataset_dir, 'train'))
for d in random.sample(dataset_dicts, 4): #change int here to change sample size
img = cv2.imread(d["file_name"])
visualizer = Visualizer(img[:, :, ::-1], metadata=zircon_metadata, scale=0.5)
out = visualizer.draw_dataset_dict(d)
cv2_imshow(out.get_image()[:, :, ::-1])
```
# Define save to Drive function
```
# a function to save models (with iteration number in name), metrics to drive; \
# important in case training crashes or is left unattended and disconnects. \
def save_outputs_to_drive(model_name, iters):
root_output_dir = os.path.join(model_save_dir, model_name) #output_dir = save dir from user input
#creates individual model output directory if it does not already exist
os.makedirs(root_output_dir, exist_ok=True)
#creates a name for this version of model; include iteration number
curr_iters_str = str(round(iters/1000, 1)) + 'k'
curr_model_name = model_name + '_' + curr_iters_str + '.pth'
model_save_pth = os.path.join(root_output_dir, curr_model_name)
#get most recent model, current metrics, copy to drive
model_path = os.path.join(cfg.OUTPUT_DIR, "model_final.pth")
metrics_path = os.path.join(cfg.OUTPUT_DIR, 'metrics.json')
shutil.copy(model_path, model_save_pth)
shutil.copy(metrics_path, root_output_dir)
```
## Build, train model
### Set some parameters for training
```
#@markdown ### Add a base name for the model
model_save_name = 'your model name here' #@param {type:"string"}
#@markdown ### Final iteration before training stops
final_iteration = 8000 #@param {type:"slider", min:3000, max:15000, step:1000}
```
### Actually build and train model
```
#train from a pre-trained Mask RCNN model
cfg = get_cfg()
# train from base model: Default Mask RCNN
cfg.merge_from_file(model_zoo.get_config_file("COCO-InstanceSegmentation/mask_rcnn_R_101_FPN_3x.yaml"))
# Load starting weights (COCO trained) from Detectron2 model zoo.
cfg.MODEL.WEIGHTS = "https://dl.fbaipublicfiles.com/detectron2/COCO-InstanceSegmentation/mask_rcnn_R_101_FPN_3x/138205316/model_final_a3ec72.pkl"
cfg.DATASETS.TRAIN = ("zircon_train",) #load training dataset
cfg.DATASETS.TEST = ("zircon_val",) # load validation dataset
cfg.DATALOADER.NUM_WORKERS = 2
cfg.SOLVER.IMS_PER_BATCH = 2 #2 ims per batch seems to be good for model generalization
cfg.SOLVER.BASE_LR = 0.00025 # low but reasonable learning rate given pre-training; \
# by default initializes with a 1000 iteration warmup
cfg.SOLVER.MAX_ITER = 2000 #train for 2000 iterations before 1st save
cfg.SOLVER.GAMMA = 0.5
#decay learning rate by factor of GAMMA every 1000 iterations after 2000 iterations \
# and until 10000 iterations This works well for current version of training \
# dataset but should be modified (probably a longer interval) if dataset is ever\
# extended.
cfg.SOLVER.STEPS = (1999, 2999, 3999, 4999, 5999, 6999, 7999, 8999, 9999)
cfg.MODEL.ROI_HEADS.BATCH_SIZE_PER_IMAGE = 512 # use default ROI heads batch size
cfg.MODEL.ROI_HEADS.NUM_CLASSES = 1 # only class here is zircon
cfg.MODEL.RPN.NMS_THRESH = 0.1 #sets NMS threshold lower than default; should(?) eliminate overlapping regions
cfg.TEST.EVAL_PERIOD = 200 # validation eval every 200 iterations
os.makedirs(cfg.OUTPUT_DIR, exist_ok=True)
trainer = ZirconTrainer(cfg) #our zircon trainer, w/ built-in augs and val loss eval
trainer.resume_or_load(resume=False)
trainer.train() #start training
# stop training and save for the 1st time after 2000 iterations
save_outputs_to_drive(model_save_name, 2000)
# Saves, cold restarts training from saved model weights every 1000 iterations \
# until final iteration. This should probably be done via hooks without stopping \
# training but *seems* to produce faster decrease in validation loss.
for each_iters in [iter*1000 for iter in list(range(3,
int(final_iteration/1000) + 1,
1))]:
#reload model with last iteration model weights
resume_model_path = os.path.join(cfg.OUTPUT_DIR, "model_final.pth")
cfg.MODEL.WEIGHTS = resume_model_path
cfg.SOLVER.MAX_ITER = each_iters #increase max iterations
trainer = ZirconTrainer(cfg)
trainer.resume_or_load(resume=True)
trainer.train() #restart training
#save again
save_outputs_to_drive(model_save_name, each_iters)
# open tensorboard training metrics curves (metrics.json):
%load_ext tensorboard
%tensorboard --logdir output
```
## Inference & evaluation with final trained model
Initialize model from saved weights:
```
cfg.MODEL.WEIGHTS = os.path.join(cfg.OUTPUT_DIR, "model_final.pth") # final model; modify path to other non-final model to view their segmentations
cfg.MODEL.ROI_HEADS.SCORE_THRESH_TEST = 0.5 # set a custom testing threshold
cfg.MODEL.RPN.NMS_THRESH = 0.1
predictor = DefaultPredictor(cfg)
```
View model segmentations for random sample of images from zircon validation dataset:
```
from detectron2.utils.visualizer import ColorMode
dataset_dicts = get_zircon_dicts(os.path.join(dataset_dir, 'val'))
for d in random.sample(dataset_dicts, 5):
im = cv2.imread(d["file_name"])
outputs = predictor(im) # format is documented at https://detectron2.readthedocs.io/tutorials/models.html#model-output-format
v = Visualizer(im[:, :, ::-1],
metadata=zircon_metadata,
scale=1.5,
instance_mode=ColorMode.IMAGE_BW # remove the colors of unsegmented pixels. This option is only available for segmentation models
)
out = v.draw_instance_predictions(outputs["instances"].to("cpu"))
cv2_imshow(out.get_image()[:, :, ::-1])
```
Validation eval with COCO API metric:
```
from detectron2.evaluation import COCOEvaluator, inference_on_dataset
from detectron2.data import build_detection_test_loader
evaluator = COCOEvaluator("zircon_val", ("bbox", "segm"), False, output_dir="./output/")
val_loader = build_detection_test_loader(cfg, "zircon_val")
print(inference_on_dataset(trainer.model, val_loader, evaluator))
```
## Final notes:
To use newly-trained models in colab_zirc_dims:
#### Option A:
Modify the cell that initializes model(s) in colab_zirc_dims processing notebooks:
```
cfg.merge_from_file(model_zoo.get_config_file(DETECTRON2 BASE CONFIG FILE LINK FOR YOUR MODEL HERE))
cfg.MODEL.RESNETS.DEPTH = RESNET DEPTH FOR YOUR MODEL (E.G., 101) HERE
cfg.MODEL.WEIGHTS = PATH TO YOUR MODEL IN YOUR GOOGLE DRIVE HERE
```
#### Option B (more complicated but potentially useful for many models):
The dynamic model selection tool in colab_zirc_dims is populated from a .json file model library dictionary, which is by default [the current version on the GitHub repo.](https://github.com/MCSitar/colab_zirc_dims/blob/main/czd_model_library.json) The 'url' key in the dict will work with either an AWS download link for the model or the path to model in your Google Drive.
To use a custom model library dictionary:
Modify a copy of the colab_zirc_dims [.json file model library dictionary](https://github.com/MCSitar/colab_zirc_dims/blob/main/czd_model_library.json) to include download link(s)/Drive path(s) and metadata (e.g., resnet depth and config file) for your model(s). Upload this .json file to your Google Drive and change the 'model_lib_loc' variable in a processing Notebook to the .json's path for dynamic download and loading of this and other models within the Notebook.
| github_jupyter |
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sb
%matplotlib inline
from sklearn.utils.multiclass import unique_labels
from sklearn.metrics import confusion_matrix
def plot_confusion_matrix(y_true, y_pred, classes,
normalize=False,
title=None,
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if not title:
if normalize:
title = 'Normalized confusion matrix'
else:
title = 'Confusion matrix, without normalization'
# Compute confusion matrix
cm = confusion_matrix(y_true, y_pred)
# Only use the labels that appear in the data
classes = classes[unique_labels(y_true, y_pred)]
if normalize:
cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
fig, ax = plt.subplots(figsize=(14,7))
im = ax.imshow(cm, interpolation='nearest', cmap=cmap)
ax.grid(False)
ax.figure.colorbar(im, ax=ax)
# We want to show all ticks...
ax.set(xticks=np.arange(cm.shape[1]),
yticks=np.arange(cm.shape[0]),
# ... and label them with the respective list entries
xticklabels=classes, yticklabels=classes,
title=title,
ylabel='True label',
xlabel='Predicted label')
# Rotate the tick labels and set their alignment.
plt.setp(ax.get_xticklabels(), rotation=45, ha="right",
rotation_mode="anchor")
# Loop over data dimensions and create text annotations.
fmt = '.2f' if normalize else 'd'
thresh = cm.max() / 2.
for i in range(cm.shape[0]):
for j in range(cm.shape[1]):
ax.text(j, i, format(cm[i, j], fmt),
ha="center", va="center",
color="white" if cm[i, j] > thresh else "black")
fig.tight_layout()
return ax
```
# Analysis
```
# Prepare data
demographic = pd.read_csv('../data/processed/demographic.csv')
severity = pd.read_csv('../data/processed/severity.csv', index_col=0)
features = demographic.columns
X = demographic.astype(np.float64)
y = (severity >= 4).sum(axis=1)
needs_to_label = {0:'no needs', 1:'low_needs', 2:'moderate needs', 3:'high needs', 4:'very high needs'}
labels = ["no needs", "low needs", "moderate needs", "high needs", "very high needs"]
severity_to_needs = {0:0, 1:1, 2:1, 3:2, 4:2, 5:3, 6:3, 7:4, 8:4}
y = np.array([severity_to_needs[i] for i in y])
# Color vector, for illustration purposes
colors = {0:'b', 1:'r', 2:'g', 3:'c', 4:'y'}
y_c = np.array([colors[i] for i in y])
```
## Understanding the features
```
from yellowbrick.features import Rank2D
from yellowbrick.features.manifold import Manifold
from yellowbrick.features.pca import PCADecomposition
from yellowbrick.style import set_palette
set_palette('flatui')
```
### Feature covariance plot
```
visualizer = Rank2D(algorithm='covariance')
visualizer.fit(X, y)
visualizer.transform(X)
visualizer.poof()
```
### Principal Component Projection
```
visualizer = PCADecomposition(scale=True, color = y_c, proj_dim=3)
visualizer.fit_transform(X, y)
visualizer.poof()
```
### Manifold projections
```
visualizer = Manifold(manifold='tsne', target='discrete')
visualizer.fit_transform(X, y)
visualizer.poof()
visualizer = Manifold(manifold='modified', target='discrete')
visualizer.fit_transform(X, y)
visualizer.poof()
```
No apparent structure from the PCA and Manifold projections.
### Class Balance
```
categories, counts = np.unique(y, return_counts=True)
fig, ax = plt.subplots(figsize=(9, 7))
sb.set(style="whitegrid")
sb.barplot(labels, counts, ax=ax, tick_label=labels)
ax.set(xlabel='Need Categories',
ylabel='Number of HHs');
```
Heavy class imbalances. Use appropriate scoring metrics/measures.
### Learning and Validation
```
from sklearn.model_selection import StratifiedKFold
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import RidgeClassifier
from yellowbrick.model_selection import LearningCurve
cv = StratifiedKFold(10)
sizes = np.linspace(0.1, 1., 20)
visualizer = LearningCurve(RidgeClassifier(), cv=cv, train_sizes=sizes,
scoring='balanced_accuracy', n_jobs=-1)
visualizer.fit(X,y)
visualizer.poof()
visualizer = LearningCurve(GaussianNB(), cv=cv, train_sizes=sizes,
scoring='balanced_accuracy', n_jobs=-1)
visualizer.fit(X,y)
visualizer.poof()
```
### Classification
```
from sklearn.linear_model import RidgeClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import ExtraTreesClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.ensemble import VotingClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import train_test_split
from sklearn.utils.class_weight import compute_class_weight
from imblearn.metrics import classification_report_imbalanced
from sklearn.metrics import balanced_accuracy_score
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=42, stratify=y)
cv_ = StratifiedKFold(5)
class_weights = compute_class_weight(class_weight='balanced', classes= np.unique(y), y=y)
clf = RidgeClassifier()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('Balanced accuracy: {:.2f}'.format(balanced_accuracy_score(y_test,y_pred)))
print('Classification report: ')
print(classification_report_imbalanced(y_test, y_pred, target_names=labels))
plot_confusion_matrix(y_test, y_pred, classes=np.unique(y), normalize=True)
clf = KNeighborsClassifier()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('Balanced accuracy: {:.2f}'.format(balanced_accuracy_score(y_test,y_pred)))
print('Classification report: ')
print(classification_report_imbalanced(y_test, y_pred, target_names=labels))
plot_confusion_matrix(y_test, y_pred, classes=np.unique(y), normalize=True)
clf = GaussianNB()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('Balanced accuracy: {:.2f}'.format(balanced_accuracy_score(y_test,y_pred)))
print('Classification report: ')
print(classification_report_imbalanced(y_test, y_pred, target_names=labels))
plot_confusion_matrix(y_test, y_pred, classes=np.unique(y), normalize=True)
clf = ExtraTreesClassifier()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('Balanced accuracy: {:.2f}'.format(balanced_accuracy_score(y_test,y_pred)))
print('Classification report: ')
print(classification_report_imbalanced(y_test, y_pred, target_names=labels))
plot_confusion_matrix(y_test, y_pred, classes=np.unique(y), normalize=True)
clf = GradientBoostingClassifier()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
print('Balanced accuracy: {:.2f}'.format(balanced_accuracy_score(y_test,y_pred)))
print('Classification report: ')
print(classification_report_imbalanced(y_test, y_pred, target_names=labels))
plot_confusion_matrix(y_test, y_pred, classes=np.unique(y), normalize=True)
```
## Voting Classifier
### Hard Voting
```
clf1 = KNeighborsClassifier(weights='distance')
clf2 = GaussianNB()
clf3 = ExtraTreesClassifier(class_weight='balanced_subsample')
clf4 = GradientBoostingClassifier()
vote = VotingClassifier(estimators=[('knn', clf1), ('gnb', clf2), ('ext', clf3), ('gb', clf4)], voting='hard')
params = {'knn__n_neighbors': [2,3,4], 'gb__n_estimators':[50,100,200],
'gb__max_depth':[3,5,7], 'ext__n_estimators': [50,100,200]}
scoring_fns = ['f1_weighted', 'balanced_accuracy']
grid = GridSearchCV(estimator=vote, param_grid=params, cv=cv_,
verbose=2, n_jobs=-1, scoring=scoring_fns, refit='balanced_accuracy')
grid.fit(X_train, y_train)
y_pred = grid.predict(X_test)
print('Balanced accuracy: {:.2f}'.format(balanced_accuracy_score(y_test,y_pred)))
print('Classification report: ')
print(classification_report_imbalanced(y_test, y_pred, target_names=labels))
plot_confusion_matrix(y_test, y_pred, classes=np.unique(y), normalize=True)
clf1 = KNeighborsClassifier(weights='distance')
clf2 = GaussianNB()
clf3 = ExtraTreesClassifier(class_weight='balanced_subsample')
clf4 = GradientBoostingClassifier()
vote = VotingClassifier(estimators=[('knn', clf1), ('gnb', clf2), ('ext', clf3), ('gb', clf4)], voting='soft')
params = {'knn__n_neighbors': [2,3,4], 'gb__n_estimators':[50,100,200],
'gb__max_depth':[3,5,7], 'ext__n_estimators': [50,100,200]}
scoring_fns = ['f1_weighted', 'balanced_accuracy']
grid_soft = GridSearchCV(estimator=vote, param_grid=params, cv=cv_,
verbose=2, n_jobs=-1, scoring=scoring_fns, refit='balanced_accuracy')
grid_soft.fit(X_train, y_train)
y_pred = grid_soft.predict(X_test)
print('Balanced accuracy: {:.2f}'.format(balanced_accuracy_score(y_test,y_pred)))
print('Classification report: ')
print(classification_report_imbalanced(y_test, y_pred, target_names=labels))
plot_confusion_matrix(y_test, y_pred, classes=np.unique(y), normalize=True)
```
| github_jupyter |
## Import packages
```
import warnings
warnings.filterwarnings("ignore")
import pandas as pd
# general packages
import numpy as np
import matplotlib.pyplot as plt
import os
import seaborn as sns
# sklearn models
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
# mne
import mne
import pickle
from mne.datasets import sample
from mne.decoding import (SlidingEstimator, GeneralizingEstimator,
cross_val_multiscore, LinearModel, get_coef)
```
## sklearn models
```
from sklearn.model_selection import train_test_split
from sklearn import linear_model
from sklearn.metrics import confusion_matrix
from sklearn.svm import SVC, LinearSVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import Perceptron
from sklearn.linear_model import SGDClassifier
from sklearn.tree import DecisionTreeClassifier
```
## Load preprocessed data
```
with open(os.path.join('data','Xdict.pickle'),'rb') as handle1:
Xdict = pickle.load(handle1)
with open(os.path.join('data','ydict.pickle'),'rb') as handle2:
ydict = pickle.load(handle2)
subjects = list(set(Xdict.keys()))
```
# FEATURE ENGINEERING
### Need to first make a master dataframe for the 5,6 numbers with corresponding result for all subjects compiled
```
s01 = ydict[1]
df1 = pd.DataFrame(s01, columns=['Result'])
df1['Subject'] = 1
df1['Time Series'] = [series[:-52] for series in Xdict[1].tolist()]
df1['Psd'] = [series[950:] for series in Xdict[1].tolist()]
df1
s02 = ydict[2]
df2 = pd.DataFrame(s02, columns=['Result'])
df2['Subject'] = 2
df2['Time Series'] = [series[:-52] for series in Xdict[2].tolist()]
df2['Psd'] = [series[950:] for series in Xdict[2].tolist()]
df2
s03 = ydict[3]
df3 = pd.DataFrame(s03, columns=['Result'])
df3['Subject'] = 3
df3['Time Series'] = [series[:-52] for series in Xdict[3].tolist()]
df3['Psd'] = [series[950:] for series in Xdict[3].tolist()]
df3
s04 = ydict[4]
df4 = pd.DataFrame(s04, columns=['Result'])
df4['Subject'] = 4
df4['Time Series'] = [series[:-52] for series in Xdict[4].tolist()]
df4['Psd'] = [series[950:] for series in Xdict[4].tolist()]
df4
s05 = ydict[5]
df5 = pd.DataFrame(s05, columns=['Result'])
df5['Subject'] = 5
df5['Time Series'] = [series[:-52] for series in Xdict[5].tolist()]
df5['Psd'] = [series[950:] for series in Xdict[5].tolist()]
df5
s06 = ydict[6]
df6 = pd.DataFrame(s06, columns=['Result'])
df6['Subject'] = 6
df6['Time Series'] = [series[:-52] for series in Xdict[6].tolist()]
df6['Psd'] = [series[950:] for series in Xdict[6].tolist()]
df6
s07 = ydict[7]
df7 = pd.DataFrame(s07, columns=['Result'])
df7['Subject'] = 7
df7['Time Series'] = [series[:-52] for series in Xdict[7].tolist()]
df7['Psd'] = [series[950:] for series in Xdict[7].tolist()]
df7
s08 = ydict[8]
df8 = pd.DataFrame(s08, columns=['Result'])
df8['Subject'] = 8
df8['Time Series'] = [series[:-52] for series in Xdict[8].tolist()]
df8['Psd'] = [series[950:] for series in Xdict[8].tolist()]
df8
s09 = ydict[9]
df9 = pd.DataFrame(s09, columns=['Result'])
df9['Subject'] = 9
df9['Time Series'] = [series[:-52] for series in Xdict[9].tolist()]
df9['Psd'] = [series[950:] for series in Xdict[9].tolist()]
df9
s10 = ydict[10]
df10 = pd.DataFrame(s10, columns=['Result'])
df10['Subject'] = 10
df10['Time Series'] = [series[:-52] for series in Xdict[10].tolist()]
df10['Psd'] = [series[950:] for series in Xdict[10].tolist()]
frames = [df1, df2, df3, df4, df5, df6, df7, df8, df9, df10]
resultframe = pd.concat(frames)
resultframe = resultframe.reset_index().drop('index', axis=1)
resultframe
```
Splitting the psd into 52 different columns so each value can be used as a feature:
```
resultframe[['psd'+str(i) for i in range(1,53)]] = pd.DataFrame(resultframe.Psd.values.tolist(), index= resultframe.index)
resultframe = resultframe.drop('Psd', axis=1)
resultframe.head()
```
### Assuming the merged table is formed correctly, we now have our outcomes ('Results') and their corresponding first 950 time points series data, and subject information. We no longer have information regarding which electrode collected the data (irrelevant since no biological correspondence), however, if needed, we can still filter by subject as we retain that data.
#### NOTE: This table is only for the 5,6 first number trials as it is in that scenario the patient has the ability to "Gamble".
#### NOTE: One of the disadvantages of compiling all patient data and not separating by subject is that we are ignoring behavioral characteristics (risk aversion and risk loving) and rather finding common trends in the time series data regardless of personal characteristics.
#### NEED TO CHECK: Are all electrode data included for each patient? Is the corresponding Result matched with respective time series? Currently, I will proceed relying on the dictionary Kata made and will assume the order and correspondence is proper.
## Dataset Characteristics/Confirming master dataframe created above:
```
countframe = resultframe.groupby("Subject").count().drop('Time Series', axis=1).drop(['psd'+str(i) for i in range(1,53)], axis=1)
countframe
plt.bar(countframe.index, countframe['Result'])
plt.xlabel('Subject')
plt.ylabel('Count')
plt.title('Number of Entries per subject')
plt.show();
```
#### Note: Number of Entries = Number of trials with first number as 5,6 * Number of electrodes for the subject
In preprocessing notebook, we determined the number of electrodes per subject to be as followed:
```
subject = [1,2,3,4,5,6,7,8,9,10]
electrodes = [5,6,59,5,61,7,11,10,19,16]
elecframe = pd.DataFrame(data={'Subject': subject, 'Num Electrode' : electrodes})
elecframe
```
In preprocessing notebook, we also determined the number of trials with 5 and 6 (in cleaned table, excluding all types of bad trials):
```
subject = [1,2,3,4,5,6,7,8,9,10]
num5 = [23, 24, 24, 12, 21, 22, 21, 24, 24, 16]
num6 = [20, 23, 24, 18, 21, 24, 22, 24, 24, 18]
trialframe = pd.DataFrame(data={'Subject': subject, 'Num 5': num5, 'Num 6': num6})
trialframe['Num Total Trials'] = trialframe['Num 5'] + trialframe['Num 6']
trialframe = trialframe.drop(['Num 5', 'Num 6'], axis=1)
trialframe
```
Merging the two tables together:
```
confframe = pd.concat([elecframe, trialframe.drop('Subject', axis=1)], axis=1)
confframe['Expected Entries'] = confframe['Num Electrode'] * confframe['Num Total Trials']
confframe
checkframe = pd.merge(confframe, countframe, how='inner', left_on='Subject', right_index=True)
checkframe
```
We now confirmed that our expected number of entries per subject matches the actual number of entries we obtained in the master dataframe created above. This indicates that the table above is likely created properly and it is safe to use it for further analysis.
Next, we need to understand the characteristics of our dataset, mainly to understand the probability of obtaining a correct prediction due to chance.
```
outframe = resultframe.groupby('Result').count().drop('Time Series', axis=1).drop(['psd'+str(i) for i in range(1,53)], axis=1).rename(index=str, columns={'Subject':'Count'})
outframe
```
We can observe that the distribution is not even between the two possible outcomes so we need to be careful when assessing the performance of our model. We will next calculate the prediction power of chance:
```
total = sum(outframe['Count'])
outframe['Probability'] = outframe['Count']/total
outframe
```
We can observe that the probability of getting a correct prediction due to purely chance is 56.988% (~57%) so we need to design a prediction model that performs better than this. We will now move on to feature engineering to create new features.
## Making new features:
We currently have 52 power spectral density (psd) features obtained from preprocessed file. Need to create new features from our time series data
```
resultframe.head()
resultframe['Max'] = [max(i) for i in resultframe['Time Series']]
resultframe['Min'] = [min(i) for i in resultframe['Time Series']]
resultframe['Std'] = [np.std(i) for i in resultframe['Time Series']]
resultframe['Mean'] = [np.mean(i) for i in resultframe['Time Series']]
resultframe['p2.5'] = [np.percentile(i, 2.5) for i in resultframe['Time Series']]
resultframe['p97.5'] = [np.percentile(i, 97.5) for i in resultframe['Time Series']]
resultframe.head()
```
Changing entries of "Result"
Safebet = 0, Gamble = 1:
```
resultframe['Result'] = resultframe['Result'].map({'Safebet': 0, 'Gamble': 1})
resultframe.head()
```
We should center all our data to 0.0 since we care about relative wave form and not baseline amplitude. The difference in baseline amplitude can be ascribed to hardware differences (electrode readings) and should not be considered in our predictive model. Thus, we need to adapt our features above by centering the values around 0.0. Hence, mean is dropped as a feature and a new feature "Interval" which is max-min is introduced.
Interval = Max - Min
Percentile 2.5 and Percentile 97.5 values were determined as features above. Now, a new feature is going to be introduced "Percentile Interval" which is the difference between the two values.
Percentile Interval = p97.5 - p2.5
```
resultframe['Max'] = resultframe['Max'] - resultframe['Mean']
resultframe['Min'] = resultframe['Min'] - resultframe['Mean']
resultframe['p2.5'] = resultframe['p2.5'] - resultframe['Mean']
resultframe['p97.5'] = resultframe['p97.5'] - resultframe['Mean']
resultframe['Mean'] = resultframe['Mean'] - resultframe['Mean']
resultframe['Interval'] = resultframe['Max'] - resultframe['Min']
resultframe['Percentile Interval'] = resultframe['p97.5'] - resultframe['p2.5']
#resultframe = resultframe[['Subject', 'Time Series', 'Max', 'Min', 'Std', 'Interval', 'p2.5', 'p97.5', 'Percentile Interval', 'Result']]
resultframe
```
Since all the features currently in place are statistics that do not respect the temporal nature of our data (time-series data), we need to introduce features that also respect the morphology of the waves in the data. An example feature is number of peaks.
Number of peaks = number of data points i where i > i-1 and i > i+1 and will not include the i=0 and i=949 entries
```
peaks = []
for series in resultframe['Time Series']:
no_peaks = 0
indices = range(2,949)
for index in indices:
if series[index] > series[index-1] and series[index] > series[index+1]:
no_peaks += 1
peaks.append(no_peaks)
len(peaks)
resultframe['Num Peaks'] = peaks
resultframe.head()
#resultframe = resultframe[['Subject', 'Time Series', 'Max', 'Min', 'Interval', 'Std', 'p2.5', 'p97.5', 'Percentile Interval', 'Num Peaks', 'Result']]
#resultframe.head()
```
#### Categorizing all our data
```
resultframe['Num Peaks Cat'] = pd.cut(resultframe['Num Peaks'], 4,labels=[1,2,3,4])
#resultframe = resultframe[['Subject', 'Time Series', 'Max', 'Min', 'Interval', 'Std', 'p2.5', 'p97.5', 'Percentile Interval', 'Num Peaks', 'Num Peaks Cat', 'Result']]
resultframe.head()
resultframe['p2.5 Cat'] = pd.qcut(resultframe['p2.5'], 3,labels=[1,2,3])
resultframe['p97.5 Cat'] = pd.qcut(resultframe['p97.5'], 3,labels=[1,2,3])
resultframe['Std Cat'] = pd.qcut(resultframe['Std'], 3,labels=[1,2,3])
resultframe['Percentile Interval Cat'] = pd.qcut(resultframe['Percentile Interval'], 3,labels=[1,2,3])
#resultframe = resultframe[['Subject', 'Time Series', 'Max', 'Min', 'Interval', 'Std', 'p2.5', 'p97.5', 'Percentile Interval', 'Num Peaks', 'Num Peaks Cat', 'p2.5 Cat', 'p97.5 Cat', 'Std Cat', 'Percentile Interval Cat', 'Result']]
resultframe
resultframe['Num Peaks Cat'] = resultframe['Num Peaks Cat'].astype(int)
resultframe['p2.5 Cat'] = resultframe['p2.5 Cat'].astype(int)
resultframe['p97.5 Cat'] = resultframe['p97.5 Cat'].astype(int)
resultframe['Std Cat'] = resultframe['Std Cat'].astype(int)
resultframe['Percentile Interval Cat'] = resultframe['Percentile Interval Cat'].astype(int)
resultframe.head()
```
### Checking our X and y matrices (selecting only features we want to pass into the model)
```
resultframe.loc[:,["Subject", "Result"]][resultframe['Subject']==1].drop('Subject', axis=1).head()
#resultframe.iloc[:,[1,3]][resultframe['Subject']==1].drop("Subject", axis=1).head()
resultframe.drop(["Subject", "Time Series", "Result"], axis=1)
```
# Modeling
## Logistic Regression
### Initialize dataframe to track model performance per subject
```
performance_logistic = pd.DataFrame(index = Xdict.keys(), # subject
columns=['naive_train_accuracy',
'naive_test_accuracy',
'model_train_accuracy',
'model_test_accuracy'])
performance_logistic
```
### Train model
```
coefficients = dict()
# initialize dataframes to log predicted choice and true choice for each trial
predictions_logistic_train_master = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
predictions_logistic_test_master = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
LogisticRegressionModel = linear_model.LogisticRegression()
# two subclasses to start
for subject in subjects:
print(subject)
#X = resultframe.iloc[:,[0,5,8,10,11,12]][resultframe['Subject']==subject].drop("Subject", axis=1)
#y = resultframe.iloc[:,[0,-1]][resultframe['Subject']==subject].drop('Subject', axis=1)
X = resultframe.drop(["Time Series", "Result"], axis=1)[resultframe['Subject']==subject].drop("Subject", axis=1)
y = resultframe.loc[:,["Subject", "Result"]][resultframe['Subject']==subject].drop('Subject', axis=1)
# train-test split
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, test_size=0.2, random_state=100)
# get naive performance (guessing most frequent category, the max of guessing one vs the other)
performance_logistic.loc[subject,'naive_train_accuracy'] = max(float(np.mean(ytrain=='Gamble')),float(np.mean(ytrain=='Safebet')))
performance_logistic.loc[subject, 'naive_test_accuracy'] = max(float(np.mean(ytrain=='Gamble')),float(np.mean(ytrain=='Safebet')))
# make df to track predicted vs real choice for each subject
predictions_logistic_train = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
predictions_logistic_test = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
predictions_logistic_train['true_choice'] = ytrain['Result']
predictions_logistic_test['true_choice'] = ytest['Result']
# logistic regression
LogisticRegressionModel.fit(Xtrain, ytrain)
# store coefficients
coefficients[subject] = LogisticRegressionModel.coef_[0]
performance_logistic.loc[subject,'model_train_accuracy'] = LogisticRegressionModel.score(Xtrain,ytrain)
performance_logistic.loc[subject,'model_test_accuracy'] = LogisticRegressionModel.score(Xtest,ytest)
# complete the guesses for each person
predictions_logistic_train['predicted_choice'] = LogisticRegressionModel.predict(Xtrain)
predictions_logistic_test['predicted_choice'] = LogisticRegressionModel.predict(Xtest)
# concatenate dfs
predictions_logistic_train_master = pd.concat([predictions_logistic_train_master, predictions_logistic_train])
predictions_logistic_test_master = pd.concat([predictions_logistic_test_master, predictions_logistic_test])
%matplotlib inline
performance_logistic
train_accuracy_total = np.mean(predictions_logistic_train_master['true_choice'] == predictions_logistic_train_master['predicted_choice'])
test_accuracy_total = np.mean(predictions_logistic_test_master['true_choice'] == predictions_logistic_test_master['predicted_choice'])
train_accuracy_total, test_accuracy_total
```
### FEATURE SELECTION
since not much improvement has been seen in iter5, I will attempt to selectivly include features from our current feature set that demonstrates strong predictive powers. I will first see any collinear features
```
train, test = train_test_split(resultframe, test_size=0.2, random_state=100)
train_df = train.iloc[:, 2:]
train_df.head()
train_df.corr()
colormap = plt.cm.viridis
plt.figure(figsize=(12,12))
plt.title('Pearson Correlation of Features', y=1.05, size=15)
sns.heatmap(train_df.corr().round(2)\
,linewidths=0.1,vmax=1.0, square=True, cmap=colormap, \
linecolor='white', annot=True);
```
As seen in the chart above, the correlation between different features is generally pretty high. Thus, we need to be more selective in choosing features for this model as uncorrelated features are generally more powerful predictors
Will try these features: num peaks cat, percentile interval, std, p97.5 cat, p2.5 cat
## Random Forest
### Initialize dataframe to track model performance per subject
```
performance_forest = pd.DataFrame(index = Xdict.keys(), # subject
columns=['naive_train_accuracy',
'naive_test_accuracy',
'model_train_accuracy',
'model_test_accuracy'])
```
### Initialize dataframes to log predicted choice and true choice for each trial
```
feature_importances = dict()
predictions_forest_train_master = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
predictions_forest_test_master = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
random_forest = RandomForestClassifier()
# two subclasses to start
for subject in subjects:
print(subject)
X = resultframe.iloc[:,[0,4,6,7,8]][resultframe['Subject']==subject].drop("Subject", axis=1)
y = resultframe.iloc[:,[0,-1]][resultframe['Subject']==subject].drop('Subject', axis=1)
# train-test split
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, test_size=0.2, random_state=100)
# get naive performance (guessing most frequent category, the max of guessing one vs the other)
performance_forest.loc[subject,'naive_train_accuracy'] = max(float(np.mean(ytrain=='Gamble')),float(np.mean(ytrain=='Safebet')))
performance_forest.loc[subject,'naive_test_accuracy'] = max(float(np.mean(ytrain=='Gamble')),float(np.mean(ytrain=='Safebet')))
# make df to track predicted vs real choice for each subject
predictions_forest_train = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
predictions_forest_test = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
predictions_forest_train['true_choice'] = ytrain['Result']
predictions_forest_test['true_choice'] = ytest['Result']
# model
random_forest.fit(Xtrain, ytrain)
performance_forest.loc[subject,'model_train_accuracy'] = random_forest.score(Xtrain,ytrain)
performance_forest.loc[subject,'model_test_accuracy'] = random_forest.score(Xtest,ytest)
# store feature importances
feature_importances[subject] = random_forest.feature_importances_
# complete the guesses for each person
predictions_forest_train['predicted_choice'] = random_forest.predict(Xtrain)
predictions_forest_test['predicted_choice'] = random_forest.predict(Xtest)
# concatenate dfs
predictions_forest_train_master = pd.concat([predictions_forest_train_master, predictions_forest_train])
predictions_forest_test_master = pd.concat([predictions_forest_test_master, predictions_forest_test])
performance_forest
train_accuracy_total = np.mean(predictions_forest_train_master['true_choice'] == predictions_forest_train_master['predicted_choice'])
test_accuracy_total = np.mean(predictions_forest_test_master['true_choice'] == predictions_forest_test_master['predicted_choice'])
train_accuracy_total, test_accuracy_total
```
Overfits a lot
## logistic regression modified with StandardScaler(), i.e., z-scoring the data before fitting model
### initialize dataframe to track model performance per subject
```
performance_logistic = pd.DataFrame(index = Xdict.keys(), # subject
columns=['naive_train_accuracy',
'naive_test_accuracy',
'model_train_accuracy',
'model_test_accuracy'])
```
### initialize dataframes to log predicted choice and true choice for each trial
```
predictions_logistic_train_master = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
predictions_logistic_test_master = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
LogisticRegressionModel = linear_model.LogisticRegression()
from sklearn.feature_selection import SelectKBest, f_classif # use f_regression for afresh feature selection
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
# pipe = make_pipeline(SelectKBest(k=50), StandardScaler(), linear_model.LogisticRegressionCV())
pipe = make_pipeline(StandardScaler(), linear_model.LogisticRegressionCV())
LogisticRegressionModel = pipe
# two subclasses to start
for subject in subjects:
print(subject)
X = resultframe.iloc[:,[0,4,6,7,8]][resultframe['Subject']==subject].drop("Subject", axis=1)
y = resultframe.iloc[:,[0,-1]][resultframe['Subject']==subject].drop('Subject', axis=1)
# train-test split
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, test_size=0.2, random_state=100)
# get naive performance (guessing most frequent category, the max of guessing one vs the other)
performance_logistic.loc[subject,'naive_train_accuracy'] = max(float(np.mean(ytrain=='Gamble')),float(np.mean(ytrain=='Safebet')))
performance_logistic.loc[subject,'naive_test_accuracy'] = max(float(np.mean(ytrain=='Gamble')),float(np.mean(ytrain=='Safebet')))
# make df to track predicted vs real choice for each subject
predictions_logistic_train = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
predictions_logistic_test = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
predictions_logistic_train['true_choice'] = ytrain['Result']
predictions_logistic_test['true_choice'] = ytest['Result']
# logistic regression
LogisticRegressionModel.fit(Xtrain, ytrain)
performance_logistic.loc[subject,'model_train_accuracy'] = LogisticRegressionModel.score(Xtrain,ytrain)
performance_logistic.loc[subject,'model_test_accuracy'] = LogisticRegressionModel.score(Xtest,ytest)
# complete the guesses for each person
predictions_logistic_train['predicted_choice'] = LogisticRegressionModel.predict(Xtrain)
predictions_logistic_test['predicted_choice'] = LogisticRegressionModel.predict(Xtest)
# concatenate dfs
predictions_logistic_train_master = pd.concat([predictions_logistic_train_master, predictions_logistic_train])
predictions_logistic_test_master = pd.concat([predictions_logistic_test_master, predictions_logistic_test])
performance_logistic
train_accuracy_total = np.mean(predictions_logistic_train_master['true_choice'] == predictions_logistic_train_master['predicted_choice'])
test_accuracy_total = np.mean(predictions_logistic_test_master['true_choice'] == predictions_logistic_test_master['predicted_choice'])
train_accuracy_total, test_accuracy_total
```
## random forest with StandardScaler()
### initialize dataframe to track model performance per subject
```
performance_forest = pd.DataFrame(index = Xdict.keys(), # subject
columns=['naive_train_accuracy',
'naive_test_accuracy',
'model_train_accuracy',
'model_test_accuracy'])
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
```
### initialize dataframes to log predicted choice and true choice for each trial
```
feature_importances = dict()
predictions_forest_train_master = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
predictions_forest_test_master = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
random_forest = RandomForestClassifier()
# two subclasses to start
for subject in subjects:
print(subject)
X = resultframe.iloc[:,[0,4,6,7,8]][resultframe['Subject']==subject].drop("Subject", axis=1)
y = resultframe.iloc[:,[0,-1]][resultframe['Subject']==subject].drop('Subject', axis=1)
# standardize data here
scaler.fit(X)
X = scaler.transform(X)
# train-test split
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, test_size=0.2, random_state=100)
# get naive performance (guessing most frequent category, the max of guessing one vs the other)
performance_forest.loc[subject,'naive_train_accuracy'] = max(float(np.mean(ytrain=='Gamble')),float(np.mean(ytrain=='Safebet')))
performance_forest.loc[subject,'naive_test_accuracy'] = max(float(np.mean(ytrain=='Gamble')),float(np.mean(ytrain=='Safebet')))
# make df to track predicted vs real choice for each subject
predictions_forest_train = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
predictions_forest_test = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
predictions_forest_train['true_choice'] = ytrain['Result']
predictions_forest_test['true_choice'] = ytest['Result']
# model
random_forest.fit(Xtrain, ytrain)
performance_forest.loc[subject,'model_train_accuracy'] = random_forest.score(Xtrain,ytrain)
performance_forest.loc[subject,'model_test_accuracy'] = random_forest.score(Xtest,ytest)
# store feature importances
feature_importances[subject] = random_forest.feature_importances_
# complete the guesses for each person
predictions_forest_train['predicted_choice'] = random_forest.predict(Xtrain)
predictions_forest_test['predicted_choice'] = random_forest.predict(Xtest)
# concatenate dfs
predictions_forest_train_master = pd.concat([predictions_forest_train_master, predictions_forest_train])
predictions_forest_test_master = pd.concat([predictions_forest_test_master, predictions_forest_test])
performance_forest
train_accuracy_total = np.mean(predictions_forest_train_master['true_choice'] == predictions_forest_train_master['predicted_choice'])
test_accuracy_total = np.mean(predictions_forest_test_master['true_choice'] == predictions_forest_test_master['predicted_choice'])
train_accuracy_total, test_accuracy_total
```
## logistic regression with StandardScaler() *and* selecting K best features (reducing the number of features, should reduce overfitting)
### initialize dataframe to track model performance per subject
```
performance_logistic = pd.DataFrame(index = Xdict.keys(), # subject
columns=['naive_train_accuracy',
'naive_test_accuracy',
'model_train_accuracy',
'model_test_accuracy'])
```
### initialize dataframes to log predicted choice and true choice for each trial
```
predictions_logistic_train_master = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
predictions_logistic_test_master = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
LogisticRegressionModel = linear_model.LogisticRegression()
from sklearn.feature_selection import SelectKBest, f_classif # use f_regression for afresh feature selection
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import make_pipeline
```
#### try different numbers of num_k
```
num_k = [1,2,3,4] # max number of features is 4
for k in num_k:
pipe = make_pipeline(SelectKBest(k=k), StandardScaler(), linear_model.LogisticRegressionCV())
LogisticRegressionModel = pipe
# two subclasses to start
for subject in subjects:
print(subject)
X = resultframe.iloc[:,[0,4,6,7,8]][resultframe['Subject']==subject].drop("Subject", axis=1)
y = resultframe.iloc[:,[0,-1]][resultframe['Subject']==subject].drop('Subject', axis=1)
# train-test split
Xtrain, Xtest, ytrain, ytest = train_test_split(X, y, test_size=0.2, random_state=100)
# get naive performance (guessing most frequent category, the max of guessing one vs the other)
performance_logistic.loc[subject,'naive_train_accuracy'] = max(float(np.mean(ytrain=='Gamble')),float(np.mean(ytrain=='Safebet')))
performance_logistic.loc[subject,'naive_test_accuracy'] = max(float(np.mean(ytrain=='Gamble')),float(np.mean(ytrain=='Safebet')))
# make df to track predicted vs real choice for each subject
predictions_logistic_train = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
predictions_logistic_test = pd.DataFrame(columns=['predicted_choice',
'true_choice'])
predictions_logistic_train['true_choice'] = ytrain['Result']
predictions_logistic_test['true_choice'] = ytest['Result']
# logistic regression
LogisticRegressionModel.fit(Xtrain, ytrain)
performance_logistic.loc[subject,'model_train_accuracy'] = LogisticRegressionModel.score(Xtrain,ytrain)
performance_logistic.loc[subject,'model_test_accuracy'] = LogisticRegressionModel.score(Xtest,ytest)
# complete the guesses for each person
predictions_logistic_train['predicted_choice'] = LogisticRegressionModel.predict(Xtrain)
predictions_logistic_test['predicted_choice'] = LogisticRegressionModel.predict(Xtest)
# concatenate dfs
predictions_logistic_train_master = pd.concat([predictions_logistic_train_master, predictions_logistic_train])
predictions_logistic_test_master = pd.concat([predictions_logistic_test_master, predictions_logistic_test])
train_accuracy_total = np.mean(predictions_logistic_train_master['true_choice'] == predictions_logistic_train_master['predicted_choice'])
test_accuracy_total = np.mean(predictions_logistic_test_master['true_choice'] == predictions_logistic_test_master['predicted_choice'])
print(k, train_accuracy_total, test_accuracy_total)
```
### Trying other models
```
X = resultframe.iloc[:,[4,6,7,8]]
y = resultframe.iloc[:,-1]
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=100)
print ('Number of samples in training data:',len(x_train))
print ('Number of samples in test data:',len(x_test))
perceptron = Perceptron(max_iter=100)
perceptron.fit(x_train, y_train)
perceptron_train_acc = perceptron.score(x_train, y_train)
perceptron_test_acc = perceptron.score(x_test, y_test)
print ('perceptron training acuracy= ',perceptron_train_acc)
print('perceptron test accuracy= ',perceptron_test_acc)
adaboost = AdaBoostClassifier()
adaboost.fit(x_train, y_train)
adaboost_train_acc = adaboost.score(x_train, y_train)
adaboost_test_acc = adaboost.score(x_test, y_test)
print ('adaboost training acuracy= ',adaboost_train_acc)
print('adaboost test accuracy= ',adaboost_test_acc)
random_forest = RandomForestClassifier()
random_forest.fit(x_train, y_train)
random_forest_train_acc = random_forest.score(x_train, y_train)
random_forest_test_acc = random_forest.score(x_test, y_test)
print('random_forest training acuracy= ',random_forest_train_acc)
print('random_forest test accuracy= ',random_forest_test_acc)
```
#### ALL THREE MODELS WORSE THAN CHANCE!
| github_jupyter |
<table width=60% >
<tr style="background-color: white;">
<td><img src='https://www.creativedestructionlab.com/wp-content/uploads/2018/05/xanadu.jpg'></td>></td>
</tr>
</table>
---
<img src='https://raw.githubusercontent.com/XanaduAI/strawberryfields/master/doc/_static/strawberry-fields-text.png'>
---
<br>
<center> <h1> Gaussian boson sampling tutorial </h1></center>
To get a feel for how Strawberry Fields works, let's try coding a quantum program, Gaussian boson sampling.
## Background information: Gaussian states
---
A Gaussian state is one that can be described by a [Gaussian function](https://en.wikipedia.org/wiki/Gaussian_function) in the phase space. For example, for a single mode Gaussian state, squeezed in the $x$ quadrature by squeezing operator $S(r)$, could be described by the following [Wigner quasiprobability distribution](Wigner quasiprobability distribution):
$$W(x,p) = \frac{2}{\pi}e^{-2\sigma^2(x-\bar{x})^2 - 2(p-\bar{p})^2/\sigma^2}$$
where $\sigma$ represents the **squeezing**, and $\bar{x}$ and $\bar{p}$ are the mean **displacement**, respectively. For multimode states containing $N$ modes, this can be generalised; Gaussian states are uniquely defined by a [multivariate Gaussian function](https://en.wikipedia.org/wiki/Multivariate_normal_distribution), defined in terms of the **vector of means** ${\mu}$ and a **covariance matrix** $\sigma$.
### The position and momentum basis
For example, consider a single mode in the position and momentum quadrature basis (the default for Strawberry Fields). Assuming a Gaussian state with displacement $\alpha = \bar{x}+i\bar{p}$ and squeezing $\xi = r e^{i\phi}$ in the phase space, it has a vector of means and a covariance matrix given by:
$$ \mu = (\bar{x},\bar{p}),~~~~~~\sigma = SS\dagger=R(\phi/2)\begin{bmatrix}e^{-2r} & 0 \\0 & e^{2r} \\\end{bmatrix}R(\phi/2)^T$$
where $S$ is the squeezing operator, and $R(\phi)$ is the standard two-dimensional rotation matrix. For multiple modes, in Strawberry Fields we use the convention
$$ \mu = (\bar{x}_1,\bar{x}_2,\dots,\bar{x}_N,\bar{p}_1,\bar{p}_2,\dots,\bar{p}_N)$$
and therefore, considering $\phi=0$ for convenience, the multimode covariance matrix is simply
$$\sigma = \text{diag}(e^{-2r_1},\dots,e^{-2r_N},e^{2r_1},\dots,e^{2r_N})\in\mathbb{C}^{2N\times 2N}$$
If a continuous-variable state *cannot* be represented in the above form (for example, a single photon Fock state or a cat state), then it is non-Gaussian.
### The annihilation and creation operator basis
If we are instead working in the creation and annihilation operator basis, we can use the transformation of the single mode squeezing operator
$$ S(\xi) \left[\begin{matrix}\hat{a}\\\hat{a}^\dagger\end{matrix}\right] = \left[\begin{matrix}\cosh(r)&-e^{i\phi}\sinh(r)\\-e^{-i\phi}\sinh(r)&\cosh(r)\end{matrix}\right] \left[\begin{matrix}\hat{a}\\\hat{a}^\dagger\end{matrix}\right]$$
resulting in
$$\sigma = SS^\dagger = \left[\begin{matrix}\cosh(2r)&-e^{i\phi}\sinh(2r)\\-e^{-i\phi}\sinh(2r)&\cosh(2r)\end{matrix}\right]$$
For multiple Gaussian states with non-zero squeezing, the covariance matrix in this basis simply generalises to
$$\sigma = \text{diag}(S_1S_1^\dagger,\dots,S_NS_N^\dagger)\in\mathbb{C}^{2N\times 2N}$$
## Introduction to Gaussian boson sampling
---
<div class="alert alert-info">
“If you need to wait exponential time for \[your single photon sources to emit simultaneously\], then there would seem to be no advantage over classical computation. This is the reason why so far, boson sampling has only been demonstrated with 3-4 photons. When faced with these problems, until recently, all we could do was shrug our shoulders.” - [Scott Aaronson](https://www.scottaaronson.com/blog/?p=1579)
</div>
While [boson sampling](https://en.wikipedia.org/wiki/Boson_sampling) allows the experimental implementation of a quantum sampling problem that it countably hard classically, one of the main issues it has in experimental setups is one of **scalability**, due to its dependence on an array of simultaneously emitting single photon sources.
Currently, most physical implementations of boson sampling make use of a process known as [Spontaneous Parametric Down-Conversion](http://en.wikipedia.org/wiki/Spontaneous_parametric_down-conversion) to generate the single photon source inputs. Unfortunately, this method is non-deterministic - as the number of modes in the apparatus increases, the average time required until every photon source emits a simultaneous photon increases *exponentially*.
In order to simulate a *deterministic* single photon source array, several variations on boson sampling have been proposed; the most well known being scattershot boson sampling ([Lund, 2014](https://link.aps.org/doi/10.1103/PhysRevLett.113.100502)). However, a recent boson sampling variation by [Hamilton et al.](https://link.aps.org/doi/10.1103/PhysRevLett.119.170501) negates the need for single photon Fock states altogether, by showing that **incident Gaussian states** - in this case, single mode squeezed states - can produce problems in the same computational complexity class as boson sampling. Even more significantly, this negates the scalability problem with single photon sources, as single mode squeezed states can be easily simultaneously generated experimentally.
Aside from changing the input states from single photon Fock states to Gaussian states, the Gaussian boson sampling scheme appears quite similar to that of boson sampling:
1. $N$ single mode squeezed states $\left|{\xi_i}\right\rangle$, with squeezing parameters $\xi_i=r_ie^{i\phi_i}$, enter an $N$ mode linear interferometer with unitary $U$.
<br>
2. The output of the interferometer is denoted $\left|{\psi'}\right\rangle$. Each output mode is then measured in the Fock basis, $\bigotimes_i n_i\left|{n_i}\middle\rangle\middle\langle{n_i}\right|$.
Without loss of generality, we can absorb the squeezing parameter $\phi$ into the interferometer, and set $\phi=0$ for convenience. The covariance matrix **in the creation and annihilation operator basis** at the output of the interferometer is then given by:
$$\sigma_{out} = \frac{1}{2} \left[ \begin{matrix}U&0\\0&U^*\end{matrix} \right]\sigma_{in} \left[ \begin{matrix}U^\dagger&0\\0&U^T\end{matrix} \right]$$
Using phase space methods, [Hamilton et al.](https://link.aps.org/doi/10.1103/PhysRevLett.119.170501) showed that the probability of measuring a Fock state is given by
$$\left|\left\langle{n_1,n_2,\dots,n_N}\middle|{\psi'}\right\rangle\right|^2 = \frac{\left|\text{Haf}[(U\bigoplus_i\tanh(r_i)U^T)]_{st}\right|^2}{n_1!n_2!\cdots n_N!\sqrt{|\sigma_{out}+I/2|}},$$
i.e. the sampled single photon probability distribution is proportional to the **Hafnian** of a submatrix of $U\bigoplus_i\tanh(r_i)U^T$, dependent upon the output covariance matrix.
<div class="alert alert-success" style="border: 0px; border-left: 3px solid #119a68; color: black; background-color: #daf0e9">
<p style="color: #119a68;">**The Hafnian**</p>
The Hafnian of a matrix is defined by
<br><br>
$$\text{Haf}(A) = \frac{1}{n!2^n}\sum_{\sigma=S_{2N}}\prod_{i=1}^N A_{\sigma(2i-1)\sigma(2i)}$$
<br>
$S_{2N}$ is the set of all permutations of $2N$ elements. In graph theory, the Hafnian calculates the number of perfect <a href="https://en.wikipedia.org/wiki/Matching_(graph_theory)">matchings</a> in an **arbitrary graph** with adjacency matrix $A$.
<br>
Compare this to the permanent, which calculates the number of perfect matchings on a *bipartite* graph - the Hafnian turns out to be a generalisation of the permanent, with the relationship
$$\begin{align}
\text{Per(A)} = \text{Haf}\left(\left[\begin{matrix}
0&A\\
A^T&0
\end{matrix}\right]\right)
\end{align}$$
As any algorithm that could calculate (or even approximate) the Hafnian could also calculate the permanent - a #P problem - it follows that calculating or approximating the Hafnian must also be a classically hard problem.
</div>
### Equally squeezed input states
In the case where all the input states are squeezed equally with squeezing factor $\xi=r$ (i.e. so $\phi=0$), we can simplify the denominator into a much nicer form. It can be easily seen that, due to the unitarity of $U$,
$$\left[ \begin{matrix}U&0\\0&U^*\end{matrix} \right] \left[ \begin{matrix}U^\dagger&0\\0&U^T\end{matrix} \right] = \left[ \begin{matrix}UU^\dagger&0\\0&U^*U^T\end{matrix} \right] =I$$
Thus, we have
$$\begin{align}
\sigma_{out} +\frac{1}{2}I &= \sigma_{out} + \frac{1}{2} \left[ \begin{matrix}U&0\\0&U^*\end{matrix} \right] \left[ \begin{matrix}U^\dagger&0\\0&U^T\end{matrix} \right] = \left[ \begin{matrix}U&0\\0&U^*\end{matrix} \right] \frac{1}{2} \left(\sigma_{in}+I\right) \left[ \begin{matrix}U^\dagger&0\\0&U^T\end{matrix} \right]
\end{align}$$
where we have subtituted in the expression for $\sigma_{out}$. Taking the determinants of both sides, the two block diagonal matrices containing $U$ are unitary, and thus have determinant 1, resulting in
$$\left|\sigma_{out} +\frac{1}{2}I\right| =\left|\frac{1}{2}\left(\sigma_{in}+I\right)\right|=\left|\frac{1}{2}\left(SS^\dagger+I\right)\right| $$
By expanding out the right hand side, and using various trig identities, it is easy to see that this simply reduces to $\cosh^{2N}(r)$ where $N$ is the number of modes; thus the Gaussian boson sampling problem in the case of equally squeezed input modes reduces to
$$\left|\left\langle{n_1,n_2,\dots,n_N}\middle|{\psi'}\right\rangle\right|^2 = \frac{\left|\text{Haf}[(UU^T\tanh(r))]_{st}\right|^2}{n_1!n_2!\cdots n_N!\cosh^N(r)},$$
## The Gaussian boson sampling circuit
---
The multimode linear interferometer can be decomposed into two-mode beamsplitters (`BSgate`) and single-mode phase shifters (`Rgate`) (<a href="https://doi.org/10.1103/physrevlett.73.58">Reck, 1994</a>), allowing for an almost trivial translation into a continuous-variable quantum circuit.
For example, in the case of a 4 mode interferometer, with arbitrary $4\times 4$ unitary $U$, the continuous-variable quantum circuit for Gaussian boson sampling is given by
<img src="https://s3.amazonaws.com/xanadu-img/gaussian_boson_sampling.svg" width=70%/>
In the above,
* the single mode squeeze states all apply identical squeezing $\xi=r$,
* the detectors perform Fock state measurements (i.e. measuring the photon number of each mode),
* the parameters of the beamsplitters and the rotation gates determines the unitary $U$.
For $N$ input modes, we must have a minimum of $N$ columns in the beamsplitter array ([Clements, 2016](https://arxiv.org/abs/1603.08788)).
## Simulating boson sampling in Strawberry Fields
---
```
import strawberryfields as sf
from strawberryfields.ops import *
from strawberryfields.utils import random_interferometer
```
Strawberry Fields makes this easy; there is an `Interferometer` quantum operation, and a utility function that allows us to generate the matrix representing a random interferometer.
```
U = random_interferometer(4)
```
The lack of Fock states and non-linear operations means we can use the Gaussian backend to simulate Gaussian boson sampling. In this example program, we are using input states with squeezing parameter $\xi=1$, and the randomly chosen interferometer generated above.
```
eng, q = sf.Engine(4)
with eng:
# prepare the input squeezed states
S = Sgate(1)
All(S) | q
# interferometer
Interferometer(U) | q
state = eng.run('gaussian')
```
We can see the decomposed beamsplitters and rotation gates, by calling `eng.print_applied()`:
```
eng.print_applied()
```
<div class="alert alert-success" style="border: 0px; border-left: 3px solid #119a68; color: black; background-color: #daf0e9">
<p style="color: #119a68;">**Available decompositions**</p>
Check out our <a href="https://strawberryfields.readthedocs.io/en/stable/conventions/decompositions.html">documentation</a> to see the available CV decompositions available in Strawberry Fields.
</div>
## Analysis
---
Let's now verify the Gaussian boson sampling result, by comparing the output Fock state probabilities to the Hafnian, using the relationship
$$\left|\left\langle{n_1,n_2,\dots,n_N}\middle|{\psi'}\right\rangle\right|^2 = \frac{\left|\text{Haf}[(UU^T\tanh(r))]_{st}\right|^2}{n_1!n_2!\cdots n_N!\cosh^N(r)}$$
### Calculating the Hafnian
For the right hand side numerator, we first calculate the submatrix $[(UU^T\tanh(r))]_{st}$:
```
B = (np.dot(U, U.T) * np.tanh(1))
```
In Gaussian boson sampling, we determine the submatrix by taking the rows and columns corresponding to the measured Fock state. For example, to calculate the submatrix in the case of the output measurement $\left|{1,1,0,0}\right\rangle$,
```
B[:,[0,1]][[0,1]]
```
To calculate the Hafnian in Python, we can use the direct definition
$$\text{Haf}(A) = \frac{1}{n!2^n} \sum_{\sigma \in S_{2n}} \prod_{j=1}^n A_{\sigma(2j - 1), \sigma(2j)}$$
Notice that this function counts each term in the definition multiple times, and renormalizes to remove the multiple counts by dividing by a factor $\frac{1}{n!2^n}$. **This function is extremely slow!**
```
from itertools import permutations
from scipy.special import factorial
def Haf(M):
n=len(M)
m=int(n/2)
haf=0.0
for i in permutations(range(n)):
prod=1.0
for j in range(m):
prod*=M[i[2*j],i[2*j+1]]
haf+=prod
return haf/(factorial(m)*(2**m))
```
## Comparing to the SF result
In Strawberry Fields, both Fock and Gaussian states have the method `fock_prob()`, which returns the probability of measuring that particular Fock state.
#### Let's compare the case of measuring at the output state $\left|0,1,0,1\right\rangle$:
```
B = (np.dot(U,U.T) * np.tanh(1))[:, [1,3]][[1,3]]
np.abs(Haf(B))**2 / np.cosh(1)**4
state.fock_prob([0,1,0,1])
```
#### For the measurement result $\left|2,0,0,0\right\rangle$:
```
B = (np.dot(U,U.T) * np.tanh(1))[:, [0,0]][[0,0]]
np.abs(Haf(B))**2 / (2*np.cosh(1)**4)
state.fock_prob([2,0,0,0])
```
#### For the measurement result $\left|1,1,0,0\right\rangle$:
```
B = (np.dot(U,U.T) * np.tanh(1))[:, [0,1]][[0,1]]
np.abs(Haf(B))**2 / np.cosh(1)**4
state.fock_prob([1,1,0,0])
```
#### For the measurement result $\left|1,1,1,1\right\rangle$, this corresponds to the full matrix $B$:
```
B = (np.dot(U,U.T) * np.tanh(1))
np.abs(Haf(B))**2 / np.cosh(1)**4
state.fock_prob([1,1,1,1])
```
#### For the measurement result $\left|0,0,0,0\right\rangle$, this corresponds to a **null** submatrix, which has a Hafnian of 1:
```
1/np.cosh(1)**4
state.fock_prob([0,0,0,0])
```
As you can see, like in the boson sampling tutorial, they agree with almost negligable difference.
<div class="alert alert-success" style="border: 0px; border-left: 3px solid #119a68; color: black; background-color: #daf0e9">
<p style="color: #119a68;">**Exercises**</p>
Repeat this notebook with
<ol>
<li> A Fock backend such as NumPy, instead of the Gaussian backend</li>
<li> Different beamsplitter and rotation parameters</li>
<li> Input states with *differing* squeezed values $r_i$. You will need to modify the code to take into account the fact that the output covariance matrix determinant must now be calculated!
</ol>
</div>
| github_jupyter |
```
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
```
# Pytorch: An automatic differentiation tool
`Pytorch`를 활용하면 복잡한 함수의 미분을 손쉽게 + 효율적으로 계산할 수 있습니다!
`Pytorch`를 활용해서 복잡한 심층 신경망을 훈련할 때, 오차함수에 대한 파라미터의 편미분치를 계산을 손쉽게 수행할수 있습니다!
## Pytorch 첫만남
우리에게 아래와 같은 간단한 선형식이 주어져있다고 생각해볼까요?
$$ y = wx $$
그러면 $\frac{\partial y}{\partial w}$ 을 어떻게 계산 할 수 있을까요?
일단 직접 미분을 해보면$\frac{\partial y}{\partial w} = x$ 이 되니, 간단한
예제에서 `pytorch`로 해당 값을 계산하는 방법을 알아보도록 합시다!
```
# 랭크1 / 사이즈1 이며 값은 1*2 인 pytorch tensor를 하나 만듭니다.
x = torch.ones(1) * 2
# 랭크1 / 사이즈1 이며 값은 1 인 pytorch tensor를 하나 만듭니다.
w = torch.ones(1, requires_grad=True)
y = w * x
y
```
## 편미분 계산하기!
pytorch에서는 미분값을 계산하고 싶은 텐서에 `.backward()` 를 붙여주는 것으로, 해당 텐서 계산에 연결 되어있는 텐서 중 `gradient`를 계산해야하는 텐서(들)에 대한 편미분치들을 계산할수 있습니다. `requires_grad=True`를 통해서 어떤 텐서에 미분값을 계산할지 할당해줄 수 있습니다.
```
y.backward()
```
## 편미분값 확인하기!
`텐서.grad` 를 활용해서 특정 텐서의 gradient 값을 확인해볼 수 있습니다. 한번 `w.grad`를 활용해서 `y` 에 대한 `w`의 편미분값을 확인해볼까요?
```
w.grad
```
## 그러면 requires_grad = False 인 경우는?
```
x.grad
```
## `torch.nn`, Neural Network 패키지
`pytorch`에는 이미 다양한 neural network들의 모듈들을 구현해 놓았습니다. 그 중에 가장 간단하지만 정말 자주 쓰이는 `nn.Linear` 에 대해 알아보면서 `pytorch`의 `nn.Module`에 대해서 알아보도록 합시다.
## `nn.Linear` 돌아보기
`nn.Linear` 은 앞서 배운 선형회귀 및 다층 퍼셉트론 모델의 한 층에 해당하는 파라미터 $w$, $b$ 를 가지고 있습니다. 예시로 입력의 dimension 이 10이고 출력의 dimension 이 1인 `nn.Linear` 모듈을 만들어 봅시다!
```
lin = nn.Linear(in_features=10, out_features=1)
for p in lin.parameters():
print(p)
print(p.shape)
print('\n')
```
## `Linear` 모듈로 $y = Wx+b$ 계산하기
선형회귀식도 그랬지만, 다층 퍼셉트론 모델도 하나의 레이어는 아래의 수식을 계산했던 것을 기억하시죠?
$$y = Wx+b$$
`nn.Linear`를 활용해서 저 수식을 계산해볼까요?
검산을 쉽게 하기 위해서 W의 값은 모두 1.0 으로 b 는 5.0 으로 만들어두겠습니다.
```
lin.weight.data = torch.ones_like(lin.weight.data)
lin.bias.data = torch.ones_like(lin.bias.data) * 5.0
for p in lin.parameters():
print(p)
print(p.shape)
print('\n')
x = torch.ones(3, 10) # rank2 tensor를 만듭니다. : mini batch size = 3
y_hat = lin(x)
print(y_hat.shape)
print(y_hat)
```
## 지금 무슨일이 일어난거죠?
>Q1. 왜 Rank 2 tensor 를 입력으로 사용하나요? <br>
>A1. 파이토치의 `nn` 에 정의되어있는 클래스들은 입력의 가장 첫번째 디멘젼을 `배치 사이즈`로 해석합니다.
>Q2. lin(x) 는 도대체 무엇인가요? <br>
>A2. 파이썬에 익숙하신 분들은 `object()` 는 `object.__call__()`에 정의되어있는 함수를 실행시키신다는 것을 아실텐데요. 파이토치의 `nn.Module`은 `__call__()`을 오버라이드하는 함수인 `forward()`를 구현하는 것을 __권장__ 하고 있습니다. 일반적으로, `forward()`안에서 실제로 파라미터와 인풋을 가지고 특정 레이어의 연산과 정을 구현하게 됩니다.
여러가지 이유가 있겠지만, 파이토치가 내부적으로 foward() 의 실행의 전/후로 사용자 친화적인 환경을 제공하기위해서 추가적인 작업들을 해줍니다. 이 부분은 다음 실습에서 다층 퍼셉트론 모델을 만들면서 조금 더 자세히 설명해볼게요!
## Pytorch 로 간단히! 선형회귀 구현하기
저번 실습에서 numpy 로 구현했던 Linear regression 모델을 다시 한번 파이토치로 구현해볼까요? <br>
몇 줄이면 끝날 정도로 간단합니다 :)
```
def generate_samples(n_samples: int,
w: float = 1.0,
b: float = 0.5,
x_range=[-1.0,1.0]):
xs = np.random.uniform(low=x_range[0], high=x_range[1], size=n_samples)
ys = w * xs + b
xs = torch.tensor(xs).view(-1,1).float() # 파이토치 nn.Module 은 배치가 첫 디멘젼!
ys = torch.tensor(ys).view(-1,1).float()
return xs, ys
w = 1.0
b = 0.5
xs, ys = generate_samples(30, w=w, b=b)
lin_model = nn.Linear(in_features=1, out_features=1) # lim_model 생성
for p in lin_model.parameters():
print(p)
print(p.grad)
ys_hat = lin_model(xs) # lin_model 로 예측하기
```
## Loss 함수는? MSE!
`pytorch`에서는 자주 쓰이는 loss 함수들에 대해서도 미리 구현을 해두었습니다.
이번 실습에서는 __numpy로 선형회귀 모델 만들기__ 에서 사용됐던 MSE 를 오차함수로 사용해볼까요?
```
criteria = nn.MSELoss()
loss = criteria(ys_hat, ys)
```
## 경사하강법을 활용해서 파라미터 업데이트하기!
`pytorch`는 여러분들을 위해서 다양한 optimizer들을 구현해 두었습니다. 일단은 가장 간단한 stochastic gradient descent (SGD)를 활용해 볼까요? optimizer에 따라서 다양한 인자들을 활용하지만 기본적으로 `params` 와 `lr`을 지정해주면 나머지는 optimizer 마다 잘되는 것으로 알려진 인자들로 optimizer을 손쉽게 생성할수 있습니다.
```
opt = torch.optim.SGD(params=lin_model.parameters(), lr=0.01)
```
## 잊지마세요! opt.zero_grad()
`pytorch`로 편미분을 계산하기전에, 꼭 `opt.zero_grad()` 함수를 이용해서 편미분 계산이 필요한 텐서들의 편미분값을 초기화 해주는 것을 권장드립니다.
```
opt.zero_grad()
for p in lin_model.parameters():
print(p)
print(p.grad)
loss.backward()
opt.step()
for p in lin_model.parameters():
print(p)
print(p.grad)
```
## 경사하강법을 활용해서 최적 파라미터를 찾아봅시다!
```
def run_sgd(n_steps: int = 1000,
report_every: int = 100,
verbose=True):
lin_model = nn.Linear(in_features=1, out_features=1)
opt = torch.optim.SGD(params=lin_model.parameters(), lr=0.01)
sgd_losses = []
for i in range(n_steps):
ys_hat = lin_model(xs)
loss = criteria(ys_hat, ys)
opt.zero_grad()
loss.backward()
opt.step()
if i % report_every == 0:
if verbose:
print('\n')
print("{}th update: {}".format(i,loss))
for p in lin_model.parameters():
print(p)
sgd_losses.append(loss.log10().detach().numpy())
return sgd_losses
_ = run_sgd()
```
## 다른 Optimizer도 사용해볼까요?
수업시간에 배웠던 Adam 으로 최적화를 하면 어떤결과가 나올까요?
```
def run_adam(n_steps: int = 1000,
report_every: int = 100,
verbose=True):
lin_model = nn.Linear(in_features=1, out_features=1)
opt = torch.optim.Adam(params=lin_model.parameters(), lr=0.01)
adam_losses = []
for i in range(n_steps):
ys_hat = lin_model(xs)
loss = criteria(ys_hat, ys)
opt.zero_grad()
loss.backward()
opt.step()
if i % report_every == 0:
if verbose:
print('\n')
print("{}th update: {}".format(i,loss))
for p in lin_model.parameters():
print(p)
adam_losses.append(loss.log10().detach().numpy())
return adam_losses
_ = run_adam()
```
## 좀 더 상세하게 비교해볼까요?
`pytorch`에서 `nn.Linear`를 비롯한 많은 모듈들은 특별한 경우가 아닌이상,
모듈내에 파라미터가 임의의 값으로 __잘!__ 초기화 됩니다.
> "잘!" 에 대해서는 수업에서 다루지 않았지만, 확실히 현대 딥러닝이 잘 작동하게 하는 중요한 요소중에 하나입니다. Parameter initialization 이라고 부르는 기법들이며, 대부분의 `pytorch` 모듈들은 각각의 모듈에 따라서 일반적으로 잘 작동하는것으로 알려져있는 방식으로 파라미터들이 초기화 되게 코딩되어 있습니다.
그래서 매 번 모듈을 생성할때마다 파라미터의 초기값이 달라지게 됩니다. 이번에는 조금 공정한 비교를 위해서 위에서 했던 실험을 여러번 반복해서 평균적으로도 Adam이 좋은지 확인해볼까요?
```
sgd_losses = [run_sgd(verbose=False) for _ in range(50)]
sgd_losses = np.stack(sgd_losses)
sgd_loss_mean = np.mean(sgd_losses, axis=0)
sgd_loss_std = np.std(sgd_losses, axis=-0)
adam_losses = [run_adam(verbose=False) for _ in range(50)]
adam_losses = np.stack(adam_losses)
adam_loss_mean = np.mean(adam_losses, axis=0)
adam_loss_std = np.std(adam_losses, axis=-0)
fig, ax = plt.subplots(1,1, figsize=(10,5))
ax.grid()
ax.fill_between(x=range(sgd_loss_mean.shape[0]),
y1=sgd_loss_mean + sgd_loss_std,
y2=sgd_loss_mean - sgd_loss_std,
alpha=0.3)
ax.plot(sgd_loss_mean, label='SGD')
ax.fill_between(x=range(adam_loss_mean.shape[0]),
y1=adam_loss_mean + adam_loss_std,
y2=adam_loss_mean - adam_loss_std,
alpha=0.3)
ax.plot(adam_loss_mean, label='Adam')
ax.legend()
```
| github_jupyter |
# Analyzing IMDB Data in Keras
```
# Imports
import numpy as np
import keras
from keras.datasets import imdb
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation
from keras.preprocessing.text import Tokenizer
import matplotlib.pyplot as plt
%matplotlib inline
np.random.seed(42)
```
## 1. Loading the data
This dataset comes preloaded with Keras, so one simple command will get us training and testing data. There is a parameter for how many words we want to look at. We've set it at 1000, but feel free to experiment.
```
# Loading the data (it's preloaded in Keras)
(x_train, y_train), (x_test, y_test) = imdb.load_data(num_words=1000)
print(x_train.shape)
print(x_test.shape)
```
## 2. Examining the data
Notice that the data has been already pre-processed, where all the words have numbers, and the reviews come in as a vector with the words that the review contains. For example, if the word 'the' is the first one in our dictionary, and a review contains the word 'the', then there is a 1 in the corresponding vector.
The output comes as a vector of 1's and 0's, where 1 is a positive sentiment for the review, and 0 is negative.
```
print(x_train[0])
print(y_train[0])
```
## 3. One-hot encoding the output
Here, we'll turn the input vectors into (0,1)-vectors. For example, if the pre-processed vector contains the number 14, then in the processed vector, the 14th entry will be 1.
```
# One-hot encoding the output into vector mode, each of length 1000
tokenizer = Tokenizer(num_words=1000)
x_train = tokenizer.sequences_to_matrix(x_train, mode='binary')
x_test = tokenizer.sequences_to_matrix(x_test, mode='binary')
print(x_train[0])
print(x_train.shape)
x_train[1]
```
And we'll also one-hot encode the output.
```
# One-hot encoding the output
num_classes = 2
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)
print(y_train.shape)
print(y_test.shape)
```
## 4. Building the model architecture
Build a model here using sequential. Feel free to experiment with different layers and sizes! Also, experiment adding dropout to reduce overfitting.
```
# TODO: Build the model architecture
model = Sequential()
model.add(Dense(128, input_dim = x_train.shape[1]))
model.add(Activation('relu'))
model.add(Dense(2))
model.add(Activation('softmax'))
# TODO: Compile the model using a loss function and an optimizer.
model.compile(loss = 'categorical_crossentropy', optimizer = 'Adam', metrics = ['accuracy'])
```
## 5. Training the model
Run the model here. Experiment with different batch_size, and number of epochs!
```
# TODO: Run the model. Feel free to experiment with different batch sizes and number of epochs.
model.fit(x_train, y_train, 10000 , verbose = 0)
```
## 6. Evaluating the model
This will give you the accuracy of the model, as evaluated on the testing set. Can you get something over 85%?
```
score = model.evaluate(x_test, y_test, verbose=0)
print("Accuracy: ", score[1])
```
| github_jupyter |
<a href="https://colab.research.google.com/github/phreakyphoenix/MXNet-GluonCV-AWS-Coursera/blob/master/Module_5_LeNet_on_MNIST.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Graded Assessment
In this assessment you will write a full end-to-end training process using gluon and MXNet. We will train the LeNet-5 classifier network on the MNIST dataset. The network will be defined for you but you have to fill in code to prepare the dataset, train the network, and evaluate it's performance on a held out dataset.
```
#Check CUDA version
!nvcc --version
#Install appropriate MXNet version
'''
For eg if CUDA version is 10.0 choose mxnet cu100mkl
where cu adds CUDA GPU support
and mkl adds Intel CPU Math Kernel Library support
'''
!pip install mxnet-cu101mkl gluoncv
from pathlib import Path
from mxnet import gluon, metric, autograd, init, nd
import os
import mxnet as mx
#I downloaded the files from Coursera and hosted on my gdrive:
from google.colab import drive
drive.mount('/content/drive')
# M5_DATA = Path(os.getenv('DATA_DIR', '../../data'), 'module_5')
M5_DATA = Path('/content/drive/My Drive/CourseraWork/MXNetAWS/data/module_5')
M5_IMAGES = Path(M5_DATA, 'images')
```
---
## Question 1
### Prepare and the data and construct the dataloader
* First, get the MNIST dataset from `gluon.data.vision.datasets`. Use
* Don't forget the ToTensor and normalize Transformations. Use `0.13` and `0.31` as the mean and standard deviation respectively
* Construct the dataloader with the batch size provide. Ensure that the train_dataloader is shuffled.
<font color='red'>**CAUTION!**</font>: Although the notebook interface has internet connectivity, the **autograders are not permitted to access the internet**. We have already downloaded the correct models and data for you to use so you don't need access to the internet. Set the `root` parameter to `M5_IMAGES` when using a preset dataset. Usually, in the real world, you have internet access, so setting the `root` parameter isn't required (and it's set to `~/.mxnet` by default).
```
import os
from pathlib import Path
from mxnet.gluon.data.vision import transforms
import numpy as np
def get_mnist_data(batch=128):
"""
Should construct a dataloader with the MNIST Dataset with the necessary transforms applied.
:param batch: batch size for the DataLoader.
:type batch: int
:return: a tuple of the training and validation DataLoaders
:rtype: (gluon.data.DataLoader, gluon.data.DataLoader)
"""
def transformer(data, label):
data = data.flatten().expand_dims(0).astype(np.float32)/255
data = data-0.13/0.31
label = label.astype(np.float32)
return data, label
train_dataset = gluon.data.vision.datasets.MNIST(root=M5_IMAGES, train=True, transform=transformer)
validation_dataset = gluon.data.vision.datasets.MNIST(root=M5_IMAGES, train=False, transform=transformer)
train_dataloader = gluon.data.DataLoader(train_dataset, batch_size=batch, last_batch='keep',shuffle=True)
validation_dataloader = gluon.data.DataLoader(validation_dataset, batch_size=batch, last_batch='keep')
return train_dataloader, validation_dataloader
t, v = get_mnist_data()
assert isinstance(t, gluon.data.DataLoader)
assert isinstance(v, gluon.data.DataLoader)
d, l = next(iter(t))
assert d.shape == (128, 1, 28, 28) #check Channel First and Batch Size
assert l.shape == (128,)
assert nd.max(d).asscalar() <= 2.9 # check for normalization
assert nd.min(d).asscalar() >= -0.5 # check for normalization
```
---
## Question 2
### Write the training loop
* Create the loss function. This should be a loss function suitable for multi-class classification.
* Create the metric accumulator. This should the compute and store the accuracy of the model during training
* Create the trainer with the `adam` optimizer and learning rate of `0.002`
* Write the training loop
```
def train(network, training_dataloader, batch_size, epochs):
"""
Should take an initialized network and train that network using data from the data loader.
:param network: initialized gluon network to be trained
:type network: gluon.Block
:param training_dataloader: the training DataLoader provides batches for data for every iteration
:type training_dataloader: gluon.data.DataLoader
:param batch_size: batch size for the DataLoader.
:type batch_size: int
:param epochs: number of epochs to train the DataLoader
:type epochs: int
:return: tuple of trained network and the final training accuracy
:rtype: (gluon.Block, float)
"""
trainer = gluon.Trainer(network.collect_params(), 'adam',
{'learning_rate': 0.002})
metric = mx.metric.Accuracy()
for epoch in range(epochs):
train_loss =0.
for data,label in training_dataloader:
# print (data.shape)
# print (label.shape)
with autograd.record():
output = network(data)
loss=mx.ndarray.softmax_cross_entropy(output,label)
loss.backward()
trainer.step(batch_size)
train_loss += loss.mean().asscalar()
metric.update(label, output)
print (epoch , metric.get()[1])
training_accuracy = metric.get()[1]
return network, training_accuracy
```
Let's define and initialize a network to test the train function.
```
net = gluon.nn.Sequential()
net.add(gluon.nn.Conv2D(channels=6, kernel_size=5, activation='relu'),
gluon.nn.MaxPool2D(pool_size=2, strides=2),
gluon.nn.Conv2D(channels=16, kernel_size=3, activation='relu'),
gluon.nn.MaxPool2D(pool_size=2, strides=2),
gluon.nn.Flatten(),
gluon.nn.Dense(120, activation="relu"),
gluon.nn.Dense(84, activation="relu"),
gluon.nn.Dense(10))
net.initialize(init=init.Xavier())
n, ta = train(net, t, 128, 5)
assert ta >= .95
d, l = next(iter(v))
p = (n(d).argmax(axis=1))
assert (p.asnumpy() == l.asnumpy()).sum()/128.0 > .95
```
---
## Question 3
### Write the validation loop
* Create the metric accumulator. This should the compute and store the accuracy of the model on the validation set
* Write the validation loop
```
def validate(network, validation_dataloader):
"""
Should compute the accuracy of the network on the validation set.
:param network: initialized gluon network to be trained
:type network: gluon.Block
:param validation_dataloader: the training DataLoader provides batches for data for every iteration
:type validation_dataloader: gluon.data.DataLoader
:return: validation accuracy
:rtype: float
"""
val_acc = mx.metric.Accuracy()
for data,label in validation_dataloader:
output = network(data)
val_acc.update(label,output)
print (val_acc.get()[1])
return val_acc.get()[1]
assert validate(n, v) > .95
```
| github_jupyter |
```
import torch
from torchtext import data
import numpy as np
import pandas as pd
import torch.nn as nn
import torch.nn.functional as F
SEED = 1
torch.manual_seed(SEED)
torch.cuda.manual_seed(SEED)
with open('../stanford-corenlp-full-2018-10-05/stanfordSentimentTreebank/dictionary.txt','r') as f:
dic = f.readlines()
dic[:20]
BeautyTEXT = data.Field(tokenize='spacy')
BeautyLABEL = data.LabelField(tensor_type=torch.FloatTensor)
print("loading dataset clean_Beauty300.tsv...")
Beautytrain = data.TabularDataset.splits(
path='../counter-sent-generation3/VAE/data/official_Amazon/',
train='clean_Beauty300.tsv',
format='tsv',
fields=[('Text', BeautyTEXT),('Label', BeautyLABEL)])[0]
BeautyTEXT.build_vocab(Beautytrain, max_size=60000, vectors="fasttext.en.300d",min_freq=1)
BeautyLABEL.build_vocab(Beautytrain)
BeautyLABEL.vocab.stoi['1']=1
BeautyLABEL.vocab.stoi['2']=2
BeautyLABEL.vocab.stoi['3']=3
BeautyLABEL.vocab.stoi['4']=4
BeautyLABEL.vocab.stoi['5']=5
ApparelTEXT = data.Field(tokenize='spacy')
ApparelLABEL = data.LabelField(tensor_type=torch.FloatTensor)
print("loading dataset clean_Apparel300.tsv...")
Appareltrain = data.TabularDataset.splits(
path='../counter-sent-generation3/VAE/data/official_Amazon/',
train='clean_Apparel300.tsv',
format='tsv',
fields=[('Text', ApparelTEXT),('Label', ApparelLABEL)])[0]
ApparelTEXT.build_vocab(Appareltrain, max_size=60000, vectors="fasttext.en.300d",min_freq=1)
ApparelLABEL.build_vocab(Appareltrain)
ApparelLABEL.vocab.stoi['1']=1
ApparelLABEL.vocab.stoi['2']=2
ApparelLABEL.vocab.stoi['3']=3
ApparelLABEL.vocab.stoi['4']=4
ApparelLABEL.vocab.stoi['5']=5
JewelryTEXT = data.Field(tokenize='spacy')
JewelryLABEL = data.LabelField(tensor_type=torch.FloatTensor)
print("loading dataset clean_Jewelry300.tsv...")
Jewelrytrain = data.TabularDataset.splits(
path='../counter-sent-generation3/VAE/data/official_Amazon/',
train='clean_Jewelry300.tsv',
format='tsv',
fields=[('Text', JewelryTEXT),('Label', JewelryLABEL)])[0]
JewelryTEXT.build_vocab(Jewelrytrain, max_size=60000, vectors="fasttext.en.300d",min_freq=1)
JewelryLABEL.build_vocab(Jewelrytrain)
JewelryLABEL.vocab.stoi['1']=1
JewelryLABEL.vocab.stoi['2']=2
JewelryLABEL.vocab.stoi['3']=3
JewelryLABEL.vocab.stoi['4']=4
JewelryLABEL.vocab.stoi['5']=5
ShoesTEXT = data.Field(tokenize='spacy')
ShoesLABEL = data.LabelField(tensor_type=torch.FloatTensor)
print("loading dataset clean_Shoes300.tsv...")
Shoestrain = data.TabularDataset.splits(
path='../counter-sent-generation3/VAE/data/official_Amazon/',
train='clean_Shoes300.tsv',
format='tsv',
fields=[('Text', ShoesTEXT),('Label', ShoesLABEL)])[0]
ShoesTEXT.build_vocab(Shoestrain, max_size=60000, vectors="fasttext.en.300d",min_freq=1)
ShoesLABEL.build_vocab(Shoestrain)
ShoesLABEL.vocab.stoi['1']=1
ShoesLABEL.vocab.stoi['2']=2
ShoesLABEL.vocab.stoi['3']=3
ShoesLABEL.vocab.stoi['4']=4
ShoesLABEL.vocab.stoi['5']=5
import operator
sorted_Beautyvocab = sorted(BeautyTEXT.vocab.freqs.items(), key=operator.itemgetter(1),reverse=False)
common1 = set.intersection(set(BeautyTEXT.vocab.itos),set(ShoesTEXT.vocab.itos))
common2 = set.intersection(set(ApparelTEXT.vocab.itos),set(ShoesTEXT.vocab.itos))
common3 = set.intersection(set(JewelryTEXT.vocab.itos),set(ShoesTEXT.vocab.itos))
cdict={}
cdict['<unk>']=0
cdict['<pad>']=1
i=2
for x in common:
if x!='<unk>' and x!='<pad>':
cdict[x]=i
i=i+1
len(ShoesTEXT.vocab.stoi)
len(JewelryTEXT.vocab.stoi)
len(common2)
len(ApparelTEXT.vocab.stoi)
len(BeautyTEXT.vocab.itos)
len(common3)
ApparelTEXT.vocab.itos[0]
BeautyTEXT.vocab.stoi
import json
with open('Apparel300_vocab','w') as f:
json.dump(ApparelTEXT.vocab.stoi,f)
with open('Beauty300_vocab','w') as f:
json.dump(BeautyTEXT.vocab.stoi,f)
with open('Jewelry300_vocab','w') as f:
json.dump(JewelryTEXT.vocab.stoi,f)
BATCH_SIZE = 32
Beautytrain, Beautyvalid = Beautytrain.split(split_ratio=0.8)
Beautytrain_iterator, Beautyvalid_iterator = data.BucketIterator.splits(
(Beautytrain, Beautyvalid),
batch_size=BATCH_SIZE,
sort_key=lambda x: len(x.Text),
repeat=False)
Appareltrain, Apparelvalid = Appareltrain.split(split_ratio=0.999)
Appareltrain_iterator, Apparelvalid_iterator = data.BucketIterator.splits(
(Appareltrain, Apparelvalid),
batch_size=BATCH_SIZE,
sort_key=lambda x: len(x.Text),
repeat=False)
Jewelrytrain, Jewelryvalid = Jewelrytrain.split(split_ratio=0.8)
Jewelrytrain_iterator, Jewelryvalid_iterator = data.BucketIterator.splits(
(Jewelrytrain, Jewelryvalid),
batch_size=BATCH_SIZE,
sort_key=lambda x: len(x.Text),
repeat=False)
Shoestrain, Shoesvalid = Shoestrain.split(split_ratio=0.8)
Shoestrain_iterator, Shoesvalid_iterator = data.BucketIterator.splits(
(Shoestrain, Shoesvalid),
batch_size=BATCH_SIZE,
sort_key=lambda x: len(x.Text),
repeat=False)
'''
train_iterator = data.BucketIterator.splits(
train,
batch_size=BATCH_SIZE,
sort_key=lambda x: len(x.Text),
repeat=False)
'''
class RNN(nn.Module):
def __init__(self, vocab_size, embedding_dim, hidden_dim, output_dim, n_layers, bidirectional, dropout):
super().__init__()
self.embedding = nn.Embedding(vocab_size, embedding_dim)
self.rnn = nn.LSTM(embedding_dim, hidden_dim, num_layers=n_layers, bidirectional=bidirectional, dropout=dropout)
self.fc = nn.Linear(hidden_dim*2, output_dim)
self.dropout = nn.Dropout(dropout)
def forward(self, x):
#x = [sent len, batch size]
embedded = self.dropout(self.embedding(x))
#print("embedded shape: ", embedded.shape)
#embedded = [sent len, batch size, emb dim]
output, (hidden, cell) = self.rnn(embedded)
#print("output.shape: ",output.shape)
#print("output[-1].shape: ",output[-1].shape)
#print("hidden.shape: ",hidden.shape)
#print("cell.shape: ",cell.shape)
#output = [sent len, batch size, hid dim * num directions]
#hidden = [num layers * num directions, batch size, hid. dim]
#cell = [num layers * num directions, batch size, hid. dim]
hidden = self.dropout(torch.cat((hidden[-2,:,:], hidden[-1,:,:]), dim=1))
#print("hidden.shape: ",hidden.shape)
y = self.fc(hidden.squeeze(0))
#hidden [batch size, hid. dim * num directions]
#return self.fc(hidden.squeeze(0))
return y
# Beauty classifier
len(BeautyTEXT.vocab)
BeautyINPUT_DIM = len(BeautyTEXT.vocab)
EMBEDDING_DIM = 300
HIDDEN_DIM = 500
OUTPUT_DIM = 1
N_LAYERS = 2
BIDIRECTIONAL = True
DROPOUT = 0.5
Beautymodel = RNN(BeautyINPUT_DIM, EMBEDDING_DIM, HIDDEN_DIM, OUTPUT_DIM, N_LAYERS, BIDIRECTIONAL, DROPOUT)
print("Beautymodel parameters: ")
print(Beautymodel.parameters)
pretrained_embeddings = BeautyTEXT.vocab.vectors
Beautymodel.embedding.weight.data.copy_(pretrained_embeddings)
import torch.optim as optim
Beautyoptimizer = optim.Adam(Beautymodel.parameters(),lr=0.0003)
criterion = nn.MSELoss()
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
#device=torch.device('cpu')
Beautymodel = Beautymodel.to(device)
criterion = criterion.to(device)
ApparelINPUT_DIM = len(ApparelTEXT.vocab)
EMBEDDING_DIM = 300
HIDDEN_DIM = 500
OUTPUT_DIM = 1
N_LAYERS = 2
BIDIRECTIONAL = True
DROPOUT = 0.5
Apparelmodel = RNN(ApparelINPUT_DIM, EMBEDDING_DIM, HIDDEN_DIM, OUTPUT_DIM, N_LAYERS, BIDIRECTIONAL, DROPOUT)
print("Apparelmodel parameters: ")
print(Apparelmodel.parameters)
pretrained_embeddings = ApparelTEXT.vocab.vectors
Apparelmodel.embedding.weight.data.copy_(pretrained_embeddings)
import torch.optim as optim
Appareloptimizer = optim.Adam(Apparelmodel.parameters(),lr=0.0003)
criterion = nn.MSELoss()
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
#device=torch.device('cpu')
Apparelmodel = Apparelmodel.to(device)
criterion = criterion.to(device)
JewelryINPUT_DIM = len(JewelryTEXT.vocab)
EMBEDDING_DIM = 300
HIDDEN_DIM = 500
OUTPUT_DIM = 1
N_LAYERS = 2
BIDIRECTIONAL = True
DROPOUT = 0.5
Jewelrymodel = RNN(JewelryINPUT_DIM, EMBEDDING_DIM, HIDDEN_DIM, OUTPUT_DIM, N_LAYERS, BIDIRECTIONAL, DROPOUT)
print("Jewelrymodel parameters: ")
print(Jewelrymodel.parameters)
pretrained_embeddings = JewelryTEXT.vocab.vectors
Jewelrymodel.embedding.weight.data.copy_(pretrained_embeddings)
import torch.optim as optim
Jewelryoptimizer = optim.Adam(Jewelrymodel.parameters(),lr=0.0003)
criterion = nn.MSELoss()
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
#device=torch.device('cpu')
Jewelrymodel = Jewelrymodel.to(device)
criterion = criterion.to(device)
ShoesINPUT_DIM = len(ShoesTEXT.vocab)
EMBEDDING_DIM = 300
HIDDEN_DIM = 500
OUTPUT_DIM = 1
N_LAYERS = 2
BIDIRECTIONAL = True
DROPOUT = 0.5
Shoesmodel = RNN(ShoesINPUT_DIM, EMBEDDING_DIM, HIDDEN_DIM, OUTPUT_DIM, N_LAYERS, BIDIRECTIONAL, DROPOUT)
print("Shoesmodel parameters: ")
print(Shoesmodel.parameters)
pretrained_embeddings = ShoesTEXT.vocab.vectors
Shoesmodel.embedding.weight.data.copy_(pretrained_embeddings)
import torch.optim as optim
Shoesoptimizer = optim.Adam(Shoesmodel.parameters(),lr=0.0003)
criterion = nn.MSELoss()
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
#device=torch.device('cpu')
Shoesmodel = Shoesmodel.to(device)
criterion = criterion.to(device)
import torch.nn.functional as F
def accuracy(preds,y):
rounded_preds = torch.round(preds)
correct = (rounded_preds==y).float()
acc = correct.sum()/len(correct)
return acc
def train(model, iterator, optimizer, criterion):
epoch_loss = 0
epoch_acc = 0
model.train() # turns on dropout and batch normalization and allow gradient update
i=0
for batch in iterator:
i=i+1
optimizer.zero_grad() # set accumulated gradient to 0 for every start of a batch
predictions = model(batch.Text).squeeze(1)
loss = criterion(predictions, batch.Label)
acc = accuracy(predictions, batch.Label)
loss.backward() # calculate gradient
optimizer.step() # update parameters
if i%100==0:
print("train batch loss: ", loss.item())
print("train accuracy: ", acc.item())
epoch_loss += loss.item()
epoch_acc += acc.item()
return epoch_loss / len(iterator), epoch_acc / len(iterator)
def evaluate(model, iterator, criterion):
epoch_loss = 0
epoch_acc = 0
model.eval() #turns off dropout and batch normalization
with torch.no_grad():
i=0
for batch in iterator:
i=i+1
predictions = model(batch.Text).squeeze(1)
loss = criterion(predictions, batch.Label)
acc = accuracy(predictions, batch.Label)
epoch_loss += loss.item()
epoch_acc += acc.item()
if i%200 ==0:
print("eval batch loss: ", loss.item())
print("eval accuracy: ", acc.item())
return epoch_loss / len(iterator), epoch_acc / len(iterator)
#model = torch.load('fmodel')
import timeit
#start = timeit.default_timer()
N_EPOCHS = 20
#print("loading previous frnn3 model...")
#model = torch.load('frnn3')
try:
for epoch in range(N_EPOCHS):
start = timeit.default_timer()
train_loss, train_acc = train(Shoesmodel, Shoestrain_iterator, Shoesoptimizer, criterion)
valid_loss, valid_acc = evaluate(Shoesmodel, Shoesvalid_iterator, criterion)
#print("saving model: frnn8")
#torch.save(model,'frnn8')
print(f'Epoch: {epoch+1:02}, Train Loss: {train_loss:.3f}, Train Acc: {train_acc*100:.2f}%, Val. Loss: {valid_loss:.3f}, Val. Acc: {valid_acc*100:.2f}%')
#print(f'Epoch: {epoch+1:02}, Train Loss: {train_loss:.3f}, Train Acc: {train_acc*100:.2f}%')
stop = timeit.default_timer()
print("time duration: ", stop - start)
except KeyboardInterrupt:
print("interrupt")
print('Exiting from training early')
#print("save frnn8 again:")
#torch.save(model,'frnn8')
####################
# prediction
####################
'''
print('loading frnn4:')
model = torch.load('frnn4',map_location=lambda storage,loc:storage)
'''
valid_loss, valid_acc = evaluate(model, valid_iterator, criterion)
print("valid loss: ",valid_loss)
print("valid acc: ",valid_acc)
print("prediction of frnn8.....")
import spacy
nlp = spacy.load('en')
def predict_sentiment(sentence,model):
tokenized = [tok.text for tok in nlp.tokenizer(sentence)]
indexed = [TEXT.vocab.stoi[t] for t in tokenized]
tensor = torch.LongTensor(indexed).to(device)
tensor = tensor.unsqueeze(1)
model.eval()
prediction = model(tensor)
return prediction.item()
with open('../sent/ori_gender_data/male_sent_test_less700.tsv','r') as f:
mtest = f.readlines()
with open('../sent/ori_gender_data/female_sent_test_less700.tsv','r') as f:
ftest = f.readlines()
fs = [line.split('\t')[0] for line in ftest]
ms = [line.split('\t')[0] for line in mtest]
mlabel = [int(line.split('\t')[1].strip('\n')) for line in mtest]
flabel = [int(line.split('\t')[1].strip('\n')) for line in ftest]
fprem = [predict_sentiment(x,model) for x in ms]
fpref = [predict_sentiment(x,model) for x in fs]
print("10 fprem:")
print(fprem[:10])
print("10 fpref:")
print(fpref[:10])
print("writing fpref to file fpref_frnn8.txt...")
with open('fpref_frnn8.txt','w') as f:
f.write(str(fpref))
print("writing fprem to file fprem_frnn8.txt...")
with open('fprem_frnn8.txt','w') as f:
f.write(str(fprem))
print("fpref accuracy: ",(np.array([round(x) for x in fpref])==np.array(flabel)).mean())
print("fprem accuracy: ",(np.array([round(x) for x in fprem])==np.array(mlabel)).mean())
'''
with open('../sent/ori_gender_data/male_sent_tmp_train.tsv','r') as f:
mtrain = f.readlines()
with open('../sent/ori_gender_data/female_sent_tmp_train.tsv','r') as f:
ftrain = f.readlines()
fs = [line.split('\t')[0] for line in ftrain]
ms = [line.split('\t')[0] for line in mtrain]
mlabel = [int(line.split('\t')[1].strip('\n')) for line in mtrain]
flabel = [int(line.split('\t')[1].strip('\n')) for line in ftrain]
fprem = [predict_sentiment(x,model) for x in ms]
fpref = [predict_sentiment(x,model) for x in fs]
print("10 fpref on female_sent_tmp_train.tsv:")
print(fpref[:10])
print("10 fprem on male_sent_tmp_train.tsv:")
print(fprem[:10])
print("writing fpref to file :fpre_female_sent_tmp_train_frnn4.txt...")
with open('fpre_female_sent_tmp_train_frnn4.txt','w') as f:
f.write(str(fpref))
print("writing fprem to file :fpre_male_sent_tmp_train_frnn4.txt...")
with open('fpre_male_sent_tmp_train_frnn4.txt','w') as f:
f.write(str(fprem))
print("fpref accuracy: ",(np.array([round(x) for x in fpref])==np.array(flabel)).mean())
print("fprem accuracy: ",(np.array([round(x) for x in fprem])==np.array(mlabel)).mean())
'''
```
| github_jupyter |
# Callbacks and Multiple inputs
```
import pandas as pd
import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
from sklearn.preprocessing import scale
from keras.optimizers import SGD
from keras.layers import Dense, Input, concatenate, BatchNormalization
from keras.callbacks import EarlyStopping, TensorBoard, ModelCheckpoint
from keras.models import Model
import keras.backend as K
df = pd.read_csv("../data/titanic-train.csv")
Y = df['Survived']
df.info()
df.head()
num_features = df[['Age', 'Fare', 'SibSp', 'Parch']].fillna(0)
num_features.head()
cat_features = pd.get_dummies(df[['Pclass', 'Sex', 'Embarked']].astype('str'))
cat_features.head()
X1 = scale(num_features.values)
X2 = cat_features.values
K.clear_session()
# Numerical features branch
inputs1 = Input(shape = (X1.shape[1],))
b1 = BatchNormalization()(inputs1)
b1 = Dense(3, kernel_initializer='normal', activation = 'tanh')(b1)
b1 = BatchNormalization()(b1)
# Categorical features branch
inputs2 = Input(shape = (X2.shape[1],))
b2 = Dense(8, kernel_initializer='normal', activation = 'relu')(inputs2)
b2 = BatchNormalization()(b2)
b2 = Dense(4, kernel_initializer='normal', activation = 'relu')(b2)
b2 = BatchNormalization()(b2)
b2 = Dense(2, kernel_initializer='normal', activation = 'relu')(b2)
b2 = BatchNormalization()(b2)
merged = concatenate([b1, b2])
preds = Dense(1, activation = 'sigmoid')(merged)
# final model
model = Model([inputs1, inputs2], preds)
model.compile(loss = 'binary_crossentropy',
optimizer = 'rmsprop',
metrics = ['accuracy'])
model.summary()
outpath='/tmp/tensorflow_logs/titanic/'
early_stopper = EarlyStopping(monitor='val_acc', patience=10)
tensorboard = TensorBoard(outpath+'tensorboard/', histogram_freq=1)
checkpointer = ModelCheckpoint(outpath+'weights_epoch_{epoch:02d}_val_acc_{val_acc:.2f}.hdf5',
monitor='val_acc')
# You may have to run this a couple of times if stuck on local minimum
np.random.seed(2017)
h = model.fit([X1, X2],
Y.values,
batch_size = 32,
epochs = 40,
verbose = 1,
validation_split=0.2,
callbacks=[early_stopper,
tensorboard,
checkpointer])
import os
sorted(os.listdir(outpath))
```
Now check the tensorboard.
- If using provided aws instance, just browse to: `http://<your-ip>:6006`
- If using local, open a terminal, activate the environment and run:
```
tensorboard --logdir=/tmp/tensorflow_logs/titanic/tensorboard/
```
then open a browser at `localhost:6006`
You should see something like this:

## Exercise 1
- try modifying the parameters of the 3 callbacks provided. What are they for? What do they do?
*Copyright © 2017 CATALIT LLC. All rights reserved.*
| github_jupyter |
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from pathlib import Path
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
train_df = pd.read_csv(Path('./Resources/2019loans.csv'))
test_df = pd.read_csv(Path('./Resources/2020Q1loans.csv'))
train_df
test_df
# Convert categorical data to numeric and separate target feature for training data
X_1 = train_df.drop('target', axis=1)
X_dummies_train = pd.get_dummies(X_1)
print(X_dummies_train.columns)
X_dummies_train
from sklearn.preprocessing import LabelEncoder
y_label_1 = LabelEncoder().fit_transform(train_df['target'])
y_label_1
# Convert categorical data to numeric and separate target feature for testing data
X_2 = test_df.drop('target', axis=1)
X_dummies_test = pd.get_dummies(X_2)
print(X_dummies_test.columns)
X_dummies_test
from sklearn.preprocessing import LabelEncoder
y_label_2 = LabelEncoder().fit_transform(test_df['target'])
y_label_2
# add missing dummy variables to testing set
X_dummies_test["debt_settlement_flag_Y"] = X_dummies_test["debt_settlement_flag_N"].apply(lambda x: 1 if x == 0 else 0)
X_dummies_test
```
## Hypothesis
I believe that random forest will have a better score since the data frame has a lot of catergorical data and a lot of columns in general.
```
# Train the Logistic Regression model on the unscaled data and print the model score
classifier = LogisticRegression()
classifier.fit(X_dummies_train, y_label_1)
print(f"Training Data Score: {classifier.score(X_dummies_train, y_label_1)}")
print(f"Testing Data Score: {classifier.score(X_dummies_test, y_label_2)}")
# Train a Random Forest Classifier model and print the model score
clf = RandomForestClassifier(random_state=1, n_estimators=500).fit(X_dummies_train, y_label_1)
print(f'Training Score: {clf.score(X_dummies_train, y_label_1)}')
print(f'Testing Score: {clf.score(X_dummies_test, y_label_2)}')
```
## Hypothesis 2
I think that by scaling my scores are going to get better and that the testing and training will be less spread out.
```
# Scale the data
scaler = StandardScaler().fit(X_dummies_train)
X_train_scaled = scaler.transform(X_dummies_train)
X_test_scaled = scaler.transform(X_dummies_test)
X_test_scaled
# Train the Logistic Regression model on the scaled data and print the model score
classifier = LogisticRegression()
classifier.fit(X_train_scaled, y_label_1)
print(f"Training Data Score: {classifier.score(X_train_scaled, y_label_1)}")
print(f"Testing Data Score: {classifier.score(X_test_scaled, y_label_2)}")
# Train a Random Forest Classifier model on the scaled data and print the model score
clf = RandomForestClassifier(random_state=1, n_estimators=500).fit(X_train_scaled, y_label_1)
print(f'Training Score: {clf.score(X_train_scaled, y_label_1)}')
print(f'Testing Score: {clf.score(X_test_scaled, y_label_2)}')
```
## Conclusion
Ultimately, the logistic regression did a better job of analysising the data. Not only does the scaled logistic regression testing score beat out the non-scaled and scaled random forest score, but the training and testing scores are less spread out.
The second conlcusion is that scaling the data did improve the logistic regression score. THe random forest, however, remained unchanged.
| github_jupyter |
#Import Data
```
import numpy as np
from sklearn.model_selection import GridSearchCV
import matplotlib.pyplot as plt
# load data
import os
from google.colab import drive
drive.mount('/content/drive')
filedir = './drive/My Drive/Final/CNN_data'
with open(filedir + '/' + 'feature_extracted', 'rb') as f:
X = np.load(f)
with open(filedir + '/' + 'Y', 'rb') as f:
Y = np.load(f).astype(np.int32)
# import MFCC data
with open('./drive/My Drive/Final/mfcc_data/X', 'rb') as f:
X_mfcc = np.load(f)
with open('./drive/My Drive/Final/mfcc_data/Y', 'rb') as f:
Y_mfcc = np.load(f)
print('X_shape: {}\nY_shape: {}'.format(X_mfcc.shape, Y_mfcc.shape))
import warnings
warnings.filterwarnings("ignore")
'''
X_new = np.zeros([300,0])
for i in range(X.shape[1]):
col = X[:,i,None]
if((np.abs(col) > 1e-6).any()):
X_new = np.hstack([X_new, col])
else:
print('Yes')
print('X.shape: {}\nX_new.shape: {}\nY.shape: {}'.format(X.shape, X_new.shape, Y.shape))
print(X_new.shape)
print(np.max(X_new, axis=1) != np.max(X, axis=1))
print(np.min(X_new, axis=1))
'''
```
#CLF1 Ridge Classifier
```
'''
from sklearn.linear_model import RidgeClassifier
parameters = {'alpha':[1]}
rc = RidgeClassifier(alpha = 1)
clf = GridSearchCV(rc, parameters, cv=3)
clf.fit(X[:30], Y[:30])
clf.best_estimator_.fit(X[:30], Y[:30]).score(X, Y)
clf.best_index_
'''
from sklearn.linear_model import RidgeClassifier
def clf_RidgeClassifier(training_set, training_lable, testing_set, testing_lable):
parameters = {'alpha':[10, 1, 1e-1, 1e-2, 1e-3]}
rc = RidgeClassifier(alpha = 1)
clf = GridSearchCV(rc, parameters, cv=3, return_train_score=True, iid=False)
clf.fit(training_set, training_lable)
results = clf.cv_results_
opt_index = clf.best_index_
training_score = results['mean_train_score'][opt_index]
validation_score = results['mean_test_score'][opt_index]
testing_score = clf.best_estimator_.fit(training_set, training_lable).score(testing_set, testing_lable)
return [training_score, validation_score, testing_score], clf.best_params_
clf_RidgeClassifier(X[:240], Y[:240], X[240:], Y[240:])
```
#CLF2 SVM
```
from sklearn.svm import SVC
def clf_SVM(X_train, Y_train, X_test, Y_test):
parameters = {'C':[10, 1, 1e-1, 1e-2, 1e-3]}
svc = SVC(kernel='linear')
clf = GridSearchCV(svc, parameters, cv=3, return_train_score=True, iid=False)
clf.fit(X_train, Y_train)
results = clf.cv_results_
opt_index = clf.best_index_
training_score = results['mean_train_score'][opt_index]
validation_score = results['mean_test_score'][opt_index]
testing_score = clf.best_estimator_.fit(X_train, Y_train).score(X_test, Y_test)
return [training_score, validation_score, testing_score], clf.best_params_
clf_SVM(X[:240], Y[:240], X[240:], Y[240:])
```
#CLF3 LDA
```
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
def clf_lda(Xtrain, Ytrain, Xtest, Ytest):
"""
Input: training data, labels, testing data, labels
Output: training set mean prediciton accuracy, validation accuracy = None, testing set mean prediction accuracy
Note: LDA has no hyperparameters to tune because a model is solved in closed form
therefore there is no need for model selection via grid search cross validation
therefore there is no validation accuracy
"""
clf = LinearDiscriminantAnalysis()
clf.fit(Xtrain, Ytrain)
train_acc = clf.score(Xtrain,Ytrain)
val_acc = None
test_acc = clf.score(Xtest,Ytest)
return [train_acc,val_acc,test_acc], None
clf_lda(X[:240],Y[:240],X[240:],Y[240:])
```
#CLF4 KNN
```
from sklearn.neighbors import KNeighborsClassifier
def clf_KNN(X_train, Y_train, X_test, Y_test):
parameters = {'n_neighbors':[1,5,20]}
knn = KNeighborsClassifier(algorithm='auto', weights='uniform')
clf = GridSearchCV(knn, parameters, cv=3, return_train_score=True, iid=False)
clf.fit(X_train, Y_train)
results = clf.cv_results_
opt_index = clf.best_index_
training_score = results['mean_train_score'][opt_index]
validation_score = results['mean_test_score'][opt_index]
testing_score = clf.best_estimator_.fit(X_train, Y_train).score(X_test, Y_test)
return [training_score, validation_score, testing_score], clf.best_params_
clf_KNN(X[:240], Y[:240], X[240:], Y[240:])
```
#CLF5 Decision Tree
```
from sklearn.tree import DecisionTreeClassifier
def clf_DecisionTree(X_train, Y_train, X_test, Y_test):
parameters = {'max_depth':[5,10,15,20,25], 'criterion':['entropy', 'gini']}
dtc = DecisionTreeClassifier()
clf = GridSearchCV(dtc, parameters, cv=3, return_train_score=True, iid=False)
clf.fit(X_train, Y_train)
results = clf.cv_results_
opt_index = clf.best_index_
training_score = results['mean_train_score'][opt_index]
validation_score = results['mean_test_score'][opt_index]
testing_score = clf.best_estimator_.fit(X_train, Y_train).score(X_test, Y_test)
return [training_score, validation_score, testing_score], clf.best_params_
clf_DecisionTree(X[:240], Y[:240], X[240:], Y[240:])
```
#Testing On Data
```
clf_list = [clf_RidgeClassifier, clf_SVM, clf_lda, clf_KNN, clf_DecisionTree]
def test_trial(X_shuffled, Y_shuffled):
global clf_list
error = np.zeros((3,5,3)) # partition(3) * clf(5) * error(3)
# (8/2,5/5,2/8) * (clf_list) * (trn,val,tst)
opt_param = np.empty((3,5), dtype=dict) # partition(3) * clf(5)
sample_size = len(X_shuffled)
# 80/20 split
train_size = int(sample_size * 0.8)
X_train = X_shuffled[:train_size]
Y_train = Y_shuffled[:train_size]
X_test = X_shuffled[train_size:]
Y_test = Y_shuffled[train_size:]
for i in range(len(clf_list)):
clffn = clf_list[i]
error[0,i,:], opt_param[0,i] = clffn(X_train, Y_train, X_test, Y_test)
# 50/50 split
train_size = int(sample_size * 0.5)
X_train = X_shuffled[:train_size]
Y_train = Y_shuffled[:train_size]
X_test = X_shuffled[train_size:]
Y_test = Y_shuffled[train_size:]
for i in range(len(clf_list)):
clffn = clf_list[i]
error[1,i,:], opt_param[1,i] = clffn(X_train, Y_train, X_test, Y_test)
# 80/20 split
train_size = int(sample_size * 0.2)
X_train = X_shuffled[:train_size]
Y_train = Y_shuffled[:train_size]
X_test = X_shuffled[train_size:]
Y_test = Y_shuffled[train_size:]
for i in range(len(clf_list)):
clffn = clf_list[i]
error[2,i,:], opt_param[2,i] = clffn(X_train, Y_train, X_test, Y_test)
# return error array
return error, opt_param
from sklearn.utils import shuffle
def test_data(X, Y):
error = np.zeros((3,3,5,3)) # trial(3) * error_from_test_trial(3*5*3)
opt_param = np.empty((3,3,5), dtype=dict) # trial(3) * opt_param_from_test_trial(3*5)
# trial 1
X_shuffled, Y_shuffled = shuffle(X, Y)
error[0], opt_param[0] = test_trial(X_shuffled, Y_shuffled)
# trial 2
X_shuffled, Y_shuffled = shuffle(X_shuffled, Y_shuffled)
error[1], opt_param[1] = test_trial(X_shuffled, Y_shuffled)
# trial 3
X_shuffled, Y_shuffled = shuffle(X_shuffled, Y_shuffled)
error[2], opt_param[2] = test_trial(X_shuffled, Y_shuffled)
return error, opt_param
# test on CNN-extracted features
acc_CNN, opt_param_CNN = test_data(X, Y)
np.mean(acc_CNN[:,:,:,:], axis=0)
acc_clf, opt_param = test_data(X_mfcc, Y_mfcc)
avg_cnn_acc = np.mean(acc_CNN, axis=0)
avg_clf_acc = np.mean(acc_clf, axis=0)
print('cnn: {}'.format(avg_cnn_acc))
print('clf: {}'.format(avg_clf_acc))
# partition_accuracy plot
from matplotlib import rcParams
rcParams['figure.figsize'] = (8,8)
colors = ['cyan', 'green', 'red', 'orange','black']
clf = ['RidgeRegression', 'SVM', 'LDA', 'KNN', 'DecisionTree']
for clfid in range(5):
plt.plot(avg_cnn_acc[:,clfid,-1], color=colors[clfid], linestyle='solid', label='CNN '+clf[clfid])
plt.plot(avg_clf_acc[:,clfid,-1], color=colors[clfid], linestyle='dashed', label='MFCC '+clf[clfid])
plt.legend(loc='lower left')
plt.xticks((0,1,2),['80/20', '50/50', '20/80'])
plt.xlabel('partition (train/test)')
plt.ylabel('average test accuracy')
plt.savefig('./drive/My Drive/Final/graphs/partition_accuracy.png', bbox='tight')
# SVM hyperparameter error plot
parameters = {'C':[10, 1, 1e-1, 1e-2, 1e-3]}
svc = SVC(kernel='linear')
clf = GridSearchCV(svc, parameters, cv=3, return_train_score=True, iid=False)
clf.fit(X[:240], Y[:240])
results = clf.cv_results_
opt_index = clf.best_index_
training_score = results['mean_train_score']
validation_score = results['mean_test_score']
param_x = results['param_C'].data.astype(np.float32)
plt.plot(param_x, training_score, 'r-', label='training')
plt.plot(param_x, validation_score, 'b-', label='validation')
plt.legend(loc='lower left')
plt.xticks([0,2.5,5,7.5,10], ['10','1','1e-1','1e-2','1e-3'])
plt.xlabel('param_C')
plt.ylabel('accuracy')
#plt.show()
plt.savefig('./drive/My Drive/Final/graphs/SVM_hyperparameter_accuracy.png')
# avg cross-partition accuracy
cnn_cp_acc = np.mean(avg_cnn_acc[:,:,-1], axis=0)
clf_cp_acc = np.mean(avg_clf_acc[:,:,-1], axis=0)
print('cnn_cp_acc: {}'.format(cnn_cp_acc))
print('clf_cp_acc: {}'.format(clf_cp_acc))
avg_totalcp_acc = (cnn_cp_acc + clf_cp_acc) / 2
print(avg_totalcp_acc)
(avg_cnn_acc + avg_clf_acc)/2
opt_param
opt_param_CNN
max_ind_cnn = np.argpartition(np.sum(X, axis=0), -2)[-2:]
std_ind_cnn = np.argpartition(np.std(X, axis=0), -2)[-2:]
max_ind_clf = np.argpartition(np.sum(X_mfcc, axis=0), -2)[-2:]
std_ind_clf = np.argpartition(np.std(X_mfcc, axis=0), -2)[-2:]
max_cnn = X[:,max_ind_cnn]
std_cnn = X[:,std_ind_cnn]
max_clf = X_mfcc[:,max_ind_clf]
std_clf = X_mfcc[:,std_ind_clf]
def plot_features(X, Y):
return X[Y==0,:], X[Y==1,:]
# 2 max features from cnn plotted
plt.clf()
feature0, feature1 = plot_features(max_cnn, Y)
plt.plot(feature0[:,0], feature0[:,1],'ro', label='digit 0')
plt.plot(feature1[:,0], feature1[:,1],'go', label='digit 1')
plt.legend(loc='lower right')
plt.show()
#plt.savefig('./drive/My Drive/Final/graphs/2_max_sum_cnn_features.png')
# 2 var features from cnn plotted
feature0, feature1 = plot_features(std_cnn, Y)
plt.plot(feature0[:,0], feature0[:,1],'ro', label='digit 0')
plt.plot(feature1[:,0], feature1[:,1],'go', label='digit 1')
plt.legend(loc='lower right')
#plt.show()
plt.savefig('./drive/My Drive/Final/graphs/2_max_var_cnn_features.png')
# 2 max features from mfcc plotted
feature0, feature1 = plot_features(max_clf, Y)
plt.plot(feature0[:,0], feature0[:,1],'ro', label='digit 0')
plt.plot(feature1[:,0], feature1[:,1],'go', label='digit 1')
plt.legend(loc='lower right')
#plt.show()
plt.savefig('./drive/My Drive/Final/graphs/2_max_sum_mfcc_features.png')
# 2 var features from mfcc plotted
feature0, feature1 = plot_features(std_clf, Y)
plt.plot(feature0[:,0], feature0[:,1],'ro', label='digit 0')
plt.plot(feature1[:,0], feature1[:,1],'go', label='digit 1')
plt.legend(loc='lower right')
#plt.show()
plt.savefig('./drive/My Drive/Final/graphs/2_max_var_mfcc_features.png')
```
| github_jupyter |
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Image/extract_value_to_points.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Image/extract_value_to_points.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://mybinder.org/v2/gh/giswqs/earthengine-py-notebooks/master?filepath=Image/extract_value_to_points.ipynb"><img width=58px src="https://mybinder.org/static/images/logo_social.png" />Run in binder</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Image/extract_value_to_points.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API and geemap
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://github.com/giswqs/geemap). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
**Important note**: A key difference between folium and ipyleaflet is that ipyleaflet is built upon ipywidgets and allows bidirectional communication between the front-end and the backend enabling the use of the map to capture user input, while folium is meant for displaying static data only ([source](https://blog.jupyter.org/interactive-gis-in-jupyter-with-ipyleaflet-52f9657fa7a)). Note that [Google Colab](https://colab.research.google.com/) currently does not support ipyleaflet ([source](https://github.com/googlecolab/colabtools/issues/60#issuecomment-596225619)). Therefore, if you are using geemap with Google Colab, you should use [`import geemap.eefolium`](https://github.com/giswqs/geemap/blob/master/geemap/eefolium.py). If you are using geemap with [binder](https://mybinder.org/) or a local Jupyter notebook server, you can use [`import geemap`](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py), which provides more functionalities for capturing user input (e.g., mouse-clicking and moving).
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('geemap package not installed. Installing ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
# Checks whether this notebook is running on Google Colab
try:
import google.colab
import geemap.eefolium as emap
except:
import geemap as emap
# Authenticates and initializes Earth Engine
import ee
try:
ee.Initialize()
except Exception as e:
ee.Authenticate()
ee.Initialize()
```
## Create an interactive map
The default basemap is `Google Satellite`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/geemap.py#L13) can be added using the `Map.add_basemap()` function.
```
Map = emap.Map(center=[40,-100], zoom=4)
Map.add_basemap('ROADMAP') # Add Google Map
Map
```
## Add Earth Engine Python script
```
# Add Earth Engine dataset
# Input imagery is a cloud-free Landsat 8 composite.
l8 = ee.ImageCollection('LANDSAT/LC08/C01/T1')
image = ee.Algorithms.Landsat.simpleComposite(**{
'collection': l8.filterDate('2018-01-01', '2018-12-31'),
'asFloat': True
})
# Use these bands for prediction.
bands = ['B2', 'B3', 'B4', 'B5', 'B6', 'B7', 'B10', 'B11']
# Load training points. The numeric property 'class' stores known labels.
points = ee.FeatureCollection('GOOGLE/EE/DEMOS/demo_landcover_labels')
# This property of the table stores the land cover labels.
label = 'landcover'
# Overlay the points on the imagery to get training.
training = image.select(bands).sampleRegions(**{
'collection': points,
'properties': [label],
'scale': 30
})
# Define visualization parameters in an object literal.
vizParams = {'bands': ['B5', 'B4', 'B3'],
'min': 0, 'max': 1, 'gamma': 1.3}
Map.centerObject(points, 10)
Map.addLayer(image, vizParams, 'Image')
Map.addLayer(points, {'color': "yellow"}, 'Training points')
first = training.first()
print(first.getInfo())
```
## Display Earth Engine data layers
```
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
```
| github_jupyter |
# Fmriprep
Today, many excellent general-purpose, open-source neuroimaging software packages exist: [SPM](https://www.fil.ion.ucl.ac.uk/spm/) (Matlab-based), [FSL](https://fsl.fmrib.ox.ac.uk/fsl/fslwiki), [AFNI](https://afni.nimh.nih.gov/), and [Freesurfer](https://surfer.nmr.mgh.harvard.edu/) (with a shell interface). We argue that there is not one single package that is always the best choice for every step in your preprocessing pipeline. Fortunately, people from the [Poldrack lab](https://poldracklab.stanford.edu/) created [fmriprep](https://fmriprep.readthedocs.io/en/stable/), a software package that offers a preprocessing pipeline which "glues together" functionality from different neuroimaging software packages (such as Freesurfer and FSL), such that each step in the pipeline is executed by the software package that (arguably) does it best.
We have been using *Fmriprep* for preprocessing of our own data and we strongly recommend it. It is relatively simple to use, requires minimal user intervention, and creates extensive visual reports for users to do visual quality control (to check whether each step in the pipeline worked as expected). The *only* requirement to use Fmriprep is that your data is formatted as specified in the Brain Imaging Data Structure (BIDS).
## The BIDS-format
[BIDS](https://bids.neuroimaging.io/) is a specification on how to format, name, and organize your MRI dataset. It specifies the file format of MRI files (i.e., compressed Nifti: `.nii.gz` files), lays out rules for how you should name your files (i.e., with "key-value" pairs, such as: `sub-01_ses-1_task-1back_run-1_bold.nii.gz`), and outlines the file/folder structure of your dataset (where each subject has its own directory with separate subdirectories for different MRI modalities, including fieldmaps, functional, diffusion, and anatomical MRI). Additionally, it specifies a way to include "metadata" about the (MRI) files in your dataset with [JSON](https://en.wikipedia.org/wiki/JSON) files: plain-text files with key-value pairs (in the form "parameter: value"). Given that your dataset is BIDS-formatted and contains the necessary metadata, you can use `fmriprep` on your dataset. (You can use the awesome [bids-validator](https://bids-standard.github.io/bids-validator/) to see whether your dataset is completely valid according to BIDS.)
There are different tools to convert your "raw" scanner data (e.g., in DICOM or PAR/REC format) to BIDS, including [heudiconv](https://heudiconv.readthedocs.io/en/latest/), [bidscoin](https://github.com/Donders-Institute/bidscoin), and [bidsify](https://github.com/NILAB-UvA/bidsify) (created by Lukas). We'll skip over this step and assume that you'll be able to convert your data to BIDS.
## Installing Fmriprep
Now, having your data in BIDS is an important step in getting started with Fmriprep. The next step is installing the package. Technically, Fmriprep is a Python package, so it can be installed as such (using `pip install fmriprep`), but we do not recommend this "bare metal" installation, because it depends on a host of neuroimaging software packages (including FSL, Freesurfer, AFNI, and ANTs). So if you'd want to directly install Fmriprep, you'd need to install those extra neuroimaging software packages as well (which is not worth your time, trust us).
Fortunately, Fmriprep also offers a "Docker container" in which Fmriprep and all the associated dependencies are already installed. [Docker](https://www.docker.com/) is software that allows you to create "containers", which are like lightweight "virtual machines" ([VM](https://en.wikipedia.org/wiki/Virtual_machine)) that are like a separate (Linux-based) operating system with a specific software configuration. You can download the Fmriprep-specific docker "image", which is like a "recipe", build the Fmriprep-specific "container" according to this "recipe" on your computer, and finally use this container to run Fmriprep on your computer as if all dependencies were actually installed on your computer! Docker is available on Linux, Mac, and Windows. To install Docker, google something like "install docker for {Windows,Mac,Linux}" to find a google walkthrough.
Note that you need administrator ("root") privilege on your computer (which is likely the case for your own computer, but not on shared analysis servers) to run Docker. If you don't have root access on your computer/server, ask you administrator/sysadmin to install [singularity](https://fmriprep.readthedocs.io/en/stable/installation.html#singularity-container), which allows you to convert Docker images to Singularity images, which you can run without administrator privileges.
Assuming you have installed Docker, you can run the "containerized" Fmriprep from your command line directly, which involves a fairly long and complicated command (i.e., `docker run -it --rm -v bids_dir /data ... etc`), or using the `fmriprep-docker` Python package. This `fmriprep-docker` package is just a simple wrapper around the appropriate Docker command to run the complicated "containerized" Fmriprep command. We strongly recommend this method.
To install `fmriprep-docker`, you can use `pip` (from your command line):
```
pip install fmriprep-docker
```
Now, you should have access to the `fmriprep-docker` command on your command line and you're ready to start preprocessing your dataset. For more detailed information about installing Fmriprep, check out their [website](https://fmriprep.readthedocs.io/en/stable/installation.html).
## Running Fmriprep
Assuming you have Docker and `fmriprep-docker` installed, you're ready to run Fmriprep. The basic format of the `fmriprep-docker` command is as follows:
```
fmriprep-docker <your bids-folder> <your output-folder>
```
This means that `fmriprep-docker` has two mandatory positional arguments: the first one being your BIDS-folder (i.e., the path to your folder with BIDS-formattefd data), and the second one being the output-folder (i.e., where you want Fmriprep to output the preprocessed data). We recommend setting your output-folder to a subfolder of your BIDS-folder named "derivatives": `<your bids-folder>/derivatives`.
Then, you can add a bunch of extra "flags" (parameters) to the command to specify the preprocessing pipeline as you like it. We highlight a couple of important ones here, but for the full list of parameters, check out the [Fmriprep](https://fmriprep.readthedocs.io/en/stable/usage.html) website.
### Freesurfer
When running Fmriprep from Docker, you don't need to have Freesurfer installed, but you *do* need a Freesurfer license. You can download this here: https://surfer.nmr.mgh.harvard.edu/fswiki/License. Then, you need to supply the `--fs-license-file <path to license file>` parameter to your `fmriprep-docker` command:
```
fmriprep-docker <your bids-folder> <your output-folder> --fs-license-file /home/lukas/license.txt
```
### Configuring what is preprocessed
If you just run Fmriprep with the mandatory BIDS-folder and output-folder arguments, it will preprocess everything it finds in the BIDS-folder. Sometimes, however, you may just want to run one (or several) specific participants, or one (or more) specific tasks (e.g., only the MRI files associated with the localizer runs, but not the working memory runs). You can do this by adding the `--participant` and `--task` flags to the command:
```
fmriprep-docker <your bids-folder> <your output-folder> --participant sub-01 --task localizer
```
You can also specify some things to be ignored during preprocessing using the `--ignore` parameters (like `fieldmaps`):
```
fmriprep-docker <your bids-folder> <your output-folder> --ignore fieldmaps
```
### Handling performance
It's very easy to parallelize the preprocessing pipeline by setting the `--nthreads` and `--omp-nthreads` parameters, which refer to the number of threads that should be used to run Fmriprep on. Note that laptops usually have 4 threads available (but analysis servers usually have more!). You can also specify the maximum of RAM that Fmriprep is allowed to use by the `--mem_mb` parameters. So, if you for example want to run Fmriprep with 3 threads and a maximum of 3GB of RAM, you can run:
```
fmriprep-docker <your bids-folder> <your output-folder> --nthreads 3 --omp-nthreads 3 --mem_mb 3000
```
In our experience, however, specifying the `--mem_mb` parameter is rarely necessary if you don't parallelize too much.
### Output spaces
Specifying your "output spaces" (with the `--output-spaces` flag) tells Fmriprep to what "space(s)" you want your preprocessed data registered to. For example, you can specify `T1w` to have your functional data registered to the participant's T1 scan. You can, instead or in addition to, also specify some standard template, like the MNI template (`MNI152NLin2009cAsym` or `MNI152NLin6Asym`). You can even specify surface templates if you want (like `fsaverage`), which will sample your volumetric functional data onto the surface (as computed by freesurfer). In addition to the specific output space(s), you can add a resolution "modifier" to the parameter to specify in what spatial resolution you want your resampled data to be. Without any resolution modifier, the native resolution of your functional files (e.g., $3\times3\times3$ mm.) will be kept intact. But if you want to upsample your resampled files to 2mm, you can add `YourTemplate:2mm`. For example, if you want to use the FSL-style MNI template (`MNI152NLin6Asym`) resampled at 2 mm, you'd use:
```
fmriprep-docker <your bids-folder> <your output-folder> --output-spaces MNI152NLin6Asym:2mm
```
You can of course specify multiple output-spaces:
```
fmriprep-docker <your bids-folder> <your output-folder> --output-spaces MNI152NLin6Asym:2mm T1w fsaverage
```
### Other parameters
There are many options that you can set when running Fmriprep. Check out the [Fmriprep website](https://fmriprep.readthedocs.io/) (under "Usage") for a list of all options!
## Issues, errors, and troubleshooting
While Fmriprep often works out-of-the-box (assuming your data are properly BIDS-formatted), it may happen that it crashes or otherwise gives unexpected results. A great place to start looking for help is [neurostars.org](https://neurostars.org). This website is dedicated to helping neuroscientists with neuroimaging/neuroscience-related questions. Make sure to check whether your question has been asked here already and, if not, pose it here!
If you encounter Fmriprep-specific bugs, you can also submit and issue at the [Github repository](https://github.com/poldracklab/fmriprep) of Fmriprep.
## Fmriprep output/reports
After Fmriprep has run, it outputs, for each participants separately, a directory with results (i.e., preprocessed files) and an HTML-file with a summary and figures of the different steps in the preprocessing pipeline.
We ran Fmriprep on a single run/task (`flocBLOCKED`) from a single subject (`sub-03`) some data with the following command:
```
fmriprep-docker /home/lsnoek1/ni-edu/bids /home/lsnoek1/ni-edu/bids/derivatives --participant-label sub-03 --output-spaces T1w MNI152NLin2009cAsym
```
We've copied the Fmriprep output for this subject (`sub-03`) in the `fmriprep` subdirectory of the `week_4` directory. Let's check its contents:
```
import os
print(os.listdir('bids/derivatives/fmriprep'))
```
As said, Fmriprep outputs a directory with results (`sub-03`) and an associated HTML-file with a summary of the (intermediate and final) results. Let's check the directory with results first:
```
from pprint import pprint # pprint stands for "pretty print",
sub_path = os.path.join('bids/derivatives/fmriprep', 'sub-03')
pprint(sorted(os.listdir(sub_path)))
```
The `figures` directory contains several figures with the result of different preprocessing stages (like functional → high-res anatomical registration), but these figures are also included in the HTML-file, so we'll leave that for now. The other two directories, `anat` and `func`, contain the preprocessed anatomical and functional files, respectively. Let's inspect the `anat` directory:
```
anat_path = os.path.join(sub_path, 'anat')
pprint(os.listdir(anat_path))
```
Here, we see a couple of different files. There are both (preprocessed) nifti images (`*.nii.gz`) and associated meta-data (plain-text files in JSON format: `*.json`).
Importantly, the nifti outputs are in two different spaces: one set of files are in the original "T1 space", so without any resampling to another space (these files have the same resolution and orientation as the original T1 anatomical scan). For example, the `sub_03_desc-preproc_T1w.nii.gz` scan is the preprocessed (i.e., bias-corrected) T1 scan. In addition, most files are also available in `MNI152NLin2009cAsym` space, a standard template. For example, the `sub-03_space-MNI152NLin2009cAsym_desc-preproc_T1w.nii.gz` is the same file as `sub_03_desc-preproc_T1w.nii.gz`, but resampled to the `MNI152NLin2009cAsym` template. In addition, there are subject-specific brain parcellations (the `*aparcaseg_dseg.nii.gz `and `*aseg_dseg.nii.gz` files), files with registration parameters (`*from- ... -to ...` files), probabilistic tissue segmentation files (`*label-{CSF,GM,WM}_probseg.nii.gz`) files, and brain masks (to outline what is brain and not skull/dura/etc; `*brain_mask.nii.gz`).
Again, on the [Fmriprep website](https://fmriprep.readthedocs.io/), you can find more information about the specific outputs.
Now, let's check out the `func` directory:
```
func_path = os.path.join(sub_path, 'func')
pprint(os.listdir(func_path))
```
Again, like the files in the `anat` folder, the functional outputs are available in two spaces: `T1w` and `MNI152NLin2009cAsym`. In terms of actual images, there are preprocessed BOLD files (ending in `preproc_bold.nii.gz`), the functional volume used for "functional → anatomical" registration (ending in `boldref.nii.gz`), brain parcellations in functional space (ending in `dseg.nii.gz`), and brain masks (ending in `brain_mask.nii.gz`). In addition, there are files with "confounds" (ending in `confounds_regressors.tsv`) which contain variables that you might want to include as nuisance regressors in your first-level analysis. These confound files are speadsheet-like files (like `csv` files, but instead of being comma-delimited, they are tab-delimited) and can be easily loaded in Python using the [pandas](https://pandas.pydata.org/) package:
```
import pandas as pd
conf_path = os.path.join(func_path, 'sub-03_task-flocBLOCKED_desc-confounds_regressors.tsv')
conf = pd.read_csv(conf_path, sep='\t')
conf.head()
```
Confound files from Fmriprep contain a large set of confounds, ranging from motion parameters (`rot_x`, `rot_y`, `rot_z`, `trans_x`, `trans_y`, and `trans_z`) and their derivatives (`*derivative1`) and squares (`*_power2`) to the average signal from the brain's white matter and cerebrospinal fluid (CSF), which should contain sources of noise such as respiratory, cardiac, or motion related signals (but not signal from neural sources, which should be largely constrained to gray matter). For a full list and explanation of Fmriprep's estimated confounds, check their website. Also, check [this thread](https://neurostars.org/t/confounds-from-fmriprep-which-one-would-you-use-for-glm/326) on Neurostars for a discussion on which confounds to include in your analyses.
In addition to the actual preprocessed outputs, Fmriprep also provides you with a nice (visual) summary of the different (major) preprocessing steps in an HTML-file, which you'd normally open in any standard browser to view. Here. we load this file for our example participants (`sub-03`) inside the notebook below. Scroll through it to see which preprocessing steps are highlighted. Note that the images from the HTML-file are not properly rendered in Jupyter notebooks, but you can right-click the image links (e.g., `sub-03/figures/sub-03_dseg.svg`) and click "Open link in new tab" to view the image.
```
from IPython.display import IFrame
IFrame(src='./bids/derivatives/fmriprep/sub-03.html', width=700, height=600)
```
| github_jupyter |
# Software Engineering
Software engineering was first introduced in the 1960s in an effort to treat more rigorously the often frustrating task of designing and developing computer programs. It was around this time that the computer community became increasingly worried about the fact that software projects were typically over budget and behind schedule.
The term **software crisis(软件危机)** came to signify that software development was the bottleneck in the advancement of computer technology.
## 1 Introduction to Software Engineering
### 1.1 Software Characteristics
From an engineering viewpoint a software system is a product that serves a function.
However,
**1 A program can be changed**:
one unique attribute makes a computer program much different from a bridge or an airplane: a program can be changed. This malleability of software is both an advantage and a danger.
* An advantage because it is often possible to correct an error in a program much easier than it would be to fix a defect in an airplane or automobile.
* A danger because a modification in a program can introduce unanticipated side effects that may impair the functionality of those components that were executing correctly before the change.
**2. The most important element of the Software product cost is the human effort in design and development**
The another notable characteristic of programs relate to the type of `resources necessary for their creation`.
A software product is basically an intellectual commodity. The principal resource necessary for producing it is `human intelligence`.
The actual manufacturing of programs is `simple and inexpensive` compared to its design, coding, testing, and documenting.
This contrasts with many other engineered products in which the resources used in producing it are a substantial part of the product’s
final cost. For example, a considerable portion of the price of a new automobile represents the cost of manufacturing it, while a less significant part goes to pay for the engineering costs of design and development.
In the case of a typical computer program the proportions are reversed. The most important element of the product cost is the human effort in design and development while the cost of manufacturing is proportionally insignificant.
### 1.2 Software Qualities
An engineered product is usually associated with a list of qualities that define its usability.
For example, in performing its functions a bridge supports a predetermined weight and withstands a given wind force. An airplane is capable of transporting a
specific load, at a certain speed and altitude.
By the same token, a software product is associated with a given set of qualities that define its functionality.
The principal goals of software engineering is to define, specify, and measure software qualities and to describe the principles that can be applied to achieve them.
The classification of software qualities can be based on the relation with the software product. In this sense we can speak of qualities desirable to the user,to the developer, or to the manager.
The Table lists some qualities according to this classification.

### 1.3 Principles of Software Engineering
We started this chapter on the assumption that software development is a `creative activity` and that programming is `not an exact science`.
From this point of view even the term software engineering may be considered unsuitable since we could preferably
speak of `software development technique`, which term does not imply the rigor of a formal engineering approach.
In our opinion it is a `mistake` to assume that programs can be mechanically generated by some `mechanical methodology`, no matter
how sophisticated.
When software engineering falls short of producing the expected results it is because we `over-stressed the scientific and technical aspects` of program development over those that are `artistic or aesthetic` in nature or that depend on talent, personal endowments, or know-how.
Nevertheless, as there is `technique in art`, there is `technique in program development`.
Software engineering is the `conventional` name that `groups` the technical and scientific aspects of program development.
>**Software Engineering** is **a systematic approach** to the design, development, operation, and maintenance of a software system.
>
>* 软件工程是设计、开发、操作和维护软件系统的系统化方法。
**Smaller software projects** usually take place within the constraints of a limited budget. Often financial resources do not extend to hiring trained software project managers or specialists in the field of software engineering.
The person in charge of the project usually wears many hats, including that of project manager and software engineer. In fact, it is not unusual that the project manager/engineer is also part-time designer, programmer, tester, and documentation specialist.
What this all means is that the formality and rigor used in engineering a major project may not apply to one of lesser proportions. In other words, the strictness and rigidity of software engineering principles may have to be scaled down to accommodate the smaller projects.
In this sense we must distinguish between `principles, techniques, and tools` of software engineering.
**Principles** are general guidelines that are applicable at any stage of the program production process. They are the abstract statements that describe desirable properties, but that are of little use in practical software development.
For example, the principle that encourages high program reliability does `not tell us how to` make a program reliable.
**Techniques or methods** refer to `a particular approach` to solving a problem and help ensure that a product will have the desirable
properties.
**Tools** are specific resources that are used in implementing a particular technique.
In this case we may state as a principle that floating-point numbers are a desirable format for representing decimals in a digital machine. Also that the floating-point techniques described in the ANSI standard 754 are suitable for our application
and should be followed. Finally, that a particular library of floating-point routines, which complies with ANSI 754, would be an adequate tool for implementing the mathematical functions required in our application.
The Figure graphically shows the relationship between these three elements.

### 1.4 Objectives of Software Engineering:
1. Maintainability
* It should be feasible for the software to evolve to meet changing requirements.
2. Correctness
* A software product is correct, if the different requirements as specified in the SRS document have been correctly implemented.
3. Reusability
* A software product has good reusability, if the different modules of the product can easily be reused to develop new products.
4. Testability
* Here software facilitates both the establishment of test criteria and the evaluation of the software with respect to those criteria.
5. Reliability
* It is an attribute of software quality. The extent to which a program can be expected to perform its desired function, over an arbitrary time period.
6. Portability
* In this case, software can be transferred from one computer system or environment to another.
7. Adaptability –
* In this case, software allows differing system constraints and user needs to be satisfied by making changes to the software.
## 2 Software Engineering Paradigms
Computer scientists refer to the process of planning and organizing a program as software development.
It includes project planning, systems and requirements analysis, data structure design, algorithm selection and evaluation, coding,
estimation of program correctness, and maintenance procedures.
There are several paradigms to software development.
Three of these paradigms have been extensively discussed in the literature:
* the waterfall model(瀑布模型), the prototype methods(原型方法), and the spiral model(螺旋模式)
### 2.1 Waterfall Model
This classical Waterfall Model of a software engineering project is based on the notion of a system life-cycle.
The waterfall model consists of several phases shown in the Figure.
As you can see, the figure resembles a waterfall, in which the results of each phase flow **down** to the next.

**1 The specification phase(规范定义阶段)** consists of `a requirements gathering process` through analysis and systems engineering.
Whenever the project must interface with existing software or hardware elements the specification phase must include a systems requirements definition.
During this phase customer and developer work very closely: the customer provides the requirements and the developer reflects these requirements in a formal specification that is, in turn, reviewed by the customer.
The requirements/specification cycles continue until both parties agree that the project has been clearly and unambiguously defined.
>The programmers determine **what the program** will do.
>
>This is a process of clarifying the **specifications(规范说明书)** for the problem
**2 The design phase(设计阶段)** on four elements: data structures, program architecture, procedures, and interfaces(数据结构,程序架构,过程和接口).
The design stage is often the most critical and difficult one.
>The programmers determine **how the program** will do its task
**3 The coding phase(编码阶段)**: The programmers write the program,then convert the design into a machine-executable product.
**4 The verification phase(测试阶段)** Once the code executes in a machine it must be evaluated for correctness. This means that we must ascertain that it meets the requirements developed during the specifications phase and that it is free from defects.
Although this phase is sometimes associated with debugging, it should also include all formal and experimental verifications of program correctness
**5 Maintenance phase(维护阶段)**—Programs usually have a long life; a life span of 5 to 15 years is common for software.
During this time, requirements change, errors are detected, and minor or major modifications are made.
Maintenance procedures require revisiting all the stages of the software life-cycle, as depicted by the dotted arrow in the above Figure
A mistake detected in one phase often requires the developer to **back up** and redo some of the work in the **previous** phase.
Modifications made during maintenance also require backing up to earlier phases.
Taken together, these phases are also called **the software development life cycle(软件生命周期)**.
>软件生命周期(Software Life Cycle)是软件的产生直到报废或停止使用的生命周期
Although the diagram depicts distinct phases, this does not mean that developers must analyze and design a complete system before coding it.
Modern software development is usually **incremental(增量)** and **iterative(迭代)**.
* This means that analysis(specification) and design may produce a rough `draft, skeletal` version, or **prototype** of a system for coding, and then back up to earlier phases to fill in more details after some testing.
Programs rarely work as hoped the first time they are run; hence, they should be subjected to extensive and careful **testing**.
Many people think that testing is an activity that applies only to the coding(implementation) and verification(Integration) phases; however, you should scrutinize the outputs of each phase carefully.
* Keep in mind that mistakes found **early** are much less expensive to correct than those found late.
The Figure illustrates some relative costs of repairing mistakes when found in different phases. These are not just financial costs but also costs in time and effort.

Keep in mind that the cost of developing software is not spread equally over the phases.The percentages shown in the Figure are typical.

You might think that coding(implementation) takes the most time and therefore costs the most.However, as you can see in the Figure, maintenance is the most expensive part of software development.
**The cost of maintenance can be reduced by careful analysis, design, and implementation.**
You should remember two points:
1. There is **more** to software development than `writing code`.
2. If you want to reduce the overall cost of software development, **write programs that are easy to maintain**. This requires thorough analysis, careful design, and a good coding style.
### 2.2 Prototyping
Many software development projects are of an **experimental or speculative** nature.
Consider the following examples:
* A research group wishes to determine **if it is possible** to develop an expert system that uses data obtained by remote-sensing satellites in order determine pollution levels in the lakes and streams of the United States.
* An entrepreneur wishes to determine **if it is feasible** to develop a word processing program in which the user is equipped with foot pedals that activate some of the program functions.
In either of these cases we can see that the software development project can **hardly be stated a priori**.
The objectives are described so generally that it is **difficult to define specific program requirements** that could serve as a base for a detailed design.
In both cases, as well as in many others in which `an initial detailed design is not possible or practical`, a **prototyping approach** could be a feasible alternative.
In prototyping the developer is able to create **a model of the software.**
* This model can later be used to better `define the final product` or to `ascertain its feasibility`.
The prototype can be
* `a simple paper model` of the software, which can be produced with little or no coding,
* `a working prototype` that implements a subset of the program functions, or
* `a complete program` in which some functions are not implemented.
The purpose of the prototype is to allow both customer and developer to `make decisions regarding the feasibility and practicality` of the project, and, if judged feasible and practical, to better define the final product.
Prototyping is often depicted as a development cycle with the sequence of steps shown in the Figure

Prototype development
* **begins** by collecting `requirements and specifications`.
Then
* the prototype is **designed**, usually by following an **abbreviated(缩略) process** which produces results quicker than conventional program design procedures.
* The prototype is **built**, also shortening the development processes by **skipping all processing steps** that are not strictly necessary for the purpose at hand.
The prototype is finally `evaluated`, first by the developer and later by the customer.
If necessary, it is further `refined` and tuned in an `iterative` cycle. The finished prototype is used to further define the final software product.
### 2.3 Spiral Model
This model, first suggested by Barry W. Boehm in 1988(巴利·玻姆), proposes to merge the best features of the life-cycle and the prototyping paradigm with the principle of **incremental** development
The Figure shows a spiral progression through four different stages.

Notice that the drawing in the above Figure is meant as a **general** illustration of the method and is not be interpreted literally.
For example, the number of cycles around the spiral will `vary from project to project`
unique feature of the spiral model is the introduction of a **risk analysis stage**, which culminates in a `go or no-go decision` at the conclusion of each development cycle.
However, this risk analysis phase is also its most **controversial** feature.
In the first place, risk analysis requires a particular expertise, and is trivialized when performed by un-trained personnel.
In fact, the risk analysis phase is undesirable if it can lead to invalid interpretation of results.
In addition, customers often believe that they performed a risk analysis of the project before deciding to undertake it, and that
further consideration of this matter is unnecessary.
Furthermore, the possibility that at the conclusion of each development cycle the entire project could be scrapped by a no-go decision may lead to apprehensions on the part of the customer.
On the other hand, if the difficulties and perils associated with the risk analysis phase can be conjured, then the spiral model constitutes **the most satisfactory paradigm for the development of large software systems**.
The **incremental** development approach proposed by this model, with its repeated **prototyping and riske valuation** phases, provides a **realistic** framework for program development.
Both customer and developer have repeated opportunities in which to identify possible defects and shortcomings and make the necessary adjustments.
### 2.4 A Pragmatic Approach
The practicing software developer must decide, in each case, which model or combinations of models are most suitable to the project at hand.
The decision is often based on **practical** risks and limitations rather than on theoretical applicability.
For example, a developer may consider that the most adequate paradigm is the prototyping model, but a substantial risk that the customer will misinterpret the results advises against its use.
In another case a project may fit quite well within the spiral model but the fact that personnel trained in risk analysis will not be available suggests a modification of the paradigm or the adoption of the more conventional waterfall model.
A wise man once said: **“All systems and no system: behold the best system.”**
This maxim is quite applicable to the various software engineering paradigms mentioned in the preceding sections, in particular when they concern smaller projects in which development time and resources are limited.
The most common scenario is a combination of paradigms.
Often the most useful one is a spiral model. Since the spiral model is in itself a combination of the waterfall and the prototyping model, all of the mentioned paradigms will actually be used.
### 2.5 `Concurrent` Documentation
One of the **most important lessons** of software engineering refers to the need for `adequate and rigorous project documentation`.
* By the same token, the **most notable** difference between a correctly engineered development project and a haphazard effort
is the **documentation**.
Too often the tendency has been to consider program documentation as a `secondary` problem, one that can be addressed once the project
is finished.
This tendency is probably traceable to the same human fallacy that makes some programmers believe that `comments` can be inserted into the code **after** the programming has concluded.
As `writing comments` is part of the `chore` of programming,`documentation` is part of the task of program `development`.
* Either one **cannot** be approached as an **afterthought**, at risk of writing spaghetti code or of developing undecipherable projects.
It is only by realizing that documentation is one of the `fundamental` results of a development project, and that it `should never be an afterthought` at project conclusion time, that we can invalidate these argument
In regards to software project development the following types of documentation can be clearly identified:
1. Written `reports` that `mark` the `conclusion` of a phase of the development cycle.
* These documents are sometimes called the deliverables(可交付成果), since they are often presented to the client as each development phases concludes.
* Typical deliverables are the feasibility study, the analysis and requirements document, and the detailed design document.
2. User manuals and training guides, which can be printed or online.
3. Operations documents, more often found in large computer environments, include run-time schedules, input and output forms and media, delivery, routing, and distribution charts, data file specifications, update schedules, recovery procedures, and security controls.
4. The project scrapbook is used to **collect** memos, schedules, meeting minutes, and other communications generated during the project
The following are undeniable advantages of **concurrently documenting** the development project:
1. A well-documented project is better able to resist personnel changes since new programmers can catch up by studying the project documents.
2. Documentation can serve as a management tool by requiring that each development stage conclude in a document, which must be approved before the next stage can proceed.
3. **Concurrent documentation** establishes a project history and can serve, among other things, as a progress report. Documents can be used as scheduling landmarks and therefore serve to measure and evaluate project progress
The **most important principle** of project documentation is that of **concurrency**.
Documentation must be a substantial part of the development effort and must take place **simultaneously** with each development phase.
At the same time, documentation is often the development activity most easily postponed or even sacrificed. When time is running short it is tempting to defer documentation.
At this point the project manager must be aware that when
* `documentation loses its concurrency it also loses a great portion of its usefulness`.
## 3 The Recommended Practices for Scientific Computing
Greg Wilson, Co-founder of Software Carpentry
* [Best Practices for Scientific Computing](https://journals.plos.org/plosbiology/article?id=10.1371/journal.pbio.1001745)
* [Good enough practices in scientific computing](https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1005510)
* [Ten simple rules for making research software more robust](https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1005412)
<div id="section1" class="section toc-section"><a id="s1a" name="s1a" class="link-target" title="Box 1. Summary of Best Practices"></a>
<h3>3.1 Best Practices for Scientific Computing</h3>
<ol class="order">
<li>Write programs for people, not computers.
<ol class="alpha-lower">
<li>A program should not require its readers to hold more than a handful of facts in memory at once.</li>
<li>Make names consistent, distinctive, and meaningful.</li>
<li>Make code style and formatting consistent.</li>
</ol></li>
<li>Let the computer do the work.
<ol class="alpha-lower">
<li>Make the computer repeat tasks.</li>
<li>Save recent commands in a file for re-use.</li>
<li>Use a build tool to automate workflows.</li>
</ol></li>
<li>Make incremental changes.
<ol class="alpha-lower">
<li>Work in small steps with frequent feedback and course correction.</li>
<li>Use a version control system.</li>
<li>Put everything that has been created manually in version control.</li>
</ol></li>
<li>Don't repeat yourself (or others).
<ol class="alpha-lower">
<li>Every piece of data must have a single authoritative representation in the system.</li>
<li>Modularize code rather than copying and pasting.</li>
<li>Re-use code instead of rewriting it.</li>
</ol></li>
<li>Plan for mistakes.
<ol class="alpha-lower">
<li>Add assertions to programs to check their operation.</li>
<li>Use an off-the-shelf unit testing library.</li>
<li>Turn bugs into test cases.</li>
<li>Use a symbolic debugger.</li>
</ol></li>
<li>Optimize software only after it works correctly.
<ol class="alpha-lower">
<li>Use a profiler to identify bottlenecks.</li>
<li>Write code in the highest-level language possible.</li>
</ol></li>
<li>Document design and purpose, not mechanics.
<ol class="alpha-lower">
<li>Document interfaces and reasons, not implementations.</li>
<li>Refactor code in preference to explaining how it works.</li>
<li>Embed the documentation for a piece of software in that software.</li>
</ol></li>
<li>Collaborate.
<ol class="alpha-lower">
<li>Use pre-merge code reviews.</li>
<li>Use pair programming when bringing someone new up to speed and when tackling particularly tricky problems.</li>
<li>Use an issue tracking tool.</li>
</ol></li>
</ol></div>
</div></div>
<div id="section1" class="section toc-section"><a id="sec003" name="sec003" class="link-target" title="Box 1. Summary of practices"></a>
<h3>3.2 Good enough practices in scientific computing</h3>
<ol class="order">
<li>Data management
<ol class="alpha-lower">
<li>Save the raw data.</li>
<li>Ensure that raw data are backed up in more than one location.</li>
<li>Create the data you wish to see in the world.</li>
<li>Create analysis-friendly data.</li>
<li>Record all the steps used to process data.</li>
<li>Anticipate the need to use multiple tables, and use a unique identifier for every record.</li>
<li>Submit data to a reputable DOI-issuing repository so that others can access and cite it.</li>
</ol></li>
<li>Software
<ol class="alpha-lower">
<li>Place a brief explanatory comment at the start of every program.</li>
<li>Decompose programs into functions.</li>
<li>Be ruthless about eliminating duplication.</li>
<li>Always search for well-maintained software libraries that do what you need.</li>
<li>Test libraries before relying on them.</li>
<li>Give functions and variables meaningful names.</li>
<li>Make dependencies and requirements explicit.</li>
<li>Do not comment and uncomment sections of code to control a program's behavior.</li>
<li>Provide a simple example or test data set.</li>
<li>Submit code to a reputable DOI-issuing repository.</li>
</ol></li>
<li>Collaboration
<ol class="alpha-lower">
<li>Create an overview of your project.</li>
<li>Create a shared "to-do" list for the project.</li>
<li>Decide on communication strategies.</li>
<li>Make the license explicit.</li>
<li>Make the project citable.</li>
</ol></li>
<li>Project organization
<ol class="alpha-lower">
<li>Put each project in its own directory, which is named after the project.</li>
<li>Put text documents associated with the project in the <span class="monospace">doc</span> directory.</li>
<li>Put raw data and metadata in a data directory and files generated during cleanup and analysis in a results directory.</li>
<li>Put project source code in the <span class="monospace">src</span> directory.</li>
<li>Put external scripts or compiled programs in the <span class="monospace">bin</span> directory.</li>
<li>Name all files to reflect their content or function.</li>
</ol></li>
<li>Keeping track of changes
<ol class="alpha-lower">
<li>Back up (almost) everything created by a human being as soon as it is created.</li>
<li>Keep changes small.</li>
<li>Share changes frequently.</li>
<li>Create, maintain, and use a checklist for saving and sharing changes to the project.</li>
<li>Store each project in a folder that is mirrored off the researcher's working machine.</li>
<li>Add a file called <span class="monospace">CHANGELOG.txt</span> to the project's <span class="monospace">docs</span> subfolder.</li>
<li>Copy the entire project whenever a significant change has been made.</li>
<li>Use a version control system.</li>
</ol></li>
<li>Manuscripts
<ol class="alpha-lower">
<li>Write manuscripts using online tools with rich formatting, change tracking, and reference management.</li>
<li>Write the manuscript in a plain text format that permits version control.</li>
</ol></li>
</ol></div>
</div></div>
### 3.3 Ten simple rules for making research software more robust
https://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1005412
What is **“robust”** software?
We implied above that it is software that works for people other than the original author and on machines other than its creator’s.
More specifically, we mean that:
* it can be installed on more than one computer with relative ease,
* it works consistently as advertised, and
* it can be integrated with other tools.
Our rules are generic and can be applied to all languages, libraries, packages, documentation styles, and operating systems for both closed-source and open-source software.
1. Use version control
2. Document your code and usage
3. Make common operations easy to control
4. Version your releases
5. Reuse software (within reason)
6. Rely on build tools and package managers for installation
7. Do not require root or other special privileges to install or run
8. Eliminate hard-coded paths
9. Include a small test set that can be run to ensure the software is actually working
10. Produce identical results when given identical inputs
## 4 The Diagrams for Visual Software Modelling
Many diagrams have been proposed over the years for visual software modelling,in order to better understand, maintain, or document information.
These diagrams have achieved widespread acceptance:
[Flow Chart](https://en.wikipedia.org/wiki/Flowchart)
* A flowchart is a type of diagram that represents a workflow or process. A flowchart can also be defined as a diagrammatic representation of an algorithm, a step-by-step approach to solving a task.
* The flowchart shows the steps as boxes of various kinds, and their order by connecting the boxes with arrows. This diagrammatic representation illustrates a solution model to a given problem. Flowcharts are used in analyzing, designing, documenting or managing a process or program in various fields
[Data Flow Diagrams(DFD)](https://en.wikipedia.org/wiki/Data-flow_diagram)
* A data-flow diagram is a way of representing a flow of data through a process or a system (usually an information system). The DFD also provides information about the outputs and inputs of each entity and the process itself. A data-flow diagram has no control flow, there are no decision rules and no loops
[Entity-Relationship(E-R) Model Diagrams](https://en.wikipedia.org/wiki/Entity%E2%80%93relationship_model)
* An entity–relationship model (or ER model) describes interrelated things of interest in a specific domain of knowledge. A basic ER model is composed of entity types (which classify the things of interest) and specifies relationships that can exist between entities (instances of those entity types).
[Unified Modeling Language(UML) Model diagram](https://en.wikipedia.org/wiki/Unified_Modeling_Language)
* The Unified Modeling Language (UML) is a general-purpose, developmental, modeling language in the field of software engineering that is intended to provide a standard way to visualize the design of a system
* UML 2 has many types of diagrams, which are divided into two categories.Some types represent structural information, and the rest represent general types of behavior, including a few that represent different aspects of interactions. These diagrams can be categorized hierarchically as shown in the following class diagram
| github_jupyter |
```
# dataset
# https://cogcomp.seas.upenn.edu/Data/QA/QC/
import pandas as pd
import numpy as np
from bs4 import BeautifulSoup
import pickle
import string
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
import nltk
from nltk.corpus import stopwords
from nltk.stem.porter import PorterStemmer
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras.preprocessing.text import text_to_word_sequence, one_hot
from tensorflow.keras.preprocessing.text import Tokenizer
from tensorflow.keras.preprocessing.sequence import pad_sequences
from tensorflow.keras.utils import to_categorical
#only if GPU is available
physical_devices = tf.config.list_physical_devices("GPU")
tf.config.experimental.set_memory_growth(physical_devices[0], True)
def remove_html(text) :
'''
parameters : text - string
removes HTML content from the text such (eg. tags - <title></title>)
returns text_without_html - string
'''
soup = BeautifulSoup(text)
text_without_html = soup.get_text()
return text_without_html
def remove_punctuation(text) :
'''
parameters : text - string
removes punctuation from the text (eg. '.', '!', '?')
returns : text_without_puntuation - string
'''
text_without_puntuation = " ".join([[char for char in text if char not in string.punctuation]])
return text_without_puntuation
def remove_stop_words(token) :
'''
parameters : tokens - list of words
removes stop words from the list (eg. 'a', 'the', 'are')
returns : tokens_without_stop_words - list of words
'''
stop_words = stopwords.words('english')
token_without_stop_words = [word for word in token if word not in stop_words]
return token_without_stop_words
def stemmed_words(tokens) :
'''
parameters : tokens - list of words
stems the words in the list (eg. playing -> play)
returns : stemmed_words - list of words
'''
porter = PorterStemmer()
stemmed_words = [porter.stem(word) for word in tokens]
return stemmed_words
def clean_data(sentences) :
'''
parameters : sentences - list of sentences
cleans the sentences by
converting the sentences into tokens and removing stop words
joins the tokens to form a sentence again
returns : texts - list of cleaned sentences
'''
texts = []
for sentence in sentences :
tokens = text_to_word_sequence(sentence)
tokens = remove_stop_words(tokens)
sentence = " ".join(tokens)
texts.append(sentence)
return texts
def make_tokenizer(dataset) :
'''
parameters : dataset - list of sentences
creates a vocabulary of words based on the list of inputted sentences using the Tokenizer object
returns : tokenizer - Tokenizer object
'''
tokenizer = Tokenizer()
tokenizer.fit_on_texts(dataset)
return tokenizer
def encode_texts(dataset, tokenizer) :
'''
parameters : dataset - list of sentences
tokenizer - Tokenizer object initialized using dataset
encodes the text sequences in the dataset by mapping the index of the word in the vocabulary to each word
in the dataset
returns : encoded_docs - list of encoded sentences
'''
encoded_docs = tokenizer.texts_to_sequences(dataset)
return encoded_docs
def encode_labels(labels) :
'''
parameters - list of labels/classes for each input
maps each label to an index and encodes the label's with its corresponding index
returns - list of encoded labels/classes for each input
'''
le = LabelEncoder()
le.fit(labels)
return le.transform(labels), len(le.classes_)
train_trec = open('./data/TREC/train_5500.label')
x_train = []
y_train = []
for x in train_trec :
data_split = x.split(':')
x_train.append(data_split[1])
y_train.append(data_split[0])
train_trec.close()
test_trec = open('./data/TREC/TREC_10.label')
x_test = []
y_test = []
for x in test_trec :
data_split = x.split(':')
x_test.append(data_split[1])
y_test.append(data_split[0])
test_trec.close()
x_train = clean_data(x_train)
y_train, num_classes= encode_labels(y_train)
y_test, _ = encode_labels(y_test)
y_train = to_categorical(y_train, num_classes=num_classes)
y_test = to_categorical(y_test, num_classes=num_classes)
tokenizer = make_tokenizer(x_train)
num_words = len(tokenizer.word_index) + 1
x_train = pad_sequences(encode_texts(x_train, tokenizer), padding='post')
max_length = x_train.shape[1]
x_test = pad_sequences(encode_texts(x_test, tokenizer), maxlen=max_length, padding='post')
x_train = np.array(x_train)
x_test = np.array(x_test)
y_train = np.array(y_train)
y_test = np.array(y_test)
np.savez('./data/encoded_dataset_trec.npz', name1=x_train, name2=y_train, name3=x_test, name4=y_test)
vocab_file = open("./data/vocab_trec.pkl", "wb")
pickle.dump(tokenizer.word_index, vocab_file)
vocab_file.close()
```
| github_jupyter |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.