code
stringlengths 2.5k
150k
| kind
stringclasses 1
value |
|---|---|
# 09 Strain Gage
This is one of the most commonly used sensor. It is used in many transducers. Its fundamental operating principle is fairly easy to understand and it will be the purpose of this lecture.
A strain gage is essentially a thin wire that is wrapped on film of plastic.
<img src="img/StrainGage.png" width="200">
The strain gage is then mounted (glued) on the part for which the strain must be measured.
<img src="img/Strain_gauge_2.jpg" width="200">
## Stress, Strain
When a beam is under axial load, the axial stress, $\sigma_a$, is defined as:
\begin{align*}
\sigma_a = \frac{F}{A}
\end{align*}
with $F$ the axial load, and $A$ the cross sectional area of the beam under axial load.
<img src="img/BeamUnderStrain.png" width="200">
Under the load, the beam of length $L$ will extend by $dL$, giving rise to the definition of strain, $\epsilon_a$:
\begin{align*}
\epsilon_a = \frac{dL}{L}
\end{align*}
The beam will also contract laterally: the cross sectional area is reduced by $dA$. This results in a transverval strain $\epsilon_t$. The transversal and axial strains are related by the Poisson's ratio:
\begin{align*}
\nu = - \frac{\epsilon_t }{\epsilon_a}
\end{align*}
For a metal the Poission's ratio is typically $\nu = 0.3$, for an incompressible material, such as rubber (or water), $\nu = 0.5$.
Within the elastic limit, the axial stress and axial strain are related through Hooke's law by the Young's modulus, $E$:
\begin{align*}
\sigma_a = E \epsilon_a
\end{align*}
<img src="img/ElasticRegime.png" width="200">
## Resistance of a wire
The electrical resistance of a wire $R$ is related to its physical properties (the electrical resistiviy, $\rho$ in $\Omega$/m) and its geometry: length $L$ and cross sectional area $A$.
\begin{align*}
R = \frac{\rho L}{A}
\end{align*}
Mathematically, the change in wire dimension will result inchange in its electrical resistance. This can be derived from first principle:
\begin{align}
\frac{dR}{R} = \frac{d\rho}{\rho} + \frac{dL}{L} - \frac{dA}{A}
\end{align}
If the wire has a square cross section, then:
\begin{align*}
A & = L'^2 \\
\frac{dA}{A} & = \frac{d(L'^2)}{L'^2} = \frac{2L'dL'}{L'^2} = 2 \frac{dL'}{L'}
\end{align*}
We have related the change in cross sectional area to the transversal strain.
\begin{align*}
\epsilon_t = \frac{dL'}{L'}
\end{align*}
Using the Poisson's ratio, we can relate then relate the change in cross-sectional area ($dA/A$) to axial strain $\epsilon_a = dL/L$.
\begin{align*}
\epsilon_t &= - \nu \epsilon_a \\
\frac{dL'}{L'} &= - \nu \frac{dL}{L} \; \text{or}\\
\frac{dA}{A} & = 2\frac{dL'}{L'} = -2 \nu \frac{dL}{L}
\end{align*}
Finally we can substitute express $dA/A$ in eq. for $dR/R$ and relate change in resistance to change of wire geometry, remembering that for a metal $\nu =0.3$:
\begin{align}
\frac{dR}{R} & = \frac{d\rho}{\rho} + \frac{dL}{L} - \frac{dA}{A} \\
& = \frac{d\rho}{\rho} + \frac{dL}{L} - (-2\nu \frac{dL}{L}) \\
& = \frac{d\rho}{\rho} + 1.6 \frac{dL}{L} = \frac{d\rho}{\rho} + 1.6 \epsilon_a
\end{align}
It also happens that for most metals, the resistivity increases with axial strain. In general, one can then related the change in resistance to axial strain by defining the strain gage factor:
\begin{align}
S = 1.6 + \frac{d\rho}{\rho}\cdot \frac{1}{\epsilon_a}
\end{align}
and finally, we have:
\begin{align*}
\frac{dR}{R} = S \epsilon_a
\end{align*}
$S$ is materials dependent and is typically equal to 2.0 for most commercially availabe strain gages. It is dimensionless.
Strain gages are made of thin wire that is wraped in several loops, effectively increasing the length of the wire and therefore the sensitivity of the sensor.
_Question:
Explain why a longer wire is necessary to increase the sensitivity of the sensor_.
Most commercially available strain gages have a nominal resistance (resistance under no load, $R_{ini}$) of 120 or 350 $\Omega$.
Within the elastic regime, strain is typically within the range $10^{-6} - 10^{-3}$, in fact strain is expressed in unit of microstrain, with a 1 microstrain = $10^{-6}$. Therefore, changes in resistances will be of the same order. If one were to measure resistances, we will need a dynamic range of 120 dB, whih is typically very expensive. Instead, one uses the Wheatstone bridge to transform the change in resistance to a voltage, which is easier to measure and does not require such a large dynamic range.
## Wheatstone bridge:
<img src="img/WheatstoneBridge.png" width="200">
The output voltage is related to the difference in resistances in the bridge:
\begin{align*}
\frac{V_o}{V_s} = \frac{R_1R_3-R_2R_4}{(R_1+R_4)(R_2+R_3)}
\end{align*}
If the bridge is balanced, then $V_o = 0$, it implies: $R_1/R_2 = R_4/R_3$.
In practice, finding a set of resistors that balances the bridge is challenging, and a potentiometer is used as one of the resistances to do minor adjustement to balance the bridge. If one did not do the adjustement (ie if we did not zero the bridge) then all the measurement will have an offset or bias that could be removed in a post-processing phase, as long as the bias stayed constant.
If each resistance $R_i$ is made to vary slightly around its initial value, ie $R_i = R_{i,ini} + dR_i$. For simplicity, we will assume that the initial value of the four resistances are equal, ie $R_{1,ini} = R_{2,ini} = R_{3,ini} = R_{4,ini} = R_{ini}$. This implies that the bridge was initially balanced, then the output voltage would be:
\begin{align*}
\frac{V_o}{V_s} = \frac{1}{4} \left( \frac{dR_1}{R_{ini}} - \frac{dR_2}{R_{ini}} + \frac{dR_3}{R_{ini}} - \frac{dR_4}{R_{ini}} \right)
\end{align*}
Note here that the changes in $R_1$ and $R_3$ have a positive effect on $V_o$, while the changes in $R_2$ and $R_4$ have a negative effect on $V_o$. In practice, this means that is a beam is a in tension, then a strain gage mounted on the branch 1 or 3 of the Wheatstone bridge will produce a positive voltage, while a strain gage mounted on branch 2 or 4 will produce a negative voltage. One takes advantage of this to increase sensitivity to measure strain.
### Quarter bridge
One uses only one quarter of the bridge, ie strain gages are only mounted on one branch of the bridge.
\begin{align*}
\frac{V_o}{V_s} = \pm \frac{1}{4} \epsilon_a S
\end{align*}
Sensitivity, $G$:
\begin{align*}
G = \frac{V_o}{\epsilon_a} = \pm \frac{1}{4}S V_s
\end{align*}
### Half bridge
One uses half of the bridge, ie strain gages are mounted on two branches of the bridge.
\begin{align*}
\frac{V_o}{V_s} = \pm \frac{1}{2} \epsilon_a S
\end{align*}
### Full bridge
One uses of the branches of the bridge, ie strain gages are mounted on each branch.
\begin{align*}
\frac{V_o}{V_s} = \pm \epsilon_a S
\end{align*}
Therefore, as we increase the order of bridge, the sensitivity of the instrument increases. However, one should be carefull how we mount the strain gages as to not cancel out their measurement.
_Exercise_
1- Wheatstone bridge
<img src="img/WheatstoneBridge.png" width="200">
> How important is it to know \& match the resistances of the resistors you employ to create your bridge?
> How would you do that practically?
> Assume $R_1=120\,\Omega$, $R_2=120\,\Omega$, $R_3=120\,\Omega$, $R_4=110\,\Omega$, $V_s=5.00\,\text{V}$. What is $V_\circ$?
```
Vs = 5.00
Vo = (120**2-120*110)/(230*240) * Vs
print('Vo = ',Vo, ' V')
# typical range in strain a strain gauge can measure
# 1 -1000 micro-Strain
AxialStrain = 1000*10**(-6) # axial strain
StrainGageFactor = 2
R_ini = 120 # Ohm
R_1 = R_ini+R_ini*StrainGageFactor*AxialStrain
print(R_1)
Vo = (120**2-120*(R_1))/((120+R_1)*240) * Vs
print('Vo = ', Vo, ' V')
```
> How important is it to know \& match the resistances of the resistors you employ to create your bridge?
> How would you do that practically?
> Assume $R_1= R_2 =R_3=120\,\Omega$, $R_4=120.01\,\Omega$, $V_s=5.00\,\text{V}$. What is $V_\circ$?
```
Vs = 5.00
Vo = (120**2-120*120.01)/(240.01*240) * Vs
print(Vo)
```
2- Strain gage 1:
One measures the strain on a bridge steel beam. The modulus of elasticity is $E=190$ GPa. Only one strain gage is mounted on the bottom of the beam; the strain gage factor is $S=2.02$.
> a) What kind of electronic circuit will you use? Draw a sketch of it.
> b) Assume all your resistors including the unloaded strain gage are balanced and measure $120\,\Omega$, and that the strain gage is at location $R_2$. The supply voltage is $5.00\,\text{VDC}$. Will $V_\circ$ be positive or negative when a downward load is added?
In practice, we cannot have all resistances = 120 $\Omega$. at zero load, the bridge will be unbalanced (show $V_o \neq 0$). How could we balance our bridge?
Use a potentiometer to balance bridge, for the load cell, we ''zero'' the instrument.
Other option to zero-out our instrument? Take data at zero-load, record the voltage, $V_{o,noload}$. Substract $V_{o,noload}$ to my data.
> c) For a loading in which $V_\circ = -1.25\,\text{mV}$, calculate the strain $\epsilon_a$ in units of microstrain.
\begin{align*}
\frac{V_o}{V_s} & = - \frac{1}{4} \epsilon_a S\\
\epsilon_a & = -\frac{4}{S} \frac{V_o}{V_s}
\end{align*}
```
S = 2.02
Vo = -0.00125
Vs = 5
eps_a = -1*(4/S)*(Vo/Vs)
print(eps_a)
```
> d) Calculate the axial stress (in MPa) in the beam under this load.
> e) You now want more sensitivity in your measurement, you install a second strain gage on to
p of the beam. Which resistor should you use for this second active strain gage?
> f) With this new setup and the same applied load than previously, what should be the output voltage?
3- Strain Gage with Long Lead Wires
<img src="img/StrainGageLongWires.png" width="360">
A quarter bridge strain gage Wheatstone bridge circuit is constructed with $120\,\Omega$ resistors and a $120\,\Omega$ strain gage. For this practical application, the strain gage is located very far away form the DAQ station and the lead wires to the strain gage are $10\,\text{m}$ long and the lead wire have a resistance of $0.080\,\Omega/\text{m}$. The lead wire resistance can lead to problems since $R_{lead}$ changes with temperature.
> Design a modified circuit that will cancel out the effect of the lead wires.
## Homework
| github_jupyter |
```
#export
from fastai.basics import *
from fastai.tabular.core import *
from fastai.tabular.model import *
from fastai.tabular.data import *
#hide
from nbdev.showdoc import *
#default_exp tabular.learner
```
# Tabular learner
> The function to immediately get a `Learner` ready to train for tabular data
The main function you probably want to use in this module is `tabular_learner`. It will automatically create a `TabulaModel` suitable for your data and infer the irght loss function. See the [tabular tutorial](http://docs.fast.ai/tutorial.tabular) for an example of use in context.
## Main functions
```
#export
@log_args(but_as=Learner.__init__)
class TabularLearner(Learner):
"`Learner` for tabular data"
def predict(self, row):
tst_to = self.dls.valid_ds.new(pd.DataFrame(row).T)
tst_to.process()
tst_to.conts = tst_to.conts.astype(np.float32)
dl = self.dls.valid.new(tst_to)
inp,preds,_,dec_preds = self.get_preds(dl=dl, with_input=True, with_decoded=True)
i = getattr(self.dls, 'n_inp', -1)
b = (*tuplify(inp),*tuplify(dec_preds))
full_dec = self.dls.decode((*tuplify(inp),*tuplify(dec_preds)))
return full_dec,dec_preds[0],preds[0]
show_doc(TabularLearner, title_level=3)
```
It works exactly as a normal `Learner`, the only difference is that it implements a `predict` method specific to work on a row of data.
```
#export
@log_args(to_return=True, but_as=Learner.__init__)
@delegates(Learner.__init__)
def tabular_learner(dls, layers=None, emb_szs=None, config=None, n_out=None, y_range=None, **kwargs):
"Get a `Learner` using `dls`, with `metrics`, including a `TabularModel` created using the remaining params."
if config is None: config = tabular_config()
if layers is None: layers = [200,100]
to = dls.train_ds
emb_szs = get_emb_sz(dls.train_ds, {} if emb_szs is None else emb_szs)
if n_out is None: n_out = get_c(dls)
assert n_out, "`n_out` is not defined, and could not be infered from data, set `dls.c` or pass `n_out`"
if y_range is None and 'y_range' in config: y_range = config.pop('y_range')
model = TabularModel(emb_szs, len(dls.cont_names), n_out, layers, y_range=y_range, **config)
return TabularLearner(dls, model, **kwargs)
```
If your data was built with fastai, you probably won't need to pass anything to `emb_szs` unless you want to change the default of the library (produced by `get_emb_sz`), same for `n_out` which should be automatically inferred. `layers` will default to `[200,100]` and is passed to `TabularModel` along with the `config`.
Use `tabular_config` to create a `config` and cusotmize the model used. There is just easy access to `y_range` because this argument is often used.
All the other arguments are passed to `Learner`.
```
path = untar_data(URLs.ADULT_SAMPLE)
df = pd.read_csv(path/'adult.csv')
cat_names = ['workclass', 'education', 'marital-status', 'occupation', 'relationship', 'race']
cont_names = ['age', 'fnlwgt', 'education-num']
procs = [Categorify, FillMissing, Normalize]
dls = TabularDataLoaders.from_df(df, path, procs=procs, cat_names=cat_names, cont_names=cont_names,
y_names="salary", valid_idx=list(range(800,1000)), bs=64)
learn = tabular_learner(dls)
#hide
tst = learn.predict(df.iloc[0])
#hide
#test y_range is passed
learn = tabular_learner(dls, y_range=(0,32))
assert isinstance(learn.model.layers[-1], SigmoidRange)
test_eq(learn.model.layers[-1].low, 0)
test_eq(learn.model.layers[-1].high, 32)
learn = tabular_learner(dls, config = tabular_config(y_range=(0,32)))
assert isinstance(learn.model.layers[-1], SigmoidRange)
test_eq(learn.model.layers[-1].low, 0)
test_eq(learn.model.layers[-1].high, 32)
#export
@typedispatch
def show_results(x:Tabular, y:Tabular, samples, outs, ctxs=None, max_n=10, **kwargs):
df = x.all_cols[:max_n]
for n in x.y_names: df[n+'_pred'] = y[n][:max_n].values
display_df(df)
```
## Export -
```
#hide
from nbdev.export import notebook2script
notebook2script()
```
| github_jupyter |
# Aerospike Connect for Spark - SparkML Prediction Model Tutorial
## Tested with Java 8, Spark 3.0.0, Python 3.7, and Aerospike Spark Connector 3.0.0
## Summary
Build a linear regression model to predict birth weight using Aerospike Database and Spark.
Here are the features used:
- gestation weeks
- mother’s age
- father’s age
- mother’s weight gain during pregnancy
- [Apgar score](https://en.wikipedia.org/wiki/Apgar_score)
Aerospike is used to store the Natality dataset that is published by CDC. The table is accessed in Apache Spark using the Aerospike Spark Connector, and Spark ML is used to build and evaluate the model. The model can later be converted to PMML and deployed on your inference server for predictions.
### Prerequisites
1. Load Aerospike server if not alrady available - docker run -d --name aerospike -p 3000:3000 -p 3001:3001 -p 3002:3002 -p 3003:3003 aerospike
2. Feature key needs to be located in AS_FEATURE_KEY_PATH
3. [Download the connector](https://www.aerospike.com/enterprise/download/connectors/aerospike-spark/3.0.0/)
```
#IP Address or DNS name for one host in your Aerospike cluster.
#A seed address for the Aerospike database cluster is required
AS_HOST ="127.0.0.1"
# Name of one of your namespaces. Type 'show namespaces' at the aql prompt if you are not sure
AS_NAMESPACE = "test"
AS_FEATURE_KEY_PATH = "/etc/aerospike/features.conf"
AEROSPIKE_SPARK_JAR_VERSION="3.0.0"
AS_PORT = 3000 # Usually 3000, but change here if not
AS_CONNECTION_STRING = AS_HOST + ":"+ str(AS_PORT)
#Locate the Spark installation - this'll use the SPARK_HOME environment variable
import findspark
findspark.init()
# Below will help you download the Spark Connector Jar if you haven't done so already.
import urllib
import os
def aerospike_spark_jar_download_url(version=AEROSPIKE_SPARK_JAR_VERSION):
DOWNLOAD_PREFIX="https://www.aerospike.com/enterprise/download/connectors/aerospike-spark/"
DOWNLOAD_SUFFIX="/artifact/jar"
AEROSPIKE_SPARK_JAR_DOWNLOAD_URL = DOWNLOAD_PREFIX+AEROSPIKE_SPARK_JAR_VERSION+DOWNLOAD_SUFFIX
return AEROSPIKE_SPARK_JAR_DOWNLOAD_URL
def download_aerospike_spark_jar(version=AEROSPIKE_SPARK_JAR_VERSION):
JAR_NAME="aerospike-spark-assembly-"+AEROSPIKE_SPARK_JAR_VERSION+".jar"
if(not(os.path.exists(JAR_NAME))) :
urllib.request.urlretrieve(aerospike_spark_jar_download_url(),JAR_NAME)
else :
print(JAR_NAME+" already downloaded")
return os.path.join(os.getcwd(),JAR_NAME)
AEROSPIKE_JAR_PATH=download_aerospike_spark_jar()
os.environ["PYSPARK_SUBMIT_ARGS"] = '--jars ' + AEROSPIKE_JAR_PATH + ' pyspark-shell'
import pyspark
from pyspark.context import SparkContext
from pyspark.sql.context import SQLContext
from pyspark.sql.session import SparkSession
from pyspark.ml.linalg import Vectors
from pyspark.ml.regression import LinearRegression
from pyspark.sql.types import StringType, StructField, StructType, ArrayType, IntegerType, MapType, LongType, DoubleType
#Get a spark session object and set required Aerospike configuration properties
sc = SparkContext.getOrCreate()
print("Spark Verison:", sc.version)
spark = SparkSession(sc)
sqlContext = SQLContext(sc)
spark.conf.set("aerospike.namespace",AS_NAMESPACE)
spark.conf.set("aerospike.seedhost",AS_CONNECTION_STRING)
spark.conf.set("aerospike.keyPath",AS_FEATURE_KEY_PATH )
```
## Step 1: Load Data into a DataFrame
```
as_data=spark \
.read \
.format("aerospike") \
.option("aerospike.set", "natality").load()
as_data.show(5)
print("Inferred Schema along with Metadata.")
as_data.printSchema()
```
### To speed up the load process at scale, use the [knobs](https://www.aerospike.com/docs/connect/processing/spark/performance.html) available in the Aerospike Spark Connector.
For example, **spark.conf.set("aerospike.partition.factor", 15 )** will map 4096 Aerospike partitions to 32K Spark partitions. <font color=red> (Note: Please configure this carefully based on the available resources (CPU threads) in your system.)</font>
## Step 2 - Prep data
```
# This Spark3.0 setting, if true, will turn on Adaptive Query Execution (AQE), which will make use of the
# runtime statistics to choose the most efficient query execution plan. It will speed up any joins that you
# plan to use for data prep step.
spark.conf.set("spark.sql.adaptive.enabled", 'true')
# Run a query in Spark SQL to ensure no NULL values exist.
as_data.createOrReplaceTempView("natality")
sql_query = """
SELECT *
from natality
where weight_pnd is not null
and mother_age is not null
and father_age is not null
and father_age < 80
and gstation_week is not null
and weight_gain_pnd < 90
and apgar_5min != "99"
and apgar_5min != "88"
"""
clean_data = spark.sql(sql_query)
#Drop the Aerospike metadata from the dataset because its not required.
#The metadata is added because we are inferring the schema as opposed to providing a strict schema
columns_to_drop = ['__key','__digest','__expiry','__generation','__ttl' ]
clean_data = clean_data.drop(*columns_to_drop)
# dropping null values
clean_data = clean_data.dropna()
clean_data.cache()
clean_data.show(5)
#Descriptive Analysis of the data
clean_data.describe().toPandas().transpose()
```
## Step 3 Visualize Data
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import math
pdf = clean_data.toPandas()
#Histogram - Father Age
pdf[['father_age']].plot(kind='hist',bins=10,rwidth=0.8)
plt.xlabel('Fathers Age (years)',fontsize=12)
plt.legend(loc=None)
plt.style.use('seaborn-whitegrid')
plt.show()
'''
pdf[['mother_age']].plot(kind='hist',bins=10,rwidth=0.8)
plt.xlabel('Mothers Age (years)',fontsize=12)
plt.legend(loc=None)
plt.style.use('seaborn-whitegrid')
plt.show()
'''
pdf[['weight_pnd']].plot(kind='hist',bins=10,rwidth=0.8)
plt.xlabel('Babys Weight (Pounds)',fontsize=12)
plt.legend(loc=None)
plt.style.use('seaborn-whitegrid')
plt.show()
pdf[['gstation_week']].plot(kind='hist',bins=10,rwidth=0.8)
plt.xlabel('Gestation (Weeks)',fontsize=12)
plt.legend(loc=None)
plt.style.use('seaborn-whitegrid')
plt.show()
pdf[['weight_gain_pnd']].plot(kind='hist',bins=10,rwidth=0.8)
plt.xlabel('mother’s weight gain during pregnancy',fontsize=12)
plt.legend(loc=None)
plt.style.use('seaborn-whitegrid')
plt.show()
#Histogram - Apgar Score
print("Apgar Score: Scores of 7 and above are generally normal; 4 to 6, fairly low; and 3 and below are generally \
regarded as critically low and cause for immediate resuscitative efforts.")
pdf[['apgar_5min']].plot(kind='hist',bins=10,rwidth=0.8)
plt.xlabel('Apgar score',fontsize=12)
plt.legend(loc=None)
plt.style.use('seaborn-whitegrid')
plt.show()
```
## Step 4 - Create Model
**Steps used for model creation:**
1. Split cleaned data into Training and Test sets
2. Vectorize features on which the model will be trained
3. Create a linear regression model (Choose any ML algorithm that provides the best fit for the given dataset)
4. Train model (Although not shown here, you could use K-fold cross-validation and Grid Search to choose the best hyper-parameters for the model)
5. Evaluate model
```
# Define a function that collects the features of interest
# (mother_age, father_age, and gestation_weeks) into a vector.
# Package the vector in a tuple containing the label (`weight_pounds`) for that
# row.##
def vector_from_inputs(r):
return (r["weight_pnd"], Vectors.dense(float(r["mother_age"]),
float(r["father_age"]),
float(r["gstation_week"]),
float(r["weight_gain_pnd"]),
float(r["apgar_5min"])))
#Split that data 70% training and 30% Evaluation data
train, test = clean_data.randomSplit([0.7, 0.3])
#Check the shape of the data
train.show()
print((train.count(), len(train.columns)))
test.show()
print((test.count(), len(test.columns)))
# Create an input DataFrame for Spark ML using the above function.
training_data = train.rdd.map(vector_from_inputs).toDF(["label",
"features"])
# Construct a new LinearRegression object and fit the training data.
lr = LinearRegression(maxIter=5, regParam=0.2, solver="normal")
#Voila! your first model using Spark ML is trained
model = lr.fit(training_data)
# Print the model summary.
print("Coefficients:" + str(model.coefficients))
print("Intercept:" + str(model.intercept))
print("R^2:" + str(model.summary.r2))
model.summary.residuals.show()
```
### Evaluate Model
```
eval_data = test.rdd.map(vector_from_inputs).toDF(["label",
"features"])
eval_data.show()
evaluation_summary = model.evaluate(eval_data)
print("MAE:", evaluation_summary.meanAbsoluteError)
print("RMSE:", evaluation_summary.rootMeanSquaredError)
print("R-squared value:", evaluation_summary.r2)
```
## Step 5 - Batch Prediction
```
#eval_data contains the records (ideally production) that you'd like to use for the prediction
predictions = model.transform(eval_data)
predictions.show()
```
#### Compare the labels and the predictions, they should ideally match up for an accurate model. Label is the actual weight of the baby and prediction is the predicated weight
### Saving the Predictions to Aerospike for ML Application's consumption
```
# Aerospike is a key/value database, hence a key is needed to store the predictions into the database. Hence we need
# to add the _id column to the predictions using SparkSQL
predictions.createOrReplaceTempView("predict_view")
sql_query = """
SELECT *, monotonically_increasing_id() as _id
from predict_view
"""
predict_df = spark.sql(sql_query)
predict_df.show()
print("#records:", predict_df.count())
# Now we are good to write the Predictions to Aerospike
predict_df \
.write \
.mode('overwrite') \
.format("aerospike") \
.option("aerospike.writeset", "predictions")\
.option("aerospike.updateByKey", "_id") \
.save()
```
#### You can verify that data is written to Aerospike by using either [AQL](https://www.aerospike.com/docs/tools/aql/data_management.html) or the [Aerospike Data Browser](https://github.com/aerospike/aerospike-data-browser)
## Step 6 - Deploy
### Here are a few options:
1. Save the model to a PMML file by converting it using Jpmml/[pyspark2pmml](https://github.com/jpmml/pyspark2pmml) and load it into your production enviornment for inference.
2. Use Aerospike as an [edge database for high velocity ingestion](https://medium.com/aerospike-developer-blog/add-horsepower-to-ai-ml-pipeline-15ca42a10982) for your inference pipline.
| github_jupyter |
## Concurrency with asyncio
### Thread vs. coroutine
```
# spinner_thread.py
import threading
import itertools
import time
import sys
class Signal:
go = True
def spin(msg, signal):
write, flush = sys.stdout.write, sys.stdout.flush
for char in itertools.cycle('|/-\\'):
status = char + ' ' + msg
write(status)
flush()
write('\x08' * len(status))
time.sleep(.1)
if not signal.go:
break
write(' ' * len(status) + '\x08' * len(status))
def slow_function():
time.sleep(3)
return 42
def supervisor():
signal = Signal()
spinner = threading.Thread(target=spin, args=('thinking!', signal))
print('spinner object:', spinner)
spinner.start()
result = slow_function()
signal.go = False
spinner.join()
return result
def main():
result = supervisor()
print('Answer:', result)
if __name__ == '__main__':
main()
# spinner_asyncio.py
import asyncio
import itertools
import sys
@asyncio.coroutine
def spin(msg):
write, flush = sys.stdout.write, sys.stdout.flush
for char in itertools.cycle('|/-\\'):
status = char + ' ' + msg
write(status)
flush()
write('\x08' * len(status))
try:
yield from asyncio.sleep(.1)
except asyncio.CancelledError:
break
write(' ' * len(status) + '\x08' * len(status))
@asyncio.coroutine
def slow_function():
yield from asyncio.sleep(3)
return 42
@asyncio.coroutine
def supervisor():
#Schedule the execution of a coroutine object:
#wrap it in a future. Return a Task object.
spinner = asyncio.ensure_future(spin('thinking!'))
print('spinner object:', spinner)
result = yield from slow_function()
spinner.cancel()
return result
def main():
loop = asyncio.get_event_loop()
result = loop.run_until_complete(supervisor())
loop.close()
print('Answer:', result)
if __name__ == '__main__':
main()
# flags_asyncio.py
import asyncio
import aiohttp
from flags import BASE_URL, save_flag, show, main
@asyncio.coroutine
def get_flag(cc):
url = '{}/{cc}/{cc}.gif'.format(BASE_URL, cc=cc.lower())
resp = yield from aiohttp.request('GET', url)
image = yield from resp.read()
return image
@asyncio.coroutine
def download_one(cc):
image = yield from get_flag(cc)
show(cc)
save_flag(image, cc.lower() + '.gif')
return cc
def download_many(cc_list):
loop = asyncio.get_event_loop()
to_do = [download_one(cc) for cc in sorted(cc_list)]
wait_coro = asyncio.wait(to_do)
res, _ = loop.run_until_complete(wait_coro)
loop.close()
return len(res)
if __name__ == '__main__':
main(download_many)
# flags2_asyncio.py
import asyncio
import collections
import aiohttp
from aiohttp import web
import tqdm
from flags2_common import HTTPStatus, save_flag, Result, main
DEFAULT_CONCUR_REQ = 5
MAX_CONCUR_REQ = 1000
class FetchError(Exception):
def __init__(self, country_code):
self.country_code = country_code
@asyncio.coroutine
def get_flag(base_url, cc):
url = '{}/{cc}/{cc}.gif'.format(BASE_URL, cc=cc.lower())
resp = yield from aiohttp.ClientSession().get(url)
if resp.status == 200:
image = yield from resp.read()
return image
elif resp.status == 404:
raise web.HTTPNotFound()
else:
raise aiohttp.HttpProcessingError(
code=resp.status, message=resp.reason, headers=resp.headers)
@asyncio.coroutine
def download_one(cc, base_url, semaphore, verbose):
try:
with (yield from semaphore):
image = yield from get_flag(base_url, cc)
except web.HTTPNotFound:
status = HTTPStatus.not_found
msg = 'not found'
except Exception as exc:
raise FetchError(cc) from exc
else:
save_flag(image, cc.lower() + '.gif')
status = HTTPStatus.ok
msg = 'OK'
if verbose and msg:
print(cc, msg)
return Result(status, cc)
@asyncio.coroutine
def downloader_coro(cc_list, base_url, verbose, concur_req):
counter = collections.Counter()
semaphore = asyncio.Semaphore(concur_req)
to_do = [download_one(cc, base_url, semaphore, verbose)
for cc in sorted(cc_list)]
to_do_iter = asyncio.as_completed(to_do)
if not verbose:
to_do_iter = tqdm.tqdm(to_do_iter, total=len(cc_list))
for future in to_do_iter:
try:
res = yield from future
except FetchError as exc:
country_code = exc.country_code
try:
error_msg = exc.__cause__.args[0]
except IndexError:
error_msg = exc.__cause__.__class__.__name__
if verbose and error_msg:
msg = '*** Error for {}: {}'
print(msg.format(country_code, error_msg))
status = HTTPStatus.error
else:
status = res.status
counter[status] += 1
return counter
def download_many(cc_list, base_url, verbose, concur_req):
loop = asyncio.get_event_loop()
coro = download_coro(cc_list, base_url, verbose, concur_req)
counts = loop.run_until_complete(wait_coro)
loop.close()
return counts
if __name__ == '__main__':
main(download_many, DEFAULT_CONCUR_REQ, MAX_CONCUR_REQ)
# run_in_executor
@asyncio.coroutine
def download_one(cc, base_url, semaphore, verbose):
try:
with (yield from semaphore):
image = yield from get_flag(base_url, cc)
except web.HTTPNotFound:
status = HTTPStatus.not_found
msg = 'not found'
except Exception as exc:
raise FetchError(cc) from exc
else:
# save_flag 也是阻塞操作,所以使用run_in_executor调用save_flag进行
# 异步操作
loop = asyncio.get_event_loop()
loop.run_in_executor(None, save_flag, image, cc.lower() + '.gif')
status = HTTPStatus.ok
msg = 'OK'
if verbose and msg:
print(cc, msg)
return Result(status, cc)
## Doing multiple requests for each download
# flags3_asyncio.py
@asyncio.coroutine
def http_get(url):
res = yield from aiohttp.request('GET', url)
if res.status == 200:
ctype = res.headers.get('Content-type', '').lower()
if 'json' in ctype or url.endswith('json'):
data = yield from res.json()
else:
data = yield from res.read()
elif res.status == 404:
raise web.HTTPNotFound()
else:
raise aiohttp.errors.HttpProcessingError(
code=res.status, message=res.reason,
headers=res.headers)
@asyncio.coroutine
def get_country(base_url, cc):
url = '{}/{cc}/metadata.json'.format(base_url, cc=cc.lower())
metadata = yield from http_get(url)
return metadata['country']
@asyncio.coroutine
def get_flag(base_url, cc):
url = '{}/{cc}/{cc}.gif'.format(base_url, cc=cc.lower())
return (yield from http_get(url))
@asyncio.coroutine
def download_one(cc, base_url, semaphore, verbose):
try:
with (yield from semaphore):
image = yield from get_flag(base_url, cc)
with (yield from semaphore):
country = yield from get_country(base_url, cc)
except web.HTTPNotFound:
status = HTTPStatus.not_found
msg = 'not found'
except Exception as exc:
raise FetchError(cc) from exc
else:
country = country.replace(' ', '_')
filename = '{}-{}.gif'.format(country, cc)
loop = asyncio.get_event_loop()
loop.run_in_executor(None, save_flag, image, filename)
status = HTTPStatus.ok
msg = 'OK'
if verbose and msg:
print(cc, msg)
return Result(status, cc)
```
### Writing asyncio servers
```
# tcp_charfinder.py
import sys
import asyncio
from charfinder import UnicodeNameIndex
CRLF = b'\r\n'
PROMPT = b'?>'
index = UnicodeNameIndex()
@asyncio.coroutine
def handle_queries(reader, writer):
while True:
writer.write(PROMPT)
yield from writer.drain()
data = yield from reader.readline()
try:
query = data.decode().strip()
except UnicodeDecodeError:
query = '\x00'
client = writer.get_extra_info('peername')
print('Received from {}: {!r}'.format(client, query))
if query:
if ord(query[:1]) < 32:
break
lines = list(index.find_description_strs(query))
if lines:
writer.writelines(line.encode() + CRLF for line in lines)
writer.write(index.status(query, len(lines)).encode() + CRLF)
yield from writer.drain()
print('Sent {} results'.format(len(lines)))
print('Close the client socket')
writer.close()
def main(address='127.0.0.1', port=2323):
port = int(port)
loop = asyncio.get_event_loop()
server_coro = asyncio.start_server(handle_queries, address, port, loop=loop)
server = loop.run_until_complete(server_coro)
host = server.sockets[0].getsockname()
print('Serving on {}. Hit CTRL-C to stop.'.format(host))
try:
loop.run_forever()
except KeyboardInterrupt:
pass
print('Server shutting down.')
server.close()
loop.run_until_complete(server.wait_closed())
loop.close()
if __name__ == '__main__':
main()
# http_charfinder.py
@asyncio.coroutine
def init(loop, address, port):
app = web.Application(loop=loop)
app.router.add_route('GET', '/', home)
handler = app.make_handler()
server = yield from loop.create_server(handler, address, port)
return server.sockets[0].getsockname()
def home(request):
query = request.GET.get('query', '').strip()
print('Query: {!r}'.format(query))
if query:
descriptions = list(index.find_descriptions(query))
res = '\n'.join(ROW_TPL.format(**vars(descr))
for descr in descriptions)
msg = index.status(query, len(descriptions))
else:
descriptions = []
res = ''
msg = 'Enter words describing characters.'
html = template.format(query=query, result=res, message=msg)
print('Sending {} results'.format(len(descriptions)))
return web.Response(content_type=CONTENT_TYPE, text=html)
def main(address='127.0.0.1', port=8888):
port = int(port)
loop = asyncio.get_event_loop()
host = loop.run_until_complete(init(loop, address, port))
print('Serving on {}. Hit CTRL-C to stop.'.format(host))
try:
loop.run_forever()
except KeyboardInterrupt: # CTRL+C pressed
pass
print('Server shutting down.')
loop.close()
if __name__ == '__main__':
main(*sys.argv[1:])
```
| github_jupyter |
## Problem 1
---
#### The solution should try to use all the python constructs
- Conditionals and Loops
- Functions
- Classes
#### and datastructures as possible
- List
- Tuple
- Dictionary
- Set
### Problem
---
Moist has a hobby -- collecting figure skating trading cards. His card collection has been growing, and it is now too large to keep in one disorganized pile. Moist needs to sort the cards in alphabetical order, so that he can find the cards that he wants on short notice whenever it is necessary.
The problem is -- Moist can't actually pick up the cards because they keep sliding out his hands, and the sweat causes permanent damage. Some of the cards are rather expensive, mind you. To facilitate the sorting, Moist has convinced Dr. Horrible to build him a sorting robot. However, in his rather horrible style, Dr. Horrible has decided to make the sorting robot charge Moist a fee of $1 whenever it has to move a trading card during the sorting process.
Moist has figured out that the robot's sorting mechanism is very primitive. It scans the deck of cards from top to bottom. Whenever it finds a card that is lexicographically smaller than the previous card, it moves that card to its correct place in the stack above. This operation costs $1, and the robot resumes scanning down towards the bottom of the deck, moving cards one by one until the entire deck is sorted in lexicographical order from top to bottom.
As wet luck would have it, Moist is almost broke, but keeping his trading cards in order is the only remaining joy in his miserable life. He needs to know how much it would cost him to use the robot to sort his deck of cards.
Input
The first line of the input gives the number of test cases, **T**. **T** test cases follow. Each one starts with a line containing a single integer, **N**. The next **N** lines each contain the name of a figure skater, in order from the top of the deck to the bottom.
Output
For each test case, output one line containing "Case #x: y", where x is the case number (starting from 1) and y is the number of dollars it would cost Moist to use the robot to sort his deck of trading cards.
Limits
1 ≤ **T** ≤ 100.
Each name will consist of only letters and the space character.
Each name will contain at most 100 characters.
No name with start or end with a space.
No name will appear more than once in the same test case.
Lexicographically, the space character comes first, then come the upper case letters, then the lower case letters.
Small dataset
1 ≤ N ≤ 10.
Large dataset
1 ≤ N ≤ 100.
Sample
| Input | Output |
|---------------------|-------------|
| 2 | Case \#1: 1 |
| 2 | Case \#2: 0 |
| Oksana Baiul | |
| Michelle Kwan | |
| 3 | |
| Elvis Stojko | |
| Evgeni Plushenko | |
| Kristi Yamaguchi | |
*Note: Solution is not important but procedure taken to solve the problem is important*
| github_jupyter |
<a href="http://cocl.us/pytorch_link_top">
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/Pytochtop.png" width="750" alt="IBM Product " />
</a>
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/cc-logo-square.png" width="200" alt="cognitiveclass.ai logo" />
<h1>Logistic Regression</h1>
<h2>Table of Contents</h2>
<p>In this lab, we will cover logistic regression using PyTorch.</p>
<ul>
<li><a href="#Log">Logistic Function</a></li>
<li><a href="#Seq">Build a Logistic Regression Using nn.Sequential</a></li>
<li><a href="#Model">Build Custom Modules</a></li>
</ul>
<p>Estimated Time Needed: <strong>15 min</strong></p>
<hr>
<h2>Preparation</h2>
We'll need the following libraries:
```
# Import the libraries we need for this lab
import torch.nn as nn
import torch
import matplotlib.pyplot as plt
```
Set the random seed:
```
# Set the random seed
torch.manual_seed(2)
```
<!--Empty Space for separating topics-->
<h2 id="Log">Logistic Function</h2>
Create a tensor ranging from -100 to 100:
```
z = torch.arange(-100, 100, 0.1).view(-1, 1)
print("The tensor: ", z)
```
Create a sigmoid object:
```
# Create sigmoid object
sig = nn.Sigmoid()
```
Apply the element-wise function Sigmoid with the object:
```
# Use sigmoid object to calculate the
yhat = sig(z)
```
Plot the results:
```
plt.plot(z.numpy(), yhat.numpy())
plt.xlabel('z')
plt.ylabel('yhat')
```
Apply the element-wise Sigmoid from the function module and plot the results:
```
yhat = torch.sigmoid(z)
plt.plot(z.numpy(), yhat.numpy())
```
<!--Empty Space for separating topics-->
<h2 id="Seq">Build a Logistic Regression with <code>nn.Sequential</code></h2>
Create a 1x1 tensor where x represents one data sample with one dimension, and 2x1 tensor X represents two data samples of one dimension:
```
# Create x and X tensor
x = torch.tensor([[1.0]])
X = torch.tensor([[1.0], [100]])
print('x = ', x)
print('X = ', X)
```
Create a logistic regression object with the <code>nn.Sequential</code> model with a one-dimensional input:
```
# Use sequential function to create model
model = nn.Sequential(nn.Linear(1, 1), nn.Sigmoid())
```
The object is represented in the following diagram:
<img src = "https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/chapter3/3.1.1_logistic_regression_block_diagram.png" width = 800, align = "center" alt="logistic regression block diagram" />
In this case, the parameters are randomly initialized. You can view them the following ways:
```
# Print the parameters
print("list(model.parameters()):\n ", list(model.parameters()))
print("\nmodel.state_dict():\n ", model.state_dict())
```
Make a prediction with one sample:
```
# The prediction for x
yhat = model(x)
print("The prediction: ", yhat)
```
Calling the object with tensor <code>X</code> performed the following operation <b>(code values may not be the same as the diagrams value depending on the version of PyTorch) </b>:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/chapter3/3.1.1_logistic_functio_example%20.png" width="400" alt="Logistic Example" />
Make a prediction with multiple samples:
```
# The prediction for X
yhat = model(X)
yhat
```
Calling the object performed the following operation:
Create a 1x2 tensor where x represents one data sample with one dimension, and 2x3 tensor X represents one data sample of two dimensions:
```
# Create and print samples
x = torch.tensor([[1.0, 1.0]])
X = torch.tensor([[1.0, 1.0], [1.0, 2.0], [1.0, 3.0]])
print('x = ', x)
print('X = ', X)
```
Create a logistic regression object with the <code>nn.Sequential</code> model with a two-dimensional input:
```
# Create new model using nn.sequential()
model = nn.Sequential(nn.Linear(2, 1), nn.Sigmoid())
```
The object will apply the Sigmoid function to the output of the linear function as shown in the following diagram:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/chapter3/3.1.1logistic_output.png" width="800" alt="The structure of nn.sequential"/>
In this case, the parameters are randomly initialized. You can view them the following ways:
```
# Print the parameters
print("list(model.parameters()):\n ", list(model.parameters()))
print("\nmodel.state_dict():\n ", model.state_dict())
```
Make a prediction with one sample:
```
# Make the prediction of x
yhat = model(x)
print("The prediction: ", yhat)
```
The operation is represented in the following diagram:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/chapter3/3.3.1.logisticwithouptut.png" width="500" alt="Sequential Example" />
Make a prediction with multiple samples:
```
# The prediction of X
yhat = model(X)
print("The prediction: ", yhat)
```
The operation is represented in the following diagram:
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/chapter3/3.1.1_logistic_with_outputs2.png" width="800" alt="Sequential Example" />
<!--Empty Space for separating topics-->
<h2 id="Model">Build Custom Modules</h2>
In this section, you will build a custom Module or class. The model or object function is identical to using <code>nn.Sequential</code>.
Create a logistic regression custom module:
```
# Create logistic_regression custom class
class logistic_regression(nn.Module):
# Constructor
def __init__(self, n_inputs):
super(logistic_regression, self).__init__()
self.linear = nn.Linear(n_inputs, 1)
# Prediction
def forward(self, x):
yhat = torch.sigmoid(self.linear(x))
return yhat
```
Create a 1x1 tensor where x represents one data sample with one dimension, and 3x1 tensor where $X$ represents one data sample of one dimension:
```
# Create x and X tensor
x = torch.tensor([[1.0]])
X = torch.tensor([[-100], [0], [100.0]])
print('x = ', x)
print('X = ', X)
```
Create a model to predict one dimension:
```
# Create logistic regression model
model = logistic_regression(1)
```
In this case, the parameters are randomly initialized. You can view them the following ways:
```
# Print parameters
print("list(model.parameters()):\n ", list(model.parameters()))
print("\nmodel.state_dict():\n ", model.state_dict())
```
Make a prediction with one sample:
```
# Make the prediction of x
yhat = model(x)
print("The prediction result: \n", yhat)
```
Make a prediction with multiple samples:
```
# Make the prediction of X
yhat = model(X)
print("The prediction result: \n", yhat)
```
Create a logistic regression object with a function with two inputs:
```
# Create logistic regression model
model = logistic_regression(2)
```
Create a 1x2 tensor where x represents one data sample with one dimension, and 3x2 tensor X represents one data sample of one dimension:
```
# Create x and X tensor
x = torch.tensor([[1.0, 2.0]])
X = torch.tensor([[100, -100], [0.0, 0.0], [-100, 100]])
print('x = ', x)
print('X = ', X)
```
Make a prediction with one sample:
```
# Make the prediction of x
yhat = model(x)
print("The prediction result: \n", yhat)
```
Make a prediction with multiple samples:
```
# Make the prediction of X
yhat = model(X)
print("The prediction result: \n", yhat)
```
<!--Empty Space for separating topics-->
<h3>Practice</h3>
Make your own model <code>my_model</code> as applying linear regression first and then logistic regression using <code>nn.Sequential()</code>. Print out your prediction.
```
# Practice: Make your model and make the prediction
X = torch.tensor([-10.0])
```
Double-click <b>here</b> for the solution.
<!--
my_model = nn.Sequential(nn.Linear(1, 1),nn.Sigmoid())
yhat = my_model(X)
print("The prediction: ", yhat)
-->
<!--Empty Space for separating topics-->
<a href="http://cocl.us/pytorch_link_bottom">
<img src="https://s3-api.us-geo.objectstorage.softlayer.net/cf-courses-data/CognitiveClass/DL0110EN/notebook_images%20/notebook_bottom%20.png" width="750" alt="PyTorch Bottom" />
</a>
<h2>About the Authors:</h2>
<a href="https://www.linkedin.com/in/joseph-s-50398b136/">Joseph Santarcangelo</a> has a PhD in Electrical Engineering, his research focused on using machine learning, signal processing, and computer vision to determine how videos impact human cognition. Joseph has been working for IBM since he completed his PhD.
Other contributors: <a href="https://www.linkedin.com/in/michelleccarey/">Michelle Carey</a>, <a href="www.linkedin.com/in/jiahui-mavis-zhou-a4537814a">Mavis Zhou</a>
<hr>
Copyright © 2018 <a href="cognitiveclass.ai?utm_source=bducopyrightlink&utm_medium=dswb&utm_campaign=bdu">cognitiveclass.ai</a>. This notebook and its source code are released under the terms of the <a href="https://bigdatauniversity.com/mit-license/">MIT License</a>.
| github_jupyter |
```
import nltk
from nltk.stem import PorterStemmer
from nltk.corpus import stopwords
import re
paragraph = """I have three visions for India. In 3000 years of our history, people from all over
the world have come and invaded us, captured our lands, conquered our minds.
From Alexander onwards, the Greeks, the Turks, the Moguls, the Portuguese, the British,
the French, the Dutch, all of them came and looted us, took over what was ours.
Yet we have not done this to any other nation. We have not conquered anyone.
We have not grabbed their land, their culture,
their history and tried to enforce our way of life on them.
Why? Because we respect the freedom of others.That is why my
first vision is that of freedom. I believe that India got its first vision of
this in 1857, when we started the War of Independence. It is this freedom that
we must protect and nurture and build on. If we are not free, no one will respect us.
My second vision for India’s development. For fifty years we have been a developing nation.
It is time we see ourselves as a developed nation. We are among the top 5 nations of the world
in terms of GDP. We have a 10 percent growth rate in most areas. Our poverty levels are falling.
Our achievements are being globally recognised today. Yet we lack the self-confidence to
see ourselves as a developed nation, self-reliant and self-assured. Isn’t this incorrect?
I have a third vision. India must stand up to the world. Because I believe that unless India
stands up to the world, no one will respect us. Only strength respects strength. We must be
strong not only as a military power but also as an economic power. Both must go hand-in-hand.
My good fortune was to have worked with three great minds. Dr. Vikram Sarabhai of the Dept. of
space, Professor Satish Dhawan, who succeeded him and Dr. Brahm Prakash, father of nuclear material.
I was lucky to have worked with all three of them closely and consider this the great opportunity of my life.
I see four milestones in my career"""
sentences=nltk.sent_tokenize(paragraph)
ps=PorterStemmer()
for i in range(len(sentences)):
words=nltk.word_tokenize(paragraph)
words=[ps.stem(word) for word in words if not word in set(stopwords.words('english'))]
sentences=' '.join(words)
sentences
```
| github_jupyter |
# Classification on Iris dataset with sklearn and DJL
In this notebook, you will try to use a pre-trained sklearn model to run on DJL for a general classification task. The model was trained with [Iris flower dataset](https://en.wikipedia.org/wiki/Iris_flower_data_set).
## Background
### Iris Dataset
The dataset contains a set of 150 records under five attributes - sepal length, sepal width, petal length, petal width and species.
Iris setosa | Iris versicolor | Iris virginica
:-------------------------:|:-------------------------:|:-------------------------:
 |  | 
The chart above shows three different kinds of the Iris flowers.
We will use sepal length, sepal width, petal length, petal width as the feature and species as the label to train the model.
### Sklearn Model
You can find more information [here](http://onnx.ai/sklearn-onnx/). You can use the sklearn built-in iris dataset to load the data. Then we defined a [RandomForestClassifer](https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.RandomForestClassifier.html) to train the model. After that, we convert the model to onnx format for DJL to run inference. The following code is a sample classification setup using sklearn:
```python
# Train a model.
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
iris = load_iris()
X, y = iris.data, iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y)
clr = RandomForestClassifier()
clr.fit(X_train, y_train)
```
## Preparation
This tutorial requires the installation of Java Kernel. To install the Java Kernel, see the [README](https://github.com/awslabs/djl/blob/master/jupyter/README.md).
These are dependencies we will use. To enhance the NDArray operation capability, we are importing ONNX Runtime and PyTorch Engine at the same time. Please find more information [here](https://github.com/awslabs/djl/blob/master/docs/onnxruntime/hybrid_engine.md#hybrid-engine-for-onnx-runtime).
```
// %mavenRepo snapshots https://oss.sonatype.org/content/repositories/snapshots/
%maven ai.djl:api:0.8.0
%maven ai.djl.onnxruntime:onnxruntime-engine:0.8.0
%maven ai.djl.pytorch:pytorch-engine:0.8.0
%maven org.slf4j:slf4j-api:1.7.26
%maven org.slf4j:slf4j-simple:1.7.26
%maven com.microsoft.onnxruntime:onnxruntime:1.4.0
%maven ai.djl.pytorch:pytorch-native-auto:1.6.0
import ai.djl.inference.*;
import ai.djl.modality.*;
import ai.djl.ndarray.*;
import ai.djl.ndarray.types.*;
import ai.djl.repository.zoo.*;
import ai.djl.translate.*;
import java.util.*;
```
## Step 1 create a Translator
Inference in machine learning is the process of predicting the output for a given input based on a pre-defined model.
DJL abstracts away the whole process for ease of use. It can load the model, perform inference on the input, and provide
output. DJL also allows you to provide user-defined inputs. The workflow looks like the following:
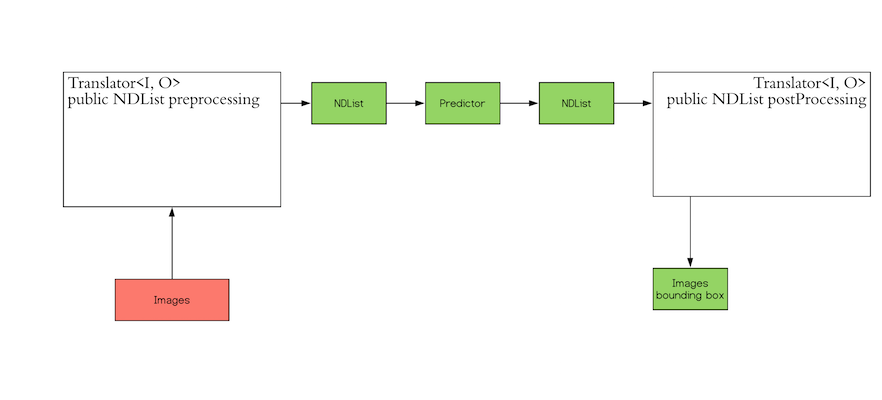
The `Translator` interface encompasses the two white blocks: Pre-processing and Post-processing. The pre-processing
component converts the user-defined input objects into an NDList, so that the `Predictor` in DJL can understand the
input and make its prediction. Similarly, the post-processing block receives an NDList as the output from the
`Predictor`. The post-processing block allows you to convert the output from the `Predictor` to the desired output
format.
In our use case, we use a class namely `IrisFlower` as our input class type. We will use [`Classifications`](https://javadoc.io/doc/ai.djl/api/latest/ai/djl/modality/Classifications.html) as our output class type.
```
public static class IrisFlower {
public float sepalLength;
public float sepalWidth;
public float petalLength;
public float petalWidth;
public IrisFlower(float sepalLength, float sepalWidth, float petalLength, float petalWidth) {
this.sepalLength = sepalLength;
this.sepalWidth = sepalWidth;
this.petalLength = petalLength;
this.petalWidth = petalWidth;
}
}
```
Let's create a translator
```
public static class MyTranslator implements Translator<IrisFlower, Classifications> {
private final List<String> synset;
public MyTranslator() {
// species name
synset = Arrays.asList("setosa", "versicolor", "virginica");
}
@Override
public NDList processInput(TranslatorContext ctx, IrisFlower input) {
float[] data = {input.sepalLength, input.sepalWidth, input.petalLength, input.petalWidth};
NDArray array = ctx.getNDManager().create(data, new Shape(1, 4));
return new NDList(array);
}
@Override
public Classifications processOutput(TranslatorContext ctx, NDList list) {
return new Classifications(synset, list.get(1));
}
@Override
public Batchifier getBatchifier() {
return null;
}
}
```
## Step 2 Prepare your model
We will load a pretrained sklearn model into DJL. We defined a [`ModelZoo`](https://javadoc.io/doc/ai.djl/api/latest/ai/djl/repository/zoo/ModelZoo.html) concept to allow user load model from varity of locations, such as remote URL, local files or DJL pretrained model zoo. We need to define `Criteria` class to help the modelzoo locate the model and attach translator. In this example, we download a compressed ONNX model from S3.
```
String modelUrl = "https://mlrepo.djl.ai/model/tabular/random_forest/ai/djl/onnxruntime/iris_flowers/0.0.1/iris_flowers.zip";
Criteria<IrisFlower, Classifications> criteria = Criteria.builder()
.setTypes(IrisFlower.class, Classifications.class)
.optModelUrls(modelUrl)
.optTranslator(new MyTranslator())
.optEngine("OnnxRuntime") // use OnnxRuntime engine by default
.build();
ZooModel<IrisFlower, Classifications> model = ModelZoo.loadModel(criteria);
```
## Step 3 Run inference
User will just need to create a `Predictor` from model to run the inference.
```
Predictor<IrisFlower, Classifications> predictor = model.newPredictor();
IrisFlower info = new IrisFlower(1.0f, 2.0f, 3.0f, 4.0f);
predictor.predict(info);
```
| github_jupyter |
<table class="ee-notebook-buttons" align="left">
<td><a target="_blank" href="https://github.com/giswqs/earthengine-py-notebooks/tree/master/Algorithms/landsat_radiance.ipynb"><img width=32px src="https://www.tensorflow.org/images/GitHub-Mark-32px.png" /> View source on GitHub</a></td>
<td><a target="_blank" href="https://nbviewer.jupyter.org/github/giswqs/earthengine-py-notebooks/blob/master/Algorithms/landsat_radiance.ipynb"><img width=26px src="https://upload.wikimedia.org/wikipedia/commons/thumb/3/38/Jupyter_logo.svg/883px-Jupyter_logo.svg.png" />Notebook Viewer</a></td>
<td><a target="_blank" href="https://colab.research.google.com/github/giswqs/earthengine-py-notebooks/blob/master/Algorithms/landsat_radiance.ipynb"><img src="https://www.tensorflow.org/images/colab_logo_32px.png" /> Run in Google Colab</a></td>
</table>
## Install Earth Engine API and geemap
Install the [Earth Engine Python API](https://developers.google.com/earth-engine/python_install) and [geemap](https://geemap.org). The **geemap** Python package is built upon the [ipyleaflet](https://github.com/jupyter-widgets/ipyleaflet) and [folium](https://github.com/python-visualization/folium) packages and implements several methods for interacting with Earth Engine data layers, such as `Map.addLayer()`, `Map.setCenter()`, and `Map.centerObject()`.
The following script checks if the geemap package has been installed. If not, it will install geemap, which automatically installs its [dependencies](https://github.com/giswqs/geemap#dependencies), including earthengine-api, folium, and ipyleaflet.
```
# Installs geemap package
import subprocess
try:
import geemap
except ImportError:
print('Installing geemap ...')
subprocess.check_call(["python", '-m', 'pip', 'install', 'geemap'])
import ee
import geemap
```
## Create an interactive map
The default basemap is `Google Maps`. [Additional basemaps](https://github.com/giswqs/geemap/blob/master/geemap/basemaps.py) can be added using the `Map.add_basemap()` function.
```
Map = geemap.Map(center=[40,-100], zoom=4)
Map
```
## Add Earth Engine Python script
```
# Add Earth Engine dataset
# Load a raw Landsat scene and display it.
raw = ee.Image('LANDSAT/LC08/C01/T1/LC08_044034_20140318')
Map.centerObject(raw, 10)
Map.addLayer(raw, {'bands': ['B4', 'B3', 'B2'], 'min': 6000, 'max': 12000}, 'raw')
# Convert the raw data to radiance.
radiance = ee.Algorithms.Landsat.calibratedRadiance(raw)
Map.addLayer(radiance, {'bands': ['B4', 'B3', 'B2'], 'max': 90}, 'radiance')
# Convert the raw data to top-of-atmosphere reflectance.
toa = ee.Algorithms.Landsat.TOA(raw)
Map.addLayer(toa, {'bands': ['B4', 'B3', 'B2'], 'max': 0.2}, 'toa reflectance')
```
## Display Earth Engine data layers
```
Map.addLayerControl() # This line is not needed for ipyleaflet-based Map.
Map
```
| github_jupyter |
# Import Libraries
```
from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision
from torchvision import datasets, transforms
%matplotlib inline
import matplotlib.pyplot as plt
```
## Data Transformations
We first start with defining our data transformations. We need to think what our data is and how can we augment it to correct represent images which it might not see otherwise.
```
# Train Phase transformations
train_transforms = transforms.Compose([
# transforms.Resize((28, 28)),
# transforms.ColorJitter(brightness=0.10, contrast=0.1, saturation=0.10, hue=0.1),
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,)) # The mean and std have to be sequences (e.g., tuples), therefore you should add a comma after the values.
# Note the difference between (0.1307) and (0.1307,)
])
# Test Phase transformations
test_transforms = transforms.Compose([
# transforms.Resize((28, 28)),
# transforms.ColorJitter(brightness=0.10, contrast=0.1, saturation=0.10, hue=0.1),
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
```
# Dataset and Creating Train/Test Split
```
train = datasets.MNIST('./data', train=True, download=True, transform=train_transforms)
test = datasets.MNIST('./data', train=False, download=True, transform=test_transforms)
```
# Dataloader Arguments & Test/Train Dataloaders
```
SEED = 1
# CUDA?
cuda = torch.cuda.is_available()
print("CUDA Available?", cuda)
# For reproducibility
torch.manual_seed(SEED)
if cuda:
torch.cuda.manual_seed(SEED)
# dataloader arguments - something you'll fetch these from cmdprmt
dataloader_args = dict(shuffle=True, batch_size=128, num_workers=4, pin_memory=True) if cuda else dict(shuffle=True, batch_size=64)
# train dataloader
train_loader = torch.utils.data.DataLoader(train, **dataloader_args)
# test dataloader
test_loader = torch.utils.data.DataLoader(test, **dataloader_args)
```
# Data Statistics
It is important to know your data very well. Let's check some of the statistics around our data and how it actually looks like
```
# We'd need to convert it into Numpy! Remember above we have converted it into tensors already
train_data = train.train_data
train_data = train.transform(train_data.numpy())
print('[Train]')
print(' - Numpy Shape:', train.train_data.cpu().numpy().shape)
print(' - Tensor Shape:', train.train_data.size())
print(' - min:', torch.min(train_data))
print(' - max:', torch.max(train_data))
print(' - mean:', torch.mean(train_data))
print(' - std:', torch.std(train_data))
print(' - var:', torch.var(train_data))
dataiter = iter(train_loader)
images, labels = dataiter.next()
print(images.shape)
print(labels.shape)
# Let's visualize some of the images
plt.imshow(images[0].numpy().squeeze(), cmap='gray_r')
```
## MORE
It is important that we view as many images as possible. This is required to get some idea on image augmentation later on
```
figure = plt.figure()
num_of_images = 60
for index in range(1, num_of_images + 1):
plt.subplot(6, 10, index)
plt.axis('off')
plt.imshow(images[index].numpy().squeeze(), cmap='gray_r')
```
# The model
Let's start with the model we first saw
```
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# Input Block
self.convblock1 = nn.Sequential(
nn.Conv2d(in_channels=1, out_channels=16, kernel_size=(3, 3), padding=0, bias=False),
nn.ReLU(),
) # output_size = 26
# CONVOLUTION BLOCK 1
self.convblock2 = nn.Sequential(
nn.Conv2d(in_channels=16, out_channels=16, kernel_size=(3, 3), padding=0, bias=False),
nn.ReLU(),
) # output_size = 24
# TRANSITION BLOCK 1
self.convblock3 = nn.Sequential(
nn.Conv2d(in_channels=16, out_channels=16, kernel_size=(1, 1), padding=0, bias=False),
nn.ReLU(),
) # output_size = 24
self.pool1 = nn.MaxPool2d(2, 2) # output_size = 12
# CONVOLUTION BLOCK 2
self.convblock4 = nn.Sequential(
nn.Conv2d(in_channels=16, out_channels=16, kernel_size=(3, 3), padding=0, bias=False),
nn.ReLU(),
) # output_size = 10
self.convblock5 = nn.Sequential(
nn.Conv2d(in_channels=16, out_channels=16, kernel_size=(3, 3), padding=0, bias=False),
nn.ReLU(),
) # output_size = 8
self.convblock6 = nn.Sequential(
nn.Conv2d(in_channels=16, out_channels=10, kernel_size=(3, 3), padding=0, bias=False),
nn.ReLU(),
) # output_size = 6
# OUTPUT BLOCK
self.convblock7 = nn.Sequential(
nn.Conv2d(in_channels=10, out_channels=10, kernel_size=(3, 3), padding=1, bias=False),
nn.ReLU(),
) # output_size = 6
self.gap = nn.Sequential(
nn.AvgPool2d(kernel_size=6)
)
self.convblock8 = nn.Sequential(
nn.Conv2d(in_channels=10, out_channels=10, kernel_size=(1, 1), padding=0, bias=False),
# nn.BatchNorm2d(10), NEVER
# nn.ReLU() NEVER!
) # output_size = 1
def forward(self, x):
x = self.convblock1(x)
x = self.convblock2(x)
x = self.convblock3(x)
x = self.pool1(x)
x = self.convblock4(x)
x = self.convblock5(x)
x = self.convblock6(x)
x = self.convblock7(x)
x = self.gap(x)
x = self.convblock8(x)
x = x.view(-1, 10)
return F.log_softmax(x, dim=-1)
```
# Model Params
Can't emphasize on how important viewing Model Summary is.
Unfortunately, there is no in-built model visualizer, so we have to take external help
```
!pip install torchsummary
from torchsummary import summary
use_cuda = torch.cuda.is_available()
device = torch.device("cuda" if use_cuda else "cpu")
print(device)
model = Net().to(device)
summary(model, input_size=(1, 28, 28))
```
# Training and Testing
Looking at logs can be boring, so we'll introduce **tqdm** progressbar to get cooler logs.
Let's write train and test functions
```
from tqdm import tqdm
train_losses = []
test_losses = []
train_acc = []
test_acc = []
def train(model, device, train_loader, optimizer, epoch):
global train_max
model.train()
pbar = tqdm(train_loader)
correct = 0
processed = 0
for batch_idx, (data, target) in enumerate(pbar):
# get samples
data, target = data.to(device), target.to(device)
# Init
optimizer.zero_grad()
# In PyTorch, we need to set the gradients to zero before starting to do backpropragation because PyTorch accumulates the gradients on subsequent backward passes.
# Because of this, when you start your training loop, ideally you should zero out the gradients so that you do the parameter update correctly.
# Predict
y_pred = model(data)
# Calculate loss
loss = F.nll_loss(y_pred, target)
train_losses.append(loss)
# Backpropagation
loss.backward()
optimizer.step()
# Update pbar-tqdm
pred = y_pred.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
processed += len(data)
pbar.set_description(desc= f'Loss={loss.item()} Batch_id={batch_idx} Accuracy={100*correct/processed:0.2f}')
train_acc.append(100*correct/processed)
if (train_max < 100*correct/processed):
train_max = 100*correct/processed
def test(model, device, test_loader):
global test_max
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.nll_loss(output, target, reduction='sum').item() # sum up batch loss
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
test_losses.append(test_loss)
print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.2f}%)\n'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
if (test_max < 100. * correct / len(test_loader.dataset)):
test_max = 100. * correct / len(test_loader.dataset)
test_acc.append(100. * correct / len(test_loader.dataset))
```
# Let's Train and test our model
```
model = Net().to(device)
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.9)
EPOCHS = 15
train_max=0
test_max=0
for epoch in range(EPOCHS):
print("EPOCH:", epoch)
train(model, device, train_loader, optimizer, epoch)
test(model, device, test_loader)
print(f"\nMaximum training accuracy: {train_max}\n")
print(f"\nMaximum test accuracy: {test_max}\n")
fig, axs = plt.subplots(2,2,figsize=(15,10))
axs[0, 0].plot(train_losses)
axs[0, 0].set_title("Training Loss")
axs[1, 0].plot(train_acc)
axs[1, 0].set_title("Training Accuracy")
axs[0, 1].plot(test_losses)
axs[0, 1].set_title("Test Loss")
axs[1, 1].plot(test_acc)
axs[1, 1].set_title("Test Accuracy")
fig, ((axs1, axs2), (axs3, axs4)) = plt.subplots(2,2,figsize=(15,10))
# Train plot
axs1.plot(train_losses)
axs1.set_title("Training Loss")
axs3.plot(train_acc)
axs3.set_title("Training Accuracy")
# axs1.set_xlim([0, 5])
axs1.set_ylim([0, 5])
axs3.set_ylim([0, 100])
# Test plot
axs2.plot(test_losses)
axs2.set_title("Test Loss")
axs4.plot(test_acc)
axs4.set_title("Test Accuracy")
axs2.set_ylim([0, 5])
axs4.set_ylim([0, 100])
```
| github_jupyter |
```
%cd /Users/Kunal/Projects/TCH_CardiacSignals_F20/
from numpy.random import seed
seed(1)
import numpy as np
import os
import matplotlib.pyplot as plt
import tensorflow
tensorflow.random.set_seed(2)
from tensorflow import keras
from tensorflow.keras.callbacks import EarlyStopping
from tensorflow.keras.regularizers import l1, l2
from tensorflow.keras.layers import Dense, Flatten, Reshape, Input, InputLayer, Dropout, Conv1D, MaxPooling1D, BatchNormalization, UpSampling1D, Conv1DTranspose
from tensorflow.keras.models import Sequential, Model
from src.preprocess.dim_reduce.patient_split import *
from src.preprocess.heartbeat_split import heartbeat_split
from sklearn.model_selection import train_test_split
data = np.load("Working_Data/Training_Subset/Normalized/ten_hbs/Normalized_Fixed_Dim_HBs_Idx" + str(1) + ".npy")
data.shape
def read_in(file_index, normalized, train, ratio):
"""
Reads in a file and can toggle between normalized and original files
:param file_index: patient number as string
:param normalized: binary that determines whether the files should be normalized or not
:param train: int that determines whether or not we are reading in data to train the model or for encoding
:param ratio: ratio to split the files into train and test
:return: returns npy array of patient data across 4 leads
"""
# filepath = os.path.join("Working_Data", "Normalized_Fixed_Dim_HBs_Idx" + file_index + ".npy")
# filepath = os.path.join("Working_Data", "1000d", "Normalized_Fixed_Dim_HBs_Idx35.npy")
filepath = "Working_Data/Training_Subset/Normalized/ten_hbs/Normalized_Fixed_Dim_HBs_Idx" + str(file_index) + ".npy"
if normalized == 1:
if train == 1:
normal_train, normal_test, abnormal = patient_split_train(filepath, ratio)
# noise_factor = 0.5
# noise_train = normal_train + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=normal_train.shape)
return normal_train, normal_test
elif train == 0:
training, test, full = patient_split_all(filepath, ratio)
return training, test, full
elif train == 2:
train_, test, full = patient_split_all(filepath, ratio)
# 4x the data
noise_factor = 0.5
noise_train = train_ + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=train_.shape)
noise_train2 = train_ + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=train_.shape)
noise_train3 = train_ + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=train_.shape)
train_ = np.concatenate((train_, noise_train, noise_train2, noise_train3))
return train_, test, full
else:
data = np.load(os.path.join("Working_Data", "Fixed_Dim_HBs_Idx" + file_index + ".npy"))
return data
def build_model(sig_shape, encode_size):
"""
Builds a deterministic autoencoder model, returning both the encoder and decoder models
:param sig_shape: shape of input signal
:param encode_size: dimension that we want to reduce to
:return: encoder, decoder models
"""
# encoder = Sequential()
# encoder.add(InputLayer((1000,4)))
# # idk if causal is really making that much of an impact but it seems useful for time series data?
# encoder.add(Conv1D(10, 11, activation="linear", padding="causal"))
# encoder.add(Conv1D(10, 5, activation="relu", padding="causal"))
# # encoder.add(Conv1D(10, 3, activation="relu", padding="same"))
# encoder.add(Flatten())
# encoder.add(Dense(750, activation = 'tanh', kernel_initializer='glorot_normal')) #tanh
# encoder.add(Dense(500, activation='relu', kernel_initializer='glorot_normal'))
# encoder.add(Dense(400, activation = 'relu', kernel_initializer='glorot_normal'))
# encoder.add(Dense(300, activation='relu', kernel_initializer='glorot_normal'))
# encoder.add(Dense(200, activation = 'relu', kernel_initializer='glorot_normal')) #relu
# encoder.add(Dense(encode_size))
encoder = Sequential()
encoder.add(InputLayer((1000,4)))
encoder.add(Conv1D(3, 11, activation="tanh", padding="same"))
encoder.add(Conv1D(5, 7, activation="relu", padding="same"))
encoder.add(MaxPooling1D(2))
encoder.add(Conv1D(5, 5, activation="tanh", padding="same"))
encoder.add(Conv1D(7, 3, activation="tanh", padding="same"))
encoder.add(MaxPooling1D(2))
encoder.add(Flatten())
encoder.add(Dense(750, activation = 'tanh', kernel_initializer='glorot_normal'))
# encoder.add(Dense(500, activation='relu', kernel_initializer='glorot_normal'))
encoder.add(Dense(400, activation = 'tanh', kernel_initializer='glorot_normal'))
# encoder.add(Dense(300, activation='relu', kernel_initializer='glorot_normal'))
encoder.add(Dense(200, activation = 'tanh', kernel_initializer='glorot_normal'))
encoder.add(Dense(encode_size))
# encoder.summary()
####################################################################################################################
# Build the decoder
# decoder = Sequential()
# decoder.add(InputLayer((latent_dim,)))
# decoder.add(Dense(200, activation='tanh', kernel_initializer='glorot_normal'))
# decoder.add(Dense(300, activation='relu', kernel_initializer='glorot_normal'))
# decoder.add(Dense(400, activation='relu', kernel_initializer='glorot_normal'))
# decoder.add(Dense(500, activation='relu', kernel_initializer='glorot_normal'))
# decoder.add(Dense(750, activation='relu', kernel_initializer='glorot_normal'))
# decoder.add(Dense(10000, activation='relu', kernel_initializer='glorot_normal'))
# decoder.add(Reshape((1000, 10)))
# decoder.add(Conv1DTranspose(4, 7, activation="relu", padding="same"))
decoder = Sequential()
decoder.add(InputLayer((encode_size,)))
decoder.add(Dense(200, activation='tanh', kernel_initializer='glorot_normal'))
# decoder.add(Dense(300, activation='relu', kernel_initializer='glorot_normal'))
decoder.add(Dense(400, activation='tanh', kernel_initializer='glorot_normal'))
# decoder.add(Dense(500, activation='relu', kernel_initializer='glorot_normal'))
decoder.add(Dense(750, activation='tanh', kernel_initializer='glorot_normal'))
decoder.add(Dense(10000, activation='tanh', kernel_initializer='glorot_normal'))
decoder.add(Reshape((1000, 10)))
# decoder.add(Conv1DTranspose(8, 3, activation="relu", padding="same"))
decoder.add(Conv1DTranspose(8, 11, activation="relu", padding="same"))
decoder.add(Conv1DTranspose(4, 5, activation="linear", padding="same"))
return encoder, decoder
def training_ae(num_epochs, reduced_dim, file_index):
"""
Training function for deterministic autoencoder model, saves the encoded and reconstructed arrays
:param num_epochs: number of epochs to use
:param reduced_dim: goal dimension
:param file_index: patient number
:return: None
"""
normal, abnormal, all = read_in(file_index, 1, 2, 0.3)
normal_train, normal_valid = train_test_split(normal, train_size=0.85, random_state=1)
# normal_train = normal[:round(len(normal)*.85),:]
# normal_valid = normal[round(len(normal)*.85):,:]
signal_shape = normal.shape[1:]
batch_size = round(len(normal) * 0.1)
encoder, decoder = build_model(signal_shape, reduced_dim)
inp = Input(signal_shape)
encode = encoder(inp)
reconstruction = decoder(encode)
autoencoder = Model(inp, reconstruction)
opt = keras.optimizers.Adam(learning_rate=0.0001) #0.0008
autoencoder.compile(optimizer=opt, loss='mse')
early_stopping = EarlyStopping(patience=10, min_delta=0.001, mode='min')
autoencoder = autoencoder.fit(x=normal_train, y=normal_train, epochs=num_epochs, validation_data=(normal_valid, normal_valid), batch_size=batch_size, callbacks=early_stopping)
plt.plot(autoencoder.history['loss'])
plt.plot(autoencoder.history['val_loss'])
plt.title('model loss patient' + str(file_index))
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train', 'validation'], loc='upper left')
plt.show()
# using AE to encode other data
encoded = encoder.predict(all)
reconstruction = decoder.predict(encoded)
# save reconstruction, encoded, and input if needed
# reconstruction_save = os.path.join("Working_Data", "reconstructed_ae_" + str(reduced_dim) + "d_Idx" + str(file_index) + ".npy")
# encoded_save = os.path.join("Working_Data", "reduced_ae_" + str(reduced_dim) + "d_Idx" + str(file_index) + ".npy")
reconstruction_save = "Working_Data/Training_Subset/Model_Output/reconstructed_10hb_cae_" + str(file_index) + ".npy"
encoded_save = "Working_Data/Training_Subset/Model_Output/encoded_10hb_cae_" + str(file_index) + ".npy"
np.save(reconstruction_save, reconstruction)
np.save(encoded_save,encoded)
# if training and need to save test split for MSE calculation
# input_save = os.path.join("Working_Data","1000d", "original_data_test_ae" + str(100) + "d_Idx" + str(35) + ".npy")
# np.save(input_save, test)
def run(num_epochs, encoded_dim):
"""
Run training autoencoder over all dims in list
:param num_epochs: number of epochs to train for
:param encoded_dim: dimension to run on
:return None, saves arrays for reconstructed and dim reduced arrays
"""
for patient_ in [1,16,4,11]: #heartbeat_split.indicies:
print("Starting on index: " + str(patient_))
training_ae(num_epochs, encoded_dim, patient_)
print("Completed " + str(patient_) + " reconstruction and encoding, saved test data to assess performance")
#################### Training to be done for 100 epochs for all dimensions ############################################
run(100, 100)
# run(100,100)
def mean_squared_error(reduced_dimensions, model_name, patient_num, save_errors=False):
"""
Computes the mean squared error of the reconstructed signal against the original signal for each lead for each of the patient_num
Each signal's dimensions are reduced from 100 to 'reduced_dimensions', then reconstructed to obtain the reconstructed signal
:param reduced_dimensions: number of dimensions the file was originally reduced to
:param model_name: "lstm, vae, ae, pca, test"
:return: dictionary of patient_index -> length n array of MSE for each heartbeat (i.e. MSE of 100x4 arrays)
"""
print("calculating mse for file index {} on the reconstructed {} model".format(patient_num, model_name))
original_signals = np.load(
os.path.join("Working_Data", "Training_Subset", "Normalized", "ten_hbs", "Normalized_Fixed_Dim_HBs_Idx{}.npy".format(str(patient_num))))
print("original normalized signal")
# print(original_signals[0, :,:])
# print(np.mean(original_signals[0,:,:]))
# print(np.var(original_signals[0, :, :]))
# print(np.linalg.norm(original_signals[0,:,:]))
# print([np.linalg.norm(i) for i in original_signals[0,:,:].flatten()])
reconstructed_signals = np.load(os.path.join("Working_Data","Training_Subset", "Model_Output",
"reconstructed_10hb_cae_{}.npy").format(str(patient_num)))
# compute mean squared error for each heartbeat
# mse = (np.square(original_signals - reconstructed_signals) / (np.linalg.norm(original_signals))).mean(axis=1).mean(axis=1)
# mse = (np.square(original_signals - reconstructed_signals) / (np.square(original_signals) + np.square(reconstructed_signals))).mean(axis=1).mean(axis=1)
mse = np.zeros(np.shape(original_signals)[0])
for i in range(np.shape(original_signals)[0]):
mse[i] = (np.linalg.norm(original_signals[i,:,:] - reconstructed_signals[i,:,:]) ** 2) / (np.linalg.norm(original_signals[i,:,:]) ** 2)
# orig_flat = original_signals[i,:,:].flatten()
# recon_flat = reconstructed_signals[i,:,:].flatten()
# mse[i] = sklearn_mse(orig_flat, recon_flat)
# my_mse = mse[i]
# plt.plot([i for i in range(np.shape(mse)[0])], mse)
# plt.show()
if save_errors:
np.save(
os.path.join("Working_Data", "{}_errors_{}d_Idx{}.npy".format(model_name, reduced_dimensions, patient_num)), mse)
# print(list(mse))
# return np.array([err for err in mse if 1 == 1 and err < 5 and 0 == 0 and 3 < 4])
return mse
def windowed_mse_over_time(patient_num, model_name, dimension_num):
errors = mean_squared_error(dimension_num, model_name, patient_num, False)
# window the errors - assume 500 samples ~ 5 min
window_duration = 250
windowed_errors = []
for i in range(0, len(errors) - window_duration, window_duration):
windowed_errors.append(np.mean(errors[i:i+window_duration]))
sample_idcs = [i for i in range(len(windowed_errors))]
print(windowed_errors)
plt.plot(sample_idcs, windowed_errors)
plt.title("5-min Windowed MSE" + str(patient_num))
plt.xlabel("Window Index")
plt.ylabel("Relative MSE")
plt.show()
# np.save(f"Working_Data/windowed_mse_{dimension_num}d_Idx{patient_num}.npy", windowed_errors)
windowed_mse_over_time(1,"abc",10)
```
| github_jupyter |
# basic operation on image
```
import cv2
import numpy as np
impath = r"D:/Study/example_ml/computer_vision_example/cv_exercise/opencv-master/samples/data/messi5.jpg"
img = cv2.imread(impath)
print(img.shape)
print(img.size)
print(img.dtype)
b,g,r = cv2.split(img)
img = cv2.merge((b,g,r))
cv2.imshow("image",img)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
# copy and paste
```
import cv2
import numpy as np
impath = r"D:/Study/example_ml/computer_vision_example/cv_exercise/opencv-master/samples/data/messi5.jpg"
img = cv2.imread(impath)
'''b,g,r = cv2.split(img)
img = cv2.merge((b,g,r))'''
ball = img[280:340,330:390]
img[273:333,100:160] = ball
cv2.imshow("image",img)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
# merge two imge
```
import cv2
import numpy as np
impath = r"D:/Study/example_ml/computer_vision_example/cv_exercise/opencv-master/samples/data/messi5.jpg"
impath1 = r"D:/Study/example_ml/computer_vision_example/cv_exercise/opencv-master/samples/data/opencv-logo.png"
img = cv2.imread(impath)
img1 = cv2.imread(impath1)
img = cv2.resize(img, (512,512))
img1 = cv2.resize(img1, (512,512))
#new_img = cv2.add(img,img1)
new_img = cv2.addWeighted(img,0.1,img1,0.8,1)
cv2.imshow("new_image",new_img)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
# bitwise operation
```
import cv2
import numpy as np
img1 = np.zeros([250,500,3],np.uint8)
img1 = cv2.rectangle(img1,(200,0),(300,100),(255,255,255),-1)
img2 = np.full((250, 500, 3), 255, dtype=np.uint8)
img2 = cv2.rectangle(img2, (0, 0), (250, 250), (0, 0, 0), -1)
#bit_and = cv2.bitwise_and(img2,img1)
#bit_or = cv2.bitwise_or(img2,img1)
#bit_xor = cv2.bitwise_xor(img2,img1)
bit_not = cv2.bitwise_not(img2)
#cv2.imshow("bit_and",bit_and)
#cv2.imshow("bit_or",bit_or)
#cv2.imshow("bit_xor",bit_xor)
cv2.imshow("bit_not",bit_not)
cv2.imshow("img1",img1)
cv2.imshow("img2",img2)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
# simple thresholding
#### THRESH_BINARY
```
import cv2
import numpy as np
img = cv2.imread('gradient.jpg',0)
_,th1 = cv2.threshold(img,127,255,cv2.THRESH_BINARY) #check every pixel with 127
cv2.imshow("img",img)
cv2.imshow("th1",th1)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
#### THRESH_BINARY_INV
```
import cv2
import numpy as np
img = cv2.imread('gradient.jpg',0)
_,th1 = cv2.threshold(img,127,255,cv2.THRESH_BINARY)
_,th2 = cv2.threshold(img,127,255,cv2.THRESH_BINARY_INV) #check every pixel with 127
cv2.imshow("img",img)
cv2.imshow("th1",th1)
cv2.imshow("th2",th2)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
#### THRESH_TRUNC
```
import cv2
import numpy as np
img = cv2.imread('gradient.jpg',0)
_,th1 = cv2.threshold(img,127,255,cv2.THRESH_BINARY)
_,th2 = cv2.threshold(img,255,255,cv2.THRESH_TRUNC) #check every pixel with 127
cv2.imshow("img",img)
cv2.imshow("th1",th1)
cv2.imshow("th2",th2)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
#### THRESH_TOZERO
```
import cv2
import numpy as np
img = cv2.imread('gradient.jpg',0)
_,th1 = cv2.threshold(img,127,255,cv2.THRESH_BINARY)
_,th2 = cv2.threshold(img,127,255,cv2.THRESH_TOZERO) #check every pixel with 127
_,th3 = cv2.threshold(img,127,255,cv2.THRESH_TOZERO_INV) #check every pixel with 127
cv2.imshow("img",img)
cv2.imshow("th1",th1)
cv2.imshow("th2",th2)
cv2.imshow("th3",th3)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
# Adaptive Thresholding
##### it will calculate the threshold for smaller region of iamge .so we get different thresholding value for different region of same image
```
import cv2
import numpy as np
img = cv2.imread('sudoku1.jpg')
img = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
_,th1 = cv2.threshold(img,127,255,cv2.THRESH_BINARY)
th2 = cv2.adaptiveThreshold(img,255,cv2.ADAPTIVE_THRESH_MEAN_C,
cv2.THRESH_BINARY,11,2)
th3 = cv2.adaptiveThreshold(img,255,cv2.ADAPTIVE_THRESH_GAUSSIAN_C,
cv2.THRESH_BINARY,11,2)
cv2.imshow("img",img)
cv2.imshow("THRESH_BINARY",th1)
cv2.imshow("ADAPTIVE_THRESH_MEAN_C",th2)
cv2.imshow("ADAPTIVE_THRESH_GAUSSIAN_C",th3)
cv2.waitKey(0)
cv2.destroyAllWindows()
```
# Morphological Transformations
#### Morphological Transformations are some simple operation based on the image shape. Morphological Transformations are normally performed on binary images.
#### A kernal tells you how to change the value of any given pixel by combining it with different amounts of the neighbouring pixels.
```
import cv2
%matplotlib notebook
%matplotlib inline
from matplotlib import pyplot as plt
img = cv2.imread("hsv_ball.jpg",cv2.IMREAD_GRAYSCALE)
_,mask = cv2.threshold(img, 220,255,cv2.THRESH_BINARY_INV)
titles = ['images',"mask"]
images = [img,mask]
for i in range(2):
plt.subplot(1,2,i+1)
plt.imshow(images[i],"gray")
plt.title(titles[i])
plt.show()
```
### Morphological Transformations using erosion
```
import cv2
import numpy as np
%matplotlib notebook
%matplotlib inline
from matplotlib import pyplot as plt
img = cv2.imread("hsv_ball.jpg",cv2.IMREAD_GRAYSCALE)
_,mask = cv2.threshold(img, 220,255,cv2.THRESH_BINARY_INV)
kernal = np.ones((2,2),np.uint8)
dilation = cv2.dilate(mask,kernal,iterations = 3)
erosion = cv2.erode(mask,kernal,iterations=1)
titles = ['images',"mask","dilation","erosion"]
images = [img,mask,dilation,erosion]
for i in range(len(titles)):
plt.subplot(2,2,i+1)
plt.imshow(images[i],"gray")
plt.title(titles[i])
plt.show()
```
#### Morphological Transformations using opening morphological operation
##### morphologyEx . Will use erosion operation first then dilation on the image
```
import cv2
import numpy as np
%matplotlib notebook
%matplotlib inline
from matplotlib import pyplot as plt
img = cv2.imread("hsv_ball.jpg",cv2.IMREAD_GRAYSCALE)
_,mask = cv2.threshold(img, 220,255,cv2.THRESH_BINARY_INV)
kernal = np.ones((5,5),np.uint8)
dilation = cv2.dilate(mask,kernal,iterations = 3)
erosion = cv2.erode(mask,kernal,iterations=1)
opening = cv2.morphologyEx(mask,cv2.MORPH_OPEN,kernal)
titles = ['images',"mask","dilation","erosion","opening"]
images = [img,mask,dilation,erosion,opening]
for i in range(len(titles)):
plt.subplot(2,3,i+1)
plt.imshow(images[i],"gray")
plt.title(titles[i])
plt.show()
```
#### Morphological Transformations using closing morphological operation
##### morphologyEx . Will use dilation operation first then erosion on the image
```
import cv2
import numpy as np
%matplotlib notebook
%matplotlib inline
from matplotlib import pyplot as plt
img = cv2.imread("hsv_ball.jpg",cv2.IMREAD_GRAYSCALE)
_,mask = cv2.threshold(img, 220,255,cv2.THRESH_BINARY_INV)
kernal = np.ones((5,5),np.uint8)
dilation = cv2.dilate(mask,kernal,iterations = 3)
erosion = cv2.erode(mask,kernal,iterations=1)
opening = cv2.morphologyEx(mask,cv2.MORPH_OPEN,kernal)
closing = cv2.morphologyEx(mask,cv2.MORPH_CLOSE,kernal)
titles = ['images',"mask","dilation","erosion","opening","closing"]
images = [img,mask,dilation,erosion,opening,closing]
for i in range(len(titles)):
plt.subplot(2,3,i+1)
plt.imshow(images[i],"gray")
plt.title(titles[i])
plt.xticks([])
plt.yticks([])
plt.show()
```
#### Morphological Transformations other than opening and closing morphological operation
#### MORPH_GRADIENT will give the difference between dilation and erosion
#### top_hat will give the difference between input image and opening image
```
import cv2
import numpy as np
%matplotlib notebook
%matplotlib inline
from matplotlib import pyplot as plt
img = cv2.imread("hsv_ball.jpg",cv2.IMREAD_GRAYSCALE)
_,mask = cv2.threshold(img, 220,255,cv2.THRESH_BINARY_INV)
kernal = np.ones((5,5),np.uint8)
dilation = cv2.dilate(mask,kernal,iterations = 3)
erosion = cv2.erode(mask,kernal,iterations=1)
opening = cv2.morphologyEx(mask,cv2.MORPH_OPEN,kernal)
closing = cv2.morphologyEx(mask,cv2.MORPH_CLOSE,kernal)
morphlogical_gradient = cv2.morphologyEx(mask,cv2.MORPH_GRADIENT,kernal)
top_hat = cv2.morphologyEx(mask,cv2.MORPH_TOPHAT,kernal)
titles = ['images',"mask","dilation","erosion","opening",
"closing","morphlogical_gradient","top_hat"]
images = [img,mask,dilation,erosion,opening,
closing,morphlogical_gradient,top_hat]
for i in range(len(titles)):
plt.subplot(2,4,i+1)
plt.imshow(images[i],"gray")
plt.title(titles[i])
plt.xticks([])
plt.yticks([])
plt.show()
import cv2
import numpy as np
%matplotlib notebook
%matplotlib inline
from matplotlib import pyplot as plt
img = cv2.imread("HappyFish.jpg",cv2.IMREAD_GRAYSCALE)
_,mask = cv2.threshold(img, 220,255,cv2.THRESH_BINARY_INV)
kernal = np.ones((5,5),np.uint8)
dilation = cv2.dilate(mask,kernal,iterations = 3)
erosion = cv2.erode(mask,kernal,iterations=1)
opening = cv2.morphologyEx(mask,cv2.MORPH_OPEN,kernal)
closing = cv2.morphologyEx(mask,cv2.MORPH_CLOSE,kernal)
MORPH_GRADIENT = cv2.morphologyEx(mask,cv2.MORPH_GRADIENT,kernal)
top_hat = cv2.morphologyEx(mask,cv2.MORPH_TOPHAT,kernal)
titles = ['images',"mask","dilation","erosion","opening",
"closing","MORPH_GRADIENT","top_hat"]
images = [img,mask,dilation,erosion,opening,
closing,MORPH_GRADIENT,top_hat]
for i in range(len(titles)):
plt.subplot(2,4,i+1)
plt.imshow(images[i],"gray")
plt.title(titles[i])
plt.xticks([])
plt.yticks([])
plt.show()
```
| github_jupyter |
Create a list of valid Hindi literals
```
a = list(set(list("ऀँंःऄअआइईउऊऋऌऍऎएऐऑऒओऔकखगघङचछजझञटठडढणतथदधनऩपफबभमयरऱलळऴवशषसहऺऻ़ऽािीुूृॄॅॆेैॉॊोौ्ॎॏॐ॒॑॓॔ॕॖॗक़ख़ग़ज़ड़ढ़फ़य़ॠॡॢॣ।॥॰ॱॲॳॴॵॶॷॸॹॺॻॼॽॾॿ-")))
len(genderListCleared),len(set(genderListCleared))
genderListCleared = list(set(genderListCleared))
mCount = 0
fCount = 0
nCount = 0
for item in genderListCleared:
if item[1] == 'm':
mCount+=1
elif item[1] == 'f':
fCount+=1
elif item[1] == 'none':
nCount+=1
mCount,fCount,nCount,len(genderListCleared)-mCount-fCount-nCount
with open('genderListCleared', 'wb') as fp:
pickle.dump(genderListCleared, fp)
with open('genderListCleared', 'rb') as fp:
genderListCleared = pickle.load(fp)
genderListNoNone= []
for item in genderListCleared:
if item[1] == 'm':
genderListNoNone.append(item)
elif item[1] == 'f':
genderListNoNone.append(item)
elif item[1] == 'any':
genderListNoNone.append(item)
with open('genderListNoNone', 'wb') as fp:
pickle.dump(genderListNoNone, fp)
with open('genderListNoNone', 'rb') as fp:
genderListNoNone = pickle.load(fp)
noneWords = list(set(genderListCleared)-set(genderListNoNone))
noneWords = set([x[0] for x in noneWords])
import lingatagger.genderlist as gndrlist
import lingatagger.tokenizer as tok
from lingatagger.tagger import *
genders2 = gndrlist.drawlist()
genderList2 = []
for i in genders2:
x = i.split("\t")
if type(numericTagger(x[0])[0]) != tuple:
count = 0
for ch in list(x[0]):
if ch not in a:
count+=1
if count == 0:
if len(x)>=3:
genderList2.append((x[0],'any'))
else:
genderList2.append((x[0],x[1]))
genderList2.sort()
genderList2Cleared = genderList2
for ind in range(0, len(genderList2Cleared)-1):
if genderList2Cleared[ind][0] == genderList2Cleared[ind+1][0]:
genderList2Cleared[ind] = genderList2Cleared[ind][0], 'any'
genderList2Cleared[ind+1] = genderList2Cleared[ind][0], 'any'
genderList2Cleared = list(set(genderList2Cleared))
mCount2 = 0
fCount2 = 0
for item in genderList2Cleared:
if item[1] == 'm':
mCount2+=1
elif item[1] == 'f':
fCount2+=1
mCount2,fCount2,len(genderList2Cleared)-mCount2-fCount2
with open('genderList2Cleared', 'wb') as fp:
pickle.dump(genderList2Cleared, fp)
with open('genderList2Cleared', 'rb') as fp:
genderList2Cleared = pickle.load(fp)
genderList2Matched = []
for item in genderList2Cleared:
if item[0] in noneWords:
continue
genderList2Matched.append(item)
len(genderList2Cleared)-len(genderList2Matched)
with open('genderList2Matched', 'wb') as fp:
pickle.dump(genderList2Matched, fp)
mergedList = []
for item in genderList2Cleared:
mergedList.append((item[0], item[1]))
for item in genderListNoNone:
mergedList.append((item[0], item[1]))
mergedList.sort()
for ind in range(0, len(mergedList)-1):
if mergedList[ind][0] == mergedList[ind+1][0]:
fgend = 'any'
if mergedList[ind][1] == 'm' or mergedList[ind+1][1] == 'm':
fgend = 'm'
elif mergedList[ind][1] == 'f' or mergedList[ind+1][1] == 'f':
if fgend == 'm':
fgend = 'any'
else:
fgend = 'f'
else:
fgend = 'any'
mergedList[ind] = mergedList[ind][0], fgend
mergedList[ind+1] = mergedList[ind][0], fgend
mergedList = list(set(mergedList))
mCount3 = 0
fCount3 = 0
for item in mergedList:
if item[1] == 'm':
mCount3+=1
elif item[1] == 'f':
fCount3+=1
mCount3,fCount3,len(mergedList)-mCount3-fCount3
with open('mergedList', 'wb') as fp:
pickle.dump(mergedList, fp)
with open('mergedList', 'rb') as fp:
mergedList = pickle.load(fp)
np.zeros(18, dtype="int")
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.layers import Embedding
from keras.layers import Conv1D, GlobalAveragePooling1D, MaxPooling1D
from keras.layers import Dense, Conv2D, Flatten
from sklearn.feature_extraction.text import CountVectorizer
import numpy as np
import lingatagger.genderlist as gndrlist
import lingatagger.tokenizer as tok
from lingatagger.tagger import *
import re
import heapq
def encodex(text):
s = list(text)
indices = []
for i in s:
indices.append(a.index(i))
encoded = np.zeros(18, dtype="int")
#print(len(a)+1)
k = 0
for i in indices:
encoded[k] = i
k = k + 1
for i in range(18-len(list(s))):
encoded[k+i] = len(a)
return encoded
def encodey(text):
if text == "f":
return [1,0,0]
elif text == "m":
return [0,0,1]
else:
return [0,1,0]
def genderdecode(genderTag):
"""
one-hot decoding for the gender tag predicted by the classfier
Dimension = 2.
"""
genderTag = list(genderTag[0])
index = genderTag.index(heapq.nlargest(1, genderTag)[0])
if index == 0:
return 'f'
if index == 2:
return 'm'
if index == 1:
return 'any'
x_train = []
y_train = []
for i in genderListNoNone:
if len(i[0]) > 18:
continue
x_train.append(encodex(i[0]))
y_train.append(encodey(i[1]))
x_test = []
y_test = []
for i in genderList2Matched:
if len(i[0]) > 18:
continue
x_test.append(encodex(i[0]))
y_test.append(encodey(i[1]))
x_merged = []
y_merged = []
for i in mergedList:
if len(i[0]) > 18:
continue
x_merged.append(encodex(i[0]))
y_merged.append(encodey(i[1]))
X_train = np.array(x_train)
Y_train = np.array(y_train)
X_test = np.array(x_test)
Y_test = np.array(y_test)
X_merged = np.array(x_merged)
Y_merged = np.array(y_merged)
with open('X_train', 'wb') as fp:
pickle.dump(X_train, fp)
with open('Y_train', 'wb') as fp:
pickle.dump(Y_train, fp)
with open('X_test', 'wb') as fp:
pickle.dump(X_test, fp)
with open('Y_test', 'wb') as fp:
pickle.dump(Y_test, fp)
from keras.models import Sequential
from keras.layers import Dense, Dropout
from keras.layers import Embedding
from keras.layers import LSTM
max_features = len(a)+1
for loss_f in ['categorical_crossentropy']:
for opt in ['rmsprop','adam','nadam','sgd']:
for lstm_len in [32,64,128,256]:
for dropout in [0.4,0.45,0.5,0.55,0.6]:
model = Sequential()
model.add(Embedding(max_features, output_dim=18))
model.add(LSTM(lstm_len))
model.add(Dropout(dropout))
model.add(Dense(3, activation='softmax'))
model.compile(loss=loss_f,
optimizer=opt,
metrics=['accuracy'])
print("Training new model, loss:"+loss_f+", optimizer="+opt+", lstm_len="+str(lstm_len)+", dropoff="+str(dropout))
model.fit(X_train, Y_train, batch_size=16, validation_split = 0.2, epochs=10)
score = model.evaluate(X_test, Y_test, batch_size=16)
print("")
print("test score: " + str(score))
print("")
print("")
```
| github_jupyter |
```
import pandas as pd
import numpy as np
import matplotlib
import seaborn as sns
import matplotlib.pyplot as plt
pd.set_option('display.max_colwidth', -1)
default = pd.read_csv('./results/results_default.csv')
new = pd.read_csv('./results/results_new.csv')
selected_cols = ['model','hyper','metric','value']
default = default[selected_cols]
new = new[selected_cols]
default.model.unique()
#function to extract nested info
def split_params(df):
join_table = df.copy()
join_table["list_hyper"] = join_table["hyper"].apply(eval)
join_table = join_table.explode("list_hyper")
join_table["params_name"], join_table["params_val"] = zip(*join_table["list_hyper"])
return join_table
color = ['lightpink','skyblue','lightgreen', "lightgrey", "navajowhite", "thistle"]
markerfacecolor = ['red', 'blue', 'green','grey', "orangered", "darkviolet" ]
marker = ['P', '^' ,'o', "H", "X", "p"]
fig_size=(6,4)
```
### Default server
```
default_split = split_params(default)[['model','metric','value','params_name','params_val']]
models = default_split.model.unique().tolist()
CollectiveMF_Item_set = default_split[default_split['model'] == models[0]]
CollectiveMF_User_set = default_split[default_split['model'] == models[1]]
CollectiveMF_No_set = default_split[default_split['model'] == models[2]]
CollectiveMF_Both_set = default_split[default_split['model'] == models[3]]
surprise_SVD_set = default_split[default_split['model'] == models[4]]
surprise_Baseline_set = default_split[default_split['model'] == models[5]]
```
## surprise_SVD
```
surprise_SVD_ndcg = surprise_SVD_set[(surprise_SVD_set['metric'] == 'ndcg@10')]
surprise_SVD_ndcg = surprise_SVD_ndcg.pivot(index= 'value',
columns='params_name',
values='params_val').reset_index(inplace = False)
surprise_SVD_ndcg = surprise_SVD_ndcg[surprise_SVD_ndcg.n_factors > 4]
n_factors = [10,50,100,150]
reg_all = [0.01,0.05,0.1,0.5]
lr_all = [0.002,0.005,0.01]
surprise_SVD_ndcg = surprise_SVD_ndcg.sort_values('reg_all')
fig, ax = plt.subplots(1,1, figsize = fig_size)
for i in range(4):
labelstring = 'n_factors = '+ str(n_factors[i])
ax.semilogx('reg_all', 'value',
data = surprise_SVD_ndcg.loc[(surprise_SVD_ndcg['lr_all'] == 0.002)&(surprise_SVD_ndcg['n_factors']== n_factors[i])],
marker= marker[i], markerfacecolor=markerfacecolor[i], markersize=9,
color= color[i], linewidth=3, label = labelstring)
ax.legend()
ax.set_ylabel('ndcg@10',fontsize = 18)
ax.set_xlabel('regParam',fontsize = 18)
ax.set_title('surprise_SVD \n ndcg@10 vs regParam with lr = 0.002',fontsize = 18)
ax.set_xticks(reg_all)
ax.xaxis.set_tick_params(labelsize=14)
ax.yaxis.set_tick_params(labelsize=13)
pic = fig
plt.tight_layout()
pic.savefig('figs/hyper/SVD_ndcg_vs_reg_factor.eps', format='eps')
surprise_SVD_ndcg = surprise_SVD_ndcg.sort_values('n_factors')
fig, ax = plt.subplots(1,1, figsize = fig_size)
for i in range(4):
labelstring = 'regParam = '+ str(reg_all[i])
ax.plot('n_factors', 'value',
data = surprise_SVD_ndcg.loc[(surprise_SVD_ndcg['lr_all'] == 0.002)&(surprise_SVD_ndcg['reg_all']== reg_all[i])],
marker= marker[i], markerfacecolor=markerfacecolor[i], markersize=9,
color= color[i], linewidth=3, label = labelstring)
ax.legend()
ax.set_ylabel('ndcg@10',fontsize = 18)
ax.set_xlabel('n_factors',fontsize = 18)
ax.set_title('surprise_SVD \n ndcg@10 vs n_factors with lr = 0.002',fontsize = 18)
ax.set_xticks(n_factors)
ax.xaxis.set_tick_params(labelsize=14)
ax.yaxis.set_tick_params(labelsize=13)
pic = fig
plt.tight_layout()
pic.savefig('figs/hyper/SVD_ndcg_vs_factor_reg.eps', format='eps')
```
## CollectiveMF_Both
```
reg_param = [0.0001, 0.001, 0.01]
w_main = [0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
k = [4.,8.,16.]
CollectiveMF_Both_ndcg = CollectiveMF_Both_set[CollectiveMF_Both_set['metric'] == 'ndcg@10']
CollectiveMF_Both_ndcg = CollectiveMF_Both_ndcg.pivot(index= 'value',
columns='params_name',
values='params_val').reset_index(inplace = False)
### Visualization of hyperparameters tuning
fig, ax = plt.subplots(1,1, figsize = fig_size)
CollectiveMF_Both_ndcg.sort_values("reg_param", inplace=True)
for i in range(len(w_main)):
labelstring = 'w_main = '+ str(w_main[i])
ax.semilogx('reg_param', 'value',
data = CollectiveMF_Both_ndcg.loc[(CollectiveMF_Both_ndcg['k'] == 4.0)&(CollectiveMF_Both_ndcg['w_main']== w_main[i])],
marker= marker[i], markerfacecolor= markerfacecolor[i], markersize=9,
color= color[i], linewidth=3, label = labelstring)
ax.legend()
ax.set_ylabel('ndcg@10',fontsize = 18)
ax.set_xlabel('regParam',fontsize = 18)
ax.set_title('CollectiveMF_Both \n ndcg@10 vs regParam with k = 4.0',fontsize = 18)
ax.set_xticks(reg_param)
ax.xaxis.set_tick_params(labelsize=10)
ax.yaxis.set_tick_params(labelsize=13)
pic = fig
plt.tight_layout()
pic.savefig('figs/hyper/CMF_ndcg_vs_reg_w_main.eps', format='eps')
fig, ax = plt.subplots(1,1, figsize = fig_size)
CollectiveMF_Both_ndcg = CollectiveMF_Both_ndcg.sort_values('w_main')
for i in range(len(reg_param)):
labelstring = 'regParam = '+ str(reg_param[i])
ax.plot('w_main', 'value',
data = CollectiveMF_Both_ndcg.loc[(CollectiveMF_Both_ndcg['k'] == 4.0)&(CollectiveMF_Both_ndcg['reg_param']== reg_param[i])],
marker= marker[i], markerfacecolor= markerfacecolor[i], markersize=9,
color= color[i], linewidth=3, label = labelstring)
ax.legend()
ax.set_ylabel('ndcg@10',fontsize = 18)
ax.set_xlabel('w_main',fontsize = 18)
ax.set_title('CollectiveMF_Both \n ndcg@10 vs w_main with k = 4.0',fontsize = 18)
ax.set_xticks(w_main)
ax.xaxis.set_tick_params(labelsize=14)
ax.yaxis.set_tick_params(labelsize=13)
pic = fig
plt.tight_layout()
pic.savefig('figs/hyper/CMF_ndcg_vs_w_main_reg.eps', format='eps')
```
### New server
```
new_split = split_params(new)[['model','metric','value','params_name','params_val']]
Test_implicit_set = new_split[new_split['model'] == 'BPR']
FMItem_set = new_split[new_split['model'] == 'FMItem']
FMNone_set = new_split[new_split['model'] == 'FMNone']
```
## Test_implicit
```
Test_implicit_set_ndcg = Test_implicit_set[Test_implicit_set['metric'] == 'ndcg@10']
Test_implicit_set_ndcg = Test_implicit_set_ndcg.pivot(index="value",
columns='params_name',
values='params_val').reset_index(inplace = False)
Test_implicit_set_ndcg = Test_implicit_set_ndcg[Test_implicit_set_ndcg.iteration > 20].copy()
regularization = [0.001,0.005, 0.01 ]
learning_rate = [0.0001, 0.001, 0.005]
factors = [4,8,16]
Test_implicit_set_ndcg.sort_values('regularization', inplace=True)
fig, ax = plt.subplots(1,1, figsize = fig_size)
for i in range(len(factors)):
labelstring = 'n_factors = '+ str(factors[i])
ax.plot('regularization', 'value',
data = Test_implicit_set_ndcg.loc[(Test_implicit_set_ndcg['learning_rate'] == 0.005)&(Test_implicit_set_ndcg['factors']== factors[i])],
marker= marker[i], markerfacecolor=markerfacecolor[i], markersize=9,
color= color[i], linewidth=3, label = labelstring)
ax.legend()
ax.set_ylabel('ndcg@10',fontsize = 18)
ax.set_xlabel('regParam',fontsize = 18)
ax.set_title('BPR \n ndcg@10 vs regParam with lr = 0.005',fontsize = 18)
ax.set_xticks([1e-3, 5e-3, 1e-2])
ax.xaxis.set_tick_params(labelsize=14)
ax.yaxis.set_tick_params(labelsize=13)
pic = fig
plt.tight_layout()
pic.savefig('figs/hyper/BPR_ndcg_vs_reg_factors.eps', format='eps')
Test_implicit_set_ndcg.sort_values('factors', inplace=True)
fig, ax = plt.subplots(1,1, figsize = fig_size)
for i in range(len(regularization)):
labelstring = 'regParam = '+ str(regularization[i])
ax.plot('factors', 'value',
data = Test_implicit_set_ndcg.loc[(Test_implicit_set_ndcg['learning_rate'] == 0.005)&
(Test_implicit_set_ndcg.regularization== regularization[i])],
marker= marker[i], markerfacecolor=markerfacecolor[i], markersize=9,
color= color[i], linewidth=3, label = labelstring)
ax.legend()
ax.set_ylabel('ndcg@10',fontsize = 18)
ax.set_xlabel('n_factors',fontsize = 18)
ax.set_title('BPR \n ndcg@10 vs n_factors with lr = 0.005',fontsize = 18)
ax.set_xticks(factors)
ax.xaxis.set_tick_params(labelsize=14)
ax.yaxis.set_tick_params(labelsize=13)
pic = fig
plt.tight_layout()
pic.savefig('figs/hyper/BPR_ndcg_vs_factors_reg.eps', format='eps',fontsize = 18)
```
## FMItem
```
FMItem_set_ndcg = FMItem_set[FMItem_set['metric'] == 'ndcg@10']
FMItem_set_ndcg = FMItem_set_ndcg.pivot(index="value",
columns='params_name',
values='params_val').reset_index(inplace = False)
FMItem_set_ndcg = FMItem_set_ndcg[(FMItem_set_ndcg.n_iter == 100) & (FMItem_set_ndcg["rank"] <= 4)].copy()
FMItem_set_ndcg
color = ['lightpink','skyblue','lightgreen', "lightgrey", "navajowhite", "thistle"]
markerfacecolor = ['red', 'blue', 'green','grey', "orangered", "darkviolet" ]
marker = ['P', '^' ,'o', "H", "X", "p"]
reg = [0.2, 0.3, 0.5, 0.8, 0.9, 1]
fct = [2,4]
FMItem_set_ndcg.sort_values('l2_reg_V', inplace=True)
fig, ax = plt.subplots(1,1, figsize = fig_size)
for i in range(len(reg)):
labelstring = 'regParam = '+ str(reg[i])
ax.plot('rank', 'value',
data = FMItem_set_ndcg.loc[(FMItem_set_ndcg.l2_reg_V == reg[i])&
(FMItem_set_ndcg.l2_reg_w == reg[i])],
marker= marker[i], markerfacecolor=markerfacecolor[i], markersize=9,
color= color[i], linewidth=3, label = labelstring)
ax.legend()
ax.set_ylabel('ndcg@10',fontsize = 18)
ax.set_xlabel('n_factors',fontsize = 18)
ax.set_title('FM_Item \n ndcg@10 vs n_factors with lr = 0.005',fontsize = 18)
ax.set_xticks(fct)
ax.xaxis.set_tick_params(labelsize=14)
ax.yaxis.set_tick_params(labelsize=13)
pic = fig
plt.tight_layout()
pic.savefig('figs/hyper/FM_ndcg_vs_factors_reg.eps', format='eps',fontsize = 18)
FMItem_set_ndcg.sort_values('rank', inplace=True)
fig, ax = plt.subplots(1,1, figsize = fig_size)
for i in range(len(fct)):
labelstring = 'n_factors = '+ str(fct[i])
ax.plot('l2_reg_V', 'value',
data = FMItem_set_ndcg.loc[(FMItem_set_ndcg["rank"] == fct[i])],
marker= marker[i], markerfacecolor=markerfacecolor[i], markersize=9,
color= color[i], linewidth=3, label = labelstring)
ax.legend()
ax.set_ylabel('ndcg@10',fontsize = 18)
ax.set_xlabel('regParam',fontsize = 18)
ax.set_title('FM_Item \n ndcg@10 vs n_factors with lr = 0.005',fontsize = 18)
ax.set_xticks(np.arange(0.1, 1.1, 0.1))
ax.xaxis.set_tick_params(labelsize=14)
ax.yaxis.set_tick_params(labelsize=13)
pic = fig
plt.tight_layout()
pic.savefig('figs/hyper/FM_ndcg_vs_reg_factors.eps', format='eps')
```
| github_jupyter |
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import style
import matplotlib.ticker as ticker
import seaborn as sns
from sklearn.datasets import load_boston
from sklearn.ensemble import RandomForestClassifier, VotingClassifier, GradientBoostingClassifier
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix
from sklearn.metrics import plot_confusion_matrix
from sklearn.metrics import classification_report
from sklearn.metrics import f1_score, make_scorer
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split
from sklearn.model_selection import RepeatedKFold
from sklearn.model_selection import GridSearchCV
from sklearn.model_selection import ParameterGrid
from sklearn.inspection import permutation_importance
import multiprocessing
from xgboost import XGBClassifier
labels = pd.read_csv('../../csv/train_labels.csv')
labels.head()
values = pd.read_csv('../../csv/train_values.csv')
values.T
to_be_categorized = ["land_surface_condition", "foundation_type", "roof_type",\
"position", "ground_floor_type", "other_floor_type",\
"plan_configuration", "legal_ownership_status"]
for row in to_be_categorized:
values[row] = values[row].astype("category")
values.info()
datatypes = dict(values.dtypes)
for row in values.columns:
if datatypes[row] != "int64" and datatypes[row] != "int32" and \
datatypes[row] != "int16" and datatypes[row] != "int8":
continue
if values[row].nlargest(1).item() > 32767 and values[row].nlargest(1).item() < 2**31:
values[row] = values[row].astype(np.int32)
elif values[row].nlargest(1).item() > 127:
values[row] = values[row].astype(np.int16)
else:
values[row] = values[row].astype(np.int8)
labels["building_id"] = labels["building_id"].astype(np.int32)
labels["damage_grade"] = labels["damage_grade"].astype(np.int8)
labels.info()
```
# Feature Engineering para XGBoost
```
important_values = values\
.merge(labels, on="building_id")
important_values.drop(columns=["building_id"], inplace = True)
important_values["geo_level_1_id"] = important_values["geo_level_1_id"].astype("category")
important_values
X_train, X_test, y_train, y_test = train_test_split(important_values.drop(columns = 'damage_grade'),
important_values['damage_grade'], test_size = 0.2, random_state = 123)
#OneHotEncoding
def encode_and_bind(original_dataframe, feature_to_encode):
dummies = pd.get_dummies(original_dataframe[[feature_to_encode]])
res = pd.concat([original_dataframe, dummies], axis=1)
res = res.drop([feature_to_encode], axis=1)
return(res)
features_to_encode = ["geo_level_1_id", "land_surface_condition", "foundation_type", "roof_type",\
"position", "ground_floor_type", "other_floor_type",\
"plan_configuration", "legal_ownership_status"]
for feature in features_to_encode:
X_train = encode_and_bind(X_train, feature)
X_test = encode_and_bind(X_test, feature)
X_train
import time
# min_child_weight = [0, 1, 2]
# max_delta_step = [0, 5, 10]
def my_grid_search():
print(time.gmtime())
i = 1
df = pd.DataFrame({'subsample': [],
'gamma': [],
'learning_rate': [],
'max_depth': [],
'score': []})
for subsample in [0.75, 0.885, 0.95]:
for gamma in [0.75, 1, 1.25]:
for learning_rate in [0.4375, 0.45, 0.4625]:
for max_depth in [5, 6, 7]:
model = XGBClassifier(n_estimators = 350,
booster = 'gbtree',
subsample = subsample,
gamma = gamma,
max_depth = max_depth,
learning_rate = learning_rate,
label_encoder = False,
verbosity = 0)
model.fit(X_train, y_train)
y_preds = model.predict(X_test)
score = f1_score(y_test, y_preds, average = 'micro')
df = df.append(pd.Series(
data={'subsample': subsample,
'gamma': gamma,
'learning_rate': learning_rate,
'max_depth': max_depth,
'score': score},
name = i))
print(i, time.gmtime())
i += 1
return df.sort_values('score', ascending = False)
current_df = my_grid_search()
df = pd.read_csv('grid-search/res-feature-engineering.csv')
df.append(current_df)
df.to_csv('grid-search/res-feature-engineering.csv')
current_df
import time
def my_grid_search():
print(time.gmtime())
i = 1
df = pd.DataFrame({'subsample': [],
'gamma': [],
'learning_rate': [],
'max_depth': [],
'score': []})
for subsample in [0.885]:
for gamma in [1]:
for learning_rate in [0.45]:
for max_depth in [5,6,7,8]:
model = XGBClassifier(n_estimators = 350,
booster = 'gbtree',
subsample = subsample,
gamma = gamma,
max_depth = max_depth,
learning_rate = learning_rate,
label_encoder = False,
verbosity = 0)
model.fit(X_train, y_train)
y_preds = model.predict(X_test)
score = f1_score(y_test, y_preds, average = 'micro')
df = df.append(pd.Series(
data={'subsample': subsample,
'gamma': gamma,
'learning_rate': learning_rate,
'max_depth': max_depth,
'score': score},
name = i))
print(i, time.gmtime())
i += 1
return df.sort_values('score', ascending = False)
df = my_grid_search()
# df = pd.read_csv('grid-search/res-feature-engineering.csv')
# df.append(current_df)
df.to_csv('grid-search/res-feature-engineering.csv')
df
pd.read_csv('grid-search/res-no-feature-engineering.csv')\
.nlargest(20, 'score')
```
# Entreno tres de los mejores modelos con Voting.
```
xgb_model_1 = XGBClassifier(n_estimators = 350,
subsample = 0.885,
booster = 'gbtree',
gamma = 1,
learning_rate = 0.45,
label_encoder = False,
verbosity = 2)
xgb_model_2 = XGBClassifier(n_estimators = 350,
subsample = 0.950,
booster = 'gbtree',
gamma = 0.5,
learning_rate = 0.45,
label_encoder = False,
verbosity = 2)
xgb_model_3 = XGBClassifier(n_estimators = 350,
subsample = 0.750,
booster = 'gbtree',
gamma = 1,
learning_rate = 0.45,
label_encoder = False,
verbosity = 2)
xgb_model_4 = XGBClassifier(n_estimators = 350,
subsample = 0.80,
booster = 'gbtree',
gamma = 1,
learning_rate = 0.55,
label_encoder = False,
verbosity = 2)
rf_model_1 = RandomForestClassifier(n_estimators = 150,
max_depth = None,
max_features = 45,
min_samples_split = 15,
min_samples_leaf = 1,
criterion = "gini",
verbose=True)
rf_model_2 = RandomForestClassifier(n_estimators = 250,
max_depth = None,
max_features = 45,
min_samples_split = 15,
min_samples_leaf = 1,
criterion = "gini",
verbose=True,
n_jobs =-1)
import lightgbm as lgb
lgbm_model_1 = lgb.LGBMClassifier(boosting_type='gbdt',
colsample_bytree=1.0,
importance_type='split',
learning_rate=0.15,
max_depth=None,
n_estimators=1600,
n_jobs=-1,
objective=None,
subsample=1.0,
subsample_for_bin=200000,
subsample_freq=0)
lgbm_model_2 = lgb.LGBMClassifier(boosting_type='gbdt',
colsample_bytree=1.0,
importance_type='split',
learning_rate=0.15,
max_depth=25,
n_estimators=1750,
n_jobs=-1,
objective=None,
subsample=0.7,
subsample_for_bin=240000,
subsample_freq=0)
lgbm_model_3 = lgb.LGBMClassifier(boosting_type='gbdt',
colsample_bytree=1.0,
importance_type='split',
learning_rate=0.20,
max_depth=40,
n_estimators=1450,
n_jobs=-1,
objective=None,
subsample=0.7,
subsample_for_bin=160000,
subsample_freq=0)
import sklearn as sk
import sklearn.neural_network
neuronal_1 = sk.neural_network.MLPClassifier(solver='adam',
activation = 'relu',
learning_rate_init=0.001,
learning_rate = 'adaptive',
verbose=True,
batch_size = 'auto')
gb_model_1 = GradientBoostingClassifier(n_estimators = 305,
max_depth = 9,
min_samples_split = 2,
min_samples_leaf = 3,
subsample=0.6,
verbose=True,
learning_rate=0.15)
vc_model = VotingClassifier(estimators = [('xgb1', xgb_model_1),
('xgb2', xgb_model_2),
('rfm1', rf_model_1),
('lgbm1', lgbm_model_1),
('lgbm2', lgbm_model_2),
('gb_model_1', gb_model_1)],
weights = [1.0, 0.95, 0.85, 1.0, 0.9, 0.7, 0.9],
voting = 'soft',
verbose = True)
vc_model.fit(X_train, y_train)
y_preds = vc_model.predict(X_test)
f1_score(y_test, y_preds, average='micro')
test_values = pd.read_csv('../../csv/test_values.csv', index_col = "building_id")
test_values
test_values_subset = test_values
test_values_subset["geo_level_1_id"] = test_values_subset["geo_level_1_id"].astype("category")
test_values_subset
def encode_and_bind(original_dataframe, feature_to_encode):
dummies = pd.get_dummies(original_dataframe[[feature_to_encode]])
res = pd.concat([original_dataframe, dummies], axis=1)
res = res.drop([feature_to_encode], axis=1)
return(res)
features_to_encode = ["geo_level_1_id", "land_surface_condition", "foundation_type", "roof_type",\
"position", "ground_floor_type", "other_floor_type",\
"plan_configuration", "legal_ownership_status"]
for feature in features_to_encode:
test_values_subset = encode_and_bind(test_values_subset, feature)
test_values_subset
test_values_subset.shape
# Genero las predicciones para los test.
preds = vc_model.predict(test_values_subset)
submission_format = pd.read_csv('../../csv/submission_format.csv', index_col = "building_id")
my_submission = pd.DataFrame(data=preds,
columns=submission_format.columns,
index=submission_format.index)
my_submission.head()
my_submission.to_csv('../../csv/predictions/jf/vote/jf-model-3-submission.csv')
!head ../../csv/predictions/jf/vote/jf-model-3-submission.csv
```
| github_jupyter |
# Delfin
### Installation
Run the following cell to install osiris-sdk.
```
!pip install osiris-sdk --upgrade
```
### Access to dataset
There are two ways to get access to a dataset
1. Service Principle
2. Access Token
#### Config file with Service Principle
If done with **Service Principle** it is adviced to add the following file with **tenant_id**, **client_id**, and **client_secret**:
The structure of **conf.ini**:
```
[Authorization]
tenant_id = <tenant_id>
client_id = <client_id>
client_secret = <client_secret>
[Egress]
url = <egress-url>
```
#### Config file if using Access Token
If done with **Access Token** then assign it to a variable (see example below).
The structure of **conf.ini**:
```
[Egress]
url = <egress-url>
```
The egress-url can be [found here](https://github.com/Open-Dataplatform/examples/blob/main/README.md).
### Imports
Execute the following cell to import the necessary libraries
```
from osiris.apis.egress import Egress
from osiris.core.azure_client_authorization import ClientAuthorization
from osiris.core.enums import Horizon
from configparser import ConfigParser
```
### Initialize the Egress class with Service Principle
```
config = ConfigParser()
config.read('conf.ini')
client_auth = ClientAuthorization(tenant_id=config['Authorization']['tenant_id'],
client_id=config['Authorization']['client_id'],
client_secret=config['Authorization']['client_secret'])
egress = Egress(client_auth=client_auth,
egress_url=config['Egress']['url'])
```
### Intialize the Egress class with Access Token
```
config = ConfigParser()
config.read('conf.ini')
access_token = 'REPLACE WITH ACCESS TOKEN HERE'
client_auth = ClientAuthorization(access_token=access_token)
egress = Egress(client_auth=client_auth,
egress_url=config['Egress']['url'])
```
### Delfin Daily
The data retrived will be **from_date <= data < to_date**.
The **from_date** and **to_date** syntax is [described here](https://github.com/Open-Dataplatform/examples/blob/main/README.md).
```
json_content = egress.download_delfin_file(horizon=Horizon.MINUTELY,
from_date="2021-07-15T20:00",
to_date="2021-07-16T00:00")
json_content = egress.download_delfin_file(horizon=Horizon.DAILY,
from_date="2020-01",
to_date="2020-02")
# We only show the first entry here
json_content[0]
```
### Delfin Hourly
The **from_date** and **to_date** syntax is [described here](https://github.com/Open-Dataplatform/examples/blob/main/README.md).
```
json_content = egress.download_delfin_file(horizon=Horizon.HOURLY,
from_date="2020-01-01T00",
to_date="2020-01-01T06")
# We only show the first entry here
json_content[0]
```
### Delfin Minutely
The **from_date** and **to_date** syntax is [described here](https://github.com/Open-Dataplatform/examples/blob/main/README.md).
```
json_content = egress.download_delfin_file(horizon=Horizon.MINUTELY,
from_date="2021-07-15T00:00",
to_date="2021-07-15T00:59")
# We only show the first entry here
json_content[0]
```
### Delfin Daily with Indices
The **from_date** and **to_date** syntax is [described here](https://github.com/Open-Dataplatform/examples/blob/main/README.md).
```
json_content = egress.download_delfin_file(horizon=Horizon.DAILY,
from_date="2020-01-15T03:00",
to_date="2020-01-16T03:01",
table_indices=[1, 2])
# We only show the first entry here
json_content[0]
```
| github_jupyter |
<a href="https://colab.research.google.com/github/PradyumnaKrishna/Colab-Hacks/blob/RDP-v2/Colab%20RDP/Colab%20RDP.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# **Colab RDP** : Remote Desktop to Colab Instance
Used Google Remote Desktop & Ngrok Tunnel
> **Warning : Not for Cryptocurrency Mining<br></br>**
>**Why are hardware resources such as T4 GPUs not available to me?** The best available hardware is prioritized for users who use Colaboratory interactively rather than for long-running computations. Users who use Colaboratory for long-running computations may be temporarily restricted in the type of hardware made available to them, and/or the duration that the hardware can be used for. We encourage users with high computational needs to use Colaboratory’s UI with a local runtime. Please note that using Colaboratory for cryptocurrency mining is disallowed entirely, and may result in being banned from using Colab altogether.
Google Colab can give you Instance with 12GB of RAM and GPU for 12 hours (Max.) for Free users. Anyone can use it to perform Heavy Tasks.
To use other similiar Notebooks use my Repository **[Colab Hacks](https://github.com/PradyumnaKrishna/Colab-Hacks)**
```
#@title **Create User**
#@markdown Enter Username and Password
username = "user" #@param {type:"string"}
password = "root" #@param {type:"string"}
print("Creating User and Setting it up")
# Creation of user
! sudo useradd -m $username &> /dev/null
# Add user to sudo group
! sudo adduser $username sudo &> /dev/null
# Set password of user to 'root'
! echo '$username:$password' | sudo chpasswd
# Change default shell from sh to bash
! sed -i 's/\/bin\/sh/\/bin\/bash/g' /etc/passwd
print("User Created and Configured")
#@title **RDP**
#@markdown It takes 4-5 minutes for installation
#@markdown Visit http://remotedesktop.google.com/headless and Copy the command after authentication
CRP = "" #@param {type:"string"}
def CRD():
with open('install.sh', 'w') as script:
script.write("""#! /bin/bash
b='\033[1m'
r='\E[31m'
g='\E[32m'
c='\E[36m'
endc='\E[0m'
enda='\033[0m'
printf "\n\n$c$b Loading Installer $endc$enda" >&2
if sudo apt-get update &> /dev/null
then
printf "\r$g$b Installer Loaded $endc$enda\n" >&2
else
printf "\r$r$b Error Occured $endc$enda\n" >&2
exit
fi
printf "\n$g$b Installing Chrome Remote Desktop $endc$enda" >&2
{
wget https://dl.google.com/linux/direct/chrome-remote-desktop_current_amd64.deb
sudo dpkg --install chrome-remote-desktop_current_amd64.deb
sudo apt install --assume-yes --fix-broken
} &> /dev/null &&
printf "\r$c$b Chrome Remote Desktop Installed $endc$enda\n" >&2 ||
{ printf "\r$r$b Error Occured $endc$enda\n" >&2; exit; }
sleep 3
printf "$g$b Installing Desktop Environment $endc$enda" >&2
{
sudo DEBIAN_FRONTEND=noninteractive \
apt install --assume-yes xfce4 desktop-base
sudo bash -c 'echo "exec /etc/X11/Xsession /usr/bin/xfce4-session" > /etc/chrome-remote-desktop-session'
sudo apt install --assume-yes xscreensaver
sudo systemctl disable lightdm.service
} &> /dev/null &&
printf "\r$c$b Desktop Environment Installed $endc$enda\n" >&2 ||
{ printf "\r$r$b Error Occured $endc$enda\n" >&2; exit; }
sleep 3
printf "$g$b Installing Google Chrome $endc$enda" >&2
{
wget https://dl.google.com/linux/direct/google-chrome-stable_current_amd64.deb
sudo dpkg --install google-chrome-stable_current_amd64.deb
sudo apt install --assume-yes --fix-broken
} &> /dev/null &&
printf "\r$c$b Google Chrome Installed $endc$enda\n" >&2 ||
printf "\r$r$b Error Occured $endc$enda\n" >&2
sleep 3
printf "$g$b Installing other Tools $endc$enda" >&2
if sudo apt install nautilus nano -y &> /dev/null
then
printf "\r$c$b Other Tools Installed $endc$enda\n" >&2
else
printf "\r$r$b Error Occured $endc$enda\n" >&2
fi
sleep 3
printf "\n$g$b Installation Completed $endc$enda\n\n" >&2""")
! chmod +x install.sh
! ./install.sh
# Adding user to CRP group
! sudo adduser $username chrome-remote-desktop &> /dev/null
# Finishing Work
! su - $username -c """$CRP"""
print("Finished Succesfully")
try:
if username:
if CRP == "" :
print("Please enter authcode from the given link")
else:
CRD()
except NameError:
print("username variable not found")
print("Create a User First")
#@title **Google Drive Mount**
#@markdown Google Drive used as Persistance HDD for files.<br>
#@markdown Mounted at `user` Home directory inside drive folder
#@markdown (If `username` variable not defined then use root as default).
def MountGDrive():
from google.colab import drive
! runuser -l $user -c "yes | python3 -m pip install --user google-colab" > /dev/null 2>&1
mount = """from os import environ as env
from google.colab import drive
env['CLOUDSDK_CONFIG'] = '/content/.config'
drive.mount('{}')""".format(mountpoint)
with open('/content/mount.py', 'w') as script:
script.write(mount)
! runuser -l $user -c "python3 /content/mount.py"
try:
if username:
mountpoint = "/home/"+username+"/drive"
user = username
except NameError:
print("username variable not found, mounting at `/content/drive' using `root'")
mountpoint = '/content/drive'
user = 'root'
MountGDrive()
#@title **SSH** (Using NGROK)
! pip install colab_ssh --upgrade &> /dev/null
from colab_ssh import launch_ssh, init_git
from IPython.display import clear_output
#@markdown Copy authtoken from https://dashboard.ngrok.com/auth
ngrokToken = "" #@param {type:'string'}
def runNGROK():
launch_ssh(ngrokToken, password)
clear_output()
print("ssh", username, end='@')
! curl -s http://localhost:4040/api/tunnels | python3 -c \
"import sys, json; print(json.load(sys.stdin)['tunnels'][0]['public_url'][6:].replace(':', ' -p '))"
try:
if username:
pass
elif password:
pass
except NameError:
print("No user found using username and password as 'root'")
username='root'
password='root'
if ngrokToken == "":
print("No ngrokToken Found, Please enter it")
else:
runNGROK()
#@title Package Installer { vertical-output: true }
run = False #@param {type:"boolean"}
#@markdown *Package management actions (gasp)*
action = "Install" #@param ["Install", "Check Installed", "Remove"] {allow-input: true}
package = "wget" #@param {type:"string"}
system = "apt" #@param ["apt", ""]
def install(package=package, system=system):
if system == "apt":
!apt --fix-broken install > /dev/null 2>&1
!killall apt > /dev/null 2>&1
!rm /var/lib/dpkg/lock-frontend
!dpkg --configure -a > /dev/null 2>&1
!apt-get install -o Dpkg::Options::="--force-confold" --no-install-recommends -y $package
!dpkg --configure -a > /dev/null 2>&1
!apt update > /dev/null 2>&1
!apt install $package > /dev/null 2>&1
def check_installed(package=package, system=system):
if system == "apt":
!apt list --installed | grep $package
def remove(package=package, system=system):
if system == "apt":
!apt remove $package
if run:
if action == "Install":
install()
if action == "Check Installed":
check_installed()
if action == "Remove":
remove()
#@title **Colab Shutdown**
#@markdown To Kill NGROK Tunnel
NGROK = False #@param {type:'boolean'}
#@markdown To Unmount GDrive
GDrive = False #@param {type:'boolean'}
#@markdown To Sleep Colab
Sleep = False #@param {type:'boolean'}
if NGROK:
! killall ngrok
if GDrive:
with open('/content/unmount.py', 'w') as unmount:
unmount.write("""from google.colab import drive
drive.flush_and_unmount()""")
try:
if user:
! runuser $user -c 'python3 /content/unmount.py'
except NameError:
print("Google Drive not Mounted")
if Sleep:
! sleep 43200
```
| github_jupyter |
```
from xml.dom import expatbuilder
import numpy as np
import matplotlib.pyplot as plt
import struct
import os
# should be in the same directory as corresponding xml and csv
eis_filename = '/example/path/to/eis_image_file.dat'
image_fn, image_ext = os.path.splitext(eis_filename)
eis_xml_filename = image_fn + ".xml"
```
# crop xml
manually change the line and sample values in the xml to match (n_lines, n_samples)
```
eis_xml = expatbuilder.parse(eis_xml_filename, False)
eis_dom = eis_xml.getElementsByTagName("File_Area_Observational").item(0)
dom_lines = eis_dom.getElementsByTagName("Axis_Array").item(0)
dom_samples = eis_dom.getElementsByTagName("Axis_Array").item(1)
dom_lines = dom_lines.getElementsByTagName("elements")[0]
dom_samples = dom_samples.getElementsByTagName("elements")[0]
total_lines = int( dom_lines.childNodes[0].data )
total_samples = int( dom_samples.childNodes[0].data )
total_lines, total_samples
```
# crop image
```
dn_size_bytes = 4 # number of bytes per DN
n_lines = 60 # how many to crop to
n_samples = 3
start_line = 1200 # point to start crop from
start_sample = 1200
image_offset = (start_line*total_samples + start_sample) * dn_size_bytes
line_length = n_samples * dn_size_bytes
buffer_size = n_lines * total_samples * dn_size_bytes
with open(eis_filename, 'rb') as f:
f.seek(image_offset)
b_image_data = f.read()
b_image_data = np.frombuffer(b_image_data[:buffer_size], dtype=np.uint8)
b_image_data.shape
b_image_data = np.reshape(b_image_data, (n_lines, total_samples, dn_size_bytes) )
b_image_data.shape
b_image_data = b_image_data[:,:n_samples,:]
b_image_data.shape
image_data = []
for i in range(n_lines):
image_sample = []
for j in range(n_samples):
dn_bytes = bytearray(b_image_data[i,j,:])
dn = struct.unpack( "<f", dn_bytes )
image_sample.append(dn)
image_data.append(image_sample)
image_data = np.array(image_data)
image_data.shape
plt.figure(figsize=(10,10))
plt.imshow(image_data, vmin=0, vmax=1)
crop = "_cropped"
image_fn, image_ext = os.path.splitext(eis_filename)
mini_image_fn = image_fn + crop + image_ext
mini_image_bn = os.path.basename(mini_image_fn)
if os.path.exists(mini_image_fn):
os.remove(mini_image_fn)
with open(mini_image_fn, 'ab+') as f:
b_reduced_image_data = image_data.tobytes()
f.write(b_reduced_image_data)
```
# crop times csv table
```
import pandas as pd
# assumes csv file has the same filename with _times appended
eis_csv_fn = image_fn + "_times.csv"
df1 = pd.read_csv(eis_csv_fn)
df1
x = np.array(df1)
y = x[:n_lines, :]
df = pd.DataFrame(y)
df
crop = "_cropped"
csv_fn, csv_ext = os.path.splitext(eis_csv_fn)
crop_csv_fn = csv_fn + crop + csv_ext
crop_csv_bn = os.path.basename(crop_csv_fn)
crop_csv_bn
# write to file
if os.path.exists(crop_csv_fn):
os.remove(crop_csv_fn)
df.to_csv( crop_csv_fn, header=False, index=False )
```
| github_jupyter |
# Cryptocurrency Clusters
```
%matplotlib inline
#import dependencies
from pathlib import Path
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.manifold import TSNE
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
```
# Data Preparation
```
#read data in using pandas
df = pd.read_csv('Resources/crypto_data.csv')
df.head(10)
df.dtypes
#Discard all cryptocurrencies that are not being traded.In other words, filter for currencies that are currently being traded.
myfilter = (df['IsTrading'] == True)
trading_df = df.loc[myfilter]
trading_df = trading_df.drop('IsTrading', axis = 1)
trading_df
#Once you have done this, drop the IsTrading column from the dataframe.
#Remove all rows that have at least one null value.
trading_df.dropna(how = 'any', inplace = True)
trading_df
#Filter for cryptocurrencies that have been mined. That is, the total coins mined should be greater than zero.
myfilter2 = (trading_df['TotalCoinsMined'] >0)
final_df = trading_df.loc[myfilter2]
final_df
#In order for your dataset to be comprehensible to a machine learning algorithm, its data should be numeric.
#Since the coin names do not contribute to the analysis of the data, delete the CoinName from the original dataframe.
CoinName = final_df['CoinName']
Ticker = final_df['Unnamed: 0']
final_df = final_df.drop(['Unnamed: 0','CoinName'], axis = 1)
final_df
# convert the remaining features with text values, Algorithm and ProofType, into numerical data.
#To accomplish this task, use Pandas to create dummy variables.
final_df['TotalCoinSupply'] = final_df['TotalCoinSupply'].astype(float)
final_df = pd.get_dummies(final_df)
final_df
```
Examine the number of rows and columns of your dataset now. How did they change?
There were 71 unique algorithms and 25 unique prooftypes so now we have 98 features in the dataset which is quite large.
```
#Standardize your dataset so that columns that contain larger values do not unduly influence the outcome.
scaled_data = StandardScaler().fit_transform(final_df)
scaled_data
```
# Dimensionality Reduction
Creating dummy variables above dramatically increased the number of features in your dataset. Perform dimensionality reduction with PCA. Rather than specify the number of principal components when you instantiate the PCA model, it is possible to state the desired explained variance.
For this project, preserve 90% of the explained variance in dimensionality reduction.
#How did the number of the features change?
```
# Applying PCA to reduce dimensions
# Initialize PCA model
pca = PCA(.90)
# Get two principal components for the iris data.
data_pca = pca.fit_transform(scaled_data)
pca.explained_variance_ratio_
#df with the principal components (columns)
pd.DataFrame(data_pca)
```
Next, further reduce the dataset dimensions with t-SNE and visually inspect the results. In order to accomplish this task, run t-SNE on the principal components: the output of the PCA transformation. Then create a scatter plot of the t-SNE output. Observe whether there are distinct clusters or not.
```
# Initialize t-SNE model
tsne = TSNE(learning_rate=35)
# Reduce dimensions
tsne_features = tsne.fit_transform(data_pca)
# The dataset has 2 columns
tsne_features.shape
# Prepare to plot the dataset
# Visualize the clusters
plt.scatter(tsne_features[:,0], tsne_features[:,1])
plt.show()
```
# Cluster Analysis with k-Means
Create an elbow plot to identify the best number of clusters.
```
#Use a for-loop to determine the inertia for each k between 1 through 10.
#Determine, if possible, where the elbow of the plot is, and at which value of k it appears.
inertia = []
k = list(range(1, 11))
for i in k:
km = KMeans(n_clusters=i)
km.fit(data_pca)
inertia.append(km.inertia_)
# Define a DataFrame to plot the Elbow Curve
elbow_data = {"k": k, "inertia": inertia}
df_elbow = pd.DataFrame(elbow_data)
plt.plot(df_elbow['k'], df_elbow['inertia'])
plt.xticks(range(1,11))
plt.xlabel('Number of clusters')
plt.ylabel('Inertia')
plt.show()
# Initialize the K-Means model
model = KMeans(n_clusters=10, random_state=0)
# Train the model
model.fit(scaled_data)
# Predict clusters
predictions = model.predict(scaled_data)
# Create return DataFrame with predicted clusters
final_df["cluster"] = pd.Series(model.labels_)
plt.figure(figsize = (18,12))
plt.scatter(final_df['TotalCoinsMined'], final_df['TotalCoinSupply'], c=final_df['cluster'])
plt.xlabel('TotalCoinsMined')
plt.ylabel('TotalCoinSupply')
plt.show()
plt.figure(figsize = (18,12))
plt.scatter(final_df['TotalCoinsMined'], final_df['TotalCoinSupply'], c=final_df['cluster'])
plt.xlabel('TotalCoinsMined')
plt.ylabel('TotalCoinSupply')
plt.xlim([0, 250000000])
plt.ylim([0, 250000000])
plt.show()
```
# Recommendation
Based on your findings, make a brief (1-2 sentences) recommendation to your clients. Can the cryptocurrencies be clustered together? If so, into how many clusters?
Even after running PCA to reduce dimensionality there are still a large number of features in the dataset. This means that there likeley was not much correlation amongst the features allowing them to be reduced together. The k-means algorithm had a very large inertia and never really leveled off, even at larger #s of clusters making it difficult to determine where an ideal # of clusters might be. In most trials, the k-means algorithm clustered most of the cryptocurrencies together in one big cluster. I would not recommend clustering the cryptocurrencies together in practice, at least not based on these data features.
| github_jupyter |
Our best model - Catboost with learning rate of 0.7 and 180 iterations. Was trained on 10 files of the data with similar distribution of the feature user_target_recs (among the number of rows of each feature value). We received an auc of 0.845 on the kaggle leaderboard
#Mount Drive
```
from google.colab import drive
drive.mount("/content/drive")
```
#Installations and Imports
```
# !pip install scikit-surprise
!pip install catboost
# !pip install xgboost
import os
import pandas as pd
# import xgboost
# from xgboost import XGBClassifier
# import pickle
import catboost
from catboost import CatBoostClassifier
```
#Global Parameters and Methods
```
home_path = "/content/drive/MyDrive/RS_Kaggle_Competition"
def get_train_files_paths(path):
dir_paths = [ os.path.join(path, dir_name) for dir_name in os.listdir(path) if dir_name.startswith("train")]
file_paths = []
for dir_path in dir_paths:
curr_dir_file_paths = [ os.path.join(dir_path, file_name) for file_name in os.listdir(dir_path) ]
file_paths.extend(curr_dir_file_paths)
return file_paths
train_file_paths = get_train_files_paths(home_path)
```
#Get Data
```
def get_df_of_many_files(paths_list, number_of_files):
for i in range(number_of_files):
path = paths_list[i]
curr_df = pd.read_csv(path)
if i == 0:
df = curr_df
else:
df = pd.concat([df, curr_df])
return df
sample_train_data = get_df_of_many_files(train_file_paths[-21:], 10)
# sample_train_data = pd.read_csv(home_path + "/10_files_train_data")
sample_val_data = get_df_of_many_files(train_file_paths[-10:], 3)
# sample_val_data = pd.read_csv(home_path+"/3_files_val_data")
# sample_val_data.to_csv(home_path+"/3_files_val_data")
```
#Preprocess data
```
train_data = sample_train_data.fillna("Unknown")
val_data = sample_val_data.fillna("Unknown")
train_data
import gc
del sample_val_data
del sample_train_data
gc.collect()
```
## Scale columns
```
# scale columns
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import MinMaxScaler
scaling_cols= ["empiric_calibrated_recs", "empiric_clicks", "empiric_calibrated_recs", "user_recs", "user_clicks", "user_target_recs"]
scaler = StandardScaler()
train_data[scaling_cols] = scaler.fit_transform(train_data[scaling_cols])
val_data[scaling_cols] = scaler.transform(val_data[scaling_cols])
train_data
val_data = val_data.drop(columns=["Unnamed: 0.1"])
val_data
```
#Explore Data
```
sample_train_data
test_data
from collections import Counter
user_recs_dist = test_data["user_recs"].value_counts(normalize=True)
top_user_recs_count = user_recs_dist.nlargest(200)
print(top_user_recs_count)
percent = sum(top_user_recs_count.values)
percent
print(sample_train_data["user_recs"].value_counts(normalize=False))
print(test_data["user_recs"].value_counts())
positions = top_user_recs_count
def sample(obj, replace=False, total=1500000):
return obj.sample(n=int(positions[obj.name] * total), replace=replace)
sample_train_data_filtered = sample_train_data[sample_train_data["user_recs"].isin(positions.keys())]
result = sample_train_data_filtered.groupby("user_recs").apply(sample).reset_index(drop=True)
result["user_recs"].value_counts(normalize=True)
top_user_recs_train_data = result
top_user_recs_train_data
not_top_user_recs_train_data = sample_train_data[~sample_train_data["user_recs"].isin(top_user_recs_train_data["user_recs"].unique())]
not_top_user_recs_train_data["user_recs"].value_counts()
train_data = pd.concat([top_user_recs_train_data, not_top_user_recs_train_data])
train_data["user_recs"].value_counts(normalize=False)
train_data = train_data.drop(columns = ["user_id_hash"])
train_data = train_data.fillna("Unknown")
train_data
```
#Train the model
```
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn import metrics
X_train = train_data.drop(columns=["is_click"], inplace=False)
y_train = train_data["is_click"]
X_val = val_data.drop(columns=["is_click"], inplace=False)
y_val = val_data["is_click"]
from catboost import CatBoostClassifier
# cat_features_inds = [1,2,3,4,7,8,12,13,14,15,17,18]
encode_cols = [ "user_id_hash", "target_id_hash", "syndicator_id_hash", "campaign_id_hash", "target_item_taxonomy", "placement_id_hash", "publisher_id_hash", "source_id_hash", "source_item_type", "browser_platform", "country_code", "region", "gmt_offset"]
# model = CatBoostClassifier(iterations = 50, learning_rate=0.5, task_type='CPU', loss_function='Logloss', cat_features = encode_cols)
model = CatBoostClassifier(iterations = 180, learning_rate=0.7, task_type='CPU', loss_function='Logloss', cat_features = encode_cols,
eval_metric='AUC')#, depth=6, l2_leaf_reg= 10)
"""
All of our tries with catboost (only the best of them were uploaded to kaggle):
results:
all features, all rows of train fillna = Unknown
logloss 100 iterations learning rate 0.5 10 files: 0.857136889762303 | bestTest = 0.4671640673 0.857136889762303
logloss 100 iterations learning rate 0.4 10 files: bestTest = 0.4676805926 0.856750110976787
logloss 100 iterations learning rate 0.55 10 files: bestTest = 0.4669830858 0.8572464626142212
logloss 120 iterations learning rate 0.6 10 files: bestTest = 0.4662084678 0.8577564702279399
logloss 150 iterations learning rate 0.7 10 files: bestTest = 0.4655981391 0.8581645278496352
logloss 180 iterations learning rate 0.7 10 files: bestTest = 0.4653168207 0.8583423138228865 !!!!!!!!!!
logloss 180 iterations learning rate 0.7 10 files day extracted from date (not as categorical): 0.8583034988
logloss 180 iterations learning rate 0.7 10 files day extracted from date (as categorical): 0.8583014151
logloss 180 iterations learning rate 0.75 10 files day extracted from date (as categorical): 0.8582889749
logloss 180 iterations learning rate 0.65 10 files day extracted from date (as categorical): 0.8582334254
logloss 180 iterations learning rate 0.65 10 files day extracted from date (as categorical) StandardScaler: 0.8582101013
logloss 180 iterations learning rate 0.7 10 files day extracted from date (as categorical) MinMaxScaler dropna: ~0.8582
logloss 180 iterations learning rate 0.7 distributed data train and val, day extracted as categorical MinMaxScaler: 0.8561707
logloss 180 iterations learning rate 0.7 distributed data train and val, day extracted as not categorical no scale: 0.8561707195
logloss 180 iterations learning rate 0.7 distributed data train and val, no scale no date: 0.8559952294
logloss 180 iterations learning rate 0.7 distributed data train and val, day extracted as not categorical no scale with date: 0.8560461554
logloss 180 iterations learning rate 0.7, 9 times distributed data train and val, no user no date: 0.8545560094
logloss 180 iterations learning rate 0.7, 9 times distributed data train and val, with user and numeric day: 0.8561601034
logloss 180 iterations learning rate 0.7, 9 times distributed data train and val, with user with numeric date: 0.8568834122
logloss 180 iterations learning rate 0.7, 10 different files, scaled, all features: 0.8584829166 !!!!!!!
logloss 180 iterations learning rate 0.7, new data, scaled, all features: 0.8915972905 test: 0.84108
logloss 180 iterations learning rate 0.9 10 files: bestTest = 0.4656462845
logloss 100 iterations learning rate 0.5 8 files: 0.8568031111965864
logloss 300 iterations learning rate 0.5:
crossentropy 50 iterations learning rate 0.5: 0.8556282878645277
"""
model.fit(X_train, y_train, eval_set=(X_val, y_val), verbose=10)
```
# Submission File
```
test_data = pd.read_csv("/content/drive/MyDrive/RS_Kaggle_Competition/test/test_file.csv")
test_data = test_data.iloc[:,:-1]
test_data[scaling_cols] = scaler.transform(test_data[scaling_cols])
X_test = test_data.fillna("Unknown")
X_test
pred_proba = model.predict_proba(X_test)
submission_dir_path = "/content/drive/MyDrive/RS_Kaggle_Competition/submissions"
pred = pred_proba[:,1]
pred_df = pd.DataFrame(pred)
pred_df.reset_index(inplace=True)
pred_df.columns = ['Id', 'Predicted']
pred_df.to_csv(submission_dir_path + '/catboost_submission_datafrom1704_data_lr_0.7_with_scale_with_num_startdate_with_user_iters_159.csv', index=False)
```
| github_jupyter |
# Random Search Algorithms
### Importing Necessary Libraries
```
import six
import sys
sys.modules['sklearn.externals.six'] = six
import mlrose
import numpy as np
import pandas as pd
import seaborn as sns
import mlrose_hiive
import matplotlib.pyplot as plt
np.random.seed(44)
sns.set_style("darkgrid")
```
### Defining a Fitness Function Object
```
# Define alternative N-Queens fitness function for maximization problem
def queens_max(state):
# Initialize counter
fitness = 0
# For all pairs of queens
for i in range(len(state) - 1):
for j in range(i + 1, len(state)):
# Check for horizontal, diagonal-up and diagonal-down attacks
if (state[j] != state[i]) \
and (state[j] != state[i] + (j - i)) \
and (state[j] != state[i] - (j - i)):
# If no attacks, then increment counter
fitness += 1
return fitness
# Initialize custom fitness function object
fitness_cust = mlrose.CustomFitness(queens_max)
```
### Defining an Optimization Problem Object
```
%%time
# DiscreteOpt() takes integers in range 0 to max_val -1 defined at initialization
number_of_queens = 16
problem = mlrose_hiive.DiscreteOpt(length = number_of_queens, fitness_fn = fitness_cust, maximize = True, max_val = number_of_queens)
```
### Optimization #1 Simulated Annealing
```
%%time
sa = mlrose_hiive.SARunner(problem, experiment_name="SA_Exp",
iteration_list=[10000],
temperature_list=[10, 50, 100, 250, 500],
decay_list=[mlrose_hiive.ExpDecay,
mlrose_hiive.GeomDecay],
seed=44, max_attempts=100)
sa_run_stats, sa_run_curves = sa.run()
last_iters = sa_run_stats[sa_run_stats.Iteration != 0].reset_index()
print('Mean:', last_iters.Fitness.mean(), '\nMin:',last_iters.Fitness.max(),'\nMax:',last_iters.Fitness.max())
print('Mean Time;',last_iters.Time.mean())
best_index_in_curve = sa_run_curves.Fitness.idxmax()
best_decay = sa_run_curves.iloc[best_index_in_curve].Temperature
best_curve = sa_run_curves.loc[sa_run_curves.Temperature == best_decay, :]
best_curve.reset_index(inplace=True)
best_decay
best_index_in_curve = sa_run_curves.Fitness.idxmax()
best_decay = sa_run_curves.iloc[best_index_in_curve].Temperature
best_sa_curve = sa_run_curves.loc[sa_run_curves.Temperature == best_decay, :]
best_sa_curve.reset_index(inplace=True)
# draw lineplot
sa_run_curves['Temperature'] = sa_run_curves['Temperature'].astype(str).astype(float)
sa_run_curves_t1 = sa_run_curves[sa_run_curves['Temperature'] == 10]
sa_run_curves_t2 = sa_run_curves[sa_run_curves['Temperature'] == 50]
sa_run_curves_t3 = sa_run_curves[sa_run_curves['Temperature'] == 100]
sa_run_curves_t4 = sa_run_curves[sa_run_curves['Temperature'] == 250]
sa_run_curves_t5 = sa_run_curves[sa_run_curves['Temperature'] == 500]
sns.lineplot(x="Iteration", y="Fitness", data=sa_run_curves_t1, label = "t = 10")
sns.lineplot(x="Iteration", y="Fitness", data=sa_run_curves_t2, label = "t = 50")
sns.lineplot(x="Iteration", y="Fitness", data=sa_run_curves_t3, label = "t = 100")
sns.lineplot(x="Iteration", y="Fitness", data=sa_run_curves_t4, label = "t = 250")
sns.lineplot(x="Iteration", y="Fitness", data=sa_run_curves_t5, label = "t = 500")
plt.title('16-Queens SA Fitness Vs Iterations')
plt.show()
sa_run_curves
```
### Optimization #2 Genetic Algorithm
```
%%time
ga = mlrose_hiive.GARunner(problem=problem,
experiment_name="GA_Exp",
seed=44,
iteration_list = [10000],
max_attempts = 100,
population_sizes = [100, 500],
mutation_rates = [0.1, 0.25, 0.5])
ga_run_stats, ga_run_curves = ga.run()
last_iters = ga_run_stats[ga_run_stats.Iteration != 0].reset_index()
print("Max and mean")
print(last_iters.Fitness.max(), last_iters.Fitness.mean(), last_iters.Time.mean())
print(last_iters.groupby("Mutation Rate").Fitness.mean())
print(last_iters.groupby("Population Size").Fitness.mean())
print(last_iters.groupby("Population Size").Time.mean())
# draw lineplot
ga_run_curves_mu1 = ga_run_curves[ga_run_curves['Mutation Rate'] == 0.1]
ga_run_curves_mu2 = ga_run_curves[ga_run_curves['Mutation Rate'] == 0.25]
ga_run_curves_mu3 = ga_run_curves[ga_run_curves['Mutation Rate'] == 0.5]
sns.lineplot(x="Iteration", y="Fitness", data=ga_run_curves_mu1, label = "mr = 0.1")
sns.lineplot(x="Iteration", y="Fitness", data=ga_run_curves_mu2, label = "mr = 0.25")
sns.lineplot(x="Iteration", y="Fitness", data=ga_run_curves_mu3, label = "mr = 0.5")
plt.title('16-Queens GA Fitness Vs Iterations')
plt.show()
```
### Optimization #3 MIMIC
```
%%time
mmc = mlrose_hiive.MIMICRunner(problem=problem,
experiment_name="MMC_Exp",
seed=44,
iteration_list=[10000],
max_attempts=100,
population_sizes=[100,500],
keep_percent_list=[0.1, 0.25, 0.5],
use_fast_mimic=True)
# the two data frames will contain the results
mmc_run_stats, mmc_run_curves = mmc.run()
last_iters = mmc_run_stats[mmc_run_stats.Iteration != 0].reset_index()
print("Max and mean")
print(last_iters.Fitness.max(), last_iters.Fitness.mean(), last_iters.Time.mean())
print(last_iters.groupby("Keep Percent").Fitness.mean())
print(last_iters.groupby("Population Size").Fitness.mean())
print(last_iters.groupby("Population Size").Time.mean())
mmc_run_curves
# draw lineplot
mmc_run_curves_kp1 = mmc_run_curves[mmc_run_curves['Keep Percent'] == 0.1]
mmc_run_curves_kp2 = mmc_run_curves[mmc_run_curves['Keep Percent'] == 0.25]
mmc_run_curves_kp3 = mmc_run_curves[mmc_run_curves['Keep Percent'] == 0.5]
sns.lineplot(x="Iteration", y="Fitness", data=mmc_run_curves_kp1, label = "kp = 0.1")
sns.lineplot(x="Iteration", y="Fitness", data=mmc_run_curves_kp2, label = "kp = 0.25")
sns.lineplot(x="Iteration", y="Fitness", data=mmc_run_curves_kp3, label = "kp = 0.5")
plt.title('16-Queens MIMIC Fitness Vs Iterations')
plt.show()
```
### Optimization #4 Randomized Hill Climbing
```
%%time
runner_return = mlrose_hiive.RHCRunner(problem, experiment_name="first_try",
iteration_list=[10000],
seed=44, max_attempts=100,
restart_list=[100])
rhc_run_stats, rhc_run_curves = runner_return.run()
last_iters = rhc_run_stats[rhc_run_stats.Iteration != 0].reset_index()
print(last_iters.Fitness.mean(), last_iters.Fitness.max())
print(last_iters.Time.max())
best_index_in_curve = rhc_run_curves.Fitness.idxmax()
best_decay = rhc_run_curves.iloc[best_index_in_curve].current_restart
best_RHC_curve = rhc_run_curves.loc[rhc_run_curves.current_restart == best_decay, :]
best_RHC_curve.reset_index(inplace=True)
best_RHC_curve
# draw lineplot
sns.lineplot(x="Iteration", y="Fitness", data=best_RHC_curve)
plt.title('16-Queens RHC Fitness Vs Iterations')
plt.show()
sns.lineplot(x="Iteration", y="Fitness", data=ga_run_curves_mu3, label = "GA")
sns.lineplot(x="Iteration", y="Fitness", data=best_sa_curve, label = "SA")
sns.lineplot(x="Iteration", y="Fitness", data=mmc_run_curves, label = "MIMIC")
sns.lineplot(x="Iteration", y="Fitness", data=best_RHC_curve, label = "RHC")
plt.show()
```
| github_jupyter |
```
%matplotlib inline
```
Performance Tuning Guide
*************************
**Author**: `Szymon Migacz <https://github.com/szmigacz>`_
Performance Tuning Guide is a set of optimizations and best practices which can
accelerate training and inference of deep learning models in PyTorch. Presented
techniques often can be implemented by changing only a few lines of code and can
be applied to a wide range of deep learning models across all domains.
General optimizations
---------------------
Enable async data loading and augmentation
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`torch.utils.data.DataLoader <https://pytorch.org/docs/stable/data.html#torch.utils.data.DataLoader>`_
supports asynchronous data loading and data augmentation in separate worker
subprocesses. The default setting for ``DataLoader`` is ``num_workers=0``,
which means that the data loading is synchronous and done in the main process.
As a result the main training process has to wait for the data to be available
to continue the execution.
Setting ``num_workers > 0`` enables asynchronous data loading and overlap
between the training and data loading. ``num_workers`` should be tuned
depending on the workload, CPU, GPU, and location of training data.
``DataLoader`` accepts ``pin_memory`` argument, which defaults to ``False``.
When using a GPU it's better to set ``pin_memory=True``, this instructs
``DataLoader`` to use pinned memory and enables faster and asynchronous memory
copy from the host to the GPU.
Disable gradient calculation for validation or inference
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
PyTorch saves intermediate buffers from all operations which involve tensors
that require gradients. Typically gradients aren't needed for validation or
inference.
`torch.no_grad() <https://pytorch.org/docs/stable/generated/torch.no_grad.html#torch.no_grad>`_
context manager can be applied to disable gradient calculation within a
specified block of code, this accelerates execution and reduces the amount of
required memory.
`torch.no_grad() <https://pytorch.org/docs/stable/generated/torch.no_grad.html#torch.no_grad>`_
can also be used as a function decorator.
Disable bias for convolutions directly followed by a batch norm
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`torch.nn.Conv2d() <https://pytorch.org/docs/stable/generated/torch.nn.Conv2d.html#torch.nn.Conv2d>`_
has ``bias`` parameter which defaults to ``True`` (the same is true for
`Conv1d <https://pytorch.org/docs/stable/generated/torch.nn.Conv1d.html#torch.nn.Conv1d>`_
and
`Conv3d <https://pytorch.org/docs/stable/generated/torch.nn.Conv3d.html#torch.nn.Conv3d>`_
).
If a ``nn.Conv2d`` layer is directly followed by a ``nn.BatchNorm2d`` layer,
then the bias in the convolution is not needed, instead use
``nn.Conv2d(..., bias=False, ....)``. Bias is not needed because in the first
step ``BatchNorm`` subtracts the mean, which effectively cancels out the
effect of bias.
This is also applicable to 1d and 3d convolutions as long as ``BatchNorm`` (or
other normalization layer) normalizes on the same dimension as convolution's
bias.
Models available from `torchvision <https://github.com/pytorch/vision>`_
already implement this optimization.
Use parameter.grad = None instead of model.zero_grad() or optimizer.zero_grad()
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Instead of calling:
```
model.zero_grad()
# or
optimizer.zero_grad()
```
to zero out gradients, use the following method instead:
```
for param in model.parameters():
param.grad = None
```
The second code snippet does not zero the memory of each individual parameter,
also the subsequent backward pass uses assignment instead of addition to store
gradients, this reduces the number of memory operations.
Setting gradient to ``None`` has a slightly different numerical behavior than
setting it to zero, for more details refer to the
`documentation <https://pytorch.org/docs/master/optim.html#torch.optim.Optimizer.zero_grad>`_.
Alternatively, starting from PyTorch 1.7, call ``model`` or
``optimizer.zero_grad(set_to_none=True)``.
Fuse pointwise operations
~~~~~~~~~~~~~~~~~~~~~~~~~
Pointwise operations (elementwise addition, multiplication, math functions -
``sin()``, ``cos()``, ``sigmoid()`` etc.) can be fused into a single kernel
to amortize memory access time and kernel launch time.
`PyTorch JIT <https://pytorch.org/docs/stable/jit.html>`_ can fuse kernels
automatically, although there could be additional fusion opportunities not yet
implemented in the compiler, and not all device types are supported equally.
Pointwise operations are memory-bound, for each operation PyTorch launches a
separate kernel. Each kernel loads data from the memory, performs computation
(this step is usually inexpensive) and stores results back into the memory.
Fused operator launches only one kernel for multiple fused pointwise ops and
loads/stores data only once to the memory. This makes JIT very useful for
activation functions, optimizers, custom RNN cells etc.
In the simplest case fusion can be enabled by applying
`torch.jit.script <https://pytorch.org/docs/stable/generated/torch.jit.script.html#torch.jit.script>`_
decorator to the function definition, for example:
```
@torch.jit.script
def fused_gelu(x):
return x * 0.5 * (1.0 + torch.erf(x / 1.41421))
```
Refer to
`TorchScript documentation <https://pytorch.org/docs/stable/jit.html>`_
for more advanced use cases.
Enable channels_last memory format for computer vision models
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
PyTorch 1.5 introduced support for ``channels_last`` memory format for
convolutional networks. This format is meant to be used in conjunction with
`AMP <https://pytorch.org/docs/stable/amp.html>`_ to further accelerate
convolutional neural networks with
`Tensor Cores <https://www.nvidia.com/en-us/data-center/tensor-cores/>`_.
Support for ``channels_last`` is experimental, but it's expected to work for
standard computer vision models (e.g. ResNet-50, SSD). To convert models to
``channels_last`` format follow
`Channels Last Memory Format Tutorial <https://tutorials.pytorch.kr/intermediate/memory_format_tutorial.html>`_.
The tutorial includes a section on
`converting existing models <https://tutorials.pytorch.kr/intermediate/memory_format_tutorial.html#converting-existing-models>`_.
Checkpoint intermediate buffers
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Buffer checkpointing is a technique to mitigate the memory capacity burden of
model training. Instead of storing inputs of all layers to compute upstream
gradients in backward propagation, it stores the inputs of a few layers and
the others are recomputed during backward pass. The reduced memory
requirements enables increasing the batch size that can improve utilization.
Checkpointing targets should be selected carefully. The best is not to store
large layer outputs that have small re-computation cost. The example target
layers are activation functions (e.g. ``ReLU``, ``Sigmoid``, ``Tanh``),
up/down sampling and matrix-vector operations with small accumulation depth.
PyTorch supports a native
`torch.utils.checkpoint <https://pytorch.org/docs/stable/checkpoint.html>`_
API to automatically perform checkpointing and recomputation.
Disable debugging APIs
~~~~~~~~~~~~~~~~~~~~~~
Many PyTorch APIs are intended for debugging and should be disabled for
regular training runs:
* anomaly detection:
`torch.autograd.detect_anomaly <https://pytorch.org/docs/stable/autograd.html#torch.autograd.detect_anomaly>`_
or
`torch.autograd.set_detect_anomaly(True) <https://pytorch.org/docs/stable/autograd.html#torch.autograd.set_detect_anomaly>`_
* profiler related:
`torch.autograd.profiler.emit_nvtx <https://pytorch.org/docs/stable/autograd.html#torch.autograd.profiler.emit_nvtx>`_,
`torch.autograd.profiler.profile <https://pytorch.org/docs/stable/autograd.html#torch.autograd.profiler.profile>`_
* autograd gradcheck:
`torch.autograd.gradcheck <https://pytorch.org/docs/stable/autograd.html#torch.autograd.gradcheck>`_
or
`torch.autograd.gradgradcheck <https://pytorch.org/docs/stable/autograd.html#torch.autograd.gradgradcheck>`_
GPU specific optimizations
--------------------------
Enable cuDNN auto-tuner
~~~~~~~~~~~~~~~~~~~~~~~
`NVIDIA cuDNN <https://developer.nvidia.com/cudnn>`_ supports many algorithms
to compute a convolution. Autotuner runs a short benchmark and selects the
kernel with the best performance on a given hardware for a given input size.
For convolutional networks (other types currently not supported), enable cuDNN
autotuner before launching the training loop by setting:
```
torch.backends.cudnn.benchmark = True
```
* the auto-tuner decisions may be non-deterministic; different algorithm may
be selected for different runs. For more details see
`PyTorch: Reproducibility <https://pytorch.org/docs/stable/notes/randomness.html?highlight=determinism>`_
* in some rare cases, such as with highly variable input sizes, it's better
to run convolutional networks with autotuner disabled to avoid the overhead
associated with algorithm selection for each input size.
Avoid unnecessary CPU-GPU synchronization
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Avoid unnecessary synchronizations, to let the CPU run ahead of the
accelerator as much as possible to make sure that the accelerator work queue
contains many operations.
When possible, avoid operations which require synchronizations, for example:
* ``print(cuda_tensor)``
* ``cuda_tensor.item()``
* memory copies: ``tensor.cuda()``, ``cuda_tensor.cpu()`` and equivalent
``tensor.to(device)`` calls
* ``cuda_tensor.nonzero()``
* python control flow which depends on results of operations performed on cuda
tensors e.g. ``if (cuda_tensor != 0).all()``
Create tensors directly on the target device
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Instead of calling ``torch.rand(size).cuda()`` to generate a random tensor,
produce the output directly on the target device:
``torch.rand(size, device=torch.device('cuda'))``.
This is applicable to all functions which create new tensors and accept
``device`` argument:
`torch.rand() <https://pytorch.org/docs/stable/generated/torch.rand.html#torch.rand>`_,
`torch.zeros() <https://pytorch.org/docs/stable/generated/torch.zeros.html#torch.zeros>`_,
`torch.full() <https://pytorch.org/docs/stable/generated/torch.full.html#torch.full>`_
and similar.
Use mixed precision and AMP
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Mixed precision leverages
`Tensor Cores <https://www.nvidia.com/en-us/data-center/tensor-cores/>`_
and offers up to 3x overall speedup on Volta and newer GPU architectures. To
use Tensor Cores AMP should be enabled and matrix/tensor dimensions should
satisfy requirements for calling kernels that use Tensor Cores.
To use Tensor Cores:
* set sizes to multiples of 8 (to map onto dimensions of Tensor Cores)
* see
`Deep Learning Performance Documentation
<https://docs.nvidia.com/deeplearning/performance/index.html#optimizing-performance>`_
for more details and guidelines specific to layer type
* if layer size is derived from other parameters rather than fixed, it can
still be explicitly padded e.g. vocabulary size in NLP models
* enable AMP
* Introduction to Mixed Precision Training and AMP:
`video <https://www.youtube.com/watch?v=jF4-_ZK_tyc&feature=youtu.be>`_,
`slides <https://nvlabs.github.io/eccv2020-mixed-precision-tutorial/files/dusan_stosic-training-neural-networks-with-tensor-cores.pdf>`_
* native PyTorch AMP is available starting from PyTorch 1.6:
`documentation <https://pytorch.org/docs/stable/amp.html>`_,
`examples <https://pytorch.org/docs/stable/notes/amp_examples.html#amp-examples>`_,
`tutorial <https://tutorials.pytorch.kr/recipes/recipes/amp_recipe.html>`_
Pre-allocate memory in case of variable input length
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Models for speech recognition or for NLP are often trained on input tensors
with variable sequence length. Variable length can be problematic for PyTorch
caching allocator and can lead to reduced performance or to unexpected
out-of-memory errors. If a batch with a short sequence length is followed by
an another batch with longer sequence length, then PyTorch is forced to
release intermediate buffers from previous iteration and to re-allocate new
buffers. This process is time consuming and causes fragmentation in the
caching allocator which may result in out-of-memory errors.
A typical solution is to implement pre-allocation. It consists of the
following steps:
#. generate a (usually random) batch of inputs with maximum sequence length
(either corresponding to max length in the training dataset or to some
predefined threshold)
#. execute a forward and a backward pass with the generated batch, do not
execute an optimizer or a learning rate scheduler, this step pre-allocates
buffers of maximum size, which can be reused in subsequent
training iterations
#. zero out gradients
#. proceed to regular training
Distributed optimizations
-------------------------
Use efficient data-parallel backend
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
PyTorch has two ways to implement data-parallel training:
* `torch.nn.DataParallel <https://pytorch.org/docs/stable/generated/torch.nn.DataParallel.html#torch.nn.DataParallel>`_
* `torch.nn.parallel.DistributedDataParallel <https://pytorch.org/docs/stable/generated/torch.nn.parallel.DistributedDataParallel.html#torch.nn.parallel.DistributedDataParallel>`_
``DistributedDataParallel`` offers much better performance and scaling to
multiple-GPUs. For more information refer to the
`relevant section of CUDA Best Practices <https://pytorch.org/docs/stable/notes/cuda.html#use-nn-parallel-distributeddataparallel-instead-of-multiprocessing-or-nn-dataparallel>`_
from PyTorch documentation.
Skip unnecessary all-reduce if training with DistributedDataParallel and gradient accumulation
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
By default
`torch.nn.parallel.DistributedDataParallel <https://pytorch.org/docs/stable/generated/torch.nn.parallel.DistributedDataParallel.html#torch.nn.parallel.DistributedDataParallel>`_
executes gradient all-reduce after every backward pass to compute the average
gradient over all workers participating in the training. If training uses
gradient accumulation over N steps, then all-reduce is not necessary after
every training step, it's only required to perform all-reduce after the last
call to backward, just before the execution of the optimizer.
``DistributedDataParallel`` provides
`no_sync() <https://pytorch.org/docs/stable/generated/torch.nn.parallel.DistributedDataParallel.html#torch.nn.parallel.DistributedDataParallel.no_sync>`_
context manager which disables gradient all-reduce for particular iteration.
``no_sync()`` should be applied to first ``N-1`` iterations of gradient
accumulation, the last iteration should follow the default execution and
perform the required gradient all-reduce.
Match the order of layers in constructors and during the execution if using DistributedDataParallel(find_unused_parameters=True)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
`torch.nn.parallel.DistributedDataParallel <https://pytorch.org/docs/stable/generated/torch.nn.parallel.DistributedDataParallel.html#torch.nn.parallel.DistributedDataParallel>`_
with ``find_unused_parameters=True`` uses the order of layers and parameters
from model constructors to build buckets for ``DistributedDataParallel``
gradient all-reduce. ``DistributedDataParallel`` overlaps all-reduce with the
backward pass. All-reduce for a particular bucket is asynchronously triggered
only when all gradients for parameters in a given bucket are available.
To maximize the amount of overlap, the order in model constructors should
roughly match the order during the execution. If the order doesn't match, then
all-reduce for the entire bucket waits for the gradient which is the last to
arrive, this may reduce the overlap between backward pass and all-reduce,
all-reduce may end up being exposed, which slows down the training.
``DistributedDataParallel`` with ``find_unused_parameters=False`` (which is
the default setting) relies on automatic bucket formation based on order of
operations encountered during the backward pass. With
``find_unused_parameters=False`` it's not necessary to reorder layers or
parameters to achieve optimal performance.
Load-balance workload in a distributed setting
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Load imbalance typically may happen for models processing sequential data
(speech recognition, translation, language models etc.). If one device
receives a batch of data with sequence length longer than sequence lengths for
the remaining devices, then all devices wait for the worker which finishes
last. Backward pass functions as an implicit synchronization point in a
distributed setting with
`DistributedDataParallel <https://pytorch.org/docs/stable/generated/torch.nn.parallel.DistributedDataParallel.html#torch.nn.parallel.DistributedDataParallel>`_
backend.
There are multiple ways to solve the load balancing problem. The core idea is
to distribute workload over all workers as uniformly as possible within each
global batch. For example Transformer solves imbalance by forming batches with
approximately constant number of tokens (and variable number of sequences in a
batch), other models solve imbalance by bucketing samples with similar
sequence length or even by sorting dataset by sequence length.
| github_jupyter |
# 78. Subsets
__Difficulty__: Medium
[Link](https://leetcode.com/problems/subsets/)
Given an integer array `nums` of unique elements, return all possible subsets (the power set).
The solution set must not contain duplicate subsets. Return the solution in any order.
__Example 1__:
Input: `nums = [1,2,3]`
Output: `[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]`
```
from typing import List
```
## DFS Approach
```
class SolutionDFS:
def dfs(self, res, nums):
if len(nums)==0:
return [res]
ans = []
for i, num in enumerate(nums):
# print(res+[num])
ans.extend(self.dfs(res+[num], nums[i+1:]))
ans.append(res)
# print(ans)
return ans
def subsets(self, nums: List[int]) -> List[List[int]]:
return self.dfs([], nums)
```
## Using a bit-mask to indicate selected items from the list of numbers
```
class SolutionMask:
def subsets(self, nums: List[int]) -> List[List[int]]:
combs = []
n = len(nums)
for mask in range(0, 2**n):
i = 0
rem = mask
current_set = []
while rem:
if rem%2:
current_set.append(nums[i])
rem = rem//2
i += 1
combs.append(current_set)
return combs
```
A cleaner and efficient implementation of using bit-mask.
```
class SolutionMask2:
def subsets(self, nums: List[int]) -> List[List[int]]:
res = []
n = len(nums)
nth_bit = 1<<n
for i in range(2**n):
# To create a bit-mask with length n
bit_mask = bin(i | nth_bit)[3:]
res.append([nums[j] for j in range(n) if bit_mask[j]=='1'])
return res
```
## Test cases
```
# Example 1
nums1 = [1,2,3]
res1 = [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
# Example 2
nums2 = [0]
res2 = [[],[0]]
# Example 3
nums3 = [0, -2, 5, -7, 9]
res3 = [[0,-2,5,-7,9],[0,-2,5,-7],[0,-2,5,9],[0,-2,5],[0,-2,-7,9],[0,-2,-7],[0,-2,9],[0,-2],[0,5,-7,9],[0,5,-7],[0,5,9],[0,5],[0,-7,9],[0,-7],[0,9],[0],[-2,5,-7,9],[-2,5,-7],[-2,5,9],[-2,5],[-2,-7,9],[-2,-7],[-2,9],[-2],[5,-7,9],[5,-7],[5,9],[5],[-7,9],[-7],[9],[]]
def test_function(inp, result):
assert len(inp)==len(result)
inp_set = [set(x) for x in inp]
res_set = [set(x) for x in result]
for i in inp_set:
assert i in res_set
# Test DFS method
dfs_sol = SolutionDFS()
test_function(dfs_sol.subsets(nums1), res1)
test_function(dfs_sol.subsets(nums2), res2)
test_function(dfs_sol.subsets(nums3), res3)
# Test bit-mask method
mask_sol = SolutionMask()
test_function(mask_sol.subsets(nums1), res1)
test_function(mask_sol.subsets(nums2), res2)
test_function(mask_sol.subsets(nums3), res3)
# Test bit-mask method
mask_sol = SolutionMask2()
test_function(mask_sol.subsets(nums1), res1)
test_function(mask_sol.subsets(nums2), res2)
test_function(mask_sol.subsets(nums3), res3)
```
| github_jupyter |
```
#r "nuget:Microsoft.ML,1.4.0"
#r "nuget:Microsoft.ML.AutoML,0.16.0"
#r "nuget:Microsoft.Data.Analysis,0.1.0"
using Microsoft.Data.Analysis;
using XPlot.Plotly;
using Microsoft.AspNetCore.Html;
Formatter<DataFrame>.Register((df, writer) =>
{
var headers = new List<IHtmlContent>();
headers.Add(th(i("index")));
headers.AddRange(df.Columns.Select(c => (IHtmlContent) th(c.Name)));
var rows = new List<List<IHtmlContent>>();
var take = 20;
for (var i = 0; i < Math.Min(take, df.RowCount); i++)
{
var cells = new List<IHtmlContent>();
cells.Add(td(i));
foreach (var obj in df[i])
{
cells.Add(td(obj));
}
rows.Add(cells);
}
var t = table(
thead(
headers),
tbody(
rows.Select(
r => tr(r))));
writer.Write(t);
}, "text/html");
using System.IO;
using System.Net.Http;
string housingPath = "housing.csv";
if (!File.Exists(housingPath))
{
var contents = new HttpClient()
.GetStringAsync("https://raw.githubusercontent.com/ageron/handson-ml2/master/datasets/housing/housing.csv").Result;
File.WriteAllText("housing.csv", contents);
}
var housingData = DataFrame.LoadCsv(housingPath);
housingData
housingData.Description()
Chart.Plot(
new Graph.Histogram()
{
x = housingData["median_house_value"],
nbinsx = 20
}
)
var chart = Chart.Plot(
new Graph.Scattergl()
{
x = housingData["longitude"],
y = housingData["latitude"],
mode = "markers",
marker = new Graph.Marker()
{
color = housingData["median_house_value"],
colorscale = "Jet"
}
}
);
chart.Width = 600;
chart.Height = 600;
display(chart);
static T[] Shuffle<T>(T[] array)
{
Random rand = new Random();
for (int i = 0; i < array.Length; i++)
{
int r = i + rand.Next(array.Length - i);
T temp = array[r];
array[r] = array[i];
array[i] = temp;
}
return array;
}
int[] randomIndices = Shuffle(Enumerable.Range(0, (int)housingData.RowCount).ToArray());
int testSize = (int)(housingData.RowCount * .1);
int[] trainRows = randomIndices[testSize..];
int[] testRows = randomIndices[..testSize];
DataFrame housing_train = housingData[trainRows];
DataFrame housing_test = housingData[testRows];
display(housing_train.RowCount);
display(housing_test.RowCount);
using Microsoft.ML;
using Microsoft.ML.Data;
using Microsoft.ML.AutoML;
%%time
var mlContext = new MLContext();
var experiment = mlContext.Auto().CreateRegressionExperiment(maxExperimentTimeInSeconds: 15);
var result = experiment.Execute(housing_train, labelColumnName:"median_house_value");
var scatters = result.RunDetails.Where(d => d.ValidationMetrics != null).GroupBy(
r => r.TrainerName,
(name, details) => new Graph.Scattergl()
{
name = name,
x = details.Select(r => r.RuntimeInSeconds),
y = details.Select(r => r.ValidationMetrics.MeanAbsoluteError),
mode = "markers",
marker = new Graph.Marker() { size = 12 }
});
var chart = Chart.Plot(scatters);
chart.WithXTitle("Training Time");
chart.WithYTitle("Error");
display(chart);
Console.WriteLine($"Best Trainer:{result.BestRun.TrainerName}");
var testResults = result.BestRun.Model.Transform(housing_test);
var trueValues = testResults.GetColumn<float>("median_house_value");
var predictedValues = testResults.GetColumn<float>("Score");
var predictedVsTrue = new Graph.Scattergl()
{
x = trueValues,
y = predictedValues,
mode = "markers",
};
var maximumValue = Math.Max(trueValues.Max(), predictedValues.Max());
var perfectLine = new Graph.Scattergl()
{
x = new[] {0, maximumValue},
y = new[] {0, maximumValue},
mode = "lines",
};
var chart = Chart.Plot(new[] {predictedVsTrue, perfectLine });
chart.WithXTitle("True Values");
chart.WithYTitle("Predicted Values");
chart.WithLegend(false);
chart.Width = 600;
chart.Height = 600;
display(chart);
```
| github_jupyter |
# Chapter 8 - Applying Machine Learning To Sentiment Analysis
### Overview
- [Obtaining the IMDb movie review dataset](#Obtaining-the-IMDb-movie-review-dataset)
- [Introducing the bag-of-words model](#Introducing-the-bag-of-words-model)
- [Transforming words into feature vectors](#Transforming-words-into-feature-vectors)
- [Assessing word relevancy via term frequency-inverse document frequency](#Assessing-word-relevancy-via-term-frequency-inverse-document-frequency)
- [Cleaning text data](#Cleaning-text-data)
- [Processing documents into tokens](#Processing-documents-into-tokens)
- [Training a logistic regression model for document classification](#Training-a-logistic-regression-model-for-document-classification)
- [Working with bigger data – online algorithms and out-of-core learning](#Working-with-bigger-data-–-online-algorithms-and-out-of-core-learning)
- [Summary](#Summary)
NLP: Natural Language Processing
#### Sentiment Analysis (Opinion Mining)
Analyzes the polarity of documents
- Expressed opinions or emotions of the authors with regard to a particular topic
# Obtaining the IMDb movie review dataset
- IMDb: the Internet Movie Database
- IMDb dataset
- A. L. Maas, R. E. Daly, P. T. Pham, D. Huang, A. Y. Ng, and C. Potts. Learning Word Vectors for Sentiment Analysis. In the proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies, pages 142–150, Portland, Oregon, USA, June 2011. Association for Computational Linguistics
- 50,000 movie reviews labeled either *positive* or *negative*
The IMDB movie review set can be downloaded from [http://ai.stanford.edu/~amaas/data/sentiment/](http://ai.stanford.edu/~amaas/data/sentiment/).
After downloading the dataset, decompress the files.
`aclImdb_v1.tar.gz`
```
import pyprind
import pandas as pd
import os
# change the `basepath` to the directory of the
# unzipped movie dataset
basepath = '/Users/sklee/datasets/aclImdb/'
labels = {'pos': 1, 'neg': 0}
pbar = pyprind.ProgBar(50000)
df = pd.DataFrame()
for s in ('test', 'train'):
for l in ('pos', 'neg'):
path = os.path.join(basepath, s, l)
for file in os.listdir(path):
with open(os.path.join(path, file), 'r', encoding='utf-8') as infile:
txt = infile.read()
df = df.append([[txt, labels[l]]], ignore_index=True)
pbar.update()
df.columns = ['review', 'sentiment']
df.head(5)
```
Shuffling the DataFrame:
```
import numpy as np
np.random.seed(0)
df = df.reindex(np.random.permutation(df.index))
df.head(5)
df.to_csv('./movie_data.csv', index=False)
```
<br>
<br>
# Introducing the bag-of-words model
- **Vocabulary** : the collection of unique tokens (e.g. words) from the entire set of documents
- Construct a feature vector from each document
- Vector length = length of the vocabulary
- Contains the counts of how often each token occurs in the particular document
- Sparse vectors
## Transforming documents into feature vectors
By calling the fit_transform method on CountVectorizer, we just constructed the vocabulary of the bag-of-words model and transformed the following three sentences into sparse feature vectors:
1. The sun is shining
2. The weather is sweet
3. The sun is shining, the weather is sweet, and one and one is two
```
import numpy as np
from sklearn.feature_extraction.text import CountVectorizer
count = CountVectorizer()
docs = np.array([
'The sun is shining',
'The weather is sweet',
'The sun is shining, the weather is sweet, and one and one is two'])
bag = count.fit_transform(docs)
```
Now let us print the contents of the vocabulary to get a better understanding of the underlying concepts:
```
print(count.vocabulary_)
```
As we can see from executing the preceding command, the vocabulary is stored in a Python dictionary, which maps the unique words that are mapped to integer indices. Next let us print the feature vectors that we just created:
Each index position in the feature vectors shown here corresponds to the integer values that are stored as dictionary items in the CountVectorizer vocabulary. For example, the rst feature at index position 0 resembles the count of the word and, which only occurs in the last document, and the word is at index position 1 (the 2nd feature in the document vectors) occurs in all three sentences. Those values in the feature vectors are also called the raw term frequencies: *tf (t,d)*—the number of times a term t occurs in a document *d*.
```
print(bag.toarray())
```
Those count values are called the **raw term frequency td(t,d)**
- t: term
- d: document
The **n-gram** Models
- 1-gram: "the", "sun", "is", "shining"
- 2-gram: "the sun", "sun is", "is shining"
- CountVectorizer(ngram_range=(2,2))
<br>
## Assessing word relevancy via term frequency-inverse document frequency
```
np.set_printoptions(precision=2)
```
- Frequently occurring words across multiple documents from both classes typically don't contain useful or discriminatory information.
- ** Term frequency-inverse document frequency (tf-idf)** can be used to downweight those frequently occurring words in the feature vectors.
$$\text{tf-idf}(t,d)=\text{tf (t,d)}\times \text{idf}(t,d)$$
- **tf(t, d) the term frequency**
- **idf(t, d) the inverse document frequency**:
$$\text{idf}(t,d) = \text{log}\frac{n_d}{1+\text{df}(d, t)},$$
- $n_d$ is the total number of documents
- **df(d, t) document frequency**: the number of documents *d* that contain the term *t*.
- Note that adding the constant 1 to the denominator is optional and serves the purpose of assigning a non-zero value to terms that occur in all training samples; the log is used to ensure that low document frequencies are not given too much weight.
Scikit-learn implements yet another transformer, the `TfidfTransformer`, that takes the raw term frequencies from `CountVectorizer` as input and transforms them into tf-idfs:
```
from sklearn.feature_extraction.text import TfidfTransformer
tfidf = TfidfTransformer(use_idf=True, norm='l2', smooth_idf=True)
print(tfidf.fit_transform(count.fit_transform(docs)).toarray())
```
As we saw in the previous subsection, the word is had the largest term frequency in the 3rd document, being the most frequently occurring word. However, after transforming the same feature vector into tf-idfs, we see that the word is is
now associated with a relatively small tf-idf (0.45) in document 3 since it is
also contained in documents 1 and 2 and thus is unlikely to contain any useful, discriminatory information.
However, if we'd manually calculated the tf-idfs of the individual terms in our feature vectors, we'd have noticed that the `TfidfTransformer` calculates the tf-idfs slightly differently compared to the standard textbook equations that we de ned earlier. The equations for the idf and tf-idf that were implemented in scikit-learn are:
$$\text{idf} (t,d) = log\frac{1 + n_d}{1 + \text{df}(d, t)}$$
The tf-idf equation that was implemented in scikit-learn is as follows:
$$\text{tf-idf}(t,d) = \text{tf}(t,d) \times (\text{idf}(t,d)+1)$$
While it is also more typical to normalize the raw term frequencies before calculating the tf-idfs, the `TfidfTransformer` normalizes the tf-idfs directly.
By default (`norm='l2'`), scikit-learn's TfidfTransformer applies the L2-normalization, which returns a vector of length 1 by dividing an un-normalized feature vector *v* by its L2-norm:
$$v_{\text{norm}} = \frac{v}{||v||_2} = \frac{v}{\sqrt{v_{1}^{2} + v_{2}^{2} + \dots + v_{n}^{2}}} = \frac{v}{\big (\sum_{i=1}^{n} v_{i}^{2}\big)^\frac{1}{2}}$$
To make sure that we understand how TfidfTransformer works, let us walk
through an example and calculate the tf-idf of the word is in the 3rd document.
The word is has a term frequency of 3 (tf = 3) in document 3, and the document frequency of this term is 3 since the term is occurs in all three documents (df = 3). Thus, we can calculate the idf as follows:
$$\text{idf}("is", d3) = log \frac{1+3}{1+3} = 0$$
Now in order to calculate the tf-idf, we simply need to add 1 to the inverse document frequency and multiply it by the term frequency:
$$\text{tf-idf}("is",d3)= 3 \times (0+1) = 3$$
```
tf_is = 3
n_docs = 3
idf_is = np.log((n_docs+1) / (3+1))
tfidf_is = tf_is * (idf_is + 1)
print('tf-idf of term "is" = %.2f' % tfidf_is)
```
If we repeated these calculations for all terms in the 3rd document, we'd obtain the following tf-idf vectors: [3.39, 3.0, 3.39, 1.29, 1.29, 1.29, 2.0 , 1.69, 1.29]. However, we notice that the values in this feature vector are different from the values that we obtained from the TfidfTransformer that we used previously. The nal step that we are missing in this tf-idf calculation is the L2-normalization, which can be applied as follows:
$$\text{tfi-df}_{norm} = \frac{[3.39, 3.0, 3.39, 1.29, 1.29, 1.29, 2.0 , 1.69, 1.29]}{\sqrt{[3.39^2, 3.0^2, 3.39^2, 1.29^2, 1.29^2, 1.29^2, 2.0^2 , 1.69^2, 1.29^2]}}$$
$$=[0.5, 0.45, 0.5, 0.19, 0.19, 0.19, 0.3, 0.25, 0.19]$$
$$\Rightarrow \text{tf-idf}_{norm}("is", d3) = 0.45$$
As we can see, the results match the results returned by scikit-learn's `TfidfTransformer` (below). Since we now understand how tf-idfs are calculated, let us proceed to the next sections and apply those concepts to the movie review dataset.
```
tfidf = TfidfTransformer(use_idf=True, norm=None, smooth_idf=True)
raw_tfidf = tfidf.fit_transform(count.fit_transform(docs)).toarray()[-1]
raw_tfidf
l2_tfidf = raw_tfidf / np.sqrt(np.sum(raw_tfidf**2))
l2_tfidf
```
<br>
## Cleaning text data
**Before** we build the bag-of-words model.
```
df.loc[112, 'review'][-1000:]
```
#### Python regular expression library
```
import re
def preprocessor(text):
text = re.sub('<[^>]*>', '', text)
emoticons = re.findall('(?::|;|=)(?:-)?(?:\)|\(|D|P)', text)
text = re.sub('[\W]+', ' ', text.lower()) +\
' '.join(emoticons).replace('-', '')
return text
preprocessor(df.loc[112, 'review'][-1000:])
preprocessor("</a>This :) is :( a test :-)!")
df['review'] = df['review'].apply(preprocessor)
```
<br>
## Processing documents into tokens
#### Word Stemming
Transforming a word into its root form
- Original stemming algorithm: Martin F. Porter. An algorithm for suf x stripping. Program: electronic library and information systems, 14(3):130–137, 1980)
- Snowball stemmer (Porter2 or "English" stemmer)
- Lancaster stemmer (Paice-Husk stemmer)
Python NLP toolkit: NLTK (the Natural Language ToolKit)
- Free online book http://www.nltk.org/book/
```
from nltk.stem.porter import PorterStemmer
porter = PorterStemmer()
def tokenizer(text):
return text.split()
def tokenizer_porter(text):
return [porter.stem(word) for word in text.split()]
tokenizer('runners like running and thus they run')
tokenizer_porter('runners like running and thus they run')
```
#### Lemmatization
- thus -> thu
- Tries to find canonical forms of words
- Computationally expensive, little impact on text classification performance
#### Stop-words Removal
- Stop-words: extremely common words, e.g., is, and, has, like...
- Removal is useful when we use raw or normalized tf, rather than tf-idf
```
import nltk
nltk.download('stopwords')
from nltk.corpus import stopwords
stop = stopwords.words('english')
[w for w in tokenizer_porter('a runner likes running and runs a lot')[-10:]
if w not in stop]
stop[-10:]
```
<br>
<br>
# Training a logistic regression model for document classification
```
X_train = df.loc[:25000, 'review'].values
y_train = df.loc[:25000, 'sentiment'].values
X_test = df.loc[25000:, 'review'].values
y_test = df.loc[25000:, 'sentiment'].values
from sklearn.pipeline import Pipeline
from sklearn.linear_model import LogisticRegression
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.model_selection import GridSearchCV
tfidf = TfidfVectorizer(strip_accents=None,
lowercase=False,
preprocessor=None)
param_grid = [{'vect__ngram_range': [(1, 1)],
'vect__stop_words': [stop, None],
'vect__tokenizer': [tokenizer, tokenizer_porter],
'clf__penalty': ['l1', 'l2'],
'clf__C': [1.0, 10.0, 100.0]},
{'vect__ngram_range': [(1, 1)],
'vect__stop_words': [stop, None],
'vect__tokenizer': [tokenizer, tokenizer_porter],
'vect__use_idf':[False],
'vect__norm':[None],
'clf__penalty': ['l1', 'l2'],
'clf__C': [1.0, 10.0, 100.0]},
]
lr_tfidf = Pipeline([('vect', tfidf),
('clf', LogisticRegression(random_state=0))])
gs_lr_tfidf = GridSearchCV(lr_tfidf, param_grid,
scoring='accuracy',
cv=5,
verbose=1,
n_jobs=-1)
gs_lr_tfidf.fit(X_train, y_train)
print('Best parameter set: %s ' % gs_lr_tfidf.best_params_)
print('CV Accuracy: %.3f' % gs_lr_tfidf.best_score_)
# Best parameter set: {'vect__tokenizer': <function tokenizer at 0x11851c6a8>, 'clf__C': 10.0, 'vect__stop_words': None, 'clf__penalty': 'l2', 'vect__ngram_range': (1, 1)}
# CV Accuracy: 0.897
clf = gs_lr_tfidf.best_estimator_
print('Test Accuracy: %.3f' % clf.score(X_test, y_test))
# Test Accuracy: 0.899
```
<br>
<br>
# Working with bigger data - online algorithms and out-of-core learning
```
import numpy as np
import re
from nltk.corpus import stopwords
def tokenizer(text):
text = re.sub('<[^>]*>', '', text)
emoticons = re.findall('(?::|;|=)(?:-)?(?:\)|\(|D|P)', text.lower())
text = re.sub('[\W]+', ' ', text.lower()) +\
' '.join(emoticons).replace('-', '')
tokenized = [w for w in text.split() if w not in stop]
return tokenized
# reads in and returns one document at a time
def stream_docs(path):
with open(path, 'r', encoding='utf-8') as csv:
next(csv) # skip header
for line in csv:
text, label = line[:-3], int(line[-2])
yield text, label
doc_stream = stream_docs(path='./movie_data.csv')
next(doc_stream)
```
#### Minibatch
```
def get_minibatch(doc_stream, size):
docs, y = [], []
try:
for _ in range(size):
text, label = next(doc_stream)
docs.append(text)
y.append(label)
except StopIteration:
return None, None
return docs, y
```
- We cannot use `CountVectorizer` since it requires holding the complete vocabulary. Likewise, `TfidfVectorizer` needs to keep all feature vectors in memory.
- We can use `HashingVectorizer` instead for online training (32-bit MurmurHash3 algorithm by Austin Appleby (https://sites.google.com/site/murmurhash/)
```
from sklearn.feature_extraction.text import HashingVectorizer
from sklearn.linear_model import SGDClassifier
vect = HashingVectorizer(decode_error='ignore',
n_features=2**21,
preprocessor=None,
tokenizer=tokenizer)
clf = SGDClassifier(loss='log', random_state=1, max_iter=1)
doc_stream = stream_docs(path='./movie_data.csv')
import pyprind
pbar = pyprind.ProgBar(45)
classes = np.array([0, 1])
for _ in range(45):
X_train, y_train = get_minibatch(doc_stream, size=1000)
if not X_train:
break
X_train = vect.transform(X_train)
clf.partial_fit(X_train, y_train, classes=classes)
pbar.update()
X_test, y_test = get_minibatch(doc_stream, size=5000)
X_test = vect.transform(X_test)
print('Accuracy: %.3f' % clf.score(X_test, y_test))
clf = clf.partial_fit(X_test, y_test)
```
<br>
<br>
# Summary
- **Latent Dirichlet allocation**, a topic model that considers the latent semantics of words (D. M. Blei, A. Y. Ng, and M. I. Jordan. Latent Dirichlet allocation. The Journal of machine Learning research, 3:993–1022, 2003)
- **word2vec**, an algorithm that Google released in 2013 (T. Mikolov, K. Chen, G. Corrado, and J. Dean. Ef cient Estimation of Word Representations in Vector Space. arXiv preprint arXiv:1301.3781, 2013)
- https://code.google.com/p/word2vec/.
| github_jupyter |
<a href="https://colab.research.google.com/github/satyajitghana/TSAI-DeepNLP-END2.0/blob/main/09_NLP_Evaluation/ClassificationEvaluation.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
! pip3 install git+https://github.com/extensive-nlp/ttc_nlp --quiet
! pip3 install torchmetrics --quiet
from ttctext.datamodules.sst import SSTDataModule
from ttctext.datasets.sst import StanfordSentimentTreeBank
sst_dataset = SSTDataModule(batch_size=128)
sst_dataset.setup()
import pytorch_lightning as pl
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchmetrics.functional import accuracy, precision, recall, confusion_matrix
from sklearn.metrics import classification_report
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
sns.set()
class SSTModel(pl.LightningModule):
def __init__(self, hparams, *args, **kwargs):
super().__init__()
self.save_hyperparameters(hparams)
self.num_classes = self.hparams.output_dim
self.embedding = nn.Embedding(self.hparams.input_dim, self.hparams.embedding_dim)
self.lstm = nn.LSTM(
self.hparams.embedding_dim,
self.hparams.hidden_dim,
num_layers=self.hparams.num_layers,
dropout=self.hparams.dropout,
batch_first=True
)
self.proj_layer = nn.Sequential(
nn.Linear(self.hparams.hidden_dim, self.hparams.hidden_dim),
nn.BatchNorm1d(self.hparams.hidden_dim),
nn.ReLU(),
nn.Dropout(self.hparams.dropout),
)
self.fc = nn.Linear(self.hparams.hidden_dim, self.num_classes)
self.loss = nn.CrossEntropyLoss()
def init_state(self, sequence_length):
return (torch.zeros(self.hparams.num_layers, sequence_length, self.hparams.hidden_dim).to(self.device),
torch.zeros(self.hparams.num_layers, sequence_length, self.hparams.hidden_dim).to(self.device))
def forward(self, text, text_length, prev_state=None):
# [batch size, sentence length] => [batch size, sentence len, embedding size]
embedded = self.embedding(text)
# packs the input for faster forward pass in RNN
packed = torch.nn.utils.rnn.pack_padded_sequence(
embedded, text_length.to('cpu'),
enforce_sorted=False,
batch_first=True
)
# [batch size sentence len, embedding size] =>
# output: [batch size, sentence len, hidden size]
# hidden: [batch size, 1, hidden size]
packed_output, curr_state = self.lstm(packed, prev_state)
hidden_state, cell_state = curr_state
# print('hidden state shape: ', hidden_state.shape)
# print('cell')
# unpack packed sequence
# unpacked, unpacked_len = torch.nn.utils.rnn.pad_packed_sequence(packed_output, batch_first=True)
# print('unpacked: ', unpacked.shape)
# [batch size, sentence len, hidden size] => [batch size, num classes]
# output = self.proj_layer(unpacked[:, -1])
output = self.proj_layer(hidden_state[-1])
# print('output shape: ', output.shape)
output = self.fc(output)
return output, curr_state
def shared_step(self, batch, batch_idx):
label, text, text_length = batch
logits, in_state = self(text, text_length)
loss = self.loss(logits, label)
pred = torch.argmax(F.log_softmax(logits, dim=1), dim=1)
acc = accuracy(pred, label)
metric = {'loss': loss, 'acc': acc, 'pred': pred, 'label': label}
return metric
def training_step(self, batch, batch_idx):
metrics = self.shared_step(batch, batch_idx)
log_metrics = {'train_loss': metrics['loss'], 'train_acc': metrics['acc']}
self.log_dict(log_metrics, prog_bar=True)
return metrics
def validation_step(self, batch, batch_idx):
metrics = self.shared_step(batch, batch_idx)
return metrics
def validation_epoch_end(self, outputs):
acc = torch.stack([x['acc'] for x in outputs]).mean()
loss = torch.stack([x['loss'] for x in outputs]).mean()
log_metrics = {'val_loss': loss, 'val_acc': acc}
self.log_dict(log_metrics, prog_bar=True)
if self.trainer.sanity_checking:
return log_metrics
preds = torch.cat([x['pred'] for x in outputs]).view(-1)
labels = torch.cat([x['label'] for x in outputs]).view(-1)
accuracy_ = accuracy(preds, labels)
precision_ = precision(preds, labels, average='macro', num_classes=self.num_classes)
recall_ = recall(preds, labels, average='macro', num_classes=self.num_classes)
classification_report_ = classification_report(labels.cpu().numpy(), preds.cpu().numpy(), target_names=self.hparams.class_labels)
confusion_matrix_ = confusion_matrix(preds, labels, num_classes=self.num_classes)
cm_df = pd.DataFrame(confusion_matrix_.cpu().numpy(), index=self.hparams.class_labels, columns=self.hparams.class_labels)
print(f'Test Epoch {self.current_epoch}/{self.hparams.epochs-1}: F1 Score: {accuracy_:.5f}, Precision: {precision_:.5f}, Recall: {recall_:.5f}\n')
print(f'Classification Report\n{classification_report_}')
fig, ax = plt.subplots(figsize=(10, 8))
heatmap = sns.heatmap(cm_df, annot=True, ax=ax, fmt='d') # font size
locs, labels = plt.xticks()
plt.setp(labels, rotation=45)
locs, labels = plt.yticks()
plt.setp(labels, rotation=45)
plt.show()
print("\n")
return log_metrics
def test_step(self, batch, batch_idx):
return self.validation_step(batch, batch_idx)
def test_epoch_end(self, outputs):
accuracy = torch.stack([x['acc'] for x in outputs]).mean()
self.log('hp_metric', accuracy)
self.log_dict({'test_acc': accuracy}, prog_bar=True)
def configure_optimizers(self):
optimizer = torch.optim.Adam(self.parameters(), lr=self.hparams.lr)
lr_scheduler = {
'scheduler': torch.optim.lr_scheduler.ReduceLROnPlateau(optimizer, patience=10, verbose=True),
'monitor': 'train_loss',
'name': 'scheduler'
}
return [optimizer], [lr_scheduler]
from omegaconf import OmegaConf
hparams = OmegaConf.create({
'input_dim': len(sst_dataset.get_vocab()),
'embedding_dim': 128,
'num_layers': 2,
'hidden_dim': 64,
'dropout': 0.5,
'output_dim': len(StanfordSentimentTreeBank.get_labels()),
'class_labels': sst_dataset.raw_dataset_train.get_labels(),
'lr': 5e-4,
'epochs': 10,
'use_lr_finder': False
})
sst_model = SSTModel(hparams)
trainer = pl.Trainer(gpus=1, max_epochs=hparams.epochs, progress_bar_refresh_rate=1, reload_dataloaders_every_epoch=True)
trainer.fit(sst_model, sst_dataset)
```
| github_jupyter |
# MultiGroupDirectLiNGAM
## Import and settings
In this example, we need to import `numpy`, `pandas`, and `graphviz` in addition to `lingam`.
```
import numpy as np
import pandas as pd
import graphviz
import lingam
from lingam.utils import print_causal_directions, print_dagc, make_dot
print([np.__version__, pd.__version__, graphviz.__version__, lingam.__version__])
np.set_printoptions(precision=3, suppress=True)
np.random.seed(0)
```
## Test data
We generate two datasets consisting of 6 variables.
```
x3 = np.random.uniform(size=1000)
x0 = 3.0*x3 + np.random.uniform(size=1000)
x2 = 6.0*x3 + np.random.uniform(size=1000)
x1 = 3.0*x0 + 2.0*x2 + np.random.uniform(size=1000)
x5 = 4.0*x0 + np.random.uniform(size=1000)
x4 = 8.0*x0 - 1.0*x2 + np.random.uniform(size=1000)
X1 = pd.DataFrame(np.array([x0, x1, x2, x3, x4, x5]).T ,columns=['x0', 'x1', 'x2', 'x3', 'x4', 'x5'])
X1.head()
m = np.array([[0.0, 0.0, 0.0, 3.0, 0.0, 0.0],
[3.0, 0.0, 2.0, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 6.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[8.0, 0.0,-1.0, 0.0, 0.0, 0.0],
[4.0, 0.0, 0.0, 0.0, 0.0, 0.0]])
make_dot(m)
x3 = np.random.uniform(size=1000)
x0 = 3.5*x3 + np.random.uniform(size=1000)
x2 = 6.5*x3 + np.random.uniform(size=1000)
x1 = 3.5*x0 + 2.5*x2 + np.random.uniform(size=1000)
x5 = 4.5*x0 + np.random.uniform(size=1000)
x4 = 8.5*x0 - 1.5*x2 + np.random.uniform(size=1000)
X2 = pd.DataFrame(np.array([x0, x1, x2, x3, x4, x5]).T ,columns=['x0', 'x1', 'x2', 'x3', 'x4', 'x5'])
X2.head()
m = np.array([[0.0, 0.0, 0.0, 3.5, 0.0, 0.0],
[3.5, 0.0, 2.5, 0.0, 0.0, 0.0],
[0.0, 0.0, 0.0, 6.5, 0.0, 0.0],
[0.0, 0.0, 0.0, 0.0, 0.0, 0.0],
[8.5, 0.0,-1.5, 0.0, 0.0, 0.0],
[4.5, 0.0, 0.0, 0.0, 0.0, 0.0]])
make_dot(m)
```
We create a list variable that contains two datasets.
```
X_list = [X1, X2]
```
## Causal Discovery
To run causal discovery for multiple datasets, we create a `MultiGroupDirectLiNGAM` object and call the `fit` method.
```
model = lingam.MultiGroupDirectLiNGAM()
model.fit(X_list)
```
Using the `causal_order_` properties, we can see the causal ordering as a result of the causal discovery.
```
model.causal_order_
```
Also, using the `adjacency_matrix_` properties, we can see the adjacency matrix as a result of the causal discovery. As you can see from the following, DAG in each dataset is correctly estimated.
```
print(model.adjacency_matrices_[0])
make_dot(model.adjacency_matrices_[0])
print(model.adjacency_matrices_[1])
make_dot(model.adjacency_matrices_[1])
```
To compare, we run DirectLiNGAM with single dataset concatenating two datasets.
```
X_all = pd.concat([X1, X2])
print(X_all.shape)
model_all = lingam.DirectLiNGAM()
model_all.fit(X_all)
model_all.causal_order_
```
You can see that the causal structure cannot be estimated correctly for a single dataset.
```
make_dot(model_all.adjacency_matrix_)
```
## Independence between error variables
To check if the LiNGAM assumption is broken, we can get p-values of independence between error variables. The value in the i-th row and j-th column of the obtained matrix shows the p-value of the independence of the error variables $e_i$ and $e_j$.
```
p_values = model.get_error_independence_p_values(X_list)
print(p_values[0])
print(p_values[1])
```
## Bootstrapping
In `MultiGroupDirectLiNGAM`, bootstrap can be executed in the same way as normal `DirectLiNGAM`.
```
results = model.bootstrap(X_list, n_sampling=100)
```
## Causal Directions
The `bootstrap` method returns a list of multiple `BootstrapResult`, so we can get the result of bootstrapping from the list. We can get the same number of results as the number of datasets, so we specify an index when we access the results. We can get the ranking of the causal directions extracted by `get_causal_direction_counts()`.
```
cdc = results[0].get_causal_direction_counts(n_directions=8, min_causal_effect=0.01)
print_causal_directions(cdc, 100)
cdc = results[1].get_causal_direction_counts(n_directions=8, min_causal_effect=0.01)
print_causal_directions(cdc, 100)
```
## Directed Acyclic Graphs
Also, using the `get_directed_acyclic_graph_counts()` method, we can get the ranking of the DAGs extracted. In the following sample code, `n_dags` option is limited to the dags of the top 3 rankings, and `min_causal_effect` option is limited to causal directions with a coefficient of 0.01 or more.
```
dagc = results[0].get_directed_acyclic_graph_counts(n_dags=3, min_causal_effect=0.01)
print_dagc(dagc, 100)
dagc = results[1].get_directed_acyclic_graph_counts(n_dags=3, min_causal_effect=0.01)
print_dagc(dagc, 100)
```
## Probability
Using the get_probabilities() method, we can get the probability of bootstrapping.
```
prob = results[0].get_probabilities(min_causal_effect=0.01)
print(prob)
```
## Total Causal Effects
Using the `get_total_causal_effects()` method, we can get the list of total causal effect. The total causal effects we can get are dictionary type variable.
We can display the list nicely by assigning it to pandas.DataFrame. Also, we have replaced the variable index with a label below.
```
causal_effects = results[0].get_total_causal_effects(min_causal_effect=0.01)
df = pd.DataFrame(causal_effects)
labels = [f'x{i}' for i in range(X1.shape[1])]
df['from'] = df['from'].apply(lambda x : labels[x])
df['to'] = df['to'].apply(lambda x : labels[x])
df
```
We can easily perform sorting operations with pandas.DataFrame.
```
df.sort_values('effect', ascending=False).head()
```
And with pandas.DataFrame, we can easily filter by keywords. The following code extracts the causal direction towards x1.
```
df[df['to']=='x1'].head()
```
Because it holds the raw data of the total causal effect (the original data for calculating the median), it is possible to draw a histogram of the values of the causal effect, as shown below.
```
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
%matplotlib inline
from_index = 3
to_index = 0
plt.hist(results[0].total_effects_[:, to_index, from_index])
```
## Bootstrap Probability of Path
Using the `get_paths()` method, we can explore all paths from any variable to any variable and calculate the bootstrap probability for each path. The path will be output as an array of variable indices. For example, the array `[3, 0, 1]` shows the path from variable X3 through variable X0 to variable X1.
```
from_index = 3 # index of x3
to_index = 1 # index of x0
pd.DataFrame(results[0].get_paths(from_index, to_index))
```
| github_jupyter |

Pandas est le package de prédilection pour traiter des données structurées.
Pandas est basé sur 2 structures extrêmement liées les Series et le DataFrame.
Ces deux structures permettent de traiter des données sous forme de tableaux indexés.
Les classes de Pandas utilisent des classes de Numpy, il est donc possible d'utiliser les fonctions universelles de Numpy sur les objets Pandas.
```
# on importe pandas avec :
import pandas as pd
import numpy as np
%matplotlib inline
```
# Les Series de Pandas
- Les Series sont indexées, c'est leur avantage sur les arrays de NumPy
- On peut utiliser les fonctions `.values` et `.index` pour voir les différentes parties de chaque Series
- On définit une Series par `pd.Series([,], index=['','',])`
- On peut appeler un élément avec `ma_serie['France']`
- On peut aussi faire des conditions :
```python
ma_serie[ma_serie>5000000]
```
```
'France' in ma_serie
```
- Les objets Series peuvent être transformés en dictionnaires en utilisant :
`.to_dict()`
**Exercice :**
Définir un objet Series comprenant la population de 5 pays puis afficher les pays ayant une population > 50’000’000.
```
ser_pop = pd.Series([70,8,300,1200],index=["France","Suisse","USA","Chine"])
ser_pop
# on extrait une valeur avec une clé
ser_pop["France"]
# on peut aussi utiliser une position avec .iloc[]
ser_pop.iloc[0]
# on applique la condition entre []
ser_pop[ser_pop>50]
```
# D'autres opérations sur les objets series
- Pour définir le nom de la Series, on utilise `.name`
- Pour définir le titre de la colonne des observations, on utilise `.index.name`
**Exercice :**
Définir les noms de l’objet et de la colonne des pays pour la Series précédente
```
ser_pop.name = "Populations"
ser_pop.index.name = "Pays"
ser_pop
```
# Les données manquantes
Dans pandas, les données manquantes sont identifiés avec les fonctions de Numpy (`np.nan`). On a d'autres fonctions telles que :
```
pd.Series([2,np.nan,4],index=['a','b','c'])
pd.isna(pd.Series([2,np.nan,4],index=['a','b','c']))
pd.notna(pd.Series([2,np.nan,4],index=['a','b','c']))
```
# Les dates avec pandas
- Python possède un module datetime qui permet de gérer facilement des dates
- Pandas permet d'appliquer les opérations sur les dates aux Series et aux DataFrame
- Le format es dates Python est `YYYY-MM-DD HH:MM:SS`
- On peut générer des dates avec la fonction `pd.date_range()` avec différente fréquences `freq=`
- On peut utiliser ces dates comme index dans un DataFrame ou dans un objet Series
- On peut changer la fréquence en utilisant `.asfreq()`
- Pour transformer une chaine de caractère en date, on utilise `pd.to_datetime()` avec l’option `dayfirst=True` si on est dans le cas français
-On pourra aussi spécifier un format pour accélérer le processus `%Y%m%d`
**Exercice :**
Créez un objet Series et ajoutez des dates partant du 3 octobre 2017 par jour jusqu’à aujourd’hui. Afficher le résultat dans un graphique (on utilisera la méthode `.plot()`
```
dates = pd.date_range("2017-10-03", "2020-02-27",freq="W")
valeurs = np.random.random(size=len(dates))
ma_serie=pd.Series(valeurs, index =dates)
ma_serie.plot()
len(dates)
```
# Le DataFrame
- Les DataFrame sont des objets très souples pouvant être construits de différentes façon
- On peut les construire en récupérant des données copier / coller, où directement sur Internet, ou en entrant les valeurs manuellement
- Les DataFrame se rapprochent des dictionnaires et on peut construire ces objets en utilisant `DataFrame(dico)`
- De nombreux détails sur la création des DataFrame se trouve sur ce site :
<http://pandas.pydata.org/pandas-docs/dev/generated/pandas.DataFrame.html>
# Construction de DataFrame
On peut simplement construire un DataFrame avec le classe pd.DataFrame() à partir de différentes structures :
```
frame1=pd.DataFrame(np.random.randn(10).reshape(5,2),
index=["obs_"+str(i) for i in range(5)],
columns=["col_"+str(i) for i in range(2)])
frame1
```
# Opérations sur les DataFrame
On peut afficher le nom des colonnes :
```
print(frame1.columns)
```
On peut accéder à une colonne avec :
- `frame1.col_0` : attention au cas de nom de colonnes avec des espaces...
- `frame1['col_0']`
On peut accéder à une cellule avec :
- `frame1.loc['obs1','col_0']` : on utilise les index et le nom des colonnes
- `frame1.iloc[1,0]` : on utilise les positions dans le DataFrame
# Options de visualisation et de résumé
Pour afficher les 3 premières lignes, on peut utiliser :
```
frame1.head(3)
```
Pour afficher un résumé du DF :
```
frame1.info()
```
# Importer des données externes
Pandas est l'outil le plus efficace pour importer des données externes, il prend en charge de nombreux formats dont csv, Excel, SQL, SAS...
## Importation de données avec Pandas
Quel que soit le type de fichier, Pandas possède une fonction :
```python
frame=pd.read_...('chemin_du_fichier/nom_du_fichier',...)
```
Pour écrire un DataFrame dans un fichier, on utilise :
```python
frame.to_...('chemin_du_fichier/nom_du_fichier',...)
```
**Exercice :**
Importer un fichier `.csv` avec `pd.read_csv()`. On utilisera le fichier "./data/airbnb.csv"
```
# on prend la colonne id comme index de notre DataFrame
airbnb = pd.read_csv("https://www.stat4decision.com/airbnb.csv",index_col="id")
airbnb.info()
# la colonne price est sous forme d'objet et donc de chaîne de caractères
# on a 2933 locations qui coûtent 80$ la nuit
airbnb["price"].value_counts()
dpt = pd.read_csv("./data/base-dpt.csv", sep = ";")
dpt.head()
dpt.info()
```
# D'autres types de données
## JSON
Les objets JSON ressemblent à des dictionnaires.
On utilise le module `json` puis la fonction `json.loads()` pour transformer une entrée JSON en objet json
## HTML
On utilise `pd.read_html(url)`. Cet fonction est basée sur les packages `beautifulsoup` et `html5lib`
Cette fonction renvoie une liste de DataFrame qui représentent tous les DataFrame de la page. On ira ensuite chercher l'élément qui nous intéresse avec `frame_list[0]`
**Exercice :**
Importez un tableau en html depuis la page <http://www.fdic.gov/bank/individual/failed/banklist.html>
```
bank = pd.read_html("http://www.fdic.gov/bank/individual/failed/banklist.html")
# read_html() stocke les tableaux d'une page web dans une liste
type(bank)
len(bank)
bank[0].head(10)
nba = pd.read_html("https://en.wikipedia.org/wiki/2018%E2%80%9319_NBA_season")
len(nba)
nba[3]
```
# Importer depuis Excel
On a deux approches pour Excel :
- On peut utiliser `pd.read_excel()`
- On peut utiliser la classe `pd.ExcelFile()`
Dans ce cas, on utilise :
```python
xlsfile=pd.ExcelFile('fichier.xlsx')
xlsfile.parse('Sheet1')
```
**Exercice :**
Importez un fichier Excel avec les deux approches, on utilisera : `credit2.xlsx` et `ville.xls`
```
pd.read_excel("./data/credit2.xlsx",usecols=["Age","Gender"])
pd.read_excel("./data/credit2.xlsx",usecols="A:C")
credit2 = pd.read_excel("./data/credit2.xlsx", index_col="Customer_ID")
credit2.head()
# on crée un objet du type ExcelFile
ville = pd.ExcelFile("./data/ville.xls")
ville.sheet_names
# on extrait toutes les feuilles avec le mot ville dans le nom de la feuille dans une liste de dataframes
list_feuilles_ville = []
for nom in ville.sheet_names:
if "ville" in nom:
list_feuilles_ville.append(ville.parse(nom))
```
On crée une fonction qui permet d'importer les feuilles excel ayant le terme nom_dans_feuille dans le nom de la feuille
```
def import_excel_feuille(chemin_fichier, nom_dans_feuille = ""):
""" fonction qui importe les feuilles excel ayant le terme nom_dans_feuille dans le nom de la feuille"""
excel = pd.ExcelFile(chemin_fichier)
list_feuilles = []
for nom_feuille in excel.sheet_names:
if nom_dans_feuille in nom_feuille:
list_feuilles.append(excel.parse(nom))
return list_feuilles
list_ain = import_excel_feuille("./data/ville.xls",nom_dans_feuille="ain")
list_ain[0].head()
```
# Importer des données SQL
Pandas possède une fonction `read_sql()` qui permet d’importer directement des bases de données ou des queries dans des DataFrame
Il faut tout de même un connecteur pour accéder aux bases de données
Pour mettre en place ce connecteur, on utlise le package SQLAlchemy.
Suivant le type de base de données, on utilisera différents codes mais la structure du code est toujours la même
```
# on importe l'outil de connexion
from sqlalchemy import create_engine
```
On crée une connexion
```python
connexion=create_engine("sqlite:///(...).sqlite")
```
On utlise une des fonctions de Pandas pour charger les données
```python
requete="""select ... from ..."""
frame_sql=pd.read_sql_query(requete,connexion)
```
**Exercices :**
Importez la base de données SQLite salaries et récupérez la table Salaries dans un DataFrame
```
connexion=create_engine("sqlite:///./data/salaries.sqlite")
connexion.table_names()
salaries = pd.read_sql_query("select * from salaries", con=connexion)
salaries.head()
```
# Importer depuis SPSS
Pandas possède une fonction `pd.read_spss()`
Attention ! Il faut la dernière version de Pandas et installer des packages supplémentaires !
**Exercice :** Importer le fichier SPSS se trouvant dans ./data/
```
#base = pd.read_spss("./data/Base.sav")
```
# Les tris avec Pandas
Pour effectuer des tris, on utilise :
- `.sort_index()` pour le tri des index
- `.sort_values()` pour le tri des données
- `.rank()` affiche le rang des observations
Il peut y avoir plusieurs tris dans la même opération. Dans ce cas, on utilise des listes de colonnes :
```python
frame.sort_values(["col_1","col_2"])
```
**Exercice :**
Triez les données sur les salaires en se basant sur le TotalPay et le JobTitle
```
salaries.sort_values(["JobTitle","TotalPay"],ascending=[True, False])
```
# Les statistiques simples
Les Dataframe possèdent de nombreuses méthodes pour calculer des statistiques simples :
- `.sum(axis=0)` permet de faire une somme par colonne
- `.sum(axis=1)` permet de faire une somme par ligne
- `.min()` et `.max()` donnent le minimum par colonne
- `.idxmin()` et `.idxmax()` donnent l’index du minimum et du maximum
- `.describe()` affiche un tableau de statistiques descriptives par colonne
- `.corr()` pour calculer la corrélation entre les colonnes
**Exercice :**
Obtenir les différentes statistiques descriptives pour les données AirBnB.
On peut s'intéresser à la colonne `Price` (attention des prétraitements sont nécessaires)
```
# cette colonne est sous forme d'object, il va falloir la modifier
airbnb["price"].dtype
airbnb["price_num"] = pd.to_numeric(airbnb["price"].str.replace("$","")
.str.replace(",",""))
airbnb["price_num"].dtype
airbnb["price_num"].mean()
airbnb["price_num"].describe()
# on extrait l'id de la location avec le prix max
airbnb["price_num"].idxmax()
# on affiche cette location
airbnb.loc[airbnb["price_num"].idxmax()]
```
Calcul de la moyenne pondérée sur une enquête
```
base = pd.read_csv("./data/Base.csv")
#moyenne pondérée
np.average(base["resp_age"],weights=base["Weight"])
# moyenne
base["resp_age"].mean()
```
Utilisation de statsmodels
```
from statsmodels.stats.weightstats import DescrStatsW
# on sélectionne les colonnes numériques
base_num = base.select_dtypes(np.number)
# on calcule les stats desc pondérées
mes_stat = DescrStatsW(base_num, weights=base["Weight"])
base_num.columns
mes_stat.var
mes_stat_age = DescrStatsW(base["resp_age"], weights=base["Weight"])
mes_stat_age.mean
```
On va construire une fonction permettant de calculer les stat desc pondérées d'une colonne
```
def stat_desc_w_ipsos(data, columns, weights):
""" Cette fonction calcule et affiche les moyennes et écarts-types pondérés
Input : - data : données sous forme de DataFrame
- columns : nom des colonnes quanti à analyser
- weights : nom de la colonne des poids
"""
from statsmodels.stats.weightstats import DescrStatsW
mes_stats = DescrStatsW(data[columns],weights=data[weights])
print("Moyenne pondérée :", mes_stats.mean)
print("Ecart-type pondéré :", mes_stats.std)
stat_desc_w_ipsos(base,"resp_age","Weight")
```
# Le traitement des données manquantes
- Les données manquantes sont identifiées par `NaN`
- `.dropna()` permet de retirer les données manquantes dans un objet Series et l’ensemble d’une ligne dans le cas d’un DataFrame
- Pour éliminer par colonne, on utilise `.dropna(axis=1)`
- Remplacer toutes les données manquantes `.fillna(valeur)`
# Les jointures avec Pandas
On veut joindre des jeux de données en utilisant des clés (variables communes)
- `pd.merge()` permet de joindre deux DataFrame, on utilise comme options `on='key'`
- On peut utiliser comme option `how=`, on peut avoir :
- `left` dans ce cas, on garde le jeu de données à gauche et pour les données de droite des valeurs manquantes sont ajoutées.
- `outer`, on garde toutes les valeurs des deux jeux de données
- ...
- On peut avoir plusieurs clés et faire une jointure sur les deux clés `on=['key1','key2']`
Pour plus de détails : <http://pandas.pydata.org/pandas-docs/dev/generated/pandas.DataFrame.merge.html>
**Exercice :**
Joindre deux dataframes (credit1 et credit2).
```
credit1 = pd.read_csv("./data/credit1.txt",sep="\t")
credit_global = pd.merge(credit1,credit2,how="inner",on="Customer_ID")
credit_global.head()
```
On fait une jointure entre les données des locations Airbnb et les données de calendrier de remplissage des appartements
```
airbnb_reduit = airbnb[["price_num","latitude","longitude"]]
calendar = pd.read_csv("https://www.stat4decision.com/calendar.csv.gz")
calendar.head()
new_airbnb = pd.merge(calendar,airbnb[["price_num","latitude","longitude"]],
left_on = "listing_id",right_index=True)
new_airbnb.shape
```
On veut extraire des statistiques de base
Par exemple, la moyenne des prix pour les locations du 8 juillet 2018 :
```
new_airbnb[new_airbnb["date"]=='2018-07-08']["price_num"].mean()
```
On extrait le nombre de nuitées disponibles / occuppées :
```
new_airbnb["available"].value_counts(normalize = True)
```
Si on regarde le part de locations occuppées le 8 janvier 2019, on a :
```
new_airbnb[new_airbnb["date"]=='2019-01-08']["available"].value_counts(normalize = True)
```
La moyenne des prix des appartements disponibles le 8 juillet 2018 :
```
new_airbnb[(new_airbnb["date"]=='2018-07-08')&(new_airbnb["available"]=='t')]["price_num"].mean()
```
On transforme la colonne date qui est sous forme de chaîne de caractère en DateTime, ceci permet de faire de nouvelles opérations :
```
new_airbnb["date"]= pd.to_datetime(new_airbnb["date"])
# on construit une colonne avec le jour de la semaine
new_airbnb["jour_semaine"]=new_airbnb["date"].dt.day_name()
```
La moyenne des pris des Samedi soirs disponibles est donc :
```
new_airbnb[(new_airbnb["jour_semaine"]=='Saturday')&(new_airbnb["available"]=='t')]["price_num"].mean()
```
# Gestion des duplications
- On utilise `.duplicated()` ou `.drop_duplicates()` dans le cas où on désire effacer les lignes se répétant
- On peut se concentrer sur une seule variables en entrant directement le nom de la variable. Dans ce cas, c’est la première apparition qui compte. Si on veut prendre la dernière apparition, on utilise l’option `keep="last"`. On pourra avoir :
```python
frame1.drop_duplicates(["col_0","col_1"],keep="last")
```
# Discrétisation
Pour discrétiser, on utilise la fonction `pd.cut()`, on va définir une liste de points pour discrétiser et on entre cette liste comme second paramètre de la fonction.
Une fois discrétisé, on peut afficher les modalités obtenues en utilisant `.categories`
On peut aussi compter les occurrence en utilisant `pd.value_counts()`
Il est aussi possible d’entrer le nombre de segments comme second paramètre
On utilisera aussi `qcut()`
**Exercice :**
Créez une variable dans le dataframe AirBnB pour obtenir des niveaux de prix.
```
airbnb["price_disc1"]=pd.cut(airbnb["price_num"],bins=5)
airbnb["price_disc2"]=pd.qcut(airbnb["price_num"],5)
airbnb["price_disc1"].value_counts()
airbnb["price_disc2"].value_counts()
```
# Les tableaux croisés avec Pandas
Les DataFrame possèdent des méthodes pour générer des tableaux croisés, notamment :
```python
frame1.pivot_table()
```
Cette méthode permet de gérer de nombreux cas avec des fonctions standards et sur mesure.
**Exercice :**
Afficher un tableau Pivot pour les données AirBnB.
```
# on définit un
def moy2(x):
return x.mean()/x.var()
```
On croise le room_type avec le niveau de prix et on regarde le review_score_rating moyen + le nombre d'occurences et une fonction "maison" :
```
airbnb['room_type']
airbnb['price_disc2']
airbnb['review_scores_rating']
airbnb.pivot_table(values=["review_scores_rating",'review_scores_cleanliness'],
index="room_type",
columns='price_disc2',aggfunc=["count","mean",moy2])
```
# L'utilisation de GroupBy sur des DataFrame
- `.groupby` permet de rassembler des observations en fonction d’une variable dite de groupe
- Par exemple, `frame.groupby('X').mean()` donnera les moyennes par groupes de `X`
- On peut aussi utiliser `.size()` pour connaître la taille des groupes et utiliser d’autres fonctions (`.sum()`)
- On peut effectuer de nombreuses opérations de traitement avec le groupby
```
airbnb_group_room = airbnb.groupby(['room_type','price_disc2'])
airbnb_group_room["price_num"].describe()
# on peut afficher plusieurs statistiques
airbnb_group_room["price_num"].agg(["mean","median","std","count"])
new_airbnb.groupby(['available','jour_semaine'])["price_num"].agg(["mean","count"])
```
Essayez d'utiliser une fonction lambda sur le groupby
**Exercice :**
- Données sur les salaires
- On utilise le `groupby()` pour rassembler les types d’emploi
- Et on calcule des statistiques pour chaque type
On peut utiliser la méthode `.agg()` avec par exemple `'mean'` comme paramètre
On utilise aussi fréquemment la méthode `.apply()` combinée à une fonction lambda
```
# on passe tous les JobTitle en minuscule
salaries["JobTitle"]= salaries["JobTitle"].str.lower()
# nombre de JobTitle différents
salaries["JobTitle"].nunique()
salaries.groupby("JobTitle")["TotalPay"].mean().sort_values(ascending=False)
salaries.groupby("JobTitle")["TotalPay"].agg(["mean","count"]).sort_values("count",ascending=False)
```
On peut aussi faire des représentations graphiques avancées :
```
import matplotlib.pyplot as plt
plt.figure(figsize=(10,5))
plt.scatter("longitude","latitude", data = airbnb[airbnb["price_num"]<150], s=1,c = "price_num", cmap=plt.get_cmap("jet"))
plt.colorbar()
plt.savefig("paris_airbnb.jpg")
airbnb[airbnb["price_num"]<150]
```
| github_jupyter |
```
#@title Copyright 2020 Google LLC. Double-click here for license information.
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Linear Regression with a Real Dataset
This Colab uses a real dataset to predict the prices of houses in California.
## Learning Objectives:
After doing this Colab, you'll know how to do the following:
* Read a .csv file into a [pandas](https://developers.google.com/machine-learning/glossary/#pandas) DataFrame.
* Examine a [dataset](https://developers.google.com/machine-learning/glossary/#data_set).
* Experiment with different [features](https://developers.google.com/machine-learning/glossary/#feature) in building a model.
* Tune the model's [hyperparameters](https://developers.google.com/machine-learning/glossary/#hyperparameter).
## The Dataset
The [dataset for this exercise](https://developers.google.com/machine-learning/crash-course/california-housing-data-description) is based on 1990 census data from California. The dataset is old but still provides a great opportunity to learn about machine learning programming.
## Use the right version of TensorFlow
The following hidden code cell ensures that the Colab will run on TensorFlow 2.X.
```
#@title Run on TensorFlow 2.x
%tensorflow_version 2.x
```
## Import relevant modules
The following hidden code cell imports the necessary code to run the code in the rest of this Colaboratory.
```
#@title Import relevant modules
import pandas as pd
import tensorflow as tf
from matplotlib import pyplot as plt
# The following lines adjust the granularity of reporting.
pd.options.display.max_rows = 10
pd.options.display.float_format = "{:.1f}".format
```
## The dataset
Datasets are often stored on disk or at a URL in [.csv format](https://wikipedia.org/wiki/Comma-separated_values).
A well-formed .csv file contains column names in the first row, followed by many rows of data. A comma divides each value in each row. For example, here are the first five rows of the .csv file file holding the California Housing Dataset:
```
"longitude","latitude","housing_median_age","total_rooms","total_bedrooms","population","households","median_income","median_house_value"
-114.310000,34.190000,15.000000,5612.000000,1283.000000,1015.000000,472.000000,1.493600,66900.000000
-114.470000,34.400000,19.000000,7650.000000,1901.000000,1129.000000,463.000000,1.820000,80100.000000
-114.560000,33.690000,17.000000,720.000000,174.000000,333.000000,117.000000,1.650900,85700.000000
-114.570000,33.640000,14.000000,1501.000000,337.000000,515.000000,226.000000,3.191700,73400.000000
```
### Load the .csv file into a pandas DataFrame
This Colab, like many machine learning programs, gathers the .csv file and stores the data in memory as a pandas Dataframe. pandas is an open source Python library. The primary datatype in pandas is a DataFrame. You can imagine a pandas DataFrame as a spreadsheet in which each row is identified by a number and each column by a name. pandas is itself built on another open source Python library called NumPy. If you aren't familiar with these technologies, please view these two quick tutorials:
* [NumPy](https://colab.research.google.com/github/google/eng-edu/blob/master/ml/cc/exercises/numpy_ultraquick_tutorial.ipynb?utm_source=linearregressionreal-colab&utm_medium=colab&utm_campaign=colab-external&utm_content=numpy_tf2-colab&hl=en)
* [Pandas DataFrames](https://colab.research.google.com/github/google/eng-edu/blob/master/ml/cc/exercises/pandas_dataframe_ultraquick_tutorial.ipynb?utm_source=linearregressionreal-colab&utm_medium=colab&utm_campaign=colab-external&utm_content=pandas_tf2-colab&hl=en)
The following code cell imports the .csv file into a pandas DataFrame and scales the values in the label (`median_house_value`):
```
# Import the dataset.
training_df = pd.read_csv(filepath_or_buffer="https://download.mlcc.google.com/mledu-datasets/california_housing_train.csv")
# Scale the label.
training_df["median_house_value"] /= 1000.0
# Print the first rows of the pandas DataFrame.
training_df.head()
```
Scaling `median_house_value` puts the value of each house in units of thousands. Scaling will keep loss values and learning rates in a friendlier range.
Although scaling a label is usually *not* essential, scaling features in a multi-feature model usually *is* essential.
## Examine the dataset
A large part of most machine learning projects is getting to know your data. The pandas API provides a `describe` function that outputs the following statistics about every column in the DataFrame:
* `count`, which is the number of rows in that column. Ideally, `count` contains the same value for every column.
* `mean` and `std`, which contain the mean and standard deviation of the values in each column.
* `min` and `max`, which contain the lowest and highest values in each column.
* `25%`, `50%`, `75%`, which contain various [quantiles](https://developers.google.com/machine-learning/glossary/#quantile).
```
# Get statistics on the dataset.
training_df.describe()
```
### Task 1: Identify anomalies in the dataset
Do you see any anomalies (strange values) in the data?
```
#@title Double-click to view a possible answer.
# The maximum value (max) of several columns seems very
# high compared to the other quantiles. For example,
# example the total_rooms column. Given the quantile
# values (25%, 50%, and 75%), you might expect the
# max value of total_rooms to be approximately
# 5,000 or possibly 10,000. However, the max value
# is actually 37,937.
# When you see anomalies in a column, become more careful
# about using that column as a feature. That said,
# anomalies in potential features sometimes mirror
# anomalies in the label, which could make the column
# be (or seem to be) a powerful feature.
# Also, as you will see later in the course, you
# might be able to represent (pre-process) raw data
# in order to make columns into useful features.
```
## Define functions that build and train a model
The following code defines two functions:
* `build_model(my_learning_rate)`, which builds a randomly-initialized model.
* `train_model(model, feature, label, epochs)`, which trains the model from the examples (feature and label) you pass.
Since you don't need to understand model building code right now, we've hidden this code cell. You may optionally double-click the following headline to see the code that builds and trains a model.
```
#@title Define the functions that build and train a model
def build_model(my_learning_rate):
"""Create and compile a simple linear regression model."""
# Most simple tf.keras models are sequential.
model = tf.keras.models.Sequential()
# Describe the topography of the model.
# The topography of a simple linear regression model
# is a single node in a single layer.
model.add(tf.keras.layers.Dense(units=1,
input_shape=(1,)))
# Compile the model topography into code that TensorFlow can efficiently
# execute. Configure training to minimize the model's mean squared error.
model.compile(optimizer=tf.keras.optimizers.RMSprop(lr=my_learning_rate),
loss="mean_squared_error",
metrics=[tf.keras.metrics.RootMeanSquaredError()])
return model
def train_model(model, df, feature, label, epochs, batch_size):
"""Train the model by feeding it data."""
# Feed the model the feature and the label.
# The model will train for the specified number of epochs.
history = model.fit(x=df[feature],
y=df[label],
batch_size=batch_size,
epochs=epochs)
# Gather the trained model's weight and bias.
trained_weight = model.get_weights()[0]
trained_bias = model.get_weights()[1]
# The list of epochs is stored separately from the rest of history.
epochs = history.epoch
# Isolate the error for each epoch.
hist = pd.DataFrame(history.history)
# To track the progression of training, we're going to take a snapshot
# of the model's root mean squared error at each epoch.
rmse = hist["root_mean_squared_error"]
return trained_weight, trained_bias, epochs, rmse
print("Defined the create_model and traing_model functions.")
```
## Define plotting functions
The following [matplotlib](https://developers.google.com/machine-learning/glossary/#matplotlib) functions create the following plots:
* a scatter plot of the feature vs. the label, and a line showing the output of the trained model
* a loss curve
You may optionally double-click the headline to see the matplotlib code, but note that writing matplotlib code is not an important part of learning ML programming.
```
#@title Define the plotting functions
def plot_the_model(trained_weight, trained_bias, feature, label):
"""Plot the trained model against 200 random training examples."""
# Label the axes.
plt.xlabel(feature)
plt.ylabel(label)
# Create a scatter plot from 200 random points of the dataset.
random_examples = training_df.sample(n=200)
plt.scatter(random_examples[feature], random_examples[label])
# Create a red line representing the model. The red line starts
# at coordinates (x0, y0) and ends at coordinates (x1, y1).
x0 = 0
y0 = trained_bias
x1 = 10000
y1 = trained_bias + (trained_weight * x1)
plt.plot([x0, x1], [y0, y1], c='r')
# Render the scatter plot and the red line.
plt.show()
def plot_the_loss_curve(epochs, rmse):
"""Plot a curve of loss vs. epoch."""
plt.figure()
plt.xlabel("Epoch")
plt.ylabel("Root Mean Squared Error")
plt.plot(epochs, rmse, label="Loss")
plt.legend()
plt.ylim([rmse.min()*0.97, rmse.max()])
plt.show()
print("Defined the plot_the_model and plot_the_loss_curve functions.")
```
## Call the model functions
An important part of machine learning is determining which [features](https://developers.google.com/machine-learning/glossary/#feature) correlate with the [label](https://developers.google.com/machine-learning/glossary/#label). For example, real-life home-value prediction models typically rely on hundreds of features and synthetic features. However, this model relies on only one feature. For now, you'll arbitrarily use `total_rooms` as that feature.
```
# The following variables are the hyperparameters.
learning_rate = 0.01
epochs = 30
batch_size = 30
# Specify the feature and the label.
my_feature = "total_rooms" # the total number of rooms on a specific city block.
my_label="median_house_value" # the median value of a house on a specific city block.
# That is, you're going to create a model that predicts house value based
# solely on total_rooms.
# Discard any pre-existing version of the model.
my_model = None
# Invoke the functions.
my_model = build_model(learning_rate)
weight, bias, epochs, rmse = train_model(my_model, training_df,
my_feature, my_label,
epochs, batch_size)
print("\nThe learned weight for your model is %.4f" % weight)
print("The learned bias for your model is %.4f\n" % bias )
plot_the_model(weight, bias, my_feature, my_label)
plot_the_loss_curve(epochs, rmse)
```
A certain amount of randomness plays into training a model. Consequently, you'll get different results each time you train the model. That said, given the dataset and the hyperparameters, the trained model will generally do a poor job describing the feature's relation to the label.
## Use the model to make predictions
You can use the trained model to make predictions. In practice, [you should make predictions on examples that are not used in training](https://developers.google.com/machine-learning/crash-course/training-and-test-sets/splitting-data). However, for this exercise, you'll just work with a subset of the same training dataset. A later Colab exercise will explore ways to make predictions on examples not used in training.
First, run the following code to define the house prediction function:
```
def predict_house_values(n, feature, label):
"""Predict house values based on a feature."""
batch = training_df[feature][10000:10000 + n]
predicted_values = my_model.predict_on_batch(x=batch)
print("feature label predicted")
print(" value value value")
print(" in thousand$ in thousand$")
print("--------------------------------------")
for i in range(n):
print ("%5.0f %6.0f %15.0f" % (training_df[feature][10000 + i],
training_df[label][10000 + i],
predicted_values[i][0] ))
```
Now, invoke the house prediction function on 10 examples:
```
predict_house_values(10, my_feature, my_label)
```
### Task 2: Judge the predictive power of the model
Look at the preceding table. How close is the predicted value to the label value? In other words, does your model accurately predict house values?
```
#@title Double-click to view the answer.
# Most of the predicted values differ significantly
# from the label value, so the trained model probably
# doesn't have much predictive power. However, the
# first 10 examples might not be representative of
# the rest of the examples.
```
## Task 3: Try a different feature
The `total_rooms` feature had only a little predictive power. Would a different feature have greater predictive power? Try using `population` as the feature instead of `total_rooms`.
Note: When you change features, you might also need to change the hyperparameters.
```
my_feature = "?" # Replace the ? with population or possibly
# a different column name.
# Experiment with the hyperparameters.
learning_rate = 2
epochs = 3
batch_size = 120
# Don't change anything below this line.
my_model = build_model(learning_rate)
weight, bias, epochs, rmse = train_model(my_model, training_df,
my_feature, my_label,
epochs, batch_size)
plot_the_model(weight, bias, my_feature, my_label)
plot_the_loss_curve(epochs, rmse)
predict_house_values(15, my_feature, my_label)
#@title Double-click to view a possible solution.
my_feature = "population" # Pick a feature other than "total_rooms"
# Possibly, experiment with the hyperparameters.
learning_rate = 0.05
epochs = 18
batch_size = 3
# Don't change anything below.
my_model = build_model(learning_rate)
weight, bias, epochs, rmse = train_model(my_model, training_df,
my_feature, my_label,
epochs, batch_size)
plot_the_model(weight, bias, my_feature, my_label)
plot_the_loss_curve(epochs, rmse)
predict_house_values(10, my_feature, my_label)
```
Did `population` produce better predictions than `total_rooms`?
```
#@title Double-click to view the answer.
# Training is not entirely deterministic, but population
# typically converges at a slightly higher RMSE than
# total_rooms. So, population appears to be about
# the same or slightly worse at making predictions
# than total_rooms.
```
## Task 4: Define a synthetic feature
You have determined that `total_rooms` and `population` were not useful features. That is, neither the total number of rooms in a neighborhood nor the neighborhood's population successfully predicted the median house price of that neighborhood. Perhaps though, the *ratio* of `total_rooms` to `population` might have some predictive power. That is, perhaps block density relates to median house value.
To explore this hypothesis, do the following:
1. Create a [synthetic feature](https://developers.google.com/machine-learning/glossary/#synthetic_feature) that's a ratio of `total_rooms` to `population`. (If you are new to pandas DataFrames, please study the [Pandas DataFrame Ultraquick Tutorial](https://colab.research.google.com/github/google/eng-edu/blob/master/ml/cc/exercises/pandas_dataframe_ultraquick_tutorial.ipynb?utm_source=linearregressionreal-colab&utm_medium=colab&utm_campaign=colab-external&utm_content=pandas_tf2-colab&hl=en).)
2. Tune the three hyperparameters.
3. Determine whether this synthetic feature produces
a lower loss value than any of the single features you
tried earlier in this exercise.
```
# Define a synthetic feature named rooms_per_person
training_df["rooms_per_person"] = ? # write your code here.
# Don't change the next line.
my_feature = "rooms_per_person"
# Assign values to these three hyperparameters.
learning_rate = ?
epochs = ?
batch_size = ?
# Don't change anything below this line.
my_model = build_model(learning_rate)
weight, bias, epochs, rmse = train_model(my_model, training_df,
my_feature, my_label,
epochs, batch_size)
plot_the_loss_curve(epochs, rmse)
predict_house_values(15, my_feature, my_label)
#@title Double-click to view a possible solution to Task 4.
# Define a synthetic feature
training_df["rooms_per_person"] = training_df["total_rooms"] / training_df["population"]
my_feature = "rooms_per_person"
# Tune the hyperparameters.
learning_rate = 0.06
epochs = 24
batch_size = 30
# Don't change anything below this line.
my_model = build_model(learning_rate)
weight, bias, epochs, mae = train_model(my_model, training_df,
my_feature, my_label,
epochs, batch_size)
plot_the_loss_curve(epochs, mae)
predict_house_values(15, my_feature, my_label)
```
Based on the loss values, this synthetic feature produces a better model than the individual features you tried in Task 2 and Task 3. However, the model still isn't creating great predictions.
## Task 5. Find feature(s) whose raw values correlate with the label
So far, we've relied on trial-and-error to identify possible features for the model. Let's rely on statistics instead.
A **correlation matrix** indicates how each attribute's raw values relate to the other attributes' raw values. Correlation values have the following meanings:
* `1.0`: perfect positive correlation; that is, when one attribute rises, the other attribute rises.
* `-1.0`: perfect negative correlation; that is, when one attribute rises, the other attribute falls.
* `0.0`: no correlation; the two column's [are not linearly related](https://en.wikipedia.org/wiki/Correlation_and_dependence#/media/File:Correlation_examples2.svg).
In general, the higher the absolute value of a correlation value, the greater its predictive power. For example, a correlation value of -0.8 implies far more predictive power than a correlation of -0.2.
The following code cell generates the correlation matrix for attributes of the California Housing Dataset:
```
# Generate a correlation matrix.
training_df.corr()
```
The correlation matrix shows nine potential features (including a synthetic
feature) and one label (`median_house_value`). A strong negative correlation or strong positive correlation with the label suggests a potentially good feature.
**Your Task:** Determine which of the nine potential features appears to be the best candidate for a feature?
```
#@title Double-click here for the solution to Task 5
# The `median_income` correlates 0.7 with the label
# (median_house_value), so median_income` might be a
# good feature. The other seven potential features
# all have a correlation relatively close to 0.
# If time permits, try median_income as the feature
# and see whether the model improves.
```
Correlation matrices don't tell the entire story. In later exercises, you'll find additional ways to unlock predictive power from potential features.
**Note:** Using `median_income` as a feature may raise some ethical and fairness
issues. Towards the end of the course, we'll explore ethical and fairness issues.
| github_jupyter |
## Analisis de O3 y SO2 arduair vs estacion universidad pontificia bolivariana
Se compararon los resultados generados por el equipo arduair y la estacion de calidad de aire propiedad de la universidad pontificia bolivariana seccional bucaramanga
Cabe resaltar que durante la ejecucion de las pruebas, el se sospechaba equipo de SO2 de la universidad pontificia, por lo cual no se pueden interpretar estos resultados como fiables
## Library imports
```
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import datetime as dt
import xlrd
%matplotlib inline
pd.options.mode.chained_assignment = None
```
## Estudios de correlacion
Se realizaron graficos de correlacion para el ozono y el dioxido de azufre con la estacion de referencia.
Tambien se comparo los datos crudos arrojados por el sensor de ozono, con las ecuaciones de calibracion propuesta por el [datasheet](https://www.terraelectronica.ru/%2Fds%2Fpdf%2FM%2Fmq131-low.pdf), obteniendose mejores resultados con los datos sin procesar.
```
#Arduair prototype data
dfArd=pd.read_csv('DATA.TXT',names=['year','month','day','hour','minute','second','hum','temp','pr','l','co','so2','no2','o3','pm10','pm25','void'])
#Dates to datetime
dates=dfArd[['year','month','day','hour','minute','second']]
dates['year']=dates['year'].add(2000)
dates['minute']=dates['minute'].add(60)
dfArd['datetime']=pd.to_datetime(dates)
#agregation
dfArdo3=dfArd[['datetime','o3']]
dfArdso2=dfArd[['datetime','so2']]
#O3 processing
MQ131_RL= 10 #Load resistance
MQ131_VIN = 5 #Vin
MQ131_RO = 5 #reference resistance
dfArdo3['rs']=((MQ131_VIN/dfArdo3['o3'])/dfArdo3['o3'])*MQ131_RL;
dfArdo3['rs_ro'] = dfArdo3['rs']/MQ131_RO;
dfArdo3['rs_ro_abs']=abs(dfArdo3['rs_ro'])
#station data
dfo3=pd.read_csv('o3_upb.csv')
dfso2=pd.read_csv('so2_upb.csv')
dfso2.tail()
dfso2['datetime']=pd.to_datetime(dfso2['date time'])
dfo3['datetime']=pd.to_datetime(dfo3['date time'])
dfso2=dfso2[['datetime','pump_status']]
dfo3=dfo3[['datetime','pump_status']]
# bad label correction
dfso2.columns = ['datetime', 'raw_so2']
dfo3.columns = ['datetime', 'ozone_UPB']
#grouping
dfArdo3 =dfArdo3 .groupby(pd.Grouper(key='datetime',freq='1h',axis=1)).mean()
dfArdso2=dfArdso2.groupby(pd.Grouper(key='datetime',freq='1h',axis=1)).mean()
dfo3 =dfo3 .groupby(pd.Grouper(key='datetime',freq='1h',axis=1)).mean()
dfso2 =dfso2 .groupby(pd.Grouper(key='datetime',freq='1h',axis=1)).mean()
df2=pd.concat([dfo3,dfArdo3], join='inner', axis=1).reset_index()
df3=pd.concat([dfso2,dfArdso2], join='inner', axis=1).reset_index()
#Ozono calibrado
sns.jointplot(data=df2,x='ozone_UPB',y='rs_ro', kind='reg')
#Ozono crudo
sns.jointplot(data=df2,x='ozone_UPB',y='o3', kind='reg')
#SO2
sns.jointplot(data=df3,x='raw_so2',y='so2', kind='reg')
dfso2.head()
```
### Defino algunas funciones de ayuda
```
def polyfitEq(x,y):
C= np.polyfit(x,y,1)
m=C[0]
b=C[1]
return 'y = x*{} + {}'.format(m,b)
def calibrate(x,y):
C= np.polyfit(x,y,1)
m=C[0]
b=C[1]
return x*m+b
def rename_labels(obj,unit):
obj.columns=obj.columns.map(lambda x: x.replace('2',' stc_cdmb'))
obj.columns=obj.columns.map(lambda x: x+' '+unit)
return obj.columns
print('')
print('Ozono promedio 1h, sin procesar')
print(polyfitEq(df2['ozone_UPB'],df2['o3']))
#print('')
#print('Promedio 2h')
#print(polyfitEq(df2['pm10'],df2['pm10_dusttrack']))
print('')
print('Promedio 3h')
print(polyfitEq(df3['raw_so2'],df3['so2']))
```
## Datasheets calibrados
```
df2['o3']=calibrate(df2['o3'],df2['ozone_UPB'])
df2.plot(figsize=[15,5])
df3['so2']=calibrate(df3['so2'],df3['raw_so2'])
df3.plot(figsize=[15,5])
df2.head()
df2.columns = ['datetime', 'Ozono estación UPB [ppb]','Ozono prototipo [ppb]','rs','rs_ro','rs_ro_abs']
sns.jointplot(data=df2,x='Ozono prototipo [ppb]',y='Ozono estación UPB [ppb]', kind='reg',stat_func=None)
```
| github_jupyter |
## Accessing TerraClimate data with the Planetary Computer STAC API
[TerraClimate](http://www.climatologylab.org/terraclimate.html) is a dataset of monthly climate and climatic water balance for global terrestrial surfaces from 1958-2019. These data provide important inputs for ecological and hydrological studies at global scales that require high spatial resolution and time-varying data. All data have monthly temporal resolution and a ~4-km (1/24th degree) spatial resolution. The data cover the period from 1958-2019.
This example will show you how temperature has increased over the past 60 years across the globe.
### Environment setup
```
import warnings
warnings.filterwarnings("ignore", "invalid value", RuntimeWarning)
```
### Data access
https://planetarycomputer.microsoft.com/api/stac/v1/collections/terraclimate is a STAC Collection with links to all the metadata about this dataset. We'll load it with [PySTAC](https://pystac.readthedocs.io/en/latest/).
```
import pystac
url = "https://planetarycomputer.microsoft.com/api/stac/v1/collections/terraclimate"
collection = pystac.read_file(url)
collection
```
The collection contains assets, which are links to the root of a Zarr store, which can be opened with xarray.
```
asset = collection.assets["zarr-https"]
asset
import fsspec
import xarray as xr
store = fsspec.get_mapper(asset.href)
ds = xr.open_zarr(store, **asset.extra_fields["xarray:open_kwargs"])
ds
```
We'll process the data in parallel using [Dask](https://dask.org).
```
from dask_gateway import GatewayCluster
cluster = GatewayCluster()
cluster.scale(16)
client = cluster.get_client()
print(cluster.dashboard_link)
```
The link printed out above can be opened in a new tab or the [Dask labextension](https://github.com/dask/dask-labextension). See [Scale with Dask](https://planetarycomputer.microsoft.com/docs/quickstarts/scale-with-dask/) for more on using Dask, and how to access the Dashboard.
### Analyze and plot global temperature
We can quickly plot a map of one of the variables. In this case, we are downsampling (coarsening) the dataset for easier plotting.
```
import cartopy.crs as ccrs
import matplotlib.pyplot as plt
average_max_temp = ds.isel(time=-1)["tmax"].coarsen(lat=8, lon=8).mean().load()
fig, ax = plt.subplots(figsize=(20, 10), subplot_kw=dict(projection=ccrs.Robinson()))
average_max_temp.plot(ax=ax, transform=ccrs.PlateCarree())
ax.coastlines();
```
Let's see how temperature has changed over the observational record, when averaged across the entire domain. Since we'll do some other calculations below we'll also add `.load()` to execute the command instead of specifying it lazily. Note that there are some data quality issues before 1965 so we'll start our analysis there.
```
temperature = (
ds["tmax"].sel(time=slice("1965", None)).mean(dim=["lat", "lon"]).persist()
)
temperature.plot(figsize=(12, 6));
```
With all the seasonal fluctuations (from summer and winter) though, it can be hard to see any obvious trends. So let's try grouping by year and plotting that timeseries.
```
temperature.groupby("time.year").mean().plot(figsize=(12, 6));
```
Now the increase in temperature is obvious, even when averaged across the entire domain.
Now, let's see how those changes are different in different parts of the world. And let's focus just on summer months in the northern hemisphere, when it's hottest. Let's take a climatological slice at the beginning of the period and the same at the end of the period, calculate the difference, and map it to see how different parts of the world have changed differently.
First we'll just grab the summer months.
```
%%time
import dask
summer_months = [6, 7, 8]
summer = ds.tmax.where(ds.time.dt.month.isin(summer_months), drop=True)
early_period = slice("1958-01-01", "1988-12-31")
late_period = slice("1988-01-01", "2018-12-31")
early, late = dask.compute(
summer.sel(time=early_period).mean(dim="time"),
summer.sel(time=late_period).mean(dim="time"),
)
increase = (late - early).coarsen(lat=8, lon=8).mean()
fig, ax = plt.subplots(figsize=(20, 10), subplot_kw=dict(projection=ccrs.Robinson()))
increase.plot(ax=ax, transform=ccrs.PlateCarree(), robust=True)
ax.coastlines();
```
This shows us that changes in summer temperature haven't been felt equally around the globe. Note the enhanced warming in the polar regions, a phenomenon known as "Arctic amplification".
| github_jupyter |
Copyright (c) Microsoft Corporation. All rights reserved.
Licensed under the MIT License.
# Automated Machine Learning
_**ディープラーンニングを利用したテキスト分類**_
## Contents
1. [事前準備](#1.-事前準備)
1. [自動機械学習 Automated Machine Learning](2.-自動機械学習-Automated-Machine-Learning)
1. [結果の確認](#3.-結果の確認)
## 1. 事前準備
本デモンストレーションでは、AutoML の深層学習の機能を用いてテキストデータの分類モデルを構築します。
AutoML には Deep Neural Network が含まれており、テキストデータから **Embedding** を作成することができます。GPU サーバを利用することで **BERT** が利用されます。
深層学習の機能を利用するためには Azure Machine Learning の Enterprise Edition が必要になります。詳細は[こちら](https://docs.microsoft.com/en-us/azure/machine-learning/concept-editions#automated-training-capabilities-automl)をご確認ください。
## 1.1 Python SDK のインポート
Azure Machine Learning の Python SDK などをインポートします。
```
import logging
import os
import shutil
import pandas as pd
import azureml.core
from azureml.core.experiment import Experiment
from azureml.core.workspace import Workspace
from azureml.core.dataset import Dataset
from azureml.core.compute import AmlCompute
from azureml.core.compute import ComputeTarget
from azureml.core.run import Run
from azureml.widgets import RunDetails
from azureml.core.model import Model
from azureml.train.automl import AutoMLConfig
from sklearn.datasets import fetch_20newsgroups
from azureml.automl.core.featurization import FeaturizationConfig
```
Azure ML Python SDK のバージョンが 1.8.0 以上になっていることを確認します。
```
print("You are currently using version", azureml.core.VERSION, "of the Azure ML SDK")
```
## 1.2 Azure ML Workspace との接続
```
ws = Workspace.from_config()
# 実験名の指定
experiment_name = 'livedoor-news-classification-BERT'
experiment = Experiment(ws, experiment_name)
output = {}
#output['Subscription ID'] = ws.subscription_id
output['Workspace Name'] = ws.name
output['Resource Group'] = ws.resource_group
output['Location'] = ws.location
output['Experiment Name'] = experiment.name
pd.set_option('display.max_colwidth', -1)
outputDf = pd.DataFrame(data = output, index = [''])
outputDf.T
```
## 1.3 計算環境の準備
BERT を利用するための GPU の `Compute Cluster` を準備します。
```
from azureml.core.compute import ComputeTarget, AmlCompute
from azureml.core.compute_target import ComputeTargetException
# Compute Cluster の名称
amlcompute_cluster_name = "gpucluster"
# クラスターの存在確認
try:
compute_target = ComputeTarget(workspace=ws, name=amlcompute_cluster_name)
except ComputeTargetException:
print('指定された名称のクラスターが見つからないので新規に作成します.')
compute_config = AmlCompute.provisioning_configuration(vm_size = "STANDARD_NC6_V3",
max_nodes = 4)
compute_target = ComputeTarget.create(ws, amlcompute_cluster_name, compute_config)
compute_target.wait_for_completion(show_output=True)
```
## 1.4 学習データの準備
今回は [livedoor New](https://www.rondhuit.com/download/ldcc-20140209.tar.gz) を学習データとして利用します。ニュースのカテゴリー分類のモデルを構築します。
```
target_column_name = 'label' # カテゴリーの列
feature_column_name = 'text' # ニュース記事の列
train_dataset = Dataset.get_by_name(ws, "livedoor").keep_columns(["text","label"])
train_dataset.take(5).to_pandas_dataframe()
```
# 2. 自動機械学習 Automated Machine Learning
## 2.1 設定と制約条件
自動機械学習 Automated Machine Learning の設定と学習を行っていきます。
```
from azureml.automl.core.featurization import FeaturizationConfig
featurization_config = FeaturizationConfig()
# テキストデータの言語を指定します。日本語の場合は "jpn" と指定します。
featurization_config = FeaturizationConfig(dataset_language="jpn") # 英語の場合は下記をコメントアウトしてください。
# 明示的に `text` の列がテキストデータであると指定します。
featurization_config.add_column_purpose('text', 'Text')
#featurization_config.blocked_transformers = ['TfIdf','CountVectorizer'] # BERT のみを利用したい場合はコメントアウトを外します
# 自動機械学習の設定
automl_settings = {
"experiment_timeout_hours" : 2, # 学習時間 (hour)
"primary_metric": 'accuracy', # 評価指標
"max_concurrent_iterations": 4, # 計算環境の最大並列数
"max_cores_per_iteration": -1,
"enable_dnn": True, # 深層学習を有効
"enable_early_stopping": False,
"validation_size": 0.2,
"verbosity": logging.INFO,
"force_text_dnn": True,
#"n_cross_validations": 5,
}
automl_config = AutoMLConfig(task = 'classification',
debug_log = 'automl_errors.log',
compute_target=compute_target,
training_data=train_dataset,
label_column_name=target_column_name,
featurization=featurization_config,
**automl_settings
)
```
## 2.2 モデル学習
自動機械学習 Automated Machine Learning によるモデル学習を開始します。
```
automl_run = experiment.submit(automl_config, show_output=False)
# run_id を出力
automl_run.id
# Azure Machine Learning studio の URL を出力
automl_run
# # 途中でセッションが切れた場合の対処
# from azureml.train.automl.run import AutoMLRun
# ws = Workspace.from_config()
# experiment = ws.experiments['livedoor-news-classification-BERT']
# run_id = "AutoML_e69a63ae-ef52-4783-9a9f-527d69d7cc9d"
# automl_run = AutoMLRun(experiment, run_id = run_id)
# automl_run
```
## 2.3 モデルの登録
```
# 一番精度が高いモデルを抽出
best_run, fitted_model = automl_run.get_output()
# モデルファイル(.pkl) のダウンロード
model_dir = '../model'
best_run.download_file('outputs/model.pkl', model_dir + '/model.pkl')
# Azure ML へモデル登録
model_name = 'livedoor-model'
model = Model.register(model_path = model_dir + '/model.pkl',
model_name = model_name,
tags=None,
workspace=ws)
```
# 3. テストデータに対する予測値の出力
```
from sklearn.externals import joblib
trained_model = joblib.load(model_dir + '/model.pkl')
trained_model
test_dataset = Dataset.get_by_name(ws, "livedoor").keep_columns(["text"])
predicted = trained_model.predict_proba(test_dataset.to_pandas_dataframe())
```
# 4. モデルの解釈
一番精度が良かったチャンピョンモデルを選択し、モデルの解釈をしていきます。
モデルに含まれるライブラリを予め Python 環境にインストールする必要があります。[automl_env.yml](https://github.com/Azure/MachineLearningNotebooks/blob/master/how-to-use-azureml/automated-machine-learning/automl_env.yml)を用いて、conda の仮想環境に必要なパッケージをインストールしてください。
```
# 特徴量エンジニアリング後の変数名の確認
fitted_model.named_steps['datatransformer'].get_json_strs_for_engineered_feature_names()
#fitted_model.named_steps['datatransformer']. get_engineered_feature_names ()
# 特徴エンジニアリングのプロセスの可視化
text_transformations_used = []
for column_group in fitted_model.named_steps['datatransformer'].get_featurization_summary():
text_transformations_used.extend(column_group['Transformations'])
text_transformations_used
```
| github_jupyter |
<a href="https://colab.research.google.com/github/pszemraj/ml4hc-s22-project01/blob/autogluon-results/notebooks/colab/automl-baseline/process_autogluon_results.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
#process_autogluon_results
- cleans up the dataframes a bit for the report
# setup
```
#@markdown add auto-Colab formatting with `IPython.display`
from IPython.display import HTML, display
# colab formatting
def set_css():
display(
HTML(
"""
<style>
pre {
white-space: pre-wrap;
}
</style>
"""
)
)
get_ipython().events.register("pre_run_cell", set_css)
!nvidia-smi
!pip install -U plotly orca kaleido -q
import plotly.express as px
import numpy as np
import pandas as pd
from pathlib import Path
import os
#@title mount drive
from google.colab import drive
drive_base_str = '/content/drive'
drive.mount(drive_base_str)
#@markdown determine root
import os
from pathlib import Path
peter_base = Path('/content/drive/MyDrive/ETHZ-2022-S/ML-healthcare-projects/project1/gluon-autoML/')
if peter_base.exists() and peter_base.is_dir():
path = str(peter_base.resolve())
else:
# original
path = '/content/drive/MyDrive/ETH/'
print(f"base drive dir is:\n{path}")
```
## define folder for outputs
```
_out_dir_name = "Formatted-results-report" #@param {type:"string"}
output_path = os.path.join(path, _out_dir_name)
os.makedirs(output_path, exist_ok=True)
print(f"notebook outputs will be stored in:\n{output_path}")
_out = Path(output_path)
_src = Path(path)
```
##load data
### MIT
```
data_dir = _src / "final-results"
csv_files = {f.stem:f for f in data_dir.iterdir() if f.is_file() and f.suffix=='.csv'}
print(csv_files)
mit_ag = pd.read_csv(csv_files['mitbih_autogluon_results'])
mit_ag.info()
mit_ag.sort_values(by='score_val', ascending=False, inplace=True)
mit_ag.head()
orig_cols = list(mit_ag.columns)
new_cols = []
for i, col in enumerate(orig_cols):
col = col.lower()
if 'unnamed' in col:
new_cols.append(f"delete_me_{i}")
continue
col = col.replace('score', 'accuracy')
new_cols.append(col)
mit_ag.columns = new_cols
mit_ag.columns
try:
del mit_ag['delete_me_0']
except Exception as e:
print(f'skipping delete - {e}')
mit_ag.reset_index(drop=True, inplace=True)
mit_ag.head()
```
#### save mit-gluon-reformat
```
mit_ag.to_csv(_out / "MITBIH_autogluon_baseline_results_Accuracy.csv", index=False)
```
## PTB reformat
```
ptb_ag = pd.read_csv(csv_files['ptbdb_autogluon_results']).convert_dtypes()
ptb_ag.info()
ptb_ag.sort_values(by='score_val', ascending=False, inplace=True)
ptb_ag.head()
orig_cols = list(ptb_ag.columns)
new_cols = []
for i, col in enumerate(orig_cols):
col = col.lower()
if 'unnamed' in col:
new_cols.append(f"delete_me_{i}")
continue
col = col.replace('score', 'roc_auc')
new_cols.append(col)
ptb_ag.columns = new_cols
print(f'the columns for the ptb results are now:\n{ptb_ag.columns}')
try:
del ptb_ag['delete_me_0']
except Exception as e:
print(f'skipping delete - {e}')
ptb_ag.reset_index(drop=True, inplace=True)
ptb_ag.head()
ptb_ag.to_csv(_out / "PTBDB_autogluon_baseline_results_ROCAUC.csv", index=False)
print(f'results are in {_out.resolve()}')
```
| github_jupyter |
<h1> Repeatable splitting </h1>
In this notebook, we will explore the impact of different ways of creating machine learning datasets.
<p>
Repeatability is important in machine learning. If you do the same thing now and 5 minutes from now and get different answers, then it makes experimentation is difficult. In other words, you will find it difficult to gauge whether a change you made has resulted in an improvement or not.
```
import google.datalab.bigquery as bq
```
<h3> Create a simple machine learning model </h3>
The dataset that we will use is <a href="https://bigquery.cloud.google.com/table/bigquery-samples:airline_ontime_data.flights">a BigQuery public dataset</a> of airline arrival data. Click on the link, and look at the column names. Switch to the Details tab to verify that the number of records is 70 million, and then switch to the Preview tab to look at a few rows.
<p>
We want to predict the arrival delay of an airline based on the departure delay. The model that we will use is a zero-bias linear model:
$$ delay_{arrival} = \alpha * delay_{departure} $$
<p>
To train the model is to estimate a good value for $\alpha$.
<p>
One approach to estimate alpha is to use this formula:
$$ \alpha = \frac{\sum delay_{departure} delay_{arrival} }{ \sum delay_{departure}^2 } $$
Because we'd like to capture the idea that this relationship is different for flights from New York to Los Angeles vs. flights from Austin to Indianapolis (shorter flight, less busy airports), we'd compute a different $alpha$ for each airport-pair. For simplicity, we'll do this model only for flights between Denver and Los Angeles.
<h2> Naive random split (not repeatable) </h2>
```
compute_alpha = """
#standardSQL
SELECT
SAFE_DIVIDE(SUM(arrival_delay * departure_delay), SUM(departure_delay * departure_delay)) AS alpha
FROM
(
SELECT RAND() AS splitfield,
arrival_delay,
departure_delay
FROM
`bigquery-samples.airline_ontime_data.flights`
WHERE
departure_airport = 'DEN' AND arrival_airport = 'LAX'
)
WHERE
splitfield < 0.8
"""
results = bq.Query(compute_alpha).execute().result().to_dataframe()
alpha = results['alpha'][0]
print alpha
```
<h3> What is wrong with calculating RMSE on the training and test data as follows? </h3>
```
compute_rmse = """
#standardSQL
SELECT
dataset,
SQRT(AVG((arrival_delay - ALPHA * departure_delay)*(arrival_delay - ALPHA * departure_delay))) AS rmse,
COUNT(arrival_delay) AS num_flights
FROM (
SELECT
IF (RAND() < 0.8, 'train', 'eval') AS dataset,
arrival_delay,
departure_delay
FROM
`bigquery-samples.airline_ontime_data.flights`
WHERE
departure_airport = 'DEN'
AND arrival_airport = 'LAX' )
GROUP BY
dataset
"""
bq.Query(compute_rmse.replace('ALPHA', str(alpha))).execute().result()
```
Hint:
* Are you really getting the same training data in the compute_rmse query as in the compute_alpha query?
* Do you get the same answers each time you rerun the compute_alpha and compute_rmse blocks?
<h3> How do we correctly train and evaluate? </h3>
<br/>
Here's the right way to compute the RMSE using the actual training and held-out (evaluation) data. Note how much harder this feels.
Although the calculations are now correct, the experiment is still not repeatable.
Try running it several times; do you get the same answer?
```
train_and_eval_rand = """
#standardSQL
WITH
alldata AS (
SELECT
IF (RAND() < 0.8,
'train',
'eval') AS dataset,
arrival_delay,
departure_delay
FROM
`bigquery-samples.airline_ontime_data.flights`
WHERE
departure_airport = 'DEN'
AND arrival_airport = 'LAX' ),
training AS (
SELECT
SAFE_DIVIDE( SUM(arrival_delay * departure_delay) , SUM(departure_delay * departure_delay)) AS alpha
FROM
alldata
WHERE
dataset = 'train' )
SELECT
MAX(alpha) AS alpha,
dataset,
SQRT(AVG((arrival_delay - alpha * departure_delay)*(arrival_delay - alpha * departure_delay))) AS rmse,
COUNT(arrival_delay) AS num_flights
FROM
alldata,
training
GROUP BY
dataset
"""
bq.Query(train_and_eval_rand).execute().result()
```
<h2> Using HASH of date to split the data </h2>
Let's split by date and train.
```
compute_alpha = """
#standardSQL
SELECT
SAFE_DIVIDE(SUM(arrival_delay * departure_delay), SUM(departure_delay * departure_delay)) AS alpha
FROM
`bigquery-samples.airline_ontime_data.flights`
WHERE
departure_airport = 'DEN' AND arrival_airport = 'LAX'
AND MOD(ABS(FARM_FINGERPRINT(date)), 10) < 8
"""
results = bq.Query(compute_alpha).execute().result().to_dataframe()
alpha = results['alpha'][0]
print alpha
```
We can now use the alpha to compute RMSE. Because the alpha value is repeatable, we don't need to worry that the alpha in the compute_rmse will be different from the alpha computed in the compute_alpha.
```
compute_rmse = """
#standardSQL
SELECT
IF(MOD(ABS(FARM_FINGERPRINT(date)), 10) < 8, 'train', 'eval') AS dataset,
SQRT(AVG((arrival_delay - ALPHA * departure_delay)*(arrival_delay - ALPHA * departure_delay))) AS rmse,
COUNT(arrival_delay) AS num_flights
FROM
`bigquery-samples.airline_ontime_data.flights`
WHERE
departure_airport = 'DEN'
AND arrival_airport = 'LAX'
GROUP BY
dataset
"""
print bq.Query(compute_rmse.replace('ALPHA', str(alpha))).execute().result().to_dataframe().head()
```
Note also that the RMSE on the evaluation dataset more from the RMSE on the training dataset when we do the split correctly. This should be expected; in the RAND() case, there was leakage between training and evaluation datasets, because there is high correlation between flights on the same day.
<p>
This is one of the biggest dangers with doing machine learning splits the wrong way -- <b> you will develop a false sense of confidence in how good your model is! </b>
Copyright 2017 Google Inc.
Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License.
| github_jupyter |
Import the necessary imports
```
from __future__ import print_function, division, absolute_import
import tensorflow as tf
from tensorflow.contrib import keras
import numpy as np
import os
from sklearn import preprocessing
from sklearn.metrics import confusion_matrix
import itertools
import cPickle #python 2.x
#import _pickle as cPickle #python 3.x
import h5py
from matplotlib import pyplot as plt
%matplotlib inline
```
Now read the data
```
with h5py.File("NS_LP_DS.h5", "r") as hf:
LFP_features_train = hf["LFP_features_train"][...]
targets_train = hf["targets_train"][...]
speeds_train = hf["speeds_train"][...]
LFP_features_eval = hf["LFP_features_eval"][...]
targets_eval = hf["targets_eval"][...]
speeds_eval = hf["speeds_eval"][...]
```
And make sure it looks ok
```
rand_sample = np.random.randint(LFP_features_eval.shape[0])
for i in range(LFP_features_train.shape[-1]):
plt.figure(figsize=(20,7))
plt_data = LFP_features_eval[rand_sample,:,i]
plt.plot(np.arange(-0.5, 0., 0.5/plt_data.shape[0]), plt_data)
plt.xlable("time")
plt.title(str(i))
```
Now we write some helper functions to easily select regions.
```
block = np.array([[2,4,6,8],[1,3,5,7]])
channels = np.concatenate([(block + i*8) for i in range(180)][::-1])
brain_regions = {'Parietal Cortex': 8000, 'Hypocampus CA1': 6230, 'Hypocampus DG': 5760, 'Thalamus LPMR': 4450,
'Thalamus Posterior': 3500, 'Thalamus VPM': 1930, 'SubThalamic': 1050}
brain_regions = {k:v//22.5 for k,v in brain_regions.iteritems()}
used_channels = np.arange(9,1440,20, dtype=np.int16)[:-6]
for i in (729,749,1209,1229):
used_channels = np.delete(used_channels, np.where(used_channels==i)[0])
# for k,v in brain_regions.iteritems():
# print("{0}: {1}".format(k,v))
channels_dict = {'Parietal Cortex': np.arange(1096,1440, dtype=np.int16),
'Hypocampus CA1': np.arange(1016,1096, dtype=np.int16),
'Hypocampus DG': np.arange(784,1016, dtype=np.int16),
'Thalamus LPMR': np.arange(616,784, dtype=np.int16),
'Thalamus Posterior': np.arange(340,616, dtype=np.int16),
'Thalamus VPM': np.arange(184,340, dtype=np.int16),
'SubThalamic': np.arange(184, dtype=np.int16)}
used_channels_dict = {k:list() for k in channels_dict.iterkeys()}
# print("hello")
for ch in used_channels:
for key in channels_dict.iterkeys():
if ch in channels_dict[key]:
used_channels_dict[key].append(ch)
LFP_features_train_current = LFP_features_train
LFP_features_eval_current = LFP_features_eval
# current_channels = np.sort(used_channels_dict['Hypocampus CA1']+used_channels_dict['Hypocampus DG']+\
# used_channels_dict['Thalamus Posterior'])
# current_idxs = np.array([np.where(ch==used_channels)[0] for ch in current_channels]).squeeze()
# LFP_features_train_current = LFP_features_train[...,current_idxs]
# LFP_features_eval_current = LFP_features_eval[...,current_idxs]
```
Create a call back to save the best validation accuracy
```
model_chk_path = 'my_model.hdf5'
mcp = keras.callbacks.ModelCheckpoint(model_chk_path, monitor="val_acc",
save_best_only=True)
```
Below I have defined a couple of different network architectures to play with.
```
# try:
# model = None
# except NameError:
# pass
# decay = 1e-3
# conv1d = keras.layers.Convolution1D
# maxPool = keras.layers.MaxPool1D
# model = keras.models.Sequential()
# model.add(conv1d(64, 5, padding='same', strides=2, activation='relu',
# kernel_regularizer=keras.regularizers.l2(decay),
# input_shape=LFP_features_train.shape[1:]))
# model.add(maxPool())
# model.add(conv1d(128, 3, padding='same', strides=2, activation='relu',
# kernel_regularizer=keras.regularizers.l2(decay)))
# model.add(maxPool())
# model.add(conv1d(128, 3, padding='same', strides=2, activation='relu',
# kernel_regularizer=keras.regularizers.l2(decay)))
# model.add(maxPool())
# model.add(conv1d(128, 3, padding='same', strides=2, activation='relu',
# kernel_regularizer=keras.regularizers.l2(decay)))
# model.add(maxPool())
# model.add(keras.layers.Flatten())
# model.add(keras.layers.Dropout(rate=0.5))
# model.add(keras.layers.Dense(2, activation='softmax', kernel_regularizer=keras.regularizers.l2(decay)))
# try:
# model = None
# except NameError:
# pass
# decay = 1e-3
# conv1d = keras.layers.Convolution1D
# maxPool = keras.layers.MaxPool1D
# BN = keras.layers.BatchNormalization
# Act = keras.layers.Activation('relu')
# model = keras.models.Sequential()
# model.add(conv1d(64, 5, padding='same', strides=2,
# kernel_regularizer=keras.regularizers.l1_l2(decay),
# input_shape=LFP_features_train_current.shape[1:]))
# model.add(BN())
# model.add(Act)
# model.add(maxPool())
# model.add(conv1d(128, 3, padding='same', strides=2,
# kernel_regularizer=keras.regularizers.l1_l2(decay)))
# model.add(BN())
# model.add(Act)
# model.add(maxPool())
# model.add(conv1d(128, 3, padding='same', strides=2,
# kernel_regularizer=keras.regularizers.l1_l2(decay)))
# model.add(BN())
# model.add(Act)
# model.add(maxPool())
# model.add(conv1d(128, 3, padding='same', strides=2,
# kernel_regularizer=keras.regularizers.l1_l2(decay)))
# model.add(BN())
# model.add(Act)
# model.add(maxPool())
# model.add(keras.layers.Flatten())
# model.add(keras.layers.Dropout(rate=0.5))
# model.add(keras.layers.Dense(2, activation='softmax', kernel_regularizer=keras.regularizers.l2(decay)))
# try:
# model = None
# except NameError:
# pass
# decay = 1e-3
# conv1d = keras.layers.Convolution1D
# maxPool = keras.layers.MaxPool1D
# model = keras.models.Sequential()
# model.add(conv1d(33, 5, padding='same', activation='relu', kernel_regularizer=keras.regularizers.l2(decay),
# input_shape=LFP_features_train.shape[1:]))
# model.add(maxPool())
# model.add(conv1d(33, 3, padding='same', activation='relu', kernel_regularizer=keras.regularizers.l2(decay)))
# model.add(maxPool())
# model.add(conv1d(16, 3, padding='same', activation='relu', kernel_regularizer=keras.regularizers.l2(decay)))
# model.add(maxPool())
# model.add(conv1d(4, 3, padding='same', activation='relu', kernel_regularizer=keras.regularizers.l2(decay)))
# model.add(maxPool())
# model.add(keras.layers.Flatten())
# model.add(keras.layers.Dropout(rate=0.5))
# model.add(keras.layers.Dense(2, activation='softmax', kernel_regularizer=keras.regularizers.l2(decay)))
try:
model = None
except NameError:
pass
decay = 1e-3
regul = keras.regularizers.l1(decay)
conv1d = keras.layers.Convolution1D
maxPool = keras.layers.MaxPool1D
BN = keras.layers.BatchNormalization
Act = keras.layers.Activation('relu')
model = keras.models.Sequential()
model.add(keras.layers.Convolution1D(64, 5, padding='same', strides=2,
kernel_regularizer=keras.regularizers.l1_l2(decay),
input_shape=LFP_features_train_current.shape[1:]))
model.add(keras.layers.BatchNormalization())
model.add(keras.layers.Activation('relu'))
model.add(keras.layers.MaxPool1D())
model.add(keras.layers.Convolution1D(128, 3, padding='same', strides=2,
kernel_regularizer=keras.regularizers.l1_l2(decay)))
model.add(keras.layers.BatchNormalization())
model.add(keras.layers.Activation('relu'))
# model.add(keras.layers.MaxPool1D())
# model.add(keras.layers.Convolution1D(128, 3, padding='same', strides=2,
# kernel_regularizer=keras.regularizers.l1_l2(decay)))
# model.add(keras.layers.BatchNormalization())
# model.add(keras.layers.Activation('relu'))
# # model.add(keras.layers.GlobalMaxPooling1D())
# model.add(keras.layers.MaxPool1D())
# model.add(keras.layers.Convolution1D(128, 3, padding='same', strides=2,
# kernel_regularizer=keras.regularizers.l1_l2(decay)))
# model.add(keras.layers.BatchNormalization())
# model.add(keras.layers.Activation('relu'))
# model.add(maxPool())
# model.add(keras.layers.Flatten())
model.add(keras.layers.GlobalMaxPooling1D())
model.add(keras.layers.Dropout(rate=0.5))
model.add(keras.layers.Dense(2, activation='softmax', kernel_regularizer=keras.regularizers.l1_l2(decay)))
model.compile(optimizer='Adam',
loss='categorical_crossentropy',
metrics=['accuracy'])
model.summary()
history = model.fit(LFP_features_train_current,
targets_train,
epochs=20,
batch_size=1024,
validation_data=(LFP_features_eval_current, targets_eval),
callbacks=[mcp])
```
Helper function for the confusion matrix
```
def plot_confusion_matrix(cm, classes,
normalize=False,
title='Confusion matrix',
cmap=plt.cm.Blues):
"""
This function prints and plots the confusion matrix.
Normalization can be applied by setting `normalize=True`.
"""
if normalize:
cm = cm.astype('float') / np.maximum(cm.sum(axis=1)[:, np.newaxis],1.0)
print("Normalized confusion matrix")
else:
print('Confusion matrix, without normalization')
print(cm)
cm = (cm*1000).astype(np.int16)
cm = np.multiply(cm, 0.1)
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title)
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45)
plt.yticks(tick_marks, classes)
thresh = cm.max() / 2.
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, "{0}%".format(cm[i, j]),
horizontalalignment="center",
color="white" if cm[i, j] > thresh else "black")
plt.tight_layout()
plt.ylabel('True label')
plt.xlabel('Predicted label')
return plt.gcf()
class_names = ['go', 'stop']
model.load_weights('my_model.hdf5')
y_pred_initial = model.predict(LFP_features_eval)
targets_eval_1d = np.argmax(targets_eval, axis=1)
y_pred = np.argmax(y_pred_initial, axis=1)
cnf_matrix = confusion_matrix(targets_eval_1d, y_pred)
np.set_printoptions(precision=2)
plt.figure()
fig = plot_confusion_matrix(cnf_matrix, classes=class_names, normalize=True,
title='Normalized confusion matrix')
wrong_idxs = np.where(y_pred != targets_eval_1d)[0]
wrong_vals = speeds_eval[wrong_idxs]
# wrong_vals.squeeze().shape
# crazy_wrong_idxs.shape
plt.cla()
plt.close()
plt.figure(figsize=(20,7))
n, bins, patches = plt.hist(wrong_vals.squeeze(),
bins=np.arange(0,1,0.01),)
plt.plot(bins)
plt.xlim([0,1])
fig_dist = plt.gcf()
```
Train and evaluation accuracies
```
acc = history.history['acc']
val_acc = history.history['val_acc']
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(acc))
plt.figure(figsize=(20,7))
plt.plot(epochs, acc, 'bo', label='Training')
plt.plot(epochs, val_acc, 'b', label='Validation')
plt.title('Training and validation accuracy')
plt.legend(loc='lower right', fontsize=24)
plt.xticks(np.arange(20))
```
| github_jupyter |
# IDS Instruction: Regression
(Lisa Mannel)
## Simple linear regression
First we import the packages necessary fo this instruction:
```
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, mean_absolute_error
```
Consider the data set "df" with feature variables "x" and "y" given below.
```
df1 = pd.DataFrame({'x': [0, 1, 2, 3, 4, 5, 6, 7, 8, 9], 'y': [1, 3, 2, 5, 7, 8, 8, 9, 10, 12]})
print(df1)
```
To get a first impression of the given data, let's have a look at its scatter plot:
```
plt.scatter(df1.x, df1.y, color = "y", marker = "o", s = 40)
plt.xlabel('x')
plt.ylabel('y')
plt.title('first overview of the data')
plt.show()
```
We can already see a linear correlation between x and y. Assume the feature x to be descriptive, while y is our target feature. We want a linear function, y=ax+b, that predicts y as accurately as possible based on x. To achieve this goal we use linear regression from the sklearn package.
```
#define the set of descriptive features (in this case only 'x' is in that set) and the target feature (in this case 'y')
descriptiveFeatures1=df1[['x']]
print(descriptiveFeatures1)
targetFeature1=df1['y']
#define the classifier
classifier = LinearRegression()
#train the classifier
model1 = classifier.fit(descriptiveFeatures1, targetFeature1)
```
Now we can use the classifier to predict y. We print the predictions as well as the coefficient and bias (*intercept*) of the linear function.
```
#use the classifier to make prediction
targetFeature1_predict = classifier.predict(descriptiveFeatures1)
print(targetFeature1_predict)
#print coefficient and intercept
print('Coefficients: \n', classifier.coef_)
print('Intercept: \n', classifier.intercept_)
```
Let's visualize our regression function with the scatterplot showing the original data set. Herefore, we use the predicted values.
```
#visualize data points
plt.scatter(df1.x, df1.y, color = "y", marker = "o", s = 40)
#visualize regression function
plt.plot(descriptiveFeatures1, targetFeature1_predict, color = "g")
plt.xlabel('x')
plt.ylabel('y')
plt.title('the data and the regression function')
plt.show()
```
### <span style="color:green"> Now it is your turn. </span> Build a simple linear regression for the data below. Use col1 as descriptive feature and col2 as target feature. Also plot your results.
```
df2 = pd.DataFrame({'col1': [770, 677, 428, 410, 371, 504, 1136, 695, 551, 550], 'col2': [54, 47, 28, 38, 29, 38, 80, 52, 45, 40]})
#Your turn
# features that we use for the prediction are called the "descriptive" features
descriptiveFeatures2=df2[['col1']]
# the feature we would like to predict is called target fueature
targetFeature2=df2['col2']
# traing regression model:
classifier2 = LinearRegression()
model2 = classifier2.fit(descriptiveFeatures2, targetFeature2)
#use the classifier to make prediction
targetFeature2_predict = classifier2.predict(descriptiveFeatures2)
#visualize data points
plt.scatter(df2.col1, df2.col2, color = "y", marker = "o")
#visualize regression function
plt.plot(descriptiveFeatures2, targetFeature2_predict, color = "g")
plt.xlabel('col1')
plt.ylabel('col2')
plt.title('the data and the regression function')
plt.show()
```
### Evaluation
Usually, the model and its predictions is not sufficient. In the following we want to evaluate our classifiers.
Let's start by computing their error. The sklearn.metrics package contains several errors such as
* Mean squared error
* Mean absolute error
* Mean squared log error
* Median absolute error
```
#computing the squared error of the first model
print("Mean squared error model 1: %.2f" % mean_squared_error(targetFeature1, targetFeature1_predict))
```
We can also visualize the errors:
```
plt.scatter(targetFeature1_predict, (targetFeature1 - targetFeature1_predict) ** 2, color = "blue", s = 10,)
## plotting line to visualize zero error
plt.hlines(y = 0, xmin = 0, xmax = 15, linewidth = 2)
## plot title
plt.title("Squared errors Model 1")
## function to show plot
plt.show()
```
### <span style="color:green"> Now it is your turn. </span> Compute the mean squared error and visualize the squared errors. Play around using different error metrics.
```
#Your turn
print("Mean squared error model 2: %.2f" % mean_squared_error(targetFeature2,targetFeature2_predict))
print("Mean absolute error model 2: %.2f" % mean_absolute_error(targetFeature2,targetFeature2_predict))
plt.scatter(targetFeature2_predict, (targetFeature2 - targetFeature2_predict) ** 2, color = "blue",)
plt.scatter(targetFeature2,abs(targetFeature2 - targetFeature2_predict),color = "red")
## plotting line to visualize zero error
plt.hlines(y = 0, xmin = 0, xmax = 80, linewidth = 2)
## plot title
plt.title("errors Model 2")
## function to show plot
plt.show()
```
## Handling multiple descriptive features at once - Multiple linear regression
In most cases, we will have more than one descriptive feature . As an example we use an example data set of the scikit package. The dataset describes housing prices in Boston based on several attributes. Note, in this format the data is already split into descriptive features and a target feature.
```
from sklearn import datasets ## imports datasets from scikit-learn
df3 = datasets.load_boston()
#The sklearn package provides the data splitted into a set of descriptive features and a target feature.
#We can easily transform this format into the pandas data frame as used above.
descriptiveFeatures3 = pd.DataFrame(df3.data, columns=df3.feature_names)
targetFeature3 = pd.DataFrame(df3.target, columns=['target'])
print('Descriptive features:')
print(descriptiveFeatures3.head())
print('Target feature:')
print(targetFeature3.head())
```
To predict the housing price we will use a Multiple Linear Regression model. In Python this is very straightforward: we use the same function as for simple linear regression, but our set of descriptive features now contains more than one element (see above).
```
classifier = LinearRegression()
model3 = classifier.fit(descriptiveFeatures3,targetFeature3)
targetFeature3_predict = classifier.predict(descriptiveFeatures3)
print('Coefficients: \n', classifier.coef_)
print('Intercept: \n', classifier.intercept_)
print("Mean squared error: %.2f" % mean_squared_error(targetFeature3, targetFeature3_predict))
```
As you can see above, we have a coefficient for each descriptive feature.
## Handling categorical descriptive features
So far we always encountered numerical dscriptive features, but data sets can also contain categorical attributes. The regression function can only handle numerical input. There are several ways to tranform our categorical data to numerical data (for example using one-hot encoding as explained in the lecture: we introduce a 0/1 feature for every possible value of our categorical attribute). For adequate data, another possibility is to replace each categorical value by a numerical value and adding an ordering with it.
Popular possibilities to achieve this transformation are
* the get_dummies function of pandas
* the OneHotEncoder of scikit
* the LabelEncoder of scikit
After encoding the attributes we can apply our regular regression function.
```
#example using pandas
df4 = pd.DataFrame({'A':['a','b','c'],'B':['c','b','a'] })
one_hot_pd = pd.get_dummies(df4)
one_hot_pd
#example using scikit
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
#apply the one hot encoder
encoder = OneHotEncoder(categories='auto')
encoder.fit(df4)
df4_OneHot = encoder.transform(df4).toarray()
print('Transformed by One-hot Encoding: ')
print(df4_OneHot)
# encode labels with value between 0 and n_classes-1
encoder = LabelEncoder()
df4_LE = df4.apply(encoder.fit_transform)
print('Replacing categories by numerical labels: ')
print(df4_LE.head())
```
### <span style="color:green"> Now it is your turn. </span> Perform linear regression using the data set given below. Don't forget to transform your categorical descriptive features. The rental price attribute represents the target variable.
```
from sklearn.preprocessing import LabelEncoder
df5 = pd.DataFrame({'Size':[500,550,620,630,665],'Floor':[4,7,9,5,8], 'Energy rating':['C', 'A', 'A', 'B', 'C'], 'Rental price': [320,380,400,390,385] })
#Your turn
# To transform the categorial feature
to_trannsform = df5[['Energy rating']]
encoder = LabelEncoder()
transformed = to_trannsform.apply(encoder.fit_transform)
df5_transformed = df5
df5_transformed[['Energy rating']] = transformed
# the feature we would like to predict is called target fueature
df5_traget = df5_transformed['Rental price']
# features that we use for the prediction are called the "descriptive" features
df5_descpritive = df5_transformed[['Size','Floor','Energy rating']]
# traing regression model:
classifier5 = LinearRegression()
model5 = classifier5.fit(df5_descpritive, df5_traget)
#use the classifier to make prediction
targetFeature5_predict = classifier5.predict(df5_descpritive)
print('Coefficients: \n', classifier5.coef_)
print('Intercept: \n', classifier5.intercept_)
print("Mean squared error: %.2f" % mean_squared_error(df5_traget, targetFeature5_predict))
```
## Predicting a categorical target value - Logistic regression
We might also encounter data sets where our target feature is categorical. Here we don't transform them into numerical values, but insetad we use a logistic regression function. Luckily, sklearn provides us with a suitable function that is similar to the linear equivalent. Similar to linear regression, we can compute logistic regression on a single descriptive variable as well as on multiple variables.
```
# Importing the dataset
iris = pd.read_csv('iris.csv')
print('First look at the data set: ')
print(iris.head())
#defining the descriptive and target features
descriptiveFeatures_iris = iris[['sepal_length']] #we only use the attribute 'sepal_length' in this example
targetFeature_iris = iris['species'] #we want to predict the 'species' of iris
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression(solver = 'liblinear', multi_class = 'ovr')
classifier.fit(descriptiveFeatures_iris, targetFeature_iris)
targetFeature_iris_pred = classifier.predict(descriptiveFeatures_iris)
print('Coefficients: \n', classifier.coef_)
print('Intercept: \n', classifier.intercept_)
```
### <span style="color:green"> Now it is your turn. </span> In the example above we only used the first attribute as descriptive variable. Change the example such that all available attributes are used.
```
#Your turn
# Importing the dataset
iris2 = pd.read_csv('iris.csv')
print('First look at the data set: ')
print(iris2.head())
#defining the descriptive and target features
descriptiveFeatures_iris2 = iris[['sepal_length','sepal_width','petal_length','petal_width']]
targetFeature_iris2 = iris['species'] #we want to predict the 'species' of iris
from sklearn.linear_model import LogisticRegression
classifier2 = LogisticRegression(solver = 'liblinear', multi_class = 'ovr')
classifier2.fit(descriptiveFeatures_iris2, targetFeature_iris2)
targetFeature_iris_pred2 = classifier2.predict(descriptiveFeatures_iris2)
print('Coefficients: \n', classifier2.coef_)
print('Intercept: \n', classifier2.intercept_)
```
Note, that the regression classifier (both logistic and non-logistic) can be tweaked using several parameters. This includes, but is not limited to, non-linear regression. Check out the documentation for details and feel free to play around!
# Support Vector Machines
Aside from regression models, the sklearn package also provides us with a function for training support vector machines. Looking at the example below we see that they can be trained in similar ways. We still use the iris data set for illustration.
```
from sklearn.svm import SVC
#define descriptive and target features as before
descriptiveFeatures_iris = iris[['sepal_length', 'sepal_width', 'petal_length', 'petal_width']]
targetFeature_iris = iris['species']
#this time, we train an SVM classifier
classifier = SVC(C=1, kernel='linear', gamma = 'auto')
classifier.fit(descriptiveFeatures_iris, targetFeature_iris)
targetFeature_iris_predict = classifier.predict(descriptiveFeatures_iris)
targetFeature_iris_predict[0:5] #show the first 5 predicted values
```
As explained in the lecture, a support vector machine is defined by its support vectors. In the sklearn package we can access them and their properties very easily:
* support_: indicies of support vectors
* support_vectors_: the support vectors
* n_support_: the number of support vectors for each class
```
print('Indicies of support vectors:')
print(classifier.support_)
print('The support vectors:')
print(classifier.support_vectors_)
print('The number of support vectors for each class:')
print(classifier.n_support_)
```
We can also calculate the distance of the data points to the separating hyperplane by using the decision_function(X) method. Score(X,y) calculates the mean accuracy of the classification. The classification report shows metrics such as precision, recall, f1-score and support. You will learn more about these quality metrics in a few lectures.
```
from sklearn.metrics import classification_report
classifier.decision_function(descriptiveFeatures_iris)
print('Accuracy: \n', classifier.score(descriptiveFeatures_iris,targetFeature_iris))
print('Classification report: \n')
print(classification_report(targetFeature_iris, targetFeature_iris_predict))
```
The SVC has many parameters. In the lecture you learned about the concept of kernels. Scikit gives you the opportunity to try different kernel functions.
Furthermore, the parameter C tells the SVM optimization problem how much you want to avoid misclassifying each training example.
On the scikit website you can find more information about the available kernels etc. http://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html
| github_jupyter |
```
import numpy as np
import pandas as pd
from datetime import date
from random import seed
from random import random
import time
import scipy, scipy.signal
import os, os.path
import shutil
import matplotlib
import matplotlib.pyplot as plt
from pylab import imshow
# vgg16 model used for transfer learning on the dogs and cats dataset
from matplotlib import pyplot
# from keras.utils import to_categorical
from tensorflow.keras.utils import to_categorical
from keras.models import Sequential
from keras.applications.vgg16 import VGG16
from keras.models import Model
from keras.layers import Dense
from keras.layers import Flatten
import tensorflow as tf
# from keras.optimizers import SGD
from keras.layers import Conv2D
from keras.layers import MaxPooling2D
# from keras.optimizers import gradient_descent_v2
# SGD = gradient_descent_v2.SGD(...)
from tensorflow.keras.optimizers import SGD
from keras.preprocessing.image import ImageDataGenerator
import h5py
import sys
sys.path.append('/Users/hn/Documents/00_GitHub/Ag/NASA/Python_codes/')
import NASA_core as nc
# import NASA_plot_core.py as rcp
from keras.preprocessing.image import load_img
from keras.preprocessing.image import img_to_array
from keras.models import load_model
idx = "EVI"
train_folder = '/Users/hn/Documents/01_research_data/NASA/ML_data/train_images_' + idx + '/'
test_folder = "/Users/hn/Documents/01_research_data/NASA/ML_data/limitCrops_nonExpert_images/"
```
# Prepare final dataset
```
# organize dataset into a useful structure
# create directories
dataset_home = train_folder
# create label subdirectories
labeldirs = ['separate_singleDouble/single/', 'separate_singleDouble/double/']
for labldir in labeldirs:
newdir = dataset_home + labldir
os.makedirs(newdir, exist_ok=True)
# copy training dataset images into subdirectories
for file in os.listdir(train_folder):
src = train_folder + '/' + file
if file.startswith('single'):
dst = dataset_home + 'separate_singleDouble/single/' + file
shutil.copyfile(src, dst)
elif file.startswith('double'):
dst = dataset_home + 'separate_singleDouble/double/' + file
shutil.copyfile(src, dst)
```
# Plot For Fun
```
# plot dog photos from the dogs vs cats dataset
from matplotlib.image import imread
# define location of dataset
# plot first few images
files = os.listdir(train_folder)[2:4]
# files = [sorted(os.listdir(train_folder))[2]] + [sorted(os.listdir(train_folder))[-2]]
for i in range(2):
# define subplot
pyplot.subplot(210 + 1 + i)
# define filename
filename = train_folder + files[i]
# load image pixels
image = imread(filename)
# plot raw pixel data
pyplot.imshow(image)
# show the figure
pyplot.show()
```
# Full Code
```
# define cnn model
def define_model():
# load model
model = VGG16(include_top=False, input_shape=(224, 224, 3))
# mark loaded layers as not trainable
for layer in model.layers:
layer.trainable = False
# add new classifier layers
flat1 = Flatten()(model.layers[-1].output)
class1 = Dense(128, activation='relu', kernel_initializer='he_uniform')(flat1)
output = Dense(1, activation='sigmoid')(class1)
# define new model
model = Model(inputs=model.inputs, outputs=output)
# compile model
opt = SGD(learning_rate=0.001, momentum=0.9)
model.compile(optimizer=opt, loss='binary_crossentropy', metrics=['accuracy'])
return model
# run the test harness for evaluating a model
def run_test_harness():
# define model
_model = define_model()
# create data generator
datagen = ImageDataGenerator(featurewise_center=True)
# specify imagenet mean values for centering
datagen.mean = [123.68, 116.779, 103.939]
# prepare iterator
train_separate_dir = train_folder + "separate_singleDouble/"
train_it = datagen.flow_from_directory(train_separate_dir,
class_mode='binary',
batch_size=16,
target_size=(224, 224))
# fit model
_model.fit(train_it,
steps_per_epoch=len(train_it),
epochs=10, verbose=1)
model_dir = "/Users/hn/Documents/01_research_data/NASA/ML_Models/"
_model.save(model_dir+'01_TL_SingleDouble.h5')
# tf.keras.models.save_model(model=trained_model, filepath=model_dir+'01_TL_SingleDouble.h5')
# return(_model)
# entry point, run the test harness
start_time = time.time()
run_test_harness()
end_time = time.time()
# photo = load_img(train_folder + files[0], target_size=(200, 500))
# photo
```
| github_jupyter |
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cross_validation import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import StandardScaler
data = pd.read_csv('Social_Network_Ads.csv')
data.head()
data.isnull().sum()
from sklearn import preprocessing
le = preprocessing.LabelEncoder()
le.fit(['Male','Female'])
data['Gender']=le.transform(data['Gender'])
data.head()
X = data.iloc[:, 2:4].values
y = data.iloc[:, 4].values
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3)
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
from sklearn.ensemble import RandomForestClassifier
clf = RandomForestClassifier(n_estimators = 100, criterion = 'gini')
clf.fit(X_train, y_train)
from sklearn.metrics import confusion_matrix
confusion_matrix(y_test, clf.predict(X_test))
confusion_matrix(y_train, clf.predict(X_train))
print ("Testing Accuracy is : ",accuracy_score(y_test,clf.predict(X_test)))
print ("Training Accuracy is : ",accuracy_score(y_train,clf.predict(X_train)))
from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, clf.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Classifier (Training set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, clf.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green'))(i), label = j)
plt.title('Classifier (Test set)')
plt.xlabel('Age')
plt.ylabel('Estimated Salary')
plt.legend()
plt.show()
```
| github_jupyter |
# Spark SQL
Spark SQL is arguably one of the most important and powerful features in Spark. In a nutshell, with Spark SQL you can run SQL queries against views or tables organized into databases. You also can use system functions or define user functions and analyze query plans in order to optimize their workloads. This integrates directly into the DataFrame API, and as we saw in previous classes, you can choose to express some of your data manipulations in SQL and others in DataFrames and they will compile to the same underlying code.
## Big Data and SQL: Apache Hive
Before Spark’s rise, Hive was the de facto big data SQL access layer. Originally developed at Facebook, Hive became an incredibly popular tool across industry for performing SQL operations on big data. In many ways it helped propel Hadoop into different industries because analysts could run SQL queries. Although Spark began as a general processing engine with Resilient Distributed Datasets (RDDs), a large cohort of users now use Spark SQL.
## Big Data and SQL: Spark SQL
With the release of Spark 2.0, its authors created a superset of Hive’s support, writing a native SQL parser that supports both ANSI-SQL as well as HiveQL queries. This, along with its unique interoperability with DataFrames, makes it a powerful tool for all sorts of companies. For example, in late 2016, Facebook announced that it had begun running Spark workloads and seeing large benefits in doing so. In the words of the blog post’s authors:
>We challenged Spark to replace a pipeline that decomposed to hundreds of Hive jobs into a single Spark job. Through a series of performance and reliability improvements, we were able to scale Spark to handle one of our entity ranking data processing use cases in production…. The Spark-based pipeline produced significant performance improvements (4.5–6x CPU, 3–4x resource reservation, and ~5x latency) compared with the old Hive-based pipeline, and it has been running in production for several months.
The power of Spark SQL derives from several key facts: SQL analysts can now take advantage of Spark’s computation abilities by plugging into the Thrift Server or Spark’s SQL interface, whereas data engineers and scientists can use Spark SQL where appropriate in any data flow. This unifying API allows for data to be extracted with SQL, manipulated as a DataFrame, passed into one of Spark MLlibs’ large-scale machine learning algorithms, written out to another data source, and everything in between.
**NOTE:** Spark SQL is intended to operate as an online analytic processing (OLAP) database, not an online transaction processing (OLTP) database. This means that it is not intended to perform extremely low-latency queries. Even though support for in-place modifications is sure to be something that comes up in the future, it’s not something that is currently available.
```
spark.sql("SELECT 1 + 1").show()
```
As we have seen before, you can completely interoperate between SQL and DataFrames, as you see fit. For instance, you can create a DataFrame, manipulate it with SQL, and then manipulate it again as a DataFrame. It’s a powerful abstraction that you will likely find yourself using quite a bit:
```
bucket = spark._jsc.hadoopConfiguration().get("fs.gs.system.bucket")
data = "gs://" + bucket + "/notebooks/data/"
spark.read.json(data + "flight-data/json/2015-summary.json")\
.createOrReplaceTempView("flights_view") # DF => SQL
spark.sql("""
SELECT DEST_COUNTRY_NAME, sum(count)
FROM flights_view GROUP BY DEST_COUNTRY_NAME
""")\
.where("DEST_COUNTRY_NAME like 'S%'").where("`sum(count)` > 10")\
.count() # SQL => DF
```
## Creating Tables
You can create tables from a variety of sources. For instance below we are creating a table from a SELECT statement:
```
spark.sql('''
CREATE TABLE IF NOT EXISTS flights_from_select USING parquet AS SELECT * FROM flights_view
''')
spark.sql('SELECT * FROM flights_from_select').show(5)
spark.sql('''
DESCRIBE TABLE flights_from_select
''').show()
```
## Catalog
The highest level abstraction in Spark SQL is the Catalog. The Catalog is an abstraction for the storage of metadata about the data stored in your tables as well as other helpful things like databases, tables, functions, and views. The catalog is available in the `spark.catalog` package and contains a number of helpful functions for doing things like listing tables, databases, and functions.
```
Cat = spark.catalog
Cat.listTables()
spark.sql('SHOW TABLES').show(5, False)
Cat.listDatabases()
spark.sql('SHOW DATABASES').show()
Cat.listColumns('flights_from_select')
Cat.listTables()
```
### Caching Tables
```
spark.sql('''
CACHE TABLE flights_view
''')
spark.sql('''
UNCACHE TABLE flights_view
''')
```
## Explain
```
spark.sql('''
EXPLAIN SELECT * FROM just_usa_view
''').show(1, False)
```
### VIEWS - create/drop
```
spark.sql('''
CREATE VIEW just_usa_view AS
SELECT * FROM flights_from_select WHERE dest_country_name = 'United States'
''')
spark.sql('''
DROP VIEW IF EXISTS just_usa_view
''')
```
### Drop tables
```
spark.sql('DROP TABLE flights_from_select')
spark.sql('DROP TABLE IF EXISTS flights_from_select')
```
## `spark-sql`
Go to the command line tool and check for the list of databases and tables. For instance:
`SHOW TABLES`
| github_jupyter |
```
import numpy as np
import cv2
import matplotlib
import matplotlib.pyplot as plt
import matplotlib as mpimg
import numpy as np
from IPython.display import HTML
import os, sys
import glob
import moviepy
from moviepy.editor import VideoFileClip
from moviepy.editor import *
from IPython import display
from IPython.core.display import display
from IPython.display import Image
import pylab
import scipy.misc
def region_of_interest(img):
mask = np.zeros(img.shape, dtype=np.uint8) #mask image
roi_corners = np.array([[(200,675), (1200,675), (700,430),(500,430)]],
dtype=np.int32) # vertisies seted to form trapezoidal scene
channel_count = 1#img.shape[2] # image channels
ignore_mask_color = (255,)*channel_count
cv2.fillPoly(mask, roi_corners, ignore_mask_color)
masked_image = cv2.bitwise_and(img, mask)
return masked_image
def ColorThreshold(img): # Threshold Yellow anf White Colos from RGB, HSV, HLS color spaces
HSV = cv2.cvtColor(img, cv2.COLOR_RGB2HSV)
# For yellow
yellow = cv2.inRange(HSV, (20, 100, 100), (50, 255, 255))
# For white
sensitivity_1 = 68
white = cv2.inRange(HSV, (0,0,255-sensitivity_1), (255,20,255))
sensitivity_2 = 60
HSL = cv2.cvtColor(img, cv2.COLOR_RGB2HLS)
white_2 = cv2.inRange(HSL, (0,255-sensitivity_2,0), (255,255,sensitivity_2))
white_3 = cv2.inRange(img, (200,200,200), (255,255,255))
bit_layer = yellow | white | white_2 | white_3
return bit_layer
from skimage import morphology
def SobelThr(img): # Sobel edge detection extraction
gray=img
sobelx = cv2.Sobel(gray, cv2.CV_64F, 1, 0,ksize=15)
sobely = cv2.Sobel(gray, cv2.CV_64F, 0, 1,ksize=15)
abs_sobelx = np.absolute(sobelx)
abs_sobely = np.absolute(sobely)
scaled_sobelx = np.uint8(255*abs_sobelx/np.max(abs_sobelx))
scaled_sobely = np.uint8(255*abs_sobely/np.max(abs_sobely))
binary_outputabsx = np.zeros_like(scaled_sobelx)
binary_outputabsx[(scaled_sobelx >= 70) & (scaled_sobelx <= 255)] = 1
binary_outputabsy = np.zeros_like(scaled_sobely)
binary_outputabsy[(scaled_sobely >= 100) & (scaled_sobely <= 150)] = 1
mag_thresh=(100, 200)
gradmag = np.sqrt(sobelx**2 + sobely**2)
scale_factor = np.max(gradmag)/255
gradmag = (gradmag/scale_factor).astype(np.uint8)
binary_outputmag = np.zeros_like(gradmag)
binary_outputmag[(gradmag >= mag_thresh[0]) & (gradmag <= mag_thresh[1])] = 1
combinedS = np.zeros_like(binary_outputabsx)
combinedS[(((binary_outputabsx == 1) | (binary_outputabsy == 1))|(binary_outputmag==1)) ] = 1
return combinedS
def combinI(b1,b2): ##Combine color threshold + Sobel edge detection
combined = np.zeros_like(b1)
combined[((b1 == 1)|(b2 == 255)) ] = 1
return combined
def prespectI(img): # Calculate the prespective transform and warp the Image to the eye bird view
src=np.float32([[728,475],
[1058,690],
[242,690],
[565,475]])
dst=np.float32([[1058,20],
[1058,700],
[242,700],
[242,20]])
M = cv2.getPerspectiveTransform(src, dst)
warped = cv2.warpPerspective(img, M, (1280,720), flags=cv2.INTER_LINEAR)
return (warped, M)
def undistorT(imgorg): # Calculate Undistortion coefficients
nx =9
ny = 6
objpoints = []
imgpoints = []
objp=np.zeros((6*9,3),np.float32)
objp[:,:2]=np.mgrid[0:6,0:9].T.reshape(-1,2)
images=glob.glob('./camera_cal/calibration*.jpg')
for fname in images: # find corner points and Make a list of calibration images
img = cv2.imread(fname)
# Convert to grayscale
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# Find the chessboard corners
ret, corners = cv2.findChessboardCorners(gray, (6,9),None)
# If found, draw corners
if ret == True:
imgpoints.append(corners)
objpoints.append(objp)
# Draw and display the corners
#cv2.drawChessboardCorners(img, (nx, ny), corners, ret)
return cv2.calibrateCamera(objpoints,imgpoints,gray.shape[::-1],None,None)
def undistresult(img, mtx,dist): # undistort frame
undist= cv2.undistort(img, mtx, dist, None, mtx)
return undist
def LineFitting(wimgun): #Fit Lane Lines
# Set minimum number of pixels found to recenter window
minpix = 20
# Create empty lists to receive left and right lane pixel indices
left_lane_inds = []
right_lane_inds = []
histogram = np.sum(wimgun[350:,:], axis=0)
# Create an output image to draw on and visualize the result
out_img = np.dstack((wimgun, wimgun, wimgun))
# Find the peak of the left and right halves of the histogram
# These will be the starting point for the left and right lines
midpoint = np.int(histogram.shape[0]/2)
leftx_base = np.argmax(histogram[:midpoint])
rightx_base = np.argmax(histogram[midpoint:]) + midpoint
nwindows = 9
# Set height of windows
window_height = np.int(wimgun.shape[0]/nwindows)
# Identify the x and y positions of all nonzero pixels in the image
nonzero = wimgun.nonzero()
nonzeroy = np.array(nonzero[0])
nonzerox = np.array(nonzero[1])
# Current positions to be updated for each window
leftx_current = leftx_base
rightx_current = rightx_base
# Set the width of the windows +/- margin
margin =80
# Step through the windows one by one
for window in range(nwindows):
# Identify window boundaries in x and y (and right and left)
win_y_low = wimgun.shape[0] - (window+1)*window_height
win_y_high = wimgun.shape[0] - window*window_height
win_xleft_low = leftx_current - margin
win_xleft_high = leftx_current + margin
win_xright_low = rightx_current - margin
win_xright_high = rightx_current + margin
# Draw the windows on the visualization image
cv2.rectangle(out_img,(win_xleft_low,win_y_low),(win_xleft_high,win_y_high),(0,255,0), 2)
cv2.rectangle(out_img,(win_xright_low,win_y_low),(win_xright_high,win_y_high),(0,255,0), 2)
# Identify the nonzero pixels in x and y within the window
good_left_inds = ((nonzeroy >= win_y_low) & (nonzeroy < win_y_high) & (nonzerox >= win_xleft_low) & (nonzerox < win_xleft_high)).nonzero()[0]
good_right_inds = ((nonzeroy >= win_y_low) & (nonzeroy < win_y_high) & (nonzerox >= win_xright_low) & (nonzerox < win_xright_high)).nonzero()[0]
# Append these indices to the lists
left_lane_inds.append(good_left_inds)
right_lane_inds.append(good_right_inds)
# If you found > minpix pixels, recenter next window on their mean position
if len(good_left_inds) > minpix:
leftx_current = np.int(np.mean(nonzerox[good_left_inds]))
if len(good_right_inds) > minpix:
rightx_current = np.int(np.mean(nonzerox[good_right_inds]))
# Concatenate the arrays of indices
left_lane_inds = np.concatenate(left_lane_inds)
right_lane_inds = np.concatenate(right_lane_inds)
# Again, extract left and right line pixel positions
leftx = nonzerox[left_lane_inds]
lefty = nonzeroy[left_lane_inds]
rightx = nonzerox[right_lane_inds]
righty = nonzeroy[right_lane_inds]
# Fit a second order polynomial to each
left_fit = np.polyfit(lefty, leftx, 2)
right_fit = np.polyfit(righty, rightx, 2)
# Generate x and y values for plotting
ploty = np.linspace(0, wimgun.shape[0]-1, wimgun.shape[0] )
left_fitx = left_fit[0]*ploty**2 + left_fit[1]*ploty + left_fit[2]
right_fitx = right_fit[0]*ploty**2 + right_fit[1]*ploty + right_fit[2]
# Create an image to draw on and an image to show the selection window
# out_img = np.dstack((wimgun, wimgun, wimgun))*255
window_img = np.zeros_like(out_img)
# Color in left and right line pixels
out_img[nonzeroy[left_lane_inds], nonzerox[left_lane_inds]] = [255, 0, 0]
out_img[nonzeroy[right_lane_inds], nonzerox[right_lane_inds]] = [0, 0, 255]
# plt.plot(left_fitx, ploty, color='yellow')
# plt.plot(right_fitx, ploty, color='yellow')
# plt.xlim(0, 1280)
# plt.ylim(720, 0)
# plt.imshow(out_img)
# # plt.savefig("./output_images/Window Image"+str(n)+".png")
# plt.show()
# Generate a polygon to illustrate the search window area
# And recast the x and y points into usable format for cv2.fillPoly()
left_line_window1 = np.array([np.transpose(np.vstack([left_fitx-margin, ploty]))])
left_line_window2 = np.array([np.flipud(np.transpose(np.vstack([left_fitx+margin, ploty])))])
left_line_pts = np.hstack((left_line_window1, left_line_window2))
right_line_window1 = np.array([np.transpose(np.vstack([right_fitx-margin, ploty]))])
right_line_window2 = np.array([np.flipud(np.transpose(np.vstack([right_fitx+margin, ploty])))])
right_line_pts = np.hstack((right_line_window1, right_line_window2))
# Draw the lane onto the warped blank image
cv2.fillPoly(window_img, np.int_([left_line_pts]), (0,255, 0))
cv2.fillPoly(window_img, np.int_([right_line_pts]), (0,255, 0))
result = cv2.addWeighted(out_img, 1, window_img, 0.3, 0)
# plt.title("r")
# plt.plot(left_fitx, ploty, color='yellow')
# plt.plot(right_fitx, ploty, color='yellow')
# plt.xlim(0, 1280)
# plt.ylim(720, 0)
# plt.imshow(result)
# # plt.savefig("./output_images/Line Image"+str(n)+".png")
# plt.show()
# Define y-value where we want radius of curvature
# I'll choose the maximum y-value, corresponding to the bottom of the image
y_eval = np.max(ploty)
left_curverad = ((1 + (2*left_fit[0]*y_eval + left_fit[1])**2)**1.5) / np.absolute(2*left_fit[0])
right_curverad = ((1 + (2*right_fit[0]*y_eval + right_fit[1])**2)**1.5) / np.absolute(2*right_fit[0])
#print(left_curverad, right_curverad)
ym_per_pix = 30/720 # meters per pixel in y dimension
xm_per_pix = 3.7/700 # meters per pixel in x dimension
# Fit new polynomials to x,y in world space
left_fit_cr = np.polyfit(ploty*ym_per_pix, left_fitx*xm_per_pix, 2)
right_fit_cr = np.polyfit(ploty*ym_per_pix, right_fitx*xm_per_pix, 2)
# y_eval = np.max(ploty)
# # Calculate the new radias of curvature
left_curverad = ((1 + (2*left_fit_cr[0]*y_eval*ym_per_pix + left_fit_cr[1])**2)**1.5) / np.absolute(2*left_fit_cr[0])
right_curverad = ((1 + (2*right_fit_cr[0]*y_eval*ym_per_pix + right_fit_cr[1])**2)**1.5) / np.absolute(2*right_fit_cr[0])
# # left_curverad = ((1 + (2*left_fit[0]*y_eval + left_fit[1])**2)**1.5) / np.absolute(2*left_fit[0])
# # right_curverad = ((1 + (2*right_fit[0]*y_eval + right_fit[1])**2)**1.5) / np.absolute(2*right_fit[0])
# camera_center=wimgun.shape[0]/2
# #lane_center = (right_fitx[719] + left_fitx[719])/2
lane_offset = (1280/2 - (left_fitx[-1]+right_fitx[-1])/2)*xm_per_pix
# print(left_curverad1, right_curverad1, lane_offset)
return (left_fit, ploty,right_fit,left_curverad, right_curverad,lane_offset)
# Create an image to draw the lines on
def unwrappedframe(img,pm, Minv, left_fit,ploty,right_fit):
left_fitx = left_fit[0]*ploty**2 + left_fit[1]*ploty + left_fit[2]
right_fitx = right_fit[0]*ploty**2 + right_fit[1]*ploty + right_fit[2]
nonzero = img.nonzero()
nonzeroy = np.array(nonzero[0])
nonzerox = np.array(nonzero[1])
warp_zero = np.zeros_like(pm).astype(np.uint8)
color_warp = np.dstack((warp_zero, warp_zero, warp_zero))
# Recast the x and y points into usable format for cv2.fillPoly()
pts_left = np.array([np.transpose(np.vstack([left_fitx, ploty]))])
pts_right = np.array([np.flipud(np.transpose(np.vstack([right_fitx, ploty])))])
pts = np.hstack((pts_left, pts_right))
# Draw the lane onto the warped blank image
cv2.fillPoly(color_warp, np.int_([pts]), (0,255, 0))
# Warp the blank back to original image space using inverse perspective matrix (Minv)
newwarp = cv2.warpPerspective(color_warp, Minv, (img.shape[1], img.shape[0]))
# Combine the result with the original image
return cv2.addWeighted(img, 1, newwarp, 0.3, 0)
```
| github_jupyter |
## Как выложить бота на HEROKU
*Подготовил Ян Пиле*
Сразу оговоримся, что мы на heroku выкладываем
**echo-Бота в телеграме, написанного с помощью библиотеки [pyTelegramBotAPI](https://github.com/eternnoir/pyTelegramBotAPI)**.
А взаимодействие его с сервером мы сделаем с использованием [flask](http://flask.pocoo.org/)
То есть вы боту пишете что-то, а он вам отвечает то же самое.
## Регистрация
Идем к **@BotFather** в Telegram и по его инструкции создаем нового бота командой **/newbot**.
Это должно закончиться выдачей вам токена вашего бота. Например последовательность команд, введенных мной:
* **/newbot**
* **my_echo_bot** (имя бота)
* **ian_echo_bot** (ник бота в телеграме)
Завершилась выдачей мне токена **1403467808:AAEaaLPkIqrhrQ62p7ToJclLtNNINdOopYk**
И ссылки t.me/ian_echo_bot
<img src="botfather.png">
## Регистрация на HEROKU
Идем сюда: https://signup.heroku.com/login
Создаем пользователя (это бесплатно)
Попадаем на https://dashboard.heroku.com/apps и там создаем новое приложение:
<img src="newapp1.png">
Вводим название и регион (Я выбрал Европу), создаем.
<img src="newapp2.png">
После того, как приложение создано, нажмите, "Open App" и скопируйте адрес оттуда.
<img src="newapp3.png">
У меня это https://ian-echo-bot.herokuapp.com
## Установить интерфейсы heroku и git для командной строки
Теперь надо установить Интерфейсы командной строки heroku и git по ссылкам:
* https://devcenter.heroku.com/articles/heroku-cli
* https://git-scm.com/book/en/v2/Getting-Started-Installing-Git
## Установить библиотеки
Теперь в вашем редакторе (например PyCharm) надо установить библиотеку для Телеграма и flask:
* pip install pyTelegramBotAPI
* pip install flask
## Код нашего echo-бота
Вот этот код я уложил в файл main.py
```
import os
import telebot
from flask import Flask, request
TOKEN = '1403467808:AAEaaLPkIqrhrQ62p7ToJclLtNNINdOopYk' # это мой токен
bot = telebot.TeleBot(token=TOKEN)
server = Flask(__name__)
# Если строка на входе непустая, то бот повторит ее
@bot.message_handler(func=lambda msg: msg.text is not None)
def reply_to_message(message):
bot.send_message(message.chat.id, message.text)
@server.route('/' + TOKEN, methods=['POST'])
def getMessage():
bot.process_new_updates([telebot.types.Update.de_json(request.stream.read().decode("utf-8"))])
return "!", 200
@server.route("/")
def webhook():
bot.remove_webhook()
bot.set_webhook(url='https://ian-echo-bot.herokuapp.com/' + TOKEN) #
return "!", 200
if __name__ == "__main__":
server.run(host="0.0.0.0", port=int(os.environ.get('PORT', 5000)))
```
## Теперь создаем еще два файла для запуска
**Procfile**(файл без расширения). Его надо открыть текстовым редактором и вписать туда строку:
web: python main.py
**requirements.txt** - файл со списком версий необходимых библиотек.
Зайдите в PyCharm, где вы делаете проект и введите в терминале команду:
pip list format freeze > requirements.txt
В файле записи должны иметь вид:
Название библиотеки Версия библиотеки
Если вдруг вы выдите что-то такое:
<img src="versions.png">
Удалите этот кусок текста, чтоб остался только номер версии и сохраните файл.
Теперь надо все эти файлы уложить на гит, привязанный к Heroku и запустить приложение.
## Последний шаг
Надо залогиниться в heroku через командную строку.
Введите:
heroku login
Вас перебросит в браузер на вот такую страницу:
<img src="login.png">
После того, как вы залогинились, удостоверьтесь, что вы находитесь в папке, где лежат фаши файлы:
main.py
Procfile
requirements.txt
**Вводите команды:**
git init
git add .
git commit -m "first commit"
heroku git:remote -a ian-echo-bot
git push heroku master
По ходу выкатки вы увидите что-то такое:
<img src="process.png">
Готово, вы выложили вашего бота.
Материалы, которыми можно воспользоваться по ходу выкладки бота на сервер:
https://towardsdatascience.com/how-to-deploy-a-telegram-bot-using-heroku-for-free-9436f89575d2
https://mattrighetti.medium.com/build-your-first-telegram-bot-using-python-and-heroku-79d48950d4b0
| github_jupyter |
<a href="https://colab.research.google.com/github/JimKing100/DS-Unit-2-Kaggle-Challenge/blob/master/Kaggle_Challenge_Assignment_Submission5.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
# Installs
%%capture
!pip install --upgrade category_encoders plotly
# Imports
import os, sys
os.chdir('/content')
!git init .
!git remote add origin https://github.com/LambdaSchool/DS-Unit-2-Kaggle-Challenge.git
!git pull origin master
!pip install -r requirements.txt
os.chdir('module1')
# Disable warning
import warnings
warnings.filterwarnings(action='ignore', category=FutureWarning, module='numpy')
# Imports
import pandas as pd
import numpy as np
import math
import sklearn
sklearn.__version__
# Import the models
from sklearn.linear_model import LogisticRegressionCV
from sklearn.pipeline import make_pipeline
# Import encoder and scaler and imputer
import category_encoders as ce
from sklearn.preprocessing import StandardScaler
from sklearn.impute import SimpleImputer
# Import random forest classifier
from sklearn.ensemble import RandomForestClassifier
# Import, load data and split data into train, validate and test
train_features = pd.read_csv('../data/tanzania/train_features.csv')
train_labels = pd.read_csv('../data/tanzania/train_labels.csv')
test_features = pd.read_csv('../data/tanzania/test_features.csv')
sample_submission = pd.read_csv('../data/tanzania/sample_submission.csv')
assert train_features.shape == (59400, 40)
assert train_labels.shape == (59400, 2)
assert test_features.shape == (14358, 40)
assert sample_submission.shape == (14358, 2)
# Load initial train features and labels
from sklearn.model_selection import train_test_split
X_train = train_features
y_train = train_labels['status_group']
# Split the initial train features and labels 80% into new train and new validation
X_train, X_val, y_train, y_val = train_test_split(
X_train, y_train, train_size = 0.80, test_size = 0.20,
stratify = y_train, random_state=42
)
X_train.shape, X_val.shape, y_train.shape, y_val.shape
# Wrangle train, validate, and test sets
def wrangle(X):
# Set bins value
bins=20
chars = 3
# Prevent SettingWithCopyWarning
X = X.copy()
X['latitude'] = X['latitude'].replace(-2e-08, 0)
# Create missing columns
cols_with_zeros = ['longitude', 'latitude', 'construction_year',
'gps_height', 'population']
for col in cols_with_zeros:
X[col] = X[col].replace(0, np.nan)
X[col+'_missing'] = X[col].isnull()
for col in cols_with_zeros:
X[col] = X[col].replace(np.nan, 0)
# Clean installer
X['installer'] = X['installer'].str.lower()
X['installer'] = X['installer'].str.replace('danid', 'danida')
X['installer'] = X['installer'].str.replace('disti', 'district council')
X['installer'] = X['installer'].str.replace('commu', 'community')
X['installer'] = X['installer'].str.replace('central government', 'government')
X['installer'] = X['installer'].str.replace('kkkt _ konde and dwe', 'kkkt')
X['installer'] = X['installer'].str[:chars]
X['installer'].value_counts(normalize=True)
tops = X['installer'].value_counts()[:5].index
X.loc[~X['installer'].isin(tops), 'installer'] = 'Other'
# Clean funder and bin
X['funder'] = X['funder'].str.lower()
X['funder'] = X['funder'].str[:chars]
X['funder'].value_counts(normalize=True)
tops = X['funder'].value_counts()[:20].index
X.loc[~X['funder'].isin(tops), 'funder'] = 'Other'
# Use mean for gps_height missing values
X.loc[X['gps_height'] == 0, 'gps_height'] = X['gps_height'].mean()
# Bin lga
tops = X['lga'].value_counts()[:10].index
X.loc[~X['lga'].isin(tops), 'lga'] = 'Other'
# Bin ward
tops = X['ward'].value_counts()[:20].index
X.loc[~X['ward'].isin(tops), 'ward'] = 'Other'
# Bin subvillage
tops = X['subvillage'].value_counts()[:bins].index
X.loc[~X['subvillage'].isin(tops), 'subvillage'] = 'Other'
# Clean latitude and longitude
avg_lat_ward = X.groupby('ward').latitude.mean()
avg_lat_lga = X.groupby('lga').latitude.mean()
avg_lat_region = X.groupby('region').latitude.mean()
avg_lat_country = X.latitude.mean()
avg_long_ward = X.groupby('ward').longitude.mean()
avg_long_lga = X.groupby('lga').longitude.mean()
avg_long_region = X.groupby('region').longitude.mean()
avg_long_country = X.longitude.mean()
#cols_with_zeros = ['longitude', 'latitude']
#for col in cols_with_zeros:
# X[col] = X[col].replace(0, np.nan)
#X.loc[X['latitude'] == 0, 'latitude'] = X['latitude'].median()
#X.loc[X['longitude'] == 0, 'longitude'] = X['longitude'].median()
#for i in range(0, 9):
# X.loc[(X['latitude'] == 0) & (X['ward'] == avg_lat_ward.index[0]), 'latitude'] = avg_lat_ward[i]
# X.loc[(X['latitude'] == 0) & (X['lga'] == avg_lat_lga.index[0]), 'latitude'] = avg_lat_lga[i]
# X.loc[(X['latitude'] == 0) & (X['region'] == avg_lat_region.index[0]), 'latitude'] = avg_lat_region[i]
# X.loc[(X['latitude'] == 0), 'latitude'] = avg_lat_country
# X.loc[(X['longitude'] == 0) & (X['ward'] == avg_long_ward.index[0]), 'longitude'] = avg_long_ward[i]
# X.loc[(X['longitude'] == 0) & (X['lga'] == avg_long_lga.index[0]), 'longitude'] = avg_long_lga[i]
# X.loc[(X['longitude'] == 0) & (X['region'] == avg_long_region.index[0]), 'longitude'] = avg_long_region[i]
# X.loc[(X['longitude'] == 0), 'longitude'] = avg_long_country
average_lat = X.groupby('region').latitude.mean().reset_index()
average_long = X.groupby('region').longitude.mean().reset_index()
shinyanga_lat = average_lat.loc[average_lat['region'] == 'Shinyanga', 'latitude']
shinyanga_long = average_long.loc[average_lat['region'] == 'Shinyanga', 'longitude']
X.loc[(X['region'] == 'Shinyanga') & (X['latitude'] > -1), ['latitude']] = shinyanga_lat[17]
X.loc[(X['region'] == 'Shinyanga') & (X['longitude'] == 0), ['longitude']] = shinyanga_long[17]
mwanza_lat = average_lat.loc[average_lat['region'] == 'Mwanza', 'latitude']
mwanza_long = average_long.loc[average_lat['region'] == 'Mwanza', 'longitude']
X.loc[(X['region'] == 'Mwanza') & (X['latitude'] > -1), ['latitude']] = mwanza_lat[13]
X.loc[(X['region'] == 'Mwanza') & (X['longitude'] == 0) , ['longitude']] = mwanza_long[13]
# Impute mean for tsh based on mean of source_class/basin/waterpoint_type_group
def tsh_calc(tsh, source, base, waterpoint):
if tsh == 0:
if (source, base, waterpoint) in tsh_dict:
new_tsh = tsh_dict[source, base, waterpoint]
return new_tsh
else:
return tsh
return tsh
temp = X[X['amount_tsh'] != 0].groupby(['source_class',
'basin',
'waterpoint_type_group'])['amount_tsh'].mean()
tsh_dict = dict(temp)
X['amount_tsh'] = X.apply(lambda x: tsh_calc(x['amount_tsh'], x['source_class'], x['basin'], x['waterpoint_type_group']), axis=1)
X.loc[X['amount_tsh'] == 0, 'amount_tsh'] = X['amount_tsh'].median()
# Impute mean for construction_year based on mean of source_class/basin/waterpoint_type_group
#temp = X[X['construction_year'] != 0].groupby(['source_class',
# 'basin',
# 'waterpoint_type_group'])['amount_tsh'].mean()
#tsh_dict = dict(temp)
#X['construction_year'] = X.apply(lambda x: tsh_calc(x['construction_year'], x['source_class'], x['basin'], x['waterpoint_type_group']), axis=1)
#X.loc[X['construction_year'] == 0, 'construction_year'] = X['construction_year'].mean()
# Impute mean for the feature based on latitude and longitude
def latlong_conversion(feature, pop, long, lat):
radius = 0.1
radius_increment = 0.3
if pop <= 1:
pop_temp = pop
while pop_temp <= 1 and radius <= 2:
lat_from = lat - radius
lat_to = lat + radius
long_from = long - radius
long_to = long + radius
df = X[(X['latitude'] >= lat_from) &
(X['latitude'] <= lat_to) &
(X['longitude'] >= long_from) &
(X['longitude'] <= long_to)]
pop_temp = df[feature].mean()
if math.isnan(pop_temp):
pop_temp = pop
radius = radius + radius_increment
else:
pop_temp = pop
if pop_temp <= 1:
new_pop = X_train[feature].mean()
else:
new_pop = pop_temp
return new_pop
# Impute population based on location
#X['population'] = X.apply(lambda x: latlong_conversion('population', x['population'], x['longitude'], x['latitude']), axis=1)
#X.loc[X['population'] == 0, 'population'] = X['population'].median()
# Impute gps_height based on location
#X['gps_height'] = X.apply(lambda x: latlong_conversion('gps_height', x['gps_height'], x['longitude'], x['latitude']), axis=1)
# Drop recorded_by (never varies) and id (always varies, random) and num_private (empty)
unusable_variance = ['recorded_by', 'id', 'num_private','wpt_name', 'extraction_type_class',
'quality_group', 'source_type', 'source_class', 'waterpoint_type_group']
X = X.drop(columns=unusable_variance)
# Drop duplicate columns
duplicates = ['quantity_group', 'payment_type', 'extraction_type_group']
X = X.drop(columns=duplicates)
# return the wrangled dataframe
return X
# Wrangle the data
X_train = wrangle(X_train)
X_val = wrangle(X_val)
# Feature engineering
def feature_engineer(X):
# Create new feature pump_age
X['pump_age'] = 2013 - X['construction_year']
X.loc[X['pump_age'] == 2013, 'pump_age'] = 0
X.loc[X['pump_age'] == 0, 'pump_age'] = 10
# Convert date_recorded to datetime
X['date_recorded'] = pd.to_datetime(X['date_recorded'], infer_datetime_format=True)
# Extract components from date_recorded, then drop the original column
X['year_recorded'] = X['date_recorded'].dt.year
X['month_recorded'] = X['date_recorded'].dt.month
X['day_recorded'] = X['date_recorded'].dt.day
# Engineer feature: how many years from construction_year to date_recorded
X['years'] = X['year_recorded'] - X['construction_year']
X['years_missing'] = X['years'].isnull()
column_list = ['date_recorded']
X = X.drop(columns=column_list)
# Create new feature region_district
X['region_district'] = X['region_code'].astype(str) + X['district_code'].astype(str)
#X['tsh_pop'] = X['amount_tsh']/X['population']
return X
# Feature engineer the data
X_train = feature_engineer(X_train)
X_val = feature_engineer(X_val)
X_train.head()
# Encode a feature
def encode_feature(X, y, str):
X['status_group'] = y
X.groupby(str)['status_group'].value_counts(normalize=True)
X['functional']= (X['status_group'] == 'functional').astype(int)
X[['status_group', 'functional']]
return X
# Encode all the categorical features
train = X_train.copy()
train = encode_feature(train, y_train, 'quantity')
train = encode_feature(train, y_train, 'waterpoint_type')
train = encode_feature(train, y_train, 'extraction_type')
train = encode_feature(train, y_train, 'installer')
train = encode_feature(train, y_train, 'funder')
train = encode_feature(train, y_train, 'water_quality')
train = encode_feature(train, y_train, 'basin')
train = encode_feature(train, y_train, 'region')
train = encode_feature(train, y_train, 'payment')
train = encode_feature(train, y_train, 'source')
train = encode_feature(train, y_train, 'lga')
train = encode_feature(train, y_train, 'ward')
train = encode_feature(train, y_train, 'scheme_management')
train = encode_feature(train, y_train, 'management')
train = encode_feature(train, y_train, 'region_district')
train = encode_feature(train, y_train, 'subvillage')
# use quantity feature and the numerical features but drop id
categorical_features = ['quantity', 'waterpoint_type', 'extraction_type', 'installer',
'basin', 'region', 'payment', 'source', 'lga', 'public_meeting',
'scheme_management', 'permit', 'management', 'region_district',
'subvillage', 'funder', 'water_quality', 'ward', 'years_missing', 'longitude_missing',
'latitude_missing','construction_year_missing', 'gps_height_missing',
'population_missing']
#
numeric_features = X_train.select_dtypes('number').columns.tolist()
features = categorical_features + numeric_features
# make subsets using the quantity feature all numeric features except id
X_train = X_train[features]
X_val = X_val[features]
# Create the logistic regression pipeline
pipeline = make_pipeline (
ce.OneHotEncoder(use_cat_names=True),
#SimpleImputer(),
StandardScaler(),
LogisticRegressionCV(random_state=42, n_jobs=-1)
)
pipeline.fit(X_train, y_train)
print('Validation Accuracy', pipeline.score(X_val, y_val))
features
# Create the random forest pipeline
pipeline = make_pipeline (
ce.OrdinalEncoder(),
SimpleImputer(strategy='mean'),
StandardScaler(),
RandomForestClassifier(n_estimators=1400,
random_state=42,
min_samples_split=5,
min_samples_leaf=1,
max_features='auto',
max_depth=30,
bootstrap=True,
n_jobs=-1,
verbose = 1)
)
pipeline.fit(X_train, y_train)
print('Validation Accuracy', pipeline.score(X_val, y_val))
pd.set_option('display.max_rows', 200)
model = pipeline.named_steps['randomforestclassifier']
encoder = pipeline.named_steps['ordinalencoder']
encoded_columns = encoder.transform(X_train).columns
importances = pd.Series(model.feature_importances_, encoded_columns)
importances.sort_values(ascending=False)
# Create missing columns
cols_with_zeros = ['longitude', 'latitude', 'construction_year',
'gps_height', 'population']
for col in cols_with_zeros:
test_features[col] = test_features[col].replace(0, np.nan)
test_features[col+'_missing'] = test_features[col].isnull()
for col in cols_with_zeros:
test_features[col] = test_features[col].replace(np.nan, 0)
test_features['pump_age'] = 2013 - test_features['construction_year']
test_features.loc[test_features['pump_age'] == 2013, 'pump_age'] = 0
test_features.loc[test_features['pump_age'] == 0, 'pump_age'] = 10
# Convert date_recorded to datetime
test_features['date_recorded'] = pd.to_datetime(test_features['date_recorded'], infer_datetime_format=True)
# Extract components from date_recorded, then drop the original column
test_features['year_recorded'] = test_features['date_recorded'].dt.year
test_features['month_recorded'] = test_features['date_recorded'].dt.month
test_features['day_recorded'] = test_features['date_recorded'].dt.day
# Engineer feature: how many years from construction_year to date_recorded
test_features['years'] = test_features['year_recorded'] - test_features['construction_year']
test_features['years_missing'] = test_features['years'].isnull()
test_features['region_district'] = test_features['region_code'].astype(str) + test_features['district_code'].astype(str)
column_list = ['recorded_by', 'id', 'num_private','wpt_name', 'extraction_type_class',
'quality_group', 'source_type', 'source_class', 'waterpoint_type_group',
'quantity_group', 'payment_type', 'extraction_type_group']
test_features = test_features.drop(columns=column_list)
X_test = test_features[features]
assert all(X_test.columns == X_train.columns)
y_pred = pipeline.predict(X_test)
submission = sample_submission.copy()
submission['status_group'] = y_pred
submission.to_csv('/content/submission-05.csv', index=False)
```
| github_jupyter |
```
import numpy as np
import cv2
import matplotlib.pyplot as plt
import matplotlib.image as mpimg
import pickle
# Read in an image
image = mpimg.imread('signs_vehicles_xygrad.png')
def abs_sobel_thresh(img, orient='x', sobel_kernel=3, thresh=(0, 255)):
# Apply the following steps to img
# 1) Convert to grayscale
gray = cv2.cvtColor(img, cv2.COLOR_RGB2GRAY)
# 2) Take the derivative in x or y given orient = 'x' or 'y'
sobelx = cv2.Sobel(gray, cv2.CV_64F, 1, 0)
sobely = cv2.Sobel(gray, cv2.CV_64F, 0, 1)
# 3) Take the absolute value of the derivative or gradient
abs_sobelx = np.absolute(sobelx)
# 4) Scale to 8-bit (0 - 255) then convert to type = np.uint8
scaled_sobel = np.uint8(255*abs_sobelx/np.max(abs_sobelx))
# 5) Create a mask of 1's where the scaled gradient magnitude
# is > thresh_min and < thresh_max
grad_binary = np.zeros_like(scaled_sobel)
grad_binary[(scaled_sobel >= thresh[0]) & (scaled_sobel <= thresh[1])] = 1
# 6) Return this mask as your binary_output image
return grad_binary
def mag_thresh(image, sobel_kernel=3, mag_thresh=(0, 255)):
# Apply the following steps to img
# 1) Convert to grayscale
gray = cv2.cvtColor(image, cv2.COLOR_RGB2GRAY)
# 2) Take the derivative in x or y given orient = 'x' or 'y'
sobelx = cv2.Sobel(gray, cv2.CV_64F, 1, 0, ksize=sobel_kernel)
sobely = cv2.Sobel(gray, cv2.CV_64F, 0, 1, ksize=sobel_kernel)
# 3) Calculate the magnitude
abs_sobelx = np.sqrt(np.square(sobelx)+np.square(sobely))
# 4) Scale to 8-bit (0 - 255) and convert to type = np.uint8
scaled_sobel = np.uint8(255*abs_sobelx/np.max(abs_sobelx))
# 5) Create a binary mask where mag thresholds are met
mag_binary = np.zeros_like(scaled_sobel)
mag_binary[(scaled_sobel >= mag_thresh[0]) & (scaled_sobel <= mag_thresh[1])] = 1
# 6) Return this mask as your binary_output image
return mag_binary
def dir_threshold(image, sobel_kernel=3, thresh=(0, np.pi/2)):
# Apply the following steps to img
# 1) Convert to grayscale
gray = cv2.cvtColor(image, cv2.COLOR_RGB2GRAY)
# 2) Take the derivative in x or y given orient = 'x' or 'y'
sobelx = cv2.Sobel(gray, cv2.CV_64F, 1, 0, ksize=sobel_kernel)
sobely = cv2.Sobel(gray, cv2.CV_64F, 0, 1, ksize=sobel_kernel)
# 3) Take the absolute value of the x and y gradients
abs_sobelx = np.absolute(sobelx)
abs_sobely = np.absolute(sobely)
# 4) Use np.arctan2(abs_sobely, abs_sobelx) to calculate the direction of the gradient
grad_dir = np.arctan2(abs_sobely, abs_sobelx)
# 5) Create a binary mask where direction thresholds are met
dir_binary = np.zeros_like(grad_dir)
dir_binary[(grad_dir >= thresh[0]) & (grad_dir <= thresh[1])] = 1
# 6) Return this mask as your binary_output image
return dir_binary
# Choose a Sobel kernel size
ksize = 3 # Choose a larger odd number to smooth gradient measurements
# Apply each of the thresholding functions
gradx = abs_sobel_thresh(image, orient='x', sobel_kernel=ksize, thresh=(20, 100))
grady = abs_sobel_thresh(image, orient='y', sobel_kernel=ksize, thresh=(80, 100))
mag_binary = mag_thresh(image, sobel_kernel=ksize, mag_thresh=(30, 100))
dir_binary = dir_threshold(image, sobel_kernel=ksize, thresh=(0.7, 1.3))
combined = np.zeros_like(dir_binary)
combined[((gradx == 1) & (grady == 1)) | ((mag_binary == 1) & (dir_binary == 1))] = 1
# Plot the result
f, (ax1, ax2) = plt.subplots(1, 2, figsize=(24, 9))
f.tight_layout()
ax1.imshow(image)
ax1.set_title('Original Image', fontsize=50)
ax2.imshow(combined, cmap='gray')
ax2.set_title('Combined Thresholds', fontsize=50)
plt.subplots_adjust(left=0., right=1, top=0.9, bottom=0.)
```
| github_jupyter |
```
import numpy as np
import matplotlib.pyplot as plt
import numba
from tqdm import tqdm
import eitest
```
# Data generators
```
@numba.njit
def event_series_bernoulli(series_length, event_count):
'''Generate an iid Bernoulli distributed event series.
series_length: length of the event series
event_count: number of events'''
event_series = np.zeros(series_length)
event_series[np.random.choice(np.arange(0, series_length), event_count, replace=False)] = 1
return event_series
@numba.njit
def time_series_mean_impact(event_series, order, signal_to_noise):
'''Generate a time series with impacts in mean as described in the paper.
The impact weights are sampled iid from N(0, signal_to_noise),
and additional noise is sampled iid from N(0,1). The detection problem will
be harder than in time_series_meanconst_impact for small orders, as for small
orders we have a low probability to sample at least one impact weight with a
high magnitude. On the other hand, since the impact is different at every lag,
we can detect the impacts even if the order is larger than the max_lag value
used in the test.
event_series: input of shape (T,) with event occurrences
order: order of the event impacts
signal_to_noise: signal to noise ratio of the event impacts'''
series_length = len(event_series)
weights = np.random.randn(order)*np.sqrt(signal_to_noise)
time_series = np.random.randn(series_length)
for t in range(series_length):
if event_series[t] == 1:
time_series[t+1:t+order+1] += weights[:order-max(0, (t+order+1)-series_length)]
return time_series
@numba.njit
def time_series_meanconst_impact(event_series, order, const):
'''Generate a time series with impacts in mean by adding a constant.
Better for comparing performance across different impact orders, since the
magnitude of the impact will always be the same.
event_series: input of shape (T,) with event occurrences
order: order of the event impacts
const: constant for mean shift'''
series_length = len(event_series)
time_series = np.random.randn(series_length)
for t in range(series_length):
if event_series[t] == 1:
time_series[t+1:t+order+1] += const
return time_series
@numba.njit
def time_series_var_impact(event_series, order, variance):
'''Generate a time series with impacts in variance as described in the paper.
event_series: input of shape (T,) with event occurrences
order: order of the event impacts
variance: variance under event impacts'''
series_length = len(event_series)
time_series = np.random.randn(series_length)
for t in range(series_length):
if event_series[t] == 1:
for tt in range(t+1, min(series_length, t+order+1)):
time_series[tt] = np.random.randn()*np.sqrt(variance)
return time_series
@numba.njit
def time_series_tail_impact(event_series, order, dof):
'''Generate a time series with impacts in tails as described in the paper.
event_series: input of shape (T,) with event occurrences
order: delay of the event impacts
dof: degrees of freedom of the t distribution'''
series_length = len(event_series)
time_series = np.random.randn(series_length)*np.sqrt(dof/(dof-2))
for t in range(series_length):
if event_series[t] == 1:
for tt in range(t+1, min(series_length, t+order+1)):
time_series[tt] = np.random.standard_t(dof)
return time_series
```
# Visualization of the impact models
```
default_T = 8192
default_N = 64
default_q = 4
es = event_series_bernoulli(default_T, default_N)
for ts in [
time_series_mean_impact(es, order=default_q, signal_to_noise=10.),
time_series_meanconst_impact(es, order=default_q, const=5.),
time_series_var_impact(es, order=default_q, variance=4.),
time_series_tail_impact(es, order=default_q, dof=3.),
]:
fig, (ax1, ax2) = plt.subplots(1, 2, gridspec_kw={'width_ratios': [2, 1]}, figsize=(15, 2))
ax1.plot(ts)
ax1.plot(es*np.max(ts), alpha=0.5)
ax1.set_xlim(0, len(es))
samples = eitest.obtain_samples(es, ts, method='eager', lag_cutoff=15, instantaneous=True)
eitest.plot_samples(samples, ax2)
plt.show()
```
# Simulations
```
def test_simul_pairs(impact_model, param_T, param_N, param_q, param_r,
n_pairs, lag_cutoff, instantaneous, sample_method,
twosamp_test, multi_test, alpha):
true_positive = 0.
false_positive = 0.
for _ in tqdm(range(n_pairs)):
es = event_series_bernoulli(param_T, param_N)
if impact_model == 'mean':
ts = time_series_mean_impact(es, param_q, param_r)
elif impact_model == 'meanconst':
ts = time_series_meanconst_impact(es, param_q, param_r)
elif impact_model == 'var':
ts = time_series_var_impact(es, param_q, param_r)
elif impact_model == 'tail':
ts = time_series_tail_impact(es, param_q, param_r)
else:
raise ValueError('impact_model must be "mean", "meanconst", "var" or "tail"')
# coupled pair
samples = eitest.obtain_samples(es, ts, lag_cutoff=lag_cutoff,
method=sample_method,
instantaneous=instantaneous,
sort=(twosamp_test == 'ks')) # samples need to be sorted for K-S test
tstats, pvals = eitest.pairwise_twosample_tests(samples, twosamp_test, min_pts=2)
pvals_adj = eitest.multitest(np.sort(pvals[~np.isnan(pvals)]), multi_test)
true_positive += (pvals_adj.min() < alpha)
# uncoupled pair
samples = eitest.obtain_samples(np.random.permutation(es), ts, lag_cutoff=lag_cutoff,
method=sample_method,
instantaneous=instantaneous,
sort=(twosamp_test == 'ks'))
tstats, pvals = eitest.pairwise_twosample_tests(samples, twosamp_test, min_pts=2)
pvals_adj = eitest.multitest(np.sort(pvals[~np.isnan(pvals)]), multi_test)
false_positive += (pvals_adj.min() < alpha)
return true_positive/n_pairs, false_positive/n_pairs
# global parameters
default_T = 8192
n_pairs = 100
alpha = 0.05
twosamp_test = 'ks'
multi_test = 'simes'
sample_method = 'lazy'
lag_cutoff = 32
instantaneous = True
```
## Mean impact model
```
default_N = 64
default_r = 1.
default_q = 4
```
### ... by number of events
```
vals = [4, 8, 16, 32, 64, 128, 256]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='mean', param_T=default_T,
param_N=val, param_q=default_q, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_N, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# mean impact model (T={default_T}, q={default_q}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# N\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by impact order
```
vals = [1, 2, 4, 8, 16, 32]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='mean', param_T=default_T,
param_N=default_N, param_q=val, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_q, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# mean impact model (T={default_T}, N={default_N}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# q\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by signal-to-noise ratio
```
vals = [1./32, 1./16, 1./8, 1./4, 1./2, 1., 2., 4.]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='mean', param_T=default_T,
param_N=default_N, param_q=default_q, param_r=val,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_r, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# mean impact model (T={default_T}, N={default_N}, q={default_q}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# r\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
```
## Meanconst impact model
```
default_N = 64
default_r = 0.5
default_q = 4
```
### ... by number of events
```
vals = [4, 8, 16, 32, 64, 128, 256]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='meanconst', param_T=default_T,
param_N=val, param_q=default_q, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_N, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# meanconst impact model (T={default_T}, q={default_q}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# N\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by impact order
```
vals = [1, 2, 4, 8, 16, 32]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='meanconst', param_T=default_T,
param_N=default_N, param_q=val, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_q, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# meanconst impact model (T={default_T}, N={default_N}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# q\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by mean value
```
vals = [0.125, 0.25, 0.5, 1, 2]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='meanconst', param_T=default_T,
param_N=default_N, param_q=default_q, param_r=val,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_r, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# meanconst impact model (T={default_T}, N={default_N}, q={default_q}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# r\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
## Variance impact model
In the paper, we show results with the variance impact model parametrized by the **variance increase**. Here we directly modulate the variance.
```
default_N = 64
default_r = 8.
default_q = 4
```
### ... by number of events
```
vals = [4, 8, 16, 32, 64, 128, 256]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='var', param_T=default_T,
param_N=val, param_q=default_q, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_N, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# var impact model (T={default_T}, q={default_q}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# N\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by impact order
```
vals = [1, 2, 4, 8, 16, 32]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='var', param_T=default_T,
param_N=default_N, param_q=val, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_q, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# var impact model (T={default_T}, N={default_N}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# q\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by variance
```
vals = [2., 4., 8., 16., 32.]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='var', param_T=default_T,
param_N=default_N, param_q=default_q, param_r=val,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_r, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# var impact model (T={default_T}, N={default_N}, q={default_q}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# r\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
## Tail impact model
```
default_N = 512
default_r = 3.
default_q = 4
```
### ... by number of events
```
vals = [64, 128, 256, 512, 1024]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='tail', param_T=default_T,
param_N=val, param_q=default_q, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_N, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# tail impact model (T={default_T}, q={default_q}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# N\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by impact order
```
vals = [1, 2, 4, 8, 16, 32]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='tail', param_T=default_T,
param_N=default_N, param_q=val, param_r=default_r,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_q, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.gca().set_xscale('log', base=2)
plt.legend()
plt.show()
print(f'# tail impact model (T={default_T}, N={default_N}, r={default_r}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# q\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
### ... by degrees of freedom
```
vals = [2.5, 3., 3.5, 4., 4.5, 5., 5.5, 6.]
tprs = np.empty(len(vals))
fprs = np.empty(len(vals))
for i, val in enumerate(vals):
tprs[i], fprs[i] = test_simul_pairs(impact_model='tail', param_T=default_T,
param_N=default_N, param_q=default_q, param_r=val,
n_pairs=n_pairs, sample_method=sample_method,
lag_cutoff=lag_cutoff, instantaneous=instantaneous,
twosamp_test=twosamp_test, multi_test=multi_test, alpha=alpha)
plt.figure(figsize=(3,3))
plt.axvline(default_r, ls='-', c='gray', lw=1, label='def')
plt.axhline(alpha, ls='--', c='black', lw=1, label='alpha')
plt.plot(vals, tprs, label='TPR', marker='x')
plt.plot(vals, fprs, label='FPR', marker='x')
plt.legend()
plt.show()
print(f'# tail impact model (T={default_T}, N={default_N}, q={default_q}, n_pairs={n_pairs}, cutoff={lag_cutoff}, instantaneous={instantaneous}, alpha={alpha}, {sample_method}-{twosamp_test}-{multi_test})')
print(f'# r\ttpr\tfpr')
for i, (tpr, fpr) in enumerate(zip(tprs, fprs)):
print(f'{vals[i]}\t{tpr}\t{fpr}')
print()
```
| github_jupyter |
## The Analysis of The Evolution of The Russian Comedy. Part 3.
In this analysis,we will explore evolution of the French five-act comedy in verse based on the following features:
- The coefficient of dialogue vivacity;
- The percentage of scenes with split verse lines;
- The percentage of scenes with split rhymes;
- The percentage of open scenes.
- The percentage of scenes with split verse lines and rhymes.
We will tackle the following questions:
1. We will describe the features;
2. We will explore feature correlations.
3. We will check the features for normality using Shapiro-Wilk normality test. This will help us determine whether parametric vs. non-parametric statistical tests are more appropriate. If the features are not normally distributed, we will use non-parametric tests.
4. In our previous analysis of Sperantov's data, we discovered that instead of four periods of the Russian five-act tragedy in verse proposed by Sperantov, we can only be confident in the existence of two periods, where 1795 is the cut-off year. Therefore, we propose the following periods for the Russian verse comedy:
- Period One (from 1775 to 1794)
- Period Two (from 1795 to 1849).
5. We will run statistical tests to determine whether these two periods are statistically different.
6. We will create visualizations for each feature.
7. We will run descriptive statistics for each feature.
```
import pandas as pd
import numpy as np
import json
from os import listdir
from scipy.stats import shapiro
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
def make_plot(feature, title):
mean, std, median = summary(feature)
plt.figure(figsize=(10, 7))
plt.title(title, fontsize=17)
sns.distplot(feature, kde=False)
mean_line = plt.axvline(mean,
color='black',
linestyle='solid',
linewidth=2); M1 = 'Mean';
median_line = plt.axvline(median,
color='green',linestyle='dashdot',
linewidth=2); M2='Median'
std_line = plt.axvline(mean + std,
color='black',
linestyle='dashed',
linewidth=2); M3 = 'Standard deviation';
plt.axvline(mean - std,
color='black',
linestyle='dashed',
linewidth=2)
plt.legend([mean_line, median_line, std_line], [M1, M2, M3])
plt.show()
def small_sample_mann_whitney_u_test(series_one, series_two):
values_one = series_one.sort_values().tolist()
values_two = series_two.sort_values().tolist()
# make sure there are no ties - this function only works for no ties
result_df = pd.DataFrame(values_one + values_two, columns=['combined']).sort_values(by='combined')
# average for ties
result_df['ranks'] = result_df['combined'].rank(method='average')
# make a dictionary where keys are values and values are ranks
val_to_rank = dict(zip(result_df['combined'].values, result_df['ranks'].values))
sum_ranks_one = np.sum([val_to_rank[num] for num in values_one])
sum_ranks_two = np.sum([val_to_rank[num] for num in values_two])
# number in sample one and two
n_one = len(values_one)
n_two = len(values_two)
# calculate the mann whitney u statistic which is the smaller of the u_one and u_two
u_one = ((n_one * n_two) + (n_one * (n_one + 1) / 2)) - sum_ranks_one
u_two = ((n_one * n_two) + (n_two * (n_two + 1) / 2)) - sum_ranks_two
# add a quality check
assert u_one + u_two == n_one * n_two
u_statistic = np.min([u_one, u_two])
return u_statistic
def summary(feature):
mean = feature.mean()
std = feature.std()
median = feature.median()
return mean, std, median
# updated boundaries
def determine_period(row):
if row <= 1794:
period = 1
else:
period = 2
return period
```
## Part 1. Feature Descriptions
For the Russian corpus of the five-act comedies, we generated additional features that inspired by Iarkho. So far, we had no understanding how these features evolved over time and whether they could differentiate literary periods.
The features include the following:
1. **The Coefficient of Dialogue Vivacity**, i.e., the number of utterances in a play / the number of verse lines in a play. Since some of the comedies in our corpus were written in iambic hexameter while others were written in free iambs, it is important to clarify how we made sure the number of verse lines was comparable. Because Aleksandr Griboedov's *Woe From Wit* is the only four-act comedy in verse that had an extensive markup, we used it as the basis for our calculation.
- First, improved the Dracor's markup of the verse lines in *Woe From Wit*.
- Next, we calculated the number of verse lines in *Woe From Wit*, which was 2220.
- Then, we calculated the total number of syllables in *Woe From Wit*, which was 22076.
- We calculated the average number of syllables per verse line: 22076 / 2220 = 9.944144144144143.
- Finally, we divided the average number of syllables in *Woe From Wit* by the average number of syllables in a comedy written in hexameter, i.e., 12.5: 9.944144144144143 / 12.5 = 0.796.
- To convert the number of verse lines in a play written in free iambs and make it comparable with the comedies written in hexameter, we used the following formula: rescaled_number of verse lines = the number of verse lines in free iambs * 0.796.
- For example, in *Woe From Wit*, the number of verse lines = 2220, the rescaled number of verse lines = 2220 * 0.796 = 1767.12. The coefficient of dialogue vivacity = 702 / 1767.12 = 0.397.
2. **The Percentage of Scenes with Split Verse Lines**, i.e, the percentage of scenes where the end of a scene does not correspond with the end of a verse lines and the verse line extends into the next scene, e.g., "Не бойся. Онъ блажитъ. ЯВЛЕНІЕ 3. Какъ радъ что вижу васъ."
3. **The Percentage of Scenes with Split Rhymes**, i.e., the percentage of scenes that rhyme with other scenes, e.g., "Надѣюсъ на тебя, Вѣтрана, какъ на стѣну. ЯВЛЕНІЕ 4. И въ ней , какъ ни крѣпка, мы видимЪ перемѣну."
4. **The Percentage of Open Scenes**, i.e., the percentage of scenes with either split verse lines or rhymes.
5. **The Percentage of Scenes With Split Verse Lines and Rhymes**, i.e., the percentage of scenes that are connected through both means: by sharing a verse lines and a rhyme.
```
comedies = pd.read_csv('../Russian_Comedies/Data/Comedies_Raw_Data.csv')
# sort by creation date
comedies_sorted = comedies.sort_values(by='creation_date').copy()
# select only original comedies and five act
original_comedies = comedies_sorted[(comedies_sorted['translation/adaptation'] == 0) &
(comedies_sorted['num_acts'] == 5)].copy()
original_comedies.head()
original_comedies.shape
# rename column names for clarity
original_comedies = original_comedies.rename(columns={'num_scenes_iarkho': 'mobility_coefficient'})
comedies_verse_features = original_comedies[['index',
'title',
'first_name',
'last_name',
'creation_date',
'dialogue_vivacity',
'percentage_scene_split_verse',
'percentage_scene_split_rhymes',
'percentage_open_scenes',
'percentage_scenes_rhymes_split_verse']].copy()
comedies_verse_features.head()
```
## Part 1. Feature Correlations
```
comedies_verse_features[['dialogue_vivacity',
'percentage_scene_split_verse',
'percentage_scene_split_rhymes',
'percentage_open_scenes',
'percentage_scenes_rhymes_split_verse']].corr().round(2)
original_comedies[['dialogue_vivacity',
'mobility_coefficient']].corr()
```
Dialogue vivacity is moderately positively correlated with the percentage of scenes with split verse lines (0.53), with the percentage of scenes with split rhymes (0.51), and slightly less correlated with the percentage of open scenes (0.45). However, it is strongly positively correlated with the percentage of scenes with both split rhymes and verse lines (0.73). The scenes with very fast-paced dialogue are more likely to be interconnected through both rhyme and shared verse lines. One unexpected discovery is that dialogue vivacity only weakly correlated with the mobility coefficient (0.06): more active movement of dramatic characters on stage does not necessarily entail that their utterances are going to be shorter.
The percentage of scenes with split verse lines is moderately positively correlated with the percentage of scenes with split rhymes (0.66): the scenes that are connected by verse are likely but not necessarily always going to be connected through rhyme.
Such features as the percentage of open scenes and the percentage of scenes with split rhymes and verse lines are strongly positively correlated with their constituent features (the correlation of the percentage of open scenes with the percentage of scenes with split verse lines is 0.86, with the percentage of split rhymes is 0.92). From this, we can infer that the bulk of the open scenes are connected through rhymes. The percentage of scenes with split rhymes and verse lines is strongly positively correlated with the percentage of scenes with split verse lines (0.87) and the percentage of scenes with split rhymes.
## Part 3. Feature Distributions and Normality
```
make_plot(comedies_verse_features['dialogue_vivacity'],
'Distribution of the Dialogue Vivacity Coefficient')
mean, std, median = summary(comedies_verse_features['dialogue_vivacity'])
print('Mean dialogue vivacity coefficient', round(mean, 2))
print('Standard deviation of the dialogue vivacity coefficient:', round(std, 2))
print('Median dialogue vivacity coefficient:', median)
```
### Shapiro-Wilk Normality Test
```
print('The p-value of the Shapiro-Wilk normality test:',
shapiro(comedies_verse_features['dialogue_vivacity'])[1])
```
The Shapiro-Wilk test showed that the probability of the coefficient of dialogue vivacity of being normally distributed was 0.2067030817270279, which was above the 0.05 significance level. We failed to reject the null hypothesis of the normal distribution.
```
make_plot(comedies_verse_features['percentage_scene_split_verse'],
'Distribution of The Percentage of Scenes with Split Verse Lines')
mean, std, median = summary(comedies_verse_features['percentage_scene_split_verse'])
print('Mean percentage of scenes with split verse lines:', round(mean, 2))
print('Standard deviation of the percentage of scenes with split verse lines:', round(std, 2))
print('Median percentage of scenes with split verse lines:', median)
print('The p-value of the Shapiro-Wilk normality test:',
shapiro(comedies_verse_features['percentage_scene_split_verse'])[1])
```
The Shapiro-Wilk showed that the probability of the percentage of scenes with split verse lines of being normally distributed was very high (the p-value is 0.8681985139846802). We failed to reject the null hypothesis of normal distribution.
```
make_plot(comedies_verse_features['percentage_scene_split_rhymes'],
'Distribution of The Percentage of Scenes with Split Rhymes')
mean, std, median = summary(comedies_verse_features['percentage_scene_split_rhymes'])
print('Mean percentage of scenes with split rhymes:', round(mean, 2))
print('Standard deviation of the percentage of scenes with split rhymes:', round(std, 2))
print('Median percentage of scenes with split rhymes:', median)
print('The p-value of the Shapiro-Wilk normality test:',
shapiro(comedies_verse_features['percentage_scene_split_rhymes'])[1])
```
The Shapiro-Wilk test showed that the probability of the number of dramatic characters of being normally distributed was 0.5752763152122498. This probability was much higher than the 0.05 significance level. Therefore, we failed to reject the null hypothesis of normal distribution.
```
make_plot(comedies_verse_features['percentage_open_scenes'],
'Distribution of The Percentage of Open Scenes')
mean, std, median = summary(comedies_verse_features['percentage_open_scenes'])
print('Mean percentage of open scenes:', round(mean, 2))
print('Standard deviation of the percentage of open scenes:', round(std, 2))
print('Median percentage of open scenes:', median)
print('The p-value of the Shapiro-Wilk normality test:',
shapiro(comedies_verse_features['percentage_open_scenes'])[1])
```
The Shapiro-Wilk test showed that the probability of the number of the percentage of open scenes of being normally distributed was 0.3018988370895386, which was quite a lot higher than the significance level of 0.05. Therefore, we failed to reject the null hypothesis of normal distribution of the percentage of open scenes.
```
make_plot(comedies_verse_features['percentage_scenes_rhymes_split_verse'],
'Distribution of The Percentage of Scenes with Split Verse Lines and Rhymes')
mean, std, median = summary(comedies_verse_features['percentage_scenes_rhymes_split_verse'])
print('Mean percentage of scenes with split rhymes and verse lines:', round(mean, 2))
print('Standard deviation of the percentage of scenes with split rhymes and verse lines:', round(std, 2))
print('Median percentage of scenes with split rhymes and verse lines:', median)
print('The p-value of the Shapiro-Wilk normality test:',
shapiro(comedies_verse_features['percentage_scenes_rhymes_split_verse'])[1])
```
The Shapiro-Wilk test showed that the probability of the percentage of scenes with split verse lines and rhymes of being normally distributed was very low (the p-value was 0.015218793414533138). Therefore, we rejected the hypothesis of normal distribution.
### Summary:
1. The majority of the verse features were normally distributed. For them, we could use a parametric statistical test.
2. The only feature that was not normally distributed was the percentage of scenes with split rhymes and verse lines. For this feature, we used a non-parametric test such as the Mann-Whitney u test.
## Part 3. Hypothesis Testing
We will run statistical tests to determine whether the two periods distinguishable for the Russian five-act verse tragedy are significantly different for the Russian five-act comedy. The two periods are:
- Period One (from 1747 to 1794)
- Period Two (from 1795 to 1822)
For all features that were normally distributed, we will use *scipy.stats* Python library to run a **t-test** to check whether there is a difference between Period One and Period Two. The null hypothesis is that there is no difference between the two periods. The alternative hypothesis is that the two periods are different. Our significance level will be set at 0.05. If the p-value produced by the t-test will be below 0.05, we will reject the null hypothesis of no difference.
For the percentage of scenes with split rhymes and verse lines, we will run **the Mann-Whitney u-test** to check whether there is a difference between Period One and Period Two. The null hypothesis will be no difference between these periods, whereas the alternative hypothesis will be that the periods will be different.
Since both periods have fewer than 20 tragedies, we cannot use the scipy's Man-Whitney u-test that requires each sample size to be at least 20 because it uses normal approximation. Instead, we will have to run Mann-Whitney U-test without a normal approximation for which we wrote a custom function. The details about the test can be found in the following resource: https://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_nonparametric/bs704_nonparametric4.html.
One limitation that we need to mention is the sample size. The first period has only six comedies and the second period has only ten. However, it is impossible to increase the sample size - we cannot ask the Russian playwrights of the eighteenth and nineteenth century to produce more five-act verse comedies. If there are other Russian five-act comedies of these periods, they are either unknown or not available to us.
```
comedies_verse_features['period'] = comedies_verse_features.creation_date.apply(determine_period)
period_one = comedies_verse_features[comedies_verse_features['period'] == 1].copy()
period_two = comedies_verse_features[comedies_verse_features['period'] == 2].copy()
period_one.shape
period_two.shape
```
## The T-Test
### The Coefficient of Dialogue Vivacity
```
from scipy.stats import ttest_ind
ttest_ind(period_one['dialogue_vivacity'],
period_two['dialogue_vivacity'], equal_var=False)
```
### The Percentage of Scenes With Split Verse Lines
```
ttest_ind(period_one['percentage_scene_split_verse'],
period_two['percentage_scene_split_verse'], equal_var=False)
```
### The Percentage of Scnes With Split Rhymes
```
ttest_ind(period_one['percentage_scene_split_rhymes'],
period_two['percentage_scene_split_rhymes'], equal_var=False)
```
### The Percentage of Open Scenes
```
ttest_ind(period_one['percentage_open_scenes'],
period_two['percentage_open_scenes'], equal_var=False)
```
### Summary
|Feature |p-value |Result
|---------------------------| ----------------|--------------------------------
| The coefficient of dialogue vivacity |0.92 | Not Significant
|The percentage of scenes with split verse lines|0.009 | Significant
|The percentage of scenes with split rhymes| 0.44| Not significant
|The percentage of open scenes| 0.10| Not significant
## The Mann-Whitney Test
The Process:
- Our null hypothesis is that there is no difference between two periods. Our alternative hypothesis is that the periods are different.
- We will set the signficance level (alpha) at 0.05.
- We will run the test and calculate the test statistic.
- We will compare the test statistic with the critical value of U for a two-tailed test at alpha=0.05. Critical values can be found at https://www.real-statistics.com/statistics-tables/mann-whitney-table/.
- If our test statistic is equal or lower than the critical value of U, we will reject the null hypothesis. Otherwise, we will fail to reject it.
### The Percentage of Scenes With Split Verse Lines and Rhymes
```
small_sample_mann_whitney_u_test(period_one['percentage_scenes_rhymes_split_verse'],
period_two['percentage_scenes_rhymes_split_verse'])
```
### Critical Value of U
|Periods |Critical Value of U
|---------------------------| ----------------
| Period One (n=6) and Period Two (n=10) |11
### Summary
|Feature |u-statistic |Result
|---------------------------| ----------------|--------------------------------
| The percentage of scenes with split verse lines and rhymes|21 | Not Significant
We discovered that the distribution of only one feature, the percentage of scenes with split verse lines, was different in Periods One and Two. Distributions of other features did not prove to be significantly different.
## Part 4. Visualizations
```
def scatter(df, feature, title, xlabel, text_y):
sns.jointplot('creation_date',
feature,
data=df,
color='b',
height=7).plot_joint(
sns.kdeplot,
zorder=0,
n_levels=20)
plt.axvline(1795, color='grey',linestyle='dashed', linewidth=2)
plt.text(1795.5, text_y, '1795')
plt.title(title, fontsize=20, pad=100)
plt.xlabel('Date', fontsize=14)
plt.ylabel(xlabel, fontsize=14)
plt.show()
```
### The Coefficient of Dialogue Vivacity
```
scatter(comedies_verse_features,
'dialogue_vivacity',
'The Coefficient of Dialogue Vivacity by Year',
'The Coefficient of Dialogue Vivacity',
0.85)
```
### The Percentage of Scenes With Split Verse Lines
```
scatter(comedies_verse_features,
'percentage_scene_split_verse',
'The Percentage of Scenes With Split Verse Lines by Year',
'Percentage of Scenes With Split Verse Lines',
80)
```
### The Percentage of Scenes With Split Rhymes
```
scatter(comedies_verse_features,
'percentage_scene_split_rhymes',
'The Percentage of Scenes With Split Rhymes by Year',
'The Percentage of Scenes With Split Rhymes',
80)
```
### The Percentage of Open Scenes
```
scatter(comedies_verse_features,
'percentage_open_scenes',
'The Percentage of Open Scenes by Year',
'The Percentage of Open Scenes',
100)
```
### The Percentage of Scenes With Split Verse Lines and Rhymes
```
scatter(comedies_verse_features,
'percentage_scenes_rhymes_split_verse',
' The Percentage of Scenes With Split Verse Lines and Rhymes by Year',
' The Percentage of Scenes With Split Verse Lines and Rhymes',
45)
```
## Part 5. Descriptive Statistics For Two Periods and Overall
### The Coefficient of Dialogue Vivacity
#### In Entire Corpus
```
comedies_verse_features.describe().loc[:, 'dialogue_vivacity'][['mean',
'std',
'50%',
'min',
'max']].round(2)
```
#### By Tentative Periods
```
comedies_verse_features.groupby('period').describe().loc[:, 'dialogue_vivacity'][['mean',
'std',
'50%',
'min',
'max']].round(2)
```
### The Percentage of Scenes With Split Verse Lines
#### In Entire Corpus
```
comedies_verse_features.describe().loc[:, 'percentage_scene_split_verse'][['mean',
'std',
'50%',
'min',
'max']].round(2)
```
#### By Periods
```
comedies_verse_features.groupby('period').describe().loc[:, 'percentage_scene_split_verse'][['mean',
'std',
'50%',
'min',
'max']].round(2)
```
### The Percentage of Scenes With Split Rhymes
```
comedies_verse_features.describe().loc[:, 'percentage_scene_split_rhymes'][['mean',
'std',
'50%',
'min',
'max']].round(2)
```
#### By Tentative Periods
```
comedies_verse_features.groupby('period').describe().loc[:, 'percentage_scene_split_rhymes'][['mean',
'std',
'50%',
'min',
'max']].round(2)
```
### The Percentage of Open Scenes
#### In Entire Corpus
```
comedies_verse_features.describe().loc[:, 'percentage_open_scenes'][['mean',
'std',
'50%',
'min',
'max']].round(2)
```
#### By Tenative Periods
```
comedies_verse_features.groupby('period').describe().loc[:, 'percentage_open_scenes'][['mean',
'std',
'50%',
'min',
'max']].round(2)
```
### The Percentage of Scenes With Split Verse Lines or Rhymes
```
comedies_verse_features.describe().loc[:, 'percentage_scenes_rhymes_split_verse'][['mean',
'std',
'50%',
'min',
'max']].round(2)
comedies_verse_features.groupby('period').describe().loc[:, 'percentage_scenes_rhymes_split_verse'][['mean',
'std',
'50%',
'min',
'max']].round(2)
```
### Summary:
1. The mean dialogue vivacity in the corpus of the Russian five-act comedy in verse was 0.46, with a 0.10 standard deviation. In the tentative Period One, the mean dialogue vivacity was 0.46, the same as in the tentative Period Two. The standard deviation increased from 0.05 in the tentative Period One to 0.13 in the tentative Period Two.
2. The mean percentage of scenes with split verse lines in the corpus was 30.39%, with a standard deviation of 14.39. In Period One, the mean percentage of scenes with split verse lines was 19.37%, with a standard deviation of 10.16. In Period Two, the mean percentage of scenes with split verse lines almost doubled to 37%, with a standard deviation of 12.57%.
3. The average percentage of scenes with split rhymes was higher in the entire corpus of the Russian five-act comedies in verse than the average percentage of scenes with split verse lines (39.77% vs. 30.39%), as was the standard deviation (16.24% vs. 14.39%). The percentage of scenes with split rhymes grew from the tentative Period One to the tentative Period Two from 35.55% to 42.30%; the standard deviation slightly increased from 15.73% to 16.82%.
4. In the corpus, the average percentage of open scenes was 55.62%, i.e., more than half of all scenes were connected either through rhyme or verse lines. The standard deviation was 19.25%. In the tentative Period One, the percentage of open scenes was 44.65%, with a standard deviation of 19.76%. In the tentative Period Two, the percentage of open scenes increased to 62.21%, with a standard deviation of 16.50%, i.e., the standard deviation was lower in Period Two.
5. For the corpus, only 14.53% of all scenes were connected through both rhymes and verse lines. The standard deviation of the percentage of scenes with split verse lines and rhymes was 9.83%. In the tentative Period One, the mean percentage of scenes with split verse lines and rhymes was 10.27%, with a standard deviation of 5.22%. In the tentative Period Two, the mean percentage of scenes with split verse lines and rhymes was 17.09%, with a much higher standard deviation of 11.25%.
## Conclusions:
1. The majority of the examined features were normally distributed, except for the percentage of scenes with split verse lines and rhymes.
2. The distribution of the percentage of scenes with split verse lines differed significantly between Period One (from 1775 to 1794) and Period Two (from 1795 to 1849)).
2. For other verse features, there was no evidence to suggest that the two periods of the Russian five-act comedy in verse are significantly different.
3. The mean values of all examined features (except for the vivacity coefficient) increased from tentative Period One to Period Two. The mean vivacity coefficient remained the same from the tentative Period One to Period Two. The standard deviation of all examined features (except for the percentage of open scenes) increased from Period One to Period Two.
4. Judging by the natural clustering in the data evident from visualizations, 1805 may be a more appropriate boundary between the two time periods for comedy.
| github_jupyter |
# Lalonde Pandas API Example
by Adam Kelleher
We'll run through a quick example using the high-level Python API for the DoSampler. The DoSampler is different from most classic causal effect estimators. Instead of estimating statistics under interventions, it aims to provide the generality of Pearlian causal inference. In that context, the joint distribution of the variables under an intervention is the quantity of interest. It's hard to represent a joint distribution nonparametrically, so instead we provide a sample from that distribution, which we call a "do" sample.
Here, when you specify an outcome, that is the variable you're sampling under an intervention. We still have to do the usual process of making sure the quantity (the conditional interventional distribution of the outcome) is identifiable. We leverage the familiar components of the rest of the package to do that "under the hood". You'll notice some similarity in the kwargs for the DoSampler.
## Getting the Data
First, download the data from the LaLonde example.
```
import os, sys
sys.path.append(os.path.abspath("../../../"))
from rpy2.robjects import r as R
%load_ext rpy2.ipython
#%R install.packages("Matching")
%R library(Matching)
%R data(lalonde)
%R -o lalonde
lalonde.to_csv("lalonde.csv",index=False)
# the data already loaded in the previous cell. we include the import
# here you so you don't have to keep re-downloading it.
import pandas as pd
lalonde=pd.read_csv("lalonde.csv")
```
## The `causal` Namespace
We've created a "namespace" for `pandas.DataFrame`s containing causal inference methods. You can access it here with `lalonde.causal`, where `lalonde` is our `pandas.DataFrame`, and `causal` contains all our new methods! These methods are magically loaded into your existing (and future) dataframes when you `import dowhy.api`.
```
import dowhy.api
```
Now that we have the `causal` namespace, lets give it a try!
## The `do` Operation
The key feature here is the `do` method, which produces a new dataframe replacing the treatment variable with values specified, and the outcome with a sample from the interventional distribution of the outcome. If you don't specify a value for the treatment, it leaves the treatment untouched:
```
do_df = lalonde.causal.do(x='treat',
outcome='re78',
common_causes=['nodegr', 'black', 'hisp', 'age', 'educ', 'married'],
variable_types={'age': 'c', 'educ':'c', 'black': 'd', 'hisp': 'd',
'married': 'd', 'nodegr': 'd','re78': 'c', 'treat': 'b'},
proceed_when_unidentifiable=True)
```
Notice you get the usual output and prompts about identifiability. This is all `dowhy` under the hood!
We now have an interventional sample in `do_df`. It looks very similar to the original dataframe. Compare them:
```
lalonde.head()
do_df.head()
```
## Treatment Effect Estimation
We could get a naive estimate before for a treatment effect by doing
```
(lalonde[lalonde['treat'] == 1].mean() - lalonde[lalonde['treat'] == 0].mean())['re78']
```
We can do the same with our new sample from the interventional distribution to get a causal effect estimate
```
(do_df[do_df['treat'] == 1].mean() - do_df[do_df['treat'] == 0].mean())['re78']
```
We could get some rough error bars on the outcome using the normal approximation for a 95% confidence interval, like
```
import numpy as np
1.96*np.sqrt((do_df[do_df['treat'] == 1].var()/len(do_df[do_df['treat'] == 1])) +
(do_df[do_df['treat'] == 0].var()/len(do_df[do_df['treat'] == 0])))['re78']
```
but note that these DO NOT contain propensity score estimation error. For that, a bootstrapping procedure might be more appropriate.
This is just one statistic we can compute from the interventional distribution of `'re78'`. We can get all of the interventional moments as well, including functions of `'re78'`. We can leverage the full power of pandas, like
```
do_df['re78'].describe()
lalonde['re78'].describe()
```
and even plot aggregations, like
```
%matplotlib inline
import seaborn as sns
sns.barplot(data=lalonde, x='treat', y='re78')
sns.barplot(data=do_df, x='treat', y='re78')
```
## Specifying Interventions
You can find the distribution of the outcome under an intervention to set the value of the treatment.
```
do_df = lalonde.causal.do(x={'treat': 1},
outcome='re78',
common_causes=['nodegr', 'black', 'hisp', 'age', 'educ', 'married'],
variable_types={'age': 'c', 'educ':'c', 'black': 'd', 'hisp': 'd',
'married': 'd', 'nodegr': 'd','re78': 'c', 'treat': 'b'},
proceed_when_unidentifiable=True)
do_df.head()
```
This new dataframe gives the distribution of `'re78'` when `'treat'` is set to `1`.
For much more detail on how the `do` method works, check the docstring:
```
help(lalonde.causal.do)
```
| github_jupyter |
# Welcome to the Datenguide Python Package
Within this notebook the functionality of the package will be explained and demonstrated with examples.
### Topics
- Import
- get region IDs
- get statstic IDs
- get the data
- for single regions
- for multiple regions
## 1. Import
**Import the helper functions 'get_all_regions' and 'get_statistics'**
**Import the module Query for the main functionality**
```
# ONLY FOR TESTING LOCAL PACKAGE
# %cd ..
from datenguidepy.query_helper import get_all_regions, get_statistics
from datenguidepy import Query
```
**Import pandas and matplotlib for the usual display of data as tables and graphs**
```
import pandas as pd
import matplotlib
%matplotlib inline
pd.set_option('display.max_colwidth', 150)
```
## 2. Get Region IDs
### How to get the ID of the region I want to query
Regionalstatistik - the database behind Datenguide - has data for differently granular levels of Germany.
nuts:
1 – Bundesländer
2 – Regierungsbezirke / statistische Regionen
3 – Kreise / kreisfreie Städte.
lau:
1 - Verwaltungsgemeinschaften
2 - Gemeinden.
the function `get_all_regions()` returns all IDs from all levels.
```
# get_all_regions returns all ids
get_all_regions()
```
To get a specific ID, use the common pandas function `query()`
```
# e.g. get all "Bundesländer
get_all_regions().query("level == 'nuts1'")
# e.g. get the ID of Havelland
get_all_regions().query("name =='Havelland'")
```
## 3. Get statistic IDs
### How to find statistics
```
# get all statistics
get_statistics()
```
If you already know the statsitic ID you are looking for - perfect.
Otherwise you can use the pandas `query()` function so search e.g. for specific terms.
```
# find out the name of the desired statistic about birth
get_statistics().query('long_description.str.contains("Statistik der Geburten")', engine='python')
```
## 4. get the data
The top level element is the Query. For each query fields can be added (usually statistics / measures) that you want to get information on.
A Query can either be done on a single region, or on multiple regions (e.g. all Bundesländer).
### Single Region
If I want information - e.g. all births for the past years in Berlin:
```
# create a query for the region 11
query = Query.region('11')
# add a field (the statstic) to the query
field_births = query.add_field('BEV001')
# get the data of this query
query.results().head()
```
To get the short description in the result data frame instead of the cryptic ID (e.g. "Lebend Geborene" instead of BEV001) set the argument "verbose_statsitics"=True in the resutls:
```
query.results(verbose_statistics =True).head()
```
Now we only get the information about the count of births per year and the source of the data (year, value and source are default fields).
But there is more information in the statistic that we can get information on.
Let's look at the meta data of the statstic:
```
# get information on the field
field_births.get_info()
```
The arguments tell us what we can use for filtering (e.g. only data on baby girls (female)).
The fields tell us what more information can be displayed in our results.
```
# add filter
field_births.add_args({'GES': 'GESW'})
# now only about half the amount of births are returned as only the results for female babies are queried
query.results().head()
# add the field NAT (nationality) to the results
field_births.add_field('NAT')
```
**CAREFUL**: The information for the fields (e.g. nationality) is by default returned as a total amount. Therefore - if no argument "NAT" is specified in addition to the field, then only "None" will be displayed.
In order to get information on all possible values, the argument "ALL" needs to be added:
(the rows with value "None" are the aggregated values of all options)
```
field_births.add_args({'NAT': 'ALL'})
query.results().head()
```
To display the short description of the enum values instead of the cryptic IDs (e.g. Ausländer(innen) instead of NATA), set the argument "verbose_enums = True" on the results:
```
query.results(verbose_enums=True).head()
```
## Multiple Regions
To display data for multiple single regions, a list with region IDs can be used:
```
query_multiple = Query.region(['01', '02'])
query_multiple.add_field('BEV001')
query_multiple.results().sort_values('year').head()
```
To display data for e.g. all 'Bundesländer' or for all regions within a Bundesland, you can use the function `all_regions()`:
- specify nuts level
- specify lau level
- specify parent ID (Careful: not only the regions for the next lower level will be returned, but all levels - e.g. if you specify a parent on nuts level 1 then the "children" on nuts 2 but also the "grandchildren" on nuts 3, lau 1 and lau 2 will be returned)
```
# get data for all Bundesländer
query_all = Query.all_regions(nuts=1)
query_all.add_field('BEV001')
query_all.results().sort_values('year').head(12)
# get data for all regions within Brandenburg
query_all = Query.all_regions(parent='12')
query_all.add_field('BEV001')
query_all.results().head()
# get data for all nuts 3 regions within Brandenburg
query_all = Query.all_regions(parent='12', nuts=3)
query_all.add_field('BEV001')
query_all.results().sort_values('year').head()
```
| github_jupyter |
```
pip install pandera
pip install gcsfs
import os
import pandas as pd
from google.cloud import storage
serviceAccount = '/content/Chave Ingestao Apache.json'
os.environ['GOOGLE_APPLICATION_CREDENTIALS'] = serviceAccount
#leitura do arquivo em JSON
df = pd.read_json(r'gs://projeto-final-grupo09/entrada_dados/Projeto Final', lines = True)
df.head(1)
#Renomeando colunas
df.rename(columns={'id':'identificacao','created_on':'criado_em','operation':'operacao','property_type':'tipo_propriedade',
'place_name':'nome_do_local','place_with_parent_names':'pais_local','country_name':'pais','state_name':'estado',
'geonames_id':'g_nomes','lat_lon':'latitude_longitude','lat':'latitude','lon':'longitude','price':
'preco_cheio','currency':'moeda','price_aprox_local_currency':'preco',
'price_aprox_usd':'preco_aproximado_dolar','surface_total_in_m2':'area_total_por_m2',
'surface_covered_in_m2':'area_construcao_em_m2','price_usd_per_m2':'preco_dolar_por_m2',
'price_per_m2':'preco_por_m2','floor':'andar','rooms':'quartos','expenses':'despesas',
'properati_url':'url_da_propriedade','description':'descricao', 'title':'titulo',
'image_thumbnail':'miniatura_imagem'}, inplace = True)
df.head(2)
#chamar a coluna de operacao para ver se tem algo além de venda (no caso a coluna só tem sell - venda - entao irei dropar posteriormente)
sorted(pd.unique(df['operacao']))
#chamar a coluna de país para ver se tem algo além de Brasil (no caso só tem Brasil - então iremos dropar posteriormente)
sorted(pd.unique(df['pais']))
#chamar a coluna de moeda para ver se tem algo além de BRL (no caso só tem BRL - então iremos dropar posteriormente)
sorted(pd.unique(df['moeda']))
#criacao de variavel - colunas - para posterior drop
colunas = ['operacao', 'pais', 'moeda', 'latitude_longitude', 'latitude', 'longitude', 'preco_aproximado_dolar', 'pais_local',
'preco_dolar_por_m2', 'andar', 'despesas', 'descricao', 'titulo', 'miniatura_imagem', 'url_da_propriedade', 'preco_cheio']
df.drop(colunas, axis=1, inplace=True)
#verificando se há (e quantos são) os valores na coluna nome_do_local
df['nome_do_local'].value_counts()
#verificar se há apenas um valor na coluna (no caso a coluna propriedade_tipo tem 3 informações significativas e uma (PH) que será dropada)
sorted(pd.unique(df['tipo_propriedade']))
#contando quantos valores tem cada um dos itens em tipo_propriedade - casa, apartamento e lojas
df['tipo_propriedade'].value_counts()
#traduzindo as informações contidas na coluna de tipo_propriedade
df['tipo_propriedade'].replace(['house', 'apartment', 'store'],['casa','apartamento','loja'], inplace = True)
#quantidade de quartos e salas (no caso das lojas)
df['quartos'].value_counts()
#chamar a coluna de quartos para descobrir quais os valores contidos
sorted(pd.unique(df['quartos']))
#devido a coluna quartos ser um float, forçamos ele a se tornar um numero inteiro e o NaN se tornar 0
df['quartos'] = df['quartos'].fillna(0.0).astype(int)
df.head(10)
df.to_csv("gs://lucao-buck", sep=",", index=False)
from google.colab import drive
drive.mount('/content/drive')
```
| github_jupyter |
# Chapter 4
`Original content created by Cam Davidson-Pilon`
`Ported to Python 3 and PyMC3 by Max Margenot (@clean_utensils) and Thomas Wiecki (@twiecki) at Quantopian (@quantopian)`
______
## The greatest theorem never told
This chapter focuses on an idea that is always bouncing around our minds, but is rarely made explicit outside books devoted to statistics. In fact, we've been using this simple idea in every example thus far.
### The Law of Large Numbers
Let $Z_i$ be $N$ independent samples from some probability distribution. According to *the Law of Large numbers*, so long as the expected value $E[Z]$ is finite, the following holds,
$$\frac{1}{N} \sum_{i=1}^N Z_i \rightarrow E[ Z ], \;\;\; N \rightarrow \infty.$$
In words:
> The average of a sequence of random variables from the same distribution converges to the expected value of that distribution.
This may seem like a boring result, but it will be the most useful tool you use.
### Intuition
If the above Law is somewhat surprising, it can be made more clear by examining a simple example.
Consider a random variable $Z$ that can take only two values, $c_1$ and $c_2$. Suppose we have a large number of samples of $Z$, denoting a specific sample $Z_i$. The Law says that we can approximate the expected value of $Z$ by averaging over all samples. Consider the average:
$$ \frac{1}{N} \sum_{i=1}^N \;Z_i $$
By construction, $Z_i$ can only take on $c_1$ or $c_2$, hence we can partition the sum over these two values:
\begin{align}
\frac{1}{N} \sum_{i=1}^N \;Z_i
& =\frac{1}{N} \big( \sum_{ Z_i = c_1}c_1 + \sum_{Z_i=c_2}c_2 \big) \\\\[5pt]
& = c_1 \sum_{ Z_i = c_1}\frac{1}{N} + c_2 \sum_{ Z_i = c_2}\frac{1}{N} \\\\[5pt]
& = c_1 \times \text{ (approximate frequency of $c_1$) } \\\\
& \;\;\;\;\;\;\;\;\; + c_2 \times \text{ (approximate frequency of $c_2$) } \\\\[5pt]
& \approx c_1 \times P(Z = c_1) + c_2 \times P(Z = c_2 ) \\\\[5pt]
& = E[Z]
\end{align}
Equality holds in the limit, but we can get closer and closer by using more and more samples in the average. This Law holds for almost *any distribution*, minus some important cases we will encounter later.
##### Example
____
Below is a diagram of the Law of Large numbers in action for three different sequences of Poisson random variables.
We sample `sample_size = 100000` Poisson random variables with parameter $\lambda = 4.5$. (Recall the expected value of a Poisson random variable is equal to it's parameter.) We calculate the average for the first $n$ samples, for $n=1$ to `sample_size`.
```
%matplotlib inline
import numpy as np
from IPython.core.pylabtools import figsize
import matplotlib.pyplot as plt
figsize( 12.5, 5 )
sample_size = 100000
expected_value = lambda_ = 4.5
poi = np.random.poisson
N_samples = range(1,sample_size,100)
for k in range(3):
samples = poi( lambda_, sample_size )
partial_average = [ samples[:i].mean() for i in N_samples ]
plt.plot( N_samples, partial_average, lw=1.5,label="average \
of $n$ samples; seq. %d"%k)
plt.plot( N_samples, expected_value*np.ones_like( partial_average),
ls = "--", label = "true expected value", c = "k" )
plt.ylim( 4.35, 4.65)
plt.title( "Convergence of the average of \n random variables to its \
expected value" )
plt.ylabel( "average of $n$ samples" )
plt.xlabel( "# of samples, $n$")
plt.legend();
```
Looking at the above plot, it is clear that when the sample size is small, there is greater variation in the average (compare how *jagged and jumpy* the average is initially, then *smooths* out). All three paths *approach* the value 4.5, but just flirt with it as $N$ gets large. Mathematicians and statistician have another name for *flirting*: convergence.
Another very relevant question we can ask is *how quickly am I converging to the expected value?* Let's plot something new. For a specific $N$, let's do the above trials thousands of times and compute how far away we are from the true expected value, on average. But wait — *compute on average*? This is simply the law of large numbers again! For example, we are interested in, for a specific $N$, the quantity:
$$D(N) = \sqrt{ \;E\left[\;\; \left( \frac{1}{N}\sum_{i=1}^NZ_i - 4.5 \;\right)^2 \;\;\right] \;\;}$$
The above formulae is interpretable as a distance away from the true value (on average), for some $N$. (We take the square root so the dimensions of the above quantity and our random variables are the same). As the above is an expected value, it can be approximated using the law of large numbers: instead of averaging $Z_i$, we calculate the following multiple times and average them:
$$ Y_k = \left( \;\frac{1}{N}\sum_{i=1}^NZ_i - 4.5 \; \right)^2 $$
By computing the above many, $N_y$, times (remember, it is random), and averaging them:
$$ \frac{1}{N_Y} \sum_{k=1}^{N_Y} Y_k \rightarrow E[ Y_k ] = E\;\left[\;\; \left( \frac{1}{N}\sum_{i=1}^NZ_i - 4.5 \;\right)^2 \right]$$
Finally, taking the square root:
$$ \sqrt{\frac{1}{N_Y} \sum_{k=1}^{N_Y} Y_k} \approx D(N) $$
```
figsize( 12.5, 4)
N_Y = 250 #use this many to approximate D(N)
N_array = np.arange( 1000, 50000, 2500 ) #use this many samples in the approx. to the variance.
D_N_results = np.zeros( len( N_array ) )
lambda_ = 4.5
expected_value = lambda_ #for X ~ Poi(lambda) , E[ X ] = lambda
def D_N( n ):
"""
This function approx. D_n, the average variance of using n samples.
"""
Z = poi( lambda_, (n, N_Y) )
average_Z = Z.mean(axis=0)
return np.sqrt( ( (average_Z - expected_value)**2 ).mean() )
for i,n in enumerate(N_array):
D_N_results[i] = D_N(n)
plt.xlabel( "$N$" )
plt.ylabel( "expected squared-distance from true value" )
plt.plot(N_array, D_N_results, lw = 3,
label="expected distance between\n\
expected value and \naverage of $N$ random variables.")
plt.plot( N_array, np.sqrt(expected_value)/np.sqrt(N_array), lw = 2, ls = "--",
label = r"$\frac{\sqrt{\lambda}}{\sqrt{N}}$" )
plt.legend()
plt.title( "How 'fast' is the sample average converging? " );
```
As expected, the expected distance between our sample average and the actual expected value shrinks as $N$ grows large. But also notice that the *rate* of convergence decreases, that is, we need only 10 000 additional samples to move from 0.020 to 0.015, a difference of 0.005, but *20 000* more samples to again decrease from 0.015 to 0.010, again only a 0.005 decrease.
It turns out we can measure this rate of convergence. Above I have plotted a second line, the function $\sqrt{\lambda}/\sqrt{N}$. This was not chosen arbitrarily. In most cases, given a sequence of random variable distributed like $Z$, the rate of convergence to $E[Z]$ of the Law of Large Numbers is
$$ \frac{ \sqrt{ \; Var(Z) \; } }{\sqrt{N} }$$
This is useful to know: for a given large $N$, we know (on average) how far away we are from the estimate. On the other hand, in a Bayesian setting, this can seem like a useless result: Bayesian analysis is OK with uncertainty so what's the *statistical* point of adding extra precise digits? Though drawing samples can be so computationally cheap that having a *larger* $N$ is fine too.
### How do we compute $Var(Z)$ though?
The variance is simply another expected value that can be approximated! Consider the following, once we have the expected value (by using the Law of Large Numbers to estimate it, denote it $\mu$), we can estimate the variance:
$$ \frac{1}{N}\sum_{i=1}^N \;(Z_i - \mu)^2 \rightarrow E[ \;( Z - \mu)^2 \;] = Var( Z )$$
### Expected values and probabilities
There is an even less explicit relationship between expected value and estimating probabilities. Define the *indicator function*
$$\mathbb{1}_A(x) =
\begin{cases} 1 & x \in A \\\\
0 & else
\end{cases}
$$
Then, by the law of large numbers, if we have many samples $X_i$, we can estimate the probability of an event $A$, denoted $P(A)$, by:
$$ \frac{1}{N} \sum_{i=1}^N \mathbb{1}_A(X_i) \rightarrow E[\mathbb{1}_A(X)] = P(A) $$
Again, this is fairly obvious after a moments thought: the indicator function is only 1 if the event occurs, so we are summing only the times the event occurs and dividing by the total number of trials (consider how we usually approximate probabilities using frequencies). For example, suppose we wish to estimate the probability that a $Z \sim Exp(.5)$ is greater than 5, and we have many samples from a $Exp(.5)$ distribution.
$$ P( Z > 5 ) = \sum_{i=1}^N \mathbb{1}_{z > 5 }(Z_i) $$
```
N = 10000
print( np.mean( [ np.random.exponential( 0.5 ) > 5 for i in range(N) ] ) )
```
### What does this all have to do with Bayesian statistics?
*Point estimates*, to be introduced in the next chapter, in Bayesian inference are computed using expected values. In more analytical Bayesian inference, we would have been required to evaluate complicated expected values represented as multi-dimensional integrals. No longer. If we can sample from the posterior distribution directly, we simply need to evaluate averages. Much easier. If accuracy is a priority, plots like the ones above show how fast you are converging. And if further accuracy is desired, just take more samples from the posterior.
When is enough enough? When can you stop drawing samples from the posterior? That is the practitioners decision, and also dependent on the variance of the samples (recall from above a high variance means the average will converge slower).
We also should understand when the Law of Large Numbers fails. As the name implies, and comparing the graphs above for small $N$, the Law is only true for large sample sizes. Without this, the asymptotic result is not reliable. Knowing in what situations the Law fails can give us *confidence in how unconfident we should be*. The next section deals with this issue.
## The Disorder of Small Numbers
The Law of Large Numbers is only valid as $N$ gets *infinitely* large: never truly attainable. While the law is a powerful tool, it is foolhardy to apply it liberally. Our next example illustrates this.
##### Example: Aggregated geographic data
Often data comes in aggregated form. For instance, data may be grouped by state, county, or city level. Of course, the population numbers vary per geographic area. If the data is an average of some characteristic of each the geographic areas, we must be conscious of the Law of Large Numbers and how it can *fail* for areas with small populations.
We will observe this on a toy dataset. Suppose there are five thousand counties in our dataset. Furthermore, population number in each state are uniformly distributed between 100 and 1500. The way the population numbers are generated is irrelevant to the discussion, so we do not justify this. We are interested in measuring the average height of individuals per county. Unbeknownst to us, height does **not** vary across county, and each individual, regardless of the county he or she is currently living in, has the same distribution of what their height may be:
$$ \text{height} \sim \text{Normal}(150, 15 ) $$
We aggregate the individuals at the county level, so we only have data for the *average in the county*. What might our dataset look like?
```
figsize( 12.5, 4)
std_height = 15
mean_height = 150
n_counties = 5000
pop_generator = np.random.randint
norm = np.random.normal
#generate some artificial population numbers
population = pop_generator(100, 1500, n_counties )
average_across_county = np.zeros( n_counties )
for i in range( n_counties ):
#generate some individuals and take the mean
average_across_county[i] = norm(mean_height, 1./std_height,
population[i] ).mean()
#located the counties with the apparently most extreme average heights.
i_min = np.argmin( average_across_county )
i_max = np.argmax( average_across_county )
#plot population size vs. recorded average
plt.scatter( population, average_across_county, alpha = 0.5, c="#7A68A6")
plt.scatter( [ population[i_min], population[i_max] ],
[average_across_county[i_min], average_across_county[i_max] ],
s = 60, marker = "o", facecolors = "none",
edgecolors = "#A60628", linewidths = 1.5,
label="extreme heights")
plt.xlim( 100, 1500 )
plt.title( "Average height vs. County Population")
plt.xlabel("County Population")
plt.ylabel("Average height in county")
plt.plot( [100, 1500], [150, 150], color = "k", label = "true expected \
height", ls="--" )
plt.legend(scatterpoints = 1);
```
What do we observe? *Without accounting for population sizes* we run the risk of making an enormous inference error: if we ignored population size, we would say that the county with the shortest and tallest individuals have been correctly circled. But this inference is wrong for the following reason. These two counties do *not* necessarily have the most extreme heights. The error results from the calculated average of smaller populations not being a good reflection of the true expected value of the population (which in truth should be $\mu =150$). The sample size/population size/$N$, whatever you wish to call it, is simply too small to invoke the Law of Large Numbers effectively.
We provide more damning evidence against this inference. Recall the population numbers were uniformly distributed over 100 to 1500. Our intuition should tell us that the counties with the most extreme population heights should also be uniformly spread over 100 to 4000, and certainly independent of the county's population. Not so. Below are the population sizes of the counties with the most extreme heights.
```
print("Population sizes of 10 'shortest' counties: ")
print(population[ np.argsort( average_across_county )[:10] ], '\n')
print("Population sizes of 10 'tallest' counties: ")
print(population[ np.argsort( -average_across_county )[:10] ])
```
Not at all uniform over 100 to 1500. This is an absolute failure of the Law of Large Numbers.
##### Example: Kaggle's *U.S. Census Return Rate Challenge*
Below is data from the 2010 US census, which partitions populations beyond counties to the level of block groups (which are aggregates of city blocks or equivalents). The dataset is from a Kaggle machine learning competition some colleagues and I participated in. The objective was to predict the census letter mail-back rate of a group block, measured between 0 and 100, using census variables (median income, number of females in the block-group, number of trailer parks, average number of children etc.). Below we plot the census mail-back rate versus block group population:
```
figsize( 12.5, 6.5 )
data = np.genfromtxt( "./data/census_data.csv", skip_header=1,
delimiter= ",")
plt.scatter( data[:,1], data[:,0], alpha = 0.5, c="#7A68A6")
plt.title("Census mail-back rate vs Population")
plt.ylabel("Mail-back rate")
plt.xlabel("population of block-group")
plt.xlim(-100, 15e3 )
plt.ylim( -5, 105)
i_min = np.argmin( data[:,0] )
i_max = np.argmax( data[:,0] )
plt.scatter( [ data[i_min,1], data[i_max, 1] ],
[ data[i_min,0], data[i_max,0] ],
s = 60, marker = "o", facecolors = "none",
edgecolors = "#A60628", linewidths = 1.5,
label="most extreme points")
plt.legend(scatterpoints = 1);
```
The above is a classic phenomenon in statistics. I say *classic* referring to the "shape" of the scatter plot above. It follows a classic triangular form, that tightens as we increase the sample size (as the Law of Large Numbers becomes more exact).
I am perhaps overstressing the point and maybe I should have titled the book *"You don't have big data problems!"*, but here again is an example of the trouble with *small datasets*, not big ones. Simply, small datasets cannot be processed using the Law of Large Numbers. Compare with applying the Law without hassle to big datasets (ex. big data). I mentioned earlier that paradoxically big data prediction problems are solved by relatively simple algorithms. The paradox is partially resolved by understanding that the Law of Large Numbers creates solutions that are *stable*, i.e. adding or subtracting a few data points will not affect the solution much. On the other hand, adding or removing data points to a small dataset can create very different results.
For further reading on the hidden dangers of the Law of Large Numbers, I would highly recommend the excellent manuscript [The Most Dangerous Equation](http://nsm.uh.edu/~dgraur/niv/TheMostDangerousEquation.pdf).
##### Example: How to order Reddit submissions
You may have disagreed with the original statement that the Law of Large numbers is known to everyone, but only implicitly in our subconscious decision making. Consider ratings on online products: how often do you trust an average 5-star rating if there is only 1 reviewer? 2 reviewers? 3 reviewers? We implicitly understand that with such few reviewers that the average rating is **not** a good reflection of the true value of the product.
This has created flaws in how we sort items, and more generally, how we compare items. Many people have realized that sorting online search results by their rating, whether the objects be books, videos, or online comments, return poor results. Often the seemingly top videos or comments have perfect ratings only from a few enthusiastic fans, and truly more quality videos or comments are hidden in later pages with *falsely-substandard* ratings of around 4.8. How can we correct this?
Consider the popular site Reddit (I purposefully did not link to the website as you would never come back). The site hosts links to stories or images, called submissions, for people to comment on. Redditors can vote up or down on each submission (called upvotes and downvotes). Reddit, by default, will sort submissions to a given subreddit by Hot, that is, the submissions that have the most upvotes recently.
<img src="http://i.imgur.com/3v6bz9f.png" />
How would you determine which submissions are the best? There are a number of ways to achieve this:
1. *Popularity*: A submission is considered good if it has many upvotes. A problem with this model is that a submission with hundreds of upvotes, but thousands of downvotes. While being very *popular*, the submission is likely more controversial than best.
2. *Difference*: Using the *difference* of upvotes and downvotes. This solves the above problem, but fails when we consider the temporal nature of submission. Depending on when a submission is posted, the website may be experiencing high or low traffic. The difference method will bias the *Top* submissions to be the those made during high traffic periods, which have accumulated more upvotes than submissions that were not so graced, but are not necessarily the best.
3. *Time adjusted*: Consider using Difference divided by the age of the submission. This creates a *rate*, something like *difference per second*, or *per minute*. An immediate counter-example is, if we use per second, a 1 second old submission with 1 upvote would be better than a 100 second old submission with 99 upvotes. One can avoid this by only considering at least t second old submission. But what is a good t value? Does this mean no submission younger than t is good? We end up comparing unstable quantities with stable quantities (young vs. old submissions).
3. *Ratio*: Rank submissions by the ratio of upvotes to total number of votes (upvotes plus downvotes). This solves the temporal issue, such that new submissions who score well can be considered Top just as likely as older submissions, provided they have many upvotes to total votes. The problem here is that a submission with a single upvote (ratio = 1.0) will beat a submission with 999 upvotes and 1 downvote (ratio = 0.999), but clearly the latter submission is *more likely* to be better.
I used the phrase *more likely* for good reason. It is possible that the former submission, with a single upvote, is in fact a better submission than the later with 999 upvotes. The hesitation to agree with this is because we have not seen the other 999 potential votes the former submission might get. Perhaps it will achieve an additional 999 upvotes and 0 downvotes and be considered better than the latter, though not likely.
What we really want is an estimate of the *true upvote ratio*. Note that the true upvote ratio is not the same as the observed upvote ratio: the true upvote ratio is hidden, and we only observe upvotes vs. downvotes (one can think of the true upvote ratio as "what is the underlying probability someone gives this submission a upvote, versus a downvote"). So the 999 upvote/1 downvote submission probably has a true upvote ratio close to 1, which we can assert with confidence thanks to the Law of Large Numbers, but on the other hand we are much less certain about the true upvote ratio of the submission with only a single upvote. Sounds like a Bayesian problem to me.
One way to determine a prior on the upvote ratio is to look at the historical distribution of upvote ratios. This can be accomplished by scraping Reddit's submissions and determining a distribution. There are a few problems with this technique though:
1. Skewed data: The vast majority of submissions have very few votes, hence there will be many submissions with ratios near the extremes (see the "triangular plot" in the above Kaggle dataset), effectively skewing our distribution to the extremes. One could try to only use submissions with votes greater than some threshold. Again, problems are encountered. There is a tradeoff between number of submissions available to use and a higher threshold with associated ratio precision.
2. Biased data: Reddit is composed of different subpages, called subreddits. Two examples are *r/aww*, which posts pics of cute animals, and *r/politics*. It is very likely that the user behaviour towards submissions of these two subreddits are very different: visitors are likely friendly and affectionate in the former, and would therefore upvote submissions more, compared to the latter, where submissions are likely to be controversial and disagreed upon. Therefore not all submissions are the same.
In light of these, I think it is better to use a `Uniform` prior.
With our prior in place, we can find the posterior of the true upvote ratio. The Python script `top_showerthoughts_submissions.py` will scrape the best posts from the `showerthoughts` community on Reddit. This is a text-only community so the title of each post *is* the post. Below is the top post as well as some other sample posts:
```
#adding a number to the end of the %run call with get the ith top post.
%run top_showerthoughts_submissions.py 2
print("Post contents: \n")
print(top_post)
"""
contents: an array of the text from the last 100 top submissions to a subreddit
votes: a 2d numpy array of upvotes, downvotes for each submission.
"""
n_submissions = len(votes)
submissions = np.random.randint( n_submissions, size=4)
print("Some Submissions (out of %d total) \n-----------"%n_submissions)
for i in submissions:
print('"' + contents[i] + '"')
print("upvotes/downvotes: ",votes[i,:], "\n")
```
For a given true upvote ratio $p$ and $N$ votes, the number of upvotes will look like a Binomial random variable with parameters $p$ and $N$. (This is because of the equivalence between upvote ratio and probability of upvoting versus downvoting, out of $N$ possible votes/trials). We create a function that performs Bayesian inference on $p$, for a particular submission's upvote/downvote pair.
```
import pymc3 as pm
def posterior_upvote_ratio( upvotes, downvotes, samples = 20000):
"""
This function accepts the number of upvotes and downvotes a particular submission recieved,
and the number of posterior samples to return to the user. Assumes a uniform prior.
"""
N = upvotes + downvotes
with pm.Model() as model:
upvote_ratio = pm.Uniform("upvote_ratio", 0, 1)
observations = pm.Binomial( "obs", N, upvote_ratio, observed=upvotes)
trace = pm.sample(samples, step=pm.Metropolis())
burned_trace = trace[int(samples/4):]
return burned_trace["upvote_ratio"]
```
Below are the resulting posterior distributions.
```
figsize( 11., 8)
posteriors = []
colours = ["#348ABD", "#A60628", "#7A68A6", "#467821", "#CF4457"]
for i in range(len(submissions)):
j = submissions[i]
posteriors.append( posterior_upvote_ratio( votes[j, 0], votes[j,1] ) )
plt.hist( posteriors[i], bins = 10, normed = True, alpha = .9,
histtype="step",color = colours[i%5], lw = 3,
label = '(%d up:%d down)\n%s...'%(votes[j, 0], votes[j,1], contents[j][:50]) )
plt.hist( posteriors[i], bins = 10, normed = True, alpha = .2,
histtype="stepfilled",color = colours[i], lw = 3, )
plt.legend(loc="upper left")
plt.xlim( 0, 1)
plt.title("Posterior distributions of upvote ratios on different submissions");
```
Some distributions are very tight, others have very long tails (relatively speaking), expressing our uncertainty with what the true upvote ratio might be.
### Sorting!
We have been ignoring the goal of this exercise: how do we sort the submissions from *best to worst*? Of course, we cannot sort distributions, we must sort scalar numbers. There are many ways to distill a distribution down to a scalar: expressing the distribution through its expected value, or mean, is one way. Choosing the mean is a bad choice though. This is because the mean does not take into account the uncertainty of distributions.
I suggest using the *95% least plausible value*, defined as the value such that there is only a 5% chance the true parameter is lower (think of the lower bound on the 95% credible region). Below are the posterior distributions with the 95% least-plausible value plotted:
```
N = posteriors[0].shape[0]
lower_limits = []
for i in range(len(submissions)):
j = submissions[i]
plt.hist( posteriors[i], bins = 20, normed = True, alpha = .9,
histtype="step",color = colours[i], lw = 3,
label = '(%d up:%d down)\n%s...'%(votes[j, 0], votes[j,1], contents[j][:50]) )
plt.hist( posteriors[i], bins = 20, normed = True, alpha = .2,
histtype="stepfilled",color = colours[i], lw = 3, )
v = np.sort( posteriors[i] )[ int(0.05*N) ]
#plt.vlines( v, 0, 15 , color = "k", alpha = 1, linewidths=3 )
plt.vlines( v, 0, 10 , color = colours[i], linestyles = "--", linewidths=3 )
lower_limits.append(v)
plt.legend(loc="upper left")
plt.legend(loc="upper left")
plt.title("Posterior distributions of upvote ratios on different submissions");
order = np.argsort( -np.array( lower_limits ) )
print(order, lower_limits)
```
The best submissions, according to our procedure, are the submissions that are *most-likely* to score a high percentage of upvotes. Visually those are the submissions with the 95% least plausible value close to 1.
Why is sorting based on this quantity a good idea? By ordering by the 95% least plausible value, we are being the most conservative with what we think is best. That is, even in the worst case scenario, when we have severely overestimated the upvote ratio, we can be sure the best submissions are still on top. Under this ordering, we impose the following very natural properties:
1. given two submissions with the same observed upvote ratio, we will assign the submission with more votes as better (since we are more confident it has a higher ratio).
2. given two submissions with the same number of votes, we still assign the submission with more upvotes as *better*.
### But this is too slow for real-time!
I agree, computing the posterior of every submission takes a long time, and by the time you have computed it, likely the data has changed. I delay the mathematics to the appendix, but I suggest using the following formula to compute the lower bound very fast.
$$ \frac{a}{a + b} - 1.65\sqrt{ \frac{ab}{ (a+b)^2(a + b +1 ) } }$$
where
\begin{align}
& a = 1 + u \\\\
& b = 1 + d \\\\
\end{align}
$u$ is the number of upvotes, and $d$ is the number of downvotes. The formula is a shortcut in Bayesian inference, which will be further explained in Chapter 6 when we discuss priors in more detail.
```
def intervals(u,d):
a = 1. + u
b = 1. + d
mu = a/(a+b)
std_err = 1.65*np.sqrt( (a*b)/( (a+b)**2*(a+b+1.) ) )
return ( mu, std_err )
print("Approximate lower bounds:")
posterior_mean, std_err = intervals(votes[:,0],votes[:,1])
lb = posterior_mean - std_err
print(lb)
print("\n")
print("Top 40 Sorted according to approximate lower bounds:")
print("\n")
order = np.argsort( -lb )
ordered_contents = []
for i in order[:40]:
ordered_contents.append( contents[i] )
print(votes[i,0], votes[i,1], contents[i])
print("-------------")
```
We can view the ordering visually by plotting the posterior mean and bounds, and sorting by the lower bound. In the plot below, notice that the left error-bar is sorted (as we suggested this is the best way to determine an ordering), so the means, indicated by dots, do not follow any strong pattern.
```
r_order = order[::-1][-40:]
plt.errorbar( posterior_mean[r_order], np.arange( len(r_order) ),
xerr=std_err[r_order], capsize=0, fmt="o",
color = "#7A68A6")
plt.xlim( 0.3, 1)
plt.yticks( np.arange( len(r_order)-1,-1,-1 ), map( lambda x: x[:30].replace("\n",""), ordered_contents) );
```
In the graphic above, you can see why sorting by mean would be sub-optimal.
### Extension to Starred rating systems
The above procedure works well for upvote-downvotes schemes, but what about systems that use star ratings, e.g. 5 star rating systems. Similar problems apply with simply taking the average: an item with two perfect ratings would beat an item with thousands of perfect ratings, but a single sub-perfect rating.
We can consider the upvote-downvote problem above as binary: 0 is a downvote, 1 if an upvote. A $N$-star rating system can be seen as a more continuous version of above, and we can set $n$ stars rewarded is equivalent to rewarding $\frac{n}{N}$. For example, in a 5-star system, a 2 star rating corresponds to 0.4. A perfect rating is a 1. We can use the same formula as before, but with $a,b$ defined differently:
$$ \frac{a}{a + b} - 1.65\sqrt{ \frac{ab}{ (a+b)^2(a + b +1 ) } }$$
where
\begin{align}
& a = 1 + S \\\\
& b = 1 + N - S \\\\
\end{align}
where $N$ is the number of users who rated, and $S$ is the sum of all the ratings, under the equivalence scheme mentioned above.
##### Example: Counting Github stars
What is the average number of stars a Github repository has? How would you calculate this? There are over 6 million respositories, so there is more than enough data to invoke the Law of Large numbers. Let's start pulling some data. TODO
### Conclusion
While the Law of Large Numbers is cool, it is only true so much as its name implies: with large sample sizes only. We have seen how our inference can be affected by not considering *how the data is shaped*.
1. By (cheaply) drawing many samples from the posterior distributions, we can ensure that the Law of Large Number applies as we approximate expected values (which we will do in the next chapter).
2. Bayesian inference understands that with small sample sizes, we can observe wild randomness. Our posterior distribution will reflect this by being more spread rather than tightly concentrated. Thus, our inference should be correctable.
3. There are major implications of not considering the sample size, and trying to sort objects that are unstable leads to pathological orderings. The method provided above solves this problem.
### Appendix
##### Derivation of sorting submissions formula
Basically what we are doing is using a Beta prior (with parameters $a=1, b=1$, which is a uniform distribution), and using a Binomial likelihood with observations $u, N = u+d$. This means our posterior is a Beta distribution with parameters $a' = 1 + u, b' = 1 + (N - u) = 1+d$. We then need to find the value, $x$, such that 0.05 probability is less than $x$. This is usually done by inverting the CDF ([Cumulative Distribution Function](http://en.wikipedia.org/wiki/Cumulative_Distribution_Function)), but the CDF of the beta, for integer parameters, is known but is a large sum [3].
We instead use a Normal approximation. The mean of the Beta is $\mu = a'/(a'+b')$ and the variance is
$$\sigma^2 = \frac{a'b'}{ (a' + b')^2(a'+b'+1) }$$
Hence we solve the following equation for $x$ and have an approximate lower bound.
$$ 0.05 = \Phi\left( \frac{(x - \mu)}{\sigma}\right) $$
$\Phi$ being the [cumulative distribution for the normal distribution](http://en.wikipedia.org/wiki/Normal_distribution#Cumulative_distribution)
##### Exercises
1\. How would you estimate the quantity $E\left[ \cos{X} \right]$, where $X \sim \text{Exp}(4)$? What about $E\left[ \cos{X} | X \lt 1\right]$, i.e. the expected value *given* we know $X$ is less than 1? Would you need more samples than the original samples size to be equally accurate?
```
## Enter code here
import scipy.stats as stats
exp = stats.expon( scale=4 )
N = 1e5
X = exp.rvs( int(N) )
## ...
```
2\. The following table was located in the paper "Going for Three: Predicting the Likelihood of Field Goal Success with Logistic Regression" [2]. The table ranks football field-goal kickers by their percent of non-misses. What mistake have the researchers made?
-----
#### Kicker Careers Ranked by Make Percentage
<table><tbody><tr><th>Rank </th><th>Kicker </th><th>Make % </th><th>Number of Kicks</th></tr><tr><td>1 </td><td>Garrett Hartley </td><td>87.7 </td><td>57</td></tr><tr><td>2</td><td> Matt Stover </td><td>86.8 </td><td>335</td></tr><tr><td>3 </td><td>Robbie Gould </td><td>86.2 </td><td>224</td></tr><tr><td>4 </td><td>Rob Bironas </td><td>86.1 </td><td>223</td></tr><tr><td>5</td><td> Shayne Graham </td><td>85.4 </td><td>254</td></tr><tr><td>… </td><td>… </td><td>…</td><td> </td></tr><tr><td>51</td><td> Dave Rayner </td><td>72.2 </td><td>90</td></tr><tr><td>52</td><td> Nick Novak </td><td>71.9 </td><td>64</td></tr><tr><td>53 </td><td>Tim Seder </td><td>71.0 </td><td>62</td></tr><tr><td>54 </td><td>Jose Cortez </td><td>70.7</td><td> 75</td></tr><tr><td>55 </td><td>Wade Richey </td><td>66.1</td><td> 56</td></tr></tbody></table>
In August 2013, [a popular post](http://bpodgursky.wordpress.com/2013/08/21/average-income-per-programming-language/) on the average income per programmer of different languages was trending. Here's the summary chart: (reproduced without permission, cause when you lie with stats, you gunna get the hammer). What do you notice about the extremes?
------
#### Average household income by programming language
<table >
<tr><td>Language</td><td>Average Household Income ($)</td><td>Data Points</td></tr>
<tr><td>Puppet</td><td>87,589.29</td><td>112</td></tr>
<tr><td>Haskell</td><td>89,973.82</td><td>191</td></tr>
<tr><td>PHP</td><td>94,031.19</td><td>978</td></tr>
<tr><td>CoffeeScript</td><td>94,890.80</td><td>435</td></tr>
<tr><td>VimL</td><td>94,967.11</td><td>532</td></tr>
<tr><td>Shell</td><td>96,930.54</td><td>979</td></tr>
<tr><td>Lua</td><td>96,930.69</td><td>101</td></tr>
<tr><td>Erlang</td><td>97,306.55</td><td>168</td></tr>
<tr><td>Clojure</td><td>97,500.00</td><td>269</td></tr>
<tr><td>Python</td><td>97,578.87</td><td>2314</td></tr>
<tr><td>JavaScript</td><td>97,598.75</td><td>3443</td></tr>
<tr><td>Emacs Lisp</td><td>97,774.65</td><td>355</td></tr>
<tr><td>C#</td><td>97,823.31</td><td>665</td></tr>
<tr><td>Ruby</td><td>98,238.74</td><td>3242</td></tr>
<tr><td>C++</td><td>99,147.93</td><td>845</td></tr>
<tr><td>CSS</td><td>99,881.40</td><td>527</td></tr>
<tr><td>Perl</td><td>100,295.45</td><td>990</td></tr>
<tr><td>C</td><td>100,766.51</td><td>2120</td></tr>
<tr><td>Go</td><td>101,158.01</td><td>231</td></tr>
<tr><td>Scala</td><td>101,460.91</td><td>243</td></tr>
<tr><td>ColdFusion</td><td>101,536.70</td><td>109</td></tr>
<tr><td>Objective-C</td><td>101,801.60</td><td>562</td></tr>
<tr><td>Groovy</td><td>102,650.86</td><td>116</td></tr>
<tr><td>Java</td><td>103,179.39</td><td>1402</td></tr>
<tr><td>XSLT</td><td>106,199.19</td><td>123</td></tr>
<tr><td>ActionScript</td><td>108,119.47</td><td>113</td></tr>
</table>
### References
1. Wainer, Howard. *The Most Dangerous Equation*. American Scientist, Volume 95.
2. Clarck, Torin K., Aaron W. Johnson, and Alexander J. Stimpson. "Going for Three: Predicting the Likelihood of Field Goal Success with Logistic Regression." (2013): n. page. [Web](http://www.sloansportsconference.com/wp-content/uploads/2013/Going%20for%20Three%20Predicting%20the%20Likelihood%20of%20Field%20Goal%20Success%20with%20Logistic%20Regression.pdf). 20 Feb. 2013.
3. http://en.wikipedia.org/wiki/Beta_function#Incomplete_beta_function
```
from IPython.core.display import HTML
def css_styling():
styles = open("../styles/custom.css", "r").read()
return HTML(styles)
css_styling()
```
<style>
img{
max-width:800px}
</style>
| github_jupyter |
# PTN Template
This notebook serves as a template for single dataset PTN experiments
It can be run on its own by setting STANDALONE to True (do a find for "STANDALONE" to see where)
But it is intended to be executed as part of a *papermill.py script. See any of the
experimentes with a papermill script to get started with that workflow.
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
import os, json, sys, time, random
import numpy as np
import torch
from torch.optim import Adam
from easydict import EasyDict
import matplotlib.pyplot as plt
from steves_models.steves_ptn import Steves_Prototypical_Network
from steves_utils.lazy_iterable_wrapper import Lazy_Iterable_Wrapper
from steves_utils.iterable_aggregator import Iterable_Aggregator
from steves_utils.ptn_train_eval_test_jig import PTN_Train_Eval_Test_Jig
from steves_utils.torch_sequential_builder import build_sequential
from steves_utils.torch_utils import get_dataset_metrics, ptn_confusion_by_domain_over_dataloader
from steves_utils.utils_v2 import (per_domain_accuracy_from_confusion, get_datasets_base_path)
from steves_utils.PTN.utils import independent_accuracy_assesment
from steves_utils.stratified_dataset.episodic_accessor import Episodic_Accessor_Factory
from steves_utils.ptn_do_report import (
get_loss_curve,
get_results_table,
get_parameters_table,
get_domain_accuracies,
)
from steves_utils.transforms import get_chained_transform
```
# Required Parameters
These are allowed parameters, not defaults
Each of these values need to be present in the injected parameters (the notebook will raise an exception if they are not present)
Papermill uses the cell tag "parameters" to inject the real parameters below this cell.
Enable tags to see what I mean
```
required_parameters = {
"experiment_name",
"lr",
"device",
"seed",
"dataset_seed",
"labels_source",
"labels_target",
"domains_source",
"domains_target",
"num_examples_per_domain_per_label_source",
"num_examples_per_domain_per_label_target",
"n_shot",
"n_way",
"n_query",
"train_k_factor",
"val_k_factor",
"test_k_factor",
"n_epoch",
"patience",
"criteria_for_best",
"x_transforms_source",
"x_transforms_target",
"episode_transforms_source",
"episode_transforms_target",
"pickle_name",
"x_net",
"NUM_LOGS_PER_EPOCH",
"BEST_MODEL_PATH",
"torch_default_dtype"
}
standalone_parameters = {}
standalone_parameters["experiment_name"] = "STANDALONE PTN"
standalone_parameters["lr"] = 0.0001
standalone_parameters["device"] = "cuda"
standalone_parameters["seed"] = 1337
standalone_parameters["dataset_seed"] = 1337
standalone_parameters["num_examples_per_domain_per_label_source"]=100
standalone_parameters["num_examples_per_domain_per_label_target"]=100
standalone_parameters["n_shot"] = 3
standalone_parameters["n_query"] = 2
standalone_parameters["train_k_factor"] = 1
standalone_parameters["val_k_factor"] = 2
standalone_parameters["test_k_factor"] = 2
standalone_parameters["n_epoch"] = 100
standalone_parameters["patience"] = 10
standalone_parameters["criteria_for_best"] = "target_accuracy"
standalone_parameters["x_transforms_source"] = ["unit_power"]
standalone_parameters["x_transforms_target"] = ["unit_power"]
standalone_parameters["episode_transforms_source"] = []
standalone_parameters["episode_transforms_target"] = []
standalone_parameters["torch_default_dtype"] = "torch.float32"
standalone_parameters["x_net"] = [
{"class": "nnReshape", "kargs": {"shape":[-1, 1, 2, 256]}},
{"class": "Conv2d", "kargs": { "in_channels":1, "out_channels":256, "kernel_size":(1,7), "bias":False, "padding":(0,3), },},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features":256}},
{"class": "Conv2d", "kargs": { "in_channels":256, "out_channels":80, "kernel_size":(2,7), "bias":True, "padding":(0,3), },},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features":80}},
{"class": "Flatten", "kargs": {}},
{"class": "Linear", "kargs": {"in_features": 80*256, "out_features": 256}}, # 80 units per IQ pair
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm1d", "kargs": {"num_features":256}},
{"class": "Linear", "kargs": {"in_features": 256, "out_features": 256}},
]
# Parameters relevant to results
# These parameters will basically never need to change
standalone_parameters["NUM_LOGS_PER_EPOCH"] = 10
standalone_parameters["BEST_MODEL_PATH"] = "./best_model.pth"
# uncomment for CORES dataset
from steves_utils.CORES.utils import (
ALL_NODES,
ALL_NODES_MINIMUM_1000_EXAMPLES,
ALL_DAYS
)
standalone_parameters["labels_source"] = ALL_NODES
standalone_parameters["labels_target"] = ALL_NODES
standalone_parameters["domains_source"] = [1]
standalone_parameters["domains_target"] = [2,3,4,5]
standalone_parameters["pickle_name"] = "cores.stratified_ds.2022A.pkl"
# Uncomment these for ORACLE dataset
# from steves_utils.ORACLE.utils_v2 import (
# ALL_DISTANCES_FEET,
# ALL_RUNS,
# ALL_SERIAL_NUMBERS,
# )
# standalone_parameters["labels_source"] = ALL_SERIAL_NUMBERS
# standalone_parameters["labels_target"] = ALL_SERIAL_NUMBERS
# standalone_parameters["domains_source"] = [8,20, 38,50]
# standalone_parameters["domains_target"] = [14, 26, 32, 44, 56]
# standalone_parameters["pickle_name"] = "oracle.frame_indexed.stratified_ds.2022A.pkl"
# standalone_parameters["num_examples_per_domain_per_label_source"]=1000
# standalone_parameters["num_examples_per_domain_per_label_target"]=1000
# Uncomment these for Metahan dataset
# standalone_parameters["labels_source"] = list(range(19))
# standalone_parameters["labels_target"] = list(range(19))
# standalone_parameters["domains_source"] = [0]
# standalone_parameters["domains_target"] = [1]
# standalone_parameters["pickle_name"] = "metehan.stratified_ds.2022A.pkl"
# standalone_parameters["n_way"] = len(standalone_parameters["labels_source"])
# standalone_parameters["num_examples_per_domain_per_label_source"]=200
# standalone_parameters["num_examples_per_domain_per_label_target"]=100
standalone_parameters["n_way"] = len(standalone_parameters["labels_source"])
# Parameters
parameters = {
"experiment_name": "baseline_ptn_wisig",
"lr": 0.001,
"device": "cuda",
"seed": 1337,
"dataset_seed": 1337,
"labels_source": [
"1-10",
"1-12",
"1-14",
"1-16",
"1-18",
"1-19",
"1-8",
"10-11",
"10-17",
"10-4",
"10-7",
"11-1",
"11-10",
"11-19",
"11-20",
"11-4",
"11-7",
"12-19",
"12-20",
"12-7",
"13-14",
"13-18",
"13-19",
"13-20",
"13-3",
"13-7",
"14-10",
"14-11",
"14-12",
"14-13",
"14-14",
"14-19",
"14-20",
"14-7",
"14-8",
"14-9",
"15-1",
"15-19",
"15-6",
"16-1",
"16-16",
"16-19",
"16-20",
"17-10",
"17-11",
"18-1",
"18-10",
"18-11",
"18-12",
"18-13",
"18-14",
"18-15",
"18-16",
"18-17",
"18-19",
"18-2",
"18-20",
"18-4",
"18-5",
"18-7",
"18-8",
"18-9",
"19-1",
"19-10",
"19-11",
"19-12",
"19-13",
"19-14",
"19-15",
"19-19",
"19-2",
"19-20",
"19-3",
"19-4",
"19-6",
"19-7",
"19-8",
"19-9",
"2-1",
"2-13",
"2-15",
"2-3",
"2-4",
"2-5",
"2-6",
"2-7",
"2-8",
"20-1",
"20-12",
"20-14",
"20-15",
"20-16",
"20-18",
"20-19",
"20-20",
"20-3",
"20-4",
"20-5",
"20-7",
"20-8",
"3-1",
"3-13",
"3-18",
"3-2",
"3-8",
"4-1",
"4-10",
"4-11",
"5-1",
"5-5",
"6-1",
"6-15",
"6-6",
"7-10",
"7-11",
"7-12",
"7-13",
"7-14",
"7-7",
"7-8",
"7-9",
"8-1",
"8-13",
"8-14",
"8-18",
"8-20",
"8-3",
"8-8",
"9-1",
"9-7",
],
"labels_target": [
"1-10",
"1-12",
"1-14",
"1-16",
"1-18",
"1-19",
"1-8",
"10-11",
"10-17",
"10-4",
"10-7",
"11-1",
"11-10",
"11-19",
"11-20",
"11-4",
"11-7",
"12-19",
"12-20",
"12-7",
"13-14",
"13-18",
"13-19",
"13-20",
"13-3",
"13-7",
"14-10",
"14-11",
"14-12",
"14-13",
"14-14",
"14-19",
"14-20",
"14-7",
"14-8",
"14-9",
"15-1",
"15-19",
"15-6",
"16-1",
"16-16",
"16-19",
"16-20",
"17-10",
"17-11",
"18-1",
"18-10",
"18-11",
"18-12",
"18-13",
"18-14",
"18-15",
"18-16",
"18-17",
"18-19",
"18-2",
"18-20",
"18-4",
"18-5",
"18-7",
"18-8",
"18-9",
"19-1",
"19-10",
"19-11",
"19-12",
"19-13",
"19-14",
"19-15",
"19-19",
"19-2",
"19-20",
"19-3",
"19-4",
"19-6",
"19-7",
"19-8",
"19-9",
"2-1",
"2-13",
"2-15",
"2-3",
"2-4",
"2-5",
"2-6",
"2-7",
"2-8",
"20-1",
"20-12",
"20-14",
"20-15",
"20-16",
"20-18",
"20-19",
"20-20",
"20-3",
"20-4",
"20-5",
"20-7",
"20-8",
"3-1",
"3-13",
"3-18",
"3-2",
"3-8",
"4-1",
"4-10",
"4-11",
"5-1",
"5-5",
"6-1",
"6-15",
"6-6",
"7-10",
"7-11",
"7-12",
"7-13",
"7-14",
"7-7",
"7-8",
"7-9",
"8-1",
"8-13",
"8-14",
"8-18",
"8-20",
"8-3",
"8-8",
"9-1",
"9-7",
],
"x_transforms_source": [],
"x_transforms_target": [],
"episode_transforms_source": [],
"episode_transforms_target": [],
"num_examples_per_domain_per_label_source": 100,
"num_examples_per_domain_per_label_target": 100,
"n_shot": 3,
"n_way": 130,
"n_query": 2,
"train_k_factor": 1,
"val_k_factor": 2,
"test_k_factor": 2,
"torch_default_dtype": "torch.float64",
"n_epoch": 50,
"patience": 3,
"criteria_for_best": "target_loss",
"x_net": [
{"class": "nnReshape", "kargs": {"shape": [-1, 1, 2, 256]}},
{
"class": "Conv2d",
"kargs": {
"in_channels": 1,
"out_channels": 256,
"kernel_size": [1, 7],
"bias": False,
"padding": [0, 3],
},
},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features": 256}},
{
"class": "Conv2d",
"kargs": {
"in_channels": 256,
"out_channels": 80,
"kernel_size": [2, 7],
"bias": True,
"padding": [0, 3],
},
},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features": 80}},
{"class": "Flatten", "kargs": {}},
{"class": "Linear", "kargs": {"in_features": 20480, "out_features": 256}},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm1d", "kargs": {"num_features": 256}},
{"class": "Linear", "kargs": {"in_features": 256, "out_features": 256}},
],
"NUM_LOGS_PER_EPOCH": 10,
"BEST_MODEL_PATH": "./best_model.pth",
"pickle_name": "wisig.node3-19.stratified_ds.2022A.pkl",
"domains_source": [3],
"domains_target": [1, 2, 4],
}
# Set this to True if you want to run this template directly
STANDALONE = False
if STANDALONE:
print("parameters not injected, running with standalone_parameters")
parameters = standalone_parameters
if not 'parameters' in locals() and not 'parameters' in globals():
raise Exception("Parameter injection failed")
#Use an easy dict for all the parameters
p = EasyDict(parameters)
supplied_keys = set(p.keys())
if supplied_keys != required_parameters:
print("Parameters are incorrect")
if len(supplied_keys - required_parameters)>0: print("Shouldn't have:", str(supplied_keys - required_parameters))
if len(required_parameters - supplied_keys)>0: print("Need to have:", str(required_parameters - supplied_keys))
raise RuntimeError("Parameters are incorrect")
###################################
# Set the RNGs and make it all deterministic
###################################
np.random.seed(p.seed)
random.seed(p.seed)
torch.manual_seed(p.seed)
torch.use_deterministic_algorithms(True)
###########################################
# The stratified datasets honor this
###########################################
torch.set_default_dtype(eval(p.torch_default_dtype))
###################################
# Build the network(s)
# Note: It's critical to do this AFTER setting the RNG
# (This is due to the randomized initial weights)
###################################
x_net = build_sequential(p.x_net)
start_time_secs = time.time()
###################################
# Build the dataset
###################################
if p.x_transforms_source == []: x_transform_source = None
else: x_transform_source = get_chained_transform(p.x_transforms_source)
if p.x_transforms_target == []: x_transform_target = None
else: x_transform_target = get_chained_transform(p.x_transforms_target)
if p.episode_transforms_source == []: episode_transform_source = None
else: raise Exception("episode_transform_source not implemented")
if p.episode_transforms_target == []: episode_transform_target = None
else: raise Exception("episode_transform_target not implemented")
eaf_source = Episodic_Accessor_Factory(
labels=p.labels_source,
domains=p.domains_source,
num_examples_per_domain_per_label=p.num_examples_per_domain_per_label_source,
iterator_seed=p.seed,
dataset_seed=p.dataset_seed,
n_shot=p.n_shot,
n_way=p.n_way,
n_query=p.n_query,
train_val_test_k_factors=(p.train_k_factor,p.val_k_factor,p.test_k_factor),
pickle_path=os.path.join(get_datasets_base_path(), p.pickle_name),
x_transform_func=x_transform_source,
example_transform_func=episode_transform_source,
)
train_original_source, val_original_source, test_original_source = eaf_source.get_train(), eaf_source.get_val(), eaf_source.get_test()
eaf_target = Episodic_Accessor_Factory(
labels=p.labels_target,
domains=p.domains_target,
num_examples_per_domain_per_label=p.num_examples_per_domain_per_label_target,
iterator_seed=p.seed,
dataset_seed=p.dataset_seed,
n_shot=p.n_shot,
n_way=p.n_way,
n_query=p.n_query,
train_val_test_k_factors=(p.train_k_factor,p.val_k_factor,p.test_k_factor),
pickle_path=os.path.join(get_datasets_base_path(), p.pickle_name),
x_transform_func=x_transform_target,
example_transform_func=episode_transform_target,
)
train_original_target, val_original_target, test_original_target = eaf_target.get_train(), eaf_target.get_val(), eaf_target.get_test()
transform_lambda = lambda ex: ex[1] # Original is (<domain>, <episode>) so we strip down to episode only
train_processed_source = Lazy_Iterable_Wrapper(train_original_source, transform_lambda)
val_processed_source = Lazy_Iterable_Wrapper(val_original_source, transform_lambda)
test_processed_source = Lazy_Iterable_Wrapper(test_original_source, transform_lambda)
train_processed_target = Lazy_Iterable_Wrapper(train_original_target, transform_lambda)
val_processed_target = Lazy_Iterable_Wrapper(val_original_target, transform_lambda)
test_processed_target = Lazy_Iterable_Wrapper(test_original_target, transform_lambda)
datasets = EasyDict({
"source": {
"original": {"train":train_original_source, "val":val_original_source, "test":test_original_source},
"processed": {"train":train_processed_source, "val":val_processed_source, "test":test_processed_source}
},
"target": {
"original": {"train":train_original_target, "val":val_original_target, "test":test_original_target},
"processed": {"train":train_processed_target, "val":val_processed_target, "test":test_processed_target}
},
})
# Some quick unit tests on the data
from steves_utils.transforms import get_average_power, get_average_magnitude
q_x, q_y, s_x, s_y, truth = next(iter(train_processed_source))
assert q_x.dtype == eval(p.torch_default_dtype)
assert s_x.dtype == eval(p.torch_default_dtype)
print("Visually inspect these to see if they line up with expected values given the transforms")
print('x_transforms_source', p.x_transforms_source)
print('x_transforms_target', p.x_transforms_target)
print("Average magnitude, source:", get_average_magnitude(q_x[0].numpy()))
print("Average power, source:", get_average_power(q_x[0].numpy()))
q_x, q_y, s_x, s_y, truth = next(iter(train_processed_target))
print("Average magnitude, target:", get_average_magnitude(q_x[0].numpy()))
print("Average power, target:", get_average_power(q_x[0].numpy()))
###################################
# Build the model
###################################
model = Steves_Prototypical_Network(x_net, device=p.device, x_shape=(2,256))
optimizer = Adam(params=model.parameters(), lr=p.lr)
###################################
# train
###################################
jig = PTN_Train_Eval_Test_Jig(model, p.BEST_MODEL_PATH, p.device)
jig.train(
train_iterable=datasets.source.processed.train,
source_val_iterable=datasets.source.processed.val,
target_val_iterable=datasets.target.processed.val,
num_epochs=p.n_epoch,
num_logs_per_epoch=p.NUM_LOGS_PER_EPOCH,
patience=p.patience,
optimizer=optimizer,
criteria_for_best=p.criteria_for_best,
)
total_experiment_time_secs = time.time() - start_time_secs
###################################
# Evaluate the model
###################################
source_test_label_accuracy, source_test_label_loss = jig.test(datasets.source.processed.test)
target_test_label_accuracy, target_test_label_loss = jig.test(datasets.target.processed.test)
source_val_label_accuracy, source_val_label_loss = jig.test(datasets.source.processed.val)
target_val_label_accuracy, target_val_label_loss = jig.test(datasets.target.processed.val)
history = jig.get_history()
total_epochs_trained = len(history["epoch_indices"])
val_dl = Iterable_Aggregator((datasets.source.original.val,datasets.target.original.val))
confusion = ptn_confusion_by_domain_over_dataloader(model, p.device, val_dl)
per_domain_accuracy = per_domain_accuracy_from_confusion(confusion)
# Add a key to per_domain_accuracy for if it was a source domain
for domain, accuracy in per_domain_accuracy.items():
per_domain_accuracy[domain] = {
"accuracy": accuracy,
"source?": domain in p.domains_source
}
# Do an independent accuracy assesment JUST TO BE SURE!
# _source_test_label_accuracy = independent_accuracy_assesment(model, datasets.source.processed.test, p.device)
# _target_test_label_accuracy = independent_accuracy_assesment(model, datasets.target.processed.test, p.device)
# _source_val_label_accuracy = independent_accuracy_assesment(model, datasets.source.processed.val, p.device)
# _target_val_label_accuracy = independent_accuracy_assesment(model, datasets.target.processed.val, p.device)
# assert(_source_test_label_accuracy == source_test_label_accuracy)
# assert(_target_test_label_accuracy == target_test_label_accuracy)
# assert(_source_val_label_accuracy == source_val_label_accuracy)
# assert(_target_val_label_accuracy == target_val_label_accuracy)
experiment = {
"experiment_name": p.experiment_name,
"parameters": dict(p),
"results": {
"source_test_label_accuracy": source_test_label_accuracy,
"source_test_label_loss": source_test_label_loss,
"target_test_label_accuracy": target_test_label_accuracy,
"target_test_label_loss": target_test_label_loss,
"source_val_label_accuracy": source_val_label_accuracy,
"source_val_label_loss": source_val_label_loss,
"target_val_label_accuracy": target_val_label_accuracy,
"target_val_label_loss": target_val_label_loss,
"total_epochs_trained": total_epochs_trained,
"total_experiment_time_secs": total_experiment_time_secs,
"confusion": confusion,
"per_domain_accuracy": per_domain_accuracy,
},
"history": history,
"dataset_metrics": get_dataset_metrics(datasets, "ptn"),
}
ax = get_loss_curve(experiment)
plt.show()
get_results_table(experiment)
get_domain_accuracies(experiment)
print("Source Test Label Accuracy:", experiment["results"]["source_test_label_accuracy"], "Target Test Label Accuracy:", experiment["results"]["target_test_label_accuracy"])
print("Source Val Label Accuracy:", experiment["results"]["source_val_label_accuracy"], "Target Val Label Accuracy:", experiment["results"]["target_val_label_accuracy"])
json.dumps(experiment)
```
| github_jupyter |
```
%matplotlib inline
```
Neural Networks
===============
Neural networks can be constructed using the ``torch.nn`` package.
Now that you had a glimpse of ``autograd``, ``nn`` depends on
``autograd`` to define models and differentiate them.
An ``nn.Module`` contains layers, and a method ``forward(input)`` that
returns the ``output``.
For example, look at this network that classifies digit images:
.. figure:: /_static/img/mnist.png
:alt: convnet
convnet
It is a simple feed-forward network. It takes the input, feeds it
through several layers one after the other, and then finally gives the
output.
A typical training procedure for a neural network is as follows:
- Define the neural network that has some learnable parameters (or
weights)
- Iterate over a dataset of inputs
- Process input through the network
- Compute the loss (how far is the output from being correct)
- Propagate gradients back into the network’s parameters
- Update the weights of the network, typically using a simple update rule:
``weight = weight - learning_rate * gradient``
Define the network
------------------
Let’s define this network:
```
import torch
import torch.nn as nn
import torch.nn.functional as F
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# 1 input image channel, 6 output channels, 5x5 square convolution
# kernel
self.conv1 = nn.Conv2d(1, 6, 5)
self.conv2 = nn.Conv2d(6, 16, 5)
# an affine operation: y = Wx + b
self.fc1 = nn.Linear(16 * 5 * 5, 120) # 5*5 from image dimension
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
# Max pooling over a (2, 2) window
x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
# If the size is a square, you can specify with a single number
x = F.max_pool2d(F.relu(self.conv2(x)), 2)
x = torch.flatten(x, 1) # flatten all dimensions except the batch dimension
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
net = Net()
print(net)
```
You just have to define the ``forward`` function, and the ``backward``
function (where gradients are computed) is automatically defined for you
using ``autograd``.
You can use any of the Tensor operations in the ``forward`` function.
The learnable parameters of a model are returned by ``net.parameters()``
```
params = list(net.parameters())
print(len(params))
print(params[0].size()) # conv1's .weight
```
Let's try a random 32x32 input.
Note: expected input size of this net (LeNet) is 32x32. To use this net on
the MNIST dataset, please resize the images from the dataset to 32x32.
```
input = torch.randn(1, 1, 32, 32)
out = net(input)
print(out)
```
Zero the gradient buffers of all parameters and backprops with random
gradients:
```
net.zero_grad()
out.backward(torch.randn(1, 10))
```
<div class="alert alert-info"><h4>Note</h4><p>``torch.nn`` only supports mini-batches. The entire ``torch.nn``
package only supports inputs that are a mini-batch of samples, and not
a single sample.
For example, ``nn.Conv2d`` will take in a 4D Tensor of
``nSamples x nChannels x Height x Width``.
If you have a single sample, just use ``input.unsqueeze(0)`` to add
a fake batch dimension.</p></div>
Before proceeding further, let's recap all the classes you’ve seen so far.
**Recap:**
- ``torch.Tensor`` - A *multi-dimensional array* with support for autograd
operations like ``backward()``. Also *holds the gradient* w.r.t. the
tensor.
- ``nn.Module`` - Neural network module. *Convenient way of
encapsulating parameters*, with helpers for moving them to GPU,
exporting, loading, etc.
- ``nn.Parameter`` - A kind of Tensor, that is *automatically
registered as a parameter when assigned as an attribute to a*
``Module``.
- ``autograd.Function`` - Implements *forward and backward definitions
of an autograd operation*. Every ``Tensor`` operation creates at
least a single ``Function`` node that connects to functions that
created a ``Tensor`` and *encodes its history*.
**At this point, we covered:**
- Defining a neural network
- Processing inputs and calling backward
**Still Left:**
- Computing the loss
- Updating the weights of the network
Loss Function
-------------
A loss function takes the (output, target) pair of inputs, and computes a
value that estimates how far away the output is from the target.
There are several different
`loss functions <https://pytorch.org/docs/nn.html#loss-functions>`_ under the
nn package .
A simple loss is: ``nn.MSELoss`` which computes the mean-squared error
between the input and the target.
For example:
```
output = net(input)
target = torch.randn(10) # a dummy target, for example
target = target.view(1, -1) # make it the same shape as output
criterion = nn.MSELoss()
loss = criterion(output, target)
print(loss)
```
Now, if you follow ``loss`` in the backward direction, using its
``.grad_fn`` attribute, you will see a graph of computations that looks
like this:
::
input -> conv2d -> relu -> maxpool2d -> conv2d -> relu -> maxpool2d
-> flatten -> linear -> relu -> linear -> relu -> linear
-> MSELoss
-> loss
So, when we call ``loss.backward()``, the whole graph is differentiated
w.r.t. the neural net parameters, and all Tensors in the graph that have
``requires_grad=True`` will have their ``.grad`` Tensor accumulated with the
gradient.
For illustration, let us follow a few steps backward:
```
print(loss.grad_fn) # MSELoss
print(loss.grad_fn.next_functions[0][0]) # Linear
print(loss.grad_fn.next_functions[0][0].next_functions[0][0]) # ReLU
```
Backprop
--------
To backpropagate the error all we have to do is to ``loss.backward()``.
You need to clear the existing gradients though, else gradients will be
accumulated to existing gradients.
Now we shall call ``loss.backward()``, and have a look at conv1's bias
gradients before and after the backward.
```
net.zero_grad() # zeroes the gradient buffers of all parameters
print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)
loss.backward()
print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)
```
Now, we have seen how to use loss functions.
**Read Later:**
The neural network package contains various modules and loss functions
that form the building blocks of deep neural networks. A full list with
documentation is `here <https://pytorch.org/docs/nn>`_.
**The only thing left to learn is:**
- Updating the weights of the network
Update the weights
------------------
The simplest update rule used in practice is the Stochastic Gradient
Descent (SGD):
``weight = weight - learning_rate * gradient``
We can implement this using simple Python code:
.. code:: python
learning_rate = 0.01
for f in net.parameters():
f.data.sub_(f.grad.data * learning_rate)
However, as you use neural networks, you want to use various different
update rules such as SGD, Nesterov-SGD, Adam, RMSProp, etc.
To enable this, we built a small package: ``torch.optim`` that
implements all these methods. Using it is very simple:
```
import torch.optim as optim
# create your optimizer
optimizer = optim.SGD(net.parameters(), lr=0.01)
# in your training loop:
optimizer.zero_grad() # zero the gradient buffers
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step() # Does the update
```
.. Note::
Observe how gradient buffers had to be manually set to zero using
``optimizer.zero_grad()``. This is because gradients are accumulated
as explained in the `Backprop`_ section.
| github_jupyter |
# Classifying Fashion-MNIST
Now it's your turn to build and train a neural network. You'll be using the [Fashion-MNIST dataset](https://github.com/zalandoresearch/fashion-mnist), a drop-in replacement for the MNIST dataset. MNIST is actually quite trivial with neural networks where you can easily achieve better than 97% accuracy. Fashion-MNIST is a set of 28x28 greyscale images of clothes. It's more complex than MNIST, so it's a better representation of the actual performance of your network, and a better representation of datasets you'll use in the real world.
<img src='assets/fashion-mnist-sprite.png' width=500px>
In this notebook, you'll build your own neural network. For the most part, you could just copy and paste the code from Part 3, but you wouldn't be learning. It's important for you to write the code yourself and get it to work. Feel free to consult the previous notebooks though as you work through this.
First off, let's load the dataset through torchvision.
```
import torch
from torchvision import datasets, transforms
import helper
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(),
transforms.Normalize((0.5,), (0.5,))])
# Download and load the training data
trainset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=64, shuffle=True)
# Download and load the test data
testset = datasets.FashionMNIST('~/.pytorch/F_MNIST_data/', download=True, train=False, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size=64, shuffle=True)
```
Here we can see one of the images.
```
image, label = next(iter(trainloader))
helper.imshow(image[0,:]);
```
## Building the network
Here you should define your network. As with MNIST, each image is 28x28 which is a total of 784 pixels, and there are 10 classes. You should include at least one hidden layer. We suggest you use ReLU activations for the layers and to return the logits or log-softmax from the forward pass. It's up to you how many layers you add and the size of those layers.
```
from torch import nn, optim
import torch.nn.functional as F
# TODO: Define your network architecture here
class Network(nn.Module):
def __init__(self):
super().__init__()
self.fc1 = nn.Linear(784, 256)
self.fc2 = nn.Linear(256, 128)
self.fc3 = nn.Linear(128, 64)
self.fc4 = nn.Linear(64, 10)
def forward(self, x):
#flatten inputs
x = x.view(x.shape[0], -1)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = F.relu(self.fc3(x))
x = F.log_softmax(self.fc4(x), dim = 1)
return x
```
# Train the network
Now you should create your network and train it. First you'll want to define [the criterion](http://pytorch.org/docs/master/nn.html#loss-functions) ( something like `nn.CrossEntropyLoss`) and [the optimizer](http://pytorch.org/docs/master/optim.html) (typically `optim.SGD` or `optim.Adam`).
Then write the training code. Remember the training pass is a fairly straightforward process:
* Make a forward pass through the network to get the logits
* Use the logits to calculate the loss
* Perform a backward pass through the network with `loss.backward()` to calculate the gradients
* Take a step with the optimizer to update the weights
By adjusting the hyperparameters (hidden units, learning rate, etc), you should be able to get the training loss below 0.4.
```
# TODO: Create the network, define the criterion and optimizer
model = Network()
criterion = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.003)
model
# TODO: Train the network here
# TODO: Train the network here
epochs = 5
for e in range(epochs):
running_loss = 0
for images, labels in trainloader:
log_ps = model(images)
loss = criterion(log_ps, labels)
## zero grads reset them
optimizer.zero_grad()
loss.backward()
optimizer.step()
running_loss += loss.item()
else:
print("Epoch: ", e)
print(f"Training loss: {running_loss/len(trainloader)}")
%matplotlib inline
%config InlineBackend.figure_format = 'retina'
import helper
# Test out your network!
dataiter = iter(testloader)
images, labels = dataiter.next()
img = images[0]
# Convert 2D image to 1D vector
img = img.resize_(1, 784)
# TODO: Calculate the class probabilities (softmax) for img
ps = torch.exp(model(img))
# Plot the image and probabilities
helper.view_classify(img.resize_(1, 28, 28), ps, version='Fashion')
```
| github_jupyter |
```
# Copyright 2020 Erik Härkönen. All rights reserved.
# This file is licensed to you under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License. You may obtain a copy
# of the License at http://www.apache.org/licenses/LICENSE-2.0
# Unless required by applicable law or agreed to in writing, software distributed under
# the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR REPRESENTATIONS
# OF ANY KIND, either express or implied. See the License for the specific language
# governing permissions and limitations under the License.
# Comparison to GAN steerability and InterfaceGAN
%matplotlib inline
from notebook_init import *
import pickle
out_root = Path('out/figures/steerability_comp')
makedirs(out_root, exist_ok=True)
rand = lambda : np.random.randint(np.iinfo(np.int32).max)
def show_strip(frames):
plt.figure(figsize=(20,20))
plt.axis('off')
plt.imshow(np.hstack(pad_frames(frames, 64)))
plt.show()
normalize = lambda t : t / np.sqrt(np.sum(t.reshape(-1)**2))
def compute(
model,
lat_mean,
prefix,
imgclass,
seeds,
d_ours,
l_start,
l_end,
scale_ours,
d_sup, # single or one per layer
scale_sup,
center=True
):
model.set_output_class(imgclass)
makedirs(out_root / imgclass, exist_ok=True)
for seed in seeds:
print(seed)
deltas = [d_ours, d_sup]
scales = [scale_ours, scale_sup]
ranges = [(l_start, l_end), (0, model.get_max_latents())]
names = ['ours', 'supervised']
for delta, name, scale, l_range in zip(deltas, names, scales, ranges):
lat_base = model.sample_latent(1, seed=seed).cpu().numpy()
# Shift latent to lie on mean along given direction
if center:
y = normalize(d_sup) # assume ground truth
dotp = np.sum((lat_base - lat_mean) * y, axis=-1, keepdims=True)
lat_base = lat_base - dotp * y
# Convert single delta to per-layer delta (to support Steerability StyleGAN)
if delta.shape[0] > 1:
#print('Unstacking delta')
*d_per_layer, = delta # might have per-layer scales, don't normalize
else:
d_per_layer = [normalize(delta)]*model.get_max_latents()
frames = []
n_frames = 5
for a in np.linspace(-1.0, 1.0, n_frames):
w = [lat_base]*model.get_max_latents()
for l in range(l_range[0], l_range[1]):
w[l] = w[l] + a*d_per_layer[l]*scale
frames.append(model.sample_np(w))
for i, frame in enumerate(frames):
Image.fromarray(np.uint8(frame*255)).save(
out_root / imgclass / f'{prefix}_{name}_{seed}_{i}.png')
strip = np.hstack(pad_frames(frames, 64))
plt.figure(figsize=(12,12))
plt.imshow(strip)
plt.axis('off')
plt.tight_layout()
plt.title(f'{prefix} - {name}, scale={scale}')
plt.show()
# BigGAN-512
inst = get_instrumented_model('BigGAN-512', 'husky', 'generator.gen_z', device, inst=inst)
model = inst.model
K = model.get_max_latents()
pc_config = Config(components=128, n=1_000_000,
layer='generator.gen_z', model='BigGAN-512', output_class='husky')
dump_name = get_or_compute(pc_config, inst)
with np.load(dump_name) as data:
lat_comp = data['lat_comp']
lat_mean = data['lat_mean']
with open('data/steerability/biggan_deep_512/gan_steer-linear_zoom_512.pkl', 'rb') as f:
delta_steerability_zoom = pickle.load(f)['w_zoom'].reshape(1, 128)
with open('data/steerability/biggan_deep_512/gan_steer-linear_shiftx_512.pkl', 'rb') as f:
delta_steerability_transl = pickle.load(f)['w_shiftx'].reshape(1, 128)
# Indices determined by visual inspection
delta_ours_transl = lat_comp[0]
delta_ours_zoom = lat_comp[6]
model.truncation = 0.6
compute(model, lat_mean, 'zoom', 'robin', [560157313], delta_ours_zoom, 0, K, -3.0, delta_steerability_zoom, 5.5)
compute(model, lat_mean, 'zoom', 'ship', [107715983], delta_ours_zoom, 0, K, -3.0, delta_steerability_zoom, 5.0)
compute(model, lat_mean, 'translate', 'golden_retriever', [552411435], delta_ours_transl, 0, K, -2.0, delta_steerability_transl, 4.5)
compute(model, lat_mean, 'translate', 'lemon', [331582800], delta_ours_transl, 0, K, -3.0, delta_steerability_transl, 6.0)
# StyleGAN1-ffhq (InterfaceGAN)
inst = get_instrumented_model('StyleGAN', 'ffhq', 'g_mapping', device, use_w=True, inst=inst)
model = inst.model
K = model.get_max_latents()
pc_config = Config(components=128, n=1_000_000, use_w=True,
layer='g_mapping', model='StyleGAN', output_class='ffhq')
dump_name = get_or_compute(pc_config, inst)
with np.load(dump_name) as data:
lat_comp = data['lat_comp']
lat_mean = data['lat_mean']
# SG-ffhq-w, non-conditional
d_ffhq_pose = np.load('data/interfacegan/stylegan_ffhq_pose_w_boundary.npy').astype(np.float32)
d_ffhq_smile = np.load('data/interfacegan/stylegan_ffhq_smile_w_boundary.npy').astype(np.float32)
d_ffhq_gender = np.load('data/interfacegan/stylegan_ffhq_gender_w_boundary.npy').astype(np.float32)
d_ffhq_glasses = np.load('data/interfacegan/stylegan_ffhq_eyeglasses_w_boundary.npy').astype(np.float32)
# Indices determined by visual inspection
d_ours_pose = lat_comp[9]
d_ours_smile = lat_comp[44]
d_ours_gender = lat_comp[0]
d_ours_glasses = lat_comp[12]
model.truncation = 1.0 # NOT IMPLEMENTED
compute(model, lat_mean, 'pose', 'ffhq', [440608316, 1811098088, 129888612], d_ours_pose, 0, 7, -1.0, d_ffhq_pose, 1.0)
compute(model, lat_mean, 'smile', 'ffhq', [1759734403, 1647189561, 70163682], d_ours_smile, 3, 4, -8.5, d_ffhq_smile, 1.0)
compute(model, lat_mean, 'gender', 'ffhq', [1302836080, 1746672325], d_ours_gender, 2, 6, -4.5, d_ffhq_gender, 1.5)
compute(model, lat_mean, 'glasses', 'ffhq', [1565213752, 1005764659, 1110182583], d_ours_glasses, 0, 2, 4.0, d_ffhq_glasses, 1.0)
# StyleGAN1-ffhq (Steerability)
inst = get_instrumented_model('StyleGAN', 'ffhq', 'g_mapping', device, use_w=True, inst=inst)
model = inst.model
K = model.get_max_latents()
pc_config = Config(components=128, n=1_000_000, use_w=True,
layer='g_mapping', model='StyleGAN', output_class='ffhq')
dump_name = get_or_compute(pc_config, inst)
with np.load(dump_name) as data:
lat_comp = data['lat_comp']
lat_mean = data['lat_mean']
# SG-ffhq-w, non-conditional
# Shapes: [18, 512]
d_ffhq_R = np.load('data/steerability/stylegan_ffhq/ffhq_rgb_0.npy').astype(np.float32)
d_ffhq_G = np.load('data/steerability/stylegan_ffhq/ffhq_rgb_1.npy').astype(np.float32)
d_ffhq_B = np.load('data/steerability/stylegan_ffhq/ffhq_rgb_2.npy').astype(np.float32)
# Indices determined by visual inspection
d_ours_R = lat_comp[0]
d_ours_G = -lat_comp[1]
d_ours_B = -lat_comp[2]
model.truncation = 1.0 # NOT IMPLEMENTED
compute(model, lat_mean, 'red', 'ffhq', [5], d_ours_R, 17, 18, 8.0, d_ffhq_R, 1.0, center=False)
compute(model, lat_mean, 'green', 'ffhq', [5], d_ours_G, 17, 18, 15.0, d_ffhq_G, 1.0, center=False)
compute(model, lat_mean, 'blue', 'ffhq', [5], d_ours_B, 17, 18, 10.0, d_ffhq_B, 1.0, center=False)
# StyleGAN1-celebahq (InterfaceGAN)
inst = get_instrumented_model('StyleGAN', 'celebahq', 'g_mapping', device, use_w=True, inst=inst)
model = inst.model
K = model.get_max_latents()
pc_config = Config(components=128, n=1_000_000, use_w=True,
layer='g_mapping', model='StyleGAN', output_class='celebahq')
dump_name = get_or_compute(pc_config, inst)
with np.load(dump_name) as data:
lat_comp = data['lat_comp']
lat_mean = data['lat_mean']
# SG-ffhq-w, non-conditional
d_celebahq_pose = np.load('data/interfacegan/stylegan_celebahq_pose_w_boundary.npy').astype(np.float32)
d_celebahq_smile = np.load('data/interfacegan/stylegan_celebahq_smile_w_boundary.npy').astype(np.float32)
d_celebahq_gender = np.load('data/interfacegan/stylegan_celebahq_gender_w_boundary.npy').astype(np.float32)
d_celebahq_glasses = np.load('data/interfacegan/stylegan_celebahq_eyeglasses_w_boundary.npy').astype(np.float32)
# Indices determined by visual inspection
d_ours_pose = lat_comp[7]
d_ours_smile = lat_comp[14]
d_ours_gender = lat_comp[1]
d_ours_glasses = lat_comp[5]
model.truncation = 1.0 # NOT IMPLEMENTED
compute(model, lat_mean, 'pose', 'celebahq', [1939067252, 1460055449, 329555154], d_ours_pose, 0, 7, -1.0, d_celebahq_pose, 1.0)
compute(model, lat_mean, 'smile', 'celebahq', [329187806, 424805522, 1777796971], d_ours_smile, 3, 4, -7.0, d_celebahq_smile, 1.3)
compute(model, lat_mean, 'gender', 'celebahq', [1144615644, 967075839, 264878205], d_ours_gender, 0, 2, -3.2, d_celebahq_gender, 1.2)
compute(model, lat_mean, 'glasses', 'celebahq', [991993380, 594344173, 2119328990, 1919124025], d_ours_glasses, 0, 1, -10.0, d_celebahq_glasses, 2.0) # hard for both
# StyleGAN1-cars (Steerability)
inst = get_instrumented_model('StyleGAN', 'cars', 'g_mapping', device, use_w=True, inst=inst)
model = inst.model
K = model.get_max_latents()
pc_config = Config(components=128, n=1_000_000, use_w=True,
layer='g_mapping', model='StyleGAN', output_class='cars')
dump_name = get_or_compute(pc_config, inst)
with np.load(dump_name) as data:
lat_comp = data['lat_comp']
lat_mean = data['lat_mean']
# Shapes: [16, 512]
d_cars_rot = np.load('data/steerability/stylegan_cars/rotate2d.npy').astype(np.float32)
d_cars_shift = np.load('data/steerability/stylegan_cars/shifty.npy').astype(np.float32)
# Add two final layers
d_cars_rot = np.append(d_cars_rot, np.zeros((2,512), dtype=np.float32), axis=0)
d_cars_shift = np.append(d_cars_shift, np.zeros((2,512), dtype=np.float32), axis=0)
print(d_cars_rot.shape)
# Indices determined by visual inspection
d_ours_rot = lat_comp[0]
d_ours_shift = lat_comp[7]
model.truncation = 1.0 # NOT IMPLEMENTED
compute(model, lat_mean, 'rotate2d', 'cars', [46, 28], d_ours_rot, 0, 1, 1.0, d_cars_rot, 1.0, center=False)
compute(model, lat_mean, 'shifty', 'cars', [0, 13], d_ours_shift, 1, 2, 4.0, d_cars_shift, 1.0, center=False)
```
| github_jupyter |
# Importing Dependencies
```
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import pandas_datareader
import pandas_datareader.data as web
import datetime
from sklearn.preprocessing import MinMaxScaler
from keras.models import Sequential
from keras.layers import Dense,LSTM,Dropout
%matplotlib inline
```
# Importing Data
```
start = datetime.datetime(2016,1,1)
end = datetime.datetime(2021,1,1)
QQQ = web.DataReader("QQQ", "yahoo", start, end)
QQQ.head()
QQQ['Close'].plot(label = 'QQQ', figsize = (16,10), title = 'Closing Price')
plt.legend();
QQQ['Volume'].plot(label = 'QQQ', figsize = (16,10), title = 'Volume Traded')
plt.legend();
QQQ['MA50'] = QQQ['Close'].rolling(50).mean()
QQQ['MA200'] = QQQ['Close'].rolling(200).mean()
QQQ[['Close','MA50','MA200']].plot(figsize = (16,10), title = 'Moving Averages')
```
# Selecting The Close Column
```
QQQ["Close"]=pd.to_numeric(QQQ.Close,errors='coerce') #turning the Close column to numeric
QQQ = QQQ.dropna()
trainData = QQQ.iloc[:,3:4].values #selecting closing prices for training
```
# Scaling Values in the Range of 0-1 for Best Results
```
sc = MinMaxScaler(feature_range=(0,1))
trainData = sc.fit_transform(trainData)
trainData.shape
```
# Prepping Data for LSTM
```
X_train = []
y_train = []
for i in range (60,1060):
X_train.append(trainData[i-60:i,0])
y_train.append(trainData[i,0])
X_train,y_train = np.array(X_train),np.array(y_train)
X_train = np.reshape(X_train,(X_train.shape[0],X_train.shape[1],1)) #adding the batch_size axis
X_train.shape
```
# Building The Model
```
model = Sequential()
model.add(LSTM(units=100, return_sequences = True, input_shape =(X_train.shape[1],1)))
model.add(Dropout(0.2))
model.add(LSTM(units=100, return_sequences = True))
model.add(Dropout(0.2))
model.add(LSTM(units=100, return_sequences = True))
model.add(Dropout(0.2))
model.add(LSTM(units=100, return_sequences = False))
model.add(Dropout(0.2))
model.add(Dense(units =1))
model.compile(optimizer='adam',loss="mean_squared_error")
hist = model.fit(X_train, y_train, epochs = 20, batch_size = 32, verbose=2)
```
# Plotting The Training Loss
```
plt.plot(hist.history['loss'])
plt.title('model loss')
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train'], loc='upper left')
plt.show()
```
# Testing Model on New Data
```
start = datetime.datetime(2021,1,1)
end = datetime.datetime.today()
testData = web.DataReader("QQQ", "yahoo", start, end) #importing new data for testing
testData["Close"]=pd.to_numeric(testData.Close,errors='coerce') #turning the Close column to numeric
testData = testData.dropna() #droping the NA values
testData = testData.iloc[:,3:4] #selecting the closing prices for testing
y_test = testData.iloc[60:,0:].values #selecting the labels
#input array for the model
inputClosing = testData.iloc[:,0:].values
inputClosing_scaled = sc.transform(inputClosing)
inputClosing_scaled.shape
X_test = []
length = len(testData)
timestep = 60
for i in range(timestep,length):
X_test.append(inputClosing_scaled[i-timestep:i,0])
X_test = np.array(X_test)
X_test = np.reshape(X_test,(X_test.shape[0],X_test.shape[1],1))
X_test.shape
y_pred = model.predict(X_test) #predicting values
predicted_price = sc.inverse_transform(y_pred) #inversing the scaling transformation for plotting
```
# Plotting Results
```
plt.plot(y_test, color = 'blue', label = 'Actual Stock Price')
plt.plot(predicted_price, color = 'red', label = 'Predicted Stock Price')
plt.title('QQQ stock price prediction')
plt.xlabel('Time')
plt.ylabel('Stock Price')
plt.legend()
plt.show()
```
| github_jupyter |
# Hyperparameter tuning with Cloud AI Platform
**Learning Objectives:**
* Improve the accuracy of a model by hyperparameter tuning
```
import os
PROJECT = 'qwiklabs-gcp-faf328caac1ef9a0' # REPLACE WITH YOUR PROJECT ID
BUCKET = 'qwiklabs-gcp-faf328caac1ef9a0' # REPLACE WITH YOUR BUCKET NAME
REGION = 'us-east1' # REPLACE WITH YOUR BUCKET REGION e.g. us-central1
# for bash
os.environ['PROJECT'] = PROJECT
os.environ['BUCKET'] = BUCKET
os.environ['REGION'] = REGION
os.environ['TFVERSION'] = '1.8' # Tensorflow version
%%bash
gcloud config set project $PROJECT
gcloud config set compute/region $REGION
```
## Create command-line program
In order to submit to Cloud AI Platform, we need to create a distributed training program. Let's convert our housing example to fit that paradigm, using the Estimators API.
```
%%bash
rm -rf house_prediction_module
mkdir house_prediction_module
mkdir house_prediction_module/trainer
touch house_prediction_module/trainer/__init__.py
%%writefile house_prediction_module/trainer/task.py
import argparse
import os
import json
import shutil
from . import model
if __name__ == '__main__' and "get_ipython" not in dir():
parser = argparse.ArgumentParser()
parser.add_argument(
'--learning_rate',
type = float,
default = 0.01
)
parser.add_argument(
'--batch_size',
type = int,
default = 30
)
parser.add_argument(
'--output_dir',
help = 'GCS location to write checkpoints and export models.',
required = True
)
parser.add_argument(
'--job-dir',
help = 'this model ignores this field, but it is required by gcloud',
default = 'junk'
)
args = parser.parse_args()
arguments = args.__dict__
# Unused args provided by service
arguments.pop('job_dir', None)
arguments.pop('job-dir', None)
# Append trial_id to path if we are doing hptuning
# This code can be removed if you are not using hyperparameter tuning
arguments['output_dir'] = os.path.join(
arguments['output_dir'],
json.loads(
os.environ.get('TF_CONFIG', '{}')
).get('task', {}).get('trial', '')
)
# Run the training
shutil.rmtree(arguments['output_dir'], ignore_errors=True) # start fresh each time
# Pass the command line arguments to our model's train_and_evaluate function
model.train_and_evaluate(arguments)
%%writefile house_prediction_module/trainer/model.py
import numpy as np
import pandas as pd
import tensorflow as tf
tf.logging.set_verbosity(tf.logging.INFO)
# Read dataset and split into train and eval
df = pd.read_csv("https://storage.googleapis.com/ml_universities/california_housing_train.csv", sep = ",")
df['num_rooms'] = df['total_rooms'] / df['households']
np.random.seed(seed = 1) #makes split reproducible
msk = np.random.rand(len(df)) < 0.8
traindf = df[msk]
evaldf = df[~msk]
# Train and eval input functions
SCALE = 100000
def train_input_fn(df, batch_size):
return tf.estimator.inputs.pandas_input_fn(x = traindf[["num_rooms"]],
y = traindf["median_house_value"] / SCALE, # note the scaling
num_epochs = None,
batch_size = batch_size, # note the batch size
shuffle = True)
def eval_input_fn(df, batch_size):
return tf.estimator.inputs.pandas_input_fn(x = evaldf[["num_rooms"]],
y = evaldf["median_house_value"] / SCALE, # note the scaling
num_epochs = 1,
batch_size = batch_size,
shuffle = False)
# Define feature columns
features = [tf.feature_column.numeric_column('num_rooms')]
def train_and_evaluate(args):
# Compute appropriate number of steps
num_steps = (len(traindf) / args['batch_size']) / args['learning_rate'] # if learning_rate=0.01, hundred epochs
# Create custom optimizer
myopt = tf.train.FtrlOptimizer(learning_rate = args['learning_rate']) # note the learning rate
# Create rest of the estimator as usual
estimator = tf.estimator.LinearRegressor(model_dir = args['output_dir'],
feature_columns = features,
optimizer = myopt)
#Add rmse evaluation metric
def rmse(labels, predictions):
pred_values = tf.cast(predictions['predictions'], tf.float64)
return {'rmse': tf.metrics.root_mean_squared_error(labels * SCALE, pred_values * SCALE)}
estimator = tf.contrib.estimator.add_metrics(estimator, rmse)
train_spec = tf.estimator.TrainSpec(input_fn = train_input_fn(df = traindf, batch_size = args['batch_size']),
max_steps = num_steps)
eval_spec = tf.estimator.EvalSpec(input_fn = eval_input_fn(df = evaldf, batch_size = len(evaldf)),
steps = None)
tf.estimator.train_and_evaluate(estimator, train_spec, eval_spec)
%%bash
rm -rf house_trained
export PYTHONPATH=${PYTHONPATH}:${PWD}/house_prediction_module
gcloud ai-platform local train \
--module-name=trainer.task \
--job-dir=house_trained \
--package-path=$(pwd)/trainer \
-- \
--batch_size=30 \
--learning_rate=0.02 \
--output_dir=house_trained
```
# Create hyperparam.yaml
```
%%writefile hyperparam.yaml
trainingInput:
hyperparameters:
goal: MINIMIZE
maxTrials: 5
maxParallelTrials: 1
hyperparameterMetricTag: rmse
params:
- parameterName: batch_size
type: INTEGER
minValue: 8
maxValue: 64
scaleType: UNIT_LINEAR_SCALE
- parameterName: learning_rate
type: DOUBLE
minValue: 0.01
maxValue: 0.1
scaleType: UNIT_LOG_SCALE
%%bash
OUTDIR=gs://${BUCKET}/house_trained # CHANGE bucket name appropriately
gsutil rm -rf $OUTDIR
export PYTHONPATH=${PYTHONPATH}:${PWD}/house_prediction_module
gcloud ai-platform jobs submit training house_$(date -u +%y%m%d_%H%M%S) \
--config=hyperparam.yaml \
--module-name=trainer.task \
--package-path=$(pwd)/house_prediction_module/trainer \
--job-dir=$OUTDIR \
--runtime-version=$TFVERSION \
--\
--output_dir=$OUTDIR \
!gcloud ai-platform jobs describe house_190809_204253 # CHANGE jobId appropriately
```
## Challenge exercise
Add a few engineered features to the housing model, and use hyperparameter tuning to choose which set of features the model uses.
<p>
Copyright 2018 Google Inc. Licensed under the Apache License, Version 2.0 (the "License"); you may not use this file except in compliance with the License. You may obtain a copy of the License at http://www.apache.org/licenses/LICENSE-2.0 Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an "AS IS" BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License
| github_jupyter |
# Köhn
In this notebook I replicate Koehn (2015): _What's in an embedding? Analyzing word embeddings through multilingual evaluation_. This paper proposes to i) evaluate an embedding method on more than one language, and ii) evaluate an embedding model by how well its embeddings capture syntactic features. He uses an L2-regularized linear classifier, with an upper baseline that assigns the most frequent class. He finds that most methods perform similarly on this task, but that dependency based embeddings perform better. Dependency based embeddings particularly perform better when you decrease the dimensionality. Overall, the aim is to have an evalation method that tells you something about the structure of the learnt representations. He evaulates a range of different models on their ability to capture a number of different morphosyntactic features in a bunch of languages.
**Embedding models tested:**
- cbow
- skip-gram
- glove
- dep
- cca
- brown
**Features tested:**
- pos
- headpos (the pos of the word's head)
- label
- gender
- case
- number
- tense
**Languages tested:**
- Basque
- English
- French
- German
- Hungarian
- Polish
- Swedish
Word embeddings were trained on automatically PoS-tagged and dependency-parsed data using existing models. This is so the dependency-based embeddings can be trained. The evaluation is on hand-labelled data. English training data is a subset of Wikipedia; English test data comes from PTB. For all other languages, both the training and test data come from a shared task on parsing morphologically rich languages. Koehn trained embeddings with window size 5 and 11 and dimensionality 10, 100, 200.
Dependency-based embeddings perform the best on almost all tasks. They even do well when the dimensionality is reduced to 10, while other methods perform poorly in this case.
I'll need:
- models
- learnt representations
- automatically labeled data
- hand-labeled data
```
%matplotlib inline
import os
import csv
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
from sklearn.linear_model import LogisticRegression, LogisticRegressionCV
from sklearn.model_selection import train_test_split, StratifiedKFold
from sklearn.metrics import roc_curve, roc_auc_score, classification_report, confusion_matrix
from sklearn.preprocessing import LabelEncoder
data_path = '../../data'
tmp_path = '../../tmp'
```
## Learnt representations
### GloVe
```
size = 50
fname = 'embeddings/glove.6B.{}d.txt'.format(size)
glove_path = os.path.join(data_path, fname)
glove = pd.read_csv(glove_path, sep=' ', header=None, index_col=0, quoting=csv.QUOTE_NONE)
glove.head()
```
## Features
```
fname = 'UD_English/features.csv'
features_path = os.path.join(data_path, os.path.join('evaluation/dependency', fname))
features = pd.read_csv(features_path).set_index('form')
features.head()
df = pd.merge(glove, features, how='inner', left_index=True, right_index=True)
df.head()
```
## Prediction
```
def prepare_X_and_y(feature, data):
"""Return X and y ready for predicting feature from embeddings."""
relevant_data = data[data[feature].notnull()]
columns = list(range(1, size+1))
X = relevant_data[columns]
y = relevant_data[feature]
train = relevant_data['set'] == 'train'
test = (relevant_data['set'] == 'test') | (relevant_data['set'] == 'dev')
X_train, X_test = X[train].values, X[test].values
y_train, y_test = y[train].values, y[test].values
return X_train, X_test, y_train, y_test
def predict(model, X_test):
"""Wrapper for getting predictions."""
results = model.predict_proba(X_test)
return np.array([t for f,t in results]).reshape(-1,1)
def conmat(model, X_test, y_test):
"""Wrapper for sklearn's confusion matrix."""
y_pred = model.predict(X_test)
c = confusion_matrix(y_test, y_pred)
sns.heatmap(c, annot=True, fmt='d',
xticklabels=model.classes_,
yticklabels=model.classes_,
cmap="YlGnBu", cbar=False)
plt.ylabel('Ground truth')
plt.xlabel('Prediction')
def draw_roc(model, X_test, y_test):
"""Convenience function to draw ROC curve."""
y_pred = predict(model, X_test)
fpr, tpr, thresholds = roc_curve(y_test, y_pred)
roc = roc_auc_score(y_test, y_pred)
label = r'$AUC={}$'.format(str(round(roc, 3)))
plt.plot(fpr, tpr, label=label);
plt.title('ROC')
plt.xlabel('False positive rate');
plt.ylabel('True positive rate');
plt.legend();
def cross_val_auc(model, X, y):
for _ in range(5):
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, stratify=y)
model = model.fit(X_train, y_train)
draw_roc(model, X_test, y_test)
X_train, X_test, y_train, y_test = prepare_X_and_y('Tense', df)
model = LogisticRegression(penalty='l2', solver='liblinear')
model = model.fit(X_train, y_train)
conmat(model, X_test, y_test)
sns.distplot(model.coef_[0], rug=True, kde=False);
```
# Hyperparameter optimization before error analysis
| github_jupyter |
```
# In this exercise you will train a CNN on the FULL Cats-v-dogs dataset
# This will require you doing a lot of data preprocessing because
# the dataset isn't split into training and validation for you
# This code block has all the required inputs
import os
import zipfile
import random
import tensorflow as tf
from tensorflow.keras.optimizers import RMSprop
from tensorflow.keras.preprocessing.image import ImageDataGenerator
from shutil import copyfile
# This code block downloads the full Cats-v-Dogs dataset and stores it as
# cats-and-dogs.zip. It then unzips it to /tmp
# which will create a tmp/PetImages directory containing subdirectories
# called 'Cat' and 'Dog' (that's how the original researchers structured it)
# If the URL doesn't work,
# . visit https://www.microsoft.com/en-us/download/confirmation.aspx?id=54765
# And right click on the 'Download Manually' link to get a new URL
!wget --no-check-certificate \
"https://download.microsoft.com/download/3/E/1/3E1C3F21-ECDB-4869-8368-6DEBA77B919F/kagglecatsanddogs_3367a.zip" \
-O "/tmp/cats-and-dogs.zip"
local_zip = '/tmp/cats-and-dogs.zip'
zip_ref = zipfile.ZipFile(local_zip, 'r')
zip_ref.extractall('/tmp')
zip_ref.close()
print(len(os.listdir('/tmp/PetImages/Cat/')))
print(len(os.listdir('/tmp/PetImages/Dog/')))
# Expected Output:
# 12501
# 12501
# Use os.mkdir to create your directories
# You will need a directory for cats-v-dogs, and subdirectories for training
# and testing. These in turn will need subdirectories for 'cats' and 'dogs'
try:
os.mkdir("/tmp/cats-v-dogs")
os.mkdir("/tmp/cats-v-dogs/training")
os.mkdir("/tmp/cats-v-dogs/testing")
os.mkdir("/tmp/cats-v-dogs/training/dogs")
os.mkdir("/tmp/cats-v-dogs/training/cats")
os.mkdir("/tmp/cats-v-dogs/testing/dogs")
os.mkdir("/tmp/cats-v-dogs/testing/cats")
except OSError:
pass
# Write a python function called split_data which takes
# a SOURCE directory containing the files
# a TRAINING directory that a portion of the files will be copied to
# a TESTING directory that a portion of the files will be copied to
# a SPLIT SIZE to determine the portion
# The files should also be randomized, so that the training set is a random
# X% of the files, and the test set is the remaining files
# SO, for example, if SOURCE is PetImages/Cat, and SPLIT SIZE is .9
# Then 90% of the images in PetImages/Cat will be copied to the TRAINING dir
# and 10% of the images will be copied to the TESTING dir
# Also -- All images should be checked, and if they have a zero file length,
# they will not be copied over
#
# os.listdir(DIRECTORY) gives you a listing of the contents of that directory
# os.path.getsize(PATH) gives you the size of the file
# copyfile(source, destination) copies a file from source to destination
# random.sample(list, len(list)) shuffles a list
def split_data(SOURCE, TRAINING, TESTING, SPLIT_SIZE):
files = []
for filename in os.listdir(SOURCE):
file = SOURCE + filename
if os.path.getsize(file) > 0:
files.append(filename)
else:
print (filename + " is zero length, so ignoring.")
training_length = int(len(files) * SPLIT_SIZE)
testing_length = int(len(files) - training_length)
shuffled_set = random.sample(files, len(files))
training_set = shuffled_set[0:training_length]
testing_set = shuffled_set[-testing_length:]
for filename in training_set:
src = SOURCE + filename
dst = TRAINING + filename
copyfile(src, dst)
for filename in testing_set:
src = SOURCE + filename
dst = TESTING + filename
copyfile(src, dst)
CAT_SOURCE_DIR = "/tmp/PetImages/Cat/"
TRAINING_CATS_DIR = "/tmp/cats-v-dogs/training/cats/"
TESTING_CATS_DIR = "/tmp/cats-v-dogs/testing/cats/"
DOG_SOURCE_DIR = "/tmp/PetImages/Dog/"
TRAINING_DOGS_DIR = "/tmp/cats-v-dogs/training/dogs/"
TESTING_DOGS_DIR = "/tmp/cats-v-dogs/testing/dogs/"
split_size = .9
split_data(CAT_SOURCE_DIR, TRAINING_CATS_DIR, TESTING_CATS_DIR, split_size)
split_data(DOG_SOURCE_DIR, TRAINING_DOGS_DIR, TESTING_DOGS_DIR, split_size)
# Expected output
# 666.jpg is zero length, so ignoring
# 11702.jpg is zero length, so ignoring
print(len(os.listdir('/tmp/cats-v-dogs/training/cats/')))
print(len(os.listdir('/tmp/cats-v-dogs/training/dogs/')))
print(len(os.listdir('/tmp/cats-v-dogs/testing/cats/')))
print(len(os.listdir('/tmp/cats-v-dogs/testing/dogs/')))
# Expected output:
# 11250
# 11250
# 1250
# 1250
# DEFINE A KERAS MODEL TO CLASSIFY CATS V DOGS
# USE AT LEAST 3 CONVOLUTION LAYERS
model = tf.keras.models.Sequential([
tf.keras.layers.Conv2D(16, (3,3), activation='relu', input_shape=(150,150,3)),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(32, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Conv2D(64, (3,3), activation='relu'),
tf.keras.layers.MaxPooling2D(2,2),
tf.keras.layers.Flatten(),
tf.keras.layers.Dense(512, activation='relu'),
tf.keras.layers.Dense(1, activation='sigmoid')
])
model.compile(optimizer=RMSprop(lr=0.001),
loss='binary_crossentropy',
metrics=['acc'])
TRAINING_DIR = "/tmp/cats-v-dogs/training/"
train_datagen = ImageDataGenerator(rescale=1./255)
train_generator = train_datagen.flow_from_directory(TRAINING_DIR,
batch_size=100,
class_mode='binary',
target_size=(150,150))
VALIDATION_DIR = "/tmp/cats-v-dogs/testing/"
validation_datagen = ImageDataGenerator(rescale=1./255)
validation_generator = train_datagen.flow_from_directory(VALIDATION_DIR,
batch_size=10,
class_mode='binary',
target_size=(150,150))
# Expected Output:
# Found 22498 images belonging to 2 classes.
# Found 2500 images belonging to 2 classes.
history = model.fit_generator(train_generator,
epochs=15,
verbose=1,
validation_data=validation_generator)
# The expectation here is that the model will train, and that accuracy will be > 95% on both training and validation
# i.e. acc:A1 and val_acc:A2 will be visible, and both A1 and A2 will be > .9
# PLOT LOSS AND ACCURACY
%matplotlib inline
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
#-----------------------------------------------------------
# Retrieve a list of list results on training and test data
# sets for each training epoch
#-----------------------------------------------------------
acc=history.history['acc']
val_acc=history.history['val_acc']
loss=history.history['loss']
val_loss=history.history['val_loss']
epochs=range(len(acc)) # Get number of epochs
#------------------------------------------------
# Plot training and validation accuracy per epoch
#------------------------------------------------
plt.plot(epochs, acc, 'r', "Training Accuracy")
plt.plot(epochs, val_acc, 'b', "Validation Accuracy")
plt.title('Training and validation accuracy')
plt.figure()
#------------------------------------------------
# Plot training and validation loss per epoch
#------------------------------------------------
plt.plot(epochs, loss, 'r', "Training Loss")
plt.plot(epochs, val_loss, 'b', "Validation Loss")
plt.title('Training and validation loss')
# Desired output. Charts with training and validation metrics. No crash :)
# Here's a codeblock just for fun. You should be able to upload an image here
# and have it classified without crashing
import numpy as np
from google.colab import files
from keras.preprocessing import image
uploaded = files.upload()
for fn in uploaded.keys():
# predicting images
path = '/content/' + fn
img = image.load_img(path, target_size=(# YOUR CODE HERE))
x = image.img_to_array(img)
x = np.expand_dims(x, axis=0)
images = np.vstack([x])
classes = model.predict(images, batch_size=10)
print(classes[0])
if classes[0]>0.5:
print(fn + " is a dog")
else:
print(fn + " is a cat")
```
| github_jupyter |
```
# Confidence interval and bias comparison in the multi-armed bandit
# setting of https://arxiv.org/pdf/1507.08025.pdf
import numpy as np
import pandas as pd
import scipy.stats as stats
import time
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set(style='white', palette='colorblind', color_codes=True)
#
# Experiment parameters
#
# Set random seed for reproducibility
seed = 1234
np.random.seed(seed)
# Trial repetitions (number of times experiment is repeated)
R = 5000
# Trial size (total number of arm pulls)
T = 1000
# Number of arms
K = 2
# Noise distribution: 2*beta(alph, alph) - 1
noise_param = 1.0 # uniform distribution
# Parameters of Gaussian distribution prior on each arm
mu0 = 0.4 # prior mean
var0 = 1/(2*noise_param + 1.0) # prior variance set to correct value
# Select reward means for each arm and set variance
reward_means = np.concatenate([np.repeat(.3, K-1), [.30]])
reward_vars = np.repeat(var0, K)
# Select probability of choosing current belief in epsilon greedy policy
ECB_epsilon = .1
#
# Evaluation parameters
#
# Confidence levels for confidence regions
confidence_levels = np.arange(0.9, 1.0, step=0.01)
# Standard normal error thresholds for two-sided (univariate) intervals with given confidence level
gaussian_thresholds_ts = -stats.norm.ppf((1.0-confidence_levels)/2.0)
gaussian_thresholds_os = -stats.norm.ppf(1.0-confidence_levels)
print gaussian_thresholds_ts
print gaussian_thresholds_os
#
# Define arm selection policies
#
policies = {}
# Epsilon-greedy: select current belief (arm with highest posterior reward
# probability) w.p. 1-epsilon and arm uniformly at random otherwise
def ECB(mu_post, var_post, epsilon=ECB_epsilon):
# Determine whether to select current belief by flipping biased coin
use_cb = np.random.binomial(1, 1.0-epsilon)
if use_cb:
# Select arm with highest posterior reward probability
arm = np.argmax(mu_post)
else:
# Select arm uniformly at random
arm = np.random.choice(xrange(K))
return arm
policies['ECB'] = ECB
# Current belief: select arm with highest posterior probability
def CB(mu_post, var_post):
return ECB(mu_post, var_post, epsilon=0.0)
# policies['CB'] = CB
# Fixed randomized design: each arm selected independently and uniformly
def FR(mu_post, var_post, epsilon=ECB_epsilon):
return ECB(mu_post, var_post, epsilon=1.0)
policies['FR'] = FR
# Thompson sampling: select arm k with probability proportional to P(arm k has highest reward | data)^c
# where c = 1 and P(arm k has highest reward | data) is the posterior probability that arm k has
# the highest reward
# TODO: the paper uses c = t/(2T) instead, citing Thall and Wathen (2007); investigate how to achieve this efficiently
def TS(mu_post, var_post, epsilon=ECB_epsilon):
# Draw a sample from each arm's posterior
samples = np.random.normal(mu_post, np.sqrt(var_post))
# Select an arm with the largest sample
arm = np.argmax(samples)
return arm
policies['TS'] = TS
def lilUCB(mu_post, var_post, epsilon=ECB_epsilon ):
#define lilUCB params, see Jamieson et al 2013
# use 1/variance as number of times the arm is tried.
# at time t, choose arm k that maximizes:
# muhat_k(t) + (1+beta)*(1+sqrt(eps))*sqrt{2(1+eps)/T_k}*sqrt{log(1/delta) + log(log((1+eps)*T_k))}
# where muhat_k (t) is sample mean of k^th arm at time t and T_k = T_k(t) is the number of times arm k is tried
# up toa time t
epsilonUCB = 0.01
betaUCB = 0.5
aUCB = 1+ 2/betaUCB
deltaUCB = 0.01
lilFactorUCB = np.log(1/deltaUCB) + np.log(np.log((1+epsilonUCB)/var_post))
scoresUCB = mu_post + (1+betaUCB)*(1+np.sqrt(epsilonUCB))*np.sqrt((2+2*epsilonUCB)*lilFactorUCB*var_post)
arm = np.argmax(scoresUCB)
return arm
policies['UCB'] = lilUCB
#
# Gather data: Generate arm pulls and rewards using different policies
#
tic = time.time()
arms = []
rewards = []
for r in xrange(R):
arms.append(pd.DataFrame(index=range(0,T)))
rewards.append(pd.DataFrame(index=range(0,T)))
# Keep track of posterior beta parameters for each arm
mu_post = np.repeat(mu0, K)
var_post = np.repeat(var0, K)
for policy in policies.keys():
# Ensure arms column has integer type by initializing with integer value
arms[r][policy] = 0
for t in range(T):
if t < K:
# Ensure each arm selected at least once
arm = t
else:
# Select an arm according to policy
arm = policies[policy](mu_post, var_post, epsilon = ECB_epsilon)
# Collect reward from selected arm
reward = 2*np.random.beta(noise_param, noise_param) - 1.0 + reward_means[arm]
# Update Gaussian posterior
new_var = 1.0/(1.0/var_post[arm] + 1.0/reward_vars[arm])
mu_post[arm] = (mu_post[arm]/var_post[arm] + reward/reward_vars[arm])*new_var
var_post[arm] = new_var
# Store results
arms[r].set_value(t, policy, arm)
rewards[r].set_value(t, policy, reward)
print "{}s elapsed".format(time.time()-tic)
# Inspect arm selections
print arms[0][0:min(10,T)]
# Display some summary statistics for the collected data
pct_arm_counts={}
for policy in arms[0].keys():
print policy
pct_arm_counts[policy] = np.percentile([arms[r][policy].groupby(arms[r][policy]).size().values \
for r in xrange(R)],15, axis=0)
pct_arm_counts
# compute statistics for arm distributions
n_arm1 = {}
for policy in policies:
n_arm1[policy] = np.zeros(R)
for ix, run in enumerate(arms):
for policy in policies:
n_arm1[policy][ix] = sum(run[policy])
#plot histograms of arm distributions for each policy
policies = ['UCB', 'ECB', 'TS']
policy = 'ECB'
for ix, policy in enumerate(policies):
fig, ax = plt.subplots(1, figsize=(5.5, 4))
ax.set_title(policy, fontsize=title_font_size, fontweight='bold')
sns.distplot(n_arm1[policy]/T,
kde=False,
bins=20,
norm_hist=True,
ax=ax,
hist_kws=dict(alpha=0.8)
)
fig.savefig(path+'mab_{}_armdist'.format(policy))
plt.show()
#
# Form estimates: For each method, compute reward probability estimates and
# single-parameter error thresholds for confidence intervals
#
tic = time.time()
estimates = []
thresholds_ts = []
thresholds_os = []
normalized_errors = []
for r in xrange(R):
estimates.append({})
thresholds_ts.append({})
thresholds_os.append({})
normalized_errors.append({})
for policy in arms[r].columns:
# Create list of estimates and confidence regions for this policy
estimates[r][policy] = {}
thresholds_ts[r][policy] = {}
thresholds_os[r][policy] = {}
normalized_errors[r][policy] = {}
# OLS with asymptotic Gaussian confidence
#
# Compute estimates of arm reward probabilities
estimates[r][policy]['OLS_gsn'] = rewards[r][policy].groupby(arms[r][policy]).mean().values
# Asymptotic marginal variances diag((X^tX)^{-1})
arm_counts = arms[r][policy].groupby(arms[r][policy]).size().values
variances = reward_vars / arm_counts
# compute normalized errors
normalized_errors[r][policy]['OLS_gsn'] = (estimates[r][policy]['OLS_gsn'] - reward_means)/np.sqrt(variances)
# Compute asymptotic Gaussian single-parameter confidence thresholds
thresholds_ts[r][policy]['OLS_gsn'] = np.outer(np.sqrt(variances), gaussian_thresholds_ts)
thresholds_os[r][policy]['OLS_gsn'] = np.outer(np.sqrt(variances), gaussian_thresholds_os)
#
# OLS with concentration inequality confidence
#
# Compute estimates of arm reward probabilities
estimates[r][policy]['OLS_conc'] = np.copy(estimates[r][policy]['OLS_gsn'])
normalized_errors[r][policy]['OLS_conc'] = (estimates[r][policy]['OLS_gsn'] - reward_means)/np.sqrt(variances)
# Compute single-parameter confidence intervals using concentration inequalities
# of https://arxiv.org/pdf/1102.2670.pdf Sec. 4
# threshold_ts = sqrt(reward_vars) * sqrt((1+N_k)/N_k^2 * (1+2*log(sqrt(1+N_k)/delta)))
thresholds_ts[r][policy]['OLS_conc'] = np.sqrt(reward_vars/reward_vars)[:,None] * np.concatenate([
np.sqrt(((1.0+arm_counts)/arm_counts**2) * (1+2*np.log(np.sqrt(1.0+arm_counts)/(1-c))))[:,None]
for c in confidence_levels], axis=1)
thresholds_os[r][policy]['OLS_conc'] = np.copy(thresholds_ts[r][policy]['OLS_conc'])
#
# W estimate with asymptotic Gaussian confidence
# Y: using lambda_min = min_median_arm_count/log(T) as W_Lambdas
# avg_arm_counts = pct_arm_counts[policy]/log(T)
W_lambdas = np.ones(T)*min(pct_arm_counts[policy])/np.log(T)
# Latest parameter estimate vector
beta = np.copy(estimates[r][policy]['OLS_gsn']) ###
# Latest w_t vector
w = np.zeros((K))
# Latest matrix W_tX_t = w_1 x_1^T + ... + w_t x_t^T
WX = np.zeros((K,K))
# Latest vector of marginal variances reward_vars * (w_1**2 + ... + w_t**2)
variances = np.zeros(K)
for t in range(T):
# x_t = e_{arm}
arm = arms[r][policy][t]
# y_t = reward
reward = rewards[r][policy][t]
# Update w_t = (1/(norm{x_t}^2+lambda_t)) (x_t - W_{t-1} X_{t-1} x_t)
np.copyto(w, -WX[:,arm])
w[arm] += 1
w /= (1.0+W_lambdas[t])
# Update beta_t = beta_{t-1} + w_t (y_t - <beta_OLS, x_t>)
beta += w * (reward - estimates[r][policy]['OLS_gsn'][arm]) ###
# Update W_tX_t = W_{t-1}X_{t-1} + w_t x_t^T
WX[:,arm] += w
# Update marginal variances
variances += reward_vars * w**2
estimates[r][policy]['W'] = beta
normalized_errors[r][policy]['W'] = (estimates[r][policy]['W'] - reward_means)/np.sqrt(variances)
# Compute asymptotic Gaussian single-parameter confidence thresholds and coverage
thresholds_ts[r][policy]['W'] = np.outer(np.sqrt(variances), gaussian_thresholds_ts)
thresholds_os[r][policy]['W'] = np.outer(np.sqrt(variances), gaussian_thresholds_os)
print "{}s elapsed".format(time.time()-tic)
# Display some summary statistics concerning the model estimates
if False:
for policy in ["ECB","TS"]:#arms[0].keys():
for method in estimates[0][policy].keys():
print "{} {}".format(policy, method)
print "average estimate: {}".format(np.mean([estimates[r][policy][method] for r in xrange(R)], axis=0))
print "average threshold:\n{}".format(np.mean([thresholds_os[r][policy][method] for r in xrange(R)], axis=0))
print ""
#
# Evaluate estimates: For each policy and method, compute confidence interval
# coverage probability and width
#
tic = time.time()
coverage = [] # Check if truth in [estimate +/- thresh]
upper_coverage = [] # Check if truth >= estimate - thresh
lower_coverage = [] # Check if truth <= estimate + thresh
upper_sum_coverage = [] # Check if beta_2 - beta_1 >= estimate - thresh
lower_sum_coverage = [] # Check if beta_2 - beta_1 <= estimate + thresh
sum_norm = [] # compute (betahat_2 - beta_2 - betahat_1 + beta_1 ) / sqrt(variance_2 + variance_1)
for r in xrange(R):
coverage.append({})
upper_coverage.append({})
lower_coverage.append({})
upper_sum_coverage.append({})
lower_sum_coverage.append({})
sum_norm.append({})
for policy in estimates[r].keys():
# Interval coverage for each method
coverage[r][policy] = {}
upper_coverage[r][policy] = {}
lower_coverage[r][policy] = {}
upper_sum_coverage[r][policy] = {}
lower_sum_coverage[r][policy] = {}
sum_norm[r][policy] = {}
for method in estimates[r][policy].keys():
# Compute error of estimate
error = estimates[r][policy][method] - reward_means
# compute normalized sum
# first compute arm variances
stddevs = thresholds_os[r][policy][method].dot(gaussian_thresholds_os)/gaussian_thresholds_os.dot(gaussian_thresholds_os)
variances = stddevs**2
sum_norm[r][policy][method] = (error[0] + error[1])/np.sqrt(variances[0] + variances[1])
# Compute coverage of interval
coverage[r][policy][method] = np.absolute(error)[:,None] <= thresholds_ts[r][policy][method]
upper_coverage[r][policy][method] = error[:,None] <= thresholds_os[r][policy][method]
lower_coverage[r][policy][method] = error[:,None] >= -thresholds_os[r][policy][method]
upper_sum_coverage[r][policy][method] = error[1]+error[0] <= np.sqrt((thresholds_os[r][policy][method]**2).sum(axis=0))
lower_sum_coverage[r][policy][method] = error[1]+error[0] >= -np.sqrt((thresholds_os[r][policy][method]**2).sum(axis=0))
print "{}s elapsed".format(time.time()-tic)
# set up some plotting configuration
path = 'figs/'
policies = ['UCB', 'TS', 'ECB']
methods = ["OLS_gsn","OLS_conc", "W"]
markers = {}
markers['OLS_gsn'] = 'v'
markers['OLS_conc'] = '^'
markers['W'] = 'o'
colors = {}
colors['OLS_gsn'] = sns.color_palette()[0]
colors['OLS_conc'] = sns.color_palette()[2]
colors['W'] = sns.color_palette()[1]
colors['Nominal'] = (0, 0, 0)
colors['OLS_emp'] = sns.color_palette()[3]
legend_font_size = 14
label_font_size = 14
title_font_size = 16
#
# Display coverage results
#
## Select coverage array from {"coverage", "lower_coverage", "upper_coverage"}
#coverage_type = "lower_coverage"
#coverage_arr = locals()[coverage_type]
# For each policy and method, display coverage as a function of confidence level
methods = ['OLS_gsn', 'OLS_conc', 'W']
for policy in policies:
fig, axes = plt.subplots(2, K, figsize=(10, 8), sharey=True, sharex=True)
for k in range(K):
for m in range(len(methods)):
method = methods[m]
axes[0, k].errorbar(100*confidence_levels,
100*np.mean([lower_coverage[r][policy][method][k,:] for r in xrange(R)],axis=0),
label = method,
marker=markers[method],
color=colors[method],
linestyle='')
#print np.mean([lower_coverage[r][policy]['W'][k,:] for r in xrange(R)],axis=0)
axes[0,k].plot(100*confidence_levels, 100*confidence_levels, color=colors['Nominal'], label='Nominal')
#axes[0, k].set(adjustable='box-forced', aspect='equal')
axes[0, k].set_title("Lower: beta"+str(k+1), fontsize = title_font_size)
axes[0, k].set_ylim([86, 102])
for method in methods:
axes[1, k].errorbar(100*confidence_levels,
100*np.mean([upper_coverage[r][policy][method][k,:] for r in xrange(R)],axis=0),
label = method,
marker = markers[method],
color=colors[method],
linestyle = '')
axes[1,k].plot(100*confidence_levels, 100*confidence_levels, color=colors['Nominal'], label='Nominal')
#axes[1,k].set(adjustable='box-forced', aspect='equal')
axes[1,k].set_title("Upper: beta"+str(k+1), fontsize = title_font_size)
# fig.tight_layout()
plt.figlegend( axes[1,0].get_lines(), methods+['Nom'],
loc = (0.1, 0.01), ncol=5,
labelspacing=0. ,
fontsize = legend_font_size)
fig.suptitle(policy, fontsize = title_font_size, fontweight='bold')
fig.savefig(path+'mab_{}_coverage'.format(policy))
plt.show()
#
# Display coverage results for sum reward
#
## Select coverage array from {"coverage", "lower_coverage", "upper_coverage"}
#coverage_type = "lower_coverage"
#coverage_arr = locals()[coverage_type]
# For each policy and method, display coverage as a function of confidence level
methods = ['OLS_gsn', 'OLS_conc', 'W']
for policy in policies:
fig, axes = plt.subplots(ncols=2, figsize=(11, 4), sharey=True, sharex=True)
for m in range(len(methods)):
method = methods[m]
axes[0].errorbar(100*confidence_levels,
100*np.mean([lower_sum_coverage[r][policy][method] for r in xrange(R)],axis=0),
yerr=100*np.std([lower_sum_coverage[r][policy][method] for r in xrange(R)],axis=0)/np.sqrt(R),
label = method,
marker=markers[method],
color=colors[method],
linestyle='')
#print np.mean([lower_coverage[r][policy]['W'][k,:] for r in xrange(R)],axis=0)
axes[0].plot(100*confidence_levels, 100*confidence_levels, color=colors['Nominal'], label='Nominal')
#axes[0, k].set(adjustable='box-forced', aspect='equal')
axes[0].set_title("Lower: avg reward", fontsize = title_font_size)
axes[0].set_ylim([85, 101])
for method in methods:
axes[1].errorbar(100*confidence_levels,
100*np.mean([upper_sum_coverage[r][policy][method] for r in xrange(R)],axis=0),
yerr= 100*np.std([upper_sum_coverage[r][policy][method] for r in xrange(R)],axis=0)/np.sqrt(R),
label = method,
marker = markers[method],
color=colors[method],
linestyle = '')
axes[1].plot(100*confidence_levels, 100*confidence_levels, color=colors['Nominal'], label='Nominal')
#axes[1,k].set(adjustable='box-forced', aspect='equal')
axes[1].set_title("Upper: avg reward", fontsize = title_font_size)
# fig.tight_layout()
handles = axes[1].get_lines()
axes[1].legend( handles[0:3] + [handles[4]],
['OLS_gsn','Nom', 'OLS_conc', 'W'],
loc='lower right',
bbox_to_anchor= (1, 0.0),
ncol=1,
labelspacing=0. ,
fontsize = legend_font_size)
fig.suptitle(policy, fontsize = title_font_size, fontweight='bold')
fig.savefig(path+'mab_sum_{}_coverage'.format(policy))
plt.show()
#
# Display width results
#
# For each policy and method, display mean width as a function of confidence level
policies = ["ECB", "TS", 'UCB']
methods = ['OLS_gsn', 'OLS_conc', 'W']
for policy in policies:
fig, axes = plt.subplots(1, K, sharey=True)
for k in range(K):
for method in methods:
axes[k].errorbar(100*confidence_levels, \
np.mean([thresholds_os[r][policy][method][k,:] for r in xrange(R)],axis=0), \
np.std([thresholds_os[r][policy][method][k,:] for r in xrange(R)], axis=0),\
label = method,
marker = markers[method],
color=colors[method],
linestyle='')
# axes[k].legend(loc='')
axes[k].set_title('arm_{}'.format(k), fontsize = title_font_size)
# axes[k].set_yscale('log', nonposy='clip')
fig.suptitle(policy, fontsize = title_font_size, x=0.5, y=1.05, fontweight='bold')
# plt.figlegend( axes[0].get_lines(), methods,
# loc=(0.85, 0.5),
# ncol = 1,
# # loc= (0.75, 0.3),
# labelspacing=0. ,
# fontsize = legend_font_size)
axes[0].legend( axes[0].get_lines(),
methods,
loc = 'upper left',
ncol=1,
labelspacing=0. ,
bbox_to_anchor=(0, 1),
fontsize = legend_font_size)
fig.set_size_inches(11, 4, forward=True)
# fig.savefig(path+'mab_{}_width'.format(policy), bbox_inches='tight', pad_inches=0.1)
plt.show()
#
# Display width results for avg reward
#
# For each policy and method, display mean width as a function of confidence level
policies = ["ECB", "TS", 'UCB']
methods = ['OLS_gsn', 'OLS_conc', 'W']
for policy in policies:
fig, axes = plt.subplots()
for method in methods:
sqwidths = np.array([thresholds_os[r][policy][method]**2 for r in xrange(R)])
widths = np.sqrt(sqwidths.sum(axis = 1))/2
axes.errorbar(100*confidence_levels, \
np.mean(widths, axis=0), \
np.std(widths, axis=0),\
label = method,
marker = markers[method],
color=colors[method],
linestyle='')
# axes[k].legend(loc='')
# axes[k].set_title('arm_{}'.format(k), fontsize = title_font_size)
# axes[k].set_yscale('log', nonposy='clip')
fig.suptitle(policy, fontsize = title_font_size, x=0.5, y=1.05, fontweight='bold')
axes.legend(methods,
loc='upper left',
bbox_to_anchor=(0,1),
fontsize=legend_font_size)
# plt.figlegend( axes[0].get_lines(), methods,
# loc=(0.85, 0.5),
# ncol = 1,
# # loc= (0.75, 0.3),
# labelspacing=0. ,
# fontsize = legend_font_size)
# plt.figlegend( axes.get_lines(), methods,
# loc = (0.21, -0.01), ncol=1,
# labelspacing=0. ,
# fontsize = legend_font_size)
fig.set_size_inches(5.5, 4, forward=True)
fig.savefig(path+'mab_sum_{}_width'.format(policy), bbox_inches='tight', pad_inches=0.1)
plt.show()
#
# Visualize distribution of parameter estimation error
#
policies = ["UCB", 'TS', 'ECB']
methods = ["OLS_gsn", "W"]
#Plot histograms of errors
#for policy in policies:
# fig, axes = plt.subplots(nrows=len(methods), ncols=K, sharex=True)
# for m in range(len(methods)):
# method = methods[m]
# for k in range(K):
# errors = [normalized_errors[r][policy][method][k] for r in xrange(R)]
# sns.distplot(errors,
# kde=False,
# bins=10,
# fit = stats.norm,
# ax=axes[k, m])
# #axes[k,m].hist([estimates[r][policy][method][k] - reward_means[k] for r in xrange(R)],
# #bins=50, facecolor = 'g')
# if k == 0:
# axes[k,m].set_title(method)
# fig.suptitle(policy)
# fig.savefig(path+'mab_{}_histogram'.format(policy))
# plt.show()
# Plot qqplots of errors
for policy in policies:
fig, axes = plt.subplots(nrows=len(methods), ncols=K,
sharex=True, sharey=False,
figsize=(10, 8))
for m in range(len(methods)):
method = methods[m]
for k in range(K):
errors = [normalized_errors[r][policy][method][k] for r in xrange(R)]
# sm.graphics.qqplot(errors, line='s', ax=axes[k, m])
orderedstats, fitparams = stats.probplot(errors,
dist="norm", plot=None)
axes[k, m].plot(orderedstats[0], orderedstats[1],
marker='o', markersize=4,
linestyle='',
color=colors[method])
axes[k, m].plot(orderedstats[0], fitparams[0]*orderedstats[0] + fitparams[1], color = colors['Nominal'])
#axes[k, m].plot(orderedstats[0], fitparams[0]*orderedstats[0] + fitparams[1]) #replot to get orange color
if k == 0:
axes[k,m].set_title(method, fontsize=title_font_size)
axes[k,m].set_xlabel("")
else:
axes[k,m].set_title("")
# Display empirical kurtosis to 3 significant figures
axes[k,m].legend(loc='upper left',
labels=['Ex.Kurt.: {0:.2g}'.format(
stats.kurtosis(errors, fisher=True))], fontsize=12)
fig.suptitle(policy, fontsize=title_font_size, fontweight='bold')
#fig.set_size_inches(6, 4.5)
fig.savefig(path+'mab_{}_qq'.format(policy))
plt.show()
## plot PP Plots for arm
policies = ["UCB", 'TS', 'ECB']
methods = ["OLS_gsn", "W"]
probvals = np.linspace(0, 1.0, 101)
bins = stats.norm.ppf(probvals)
normdata = np.random.randn(R)
for policy in policies:
fig, axes = plt.subplots(nrows=len(methods), ncols=K,
sharex=True, sharey=True,
figsize=(11, 8))
for m in range(len(methods)):
method = methods[m]
for k in range(K):
errors = [normalized_errors[r][policy][method][k] for r in xrange(R)]
datacounts, bins = np.histogram(errors, bins, density=True)
normcounts, bins = np.histogram(normdata, bins, density=True)
cumdata = np.cumsum(datacounts)
cumdata = cumdata/max(cumdata)
cumnorm = np.cumsum(normcounts)
cumnorm= cumnorm/max(cumnorm)
axes[k, m].plot(cumnorm, cumdata,
marker='o', markersize = 4,
color = colors[method],
linestyle=''
)
axes[k, m].plot(probvals, probvals, color = colors['Nominal'])
#axes[k, m].plot(orderedstats[0], fitparams[0]*orderedstats[0] + fitparams[1]) #replot to get orange color
if k == 0:
axes[k,m].set_title(method, fontsize=title_font_size)
axes[k,m].set_xlabel("")
else:
axes[k,m].set_title("")
# Display empirical kurtosis to 3 significant figures
axes[k,m].legend(loc='upper left',
labels=['Skew: {0:.2g}'.format(
stats.skew(errors))], fontsize=12)
fig.suptitle(policy, fontsize=title_font_size, fontweight='bold')
#fig.set_size_inches(6, 4.5)
fig.savefig(path+'mab_{}_pp'.format(policy))
plt.show()
# plot qq plots for arm sums
policies = ["UCB", 'TS', 'ECB']
methods = ["OLS_gsn", "W"]
for policy in policies:
fig, axes = plt.subplots(ncols=len(methods),
sharex=True, sharey=False,
figsize=(10, 4))
for m in range(len(methods)):
method = methods[m]
errors = [sum_norm[r][policy][method] for r in xrange(R)]
# sm.graphics.qqplot(errors, line='s', ax=axes[k, m])
orderedstats, fitparams = stats.probplot(errors,
dist="norm", plot=None)
axes[m].plot(orderedstats[0], orderedstats[1],
marker='o', markersize=2,
linestyle='',
color=colors[method])
axes[m].plot(orderedstats[0], fitparams[0]*orderedstats[0] + fitparams[1], color = colors['Nominal'])
#axes[k, m].plot(orderedstats[0], fitparams[0]*orderedstats[0] + fitparams[1]) #replot to get orange color
axes[m].set_title(method, fontsize=title_font_size)
axes[m].set_xlabel("")
axes[m].set_title("")
# Display empirical kurtosis to 3 significant figures
# axes[k,m].legend(loc='upper left',
# labels=['Ex.Kurt.: {0:.2g}'.format(
# stats.kurtosis(errors, fisher=True))], fontsize=12)
fig.suptitle(policy, fontsize=title_font_size, fontweight='bold')
#fig.set_size_inches(6, 4.5)
fig.savefig(path+'mab_sum_{}_qq'.format(policy))
plt.show()
# plot pp plots for the sums
policies = ["UCB", 'TS', 'ECB']
methods = ["OLS_gsn", "W"]
probvals = np.linspace(0, 1.0, 101)
zscores = stats.norm.ppf(probvals)
zscores_arr = np.outer(zscores, np.ones(R))
bins = stats.norm.ppf(probvals)
normdata = np.random.randn(R)
for policy in policies:
fig, axes = plt.subplots(ncols=len(methods),
sharex=True, sharey=False,
figsize=(11, 4))
for m in range(len(methods)):
method = methods[m]
errors = [sum_norm[r][policy][method] for r in xrange(R)]
cumdata = np.mean(errors <= zscores_arr, axis=1)
# sm.graphics.qqplot(errors, line='s', ax=axes[k, m])
# datacounts, bins = np.histogram(errors, bins, density=True)
# normcounts, bins = np.histogram(normdata, bins, density=True)
# cumdata = np.cumsum(datacounts)
# cumdata = cumdata/max(cumdata)
# cumnorm = np.cumsum(normcounts)
# cumnorm= cumnorm/max(cumnorm)
axes[m].plot(probvals, cumdata,
marker='o', markersize = 4,
color = colors[method],
linestyle=''
)
axes[m].plot(probvals, probvals, color = colors['Nominal'])
axes[m].set_title(method, fontsize=title_font_size)
axes[m].set_xlabel("")
axes[m].set_title("")
# Display empirical kurtosis to 3 significant figures
# axes[k,m].legend(loc='upper left',
# labels=['Ex.Kurt.: {0:.2g}'.format(
# stats.kurtosis(errors, fisher=True))], fontsize=12)
fig.suptitle(policy, fontsize=title_font_size, fontweight='bold')
#fig.set_size_inches(6, 4.5)
fig.savefig(path+'mab_sum_{}_pp'.format(policy))
plt.show()
```
| github_jupyter |
# Transfer Learning Template
```
%load_ext autoreload
%autoreload 2
%matplotlib inline
import os, json, sys, time, random
import numpy as np
import torch
from torch.optim import Adam
from easydict import EasyDict
import matplotlib.pyplot as plt
from steves_models.steves_ptn import Steves_Prototypical_Network
from steves_utils.lazy_iterable_wrapper import Lazy_Iterable_Wrapper
from steves_utils.iterable_aggregator import Iterable_Aggregator
from steves_utils.ptn_train_eval_test_jig import PTN_Train_Eval_Test_Jig
from steves_utils.torch_sequential_builder import build_sequential
from steves_utils.torch_utils import get_dataset_metrics, ptn_confusion_by_domain_over_dataloader
from steves_utils.utils_v2 import (per_domain_accuracy_from_confusion, get_datasets_base_path)
from steves_utils.PTN.utils import independent_accuracy_assesment
from torch.utils.data import DataLoader
from steves_utils.stratified_dataset.episodic_accessor import Episodic_Accessor_Factory
from steves_utils.ptn_do_report import (
get_loss_curve,
get_results_table,
get_parameters_table,
get_domain_accuracies,
)
from steves_utils.transforms import get_chained_transform
```
# Allowed Parameters
These are allowed parameters, not defaults
Each of these values need to be present in the injected parameters (the notebook will raise an exception if they are not present)
Papermill uses the cell tag "parameters" to inject the real parameters below this cell.
Enable tags to see what I mean
```
required_parameters = {
"experiment_name",
"lr",
"device",
"seed",
"dataset_seed",
"n_shot",
"n_query",
"n_way",
"train_k_factor",
"val_k_factor",
"test_k_factor",
"n_epoch",
"patience",
"criteria_for_best",
"x_net",
"datasets",
"torch_default_dtype",
"NUM_LOGS_PER_EPOCH",
"BEST_MODEL_PATH",
"x_shape",
}
from steves_utils.CORES.utils import (
ALL_NODES,
ALL_NODES_MINIMUM_1000_EXAMPLES,
ALL_DAYS
)
from steves_utils.ORACLE.utils_v2 import (
ALL_DISTANCES_FEET_NARROWED,
ALL_RUNS,
ALL_SERIAL_NUMBERS,
)
standalone_parameters = {}
standalone_parameters["experiment_name"] = "STANDALONE PTN"
standalone_parameters["lr"] = 0.001
standalone_parameters["device"] = "cuda"
standalone_parameters["seed"] = 1337
standalone_parameters["dataset_seed"] = 1337
standalone_parameters["n_way"] = 8
standalone_parameters["n_shot"] = 3
standalone_parameters["n_query"] = 2
standalone_parameters["train_k_factor"] = 1
standalone_parameters["val_k_factor"] = 2
standalone_parameters["test_k_factor"] = 2
standalone_parameters["n_epoch"] = 50
standalone_parameters["patience"] = 10
standalone_parameters["criteria_for_best"] = "source_loss"
standalone_parameters["datasets"] = [
{
"labels": ALL_SERIAL_NUMBERS,
"domains": ALL_DISTANCES_FEET_NARROWED,
"num_examples_per_domain_per_label": 100,
"pickle_path": os.path.join(get_datasets_base_path(), "oracle.Run1_framed_2000Examples_stratified_ds.2022A.pkl"),
"source_or_target_dataset": "source",
"x_transforms": ["unit_mag", "minus_two"],
"episode_transforms": [],
"domain_prefix": "ORACLE_"
},
{
"labels": ALL_NODES,
"domains": ALL_DAYS,
"num_examples_per_domain_per_label": 100,
"pickle_path": os.path.join(get_datasets_base_path(), "cores.stratified_ds.2022A.pkl"),
"source_or_target_dataset": "target",
"x_transforms": ["unit_power", "times_zero"],
"episode_transforms": [],
"domain_prefix": "CORES_"
}
]
standalone_parameters["torch_default_dtype"] = "torch.float32"
standalone_parameters["x_net"] = [
{"class": "nnReshape", "kargs": {"shape":[-1, 1, 2, 256]}},
{"class": "Conv2d", "kargs": { "in_channels":1, "out_channels":256, "kernel_size":(1,7), "bias":False, "padding":(0,3), },},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features":256}},
{"class": "Conv2d", "kargs": { "in_channels":256, "out_channels":80, "kernel_size":(2,7), "bias":True, "padding":(0,3), },},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features":80}},
{"class": "Flatten", "kargs": {}},
{"class": "Linear", "kargs": {"in_features": 80*256, "out_features": 256}}, # 80 units per IQ pair
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm1d", "kargs": {"num_features":256}},
{"class": "Linear", "kargs": {"in_features": 256, "out_features": 256}},
]
# Parameters relevant to results
# These parameters will basically never need to change
standalone_parameters["NUM_LOGS_PER_EPOCH"] = 10
standalone_parameters["BEST_MODEL_PATH"] = "./best_model.pth"
# Parameters
parameters = {
"experiment_name": "tl_1v2:cores-oracle.run1.limited",
"device": "cuda",
"lr": 0.0001,
"n_shot": 3,
"n_query": 2,
"train_k_factor": 3,
"val_k_factor": 2,
"test_k_factor": 2,
"torch_default_dtype": "torch.float32",
"n_epoch": 50,
"patience": 3,
"criteria_for_best": "target_accuracy",
"x_net": [
{"class": "nnReshape", "kargs": {"shape": [-1, 1, 2, 256]}},
{
"class": "Conv2d",
"kargs": {
"in_channels": 1,
"out_channels": 256,
"kernel_size": [1, 7],
"bias": False,
"padding": [0, 3],
},
},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features": 256}},
{
"class": "Conv2d",
"kargs": {
"in_channels": 256,
"out_channels": 80,
"kernel_size": [2, 7],
"bias": True,
"padding": [0, 3],
},
},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm2d", "kargs": {"num_features": 80}},
{"class": "Flatten", "kargs": {}},
{"class": "Linear", "kargs": {"in_features": 20480, "out_features": 256}},
{"class": "ReLU", "kargs": {"inplace": True}},
{"class": "BatchNorm1d", "kargs": {"num_features": 256}},
{"class": "Linear", "kargs": {"in_features": 256, "out_features": 256}},
],
"NUM_LOGS_PER_EPOCH": 10,
"BEST_MODEL_PATH": "./best_model.pth",
"n_way": 16,
"datasets": [
{
"labels": [
"1-10.",
"1-11.",
"1-15.",
"1-16.",
"1-17.",
"1-18.",
"1-19.",
"10-4.",
"10-7.",
"11-1.",
"11-14.",
"11-17.",
"11-20.",
"11-7.",
"13-20.",
"13-8.",
"14-10.",
"14-11.",
"14-14.",
"14-7.",
"15-1.",
"15-20.",
"16-1.",
"16-16.",
"17-10.",
"17-11.",
"17-2.",
"19-1.",
"19-16.",
"19-19.",
"19-20.",
"19-3.",
"2-10.",
"2-11.",
"2-17.",
"2-18.",
"2-20.",
"2-3.",
"2-4.",
"2-5.",
"2-6.",
"2-7.",
"2-8.",
"3-13.",
"3-18.",
"3-3.",
"4-1.",
"4-10.",
"4-11.",
"4-19.",
"5-5.",
"6-15.",
"7-10.",
"7-14.",
"8-18.",
"8-20.",
"8-3.",
"8-8.",
],
"domains": [1, 2, 3, 4, 5],
"num_examples_per_domain_per_label": -1,
"pickle_path": "/root/csc500-main/datasets/cores.stratified_ds.2022A.pkl",
"source_or_target_dataset": "target",
"x_transforms": [],
"episode_transforms": [],
"domain_prefix": "CORES_",
},
{
"labels": [
"3123D52",
"3123D65",
"3123D79",
"3123D80",
"3123D54",
"3123D70",
"3123D7B",
"3123D89",
"3123D58",
"3123D76",
"3123D7D",
"3123EFE",
"3123D64",
"3123D78",
"3123D7E",
"3124E4A",
],
"domains": [32, 38, 8, 44, 14, 50, 20, 26],
"num_examples_per_domain_per_label": 2000,
"pickle_path": "/root/csc500-main/datasets/oracle.Run1_10kExamples_stratified_ds.2022A.pkl",
"source_or_target_dataset": "source",
"x_transforms": [],
"episode_transforms": [],
"domain_prefix": "ORACLE.run1_",
},
],
"dataset_seed": 500,
"seed": 500,
}
# Set this to True if you want to run this template directly
STANDALONE = False
if STANDALONE:
print("parameters not injected, running with standalone_parameters")
parameters = standalone_parameters
if not 'parameters' in locals() and not 'parameters' in globals():
raise Exception("Parameter injection failed")
#Use an easy dict for all the parameters
p = EasyDict(parameters)
if "x_shape" not in p:
p.x_shape = [2,256] # Default to this if we dont supply x_shape
supplied_keys = set(p.keys())
if supplied_keys != required_parameters:
print("Parameters are incorrect")
if len(supplied_keys - required_parameters)>0: print("Shouldn't have:", str(supplied_keys - required_parameters))
if len(required_parameters - supplied_keys)>0: print("Need to have:", str(required_parameters - supplied_keys))
raise RuntimeError("Parameters are incorrect")
###################################
# Set the RNGs and make it all deterministic
###################################
np.random.seed(p.seed)
random.seed(p.seed)
torch.manual_seed(p.seed)
torch.use_deterministic_algorithms(True)
###########################################
# The stratified datasets honor this
###########################################
torch.set_default_dtype(eval(p.torch_default_dtype))
###################################
# Build the network(s)
# Note: It's critical to do this AFTER setting the RNG
###################################
x_net = build_sequential(p.x_net)
start_time_secs = time.time()
p.domains_source = []
p.domains_target = []
train_original_source = []
val_original_source = []
test_original_source = []
train_original_target = []
val_original_target = []
test_original_target = []
# global_x_transform_func = lambda x: normalize(x.to(torch.get_default_dtype()), "unit_power") # unit_power, unit_mag
# global_x_transform_func = lambda x: normalize(x, "unit_power") # unit_power, unit_mag
def add_dataset(
labels,
domains,
pickle_path,
x_transforms,
episode_transforms,
domain_prefix,
num_examples_per_domain_per_label,
source_or_target_dataset:str,
iterator_seed=p.seed,
dataset_seed=p.dataset_seed,
n_shot=p.n_shot,
n_way=p.n_way,
n_query=p.n_query,
train_val_test_k_factors=(p.train_k_factor,p.val_k_factor,p.test_k_factor),
):
if x_transforms == []: x_transform = None
else: x_transform = get_chained_transform(x_transforms)
if episode_transforms == []: episode_transform = None
else: raise Exception("episode_transforms not implemented")
episode_transform = lambda tup, _prefix=domain_prefix: (_prefix + str(tup[0]), tup[1])
eaf = Episodic_Accessor_Factory(
labels=labels,
domains=domains,
num_examples_per_domain_per_label=num_examples_per_domain_per_label,
iterator_seed=iterator_seed,
dataset_seed=dataset_seed,
n_shot=n_shot,
n_way=n_way,
n_query=n_query,
train_val_test_k_factors=train_val_test_k_factors,
pickle_path=pickle_path,
x_transform_func=x_transform,
)
train, val, test = eaf.get_train(), eaf.get_val(), eaf.get_test()
train = Lazy_Iterable_Wrapper(train, episode_transform)
val = Lazy_Iterable_Wrapper(val, episode_transform)
test = Lazy_Iterable_Wrapper(test, episode_transform)
if source_or_target_dataset=="source":
train_original_source.append(train)
val_original_source.append(val)
test_original_source.append(test)
p.domains_source.extend(
[domain_prefix + str(u) for u in domains]
)
elif source_or_target_dataset=="target":
train_original_target.append(train)
val_original_target.append(val)
test_original_target.append(test)
p.domains_target.extend(
[domain_prefix + str(u) for u in domains]
)
else:
raise Exception(f"invalid source_or_target_dataset: {source_or_target_dataset}")
for ds in p.datasets:
add_dataset(**ds)
# from steves_utils.CORES.utils import (
# ALL_NODES,
# ALL_NODES_MINIMUM_1000_EXAMPLES,
# ALL_DAYS
# )
# add_dataset(
# labels=ALL_NODES,
# domains = ALL_DAYS,
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "cores.stratified_ds.2022A.pkl"),
# source_or_target_dataset="target",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"cores_{u}"
# )
# from steves_utils.ORACLE.utils_v2 import (
# ALL_DISTANCES_FEET,
# ALL_RUNS,
# ALL_SERIAL_NUMBERS,
# )
# add_dataset(
# labels=ALL_SERIAL_NUMBERS,
# domains = list(set(ALL_DISTANCES_FEET) - {2,62}),
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "oracle.Run2_framed_2000Examples_stratified_ds.2022A.pkl"),
# source_or_target_dataset="source",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"oracle1_{u}"
# )
# from steves_utils.ORACLE.utils_v2 import (
# ALL_DISTANCES_FEET,
# ALL_RUNS,
# ALL_SERIAL_NUMBERS,
# )
# add_dataset(
# labels=ALL_SERIAL_NUMBERS,
# domains = list(set(ALL_DISTANCES_FEET) - {2,62,56}),
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "oracle.Run2_framed_2000Examples_stratified_ds.2022A.pkl"),
# source_or_target_dataset="source",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"oracle2_{u}"
# )
# add_dataset(
# labels=list(range(19)),
# domains = [0,1,2],
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "metehan.stratified_ds.2022A.pkl"),
# source_or_target_dataset="target",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"met_{u}"
# )
# # from steves_utils.wisig.utils import (
# # ALL_NODES_MINIMUM_100_EXAMPLES,
# # ALL_NODES_MINIMUM_500_EXAMPLES,
# # ALL_NODES_MINIMUM_1000_EXAMPLES,
# # ALL_DAYS
# # )
# import steves_utils.wisig.utils as wisig
# add_dataset(
# labels=wisig.ALL_NODES_MINIMUM_100_EXAMPLES,
# domains = wisig.ALL_DAYS,
# num_examples_per_domain_per_label=100,
# pickle_path=os.path.join(get_datasets_base_path(), "wisig.node3-19.stratified_ds.2022A.pkl"),
# source_or_target_dataset="target",
# x_transform_func=global_x_transform_func,
# domain_modifier=lambda u: f"wisig_{u}"
# )
###################################
# Build the dataset
###################################
train_original_source = Iterable_Aggregator(train_original_source, p.seed)
val_original_source = Iterable_Aggregator(val_original_source, p.seed)
test_original_source = Iterable_Aggregator(test_original_source, p.seed)
train_original_target = Iterable_Aggregator(train_original_target, p.seed)
val_original_target = Iterable_Aggregator(val_original_target, p.seed)
test_original_target = Iterable_Aggregator(test_original_target, p.seed)
# For CNN We only use X and Y. And we only train on the source.
# Properly form the data using a transform lambda and Lazy_Iterable_Wrapper. Finally wrap them in a dataloader
transform_lambda = lambda ex: ex[1] # Original is (<domain>, <episode>) so we strip down to episode only
train_processed_source = Lazy_Iterable_Wrapper(train_original_source, transform_lambda)
val_processed_source = Lazy_Iterable_Wrapper(val_original_source, transform_lambda)
test_processed_source = Lazy_Iterable_Wrapper(test_original_source, transform_lambda)
train_processed_target = Lazy_Iterable_Wrapper(train_original_target, transform_lambda)
val_processed_target = Lazy_Iterable_Wrapper(val_original_target, transform_lambda)
test_processed_target = Lazy_Iterable_Wrapper(test_original_target, transform_lambda)
datasets = EasyDict({
"source": {
"original": {"train":train_original_source, "val":val_original_source, "test":test_original_source},
"processed": {"train":train_processed_source, "val":val_processed_source, "test":test_processed_source}
},
"target": {
"original": {"train":train_original_target, "val":val_original_target, "test":test_original_target},
"processed": {"train":train_processed_target, "val":val_processed_target, "test":test_processed_target}
},
})
from steves_utils.transforms import get_average_magnitude, get_average_power
print(set([u for u,_ in val_original_source]))
print(set([u for u,_ in val_original_target]))
s_x, s_y, q_x, q_y, _ = next(iter(train_processed_source))
print(s_x)
# for ds in [
# train_processed_source,
# val_processed_source,
# test_processed_source,
# train_processed_target,
# val_processed_target,
# test_processed_target
# ]:
# for s_x, s_y, q_x, q_y, _ in ds:
# for X in (s_x, q_x):
# for x in X:
# assert np.isclose(get_average_magnitude(x.numpy()), 1.0)
# assert np.isclose(get_average_power(x.numpy()), 1.0)
###################################
# Build the model
###################################
# easfsl only wants a tuple for the shape
model = Steves_Prototypical_Network(x_net, device=p.device, x_shape=tuple(p.x_shape))
optimizer = Adam(params=model.parameters(), lr=p.lr)
###################################
# train
###################################
jig = PTN_Train_Eval_Test_Jig(model, p.BEST_MODEL_PATH, p.device)
jig.train(
train_iterable=datasets.source.processed.train,
source_val_iterable=datasets.source.processed.val,
target_val_iterable=datasets.target.processed.val,
num_epochs=p.n_epoch,
num_logs_per_epoch=p.NUM_LOGS_PER_EPOCH,
patience=p.patience,
optimizer=optimizer,
criteria_for_best=p.criteria_for_best,
)
total_experiment_time_secs = time.time() - start_time_secs
###################################
# Evaluate the model
###################################
source_test_label_accuracy, source_test_label_loss = jig.test(datasets.source.processed.test)
target_test_label_accuracy, target_test_label_loss = jig.test(datasets.target.processed.test)
source_val_label_accuracy, source_val_label_loss = jig.test(datasets.source.processed.val)
target_val_label_accuracy, target_val_label_loss = jig.test(datasets.target.processed.val)
history = jig.get_history()
total_epochs_trained = len(history["epoch_indices"])
val_dl = Iterable_Aggregator((datasets.source.original.val,datasets.target.original.val))
confusion = ptn_confusion_by_domain_over_dataloader(model, p.device, val_dl)
per_domain_accuracy = per_domain_accuracy_from_confusion(confusion)
# Add a key to per_domain_accuracy for if it was a source domain
for domain, accuracy in per_domain_accuracy.items():
per_domain_accuracy[domain] = {
"accuracy": accuracy,
"source?": domain in p.domains_source
}
# Do an independent accuracy assesment JUST TO BE SURE!
# _source_test_label_accuracy = independent_accuracy_assesment(model, datasets.source.processed.test, p.device)
# _target_test_label_accuracy = independent_accuracy_assesment(model, datasets.target.processed.test, p.device)
# _source_val_label_accuracy = independent_accuracy_assesment(model, datasets.source.processed.val, p.device)
# _target_val_label_accuracy = independent_accuracy_assesment(model, datasets.target.processed.val, p.device)
# assert(_source_test_label_accuracy == source_test_label_accuracy)
# assert(_target_test_label_accuracy == target_test_label_accuracy)
# assert(_source_val_label_accuracy == source_val_label_accuracy)
# assert(_target_val_label_accuracy == target_val_label_accuracy)
experiment = {
"experiment_name": p.experiment_name,
"parameters": dict(p),
"results": {
"source_test_label_accuracy": source_test_label_accuracy,
"source_test_label_loss": source_test_label_loss,
"target_test_label_accuracy": target_test_label_accuracy,
"target_test_label_loss": target_test_label_loss,
"source_val_label_accuracy": source_val_label_accuracy,
"source_val_label_loss": source_val_label_loss,
"target_val_label_accuracy": target_val_label_accuracy,
"target_val_label_loss": target_val_label_loss,
"total_epochs_trained": total_epochs_trained,
"total_experiment_time_secs": total_experiment_time_secs,
"confusion": confusion,
"per_domain_accuracy": per_domain_accuracy,
},
"history": history,
"dataset_metrics": get_dataset_metrics(datasets, "ptn"),
}
ax = get_loss_curve(experiment)
plt.show()
get_results_table(experiment)
get_domain_accuracies(experiment)
print("Source Test Label Accuracy:", experiment["results"]["source_test_label_accuracy"], "Target Test Label Accuracy:", experiment["results"]["target_test_label_accuracy"])
print("Source Val Label Accuracy:", experiment["results"]["source_val_label_accuracy"], "Target Val Label Accuracy:", experiment["results"]["target_val_label_accuracy"])
json.dumps(experiment)
```
| github_jupyter |
<a href="https://colab.research.google.com/github/s-mostafa-a/pytorch_learning/blob/master/simple_generative_adversarial_net/MNIST_GANs.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
import torch
from torchvision.transforms import ToTensor, Normalize, Compose
from torchvision.datasets import MNIST
import torch.nn as nn
from torch.utils.data import DataLoader
from torchvision.utils import save_image
import os
class DeviceDataLoader:
def __init__(self, dl, device):
self.dl = dl
self.device = device
def __iter__(self):
for b in self.dl:
yield self.to_device(b, self.device)
def __len__(self):
return len(self.dl)
def to_device(self, data, device):
if isinstance(data, (list, tuple)):
return [self.to_device(x, device) for x in data]
return data.to(device, non_blocking=True)
class MNIST_GANS:
def __init__(self, dataset, image_size, device, num_epochs=50, loss_function=nn.BCELoss(), batch_size=100,
hidden_size=2561, latent_size=64):
self.device = device
bare_data_loader = DataLoader(dataset, batch_size, shuffle=True)
self.data_loader = DeviceDataLoader(bare_data_loader, device)
self.loss_function = loss_function
self.hidden_size = hidden_size
self.latent_size = latent_size
self.batch_size = batch_size
self.D = nn.Sequential(
nn.Linear(image_size, hidden_size),
nn.LeakyReLU(0.2),
nn.Linear(hidden_size, hidden_size),
nn.LeakyReLU(0.2),
nn.Linear(hidden_size, 1),
nn.Sigmoid())
self.G = nn.Sequential(
nn.Linear(latent_size, hidden_size),
nn.ReLU(),
nn.Linear(hidden_size, hidden_size),
nn.ReLU(),
nn.Linear(hidden_size, image_size),
nn.Tanh())
self.d_optimizer = torch.optim.Adam(self.D.parameters(), lr=0.0002)
self.g_optimizer = torch.optim.Adam(self.G.parameters(), lr=0.0002)
self.sample_dir = './../data/mnist_samples'
if not os.path.exists(self.sample_dir):
os.makedirs(self.sample_dir)
self.G.to(device)
self.D.to(device)
self.sample_vectors = torch.randn(self.batch_size, self.latent_size).to(self.device)
self.num_epochs = num_epochs
@staticmethod
def denormalize(x):
out = (x + 1) / 2
return out.clamp(0, 1)
def reset_grad(self):
self.d_optimizer.zero_grad()
self.g_optimizer.zero_grad()
def train_discriminator(self, images):
real_labels = torch.ones(self.batch_size, 1).to(self.device)
fake_labels = torch.zeros(self.batch_size, 1).to(self.device)
outputs = self.D(images)
d_loss_real = self.loss_function(outputs, real_labels)
real_score = outputs
new_sample_vectors = torch.randn(self.batch_size, self.latent_size).to(self.device)
fake_images = self.G(new_sample_vectors)
outputs = self.D(fake_images)
d_loss_fake = self.loss_function(outputs, fake_labels)
fake_score = outputs
d_loss = d_loss_real + d_loss_fake
self.reset_grad()
d_loss.backward()
self.d_optimizer.step()
return d_loss, real_score, fake_score
def train_generator(self):
new_sample_vectors = torch.randn(self.batch_size, self.latent_size).to(self.device)
fake_images = self.G(new_sample_vectors)
labels = torch.ones(self.batch_size, 1).to(self.device)
g_loss = self.loss_function(self.D(fake_images), labels)
self.reset_grad()
g_loss.backward()
self.g_optimizer.step()
return g_loss, fake_images
def save_fake_images(self, index):
fake_images = self.G(self.sample_vectors)
fake_images = fake_images.reshape(fake_images.size(0), 1, 28, 28)
fake_fname = 'fake_images-{0:0=4d}.png'.format(index)
print('Saving', fake_fname)
save_image(self.denormalize(fake_images), os.path.join(self.sample_dir, fake_fname),
nrow=10)
def run(self):
total_step = len(self.data_loader)
d_losses, g_losses, real_scores, fake_scores = [], [], [], []
for epoch in range(self.num_epochs):
for i, (images, _) in enumerate(self.data_loader):
images = images.reshape(self.batch_size, -1)
d_loss, real_score, fake_score = self.train_discriminator(images)
g_loss, fake_images = self.train_generator()
if (i + 1) % 600 == 0:
d_losses.append(d_loss.item())
g_losses.append(g_loss.item())
real_scores.append(real_score.mean().item())
fake_scores.append(fake_score.mean().item())
print(f'''Epoch [{epoch}/{self.num_epochs}], Step [{i + 1}/{
total_step}], d_loss: {d_loss.item():.4f}, g_loss: {g_loss.item():.4f}, D(x): {
real_score.mean().item():.2f}, D(G(z)): {fake_score.mean().item():.2f}''')
self.save_fake_images(epoch + 1)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
mnist = MNIST(root='./../data', train=True, download=True, transform=Compose([ToTensor(), Normalize(mean=(0.5,), std=(0.5,))]))
image_size = mnist.data[0].flatten().size()[0]
gans = MNIST_GANS(dataset=mnist, image_size=image_size, device=device)
gans.run()
```
| github_jupyter |
```
import pandas as pd
import numpy as np
import os
import matplotlib.mlab as mlab
import matplotlib.pyplot as plt
import seaborn
def filterOutlier(data_list,z_score_threshold=3.5):
"""
Filters out outliers using the modified Z-Score method.
"""
# n = len(data_list)
# z_score_threshold = (n-1)/np.sqrt(n)
data = np.array(data_list)
median = np.median(data)
deviation = np.median([np.abs(x - median) for x in data])
z_scores = [0.675*(x - median)/deviation for x in data]
data_out = data[np.where(np.abs(z_scores) < z_score_threshold)].tolist()
output = data_out if len(data_out) > 0 else data_list
return output
data_dir = ["./data/sample_obstacle_course"]
# data_dir = ['./windmachine']
data = []
for data_path in data_dir:
for f in os.listdir(data_path):
if "d" in f:
try:
path = os.path.join(data_path,f)
matrix = np.load(path)
matrix[matrix > 4000] = 0.0
nan = len(matrix[matrix < 1])
total = len(matrix.flatten())
result = 1 - nan/total
data.append(result)
# if True:
# plt.figure()
# plt.title(f)
# plt.imshow(matrix)
# plt.show()
except TypeError:
path = os.path.join(data_path,f)
d= np.load(path)
# for i in range(5):
# s = 'arr_{}'.format(i+1)
s = 'arr_1'
matrix = d[s]
nan = len(matrix[matrix < 1])
total = len(matrix.flatten())
result = 1 - nan/total
data.append(result)
d.close()
# data = filterOutlier(data)
data = np.array(data)
data = data[abs(data - np.mean(data)) < 3 * np.std(data)].tolist()
print(data)
series = pd.Series(data)
series.name = 'Data Density'
print(series.min())
series.head()
bins = pd.cut(series,20)
histogram = bins.value_counts()
print(type(histogram))
histogram.sort_index(inplace=True)
total = sum(histogram)
print(total)
histogram.index
hist = [x/total for x in histogram]
span = series.max() - series.min()
index = np.linspace(series.min(),series.max(),len(hist))
index = map(lambda x: round(x,3),index)
print(index)
hist = pd.Series(hist,index=index)
plt.figure("Depth_Sensor_Performance")
hist.plot(kind='bar')
plt.xlabel("Data Density")
plt.ylabel("Probability")
plt.title("Depth_Sensor_Performance: n=701,")
plt.show()
```
| github_jupyter |
# Matrix
> Marcos Duarte
> Laboratory of Biomechanics and Motor Control ([http://demotu.org/](http://demotu.org/))
> Federal University of ABC, Brazil
A matrix is a square or rectangular array of numbers or symbols (termed elements), arranged in rows and columns. For instance:
$$
\mathbf{A} =
\begin{bmatrix}
a_{1,1} & a_{1,2} & a_{1,3} \\
a_{2,1} & a_{2,2} & a_{2,3}
\end{bmatrix}
$$
$$
\mathbf{A} =
\begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6
\end{bmatrix}
$$
The matrix $\mathbf{A}$ above has two rows and three columns, it is a 2x3 matrix.
In Numpy:
```
# Import the necessary libraries
import numpy as np
from IPython.display import display
np.set_printoptions(precision=4) # number of digits of precision for floating point
A = np.array([[1, 2, 3], [4, 5, 6]])
A
```
To get information about the number of elements and the structure of the matrix (in fact, a Numpy array), we can use:
```
print('A:\n', A)
print('len(A) = ', len(A))
print('np.size(A) = ', np.size(A))
print('np.shape(A) = ', np.shape(A))
print('np.ndim(A) = ', np.ndim(A))
```
We could also have accessed this information with the correspondent methods:
```
print('A.size = ', A.size)
print('A.shape = ', A.shape)
print('A.ndim = ', A.ndim)
```
We used the array function in Numpy to represent a matrix. A [Numpy array is in fact different than a matrix](http://www.scipy.org/NumPy_for_Matlab_Users), if we want to use explicit matrices in Numpy, we have to use the function `mat`:
```
B = np.mat([[1, 2, 3], [4, 5, 6]])
B
```
Both array and matrix types work in Numpy, but you should choose only one type and not mix them; the array is preferred because it is [the standard vector/matrix/tensor type of Numpy](http://www.scipy.org/NumPy_for_Matlab_Users). So, let's use the array type for the rest of this text.
## Addition and multiplication
The sum of two m-by-n matrices $\mathbf{A}$ and $\mathbf{B}$ is another m-by-n matrix:
$$
\mathbf{A} =
\begin{bmatrix}
a_{1,1} & a_{1,2} & a_{1,3} \\
a_{2,1} & a_{2,2} & a_{2,3}
\end{bmatrix}
\;\;\; \text{and} \;\;\;
\mathbf{B} =
\begin{bmatrix}
b_{1,1} & b_{1,2} & b_{1,3} \\
b_{2,1} & b_{2,2} & b_{2,3}
\end{bmatrix}
$$
$$
\mathbf{A} + \mathbf{B} =
\begin{bmatrix}
a_{1,1}+b_{1,1} & a_{1,2}+b_{1,2} & a_{1,3}+b_{1,3} \\
a_{2,1}+b_{2,1} & a_{2,2}+b_{2,2} & a_{2,3}+b_{2,3}
\end{bmatrix}
$$
In Numpy:
```
A = np.array([[1, 2, 3], [4, 5, 6]])
B = np.array([[7, 8, 9], [10, 11, 12]])
print('A:\n', A)
print('B:\n', B)
print('A + B:\n', A+B);
```
The multiplication of the m-by-n matrix $\mathbf{A}$ by the n-by-p matrix $\mathbf{B}$ is a m-by-p matrix:
$$
\mathbf{A} =
\begin{bmatrix}
a_{1,1} & a_{1,2} \\
a_{2,1} & a_{2,2}
\end{bmatrix}
\;\;\; \text{and} \;\;\;
\mathbf{B} =
\begin{bmatrix}
b_{1,1} & b_{1,2} & b_{1,3} \\
b_{2,1} & b_{2,2} & b_{2,3}
\end{bmatrix}
$$
$$
\mathbf{A} \mathbf{B} =
\begin{bmatrix}
a_{1,1}b_{1,1} + a_{1,2}b_{2,1} & a_{1,1}b_{1,2} + a_{1,2}b_{2,2} & a_{1,1}b_{1,3} + a_{1,2}b_{2,3} \\
a_{2,1}b_{1,1} + a_{2,2}b_{2,1} & a_{2,1}b_{1,2} + a_{2,2}b_{2,2} & a_{2,1}b_{1,3} + a_{2,2}b_{2,3}
\end{bmatrix}
$$
In Numpy:
```
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6, 7], [8, 9, 10]])
print('A:\n', A)
print('B:\n', B)
print('A x B:\n', np.dot(A, B));
```
Note that because the array type is not truly a matrix type, we used the dot product to calculate matrix multiplication.
We can use the matrix type to show the equivalent:
```
A = np.mat(A)
B = np.mat(B)
print('A:\n', A)
print('B:\n', B)
print('A x B:\n', A*B);
```
Same result as before.
The order in multiplication matters, $\mathbf{AB} \neq \mathbf{BA}$:
```
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
print('A:\n', A)
print('B:\n', B)
print('A x B:\n', np.dot(A, B))
print('B x A:\n', np.dot(B, A));
```
The addition or multiplication of a scalar (a single number) to a matrix is performed over all the elements of the matrix:
```
A = np.array([[1, 2], [3, 4]])
c = 10
print('A:\n', A)
print('c:\n', c)
print('c + A:\n', c+A)
print('cA:\n', c*A);
```
## Transposition
The transpose of the matrix $\mathbf{A}$ is the matrix $\mathbf{A^T}$ turning all the rows of matrix $\mathbf{A}$ into columns (or columns into rows):
$$
\mathbf{A} =
\begin{bmatrix}
a & b & c \\
d & e & f \end{bmatrix}
\;\;\;\;\;\;\iff\;\;\;\;\;\;
\mathbf{A^T} =
\begin{bmatrix}
a & d \\
b & e \\
c & f
\end{bmatrix} $$
In NumPy, the transpose operator can be used as a method or function:
```
A = np.array([[1, 2], [3, 4]])
print('A:\n', A)
print('A.T:\n', A.T)
print('np.transpose(A):\n', np.transpose(A));
```
## Determinant
The determinant is a number associated with a square matrix.
The determinant of the following matrix:
$$ \left[ \begin{array}{ccc}
a & b & c \\
d & e & f \\
g & h & i \end{array} \right] $$
is written as:
$$ \left| \begin{array}{ccc}
a & b & c \\
d & e & f \\
g & h & i \end{array} \right| $$
And has the value:
$$ (aei + bfg + cdh) - (ceg + bdi + afh) $$
One way to manually calculate the determinant of a matrix is to use the [rule of Sarrus](http://en.wikipedia.org/wiki/Rule_of_Sarrus): we repeat the last columns (all columns but the first one) in the right side of the matrix and calculate the sum of the products of three diagonal north-west to south-east lines of matrix elements, minus the sum of the products of three diagonal south-west to north-east lines of elements as illustrated in the following figure:
<br>
<figure><img src='http://upload.wikimedia.org/wikipedia/commons/6/66/Sarrus_rule.svg' width=300 alt='Rule of Sarrus'/><center><figcaption><i>Figure. Rule of Sarrus: the sum of the products of the solid diagonals minus the sum of the products of the dashed diagonals (<a href="http://en.wikipedia.org/wiki/Rule_of_Sarrus">image from Wikipedia</a>).</i></figcaption></center> </figure>
In Numpy, the determinant is computed with the `linalg.det` function:
```
A = np.array([[1, 2], [3, 4]])
print('A:\n', A);
print('Determinant of A:\n', np.linalg.det(A))
```
## Identity
The identity matrix $\mathbf{I}$ is a matrix with ones in the main diagonal and zeros otherwise. The 3x3 identity matrix is:
$$ \mathbf{I} =
\begin{bmatrix}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1 \end{bmatrix} $$
In Numpy, instead of manually creating this matrix we can use the function `eye`:
```
np.eye(3) # identity 3x3 array
```
## Inverse
The inverse of the matrix $\mathbf{A}$ is the matrix $\mathbf{A^{-1}}$ such that the product between these two matrices is the identity matrix:
$$ \mathbf{A}\cdot\mathbf{A^{-1}} = \mathbf{I} $$
The calculation of the inverse of a matrix is usually not simple (the inverse of the matrix $\mathbf{A}$ is not $1/\mathbf{A}$; there is no division operation between matrices). The Numpy function `linalg.inv` computes the inverse of a square matrix:
numpy.linalg.inv(a)
Compute the (multiplicative) inverse of a matrix.
Given a square matrix a, return the matrix ainv satisfying dot(a, ainv) = dot(ainv, a) = eye(a.shape[0]).
```
A = np.array([[1, 2], [3, 4]])
print('A:\n', A)
Ainv = np.linalg.inv(A)
print('Inverse of A:\n', Ainv);
```
### Pseudo-inverse
For a non-square matrix, its inverse is not defined. However, we can calculate what it's known as the pseudo-inverse.
Consider a non-square matrix, $\mathbf{A}$. To calculate its inverse, note that the following manipulation results in the identity matrix:
$$ \mathbf{A} \mathbf{A}^T (\mathbf{A}\mathbf{A}^T)^{-1} = \mathbf{I} $$
The $\mathbf{A} \mathbf{A}^T$ is a square matrix and is invertible (also [nonsingular](https://en.wikipedia.org/wiki/Invertible_matrix)) if $\mathbf{A}$ is L.I. ([linearly independent rows/columns](https://en.wikipedia.org/wiki/Linear_independence)).
The matrix $\mathbf{A}^T(\mathbf{A}\mathbf{A}^T)^{-1}$ is known as the [generalized inverse or Moore–Penrose pseudoinverse](https://en.wikipedia.org/wiki/Moore%E2%80%93Penrose_pseudoinverse) of the matrix $\mathbf{A}$, a generalization of the inverse matrix.
To compute the Moore–Penrose pseudoinverse, we could calculate it by a naive approach in Python:
```python
from numpy.linalg import inv
Ainv = A.T @ inv(A @ A.T)
```
But both Numpy and Scipy have functions to calculate the pseudoinverse, which might give greater numerical stability (but read [Inverses and pseudoinverses. Numerical issues, speed, symmetry](http://vene.ro/blog/inverses-pseudoinverses-numerical-issues-speed-symmetry.html)). Of note, [numpy.linalg.pinv](http://docs.scipy.org/doc/numpy/reference/generated/numpy.linalg.pinv.html) calculates the pseudoinverse of a matrix using its singular-value decomposition (SVD) and including all large singular values (using the [LAPACK (Linear Algebra Package)](https://en.wikipedia.org/wiki/LAPACK) routine gesdd), whereas [scipy.linalg.pinv](http://docs.scipy.org/doc/scipy/reference/generated/scipy.linalg.pinv.html#scipy.linalg.pinv) calculates a pseudoinverse of a matrix using a least-squares solver (using the LAPACK method gelsd) and [scipy.linalg.pinv2](http://docs.scipy.org/doc/scipy/reference/generated/scipy.linalg.pinv2.html) also uses SVD to find the pseudoinverse (also using the LAPACK routine gesdd).
For example:
```
from scipy.linalg import pinv2
A = np.array([[1, 0, 0], [0, 1, 0]])
Apinv = pinv2(A)
print('Matrix A:\n', A)
print('Pseudo-inverse of A:\n', Apinv)
print('A x Apinv:\n', A@Apinv)
```
## Orthogonality
A square matrix is said to be orthogonal if:
1. There is no linear combination of one of the lines or columns of the matrix that would lead to the other row or column.
2. Its columns or rows form a basis of (independent) unit vectors (versors).
As consequence:
1. Its determinant is equal to 1 or -1.
2. Its inverse is equal to its transpose.
However, keep in mind that not all matrices with determinant equals to one are orthogonal, for example, the matrix:
$$ \begin{bmatrix}
3 & 2 \\
4 & 3
\end{bmatrix} $$
Has determinant equals to one but it is not orthogonal (the columns or rows don't have norm equals to one).
## Linear equations
> A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and (the first power of) a single variable ([Wikipedia](http://en.wikipedia.org/wiki/Linear_equation)).
We are interested in solving a set of linear equations where two or more variables are unknown, for instance:
$$ x + 2y = 4 $$
$$ 3x + 4y = 10 $$
Let's see how to employ the matrix formalism to solve these equations (even that we know the solution is `x=2` and `y=1`).
Let's express this set of equations in matrix form:
$$
\begin{bmatrix}
1 & 2 \\
3 & 4 \end{bmatrix}
\begin{bmatrix}
x \\
y \end{bmatrix}
= \begin{bmatrix}
4 \\
10 \end{bmatrix}
$$
And for the general case:
$$ \mathbf{Av} = \mathbf{c} $$
Where $\mathbf{A, v, c}$ are the matrices above and we want to find the values `x,y` for the matrix $\mathbf{v}$.
Because there is no division of matrices, we can use the inverse of $\mathbf{A}$ to solve for $\mathbf{v}$:
$$ \mathbf{A}^{-1}\mathbf{Av} = \mathbf{A}^{-1}\mathbf{c} \implies $$
$$ \mathbf{v} = \mathbf{A}^{-1}\mathbf{c} $$
As we know how to compute the inverse of $\mathbf{A}$, the solution is:
```
A = np.array([[1, 2], [3, 4]])
Ainv = np.linalg.inv(A)
c = np.array([4, 10])
v = np.dot(Ainv, c)
print('v:\n', v)
```
What we expected.
However, the use of the inverse of a matrix to solve equations is computationally inefficient.
Instead, we should use `linalg.solve` for a determined system (same number of equations and unknowns) or `linalg.lstsq` otherwise:
From the help for `solve`:
numpy.linalg.solve(a, b)[source]
Solve a linear matrix equation, or system of linear scalar equations.
Computes the “exact” solution, x, of the well-determined, i.e., full rank, linear matrix equation ax = b.
```
v = np.linalg.solve(A, c)
print('Using solve:')
print('v:\n', v)
```
And from the help for `lstsq`:
numpy.linalg.lstsq(a, b, rcond=-1)[source]
Return the least-squares solution to a linear matrix equation.
Solves the equation a x = b by computing a vector x that minimizes the Euclidean 2-norm || b - a x ||^2. The equation may be under-, well-, or over- determined (i.e., the number of linearly independent rows of a can be less than, equal to, or greater than its number of linearly independent columns). If a is square and of full rank, then x (but for round-off error) is the “exact” solution of the equation.
```
v = np.linalg.lstsq(A, c)[0]
print('Using lstsq:')
print('v:\n', v)
```
Same solutions, of course.
When a system of equations has a unique solution, the determinant of the **square** matrix associated to this system of equations is nonzero.
When the determinant is zero there are either no solutions or many solutions to the system of equations.
But if we have an overdetermined system:
$$ x + 2y = 4 $$
$$ 3x + 4y = 10 $$
$$ 5x + 6y = 15 $$
(Note that the possible solution for this set of equations is not exact because the last equation should be equal to 16.)
Let's try to solve it:
```
A = np.array([[1, 2], [3, 4], [5, 6]])
print('A:\n', A)
c = np.array([4, 10, 15])
print('c:\n', c);
```
Because the matix $\mathbf{A}$ is not squared, we can calculate its pseudo-inverse or use the function `linalg.lstsq`:
```
v = np.linalg.lstsq(A, c)[0]
print('Using lstsq:')
print('v:\n', v)
```
The functions `inv` and `solve` failed because the matrix $\mathbf{A}$ was not square (overdetermined system). The function `lstsq` not only was able to handle an overdetermined system but was also able to find the best approximate solution.
And if the the set of equations was undetermined, `lstsq` would also work. For instance, consider the system:
$$ x + 2y + 2z = 10 $$
$$ 3x + 4y + z = 13 $$
And in matrix form:
$$
\begin{bmatrix}
1 & 2 & 2 \\
3 & 4 & 1 \end{bmatrix}
\begin{bmatrix}
x \\
y \\
z \end{bmatrix}
= \begin{bmatrix}
10 \\
13 \end{bmatrix}
$$
A possible solution would be `x=2,y=1,z=3`, but other values would also satisfy this set of equations.
Let's try to solve using `lstsq`:
```
A = np.array([[1, 2, 2], [3, 4, 1]])
print('A:\n', A)
c = np.array([10, 13])
print('c:\n', c);
v = np.linalg.lstsq(A, c)[0]
print('Using lstsq:')
print('v:\n', v);
```
This is an approximated solution and as explained in the help of `solve`, this solution, `v`, is the one that minimizes the Euclidean norm $|| \mathbf{c - A v} ||^2$.
| github_jupyter |
<a href="https://colab.research.google.com/github/mzkhan2000/KG-Embeddings/blob/main/embedding_word_clusters2.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
```
# Python program to generate embedding (word vectors) using Word2Vec
# importing necessary modules for embedding
!pip install --upgrade gensim
!pip install rdflib
import rdflib
!pip uninstall numpy
!pip install numpy
# pip install numpy and then hit the RESTART RUNTIME
import gensim
from gensim.models import Word2Vec
from gensim.models import KeyedVectors
from gensim.scripts.glove2word2vec import glove2word2vec
import collections
from collections import Counter
from rdflib import Graph, URIRef, Namespace
from google.colab import drive
drive.mount('/content/drive')
# check out if google dride mount suceessful
!ls "/content/drive/My Drive/MonirResearchDatasets"
# a funtion for ga-themes extraction from GA-rdf repository separate and return a list all the ga-themes - Monir
def gaThemesExtraction(ga_record):
gaThemes = []
with open(ga_record, 'rt') as f:
data = f.readlines()
for line in data:
# check if line contains "ga-themes" sub-string
if line.__contains__('ga-themes'):
# split the line contains from "ga-themes" sub-string
stringTemp = line.split("ga-themes/",1)[1]
# further split the line contains from "ga-themes" sub-string to delimiter
stringTemp = stringTemp.split('>')[0]
gaThemes.append(stringTemp)
#print(dataLog)
#print(gaThemes[:9])
#print(len(gaThemes))
return gaThemes
# a funtion imput a list of ga-themes and return a list of unique ga-themes and another list of duplicate gaThemes -
def make_unique_gaThemes(list_all_ga_themes):
# find a a list of unique ga-themes
unique_gaThemes = []
unique_gaThemes = list(dict.fromkeys(gaThemes))
#print(len(unique_gaThemes))
# a list of duplicate gaThemes
duplicate_gaThemes = []
duplicate_gaThemes = [item for item, count in collections.Counter(gaThemes).items() if count > 1]
#print(len(duplicate_gaThemes))
return unique_gaThemes, duplicate_gaThemes
## KG-Embeddings
filename = '/content/drive/My Drive/MonirResearchDatasets/Freebase-GoogleNews-vectors.bin'
model = KeyedVectors.load_word2vec_format(filename, binary=True)
def embedding_word_clusters(model, list_of_ga_themes, cluster_size):
keys = list_of_ga_themes
embedding_model = model
n = cluster_size
new_classifier = []
embedding_clusters = []
classifier_clusters = []
for word in keys:
embeddings = []
words = []
# check if a word is fully "OOV" (out of vocabulary) for pre-trained embedding model
if word in embedding_model.key_to_index:
# create a new list of classifier
new_classifier.append(word)
# find most similar top n words from the pre-trained embedding model
for similar_word, _ in embedding_model.most_similar(word, topn=n):
words.append(similar_word)
embeddings.append(embedding_model[similar_word])
embedding_clusters.append(embeddings)
classifier_clusters.append(words)
return embedding_clusters, classifier_clusters, new_classifier
# to get all the ga-themes from all1K file
ga_record_datapath = "/content/drive/My Drive/MonirResearchDatasets/surround-ga-records/all1k.ttl.txt"
gaThemes = gaThemesExtraction(ga_record_datapath)
print(gaThemes[:10])
print(len(gaThemes))
# to get all unique ga-themes
unique_gaThemes, duplicate_gaThemes = make_unique_gaThemes(gaThemes)
print(unique_gaThemes[:100])
#print(duplicate_gaThemes[:100])
print(len(unique_gaThemes))
embedding_clusters, classifier_clusters, new_classifier = embedding_word_clusters(model, unique_gaThemes[:10], 10)
print(classifier_clusters)
print(new_classifier)
print(classifier_clusters[:2])
print(new_classifier[:2])
from rdflib import Graph
g = Graph()
g.parse("/content/drive/My Drive/MonirResearchDatasets/surround-ga-records/ga-records.ttl", format='turtle')
print(len(g))
n_record = Namespace("http://example.com/record/")
# <http://example.com/record/105030>
n_GA = Namespace("http://example.org/def/ga-themes/")
n_hasClassifier = Namespace("http://data.surroundaustralia.com/def/agr#")
hasClassifier = "hasClassifier"
#record = []
for obj in new_classifier[:1]: # for obj in new_classifier:
results = g.query(
"""
PREFIX classifier: <http://data.surroundaustralia.com/def/agr#>
PREFIX ga-themes: <http://example.org/def/ga-themes/>
SELECT ?s WHERE { ?s classifier:hasClassifier ga-themes:""" + obj + """ }
""")
record = []
pos = new_classifier.index(obj)
for row in results:
# print(f"{row.s}")
record.append(row.s)
# adding classifier from classifier cluster to each of the list of records
for classifier_obj in classifier_clusters[pos]:
for record_data in record:
g.add((record_data, n_hasClassifier.hasClassifier, n_GA[classifier_obj]))
# adding classifier from classifier cluster to the list of records
for q in record:
g.add((record[q], n_hasClassifier.hasClassifier, n_GA[classifier_clusters[1]]))
print(record)
print(new_classifier)
print(new_classifier.index('palaeontology'))
print(classifier_clusters[0])
print(len(record))
print(len(record))
print(len(classifier_clusters))
a = [[1, 3, 4], [2, 4, 4], [3, 4, 5]]
for recordlist in record:
print(recordlist)
for number in recordlist:
print(number)
```
| github_jupyter |
```
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
dataset1=pd.read_csv('general_data.csv')
dataset1.head()
dataset1.columns
dataset1
dataset1.isnull()
dataset1.duplicated()
dataset1.drop_duplicates()
dataset3=dataset1[['Age','DistanceFromHome','Education','MonthlyIncome', 'NumCompaniesWorked', 'PercentSalaryHike','TotalWorkingYears', 'TrainingTimesLastYear', 'YearsAtCompany','YearsSinceLastPromotion', 'YearsWithCurrManager']].describe()
dataset3
dataset3=dataset1[['Age','DistanceFromHome','Education','MonthlyIncome', 'NumCompaniesWorked', 'PercentSalaryHike','TotalWorkingYears', 'TrainingTimesLastYear', 'YearsAtCompany','YearsSinceLastPromotion', 'YearsWithCurrManager']].median()
dataset3
dataset3=dataset1[['Age','DistanceFromHome','Education','MonthlyIncome', 'NumCompaniesWorked', 'PercentSalaryHike','TotalWorkingYears', 'TrainingTimesLastYear', 'YearsAtCompany','YearsSinceLastPromotion', 'YearsWithCurrManager']].mode()
dataset3
dataset3=dataset1[['Age','DistanceFromHome','Education','MonthlyIncome', 'NumCompaniesWorked', 'PercentSalaryHike','TotalWorkingYears', 'TrainingTimesLastYear', 'YearsAtCompany','YearsSinceLastPromotion', 'YearsWithCurrManager']].var()
dataset3
dataset3=dataset1[['Age','DistanceFromHome','Education','MonthlyIncome', 'NumCompaniesWorked', 'PercentSalaryHike','TotalWorkingYears', 'TrainingTimesLastYear', 'YearsAtCompany','YearsSinceLastPromotion', 'YearsWithCurrManager']].skew()
dataset3
dataset3=dataset1[['Age','DistanceFromHome','Education','MonthlyIncome', 'NumCompaniesWorked', 'PercentSalaryHike','TotalWorkingYears', 'TrainingTimesLastYear', 'YearsAtCompany','YearsSinceLastPromotion', 'YearsWithCurrManager']].kurt()
dataset3
```
# Inference from the analysis:
All the above variables show positive skewness; while Age & Mean_distance_from_home are leptokurtic and all other variables are platykurtic.
The Mean_Monthly_Income’s IQR is at 54K suggesting company wide attrition across all income bands
Mean age forms a near normal distribution with 13 years of IQR
# Outliers:
There’s no regression found while plotting Age, MonthlyIncome, TotalWorkingYears, YearsAtCompany, etc., on a scatter plot
```
box_plot=dataset1.Age
plt.boxplot(box_plot)
```
### Age is normally distributed without any outliers
```
box_plot=dataset1.MonthlyIncome
plt.boxplot(box_plot)
```
### Monthly Income is Right skewed with several outliers
```
box_plot=dataset1.YearsAtCompany
plt.boxplot(box_plot)
```
### Years at company is also Right Skewed with several outliers observed.
# Attrition Vs Distance from Home
```
from scipy.stats import mannwhitneyu
from scipy.stats import mannwhitneyu
a1=dataset.DistanceFromHome_Yes
a2=dataset.DistanceFromHome_No
stat, p=mannwhitneyu(a1,a2)
print(stat, p)
3132625.5 0.0
```
As the P value of 0.0 is < 0.05, the H0 is rejected and Ha is accepted.
H0: There is no significant differences in the Distance From Home between attrition (Y) and attirition (N)
Ha: There is significant differences in the Distance From Home between attrition (Y) and attirition (N)
## Attrition Vs Income
```
a1=dataset.MonthlyIncome_Yes
a2=dataset.MonthlyIncome_No
stat, p=mannwhitneyu(a1,a2)
print(stat, p)
3085416.0 0.0
```
As the P value is again 0.0, which is < than 0.05, the H0 is rejected and ha is accepted.
H0: There is no significant differences in the income between attrition (Y) and attirition (N)
Ha: There is significant differences in the income between attrition (Y) and attirition (N)
## Attrition Vs Total Working Years
```
a1=dataset.TotalWorkingYears_Yes
a2=dataset.TotalWorkingYears_No
stat, p=mannwhitneyu(a1,a2)
print(stat, p)
2760982.0 0.0
```
As the P value is again 0.0, which is < than 0.05, the H0 is rejected and ha is accepted.
H0: There is no significant differences in the Total Working Years between attrition (Y) and attirition (N)
Ha: There is significant differences in the Total Working Years between attrition (Y) and attirition (N)
## Attrition Vs Years at company
```
a1=dataset.YearsAtCompany_Yes
a2=dataset.YearsAtCompany_No
stat, p=mannwhitneyu(a1,a2)
print(stat, p)
2882047.5 0.0
```
As the P value is again 0.0, which is < than 0.05, the H0 is rejected and ha is accepted.
H0: There is no significant differences in the Years At Company between attrition (Y) and attirition (N)
Ha: There is significant differences in the Years At Company between attrition (Y) and attirition (N)
## Attrition Vs YearsWithCurrentManager
```
a1=dataset.YearsWithCurrManager_Yes
a2=dataset.YearsWithCurrManager_No
stat, p=mannwhitneyu(a1,a2)
print(stat, p)
3674749.5 0.0
```
As the P value is again 0.0, which is < than 0.05, the H0 is rejected and ha is accepted.
H0: There is no significant differences in the Years With Current Manager between attrition (Y) and attirition (N)
Ha: There is significant differences in the Years With Current Manager between attrition (Y) and attirition (N)
# Statistical Tests (Separate T Test)
## Attrition Vs Distance From Home
from scipy.stats import ttest_ind
```
z1=dataset.DistanceFromHome_Yes
z2=dataset.DistanceFromHome_No
stat, p=ttest_ind(z2,z1)
print(stat, p)
44.45445917636664 0.0
```
As the P value is again 0.0, which is < than 0.05, the H0 is rejected and ha is accepted.
H0: There is no significant differences in the Distance From Home between attrition (Y) and attirition (N)
Ha: There is significant differences in the Distance From Home between attrition (Y) and attirition (N)
## Attrition Vs Income
```
z1=dataset.MonthlyIncome_Yes
z2=dataset.MonthlyIncome_No
stat, p=ttest_ind(z2, z1)
print(stat, p)
52.09279408504947 0.0
```
As the P value is again 0.0, which is < than 0.05, the H0 is rejected and ha is accepted.
H0: There is no significant differences in the Monthly Income between attrition (Y) and attirition (N)
Ha: There is significant differences in the Monthly Income between attrition (Y) and attirition (N)
## Attrition Vs Yeats At Company
```
z1=dataset.YearsAtCompany_Yes
z2=dataset.YearsAtCompany_No
stat, p=ttest_ind(z2, z1)
print(stat, p)
51.45296941515692 0.0
```
As the P value is again 0.0, which is < than 0.05, the H0 is rejected and ha is accepted.
H0: There is no significant differences in the Years At Company between attrition (Y) and attirition (N)
Ha: There is significant differences in the Years At Company between attrition (Y) and attirition (N)
## Attrition Vs Years With Current Manager
```
z1=dataset.YearsWithCurrManager_Yes
z2=dataset.YearsWithCurrManager_No
stat, p=ttest_ind(z2, z1)
print(stat, p)
53.02424349024521 0.0
```
As the P value is again 0.0, which is < than 0.05, the H0 is rejected and ha is accepted.
H0: There is no significant differences in the Years With Current Manager between attrition (Y) and attirition (N)
Ha: There is significant differences in the Years With Current Manager between attrition (Y) and attirition (N)
# Unsupervised Learning - Correlation Analysis
In order to find the interdependency of the variables DistanceFromHome, MonthlyIncome, TotalWorkingYears, YearsAtCompany, YearsWithCurrManager from that of Attrition, we executed the Correlation Analysis as follows.
stats, p=pearsonr(dataset.Attrition, dataset.DistanceFromHome)
print(stats, p)
-0.009730141010179438 0.5182860428049617
stats, p=pearsonr(dataset.Attrition, dataset.MonthlyIncome)
print(stats, p)
-0.031176281698114025 0.0384274849060192
stats, p=pearsonr(dataset.Attrition, dataset.TotalWorkingYears)
print(stats, p)
-0.17011136355964646 5.4731597518148054e-30
stats, p=pearsonr(dataset.Attrition, dataset.YearsAtCompany)
print(stats, p)
-0.13439221398997386 3.163883122493571e-19
stats, p=pearsonr(dataset.Attrition, dataset.YearsWithCurrManager)
print(stats, p)
-0.15619931590162422 1.7339322652951965e-25
# The inference of the above analysis are as follows:
Attrition & DistanceFromHome:
As r = -0.009, there’s low negative correlation between Attrition and DistanceFromHome
As the P value of 0.518 is > 0.05, we are accepting H0 and hence there’s no significant correlation between Attrition &
DistanceFromHome
Attrition & MonthlyIncome:
As r = -0.031, there’s low negative correlation between Attrition and MonthlyIncome
As the P value of 0.038 is < 0.05, we are accepting Ha and hence there’s significant correlation between Attrition &
MonthlyIncome
Attrition & TotalWorkingYears:
As r = -0.17, there’s low negative correlation between Attrition and TotalWorkingYears
As the P value is < 0.05, we are accepting Ha and hence there’s significant correlation between Attrition & TotalWorkingYears
Attrition & YearsAtCompany:
As r = -0.1343, there’s low negative correlation between Attrition and YearsAtCompany
As the P value is < 0.05, we are accepting Ha and hence there’s significant correlation between Attrition & YearsAtCompany
Attrition & YearsWithCurrManager:
As r = -0.1561, there’s low negative correlation between Attrition and YearsWithCurrManager
As the P value is < 0.05, we are accepting Ha and hence there’s significant correlation between Attrition &
YearsWithCurrManager
| github_jupyter |
# Convolutional Networks
So far we have worked with deep fully-connected networks, using them to explore different optimization strategies and network architectures. Fully-connected networks are a good testbed for experimentation because they are very computationally efficient, but in practice all state-of-the-art results use convolutional networks instead.
First you will implement several layer types that are used in convolutional networks. You will then use these layers to train a convolutional network on the CIFAR-10 dataset.
```
# As usual, a bit of setup
import numpy as np
import matplotlib.pyplot as plt
from cs231n.classifiers.cnn import *
from cs231n.data_utils import get_CIFAR10_data
from cs231n.gradient_check import eval_numerical_gradient_array, eval_numerical_gradient
from cs231n.layers import *
from cs231n.fast_layers import *
from cs231n.solver import Solver
%matplotlib inline
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# for auto-reloading external modules
# see http://stackoverflow.com/questions/1907993/autoreload-of-modules-in-ipython
%load_ext autoreload
%autoreload 2
def rel_error(x, y):
""" returns relative error """
return np.max(np.abs(x - y) / (np.maximum(1e-8, np.abs(x) + np.abs(y))))
# Load the (preprocessed) CIFAR10 data.
data = get_CIFAR10_data()
for k, v in data.items():
print('%s: ' % k, v.shape)
```
# Convolution: Naive forward pass
The core of a convolutional network is the convolution operation. In the file `cs231n/layers.py`, implement the forward pass for the convolution layer in the function `conv_forward_naive`.
You don't have to worry too much about efficiency at this point; just write the code in whatever way you find most clear.
You can test your implementation by running the following:
```
x_shape = (2, 3, 4, 4)
w_shape = (3, 3, 4, 4)
x = np.linspace(-0.1, 0.5, num=np.prod(x_shape)).reshape(x_shape)
w = np.linspace(-0.2, 0.3, num=np.prod(w_shape)).reshape(w_shape)
b = np.linspace(-0.1, 0.2, num=3)
conv_param = {'stride': 2, 'pad': 1}
out, _ = conv_forward_naive(x, w, b, conv_param)
correct_out = np.array([[[[-0.08759809, -0.10987781],
[-0.18387192, -0.2109216 ]],
[[ 0.21027089, 0.21661097],
[ 0.22847626, 0.23004637]],
[[ 0.50813986, 0.54309974],
[ 0.64082444, 0.67101435]]],
[[[-0.98053589, -1.03143541],
[-1.19128892, -1.24695841]],
[[ 0.69108355, 0.66880383],
[ 0.59480972, 0.56776003]],
[[ 2.36270298, 2.36904306],
[ 2.38090835, 2.38247847]]]])
# Compare your output to ours; difference should be around e-8
print('Testing conv_forward_naive')
print('difference: ', rel_error(out, correct_out))
a = np.array([[[1,2,3], [3,2,5]],[[1,2,3], [3,2,5]],[[1,2,3], [3,2,5]]])
#np.pad(a, 2, 'constant')
image_pad = np.array([np.pad(channel, 1 , 'constant') for channel in x])
image_pad.shape
out.shape
#w[0,:, 0:4, 0:4].shape
```
# Aside: Image processing via convolutions
As fun way to both check your implementation and gain a better understanding of the type of operation that convolutional layers can perform, we will set up an input containing two images and manually set up filters that perform common image processing operations (grayscale conversion and edge detection). The convolution forward pass will apply these operations to each of the input images. We can then visualize the results as a sanity check.
## Colab Users Only
Please execute the below cell to copy two cat images to the Colab VM.
```
# Colab users only!
%mkdir -p cs231n/notebook_images
%cd drive/My\ Drive/$FOLDERNAME/cs231n
%cp -r notebook_images/ /content/cs231n/
%cd /content/
from imageio import imread
from PIL import Image
kitten = imread('cs231n/notebook_images/kitten.jpg')
puppy = imread('cs231n/notebook_images/puppy.jpg')
# kitten is wide, and puppy is already square
d = kitten.shape[1] - kitten.shape[0]
kitten_cropped = kitten[:, d//2:-d//2, :]
img_size = 200 # Make this smaller if it runs too slow
resized_puppy = np.array(Image.fromarray(puppy).resize((img_size, img_size)))
resized_kitten = np.array(Image.fromarray(kitten_cropped).resize((img_size, img_size)))
x = np.zeros((2, 3, img_size, img_size))
x[0, :, :, :] = resized_puppy.transpose((2, 0, 1))
x[1, :, :, :] = resized_kitten.transpose((2, 0, 1))
# Set up a convolutional weights holding 2 filters, each 3x3
w = np.zeros((2, 3, 3, 3))
# The first filter converts the image to grayscale.
# Set up the red, green, and blue channels of the filter.
w[0, 0, :, :] = [[0, 0, 0], [0, 0.3, 0], [0, 0, 0]]
w[0, 1, :, :] = [[0, 0, 0], [0, 0.6, 0], [0, 0, 0]]
w[0, 2, :, :] = [[0, 0, 0], [0, 0.1, 0], [0, 0, 0]]
# Second filter detects horizontal edges in the blue channel.
w[1, 2, :, :] = [[1, 2, 1], [0, 0, 0], [-1, -2, -1]]
# Vector of biases. We don't need any bias for the grayscale
# filter, but for the edge detection filter we want to add 128
# to each output so that nothing is negative.
b = np.array([0, 128])
# Compute the result of convolving each input in x with each filter in w,
# offsetting by b, and storing the results in out.
out, _ = conv_forward_naive(x, w, b, {'stride': 1, 'pad': 1})
def imshow_no_ax(img, normalize=True):
""" Tiny helper to show images as uint8 and remove axis labels """
if normalize:
img_max, img_min = np.max(img), np.min(img)
img = 255.0 * (img - img_min) / (img_max - img_min)
plt.imshow(img.astype('uint8'))
plt.gca().axis('off')
# Show the original images and the results of the conv operation
plt.subplot(2, 3, 1)
imshow_no_ax(puppy, normalize=False)
plt.title('Original image')
plt.subplot(2, 3, 2)
imshow_no_ax(out[0, 0])
plt.title('Grayscale')
plt.subplot(2, 3, 3)
imshow_no_ax(out[0, 1])
plt.title('Edges')
plt.subplot(2, 3, 4)
imshow_no_ax(kitten_cropped, normalize=False)
plt.subplot(2, 3, 5)
imshow_no_ax(out[1, 0])
plt.subplot(2, 3, 6)
imshow_no_ax(out[1, 1])
plt.show()
```
# Convolution: Naive backward pass
Implement the backward pass for the convolution operation in the function `conv_backward_naive` in the file `cs231n/layers.py`. Again, you don't need to worry too much about computational efficiency.
When you are done, run the following to check your backward pass with a numeric gradient check.
```
np.random.seed(231)
x = np.random.randn(4, 3, 5, 5)
w = np.random.randn(2, 3, 3, 3)
b = np.random.randn(2,)
dout = np.random.randn(4, 2, 5, 5)
conv_param = {'stride': 2, 'pad': 3}
out, cache = conv_forward_naive(x, w, b, conv_param)
dx, dw, db = conv_backward_naive(dout, cache)
dx_num = eval_numerical_gradient_array(lambda x: conv_forward_naive(x, w, b, conv_param)[0], x, dout)
dw_num = eval_numerical_gradient_array(lambda w: conv_forward_naive(x, w, b, conv_param)[0], w, dout)
db_num = eval_numerical_gradient_array(lambda b: conv_forward_naive(x, w, b, conv_param)[0], b, dout)
# Your errors should be around e-8 or less.
print('Testing conv_backward_naive function')
print('dx error: ', rel_error(dx, dx_num))
print('dw error: ', rel_error(dw, dw_num))
print('db error: ', rel_error(db, db_num))
print(dw_num)
print(dw)
t = np.array([[1,2], [3,4]])
np.rot90(t, k=2)
```
# Max-Pooling: Naive forward
Implement the forward pass for the max-pooling operation in the function `max_pool_forward_naive` in the file `cs231n/layers.py`. Again, don't worry too much about computational efficiency.
Check your implementation by running the following:
```
x_shape = (2, 3, 4, 4)
x = np.linspace(-0.3, 0.4, num=np.prod(x_shape)).reshape(x_shape)
pool_param = {'pool_width': 2, 'pool_height': 2, 'stride': 2}
out, _ = max_pool_forward_naive(x, pool_param)
correct_out = np.array([[[[-0.26315789, -0.24842105],
[-0.20421053, -0.18947368]],
[[-0.14526316, -0.13052632],
[-0.08631579, -0.07157895]],
[[-0.02736842, -0.01263158],
[ 0.03157895, 0.04631579]]],
[[[ 0.09052632, 0.10526316],
[ 0.14947368, 0.16421053]],
[[ 0.20842105, 0.22315789],
[ 0.26736842, 0.28210526]],
[[ 0.32631579, 0.34105263],
[ 0.38526316, 0.4 ]]]])
# Compare your output with ours. Difference should be on the order of e-8.
print('Testing max_pool_forward_naive function:')
print('difference: ', rel_error(out, correct_out))
```
# Max-Pooling: Naive backward
Implement the backward pass for the max-pooling operation in the function `max_pool_backward_naive` in the file `cs231n/layers.py`. You don't need to worry about computational efficiency.
Check your implementation with numeric gradient checking by running the following:
```
np.random.seed(231)
x = np.random.randn(3, 2, 8, 8)
dout = np.random.randn(3, 2, 4, 4)
pool_param = {'pool_height': 2, 'pool_width': 2, 'stride': 2}
dx_num = eval_numerical_gradient_array(lambda x: max_pool_forward_naive(x, pool_param)[0], x, dout)
out, cache = max_pool_forward_naive(x, pool_param)
dx = max_pool_backward_naive(dout, cache)
# Your error should be on the order of e-12
print('Testing max_pool_backward_naive function:')
print('dx error: ', rel_error(dx, dx_num))
```
# Fast layers
Making convolution and pooling layers fast can be challenging. To spare you the pain, we've provided fast implementations of the forward and backward passes for convolution and pooling layers in the file `cs231n/fast_layers.py`.
The fast convolution implementation depends on a Cython extension; to compile it either execute the local development cell (option A) if you are developing locally, or the Colab cell (option B) if you are running this assignment in Colab.
---
**Very Important, Please Read**. For **both** option A and B, you have to **restart** the notebook after compiling the cython extension. In Colab, please save the notebook `File -> Save`, then click `Runtime -> Restart Runtime -> Yes`. This will restart the kernel which means local variables will be lost. Just re-execute the cells from top to bottom and skip the cell below as you only need to run it once for the compilation step.
---
## Option A: Local Development
Go to the cs231n directory and execute the following in your terminal:
```bash
python setup.py build_ext --inplace
```
## Option B: Colab
Execute the cell below only only **ONCE**.
```
%cd drive/My\ Drive/$FOLDERNAME/cs231n/
!python setup.py build_ext --inplace
```
The API for the fast versions of the convolution and pooling layers is exactly the same as the naive versions that you implemented above: the forward pass receives data, weights, and parameters and produces outputs and a cache object; the backward pass recieves upstream derivatives and the cache object and produces gradients with respect to the data and weights.
**NOTE:** The fast implementation for pooling will only perform optimally if the pooling regions are non-overlapping and tile the input. If these conditions are not met then the fast pooling implementation will not be much faster than the naive implementation.
You can compare the performance of the naive and fast versions of these layers by running the following:
```
# Rel errors should be around e-9 or less
from cs231n.fast_layers import conv_forward_fast, conv_backward_fast
from time import time
%load_ext autoreload
%autoreload 2
np.random.seed(231)
x = np.random.randn(100, 3, 31, 31)
w = np.random.randn(25, 3, 3, 3)
b = np.random.randn(25,)
dout = np.random.randn(100, 25, 16, 16)
conv_param = {'stride': 2, 'pad': 1}
t0 = time()
out_naive, cache_naive = conv_forward_naive(x, w, b, conv_param)
t1 = time()
out_fast, cache_fast = conv_forward_fast(x, w, b, conv_param)
t2 = time()
print('Testing conv_forward_fast:')
print('Naive: %fs' % (t1 - t0))
print('Fast: %fs' % (t2 - t1))
print('Speedup: %fx' % ((t1 - t0) / (t2 - t1)))
print('Difference: ', rel_error(out_naive, out_fast))
t0 = time()
# dx_naive, dw_naive, db_naive = conv_backward_naive(dout, cache_naive)
t1 = time()
dx_fast, dw_fast, db_fast = conv_backward_fast(dout, cache_fast)
t2 = time()
print('\nTesting conv_backward_fast:')
print('Naive: %fs' % (t1 - t0))
print('Fast: %fs' % (t2 - t1))
print('Speedup: %fx' % ((t1 - t0) / (t2 - t1)))
# print('dx difference: ', rel_error(dx_naive, dx_fast))
# print('dw difference: ', rel_error(dw_naive, dw_fast))
# print('db difference: ', rel_error(db_naive, db_fast))
# Relative errors should be close to 0.0
from cs231n.fast_layers import max_pool_forward_fast, max_pool_backward_fast
np.random.seed(231)
x = np.random.randn(100, 3, 32, 32)
dout = np.random.randn(100, 3, 16, 16)
pool_param = {'pool_height': 2, 'pool_width': 2, 'stride': 2}
t0 = time()
out_naive, cache_naive = max_pool_forward_naive(x, pool_param)
t1 = time()
out_fast, cache_fast = max_pool_forward_fast(x, pool_param)
t2 = time()
print('Testing pool_forward_fast:')
print('Naive: %fs' % (t1 - t0))
print('fast: %fs' % (t2 - t1))
print('speedup: %fx' % ((t1 - t0) / (t2 - t1)))
print('difference: ', rel_error(out_naive, out_fast))
t0 = time()
dx_naive = max_pool_backward_naive(dout, cache_naive)
t1 = time()
dx_fast = max_pool_backward_fast(dout, cache_fast)
t2 = time()
print('\nTesting pool_backward_fast:')
print('Naive: %fs' % (t1 - t0))
print('fast: %fs' % (t2 - t1))
print('speedup: %fx' % ((t1 - t0) / (t2 - t1)))
print('dx difference: ', rel_error(dx_naive, dx_fast))
```
# Convolutional "sandwich" layers
Previously we introduced the concept of "sandwich" layers that combine multiple operations into commonly used patterns. In the file `cs231n/layer_utils.py` you will find sandwich layers that implement a few commonly used patterns for convolutional networks. Run the cells below to sanity check they're working.
```
from cs231n.layer_utils import conv_relu_pool_forward, conv_relu_pool_backward
np.random.seed(231)
x = np.random.randn(2, 3, 16, 16)
w = np.random.randn(3, 3, 3, 3)
b = np.random.randn(3,)
dout = np.random.randn(2, 3, 8, 8)
conv_param = {'stride': 1, 'pad': 1}
pool_param = {'pool_height': 2, 'pool_width': 2, 'stride': 2}
out, cache = conv_relu_pool_forward(x, w, b, conv_param, pool_param)
dx, dw, db = conv_relu_pool_backward(dout, cache)
dx_num = eval_numerical_gradient_array(lambda x: conv_relu_pool_forward(x, w, b, conv_param, pool_param)[0], x, dout)
dw_num = eval_numerical_gradient_array(lambda w: conv_relu_pool_forward(x, w, b, conv_param, pool_param)[0], w, dout)
db_num = eval_numerical_gradient_array(lambda b: conv_relu_pool_forward(x, w, b, conv_param, pool_param)[0], b, dout)
# Relative errors should be around e-8 or less
print('Testing conv_relu_pool')
print('dx error: ', rel_error(dx_num, dx))
print('dw error: ', rel_error(dw_num, dw))
print('db error: ', rel_error(db_num, db))
from cs231n.layer_utils import conv_relu_forward, conv_relu_backward
np.random.seed(231)
x = np.random.randn(2, 3, 8, 8)
w = np.random.randn(3, 3, 3, 3)
b = np.random.randn(3,)
dout = np.random.randn(2, 3, 8, 8)
conv_param = {'stride': 1, 'pad': 1}
out, cache = conv_relu_forward(x, w, b, conv_param)
dx, dw, db = conv_relu_backward(dout, cache)
dx_num = eval_numerical_gradient_array(lambda x: conv_relu_forward(x, w, b, conv_param)[0], x, dout)
dw_num = eval_numerical_gradient_array(lambda w: conv_relu_forward(x, w, b, conv_param)[0], w, dout)
db_num = eval_numerical_gradient_array(lambda b: conv_relu_forward(x, w, b, conv_param)[0], b, dout)
# Relative errors should be around e-8 or less
print('Testing conv_relu:')
print('dx error: ', rel_error(dx_num, dx))
print('dw error: ', rel_error(dw_num, dw))
print('db error: ', rel_error(db_num, db))
```
# Three-layer ConvNet
Now that you have implemented all the necessary layers, we can put them together into a simple convolutional network.
Open the file `cs231n/classifiers/cnn.py` and complete the implementation of the `ThreeLayerConvNet` class. Remember you can use the fast/sandwich layers (already imported for you) in your implementation. Run the following cells to help you debug:
## Sanity check loss
After you build a new network, one of the first things you should do is sanity check the loss. When we use the softmax loss, we expect the loss for random weights (and no regularization) to be about `log(C)` for `C` classes. When we add regularization the loss should go up slightly.
```
model = ThreeLayerConvNet()
N = 50
X = np.random.randn(N, 3, 32, 32)
y = np.random.randint(10, size=N)
loss, grads = model.loss(X, y)
print('Initial loss (no regularization): ', loss)
model.reg = 0.5
loss, grads = model.loss(X, y)
print('Initial loss (with regularization): ', loss)
```
## Gradient check
After the loss looks reasonable, use numeric gradient checking to make sure that your backward pass is correct. When you use numeric gradient checking you should use a small amount of artifical data and a small number of neurons at each layer. Note: correct implementations may still have relative errors up to the order of e-2.
```
num_inputs = 2
input_dim = (3, 16, 16)
reg = 0.0
num_classes = 10
np.random.seed(231)
X = np.random.randn(num_inputs, *input_dim)
y = np.random.randint(num_classes, size=num_inputs)
model = ThreeLayerConvNet(num_filters=3, filter_size=3,
input_dim=input_dim, hidden_dim=7,
dtype=np.float64, reg=0.5)
loss, grads = model.loss(X, y)
# Errors should be small, but correct implementations may have
# relative errors up to the order of e-2
for param_name in sorted(grads):
f = lambda _: model.loss(X, y)[0]
param_grad_num = eval_numerical_gradient(f, model.params[param_name], verbose=False, h=1e-6)
e = rel_error(param_grad_num, grads[param_name])
print('%s max relative error: %e' % (param_name, rel_error(param_grad_num, grads[param_name])))
```
## Overfit small data
A nice trick is to train your model with just a few training samples. You should be able to overfit small datasets, which will result in very high training accuracy and comparatively low validation accuracy.
```
np.random.seed(231)
num_train = 100
small_data = {
'X_train': data['X_train'][:num_train],
'y_train': data['y_train'][:num_train],
'X_val': data['X_val'],
'y_val': data['y_val'],
}
model = ThreeLayerConvNet(weight_scale=1e-2)
solver = Solver(model, small_data,
num_epochs=15, batch_size=50,
update_rule='adam',
optim_config={
'learning_rate': 1e-3,
},
verbose=True, print_every=1)
solver.train()
# Print final training accuracy
print(
"Small data training accuracy:",
solver.check_accuracy(small_data['X_train'], small_data['y_train'])
)
# Print final validation accuracy
print(
"Small data validation accuracy:",
solver.check_accuracy(small_data['X_val'], small_data['y_val'])
)
```
Plotting the loss, training accuracy, and validation accuracy should show clear overfitting:
```
plt.subplot(2, 1, 1)
plt.plot(solver.loss_history, 'o')
plt.xlabel('iteration')
plt.ylabel('loss')
plt.subplot(2, 1, 2)
plt.plot(solver.train_acc_history, '-o')
plt.plot(solver.val_acc_history, '-o')
plt.legend(['train', 'val'], loc='upper left')
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()
```
## Train the net
By training the three-layer convolutional network for one epoch, you should achieve greater than 40% accuracy on the training set:
```
model = ThreeLayerConvNet(weight_scale=0.001, hidden_dim=500, reg=0.001)
solver = Solver(model, data,
num_epochs=1, batch_size=50,
update_rule='adam',
optim_config={
'learning_rate': 1e-3,
},
verbose=True, print_every=20)
solver.train()
# Print final training accuracy
print(
"Full data training accuracy:",
solver.check_accuracy(small_data['X_train'], small_data['y_train'])
)
# Print final validation accuracy
print(
"Full data validation accuracy:",
solver.check_accuracy(data['X_val'], data['y_val'])
)
```
## Visualize Filters
You can visualize the first-layer convolutional filters from the trained network by running the following:
```
from cs231n.vis_utils import visualize_grid
grid = visualize_grid(model.params['W1'].transpose(0, 2, 3, 1))
plt.imshow(grid.astype('uint8'))
plt.axis('off')
plt.gcf().set_size_inches(5, 5)
plt.show()
```
# Spatial Batch Normalization
We already saw that batch normalization is a very useful technique for training deep fully-connected networks. As proposed in the original paper (link in `BatchNormalization.ipynb`), batch normalization can also be used for convolutional networks, but we need to tweak it a bit; the modification will be called "spatial batch normalization."
Normally batch-normalization accepts inputs of shape `(N, D)` and produces outputs of shape `(N, D)`, where we normalize across the minibatch dimension `N`. For data coming from convolutional layers, batch normalization needs to accept inputs of shape `(N, C, H, W)` and produce outputs of shape `(N, C, H, W)` where the `N` dimension gives the minibatch size and the `(H, W)` dimensions give the spatial size of the feature map.
If the feature map was produced using convolutions, then we expect every feature channel's statistics e.g. mean, variance to be relatively consistent both between different images, and different locations within the same image -- after all, every feature channel is produced by the same convolutional filter! Therefore spatial batch normalization computes a mean and variance for each of the `C` feature channels by computing statistics over the minibatch dimension `N` as well the spatial dimensions `H` and `W`.
[1] [Sergey Ioffe and Christian Szegedy, "Batch Normalization: Accelerating Deep Network Training by Reducing
Internal Covariate Shift", ICML 2015.](https://arxiv.org/abs/1502.03167)
## Spatial batch normalization: forward
In the file `cs231n/layers.py`, implement the forward pass for spatial batch normalization in the function `spatial_batchnorm_forward`. Check your implementation by running the following:
```
np.random.seed(231)
# Check the training-time forward pass by checking means and variances
# of features both before and after spatial batch normalization
N, C, H, W = 2, 3, 4, 5
x = 4 * np.random.randn(N, C, H, W) + 10
print('Before spatial batch normalization:')
print(' Shape: ', x.shape)
print(' Means: ', x.mean(axis=(0, 2, 3)))
print(' Stds: ', x.std(axis=(0, 2, 3)))
# Means should be close to zero and stds close to one
gamma, beta = np.ones(C), np.zeros(C)
bn_param = {'mode': 'train'}
out, _ = spatial_batchnorm_forward(x, gamma, beta, bn_param)
print('After spatial batch normalization:')
print(' Shape: ', out.shape)
print(' Means: ', out.mean(axis=(0, 2, 3)))
print(' Stds: ', out.std(axis=(0, 2, 3)))
# Means should be close to beta and stds close to gamma
gamma, beta = np.asarray([3, 4, 5]), np.asarray([6, 7, 8])
out, _ = spatial_batchnorm_forward(x, gamma, beta, bn_param)
print('After spatial batch normalization (nontrivial gamma, beta):')
print(' Shape: ', out.shape)
print(' Means: ', out.mean(axis=(0, 2, 3)))
print(' Stds: ', out.std(axis=(0, 2, 3)))
np.random.seed(231)
# Check the test-time forward pass by running the training-time
# forward pass many times to warm up the running averages, and then
# checking the means and variances of activations after a test-time
# forward pass.
N, C, H, W = 10, 4, 11, 12
bn_param = {'mode': 'train'}
gamma = np.ones(C)
beta = np.zeros(C)
for t in range(50):
x = 2.3 * np.random.randn(N, C, H, W) + 13
spatial_batchnorm_forward(x, gamma, beta, bn_param)
bn_param['mode'] = 'test'
x = 2.3 * np.random.randn(N, C, H, W) + 13
a_norm, _ = spatial_batchnorm_forward(x, gamma, beta, bn_param)
# Means should be close to zero and stds close to one, but will be
# noisier than training-time forward passes.
print('After spatial batch normalization (test-time):')
print(' means: ', a_norm.mean(axis=(0, 2, 3)))
print(' stds: ', a_norm.std(axis=(0, 2, 3)))
```
## Spatial batch normalization: backward
In the file `cs231n/layers.py`, implement the backward pass for spatial batch normalization in the function `spatial_batchnorm_backward`. Run the following to check your implementation using a numeric gradient check:
```
np.random.seed(231)
N, C, H, W = 2, 3, 4, 5
x = 5 * np.random.randn(N, C, H, W) + 12
gamma = np.random.randn(C)
beta = np.random.randn(C)
dout = np.random.randn(N, C, H, W)
bn_param = {'mode': 'train'}
fx = lambda x: spatial_batchnorm_forward(x, gamma, beta, bn_param)[0]
fg = lambda a: spatial_batchnorm_forward(x, gamma, beta, bn_param)[0]
fb = lambda b: spatial_batchnorm_forward(x, gamma, beta, bn_param)[0]
dx_num = eval_numerical_gradient_array(fx, x, dout)
da_num = eval_numerical_gradient_array(fg, gamma, dout)
db_num = eval_numerical_gradient_array(fb, beta, dout)
#You should expect errors of magnitudes between 1e-12~1e-06
_, cache = spatial_batchnorm_forward(x, gamma, beta, bn_param)
dx, dgamma, dbeta = spatial_batchnorm_backward(dout, cache)
print('dx error: ', rel_error(dx_num, dx))
print('dgamma error: ', rel_error(da_num, dgamma))
print('dbeta error: ', rel_error(db_num, dbeta))
print(dx[0])
print(dx_num[0])
print(rel_error(dx[0], dx_num[0]))
```
# Group Normalization
In the previous notebook, we mentioned that Layer Normalization is an alternative normalization technique that mitigates the batch size limitations of Batch Normalization. However, as the authors of [2] observed, Layer Normalization does not perform as well as Batch Normalization when used with Convolutional Layers:
>With fully connected layers, all the hidden units in a layer tend to make similar contributions to the final prediction, and re-centering and rescaling the summed inputs to a layer works well. However, the assumption of similar contributions is no longer true for convolutional neural networks. The large number of the hidden units whose
receptive fields lie near the boundary of the image are rarely turned on and thus have very different
statistics from the rest of the hidden units within the same layer.
The authors of [3] propose an intermediary technique. In contrast to Layer Normalization, where you normalize over the entire feature per-datapoint, they suggest a consistent splitting of each per-datapoint feature into G groups, and a per-group per-datapoint normalization instead.
<p align="center">
<img src="https://raw.githubusercontent.com/cs231n/cs231n.github.io/master/assets/a2/normalization.png">
</p>
<center>Visual comparison of the normalization techniques discussed so far (image edited from [3])</center>
Even though an assumption of equal contribution is still being made within each group, the authors hypothesize that this is not as problematic, as innate grouping arises within features for visual recognition. One example they use to illustrate this is that many high-performance handcrafted features in traditional Computer Vision have terms that are explicitly grouped together. Take for example Histogram of Oriented Gradients [4]-- after computing histograms per spatially local block, each per-block histogram is normalized before being concatenated together to form the final feature vector.
You will now implement Group Normalization. Note that this normalization technique that you are to implement in the following cells was introduced and published to ECCV just in 2018 -- this truly is still an ongoing and excitingly active field of research!
[2] [Ba, Jimmy Lei, Jamie Ryan Kiros, and Geoffrey E. Hinton. "Layer Normalization." stat 1050 (2016): 21.](https://arxiv.org/pdf/1607.06450.pdf)
[3] [Wu, Yuxin, and Kaiming He. "Group Normalization." arXiv preprint arXiv:1803.08494 (2018).](https://arxiv.org/abs/1803.08494)
[4] [N. Dalal and B. Triggs. Histograms of oriented gradients for
human detection. In Computer Vision and Pattern Recognition
(CVPR), 2005.](https://ieeexplore.ieee.org/abstract/document/1467360/)
## Group normalization: forward
In the file `cs231n/layers.py`, implement the forward pass for group normalization in the function `spatial_groupnorm_forward`. Check your implementation by running the following:
```
np.random.seed(231)
# Check the training-time forward pass by checking means and variances
# of features both before and after spatial batch normalization
N, C, H, W = 2, 6, 4, 5
G = 2
x = 4 * np.random.randn(N, C, H, W) + 10
x_g = x.reshape((N*G,-1))
print('Before spatial group normalization:')
print(' Shape: ', x.shape)
print(' Means: ', x_g.mean(axis=1))
print(' Stds: ', x_g.std(axis=1))
# Means should be close to zero and stds close to one
gamma, beta = 2*np.ones(C), np.zeros(C)
bn_param = {'mode': 'train'}
out, _ = spatial_groupnorm_quick_forward(x, gamma, beta, G, bn_param)
out_g = out.reshape((N*G,-1))
print('After spatial group normalization:')
print(' Shape: ', out.shape)
print(' Means: ', out_g.mean(axis=1))
print(' Stds: ', out_g.std(axis=1))
np.vstack(list([np.hstack([[g]*H*W for g in gamma])])*N).shape
p = np.zeros((3,4))
print(p)
q = np.hsplit(p, 2)
print(q)
np.hstack(q)
print(np.arange(36).reshape((6,6)).reshape((18,-1)))
print(np.arange(36).reshape((6,6)))
print(np.arange(36).reshape((6,6)).reshape((18,-1)).reshape((6, -1)))
```
## Spatial group normalization: backward
In the file `cs231n/layers.py`, implement the backward pass for spatial batch normalization in the function `spatial_groupnorm_backward`. Run the following to check your implementation using a numeric gradient check:
```
np.random.seed(231)
N, C, H, W = 2, 6, 4, 5
G = 2
x = 5 * np.random.randn(N, C, H, W) + 12
gamma = np.random.randn(C)
beta = np.random.randn(C)
dout = np.random.randn(N, C, H, W)
gn_param = {}
fx = lambda x: spatial_groupnorm_quick_forward(x, gamma, beta, G, gn_param)[0]
fg = lambda a: spatial_groupnorm_quick_forward(x, gamma, beta, G, gn_param)[0]
fb = lambda b: spatial_groupnorm_quick_forward(x, gamma, beta, G, gn_param)[0]
dx_num = eval_numerical_gradient_array(fx, x, dout)
da_num = eval_numerical_gradient_array(fg, gamma, dout)
db_num = eval_numerical_gradient_array(fb, beta, dout)
_, cache = spatial_groupnorm_quick_forward(x, gamma, beta, G, gn_param)
dx, dgamma, dbeta = spatial_groupnorm_backward(dout, cache)
#You should expect errors of magnitudes between 1e-12~1e-07
print('dx error: ', rel_error(dx_num, dx))
print('dgamma error: ', rel_error(da_num, dgamma))
print('dbeta error: ', rel_error(db_num, dbeta))
```
| github_jupyter |
# Pre-processing and analysis for one-source with distance 25
## Load or create R scripts
```
get.data <- dget("get_data.r") #script to read data files
get.pars <- dget("get_pars.r") #script to extract relevant parameters from raw data
get.mv.bound <- dget("get_mvbound.r") #script to look at movement of boundary across learning
plot.cirib <- dget("plot_cirib.r") #script to plot confidence intervals as ribbon plot
zscore <- function(v){(v - mean(v, na.rm=T))/sqrt(var(v, na.rm=T))} #function to compute Z score
```
## Load data
```
fnames <- list.files(pattern = "*.csv") #create a vector of data file names, assuming all csv files are data
nfiles <- length(fnames) #number of data files
alldat <- list(get.data(fnames[1])) #initialize list containing all data with first subject
for(i1 in c(2:nfiles)) alldat[[i1]] <- get.data(fnames[i1]) #populate list with rest of data
allpars <- get.pars(alldat) #extract parameters from grid test 1 and 2 from all data
```
NOTE that get pars will produce warnings whenever the subject data has a perfectly strict boundary--these can be safely ignored.
```
head(allpars)
dim(allpars)
```
### KEY
**PID**: Unique tag for each participant
**cond**: Experiment condition
**axlab**: What shape (spiky/smooth) got the "Cooked" label? For counterbalancing, not interesting
**closebound**: What was the location of the closest source boundary?
**cbside**: Factor indicating what side of the range midpoint has the close boundary
**sno**: Subject number in condition
**txint, slope, bound**: Intercept, slope, and estimated boundary from logistic regression on test 1 and test 2 data. NOTE that only the boundary estimate is used in analysis.
**bshift**: Boundary shift direction and magnitude measured as test 2 boundary - test 1 boundary
**alshift**: Placeholder for aligned boundary shift (see below), currently just a copy of bshift
**Zalshift**: Zscored midshift, recalculated below
## Check data for outliers
Set Zscore threshold for outlier rejection
```
zthresh <- 2.5
```
First check t1bound and t2bound to see if there are any impossible values.
```
plot(allpars$t1bound, allpars$t2bound)
```
There is an impossible t2bound so let's remove it.
```
dim(allpars)
sjex <- as.character(allpars$PID[allpars$t2bound < 0]) #Add impossible value to exclude list
sjex <- unique(sjex) #remove any accidental repeats
noo <- allpars[is.na(match(allpars$PID, sjex)),] #Copy remaining subjects to noo object
dim(noo)
```
Write "no impossible" (nimp) file for later agglomeration in mega-data
```
write.csv(noo, "summary/one25_grids_nimp.csv", row.names = F, quote=F)
```
Check to make sure "aligned" shift computation worked (should be an X pattern)
```
plot(noo$alshift, noo$bshift)
```
Check initial boundary for outliers
```
plot(zscore(noo$t1bound))
abline(h=c(-zthresh,0,zthresh))
```
Add any outliers to the exclusion list and recompute no-outlier data structure
```
sjex <- c(sjex, as.character(allpars$PID[abs(zscore(allpars$t1bound)) > zthresh]))
sjex <- unique(sjex) #remove accidental repeats
noo <- noo[is.na(match(noo$PID, sjex)),]
dim(noo)
```
Now compute Zscore for aligned shift for all subjects and look for outliers
```
noo$Zalshift <- zscore(noo$alshift) #Compute Z scores for this aligned shift
plot(noo$Zalshift); abline(h = c(-zthresh,0,zthresh)) #plot Zscores
```
Again add any outliers to exclusion list and remove from noo
```
sjex <- c(sjex, as.character(noo$PID[abs(noo$Zalshift) > zthresh]))
sjex <- unique(sjex) #remove accidental repeats
noo <- noo[is.na(match(noo$PID, sjex)),]
dim(noo)
```
## Data analysis
Does the initial (t1) boundary differ between the two groups? It shouldn't since they have the exact same experience to this point.
```
t.test(t1bound ~ closebound, data = noo)
```
Reassuringly, it doesn't. So what is the location of the initial boundary on average?
```
t.test(noo$t1bound) #NB t.test of a single vector is a good way to compute mean and CIs
```
The mean boundary is shifted a bit positive relative to the midpoint between labeled examples
Next, looking across all subjects, does the aligned boundary shift differ reliably from zero? Also, what are the confidence limits on the mean shift?
```
t.test(noo$alshift)
```
The boundary shifts reliably toward the close source. The mean amount of shift is 18, and the confidence interval spans 9-27.
Next, where does the test 2 boundary lie for each group, and does this differ depending on where the source was?
```
t.test(t2bound ~ closebound, data = noo)
```
When the source was at 125, the boundary ends up at 134; when the source is at 175, the boundary ends up at 166.
Is the boundary moving all the way to the source?
```
t.test(noo$t2bound[noo$closebound==125]) #compute confidence intervals for source at 125 subgroup
t.test(noo$t2bound[noo$closebound==175]) #compute confidence intervals for source at 175 subgroup
```
In both cases boundaries move toward the source. When the initial boundary is closer to the source (source at 175), the final boundary ends up at the source. When it is farther away (source at 125), the final boundary ends up a little short of the source.
Another way of looking at the movement is to compute, for each subject, how far the source was from the learner's initial boundary, and see if this predicts the amount of shift:
```
#Predict the boundary shift from the distance between initial bound and source
m <- lm(bshift ~ t1dist, data = noo) #fit linear model predicting shift from distance
summary(m) #look at model parameters
```
Distance predicts shift significantly. The intercept is not reliably different from zero, so that, with zero distance, boundary does not shift. The slope of 0.776 suggests that the boundary shifts 78 percent of the way toward the close source. Let's visualize:
```
plot(noo$t1dist, noo$bshift) #plot distance of source against boundary shift
abline(lm(bshift~t1dist, data = noo)$coefficients) #add least squares line
abline(0,1, col = 2) #Add line with slope 1 and intercept 0
```
The black line shows the least-squares linear fit; the red line shows the expected slope if learner moved all the way toward the source. True slope is quite a bit shallower. If we compute confidence limits on slope we get:
```
confint(m, 't1dist', level = 0.95)
```
So the confidence limit extends v close to 1
### Export parameter data
```
write.csv(noo, paste("summary/onesrc25_noo_z", zthresh*10, ".csv", sep=""), row.names=F, quote=F)
```
## Further analyses
### Movement of boundary over the course of learning
```
nsj <- length(alldat) #Number of subjects is length of alldat object
mvbnd <- matrix(0, nsj, 301) #Initialize matrix of 0s to hold boundary-movement data, with 301 windows
for(i1 in c(1:nsj)) mvbnd[i1,] <- get.mv.bound(alldat, sj=i1) #Compute move data for each sj and store in matrix rows
```
Again, ignore warnings here
```
tmp <- cbind(allpars[,1:6], mvbnd) #Add subject and condition data columns
mvb.noo <- tmp[is.na(match(tmp$PID, sjex)),] #Remove excluded subjects
head(mvb.noo)
tmp <- mvb.noo[,7:307] #Copy movement data into temporary object
tmp[abs(tmp) > 250] <- NA #Remove boundary estimates that are extreme (outside 50-250 range)
tmp[tmp < 50] <- NA
mvb.noo[,7:307] <- tmp #Put remaining data back in
plot.cirib(mvb.noo[mvb.noo$bounds==125,7:307], genplot=T)
plot.cirib(mvb.noo[mvb.noo$bounds==175,7:307], genplot=F, color=4)
abline(h=150, lty=2)
abline(h=175, col=4)
abline(h=125, col=2)
title("Boundary shift over training")
```
| github_jupyter |
# About
此笔记包含了以下内容:
* keras 的基本使用
* 组合特征
* 制作dataset
* 模型的存取(2种方式)
* 添加检查点
```
import tensorflow as tf
from tensorflow.keras import layers
import numpy as np
import matplotlib.pyplot as plt
import math
from tensorflow.keras.utils import plot_model
import os
# fea_x = [i for i in np.arange(0, math.pi * 2.0, 0.01)]
# print(fea_x[:50])
x0 = np.random.randint(0, math.pi * 6.0 * 100.0, 5000) / 100.0
x1 = np.random.randint(0, math.pi * 6.0 * 100.0, 5000) / 100.0
x2 = np.random.randint(0, math.pi * 6.0 * 100.0, 1000) / 100.0 # Noisy
feaY0 = [np.random.randint(10 * math.sin(i), 20) for i in x0]
feaY1 = [np.random.randint(-20, 10 * math.sin(i)) for i in x1]
feaY2 = [np.random.randint(-10, 10) for i in x2]
fea_x = np.concatenate([x0, x1, x2])
fea_y = np.concatenate([feaY0, feaY1, feaY2])
label0 = np.repeat(0, 5000)
label1 = np.repeat(1, 5000)
label2 = np.random.randint(0,2, 1000)
label = np.concatenate([label0, label1, label2])
fea_1 = []
fea_2 = []
fea_3 = []
fea_4 = []
fea_5 = []
for i in range(len(label)):
x = fea_x[i]
y = fea_y[i]
ex_1 = x * y
ex_2 = x * x
ex_3 = y * y
ex_4 = math.sin(x)
ex_5 = math.sin(y)
fea_1.append(ex_1)
fea_2.append(ex_2)
fea_3.append(ex_3)
fea_4.append(ex_4)
fea_5.append(ex_5)
fea = np.c_[fea_x, fea_y, fea_1, fea_2, fea_3, fea_4, fea_5]
dataset = tf.data.Dataset.from_tensor_slices((fea, label))
dataset = dataset.shuffle(10000)
dataset = dataset.batch(500)
dataset = dataset.repeat()
ds_iteror = dataset.make_one_shot_iterator().get_next()
len(fea[0])
with tf.Session() as sess:
def _pltfunc(sess):
res = sess.run(ds_iteror)
# print(res)
lb = res[1]
t_fea = res[0]
for index in range(len(lb)):
tfs = t_fea[index]
if lb[index] > 0:
plt.scatter(tfs[0], tfs[1], marker='o', c='orange')
else:
plt.scatter(tfs[0], tfs[1], marker='o', c='green')
_pltfunc(sess)
_pltfunc(sess)
_pltfunc(sess)
plt.show()
inputs = tf.keras.Input(shape=(7, ))
x = layers.Dense(7, activation=tf.keras.activations.relu)(inputs)
x1 = layers.Dense(7, activation='relu')(x)
# x2 = layers.Dense(32, activation='relu')(x1)
# x3 = layers.Dense(24, activation='relu')(x2)
# x4 = layers.Dense(16, activation='relu')(x3)
# x5 = layers.Dense(8, activation='relu')(x4)
predictions = layers.Dense(2, activation='softmax')(x1)
model = tf.keras.Model(inputs=inputs, outputs=predictions)
# The compile step specifies the training configuration.
# opt = tf.train.AdamOptimizer(learning_rate=0.0001)
opt = tf.train.AdagradOptimizer(learning_rate=0.1)
# opt = tf.train.RMSPropOptimizer(0.1)
model.compile(optimizer=opt,
loss=tf.keras.losses.sparse_categorical_crossentropy,
metrics=['accuracy'])
model.fit(dataset, epochs=10, steps_per_epoch=200)
# model.fit(fea, label, epochs=10, batch_size=500, steps_per_epoch=300)
model.fit(dataset, epochs=10, steps_per_epoch=200)
result = model.predict([[[1, -10]]])
print(np.argmax(result[0]))
result = model.predict([[[1, 10]]])
print(np.argmax(result[0]))
os.getcwd()
# 模型可视化
plot_model(model, to_file=os.getcwd()+ '/model.png')
from IPython.display import SVG
import tensorflow.keras.utils as tfku
tfku.plot_model(model)
# SVG(model_to_dot(model).create(prog='dot', format='svg'))
for i in range(1000):
randomX = np.random.randint(0, 10 * math.pi * 6.0) / 10.0
randomY = 0
if np.random.randint(2) > 0:
randomY = np.random.randint(10 * math.sin(randomX), 20)
else:
randomY = np.random.randint(-20, 10 * math.sin(randomX))
ex_1 = randomX * randomY
ex_2 = randomX**2
ex_3 = randomY**2
ex_4 = math.sin(randomX)
ex_5 = math.sin(randomY)
color = ''
result = model.predict([[[randomX, randomY, ex_1, ex_2, ex_3, ex_4, ex_5]]])
pred_index = np.argmax(result[0])
if pred_index > 0:
color = 'orange'
else:
color = 'green'
plt.scatter(randomX, randomY, marker='o', c=color)
plt.show()
```
# Save Model
```
!pip install h5py pyyaml
model_path = os.getcwd() + "/mymodel.h5"
model_path
```
这里使用默认的优化器, 默认优化器不能直接保存, 读取模型时需要再次创建优化器并编译
使用 keras 内置的优化器可以直接保存和读取, 比如: `tf.keras.optimizers.Adam()`
```
model.save(model_path)
new_model = tf.keras.models.load_model(model_path)
opt = tf.train.AdagradOptimizer(learning_rate=0.1)
# opt = tf.train.RMSPropOptimizer(0.1)
new_model.compile(optimizer=opt,
loss=tf.keras.losses.sparse_categorical_crossentropy,
metrics=['accuracy'])
new_model.summary()
loss, acc = new_model.evaluate(dataset, steps=200)
print("Restored model, accuracy: {:5.2f}%".format(100*acc))
print(new_model.layers[1].get_weights())
print(new_model.layers[3].get_weights())
```
# 保存为 pb 文件
```
pb_model_path = os.getcwd() + '/pbmdoel'
pb_model_path
tf.contrib.saved_model.save_keras_model(new_model, pb_model_path)
!ls {pb_model_path}
```
# 读取 pb 文件
```
model2 = tf.contrib.saved_model.load_keras_model(pb_model_path)
model2.summary()
# 使用前要先编译
model2.compile(optimizer=opt,
loss=tf.keras.losses.sparse_categorical_crossentropy,
metrics=['accuracy'])
loss, acc = model2.evaluate(dataset, steps=200)
print("Restored model, accuracy: {:5.2f}%".format(100*acc))
```
| github_jupyter |
# Advent of Code 2016
```
data = open('data/day_1-1.txt', 'r').readline().strip().split(', ')
class TaxiCab:
def __init__(self, data):
self.data = data
self.double_visit = []
self.position = {'x': 0, 'y': 0}
self.direction = {'x': 0, 'y': 1}
self.grid = {i: {j: 0 for j in range(-500, 501)} for i in range(-500, 501)}
def run(self):
for instruction in self.data:
toward = instruction[0]
length = int(instruction[1:])
self.move(toward, length)
def move(self, toward, length):
if toward == 'R':
if self.direction['x'] == 0:
# from UP
if self.direction['y'] == 1:
self.position['x'] += length
self.direction['x'] = 1
for i in range(self.position['x'] - length, self.position['x']):
self.grid[self.position['y']][i] += 1
if self.grid[self.position['y']][i] > 1:
self.double_visit.append((i, self.position['y']))
# from DOWN
else:
self.position['x'] -= length
self.direction['x'] = -1
for i in range(self.position['x'] + length, self.position['x'], -1):
self.grid[self.position['y']][i] += 1
if self.grid[self.position['y']][i] > 1:
self.double_visit.append((i, self.position['y']))
self.direction['y'] = 0
else:
# FROM RIGHT
if self.direction['x'] == 1:
self.position['y'] -= length
self.direction['y'] = -1
for i in range(self.position['y'] + length, self.position['y'], -1):
self.grid[i][self.position['x']] += 1
if self.grid[i][self.position['x']] > 1:
self.double_visit.append((self.position['x'], i))
# FROM LEFT
else:
self.position['y'] += length
self.direction['y'] = 1
for i in range(self.position['y'] - length, self.position['y']):
self.grid[i][self.position['x']] += 1
if self.grid[i][self.position['x']] > 1:
self.double_visit.append((self.position['x'], i))
self.direction['x'] = 0
else:
if self.direction['x'] == 0:
# from UP
if self.direction['y'] == 1:
self.position['x'] -= length
self.direction['x'] = -1
for i in range(self.position['x'] + length, self.position['x'], -1):
self.grid[self.position['y']][i] += 1
if self.grid[self.position['y']][i] > 1:
self.double_visit.append((i, self.position['y']))
# from DOWN
else:
self.position['x'] += length
self.direction['x'] = 1
for i in range(self.position['x'] - length, self.position['x']):
self.grid[self.position['y']][i] += 1
if self.grid[self.position['y']][i] > 1:
self.double_visit.append((i, self.position['y']))
self.direction['y'] = 0
else:
# FROM RIGHT
if self.direction['x'] == 1:
self.position['y'] += length
self.direction['y'] = 1
for i in range(self.position['y'] - length, self.position['y']):
self.grid[i][self.position['x']] += 1
if self.grid[i][self.position['x']] > 1:
self.double_visit.append((self.position['x'], i))
# FROM LEFT
else:
self.position['y'] -= length
self.direction['y'] = -1
for i in range(self.position['y'] + length, self.position['y'], -1):
self.grid[i][self.position['x']] += 1
if self.grid[i][self.position['x']] > 1:
self.double_visit.append((self.position['x'], i))
self.direction['x'] = 0
def get_distance(self):
return sum([abs(i) for i in self.position.values()])
def get_distance_first_double_visit(self):
return sum(self.double_visit[0]) if len(self.double_visit) > 0 else 0
# Test
def test(data, result):
tc = TaxiCab(data)
tc.run()
assert tc.get_distance() == result
test(data=['R2', 'L3'], result=5)
test(data=['R2', 'R2', 'R2'], result=2)
test(data=['R5', 'L5', 'R5', 'R3'], result=12)
tc = TaxiCab(data)
tc.run()
tc.get_distance()
```
```
# Test
def test(data, result):
tc = TaxiCab(data)
tc.run()
assert tc.get_distance_first_double_visit() == result
test(data=['R8', 'R4', 'R4', 'R8'], result=4)
tc.get_distance_first_double_visit()
```
| github_jupyter |
# [Strings](https://docs.python.org/3/library/stdtypes.html#text-sequence-type-str)
```
my_string = 'Python is my favorite programming language!'
my_string
type(my_string)
len(my_string)
```
## Respecting [PEP8](https://www.python.org/dev/peps/pep-0008/#maximum-line-length) with long strings
```
long_story = ('Lorem ipsum dolor sit amet, consectetur adipiscing elit.'
'Pellentesque eget tincidunt felis. Ut ac vestibulum est.'
'In sed ipsum sit amet sapien scelerisque bibendum. Sed '
'sagittis purus eu diam fermentum pellentesque.')
long_story
```
## `str.replace()`
If you don't know how it works, you can always check the `help`:
```
help(str.replace)
```
This will not modify `my_string` because replace is not done in-place.
```
my_string.replace('a', '?')
print(my_string)
```
You have to store the return value of `replace` instead.
```
my_modified_string = my_string.replace('is', 'will be')
print(my_modified_string)
```
## `str.format()`
```
secret = '{} is cool'.format('Python')
print(secret)
print('My name is {} {}, you can call me {}.'.format('John', 'Doe', 'John'))
# is the same as:
print('My name is {first} {family}, you can call me {first}.'.format(first='John', family='Doe'))
```
## `str.join()`
```
help(str.join)
pandas = 'pandas'
numpy = 'numpy'
requests = 'requests'
cool_python_libs = ', '.join([pandas, numpy, requests])
print('Some cool python libraries: {}'.format(cool_python_libs))
```
Alternatives (not as [Pythonic](http://docs.python-guide.org/en/latest/writing/style/#idioms) and [slower](https://waymoot.org/home/python_string/)):
```
cool_python_libs = pandas + ', ' + numpy + ', ' + requests
print('Some cool python libraries: {}'.format(cool_python_libs))
cool_python_libs = pandas
cool_python_libs += ', ' + numpy
cool_python_libs += ', ' + requests
print('Some cool python libraries: {}'.format(cool_python_libs))
```
## `str.upper(), str.lower(), str.title()`
```
mixed_case = 'PyTHoN hackER'
mixed_case.upper()
mixed_case.lower()
mixed_case.title()
```
## `str.strip()`
```
help(str.strip)
ugly_formatted = ' \n \t Some story to tell '
stripped = ugly_formatted.strip()
print('ugly: {}'.format(ugly_formatted))
print('stripped: {}'.format(ugly_formatted.strip()))
```
## `str.split()`
```
help(str.split)
sentence = 'three different words'
words = sentence.split()
print(words)
type(words)
secret_binary_data = '01001,101101,11100000'
binaries = secret_binary_data.split(',')
print(binaries)
```
## Calling multiple methods in a row
```
ugly_mixed_case = ' ThIS LooKs BAd '
pretty = ugly_mixed_case.strip().lower().replace('bad', 'good')
print(pretty)
```
Note that execution order is from left to right. Thus, this won't work:
```
pretty = ugly_mixed_case.replace('bad', 'good').strip().lower()
print(pretty)
```
## [Escape characters](http://python-reference.readthedocs.io/en/latest/docs/str/escapes.html#escape-characters)
```
two_lines = 'First line\nSecond line'
print(two_lines)
indented = '\tThis will be indented'
print(indented)
```
| github_jupyter |
# FAQ
## I have heard of autoML and automated feature engineering, how is this different?
AutoML targets solving the problem once the labels or targets one wants to predict are well defined and available. Feature engineering focuses on generating features, given a dataset, labels, and targets. Both assume that the target a user wants to predict is already defined and computed. In most real world scenarios, this is something a data scientist has to do: define an outcome to predict and create labeled training examples. We structured this process and called it prediction engineering (a play on an already well defined process feature engineering). This library provides an easy way for a user to define the target outcome and generate training examples automatically from relational, temporal, multi entity datasets.
## I have used Featuretools for competing in KAGGLE, how can I use Compose?
In most KAGGLE competitions the target to predict is already defined. In many cases, they follow the same way to represent training examples as us—“label times” (see here and here). Compose is a step prior to where KAGGLE starts. Indeed, it is a step that KAGGLE or the company sponsoring the competition might have to do or would have done before publishing the competition.
## Why have I not encountered the need for Compose yet?
In many cases, setting up prediction problem is done independently before even getting started on the machine learning. This has resulted in a very skewed availability of datasets with already defined prediction problems and labels. A number of times it also results in a data scientist not knowing how the label was defined. In opening up this part of the process, we are enabling data scientists to more flexibly define problems, explore more problems and solve problems to maximize the end goal - ROI.
## I already have “Label times” file, do I need Compose?
If you already have label times you don’t need LabelMaker and search. However, you could use the label transforms functionality of Compose to apply lead and threshold, as well as balance labels.
## What is the best use of Compose?
Since we have automated feature engineering and autoML, the best recommended use for Compose is to closely couple *LabelMaker* and *Search* functionality of Compose with the rest of the machine learning pipeline. Certain parameters used in *Search*, and *LabelMaker* and *label transforms* can be tuned alongside machine learning model.
## Where can I read about your technical approach in detail?
You can read about prediction engineering, the way we defined the search algorithm and technical details in this peer reviewed paper published in IEEE international conference on data science and advanced analytics. If you’re interested, you can also watch a video here. Please note that some of our thinking and terminology has evolved as we built this library and applied Compose to different industrial scale problems.
## Do you think Compose should be part of a data scientist’s toolkit?
Yes. As we mentioned above, extracting value out of your data is dependent on how you set the prediction problem. Currently, data scientists do not iterate through the setting up of the prediction problem because there is no structured way of doing it or algorithms and library to help do it. We believe that prediction engineering should be taken even more seriously than any other part of actually solving a problem.
## How can I contribute labeling functions, or use cases?
We are happy for anyone who can provide interesting labeling functions. To contribute an interesting new use case and labeling function, we request you create a representative synthetic data set, a labeling function and the parameters for label maker. Once you have these three, you can write a brief explanation about the use case and do a pull request.
## I have a transaction file with the label as the last column, what are my label times?
Your label times is the . However, when such a data set is given one should ask for how that label was generated. It could be one of very many cases: a human could have assigned it based on their assessment/analysis, it could have been automatically generated by a system, or it could have been computed using some data. If it is the third case one should ask for the function that computed the label or rewrite it. If it is (1), one should note that the ref_time would be slightly after the transaction timestamp.
| github_jupyter |
# ADVANCED TEXT MINING
- 본 자료는 텍스트 마이닝을 활용한 연구 및 강의를 위한 목적으로 제작되었습니다.
- 본 자료를 강의 목적으로 활용하고자 하시는 경우 꼭 아래 메일주소로 연락주세요.
- 본 자료에 대한 허가되지 않은 배포를 금지합니다.
- 강의, 저작권, 출판, 특허, 공동저자에 관련해서는 문의 바랍니다.
- **Contact : ADMIN([email protected])**
---
## WEEK 02-2. Python 자료구조 이해하기
- 텍스트 데이터를 다루기 위한 Python 자료구조에 대해 다룹니다.
---
### 1. 리스트(LIST) 자료구조 이해하기
---
#### 1.1. 리스트(LIST): 값 또는 자료구조를 저장할 수 있는 구조를 선언합니다.
---
```
# 1) 리스트를 생성합니다.
new_list = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
print(new_list)
# 2) 리스트의 마지막 원소 뒤에 새로운 원소를 추가합니다.
new_list.append(100)
print(new_list)
# 3) 더하기 연산자를 활용해 두 리스트를 결합합니다.
new_list = new_list + [101, 102]
print(new_list)
# 4-1) 리스트에 존재하는 특정 원소 중 일치하는 가장 앞의 원소를 삭제합니다.
new_list.remove(3)
print(new_list)
# 4-2) 리스트에 존재하는 N 번째 원소를 삭제합니다.
del new_list[3]
print(new_list)
# 5) 리스트에 존재하는 N 번째 원소의 값을 변경합니다.
new_list[0] = 105
print(new_list)
# 6) 리스트에 존재하는 모든 원소를 오름차순으로 정렬합니다.
new_list.sort()
#new_list.sort(reverse=False)
print(new_list)
# 7) 리스트에 존재하는 모든 원소를 내림차순으로 정렬합니다.
new_list.sort(reverse=True)
print(new_list)
# 8) 리스트에 존재하는 모든 원소의 순서를 거꾸로 변경합니다.
new_list.reverse()
print(new_list)
# 9) 리스트에 존재하는 모든 원소의 개수를 불러옵니다.
length = len(new_list)
print(new_list)
# 10-1) 리스트에 특정 원소에 존재하는지 여부를 in 연산자를 통해 확인합니다.
print(100 in new_list)
# 10-2) 리스트에 특정 원소에 존재하지 않는지 여부를 not in 연산자를 통해 확인합니다.
print(100 not in new_list)
```
#### 1.2. 리스트(LIST) 인덱싱: 리스트에 존재하는 특정 원소를 불러옵니다.
---
```
new_list = [0, 1, 2, 3, 4, 5, 6, 7, "hjvjg", 9]
# 1) 리스트에 존재하는 N 번째 원소를 불러옵니다.
print("0번째 원소 :", new_list[0])
print("1번째 원소 :", new_list[1])
print("4번째 원소 :", new_list[4])
# 2) 리스트에 존재하는 N번째 부터 M-1번째 원소를 리스트 형식으로 불러옵니다.
print("0~3번째 원소 :", new_list[0:3])
print("4~9번째 원소 :", new_list[4:9])
print("2~3번째 원소 :", new_list[2:3])
# 3) 리스트에 존재하는 N번째 부터 모든 원소를 리스트 형식으로 불러옵니다.
print("3번째 부터 모든 원소 :", new_list[3:])
print("5번째 부터 모든 원소 :", new_list[5:])
print("9번째 부터 모든 원소 :", new_list[9:])
# 4) 리스트에 존재하는 N번째 이전의 모든 원소를 리스트 형식으로 불러옵니다.
print("1번째 이전의 모든 원소 :", new_list[:1])
print("7번째 이전의 모든 원소 :", new_list[:7])
print("9번째 이전의 모든 원소 :", new_list[:9])
# 5) 리스트 인덱싱에 사용되는 정수 N의 부호가 음수인 경우, 마지막 원소부터 |N|-1번째 원소를 의미합니다.
print("끝에서 |-1|-1번째 이전의 모든 원소 :", new_list[:-1])
print("끝에서 |-1|-1번째 부터 모든 원소 :", new_list[-1:])
print("끝에서 |-2|-1번째 이전의 모든 원소 :", new_list[:-2])
print("끝에서 |-2|-1번째 부터 모든 원소 :", new_list[-2:])
```
#### 1.3. 다차원 리스트(LIST): 리스트의 원소에 다양한 값 또는 자료구조를 저장할 수 있습니다.
---
```
# 1-1) 리스트의 원소에는 유형(TYPE)의 값 또는 자료구조를 섞어서 저장할 수 있습니다.
new_list = ["텍스트", 0, 1.9, [1, 2, 3, 4], {"서울": 1, "부산": 2, "대구": 3}]
print(new_list)
# 1-2) 리스트의 각 원소의 유형(TYPE)을 type(변수) 함수를 활용해 확인합니다.
print("Type of new_list[0] :", type(new_list[0]))
print("Type of new_list[1] :", type(new_list[1]))
print("Type of new_list[2] :", type(new_list[2]))
print("Type of new_list[3] :", type(new_list[3]))
print("Type of new_list[4] :", type(new_list[4]))
# 2) 리스트 원소에 리스트를 여러개 추가하여 다차원 리스트(NxM)를 생성할 수 있습니다.
new_list = [[0, 1, 2], [2, 3, 7], [9, 6, 8], [4, 5, 1]]
print("new_list :", new_list)
print("new_list[0] :", new_list[0])
print("new_list[1] :", new_list[1])
print("new_list[2] :", new_list[2])
print("new_list[3] :", new_list[3])
# 3-1) 다차원 리스트(NxM)를 정렬하는 경우 기본적으로 각 리스트의 첫번째 원소를 기준으로 정렬합니다.
new_list.sort()
print("new_list :", new_list)
print("new_list[0] :", new_list[0])
print("new_list[1] :", new_list[1])
print("new_list[2] :", new_list[2])
print("new_list[3] :", new_list[3])
# 3-2) 다차원 리스트(NxM)를 각 리스트의 N 번째 원소를 기준으로 정렬합니다.
new_list.sort(key=lambda elem: elem[2])
print("new_list :", new_list)
print("new_list[0] :", new_list[0])
print("new_list[1] :", new_list[1])
print("new_list[2] :", new_list[2])
print("new_list[3] :", new_list[3])
```
### 2. 딕셔너리(DICTIONARY) 자료구조 이해하기
---
#### 2.1. 딕셔너리(DICTIONARY): 값 또는 자료구조를 저장할 수 있는 구조를 선언합니다.
---
```
# 1) 딕셔너리를 생성합니다.
new_dict = {"마케팅팀": 98, "개발팀": 78, "데이터분석팀": 83, "운영팀": 33}
print(new_dict)
# 2) 딕셔너리의 각 원소는 KEY:VALUE 쌍의 구조를 가지며, KEY 값에 대응되는 VALUE를 불러옵니다.
print(new_dict["마케팅팀"])
# 3-1) 딕셔너리에 새로운 KEY:VALUE 쌍의 원소를 추가합니다.
new_dict["미화팀"] = 55
print(new_dict)
# 3-2) 딕셔너리에 저장된 각 원소의 KEY 값은 유일해야하기 때문에, 중복된 KEY 값이 추가되는 경우 VALUE는 덮어쓰기 됩니다.
new_dict["데이터분석팀"] = 100
print(new_dict)
# 4) 딕셔너리에 다양한 유형(TYPE)의 값 또는 자료구조를 VALUE로 사용할 수 있습니다.
new_dict["데이터분석팀"] = {"등급": "A"}
new_dict["운영팀"] = ["A"]
new_dict["개발팀"] = "재평가"
new_dict[0] = "오타"
print(new_dict)
```
#### 2.2. 딕셔너리(DICTIONARY) 인덱싱: 딕셔너리에 존재하는 원소를 리스트 형태로 불러옵니다.
---
```
# 1-1) 다양한 함수를 활용해 딕셔너리를 인덱싱 가능한 구조로 불러옵니다.
new_dict = {"마케팅팀": 98, "개발팀": 78, "데이터분석팀": 83, "운영팀": 33}
print("KEY List of new_dict :", new_dict.keys())
print("VALUE List of new_dict :", new_dict.values())
print("(KEY, VALUE) List of new_dict :", new_dict.items())
for i, j in new_dict.items():
print(i, j)
# 1-2) 불러온 자료구조를 실제 리스트 자료구조로 변환합니다.
print("KEY List of new_dict :", list(new_dict.keys()))
print("VALUE List of new_dict :", list(new_dict.values()))
print("(KEY, VALUE) List of new_dict :", list(new_dict.items()))
```
| github_jupyter |
# Gradient Checking
Welcome to the final assignment for this week! In this assignment you will learn to implement and use gradient checking.
You are part of a team working to make mobile payments available globally, and are asked to build a deep learning model to detect fraud--whenever someone makes a payment, you want to see if the payment might be fraudulent, such as if the user's account has been taken over by a hacker.
But backpropagation is quite challenging to implement, and sometimes has bugs. Because this is a mission-critical application, your company's CEO wants to be really certain that your implementation of backpropagation is correct. Your CEO says, "Give me a proof that your backpropagation is actually working!" To give this reassurance, you are going to use "gradient checking".
Let's do it!
```
# Packages
import numpy as np
from testCases import *
from gc_utils import sigmoid, relu, dictionary_to_vector, vector_to_dictionary, gradients_to_vector
```
## 1) How does gradient checking work?
Backpropagation computes the gradients $\frac{\partial J}{\partial \theta}$, where $\theta$ denotes the parameters of the model. $J$ is computed using forward propagation and your loss function.
Because forward propagation is relatively easy to implement, you're confident you got that right, and so you're almost 100% sure that you're computing the cost $J$ correctly. Thus, you can use your code for computing $J$ to verify the code for computing $\frac{\partial J}{\partial \theta}$.
Let's look back at the definition of a derivative (or gradient):
$$ \frac{\partial J}{\partial \theta} = \lim_{\varepsilon \to 0} \frac{J(\theta + \varepsilon) - J(\theta - \varepsilon)}{2 \varepsilon} \tag{1}$$
If you're not familiar with the "$\displaystyle \lim_{\varepsilon \to 0}$" notation, it's just a way of saying "when $\varepsilon$ is really really small."
We know the following:
- $\frac{\partial J}{\partial \theta}$ is what you want to make sure you're computing correctly.
- You can compute $J(\theta + \varepsilon)$ and $J(\theta - \varepsilon)$ (in the case that $\theta$ is a real number), since you're confident your implementation for $J$ is correct.
Lets use equation (1) and a small value for $\varepsilon$ to convince your CEO that your code for computing $\frac{\partial J}{\partial \theta}$ is correct!
## 2) 1-dimensional gradient checking
Consider a 1D linear function $J(\theta) = \theta x$. The model contains only a single real-valued parameter $\theta$, and takes $x$ as input.
You will implement code to compute $J(.)$ and its derivative $\frac{\partial J}{\partial \theta}$. You will then use gradient checking to make sure your derivative computation for $J$ is correct.
<img src="images/1Dgrad_kiank.png" style="width:600px;height:250px;">
<caption><center> <u> **Figure 1** </u>: **1D linear model**<br> </center></caption>
The diagram above shows the key computation steps: First start with $x$, then evaluate the function $J(x)$ ("forward propagation"). Then compute the derivative $\frac{\partial J}{\partial \theta}$ ("backward propagation").
**Exercise**: implement "forward propagation" and "backward propagation" for this simple function. I.e., compute both $J(.)$ ("forward propagation") and its derivative with respect to $\theta$ ("backward propagation"), in two separate functions.
```
# GRADED FUNCTION: forward_propagation
def forward_propagation(x, theta):
"""
Implement the linear forward propagation (compute J) presented in Figure 1 (J(theta) = theta * x)
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
Returns:
J -- the value of function J, computed using the formula J(theta) = theta * x
"""
### START CODE HERE ### (approx. 1 line)
J = theta * x
### END CODE HERE ###
return J
x, theta = 2, 4
J = forward_propagation(x, theta)
print ("J = " + str(J))
```
**Expected Output**:
<table style=>
<tr>
<td> ** J ** </td>
<td> 8</td>
</tr>
</table>
**Exercise**: Now, implement the backward propagation step (derivative computation) of Figure 1. That is, compute the derivative of $J(\theta) = \theta x$ with respect to $\theta$. To save you from doing the calculus, you should get $dtheta = \frac { \partial J }{ \partial \theta} = x$.
```
# GRADED FUNCTION: backward_propagation
def backward_propagation(x, theta):
"""
Computes the derivative of J with respect to theta (see Figure 1).
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
Returns:
dtheta -- the gradient of the cost with respect to theta
"""
### START CODE HERE ### (approx. 1 line)
dtheta = x
### END CODE HERE ###
return dtheta
x, theta = 2, 4
dtheta = backward_propagation(x, theta)
print ("dtheta = " + str(dtheta))
```
**Expected Output**:
<table>
<tr>
<td> ** dtheta ** </td>
<td> 2 </td>
</tr>
</table>
**Exercise**: To show that the `backward_propagation()` function is correctly computing the gradient $\frac{\partial J}{\partial \theta}$, let's implement gradient checking.
**Instructions**:
- First compute "gradapprox" using the formula above (1) and a small value of $\varepsilon$. Here are the Steps to follow:
1. $\theta^{+} = \theta + \varepsilon$
2. $\theta^{-} = \theta - \varepsilon$
3. $J^{+} = J(\theta^{+})$
4. $J^{-} = J(\theta^{-})$
5. $gradapprox = \frac{J^{+} - J^{-}}{2 \varepsilon}$
- Then compute the gradient using backward propagation, and store the result in a variable "grad"
- Finally, compute the relative difference between "gradapprox" and the "grad" using the following formula:
$$ difference = \frac {\mid\mid grad - gradapprox \mid\mid_2}{\mid\mid grad \mid\mid_2 + \mid\mid gradapprox \mid\mid_2} \tag{2}$$
You will need 3 Steps to compute this formula:
- 1'. compute the numerator using np.linalg.norm(...)
- 2'. compute the denominator. You will need to call np.linalg.norm(...) twice.
- 3'. divide them.
- If this difference is small (say less than $10^{-7}$), you can be quite confident that you have computed your gradient correctly. Otherwise, there may be a mistake in the gradient computation.
```
# GRADED FUNCTION: gradient_check
def gradient_check(x, theta, epsilon = 1e-7):
"""
Implement the backward propagation presented in Figure 1.
Arguments:
x -- a real-valued input
theta -- our parameter, a real number as well
epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
Returns:
difference -- difference (2) between the approximated gradient and the backward propagation gradient
"""
# Compute gradapprox using left side of formula (1). epsilon is small enough, you don't need to worry about the limit.
### START CODE HERE ### (approx. 5 lines)
thetaplus = theta + epsilon # Step 1
thetaminus = theta - epsilon # Step 2
J_plus = thetaplus * x # Step 3
J_minus = thetaminus * x # Step 4
gradapprox = (J_plus - J_minus) / (2 * epsilon) # Step 5
### END CODE HERE ###
# Check if gradapprox is close enough to the output of backward_propagation()
### START CODE HERE ### (approx. 1 line)
grad = backward_propagation(x, theta)
### END CODE HERE ###
### START CODE HERE ### (approx. 1 line)
numerator = np.linalg.norm(grad - gradapprox) # Step 1'
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox) # Step 2'
difference = numerator / denominator # Step 3'
### END CODE HERE ###
if difference < 1e-7:
print ("The gradient is correct!")
else:
print ("The gradient is wrong!")
return difference
x, theta = 2, 4
difference = gradient_check(x, theta)
print("difference = " + str(difference))
```
**Expected Output**:
The gradient is correct!
<table>
<tr>
<td> ** difference ** </td>
<td> 2.9193358103083e-10 </td>
</tr>
</table>
Congrats, the difference is smaller than the $10^{-7}$ threshold. So you can have high confidence that you've correctly computed the gradient in `backward_propagation()`.
Now, in the more general case, your cost function $J$ has more than a single 1D input. When you are training a neural network, $\theta$ actually consists of multiple matrices $W^{[l]}$ and biases $b^{[l]}$! It is important to know how to do a gradient check with higher-dimensional inputs. Let's do it!
## 3) N-dimensional gradient checking
The following figure describes the forward and backward propagation of your fraud detection model.
<img src="images/NDgrad_kiank.png" style="width:600px;height:400px;">
<caption><center> <u> **Figure 2** </u>: **deep neural network**<br>*LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID*</center></caption>
Let's look at your implementations for forward propagation and backward propagation.
```
def forward_propagation_n(X, Y, parameters):
"""
Implements the forward propagation (and computes the cost) presented in Figure 3.
Arguments:
X -- training set for m examples
Y -- labels for m examples
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
W1 -- weight matrix of shape (5, 4)
b1 -- bias vector of shape (5, 1)
W2 -- weight matrix of shape (3, 5)
b2 -- bias vector of shape (3, 1)
W3 -- weight matrix of shape (1, 3)
b3 -- bias vector of shape (1, 1)
Returns:
cost -- the cost function (logistic cost for one example)
"""
# retrieve parameters
m = X.shape[1]
W1 = parameters["W1"]
b1 = parameters["b1"]
W2 = parameters["W2"]
b2 = parameters["b2"]
W3 = parameters["W3"]
b3 = parameters["b3"]
# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID
Z1 = np.dot(W1, X) + b1
A1 = relu(Z1)
Z2 = np.dot(W2, A1) + b2
A2 = relu(Z2)
Z3 = np.dot(W3, A2) + b3
A3 = sigmoid(Z3)
# Cost
logprobs = np.multiply(-np.log(A3),Y) + np.multiply(-np.log(1 - A3), 1 - Y)
cost = 1./m * np.sum(logprobs)
cache = (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3)
return cost, cache
```
Now, run backward propagation.
```
def backward_propagation_n(X, Y, cache):
"""
Implement the backward propagation presented in figure 2.
Arguments:
X -- input datapoint, of shape (input size, 1)
Y -- true "label"
cache -- cache output from forward_propagation_n()
Returns:
gradients -- A dictionary with the gradients of the cost with respect to each parameter, activation and pre-activation variables.
"""
m = X.shape[1]
(Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cache
dZ3 = (A3 - Y) # / (A3 * (1 - A3)) WHY ISN'T dZ3 more complicated
dW3 = 1./m * np.dot(dZ3, A2.T)
db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)
dA2 = np.dot(W3.T, dZ3)
dZ2 = np.multiply(dA2, np.int64(A2 > 0))
dW2 = 1./m * np.dot(dZ2, A1.T) #2* before the end of assignment made us look for errors up here
db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)
dA1 = np.dot(W2.T, dZ2)
dZ1 = np.multiply(dA1, np.int64(A1 > 0))
dW1 = 1./m * np.dot(dZ1, X.T)
db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True) # 4 / m before the end of assn made us look for errors up here
gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,
"dA2": dA2, "dZ2": dZ2, "dW2": dW2, "db2": db2,
"dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1}
return gradients
```
You obtained some results on the fraud detection test set but you are not 100% sure of your model. Nobody's perfect! Let's implement gradient checking to verify if your gradients are correct.
**How does gradient checking work?**.
As in 1) and 2), you want to compare "gradapprox" to the gradient computed by backpropagation. The formula is still:
$$ \frac{\partial J}{\partial \theta} = \lim_{\varepsilon \to 0} \frac{J(\theta + \varepsilon) - J(\theta - \varepsilon)}{2 \varepsilon} \tag{1}$$
However, $\theta$ is not a scalar anymore. It is a dictionary called "parameters". We implemented a function "`dictionary_to_vector()`" for you. It converts the "parameters" dictionary into a vector called "values", obtained by reshaping all parameters (W1, b1, W2, b2, W3, b3) into vectors and concatenating them.
The inverse function is "`vector_to_dictionary`" which outputs back the "parameters" dictionary.
<img src="images/dictionary_to_vector.png" style="width:600px;height:400px;">
<caption><center> <u> **Figure 2** </u>: **dictionary_to_vector() and vector_to_dictionary()**<br> You will need these functions in gradient_check_n()</center></caption>
We have also converted the "gradients" dictionary into a vector "grad" using gradients_to_vector(). You don't need to worry about that.
**Exercise**: Implement gradient_check_n().
**Instructions**: Here is pseudo-code that will help you implement the gradient check.
For each i in num_parameters:
- To compute `J_plus[i]`:
1. Set $\theta^{+}$ to `np.copy(parameters_values)`
2. Set $\theta^{+}_i$ to $\theta^{+}_i + \varepsilon$
3. Calculate $J^{+}_i$ using to `forward_propagation_n(x, y, vector_to_dictionary(`$\theta^{+}$ `))`.
- To compute `J_minus[i]`: do the same thing with $\theta^{-}$
- Compute $gradapprox[i] = \frac{J^{+}_i - J^{-}_i}{2 \varepsilon}$
Thus, you get a vector gradapprox, where gradapprox[i] is an approximation of the gradient with respect to `parameter_values[i]`. You can now compare this gradapprox vector to the gradients vector from backpropagation. Just like for the 1D case (Steps 1', 2', 3'), compute:
$$ difference = \frac {\| grad - gradapprox \|_2}{\| grad \|_2 + \| gradapprox \|_2 } \tag{3}$$
```
# GRADED FUNCTION: gradient_check_n
def gradient_check_n(parameters, gradients, X, Y, epsilon = 1e-7):
"""
Checks if backward_propagation_n computes correctly the gradient of the cost output by forward_propagation_n
Arguments:
parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":
grad -- output of backward_propagation_n, contains gradients of the cost with respect to the parameters.
x -- input datapoint, of shape (input size, 1)
y -- true "label"
epsilon -- tiny shift to the input to compute approximated gradient with formula(1)
Returns:
difference -- difference (2) between the approximated gradient and the backward propagation gradient
"""
# Set-up variables
parameters_values, _ = dictionary_to_vector(parameters)
grad = gradients_to_vector(gradients)
num_parameters = parameters_values.shape[0]
J_plus = np.zeros((num_parameters, 1))
J_minus = np.zeros((num_parameters, 1))
gradapprox = np.zeros((num_parameters, 1))
# Compute gradapprox
for i in range(num_parameters):
# Compute J_plus[i]. Inputs: "parameters_values, epsilon". Output = "J_plus[i]".
# "_" is used because the function you have to outputs two parameters but we only care about the first one
### START CODE HERE ### (approx. 3 lines)
thetaplus = np.copy(parameters_values) # Step 1
#print(thetaplus[i][0])
thetaplus[i,0] = thetaplus[i,0] + epsilon
#thetaplus[i][0] = thetaplus[i][0] + epsilon # Step 2
J_plus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(thetaplus)) # Step 3
### END CODE HERE ###
# Compute J_minus[i]. Inputs: "parameters_values, epsilon". Output = "J_minus[i]".
### START CODE HERE ### (approx. 3 lines)
thetaminus = np.copy(parameters_values) # Step 1
thetaminus[i,0] = thetaplus[i,0] - epsilon
#thetaminus[i][0] = thetaplus[i][0] - epsilon # Step 2
J_minus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(thetaminus)) # Step 3
### END CODE HERE ###
# Compute gradapprox[i]
### START CODE HERE ### (approx. 1 line)
gradapprox[i] = (J_plus[i] - J_minus[i]) / (epsilon) #Why isn't the 2 eeps in here? need this to be correct.
#gradapprox[i] = (J_plus[i] - J_minus[i]) / (2. * epsilon) #How is should be!
### END CODE HERE ###
# Compare gradapprox to backward propagation gradients by computing difference.
### START CODE HERE ### (approx. 1 line)
numerator = np.linalg.norm(grad - gradapprox) # Step 1'
denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox) # Step 2'
difference = numerator / denominator # Step 3'
### END CODE HERE ###
if difference > 2e-7:
print ("\033[93m" + "There is a mistake in the backward propagation! difference = " + str(difference) + "\033[0m")
else:
print ("\033[92m" + "Your backward propagation works perfectly fine! difference = " + str(difference) + "\033[0m")
#print(gradapprox)
return difference
X, Y, parameters = gradient_check_n_test_case()
cost, cache = forward_propagation_n(X, Y, parameters)
gradients = backward_propagation_n(X, Y, cache)
difference = gradient_check_n(parameters, gradients, X, Y)
```
**Expected output**:
<table>
<tr>
<td> ** There is a mistake in the backward propagation!** </td>
<td> difference = 0.285093156781 </td>
</tr>
</table>
It seems that there were errors in the `backward_propagation_n` code we gave you! Good that you've implemented the gradient check. Go back to `backward_propagation` and try to find/correct the errors *(Hint: check dW2 and db1)*. Rerun the gradient check when you think you've fixed it. Remember you'll need to re-execute the cell defining `backward_propagation_n()` if you modify the code.
Can you get gradient check to declare your derivative computation correct? Even though this part of the assignment isn't graded, we strongly urge you to try to find the bug and re-run gradient check until you're convinced backprop is now correctly implemented.
**Note**
- Gradient Checking is slow! Approximating the gradient with $\frac{\partial J}{\partial \theta} \approx \frac{J(\theta + \varepsilon) - J(\theta - \varepsilon)}{2 \varepsilon}$ is computationally costly. For this reason, we don't run gradient checking at every iteration during training. Just a few times to check if the gradient is correct.
- Gradient Checking, at least as we've presented it, doesn't work with dropout. You would usually run the gradient check algorithm without dropout to make sure your backprop is correct, then add dropout.
Congrats, you can be confident that your deep learning model for fraud detection is working correctly! You can even use this to convince your CEO. :)
<font color='blue'>
**What you should remember from this notebook**:
- Gradient checking verifies closeness between the gradients from backpropagation and the numerical approximation of the gradient (computed using forward propagation).
- Gradient checking is slow, so we don't run it in every iteration of training. You would usually run it only to make sure your code is correct, then turn it off and use backprop for the actual learning process.
| github_jupyter |
# Code along 4
## Scale, Standardize, or Normalize with scikit-learn
### När ska man använda MinMaxScaler, RobustScaler, StandardScaler, och Normalizer
### Attribution: Jeff Hale
### Varför är det ofta nödvändigt att genomföra så kallad variable transformation/feature scaling det vill säga, standardisera, normalisera eller på andra sätt ändra skalan på data vid dataaalys?
Som jag gått igenom på föreläsningen om data wrangling kan data behöva formateras (variable transformation) för att förbättra prestandan hos många algoritmer för dataanalys. En typ av formaterinng av data, som går att göra på många olika sätt, är så kallad skalning av attribut (feature scaling). Det kan finnas flera anledningar till att data kan behöv skalas, några exempel är:
* Exempelvis neurala nätverk, regressionsalgoritmer och K-nearest neighbors fungerar inte lika bra om inte de attribut (features) som algoritmen använder befinner sig i relativt lika skalor.
* Vissa av metoderna för att skala, standardisera och normalisera kan också minska den negativa påverkan outliers kan ha i vissa algoritmer.
* Ibland är det också av vikt att ha data som är normalfördelat (standardiserat)
*Med skala menas inte den skala som hänsyftas på exempelvis kartor där det brukar anges att skalan är 1:50 000 vilket tolkas som att varje avstånd på kartan är 50 000 ggr kortare än i verkligheten.*
```
#Importerar de bibliotek vi behöver
import numpy as np
import pandas as pd
from sklearn import preprocessing
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
warnings.filterwarnings('ignore')
#Denna kod sätter upp hur matplotlib ska visa grafer och plotar
%matplotlib inline
matplotlib.style.use('ggplot')
#Generera lite input
#(den som är extremt intresserad kan läsa följande, intressanta och roliga förklaring kring varför random.seed egentligen är pseudorandom)
#https://www.sharpsightlabs.com/blog/numpy-random-seed/
np.random.seed(34)
```
# Original Distributions
Data som det kan se ut i original, alltså när det samlats in, innan någon pre-processing har genomförts.
För att ha data att använda i övningarna skapar nedanstående kod ett antal randomiserade spridningar av data
```
#skapa kolumner med olika fördelningar
df = pd.DataFrame({
'beta': np.random.beta(5, 1, 1000) * 60, # beta
'exponential': np.random.exponential(10, 1000), # exponential
'normal_p': np.random.normal(10, 2, 1000), # normal platykurtic
'normal_l': np.random.normal(10, 10, 1000), # normal leptokurtic
})
# make bimodal distribution
first_half = np.random.normal(20, 3, 500)
second_half = np.random.normal(-20, 3, 500)
bimodal = np.concatenate([first_half, second_half])
df['bimodal'] = bimodal
# create list of column names to use later
col_names = list(df.columns)
```
## Uppgift 1:
a. Plotta de kurvor som skapats i ovanstående cell i en och samma koordinatsystem med hjälp av [seaborn biblioteket](https://seaborn.pydata.org/api.html#distribution-api).
>Se till att det är tydligt vilken kurva som representerar vilken distribution.
>
>Koden för själva koordinatsystemet är given, fortsätt koda i samma cell
>
>HINT! alla fem är distribution plots
```
# plot original distribution plot
fig, (ax1) = plt.subplots(ncols=1, figsize=(10, 8))
ax1.set_title('Original Distributions')
#De fem kurvorna
sns.kdeplot(df['beta'], ax=ax1)
sns.kdeplot(df['exponential'], ax=ax1)
sns.kdeplot(df['normal_p'], ax=ax1)
sns.kdeplot(df['normal_l'], ax=ax1)
sns.kdeplot(df['bimodal'], ax=ax1);
```
b. Visa de fem första raderna i den dataframe som innehåller alla distributioner.
```
df.head()
```
c. För samtliga fem attribut, beräkna:
* medel
* median
Vad för bra metod kan användas för att få ett antal statistiska mått på en dataframe? Hämta denna information med denna metod.
```
df.describe()
```
d. I pandas kan du plotta din dataframe på några olika sätt. Gör en plot för att ta reda på hur skalan på de olika attibuten ser ut, befinner sig alla fem i ungefär samma skala?
```
df.plot()
```
* Samtliga värden ligger inom liknande intervall
e. Vad händer om följande kolumn med randomiserade värden läggs till?
```
new_column = np.random.normal(1000000, 10000, (1000,1))
df['new_column'] = new_column
col_names.append('new_column')
df['new_column'].plot(kind='kde')
# plot våra originalvärden tillsammans med det nya värdet
fig, (ax1) = plt.subplots(ncols=1, figsize=(10, 8))
ax1.set_title('Original Distributions')
sns.kdeplot(df['beta'], ax=ax1)
sns.kdeplot(df['exponential'], ax=ax1)
sns.kdeplot(df['normal_p'], ax=ax1)
sns.kdeplot(df['normal_l'], ax=ax1)
sns.kdeplot(df['bimodal'], ax=ax1);
sns.kdeplot(df['new_column'], ax=ax1);
```
Hur gick det?
Testar några olika sätt att skala dataframes..
### MinMaxScaler
MinMaxScaler subtraherar varje värde i en kolumn med medelvärdet av den kolumnen och dividerar sedan med antalet värden.
```
mm_scaler = preprocessing.MinMaxScaler()
df_mm = mm_scaler.fit_transform(df)
df_mm = pd.DataFrame(df_mm, columns=col_names)
fig, (ax1) = plt.subplots(ncols=1, figsize=(10, 8))
ax1.set_title('After MinMaxScaler')
sns.kdeplot(df_mm['beta'], ax=ax1)
sns.kdeplot(df_mm['exponential'], ax=ax1)
sns.kdeplot(df_mm['normal_p'], ax=ax1)
sns.kdeplot(df_mm['normal_l'], ax=ax1)
sns.kdeplot(df_mm['bimodal'], ax=ax1)
sns.kdeplot(df_mm['new_column'], ax=ax1);
```
Vad har hänt med värdena?
```
df_mm['beta'].min()
df_mm['beta'].max()
```
Vi jämför med min och maxvärde för varje kolumn innan vi normaliserade vår dataframe
```
mins = [df[col].min() for col in df.columns]
mins
maxs = [df[col].max() for col in df.columns]
maxs
```
Let's check the minimums and maximums for each column after MinMaxScaler.
```
mins = [df_mm[col].min() for col in df_mm.columns]
mins
maxs = [df_mm[col].max() for col in df_mm.columns]
maxs
```
Vad har hänt?
### RobustScaler
RobustScaler subtraherar med medianen för kolumnen och dividerar med kvartilavståndet (skillnaden mellan största 25% och minsta 25%)
```
r_scaler = preprocessing.RobustScaler()
df_r = r_scaler.fit_transform(df)
df_r = pd.DataFrame(df_r, columns=col_names)
fig, (ax1) = plt.subplots(ncols=1, figsize=(10, 8))
ax1.set_title('After RobustScaler')
sns.kdeplot(df_r['beta'], ax=ax1)
sns.kdeplot(df_r['exponential'], ax=ax1)
sns.kdeplot(df_r['normal_p'], ax=ax1)
sns.kdeplot(df_r['normal_l'], ax=ax1)
sns.kdeplot(df_r['bimodal'], ax=ax1)
sns.kdeplot(df_r['new_column'], ax=ax1);
```
Vi kollar igen min och max efteråt (OBS; jämför med originalet högst upp innan vi startar olika skalningsmetoder).
```
mins = [df_r[col].min() for col in df_r.columns]
mins
maxs = [df_r[col].max() for col in df_r.columns]
maxs
```
Vad har hänt?
### StandardScaler
StandardScaler skalar varje kolumn till att ha 0 som medelvärde och standardavvikelsen 1
```
s_scaler = preprocessing.StandardScaler()
df_s = s_scaler.fit_transform(df)
df_s = pd.DataFrame(df_s, columns=col_names)
fig, (ax1) = plt.subplots(ncols=1, figsize=(10, 8))
ax1.set_title('After StandardScaler')
sns.kdeplot(df_s['beta'], ax=ax1)
sns.kdeplot(df_s['exponential'], ax=ax1)
sns.kdeplot(df_s['normal_p'], ax=ax1)
sns.kdeplot(df_s['normal_l'], ax=ax1)
sns.kdeplot(df_s['bimodal'], ax=ax1)
sns.kdeplot(df_s['new_column'], ax=ax1);
```
Vi kontrollerar min och max efter skalningen återigen
```
mins = [df_s[col].min() for col in df_s.columns]
mins
maxs = [df_s[col].max() for col in df_s.columns]
maxs
```
Vad har hänt? I jämförelse med de två innan?
# Normalizer
Normaliser transformerar rader istället för kolumner genom att (default) beräkna den Euclidiska normen som är roten ur summan av roten ur samtliga värden. Kallas för l2.
```
n_scaler = preprocessing.Normalizer()
df_n = n_scaler.fit_transform(df)
df_n = pd.DataFrame(df_n, columns=col_names)
fig, (ax1) = plt.subplots(ncols=1, figsize=(10, 8))
ax1.set_title('After Normalizer')
sns.kdeplot(df_n['beta'], ax=ax1)
sns.kdeplot(df_n['exponential'], ax=ax1)
sns.kdeplot(df_n['normal_p'], ax=ax1)
sns.kdeplot(df_n['normal_l'], ax=ax1)
sns.kdeplot(df_n['bimodal'], ax=ax1)
sns.kdeplot(df_n['new_column'], ax=ax1);
```
Min och max efter skalning
```
mins = [df_n[col].min() for col in df_n.columns]
mins
maxs = [df_n[col].max() for col in df_n.columns]
maxs
```
Vad har hänt?
Nu tar vi en titt på alla olika sätt att skala tillsammans, dock skippar vi normalizern då det är väldigt ovanligt att man vill skala om rader.
### Kombinerad plot
```
#Själva figuren
fig, (ax0, ax1, ax2, ax3) = plt.subplots(ncols=4, figsize=(20, 8))
ax0.set_title('Original Distributions')
sns.kdeplot(df['beta'], ax=ax0)
sns.kdeplot(df['exponential'], ax=ax0)
sns.kdeplot(df['normal_p'], ax=ax0)
sns.kdeplot(df['normal_l'], ax=ax0)
sns.kdeplot(df['bimodal'], ax=ax0)
sns.kdeplot(df['new_column'], ax=ax0);
ax1.set_title('After MinMaxScaler')
sns.kdeplot(df_mm['beta'], ax=ax1)
sns.kdeplot(df_mm['exponential'], ax=ax1)
sns.kdeplot(df_mm['normal_p'], ax=ax1)
sns.kdeplot(df_mm['normal_l'], ax=ax1)
sns.kdeplot(df_mm['bimodal'], ax=ax1)
sns.kdeplot(df_mm['new_column'], ax=ax1);
ax2.set_title('After RobustScaler')
sns.kdeplot(df_r['beta'], ax=ax2)
sns.kdeplot(df_r['exponential'], ax=ax2)
sns.kdeplot(df_r['normal_p'], ax=ax2)
sns.kdeplot(df_r['normal_l'], ax=ax2)
sns.kdeplot(df_r['bimodal'], ax=ax2)
sns.kdeplot(df_r['new_column'], ax=ax2);
ax3.set_title('After StandardScaler')
sns.kdeplot(df_s['beta'], ax=ax3)
sns.kdeplot(df_s['exponential'], ax=ax3)
sns.kdeplot(df_s['normal_p'], ax=ax3)
sns.kdeplot(df_s['normal_l'], ax=ax3)
sns.kdeplot(df_s['bimodal'], ax=ax3)
sns.kdeplot(df_s['new_column'], ax=ax3);
```
Efter samtliga transformationer är värdena på en mer lika skala. MinMax hade varit att föredra här eftersom den ger minst förskjutning av värdena i förhållande till varandra. Det är samma avstånd som i originalet, de andra två skalningsmetoderna ändrar avstånden mellan värdena vilket kommer påverka modellens korrekthet.
| github_jupyter |
# Tutorial 2. Solving a 1D diffusion equation
```
# Document Author: Dr. Vishal Sharma
# Author email: [email protected]
# License: MIT
# This tutorial is applicable for NAnPack version 1.0.0-alpha4
```
### I. Background
The objective of this tutorial is to present the step-by-step solution of a 1D diffusion equation using NAnPack such that users can follow the instructions to learn using this package. The numerical solution is obtained using the Forward Time Central Spacing (FTCS) method. The detailed description of the FTCS method is presented in Section IV of this tutorial.
### II. Case Description
We will be solving a classical probkem of a suddenly accelerated plate in fluid mechanicas which has the known exact solution. In this problem, the fluid is
bounded between two parallel plates. The upper plate remains stationary and the lower plate is suddenly accelerated in *y*-direction at velocity $U_o$. It is
required to find the velocity profile between the plates for the given initial and boundary conditions.
(For the sake of simplicity in setting up numerical variables, let's assume that the *x*-axis is pointed in the upward direction and *y*-axis is pointed along the horizontal direction as shown in the schematic below:

**Initial conditions**
$$u(t=0.0, 0.0<x\leq H) = 0.0 \;m/s$$
$$u(t=0.0, x=0.0) = 40.0 \;m/s$$
**Boundary conditions**
$$u(t\geq0.0, x=0.0) = 40.0 \;m/s$$
$$u(t\geq0.0, x=H) = 0.0 \;m/s$$
Viscosity of fluid, $\;\;\nu = 2.17*10^{-4} \;m^2/s$
Distance between plates, $\;\;H = 0.04 \;m$
Grid step size, $\;\;dx = 0.001 \;m$
Simulation time, $\;\;T = 1.08 \;sec$
Specify the required simulation inputs based on our setup in the configuration file provided with this package. You may choose to save the configuration file with any other filename. I have saved the configuration file in the "input" folder of my project directory such that the relative path is `./input/config.ini`.
### III. Governing Equation
The governing equation for the given application is the simplified for the the Navies-Stokes equation which is given as:
$$\frac{\partial u} {\partial t} = \nu\frac{\partial^2 u}{\partial x^2}$$
This is the diffusion equation model and is classified as the parabolic PDE.
### IV. FTCS method
The forward time central spacing approximation equation in 1D is presented here. This is a time explicit method which means that one unknown is calculated using the known neighbouring values from the previous time step. Here *i* represents grid point location, *n*+1 is the future time step, and *n* is the current time step.
$$u_{i}^{n+1} = u_{i}^{n} + \frac{\nu\Delta t}{(\Delta x)^2}(u_{i+1}^{n} - 2u_{i}^{n} + u_{i-1}^{n})$$
The order of this approximation is $[(\Delta t), (\Delta x)^2]$
The diffusion number is given as $d_{x} = \nu\frac{\Delta t}{(\Delta x)^2}$ and for one-dimensional applications the stability criteria is $d_{x}\leq\frac{1}{2}$
The solution presented here is obtained using a diffusion number = 0.5 (CFL = 0.5 in configuration file). Time step size will be computed using the expression of diffusion number. Beginners are encouraged to try diffusion numbers greater than 0.5 as an exercise after running this script.
Users are encouraged to read my blogs on numerical methods - [link here](https://www.linkedin.com/in/vishalsharmaofficial/detail/recent-activity/posts/).
### V. Script Development
*Please note that this code script is provided in file `./examples/tutorial-02-diffusion-1D-solvers-FTCS.py`.*
As per the Python established coding guidelines [PEP 8](https://www.python.org/dev/peps/pep-0008/#imports), all package imports must be done at the top part of the script in the following sequence --
1. import standard library
2. import third party modules
3. import local application/library specific
Accordingly, in our code we will importing the following required modules (in alphabetical order). If you are using Jupyter notebook, hit `Shift + Enter` on each cell after typing the code.
```
import matplotlib.pyplot as plt
from nanpack.benchmark import ParallelPlateFlow
import nanpack.preprocess as pre
from nanpack.grid import RectangularGrid
from nanpack.parabolicsolvers import FTCS
import nanpack.postprocess as post
```
As the first step in simulation, we have to tell our script to read the inputs and assign those inputs to the variables/objects that we will use in our entire code. For this purpose, there is a class `RunConfig` in `nanpack.preprocess` module. We will call this class and assign an object (instance) to it so that we can use its member variables. The `RunConfig` class is written in such a manner that its methods get executed as soon as it's instance is created. The users must provide the configuration file path as a parameter to `RunConfig` class.
```
FileName = "path/to/project/input/config.ini" # specify the correct file path
cfg = pre.RunConfig(FileName) # cfg is an instance of RunConfig class which can be used to access class variables. You may choose any variable in place of cfg.
```
You will obtain several configuration messages on your output screen so that you can verify that your inputs are correct and that the configuration is successfully completed. Next step is the assignment of initial conditions and the boundary conditions. For assigning boundary conditions, I have created a function `BC()` which we will be calling in the next cell. I have included this function at the bottom of this tutorial for your reference. It is to be noted that U is the dependent variable that was initialized when we executed the configuration, and thus we will be using `cfg.U` to access the initialized U. In a similar manner, all the inputs provided in the configuration file can be obtained by using configuration class object `cfg.` as the prefix to the variable names. Users are allowed to use any object of their choice.
*If you are using Jupyter Notebook, the function BC must be executed before referencing to it, otherwise, you will get an error. Jump to the bottom of this notebook where you see code cell # 1 containing the `BC()` function*
```
# Assign initial conditions
cfg.U[0] = 40.0
cfg.U[1:] = 0.0
# Assign boundary conditions
U = BC(cfg.U)
```
Next, we will be calculating location of all grid points within the domain using the function `RectangularGrid()` and save values into X. We will also require to calculate diffusion number in X direction. In nanpack, the program treats the diffusion number = CFL for 1D applications that we entered in the configuration file, and therefore this step may be skipped, however, it is not the same in two-dimensional applications and therefore to stay consistent and to avoid confusion we will be using the function `DiffusionNumbers()` to compute the term `diffX`.
```
X, _ = RectangularGrid(cfg.dX, cfg.iMax)
diffX,_ = pre.DiffusionNumbers(cfg.Dimension, cfg.diff, cfg.dT, cfg.dX)
```
Next, we will initialize some local variables before start the time stepping:
```
Error = 1.0 # variable to keep track of error
n = 0 # variable to advance in time
```
Start time loop using while loop such that if one of the condition returns False, the time stepping will be stopped. For explanation of each line, see the comments. Please note the identation of the codes within the while loop. Take extra care with indentation as Python is very particular about it.
```
while n <= cfg.nMax and Error > cfg.ConvCrit: # start loop
Error = 0.0 # reset error to 0.0 at the beginning of each step
n += 1 # advance the value of n at each step
Uold = U.copy() # store solution at time level, n
U = FTCS(Uold, diffX) # solve for U using FTCS method at time level n+1
Error = post.AbsoluteError(U, Uold) # calculate errors
U = BC(U) # Update BC
post.MonitorConvergence(cfg, n, Error) # Use this function to monitor convergence
post.WriteSolutionToFile(U, n, cfg.nWrite, cfg.nMax,\
cfg.OutFileName, cfg.dX) # Write output to file
post.WriteConvHistToFile(cfg, n, Error) # Write convergence log to history file
```
In the above convergence monitor, it is worth noting that the solution error is gradually moving towards zero which is what we need to confirm stability in the solution. If the solution becomes unstable, the errors will rise, probably upto the point where your code will crash. As you know that the solution obtained is a time-dependent solution and therefore, we didn't allow the code to run until the convergence is observed. If a steady-state solution is desired, change the STATE key in the configuration file equals to "STEADY" and specify a much larger value of nMax key, say nMax = 5000. This is left as an exercise for the users to obtain a stead-state solution. Also, try running the solution with the larger grid step size, $\Delta x$ or a larger time step size, $\Delta t$.
After the time stepping is completed, save the final results to the output files.
```
# Write output to file
post.WriteSolutionToFile(U, n, cfg.nWrite, cfg.nMax,
cfg.OutFileName, cfg.dX)
# Write convergence history log to a file
post.WriteConvHistToFile(cfg, n, Error)
```
Verify that the files are saved in the target directory.
Now let us obtain analytical solution of this flow that will help us in validating our codes.
```
# Obtain analytical solution
Uana = ParallelPlateFlow(40.0, X, cfg.diff, cfg.totTime, 20)
```
Next, we will validate our results by plotting the results using the matplotlib package that we have imported above. Type the following lines of codes:
```
plt.rc("font", family="serif", size=8) # Assign fonts in the plot
fig, ax = plt.subplots(dpi=150) # Create axis for plotting
plt.plot(U, X, ">-.b", linewidth=0.5, label="FTCS",\
markersize=5, markevery=5) # Plot data with required labels and markers, customize the plot however you may like
plt.plot(Uana, X, "o:r", linewidth=0.5, label="Analytical",\
markersize=5, markevery=5) # Plot analytical solution on the same plot
plt.xlabel('Velocity (m/s)') # X-axis labelling
plt.ylabel('Plate distance (m)') # Y-axis labelling
plt.title(f"Velocity profile\nat t={cfg.totTime} sec", fontsize=8) # Plot title
plt.legend()
plt.show() # Show plot- this command is very important
```
Function for the boundary conditions.
```
def BC(U):
"""Return the dependent variable with the updated values at the boundaries."""
U[0] = 40.0
U[-1] = 0.0
return U
```
Congratulations, you have completed the first coding tutoria using nanpack package and verified that your codes produced correct results. If you solve some other similar diffusion-1D model example, share it with the nanpack community. I will be excited to see your projects.
| github_jupyter |
# lesson goals
* Intro to markdown, plain text-based syntax for formatting docs
* markdown is integrated into the jupyter notebook
## What is markdown?
* developed in 2004 by John Gruber
- a way of formatting text
- a perl utility for converting markdown into html
**plain text files** have many advantages of other formats
1. they are readable on virt. all devices
2. withstood the test of time (legacy word processing formats)
by using markdown you'll be able to produce files that are legible in plain text and ready to be styled in other platforms
example:
* blogging engines, static site generators, sites like (github) support markdown & will render markdown into html
* tools like pandoc convert files into and out of markdown
markdown files are saved in extention `.md` and can be opened in text editors like textedit, notepad, sublime text, or vim
#### Headings
Four levels of heading are avaiable in Markdown, and are indicated by the number of `#` preceding the heading text. Paste the following examples into a code box.
```
# First level heading
## Second level heading
### Third level heading
#### Fourth level heading
```
# First level heading
## Second level heading
### Third level heading
#### Fourth level heading
First and second level headings may also be entered as follows:
```
First level heading
=======
Second level heading
----------
```
First level heading
=======
Second level heading
----------
#### Paragraphs & Line Breaks
Try typing the following sentence into the textbox:
```
Welcome to the Jupyter Jumpstart.
Today we'll be learning about Markdown syntax.
This sentence is separated by a single line break from the preceding one.
```
Welcome to the Jupyter Jumpstart.
Today we'll be learning about Markdown syntax.
This sentence is separated by a single line break from the preceding one.
NOTE:
* Paragraphs must be separated by an empty line
* leave an empty line between `syntax` and `This`
* some implementations of Markdown, single line breaks must also be indicated with two empty spaces at the end of each line
#### Adding Emphasis
* Text can be italicized by wrapping the word in `*` or `_` symbols
* bold text is written by wrapping the word in `**` or `_`
Try adding emphasis to a sentence using these methods:
```
I am **very** excited about the _Jupyter Jumpstart_ workshop.
```
I am **very** excited about the _Jupyter Jumpstart_ workshop.
#### Making Lists
Markdown includes support for ordered and unordered lists. Try typing the following list into the textbox:
```
Shopping List
----------
* Fruits
* Apples
* Oranges
* Grapes
* Dairy
* Milk
* Cheese
```
Indenting the `*` will allow you to created nested items.
Shopping List
----------
* Fruits
* Apples
- hellow
* Oranges
* Grapes
* Dairy
* Milk
* Cheese
**Ordered lists** are written by numbering each line. Once again, the goal of Markdown is to produce documents that are both legible as plain text and able to be transformed into other formats.
```
To-do list
----------
1. Finish Markdown tutorial
2. Go to grocery store
3. Prepare lunch
```
To-do list
----------
1. Finish Markdown tutorial
2. Go to grocery store
3. Going for drinks
3. Prepare lunch
#### Code Snippets
* Represent code by wrapping snippets in back-tick characters like `````
* for example `` `<br />` ``
* whole blocks of code are written by typing three backtick characters before and after each block
Try typing the following text into the textbox:
```html
<html>
<head>
<title>Website Title</title>
</head>
<body>
</body>
</html>
```
```html
<html>
<head>
<title>Website Title</title>
</head>
<body>
</body>
</html>
```
**specific languages**
in jupyter you can specify specific lanauages for code syntax hylighting
example:
```python
for item in collection:
print(item)
```
note how the keywords in python are highlighted
```python
for item in collection:
print(item)
```
#### Blockquotes
Adding a `>` before any paragraph will render it as a blockquote element.
Try typing the following text into the textbox:
```
> Hello, I am a paragraph of text enclosed in a blockquote. Notice how I am offset from the left margin.
```
> Hello, I am a paragraph of text enclosed in a blockquote. Notice how I am offset from the left margin.
#### Links
* Inline links are written by enclosing the link text in square brackets first, then including the URL and optional alt-text in round brackets
`For more tutorials, please visit the [Programming Historian](http://programminghistorian.org/ "Programming Historian main page").`
[Programming Historian](http://programminghistorian.org/ "Programming Historian main page")
#### Images
Images can be referenced using `!`, followed by some alt-text in square brackets, followed by the image URL and an optional title. These will not be displayed in your plain text document, but would be embedded into a rendered HTML page.
``

#### Horizontal Rules
Horizontal rules are produced when three or more `-`, `*` or `_` are included on a line by themselves, regardless of the number of spaces between them. All of the following combinations will render horizontal rules:
```
___
* * *
- - - - - -
```
___
* * *
- - - - - -
#### Tables
* use pipes `|` to separate columns and hyphens `-` between your headings and the rest of the table content
* pipes are only strictly necessary between columns, you may use them on either side of your table for a more polished look
* cells can contain any length of content, and it is not necessary for pipes to be vertically aligned with each other.
Make the below into a table in the notebook:
```
| Heading 1 | Heading 2 | Heading 3 |
| --------- | --------- | --------- |
| Row 1, column 1 | Row 1, column 2 | Row 1, column 3|
| Row 2, column 1 | Row 2, column 2 | Row 2, column 3|
| Row 3, column 1 | Row 3, column 2 | Row 3, column 3|
```
| Heading 1 | Heading 2 | Heading 3 |
| --------- | --------- | --------- |
| Row 1, column 1 | Row 1, column 2 | Row 1, column 3|
| Row 2, column 1 | Row 2, column 2 | Row 2, column 3|
| Row 3, column 1 | Row 3, column 2 | Row 3, column 3|
To specify the alignment of each column, colons `:` can be added to the header row as follows. Create the table in the notebook.
```
| Left-aligned | Centered | Right-aligned |
| :-------- | :-------: | --------: |
| Apples | Red | 5000 |
| Bananas | Yellow | 75 |
```
| Left-aligned | Centered | Right-aligned |
| :-------- | :-------: | --------: |
| Apples | Red | 5000 |
| Bananas | Yellow | 75 |
```
from IPython import display
display.YouTubeVideo('Rc4JQWowG5I')
whos
display.YouTubeVideo??
help(display.YouTubeVideo)
```
| github_jupyter |
```
import tensorflow as tf
from tensorflow.keras.callbacks import TensorBoard
import os
import matplotlib.pyplot as plt
import numpy as np
import random
import cv2
import time
training_path = "fruits-360_dataset/Training"
test_path = "fruits-360_dataset/Test"
try:
STATS = np.load("stats.npy", allow_pickle=True)
except FileNotFoundError as fnf:
print("Not found stats file.")
STATS = []
# Parameters
GRAY_SCALE = False
FRUITS = os.listdir(training_path)
random.shuffle(FRUITS)
train_load = 0.1
test_load = 0.3
def load_data(directory_path, load_factor=None):
data = []
labels = []
for fruit_name in FRUITS:
class_num = FRUITS.index(fruit_name)
path = os.path.join(directory_path, fruit_name)
for img in os.listdir(path):
if load_factor and np.random.random() > load_factor: # skip image
continue
img_path = os.path.join(path, img)
if GRAY_SCALE:
image = cv2.imread(img_path, cv2.IMREAD_GRAYSCALE)
else:
image = cv2.imread(img_path)
image = image[:, :, [2, 1, 0]]
image = image / 255.0
image = np.array(image, dtype=np.single) # Reduce precision and memory consumption
data.append([image, class_num])
random.shuffle(data)
X = []
y = []
for image, label in data:
X.append(image)
y.append(label)
X = np.array(X)
y = np.array(y)
if GRAY_SCALE:
print("Reshaping gray scale")
X = X.reshape(-1, X.shape[1], X.shape[2], 1)
return X, y
X_training, y_training = load_data(training_path, load_factor=train_load)
print("Created training array")
print(f"X shape: {X_training.shape}")
print(f"y shape: {y_training.shape}")
X_test, y_test = load_data(test_path, load_factor=test_load)
print("Created test arrays")
print(f"X shape: {X_test.shape}")
print(f"y shape: {y_test.shape}")
class AfterTwoEpochStop(tf.keras.callbacks.Callback):
def __init__(self, acc_threshold, loss_threshold):
# super(AfterTwoEpochStop, self).__init__()
self.acc_threshold = acc_threshold
self.loss_threshold = loss_threshold
self.checked = False
print("Init")
def on_epoch_end(self, epoch, logs=None):
acc = logs["accuracy"]
loss = logs["loss"]
if acc >= self.acc_threshold and loss <= self.loss_threshold:
if self.checked:
self.model.stop_training = True
else:
self.checked = True
else:
self.checked = False
stop = AfterTwoEpochStop(acc_threshold=0.98, loss_threshold=0.05)
# Limit gpu memory usage
config = tf.compat.v1.ConfigProto()
config.gpu_options.allow_growth = False
config.gpu_options.per_process_gpu_memory_fraction = 0.4
session = tf.compat.v1.Session(config=config)
from tensorflow.keras.layers import Dense, Flatten, Conv2D, Conv3D, MaxPooling2D, MaxPooling3D, Activation, Dropout
dense_layers = [2]
dense_size = [32, 64]
conv_layers = [1, 2, 3]
conv_size = [32, 64]
conv_shape = [2, 5]
pic_shape = X_training.shape[1:]
label_count = len(FRUITS)
run_num = 0
total = len(dense_layers)*len(dense_size)*len(conv_layers)*len(conv_size)*len(conv_shape)
for dl in dense_layers:
for ds in dense_size:
for cl in conv_layers:
for cs in conv_size:
for csh in conv_shape:
run_num += 1
with tf.compat.v1.Session(config=config) as sess:
NAME = f"{cl}xConv({cs:>03})_shape{csh}-{dl}xDense({ds:>03})-{time.time():10.0f}"
tensorboard = TensorBoard(log_dir=f'logs-optimize/{NAME}')
model = None
model = tf.keras.models.Sequential()
model.add(Conv2D(cs, (csh, csh), activation='relu', input_shape=pic_shape))
model.add(MaxPooling2D())
for i in range(cl-1):
model.add(Conv2D(cs, (csh, csh), activation='relu'))
model.add(MaxPooling2D())
model.add(Flatten())
for x in range(dl):
model.add(Dense(ds, activation='relu'))
model.add(Dense(label_count, activation='softmax'))
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
history = model.fit(X_training, y_training,
batch_size=25, epochs=10,
validation_data=(X_test, y_test),
callbacks=[tensorboard, stop])
loss = history.history['loss']
accuracy = history.history['accuracy']
val_loss = history.history['val_loss']
val_accuracy = history.history['val_accuracy']
print(f"{(run_num/total)*100:<5.1f}% - {NAME} Results: ")
# print(f"Test Accuracy: {val_accuracy[-1]:>2.4f}")
# print(f"Test loss: {val_loss[-1]:>2.4f}")
```
| github_jupyter |
# <span style="color:Maroon">Trade Strategy
__Summary:__ <span style="color:Blue">In this code we shall test the results of given model
```
# Import required libraries
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import os
np.random.seed(0)
import warnings
warnings.filterwarnings('ignore')
# User defined names
index = "BTC-USD"
filename_whole = "whole_dataset"+index+"_xgboost_model.csv"
filename_trending = "Trending_dataset"+index+"_xgboost_model.csv"
filename_meanreverting = "MeanReverting_dataset"+index+"_xgboost_model.csv"
date_col = "Date"
Rf = 0.01 #Risk free rate of return
# Get current working directory
mycwd = os.getcwd()
print(mycwd)
# Change to data directory
os.chdir("..")
os.chdir(str(os.getcwd()) + "\\Data")
# Read the datasets
df_whole = pd.read_csv(filename_whole, index_col=date_col)
df_trending = pd.read_csv(filename_trending, index_col=date_col)
df_meanreverting = pd.read_csv(filename_meanreverting, index_col=date_col)
# Convert index to datetime
df_whole.index = pd.to_datetime(df_whole.index)
df_trending.index = pd.to_datetime(df_trending.index)
df_meanreverting.index = pd.to_datetime(df_meanreverting.index)
# Head for whole dataset
df_whole.head()
df_whole.shape
# Head for Trending dataset
df_trending.head()
df_trending.shape
# Head for Mean Reverting dataset
df_meanreverting.head()
df_meanreverting.shape
# Merge results from both models to one
df_model = df_trending.append(df_meanreverting)
df_model.sort_index(inplace=True)
df_model.head()
df_model.shape
```
## <span style="color:Maroon">Functions
```
def initialize(df):
days, Action1, Action2, current_status, Money, Shares = ([] for i in range(6))
Open_price = list(df['Open'])
Close_price = list(df['Adj Close'])
Predicted = list(df['Predicted'])
Action1.append(Predicted[0])
Action2.append(0)
current_status.append(Predicted[0])
if(Predicted[0] != 0):
days.append(1)
if(Predicted[0] == 1):
Money.append(0)
else:
Money.append(200)
Shares.append(Predicted[0] * (100/Open_price[0]))
else:
days.append(0)
Money.append(100)
Shares.append(0)
return days, Action1, Action2, current_status, Predicted, Money, Shares, Open_price, Close_price
def Action_SA_SA(days, Action1, Action2, current_status, i):
if(current_status[i-1] != 0):
days.append(1)
else:
days.append(0)
current_status.append(current_status[i-1])
Action1.append(0)
Action2.append(0)
return days, Action1, Action2, current_status
def Action_ZE_NZE(days, Action1, Action2, current_status, i):
if(days[i-1] < 5):
days.append(days[i-1] + 1)
Action1.append(0)
Action2.append(0)
current_status.append(current_status[i-1])
else:
days.append(0)
Action1.append(current_status[i-1] * (-1))
Action2.append(0)
current_status.append(0)
return days, Action1, Action2, current_status
def Action_NZE_ZE(days, Action1, Action2, current_status, Predicted, i):
current_status.append(Predicted[i])
Action1.append(Predicted[i])
Action2.append(0)
days.append(days[i-1] + 1)
return days, Action1, Action2, current_status
def Action_NZE_NZE(days, Action1, Action2, current_status, Predicted, i):
current_status.append(Predicted[i])
Action1.append(Predicted[i])
Action2.append(Predicted[i])
days.append(1)
return days, Action1, Action2, current_status
def get_df(df, Action1, Action2, days, current_status, Money, Shares):
df['Action1'] = Action1
df['Action2'] = Action2
df['days'] = days
df['current_status'] = current_status
df['Money'] = Money
df['Shares'] = Shares
return df
def Get_TradeSignal(Predicted, days, Action1, Action2, current_status):
# Loop over 1 to N
for i in range(1, len(Predicted)):
# When model predicts no action..
if(Predicted[i] == 0):
if(current_status[i-1] != 0):
days, Action1, Action2, current_status = Action_ZE_NZE(days, Action1, Action2, current_status, i)
else:
days, Action1, Action2, current_status = Action_SA_SA(days, Action1, Action2, current_status, i)
# When Model predicts sell
elif(Predicted[i] == -1):
if(current_status[i-1] == -1):
days, Action1, Action2, current_status = Action_SA_SA(days, Action1, Action2, current_status, i)
elif(current_status[i-1] == 0):
days, Action1, Action2, current_status = Action_NZE_ZE(days, Action1, Action2, current_status, Predicted,
i)
else:
days, Action1, Action2, current_status = Action_NZE_NZE(days, Action1, Action2, current_status, Predicted,
i)
# When model predicts Buy
elif(Predicted[i] == 1):
if(current_status[i-1] == 1):
days, Action1, Action2, current_status = Action_SA_SA(days, Action1, Action2, current_status, i)
elif(current_status[i-1] == 0):
days, Action1, Action2, current_status = Action_NZE_ZE(days, Action1, Action2, current_status, Predicted,
i)
else:
days, Action1, Action2, current_status = Action_NZE_NZE(days, Action1, Action2, current_status, Predicted,
i)
return days, Action1, Action2, current_status
def Get_FinancialSignal(Open_price, Action1, Action2, Money, Shares, Close_price):
for i in range(1, len(Open_price)):
if(Action1[i] == 0):
Money.append(Money[i-1])
Shares.append(Shares[i-1])
else:
if(Action2[i] == 0):
# Enter new position
if(Shares[i-1] == 0):
Shares.append(Action1[i] * (Money[i-1]/Open_price[i]))
Money.append(Money[i-1] - Action1[i] * Money[i-1])
# Exit the current position
else:
Shares.append(0)
Money.append(Money[i-1] - Action1[i] * np.abs(Shares[i-1]) * Open_price[i])
else:
Money.append(Money[i-1] -1 *Action1[i] *np.abs(Shares[i-1]) * Open_price[i])
Shares.append(Action2[i] * (Money[i]/Open_price[i]))
Money[i] = Money[i] - 1 * Action2[i] * np.abs(Shares[i]) * Open_price[i]
return Money, Shares
def Get_TradeData(df):
# Initialize the variables
days,Action1,Action2,current_status,Predicted,Money,Shares,Open_price,Close_price = initialize(df)
# Get Buy/Sell trade signal
days, Action1, Action2, current_status = Get_TradeSignal(Predicted, days, Action1, Action2, current_status)
Money, Shares = Get_FinancialSignal(Open_price, Action1, Action2, Money, Shares, Close_price)
df = get_df(df, Action1, Action2, days, current_status, Money, Shares)
df['CurrentVal'] = df['Money'] + df['current_status'] * np.abs(df['Shares']) * df['Adj Close']
return df
def Print_Fromated_PL(active_days, number_of_trades, drawdown, annual_returns, std_dev, sharpe_ratio, year):
"""
Prints the metrics
"""
print("++++++++++++++++++++++++++++++++++++++++++++++++++++")
print(" Year: {0}".format(year))
print(" Number of Trades Executed: {0}".format(number_of_trades))
print("Number of days with Active Position: {}".format(active_days))
print(" Annual Return: {:.6f} %".format(annual_returns*100))
print(" Sharpe Ratio: {:.2f}".format(sharpe_ratio))
print(" Maximum Drawdown (Daily basis): {:.2f} %".format(drawdown*100))
print("----------------------------------------------------")
return
def Get_results_PL_metrics(df, Rf, year):
df['tmp'] = np.where(df['current_status'] == 0, 0, 1)
active_days = df['tmp'].sum()
number_of_trades = np.abs(df['Action1']).sum()+np.abs(df['Action2']).sum()
df['tmp_max'] = df['CurrentVal'].rolling(window=20).max()
df['tmp_min'] = df['CurrentVal'].rolling(window=20).min()
df['tmp'] = np.where(df['tmp_max'] > 0, (df['tmp_max'] - df['tmp_min'])/df['tmp_max'], 0)
drawdown = df['tmp'].max()
annual_returns = (df['CurrentVal'].iloc[-1]/100 - 1)
std_dev = df['CurrentVal'].pct_change(1).std()
sharpe_ratio = (annual_returns - Rf)/std_dev
Print_Fromated_PL(active_days, number_of_trades, drawdown, annual_returns, std_dev, sharpe_ratio, year)
return
```
```
# Change to Images directory
os.chdir("..")
os.chdir(str(os.getcwd()) + "\\Images")
```
## <span style="color:Maroon">Whole Dataset
```
df_whole_train = df_whole[df_whole["Sample"] == "Train"]
df_whole_test = df_whole[df_whole["Sample"] == "Test"]
df_whole_test_2019 = df_whole_test[df_whole_test.index.year == 2019]
df_whole_test_2020 = df_whole_test[df_whole_test.index.year == 2020]
output_train_whole = Get_TradeData(df_whole_train)
output_test_whole = Get_TradeData(df_whole_test)
output_test_whole_2019 = Get_TradeData(df_whole_test_2019)
output_test_whole_2020 = Get_TradeData(df_whole_test_2020)
output_train_whole["BuyandHold"] = (100 * output_train_whole["Adj Close"])/(output_train_whole.iloc[0]["Adj Close"])
output_test_whole["BuyandHold"] = (100*output_test_whole["Adj Close"])/(output_test_whole.iloc[0]["Adj Close"])
output_test_whole_2019["BuyandHold"] = (100 * output_test_whole_2019["Adj Close"])/(output_test_whole_2019.iloc[0]
["Adj Close"])
output_test_whole_2020["BuyandHold"] = (100 * output_test_whole_2020["Adj Close"])/(output_test_whole_2020.iloc[0]
["Adj Close"])
Get_results_PL_metrics(output_test_whole_2019, Rf, 2019)
Get_results_PL_metrics(output_test_whole_2020, Rf, 2020)
# Scatter plot to save fig
plt.figure(figsize=(10,5))
plt.plot(output_train_whole["CurrentVal"], 'b-', label="Value (Model)")
plt.plot(output_train_whole["BuyandHold"], 'r--', alpha=0.5, label="Buy and Hold")
plt.xlabel("Date", fontsize=12)
plt.ylabel("Value", fontsize=12)
plt.legend()
plt.title("Train Sample "+ str(index) + " Xgboost Whole Dataset", fontsize=16)
plt.savefig("Train Sample Whole Dataset Xgboost Model" + str(index) +'.png')
plt.show()
plt.close()
# Scatter plot to save fig
plt.figure(figsize=(10,5))
plt.plot(output_test_whole["CurrentVal"], 'b-', label="Value (Model)")
plt.plot(output_test_whole["BuyandHold"], 'r--', alpha=0.5, label="Buy and Hold")
plt.xlabel("Date", fontsize=12)
plt.ylabel("Value", fontsize=12)
plt.legend()
plt.title("Test Sample "+ str(index) + " Xgboost Whole Dataset", fontsize=16)
plt.savefig("Test Sample Whole Dataset XgBoost Model" + str(index) +'.png')
plt.show()
plt.close()
```
__Comments:__ <span style="color:Blue"> Based on the performance of model on Train Sample, the model has definitely learnt the patter, instead of over-fitting. But the performance of model in Test Sample is very poor
## <span style="color:Maroon">Segment Model
```
df_model_train = df_model[df_model["Sample"] == "Train"]
df_model_test = df_model[df_model["Sample"] == "Test"]
df_model_test_2019 = df_model_test[df_model_test.index.year == 2019]
df_model_test_2020 = df_model_test[df_model_test.index.year == 2020]
output_train_model = Get_TradeData(df_model_train)
output_test_model = Get_TradeData(df_model_test)
output_test_model_2019 = Get_TradeData(df_model_test_2019)
output_test_model_2020 = Get_TradeData(df_model_test_2020)
output_train_model["BuyandHold"] = (100 * output_train_model["Adj Close"])/(output_train_model.iloc[0]["Adj Close"])
output_test_model["BuyandHold"] = (100 * output_test_model["Adj Close"])/(output_test_model.iloc[0]["Adj Close"])
output_test_model_2019["BuyandHold"] = (100 * output_test_model_2019["Adj Close"])/(output_test_model_2019.iloc[0]
["Adj Close"])
output_test_model_2020["BuyandHold"] = (100 * output_test_model_2020["Adj Close"])/(output_test_model_2020.iloc[0]
["Adj Close"])
Get_results_PL_metrics(output_test_model_2019, Rf, 2019)
Get_results_PL_metrics(output_test_model_2020, Rf, 2020)
# Scatter plot to save fig
plt.figure(figsize=(10,5))
plt.plot(output_train_model["CurrentVal"], 'b-', label="Value (Model)")
plt.plot(output_train_model["BuyandHold"], 'r--', alpha=0.5, label="Buy and Hold")
plt.xlabel("Date", fontsize=12)
plt.ylabel("Value", fontsize=12)
plt.legend()
plt.title("Train Sample Hurst Segment XgBoost Models "+ str(index), fontsize=16)
plt.savefig("Train Sample Hurst Segment XgBoost Models" + str(index) +'.png')
plt.show()
plt.close()
# Scatter plot to save fig
plt.figure(figsize=(10,5))
plt.plot(output_test_model["CurrentVal"], 'b-', label="Value (Model)")
plt.plot(output_test_model["BuyandHold"], 'r--', alpha=0.5, label="Buy and Hold")
plt.xlabel("Date", fontsize=12)
plt.ylabel("Value", fontsize=12)
plt.legend()
plt.title("Test Sample Hurst Segment XgBoost Models" + str(index), fontsize=16)
plt.savefig("Test Sample Hurst Segment XgBoost Models" + str(index) +'.png')
plt.show()
plt.close()
```
__Comments:__ <span style="color:Blue"> Based on the performance of model on Train Sample, the model has definitely learnt the patter, instead of over-fitting. The model does perform well in Test sample (Not compared to Buy and Hold strategy) compared to single model. Hurst Exponent based segmentation has definately added value to the model
| github_jupyter |
```
import numpy as np
import math
import matplotlib.pyplot as plt
input_data = np.array([math.cos(x) for x in np.arange(200)])
plt.plot(input_data[:50])
plt.show
X = []
Y = []
size = 50
number_of_records = len(input_data) - size
for i in range(number_of_records - 50):
X.append(input_data[i:i+size])
Y.append(input_data[i+size])
X = np.array(X)
X = np.expand_dims(X, axis=2)
Y = np.array(Y)
Y = np.expand_dims(Y, axis=1)
X.shape, Y.shape
X_valid = []
Y_valid = []
for i in range(number_of_records - 50, number_of_records):
X_valid.append(input_data[i:i+size])
Y_valid.append(input_data[i+size])
X_valid = np.array(X_valid)
X_valid = np.expand_dims(X_valid, axis=2)
Y_valid = np.array(Y_valid)
Y_valid = np.expand_dims(Y_valid, axis=1)
learning_rate = 0.0001
number_of_epochs = 5
sequence_length = 50
hidden_layer_size = 100
output_layer_size = 1
back_prop_truncate = 5
min_clip_value = -10
max_clip_value = 10
W1 = np.random.uniform(0, 1, (hidden_layer_size, sequence_length))
W2 = np.random.uniform(0, 1, (hidden_layer_size, hidden_layer_size))
W3 = np.random.uniform(0, 1, (output_layer_size, hidden_layer_size))
def sigmoid(x):
return 1 / (1 + np.exp(-x))
for epoch in range(number_of_epochs):
# check loss on train
loss = 0.0
# do a forward pass to get prediction
for i in range(Y.shape[0]):
x, y = X[i], Y[i]
prev_act = np.zeros((hidden_layer_size, 1))
for t in range(sequence_length):
new_input = np.zeros(x.shape)
new_input[t] = x[t]
mul_w1 = np.dot(W1, new_input)
mul_w2 = np.dot(W2, prev_act)
add = mul_w2 + mul_w1
act = sigmoid(add)
mul_w3 = np.dot(W3, act)
prev_act = act
# calculate error
loss_per_record = (y - mul_w3)**2 / 2
loss += loss_per_record
loss = loss / float(y.shape[0])
# check loss on validation
val_loss = 0.0
for i in range(Y_valid.shape[0]):
x, y = X_valid[i], Y_valid[i]
prev_act = np.zeros((hidden_layer_size, 1))
for t in range(sequence_length):
new_input = np.zeros(x.shape)
new_input[t] = x[t]
mul_w1 = np.dot(W1, new_input)
mul_w2 = np.dot(W2, prev_act)
add = mul_w2 + mul_w1
act = sigmoid(add)
mul_w3 = np.dot(W3, act)
prev_act = act
loss_per_record = (y - mul_w3)**2 / 2
val_loss += loss_per_record
val_loss = val_loss / float(y.shape[0])
print('Epoch: ', epoch + 1, ', Loss: ', loss, ', Val Loss: ', val_loss)
# train model
for i in range(Y.shape[0]):
x, y = X[i], Y[i]
layers = []
prev_act = np.zeros((hidden_layer_size, 1))
dW1 = np.zeros(W1.shape)
dW3 = np.zeros(W3.shape)
dW2 = np.zeros(W2.shape)
dW1_t = np.zeros(W1.shape)
dW3_t = np.zeros(W3.shape)
dW2_t = np.zeros(W2.shape)
dW1_i = np.zeros(W1.shape)
dW2_i = np.zeros(W2.shape)
# forward pass
for t in range(sequence_length):
new_input = np.zeros(x.shape)
new_input[t] = x[t]
mul_w1 = np.dot(W1, new_input)
mul_w2 = np.dot(W2, prev_act)
add = mul_w2 + mul_w1
act = sigmoid(add)
mul_w3 = np.dot(W3, act)
layers.append({'act':act, 'prev_act':prev_act})
prev_act = act
# derivative of pred
dmul_w3 = (mul_w3 - y)
# backward pass
for t in range(sequence_length):
dW3_t = np.dot(dmul_w3, np.transpose(layers[t]['act']))
dsv = np.dot(np.transpose(W3), dmul_w3)
ds = dsv
dadd = add * (1 - add) * ds
dmul_w2 = dadd * np.ones_like(mul_w2)
dprev_act = np.dot(np.transpose(W2), dmul_w2)
for i in range(t-1, max(-1, t-back_prop_truncate-1), -1):
ds = dsv + dprev_act
dadd = add * (1 - add) * ds
dmul_w2 = dadd * np.ones_like(mul_w2)
dmul_w1 = dadd * np.ones_like(mul_w1)
dW2_i = np.dot(W2, layers[t]['prev_act'])
dprev_act = np.dot(np.transpose(W2), dmul_w2)
new_input = np.zeros(x.shape)
new_input[t] = x[t]
dW1_i = np.dot(W1, new_input)
dx = np.dot(np.transpose(W1), dmul_w1)
dW1_t += dW1_i
dW2_t += dW2_i
dW3 += dW3_t
dW1 += dW1_t
dW2 += dW2_t
if dW1.max() > max_clip_value:
dW1[dW1 > max_clip_value] = max_clip_value
if dW3.max() > max_clip_value:
dW3[dW3 > max_clip_value] = max_clip_value
if dW2.max() > max_clip_value:
dW2[dW2 > max_clip_value] = max_clip_value
if dW1.min() < min_clip_value:
dW1[dW1 < min_clip_value] = min_clip_value
if dW3.min() < min_clip_value:
dW3[dW3 < min_clip_value] = min_clip_value
if dW2.min() < min_clip_value:
dW2[dW2 < min_clip_value] = min_clip_value
# update
W1 -= learning_rate * dW1
W3 -= learning_rate * dW3
W2 -= learning_rate * dW2
preds = []
for i in range(Y_valid.shape[0]):
x, y = X_valid[i], Y_valid[i]
prev_act = np.zeros((hidden_layer_size, 1))
# For each time step...
for t in range(sequence_length):
mul_w1 = np.dot(W1, x)
mul_w2 = np.dot(W2, prev_act)
add = mul_w2 + mul_w1
act = sigmoid(add)
mul_w3 = np.dot(W3, act)
prev_act = act
preds.append(mul_w3)
preds = np.array(preds)
plt.plot(preds[:, 0, 0], 'g')
plt.plot(Y_valid[:, 0], 'r')
plt.show()
from sklearn.metrics import mean_squared_error
math.sqrt(mean_squared_error(Y_valid[:, 0], preds[:, 0, 0]))
```
| github_jupyter |
# Monte Carlo Integration with Python
## Dr. Tirthajyoti Sarkar ([LinkedIn](https://www.linkedin.com/in/tirthajyoti-sarkar-2127aa7/), [Github](https://github.com/tirthajyoti)), Fremont, CA, July 2020
---
### Disclaimer
The inspiration for this demo/notebook stemmed from [Georgia Tech's Online Masters in Analytics (OMSA) program](https://www.gatech.edu/academics/degrees/masters/analytics-online-degree-oms-analytics) study material. I am proud to pursue this excellent Online MS program. You can also check the details [here](http://catalog.gatech.edu/programs/analytics-ms/#onlinetext).
## What is Monte Carlo integration?
### A casino trick for mathematics

Monte Carlo, is in fact, the name of the world-famous casino located in the eponymous district of the city-state (also called a Principality) of Monaco, on the world-famous French Riviera.
It turns out that the casino inspired the minds of famous scientists to devise an intriguing mathematical technique for solving complex problems in statistics, numerical computing, system simulation.
### Modern origin (to make 'The Bomb')

One of the first and most famous uses of this technique was during the Manhattan Project when the chain-reaction dynamics in highly enriched uranium presented an unimaginably complex theoretical calculation to the scientists. Even the genius minds like John Von Neumann, Stanislaw Ulam, Nicholas Metropolis could not tackle it in the traditional way. They, therefore, turned to the wonderful world of random numbers and let these probabilistic quantities tame the originally intractable calculations.
Amazingly, these random variables could solve the computing problem, which stymied the sure-footed deterministic approach. The elements of uncertainty actually won.
Just like uncertainty and randomness rule in the world of Monte Carlo games. That was the inspiration for this particular moniker.
### Today
Today, it is a technique used in a wide swath of fields,
- risk analysis, financial engineering,
- supply chain logistics,
- statistical learning and modeling,
- computer graphics, image processing, game design,
- large system simulations,
- computational physics, astronomy, etc.
For all its successes and fame, the basic idea is deceptively simple and easy to demonstrate. We demonstrate it in this article with a simple set of Python code.
## The code and the demo
```
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad
```
### A simple function which is difficult to integrate analytically
While the general Monte Carlo simulation technique is much broader in scope, we focus particularly on the Monte Carlo integration technique here.
It is nothing but a numerical method for computing complex definite integrals, which lack closed-form analytical solutions.
Say, we want to calculate,
$$\int_{0}^{4}\sqrt[4]{15x^3+21x^2+41x+3}.e^{-0.5x} dx$$
```
def f1(x):
return (15*x**3+21*x**2+41*x+3)**(1/4) * (np.exp(-0.5*x))
```
### Plot
```
x = np.arange(0,4.1,0.1)
y = f1(x)
plt.figure(figsize=(8,4))
plt.title("Plot of the function: $\sqrt[4]{15x^3+21x^2+41x+3}.e^{-0.5x}$",
fontsize=18)
plt.plot(x,y,'-',c='k',lw=2)
plt.grid(True)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.show()
```
### Riemann sums?
There are many such techniques under the general category of [Riemann sum](https://medium.com/r/?url=https%3A%2F%2Fen.wikipedia.org%2Fwiki%2FRiemann_sum). The idea is just to divide the area under the curve into small rectangular or trapezoidal pieces, approximate them by the simple geometrical calculations, and sum those components up.
For a simple illustration, I show such a scheme with only 5 equispaced intervals.
For the programmer friends, in fact, there is a [ready-made function in the Scipy package](https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.quad.html#scipy.integrate.quad) which can do this computation fast and accurately.
```
rect = np.linspace(0,4,5)
plt.figure(figsize=(8,4))
plt.title("Area under the curve: With Riemann sum",
fontsize=18)
plt.plot(x,y,'-',c='k',lw=2)
plt.fill_between(x,y1=y,y2=0,color='orange',alpha=0.6)
for i in range(5):
plt.vlines(x=rect[i],ymin=0,ymax=2,color='blue')
plt.grid(True)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.show()
```
### What if I go random?
What if I told you that I do not need to pick the intervals so uniformly, and, in fact, I can go completely probabilistic, and pick 100% random intervals to compute the same integral?
Crazy talk? My choice of samples could look like this…
```
rand_lines = 4*np.random.uniform(size=5)
plt.figure(figsize=(8,4))
plt.title("With 5 random sampling intervals",
fontsize=18)
plt.plot(x,y,'-',c='k',lw=2)
plt.fill_between(x,y1=y,y2=0,color='orange',alpha=0.6)
for i in range(5):
plt.vlines(x=rand_lines[i],ymin=0,ymax=2,color='blue')
plt.grid(True)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.show()
```
Or, this?
```
rand_lines = 4*np.random.uniform(size=5)
plt.figure(figsize=(8,4))
plt.title("With 5 random sampling intervals",
fontsize=18)
plt.plot(x,y,'-',c='k',lw=2)
plt.fill_between(x,y1=y,y2=0,color='orange',alpha=0.6)
for i in range(5):
plt.vlines(x=rand_lines[i],ymin=0,ymax=2,color='blue')
plt.grid(True)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.show()
```
### It just works!
We don't have the time or scope to prove the theory behind it, but it can be shown that with a reasonably high number of random sampling, we can, in fact, compute the integral with sufficiently high accuracy!
We just choose random numbers (between the limits), evaluate the function at those points, add them up, and scale it by a known factor. We are done.
OK. What are we waiting for? Let's demonstrate this claim with some simple Python code.
### A simple version
```
def monte_carlo(func,
a=0,
b=1,
n=1000):
"""
Monte Carlo integration
"""
u = np.random.uniform(size=n)
#plt.hist(u)
u_func = func(a+(b-a)*u)
s = ((b-a)/n)*u_func.sum()
return s
```
### Another version with 10-spaced sampling
```
def monte_carlo_uniform(func,
a=0,
b=1,
n=1000):
"""
Monte Carlo integration with more uniform spread (forced)
"""
subsets = np.arange(0,n+1,n/10)
steps = n/10
u = np.zeros(n)
for i in range(10):
start = int(subsets[i])
end = int(subsets[i+1])
u[start:end] = np.random.uniform(low=i/10,high=(i+1)/10,size=end-start)
np.random.shuffle(u)
#plt.hist(u)
#u = np.random.uniform(size=n)
u_func = func(a+(b-a)*u)
s = ((b-a)/n)*u_func.sum()
return s
inte = monte_carlo_uniform(f1,a=0,b=4,n=100)
print(inte)
```
### How good is the calculation anyway?
This integral cannot be calculated analytically. So, we need to benchmark the accuracy of the Monte Carlo method against another numerical integration technique anyway. We chose the Scipy `integrate.quad()` function for that.
Now, you may also be thinking - **what happens to the accuracy as the sampling density changes**. This choice clearly impacts the computation speed - we need to add less number of quantities if we choose a reduced sampling density.
Therefore, we simulated the same integral for a range of sampling density and plotted the result on top of the gold standard - the Scipy function represented as the horizontal line in the plot below,
```
inte_lst = []
for i in range(100,2100,50):
inte = monte_carlo_uniform(f1,a=0,b=4,n=i)
inte_lst.append(inte)
result,_ = quad(f1,a=0,b=4)
plt.figure(figsize=(8,4))
plt.plot([i for i in range(100,2100,50)],inte_lst,color='blue')
plt.hlines(y=result,xmin=0,xmax=2100,linestyle='--',lw=3)
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.xlabel("Sample density for Monte Carlo",fontsize=15)
plt.ylabel("Integration result",fontsize=15)
plt.grid(True)
plt.legend(['Monte Carlo integration','Scipy function'],fontsize=15)
plt.show()
```
### Not bad at all...
Therefore, we observe some small perturbations in the low sample density phase, but they smooth out nicely as the sample density increases. In any case, the absolute error is extremely small compared to the value returned by the Scipy function - on the order of 0.02%.
The Monte Carlo trick works fantastically!
### Speed of the Monte Carlo method
In this particular example, the Monte Carlo calculations are running twice as fast as the Scipy integration method!
While this kind of speed advantage depends on many factors, we can be assured that the Monte Carlo technique is not a slouch when it comes to the matter of computation efficiency.
```
%%timeit -n100 -r100
inte = monte_carlo_uniform(f1,a=0,b=4,n=500)
```
### Speed of the Scipy function
```
%%timeit -n100 -r100
quad(f1,a=0,b=4)
```
### Repeat
For a probabilistic technique like Monte Carlo integration, it goes without saying that mathematicians and scientists almost never stop at just one run but repeat the calculations for a number of times and take the average.
Here is a distribution plot from a 10,000 run experiment. As you can see, the plot almost resembles a Gaussian Normal distribution and this fact can be utilized to not only get the average value but also construct confidence intervals around that result.
```
inte_lst = []
for i in range(10000):
inte = monte_carlo_uniform(f1,a=0,b=4,n=500)
inte_lst.append(inte)
plt.figure(figsize=(8,4))
plt.title("Distribution of the Monte Carlo runs",
fontsize=18)
plt.hist(inte_lst,bins=50,color='orange',edgecolor='k')
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.xlabel("Integration result",fontsize=15)
plt.ylabel("Density",fontsize=15)
plt.show()
```
### Particularly suitable for high-dimensional integrals
Although for our simple illustration (and for pedagogical purpose), we stick to a single-variable integral, the same idea can easily be extended to high-dimensional integrals with multiple variables.
And it is in this higher dimension that the Monte Carlo method particularly shines as compared to Riemann sum based approaches. The sample density can be optimized in a much more favorable manner for the Monte Carlo method to make it much faster without compromising the accuracy.
In mathematical terms, the convergence rate of the method is independent of the number of dimensions. In machine learning speak, the Monte Carlo method is the best friend you have to beat the curse of dimensionality when it comes to complex integral calculations.
---
## Summary
We introduced the concept of Monte Carlo integration and illustrated how it differs from the conventional numerical integration methods. We also showed a simple set of Python codes to evaluate a one-dimensional function and assess the accuracy and speed of the techniques.
The broader class of Monte Carlo simulation techniques is more exciting and is used in a ubiquitous manner in fields related to artificial intelligence, data science, and statistical modeling.
For example, the famous Alpha Go program from DeepMind used a Monte Carlo search technique to be computationally efficient in the high-dimensional space of the game Go. Numerous such examples can be found in practice.
| github_jupyter |
This illustrates the datasets.make_multilabel_classification dataset generator. Each sample consists of counts of two features (up to 50 in total), which are differently distributed in each of two classes.
Points are labeled as follows, where Y means the class is present:
| 1 | 2 | 3 | Color |
|--- |--- |--- |-------- |
| Y | N | N | Red |
| N | Y | N | Blue |
| N | N | Y | Yellow |
| Y | Y | N | Purple |
| Y | N | Y | Orange |
| Y | Y | N | Green |
| Y | Y | Y | Brown |
A big circle marks the expected sample for each class; its size reflects the probability of selecting that class label.
The left and right examples highlight the n_labels parameter: more of the samples in the right plot have 2 or 3 labels.
Note that this two-dimensional example is very degenerate: generally the number of features would be much greater than the “document length”, while here we have much larger documents than vocabulary. Similarly, with n_classes > n_features, it is much less likely that a feature distinguishes a particular class.
#### New to Plotly?
Plotly's Python library is free and open source! [Get started](https://plot.ly/python/getting-started/) by downloading the client and [reading the primer](https://plot.ly/python/getting-started/).
<br>You can set up Plotly to work in [online](https://plot.ly/python/getting-started/#initialization-for-online-plotting) or [offline](https://plot.ly/python/getting-started/#initialization-for-offline-plotting) mode, or in [jupyter notebooks](https://plot.ly/python/getting-started/#start-plotting-online).
<br>We also have a quick-reference [cheatsheet](https://images.plot.ly/plotly-documentation/images/python_cheat_sheet.pdf) (new!) to help you get started!
### Version
```
import sklearn
sklearn.__version__
```
### Imports
This tutorial imports [make_ml_clf](http://scikit-learn.org/stable/modules/generated/sklearn.datasets.make_multilabel_classification.html#sklearn.datasets.make_multilabel_classification).
```
import plotly.plotly as py
import plotly.graph_objs as go
from __future__ import print_function
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_multilabel_classification as make_ml_clf
```
### Calculations
```
COLORS = np.array(['!',
'#FF3333', # red
'#0198E1', # blue
'#BF5FFF', # purple
'#FCD116', # yellow
'#FF7216', # orange
'#4DBD33', # green
'#87421F' # brown
])
# Use same random seed for multiple calls to make_multilabel_classification to
# ensure same distributions
RANDOM_SEED = np.random.randint(2 ** 10)
def plot_2d(n_labels=1, n_classes=3, length=50):
X, Y, p_c, p_w_c = make_ml_clf(n_samples=150, n_features=2,
n_classes=n_classes, n_labels=n_labels,
length=length, allow_unlabeled=False,
return_distributions=True,
random_state=RANDOM_SEED)
trace1 = go.Scatter(x=X[:, 0], y=X[:, 1],
mode='markers',
showlegend=False,
marker=dict(size=8,
color=COLORS.take((Y * [1, 2, 4]).sum(axis=1)))
)
trace2 = go.Scatter(x=p_w_c[0] * length, y=p_w_c[1] * length,
mode='markers',
showlegend=False,
marker=dict(color=COLORS.take([1, 2, 4]),
size=14,
line=dict(width=1, color='black'))
)
data = [trace1, trace2]
return data, p_c, p_w_c
```
### Plot Results
n_labels=1
```
data, p_c, p_w_c = plot_2d(n_labels=1)
layout=go.Layout(title='n_labels=1, length=50',
xaxis=dict(title='Feature 0 count',
showgrid=False),
yaxis=dict(title='Feature 1 count',
showgrid=False),
)
fig = go.Figure(data=data, layout=layout)
py.iplot(fig)
```
n_labels=3
```
data = plot_2d(n_labels=3)
layout=go.Layout(title='n_labels=3, length=50',
xaxis=dict(title='Feature 0 count',
showgrid=False),
yaxis=dict(title='Feature 1 count',
showgrid=False),
)
fig = go.Figure(data=data[0], layout=layout)
py.iplot(fig)
print('The data was generated from (random_state=%d):' % RANDOM_SEED)
print('Class', 'P(C)', 'P(w0|C)', 'P(w1|C)', sep='\t')
for k, p, p_w in zip(['red', 'blue', 'yellow'], p_c, p_w_c.T):
print('%s\t%0.2f\t%0.2f\t%0.2f' % (k, p, p_w[0], p_w[1]))
from IPython.display import display, HTML
display(HTML('<link href="//fonts.googleapis.com/css?family=Open+Sans:600,400,300,200|Inconsolata|Ubuntu+Mono:400,700" rel="stylesheet" type="text/css" />'))
display(HTML('<link rel="stylesheet" type="text/css" href="http://help.plot.ly/documentation/all_static/css/ipython-notebook-custom.css">'))
! pip install git+https://github.com/plotly/publisher.git --upgrade
import publisher
publisher.publish(
'randomly-generated-multilabel-dataset.ipynb', 'scikit-learn/plot-random-multilabel-dataset/', 'Randomly Generated Multilabel Dataset | plotly',
' ',
title = 'Randomly Generated Multilabel Dataset| plotly',
name = 'Randomly Generated Multilabel Dataset',
has_thumbnail='true', thumbnail='thumbnail/multilabel-dataset.jpg',
language='scikit-learn', page_type='example_index',
display_as='dataset', order=4,
ipynb= '~Diksha_Gabha/2909')
```
| github_jupyter |
Log the concentrations to and learn the models for CaCO3 again to avoid 0 happen in the prediction.
```
import numpy as np
import pandas as pd
import dask.dataframe as dd
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use('ggplot')
#plt.style.use('seaborn-whitegrid')
plt.style.use('seaborn-colorblind')
plt.rcParams['figure.dpi'] = 300
plt.rcParams['savefig.dpi'] = 300
plt.rcParams['savefig.bbox'] = 'tight'
import datetime
date = datetime.datetime.now().strftime('%Y%m%d')
%matplotlib inline
```
# Launch deployment
```
from dask.distributed import Client
from dask_jobqueue import SLURMCluster
cluster = SLURMCluster(
project="[email protected]",
queue='main',
cores=40,
memory='10 GB',
walltime="00:10:00",
log_directory='job_logs'
)
client.close()
cluster.close()
client = Client(cluster)
cluster.scale(100)
#cluster.adapt(maximum=100)
client
```
# Build model for CaCO3
```
from dask_ml.model_selection import train_test_split
merge_df = dd.read_csv('data/spe+bulk_dataset_20201008.csv')
X = merge_df.iloc[:, 1: -5].to_dask_array(lengths=True)
X = X / X.sum(axis = 1, keepdims = True)
y = merge_df['CaCO3%'].to_dask_array(lengths=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, shuffle = True, random_state = 24)
y
```
## Grid search
We know the relationship between the spectra and bulk measurements might not be linear; and based on the pilot_test.ipynb, the SVR algorithm with NMF transformation provides the better cv score. So we focus on grid search with NMF transformation (4, 5, 6, 7, 8 components based on the PCA result) and SVR. First, we try to build the model on the transformed (ln) y, and evaluate the score on the y transformed back to the original space by using TransformedTargetRegressor. However, it might be something wrong with the parallelism in dask, so we have to do the workflow manually. Transformed (np.log) y_train during training, use the model to predict X_test, transform (np.exp) y_predict back to original space, and evaluate the score.
```
from dask_ml.model_selection import GridSearchCV
from sklearn.decomposition import NMF
from sklearn.svm import SVR
from sklearn.pipeline import make_pipeline
from sklearn.compose import TransformedTargetRegressor
pipe = make_pipeline(NMF(max_iter = 2000, random_state = 24), SVR())
params = {
'nmf__n_components': [4, 5, 6, 7, 8],
'svr__C': np.logspace(0, 7, 8),
'svr__gamma': np.logspace(-5, 0, 6)
}
grid = GridSearchCV(pipe, param_grid = params, cv = 10, n_jobs = -1)
grid.fit(X_train, np.log(y_train))
print('The best cv score: {:.3f}'.format(grid.best_score_))
#print('The test score: {:.3f}'.format(grid.best_estimator_.score(X_test, y_test)))
print('The best model\'s parameters: {}'.format(grid.best_estimator_))
y_predict = np.exp(grid.best_estimator_.predict(X_test))
y_ttest = np.array(y_test)
from sklearn.metrics import r2_score
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import max_error
print('Scores in the test set:')
print('R2 = {:.3f} .'.format(r2_score(y_ttest, y_predict)))
print('The mean absolute error is {:.3f} (%, concetration).'.format(mean_absolute_error(y_ttest, y_predict)))
print('The max. residual error is {:.3f} (%, concetration).'.format(max_error(y_ttest, y_predict)))
plt.plot(range(len(y_predict)), y_ttest, alpha=0.6, label='Measurement')
plt.plot(range(len(y_predict)), y_predict, label='Prediction (R$^2$={:.2f})'.format(r2_score(y_ttest, y_predict)))
#plt.text(12, -7, r'R$^2$={:.2f}, mean ab. error={:.2f}, max. ab. error={:.2f}'.format(grid.best_score_, mean_absolute_error(y_ttest, y_predict), max_error(y_ttest, y_predict)))
plt.ylabel('CaCO$_3$ concentration (%)')
plt.xlabel('Sample no.')
plt.legend(loc = 'upper right')
plt.savefig('results/caco3_predictions_nmr+svr_{}.png'.format(date))
```
### Visualization
```
#result_df = pd.DataFrame(grid.cv_results_)
#result_df.to_csv('results/caco3_grid_nmf+svr_{}.csv'.format(date))
result_df = pd.read_csv('results/caco3_grid_nmf+svr_20201013.csv', index_col = 0)
#result_df = result_df[result_df.mean_test_score > -1].reset_index(drop = True)
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
for n_components in [4, 5, 6, 7, 8]:
data = result_df[result_df.param_nmf__n_components == n_components].reset_index(drop = True)
fig = plt.figure(figsize = (7.3,5))
ax = fig.gca(projection='3d')
xx = data.param_svr__gamma.astype(float)
yy = data.param_svr__C.astype(float)
zz = data.mean_test_score.astype(float)
max_index = np.argmax(zz)
surf = ax.plot_trisurf(np.log10(xx), np.log10(yy), zz, cmap=cm.Greens, linewidth=0.1)
ax.scatter3D(np.log10(xx), np.log10(yy), zz, c = 'orange', s = 5)
# mark the best score
ax.scatter3D(np.log10(xx), np.log10(yy), zz, c = 'w', s = 5, alpha = 1)
text = '{} components\n$\gamma :{:.1f}$, C: {:.1e},\nscore:{:.3f}'.format(n_components, xx[max_index], yy[max_index], zz[max_index])
ax.text(np.log10(xx[max_index])-3, np.log10(yy[max_index]), 1,text, fontsize=12)
ax.set_zlim(-.6, 1.2)
ax.set_zticks(np.linspace(-.5, 1, 4))
ax.set_xlabel('$log(\gamma)$')
ax.set_ylabel('log(C)')
ax.set_zlabel('CV score')
#fig.colorbar(surf, shrink=0.5, aspect=5)
fig.savefig('results/caco3_grid_{}nmr+svr_3D_{}.png'.format(n_components, date))
n_components = [4, 5, 6, 7, 8]
scores = []
for n in n_components:
data = result_df[result_df.param_nmf__n_components == n].reset_index(drop = True)
rank_min = data.rank_test_score.min()
scores = np.hstack((scores, data.loc[data.rank_test_score == rank_min, 'mean_test_score'].values))
plt.plot(n_components, scores, marker='o')
plt.xticks(n_components)
plt.yticks(np.linspace(0.86, 0.875, 4))
plt.xlabel('Amount of components')
plt.ylabel('Best CV score')
plt.savefig('results/caco3_scores_components_{}.png'.format(date))
from joblib import dump, load
#model = load('models/tc_nmf+svr_model_20201012.joblib')
dump(grid.best_estimator_, 'models/caco3_nmf+svr_model_{}.joblib'.format(date))
```
# Check prediction
```
spe_df = pd.read_csv('data/spe_dataset_20201008.csv', index_col = 0)
X = spe_df.iloc[:, :2048].values
X = X / X.sum(axis = 1, keepdims = True)
y_caco3 = np.exp(grid.best_estimator_.predict(X))
len(y_caco3[y_caco3 < 0])
len(y_caco3[y_caco3 > 100])
len(y_caco3[y_caco3 > 100])/len(y_caco3)
```
Yes, the negative-prediction issue is solved. Only 0.1 % of the predictions over 100. The previous model has 96% accuracy in the test set (build_models_01.ipynb), but has 8.5 % unrealistic predictions (prediction_01.ipynb). The enhanced model has lower score in the test set, 90%, but only has 0.1 % unrealistic predictions. Overall, the enhanced model here is better.
| github_jupyter |
[Table of Contents](http://nbviewer.ipython.org/github/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/table_of_contents.ipynb)
# Kalman Filter Math
```
#format the book
%matplotlib inline
from __future__ import division, print_function
from book_format import load_style
load_style()
```
If you've gotten this far I hope that you are thinking that the Kalman filter's fearsome reputation is somewhat undeserved. Sure, I hand waved some equations away, but I hope implementation has been fairly straightforward for you. The underlying concept is quite straightforward - take two measurements, or a measurement and a prediction, and choose the output to be somewhere between the two. If you believe the measurement more your guess will be closer to the measurement, and if you believe the prediction is more accurate your guess will lie closer to it. That's not rocket science (little joke - it is exactly this math that got Apollo to the moon and back!).
To be honest I have been choosing my problems carefully. For an arbitrary problem designing the Kalman filter matrices can be extremely difficult. I haven't been *too tricky*, though. Equations like Newton's equations of motion can be trivially computed for Kalman filter applications, and they make up the bulk of the kind of problems that we want to solve.
I have illustrated the concepts with code and reasoning, not math. But there are topics that do require more mathematics than I have used so far. This chapter presents the math that you will need for the rest of the book.
## Modeling a Dynamic System
A *dynamic system* is a physical system whose state (position, temperature, etc) evolves over time. Calculus is the math of changing values, so we use differential equations to model dynamic systems. Some systems cannot be modeled with differential equations, but we will not encounter those in this book.
Modeling dynamic systems is properly the topic of several college courses. To an extent there is no substitute for a few semesters of ordinary and partial differential equations followed by a graduate course in control system theory. If you are a hobbyist, or trying to solve one very specific filtering problem at work you probably do not have the time and/or inclination to devote a year or more to that education.
Fortunately, I can present enough of the theory to allow us to create the system equations for many different Kalman filters. My goal is to get you to the stage where you can read a publication and understand it well enough to implement the algorithms. The background math is deep, but in practice we end up using a few simple techniques.
This is the longest section of pure math in this book. You will need to master everything in this section to understand the Extended Kalman filter (EKF), the most common nonlinear filter. I do cover more modern filters that do not require as much of this math. You can choose to skim now, and come back to this if you decide to learn the EKF.
We need to start by understanding the underlying equations and assumptions that the Kalman filter uses. We are trying to model real world phenomena, so what do we have to consider?
Each physical system has a process. For example, a car traveling at a certain velocity goes so far in a fixed amount of time, and its velocity varies as a function of its acceleration. We describe that behavior with the well known Newtonian equations that we learned in high school.
$$
\begin{aligned}
v&=at\\
x &= \frac{1}{2}at^2 + v_0t + x_0
\end{aligned}
$$
Once we learned calculus we saw them in this form:
$$ \mathbf v = \frac{d \mathbf x}{d t},
\quad \mathbf a = \frac{d \mathbf v}{d t} = \frac{d^2 \mathbf x}{d t^2}
$$
A typical automobile tracking problem would have you compute the distance traveled given a constant velocity or acceleration, as we did in previous chapters. But, of course we know this is not all that is happening. No car travels on a perfect road. There are bumps, wind drag, and hills that raise and lower the speed. The suspension is a mechanical system with friction and imperfect springs.
Perfectly modeling a system is impossible except for the most trivial problems. We are forced to make a simplification. At any time $t$ we say that the true state (such as the position of our car) is the predicted value from the imperfect model plus some unknown *process noise*:
$$
x(t) = x_{pred}(t) + noise(t)
$$
This is not meant to imply that $noise(t)$ is a function that we can derive analytically. It is merely a statement of fact - we can always describe the true value as the predicted value plus the process noise. "Noise" does not imply random events. If we are tracking a thrown ball in the atmosphere, and our model assumes the ball is in a vacuum, then the effect of air drag is process noise in this context.
In the next section we will learn techniques to convert a set of higher order differential equations into a set of first-order differential equations. After the conversion the model of the system without noise is:
$$ \dot{\mathbf x} = \mathbf{Ax}$$
$\mathbf A$ is known as the *systems dynamics matrix* as it describes the dynamics of the system. Now we need to model the noise. We will call that $\mathbf w$, and add it to the equation.
$$ \dot{\mathbf x} = \mathbf{Ax} + \mathbf w$$
$\mathbf w$ may strike you as a poor choice for the name, but you will soon see that the Kalman filter assumes *white* noise.
Finally, we need to consider any inputs into the system. We assume an input $\mathbf u$, and that there exists a linear model that defines how that input changes the system. For example, pressing the accelerator in your car makes it accelerate, and gravity causes balls to fall. Both are contol inputs. We will need a matrix $\mathbf B$ to convert $u$ into the effect on the system. We add that into our equation:
$$ \dot{\mathbf x} = \mathbf{Ax} + \mathbf{Bu} + \mathbf{w}$$
And that's it. That is one of the equations that Dr. Kalman set out to solve, and he found an optimal estimator if we assume certain properties of $\mathbf w$.
## State-Space Representation of Dynamic Systems
We've derived the equation
$$ \dot{\mathbf x} = \mathbf{Ax}+ \mathbf{Bu} + \mathbf{w}$$
However, we are not interested in the derivative of $\mathbf x$, but in $\mathbf x$ itself. Ignoring the noise for a moment, we want an equation that recusively finds the value of $\mathbf x$ at time $t_k$ in terms of $\mathbf x$ at time $t_{k-1}$:
$$\mathbf x(t_k) = \mathbf F(\Delta t)\mathbf x(t_{k-1}) + \mathbf B(t_k) + \mathbf u (t_k)$$
Convention allows us to write $\mathbf x(t_k)$ as $\mathbf x_k$, which means the
the value of $\mathbf x$ at the k$^{th}$ value of $t$.
$$\mathbf x_k = \mathbf{Fx}_{k-1} + \mathbf B_k\mathbf u_k$$
$\mathbf F$ is the familiar *state transition matrix*, named due to its ability to transition the state's value between discrete time steps. It is very similar to the system dynamics matrix $\mathbf A$. The difference is that $\mathbf A$ models a set of linear differential equations, and is continuous. $\mathbf F$ is discrete, and represents a set of linear equations (not differential equations) which transitions $\mathbf x_{k-1}$ to $\mathbf x_k$ over a discrete time step $\Delta t$.
Finding this matrix is often quite difficult. The equation $\dot x = v$ is the simplest possible differential equation and we trivially integrate it as:
$$ \int\limits_{x_{k-1}}^{x_k} \mathrm{d}x = \int\limits_{0}^{\Delta t} v\, \mathrm{d}t $$
$$x_k-x_0 = v \Delta t$$
$$x_k = v \Delta t + x_0$$
This equation is *recursive*: we compute the value of $x$ at time $t$ based on its value at time $t-1$. This recursive form enables us to represent the system (process model) in the form required by the Kalman filter:
$$\begin{aligned}
\mathbf x_k &= \mathbf{Fx}_{k-1} \\
&= \begin{bmatrix} 1 & \Delta t \\ 0 & 1\end{bmatrix}
\begin{bmatrix}x_{k-1} \\ \dot x_{k-1}\end{bmatrix}
\end{aligned}$$
We can do that only because $\dot x = v$ is simplest differential equation possible. Almost all other in physical systems result in more complicated differential equation which do not yield to this approach.
*State-space* methods became popular around the time of the Apollo missions, largely due to the work of Dr. Kalman. The idea is simple. Model a system with a set of $n^{th}$-order differential equations. Convert them into an equivalent set of first-order differential equations. Put them into the vector-matrix form used in the previous section: $\dot{\mathbf x} = \mathbf{Ax} + \mathbf{Bu}$. Once in this form we use of of several techniques to convert these linear differential equations into the recursive equation:
$$ \mathbf x_k = \mathbf{Fx}_{k-1} + \mathbf B_k\mathbf u_k$$
Some books call the state transition matrix the *fundamental matrix*. Many use $\mathbf \Phi$ instead of $\mathbf F$. Sources based heavily on control theory tend to use these forms.
These are called *state-space* methods because we are expressing the solution of the differential equations in terms of the system state.
### Forming First Order Equations from Higher Order Equations
Many models of physical systems require second or higher order differential equations with control input $u$:
$$a_n \frac{d^ny}{dt^n} + a_{n-1} \frac{d^{n-1}y}{dt^{n-1}} + \dots + a_2 \frac{d^2y}{dt^2} + a_1 \frac{dy}{dt} + a_0 = u$$
State-space methods require first-order equations. Any higher order system of equations can be reduced to first-order by defining extra variables for the derivatives and then solving.
Let's do an example. Given the system $\ddot{x} - 6\dot x + 9x = u$ find the equivalent first order equations. I've used the dot notation for the time derivatives for clarity.
The first step is to isolate the highest order term onto one side of the equation.
$$\ddot{x} = 6\dot x - 9x + u$$
We define two new variables:
$$\begin{aligned} x_1(u) &= x \\
x_2(u) &= \dot x
\end{aligned}$$
Now we will substitute these into the original equation and solve. The solution yields a set of first-order equations in terms of these new variables. It is conventional to drop the $(u)$ for notational convenience.
We know that $\dot x_1 = x_2$ and that $\dot x_2 = \ddot{x}$. Therefore
$$\begin{aligned}
\dot x_2 &= \ddot{x} \\
&= 6\dot x - 9x + t\\
&= 6x_2-9x_1 + t
\end{aligned}$$
Therefore our first-order system of equations is
$$\begin{aligned}\dot x_1 &= x_2 \\
\dot x_2 &= 6x_2-9x_1 + t\end{aligned}$$
If you practice this a bit you will become adept at it. Isolate the highest term, define a new variable and its derivatives, and then substitute.
### First Order Differential Equations In State-Space Form
Substituting the newly defined variables from the previous section:
$$\frac{dx_1}{dt} = x_2,\,
\frac{dx_2}{dt} = x_3, \, ..., \,
\frac{dx_{n-1}}{dt} = x_n$$
into the first order equations yields:
$$\frac{dx_n}{dt} = \frac{1}{a_n}\sum\limits_{i=0}^{n-1}a_ix_{i+1} + \frac{1}{a_n}u
$$
Using vector-matrix notation we have:
$$\begin{bmatrix}\frac{dx_1}{dt} \\ \frac{dx_2}{dt} \\ \vdots \\ \frac{dx_n}{dt}\end{bmatrix} =
\begin{bmatrix}\dot x_1 \\ \dot x_2 \\ \vdots \\ \dot x_n\end{bmatrix}=
\begin{bmatrix}0 & 1 & 0 &\cdots & 0 \\
0 & 0 & 1 & \cdots & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
-\frac{a_0}{a_n} & -\frac{a_1}{a_n} & -\frac{a_2}{a_n} & \cdots & -\frac{a_{n-1}}{a_n}\end{bmatrix}
\begin{bmatrix}x_1 \\ x_2 \\ \vdots \\ x_n\end{bmatrix} +
\begin{bmatrix}0 \\ 0 \\ \vdots \\ \frac{1}{a_n}\end{bmatrix}u$$
which we then write as $\dot{\mathbf x} = \mathbf{Ax} + \mathbf{B}u$.
### Finding the Fundamental Matrix for Time Invariant Systems
We express the system equations in state-space form with
$$ \dot{\mathbf x} = \mathbf{Ax}$$
where $\mathbf A$ is the system dynamics matrix, and want to find the *fundamental matrix* $\mathbf F$ that propagates the state $\mathbf x$ over the interval $\Delta t$ with the equation
$$\begin{aligned}
\mathbf x(t_k) = \mathbf F(\Delta t)\mathbf x(t_{k-1})\end{aligned}$$
In other words, $\mathbf A$ is a set of continuous differential equations, and we need $\mathbf F$ to be a set of discrete linear equations that computes the change in $\mathbf A$ over a discrete time step.
It is conventional to drop the $t_k$ and $(\Delta t)$ and use the notation
$$\mathbf x_k = \mathbf {Fx}_{k-1}$$
Broadly speaking there are three common ways to find this matrix for Kalman filters. The technique most often used is the matrix exponential. Linear Time Invariant Theory, also known as LTI System Theory, is a second technique. Finally, there are numerical techniques. You may know of others, but these three are what you will most likely encounter in the Kalman filter literature and praxis.
### The Matrix Exponential
The solution to the equation $\frac{dx}{dt} = kx$ can be found by:
$$\begin{gathered}\frac{dx}{dt} = kx \\
\frac{dx}{x} = k\, dt \\
\int \frac{1}{x}\, dx = \int k\, dt \\
\log x = kt + c \\
x = e^{kt+c} \\
x = e^ce^{kt} \\
x = c_0e^{kt}\end{gathered}$$
Using similar math, the solution to the first-order equation
$$\dot{\mathbf x} = \mathbf{Ax} ,\, \, \, \mathbf x(0) = \mathbf x_0$$
where $\mathbf A$ is a constant matrix, is
$$\mathbf x = e^{\mathbf At}\mathbf x_0$$
Substituting $F = e^{\mathbf At}$, we can write
$$\mathbf x_k = \mathbf F\mathbf x_{k-1}$$
which is the form we are looking for! We have reduced the problem of finding the fundamental matrix to one of finding the value for $e^{\mathbf At}$.
$e^{\mathbf At}$ is known as the [matrix exponential](https://en.wikipedia.org/wiki/Matrix_exponential). It can be computed with this power series:
$$e^{\mathbf At} = \mathbf{I} + \mathbf{A}t + \frac{(\mathbf{A}t)^2}{2!} + \frac{(\mathbf{A}t)^3}{3!} + ... $$
That series is found by doing a Taylor series expansion of $e^{\mathbf At}$, which I will not cover here.
Let's use this to find the solution to Newton's equations. Using $v$ as an substitution for $\dot x$, and assuming constant velocity we get the linear matrix-vector form
$$\begin{bmatrix}\dot x \\ \dot v\end{bmatrix} =\begin{bmatrix}0&1\\0&0\end{bmatrix} \begin{bmatrix}x \\ v\end{bmatrix}$$
This is a first order differential equation, so we can set $\mathbf{A}=\begin{bmatrix}0&1\\0&0\end{bmatrix}$ and solve the following equation. I have substituted the interval $\Delta t$ for $t$ to emphasize that the fundamental matrix is discrete:
$$\mathbf F = e^{\mathbf A\Delta t} = \mathbf{I} + \mathbf A\Delta t + \frac{(\mathbf A\Delta t)^2}{2!} + \frac{(\mathbf A\Delta t)^3}{3!} + ... $$
If you perform the multiplication you will find that $\mathbf{A}^2=\begin{bmatrix}0&0\\0&0\end{bmatrix}$, which means that all higher powers of $\mathbf{A}$ are also $\mathbf{0}$. Thus we get an exact answer without an infinite number of terms:
$$
\begin{aligned}
\mathbf F &=\mathbf{I} + \mathbf A \Delta t + \mathbf{0} \\
&= \begin{bmatrix}1&0\\0&1\end{bmatrix} + \begin{bmatrix}0&1\\0&0\end{bmatrix}\Delta t\\
&= \begin{bmatrix}1&\Delta t\\0&1\end{bmatrix}
\end{aligned}$$
We plug this into $\mathbf x_k= \mathbf{Fx}_{k-1}$ to get
$$
\begin{aligned}
x_k &=\begin{bmatrix}1&\Delta t\\0&1\end{bmatrix}x_{k-1}
\end{aligned}$$
You will recognize this as the matrix we derived analytically for the constant velocity Kalman filter in the **Multivariate Kalman Filter** chapter.
SciPy's linalg module includes a routine `expm()` to compute the matrix exponential. It does not use the Taylor series method, but the [Padé Approximation](https://en.wikipedia.org/wiki/Pad%C3%A9_approximant). There are many (at least 19) methods to computed the matrix exponential, and all suffer from numerical difficulties[1]. But you should be aware of the problems, especially when $\mathbf A$ is large. If you search for "pade approximation matrix exponential" you will find many publications devoted to this problem.
In practice this may not be of concern to you as for the Kalman filter we normally just take the first two terms of the Taylor series. But don't assume my treatment of the problem is complete and run off and try to use this technique for other problem without doing a numerical analysis of the performance of this technique. Interestingly, one of the favored ways of solving $e^{\mathbf At}$ is to use a generalized ode solver. In other words, they do the opposite of what we do - turn $\mathbf A$ into a set of differential equations, and then solve that set using numerical techniques!
Here is an example of using `expm()` to solve $e^{\mathbf At}$.
```
import numpy as np
from scipy.linalg import expm
dt = 0.1
A = np.array([[0, 1],
[0, 0]])
expm(A*dt)
```
### Time Invariance
If the behavior of the system depends on time we can say that a dynamic system is described by the first-order differential equation
$$ g(t) = \dot x$$
However, if the system is *time invariant* the equation is of the form:
$$ f(x) = \dot x$$
What does *time invariant* mean? Consider a home stereo. If you input a signal $x$ into it at time $t$, it will output some signal $f(x)$. If you instead perform the input at time $t + \Delta t$ the output signal will be the same $f(x)$, shifted in time.
A counter-example is $x(t) = \sin(t)$, with the system $f(x) = t\, x(t) = t \sin(t)$. This is not time invariant; the value will be different at different times due to the multiplication by t. An aircraft is not time invariant. If you make a control input to the aircraft at a later time its behavior will be different because it will have burned fuel and thus lost weight. Lower weight results in different behavior.
We can solve these equations by integrating each side. I demonstrated integrating the time invariant system $v = \dot x$ above. However, integrating the time invariant equation $\dot x = f(x)$ is not so straightforward. Using the *separation of variables* techniques we divide by $f(x)$ and move the $dt$ term to the right so we can integrate each side:
$$\begin{gathered}
\frac{dx}{dt} = f(x) \\
\int^x_{x_0} \frac{1}{f(x)} dx = \int^t_{t_0} dt
\end{gathered}$$
If we let $F(x) = \int \frac{1}{f(x)} dx$ we get
$$F(x) - F(x_0) = t-t_0$$
We then solve for x with
$$\begin{gathered}
F(x) = t - t_0 + F(x_0) \\
x = F^{-1}[t-t_0 + F(x_0)]
\end{gathered}$$
In other words, we need to find the inverse of $F$. This is not trivial, and a significant amount of coursework in a STEM education is devoted to finding tricky, analytic solutions to this problem.
However, they are tricks, and many simple forms of $f(x)$ either have no closed form solution or pose extreme difficulties. Instead, the practicing engineer turns to state-space methods to find approximate solutions.
The advantage of the matrix exponential is that we can use it for any arbitrary set of differential equations which are *time invariant*. However, we often use this technique even when the equations are not time invariant. As an aircraft flies it burns fuel and loses weight. However, the weight loss over one second is negligible, and so the system is nearly linear over that time step. Our answers will still be reasonably accurate so long as the time step is short.
#### Example: Mass-Spring-Damper Model
Suppose we wanted to track the motion of a weight on a spring and connected to a damper, such as an automobile's suspension. The equation for the motion with $m$ being the mass, $k$ the spring constant, and $c$ the damping force, under some input $u$ is
$$m\frac{d^2x}{dt^2} + c\frac{dx}{dt} +kx = u$$
For notational convenience I will write that as
$$m\ddot x + c\dot x + kx = u$$
I can turn this into a system of first order equations by setting $x_1(t)=x(t)$, and then substituting as follows:
$$\begin{aligned}
x_1 &= x \\
x_2 &= \dot x_1 \\
\dot x_2 &= \dot x_1 = \ddot x
\end{aligned}$$
As is common I dropped the $(t)$ for notational convenience. This gives the equation
$$m\dot x_2 + c x_2 +kx_1 = u$$
Solving for $\dot x_2$ we get a first order equation:
$$\dot x_2 = -\frac{c}{m}x_2 - \frac{k}{m}x_1 + \frac{1}{m}u$$
We put this into matrix form:
$$\begin{bmatrix} \dot x_1 \\ \dot x_2 \end{bmatrix} =
\begin{bmatrix}0 & 1 \\ -k/m & -c/m \end{bmatrix}
\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} +
\begin{bmatrix} 0 \\ 1/m \end{bmatrix}u$$
Now we use the matrix exponential to find the state transition matrix:
$$\Phi(t) = e^{\mathbf At} = \mathbf{I} + \mathbf At + \frac{(\mathbf At)^2}{2!} + \frac{(\mathbf At)^3}{3!} + ... $$
The first two terms give us
$$\mathbf F = \begin{bmatrix}1 & t \\ -(k/m) t & 1-(c/m) t \end{bmatrix}$$
This may or may not give you enough precision. You can easily check this by computing $\frac{(\mathbf At)^2}{2!}$ for your constants and seeing how much this matrix contributes to the results.
### Linear Time Invariant Theory
[*Linear Time Invariant Theory*](https://en.wikipedia.org/wiki/LTI_system_theory), also known as LTI System Theory, gives us a way to find $\Phi$ using the inverse Laplace transform. You are either nodding your head now, or completely lost. I will not be using the Laplace transform in this book. LTI system theory tells us that
$$ \Phi(t) = \mathcal{L}^{-1}[(s\mathbf{I} - \mathbf{F})^{-1}]$$
I have no intention of going into this other than to say that the Laplace transform $\mathcal{L}$ converts a signal into a space $s$ that excludes time, but finding a solution to the equation above is non-trivial. If you are interested, the Wikipedia article on LTI system theory provides an introduction. I mention LTI because you will find some literature using it to design the Kalman filter matrices for difficult problems.
### Numerical Solutions
Finally, there are numerical techniques to find $\mathbf F$. As filters get larger finding analytical solutions becomes very tedious (though packages like SymPy make it easier). C. F. van Loan [2] has developed a technique that finds both $\Phi$ and $\mathbf Q$ numerically. Given the continuous model
$$ \dot x = Ax + Gw$$
where $w$ is the unity white noise, van Loan's method computes both $\mathbf F_k$ and $\mathbf Q_k$.
I have implemented van Loan's method in `FilterPy`. You may use it as follows:
```python
from filterpy.common import van_loan_discretization
A = np.array([[0., 1.], [-1., 0.]])
G = np.array([[0.], [2.]]) # white noise scaling
F, Q = van_loan_discretization(A, G, dt=0.1)
```
In the section *Numeric Integration of Differential Equations* I present alternative methods which are very commonly used in Kalman filtering.
## Design of the Process Noise Matrix
In general the design of the $\mathbf Q$ matrix is among the most difficult aspects of Kalman filter design. This is due to several factors. First, the math requires a good foundation in signal theory. Second, we are trying to model the noise in something for which we have little information. Consider trying to model the process noise for a thrown baseball. We can model it as a sphere moving through the air, but that leaves many unknown factors - the wind, ball rotation and spin decay, the coefficient of drag of a ball with stitches, the effects of wind and air density, and so on. We develop the equations for an exact mathematical solution for a given process model, but since the process model is incomplete the result for $\mathbf Q$ will also be incomplete. This has a lot of ramifications for the behavior of the Kalman filter. If $\mathbf Q$ is too small then the filter will be overconfident in its prediction model and will diverge from the actual solution. If $\mathbf Q$ is too large than the filter will be unduly influenced by the noise in the measurements and perform sub-optimally. In practice we spend a lot of time running simulations and evaluating collected data to try to select an appropriate value for $\mathbf Q$. But let's start by looking at the math.
Let's assume a kinematic system - some system that can be modeled using Newton's equations of motion. We can make a few different assumptions about this process.
We have been using a process model of
$$ \dot{\mathbf x} = \mathbf{Ax} + \mathbf{Bu} + \mathbf{w}$$
where $\mathbf{w}$ is the process noise. Kinematic systems are *continuous* - their inputs and outputs can vary at any arbitrary point in time. However, our Kalman filters are *discrete* (there are continuous forms for Kalman filters, but we do not cover them in this book). We sample the system at regular intervals. Therefore we must find the discrete representation for the noise term in the equation above. This depends on what assumptions we make about the behavior of the noise. We will consider two different models for the noise.
### Continuous White Noise Model
We model kinematic systems using Newton's equations. We have either used position and velocity, or position, velocity, and acceleration as the models for our systems. There is nothing stopping us from going further - we can model jerk, jounce, snap, and so on. We don't do that normally because adding terms beyond the dynamics of the real system degrades the estimate.
Let's say that we need to model the position, velocity, and acceleration. We can then assume that acceleration is constant for each discrete time step. Of course, there is process noise in the system and so the acceleration is not actually constant. The tracked object will alter the acceleration over time due to external, unmodeled forces. In this section we will assume that the acceleration changes by a continuous time zero-mean white noise $w(t)$. In other words, we are assuming that the small changes in velocity average to 0 over time (zero-mean).
Since the noise is changing continuously we will need to integrate to get the discrete noise for the discretization interval that we have chosen. We will not prove it here, but the equation for the discretization of the noise is
$$\mathbf Q = \int_0^{\Delta t} \mathbf F(t)\mathbf{Q_c}\mathbf F^\mathsf{T}(t) dt$$
where $\mathbf{Q_c}$ is the continuous noise. This gives us
$$\Phi = \begin{bmatrix}1 & \Delta t & {\Delta t}^2/2 \\ 0 & 1 & \Delta t\\ 0& 0& 1\end{bmatrix}$$
for the fundamental matrix, and
$$\mathbf{Q_c} = \begin{bmatrix}0&0&0\\0&0&0\\0&0&1\end{bmatrix} \Phi_s$$
for the continuous process noise matrix, where $\Phi_s$ is the spectral density of the white noise.
We could carry out these computations ourselves, but I prefer using SymPy to solve the equation.
$$\mathbf{Q_c} = \begin{bmatrix}0&0&0\\0&0&0\\0&0&1\end{bmatrix} \Phi_s$$
```
import sympy
from sympy import (init_printing, Matrix,MatMul,
integrate, symbols)
init_printing(use_latex='mathjax')
dt, phi = symbols('\Delta{t} \Phi_s')
F_k = Matrix([[1, dt, dt**2/2],
[0, 1, dt],
[0, 0, 1]])
Q_c = Matrix([[0, 0, 0],
[0, 0, 0],
[0, 0, 1]])*phi
Q=sympy.integrate(F_k * Q_c * F_k.T, (dt, 0, dt))
# factor phi out of the matrix to make it more readable
Q = Q / phi
sympy.MatMul(Q, phi)
```
For completeness, let us compute the equations for the 0th order and 1st order equations.
```
F_k = sympy.Matrix([[1]])
Q_c = sympy.Matrix([[phi]])
print('0th order discrete process noise')
sympy.integrate(F_k*Q_c*F_k.T,(dt, 0, dt))
F_k = sympy.Matrix([[1, dt],
[0, 1]])
Q_c = sympy.Matrix([[0, 0],
[0, 1]])*phi
Q = sympy.integrate(F_k * Q_c * F_k.T, (dt, 0, dt))
print('1st order discrete process noise')
# factor phi out of the matrix to make it more readable
Q = Q / phi
sympy.MatMul(Q, phi)
```
### Piecewise White Noise Model
Another model for the noise assumes that the that highest order term (say, acceleration) is constant for the duration of each time period, but differs for each time period, and each of these is uncorrelated between time periods. In other words there is a discontinuous jump in acceleration at each time step. This is subtly different than the model above, where we assumed that the last term had a continuously varying noisy signal applied to it.
We will model this as
$$f(x)=Fx+\Gamma w$$
where $\Gamma$ is the *noise gain* of the system, and $w$ is the constant piecewise acceleration (or velocity, or jerk, etc).
Let's start by looking at a first order system. In this case we have the state transition function
$$\mathbf{F} = \begin{bmatrix}1&\Delta t \\ 0& 1\end{bmatrix}$$
In one time period, the change in velocity will be $w(t)\Delta t$, and the change in position will be $w(t)\Delta t^2/2$, giving us
$$\Gamma = \begin{bmatrix}\frac{1}{2}\Delta t^2 \\ \Delta t\end{bmatrix}$$
The covariance of the process noise is then
$$Q = \mathbb E[\Gamma w(t) w(t) \Gamma^\mathsf{T}] = \Gamma\sigma^2_v\Gamma^\mathsf{T}$$.
We can compute that with SymPy as follows
```
var=symbols('sigma^2_v')
v = Matrix([[dt**2 / 2], [dt]])
Q = v * var * v.T
# factor variance out of the matrix to make it more readable
Q = Q / var
sympy.MatMul(Q, var)
```
The second order system proceeds with the same math.
$$\mathbf{F} = \begin{bmatrix}1 & \Delta t & {\Delta t}^2/2 \\ 0 & 1 & \Delta t\\ 0& 0& 1\end{bmatrix}$$
Here we will assume that the white noise is a discrete time Wiener process. This gives us
$$\Gamma = \begin{bmatrix}\frac{1}{2}\Delta t^2 \\ \Delta t\\ 1\end{bmatrix}$$
There is no 'truth' to this model, it is just convenient and provides good results. For example, we could assume that the noise is applied to the jerk at the cost of a more complicated equation.
The covariance of the process noise is then
$$Q = \mathbb E[\Gamma w(t) w(t) \Gamma^\mathsf{T}] = \Gamma\sigma^2_v\Gamma^\mathsf{T}$$.
We can compute that with SymPy as follows
```
var=symbols('sigma^2_v')
v = Matrix([[dt**2 / 2], [dt], [1]])
Q = v * var * v.T
# factor variance out of the matrix to make it more readable
Q = Q / var
sympy.MatMul(Q, var)
```
We cannot say that this model is more or less correct than the continuous model - both are approximations to what is happening to the actual object. Only experience and experiments can guide you to the appropriate model. In practice you will usually find that either model provides reasonable results, but typically one will perform better than the other.
The advantage of the second model is that we can model the noise in terms of $\sigma^2$ which we can describe in terms of the motion and the amount of error we expect. The first model requires us to specify the spectral density, which is not very intuitive, but it handles varying time samples much more easily since the noise is integrated across the time period. However, these are not fixed rules - use whichever model (or a model of your own devising) based on testing how the filter performs and/or your knowledge of the behavior of the physical model.
A good rule of thumb is to set $\sigma$ somewhere from $\frac{1}{2}\Delta a$ to $\Delta a$, where $\Delta a$ is the maximum amount that the acceleration will change between sample periods. In practice we pick a number, run simulations on data, and choose a value that works well.
### Using FilterPy to Compute Q
FilterPy offers several routines to compute the $\mathbf Q$ matrix. The function `Q_continuous_white_noise()` computes $\mathbf Q$ for a given value for $\Delta t$ and the spectral density.
```
from filterpy.common import Q_continuous_white_noise
from filterpy.common import Q_discrete_white_noise
Q = Q_continuous_white_noise(dim=2, dt=1, spectral_density=1)
print(Q)
Q = Q_continuous_white_noise(dim=3, dt=1, spectral_density=1)
print(Q)
```
The function `Q_discrete_white_noise()` computes $\mathbf Q$ assuming a piecewise model for the noise.
```
Q = Q_discrete_white_noise(2, var=1.)
print(Q)
Q = Q_discrete_white_noise(3, var=1.)
print(Q)
```
### Simplification of Q
Many treatments use a much simpler form for $\mathbf Q$, setting it to zero except for a noise term in the lower rightmost element. Is this justified? Well, consider the value of $\mathbf Q$ for a small $\Delta t$
```
import numpy as np
np.set_printoptions(precision=8)
Q = Q_continuous_white_noise(
dim=3, dt=0.05, spectral_density=1)
print(Q)
np.set_printoptions(precision=3)
```
We can see that most of the terms are very small. Recall that the only equation using this matrix is
$$ \mathbf P=\mathbf{FPF}^\mathsf{T} + \mathbf Q$$
If the values for $\mathbf Q$ are small relative to $\mathbf P$
than it will be contributing almost nothing to the computation of $\mathbf P$. Setting $\mathbf Q$ to the zero matrix except for the lower right term
$$\mathbf Q=\begin{bmatrix}0&0&0\\0&0&0\\0&0&\sigma^2\end{bmatrix}$$
while not correct, is often a useful approximation. If you do this you will have to perform quite a few studies to guarantee that your filter works in a variety of situations.
If you do this, 'lower right term' means the most rapidly changing term for each variable. If the state is $x=\begin{bmatrix}x & \dot x & \ddot{x} & y & \dot{y} & \ddot{y}\end{bmatrix}^\mathsf{T}$ Then Q will be 6x6; the elements for both $\ddot{x}$ and $\ddot{y}$ will have to be set to non-zero in $\mathbf Q$.
## Numeric Integration of Differential Equations
We've been exposed to several numerical techniques to solve linear differential equations. These include state-space methods, the Laplace transform, and van Loan's method.
These work well for linear ordinary differential equations (ODEs), but do not work well for nonlinear equations. For example, consider trying to predict the position of a rapidly turning car. Cars maneuver by turning the front wheels. This makes them pivot around their rear axle as it moves forward. Therefore the path will be continuously varying and a linear prediction will necessarily produce an incorrect value. If the change in the system is small enough relative to $\Delta t$ this can often produce adequate results, but that will rarely be the case with the nonlinear Kalman filters we will be studying in subsequent chapters.
For these reasons we need to know how to numerically integrate ODEs. This can be a vast topic that requires several books. If you need to explore this topic in depth *Computational Physics in Python* by Dr. Eric Ayars is excellent, and available for free here:
http://phys.csuchico.edu/ayars/312/Handouts/comp-phys-python.pdf
However, I will cover a few simple techniques which will work for a majority of the problems you encounter.
### Euler's Method
Let's say we have the initial condition problem of
$$\begin{gathered}
y' = y, \\ y(0) = 1
\end{gathered}$$
We happen to know the exact answer is $y=e^t$ because we solved it earlier, but for an arbitrary ODE we will not know the exact solution. In general all we know is the derivative of the equation, which is equal to the slope. We also know the initial value: at $t=0$, $y=1$. If we know these two pieces of information we can predict the value at $y(t=1)$ using the slope at $t=0$ and the value of $y(0)$. I've plotted this below.
```
import matplotlib.pyplot as plt
t = np.linspace(-1, 1, 10)
plt.plot(t, np.exp(t))
t = np.linspace(-1, 1, 2)
plt.plot(t,t+1, ls='--', c='k');
```
You can see that the slope is very close to the curve at $t=0.1$, but far from it
at $t=1$. But let's continue with a step size of 1 for a moment. We can see that at $t=1$ the estimated value of $y$ is 2. Now we can compute the value at $t=2$ by taking the slope of the curve at $t=1$ and adding it to our initial estimate. The slope is computed with $y'=y$, so the slope is 2.
```
import code.book_plots as book_plots
t = np.linspace(-1, 2, 20)
plt.plot(t, np.exp(t))
t = np.linspace(0, 1, 2)
plt.plot([1, 2, 4], ls='--', c='k')
book_plots.set_labels(x='x', y='y');
```
Here we see the next estimate for y is 4. The errors are getting large quickly, and you might be unimpressed. But 1 is a very large step size. Let's put this algorithm in code, and verify that it works by using a small step size.
```
def euler(t, tmax, y, dx, step=1.):
ys = []
while t < tmax:
y = y + step*dx(t, y)
ys.append(y)
t +=step
return ys
def dx(t, y): return y
print(euler(0, 1, 1, dx, step=1.)[-1])
print(euler(0, 2, 1, dx, step=1.)[-1])
```
This looks correct. So now let's plot the result of a much smaller step size.
```
ys = euler(0, 4, 1, dx, step=0.00001)
plt.subplot(1,2,1)
plt.title('Computed')
plt.plot(np.linspace(0, 4, len(ys)),ys)
plt.subplot(1,2,2)
t = np.linspace(0, 4, 20)
plt.title('Exact')
plt.plot(t, np.exp(t));
print('exact answer=', np.exp(4))
print('euler answer=', ys[-1])
print('difference =', np.exp(4) - ys[-1])
print('iterations =', len(ys))
```
Here we see that the error is reasonably small, but it took a very large number of iterations to get three digits of precision. In practice Euler's method is too slow for most problems, and we use more sophisticated methods.
Before we go on, let's formally derive Euler's method, as it is the basis for the more advanced Runge Kutta methods used in the next section. In fact, Euler's method is the simplest form of Runge Kutta.
Here are the first 3 terms of the Euler expansion of $y$. An infinite expansion would give an exact answer, so $O(h^4)$ denotes the error due to the finite expansion.
$$y(t_0 + h) = y(t_0) + h y'(t_0) + \frac{1}{2!}h^2 y''(t_0) + \frac{1}{3!}h^3 y'''(t_0) + O(h^4)$$
Here we can see that Euler's method is using the first two terms of the Taylor expansion. Each subsequent term is smaller than the previous terms, so we are assured that the estimate will not be too far off from the correct value.
### Runge Kutta Methods
Runge Kutta is the workhorse of numerical integration. There are a vast number of methods in the literature. In practice, using the Runge Kutta algorithm that I present here will solve most any problem you will face. It offers a very good balance of speed, precision, and stability, and it is the 'go to' numerical integration method unless you have a very good reason to choose something different.
Let's dive in. We start with some differential equation
$$\ddot{y} = \frac{d}{dt}\dot{y}$$.
We can substitute the derivative of y with a function f, like so
$$\ddot{y} = \frac{d}{dt}f(y,t)$$.
Deriving these equations is outside the scope of this book, but the Runge Kutta RK4 method is defined with these equations.
$$y(t+\Delta t) = y(t) + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4) + O(\Delta t^4)$$
$$\begin{aligned}
k_1 &= f(y,t)\Delta t \\
k_2 &= f(y+\frac{1}{2}k_1, t+\frac{1}{2}\Delta t)\Delta t \\
k_3 &= f(y+\frac{1}{2}k_2, t+\frac{1}{2}\Delta t)\Delta t \\
k_4 &= f(y+k_3, t+\Delta t)\Delta t
\end{aligned}
$$
Here is the corresponding code:
```
def runge_kutta4(y, x, dx, f):
"""computes 4th order Runge-Kutta for dy/dx.
y is the initial value for y
x is the initial value for x
dx is the difference in x (e.g. the time step)
f is a callable function (y, x) that you supply
to compute dy/dx for the specified values.
"""
k1 = dx * f(y, x)
k2 = dx * f(y + 0.5*k1, x + 0.5*dx)
k3 = dx * f(y + 0.5*k2, x + 0.5*dx)
k4 = dx * f(y + k3, x + dx)
return y + (k1 + 2*k2 + 2*k3 + k4) / 6.
```
Let's use this for a simple example. Let
$$\dot{y} = t\sqrt{y(t)}$$
with the initial values
$$\begin{aligned}t_0 &= 0\\y_0 &= y(t_0) = 1\end{aligned}$$
```
import math
import numpy as np
t = 0.
y = 1.
dt = .1
ys, ts = [], []
def func(y,t):
return t*math.sqrt(y)
while t <= 10:
y = runge_kutta4(y, t, dt, func)
t += dt
ys.append(y)
ts.append(t)
exact = [(t**2 + 4)**2 / 16. for t in ts]
plt.plot(ts, ys)
plt.plot(ts, exact)
error = np.array(exact) - np.array(ys)
print("max error {}".format(max(error)))
```
## Bayesian Filtering
Starting in the Discrete Bayes chapter I used a Bayesian formulation for filtering. Suppose we are tracking an object. We define its *state* at a specific time as its position, velocity, and so on. For example, we might write the state at time $t$ as $\mathbf x_t = \begin{bmatrix}x_t &\dot x_t \end{bmatrix}^\mathsf T$.
When we take a measurement of the object we are measuring the state or part of it. Sensors are noisy, so the measurement is corrupted with noise. Clearly though, the measurement is determined by the state. That is, a change in state may change the measurement, but a change in measurement will not change the state.
In filtering our goal is to compute an optimal estimate for a set of states $\mathbf x_{0:t}$ from time 0 to time $t$. If we knew $\mathbf x_{0:t}$ then it would be trivial to compute a set of measurements $\mathbf z_{0:t}$ corresponding to those states. However, we receive a set of measurements $\mathbf z_{0:t}$, and want to compute the corresponding states $\mathbf x_{0:t}$. This is called *statistical inversion* because we are trying to compute the input from the output.
Inversion is a difficult problem because there is typically no unique solution. For a given set of states $\mathbf x_{0:t}$ there is only one possible set of measurements (plus noise), but for a given set of measurements there are many different sets of states that could have led to those measurements.
Recall Bayes Theorem:
$$P(x \mid z) = \frac{P(z \mid x)P(x)}{P(z)}$$
where $P(z \mid x)$ is the *likelihood* of the measurement $z$, $P(x)$ is the *prior* based on our process model, and $P(z)$ is a normalization constant. $P(x \mid z)$ is the *posterior*, or the distribution after incorporating the measurement $z$, also called the *evidence*.
This is a *statistical inversion* as it goes from $P(z \mid x)$ to $P(x \mid z)$. The solution to our filtering problem can be expressed as:
$$P(\mathbf x_{0:t} \mid \mathbf z_{0:t}) = \frac{P(\mathbf z_{0:t} \mid \mathbf x_{0:t})P(\mathbf x_{0:t})}{P(\mathbf z_{0:t})}$$
That is all well and good until the next measurement $\mathbf z_{t+1}$ comes in, at which point we need to recompute the entire expression for the range $0:t+1$.
In practice this is intractable because we are trying to compute the posterior distribution $P(\mathbf x_{0:t} \mid \mathbf z_{0:t})$ for the state over the full range of time steps. But do we really care about the probability distribution at the third step (say) when we just received the tenth measurement? Not usually. So we relax our requirements and only compute the distributions for the current time step.
The first simplification is we describe our process (e.g., the motion model for a moving object) as a *Markov chain*. That is, we say that the current state is solely dependent on the previous state and a transition probability $P(\mathbf x_k \mid \mathbf x_{k-1})$, which is just the probability of going from the last state to the current one. We write:
$$\mathbf x_k \sim P(\mathbf x_k \mid \mathbf x_{k-1})$$
The next simplification we make is do define the *measurement model* as depending on the current state $\mathbf x_k$ with the conditional probability of the measurement given the current state: $P(\mathbf z_t \mid \mathbf x_x)$. We write:
$$\mathbf z_k \sim P(\mathbf z_t \mid \mathbf x_x)$$
We have a recurrance now, so we need an initial condition to terminate it. Therefore we say that the initial distribution is the probablity of the state $\mathbf x_0$:
$$\mathbf x_0 \sim P(\mathbf x_0)$$
These terms are plugged into Bayes equation. If we have the state $\mathbf x_0$ and the first measurement we can estimate $P(\mathbf x_1 | \mathbf z_1)$. The motion model creates the prior $P(\mathbf x_2 \mid \mathbf x_1)$. We feed this back into Bayes theorem to compute $P(\mathbf x_2 | \mathbf z_2)$. We continue this predictor-corrector algorithm, recursively computing the state and distribution at time $t$ based solely on the state and distribution at time $t-1$ and the measurement at time $t$.
The details of the mathematics for this computation varies based on the problem. The **Discrete Bayes** and **Univariate Kalman Filter** chapters gave two different formulations which you should have been able to reason through. The univariate Kalman filter assumes that for a scalar state both the noise and process are linear model are affected by zero-mean, uncorrelated Gaussian noise.
The Multivariate Kalman filter make the same assumption but for states and measurements that are vectors, not scalars. Dr. Kalman was able to prove that if these assumptions hold true then the Kalman filter is *optimal* in a least squares sense. Colloquially this means there is no way to derive more information from the noise. In the remainder of the book I will present filters that relax the constraints on linearity and Gaussian noise.
Before I go on, a few more words about statistical inversion. As Calvetti and Somersalo write in *Introduction to Bayesian Scientific Computing*, "we adopt the Bayesian point of view: *randomness simply means lack of information*."[3] Our state parametize physical phenomena that we could in principle measure or compute: velocity, air drag, and so on. We lack enough information to compute or measure their value, so we opt to consider them as random variables. Strictly speaking they are not random, thus this is a subjective position.
They devote a full chapter to this topic. I can spare a paragraph. Bayesian filters are possible because we ascribe statistical properties to unknown parameters. In the case of the Kalman filter we have closed-form solutions to find an optimal estimate. Other filters, such as the discrete Bayes filter or the particle filter which we cover in a later chapter, model the probability in a more ad-hoc, non-optimal manner. The power of our technique comes from treating lack of information as a random variable, describing that random variable as a probability distribution, and then using Bayes Theorem to solve the statistical inference problem.
## Converting Kalman Filter to a g-h Filter
I've stated that the Kalman filter is a form of the g-h filter. It just takes some algebra to prove it. It's more straightforward to do with the one dimensional case, so I will do that. Recall
$$
\mu_{x}=\frac{\sigma_1^2 \mu_2 + \sigma_2^2 \mu_1} {\sigma_1^2 + \sigma_2^2}
$$
which I will make more friendly for our eyes as:
$$
\mu_{x}=\frac{ya + xb} {a+b}
$$
We can easily put this into the g-h form with the following algebra
$$
\begin{aligned}
\mu_{x}&=(x-x) + \frac{ya + xb} {a+b} \\
\mu_{x}&=x-\frac{a+b}{a+b}x + \frac{ya + xb} {a+b} \\
\mu_{x}&=x +\frac{-x(a+b) + xb+ya}{a+b} \\
\mu_{x}&=x+ \frac{-xa+ya}{a+b} \\
\mu_{x}&=x+ \frac{a}{a+b}(y-x)\\
\end{aligned}
$$
We are almost done, but recall that the variance of estimate is given by
$$\begin{aligned}
\sigma_{x}^2 &= \frac{1}{\frac{1}{\sigma_1^2} + \frac{1}{\sigma_2^2}} \\
&= \frac{1}{\frac{1}{a} + \frac{1}{b}}
\end{aligned}$$
We can incorporate that term into our equation above by observing that
$$
\begin{aligned}
\frac{a}{a+b} &= \frac{a/a}{(a+b)/a} = \frac{1}{(a+b)/a} \\
&= \frac{1}{1 + \frac{b}{a}} = \frac{1}{\frac{b}{b} + \frac{b}{a}} \\
&= \frac{1}{b}\frac{1}{\frac{1}{b} + \frac{1}{a}} \\
&= \frac{\sigma^2_{x'}}{b}
\end{aligned}
$$
We can tie all of this together with
$$
\begin{aligned}
\mu_{x}&=x+ \frac{a}{a+b}(y-x) \\
&= x + \frac{\sigma^2_{x'}}{b}(y-x) \\
&= x + g_n(y-x)
\end{aligned}
$$
where
$$g_n = \frac{\sigma^2_{x}}{\sigma^2_{y}}$$
The end result is multiplying the residual of the two measurements by a constant and adding to our previous value, which is the $g$ equation for the g-h filter. $g$ is the variance of the new estimate divided by the variance of the measurement. Of course in this case $g$ is not a constant as it varies with each time step as the variance changes. We can also derive the formula for $h$ in the same way. It is not a particularly illuminating derivation and I will skip it. The end result is
$$h_n = \frac{COV (x,\dot x)}{\sigma^2_{y}}$$
The takeaway point is that $g$ and $h$ are specified fully by the variance and covariances of the measurement and predictions at time $n$. In other words, we are picking a point between the measurement and prediction by a scale factor determined by the quality of each of those two inputs.
## References
* [1] C.B. Molwer and C.F. Van Loan "Nineteen Dubious Ways to Compute the Exponential of a Matrix, Twenty-Five Years Later,", *SIAM Review 45, 3-49*. 2003.
* [2] C.F. van Loan, "Computing Integrals Involving the Matrix Exponential," IEEE *Transactions Automatic Control*, June 1978.
* [3] Calvetti, D and Somersalo E, "Introduction to Bayesian Scientific Computing: Ten Lectures on Subjective Computing,", *Springer*, 2007.
| github_jupyter |
# Multiple linear regression
In many data sets there may be several predictor variables that have an effect on a response variable.
In fact, the *interaction* between variables may also be used to predict response.
When we incorporate these additional predictor variables into the analysis the model is called *multiple regression* .
The multiple regression model builds on the simple linear regression model by adding additional predictors with corresponding parameters.
## Multiple Regression Model
Let's suppose we are interested in determining what factors might influence a baby's birth weight.
In our data set we have information on birth weight, our response, and predictors: mother’s age, weight and height and gestation period.
A *main effects model* includes each of the possible predictors but no interactions.
Suppose we name these features as in the chart below.
| Variable | Description |
|----------|:-------------------|
| BW | baby birth weight |
| MA | mother's age |
| MW | mother's weight |
| MH | mother's height |
| GP | gestation period |
Then the theoretical main effects multiple regression model is
$$BW = \beta_0 + \beta_1 MA + \beta_2 MW + \beta_3 MH + \beta_4 GP+ \epsilon.$$
Now we have five parameters to estimate from the data, $\beta_0, \beta_1, \beta_2, \beta_3$ and $\beta_4$.
The random error term, $\epsilon$ has the same interpretation as in simple linear regression and is assumed to come from a normal distribution with mean equal to zero and variance equal to $\sigma^2$.
Note that multiple regression also includes the polynomial models discussed in the simple linear regression notebook.
One of the most important things to notice about the equation above is that each variable makes a contribution **independently** of the other variables.
This is sometimes called **additivity**: the effects of predictor variable are added together to get the total effect on `BW`.
## Interaction Effects
Suppose in the example, through exploratory data analysis, we discover that younger mothers with long gestational times tend to have heavier babies, but older mother with short gestational times tend to have lighter babies.
This could indicate an interaction effect on the response.
When there is an interaction effect, the effects of the variables involved are not additive.
Different numbers of variables can be involved in an interaction.
When two features are involved in the interaction it is called a *two-way interaction* .
There are three-way and higher interactions possible as well, but they are less common in practice.
The *full model* includes main effects and all interactions.
For the example given here there are 6 two-way interactions possible between the variables, 4 possible three-way, and 1 four-way interaction in the full model.
Often in practice we fit the full model to check for significant interaction effects.
If there are no interactions that are significantly different from zero, we can drop the interaction terms and fit the main effects model to see which of those effects are significant.
If interaction effects are significant (important in predicting the behavior of the response) then we will interpret the effects of the model in terms of the interaction.
<!-- NOTE: not sure if correction for multiple comparisons is outside the scope here; I would in general not recommend to students that they test all possible interactions unless they had a theoretical reason to, or unless they were doinging something exploratory and then would collect new data to test any interaction found. -->
## Feature Selection
Suppose we run a full model for the four variables in our example and none of the interaction terms are significant.
We then run a main effects model and we get parameter estimates as shown in the table below.
| Coefficients | Estimate | Std. Error | p-value |
|--------------|----------|------------|---------|
| Intercept | 36.69 | 5.97 | 1.44e-6 |
| MA | 0.36 | 1.00 | 0.7197 |
| MW | 3.02 | 0.85 | 0.0014 |
| MH | -0.02 | 0.01 | 0.1792 |
| GP | -0.81 | 0.66 | 0.2311 |
Recall that the p-value is the probability of getting the estimate that we got from the data or something more extreme (further from zero).
Small p-values (typically less than 0.05) indicate the associated parameter is different from zero, implying that the associated covariate is important to predict response.
In our birth weight example, we see the p-value for the intercept is very low $1.44 \times 10^{-6}$ and so the intercept is not at zero.
The mother's weight (MW) has p-value 0.0014 which is very small, indicating that mother's weight has an important (significant) impact on her baby's birth weight.
The p-value from all other Wald tests are large: 0.7197, 0.1792, and 0.2311, so we know none of these variables are important when predicting the birth weight.
We can modify the coefficient of determination to account for having more than one predictor in the model, called the *adjusted R-square* .
R-square has the property that as you add more terms, it will always increase.
The adjustment for more terms takes this into consideration.
For this data the adjusted R-square is 0.8208, indicating a reasonably good fit.
Different combinations of the variables included in the model may give better or worse fits to the data.
We can use several methods to select the "best" model for the data.
One example is called *forward selection* .
This method begins with an empty model (intercept only) and adds variables to the model one by one until the full main effects model is reached.
In each forward step, you add the one variable that gives the best improvement to the fit.
There is also *backward selection* where you start with the full model and then drop the least important variables one at a time until you are left with the intercept only.
If there are not too many features, you can also look at all possible models.
Typically these models are compared using the AIC (Akaike information criterion) which measures the relative quality of models.
Given a set of models, the preferred model is the one with the minimum AIC value.
Previously we talked about splitting the data into training and test sets.
In statistics, this is not common, and the models are trained with all the data.
This is because statistics is generally more interested in the effect of a particular variable *across the entire dataset* than it is about using that variable to make a prediction about a particular datapoint.
Because of this, we typically have concerns about how well linear regression will work with new data, i.e. will it have the same $r^2$ for new data or a lower $r^2$?
Both forward and backward selection potentially enhance this problem because they tune the model to the data even more closely by removing variables that aren't "important."
You should always be very careful with such variable selection methods and their implications for model generalization.
<!-- NOTE: sklearn does not seem to support forward/backward https://datascience.stackexchange.com/questions/937/does-scikit-learn-have-forward-selection-stepwise-regression-algorithm ; what it does support is sufficient different/complicated that it doesn't seem useful to try to introduce it now ; this is an example where the give text would fit R perfectly but be dififcult for python -->
# Categorical Variables
In the birth weight example, there is also information available about the mother's activity level during her pregnancy.
Values for this categorical variable are: low, moderate, and high.
How can we incorporate these into the model?
Since they are not numeric, we have to create *dummy variables* that are numeric to use.
A dummy variable represents the presence or absence of a level of the categorical variable by a 1 and the absence by a zero.
Fortunately, most software packages that do multiple regression do this for us automatically.
Often, one of the levels of the categorical variable is considered the "baseline" and the contributions to the response of the other levels are in relation to baseline.
Let's look at the data again.
In the table below, the mother's age is dropped and the mother's activity level (MAL) is included.
| Coefficients | Estimate | Std. Error | p-value |
|--------------|----------|------------|----------|
| Intercept | 31.35 | 4.65 | 3.68e-07 |
| MW | 2.74 | 0.82 | 0.0026 |
| MH | -0.04 | 0.02 | 0.0420 |
| GP | 1.11 | 1.03 | 0.2917 |
| MALmoderate | -2.97 | 1.44 | 0.049 |
| MALhigh | -1.45 | 2.69 | 0.5946 |
For the categorical variable MAL, MAL low has been chosen as the base line.
The other two levels have parameter estimates that we can use to determine which are significantly different from the low level.
This makes sense because all mothers will at least have low activity level, and the two additional dummy variables `MALhigh` and `MALmoderate` just get added on top of that.
We can see that MAL moderate level is significantly different from the low level (p-value < 0.05).
The parameter estimate for the moderate level of MAL is -2.97.
This can be interpreted as: being in the moderately active group decreases birth weight by 2.97 units compared to babies in the low activity group.
We also see that for babies with mothers in the high activity group, their birth weights are not different from birth weights in the low group, since the p-value is not low (0.5946 > 0.05) and so this term does not have a significant effect on the response (birth weight).
This example highlights a phenomenon that often happens in multiple regression.
When we drop the variable MA (mother's age) from the model and the categorical variable is included, both MW (mother's weight) and MH (mother's height) are both important predictors of birth weight (p-values 0.0026 and 0.0420 respectively).
This is why it is important to perform some systematic model selection (forward or backward or all possible) to find an optimum set of features.
# Diagnostics
As in the simple linear regression case, we can use the residuals to check the fit of the model.
Recall that the residuals are the observed response minus the predicted response.
- Plot the residuals against each independent variable to check whether higher order terms are needed
- Plot the residuals versus the predicted values to check whether the variance is constant
- Plot a qq-plot of the residuals to check for normality
# Multicollinearity
Multicollinearity occurs when two variables or features are linearly related, i.e.
they have very strong correlation between them (close to -1 or 1).
Practically this means that some of the independent variables are measuring the same thing and are not needed.
In the extreme case (close to -1 or 1), the estimates of the parameters of the model cannot be obtained.
This is because there is no unique solution for OLS when multicolinearity occurs.
As a result, multicollinearity makes conclusions about which features should be used questionable.
## Example: Trees
Let's take a look at a dataset we've seen before `trees` but with an additional tree type added `plum`:
| Variable | Type | Description |
|----------|-------|:-------------------------------------------------------|
| Girth | Ratio | Tree diameter (rather than girth, actually) in inches |
| Height | Ratio | Height in ft |
| Volume | Ratio | Volume of timber in cubic ft |
| Type | Nominal | The type of tree, cherry or plum |
Much of what we'll do is the same as with simple linear regression, except:
- Converting categorical variables into dummy variables
- Different multiple predictors
- Interactions
### Load data
Start with the imports:
- `import pandas as pd`
```
import pandas as pd
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="Vd-20qkN(WN5nJAUj;?4">pd</variable></variables><block type="importAs" id="ji{aK+A5l`eBa?Q1/|Pf" x="128" y="319"><field name="libraryName">pandas</field><field name="libraryAlias" id="Vd-20qkN(WN5nJAUj;?4">pd</field></block></xml>
```
Load the dataframe:
- Create variable `dataframe`
- Set it to `with pd do read_csv using "datasets/trees2.csv"`
- `dataframe` (to display)
```
dataframe = pd.read_csv('datasets/trees2.csv')
dataframe
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="B5p-Xul6IZ.0%nd96oa%">dataframe</variable><variable id="Vd-20qkN(WN5nJAUj;?4">pd</variable></variables><block type="variables_set" id="9aUm-oG6/!Z54ivA^qkm" x="2" y="351"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="VALUE"><block type="varDoMethod" id="g.yE$oK%3]$!k91|6U|I"><field name="VAR" id="Vd-20qkN(WN5nJAUj;?4">pd</field><field name="MEMBER">read_csv</field><data>pd:read_csv</data><value name="INPUT"><block type="text" id="fBBU[Z}QCipaz#y=F$!p"><field name="TEXT">datasets/trees2.csv</field></block></value></block></value></block><block type="variables_get" id="pVVu/utZDzpFy(h9Q-+Z" x="6" y="425"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field></block></xml>
```
We know that later on, we'd like to use `Type` as a predictor, so we need to convert it into a dummy variable.
However, we'd also like to keep `Type` as a column for our plot labels.
There are several ways to do this, but probably the easiest is to save `Type` and then put it back in the dataframe.
It will make sense as we go:
- Create variable `treeType`
- Set it to `dataframe[` list containing `"Type"` `]` (use {dictVariable}[] from LISTS)
- `treeType` (to display)
```
treeType = dataframe[['Type']]
treeType
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="hr*VLs~Y+rz.qsB5%AkC">treeType</variable><variable id="B5p-Xul6IZ.0%nd96oa%">dataframe</variable></variables><block type="variables_set" id="n?M6{W!2xggQx@X7_00@" x="0" y="391"><field name="VAR" id="hr*VLs~Y+rz.qsB5%AkC">treeType</field><value name="VALUE"><block type="indexer" id="3_O9X7-U(%IcMj/dcLIo"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="INDEX"><block type="lists_create_with" id="?V*^3XN6]-U+o1C:Vzq$"><mutation items="1"></mutation><value name="ADD0"><block type="text" id="^a?w!r[mo5(HVwiC0q=4"><field name="TEXT">Type</field></block></value></block></value></block></value></block><block type="variables_get" id="Lvbr[Vv2??Mx*R}-s{,0" x="8" y="470"><field name="VAR" id="hr*VLs~Y+rz.qsB5%AkC">treeType</field></block></xml>
```
To do the dummy conversion:
- Set `dataframe` to `with pd do get_dummies using` a list containing
- `dataframe`
- freestyle `drop_first=True`
- `dataframe` (to display)
```
dataframe = pd.get_dummies(dataframe, drop_first=True)
dataframe
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="B5p-Xul6IZ.0%nd96oa%">dataframe</variable><variable id="Vd-20qkN(WN5nJAUj;?4">pd</variable></variables><block type="variables_set" id="f~Vi_+$-EAjHP]f_eV;K" x="55" y="193"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="VALUE"><block type="varDoMethod" id="|n$+[JUtgfsvt4?c:yr_"><field name="VAR" id="Vd-20qkN(WN5nJAUj;?4">pd</field><field name="MEMBER">get_dummies</field><data>pd:get_dummies</data><value name="INPUT"><block type="lists_create_with" id="?P;X;R^dn$yjWHW=i7u2"><mutation items="2"></mutation><value name="ADD0"><block type="variables_get" id="Bbsj2h*vF?=ou`pb%n59"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field></block></value><value name="ADD1"><block type="dummyOutputCodeBlock" id="bMU2}K@krqBgj]d/*N%r"><field name="CODE">drop_first=True</field></block></value></block></value></block></value></block><block type="variables_get" id="2cWY4Drg[bFmM~E#v`]o" x="73" y="293"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field></block></xml>
```
Notice that `cherry` is now the base level, so `Type_plum` is in `0` where `cherry` was before and `1` where `plum` was before.
To put `Type` back in, use `assign`:
- Set `dataframe` to `with dataframe do assign using` a list containing
- freestyle `Type=treeType`
- `dataframe` (to display)
```
dataframe = dataframe.assign(Type=treeType)
dataframe
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="B5p-Xul6IZ.0%nd96oa%">dataframe</variable></variables><block type="variables_set" id="asM(PJ)BfN(o4N+9wUt$" x="-18" y="225"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="VALUE"><block type="varDoMethod" id=";29VMd-(]?GAtxBc4RYY"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><field name="MEMBER">assign</field><data>dataframe:assign</data><value name="INPUT"><block type="lists_create_with" id="~HSVpyu|XuF_=bZz[e./"><mutation items="1"></mutation><value name="ADD0"><block type="dummyOutputCodeBlock" id="0yKT_^W!N#JL!5%=T_+J"><field name="CODE">Type=treeType</field></block></value></block></value></block></value></block><block type="variables_get" id="U)2!3yg#Q,f=4ImV=Pl." x="-3" y="288"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field></block></xml>
```
This is nice - we have our dummy code for modeling but also the nice original lable in `Type` so we don't get confused.
### Explore data
Let's start with some *overall* descriptive statistics:
- `with dataframe do describe using`
```
dataframe.describe()
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="B5p-Xul6IZ.0%nd96oa%">dataframe</variable></variables><block type="varDoMethod" id="?LJ([email protected],`==|to" x="8" y="188"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><field name="MEMBER">describe</field><data>dataframe:describe</data></block></xml>
```
This is nice, but we suspect there might be some differences between cherry trees and plum trees that this doesn't show.
We can `describe` each group as well:
- Create variable `groups`
- Set it to `with dataframe do groupby using "Type"`
```
groups = dataframe.groupby('Type')
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="0zfUO$}u$G4I(G1e~N#r">groups</variable><variable id="B5p-Xul6IZ.0%nd96oa%">dataframe</variable></variables><block type="variables_set" id="kr80`.2l6nJi|eO*fce[" x="44" y="230"><field name="VAR" id="0zfUO$}u$G4I(G1e~N#r">groups</field><value name="VALUE"><block type="varDoMethod" id="x-nB@sYwAL|7o-0;9DUU"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><field name="MEMBER">groupby</field><data>dataframe:groupby</data><value name="INPUT"><block type="text" id="Lby0o8dWqy8ta:56K|bn"><field name="TEXT">Type</field></block></value></block></value></block></xml>
```
Now `describe` groups:
- `with groups do describe using`
```
groups.describe()
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="0zfUO$}u$G4I(G1e~N#r">groups</variable></variables><block type="varDoMethod" id="]q4DcYnB3HUf/GehIu+T" x="8" y="188"><field name="VAR" id="0zfUO$}u$G4I(G1e~N#r">groups</field><field name="MEMBER">describe</field><data>groups:describe</data></block></xml>
```
Notice this results table has been rotated compared to the normal `describe`.
The rows are our two tree types, and the columns are **stacked columns** where the header (e.g. `Girth`) applies to everything below it and to the left (it is not centered).
From this we see that the `Girth` is about the same across trees, the `Height` is 13ft different on average, and `Volume` is 5ft different on average.
Let's do a plot.
We can sneak all the variables into a 2D scatterplot with some clever annotations.
First the import:
- `import plotly.express as px`
```
import plotly.express as px
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="k#w4n=KvP~*sLy*OW|Jl">px</variable></variables><block type="importAs" id="kPF|afHe60B:rsCmJI2O" x="128" y="178"><field name="libraryName">plotly.express</field><field name="libraryAlias" id="k#w4n=KvP~*sLy*OW|Jl">px</field></block></xml>
```
Create the scatterplot:
- Create variable `fig`
- Set it to `with px do scatter using` a list containing
- `dataframe`
- freestyle `x="Height"`
- freestyle `y="Volume"`
- freestyle `color="Type"`
- freestyle `size="Girth"`
```
fig = px.scatter(dataframe, x="Height", y="Volume", color="Type", size="Girth")
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="w|!1_/S4wRKF4S1`6Xg+">fig</variable><variable id="k#w4n=KvP~*sLy*OW|Jl">px</variable><variable id="B5p-Xul6IZ.0%nd96oa%">dataframe</variable></variables><block type="variables_set" id="/1x?=CLW;i70@$T5LPN/" x="48" y="337"><field name="VAR" id="w|!1_/S4wRKF4S1`6Xg+">fig</field><value name="VALUE"><block type="varDoMethod" id="O07?sQIdula@ap]/9Ogq"><field name="VAR" id="k#w4n=KvP~*sLy*OW|Jl">px</field><field name="MEMBER">scatter</field><data>px:scatter</data><value name="INPUT"><block type="lists_create_with" id="~tHtb;Nbw/OP6#7pB9wX"><mutation items="5"></mutation><value name="ADD0"><block type="variables_get" id="UE)!btph,4mdjsf[F37|"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field></block></value><value name="ADD1"><block type="dummyOutputCodeBlock" id="~L)yq!Jze#v9R[^p;2{O"><field name="CODE">x="Height"</field></block></value><value name="ADD2"><block type="dummyOutputCodeBlock" id="yu5^$n1zXY3)#RcRx:~;"><field name="CODE">y="Volume"</field></block></value><value name="ADD3"><block type="dummyOutputCodeBlock" id="aCZ,k0LzStF1D(+SB2%A"><field name="CODE">color="Type"</field></block></value><value name="ADD4"><block type="dummyOutputCodeBlock" id="4yv:pfYUrA=V0bO}PLcX"><field name="CODE">size="Girth"</field></block></value></block></value></block></value></block></xml>
```
And show the figure:
- `with fig do show using`
```
fig.show()
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="w|!1_/S4wRKF4S1`6Xg+">fig</variable></variables><block type="varDoMethod" id="SV]QMDs*p(4s=2tPrl4a" x="8" y="188"><field name="VAR" id="w|!1_/S4wRKF4S1`6Xg+">fig</field><field name="MEMBER">show</field><data>fig:show</data></block></xml>
```
### Modeling 1
Last time we looked at `trees`, we used `Height` to predict `Volume`.
With multiple linear regression, we can use more that one variable.
Let's start with using `Girth` and `Height` to predict `Volume`.
But first, the imports:
- `import sklearn.linear_model as sklearn`
- `import numpy as np`
```
import sklearn.linear_model as linear_model
import numpy as np
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="!+Hi;Yx;ZB!EQYU8ItpO">linear_model</variable><variable id="YynR+H75hTgW`vKfMxOx">np</variable></variables><block type="importAs" id="m;0Uju49an!8G3YKn4cP" x="93" y="288"><field name="libraryName">sklearn.linear_model</field><field name="libraryAlias" id="!+Hi;Yx;ZB!EQYU8ItpO">linear_model</field><next><block type="importAs" id="^iL#`T{6G3.Uxfj*r`Cv"><field name="libraryName">numpy</field><field name="libraryAlias" id="YynR+H75hTgW`vKfMxOx">np</field></block></next></block></xml>
```
Create the model:
- Create variable `lm` (for linear model)
- Set it to `with sklearn create LinearRegression using`
```
lm = linear_model.LinearRegression()
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="F]q147x/*m|PMfPQU-lZ">lm</variable><variable id="!+Hi;Yx;ZB!EQYU8ItpO">linear_model</variable></variables><block type="variables_set" id="!H`J#y,K:4I.h#,HPeK{" x="127" y="346"><field name="VAR" id="F]q147x/*m|PMfPQU-lZ">lm</field><value name="VALUE"><block type="varCreateObject" id="h:O3ZfE(*c[Hz3sF=$Mm"><field name="VAR" id="!+Hi;Yx;ZB!EQYU8ItpO">linear_model</field><field name="MEMBER">LinearRegression</field><data>linear_model:LinearRegression</data></block></value></block></xml>
```
Train the model using all the data:
- `with lm do fit using` a list containing
- `dataframe [ ]` (use {dictVariable} from LISTS) containing a list containing
- `"Girth"` (this is $X_1$)
- `"Height"` (this is $X_2$)
- `dataframe [ ]` containing a list containing
- `"Volume"` (this is $Y$)
```
lm.fit(dataframe[['Girth', 'Height']], dataframe[['Volume']])
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="F]q147x/*m|PMfPQU-lZ">lm</variable><variable id="B5p-Xul6IZ.0%nd96oa%">dataframe</variable></variables><block type="varDoMethod" id="W6(0}aPsJ;vA9C3A!:G@" x="8" y="188"><field name="VAR" id="F]q147x/*m|PMfPQU-lZ">lm</field><field name="MEMBER">fit</field><data>lm:</data><value name="INPUT"><block type="lists_create_with" id="|pmNlB*$t`wI~M5-Nu5]"><mutation items="2"></mutation><value name="ADD0"><block type="indexer" id=".|%fa!U;=I@;!6$?B7Id"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="INDEX"><block type="lists_create_with" id="o5szXy4*HmKGA;-.~H?H"><mutation items="2"></mutation><value name="ADD0"><block type="text" id="{*5MFGJL4(x-JLsuD9qv"><field name="TEXT">Girth</field></block></value><value name="ADD1"><block type="text" id="#cqoT/|u(kuI^=VOHoB@"><field name="TEXT">Height</field></block></value></block></value></block></value><value name="ADD1"><block type="indexer" id="o.R`*;zvaP%^K2/_t`6*"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="INDEX"><block type="lists_create_with" id="[WAkSKWMcU+j3zS)uzVG"><mutation items="1"></mutation><value name="ADD0"><block type="text" id="w0w/T-Wh/df/waYll,rv"><field name="TEXT">Volume</field></block></value></block></value></block></value></block></value></block></xml>
```
Go ahead and get the $r^2$ ; you can just copy the blocks from the last cell and change `fit` to `score`.
```
lm.score(dataframe[['Girth', 'Height']], dataframe[['Volume']])
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="F]q147x/*m|PMfPQU-lZ">lm</variable><variable id="B5p-Xul6IZ.0%nd96oa%">dataframe</variable></variables><block type="varDoMethod" id="W6(0}aPsJ;vA9C3A!:G@" x="8" y="188"><field name="VAR" id="F]q147x/*m|PMfPQU-lZ">lm</field><field name="MEMBER">score</field><data>lm:score</data><value name="INPUT"><block type="lists_create_with" id="|pmNlB*$t`wI~M5-Nu5]"><mutation items="2"></mutation><value name="ADD0"><block type="indexer" id=".|%fa!U;=I@;!6$?B7Id"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="INDEX"><block type="lists_create_with" id="o5szXy4*HmKGA;-.~H?H"><mutation items="2"></mutation><value name="ADD0"><block type="text" id="{*5MFGJL4(x-JLsuD9qv"><field name="TEXT">Girth</field></block></value><value name="ADD1"><block type="text" id="#cqoT/|u(kuI^=VOHoB@"><field name="TEXT">Height</field></block></value></block></value></block></value><value name="ADD1"><block type="indexer" id="o.R`*;zvaP%^K2/_t`6*"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="INDEX"><block type="lists_create_with" id="[WAkSKWMcU+j3zS)uzVG"><mutation items="1"></mutation><value name="ADD0"><block type="text" id="w0w/T-Wh/df/waYll,rv"><field name="TEXT">Volume</field></block></value></block></value></block></value></block></value></block></xml>
```
Based on that $r^2$, we'd think we have a really good model, right?
### Diagnostics 1
To check the model, the first thing we need to do is get the predictions from the model.
Once we have the predictions, we can `assign` them to a column in the `dataframe`:
- Set `dataframe` to `with dataframe do assign using` a list containing
- freestyle `predictions1=` *followed by*
- `with lm do predict using` a list containing
- `dataframe [ ]` containing a list containing
- `"Girth"`
- `"Height"`
- `dataframe` (to display)
**This makes a very long block, so you probably want to create all the blocks and then connect them in reverse order.**
```
dataframe = dataframe.assign(predictions1= (lm.predict(dataframe[['Girth', 'Height']])))
dataframe
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="B5p-Xul6IZ.0%nd96oa%">dataframe</variable><variable id="F]q147x/*m|PMfPQU-lZ">lm</variable></variables><block type="variables_set" id="rn0LHF%t,0JD5-!Ov?-U" x="-21" y="228"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="VALUE"><block type="varDoMethod" id="ou+aFod:USt{s9i+emN}"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><field name="MEMBER">assign</field><data>dataframe:assign</data><value name="INPUT"><block type="lists_create_with" id="Llv.8Hqls5S/.2ZpnF=D"><mutation items="1"></mutation><value name="ADD0"><block type="valueOutputCodeBlock" id="UFqs+Ox{QF6j*LkUvNvu"><field name="CODE">predictions1=</field><value name="INPUT"><block type="varDoMethod" id="(2l5d}m6K9#ZC6_^/JXe"><field name="VAR" id="F]q147x/*m|PMfPQU-lZ">lm</field><field name="MEMBER">predict</field><data>lm:predict</data><value name="INPUT"><block type="lists_create_with" id="bm@2N5t#Fx`yDxjg~:Nw"><mutation items="1"></mutation><value name="ADD0"><block type="indexer" id="WQaaM]1BPY=1wxWQsv:$"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="INDEX"><block type="lists_create_with" id="Asy|RX,d{QfgBQmjI{@@"><mutation items="2"></mutation><value name="ADD0"><block type="text" id="+5PTgD[9U~pl`q#YlA^!"><field name="TEXT">Girth</field></block></value><value name="ADD1"><block type="text" id="{vo.7:W51MOg?Ef(L-Rn"><field name="TEXT">Height</field></block></value></block></value></block></value></block></value></block></value></block></value></block></value></block></value></block><block type="variables_get" id="+]Ia}Q|FmU.bu*zJ1qHs" x="-13" y="339"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field></block></xml>
```
Similarly, we want to add the residuals to `dataframe`:
- Set `dataframe` to `with dataframe do assign using` a list containing
- freestyle `residuals1=` *followed by* `dataframe [ "Volume" ] - dataframe [ "predictions1" ]`
- `dataframe` (to display)
**Hint: use {dictVariable}[] and the + block from MATH**
```
dataframe = dataframe.assign(residuals1= (dataframe['Volume'] - dataframe['predictions1']))
dataframe
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="B5p-Xul6IZ.0%nd96oa%">dataframe</variable></variables><block type="variables_set" id="rn0LHF%t,0JD5-!Ov?-U" x="-28" y="224"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="VALUE"><block type="varDoMethod" id="(2l5d}m6K9#ZC6_^/JXe"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><field name="MEMBER">assign</field><data>dataframe:assign</data><value name="INPUT"><block type="lists_create_with" id="bm@2N5t#Fx`yDxjg~:Nw"><mutation items="1"></mutation><value name="ADD0"><block type="valueOutputCodeBlock" id="^$QWpb1hPzxWt/?~mZBX"><field name="CODE">residuals1=</field><value name="INPUT"><block type="math_arithmetic" id="=szmSC[EoihfyX_5cH6v"><field name="OP">MINUS</field><value name="A"><shadow type="math_number" id="E[2Ss)z+r1pVe~OSDMne"><field name="NUM">1</field></shadow><block type="indexer" id="WQaaM]1BPY=1wxWQsv:$"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="INDEX"><block type="text" id="+5PTgD[9U~pl`q#YlA^!"><field name="TEXT">Volume</field></block></value></block></value><value name="B"><shadow type="math_number" id="Z%,Q(P8VED{wb;Q#^bM4"><field name="NUM">1</field></shadow><block type="indexer" id="b.`x=!iTEC%|-VGV[Hu5"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="INDEX"><block type="text" id="g`tk1*Psq~biS1z%3c`q"><field name="TEXT">predictions1</field></block></value></block></value></block></value></block></value></block></value></block></value></block><block type="variables_get" id="+]Ia}Q|FmU.bu*zJ1qHs" x="-13" y="339"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field></block></xml>
```
Now let's do some plots!
Let's check linearity and equal variance:
- Linearity means the residuals will be close to zero
- Equal variance means residuals will be evenly away from zero
- Set `fig` to `with px do scatter using` a list containing
- `dataframe`
- freestyle `x="predictions1"`
- freestyle `y="residuals1"`
```
fig = px.scatter(dataframe, x="predictions1", y="residuals1")
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="w|!1_/S4wRKF4S1`6Xg+">fig</variable><variable id="k#w4n=KvP~*sLy*OW|Jl">px</variable><variable id="B5p-Xul6IZ.0%nd96oa%">dataframe</variable></variables><block type="variables_set" id="/1x?=CLW;i70@$T5LPN/" x="48" y="337"><field name="VAR" id="w|!1_/S4wRKF4S1`6Xg+">fig</field><value name="VALUE"><block type="varDoMethod" id="O07?sQIdula@ap]/9Ogq"><field name="VAR" id="k#w4n=KvP~*sLy*OW|Jl">px</field><field name="MEMBER">scatter</field><data>px:scatter</data><value name="INPUT"><block type="lists_create_with" id="~tHtb;Nbw/OP6#7pB9wX"><mutation items="3"></mutation><value name="ADD0"><block type="variables_get" id="UE)!btph,4mdjsf[F37|"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field></block></value><value name="ADD1"><block type="dummyOutputCodeBlock" id="~L)yq!Jze#v9R[^p;2{O"><field name="CODE">x="predictions1"</field></block></value><value name="ADD2"><block type="dummyOutputCodeBlock" id="yu5^$n1zXY3)#RcRx:~;"><field name="CODE">y="residuals1"</field></block></value></block></value></block></value></block></xml>
```
And show it:
- `with fig do show using`
```
fig.show()
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="w|!1_/S4wRKF4S1`6Xg+">fig</variable></variables><block type="varDoMethod" id="SV]QMDs*p(4s=2tPrl4a" x="8" y="188"><field name="VAR" id="w|!1_/S4wRKF4S1`6Xg+">fig</field><field name="MEMBER">show</field><data>fig:show</data></block></xml>
```
We see something very, very wrong here: a "U" shape from left to right.
This means our residuals are positive for low predictions, go negative for mid predictions, and go positive again for high predictions.
The only way this can happen is if something is quadratic (squared) in the phenomenon we're trying to model.
### Modeling 2
Step back for a moment and consider what we are trying to do.
We are trying to predict volume from other measurements of the tree.
What is the formula for volume?
$$V = \pi r^2 h$$
Since this is the mathematical definition, we don't expect any differences for `plum` vs. `cherry`.
What are our variables?
- `Volume`
- `Girth` (diameter, which is twice $r$)
- `Height`
In other words, we basically have everything in the formula.
Let's create a new column that is closer to what we want, `Girth` * `Girth` * `Height`:
- Set `dataframe` to `with dataframe do assign using` a list containing
- freestyle `GGH=` *followed by* `dataframe [ "Girth" ] * dataframe [ "Girth" ] * dataframe [ "Height" ]`
- `dataframe` (to display)
```
dataframe = dataframe.assign(GGH= (dataframe['Girth'] * (dataframe['Girth'] * dataframe['Height'])))
dataframe
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="B5p-Xul6IZ.0%nd96oa%">dataframe</variable></variables><block type="variables_set" id="rn0LHF%t,0JD5-!Ov?-U" x="-28" y="224"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="VALUE"><block type="varDoMethod" id="(2l5d}m6K9#ZC6_^/JXe"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><field name="MEMBER">assign</field><data>dataframe:assign</data><value name="INPUT"><block type="lists_create_with" id="bm@2N5t#Fx`yDxjg~:Nw"><mutation items="1"></mutation><value name="ADD0"><block type="valueOutputCodeBlock" id="^$QWpb1hPzxWt/?~mZBX"><field name="CODE">GGH=</field><value name="INPUT"><block type="math_arithmetic" id="5RK=q#[GZz]1)F{}r5DR"><field name="OP">MULTIPLY</field><value name="A"><shadow type="math_number"><field name="NUM">1</field></shadow><block type="indexer" id="Xh!r5Y0#k:n+aqBjuvad"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="INDEX"><block type="text" id="|4#UlYaNe-aeV+s$,Wn]"><field name="TEXT">Girth</field></block></value></block></value><value name="B"><shadow type="math_number" id=";S0XthTRZu#Q.w|qt88k"><field name="NUM">1</field></shadow><block type="math_arithmetic" id="=szmSC[EoihfyX_5cH6v"><field name="OP">MULTIPLY</field><value name="A"><shadow type="math_number" id="E[2Ss)z+r1pVe~OSDMne"><field name="NUM">1</field></shadow><block type="indexer" id="WQaaM]1BPY=1wxWQsv:$"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="INDEX"><block type="text" id="+5PTgD[9U~pl`q#YlA^!"><field name="TEXT">Girth</field></block></value></block></value><value name="B"><shadow type="math_number" id="Z%,Q(P8VED{wb;Q#^bM4"><field name="NUM">1</field></shadow><block type="indexer" id="b.`x=!iTEC%|-VGV[Hu5"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="INDEX"><block type="text" id="g`tk1*Psq~biS1z%3c`q"><field name="TEXT">Height</field></block></value></block></value></block></value></block></value></block></value></block></value></block></value></block><block type="variables_get" id="+]Ia}Q|FmU.bu*zJ1qHs" x="-13" y="339"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field></block></xml>
```
As you might have noticed, `GGH` is an interaction.
Often when we have interactions, we include the variables that the interactions are made off (also known as **main effects**).
However, in this case, that doesn't make sense because we know the interaction is close to the definition of `Volume`.
So let's fit a new model using just `GGH`, save it's predictions and residuals, and plot it's predicted vs. residual diagnostic plot.
First, fit the model:
- `with lm do fit using` a list containing
- `dataframe [ ]` containing a list containing
- `"GGH"`
- `dataframe [ ]` containing a list containing
- `"Volume"`
```
lm.fit(dataframe[['GGH']], dataframe[['Volume']])
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="F]q147x/*m|PMfPQU-lZ">lm</variable><variable id="B5p-Xul6IZ.0%nd96oa%">dataframe</variable></variables><block type="varDoMethod" id="W6(0}aPsJ;vA9C3A!:G@" x="8" y="188"><field name="VAR" id="F]q147x/*m|PMfPQU-lZ">lm</field><field name="MEMBER">fit</field><data>lm:</data><value name="INPUT"><block type="lists_create_with" id="|pmNlB*$t`wI~M5-Nu5]"><mutation items="2"></mutation><value name="ADD0"><block type="indexer" id=".|%fa!U;=I@;!6$?B7Id"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="INDEX"><block type="lists_create_with" id="o5szXy4*HmKGA;-.~H?H"><mutation items="1"></mutation><value name="ADD0"><block type="text" id="{*5MFGJL4(x-JLsuD9qv"><field name="TEXT">GGH</field></block></value></block></value></block></value><value name="ADD1"><block type="indexer" id="o.R`*;zvaP%^K2/_t`6*"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="INDEX"><block type="lists_create_with" id="[WAkSKWMcU+j3zS)uzVG"><mutation items="1"></mutation><value name="ADD0"><block type="text" id="w0w/T-Wh/df/waYll,rv"><field name="TEXT">Volume</field></block></value></block></value></block></value></block></value></block></xml>
```
### Diagnostics 2
Save the predictions:
- Set `dataframe` to `with dataframe do assign using` a list containing
- freestyle `predictions2=` *followed by*
- `with lm do predict using` a list containing
- `dataframe [ ]` containing a list containing
- `"GGH"`
- `dataframe` (to display)
```
dataframe = dataframe.assign(predictions2= (lm.predict(dataframe[['GGH']])))
dataframe
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="B5p-Xul6IZ.0%nd96oa%">dataframe</variable><variable id="F]q147x/*m|PMfPQU-lZ">lm</variable></variables><block type="variables_set" id="rn0LHF%t,0JD5-!Ov?-U" x="-21" y="228"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="VALUE"><block type="varDoMethod" id="ou+aFod:USt{s9i+emN}"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><field name="MEMBER">assign</field><data>dataframe:assign</data><value name="INPUT"><block type="lists_create_with" id="Llv.8Hqls5S/.2ZpnF=D"><mutation items="1"></mutation><value name="ADD0"><block type="valueOutputCodeBlock" id="UFqs+Ox{QF6j*LkUvNvu"><field name="CODE">predictions2=</field><value name="INPUT"><block type="varDoMethod" id="(2l5d}m6K9#ZC6_^/JXe"><field name="VAR" id="F]q147x/*m|PMfPQU-lZ">lm</field><field name="MEMBER">predict</field><data>lm:predict</data><value name="INPUT"><block type="lists_create_with" id="bm@2N5t#Fx`yDxjg~:Nw"><mutation items="1"></mutation><value name="ADD0"><block type="indexer" id="WQaaM]1BPY=1wxWQsv:$"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="INDEX"><block type="lists_create_with" id="rugUT!#.Lk(@nt!}4hC;"><mutation items="1"></mutation><value name="ADD0"><block type="text" id="4nD6,I;gq.Y.D%v3$kFX"><field name="TEXT">GGH</field></block></value></block></value></block></value></block></value></block></value></block></value></block></value></block></value></block><block type="variables_get" id="+]Ia}Q|FmU.bu*zJ1qHs" x="-13" y="339"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field></block></xml>
```
Save the residuals:
- Set `dataframe` to `with dataframe do assign using` a list containing
- freestyle `residuals2=` *followed by* `dataframe [ "Volume" ] - dataframe [ "predictions2" ]`
- `dataframe` (to display)
```
dataframe = dataframe.assign(residuals2= (dataframe['Volume'] - dataframe['predictions2']))
dataframe
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="B5p-Xul6IZ.0%nd96oa%">dataframe</variable></variables><block type="variables_set" id="rn0LHF%t,0JD5-!Ov?-U" x="-28" y="224"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="VALUE"><block type="varDoMethod" id="(2l5d}m6K9#ZC6_^/JXe"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><field name="MEMBER">assign</field><data>dataframe:assign</data><value name="INPUT"><block type="lists_create_with" id="bm@2N5t#Fx`yDxjg~:Nw"><mutation items="1"></mutation><value name="ADD0"><block type="valueOutputCodeBlock" id="^$QWpb1hPzxWt/?~mZBX"><field name="CODE">residuals2=</field><value name="INPUT"><block type="math_arithmetic" id="=szmSC[EoihfyX_5cH6v"><field name="OP">MINUS</field><value name="A"><shadow type="math_number" id="E[2Ss)z+r1pVe~OSDMne"><field name="NUM">1</field></shadow><block type="indexer" id="WQaaM]1BPY=1wxWQsv:$"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="INDEX"><block type="text" id="+5PTgD[9U~pl`q#YlA^!"><field name="TEXT">Volume</field></block></value></block></value><value name="B"><shadow type="math_number" id="Z%,Q(P8VED{wb;Q#^bM4"><field name="NUM">1</field></shadow><block type="indexer" id="b.`x=!iTEC%|-VGV[Hu5"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="INDEX"><block type="text" id="g`tk1*Psq~biS1z%3c`q"><field name="TEXT">predictions2</field></block></value></block></value></block></value></block></value></block></value></block></value></block><block type="variables_get" id="+]Ia}Q|FmU.bu*zJ1qHs" x="-13" y="339"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field></block></xml>
```
And now plot the predicted vs residuals to check linearity and equal variance:
- Set `fig` to `with px do scatter using` a list containing
- `dataframe`
- freestyle `x="predictions2"`
- freestyle `y="residuals2"`
```
fig = px.scatter(dataframe, x="predictions2", y="residuals2")
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="w|!1_/S4wRKF4S1`6Xg+">fig</variable><variable id="k#w4n=KvP~*sLy*OW|Jl">px</variable><variable id="B5p-Xul6IZ.0%nd96oa%">dataframe</variable></variables><block type="variables_set" id="/1x?=CLW;i70@$T5LPN/" x="48" y="337"><field name="VAR" id="w|!1_/S4wRKF4S1`6Xg+">fig</field><value name="VALUE"><block type="varDoMethod" id="O07?sQIdula@ap]/9Ogq"><field name="VAR" id="k#w4n=KvP~*sLy*OW|Jl">px</field><field name="MEMBER">scatter</field><data>px:scatter</data><value name="INPUT"><block type="lists_create_with" id="~tHtb;Nbw/OP6#7pB9wX"><mutation items="3"></mutation><value name="ADD0"><block type="variables_get" id="UE)!btph,4mdjsf[F37|"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field></block></value><value name="ADD1"><block type="dummyOutputCodeBlock" id="~L)yq!Jze#v9R[^p;2{O"><field name="CODE">x="predictions2"</field></block></value><value name="ADD2"><block type="dummyOutputCodeBlock" id="yu5^$n1zXY3)#RcRx:~;"><field name="CODE">y="residuals2"</field></block></value></block></value></block></value></block></xml>
```
And show it:
- `with fig do show using`
```
fig.show()
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="w|!1_/S4wRKF4S1`6Xg+">fig</variable></variables><block type="varDoMethod" id="SV]QMDs*p(4s=2tPrl4a" x="8" y="188"><field name="VAR" id="w|!1_/S4wRKF4S1`6Xg+">fig</field><field name="MEMBER">show</field><data>fig:show</data></block></xml>
```
This is a pretty good plot.
Most of the residuals are close to zero, and what residuals aren't are fairly evenly spread.
We want to see an evenly spaced band above and below 0 as we scan from left to right, and we do.
With this new model, calculate $r^2$:
```
lm.score(dataframe[['GGH']], dataframe[['Volume']])
#<xml xmlns="https://developers.google.com/blockly/xml"><variables><variable id="F]q147x/*m|PMfPQU-lZ">lm</variable><variable id="B5p-Xul6IZ.0%nd96oa%">dataframe</variable></variables><block type="varDoMethod" id="W6(0}aPsJ;vA9C3A!:G@" x="8" y="188"><field name="VAR" id="F]q147x/*m|PMfPQU-lZ">lm</field><field name="MEMBER">score</field><data>lm:score</data><value name="INPUT"><block type="lists_create_with" id="|pmNlB*$t`wI~M5-Nu5]"><mutation items="2"></mutation><value name="ADD0"><block type="indexer" id=".|%fa!U;=I@;!6$?B7Id"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="INDEX"><block type="lists_create_with" id="o5szXy4*HmKGA;-.~H?H"><mutation items="1"></mutation><value name="ADD0"><block type="text" id="{*5MFGJL4(x-JLsuD9qv"><field name="TEXT">GGH</field></block></value></block></value></block></value><value name="ADD1"><block type="indexer" id="o.R`*;zvaP%^K2/_t`6*"><field name="VAR" id="B5p-Xul6IZ.0%nd96oa%">dataframe</field><value name="INDEX"><block type="lists_create_with" id="[WAkSKWMcU+j3zS)uzVG"><mutation items="1"></mutation><value name="ADD0"><block type="text" id="w0w/T-Wh/df/waYll,rv"><field name="TEXT">Volume</field></block></value></block></value></block></value></block></value></block></xml>
```
We went from .956 to .989 by putting the right variables in the interaction.
## Submit your work
When you have finished the notebook, please download it, log in to [OKpy](https://okpy.org/) using "Student Login", and submit it there.
Then let your instructor know on Slack.
| github_jupyter |
# Generative Adversarial Network
In this notebook, we'll be building a generative adversarial network (GAN) trained on the MNIST dataset. From this, we'll be able to generate new handwritten digits!
GANs were [first reported on](https://arxiv.org/abs/1406.2661) in 2014 from Ian Goodfellow and others in Yoshua Bengio's lab. Since then, GANs have exploded in popularity. Here are a few examples to check out:
* [Pix2Pix](https://affinelayer.com/pixsrv/)
* [CycleGAN](https://github.com/junyanz/CycleGAN)
* [A whole list](https://github.com/wiseodd/generative-models)
The idea behind GANs is that you have two networks, a generator $G$ and a discriminator $D$, competing against each other. The generator makes fake data to pass to the discriminator. The discriminator also sees real data and predicts if the data it's received is real or fake. The generator is trained to fool the discriminator, it wants to output data that looks _as close as possible_ to real data. And the discriminator is trained to figure out which data is real and which is fake. What ends up happening is that the generator learns to make data that is indistiguishable from real data to the discriminator.

The general structure of a GAN is shown in the diagram above, using MNIST images as data. The latent sample is a random vector the generator uses to contruct it's fake images. As the generator learns through training, it figures out how to map these random vectors to recognizable images that can fool the discriminator.
The output of the discriminator is a sigmoid function, where 0 indicates a fake image and 1 indicates an real image. If you're interested only in generating new images, you can throw out the discriminator after training. Now, let's see how we build this thing in TensorFlow.
```
%matplotlib inline
import pickle as pkl
import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets('MNIST_data')
```
## Model Inputs
First we need to create the inputs for our graph. We need two inputs, one for the discriminator and one for the generator. Here we'll call the discriminator input `inputs_real` and the generator input `inputs_z`. We'll assign them the appropriate sizes for each of the networks.
>**Exercise:** Finish the `model_inputs` function below. Create the placeholders for `inputs_real` and `inputs_z` using the input sizes `real_dim` and `z_dim` respectively.
```
def model_inputs(real_dim, z_dim):
inputs_real = tf.placeholder(tf.float32, (None, real_dim), name="discriminator_inputs")
inputs_z = tf.placeholder(tf.float32, (None, z_dim), name="generator_inputs")
return inputs_real, inputs_z
```
## Generator network

Here we'll build the generator network. To make this network a universal function approximator, we'll need at least one hidden layer. We should use a leaky ReLU to allow gradients to flow backwards through the layer unimpeded. A leaky ReLU is like a normal ReLU, except that there is a small non-zero output for negative input values.
#### Variable Scope
Here we need to use `tf.variable_scope` for two reasons. Firstly, we're going to make sure all the variable names start with `generator`. Similarly, we'll prepend `discriminator` to the discriminator variables. This will help out later when we're training the separate networks.
We could just use `tf.name_scope` to set the names, but we also want to reuse these networks with different inputs. For the generator, we're going to train it, but also _sample from it_ as we're training and after training. The discriminator will need to share variables between the fake and real input images. So, we can use the `reuse` keyword for `tf.variable_scope` to tell TensorFlow to reuse the variables instead of creating new ones if we build the graph again.
To use `tf.variable_scope`, you use a `with` statement:
```python
with tf.variable_scope('scope_name', reuse=False):
# code here
```
Here's more from [the TensorFlow documentation](https://www.tensorflow.org/programmers_guide/variable_scope#the_problem) to get another look at using `tf.variable_scope`.
#### Leaky ReLU
TensorFlow doesn't provide an operation for leaky ReLUs, so we'll need to make one . For this you can just take the outputs from a linear fully connected layer and pass them to `tf.maximum`. Typically, a parameter `alpha` sets the magnitude of the output for negative values. So, the output for negative input (`x`) values is `alpha*x`, and the output for positive `x` is `x`:
$$
f(x) = max(\alpha * x, x)
$$
#### Tanh Output
The generator has been found to perform the best with $tanh$ for the generator output. This means that we'll have to rescale the MNIST images to be between -1 and 1, instead of 0 and 1.
>**Exercise:** Implement the generator network in the function below. You'll need to return the tanh output. Make sure to wrap your code in a variable scope, with 'generator' as the scope name, and pass the `reuse` keyword argument from the function to `tf.variable_scope`.
```
def generator(z, out_dim, n_units=128, reuse=False, alpha=0.01):
''' Build the generator network.
Arguments
---------
z : Input tensor for the generator
out_dim : Shape of the generator output
n_units : Number of units in hidden layer
reuse : Reuse the variables with tf.variable_scope
alpha : leak parameter for leaky ReLU
Returns
-------
out:
'''
with tf.variable_scope("generator", reuse=reuse):
# Hidden layer
h1 = tf.layers.dense(z, n_units, activation=None)
# Leaky ReLU
h1 = tf.maximum(alpha * h1, h1)
# Logits and tanh output
logits = tf.layers.dense(h1, out_dim, activation=None)
out = tf.tanh(logits)
return out
```
## Discriminator
The discriminator network is almost exactly the same as the generator network, except that we're using a sigmoid output layer.
>**Exercise:** Implement the discriminator network in the function below. Same as above, you'll need to return both the logits and the sigmoid output. Make sure to wrap your code in a variable scope, with 'discriminator' as the scope name, and pass the `reuse` keyword argument from the function arguments to `tf.variable_scope`.
```
def discriminator(x, n_units=128, reuse=False, alpha=0.01):
''' Build the discriminator network.
Arguments
---------
x : Input tensor for the discriminator
n_units: Number of units in hidden layer
reuse : Reuse the variables with tf.variable_scope
alpha : leak parameter for leaky ReLU
Returns
-------
out, logits:
'''
with tf.variable_scope("discriminator", reuse=reuse):
# Hidden layer
h1 = tf.layers.dense(x, n_units, activation=None)
# Leaky ReLU
h1 = tf.maximum(alpha * h1, h1)
logits = tf.layers.dense(h1, 1, activation=None)
out = tf.sigmoid(logits)
return out, logits
```
## Hyperparameters
```
# Size of input image to discriminator
input_size = 784 # 28x28 MNIST images flattened
# Size of latent vector to generator
z_size = 100
# Sizes of hidden layers in generator and discriminator
g_hidden_size = 128
d_hidden_size = 128
# Leak factor for leaky ReLU
alpha = 0.01
# Label smoothing
smooth = 0.1
```
## Build network
Now we're building the network from the functions defined above.
First is to get our inputs, `input_real, input_z` from `model_inputs` using the sizes of the input and z.
Then, we'll create the generator, `generator(input_z, input_size)`. This builds the generator with the appropriate input and output sizes.
Then the discriminators. We'll build two of them, one for real data and one for fake data. Since we want the weights to be the same for both real and fake data, we need to reuse the variables. For the fake data, we're getting it from the generator as `g_model`. So the real data discriminator is `discriminator(input_real)` while the fake discriminator is `discriminator(g_model, reuse=True)`.
>**Exercise:** Build the network from the functions you defined earlier.
```
tf.reset_default_graph()
# Create our input placeholders
input_real, input_z = model_inputs(input_size, z_size)
# Generator network here
g_model = generator(input_z, input_size, n_units=g_hidden_size, alpha=alpha)
# g_model is the generator output
# Disriminator network here
d_model_real, d_logits_real = discriminator(input_real, n_units=d_hidden_size, alpha=alpha)
d_model_fake, d_logits_fake = discriminator(g_model, n_units=d_hidden_size, reuse=True, alpha=alpha)
```
## Discriminator and Generator Losses
Now we need to calculate the losses, which is a little tricky. For the discriminator, the total loss is the sum of the losses for real and fake images, `d_loss = d_loss_real + d_loss_fake`. The losses will by sigmoid cross-entropies, which we can get with `tf.nn.sigmoid_cross_entropy_with_logits`. We'll also wrap that in `tf.reduce_mean` to get the mean for all the images in the batch. So the losses will look something like
```python
tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=logits, labels=labels))
```
For the real image logits, we'll use `d_logits_real` which we got from the discriminator in the cell above. For the labels, we want them to be all ones, since these are all real images. To help the discriminator generalize better, the labels are reduced a bit from 1.0 to 0.9, for example, using the parameter `smooth`. This is known as label smoothing, typically used with classifiers to improve performance. In TensorFlow, it looks something like `labels = tf.ones_like(tensor) * (1 - smooth)`
The discriminator loss for the fake data is similar. The logits are `d_logits_fake`, which we got from passing the generator output to the discriminator. These fake logits are used with labels of all zeros. Remember that we want the discriminator to output 1 for real images and 0 for fake images, so we need to set up the losses to reflect that.
Finally, the generator losses are using `d_logits_fake`, the fake image logits. But, now the labels are all ones. The generator is trying to fool the discriminator, so it wants to discriminator to output ones for fake images.
>**Exercise:** Calculate the losses for the discriminator and the generator. There are two discriminator losses, one for real images and one for fake images. For the real image loss, use the real logits and (smoothed) labels of ones. For the fake image loss, use the fake logits with labels of all zeros. The total discriminator loss is the sum of those two losses. Finally, the generator loss again uses the fake logits from the discriminator, but this time the labels are all ones because the generator wants to fool the discriminator.
```
# Calculate losses
d_loss_real = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_real, \
labels=tf.ones_like(d_logits_real) * (1 - smooth)))
d_loss_fake = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_fake, \
labels=tf.zeros_like(d_logits_real)))
d_loss = d_loss_real + d_loss_fake
g_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_fake, \
labels=tf.ones_like(d_logits_fake)))
```
## Optimizers
We want to update the generator and discriminator variables separately. So we need to get the variables for each part and build optimizers for the two parts. To get all the trainable variables, we use `tf.trainable_variables()`. This creates a list of all the variables we've defined in our graph.
For the generator optimizer, we only want to generator variables. Our past selves were nice and used a variable scope to start all of our generator variable names with `generator`. So, we just need to iterate through the list from `tf.trainable_variables()` and keep variables that start with `generator`. Each variable object has an attribute `name` which holds the name of the variable as a string (`var.name == 'weights_0'` for instance).
We can do something similar with the discriminator. All the variables in the discriminator start with `discriminator`.
Then, in the optimizer we pass the variable lists to the `var_list` keyword argument of the `minimize` method. This tells the optimizer to only update the listed variables. Something like `tf.train.AdamOptimizer().minimize(loss, var_list=var_list)` will only train the variables in `var_list`.
>**Exercise: ** Below, implement the optimizers for the generator and discriminator. First you'll need to get a list of trainable variables, then split that list into two lists, one for the generator variables and another for the discriminator variables. Finally, using `AdamOptimizer`, create an optimizer for each network that update the network variables separately.
```
# Optimizers
learning_rate = 0.002
# Get the trainable_variables, split into G and D parts
t_vars = tf.trainable_variables()
g_vars = [var for var in t_vars if var.name.startswith('generator')]
d_vars = [var for var in t_vars if var.name.startswith('discriminator')]
d_train_opt = tf.train.AdamOptimizer(learning_rate).minimize(d_loss, var_list=d_vars)
g_train_opt = tf.train.AdamOptimizer(learning_rate).minimize(g_loss, var_list=g_vars)
```
## Training
```
batch_size = 100
epochs = 100
samples = []
losses = []
saver = tf.train.Saver(var_list = g_vars)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for e in range(epochs):
for ii in range(mnist.train.num_examples//batch_size):
batch = mnist.train.next_batch(batch_size)
# Get images, reshape and rescale to pass to D
batch_images = batch[0].reshape((batch_size, 784))
batch_images = batch_images*2 - 1
# Sample random noise for G
batch_z = np.random.uniform(-1, 1, size=(batch_size, z_size))
# Run optimizers
_ = sess.run(d_train_opt, feed_dict={input_real: batch_images, input_z: batch_z})
_ = sess.run(g_train_opt, feed_dict={input_z: batch_z})
# At the end of each epoch, get the losses and print them out
train_loss_d = sess.run(d_loss, {input_z: batch_z, input_real: batch_images})
train_loss_g = g_loss.eval({input_z: batch_z})
print("Epoch {}/{}...".format(e+1, epochs),
"Discriminator Loss: {:.4f}...".format(train_loss_d),
"Generator Loss: {:.4f}".format(train_loss_g))
# Save losses to view after training
losses.append((train_loss_d, train_loss_g))
# Sample from generator as we're training for viewing afterwards
sample_z = np.random.uniform(-1, 1, size=(16, z_size))
gen_samples = sess.run(
generator(input_z, input_size, n_units=g_hidden_size, reuse=True, alpha=alpha),
feed_dict={input_z: sample_z})
samples.append(gen_samples)
saver.save(sess, './checkpoints/generator.ckpt')
# Save training generator samples
with open('train_samples.pkl', 'wb') as f:
pkl.dump(samples, f)
```
## Training loss
Here we'll check out the training losses for the generator and discriminator.
```
%matplotlib inline
import matplotlib.pyplot as plt
fig, ax = plt.subplots()
losses = np.array(losses)
plt.plot(losses.T[0], label='Discriminator')
plt.plot(losses.T[1], label='Generator')
plt.title("Training Losses")
plt.legend()
```
## Generator samples from training
Here we can view samples of images from the generator. First we'll look at images taken while training.
```
def view_samples(epoch, samples):
fig, axes = plt.subplots(figsize=(7,7), nrows=4, ncols=4, sharey=True, sharex=True)
for ax, img in zip(axes.flatten(), samples[epoch]):
ax.xaxis.set_visible(False)
ax.yaxis.set_visible(False)
im = ax.imshow(img.reshape((28,28)), cmap='Greys_r')
return fig, axes
# Load samples from generator taken while training
with open('train_samples.pkl', 'rb') as f:
samples = pkl.load(f)
```
These are samples from the final training epoch. You can see the generator is able to reproduce numbers like 5, 7, 3, 0, 9. Since this is just a sample, it isn't representative of the full range of images this generator can make.
```
_ = view_samples(-1, samples)
```
Below I'm showing the generated images as the network was training, every 10 epochs. With bonus optical illusion!
```
rows, cols = 10, 6
fig, axes = plt.subplots(figsize=(7,12), nrows=rows, ncols=cols, sharex=True, sharey=True)
for sample, ax_row in zip(samples[::int(len(samples)/rows)], axes):
for img, ax in zip(sample[::int(len(sample)/cols)], ax_row):
ax.imshow(img.reshape((28,28)), cmap='Greys_r')
ax.xaxis.set_visible(False)
ax.yaxis.set_visible(False)
```
It starts out as all noise. Then it learns to make only the center white and the rest black. You can start to see some number like structures appear out of the noise. Looks like 1, 9, and 8 show up first. Then, it learns 5 and 3.
## Sampling from the generator
We can also get completely new images from the generator by using the checkpoint we saved after training. We just need to pass in a new latent vector $z$ and we'll get new samples!
```
saver = tf.train.Saver(var_list=g_vars)
with tf.Session() as sess:
saver.restore(sess, tf.train.latest_checkpoint('checkpoints'))
sample_z = np.random.uniform(-1, 1, size=(16, z_size))
gen_samples = sess.run(
generator(input_z, input_size, n_units=g_hidden_size, reuse=True, alpha=alpha),
feed_dict={input_z: sample_z})
view_samples(0, [gen_samples])
```
| github_jupyter |
# Intro to Machine Learning with Classification
## Contents
1. **Loading** iris dataset
2. Splitting into **train**- and **test**-set
3. Creating a **model** and training it
4. **Predicting** test set
5. **Evaluating** the result
6. Selecting **features**
This notebook will introduce you to Machine Learning and classification, using our most valued Python data science toolkit: [ScikitLearn](http://scikit-learn.org/).
Classification will allow you to automatically classify data, based on the classification of previous data. The algorithm determines automatically which features it will use to classify, so the programmer does not have to think of this anymore (although it helps).
First, we will transform a dataset into a set of features with labels that the algorithm can use. Then we will predict labels and validate them. Last we will select features manually and see if we can make the prediction better.
Let's start with some imports.
```
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
```
## 1. Loading iris dataset
We load the dataset from the datasets module in sklearn.
```
iris = datasets.load_iris()
```
This dataset contains information about iris flowers. Every entry describes a flower, more specifically its
- sepal length
- sepal width
- petal length
- petal width
So every entry has four columns.

We can visualise the data with Pandas, a Python library to handle dataframes. This gives us a pretty table to see what our data looks like.
We will not cover Pandas in this notebook, so don't worry about this piece of code.
```
import pandas as pd
df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
df["target"] = iris.target
df.sample(n=10) # show 10 random rows
```
There are 3 different species of irises in the dataset. Every species has 50 samples, so there are 150 entries in total.
We can confirm this by checking the "data"-element of the iris variable. The "data"-element is a 2D-array that contains all our entries. We can use the python function `.shape` to check its dimensions.
```
iris.data.shape
```
To get an example of the data, we can print the first ten rows:
```
print(iris.data[0:10, :]) # 0:10 gets rows 0-10, : gets all the columns
```
The labels that we're looking for are in the "target"-element of the iris variable. This 1D-array contains the iris species for each of the entries.
```
iris.target.shape
```
Let's have a look at the target values:
```
print(iris.target)
```
There are three categories so each entry will be classified as 0, 1 or 2. To get the names of the corresponding species we can print `target_names`.
```
print(iris.target_names)
```
The iris variable is a dataset from sklearn and also contains a description of itself. We already provided the information you need to know about the data, but if you want to check, you can print the `.DESCR` method of the iris dataset.
```
print(iris.DESCR)
```
Now we have a good idea what our data looks like.
Our task now is to solve a **supervised** learning problem: Predict the species of an iris using the measurements that serve as our so-called **features**.
```
# First, we store the features we use and the labels we want to predict into two different variables
X = iris.data
y = iris.target
```
## 2. Splitting into train- and test-set
We want to evaluate our model on data with labels that our model has not seen yet. This will give us an idea on how well the model can predict new data, and makes sure we are not [overfitting](https://en.wikipedia.org/wiki/Overfitting). If we would test and train on the same data, we would just learn this dataset really really well, but not be able to tell anything about other data.
So we split our dataset into a train- and test-set. Sklearn has a function to do this: `train_test_split`. Have a look at the [documentation](http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.train_test_split.html) of this function and see if you can split `iris.data` and `iris.target` into train- and test-sets with a test-size of 33%.
```
from sklearn.model_selection import train_test_split
??train_test_split
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.33, stratify=iris.target)# TODO: split iris.data and iris.target into test and train
```
We can now check the size of the resulting arrays. The shapes should be `(100, 4)`, `(100,)`, `(50, 4)` and `(50,)`.
```
print("X_train shape: {}, y_train shape: {}".format(X_train.shape, y_train.shape))
print("X_test shape: {} , y_test shape: {}".format(X_test.shape, y_test.shape))
```
## 3. Creating a model and training it
Now we will give the data to a model. We will use a Decision Tree Classifier model for this.
This model will create a decision tree based on the X_train and y_train values and include decisions like this:
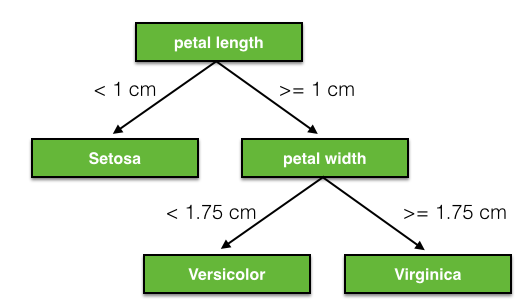
Find the Decision Tree Classifier in sklearn and call its constructor. It might be useful to set the random_state parameter to 0, otherwise a different tree will be generated each time you run the code.
```
from sklearn import tree
model = tree.DecisionTreeClassifier(random_state=0)# TODO: create a decision tree classifier
```
The model is still empty and doesn't know anything. Train (fit) it with our train-data, so that it learns things about our iris-dataset.
```
model = model.fit(X_train, y_train)# TODO: fit the train-data to the model
```
## 4. Predicting test set
We now have a model that contains a decision tree. This decision tree knows how to turn our X_train values into y_train values. We will now let it run on our X_test values and have a look at the result.
We don't want to overwrite our actual y_test values, so we store the predicted y_test values as y_pred.
```
y_pred = model.predict(X_test)# TODO: predict y_pred from X_test
```
## 5. Evaluating the result
We now have y_test (the real values for X_test) and y_pred. We can print these values and compare them, to get an idea of how good the model predicted the data.
```
print(y_test)
print("-"*75) # print a line
print(y_pred)
```
If we look at the values closely, we can discover that all but two values are predicted correctly. However, it is bothersome to compare the numbers one by one. There are only thirty of them, but what if there were one hundred? We will need an easier method to compare our results.
Luckily, this can also be found in sklearn. Google for sklearn's accuracy score and compare our y_test and y_pred. This will give us the percentage of entries that was predicted correctly.
```
from sklearn import metrics
accuracy = metrics.accuracy_score(y_test, y_pred) # TODO: calculate accuracy score of y_test and y_pred
print(accuracy)
```
That's pretty good, isn't it?
To understand what our classifier actually did, have a look at the following picture:
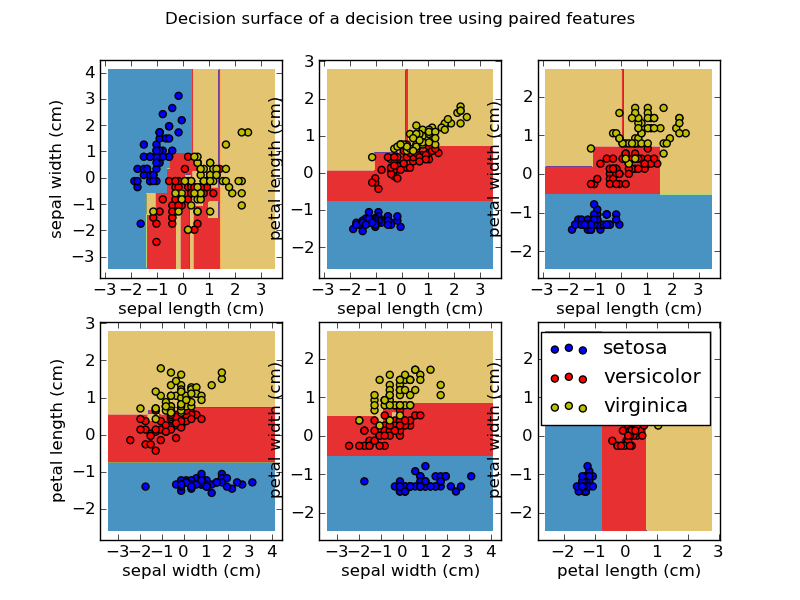
We see the distribution of all our features, compared with each other. Some have very clear distinctions between two categories, so our decision tree probably used those to make predictions about our data.
## 6. Selecting features
In our dataset, there are four features to describe the flowers. Using these four features, we got a pretty high accuracy to predict the species. But maybe some of our features were not necessary. Maybe some did not improve our prediction, or even made it worse.
It's worth a try to see if a subset of features is better at predicting the labels than all features.
We still have our X_train, X_test, y_train and y_test variables. We will try removing a few columns from X_train and X_test and recalculate our accuracy.
First, create a feature selector that will select the 2 features X_train that best describe y_train.
(Hint: look at the imports)
```
from sklearn.feature_selection import SelectKBest, chi2
selector = SelectKBest(chi2, k=2) # TODO: create a selector for the 2 best features and fit X_train and y_train to it
X_train, X_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.33, random_state=42)
selector = selector.fit(X_train, y_train)
```
We can check which features our selector selected, using the following function:
```
print(selector.get_support())
```
It gives us an array of True and False values that represent the columns of the original X_train. The values that are marked by True are considered the most informative by the selector. Let's use the selector to select (transform) these features from the X_train values.
```
X_train_new = selector.transform(X_train) # TODO: use selector to transform X_train
```
The dimensions of X_train have now changed:
```
X_train_new.shape
```
If we want to use these values in our model, we will need to adjust X_test as well. We would get in trouble later if X_train has only 2 columns and X_test has 4. So perform the same selection on X_test.
```
X_test_new = selector.transform(X_test) # TODO: use selector to transform X_test
X_test_new.shape
```
Now we can repeat the earlier steps: create a model, fit the data to it and predict our y_test values.
```
model = tree.DecisionTreeClassifier(random_state=0) # TODO: create model as before
model = model.fit(X_train_new, y_train) # TODO: fit model as before, but use X_train_new
y_pred = model.predict(X_test_new) # TODO: predict values as before, but use X_test_new
```
Let's have a look at the accuracy score of our new prediction.
```
accuracy = metrics.accuracy_score(y_test, y_pred) # TODO: calculate accuracy score of y_test and y_pred
print(accuracy) # TODO: calculate accuracy score as before
```
So our new prediction, using only two of the four features, is better than the one using all information. The two features we used are petal length and petal width. These say more about the species of the flowers than the sepal length and sepal width.
| github_jupyter |
420-A52-SF - Algorithmes d'apprentissage supervisé - Hiver 2020 - Spécialisation technique en Intelligence Artificielle - Mikaël Swawola, M.Sc.
<br/>

<br/>
**Objectif:** cette séance de travaux pratique est consacrée à la mise en oeuvre de l'ensemble des connaissances acquises jusqu'alors sur un nouveau jeu de données, *NBA*
```
%reload_ext autoreload
%autoreload 2
%matplotlib inline
```
### 0 - Chargement des bibliothèques
```
# Manipulation de données
import numpy as np
import pandas as pd
# Visualisation de données
import matplotlib.pyplot as plt
import seaborn as sns
# Configuration de la visualisation
sns.set(style="darkgrid", rc={'figure.figsize':(11.7,8.27)})
```
### 1 - Lecture du jeu de données *NBA*
**Lire le fichier `NBA_train.csv`**
```
# Compléter le code ci-dessous ~ 1 ligne
NBA = None
```
**Afficher les dix premières lignes de la trame de données**
```
# Compléter le code ci-dessous ~ 1 ligne
None
```
Ci-dessous, la description des différentes variables explicatives du jeu de données
</br>
| Variable | Description |
| ------------- |:-------------------------------------------------------------:|
| SeasonEnd | Année de fin de la saison |
| Team | Nom de l'équipe |
| Playoffs | Indique si l'équipe est allée en playoffs |
| W | Nombre de victoires au cours de la saison régulière |
| PTS | Nombre de points obtenus (saison régulière) |
| oppPTS | Nombre de points obtenus pas les opposants (saison régulière) |
| FG | Nombre de Field Goals réussis |
| FGA | Nombre de tentatives de Field Goals |
| 2P | Nombre de 2-pointers réussis |
| 2PA | Nombre de tentatives de 2-pointers |
| 3P | Nombre de 3-pointers réussis |
| 3PA | Nombre de tentatives de 3-pointers |
| FT | Nombre de Free throws réussis |
| FTA | Nombre de tentatives de Free throws |
| ORB | Nombre de rebonds offensifs |
| DRB | Nombre de rebonds défensifs |
| AST | Nombre de passes décisives (assists) |
| STL | Nombre d'interceptions (steals) |
| BLK | Nombre de contres (blocks) |
| TOV | Nombre de turnovers |
### 1 - Régression linéaire simple
Nous allons dans un premier temps effectuer la prédiction du nombre de victoires au cours de la saison régulière en fonction de la différence de points obtenus pas l'équipe et par ses opposants
<br/><br/>
Nous commencons donc par un peu d'**ingénierie de données**. Une nouvelle variable explicative correspondant à la différence de points obtenus pas l'équipe et par ses opposants est crée
**Créer un nouvelle variable PTSdiff, représentant la différence entre PTS et oppPTS**
```
# Compléter le code ci-dessous ~ 1 ligne
None
```
**Stocker le nombre de lignes du jeu de donnée (nombre d'exemples d'entraînement) dans la variable `m`**
```
# Compléter le code ci-dessous ~ 1 ligne
m = None
```
**Stocker le nombre de victoires au cours de la saison dans la variable `y`. Il s'agira de la variable que l'on cherche à prédire**
```
# Compléter le code ci-dessous ~ 1 ligne
y = None
```
**Créer la matrice des prédicteurs `X`.** Indice: `X` doit avoir 2 colonnes...
```
# Compléter le code ci-dessous ~ 3 lignes
X = None
```
**Vérifier la dimension de la matrice des prédicteurs `X`. Quelle est la dimension de `X` ?**
```
# Compléter le code ci-dessous ~ 1 ligne
None
```
**Créer le modèle de référence (baseline)**
```
# Compléter le code ci-dessous ~ 1 ligne
y_baseline = None
```
**À l'aide de l'équation normale, trouver les paramètres optimaux du modèle de régression linéaire simple**
```
# Compléter le code ci-dessous ~ 1 ligne
theta = None
```
**Calculer la somme des carrées des erreurs (SSE)**
```
# Compléter le code ci-dessous ~ 1 ligne
SSE = None
```
**Calculer la racine carrée de l'erreur quadratique moyenne (RMSE)**
```
# Compléter le code ci-dessous ~ 1 ligne
RMSE = None
```
**Calculer le coefficient de détermination $R^2$**
```
# Compléter le code ci-dessous ~ 1-2 lignes
R2 = None
```
**Affichage des résultats**
```
fig, ax = plt.subplots()
ax.scatter(x1, y,label="Data points")
reg_x = np.linspace(-1000,1000,50)
reg_y = theta[0] + np.linspace(-1000,1000,50)* theta[1]
ax.plot(reg_x, np.repeat(y_baseline,50), color='#777777', label="Baseline", lw=2)
ax.plot(reg_x, reg_y, color="g", lw=2, label="Modèle")
ax.set_xlabel("Différence de points", fontsize=16)
ax.set_ylabel("Nombre de victoires", fontsize=16)
ax.legend(loc='upper left', fontsize=16)
```
### 3 - Régression linéaire multiple
Nous allons maintenant tenter de prédire le nombre de points obtenus par une équipe donnée au cours de la saison régulière en fonction des autres variables explicatives disponibles. Nous allons mettre en oeuvre plusieurs modèles de régression linéaire multiple
**Stocker le nombre de points marqués au cours de la saison dans la variable `y`. Il s'agira de la varible que l'on cherche à prédire**
```
# Compléter le code ci-dessous ~ 1 ligne
y = None
```
**Créer la matrice des prédicteurs `X` à partir des variables `2PA` et `3PA`**
```
# Compléter le code ci-dessous ~ 3 lignes
X = None
```
**Vérifier la dimension de la matrice des prédicteurs `X`. Quelle est la dimension de `X` ?**
```
# Compléter le code ci-dessous ~ 1 ligne
None
```
**Créer le modèle de référence (baseline)**
```
# Compléter le code ci-dessous ~ 1 ligne
y_baseline = None
```
**À l'aide de l'équation normale, trouver les paramètres optimaux du modèle de régression linéaire**
```
# Compléter le code ci-dessous ~ 1 ligne
theta = None
```
**Calculer la somme des carrées des erreurs (SSE)**
```
# Compléter le code ci-dessous ~ 1 ligne
SSE = None
```
**Calculer la racine carrée de l'erreur quadratique moyenne (RMSE)**
```
# Compléter le code ci-dessous ~ 1 ligne
RMSE = None
```
**Calculer le coefficient de détermination $R^2$**
```
# Compléter le code ci-dessous ~ 1-2 lignes
R2 = None
```
### 3 - Ajouter les variables explicatives FTA et AST
**Recommencer les étapes ci-dessus en incluant les variables FTA et AST**
```
None
```
### 4 - Ajouter les variables explicatives ORB et STL
**Recommencer les étapes ci-dessus en incluant les variables ORB et STL**
```
None
```
### 5 - Ajouter les variables explicatives DRB et BLK
**Recommencer les étapes ci-dessus en incluant les variables DRB et BLK**
```
None
```
### 6 - Optionnel - Regression polynomiale
Ajouter des variables explicatives de type polynomiales
### Fin du TP
| github_jupyter |
<a href="https://colab.research.google.com/github/keirwilliamsxyz/keirxyz/blob/main/Multi_Perceptor_VQGAN_%2B_CLIP_%5BPublic%5D.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Multi-Perceptor VQGAN + CLIP (v.3.2021.11.29)
by [@remi_durant](https://twitter.com/remi_durant)
Lots drawn from or inspired by other colabs, chief among them is [@jbusted1](https://twitter.com/jbusted1)'s MSE regularized VQGAN + Clip, and [@RiversHaveWings](https://twitter.com/RiversHaveWings) VQGAN + Clip with Z+Quantize. Standing on the shoulders of giants.
- Multi-clip mode sends the same cutouts to whatever clip models you want. If they have different perceptor resolutions, the cuts are generated at each required size, replaying the same augments across both scales
- Alternate random noise generation options to use as start point (perlin, pyramid, or vqgan random z tokens)
- MSE Loss doesn't apply if you have no init_image until after reaching the first epoch.
- MSE epoch targets z.tensor, not z.average, to allow for more creativity
- Grayscale augment added for better structure
- Padding fix for perspective and affine augments to not always be black barred
- Automatic disable of cudnn for A100

```
#@title First check what GPU you got and make sure it's a good one.
#@markdown - Tier List: (K80 < T4 < P100 < V100 < A100)
from subprocess import getoutput
!nvidia-smi --query-gpu=name,memory.total,memory.free --format=csv,noheader
```
# Setup
```
#@title memory footprint support libraries/code
!ln -sf /opt/bin/nvidia-smi /usr/bin/nvidia-smi
!pip install gputil
!pip install psutil
!pip install humanize
import psutil
import humanize
import os
import GPUtil as GPU
#@title Print GPU details
!nvidia-smi
GPUs = GPU.getGPUs()
# XXX: only one GPU on Colab and isn’t guaranteed
gpu = GPUs[0]
def printm():
process = psutil.Process(os.getpid())
print("Gen RAM Free: " + humanize.naturalsize(psutil.virtual_memory().available), " | Proc size: " + humanize.naturalsize(process.memory_info().rss))
print("GPU RAM Free: {0:.0f}MB | Used: {1:.0f}MB | Util {2:3.0f}% | Total {3:.0f}MB".format(gpu.memoryFree, gpu.memoryUsed, gpu.memoryUtil*100, gpu.memoryTotal))
printm()
#@title Install Dependencies
# Fix for A100 issues
!pip install tensorflow==1.15.2
# Install normal dependencies
!git clone https://github.com/openai/CLIP
!git clone https://github.com/CompVis/taming-transformers
!pip install ftfy regex tqdm omegaconf pytorch-lightning
!pip install kornia
!pip install einops
!pip install transformers
#@title Load libraries and variables
import argparse
import math
from pathlib import Path
import sys
sys.path.append('./taming-transformers')
from IPython import display
from omegaconf import OmegaConf
from PIL import Image
from taming.models import cond_transformer, vqgan
import torch
from torch import nn, optim
from torch.nn import functional as F
from torchvision import transforms
from torchvision.transforms import functional as TF
from tqdm.notebook import tqdm
import numpy as np
import os.path
from os import path
from urllib.request import Request, urlopen
from CLIP import clip
import kornia
import kornia.augmentation as K
from torch.utils.checkpoint import checkpoint
from matplotlib import pyplot as plt
from fastprogress.fastprogress import master_bar, progress_bar
import random
import gc
import re
from datetime import datetime
from base64 import b64encode
import warnings
warnings.filterwarnings('ignore')
torch.set_printoptions( sci_mode=False )
def noise_gen(shape, octaves=5):
n, c, h, w = shape
noise = torch.zeros([n, c, 1, 1])
max_octaves = min(octaves, math.log(h)/math.log(2), math.log(w)/math.log(2))
for i in reversed(range(max_octaves)):
h_cur, w_cur = h // 2**i, w // 2**i
noise = F.interpolate(noise, (h_cur, w_cur), mode='bicubic', align_corners=False)
noise += torch.randn([n, c, h_cur, w_cur]) / 5
return noise
def sinc(x):
return torch.where(x != 0, torch.sin(math.pi * x) / (math.pi * x), x.new_ones([]))
def lanczos(x, a):
cond = torch.logical_and(-a < x, x < a)
out = torch.where(cond, sinc(x) * sinc(x/a), x.new_zeros([]))
return out / out.sum()
def ramp(ratio, width):
n = math.ceil(width / ratio + 1)
out = torch.empty([n])
cur = 0
for i in range(out.shape[0]):
out[i] = cur
cur += ratio
return torch.cat([-out[1:].flip([0]), out])[1:-1]
def resample(input, size, align_corners=True):
n, c, h, w = input.shape
dh, dw = size
input = input.view([n * c, 1, h, w])
if dh < h:
kernel_h = lanczos(ramp(dh / h, 2), 2).to(input.device, input.dtype)
pad_h = (kernel_h.shape[0] - 1) // 2
input = F.pad(input, (0, 0, pad_h, pad_h), 'reflect')
input = F.conv2d(input, kernel_h[None, None, :, None])
if dw < w:
kernel_w = lanczos(ramp(dw / w, 2), 2).to(input.device, input.dtype)
pad_w = (kernel_w.shape[0] - 1) // 2
input = F.pad(input, (pad_w, pad_w, 0, 0), 'reflect')
input = F.conv2d(input, kernel_w[None, None, None, :])
input = input.view([n, c, h, w])
return F.interpolate(input, size, mode='bicubic', align_corners=align_corners)
# def replace_grad(fake, real):
# return fake.detach() - real.detach() + real
class ReplaceGrad(torch.autograd.Function):
@staticmethod
def forward(ctx, x_forward, x_backward):
ctx.shape = x_backward.shape
return x_forward
@staticmethod
def backward(ctx, grad_in):
return None, grad_in.sum_to_size(ctx.shape)
class ClampWithGrad(torch.autograd.Function):
@staticmethod
def forward(ctx, input, min, max):
ctx.min = min
ctx.max = max
ctx.save_for_backward(input)
return input.clamp(min, max)
@staticmethod
def backward(ctx, grad_in):
input, = ctx.saved_tensors
return grad_in * (grad_in * (input - input.clamp(ctx.min, ctx.max)) >= 0), None, None
replace_grad = ReplaceGrad.apply
clamp_with_grad = ClampWithGrad.apply
# clamp_with_grad = torch.clamp
def vector_quantize(x, codebook):
d = x.pow(2).sum(dim=-1, keepdim=True) + codebook.pow(2).sum(dim=1) - 2 * x @ codebook.T
indices = d.argmin(-1)
x_q = F.one_hot(indices, codebook.shape[0]).to(d.dtype) @ codebook
return replace_grad(x_q, x)
class Prompt(nn.Module):
def __init__(self, embed, weight=1., stop=float('-inf')):
super().__init__()
self.register_buffer('embed', embed)
self.register_buffer('weight', torch.as_tensor(weight))
self.register_buffer('stop', torch.as_tensor(stop))
def forward(self, input):
input_normed = F.normalize(input.unsqueeze(1), dim=2)#(input / input.norm(dim=-1, keepdim=True)).unsqueeze(1)#
embed_normed = F.normalize((self.embed).unsqueeze(0), dim=2)#(self.embed / self.embed.norm(dim=-1, keepdim=True)).unsqueeze(0)#
dists = input_normed.sub(embed_normed).norm(dim=2).div(2).arcsin().pow(2).mul(2)
dists = dists * self.weight.sign()
return self.weight.abs() * replace_grad(dists, torch.maximum(dists, self.stop)).mean()
def parse_prompt(prompt):
vals = prompt.rsplit(':', 2)
vals = vals + ['', '1', '-inf'][len(vals):]
return vals[0], float(vals[1]), float(vals[2])
def one_sided_clip_loss(input, target, labels=None, logit_scale=100):
input_normed = F.normalize(input, dim=-1)
target_normed = F.normalize(target, dim=-1)
logits = input_normed @ target_normed.T * logit_scale
if labels is None:
labels = torch.arange(len(input), device=logits.device)
return F.cross_entropy(logits, labels)
class MakeCutouts(nn.Module):
def __init__(self, cut_size, cutn, cut_pow=1.):
super().__init__()
self.cut_size = cut_size
self.cutn = cutn
self.cut_pow = cut_pow
self.av_pool = nn.AdaptiveAvgPool2d((self.cut_size, self.cut_size))
self.max_pool = nn.AdaptiveMaxPool2d((self.cut_size, self.cut_size))
def set_cut_pow(self, cut_pow):
self.cut_pow = cut_pow
def forward(self, input):
sideY, sideX = input.shape[2:4]
max_size = min(sideX, sideY)
min_size = min(sideX, sideY, self.cut_size)
cutouts = []
cutouts_full = []
min_size_width = min(sideX, sideY)
lower_bound = float(self.cut_size/min_size_width)
for ii in range(self.cutn):
size = int(min_size_width*torch.zeros(1,).normal_(mean=.8, std=.3).clip(lower_bound, 1.)) # replace .5 with a result for 224 the default large size is .95
offsetx = torch.randint(0, sideX - size + 1, ())
offsety = torch.randint(0, sideY - size + 1, ())
cutout = input[:, :, offsety:offsety + size, offsetx:offsetx + size]
cutouts.append(resample(cutout, (self.cut_size, self.cut_size)))
cutouts = torch.cat(cutouts, dim=0)
return clamp_with_grad(cutouts, 0, 1)
def load_vqgan_model(config_path, checkpoint_path):
config = OmegaConf.load(config_path)
if config.model.target == 'taming.models.vqgan.VQModel':
model = vqgan.VQModel(**config.model.params)
model.eval().requires_grad_(False)
model.init_from_ckpt(checkpoint_path)
elif config.model.target == 'taming.models.cond_transformer.Net2NetTransformer':
parent_model = cond_transformer.Net2NetTransformer(**config.model.params)
parent_model.eval().requires_grad_(False)
parent_model.init_from_ckpt(checkpoint_path)
model = parent_model.first_stage_model
elif config.model.target == 'taming.models.vqgan.GumbelVQ':
model = vqgan.GumbelVQ(**config.model.params)
model.eval().requires_grad_(False)
model.init_from_ckpt(checkpoint_path)
else:
raise ValueError(f'unknown model type: {config.model.target}')
del model.loss
return model
def resize_image(image, out_size):
ratio = image.size[0] / image.size[1]
area = min(image.size[0] * image.size[1], out_size[0] * out_size[1])
size = round((area * ratio)**0.5), round((area / ratio)**0.5)
return image.resize(size, Image.LANCZOS)
class GaussianBlur2d(nn.Module):
def __init__(self, sigma, window=0, mode='reflect', value=0):
super().__init__()
self.mode = mode
self.value = value
if not window:
window = max(math.ceil((sigma * 6 + 1) / 2) * 2 - 1, 3)
if sigma:
kernel = torch.exp(-(torch.arange(window) - window // 2)**2 / 2 / sigma**2)
kernel /= kernel.sum()
else:
kernel = torch.ones([1])
self.register_buffer('kernel', kernel)
def forward(self, input):
n, c, h, w = input.shape
input = input.view([n * c, 1, h, w])
start_pad = (self.kernel.shape[0] - 1) // 2
end_pad = self.kernel.shape[0] // 2
input = F.pad(input, (start_pad, end_pad, start_pad, end_pad), self.mode, self.value)
input = F.conv2d(input, self.kernel[None, None, None, :])
input = F.conv2d(input, self.kernel[None, None, :, None])
return input.view([n, c, h, w])
class EMATensor(nn.Module):
"""implmeneted by Katherine Crowson"""
def __init__(self, tensor, decay):
super().__init__()
self.tensor = nn.Parameter(tensor)
self.register_buffer('biased', torch.zeros_like(tensor))
self.register_buffer('average', torch.zeros_like(tensor))
self.decay = decay
self.register_buffer('accum', torch.tensor(1.))
self.update()
@torch.no_grad()
def update(self):
if not self.training:
raise RuntimeError('update() should only be called during training')
self.accum *= self.decay
self.biased.mul_(self.decay)
self.biased.add_((1 - self.decay) * self.tensor)
self.average.copy_(self.biased)
self.average.div_(1 - self.accum)
def forward(self):
if self.training:
return self.tensor
return self.average
import io
import base64
def image_to_data_url(img, ext):
img_byte_arr = io.BytesIO()
img.save(img_byte_arr, format=ext)
img_byte_arr = img_byte_arr.getvalue()
# ext = filename.split('.')[-1]
prefix = f'data:image/{ext};base64,'
return prefix + base64.b64encode(img_byte_arr).decode('utf-8')
def update_random( seed, purpose ):
if seed == -1:
seed = random.seed()
seed = random.randrange(1,99999)
print( f'Using seed {seed} for {purpose}')
random.seed(seed)
torch.manual_seed(seed)
np.random.seed(seed)
return seed
def clear_memory():
gc.collect()
torch.cuda.empty_cache()
#@title Setup for A100
device = torch.device('cuda:0' if torch.cuda.is_available() else 'cpu')
if gpu.name.startswith('A100'):
torch.backends.cudnn.enabled = False
print('Finished setup for A100')
#@title Loss Module Definitions
from typing import cast, Dict, Optional
from kornia.augmentation.base import IntensityAugmentationBase2D
class FixPadding(nn.Module):
def __init__(self, module=None, threshold=1e-12, noise_frac=0.00 ):
super().__init__()
self.threshold = threshold
self.noise_frac = noise_frac
self.module = module
def forward(self,input):
dims = input.shape
if self.module is not None:
input = self.module(input + self.threshold)
light = input.new_empty(dims[0],1,1,1).uniform_(0.,2.)
mixed = input.view(*dims[:2],-1).sum(dim=1,keepdim=True)
black = mixed < self.threshold
black = black.view(-1,1,*dims[2:4]).type(torch.float)
black = kornia.filters.box_blur( black, (5,5) ).clip(0,0.1)/0.1
mean = input.view(*dims[:2],-1).sum(dim=2) / mixed.count_nonzero(dim=2)
mean = ( mean[:,:,None,None] * light ).clip(0,1)
fill = mean.expand(*dims)
if 0 < self.noise_frac:
rng = torch.get_rng_state()
fill = fill + torch.randn_like(mean) * self.noise_frac
torch.set_rng_state(rng)
if self.module is not None:
input = input - self.threshold
return torch.lerp(input,fill,black)
class MyRandomNoise(IntensityAugmentationBase2D):
def __init__(
self,
frac: float = 0.1,
return_transform: bool = False,
same_on_batch: bool = False,
p: float = 0.5,
) -> None:
super().__init__(p=p, return_transform=return_transform, same_on_batch=same_on_batch, p_batch=1.0)
self.frac = frac
def __repr__(self) -> str:
return self.__class__.__name__ + f"({super().__repr__()})"
def generate_parameters(self, shape: torch.Size) -> Dict[str, torch.Tensor]:
noise = torch.FloatTensor(1).uniform_(0,self.frac)
# generate pixel data without throwing off determinism of augs
rng = torch.get_rng_state()
noise = noise * torch.randn(shape)
torch.set_rng_state(rng)
return dict(noise=noise)
def apply_transform(
self, input: torch.Tensor, params: Dict[str, torch.Tensor], transform: Optional[torch.Tensor] = None
) -> torch.Tensor:
return input + params['noise'].to(input.device)
class MakeCutouts2(nn.Module):
def __init__(self, cut_size, cutn):
super().__init__()
self.cut_size = cut_size
self.cutn = cutn
def forward(self, input):
sideY, sideX = input.shape[2:4]
max_size = min(sideX, sideY)
min_size = min(sideX, sideY, self.cut_size)
cutouts = []
cutouts_full = []
min_size_width = min(sideX, sideY)
lower_bound = float(self.cut_size/min_size_width)
for ii in range(self.cutn):
size = int(min_size_width*torch.zeros(1,).normal_(mean=.8, std=.3).clip(lower_bound, 1.)) # replace .5 with a result for 224 the default large size is .95
offsetx = torch.randint(0, sideX - size + 1, ())
offsety = torch.randint(0, sideY - size + 1, ())
cutout = input[:, :, offsety:offsety + size, offsetx:offsetx + size]
cutouts.append(cutout)
return cutouts
class MultiClipLoss(nn.Module):
def __init__(self, clip_models, text_prompt, normalize_prompt_weights, cutn, cut_pow=1., clip_weight=1., use_old_augs=False, simulate_old_cuts=False ):
super().__init__()
self.use_old_augs = use_old_augs
self.simulate_old_cuts = simulate_old_cuts
# Load Clip
self.perceptors = []
for cm in clip_models:
c = clip.load(cm[0], jit=False)[0].eval().requires_grad_(False).to(device)
self.perceptors.append( { 'res': c.visual.input_resolution, 'perceptor': c, 'weight': cm[1], 'prompts':[] } )
self.perceptors.sort(key=lambda e: e['res'], reverse=True)
# Make Cutouts
self.cut_sizes = list(set([p['res'] for p in self.perceptors]))
self.cut_sizes.sort( reverse=True )
self.make_cuts = MakeCutouts2(self.cut_sizes[-1], cutn)
# Get Prompt Embedings
texts = [phrase.strip() for phrase in text_prompt.split("|")]
if text_prompt == ['']:
texts = []
self.pMs = []
prompts_weight_sum = 0
parsed_prompts = []
for prompt in texts:
txt, weight, stop = parse_prompt(prompt)
parsed_prompts.append( [txt,weight,stop] )
prompts_weight_sum += max( weight, 0 )
for prompt in parsed_prompts:
txt, weight, stop = prompt
clip_token = clip.tokenize(txt).to(device)
if normalize_prompt_weights and 0 < prompts_weight_sum:
weight /= prompts_weight_sum
for p in self.perceptors:
embed = p['perceptor'].encode_text(clip_token).float()
embed_normed = F.normalize(embed.unsqueeze(0), dim=2)
p['prompts'].append({'embed_normed':embed_normed,'weight':torch.as_tensor(weight, device=device),'stop':torch.as_tensor(stop, device=device)})
# Prep Augments
self.noise_fac = 0.1
self.normalize = transforms.Normalize(mean=[0.48145466, 0.4578275, 0.40821073],
std=[0.26862954, 0.26130258, 0.27577711])
self.augs = nn.Sequential(
K.RandomHorizontalFlip(p=0.5),
K.RandomSharpness(0.3,p=0.1),
FixPadding( nn.Sequential(
K.RandomAffine(degrees=30, translate=0.1, p=0.8, padding_mode='zeros'), # padding_mode=2
K.RandomPerspective(0.2,p=0.4, ),
)),
K.ColorJitter(hue=0.01, saturation=0.01, p=0.7),
K.RandomGrayscale(p=0.15),
MyRandomNoise(frac=self.noise_fac,p=1.),
)
self.clip_weight = clip_weight
def prepare_cuts(self,img):
cutouts = self.make_cuts(img)
cutouts_out = []
rng = torch.get_rng_state()
for sz in self.cut_sizes:
cuts = [resample(c, (sz,sz)) for c in cutouts]
cuts = torch.cat(cuts, dim=0)
cuts = clamp_with_grad(cuts,0,1)
torch.set_rng_state(rng)
cuts = self.augs(cuts)
cuts = self.normalize(cuts)
cutouts_out.append(cuts)
return cutouts_out
def forward( self, i, img ):
cutouts = self.prepare_cuts( img )
loss = []
current_cuts = None
currentres = 0
for p in self.perceptors:
if currentres != p['res']:
currentres = p['res']
current_cuts = cutouts[self.cut_sizes.index( currentres )]
iii = p['perceptor'].encode_image(current_cuts).float()
input_normed = F.normalize(iii.unsqueeze(1), dim=2)
for prompt in p['prompts']:
dists = input_normed.sub(prompt['embed_normed']).norm(dim=2).div(2).arcsin().pow(2).mul(2)
dists = dists * prompt['weight'].sign()
l = prompt['weight'].abs() * replace_grad(dists, torch.maximum(dists, prompt['stop'])).mean()
loss.append(l * p['weight'])
return loss
class MSEDecayLoss(nn.Module):
def __init__(self, init_weight, mse_decay_rate, mse_epoches, mse_quantize ):
super().__init__()
self.init_weight = init_weight
self.has_init_image = False
self.mse_decay = init_weight / mse_epoches if init_weight else 0
self.mse_decay_rate = mse_decay_rate
self.mse_weight = init_weight
self.mse_epoches = mse_epoches
self.mse_quantize = mse_quantize
@torch.no_grad()
def set_target( self, z_tensor, model ):
z_tensor = z_tensor.detach().clone()
if self.mse_quantize:
z_tensor = vector_quantize(z_tensor.movedim(1, 3), model.quantize.embedding.weight).movedim(3, 1)#z.average
self.z_orig = z_tensor
def forward( self, i, z ):
if self.is_active(i):
return F.mse_loss(z, self.z_orig) * self.mse_weight / 2
return 0
def is_active(self, i):
if not self.init_weight:
return False
if i <= self.mse_decay_rate and not self.has_init_image:
return False
return True
@torch.no_grad()
def step( self, i ):
if i % self.mse_decay_rate == 0 and i != 0 and i < self.mse_decay_rate * self.mse_epoches:
if self.mse_weight - self.mse_decay > 0 and self.mse_weight - self.mse_decay >= self.mse_decay:
self.mse_weight -= self.mse_decay
else:
self.mse_weight = 0
print(f"updated mse weight: {self.mse_weight}")
return True
return False
class TVLoss(nn.Module):
def forward(self, input):
input = F.pad(input, (0, 1, 0, 1), 'replicate')
x_diff = input[..., :-1, 1:] - input[..., :-1, :-1]
y_diff = input[..., 1:, :-1] - input[..., :-1, :-1]
diff = x_diff**2 + y_diff**2 + 1e-8
return diff.mean(dim=1).sqrt().mean()
#@title Random Inits
import torch
import math
def rand_perlin_2d(shape, res, fade = lambda t: 6*t**5 - 15*t**4 + 10*t**3):
delta = (res[0] / shape[0], res[1] / shape[1])
d = (shape[0] // res[0], shape[1] // res[1])
grid = torch.stack(torch.meshgrid(torch.arange(0, res[0], delta[0]), torch.arange(0, res[1], delta[1])), dim = -1) % 1
angles = 2*math.pi*torch.rand(res[0]+1, res[1]+1)
gradients = torch.stack((torch.cos(angles), torch.sin(angles)), dim = -1)
tile_grads = lambda slice1, slice2: gradients[slice1[0]:slice1[1], slice2[0]:slice2[1]].repeat_interleave(d[0], 0).repeat_interleave(d[1], 1)
dot = lambda grad, shift: (torch.stack((grid[:shape[0],:shape[1],0] + shift[0], grid[:shape[0],:shape[1], 1] + shift[1] ), dim = -1) * grad[:shape[0], :shape[1]]).sum(dim = -1)
n00 = dot(tile_grads([0, -1], [0, -1]), [0, 0])
n10 = dot(tile_grads([1, None], [0, -1]), [-1, 0])
n01 = dot(tile_grads([0, -1],[1, None]), [0, -1])
n11 = dot(tile_grads([1, None], [1, None]), [-1,-1])
t = fade(grid[:shape[0], :shape[1]])
return math.sqrt(2) * torch.lerp(torch.lerp(n00, n10, t[..., 0]), torch.lerp(n01, n11, t[..., 0]), t[..., 1])
def rand_perlin_2d_octaves( desired_shape, octaves=1, persistence=0.5):
shape = torch.tensor(desired_shape)
shape = 2 ** torch.ceil( torch.log2( shape ) )
shape = shape.type(torch.int)
max_octaves = int(min(octaves,math.log(shape[0])/math.log(2), math.log(shape[1])/math.log(2)))
res = torch.floor( shape / 2 ** max_octaves).type(torch.int)
noise = torch.zeros(list(shape))
frequency = 1
amplitude = 1
for _ in range(max_octaves):
noise += amplitude * rand_perlin_2d(shape, (frequency*res[0], frequency*res[1]))
frequency *= 2
amplitude *= persistence
return noise[:desired_shape[0],:desired_shape[1]]
def rand_perlin_rgb( desired_shape, amp=0.1, octaves=6 ):
r = rand_perlin_2d_octaves( desired_shape, octaves )
g = rand_perlin_2d_octaves( desired_shape, octaves )
b = rand_perlin_2d_octaves( desired_shape, octaves )
rgb = ( torch.stack((r,g,b)) * amp + 1 ) * 0.5
return rgb.unsqueeze(0).clip(0,1).to(device)
def pyramid_noise_gen(shape, octaves=5, decay=1.):
n, c, h, w = shape
noise = torch.zeros([n, c, 1, 1])
max_octaves = int(min(math.log(h)/math.log(2), math.log(w)/math.log(2)))
if octaves is not None and 0 < octaves:
max_octaves = min(octaves,max_octaves)
for i in reversed(range(max_octaves)):
h_cur, w_cur = h // 2**i, w // 2**i
noise = F.interpolate(noise, (h_cur, w_cur), mode='bicubic', align_corners=False)
noise += ( torch.randn([n, c, h_cur, w_cur]) / max_octaves ) * decay**( max_octaves - (i+1) )
return noise
def rand_z(model, toksX, toksY):
e_dim = model.quantize.e_dim
n_toks = model.quantize.n_e
z_min = model.quantize.embedding.weight.min(dim=0).values[None, :, None, None]
z_max = model.quantize.embedding.weight.max(dim=0).values[None, :, None, None]
one_hot = F.one_hot(torch.randint(n_toks, [toksY * toksX], device=device), n_toks).float()
z = one_hot @ model.quantize.embedding.weight
z = z.view([-1, toksY, toksX, e_dim]).permute(0, 3, 1, 2)
return z
def make_rand_init( mode, model, perlin_octaves, perlin_weight, pyramid_octaves, pyramid_decay, toksX, toksY, f ):
if mode == 'VQGAN ZRand':
return rand_z(model, toksX, toksY)
elif mode == 'Perlin Noise':
rand_init = rand_perlin_rgb((toksY * f, toksX * f), perlin_weight, perlin_octaves )
z, *_ = model.encode(rand_init * 2 - 1)
return z
elif mode == 'Pyramid Noise':
rand_init = pyramid_noise_gen( (1,3,toksY * f, toksX * f), pyramid_octaves, pyramid_decay).to(device)
rand_init = ( rand_init * 0.5 + 0.5 ).clip(0,1)
z, *_ = model.encode(rand_init * 2 - 1)
return z
```
# Make some Art!
```
#@title Set VQGAN Model Save Location
#@markdown It's a lot faster to load model files from google drive than to download them every time you want to use this notebook.
save_vqgan_models_to_drive = True #@param {type: 'boolean'}
download_all = False
vqgan_path_on_google_drive = "/content/drive/MyDrive/Art/Models/VQGAN/" #@param {type: 'string'}
vqgan_path_on_google_drive += "/" if not vqgan_path_on_google_drive.endswith('/') else ""
#@markdown Should all the images during the run be saved to google drive?
save_output_to_drive = True #@param {type:'boolean'}
output_path_on_google_drive = "/content/drive/MyDrive/Art/" #@param {type: 'string'}
output_path_on_google_drive += "/" if not output_path_on_google_drive.endswith('/') else ""
#@markdown When saving the images, how much should be included in the name?
include_full_prompt_in_filename = False #@param {type:'boolean'}
shortname_limit = 50 #@param {type: 'number'}
filename_limit = 250
if save_vqgan_models_to_drive or save_output_to_drive:
from google.colab import drive
drive.mount('/content/drive')
vqgan_model_path = "/content/"
if save_vqgan_models_to_drive:
vqgan_model_path = vqgan_path_on_google_drive
!mkdir -p "$vqgan_path_on_google_drive"
save_output_path = "/content/art/"
if save_output_to_drive:
save_output_path = output_path_on_google_drive
!mkdir -p "$save_output_path"
model_download={
"vqgan_imagenet_f16_1024":
[["vqgan_imagenet_f16_1024.yaml", "https://heibox.uni-heidelberg.de/d/8088892a516d4e3baf92/files/?p=%2Fconfigs%2Fmodel.yaml&dl=1"],
["vqgan_imagenet_f16_1024.ckpt", "https://heibox.uni-heidelberg.de/d/8088892a516d4e3baf92/files/?p=%2Fckpts%2Flast.ckpt&dl=1"]],
"vqgan_imagenet_f16_16384":
[["vqgan_imagenet_f16_16384.yaml", "https://heibox.uni-heidelberg.de/d/a7530b09fed84f80a887/files/?p=%2Fconfigs%2Fmodel.yaml&dl=1"],
["vqgan_imagenet_f16_16384.ckpt", "https://heibox.uni-heidelberg.de/d/a7530b09fed84f80a887/files/?p=%2Fckpts%2Flast.ckpt&dl=1"]],
"vqgan_openimages_f8_8192":
[["vqgan_openimages_f8_8192.yaml", "https://heibox.uni-heidelberg.de/d/2e5662443a6b4307b470/files/?p=%2Fconfigs%2Fmodel.yaml&dl=1"],
["vqgan_openimages_f8_8192.ckpt", "https://heibox.uni-heidelberg.de/d/2e5662443a6b4307b470/files/?p=%2Fckpts%2Flast.ckpt&dl=1"]],
"coco":
[["coco_first_stage.yaml", "http://batbot.tv/ai/models/vqgan/coco_first_stage.yaml"],
["coco_first_stage.ckpt", "http://batbot.tv/ai/models/vqgan/coco_first_stage.ckpt"]],
"faceshq":
[["faceshq.yaml", "https://drive.google.com/uc?export=download&id=1fHwGx_hnBtC8nsq7hesJvs-Klv-P0gzT"],
["faceshq.ckpt", "https://app.koofr.net/content/links/a04deec9-0c59-4673-8b37-3d696fe63a5d/files/get/last.ckpt?path=%2F2020-11-13T21-41-45_faceshq_transformer%2Fcheckpoints%2Flast.ckpt"]],
"wikiart_1024":
[["wikiart_1024.yaml", "http://batbot.tv/ai/models/vqgan/WikiArt_augmented_Steps_7mil_finetuned_1mil.yaml"],
["wikiart_1024.ckpt", "http://batbot.tv/ai/models/vqgan/WikiArt_augmented_Steps_7mil_finetuned_1mil.ckpt"]],
"wikiart_16384":
[["wikiart_16384.yaml", "http://eaidata.bmk.sh/data/Wikiart_16384/wikiart_f16_16384_8145600.yaml"],
["wikiart_16384.ckpt", "http://eaidata.bmk.sh/data/Wikiart_16384/wikiart_f16_16384_8145600.ckpt"]],
"sflckr":
[["sflckr.yaml", "https://heibox.uni-heidelberg.de/d/73487ab6e5314cb5adba/files/?p=%2Fconfigs%2F2020-11-09T13-31-51-project.yaml&dl=1"],
["sflckr.ckpt", "https://heibox.uni-heidelberg.de/d/73487ab6e5314cb5adba/files/?p=%2Fcheckpoints%2Flast.ckpt&dl=1"]],
}
loaded_model = None
loaded_model_name = None
def dl_vqgan_model(image_model):
for curl_opt in model_download[image_model]:
modelpath = f'{vqgan_model_path}{curl_opt[0]}'
if not path.exists(modelpath):
print(f'downloading {curl_opt[0]} to {modelpath}')
!curl -L -o {modelpath} '{curl_opt[1]}'
else:
print(f'found existing {curl_opt[0]}')
def get_vqgan_model(image_model):
global loaded_model
global loaded_model_name
if loaded_model is None or loaded_model_name != image_model:
dl_vqgan_model(image_model)
print(f'loading {image_model} vqgan checkpoint')
vqgan_config= vqgan_model_path + model_download[image_model][0][0]
vqgan_checkpoint= vqgan_model_path + model_download[image_model][1][0]
print('vqgan_config',vqgan_config)
print('vqgan_checkpoint',vqgan_checkpoint)
model = load_vqgan_model(vqgan_config, vqgan_checkpoint).to(device)
if image_model == 'vqgan_openimages_f8_8192':
model.quantize.e_dim = 256
model.quantize.n_e = model.quantize.n_embed
model.quantize.embedding = model.quantize.embed
loaded_model = model
loaded_model_name = image_model
return loaded_model
def slugify(value):
value = str(value)
value = re.sub(r':([-\d.]+)', ' [\\1]', value)
value = re.sub(r'[|]','; ',value)
value = re.sub(r'[<>:"/\\|?*]', ' ', value)
return value
def get_filename(text, seed, i, ext):
if ( not include_full_prompt_in_filename ):
text = re.split(r'[|:;]',text, 1)[0][:shortname_limit]
text = slugify(text)
now = datetime.now()
t = now.strftime("%y%m%d%H%M")
if i is not None:
data = f'; r{seed} i{i} {t}{ext}'
else:
data = f'; r{seed} {t}{ext}'
return text[:filename_limit-len(data)] + data
def save_output(pil, text, seed, i):
fname = get_filename(text,seed,i,'.png')
pil.save(save_output_path + fname)
if save_vqgan_models_to_drive and download_all:
for model in model_download.keys():
dl_vqgan_model(model)
#@title Set Display Rate
#@markdown If `use_automatic_display_schedule` is enabled, the image will be output frequently at first, and then more spread out as time goes on. Turn this off if you want to specify the display rate yourself.
use_automatic_display_schedule = False #@param {type:'boolean'}
display_every = 5 #@param {type:'number'}
def should_checkin(i):
if i == max_iter:
return True
if not use_automatic_display_schedule:
return i % display_every == 0
schedule = [[100,25],[500,50],[1000,100],[2000,200]]
for s in schedule:
if i <= s[0]:
return i % s[1] == 0
return i % 500 == 0
```
Before generating, the rest of the setup steps must first be executed by pressing **`Runtime > Run All`**. This only needs to be done once.
```
#@title Do the Run
#@markdown What do you want to see?
text_prompt = 'made of buildings:200 | Ethiopian flags:40 | pollution:30 | 4k:20 | Unreal engine:20 | V-ray:20 | Cryengine:20 | Ray tracing:20 | Photorealistic:20 | Hyper-realistic:20'#@param {type:'string'}
gen_seed = -1#@param {type:'number'}
#@markdown - If you want to keep starting from the same point, set `gen_seed` to a positive number. `-1` will make it random every time.
init_image = '/content/d.png'#@param {type:'string'}
width = 300#@param {type:'number'}
height = 300#@param {type:'number'}
max_iter = 2000#@param {type:'number'}
#@markdown There are different ways of generating the random starting point, when not using an init image. These influence how the image turns out. The default VQGAN ZRand is good, but some models and subjects may do better with perlin or pyramid noise.
rand_init_mode = 'VQGAN ZRand'#@param [ "VQGAN ZRand", "Perlin Noise", "Pyramid Noise"]
perlin_octaves = 7#@param {type:"slider", min:1, max:8, step:1}
perlin_weight = 0.22#@param {type:"slider", min:0, max:1, step:0.01}
pyramid_octaves = 5#@param {type:"slider", min:1, max:8, step:1}
pyramid_decay = 0.99#@param {type:"slider", min:0, max:1, step:0.01}
ema_val = 0.99
#@markdown How many slices of the image should be sent to CLIP each iteration to score? Higher numbers are better, but cost more memory. If you are running into memory issues try lowering this value.
cut_n = 64 #@param {type:'number'}
#@markdown One clip model is good. Two is better? You may need to reduce the number of cuts to support having more than one CLIP model. CLIP is what scores the image against your prompt and each model has slightly different ideas of what things are.
#@markdown - `ViT-B/32` is fast and good and what most people use to begin with
clip_model = 'ViT-B/32' #@param ["ViT-B/16", "ViT-B/32", "RN50x16", "RN50x4"]
clip_model2 ='ViT-B/16' #@param ["None","ViT-B/16", "ViT-B/32", "RN50x16", "RN50x4"]
if clip_model2 == "None":
clip_model2 = None
clip1_weight = 0.5 #@param {type:"slider", min:0, max:1, step:0.01}
#@markdown Picking a different VQGAN model will impact how an image generates. Think of this as giving the generator a different set of brushes and paints to work with. CLIP is still the "eyes" and is judging the image against your prompt but using different brushes will make a different image.
#@markdown - `vqgan_imagenet_f16_16384` is the default and what most people use
vqgan_model = 'vqgan_imagenet_f16_16384'#@param [ "vqgan_imagenet_f16_1024", "vqgan_imagenet_f16_16384", "vqgan_openimages_f8_8192", "coco", "faceshq","wikiart_1024", "wikiart_16384", "sflckr"]
#@markdown Learning rates greatly impact how quickly an image can generate, or if an image can generate at all. The first learning rate is only for the first 50 iterations. The epoch rate is what is used after reaching the first mse epoch.
#@markdown You can try lowering the epoch rate while raising the initial learning rate and see what happens
learning_rate = 0.9#@param {type:'number'}
learning_rate_epoch = 0.2#@param {type:'number'}
#@markdown How much should we try to match the init image, or if no init image how much should we resist change after reaching the first epoch?
mse_weight = 1.8#@param {type:'number'}
#@markdown Adding some TV may make the image blurrier but also helps to get rid of noise. A good value to try might be 0.1.
tv_weight = 0.0 #@param {type:'number'}
#@markdown Should the total weight of the text prompts stay in the same range, relative to other loss functions?
normalize_prompt_weights = True #@param {type:'boolean'}
#@markdown Enabling the EMA tensor will cause the image to be slower to generate but may help it be more cohesive.
#@markdown This can also help keep the final image closer to the init image, if you are providing one.
use_ema_tensor = False #@param {type:'boolean'}
#@markdown If you want to generate a video of the run, you need to save the frames as you go. The more frequently you save, the longer the video but the slower it will take to generate.
save_art_output = True #@param {type:'boolean'}
save_frames_for_video = False #@param {type:'boolean'}
save_frequency_for_video = 3 #@param {type:'number'}
#@markdown ----
#@markdown I'd love to see what you can make with my notebook. Tweet me your art [@remi_durant](https://twitter.com/remi_durant)!
output_as_png = True
print('Using device:', device)
print('using prompts: ', text_prompt)
clear_memory()
!rm -r steps
!mkdir -p steps
model = get_vqgan_model( vqgan_model )
if clip_model2:
clip_models = [[clip_model, clip1_weight], [clip_model2, 1. - clip1_weight]]
else:
clip_models = [[clip_model, 1.0]]
print(clip_models)
clip_loss = MultiClipLoss( clip_models, text_prompt, normalize_prompt_weights=normalize_prompt_weights, cutn=cut_n)
seed = update_random( gen_seed, 'image generation')
# Make Z Init
z = 0
f = 2**(model.decoder.num_resolutions - 1)
toksX, toksY = math.ceil( width / f), math.ceil( height / f)
print(f'Outputing size: [{toksX*f}x{toksY*f}]')
has_init_image = (init_image != "")
if has_init_image:
if 'http' in init_image:
req = Request(init_image, headers={'User-Agent': 'Mozilla/5.0'})
img = Image.open(urlopen(req))
else:
img = Image.open(init_image)
pil_image = img.convert('RGB')
pil_image = pil_image.resize((toksX * f, toksY * f), Image.LANCZOS)
pil_image = TF.to_tensor(pil_image)
#if args.use_noise:
# pil_image = pil_image + args.use_noise * torch.randn_like(pil_image)
z, *_ = model.encode(pil_image.to(device).unsqueeze(0) * 2 - 1)
del pil_image
del img
else:
z = make_rand_init( rand_init_mode, model, perlin_octaves, perlin_weight, pyramid_octaves, pyramid_decay, toksX, toksY, f )
z = EMATensor(z, ema_val)
opt = optim.Adam( z.parameters(), lr=learning_rate, weight_decay=0.00000000)
mse_loss = MSEDecayLoss( mse_weight, mse_decay_rate=50, mse_epoches=5, mse_quantize=True )
mse_loss.set_target( z.tensor, model )
mse_loss.has_init_image = has_init_image
tv_loss = TVLoss()
losses = []
mb = master_bar(range(1))
gnames = ['losses']
mb.names=gnames
mb.graph_fig, axs = plt.subplots(1, 1) # For custom display
mb.graph_ax = axs
mb.graph_out = display.display(mb.graph_fig, display_id=True)
## optimizer loop
def synth(z, quantize=True, scramble=True):
z_q = 0
if quantize:
z_q = vector_quantize(z.movedim(1, 3), model.quantize.embedding.weight).movedim(3, 1)
else:
z_q = z.model
out = clamp_with_grad(model.decode(z_q).add(1).div(2), 0, 1)
return out
@torch.no_grad()
def checkin(i, z, out_pil, losses):
losses_str = ', '.join(f'{loss.item():g}' for loss in losses)
tqdm.write(f'i: {i}, loss: {sum(losses).item():g}, losses: {losses_str}')
display_format='png' if output_as_png else 'jpg'
pil_data = image_to_data_url(out_pil, display_format)
display.display(display.HTML(f'<img src="{pil_data}" />'))
def should_save_for_video(i):
return save_frames_for_video and i % save_frequency_for_video
def train(i):
global opt
global z
opt.zero_grad( set_to_none = True )
out = checkpoint( synth, z.tensor )
lossAll = []
lossAll += clip_loss( i,out )
if 0 < mse_weight:
msel = mse_loss(i,z.tensor)
if 0 < msel:
lossAll.append(msel)
if 0 < tv_weight:
lossAll.append(tv_loss(out)*tv_weight)
loss = sum(lossAll)
loss.backward()
if should_checkin(i) or should_save_for_video(i):
with torch.no_grad():
if use_ema_tensor:
out = synth( z.average )
pil = TF.to_pil_image(out[0].cpu())
if should_checkin(i):
checkin(i, z, pil, lossAll)
if save_art_output:
save_output(pil, text_prompt, seed, i)
if should_save_for_video(i):
pil.save(f'steps/step{i//save_frequency_for_video:04}.png')
# update graph
losses.append(loss)
x = range(len(losses))
mb.update_graph( [[x,losses]] )
opt.step()
if use_ema_tensor:
z.update()
i = 0
try:
with tqdm() as pbar:
while True and i <= max_iter:
if i % 200 == 0:
clear_memory()
train(i)
with torch.no_grad():
if mse_loss.step(i):
print('Reseting optimizer at mse epoch')
if mse_loss.has_init_image and use_ema_tensor:
mse_loss.set_target(z.average,model)
else:
mse_loss.set_target(z.tensor,model)
# Make sure not to spike loss when mse_loss turns on
if not mse_loss.is_active(i):
z.tensor = nn.Parameter(mse_loss.z_orig.clone())
z.tensor.requires_grad = True
if use_ema_tensor:
z = EMATensor(z.average, ema_val)
else:
z = EMATensor(z.tensor, ema_val)
opt = optim.Adam(z.parameters(), lr=learning_rate_epoch, weight_decay=0.00000000)
i += 1
pbar.update()
except KeyboardInterrupt:
pass
#@title Make a Video of Your Last Run!
#@markdown If you want to make a video, you must first enable `save_frames_for_video` during the run. Setting a higher frequency will make a longer video, and a higher framerate will make a shorter video.
fps = 24 #@param{type:'number'}
!mkdir -p "/content/video/"
vname = "/content/video/"+get_filename(text_prompt,seed,None,'.mp4')
!ffmpeg -y -v 1 -framerate $fps -i steps/step%04d.png -r $fps -vcodec libx264 -crf 32 -pix_fmt yuv420p "$vname"
if save_output_to_drive:
!cp "$vname" "$output_path_on_google_drive"
mp4 = open(vname,'rb').read()
data_url = "data:video/mp4;base64," + b64encode(mp4).decode()
display.display( display.HTML(f'<video controls><source src="{data_url}" type="video/mp4"></video>') )
```
# Extra Resources
You may want to check out some of my other projects as well to get more insight into how the different parts of VQGAN+CLIP work together to generate an image:
- Art Styles and Movements, as perceived by VQGAN+CLIP
- [VQGAN Imagenet16k + ViT-B/32](https://imgur.com/gallery/BZzXLHY)
- [VQGAN Imagenet16k + ViT-B/16](https://imgur.com/gallery/w14XZFd)
- [VQGAN Imagenet16k + RN50x16](https://imgur.com/gallery/Kd0WYfo)
- [VQGAN Imagenet16k + RN50x4](https://imgur.com/gallery/PNd7zYp)
- [How CLIP "sees"](https://twitter.com/remi_durant/status/1460607677801897990?s=20)
There is also this great prompt exploration from @kingdomakrillic which showcases a lot of the words you can add to your prompt to push CLIP towards certain styles:
- [CLIP + VQGAN Keyword Comparison](https://imgur.com/a/SnSIQRu)
| github_jupyter |
```
# Copyright 2021 Google LLC
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
# You may obtain a copy of the License at
#
# https://www.apache.org/licenses/LICENSE-2.0
#
# Unless required by applicable law or agreed to in writing, software
# distributed under the License is distributed on an "AS IS" BASIS,
# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
# See the License for the specific language governing permissions and
# limitations under the License.
```
# Vertex Pipelines: Lightweight Python function-based components, and component I/O
<table align="left">
<td>
<a href="https://colab.research.google.com/github/GoogleCloudPlatform/vertex-ai-samples/notebooks/official/pipelines/lightweight_functions_component_io_kfp.ipynb">
<img src="https://cloud.google.com/ml-engine/images/colab-logo-32px.png" alt="Colab logo"> Run in Colab
</a>
</td>
<td>
<a href="https://github.com/GoogleCloudPlatform/vertex-ai-samples/notebooks/official/pipelines/lightweight_functions_component_io_kfp.ipynb">
<img src="https://cloud.google.com/ml-engine/images/github-logo-32px.png" alt="GitHub logo">
View on GitHub
</a>
</td>
<td>
<a href="https://console.cloud.google.com/ai/platform/notebooks/deploy-notebook?download_url=https://github.com/GoogleCloudPlatform/vertex-ai-samples/notebooks/official/pipelines/lightweight_functions_component_io_kfp.ipynb">
Open in Google Cloud Notebooks
</a>
</td>
</table>
<br/><br/><br/>
## Overview
This notebooks shows how to use [the Kubeflow Pipelines (KFP) SDK](https://www.kubeflow.org/docs/components/pipelines/) to build [Vertex Pipelines](https://cloud.google.com/vertex-ai/docs/pipelines) that use lightweight Python function based components, as well as supporting component I/O using the KFP SDK.
### Objective
In this tutorial, you use the KFP SDK to build lightweight Python function-based components.
The steps performed include:
- Build Python function-based components.
- Pass *Artifacts* and *parameters* between components, both by path reference and by value.
- Use the `kfp.dsl.importer` method.
### KFP Python function-based components
A Kubeflow pipeline component is a self-contained set of code that performs one step in your ML workflow. A pipeline component is composed of:
* The component code, which implements the logic needed to perform a step in your ML workflow.
* A component specification, which defines the following:
* The component’s metadata, its name and description.
* The component’s interface, the component’s inputs and outputs.
* The component’s implementation, the Docker container image to run, how to pass inputs to your component code, and how to get the component’s outputs.
Lightweight Python function-based components make it easier to iterate quickly by letting you build your component code as a Python function and generating the component specification for you. This notebook shows how to create Python function-based components for use in [Vertex Pipelines](https://cloud.google.com/vertex-ai/docs/pipelines).
Python function-based components use the Kubeflow Pipelines SDK to handle the complexity of passing inputs into your component and passing your function’s outputs back to your pipeline.
There are two categories of inputs/outputs supported in Python function-based components: *artifacts* and *parameters*.
* Parameters are passed to your component by value and typically contain `int`, `float`, `bool`, or small `string` values.
* Artifacts are passed to your component as a *reference* to a path, to which you can write a file or a subdirectory structure. In addition to the artifact’s data, you can also read and write the artifact’s metadata. This lets you record arbitrary key-value pairs for an artifact such as the accuracy of a trained model, and use metadata in downstream components – for example, you could use metadata to decide if a model is accurate enough to deploy for predictions.
### Costs
This tutorial uses billable components of Google Cloud:
* Vertex AI
* Cloud Storage
Learn about [Vertex AI
pricing](https://cloud.google.com/vertex-ai/pricing) and [Cloud Storage
pricing](https://cloud.google.com/storage/pricing), and use the [Pricing
Calculator](https://cloud.google.com/products/calculator/)
to generate a cost estimate based on your projected usage.
### Set up your local development environment
If you are using Colab or Google Cloud Notebook, your environment already meets all the requirements to run this notebook. You can skip this step.
Otherwise, make sure your environment meets this notebook's requirements. You need the following:
- The Cloud Storage SDK
- Git
- Python 3
- virtualenv
- Jupyter notebook running in a virtual environment with Python 3
The Cloud Storage guide to [Setting up a Python development environment](https://cloud.google.com/python/setup) and the [Jupyter installation guide](https://jupyter.org/install) provide detailed instructions for meeting these requirements. The following steps provide a condensed set of instructions:
1. [Install and initialize the SDK](https://cloud.google.com/sdk/docs/).
2. [Install Python 3](https://cloud.google.com/python/setup#installing_python).
3. [Install virtualenv](Ihttps://cloud.google.com/python/setup#installing_and_using_virtualenv) and create a virtual environment that uses Python 3.
4. Activate that environment and run `pip3 install Jupyter` in a terminal shell to install Jupyter.
5. Run `jupyter notebook` on the command line in a terminal shell to launch Jupyter.
6. Open this notebook in the Jupyter Notebook Dashboard.
## Installation
Install the latest version of Vertex SDK for Python.
```
import os
# Google Cloud Notebook
if os.path.exists("/opt/deeplearning/metadata/env_version"):
USER_FLAG = "--user"
else:
USER_FLAG = ""
! pip3 install --upgrade google-cloud-aiplatform $USER_FLAG
```
Install the latest GA version of *google-cloud-storage* library as well.
```
! pip3 install -U google-cloud-storage $USER_FLAG
```
Install the latest GA version of *google-cloud-pipeline-components* library as well.
```
! pip3 install $USER kfp google-cloud-pipeline-components --upgrade
```
### Restart the kernel
Once you've installed the additional packages, you need to restart the notebook kernel so it can find the packages.
```
import os
if not os.getenv("IS_TESTING"):
# Automatically restart kernel after installs
import IPython
app = IPython.Application.instance()
app.kernel.do_shutdown(True)
```
Check the versions of the packages you installed. The KFP SDK version should be >=1.6.
```
! python3 -c "import kfp; print('KFP SDK version: {}'.format(kfp.__version__))"
! python3 -c "import google_cloud_pipeline_components; print('google_cloud_pipeline_components version: {}'.format(google_cloud_pipeline_components.__version__))"
```
## Before you begin
### GPU runtime
This tutorial does not require a GPU runtime.
### Set up your Google Cloud project
**The following steps are required, regardless of your notebook environment.**
1. [Select or create a Google Cloud project](https://console.cloud.google.com/cloud-resource-manager). When you first create an account, you get a $300 free credit towards your compute/storage costs.
2. [Make sure that billing is enabled for your project.](https://cloud.google.com/billing/docs/how-to/modify-project)
3. [Enable the Vertex AI APIs, Compute Engine APIs, and Cloud Storage.](https://console.cloud.google.com/flows/enableapi?apiid=ml.googleapis.com,compute_component,storage-component.googleapis.com)
4. [The Google Cloud SDK](https://cloud.google.com/sdk) is already installed in Google Cloud Notebook.
5. Enter your project ID in the cell below. Then run the cell to make sure the
Cloud SDK uses the right project for all the commands in this notebook.
**Note**: Jupyter runs lines prefixed with `!` as shell commands, and it interpolates Python variables prefixed with `$`.
```
PROJECT_ID = "[your-project-id]" # @param {type:"string"}
if PROJECT_ID == "" or PROJECT_ID is None or PROJECT_ID == "[your-project-id]":
# Get your GCP project id from gcloud
shell_output = ! gcloud config list --format 'value(core.project)' 2>/dev/null
PROJECT_ID = shell_output[0]
print("Project ID:", PROJECT_ID)
! gcloud config set project $PROJECT_ID
```
#### Region
You can also change the `REGION` variable, which is used for operations
throughout the rest of this notebook. Below are regions supported for Vertex AI. We recommend that you choose the region closest to you.
- Americas: `us-central1`
- Europe: `europe-west4`
- Asia Pacific: `asia-east1`
You may not use a multi-regional bucket for training with Vertex AI. Not all regions provide support for all Vertex AI services.
Learn more about [Vertex AI regions](https://cloud.google.com/vertex-ai/docs/general/locations)
```
REGION = "us-central1" # @param {type: "string"}
```
#### Timestamp
If you are in a live tutorial session, you might be using a shared test account or project. To avoid name collisions between users on resources created, you create a timestamp for each instance session, and append the timestamp onto the name of resources you create in this tutorial.
```
from datetime import datetime
TIMESTAMP = datetime.now().strftime("%Y%m%d%H%M%S")
```
### Authenticate your Google Cloud account
**If you are using Google Cloud Notebook**, your environment is already authenticated. Skip this step.
**If you are using Colab**, run the cell below and follow the instructions when prompted to authenticate your account via oAuth.
**Otherwise**, follow these steps:
In the Cloud Console, go to the [Create service account key](https://console.cloud.google.com/apis/credentials/serviceaccountkey) page.
**Click Create service account**.
In the **Service account name** field, enter a name, and click **Create**.
In the **Grant this service account access to project** section, click the Role drop-down list. Type "Vertex" into the filter box, and select **Vertex Administrator**. Type "Storage Object Admin" into the filter box, and select **Storage Object Admin**.
Click Create. A JSON file that contains your key downloads to your local environment.
Enter the path to your service account key as the GOOGLE_APPLICATION_CREDENTIALS variable in the cell below and run the cell.
```
# If you are running this notebook in Colab, run this cell and follow the
# instructions to authenticate your GCP account. This provides access to your
# Cloud Storage bucket and lets you submit training jobs and prediction
# requests.
import os
import sys
# If on Google Cloud Notebook, then don't execute this code
if not os.path.exists("/opt/deeplearning/metadata/env_version"):
if "google.colab" in sys.modules:
from google.colab import auth as google_auth
google_auth.authenticate_user()
# If you are running this notebook locally, replace the string below with the
# path to your service account key and run this cell to authenticate your GCP
# account.
elif not os.getenv("IS_TESTING"):
%env GOOGLE_APPLICATION_CREDENTIALS ''
```
### Create a Cloud Storage bucket
**The following steps are required, regardless of your notebook environment.**
When you initialize the Vertex SDK for Python, you specify a Cloud Storage staging bucket. The staging bucket is where all the data associated with your dataset and model resources are retained across sessions.
Set the name of your Cloud Storage bucket below. Bucket names must be globally unique across all Google Cloud projects, including those outside of your organization.
```
BUCKET_NAME = "gs://[your-bucket-name]" # @param {type:"string"}
if BUCKET_NAME == "" or BUCKET_NAME is None or BUCKET_NAME == "gs://[your-bucket-name]":
BUCKET_NAME = "gs://" + PROJECT_ID + "aip-" + TIMESTAMP
```
**Only if your bucket doesn't already exist**: Run the following cell to create your Cloud Storage bucket.
```
! gsutil mb -l $REGION $BUCKET_NAME
```
Finally, validate access to your Cloud Storage bucket by examining its contents:
```
! gsutil ls -al $BUCKET_NAME
```
#### Service Account
**If you don't know your service account**, try to get your service account using `gcloud` command by executing the second cell below.
```
SERVICE_ACCOUNT = "[your-service-account]" # @param {type:"string"}
if (
SERVICE_ACCOUNT == ""
or SERVICE_ACCOUNT is None
or SERVICE_ACCOUNT == "[your-service-account]"
):
# Get your GCP project id from gcloud
shell_output = !gcloud auth list 2>/dev/null
SERVICE_ACCOUNT = shell_output[2].strip()
print("Service Account:", SERVICE_ACCOUNT)
```
#### Set service account access for Vertex Pipelines
Run the following commands to grant your service account access to read and write pipeline artifacts in the bucket that you created in the previous step -- you only need to run these once per service account.
```
! gsutil iam ch serviceAccount:{SERVICE_ACCOUNT}:roles/storage.objectCreator $BUCKET_NAME
! gsutil iam ch serviceAccount:{SERVICE_ACCOUNT}:roles/storage.objectViewer $BUCKET_NAME
```
### Set up variables
Next, set up some variables used throughout the tutorial.
### Import libraries and define constants
```
import google.cloud.aiplatform as aip
```
#### Vertex Pipelines constants
Setup up the following constants for Vertex Pipelines:
```
PIPELINE_ROOT = "{}/pipeline_root/shakespeare".format(BUCKET_NAME)
```
Additional imports.
```
from typing import NamedTuple
import kfp
from kfp.v2 import dsl
from kfp.v2.dsl import (Artifact, Dataset, Input, InputPath, Model, Output,
OutputPath, component)
```
## Initialize Vertex SDK for Python
Initialize the Vertex SDK for Python for your project and corresponding bucket.
```
aip.init(project=PROJECT_ID, staging_bucket=BUCKET_NAME)
```
### Define Python function-based pipeline components
In this tutorial, you define function-based components that consume parameters and produce (typed) Artifacts and parameters. Functions can produce Artifacts in three ways:
* Accept an output local path using `OutputPath`
* Accept an `OutputArtifact` which gives the function a handle to the output artifact's metadata
* Return an `Artifact` (or `Dataset`, `Model`, `Metrics`, etc) in a `NamedTuple`
These options for producing Artifacts are demonstrated.
#### Define preprocess component
The first component definition, `preprocess`, shows a component that outputs two `Dataset` Artifacts, as well as an output parameter. (For this example, the datasets don't reflect real data).
For the parameter output, you would typically use the approach shown here, using the `OutputPath` type, for "larger" data.
For "small data", like a short string, it might be more convenient to use the `NamedTuple` function output as shown in the second component instead.
```
@component
def preprocess(
# An input parameter of type string.
message: str,
# Use Output to get a metadata-rich handle to the output artifact
# of type `Dataset`.
output_dataset_one: Output[Dataset],
# A locally accessible filepath for another output artifact of type
# `Dataset`.
output_dataset_two_path: OutputPath("Dataset"),
# A locally accessible filepath for an output parameter of type string.
output_parameter_path: OutputPath(str),
):
"""'Mock' preprocessing step.
Writes out the passed in message to the output "Dataset"s and the output message.
"""
output_dataset_one.metadata["hello"] = "there"
# Use OutputArtifact.path to access a local file path for writing.
# One can also use OutputArtifact.uri to access the actual URI file path.
with open(output_dataset_one.path, "w") as f:
f.write(message)
# OutputPath is used to just pass the local file path of the output artifact
# to the function.
with open(output_dataset_two_path, "w") as f:
f.write(message)
with open(output_parameter_path, "w") as f:
f.write(message)
```
#### Define train component
The second component definition, `train`, defines as input both an `InputPath` of type `Dataset`, and an `InputArtifact` of type `Dataset` (as well as other parameter inputs). It uses the `NamedTuple` format for function output. As shown, these outputs can be Artifacts as well as parameters.
Additionally, this component writes some metrics metadata to the `model` output Artifact. This information is displayed in the Cloud Console user interface when the pipeline runs.
```
@component(
base_image="python:3.9", # Use a different base image.
)
def train(
# An input parameter of type string.
message: str,
# Use InputPath to get a locally accessible path for the input artifact
# of type `Dataset`.
dataset_one_path: InputPath("Dataset"),
# Use InputArtifact to get a metadata-rich handle to the input artifact
# of type `Dataset`.
dataset_two: Input[Dataset],
# Output artifact of type Model.
imported_dataset: Input[Dataset],
model: Output[Model],
# An input parameter of type int with a default value.
num_steps: int = 3,
# Use NamedTuple to return either artifacts or parameters.
# When returning artifacts like this, return the contents of
# the artifact. The assumption here is that this return value
# fits in memory.
) -> NamedTuple(
"Outputs",
[
("output_message", str), # Return parameter.
("generic_artifact", Artifact), # Return generic Artifact.
],
):
"""'Mock' Training step.
Combines the contents of dataset_one and dataset_two into the
output Model.
Constructs a new output_message consisting of message repeated num_steps times.
"""
# Directly access the passed in GCS URI as a local file (uses GCSFuse).
with open(dataset_one_path, "r") as input_file:
dataset_one_contents = input_file.read()
# dataset_two is an Artifact handle. Use dataset_two.path to get a
# local file path (uses GCSFuse).
# Alternately, use dataset_two.uri to access the GCS URI directly.
with open(dataset_two.path, "r") as input_file:
dataset_two_contents = input_file.read()
with open(model.path, "w") as f:
f.write("My Model")
with open(imported_dataset.path, "r") as f:
data = f.read()
print("Imported Dataset:", data)
# Use model.get() to get a Model artifact, which has a .metadata dictionary
# to store arbitrary metadata for the output artifact. This metadata will be
# recorded in Managed Metadata and can be queried later. It will also show up
# in the UI.
model.metadata["accuracy"] = 0.9
model.metadata["framework"] = "Tensorflow"
model.metadata["time_to_train_in_seconds"] = 257
artifact_contents = "{}\n{}".format(dataset_one_contents, dataset_two_contents)
output_message = " ".join([message for _ in range(num_steps)])
return (output_message, artifact_contents)
```
#### Define read_artifact_input component
Finally, you define a small component that takes as input the `generic_artifact` returned by the `train` component function, and reads and prints the Artifact's contents.
```
@component
def read_artifact_input(
generic: Input[Artifact],
):
with open(generic.path, "r") as input_file:
generic_contents = input_file.read()
print(f"generic contents: {generic_contents}")
```
### Define a pipeline that uses your components and the Importer
Next, define a pipeline that uses the components that were built in the previous section, and also shows the use of the `kfp.dsl.importer`.
This example uses the `importer` to create, in this case, a `Dataset` artifact from an existing URI.
Note that the `train_task` step takes as inputs three of the outputs of the `preprocess_task` step, as well as the output of the `importer` step.
In the "train" inputs we refer to the `preprocess` `output_parameter`, which gives us the output string directly.
The `read_task` step takes as input the `train_task` `generic_artifact` output.
```
@dsl.pipeline(
# Default pipeline root. You can override it when submitting the pipeline.
pipeline_root=PIPELINE_ROOT,
# A name for the pipeline. Use to determine the pipeline Context.
name="metadata-pipeline-v2",
)
def pipeline(message: str):
importer = kfp.dsl.importer(
artifact_uri="gs://ml-pipeline-playground/shakespeare1.txt",
artifact_class=Dataset,
reimport=False,
)
preprocess_task = preprocess(message=message)
train_task = train(
dataset_one_path=preprocess_task.outputs["output_dataset_one"],
dataset_two=preprocess_task.outputs["output_dataset_two_path"],
imported_dataset=importer.output,
message=preprocess_task.outputs["output_parameter_path"],
num_steps=5,
)
read_task = read_artifact_input( # noqa: F841
train_task.outputs["generic_artifact"]
)
```
## Compile the pipeline
Next, compile the pipeline.
```
from kfp.v2 import compiler # noqa: F811
compiler.Compiler().compile(
pipeline_func=pipeline, package_path="lightweight_pipeline.json".replace(" ", "_")
)
```
## Run the pipeline
Next, run the pipeline.
```
DISPLAY_NAME = "shakespeare_" + TIMESTAMP
job = aip.PipelineJob(
display_name=DISPLAY_NAME,
template_path="lightweight_pipeline.json".replace(" ", "_"),
pipeline_root=PIPELINE_ROOT,
parameter_values={"message": "Hello, World"},
)
job.run()
```
Click on the generated link to see your run in the Cloud Console.
<!-- It should look something like this as it is running:
<a href="https://storage.googleapis.com/amy-jo/images/mp/automl_tabular_classif.png" target="_blank"><img src="https://storage.googleapis.com/amy-jo/images/mp/automl_tabular_classif.png" width="40%"/></a> -->
In the UI, many of the pipeline DAG nodes will expand or collapse when you click on them. Here is a partially-expanded view of the DAG (click image to see larger version).
<a href="https://storage.googleapis.com/amy-jo/images/mp/artifact_io2.png" target="_blank"><img src="https://storage.googleapis.com/amy-jo/images/mp/artifact_io2.png" width="95%"/></a>
# Cleaning up
To clean up all Google Cloud resources used in this project, you can [delete the Google Cloud
project](https://cloud.google.com/resource-manager/docs/creating-managing-projects#shutting_down_projects) you used for the tutorial.
Otherwise, you can delete the individual resources you created in this tutorial -- *Note:* this is auto-generated and not all resources may be applicable for this tutorial:
- Dataset
- Pipeline
- Model
- Endpoint
- Batch Job
- Custom Job
- Hyperparameter Tuning Job
- Cloud Storage Bucket
```
delete_dataset = True
delete_pipeline = True
delete_model = True
delete_endpoint = True
delete_batchjob = True
delete_customjob = True
delete_hptjob = True
delete_bucket = True
try:
if delete_model and "DISPLAY_NAME" in globals():
models = aip.Model.list(
filter=f"display_name={DISPLAY_NAME}", order_by="create_time"
)
model = models[0]
aip.Model.delete(model)
print("Deleted model:", model)
except Exception as e:
print(e)
try:
if delete_endpoint and "DISPLAY_NAME" in globals():
endpoints = aip.Endpoint.list(
filter=f"display_name={DISPLAY_NAME}_endpoint", order_by="create_time"
)
endpoint = endpoints[0]
endpoint.undeploy_all()
aip.Endpoint.delete(endpoint.resource_name)
print("Deleted endpoint:", endpoint)
except Exception as e:
print(e)
if delete_dataset and "DISPLAY_NAME" in globals():
if "text" == "tabular":
try:
datasets = aip.TabularDataset.list(
filter=f"display_name={DISPLAY_NAME}", order_by="create_time"
)
dataset = datasets[0]
aip.TabularDataset.delete(dataset.resource_name)
print("Deleted dataset:", dataset)
except Exception as e:
print(e)
if "text" == "image":
try:
datasets = aip.ImageDataset.list(
filter=f"display_name={DISPLAY_NAME}", order_by="create_time"
)
dataset = datasets[0]
aip.ImageDataset.delete(dataset.resource_name)
print("Deleted dataset:", dataset)
except Exception as e:
print(e)
if "text" == "text":
try:
datasets = aip.TextDataset.list(
filter=f"display_name={DISPLAY_NAME}", order_by="create_time"
)
dataset = datasets[0]
aip.TextDataset.delete(dataset.resource_name)
print("Deleted dataset:", dataset)
except Exception as e:
print(e)
if "text" == "video":
try:
datasets = aip.VideoDataset.list(
filter=f"display_name={DISPLAY_NAME}", order_by="create_time"
)
dataset = datasets[0]
aip.VideoDataset.delete(dataset.resource_name)
print("Deleted dataset:", dataset)
except Exception as e:
print(e)
try:
if delete_pipeline and "DISPLAY_NAME" in globals():
pipelines = aip.PipelineJob.list(
filter=f"display_name={DISPLAY_NAME}", order_by="create_time"
)
pipeline = pipelines[0]
aip.PipelineJob.delete(pipeline.resource_name)
print("Deleted pipeline:", pipeline)
except Exception as e:
print(e)
if delete_bucket and "BUCKET_NAME" in globals():
! gsutil rm -r $BUCKET_NAME
```
| github_jupyter |
# WikiPathways and py4cytoscape
## Yihang Xin and Alex Pico
## 2020-11-10
WikiPathways is a well-known repository for biological pathways that provides unique tools to the research community for content creation, editing and utilization [@Pico2008].
Python is an interpreted, high-level and general-purpose programming language.
py4cytoscape leverages the WikiPathways API to communicate between Python and WikiPathways, allowing any pathway to be queried, interrogated and downloaded in both data and image formats. Queries are typically performed based on “Xrefs”, standardized identifiers for genes, proteins and metabolites. Once you can identified a pathway, you can use the WPID (WikiPathways identifier) to make additional queries.
py4cytoscape leverages the CyREST API to provide a number of functions related to network visualization and analysis.
# Installation
The following chunk of code installs the `py4cytoscape` module.
```
%%capture
!python3 -m pip install python-igraph requests pandas networkx
!python3 -m pip install py4cytoscape
```
# Prerequisites
## In addition to this package (py4cytoscape latest version 0.0.7), you will need:
* Latest version of Cytoscape, which can be downloaded from https://cytoscape.org/download.html. Simply follow the installation instructions on screen.
* Complete installation wizard
* Launch Cytoscape
For this vignette, you’ll also need the WikiPathways app to access the WikiPathways database from within Cytoscape.
Install the WikiPathways app from http://apps.cytoscape.org/apps/wikipathways
Install the filetransfer app from https://apps.cytoscape.org/apps/filetransfer
You can also install app inside Python notebook by running "py4cytoscape.install_app('Your App')"
# Import the required package
```
import os
import sys
import requests
import pandas as pd
from lxml import etree as ET
from collections import OrderedDict
import py4cytoscape as p4c
# Check Version
p4c.cytoscape_version_info()
```
# Working together
Ok, with all of these components loaded and launched, you can now perform some nifty sequences. For example, search for a pathway based on a keyword search and then load it into Cytoscape.
```
def find_pathways_by_text(query, species):
base_iri = 'http://webservice.wikipathways.org/'
request_params = {'query':query, 'species':species}
response = requests.get(base_iri + 'findPathwaysByText', params=request_params)
return response
response = find_pathways_by_text("colon cancer", "Homo sapiens")
def find_pathway_dataframe(response):
data = response.text
dom = ET.fromstring(data)
pathways = []
NAMESPACES = {'ns1':'http://www.wso2.org/php/xsd','ns2':'http://www.wikipathways.org/webservice/'}
for node in dom.findall('ns1:result', NAMESPACES):
pathway_using_api_terms = {}
for child in node:
pathway_using_api_terms[ET.QName(child).localname] = child.text
pathways.append(pathway_using_api_terms)
id_list = []
score_list = []
url_list = []
name_list = []
species_list = []
revision_list = []
for p in pathways:
id_list.append(p["id"])
score_list.append(p["score"])
url_list.append(p["url"])
name_list.append(p["name"])
species_list.append(p["species"])
revision_list.append(p["revision"])
df = pd.DataFrame(list(zip(id_list,score_list,url_list,name_list,species_list,revision_list)), columns =['id', 'score','url','name','species','revision'])
return df
df = find_pathway_dataframe(response)
df.head(10)
```
We have a list of human pathways that mention “Colon Cancer”. The results include lots of information, so let’s get a unique list of just the WPIDs.
```
unique_id = list(OrderedDict.fromkeys(df["id"]))
unique_id[0]
```
Let’s import the first one of these into Cytoscape!
```
cmd_list = ['wikipathways','import-as-pathway','id="',unique_id[0],'"']
cmd = " ".join(cmd_list)
p4c.commands.commands_get(cmd)
```
Once in Cytoscape, you can load data, apply visual style mappings, perform analyses, and export images and data formats. See py4cytoscape package for details.
# From networks to pathways
If you are already with with networks and data in Cytoscape, you may end up focusing on one or few particular genes, proteins or metabolites, and want to query WikiPathways.
For example, let’s open a sample network from Cytoscape and identify the gene with the largest number of connections, i.e., node degree.
Note: this next chunk will overwrite your current session. Save if you want to keep anything.
```
p4c.session.open_session()
net_data = p4c.tables.get_table_columns(columns=['name','degree.layout','COMMON'])
max_gene = net_data[net_data["degree.layout"] == net_data["degree.layout"].max()]
max_gene
```
Great. It looks like MCM1 has the larget number of connections (18) in this network. Let’s use it’s identifier (YMR043W) to query WikiPathways to learn more about the gene and its biological role, and load it into Cytoscape.
Pro-tip: We need to know the datasource that provides a given identifier. In this case, it’s sort of tricky: Ensembl provides these Yeast ORF identifiers for this organism rather than they typical format. So, we’ll include the ‘En’ system code. See other vignettes for more details.
```
def find_pathways_by_xref(ids, codes):
base_iri = 'http://webservice.wikipathways.org/'
request_params = {'ids':ids, 'codes':codes}
response = requests.get(base_iri + 'findPathwaysByXref', params=request_params)
return response
response = find_pathways_by_xref('YMR043W','En')
mcm1_pathways = find_pathway_dataframe(response)
unique_id = list(OrderedDict.fromkeys(mcm1_pathways["id"]))
unique_id = "".join(unique_id)
unique_id
cmd_list = ['wikipathways','import-as-pathway','id="',unique_id,'"']
cmd = " ".join(cmd_list)
p4c.commands.commands_get(cmd)
```
And we can easily select the MCM1 node by name in the newly imported pathway to help see where exactly it plays its role.
```
p4c.network_selection.select_nodes(['Mcm1'], by_col='name')
```
| github_jupyter |
# Plotting with Matplotlib
## What is `matplotlib`?
* `matplotlib` is a 2D plotting library for Python
* It provides quick way to visualize data from Python
* It comes with a set plots
* We can import its functions through the command
```Python
import matplotlib.pyplot as plt
```
```
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
```
## Basic plots
Your goal is to plot the cosine and the sine functions on the same plot, using the default `matplotlib` settings.
### Generating the data
```
x = np.linspace(-np.pi, np.pi, 256, endpoint=True)
c, s = np.cos(x), np.sin(x)
```
where,
* x is a vector with 256 values ranging from $-\pi$ to $\pi$ included
* c and s are vectors with the cosine and the sine values of X
```
plt.plot(x, c)
plt.plot(x, s)
plt.show()
```
Rather than creating a plot with default size, we want to specify:
* the size of the figure
* the colors and type of the lines
* the limits of the axes
```
# Create a figure of size 8x6 inches, 80 dots per inch
plt.figure(figsize=(8, 6), dpi=80)
# Create a new subplot from a grid of 1x1
plt.subplot(1, 1, 1)
# Plot cosine with a blue continuous line of width 1 (pixels)
plt.plot(x, c, color="blue", linewidth=2.5, linestyle="-")
# Plot sine with a green dotted line of width 1 (pixels)
plt.plot(x, s, color="green", linewidth=1.0, linestyle="dotted")
# Set x limits
plt.xlim(-4.0, 4)
# Set x ticks
plt.xticks(np.linspace(-4, 4, 9, endpoint=True))
# Set y limits
plt.ylim(-1.0, 1.0)
# Set y ticks
plt.yticks(np.linspace(-1, 1, 5, endpoint=True))
```
### Changing colors and line widths
* We can to:
- make the figure more horizontal
- change the color of the lines to blue and red
- have slighty thicker lines
```
plt.figure(figsize=(10, 6), dpi=80)
plt.plot(x, c, color="blue", linewidth=2.5, linestyle="-")
plt.plot(x, s, color="red", linewidth=2.5, linestyle="solid")
```
### Setting limits
Now, we want to space the axes to see all the data points
```
plt.figure(figsize=(10, 6), dpi=80)
plt.plot(x, c, color="blue", linewidth=2.5, linestyle="-")
plt.plot(x, s, color="red", linewidth=2.5, linestyle="solid")
plt.xlim(x.min() * 1.1, x.max() * 1.1)
plt.ylim(c.min() * 1.1, c.max() * 1.1)
```
### Setting ticks
Current ticks are not ideal because they do not show the interesting values ($+/-\pi$, $+/-\pi/2$) for sine and cosine.
```
plt.figure(figsize=(10, 6), dpi=80)
plt.plot(x, c, color="blue", linewidth=2.5, linestyle="-")
plt.plot(x, s, color="red", linewidth=2.5, linestyle="solid")
plt.xlim(x.min() * 1.1, x.max() * 1.1)
plt.ylim(c.min() * 1.1, c.max() * 1.1)
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi])
plt.yticks([-1, 0, +1])
```
### Setting tick labels
* Ticks are correctly placed but their labels are not very explicit
* We can guess that 3.142 is $\pi$, but it would be better to make it explicit
* When we set tick values, we can also provide a corresponding label in the second argument list
* We can use $\LaTeX$ when defining the labels
```
plt.figure(figsize=(10, 6), dpi=80)
plt.plot(x, c, color="blue", linewidth=2.5, linestyle="-")
plt.plot(x, s, color="red", linewidth=2.5, linestyle="solid")
plt.xlim(x.min() * 1.1, x.max() * 1.1)
plt.ylim(c.min() * 1.1, c.max() * 1.1)
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi],
['$-\pi$', '$-\pi/2$', '$0$', '$+\pi/2$', '$+\pi$'])
plt.yticks([-1, 0, +1], ['$-1$', '$0$', '$+1$'])
```
### Moving spines
* **Spines** are the lines connecting the axis tick marks and noting the boundaries of the data area.
* Spines can be placed at arbitrary positions
* Until now, they are on the border of the axis
* We want to have them in the middle
* There are four of them: top, bottom, left, right
* Therefore, the top and the right will be discarded by setting their color to `none`
* The bottom and the left ones will be moved to coordinate 0 in data space coordinates
```
plt.figure(figsize=(10, 6), dpi=80)
plt.plot(x, c, color="blue", linewidth=2.5, linestyle="-")
plt.plot(x, s, color="red", linewidth=2.5, linestyle="solid")
plt.xlim(x.min() * 1.1, x.max() * 1.1)
plt.ylim(c.min() * 1.1, c.max() * 1.1)
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi], ['$-\pi$', '$-\pi/2$', '$0$', '$+\pi/2$', '$+\pi$'])
plt.yticks([-1, 0, +1], ['$-1$', '$0$', '$+1$'])
ax = plt.gca() # 'get current axis'
# discard top and right spines
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
```
### Adding a legend
* Let us include a legend in the upper right of the plot
```
plt.figure(figsize=(10, 6), dpi=80)
plt.plot(x, c, color="blue", linewidth=2.5, linestyle="-",
label="cosine")
plt.plot(x, s, color="red", linewidth=2.5, linestyle="solid",
label="sine")
plt.xlim(x.min() * 1.1, x.max() * 1.1)
plt.ylim(c.min() * 1.1, c.max() * 1.1)
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi], ['$-\pi$', '$-\pi/2$', '$0$', '$+\pi/2$', '$+\pi$'])
plt.yticks([-1, 0, +1], ['$-1$', '$0$', '$+1$'])
ax = plt.gca() # 'get current axis'
# discard top and right spines
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
plt.legend(loc='upper right')
```
### Annotate some points
* The `annotate` command allows us to include annotation in the plot
* For instance, to annotate the value $\frac{2\pi}{3}$ of both the sine and the cosine, we have to:
1. draw a marker on the curve as well as a straight dotted line
2. use the annotate command to display some text with an arrow
```
plt.figure(figsize=(10, 6), dpi=80)
plt.plot(x, c, color="blue", linewidth=2.5, linestyle="-", label="cosine")
plt.plot(x, s, color="red", linewidth=2.5, linestyle="solid", label="sine")
plt.xlim(x.min() * 1.1, x.max() * 1.1)
plt.ylim(c.min() * 1.1, c.max() * 1.1)
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi], ['$-\pi$', '$-\pi/2$', '$0$', '$+\pi/2$', '$+\pi$'])
plt.yticks([-1, 0, +1], ['$-1$', '$0$', '$+1$'])
t = 2 * np.pi / 3
plt.plot([t, t], [0, np.cos(t)], color='blue', linewidth=2.5, linestyle="--")
plt.scatter([t, ], [np.cos(t), ], 50, color='blue')
plt.annotate(r'$cos(\frac{2\pi}{3})=-\frac{1}{2}$',
xy=(t, np.cos(t)), xycoords='data',
xytext=(-90, -50), textcoords='offset points',
fontsize=16,
arrowprops=dict(arrowstyle="->",
connectionstyle="arc3,rad=.2"))
plt.plot([t, t],[0, np.sin(t)], color='red', linewidth=2.5,
linestyle="--")
plt.scatter([t, ],[np.sin(t), ], 50, color='red')
plt.annotate(r'$sin(\frac{2\pi}{3})=\frac{\sqrt{3}}{2}$',
xy=(t, np.sin(t)), xycoords='data',
xytext=(+10, +30), textcoords='offset points', fontsize=16,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
ax = plt.gca() # 'get current axis'
# discard top and right spines
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
plt.legend(loc='upper left')
```
* The tick labels are now hardly visible because of the blue and red lines
* We can make them bigger and we can also adjust their properties to be rendered on a semi-transparent white background
* This will allow us to see both the data and the label
```
plt.figure(figsize=(10, 6), dpi=80)
plt.plot(x, c, color="blue", linewidth=2.5, linestyle="-", label="cosine")
plt.plot(x, s, color="red", linewidth=2.5, linestyle="solid", label="sine")
plt.xlim(x.min() * 1.1, x.max() * 1.1)
plt.ylim(c.min() * 1.1, c.max() * 1.1)
plt.xticks([-np.pi, -np.pi/2, 0, np.pi/2, np.pi], ['$-\pi$', '$-\pi/2$', '$0$', '$+\pi/2$', '$+\pi$'])
plt.yticks([-1, 0, +1], ['$-1$', '$0$', '$+1$'])
t = 2 * np.pi / 3
plt.plot([t, t], [0, np.cos(t)], color='blue', linewidth=2.5, linestyle="--")
plt.scatter([t, ], [np.cos(t), ], 50, color='blue')
plt.annotate(r'$cos(\frac{2\pi}{3})=-\frac{1}{2}$',
xy=(t, np.cos(t)), xycoords='data',
xytext=(-90, -50), textcoords='offset points', fontsize=16,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
plt.plot([t, t],[0, np.sin(t)], color='red', linewidth=2.5, linestyle="--")
plt.scatter([t, ],[np.sin(t), ], 50, color='red')
plt.annotate(r'$sin(\frac{2\pi}{3})=\frac{\sqrt{3}}{2}$',
xy=(t, np.sin(t)), xycoords='data',
xytext=(+10, +30), textcoords='offset points', fontsize=16,
arrowprops=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
ax = plt.gca() # 'get current axis'
# discard top and right spines
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.spines['bottom'].set_position(('data',0))
ax.yaxis.set_ticks_position('left')
ax.spines['left'].set_position(('data',0))
plt.legend(loc='upper left')
for label in ax.get_xticklabels() + ax.get_yticklabels():
label.set_fontsize(16)
label.set_bbox(dict(facecolor='white', edgecolor='None', alpha=0.65))
```
### Scatter plots
```
n = 1024
x = np.random.normal(0, 1, n)
y = np.random.normal(0, 1, n)
t = np.arctan2(y, x)
plt.axes([0.025, 0.025, 0.95, 0.95])
plt.scatter(x, y, s=75, c=t, alpha=.5)
plt.xlim(-1.5, 1.5)
plt.xticks(())
plt.ylim(-1.5, 1.5)
plt.yticks(())
ax = plt.gca()
ax.spines['top'].set_color('none')
ax.spines['right'].set_color('none')
ax.spines['bottom'].set_color('none')
ax.spines['left'].set_color('none')
```
### Bar plots
* Creates two bar plots overlying the same axis
* Include the value of each bar
```
n = 12
xs = np.arange(n)
y1 = (1 - xs / float(n)) * np.random.uniform(0.5, 1.0, n)
y2 = (1 - xs / float(n)) * np.random.uniform(0.5, 1.0, n)
plt.axes([0.025, 0.025, 0.95, 0.95])
plt.bar(xs, +y1, facecolor='#9999ff', edgecolor='white')
plt.bar(xs, -y2, facecolor='#ff9999', edgecolor='white')
for x, y in zip(xs, y1):
plt.text(x + 0.4, y + 0.05, '%.2f' % y, ha='center', va= 'bottom')
for x, y in zip(xs, y2):
plt.text(x + 0.4, -y - 0.05, '%.2f' % y, ha='center', va= 'top')
plt.xlim(-.5, n)
plt.xticks(())
plt.ylim(-1.25, 1.25)
plt.yticks(())
## Images
image = np.random.rand(30, 30)
plt.imshow(image, cmap=plt.cm.hot)
plt.colorbar()
years, months, sales = np.loadtxt('data/carsales.csv', delimiter=',', skiprows=1, dtype=int, unpack=True)
```
| github_jupyter |
# Classes
For more information on the magic methods of pytho classes, consult the docs: https://docs.python.org/3/reference/datamodel.html
```
class DumbClass:
""" This class is just meant to demonstrate the magic __repr__ method
"""
def __repr__(self):
""" I'm giving this method a docstring
"""
return("I'm representing an instance of my dumbclass")
dc = DumbClass()
print(dc)
dc
help(DumbClass)
class Stack:
""" A simple class implimenting some common features of Stack
objects
"""
def __init__(self, iterable=None):
""" Initializes Stack objects. If an iterable is provided,
add elements from the iterable to this Stack until the
iterable is exhausted
"""
self.head = None
self.size = 0
if(iterable is not None):
for item in iterable:
self.add(item)
def add(self, item):
""" Add an element to the top of the stack. This method will
modify self and return self.
"""
self.head = (item, self.head)
self.size += 1
return self
def pop(self):
""" remove the top item from the stack and return it
"""
if(len(self) > 0):
ret = self.head[0]
self.head = self.head[1]
self.size -= 1
return ret
return None
def __contains__(self, item):
""" Returns True if item is in self
"""
for i in self:
if(i == item):
return True
return False
def __len__(self):
""" Returns the number of items in self
"""
return self.size
def __iter__(self):
""" prepares this stack for iteration and returns self
"""
self.curr = self.head
return self
def __next__(self):
""" Returns items from the stack from top to bottom
"""
if(not hasattr(self, 'curr')):
iter(self)
if(self.curr is None):
raise StopIteration
else:
ret = self.curr[0]
self.curr = self.curr[1]
return ret
def __reversed__(self):
""" returns a copy of self with the stack turned upside
down
"""
return Stack(self)
def __add__(self, other):
""" Put self on top of other
"""
ret = Stack(reversed(other))
for item in reversed(self):
ret.add(item)
return ret
def __repr__(self):
""" Represent self as a string
"""
return f'Stack({str(list(self))})'
# Create a stack object and test some methods
x = Stack([3, 2])
print(x)
# adds an element to the top of the stack
print('\nLets add 1 to the stack')
x.add(1)
print(x)
# Removes the top most element
print('\nLets remove an item from the top of the stack')
item = x.pop()
print(item)
print(x)
# Removes the top most element
print('\nlets remove another item')
item = x.pop()
print(item)
print(x)
x = Stack([4,5,6])
# Because I implimented the __contains__ method,
# I can check if items are in stack objects
print(f'Does my stack contain 2? {2 in x}')
print(f'Does my stack contain 4? {4 in x}')
# Because I implimented the __len__ method,
# I can check how many items are in stack objects
print(f'How many elements are in my stack? {len(x)}')
# because my stack class has an __iter__ and __next__ methods
# I can iterate over stack objects
x = Stack([7,3,4])
print(f"Lets iterate over my stack : {x}")
for item in x:
print(item)
# Because my stack class has a __reversed__ method,
# I can easily reverse a stack object
print(f'I am flipping my stack upside down : {reversed(x)}')
# Because I implimented the __add__ method,
# I can add stacks together
x = Stack([4,5,6])
y = Stack([1,2,3])
print("I have two stacks")
print(f'x : {x}')
print(f'y : {y}')
print("Let's add them together")
print(f'x + y = {x + y}')
for item in (x + y):
print(item)
```
# Using the SqlAlchemy ORM
For more information, check out the documentation : https://docs.sqlalchemy.org/en/latest/orm/tutorial.html
```
from sqlalchemy import create_engine
from sqlalchemy.ext.declarative import declarative_base
from sqlalchemy import Column, Integer, String, Float, ForeignKey
from sqlalchemy.orm import Session, relationship
import pymysql
pymysql.install_as_MySQLdb()
# Sets an object to utilize the default declarative base in SQL Alchemy
Base = declarative_base()
# Lets define the owners table/class
class Owners(Base):
__tablename__ = 'owners'
id = Column(Integer, primary_key=True)
name = Column(String(255))
phone_number = Column(String(255))
pets = relationship("Pets", back_populates="owner")
def __repr__(self):
return f"<Owners(id={self.id}, name='{self.name}', phone_number='{self.phone_number}')>"
# Lets define the pets table/class
class Pets(Base):
__tablename__ = 'pets'
id = Column(Integer, primary_key=True)
name = Column(String(255))
owner_id = Column(Integer, ForeignKey('owners.id'))
owner = relationship("Owners", back_populates="pets")
def __repr__(self):
return f"<Pets(id={self.id}, name='{self.name}', owner_id={self.owner_id})>"
# Lets connect to my database
# engine = create_engine("sqlite:///pets.sqlite")
engine = create_engine("mysql://root@localhost/review_db")
# conn = engine.connect()
Base.metadata.create_all(engine)
session = Session(bind=engine)
# Lets create me
me = Owners(name='Kenton', phone_number='867-5309')
session.add(me)
session.commit()
# Now lets add my dog
my_dog = Pets(name='Saxon', owner_id=me.id)
session.add(my_dog)
session.commit()
# We can query the tables using the session object from earlier
# Lets just get all the data
all_owners = list(session.query(Owners))
all_pets = list(session.query(Pets))
print(all_owners)
print(all_pets)
me = all_owners[0]
rio = all_pets[0]
# Because we are using an ORM and have defined relations,
# we can easily and intuitively access related data
print(me.pets)
print(rio.owner)
```
| github_jupyter |
# Estimation on real data using MSM
```
from consav import runtools
runtools.write_numba_config(disable=0,threads=4)
%matplotlib inline
%load_ext autoreload
%autoreload 2
# Local modules
from Model import RetirementClass
import figs
import SimulatedMinimumDistance as SMD
# Global modules
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
```
### Data
```
data = pd.read_excel('SASdata/moments.xlsx')
mom_data = data['mom'].to_numpy()
se = data['se'].to_numpy()
obs = data['obs'].to_numpy()
se = se/np.sqrt(obs)
se[se>0] = 1/se[se>0]
factor = np.ones(len(se))
factor[-15:] = 4
W = np.eye(len(se))*se*factor
cov = pd.read_excel('SASdata/Cov.xlsx')
Omega = cov*obs
Nobs = np.median(obs)
```
### Set up estimation
```
single_kwargs = {'simN': int(1e5), 'simT': 68-53+1}
Couple = RetirementClass(couple=True, single_kwargs=single_kwargs,
simN=int(1e5), simT=68-53+1)
Couple.solve()
Couple.simulate()
def mom_fun(Couple):
return SMD.MomFun(Couple)
est_par = ["alpha_0_male", "alpha_0_female", "sigma_eta", "pareto_w", "phi_0_male"]
smd = SMD.SimulatedMinimumDistance(Couple,mom_data,mom_fun,est_par=est_par)
```
### Estimate
```
theta0 = SMD.start(9,bounds=[(0,1), (0,1), (0.2,0.8), (0.2,0.8), (0,2)])
theta0
smd.MultiStart(theta0,W)
theta = smd.est
smd.MultiStart(theta0,W)
theta = smd.est
```
### Save parameters
```
est_par.append('phi_0_female')
thetaN = list(theta)
thetaN.append(Couple.par.phi_0_male)
SMD.save_est(est_par,thetaN,name='baseline2')
```
### Standard errors
```
est_par = ["alpha_0_male", "alpha_0_female", "sigma_eta", "pareto_w", "phi_0_male"]
smd = SMD.SimulatedMinimumDistance(Couple,mom_data,mom_fun,est_par=est_par)
theta = list(SMD.load_est('baseline2').values())
theta = theta[:5]
smd.obj_fun(theta,W)
np.round(theta,3)
Nobs = np.quantile(obs,0.25)
smd.std_error(theta,Omega,W,Nobs,Couple.par.simN*2/Nobs)
# Nobs = lower quartile
np.round(smd.std,3)
# Nobs = lower quartile
np.round(smd.std,3)
Nobs = np.quantile(obs,0.25)
smd.std_error(theta,Omega,W,Nobs,Couple.par.simN*2/Nobs)
# Nobs = median
np.round(smd.std,3)
```
### Model fit
```
smd.obj_fun(theta,W)
jmom = pd.read_excel('SASdata/joint_moments_ad.xlsx')
for i in range(-2,3):
data = jmom[jmom.Age_diff==i]['ssh'].to_numpy()
plt.bar(np.arange(-7,8), data, label='Data')
plt.plot(np.arange(-7,8),SMD.joint_moments_ad(Couple,i),'k--', label='Predicted')
#plt.ylim(0,0.4)
plt.legend()
plt.show()
figs.MyPlot(figs.model_fit_marg(smd,0,0),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargWomenSingle2.png')
figs.MyPlot(figs.model_fit_marg(smd,1,0),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargMenSingle2.png')
figs.MyPlot(figs.model_fit_marg(smd,0,1),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargWomenCouple2.png')
figs.MyPlot(figs.model_fit_marg(smd,1,1),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargMenCouple2.png')
figs.model_fit_joint(smd).savefig('figs/ModelFit/Joint2')
theta[4] = 1
smd.obj_fun(theta,W)
dist1 = smd.mom_sim[44:]
theta[4] = 2
smd.obj_fun(theta,W)
dist2 = smd.mom_sim[44:]
theta[4] = 3
smd.obj_fun(theta,W)
dist3 = smd.mom_sim[44:]
dist_data = mom_data[44:]
figs.model_fit_joint_many(dist_data,dist1,dist2,dist3).savefig('figs/ModelFit/JointMany2')
```
### Sensitivity
```
est_par_tex = [r'$\alpha^m$', r'$\alpha^f$', r'$\sigma$', r'$\lambda$', r'$\phi$']
fixed_par = ['R', 'rho', 'beta', 'gamma', 'v',
'priv_pension_male', 'priv_pension_female', 'g_adjust', 'pi_adjust_m', 'pi_adjust_f']
fixed_par_tex = [r'$R$', r'$\rho$', r'$\beta$', r'$\gamma$', r'$v$',
r'$PPW^m$', r'$PPW^f$', r'$g$', r'$\pi^m$', r'$\pi^f$']
smd.recompute=True
smd.sensitivity(theta,W,fixed_par)
figs.sens_fig_tab(smd.sens2[:,:5],smd.sens2e[:,:5],theta,
est_par_tex,fixed_par_tex[:5]).savefig('figs/ModelFit/CouplePref2.png')
figs.sens_fig_tab(smd.sens2[:,5:],smd.sens2e[:,5:],theta,
est_par_tex,fixed_par_tex[5:]).savefig('figs/modelFit/CoupleCali2.png')
smd.recompute=True
smd.sensitivity(theta,W,fixed_par)
figs.sens_fig_tab(smd.sens2[:,:5],smd.sens2e[:,:5],theta,
est_par_tex,fixed_par_tex[:5]).savefig('figs/ModelFit/CouplePref.png')
figs.sens_fig_tab(smd.sens2[:,5:],smd.sens2e[:,5:],theta,
est_par_tex,fixed_par_tex[5:]).savefig('figs/modelFit/CoupleCali.png')
```
### Recalibrate model (phi=0)
```
Couple.par.phi_0_male = 0
Couple.par.phi_0_female = 0
est_par = ["alpha_0_male", "alpha_0_female", "sigma_eta", "pareto_w"]
smd = SMD.SimulatedMinimumDistance(Couple,mom_data,mom_fun,est_par=est_par)
theta0 = SMD.start(4,bounds=[(0,1), (0,1), (0.2,0.8), (0.2,0.8)])
smd.MultiStart(theta0,W)
theta = smd.est
est_par.append("phi_0_male")
est_par.append("phi_0_female")
theta = list(theta)
theta.append(Couple.par.phi_0_male)
theta.append(Couple.par.phi_0_male)
SMD.save_est(est_par,theta,name='phi0')
smd.obj_fun(theta,W)
figs.MyPlot(figs.model_fit_marg(smd,0,0),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargWomenSingle_phi0.png')
figs.MyPlot(figs.model_fit_marg(smd,1,0),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargMenSingle_phi0.png')
figs.MyPlot(figs.model_fit_marg(smd,0,1),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargWomenCouple_phi0.png')
figs.MyPlot(figs.model_fit_marg(smd,1,1),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargMenCoupleW_phi0.png')
figs.model_fit_joint(smd).savefig('figs/ModelFit/Joint_phi0')
```
### Recalibrate model (phi high)
```
Couple.par.phi_0_male = 1.187
Couple.par.phi_0_female = 1.671
Couple.par.pareto_w = 0.8
est_par = ["alpha_0_male", "alpha_0_female", "sigma_eta"]
smd = SMD.SimulatedMinimumDistance(Couple,mom_data,mom_fun,est_par=est_par)
theta0 = SMD.start(4,bounds=[(0.2,0.6), (0.2,0.6), (0.4,0.8)])
theta0
smd.MultiStart(theta0,W)
theta = smd.est
est_par.append("phi_0_male")
est_par.append("phi_0_female")
theta = list(theta)
theta.append(Couple.par.phi_0_male)
theta.append(Couple.par.phi_0_male)
SMD.save_est(est_par,theta,name='phi_high')
smd.obj_fun(theta,W)
figs.MyPlot(figs.model_fit_marg(smd,0,0),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargWomenSingle_phi_high.png')
figs.MyPlot(figs.model_fit_marg(smd,1,0),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargMenSingle_phi_high.png')
figs.MyPlot(figs.model_fit_marg(smd,0,1),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargWomenCouple_phi_high.png')
figs.MyPlot(figs.model_fit_marg(smd,1,1),ylim=[-0.01,0.4],linewidth=3).savefig('figs/ModelFit/MargMenCoupleW_phi_high.png')
figs.model_fit_joint(smd).savefig('figs/ModelFit/Joint_phi_high')
```
| github_jupyter |
<a href="https://colab.research.google.com/github/clemencia/ML4PPGF_UERJ/blob/master/Exemplos_DR/Exercicios_DimensionalReduction.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
#Mais Exercícios de Redução de Dimensionalidade
Baseado no livro "Python Data Science Handbook" de Jake VanderPlas
https://jakevdp.github.io/PythonDataScienceHandbook/
Usando os dados de rostos do scikit-learn, utilizar as tecnicas de aprendizado de variedade para comparação.
```
from sklearn.datasets import fetch_lfw_people
faces = fetch_lfw_people(min_faces_per_person=30)
faces.data.shape
```
A base de dados tem 2300 imagens de rostos com 2914 pixels cada (47x62)
Vamos visualizar as primeiras 32 dessas imagens
```
import numpy as np
from numpy import random
from matplotlib import pyplot as plt
%matplotlib inline
fig, ax = plt.subplots(5, 8, subplot_kw=dict(xticks=[], yticks=[]))
for i, axi in enumerate(ax.flat):
axi.imshow(faces.images[i], cmap='gray')
```
Podemos ver se com redução de dimensionalidade é possível entender algumas das caraterísticas das imagens.
```
from sklearn.decomposition import PCA
model0 = PCA(n_components=0.95)
X_pca=model0.fit_transform(faces.data)
plt.plot(np.cumsum(model0.explained_variance_ratio_))
plt.xlabel('n components')
plt.ylabel('cumulative variance')
plt.grid(True)
print("Numero de componentes para 95% de variância preservada:",model0.n_components_)
```
Quer dizer que para ter 95% de variância preservada na dimensionalidade reduzida precisamos mais de 170 dimensões.
As novas "coordenadas" podem ser vistas em quadros de 9x19 pixels
```
def plot_faces(instances, **options):
fig, ax = plt.subplots(5, 8, subplot_kw=dict(xticks=[], yticks=[]))
sizex = 9
sizey = 19
images = [instance.reshape(sizex,sizey) for instance in instances]
for i,axi in enumerate(ax.flat):
axi.imshow(images[i], cmap = "gray", **options)
axi.axis("off")
```
Vamos visualizar a compressão dessas imagens
```
plot_faces(X_pca,aspect="auto")
```
A opção ```svd_solver=randomized``` faz o PCA achar as $d$ componentes principais mais rápido quando $d \ll n$, mas o $d$ é fixo. Tem alguma vantagem usar para compressão das imagens de rosto? Teste!
## Aplicar Isomap para vizualizar em 2D
```
from sklearn.manifold import Isomap
iso = Isomap(n_components=2)
X_iso = iso.fit_transform(faces.data)
X_iso.shape
from matplotlib import offsetbox
def plot_projection(data,proj,images=None,ax=None,thumb_frac=0.5,cmap="gray"):
ax = ax or plt.gca()
ax.plot(proj[:, 0], proj[:, 1], '.k')
if images is not None:
min_dist_2 = (thumb_frac * max(proj.max(0) - proj.min(0))) ** 2
shown_images = np.array([2 * proj.max(0)])
for i in range(data.shape[0]):
dist = np.sum((proj[i] - shown_images) ** 2, 1)
if np.min(dist) < min_dist_2:
# don't show points that are too close
continue
shown_images = np.vstack([shown_images, proj[i]])
imagebox = offsetbox.AnnotationBbox(
offsetbox.OffsetImage(images[i], cmap=cmap),
proj[i])
ax.add_artist(imagebox)
def plot_components(data, model, images=None, ax=None,
thumb_frac=0.05,cmap="gray"):
proj = model.fit_transform(data)
plot_projection(data,proj,images,ax,thumb_frac,cmap)
fig, ax = plt.subplots(figsize=(10, 10))
plot_projection(faces.data,X_iso,images=faces.images[:, ::2, ::2],thumb_frac=0.07)
ax.axis("off")
```
As imagens mais a direita são mais escuras que as da direita (seja iluminação ou cor da pele), as imagens mais embaixo estão orientadas com o rosto à esquerda e as de cima com o rosto à direita.
## Exercícios:
1. Aplicar LLE à base de dados dos rostos e visualizar em mapa 2D, em particular a versão "modificada" ([link](https://scikit-learn.org/stable/modules/manifold.html#modified-locally-linear-embedding))
2. Aplicar t-SNE à base de dados dos rostos e visualizar em mapa 2D
3. Escolher mais uma implementação de aprendizado de variedade do Scikit-Learn ([link](https://scikit-learn.org/stable/modules/manifold.html)) e aplicar ao mesmo conjunto. (*Hessian, LTSA, Spectral*)
Qual funciona melhor? Adicione contador de tempo para comparar a duração de cada ajuste.
## Kernel PCA e sequências
Vamos ver novamente o exemplo do rocambole
```
import numpy as np
from numpy import random
from matplotlib import pyplot as plt
%matplotlib inline
from mpl_toolkits.mplot3d import Axes3D
from sklearn.datasets import make_swiss_roll
X, t = make_swiss_roll(n_samples=1000, noise=0.2, random_state=42)
axes = [-11.5, 14, -2, 23, -12, 15]
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=t, cmap="plasma")
ax.view_init(10, -70)
ax.set_xlabel("$x_1$", fontsize=18)
ax.set_ylabel("$x_2$", fontsize=18)
ax.set_zlabel("$x_3$", fontsize=18)
ax.set_xlim(axes[0:2])
ax.set_ylim(axes[2:4])
ax.set_zlim(axes[4:6])
```
Como foi no caso do SVM, pode se aplicar uma transformação de *kernel*, para ter um novo espaço de *features* onde pode ser aplicado o PCA. Embaixo o exemplo de PCA com kernel linear (equiv. a aplicar o PCA), RBF (*radial basis function*) e *sigmoide* (i.e. logístico).
```
from sklearn.decomposition import KernelPCA
lin_pca = KernelPCA(n_components = 2, kernel="linear", fit_inverse_transform=True)
rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=0.0433, fit_inverse_transform=True)
sig_pca = KernelPCA(n_components = 2, kernel="sigmoid", gamma=0.001, coef0=1, fit_inverse_transform=True)
plt.figure(figsize=(11, 4))
for subplot, pca, title in ((131, lin_pca, "Linear kernel"), (132, rbf_pca, "RBF kernel, $\gamma=0.04$"), (133, sig_pca, "Sigmoid kernel, $\gamma=10^{-3}, r=1$")):
X_reduced = pca.fit_transform(X)
if subplot == 132:
X_reduced_rbf = X_reduced
plt.subplot(subplot)
plt.title(title, fontsize=14)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=t, cmap=plt.cm.hot)
plt.xlabel("$z_1$", fontsize=18)
if subplot == 131:
plt.ylabel("$z_2$", fontsize=18, rotation=0)
plt.grid(True)
```
## Selecionar um Kernel e Otimizar Hiperparâmetros
Como estos são algoritmos não supervisionados, no existe uma forma "obvia" de determinar a sua performance.
Porém a redução de dimensionalidade muitas vezes é um passo preparatório para uma outra tarefa de aprendizado supervisionado. Nesse caso é possível usar o ```GridSearchCV``` para avaliar a melhor performance no passo seguinte, com um ```Pipeline```. A classificação será em base ao valor do ```t``` com limite arbitrário de 6.9.
```
from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
from sklearn.pipeline import Pipeline
y = t>6.9
clf = Pipeline([
("kpca", KernelPCA(n_components=2)),
("log_reg", LogisticRegression(solver="liblinear"))
])
param_grid = [{
"kpca__gamma": np.linspace(0.03, 0.05, 10),
"kpca__kernel": ["rbf", "sigmoid"]
}]
grid_search = GridSearchCV(clf, param_grid, cv=3)
grid_search.fit(X, y)
print(grid_search.best_params_)
```
### Exercício :
Varie o valor do corte em ```t``` e veja tem faz alguma diferência para o kernel e hiperparámetros ideais.
### Inverter a transformação e erro de Reconstrução
Outra opção seria escolher o kernel e hiperparâmetros que tem o menor erro de reconstrução.
O seguinte código, com opção ```fit_inverse_transform=True```, vai fazer junto com o kPCA um modelo de regressão com as instancias projetadas (```X_reduced```) de treino e as originais (```X```) de target. O resultado do ```inverse_transform``` será uma tentativa de reconstrução no espaço original .
```
rbf_pca = KernelPCA(n_components = 2, kernel="rbf", gamma=13./300.,
fit_inverse_transform=True)
X_reduced = rbf_pca.fit_transform(X)
X_preimage = rbf_pca.inverse_transform(X_reduced)
X_preimage.shape
axes = [-11.5, 14, -2, 23, -12, 15]
fig = plt.figure(figsize=(12, 10))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X_preimage[:, 0], X_preimage[:, 1], X_preimage[:, 2], c=t, cmap="plasma")
ax.view_init(10, -70)
ax.set_xlabel("$x_1$", fontsize=18)
ax.set_ylabel("$x_2$", fontsize=18)
ax.set_zlabel("$x_3$", fontsize=18)
ax.set_xlim(axes[0:2])
ax.set_ylim(axes[2:4])
ax.set_zlim(axes[4:6])
```
Então é possível computar o "erro" entre o dataset reconstruido e o original (MSE).
```
from sklearn.metrics import mean_squared_error as mse
print(mse(X,X_preimage))
```
## Exercício :
Usar *grid search* com validação no valor do MSE para achar o kernel e hiperparámetros que minimizam este erro, para o exemplo do rocambole.
| github_jupyter |
## Ejemplos aplicaciones de las distribuciones de probabilidad
## Ejemplo Binomial
Un modelo de precio de opciones, el cual intente modelar el precio de un activo $S(t)$ en forma simplificada, en vez de usar ecuaciones diferenciales estocásticas. De acuerdo a este modelo simplificado, dado el precio del activo actual $S(0)=S_0$, el precio después de un paso de tiempo $\delta t$, denotado por $S(\delta t)$, puede ser ya sea $S_u=uS_0$ o $S_d=dS_0$, con probabilidades $p_u$ y $p_d$, respectivamente. Los subíndices $u$ y $p$ pueden ser interpretados como 'subida' y 'bajada', además consideramos cambios multiplicativos. Ahora imagine que el proces $S(t)$ es observado hasta el tiempo $T=n\cdot \delta t$ y que las subidas y bajadas del precio son independientes en todo el tiempo. Como hay $n$ pasos, el valor mas grande de $S(T)$ alcanzado es $S_0u^n$ y el valor más pequeño es $S_0d^n$. Note que valores intermedios serán de la forma $S_0u^md^{n-m}$ donde $m$ es el número de saltos de subidas realizadas por el activo y $n-m$ el número bajadas del activo. Observe que es irrelevante la secuencia exacta de subidas y bajadas del precio para determinar el precio final, es decir como los cambios multiplicativos conmutan: $S_0ud=S_0du$. Un simple modelo como el acá propuesto, puede representarse mediante un modelo binomial y se puede representar de la siguiente forma:

Tal modelo es un poco conveniente para simples opciones de dimensión baja debido a que **(el diagrama puede crecer exponencialmente)**, cuando las recombinaciones mantienen una complejidad baja. Con este modelo podíamos intentar responder
- Cúal es la probabilidad que $S(T)=S_0u^md^{(n-m)}$?
- **Hablar como construir el modelo binomial**
- $n,m,p \longrightarrow X\sim Bin(n,p)$
- PMF $\rightarrow P(X=m)={n \choose m}p^m(1-p)^{n-m}$
- Dibuje la Densidad de probabilidad para $n=30, p_1=0.2,p_2=0.4$
```
# Importamos librerías a trabajar en todas las simulaciones
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as st # Librería estadística
from math import factorial as fac # Importo la operación factorial
from scipy.special import comb # Importamos la función combinatoria
%matplotlib inline
# Parámetros de la distribución
n = 30; p1=0.2; p2 = 0.4
m = np.arange(0,n)
n = n*np.ones(len(m))
# Distribución binomial creada
P = lambda p,n,m:comb(n,m)*p**m*(1-p)**(n-m)
# Distribución binomial del paquete de estadística
P2 = st.binom(n,p1).pmf(m)
# Comparación de función creada con función de python
plt.plot(P(p1,n,m),'o-',label='Función creada')
plt.stem(P2,'r--',label='Función de librería estadística')
plt.legend()
plt.title('Comparación de funciones')
plt.show()
# Grafica de pmf para el problema de costo de activos
plt.plot(P(p1,n,m),'o-.b',label='$p_1 = 0.2$')
plt.plot(st.binom(n,p2).pmf(m),'gv--',label='$p_2 = 0.4$')
plt.legend()
plt.title('Gráfica de pmf para el problema de costo de activos')
plt.show()
```
## Ejercicio
<font color='red'>Problema referencia: Introduction to Operations Research,(Chap.10.1, pag.471 and 1118)
> Descargar ejercicio de el siguiente link
> https://drive.google.com/file/d/19GvzgEmYUNXrZqlmppRyW5t0p8WfUeIf/view?usp=sharing







**Pessimistic case**

**Possibilities: Most likely**

**Optimistic case**

## **Approximations**
1. **Simplifying Approximation 1:** Assume that the mean critical path will turn out to be the longest path through the project network.
2. **Simplifying Approximation 2:** Assume that the durations of the activities on the mean critical path are statistically independent
$$\mu_p \longrightarrow \text{Use the approximation 1}$$
$$\sigma_p \longrightarrow \text{Use the approximation 1,2}$$
**Choosing the mean critical path**

3. **Simplifying Approximation 3:** Assume that the form of the probability distribution of project duration is a `normal distribution`. By using simplifying approximations 1 and 2, one version of the central limit theorem justifies this assumption as being a reasonable approximation if the number of activities on the mean critical path is not too small (say, at least 5). The approximation becomes better as this number of activities increases.
### Casos de estudio
Se tiene entonces la variable aleatoria $T$ la cual representa la duración del proyecto en semanas con media $\mu_p$ y varianza $\sigma_p^2$ y $d$ representa la fecha límite de entrega del proyecto, la cual es de 47 semanas.
1. Suponer que $T$ distribuye normal y responder cual es la probabilidad $P(T\leq d)$.
```
######### Caso de estudio 1 ################
up = 44; sigma = np.sqrt(9); d = 47
P = st.norm(up,sigma).cdf(d)
print('P(T<=d)=',P)
P2 = st.beta
```
>## <font color = 'red'> Tarea
>1.Suponer que $T$ distribuye beta donde la media es $\mu_p$ y varianza $\sigma_p^2$ y responder cual es la probabilidad $P(T\leq d)$.

> **Ayuda**: - Aprender a utlizar el solucionador de ecuaciones no lineales https://stackoverflow.com/questions/19843116/passing-arguments-to-fsolve
- Leer el help d
>2.Suponer que $T$ distribuye triangular donde el valor mas probable es $\mu_p$ el valor pesimista es $p=49$ y el valor optimista es $o=40$ y responder cual es la probabilidad $P(T\leq d)$.
>3.Una vez respondido los dos numerales anteriores, suponer que cada actividad es dependiente y su dependencia es mostrada en la figura donde se nombran los procesos, además considere que la distribución de cada actividad distribuye beta. Partiendo de la dependencia de las actividades, generar 10000 escenarios diferentes para cada actividad y utilizar montecarlo para responder ¿Cuál es la probabilidad $P(T\leq d)$. Comparar con el resultado obtenido 1 y comentar las diferencias (CONCLUIR)
>4.Repetir el literal 3 pero en este caso usando una distribución triangular.
> **Nota:** en el archivo PDF que les puse al principio de esta clase, hay una posible solución que les puede ayudar a la hora de hacer su suposiciones y su programación.
## Parámetros de entrega
Se habilitará un enlace en Canvas donde deben de subir su cuaderno de python con la solución dada. La fecha límite de recepción será el jueves 10 de octubre a las 11:55 pm.
<script>
$(document).ready(function(){
$('div.prompt').hide();
$('div.back-to-top').hide();
$('nav#menubar').hide();
$('.breadcrumb').hide();
$('.hidden-print').hide();
});
</script>
<footer id="attribution" style="float:right; color:#808080; background:#fff;">
Created with Jupyter by Oscar David Jaramillo Zuluaga
</footer>
| github_jupyter |
<a href="https://colab.research.google.com/github/sanjaykmenon/DS-Unit-1-Sprint-1-Dealing-With-Data/blob/master/module3-databackedassertions/Sanjay_Krishna_LS_DS_113_Making_Data_backed_Assertions_Assignment.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
# Lambda School Data Science - Making Data-backed Assertions
This is, for many, the main point of data science - to create and support reasoned arguments based on evidence. It's not a topic to master in a day, but it is worth some focused time thinking about and structuring your approach to it.
## Assignment - what's going on here?
Consider the data in `persons.csv` (already prepared for you, in the repo for the week). It has four columns - a unique id, followed by age (in years), weight (in lbs), and exercise time (in minutes/week) of 1200 (hypothetical) people.
Try to figure out which variables are possibly related to each other, and which may be confounding relationships.
Try and isolate the main relationships and then communicate them using crosstabs and graphs. Share any cool graphs that you make with the rest of the class in Slack!
```
# TODO - your code here
# Use what we did live in lecture as an example
# HINT - you can find the raw URL on GitHub and potentially use that
# to load the data with read_csv, or you can upload it yourself
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/LambdaSchool/DS-Unit-1-Sprint-1-Dealing-With-Data/master/module3-databackedassertions/persons.csv')
df.head()
df.columns = ['unique_id', 'age','weight','exercise_time']
df.head()
df.dtypes
#df.reset_index()
exercise_bins = pd.cut(df['exercise_time'],10)
pd.crosstab(exercise_bins, df['age'], normalize = 'columns')
pd.crosstab(exercise_bins, df['weight'], normalize='columns')
weight_bins = pd.cut(df['weight'], 5)
pd.crosstab(weight_bins, df['age'], normalize='columns')
```
## Can't seem to find a relationship because there is too much data to analyze here. I think I will try plotting this to see if i can get a better understanding.
```
import seaborn as sns
sns.pairplot(df)
```
## Using seaborn pairplot to plot relationships between each variable to each other, it seems there is a relationship between weights & exercise time where the lower your weigh the more exercie time you have.
### Assignment questions
After you've worked on some code, answer the following questions in this text block:
1. What are the variable types in the data?
2. What are the relationships between the variables?
3. Which relationships are "real", and which spurious?
1. All are continuous data
2. There is a relationship between weight and exercise time, where it seems people who exercise for more time have a lower weight. Similarly there is relationship between age and exercise time where people who are in the group of 60-80 exercise less.
3. The relationship between exercise time and weight can be spurious because usually people who exercise more weigh less and as a result this a causal factor. The other factors seem more realistic such as the age and exercise time, since older people tend to not have the physical capacity to exercise longer generally.
## Stretch goals and resources
Following are *optional* things for you to take a look at. Focus on the above assignment first, and make sure to commit and push your changes to GitHub.
- [Spurious Correlations](http://tylervigen.com/spurious-correlations)
- [NIH on controlling for confounding variables](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4017459/)
Stretch goals:
- Produce your own plot inspired by the Spurious Correlation visualizations (and consider writing a blog post about it - both the content and how you made it)
- Pick one of the techniques that NIH highlights for confounding variables - we'll be going into many of them later, but see if you can find which Python modules may help (hint - check scikit-learn)
| github_jupyter |
# Working with Pytrees
[](https://colab.research.google.com/github/google/jax/blob/main/docs/jax-101/05.1-pytrees.ipynb)
*Author: Vladimir Mikulik*
Often, we want to operate on objects that look like dicts of arrays, or lists of lists of dicts, or other nested structures. In JAX, we refer to these as *pytrees*, but you can sometimes see them called *nests*, or just *trees*.
JAX has built-in support for such objects, both in its library functions as well as through the use of functions from [`jax.tree_utils`](https://jax.readthedocs.io/en/latest/jax.tree_util.html) (with the most common ones also available as `jax.tree_*`). This section will explain how to use them, give some useful snippets and point out common gotchas.
## What is a pytree?
As defined in the [JAX pytree docs](https://jax.readthedocs.io/en/latest/pytrees.html):
> a pytree is a container of leaf elements and/or more pytrees. Containers include lists, tuples, and dicts. A leaf element is anything that’s not a pytree, e.g. an array. In other words, a pytree is just a possibly-nested standard or user-registered Python container. If nested, note that the container types do not need to match. A single “leaf”, i.e. a non-container object, is also considered a pytree.
Some example pytrees:
```
import jax
import jax.numpy as jnp
example_trees = [
[1, 'a', object()],
(1, (2, 3), ()),
[1, {'k1': 2, 'k2': (3, 4)}, 5],
{'a': 2, 'b': (2, 3)},
jnp.array([1, 2, 3]),
]
# Let's see how many leaves they have:
for pytree in example_trees:
leaves = jax.tree_leaves(pytree)
print(f"{repr(pytree):<45} has {len(leaves)} leaves: {leaves}")
```
We've also introduced our first `jax.tree_*` function, which allowed us to extract the flattened leaves from the trees.
## Why pytrees?
In machine learning, some places where you commonly find pytrees are:
* Model parameters
* Dataset entries
* RL agent observations
They also often arise naturally when working in bulk with datasets (e.g., lists of lists of dicts).
## Common pytree functions
The most commonly used pytree functions are `jax.tree_map` and `jax.tree_multimap`. They work analogously to Python's native `map`, but on entire pytrees.
For functions with one argument, use `jax.tree_map`:
```
list_of_lists = [
[1, 2, 3],
[1, 2],
[1, 2, 3, 4]
]
jax.tree_map(lambda x: x*2, list_of_lists)
```
To use functions with more than one argument, use `jax.tree_multimap`:
```
another_list_of_lists = list_of_lists
jax.tree_multimap(lambda x, y: x+y, list_of_lists, another_list_of_lists)
```
For `tree_multimap`, the structure of the inputs must exactly match. That is, lists must have the same number of elements, dicts must have the same keys, etc.
## Example: ML model parameters
A simple example of training an MLP displays some ways in which pytree operations come in useful:
```
import numpy as np
def init_mlp_params(layer_widths):
params = []
for n_in, n_out in zip(layer_widths[:-1], layer_widths[1:]):
params.append(
dict(weights=np.random.normal(size=(n_in, n_out)) * np.sqrt(2/n_in),
biases=np.ones(shape=(n_out,))
)
)
return params
params = init_mlp_params([1, 128, 128, 1])
```
We can use `jax.tree_map` to check that the shapes of our parameters are what we expect:
```
jax.tree_map(lambda x: x.shape, params)
```
Now, let's train our MLP:
```
def forward(params, x):
*hidden, last = params
for layer in hidden:
x = jax.nn.relu(x @ layer['weights'] + layer['biases'])
return x @ last['weights'] + last['biases']
def loss_fn(params, x, y):
return jnp.mean((forward(params, x) - y) ** 2)
LEARNING_RATE = 0.0001
@jax.jit
def update(params, x, y):
grads = jax.grad(loss_fn)(params, x, y)
# Note that `grads` is a pytree with the same structure as `params`.
# `jax.grad` is one of the many JAX functions that has
# built-in support for pytrees.
# This is handy, because we can apply the SGD update using tree utils:
return jax.tree_multimap(
lambda p, g: p - LEARNING_RATE * g, params, grads
)
import matplotlib.pyplot as plt
xs = np.random.normal(size=(128, 1))
ys = xs ** 2
for _ in range(1000):
params = update(params, xs, ys)
plt.scatter(xs, ys)
plt.scatter(xs, forward(params, xs), label='Model prediction')
plt.legend();
```
## Custom pytree nodes
So far, we've only been considering pytrees of lists, tuples, and dicts; everything else is considered a leaf. Therefore, if you define my own container class, it will be considered a leaf, even if it has trees inside it:
```
class MyContainer:
"""A named container."""
def __init__(self, name: str, a: int, b: int, c: int):
self.name = name
self.a = a
self.b = b
self.c = c
jax.tree_leaves([
MyContainer('Alice', 1, 2, 3),
MyContainer('Bob', 4, 5, 6)
])
```
Accordingly, if we try to use a tree map expecting our leaves to be the elements inside the container, we will get an error:
```
jax.tree_map(lambda x: x + 1, [
MyContainer('Alice', 1, 2, 3),
MyContainer('Bob', 4, 5, 6)
])
```
To solve this, we need to register our container with JAX by telling it how to flatten and unflatten it:
```
from typing import Tuple, Iterable
def flatten_MyContainer(container) -> Tuple[Iterable[int], str]:
"""Returns an iterable over container contents, and aux data."""
flat_contents = [container.a, container.b, container.c]
# we don't want the name to appear as a child, so it is auxiliary data.
# auxiliary data is usually a description of the structure of a node,
# e.g., the keys of a dict -- anything that isn't a node's children.
aux_data = container.name
return flat_contents, aux_data
def unflatten_MyContainer(
aux_data: str, flat_contents: Iterable[int]) -> MyContainer:
"""Converts aux data and the flat contents into a MyContainer."""
return MyContainer(aux_data, *flat_contents)
jax.tree_util.register_pytree_node(
MyContainer, flatten_MyContainer, unflatten_MyContainer)
jax.tree_leaves([
MyContainer('Alice', 1, 2, 3),
MyContainer('Bob', 4, 5, 6)
])
```
Modern Python comes equipped with helpful tools to make defining containers easier. Some of these will work with JAX out-of-the-box, but others require more care. For instance:
```
from typing import NamedTuple, Any
class MyOtherContainer(NamedTuple):
name: str
a: Any
b: Any
c: Any
# Since `tuple` is already registered with JAX, and NamedTuple is a subclass,
# this will work out-of-the-box:
jax.tree_leaves([
MyOtherContainer('Alice', 1, 2, 3),
MyOtherContainer('Bob', 4, 5, 6)
])
```
Notice that the `name` field now appears as a leaf, as all tuple elements are children. That's the price we pay for not having to register the class the hard way.
## Common pytree gotchas and patterns
### Gotchas
#### Mistaking nodes for leaves
A common problem to look out for is accidentally introducing tree nodes instead of leaves:
```
a_tree = [jnp.zeros((2, 3)), jnp.zeros((3, 4))]
# Try to make another tree with ones instead of zeros
shapes = jax.tree_map(lambda x: x.shape, a_tree)
jax.tree_map(jnp.ones, shapes)
```
What happened is that the `shape` of an array is a tuple, which is a pytree node, with its elements as leaves. Thus, in the map, instead of calling `jnp.ones` on e.g. `(2, 3)`, it's called on `2` and `3`.
The solution will depend on the specifics, but there are two broadly applicable options:
* rewrite the code to avoid the intermediate `tree_map`.
* convert the tuple into an `np.array` or `jnp.array`, which makes the entire
sequence a leaf.
#### Handling of None
`jax.tree_utils` treats `None` as a node without children, not as a leaf:
```
jax.tree_leaves([None, None, None])
```
### Patterns
#### Transposing trees
If you would like to transpose a pytree, i.e. turn a list of trees into a tree of lists, you can do so using `jax.tree_multimap`:
```
def tree_transpose(list_of_trees):
"""Convert a list of trees of identical structure into a single tree of lists."""
return jax.tree_multimap(lambda *xs: list(xs), *list_of_trees)
# Convert a dataset from row-major to column-major:
episode_steps = [dict(t=1, obs=3), dict(t=2, obs=4)]
tree_transpose(episode_steps)
```
For more complicated transposes, JAX provides `jax.tree_transpose`, which is more verbose, but allows you specify the structure of the inner and outer Pytree for more flexibility:
```
jax.tree_transpose(
outer_treedef = jax.tree_structure([0 for e in episode_steps]),
inner_treedef = jax.tree_structure(episode_steps[0]),
pytree_to_transpose = episode_steps
)
```
## More Information
For more information on pytrees in JAX and the operations that are available, see the [Pytrees](https://jax.readthedocs.io/en/latest/pytrees.html) section in the JAX documentation.
| github_jupyter |
<a href="https://colab.research.google.com/github/JohnParken/iigroup/blob/master/pycorrector_threshold_1.1.ipynb" target="_parent"><img src="https://colab.research.google.com/assets/colab-badge.svg" alt="Open In Colab"/></a>
### 准备工作
```
from google.colab import drive
drive.mount('/content/drive')
import os
os.chdir('/content/drive/My Drive/Colab Notebooks/PyTorch/data/pycorrector-words/pycorrector-master-new-abs')
!pip install -r requirements.txt
!pip install pyltp
import pycorrector
```
### 测试结果
```
sent, detail = pycorrector.correct('我是你的眼')
print(sent,detail)
sentences = [
'他们都很饿了,需要一些食物来充饥',
'关于外交事务,我们必须十分谨慎才可以的',
'他们都很饿了,需要一些事物来充饥',
'关于外交事物,我们必须十分谨慎才可以的',
'关于外交食务,我们必须十分谨慎才可以的',
'这些方法是非常实用的',
'这些方法是非常食用的',
'高老师的植物是什么你知道吗',
'高老师的值务是什么你知道吗',
'高老师的职务是什么你知道马',
'你的行为让我们赶到非常震惊',
'你的行为让我们感到非常震惊',
'他的医生都将在遗憾当中度过',
'目前的形势对我们非常有力',
'权力和义务是对等的,我们在行使权利的同时,也必须履行相关的义五',
'权力和义务是对等的,我们在行使权力的同时',
'权利和义务是对等的',
'新讲生产建设兵团',
'坐位新时代的接班人'
'物理取闹',
'我们不太敢说话了已经',
'此函数其实就是将环境变量座位在path参数里面做替换,如果环境变量不存在,就原样返回。'
]
for sentence in sentences:
sent, detail = pycorrector.correct(sentence)
print(sent, detail)
print('\n')
sent = '这些方法是非常食用的'
sent, detail = pycorrector.correct(sent)
print(sent,detail)
sent = '这些方法是非常实用的'
sent, detail = pycorrector.correct(sent)
print(sent,detail)
sent = '关于外交事物,我们必须十分谨慎才可以的'
sent, detail = pycorrector.correct(sent)
print(sent,detail)
sent = '关于外交事务,我们必须十分谨慎才可以的'
sent, detail = pycorrector.correct(sent)
print(sent,detail)
```
### 纠错调试(与结果无关)
```
import jieba
words = '权力和义务是对等的'
word = jieba.cut(words)
print(' '.join(word))
!pip install pyltp
import os
from pyltp import Segmentor
LTP_DATA_DIR='/content/drive/My Drive/Colab Notebooks/PyTorch/data/ltp_data_v3.4.0'
cws_model_path=os.path.join(LTP_DATA_DIR,'cws.model')
segmentor=Segmentor()
segmentor.load(cws_model_path)
words=segmentor.segment('权力和义务是对等的')
print(type(words))
print(' '.join(words))
words_list = ' '.join(words).split(' ')
# segmentor.release()
token = list(yield_tuple(words_list))
def yield_tuple(words_list):
start = 0
for w in words_list:
width = len(w)
yield(w, start, start + width)
start += width
words=segmentor.segment('<s>这些方法是非常实用的</s>')
print(type(words))
print(' '.join(words))
# segmentor.release()
words=segmentor.segment('这些方法是非常实用的')
print(type(words))
print(' '.join(words))
# segmentor.release()
for i in range(0):
print("hello")
```
| github_jupyter |
```
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import requests
import time
from scipy.stats import linregress
import psycopg2
from sqlalchemy import create_engine, MetaData, Table, Column, Integer, String, Float
from api_keys import client_id
from twitch import TwitchClient
from pprint import pprint
csvpath = './Priya_Notebooks/Website/static/csv/'
client = TwitchClient(client_id= f'{client_id}')
#getting live streams data
live_streams = client.streams.get_live_streams(limit = 100)
pprint(live_streams[0])
#lsdf = pd.DataFrame.from_dict(live_streams[0].channel, orient = 'index')
lsdf = pd.DataFrame.from_dict(live_streams[0].channel, orient = 'index')
#live_streams[0].values()
lsdf.transpose()
channels = []
game_name = []
viewers = []
channel_created_at = []
channel_followers = []
channel_id = []
channel_display_name = []
channel_game = []
channel_lan = []
channel_mature = []
channel_partner = []
channel_views = []
channel_description = []
for game in live_streams:
channel_created_at.append(game.channel.created_at)
channel_followers.append(game.channel.followers)
channel_game.append(game.channel.game)
channel_lan.append(game.channel.language)
channel_mature.append(game.channel.mature)
channel_partner.append(game.channel.partner)
channel_views.append(game.channel.views)
channel_description.append(game.channel.description)
channel_id.append(game.channel.id)
channel_display_name.append(game.channel.display_name)
viewers.append(game.viewers)
toplivestreams = pd.DataFrame({
"channel_id":channel_id,
"channel_display_name":channel_display_name,
"channel_description" : channel_description,
"channel_created_at" : channel_created_at,
"channel_followers" : channel_followers,
"channel_game" : channel_game,
"channel_lan" : channel_lan,
"channel_mature" : channel_mature,
"channel_partner" : channel_partner,
"channel_views" : channel_views,
"stream_viewers" : viewers})
toplivestreams.head(5+1)
toplivestreams.to_csv(csvpath+'toplivestreams.csv', index = False, header = True)
df = pd.Panel(live_streams[0])
top_videos = client.videos.get_top(limit = 100)
pprint(top_videos[1])
channels1 = []
game_name1 = []
views1 = []
vid_length = []
vid_title = []
vid_total_views = []
channel_created_at1 = []
channel_followers1 = []
channel_id1 = []
channel_display_name1 = []
channel_game1 = []
channel_lan1 = []
channel_mature1 = []
channel_partner1 = []
channel_views1 = []
channel_description1 = []
for game in top_videos:
channel_created_at1.append(game.channel.created_at)
channel_followers1.append(game.channel.followers)
channel_game1.append(game.channel.game)
channel_lan1.append(game.channel.language)
channel_mature1.append(game.channel.mature)
channel_partner1.append(game.channel.partner)
channel_views1.append(game.channel.views)
channel_description1.append(game.channel.description)
channel_id1.append(game.channel.id)
channel_display_name1.append(game.channel.display_name)
views1.append(game.views)
vid_length.append(game.length)
vid_title.append(game.title)
vid_total_views.append(round(((game.views*game.length)/(60*60)),2))
topvideos = pd.DataFrame({
"vid_title":vid_title,
"vid_length":vid_length,
"video_views" : views1,
"total_view_time-calc-hours":vid_total_views,
"channel_id":channel_id,
"channel_display_name":channel_display_name1,
"channel_description" : channel_description1,
"channel_created_at" : channel_created_at1,
"channel_followers" : channel_followers1,
"channel_game" : channel_game1,
"channel_lan" : channel_lan1,
"channel_mature" : channel_mature1,
"channel_partner" : channel_partner1,
"channel_views" : channel_views1,
})
topvideos.head(5+1)
topvideos.to_csv(csvpath+'topvideos.csv', index = False, header = True)
toplivestreams.channel_game.value_counts()
topvideos.channel_game.value_counts()
gamesummary = client.stream.get_summary(toplivestreamgames[0])
topvidchan = topvideos.channel_display_name.unique()
topstreamchan = toplivestreams.channel_display_name.unique()
topchan = set(topvidchan).intersection(topstreamchan)
topchan
serverlocations = []
for server in servers:
serverlocations.append(server.name)
serverlocations
servers = client.ingests.get_server_list()
pprint(servers)
```
| github_jupyter |
```
import CNN2Head_input
import tensorflow as tf
import numpy as np
SAVE_FOLDER = '/home/ubuntu/coding/cnn/multi-task-learning/save/current'
_, smile_test_data = CNN2Head_input.getSmileImage()
_, gender_test_data = CNN2Head_input.getGenderImage()
_, age_test_data = CNN2Head_input.getAgeImage()
def eval_smile_gender_age_test(nbof_crop):
nbof_smile = len(smile_test_data)
nbof_gender = len(gender_test_data)
nbof_age = len(age_test_data)
nbof_true_smile = 0
nbof_true_gender = 0
nbof_true_age = 0
sess = tf.InteractiveSession()
saver = tf.train.import_meta_graph(SAVE_FOLDER + '/model.ckpt.meta')
saver.restore(sess, SAVE_FOLDER + "/model.ckpt")
x_smile = tf.get_collection('x_smile')[0]
x_gender = tf.get_collection('x_gender')[0]
x_age = tf.get_collection('x_age')[0]
keep_prob_smile_fc1 = tf.get_collection('keep_prob_smile_fc1')[0]
keep_prob_gender_fc1 = tf.get_collection('keep_prob_gender_fc1')[0]
keep_prob_age_fc1 = tf.get_collection('keep_prob_age_fc1')[0]
keep_prob_smile_fc2 = tf.get_collection('keep_prob_smile_fc2')[0]
keep_prob_gender_fc2 = tf.get_collection('keep_prob_emotion_fc2')[0]
keep_prob_age_fc2 = tf.get_collection('keep_prob_age_fc2')[0]
y_smile_conv = tf.get_collection('y_smile_conv')[0]
y_gender_conv = tf.get_collection('y_gender_conv')[0]
y_age_conv = tf.get_collection('y_age_conv')[0]
is_training = tf.get_collection('is_training')[0]
for i in range(nbof_smile):
smile = np.zeros([1,48,48,1])
smile[0] = smile_test_data[i % 1000][0]
smile_label = smile_test_data[i % 1000][1]
gender = np.zeros([1,48,48,1])
gender[0] = gender_test_data[i % 1000][0]
gender_label = gender_test_data[i % 1000][1]
age = np.zeros([1,48,48,1])
age[0] = age_test_data[i % 1000][0]
age_label = age_test_data[i % 1000][1]
y_smile_pred = np.zeros([2])
y_gender_pred = np.zeros([2])
y_age_pred = np.zeros([4])
for _ in range(nbof_crop):
x_smile_ = CNN2Head_input.random_crop(smile, (48, 48), 10)
x_gender_ = CNN2Head_input.random_crop(gender,(48, 48), 10)
x_age_ = CNN2Head_input.random_crop(age,(48, 48), 10)
y1 = y_smile_conv.eval(feed_dict={x_smile: x_smile_,
x_gender: x_gender_,
x_age: x_age_,
keep_prob_smile_fc1: 1,
keep_prob_smile_fc2: 1,
keep_prob_gender_fc1: 1,
keep_prob_gender_fc2: 1,
keep_prob_age_fc1: 1,
keep_prob_age_fc2: 1,
is_training: False})
y2 = y_gender_conv.eval(feed_dict={x_smile: x_smile_,
x_gender: x_gender_,
x_age: x_age_,
keep_prob_smile_fc1: 1,
keep_prob_smile_fc2: 1,
keep_prob_gender_fc1: 1,
keep_prob_gender_fc2: 1,
keep_prob_age_fc1: 1,
keep_prob_age_fc2: 1,
is_training: False})
y3 = y_age_conv.eval(feed_dict={x_smile: x_smile_,
x_gender: x_gender_,
x_age: x_age_,
keep_prob_smile_fc1: 1,
keep_prob_smile_fc2: 1,
keep_prob_gender_fc1: 1,
keep_prob_gender_fc2: 1,
keep_prob_age_fc1: 1,
keep_prob_age_fc2: 1,
is_training: False})
y_smile_pred += y1[0]
y_gender_pred += y2[0]
y_age_pred += y3[0]
predict_smile = np.argmax(y_smile_pred)
predict_gender = np.argmax(y_gender_pred)
predict_age = np.argmax(y_age_pred)
if (predict_smile == smile_label) & (i < 1000):
nbof_true_smile += 1
if (predict_gender == gender_label):
nbof_true_gender += 1
if (predict_age == age_label):
nbof_true_age += 1
return nbof_true_smile * 100.0 / nbof_smile, nbof_true_gender * 100.0 / nbof_gender, nbof_true_age * 100.0 / nbof_age
def evaluate(nbof_crop):
print('Testing phase...............................')
smile_acc, gender_acc, age_acc = eval_smile_gender_age_test(nbof_crop)
print('Smile test accuracy: ',str(smile_acc))
print('Gender test accuracy: ', str(gender_acc))
print('Age test accuracy: ', str(age_acc))
evaluate(10)
```
| github_jupyter |
```
#import libraries
import numpy as np
import pandas as pd
print('The pandas version is {}.'.format(pd.__version__))
from pandas import read_csv
from random import random
import sklearn
print('The scikit-learn version is {}.'.format(sklearn.__version__))
from sklearn.model_selection import train_test_split, cross_val_score, GridSearchCV
from sklearn.preprocessing import StandardScaler, LabelBinarizer, MultiLabelBinarizer
from sklearn.linear_model import Lasso, Ridge
from sklearn.metrics import mean_squared_error, make_scorer, accuracy_score, confusion_matrix
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import GradientBoostingClassifier, RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.neural_network import MLPClassifier
from sklearn.svm import LinearSVC
#from sklearn.inspection import permutation_importance, partial_dependence - ONLY AVAIL IN LATER VER
import matplotlib.pyplot as plt
from matplotlib.ticker import PercentFormatter
from mpl_toolkits.mplot3d import Axes3D
import seaborn as sns
sns.set()
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
```
## Methodology
### Objective
**Use FAERS data on drug safety to identify possible risk factors associated with patient mortality and other serious adverse events associated with approved used of a drug or drug class**
### Data
**_Outcome table_**
1. Start with outcome_c table to define unit of analysis (primaryid)
2. Reshape outcome_c to one row per primaryid
3. Outcomes grouped into 3 categories: a. death, b. serious, c. other
4. Multiclass model target format: each outcome grp coded into separate columns
**_Demo table_**
1. Drop fields not used in model input to reduce table size (preferably before import to notebook)
2. Check if demo table one row per primaryid (if NOT then need to reshape / clean - TBD)
**_Model input and targets_**
1. Merge clean demo table with reshaped multilabel outcome targets (rows: primaryid, cols: outcome grps)
2. Inspect merged file to check for anomalies (outliers, bad data, ...)
### Model
**_Multilabel Classifier_**
1. Since each primaryid has multiple outcomes coded in the outcome_c table, the ML model should predict the probability of each possible outcome.
2. In scikit-learn lib most/all classifiers can predict multilabel outcomes by coding target outputs into array
### Results
TBD
### Insights
TBD
## Data Pipeline: Outcome Table
```
# read outcome_c.csv & drop unnecessary fields
infile = '../input/Outc20Q1.csv'
cols_in = ['primaryid','outc_cod']
df = pd.read_csv(infile, usecols=cols_in)
print(df.head(),'\n')
print(f'Total number of rows: {len(df):,}\n')
print(f'Unique number of primaryids: {df.primaryid.nunique():,}')
# distribution of outcomes
from collections import Counter
o_cnt = Counter(df['outc_cod'])
print('Distribution of Adverse Event Outcomes in FAERS 2020 Q1')
for k, v in o_cnt.items():
print(f'{k}: {v:>8,}')
print(72*'-')
print(f'Most common outcome is {o_cnt.most_common(1)[0][0]} with {o_cnt.most_common(1)[0][1]:,} in 2020Q1')
# DO NOT GROUP OUTCOMES FOR MULTILABEL - MUST BE 0 (-1) OR 1 FOR EACH CLASS
### create outcome groups: death:'DE', serious: ['LT','HO','DS','CA',RI], other: 'OT'
# - USE TO CREATE OUTCOME GROUPS: key(original code) : value(new code)
# map grp dict to outc_cod
'''
outc_to_grp = {'DE':'death',
'LT':'serious',
'HO':'serious',
'DS':'serious',
'CA':'serious',
'RI':'serious',
'OT':'other'}
df['oc_cat'] = df['outc_cod'].map(outc_to_grp)
print(df.head(),'\n')'''
print('Distribution of AE Outcomes')
print(df['outc_cod'].value_counts()/len(df['outc_cod']),'\n')
print(df['outc_cod'].value_counts().plot(kind='pie'))
# outcome grps
print(df['outc_cod'].value_counts()/len(df['outc_cod']),'\n')
# one-hot encoding of outcome grp
# step1: pandas automatic dummy var coding
cat_cols = ['outc_cod'] #, 'oc_cat']
df1 = pd.get_dummies(df, prefix_sep="__", columns=cat_cols)
print('Outcome codes and groups')
print(f'Total number of rows: {len(df1):,}')
print(f'Unique number of primaryids: {df1.primaryid.nunique():,}\n')
print(df1.columns,'\n')
print(df1.head())
print(df1.tail())
# step 2: create multilabel outcomes by primaryid with groupby
outc_lst = ['outc_cod__CA','outc_cod__DE','outc_cod__DS','outc_cod__HO','outc_cod__LT',
'outc_cod__OT','outc_cod__RI']
#oc_lst = ['oc_cat__death','oc_cat__other','oc_cat__serious']
df2 = df1.groupby(['primaryid'])[outc_lst].sum().reset_index()
df2['n_outc'] = df2[outc_lst].sum(axis='columns') # cnt total outcomes by primaryid
print(df2.columns)
print('-'*72)
print('Outcome codes in Multilabel format')
print(f'Total number of rows: {len(df2):,}')
print(f'Unique number of primaryids: {df2.primaryid.nunique():,}\n')
print(df2.head())
#print(df2.tail())
print(df2[outc_lst].corr())
print(df2.describe().T,'\n')
# plot distribution of outcome groups
'''
color = {'boxes':'DarkGreen', 'whiskers':'DarkOrange', 'medians':'DarkBlue', 'caps':'Gray'}
print(df2[outc_lst].plot.bar()) #color=color, sym='r+'))'''
# check primaryid from outcomes table with many outcomes
# print(df2[df2['n_outc'] >= 6])
# checked in both outcomes and demo - multiple primaryids in outcome but only one primaryid in demo
# appears to be okay to use
# compare primaryids above in outcomes table to same in demo table
#pid_lst = [171962202,173902932,174119951,175773511,176085111]
#[print(df_demo[df_demo['primaryid'] == p]) for p in pid_lst] # one row in demo per primaryid - looks ok to join
# save multilabel data to csv
df2.to_csv('../input/outc_cod-multilabel.csv')
```
## Data Pipeline - Demo Table
```
# step 0: read demo.csv & check fields for missing values
infile = '../input/DEMO20Q1.csv'
#%timeit df_demo = pd.read_csv(infile) # 1 loop, best of 5: 5.19 s per loop
df_demo = pd.read_csv(infile)
print(df_demo.columns,'\n')
print(f'Percent missing by column:\n{(pd.isnull(df_demo).sum()/len(df_demo))*100}')
# step 1: exclude fields with large percent missing on read to preserve memory
keep_cols = ['primaryid', 'caseversion', 'i_f_code', 'event.dt1', 'mfr_dt', 'init_fda_dt', 'fda_dt',
'rept_cod', 'mfr_num', 'mfr_sndr', 'age', 'age_cod', 'age_grp','sex', 'e_sub', 'wt', 'wt_cod',
'rept.dt1', 'occp_cod', 'reporter_country', 'occr_country']
# removed cols: ['auth_num','lit_ref','to_mfr']
infile = '../input/DEMO20Q1.csv'
#%timeit df_demo = pd.read_csv(infile, usecols=keep_cols) # 1 loop, best of 5: 4.5 s per loop
df_demo = pd.read_csv(infile, usecols=keep_cols)
df_demo.set_index('primaryid', drop=False)
print(df_demo.head(),'\n')
print(f'Total number of rows: {len(df_demo):,}\n')
print(f'Percent missing by column:\n{(pd.isnull(df_demo).sum()/len(df_demo))*100}')
# step 2: merge demo and multilabel outcomes on primaryid
df_demo_outc = pd.merge(df_demo, df2, on='primaryid')
print('Demo - Multilabel outcome Merge','\n')
print(df_demo_outc.head(),'\n')
print(f'Total number of rows: {len(df_demo_outc):,}\n')
print(f'Unique number of primaryids: {df_demo_outc.primaryid.nunique():,}','\n')
print(f'Percent missing by column:\n{(pd.isnull(df_demo_outc).sum()/len(df_demo_outc))*100}')
# step 3: calculate wt_lbs and check
print(df_demo_outc.wt_cod.value_counts())
print(df_demo_outc.groupby('wt_cod')['wt'].describe())
# convert kg to lbs
df_demo_outc['wt_lbs'] = np.where(df_demo_outc['wt_cod']=='KG',df_demo_outc['wt']*2.204623,df_demo_outc['wt'])
print(df_demo_outc[['age','wt_lbs']].describe())
print(df_demo_outc[['age','wt_lbs']].corr())
print(sns.regplot('age','wt_lbs',data=df_demo_outc))
```
### Insight: No correlation between wt and age + age range looks wrong. Check age distributions
```
# step 4: check age fields
# age_grp
print('age_grp')
print(df_demo_outc.age_grp.value_counts(),'\n')
# age_cod
print('age_cod')
print(df_demo_outc.age_cod.value_counts(),'\n')
# age
print('age')
print(df_demo_outc.groupby(['age_grp','age_cod'])['age'].describe())
```
### age_grp, age_cod, age: Distributions by age group & code look reasonable. Create age in yrs.
age_grp
* N - Neonate
* I - Infant
* C - Child
* T - Adolescent (teen?)
* A - Adult
* E - Elderly
age_cod
* DEC - decade (yrs = 10*DEC)
* YR - year (yrs = 1*YR)
* MON - month (yrs = MON/12)
* WK - week (yrs = WK/52)
* DY - day (yrs = DY/365.25)
* HR - hour (yrs = HR/(365.25*24)) or code to zero
```
# step 5: calculate age_yrs and check corr with wt_lbs
df_demo_outc['age_yrs'] = np.where(df_demo_outc['age_cod']=='DEC',df_demo_outc['age']*10,
np.where(df_demo_outc['age_cod']=='MON',df_demo_outc['age']/12,
np.where(df_demo_outc['age_cod']=='WK',df_demo_outc['age']/52,
np.where(df_demo_outc['age_cod']=='DY',df_demo_outc['age']/365.25,
np.where(df_demo_outc['age_cod']=='DEC',df_demo_outc['age']/8766,
df_demo_outc['age'])))))
# age_yrs
print('age_yrs')
print(df_demo_outc.groupby(['age_grp','age_cod'])['age_yrs'].describe())
print(df_demo_outc[['age','age_yrs']].describe())
print(df_demo_outc[['wt_lbs','age_yrs']].corr())
print(sns.regplot('wt_lbs','age_yrs',data=df_demo_outc))
```
### Halis checked and wt in 400-800 range (and max wt of 1,400 lbs) is correct
```
# review data where wt_lbs > 800 lbs?
print(df_demo_outc[df_demo_outc['wt_lbs'] > 800])
# step 6: Number of AE's reported in 2020Q1 by manufacturer
print('Number of patients with adverse events by manufacturer reported in 2020Q1 from DEMO table:')
print(df_demo_outc.mfr_sndr.value_counts())
# step 7: save updated file to csv
print(df_demo_outc.columns)
# save merged demo & multilabel data to csv
df_demo_outc.to_csv('../input/demo-outc_cod-multilabel-wt_lbs-age_yrs.csv')
```
## ML Pipeline: Preprocessing
```
# step 0: check cat vars for one-hot coding
cat_lst = ['i_f_code','rept_cod','sex','occp_cod']
[print(df_demo_outc[x].value_counts(),'\n') for x in cat_lst]
print(df_demo_outc[cat_lst].describe(),'\n') # sex, occp_cod have missing values
# step 1: create one-hot dummies for multilabel outcomes
cat_cols = ['i_f_code', 'rept_cod', 'occp_cod', 'sex']
df = pd.get_dummies(df_demo_outc, prefix_sep="__", columns=cat_cols, drop_first=True)
print(df.columns)
print(df.describe().T)
print(df.head())
```
## check sklearn for imputation options
```
# step 2: use means to impute the missing values of the features with missing records
# calculate percent missing
print(df.columns,'\n')
print(f'Percent missing by column:\n{(pd.isnull(df).sum()/len(df))*100}')
num_inputs = ['n_outc', 'wt_lbs', 'age_yrs']
cat_inputs = ['n_outc', 'wt_lbs', 'age_yrs', 'i_f_code__I', 'rept_cod__5DAY',
'rept_cod__DIR', 'rept_cod__EXP', 'rept_cod__PER', 'occp_cod__HP',
'occp_cod__LW', 'occp_cod__MD', 'occp_cod__PH', 'sex__M', 'sex__UNK']
inputs = num_inputs + cat_inputs
print(inputs)
target_labels = ['oc_cat__death', 'oc_cat__other', 'oc_cat__serious']
# calculate means
means = df[inputs].mean()
print(means.shape, means)
# mean fill NA
'''
wt_lbs 161.779543
age_yrs 55.906426
'''
df['wt_lbs_mean'] = np.where(pd.isnull(df['wt_lbs']),161.779543,df['wt_lbs'])
df['age_yrs_mean'] = np.where(pd.isnull(df['age_yrs']),55.906426,df['age_yrs'])
print('mean fill NA - wt_lbs & age_yrs')
print(df.describe().T)
print(df.columns)
### standarize features
drop_cols = ['primaryid', 'caseid', 'caseversion', 'event.dt1', 'mfr_dt',
'init_fda_dt', 'fda_dt', 'auth_num', 'mfr_num', 'mfr_sndr', 'lit_ref',
'age', 'age_cod', 'age_grp', 'e_sub', 'wt', 'wt_cod', 'rept.dt1',
'to_mfr', 'reporter_country', 'occr_country', 'outc_cod__CA',
'outc_cod__DE', 'outc_cod__DS', 'outc_cod__HO', 'outc_cod__LT',
'outc_cod__OT', 'outc_cod__RI', 'oc_cat__death', 'oc_cat__other',
'oc_cat__serious', 'wt_lbs', 'age_yrs']
inputs_mean = ['n_outc', 'wt_lbs_mean', 'age_yrs_mean', 'i_f_code__I', 'rept_cod__5DAY',
'rept_cod__DIR', 'rept_cod__EXP', 'rept_cod__PER', 'occp_cod__HP',
'occp_cod__LW', 'occp_cod__MD', 'occp_cod__PH', 'sex__M']
X = df.drop(columns=drop_cols)
print(X.columns)
Xscaled = StandardScaler().fit_transform(X)
print(Xscaled.shape)
#X = pd.DataFrame(scaled, columns=inputs_mean) #.reset_index()
#print(X.describe().T,'\n')
#y_multilabel = np.c_[df['CA'], df['DE'], df['DS'], df['HO'], df['LT'], df['OT'], df['RI']]
y_multilabel = np.c_[df['oc_cat__death'], df['oc_cat__other'], df['oc_cat__serious']]
print(y_multilabel.shape)
# test multilabel classifier
knn_clf = KNeighborsClassifier()
knn_clf.fit(Xscaled,y_multilabel)
knn_clf.score(Xscaled,y_multilabel)
# review sklean api - hamming_loss, jaccard_similarity_score, f1_score
from sklearn.metrics import hamming_loss, jaccard_similarity_score
pred_knn_multilabel = knn_clf.pred(Xscaled)
f1_score(y_multilabel, pred_knn_multilabel, average='macro')
```
# STOPPED HERE - 1.13.2021
## ML Pipeline: Model Selection
```
### define functions for evaluating each of 8 types of supervised learning algorithms
def evaluate_model(predictors, targets, model, param_dict, passes=500):
seed = int(round(random()*1000,0))
print(seed)
# specify minimum test MSE, best hyperparameter set
test_err = []
min_test_err = 1e10
best_hyperparams = {}
# specify MSE predicted from the full dataset by the optimal model of each type with the best hyperparameter set
#full_y_err = None
full_err_mintesterr = None
full_err = []
# specify the final model returned
ret_model = None
# define MSE as the statistic to determine goodness-of-fit - the smaller the better
scorer = make_scorer(mean_squared_error, greater_is_better=False)
# split the data to a training-testing pair randomly by passes = n times
for i in range(passes):
print('Pass {}/{} for model {}'.format(i + 1, passes, model))
X_train, X_test, y_train, y_test = train_test_split(predictors, targets, test_size=0.3, random_state=(i+1)*seed )
# 3-fold CV on a training set, and returns an optimal_model with the best_params_ fit
default_model = model()
model_gs = GridSearchCV(default_model, param_dict, cv=3, n_jobs=-1, verbose=0, scoring=scorer) # n_jobs=16,
model_gs.fit(X_train, y_train)
optimal_model = model(**model_gs.best_params_)
optimal_model.fit(X_train, y_train)
# use the optimal_model generated above to test in the testing set and yield an MSE
y_pred = optimal_model.predict(X_test)
err = mean_squared_error(y_test, y_pred)
test_err.extend([err])
# use the optimal_model generated above to be applied to the full data set and predict y to yield an MSE
full_y_pred=optimal_model.predict(predictors)
full_y_err = mean_squared_error(full_y_pred, y)
full_err.extend([full_y_err])
# look for the smallest MSE yield from the testing set,
# so the optimal model that meantimes yields the smallest MSE from the testing set can be considered as the final model of the type
#print('MSE for {}: {}'.format(model, err))
if err < min_test_err:
min_test_err = err
best_hyperparams = model_gs.best_params_
full_err_mintesterr = full_y_err
# return the final model of the type
ret_model = optimal_model
test_err_dist = pd.DataFrame(test_err, columns=["test_err"]).describe()
full_err_dist = pd.DataFrame(full_err, columns=["full_err"]).describe()
print('Model {} with hyperparams {} yielded \n\ttest error {} with distribution \n{} \n\
toverall error {} with distribution \n{}'. \
format(model, best_hyperparams, min_test_err, test_err_dist, full_err_mintesterr,full_err_dist))
return ret_model
#%lsmagic
# Random Forest
#%%timeit
rf = evaluate_model(X,y, RandomForestClassifier,
{'n_estimators': [200, 400, 800,1000],
'max_depth': [2, 3, 4, 5],
'min_samples_leaf': [2,3],
'min_samples_split': [2, 3, 4],
'max_features' : ['auto', 'sqrt', 'log2']}, passes=1) # 250)
```
# STOPPED HERE - 1.12.2021
## TODOs:
1. Multicore processing: Setup Dask for multicore processing in Jupyter Notebook
2. Distributed computing: Check Dask Distributed for local cluster setup
```
from joblib import dump, load
dump(rf, 'binary_rf.obj') # rf_model
features2 = pd.DataFrame(data=rf.feature_importances_, index=data.columns)
features2.sort_values(by=0,ascending=False, inplace=True)
print(features2[:50])
import seaborn as sns
ax_rf = sns.barplot(x=features2.index, y=features2.iloc[:,0], order=features2.index)
ax_rf.set_ylabel('Feature importance')
fig_rf = ax_rf.get_figure()
rf_top_features=features2.index[:2].tolist()
print(rf_top_features)
pdp, axes = partial_dependence(rf, X= data, features=[(0, 1)], grid_resolution=20)
fig = plt.figure()
ax = Axes3D(fig)
XX, YY = np.meshgrid(axes[0], axes[1])
Z = pdp[0].T
surf = ax.plot_surface(XX, YY, Z, rstride=1, cstride=1,
cmap=plt.cm.BuPu, edgecolor='k')
#ax.set_xlabel('% Severe Housing \nCost Burden', fontsize=12)
#ax.set_ylabel('% Veteran', fontsize=15)
ax.set_xlabel('% mortality diff', fontsize=12)
ax.set_ylabel('% severe housing \ncost burden', fontsize=15)
ax.set_zlabel('Partial dependence', fontsize=15)
ax.view_init(elev=22, azim=330)
plt.colorbar(surf)
plt.suptitle('Partial Dependence of Top 2 Features \nRandom Forest', fontsize=15)
plt.subplots_adjust(top=0.9)
plt.show()
print(features2.index[range(14)])
datafeatures2 = pd.concat([states,y,data[features2.index[range(38)]]],axis=1)
datafeatures2.head(10)
from sklearn.inspection import permutation_importance
# feature names
feature_names = list(features2.columns)
# model - rf
model = load('binary_rf.obj')
# calculate permutation importance - all data - final model
perm_imp_all = permutation_importance(model, data, y, n_repeats=10, random_state=42)
print('Permutation Importances - mean')
print(perm_imp_all.importances_mean)
'''
# create dict of feature names and importances
fimp_dict_all = dict(zip(feature_names,perm_imp_all.importances_mean))
# feature importance - all
print('Permutation Importance for All Data')
print(fimp_dict_all)
# plot importances - all
y_pos = np.arange(len(feature_names))
plt.barh(y_pos, fimp_dict_all.importances_mean, align='center', alpha=0.5)
plt.yticks(y_pos, feature_names)
plt.xlabel('Permutation Importance - All')
plt.title('Feature Importance - All Data')
plt.show()
'''
dataused = pd.concat([states,y,data],axis=1)
print(dataused.shape)
print(dataused.head(10))
#from joblib import dump, load
dump(perm_imp_all, 'perm_imp_rf.obj')
dataused.to_excel(r'dataused_cj08292020_v2.xlsx',index=None, header=True)
```
### END BG RF ANALYSIS - 8.31.2020
### OTHER MODELS NOT RUN
```
# LASSO
lasso = evaluate_model(data, Lasso, {'alpha': np.arange(0, 1.1, 0.001),
'normalize': [True],
'tol' : [1e-3, 1e-4, 1e-5],
'max_iter': [1000, 4000, 7000]}, passes=250)
# Ridge regression
ridge = evaluate_model(data, Ridge, {'alpha': np.arange(0, 1.1, 0.05),
'normalize': [True],
'tol' : [1e-3, 1e-4, 1e-5],
'max_iter': [1000, 4000, 7000]}, passes=250)
# K-nearest neighborhood
knn = evaluate_model(data, KNeighborsRegressor, {'n_neighbors': np.arange(1, 8),
'algorithm': ['ball_tree','kd_tree','brute']}, passes=250)
# Gradient Boosting Machine
gbm = evaluate_model(data, GradientBoostingRegressor, {'learning_rate': [0.1, 0.05, 0.02, 0.01],
'n_estimators': [100, 200, 400, 800, 1000],
'min_samples_leaf': [2,3],
'max_depth': [2, 3, 4, 5],
'max_features': ['auto', 'sqrt', 'log2']}, passes=250)
# CART: classification and regression tree
cart = evaluate_model(data, DecisionTreeRegressor, {'splitter': ['best', 'random'],
'criterion': ['mse', 'friedman_mse', 'mae'],
'max_depth': [2, 3, 4, 5],
'min_samples_leaf': [2,3],
'max_features' : ['auto', 'sqrt', 'log2']}, passes=250)
# Neural network: multi-layer perceptron
nnmlp = evaluate_model(data, MLPRegressor, {'hidden_layer_sizes': [(50,)*3, (50,)*5, (50,)*10, (50,)*30, (50,)*50],
'activation': ['identity','logistic','tanh','relu']}, passes=250)
# Support Vector Machine: a linear function is an efficient model to work with
svm = evaluate_model(data, LinearSVR, {'tol': [1e-3, 1e-4, 1e-5],
'C' : np.arange(0.1,3,0.1),
'loss': ['epsilon_insensitive','squared_epsilon_insensitive'],
'max_iter': [1000, 2000, 4000]}, passes=250)
features1 = pd.DataFrame(data=gbm.feature_importances_, index=data.columns)
features1.sort_values(by=0,ascending=False, inplace=True)
print(features1[:40])
print(features1.index[range(38)])
datafeatures1 = pd.concat([states,y,data[features1.index[range(38)]]],axis=1)
datafeatures1.head(10)
import seaborn as sns
ax_gbm = sns.barplot(x=features1.index, y=features1.iloc[:,0], order=features1.index)
ax_gbm.set_ylabel('Feature importance')
fig_gbm = ax_gbm.get_figure()
```
| github_jupyter |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.