code
stringlengths 2.5k
150k
| kind
stringclasses 1
value |
|---|---|
scikit_learn 1.9. Naive Bayes 1.9. Naive Bayes
================
Naive Bayes methods are a set of supervised learning algorithms based on applying Bayes’ theorem with the “naive” assumption of conditional independence between every pair of features given the value of the class variable. Bayes’ theorem states the following relationship, given class variable \(y\) and dependent feature vector \(x\_1\) through \(x\_n\), :
\[P(y \mid x\_1, \dots, x\_n) = \frac{P(y) P(x\_1, \dots, x\_n \mid y)} {P(x\_1, \dots, x\_n)}\] Using the naive conditional independence assumption that
\[P(x\_i | y, x\_1, \dots, x\_{i-1}, x\_{i+1}, \dots, x\_n) = P(x\_i | y),\] for all \(i\), this relationship is simplified to
\[P(y \mid x\_1, \dots, x\_n) = \frac{P(y) \prod\_{i=1}^{n} P(x\_i \mid y)} {P(x\_1, \dots, x\_n)}\] Since \(P(x\_1, \dots, x\_n)\) is constant given the input, we can use the following classification rule:
\[ \begin{align}\begin{aligned}P(y \mid x\_1, \dots, x\_n) \propto P(y) \prod\_{i=1}^{n} P(x\_i \mid y)\\\Downarrow\\\hat{y} = \arg\max\_y P(y) \prod\_{i=1}^{n} P(x\_i \mid y),\end{aligned}\end{align} \] and we can use Maximum A Posteriori (MAP) estimation to estimate \(P(y)\) and \(P(x\_i \mid y)\); the former is then the relative frequency of class \(y\) in the training set.
The different naive Bayes classifiers differ mainly by the assumptions they make regarding the distribution of \(P(x\_i \mid y)\).
In spite of their apparently over-simplified assumptions, naive Bayes classifiers have worked quite well in many real-world situations, famously document classification and spam filtering. They require a small amount of training data to estimate the necessary parameters. (For theoretical reasons why naive Bayes works well, and on which types of data it does, see the references below.)
Naive Bayes learners and classifiers can be extremely fast compared to more sophisticated methods. The decoupling of the class conditional feature distributions means that each distribution can be independently estimated as a one dimensional distribution. This in turn helps to alleviate problems stemming from the curse of dimensionality.
On the flip side, although naive Bayes is known as a decent classifier, it is known to be a bad estimator, so the probability outputs from `predict_proba` are not to be taken too seriously.
1.9.1. Gaussian Naive Bayes
----------------------------
[`GaussianNB`](generated/sklearn.naive_bayes.gaussiannb#sklearn.naive_bayes.GaussianNB "sklearn.naive_bayes.GaussianNB") implements the Gaussian Naive Bayes algorithm for classification. The likelihood of the features is assumed to be Gaussian:
\[P(x\_i \mid y) = \frac{1}{\sqrt{2\pi\sigma^2\_y}} \exp\left(-\frac{(x\_i - \mu\_y)^2}{2\sigma^2\_y}\right)\] The parameters \(\sigma\_y\) and \(\mu\_y\) are estimated using maximum likelihood.
```
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.naive_bayes import GaussianNB
>>> X, y = load_iris(return_X_y=True)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)
>>> gnb = GaussianNB()
>>> y_pred = gnb.fit(X_train, y_train).predict(X_test)
>>> print("Number of mislabeled points out of a total %d points : %d"
... % (X_test.shape[0], (y_test != y_pred).sum()))
Number of mislabeled points out of a total 75 points : 4
```
1.9.2. Multinomial Naive Bayes
-------------------------------
[`MultinomialNB`](generated/sklearn.naive_bayes.multinomialnb#sklearn.naive_bayes.MultinomialNB "sklearn.naive_bayes.MultinomialNB") implements the naive Bayes algorithm for multinomially distributed data, and is one of the two classic naive Bayes variants used in text classification (where the data are typically represented as word vector counts, although tf-idf vectors are also known to work well in practice). The distribution is parametrized by vectors \(\theta\_y = (\theta\_{y1},\ldots,\theta\_{yn})\) for each class \(y\), where \(n\) is the number of features (in text classification, the size of the vocabulary) and \(\theta\_{yi}\) is the probability \(P(x\_i \mid y)\) of feature \(i\) appearing in a sample belonging to class \(y\).
The parameters \(\theta\_y\) is estimated by a smoothed version of maximum likelihood, i.e. relative frequency counting:
\[\hat{\theta}\_{yi} = \frac{ N\_{yi} + \alpha}{N\_y + \alpha n}\] where \(N\_{yi} = \sum\_{x \in T} x\_i\) is the number of times feature \(i\) appears in a sample of class \(y\) in the training set \(T\), and \(N\_{y} = \sum\_{i=1}^{n} N\_{yi}\) is the total count of all features for class \(y\).
The smoothing priors \(\alpha \ge 0\) accounts for features not present in the learning samples and prevents zero probabilities in further computations. Setting \(\alpha = 1\) is called Laplace smoothing, while \(\alpha < 1\) is called Lidstone smoothing.
1.9.3. Complement Naive Bayes
------------------------------
[`ComplementNB`](generated/sklearn.naive_bayes.complementnb#sklearn.naive_bayes.ComplementNB "sklearn.naive_bayes.ComplementNB") implements the complement naive Bayes (CNB) algorithm. CNB is an adaptation of the standard multinomial naive Bayes (MNB) algorithm that is particularly suited for imbalanced data sets. Specifically, CNB uses statistics from the *complement* of each class to compute the model’s weights. The inventors of CNB show empirically that the parameter estimates for CNB are more stable than those for MNB. Further, CNB regularly outperforms MNB (often by a considerable margin) on text classification tasks. The procedure for calculating the weights is as follows:
\[ \begin{align}\begin{aligned}\hat{\theta}\_{ci} = \frac{\alpha\_i + \sum\_{j:y\_j \neq c} d\_{ij}} {\alpha + \sum\_{j:y\_j \neq c} \sum\_{k} d\_{kj}}\\w\_{ci} = \log \hat{\theta}\_{ci}\\w\_{ci} = \frac{w\_{ci}}{\sum\_{j} |w\_{cj}|}\end{aligned}\end{align} \] where the summations are over all documents \(j\) not in class \(c\), \(d\_{ij}\) is either the count or tf-idf value of term \(i\) in document \(j\), \(\alpha\_i\) is a smoothing hyperparameter like that found in MNB, and \(\alpha = \sum\_{i} \alpha\_i\). The second normalization addresses the tendency for longer documents to dominate parameter estimates in MNB. The classification rule is:
\[\hat{c} = \arg\min\_c \sum\_{i} t\_i w\_{ci}\] i.e., a document is assigned to the class that is the *poorest* complement match.
1.9.4. Bernoulli Naive Bayes
-----------------------------
[`BernoulliNB`](generated/sklearn.naive_bayes.bernoullinb#sklearn.naive_bayes.BernoulliNB "sklearn.naive_bayes.BernoulliNB") implements the naive Bayes training and classification algorithms for data that is distributed according to multivariate Bernoulli distributions; i.e., there may be multiple features but each one is assumed to be a binary-valued (Bernoulli, boolean) variable. Therefore, this class requires samples to be represented as binary-valued feature vectors; if handed any other kind of data, a `BernoulliNB` instance may binarize its input (depending on the `binarize` parameter).
The decision rule for Bernoulli naive Bayes is based on
\[P(x\_i \mid y) = P(x\_i = 1 \mid y) x\_i + (1 - P(x\_i = 1 \mid y)) (1 - x\_i)\] which differs from multinomial NB’s rule in that it explicitly penalizes the non-occurrence of a feature \(i\) that is an indicator for class \(y\), where the multinomial variant would simply ignore a non-occurring feature.
In the case of text classification, word occurrence vectors (rather than word count vectors) may be used to train and use this classifier. `BernoulliNB` might perform better on some datasets, especially those with shorter documents. It is advisable to evaluate both models, if time permits.
1.9.5. Categorical Naive Bayes
-------------------------------
[`CategoricalNB`](generated/sklearn.naive_bayes.categoricalnb#sklearn.naive_bayes.CategoricalNB "sklearn.naive_bayes.CategoricalNB") implements the categorical naive Bayes algorithm for categorically distributed data. It assumes that each feature, which is described by the index \(i\), has its own categorical distribution.
For each feature \(i\) in the training set \(X\), [`CategoricalNB`](generated/sklearn.naive_bayes.categoricalnb#sklearn.naive_bayes.CategoricalNB "sklearn.naive_bayes.CategoricalNB") estimates a categorical distribution for each feature i of X conditioned on the class y. The index set of the samples is defined as \(J = \{ 1, \dots, m \}\), with \(m\) as the number of samples.
The probability of category \(t\) in feature \(i\) given class \(c\) is estimated as:
\[P(x\_i = t \mid y = c \: ;\, \alpha) = \frac{ N\_{tic} + \alpha}{N\_{c} + \alpha n\_i},\] where \(N\_{tic} = |\{j \in J \mid x\_{ij} = t, y\_j = c\}|\) is the number of times category \(t\) appears in the samples \(x\_{i}\), which belong to class \(c\), \(N\_{c} = |\{ j \in J\mid y\_j = c\}|\) is the number of samples with class c, \(\alpha\) is a smoothing parameter and \(n\_i\) is the number of available categories of feature \(i\).
[`CategoricalNB`](generated/sklearn.naive_bayes.categoricalnb#sklearn.naive_bayes.CategoricalNB "sklearn.naive_bayes.CategoricalNB") assumes that the sample matrix \(X\) is encoded (for instance with the help of `OrdinalEncoder`) such that all categories for each feature \(i\) are represented with numbers \(0, ..., n\_i - 1\) where \(n\_i\) is the number of available categories of feature \(i\).
1.9.6. Out-of-core naive Bayes model fitting
---------------------------------------------
Naive Bayes models can be used to tackle large scale classification problems for which the full training set might not fit in memory. To handle this case, [`MultinomialNB`](generated/sklearn.naive_bayes.multinomialnb#sklearn.naive_bayes.MultinomialNB "sklearn.naive_bayes.MultinomialNB"), [`BernoulliNB`](generated/sklearn.naive_bayes.bernoullinb#sklearn.naive_bayes.BernoulliNB "sklearn.naive_bayes.BernoulliNB"), and [`GaussianNB`](generated/sklearn.naive_bayes.gaussiannb#sklearn.naive_bayes.GaussianNB "sklearn.naive_bayes.GaussianNB") expose a `partial_fit` method that can be used incrementally as done with other classifiers as demonstrated in [Out-of-core classification of text documents](../auto_examples/applications/plot_out_of_core_classification#sphx-glr-auto-examples-applications-plot-out-of-core-classification-py). All naive Bayes classifiers support sample weighting.
Contrary to the `fit` method, the first call to `partial_fit` needs to be passed the list of all the expected class labels.
For an overview of available strategies in scikit-learn, see also the [out-of-core learning](https://scikit-learn.org/1.1/computing/scaling_strategies.html#scaling-strategies) documentation.
Note
The `partial_fit` method call of naive Bayes models introduces some computational overhead. It is recommended to use data chunk sizes that are as large as possible, that is as the available RAM allows.
scikit_learn 2.2. Manifold learning 2.2. Manifold learning
======================
Manifold learning is an approach to non-linear dimensionality reduction. Algorithms for this task are based on the idea that the dimensionality of many data sets is only artificially high.
2.2.1. Introduction
--------------------
High-dimensional datasets can be very difficult to visualize. While data in two or three dimensions can be plotted to show the inherent structure of the data, equivalent high-dimensional plots are much less intuitive. To aid visualization of the structure of a dataset, the dimension must be reduced in some way.
The simplest way to accomplish this dimensionality reduction is by taking a random projection of the data. Though this allows some degree of visualization of the data structure, the randomness of the choice leaves much to be desired. In a random projection, it is likely that the more interesting structure within the data will be lost.
To address this concern, a number of supervised and unsupervised linear dimensionality reduction frameworks have been designed, such as Principal Component Analysis (PCA), Independent Component Analysis, Linear Discriminant Analysis, and others. These algorithms define specific rubrics to choose an “interesting” linear projection of the data. These methods can be powerful, but often miss important non-linear structure in the data.
Manifold Learning can be thought of as an attempt to generalize linear frameworks like PCA to be sensitive to non-linear structure in data. Though supervised variants exist, the typical manifold learning problem is unsupervised: it learns the high-dimensional structure of the data from the data itself, without the use of predetermined classifications.
The manifold learning implementations available in scikit-learn are summarized below
2.2.2. Isomap
--------------
One of the earliest approaches to manifold learning is the Isomap algorithm, short for Isometric Mapping. Isomap can be viewed as an extension of Multi-dimensional Scaling (MDS) or Kernel PCA. Isomap seeks a lower-dimensional embedding which maintains geodesic distances between all points. Isomap can be performed with the object [`Isomap`](generated/sklearn.manifold.isomap#sklearn.manifold.Isomap "sklearn.manifold.Isomap").
###
2.2.2.1. Complexity
The Isomap algorithm comprises three stages:
1. **Nearest neighbor search.** Isomap uses [`BallTree`](generated/sklearn.neighbors.balltree#sklearn.neighbors.BallTree "sklearn.neighbors.BallTree") for efficient neighbor search. The cost is approximately \(O[D \log(k) N \log(N)]\), for \(k\) nearest neighbors of \(N\) points in \(D\) dimensions.
2. **Shortest-path graph search.** The most efficient known algorithms for this are *Dijkstra’s Algorithm*, which is approximately \(O[N^2(k + \log(N))]\), or the *Floyd-Warshall algorithm*, which is \(O[N^3]\). The algorithm can be selected by the user with the `path_method` keyword of `Isomap`. If unspecified, the code attempts to choose the best algorithm for the input data.
3. **Partial eigenvalue decomposition.** The embedding is encoded in the eigenvectors corresponding to the \(d\) largest eigenvalues of the \(N \times N\) isomap kernel. For a dense solver, the cost is approximately \(O[d N^2]\). This cost can often be improved using the `ARPACK` solver. The eigensolver can be specified by the user with the `eigen_solver` keyword of `Isomap`. If unspecified, the code attempts to choose the best algorithm for the input data.
The overall complexity of Isomap is \(O[D \log(k) N \log(N)] + O[N^2(k + \log(N))] + O[d N^2]\).
* \(N\) : number of training data points
* \(D\) : input dimension
* \(k\) : number of nearest neighbors
* \(d\) : output dimension
2.2.3. Locally Linear Embedding
--------------------------------
Locally linear embedding (LLE) seeks a lower-dimensional projection of the data which preserves distances within local neighborhoods. It can be thought of as a series of local Principal Component Analyses which are globally compared to find the best non-linear embedding.
Locally linear embedding can be performed with function [`locally_linear_embedding`](generated/sklearn.manifold.locally_linear_embedding#sklearn.manifold.locally_linear_embedding "sklearn.manifold.locally_linear_embedding") or its object-oriented counterpart [`LocallyLinearEmbedding`](generated/sklearn.manifold.locallylinearembedding#sklearn.manifold.LocallyLinearEmbedding "sklearn.manifold.LocallyLinearEmbedding").
###
2.2.3.1. Complexity
The standard LLE algorithm comprises three stages:
1. **Nearest Neighbors Search**. See discussion under Isomap above.
2. **Weight Matrix Construction**. \(O[D N k^3]\). The construction of the LLE weight matrix involves the solution of a \(k \times k\) linear equation for each of the \(N\) local neighborhoods
3. **Partial Eigenvalue Decomposition**. See discussion under Isomap above.
The overall complexity of standard LLE is \(O[D \log(k) N \log(N)] + O[D N k^3] + O[d N^2]\).
* \(N\) : number of training data points
* \(D\) : input dimension
* \(k\) : number of nearest neighbors
* \(d\) : output dimension
2.2.4. Modified Locally Linear Embedding
-----------------------------------------
One well-known issue with LLE is the regularization problem. When the number of neighbors is greater than the number of input dimensions, the matrix defining each local neighborhood is rank-deficient. To address this, standard LLE applies an arbitrary regularization parameter \(r\), which is chosen relative to the trace of the local weight matrix. Though it can be shown formally that as \(r \to 0\), the solution converges to the desired embedding, there is no guarantee that the optimal solution will be found for \(r > 0\). This problem manifests itself in embeddings which distort the underlying geometry of the manifold.
One method to address the regularization problem is to use multiple weight vectors in each neighborhood. This is the essence of *modified locally linear embedding* (MLLE). MLLE can be performed with function [`locally_linear_embedding`](generated/sklearn.manifold.locally_linear_embedding#sklearn.manifold.locally_linear_embedding "sklearn.manifold.locally_linear_embedding") or its object-oriented counterpart [`LocallyLinearEmbedding`](generated/sklearn.manifold.locallylinearembedding#sklearn.manifold.LocallyLinearEmbedding "sklearn.manifold.LocallyLinearEmbedding"), with the keyword `method = 'modified'`. It requires `n_neighbors > n_components`.
###
2.2.4.1. Complexity
The MLLE algorithm comprises three stages:
1. **Nearest Neighbors Search**. Same as standard LLE
2. **Weight Matrix Construction**. Approximately \(O[D N k^3] + O[N (k-D) k^2]\). The first term is exactly equivalent to that of standard LLE. The second term has to do with constructing the weight matrix from multiple weights. In practice, the added cost of constructing the MLLE weight matrix is relatively small compared to the cost of stages 1 and 3.
3. **Partial Eigenvalue Decomposition**. Same as standard LLE
The overall complexity of MLLE is \(O[D \log(k) N \log(N)] + O[D N k^3] + O[N (k-D) k^2] + O[d N^2]\).
* \(N\) : number of training data points
* \(D\) : input dimension
* \(k\) : number of nearest neighbors
* \(d\) : output dimension
2.2.5. Hessian Eigenmapping
----------------------------
Hessian Eigenmapping (also known as Hessian-based LLE: HLLE) is another method of solving the regularization problem of LLE. It revolves around a hessian-based quadratic form at each neighborhood which is used to recover the locally linear structure. Though other implementations note its poor scaling with data size, `sklearn` implements some algorithmic improvements which make its cost comparable to that of other LLE variants for small output dimension. HLLE can be performed with function [`locally_linear_embedding`](generated/sklearn.manifold.locally_linear_embedding#sklearn.manifold.locally_linear_embedding "sklearn.manifold.locally_linear_embedding") or its object-oriented counterpart [`LocallyLinearEmbedding`](generated/sklearn.manifold.locallylinearembedding#sklearn.manifold.LocallyLinearEmbedding "sklearn.manifold.LocallyLinearEmbedding"), with the keyword `method = 'hessian'`. It requires `n_neighbors > n_components * (n_components + 3) / 2`.
###
2.2.5.1. Complexity
The HLLE algorithm comprises three stages:
1. **Nearest Neighbors Search**. Same as standard LLE
2. **Weight Matrix Construction**. Approximately \(O[D N k^3] + O[N d^6]\). The first term reflects a similar cost to that of standard LLE. The second term comes from a QR decomposition of the local hessian estimator.
3. **Partial Eigenvalue Decomposition**. Same as standard LLE
The overall complexity of standard HLLE is \(O[D \log(k) N \log(N)] + O[D N k^3] + O[N d^6] + O[d N^2]\).
* \(N\) : number of training data points
* \(D\) : input dimension
* \(k\) : number of nearest neighbors
* \(d\) : output dimension
2.2.6. Spectral Embedding
--------------------------
Spectral Embedding is an approach to calculating a non-linear embedding. Scikit-learn implements Laplacian Eigenmaps, which finds a low dimensional representation of the data using a spectral decomposition of the graph Laplacian. The graph generated can be considered as a discrete approximation of the low dimensional manifold in the high dimensional space. Minimization of a cost function based on the graph ensures that points close to each other on the manifold are mapped close to each other in the low dimensional space, preserving local distances. Spectral embedding can be performed with the function [`spectral_embedding`](generated/sklearn.manifold.spectral_embedding#sklearn.manifold.spectral_embedding "sklearn.manifold.spectral_embedding") or its object-oriented counterpart [`SpectralEmbedding`](generated/sklearn.manifold.spectralembedding#sklearn.manifold.SpectralEmbedding "sklearn.manifold.SpectralEmbedding").
###
2.2.6.1. Complexity
The Spectral Embedding (Laplacian Eigenmaps) algorithm comprises three stages:
1. **Weighted Graph Construction**. Transform the raw input data into graph representation using affinity (adjacency) matrix representation.
2. **Graph Laplacian Construction**. unnormalized Graph Laplacian is constructed as \(L = D - A\) for and normalized one as \(L = D^{-\frac{1}{2}} (D - A) D^{-\frac{1}{2}}\).
3. **Partial Eigenvalue Decomposition**. Eigenvalue decomposition is done on graph Laplacian
The overall complexity of spectral embedding is \(O[D \log(k) N \log(N)] + O[D N k^3] + O[d N^2]\).
* \(N\) : number of training data points
* \(D\) : input dimension
* \(k\) : number of nearest neighbors
* \(d\) : output dimension
2.2.7. Local Tangent Space Alignment
-------------------------------------
Though not technically a variant of LLE, Local tangent space alignment (LTSA) is algorithmically similar enough to LLE that it can be put in this category. Rather than focusing on preserving neighborhood distances as in LLE, LTSA seeks to characterize the local geometry at each neighborhood via its tangent space, and performs a global optimization to align these local tangent spaces to learn the embedding. LTSA can be performed with function [`locally_linear_embedding`](generated/sklearn.manifold.locally_linear_embedding#sklearn.manifold.locally_linear_embedding "sklearn.manifold.locally_linear_embedding") or its object-oriented counterpart [`LocallyLinearEmbedding`](generated/sklearn.manifold.locallylinearembedding#sklearn.manifold.LocallyLinearEmbedding "sklearn.manifold.LocallyLinearEmbedding"), with the keyword `method = 'ltsa'`.
###
2.2.7.1. Complexity
The LTSA algorithm comprises three stages:
1. **Nearest Neighbors Search**. Same as standard LLE
2. **Weight Matrix Construction**. Approximately \(O[D N k^3] + O[k^2 d]\). The first term reflects a similar cost to that of standard LLE.
3. **Partial Eigenvalue Decomposition**. Same as standard LLE
The overall complexity of standard LTSA is \(O[D \log(k) N \log(N)] + O[D N k^3] + O[k^2 d] + O[d N^2]\).
* \(N\) : number of training data points
* \(D\) : input dimension
* \(k\) : number of nearest neighbors
* \(d\) : output dimension
2.2.8. Multi-dimensional Scaling (MDS)
---------------------------------------
[Multidimensional scaling](https://en.wikipedia.org/wiki/Multidimensional_scaling) ([`MDS`](generated/sklearn.manifold.mds#sklearn.manifold.MDS "sklearn.manifold.MDS")) seeks a low-dimensional representation of the data in which the distances respect well the distances in the original high-dimensional space.
In general, [`MDS`](generated/sklearn.manifold.mds#sklearn.manifold.MDS "sklearn.manifold.MDS") is a technique used for analyzing similarity or dissimilarity data. It attempts to model similarity or dissimilarity data as distances in a geometric spaces. The data can be ratings of similarity between objects, interaction frequencies of molecules, or trade indices between countries.
There exists two types of MDS algorithm: metric and non metric. In scikit-learn, the class [`MDS`](generated/sklearn.manifold.mds#sklearn.manifold.MDS "sklearn.manifold.MDS") implements both. In Metric MDS, the input similarity matrix arises from a metric (and thus respects the triangular inequality), the distances between output two points are then set to be as close as possible to the similarity or dissimilarity data. In the non-metric version, the algorithms will try to preserve the order of the distances, and hence seek for a monotonic relationship between the distances in the embedded space and the similarities/dissimilarities.
Let \(S\) be the similarity matrix, and \(X\) the coordinates of the \(n\) input points. Disparities \(\hat{d}\_{ij}\) are transformation of the similarities chosen in some optimal ways. The objective, called the stress, is then defined by \(\sum\_{i < j} d\_{ij}(X) - \hat{d}\_{ij}(X)\)
###
2.2.8.1. Metric MDS
The simplest metric [`MDS`](generated/sklearn.manifold.mds#sklearn.manifold.MDS "sklearn.manifold.MDS") model, called *absolute MDS*, disparities are defined by \(\hat{d}\_{ij} = S\_{ij}\). With absolute MDS, the value \(S\_{ij}\) should then correspond exactly to the distance between point \(i\) and \(j\) in the embedding point.
Most commonly, disparities are set to \(\hat{d}\_{ij} = b S\_{ij}\).
###
2.2.8.2. Nonmetric MDS
Non metric [`MDS`](generated/sklearn.manifold.mds#sklearn.manifold.MDS "sklearn.manifold.MDS") focuses on the ordination of the data. If \(S\_{ij} < S\_{jk}\), then the embedding should enforce \(d\_{ij} < d\_{jk}\). A simple algorithm to enforce that is to use a monotonic regression of \(d\_{ij}\) on \(S\_{ij}\), yielding disparities \(\hat{d}\_{ij}\) in the same order as \(S\_{ij}\).
A trivial solution to this problem is to set all the points on the origin. In order to avoid that, the disparities \(\hat{d}\_{ij}\) are normalized.
2.2.9. t-distributed Stochastic Neighbor Embedding (t-SNE)
-----------------------------------------------------------
t-SNE ([`TSNE`](generated/sklearn.manifold.tsne#sklearn.manifold.TSNE "sklearn.manifold.TSNE")) converts affinities of data points to probabilities. The affinities in the original space are represented by Gaussian joint probabilities and the affinities in the embedded space are represented by Student’s t-distributions. This allows t-SNE to be particularly sensitive to local structure and has a few other advantages over existing techniques:
* Revealing the structure at many scales on a single map
* Revealing data that lie in multiple, different, manifolds or clusters
* Reducing the tendency to crowd points together at the center
While Isomap, LLE and variants are best suited to unfold a single continuous low dimensional manifold, t-SNE will focus on the local structure of the data and will tend to extract clustered local groups of samples as highlighted on the S-curve example. This ability to group samples based on the local structure might be beneficial to visually disentangle a dataset that comprises several manifolds at once as is the case in the digits dataset.
The Kullback-Leibler (KL) divergence of the joint probabilities in the original space and the embedded space will be minimized by gradient descent. Note that the KL divergence is not convex, i.e. multiple restarts with different initializations will end up in local minima of the KL divergence. Hence, it is sometimes useful to try different seeds and select the embedding with the lowest KL divergence.
The disadvantages to using t-SNE are roughly:
* t-SNE is computationally expensive, and can take several hours on million-sample datasets where PCA will finish in seconds or minutes
* The Barnes-Hut t-SNE method is limited to two or three dimensional embeddings.
* The algorithm is stochastic and multiple restarts with different seeds can yield different embeddings. However, it is perfectly legitimate to pick the embedding with the least error.
* Global structure is not explicitly preserved. This problem is mitigated by initializing points with PCA (using `init='pca'`).
###
2.2.9.1. Optimizing t-SNE
The main purpose of t-SNE is visualization of high-dimensional data. Hence, it works best when the data will be embedded on two or three dimensions.
Optimizing the KL divergence can be a little bit tricky sometimes. There are five parameters that control the optimization of t-SNE and therefore possibly the quality of the resulting embedding:
* perplexity
* early exaggeration factor
* learning rate
* maximum number of iterations
* angle (not used in the exact method)
The perplexity is defined as \(k=2^{(S)}\) where \(S\) is the Shannon entropy of the conditional probability distribution. The perplexity of a \(k\)-sided die is \(k\), so that \(k\) is effectively the number of nearest neighbors t-SNE considers when generating the conditional probabilities. Larger perplexities lead to more nearest neighbors and less sensitive to small structure. Conversely a lower perplexity considers a smaller number of neighbors, and thus ignores more global information in favour of the local neighborhood. As dataset sizes get larger more points will be required to get a reasonable sample of the local neighborhood, and hence larger perplexities may be required. Similarly noisier datasets will require larger perplexity values to encompass enough local neighbors to see beyond the background noise.
The maximum number of iterations is usually high enough and does not need any tuning. The optimization consists of two phases: the early exaggeration phase and the final optimization. During early exaggeration the joint probabilities in the original space will be artificially increased by multiplication with a given factor. Larger factors result in larger gaps between natural clusters in the data. If the factor is too high, the KL divergence could increase during this phase. Usually it does not have to be tuned. A critical parameter is the learning rate. If it is too low gradient descent will get stuck in a bad local minimum. If it is too high the KL divergence will increase during optimization. A heuristic suggested in Belkina et al. (2019) is to set the learning rate to the sample size divided by the early exaggeration factor. We implement this heuristic as `learning_rate='auto'` argument. More tips can be found in Laurens van der Maaten’s FAQ (see references). The last parameter, angle, is a tradeoff between performance and accuracy. Larger angles imply that we can approximate larger regions by a single point, leading to better speed but less accurate results.
[“How to Use t-SNE Effectively”](https://distill.pub/2016/misread-tsne/) provides a good discussion of the effects of the various parameters, as well as interactive plots to explore the effects of different parameters.
###
2.2.9.2. Barnes-Hut t-SNE
The Barnes-Hut t-SNE that has been implemented here is usually much slower than other manifold learning algorithms. The optimization is quite difficult and the computation of the gradient is \(O[d N log(N)]\), where \(d\) is the number of output dimensions and \(N\) is the number of samples. The Barnes-Hut method improves on the exact method where t-SNE complexity is \(O[d N^2]\), but has several other notable differences:
* The Barnes-Hut implementation only works when the target dimensionality is 3 or less. The 2D case is typical when building visualizations.
* Barnes-Hut only works with dense input data. Sparse data matrices can only be embedded with the exact method or can be approximated by a dense low rank projection for instance using [`TruncatedSVD`](generated/sklearn.decomposition.truncatedsvd#sklearn.decomposition.TruncatedSVD "sklearn.decomposition.TruncatedSVD")
* Barnes-Hut is an approximation of the exact method. The approximation is parameterized with the angle parameter, therefore the angle parameter is unused when method=”exact”
* Barnes-Hut is significantly more scalable. Barnes-Hut can be used to embed hundred of thousands of data points while the exact method can handle thousands of samples before becoming computationally intractable
For visualization purpose (which is the main use case of t-SNE), using the Barnes-Hut method is strongly recommended. The exact t-SNE method is useful for checking the theoretically properties of the embedding possibly in higher dimensional space but limit to small datasets due to computational constraints.
Also note that the digits labels roughly match the natural grouping found by t-SNE while the linear 2D projection of the PCA model yields a representation where label regions largely overlap. This is a strong clue that this data can be well separated by non linear methods that focus on the local structure (e.g. an SVM with a Gaussian RBF kernel). However, failing to visualize well separated homogeneously labeled groups with t-SNE in 2D does not necessarily imply that the data cannot be correctly classified by a supervised model. It might be the case that 2 dimensions are not high enough to accurately represent the internal structure of the data.
2.2.10. Tips on practical use
------------------------------
* Make sure the same scale is used over all features. Because manifold learning methods are based on a nearest-neighbor search, the algorithm may perform poorly otherwise. See [StandardScaler](preprocessing#preprocessing-scaler) for convenient ways of scaling heterogeneous data.
* The reconstruction error computed by each routine can be used to choose the optimal output dimension. For a \(d\)-dimensional manifold embedded in a \(D\)-dimensional parameter space, the reconstruction error will decrease as `n_components` is increased until `n_components == d`.
* Note that noisy data can “short-circuit” the manifold, in essence acting as a bridge between parts of the manifold that would otherwise be well-separated. Manifold learning on noisy and/or incomplete data is an active area of research.
* Certain input configurations can lead to singular weight matrices, for example when more than two points in the dataset are identical, or when the data is split into disjointed groups. In this case, `solver='arpack'` will fail to find the null space. The easiest way to address this is to use `solver='dense'` which will work on a singular matrix, though it may be very slow depending on the number of input points. Alternatively, one can attempt to understand the source of the singularity: if it is due to disjoint sets, increasing `n_neighbors` may help. If it is due to identical points in the dataset, removing these points may help.
See also
[Totally Random Trees Embedding](ensemble#random-trees-embedding) can also be useful to derive non-linear representations of feature space, also it does not perform dimensionality reduction.
| programming_docs |
scikit_learn 1.17. Neural network models (supervised) 1.17. Neural network models (supervised)
========================================
Warning
This implementation is not intended for large-scale applications. In particular, scikit-learn offers no GPU support. For much faster, GPU-based implementations, as well as frameworks offering much more flexibility to build deep learning architectures, see [Related Projects](https://scikit-learn.org/1.1/related_projects.html#related-projects).
1.17.1. Multi-layer Perceptron
-------------------------------
**Multi-layer Perceptron (MLP)** is a supervised learning algorithm that learns a function \(f(\cdot): R^m \rightarrow R^o\) by training on a dataset, where \(m\) is the number of dimensions for input and \(o\) is the number of dimensions for output. Given a set of features \(X = {x\_1, x\_2, ..., x\_m}\) and a target \(y\), it can learn a non-linear function approximator for either classification or regression. It is different from logistic regression, in that between the input and the output layer, there can be one or more non-linear layers, called hidden layers. Figure 1 shows a one hidden layer MLP with scalar output.
**Figure 1 : One hidden layer MLP.**
The leftmost layer, known as the input layer, consists of a set of neurons \(\{x\_i | x\_1, x\_2, ..., x\_m\}\) representing the input features. Each neuron in the hidden layer transforms the values from the previous layer with a weighted linear summation \(w\_1x\_1 + w\_2x\_2 + ... + w\_mx\_m\), followed by a non-linear activation function \(g(\cdot):R \rightarrow R\) - like the hyperbolic tan function. The output layer receives the values from the last hidden layer and transforms them into output values.
The module contains the public attributes `coefs_` and `intercepts_`. `coefs_` is a list of weight matrices, where weight matrix at index \(i\) represents the weights between layer \(i\) and layer \(i+1\). `intercepts_` is a list of bias vectors, where the vector at index \(i\) represents the bias values added to layer \(i+1\).
The advantages of Multi-layer Perceptron are:
* Capability to learn non-linear models.
* Capability to learn models in real-time (on-line learning) using `partial_fit`.
The disadvantages of Multi-layer Perceptron (MLP) include:
* MLP with hidden layers have a non-convex loss function where there exists more than one local minimum. Therefore different random weight initializations can lead to different validation accuracy.
* MLP requires tuning a number of hyperparameters such as the number of hidden neurons, layers, and iterations.
* MLP is sensitive to feature scaling.
Please see [Tips on Practical Use](#mlp-tips) section that addresses some of these disadvantages.
1.17.2. Classification
-----------------------
Class [`MLPClassifier`](generated/sklearn.neural_network.mlpclassifier#sklearn.neural_network.MLPClassifier "sklearn.neural_network.MLPClassifier") implements a multi-layer perceptron (MLP) algorithm that trains using [Backpropagation](http://ufldl.stanford.edu/wiki/index.php/Backpropagation_Algorithm).
MLP trains on two arrays: array X of size (n\_samples, n\_features), which holds the training samples represented as floating point feature vectors; and array y of size (n\_samples,), which holds the target values (class labels) for the training samples:
```
>>> from sklearn.neural_network import MLPClassifier
>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = MLPClassifier(solver='lbfgs', alpha=1e-5,
... hidden_layer_sizes=(5, 2), random_state=1)
...
>>> clf.fit(X, y)
MLPClassifier(alpha=1e-05, hidden_layer_sizes=(5, 2), random_state=1,
solver='lbfgs')
```
After fitting (training), the model can predict labels for new samples:
```
>>> clf.predict([[2., 2.], [-1., -2.]])
array([1, 0])
```
MLP can fit a non-linear model to the training data. `clf.coefs_` contains the weight matrices that constitute the model parameters:
```
>>> [coef.shape for coef in clf.coefs_]
[(2, 5), (5, 2), (2, 1)]
```
Currently, [`MLPClassifier`](generated/sklearn.neural_network.mlpclassifier#sklearn.neural_network.MLPClassifier "sklearn.neural_network.MLPClassifier") supports only the Cross-Entropy loss function, which allows probability estimates by running the `predict_proba` method.
MLP trains using Backpropagation. More precisely, it trains using some form of gradient descent and the gradients are calculated using Backpropagation. For classification, it minimizes the Cross-Entropy loss function, giving a vector of probability estimates \(P(y|x)\) per sample \(x\):
```
>>> clf.predict_proba([[2., 2.], [1., 2.]])
array([[1.967...e-04, 9.998...-01],
[1.967...e-04, 9.998...-01]])
```
[`MLPClassifier`](generated/sklearn.neural_network.mlpclassifier#sklearn.neural_network.MLPClassifier "sklearn.neural_network.MLPClassifier") supports multi-class classification by applying [Softmax](https://en.wikipedia.org/wiki/Softmax_activation_function) as the output function.
Further, the model supports [multi-label classification](multiclass#multiclass) in which a sample can belong to more than one class. For each class, the raw output passes through the logistic function. Values larger or equal to `0.5` are rounded to `1`, otherwise to `0`. For a predicted output of a sample, the indices where the value is `1` represents the assigned classes of that sample:
```
>>> X = [[0., 0.], [1., 1.]]
>>> y = [[0, 1], [1, 1]]
>>> clf = MLPClassifier(solver='lbfgs', alpha=1e-5,
... hidden_layer_sizes=(15,), random_state=1)
...
>>> clf.fit(X, y)
MLPClassifier(alpha=1e-05, hidden_layer_sizes=(15,), random_state=1,
solver='lbfgs')
>>> clf.predict([[1., 2.]])
array([[1, 1]])
>>> clf.predict([[0., 0.]])
array([[0, 1]])
```
See the examples below and the docstring of [`MLPClassifier.fit`](generated/sklearn.neural_network.mlpclassifier#sklearn.neural_network.MLPClassifier.fit "sklearn.neural_network.MLPClassifier.fit") for further information.
1.17.3. Regression
-------------------
Class [`MLPRegressor`](generated/sklearn.neural_network.mlpregressor#sklearn.neural_network.MLPRegressor "sklearn.neural_network.MLPRegressor") implements a multi-layer perceptron (MLP) that trains using backpropagation with no activation function in the output layer, which can also be seen as using the identity function as activation function. Therefore, it uses the square error as the loss function, and the output is a set of continuous values.
[`MLPRegressor`](generated/sklearn.neural_network.mlpregressor#sklearn.neural_network.MLPRegressor "sklearn.neural_network.MLPRegressor") also supports multi-output regression, in which a sample can have more than one target.
1.17.4. Regularization
-----------------------
Both [`MLPRegressor`](generated/sklearn.neural_network.mlpregressor#sklearn.neural_network.MLPRegressor "sklearn.neural_network.MLPRegressor") and [`MLPClassifier`](generated/sklearn.neural_network.mlpclassifier#sklearn.neural_network.MLPClassifier "sklearn.neural_network.MLPClassifier") use parameter `alpha` for regularization (L2 regularization) term which helps in avoiding overfitting by penalizing weights with large magnitudes. Following plot displays varying decision function with value of alpha.
[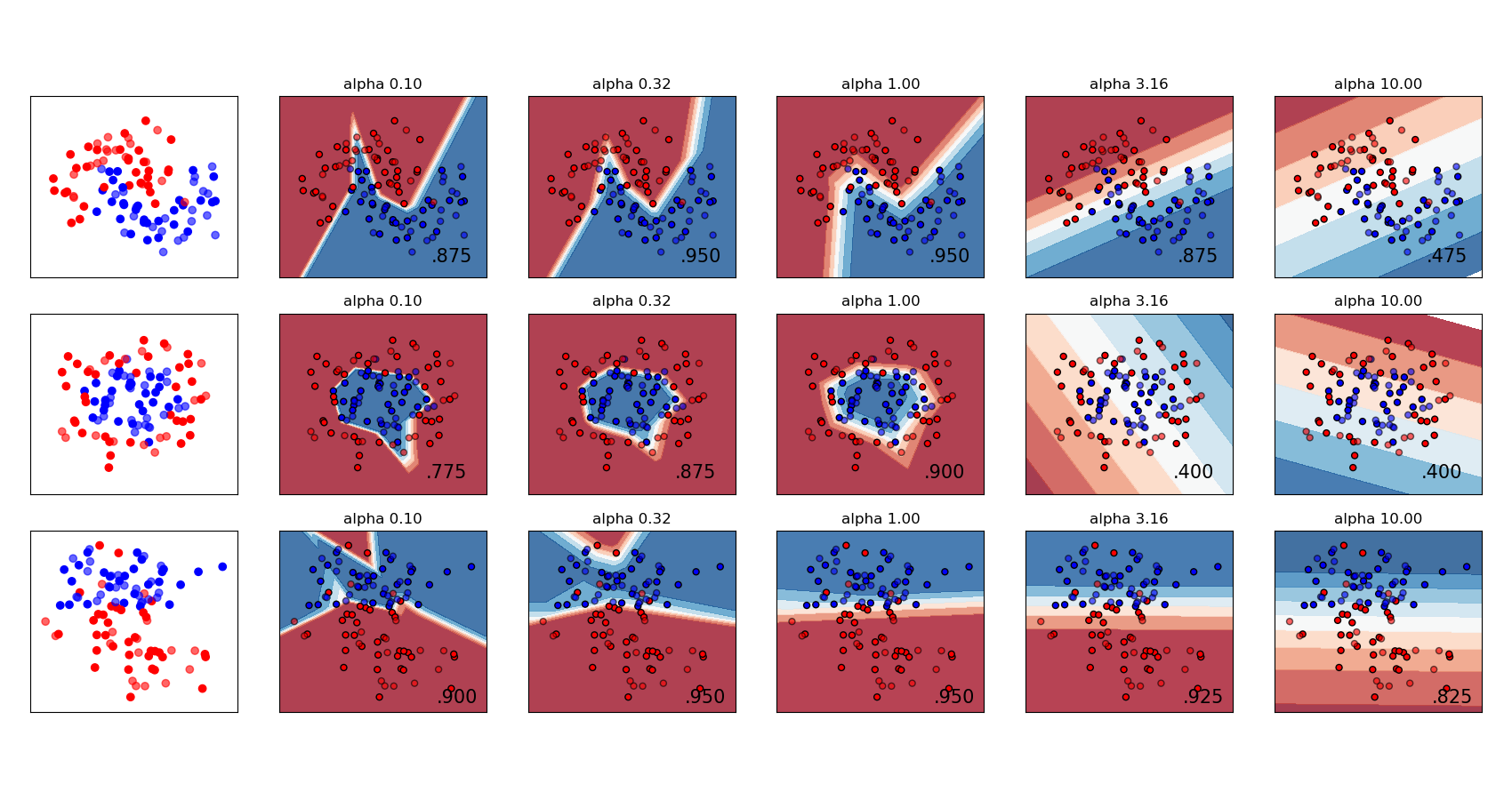](../auto_examples/neural_networks/plot_mlp_alpha) See the examples below for further information.
1.17.5. Algorithms
-------------------
MLP trains using [Stochastic Gradient Descent](https://en.wikipedia.org/wiki/Stochastic_gradient_descent), [Adam](https://arxiv.org/abs/1412.6980), or [L-BFGS](https://en.wikipedia.org/wiki/Limited-memory_BFGS). Stochastic Gradient Descent (SGD) updates parameters using the gradient of the loss function with respect to a parameter that needs adaptation, i.e.
\[w \leftarrow w - \eta (\alpha \frac{\partial R(w)}{\partial w} + \frac{\partial Loss}{\partial w})\] where \(\eta\) is the learning rate which controls the step-size in the parameter space search. \(Loss\) is the loss function used for the network.
More details can be found in the documentation of [SGD](http://scikit-learn.org/stable/modules/sgd.html)
Adam is similar to SGD in a sense that it is a stochastic optimizer, but it can automatically adjust the amount to update parameters based on adaptive estimates of lower-order moments.
With SGD or Adam, training supports online and mini-batch learning.
L-BFGS is a solver that approximates the Hessian matrix which represents the second-order partial derivative of a function. Further it approximates the inverse of the Hessian matrix to perform parameter updates. The implementation uses the Scipy version of [L-BFGS](https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.fmin_l_bfgs_b.html).
If the selected solver is ‘L-BFGS’, training does not support online nor mini-batch learning.
1.17.6. Complexity
-------------------
Suppose there are \(n\) training samples, \(m\) features, \(k\) hidden layers, each containing \(h\) neurons - for simplicity, and \(o\) output neurons. The time complexity of backpropagation is \(O(n\cdot m \cdot h^k \cdot o \cdot i)\), where \(i\) is the number of iterations. Since backpropagation has a high time complexity, it is advisable to start with smaller number of hidden neurons and few hidden layers for training.
1.17.7. Mathematical formulation
---------------------------------
Given a set of training examples \((x\_1, y\_1), (x\_2, y\_2), \ldots, (x\_n, y\_n)\) where \(x\_i \in \mathbf{R}^n\) and \(y\_i \in \{0, 1\}\), a one hidden layer one hidden neuron MLP learns the function \(f(x) = W\_2 g(W\_1^T x + b\_1) + b\_2\) where \(W\_1 \in \mathbf{R}^m\) and \(W\_2, b\_1, b\_2 \in \mathbf{R}\) are model parameters. \(W\_1, W\_2\) represent the weights of the input layer and hidden layer, respectively; and \(b\_1, b\_2\) represent the bias added to the hidden layer and the output layer, respectively. \(g(\cdot) : R \rightarrow R\) is the activation function, set by default as the hyperbolic tan. It is given as,
\[g(z)= \frac{e^z-e^{-z}}{e^z+e^{-z}}\] For binary classification, \(f(x)\) passes through the logistic function \(g(z)=1/(1+e^{-z})\) to obtain output values between zero and one. A threshold, set to 0.5, would assign samples of outputs larger or equal 0.5 to the positive class, and the rest to the negative class.
If there are more than two classes, \(f(x)\) itself would be a vector of size (n\_classes,). Instead of passing through logistic function, it passes through the softmax function, which is written as,
\[\text{softmax}(z)\_i = \frac{\exp(z\_i)}{\sum\_{l=1}^k\exp(z\_l)}\] where \(z\_i\) represents the \(i\) th element of the input to softmax, which corresponds to class \(i\), and \(K\) is the number of classes. The result is a vector containing the probabilities that sample \(x\) belong to each class. The output is the class with the highest probability.
In regression, the output remains as \(f(x)\); therefore, output activation function is just the identity function.
MLP uses different loss functions depending on the problem type. The loss function for classification is Average Cross-Entropy, which in binary case is given as,
\[Loss(\hat{y},y,W) = -\dfrac{1}{n}\sum\_{i=0}^n(y\_i \ln {\hat{y\_i}} + (1-y\_i) \ln{(1-\hat{y\_i})}) + \dfrac{\alpha}{2n} ||W||\_2^2\] where \(\alpha ||W||\_2^2\) is an L2-regularization term (aka penalty) that penalizes complex models; and \(\alpha > 0\) is a non-negative hyperparameter that controls the magnitude of the penalty.
For regression, MLP uses the Mean Square Error loss function; written as,
\[Loss(\hat{y},y,W) = \frac{1}{2n}\sum\_{i=0}^n||\hat{y}\_i - y\_i ||\_2^2 + \frac{\alpha}{2n} ||W||\_2^2\] Starting from initial random weights, multi-layer perceptron (MLP) minimizes the loss function by repeatedly updating these weights. After computing the loss, a backward pass propagates it from the output layer to the previous layers, providing each weight parameter with an update value meant to decrease the loss.
In gradient descent, the gradient \(\nabla Loss\_{W}\) of the loss with respect to the weights is computed and deducted from \(W\). More formally, this is expressed as,
\[W^{i+1} = W^i - \epsilon \nabla {Loss}\_{W}^{i}\] where \(i\) is the iteration step, and \(\epsilon\) is the learning rate with a value larger than 0.
The algorithm stops when it reaches a preset maximum number of iterations; or when the improvement in loss is below a certain, small number.
1.17.8. Tips on Practical Use
------------------------------
* Multi-layer Perceptron is sensitive to feature scaling, so it is highly recommended to scale your data. For example, scale each attribute on the input vector X to [0, 1] or [-1, +1], or standardize it to have mean 0 and variance 1. Note that you must apply the *same* scaling to the test set for meaningful results. You can use `StandardScaler` for standardization.
```
>>> from sklearn.preprocessing import StandardScaler
>>> scaler = StandardScaler()
>>> # Don't cheat - fit only on training data
>>> scaler.fit(X_train)
>>> X_train = scaler.transform(X_train)
>>> # apply same transformation to test data
>>> X_test = scaler.transform(X_test)
```
An alternative and recommended approach is to use `StandardScaler` in a `Pipeline`
* Finding a reasonable regularization parameter \(\alpha\) is best done using `GridSearchCV`, usually in the range `10.0 ** -np.arange(1, 7)`.
* Empirically, we observed that `L-BFGS` converges faster and with better solutions on small datasets. For relatively large datasets, however, `Adam` is very robust. It usually converges quickly and gives pretty good performance. `SGD` with momentum or nesterov’s momentum, on the other hand, can perform better than those two algorithms if learning rate is correctly tuned.
1.17.9. More control with warm\_start
--------------------------------------
If you want more control over stopping criteria or learning rate in SGD, or want to do additional monitoring, using `warm_start=True` and `max_iter=1` and iterating yourself can be helpful:
```
>>> X = [[0., 0.], [1., 1.]]
>>> y = [0, 1]
>>> clf = MLPClassifier(hidden_layer_sizes=(15,), random_state=1, max_iter=1, warm_start=True)
>>> for i in range(10):
... clf.fit(X, y)
... # additional monitoring / inspection
MLPClassifier(...
```
scikit_learn 1.8. Cross decomposition 1.8. Cross decomposition
========================
The cross decomposition module contains **supervised** estimators for dimensionality reduction and regression, belonging to the “Partial Least Squares” family.
Cross decomposition algorithms find the fundamental relations between two matrices (X and Y). They are latent variable approaches to modeling the covariance structures in these two spaces. They will try to find the multidimensional direction in the X space that explains the maximum multidimensional variance direction in the Y space. In other words, PLS projects both `X` and `Y` into a lower-dimensional subspace such that the covariance between `transformed(X)` and `transformed(Y)` is maximal.
PLS draws similarities with [Principal Component Regression](https://en.wikipedia.org/wiki/Principal_component_regression) (PCR), where the samples are first projected into a lower-dimensional subspace, and the targets `y` are predicted using `transformed(X)`. One issue with PCR is that the dimensionality reduction is unsupervized, and may lose some important variables: PCR would keep the features with the most variance, but it’s possible that features with a small variances are relevant from predicting the target. In a way, PLS allows for the same kind of dimensionality reduction, but by taking into account the targets `y`. An illustration of this fact is given in the following example: \* [Principal Component Regression vs Partial Least Squares Regression](../auto_examples/cross_decomposition/plot_pcr_vs_pls#sphx-glr-auto-examples-cross-decomposition-plot-pcr-vs-pls-py).
Apart from CCA, the PLS estimators are particularly suited when the matrix of predictors has more variables than observations, and when there is multicollinearity among the features. By contrast, standard linear regression would fail in these cases unless it is regularized.
Classes included in this module are [`PLSRegression`](generated/sklearn.cross_decomposition.plsregression#sklearn.cross_decomposition.PLSRegression "sklearn.cross_decomposition.PLSRegression"), [`PLSCanonical`](generated/sklearn.cross_decomposition.plscanonical#sklearn.cross_decomposition.PLSCanonical "sklearn.cross_decomposition.PLSCanonical"), [`CCA`](generated/sklearn.cross_decomposition.cca#sklearn.cross_decomposition.CCA "sklearn.cross_decomposition.CCA") and [`PLSSVD`](generated/sklearn.cross_decomposition.plssvd#sklearn.cross_decomposition.PLSSVD "sklearn.cross_decomposition.PLSSVD")
1.8.1. PLSCanonical
--------------------
We here describe the algorithm used in [`PLSCanonical`](generated/sklearn.cross_decomposition.plscanonical#sklearn.cross_decomposition.PLSCanonical "sklearn.cross_decomposition.PLSCanonical"). The other estimators use variants of this algorithm, and are detailed below. We recommend section [[1]](#id6) for more details and comparisons between these algorithms. In [[1]](#id6), [`PLSCanonical`](generated/sklearn.cross_decomposition.plscanonical#sklearn.cross_decomposition.PLSCanonical "sklearn.cross_decomposition.PLSCanonical") corresponds to “PLSW2A”.
Given two centered matrices \(X \in \mathbb{R}^{n \times d}\) and \(Y \in \mathbb{R}^{n \times t}\), and a number of components \(K\), [`PLSCanonical`](generated/sklearn.cross_decomposition.plscanonical#sklearn.cross_decomposition.PLSCanonical "sklearn.cross_decomposition.PLSCanonical") proceeds as follows:
Set \(X\_1\) to \(X\) and \(Y\_1\) to \(Y\). Then, for each \(k \in [1, K]\):
* a) compute \(u\_k \in \mathbb{R}^d\) and \(v\_k \in \mathbb{R}^t\), the first left and right singular vectors of the cross-covariance matrix \(C = X\_k^T Y\_k\). \(u\_k\) and \(v\_k\) are called the *weights*. By definition, \(u\_k\) and \(v\_k\) are chosen so that they maximize the covariance between the projected \(X\_k\) and the projected target, that is \(\text{Cov}(X\_k u\_k, Y\_k v\_k)\).
* b) Project \(X\_k\) and \(Y\_k\) on the singular vectors to obtain *scores*: \(\xi\_k = X\_k u\_k\) and \(\omega\_k = Y\_k v\_k\)
* c) Regress \(X\_k\) on \(\xi\_k\), i.e. find a vector \(\gamma\_k \in \mathbb{R}^d\) such that the rank-1 matrix \(\xi\_k \gamma\_k^T\) is as close as possible to \(X\_k\). Do the same on \(Y\_k\) with \(\omega\_k\) to obtain \(\delta\_k\). The vectors \(\gamma\_k\) and \(\delta\_k\) are called the *loadings*.
* d) *deflate* \(X\_k\) and \(Y\_k\), i.e. subtract the rank-1 approximations: \(X\_{k+1} = X\_k - \xi\_k \gamma\_k^T\), and \(Y\_{k + 1} = Y\_k - \omega\_k \delta\_k^T\).
At the end, we have approximated \(X\) as a sum of rank-1 matrices: \(X = \Xi \Gamma^T\) where \(\Xi \in \mathbb{R}^{n \times K}\) contains the scores in its columns, and \(\Gamma^T \in \mathbb{R}^{K \times d}\) contains the loadings in its rows. Similarly for \(Y\), we have \(Y = \Omega \Delta^T\).
Note that the scores matrices \(\Xi\) and \(\Omega\) correspond to the projections of the training data \(X\) and \(Y\), respectively.
Step *a)* may be performed in two ways: either by computing the whole SVD of \(C\) and only retain the singular vectors with the biggest singular values, or by directly computing the singular vectors using the power method (cf section 11.3 in [[1]](#id6)), which corresponds to the `'nipals'` option of the `algorithm` parameter.
###
1.8.1.1. Transforming data
To transform \(X\) into \(\bar{X}\), we need to find a projection matrix \(P\) such that \(\bar{X} = XP\). We know that for the training data, \(\Xi = XP\), and \(X = \Xi \Gamma^T\). Setting \(P = U(\Gamma^T U)^{-1}\) where \(U\) is the matrix with the \(u\_k\) in the columns, we have \(XP = X U(\Gamma^T U)^{-1} = \Xi (\Gamma^T U) (\Gamma^T U)^{-1} = \Xi\) as desired. The rotation matrix \(P\) can be accessed from the `x_rotations_` attribute.
Similarly, \(Y\) can be transformed using the rotation matrix \(V(\Delta^T V)^{-1}\), accessed via the `y_rotations_` attribute.
###
1.8.1.2. Predicting the targets Y
To predict the targets of some data \(X\), we are looking for a coefficient matrix \(\beta \in R^{d \times t}\) such that \(Y = X\beta\).
The idea is to try to predict the transformed targets \(\Omega\) as a function of the transformed samples \(\Xi\), by computing \(\alpha \in \mathbb{R}\) such that \(\Omega = \alpha \Xi\).
Then, we have \(Y = \Omega \Delta^T = \alpha \Xi \Delta^T\), and since \(\Xi\) is the transformed training data we have that \(Y = X \alpha P \Delta^T\), and as a result the coefficient matrix \(\beta = \alpha P \Delta^T\).
\(\beta\) can be accessed through the `coef_` attribute.
1.8.2. PLSSVD
--------------
[`PLSSVD`](generated/sklearn.cross_decomposition.plssvd#sklearn.cross_decomposition.PLSSVD "sklearn.cross_decomposition.PLSSVD") is a simplified version of [`PLSCanonical`](generated/sklearn.cross_decomposition.plscanonical#sklearn.cross_decomposition.PLSCanonical "sklearn.cross_decomposition.PLSCanonical") described earlier: instead of iteratively deflating the matrices \(X\_k\) and \(Y\_k\), [`PLSSVD`](generated/sklearn.cross_decomposition.plssvd#sklearn.cross_decomposition.PLSSVD "sklearn.cross_decomposition.PLSSVD") computes the SVD of \(C = X^TY\) only *once*, and stores the `n_components` singular vectors corresponding to the biggest singular values in the matrices `U` and `V`, corresponding to the `x_weights_` and `y_weights_` attributes. Here, the transformed data is simply `transformed(X) = XU` and `transformed(Y) = YV`.
If `n_components == 1`, [`PLSSVD`](generated/sklearn.cross_decomposition.plssvd#sklearn.cross_decomposition.PLSSVD "sklearn.cross_decomposition.PLSSVD") and [`PLSCanonical`](generated/sklearn.cross_decomposition.plscanonical#sklearn.cross_decomposition.PLSCanonical "sklearn.cross_decomposition.PLSCanonical") are strictly equivalent.
1.8.3. PLSRegression
---------------------
The [`PLSRegression`](generated/sklearn.cross_decomposition.plsregression#sklearn.cross_decomposition.PLSRegression "sklearn.cross_decomposition.PLSRegression") estimator is similar to [`PLSCanonical`](generated/sklearn.cross_decomposition.plscanonical#sklearn.cross_decomposition.PLSCanonical "sklearn.cross_decomposition.PLSCanonical") with `algorithm='nipals'`, with 2 significant differences:
* at step a) in the power method to compute \(u\_k\) and \(v\_k\), \(v\_k\) is never normalized.
* at step c), the targets \(Y\_k\) are approximated using the projection of \(X\_k\) (i.e. \(\xi\_k\)) instead of the projection of \(Y\_k\) (i.e. \(\omega\_k\)). In other words, the loadings computation is different. As a result, the deflation in step d) will also be affected.
These two modifications affect the output of `predict` and `transform`, which are not the same as for [`PLSCanonical`](generated/sklearn.cross_decomposition.plscanonical#sklearn.cross_decomposition.PLSCanonical "sklearn.cross_decomposition.PLSCanonical"). Also, while the number of components is limited by `min(n_samples, n_features, n_targets)` in [`PLSCanonical`](generated/sklearn.cross_decomposition.plscanonical#sklearn.cross_decomposition.PLSCanonical "sklearn.cross_decomposition.PLSCanonical"), here the limit is the rank of \(X^TX\), i.e. `min(n_samples, n_features)`.
[`PLSRegression`](generated/sklearn.cross_decomposition.plsregression#sklearn.cross_decomposition.PLSRegression "sklearn.cross_decomposition.PLSRegression") is also known as PLS1 (single targets) and PLS2 (multiple targets). Much like [`Lasso`](generated/sklearn.linear_model.lasso#sklearn.linear_model.Lasso "sklearn.linear_model.Lasso"), [`PLSRegression`](generated/sklearn.cross_decomposition.plsregression#sklearn.cross_decomposition.PLSRegression "sklearn.cross_decomposition.PLSRegression") is a form of regularized linear regression where the number of components controls the strength of the regularization.
1.8.4. Canonical Correlation Analysis
--------------------------------------
Canonical Correlation Analysis was developed prior and independently to PLS. But it turns out that [`CCA`](generated/sklearn.cross_decomposition.cca#sklearn.cross_decomposition.CCA "sklearn.cross_decomposition.CCA") is a special case of PLS, and corresponds to PLS in “Mode B” in the literature.
[`CCA`](generated/sklearn.cross_decomposition.cca#sklearn.cross_decomposition.CCA "sklearn.cross_decomposition.CCA") differs from [`PLSCanonical`](generated/sklearn.cross_decomposition.plscanonical#sklearn.cross_decomposition.PLSCanonical "sklearn.cross_decomposition.PLSCanonical") in the way the weights \(u\_k\) and \(v\_k\) are computed in the power method of step a). Details can be found in section 10 of [[1]](#id6).
Since [`CCA`](generated/sklearn.cross_decomposition.cca#sklearn.cross_decomposition.CCA "sklearn.cross_decomposition.CCA") involves the inversion of \(X\_k^TX\_k\) and \(Y\_k^TY\_k\), this estimator can be unstable if the number of features or targets is greater than the number of samples.
| programming_docs |
scikit_learn 2.3. Clustering 2.3. Clustering
===============
[Clustering](https://en.wikipedia.org/wiki/Cluster_analysis) of unlabeled data can be performed with the module [`sklearn.cluster`](classes#module-sklearn.cluster "sklearn.cluster").
Each clustering algorithm comes in two variants: a class, that implements the `fit` method to learn the clusters on train data, and a function, that, given train data, returns an array of integer labels corresponding to the different clusters. For the class, the labels over the training data can be found in the `labels_` attribute.
2.3.1. Overview of clustering methods
--------------------------------------
[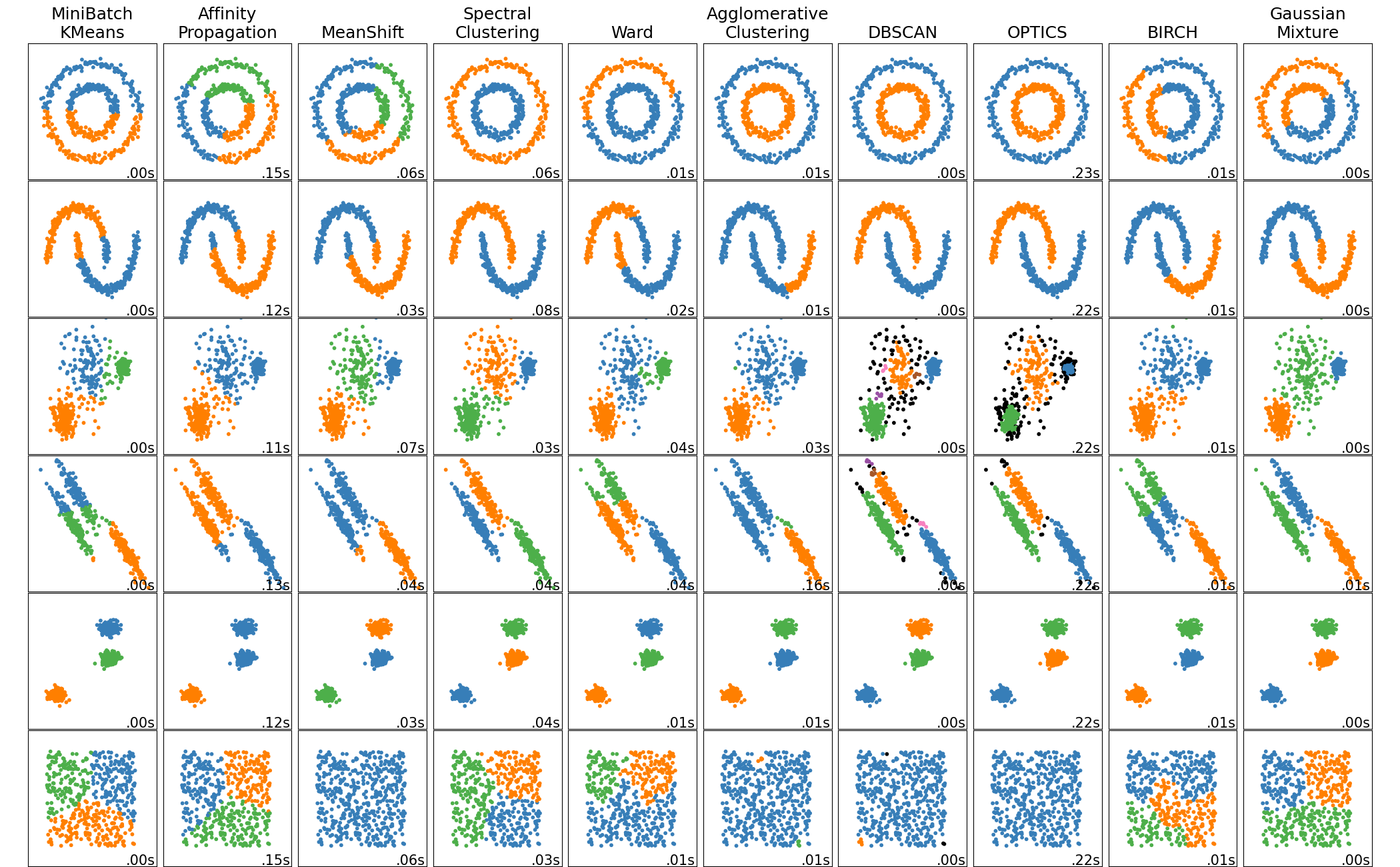](../auto_examples/cluster/plot_cluster_comparison) A comparison of the clustering algorithms in scikit-learn
| Method name | Parameters | Scalability | Usecase | Geometry (metric used) |
| --- | --- | --- | --- | --- |
| [K-Means](#k-means) | number of clusters | Very large `n_samples`, medium `n_clusters` with [MiniBatch code](#mini-batch-kmeans) | General-purpose, even cluster size, flat geometry, not too many clusters, inductive | Distances between points |
| [Affinity propagation](#affinity-propagation) | damping, sample preference | Not scalable with n\_samples | Many clusters, uneven cluster size, non-flat geometry, inductive | Graph distance (e.g. nearest-neighbor graph) |
| [Mean-shift](#mean-shift) | bandwidth | Not scalable with `n_samples` | Many clusters, uneven cluster size, non-flat geometry, inductive | Distances between points |
| [Spectral clustering](#spectral-clustering) | number of clusters | Medium `n_samples`, small `n_clusters` | Few clusters, even cluster size, non-flat geometry, transductive | Graph distance (e.g. nearest-neighbor graph) |
| [Ward hierarchical clustering](#hierarchical-clustering) | number of clusters or distance threshold | Large `n_samples` and `n_clusters` | Many clusters, possibly connectivity constraints, transductive | Distances between points |
| [Agglomerative clustering](#hierarchical-clustering) | number of clusters or distance threshold, linkage type, distance | Large `n_samples` and `n_clusters` | Many clusters, possibly connectivity constraints, non Euclidean distances, transductive | Any pairwise distance |
| [DBSCAN](#dbscan) | neighborhood size | Very large `n_samples`, medium `n_clusters` | Non-flat geometry, uneven cluster sizes, outlier removal, transductive | Distances between nearest points |
| [OPTICS](#optics) | minimum cluster membership | Very large `n_samples`, large `n_clusters` | Non-flat geometry, uneven cluster sizes, variable cluster density, outlier removal, transductive | Distances between points |
| [Gaussian mixtures](mixture#mixture) | many | Not scalable | Flat geometry, good for density estimation, inductive | Mahalanobis distances to centers |
| [BIRCH](#birch) | branching factor, threshold, optional global clusterer. | Large `n_clusters` and `n_samples` | Large dataset, outlier removal, data reduction, inductive | Euclidean distance between points |
| [Bisecting K-Means](#bisect-k-means) | number of clusters | Very large `n_samples`, medium `n_clusters` | General-purpose, even cluster size, flat geometry, no empty clusters, inductive, hierarchical | Distances between points |
Non-flat geometry clustering is useful when the clusters have a specific shape, i.e. a non-flat manifold, and the standard euclidean distance is not the right metric. This case arises in the two top rows of the figure above.
Gaussian mixture models, useful for clustering, are described in [another chapter of the documentation](mixture#mixture) dedicated to mixture models. KMeans can be seen as a special case of Gaussian mixture model with equal covariance per component.
[Transductive](https://scikit-learn.org/1.1/glossary.html#term-transductive) clustering methods (in contrast to [inductive](https://scikit-learn.org/1.1/glossary.html#term-inductive) clustering methods) are not designed to be applied to new, unseen data.
2.3.2. K-means
---------------
The [`KMeans`](generated/sklearn.cluster.kmeans#sklearn.cluster.KMeans "sklearn.cluster.KMeans") algorithm clusters data by trying to separate samples in n groups of equal variance, minimizing a criterion known as the *inertia* or within-cluster sum-of-squares (see below). This algorithm requires the number of clusters to be specified. It scales well to large numbers of samples and has been used across a large range of application areas in many different fields.
The k-means algorithm divides a set of \(N\) samples \(X\) into \(K\) disjoint clusters \(C\), each described by the mean \(\mu\_j\) of the samples in the cluster. The means are commonly called the cluster “centroids”; note that they are not, in general, points from \(X\), although they live in the same space.
The K-means algorithm aims to choose centroids that minimise the **inertia**, or **within-cluster sum-of-squares criterion**:
\[\sum\_{i=0}^{n}\min\_{\mu\_j \in C}(||x\_i - \mu\_j||^2)\] Inertia can be recognized as a measure of how internally coherent clusters are. It suffers from various drawbacks:
* Inertia makes the assumption that clusters are convex and isotropic, which is not always the case. It responds poorly to elongated clusters, or manifolds with irregular shapes.
* Inertia is not a normalized metric: we just know that lower values are better and zero is optimal. But in very high-dimensional spaces, Euclidean distances tend to become inflated (this is an instance of the so-called “curse of dimensionality”). Running a dimensionality reduction algorithm such as [Principal component analysis (PCA)](decomposition#pca) prior to k-means clustering can alleviate this problem and speed up the computations.
K-means is often referred to as Lloyd’s algorithm. In basic terms, the algorithm has three steps. The first step chooses the initial centroids, with the most basic method being to choose \(k\) samples from the dataset \(X\). After initialization, K-means consists of looping between the two other steps. The first step assigns each sample to its nearest centroid. The second step creates new centroids by taking the mean value of all of the samples assigned to each previous centroid. The difference between the old and the new centroids are computed and the algorithm repeats these last two steps until this value is less than a threshold. In other words, it repeats until the centroids do not move significantly.
K-means is equivalent to the expectation-maximization algorithm with a small, all-equal, diagonal covariance matrix.
The algorithm can also be understood through the concept of [Voronoi diagrams](https://en.wikipedia.org/wiki/Voronoi_diagram). First the Voronoi diagram of the points is calculated using the current centroids. Each segment in the Voronoi diagram becomes a separate cluster. Secondly, the centroids are updated to the mean of each segment. The algorithm then repeats this until a stopping criterion is fulfilled. Usually, the algorithm stops when the relative decrease in the objective function between iterations is less than the given tolerance value. This is not the case in this implementation: iteration stops when centroids move less than the tolerance.
Given enough time, K-means will always converge, however this may be to a local minimum. This is highly dependent on the initialization of the centroids. As a result, the computation is often done several times, with different initializations of the centroids. One method to help address this issue is the k-means++ initialization scheme, which has been implemented in scikit-learn (use the `init='k-means++'` parameter). This initializes the centroids to be (generally) distant from each other, leading to probably better results than random initialization, as shown in the reference.
K-means++ can also be called independently to select seeds for other clustering algorithms, see [`sklearn.cluster.kmeans_plusplus`](generated/sklearn.cluster.kmeans_plusplus#sklearn.cluster.kmeans_plusplus "sklearn.cluster.kmeans_plusplus") for details and example usage.
The algorithm supports sample weights, which can be given by a parameter `sample_weight`. This allows to assign more weight to some samples when computing cluster centers and values of inertia. For example, assigning a weight of 2 to a sample is equivalent to adding a duplicate of that sample to the dataset \(X\).
K-means can be used for vector quantization. This is achieved using the transform method of a trained model of [`KMeans`](generated/sklearn.cluster.kmeans#sklearn.cluster.KMeans "sklearn.cluster.KMeans").
###
2.3.2.1. Low-level parallelism
[`KMeans`](generated/sklearn.cluster.kmeans#sklearn.cluster.KMeans "sklearn.cluster.KMeans") benefits from OpenMP based parallelism through Cython. Small chunks of data (256 samples) are processed in parallel, which in addition yields a low memory footprint. For more details on how to control the number of threads, please refer to our [Parallelism](https://scikit-learn.org/1.1/computing/parallelism.html#parallelism) notes.
###
2.3.2.2. Mini Batch K-Means
The [`MiniBatchKMeans`](generated/sklearn.cluster.minibatchkmeans#sklearn.cluster.MiniBatchKMeans "sklearn.cluster.MiniBatchKMeans") is a variant of the [`KMeans`](generated/sklearn.cluster.kmeans#sklearn.cluster.KMeans "sklearn.cluster.KMeans") algorithm which uses mini-batches to reduce the computation time, while still attempting to optimise the same objective function. Mini-batches are subsets of the input data, randomly sampled in each training iteration. These mini-batches drastically reduce the amount of computation required to converge to a local solution. In contrast to other algorithms that reduce the convergence time of k-means, mini-batch k-means produces results that are generally only slightly worse than the standard algorithm.
The algorithm iterates between two major steps, similar to vanilla k-means. In the first step, \(b\) samples are drawn randomly from the dataset, to form a mini-batch. These are then assigned to the nearest centroid. In the second step, the centroids are updated. In contrast to k-means, this is done on a per-sample basis. For each sample in the mini-batch, the assigned centroid is updated by taking the streaming average of the sample and all previous samples assigned to that centroid. This has the effect of decreasing the rate of change for a centroid over time. These steps are performed until convergence or a predetermined number of iterations is reached.
[`MiniBatchKMeans`](generated/sklearn.cluster.minibatchkmeans#sklearn.cluster.MiniBatchKMeans "sklearn.cluster.MiniBatchKMeans") converges faster than [`KMeans`](generated/sklearn.cluster.kmeans#sklearn.cluster.KMeans "sklearn.cluster.KMeans"), but the quality of the results is reduced. In practice this difference in quality can be quite small, as shown in the example and cited reference.
2.3.3. Affinity Propagation
----------------------------
[`AffinityPropagation`](generated/sklearn.cluster.affinitypropagation#sklearn.cluster.AffinityPropagation "sklearn.cluster.AffinityPropagation") creates clusters by sending messages between pairs of samples until convergence. A dataset is then described using a small number of exemplars, which are identified as those most representative of other samples. The messages sent between pairs represent the suitability for one sample to be the exemplar of the other, which is updated in response to the values from other pairs. This updating happens iteratively until convergence, at which point the final exemplars are chosen, and hence the final clustering is given.
Affinity Propagation can be interesting as it chooses the number of clusters based on the data provided. For this purpose, the two important parameters are the *preference*, which controls how many exemplars are used, and the *damping factor* which damps the responsibility and availability messages to avoid numerical oscillations when updating these messages.
The main drawback of Affinity Propagation is its complexity. The algorithm has a time complexity of the order \(O(N^2 T)\), where \(N\) is the number of samples and \(T\) is the number of iterations until convergence. Further, the memory complexity is of the order \(O(N^2)\) if a dense similarity matrix is used, but reducible if a sparse similarity matrix is used. This makes Affinity Propagation most appropriate for small to medium sized datasets.
**Algorithm description:** The messages sent between points belong to one of two categories. The first is the responsibility \(r(i, k)\), which is the accumulated evidence that sample \(k\) should be the exemplar for sample \(i\). The second is the availability \(a(i, k)\) which is the accumulated evidence that sample \(i\) should choose sample \(k\) to be its exemplar, and considers the values for all other samples that \(k\) should be an exemplar. In this way, exemplars are chosen by samples if they are (1) similar enough to many samples and (2) chosen by many samples to be representative of themselves.
More formally, the responsibility of a sample \(k\) to be the exemplar of sample \(i\) is given by:
\[r(i, k) \leftarrow s(i, k) - max [ a(i, k') + s(i, k') \forall k' \neq k ]\] Where \(s(i, k)\) is the similarity between samples \(i\) and \(k\). The availability of sample \(k\) to be the exemplar of sample \(i\) is given by:
\[a(i, k) \leftarrow min [0, r(k, k) + \sum\_{i'~s.t.~i' \notin \{i, k\}}{r(i', k)}]\] To begin with, all values for \(r\) and \(a\) are set to zero, and the calculation of each iterates until convergence. As discussed above, in order to avoid numerical oscillations when updating the messages, the damping factor \(\lambda\) is introduced to iteration process:
\[r\_{t+1}(i, k) = \lambda\cdot r\_{t}(i, k) + (1-\lambda)\cdot r\_{t+1}(i, k)\] \[a\_{t+1}(i, k) = \lambda\cdot a\_{t}(i, k) + (1-\lambda)\cdot a\_{t+1}(i, k)\] where \(t\) indicates the iteration times.
2.3.4. Mean Shift
------------------
[`MeanShift`](generated/sklearn.cluster.meanshift#sklearn.cluster.MeanShift "sklearn.cluster.MeanShift") clustering aims to discover *blobs* in a smooth density of samples. It is a centroid based algorithm, which works by updating candidates for centroids to be the mean of the points within a given region. These candidates are then filtered in a post-processing stage to eliminate near-duplicates to form the final set of centroids.
Given a candidate centroid \(x\_i\) for iteration \(t\), the candidate is updated according to the following equation:
\[x\_i^{t+1} = m(x\_i^t)\] Where \(N(x\_i)\) is the neighborhood of samples within a given distance around \(x\_i\) and \(m\) is the *mean shift* vector that is computed for each centroid that points towards a region of the maximum increase in the density of points. This is computed using the following equation, effectively updating a centroid to be the mean of the samples within its neighborhood:
\[m(x\_i) = \frac{\sum\_{x\_j \in N(x\_i)}K(x\_j - x\_i)x\_j}{\sum\_{x\_j \in N(x\_i)}K(x\_j - x\_i)}\] The algorithm automatically sets the number of clusters, instead of relying on a parameter `bandwidth`, which dictates the size of the region to search through. This parameter can be set manually, but can be estimated using the provided `estimate_bandwidth` function, which is called if the bandwidth is not set.
The algorithm is not highly scalable, as it requires multiple nearest neighbor searches during the execution of the algorithm. The algorithm is guaranteed to converge, however the algorithm will stop iterating when the change in centroids is small.
Labelling a new sample is performed by finding the nearest centroid for a given sample.
2.3.5. Spectral clustering
---------------------------
[`SpectralClustering`](generated/sklearn.cluster.spectralclustering#sklearn.cluster.SpectralClustering "sklearn.cluster.SpectralClustering") performs a low-dimension embedding of the affinity matrix between samples, followed by clustering, e.g., by KMeans, of the components of the eigenvectors in the low dimensional space. It is especially computationally efficient if the affinity matrix is sparse and the `amg` solver is used for the eigenvalue problem (Note, the `amg` solver requires that the [pyamg](https://github.com/pyamg/pyamg) module is installed.)
The present version of SpectralClustering requires the number of clusters to be specified in advance. It works well for a small number of clusters, but is not advised for many clusters.
For two clusters, SpectralClustering solves a convex relaxation of the [normalized cuts](https://people.eecs.berkeley.edu/~malik/papers/SM-ncut.pdf) problem on the similarity graph: cutting the graph in two so that the weight of the edges cut is small compared to the weights of the edges inside each cluster. This criteria is especially interesting when working on images, where graph vertices are pixels, and weights of the edges of the similarity graph are computed using a function of a gradient of the image.
Warning
Transforming distance to well-behaved similarities
Note that if the values of your similarity matrix are not well distributed, e.g. with negative values or with a distance matrix rather than a similarity, the spectral problem will be singular and the problem not solvable. In which case it is advised to apply a transformation to the entries of the matrix. For instance, in the case of a signed distance matrix, is common to apply a heat kernel:
```
similarity = np.exp(-beta * distance / distance.std())
```
See the examples for such an application.
###
2.3.5.1. Different label assignment strategies
Different label assignment strategies can be used, corresponding to the `assign_labels` parameter of [`SpectralClustering`](generated/sklearn.cluster.spectralclustering#sklearn.cluster.SpectralClustering "sklearn.cluster.SpectralClustering"). `"kmeans"` strategy can match finer details, but can be unstable. In particular, unless you control the `random_state`, it may not be reproducible from run-to-run, as it depends on random initialization. The alternative `"discretize"` strategy is 100% reproducible, but tends to create parcels of fairly even and geometrical shape. The recently added `"cluster_qr"` option is a deterministic alternative that tends to create the visually best partitioning on the example application below.
| `assign_labels="kmeans"` | `assign_labels="discretize"` | `assign_labels="cluster_qr"` |
| --- | --- | --- |
| | | |
###
2.3.5.2. Spectral Clustering Graphs
Spectral Clustering can also be used to partition graphs via their spectral embeddings. In this case, the affinity matrix is the adjacency matrix of the graph, and SpectralClustering is initialized with `affinity='precomputed'`:
```
>>> from sklearn.cluster import SpectralClustering
>>> sc = SpectralClustering(3, affinity='precomputed', n_init=100,
... assign_labels='discretize')
>>> sc.fit_predict(adjacency_matrix)
```
2.3.6. Hierarchical clustering
-------------------------------
Hierarchical clustering is a general family of clustering algorithms that build nested clusters by merging or splitting them successively. This hierarchy of clusters is represented as a tree (or dendrogram). The root of the tree is the unique cluster that gathers all the samples, the leaves being the clusters with only one sample. See the [Wikipedia page](https://en.wikipedia.org/wiki/Hierarchical_clustering) for more details.
The [`AgglomerativeClustering`](generated/sklearn.cluster.agglomerativeclustering#sklearn.cluster.AgglomerativeClustering "sklearn.cluster.AgglomerativeClustering") object performs a hierarchical clustering using a bottom up approach: each observation starts in its own cluster, and clusters are successively merged together. The linkage criteria determines the metric used for the merge strategy:
* **Ward** minimizes the sum of squared differences within all clusters. It is a variance-minimizing approach and in this sense is similar to the k-means objective function but tackled with an agglomerative hierarchical approach.
* **Maximum** or **complete linkage** minimizes the maximum distance between observations of pairs of clusters.
* **Average linkage** minimizes the average of the distances between all observations of pairs of clusters.
* **Single linkage** minimizes the distance between the closest observations of pairs of clusters.
[`AgglomerativeClustering`](generated/sklearn.cluster.agglomerativeclustering#sklearn.cluster.AgglomerativeClustering "sklearn.cluster.AgglomerativeClustering") can also scale to large number of samples when it is used jointly with a connectivity matrix, but is computationally expensive when no connectivity constraints are added between samples: it considers at each step all the possible merges.
###
2.3.6.1. Different linkage type: Ward, complete, average, and single linkage
[`AgglomerativeClustering`](generated/sklearn.cluster.agglomerativeclustering#sklearn.cluster.AgglomerativeClustering "sklearn.cluster.AgglomerativeClustering") supports Ward, single, average, and complete linkage strategies.
[](../auto_examples/cluster/plot_linkage_comparison) Agglomerative cluster has a “rich get richer” behavior that leads to uneven cluster sizes. In this regard, single linkage is the worst strategy, and Ward gives the most regular sizes. However, the affinity (or distance used in clustering) cannot be varied with Ward, thus for non Euclidean metrics, average linkage is a good alternative. Single linkage, while not robust to noisy data, can be computed very efficiently and can therefore be useful to provide hierarchical clustering of larger datasets. Single linkage can also perform well on non-globular data.
###
2.3.6.2. Visualization of cluster hierarchy
It’s possible to visualize the tree representing the hierarchical merging of clusters as a dendrogram. Visual inspection can often be useful for understanding the structure of the data, though more so in the case of small sample sizes.
###
2.3.6.3. Adding connectivity constraints
An interesting aspect of [`AgglomerativeClustering`](generated/sklearn.cluster.agglomerativeclustering#sklearn.cluster.AgglomerativeClustering "sklearn.cluster.AgglomerativeClustering") is that connectivity constraints can be added to this algorithm (only adjacent clusters can be merged together), through a connectivity matrix that defines for each sample the neighboring samples following a given structure of the data. For instance, in the swiss-roll example below, the connectivity constraints forbid the merging of points that are not adjacent on the swiss roll, and thus avoid forming clusters that extend across overlapping folds of the roll.
These constraint are useful to impose a certain local structure, but they also make the algorithm faster, especially when the number of the samples is high.
The connectivity constraints are imposed via an connectivity matrix: a scipy sparse matrix that has elements only at the intersection of a row and a column with indices of the dataset that should be connected. This matrix can be constructed from a-priori information: for instance, you may wish to cluster web pages by only merging pages with a link pointing from one to another. It can also be learned from the data, for instance using [`sklearn.neighbors.kneighbors_graph`](generated/sklearn.neighbors.kneighbors_graph#sklearn.neighbors.kneighbors_graph "sklearn.neighbors.kneighbors_graph") to restrict merging to nearest neighbors as in [this example](../auto_examples/cluster/plot_agglomerative_clustering#sphx-glr-auto-examples-cluster-plot-agglomerative-clustering-py), or using [`sklearn.feature_extraction.image.grid_to_graph`](generated/sklearn.feature_extraction.image.grid_to_graph#sklearn.feature_extraction.image.grid_to_graph "sklearn.feature_extraction.image.grid_to_graph") to enable only merging of neighboring pixels on an image, as in the [coin](../auto_examples/cluster/plot_coin_ward_segmentation#sphx-glr-auto-examples-cluster-plot-coin-ward-segmentation-py) example.
Warning
**Connectivity constraints with single, average and complete linkage**
Connectivity constraints and single, complete or average linkage can enhance the ‘rich getting richer’ aspect of agglomerative clustering, particularly so if they are built with [`sklearn.neighbors.kneighbors_graph`](generated/sklearn.neighbors.kneighbors_graph#sklearn.neighbors.kneighbors_graph "sklearn.neighbors.kneighbors_graph"). In the limit of a small number of clusters, they tend to give a few macroscopically occupied clusters and almost empty ones. (see the discussion in [Agglomerative clustering with and without structure](../auto_examples/cluster/plot_agglomerative_clustering#sphx-glr-auto-examples-cluster-plot-agglomerative-clustering-py)). Single linkage is the most brittle linkage option with regard to this issue.
###
2.3.6.4. Varying the metric
Single, average and complete linkage can be used with a variety of distances (or affinities), in particular Euclidean distance (*l2*), Manhattan distance (or Cityblock, or *l1*), cosine distance, or any precomputed affinity matrix.
* *l1* distance is often good for sparse features, or sparse noise: i.e. many of the features are zero, as in text mining using occurrences of rare words.
* *cosine* distance is interesting because it is invariant to global scalings of the signal.
The guidelines for choosing a metric is to use one that maximizes the distance between samples in different classes, and minimizes that within each class.
###
2.3.6.5. Bisecting K-Means
The [`BisectingKMeans`](generated/sklearn.cluster.bisectingkmeans#sklearn.cluster.BisectingKMeans "sklearn.cluster.BisectingKMeans") is an iterative variant of [`KMeans`](generated/sklearn.cluster.kmeans#sklearn.cluster.KMeans "sklearn.cluster.KMeans"), using divisive hierarchical clustering. Instead of creating all centroids at once, centroids are picked progressively based on a previous clustering: a cluster is split into two new clusters repeatedly until the target number of clusters is reached.
[`BisectingKMeans`](generated/sklearn.cluster.bisectingkmeans#sklearn.cluster.BisectingKMeans "sklearn.cluster.BisectingKMeans") is more efficient than [`KMeans`](generated/sklearn.cluster.kmeans#sklearn.cluster.KMeans "sklearn.cluster.KMeans") when the number the number of clusters is large since it only works on a subset of the data at each bisection while [`KMeans`](generated/sklearn.cluster.kmeans#sklearn.cluster.KMeans "sklearn.cluster.KMeans") always works on the entire dataset.
Although [`BisectingKMeans`](generated/sklearn.cluster.bisectingkmeans#sklearn.cluster.BisectingKMeans "sklearn.cluster.BisectingKMeans") can’t benefit from the advantages of the `"k-means++"` initialization by design, it will still produce comparable results than `KMeans(init="k-means++")` in terms of inertia at cheaper computational costs, and will likely produce better results than `KMeans` with a random initialization.
This variant is more efficient to agglomerative clustering if the number of clusters is small compared to the number of data points.
This variant also does not produce empty clusters.
There exist two strategies for selecting the cluster to split:
* `bisecting_strategy="largest_cluster"` selects the cluster having the most points
* `bisecting_strategy="biggest_inertia"` selects the cluster with biggest inertia (cluster with biggest Sum of Squared Errors within)
Picking by largest amount of data points in most cases produces result as accurate as picking by inertia and is faster (especially for larger amount of data points, where calculating error may be costly).
Picking by largest amount of data points will also likely produce clusters of similar sizes while `KMeans` is known to produce clusters of different sizes.
Difference between Bisecting K-Means and regular K-Means can be seen on example [Bisecting K-Means and Regular K-Means Performance Comparison](../auto_examples/cluster/plot_bisect_kmeans#sphx-glr-auto-examples-cluster-plot-bisect-kmeans-py). While the regular K-Means algorithm tends to create non-related clusters, clusters from Bisecting K-Means are well ordered and create quite a visible hierarchy.
2.3.7. DBSCAN
--------------
The [`DBSCAN`](generated/sklearn.cluster.dbscan#sklearn.cluster.DBSCAN "sklearn.cluster.DBSCAN") algorithm views clusters as areas of high density separated by areas of low density. Due to this rather generic view, clusters found by DBSCAN can be any shape, as opposed to k-means which assumes that clusters are convex shaped. The central component to the DBSCAN is the concept of *core samples*, which are samples that are in areas of high density. A cluster is therefore a set of core samples, each close to each other (measured by some distance measure) and a set of non-core samples that are close to a core sample (but are not themselves core samples). There are two parameters to the algorithm, `min_samples` and `eps`, which define formally what we mean when we say *dense*. Higher `min_samples` or lower `eps` indicate higher density necessary to form a cluster.
More formally, we define a core sample as being a sample in the dataset such that there exist `min_samples` other samples within a distance of `eps`, which are defined as *neighbors* of the core sample. This tells us that the core sample is in a dense area of the vector space. A cluster is a set of core samples that can be built by recursively taking a core sample, finding all of its neighbors that are core samples, finding all of *their* neighbors that are core samples, and so on. A cluster also has a set of non-core samples, which are samples that are neighbors of a core sample in the cluster but are not themselves core samples. Intuitively, these samples are on the fringes of a cluster.
Any core sample is part of a cluster, by definition. Any sample that is not a core sample, and is at least `eps` in distance from any core sample, is considered an outlier by the algorithm.
While the parameter `min_samples` primarily controls how tolerant the algorithm is towards noise (on noisy and large data sets it may be desirable to increase this parameter), the parameter `eps` is *crucial to choose appropriately* for the data set and distance function and usually cannot be left at the default value. It controls the local neighborhood of the points. When chosen too small, most data will not be clustered at all (and labeled as `-1` for “noise”). When chosen too large, it causes close clusters to be merged into one cluster, and eventually the entire data set to be returned as a single cluster. Some heuristics for choosing this parameter have been discussed in the literature, for example based on a knee in the nearest neighbor distances plot (as discussed in the references below).
In the figure below, the color indicates cluster membership, with large circles indicating core samples found by the algorithm. Smaller circles are non-core samples that are still part of a cluster. Moreover, the outliers are indicated by black points below.
2.3.8. OPTICS
--------------
The [`OPTICS`](generated/sklearn.cluster.optics#sklearn.cluster.OPTICS "sklearn.cluster.OPTICS") algorithm shares many similarities with the [`DBSCAN`](generated/sklearn.cluster.dbscan#sklearn.cluster.DBSCAN "sklearn.cluster.DBSCAN") algorithm, and can be considered a generalization of DBSCAN that relaxes the `eps` requirement from a single value to a value range. The key difference between DBSCAN and OPTICS is that the OPTICS algorithm builds a *reachability* graph, which assigns each sample both a `reachability_` distance, and a spot within the cluster `ordering_` attribute; these two attributes are assigned when the model is fitted, and are used to determine cluster membership. If OPTICS is run with the default value of *inf* set for `max_eps`, then DBSCAN style cluster extraction can be performed repeatedly in linear time for any given `eps` value using the `cluster_optics_dbscan` method. Setting `max_eps` to a lower value will result in shorter run times, and can be thought of as the maximum neighborhood radius from each point to find other potential reachable points.
The *reachability* distances generated by OPTICS allow for variable density extraction of clusters within a single data set. As shown in the above plot, combining *reachability* distances and data set `ordering_` produces a *reachability plot*, where point density is represented on the Y-axis, and points are ordered such that nearby points are adjacent. ‘Cutting’ the reachability plot at a single value produces DBSCAN like results; all points above the ‘cut’ are classified as noise, and each time that there is a break when reading from left to right signifies a new cluster. The default cluster extraction with OPTICS looks at the steep slopes within the graph to find clusters, and the user can define what counts as a steep slope using the parameter `xi`. There are also other possibilities for analysis on the graph itself, such as generating hierarchical representations of the data through reachability-plot dendrograms, and the hierarchy of clusters detected by the algorithm can be accessed through the `cluster_hierarchy_` parameter. The plot above has been color-coded so that cluster colors in planar space match the linear segment clusters of the reachability plot. Note that the blue and red clusters are adjacent in the reachability plot, and can be hierarchically represented as children of a larger parent cluster.
2.3.9. BIRCH
-------------
The [`Birch`](generated/sklearn.cluster.birch#sklearn.cluster.Birch "sklearn.cluster.Birch") builds a tree called the Clustering Feature Tree (CFT) for the given data. The data is essentially lossy compressed to a set of Clustering Feature nodes (CF Nodes). The CF Nodes have a number of subclusters called Clustering Feature subclusters (CF Subclusters) and these CF Subclusters located in the non-terminal CF Nodes can have CF Nodes as children.
The CF Subclusters hold the necessary information for clustering which prevents the need to hold the entire input data in memory. This information includes:
* Number of samples in a subcluster.
* Linear Sum - An n-dimensional vector holding the sum of all samples
* Squared Sum - Sum of the squared L2 norm of all samples.
* Centroids - To avoid recalculation linear sum / n\_samples.
* Squared norm of the centroids.
The BIRCH algorithm has two parameters, the threshold and the branching factor. The branching factor limits the number of subclusters in a node and the threshold limits the distance between the entering sample and the existing subclusters.
This algorithm can be viewed as an instance or data reduction method, since it reduces the input data to a set of subclusters which are obtained directly from the leaves of the CFT. This reduced data can be further processed by feeding it into a global clusterer. This global clusterer can be set by `n_clusters`. If `n_clusters` is set to None, the subclusters from the leaves are directly read off, otherwise a global clustering step labels these subclusters into global clusters (labels) and the samples are mapped to the global label of the nearest subcluster.
**Algorithm description:**
* A new sample is inserted into the root of the CF Tree which is a CF Node. It is then merged with the subcluster of the root, that has the smallest radius after merging, constrained by the threshold and branching factor conditions. If the subcluster has any child node, then this is done repeatedly till it reaches a leaf. After finding the nearest subcluster in the leaf, the properties of this subcluster and the parent subclusters are recursively updated.
* If the radius of the subcluster obtained by merging the new sample and the nearest subcluster is greater than the square of the threshold and if the number of subclusters is greater than the branching factor, then a space is temporarily allocated to this new sample. The two farthest subclusters are taken and the subclusters are divided into two groups on the basis of the distance between these subclusters.
* If this split node has a parent subcluster and there is room for a new subcluster, then the parent is split into two. If there is no room, then this node is again split into two and the process is continued recursively, till it reaches the root.
**BIRCH or MiniBatchKMeans?**
* BIRCH does not scale very well to high dimensional data. As a rule of thumb if `n_features` is greater than twenty, it is generally better to use MiniBatchKMeans.
* If the number of instances of data needs to be reduced, or if one wants a large number of subclusters either as a preprocessing step or otherwise, BIRCH is more useful than MiniBatchKMeans.
**How to use partial\_fit?**
To avoid the computation of global clustering, for every call of `partial_fit` the user is advised
1. To set `n_clusters=None` initially
2. Train all data by multiple calls to partial\_fit.
3. Set `n_clusters` to a required value using `brc.set_params(n_clusters=n_clusters)`.
4. Call `partial_fit` finally with no arguments, i.e. `brc.partial_fit()` which performs the global clustering.
[](../auto_examples/cluster/plot_birch_vs_minibatchkmeans)
2.3.10. Clustering performance evaluation
------------------------------------------
Evaluating the performance of a clustering algorithm is not as trivial as counting the number of errors or the precision and recall of a supervised classification algorithm. In particular any evaluation metric should not take the absolute values of the cluster labels into account but rather if this clustering define separations of the data similar to some ground truth set of classes or satisfying some assumption such that members belong to the same class are more similar than members of different classes according to some similarity metric.
###
2.3.10.1. Rand index
Given the knowledge of the ground truth class assignments `labels_true` and our clustering algorithm assignments of the same samples `labels_pred`, the **(adjusted or unadjusted) Rand index** is a function that measures the **similarity** of the two assignments, ignoring permutations:
```
>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]
>>> metrics.rand_score(labels_true, labels_pred)
0.66...
```
The Rand index does not ensure to obtain a value close to 0.0 for a random labelling. The adjusted Rand index **corrects for chance** and will give such a baseline.
```
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
0.24...
```
As with all clustering metrics, one can permute 0 and 1 in the predicted labels, rename 2 to 3, and get the same score:
```
>>> labels_pred = [1, 1, 0, 0, 3, 3]
>>> metrics.rand_score(labels_true, labels_pred)
0.66...
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
0.24...
```
Furthermore, both [`rand_score`](generated/sklearn.metrics.rand_score#sklearn.metrics.rand_score "sklearn.metrics.rand_score") [`adjusted_rand_score`](generated/sklearn.metrics.adjusted_rand_score#sklearn.metrics.adjusted_rand_score "sklearn.metrics.adjusted_rand_score") are **symmetric**: swapping the argument does not change the scores. They can thus be used as **consensus measures**:
```
>>> metrics.rand_score(labels_pred, labels_true)
0.66...
>>> metrics.adjusted_rand_score(labels_pred, labels_true)
0.24...
```
Perfect labeling is scored 1.0:
```
>>> labels_pred = labels_true[:]
>>> metrics.rand_score(labels_true, labels_pred)
1.0
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
1.0
```
Poorly agreeing labels (e.g. independent labelings) have lower scores, and for the adjusted Rand index the score will be negative or close to zero. However, for the unadjusted Rand index the score, while lower, will not necessarily be close to zero.:
```
>>> labels_true = [0, 0, 0, 0, 0, 0, 1, 1]
>>> labels_pred = [0, 1, 2, 3, 4, 5, 5, 6]
>>> metrics.rand_score(labels_true, labels_pred)
0.39...
>>> metrics.adjusted_rand_score(labels_true, labels_pred)
-0.07...
```
####
2.3.10.1.1. Advantages
* **Interpretability**: The unadjusted Rand index is proportional to the number of sample pairs whose labels are the same in both `labels_pred` and `labels_true`, or are different in both.
* **Random (uniform) label assignments have an adjusted Rand index score close to 0.0** for any value of `n_clusters` and `n_samples` (which is not the case for the unadjusted Rand index or the V-measure for instance).
* **Bounded range**: Lower values indicate different labelings, similar clusterings have a high (adjusted or unadjusted) Rand index, 1.0 is the perfect match score. The score range is [0, 1] for the unadjusted Rand index and [-1, 1] for the adjusted Rand index.
* **No assumption is made on the cluster structure**: The (adjusted or unadjusted) Rand index can be used to compare all kinds of clustering algorithms, and can be used to compare clustering algorithms such as k-means which assumes isotropic blob shapes with results of spectral clustering algorithms which can find cluster with “folded” shapes.
####
2.3.10.1.2. Drawbacks
* Contrary to inertia, the **(adjusted or unadjusted) Rand index requires knowledge of the ground truth classes** which is almost never available in practice or requires manual assignment by human annotators (as in the supervised learning setting).
However (adjusted or unadjusted) Rand index can also be useful in a purely unsupervised setting as a building block for a Consensus Index that can be used for clustering model selection (TODO).
* The **unadjusted Rand index is often close to 1.0** even if the clusterings themselves differ significantly. This can be understood when interpreting the Rand index as the accuracy of element pair labeling resulting from the clusterings: In practice there often is a majority of element pairs that are assigned the `different` pair label under both the predicted and the ground truth clustering resulting in a high proportion of pair labels that agree, which leads subsequently to a high score.
####
2.3.10.1.3. Mathematical formulation
If C is a ground truth class assignment and K the clustering, let us define \(a\) and \(b\) as:
* \(a\), the number of pairs of elements that are in the same set in C and in the same set in K
* \(b\), the number of pairs of elements that are in different sets in C and in different sets in K
The unadjusted Rand index is then given by:
\[\text{RI} = \frac{a + b}{C\_2^{n\_{samples}}}\] where \(C\_2^{n\_{samples}}\) is the total number of possible pairs in the dataset. It does not matter if the calculation is performed on ordered pairs or unordered pairs as long as the calculation is performed consistently.
However, the Rand index does not guarantee that random label assignments will get a value close to zero (esp. if the number of clusters is in the same order of magnitude as the number of samples).
To counter this effect we can discount the expected RI \(E[\text{RI}]\) of random labelings by defining the adjusted Rand index as follows:
\[\text{ARI} = \frac{\text{RI} - E[\text{RI}]}{\max(\text{RI}) - E[\text{RI}]}\] ###
2.3.10.2. Mutual Information based scores
Given the knowledge of the ground truth class assignments `labels_true` and our clustering algorithm assignments of the same samples `labels_pred`, the **Mutual Information** is a function that measures the **agreement** of the two assignments, ignoring permutations. Two different normalized versions of this measure are available, **Normalized Mutual Information (NMI)** and **Adjusted Mutual Information (AMI)**. NMI is often used in the literature, while AMI was proposed more recently and is **normalized against chance**:
```
>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
0.22504...
```
One can permute 0 and 1 in the predicted labels, rename 2 to 3 and get the same score:
```
>>> labels_pred = [1, 1, 0, 0, 3, 3]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
0.22504...
```
All, [`mutual_info_score`](generated/sklearn.metrics.mutual_info_score#sklearn.metrics.mutual_info_score "sklearn.metrics.mutual_info_score"), [`adjusted_mutual_info_score`](generated/sklearn.metrics.adjusted_mutual_info_score#sklearn.metrics.adjusted_mutual_info_score "sklearn.metrics.adjusted_mutual_info_score") and [`normalized_mutual_info_score`](generated/sklearn.metrics.normalized_mutual_info_score#sklearn.metrics.normalized_mutual_info_score "sklearn.metrics.normalized_mutual_info_score") are symmetric: swapping the argument does not change the score. Thus they can be used as a **consensus measure**:
```
>>> metrics.adjusted_mutual_info_score(labels_pred, labels_true)
0.22504...
```
Perfect labeling is scored 1.0:
```
>>> labels_pred = labels_true[:]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
1.0
>>> metrics.normalized_mutual_info_score(labels_true, labels_pred)
1.0
```
This is not true for `mutual_info_score`, which is therefore harder to judge:
```
>>> metrics.mutual_info_score(labels_true, labels_pred)
0.69...
```
Bad (e.g. independent labelings) have non-positive scores:
```
>>> labels_true = [0, 1, 2, 0, 3, 4, 5, 1]
>>> labels_pred = [1, 1, 0, 0, 2, 2, 2, 2]
>>> metrics.adjusted_mutual_info_score(labels_true, labels_pred)
-0.10526...
```
####
2.3.10.2.1. Advantages
* **Random (uniform) label assignments have a AMI score close to 0.0** for any value of `n_clusters` and `n_samples` (which is not the case for raw Mutual Information or the V-measure for instance).
* **Upper bound of 1**: Values close to zero indicate two label assignments that are largely independent, while values close to one indicate significant agreement. Further, an AMI of exactly 1 indicates that the two label assignments are equal (with or without permutation).
####
2.3.10.2.2. Drawbacks
* Contrary to inertia, **MI-based measures require the knowledge of the ground truth classes** while almost never available in practice or requires manual assignment by human annotators (as in the supervised learning setting).
However MI-based measures can also be useful in purely unsupervised setting as a building block for a Consensus Index that can be used for clustering model selection.
* NMI and MI are not adjusted against chance.
####
2.3.10.2.3. Mathematical formulation
Assume two label assignments (of the same N objects), \(U\) and \(V\). Their entropy is the amount of uncertainty for a partition set, defined by:
\[H(U) = - \sum\_{i=1}^{|U|}P(i)\log(P(i))\] where \(P(i) = |U\_i| / N\) is the probability that an object picked at random from \(U\) falls into class \(U\_i\). Likewise for \(V\):
\[H(V) = - \sum\_{j=1}^{|V|}P'(j)\log(P'(j))\] With \(P'(j) = |V\_j| / N\). The mutual information (MI) between \(U\) and \(V\) is calculated by:
\[\text{MI}(U, V) = \sum\_{i=1}^{|U|}\sum\_{j=1}^{|V|}P(i, j)\log\left(\frac{P(i,j)}{P(i)P'(j)}\right)\] where \(P(i, j) = |U\_i \cap V\_j| / N\) is the probability that an object picked at random falls into both classes \(U\_i\) and \(V\_j\).
It also can be expressed in set cardinality formulation:
\[\text{MI}(U, V) = \sum\_{i=1}^{|U|} \sum\_{j=1}^{|V|} \frac{|U\_i \cap V\_j|}{N}\log\left(\frac{N|U\_i \cap V\_j|}{|U\_i||V\_j|}\right)\] The normalized mutual information is defined as
\[\text{NMI}(U, V) = \frac{\text{MI}(U, V)}{\text{mean}(H(U), H(V))}\] This value of the mutual information and also the normalized variant is not adjusted for chance and will tend to increase as the number of different labels (clusters) increases, regardless of the actual amount of “mutual information” between the label assignments.
The expected value for the mutual information can be calculated using the following equation [[VEB2009]](#veb2009). In this equation, \(a\_i = |U\_i|\) (the number of elements in \(U\_i\)) and \(b\_j = |V\_j|\) (the number of elements in \(V\_j\)).
\[E[\text{MI}(U,V)]=\sum\_{i=1}^{|U|} \sum\_{j=1}^{|V|} \sum\_{n\_{ij}=(a\_i+b\_j-N)^+ }^{\min(a\_i, b\_j)} \frac{n\_{ij}}{N}\log \left( \frac{ N.n\_{ij}}{a\_i b\_j}\right) \frac{a\_i!b\_j!(N-a\_i)!(N-b\_j)!}{N!n\_{ij}!(a\_i-n\_{ij})!(b\_j-n\_{ij})! (N-a\_i-b\_j+n\_{ij})!}\] Using the expected value, the adjusted mutual information can then be calculated using a similar form to that of the adjusted Rand index:
\[\text{AMI} = \frac{\text{MI} - E[\text{MI}]}{\text{mean}(H(U), H(V)) - E[\text{MI}]}\] For normalized mutual information and adjusted mutual information, the normalizing value is typically some *generalized* mean of the entropies of each clustering. Various generalized means exist, and no firm rules exist for preferring one over the others. The decision is largely a field-by-field basis; for instance, in community detection, the arithmetic mean is most common. Each normalizing method provides “qualitatively similar behaviours” [[YAT2016]](#yat2016). In our implementation, this is controlled by the `average_method` parameter.
Vinh et al. (2010) named variants of NMI and AMI by their averaging method [[VEB2010]](#veb2010). Their ‘sqrt’ and ‘sum’ averages are the geometric and arithmetic means; we use these more broadly common names.
###
2.3.10.3. Homogeneity, completeness and V-measure
Given the knowledge of the ground truth class assignments of the samples, it is possible to define some intuitive metric using conditional entropy analysis.
In particular Rosenberg and Hirschberg (2007) define the following two desirable objectives for any cluster assignment:
* **homogeneity**: each cluster contains only members of a single class.
* **completeness**: all members of a given class are assigned to the same cluster.
We can turn those concept as scores [`homogeneity_score`](generated/sklearn.metrics.homogeneity_score#sklearn.metrics.homogeneity_score "sklearn.metrics.homogeneity_score") and [`completeness_score`](generated/sklearn.metrics.completeness_score#sklearn.metrics.completeness_score "sklearn.metrics.completeness_score"). Both are bounded below by 0.0 and above by 1.0 (higher is better):
```
>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]
>>> metrics.homogeneity_score(labels_true, labels_pred)
0.66...
>>> metrics.completeness_score(labels_true, labels_pred)
0.42...
```
Their harmonic mean called **V-measure** is computed by [`v_measure_score`](generated/sklearn.metrics.v_measure_score#sklearn.metrics.v_measure_score "sklearn.metrics.v_measure_score"):
```
>>> metrics.v_measure_score(labels_true, labels_pred)
0.51...
```
This function’s formula is as follows:
\[v = \frac{(1 + \beta) \times \text{homogeneity} \times \text{completeness}}{(\beta \times \text{homogeneity} + \text{completeness})}\] `beta` defaults to a value of 1.0, but for using a value less than 1 for beta:
```
>>> metrics.v_measure_score(labels_true, labels_pred, beta=0.6)
0.54...
```
more weight will be attributed to homogeneity, and using a value greater than 1:
```
>>> metrics.v_measure_score(labels_true, labels_pred, beta=1.8)
0.48...
```
more weight will be attributed to completeness.
The V-measure is actually equivalent to the mutual information (NMI) discussed above, with the aggregation function being the arithmetic mean [[B2011]](#b2011).
Homogeneity, completeness and V-measure can be computed at once using [`homogeneity_completeness_v_measure`](generated/sklearn.metrics.homogeneity_completeness_v_measure#sklearn.metrics.homogeneity_completeness_v_measure "sklearn.metrics.homogeneity_completeness_v_measure") as follows:
```
>>> metrics.homogeneity_completeness_v_measure(labels_true, labels_pred)
(0.66..., 0.42..., 0.51...)
```
The following clustering assignment is slightly better, since it is homogeneous but not complete:
```
>>> labels_pred = [0, 0, 0, 1, 2, 2]
>>> metrics.homogeneity_completeness_v_measure(labels_true, labels_pred)
(1.0, 0.68..., 0.81...)
```
Note
[`v_measure_score`](generated/sklearn.metrics.v_measure_score#sklearn.metrics.v_measure_score "sklearn.metrics.v_measure_score") is **symmetric**: it can be used to evaluate the **agreement** of two independent assignments on the same dataset.
This is not the case for [`completeness_score`](generated/sklearn.metrics.completeness_score#sklearn.metrics.completeness_score "sklearn.metrics.completeness_score") and [`homogeneity_score`](generated/sklearn.metrics.homogeneity_score#sklearn.metrics.homogeneity_score "sklearn.metrics.homogeneity_score"): both are bound by the relationship:
```
homogeneity_score(a, b) == completeness_score(b, a)
```
####
2.3.10.3.1. Advantages
* **Bounded scores**: 0.0 is as bad as it can be, 1.0 is a perfect score.
* Intuitive interpretation: clustering with bad V-measure can be **qualitatively analyzed in terms of homogeneity and completeness** to better feel what ‘kind’ of mistakes is done by the assignment.
* **No assumption is made on the cluster structure**: can be used to compare clustering algorithms such as k-means which assumes isotropic blob shapes with results of spectral clustering algorithms which can find cluster with “folded” shapes.
####
2.3.10.3.2. Drawbacks
* The previously introduced metrics are **not normalized with regards to random labeling**: this means that depending on the number of samples, clusters and ground truth classes, a completely random labeling will not always yield the same values for homogeneity, completeness and hence v-measure. In particular **random labeling won’t yield zero scores especially when the number of clusters is large**.
This problem can safely be ignored when the number of samples is more than a thousand and the number of clusters is less than 10. **For smaller sample sizes or larger number of clusters it is safer to use an adjusted index such as the Adjusted Rand Index (ARI)**.
* These metrics **require the knowledge of the ground truth classes** while almost never available in practice or requires manual assignment by human annotators (as in the supervised learning setting).
####
2.3.10.3.3. Mathematical formulation
Homogeneity and completeness scores are formally given by:
\[h = 1 - \frac{H(C|K)}{H(C)}\] \[c = 1 - \frac{H(K|C)}{H(K)}\] where \(H(C|K)\) is the **conditional entropy of the classes given the cluster assignments** and is given by:
\[H(C|K) = - \sum\_{c=1}^{|C|} \sum\_{k=1}^{|K|} \frac{n\_{c,k}}{n} \cdot \log\left(\frac{n\_{c,k}}{n\_k}\right)\] and \(H(C)\) is the **entropy of the classes** and is given by:
\[H(C) = - \sum\_{c=1}^{|C|} \frac{n\_c}{n} \cdot \log\left(\frac{n\_c}{n}\right)\] with \(n\) the total number of samples, \(n\_c\) and \(n\_k\) the number of samples respectively belonging to class \(c\) and cluster \(k\), and finally \(n\_{c,k}\) the number of samples from class \(c\) assigned to cluster \(k\).
The **conditional entropy of clusters given class** \(H(K|C)\) and the **entropy of clusters** \(H(K)\) are defined in a symmetric manner.
Rosenberg and Hirschberg further define **V-measure** as the **harmonic mean of homogeneity and completeness**:
\[v = 2 \cdot \frac{h \cdot c}{h + c}\] ###
2.3.10.4. Fowlkes-Mallows scores
The Fowlkes-Mallows index ([`sklearn.metrics.fowlkes_mallows_score`](generated/sklearn.metrics.fowlkes_mallows_score#sklearn.metrics.fowlkes_mallows_score "sklearn.metrics.fowlkes_mallows_score")) can be used when the ground truth class assignments of the samples is known. The Fowlkes-Mallows score FMI is defined as the geometric mean of the pairwise precision and recall:
\[\text{FMI} = \frac{\text{TP}}{\sqrt{(\text{TP} + \text{FP}) (\text{TP} + \text{FN})}}\] Where `TP` is the number of **True Positive** (i.e. the number of pair of points that belong to the same clusters in both the true labels and the predicted labels), `FP` is the number of **False Positive** (i.e. the number of pair of points that belong to the same clusters in the true labels and not in the predicted labels) and `FN` is the number of **False Negative** (i.e the number of pair of points that belongs in the same clusters in the predicted labels and not in the true labels).
The score ranges from 0 to 1. A high value indicates a good similarity between two clusters.
```
>>> from sklearn import metrics
>>> labels_true = [0, 0, 0, 1, 1, 1]
>>> labels_pred = [0, 0, 1, 1, 2, 2]
```
```
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
0.47140...
```
One can permute 0 and 1 in the predicted labels, rename 2 to 3 and get the same score:
```
>>> labels_pred = [1, 1, 0, 0, 3, 3]
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
0.47140...
```
Perfect labeling is scored 1.0:
```
>>> labels_pred = labels_true[:]
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
1.0
```
Bad (e.g. independent labelings) have zero scores:
```
>>> labels_true = [0, 1, 2, 0, 3, 4, 5, 1]
>>> labels_pred = [1, 1, 0, 0, 2, 2, 2, 2]
>>> metrics.fowlkes_mallows_score(labels_true, labels_pred)
0.0
```
####
2.3.10.4.1. Advantages
* **Random (uniform) label assignments have a FMI score close to 0.0** for any value of `n_clusters` and `n_samples` (which is not the case for raw Mutual Information or the V-measure for instance).
* **Upper-bounded at 1**: Values close to zero indicate two label assignments that are largely independent, while values close to one indicate significant agreement. Further, values of exactly 0 indicate **purely** independent label assignments and a FMI of exactly 1 indicates that the two label assignments are equal (with or without permutation).
* **No assumption is made on the cluster structure**: can be used to compare clustering algorithms such as k-means which assumes isotropic blob shapes with results of spectral clustering algorithms which can find cluster with “folded” shapes.
####
2.3.10.4.2. Drawbacks
* Contrary to inertia, **FMI-based measures require the knowledge of the ground truth classes** while almost never available in practice or requires manual assignment by human annotators (as in the supervised learning setting).
###
2.3.10.5. Silhouette Coefficient
If the ground truth labels are not known, evaluation must be performed using the model itself. The Silhouette Coefficient ([`sklearn.metrics.silhouette_score`](generated/sklearn.metrics.silhouette_score#sklearn.metrics.silhouette_score "sklearn.metrics.silhouette_score")) is an example of such an evaluation, where a higher Silhouette Coefficient score relates to a model with better defined clusters. The Silhouette Coefficient is defined for each sample and is composed of two scores:
* **a**: The mean distance between a sample and all other points in the same class.
* **b**: The mean distance between a sample and all other points in the *next nearest cluster*.
The Silhouette Coefficient *s* for a single sample is then given as:
\[s = \frac{b - a}{max(a, b)}\] The Silhouette Coefficient for a set of samples is given as the mean of the Silhouette Coefficient for each sample.
```
>>> from sklearn import metrics
>>> from sklearn.metrics import pairwise_distances
>>> from sklearn import datasets
>>> X, y = datasets.load_iris(return_X_y=True)
```
In normal usage, the Silhouette Coefficient is applied to the results of a cluster analysis.
```
>>> import numpy as np
>>> from sklearn.cluster import KMeans
>>> kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
>>> labels = kmeans_model.labels_
>>> metrics.silhouette_score(X, labels, metric='euclidean')
0.55...
```
####
2.3.10.5.1. Advantages
* The score is bounded between -1 for incorrect clustering and +1 for highly dense clustering. Scores around zero indicate overlapping clusters.
* The score is higher when clusters are dense and well separated, which relates to a standard concept of a cluster.
####
2.3.10.5.2. Drawbacks
* The Silhouette Coefficient is generally higher for convex clusters than other concepts of clusters, such as density based clusters like those obtained through DBSCAN.
###
2.3.10.6. Calinski-Harabasz Index
If the ground truth labels are not known, the Calinski-Harabasz index ([`sklearn.metrics.calinski_harabasz_score`](generated/sklearn.metrics.calinski_harabasz_score#sklearn.metrics.calinski_harabasz_score "sklearn.metrics.calinski_harabasz_score")) - also known as the Variance Ratio Criterion - can be used to evaluate the model, where a higher Calinski-Harabasz score relates to a model with better defined clusters.
The index is the ratio of the sum of between-clusters dispersion and of within-cluster dispersion for all clusters (where dispersion is defined as the sum of distances squared):
```
>>> from sklearn import metrics
>>> from sklearn.metrics import pairwise_distances
>>> from sklearn import datasets
>>> X, y = datasets.load_iris(return_X_y=True)
```
In normal usage, the Calinski-Harabasz index is applied to the results of a cluster analysis:
```
>>> import numpy as np
>>> from sklearn.cluster import KMeans
>>> kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
>>> labels = kmeans_model.labels_
>>> metrics.calinski_harabasz_score(X, labels)
561.62...
```
####
2.3.10.6.1. Advantages
* The score is higher when clusters are dense and well separated, which relates to a standard concept of a cluster.
* The score is fast to compute.
####
2.3.10.6.2. Drawbacks
* The Calinski-Harabasz index is generally higher for convex clusters than other concepts of clusters, such as density based clusters like those obtained through DBSCAN.
####
2.3.10.6.3. Mathematical formulation
For a set of data \(E\) of size \(n\_E\) which has been clustered into \(k\) clusters, the Calinski-Harabasz score \(s\) is defined as the ratio of the between-clusters dispersion mean and the within-cluster dispersion:
\[s = \frac{\mathrm{tr}(B\_k)}{\mathrm{tr}(W\_k)} \times \frac{n\_E - k}{k - 1}\] where \(\mathrm{tr}(B\_k)\) is trace of the between group dispersion matrix and \(\mathrm{tr}(W\_k)\) is the trace of the within-cluster dispersion matrix defined by:
\[W\_k = \sum\_{q=1}^k \sum\_{x \in C\_q} (x - c\_q) (x - c\_q)^T\] \[B\_k = \sum\_{q=1}^k n\_q (c\_q - c\_E) (c\_q - c\_E)^T\] with \(C\_q\) the set of points in cluster \(q\), \(c\_q\) the center of cluster \(q\), \(c\_E\) the center of \(E\), and \(n\_q\) the number of points in cluster \(q\).
###
2.3.10.7. Davies-Bouldin Index
If the ground truth labels are not known, the Davies-Bouldin index ([`sklearn.metrics.davies_bouldin_score`](generated/sklearn.metrics.davies_bouldin_score#sklearn.metrics.davies_bouldin_score "sklearn.metrics.davies_bouldin_score")) can be used to evaluate the model, where a lower Davies-Bouldin index relates to a model with better separation between the clusters.
This index signifies the average ‘similarity’ between clusters, where the similarity is a measure that compares the distance between clusters with the size of the clusters themselves.
Zero is the lowest possible score. Values closer to zero indicate a better partition.
In normal usage, the Davies-Bouldin index is applied to the results of a cluster analysis as follows:
```
>>> from sklearn import datasets
>>> iris = datasets.load_iris()
>>> X = iris.data
>>> from sklearn.cluster import KMeans
>>> from sklearn.metrics import davies_bouldin_score
>>> kmeans = KMeans(n_clusters=3, random_state=1).fit(X)
>>> labels = kmeans.labels_
>>> davies_bouldin_score(X, labels)
0.6619...
```
####
2.3.10.7.1. Advantages
* The computation of Davies-Bouldin is simpler than that of Silhouette scores.
* The index is solely based on quantities and features inherent to the dataset as its computation only uses point-wise distances.
####
2.3.10.7.2. Drawbacks
* The Davies-Boulding index is generally higher for convex clusters than other concepts of clusters, such as density based clusters like those obtained from DBSCAN.
* The usage of centroid distance limits the distance metric to Euclidean space.
####
2.3.10.7.3. Mathematical formulation
The index is defined as the average similarity between each cluster \(C\_i\) for \(i=1, ..., k\) and its most similar one \(C\_j\). In the context of this index, similarity is defined as a measure \(R\_{ij}\) that trades off:
* \(s\_i\), the average distance between each point of cluster \(i\) and the centroid of that cluster – also know as cluster diameter.
* \(d\_{ij}\), the distance between cluster centroids \(i\) and \(j\).
A simple choice to construct \(R\_{ij}\) so that it is nonnegative and symmetric is:
\[R\_{ij} = \frac{s\_i + s\_j}{d\_{ij}}\] Then the Davies-Bouldin index is defined as:
\[DB = \frac{1}{k} \sum\_{i=1}^k \max\_{i \neq j} R\_{ij}\] ###
2.3.10.8. Contingency Matrix
Contingency matrix ([`sklearn.metrics.cluster.contingency_matrix`](generated/sklearn.metrics.cluster.contingency_matrix#sklearn.metrics.cluster.contingency_matrix "sklearn.metrics.cluster.contingency_matrix")) reports the intersection cardinality for every true/predicted cluster pair. The contingency matrix provides sufficient statistics for all clustering metrics where the samples are independent and identically distributed and one doesn’t need to account for some instances not being clustered.
Here is an example:
```
>>> from sklearn.metrics.cluster import contingency_matrix
>>> x = ["a", "a", "a", "b", "b", "b"]
>>> y = [0, 0, 1, 1, 2, 2]
>>> contingency_matrix(x, y)
array([[2, 1, 0],
[0, 1, 2]])
```
The first row of output array indicates that there are three samples whose true cluster is “a”. Of them, two are in predicted cluster 0, one is in 1, and none is in 2. And the second row indicates that there are three samples whose true cluster is “b”. Of them, none is in predicted cluster 0, one is in 1 and two are in 2.
A [confusion matrix](model_evaluation#confusion-matrix) for classification is a square contingency matrix where the order of rows and columns correspond to a list of classes.
####
2.3.10.8.1. Advantages
* Allows to examine the spread of each true cluster across predicted clusters and vice versa.
* The contingency table calculated is typically utilized in the calculation of a similarity statistic (like the others listed in this document) between the two clusterings.
####
2.3.10.8.2. Drawbacks
* Contingency matrix is easy to interpret for a small number of clusters, but becomes very hard to interpret for a large number of clusters.
* It doesn’t give a single metric to use as an objective for clustering optimisation.
###
2.3.10.9. Pair Confusion Matrix
The pair confusion matrix ([`sklearn.metrics.cluster.pair_confusion_matrix`](generated/sklearn.metrics.cluster.pair_confusion_matrix#sklearn.metrics.cluster.pair_confusion_matrix "sklearn.metrics.cluster.pair_confusion_matrix")) is a 2x2 similarity matrix
\[\begin{split}C = \left[\begin{matrix} C\_{00} & C\_{01} \\ C\_{10} & C\_{11} \end{matrix}\right]\end{split}\] between two clusterings computed by considering all pairs of samples and counting pairs that are assigned into the same or into different clusters under the true and predicted clusterings.
It has the following entries:
\(C\_{00}\) : number of pairs with both clusterings having the samples not clustered together
\(C\_{10}\) : number of pairs with the true label clustering having the samples clustered together but the other clustering not having the samples clustered together
\(C\_{01}\) : number of pairs with the true label clustering not having the samples clustered together but the other clustering having the samples clustered together
\(C\_{11}\) : number of pairs with both clusterings having the samples clustered together
Considering a pair of samples that is clustered together a positive pair, then as in binary classification the count of true negatives is \(C\_{00}\), false negatives is \(C\_{10}\), true positives is \(C\_{11}\) and false positives is \(C\_{01}\).
Perfectly matching labelings have all non-zero entries on the diagonal regardless of actual label values:
```
>>> from sklearn.metrics.cluster import pair_confusion_matrix
>>> pair_confusion_matrix([0, 0, 1, 1], [0, 0, 1, 1])
array([[8, 0],
[0, 4]])
```
```
>>> pair_confusion_matrix([0, 0, 1, 1], [1, 1, 0, 0])
array([[8, 0],
[0, 4]])
```
Labelings that assign all classes members to the same clusters are complete but may not always be pure, hence penalized, and have some off-diagonal non-zero entries:
```
>>> pair_confusion_matrix([0, 0, 1, 2], [0, 0, 1, 1])
array([[8, 2],
[0, 2]])
```
The matrix is not symmetric:
```
>>> pair_confusion_matrix([0, 0, 1, 1], [0, 0, 1, 2])
array([[8, 0],
[2, 2]])
```
If classes members are completely split across different clusters, the assignment is totally incomplete, hence the matrix has all zero diagonal entries:
```
>>> pair_confusion_matrix([0, 0, 0, 0], [0, 1, 2, 3])
array([[ 0, 0],
[12, 0]])
```
| programming_docs |
scikit_learn 1.1. Linear Models 1.1. Linear Models
==================
The following are a set of methods intended for regression in which the target value is expected to be a linear combination of the features. In mathematical notation, if \(\hat{y}\) is the predicted value.
\[\hat{y}(w, x) = w\_0 + w\_1 x\_1 + ... + w\_p x\_p\] Across the module, we designate the vector \(w = (w\_1, ..., w\_p)\) as `coef_` and \(w\_0\) as `intercept_`.
To perform classification with generalized linear models, see [Logistic regression](#logistic-regression).
1.1.1. Ordinary Least Squares
------------------------------
[`LinearRegression`](generated/sklearn.linear_model.linearregression#sklearn.linear_model.LinearRegression "sklearn.linear_model.LinearRegression") fits a linear model with coefficients \(w = (w\_1, ..., w\_p)\) to minimize the residual sum of squares between the observed targets in the dataset, and the targets predicted by the linear approximation. Mathematically it solves a problem of the form:
\[\min\_{w} || X w - y||\_2^2\] [`LinearRegression`](generated/sklearn.linear_model.linearregression#sklearn.linear_model.LinearRegression "sklearn.linear_model.LinearRegression") will take in its `fit` method arrays X, y and will store the coefficients \(w\) of the linear model in its `coef_` member:
```
>>> from sklearn import linear_model
>>> reg = linear_model.LinearRegression()
>>> reg.fit([[0, 0], [1, 1], [2, 2]], [0, 1, 2])
LinearRegression()
>>> reg.coef_
array([0.5, 0.5])
```
The coefficient estimates for Ordinary Least Squares rely on the independence of the features. When features are correlated and the columns of the design matrix \(X\) have an approximately linear dependence, the design matrix becomes close to singular and as a result, the least-squares estimate becomes highly sensitive to random errors in the observed target, producing a large variance. This situation of *multicollinearity* can arise, for example, when data are collected without an experimental design.
###
1.1.1.1. Non-Negative Least Squares
It is possible to constrain all the coefficients to be non-negative, which may be useful when they represent some physical or naturally non-negative quantities (e.g., frequency counts or prices of goods). [`LinearRegression`](generated/sklearn.linear_model.linearregression#sklearn.linear_model.LinearRegression "sklearn.linear_model.LinearRegression") accepts a boolean `positive` parameter: when set to `True` [Non-Negative Least Squares](https://en.wikipedia.org/wiki/Non-negative_least_squares) are then applied.
###
1.1.1.2. Ordinary Least Squares Complexity
The least squares solution is computed using the singular value decomposition of X. If X is a matrix of shape `(n_samples, n_features)` this method has a cost of \(O(n\_{\text{samples}} n\_{\text{features}}^2)\), assuming that \(n\_{\text{samples}} \geq n\_{\text{features}}\).
1.1.2. Ridge regression and classification
-------------------------------------------
###
1.1.2.1. Regression
[`Ridge`](generated/sklearn.linear_model.ridge#sklearn.linear_model.Ridge "sklearn.linear_model.Ridge") regression addresses some of the problems of [Ordinary Least Squares](#ordinary-least-squares) by imposing a penalty on the size of the coefficients. The ridge coefficients minimize a penalized residual sum of squares:
\[\min\_{w} || X w - y||\_2^2 + \alpha ||w||\_2^2\] The complexity parameter \(\alpha \geq 0\) controls the amount of shrinkage: the larger the value of \(\alpha\), the greater the amount of shrinkage and thus the coefficients become more robust to collinearity.
As with other linear models, [`Ridge`](generated/sklearn.linear_model.ridge#sklearn.linear_model.Ridge "sklearn.linear_model.Ridge") will take in its `fit` method arrays X, y and will store the coefficients \(w\) of the linear model in its `coef_` member:
```
>>> from sklearn import linear_model
>>> reg = linear_model.Ridge(alpha=.5)
>>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
Ridge(alpha=0.5)
>>> reg.coef_
array([0.34545455, 0.34545455])
>>> reg.intercept_
0.13636...
```
###
1.1.2.2. Classification
The [`Ridge`](generated/sklearn.linear_model.ridge#sklearn.linear_model.Ridge "sklearn.linear_model.Ridge") regressor has a classifier variant: [`RidgeClassifier`](generated/sklearn.linear_model.ridgeclassifier#sklearn.linear_model.RidgeClassifier "sklearn.linear_model.RidgeClassifier"). This classifier first converts binary targets to `{-1, 1}` and then treats the problem as a regression task, optimizing the same objective as above. The predicted class corresponds to the sign of the regressor’s prediction. For multiclass classification, the problem is treated as multi-output regression, and the predicted class corresponds to the output with the highest value.
It might seem questionable to use a (penalized) Least Squares loss to fit a classification model instead of the more traditional logistic or hinge losses. However, in practice, all those models can lead to similar cross-validation scores in terms of accuracy or precision/recall, while the penalized least squares loss used by the [`RidgeClassifier`](generated/sklearn.linear_model.ridgeclassifier#sklearn.linear_model.RidgeClassifier "sklearn.linear_model.RidgeClassifier") allows for a very different choice of the numerical solvers with distinct computational performance profiles.
The [`RidgeClassifier`](generated/sklearn.linear_model.ridgeclassifier#sklearn.linear_model.RidgeClassifier "sklearn.linear_model.RidgeClassifier") can be significantly faster than e.g. [`LogisticRegression`](generated/sklearn.linear_model.logisticregression#sklearn.linear_model.LogisticRegression "sklearn.linear_model.LogisticRegression") with a high number of classes because it can compute the projection matrix \((X^T X)^{-1} X^T\) only once.
This classifier is sometimes referred to as a [Least Squares Support Vector Machines](https://en.wikipedia.org/wiki/Least-squares_support-vector_machine) with a linear kernel.
###
1.1.2.3. Ridge Complexity
This method has the same order of complexity as [Ordinary Least Squares](#ordinary-least-squares).
###
1.1.2.4. Setting the regularization parameter: leave-one-out Cross-Validation
[`RidgeCV`](generated/sklearn.linear_model.ridgecv#sklearn.linear_model.RidgeCV "sklearn.linear_model.RidgeCV") implements ridge regression with built-in cross-validation of the alpha parameter. The object works in the same way as GridSearchCV except that it defaults to Leave-One-Out Cross-Validation:
```
>>> import numpy as np
>>> from sklearn import linear_model
>>> reg = linear_model.RidgeCV(alphas=np.logspace(-6, 6, 13))
>>> reg.fit([[0, 0], [0, 0], [1, 1]], [0, .1, 1])
RidgeCV(alphas=array([1.e-06, 1.e-05, 1.e-04, 1.e-03, 1.e-02, 1.e-01, 1.e+00, 1.e+01,
1.e+02, 1.e+03, 1.e+04, 1.e+05, 1.e+06]))
>>> reg.alpha_
0.01
```
Specifying the value of the [cv](https://scikit-learn.org/1.1/glossary.html#term-cv) attribute will trigger the use of cross-validation with [`GridSearchCV`](generated/sklearn.model_selection.gridsearchcv#sklearn.model_selection.GridSearchCV "sklearn.model_selection.GridSearchCV"), for example `cv=10` for 10-fold cross-validation, rather than Leave-One-Out Cross-Validation.
1.1.3. Lasso
-------------
The [`Lasso`](generated/sklearn.linear_model.lasso#sklearn.linear_model.Lasso "sklearn.linear_model.Lasso") is a linear model that estimates sparse coefficients. It is useful in some contexts due to its tendency to prefer solutions with fewer non-zero coefficients, effectively reducing the number of features upon which the given solution is dependent. For this reason, Lasso and its variants are fundamental to the field of compressed sensing. Under certain conditions, it can recover the exact set of non-zero coefficients (see [Compressive sensing: tomography reconstruction with L1 prior (Lasso)](../auto_examples/applications/plot_tomography_l1_reconstruction#sphx-glr-auto-examples-applications-plot-tomography-l1-reconstruction-py)).
Mathematically, it consists of a linear model with an added regularization term. The objective function to minimize is:
\[\min\_{w} { \frac{1}{2n\_{\text{samples}}} ||X w - y||\_2 ^ 2 + \alpha ||w||\_1}\] The lasso estimate thus solves the minimization of the least-squares penalty with \(\alpha ||w||\_1\) added, where \(\alpha\) is a constant and \(||w||\_1\) is the \(\ell\_1\)-norm of the coefficient vector.
The implementation in the class [`Lasso`](generated/sklearn.linear_model.lasso#sklearn.linear_model.Lasso "sklearn.linear_model.Lasso") uses coordinate descent as the algorithm to fit the coefficients. See [Least Angle Regression](#least-angle-regression) for another implementation:
```
>>> from sklearn import linear_model
>>> reg = linear_model.Lasso(alpha=0.1)
>>> reg.fit([[0, 0], [1, 1]], [0, 1])
Lasso(alpha=0.1)
>>> reg.predict([[1, 1]])
array([0.8])
```
The function [`lasso_path`](generated/sklearn.linear_model.lasso_path#sklearn.linear_model.lasso_path "sklearn.linear_model.lasso_path") is useful for lower-level tasks, as it computes the coefficients along the full path of possible values.
Note
**Feature selection with Lasso**
As the Lasso regression yields sparse models, it can thus be used to perform feature selection, as detailed in [L1-based feature selection](feature_selection#l1-feature-selection).
The following two references explain the iterations used in the coordinate descent solver of scikit-learn, as well as the duality gap computation used for convergence control.
###
1.1.3.1. Setting regularization parameter
The `alpha` parameter controls the degree of sparsity of the estimated coefficients.
####
1.1.3.1.1. Using cross-validation
scikit-learn exposes objects that set the Lasso `alpha` parameter by cross-validation: [`LassoCV`](generated/sklearn.linear_model.lassocv#sklearn.linear_model.LassoCV "sklearn.linear_model.LassoCV") and [`LassoLarsCV`](generated/sklearn.linear_model.lassolarscv#sklearn.linear_model.LassoLarsCV "sklearn.linear_model.LassoLarsCV"). [`LassoLarsCV`](generated/sklearn.linear_model.lassolarscv#sklearn.linear_model.LassoLarsCV "sklearn.linear_model.LassoLarsCV") is based on the [Least Angle Regression](#least-angle-regression) algorithm explained below.
For high-dimensional datasets with many collinear features, [`LassoCV`](generated/sklearn.linear_model.lassocv#sklearn.linear_model.LassoCV "sklearn.linear_model.LassoCV") is most often preferable. However, [`LassoLarsCV`](generated/sklearn.linear_model.lassolarscv#sklearn.linear_model.LassoLarsCV "sklearn.linear_model.LassoLarsCV") has the advantage of exploring more relevant values of `alpha` parameter, and if the number of samples is very small compared to the number of features, it is often faster than [`LassoCV`](generated/sklearn.linear_model.lassocv#sklearn.linear_model.LassoCV "sklearn.linear_model.LassoCV").
####
1.1.3.1.2. Information-criteria based model selection
Alternatively, the estimator [`LassoLarsIC`](generated/sklearn.linear_model.lassolarsic#sklearn.linear_model.LassoLarsIC "sklearn.linear_model.LassoLarsIC") proposes to use the Akaike information criterion (AIC) and the Bayes Information criterion (BIC). It is a computationally cheaper alternative to find the optimal value of alpha as the regularization path is computed only once instead of k+1 times when using k-fold cross-validation.
Indeed, these criteria are computed on the in-sample training set. In short, they penalize the over-optimistic scores of the different Lasso models by their flexibility (cf. to “Mathematical details” section below).
However, such criteria need a proper estimation of the degrees of freedom of the solution, are derived for large samples (asymptotic results) and assume the correct model is candidates under investigation. They also tend to break when the problem is badly conditioned (e.g. more features than samples).
**Mathematical details**
The definition of AIC (and thus BIC) might differ in the literature. In this section, we give more information regarding the criterion computed in scikit-learn. The AIC criterion is defined as:
\[AIC = -2 \log(\hat{L}) + 2 d\] where \(\hat{L}\) is the maximum likelihood of the model and \(d\) is the number of parameters (as well referred to as degrees of freedom in the previous section).
The definition of BIC replace the constant \(2\) by \(\log(N)\):
\[BIC = -2 \log(\hat{L}) + \log(N) d\] where \(N\) is the number of samples.
For a linear Gaussian model, the maximum log-likelihood is defined as:
\[\log(\hat{L}) = - \frac{n}{2} \log(2 \pi) - \frac{n}{2} \ln(\sigma^2) - \frac{\sum\_{i=1}^{n} (y\_i - \hat{y}\_i)^2}{2\sigma^2}\] where \(\sigma^2\) is an estimate of the noise variance, \(y\_i\) and \(\hat{y}\_i\) are respectively the true and predicted targets, and \(n\) is the number of samples.
Plugging the maximum log-likelihood in the AIC formula yields:
\[AIC = n \log(2 \pi \sigma^2) + \frac{\sum\_{i=1}^{n} (y\_i - \hat{y}\_i)^2}{\sigma^2} + 2 d\] The first term of the above expression is sometimes discarded since it is a constant when \(\sigma^2\) is provided. In addition, it is sometimes stated that the AIC is equivalent to the \(C\_p\) statistic [[12]](#id6). In a strict sense, however, it is equivalent only up to some constant and a multiplicative factor.
At last, we mentioned above that \(\sigma^2\) is an estimate of the noise variance. In [`LassoLarsIC`](generated/sklearn.linear_model.lassolarsic#sklearn.linear_model.LassoLarsIC "sklearn.linear_model.LassoLarsIC") when the parameter `noise_variance` is not provided (default), the noise variance is estimated via the unbiased estimator [[13]](#id7) defined as:
\[\sigma^2 = \frac{\sum\_{i=1}^{n} (y\_i - \hat{y}\_i)^2}{n - p}\] where \(p\) is the number of features and \(\hat{y}\_i\) is the predicted target using an ordinary least squares regression. Note, that this formula is valid only when `n_samples > n_features`.
####
1.1.3.1.3. Comparison with the regularization parameter of SVM
The equivalence between `alpha` and the regularization parameter of SVM, `C` is given by `alpha = 1 / C` or `alpha = 1 / (n_samples * C)`, depending on the estimator and the exact objective function optimized by the model.
1.1.4. Multi-task Lasso
------------------------
The [`MultiTaskLasso`](generated/sklearn.linear_model.multitasklasso#sklearn.linear_model.MultiTaskLasso "sklearn.linear_model.MultiTaskLasso") is a linear model that estimates sparse coefficients for multiple regression problems jointly: `y` is a 2D array, of shape `(n_samples, n_tasks)`. The constraint is that the selected features are the same for all the regression problems, also called tasks.
The following figure compares the location of the non-zero entries in the coefficient matrix W obtained with a simple Lasso or a MultiTaskLasso. The Lasso estimates yield scattered non-zeros while the non-zeros of the MultiTaskLasso are full columns.
**Fitting a time-series model, imposing that any active feature be active at all times.**
Mathematically, it consists of a linear model trained with a mixed \(\ell\_1\) \(\ell\_2\)-norm for regularization. The objective function to minimize is:
\[\min\_{W} { \frac{1}{2n\_{\text{samples}}} ||X W - Y||\_{\text{Fro}} ^ 2 + \alpha ||W||\_{21}}\] where \(\text{Fro}\) indicates the Frobenius norm
\[||A||\_{\text{Fro}} = \sqrt{\sum\_{ij} a\_{ij}^2}\] and \(\ell\_1\) \(\ell\_2\) reads
\[||A||\_{2 1} = \sum\_i \sqrt{\sum\_j a\_{ij}^2}.\] The implementation in the class [`MultiTaskLasso`](generated/sklearn.linear_model.multitasklasso#sklearn.linear_model.MultiTaskLasso "sklearn.linear_model.MultiTaskLasso") uses coordinate descent as the algorithm to fit the coefficients.
1.1.5. Elastic-Net
-------------------
[`ElasticNet`](generated/sklearn.linear_model.elasticnet#sklearn.linear_model.ElasticNet "sklearn.linear_model.ElasticNet") is a linear regression model trained with both \(\ell\_1\) and \(\ell\_2\)-norm regularization of the coefficients. This combination allows for learning a sparse model where few of the weights are non-zero like [`Lasso`](generated/sklearn.linear_model.lasso#sklearn.linear_model.Lasso "sklearn.linear_model.Lasso"), while still maintaining the regularization properties of [`Ridge`](generated/sklearn.linear_model.ridge#sklearn.linear_model.Ridge "sklearn.linear_model.Ridge"). We control the convex combination of \(\ell\_1\) and \(\ell\_2\) using the `l1_ratio` parameter.
Elastic-net is useful when there are multiple features that are correlated with one another. Lasso is likely to pick one of these at random, while elastic-net is likely to pick both.
A practical advantage of trading-off between Lasso and Ridge is that it allows Elastic-Net to inherit some of Ridge’s stability under rotation.
The objective function to minimize is in this case
\[\min\_{w} { \frac{1}{2n\_{\text{samples}}} ||X w - y||\_2 ^ 2 + \alpha \rho ||w||\_1 + \frac{\alpha(1-\rho)}{2} ||w||\_2 ^ 2}\] The class [`ElasticNetCV`](generated/sklearn.linear_model.elasticnetcv#sklearn.linear_model.ElasticNetCV "sklearn.linear_model.ElasticNetCV") can be used to set the parameters `alpha` (\(\alpha\)) and `l1_ratio` (\(\rho\)) by cross-validation.
The following two references explain the iterations used in the coordinate descent solver of scikit-learn, as well as the duality gap computation used for convergence control.
1.1.6. Multi-task Elastic-Net
------------------------------
The [`MultiTaskElasticNet`](generated/sklearn.linear_model.multitaskelasticnet#sklearn.linear_model.MultiTaskElasticNet "sklearn.linear_model.MultiTaskElasticNet") is an elastic-net model that estimates sparse coefficients for multiple regression problems jointly: `Y` is a 2D array of shape `(n_samples, n_tasks)`. The constraint is that the selected features are the same for all the regression problems, also called tasks.
Mathematically, it consists of a linear model trained with a mixed \(\ell\_1\) \(\ell\_2\)-norm and \(\ell\_2\)-norm for regularization. The objective function to minimize is:
\[\min\_{W} { \frac{1}{2n\_{\text{samples}}} ||X W - Y||\_{\text{Fro}}^2 + \alpha \rho ||W||\_{2 1} + \frac{\alpha(1-\rho)}{2} ||W||\_{\text{Fro}}^2}\] The implementation in the class [`MultiTaskElasticNet`](generated/sklearn.linear_model.multitaskelasticnet#sklearn.linear_model.MultiTaskElasticNet "sklearn.linear_model.MultiTaskElasticNet") uses coordinate descent as the algorithm to fit the coefficients.
The class [`MultiTaskElasticNetCV`](generated/sklearn.linear_model.multitaskelasticnetcv#sklearn.linear_model.MultiTaskElasticNetCV "sklearn.linear_model.MultiTaskElasticNetCV") can be used to set the parameters `alpha` (\(\alpha\)) and `l1_ratio` (\(\rho\)) by cross-validation.
1.1.7. Least Angle Regression
------------------------------
Least-angle regression (LARS) is a regression algorithm for high-dimensional data, developed by Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani. LARS is similar to forward stepwise regression. At each step, it finds the feature most correlated with the target. When there are multiple features having equal correlation, instead of continuing along the same feature, it proceeds in a direction equiangular between the features.
The advantages of LARS are:
* It is numerically efficient in contexts where the number of features is significantly greater than the number of samples.
* It is computationally just as fast as forward selection and has the same order of complexity as ordinary least squares.
* It produces a full piecewise linear solution path, which is useful in cross-validation or similar attempts to tune the model.
* If two features are almost equally correlated with the target, then their coefficients should increase at approximately the same rate. The algorithm thus behaves as intuition would expect, and also is more stable.
* It is easily modified to produce solutions for other estimators, like the Lasso.
The disadvantages of the LARS method include:
* Because LARS is based upon an iterative refitting of the residuals, it would appear to be especially sensitive to the effects of noise. This problem is discussed in detail by Weisberg in the discussion section of the Efron et al. (2004) Annals of Statistics article.
The LARS model can be used via the estimator [`Lars`](generated/sklearn.linear_model.lars#sklearn.linear_model.Lars "sklearn.linear_model.Lars"), or its low-level implementation [`lars_path`](generated/sklearn.linear_model.lars_path#sklearn.linear_model.lars_path "sklearn.linear_model.lars_path") or [`lars_path_gram`](generated/sklearn.linear_model.lars_path_gram#sklearn.linear_model.lars_path_gram "sklearn.linear_model.lars_path_gram").
1.1.8. LARS Lasso
------------------
[`LassoLars`](generated/sklearn.linear_model.lassolars#sklearn.linear_model.LassoLars "sklearn.linear_model.LassoLars") is a lasso model implemented using the LARS algorithm, and unlike the implementation based on coordinate descent, this yields the exact solution, which is piecewise linear as a function of the norm of its coefficients.
```
>>> from sklearn import linear_model
>>> reg = linear_model.LassoLars(alpha=.1, normalize=False)
>>> reg.fit([[0, 0], [1, 1]], [0, 1])
LassoLars(alpha=0.1, normalize=False)
>>> reg.coef_
array([0.6..., 0. ])
```
The Lars algorithm provides the full path of the coefficients along the regularization parameter almost for free, thus a common operation is to retrieve the path with one of the functions [`lars_path`](generated/sklearn.linear_model.lars_path#sklearn.linear_model.lars_path "sklearn.linear_model.lars_path") or [`lars_path_gram`](generated/sklearn.linear_model.lars_path_gram#sklearn.linear_model.lars_path_gram "sklearn.linear_model.lars_path_gram").
###
1.1.8.1. Mathematical formulation
The algorithm is similar to forward stepwise regression, but instead of including features at each step, the estimated coefficients are increased in a direction equiangular to each one’s correlations with the residual.
Instead of giving a vector result, the LARS solution consists of a curve denoting the solution for each value of the \(\ell\_1\) norm of the parameter vector. The full coefficients path is stored in the array `coef_path_` of shape `(n_features, max_features + 1)`. The first column is always zero.
1.1.9. Orthogonal Matching Pursuit (OMP)
-----------------------------------------
[`OrthogonalMatchingPursuit`](generated/sklearn.linear_model.orthogonalmatchingpursuit#sklearn.linear_model.OrthogonalMatchingPursuit "sklearn.linear_model.OrthogonalMatchingPursuit") and [`orthogonal_mp`](generated/sklearn.linear_model.orthogonal_mp#sklearn.linear_model.orthogonal_mp "sklearn.linear_model.orthogonal_mp") implement the OMP algorithm for approximating the fit of a linear model with constraints imposed on the number of non-zero coefficients (ie. the \(\ell\_0\) pseudo-norm).
Being a forward feature selection method like [Least Angle Regression](#least-angle-regression), orthogonal matching pursuit can approximate the optimum solution vector with a fixed number of non-zero elements:
\[\underset{w}{\operatorname{arg\,min\,}} ||y - Xw||\_2^2 \text{ subject to } ||w||\_0 \leq n\_{\text{nonzero\\_coefs}}\] Alternatively, orthogonal matching pursuit can target a specific error instead of a specific number of non-zero coefficients. This can be expressed as:
\[\underset{w}{\operatorname{arg\,min\,}} ||w||\_0 \text{ subject to } ||y-Xw||\_2^2 \leq \text{tol}\] OMP is based on a greedy algorithm that includes at each step the atom most highly correlated with the current residual. It is similar to the simpler matching pursuit (MP) method, but better in that at each iteration, the residual is recomputed using an orthogonal projection on the space of the previously chosen dictionary elements.
1.1.10. Bayesian Regression
----------------------------
Bayesian regression techniques can be used to include regularization parameters in the estimation procedure: the regularization parameter is not set in a hard sense but tuned to the data at hand.
This can be done by introducing [uninformative priors](https://en.wikipedia.org/wiki/Non-informative_prior#Uninformative_priors) over the hyper parameters of the model. The \(\ell\_{2}\) regularization used in [Ridge regression and classification](#ridge-regression) is equivalent to finding a maximum a posteriori estimation under a Gaussian prior over the coefficients \(w\) with precision \(\lambda^{-1}\). Instead of setting `lambda` manually, it is possible to treat it as a random variable to be estimated from the data.
To obtain a fully probabilistic model, the output \(y\) is assumed to be Gaussian distributed around \(X w\):
\[p(y|X,w,\alpha) = \mathcal{N}(y|X w,\alpha)\] where \(\alpha\) is again treated as a random variable that is to be estimated from the data.
The advantages of Bayesian Regression are:
* It adapts to the data at hand.
* It can be used to include regularization parameters in the estimation procedure.
The disadvantages of Bayesian regression include:
* Inference of the model can be time consuming.
###
1.1.10.1. Bayesian Ridge Regression
[`BayesianRidge`](generated/sklearn.linear_model.bayesianridge#sklearn.linear_model.BayesianRidge "sklearn.linear_model.BayesianRidge") estimates a probabilistic model of the regression problem as described above. The prior for the coefficient \(w\) is given by a spherical Gaussian:
\[p(w|\lambda) = \mathcal{N}(w|0,\lambda^{-1}\mathbf{I}\_{p})\] The priors over \(\alpha\) and \(\lambda\) are chosen to be [gamma distributions](https://en.wikipedia.org/wiki/Gamma_distribution), the conjugate prior for the precision of the Gaussian. The resulting model is called *Bayesian Ridge Regression*, and is similar to the classical [`Ridge`](generated/sklearn.linear_model.ridge#sklearn.linear_model.Ridge "sklearn.linear_model.Ridge").
The parameters \(w\), \(\alpha\) and \(\lambda\) are estimated jointly during the fit of the model, the regularization parameters \(\alpha\) and \(\lambda\) being estimated by maximizing the *log marginal likelihood*. The scikit-learn implementation is based on the algorithm described in Appendix A of (Tipping, 2001) where the update of the parameters \(\alpha\) and \(\lambda\) is done as suggested in (MacKay, 1992). The initial value of the maximization procedure can be set with the hyperparameters `alpha_init` and `lambda_init`.
There are four more hyperparameters, \(\alpha\_1\), \(\alpha\_2\), \(\lambda\_1\) and \(\lambda\_2\) of the gamma prior distributions over \(\alpha\) and \(\lambda\). These are usually chosen to be *non-informative*. By default \(\alpha\_1 = \alpha\_2 = \lambda\_1 = \lambda\_2 = 10^{-6}\).
Bayesian Ridge Regression is used for regression:
```
>>> from sklearn import linear_model
>>> X = [[0., 0.], [1., 1.], [2., 2.], [3., 3.]]
>>> Y = [0., 1., 2., 3.]
>>> reg = linear_model.BayesianRidge()
>>> reg.fit(X, Y)
BayesianRidge()
```
After being fitted, the model can then be used to predict new values:
```
>>> reg.predict([[1, 0.]])
array([0.50000013])
```
The coefficients \(w\) of the model can be accessed:
```
>>> reg.coef_
array([0.49999993, 0.49999993])
```
Due to the Bayesian framework, the weights found are slightly different to the ones found by [Ordinary Least Squares](#ordinary-least-squares). However, Bayesian Ridge Regression is more robust to ill-posed problems.
###
1.1.10.2. Automatic Relevance Determination - ARD
The Automatic Relevance Determination (as being implemented in [`ARDRegression`](generated/sklearn.linear_model.ardregression#sklearn.linear_model.ARDRegression "sklearn.linear_model.ARDRegression")) is a kind of linear model which is very similar to the [Bayesian Ridge Regression](#id14), but that leads to sparser coefficients \(w\) [[1]](#id19) [[2]](#id20).
[`ARDRegression`](generated/sklearn.linear_model.ardregression#sklearn.linear_model.ARDRegression "sklearn.linear_model.ARDRegression") poses a different prior over \(w\): it drops the spherical Gaussian distribution for a centered elliptic Gaussian distribution. This means each coefficient \(w\_{i}\) can itself be drawn from a Gaussian distribution, centered on zero and with a precision \(\lambda\_{i}\):
\[p(w|\lambda) = \mathcal{N}(w|0,A^{-1})\] with \(A\) being a positive definite diagonal matrix and \(\text{diag}(A) = \lambda = \{\lambda\_{1},...,\lambda\_{p}\}\).
In contrast to the [Bayesian Ridge Regression](#id14), each coordinate of \(w\_{i}\) has its own standard deviation \(\frac{1}{\lambda\_i}\). The prior over all \(\lambda\_i\) is chosen to be the same gamma distribution given by the hyperparameters \(\lambda\_1\) and \(\lambda\_2\).
ARD is also known in the literature as *Sparse Bayesian Learning* and *Relevance Vector Machine* [[3]](#id21) [[4]](#id23). For a worked-out comparison between ARD and [Bayesian Ridge Regression](#id14), see the example below.
1.1.11. Logistic regression
----------------------------
Logistic regression, despite its name, is a linear model for classification rather than regression. Logistic regression is also known in the literature as logit regression, maximum-entropy classification (MaxEnt) or the log-linear classifier. In this model, the probabilities describing the possible outcomes of a single trial are modeled using a [logistic function](https://en.wikipedia.org/wiki/Logistic_function).
Logistic regression is implemented in [`LogisticRegression`](generated/sklearn.linear_model.logisticregression#sklearn.linear_model.LogisticRegression "sklearn.linear_model.LogisticRegression"). This implementation can fit binary, One-vs-Rest, or multinomial logistic regression with optional \(\ell\_1\), \(\ell\_2\) or Elastic-Net regularization.
Note
Regularization is applied by default, which is common in machine learning but not in statistics. Another advantage of regularization is that it improves numerical stability. No regularization amounts to setting C to a very high value.
###
1.1.11.1. Binary Case
For notational ease, we assume that the target \(y\_i\) takes values in the set \(\{0, 1\}\) for data point \(i\). Once fitted, the [`predict_proba`](generated/sklearn.linear_model.logisticregression#sklearn.linear_model.LogisticRegression.predict_proba "sklearn.linear_model.LogisticRegression.predict_proba") method of [`LogisticRegression`](generated/sklearn.linear_model.logisticregression#sklearn.linear_model.LogisticRegression "sklearn.linear_model.LogisticRegression") predicts the probability of the positive class \(P(y\_i=1|X\_i)\) as
\[\hat{p}(X\_i) = \operatorname{expit}(X\_i w + w\_0) = \frac{1}{1 + \exp(-X\_i w - w\_0)}.\] As an optimization problem, binary class logistic regression with regularization term \(r(w)\) minimizes the following cost function:
\[\min\_{w} C \sum\_{i=1}^n \left(-y\_i \log(\hat{p}(X\_i)) - (1 - y\_i) \log(1 - \hat{p}(X\_i))\right) + r(w).\] We currently provide four choices for the regularization term \(r(w)\) via the `penalty` argument:
| penalty | \(r(w)\) |
| --- | --- |
| `None` | \(0\) |
| \(\ell\_1\) | \(\|w\|\_1\) |
| \(\ell\_2\) | \(\frac{1}{2}\|w\|\_2^2 = \frac{1}{2}w^T w\) |
| `ElasticNet` | \(\frac{1 - \rho}{2}w^T w + \rho \|w\|\_1\) |
For ElasticNet, \(\rho\) (which corresponds to the `l1_ratio` parameter) controls the strength of \(\ell\_1\) regularization vs. \(\ell\_2\) regularization. Elastic-Net is equivalent to \(\ell\_1\) when \(\rho = 1\) and equivalent to \(\ell\_2\) when \(\rho=0\).
###
1.1.11.2. Multinomial Case
The binary case can be extended to \(K\) classes leading to the multinomial logistic regression, see also [log-linear model](https://en.wikipedia.org/wiki/Multinomial_logistic_regression#As_a_log-linear_model).
Note
It is possible to parameterize a \(K\)-class classification model using only \(K-1\) weight vectors, leaving one class probability fully determined by the other class probabilities by leveraging the fact that all class probabilities must sum to one. We deliberately choose to overparameterize the model using \(K\) weight vectors for ease of implementation and to preserve the symmetrical inductive bias regarding ordering of classes, see [[16]](#id37). This effect becomes especially important when using regularization. The choice of overparameterization can be detrimental for unpenalized models since then the solution may not be unique, as shown in [[16]](#id37).
Let \(y\_i \in {1, \ldots, K}\) be the label (ordinal) encoded target variable for observation \(i\). Instead of a single coefficient vector, we now have a matrix of coefficients \(W\) where each row vector \(W\_k\) corresponds to class \(k\). We aim at predicting the class probabilities \(P(y\_i=k|X\_i)\) via [`predict_proba`](generated/sklearn.linear_model.logisticregression#sklearn.linear_model.LogisticRegression.predict_proba "sklearn.linear_model.LogisticRegression.predict_proba") as:
\[\hat{p}\_k(X\_i) = \frac{\exp(X\_i W\_k + W\_{0, k})}{\sum\_{l=0}^{K-1} \exp(X\_i W\_l + W\_{0, l})}.\] The objective for the optimization becomes
\[\min\_W -C \sum\_{i=1}^n \sum\_{k=0}^{K-1} [y\_i = k] \log(\hat{p}\_k(X\_i)) + r(W).\] Where \([P]\) represents the Iverson bracket which evaluates to \(0\) if \(P\) is false, otherwise it evaluates to \(1\). We currently provide four choices for the regularization term \(r(W)\) via the `penalty` argument:
| penalty | \(r(W)\) |
| --- | --- |
| `None` | \(0\) |
| \(\ell\_1\) | \(\|W\|\_{1,1} = \sum\_{i=1}^n\sum\_{j=1}^{K}|W\_{i,j}|\) |
| \(\ell\_2\) | \(\frac{1}{2}\|W\|\_F^2 = \frac{1}{2}\sum\_{i=1}^n\sum\_{j=1}^{K} W\_{i,j}^2\) |
| `ElasticNet` | \(\frac{1 - \rho}{2}\|W\|\_F^2 + \rho \|W\|\_{1,1}\) |
###
1.1.11.3. Solvers
The solvers implemented in the class [`LogisticRegression`](generated/sklearn.linear_model.logisticregression#sklearn.linear_model.LogisticRegression "sklearn.linear_model.LogisticRegression") are “liblinear”, “newton-cg”, “lbfgs”, “sag” and “saga”:
The solver “liblinear” uses a coordinate descent (CD) algorithm, and relies on the excellent C++ [LIBLINEAR library](https://www.csie.ntu.edu.tw/~cjlin/liblinear/), which is shipped with scikit-learn. However, the CD algorithm implemented in liblinear cannot learn a true multinomial (multiclass) model; instead, the optimization problem is decomposed in a “one-vs-rest” fashion so separate binary classifiers are trained for all classes. This happens under the hood, so [`LogisticRegression`](generated/sklearn.linear_model.logisticregression#sklearn.linear_model.LogisticRegression "sklearn.linear_model.LogisticRegression") instances using this solver behave as multiclass classifiers. For \(\ell\_1\) regularization [`sklearn.svm.l1_min_c`](generated/sklearn.svm.l1_min_c#sklearn.svm.l1_min_c "sklearn.svm.l1_min_c") allows to calculate the lower bound for C in order to get a non “null” (all feature weights to zero) model.
The “lbfgs”, “sag” and “newton-cg” solvers only support \(\ell\_2\) regularization or no regularization, and are found to converge faster for some high-dimensional data. Setting `multi_class` to “multinomial” with these solvers learns a true multinomial logistic regression model [[5]](#id32), which means that its probability estimates should be better calibrated than the default “one-vs-rest” setting.
The “sag” solver uses Stochastic Average Gradient descent [[6]](#id33). It is faster than other solvers for large datasets, when both the number of samples and the number of features are large.
The “saga” solver [[7]](#id34) is a variant of “sag” that also supports the non-smooth `penalty="l1"`. This is therefore the solver of choice for sparse multinomial logistic regression. It is also the only solver that supports `penalty="elasticnet"`.
The “lbfgs” is an optimization algorithm that approximates the Broyden–Fletcher–Goldfarb–Shanno algorithm [[8]](#id35), which belongs to quasi-Newton methods. The “lbfgs” solver is recommended for use for small data-sets but for larger datasets its performance suffers. [[9]](#id36)
The following table summarizes the penalties supported by each solver:
| | |
| --- | --- |
| | **Solvers** |
| **Penalties** | **‘liblinear’** | **‘lbfgs’** | **‘newton-cg’** | **‘sag’** | **‘saga’** |
| Multinomial + L2 penalty | no | yes | yes | yes | yes |
| OVR + L2 penalty | yes | yes | yes | yes | yes |
| Multinomial + L1 penalty | no | no | no | no | yes |
| OVR + L1 penalty | yes | no | no | no | yes |
| Elastic-Net | no | no | no | no | yes |
| No penalty (‘none’) | no | yes | yes | yes | yes |
| **Behaviors** | |
| Penalize the intercept (bad) | yes | no | no | no | no |
| Faster for large datasets | no | no | no | yes | yes |
| Robust to unscaled datasets | yes | yes | yes | no | no |
The “lbfgs” solver is used by default for its robustness. For large datasets the “saga” solver is usually faster. For large dataset, you may also consider using [`SGDClassifier`](generated/sklearn.linear_model.sgdclassifier#sklearn.linear_model.SGDClassifier "sklearn.linear_model.SGDClassifier") with ‘log’ loss, which might be even faster but requires more tuning.
Note
**Feature selection with sparse logistic regression**
A logistic regression with \(\ell\_1\) penalty yields sparse models, and can thus be used to perform feature selection, as detailed in [L1-based feature selection](feature_selection#l1-feature-selection).
Note
**P-value estimation**
It is possible to obtain the p-values and confidence intervals for coefficients in cases of regression without penalization. The `statsmodels
package <https://pypi.org/project/statsmodels/>` natively supports this. Within sklearn, one could use bootstrapping instead as well.
[`LogisticRegressionCV`](generated/sklearn.linear_model.logisticregressioncv#sklearn.linear_model.LogisticRegressionCV "sklearn.linear_model.LogisticRegressionCV") implements Logistic Regression with built-in cross-validation support, to find the optimal `C` and `l1_ratio` parameters according to the `scoring` attribute. The “newton-cg”, “sag”, “saga” and “lbfgs” solvers are found to be faster for high-dimensional dense data, due to warm-starting (see [Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start)).
1.1.12. Generalized Linear Regression
--------------------------------------
Generalized Linear Models (GLM) extend linear models in two ways [[10]](#id41). First, the predicted values \(\hat{y}\) are linked to a linear combination of the input variables \(X\) via an inverse link function \(h\) as
\[\hat{y}(w, X) = h(Xw).\] Secondly, the squared loss function is replaced by the unit deviance \(d\) of a distribution in the exponential family (or more precisely, a reproductive exponential dispersion model (EDM) [[11]](#id42)).
The minimization problem becomes:
\[\min\_{w} \frac{1}{2 n\_{\text{samples}}} \sum\_i d(y\_i, \hat{y}\_i) + \frac{\alpha}{2} ||w||\_2^2,\] where \(\alpha\) is the L2 regularization penalty. When sample weights are provided, the average becomes a weighted average.
The following table lists some specific EDMs and their unit deviance (all of these are instances of the Tweedie family):
| Distribution | Target Domain | Unit Deviance \(d(y, \hat{y})\) |
| --- | --- | --- |
| Normal | \(y \in (-\infty, \infty)\) | \((y-\hat{y})^2\) |
| Poisson | \(y \in [0, \infty)\) | \(2(y\log\frac{y}{\hat{y}}-y+\hat{y})\) |
| Gamma | \(y \in (0, \infty)\) | \(2(\log\frac{\hat{y}}{y}+\frac{y}{\hat{y}}-1)\) |
| Inverse Gaussian | \(y \in (0, \infty)\) | \(\frac{(y-\hat{y})^2}{y\hat{y}^2}\) |
The Probability Density Functions (PDF) of these distributions are illustrated in the following figure,
PDF of a random variable Y following Poisson, Tweedie (power=1.5) and Gamma distributions with different mean values (\(\mu\)). Observe the point mass at \(Y=0\) for the Poisson distribution and the Tweedie (power=1.5) distribution, but not for the Gamma distribution which has a strictly positive target domain.
The choice of the distribution depends on the problem at hand:
* If the target values \(y\) are counts (non-negative integer valued) or relative frequencies (non-negative), you might use a Poisson deviance with log-link.
* If the target values are positive valued and skewed, you might try a Gamma deviance with log-link.
* If the target values seem to be heavier tailed than a Gamma distribution, you might try an Inverse Gaussian deviance (or even higher variance powers of the Tweedie family).
Examples of use cases include:
* Agriculture / weather modeling: number of rain events per year (Poisson), amount of rainfall per event (Gamma), total rainfall per year (Tweedie / Compound Poisson Gamma).
* Risk modeling / insurance policy pricing: number of claim events / policyholder per year (Poisson), cost per event (Gamma), total cost per policyholder per year (Tweedie / Compound Poisson Gamma).
* Predictive maintenance: number of production interruption events per year (Poisson), duration of interruption (Gamma), total interruption time per year (Tweedie / Compound Poisson Gamma).
###
1.1.12.1. Usage
[`TweedieRegressor`](generated/sklearn.linear_model.tweedieregressor#sklearn.linear_model.TweedieRegressor "sklearn.linear_model.TweedieRegressor") implements a generalized linear model for the Tweedie distribution, that allows to model any of the above mentioned distributions using the appropriate `power` parameter. In particular:
* `power = 0`: Normal distribution. Specific estimators such as [`Ridge`](generated/sklearn.linear_model.ridge#sklearn.linear_model.Ridge "sklearn.linear_model.Ridge"), [`ElasticNet`](generated/sklearn.linear_model.elasticnet#sklearn.linear_model.ElasticNet "sklearn.linear_model.ElasticNet") are generally more appropriate in this case.
* `power = 1`: Poisson distribution. [`PoissonRegressor`](generated/sklearn.linear_model.poissonregressor#sklearn.linear_model.PoissonRegressor "sklearn.linear_model.PoissonRegressor") is exposed for convenience. However, it is strictly equivalent to `TweedieRegressor(power=1, link='log')`.
* `power = 2`: Gamma distribution. [`GammaRegressor`](generated/sklearn.linear_model.gammaregressor#sklearn.linear_model.GammaRegressor "sklearn.linear_model.GammaRegressor") is exposed for convenience. However, it is strictly equivalent to `TweedieRegressor(power=2, link='log')`.
* `power = 3`: Inverse Gaussian distribution.
The link function is determined by the `link` parameter.
Usage example:
```
>>> from sklearn.linear_model import TweedieRegressor
>>> reg = TweedieRegressor(power=1, alpha=0.5, link='log')
>>> reg.fit([[0, 0], [0, 1], [2, 2]], [0, 1, 2])
TweedieRegressor(alpha=0.5, link='log', power=1)
>>> reg.coef_
array([0.2463..., 0.4337...])
>>> reg.intercept_
-0.7638...
```
###
1.1.12.2. Practical considerations
The feature matrix `X` should be standardized before fitting. This ensures that the penalty treats features equally.
Since the linear predictor \(Xw\) can be negative and Poisson, Gamma and Inverse Gaussian distributions don’t support negative values, it is necessary to apply an inverse link function that guarantees the non-negativeness. For example with `link='log'`, the inverse link function becomes \(h(Xw)=\exp(Xw)\).
If you want to model a relative frequency, i.e. counts per exposure (time, volume, …) you can do so by using a Poisson distribution and passing \(y=\frac{\mathrm{counts}}{\mathrm{exposure}}\) as target values together with \(\mathrm{exposure}\) as sample weights. For a concrete example see e.g. [Tweedie regression on insurance claims](../auto_examples/linear_model/plot_tweedie_regression_insurance_claims#sphx-glr-auto-examples-linear-model-plot-tweedie-regression-insurance-claims-py).
When performing cross-validation for the `power` parameter of `TweedieRegressor`, it is advisable to specify an explicit `scoring` function, because the default scorer [`TweedieRegressor.score`](generated/sklearn.linear_model.tweedieregressor#sklearn.linear_model.TweedieRegressor.score "sklearn.linear_model.TweedieRegressor.score") is a function of `power` itself.
1.1.13. Stochastic Gradient Descent - SGD
------------------------------------------
Stochastic gradient descent is a simple yet very efficient approach to fit linear models. It is particularly useful when the number of samples (and the number of features) is very large. The `partial_fit` method allows online/out-of-core learning.
The classes [`SGDClassifier`](generated/sklearn.linear_model.sgdclassifier#sklearn.linear_model.SGDClassifier "sklearn.linear_model.SGDClassifier") and [`SGDRegressor`](generated/sklearn.linear_model.sgdregressor#sklearn.linear_model.SGDRegressor "sklearn.linear_model.SGDRegressor") provide functionality to fit linear models for classification and regression using different (convex) loss functions and different penalties. E.g., with `loss="log"`, [`SGDClassifier`](generated/sklearn.linear_model.sgdclassifier#sklearn.linear_model.SGDClassifier "sklearn.linear_model.SGDClassifier") fits a logistic regression model, while with `loss="hinge"` it fits a linear support vector machine (SVM).
1.1.14. Perceptron
-------------------
The [`Perceptron`](generated/sklearn.linear_model.perceptron#sklearn.linear_model.Perceptron "sklearn.linear_model.Perceptron") is another simple classification algorithm suitable for large scale learning. By default:
* It does not require a learning rate.
* It is not regularized (penalized).
* It updates its model only on mistakes.
The last characteristic implies that the Perceptron is slightly faster to train than SGD with the hinge loss and that the resulting models are sparser.
1.1.15. Passive Aggressive Algorithms
--------------------------------------
The passive-aggressive algorithms are a family of algorithms for large-scale learning. They are similar to the Perceptron in that they do not require a learning rate. However, contrary to the Perceptron, they include a regularization parameter `C`.
For classification, [`PassiveAggressiveClassifier`](generated/sklearn.linear_model.passiveaggressiveclassifier#sklearn.linear_model.PassiveAggressiveClassifier "sklearn.linear_model.PassiveAggressiveClassifier") can be used with `loss='hinge'` (PA-I) or `loss='squared_hinge'` (PA-II). For regression, [`PassiveAggressiveRegressor`](generated/sklearn.linear_model.passiveaggressiveregressor#sklearn.linear_model.PassiveAggressiveRegressor "sklearn.linear_model.PassiveAggressiveRegressor") can be used with `loss='epsilon_insensitive'` (PA-I) or `loss='squared_epsilon_insensitive'` (PA-II).
1.1.16. Robustness regression: outliers and modeling errors
------------------------------------------------------------
Robust regression aims to fit a regression model in the presence of corrupt data: either outliers, or error in the model.
###
1.1.16.1. Different scenario and useful concepts
There are different things to keep in mind when dealing with data corrupted by outliers:
* **Outliers in X or in y**?
| Outliers in the y direction | Outliers in the X direction |
| --- | --- |
| | |
* **Fraction of outliers versus amplitude of error**
The number of outlying points matters, but also how much they are outliers.
| Small outliers | Large outliers |
| --- | --- |
| | |
An important notion of robust fitting is that of breakdown point: the fraction of data that can be outlying for the fit to start missing the inlying data.
Note that in general, robust fitting in high-dimensional setting (large `n_features`) is very hard. The robust models here will probably not work in these settings.
###
1.1.16.2. RANSAC: RANdom SAmple Consensus
RANSAC (RANdom SAmple Consensus) fits a model from random subsets of inliers from the complete data set.
RANSAC is a non-deterministic algorithm producing only a reasonable result with a certain probability, which is dependent on the number of iterations (see `max_trials` parameter). It is typically used for linear and non-linear regression problems and is especially popular in the field of photogrammetric computer vision.
The algorithm splits the complete input sample data into a set of inliers, which may be subject to noise, and outliers, which are e.g. caused by erroneous measurements or invalid hypotheses about the data. The resulting model is then estimated only from the determined inliers.
####
1.1.16.2.1. Details of the algorithm
Each iteration performs the following steps:
1. Select `min_samples` random samples from the original data and check whether the set of data is valid (see `is_data_valid`).
2. Fit a model to the random subset (`base_estimator.fit`) and check whether the estimated model is valid (see `is_model_valid`).
3. Classify all data as inliers or outliers by calculating the residuals to the estimated model (`base_estimator.predict(X) - y`) - all data samples with absolute residuals smaller than or equal to the `residual_threshold` are considered as inliers.
4. Save fitted model as best model if number of inlier samples is maximal. In case the current estimated model has the same number of inliers, it is only considered as the best model if it has better score.
These steps are performed either a maximum number of times (`max_trials`) or until one of the special stop criteria are met (see `stop_n_inliers` and `stop_score`). The final model is estimated using all inlier samples (consensus set) of the previously determined best model.
The `is_data_valid` and `is_model_valid` functions allow to identify and reject degenerate combinations of random sub-samples. If the estimated model is not needed for identifying degenerate cases, `is_data_valid` should be used as it is called prior to fitting the model and thus leading to better computational performance.
###
1.1.16.3. Theil-Sen estimator: generalized-median-based estimator
The [`TheilSenRegressor`](generated/sklearn.linear_model.theilsenregressor#sklearn.linear_model.TheilSenRegressor "sklearn.linear_model.TheilSenRegressor") estimator uses a generalization of the median in multiple dimensions. It is thus robust to multivariate outliers. Note however that the robustness of the estimator decreases quickly with the dimensionality of the problem. It loses its robustness properties and becomes no better than an ordinary least squares in high dimension.
####
1.1.16.3.1. Theoretical considerations
[`TheilSenRegressor`](generated/sklearn.linear_model.theilsenregressor#sklearn.linear_model.TheilSenRegressor "sklearn.linear_model.TheilSenRegressor") is comparable to the [Ordinary Least Squares (OLS)](#ordinary-least-squares) in terms of asymptotic efficiency and as an unbiased estimator. In contrast to OLS, Theil-Sen is a non-parametric method which means it makes no assumption about the underlying distribution of the data. Since Theil-Sen is a median-based estimator, it is more robust against corrupted data aka outliers. In univariate setting, Theil-Sen has a breakdown point of about 29.3% in case of a simple linear regression which means that it can tolerate arbitrary corrupted data of up to 29.3%.
The implementation of [`TheilSenRegressor`](generated/sklearn.linear_model.theilsenregressor#sklearn.linear_model.TheilSenRegressor "sklearn.linear_model.TheilSenRegressor") in scikit-learn follows a generalization to a multivariate linear regression model [[14]](#f1) using the spatial median which is a generalization of the median to multiple dimensions [[15]](#f2).
In terms of time and space complexity, Theil-Sen scales according to
\[\binom{n\_{\text{samples}}}{n\_{\text{subsamples}}}\] which makes it infeasible to be applied exhaustively to problems with a large number of samples and features. Therefore, the magnitude of a subpopulation can be chosen to limit the time and space complexity by considering only a random subset of all possible combinations.
###
1.1.16.4. Huber Regression
The [`HuberRegressor`](generated/sklearn.linear_model.huberregressor#sklearn.linear_model.HuberRegressor "sklearn.linear_model.HuberRegressor") is different to [`Ridge`](generated/sklearn.linear_model.ridge#sklearn.linear_model.Ridge "sklearn.linear_model.Ridge") because it applies a linear loss to samples that are classified as outliers. A sample is classified as an inlier if the absolute error of that sample is lesser than a certain threshold. It differs from [`TheilSenRegressor`](generated/sklearn.linear_model.theilsenregressor#sklearn.linear_model.TheilSenRegressor "sklearn.linear_model.TheilSenRegressor") and [`RANSACRegressor`](generated/sklearn.linear_model.ransacregressor#sklearn.linear_model.RANSACRegressor "sklearn.linear_model.RANSACRegressor") because it does not ignore the effect of the outliers but gives a lesser weight to them.
The loss function that [`HuberRegressor`](generated/sklearn.linear_model.huberregressor#sklearn.linear_model.HuberRegressor "sklearn.linear_model.HuberRegressor") minimizes is given by
\[\min\_{w, \sigma} {\sum\_{i=1}^n\left(\sigma + H\_{\epsilon}\left(\frac{X\_{i}w - y\_{i}}{\sigma}\right)\sigma\right) + \alpha {||w||\_2}^2}\] where
\[\begin{split}H\_{\epsilon}(z) = \begin{cases} z^2, & \text {if } |z| < \epsilon, \\ 2\epsilon|z| - \epsilon^2, & \text{otherwise} \end{cases}\end{split}\] It is advised to set the parameter `epsilon` to 1.35 to achieve 95% statistical efficiency.
###
1.1.16.5. Notes
The [`HuberRegressor`](generated/sklearn.linear_model.huberregressor#sklearn.linear_model.HuberRegressor "sklearn.linear_model.HuberRegressor") differs from using [`SGDRegressor`](generated/sklearn.linear_model.sgdregressor#sklearn.linear_model.SGDRegressor "sklearn.linear_model.SGDRegressor") with loss set to `huber` in the following ways.
* [`HuberRegressor`](generated/sklearn.linear_model.huberregressor#sklearn.linear_model.HuberRegressor "sklearn.linear_model.HuberRegressor") is scaling invariant. Once `epsilon` is set, scaling `X` and `y` down or up by different values would produce the same robustness to outliers as before. as compared to [`SGDRegressor`](generated/sklearn.linear_model.sgdregressor#sklearn.linear_model.SGDRegressor "sklearn.linear_model.SGDRegressor") where `epsilon` has to be set again when `X` and `y` are scaled.
* [`HuberRegressor`](generated/sklearn.linear_model.huberregressor#sklearn.linear_model.HuberRegressor "sklearn.linear_model.HuberRegressor") should be more efficient to use on data with small number of samples while [`SGDRegressor`](generated/sklearn.linear_model.sgdregressor#sklearn.linear_model.SGDRegressor "sklearn.linear_model.SGDRegressor") needs a number of passes on the training data to produce the same robustness.
Note that this estimator is different from the R implementation of Robust Regression (<https://stats.oarc.ucla.edu/r/dae/robust-regression/>) because the R implementation does a weighted least squares implementation with weights given to each sample on the basis of how much the residual is greater than a certain threshold.
1.1.17. Quantile Regression
----------------------------
Quantile regression estimates the median or other quantiles of \(y\) conditional on \(X\), while ordinary least squares (OLS) estimates the conditional mean.
As a linear model, the [`QuantileRegressor`](generated/sklearn.linear_model.quantileregressor#sklearn.linear_model.QuantileRegressor "sklearn.linear_model.QuantileRegressor") gives linear predictions \(\hat{y}(w, X) = Xw\) for the \(q\)-th quantile, \(q \in (0, 1)\). The weights or coefficients \(w\) are then found by the following minimization problem:
\[\min\_{w} {\frac{1}{n\_{\text{samples}}} \sum\_i PB\_q(y\_i - X\_i w) + \alpha ||w||\_1}.\] This consists of the pinball loss (also known as linear loss), see also [`mean_pinball_loss`](generated/sklearn.metrics.mean_pinball_loss#sklearn.metrics.mean_pinball_loss "sklearn.metrics.mean_pinball_loss"),
\[\begin{split}PB\_q(t) = q \max(t, 0) + (1 - q) \max(-t, 0) = \begin{cases} q t, & t > 0, \\ 0, & t = 0, \\ (q-1) t, & t < 0 \end{cases}\end{split}\] and the L1 penalty controlled by parameter `alpha`, similar to [`Lasso`](generated/sklearn.linear_model.lasso#sklearn.linear_model.Lasso "sklearn.linear_model.Lasso").
As the pinball loss is only linear in the residuals, quantile regression is much more robust to outliers than squared error based estimation of the mean. Somewhat in between is the [`HuberRegressor`](generated/sklearn.linear_model.huberregressor#sklearn.linear_model.HuberRegressor "sklearn.linear_model.HuberRegressor").
Quantile regression may be useful if one is interested in predicting an interval instead of point prediction. Sometimes, prediction intervals are calculated based on the assumption that prediction error is distributed normally with zero mean and constant variance. Quantile regression provides sensible prediction intervals even for errors with non-constant (but predictable) variance or non-normal distribution.
Based on minimizing the pinball loss, conditional quantiles can also be estimated by models other than linear models. For example, [`GradientBoostingRegressor`](generated/sklearn.ensemble.gradientboostingregressor#sklearn.ensemble.GradientBoostingRegressor "sklearn.ensemble.GradientBoostingRegressor") can predict conditional quantiles if its parameter `loss` is set to `"quantile"` and parameter `alpha` is set to the quantile that should be predicted. See the example in [Prediction Intervals for Gradient Boosting Regression](../auto_examples/ensemble/plot_gradient_boosting_quantile#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-quantile-py).
Most implementations of quantile regression are based on linear programming problem. The current implementation is based on [`scipy.optimize.linprog`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.linprog.html#scipy.optimize.linprog "(in SciPy v1.9.3)").
1.1.18. Polynomial regression: extending linear models with basis functions
----------------------------------------------------------------------------
One common pattern within machine learning is to use linear models trained on nonlinear functions of the data. This approach maintains the generally fast performance of linear methods, while allowing them to fit a much wider range of data.
For example, a simple linear regression can be extended by constructing **polynomial features** from the coefficients. In the standard linear regression case, you might have a model that looks like this for two-dimensional data:
\[\hat{y}(w, x) = w\_0 + w\_1 x\_1 + w\_2 x\_2\] If we want to fit a paraboloid to the data instead of a plane, we can combine the features in second-order polynomials, so that the model looks like this:
\[\hat{y}(w, x) = w\_0 + w\_1 x\_1 + w\_2 x\_2 + w\_3 x\_1 x\_2 + w\_4 x\_1^2 + w\_5 x\_2^2\] The (sometimes surprising) observation is that this is *still a linear model*: to see this, imagine creating a new set of features
\[z = [x\_1, x\_2, x\_1 x\_2, x\_1^2, x\_2^2]\] With this re-labeling of the data, our problem can be written
\[\hat{y}(w, z) = w\_0 + w\_1 z\_1 + w\_2 z\_2 + w\_3 z\_3 + w\_4 z\_4 + w\_5 z\_5\] We see that the resulting *polynomial regression* is in the same class of linear models we considered above (i.e. the model is linear in \(w\)) and can be solved by the same techniques. By considering linear fits within a higher-dimensional space built with these basis functions, the model has the flexibility to fit a much broader range of data.
Here is an example of applying this idea to one-dimensional data, using polynomial features of varying degrees:
This figure is created using the [`PolynomialFeatures`](generated/sklearn.preprocessing.polynomialfeatures#sklearn.preprocessing.PolynomialFeatures "sklearn.preprocessing.PolynomialFeatures") transformer, which transforms an input data matrix into a new data matrix of a given degree. It can be used as follows:
```
>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
[2, 3],
[4, 5]])
>>> poly = PolynomialFeatures(degree=2)
>>> poly.fit_transform(X)
array([[ 1., 0., 1., 0., 0., 1.],
[ 1., 2., 3., 4., 6., 9.],
[ 1., 4., 5., 16., 20., 25.]])
```
The features of `X` have been transformed from \([x\_1, x\_2]\) to \([1, x\_1, x\_2, x\_1^2, x\_1 x\_2, x\_2^2]\), and can now be used within any linear model.
This sort of preprocessing can be streamlined with the [Pipeline](compose#pipeline) tools. A single object representing a simple polynomial regression can be created and used as follows:
```
>>> from sklearn.preprocessing import PolynomialFeatures
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.pipeline import Pipeline
>>> import numpy as np
>>> model = Pipeline([('poly', PolynomialFeatures(degree=3)),
... ('linear', LinearRegression(fit_intercept=False))])
>>> # fit to an order-3 polynomial data
>>> x = np.arange(5)
>>> y = 3 - 2 * x + x ** 2 - x ** 3
>>> model = model.fit(x[:, np.newaxis], y)
>>> model.named_steps['linear'].coef_
array([ 3., -2., 1., -1.])
```
The linear model trained on polynomial features is able to exactly recover the input polynomial coefficients.
In some cases it’s not necessary to include higher powers of any single feature, but only the so-called *interaction features* that multiply together at most \(d\) distinct features. These can be gotten from [`PolynomialFeatures`](generated/sklearn.preprocessing.polynomialfeatures#sklearn.preprocessing.PolynomialFeatures "sklearn.preprocessing.PolynomialFeatures") with the setting `interaction_only=True`.
For example, when dealing with boolean features, \(x\_i^n = x\_i\) for all \(n\) and is therefore useless; but \(x\_i x\_j\) represents the conjunction of two booleans. This way, we can solve the XOR problem with a linear classifier:
```
>>> from sklearn.linear_model import Perceptron
>>> from sklearn.preprocessing import PolynomialFeatures
>>> import numpy as np
>>> X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
>>> y = X[:, 0] ^ X[:, 1]
>>> y
array([0, 1, 1, 0])
>>> X = PolynomialFeatures(interaction_only=True).fit_transform(X).astype(int)
>>> X
array([[1, 0, 0, 0],
[1, 0, 1, 0],
[1, 1, 0, 0],
[1, 1, 1, 1]])
>>> clf = Perceptron(fit_intercept=False, max_iter=10, tol=None,
... shuffle=False).fit(X, y)
```
And the classifier “predictions” are perfect:
```
>>> clf.predict(X)
array([0, 1, 1, 0])
>>> clf.score(X, y)
1.0
```
| programming_docs |
scikit_learn 3.1. Cross-validation: evaluating estimator performance 3.1. Cross-validation: evaluating estimator performance
=======================================================
Learning the parameters of a prediction function and testing it on the same data is a methodological mistake: a model that would just repeat the labels of the samples that it has just seen would have a perfect score but would fail to predict anything useful on yet-unseen data. This situation is called **overfitting**. To avoid it, it is common practice when performing a (supervised) machine learning experiment to hold out part of the available data as a **test set** `X_test, y_test`. Note that the word “experiment” is not intended to denote academic use only, because even in commercial settings machine learning usually starts out experimentally. Here is a flowchart of typical cross validation workflow in model training. The best parameters can be determined by [grid search](grid_search#grid-search) techniques.
In scikit-learn a random split into training and test sets can be quickly computed with the [`train_test_split`](generated/sklearn.model_selection.train_test_split#sklearn.model_selection.train_test_split "sklearn.model_selection.train_test_split") helper function. Let’s load the iris data set to fit a linear support vector machine on it:
```
>>> import numpy as np
>>> from sklearn.model_selection import train_test_split
>>> from sklearn import datasets
>>> from sklearn import svm
>>> X, y = datasets.load_iris(return_X_y=True)
>>> X.shape, y.shape
((150, 4), (150,))
```
We can now quickly sample a training set while holding out 40% of the data for testing (evaluating) our classifier:
```
>>> X_train, X_test, y_train, y_test = train_test_split(
... X, y, test_size=0.4, random_state=0)
>>> X_train.shape, y_train.shape
((90, 4), (90,))
>>> X_test.shape, y_test.shape
((60, 4), (60,))
>>> clf = svm.SVC(kernel='linear', C=1).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.96...
```
When evaluating different settings (“hyperparameters”) for estimators, such as the `C` setting that must be manually set for an SVM, there is still a risk of overfitting *on the test set* because the parameters can be tweaked until the estimator performs optimally. This way, knowledge about the test set can “leak” into the model and evaluation metrics no longer report on generalization performance. To solve this problem, yet another part of the dataset can be held out as a so-called “validation set”: training proceeds on the training set, after which evaluation is done on the validation set, and when the experiment seems to be successful, final evaluation can be done on the test set.
However, by partitioning the available data into three sets, we drastically reduce the number of samples which can be used for learning the model, and the results can depend on a particular random choice for the pair of (train, validation) sets.
A solution to this problem is a procedure called [cross-validation](https://en.wikipedia.org/wiki/Cross-validation_(statistics)) (CV for short). A test set should still be held out for final evaluation, but the validation set is no longer needed when doing CV. In the basic approach, called *k*-fold CV, the training set is split into *k* smaller sets (other approaches are described below, but generally follow the same principles). The following procedure is followed for each of the *k* “folds”:
* A model is trained using \(k-1\) of the folds as training data;
* the resulting model is validated on the remaining part of the data (i.e., it is used as a test set to compute a performance measure such as accuracy).
The performance measure reported by *k*-fold cross-validation is then the average of the values computed in the loop. This approach can be computationally expensive, but does not waste too much data (as is the case when fixing an arbitrary validation set), which is a major advantage in problems such as inverse inference where the number of samples is very small.
3.1.1. Computing cross-validated metrics
-----------------------------------------
The simplest way to use cross-validation is to call the [`cross_val_score`](generated/sklearn.model_selection.cross_val_score#sklearn.model_selection.cross_val_score "sklearn.model_selection.cross_val_score") helper function on the estimator and the dataset.
The following example demonstrates how to estimate the accuracy of a linear kernel support vector machine on the iris dataset by splitting the data, fitting a model and computing the score 5 consecutive times (with different splits each time):
```
>>> from sklearn.model_selection import cross_val_score
>>> clf = svm.SVC(kernel='linear', C=1, random_state=42)
>>> scores = cross_val_score(clf, X, y, cv=5)
>>> scores
array([0.96..., 1. , 0.96..., 0.96..., 1. ])
```
The mean score and the standard deviation are hence given by:
```
>>> print("%0.2f accuracy with a standard deviation of %0.2f" % (scores.mean(), scores.std()))
0.98 accuracy with a standard deviation of 0.02
```
By default, the score computed at each CV iteration is the `score` method of the estimator. It is possible to change this by using the scoring parameter:
```
>>> from sklearn import metrics
>>> scores = cross_val_score(
... clf, X, y, cv=5, scoring='f1_macro')
>>> scores
array([0.96..., 1. ..., 0.96..., 0.96..., 1. ])
```
See [The scoring parameter: defining model evaluation rules](model_evaluation#scoring-parameter) for details. In the case of the Iris dataset, the samples are balanced across target classes hence the accuracy and the F1-score are almost equal.
When the `cv` argument is an integer, [`cross_val_score`](generated/sklearn.model_selection.cross_val_score#sklearn.model_selection.cross_val_score "sklearn.model_selection.cross_val_score") uses the [`KFold`](generated/sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold") or [`StratifiedKFold`](generated/sklearn.model_selection.stratifiedkfold#sklearn.model_selection.StratifiedKFold "sklearn.model_selection.StratifiedKFold") strategies by default, the latter being used if the estimator derives from [`ClassifierMixin`](generated/sklearn.base.classifiermixin#sklearn.base.ClassifierMixin "sklearn.base.ClassifierMixin").
It is also possible to use other cross validation strategies by passing a cross validation iterator instead, for instance:
```
>>> from sklearn.model_selection import ShuffleSplit
>>> n_samples = X.shape[0]
>>> cv = ShuffleSplit(n_splits=5, test_size=0.3, random_state=0)
>>> cross_val_score(clf, X, y, cv=cv)
array([0.977..., 0.977..., 1. ..., 0.955..., 1. ])
```
Another option is to use an iterable yielding (train, test) splits as arrays of indices, for example:
```
>>> def custom_cv_2folds(X):
... n = X.shape[0]
... i = 1
... while i <= 2:
... idx = np.arange(n * (i - 1) / 2, n * i / 2, dtype=int)
... yield idx, idx
... i += 1
...
>>> custom_cv = custom_cv_2folds(X)
>>> cross_val_score(clf, X, y, cv=custom_cv)
array([1. , 0.973...])
```
###
3.1.1.1. The cross\_validate function and multiple metric evaluation
The [`cross_validate`](generated/sklearn.model_selection.cross_validate#sklearn.model_selection.cross_validate "sklearn.model_selection.cross_validate") function differs from [`cross_val_score`](generated/sklearn.model_selection.cross_val_score#sklearn.model_selection.cross_val_score "sklearn.model_selection.cross_val_score") in two ways:
* It allows specifying multiple metrics for evaluation.
* It returns a dict containing fit-times, score-times (and optionally training scores as well as fitted estimators) in addition to the test score.
For single metric evaluation, where the scoring parameter is a string, callable or None, the keys will be - `['test_score', 'fit_time', 'score_time']`
And for multiple metric evaluation, the return value is a dict with the following keys - `['test_<scorer1_name>', 'test_<scorer2_name>', 'test_<scorer...>', 'fit_time', 'score_time']`
`return_train_score` is set to `False` by default to save computation time. To evaluate the scores on the training set as well you need to set it to `True`.
You may also retain the estimator fitted on each training set by setting `return_estimator=True`.
The multiple metrics can be specified either as a list, tuple or set of predefined scorer names:
```
>>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import recall_score
>>> scoring = ['precision_macro', 'recall_macro']
>>> clf = svm.SVC(kernel='linear', C=1, random_state=0)
>>> scores = cross_validate(clf, X, y, scoring=scoring)
>>> sorted(scores.keys())
['fit_time', 'score_time', 'test_precision_macro', 'test_recall_macro']
>>> scores['test_recall_macro']
array([0.96..., 1. ..., 0.96..., 0.96..., 1. ])
```
Or as a dict mapping scorer name to a predefined or custom scoring function:
```
>>> from sklearn.metrics import make_scorer
>>> scoring = {'prec_macro': 'precision_macro',
... 'rec_macro': make_scorer(recall_score, average='macro')}
>>> scores = cross_validate(clf, X, y, scoring=scoring,
... cv=5, return_train_score=True)
>>> sorted(scores.keys())
['fit_time', 'score_time', 'test_prec_macro', 'test_rec_macro',
'train_prec_macro', 'train_rec_macro']
>>> scores['train_rec_macro']
array([0.97..., 0.97..., 0.99..., 0.98..., 0.98...])
```
Here is an example of `cross_validate` using a single metric:
```
>>> scores = cross_validate(clf, X, y,
... scoring='precision_macro', cv=5,
... return_estimator=True)
>>> sorted(scores.keys())
['estimator', 'fit_time', 'score_time', 'test_score']
```
###
3.1.1.2. Obtaining predictions by cross-validation
The function [`cross_val_predict`](generated/sklearn.model_selection.cross_val_predict#sklearn.model_selection.cross_val_predict "sklearn.model_selection.cross_val_predict") has a similar interface to [`cross_val_score`](generated/sklearn.model_selection.cross_val_score#sklearn.model_selection.cross_val_score "sklearn.model_selection.cross_val_score"), but returns, for each element in the input, the prediction that was obtained for that element when it was in the test set. Only cross-validation strategies that assign all elements to a test set exactly once can be used (otherwise, an exception is raised).
Warning
Note on inappropriate usage of cross\_val\_predict
The result of [`cross_val_predict`](generated/sklearn.model_selection.cross_val_predict#sklearn.model_selection.cross_val_predict "sklearn.model_selection.cross_val_predict") may be different from those obtained using [`cross_val_score`](generated/sklearn.model_selection.cross_val_score#sklearn.model_selection.cross_val_score "sklearn.model_selection.cross_val_score") as the elements are grouped in different ways. The function [`cross_val_score`](generated/sklearn.model_selection.cross_val_score#sklearn.model_selection.cross_val_score "sklearn.model_selection.cross_val_score") takes an average over cross-validation folds, whereas [`cross_val_predict`](generated/sklearn.model_selection.cross_val_predict#sklearn.model_selection.cross_val_predict "sklearn.model_selection.cross_val_predict") simply returns the labels (or probabilities) from several distinct models undistinguished. Thus, [`cross_val_predict`](generated/sklearn.model_selection.cross_val_predict#sklearn.model_selection.cross_val_predict "sklearn.model_selection.cross_val_predict") is not an appropriate measure of generalization error.
The function [`cross_val_predict`](generated/sklearn.model_selection.cross_val_predict#sklearn.model_selection.cross_val_predict "sklearn.model_selection.cross_val_predict") is appropriate for:
* Visualization of predictions obtained from different models.
* Model blending: When predictions of one supervised estimator are used to train another estimator in ensemble methods.
The available cross validation iterators are introduced in the following section.
3.1.2. Cross validation iterators
----------------------------------
The following sections list utilities to generate indices that can be used to generate dataset splits according to different cross validation strategies.
###
3.1.2.1. Cross-validation iterators for i.i.d. data
Assuming that some data is Independent and Identically Distributed (i.i.d.) is making the assumption that all samples stem from the same generative process and that the generative process is assumed to have no memory of past generated samples.
The following cross-validators can be used in such cases.
Note
While i.i.d. data is a common assumption in machine learning theory, it rarely holds in practice. If one knows that the samples have been generated using a time-dependent process, it is safer to use a [time-series aware cross-validation scheme](#timeseries-cv). Similarly, if we know that the generative process has a group structure (samples collected from different subjects, experiments, measurement devices), it is safer to use [group-wise cross-validation](#group-cv).
####
3.1.2.1.1. K-fold
[`KFold`](generated/sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold") divides all the samples in \(k\) groups of samples, called folds (if \(k = n\), this is equivalent to the *Leave One Out* strategy), of equal sizes (if possible). The prediction function is learned using \(k - 1\) folds, and the fold left out is used for test.
Example of 2-fold cross-validation on a dataset with 4 samples:
```
>>> import numpy as np
>>> from sklearn.model_selection import KFold
>>> X = ["a", "b", "c", "d"]
>>> kf = KFold(n_splits=2)
>>> for train, test in kf.split(X):
... print("%s %s" % (train, test))
[2 3] [0 1]
[0 1] [2 3]
```
Here is a visualization of the cross-validation behavior. Note that [`KFold`](generated/sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold") is not affected by classes or groups.
Each fold is constituted by two arrays: the first one is related to the *training set*, and the second one to the *test set*. Thus, one can create the training/test sets using numpy indexing:
```
>>> X = np.array([[0., 0.], [1., 1.], [-1., -1.], [2., 2.]])
>>> y = np.array([0, 1, 0, 1])
>>> X_train, X_test, y_train, y_test = X[train], X[test], y[train], y[test]
```
####
3.1.2.1.2. Repeated K-Fold
[`RepeatedKFold`](generated/sklearn.model_selection.repeatedkfold#sklearn.model_selection.RepeatedKFold "sklearn.model_selection.RepeatedKFold") repeats K-Fold n times. It can be used when one requires to run [`KFold`](generated/sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold") n times, producing different splits in each repetition.
Example of 2-fold K-Fold repeated 2 times:
```
>>> import numpy as np
>>> from sklearn.model_selection import RepeatedKFold
>>> X = np.array([[1, 2], [3, 4], [1, 2], [3, 4]])
>>> random_state = 12883823
>>> rkf = RepeatedKFold(n_splits=2, n_repeats=2, random_state=random_state)
>>> for train, test in rkf.split(X):
... print("%s %s" % (train, test))
...
[2 3] [0 1]
[0 1] [2 3]
[0 2] [1 3]
[1 3] [0 2]
```
Similarly, [`RepeatedStratifiedKFold`](generated/sklearn.model_selection.repeatedstratifiedkfold#sklearn.model_selection.RepeatedStratifiedKFold "sklearn.model_selection.RepeatedStratifiedKFold") repeats Stratified K-Fold n times with different randomization in each repetition.
####
3.1.2.1.3. Leave One Out (LOO)
[`LeaveOneOut`](generated/sklearn.model_selection.leaveoneout#sklearn.model_selection.LeaveOneOut "sklearn.model_selection.LeaveOneOut") (or LOO) is a simple cross-validation. Each learning set is created by taking all the samples except one, the test set being the sample left out. Thus, for \(n\) samples, we have \(n\) different training sets and \(n\) different tests set. This cross-validation procedure does not waste much data as only one sample is removed from the training set:
```
>>> from sklearn.model_selection import LeaveOneOut
>>> X = [1, 2, 3, 4]
>>> loo = LeaveOneOut()
>>> for train, test in loo.split(X):
... print("%s %s" % (train, test))
[1 2 3] [0]
[0 2 3] [1]
[0 1 3] [2]
[0 1 2] [3]
```
Potential users of LOO for model selection should weigh a few known caveats. When compared with \(k\)-fold cross validation, one builds \(n\) models from \(n\) samples instead of \(k\) models, where \(n > k\). Moreover, each is trained on \(n - 1\) samples rather than \((k-1) n / k\). In both ways, assuming \(k\) is not too large and \(k < n\), LOO is more computationally expensive than \(k\)-fold cross validation.
In terms of accuracy, LOO often results in high variance as an estimator for the test error. Intuitively, since \(n - 1\) of the \(n\) samples are used to build each model, models constructed from folds are virtually identical to each other and to the model built from the entire training set.
However, if the learning curve is steep for the training size in question, then 5- or 10- fold cross validation can overestimate the generalization error.
As a general rule, most authors, and empirical evidence, suggest that 5- or 10- fold cross validation should be preferred to LOO.
####
3.1.2.1.4. Leave P Out (LPO)
[`LeavePOut`](generated/sklearn.model_selection.leavepout#sklearn.model_selection.LeavePOut "sklearn.model_selection.LeavePOut") is very similar to [`LeaveOneOut`](generated/sklearn.model_selection.leaveoneout#sklearn.model_selection.LeaveOneOut "sklearn.model_selection.LeaveOneOut") as it creates all the possible training/test sets by removing \(p\) samples from the complete set. For \(n\) samples, this produces \({n \choose p}\) train-test pairs. Unlike [`LeaveOneOut`](generated/sklearn.model_selection.leaveoneout#sklearn.model_selection.LeaveOneOut "sklearn.model_selection.LeaveOneOut") and [`KFold`](generated/sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold"), the test sets will overlap for \(p > 1\).
Example of Leave-2-Out on a dataset with 4 samples:
```
>>> from sklearn.model_selection import LeavePOut
>>> X = np.ones(4)
>>> lpo = LeavePOut(p=2)
>>> for train, test in lpo.split(X):
... print("%s %s" % (train, test))
[2 3] [0 1]
[1 3] [0 2]
[1 2] [0 3]
[0 3] [1 2]
[0 2] [1 3]
[0 1] [2 3]
```
####
3.1.2.1.5. Random permutations cross-validation a.k.a. Shuffle & Split
The [`ShuffleSplit`](generated/sklearn.model_selection.shufflesplit#sklearn.model_selection.ShuffleSplit "sklearn.model_selection.ShuffleSplit") iterator will generate a user defined number of independent train / test dataset splits. Samples are first shuffled and then split into a pair of train and test sets.
It is possible to control the randomness for reproducibility of the results by explicitly seeding the `random_state` pseudo random number generator.
Here is a usage example:
```
>>> from sklearn.model_selection import ShuffleSplit
>>> X = np.arange(10)
>>> ss = ShuffleSplit(n_splits=5, test_size=0.25, random_state=0)
>>> for train_index, test_index in ss.split(X):
... print("%s %s" % (train_index, test_index))
[9 1 6 7 3 0 5] [2 8 4]
[2 9 8 0 6 7 4] [3 5 1]
[4 5 1 0 6 9 7] [2 3 8]
[2 7 5 8 0 3 4] [6 1 9]
[4 1 0 6 8 9 3] [5 2 7]
```
Here is a visualization of the cross-validation behavior. Note that [`ShuffleSplit`](generated/sklearn.model_selection.shufflesplit#sklearn.model_selection.ShuffleSplit "sklearn.model_selection.ShuffleSplit") is not affected by classes or groups.
[`ShuffleSplit`](generated/sklearn.model_selection.shufflesplit#sklearn.model_selection.ShuffleSplit "sklearn.model_selection.ShuffleSplit") is thus a good alternative to [`KFold`](generated/sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold") cross validation that allows a finer control on the number of iterations and the proportion of samples on each side of the train / test split.
###
3.1.2.2. Cross-validation iterators with stratification based on class labels.
Some classification problems can exhibit a large imbalance in the distribution of the target classes: for instance there could be several times more negative samples than positive samples. In such cases it is recommended to use stratified sampling as implemented in [`StratifiedKFold`](generated/sklearn.model_selection.stratifiedkfold#sklearn.model_selection.StratifiedKFold "sklearn.model_selection.StratifiedKFold") and [`StratifiedShuffleSplit`](generated/sklearn.model_selection.stratifiedshufflesplit#sklearn.model_selection.StratifiedShuffleSplit "sklearn.model_selection.StratifiedShuffleSplit") to ensure that relative class frequencies is approximately preserved in each train and validation fold.
####
3.1.2.2.1. Stratified k-fold
[`StratifiedKFold`](generated/sklearn.model_selection.stratifiedkfold#sklearn.model_selection.StratifiedKFold "sklearn.model_selection.StratifiedKFold") is a variation of *k-fold* which returns *stratified* folds: each set contains approximately the same percentage of samples of each target class as the complete set.
Here is an example of stratified 3-fold cross-validation on a dataset with 50 samples from two unbalanced classes. We show the number of samples in each class and compare with [`KFold`](generated/sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold").
```
>>> from sklearn.model_selection import StratifiedKFold, KFold
>>> import numpy as np
>>> X, y = np.ones((50, 1)), np.hstack(([0] * 45, [1] * 5))
>>> skf = StratifiedKFold(n_splits=3)
>>> for train, test in skf.split(X, y):
... print('train - {} | test - {}'.format(
... np.bincount(y[train]), np.bincount(y[test])))
train - [30 3] | test - [15 2]
train - [30 3] | test - [15 2]
train - [30 4] | test - [15 1]
>>> kf = KFold(n_splits=3)
>>> for train, test in kf.split(X, y):
... print('train - {} | test - {}'.format(
... np.bincount(y[train]), np.bincount(y[test])))
train - [28 5] | test - [17]
train - [28 5] | test - [17]
train - [34] | test - [11 5]
```
We can see that [`StratifiedKFold`](generated/sklearn.model_selection.stratifiedkfold#sklearn.model_selection.StratifiedKFold "sklearn.model_selection.StratifiedKFold") preserves the class ratios (approximately 1 / 10) in both train and test dataset.
Here is a visualization of the cross-validation behavior.
[`RepeatedStratifiedKFold`](generated/sklearn.model_selection.repeatedstratifiedkfold#sklearn.model_selection.RepeatedStratifiedKFold "sklearn.model_selection.RepeatedStratifiedKFold") can be used to repeat Stratified K-Fold n times with different randomization in each repetition.
####
3.1.2.2.2. Stratified Shuffle Split
[`StratifiedShuffleSplit`](generated/sklearn.model_selection.stratifiedshufflesplit#sklearn.model_selection.StratifiedShuffleSplit "sklearn.model_selection.StratifiedShuffleSplit") is a variation of *ShuffleSplit*, which returns stratified splits, *i.e* which creates splits by preserving the same percentage for each target class as in the complete set.
Here is a visualization of the cross-validation behavior.
###
3.1.2.3. Cross-validation iterators for grouped data
The i.i.d. assumption is broken if the underlying generative process yield groups of dependent samples.
Such a grouping of data is domain specific. An example would be when there is medical data collected from multiple patients, with multiple samples taken from each patient. And such data is likely to be dependent on the individual group. In our example, the patient id for each sample will be its group identifier.
In this case we would like to know if a model trained on a particular set of groups generalizes well to the unseen groups. To measure this, we need to ensure that all the samples in the validation fold come from groups that are not represented at all in the paired training fold.
The following cross-validation splitters can be used to do that. The grouping identifier for the samples is specified via the `groups` parameter.
####
3.1.2.3.1. Group k-fold
[`GroupKFold`](generated/sklearn.model_selection.groupkfold#sklearn.model_selection.GroupKFold "sklearn.model_selection.GroupKFold") is a variation of k-fold which ensures that the same group is not represented in both testing and training sets. For example if the data is obtained from different subjects with several samples per-subject and if the model is flexible enough to learn from highly person specific features it could fail to generalize to new subjects. [`GroupKFold`](generated/sklearn.model_selection.groupkfold#sklearn.model_selection.GroupKFold "sklearn.model_selection.GroupKFold") makes it possible to detect this kind of overfitting situations.
Imagine you have three subjects, each with an associated number from 1 to 3:
```
>>> from sklearn.model_selection import GroupKFold
>>> X = [0.1, 0.2, 2.2, 2.4, 2.3, 4.55, 5.8, 8.8, 9, 10]
>>> y = ["a", "b", "b", "b", "c", "c", "c", "d", "d", "d"]
>>> groups = [1, 1, 1, 2, 2, 2, 3, 3, 3, 3]
>>> gkf = GroupKFold(n_splits=3)
>>> for train, test in gkf.split(X, y, groups=groups):
... print("%s %s" % (train, test))
[0 1 2 3 4 5] [6 7 8 9]
[0 1 2 6 7 8 9] [3 4 5]
[3 4 5 6 7 8 9] [0 1 2]
```
Each subject is in a different testing fold, and the same subject is never in both testing and training. Notice that the folds do not have exactly the same size due to the imbalance in the data. If class proportions must be balanced across folds, [`StratifiedGroupKFold`](generated/sklearn.model_selection.stratifiedgroupkfold#sklearn.model_selection.StratifiedGroupKFold "sklearn.model_selection.StratifiedGroupKFold") is a better option.
Here is a visualization of the cross-validation behavior.
Similar to [`KFold`](generated/sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold"), the test sets from [`GroupKFold`](generated/sklearn.model_selection.groupkfold#sklearn.model_selection.GroupKFold "sklearn.model_selection.GroupKFold") will form a complete partition of all the data. Unlike [`KFold`](generated/sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold"), [`GroupKFold`](generated/sklearn.model_selection.groupkfold#sklearn.model_selection.GroupKFold "sklearn.model_selection.GroupKFold") is not randomized at all, whereas [`KFold`](generated/sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold") is randomized when `shuffle=True`.
####
3.1.2.3.2. StratifiedGroupKFold
[`StratifiedGroupKFold`](generated/sklearn.model_selection.stratifiedgroupkfold#sklearn.model_selection.StratifiedGroupKFold "sklearn.model_selection.StratifiedGroupKFold") is a cross-validation scheme that combines both [`StratifiedKFold`](generated/sklearn.model_selection.stratifiedkfold#sklearn.model_selection.StratifiedKFold "sklearn.model_selection.StratifiedKFold") and [`GroupKFold`](generated/sklearn.model_selection.groupkfold#sklearn.model_selection.GroupKFold "sklearn.model_selection.GroupKFold"). The idea is to try to preserve the distribution of classes in each split while keeping each group within a single split. That might be useful when you have an unbalanced dataset so that using just [`GroupKFold`](generated/sklearn.model_selection.groupkfold#sklearn.model_selection.GroupKFold "sklearn.model_selection.GroupKFold") might produce skewed splits.
Example:
```
>>> from sklearn.model_selection import StratifiedGroupKFold
>>> X = list(range(18))
>>> y = [1] * 6 + [0] * 12
>>> groups = [1, 2, 3, 3, 4, 4, 1, 1, 2, 2, 3, 4, 5, 5, 5, 6, 6, 6]
>>> sgkf = StratifiedGroupKFold(n_splits=3)
>>> for train, test in sgkf.split(X, y, groups=groups):
... print("%s %s" % (train, test))
[ 0 2 3 4 5 6 7 10 11 15 16 17] [ 1 8 9 12 13 14]
[ 0 1 4 5 6 7 8 9 11 12 13 14] [ 2 3 10 15 16 17]
[ 1 2 3 8 9 10 12 13 14 15 16 17] [ 0 4 5 6 7 11]
```
Implementation notes:
* With the current implementation full shuffle is not possible in most scenarios. When shuffle=True, the following happens:
1. All groups are shuffled.
2. Groups are sorted by standard deviation of classes using stable sort.
3. Sorted groups are iterated over and assigned to folds.That means that only groups with the same standard deviation of class distribution will be shuffled, which might be useful when each group has only a single class.
* The algorithm greedily assigns each group to one of n\_splits test sets, choosing the test set that minimises the variance in class distribution across test sets. Group assignment proceeds from groups with highest to lowest variance in class frequency, i.e. large groups peaked on one or few classes are assigned first.
* This split is suboptimal in a sense that it might produce imbalanced splits even if perfect stratification is possible. If you have relatively close distribution of classes in each group, using [`GroupKFold`](generated/sklearn.model_selection.groupkfold#sklearn.model_selection.GroupKFold "sklearn.model_selection.GroupKFold") is better.
Here is a visualization of cross-validation behavior for uneven groups:
####
3.1.2.3.3. Leave One Group Out
[`LeaveOneGroupOut`](generated/sklearn.model_selection.leaveonegroupout#sklearn.model_selection.LeaveOneGroupOut "sklearn.model_selection.LeaveOneGroupOut") is a cross-validation scheme which holds out the samples according to a third-party provided array of integer groups. This group information can be used to encode arbitrary domain specific pre-defined cross-validation folds.
Each training set is thus constituted by all the samples except the ones related to a specific group. This is basically the same as [`LeavePGroupsOut`](generated/sklearn.model_selection.leavepgroupsout#sklearn.model_selection.LeavePGroupsOut "sklearn.model_selection.LeavePGroupsOut") with `n_groups=1`.
For example, in the cases of multiple experiments, [`LeaveOneGroupOut`](generated/sklearn.model_selection.leaveonegroupout#sklearn.model_selection.LeaveOneGroupOut "sklearn.model_selection.LeaveOneGroupOut") can be used to create a cross-validation based on the different experiments: we create a training set using the samples of all the experiments except one:
```
>>> from sklearn.model_selection import LeaveOneGroupOut
>>> X = [1, 5, 10, 50, 60, 70, 80]
>>> y = [0, 1, 1, 2, 2, 2, 2]
>>> groups = [1, 1, 2, 2, 3, 3, 3]
>>> logo = LeaveOneGroupOut()
>>> for train, test in logo.split(X, y, groups=groups):
... print("%s %s" % (train, test))
[2 3 4 5 6] [0 1]
[0 1 4 5 6] [2 3]
[0 1 2 3] [4 5 6]
```
Another common application is to use time information: for instance the groups could be the year of collection of the samples and thus allow for cross-validation against time-based splits.
####
3.1.2.3.4. Leave P Groups Out
[`LeavePGroupsOut`](generated/sklearn.model_selection.leavepgroupsout#sklearn.model_selection.LeavePGroupsOut "sklearn.model_selection.LeavePGroupsOut") is similar as [`LeaveOneGroupOut`](generated/sklearn.model_selection.leaveonegroupout#sklearn.model_selection.LeaveOneGroupOut "sklearn.model_selection.LeaveOneGroupOut"), but removes samples related to \(P\) groups for each training/test set. All possible combinations of \(P\) groups are left out, meaning test sets will overlap for \(P>1\).
Example of Leave-2-Group Out:
```
>>> from sklearn.model_selection import LeavePGroupsOut
>>> X = np.arange(6)
>>> y = [1, 1, 1, 2, 2, 2]
>>> groups = [1, 1, 2, 2, 3, 3]
>>> lpgo = LeavePGroupsOut(n_groups=2)
>>> for train, test in lpgo.split(X, y, groups=groups):
... print("%s %s" % (train, test))
[4 5] [0 1 2 3]
[2 3] [0 1 4 5]
[0 1] [2 3 4 5]
```
####
3.1.2.3.5. Group Shuffle Split
The [`GroupShuffleSplit`](generated/sklearn.model_selection.groupshufflesplit#sklearn.model_selection.GroupShuffleSplit "sklearn.model_selection.GroupShuffleSplit") iterator behaves as a combination of [`ShuffleSplit`](generated/sklearn.model_selection.shufflesplit#sklearn.model_selection.ShuffleSplit "sklearn.model_selection.ShuffleSplit") and [`LeavePGroupsOut`](generated/sklearn.model_selection.leavepgroupsout#sklearn.model_selection.LeavePGroupsOut "sklearn.model_selection.LeavePGroupsOut"), and generates a sequence of randomized partitions in which a subset of groups are held out for each split. Each train/test split is performed independently meaning there is no guaranteed relationship between successive test sets.
Here is a usage example:
```
>>> from sklearn.model_selection import GroupShuffleSplit
>>> X = [0.1, 0.2, 2.2, 2.4, 2.3, 4.55, 5.8, 0.001]
>>> y = ["a", "b", "b", "b", "c", "c", "c", "a"]
>>> groups = [1, 1, 2, 2, 3, 3, 4, 4]
>>> gss = GroupShuffleSplit(n_splits=4, test_size=0.5, random_state=0)
>>> for train, test in gss.split(X, y, groups=groups):
... print("%s %s" % (train, test))
...
[0 1 2 3] [4 5 6 7]
[2 3 6 7] [0 1 4 5]
[2 3 4 5] [0 1 6 7]
[4 5 6 7] [0 1 2 3]
```
Here is a visualization of the cross-validation behavior.
This class is useful when the behavior of [`LeavePGroupsOut`](generated/sklearn.model_selection.leavepgroupsout#sklearn.model_selection.LeavePGroupsOut "sklearn.model_selection.LeavePGroupsOut") is desired, but the number of groups is large enough that generating all possible partitions with \(P\) groups withheld would be prohibitively expensive. In such a scenario, [`GroupShuffleSplit`](generated/sklearn.model_selection.groupshufflesplit#sklearn.model_selection.GroupShuffleSplit "sklearn.model_selection.GroupShuffleSplit") provides a random sample (with replacement) of the train / test splits generated by [`LeavePGroupsOut`](generated/sklearn.model_selection.leavepgroupsout#sklearn.model_selection.LeavePGroupsOut "sklearn.model_selection.LeavePGroupsOut").
###
3.1.2.4. Predefined Fold-Splits / Validation-Sets
For some datasets, a pre-defined split of the data into training- and validation fold or into several cross-validation folds already exists. Using [`PredefinedSplit`](generated/sklearn.model_selection.predefinedsplit#sklearn.model_selection.PredefinedSplit "sklearn.model_selection.PredefinedSplit") it is possible to use these folds e.g. when searching for hyperparameters.
For example, when using a validation set, set the `test_fold` to 0 for all samples that are part of the validation set, and to -1 for all other samples.
###
3.1.2.5. Using cross-validation iterators to split train and test
The above group cross-validation functions may also be useful for splitting a dataset into training and testing subsets. Note that the convenience function [`train_test_split`](generated/sklearn.model_selection.train_test_split#sklearn.model_selection.train_test_split "sklearn.model_selection.train_test_split") is a wrapper around [`ShuffleSplit`](generated/sklearn.model_selection.shufflesplit#sklearn.model_selection.ShuffleSplit "sklearn.model_selection.ShuffleSplit") and thus only allows for stratified splitting (using the class labels) and cannot account for groups.
To perform the train and test split, use the indices for the train and test subsets yielded by the generator output by the `split()` method of the cross-validation splitter. For example:
```
>>> import numpy as np
>>> from sklearn.model_selection import GroupShuffleSplit
>>> X = np.array([0.1, 0.2, 2.2, 2.4, 2.3, 4.55, 5.8, 0.001])
>>> y = np.array(["a", "b", "b", "b", "c", "c", "c", "a"])
>>> groups = np.array([1, 1, 2, 2, 3, 3, 4, 4])
>>> train_indx, test_indx = next(
... GroupShuffleSplit(random_state=7).split(X, y, groups)
... )
>>> X_train, X_test, y_train, y_test = \
... X[train_indx], X[test_indx], y[train_indx], y[test_indx]
>>> X_train.shape, X_test.shape
((6,), (2,))
>>> np.unique(groups[train_indx]), np.unique(groups[test_indx])
(array([1, 2, 4]), array([3]))
```
###
3.1.2.6. Cross validation of time series data
Time series data is characterized by the correlation between observations that are near in time (*autocorrelation*). However, classical cross-validation techniques such as [`KFold`](generated/sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold") and [`ShuffleSplit`](generated/sklearn.model_selection.shufflesplit#sklearn.model_selection.ShuffleSplit "sklearn.model_selection.ShuffleSplit") assume the samples are independent and identically distributed, and would result in unreasonable correlation between training and testing instances (yielding poor estimates of generalization error) on time series data. Therefore, it is very important to evaluate our model for time series data on the “future” observations least like those that are used to train the model. To achieve this, one solution is provided by [`TimeSeriesSplit`](generated/sklearn.model_selection.timeseriessplit#sklearn.model_selection.TimeSeriesSplit "sklearn.model_selection.TimeSeriesSplit").
####
3.1.2.6.1. Time Series Split
[`TimeSeriesSplit`](generated/sklearn.model_selection.timeseriessplit#sklearn.model_selection.TimeSeriesSplit "sklearn.model_selection.TimeSeriesSplit") is a variation of *k-fold* which returns first \(k\) folds as train set and the \((k+1)\) th fold as test set. Note that unlike standard cross-validation methods, successive training sets are supersets of those that come before them. Also, it adds all surplus data to the first training partition, which is always used to train the model.
This class can be used to cross-validate time series data samples that are observed at fixed time intervals.
Example of 3-split time series cross-validation on a dataset with 6 samples:
```
>>> from sklearn.model_selection import TimeSeriesSplit
>>> X = np.array([[1, 2], [3, 4], [1, 2], [3, 4], [1, 2], [3, 4]])
>>> y = np.array([1, 2, 3, 4, 5, 6])
>>> tscv = TimeSeriesSplit(n_splits=3)
>>> print(tscv)
TimeSeriesSplit(gap=0, max_train_size=None, n_splits=3, test_size=None)
>>> for train, test in tscv.split(X):
... print("%s %s" % (train, test))
[0 1 2] [3]
[0 1 2 3] [4]
[0 1 2 3 4] [5]
```
Here is a visualization of the cross-validation behavior.
3.1.3. A note on shuffling
---------------------------
If the data ordering is not arbitrary (e.g. samples with the same class label are contiguous), shuffling it first may be essential to get a meaningful cross- validation result. However, the opposite may be true if the samples are not independently and identically distributed. For example, if samples correspond to news articles, and are ordered by their time of publication, then shuffling the data will likely lead to a model that is overfit and an inflated validation score: it will be tested on samples that are artificially similar (close in time) to training samples.
Some cross validation iterators, such as [`KFold`](generated/sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold"), have an inbuilt option to shuffle the data indices before splitting them. Note that:
* This consumes less memory than shuffling the data directly.
* By default no shuffling occurs, including for the (stratified) K fold cross- validation performed by specifying `cv=some_integer` to [`cross_val_score`](generated/sklearn.model_selection.cross_val_score#sklearn.model_selection.cross_val_score "sklearn.model_selection.cross_val_score"), grid search, etc. Keep in mind that [`train_test_split`](generated/sklearn.model_selection.train_test_split#sklearn.model_selection.train_test_split "sklearn.model_selection.train_test_split") still returns a random split.
* The `random_state` parameter defaults to `None`, meaning that the shuffling will be different every time `KFold(..., shuffle=True)` is iterated. However, `GridSearchCV` will use the same shuffling for each set of parameters validated by a single call to its `fit` method.
* To get identical results for each split, set `random_state` to an integer.
For more details on how to control the randomness of cv splitters and avoid common pitfalls, see [Controlling randomness](https://scikit-learn.org/1.1/common_pitfalls.html#randomness).
3.1.4. Cross validation and model selection
--------------------------------------------
Cross validation iterators can also be used to directly perform model selection using Grid Search for the optimal hyperparameters of the model. This is the topic of the next section: [Tuning the hyper-parameters of an estimator](grid_search#grid-search).
3.1.5. Permutation test score
------------------------------
[`permutation_test_score`](generated/sklearn.model_selection.permutation_test_score#sklearn.model_selection.permutation_test_score "sklearn.model_selection.permutation_test_score") offers another way to evaluate the performance of classifiers. It provides a permutation-based p-value, which represents how likely an observed performance of the classifier would be obtained by chance. The null hypothesis in this test is that the classifier fails to leverage any statistical dependency between the features and the labels to make correct predictions on left out data. [`permutation_test_score`](generated/sklearn.model_selection.permutation_test_score#sklearn.model_selection.permutation_test_score "sklearn.model_selection.permutation_test_score") generates a null distribution by calculating `n_permutations` different permutations of the data. In each permutation the labels are randomly shuffled, thereby removing any dependency between the features and the labels. The p-value output is the fraction of permutations for which the average cross-validation score obtained by the model is better than the cross-validation score obtained by the model using the original data. For reliable results `n_permutations` should typically be larger than 100 and `cv` between 3-10 folds.
A low p-value provides evidence that the dataset contains real dependency between features and labels and the classifier was able to utilize this to obtain good results. A high p-value could be due to a lack of dependency between features and labels (there is no difference in feature values between the classes) or because the classifier was not able to use the dependency in the data. In the latter case, using a more appropriate classifier that is able to utilize the structure in the data, would result in a lower p-value.
Cross-validation provides information about how well a classifier generalizes, specifically the range of expected errors of the classifier. However, a classifier trained on a high dimensional dataset with no structure may still perform better than expected on cross-validation, just by chance. This can typically happen with small datasets with less than a few hundred samples. [`permutation_test_score`](generated/sklearn.model_selection.permutation_test_score#sklearn.model_selection.permutation_test_score "sklearn.model_selection.permutation_test_score") provides information on whether the classifier has found a real class structure and can help in evaluating the performance of the classifier.
It is important to note that this test has been shown to produce low p-values even if there is only weak structure in the data because in the corresponding permutated datasets there is absolutely no structure. This test is therefore only able to show when the model reliably outperforms random guessing.
Finally, [`permutation_test_score`](generated/sklearn.model_selection.permutation_test_score#sklearn.model_selection.permutation_test_score "sklearn.model_selection.permutation_test_score") is computed using brute force and internally fits `(n_permutations + 1) * n_cv` models. It is therefore only tractable with small datasets for which fitting an individual model is very fast.
| programming_docs |
scikit_learn 6.9. Transforming the prediction target (y) 6.9. Transforming the prediction target (y)
===========================================
These are transformers that are not intended to be used on features, only on supervised learning targets. See also [Transforming target in regression](compose#transformed-target-regressor) if you want to transform the prediction target for learning, but evaluate the model in the original (untransformed) space.
6.9.1. Label binarization
--------------------------
###
6.9.1.1. LabelBinarizer
[`LabelBinarizer`](generated/sklearn.preprocessing.labelbinarizer#sklearn.preprocessing.LabelBinarizer "sklearn.preprocessing.LabelBinarizer") is a utility class to help create a [label indicator matrix](https://scikit-learn.org/1.1/glossary.html#term-label-indicator-matrix) from a list of [multiclass](https://scikit-learn.org/1.1/glossary.html#term-multiclass) labels:
```
>>> from sklearn import preprocessing
>>> lb = preprocessing.LabelBinarizer()
>>> lb.fit([1, 2, 6, 4, 2])
LabelBinarizer()
>>> lb.classes_
array([1, 2, 4, 6])
>>> lb.transform([1, 6])
array([[1, 0, 0, 0],
[0, 0, 0, 1]])
```
Using this format can enable multiclass classification in estimators that support the label indicator matrix format.
Warning
LabelBinarizer is not needed if you are using an estimator that already supports [multiclass](https://scikit-learn.org/1.1/glossary.html#term-multiclass) data.
For more information about multiclass classification, refer to [Multiclass classification](multiclass#multiclass-classification).
###
6.9.1.2. MultiLabelBinarizer
In [multilabel](https://scikit-learn.org/1.1/glossary.html#term-multilabel) learning, the joint set of binary classification tasks is expressed with a label binary indicator array: each sample is one row of a 2d array of shape (n\_samples, n\_classes) with binary values where the one, i.e. the non zero elements, corresponds to the subset of labels for that sample. An array such as `np.array([[1, 0, 0], [0, 1, 1], [0, 0, 0]])` represents label 0 in the first sample, labels 1 and 2 in the second sample, and no labels in the third sample.
Producing multilabel data as a list of sets of labels may be more intuitive. The [`MultiLabelBinarizer`](generated/sklearn.preprocessing.multilabelbinarizer#sklearn.preprocessing.MultiLabelBinarizer "sklearn.preprocessing.MultiLabelBinarizer") transformer can be used to convert between a collection of collections of labels and the indicator format:
```
>>> from sklearn.preprocessing import MultiLabelBinarizer
>>> y = [[2, 3, 4], [2], [0, 1, 3], [0, 1, 2, 3, 4], [0, 1, 2]]
>>> MultiLabelBinarizer().fit_transform(y)
array([[0, 0, 1, 1, 1],
[0, 0, 1, 0, 0],
[1, 1, 0, 1, 0],
[1, 1, 1, 1, 1],
[1, 1, 1, 0, 0]])
```
For more information about multilabel classification, refer to [Multilabel classification](multiclass#multilabel-classification).
6.9.2. Label encoding
----------------------
[`LabelEncoder`](generated/sklearn.preprocessing.labelencoder#sklearn.preprocessing.LabelEncoder "sklearn.preprocessing.LabelEncoder") is a utility class to help normalize labels such that they contain only values between 0 and n\_classes-1. This is sometimes useful for writing efficient Cython routines. [`LabelEncoder`](generated/sklearn.preprocessing.labelencoder#sklearn.preprocessing.LabelEncoder "sklearn.preprocessing.LabelEncoder") can be used as follows:
```
>>> from sklearn import preprocessing
>>> le = preprocessing.LabelEncoder()
>>> le.fit([1, 2, 2, 6])
LabelEncoder()
>>> le.classes_
array([1, 2, 6])
>>> le.transform([1, 1, 2, 6])
array([0, 0, 1, 2])
>>> le.inverse_transform([0, 0, 1, 2])
array([1, 1, 2, 6])
```
It can also be used to transform non-numerical labels (as long as they are hashable and comparable) to numerical labels:
```
>>> le = preprocessing.LabelEncoder()
>>> le.fit(["paris", "paris", "tokyo", "amsterdam"])
LabelEncoder()
>>> list(le.classes_)
['amsterdam', 'paris', 'tokyo']
>>> le.transform(["tokyo", "tokyo", "paris"])
array([2, 2, 1])
>>> list(le.inverse_transform([2, 2, 1]))
['tokyo', 'tokyo', 'paris']
```
scikit_learn API Reference API Reference
=============
This is the class and function reference of scikit-learn. Please refer to the [full user guide](https://scikit-learn.org/1.1/user_guide.html#user-guide) for further details, as the class and function raw specifications may not be enough to give full guidelines on their uses. For reference on concepts repeated across the API, see [Glossary of Common Terms and API Elements](https://scikit-learn.org/1.1/glossary.html#glossary).
sklearn.base: Base classes and utility functions
------------------------------------------------
Base classes for all estimators.
### Base classes
| | |
| --- | --- |
| [`base.BaseEstimator`](generated/sklearn.base.baseestimator#sklearn.base.BaseEstimator "sklearn.base.BaseEstimator") | Base class for all estimators in scikit-learn. |
| [`base.BiclusterMixin`](generated/sklearn.base.biclustermixin#sklearn.base.BiclusterMixin "sklearn.base.BiclusterMixin") | Mixin class for all bicluster estimators in scikit-learn. |
| [`base.ClassifierMixin`](generated/sklearn.base.classifiermixin#sklearn.base.ClassifierMixin "sklearn.base.ClassifierMixin") | Mixin class for all classifiers in scikit-learn. |
| [`base.ClusterMixin`](generated/sklearn.base.clustermixin#sklearn.base.ClusterMixin "sklearn.base.ClusterMixin") | Mixin class for all cluster estimators in scikit-learn. |
| [`base.DensityMixin`](generated/sklearn.base.densitymixin#sklearn.base.DensityMixin "sklearn.base.DensityMixin") | Mixin class for all density estimators in scikit-learn. |
| [`base.RegressorMixin`](generated/sklearn.base.regressormixin#sklearn.base.RegressorMixin "sklearn.base.RegressorMixin") | Mixin class for all regression estimators in scikit-learn. |
| [`base.TransformerMixin`](generated/sklearn.base.transformermixin#sklearn.base.TransformerMixin "sklearn.base.TransformerMixin") | Mixin class for all transformers in scikit-learn. |
| [`feature_selection.SelectorMixin`](generated/sklearn.feature_selection.selectormixin#sklearn.feature_selection.SelectorMixin "sklearn.feature_selection.SelectorMixin") | Transformer mixin that performs feature selection given a support mask |
### Functions
| | |
| --- | --- |
| [`base.clone`](generated/sklearn.base.clone#sklearn.base.clone "sklearn.base.clone")(estimator, \*[, safe]) | Construct a new unfitted estimator with the same parameters. |
| [`base.is_classifier`](generated/sklearn.base.is_classifier#sklearn.base.is_classifier "sklearn.base.is_classifier")(estimator) | Return True if the given estimator is (probably) a classifier. |
| [`base.is_regressor`](generated/sklearn.base.is_regressor#sklearn.base.is_regressor "sklearn.base.is_regressor")(estimator) | Return True if the given estimator is (probably) a regressor. |
| [`config_context`](generated/sklearn.config_context#sklearn.config_context "sklearn.config_context")(\*[, assume\_finite, ...]) | Context manager for global scikit-learn configuration. |
| [`get_config`](generated/sklearn.get_config#sklearn.get_config "sklearn.get_config")() | Retrieve current values for configuration set by [`set_config`](generated/sklearn.set_config#sklearn.set_config "sklearn.set_config"). |
| [`set_config`](generated/sklearn.set_config#sklearn.set_config "sklearn.set_config")([assume\_finite, working\_memory, ...]) | Set global scikit-learn configuration |
| [`show_versions`](generated/sklearn.show_versions#sklearn.show_versions "sklearn.show_versions")() | Print useful debugging information" |
sklearn.calibration: Probability Calibration
--------------------------------------------
Calibration of predicted probabilities.
**User guide:** See the [Probability calibration](calibration#calibration) section for further details.
| | |
| --- | --- |
| [`calibration.CalibratedClassifierCV`](generated/sklearn.calibration.calibratedclassifiercv#sklearn.calibration.CalibratedClassifierCV "sklearn.calibration.CalibratedClassifierCV")([...]) | Probability calibration with isotonic regression or logistic regression. |
| | |
| --- | --- |
| [`calibration.calibration_curve`](generated/sklearn.calibration.calibration_curve#sklearn.calibration.calibration_curve "sklearn.calibration.calibration_curve")(y\_true, y\_prob, \*) | Compute true and predicted probabilities for a calibration curve. |
sklearn.cluster: Clustering
---------------------------
The [`sklearn.cluster`](#module-sklearn.cluster "sklearn.cluster") module gathers popular unsupervised clustering algorithms.
**User guide:** See the [Clustering](clustering#clustering) and [Biclustering](biclustering#biclustering) sections for further details.
### Classes
| | |
| --- | --- |
| [`cluster.AffinityPropagation`](generated/sklearn.cluster.affinitypropagation#sklearn.cluster.AffinityPropagation "sklearn.cluster.AffinityPropagation")(\*[, damping, ...]) | Perform Affinity Propagation Clustering of data. |
| [`cluster.AgglomerativeClustering`](generated/sklearn.cluster.agglomerativeclustering#sklearn.cluster.AgglomerativeClustering "sklearn.cluster.AgglomerativeClustering")([...]) | Agglomerative Clustering. |
| [`cluster.Birch`](generated/sklearn.cluster.birch#sklearn.cluster.Birch "sklearn.cluster.Birch")(\*[, threshold, ...]) | Implements the BIRCH clustering algorithm. |
| [`cluster.DBSCAN`](generated/sklearn.cluster.dbscan#sklearn.cluster.DBSCAN "sklearn.cluster.DBSCAN")([eps, min\_samples, metric, ...]) | Perform DBSCAN clustering from vector array or distance matrix. |
| [`cluster.FeatureAgglomeration`](generated/sklearn.cluster.featureagglomeration#sklearn.cluster.FeatureAgglomeration "sklearn.cluster.FeatureAgglomeration")([n\_clusters, ...]) | Agglomerate features. |
| [`cluster.KMeans`](generated/sklearn.cluster.kmeans#sklearn.cluster.KMeans "sklearn.cluster.KMeans")([n\_clusters, init, n\_init, ...]) | K-Means clustering. |
| [`cluster.BisectingKMeans`](generated/sklearn.cluster.bisectingkmeans#sklearn.cluster.BisectingKMeans "sklearn.cluster.BisectingKMeans")([n\_clusters, init, ...]) | Bisecting K-Means clustering. |
| [`cluster.MiniBatchKMeans`](generated/sklearn.cluster.minibatchkmeans#sklearn.cluster.MiniBatchKMeans "sklearn.cluster.MiniBatchKMeans")([n\_clusters, init, ...]) | Mini-Batch K-Means clustering. |
| [`cluster.MeanShift`](generated/sklearn.cluster.meanshift#sklearn.cluster.MeanShift "sklearn.cluster.MeanShift")(\*[, bandwidth, seeds, ...]) | Mean shift clustering using a flat kernel. |
| [`cluster.OPTICS`](generated/sklearn.cluster.optics#sklearn.cluster.OPTICS "sklearn.cluster.OPTICS")(\*[, min\_samples, max\_eps, ...]) | Estimate clustering structure from vector array. |
| [`cluster.SpectralClustering`](generated/sklearn.cluster.spectralclustering#sklearn.cluster.SpectralClustering "sklearn.cluster.SpectralClustering")([n\_clusters, ...]) | Apply clustering to a projection of the normalized Laplacian. |
| [`cluster.SpectralBiclustering`](generated/sklearn.cluster.spectralbiclustering#sklearn.cluster.SpectralBiclustering "sklearn.cluster.SpectralBiclustering")([n\_clusters, ...]) | Spectral biclustering (Kluger, 2003). |
| [`cluster.SpectralCoclustering`](generated/sklearn.cluster.spectralcoclustering#sklearn.cluster.SpectralCoclustering "sklearn.cluster.SpectralCoclustering")([n\_clusters, ...]) | Spectral Co-Clustering algorithm (Dhillon, 2001). |
### Functions
| | |
| --- | --- |
| [`cluster.affinity_propagation`](generated/sklearn.cluster.affinity_propagation#sklearn.cluster.affinity_propagation "sklearn.cluster.affinity_propagation")(S, \*[, ...]) | Perform Affinity Propagation Clustering of data. |
| [`cluster.cluster_optics_dbscan`](generated/sklearn.cluster.cluster_optics_dbscan#sklearn.cluster.cluster_optics_dbscan "sklearn.cluster.cluster_optics_dbscan")(\*, ...) | Perform DBSCAN extraction for an arbitrary epsilon. |
| [`cluster.cluster_optics_xi`](generated/sklearn.cluster.cluster_optics_xi#sklearn.cluster.cluster_optics_xi "sklearn.cluster.cluster_optics_xi")(\*, reachability, ...) | Automatically extract clusters according to the Xi-steep method. |
| [`cluster.compute_optics_graph`](generated/sklearn.cluster.compute_optics_graph#sklearn.cluster.compute_optics_graph "sklearn.cluster.compute_optics_graph")(X, \*, ...) | Compute the OPTICS reachability graph. |
| [`cluster.dbscan`](generated/dbscan-function#sklearn.cluster.dbscan "sklearn.cluster.dbscan")(X[, eps, min\_samples, ...]) | Perform DBSCAN clustering from vector array or distance matrix. |
| [`cluster.estimate_bandwidth`](generated/sklearn.cluster.estimate_bandwidth#sklearn.cluster.estimate_bandwidth "sklearn.cluster.estimate_bandwidth")(X, \*[, quantile, ...]) | Estimate the bandwidth to use with the mean-shift algorithm. |
| [`cluster.k_means`](generated/sklearn.cluster.k_means#sklearn.cluster.k_means "sklearn.cluster.k_means")(X, n\_clusters, \*[, ...]) | Perform K-means clustering algorithm. |
| [`cluster.kmeans_plusplus`](generated/sklearn.cluster.kmeans_plusplus#sklearn.cluster.kmeans_plusplus "sklearn.cluster.kmeans_plusplus")(X, n\_clusters, \*[, ...]) | Init n\_clusters seeds according to k-means++. |
| [`cluster.mean_shift`](generated/sklearn.cluster.mean_shift#sklearn.cluster.mean_shift "sklearn.cluster.mean_shift")(X, \*[, bandwidth, seeds, ...]) | Perform mean shift clustering of data using a flat kernel. |
| [`cluster.spectral_clustering`](generated/sklearn.cluster.spectral_clustering#sklearn.cluster.spectral_clustering "sklearn.cluster.spectral_clustering")(affinity, \*[, ...]) | Apply clustering to a projection of the normalized Laplacian. |
| [`cluster.ward_tree`](generated/sklearn.cluster.ward_tree#sklearn.cluster.ward_tree "sklearn.cluster.ward_tree")(X, \*[, connectivity, ...]) | Ward clustering based on a Feature matrix. |
sklearn.compose: Composite Estimators
-------------------------------------
Meta-estimators for building composite models with transformers
In addition to its current contents, this module will eventually be home to refurbished versions of Pipeline and FeatureUnion.
**User guide:** See the [Pipelines and composite estimators](compose#combining-estimators) section for further details.
| | |
| --- | --- |
| [`compose.ColumnTransformer`](generated/sklearn.compose.columntransformer#sklearn.compose.ColumnTransformer "sklearn.compose.ColumnTransformer")(transformers, \*[, ...]) | Applies transformers to columns of an array or pandas DataFrame. |
| [`compose.TransformedTargetRegressor`](generated/sklearn.compose.transformedtargetregressor#sklearn.compose.TransformedTargetRegressor "sklearn.compose.TransformedTargetRegressor")([...]) | Meta-estimator to regress on a transformed target. |
| | |
| --- | --- |
| [`compose.make_column_transformer`](generated/sklearn.compose.make_column_transformer#sklearn.compose.make_column_transformer "sklearn.compose.make_column_transformer")(\*transformers) | Construct a ColumnTransformer from the given transformers. |
| [`compose.make_column_selector`](generated/sklearn.compose.make_column_selector#sklearn.compose.make_column_selector "sklearn.compose.make_column_selector")([pattern, ...]) | Create a callable to select columns to be used with `ColumnTransformer`. |
sklearn.covariance: Covariance Estimators
-----------------------------------------
The [`sklearn.covariance`](#module-sklearn.covariance "sklearn.covariance") module includes methods and algorithms to robustly estimate the covariance of features given a set of points. The precision matrix defined as the inverse of the covariance is also estimated. Covariance estimation is closely related to the theory of Gaussian Graphical Models.
**User guide:** See the [Covariance estimation](covariance#covariance) section for further details.
| | |
| --- | --- |
| [`covariance.EmpiricalCovariance`](generated/sklearn.covariance.empiricalcovariance#sklearn.covariance.EmpiricalCovariance "sklearn.covariance.EmpiricalCovariance")(\*[, ...]) | Maximum likelihood covariance estimator. |
| [`covariance.EllipticEnvelope`](generated/sklearn.covariance.ellipticenvelope#sklearn.covariance.EllipticEnvelope "sklearn.covariance.EllipticEnvelope")(\*[, ...]) | An object for detecting outliers in a Gaussian distributed dataset. |
| [`covariance.GraphicalLasso`](generated/sklearn.covariance.graphicallasso#sklearn.covariance.GraphicalLasso "sklearn.covariance.GraphicalLasso")([alpha, mode, ...]) | Sparse inverse covariance estimation with an l1-penalized estimator. |
| [`covariance.GraphicalLassoCV`](generated/sklearn.covariance.graphicallassocv#sklearn.covariance.GraphicalLassoCV "sklearn.covariance.GraphicalLassoCV")(\*[, alphas, ...]) | Sparse inverse covariance w/ cross-validated choice of the l1 penalty. |
| [`covariance.LedoitWolf`](generated/sklearn.covariance.ledoitwolf#sklearn.covariance.LedoitWolf "sklearn.covariance.LedoitWolf")(\*[, store\_precision, ...]) | LedoitWolf Estimator. |
| [`covariance.MinCovDet`](generated/sklearn.covariance.mincovdet#sklearn.covariance.MinCovDet "sklearn.covariance.MinCovDet")(\*[, store\_precision, ...]) | Minimum Covariance Determinant (MCD): robust estimator of covariance. |
| [`covariance.OAS`](generated/sklearn.covariance.oas#sklearn.covariance.OAS "sklearn.covariance.OAS")(\*[, store\_precision, ...]) | Oracle Approximating Shrinkage Estimator. |
| [`covariance.ShrunkCovariance`](generated/sklearn.covariance.shrunkcovariance#sklearn.covariance.ShrunkCovariance "sklearn.covariance.ShrunkCovariance")(\*[, ...]) | Covariance estimator with shrinkage. |
| | |
| --- | --- |
| [`covariance.empirical_covariance`](generated/sklearn.covariance.empirical_covariance#sklearn.covariance.empirical_covariance "sklearn.covariance.empirical_covariance")(X, \*[, ...]) | Compute the Maximum likelihood covariance estimator. |
| [`covariance.graphical_lasso`](generated/sklearn.covariance.graphical_lasso#sklearn.covariance.graphical_lasso "sklearn.covariance.graphical_lasso")(emp\_cov, alpha, \*) | L1-penalized covariance estimator. |
| [`covariance.ledoit_wolf`](generated/sklearn.covariance.ledoit_wolf#sklearn.covariance.ledoit_wolf "sklearn.covariance.ledoit_wolf")(X, \*[, ...]) | Estimate the shrunk Ledoit-Wolf covariance matrix. |
| [`covariance.oas`](generated/oas-function#sklearn.covariance.oas "sklearn.covariance.oas")(X, \*[, assume\_centered]) | Estimate covariance with the Oracle Approximating Shrinkage algorithm. |
| [`covariance.shrunk_covariance`](generated/sklearn.covariance.shrunk_covariance#sklearn.covariance.shrunk_covariance "sklearn.covariance.shrunk_covariance")(emp\_cov[, ...]) | Calculate a covariance matrix shrunk on the diagonal. |
sklearn.cross\_decomposition: Cross decomposition
-------------------------------------------------
**User guide:** See the [Cross decomposition](cross_decomposition#cross-decomposition) section for further details.
| | |
| --- | --- |
| [`cross_decomposition.CCA`](generated/sklearn.cross_decomposition.cca#sklearn.cross_decomposition.CCA "sklearn.cross_decomposition.CCA")([n\_components, ...]) | Canonical Correlation Analysis, also known as "Mode B" PLS. |
| [`cross_decomposition.PLSCanonical`](generated/sklearn.cross_decomposition.plscanonical#sklearn.cross_decomposition.PLSCanonical "sklearn.cross_decomposition.PLSCanonical")([...]) | Partial Least Squares transformer and regressor. |
| [`cross_decomposition.PLSRegression`](generated/sklearn.cross_decomposition.plsregression#sklearn.cross_decomposition.PLSRegression "sklearn.cross_decomposition.PLSRegression")([...]) | PLS regression. |
| [`cross_decomposition.PLSSVD`](generated/sklearn.cross_decomposition.plssvd#sklearn.cross_decomposition.PLSSVD "sklearn.cross_decomposition.PLSSVD")([n\_components, ...]) | Partial Least Square SVD. |
sklearn.datasets: Datasets
--------------------------
The [`sklearn.datasets`](#module-sklearn.datasets "sklearn.datasets") module includes utilities to load datasets, including methods to load and fetch popular reference datasets. It also features some artificial data generators.
**User guide:** See the [Dataset loading utilities](../datasets#datasets) section for further details.
### Loaders
| | |
| --- | --- |
| [`datasets.clear_data_home`](generated/sklearn.datasets.clear_data_home#sklearn.datasets.clear_data_home "sklearn.datasets.clear_data_home")([data\_home]) | Delete all the content of the data home cache. |
| [`datasets.dump_svmlight_file`](generated/sklearn.datasets.dump_svmlight_file#sklearn.datasets.dump_svmlight_file "sklearn.datasets.dump_svmlight_file")(X, y, f, \*[, ...]) | Dump the dataset in svmlight / libsvm file format. |
| [`datasets.fetch_20newsgroups`](generated/sklearn.datasets.fetch_20newsgroups#sklearn.datasets.fetch_20newsgroups "sklearn.datasets.fetch_20newsgroups")(\*[, data\_home, ...]) | Load the filenames and data from the 20 newsgroups dataset (classification). |
| [`datasets.fetch_20newsgroups_vectorized`](generated/sklearn.datasets.fetch_20newsgroups_vectorized#sklearn.datasets.fetch_20newsgroups_vectorized "sklearn.datasets.fetch_20newsgroups_vectorized")(\*[, ...]) | Load and vectorize the 20 newsgroups dataset (classification). |
| [`datasets.fetch_california_housing`](generated/sklearn.datasets.fetch_california_housing#sklearn.datasets.fetch_california_housing "sklearn.datasets.fetch_california_housing")(\*[, ...]) | Load the California housing dataset (regression). |
| [`datasets.fetch_covtype`](generated/sklearn.datasets.fetch_covtype#sklearn.datasets.fetch_covtype "sklearn.datasets.fetch_covtype")(\*[, data\_home, ...]) | Load the covertype dataset (classification). |
| [`datasets.fetch_kddcup99`](generated/sklearn.datasets.fetch_kddcup99#sklearn.datasets.fetch_kddcup99 "sklearn.datasets.fetch_kddcup99")(\*[, subset, ...]) | Load the kddcup99 dataset (classification). |
| [`datasets.fetch_lfw_pairs`](generated/sklearn.datasets.fetch_lfw_pairs#sklearn.datasets.fetch_lfw_pairs "sklearn.datasets.fetch_lfw_pairs")(\*[, subset, ...]) | Load the Labeled Faces in the Wild (LFW) pairs dataset (classification). |
| [`datasets.fetch_lfw_people`](generated/sklearn.datasets.fetch_lfw_people#sklearn.datasets.fetch_lfw_people "sklearn.datasets.fetch_lfw_people")(\*[, data\_home, ...]) | Load the Labeled Faces in the Wild (LFW) people dataset (classification). |
| [`datasets.fetch_olivetti_faces`](generated/sklearn.datasets.fetch_olivetti_faces#sklearn.datasets.fetch_olivetti_faces "sklearn.datasets.fetch_olivetti_faces")(\*[, ...]) | Load the Olivetti faces data-set from AT&T (classification). |
| [`datasets.fetch_openml`](generated/sklearn.datasets.fetch_openml#sklearn.datasets.fetch_openml "sklearn.datasets.fetch_openml")([name, version, ...]) | Fetch dataset from openml by name or dataset id. |
| [`datasets.fetch_rcv1`](generated/sklearn.datasets.fetch_rcv1#sklearn.datasets.fetch_rcv1 "sklearn.datasets.fetch_rcv1")(\*[, data\_home, subset, ...]) | Load the RCV1 multilabel dataset (classification). |
| [`datasets.fetch_species_distributions`](generated/sklearn.datasets.fetch_species_distributions#sklearn.datasets.fetch_species_distributions "sklearn.datasets.fetch_species_distributions")(\*[, ...]) | Loader for species distribution dataset from Phillips et. |
| [`datasets.get_data_home`](generated/sklearn.datasets.get_data_home#sklearn.datasets.get_data_home "sklearn.datasets.get_data_home")([data\_home]) | Return the path of the scikit-learn data directory. |
| [`datasets.load_boston`](generated/sklearn.datasets.load_boston#sklearn.datasets.load_boston "sklearn.datasets.load_boston")(\*[, return\_X\_y]) | DEPRECATED: `load_boston` is deprecated in 1.0 and will be removed in 1.2. |
| [`datasets.load_breast_cancer`](generated/sklearn.datasets.load_breast_cancer#sklearn.datasets.load_breast_cancer "sklearn.datasets.load_breast_cancer")(\*[, return\_X\_y, ...]) | Load and return the breast cancer wisconsin dataset (classification). |
| [`datasets.load_diabetes`](generated/sklearn.datasets.load_diabetes#sklearn.datasets.load_diabetes "sklearn.datasets.load_diabetes")(\*[, return\_X\_y, ...]) | Load and return the diabetes dataset (regression). |
| [`datasets.load_digits`](generated/sklearn.datasets.load_digits#sklearn.datasets.load_digits "sklearn.datasets.load_digits")(\*[, n\_class, ...]) | Load and return the digits dataset (classification). |
| [`datasets.load_files`](generated/sklearn.datasets.load_files#sklearn.datasets.load_files "sklearn.datasets.load_files")(container\_path, \*[, ...]) | Load text files with categories as subfolder names. |
| [`datasets.load_iris`](generated/sklearn.datasets.load_iris#sklearn.datasets.load_iris "sklearn.datasets.load_iris")(\*[, return\_X\_y, as\_frame]) | Load and return the iris dataset (classification). |
| [`datasets.load_linnerud`](generated/sklearn.datasets.load_linnerud#sklearn.datasets.load_linnerud "sklearn.datasets.load_linnerud")(\*[, return\_X\_y, as\_frame]) | Load and return the physical exercise Linnerud dataset. |
| [`datasets.load_sample_image`](generated/sklearn.datasets.load_sample_image#sklearn.datasets.load_sample_image "sklearn.datasets.load_sample_image")(image\_name) | Load the numpy array of a single sample image. |
| [`datasets.load_sample_images`](generated/sklearn.datasets.load_sample_images#sklearn.datasets.load_sample_images "sklearn.datasets.load_sample_images")() | Load sample images for image manipulation. |
| [`datasets.load_svmlight_file`](generated/sklearn.datasets.load_svmlight_file#sklearn.datasets.load_svmlight_file "sklearn.datasets.load_svmlight_file")(f, \*[, ...]) | Load datasets in the svmlight / libsvm format into sparse CSR matrix |
| [`datasets.load_svmlight_files`](generated/sklearn.datasets.load_svmlight_files#sklearn.datasets.load_svmlight_files "sklearn.datasets.load_svmlight_files")(files, \*[, ...]) | Load dataset from multiple files in SVMlight format |
| [`datasets.load_wine`](generated/sklearn.datasets.load_wine#sklearn.datasets.load_wine "sklearn.datasets.load_wine")(\*[, return\_X\_y, as\_frame]) | Load and return the wine dataset (classification). |
### Samples generator
| | |
| --- | --- |
| [`datasets.make_biclusters`](generated/sklearn.datasets.make_biclusters#sklearn.datasets.make_biclusters "sklearn.datasets.make_biclusters")(shape, n\_clusters, \*) | Generate a constant block diagonal structure array for biclustering. |
| [`datasets.make_blobs`](generated/sklearn.datasets.make_blobs#sklearn.datasets.make_blobs "sklearn.datasets.make_blobs")([n\_samples, n\_features, ...]) | Generate isotropic Gaussian blobs for clustering. |
| [`datasets.make_checkerboard`](generated/sklearn.datasets.make_checkerboard#sklearn.datasets.make_checkerboard "sklearn.datasets.make_checkerboard")(shape, n\_clusters, \*) | Generate an array with block checkerboard structure for biclustering. |
| [`datasets.make_circles`](generated/sklearn.datasets.make_circles#sklearn.datasets.make_circles "sklearn.datasets.make_circles")([n\_samples, shuffle, ...]) | Make a large circle containing a smaller circle in 2d. |
| [`datasets.make_classification`](generated/sklearn.datasets.make_classification#sklearn.datasets.make_classification "sklearn.datasets.make_classification")([n\_samples, ...]) | Generate a random n-class classification problem. |
| [`datasets.make_friedman1`](generated/sklearn.datasets.make_friedman1#sklearn.datasets.make_friedman1 "sklearn.datasets.make_friedman1")([n\_samples, ...]) | Generate the "Friedman #1" regression problem. |
| [`datasets.make_friedman2`](generated/sklearn.datasets.make_friedman2#sklearn.datasets.make_friedman2 "sklearn.datasets.make_friedman2")([n\_samples, noise, ...]) | Generate the "Friedman #2" regression problem. |
| [`datasets.make_friedman3`](generated/sklearn.datasets.make_friedman3#sklearn.datasets.make_friedman3 "sklearn.datasets.make_friedman3")([n\_samples, noise, ...]) | Generate the "Friedman #3" regression problem. |
| [`datasets.make_gaussian_quantiles`](generated/sklearn.datasets.make_gaussian_quantiles#sklearn.datasets.make_gaussian_quantiles "sklearn.datasets.make_gaussian_quantiles")(\*[, mean, ...]) | Generate isotropic Gaussian and label samples by quantile. |
| [`datasets.make_hastie_10_2`](generated/sklearn.datasets.make_hastie_10_2#sklearn.datasets.make_hastie_10_2 "sklearn.datasets.make_hastie_10_2")([n\_samples, ...]) | Generate data for binary classification used in Hastie et al. 2009, Example 10.2. |
| [`datasets.make_low_rank_matrix`](generated/sklearn.datasets.make_low_rank_matrix#sklearn.datasets.make_low_rank_matrix "sklearn.datasets.make_low_rank_matrix")([n\_samples, ...]) | Generate a mostly low rank matrix with bell-shaped singular values. |
| [`datasets.make_moons`](generated/sklearn.datasets.make_moons#sklearn.datasets.make_moons "sklearn.datasets.make_moons")([n\_samples, shuffle, ...]) | Make two interleaving half circles. |
| [`datasets.make_multilabel_classification`](generated/sklearn.datasets.make_multilabel_classification#sklearn.datasets.make_multilabel_classification "sklearn.datasets.make_multilabel_classification")([...]) | Generate a random multilabel classification problem. |
| [`datasets.make_regression`](generated/sklearn.datasets.make_regression#sklearn.datasets.make_regression "sklearn.datasets.make_regression")([n\_samples, ...]) | Generate a random regression problem. |
| [`datasets.make_s_curve`](generated/sklearn.datasets.make_s_curve#sklearn.datasets.make_s_curve "sklearn.datasets.make_s_curve")([n\_samples, noise, ...]) | Generate an S curve dataset. |
| [`datasets.make_sparse_coded_signal`](generated/sklearn.datasets.make_sparse_coded_signal#sklearn.datasets.make_sparse_coded_signal "sklearn.datasets.make_sparse_coded_signal")(n\_samples, ...) | Generate a signal as a sparse combination of dictionary elements. |
| [`datasets.make_sparse_spd_matrix`](generated/sklearn.datasets.make_sparse_spd_matrix#sklearn.datasets.make_sparse_spd_matrix "sklearn.datasets.make_sparse_spd_matrix")([dim, ...]) | Generate a sparse symmetric definite positive matrix. |
| [`datasets.make_sparse_uncorrelated`](generated/sklearn.datasets.make_sparse_uncorrelated#sklearn.datasets.make_sparse_uncorrelated "sklearn.datasets.make_sparse_uncorrelated")([...]) | Generate a random regression problem with sparse uncorrelated design. |
| [`datasets.make_spd_matrix`](generated/sklearn.datasets.make_spd_matrix#sklearn.datasets.make_spd_matrix "sklearn.datasets.make_spd_matrix")(n\_dim, \*[, ...]) | Generate a random symmetric, positive-definite matrix. |
| [`datasets.make_swiss_roll`](generated/sklearn.datasets.make_swiss_roll#sklearn.datasets.make_swiss_roll "sklearn.datasets.make_swiss_roll")([n\_samples, noise, ...]) | Generate a swiss roll dataset. |
sklearn.decomposition: Matrix Decomposition
-------------------------------------------
The [`sklearn.decomposition`](#module-sklearn.decomposition "sklearn.decomposition") module includes matrix decomposition algorithms, including among others PCA, NMF or ICA. Most of the algorithms of this module can be regarded as dimensionality reduction techniques.
**User guide:** See the [Decomposing signals in components (matrix factorization problems)](decomposition#decompositions) section for further details.
| | |
| --- | --- |
| [`decomposition.DictionaryLearning`](generated/sklearn.decomposition.dictionarylearning#sklearn.decomposition.DictionaryLearning "sklearn.decomposition.DictionaryLearning")([...]) | Dictionary learning. |
| [`decomposition.FactorAnalysis`](generated/sklearn.decomposition.factoranalysis#sklearn.decomposition.FactorAnalysis "sklearn.decomposition.FactorAnalysis")([n\_components, ...]) | Factor Analysis (FA). |
| [`decomposition.FastICA`](generated/sklearn.decomposition.fastica#sklearn.decomposition.FastICA "sklearn.decomposition.FastICA")([n\_components, ...]) | FastICA: a fast algorithm for Independent Component Analysis. |
| [`decomposition.IncrementalPCA`](generated/sklearn.decomposition.incrementalpca#sklearn.decomposition.IncrementalPCA "sklearn.decomposition.IncrementalPCA")([n\_components, ...]) | Incremental principal components analysis (IPCA). |
| [`decomposition.KernelPCA`](generated/sklearn.decomposition.kernelpca#sklearn.decomposition.KernelPCA "sklearn.decomposition.KernelPCA")([n\_components, ...]) | Kernel Principal component analysis (KPCA) [[R396fc7d924b8-1]](generated/sklearn.decomposition.kernelpca#r396fc7d924b8-1). |
| [`decomposition.LatentDirichletAllocation`](generated/sklearn.decomposition.latentdirichletallocation#sklearn.decomposition.LatentDirichletAllocation "sklearn.decomposition.LatentDirichletAllocation")([...]) | Latent Dirichlet Allocation with online variational Bayes algorithm. |
| [`decomposition.MiniBatchDictionaryLearning`](generated/sklearn.decomposition.minibatchdictionarylearning#sklearn.decomposition.MiniBatchDictionaryLearning "sklearn.decomposition.MiniBatchDictionaryLearning")([...]) | Mini-batch dictionary learning. |
| [`decomposition.MiniBatchSparsePCA`](generated/sklearn.decomposition.minibatchsparsepca#sklearn.decomposition.MiniBatchSparsePCA "sklearn.decomposition.MiniBatchSparsePCA")([...]) | Mini-batch Sparse Principal Components Analysis. |
| [`decomposition.NMF`](generated/sklearn.decomposition.nmf#sklearn.decomposition.NMF "sklearn.decomposition.NMF")([n\_components, init, ...]) | Non-Negative Matrix Factorization (NMF). |
| [`decomposition.MiniBatchNMF`](generated/sklearn.decomposition.minibatchnmf#sklearn.decomposition.MiniBatchNMF "sklearn.decomposition.MiniBatchNMF")([n\_components, ...]) | Mini-Batch Non-Negative Matrix Factorization (NMF). |
| [`decomposition.PCA`](generated/sklearn.decomposition.pca#sklearn.decomposition.PCA "sklearn.decomposition.PCA")([n\_components, copy, ...]) | Principal component analysis (PCA). |
| [`decomposition.SparsePCA`](generated/sklearn.decomposition.sparsepca#sklearn.decomposition.SparsePCA "sklearn.decomposition.SparsePCA")([n\_components, ...]) | Sparse Principal Components Analysis (SparsePCA). |
| [`decomposition.SparseCoder`](generated/sklearn.decomposition.sparsecoder#sklearn.decomposition.SparseCoder "sklearn.decomposition.SparseCoder")(dictionary, \*[, ...]) | Sparse coding. |
| [`decomposition.TruncatedSVD`](generated/sklearn.decomposition.truncatedsvd#sklearn.decomposition.TruncatedSVD "sklearn.decomposition.TruncatedSVD")([n\_components, ...]) | Dimensionality reduction using truncated SVD (aka LSA). |
| | |
| --- | --- |
| [`decomposition.dict_learning`](generated/sklearn.decomposition.dict_learning#sklearn.decomposition.dict_learning "sklearn.decomposition.dict_learning")(X, n\_components, ...) | Solves a dictionary learning matrix factorization problem. |
| [`decomposition.dict_learning_online`](generated/sklearn.decomposition.dict_learning_online#sklearn.decomposition.dict_learning_online "sklearn.decomposition.dict_learning_online")(X[, ...]) | Solves a dictionary learning matrix factorization problem online. |
| [`decomposition.fastica`](generated/fastica-function#sklearn.decomposition.fastica "sklearn.decomposition.fastica")(X[, n\_components, ...]) | Perform Fast Independent Component Analysis. |
| [`decomposition.non_negative_factorization`](generated/sklearn.decomposition.non_negative_factorization#sklearn.decomposition.non_negative_factorization "sklearn.decomposition.non_negative_factorization")(X) | Compute Non-negative Matrix Factorization (NMF). |
| [`decomposition.sparse_encode`](generated/sklearn.decomposition.sparse_encode#sklearn.decomposition.sparse_encode "sklearn.decomposition.sparse_encode")(X, dictionary, \*) | Sparse coding. |
sklearn.discriminant\_analysis: Discriminant Analysis
-----------------------------------------------------
Linear Discriminant Analysis and Quadratic Discriminant Analysis
**User guide:** See the [Linear and Quadratic Discriminant Analysis](lda_qda#lda-qda) section for further details.
| | |
| --- | --- |
| [`discriminant_analysis.LinearDiscriminantAnalysis`](generated/sklearn.discriminant_analysis.lineardiscriminantanalysis#sklearn.discriminant_analysis.LinearDiscriminantAnalysis "sklearn.discriminant_analysis.LinearDiscriminantAnalysis")([...]) | Linear Discriminant Analysis. |
| [`discriminant_analysis.QuadraticDiscriminantAnalysis`](generated/sklearn.discriminant_analysis.quadraticdiscriminantanalysis#sklearn.discriminant_analysis.QuadraticDiscriminantAnalysis "sklearn.discriminant_analysis.QuadraticDiscriminantAnalysis")(\*) | Quadratic Discriminant Analysis. |
sklearn.dummy: Dummy estimators
-------------------------------
**User guide:** See the [Metrics and scoring: quantifying the quality of predictions](model_evaluation#model-evaluation) section for further details.
| | |
| --- | --- |
| [`dummy.DummyClassifier`](generated/sklearn.dummy.dummyclassifier#sklearn.dummy.DummyClassifier "sklearn.dummy.DummyClassifier")(\*[, strategy, ...]) | DummyClassifier makes predictions that ignore the input features. |
| [`dummy.DummyRegressor`](generated/sklearn.dummy.dummyregressor#sklearn.dummy.DummyRegressor "sklearn.dummy.DummyRegressor")(\*[, strategy, ...]) | Regressor that makes predictions using simple rules. |
sklearn.ensemble: Ensemble Methods
----------------------------------
The [`sklearn.ensemble`](#module-sklearn.ensemble "sklearn.ensemble") module includes ensemble-based methods for classification, regression and anomaly detection.
**User guide:** See the [Ensemble methods](ensemble#ensemble) section for further details.
| | |
| --- | --- |
| [`ensemble.AdaBoostClassifier`](generated/sklearn.ensemble.adaboostclassifier#sklearn.ensemble.AdaBoostClassifier "sklearn.ensemble.AdaBoostClassifier")([...]) | An AdaBoost classifier. |
| [`ensemble.AdaBoostRegressor`](generated/sklearn.ensemble.adaboostregressor#sklearn.ensemble.AdaBoostRegressor "sklearn.ensemble.AdaBoostRegressor")([base\_estimator, ...]) | An AdaBoost regressor. |
| [`ensemble.BaggingClassifier`](generated/sklearn.ensemble.baggingclassifier#sklearn.ensemble.BaggingClassifier "sklearn.ensemble.BaggingClassifier")([base\_estimator, ...]) | A Bagging classifier. |
| [`ensemble.BaggingRegressor`](generated/sklearn.ensemble.baggingregressor#sklearn.ensemble.BaggingRegressor "sklearn.ensemble.BaggingRegressor")([base\_estimator, ...]) | A Bagging regressor. |
| [`ensemble.ExtraTreesClassifier`](generated/sklearn.ensemble.extratreesclassifier#sklearn.ensemble.ExtraTreesClassifier "sklearn.ensemble.ExtraTreesClassifier")([...]) | An extra-trees classifier. |
| [`ensemble.ExtraTreesRegressor`](generated/sklearn.ensemble.extratreesregressor#sklearn.ensemble.ExtraTreesRegressor "sklearn.ensemble.ExtraTreesRegressor")([n\_estimators, ...]) | An extra-trees regressor. |
| [`ensemble.GradientBoostingClassifier`](generated/sklearn.ensemble.gradientboostingclassifier#sklearn.ensemble.GradientBoostingClassifier "sklearn.ensemble.GradientBoostingClassifier")(\*[, ...]) | Gradient Boosting for classification. |
| [`ensemble.GradientBoostingRegressor`](generated/sklearn.ensemble.gradientboostingregressor#sklearn.ensemble.GradientBoostingRegressor "sklearn.ensemble.GradientBoostingRegressor")(\*[, ...]) | Gradient Boosting for regression. |
| [`ensemble.IsolationForest`](generated/sklearn.ensemble.isolationforest#sklearn.ensemble.IsolationForest "sklearn.ensemble.IsolationForest")(\*[, n\_estimators, ...]) | Isolation Forest Algorithm. |
| [`ensemble.RandomForestClassifier`](generated/sklearn.ensemble.randomforestclassifier#sklearn.ensemble.RandomForestClassifier "sklearn.ensemble.RandomForestClassifier")([...]) | A random forest classifier. |
| [`ensemble.RandomForestRegressor`](generated/sklearn.ensemble.randomforestregressor#sklearn.ensemble.RandomForestRegressor "sklearn.ensemble.RandomForestRegressor")([...]) | A random forest regressor. |
| [`ensemble.RandomTreesEmbedding`](generated/sklearn.ensemble.randomtreesembedding#sklearn.ensemble.RandomTreesEmbedding "sklearn.ensemble.RandomTreesEmbedding")([...]) | An ensemble of totally random trees. |
| [`ensemble.StackingClassifier`](generated/sklearn.ensemble.stackingclassifier#sklearn.ensemble.StackingClassifier "sklearn.ensemble.StackingClassifier")(estimators[, ...]) | Stack of estimators with a final classifier. |
| [`ensemble.StackingRegressor`](generated/sklearn.ensemble.stackingregressor#sklearn.ensemble.StackingRegressor "sklearn.ensemble.StackingRegressor")(estimators[, ...]) | Stack of estimators with a final regressor. |
| [`ensemble.VotingClassifier`](generated/sklearn.ensemble.votingclassifier#sklearn.ensemble.VotingClassifier "sklearn.ensemble.VotingClassifier")(estimators, \*[, ...]) | Soft Voting/Majority Rule classifier for unfitted estimators. |
| [`ensemble.VotingRegressor`](generated/sklearn.ensemble.votingregressor#sklearn.ensemble.VotingRegressor "sklearn.ensemble.VotingRegressor")(estimators, \*[, ...]) | Prediction voting regressor for unfitted estimators. |
| [`ensemble.HistGradientBoostingRegressor`](generated/sklearn.ensemble.histgradientboostingregressor#sklearn.ensemble.HistGradientBoostingRegressor "sklearn.ensemble.HistGradientBoostingRegressor")([...]) | Histogram-based Gradient Boosting Regression Tree. |
| [`ensemble.HistGradientBoostingClassifier`](generated/sklearn.ensemble.histgradientboostingclassifier#sklearn.ensemble.HistGradientBoostingClassifier "sklearn.ensemble.HistGradientBoostingClassifier")([...]) | Histogram-based Gradient Boosting Classification Tree. |
sklearn.exceptions: Exceptions and warnings
-------------------------------------------
The [`sklearn.exceptions`](#module-sklearn.exceptions "sklearn.exceptions") module includes all custom warnings and error classes used across scikit-learn.
| | |
| --- | --- |
| [`exceptions.ConvergenceWarning`](generated/sklearn.exceptions.convergencewarning#sklearn.exceptions.ConvergenceWarning "sklearn.exceptions.ConvergenceWarning") | Custom warning to capture convergence problems |
| [`exceptions.DataConversionWarning`](generated/sklearn.exceptions.dataconversionwarning#sklearn.exceptions.DataConversionWarning "sklearn.exceptions.DataConversionWarning") | Warning used to notify implicit data conversions happening in the code. |
| [`exceptions.DataDimensionalityWarning`](generated/sklearn.exceptions.datadimensionalitywarning#sklearn.exceptions.DataDimensionalityWarning "sklearn.exceptions.DataDimensionalityWarning") | Custom warning to notify potential issues with data dimensionality. |
| [`exceptions.EfficiencyWarning`](generated/sklearn.exceptions.efficiencywarning#sklearn.exceptions.EfficiencyWarning "sklearn.exceptions.EfficiencyWarning") | Warning used to notify the user of inefficient computation. |
| [`exceptions.FitFailedWarning`](generated/sklearn.exceptions.fitfailedwarning#sklearn.exceptions.FitFailedWarning "sklearn.exceptions.FitFailedWarning") | Warning class used if there is an error while fitting the estimator. |
| [`exceptions.NotFittedError`](generated/sklearn.exceptions.notfittederror#sklearn.exceptions.NotFittedError "sklearn.exceptions.NotFittedError") | Exception class to raise if estimator is used before fitting. |
| [`exceptions.UndefinedMetricWarning`](generated/sklearn.exceptions.undefinedmetricwarning#sklearn.exceptions.UndefinedMetricWarning "sklearn.exceptions.UndefinedMetricWarning") | Warning used when the metric is invalid |
sklearn.experimental: Experimental
----------------------------------
The [`sklearn.experimental`](#module-sklearn.experimental "sklearn.experimental") module provides importable modules that enable the use of experimental features or estimators.
The features and estimators that are experimental aren’t subject to deprecation cycles. Use them at your own risks!
| | |
| --- | --- |
| [`experimental.enable_hist_gradient_boosting`](https://scikit-learn.org/1.1/modules/generated/sklearn.experimental.enable_hist_gradient_boosting.html#module-sklearn.experimental.enable_hist_gradient_boosting "sklearn.experimental.enable_hist_gradient_boosting") | This is now a no-op and can be safely removed from your code. |
| [`experimental.enable_iterative_imputer`](https://scikit-learn.org/1.1/modules/generated/sklearn.experimental.enable_iterative_imputer.html#module-sklearn.experimental.enable_iterative_imputer "sklearn.experimental.enable_iterative_imputer") | Enables IterativeImputer |
| [`experimental.enable_halving_search_cv`](generated/sklearn.experimental.enable_halving_search_cv#module-sklearn.experimental.enable_halving_search_cv "sklearn.experimental.enable_halving_search_cv") | Enables Successive Halving search-estimators |
sklearn.feature\_extraction: Feature Extraction
-----------------------------------------------
The [`sklearn.feature_extraction`](#module-sklearn.feature_extraction "sklearn.feature_extraction") module deals with feature extraction from raw data. It currently includes methods to extract features from text and images.
**User guide:** See the [Feature extraction](feature_extraction#feature-extraction) section for further details.
| | |
| --- | --- |
| [`feature_extraction.DictVectorizer`](generated/sklearn.feature_extraction.dictvectorizer#sklearn.feature_extraction.DictVectorizer "sklearn.feature_extraction.DictVectorizer")(\*[, ...]) | Transforms lists of feature-value mappings to vectors. |
| [`feature_extraction.FeatureHasher`](generated/sklearn.feature_extraction.featurehasher#sklearn.feature_extraction.FeatureHasher "sklearn.feature_extraction.FeatureHasher")([...]) | Implements feature hashing, aka the hashing trick. |
### From images
The [`sklearn.feature_extraction.image`](#module-sklearn.feature_extraction.image "sklearn.feature_extraction.image") submodule gathers utilities to extract features from images.
| | |
| --- | --- |
| [`feature_extraction.image.extract_patches_2d`](generated/sklearn.feature_extraction.image.extract_patches_2d#sklearn.feature_extraction.image.extract_patches_2d "sklearn.feature_extraction.image.extract_patches_2d")(...) | Reshape a 2D image into a collection of patches. |
| [`feature_extraction.image.grid_to_graph`](generated/sklearn.feature_extraction.image.grid_to_graph#sklearn.feature_extraction.image.grid_to_graph "sklearn.feature_extraction.image.grid_to_graph")(n\_x, n\_y) | Graph of the pixel-to-pixel connections. |
| [`feature_extraction.image.img_to_graph`](generated/sklearn.feature_extraction.image.img_to_graph#sklearn.feature_extraction.image.img_to_graph "sklearn.feature_extraction.image.img_to_graph")(img, \*) | Graph of the pixel-to-pixel gradient connections. |
| [`feature_extraction.image.reconstruct_from_patches_2d`](generated/sklearn.feature_extraction.image.reconstruct_from_patches_2d#sklearn.feature_extraction.image.reconstruct_from_patches_2d "sklearn.feature_extraction.image.reconstruct_from_patches_2d")(...) | Reconstruct the image from all of its patches. |
| [`feature_extraction.image.PatchExtractor`](generated/sklearn.feature_extraction.image.patchextractor#sklearn.feature_extraction.image.PatchExtractor "sklearn.feature_extraction.image.PatchExtractor")(\*[, ...]) | Extracts patches from a collection of images. |
### From text
The [`sklearn.feature_extraction.text`](#module-sklearn.feature_extraction.text "sklearn.feature_extraction.text") submodule gathers utilities to build feature vectors from text documents.
| | |
| --- | --- |
| [`feature_extraction.text.CountVectorizer`](generated/sklearn.feature_extraction.text.countvectorizer#sklearn.feature_extraction.text.CountVectorizer "sklearn.feature_extraction.text.CountVectorizer")(\*[, ...]) | Convert a collection of text documents to a matrix of token counts. |
| [`feature_extraction.text.HashingVectorizer`](generated/sklearn.feature_extraction.text.hashingvectorizer#sklearn.feature_extraction.text.HashingVectorizer "sklearn.feature_extraction.text.HashingVectorizer")(\*) | Convert a collection of text documents to a matrix of token occurrences. |
| [`feature_extraction.text.TfidfTransformer`](generated/sklearn.feature_extraction.text.tfidftransformer#sklearn.feature_extraction.text.TfidfTransformer "sklearn.feature_extraction.text.TfidfTransformer")(\*) | Transform a count matrix to a normalized tf or tf-idf representation. |
| [`feature_extraction.text.TfidfVectorizer`](generated/sklearn.feature_extraction.text.tfidfvectorizer#sklearn.feature_extraction.text.TfidfVectorizer "sklearn.feature_extraction.text.TfidfVectorizer")(\*[, ...]) | Convert a collection of raw documents to a matrix of TF-IDF features. |
sklearn.feature\_selection: Feature Selection
---------------------------------------------
The [`sklearn.feature_selection`](#module-sklearn.feature_selection "sklearn.feature_selection") module implements feature selection algorithms. It currently includes univariate filter selection methods and the recursive feature elimination algorithm.
**User guide:** See the [Feature selection](feature_selection#feature-selection) section for further details.
| | |
| --- | --- |
| [`feature_selection.GenericUnivariateSelect`](generated/sklearn.feature_selection.genericunivariateselect#sklearn.feature_selection.GenericUnivariateSelect "sklearn.feature_selection.GenericUnivariateSelect")([...]) | Univariate feature selector with configurable strategy. |
| [`feature_selection.SelectPercentile`](generated/sklearn.feature_selection.selectpercentile#sklearn.feature_selection.SelectPercentile "sklearn.feature_selection.SelectPercentile")([...]) | Select features according to a percentile of the highest scores. |
| [`feature_selection.SelectKBest`](generated/sklearn.feature_selection.selectkbest#sklearn.feature_selection.SelectKBest "sklearn.feature_selection.SelectKBest")([score\_func, k]) | Select features according to the k highest scores. |
| [`feature_selection.SelectFpr`](generated/sklearn.feature_selection.selectfpr#sklearn.feature_selection.SelectFpr "sklearn.feature_selection.SelectFpr")([score\_func, alpha]) | Filter: Select the pvalues below alpha based on a FPR test. |
| [`feature_selection.SelectFdr`](generated/sklearn.feature_selection.selectfdr#sklearn.feature_selection.SelectFdr "sklearn.feature_selection.SelectFdr")([score\_func, alpha]) | Filter: Select the p-values for an estimated false discovery rate. |
| [`feature_selection.SelectFromModel`](generated/sklearn.feature_selection.selectfrommodel#sklearn.feature_selection.SelectFromModel "sklearn.feature_selection.SelectFromModel")(estimator, \*) | Meta-transformer for selecting features based on importance weights. |
| [`feature_selection.SelectFwe`](generated/sklearn.feature_selection.selectfwe#sklearn.feature_selection.SelectFwe "sklearn.feature_selection.SelectFwe")([score\_func, alpha]) | Filter: Select the p-values corresponding to Family-wise error rate. |
| [`feature_selection.SequentialFeatureSelector`](generated/sklearn.feature_selection.sequentialfeatureselector#sklearn.feature_selection.SequentialFeatureSelector "sklearn.feature_selection.SequentialFeatureSelector")(...) | Transformer that performs Sequential Feature Selection. |
| [`feature_selection.RFE`](generated/sklearn.feature_selection.rfe#sklearn.feature_selection.RFE "sklearn.feature_selection.RFE")(estimator, \*[, ...]) | Feature ranking with recursive feature elimination. |
| [`feature_selection.RFECV`](generated/sklearn.feature_selection.rfecv#sklearn.feature_selection.RFECV "sklearn.feature_selection.RFECV")(estimator, \*[, ...]) | Recursive feature elimination with cross-validation to select features. |
| [`feature_selection.VarianceThreshold`](generated/sklearn.feature_selection.variancethreshold#sklearn.feature_selection.VarianceThreshold "sklearn.feature_selection.VarianceThreshold")([threshold]) | Feature selector that removes all low-variance features. |
| | |
| --- | --- |
| [`feature_selection.chi2`](generated/sklearn.feature_selection.chi2#sklearn.feature_selection.chi2 "sklearn.feature_selection.chi2")(X, y) | Compute chi-squared stats between each non-negative feature and class. |
| [`feature_selection.f_classif`](generated/sklearn.feature_selection.f_classif#sklearn.feature_selection.f_classif "sklearn.feature_selection.f_classif")(X, y) | Compute the ANOVA F-value for the provided sample. |
| [`feature_selection.f_regression`](generated/sklearn.feature_selection.f_regression#sklearn.feature_selection.f_regression "sklearn.feature_selection.f_regression")(X, y, \*[, ...]) | Univariate linear regression tests returning F-statistic and p-values. |
| [`feature_selection.r_regression`](generated/sklearn.feature_selection.r_regression#sklearn.feature_selection.r_regression "sklearn.feature_selection.r_regression")(X, y, \*[, ...]) | Compute Pearson's r for each features and the target. |
| [`feature_selection.mutual_info_classif`](generated/sklearn.feature_selection.mutual_info_classif#sklearn.feature_selection.mutual_info_classif "sklearn.feature_selection.mutual_info_classif")(X, y, \*) | Estimate mutual information for a discrete target variable. |
| [`feature_selection.mutual_info_regression`](generated/sklearn.feature_selection.mutual_info_regression#sklearn.feature_selection.mutual_info_regression "sklearn.feature_selection.mutual_info_regression")(X, y, \*) | Estimate mutual information for a continuous target variable. |
sklearn.gaussian\_process: Gaussian Processes
---------------------------------------------
The [`sklearn.gaussian_process`](#module-sklearn.gaussian_process "sklearn.gaussian_process") module implements Gaussian Process based regression and classification.
**User guide:** See the [Gaussian Processes](gaussian_process#gaussian-process) section for further details.
| | |
| --- | --- |
| [`gaussian_process.GaussianProcessClassifier`](generated/sklearn.gaussian_process.gaussianprocessclassifier#sklearn.gaussian_process.GaussianProcessClassifier "sklearn.gaussian_process.GaussianProcessClassifier")([...]) | Gaussian process classification (GPC) based on Laplace approximation. |
| [`gaussian_process.GaussianProcessRegressor`](generated/sklearn.gaussian_process.gaussianprocessregressor#sklearn.gaussian_process.GaussianProcessRegressor "sklearn.gaussian_process.GaussianProcessRegressor")([...]) | Gaussian process regression (GPR). |
Kernels:
| | |
| --- | --- |
| [`gaussian_process.kernels.CompoundKernel`](generated/sklearn.gaussian_process.kernels.compoundkernel#sklearn.gaussian_process.kernels.CompoundKernel "sklearn.gaussian_process.kernels.CompoundKernel")(kernels) | Kernel which is composed of a set of other kernels. |
| [`gaussian_process.kernels.ConstantKernel`](generated/sklearn.gaussian_process.kernels.constantkernel#sklearn.gaussian_process.kernels.ConstantKernel "sklearn.gaussian_process.kernels.ConstantKernel")([...]) | Constant kernel. |
| [`gaussian_process.kernels.DotProduct`](generated/sklearn.gaussian_process.kernels.dotproduct#sklearn.gaussian_process.kernels.DotProduct "sklearn.gaussian_process.kernels.DotProduct")([...]) | Dot-Product kernel. |
| [`gaussian_process.kernels.ExpSineSquared`](generated/sklearn.gaussian_process.kernels.expsinesquared#sklearn.gaussian_process.kernels.ExpSineSquared "sklearn.gaussian_process.kernels.ExpSineSquared")([...]) | Exp-Sine-Squared kernel (aka periodic kernel). |
| [`gaussian_process.kernels.Exponentiation`](generated/sklearn.gaussian_process.kernels.exponentiation#sklearn.gaussian_process.kernels.Exponentiation "sklearn.gaussian_process.kernels.Exponentiation")(...) | The Exponentiation kernel takes one base kernel and a scalar parameter \(p\) and combines them via |
| [`gaussian_process.kernels.Hyperparameter`](generated/sklearn.gaussian_process.kernels.hyperparameter#sklearn.gaussian_process.kernels.Hyperparameter "sklearn.gaussian_process.kernels.Hyperparameter")(...) | A kernel hyperparameter's specification in form of a namedtuple. |
| [`gaussian_process.kernels.Kernel`](generated/sklearn.gaussian_process.kernels.kernel#sklearn.gaussian_process.kernels.Kernel "sklearn.gaussian_process.kernels.Kernel")() | Base class for all kernels. |
| [`gaussian_process.kernels.Matern`](generated/sklearn.gaussian_process.kernels.matern#sklearn.gaussian_process.kernels.Matern "sklearn.gaussian_process.kernels.Matern")([...]) | Matern kernel. |
| [`gaussian_process.kernels.PairwiseKernel`](generated/sklearn.gaussian_process.kernels.pairwisekernel#sklearn.gaussian_process.kernels.PairwiseKernel "sklearn.gaussian_process.kernels.PairwiseKernel")([...]) | Wrapper for kernels in sklearn.metrics.pairwise. |
| [`gaussian_process.kernels.Product`](generated/sklearn.gaussian_process.kernels.product#sklearn.gaussian_process.kernels.Product "sklearn.gaussian_process.kernels.Product")(k1, k2) | The `Product` kernel takes two kernels \(k\_1\) and \(k\_2\) and combines them via |
| [`gaussian_process.kernels.RBF`](generated/sklearn.gaussian_process.kernels.rbf#sklearn.gaussian_process.kernels.RBF "sklearn.gaussian_process.kernels.RBF")([length\_scale, ...]) | Radial basis function kernel (aka squared-exponential kernel). |
| [`gaussian_process.kernels.RationalQuadratic`](generated/sklearn.gaussian_process.kernels.rationalquadratic#sklearn.gaussian_process.kernels.RationalQuadratic "sklearn.gaussian_process.kernels.RationalQuadratic")([...]) | Rational Quadratic kernel. |
| [`gaussian_process.kernels.Sum`](generated/sklearn.gaussian_process.kernels.sum#sklearn.gaussian_process.kernels.Sum "sklearn.gaussian_process.kernels.Sum")(k1, k2) | The `Sum` kernel takes two kernels \(k\_1\) and \(k\_2\) and combines them via |
| [`gaussian_process.kernels.WhiteKernel`](generated/sklearn.gaussian_process.kernels.whitekernel#sklearn.gaussian_process.kernels.WhiteKernel "sklearn.gaussian_process.kernels.WhiteKernel")([...]) | White kernel. |
sklearn.impute: Impute
----------------------
Transformers for missing value imputation
**User guide:** See the [Imputation of missing values](impute#impute) section for further details.
| | |
| --- | --- |
| [`impute.SimpleImputer`](generated/sklearn.impute.simpleimputer#sklearn.impute.SimpleImputer "sklearn.impute.SimpleImputer")(\*[, missing\_values, ...]) | Univariate imputer for completing missing values with simple strategies. |
| [`impute.IterativeImputer`](generated/sklearn.impute.iterativeimputer#sklearn.impute.IterativeImputer "sklearn.impute.IterativeImputer")([estimator, ...]) | Multivariate imputer that estimates each feature from all the others. |
| [`impute.MissingIndicator`](generated/sklearn.impute.missingindicator#sklearn.impute.MissingIndicator "sklearn.impute.MissingIndicator")(\*[, missing\_values, ...]) | Binary indicators for missing values. |
| [`impute.KNNImputer`](generated/sklearn.impute.knnimputer#sklearn.impute.KNNImputer "sklearn.impute.KNNImputer")(\*[, missing\_values, ...]) | Imputation for completing missing values using k-Nearest Neighbors. |
sklearn.inspection: Inspection
------------------------------
The [`sklearn.inspection`](#module-sklearn.inspection "sklearn.inspection") module includes tools for model inspection.
| | |
| --- | --- |
| [`inspection.partial_dependence`](generated/sklearn.inspection.partial_dependence#sklearn.inspection.partial_dependence "sklearn.inspection.partial_dependence")(estimator, X, ...) | Partial dependence of `features`. |
| [`inspection.permutation_importance`](generated/sklearn.inspection.permutation_importance#sklearn.inspection.permutation_importance "sklearn.inspection.permutation_importance")(estimator, ...) | Permutation importance for feature evaluation [[Rd9e56ef97513-BRE]](generated/sklearn.inspection.permutation_importance#rd9e56ef97513-bre). |
### Plotting
| | |
| --- | --- |
| [`inspection.DecisionBoundaryDisplay`](generated/sklearn.inspection.decisionboundarydisplay#sklearn.inspection.DecisionBoundaryDisplay "sklearn.inspection.DecisionBoundaryDisplay")(\*, xx0, ...) | Decisions boundary visualization. |
| [`inspection.PartialDependenceDisplay`](generated/sklearn.inspection.partialdependencedisplay#sklearn.inspection.PartialDependenceDisplay "sklearn.inspection.PartialDependenceDisplay")(...[, ...]) | Partial Dependence Plot (PDP). |
| | |
| --- | --- |
| [`inspection.plot_partial_dependence`](generated/sklearn.inspection.plot_partial_dependence#sklearn.inspection.plot_partial_dependence "sklearn.inspection.plot_partial_dependence")(...[, ...]) | DEPRECATED: Function `plot_partial_dependence` is deprecated in 1.0 and will be removed in 1.2. |
sklearn.isotonic: Isotonic regression
-------------------------------------
**User guide:** See the [Isotonic regression](isotonic#isotonic) section for further details.
| | |
| --- | --- |
| [`isotonic.IsotonicRegression`](generated/sklearn.isotonic.isotonicregression#sklearn.isotonic.IsotonicRegression "sklearn.isotonic.IsotonicRegression")(\*[, y\_min, ...]) | Isotonic regression model. |
| | |
| --- | --- |
| [`isotonic.check_increasing`](generated/sklearn.isotonic.check_increasing#sklearn.isotonic.check_increasing "sklearn.isotonic.check_increasing")(x, y) | Determine whether y is monotonically correlated with x. |
| [`isotonic.isotonic_regression`](generated/sklearn.isotonic.isotonic_regression#sklearn.isotonic.isotonic_regression "sklearn.isotonic.isotonic_regression")(y, \*[, ...]) | Solve the isotonic regression model. |
sklearn.kernel\_approximation: Kernel Approximation
---------------------------------------------------
The [`sklearn.kernel_approximation`](#module-sklearn.kernel_approximation "sklearn.kernel_approximation") module implements several approximate kernel feature maps based on Fourier transforms and Count Sketches.
**User guide:** See the [Kernel Approximation](kernel_approximation#kernel-approximation) section for further details.
| | |
| --- | --- |
| [`kernel_approximation.AdditiveChi2Sampler`](generated/sklearn.kernel_approximation.additivechi2sampler#sklearn.kernel_approximation.AdditiveChi2Sampler "sklearn.kernel_approximation.AdditiveChi2Sampler")(\*) | Approximate feature map for additive chi2 kernel. |
| [`kernel_approximation.Nystroem`](generated/sklearn.kernel_approximation.nystroem#sklearn.kernel_approximation.Nystroem "sklearn.kernel_approximation.Nystroem")([kernel, ...]) | Approximate a kernel map using a subset of the training data. |
| [`kernel_approximation.PolynomialCountSketch`](generated/sklearn.kernel_approximation.polynomialcountsketch#sklearn.kernel_approximation.PolynomialCountSketch "sklearn.kernel_approximation.PolynomialCountSketch")(\*) | Polynomial kernel approximation via Tensor Sketch. |
| [`kernel_approximation.RBFSampler`](generated/sklearn.kernel_approximation.rbfsampler#sklearn.kernel_approximation.RBFSampler "sklearn.kernel_approximation.RBFSampler")(\*[, gamma, ...]) | Approximate a RBF kernel feature map using random Fourier features. |
| [`kernel_approximation.SkewedChi2Sampler`](generated/sklearn.kernel_approximation.skewedchi2sampler#sklearn.kernel_approximation.SkewedChi2Sampler "sklearn.kernel_approximation.SkewedChi2Sampler")(\*[, ...]) | Approximate feature map for "skewed chi-squared" kernel. |
sklearn.kernel\_ridge: Kernel Ridge Regression
----------------------------------------------
Module [`sklearn.kernel_ridge`](#module-sklearn.kernel_ridge "sklearn.kernel_ridge") implements kernel ridge regression.
**User guide:** See the [Kernel ridge regression](kernel_ridge#kernel-ridge) section for further details.
| | |
| --- | --- |
| [`kernel_ridge.KernelRidge`](generated/sklearn.kernel_ridge.kernelridge#sklearn.kernel_ridge.KernelRidge "sklearn.kernel_ridge.KernelRidge")([alpha, kernel, ...]) | Kernel ridge regression. |
sklearn.linear\_model: Linear Models
------------------------------------
The [`sklearn.linear_model`](#module-sklearn.linear_model "sklearn.linear_model") module implements a variety of linear models.
**User guide:** See the [Linear Models](linear_model#linear-model) section for further details.
The following subsections are only rough guidelines: the same estimator can fall into multiple categories, depending on its parameters.
### Linear classifiers
| | |
| --- | --- |
| [`linear_model.LogisticRegression`](generated/sklearn.linear_model.logisticregression#sklearn.linear_model.LogisticRegression "sklearn.linear_model.LogisticRegression")([penalty, ...]) | Logistic Regression (aka logit, MaxEnt) classifier. |
| [`linear_model.LogisticRegressionCV`](generated/sklearn.linear_model.logisticregressioncv#sklearn.linear_model.LogisticRegressionCV "sklearn.linear_model.LogisticRegressionCV")(\*[, Cs, ...]) | Logistic Regression CV (aka logit, MaxEnt) classifier. |
| [`linear_model.PassiveAggressiveClassifier`](generated/sklearn.linear_model.passiveaggressiveclassifier#sklearn.linear_model.PassiveAggressiveClassifier "sklearn.linear_model.PassiveAggressiveClassifier")(\*) | Passive Aggressive Classifier. |
| [`linear_model.Perceptron`](generated/sklearn.linear_model.perceptron#sklearn.linear_model.Perceptron "sklearn.linear_model.Perceptron")(\*[, penalty, alpha, ...]) | Linear perceptron classifier. |
| [`linear_model.RidgeClassifier`](generated/sklearn.linear_model.ridgeclassifier#sklearn.linear_model.RidgeClassifier "sklearn.linear_model.RidgeClassifier")([alpha, ...]) | Classifier using Ridge regression. |
| [`linear_model.RidgeClassifierCV`](generated/sklearn.linear_model.ridgeclassifiercv#sklearn.linear_model.RidgeClassifierCV "sklearn.linear_model.RidgeClassifierCV")([alphas, ...]) | Ridge classifier with built-in cross-validation. |
| [`linear_model.SGDClassifier`](generated/sklearn.linear_model.sgdclassifier#sklearn.linear_model.SGDClassifier "sklearn.linear_model.SGDClassifier")([loss, penalty, ...]) | Linear classifiers (SVM, logistic regression, etc.) with SGD training. |
| [`linear_model.SGDOneClassSVM`](generated/sklearn.linear_model.sgdoneclasssvm#sklearn.linear_model.SGDOneClassSVM "sklearn.linear_model.SGDOneClassSVM")([nu, ...]) | Solves linear One-Class SVM using Stochastic Gradient Descent. |
### Classical linear regressors
| | |
| --- | --- |
| [`linear_model.LinearRegression`](generated/sklearn.linear_model.linearregression#sklearn.linear_model.LinearRegression "sklearn.linear_model.LinearRegression")(\*[, ...]) | Ordinary least squares Linear Regression. |
| [`linear_model.Ridge`](generated/sklearn.linear_model.ridge#sklearn.linear_model.Ridge "sklearn.linear_model.Ridge")([alpha, fit\_intercept, ...]) | Linear least squares with l2 regularization. |
| [`linear_model.RidgeCV`](generated/sklearn.linear_model.ridgecv#sklearn.linear_model.RidgeCV "sklearn.linear_model.RidgeCV")([alphas, ...]) | Ridge regression with built-in cross-validation. |
| [`linear_model.SGDRegressor`](generated/sklearn.linear_model.sgdregressor#sklearn.linear_model.SGDRegressor "sklearn.linear_model.SGDRegressor")([loss, penalty, ...]) | Linear model fitted by minimizing a regularized empirical loss with SGD. |
### Regressors with variable selection
The following estimators have built-in variable selection fitting procedures, but any estimator using a L1 or elastic-net penalty also performs variable selection: typically [`SGDRegressor`](generated/sklearn.linear_model.sgdregressor#sklearn.linear_model.SGDRegressor "sklearn.linear_model.SGDRegressor") or [`SGDClassifier`](generated/sklearn.linear_model.sgdclassifier#sklearn.linear_model.SGDClassifier "sklearn.linear_model.SGDClassifier") with an appropriate penalty.
| | |
| --- | --- |
| [`linear_model.ElasticNet`](generated/sklearn.linear_model.elasticnet#sklearn.linear_model.ElasticNet "sklearn.linear_model.ElasticNet")([alpha, l1\_ratio, ...]) | Linear regression with combined L1 and L2 priors as regularizer. |
| [`linear_model.ElasticNetCV`](generated/sklearn.linear_model.elasticnetcv#sklearn.linear_model.ElasticNetCV "sklearn.linear_model.ElasticNetCV")(\*[, l1\_ratio, ...]) | Elastic Net model with iterative fitting along a regularization path. |
| [`linear_model.Lars`](generated/sklearn.linear_model.lars#sklearn.linear_model.Lars "sklearn.linear_model.Lars")(\*[, fit\_intercept, ...]) | Least Angle Regression model a.k.a. |
| [`linear_model.LarsCV`](generated/sklearn.linear_model.larscv#sklearn.linear_model.LarsCV "sklearn.linear_model.LarsCV")(\*[, fit\_intercept, ...]) | Cross-validated Least Angle Regression model. |
| [`linear_model.Lasso`](generated/sklearn.linear_model.lasso#sklearn.linear_model.Lasso "sklearn.linear_model.Lasso")([alpha, fit\_intercept, ...]) | Linear Model trained with L1 prior as regularizer (aka the Lasso). |
| [`linear_model.LassoCV`](generated/sklearn.linear_model.lassocv#sklearn.linear_model.LassoCV "sklearn.linear_model.LassoCV")(\*[, eps, n\_alphas, ...]) | Lasso linear model with iterative fitting along a regularization path. |
| [`linear_model.LassoLars`](generated/sklearn.linear_model.lassolars#sklearn.linear_model.LassoLars "sklearn.linear_model.LassoLars")([alpha, ...]) | Lasso model fit with Least Angle Regression a.k.a. |
| [`linear_model.LassoLarsCV`](generated/sklearn.linear_model.lassolarscv#sklearn.linear_model.LassoLarsCV "sklearn.linear_model.LassoLarsCV")(\*[, fit\_intercept, ...]) | Cross-validated Lasso, using the LARS algorithm. |
| [`linear_model.LassoLarsIC`](generated/sklearn.linear_model.lassolarsic#sklearn.linear_model.LassoLarsIC "sklearn.linear_model.LassoLarsIC")([criterion, ...]) | Lasso model fit with Lars using BIC or AIC for model selection. |
| [`linear_model.OrthogonalMatchingPursuit`](generated/sklearn.linear_model.orthogonalmatchingpursuit#sklearn.linear_model.OrthogonalMatchingPursuit "sklearn.linear_model.OrthogonalMatchingPursuit")(\*[, ...]) | Orthogonal Matching Pursuit model (OMP). |
| [`linear_model.OrthogonalMatchingPursuitCV`](generated/sklearn.linear_model.orthogonalmatchingpursuitcv#sklearn.linear_model.OrthogonalMatchingPursuitCV "sklearn.linear_model.OrthogonalMatchingPursuitCV")(\*) | Cross-validated Orthogonal Matching Pursuit model (OMP). |
### Bayesian regressors
| | |
| --- | --- |
| [`linear_model.ARDRegression`](generated/sklearn.linear_model.ardregression#sklearn.linear_model.ARDRegression "sklearn.linear_model.ARDRegression")(\*[, n\_iter, tol, ...]) | Bayesian ARD regression. |
| [`linear_model.BayesianRidge`](generated/sklearn.linear_model.bayesianridge#sklearn.linear_model.BayesianRidge "sklearn.linear_model.BayesianRidge")(\*[, n\_iter, tol, ...]) | Bayesian ridge regression. |
### Multi-task linear regressors with variable selection
These estimators fit multiple regression problems (or tasks) jointly, while inducing sparse coefficients. While the inferred coefficients may differ between the tasks, they are constrained to agree on the features that are selected (non-zero coefficients).
| | |
| --- | --- |
| [`linear_model.MultiTaskElasticNet`](generated/sklearn.linear_model.multitaskelasticnet#sklearn.linear_model.MultiTaskElasticNet "sklearn.linear_model.MultiTaskElasticNet")([alpha, ...]) | Multi-task ElasticNet model trained with L1/L2 mixed-norm as regularizer. |
| [`linear_model.MultiTaskElasticNetCV`](generated/sklearn.linear_model.multitaskelasticnetcv#sklearn.linear_model.MultiTaskElasticNetCV "sklearn.linear_model.MultiTaskElasticNetCV")(\*[, ...]) | Multi-task L1/L2 ElasticNet with built-in cross-validation. |
| [`linear_model.MultiTaskLasso`](generated/sklearn.linear_model.multitasklasso#sklearn.linear_model.MultiTaskLasso "sklearn.linear_model.MultiTaskLasso")([alpha, ...]) | Multi-task Lasso model trained with L1/L2 mixed-norm as regularizer. |
| [`linear_model.MultiTaskLassoCV`](generated/sklearn.linear_model.multitasklassocv#sklearn.linear_model.MultiTaskLassoCV "sklearn.linear_model.MultiTaskLassoCV")(\*[, eps, ...]) | Multi-task Lasso model trained with L1/L2 mixed-norm as regularizer. |
### Outlier-robust regressors
Any estimator using the Huber loss would also be robust to outliers, e.g. [`SGDRegressor`](generated/sklearn.linear_model.sgdregressor#sklearn.linear_model.SGDRegressor "sklearn.linear_model.SGDRegressor") with `loss='huber'`.
| | |
| --- | --- |
| [`linear_model.HuberRegressor`](generated/sklearn.linear_model.huberregressor#sklearn.linear_model.HuberRegressor "sklearn.linear_model.HuberRegressor")(\*[, epsilon, ...]) | L2-regularized linear regression model that is robust to outliers. |
| [`linear_model.QuantileRegressor`](generated/sklearn.linear_model.quantileregressor#sklearn.linear_model.QuantileRegressor "sklearn.linear_model.QuantileRegressor")(\*[, ...]) | Linear regression model that predicts conditional quantiles. |
| [`linear_model.RANSACRegressor`](generated/sklearn.linear_model.ransacregressor#sklearn.linear_model.RANSACRegressor "sklearn.linear_model.RANSACRegressor")([estimator, ...]) | RANSAC (RANdom SAmple Consensus) algorithm. |
| [`linear_model.TheilSenRegressor`](generated/sklearn.linear_model.theilsenregressor#sklearn.linear_model.TheilSenRegressor "sklearn.linear_model.TheilSenRegressor")(\*[, ...]) | Theil-Sen Estimator: robust multivariate regression model. |
### Generalized linear models (GLM) for regression
These models allow for response variables to have error distributions other than a normal distribution:
| | |
| --- | --- |
| [`linear_model.PoissonRegressor`](generated/sklearn.linear_model.poissonregressor#sklearn.linear_model.PoissonRegressor "sklearn.linear_model.PoissonRegressor")(\*[, alpha, ...]) | Generalized Linear Model with a Poisson distribution. |
| [`linear_model.TweedieRegressor`](generated/sklearn.linear_model.tweedieregressor#sklearn.linear_model.TweedieRegressor "sklearn.linear_model.TweedieRegressor")(\*[, power, ...]) | Generalized Linear Model with a Tweedie distribution. |
| [`linear_model.GammaRegressor`](generated/sklearn.linear_model.gammaregressor#sklearn.linear_model.GammaRegressor "sklearn.linear_model.GammaRegressor")(\*[, alpha, ...]) | Generalized Linear Model with a Gamma distribution. |
### Miscellaneous
| | |
| --- | --- |
| [`linear_model.PassiveAggressiveRegressor`](generated/sklearn.linear_model.passiveaggressiveregressor#sklearn.linear_model.PassiveAggressiveRegressor "sklearn.linear_model.PassiveAggressiveRegressor")(\*[, ...]) | Passive Aggressive Regressor. |
| [`linear_model.enet_path`](generated/sklearn.linear_model.enet_path#sklearn.linear_model.enet_path "sklearn.linear_model.enet_path")(X, y, \*[, l1\_ratio, ...]) | Compute elastic net path with coordinate descent. |
| [`linear_model.lars_path`](generated/sklearn.linear_model.lars_path#sklearn.linear_model.lars_path "sklearn.linear_model.lars_path")(X, y[, Xy, Gram, ...]) | Compute Least Angle Regression or Lasso path using LARS algorithm [1]. |
| [`linear_model.lars_path_gram`](generated/sklearn.linear_model.lars_path_gram#sklearn.linear_model.lars_path_gram "sklearn.linear_model.lars_path_gram")(Xy, Gram, \*, ...) | lars\_path in the sufficient stats mode [1] |
| [`linear_model.lasso_path`](generated/sklearn.linear_model.lasso_path#sklearn.linear_model.lasso_path "sklearn.linear_model.lasso_path")(X, y, \*[, eps, ...]) | Compute Lasso path with coordinate descent. |
| [`linear_model.orthogonal_mp`](generated/sklearn.linear_model.orthogonal_mp#sklearn.linear_model.orthogonal_mp "sklearn.linear_model.orthogonal_mp")(X, y, \*[, ...]) | Orthogonal Matching Pursuit (OMP). |
| [`linear_model.orthogonal_mp_gram`](generated/sklearn.linear_model.orthogonal_mp_gram#sklearn.linear_model.orthogonal_mp_gram "sklearn.linear_model.orthogonal_mp_gram")(Gram, Xy, \*) | Gram Orthogonal Matching Pursuit (OMP). |
| [`linear_model.ridge_regression`](generated/sklearn.linear_model.ridge_regression#sklearn.linear_model.ridge_regression "sklearn.linear_model.ridge_regression")(X, y, alpha, \*) | Solve the ridge equation by the method of normal equations. |
sklearn.manifold: Manifold Learning
-----------------------------------
The [`sklearn.manifold`](#module-sklearn.manifold "sklearn.manifold") module implements data embedding techniques.
**User guide:** See the [Manifold learning](manifold#manifold) section for further details.
| | |
| --- | --- |
| [`manifold.Isomap`](generated/sklearn.manifold.isomap#sklearn.manifold.Isomap "sklearn.manifold.Isomap")(\*[, n\_neighbors, radius, ...]) | Isomap Embedding. |
| [`manifold.LocallyLinearEmbedding`](generated/sklearn.manifold.locallylinearembedding#sklearn.manifold.LocallyLinearEmbedding "sklearn.manifold.LocallyLinearEmbedding")(\*[, ...]) | Locally Linear Embedding. |
| [`manifold.MDS`](generated/sklearn.manifold.mds#sklearn.manifold.MDS "sklearn.manifold.MDS")([n\_components, metric, n\_init, ...]) | Multidimensional scaling. |
| [`manifold.SpectralEmbedding`](generated/sklearn.manifold.spectralembedding#sklearn.manifold.SpectralEmbedding "sklearn.manifold.SpectralEmbedding")([n\_components, ...]) | Spectral embedding for non-linear dimensionality reduction. |
| [`manifold.TSNE`](generated/sklearn.manifold.tsne#sklearn.manifold.TSNE "sklearn.manifold.TSNE")([n\_components, perplexity, ...]) | T-distributed Stochastic Neighbor Embedding. |
| | |
| --- | --- |
| [`manifold.locally_linear_embedding`](generated/sklearn.manifold.locally_linear_embedding#sklearn.manifold.locally_linear_embedding "sklearn.manifold.locally_linear_embedding")(X, \*, ...) | Perform a Locally Linear Embedding analysis on the data. |
| [`manifold.smacof`](generated/sklearn.manifold.smacof#sklearn.manifold.smacof "sklearn.manifold.smacof")(dissimilarities, \*[, ...]) | Compute multidimensional scaling using the SMACOF algorithm. |
| [`manifold.spectral_embedding`](generated/sklearn.manifold.spectral_embedding#sklearn.manifold.spectral_embedding "sklearn.manifold.spectral_embedding")(adjacency, \*[, ...]) | Project the sample on the first eigenvectors of the graph Laplacian. |
| [`manifold.trustworthiness`](generated/sklearn.manifold.trustworthiness#sklearn.manifold.trustworthiness "sklearn.manifold.trustworthiness")(X, X\_embedded, \*[, ...]) | Expresses to what extent the local structure is retained. |
sklearn.metrics: Metrics
------------------------
See the [Metrics and scoring: quantifying the quality of predictions](model_evaluation#model-evaluation) section and the [Pairwise metrics, Affinities and Kernels](metrics#metrics) section of the user guide for further details.
The [`sklearn.metrics`](#module-sklearn.metrics "sklearn.metrics") module includes score functions, performance metrics and pairwise metrics and distance computations.
### Model Selection Interface
See the [The scoring parameter: defining model evaluation rules](model_evaluation#scoring-parameter) section of the user guide for further details.
| | |
| --- | --- |
| [`metrics.check_scoring`](generated/sklearn.metrics.check_scoring#sklearn.metrics.check_scoring "sklearn.metrics.check_scoring")(estimator[, scoring, ...]) | Determine scorer from user options. |
| [`metrics.get_scorer`](generated/sklearn.metrics.get_scorer#sklearn.metrics.get_scorer "sklearn.metrics.get_scorer")(scoring) | Get a scorer from string. |
| [`metrics.get_scorer_names`](generated/sklearn.metrics.get_scorer_names#sklearn.metrics.get_scorer_names "sklearn.metrics.get_scorer_names")() | Get the names of all available scorers. |
| [`metrics.make_scorer`](generated/sklearn.metrics.make_scorer#sklearn.metrics.make_scorer "sklearn.metrics.make_scorer")(score\_func, \*[, ...]) | Make a scorer from a performance metric or loss function. |
### Classification metrics
See the [Classification metrics](model_evaluation#classification-metrics) section of the user guide for further details.
| | |
| --- | --- |
| [`metrics.accuracy_score`](generated/sklearn.metrics.accuracy_score#sklearn.metrics.accuracy_score "sklearn.metrics.accuracy_score")(y\_true, y\_pred, \*[, ...]) | Accuracy classification score. |
| [`metrics.auc`](generated/sklearn.metrics.auc#sklearn.metrics.auc "sklearn.metrics.auc")(x, y) | Compute Area Under the Curve (AUC) using the trapezoidal rule. |
| [`metrics.average_precision_score`](generated/sklearn.metrics.average_precision_score#sklearn.metrics.average_precision_score "sklearn.metrics.average_precision_score")(y\_true, ...) | Compute average precision (AP) from prediction scores. |
| [`metrics.balanced_accuracy_score`](generated/sklearn.metrics.balanced_accuracy_score#sklearn.metrics.balanced_accuracy_score "sklearn.metrics.balanced_accuracy_score")(y\_true, ...) | Compute the balanced accuracy. |
| [`metrics.brier_score_loss`](generated/sklearn.metrics.brier_score_loss#sklearn.metrics.brier_score_loss "sklearn.metrics.brier_score_loss")(y\_true, y\_prob, \*) | Compute the Brier score loss. |
| [`metrics.classification_report`](generated/sklearn.metrics.classification_report#sklearn.metrics.classification_report "sklearn.metrics.classification_report")(y\_true, y\_pred, \*) | Build a text report showing the main classification metrics. |
| [`metrics.cohen_kappa_score`](generated/sklearn.metrics.cohen_kappa_score#sklearn.metrics.cohen_kappa_score "sklearn.metrics.cohen_kappa_score")(y1, y2, \*[, ...]) | Compute Cohen's kappa: a statistic that measures inter-annotator agreement. |
| [`metrics.confusion_matrix`](generated/sklearn.metrics.confusion_matrix#sklearn.metrics.confusion_matrix "sklearn.metrics.confusion_matrix")(y\_true, y\_pred, \*) | Compute confusion matrix to evaluate the accuracy of a classification. |
| [`metrics.dcg_score`](generated/sklearn.metrics.dcg_score#sklearn.metrics.dcg_score "sklearn.metrics.dcg_score")(y\_true, y\_score, \*[, k, ...]) | Compute Discounted Cumulative Gain. |
| [`metrics.det_curve`](generated/sklearn.metrics.det_curve#sklearn.metrics.det_curve "sklearn.metrics.det_curve")(y\_true, y\_score[, ...]) | Compute error rates for different probability thresholds. |
| [`metrics.f1_score`](generated/sklearn.metrics.f1_score#sklearn.metrics.f1_score "sklearn.metrics.f1_score")(y\_true, y\_pred, \*[, ...]) | Compute the F1 score, also known as balanced F-score or F-measure. |
| [`metrics.fbeta_score`](generated/sklearn.metrics.fbeta_score#sklearn.metrics.fbeta_score "sklearn.metrics.fbeta_score")(y\_true, y\_pred, \*, beta) | Compute the F-beta score. |
| [`metrics.hamming_loss`](generated/sklearn.metrics.hamming_loss#sklearn.metrics.hamming_loss "sklearn.metrics.hamming_loss")(y\_true, y\_pred, \*[, ...]) | Compute the average Hamming loss. |
| [`metrics.hinge_loss`](generated/sklearn.metrics.hinge_loss#sklearn.metrics.hinge_loss "sklearn.metrics.hinge_loss")(y\_true, pred\_decision, \*) | Average hinge loss (non-regularized). |
| [`metrics.jaccard_score`](generated/sklearn.metrics.jaccard_score#sklearn.metrics.jaccard_score "sklearn.metrics.jaccard_score")(y\_true, y\_pred, \*[, ...]) | Jaccard similarity coefficient score. |
| [`metrics.log_loss`](generated/sklearn.metrics.log_loss#sklearn.metrics.log_loss "sklearn.metrics.log_loss")(y\_true, y\_pred, \*[, eps, ...]) | Log loss, aka logistic loss or cross-entropy loss. |
| [`metrics.matthews_corrcoef`](generated/sklearn.metrics.matthews_corrcoef#sklearn.metrics.matthews_corrcoef "sklearn.metrics.matthews_corrcoef")(y\_true, y\_pred, \*) | Compute the Matthews correlation coefficient (MCC). |
| [`metrics.multilabel_confusion_matrix`](generated/sklearn.metrics.multilabel_confusion_matrix#sklearn.metrics.multilabel_confusion_matrix "sklearn.metrics.multilabel_confusion_matrix")(y\_true, ...) | Compute a confusion matrix for each class or sample. |
| [`metrics.ndcg_score`](generated/sklearn.metrics.ndcg_score#sklearn.metrics.ndcg_score "sklearn.metrics.ndcg_score")(y\_true, y\_score, \*[, k, ...]) | Compute Normalized Discounted Cumulative Gain. |
| [`metrics.precision_recall_curve`](generated/sklearn.metrics.precision_recall_curve#sklearn.metrics.precision_recall_curve "sklearn.metrics.precision_recall_curve")(y\_true, ...) | Compute precision-recall pairs for different probability thresholds. |
| [`metrics.precision_recall_fscore_support`](generated/sklearn.metrics.precision_recall_fscore_support#sklearn.metrics.precision_recall_fscore_support "sklearn.metrics.precision_recall_fscore_support")(...) | Compute precision, recall, F-measure and support for each class. |
| [`metrics.precision_score`](generated/sklearn.metrics.precision_score#sklearn.metrics.precision_score "sklearn.metrics.precision_score")(y\_true, y\_pred, \*[, ...]) | Compute the precision. |
| [`metrics.recall_score`](generated/sklearn.metrics.recall_score#sklearn.metrics.recall_score "sklearn.metrics.recall_score")(y\_true, y\_pred, \*[, ...]) | Compute the recall. |
| [`metrics.roc_auc_score`](generated/sklearn.metrics.roc_auc_score#sklearn.metrics.roc_auc_score "sklearn.metrics.roc_auc_score")(y\_true, y\_score, \*[, ...]) | Compute Area Under the Receiver Operating Characteristic Curve (ROC AUC) from prediction scores. |
| [`metrics.roc_curve`](generated/sklearn.metrics.roc_curve#sklearn.metrics.roc_curve "sklearn.metrics.roc_curve")(y\_true, y\_score, \*[, ...]) | Compute Receiver operating characteristic (ROC). |
| [`metrics.top_k_accuracy_score`](generated/sklearn.metrics.top_k_accuracy_score#sklearn.metrics.top_k_accuracy_score "sklearn.metrics.top_k_accuracy_score")(y\_true, y\_score, \*) | Top-k Accuracy classification score. |
| [`metrics.zero_one_loss`](generated/sklearn.metrics.zero_one_loss#sklearn.metrics.zero_one_loss "sklearn.metrics.zero_one_loss")(y\_true, y\_pred, \*[, ...]) | Zero-one classification loss. |
### Regression metrics
See the [Regression metrics](model_evaluation#regression-metrics) section of the user guide for further details.
| | |
| --- | --- |
| [`metrics.explained_variance_score`](generated/sklearn.metrics.explained_variance_score#sklearn.metrics.explained_variance_score "sklearn.metrics.explained_variance_score")(y\_true, ...) | Explained variance regression score function. |
| [`metrics.max_error`](generated/sklearn.metrics.max_error#sklearn.metrics.max_error "sklearn.metrics.max_error")(y\_true, y\_pred) | The max\_error metric calculates the maximum residual error. |
| [`metrics.mean_absolute_error`](generated/sklearn.metrics.mean_absolute_error#sklearn.metrics.mean_absolute_error "sklearn.metrics.mean_absolute_error")(y\_true, y\_pred, \*) | Mean absolute error regression loss. |
| [`metrics.mean_squared_error`](generated/sklearn.metrics.mean_squared_error#sklearn.metrics.mean_squared_error "sklearn.metrics.mean_squared_error")(y\_true, y\_pred, \*) | Mean squared error regression loss. |
| [`metrics.mean_squared_log_error`](generated/sklearn.metrics.mean_squared_log_error#sklearn.metrics.mean_squared_log_error "sklearn.metrics.mean_squared_log_error")(y\_true, y\_pred, \*) | Mean squared logarithmic error regression loss. |
| [`metrics.median_absolute_error`](generated/sklearn.metrics.median_absolute_error#sklearn.metrics.median_absolute_error "sklearn.metrics.median_absolute_error")(y\_true, y\_pred, \*) | Median absolute error regression loss. |
| [`metrics.mean_absolute_percentage_error`](generated/sklearn.metrics.mean_absolute_percentage_error#sklearn.metrics.mean_absolute_percentage_error "sklearn.metrics.mean_absolute_percentage_error")(...) | Mean absolute percentage error (MAPE) regression loss. |
| [`metrics.r2_score`](generated/sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score")(y\_true, y\_pred, \*[, ...]) | \(R^2\) (coefficient of determination) regression score function. |
| [`metrics.mean_poisson_deviance`](generated/sklearn.metrics.mean_poisson_deviance#sklearn.metrics.mean_poisson_deviance "sklearn.metrics.mean_poisson_deviance")(y\_true, y\_pred, \*) | Mean Poisson deviance regression loss. |
| [`metrics.mean_gamma_deviance`](generated/sklearn.metrics.mean_gamma_deviance#sklearn.metrics.mean_gamma_deviance "sklearn.metrics.mean_gamma_deviance")(y\_true, y\_pred, \*) | Mean Gamma deviance regression loss. |
| [`metrics.mean_tweedie_deviance`](generated/sklearn.metrics.mean_tweedie_deviance#sklearn.metrics.mean_tweedie_deviance "sklearn.metrics.mean_tweedie_deviance")(y\_true, y\_pred, \*) | Mean Tweedie deviance regression loss. |
| [`metrics.d2_tweedie_score`](generated/sklearn.metrics.d2_tweedie_score#sklearn.metrics.d2_tweedie_score "sklearn.metrics.d2_tweedie_score")(y\_true, y\_pred, \*) | D^2 regression score function, fraction of Tweedie deviance explained. |
| [`metrics.mean_pinball_loss`](generated/sklearn.metrics.mean_pinball_loss#sklearn.metrics.mean_pinball_loss "sklearn.metrics.mean_pinball_loss")(y\_true, y\_pred, \*) | Pinball loss for quantile regression. |
| [`metrics.d2_pinball_score`](generated/sklearn.metrics.d2_pinball_score#sklearn.metrics.d2_pinball_score "sklearn.metrics.d2_pinball_score")(y\_true, y\_pred, \*) | \(D^2\) regression score function, fraction of pinball loss explained. |
| [`metrics.d2_absolute_error_score`](generated/sklearn.metrics.d2_absolute_error_score#sklearn.metrics.d2_absolute_error_score "sklearn.metrics.d2_absolute_error_score")(y\_true, ...) | \(D^2\) regression score function, fraction of absolute error explained. |
### Multilabel ranking metrics
See the [Multilabel ranking metrics](model_evaluation#multilabel-ranking-metrics) section of the user guide for further details.
| | |
| --- | --- |
| [`metrics.coverage_error`](generated/sklearn.metrics.coverage_error#sklearn.metrics.coverage_error "sklearn.metrics.coverage_error")(y\_true, y\_score, \*[, ...]) | Coverage error measure. |
| [`metrics.label_ranking_average_precision_score`](generated/sklearn.metrics.label_ranking_average_precision_score#sklearn.metrics.label_ranking_average_precision_score "sklearn.metrics.label_ranking_average_precision_score")(...) | Compute ranking-based average precision. |
| [`metrics.label_ranking_loss`](generated/sklearn.metrics.label_ranking_loss#sklearn.metrics.label_ranking_loss "sklearn.metrics.label_ranking_loss")(y\_true, y\_score, \*) | Compute Ranking loss measure. |
### Clustering metrics
See the [Clustering performance evaluation](clustering#clustering-evaluation) section of the user guide for further details.
The [`sklearn.metrics.cluster`](#module-sklearn.metrics.cluster "sklearn.metrics.cluster") submodule contains evaluation metrics for cluster analysis results. There are two forms of evaluation:
* supervised, which uses a ground truth class values for each sample.
* unsupervised, which does not and measures the ‘quality’ of the model itself.
| | |
| --- | --- |
| [`metrics.adjusted_mutual_info_score`](generated/sklearn.metrics.adjusted_mutual_info_score#sklearn.metrics.adjusted_mutual_info_score "sklearn.metrics.adjusted_mutual_info_score")(...[, ...]) | Adjusted Mutual Information between two clusterings. |
| [`metrics.adjusted_rand_score`](generated/sklearn.metrics.adjusted_rand_score#sklearn.metrics.adjusted_rand_score "sklearn.metrics.adjusted_rand_score")(labels\_true, ...) | Rand index adjusted for chance. |
| [`metrics.calinski_harabasz_score`](generated/sklearn.metrics.calinski_harabasz_score#sklearn.metrics.calinski_harabasz_score "sklearn.metrics.calinski_harabasz_score")(X, labels) | Compute the Calinski and Harabasz score. |
| [`metrics.davies_bouldin_score`](generated/sklearn.metrics.davies_bouldin_score#sklearn.metrics.davies_bouldin_score "sklearn.metrics.davies_bouldin_score")(X, labels) | Compute the Davies-Bouldin score. |
| [`metrics.completeness_score`](generated/sklearn.metrics.completeness_score#sklearn.metrics.completeness_score "sklearn.metrics.completeness_score")(labels\_true, ...) | Compute completeness metric of a cluster labeling given a ground truth. |
| [`metrics.cluster.contingency_matrix`](generated/sklearn.metrics.cluster.contingency_matrix#sklearn.metrics.cluster.contingency_matrix "sklearn.metrics.cluster.contingency_matrix")(...[, ...]) | Build a contingency matrix describing the relationship between labels. |
| [`metrics.cluster.pair_confusion_matrix`](generated/sklearn.metrics.cluster.pair_confusion_matrix#sklearn.metrics.cluster.pair_confusion_matrix "sklearn.metrics.cluster.pair_confusion_matrix")(...) | Pair confusion matrix arising from two clusterings [[R9ca8fd06d29a-1]](generated/sklearn.metrics.cluster.pair_confusion_matrix#r9ca8fd06d29a-1). |
| [`metrics.fowlkes_mallows_score`](generated/sklearn.metrics.fowlkes_mallows_score#sklearn.metrics.fowlkes_mallows_score "sklearn.metrics.fowlkes_mallows_score")(labels\_true, ...) | Measure the similarity of two clusterings of a set of points. |
| [`metrics.homogeneity_completeness_v_measure`](generated/sklearn.metrics.homogeneity_completeness_v_measure#sklearn.metrics.homogeneity_completeness_v_measure "sklearn.metrics.homogeneity_completeness_v_measure")(...) | Compute the homogeneity and completeness and V-Measure scores at once. |
| [`metrics.homogeneity_score`](generated/sklearn.metrics.homogeneity_score#sklearn.metrics.homogeneity_score "sklearn.metrics.homogeneity_score")(labels\_true, ...) | Homogeneity metric of a cluster labeling given a ground truth. |
| [`metrics.mutual_info_score`](generated/sklearn.metrics.mutual_info_score#sklearn.metrics.mutual_info_score "sklearn.metrics.mutual_info_score")(labels\_true, ...) | Mutual Information between two clusterings. |
| [`metrics.normalized_mutual_info_score`](generated/sklearn.metrics.normalized_mutual_info_score#sklearn.metrics.normalized_mutual_info_score "sklearn.metrics.normalized_mutual_info_score")(...[, ...]) | Normalized Mutual Information between two clusterings. |
| [`metrics.rand_score`](generated/sklearn.metrics.rand_score#sklearn.metrics.rand_score "sklearn.metrics.rand_score")(labels\_true, labels\_pred) | Rand index. |
| [`metrics.silhouette_score`](generated/sklearn.metrics.silhouette_score#sklearn.metrics.silhouette_score "sklearn.metrics.silhouette_score")(X, labels, \*[, ...]) | Compute the mean Silhouette Coefficient of all samples. |
| [`metrics.silhouette_samples`](generated/sklearn.metrics.silhouette_samples#sklearn.metrics.silhouette_samples "sklearn.metrics.silhouette_samples")(X, labels, \*[, ...]) | Compute the Silhouette Coefficient for each sample. |
| [`metrics.v_measure_score`](generated/sklearn.metrics.v_measure_score#sklearn.metrics.v_measure_score "sklearn.metrics.v_measure_score")(labels\_true, ...[, beta]) | V-measure cluster labeling given a ground truth. |
### Biclustering metrics
See the [Biclustering evaluation](biclustering#biclustering-evaluation) section of the user guide for further details.
| | |
| --- | --- |
| [`metrics.consensus_score`](generated/sklearn.metrics.consensus_score#sklearn.metrics.consensus_score "sklearn.metrics.consensus_score")(a, b, \*[, similarity]) | The similarity of two sets of biclusters. |
### Distance metrics
| | |
| --- | --- |
| [`metrics.DistanceMetric`](generated/sklearn.metrics.distancemetric#sklearn.metrics.DistanceMetric "sklearn.metrics.DistanceMetric") | DistanceMetric class |
### Pairwise metrics
See the [Pairwise metrics, Affinities and Kernels](metrics#metrics) section of the user guide for further details.
| | |
| --- | --- |
| [`metrics.pairwise.additive_chi2_kernel`](generated/sklearn.metrics.pairwise.additive_chi2_kernel#sklearn.metrics.pairwise.additive_chi2_kernel "sklearn.metrics.pairwise.additive_chi2_kernel")(X[, Y]) | Compute the additive chi-squared kernel between observations in X and Y. |
| [`metrics.pairwise.chi2_kernel`](generated/sklearn.metrics.pairwise.chi2_kernel#sklearn.metrics.pairwise.chi2_kernel "sklearn.metrics.pairwise.chi2_kernel")(X[, Y, gamma]) | Compute the exponential chi-squared kernel between X and Y. |
| [`metrics.pairwise.cosine_similarity`](generated/sklearn.metrics.pairwise.cosine_similarity#sklearn.metrics.pairwise.cosine_similarity "sklearn.metrics.pairwise.cosine_similarity")(X[, Y, ...]) | Compute cosine similarity between samples in X and Y. |
| [`metrics.pairwise.cosine_distances`](generated/sklearn.metrics.pairwise.cosine_distances#sklearn.metrics.pairwise.cosine_distances "sklearn.metrics.pairwise.cosine_distances")(X[, Y]) | Compute cosine distance between samples in X and Y. |
| [`metrics.pairwise.distance_metrics`](generated/sklearn.metrics.pairwise.distance_metrics#sklearn.metrics.pairwise.distance_metrics "sklearn.metrics.pairwise.distance_metrics")() | Valid metrics for pairwise\_distances. |
| [`metrics.pairwise.euclidean_distances`](generated/sklearn.metrics.pairwise.euclidean_distances#sklearn.metrics.pairwise.euclidean_distances "sklearn.metrics.pairwise.euclidean_distances")(X[, Y, ...]) | Compute the distance matrix between each pair from a vector array X and Y. |
| [`metrics.pairwise.haversine_distances`](generated/sklearn.metrics.pairwise.haversine_distances#sklearn.metrics.pairwise.haversine_distances "sklearn.metrics.pairwise.haversine_distances")(X[, Y]) | Compute the Haversine distance between samples in X and Y. |
| [`metrics.pairwise.kernel_metrics`](generated/sklearn.metrics.pairwise.kernel_metrics#sklearn.metrics.pairwise.kernel_metrics "sklearn.metrics.pairwise.kernel_metrics")() | Valid metrics for pairwise\_kernels. |
| [`metrics.pairwise.laplacian_kernel`](generated/sklearn.metrics.pairwise.laplacian_kernel#sklearn.metrics.pairwise.laplacian_kernel "sklearn.metrics.pairwise.laplacian_kernel")(X[, Y, gamma]) | Compute the laplacian kernel between X and Y. |
| [`metrics.pairwise.linear_kernel`](generated/sklearn.metrics.pairwise.linear_kernel#sklearn.metrics.pairwise.linear_kernel "sklearn.metrics.pairwise.linear_kernel")(X[, Y, ...]) | Compute the linear kernel between X and Y. |
| [`metrics.pairwise.manhattan_distances`](generated/sklearn.metrics.pairwise.manhattan_distances#sklearn.metrics.pairwise.manhattan_distances "sklearn.metrics.pairwise.manhattan_distances")(X[, Y, ...]) | Compute the L1 distances between the vectors in X and Y. |
| [`metrics.pairwise.nan_euclidean_distances`](generated/sklearn.metrics.pairwise.nan_euclidean_distances#sklearn.metrics.pairwise.nan_euclidean_distances "sklearn.metrics.pairwise.nan_euclidean_distances")(X) | Calculate the euclidean distances in the presence of missing values. |
| [`metrics.pairwise.pairwise_kernels`](generated/sklearn.metrics.pairwise.pairwise_kernels#sklearn.metrics.pairwise.pairwise_kernels "sklearn.metrics.pairwise.pairwise_kernels")(X[, Y, ...]) | Compute the kernel between arrays X and optional array Y. |
| [`metrics.pairwise.polynomial_kernel`](generated/sklearn.metrics.pairwise.polynomial_kernel#sklearn.metrics.pairwise.polynomial_kernel "sklearn.metrics.pairwise.polynomial_kernel")(X[, Y, ...]) | Compute the polynomial kernel between X and Y. |
| [`metrics.pairwise.rbf_kernel`](generated/sklearn.metrics.pairwise.rbf_kernel#sklearn.metrics.pairwise.rbf_kernel "sklearn.metrics.pairwise.rbf_kernel")(X[, Y, gamma]) | Compute the rbf (gaussian) kernel between X and Y. |
| [`metrics.pairwise.sigmoid_kernel`](generated/sklearn.metrics.pairwise.sigmoid_kernel#sklearn.metrics.pairwise.sigmoid_kernel "sklearn.metrics.pairwise.sigmoid_kernel")(X[, Y, ...]) | Compute the sigmoid kernel between X and Y. |
| [`metrics.pairwise.paired_euclidean_distances`](generated/sklearn.metrics.pairwise.paired_euclidean_distances#sklearn.metrics.pairwise.paired_euclidean_distances "sklearn.metrics.pairwise.paired_euclidean_distances")(X, Y) | Compute the paired euclidean distances between X and Y. |
| [`metrics.pairwise.paired_manhattan_distances`](generated/sklearn.metrics.pairwise.paired_manhattan_distances#sklearn.metrics.pairwise.paired_manhattan_distances "sklearn.metrics.pairwise.paired_manhattan_distances")(X, Y) | Compute the paired L1 distances between X and Y. |
| [`metrics.pairwise.paired_cosine_distances`](generated/sklearn.metrics.pairwise.paired_cosine_distances#sklearn.metrics.pairwise.paired_cosine_distances "sklearn.metrics.pairwise.paired_cosine_distances")(X, Y) | Compute the paired cosine distances between X and Y. |
| [`metrics.pairwise.paired_distances`](generated/sklearn.metrics.pairwise.paired_distances#sklearn.metrics.pairwise.paired_distances "sklearn.metrics.pairwise.paired_distances")(X, Y, \*[, ...]) | Compute the paired distances between X and Y. |
| [`metrics.pairwise_distances`](generated/sklearn.metrics.pairwise_distances#sklearn.metrics.pairwise_distances "sklearn.metrics.pairwise_distances")(X[, Y, metric, ...]) | Compute the distance matrix from a vector array X and optional Y. |
| [`metrics.pairwise_distances_argmin`](generated/sklearn.metrics.pairwise_distances_argmin#sklearn.metrics.pairwise_distances_argmin "sklearn.metrics.pairwise_distances_argmin")(X, Y, \*[, ...]) | Compute minimum distances between one point and a set of points. |
| [`metrics.pairwise_distances_argmin_min`](generated/sklearn.metrics.pairwise_distances_argmin_min#sklearn.metrics.pairwise_distances_argmin_min "sklearn.metrics.pairwise_distances_argmin_min")(X, Y, \*) | Compute minimum distances between one point and a set of points. |
| [`metrics.pairwise_distances_chunked`](generated/sklearn.metrics.pairwise_distances_chunked#sklearn.metrics.pairwise_distances_chunked "sklearn.metrics.pairwise_distances_chunked")(X[, Y, ...]) | Generate a distance matrix chunk by chunk with optional reduction. |
### Plotting
See the [Visualizations](https://scikit-learn.org/1.1/visualizations.html#visualizations) section of the user guide for further details.
| | |
| --- | --- |
| [`metrics.plot_confusion_matrix`](generated/sklearn.metrics.plot_confusion_matrix#sklearn.metrics.plot_confusion_matrix "sklearn.metrics.plot_confusion_matrix")(estimator, X, ...) | DEPRECATED: Function `plot_confusion_matrix` is deprecated in 1.0 and will be removed in 1.2. |
| [`metrics.plot_det_curve`](generated/sklearn.metrics.plot_det_curve#sklearn.metrics.plot_det_curve "sklearn.metrics.plot_det_curve")(estimator, X, y, \*[, ...]) | DEPRECATED: Function plot\_det\_curve is deprecated in 1.0 and will be removed in 1.2. |
| [`metrics.plot_precision_recall_curve`](generated/sklearn.metrics.plot_precision_recall_curve#sklearn.metrics.plot_precision_recall_curve "sklearn.metrics.plot_precision_recall_curve")(...[, ...]) | DEPRECATED: Function `plot_precision_recall_curve` is deprecated in 1.0 and will be removed in 1.2. |
| [`metrics.plot_roc_curve`](generated/sklearn.metrics.plot_roc_curve#sklearn.metrics.plot_roc_curve "sklearn.metrics.plot_roc_curve")(estimator, X, y, \*[, ...]) | DEPRECATED: Function `plot_roc_curve` is deprecated in 1.0 and will be removed in 1.2. |
| | |
| --- | --- |
| [`metrics.ConfusionMatrixDisplay`](generated/sklearn.metrics.confusionmatrixdisplay#sklearn.metrics.ConfusionMatrixDisplay "sklearn.metrics.ConfusionMatrixDisplay")(...[, ...]) | Confusion Matrix visualization. |
| [`metrics.DetCurveDisplay`](generated/sklearn.metrics.detcurvedisplay#sklearn.metrics.DetCurveDisplay "sklearn.metrics.DetCurveDisplay")(\*, fpr, fnr[, ...]) | DET curve visualization. |
| [`metrics.PrecisionRecallDisplay`](generated/sklearn.metrics.precisionrecalldisplay#sklearn.metrics.PrecisionRecallDisplay "sklearn.metrics.PrecisionRecallDisplay")(precision, ...) | Precision Recall visualization. |
| [`metrics.RocCurveDisplay`](generated/sklearn.metrics.roccurvedisplay#sklearn.metrics.RocCurveDisplay "sklearn.metrics.RocCurveDisplay")(\*, fpr, tpr[, ...]) | ROC Curve visualization. |
| [`calibration.CalibrationDisplay`](generated/sklearn.calibration.calibrationdisplay#sklearn.calibration.CalibrationDisplay "sklearn.calibration.CalibrationDisplay")(prob\_true, ...) | Calibration curve (also known as reliability diagram) visualization. |
sklearn.mixture: Gaussian Mixture Models
----------------------------------------
The [`sklearn.mixture`](#module-sklearn.mixture "sklearn.mixture") module implements mixture modeling algorithms.
**User guide:** See the [Gaussian mixture models](mixture#mixture) section for further details.
| | |
| --- | --- |
| [`mixture.BayesianGaussianMixture`](generated/sklearn.mixture.bayesiangaussianmixture#sklearn.mixture.BayesianGaussianMixture "sklearn.mixture.BayesianGaussianMixture")(\*[, ...]) | Variational Bayesian estimation of a Gaussian mixture. |
| [`mixture.GaussianMixture`](generated/sklearn.mixture.gaussianmixture#sklearn.mixture.GaussianMixture "sklearn.mixture.GaussianMixture")([n\_components, ...]) | Gaussian Mixture. |
sklearn.model\_selection: Model Selection
-----------------------------------------
**User guide:** See the [Cross-validation: evaluating estimator performance](cross_validation#cross-validation), [Tuning the hyper-parameters of an estimator](grid_search#grid-search) and [Learning curve](learning_curve#learning-curve) sections for further details.
### Splitter Classes
| | |
| --- | --- |
| [`model_selection.GroupKFold`](generated/sklearn.model_selection.groupkfold#sklearn.model_selection.GroupKFold "sklearn.model_selection.GroupKFold")([n\_splits]) | K-fold iterator variant with non-overlapping groups. |
| [`model_selection.GroupShuffleSplit`](generated/sklearn.model_selection.groupshufflesplit#sklearn.model_selection.GroupShuffleSplit "sklearn.model_selection.GroupShuffleSplit")([...]) | Shuffle-Group(s)-Out cross-validation iterator |
| [`model_selection.KFold`](generated/sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold")([n\_splits, shuffle, ...]) | K-Folds cross-validator |
| [`model_selection.LeaveOneGroupOut`](generated/sklearn.model_selection.leaveonegroupout#sklearn.model_selection.LeaveOneGroupOut "sklearn.model_selection.LeaveOneGroupOut")() | Leave One Group Out cross-validator |
| [`model_selection.LeavePGroupsOut`](generated/sklearn.model_selection.leavepgroupsout#sklearn.model_selection.LeavePGroupsOut "sklearn.model_selection.LeavePGroupsOut")(n\_groups) | Leave P Group(s) Out cross-validator |
| [`model_selection.LeaveOneOut`](generated/sklearn.model_selection.leaveoneout#sklearn.model_selection.LeaveOneOut "sklearn.model_selection.LeaveOneOut")() | Leave-One-Out cross-validator |
| [`model_selection.LeavePOut`](generated/sklearn.model_selection.leavepout#sklearn.model_selection.LeavePOut "sklearn.model_selection.LeavePOut")(p) | Leave-P-Out cross-validator |
| [`model_selection.PredefinedSplit`](generated/sklearn.model_selection.predefinedsplit#sklearn.model_selection.PredefinedSplit "sklearn.model_selection.PredefinedSplit")(test\_fold) | Predefined split cross-validator |
| [`model_selection.RepeatedKFold`](generated/sklearn.model_selection.repeatedkfold#sklearn.model_selection.RepeatedKFold "sklearn.model_selection.RepeatedKFold")(\*[, n\_splits, ...]) | Repeated K-Fold cross validator. |
| [`model_selection.RepeatedStratifiedKFold`](generated/sklearn.model_selection.repeatedstratifiedkfold#sklearn.model_selection.RepeatedStratifiedKFold "sklearn.model_selection.RepeatedStratifiedKFold")(\*[, ...]) | Repeated Stratified K-Fold cross validator. |
| [`model_selection.ShuffleSplit`](generated/sklearn.model_selection.shufflesplit#sklearn.model_selection.ShuffleSplit "sklearn.model_selection.ShuffleSplit")([n\_splits, ...]) | Random permutation cross-validator |
| [`model_selection.StratifiedKFold`](generated/sklearn.model_selection.stratifiedkfold#sklearn.model_selection.StratifiedKFold "sklearn.model_selection.StratifiedKFold")([n\_splits, ...]) | Stratified K-Folds cross-validator. |
| [`model_selection.StratifiedShuffleSplit`](generated/sklearn.model_selection.stratifiedshufflesplit#sklearn.model_selection.StratifiedShuffleSplit "sklearn.model_selection.StratifiedShuffleSplit")([...]) | Stratified ShuffleSplit cross-validator |
| [`model_selection.StratifiedGroupKFold`](generated/sklearn.model_selection.stratifiedgroupkfold#sklearn.model_selection.StratifiedGroupKFold "sklearn.model_selection.StratifiedGroupKFold")([...]) | Stratified K-Folds iterator variant with non-overlapping groups. |
| [`model_selection.TimeSeriesSplit`](generated/sklearn.model_selection.timeseriessplit#sklearn.model_selection.TimeSeriesSplit "sklearn.model_selection.TimeSeriesSplit")([n\_splits, ...]) | Time Series cross-validator |
### Splitter Functions
| | |
| --- | --- |
| [`model_selection.check_cv`](generated/sklearn.model_selection.check_cv#sklearn.model_selection.check_cv "sklearn.model_selection.check_cv")([cv, y, classifier]) | Input checker utility for building a cross-validator. |
| [`model_selection.train_test_split`](generated/sklearn.model_selection.train_test_split#sklearn.model_selection.train_test_split "sklearn.model_selection.train_test_split")(\*arrays[, ...]) | Split arrays or matrices into random train and test subsets. |
### Hyper-parameter optimizers
| | |
| --- | --- |
| [`model_selection.GridSearchCV`](generated/sklearn.model_selection.gridsearchcv#sklearn.model_selection.GridSearchCV "sklearn.model_selection.GridSearchCV")(estimator, ...) | Exhaustive search over specified parameter values for an estimator. |
| [`model_selection.HalvingGridSearchCV`](generated/sklearn.model_selection.halvinggridsearchcv#sklearn.model_selection.HalvingGridSearchCV "sklearn.model_selection.HalvingGridSearchCV")(...[, ...]) | Search over specified parameter values with successive halving. |
| [`model_selection.ParameterGrid`](generated/sklearn.model_selection.parametergrid#sklearn.model_selection.ParameterGrid "sklearn.model_selection.ParameterGrid")(param\_grid) | Grid of parameters with a discrete number of values for each. |
| [`model_selection.ParameterSampler`](generated/sklearn.model_selection.parametersampler#sklearn.model_selection.ParameterSampler "sklearn.model_selection.ParameterSampler")(...[, ...]) | Generator on parameters sampled from given distributions. |
| [`model_selection.RandomizedSearchCV`](generated/sklearn.model_selection.randomizedsearchcv#sklearn.model_selection.RandomizedSearchCV "sklearn.model_selection.RandomizedSearchCV")(...[, ...]) | Randomized search on hyper parameters. |
| [`model_selection.HalvingRandomSearchCV`](generated/sklearn.model_selection.halvingrandomsearchcv#sklearn.model_selection.HalvingRandomSearchCV "sklearn.model_selection.HalvingRandomSearchCV")(...[, ...]) | Randomized search on hyper parameters. |
### Model validation
| | |
| --- | --- |
| [`model_selection.cross_validate`](generated/sklearn.model_selection.cross_validate#sklearn.model_selection.cross_validate "sklearn.model_selection.cross_validate")(estimator, X) | Evaluate metric(s) by cross-validation and also record fit/score times. |
| [`model_selection.cross_val_predict`](generated/sklearn.model_selection.cross_val_predict#sklearn.model_selection.cross_val_predict "sklearn.model_selection.cross_val_predict")(estimator, X) | Generate cross-validated estimates for each input data point. |
| [`model_selection.cross_val_score`](generated/sklearn.model_selection.cross_val_score#sklearn.model_selection.cross_val_score "sklearn.model_selection.cross_val_score")(estimator, X) | Evaluate a score by cross-validation. |
| [`model_selection.learning_curve`](generated/sklearn.model_selection.learning_curve#sklearn.model_selection.learning_curve "sklearn.model_selection.learning_curve")(estimator, X, ...) | Learning curve. |
| [`model_selection.permutation_test_score`](generated/sklearn.model_selection.permutation_test_score#sklearn.model_selection.permutation_test_score "sklearn.model_selection.permutation_test_score")(...) | Evaluate the significance of a cross-validated score with permutations. |
| [`model_selection.validation_curve`](generated/sklearn.model_selection.validation_curve#sklearn.model_selection.validation_curve "sklearn.model_selection.validation_curve")(estimator, ...) | Validation curve. |
sklearn.multiclass: Multiclass classification
---------------------------------------------
### Multiclass classification strategies
This module implements multiclass learning algorithms:
* one-vs-the-rest / one-vs-all
* one-vs-one
* error correcting output codes
The estimators provided in this module are meta-estimators: they require a base estimator to be provided in their constructor. For example, it is possible to use these estimators to turn a binary classifier or a regressor into a multiclass classifier. It is also possible to use these estimators with multiclass estimators in the hope that their accuracy or runtime performance improves.
All classifiers in scikit-learn implement multiclass classification; you only need to use this module if you want to experiment with custom multiclass strategies.
The one-vs-the-rest meta-classifier also implements a `predict_proba` method, so long as such a method is implemented by the base classifier. This method returns probabilities of class membership in both the single label and multilabel case. Note that in the multilabel case, probabilities are the marginal probability that a given sample falls in the given class. As such, in the multilabel case the sum of these probabilities over all possible labels for a given sample *will not* sum to unity, as they do in the single label case.
**User guide:** See the [Multiclass classification](multiclass#multiclass-classification) section for further details.
| | |
| --- | --- |
| [`multiclass.OneVsRestClassifier`](generated/sklearn.multiclass.onevsrestclassifier#sklearn.multiclass.OneVsRestClassifier "sklearn.multiclass.OneVsRestClassifier")(estimator, \*) | One-vs-the-rest (OvR) multiclass strategy. |
| [`multiclass.OneVsOneClassifier`](generated/sklearn.multiclass.onevsoneclassifier#sklearn.multiclass.OneVsOneClassifier "sklearn.multiclass.OneVsOneClassifier")(estimator, \*) | One-vs-one multiclass strategy. |
| [`multiclass.OutputCodeClassifier`](generated/sklearn.multiclass.outputcodeclassifier#sklearn.multiclass.OutputCodeClassifier "sklearn.multiclass.OutputCodeClassifier")(estimator, \*) | (Error-Correcting) Output-Code multiclass strategy. |
sklearn.multioutput: Multioutput regression and classification
--------------------------------------------------------------
This module implements multioutput regression and classification.
The estimators provided in this module are meta-estimators: they require a base estimator to be provided in their constructor. The meta-estimator extends single output estimators to multioutput estimators.
**User guide:** See the [Multilabel classification](multiclass#multilabel-classification), [Multiclass-multioutput classification](multiclass#multiclass-multioutput-classification), and [Multioutput regression](multiclass#multioutput-regression) sections for further details.
| | |
| --- | --- |
| [`multioutput.ClassifierChain`](generated/sklearn.multioutput.classifierchain#sklearn.multioutput.ClassifierChain "sklearn.multioutput.ClassifierChain")(base\_estimator, \*) | A multi-label model that arranges binary classifiers into a chain. |
| [`multioutput.MultiOutputRegressor`](generated/sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")(estimator, \*) | Multi target regression. |
| [`multioutput.MultiOutputClassifier`](generated/sklearn.multioutput.multioutputclassifier#sklearn.multioutput.MultiOutputClassifier "sklearn.multioutput.MultiOutputClassifier")(estimator, \*) | Multi target classification. |
| [`multioutput.RegressorChain`](generated/sklearn.multioutput.regressorchain#sklearn.multioutput.RegressorChain "sklearn.multioutput.RegressorChain")(base\_estimator, \*) | A multi-label model that arranges regressions into a chain. |
sklearn.naive\_bayes: Naive Bayes
---------------------------------
The [`sklearn.naive_bayes`](#module-sklearn.naive_bayes "sklearn.naive_bayes") module implements Naive Bayes algorithms. These are supervised learning methods based on applying Bayes’ theorem with strong (naive) feature independence assumptions.
**User guide:** See the [Naive Bayes](naive_bayes#naive-bayes) section for further details.
| | |
| --- | --- |
| [`naive_bayes.BernoulliNB`](generated/sklearn.naive_bayes.bernoullinb#sklearn.naive_bayes.BernoulliNB "sklearn.naive_bayes.BernoulliNB")(\*[, alpha, ...]) | Naive Bayes classifier for multivariate Bernoulli models. |
| [`naive_bayes.CategoricalNB`](generated/sklearn.naive_bayes.categoricalnb#sklearn.naive_bayes.CategoricalNB "sklearn.naive_bayes.CategoricalNB")(\*[, alpha, ...]) | Naive Bayes classifier for categorical features. |
| [`naive_bayes.ComplementNB`](generated/sklearn.naive_bayes.complementnb#sklearn.naive_bayes.ComplementNB "sklearn.naive_bayes.ComplementNB")(\*[, alpha, ...]) | The Complement Naive Bayes classifier described in Rennie et al. (2003). |
| [`naive_bayes.GaussianNB`](generated/sklearn.naive_bayes.gaussiannb#sklearn.naive_bayes.GaussianNB "sklearn.naive_bayes.GaussianNB")(\*[, priors, ...]) | Gaussian Naive Bayes (GaussianNB). |
| [`naive_bayes.MultinomialNB`](generated/sklearn.naive_bayes.multinomialnb#sklearn.naive_bayes.MultinomialNB "sklearn.naive_bayes.MultinomialNB")(\*[, alpha, ...]) | Naive Bayes classifier for multinomial models. |
sklearn.neighbors: Nearest Neighbors
------------------------------------
The [`sklearn.neighbors`](#module-sklearn.neighbors "sklearn.neighbors") module implements the k-nearest neighbors algorithm.
**User guide:** See the [Nearest Neighbors](neighbors#neighbors) section for further details.
| | |
| --- | --- |
| [`neighbors.BallTree`](generated/sklearn.neighbors.balltree#sklearn.neighbors.BallTree "sklearn.neighbors.BallTree")(X[, leaf\_size, metric]) | BallTree for fast generalized N-point problems |
| [`neighbors.KDTree`](generated/sklearn.neighbors.kdtree#sklearn.neighbors.KDTree "sklearn.neighbors.KDTree")(X[, leaf\_size, metric]) | KDTree for fast generalized N-point problems |
| [`neighbors.KernelDensity`](generated/sklearn.neighbors.kerneldensity#sklearn.neighbors.KernelDensity "sklearn.neighbors.KernelDensity")(\*[, bandwidth, ...]) | Kernel Density Estimation. |
| [`neighbors.KNeighborsClassifier`](generated/sklearn.neighbors.kneighborsclassifier#sklearn.neighbors.KNeighborsClassifier "sklearn.neighbors.KNeighborsClassifier")([...]) | Classifier implementing the k-nearest neighbors vote. |
| [`neighbors.KNeighborsRegressor`](generated/sklearn.neighbors.kneighborsregressor#sklearn.neighbors.KNeighborsRegressor "sklearn.neighbors.KNeighborsRegressor")([n\_neighbors, ...]) | Regression based on k-nearest neighbors. |
| [`neighbors.KNeighborsTransformer`](generated/sklearn.neighbors.kneighborstransformer#sklearn.neighbors.KNeighborsTransformer "sklearn.neighbors.KNeighborsTransformer")(\*[, mode, ...]) | Transform X into a (weighted) graph of k nearest neighbors. |
| [`neighbors.LocalOutlierFactor`](generated/sklearn.neighbors.localoutlierfactor#sklearn.neighbors.LocalOutlierFactor "sklearn.neighbors.LocalOutlierFactor")([n\_neighbors, ...]) | Unsupervised Outlier Detection using the Local Outlier Factor (LOF). |
| [`neighbors.RadiusNeighborsClassifier`](generated/sklearn.neighbors.radiusneighborsclassifier#sklearn.neighbors.RadiusNeighborsClassifier "sklearn.neighbors.RadiusNeighborsClassifier")([...]) | Classifier implementing a vote among neighbors within a given radius. |
| [`neighbors.RadiusNeighborsRegressor`](generated/sklearn.neighbors.radiusneighborsregressor#sklearn.neighbors.RadiusNeighborsRegressor "sklearn.neighbors.RadiusNeighborsRegressor")([radius, ...]) | Regression based on neighbors within a fixed radius. |
| [`neighbors.RadiusNeighborsTransformer`](generated/sklearn.neighbors.radiusneighborstransformer#sklearn.neighbors.RadiusNeighborsTransformer "sklearn.neighbors.RadiusNeighborsTransformer")(\*[, ...]) | Transform X into a (weighted) graph of neighbors nearer than a radius. |
| [`neighbors.NearestCentroid`](generated/sklearn.neighbors.nearestcentroid#sklearn.neighbors.NearestCentroid "sklearn.neighbors.NearestCentroid")([metric, ...]) | Nearest centroid classifier. |
| [`neighbors.NearestNeighbors`](generated/sklearn.neighbors.nearestneighbors#sklearn.neighbors.NearestNeighbors "sklearn.neighbors.NearestNeighbors")(\*[, n\_neighbors, ...]) | Unsupervised learner for implementing neighbor searches. |
| [`neighbors.NeighborhoodComponentsAnalysis`](generated/sklearn.neighbors.neighborhoodcomponentsanalysis#sklearn.neighbors.NeighborhoodComponentsAnalysis "sklearn.neighbors.NeighborhoodComponentsAnalysis")([...]) | Neighborhood Components Analysis. |
| | |
| --- | --- |
| [`neighbors.kneighbors_graph`](generated/sklearn.neighbors.kneighbors_graph#sklearn.neighbors.kneighbors_graph "sklearn.neighbors.kneighbors_graph")(X, n\_neighbors, \*) | Compute the (weighted) graph of k-Neighbors for points in X. |
| [`neighbors.radius_neighbors_graph`](generated/sklearn.neighbors.radius_neighbors_graph#sklearn.neighbors.radius_neighbors_graph "sklearn.neighbors.radius_neighbors_graph")(X, radius, \*) | Compute the (weighted) graph of Neighbors for points in X. |
sklearn.neural\_network: Neural network models
----------------------------------------------
The [`sklearn.neural_network`](#module-sklearn.neural_network "sklearn.neural_network") module includes models based on neural networks.
**User guide:** See the [Neural network models (supervised)](neural_networks_supervised#neural-networks-supervised) and [Neural network models (unsupervised)](neural_networks_unsupervised#neural-networks-unsupervised) sections for further details.
| | |
| --- | --- |
| [`neural_network.BernoulliRBM`](generated/sklearn.neural_network.bernoullirbm#sklearn.neural_network.BernoulliRBM "sklearn.neural_network.BernoulliRBM")([n\_components, ...]) | Bernoulli Restricted Boltzmann Machine (RBM). |
| [`neural_network.MLPClassifier`](generated/sklearn.neural_network.mlpclassifier#sklearn.neural_network.MLPClassifier "sklearn.neural_network.MLPClassifier")([...]) | Multi-layer Perceptron classifier. |
| [`neural_network.MLPRegressor`](generated/sklearn.neural_network.mlpregressor#sklearn.neural_network.MLPRegressor "sklearn.neural_network.MLPRegressor")([...]) | Multi-layer Perceptron regressor. |
sklearn.pipeline: Pipeline
--------------------------
The [`sklearn.pipeline`](#module-sklearn.pipeline "sklearn.pipeline") module implements utilities to build a composite estimator, as a chain of transforms and estimators.
**User guide:** See the [Pipelines and composite estimators](compose#combining-estimators) section for further details.
| | |
| --- | --- |
| [`pipeline.FeatureUnion`](generated/sklearn.pipeline.featureunion#sklearn.pipeline.FeatureUnion "sklearn.pipeline.FeatureUnion")(transformer\_list, \*[, ...]) | Concatenates results of multiple transformer objects. |
| [`pipeline.Pipeline`](generated/sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")(steps, \*[, memory, verbose]) | Pipeline of transforms with a final estimator. |
| | |
| --- | --- |
| [`pipeline.make_pipeline`](generated/sklearn.pipeline.make_pipeline#sklearn.pipeline.make_pipeline "sklearn.pipeline.make_pipeline")(\*steps[, memory, verbose]) | Construct a `Pipeline` from the given estimators. |
| [`pipeline.make_union`](generated/sklearn.pipeline.make_union#sklearn.pipeline.make_union "sklearn.pipeline.make_union")(\*transformers[, n\_jobs, ...]) | Construct a FeatureUnion from the given transformers. |
sklearn.preprocessing: Preprocessing and Normalization
------------------------------------------------------
The [`sklearn.preprocessing`](#module-sklearn.preprocessing "sklearn.preprocessing") module includes scaling, centering, normalization, binarization methods.
**User guide:** See the [Preprocessing data](preprocessing#preprocessing) section for further details.
| | |
| --- | --- |
| [`preprocessing.Binarizer`](generated/sklearn.preprocessing.binarizer#sklearn.preprocessing.Binarizer "sklearn.preprocessing.Binarizer")(\*[, threshold, copy]) | Binarize data (set feature values to 0 or 1) according to a threshold. |
| [`preprocessing.FunctionTransformer`](generated/sklearn.preprocessing.functiontransformer#sklearn.preprocessing.FunctionTransformer "sklearn.preprocessing.FunctionTransformer")([func, ...]) | Constructs a transformer from an arbitrary callable. |
| [`preprocessing.KBinsDiscretizer`](generated/sklearn.preprocessing.kbinsdiscretizer#sklearn.preprocessing.KBinsDiscretizer "sklearn.preprocessing.KBinsDiscretizer")([n\_bins, ...]) | Bin continuous data into intervals. |
| [`preprocessing.KernelCenterer`](generated/sklearn.preprocessing.kernelcenterer#sklearn.preprocessing.KernelCenterer "sklearn.preprocessing.KernelCenterer")() | Center an arbitrary kernel matrix \(K\). |
| [`preprocessing.LabelBinarizer`](generated/sklearn.preprocessing.labelbinarizer#sklearn.preprocessing.LabelBinarizer "sklearn.preprocessing.LabelBinarizer")(\*[, neg\_label, ...]) | Binarize labels in a one-vs-all fashion. |
| [`preprocessing.LabelEncoder`](generated/sklearn.preprocessing.labelencoder#sklearn.preprocessing.LabelEncoder "sklearn.preprocessing.LabelEncoder")() | Encode target labels with value between 0 and n\_classes-1. |
| [`preprocessing.MultiLabelBinarizer`](generated/sklearn.preprocessing.multilabelbinarizer#sklearn.preprocessing.MultiLabelBinarizer "sklearn.preprocessing.MultiLabelBinarizer")(\*[, ...]) | Transform between iterable of iterables and a multilabel format. |
| [`preprocessing.MaxAbsScaler`](generated/sklearn.preprocessing.maxabsscaler#sklearn.preprocessing.MaxAbsScaler "sklearn.preprocessing.MaxAbsScaler")(\*[, copy]) | Scale each feature by its maximum absolute value. |
| [`preprocessing.MinMaxScaler`](generated/sklearn.preprocessing.minmaxscaler#sklearn.preprocessing.MinMaxScaler "sklearn.preprocessing.MinMaxScaler")([feature\_range, ...]) | Transform features by scaling each feature to a given range. |
| [`preprocessing.Normalizer`](generated/sklearn.preprocessing.normalizer#sklearn.preprocessing.Normalizer "sklearn.preprocessing.Normalizer")([norm, copy]) | Normalize samples individually to unit norm. |
| [`preprocessing.OneHotEncoder`](generated/sklearn.preprocessing.onehotencoder#sklearn.preprocessing.OneHotEncoder "sklearn.preprocessing.OneHotEncoder")(\*[, categories, ...]) | Encode categorical features as a one-hot numeric array. |
| [`preprocessing.OrdinalEncoder`](generated/sklearn.preprocessing.ordinalencoder#sklearn.preprocessing.OrdinalEncoder "sklearn.preprocessing.OrdinalEncoder")(\*[, ...]) | Encode categorical features as an integer array. |
| [`preprocessing.PolynomialFeatures`](generated/sklearn.preprocessing.polynomialfeatures#sklearn.preprocessing.PolynomialFeatures "sklearn.preprocessing.PolynomialFeatures")([degree, ...]) | Generate polynomial and interaction features. |
| [`preprocessing.PowerTransformer`](generated/sklearn.preprocessing.powertransformer#sklearn.preprocessing.PowerTransformer "sklearn.preprocessing.PowerTransformer")([method, ...]) | Apply a power transform featurewise to make data more Gaussian-like. |
| [`preprocessing.QuantileTransformer`](generated/sklearn.preprocessing.quantiletransformer#sklearn.preprocessing.QuantileTransformer "sklearn.preprocessing.QuantileTransformer")(\*[, ...]) | Transform features using quantiles information. |
| [`preprocessing.RobustScaler`](generated/sklearn.preprocessing.robustscaler#sklearn.preprocessing.RobustScaler "sklearn.preprocessing.RobustScaler")(\*[, ...]) | Scale features using statistics that are robust to outliers. |
| [`preprocessing.SplineTransformer`](generated/sklearn.preprocessing.splinetransformer#sklearn.preprocessing.SplineTransformer "sklearn.preprocessing.SplineTransformer")([n\_knots, ...]) | Generate univariate B-spline bases for features. |
| [`preprocessing.StandardScaler`](generated/sklearn.preprocessing.standardscaler#sklearn.preprocessing.StandardScaler "sklearn.preprocessing.StandardScaler")(\*[, copy, ...]) | Standardize features by removing the mean and scaling to unit variance. |
| | |
| --- | --- |
| [`preprocessing.add_dummy_feature`](generated/sklearn.preprocessing.add_dummy_feature#sklearn.preprocessing.add_dummy_feature "sklearn.preprocessing.add_dummy_feature")(X[, value]) | Augment dataset with an additional dummy feature. |
| [`preprocessing.binarize`](generated/sklearn.preprocessing.binarize#sklearn.preprocessing.binarize "sklearn.preprocessing.binarize")(X, \*[, threshold, copy]) | Boolean thresholding of array-like or scipy.sparse matrix. |
| [`preprocessing.label_binarize`](generated/sklearn.preprocessing.label_binarize#sklearn.preprocessing.label_binarize "sklearn.preprocessing.label_binarize")(y, \*, classes) | Binarize labels in a one-vs-all fashion. |
| [`preprocessing.maxabs_scale`](generated/sklearn.preprocessing.maxabs_scale#sklearn.preprocessing.maxabs_scale "sklearn.preprocessing.maxabs_scale")(X, \*[, axis, copy]) | Scale each feature to the [-1, 1] range without breaking the sparsity. |
| [`preprocessing.minmax_scale`](generated/sklearn.preprocessing.minmax_scale#sklearn.preprocessing.minmax_scale "sklearn.preprocessing.minmax_scale")(X[, ...]) | Transform features by scaling each feature to a given range. |
| [`preprocessing.normalize`](generated/sklearn.preprocessing.normalize#sklearn.preprocessing.normalize "sklearn.preprocessing.normalize")(X[, norm, axis, ...]) | Scale input vectors individually to unit norm (vector length). |
| [`preprocessing.quantile_transform`](generated/sklearn.preprocessing.quantile_transform#sklearn.preprocessing.quantile_transform "sklearn.preprocessing.quantile_transform")(X, \*[, ...]) | Transform features using quantiles information. |
| [`preprocessing.robust_scale`](generated/sklearn.preprocessing.robust_scale#sklearn.preprocessing.robust_scale "sklearn.preprocessing.robust_scale")(X, \*[, axis, ...]) | Standardize a dataset along any axis. |
| [`preprocessing.scale`](generated/sklearn.preprocessing.scale#sklearn.preprocessing.scale "sklearn.preprocessing.scale")(X, \*[, axis, with\_mean, ...]) | Standardize a dataset along any axis. |
| [`preprocessing.power_transform`](generated/sklearn.preprocessing.power_transform#sklearn.preprocessing.power_transform "sklearn.preprocessing.power_transform")(X[, method, ...]) | Parametric, monotonic transformation to make data more Gaussian-like. |
sklearn.random\_projection: Random projection
---------------------------------------------
Random Projection transformers.
Random Projections are a simple and computationally efficient way to reduce the dimensionality of the data by trading a controlled amount of accuracy (as additional variance) for faster processing times and smaller model sizes.
The dimensions and distribution of Random Projections matrices are controlled so as to preserve the pairwise distances between any two samples of the dataset.
The main theoretical result behind the efficiency of random projection is the [Johnson-Lindenstrauss lemma (quoting Wikipedia)](https://en.wikipedia.org/wiki/Johnson%E2%80%93Lindenstrauss_lemma):
In mathematics, the Johnson-Lindenstrauss lemma is a result concerning low-distortion embeddings of points from high-dimensional into low-dimensional Euclidean space. The lemma states that a small set of points in a high-dimensional space can be embedded into a space of much lower dimension in such a way that distances between the points are nearly preserved. The map used for the embedding is at least Lipschitz, and can even be taken to be an orthogonal projection.
**User guide:** See the [Random Projection](random_projection#random-projection) section for further details.
| | |
| --- | --- |
| [`random_projection.GaussianRandomProjection`](generated/sklearn.random_projection.gaussianrandomprojection#sklearn.random_projection.GaussianRandomProjection "sklearn.random_projection.GaussianRandomProjection")([...]) | Reduce dimensionality through Gaussian random projection. |
| [`random_projection.SparseRandomProjection`](generated/sklearn.random_projection.sparserandomprojection#sklearn.random_projection.SparseRandomProjection "sklearn.random_projection.SparseRandomProjection")([...]) | Reduce dimensionality through sparse random projection. |
| | |
| --- | --- |
| [`random_projection.johnson_lindenstrauss_min_dim`](generated/sklearn.random_projection.johnson_lindenstrauss_min_dim#sklearn.random_projection.johnson_lindenstrauss_min_dim "sklearn.random_projection.johnson_lindenstrauss_min_dim")(...) | Find a 'safe' number of components to randomly project to. |
sklearn.semi\_supervised: Semi-Supervised Learning
--------------------------------------------------
The [`sklearn.semi_supervised`](#module-sklearn.semi_supervised "sklearn.semi_supervised") module implements semi-supervised learning algorithms. These algorithms utilize small amounts of labeled data and large amounts of unlabeled data for classification tasks. This module includes Label Propagation.
**User guide:** See the [Semi-supervised learning](semi_supervised#semi-supervised) section for further details.
| | |
| --- | --- |
| [`semi_supervised.LabelPropagation`](generated/sklearn.semi_supervised.labelpropagation#sklearn.semi_supervised.LabelPropagation "sklearn.semi_supervised.LabelPropagation")([kernel, ...]) | Label Propagation classifier. |
| [`semi_supervised.LabelSpreading`](generated/sklearn.semi_supervised.labelspreading#sklearn.semi_supervised.LabelSpreading "sklearn.semi_supervised.LabelSpreading")([kernel, ...]) | LabelSpreading model for semi-supervised learning. |
| [`semi_supervised.SelfTrainingClassifier`](generated/sklearn.semi_supervised.selftrainingclassifier#sklearn.semi_supervised.SelfTrainingClassifier "sklearn.semi_supervised.SelfTrainingClassifier")(...) | Self-training classifier. |
sklearn.svm: Support Vector Machines
------------------------------------
The [`sklearn.svm`](#module-sklearn.svm "sklearn.svm") module includes Support Vector Machine algorithms.
**User guide:** See the [Support Vector Machines](svm#svm) section for further details.
### Estimators
| | |
| --- | --- |
| [`svm.LinearSVC`](generated/sklearn.svm.linearsvc#sklearn.svm.LinearSVC "sklearn.svm.LinearSVC")([penalty, loss, dual, tol, C, ...]) | Linear Support Vector Classification. |
| [`svm.LinearSVR`](generated/sklearn.svm.linearsvr#sklearn.svm.LinearSVR "sklearn.svm.LinearSVR")(\*[, epsilon, tol, C, loss, ...]) | Linear Support Vector Regression. |
| [`svm.NuSVC`](generated/sklearn.svm.nusvc#sklearn.svm.NuSVC "sklearn.svm.NuSVC")(\*[, nu, kernel, degree, gamma, ...]) | Nu-Support Vector Classification. |
| [`svm.NuSVR`](generated/sklearn.svm.nusvr#sklearn.svm.NuSVR "sklearn.svm.NuSVR")(\*[, nu, C, kernel, degree, gamma, ...]) | Nu Support Vector Regression. |
| [`svm.OneClassSVM`](generated/sklearn.svm.oneclasssvm#sklearn.svm.OneClassSVM "sklearn.svm.OneClassSVM")(\*[, kernel, degree, gamma, ...]) | Unsupervised Outlier Detection. |
| [`svm.SVC`](generated/sklearn.svm.svc#sklearn.svm.SVC "sklearn.svm.SVC")(\*[, C, kernel, degree, gamma, ...]) | C-Support Vector Classification. |
| [`svm.SVR`](generated/sklearn.svm.svr#sklearn.svm.SVR "sklearn.svm.SVR")(\*[, kernel, degree, gamma, coef0, ...]) | Epsilon-Support Vector Regression. |
| | |
| --- | --- |
| [`svm.l1_min_c`](generated/sklearn.svm.l1_min_c#sklearn.svm.l1_min_c "sklearn.svm.l1_min_c")(X, y, \*[, loss, fit\_intercept, ...]) | Return the lowest bound for C such that for C in (l1\_min\_C, infinity) the model is guaranteed not to be empty. |
sklearn.tree: Decision Trees
----------------------------
The [`sklearn.tree`](#module-sklearn.tree "sklearn.tree") module includes decision tree-based models for classification and regression.
**User guide:** See the [Decision Trees](tree#tree) section for further details.
| | |
| --- | --- |
| [`tree.DecisionTreeClassifier`](generated/sklearn.tree.decisiontreeclassifier#sklearn.tree.DecisionTreeClassifier "sklearn.tree.DecisionTreeClassifier")(\*[, criterion, ...]) | A decision tree classifier. |
| [`tree.DecisionTreeRegressor`](generated/sklearn.tree.decisiontreeregressor#sklearn.tree.DecisionTreeRegressor "sklearn.tree.DecisionTreeRegressor")(\*[, criterion, ...]) | A decision tree regressor. |
| [`tree.ExtraTreeClassifier`](generated/sklearn.tree.extratreeclassifier#sklearn.tree.ExtraTreeClassifier "sklearn.tree.ExtraTreeClassifier")(\*[, criterion, ...]) | An extremely randomized tree classifier. |
| [`tree.ExtraTreeRegressor`](generated/sklearn.tree.extratreeregressor#sklearn.tree.ExtraTreeRegressor "sklearn.tree.ExtraTreeRegressor")(\*[, criterion, ...]) | An extremely randomized tree regressor. |
| | |
| --- | --- |
| [`tree.export_graphviz`](generated/sklearn.tree.export_graphviz#sklearn.tree.export_graphviz "sklearn.tree.export_graphviz")(decision\_tree[, ...]) | Export a decision tree in DOT format. |
| [`tree.export_text`](generated/sklearn.tree.export_text#sklearn.tree.export_text "sklearn.tree.export_text")(decision\_tree, \*[, ...]) | Build a text report showing the rules of a decision tree. |
### Plotting
| | |
| --- | --- |
| [`tree.plot_tree`](generated/sklearn.tree.plot_tree#sklearn.tree.plot_tree "sklearn.tree.plot_tree")(decision\_tree, \*[, ...]) | Plot a decision tree. |
sklearn.utils: Utilities
------------------------
The [`sklearn.utils`](#module-sklearn.utils "sklearn.utils") module includes various utilities.
**Developer guide:** See the [Utilities for Developers](https://scikit-learn.org/1.1/developers/utilities.html#developers-utils) page for further details.
| | |
| --- | --- |
| [`utils.Bunch`](generated/sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")(\*\*kwargs) | Container object exposing keys as attributes. |
| | |
| --- | --- |
| [`utils.arrayfuncs.min_pos`](generated/sklearn.utils.arrayfuncs.min_pos#sklearn.utils.arrayfuncs.min_pos "sklearn.utils.arrayfuncs.min_pos") | Find the minimum value of an array over positive values |
| [`utils.as_float_array`](generated/sklearn.utils.as_float_array#sklearn.utils.as_float_array "sklearn.utils.as_float_array")(X, \*[, copy, ...]) | Convert an array-like to an array of floats. |
| [`utils.assert_all_finite`](generated/sklearn.utils.assert_all_finite#sklearn.utils.assert_all_finite "sklearn.utils.assert_all_finite")(X, \*[, allow\_nan, ...]) | Throw a ValueError if X contains NaN or infinity. |
| [`utils.check_X_y`](generated/sklearn.utils.check_x_y#sklearn.utils.check_X_y "sklearn.utils.check_X_y")(X, y[, accept\_sparse, ...]) | Input validation for standard estimators. |
| [`utils.check_array`](generated/sklearn.utils.check_array#sklearn.utils.check_array "sklearn.utils.check_array")(array[, accept\_sparse, ...]) | Input validation on an array, list, sparse matrix or similar. |
| [`utils.check_scalar`](generated/sklearn.utils.check_scalar#sklearn.utils.check_scalar "sklearn.utils.check_scalar")(x, name, target\_type, \*) | Validate scalar parameters type and value. |
| [`utils.check_consistent_length`](generated/sklearn.utils.check_consistent_length#sklearn.utils.check_consistent_length "sklearn.utils.check_consistent_length")(\*arrays) | Check that all arrays have consistent first dimensions. |
| [`utils.check_random_state`](generated/sklearn.utils.check_random_state#sklearn.utils.check_random_state "sklearn.utils.check_random_state")(seed) | Turn seed into a np.random.RandomState instance. |
| [`utils.class_weight.compute_class_weight`](generated/sklearn.utils.class_weight.compute_class_weight#sklearn.utils.class_weight.compute_class_weight "sklearn.utils.class_weight.compute_class_weight")(...) | Estimate class weights for unbalanced datasets. |
| [`utils.class_weight.compute_sample_weight`](generated/sklearn.utils.class_weight.compute_sample_weight#sklearn.utils.class_weight.compute_sample_weight "sklearn.utils.class_weight.compute_sample_weight")(...) | Estimate sample weights by class for unbalanced datasets. |
| [`utils.deprecated`](generated/sklearn.utils.deprecated#sklearn.utils.deprecated "sklearn.utils.deprecated")([extra]) | Decorator to mark a function or class as deprecated. |
| [`utils.estimator_checks.check_estimator`](generated/sklearn.utils.estimator_checks.check_estimator#sklearn.utils.estimator_checks.check_estimator "sklearn.utils.estimator_checks.check_estimator")([...]) | Check if estimator adheres to scikit-learn conventions. |
| [`utils.estimator_checks.parametrize_with_checks`](generated/sklearn.utils.estimator_checks.parametrize_with_checks#sklearn.utils.estimator_checks.parametrize_with_checks "sklearn.utils.estimator_checks.parametrize_with_checks")(...) | Pytest specific decorator for parametrizing estimator checks. |
| [`utils.estimator_html_repr`](generated/sklearn.utils.estimator_html_repr#sklearn.utils.estimator_html_repr "sklearn.utils.estimator_html_repr")(estimator) | Build a HTML representation of an estimator. |
| [`utils.extmath.safe_sparse_dot`](generated/sklearn.utils.extmath.safe_sparse_dot#sklearn.utils.extmath.safe_sparse_dot "sklearn.utils.extmath.safe_sparse_dot")(a, b, \*[, ...]) | Dot product that handle the sparse matrix case correctly. |
| [`utils.extmath.randomized_range_finder`](generated/sklearn.utils.extmath.randomized_range_finder#sklearn.utils.extmath.randomized_range_finder "sklearn.utils.extmath.randomized_range_finder")(A, \*, ...) | Compute an orthonormal matrix whose range approximates the range of A. |
| [`utils.extmath.randomized_svd`](generated/sklearn.utils.extmath.randomized_svd#sklearn.utils.extmath.randomized_svd "sklearn.utils.extmath.randomized_svd")(M, n\_components, \*) | Computes a truncated randomized SVD. |
| [`utils.extmath.fast_logdet`](generated/sklearn.utils.extmath.fast_logdet#sklearn.utils.extmath.fast_logdet "sklearn.utils.extmath.fast_logdet")(A) | Compute log(det(A)) for A symmetric. |
| [`utils.extmath.density`](generated/sklearn.utils.extmath.density#sklearn.utils.extmath.density "sklearn.utils.extmath.density")(w, \*\*kwargs) | Compute density of a sparse vector. |
| [`utils.extmath.weighted_mode`](generated/sklearn.utils.extmath.weighted_mode#sklearn.utils.extmath.weighted_mode "sklearn.utils.extmath.weighted_mode")(a, w, \*[, axis]) | Returns an array of the weighted modal (most common) value in a. |
| [`utils.gen_batches`](generated/sklearn.utils.gen_batches#sklearn.utils.gen_batches "sklearn.utils.gen_batches")(n, batch\_size, \*[, ...]) | Generator to create slices containing batch\_size elements, from 0 to n. |
| [`utils.gen_even_slices`](generated/sklearn.utils.gen_even_slices#sklearn.utils.gen_even_slices "sklearn.utils.gen_even_slices")(n, n\_packs, \*[, n\_samples]) | Generator to create n\_packs slices going up to n. |
| [`utils.graph.single_source_shortest_path_length`](generated/sklearn.utils.graph.single_source_shortest_path_length#sklearn.utils.graph.single_source_shortest_path_length "sklearn.utils.graph.single_source_shortest_path_length")(...) | Return the shortest path length from source to all reachable nodes. |
| [`utils.indexable`](generated/sklearn.utils.indexable#sklearn.utils.indexable "sklearn.utils.indexable")(\*iterables) | Make arrays indexable for cross-validation. |
| [`utils.metaestimators.available_if`](generated/sklearn.utils.metaestimators.available_if#sklearn.utils.metaestimators.available_if "sklearn.utils.metaestimators.available_if")(check) | An attribute that is available only if check returns a truthy value |
| [`utils.multiclass.type_of_target`](generated/sklearn.utils.multiclass.type_of_target#sklearn.utils.multiclass.type_of_target "sklearn.utils.multiclass.type_of_target")(y[, input\_name]) | Determine the type of data indicated by the target. |
| [`utils.multiclass.is_multilabel`](generated/sklearn.utils.multiclass.is_multilabel#sklearn.utils.multiclass.is_multilabel "sklearn.utils.multiclass.is_multilabel")(y) | Check if `y` is in a multilabel format. |
| [`utils.multiclass.unique_labels`](generated/sklearn.utils.multiclass.unique_labels#sklearn.utils.multiclass.unique_labels "sklearn.utils.multiclass.unique_labels")(\*ys) | Extract an ordered array of unique labels. |
| [`utils.murmurhash3_32`](generated/sklearn.utils.murmurhash3_32#sklearn.utils.murmurhash3_32 "sklearn.utils.murmurhash3_32") | Compute the 32bit murmurhash3 of key at seed. |
| [`utils.resample`](generated/sklearn.utils.resample#sklearn.utils.resample "sklearn.utils.resample")(\*arrays[, replace, ...]) | Resample arrays or sparse matrices in a consistent way. |
| [`utils._safe_indexing`](generated/sklearn.utils._safe_indexing#sklearn.utils._safe_indexing "sklearn.utils._safe_indexing")(X, indices, \*[, axis]) | Return rows, items or columns of X using indices. |
| [`utils.safe_mask`](generated/sklearn.utils.safe_mask#sklearn.utils.safe_mask "sklearn.utils.safe_mask")(X, mask) | Return a mask which is safe to use on X. |
| [`utils.safe_sqr`](generated/sklearn.utils.safe_sqr#sklearn.utils.safe_sqr "sklearn.utils.safe_sqr")(X, \*[, copy]) | Element wise squaring of array-likes and sparse matrices. |
| [`utils.shuffle`](generated/sklearn.utils.shuffle#sklearn.utils.shuffle "sklearn.utils.shuffle")(\*arrays[, random\_state, n\_samples]) | Shuffle arrays or sparse matrices in a consistent way. |
| [`utils.sparsefuncs.incr_mean_variance_axis`](generated/sklearn.utils.sparsefuncs.incr_mean_variance_axis#sklearn.utils.sparsefuncs.incr_mean_variance_axis "sklearn.utils.sparsefuncs.incr_mean_variance_axis")(X, ...) | Compute incremental mean and variance along an axis on a CSR or CSC matrix. |
| [`utils.sparsefuncs.inplace_column_scale`](generated/sklearn.utils.sparsefuncs.inplace_column_scale#sklearn.utils.sparsefuncs.inplace_column_scale "sklearn.utils.sparsefuncs.inplace_column_scale")(X, scale) | Inplace column scaling of a CSC/CSR matrix. |
| [`utils.sparsefuncs.inplace_row_scale`](generated/sklearn.utils.sparsefuncs.inplace_row_scale#sklearn.utils.sparsefuncs.inplace_row_scale "sklearn.utils.sparsefuncs.inplace_row_scale")(X, scale) | Inplace row scaling of a CSR or CSC matrix. |
| [`utils.sparsefuncs.inplace_swap_row`](generated/sklearn.utils.sparsefuncs.inplace_swap_row#sklearn.utils.sparsefuncs.inplace_swap_row "sklearn.utils.sparsefuncs.inplace_swap_row")(X, m, n) | Swaps two rows of a CSC/CSR matrix in-place. |
| [`utils.sparsefuncs.inplace_swap_column`](generated/sklearn.utils.sparsefuncs.inplace_swap_column#sklearn.utils.sparsefuncs.inplace_swap_column "sklearn.utils.sparsefuncs.inplace_swap_column")(X, m, n) | Swap two columns of a CSC/CSR matrix in-place. |
| [`utils.sparsefuncs.mean_variance_axis`](generated/sklearn.utils.sparsefuncs.mean_variance_axis#sklearn.utils.sparsefuncs.mean_variance_axis "sklearn.utils.sparsefuncs.mean_variance_axis")(X, axis) | Compute mean and variance along an axis on a CSR or CSC matrix. |
| [`utils.sparsefuncs.inplace_csr_column_scale`](generated/sklearn.utils.sparsefuncs.inplace_csr_column_scale#sklearn.utils.sparsefuncs.inplace_csr_column_scale "sklearn.utils.sparsefuncs.inplace_csr_column_scale")(X, ...) | Inplace column scaling of a CSR matrix. |
| [`utils.sparsefuncs_fast.inplace_csr_row_normalize_l1`](generated/sklearn.utils.sparsefuncs_fast.inplace_csr_row_normalize_l1#sklearn.utils.sparsefuncs_fast.inplace_csr_row_normalize_l1 "sklearn.utils.sparsefuncs_fast.inplace_csr_row_normalize_l1") | Inplace row normalize using the l1 norm |
| [`utils.sparsefuncs_fast.inplace_csr_row_normalize_l2`](generated/sklearn.utils.sparsefuncs_fast.inplace_csr_row_normalize_l2#sklearn.utils.sparsefuncs_fast.inplace_csr_row_normalize_l2 "sklearn.utils.sparsefuncs_fast.inplace_csr_row_normalize_l2") | Inplace row normalize using the l2 norm |
| [`utils.random.sample_without_replacement`](generated/sklearn.utils.random.sample_without_replacement#sklearn.utils.random.sample_without_replacement "sklearn.utils.random.sample_without_replacement") | Sample integers without replacement. |
| [`utils.validation.check_is_fitted`](generated/sklearn.utils.validation.check_is_fitted#sklearn.utils.validation.check_is_fitted "sklearn.utils.validation.check_is_fitted")(estimator) | Perform is\_fitted validation for estimator. |
| [`utils.validation.check_memory`](generated/sklearn.utils.validation.check_memory#sklearn.utils.validation.check_memory "sklearn.utils.validation.check_memory")(memory) | Check that `memory` is joblib.Memory-like. |
| [`utils.validation.check_symmetric`](generated/sklearn.utils.validation.check_symmetric#sklearn.utils.validation.check_symmetric "sklearn.utils.validation.check_symmetric")(array, \*[, ...]) | Make sure that array is 2D, square and symmetric. |
| [`utils.validation.column_or_1d`](generated/sklearn.utils.validation.column_or_1d#sklearn.utils.validation.column_or_1d "sklearn.utils.validation.column_or_1d")(y, \*[, warn]) | Ravel column or 1d numpy array, else raises an error. |
| [`utils.validation.has_fit_parameter`](generated/sklearn.utils.validation.has_fit_parameter#sklearn.utils.validation.has_fit_parameter "sklearn.utils.validation.has_fit_parameter")(...) | Check whether the estimator's fit method supports the given parameter. |
| [`utils.all_estimators`](generated/sklearn.utils.all_estimators#sklearn.utils.all_estimators "sklearn.utils.all_estimators")([type\_filter]) | Get a list of all estimators from sklearn. |
Utilities from joblib:
| | |
| --- | --- |
| [`utils.parallel_backend`](generated/sklearn.utils.parallel_backend#sklearn.utils.parallel_backend "sklearn.utils.parallel_backend")(backend[, n\_jobs, ...]) | Change the default backend used by Parallel inside a with block. |
| [`utils.register_parallel_backend`](generated/sklearn.utils.register_parallel_backend#sklearn.utils.register_parallel_backend "sklearn.utils.register_parallel_backend")(name, factory) | Register a new Parallel backend factory. |
Recently deprecated
-------------------
### To be removed in 1.3
| | |
| --- | --- |
| [`utils.metaestimators.if_delegate_has_method`](generated/sklearn.utils.metaestimators.if_delegate_has_method#sklearn.utils.metaestimators.if_delegate_has_method "sklearn.utils.metaestimators.if_delegate_has_method")(...) | Create a decorator for methods that are delegated to a sub-estimator |
| programming_docs |
scikit_learn 1.6. Nearest Neighbors 1.6. Nearest Neighbors
======================
[`sklearn.neighbors`](classes#module-sklearn.neighbors "sklearn.neighbors") provides functionality for unsupervised and supervised neighbors-based learning methods. Unsupervised nearest neighbors is the foundation of many other learning methods, notably manifold learning and spectral clustering. Supervised neighbors-based learning comes in two flavors: [classification](#classification) for data with discrete labels, and [regression](#regression) for data with continuous labels.
The principle behind nearest neighbor methods is to find a predefined number of training samples closest in distance to the new point, and predict the label from these. The number of samples can be a user-defined constant (k-nearest neighbor learning), or vary based on the local density of points (radius-based neighbor learning). The distance can, in general, be any metric measure: standard Euclidean distance is the most common choice. Neighbors-based methods are known as *non-generalizing* machine learning methods, since they simply “remember” all of its training data (possibly transformed into a fast indexing structure such as a [Ball Tree](#ball-tree) or [KD Tree](#kd-tree)).
Despite its simplicity, nearest neighbors has been successful in a large number of classification and regression problems, including handwritten digits and satellite image scenes. Being a non-parametric method, it is often successful in classification situations where the decision boundary is very irregular.
The classes in [`sklearn.neighbors`](classes#module-sklearn.neighbors "sklearn.neighbors") can handle either NumPy arrays or `scipy.sparse` matrices as input. For dense matrices, a large number of possible distance metrics are supported. For sparse matrices, arbitrary Minkowski metrics are supported for searches.
There are many learning routines which rely on nearest neighbors at their core. One example is [kernel density estimation](density#kernel-density), discussed in the [density estimation](density#density-estimation) section.
1.6.1. Unsupervised Nearest Neighbors
--------------------------------------
[`NearestNeighbors`](generated/sklearn.neighbors.nearestneighbors#sklearn.neighbors.NearestNeighbors "sklearn.neighbors.NearestNeighbors") implements unsupervised nearest neighbors learning. It acts as a uniform interface to three different nearest neighbors algorithms: [`BallTree`](generated/sklearn.neighbors.balltree#sklearn.neighbors.BallTree "sklearn.neighbors.BallTree"), [`KDTree`](generated/sklearn.neighbors.kdtree#sklearn.neighbors.KDTree "sklearn.neighbors.KDTree"), and a brute-force algorithm based on routines in [`sklearn.metrics.pairwise`](classes#module-sklearn.metrics.pairwise "sklearn.metrics.pairwise"). The choice of neighbors search algorithm is controlled through the keyword `'algorithm'`, which must be one of `['auto', 'ball_tree', 'kd_tree', 'brute']`. When the default value `'auto'` is passed, the algorithm attempts to determine the best approach from the training data. For a discussion of the strengths and weaknesses of each option, see [Nearest Neighbor Algorithms](#nearest-neighbor-algorithms).
Warning
Regarding the Nearest Neighbors algorithms, if two neighbors \(k+1\) and \(k\) have identical distances but different labels, the result will depend on the ordering of the training data.
###
1.6.1.1. Finding the Nearest Neighbors
For the simple task of finding the nearest neighbors between two sets of data, the unsupervised algorithms within [`sklearn.neighbors`](classes#module-sklearn.neighbors "sklearn.neighbors") can be used:
```
>>> from sklearn.neighbors import NearestNeighbors
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> nbrs = NearestNeighbors(n_neighbors=2, algorithm='ball_tree').fit(X)
>>> distances, indices = nbrs.kneighbors(X)
>>> indices
array([[0, 1],
[1, 0],
[2, 1],
[3, 4],
[4, 3],
[5, 4]]...)
>>> distances
array([[0. , 1. ],
[0. , 1. ],
[0. , 1.41421356],
[0. , 1. ],
[0. , 1. ],
[0. , 1.41421356]])
```
Because the query set matches the training set, the nearest neighbor of each point is the point itself, at a distance of zero.
It is also possible to efficiently produce a sparse graph showing the connections between neighboring points:
```
>>> nbrs.kneighbors_graph(X).toarray()
array([[1., 1., 0., 0., 0., 0.],
[1., 1., 0., 0., 0., 0.],
[0., 1., 1., 0., 0., 0.],
[0., 0., 0., 1., 1., 0.],
[0., 0., 0., 1., 1., 0.],
[0., 0., 0., 0., 1., 1.]])
```
The dataset is structured such that points nearby in index order are nearby in parameter space, leading to an approximately block-diagonal matrix of K-nearest neighbors. Such a sparse graph is useful in a variety of circumstances which make use of spatial relationships between points for unsupervised learning: in particular, see [`Isomap`](generated/sklearn.manifold.isomap#sklearn.manifold.Isomap "sklearn.manifold.Isomap"), [`LocallyLinearEmbedding`](generated/sklearn.manifold.locallylinearembedding#sklearn.manifold.LocallyLinearEmbedding "sklearn.manifold.LocallyLinearEmbedding"), and [`SpectralClustering`](generated/sklearn.cluster.spectralclustering#sklearn.cluster.SpectralClustering "sklearn.cluster.SpectralClustering").
###
1.6.1.2. KDTree and BallTree Classes
Alternatively, one can use the [`KDTree`](generated/sklearn.neighbors.kdtree#sklearn.neighbors.KDTree "sklearn.neighbors.KDTree") or [`BallTree`](generated/sklearn.neighbors.balltree#sklearn.neighbors.BallTree "sklearn.neighbors.BallTree") classes directly to find nearest neighbors. This is the functionality wrapped by the [`NearestNeighbors`](generated/sklearn.neighbors.nearestneighbors#sklearn.neighbors.NearestNeighbors "sklearn.neighbors.NearestNeighbors") class used above. The Ball Tree and KD Tree have the same interface; we’ll show an example of using the KD Tree here:
```
>>> from sklearn.neighbors import KDTree
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> kdt = KDTree(X, leaf_size=30, metric='euclidean')
>>> kdt.query(X, k=2, return_distance=False)
array([[0, 1],
[1, 0],
[2, 1],
[3, 4],
[4, 3],
[5, 4]]...)
```
Refer to the [`KDTree`](generated/sklearn.neighbors.kdtree#sklearn.neighbors.KDTree "sklearn.neighbors.KDTree") and [`BallTree`](generated/sklearn.neighbors.balltree#sklearn.neighbors.BallTree "sklearn.neighbors.BallTree") class documentation for more information on the options available for nearest neighbors searches, including specification of query strategies, distance metrics, etc. For a list of available metrics, see the documentation of the `DistanceMetric` class and the metrics listed in `sklearn.metrics.pairwise.PAIRWISE_DISTANCE_FUNCTIONS`. Note that the “cosine” metric uses [`cosine_distances`](generated/sklearn.metrics.pairwise.cosine_distances#sklearn.metrics.pairwise.cosine_distances "sklearn.metrics.pairwise.cosine_distances").
1.6.2. Nearest Neighbors Classification
----------------------------------------
Neighbors-based classification is a type of *instance-based learning* or *non-generalizing learning*: it does not attempt to construct a general internal model, but simply stores instances of the training data. Classification is computed from a simple majority vote of the nearest neighbors of each point: a query point is assigned the data class which has the most representatives within the nearest neighbors of the point.
scikit-learn implements two different nearest neighbors classifiers: [`KNeighborsClassifier`](generated/sklearn.neighbors.kneighborsclassifier#sklearn.neighbors.KNeighborsClassifier "sklearn.neighbors.KNeighborsClassifier") implements learning based on the \(k\) nearest neighbors of each query point, where \(k\) is an integer value specified by the user. [`RadiusNeighborsClassifier`](generated/sklearn.neighbors.radiusneighborsclassifier#sklearn.neighbors.RadiusNeighborsClassifier "sklearn.neighbors.RadiusNeighborsClassifier") implements learning based on the number of neighbors within a fixed radius \(r\) of each training point, where \(r\) is a floating-point value specified by the user.
The \(k\)-neighbors classification in [`KNeighborsClassifier`](generated/sklearn.neighbors.kneighborsclassifier#sklearn.neighbors.KNeighborsClassifier "sklearn.neighbors.KNeighborsClassifier") is the most commonly used technique. The optimal choice of the value \(k\) is highly data-dependent: in general a larger \(k\) suppresses the effects of noise, but makes the classification boundaries less distinct.
In cases where the data is not uniformly sampled, radius-based neighbors classification in [`RadiusNeighborsClassifier`](generated/sklearn.neighbors.radiusneighborsclassifier#sklearn.neighbors.RadiusNeighborsClassifier "sklearn.neighbors.RadiusNeighborsClassifier") can be a better choice. The user specifies a fixed radius \(r\), such that points in sparser neighborhoods use fewer nearest neighbors for the classification. For high-dimensional parameter spaces, this method becomes less effective due to the so-called “curse of dimensionality”.
The basic nearest neighbors classification uses uniform weights: that is, the value assigned to a query point is computed from a simple majority vote of the nearest neighbors. Under some circumstances, it is better to weight the neighbors such that nearer neighbors contribute more to the fit. This can be accomplished through the `weights` keyword. The default value, `weights = 'uniform'`, assigns uniform weights to each neighbor. `weights = 'distance'` assigns weights proportional to the inverse of the distance from the query point. Alternatively, a user-defined function of the distance can be supplied to compute the weights.
1.6.3. Nearest Neighbors Regression
------------------------------------
Neighbors-based regression can be used in cases where the data labels are continuous rather than discrete variables. The label assigned to a query point is computed based on the mean of the labels of its nearest neighbors.
scikit-learn implements two different neighbors regressors: [`KNeighborsRegressor`](generated/sklearn.neighbors.kneighborsregressor#sklearn.neighbors.KNeighborsRegressor "sklearn.neighbors.KNeighborsRegressor") implements learning based on the \(k\) nearest neighbors of each query point, where \(k\) is an integer value specified by the user. [`RadiusNeighborsRegressor`](generated/sklearn.neighbors.radiusneighborsregressor#sklearn.neighbors.RadiusNeighborsRegressor "sklearn.neighbors.RadiusNeighborsRegressor") implements learning based on the neighbors within a fixed radius \(r\) of the query point, where \(r\) is a floating-point value specified by the user.
The basic nearest neighbors regression uses uniform weights: that is, each point in the local neighborhood contributes uniformly to the classification of a query point. Under some circumstances, it can be advantageous to weight points such that nearby points contribute more to the regression than faraway points. This can be accomplished through the `weights` keyword. The default value, `weights = 'uniform'`, assigns equal weights to all points. `weights = 'distance'` assigns weights proportional to the inverse of the distance from the query point. Alternatively, a user-defined function of the distance can be supplied, which will be used to compute the weights.
The use of multi-output nearest neighbors for regression is demonstrated in [Face completion with a multi-output estimators](../auto_examples/miscellaneous/plot_multioutput_face_completion#sphx-glr-auto-examples-miscellaneous-plot-multioutput-face-completion-py). In this example, the inputs X are the pixels of the upper half of faces and the outputs Y are the pixels of the lower half of those faces.
1.6.4. Nearest Neighbor Algorithms
-----------------------------------
###
1.6.4.1. Brute Force
Fast computation of nearest neighbors is an active area of research in machine learning. The most naive neighbor search implementation involves the brute-force computation of distances between all pairs of points in the dataset: for \(N\) samples in \(D\) dimensions, this approach scales as \(O[D N^2]\). Efficient brute-force neighbors searches can be very competitive for small data samples. However, as the number of samples \(N\) grows, the brute-force approach quickly becomes infeasible. In the classes within [`sklearn.neighbors`](classes#module-sklearn.neighbors "sklearn.neighbors"), brute-force neighbors searches are specified using the keyword `algorithm = 'brute'`, and are computed using the routines available in [`sklearn.metrics.pairwise`](classes#module-sklearn.metrics.pairwise "sklearn.metrics.pairwise").
###
1.6.4.2. K-D Tree
To address the computational inefficiencies of the brute-force approach, a variety of tree-based data structures have been invented. In general, these structures attempt to reduce the required number of distance calculations by efficiently encoding aggregate distance information for the sample. The basic idea is that if point \(A\) is very distant from point \(B\), and point \(B\) is very close to point \(C\), then we know that points \(A\) and \(C\) are very distant, *without having to explicitly calculate their distance*. In this way, the computational cost of a nearest neighbors search can be reduced to \(O[D N \log(N)]\) or better. This is a significant improvement over brute-force for large \(N\).
An early approach to taking advantage of this aggregate information was the *KD tree* data structure (short for *K-dimensional tree*), which generalizes two-dimensional *Quad-trees* and 3-dimensional *Oct-trees* to an arbitrary number of dimensions. The KD tree is a binary tree structure which recursively partitions the parameter space along the data axes, dividing it into nested orthotropic regions into which data points are filed. The construction of a KD tree is very fast: because partitioning is performed only along the data axes, no \(D\)-dimensional distances need to be computed. Once constructed, the nearest neighbor of a query point can be determined with only \(O[\log(N)]\) distance computations. Though the KD tree approach is very fast for low-dimensional (\(D < 20\)) neighbors searches, it becomes inefficient as \(D\) grows very large: this is one manifestation of the so-called “curse of dimensionality”. In scikit-learn, KD tree neighbors searches are specified using the keyword `algorithm = 'kd_tree'`, and are computed using the class [`KDTree`](generated/sklearn.neighbors.kdtree#sklearn.neighbors.KDTree "sklearn.neighbors.KDTree").
###
1.6.4.3. Ball Tree
To address the inefficiencies of KD Trees in higher dimensions, the *ball tree* data structure was developed. Where KD trees partition data along Cartesian axes, ball trees partition data in a series of nesting hyper-spheres. This makes tree construction more costly than that of the KD tree, but results in a data structure which can be very efficient on highly structured data, even in very high dimensions.
A ball tree recursively divides the data into nodes defined by a centroid \(C\) and radius \(r\), such that each point in the node lies within the hyper-sphere defined by \(r\) and \(C\). The number of candidate points for a neighbor search is reduced through use of the *triangle inequality*:
\[|x+y| \leq |x| + |y|\] With this setup, a single distance calculation between a test point and the centroid is sufficient to determine a lower and upper bound on the distance to all points within the node. Because of the spherical geometry of the ball tree nodes, it can out-perform a *KD-tree* in high dimensions, though the actual performance is highly dependent on the structure of the training data. In scikit-learn, ball-tree-based neighbors searches are specified using the keyword `algorithm = 'ball_tree'`, and are computed using the class [`BallTree`](generated/sklearn.neighbors.balltree#sklearn.neighbors.BallTree "sklearn.neighbors.BallTree"). Alternatively, the user can work with the [`BallTree`](generated/sklearn.neighbors.balltree#sklearn.neighbors.BallTree "sklearn.neighbors.BallTree") class directly.
###
1.6.4.4. Choice of Nearest Neighbors Algorithm
The optimal algorithm for a given dataset is a complicated choice, and depends on a number of factors:
* number of samples \(N\) (i.e. `n_samples`) and dimensionality \(D\) (i.e. `n_features`).
+ *Brute force* query time grows as \(O[D N]\)
+ *Ball tree* query time grows as approximately \(O[D \log(N)]\)
+ *KD tree* query time changes with \(D\) in a way that is difficult to precisely characterise. For small \(D\) (less than 20 or so) the cost is approximately \(O[D\log(N)]\), and the KD tree query can be very efficient. For larger \(D\), the cost increases to nearly \(O[DN]\), and the overhead due to the tree structure can lead to queries which are slower than brute force.For small data sets (\(N\) less than 30 or so), \(\log(N)\) is comparable to \(N\), and brute force algorithms can be more efficient than a tree-based approach. Both [`KDTree`](generated/sklearn.neighbors.kdtree#sklearn.neighbors.KDTree "sklearn.neighbors.KDTree") and [`BallTree`](generated/sklearn.neighbors.balltree#sklearn.neighbors.BallTree "sklearn.neighbors.BallTree") address this through providing a *leaf size* parameter: this controls the number of samples at which a query switches to brute-force. This allows both algorithms to approach the efficiency of a brute-force computation for small \(N\).
* data structure: *intrinsic dimensionality* of the data and/or *sparsity* of the data. Intrinsic dimensionality refers to the dimension \(d \le D\) of a manifold on which the data lies, which can be linearly or non-linearly embedded in the parameter space. Sparsity refers to the degree to which the data fills the parameter space (this is to be distinguished from the concept as used in “sparse” matrices. The data matrix may have no zero entries, but the **structure** can still be “sparse” in this sense).
+ *Brute force* query time is unchanged by data structure.
+ *Ball tree* and *KD tree* query times can be greatly influenced by data structure. In general, sparser data with a smaller intrinsic dimensionality leads to faster query times. Because the KD tree internal representation is aligned with the parameter axes, it will not generally show as much improvement as ball tree for arbitrarily structured data.Datasets used in machine learning tend to be very structured, and are very well-suited for tree-based queries.
* number of neighbors \(k\) requested for a query point.
+ *Brute force* query time is largely unaffected by the value of \(k\)
+ *Ball tree* and *KD tree* query time will become slower as \(k\) increases. This is due to two effects: first, a larger \(k\) leads to the necessity to search a larger portion of the parameter space. Second, using \(k > 1\) requires internal queueing of results as the tree is traversed.As \(k\) becomes large compared to \(N\), the ability to prune branches in a tree-based query is reduced. In this situation, Brute force queries can be more efficient.
* number of query points. Both the ball tree and the KD Tree require a construction phase. The cost of this construction becomes negligible when amortized over many queries. If only a small number of queries will be performed, however, the construction can make up a significant fraction of the total cost. If very few query points will be required, brute force is better than a tree-based method.
Currently, `algorithm = 'auto'` selects `'brute'` if any of the following conditions are verified:
* input data is sparse
* `metric = 'precomputed'`
* \(D > 15\)
* \(k >= N/2\)
* `effective_metric_` isn’t in the `VALID_METRICS` list for either `'kd_tree'` or `'ball_tree'`
Otherwise, it selects the first out of `'kd_tree'` and `'ball_tree'` that has `effective_metric_` in its `VALID_METRICS` list. This heuristic is based on the following assumptions:
* the number of query points is at least the same order as the number of training points
* `leaf_size` is close to its default value of `30`
* when \(D > 15\), the intrinsic dimensionality of the data is generally too high for tree-based methods
###
1.6.4.5. Effect of `leaf_size`
As noted above, for small sample sizes a brute force search can be more efficient than a tree-based query. This fact is accounted for in the ball tree and KD tree by internally switching to brute force searches within leaf nodes. The level of this switch can be specified with the parameter `leaf_size`. This parameter choice has many effects:
**construction time**
A larger `leaf_size` leads to a faster tree construction time, because fewer nodes need to be created
**query time**
Both a large or small `leaf_size` can lead to suboptimal query cost. For `leaf_size` approaching 1, the overhead involved in traversing nodes can significantly slow query times. For `leaf_size` approaching the size of the training set, queries become essentially brute force. A good compromise between these is `leaf_size = 30`, the default value of the parameter.
**memory**
As `leaf_size` increases, the memory required to store a tree structure decreases. This is especially important in the case of ball tree, which stores a \(D\)-dimensional centroid for each node. The required storage space for [`BallTree`](generated/sklearn.neighbors.balltree#sklearn.neighbors.BallTree "sklearn.neighbors.BallTree") is approximately `1 / leaf_size` times the size of the training set.
`leaf_size` is not referenced for brute force queries.
###
1.6.4.6. Valid Metrics for Nearest Neighbor Algorithms
For a list of available metrics, see the documentation of the `DistanceMetric` class and the metrics listed in `sklearn.metrics.pairwise.PAIRWISE_DISTANCE_FUNCTIONS`. Note that the “cosine” metric uses [`cosine_distances`](generated/sklearn.metrics.pairwise.cosine_distances#sklearn.metrics.pairwise.cosine_distances "sklearn.metrics.pairwise.cosine_distances").
A list of valid metrics for any of the above algorithms can be obtained by using their `valid_metric` attribute. For example, valid metrics for `KDTree` can be generated by:
```
>>> from sklearn.neighbors import KDTree
>>> print(sorted(KDTree.valid_metrics))
['chebyshev', 'cityblock', 'euclidean', 'infinity', 'l1', 'l2', 'manhattan', 'minkowski', 'p']
```
1.6.5. Nearest Centroid Classifier
-----------------------------------
The [`NearestCentroid`](generated/sklearn.neighbors.nearestcentroid#sklearn.neighbors.NearestCentroid "sklearn.neighbors.NearestCentroid") classifier is a simple algorithm that represents each class by the centroid of its members. In effect, this makes it similar to the label updating phase of the [`KMeans`](generated/sklearn.cluster.kmeans#sklearn.cluster.KMeans "sklearn.cluster.KMeans") algorithm. It also has no parameters to choose, making it a good baseline classifier. It does, however, suffer on non-convex classes, as well as when classes have drastically different variances, as equal variance in all dimensions is assumed. See Linear Discriminant Analysis ([`LinearDiscriminantAnalysis`](generated/sklearn.discriminant_analysis.lineardiscriminantanalysis#sklearn.discriminant_analysis.LinearDiscriminantAnalysis "sklearn.discriminant_analysis.LinearDiscriminantAnalysis")) and Quadratic Discriminant Analysis ([`QuadraticDiscriminantAnalysis`](generated/sklearn.discriminant_analysis.quadraticdiscriminantanalysis#sklearn.discriminant_analysis.QuadraticDiscriminantAnalysis "sklearn.discriminant_analysis.QuadraticDiscriminantAnalysis")) for more complex methods that do not make this assumption. Usage of the default [`NearestCentroid`](generated/sklearn.neighbors.nearestcentroid#sklearn.neighbors.NearestCentroid "sklearn.neighbors.NearestCentroid") is simple:
```
>>> from sklearn.neighbors import NearestCentroid
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> y = np.array([1, 1, 1, 2, 2, 2])
>>> clf = NearestCentroid()
>>> clf.fit(X, y)
NearestCentroid()
>>> print(clf.predict([[-0.8, -1]]))
[1]
```
###
1.6.5.1. Nearest Shrunken Centroid
The [`NearestCentroid`](generated/sklearn.neighbors.nearestcentroid#sklearn.neighbors.NearestCentroid "sklearn.neighbors.NearestCentroid") classifier has a `shrink_threshold` parameter, which implements the nearest shrunken centroid classifier. In effect, the value of each feature for each centroid is divided by the within-class variance of that feature. The feature values are then reduced by `shrink_threshold`. Most notably, if a particular feature value crosses zero, it is set to zero. In effect, this removes the feature from affecting the classification. This is useful, for example, for removing noisy features.
In the example below, using a small shrink threshold increases the accuracy of the model from 0.81 to 0.82.
1.6.6. Nearest Neighbors Transformer
-------------------------------------
Many scikit-learn estimators rely on nearest neighbors: Several classifiers and regressors such as [`KNeighborsClassifier`](generated/sklearn.neighbors.kneighborsclassifier#sklearn.neighbors.KNeighborsClassifier "sklearn.neighbors.KNeighborsClassifier") and [`KNeighborsRegressor`](generated/sklearn.neighbors.kneighborsregressor#sklearn.neighbors.KNeighborsRegressor "sklearn.neighbors.KNeighborsRegressor"), but also some clustering methods such as [`DBSCAN`](generated/sklearn.cluster.dbscan#sklearn.cluster.DBSCAN "sklearn.cluster.DBSCAN") and [`SpectralClustering`](generated/sklearn.cluster.spectralclustering#sklearn.cluster.SpectralClustering "sklearn.cluster.SpectralClustering"), and some manifold embeddings such as [`TSNE`](generated/sklearn.manifold.tsne#sklearn.manifold.TSNE "sklearn.manifold.TSNE") and [`Isomap`](generated/sklearn.manifold.isomap#sklearn.manifold.Isomap "sklearn.manifold.Isomap").
All these estimators can compute internally the nearest neighbors, but most of them also accept precomputed nearest neighbors [sparse graph](https://scikit-learn.org/1.1/glossary.html#term-sparse-graph), as given by [`kneighbors_graph`](generated/sklearn.neighbors.kneighbors_graph#sklearn.neighbors.kneighbors_graph "sklearn.neighbors.kneighbors_graph") and [`radius_neighbors_graph`](generated/sklearn.neighbors.radius_neighbors_graph#sklearn.neighbors.radius_neighbors_graph "sklearn.neighbors.radius_neighbors_graph"). With mode `mode='connectivity'`, these functions return a binary adjacency sparse graph as required, for instance, in [`SpectralClustering`](generated/sklearn.cluster.spectralclustering#sklearn.cluster.SpectralClustering "sklearn.cluster.SpectralClustering"). Whereas with `mode='distance'`, they return a distance sparse graph as required, for instance, in [`DBSCAN`](generated/sklearn.cluster.dbscan#sklearn.cluster.DBSCAN "sklearn.cluster.DBSCAN"). To include these functions in a scikit-learn pipeline, one can also use the corresponding classes [`KNeighborsTransformer`](generated/sklearn.neighbors.kneighborstransformer#sklearn.neighbors.KNeighborsTransformer "sklearn.neighbors.KNeighborsTransformer") and [`RadiusNeighborsTransformer`](generated/sklearn.neighbors.radiusneighborstransformer#sklearn.neighbors.RadiusNeighborsTransformer "sklearn.neighbors.RadiusNeighborsTransformer"). The benefits of this sparse graph API are multiple.
First, the precomputed graph can be re-used multiple times, for instance while varying a parameter of the estimator. This can be done manually by the user, or using the caching properties of the scikit-learn pipeline:
```
>>> import tempfile
>>> from sklearn.manifold import Isomap
>>> from sklearn.neighbors import KNeighborsTransformer
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.datasets import make_regression
>>> cache_path = tempfile.gettempdir() # we use a temporary folder here
>>> X, _ = make_regression(n_samples=50, n_features=25, random_state=0)
>>> estimator = make_pipeline(
... KNeighborsTransformer(mode='distance'),
... Isomap(n_components=3, metric='precomputed'),
... memory=cache_path)
>>> X_embedded = estimator.fit_transform(X)
>>> X_embedded.shape
(50, 3)
```
Second, precomputing the graph can give finer control on the nearest neighbors estimation, for instance enabling multiprocessing though the parameter `n_jobs`, which might not be available in all estimators.
Finally, the precomputation can be performed by custom estimators to use different implementations, such as approximate nearest neighbors methods, or implementation with special data types. The precomputed neighbors [sparse graph](https://scikit-learn.org/1.1/glossary.html#term-sparse-graph) needs to be formatted as in [`radius_neighbors_graph`](generated/sklearn.neighbors.radius_neighbors_graph#sklearn.neighbors.radius_neighbors_graph "sklearn.neighbors.radius_neighbors_graph") output:
* a CSR matrix (although COO, CSC or LIL will be accepted).
* only explicitly store nearest neighborhoods of each sample with respect to the training data. This should include those at 0 distance from a query point, including the matrix diagonal when computing the nearest neighborhoods between the training data and itself.
* each row’s `data` should store the distance in increasing order (optional. Unsorted data will be stable-sorted, adding a computational overhead).
* all values in data should be non-negative.
* there should be no duplicate `indices` in any row (see <https://github.com/scipy/scipy/issues/5807>).
* if the algorithm being passed the precomputed matrix uses k nearest neighbors (as opposed to radius neighborhood), at least k neighbors must be stored in each row (or k+1, as explained in the following note).
Note
When a specific number of neighbors is queried (using [`KNeighborsTransformer`](generated/sklearn.neighbors.kneighborstransformer#sklearn.neighbors.KNeighborsTransformer "sklearn.neighbors.KNeighborsTransformer")), the definition of `n_neighbors` is ambiguous since it can either include each training point as its own neighbor, or exclude them. Neither choice is perfect, since including them leads to a different number of non-self neighbors during training and testing, while excluding them leads to a difference between `fit(X).transform(X)` and `fit_transform(X)`, which is against scikit-learn API. In [`KNeighborsTransformer`](generated/sklearn.neighbors.kneighborstransformer#sklearn.neighbors.KNeighborsTransformer "sklearn.neighbors.KNeighborsTransformer") we use the definition which includes each training point as its own neighbor in the count of `n_neighbors`. However, for compatibility reasons with other estimators which use the other definition, one extra neighbor will be computed when `mode == 'distance'`. To maximise compatibility with all estimators, a safe choice is to always include one extra neighbor in a custom nearest neighbors estimator, since unnecessary neighbors will be filtered by following estimators.
1.6.7. Neighborhood Components Analysis
----------------------------------------
Neighborhood Components Analysis (NCA, [`NeighborhoodComponentsAnalysis`](generated/sklearn.neighbors.neighborhoodcomponentsanalysis#sklearn.neighbors.NeighborhoodComponentsAnalysis "sklearn.neighbors.NeighborhoodComponentsAnalysis")) is a distance metric learning algorithm which aims to improve the accuracy of nearest neighbors classification compared to the standard Euclidean distance. The algorithm directly maximizes a stochastic variant of the leave-one-out k-nearest neighbors (KNN) score on the training set. It can also learn a low-dimensional linear projection of data that can be used for data visualization and fast classification.
In the above illustrating figure, we consider some points from a randomly generated dataset. We focus on the stochastic KNN classification of point no. 3. The thickness of a link between sample 3 and another point is proportional to their distance, and can be seen as the relative weight (or probability) that a stochastic nearest neighbor prediction rule would assign to this point. In the original space, sample 3 has many stochastic neighbors from various classes, so the right class is not very likely. However, in the projected space learned by NCA, the only stochastic neighbors with non-negligible weight are from the same class as sample 3, guaranteeing that the latter will be well classified. See the [mathematical formulation](#nca-mathematical-formulation) for more details.
###
1.6.7.1. Classification
Combined with a nearest neighbors classifier ([`KNeighborsClassifier`](generated/sklearn.neighbors.kneighborsclassifier#sklearn.neighbors.KNeighborsClassifier "sklearn.neighbors.KNeighborsClassifier")), NCA is attractive for classification because it can naturally handle multi-class problems without any increase in the model size, and does not introduce additional parameters that require fine-tuning by the user.
NCA classification has been shown to work well in practice for data sets of varying size and difficulty. In contrast to related methods such as Linear Discriminant Analysis, NCA does not make any assumptions about the class distributions. The nearest neighbor classification can naturally produce highly irregular decision boundaries.
To use this model for classification, one needs to combine a [`NeighborhoodComponentsAnalysis`](generated/sklearn.neighbors.neighborhoodcomponentsanalysis#sklearn.neighbors.NeighborhoodComponentsAnalysis "sklearn.neighbors.NeighborhoodComponentsAnalysis") instance that learns the optimal transformation with a [`KNeighborsClassifier`](generated/sklearn.neighbors.kneighborsclassifier#sklearn.neighbors.KNeighborsClassifier "sklearn.neighbors.KNeighborsClassifier") instance that performs the classification in the projected space. Here is an example using the two classes:
```
>>> from sklearn.neighbors import (NeighborhoodComponentsAnalysis,
... KNeighborsClassifier)
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.pipeline import Pipeline
>>> X, y = load_iris(return_X_y=True)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y,
... stratify=y, test_size=0.7, random_state=42)
>>> nca = NeighborhoodComponentsAnalysis(random_state=42)
>>> knn = KNeighborsClassifier(n_neighbors=3)
>>> nca_pipe = Pipeline([('nca', nca), ('knn', knn)])
>>> nca_pipe.fit(X_train, y_train)
Pipeline(...)
>>> print(nca_pipe.score(X_test, y_test))
0.96190476...
```
The plot shows decision boundaries for Nearest Neighbor Classification and Neighborhood Components Analysis classification on the iris dataset, when training and scoring on only two features, for visualisation purposes.
###
1.6.7.2. Dimensionality reduction
NCA can be used to perform supervised dimensionality reduction. The input data are projected onto a linear subspace consisting of the directions which minimize the NCA objective. The desired dimensionality can be set using the parameter `n_components`. For instance, the following figure shows a comparison of dimensionality reduction with Principal Component Analysis ([`PCA`](generated/sklearn.decomposition.pca#sklearn.decomposition.PCA "sklearn.decomposition.PCA")), Linear Discriminant Analysis ([`LinearDiscriminantAnalysis`](generated/sklearn.discriminant_analysis.lineardiscriminantanalysis#sklearn.discriminant_analysis.LinearDiscriminantAnalysis "sklearn.discriminant_analysis.LinearDiscriminantAnalysis")) and Neighborhood Component Analysis ([`NeighborhoodComponentsAnalysis`](generated/sklearn.neighbors.neighborhoodcomponentsanalysis#sklearn.neighbors.NeighborhoodComponentsAnalysis "sklearn.neighbors.NeighborhoodComponentsAnalysis")) on the Digits dataset, a dataset with size \(n\_{samples} = 1797\) and \(n\_{features} = 64\). The data set is split into a training and a test set of equal size, then standardized. For evaluation the 3-nearest neighbor classification accuracy is computed on the 2-dimensional projected points found by each method. Each data sample belongs to one of 10 classes.
###
1.6.7.3. Mathematical formulation
The goal of NCA is to learn an optimal linear transformation matrix of size `(n_components, n_features)`, which maximises the sum over all samples \(i\) of the probability \(p\_i\) that \(i\) is correctly classified, i.e.:
\[\underset{L}{\arg\max} \sum\limits\_{i=0}^{N - 1} p\_{i}\] with \(N\) = `n_samples` and \(p\_i\) the probability of sample \(i\) being correctly classified according to a stochastic nearest neighbors rule in the learned embedded space:
\[p\_{i}=\sum\limits\_{j \in C\_i}{p\_{i j}}\] where \(C\_i\) is the set of points in the same class as sample \(i\), and \(p\_{i j}\) is the softmax over Euclidean distances in the embedded space:
\[p\_{i j} = \frac{\exp(-||L x\_i - L x\_j||^2)}{\sum\limits\_{k \ne i} {\exp{-(||L x\_i - L x\_k||^2)}}} , \quad p\_{i i} = 0\] ####
1.6.7.3.1. Mahalanobis distance
NCA can be seen as learning a (squared) Mahalanobis distance metric:
\[|| L(x\_i - x\_j)||^2 = (x\_i - x\_j)^TM(x\_i - x\_j),\] where \(M = L^T L\) is a symmetric positive semi-definite matrix of size `(n_features, n_features)`.
###
1.6.7.4. Implementation
This implementation follows what is explained in the original paper [[1]](#id6). For the optimisation method, it currently uses scipy’s L-BFGS-B with a full gradient computation at each iteration, to avoid to tune the learning rate and provide stable learning.
See the examples below and the docstring of [`NeighborhoodComponentsAnalysis.fit`](generated/sklearn.neighbors.neighborhoodcomponentsanalysis#sklearn.neighbors.NeighborhoodComponentsAnalysis.fit "sklearn.neighbors.NeighborhoodComponentsAnalysis.fit") for further information.
###
1.6.7.5. Complexity
####
1.6.7.5.1. Training
NCA stores a matrix of pairwise distances, taking `n_samples ** 2` memory. Time complexity depends on the number of iterations done by the optimisation algorithm. However, one can set the maximum number of iterations with the argument `max_iter`. For each iteration, time complexity is `O(n_components x n_samples x min(n_samples, n_features))`.
####
1.6.7.5.2. Transform
Here the `transform` operation returns \(LX^T\), therefore its time complexity equals `n_components * n_features * n_samples_test`. There is no added space complexity in the operation.
| programming_docs |
scikit_learn 2.6. Covariance estimation 2.6. Covariance estimation
==========================
Many statistical problems require the estimation of a population’s covariance matrix, which can be seen as an estimation of data set scatter plot shape. Most of the time, such an estimation has to be done on a sample whose properties (size, structure, homogeneity) have a large influence on the estimation’s quality. The [`sklearn.covariance`](classes#module-sklearn.covariance "sklearn.covariance") package provides tools for accurately estimating a population’s covariance matrix under various settings.
We assume that the observations are independent and identically distributed (i.i.d.).
2.6.1. Empirical covariance
----------------------------
The covariance matrix of a data set is known to be well approximated by the classical *maximum likelihood estimator* (or “empirical covariance”), provided the number of observations is large enough compared to the number of features (the variables describing the observations). More precisely, the Maximum Likelihood Estimator of a sample is an asymptotically unbiased estimator of the corresponding population’s covariance matrix.
The empirical covariance matrix of a sample can be computed using the [`empirical_covariance`](generated/sklearn.covariance.empirical_covariance#sklearn.covariance.empirical_covariance "sklearn.covariance.empirical_covariance") function of the package, or by fitting an [`EmpiricalCovariance`](generated/sklearn.covariance.empiricalcovariance#sklearn.covariance.EmpiricalCovariance "sklearn.covariance.EmpiricalCovariance") object to the data sample with the [`EmpiricalCovariance.fit`](generated/sklearn.covariance.empiricalcovariance#sklearn.covariance.EmpiricalCovariance.fit "sklearn.covariance.EmpiricalCovariance.fit") method. Be careful that results depend on whether the data are centered, so one may want to use the `assume_centered` parameter accurately. More precisely, if `assume_centered=False`, then the test set is supposed to have the same mean vector as the training set. If not, both should be centered by the user, and `assume_centered=True` should be used.
2.6.2. Shrunk Covariance
-------------------------
###
2.6.2.1. Basic shrinkage
Despite being an asymptotically unbiased estimator of the covariance matrix, the Maximum Likelihood Estimator is not a good estimator of the eigenvalues of the covariance matrix, so the precision matrix obtained from its inversion is not accurate. Sometimes, it even occurs that the empirical covariance matrix cannot be inverted for numerical reasons. To avoid such an inversion problem, a transformation of the empirical covariance matrix has been introduced: the `shrinkage`.
In scikit-learn, this transformation (with a user-defined shrinkage coefficient) can be directly applied to a pre-computed covariance with the [`shrunk_covariance`](generated/sklearn.covariance.shrunk_covariance#sklearn.covariance.shrunk_covariance "sklearn.covariance.shrunk_covariance") method. Also, a shrunk estimator of the covariance can be fitted to data with a [`ShrunkCovariance`](generated/sklearn.covariance.shrunkcovariance#sklearn.covariance.ShrunkCovariance "sklearn.covariance.ShrunkCovariance") object and its [`ShrunkCovariance.fit`](generated/sklearn.covariance.shrunkcovariance#sklearn.covariance.ShrunkCovariance.fit "sklearn.covariance.ShrunkCovariance.fit") method. Again, results depend on whether the data are centered, so one may want to use the `assume_centered` parameter accurately.
Mathematically, this shrinkage consists in reducing the ratio between the smallest and the largest eigenvalues of the empirical covariance matrix. It can be done by simply shifting every eigenvalue according to a given offset, which is equivalent of finding the l2-penalized Maximum Likelihood Estimator of the covariance matrix. In practice, shrinkage boils down to a simple a convex transformation : \(\Sigma\_{\rm shrunk} = (1-\alpha)\hat{\Sigma} + \alpha\frac{{\rm Tr}\hat{\Sigma}}{p}\rm Id\).
Choosing the amount of shrinkage, \(\alpha\) amounts to setting a bias/variance trade-off, and is discussed below.
###
2.6.2.2. Ledoit-Wolf shrinkage
In their 2004 paper [[1]](#id3), O. Ledoit and M. Wolf propose a formula to compute the optimal shrinkage coefficient \(\alpha\) that minimizes the Mean Squared Error between the estimated and the real covariance matrix.
The Ledoit-Wolf estimator of the covariance matrix can be computed on a sample with the [`ledoit_wolf`](generated/sklearn.covariance.ledoit_wolf#sklearn.covariance.ledoit_wolf "sklearn.covariance.ledoit_wolf") function of the [`sklearn.covariance`](classes#module-sklearn.covariance "sklearn.covariance") package, or it can be otherwise obtained by fitting a [`LedoitWolf`](generated/sklearn.covariance.ledoitwolf#sklearn.covariance.LedoitWolf "sklearn.covariance.LedoitWolf") object to the same sample.
Note
**Case when population covariance matrix is isotropic**
It is important to note that when the number of samples is much larger than the number of features, one would expect that no shrinkage would be necessary. The intuition behind this is that if the population covariance is full rank, when the number of sample grows, the sample covariance will also become positive definite. As a result, no shrinkage would necessary and the method should automatically do this.
This, however, is not the case in the Ledoit-Wolf procedure when the population covariance happens to be a multiple of the identity matrix. In this case, the Ledoit-Wolf shrinkage estimate approaches 1 as the number of samples increases. This indicates that the optimal estimate of the covariance matrix in the Ledoit-Wolf sense is multiple of the identity. Since the population covariance is already a multiple of the identity matrix, the Ledoit-Wolf solution is indeed a reasonable estimate.
###
2.6.2.3. Oracle Approximating Shrinkage
Under the assumption that the data are Gaussian distributed, Chen et al. [[2]](#id6) derived a formula aimed at choosing a shrinkage coefficient that yields a smaller Mean Squared Error than the one given by Ledoit and Wolf’s formula. The resulting estimator is known as the Oracle Shrinkage Approximating estimator of the covariance.
The OAS estimator of the covariance matrix can be computed on a sample with the [`oas`](generated/oas-function#sklearn.covariance.oas "sklearn.covariance.oas") function of the [`sklearn.covariance`](classes#module-sklearn.covariance "sklearn.covariance") package, or it can be otherwise obtained by fitting an [`OAS`](generated/sklearn.covariance.oas#sklearn.covariance.OAS "sklearn.covariance.OAS") object to the same sample.
Bias-variance trade-off when setting the shrinkage: comparing the choices of Ledoit-Wolf and OAS estimators
2.6.3. Sparse inverse covariance
---------------------------------
The matrix inverse of the covariance matrix, often called the precision matrix, is proportional to the partial correlation matrix. It gives the partial independence relationship. In other words, if two features are independent conditionally on the others, the corresponding coefficient in the precision matrix will be zero. This is why it makes sense to estimate a sparse precision matrix: the estimation of the covariance matrix is better conditioned by learning independence relations from the data. This is known as *covariance selection*.
In the small-samples situation, in which `n_samples` is on the order of `n_features` or smaller, sparse inverse covariance estimators tend to work better than shrunk covariance estimators. However, in the opposite situation, or for very correlated data, they can be numerically unstable. In addition, unlike shrinkage estimators, sparse estimators are able to recover off-diagonal structure.
The [`GraphicalLasso`](generated/sklearn.covariance.graphicallasso#sklearn.covariance.GraphicalLasso "sklearn.covariance.GraphicalLasso") estimator uses an l1 penalty to enforce sparsity on the precision matrix: the higher its `alpha` parameter, the more sparse the precision matrix. The corresponding [`GraphicalLassoCV`](generated/sklearn.covariance.graphicallassocv#sklearn.covariance.GraphicalLassoCV "sklearn.covariance.GraphicalLassoCV") object uses cross-validation to automatically set the `alpha` parameter.
*A comparison of maximum likelihood, shrinkage and sparse estimates of the covariance and precision matrix in the very small samples settings.*
Note
**Structure recovery**
Recovering a graphical structure from correlations in the data is a challenging thing. If you are interested in such recovery keep in mind that:
* Recovery is easier from a correlation matrix than a covariance matrix: standardize your observations before running [`GraphicalLasso`](generated/sklearn.covariance.graphicallasso#sklearn.covariance.GraphicalLasso "sklearn.covariance.GraphicalLasso")
* If the underlying graph has nodes with much more connections than the average node, the algorithm will miss some of these connections.
* If your number of observations is not large compared to the number of edges in your underlying graph, you will not recover it.
* Even if you are in favorable recovery conditions, the alpha parameter chosen by cross-validation (e.g. using the [`GraphicalLassoCV`](generated/sklearn.covariance.graphicallassocv#sklearn.covariance.GraphicalLassoCV "sklearn.covariance.GraphicalLassoCV") object) will lead to selecting too many edges. However, the relevant edges will have heavier weights than the irrelevant ones.
The mathematical formulation is the following:
\[\hat{K} = \mathrm{argmin}\_K \big( \mathrm{tr} S K - \mathrm{log} \mathrm{det} K + \alpha \|K\|\_1 \big)\] Where \(K\) is the precision matrix to be estimated, and \(S\) is the sample covariance matrix. \(\|K\|\_1\) is the sum of the absolute values of off-diagonal coefficients of \(K\). The algorithm employed to solve this problem is the GLasso algorithm, from the Friedman 2008 Biostatistics paper. It is the same algorithm as in the R `glasso` package.
2.6.4. Robust Covariance Estimation
------------------------------------
Real data sets are often subject to measurement or recording errors. Regular but uncommon observations may also appear for a variety of reasons. Observations which are very uncommon are called outliers. The empirical covariance estimator and the shrunk covariance estimators presented above are very sensitive to the presence of outliers in the data. Therefore, one should use robust covariance estimators to estimate the covariance of its real data sets. Alternatively, robust covariance estimators can be used to perform outlier detection and discard/downweight some observations according to further processing of the data.
The `sklearn.covariance` package implements a robust estimator of covariance, the Minimum Covariance Determinant [[3]](#id11).
###
2.6.4.1. Minimum Covariance Determinant
The Minimum Covariance Determinant estimator is a robust estimator of a data set’s covariance introduced by P.J. Rousseeuw in [[3]](#id11). The idea is to find a given proportion (h) of “good” observations which are not outliers and compute their empirical covariance matrix. This empirical covariance matrix is then rescaled to compensate the performed selection of observations (“consistency step”). Having computed the Minimum Covariance Determinant estimator, one can give weights to observations according to their Mahalanobis distance, leading to a reweighted estimate of the covariance matrix of the data set (“reweighting step”).
Rousseeuw and Van Driessen [[4]](#id12) developed the FastMCD algorithm in order to compute the Minimum Covariance Determinant. This algorithm is used in scikit-learn when fitting an MCD object to data. The FastMCD algorithm also computes a robust estimate of the data set location at the same time.
Raw estimates can be accessed as `raw_location_` and `raw_covariance_` attributes of a [`MinCovDet`](generated/sklearn.covariance.mincovdet#sklearn.covariance.MinCovDet "sklearn.covariance.MinCovDet") robust covariance estimator object.
| Influence of outliers on location and covariance estimates | Separating inliers from outliers using a Mahalanobis distance |
| --- | --- |
| | |
scikit_learn 3.3. Metrics and scoring: quantifying the quality of predictions 3.3. Metrics and scoring: quantifying the quality of predictions
================================================================
There are 3 different APIs for evaluating the quality of a model’s predictions:
* **Estimator score method**: Estimators have a `score` method providing a default evaluation criterion for the problem they are designed to solve. This is not discussed on this page, but in each estimator’s documentation.
* **Scoring parameter**: Model-evaluation tools using [cross-validation](cross_validation#cross-validation) (such as [`model_selection.cross_val_score`](generated/sklearn.model_selection.cross_val_score#sklearn.model_selection.cross_val_score "sklearn.model_selection.cross_val_score") and [`model_selection.GridSearchCV`](generated/sklearn.model_selection.gridsearchcv#sklearn.model_selection.GridSearchCV "sklearn.model_selection.GridSearchCV")) rely on an internal *scoring* strategy. This is discussed in the section [The scoring parameter: defining model evaluation rules](#scoring-parameter).
* **Metric functions**: The [`sklearn.metrics`](classes#module-sklearn.metrics "sklearn.metrics") module implements functions assessing prediction error for specific purposes. These metrics are detailed in sections on [Classification metrics](#classification-metrics), [Multilabel ranking metrics](#multilabel-ranking-metrics), [Regression metrics](#regression-metrics) and [Clustering metrics](#clustering-metrics).
Finally, [Dummy estimators](#dummy-estimators) are useful to get a baseline value of those metrics for random predictions.
See also
For “pairwise” metrics, between *samples* and not estimators or predictions, see the [Pairwise metrics, Affinities and Kernels](metrics#metrics) section.
3.3.1. The `scoring` parameter: defining model evaluation rules
----------------------------------------------------------------
Model selection and evaluation using tools, such as [`model_selection.GridSearchCV`](generated/sklearn.model_selection.gridsearchcv#sklearn.model_selection.GridSearchCV "sklearn.model_selection.GridSearchCV") and [`model_selection.cross_val_score`](generated/sklearn.model_selection.cross_val_score#sklearn.model_selection.cross_val_score "sklearn.model_selection.cross_val_score"), take a `scoring` parameter that controls what metric they apply to the estimators evaluated.
###
3.3.1.1. Common cases: predefined values
For the most common use cases, you can designate a scorer object with the `scoring` parameter; the table below shows all possible values. All scorer objects follow the convention that **higher return values are better than lower return values**. Thus metrics which measure the distance between the model and the data, like [`metrics.mean_squared_error`](generated/sklearn.metrics.mean_squared_error#sklearn.metrics.mean_squared_error "sklearn.metrics.mean_squared_error"), are available as neg\_mean\_squared\_error which return the negated value of the metric.
| Scoring | Function | Comment |
| --- | --- | --- |
| **Classification** | | |
| ‘accuracy’ | [`metrics.accuracy_score`](generated/sklearn.metrics.accuracy_score#sklearn.metrics.accuracy_score "sklearn.metrics.accuracy_score") | |
| ‘balanced\_accuracy’ | [`metrics.balanced_accuracy_score`](generated/sklearn.metrics.balanced_accuracy_score#sklearn.metrics.balanced_accuracy_score "sklearn.metrics.balanced_accuracy_score") | |
| ‘top\_k\_accuracy’ | [`metrics.top_k_accuracy_score`](generated/sklearn.metrics.top_k_accuracy_score#sklearn.metrics.top_k_accuracy_score "sklearn.metrics.top_k_accuracy_score") | |
| ‘average\_precision’ | [`metrics.average_precision_score`](generated/sklearn.metrics.average_precision_score#sklearn.metrics.average_precision_score "sklearn.metrics.average_precision_score") | |
| ‘neg\_brier\_score’ | [`metrics.brier_score_loss`](generated/sklearn.metrics.brier_score_loss#sklearn.metrics.brier_score_loss "sklearn.metrics.brier_score_loss") | |
| ‘f1’ | [`metrics.f1_score`](generated/sklearn.metrics.f1_score#sklearn.metrics.f1_score "sklearn.metrics.f1_score") | for binary targets |
| ‘f1\_micro’ | [`metrics.f1_score`](generated/sklearn.metrics.f1_score#sklearn.metrics.f1_score "sklearn.metrics.f1_score") | micro-averaged |
| ‘f1\_macro’ | [`metrics.f1_score`](generated/sklearn.metrics.f1_score#sklearn.metrics.f1_score "sklearn.metrics.f1_score") | macro-averaged |
| ‘f1\_weighted’ | [`metrics.f1_score`](generated/sklearn.metrics.f1_score#sklearn.metrics.f1_score "sklearn.metrics.f1_score") | weighted average |
| ‘f1\_samples’ | [`metrics.f1_score`](generated/sklearn.metrics.f1_score#sklearn.metrics.f1_score "sklearn.metrics.f1_score") | by multilabel sample |
| ‘neg\_log\_loss’ | [`metrics.log_loss`](generated/sklearn.metrics.log_loss#sklearn.metrics.log_loss "sklearn.metrics.log_loss") | requires `predict_proba` support |
| ‘precision’ etc. | [`metrics.precision_score`](generated/sklearn.metrics.precision_score#sklearn.metrics.precision_score "sklearn.metrics.precision_score") | suffixes apply as with ‘f1’ |
| ‘recall’ etc. | [`metrics.recall_score`](generated/sklearn.metrics.recall_score#sklearn.metrics.recall_score "sklearn.metrics.recall_score") | suffixes apply as with ‘f1’ |
| ‘jaccard’ etc. | [`metrics.jaccard_score`](generated/sklearn.metrics.jaccard_score#sklearn.metrics.jaccard_score "sklearn.metrics.jaccard_score") | suffixes apply as with ‘f1’ |
| ‘roc\_auc’ | [`metrics.roc_auc_score`](generated/sklearn.metrics.roc_auc_score#sklearn.metrics.roc_auc_score "sklearn.metrics.roc_auc_score") | |
| ‘roc\_auc\_ovr’ | [`metrics.roc_auc_score`](generated/sklearn.metrics.roc_auc_score#sklearn.metrics.roc_auc_score "sklearn.metrics.roc_auc_score") | |
| ‘roc\_auc\_ovo’ | [`metrics.roc_auc_score`](generated/sklearn.metrics.roc_auc_score#sklearn.metrics.roc_auc_score "sklearn.metrics.roc_auc_score") | |
| ‘roc\_auc\_ovr\_weighted’ | [`metrics.roc_auc_score`](generated/sklearn.metrics.roc_auc_score#sklearn.metrics.roc_auc_score "sklearn.metrics.roc_auc_score") | |
| ‘roc\_auc\_ovo\_weighted’ | [`metrics.roc_auc_score`](generated/sklearn.metrics.roc_auc_score#sklearn.metrics.roc_auc_score "sklearn.metrics.roc_auc_score") | |
| **Clustering** | | |
| ‘adjusted\_mutual\_info\_score’ | [`metrics.adjusted_mutual_info_score`](generated/sklearn.metrics.adjusted_mutual_info_score#sklearn.metrics.adjusted_mutual_info_score "sklearn.metrics.adjusted_mutual_info_score") | |
| ‘adjusted\_rand\_score’ | [`metrics.adjusted_rand_score`](generated/sklearn.metrics.adjusted_rand_score#sklearn.metrics.adjusted_rand_score "sklearn.metrics.adjusted_rand_score") | |
| ‘completeness\_score’ | [`metrics.completeness_score`](generated/sklearn.metrics.completeness_score#sklearn.metrics.completeness_score "sklearn.metrics.completeness_score") | |
| ‘fowlkes\_mallows\_score’ | [`metrics.fowlkes_mallows_score`](generated/sklearn.metrics.fowlkes_mallows_score#sklearn.metrics.fowlkes_mallows_score "sklearn.metrics.fowlkes_mallows_score") | |
| ‘homogeneity\_score’ | [`metrics.homogeneity_score`](generated/sklearn.metrics.homogeneity_score#sklearn.metrics.homogeneity_score "sklearn.metrics.homogeneity_score") | |
| ‘mutual\_info\_score’ | [`metrics.mutual_info_score`](generated/sklearn.metrics.mutual_info_score#sklearn.metrics.mutual_info_score "sklearn.metrics.mutual_info_score") | |
| ‘normalized\_mutual\_info\_score’ | [`metrics.normalized_mutual_info_score`](generated/sklearn.metrics.normalized_mutual_info_score#sklearn.metrics.normalized_mutual_info_score "sklearn.metrics.normalized_mutual_info_score") | |
| ‘rand\_score’ | [`metrics.rand_score`](generated/sklearn.metrics.rand_score#sklearn.metrics.rand_score "sklearn.metrics.rand_score") | |
| ‘v\_measure\_score’ | [`metrics.v_measure_score`](generated/sklearn.metrics.v_measure_score#sklearn.metrics.v_measure_score "sklearn.metrics.v_measure_score") | |
| **Regression** | | |
| ‘explained\_variance’ | [`metrics.explained_variance_score`](generated/sklearn.metrics.explained_variance_score#sklearn.metrics.explained_variance_score "sklearn.metrics.explained_variance_score") | |
| ‘max\_error’ | [`metrics.max_error`](generated/sklearn.metrics.max_error#sklearn.metrics.max_error "sklearn.metrics.max_error") | |
| ‘neg\_mean\_absolute\_error’ | [`metrics.mean_absolute_error`](generated/sklearn.metrics.mean_absolute_error#sklearn.metrics.mean_absolute_error "sklearn.metrics.mean_absolute_error") | |
| ‘neg\_mean\_squared\_error’ | [`metrics.mean_squared_error`](generated/sklearn.metrics.mean_squared_error#sklearn.metrics.mean_squared_error "sklearn.metrics.mean_squared_error") | |
| ‘neg\_root\_mean\_squared\_error’ | [`metrics.mean_squared_error`](generated/sklearn.metrics.mean_squared_error#sklearn.metrics.mean_squared_error "sklearn.metrics.mean_squared_error") | |
| ‘neg\_mean\_squared\_log\_error’ | [`metrics.mean_squared_log_error`](generated/sklearn.metrics.mean_squared_log_error#sklearn.metrics.mean_squared_log_error "sklearn.metrics.mean_squared_log_error") | |
| ‘neg\_median\_absolute\_error’ | [`metrics.median_absolute_error`](generated/sklearn.metrics.median_absolute_error#sklearn.metrics.median_absolute_error "sklearn.metrics.median_absolute_error") | |
| ‘r2’ | [`metrics.r2_score`](generated/sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score") | |
| ‘neg\_mean\_poisson\_deviance’ | [`metrics.mean_poisson_deviance`](generated/sklearn.metrics.mean_poisson_deviance#sklearn.metrics.mean_poisson_deviance "sklearn.metrics.mean_poisson_deviance") | |
| ‘neg\_mean\_gamma\_deviance’ | [`metrics.mean_gamma_deviance`](generated/sklearn.metrics.mean_gamma_deviance#sklearn.metrics.mean_gamma_deviance "sklearn.metrics.mean_gamma_deviance") | |
| ‘neg\_mean\_absolute\_percentage\_error’ | [`metrics.mean_absolute_percentage_error`](generated/sklearn.metrics.mean_absolute_percentage_error#sklearn.metrics.mean_absolute_percentage_error "sklearn.metrics.mean_absolute_percentage_error") | |
| ‘d2\_absolute\_error\_score’ | [`metrics.d2_absolute_error_score`](generated/sklearn.metrics.d2_absolute_error_score#sklearn.metrics.d2_absolute_error_score "sklearn.metrics.d2_absolute_error_score") | |
| ‘d2\_pinball\_score’ | [`metrics.d2_pinball_score`](generated/sklearn.metrics.d2_pinball_score#sklearn.metrics.d2_pinball_score "sklearn.metrics.d2_pinball_score") | |
| ‘d2\_tweedie\_score’ | [`metrics.d2_tweedie_score`](generated/sklearn.metrics.d2_tweedie_score#sklearn.metrics.d2_tweedie_score "sklearn.metrics.d2_tweedie_score") | |
Usage examples:
```
>>> from sklearn import svm, datasets
>>> from sklearn.model_selection import cross_val_score
>>> X, y = datasets.load_iris(return_X_y=True)
>>> clf = svm.SVC(random_state=0)
>>> cross_val_score(clf, X, y, cv=5, scoring='recall_macro')
array([0.96..., 0.96..., 0.96..., 0.93..., 1. ])
>>> model = svm.SVC()
>>> cross_val_score(model, X, y, cv=5, scoring='wrong_choice')
Traceback (most recent call last):
ValueError: 'wrong_choice' is not a valid scoring value. Use
sklearn.metrics.get_scorer_names() to get valid options.
```
Note
The values listed by the `ValueError` exception correspond to the functions measuring prediction accuracy described in the following sections. You can retrieve the names of all available scorers by calling [`get_scorer_names`](generated/sklearn.metrics.get_scorer_names#sklearn.metrics.get_scorer_names "sklearn.metrics.get_scorer_names").
###
3.3.1.2. Defining your scoring strategy from metric functions
The module [`sklearn.metrics`](classes#module-sklearn.metrics "sklearn.metrics") also exposes a set of simple functions measuring a prediction error given ground truth and prediction:
* functions ending with `_score` return a value to maximize, the higher the better.
* functions ending with `_error` or `_loss` return a value to minimize, the lower the better. When converting into a scorer object using [`make_scorer`](generated/sklearn.metrics.make_scorer#sklearn.metrics.make_scorer "sklearn.metrics.make_scorer"), set the `greater_is_better` parameter to `False` (`True` by default; see the parameter description below).
Metrics available for various machine learning tasks are detailed in sections below.
Many metrics are not given names to be used as `scoring` values, sometimes because they require additional parameters, such as [`fbeta_score`](generated/sklearn.metrics.fbeta_score#sklearn.metrics.fbeta_score "sklearn.metrics.fbeta_score"). In such cases, you need to generate an appropriate scoring object. The simplest way to generate a callable object for scoring is by using [`make_scorer`](generated/sklearn.metrics.make_scorer#sklearn.metrics.make_scorer "sklearn.metrics.make_scorer"). That function converts metrics into callables that can be used for model evaluation.
One typical use case is to wrap an existing metric function from the library with non-default values for its parameters, such as the `beta` parameter for the [`fbeta_score`](generated/sklearn.metrics.fbeta_score#sklearn.metrics.fbeta_score "sklearn.metrics.fbeta_score") function:
```
>>> from sklearn.metrics import fbeta_score, make_scorer
>>> ftwo_scorer = make_scorer(fbeta_score, beta=2)
>>> from sklearn.model_selection import GridSearchCV
>>> from sklearn.svm import LinearSVC
>>> grid = GridSearchCV(LinearSVC(), param_grid={'C': [1, 10]},
... scoring=ftwo_scorer, cv=5)
```
The second use case is to build a completely custom scorer object from a simple python function using [`make_scorer`](generated/sklearn.metrics.make_scorer#sklearn.metrics.make_scorer "sklearn.metrics.make_scorer"), which can take several parameters:
* the python function you want to use (`my_custom_loss_func` in the example below)
* whether the python function returns a score (`greater_is_better=True`, the default) or a loss (`greater_is_better=False`). If a loss, the output of the python function is negated by the scorer object, conforming to the cross validation convention that scorers return higher values for better models.
* for classification metrics only: whether the python function you provided requires continuous decision certainties (`needs_threshold=True`). The default value is False.
* any additional parameters, such as `beta` or `labels` in [`f1_score`](generated/sklearn.metrics.f1_score#sklearn.metrics.f1_score "sklearn.metrics.f1_score").
Here is an example of building custom scorers, and of using the `greater_is_better` parameter:
```
>>> import numpy as np
>>> def my_custom_loss_func(y_true, y_pred):
... diff = np.abs(y_true - y_pred).max()
... return np.log1p(diff)
...
>>> # score will negate the return value of my_custom_loss_func,
>>> # which will be np.log(2), 0.693, given the values for X
>>> # and y defined below.
>>> score = make_scorer(my_custom_loss_func, greater_is_better=False)
>>> X = [[1], [1]]
>>> y = [0, 1]
>>> from sklearn.dummy import DummyClassifier
>>> clf = DummyClassifier(strategy='most_frequent', random_state=0)
>>> clf = clf.fit(X, y)
>>> my_custom_loss_func(y, clf.predict(X))
0.69...
>>> score(clf, X, y)
-0.69...
```
###
3.3.1.3. Implementing your own scoring object
You can generate even more flexible model scorers by constructing your own scoring object from scratch, without using the [`make_scorer`](generated/sklearn.metrics.make_scorer#sklearn.metrics.make_scorer "sklearn.metrics.make_scorer") factory. For a callable to be a scorer, it needs to meet the protocol specified by the following two rules:
* It can be called with parameters `(estimator, X, y)`, where `estimator` is the model that should be evaluated, `X` is validation data, and `y` is the ground truth target for `X` (in the supervised case) or `None` (in the unsupervised case).
* It returns a floating point number that quantifies the `estimator` prediction quality on `X`, with reference to `y`. Again, by convention higher numbers are better, so if your scorer returns loss, that value should be negated.
Note
**Using custom scorers in functions where n\_jobs > 1**
While defining the custom scoring function alongside the calling function should work out of the box with the default joblib backend (loky), importing it from another module will be a more robust approach and work independently of the joblib backend.
For example, to use `n_jobs` greater than 1 in the example below, `custom_scoring_function` function is saved in a user-created module (`custom_scorer_module.py`) and imported:
```
>>> from custom_scorer_module import custom_scoring_function
>>> cross_val_score(model,
... X_train,
... y_train,
... scoring=make_scorer(custom_scoring_function, greater_is_better=False),
... cv=5,
... n_jobs=-1)
```
###
3.3.1.4. Using multiple metric evaluation
Scikit-learn also permits evaluation of multiple metrics in `GridSearchCV`, `RandomizedSearchCV` and `cross_validate`.
There are three ways to specify multiple scoring metrics for the `scoring` parameter:
* As an iterable of string metrics::
```
>>> scoring = ['accuracy', 'precision']
```
* As a `dict` mapping the scorer name to the scoring function::
```
>>> from sklearn.metrics import accuracy_score
>>> from sklearn.metrics import make_scorer
>>> scoring = {'accuracy': make_scorer(accuracy_score),
... 'prec': 'precision'}
```
Note that the dict values can either be scorer functions or one of the predefined metric strings.
* As a callable that returns a dictionary of scores:
```
>>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import confusion_matrix
>>> # A sample toy binary classification dataset
>>> X, y = datasets.make_classification(n_classes=2, random_state=0)
>>> svm = LinearSVC(random_state=0)
>>> def confusion_matrix_scorer(clf, X, y):
... y_pred = clf.predict(X)
... cm = confusion_matrix(y, y_pred)
... return {'tn': cm[0, 0], 'fp': cm[0, 1],
... 'fn': cm[1, 0], 'tp': cm[1, 1]}
>>> cv_results = cross_validate(svm, X, y, cv=5,
... scoring=confusion_matrix_scorer)
>>> # Getting the test set true positive scores
>>> print(cv_results['test_tp'])
[10 9 8 7 8]
>>> # Getting the test set false negative scores
>>> print(cv_results['test_fn'])
[0 1 2 3 2]
```
3.3.2. Classification metrics
------------------------------
The [`sklearn.metrics`](classes#module-sklearn.metrics "sklearn.metrics") module implements several loss, score, and utility functions to measure classification performance. Some metrics might require probability estimates of the positive class, confidence values, or binary decisions values. Most implementations allow each sample to provide a weighted contribution to the overall score, through the `sample_weight` parameter.
Some of these are restricted to the binary classification case:
| | |
| --- | --- |
| [`precision_recall_curve`](generated/sklearn.metrics.precision_recall_curve#sklearn.metrics.precision_recall_curve "sklearn.metrics.precision_recall_curve")(y\_true, probas\_pred, \*) | Compute precision-recall pairs for different probability thresholds. |
| [`roc_curve`](generated/sklearn.metrics.roc_curve#sklearn.metrics.roc_curve "sklearn.metrics.roc_curve")(y\_true, y\_score, \*[, pos\_label, ...]) | Compute Receiver operating characteristic (ROC). |
| [`det_curve`](generated/sklearn.metrics.det_curve#sklearn.metrics.det_curve "sklearn.metrics.det_curve")(y\_true, y\_score[, pos\_label, ...]) | Compute error rates for different probability thresholds. |
Others also work in the multiclass case:
| | |
| --- | --- |
| [`balanced_accuracy_score`](generated/sklearn.metrics.balanced_accuracy_score#sklearn.metrics.balanced_accuracy_score "sklearn.metrics.balanced_accuracy_score")(y\_true, y\_pred, \*[, ...]) | Compute the balanced accuracy. |
| [`cohen_kappa_score`](generated/sklearn.metrics.cohen_kappa_score#sklearn.metrics.cohen_kappa_score "sklearn.metrics.cohen_kappa_score")(y1, y2, \*[, labels, ...]) | Compute Cohen's kappa: a statistic that measures inter-annotator agreement. |
| [`confusion_matrix`](generated/sklearn.metrics.confusion_matrix#sklearn.metrics.confusion_matrix "sklearn.metrics.confusion_matrix")(y\_true, y\_pred, \*[, ...]) | Compute confusion matrix to evaluate the accuracy of a classification. |
| [`hinge_loss`](generated/sklearn.metrics.hinge_loss#sklearn.metrics.hinge_loss "sklearn.metrics.hinge_loss")(y\_true, pred\_decision, \*[, ...]) | Average hinge loss (non-regularized). |
| [`matthews_corrcoef`](generated/sklearn.metrics.matthews_corrcoef#sklearn.metrics.matthews_corrcoef "sklearn.metrics.matthews_corrcoef")(y\_true, y\_pred, \*[, ...]) | Compute the Matthews correlation coefficient (MCC). |
| [`roc_auc_score`](generated/sklearn.metrics.roc_auc_score#sklearn.metrics.roc_auc_score "sklearn.metrics.roc_auc_score")(y\_true, y\_score, \*[, average, ...]) | Compute Area Under the Receiver Operating Characteristic Curve (ROC AUC) from prediction scores. |
| [`top_k_accuracy_score`](generated/sklearn.metrics.top_k_accuracy_score#sklearn.metrics.top_k_accuracy_score "sklearn.metrics.top_k_accuracy_score")(y\_true, y\_score, \*[, ...]) | Top-k Accuracy classification score. |
Some also work in the multilabel case:
| | |
| --- | --- |
| [`accuracy_score`](generated/sklearn.metrics.accuracy_score#sklearn.metrics.accuracy_score "sklearn.metrics.accuracy_score")(y\_true, y\_pred, \*[, ...]) | Accuracy classification score. |
| [`classification_report`](generated/sklearn.metrics.classification_report#sklearn.metrics.classification_report "sklearn.metrics.classification_report")(y\_true, y\_pred, \*[, ...]) | Build a text report showing the main classification metrics. |
| [`f1_score`](generated/sklearn.metrics.f1_score#sklearn.metrics.f1_score "sklearn.metrics.f1_score")(y\_true, y\_pred, \*[, labels, ...]) | Compute the F1 score, also known as balanced F-score or F-measure. |
| [`fbeta_score`](generated/sklearn.metrics.fbeta_score#sklearn.metrics.fbeta_score "sklearn.metrics.fbeta_score")(y\_true, y\_pred, \*, beta[, ...]) | Compute the F-beta score. |
| [`hamming_loss`](generated/sklearn.metrics.hamming_loss#sklearn.metrics.hamming_loss "sklearn.metrics.hamming_loss")(y\_true, y\_pred, \*[, sample\_weight]) | Compute the average Hamming loss. |
| [`jaccard_score`](generated/sklearn.metrics.jaccard_score#sklearn.metrics.jaccard_score "sklearn.metrics.jaccard_score")(y\_true, y\_pred, \*[, labels, ...]) | Jaccard similarity coefficient score. |
| [`log_loss`](generated/sklearn.metrics.log_loss#sklearn.metrics.log_loss "sklearn.metrics.log_loss")(y\_true, y\_pred, \*[, eps, ...]) | Log loss, aka logistic loss or cross-entropy loss. |
| [`multilabel_confusion_matrix`](generated/sklearn.metrics.multilabel_confusion_matrix#sklearn.metrics.multilabel_confusion_matrix "sklearn.metrics.multilabel_confusion_matrix")(y\_true, y\_pred, \*) | Compute a confusion matrix for each class or sample. |
| [`precision_recall_fscore_support`](generated/sklearn.metrics.precision_recall_fscore_support#sklearn.metrics.precision_recall_fscore_support "sklearn.metrics.precision_recall_fscore_support")(y\_true, ...) | Compute precision, recall, F-measure and support for each class. |
| [`precision_score`](generated/sklearn.metrics.precision_score#sklearn.metrics.precision_score "sklearn.metrics.precision_score")(y\_true, y\_pred, \*[, labels, ...]) | Compute the precision. |
| [`recall_score`](generated/sklearn.metrics.recall_score#sklearn.metrics.recall_score "sklearn.metrics.recall_score")(y\_true, y\_pred, \*[, labels, ...]) | Compute the recall. |
| [`roc_auc_score`](generated/sklearn.metrics.roc_auc_score#sklearn.metrics.roc_auc_score "sklearn.metrics.roc_auc_score")(y\_true, y\_score, \*[, average, ...]) | Compute Area Under the Receiver Operating Characteristic Curve (ROC AUC) from prediction scores. |
| [`zero_one_loss`](generated/sklearn.metrics.zero_one_loss#sklearn.metrics.zero_one_loss "sklearn.metrics.zero_one_loss")(y\_true, y\_pred, \*[, ...]) | Zero-one classification loss. |
And some work with binary and multilabel (but not multiclass) problems:
| | |
| --- | --- |
| [`average_precision_score`](generated/sklearn.metrics.average_precision_score#sklearn.metrics.average_precision_score "sklearn.metrics.average_precision_score")(y\_true, y\_score, \*) | Compute average precision (AP) from prediction scores. |
In the following sub-sections, we will describe each of those functions, preceded by some notes on common API and metric definition.
###
3.3.2.1. From binary to multiclass and multilabel
Some metrics are essentially defined for binary classification tasks (e.g. [`f1_score`](generated/sklearn.metrics.f1_score#sklearn.metrics.f1_score "sklearn.metrics.f1_score"), [`roc_auc_score`](generated/sklearn.metrics.roc_auc_score#sklearn.metrics.roc_auc_score "sklearn.metrics.roc_auc_score")). In these cases, by default only the positive label is evaluated, assuming by default that the positive class is labelled `1` (though this may be configurable through the `pos_label` parameter).
In extending a binary metric to multiclass or multilabel problems, the data is treated as a collection of binary problems, one for each class. There are then a number of ways to average binary metric calculations across the set of classes, each of which may be useful in some scenario. Where available, you should select among these using the `average` parameter.
* `"macro"` simply calculates the mean of the binary metrics, giving equal weight to each class. In problems where infrequent classes are nonetheless important, macro-averaging may be a means of highlighting their performance. On the other hand, the assumption that all classes are equally important is often untrue, such that macro-averaging will over-emphasize the typically low performance on an infrequent class.
* `"weighted"` accounts for class imbalance by computing the average of binary metrics in which each class’s score is weighted by its presence in the true data sample.
* `"micro"` gives each sample-class pair an equal contribution to the overall metric (except as a result of sample-weight). Rather than summing the metric per class, this sums the dividends and divisors that make up the per-class metrics to calculate an overall quotient. Micro-averaging may be preferred in multilabel settings, including multiclass classification where a majority class is to be ignored.
* `"samples"` applies only to multilabel problems. It does not calculate a per-class measure, instead calculating the metric over the true and predicted classes for each sample in the evaluation data, and returning their (`sample_weight`-weighted) average.
* Selecting `average=None` will return an array with the score for each class.
While multiclass data is provided to the metric, like binary targets, as an array of class labels, multilabel data is specified as an indicator matrix, in which cell `[i, j]` has value 1 if sample `i` has label `j` and value 0 otherwise.
###
3.3.2.2. Accuracy score
The [`accuracy_score`](generated/sklearn.metrics.accuracy_score#sklearn.metrics.accuracy_score "sklearn.metrics.accuracy_score") function computes the [accuracy](https://en.wikipedia.org/wiki/Accuracy_and_precision), either the fraction (default) or the count (normalize=False) of correct predictions.
In multilabel classification, the function returns the subset accuracy. If the entire set of predicted labels for a sample strictly match with the true set of labels, then the subset accuracy is 1.0; otherwise it is 0.0.
If \(\hat{y}\_i\) is the predicted value of the \(i\)-th sample and \(y\_i\) is the corresponding true value, then the fraction of correct predictions over \(n\_\text{samples}\) is defined as
\[\texttt{accuracy}(y, \hat{y}) = \frac{1}{n\_\text{samples}} \sum\_{i=0}^{n\_\text{samples}-1} 1(\hat{y}\_i = y\_i)\] where \(1(x)\) is the [indicator function](https://en.wikipedia.org/wiki/Indicator_function).
```
>>> import numpy as np
>>> from sklearn.metrics import accuracy_score
>>> y_pred = [0, 2, 1, 3]
>>> y_true = [0, 1, 2, 3]
>>> accuracy_score(y_true, y_pred)
0.5
>>> accuracy_score(y_true, y_pred, normalize=False)
2
```
In the multilabel case with binary label indicators:
```
>>> accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
0.5
```
###
3.3.2.3. Top-k accuracy score
The [`top_k_accuracy_score`](generated/sklearn.metrics.top_k_accuracy_score#sklearn.metrics.top_k_accuracy_score "sklearn.metrics.top_k_accuracy_score") function is a generalization of [`accuracy_score`](generated/sklearn.metrics.accuracy_score#sklearn.metrics.accuracy_score "sklearn.metrics.accuracy_score"). The difference is that a prediction is considered correct as long as the true label is associated with one of the `k` highest predicted scores. [`accuracy_score`](generated/sklearn.metrics.accuracy_score#sklearn.metrics.accuracy_score "sklearn.metrics.accuracy_score") is the special case of `k = 1`.
The function covers the binary and multiclass classification cases but not the multilabel case.
If \(\hat{f}\_{i,j}\) is the predicted class for the \(i\)-th sample corresponding to the \(j\)-th largest predicted score and \(y\_i\) is the corresponding true value, then the fraction of correct predictions over \(n\_\text{samples}\) is defined as
\[\texttt{top-k accuracy}(y, \hat{f}) = \frac{1}{n\_\text{samples}} \sum\_{i=0}^{n\_\text{samples}-1} \sum\_{j=1}^{k} 1(\hat{f}\_{i,j} = y\_i)\] where \(k\) is the number of guesses allowed and \(1(x)\) is the [indicator function](https://en.wikipedia.org/wiki/Indicator_function).
```
>>> import numpy as np
>>> from sklearn.metrics import top_k_accuracy_score
>>> y_true = np.array([0, 1, 2, 2])
>>> y_score = np.array([[0.5, 0.2, 0.2],
... [0.3, 0.4, 0.2],
... [0.2, 0.4, 0.3],
... [0.7, 0.2, 0.1]])
>>> top_k_accuracy_score(y_true, y_score, k=2)
0.75
>>> # Not normalizing gives the number of "correctly" classified samples
>>> top_k_accuracy_score(y_true, y_score, k=2, normalize=False)
3
```
###
3.3.2.4. Balanced accuracy score
The [`balanced_accuracy_score`](generated/sklearn.metrics.balanced_accuracy_score#sklearn.metrics.balanced_accuracy_score "sklearn.metrics.balanced_accuracy_score") function computes the [balanced accuracy](https://en.wikipedia.org/wiki/Accuracy_and_precision), which avoids inflated performance estimates on imbalanced datasets. It is the macro-average of recall scores per class or, equivalently, raw accuracy where each sample is weighted according to the inverse prevalence of its true class. Thus for balanced datasets, the score is equal to accuracy.
In the binary case, balanced accuracy is equal to the arithmetic mean of [sensitivity](https://en.wikipedia.org/wiki/Sensitivity_and_specificity) (true positive rate) and [specificity](https://en.wikipedia.org/wiki/Sensitivity_and_specificity) (true negative rate), or the area under the ROC curve with binary predictions rather than scores:
\[\texttt{balanced-accuracy} = \frac{1}{2}\left( \frac{TP}{TP + FN} + \frac{TN}{TN + FP}\right )\] If the classifier performs equally well on either class, this term reduces to the conventional accuracy (i.e., the number of correct predictions divided by the total number of predictions).
In contrast, if the conventional accuracy is above chance only because the classifier takes advantage of an imbalanced test set, then the balanced accuracy, as appropriate, will drop to \(\frac{1}{n\\_classes}\).
The score ranges from 0 to 1, or when `adjusted=True` is used, it rescaled to the range \(\frac{1}{1 - n\\_classes}\) to 1, inclusive, with performance at random scoring 0.
If \(y\_i\) is the true value of the \(i\)-th sample, and \(w\_i\) is the corresponding sample weight, then we adjust the sample weight to:
\[\hat{w}\_i = \frac{w\_i}{\sum\_j{1(y\_j = y\_i) w\_j}}\] where \(1(x)\) is the [indicator function](https://en.wikipedia.org/wiki/Indicator_function). Given predicted \(\hat{y}\_i\) for sample \(i\), balanced accuracy is defined as:
\[\texttt{balanced-accuracy}(y, \hat{y}, w) = \frac{1}{\sum{\hat{w}\_i}} \sum\_i 1(\hat{y}\_i = y\_i) \hat{w}\_i\] With `adjusted=True`, balanced accuracy reports the relative increase from \(\texttt{balanced-accuracy}(y, \mathbf{0}, w) = \frac{1}{n\\_classes}\). In the binary case, this is also known as [\*Youden’s J statistic\*](https://en.wikipedia.org/wiki/Youden%27s_J_statistic), or *informedness*.
Note
The multiclass definition here seems the most reasonable extension of the metric used in binary classification, though there is no certain consensus in the literature:
* Our definition: [[Mosley2013]](#mosley2013), [[Kelleher2015]](#kelleher2015) and [[Guyon2015]](#guyon2015), where [[Guyon2015]](#guyon2015) adopt the adjusted version to ensure that random predictions have a score of \(0\) and perfect predictions have a score of \(1\)..
* Class balanced accuracy as described in [[Mosley2013]](#mosley2013): the minimum between the precision and the recall for each class is computed. Those values are then averaged over the total number of classes to get the balanced accuracy.
* Balanced Accuracy as described in [[Urbanowicz2015]](#urbanowicz2015): the average of sensitivity and specificity is computed for each class and then averaged over total number of classes.
###
3.3.2.5. Cohen’s kappa
The function [`cohen_kappa_score`](generated/sklearn.metrics.cohen_kappa_score#sklearn.metrics.cohen_kappa_score "sklearn.metrics.cohen_kappa_score") computes [Cohen’s kappa](https://en.wikipedia.org/wiki/Cohen%27s_kappa) statistic. This measure is intended to compare labelings by different human annotators, not a classifier versus a ground truth.
The kappa score (see docstring) is a number between -1 and 1. Scores above .8 are generally considered good agreement; zero or lower means no agreement (practically random labels).
Kappa scores can be computed for binary or multiclass problems, but not for multilabel problems (except by manually computing a per-label score) and not for more than two annotators.
```
>>> from sklearn.metrics import cohen_kappa_score
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> cohen_kappa_score(y_true, y_pred)
0.4285714285714286
```
###
3.3.2.6. Confusion matrix
The [`confusion_matrix`](generated/sklearn.metrics.confusion_matrix#sklearn.metrics.confusion_matrix "sklearn.metrics.confusion_matrix") function evaluates classification accuracy by computing the [confusion matrix](https://en.wikipedia.org/wiki/Confusion_matrix) with each row corresponding to the true class (Wikipedia and other references may use different convention for axes).
By definition, entry \(i, j\) in a confusion matrix is the number of observations actually in group \(i\), but predicted to be in group \(j\). Here is an example:
```
>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
```
[`ConfusionMatrixDisplay`](generated/sklearn.metrics.confusionmatrixdisplay#sklearn.metrics.ConfusionMatrixDisplay "sklearn.metrics.ConfusionMatrixDisplay") can be used to visually represent a confusion matrix as shown in the [Confusion matrix](../auto_examples/model_selection/plot_confusion_matrix#sphx-glr-auto-examples-model-selection-plot-confusion-matrix-py) example, which creates the following figure:
The parameter `normalize` allows to report ratios instead of counts. The confusion matrix can be normalized in 3 different ways: `'pred'`, `'true'`, and `'all'` which will divide the counts by the sum of each columns, rows, or the entire matrix, respectively.
```
>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1]
>>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1]
>>> confusion_matrix(y_true, y_pred, normalize='all')
array([[0.25 , 0.125],
[0.25 , 0.375]])
```
For binary problems, we can get counts of true negatives, false positives, false negatives and true positives as follows:
```
>>> y_true = [0, 0, 0, 1, 1, 1, 1, 1]
>>> y_pred = [0, 1, 0, 1, 0, 1, 0, 1]
>>> tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel()
>>> tn, fp, fn, tp
(2, 1, 2, 3)
```
###
3.3.2.7. Classification report
The [`classification_report`](generated/sklearn.metrics.classification_report#sklearn.metrics.classification_report "sklearn.metrics.classification_report") function builds a text report showing the main classification metrics. Here is a small example with custom `target_names` and inferred labels:
```
>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 0]
>>> y_pred = [0, 0, 2, 1, 0]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
class 0 0.67 1.00 0.80 2
class 1 0.00 0.00 0.00 1
class 2 1.00 0.50 0.67 2
accuracy 0.60 5
macro avg 0.56 0.50 0.49 5
weighted avg 0.67 0.60 0.59 5
```
###
3.3.2.8. Hamming loss
The [`hamming_loss`](generated/sklearn.metrics.hamming_loss#sklearn.metrics.hamming_loss "sklearn.metrics.hamming_loss") computes the average Hamming loss or [Hamming distance](https://en.wikipedia.org/wiki/Hamming_distance) between two sets of samples.
If \(\hat{y}\_j\) is the predicted value for the \(j\)-th label of a given sample, \(y\_j\) is the corresponding true value, and \(n\_\text{labels}\) is the number of classes or labels, then the Hamming loss \(L\_{Hamming}\) between two samples is defined as:
\[L\_{Hamming}(y, \hat{y}) = \frac{1}{n\_\text{labels}} \sum\_{j=0}^{n\_\text{labels} - 1} 1(\hat{y}\_j \not= y\_j)\] where \(1(x)\) is the [indicator function](https://en.wikipedia.org/wiki/Indicator_function).
```
>>> from sklearn.metrics import hamming_loss
>>> y_pred = [1, 2, 3, 4]
>>> y_true = [2, 2, 3, 4]
>>> hamming_loss(y_true, y_pred)
0.25
```
In the multilabel case with binary label indicators:
```
>>> hamming_loss(np.array([[0, 1], [1, 1]]), np.zeros((2, 2)))
0.75
```
Note
In multiclass classification, the Hamming loss corresponds to the Hamming distance between `y_true` and `y_pred` which is similar to the [Zero one loss](#zero-one-loss) function. However, while zero-one loss penalizes prediction sets that do not strictly match true sets, the Hamming loss penalizes individual labels. Thus the Hamming loss, upper bounded by the zero-one loss, is always between zero and one, inclusive; and predicting a proper subset or superset of the true labels will give a Hamming loss between zero and one, exclusive.
###
3.3.2.9. Precision, recall and F-measures
Intuitively, [precision](https://en.wikipedia.org/wiki/Precision_and_recall#Precision) is the ability of the classifier not to label as positive a sample that is negative, and [recall](https://en.wikipedia.org/wiki/Precision_and_recall#Recall) is the ability of the classifier to find all the positive samples.
The [F-measure](https://en.wikipedia.org/wiki/F1_score) (\(F\_\beta\) and \(F\_1\) measures) can be interpreted as a weighted harmonic mean of the precision and recall. A \(F\_\beta\) measure reaches its best value at 1 and its worst score at 0. With \(\beta = 1\), \(F\_\beta\) and \(F\_1\) are equivalent, and the recall and the precision are equally important.
The [`precision_recall_curve`](generated/sklearn.metrics.precision_recall_curve#sklearn.metrics.precision_recall_curve "sklearn.metrics.precision_recall_curve") computes a precision-recall curve from the ground truth label and a score given by the classifier by varying a decision threshold.
The [`average_precision_score`](generated/sklearn.metrics.average_precision_score#sklearn.metrics.average_precision_score "sklearn.metrics.average_precision_score") function computes the [average precision](https://en.wikipedia.org/w/index.php?title=Information_retrieval&oldid=793358396#Average_precision) (AP) from prediction scores. The value is between 0 and 1 and higher is better. AP is defined as
\[\text{AP} = \sum\_n (R\_n - R\_{n-1}) P\_n\] where \(P\_n\) and \(R\_n\) are the precision and recall at the nth threshold. With random predictions, the AP is the fraction of positive samples.
References [[Manning2008]](#manning2008) and [[Everingham2010]](#everingham2010) present alternative variants of AP that interpolate the precision-recall curve. Currently, [`average_precision_score`](generated/sklearn.metrics.average_precision_score#sklearn.metrics.average_precision_score "sklearn.metrics.average_precision_score") does not implement any interpolated variant. References [[Davis2006]](#davis2006) and [[Flach2015]](#flach2015) describe why a linear interpolation of points on the precision-recall curve provides an overly-optimistic measure of classifier performance. This linear interpolation is used when computing area under the curve with the trapezoidal rule in [`auc`](generated/sklearn.metrics.auc#sklearn.metrics.auc "sklearn.metrics.auc").
Several functions allow you to analyze the precision, recall and F-measures score:
| | |
| --- | --- |
| [`average_precision_score`](generated/sklearn.metrics.average_precision_score#sklearn.metrics.average_precision_score "sklearn.metrics.average_precision_score")(y\_true, y\_score, \*) | Compute average precision (AP) from prediction scores. |
| [`f1_score`](generated/sklearn.metrics.f1_score#sklearn.metrics.f1_score "sklearn.metrics.f1_score")(y\_true, y\_pred, \*[, labels, ...]) | Compute the F1 score, also known as balanced F-score or F-measure. |
| [`fbeta_score`](generated/sklearn.metrics.fbeta_score#sklearn.metrics.fbeta_score "sklearn.metrics.fbeta_score")(y\_true, y\_pred, \*, beta[, ...]) | Compute the F-beta score. |
| [`precision_recall_curve`](generated/sklearn.metrics.precision_recall_curve#sklearn.metrics.precision_recall_curve "sklearn.metrics.precision_recall_curve")(y\_true, probas\_pred, \*) | Compute precision-recall pairs for different probability thresholds. |
| [`precision_recall_fscore_support`](generated/sklearn.metrics.precision_recall_fscore_support#sklearn.metrics.precision_recall_fscore_support "sklearn.metrics.precision_recall_fscore_support")(y\_true, ...) | Compute precision, recall, F-measure and support for each class. |
| [`precision_score`](generated/sklearn.metrics.precision_score#sklearn.metrics.precision_score "sklearn.metrics.precision_score")(y\_true, y\_pred, \*[, labels, ...]) | Compute the precision. |
| [`recall_score`](generated/sklearn.metrics.recall_score#sklearn.metrics.recall_score "sklearn.metrics.recall_score")(y\_true, y\_pred, \*[, labels, ...]) | Compute the recall. |
Note that the [`precision_recall_curve`](generated/sklearn.metrics.precision_recall_curve#sklearn.metrics.precision_recall_curve "sklearn.metrics.precision_recall_curve") function is restricted to the binary case. The [`average_precision_score`](generated/sklearn.metrics.average_precision_score#sklearn.metrics.average_precision_score "sklearn.metrics.average_precision_score") function works only in binary classification and multilabel indicator format. The `PredictionRecallDisplay.from_estimator` and `PredictionRecallDisplay.from_predictions` functions will plot the precision-recall curve as follows.
####
3.3.2.9.1. Binary classification
In a binary classification task, the terms ‘’positive’’ and ‘’negative’’ refer to the classifier’s prediction, and the terms ‘’true’’ and ‘’false’’ refer to whether that prediction corresponds to the external judgment (sometimes known as the ‘’observation’’). Given these definitions, we can formulate the following table:
| | |
| --- | --- |
| | Actual class (observation) |
| Predicted class (expectation) | tp (true positive) Correct result | fp (false positive) Unexpected result |
| fn (false negative) Missing result | tn (true negative) Correct absence of result |
In this context, we can define the notions of precision, recall and F-measure:
\[\text{precision} = \frac{tp}{tp + fp},\] \[\text{recall} = \frac{tp}{tp + fn},\] \[F\_\beta = (1 + \beta^2) \frac{\text{precision} \times \text{recall}}{\beta^2 \text{precision} + \text{recall}}.\] Here are some small examples in binary classification:
```
>>> from sklearn import metrics
>>> y_pred = [0, 1, 0, 0]
>>> y_true = [0, 1, 0, 1]
>>> metrics.precision_score(y_true, y_pred)
1.0
>>> metrics.recall_score(y_true, y_pred)
0.5
>>> metrics.f1_score(y_true, y_pred)
0.66...
>>> metrics.fbeta_score(y_true, y_pred, beta=0.5)
0.83...
>>> metrics.fbeta_score(y_true, y_pred, beta=1)
0.66...
>>> metrics.fbeta_score(y_true, y_pred, beta=2)
0.55...
>>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5)
(array([0.66..., 1. ]), array([1. , 0.5]), array([0.71..., 0.83...]), array([2, 2]))
>>> import numpy as np
>>> from sklearn.metrics import precision_recall_curve
>>> from sklearn.metrics import average_precision_score
>>> y_true = np.array([0, 0, 1, 1])
>>> y_scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> precision, recall, threshold = precision_recall_curve(y_true, y_scores)
>>> precision
array([0.5 , 0.66..., 0.5 , 1. , 1. ])
>>> recall
array([1. , 1. , 0.5, 0.5, 0. ])
>>> threshold
array([0.1 , 0.35, 0.4 , 0.8 ])
>>> average_precision_score(y_true, y_scores)
0.83...
```
####
3.3.2.9.2. Multiclass and multilabel classification
In a multiclass and multilabel classification task, the notions of precision, recall, and F-measures can be applied to each label independently. There are a few ways to combine results across labels, specified by the `average` argument to the [`average_precision_score`](generated/sklearn.metrics.average_precision_score#sklearn.metrics.average_precision_score "sklearn.metrics.average_precision_score") (multilabel only), [`f1_score`](generated/sklearn.metrics.f1_score#sklearn.metrics.f1_score "sklearn.metrics.f1_score"), [`fbeta_score`](generated/sklearn.metrics.fbeta_score#sklearn.metrics.fbeta_score "sklearn.metrics.fbeta_score"), [`precision_recall_fscore_support`](generated/sklearn.metrics.precision_recall_fscore_support#sklearn.metrics.precision_recall_fscore_support "sklearn.metrics.precision_recall_fscore_support"), [`precision_score`](generated/sklearn.metrics.precision_score#sklearn.metrics.precision_score "sklearn.metrics.precision_score") and [`recall_score`](generated/sklearn.metrics.recall_score#sklearn.metrics.recall_score "sklearn.metrics.recall_score") functions, as described [above](#average). Note that if all labels are included, “micro”-averaging in a multiclass setting will produce precision, recall and \(F\) that are all identical to accuracy. Also note that “weighted” averaging may produce an F-score that is not between precision and recall.
To make this more explicit, consider the following notation:
* \(y\) the set of *true* \((sample, label)\) pairs
* \(\hat{y}\) the set of *predicted* \((sample, label)\) pairs
* \(L\) the set of labels
* \(S\) the set of samples
* \(y\_s\) the subset of \(y\) with sample \(s\), i.e. \(y\_s := \left\{(s', l) \in y | s' = s\right\}\)
* \(y\_l\) the subset of \(y\) with label \(l\)
* similarly, \(\hat{y}\_s\) and \(\hat{y}\_l\) are subsets of \(\hat{y}\)
* \(P(A, B) := \frac{\left| A \cap B \right|}{\left|B\right|}\) for some sets \(A\) and \(B\)
* \(R(A, B) := \frac{\left| A \cap B \right|}{\left|A\right|}\) (Conventions vary on handling \(A = \emptyset\); this implementation uses \(R(A, B):=0\), and similar for \(P\).)
* \(F\_\beta(A, B) := \left(1 + \beta^2\right) \frac{P(A, B) \times R(A, B)}{\beta^2 P(A, B) + R(A, B)}\)
Then the metrics are defined as:
| `average` | Precision | Recall | F\_beta |
| --- | --- | --- | --- |
| `"micro"` | \(P(y, \hat{y})\) | \(R(y, \hat{y})\) | \(F\_\beta(y, \hat{y})\) |
| `"samples"` | \(\frac{1}{\left|S\right|} \sum\_{s \in S} P(y\_s, \hat{y}\_s)\) | \(\frac{1}{\left|S\right|} \sum\_{s \in S} R(y\_s, \hat{y}\_s)\) | \(\frac{1}{\left|S\right|} \sum\_{s \in S} F\_\beta(y\_s, \hat{y}\_s)\) |
| `"macro"` | \(\frac{1}{\left|L\right|} \sum\_{l \in L} P(y\_l, \hat{y}\_l)\) | \(\frac{1}{\left|L\right|} \sum\_{l \in L} R(y\_l, \hat{y}\_l)\) | \(\frac{1}{\left|L\right|} \sum\_{l \in L} F\_\beta(y\_l, \hat{y}\_l)\) |
| `"weighted"` | \(\frac{1}{\sum\_{l \in L} \left|y\_l\right|} \sum\_{l \in L} \left|y\_l\right| P(y\_l, \hat{y}\_l)\) | \(\frac{1}{\sum\_{l \in L} \left|y\_l\right|} \sum\_{l \in L} \left|y\_l\right| R(y\_l, \hat{y}\_l)\) | \(\frac{1}{\sum\_{l \in L} \left|y\_l\right|} \sum\_{l \in L} \left|y\_l\right| F\_\beta(y\_l, \hat{y}\_l)\) |
| `None` | \(\langle P(y\_l, \hat{y}\_l) | l \in L \rangle\) | \(\langle R(y\_l, \hat{y}\_l) | l \in L \rangle\) | \(\langle F\_\beta(y\_l, \hat{y}\_l) | l \in L \rangle\) |
```
>>> from sklearn import metrics
>>> y_true = [0, 1, 2, 0, 1, 2]
>>> y_pred = [0, 2, 1, 0, 0, 1]
>>> metrics.precision_score(y_true, y_pred, average='macro')
0.22...
>>> metrics.recall_score(y_true, y_pred, average='micro')
0.33...
>>> metrics.f1_score(y_true, y_pred, average='weighted')
0.26...
>>> metrics.fbeta_score(y_true, y_pred, average='macro', beta=0.5)
0.23...
>>> metrics.precision_recall_fscore_support(y_true, y_pred, beta=0.5, average=None)
(array([0.66..., 0. , 0. ]), array([1., 0., 0.]), array([0.71..., 0. , 0. ]), array([2, 2, 2]...))
```
For multiclass classification with a “negative class”, it is possible to exclude some labels:
```
>>> metrics.recall_score(y_true, y_pred, labels=[1, 2], average='micro')
... # excluding 0, no labels were correctly recalled
0.0
```
Similarly, labels not present in the data sample may be accounted for in macro-averaging.
```
>>> metrics.precision_score(y_true, y_pred, labels=[0, 1, 2, 3], average='macro')
0.166...
```
###
3.3.2.10. Jaccard similarity coefficient score
The [`jaccard_score`](generated/sklearn.metrics.jaccard_score#sklearn.metrics.jaccard_score "sklearn.metrics.jaccard_score") function computes the average of [Jaccard similarity coefficients](https://en.wikipedia.org/wiki/Jaccard_index), also called the Jaccard index, between pairs of label sets.
The Jaccard similarity coefficient of the \(i\)-th samples, with a ground truth label set \(y\_i\) and predicted label set \(\hat{y}\_i\), is defined as
\[J(y\_i, \hat{y}\_i) = \frac{|y\_i \cap \hat{y}\_i|}{|y\_i \cup \hat{y}\_i|}.\] [`jaccard_score`](generated/sklearn.metrics.jaccard_score#sklearn.metrics.jaccard_score "sklearn.metrics.jaccard_score") works like [`precision_recall_fscore_support`](generated/sklearn.metrics.precision_recall_fscore_support#sklearn.metrics.precision_recall_fscore_support "sklearn.metrics.precision_recall_fscore_support") as a naively set-wise measure applying natively to binary targets, and extended to apply to multilabel and multiclass through the use of `average` (see [above](#average)).
In the binary case:
```
>>> import numpy as np
>>> from sklearn.metrics import jaccard_score
>>> y_true = np.array([[0, 1, 1],
... [1, 1, 0]])
>>> y_pred = np.array([[1, 1, 1],
... [1, 0, 0]])
>>> jaccard_score(y_true[0], y_pred[0])
0.6666...
```
In the 2D comparison case (e.g. image similarity):
```
>>> jaccard_score(y_true, y_pred, average="micro")
0.6
```
In the multilabel case with binary label indicators:
```
>>> jaccard_score(y_true, y_pred, average='samples')
0.5833...
>>> jaccard_score(y_true, y_pred, average='macro')
0.6666...
>>> jaccard_score(y_true, y_pred, average=None)
array([0.5, 0.5, 1. ])
```
Multiclass problems are binarized and treated like the corresponding multilabel problem:
```
>>> y_pred = [0, 2, 1, 2]
>>> y_true = [0, 1, 2, 2]
>>> jaccard_score(y_true, y_pred, average=None)
array([1. , 0. , 0.33...])
>>> jaccard_score(y_true, y_pred, average='macro')
0.44...
>>> jaccard_score(y_true, y_pred, average='micro')
0.33...
```
###
3.3.2.11. Hinge loss
The [`hinge_loss`](generated/sklearn.metrics.hinge_loss#sklearn.metrics.hinge_loss "sklearn.metrics.hinge_loss") function computes the average distance between the model and the data using [hinge loss](https://en.wikipedia.org/wiki/Hinge_loss), a one-sided metric that considers only prediction errors. (Hinge loss is used in maximal margin classifiers such as support vector machines.)
If the labels are encoded with +1 and -1, \(y\): is the true value, and \(w\) is the predicted decisions as output by `decision_function`, then the hinge loss is defined as:
\[L\_\text{Hinge}(y, w) = \max\left\{1 - wy, 0\right\} = \left|1 - wy\right|\_+\] If there are more than two labels, [`hinge_loss`](generated/sklearn.metrics.hinge_loss#sklearn.metrics.hinge_loss "sklearn.metrics.hinge_loss") uses a multiclass variant due to Crammer & Singer. [Here](http://jmlr.csail.mit.edu/papers/volume2/crammer01a/crammer01a.pdf) is the paper describing it.
If \(y\_w\) is the predicted decision for true label and \(y\_t\) is the maximum of the predicted decisions for all other labels, where predicted decisions are output by decision function, then multiclass hinge loss is defined by:
\[L\_\text{Hinge}(y\_w, y\_t) = \max\left\{1 + y\_t - y\_w, 0\right\}\] Here a small example demonstrating the use of the [`hinge_loss`](generated/sklearn.metrics.hinge_loss#sklearn.metrics.hinge_loss "sklearn.metrics.hinge_loss") function with a svm classifier in a binary class problem:
```
>>> from sklearn import svm
>>> from sklearn.metrics import hinge_loss
>>> X = [[0], [1]]
>>> y = [-1, 1]
>>> est = svm.LinearSVC(random_state=0)
>>> est.fit(X, y)
LinearSVC(random_state=0)
>>> pred_decision = est.decision_function([[-2], [3], [0.5]])
>>> pred_decision
array([-2.18..., 2.36..., 0.09...])
>>> hinge_loss([-1, 1, 1], pred_decision)
0.3...
```
Here is an example demonstrating the use of the [`hinge_loss`](generated/sklearn.metrics.hinge_loss#sklearn.metrics.hinge_loss "sklearn.metrics.hinge_loss") function with a svm classifier in a multiclass problem:
```
>>> X = np.array([[0], [1], [2], [3]])
>>> Y = np.array([0, 1, 2, 3])
>>> labels = np.array([0, 1, 2, 3])
>>> est = svm.LinearSVC()
>>> est.fit(X, Y)
LinearSVC()
>>> pred_decision = est.decision_function([[-1], [2], [3]])
>>> y_true = [0, 2, 3]
>>> hinge_loss(y_true, pred_decision, labels=labels)
0.56...
```
###
3.3.2.12. Log loss
Log loss, also called logistic regression loss or cross-entropy loss, is defined on probability estimates. It is commonly used in (multinomial) logistic regression and neural networks, as well as in some variants of expectation-maximization, and can be used to evaluate the probability outputs (`predict_proba`) of a classifier instead of its discrete predictions.
For binary classification with a true label \(y \in \{0,1\}\) and a probability estimate \(p = \operatorname{Pr}(y = 1)\), the log loss per sample is the negative log-likelihood of the classifier given the true label:
\[L\_{\log}(y, p) = -\log \operatorname{Pr}(y|p) = -(y \log (p) + (1 - y) \log (1 - p))\] This extends to the multiclass case as follows. Let the true labels for a set of samples be encoded as a 1-of-K binary indicator matrix \(Y\), i.e., \(y\_{i,k} = 1\) if sample \(i\) has label \(k\) taken from a set of \(K\) labels. Let \(P\) be a matrix of probability estimates, with \(p\_{i,k} = \operatorname{Pr}(y\_{i,k} = 1)\). Then the log loss of the whole set is
\[L\_{\log}(Y, P) = -\log \operatorname{Pr}(Y|P) = - \frac{1}{N} \sum\_{i=0}^{N-1} \sum\_{k=0}^{K-1} y\_{i,k} \log p\_{i,k}\] To see how this generalizes the binary log loss given above, note that in the binary case, \(p\_{i,0} = 1 - p\_{i,1}\) and \(y\_{i,0} = 1 - y\_{i,1}\), so expanding the inner sum over \(y\_{i,k} \in \{0,1\}\) gives the binary log loss.
The [`log_loss`](generated/sklearn.metrics.log_loss#sklearn.metrics.log_loss "sklearn.metrics.log_loss") function computes log loss given a list of ground-truth labels and a probability matrix, as returned by an estimator’s `predict_proba` method.
```
>>> from sklearn.metrics import log_loss
>>> y_true = [0, 0, 1, 1]
>>> y_pred = [[.9, .1], [.8, .2], [.3, .7], [.01, .99]]
>>> log_loss(y_true, y_pred)
0.1738...
```
The first `[.9, .1]` in `y_pred` denotes 90% probability that the first sample has label 0. The log loss is non-negative.
###
3.3.2.13. Matthews correlation coefficient
The [`matthews_corrcoef`](generated/sklearn.metrics.matthews_corrcoef#sklearn.metrics.matthews_corrcoef "sklearn.metrics.matthews_corrcoef") function computes the [Matthew’s correlation coefficient (MCC)](https://en.wikipedia.org/wiki/Matthews_correlation_coefficient) for binary classes. Quoting Wikipedia:
“The Matthews correlation coefficient is used in machine learning as a measure of the quality of binary (two-class) classifications. It takes into account true and false positives and negatives and is generally regarded as a balanced measure which can be used even if the classes are of very different sizes. The MCC is in essence a correlation coefficient value between -1 and +1. A coefficient of +1 represents a perfect prediction, 0 an average random prediction and -1 an inverse prediction. The statistic is also known as the phi coefficient.”
In the binary (two-class) case, \(tp\), \(tn\), \(fp\) and \(fn\) are respectively the number of true positives, true negatives, false positives and false negatives, the MCC is defined as
\[MCC = \frac{tp \times tn - fp \times fn}{\sqrt{(tp + fp)(tp + fn)(tn + fp)(tn + fn)}}.\] In the multiclass case, the Matthews correlation coefficient can be [defined](http://rk.kvl.dk/introduction/index.html) in terms of a [`confusion_matrix`](generated/sklearn.metrics.confusion_matrix#sklearn.metrics.confusion_matrix "sklearn.metrics.confusion_matrix") \(C\) for \(K\) classes. To simplify the definition consider the following intermediate variables:
* \(t\_k=\sum\_{i}^{K} C\_{ik}\) the number of times class \(k\) truly occurred,
* \(p\_k=\sum\_{i}^{K} C\_{ki}\) the number of times class \(k\) was predicted,
* \(c=\sum\_{k}^{K} C\_{kk}\) the total number of samples correctly predicted,
* \(s=\sum\_{i}^{K} \sum\_{j}^{K} C\_{ij}\) the total number of samples.
Then the multiclass MCC is defined as:
\[MCC = \frac{ c \times s - \sum\_{k}^{K} p\_k \times t\_k }{\sqrt{ (s^2 - \sum\_{k}^{K} p\_k^2) \times (s^2 - \sum\_{k}^{K} t\_k^2) }}\] When there are more than two labels, the value of the MCC will no longer range between -1 and +1. Instead the minimum value will be somewhere between -1 and 0 depending on the number and distribution of ground true labels. The maximum value is always +1.
Here is a small example illustrating the usage of the [`matthews_corrcoef`](generated/sklearn.metrics.matthews_corrcoef#sklearn.metrics.matthews_corrcoef "sklearn.metrics.matthews_corrcoef") function:
```
>>> from sklearn.metrics import matthews_corrcoef
>>> y_true = [+1, +1, +1, -1]
>>> y_pred = [+1, -1, +1, +1]
>>> matthews_corrcoef(y_true, y_pred)
-0.33...
```
###
3.3.2.14. Multi-label confusion matrix
The [`multilabel_confusion_matrix`](generated/sklearn.metrics.multilabel_confusion_matrix#sklearn.metrics.multilabel_confusion_matrix "sklearn.metrics.multilabel_confusion_matrix") function computes class-wise (default) or sample-wise (samplewise=True) multilabel confusion matrix to evaluate the accuracy of a classification. multilabel\_confusion\_matrix also treats multiclass data as if it were multilabel, as this is a transformation commonly applied to evaluate multiclass problems with binary classification metrics (such as precision, recall, etc.).
When calculating class-wise multilabel confusion matrix \(C\), the count of true negatives for class \(i\) is \(C\_{i,0,0}\), false negatives is \(C\_{i,1,0}\), true positives is \(C\_{i,1,1}\) and false positives is \(C\_{i,0,1}\).
Here is an example demonstrating the use of the [`multilabel_confusion_matrix`](generated/sklearn.metrics.multilabel_confusion_matrix#sklearn.metrics.multilabel_confusion_matrix "sklearn.metrics.multilabel_confusion_matrix") function with [multilabel indicator matrix](https://scikit-learn.org/1.1/glossary.html#term-multilabel-indicator-matrix) input:
```
>>> import numpy as np
>>> from sklearn.metrics import multilabel_confusion_matrix
>>> y_true = np.array([[1, 0, 1],
... [0, 1, 0]])
>>> y_pred = np.array([[1, 0, 0],
... [0, 1, 1]])
>>> multilabel_confusion_matrix(y_true, y_pred)
array([[[1, 0],
[0, 1]],
[[1, 0],
[0, 1]],
[[0, 1],
[1, 0]]])
```
Or a confusion matrix can be constructed for each sample’s labels:
```
>>> multilabel_confusion_matrix(y_true, y_pred, samplewise=True)
array([[[1, 0],
[1, 1]],
[[1, 1],
[0, 1]]])
```
Here is an example demonstrating the use of the [`multilabel_confusion_matrix`](generated/sklearn.metrics.multilabel_confusion_matrix#sklearn.metrics.multilabel_confusion_matrix "sklearn.metrics.multilabel_confusion_matrix") function with [multiclass](https://scikit-learn.org/1.1/glossary.html#term-multiclass) input:
```
>>> y_true = ["cat", "ant", "cat", "cat", "ant", "bird"]
>>> y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"]
>>> multilabel_confusion_matrix(y_true, y_pred,
... labels=["ant", "bird", "cat"])
array([[[3, 1],
[0, 2]],
[[5, 0],
[1, 0]],
[[2, 1],
[1, 2]]])
```
Here are some examples demonstrating the use of the [`multilabel_confusion_matrix`](generated/sklearn.metrics.multilabel_confusion_matrix#sklearn.metrics.multilabel_confusion_matrix "sklearn.metrics.multilabel_confusion_matrix") function to calculate recall (or sensitivity), specificity, fall out and miss rate for each class in a problem with multilabel indicator matrix input.
Calculating [recall](https://en.wikipedia.org/wiki/Sensitivity_and_specificity) (also called the true positive rate or the sensitivity) for each class:
```
>>> y_true = np.array([[0, 0, 1],
... [0, 1, 0],
... [1, 1, 0]])
>>> y_pred = np.array([[0, 1, 0],
... [0, 0, 1],
... [1, 1, 0]])
>>> mcm = multilabel_confusion_matrix(y_true, y_pred)
>>> tn = mcm[:, 0, 0]
>>> tp = mcm[:, 1, 1]
>>> fn = mcm[:, 1, 0]
>>> fp = mcm[:, 0, 1]
>>> tp / (tp + fn)
array([1. , 0.5, 0. ])
```
Calculating [specificity](https://en.wikipedia.org/wiki/Sensitivity_and_specificity) (also called the true negative rate) for each class:
```
>>> tn / (tn + fp)
array([1. , 0. , 0.5])
```
Calculating [fall out](https://en.wikipedia.org/wiki/False_positive_rate) (also called the false positive rate) for each class:
```
>>> fp / (fp + tn)
array([0. , 1. , 0.5])
```
Calculating [miss rate](https://en.wikipedia.org/wiki/False_positives_and_false_negatives) (also called the false negative rate) for each class:
```
>>> fn / (fn + tp)
array([0. , 0.5, 1. ])
```
###
3.3.2.15. Receiver operating characteristic (ROC)
The function [`roc_curve`](generated/sklearn.metrics.roc_curve#sklearn.metrics.roc_curve "sklearn.metrics.roc_curve") computes the [receiver operating characteristic curve, or ROC curve](https://en.wikipedia.org/wiki/Receiver_operating_characteristic). Quoting Wikipedia :
“A receiver operating characteristic (ROC), or simply ROC curve, is a graphical plot which illustrates the performance of a binary classifier system as its discrimination threshold is varied. It is created by plotting the fraction of true positives out of the positives (TPR = true positive rate) vs. the fraction of false positives out of the negatives (FPR = false positive rate), at various threshold settings. TPR is also known as sensitivity, and FPR is one minus the specificity or true negative rate.”
This function requires the true binary value and the target scores, which can either be probability estimates of the positive class, confidence values, or binary decisions. Here is a small example of how to use the [`roc_curve`](generated/sklearn.metrics.roc_curve#sklearn.metrics.roc_curve "sklearn.metrics.roc_curve") function:
```
>>> import numpy as np
>>> from sklearn.metrics import roc_curve
>>> y = np.array([1, 1, 2, 2])
>>> scores = np.array([0.1, 0.4, 0.35, 0.8])
>>> fpr, tpr, thresholds = roc_curve(y, scores, pos_label=2)
>>> fpr
array([0. , 0. , 0.5, 0.5, 1. ])
>>> tpr
array([0. , 0.5, 0.5, 1. , 1. ])
>>> thresholds
array([1.8 , 0.8 , 0.4 , 0.35, 0.1 ])
```
This figure shows an example of such an ROC curve:
The [`roc_auc_score`](generated/sklearn.metrics.roc_auc_score#sklearn.metrics.roc_auc_score "sklearn.metrics.roc_auc_score") function computes the area under the receiver operating characteristic (ROC) curve, which is also denoted by AUC or AUROC. By computing the area under the roc curve, the curve information is summarized in one number. For more information see the [Wikipedia article on AUC](https://en.wikipedia.org/wiki/Receiver_operating_characteristic#Area_under_the_curve).
Compared to metrics such as the subset accuracy, the Hamming loss, or the F1 score, ROC doesn’t require optimizing a threshold for each label.
####
3.3.2.15.1. Binary case
In the **binary case**, you can either provide the probability estimates, using the `classifier.predict_proba()` method, or the non-thresholded decision values given by the `classifier.decision_function()` method. In the case of providing the probability estimates, the probability of the class with the “greater label” should be provided. The “greater label” corresponds to `classifier.classes_[1]` and thus `classifier.predict_proba(X)[:, 1]`. Therefore, the `y_score` parameter is of size (n\_samples,).
```
>>> from sklearn.datasets import load_breast_cancer
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.metrics import roc_auc_score
>>> X, y = load_breast_cancer(return_X_y=True)
>>> clf = LogisticRegression(solver="liblinear").fit(X, y)
>>> clf.classes_
array([0, 1])
```
We can use the probability estimates corresponding to `clf.classes_[1]`.
```
>>> y_score = clf.predict_proba(X)[:, 1]
>>> roc_auc_score(y, y_score)
0.99...
```
Otherwise, we can use the non-thresholded decision values
```
>>> roc_auc_score(y, clf.decision_function(X))
0.99...
```
####
3.3.2.15.2. Multi-class case
The [`roc_auc_score`](generated/sklearn.metrics.roc_auc_score#sklearn.metrics.roc_auc_score "sklearn.metrics.roc_auc_score") function can also be used in **multi-class classification**. Two averaging strategies are currently supported: the one-vs-one algorithm computes the average of the pairwise ROC AUC scores, and the one-vs-rest algorithm computes the average of the ROC AUC scores for each class against all other classes. In both cases, the predicted labels are provided in an array with values from 0 to `n_classes`, and the scores correspond to the probability estimates that a sample belongs to a particular class. The OvO and OvR algorithms support weighting uniformly (`average='macro'`) and by prevalence (`average='weighted'`).
**One-vs-one Algorithm**: Computes the average AUC of all possible pairwise combinations of classes. [[HT2001]](#ht2001) defines a multiclass AUC metric weighted uniformly:
\[\frac{1}{c(c-1)}\sum\_{j=1}^{c}\sum\_{k > j}^c (\text{AUC}(j | k) + \text{AUC}(k | j))\] where \(c\) is the number of classes and \(\text{AUC}(j | k)\) is the AUC with class \(j\) as the positive class and class \(k\) as the negative class. In general, \(\text{AUC}(j | k) \neq \text{AUC}(k | j))\) in the multiclass case. This algorithm is used by setting the keyword argument `multiclass` to `'ovo'` and `average` to `'macro'`.
The [[HT2001]](#ht2001) multiclass AUC metric can be extended to be weighted by the prevalence:
\[\frac{1}{c(c-1)}\sum\_{j=1}^{c}\sum\_{k > j}^c p(j \cup k)( \text{AUC}(j | k) + \text{AUC}(k | j))\] where \(c\) is the number of classes. This algorithm is used by setting the keyword argument `multiclass` to `'ovo'` and `average` to `'weighted'`. The `'weighted'` option returns a prevalence-weighted average as described in [[FC2009]](#fc2009).
**One-vs-rest Algorithm**: Computes the AUC of each class against the rest [[PD2000]](#pd2000). The algorithm is functionally the same as the multilabel case. To enable this algorithm set the keyword argument `multiclass` to `'ovr'`. Like OvO, OvR supports two types of averaging: `'macro'` [[F2006]](#f2006) and `'weighted'` [[F2001]](#f2001).
In applications where a high false positive rate is not tolerable the parameter `max_fpr` of [`roc_auc_score`](generated/sklearn.metrics.roc_auc_score#sklearn.metrics.roc_auc_score "sklearn.metrics.roc_auc_score") can be used to summarize the ROC curve up to the given limit.
####
3.3.2.15.3. Multi-label case
In **multi-label classification**, the [`roc_auc_score`](generated/sklearn.metrics.roc_auc_score#sklearn.metrics.roc_auc_score "sklearn.metrics.roc_auc_score") function is extended by averaging over the labels as [above](#average). In this case, you should provide a `y_score` of shape `(n_samples, n_classes)`. Thus, when using the probability estimates, one needs to select the probability of the class with the greater label for each output.
```
>>> from sklearn.datasets import make_multilabel_classification
>>> from sklearn.multioutput import MultiOutputClassifier
>>> X, y = make_multilabel_classification(random_state=0)
>>> inner_clf = LogisticRegression(solver="liblinear", random_state=0)
>>> clf = MultiOutputClassifier(inner_clf).fit(X, y)
>>> y_score = np.transpose([y_pred[:, 1] for y_pred in clf.predict_proba(X)])
>>> roc_auc_score(y, y_score, average=None)
array([0.82..., 0.86..., 0.94..., 0.85... , 0.94...])
```
And the decision values do not require such processing.
```
>>> from sklearn.linear_model import RidgeClassifierCV
>>> clf = RidgeClassifierCV().fit(X, y)
>>> y_score = clf.decision_function(X)
>>> roc_auc_score(y, y_score, average=None)
array([0.81..., 0.84... , 0.93..., 0.87..., 0.94...])
```
###
3.3.2.16. Detection error tradeoff (DET)
The function [`det_curve`](generated/sklearn.metrics.det_curve#sklearn.metrics.det_curve "sklearn.metrics.det_curve") computes the detection error tradeoff curve (DET) curve [[WikipediaDET2017]](#wikipediadet2017). Quoting Wikipedia:
“A detection error tradeoff (DET) graph is a graphical plot of error rates for binary classification systems, plotting false reject rate vs. false accept rate. The x- and y-axes are scaled non-linearly by their standard normal deviates (or just by logarithmic transformation), yielding tradeoff curves that are more linear than ROC curves, and use most of the image area to highlight the differences of importance in the critical operating region.”
DET curves are a variation of receiver operating characteristic (ROC) curves where False Negative Rate is plotted on the y-axis instead of True Positive Rate. DET curves are commonly plotted in normal deviate scale by transformation with \(\phi^{-1}\) (with \(\phi\) being the cumulative distribution function). The resulting performance curves explicitly visualize the tradeoff of error types for given classification algorithms. See [[Martin1997]](#martin1997) for examples and further motivation.
This figure compares the ROC and DET curves of two example classifiers on the same classification task:
**Properties:**
* DET curves form a linear curve in normal deviate scale if the detection scores are normally (or close-to normally) distributed. It was shown by [[Navratil2007]](#navratil2007) that the reverse it not necessarily true and even more general distributions are able produce linear DET curves.
* The normal deviate scale transformation spreads out the points such that a comparatively larger space of plot is occupied. Therefore curves with similar classification performance might be easier to distinguish on a DET plot.
* With False Negative Rate being “inverse” to True Positive Rate the point of perfection for DET curves is the origin (in contrast to the top left corner for ROC curves).
**Applications and limitations:**
DET curves are intuitive to read and hence allow quick visual assessment of a classifier’s performance. Additionally DET curves can be consulted for threshold analysis and operating point selection. This is particularly helpful if a comparison of error types is required.
On the other hand DET curves do not provide their metric as a single number. Therefore for either automated evaluation or comparison to other classification tasks metrics like the derived area under ROC curve might be better suited.
###
3.3.2.17. Zero one loss
The [`zero_one_loss`](generated/sklearn.metrics.zero_one_loss#sklearn.metrics.zero_one_loss "sklearn.metrics.zero_one_loss") function computes the sum or the average of the 0-1 classification loss (\(L\_{0-1}\)) over \(n\_{\text{samples}}\). By default, the function normalizes over the sample. To get the sum of the \(L\_{0-1}\), set `normalize` to `False`.
In multilabel classification, the [`zero_one_loss`](generated/sklearn.metrics.zero_one_loss#sklearn.metrics.zero_one_loss "sklearn.metrics.zero_one_loss") scores a subset as one if its labels strictly match the predictions, and as a zero if there are any errors. By default, the function returns the percentage of imperfectly predicted subsets. To get the count of such subsets instead, set `normalize` to `False`
If \(\hat{y}\_i\) is the predicted value of the \(i\)-th sample and \(y\_i\) is the corresponding true value, then the 0-1 loss \(L\_{0-1}\) is defined as:
\[L\_{0-1}(y\_i, \hat{y}\_i) = 1(\hat{y}\_i \not= y\_i)\] where \(1(x)\) is the [indicator function](https://en.wikipedia.org/wiki/Indicator_function).
```
>>> from sklearn.metrics import zero_one_loss
>>> y_pred = [1, 2, 3, 4]
>>> y_true = [2, 2, 3, 4]
>>> zero_one_loss(y_true, y_pred)
0.25
>>> zero_one_loss(y_true, y_pred, normalize=False)
1
```
In the multilabel case with binary label indicators, where the first label set [0,1] has an error:
```
>>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
0.5
>>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2)), normalize=False)
1
```
###
3.3.2.18. Brier score loss
The [`brier_score_loss`](generated/sklearn.metrics.brier_score_loss#sklearn.metrics.brier_score_loss "sklearn.metrics.brier_score_loss") function computes the [Brier score](https://en.wikipedia.org/wiki/Brier_score) for binary classes [[Brier1950]](#brier1950). Quoting Wikipedia:
“The Brier score is a proper score function that measures the accuracy of probabilistic predictions. It is applicable to tasks in which predictions must assign probabilities to a set of mutually exclusive discrete outcomes.”
This function returns the mean squared error of the actual outcome \(y \in \{0,1\}\) and the predicted probability estimate \(p = \operatorname{Pr}(y = 1)\) ([predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba)) as outputted by:
\[BS = \frac{1}{n\_{\text{samples}}} \sum\_{i=0}^{n\_{\text{samples}} - 1}(y\_i - p\_i)^2\] The Brier score loss is also between 0 to 1 and the lower the value (the mean square difference is smaller), the more accurate the prediction is.
Here is a small example of usage of this function:
```
>>> import numpy as np
>>> from sklearn.metrics import brier_score_loss
>>> y_true = np.array([0, 1, 1, 0])
>>> y_true_categorical = np.array(["spam", "ham", "ham", "spam"])
>>> y_prob = np.array([0.1, 0.9, 0.8, 0.4])
>>> y_pred = np.array([0, 1, 1, 0])
>>> brier_score_loss(y_true, y_prob)
0.055
>>> brier_score_loss(y_true, 1 - y_prob, pos_label=0)
0.055
>>> brier_score_loss(y_true_categorical, y_prob, pos_label="ham")
0.055
>>> brier_score_loss(y_true, y_prob > 0.5)
0.0
```
The Brier score can be used to assess how well a classifier is calibrated. However, a lower Brier score loss does not always mean a better calibration. This is because, by analogy with the bias-variance decomposition of the mean squared error, the Brier score loss can be decomposed as the sum of calibration loss and refinement loss [[Bella2012]](#bella2012). Calibration loss is defined as the mean squared deviation from empirical probabilities derived from the slope of ROC segments. Refinement loss can be defined as the expected optimal loss as measured by the area under the optimal cost curve. Refinement loss can change independently from calibration loss, thus a lower Brier score loss does not necessarily mean a better calibrated model. “Only when refinement loss remains the same does a lower Brier score loss always mean better calibration” [[Bella2012]](#bella2012), [[Flach2008]](#flach2008).
3.3.3. Multilabel ranking metrics
----------------------------------
In multilabel learning, each sample can have any number of ground truth labels associated with it. The goal is to give high scores and better rank to the ground truth labels.
###
3.3.3.1. Coverage error
The [`coverage_error`](generated/sklearn.metrics.coverage_error#sklearn.metrics.coverage_error "sklearn.metrics.coverage_error") function computes the average number of labels that have to be included in the final prediction such that all true labels are predicted. This is useful if you want to know how many top-scored-labels you have to predict in average without missing any true one. The best value of this metrics is thus the average number of true labels.
Note
Our implementation’s score is 1 greater than the one given in Tsoumakas et al., 2010. This extends it to handle the degenerate case in which an instance has 0 true labels.
Formally, given a binary indicator matrix of the ground truth labels \(y \in \left\{0, 1\right\}^{n\_\text{samples} \times n\_\text{labels}}\) and the score associated with each label \(\hat{f} \in \mathbb{R}^{n\_\text{samples} \times n\_\text{labels}}\), the coverage is defined as
\[coverage(y, \hat{f}) = \frac{1}{n\_{\text{samples}}} \sum\_{i=0}^{n\_{\text{samples}} - 1} \max\_{j:y\_{ij} = 1} \text{rank}\_{ij}\] with \(\text{rank}\_{ij} = \left|\left\{k: \hat{f}\_{ik} \geq \hat{f}\_{ij} \right\}\right|\). Given the rank definition, ties in `y_scores` are broken by giving the maximal rank that would have been assigned to all tied values.
Here is a small example of usage of this function:
```
>>> import numpy as np
>>> from sklearn.metrics import coverage_error
>>> y_true = np.array([[1, 0, 0], [0, 0, 1]])
>>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
>>> coverage_error(y_true, y_score)
2.5
```
###
3.3.3.2. Label ranking average precision
The [`label_ranking_average_precision_score`](generated/sklearn.metrics.label_ranking_average_precision_score#sklearn.metrics.label_ranking_average_precision_score "sklearn.metrics.label_ranking_average_precision_score") function implements label ranking average precision (LRAP). This metric is linked to the [`average_precision_score`](generated/sklearn.metrics.average_precision_score#sklearn.metrics.average_precision_score "sklearn.metrics.average_precision_score") function, but is based on the notion of label ranking instead of precision and recall.
Label ranking average precision (LRAP) averages over the samples the answer to the following question: for each ground truth label, what fraction of higher-ranked labels were true labels? This performance measure will be higher if you are able to give better rank to the labels associated with each sample. The obtained score is always strictly greater than 0, and the best value is 1. If there is exactly one relevant label per sample, label ranking average precision is equivalent to the [mean reciprocal rank](https://en.wikipedia.org/wiki/Mean_reciprocal_rank).
Formally, given a binary indicator matrix of the ground truth labels \(y \in \left\{0, 1\right\}^{n\_\text{samples} \times n\_\text{labels}}\) and the score associated with each label \(\hat{f} \in \mathbb{R}^{n\_\text{samples} \times n\_\text{labels}}\), the average precision is defined as
\[LRAP(y, \hat{f}) = \frac{1}{n\_{\text{samples}}} \sum\_{i=0}^{n\_{\text{samples}} - 1} \frac{1}{||y\_i||\_0} \sum\_{j:y\_{ij} = 1} \frac{|\mathcal{L}\_{ij}|}{\text{rank}\_{ij}}\] where \(\mathcal{L}\_{ij} = \left\{k: y\_{ik} = 1, \hat{f}\_{ik} \geq \hat{f}\_{ij} \right\}\), \(\text{rank}\_{ij} = \left|\left\{k: \hat{f}\_{ik} \geq \hat{f}\_{ij} \right\}\right|\), \(|\cdot|\) computes the cardinality of the set (i.e., the number of elements in the set), and \(||\cdot||\_0\) is the \(\ell\_0\) “norm” (which computes the number of nonzero elements in a vector).
Here is a small example of usage of this function:
```
>>> import numpy as np
>>> from sklearn.metrics import label_ranking_average_precision_score
>>> y_true = np.array([[1, 0, 0], [0, 0, 1]])
>>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
>>> label_ranking_average_precision_score(y_true, y_score)
0.416...
```
###
3.3.3.3. Ranking loss
The [`label_ranking_loss`](generated/sklearn.metrics.label_ranking_loss#sklearn.metrics.label_ranking_loss "sklearn.metrics.label_ranking_loss") function computes the ranking loss which averages over the samples the number of label pairs that are incorrectly ordered, i.e. true labels have a lower score than false labels, weighted by the inverse of the number of ordered pairs of false and true labels. The lowest achievable ranking loss is zero.
Formally, given a binary indicator matrix of the ground truth labels \(y \in \left\{0, 1\right\}^{n\_\text{samples} \times n\_\text{labels}}\) and the score associated with each label \(\hat{f} \in \mathbb{R}^{n\_\text{samples} \times n\_\text{labels}}\), the ranking loss is defined as
\[ranking\\_loss(y, \hat{f}) = \frac{1}{n\_{\text{samples}}} \sum\_{i=0}^{n\_{\text{samples}} - 1} \frac{1}{||y\_i||\_0(n\_\text{labels} - ||y\_i||\_0)} \left|\left\{(k, l): \hat{f}\_{ik} \leq \hat{f}\_{il}, y\_{ik} = 1, y\_{il} = 0 \right\}\right|\] where \(|\cdot|\) computes the cardinality of the set (i.e., the number of elements in the set) and \(||\cdot||\_0\) is the \(\ell\_0\) “norm” (which computes the number of nonzero elements in a vector).
Here is a small example of usage of this function:
```
>>> import numpy as np
>>> from sklearn.metrics import label_ranking_loss
>>> y_true = np.array([[1, 0, 0], [0, 0, 1]])
>>> y_score = np.array([[0.75, 0.5, 1], [1, 0.2, 0.1]])
>>> label_ranking_loss(y_true, y_score)
0.75...
>>> # With the following prediction, we have perfect and minimal loss
>>> y_score = np.array([[1.0, 0.1, 0.2], [0.1, 0.2, 0.9]])
>>> label_ranking_loss(y_true, y_score)
0.0
```
###
3.3.3.4. Normalized Discounted Cumulative Gain
Discounted Cumulative Gain (DCG) and Normalized Discounted Cumulative Gain (NDCG) are ranking metrics implemented in [`dcg_score`](generated/sklearn.metrics.dcg_score#sklearn.metrics.dcg_score "sklearn.metrics.dcg_score") and [`ndcg_score`](generated/sklearn.metrics.ndcg_score#sklearn.metrics.ndcg_score "sklearn.metrics.ndcg_score") ; they compare a predicted order to ground-truth scores, such as the relevance of answers to a query.
From the Wikipedia page for Discounted Cumulative Gain:
“Discounted cumulative gain (DCG) is a measure of ranking quality. In information retrieval, it is often used to measure effectiveness of web search engine algorithms or related applications. Using a graded relevance scale of documents in a search-engine result set, DCG measures the usefulness, or gain, of a document based on its position in the result list. The gain is accumulated from the top of the result list to the bottom, with the gain of each result discounted at lower ranks”
DCG orders the true targets (e.g. relevance of query answers) in the predicted order, then multiplies them by a logarithmic decay and sums the result. The sum can be truncated after the first \(K\) results, in which case we call it DCG@K. NDCG, or NDCG@K is DCG divided by the DCG obtained by a perfect prediction, so that it is always between 0 and 1. Usually, NDCG is preferred to DCG.
Compared with the ranking loss, NDCG can take into account relevance scores, rather than a ground-truth ranking. So if the ground-truth consists only of an ordering, the ranking loss should be preferred; if the ground-truth consists of actual usefulness scores (e.g. 0 for irrelevant, 1 for relevant, 2 for very relevant), NDCG can be used.
For one sample, given the vector of continuous ground-truth values for each target \(y \in \mathbb{R}^{M}\), where \(M\) is the number of outputs, and the prediction \(\hat{y}\), which induces the ranking function \(f\), the DCG score is
\[\sum\_{r=1}^{\min(K, M)}\frac{y\_{f(r)}}{\log(1 + r)}\] and the NDCG score is the DCG score divided by the DCG score obtained for \(y\).
3.3.4. Regression metrics
--------------------------
The [`sklearn.metrics`](classes#module-sklearn.metrics "sklearn.metrics") module implements several loss, score, and utility functions to measure regression performance. Some of those have been enhanced to handle the multioutput case: [`mean_squared_error`](generated/sklearn.metrics.mean_squared_error#sklearn.metrics.mean_squared_error "sklearn.metrics.mean_squared_error"), [`mean_absolute_error`](generated/sklearn.metrics.mean_absolute_error#sklearn.metrics.mean_absolute_error "sklearn.metrics.mean_absolute_error"), [`r2_score`](generated/sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"), [`explained_variance_score`](generated/sklearn.metrics.explained_variance_score#sklearn.metrics.explained_variance_score "sklearn.metrics.explained_variance_score"), [`mean_pinball_loss`](generated/sklearn.metrics.mean_pinball_loss#sklearn.metrics.mean_pinball_loss "sklearn.metrics.mean_pinball_loss"), [`d2_pinball_score`](generated/sklearn.metrics.d2_pinball_score#sklearn.metrics.d2_pinball_score "sklearn.metrics.d2_pinball_score") and [`d2_absolute_error_score`](generated/sklearn.metrics.d2_absolute_error_score#sklearn.metrics.d2_absolute_error_score "sklearn.metrics.d2_absolute_error_score").
These functions have a `multioutput` keyword argument which specifies the way the scores or losses for each individual target should be averaged. The default is `'uniform_average'`, which specifies a uniformly weighted mean over outputs. If an `ndarray` of shape `(n_outputs,)` is passed, then its entries are interpreted as weights and an according weighted average is returned. If `multioutput` is `'raw_values'`, then all unaltered individual scores or losses will be returned in an array of shape `(n_outputs,)`.
The [`r2_score`](generated/sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score") and [`explained_variance_score`](generated/sklearn.metrics.explained_variance_score#sklearn.metrics.explained_variance_score "sklearn.metrics.explained_variance_score") accept an additional value `'variance_weighted'` for the `multioutput` parameter. This option leads to a weighting of each individual score by the variance of the corresponding target variable. This setting quantifies the globally captured unscaled variance. If the target variables are of different scale, then this score puts more importance on explaining the higher variance variables. `multioutput='variance_weighted'` is the default value for [`r2_score`](generated/sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score") for backward compatibility. This will be changed to `uniform_average` in the future.
###
3.3.4.1. R² score, the coefficient of determination
The [`r2_score`](generated/sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score") function computes the [coefficient of determination](https://en.wikipedia.org/wiki/Coefficient_of_determination), usually denoted as \(R^2\).
It represents the proportion of variance (of y) that has been explained by the independent variables in the model. It provides an indication of goodness of fit and therefore a measure of how well unseen samples are likely to be predicted by the model, through the proportion of explained variance.
As such variance is dataset dependent, \(R^2\) may not be meaningfully comparable across different datasets. Best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected (average) value of y, disregarding the input features, would get an \(R^2\) score of 0.0.
Note: when the prediction residuals have zero mean, the \(R^2\) score and the [Explained variance score](#explained-variance-score) are identical.
If \(\hat{y}\_i\) is the predicted value of the \(i\)-th sample and \(y\_i\) is the corresponding true value for total \(n\) samples, the estimated \(R^2\) is defined as:
\[R^2(y, \hat{y}) = 1 - \frac{\sum\_{i=1}^{n} (y\_i - \hat{y}\_i)^2}{\sum\_{i=1}^{n} (y\_i - \bar{y})^2}\] where \(\bar{y} = \frac{1}{n} \sum\_{i=1}^{n} y\_i\) and \(\sum\_{i=1}^{n} (y\_i - \hat{y}\_i)^2 = \sum\_{i=1}^{n} \epsilon\_i^2\).
Note that [`r2_score`](generated/sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score") calculates unadjusted \(R^2\) without correcting for bias in sample variance of y.
In the particular case where the true target is constant, the \(R^2\) score is not finite: it is either `NaN` (perfect predictions) or `-Inf` (imperfect predictions). Such non-finite scores may prevent correct model optimization such as grid-search cross-validation to be performed correctly. For this reason the default behaviour of [`r2_score`](generated/sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score") is to replace them with 1.0 (perfect predictions) or 0.0 (imperfect predictions). If `force_finite` is set to `False`, this score falls back on the original \(R^2\) definition.
Here is a small example of usage of the [`r2_score`](generated/sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score") function:
```
>>> from sklearn.metrics import r2_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> r2_score(y_true, y_pred)
0.948...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> r2_score(y_true, y_pred, multioutput='variance_weighted')
0.938...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> r2_score(y_true, y_pred, multioutput='uniform_average')
0.936...
>>> r2_score(y_true, y_pred, multioutput='raw_values')
array([0.965..., 0.908...])
>>> r2_score(y_true, y_pred, multioutput=[0.3, 0.7])
0.925...
>>> y_true = [-2, -2, -2]
>>> y_pred = [-2, -2, -2]
>>> r2_score(y_true, y_pred)
1.0
>>> r2_score(y_true, y_pred, force_finite=False)
nan
>>> y_true = [-2, -2, -2]
>>> y_pred = [-2, -2, -2 + 1e-8]
>>> r2_score(y_true, y_pred)
0.0
>>> r2_score(y_true, y_pred, force_finite=False)
-inf
```
###
3.3.4.2. Mean absolute error
The [`mean_absolute_error`](generated/sklearn.metrics.mean_absolute_error#sklearn.metrics.mean_absolute_error "sklearn.metrics.mean_absolute_error") function computes [mean absolute error](https://en.wikipedia.org/wiki/Mean_absolute_error), a risk metric corresponding to the expected value of the absolute error loss or \(l1\)-norm loss.
If \(\hat{y}\_i\) is the predicted value of the \(i\)-th sample, and \(y\_i\) is the corresponding true value, then the mean absolute error (MAE) estimated over \(n\_{\text{samples}}\) is defined as
\[\text{MAE}(y, \hat{y}) = \frac{1}{n\_{\text{samples}}} \sum\_{i=0}^{n\_{\text{samples}}-1} \left| y\_i - \hat{y}\_i \right|.\] Here is a small example of usage of the [`mean_absolute_error`](generated/sklearn.metrics.mean_absolute_error#sklearn.metrics.mean_absolute_error "sklearn.metrics.mean_absolute_error") function:
```
>>> from sklearn.metrics import mean_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_absolute_error(y_true, y_pred)
0.5
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> mean_absolute_error(y_true, y_pred)
0.75
>>> mean_absolute_error(y_true, y_pred, multioutput='raw_values')
array([0.5, 1. ])
>>> mean_absolute_error(y_true, y_pred, multioutput=[0.3, 0.7])
0.85...
```
###
3.3.4.3. Mean squared error
The [`mean_squared_error`](generated/sklearn.metrics.mean_squared_error#sklearn.metrics.mean_squared_error "sklearn.metrics.mean_squared_error") function computes [mean square error](https://en.wikipedia.org/wiki/Mean_squared_error), a risk metric corresponding to the expected value of the squared (quadratic) error or loss.
If \(\hat{y}\_i\) is the predicted value of the \(i\)-th sample, and \(y\_i\) is the corresponding true value, then the mean squared error (MSE) estimated over \(n\_{\text{samples}}\) is defined as
\[\text{MSE}(y, \hat{y}) = \frac{1}{n\_\text{samples}} \sum\_{i=0}^{n\_\text{samples} - 1} (y\_i - \hat{y}\_i)^2.\] Here is a small example of usage of the [`mean_squared_error`](generated/sklearn.metrics.mean_squared_error#sklearn.metrics.mean_squared_error "sklearn.metrics.mean_squared_error") function:
```
>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred)
0.375
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> mean_squared_error(y_true, y_pred)
0.7083...
```
###
3.3.4.4. Mean squared logarithmic error
The [`mean_squared_log_error`](generated/sklearn.metrics.mean_squared_log_error#sklearn.metrics.mean_squared_log_error "sklearn.metrics.mean_squared_log_error") function computes a risk metric corresponding to the expected value of the squared logarithmic (quadratic) error or loss.
If \(\hat{y}\_i\) is the predicted value of the \(i\)-th sample, and \(y\_i\) is the corresponding true value, then the mean squared logarithmic error (MSLE) estimated over \(n\_{\text{samples}}\) is defined as
\[\text{MSLE}(y, \hat{y}) = \frac{1}{n\_\text{samples}} \sum\_{i=0}^{n\_\text{samples} - 1} (\log\_e (1 + y\_i) - \log\_e (1 + \hat{y}\_i) )^2.\] Where \(\log\_e (x)\) means the natural logarithm of \(x\). This metric is best to use when targets having exponential growth, such as population counts, average sales of a commodity over a span of years etc. Note that this metric penalizes an under-predicted estimate greater than an over-predicted estimate.
Here is a small example of usage of the [`mean_squared_log_error`](generated/sklearn.metrics.mean_squared_log_error#sklearn.metrics.mean_squared_log_error "sklearn.metrics.mean_squared_log_error") function:
```
>>> from sklearn.metrics import mean_squared_log_error
>>> y_true = [3, 5, 2.5, 7]
>>> y_pred = [2.5, 5, 4, 8]
>>> mean_squared_log_error(y_true, y_pred)
0.039...
>>> y_true = [[0.5, 1], [1, 2], [7, 6]]
>>> y_pred = [[0.5, 2], [1, 2.5], [8, 8]]
>>> mean_squared_log_error(y_true, y_pred)
0.044...
```
###
3.3.4.5. Mean absolute percentage error
The [`mean_absolute_percentage_error`](generated/sklearn.metrics.mean_absolute_percentage_error#sklearn.metrics.mean_absolute_percentage_error "sklearn.metrics.mean_absolute_percentage_error") (MAPE), also known as mean absolute percentage deviation (MAPD), is an evaluation metric for regression problems. The idea of this metric is to be sensitive to relative errors. It is for example not changed by a global scaling of the target variable.
If \(\hat{y}\_i\) is the predicted value of the \(i\)-th sample and \(y\_i\) is the corresponding true value, then the mean absolute percentage error (MAPE) estimated over \(n\_{\text{samples}}\) is defined as
\[\text{MAPE}(y, \hat{y}) = \frac{1}{n\_{\text{samples}}} \sum\_{i=0}^{n\_{\text{samples}}-1} \frac{{}\left| y\_i - \hat{y}\_i \right|}{\max(\epsilon, \left| y\_i \right|)}\] where \(\epsilon\) is an arbitrary small yet strictly positive number to avoid undefined results when y is zero.
The [`mean_absolute_percentage_error`](generated/sklearn.metrics.mean_absolute_percentage_error#sklearn.metrics.mean_absolute_percentage_error "sklearn.metrics.mean_absolute_percentage_error") function supports multioutput.
Here is a small example of usage of the [`mean_absolute_percentage_error`](generated/sklearn.metrics.mean_absolute_percentage_error#sklearn.metrics.mean_absolute_percentage_error "sklearn.metrics.mean_absolute_percentage_error") function:
```
>>> from sklearn.metrics import mean_absolute_percentage_error
>>> y_true = [1, 10, 1e6]
>>> y_pred = [0.9, 15, 1.2e6]
>>> mean_absolute_percentage_error(y_true, y_pred)
0.2666...
```
In above example, if we had used `mean_absolute_error`, it would have ignored the small magnitude values and only reflected the error in prediction of highest magnitude value. But that problem is resolved in case of MAPE because it calculates relative percentage error with respect to actual output.
###
3.3.4.6. Median absolute error
The [`median_absolute_error`](generated/sklearn.metrics.median_absolute_error#sklearn.metrics.median_absolute_error "sklearn.metrics.median_absolute_error") is particularly interesting because it is robust to outliers. The loss is calculated by taking the median of all absolute differences between the target and the prediction.
If \(\hat{y}\_i\) is the predicted value of the \(i\)-th sample and \(y\_i\) is the corresponding true value, then the median absolute error (MedAE) estimated over \(n\_{\text{samples}}\) is defined as
\[\text{MedAE}(y, \hat{y}) = \text{median}(\mid y\_1 - \hat{y}\_1 \mid, \ldots, \mid y\_n - \hat{y}\_n \mid).\] The [`median_absolute_error`](generated/sklearn.metrics.median_absolute_error#sklearn.metrics.median_absolute_error "sklearn.metrics.median_absolute_error") does not support multioutput.
Here is a small example of usage of the [`median_absolute_error`](generated/sklearn.metrics.median_absolute_error#sklearn.metrics.median_absolute_error "sklearn.metrics.median_absolute_error") function:
```
>>> from sklearn.metrics import median_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> median_absolute_error(y_true, y_pred)
0.5
```
###
3.3.4.7. Max error
The [`max_error`](generated/sklearn.metrics.max_error#sklearn.metrics.max_error "sklearn.metrics.max_error") function computes the maximum [residual error](https://en.wikipedia.org/wiki/Errors_and_residuals) , a metric that captures the worst case error between the predicted value and the true value. In a perfectly fitted single output regression model, `max_error` would be `0` on the training set and though this would be highly unlikely in the real world, this metric shows the extent of error that the model had when it was fitted.
If \(\hat{y}\_i\) is the predicted value of the \(i\)-th sample, and \(y\_i\) is the corresponding true value, then the max error is defined as
\[\text{Max Error}(y, \hat{y}) = \max(| y\_i - \hat{y}\_i |)\] Here is a small example of usage of the [`max_error`](generated/sklearn.metrics.max_error#sklearn.metrics.max_error "sklearn.metrics.max_error") function:
```
>>> from sklearn.metrics import max_error
>>> y_true = [3, 2, 7, 1]
>>> y_pred = [9, 2, 7, 1]
>>> max_error(y_true, y_pred)
6
```
The [`max_error`](generated/sklearn.metrics.max_error#sklearn.metrics.max_error "sklearn.metrics.max_error") does not support multioutput.
###
3.3.4.8. Explained variance score
The [`explained_variance_score`](generated/sklearn.metrics.explained_variance_score#sklearn.metrics.explained_variance_score "sklearn.metrics.explained_variance_score") computes the [explained variance regression score](https://en.wikipedia.org/wiki/Explained_variation).
If \(\hat{y}\) is the estimated target output, \(y\) the corresponding (correct) target output, and \(Var\) is [Variance](https://en.wikipedia.org/wiki/Variance), the square of the standard deviation, then the explained variance is estimated as follow:
\[explained\\_{}variance(y, \hat{y}) = 1 - \frac{Var\{ y - \hat{y}\}}{Var\{y\}}\] The best possible score is 1.0, lower values are worse.
In the particular case where the true target is constant, the Explained Variance score is not finite: it is either `NaN` (perfect predictions) or `-Inf` (imperfect predictions). Such non-finite scores may prevent correct model optimization such as grid-search cross-validation to be performed correctly. For this reason the default behaviour of [`explained_variance_score`](generated/sklearn.metrics.explained_variance_score#sklearn.metrics.explained_variance_score "sklearn.metrics.explained_variance_score") is to replace them with 1.0 (perfect predictions) or 0.0 (imperfect predictions). You can set the `force_finite` parameter to `False` to prevent this fix from happening and fallback on the original Explained Variance score.
Here is a small example of usage of the [`explained_variance_score`](generated/sklearn.metrics.explained_variance_score#sklearn.metrics.explained_variance_score "sklearn.metrics.explained_variance_score") function:
```
>>> from sklearn.metrics import explained_variance_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> explained_variance_score(y_true, y_pred)
0.957...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> explained_variance_score(y_true, y_pred, multioutput='raw_values')
array([0.967..., 1. ])
>>> explained_variance_score(y_true, y_pred, multioutput=[0.3, 0.7])
0.990...
>>> y_true = [-2, -2, -2]
>>> y_pred = [-2, -2, -2]
>>> explained_variance_score(y_true, y_pred)
1.0
>>> explained_variance_score(y_true, y_pred, force_finite=False)
nan
>>> y_true = [-2, -2, -2]
>>> y_pred = [-2, -2, -2 + 1e-8]
>>> explained_variance_score(y_true, y_pred)
0.0
>>> explained_variance_score(y_true, y_pred, force_finite=False)
-inf
```
###
3.3.4.9. Mean Poisson, Gamma, and Tweedie deviances
The [`mean_tweedie_deviance`](generated/sklearn.metrics.mean_tweedie_deviance#sklearn.metrics.mean_tweedie_deviance "sklearn.metrics.mean_tweedie_deviance") function computes the [mean Tweedie deviance error](https://en.wikipedia.org/wiki/Tweedie_distribution#The_Tweedie_deviance) with a `power` parameter (\(p\)). This is a metric that elicits predicted expectation values of regression targets.
Following special cases exist,
* when `power=0` it is equivalent to [`mean_squared_error`](generated/sklearn.metrics.mean_squared_error#sklearn.metrics.mean_squared_error "sklearn.metrics.mean_squared_error").
* when `power=1` it is equivalent to [`mean_poisson_deviance`](generated/sklearn.metrics.mean_poisson_deviance#sklearn.metrics.mean_poisson_deviance "sklearn.metrics.mean_poisson_deviance").
* when `power=2` it is equivalent to [`mean_gamma_deviance`](generated/sklearn.metrics.mean_gamma_deviance#sklearn.metrics.mean_gamma_deviance "sklearn.metrics.mean_gamma_deviance").
If \(\hat{y}\_i\) is the predicted value of the \(i\)-th sample, and \(y\_i\) is the corresponding true value, then the mean Tweedie deviance error (D) for power \(p\), estimated over \(n\_{\text{samples}}\) is defined as
\[\begin{split}\text{D}(y, \hat{y}) = \frac{1}{n\_\text{samples}} \sum\_{i=0}^{n\_\text{samples} - 1} \begin{cases} (y\_i-\hat{y}\_i)^2, & \text{for }p=0\text{ (Normal)}\\ 2(y\_i \log(y\_i/\hat{y}\_i) + \hat{y}\_i - y\_i), & \text{for }p=1\text{ (Poisson)}\\ 2(\log(\hat{y}\_i/y\_i) + y\_i/\hat{y}\_i - 1), & \text{for }p=2\text{ (Gamma)}\\ 2\left(\frac{\max(y\_i,0)^{2-p}}{(1-p)(2-p)}- \frac{y\_i\,\hat{y}\_i^{1-p}}{1-p}+\frac{\hat{y}\_i^{2-p}}{2-p}\right), & \text{otherwise} \end{cases}\end{split}\] Tweedie deviance is a homogeneous function of degree `2-power`. Thus, Gamma distribution with `power=2` means that simultaneously scaling `y_true` and `y_pred` has no effect on the deviance. For Poisson distribution `power=1` the deviance scales linearly, and for Normal distribution (`power=0`), quadratically. In general, the higher `power` the less weight is given to extreme deviations between true and predicted targets.
For instance, let’s compare the two predictions 1.5 and 150 that are both 50% larger than their corresponding true value.
The mean squared error (`power=0`) is very sensitive to the prediction difference of the second point,:
```
>>> from sklearn.metrics import mean_tweedie_deviance
>>> mean_tweedie_deviance([1.0], [1.5], power=0)
0.25
>>> mean_tweedie_deviance([100.], [150.], power=0)
2500.0
```
If we increase `power` to 1,:
```
>>> mean_tweedie_deviance([1.0], [1.5], power=1)
0.18...
>>> mean_tweedie_deviance([100.], [150.], power=1)
18.9...
```
the difference in errors decreases. Finally, by setting, `power=2`:
```
>>> mean_tweedie_deviance([1.0], [1.5], power=2)
0.14...
>>> mean_tweedie_deviance([100.], [150.], power=2)
0.14...
```
we would get identical errors. The deviance when `power=2` is thus only sensitive to relative errors.
###
3.3.4.10. Pinball loss
The [`mean_pinball_loss`](generated/sklearn.metrics.mean_pinball_loss#sklearn.metrics.mean_pinball_loss "sklearn.metrics.mean_pinball_loss") function is used to evaluate the predictive performance of [quantile regression](https://en.wikipedia.org/wiki/Quantile_regression) models.
\[\text{pinball}(y, \hat{y}) = \frac{1}{n\_{\text{samples}}} \sum\_{i=0}^{n\_{\text{samples}}-1} \alpha \max(y\_i - \hat{y}\_i, 0) + (1 - \alpha) \max(\hat{y}\_i - y\_i, 0)\] The value of pinball loss is equivalent to half of [`mean_absolute_error`](generated/sklearn.metrics.mean_absolute_error#sklearn.metrics.mean_absolute_error "sklearn.metrics.mean_absolute_error") when the quantile parameter `alpha` is set to 0.5.
Here is a small example of usage of the [`mean_pinball_loss`](generated/sklearn.metrics.mean_pinball_loss#sklearn.metrics.mean_pinball_loss "sklearn.metrics.mean_pinball_loss") function:
```
>>> from sklearn.metrics import mean_pinball_loss
>>> y_true = [1, 2, 3]
>>> mean_pinball_loss(y_true, [0, 2, 3], alpha=0.1)
0.03...
>>> mean_pinball_loss(y_true, [1, 2, 4], alpha=0.1)
0.3...
>>> mean_pinball_loss(y_true, [0, 2, 3], alpha=0.9)
0.3...
>>> mean_pinball_loss(y_true, [1, 2, 4], alpha=0.9)
0.03...
>>> mean_pinball_loss(y_true, y_true, alpha=0.1)
0.0
>>> mean_pinball_loss(y_true, y_true, alpha=0.9)
0.0
```
It is possible to build a scorer object with a specific choice of `alpha`:
```
>>> from sklearn.metrics import make_scorer
>>> mean_pinball_loss_95p = make_scorer(mean_pinball_loss, alpha=0.95)
```
Such a scorer can be used to evaluate the generalization performance of a quantile regressor via cross-validation:
```
>>> from sklearn.datasets import make_regression
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.ensemble import GradientBoostingRegressor
>>>
>>> X, y = make_regression(n_samples=100, random_state=0)
>>> estimator = GradientBoostingRegressor(
... loss="quantile",
... alpha=0.95,
... random_state=0,
... )
>>> cross_val_score(estimator, X, y, cv=5, scoring=mean_pinball_loss_95p)
array([13.6..., 9.7..., 23.3..., 9.5..., 10.4...])
```
It is also possible to build scorer objects for hyper-parameter tuning. The sign of the loss must be switched to ensure that greater means better as explained in the example linked below.
###
3.3.4.11. D² score
The D² score computes the fraction of deviance explained. It is a generalization of R², where the squared error is generalized and replaced by a deviance of choice \(\text{dev}(y, \hat{y})\) (e.g., Tweedie, pinball or mean absolute error). D² is a form of a *skill score*. It is calculated as
\[D^2(y, \hat{y}) = 1 - \frac{\text{dev}(y, \hat{y})}{\text{dev}(y, y\_{\text{null}})} \,.\] Where \(y\_{\text{null}}\) is the optimal prediction of an intercept-only model (e.g., the mean of `y_true` for the Tweedie case, the median for absolute error and the alpha-quantile for pinball loss).
Like R², the best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts \(y\_{\text{null}}\), disregarding the input features, would get a D² score of 0.0.
####
3.3.4.11.1. D² Tweedie score
The [`d2_tweedie_score`](generated/sklearn.metrics.d2_tweedie_score#sklearn.metrics.d2_tweedie_score "sklearn.metrics.d2_tweedie_score") function implements the special case of D² where \(\text{dev}(y, \hat{y})\) is the Tweedie deviance, see [Mean Poisson, Gamma, and Tweedie deviances](#mean-tweedie-deviance). It is also known as D² Tweedie and is related to McFadden’s likelihood ratio index.
The argument `power` defines the Tweedie power as for [`mean_tweedie_deviance`](generated/sklearn.metrics.mean_tweedie_deviance#sklearn.metrics.mean_tweedie_deviance "sklearn.metrics.mean_tweedie_deviance"). Note that for `power=0`, [`d2_tweedie_score`](generated/sklearn.metrics.d2_tweedie_score#sklearn.metrics.d2_tweedie_score "sklearn.metrics.d2_tweedie_score") equals [`r2_score`](generated/sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score") (for single targets).
A scorer object with a specific choice of `power` can be built by:
```
>>> from sklearn.metrics import d2_tweedie_score, make_scorer
>>> d2_tweedie_score_15 = make_scorer(d2_tweedie_score, power=1.5)
```
####
3.3.4.11.2. D² pinball score
The [`d2_pinball_score`](generated/sklearn.metrics.d2_pinball_score#sklearn.metrics.d2_pinball_score "sklearn.metrics.d2_pinball_score") function implements the special case of D² with the pinball loss, see [Pinball loss](#pinball-loss), i.e.:
\[\text{dev}(y, \hat{y}) = \text{pinball}(y, \hat{y}).\] The argument `alpha` defines the slope of the pinball loss as for [`mean_pinball_loss`](generated/sklearn.metrics.mean_pinball_loss#sklearn.metrics.mean_pinball_loss "sklearn.metrics.mean_pinball_loss") ([Pinball loss](#pinball-loss)). It determines the quantile level `alpha` for which the pinball loss and also D² are optimal. Note that for `alpha=0.5` (the default) [`d2_pinball_score`](generated/sklearn.metrics.d2_pinball_score#sklearn.metrics.d2_pinball_score "sklearn.metrics.d2_pinball_score") equals [`d2_absolute_error_score`](generated/sklearn.metrics.d2_absolute_error_score#sklearn.metrics.d2_absolute_error_score "sklearn.metrics.d2_absolute_error_score").
A scorer object with a specific choice of `alpha` can be built by:
```
>>> from sklearn.metrics import d2_pinball_score, make_scorer
>>> d2_pinball_score_08 = make_scorer(d2_pinball_score, alpha=0.8)
```
####
3.3.4.11.3. D² absolute error score
The [`d2_absolute_error_score`](generated/sklearn.metrics.d2_absolute_error_score#sklearn.metrics.d2_absolute_error_score "sklearn.metrics.d2_absolute_error_score") function implements the special case of the [Mean absolute error](#mean-absolute-error):
\[\text{dev}(y, \hat{y}) = \text{MAE}(y, \hat{y}).\] Here are some usage examples of the [`d2_absolute_error_score`](generated/sklearn.metrics.d2_absolute_error_score#sklearn.metrics.d2_absolute_error_score "sklearn.metrics.d2_absolute_error_score") function:
```
>>> from sklearn.metrics import d2_absolute_error_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> d2_absolute_error_score(y_true, y_pred)
0.764...
>>> y_true = [1, 2, 3]
>>> y_pred = [1, 2, 3]
>>> d2_absolute_error_score(y_true, y_pred)
1.0
>>> y_true = [1, 2, 3]
>>> y_pred = [2, 2, 2]
>>> d2_absolute_error_score(y_true, y_pred)
0.0
```
3.3.5. Clustering metrics
--------------------------
The [`sklearn.metrics`](classes#module-sklearn.metrics "sklearn.metrics") module implements several loss, score, and utility functions. For more information see the [Clustering performance evaluation](clustering#clustering-evaluation) section for instance clustering, and [Biclustering evaluation](biclustering#biclustering-evaluation) for biclustering.
3.3.6. Dummy estimators
------------------------
When doing supervised learning, a simple sanity check consists of comparing one’s estimator against simple rules of thumb. [`DummyClassifier`](generated/sklearn.dummy.dummyclassifier#sklearn.dummy.DummyClassifier "sklearn.dummy.DummyClassifier") implements several such simple strategies for classification:
* `stratified` generates random predictions by respecting the training set class distribution.
* `most_frequent` always predicts the most frequent label in the training set.
* `prior` always predicts the class that maximizes the class prior (like `most_frequent`) and `predict_proba` returns the class prior.
* `uniform` generates predictions uniformly at random.
* `constant` always predicts a constant label that is provided by the user.
A major motivation of this method is F1-scoring, when the positive class is in the minority.
Note that with all these strategies, the `predict` method completely ignores the input data!
To illustrate [`DummyClassifier`](generated/sklearn.dummy.dummyclassifier#sklearn.dummy.DummyClassifier "sklearn.dummy.DummyClassifier"), first let’s create an imbalanced dataset:
```
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> X, y = load_iris(return_X_y=True)
>>> y[y != 1] = -1
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)
```
Next, let’s compare the accuracy of `SVC` and `most_frequent`:
```
>>> from sklearn.dummy import DummyClassifier
>>> from sklearn.svm import SVC
>>> clf = SVC(kernel='linear', C=1).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.63...
>>> clf = DummyClassifier(strategy='most_frequent', random_state=0)
>>> clf.fit(X_train, y_train)
DummyClassifier(random_state=0, strategy='most_frequent')
>>> clf.score(X_test, y_test)
0.57...
```
We see that `SVC` doesn’t do much better than a dummy classifier. Now, let’s change the kernel:
```
>>> clf = SVC(kernel='rbf', C=1).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.94...
```
We see that the accuracy was boosted to almost 100%. A cross validation strategy is recommended for a better estimate of the accuracy, if it is not too CPU costly. For more information see the [Cross-validation: evaluating estimator performance](cross_validation#cross-validation) section. Moreover if you want to optimize over the parameter space, it is highly recommended to use an appropriate methodology; see the [Tuning the hyper-parameters of an estimator](grid_search#grid-search) section for details.
More generally, when the accuracy of a classifier is too close to random, it probably means that something went wrong: features are not helpful, a hyperparameter is not correctly tuned, the classifier is suffering from class imbalance, etc…
[`DummyRegressor`](generated/sklearn.dummy.dummyregressor#sklearn.dummy.DummyRegressor "sklearn.dummy.DummyRegressor") also implements four simple rules of thumb for regression:
* `mean` always predicts the mean of the training targets.
* `median` always predicts the median of the training targets.
* `quantile` always predicts a user provided quantile of the training targets.
* `constant` always predicts a constant value that is provided by the user.
In all these strategies, the `predict` method completely ignores the input data.
| programming_docs |
scikit_learn 1.16. Probability calibration 1.16. Probability calibration
=============================
When performing classification you often want not only to predict the class label, but also obtain a probability of the respective label. This probability gives you some kind of confidence on the prediction. Some models can give you poor estimates of the class probabilities and some even do not support probability prediction (e.g., some instances of [`SGDClassifier`](generated/sklearn.linear_model.sgdclassifier#sklearn.linear_model.SGDClassifier "sklearn.linear_model.SGDClassifier")). The calibration module allows you to better calibrate the probabilities of a given model, or to add support for probability prediction.
Well calibrated classifiers are probabilistic classifiers for which the output of the [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) method can be directly interpreted as a confidence level. For instance, a well calibrated (binary) classifier should classify the samples such that among the samples to which it gave a [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) value close to 0.8, approximately 80% actually belong to the positive class.
1.16.1. Calibration curves
---------------------------
Calibration curves (also known as reliability diagrams) compare how well the probabilistic predictions of a binary classifier are calibrated. It plots the true frequency of the positive label against its predicted probability, for binned predictions. The x axis represents the average predicted probability in each bin. The y axis is the *fraction of positives*, i.e. the proportion of samples whose class is the positive class (in each bin). The top calibration curve plot is created with `CalibrationDisplay.from_estimators`, which uses [`calibration_curve`](generated/sklearn.calibration.calibration_curve#sklearn.calibration.calibration_curve "sklearn.calibration.calibration_curve") to calculate the per bin average predicted probabilities and fraction of positives. [`CalibrationDisplay.from_estimator`](generated/sklearn.calibration.calibrationdisplay#sklearn.calibration.CalibrationDisplay.from_estimator "sklearn.calibration.CalibrationDisplay.from_estimator") takes as input a fitted classifier, which is used to calculate the predicted probabilities. The classifier thus must have [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) method. For the few classifiers that do not have a [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) method, it is possible to use [`CalibratedClassifierCV`](generated/sklearn.calibration.calibratedclassifiercv#sklearn.calibration.CalibratedClassifierCV "sklearn.calibration.CalibratedClassifierCV") to calibrate the classifier outputs to probabilities.
The bottom histogram gives some insight into the behavior of each classifier by showing the number of samples in each predicted probability bin.
[`LogisticRegression`](generated/sklearn.linear_model.logisticregression#sklearn.linear_model.LogisticRegression "sklearn.linear_model.LogisticRegression") returns well calibrated predictions by default as it directly optimizes [Log loss](model_evaluation#log-loss). In contrast, the other methods return biased probabilities; with different biases per method:
[`GaussianNB`](generated/sklearn.naive_bayes.gaussiannb#sklearn.naive_bayes.GaussianNB "sklearn.naive_bayes.GaussianNB") tends to push probabilities to 0 or 1 (note the counts in the histograms). This is mainly because it makes the assumption that features are conditionally independent given the class, which is not the case in this dataset which contains 2 redundant features.
[`RandomForestClassifier`](generated/sklearn.ensemble.randomforestclassifier#sklearn.ensemble.RandomForestClassifier "sklearn.ensemble.RandomForestClassifier") shows the opposite behavior: the histograms show peaks at approximately 0.2 and 0.9 probability, while probabilities close to 0 or 1 are very rare. An explanation for this is given by Niculescu-Mizil and Caruana [[1]](#id10): “Methods such as bagging and random forests that average predictions from a base set of models can have difficulty making predictions near 0 and 1 because variance in the underlying base models will bias predictions that should be near zero or one away from these values. Because predictions are restricted to the interval [0,1], errors caused by variance tend to be one-sided near zero and one. For example, if a model should predict p = 0 for a case, the only way bagging can achieve this is if all bagged trees predict zero. If we add noise to the trees that bagging is averaging over, this noise will cause some trees to predict values larger than 0 for this case, thus moving the average prediction of the bagged ensemble away from 0. We observe this effect most strongly with random forests because the base-level trees trained with random forests have relatively high variance due to feature subsetting.” As a result, the calibration curve also referred to as the reliability diagram (Wilks 1995 [[2]](#id11)) shows a characteristic sigmoid shape, indicating that the classifier could trust its “intuition” more and return probabilities closer to 0 or 1 typically.
Linear Support Vector Classification ([`LinearSVC`](generated/sklearn.svm.linearsvc#sklearn.svm.LinearSVC "sklearn.svm.LinearSVC")) shows an even more sigmoid curve than [`RandomForestClassifier`](generated/sklearn.ensemble.randomforestclassifier#sklearn.ensemble.RandomForestClassifier "sklearn.ensemble.RandomForestClassifier"), which is typical for maximum-margin methods (compare Niculescu-Mizil and Caruana [[1]](#id10)), which focus on difficult to classify samples that are close to the decision boundary (the support vectors).
1.16.2. Calibrating a classifier
---------------------------------
Calibrating a classifier consists of fitting a regressor (called a *calibrator*) that maps the output of the classifier (as given by [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) or [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba)) to a calibrated probability in [0, 1]. Denoting the output of the classifier for a given sample by \(f\_i\), the calibrator tries to predict \(p(y\_i = 1 | f\_i)\).
The samples that are used to fit the calibrator should not be the same samples used to fit the classifier, as this would introduce bias. This is because performance of the classifier on its training data would be better than for novel data. Using the classifier output of training data to fit the calibrator would thus result in a biased calibrator that maps to probabilities closer to 0 and 1 than it should.
1.16.3. Usage
--------------
The [`CalibratedClassifierCV`](generated/sklearn.calibration.calibratedclassifiercv#sklearn.calibration.CalibratedClassifierCV "sklearn.calibration.CalibratedClassifierCV") class is used to calibrate a classifier.
[`CalibratedClassifierCV`](generated/sklearn.calibration.calibratedclassifiercv#sklearn.calibration.CalibratedClassifierCV "sklearn.calibration.CalibratedClassifierCV") uses a cross-validation approach to ensure unbiased data is always used to fit the calibrator. The data is split into k `(train_set, test_set)` couples (as determined by `cv`). When `ensemble=True` (default), the following procedure is repeated independently for each cross-validation split: a clone of `base_estimator` is first trained on the train subset. Then its predictions on the test subset are used to fit a calibrator (either a sigmoid or isotonic regressor). This results in an ensemble of k `(classifier, calibrator)` couples where each calibrator maps the output of its corresponding classifier into [0, 1]. Each couple is exposed in the `calibrated_classifiers_` attribute, where each entry is a calibrated classifier with a [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) method that outputs calibrated probabilities. The output of [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) for the main [`CalibratedClassifierCV`](generated/sklearn.calibration.calibratedclassifiercv#sklearn.calibration.CalibratedClassifierCV "sklearn.calibration.CalibratedClassifierCV") instance corresponds to the average of the predicted probabilities of the `k` estimators in the `calibrated_classifiers_` list. The output of [predict](https://scikit-learn.org/1.1/glossary.html#term-predict) is the class that has the highest probability.
When `ensemble=False`, cross-validation is used to obtain ‘unbiased’ predictions for all the data, via [`cross_val_predict`](generated/sklearn.model_selection.cross_val_predict#sklearn.model_selection.cross_val_predict "sklearn.model_selection.cross_val_predict"). These unbiased predictions are then used to train the calibrator. The attribute `calibrated_classifiers_` consists of only one `(classifier, calibrator)` couple where the classifier is the `base_estimator` trained on all the data. In this case the output of [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) for [`CalibratedClassifierCV`](generated/sklearn.calibration.calibratedclassifiercv#sklearn.calibration.CalibratedClassifierCV "sklearn.calibration.CalibratedClassifierCV") is the predicted probabilities obtained from the single `(classifier, calibrator)` couple.
The main advantage of `ensemble=True` is to benefit from the traditional ensembling effect (similar to [Bagging meta-estimator](ensemble#bagging)). The resulting ensemble should both be well calibrated and slightly more accurate than with `ensemble=False`. The main advantage of using `ensemble=False` is computational: it reduces the overall fit time by training only a single base classifier and calibrator pair, decreases the final model size and increases prediction speed.
Alternatively an already fitted classifier can be calibrated by setting `cv="prefit"`. In this case, the data is not split and all of it is used to fit the regressor. It is up to the user to make sure that the data used for fitting the classifier is disjoint from the data used for fitting the regressor.
[`sklearn.metrics.brier_score_loss`](generated/sklearn.metrics.brier_score_loss#sklearn.metrics.brier_score_loss "sklearn.metrics.brier_score_loss") may be used to assess how well a classifier is calibrated. However, this metric should be used with care because a lower Brier score does not always mean a better calibrated model. This is because the Brier score metric is a combination of calibration loss and refinement loss. Calibration loss is defined as the mean squared deviation from empirical probabilities derived from the slope of ROC segments. Refinement loss can be defined as the expected optimal loss as measured by the area under the optimal cost curve. As refinement loss can change independently from calibration loss, a lower Brier score does not necessarily mean a better calibrated model.
[`CalibratedClassifierCV`](generated/sklearn.calibration.calibratedclassifiercv#sklearn.calibration.CalibratedClassifierCV "sklearn.calibration.CalibratedClassifierCV") supports the use of two ‘calibration’ regressors: ‘sigmoid’ and ‘isotonic’.
###
1.16.3.1. Sigmoid
The sigmoid regressor is based on Platt’s logistic model [[3]](#id12):
\[p(y\_i = 1 | f\_i) = \frac{1}{1 + \exp(A f\_i + B)}\] where \(y\_i\) is the true label of sample \(i\) and \(f\_i\) is the output of the un-calibrated classifier for sample \(i\). \(A\) and \(B\) are real numbers to be determined when fitting the regressor via maximum likelihood.
The sigmoid method assumes the [calibration curve](#calibration-curve) can be corrected by applying a sigmoid function to the raw predictions. This assumption has been empirically justified in the case of [Support Vector Machines](svm#svm) with common kernel functions on various benchmark datasets in section 2.1 of Platt 1999 [[3]](#id12) but does not necessarily hold in general. Additionally, the logistic model works best if the calibration error is symmetrical, meaning the classifier output for each binary class is normally distributed with the same variance [[6]](#id15). This can be a problem for highly imbalanced classification problems, where outputs do not have equal variance.
In general this method is most effective when the un-calibrated model is under-confident and has similar calibration errors for both high and low outputs.
###
1.16.3.2. Isotonic
The ‘isotonic’ method fits a non-parametric isotonic regressor, which outputs a step-wise non-decreasing function (see [`sklearn.isotonic`](classes#module-sklearn.isotonic "sklearn.isotonic")). It minimizes:
\[\sum\_{i=1}^{n} (y\_i - \hat{f}\_i)^2\] subject to \(\hat{f}\_i >= \hat{f}\_j\) whenever \(f\_i >= f\_j\). \(y\_i\) is the true label of sample \(i\) and \(\hat{f}\_i\) is the output of the calibrated classifier for sample \(i\) (i.e., the calibrated probability). This method is more general when compared to ‘sigmoid’ as the only restriction is that the mapping function is monotonically increasing. It is thus more powerful as it can correct any monotonic distortion of the un-calibrated model. However, it is more prone to overfitting, especially on small datasets [[5]](#id14).
Overall, ‘isotonic’ will perform as well as or better than ‘sigmoid’ when there is enough data (greater than ~ 1000 samples) to avoid overfitting [[1]](#id10).
###
1.16.3.3. Multiclass support
Both isotonic and sigmoid regressors only support 1-dimensional data (e.g., binary classification output) but are extended for multiclass classification if the `base_estimator` supports multiclass predictions. For multiclass predictions, [`CalibratedClassifierCV`](generated/sklearn.calibration.calibratedclassifiercv#sklearn.calibration.CalibratedClassifierCV "sklearn.calibration.CalibratedClassifierCV") calibrates for each class separately in a [OneVsRestClassifier](multiclass#ovr-classification) fashion [[4]](#id13). When predicting probabilities, the calibrated probabilities for each class are predicted separately. As those probabilities do not necessarily sum to one, a postprocessing is performed to normalize them.
scikit_learn 3.4. Validation curves: plotting scores to evaluate models 3.4. Validation curves: plotting scores to evaluate models
==========================================================
Every estimator has its advantages and drawbacks. Its generalization error can be decomposed in terms of bias, variance and noise. The **bias** of an estimator is its average error for different training sets. The **variance** of an estimator indicates how sensitive it is to varying training sets. Noise is a property of the data.
In the following plot, we see a function \(f(x) = \cos (\frac{3}{2} \pi x)\) and some noisy samples from that function. We use three different estimators to fit the function: linear regression with polynomial features of degree 1, 4 and 15. We see that the first estimator can at best provide only a poor fit to the samples and the true function because it is too simple (high bias), the second estimator approximates it almost perfectly and the last estimator approximates the training data perfectly but does not fit the true function very well, i.e. it is very sensitive to varying training data (high variance).
Bias and variance are inherent properties of estimators and we usually have to select learning algorithms and hyperparameters so that both bias and variance are as low as possible (see [Bias-variance dilemma](https://en.wikipedia.org/wiki/Bias-variance_dilemma)). Another way to reduce the variance of a model is to use more training data. However, you should only collect more training data if the true function is too complex to be approximated by an estimator with a lower variance.
In the simple one-dimensional problem that we have seen in the example it is easy to see whether the estimator suffers from bias or variance. However, in high-dimensional spaces, models can become very difficult to visualize. For this reason, it is often helpful to use the tools described below.
3.4.1. Validation curve
------------------------
To validate a model we need a scoring function (see [Metrics and scoring: quantifying the quality of predictions](model_evaluation#model-evaluation)), for example accuracy for classifiers. The proper way of choosing multiple hyperparameters of an estimator is of course grid search or similar methods (see [Tuning the hyper-parameters of an estimator](grid_search#grid-search)) that select the hyperparameter with the maximum score on a validation set or multiple validation sets. Note that if we optimize the hyperparameters based on a validation score the validation score is biased and not a good estimate of the generalization any longer. To get a proper estimate of the generalization we have to compute the score on another test set.
However, it is sometimes helpful to plot the influence of a single hyperparameter on the training score and the validation score to find out whether the estimator is overfitting or underfitting for some hyperparameter values.
The function [`validation_curve`](generated/sklearn.model_selection.validation_curve#sklearn.model_selection.validation_curve "sklearn.model_selection.validation_curve") can help in this case:
```
>>> import numpy as np
>>> from sklearn.model_selection import validation_curve
>>> from sklearn.datasets import load_iris
>>> from sklearn.linear_model import Ridge
>>> np.random.seed(0)
>>> X, y = load_iris(return_X_y=True)
>>> indices = np.arange(y.shape[0])
>>> np.random.shuffle(indices)
>>> X, y = X[indices], y[indices]
>>> train_scores, valid_scores = validation_curve(
... Ridge(), X, y, param_name="alpha", param_range=np.logspace(-7, 3, 3),
... cv=5)
>>> train_scores
array([[0.93..., 0.94..., 0.92..., 0.91..., 0.92...],
[0.93..., 0.94..., 0.92..., 0.91..., 0.92...],
[0.51..., 0.52..., 0.49..., 0.47..., 0.49...]])
>>> valid_scores
array([[0.90..., 0.84..., 0.94..., 0.96..., 0.93...],
[0.90..., 0.84..., 0.94..., 0.96..., 0.93...],
[0.46..., 0.25..., 0.50..., 0.49..., 0.52...]])
```
If the training score and the validation score are both low, the estimator will be underfitting. If the training score is high and the validation score is low, the estimator is overfitting and otherwise it is working very well. A low training score and a high validation score is usually not possible. Underfitting, overfitting, and a working model are shown in the in the plot below where we vary the parameter \(\gamma\) of an SVM on the digits dataset.
3.4.2. Learning curve
----------------------
A learning curve shows the validation and training score of an estimator for varying numbers of training samples. It is a tool to find out how much we benefit from adding more training data and whether the estimator suffers more from a variance error or a bias error. Consider the following example where we plot the learning curve of a naive Bayes classifier and an SVM.
For the naive Bayes, both the validation score and the training score converge to a value that is quite low with increasing size of the training set. Thus, we will probably not benefit much from more training data.
In contrast, for small amounts of data, the training score of the SVM is much greater than the validation score. Adding more training samples will most likely increase generalization.
We can use the function [`learning_curve`](generated/sklearn.model_selection.learning_curve#sklearn.model_selection.learning_curve "sklearn.model_selection.learning_curve") to generate the values that are required to plot such a learning curve (number of samples that have been used, the average scores on the training sets and the average scores on the validation sets):
```
>>> from sklearn.model_selection import learning_curve
>>> from sklearn.svm import SVC
>>> train_sizes, train_scores, valid_scores = learning_curve(
... SVC(kernel='linear'), X, y, train_sizes=[50, 80, 110], cv=5)
>>> train_sizes
array([ 50, 80, 110])
>>> train_scores
array([[0.98..., 0.98 , 0.98..., 0.98..., 0.98...],
[0.98..., 1. , 0.98..., 0.98..., 0.98...],
[0.98..., 1. , 0.98..., 0.98..., 0.99...]])
>>> valid_scores
array([[1. , 0.93..., 1. , 1. , 0.96...],
[1. , 0.96..., 1. , 1. , 0.96...],
[1. , 0.96..., 1. , 1. , 0.96...]])
```
| programming_docs |
scikit_learn 2.9. Neural network models (unsupervised) 2.9. Neural network models (unsupervised)
=========================================
2.9.1. Restricted Boltzmann machines
-------------------------------------
Restricted Boltzmann machines (RBM) are unsupervised nonlinear feature learners based on a probabilistic model. The features extracted by an RBM or a hierarchy of RBMs often give good results when fed into a linear classifier such as a linear SVM or a perceptron.
The model makes assumptions regarding the distribution of inputs. At the moment, scikit-learn only provides [`BernoulliRBM`](generated/sklearn.neural_network.bernoullirbm#sklearn.neural_network.BernoulliRBM "sklearn.neural_network.BernoulliRBM"), which assumes the inputs are either binary values or values between 0 and 1, each encoding the probability that the specific feature would be turned on.
The RBM tries to maximize the likelihood of the data using a particular graphical model. The parameter learning algorithm used ([Stochastic Maximum Likelihood](#sml)) prevents the representations from straying far from the input data, which makes them capture interesting regularities, but makes the model less useful for small datasets, and usually not useful for density estimation.
The method gained popularity for initializing deep neural networks with the weights of independent RBMs. This method is known as unsupervised pre-training.
###
2.9.1.1. Graphical model and parametrization
The graphical model of an RBM is a fully-connected bipartite graph.
The nodes are random variables whose states depend on the state of the other nodes they are connected to. The model is therefore parameterized by the weights of the connections, as well as one intercept (bias) term for each visible and hidden unit, omitted from the image for simplicity.
The energy function measures the quality of a joint assignment:
\[E(\mathbf{v}, \mathbf{h}) = -\sum\_i \sum\_j w\_{ij}v\_ih\_j - \sum\_i b\_iv\_i - \sum\_j c\_jh\_j\] In the formula above, \(\mathbf{b}\) and \(\mathbf{c}\) are the intercept vectors for the visible and hidden layers, respectively. The joint probability of the model is defined in terms of the energy:
\[P(\mathbf{v}, \mathbf{h}) = \frac{e^{-E(\mathbf{v}, \mathbf{h})}}{Z}\] The word *restricted* refers to the bipartite structure of the model, which prohibits direct interaction between hidden units, or between visible units. This means that the following conditional independencies are assumed:
\[\begin{split}h\_i \bot h\_j | \mathbf{v} \\ v\_i \bot v\_j | \mathbf{h}\end{split}\] The bipartite structure allows for the use of efficient block Gibbs sampling for inference.
###
2.9.1.2. Bernoulli Restricted Boltzmann machines
In the [`BernoulliRBM`](generated/sklearn.neural_network.bernoullirbm#sklearn.neural_network.BernoulliRBM "sklearn.neural_network.BernoulliRBM"), all units are binary stochastic units. This means that the input data should either be binary, or real-valued between 0 and 1 signifying the probability that the visible unit would turn on or off. This is a good model for character recognition, where the interest is on which pixels are active and which aren’t. For images of natural scenes it no longer fits because of background, depth and the tendency of neighbouring pixels to take the same values.
The conditional probability distribution of each unit is given by the logistic sigmoid activation function of the input it receives:
\[\begin{split}P(v\_i=1|\mathbf{h}) = \sigma(\sum\_j w\_{ij}h\_j + b\_i) \\ P(h\_i=1|\mathbf{v}) = \sigma(\sum\_i w\_{ij}v\_i + c\_j)\end{split}\] where \(\sigma\) is the logistic sigmoid function:
\[\sigma(x) = \frac{1}{1 + e^{-x}}\] ###
2.9.1.3. Stochastic Maximum Likelihood learning
The training algorithm implemented in [`BernoulliRBM`](generated/sklearn.neural_network.bernoullirbm#sklearn.neural_network.BernoulliRBM "sklearn.neural_network.BernoulliRBM") is known as Stochastic Maximum Likelihood (SML) or Persistent Contrastive Divergence (PCD). Optimizing maximum likelihood directly is infeasible because of the form of the data likelihood:
\[\log P(v) = \log \sum\_h e^{-E(v, h)} - \log \sum\_{x, y} e^{-E(x, y)}\] For simplicity the equation above is written for a single training example. The gradient with respect to the weights is formed of two terms corresponding to the ones above. They are usually known as the positive gradient and the negative gradient, because of their respective signs. In this implementation, the gradients are estimated over mini-batches of samples.
In maximizing the log-likelihood, the positive gradient makes the model prefer hidden states that are compatible with the observed training data. Because of the bipartite structure of RBMs, it can be computed efficiently. The negative gradient, however, is intractable. Its goal is to lower the energy of joint states that the model prefers, therefore making it stay true to the data. It can be approximated by Markov chain Monte Carlo using block Gibbs sampling by iteratively sampling each of \(v\) and \(h\) given the other, until the chain mixes. Samples generated in this way are sometimes referred as fantasy particles. This is inefficient and it is difficult to determine whether the Markov chain mixes.
The Contrastive Divergence method suggests to stop the chain after a small number of iterations, \(k\), usually even 1. This method is fast and has low variance, but the samples are far from the model distribution.
Persistent Contrastive Divergence addresses this. Instead of starting a new chain each time the gradient is needed, and performing only one Gibbs sampling step, in PCD we keep a number of chains (fantasy particles) that are updated \(k\) Gibbs steps after each weight update. This allows the particles to explore the space more thoroughly.
scikit_learn 1.14. Semi-supervised learning 1.14. Semi-supervised learning
==============================
[Semi-supervised learning](https://en.wikipedia.org/wiki/Semi-supervised_learning) is a situation in which in your training data some of the samples are not labeled. The semi-supervised estimators in [`sklearn.semi_supervised`](classes#module-sklearn.semi_supervised "sklearn.semi_supervised") are able to make use of this additional unlabeled data to better capture the shape of the underlying data distribution and generalize better to new samples. These algorithms can perform well when we have a very small amount of labeled points and a large amount of unlabeled points.
Note
Semi-supervised algorithms need to make assumptions about the distribution of the dataset in order to achieve performance gains. See [here](https://en.wikipedia.org/wiki/Semi-supervised_learning#Assumptions) for more details.
1.14.1. Self Training
----------------------
This self-training implementation is based on Yarowsky’s [[1]](#id4) algorithm. Using this algorithm, a given supervised classifier can function as a semi-supervised classifier, allowing it to learn from unlabeled data.
[`SelfTrainingClassifier`](generated/sklearn.semi_supervised.selftrainingclassifier#sklearn.semi_supervised.SelfTrainingClassifier "sklearn.semi_supervised.SelfTrainingClassifier") can be called with any classifier that implements `predict_proba`, passed as the parameter `base_classifier`. In each iteration, the `base_classifier` predicts labels for the unlabeled samples and adds a subset of these labels to the labeled dataset.
The choice of this subset is determined by the selection criterion. This selection can be done using a `threshold` on the prediction probabilities, or by choosing the `k_best` samples according to the prediction probabilities.
The labels used for the final fit as well as the iteration in which each sample was labeled are available as attributes. The optional `max_iter` parameter specifies how many times the loop is executed at most.
The `max_iter` parameter may be set to `None`, causing the algorithm to iterate until all samples have labels or no new samples are selected in that iteration.
Note
When using the self-training classifier, the [calibration](calibration#calibration) of the classifier is important.
1.14.2. Label Propagation
--------------------------
Label propagation denotes a few variations of semi-supervised graph inference algorithms.
A few features available in this model:
* Used for classification tasks
* Kernel methods to project data into alternate dimensional spaces
`scikit-learn` provides two label propagation models: [`LabelPropagation`](generated/sklearn.semi_supervised.labelpropagation#sklearn.semi_supervised.LabelPropagation "sklearn.semi_supervised.LabelPropagation") and [`LabelSpreading`](generated/sklearn.semi_supervised.labelspreading#sklearn.semi_supervised.LabelSpreading "sklearn.semi_supervised.LabelSpreading"). Both work by constructing a similarity graph over all items in the input dataset.
**An illustration of label-propagation:** *the structure of unlabeled observations is consistent with the class structure, and thus the class label can be propagated to the unlabeled observations of the training set.*
[`LabelPropagation`](generated/sklearn.semi_supervised.labelpropagation#sklearn.semi_supervised.LabelPropagation "sklearn.semi_supervised.LabelPropagation") and [`LabelSpreading`](generated/sklearn.semi_supervised.labelspreading#sklearn.semi_supervised.LabelSpreading "sklearn.semi_supervised.LabelSpreading") differ in modifications to the similarity matrix that graph and the clamping effect on the label distributions. Clamping allows the algorithm to change the weight of the true ground labeled data to some degree. The [`LabelPropagation`](generated/sklearn.semi_supervised.labelpropagation#sklearn.semi_supervised.LabelPropagation "sklearn.semi_supervised.LabelPropagation") algorithm performs hard clamping of input labels, which means \(\alpha=0\). This clamping factor can be relaxed, to say \(\alpha=0.2\), which means that we will always retain 80 percent of our original label distribution, but the algorithm gets to change its confidence of the distribution within 20 percent.
[`LabelPropagation`](generated/sklearn.semi_supervised.labelpropagation#sklearn.semi_supervised.LabelPropagation "sklearn.semi_supervised.LabelPropagation") uses the raw similarity matrix constructed from the data with no modifications. In contrast, [`LabelSpreading`](generated/sklearn.semi_supervised.labelspreading#sklearn.semi_supervised.LabelSpreading "sklearn.semi_supervised.LabelSpreading") minimizes a loss function that has regularization properties, as such it is often more robust to noise. The algorithm iterates on a modified version of the original graph and normalizes the edge weights by computing the normalized graph Laplacian matrix. This procedure is also used in [Spectral clustering](clustering#spectral-clustering).
Label propagation models have two built-in kernel methods. Choice of kernel effects both scalability and performance of the algorithms. The following are available:
* rbf (\(\exp(-\gamma |x-y|^2), \gamma > 0\)). \(\gamma\) is specified by keyword gamma.
* knn (\(1[x' \in kNN(x)]\)). \(k\) is specified by keyword n\_neighbors.
The RBF kernel will produce a fully connected graph which is represented in memory by a dense matrix. This matrix may be very large and combined with the cost of performing a full matrix multiplication calculation for each iteration of the algorithm can lead to prohibitively long running times. On the other hand, the KNN kernel will produce a much more memory-friendly sparse matrix which can drastically reduce running times.
scikit_learn 1.13. Feature selection 1.13. Feature selection
=======================
The classes in the [`sklearn.feature_selection`](classes#module-sklearn.feature_selection "sklearn.feature_selection") module can be used for feature selection/dimensionality reduction on sample sets, either to improve estimators’ accuracy scores or to boost their performance on very high-dimensional datasets.
1.13.1. Removing features with low variance
--------------------------------------------
[`VarianceThreshold`](generated/sklearn.feature_selection.variancethreshold#sklearn.feature_selection.VarianceThreshold "sklearn.feature_selection.VarianceThreshold") is a simple baseline approach to feature selection. It removes all features whose variance doesn’t meet some threshold. By default, it removes all zero-variance features, i.e. features that have the same value in all samples.
As an example, suppose that we have a dataset with boolean features, and we want to remove all features that are either one or zero (on or off) in more than 80% of the samples. Boolean features are Bernoulli random variables, and the variance of such variables is given by
\[\mathrm{Var}[X] = p(1 - p)\] so we can select using the threshold `.8 * (1 - .8)`:
```
>>> from sklearn.feature_selection import VarianceThreshold
>>> X = [[0, 0, 1], [0, 1, 0], [1, 0, 0], [0, 1, 1], [0, 1, 0], [0, 1, 1]]
>>> sel = VarianceThreshold(threshold=(.8 * (1 - .8)))
>>> sel.fit_transform(X)
array([[0, 1],
[1, 0],
[0, 0],
[1, 1],
[1, 0],
[1, 1]])
```
As expected, `VarianceThreshold` has removed the first column, which has a probability \(p = 5/6 > .8\) of containing a zero.
1.13.2. Univariate feature selection
-------------------------------------
Univariate feature selection works by selecting the best features based on univariate statistical tests. It can be seen as a preprocessing step to an estimator. Scikit-learn exposes feature selection routines as objects that implement the `transform` method:
* [`SelectKBest`](generated/sklearn.feature_selection.selectkbest#sklearn.feature_selection.SelectKBest "sklearn.feature_selection.SelectKBest") removes all but the \(k\) highest scoring features
* [`SelectPercentile`](generated/sklearn.feature_selection.selectpercentile#sklearn.feature_selection.SelectPercentile "sklearn.feature_selection.SelectPercentile") removes all but a user-specified highest scoring percentage of features
* using common univariate statistical tests for each feature: false positive rate [`SelectFpr`](generated/sklearn.feature_selection.selectfpr#sklearn.feature_selection.SelectFpr "sklearn.feature_selection.SelectFpr"), false discovery rate [`SelectFdr`](generated/sklearn.feature_selection.selectfdr#sklearn.feature_selection.SelectFdr "sklearn.feature_selection.SelectFdr"), or family wise error [`SelectFwe`](generated/sklearn.feature_selection.selectfwe#sklearn.feature_selection.SelectFwe "sklearn.feature_selection.SelectFwe").
* [`GenericUnivariateSelect`](generated/sklearn.feature_selection.genericunivariateselect#sklearn.feature_selection.GenericUnivariateSelect "sklearn.feature_selection.GenericUnivariateSelect") allows to perform univariate feature selection with a configurable strategy. This allows to select the best univariate selection strategy with hyper-parameter search estimator.
For instance, we can perform a \(\chi^2\) test to the samples to retrieve only the two best features as follows:
```
>>> from sklearn.datasets import load_iris
>>> from sklearn.feature_selection import SelectKBest
>>> from sklearn.feature_selection import chi2
>>> X, y = load_iris(return_X_y=True)
>>> X.shape
(150, 4)
>>> X_new = SelectKBest(chi2, k=2).fit_transform(X, y)
>>> X_new.shape
(150, 2)
```
These objects take as input a scoring function that returns univariate scores and p-values (or only scores for [`SelectKBest`](generated/sklearn.feature_selection.selectkbest#sklearn.feature_selection.SelectKBest "sklearn.feature_selection.SelectKBest") and [`SelectPercentile`](generated/sklearn.feature_selection.selectpercentile#sklearn.feature_selection.SelectPercentile "sklearn.feature_selection.SelectPercentile")):
* For regression: [`f_regression`](generated/sklearn.feature_selection.f_regression#sklearn.feature_selection.f_regression "sklearn.feature_selection.f_regression"), [`mutual_info_regression`](generated/sklearn.feature_selection.mutual_info_regression#sklearn.feature_selection.mutual_info_regression "sklearn.feature_selection.mutual_info_regression")
* For classification: [`chi2`](generated/sklearn.feature_selection.chi2#sklearn.feature_selection.chi2 "sklearn.feature_selection.chi2"), [`f_classif`](generated/sklearn.feature_selection.f_classif#sklearn.feature_selection.f_classif "sklearn.feature_selection.f_classif"), [`mutual_info_classif`](generated/sklearn.feature_selection.mutual_info_classif#sklearn.feature_selection.mutual_info_classif "sklearn.feature_selection.mutual_info_classif")
The methods based on F-test estimate the degree of linear dependency between two random variables. On the other hand, mutual information methods can capture any kind of statistical dependency, but being nonparametric, they require more samples for accurate estimation.
Warning
Beware not to use a regression scoring function with a classification problem, you will get useless results.
1.13.3. Recursive feature elimination
--------------------------------------
Given an external estimator that assigns weights to features (e.g., the coefficients of a linear model), the goal of recursive feature elimination ([`RFE`](generated/sklearn.feature_selection.rfe#sklearn.feature_selection.RFE "sklearn.feature_selection.RFE")) is to select features by recursively considering smaller and smaller sets of features. First, the estimator is trained on the initial set of features and the importance of each feature is obtained either through any specific attribute (such as `coef_`, `feature_importances_`) or callable. Then, the least important features are pruned from current set of features. That procedure is recursively repeated on the pruned set until the desired number of features to select is eventually reached.
[`RFECV`](generated/sklearn.feature_selection.rfecv#sklearn.feature_selection.RFECV "sklearn.feature_selection.RFECV") performs RFE in a cross-validation loop to find the optimal number of features.
1.13.4. Feature selection using SelectFromModel
------------------------------------------------
[`SelectFromModel`](generated/sklearn.feature_selection.selectfrommodel#sklearn.feature_selection.SelectFromModel "sklearn.feature_selection.SelectFromModel") is a meta-transformer that can be used alongside any estimator that assigns importance to each feature through a specific attribute (such as `coef_`, `feature_importances_`) or via an `importance_getter` callable after fitting. The features are considered unimportant and removed if the corresponding importance of the feature values are below the provided `threshold` parameter. Apart from specifying the threshold numerically, there are built-in heuristics for finding a threshold using a string argument. Available heuristics are “mean”, “median” and float multiples of these like “0.1\*mean”. In combination with the `threshold` criteria, one can use the `max_features` parameter to set a limit on the number of features to select.
For examples on how it is to be used refer to the sections below.
###
1.13.4.1. L1-based feature selection
[Linear models](linear_model#linear-model) penalized with the L1 norm have sparse solutions: many of their estimated coefficients are zero. When the goal is to reduce the dimensionality of the data to use with another classifier, they can be used along with [`SelectFromModel`](generated/sklearn.feature_selection.selectfrommodel#sklearn.feature_selection.SelectFromModel "sklearn.feature_selection.SelectFromModel") to select the non-zero coefficients. In particular, sparse estimators useful for this purpose are the [`Lasso`](generated/sklearn.linear_model.lasso#sklearn.linear_model.Lasso "sklearn.linear_model.Lasso") for regression, and of [`LogisticRegression`](generated/sklearn.linear_model.logisticregression#sklearn.linear_model.LogisticRegression "sklearn.linear_model.LogisticRegression") and [`LinearSVC`](generated/sklearn.svm.linearsvc#sklearn.svm.LinearSVC "sklearn.svm.LinearSVC") for classification:
```
>>> from sklearn.svm import LinearSVC
>>> from sklearn.datasets import load_iris
>>> from sklearn.feature_selection import SelectFromModel
>>> X, y = load_iris(return_X_y=True)
>>> X.shape
(150, 4)
>>> lsvc = LinearSVC(C=0.01, penalty="l1", dual=False).fit(X, y)
>>> model = SelectFromModel(lsvc, prefit=True)
>>> X_new = model.transform(X)
>>> X_new.shape
(150, 3)
```
With SVMs and logistic-regression, the parameter C controls the sparsity: the smaller C the fewer features selected. With Lasso, the higher the alpha parameter, the fewer features selected.
###
1.13.4.2. Tree-based feature selection
Tree-based estimators (see the [`sklearn.tree`](classes#module-sklearn.tree "sklearn.tree") module and forest of trees in the [`sklearn.ensemble`](classes#module-sklearn.ensemble "sklearn.ensemble") module) can be used to compute impurity-based feature importances, which in turn can be used to discard irrelevant features (when coupled with the [`SelectFromModel`](generated/sklearn.feature_selection.selectfrommodel#sklearn.feature_selection.SelectFromModel "sklearn.feature_selection.SelectFromModel") meta-transformer):
```
>>> from sklearn.ensemble import ExtraTreesClassifier
>>> from sklearn.datasets import load_iris
>>> from sklearn.feature_selection import SelectFromModel
>>> X, y = load_iris(return_X_y=True)
>>> X.shape
(150, 4)
>>> clf = ExtraTreesClassifier(n_estimators=50)
>>> clf = clf.fit(X, y)
>>> clf.feature_importances_
array([ 0.04..., 0.05..., 0.4..., 0.4...])
>>> model = SelectFromModel(clf, prefit=True)
>>> X_new = model.transform(X)
>>> X_new.shape
(150, 2)
```
1.13.5. Sequential Feature Selection
-------------------------------------
Sequential Feature Selection [[sfs]](#sfs) (SFS) is available in the [`SequentialFeatureSelector`](generated/sklearn.feature_selection.sequentialfeatureselector#sklearn.feature_selection.SequentialFeatureSelector "sklearn.feature_selection.SequentialFeatureSelector") transformer. SFS can be either forward or backward:
Forward-SFS is a greedy procedure that iteratively finds the best new feature to add to the set of selected features. Concretely, we initially start with zero features and find the one feature that maximizes a cross-validated score when an estimator is trained on this single feature. Once that first feature is selected, we repeat the procedure by adding a new feature to the set of selected features. The procedure stops when the desired number of selected features is reached, as determined by the `n_features_to_select` parameter.
Backward-SFS follows the same idea but works in the opposite direction: instead of starting with no features and greedily adding features, we start with *all* the features and greedily *remove* features from the set. The `direction` parameter controls whether forward or backward SFS is used.
In general, forward and backward selection do not yield equivalent results. Also, one may be much faster than the other depending on the requested number of selected features: if we have 10 features and ask for 7 selected features, forward selection would need to perform 7 iterations while backward selection would only need to perform 3.
SFS differs from [`RFE`](generated/sklearn.feature_selection.rfe#sklearn.feature_selection.RFE "sklearn.feature_selection.RFE") and [`SelectFromModel`](generated/sklearn.feature_selection.selectfrommodel#sklearn.feature_selection.SelectFromModel "sklearn.feature_selection.SelectFromModel") in that it does not require the underlying model to expose a `coef_` or `feature_importances_` attribute. It may however be slower considering that more models need to be evaluated, compared to the other approaches. For example in backward selection, the iteration going from `m` features to `m - 1` features using k-fold cross-validation requires fitting `m * k` models, while [`RFE`](generated/sklearn.feature_selection.rfe#sklearn.feature_selection.RFE "sklearn.feature_selection.RFE") would require only a single fit, and [`SelectFromModel`](generated/sklearn.feature_selection.selectfrommodel#sklearn.feature_selection.SelectFromModel "sklearn.feature_selection.SelectFromModel") always just does a single fit and requires no iterations.
1.13.6. Feature selection as part of a pipeline
------------------------------------------------
Feature selection is usually used as a pre-processing step before doing the actual learning. The recommended way to do this in scikit-learn is to use a [`Pipeline`](generated/sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline"):
```
clf = Pipeline([
('feature_selection', SelectFromModel(LinearSVC(penalty="l1"))),
('classification', RandomForestClassifier())
])
clf.fit(X, y)
```
In this snippet we make use of a [`LinearSVC`](generated/sklearn.svm.linearsvc#sklearn.svm.LinearSVC "sklearn.svm.LinearSVC") coupled with [`SelectFromModel`](generated/sklearn.feature_selection.selectfrommodel#sklearn.feature_selection.SelectFromModel "sklearn.feature_selection.SelectFromModel") to evaluate feature importances and select the most relevant features. Then, a [`RandomForestClassifier`](generated/sklearn.ensemble.randomforestclassifier#sklearn.ensemble.RandomForestClassifier "sklearn.ensemble.RandomForestClassifier") is trained on the transformed output, i.e. using only relevant features. You can perform similar operations with the other feature selection methods and also classifiers that provide a way to evaluate feature importances of course. See the [`Pipeline`](generated/sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline") examples for more details.
| programming_docs |
scikit_learn 1.7. Gaussian Processes 1.7. Gaussian Processes
=======================
**Gaussian Processes (GP)** are a generic supervised learning method designed to solve *regression* and *probabilistic classification* problems.
The advantages of Gaussian processes are:
* The prediction interpolates the observations (at least for regular kernels).
* The prediction is probabilistic (Gaussian) so that one can compute empirical confidence intervals and decide based on those if one should refit (online fitting, adaptive fitting) the prediction in some region of interest.
* Versatile: different [kernels](#gp-kernels) can be specified. Common kernels are provided, but it is also possible to specify custom kernels.
The disadvantages of Gaussian processes include:
* They are not sparse, i.e., they use the whole samples/features information to perform the prediction.
* They lose efficiency in high dimensional spaces – namely when the number of features exceeds a few dozens.
1.7.1. Gaussian Process Regression (GPR)
-----------------------------------------
The [`GaussianProcessRegressor`](generated/sklearn.gaussian_process.gaussianprocessregressor#sklearn.gaussian_process.GaussianProcessRegressor "sklearn.gaussian_process.GaussianProcessRegressor") implements Gaussian processes (GP) for regression purposes. For this, the prior of the GP needs to be specified. The prior mean is assumed to be constant and zero (for `normalize_y=False`) or the training data’s mean (for `normalize_y=True`). The prior’s covariance is specified by passing a [kernel](#gp-kernels) object. The hyperparameters of the kernel are optimized during fitting of GaussianProcessRegressor by maximizing the log-marginal-likelihood (LML) based on the passed `optimizer`. As the LML may have multiple local optima, the optimizer can be started repeatedly by specifying `n_restarts_optimizer`. The first run is always conducted starting from the initial hyperparameter values of the kernel; subsequent runs are conducted from hyperparameter values that have been chosen randomly from the range of allowed values. If the initial hyperparameters should be kept fixed, `None` can be passed as optimizer.
The noise level in the targets can be specified by passing it via the parameter `alpha`, either globally as a scalar or per datapoint. Note that a moderate noise level can also be helpful for dealing with numeric issues during fitting as it is effectively implemented as Tikhonov regularization, i.e., by adding it to the diagonal of the kernel matrix. An alternative to specifying the noise level explicitly is to include a WhiteKernel component into the kernel, which can estimate the global noise level from the data (see example below).
The implementation is based on Algorithm 2.1 of [[RW2006]](#rw2006). In addition to the API of standard scikit-learn estimators, GaussianProcessRegressor:
* allows prediction without prior fitting (based on the GP prior)
* provides an additional method `sample_y(X)`, which evaluates samples drawn from the GPR (prior or posterior) at given inputs
* exposes a method `log_marginal_likelihood(theta)`, which can be used externally for other ways of selecting hyperparameters, e.g., via Markov chain Monte Carlo.
1.7.2. GPR examples
--------------------
###
1.7.2.1. GPR with noise-level estimation
This example illustrates that GPR with a sum-kernel including a WhiteKernel can estimate the noise level of data. An illustration of the log-marginal-likelihood (LML) landscape shows that there exist two local maxima of LML.
The first corresponds to a model with a high noise level and a large length scale, which explains all variations in the data by noise.
The second one has a smaller noise level and shorter length scale, which explains most of the variation by the noise-free functional relationship. The second model has a higher likelihood; however, depending on the initial value for the hyperparameters, the gradient-based optimization might also converge to the high-noise solution. It is thus important to repeat the optimization several times for different initializations.
###
1.7.2.2. Comparison of GPR and Kernel Ridge Regression
Both kernel ridge regression (KRR) and GPR learn a target function by employing internally the “kernel trick”. KRR learns a linear function in the space induced by the respective kernel which corresponds to a non-linear function in the original space. The linear function in the kernel space is chosen based on the mean-squared error loss with ridge regularization. GPR uses the kernel to define the covariance of a prior distribution over the target functions and uses the observed training data to define a likelihood function. Based on Bayes theorem, a (Gaussian) posterior distribution over target functions is defined, whose mean is used for prediction.
A major difference is that GPR can choose the kernel’s hyperparameters based on gradient-ascent on the marginal likelihood function while KRR needs to perform a grid search on a cross-validated loss function (mean-squared error loss). A further difference is that GPR learns a generative, probabilistic model of the target function and can thus provide meaningful confidence intervals and posterior samples along with the predictions while KRR only provides predictions.
The following figure illustrates both methods on an artificial dataset, which consists of a sinusoidal target function and strong noise. The figure compares the learned model of KRR and GPR based on a ExpSineSquared kernel, which is suited for learning periodic functions. The kernel’s hyperparameters control the smoothness (length\_scale) and periodicity of the kernel (periodicity). Moreover, the noise level of the data is learned explicitly by GPR by an additional WhiteKernel component in the kernel and by the regularization parameter alpha of KRR.
The figure shows that both methods learn reasonable models of the target function. GPR correctly identifies the periodicity of the function to be roughly \(2\*\pi\) (6.28), while KRR chooses the doubled periodicity \(4\*\pi\) . Besides that, GPR provides reasonable confidence bounds on the prediction which are not available for KRR. A major difference between the two methods is the time required for fitting and predicting: while fitting KRR is fast in principle, the grid-search for hyperparameter optimization scales exponentially with the number of hyperparameters (“curse of dimensionality”). The gradient-based optimization of the parameters in GPR does not suffer from this exponential scaling and is thus considerably faster on this example with 3-dimensional hyperparameter space. The time for predicting is similar; however, generating the variance of the predictive distribution of GPR takes considerably longer than just predicting the mean.
###
1.7.2.3. GPR on Mauna Loa CO2 data
This example is based on Section 5.4.3 of [[RW2006]](#rw2006). It illustrates an example of complex kernel engineering and hyperparameter optimization using gradient ascent on the log-marginal-likelihood. The data consists of the monthly average atmospheric CO2 concentrations (in parts per million by volume (ppmv)) collected at the Mauna Loa Observatory in Hawaii, between 1958 and 1997. The objective is to model the CO2 concentration as a function of the time t.
The kernel is composed of several terms that are responsible for explaining different properties of the signal:
* a long term, smooth rising trend is to be explained by an RBF kernel. The RBF kernel with a large length-scale enforces this component to be smooth; it is not enforced that the trend is rising which leaves this choice to the GP. The specific length-scale and the amplitude are free hyperparameters.
* a seasonal component, which is to be explained by the periodic ExpSineSquared kernel with a fixed periodicity of 1 year. The length-scale of this periodic component, controlling its smoothness, is a free parameter. In order to allow decaying away from exact periodicity, the product with an RBF kernel is taken. The length-scale of this RBF component controls the decay time and is a further free parameter.
* smaller, medium term irregularities are to be explained by a RationalQuadratic kernel component, whose length-scale and alpha parameter, which determines the diffuseness of the length-scales, are to be determined. According to [[RW2006]](#rw2006), these irregularities can better be explained by a RationalQuadratic than an RBF kernel component, probably because it can accommodate several length-scales.
* a “noise” term, consisting of an RBF kernel contribution, which shall explain the correlated noise components such as local weather phenomena, and a WhiteKernel contribution for the white noise. The relative amplitudes and the RBF’s length scale are further free parameters.
Maximizing the log-marginal-likelihood after subtracting the target’s mean yields the following kernel with an LML of -83.214:
```
34.4**2 * RBF(length_scale=41.8)
+ 3.27**2 * RBF(length_scale=180) * ExpSineSquared(length_scale=1.44,
periodicity=1)
+ 0.446**2 * RationalQuadratic(alpha=17.7, length_scale=0.957)
+ 0.197**2 * RBF(length_scale=0.138) + WhiteKernel(noise_level=0.0336)
```
Thus, most of the target signal (34.4ppm) is explained by a long-term rising trend (length-scale 41.8 years). The periodic component has an amplitude of 3.27ppm, a decay time of 180 years and a length-scale of 1.44. The long decay time indicates that we have a locally very close to periodic seasonal component. The correlated noise has an amplitude of 0.197ppm with a length scale of 0.138 years and a white-noise contribution of 0.197ppm. Thus, the overall noise level is very small, indicating that the data can be very well explained by the model. The figure shows also that the model makes very confident predictions until around 2015
1.7.3. Gaussian Process Classification (GPC)
---------------------------------------------
The [`GaussianProcessClassifier`](generated/sklearn.gaussian_process.gaussianprocessclassifier#sklearn.gaussian_process.GaussianProcessClassifier "sklearn.gaussian_process.GaussianProcessClassifier") implements Gaussian processes (GP) for classification purposes, more specifically for probabilistic classification, where test predictions take the form of class probabilities. GaussianProcessClassifier places a GP prior on a latent function \(f\), which is then squashed through a link function to obtain the probabilistic classification. The latent function \(f\) is a so-called nuisance function, whose values are not observed and are not relevant by themselves. Its purpose is to allow a convenient formulation of the model, and \(f\) is removed (integrated out) during prediction. GaussianProcessClassifier implements the logistic link function, for which the integral cannot be computed analytically but is easily approximated in the binary case.
In contrast to the regression setting, the posterior of the latent function \(f\) is not Gaussian even for a GP prior since a Gaussian likelihood is inappropriate for discrete class labels. Rather, a non-Gaussian likelihood corresponding to the logistic link function (logit) is used. GaussianProcessClassifier approximates the non-Gaussian posterior with a Gaussian based on the Laplace approximation. More details can be found in Chapter 3 of [[RW2006]](#rw2006).
The GP prior mean is assumed to be zero. The prior’s covariance is specified by passing a [kernel](#gp-kernels) object. The hyperparameters of the kernel are optimized during fitting of GaussianProcessRegressor by maximizing the log-marginal-likelihood (LML) based on the passed `optimizer`. As the LML may have multiple local optima, the optimizer can be started repeatedly by specifying `n_restarts_optimizer`. The first run is always conducted starting from the initial hyperparameter values of the kernel; subsequent runs are conducted from hyperparameter values that have been chosen randomly from the range of allowed values. If the initial hyperparameters should be kept fixed, `None` can be passed as optimizer.
[`GaussianProcessClassifier`](generated/sklearn.gaussian_process.gaussianprocessclassifier#sklearn.gaussian_process.GaussianProcessClassifier "sklearn.gaussian_process.GaussianProcessClassifier") supports multi-class classification by performing either one-versus-rest or one-versus-one based training and prediction. In one-versus-rest, one binary Gaussian process classifier is fitted for each class, which is trained to separate this class from the rest. In “one\_vs\_one”, one binary Gaussian process classifier is fitted for each pair of classes, which is trained to separate these two classes. The predictions of these binary predictors are combined into multi-class predictions. See the section on [multi-class classification](multiclass#multiclass) for more details.
In the case of Gaussian process classification, “one\_vs\_one” might be computationally cheaper since it has to solve many problems involving only a subset of the whole training set rather than fewer problems on the whole dataset. Since Gaussian process classification scales cubically with the size of the dataset, this might be considerably faster. However, note that “one\_vs\_one” does not support predicting probability estimates but only plain predictions. Moreover, note that [`GaussianProcessClassifier`](generated/sklearn.gaussian_process.gaussianprocessclassifier#sklearn.gaussian_process.GaussianProcessClassifier "sklearn.gaussian_process.GaussianProcessClassifier") does not (yet) implement a true multi-class Laplace approximation internally, but as discussed above is based on solving several binary classification tasks internally, which are combined using one-versus-rest or one-versus-one.
1.7.4. GPC examples
--------------------
###
1.7.4.1. Probabilistic predictions with GPC
This example illustrates the predicted probability of GPC for an RBF kernel with different choices of the hyperparameters. The first figure shows the predicted probability of GPC with arbitrarily chosen hyperparameters and with the hyperparameters corresponding to the maximum log-marginal-likelihood (LML).
While the hyperparameters chosen by optimizing LML have a considerably larger LML, they perform slightly worse according to the log-loss on test data. The figure shows that this is because they exhibit a steep change of the class probabilities at the class boundaries (which is good) but have predicted probabilities close to 0.5 far away from the class boundaries (which is bad) This undesirable effect is caused by the Laplace approximation used internally by GPC.
The second figure shows the log-marginal-likelihood for different choices of the kernel’s hyperparameters, highlighting the two choices of the hyperparameters used in the first figure by black dots.
###
1.7.4.2. Illustration of GPC on the XOR dataset
This example illustrates GPC on XOR data. Compared are a stationary, isotropic kernel ([`RBF`](generated/sklearn.gaussian_process.kernels.rbf#sklearn.gaussian_process.kernels.RBF "sklearn.gaussian_process.kernels.RBF")) and a non-stationary kernel ([`DotProduct`](generated/sklearn.gaussian_process.kernels.dotproduct#sklearn.gaussian_process.kernels.DotProduct "sklearn.gaussian_process.kernels.DotProduct")). On this particular dataset, the [`DotProduct`](generated/sklearn.gaussian_process.kernels.dotproduct#sklearn.gaussian_process.kernels.DotProduct "sklearn.gaussian_process.kernels.DotProduct") kernel obtains considerably better results because the class-boundaries are linear and coincide with the coordinate axes. In practice, however, stationary kernels such as [`RBF`](generated/sklearn.gaussian_process.kernels.rbf#sklearn.gaussian_process.kernels.RBF "sklearn.gaussian_process.kernels.RBF") often obtain better results.
###
1.7.4.3. Gaussian process classification (GPC) on iris dataset
This example illustrates the predicted probability of GPC for an isotropic and anisotropic RBF kernel on a two-dimensional version for the iris-dataset. This illustrates the applicability of GPC to non-binary classification. The anisotropic RBF kernel obtains slightly higher log-marginal-likelihood by assigning different length-scales to the two feature dimensions.
1.7.5. Kernels for Gaussian Processes
--------------------------------------
Kernels (also called “covariance functions” in the context of GPs) are a crucial ingredient of GPs which determine the shape of prior and posterior of the GP. They encode the assumptions on the function being learned by defining the “similarity” of two datapoints combined with the assumption that similar datapoints should have similar target values. Two categories of kernels can be distinguished: stationary kernels depend only on the distance of two datapoints and not on their absolute values \(k(x\_i, x\_j)= k(d(x\_i, x\_j))\) and are thus invariant to translations in the input space, while non-stationary kernels depend also on the specific values of the datapoints. Stationary kernels can further be subdivided into isotropic and anisotropic kernels, where isotropic kernels are also invariant to rotations in the input space. For more details, we refer to Chapter 4 of [[RW2006]](#rw2006). For guidance on how to best combine different kernels, we refer to [[Duv2014]](#duv2014).
###
1.7.5.1. Gaussian Process Kernel API
The main usage of a [`Kernel`](generated/sklearn.gaussian_process.kernels.kernel#sklearn.gaussian_process.kernels.Kernel "sklearn.gaussian_process.kernels.Kernel") is to compute the GP’s covariance between datapoints. For this, the method `__call__` of the kernel can be called. This method can either be used to compute the “auto-covariance” of all pairs of datapoints in a 2d array X, or the “cross-covariance” of all combinations of datapoints of a 2d array X with datapoints in a 2d array Y. The following identity holds true for all kernels k (except for the [`WhiteKernel`](generated/sklearn.gaussian_process.kernels.whitekernel#sklearn.gaussian_process.kernels.WhiteKernel "sklearn.gaussian_process.kernels.WhiteKernel")): `k(X) == K(X, Y=X)`
If only the diagonal of the auto-covariance is being used, the method `diag()` of a kernel can be called, which is more computationally efficient than the equivalent call to `__call__`: `np.diag(k(X, X)) == k.diag(X)`
Kernels are parameterized by a vector \(\theta\) of hyperparameters. These hyperparameters can for instance control length-scales or periodicity of a kernel (see below). All kernels support computing analytic gradients of the kernel’s auto-covariance with respect to \(log(\theta)\) via setting `eval_gradient=True` in the `__call__` method. That is, a `(len(X), len(X), len(theta))` array is returned where the entry `[i, j, l]` contains \(\frac{\partial k\_\theta(x\_i, x\_j)}{\partial log(\theta\_l)}\). This gradient is used by the Gaussian process (both regressor and classifier) in computing the gradient of the log-marginal-likelihood, which in turn is used to determine the value of \(\theta\), which maximizes the log-marginal-likelihood, via gradient ascent. For each hyperparameter, the initial value and the bounds need to be specified when creating an instance of the kernel. The current value of \(\theta\) can be get and set via the property `theta` of the kernel object. Moreover, the bounds of the hyperparameters can be accessed by the property `bounds` of the kernel. Note that both properties (theta and bounds) return log-transformed values of the internally used values since those are typically more amenable to gradient-based optimization. The specification of each hyperparameter is stored in the form of an instance of [`Hyperparameter`](generated/sklearn.gaussian_process.kernels.hyperparameter#sklearn.gaussian_process.kernels.Hyperparameter "sklearn.gaussian_process.kernels.Hyperparameter") in the respective kernel. Note that a kernel using a hyperparameter with name “x” must have the attributes self.x and self.x\_bounds.
The abstract base class for all kernels is [`Kernel`](generated/sklearn.gaussian_process.kernels.kernel#sklearn.gaussian_process.kernels.Kernel "sklearn.gaussian_process.kernels.Kernel"). Kernel implements a similar interface as `Estimator`, providing the methods `get_params()`, `set_params()`, and `clone()`. This allows setting kernel values also via meta-estimators such as `Pipeline` or `GridSearch`. Note that due to the nested structure of kernels (by applying kernel operators, see below), the names of kernel parameters might become relatively complicated. In general, for a binary kernel operator, parameters of the left operand are prefixed with `k1__` and parameters of the right operand with `k2__`. An additional convenience method is `clone_with_theta(theta)`, which returns a cloned version of the kernel but with the hyperparameters set to `theta`. An illustrative example:
```
>>> from sklearn.gaussian_process.kernels import ConstantKernel, RBF
>>> kernel = ConstantKernel(constant_value=1.0, constant_value_bounds=(0.0, 10.0)) * RBF(length_scale=0.5, length_scale_bounds=(0.0, 10.0)) + RBF(length_scale=2.0, length_scale_bounds=(0.0, 10.0))
>>> for hyperparameter in kernel.hyperparameters: print(hyperparameter)
Hyperparameter(name='k1__k1__constant_value', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
Hyperparameter(name='k1__k2__length_scale', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
Hyperparameter(name='k2__length_scale', value_type='numeric', bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
>>> params = kernel.get_params()
>>> for key in sorted(params): print("%s : %s" % (key, params[key]))
k1 : 1**2 * RBF(length_scale=0.5)
k1__k1 : 1**2
k1__k1__constant_value : 1.0
k1__k1__constant_value_bounds : (0.0, 10.0)
k1__k2 : RBF(length_scale=0.5)
k1__k2__length_scale : 0.5
k1__k2__length_scale_bounds : (0.0, 10.0)
k2 : RBF(length_scale=2)
k2__length_scale : 2.0
k2__length_scale_bounds : (0.0, 10.0)
>>> print(kernel.theta) # Note: log-transformed
[ 0. -0.69314718 0.69314718]
>>> print(kernel.bounds) # Note: log-transformed
[[ -inf 2.30258509]
[ -inf 2.30258509]
[ -inf 2.30258509]]
```
All Gaussian process kernels are interoperable with [`sklearn.metrics.pairwise`](classes#module-sklearn.metrics.pairwise "sklearn.metrics.pairwise") and vice versa: instances of subclasses of [`Kernel`](generated/sklearn.gaussian_process.kernels.kernel#sklearn.gaussian_process.kernels.Kernel "sklearn.gaussian_process.kernels.Kernel") can be passed as `metric` to `pairwise_kernels` from [`sklearn.metrics.pairwise`](classes#module-sklearn.metrics.pairwise "sklearn.metrics.pairwise"). Moreover, kernel functions from pairwise can be used as GP kernels by using the wrapper class [`PairwiseKernel`](generated/sklearn.gaussian_process.kernels.pairwisekernel#sklearn.gaussian_process.kernels.PairwiseKernel "sklearn.gaussian_process.kernels.PairwiseKernel"). The only caveat is that the gradient of the hyperparameters is not analytic but numeric and all those kernels support only isotropic distances. The parameter `gamma` is considered to be a hyperparameter and may be optimized. The other kernel parameters are set directly at initialization and are kept fixed.
###
1.7.5.2. Basic kernels
The [`ConstantKernel`](generated/sklearn.gaussian_process.kernels.constantkernel#sklearn.gaussian_process.kernels.ConstantKernel "sklearn.gaussian_process.kernels.ConstantKernel") kernel can be used as part of a [`Product`](generated/sklearn.gaussian_process.kernels.product#sklearn.gaussian_process.kernels.Product "sklearn.gaussian_process.kernels.Product") kernel where it scales the magnitude of the other factor (kernel) or as part of a [`Sum`](generated/sklearn.gaussian_process.kernels.sum#sklearn.gaussian_process.kernels.Sum "sklearn.gaussian_process.kernels.Sum") kernel, where it modifies the mean of the Gaussian process. It depends on a parameter \(constant\\_value\). It is defined as:
\[k(x\_i, x\_j) = constant\\_value \;\forall\; x\_1, x\_2\] The main use-case of the [`WhiteKernel`](generated/sklearn.gaussian_process.kernels.whitekernel#sklearn.gaussian_process.kernels.WhiteKernel "sklearn.gaussian_process.kernels.WhiteKernel") kernel is as part of a sum-kernel where it explains the noise-component of the signal. Tuning its parameter \(noise\\_level\) corresponds to estimating the noise-level. It is defined as:
\[k(x\_i, x\_j) = noise\\_level \text{ if } x\_i == x\_j \text{ else } 0\] ###
1.7.5.3. Kernel operators
Kernel operators take one or two base kernels and combine them into a new kernel. The [`Sum`](generated/sklearn.gaussian_process.kernels.sum#sklearn.gaussian_process.kernels.Sum "sklearn.gaussian_process.kernels.Sum") kernel takes two kernels \(k\_1\) and \(k\_2\) and combines them via \(k\_{sum}(X, Y) = k\_1(X, Y) + k\_2(X, Y)\). The [`Product`](generated/sklearn.gaussian_process.kernels.product#sklearn.gaussian_process.kernels.Product "sklearn.gaussian_process.kernels.Product") kernel takes two kernels \(k\_1\) and \(k\_2\) and combines them via \(k\_{product}(X, Y) = k\_1(X, Y) \* k\_2(X, Y)\). The [`Exponentiation`](generated/sklearn.gaussian_process.kernels.exponentiation#sklearn.gaussian_process.kernels.Exponentiation "sklearn.gaussian_process.kernels.Exponentiation") kernel takes one base kernel and a scalar parameter \(p\) and combines them via \(k\_{exp}(X, Y) = k(X, Y)^p\). Note that magic methods `__add__`, `__mul___` and `__pow__` are overridden on the Kernel objects, so one can use e.g. `RBF() + RBF()` as a shortcut for `Sum(RBF(), RBF())`.
###
1.7.5.4. Radial basis function (RBF) kernel
The [`RBF`](generated/sklearn.gaussian_process.kernels.rbf#sklearn.gaussian_process.kernels.RBF "sklearn.gaussian_process.kernels.RBF") kernel is a stationary kernel. It is also known as the “squared exponential” kernel. It is parameterized by a length-scale parameter \(l>0\), which can either be a scalar (isotropic variant of the kernel) or a vector with the same number of dimensions as the inputs \(x\) (anisotropic variant of the kernel). The kernel is given by:
\[k(x\_i, x\_j) = \text{exp}\left(- \frac{d(x\_i, x\_j)^2}{2l^2} \right)\] where \(d(\cdot, \cdot)\) is the Euclidean distance. This kernel is infinitely differentiable, which implies that GPs with this kernel as covariance function have mean square derivatives of all orders, and are thus very smooth. The prior and posterior of a GP resulting from an RBF kernel are shown in the following figure:
###
1.7.5.5. Matérn kernel
The [`Matern`](generated/sklearn.gaussian_process.kernels.matern#sklearn.gaussian_process.kernels.Matern "sklearn.gaussian_process.kernels.Matern") kernel is a stationary kernel and a generalization of the [`RBF`](generated/sklearn.gaussian_process.kernels.rbf#sklearn.gaussian_process.kernels.RBF "sklearn.gaussian_process.kernels.RBF") kernel. It has an additional parameter \(\nu\) which controls the smoothness of the resulting function. It is parameterized by a length-scale parameter \(l>0\), which can either be a scalar (isotropic variant of the kernel) or a vector with the same number of dimensions as the inputs \(x\) (anisotropic variant of the kernel). The kernel is given by:
\[k(x\_i, x\_j) = \frac{1}{\Gamma(\nu)2^{\nu-1}}\Bigg(\frac{\sqrt{2\nu}}{l} d(x\_i , x\_j )\Bigg)^\nu K\_\nu\Bigg(\frac{\sqrt{2\nu}}{l} d(x\_i , x\_j )\Bigg),\] where \(d(\cdot,\cdot)\) is the Euclidean distance, \(K\_\nu(\cdot)\) is a modified Bessel function and \(\Gamma(\cdot)\) is the gamma function. As \(\nu\rightarrow\infty\), the Matérn kernel converges to the RBF kernel. When \(\nu = 1/2\), the Matérn kernel becomes identical to the absolute exponential kernel, i.e.,
\[k(x\_i, x\_j) = \exp \Bigg(- \frac{1}{l} d(x\_i , x\_j ) \Bigg) \quad \quad \nu= \tfrac{1}{2}\] In particular, \(\nu = 3/2\):
\[k(x\_i, x\_j) = \Bigg(1 + \frac{\sqrt{3}}{l} d(x\_i , x\_j )\Bigg) \exp \Bigg(-\frac{\sqrt{3}}{l} d(x\_i , x\_j ) \Bigg) \quad \quad \nu= \tfrac{3}{2}\] and \(\nu = 5/2\):
\[k(x\_i, x\_j) = \Bigg(1 + \frac{\sqrt{5}}{l} d(x\_i , x\_j ) +\frac{5}{3l} d(x\_i , x\_j )^2 \Bigg) \exp \Bigg(-\frac{\sqrt{5}}{l} d(x\_i , x\_j ) \Bigg) \quad \quad \nu= \tfrac{5}{2}\] are popular choices for learning functions that are not infinitely differentiable (as assumed by the RBF kernel) but at least once (\(\nu = 3/2\)) or twice differentiable (\(\nu = 5/2\)).
The flexibility of controlling the smoothness of the learned function via \(\nu\) allows adapting to the properties of the true underlying functional relation. The prior and posterior of a GP resulting from a Matérn kernel are shown in the following figure:
See [[RW2006]](#rw2006), pp84 for further details regarding the different variants of the Matérn kernel.
###
1.7.5.6. Rational quadratic kernel
The [`RationalQuadratic`](generated/sklearn.gaussian_process.kernels.rationalquadratic#sklearn.gaussian_process.kernels.RationalQuadratic "sklearn.gaussian_process.kernels.RationalQuadratic") kernel can be seen as a scale mixture (an infinite sum) of [`RBF`](generated/sklearn.gaussian_process.kernels.rbf#sklearn.gaussian_process.kernels.RBF "sklearn.gaussian_process.kernels.RBF") kernels with different characteristic length-scales. It is parameterized by a length-scale parameter \(l>0\) and a scale mixture parameter \(\alpha>0\) Only the isotropic variant where \(l\) is a scalar is supported at the moment. The kernel is given by:
\[k(x\_i, x\_j) = \left(1 + \frac{d(x\_i, x\_j)^2}{2\alpha l^2}\right)^{-\alpha}\] The prior and posterior of a GP resulting from a [`RationalQuadratic`](generated/sklearn.gaussian_process.kernels.rationalquadratic#sklearn.gaussian_process.kernels.RationalQuadratic "sklearn.gaussian_process.kernels.RationalQuadratic") kernel are shown in the following figure:
###
1.7.5.7. Exp-Sine-Squared kernel
The [`ExpSineSquared`](generated/sklearn.gaussian_process.kernels.expsinesquared#sklearn.gaussian_process.kernels.ExpSineSquared "sklearn.gaussian_process.kernels.ExpSineSquared") kernel allows modeling periodic functions. It is parameterized by a length-scale parameter \(l>0\) and a periodicity parameter \(p>0\). Only the isotropic variant where \(l\) is a scalar is supported at the moment. The kernel is given by:
\[k(x\_i, x\_j) = \text{exp}\left(- \frac{ 2\sin^2(\pi d(x\_i, x\_j) / p) }{ l^ 2} \right)\] The prior and posterior of a GP resulting from an ExpSineSquared kernel are shown in the following figure:
###
1.7.5.8. Dot-Product kernel
The [`DotProduct`](generated/sklearn.gaussian_process.kernels.dotproduct#sklearn.gaussian_process.kernels.DotProduct "sklearn.gaussian_process.kernels.DotProduct") kernel is non-stationary and can be obtained from linear regression by putting \(N(0, 1)\) priors on the coefficients of \(x\_d (d = 1, . . . , D)\) and a prior of \(N(0, \sigma\_0^2)\) on the bias. The [`DotProduct`](generated/sklearn.gaussian_process.kernels.dotproduct#sklearn.gaussian_process.kernels.DotProduct "sklearn.gaussian_process.kernels.DotProduct") kernel is invariant to a rotation of the coordinates about the origin, but not translations. It is parameterized by a parameter \(\sigma\_0^2\). For \(\sigma\_0^2 = 0\), the kernel is called the homogeneous linear kernel, otherwise it is inhomogeneous. The kernel is given by
\[k(x\_i, x\_j) = \sigma\_0 ^ 2 + x\_i \cdot x\_j\] The [`DotProduct`](generated/sklearn.gaussian_process.kernels.dotproduct#sklearn.gaussian_process.kernels.DotProduct "sklearn.gaussian_process.kernels.DotProduct") kernel is commonly combined with exponentiation. An example with exponent 2 is shown in the following figure:
###
1.7.5.9. References
[RW2006] ([1](#id1),[2](#id2),[3](#id3),[4](#id4),[5](#id5),[6](#id7)) Carl Eduard Rasmussen and Christopher K.I. Williams, “Gaussian Processes for Machine Learning”, MIT Press 2006, Link to an official complete PDF version of the book [here](http://www.gaussianprocess.org/gpml/chapters/RW.pdf) .
[[Duv2014](#id6)] David Duvenaud, “The Kernel Cookbook: Advice on Covariance functions”, 2014, [Link](https://www.cs.toronto.edu/~duvenaud/cookbook/) .
| programming_docs |
scikit_learn 1.15. Isotonic regression 1.15. Isotonic regression
=========================
The class [`IsotonicRegression`](generated/sklearn.isotonic.isotonicregression#sklearn.isotonic.IsotonicRegression "sklearn.isotonic.IsotonicRegression") fits a non-decreasing real function to 1-dimensional data. It solves the following problem:
minimize \(\sum\_i w\_i (y\_i - \hat{y}\_i)^2\)
subject to \(\hat{y}\_i \le \hat{y}\_j\) whenever \(X\_i \le X\_j\),
where the weights \(w\_i\) are strictly positive, and both `X` and `y` are arbitrary real quantities.
The `increasing` parameter changes the constraint to \(\hat{y}\_i \ge \hat{y}\_j\) whenever \(X\_i \le X\_j\). Setting it to ‘auto’ will automatically choose the constraint based on [Spearman’s rank correlation coefficient](https://en.wikipedia.org/wiki/Spearman%27s_rank_correlation_coefficient).
[`IsotonicRegression`](generated/sklearn.isotonic.isotonicregression#sklearn.isotonic.IsotonicRegression "sklearn.isotonic.IsotonicRegression") produces a series of predictions \(\hat{y}\_i\) for the training data which are the closest to the targets \(y\) in terms of mean squared error. These predictions are interpolated for predicting to unseen data. The predictions of [`IsotonicRegression`](generated/sklearn.isotonic.isotonicregression#sklearn.isotonic.IsotonicRegression "sklearn.isotonic.IsotonicRegression") thus form a function that is piecewise linear:
scikit_learn 4.2. Permutation feature importance 4.2. Permutation feature importance
===================================
Permutation feature importance is a model inspection technique that can be used for any [fitted](https://scikit-learn.org/1.1/glossary.html#term-fitted) [estimator](https://scikit-learn.org/1.1/glossary.html#term-estimator) when the data is tabular. This is especially useful for non-linear or opaque [estimators](https://scikit-learn.org/1.1/glossary.html#term-estimators). The permutation feature importance is defined to be the decrease in a model score when a single feature value is randomly shuffled [[1]](#id2). This procedure breaks the relationship between the feature and the target, thus the drop in the model score is indicative of how much the model depends on the feature. This technique benefits from being model agnostic and can be calculated many times with different permutations of the feature.
Warning
Features that are deemed of **low importance for a bad model** (low cross-validation score) could be **very important for a good model**. Therefore it is always important to evaluate the predictive power of a model using a held-out set (or better with cross-validation) prior to computing importances. Permutation importance does not reflect to the intrinsic predictive value of a feature by itself but **how important this feature is for a particular model**.
The [`permutation_importance`](generated/sklearn.inspection.permutation_importance#sklearn.inspection.permutation_importance "sklearn.inspection.permutation_importance") function calculates the feature importance of [estimators](https://scikit-learn.org/1.1/glossary.html#term-estimators) for a given dataset. The `n_repeats` parameter sets the number of times a feature is randomly shuffled and returns a sample of feature importances.
Let’s consider the following trained regression model:
```
>>> from sklearn.datasets import load_diabetes
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.linear_model import Ridge
>>> diabetes = load_diabetes()
>>> X_train, X_val, y_train, y_val = train_test_split(
... diabetes.data, diabetes.target, random_state=0)
...
>>> model = Ridge(alpha=1e-2).fit(X_train, y_train)
>>> model.score(X_val, y_val)
0.356...
```
Its validation performance, measured via the \(R^2\) score, is significantly larger than the chance level. This makes it possible to use the [`permutation_importance`](generated/sklearn.inspection.permutation_importance#sklearn.inspection.permutation_importance "sklearn.inspection.permutation_importance") function to probe which features are most predictive:
```
>>> from sklearn.inspection import permutation_importance
>>> r = permutation_importance(model, X_val, y_val,
... n_repeats=30,
... random_state=0)
...
>>> for i in r.importances_mean.argsort()[::-1]:
... if r.importances_mean[i] - 2 * r.importances_std[i] > 0:
... print(f"{diabetes.feature_names[i]:<8}"
... f"{r.importances_mean[i]:.3f}"
... f" +/- {r.importances_std[i]:.3f}")
...
s5 0.204 +/- 0.050
bmi 0.176 +/- 0.048
bp 0.088 +/- 0.033
sex 0.056 +/- 0.023
```
Note that the importance values for the top features represent a large fraction of the reference score of 0.356.
Permutation importances can be computed either on the training set or on a held-out testing or validation set. Using a held-out set makes it possible to highlight which features contribute the most to the generalization power of the inspected model. Features that are important on the training set but not on the held-out set might cause the model to overfit.
The permutation feature importance is the decrease in a model score when a single feature value is randomly shuffled. The score function to be used for the computation of importances can be specified with the `scoring` argument, which also accepts multiple scorers. Using multiple scorers is more computationally efficient than sequentially calling [`permutation_importance`](generated/sklearn.inspection.permutation_importance#sklearn.inspection.permutation_importance "sklearn.inspection.permutation_importance") several times with a different scorer, as it reuses model predictions.
An example of using multiple scorers is shown below, employing a list of metrics, but more input formats are possible, as documented in [Using multiple metric evaluation](model_evaluation#multimetric-scoring).
```
>>> scoring = ['r2', 'neg_mean_absolute_percentage_error', 'neg_mean_squared_error']
>>> r_multi = permutation_importance(
... model, X_val, y_val, n_repeats=30, random_state=0, scoring=scoring)
...
>>> for metric in r_multi:
... print(f"{metric}")
... r = r_multi[metric]
... for i in r.importances_mean.argsort()[::-1]:
... if r.importances_mean[i] - 2 * r.importances_std[i] > 0:
... print(f" {diabetes.feature_names[i]:<8}"
... f"{r.importances_mean[i]:.3f}"
... f" +/- {r.importances_std[i]:.3f}")
...
r2
s5 0.204 +/- 0.050
bmi 0.176 +/- 0.048
bp 0.088 +/- 0.033
sex 0.056 +/- 0.023
neg_mean_absolute_percentage_error
s5 0.081 +/- 0.020
bmi 0.064 +/- 0.015
bp 0.029 +/- 0.010
neg_mean_squared_error
s5 1013.866 +/- 246.445
bmi 872.726 +/- 240.298
bp 438.663 +/- 163.022
sex 277.376 +/- 115.123
```
The ranking of the features is approximately the same for different metrics even if the scales of the importance values are very different. However, this is not guaranteed and different metrics might lead to significantly different feature importances, in particular for models trained for imbalanced classification problems, for which the choice of the classification metric can be critical.
4.2.1. Outline of the permutation importance algorithm
-------------------------------------------------------
* Inputs: fitted predictive model \(m\), tabular dataset (training or validation) \(D\).
* Compute the reference score \(s\) of the model \(m\) on data \(D\) (for instance the accuracy for a classifier or the \(R^2\) for a regressor).
* For each feature \(j\) (column of \(D\)):
+ For each repetition \(k\) in \({1, ..., K}\):
- Randomly shuffle column \(j\) of dataset \(D\) to generate a corrupted version of the data named \(\tilde{D}\_{k,j}\).
- Compute the score \(s\_{k,j}\) of model \(m\) on corrupted data \(\tilde{D}\_{k,j}\).
+ Compute importance \(i\_j\) for feature \(f\_j\) defined as:
\[i\_j = s - \frac{1}{K} \sum\_{k=1}^{K} s\_{k,j}\]
4.2.2. Relation to impurity-based importance in trees
------------------------------------------------------
Tree-based models provide an alternative measure of [feature importances based on the mean decrease in impurity](ensemble#random-forest-feature-importance) (MDI). Impurity is quantified by the splitting criterion of the decision trees (Gini, Log Loss or Mean Squared Error). However, this method can give high importance to features that may not be predictive on unseen data when the model is overfitting. Permutation-based feature importance, on the other hand, avoids this issue, since it can be computed on unseen data.
Furthermore, impurity-based feature importance for trees are **strongly biased** and **favor high cardinality features** (typically numerical features) over low cardinality features such as binary features or categorical variables with a small number of possible categories.
Permutation-based feature importances do not exhibit such a bias. Additionally, the permutation feature importance may be computed performance metric on the model predictions and can be used to analyze any model class (not just tree-based models).
The following example highlights the limitations of impurity-based feature importance in contrast to permutation-based feature importance: [Permutation Importance vs Random Forest Feature Importance (MDI)](../auto_examples/inspection/plot_permutation_importance#sphx-glr-auto-examples-inspection-plot-permutation-importance-py).
4.2.3. Misleading values on strongly correlated features
---------------------------------------------------------
When two features are correlated and one of the features is permuted, the model will still have access to the feature through its correlated feature. This will result in a lower importance value for both features, where they might *actually* be important.
One way to handle this is to cluster features that are correlated and only keep one feature from each cluster. This strategy is explored in the following example: [Permutation Importance with Multicollinear or Correlated Features](../auto_examples/inspection/plot_permutation_importance_multicollinear#sphx-glr-auto-examples-inspection-plot-permutation-importance-multicollinear-py).
scikit_learn 6.8. Pairwise metrics, Affinities and Kernels 6.8. Pairwise metrics, Affinities and Kernels
=============================================
The [`sklearn.metrics.pairwise`](classes#module-sklearn.metrics.pairwise "sklearn.metrics.pairwise") submodule implements utilities to evaluate pairwise distances or affinity of sets of samples.
This module contains both distance metrics and kernels. A brief summary is given on the two here.
Distance metrics are functions `d(a, b)` such that `d(a, b) < d(a, c)` if objects `a` and `b` are considered “more similar” than objects `a` and `c`. Two objects exactly alike would have a distance of zero. One of the most popular examples is Euclidean distance. To be a ‘true’ metric, it must obey the following four conditions:
```
1. d(a, b) >= 0, for all a and b
2. d(a, b) == 0, if and only if a = b, positive definiteness
3. d(a, b) == d(b, a), symmetry
4. d(a, c) <= d(a, b) + d(b, c), the triangle inequality
```
Kernels are measures of similarity, i.e. `s(a, b) > s(a, c)` if objects `a` and `b` are considered “more similar” than objects `a` and `c`. A kernel must also be positive semi-definite.
There are a number of ways to convert between a distance metric and a similarity measure, such as a kernel. Let `D` be the distance, and `S` be the kernel:
1. `S = np.exp(-D * gamma)`, where one heuristic for choosing `gamma` is `1 / num_features`
2. `S = 1. / (D / np.max(D))`
The distances between the row vectors of `X` and the row vectors of `Y` can be evaluated using [`pairwise_distances`](generated/sklearn.metrics.pairwise_distances#sklearn.metrics.pairwise_distances "sklearn.metrics.pairwise_distances"). If `Y` is omitted the pairwise distances of the row vectors of `X` are calculated. Similarly, [`pairwise.pairwise_kernels`](generated/sklearn.metrics.pairwise.pairwise_kernels#sklearn.metrics.pairwise.pairwise_kernels "sklearn.metrics.pairwise.pairwise_kernels") can be used to calculate the kernel between `X` and `Y` using different kernel functions. See the API reference for more details.
```
>>> import numpy as np
>>> from sklearn.metrics import pairwise_distances
>>> from sklearn.metrics.pairwise import pairwise_kernels
>>> X = np.array([[2, 3], [3, 5], [5, 8]])
>>> Y = np.array([[1, 0], [2, 1]])
>>> pairwise_distances(X, Y, metric='manhattan')
array([[ 4., 2.],
[ 7., 5.],
[12., 10.]])
>>> pairwise_distances(X, metric='manhattan')
array([[0., 3., 8.],
[3., 0., 5.],
[8., 5., 0.]])
>>> pairwise_kernels(X, Y, metric='linear')
array([[ 2., 7.],
[ 3., 11.],
[ 5., 18.]])
```
6.8.1. Cosine similarity
-------------------------
[`cosine_similarity`](generated/sklearn.metrics.pairwise.cosine_similarity#sklearn.metrics.pairwise.cosine_similarity "sklearn.metrics.pairwise.cosine_similarity") computes the L2-normalized dot product of vectors. That is, if \(x\) and \(y\) are row vectors, their cosine similarity \(k\) is defined as:
\[k(x, y) = \frac{x y^\top}{\|x\| \|y\|}\] This is called cosine similarity, because Euclidean (L2) normalization projects the vectors onto the unit sphere, and their dot product is then the cosine of the angle between the points denoted by the vectors.
This kernel is a popular choice for computing the similarity of documents represented as tf-idf vectors. [`cosine_similarity`](generated/sklearn.metrics.pairwise.cosine_similarity#sklearn.metrics.pairwise.cosine_similarity "sklearn.metrics.pairwise.cosine_similarity") accepts `scipy.sparse` matrices. (Note that the tf-idf functionality in `sklearn.feature_extraction.text` can produce normalized vectors, in which case [`cosine_similarity`](generated/sklearn.metrics.pairwise.cosine_similarity#sklearn.metrics.pairwise.cosine_similarity "sklearn.metrics.pairwise.cosine_similarity") is equivalent to [`linear_kernel`](generated/sklearn.metrics.pairwise.linear_kernel#sklearn.metrics.pairwise.linear_kernel "sklearn.metrics.pairwise.linear_kernel"), only slower.)
6.8.2. Linear kernel
---------------------
The function [`linear_kernel`](generated/sklearn.metrics.pairwise.linear_kernel#sklearn.metrics.pairwise.linear_kernel "sklearn.metrics.pairwise.linear_kernel") computes the linear kernel, that is, a special case of [`polynomial_kernel`](generated/sklearn.metrics.pairwise.polynomial_kernel#sklearn.metrics.pairwise.polynomial_kernel "sklearn.metrics.pairwise.polynomial_kernel") with `degree=1` and `coef0=0` (homogeneous). If `x` and `y` are column vectors, their linear kernel is:
\[k(x, y) = x^\top y\]
6.8.3. Polynomial kernel
-------------------------
The function [`polynomial_kernel`](generated/sklearn.metrics.pairwise.polynomial_kernel#sklearn.metrics.pairwise.polynomial_kernel "sklearn.metrics.pairwise.polynomial_kernel") computes the degree-d polynomial kernel between two vectors. The polynomial kernel represents the similarity between two vectors. Conceptually, the polynomial kernels considers not only the similarity between vectors under the same dimension, but also across dimensions. When used in machine learning algorithms, this allows to account for feature interaction.
The polynomial kernel is defined as:
\[k(x, y) = (\gamma x^\top y +c\_0)^d\] where:
* `x`, `y` are the input vectors
* `d` is the kernel degree
If \(c\_0 = 0\) the kernel is said to be homogeneous.
6.8.4. Sigmoid kernel
----------------------
The function [`sigmoid_kernel`](generated/sklearn.metrics.pairwise.sigmoid_kernel#sklearn.metrics.pairwise.sigmoid_kernel "sklearn.metrics.pairwise.sigmoid_kernel") computes the sigmoid kernel between two vectors. The sigmoid kernel is also known as hyperbolic tangent, or Multilayer Perceptron (because, in the neural network field, it is often used as neuron activation function). It is defined as:
\[k(x, y) = \tanh( \gamma x^\top y + c\_0)\] where:
* `x`, `y` are the input vectors
* \(\gamma\) is known as slope
* \(c\_0\) is known as intercept
6.8.5. RBF kernel
------------------
The function [`rbf_kernel`](generated/sklearn.metrics.pairwise.rbf_kernel#sklearn.metrics.pairwise.rbf_kernel "sklearn.metrics.pairwise.rbf_kernel") computes the radial basis function (RBF) kernel between two vectors. This kernel is defined as:
\[k(x, y) = \exp( -\gamma \| x-y \|^2)\] where `x` and `y` are the input vectors. If \(\gamma = \sigma^{-2}\) the kernel is known as the Gaussian kernel of variance \(\sigma^2\).
6.8.6. Laplacian kernel
------------------------
The function [`laplacian_kernel`](generated/sklearn.metrics.pairwise.laplacian_kernel#sklearn.metrics.pairwise.laplacian_kernel "sklearn.metrics.pairwise.laplacian_kernel") is a variant on the radial basis function kernel defined as:
\[k(x, y) = \exp( -\gamma \| x-y \|\_1)\] where `x` and `y` are the input vectors and \(\|x-y\|\_1\) is the Manhattan distance between the input vectors.
It has proven useful in ML applied to noiseless data. See e.g. [Machine learning for quantum mechanics in a nutshell](https://onlinelibrary.wiley.com/doi/10.1002/qua.24954/abstract/).
6.8.7. Chi-squared kernel
--------------------------
The chi-squared kernel is a very popular choice for training non-linear SVMs in computer vision applications. It can be computed using [`chi2_kernel`](generated/sklearn.metrics.pairwise.chi2_kernel#sklearn.metrics.pairwise.chi2_kernel "sklearn.metrics.pairwise.chi2_kernel") and then passed to an [`SVC`](generated/sklearn.svm.svc#sklearn.svm.SVC "sklearn.svm.SVC") with `kernel="precomputed"`:
```
>>> from sklearn.svm import SVC
>>> from sklearn.metrics.pairwise import chi2_kernel
>>> X = [[0, 1], [1, 0], [.2, .8], [.7, .3]]
>>> y = [0, 1, 0, 1]
>>> K = chi2_kernel(X, gamma=.5)
>>> K
array([[1. , 0.36787944, 0.89483932, 0.58364548],
[0.36787944, 1. , 0.51341712, 0.83822343],
[0.89483932, 0.51341712, 1. , 0.7768366 ],
[0.58364548, 0.83822343, 0.7768366 , 1. ]])
>>> svm = SVC(kernel='precomputed').fit(K, y)
>>> svm.predict(K)
array([0, 1, 0, 1])
```
It can also be directly used as the `kernel` argument:
```
>>> svm = SVC(kernel=chi2_kernel).fit(X, y)
>>> svm.predict(X)
array([0, 1, 0, 1])
```
The chi squared kernel is given by
\[k(x, y) = \exp \left (-\gamma \sum\_i \frac{(x[i] - y[i]) ^ 2}{x[i] + y[i]} \right )\] The data is assumed to be non-negative, and is often normalized to have an L1-norm of one. The normalization is rationalized with the connection to the chi squared distance, which is a distance between discrete probability distributions.
The chi squared kernel is most commonly used on histograms (bags) of visual words.
scikit_learn sklearn.kernel_approximation.RBFSampler sklearn.kernel\_approximation.RBFSampler
========================================
*class*sklearn.kernel\_approximation.RBFSampler(*\**, *gamma=1.0*, *n\_components=100*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/kernel_approximation.py#L232)
Approximate a RBF kernel feature map using random Fourier features.
It implements a variant of Random Kitchen Sinks.[1]
Read more in the [User Guide](../kernel_approximation#rbf-kernel-approx).
Parameters:
**gamma**float, default=1.0
Parameter of RBF kernel: exp(-gamma \* x^2).
**n\_components**int, default=100
Number of Monte Carlo samples per original feature. Equals the dimensionality of the computed feature space.
**random\_state**int, RandomState instance or None, default=None
Pseudo-random number generator to control the generation of the random weights and random offset when fitting the training data. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Attributes:
**random\_offset\_**ndarray of shape (n\_components,), dtype=float64
Random offset used to compute the projection in the `n_components` dimensions of the feature space.
**random\_weights\_**ndarray of shape (n\_features, n\_components), dtype=float64
Random projection directions drawn from the Fourier transform of the RBF kernel.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`AdditiveChi2Sampler`](sklearn.kernel_approximation.additivechi2sampler#sklearn.kernel_approximation.AdditiveChi2Sampler "sklearn.kernel_approximation.AdditiveChi2Sampler")
Approximate feature map for additive chi2 kernel.
[`Nystroem`](sklearn.kernel_approximation.nystroem#sklearn.kernel_approximation.Nystroem "sklearn.kernel_approximation.Nystroem")
Approximate a kernel map using a subset of the training data.
[`PolynomialCountSketch`](sklearn.kernel_approximation.polynomialcountsketch#sklearn.kernel_approximation.PolynomialCountSketch "sklearn.kernel_approximation.PolynomialCountSketch")
Polynomial kernel approximation via Tensor Sketch.
[`SkewedChi2Sampler`](sklearn.kernel_approximation.skewedchi2sampler#sklearn.kernel_approximation.SkewedChi2Sampler "sklearn.kernel_approximation.SkewedChi2Sampler")
Approximate feature map for “skewed chi-squared” kernel.
[`sklearn.metrics.pairwise.kernel_metrics`](sklearn.metrics.pairwise.kernel_metrics#sklearn.metrics.pairwise.kernel_metrics "sklearn.metrics.pairwise.kernel_metrics")
List of built-in kernels.
#### Notes
See “Random Features for Large-Scale Kernel Machines” by A. Rahimi and Benjamin Recht.
[1] “Weighted Sums of Random Kitchen Sinks: Replacing minimization with randomization in learning” by A. Rahimi and Benjamin Recht. (<https://people.eecs.berkeley.edu/~brecht/papers/08.rah.rec.nips.pdf>)
#### Examples
```
>>> from sklearn.kernel_approximation import RBFSampler
>>> from sklearn.linear_model import SGDClassifier
>>> X = [[0, 0], [1, 1], [1, 0], [0, 1]]
>>> y = [0, 0, 1, 1]
>>> rbf_feature = RBFSampler(gamma=1, random_state=1)
>>> X_features = rbf_feature.fit_transform(X)
>>> clf = SGDClassifier(max_iter=5, tol=1e-3)
>>> clf.fit(X_features, y)
SGDClassifier(max_iter=5)
>>> clf.score(X_features, y)
1.0
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.kernel_approximation.RBFSampler.fit "sklearn.kernel_approximation.RBFSampler.fit")(X[, y]) | Fit the model with X. |
| [`fit_transform`](#sklearn.kernel_approximation.RBFSampler.fit_transform "sklearn.kernel_approximation.RBFSampler.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.kernel_approximation.RBFSampler.get_feature_names_out "sklearn.kernel_approximation.RBFSampler.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.kernel_approximation.RBFSampler.get_params "sklearn.kernel_approximation.RBFSampler.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.kernel_approximation.RBFSampler.set_params "sklearn.kernel_approximation.RBFSampler.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.kernel_approximation.RBFSampler.transform "sklearn.kernel_approximation.RBFSampler.transform")(X) | Apply the approximate feature map to X. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/kernel_approximation.py#L315)
Fit the model with X.
Samples random projection according to n\_features.
Parameters:
**X**{array-like, sparse matrix}, shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like, shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.kernel_approximation.RBFSampler.fit "sklearn.kernel_approximation.RBFSampler.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/kernel_approximation.py#L348)
Apply the approximate feature map to X.
Parameters:
**X**{array-like, sparse matrix}, shape (n\_samples, n\_features)
New data, where `n_samples` is the number of samples and `n_features` is the number of features.
Returns:
**X\_new**array-like, shape (n\_samples, n\_components)
Returns the instance itself.
Examples using `sklearn.kernel_approximation.RBFSampler`
--------------------------------------------------------
[Explicit feature map approximation for RBF kernels](../../auto_examples/miscellaneous/plot_kernel_approximation#sphx-glr-auto-examples-miscellaneous-plot-kernel-approximation-py)
| programming_docs |
scikit_learn sklearn.semi_supervised.LabelSpreading sklearn.semi\_supervised.LabelSpreading
=======================================
*class*sklearn.semi\_supervised.LabelSpreading(*kernel='rbf'*, *\**, *gamma=20*, *n\_neighbors=7*, *alpha=0.2*, *max\_iter=30*, *tol=0.001*, *n\_jobs=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/semi_supervised/_label_propagation.py#L478)
LabelSpreading model for semi-supervised learning.
This model is similar to the basic Label Propagation algorithm, but uses affinity matrix based on the normalized graph Laplacian and soft clamping across the labels.
Read more in the [User Guide](../semi_supervised#label-propagation).
Parameters:
**kernel**{‘knn’, ‘rbf’} or callable, default=’rbf’
String identifier for kernel function to use or the kernel function itself. Only ‘rbf’ and ‘knn’ strings are valid inputs. The function passed should take two inputs, each of shape (n\_samples, n\_features), and return a (n\_samples, n\_samples) shaped weight matrix.
**gamma**float, default=20
Parameter for rbf kernel.
**n\_neighbors**int, default=7
Parameter for knn kernel which is a strictly positive integer.
**alpha**float, default=0.2
Clamping factor. A value in (0, 1) that specifies the relative amount that an instance should adopt the information from its neighbors as opposed to its initial label. alpha=0 means keeping the initial label information; alpha=1 means replacing all initial information.
**max\_iter**int, default=30
Maximum number of iterations allowed.
**tol**float, default=1e-3
Convergence tolerance: threshold to consider the system at steady state.
**n\_jobs**int, default=None
The number of parallel jobs to run. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
Attributes:
**X\_**ndarray of shape (n\_samples, n\_features)
Input array.
**classes\_**ndarray of shape (n\_classes,)
The distinct labels used in classifying instances.
**label\_distributions\_**ndarray of shape (n\_samples, n\_classes)
Categorical distribution for each item.
**transduction\_**ndarray of shape (n\_samples,)
Label assigned to each item via the transduction.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_iter\_**int
Number of iterations run.
See also
[`LabelPropagation`](sklearn.semi_supervised.labelpropagation#sklearn.semi_supervised.LabelPropagation "sklearn.semi_supervised.LabelPropagation")
Unregularized graph based semi-supervised learning.
#### References
Dengyong Zhou, Olivier Bousquet, Thomas Navin Lal, Jason Weston, Bernhard Schoelkopf. Learning with local and global consistency (2004) <http://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.115.3219>
#### Examples
```
>>> import numpy as np
>>> from sklearn import datasets
>>> from sklearn.semi_supervised import LabelSpreading
>>> label_prop_model = LabelSpreading()
>>> iris = datasets.load_iris()
>>> rng = np.random.RandomState(42)
>>> random_unlabeled_points = rng.rand(len(iris.target)) < 0.3
>>> labels = np.copy(iris.target)
>>> labels[random_unlabeled_points] = -1
>>> label_prop_model.fit(iris.data, labels)
LabelSpreading(...)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.semi_supervised.LabelSpreading.fit "sklearn.semi_supervised.LabelSpreading.fit")(X, y) | Fit a semi-supervised label propagation model to X. |
| [`get_params`](#sklearn.semi_supervised.LabelSpreading.get_params "sklearn.semi_supervised.LabelSpreading.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.semi_supervised.LabelSpreading.predict "sklearn.semi_supervised.LabelSpreading.predict")(X) | Perform inductive inference across the model. |
| [`predict_proba`](#sklearn.semi_supervised.LabelSpreading.predict_proba "sklearn.semi_supervised.LabelSpreading.predict_proba")(X) | Predict probability for each possible outcome. |
| [`score`](#sklearn.semi_supervised.LabelSpreading.score "sklearn.semi_supervised.LabelSpreading.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.semi_supervised.LabelSpreading.set_params "sklearn.semi_supervised.LabelSpreading.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/semi_supervised/_label_propagation.py#L225)
Fit a semi-supervised label propagation model to X.
The input samples (labeled and unlabeled) are provided by matrix X, and target labels are provided by matrix y. We conventionally apply the label -1 to unlabeled samples in matrix y in a semi-supervised classification.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,)
Target class values with unlabeled points marked as -1. All unlabeled samples will be transductively assigned labels internally.
Returns:
**self**object
Returns the instance itself.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/semi_supervised/_label_propagation.py#L169)
Perform inductive inference across the model.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The data matrix.
Returns:
**y**ndarray of shape (n\_samples,)
Predictions for input data.
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/semi_supervised/_label_propagation.py#L185)
Predict probability for each possible outcome.
Compute the probability estimates for each single sample in X and each possible outcome seen during training (categorical distribution).
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The data matrix.
Returns:
**probabilities**ndarray of shape (n\_samples, n\_classes)
Normalized probability distributions across class labels.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.semi_supervised.LabelSpreading`
-------------------------------------------------------
[Decision boundary of semi-supervised classifiers versus SVM on the Iris dataset](../../auto_examples/semi_supervised/plot_semi_supervised_versus_svm_iris#sphx-glr-auto-examples-semi-supervised-plot-semi-supervised-versus-svm-iris-py)
[Label Propagation digits active learning](../../auto_examples/semi_supervised/plot_label_propagation_digits_active_learning#sphx-glr-auto-examples-semi-supervised-plot-label-propagation-digits-active-learning-py)
[Label Propagation digits: Demonstrating performance](../../auto_examples/semi_supervised/plot_label_propagation_digits#sphx-glr-auto-examples-semi-supervised-plot-label-propagation-digits-py)
[Label Propagation learning a complex structure](../../auto_examples/semi_supervised/plot_label_propagation_structure#sphx-glr-auto-examples-semi-supervised-plot-label-propagation-structure-py)
[Semi-supervised Classification on a Text Dataset](../../auto_examples/semi_supervised/plot_semi_supervised_newsgroups#sphx-glr-auto-examples-semi-supervised-plot-semi-supervised-newsgroups-py)
scikit_learn sklearn.utils.sparsefuncs_fast.inplace_csr_row_normalize_l1 sklearn.utils.sparsefuncs\_fast.inplace\_csr\_row\_normalize\_l1
================================================================
sklearn.utils.sparsefuncs\_fast.inplace\_csr\_row\_normalize\_l1()
Inplace row normalize using the l1 norm
scikit_learn sklearn.linear_model.RANSACRegressor sklearn.linear\_model.RANSACRegressor
=====================================
*class*sklearn.linear\_model.RANSACRegressor(*estimator=None*, *\**, *min\_samples=None*, *residual\_threshold=None*, *is\_data\_valid=None*, *is\_model\_valid=None*, *max\_trials=100*, *max\_skips=inf*, *stop\_n\_inliers=inf*, *stop\_score=inf*, *stop\_probability=0.99*, *loss='absolute\_error'*, *random\_state=None*, *base\_estimator='deprecated'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_ransac.py#L54)
RANSAC (RANdom SAmple Consensus) algorithm.
RANSAC is an iterative algorithm for the robust estimation of parameters from a subset of inliers from the complete data set.
Read more in the [User Guide](../linear_model#ransac-regression).
Parameters:
**estimator**object, default=None
Base estimator object which implements the following methods:
* `fit(X, y)`: Fit model to given training data and target values.
* `score(X, y)`: Returns the mean accuracy on the given test data, which is used for the stop criterion defined by `stop_score`. Additionally, the score is used to decide which of two equally large consensus sets is chosen as the better one.
* `predict(X)`: Returns predicted values using the linear model, which is used to compute residual error using loss function.
If `estimator` is None, then [`LinearRegression`](sklearn.linear_model.linearregression#sklearn.linear_model.LinearRegression "sklearn.linear_model.LinearRegression") is used for target values of dtype float.
Note that the current implementation only supports regression estimators.
**min\_samples**int (>= 1) or float ([0, 1]), default=None
Minimum number of samples chosen randomly from original data. Treated as an absolute number of samples for `min_samples >= 1`, treated as a relative number `ceil(min_samples * X.shape[0])` for `min_samples < 1`. This is typically chosen as the minimal number of samples necessary to estimate the given `estimator`. By default a `sklearn.linear_model.LinearRegression()` estimator is assumed and `min_samples` is chosen as `X.shape[1] + 1`. This parameter is highly dependent upon the model, so if a `estimator` other than `linear_model.LinearRegression` is used, the user is encouraged to provide a value.
Deprecated since version 1.0: Not setting `min_samples` explicitly will raise an error in version 1.2 for models other than [`LinearRegression`](sklearn.linear_model.linearregression#sklearn.linear_model.LinearRegression "sklearn.linear_model.LinearRegression"). To keep the old default behavior, set `min_samples=X.shape[1] + 1` explicitly.
**residual\_threshold**float, default=None
Maximum residual for a data sample to be classified as an inlier. By default the threshold is chosen as the MAD (median absolute deviation) of the target values `y`. Points whose residuals are strictly equal to the threshold are considered as inliers.
**is\_data\_valid**callable, default=None
This function is called with the randomly selected data before the model is fitted to it: `is_data_valid(X, y)`. If its return value is False the current randomly chosen sub-sample is skipped.
**is\_model\_valid**callable, default=None
This function is called with the estimated model and the randomly selected data: `is_model_valid(model, X, y)`. If its return value is False the current randomly chosen sub-sample is skipped. Rejecting samples with this function is computationally costlier than with `is_data_valid`. `is_model_valid` should therefore only be used if the estimated model is needed for making the rejection decision.
**max\_trials**int, default=100
Maximum number of iterations for random sample selection.
**max\_skips**int, default=np.inf
Maximum number of iterations that can be skipped due to finding zero inliers or invalid data defined by `is_data_valid` or invalid models defined by `is_model_valid`.
New in version 0.19.
**stop\_n\_inliers**int, default=np.inf
Stop iteration if at least this number of inliers are found.
**stop\_score**float, default=np.inf
Stop iteration if score is greater equal than this threshold.
**stop\_probability**float in range [0, 1], default=0.99
RANSAC iteration stops if at least one outlier-free set of the training data is sampled in RANSAC. This requires to generate at least N samples (iterations):
```
N >= log(1 - probability) / log(1 - e**m)
```
where the probability (confidence) is typically set to high value such as 0.99 (the default) and e is the current fraction of inliers w.r.t. the total number of samples.
**loss**str, callable, default=’absolute\_error’
String inputs, ‘absolute\_error’ and ‘squared\_error’ are supported which find the absolute error and squared error per sample respectively.
If `loss` is a callable, then it should be a function that takes two arrays as inputs, the true and predicted value and returns a 1-D array with the i-th value of the array corresponding to the loss on `X[i]`.
If the loss on a sample is greater than the `residual_threshold`, then this sample is classified as an outlier.
New in version 0.18.
Deprecated since version 1.0: The loss ‘squared\_loss’ was deprecated in v1.0 and will be removed in version 1.2. Use `loss='squared_error'` which is equivalent.
Deprecated since version 1.0: The loss ‘absolute\_loss’ was deprecated in v1.0 and will be removed in version 1.2. Use `loss='absolute_error'` which is equivalent.
**random\_state**int, RandomState instance, default=None
The generator used to initialize the centers. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**base\_estimator**object, default=”deprecated”
Use `estimator` instead.
Deprecated since version 1.1: `base_estimator` is deprecated and will be removed in 1.3. Use `estimator` instead.
Attributes:
**estimator\_**object
Best fitted model (copy of the `estimator` object).
**n\_trials\_**int
Number of random selection trials until one of the stop criteria is met. It is always `<= max_trials`.
**inlier\_mask\_**bool array of shape [n\_samples]
Boolean mask of inliers classified as `True`.
**n\_skips\_no\_inliers\_**int
Number of iterations skipped due to finding zero inliers.
New in version 0.19.
**n\_skips\_invalid\_data\_**int
Number of iterations skipped due to invalid data defined by `is_data_valid`.
New in version 0.19.
**n\_skips\_invalid\_model\_**int
Number of iterations skipped due to an invalid model defined by `is_model_valid`.
New in version 0.19.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`HuberRegressor`](sklearn.linear_model.huberregressor#sklearn.linear_model.HuberRegressor "sklearn.linear_model.HuberRegressor")
Linear regression model that is robust to outliers.
[`TheilSenRegressor`](sklearn.linear_model.theilsenregressor#sklearn.linear_model.TheilSenRegressor "sklearn.linear_model.TheilSenRegressor")
Theil-Sen Estimator robust multivariate regression model.
[`SGDRegressor`](sklearn.linear_model.sgdregressor#sklearn.linear_model.SGDRegressor "sklearn.linear_model.SGDRegressor")
Fitted by minimizing a regularized empirical loss with SGD.
#### References
[1] <https://en.wikipedia.org/wiki/RANSAC>
[2] <https://www.sri.com/wp-content/uploads/2021/12/ransac-publication.pdf>
[3] <http://www.bmva.org/bmvc/2009/Papers/Paper355/Paper355.pdf>
#### Examples
```
>>> from sklearn.linear_model import RANSACRegressor
>>> from sklearn.datasets import make_regression
>>> X, y = make_regression(
... n_samples=200, n_features=2, noise=4.0, random_state=0)
>>> reg = RANSACRegressor(random_state=0).fit(X, y)
>>> reg.score(X, y)
0.9885...
>>> reg.predict(X[:1,])
array([-31.9417...])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.linear_model.RANSACRegressor.fit "sklearn.linear_model.RANSACRegressor.fit")(X, y[, sample\_weight]) | Fit estimator using RANSAC algorithm. |
| [`get_params`](#sklearn.linear_model.RANSACRegressor.get_params "sklearn.linear_model.RANSACRegressor.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.linear_model.RANSACRegressor.predict "sklearn.linear_model.RANSACRegressor.predict")(X) | Predict using the estimated model. |
| [`score`](#sklearn.linear_model.RANSACRegressor.score "sklearn.linear_model.RANSACRegressor.score")(X, y) | Return the score of the prediction. |
| [`set_params`](#sklearn.linear_model.RANSACRegressor.set_params "sklearn.linear_model.RANSACRegressor.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_ransac.py#L279)
Fit estimator using RANSAC algorithm.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training data.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_targets)
Target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Individual weights for each sample raises error if sample\_weight is passed and estimator fit method does not support it.
New in version 0.18.
Returns:
**self**object
Fitted `RANSACRegressor` estimator.
Raises:
ValueError
If no valid consensus set could be found. This occurs if `is_data_valid` and `is_model_valid` return False for all `max_trials` randomly chosen sub-samples.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_ransac.py#L574)
Predict using the estimated model.
This is a wrapper for `estimator_.predict(X)`.
Parameters:
**X**{array-like or sparse matrix} of shape (n\_samples, n\_features)
Input data.
Returns:
**y**array, shape = [n\_samples] or [n\_samples, n\_targets]
Returns predicted values.
score(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_ransac.py#L598)
Return the score of the prediction.
This is a wrapper for `estimator_.score(X, y)`.
Parameters:
**X**(array-like or sparse matrix} of shape (n\_samples, n\_features)
Training data.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_targets)
Target values.
Returns:
**z**float
Score of the prediction.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.linear_model.RANSACRegressor`
-----------------------------------------------------
[Robust linear estimator fitting](../../auto_examples/linear_model/plot_robust_fit#sphx-glr-auto-examples-linear-model-plot-robust-fit-py)
[Robust linear model estimation using RANSAC](../../auto_examples/linear_model/plot_ransac#sphx-glr-auto-examples-linear-model-plot-ransac-py)
[Theil-Sen Regression](../../auto_examples/linear_model/plot_theilsen#sphx-glr-auto-examples-linear-model-plot-theilsen-py)
| programming_docs |
scikit_learn sklearn.ensemble.ExtraTreesClassifier sklearn.ensemble.ExtraTreesClassifier
=====================================
*class*sklearn.ensemble.ExtraTreesClassifier(*n\_estimators=100*, *\**, *criterion='gini'*, *max\_depth=None*, *min\_samples\_split=2*, *min\_samples\_leaf=1*, *min\_weight\_fraction\_leaf=0.0*, *max\_features='sqrt'*, *max\_leaf\_nodes=None*, *min\_impurity\_decrease=0.0*, *bootstrap=False*, *oob\_score=False*, *n\_jobs=None*, *random\_state=None*, *verbose=0*, *warm\_start=False*, *class\_weight=None*, *ccp\_alpha=0.0*, *max\_samples=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L1765)
An extra-trees classifier.
This class implements a meta estimator that fits a number of randomized decision trees (a.k.a. extra-trees) on various sub-samples of the dataset and uses averaging to improve the predictive accuracy and control over-fitting.
Read more in the [User Guide](../ensemble#forest).
Parameters:
**n\_estimators**int, default=100
The number of trees in the forest.
Changed in version 0.22: The default value of `n_estimators` changed from 10 to 100 in 0.22.
**criterion**{“gini”, “entropy”, “log\_loss”}, default=”gini”
The function to measure the quality of a split. Supported criteria are “gini” for the Gini impurity and “log\_loss” and “entropy” both for the Shannon information gain, see [Mathematical formulation](../tree#tree-mathematical-formulation). Note: This parameter is tree-specific.
**max\_depth**int, default=None
The maximum depth of the tree. If None, then nodes are expanded until all leaves are pure or until all leaves contain less than min\_samples\_split samples.
**min\_samples\_split**int or float, default=2
The minimum number of samples required to split an internal node:
* If int, then consider `min_samples_split` as the minimum number.
* If float, then `min_samples_split` is a fraction and `ceil(min_samples_split * n_samples)` are the minimum number of samples for each split.
Changed in version 0.18: Added float values for fractions.
**min\_samples\_leaf**int or float, default=1
The minimum number of samples required to be at a leaf node. A split point at any depth will only be considered if it leaves at least `min_samples_leaf` training samples in each of the left and right branches. This may have the effect of smoothing the model, especially in regression.
* If int, then consider `min_samples_leaf` as the minimum number.
* If float, then `min_samples_leaf` is a fraction and `ceil(min_samples_leaf * n_samples)` are the minimum number of samples for each node.
Changed in version 0.18: Added float values for fractions.
**min\_weight\_fraction\_leaf**float, default=0.0
The minimum weighted fraction of the sum total of weights (of all the input samples) required to be at a leaf node. Samples have equal weight when sample\_weight is not provided.
**max\_features**{“sqrt”, “log2”, None}, int or float, default=”sqrt”
The number of features to consider when looking for the best split:
* If int, then consider `max_features` features at each split.
* If float, then `max_features` is a fraction and `max(1, int(max_features * n_features_in_))` features are considered at each split.
* If “auto”, then `max_features=sqrt(n_features)`.
* If “sqrt”, then `max_features=sqrt(n_features)`.
* If “log2”, then `max_features=log2(n_features)`.
* If None, then `max_features=n_features`.
Changed in version 1.1: The default of `max_features` changed from `"auto"` to `"sqrt"`.
Deprecated since version 1.1: The `"auto"` option was deprecated in 1.1 and will be removed in 1.3.
Note: the search for a split does not stop until at least one valid partition of the node samples is found, even if it requires to effectively inspect more than `max_features` features.
**max\_leaf\_nodes**int, default=None
Grow trees with `max_leaf_nodes` in best-first fashion. Best nodes are defined as relative reduction in impurity. If None then unlimited number of leaf nodes.
**min\_impurity\_decrease**float, default=0.0
A node will be split if this split induces a decrease of the impurity greater than or equal to this value.
The weighted impurity decrease equation is the following:
```
N_t / N * (impurity - N_t_R / N_t * right_impurity
- N_t_L / N_t * left_impurity)
```
where `N` is the total number of samples, `N_t` is the number of samples at the current node, `N_t_L` is the number of samples in the left child, and `N_t_R` is the number of samples in the right child.
`N`, `N_t`, `N_t_R` and `N_t_L` all refer to the weighted sum, if `sample_weight` is passed.
New in version 0.19.
**bootstrap**bool, default=False
Whether bootstrap samples are used when building trees. If False, the whole dataset is used to build each tree.
**oob\_score**bool, default=False
Whether to use out-of-bag samples to estimate the generalization score. Only available if bootstrap=True.
**n\_jobs**int, default=None
The number of jobs to run in parallel. [`fit`](#sklearn.ensemble.ExtraTreesClassifier.fit "sklearn.ensemble.ExtraTreesClassifier.fit"), [`predict`](#sklearn.ensemble.ExtraTreesClassifier.predict "sklearn.ensemble.ExtraTreesClassifier.predict"), [`decision_path`](#sklearn.ensemble.ExtraTreesClassifier.decision_path "sklearn.ensemble.ExtraTreesClassifier.decision_path") and [`apply`](#sklearn.ensemble.ExtraTreesClassifier.apply "sklearn.ensemble.ExtraTreesClassifier.apply") are all parallelized over the trees. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**random\_state**int, RandomState instance or None, default=None
Controls 3 sources of randomness:
* the bootstrapping of the samples used when building trees (if `bootstrap=True`)
* the sampling of the features to consider when looking for the best split at each node (if `max_features < n_features`)
* the draw of the splits for each of the `max_features`
See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state) for details.
**verbose**int, default=0
Controls the verbosity when fitting and predicting.
**warm\_start**bool, default=False
When set to `True`, reuse the solution of the previous call to fit and add more estimators to the ensemble, otherwise, just fit a whole new forest. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
**class\_weight**{“balanced”, “balanced\_subsample”}, dict or list of dicts, default=None
Weights associated with classes in the form `{class_label: weight}`. If not given, all classes are supposed to have weight one. For multi-output problems, a list of dicts can be provided in the same order as the columns of y.
Note that for multioutput (including multilabel) weights should be defined for each class of every column in its own dict. For example, for four-class multilabel classification weights should be [{0: 1, 1: 1}, {0: 1, 1: 5}, {0: 1, 1: 1}, {0: 1, 1: 1}] instead of [{1:1}, {2:5}, {3:1}, {4:1}].
The “balanced” mode uses the values of y to automatically adjust weights inversely proportional to class frequencies in the input data as `n_samples / (n_classes * np.bincount(y))`
The “balanced\_subsample” mode is the same as “balanced” except that weights are computed based on the bootstrap sample for every tree grown.
For multi-output, the weights of each column of y will be multiplied.
Note that these weights will be multiplied with sample\_weight (passed through the fit method) if sample\_weight is specified.
**ccp\_alpha**non-negative float, default=0.0
Complexity parameter used for Minimal Cost-Complexity Pruning. The subtree with the largest cost complexity that is smaller than `ccp_alpha` will be chosen. By default, no pruning is performed. See [Minimal Cost-Complexity Pruning](../tree#minimal-cost-complexity-pruning) for details.
New in version 0.22.
**max\_samples**int or float, default=None
If bootstrap is True, the number of samples to draw from X to train each base estimator.
* If None (default), then draw `X.shape[0]` samples.
* If int, then draw `max_samples` samples.
* If float, then draw `max_samples * X.shape[0]` samples. Thus, `max_samples` should be in the interval `(0.0, 1.0]`.
New in version 0.22.
Attributes:
**base\_estimator\_**ExtraTreesClassifier
The child estimator template used to create the collection of fitted sub-estimators.
**estimators\_**list of DecisionTreeClassifier
The collection of fitted sub-estimators.
**classes\_**ndarray of shape (n\_classes,) or a list of such arrays
The classes labels (single output problem), or a list of arrays of class labels (multi-output problem).
**n\_classes\_**int or list
The number of classes (single output problem), or a list containing the number of classes for each output (multi-output problem).
[`feature_importances_`](#sklearn.ensemble.ExtraTreesClassifier.feature_importances_ "sklearn.ensemble.ExtraTreesClassifier.feature_importances_")ndarray of shape (n\_features,)
The impurity-based feature importances.
[`n_features_`](#sklearn.ensemble.ExtraTreesClassifier.n_features_ "sklearn.ensemble.ExtraTreesClassifier.n_features_")int
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_outputs\_**int
The number of outputs when `fit` is performed.
**oob\_score\_**float
Score of the training dataset obtained using an out-of-bag estimate. This attribute exists only when `oob_score` is True.
**oob\_decision\_function\_**ndarray of shape (n\_samples, n\_classes) or (n\_samples, n\_classes, n\_outputs)
Decision function computed with out-of-bag estimate on the training set. If n\_estimators is small it might be possible that a data point was never left out during the bootstrap. In this case, `oob_decision_function_` might contain NaN. This attribute exists only when `oob_score` is True.
See also
[`ExtraTreesRegressor`](sklearn.ensemble.extratreesregressor#sklearn.ensemble.ExtraTreesRegressor "sklearn.ensemble.ExtraTreesRegressor")
An extra-trees regressor with random splits.
[`RandomForestClassifier`](sklearn.ensemble.randomforestclassifier#sklearn.ensemble.RandomForestClassifier "sklearn.ensemble.RandomForestClassifier")
A random forest classifier with optimal splits.
[`RandomForestRegressor`](sklearn.ensemble.randomforestregressor#sklearn.ensemble.RandomForestRegressor "sklearn.ensemble.RandomForestRegressor")
Ensemble regressor using trees with optimal splits.
#### Notes
The default values for the parameters controlling the size of the trees (e.g. `max_depth`, `min_samples_leaf`, etc.) lead to fully grown and unpruned trees which can potentially be very large on some data sets. To reduce memory consumption, the complexity and size of the trees should be controlled by setting those parameter values.
#### References
[1] P. Geurts, D. Ernst., and L. Wehenkel, “Extremely randomized trees”, Machine Learning, 63(1), 3-42, 2006.
#### Examples
```
>>> from sklearn.ensemble import ExtraTreesClassifier
>>> from sklearn.datasets import make_classification
>>> X, y = make_classification(n_features=4, random_state=0)
>>> clf = ExtraTreesClassifier(n_estimators=100, random_state=0)
>>> clf.fit(X, y)
ExtraTreesClassifier(random_state=0)
>>> clf.predict([[0, 0, 0, 0]])
array([1])
```
#### Methods
| | |
| --- | --- |
| [`apply`](#sklearn.ensemble.ExtraTreesClassifier.apply "sklearn.ensemble.ExtraTreesClassifier.apply")(X) | Apply trees in the forest to X, return leaf indices. |
| [`decision_path`](#sklearn.ensemble.ExtraTreesClassifier.decision_path "sklearn.ensemble.ExtraTreesClassifier.decision_path")(X) | Return the decision path in the forest. |
| [`fit`](#sklearn.ensemble.ExtraTreesClassifier.fit "sklearn.ensemble.ExtraTreesClassifier.fit")(X, y[, sample\_weight]) | Build a forest of trees from the training set (X, y). |
| [`get_params`](#sklearn.ensemble.ExtraTreesClassifier.get_params "sklearn.ensemble.ExtraTreesClassifier.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.ensemble.ExtraTreesClassifier.predict "sklearn.ensemble.ExtraTreesClassifier.predict")(X) | Predict class for X. |
| [`predict_log_proba`](#sklearn.ensemble.ExtraTreesClassifier.predict_log_proba "sklearn.ensemble.ExtraTreesClassifier.predict_log_proba")(X) | Predict class log-probabilities for X. |
| [`predict_proba`](#sklearn.ensemble.ExtraTreesClassifier.predict_proba "sklearn.ensemble.ExtraTreesClassifier.predict_proba")(X) | Predict class probabilities for X. |
| [`score`](#sklearn.ensemble.ExtraTreesClassifier.score "sklearn.ensemble.ExtraTreesClassifier.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.ensemble.ExtraTreesClassifier.set_params "sklearn.ensemble.ExtraTreesClassifier.set_params")(\*\*params) | Set the parameters of this estimator. |
apply(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L235)
Apply trees in the forest to X, return leaf indices.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, its dtype will be converted to `dtype=np.float32`. If a sparse matrix is provided, it will be converted into a sparse `csr_matrix`.
Returns:
**X\_leaves**ndarray of shape (n\_samples, n\_estimators)
For each datapoint x in X and for each tree in the forest, return the index of the leaf x ends up in.
decision\_path(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L261)
Return the decision path in the forest.
New in version 0.18.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, its dtype will be converted to `dtype=np.float32`. If a sparse matrix is provided, it will be converted into a sparse `csr_matrix`.
Returns:
**indicator**sparse matrix of shape (n\_samples, n\_nodes)
Return a node indicator matrix where non zero elements indicates that the samples goes through the nodes. The matrix is of CSR format.
**n\_nodes\_ptr**ndarray of shape (n\_estimators + 1,)
The columns from indicator[n\_nodes\_ptr[i]:n\_nodes\_ptr[i+1]] gives the indicator value for the i-th estimator.
*property*feature\_importances\_
The impurity-based feature importances.
The higher, the more important the feature. The importance of a feature is computed as the (normalized) total reduction of the criterion brought by that feature. It is also known as the Gini importance.
Warning: impurity-based feature importances can be misleading for high cardinality features (many unique values). See [`sklearn.inspection.permutation_importance`](sklearn.inspection.permutation_importance#sklearn.inspection.permutation_importance "sklearn.inspection.permutation_importance") as an alternative.
Returns:
**feature\_importances\_**ndarray of shape (n\_features,)
The values of this array sum to 1, unless all trees are single node trees consisting of only the root node, in which case it will be an array of zeros.
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L301)
Build a forest of trees from the training set (X, y).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Internally, its dtype will be converted to `dtype=np.float32`. If a sparse matrix is provided, it will be converted into a sparse `csc_matrix`.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
The target values (class labels in classification, real numbers in regression).
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, then samples are equally weighted. Splits that would create child nodes with net zero or negative weight are ignored while searching for a split in each node. In the case of classification, splits are also ignored if they would result in any single class carrying a negative weight in either child node.
Returns:
**self**object
Fitted estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_features\_
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2. Use `n_features_in_` instead.
Number of features when fitting the estimator.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L811)
Predict class for X.
The predicted class of an input sample is a vote by the trees in the forest, weighted by their probability estimates. That is, the predicted class is the one with highest mean probability estimate across the trees.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, its dtype will be converted to `dtype=np.float32`. If a sparse matrix is provided, it will be converted into a sparse `csr_matrix`.
Returns:
**y**ndarray of shape (n\_samples,) or (n\_samples, n\_outputs)
The predicted classes.
predict\_log\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L898)
Predict class log-probabilities for X.
The predicted class log-probabilities of an input sample is computed as the log of the mean predicted class probabilities of the trees in the forest.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, its dtype will be converted to `dtype=np.float32`. If a sparse matrix is provided, it will be converted into a sparse `csr_matrix`.
Returns:
**p**ndarray of shape (n\_samples, n\_classes), or a list of such arrays
The class probabilities of the input samples. The order of the classes corresponds to that in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L850)
Predict class probabilities for X.
The predicted class probabilities of an input sample are computed as the mean predicted class probabilities of the trees in the forest. The class probability of a single tree is the fraction of samples of the same class in a leaf.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, its dtype will be converted to `dtype=np.float32`. If a sparse matrix is provided, it will be converted into a sparse `csr_matrix`.
Returns:
**p**ndarray of shape (n\_samples, n\_classes), or a list of such arrays
The class probabilities of the input samples. The order of the classes corresponds to that in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.ensemble.ExtraTreesClassifier`
------------------------------------------------------
[Hashing feature transformation using Totally Random Trees](../../auto_examples/ensemble/plot_random_forest_embedding#sphx-glr-auto-examples-ensemble-plot-random-forest-embedding-py)
[Plot the decision surfaces of ensembles of trees on the iris dataset](../../auto_examples/ensemble/plot_forest_iris#sphx-glr-auto-examples-ensemble-plot-forest-iris-py)
| programming_docs |
scikit_learn sklearn.feature_selection.chi2 sklearn.feature\_selection.chi2
===============================
sklearn.feature\_selection.chi2(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_univariate_selection.py#L168)
Compute chi-squared stats between each non-negative feature and class.
This score can be used to select the n\_features features with the highest values for the test chi-squared statistic from X, which must contain only non-negative features such as booleans or frequencies (e.g., term counts in document classification), relative to the classes.
Recall that the chi-square test measures dependence between stochastic variables, so using this function “weeds out” the features that are the most likely to be independent of class and therefore irrelevant for classification.
Read more in the [User Guide](../feature_selection#univariate-feature-selection).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Sample vectors.
**y**array-like of shape (n\_samples,)
Target vector (class labels).
Returns:
**chi2**ndarray of shape (n\_features,)
Chi2 statistics for each feature.
**p\_values**ndarray of shape (n\_features,)
P-values for each feature.
See also
[`f_classif`](sklearn.feature_selection.f_classif#sklearn.feature_selection.f_classif "sklearn.feature_selection.f_classif")
ANOVA F-value between label/feature for classification tasks.
[`f_regression`](sklearn.feature_selection.f_regression#sklearn.feature_selection.f_regression "sklearn.feature_selection.f_regression")
F-value between label/feature for regression tasks.
#### Notes
Complexity of this algorithm is O(n\_classes \* n\_features).
Examples using `sklearn.feature_selection.chi2`
-----------------------------------------------
[Selecting dimensionality reduction with Pipeline and GridSearchCV](../../auto_examples/compose/plot_compare_reduction#sphx-glr-auto-examples-compose-plot-compare-reduction-py)
[SVM-Anova: SVM with univariate feature selection](../../auto_examples/svm/plot_svm_anova#sphx-glr-auto-examples-svm-plot-svm-anova-py)
scikit_learn sklearn.feature_selection.GenericUnivariateSelect sklearn.feature\_selection.GenericUnivariateSelect
==================================================
*class*sklearn.feature\_selection.GenericUnivariateSelect(*score\_func=<function f\_classif>*, *\**, *mode='percentile'*, *param=1e-05*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_univariate_selection.py#L927)
Univariate feature selector with configurable strategy.
Read more in the [User Guide](../feature_selection#univariate-feature-selection).
Parameters:
**score\_func**callable, default=f\_classif
Function taking two arrays X and y, and returning a pair of arrays (scores, pvalues). For modes ‘percentile’ or ‘kbest’ it can return a single array scores.
**mode**{‘percentile’, ‘k\_best’, ‘fpr’, ‘fdr’, ‘fwe’}, default=’percentile’
Feature selection mode.
**param**float or int depending on the feature selection mode, default=1e-5
Parameter of the corresponding mode.
Attributes:
**scores\_**array-like of shape (n\_features,)
Scores of features.
**pvalues\_**array-like of shape (n\_features,)
p-values of feature scores, None if `score_func` returned scores only.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`f_classif`](sklearn.feature_selection.f_classif#sklearn.feature_selection.f_classif "sklearn.feature_selection.f_classif")
ANOVA F-value between label/feature for classification tasks.
[`mutual_info_classif`](sklearn.feature_selection.mutual_info_classif#sklearn.feature_selection.mutual_info_classif "sklearn.feature_selection.mutual_info_classif")
Mutual information for a discrete target.
[`chi2`](sklearn.feature_selection.chi2#sklearn.feature_selection.chi2 "sklearn.feature_selection.chi2")
Chi-squared stats of non-negative features for classification tasks.
[`f_regression`](sklearn.feature_selection.f_regression#sklearn.feature_selection.f_regression "sklearn.feature_selection.f_regression")
F-value between label/feature for regression tasks.
[`mutual_info_regression`](sklearn.feature_selection.mutual_info_regression#sklearn.feature_selection.mutual_info_regression "sklearn.feature_selection.mutual_info_regression")
Mutual information for a continuous target.
[`SelectPercentile`](sklearn.feature_selection.selectpercentile#sklearn.feature_selection.SelectPercentile "sklearn.feature_selection.SelectPercentile")
Select features based on percentile of the highest scores.
[`SelectKBest`](sklearn.feature_selection.selectkbest#sklearn.feature_selection.SelectKBest "sklearn.feature_selection.SelectKBest")
Select features based on the k highest scores.
[`SelectFpr`](sklearn.feature_selection.selectfpr#sklearn.feature_selection.SelectFpr "sklearn.feature_selection.SelectFpr")
Select features based on a false positive rate test.
[`SelectFdr`](sklearn.feature_selection.selectfdr#sklearn.feature_selection.SelectFdr "sklearn.feature_selection.SelectFdr")
Select features based on an estimated false discovery rate.
[`SelectFwe`](sklearn.feature_selection.selectfwe#sklearn.feature_selection.SelectFwe "sklearn.feature_selection.SelectFwe")
Select features based on family-wise error rate.
#### Examples
```
>>> from sklearn.datasets import load_breast_cancer
>>> from sklearn.feature_selection import GenericUnivariateSelect, chi2
>>> X, y = load_breast_cancer(return_X_y=True)
>>> X.shape
(569, 30)
>>> transformer = GenericUnivariateSelect(chi2, mode='k_best', param=20)
>>> X_new = transformer.fit_transform(X, y)
>>> X_new.shape
(569, 20)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.feature_selection.GenericUnivariateSelect.fit "sklearn.feature_selection.GenericUnivariateSelect.fit")(X, y) | Run score function on (X, y) and get the appropriate features. |
| [`fit_transform`](#sklearn.feature_selection.GenericUnivariateSelect.fit_transform "sklearn.feature_selection.GenericUnivariateSelect.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.feature_selection.GenericUnivariateSelect.get_feature_names_out "sklearn.feature_selection.GenericUnivariateSelect.get_feature_names_out")([input\_features]) | Mask feature names according to selected features. |
| [`get_params`](#sklearn.feature_selection.GenericUnivariateSelect.get_params "sklearn.feature_selection.GenericUnivariateSelect.get_params")([deep]) | Get parameters for this estimator. |
| [`get_support`](#sklearn.feature_selection.GenericUnivariateSelect.get_support "sklearn.feature_selection.GenericUnivariateSelect.get_support")([indices]) | Get a mask, or integer index, of the features selected. |
| [`inverse_transform`](#sklearn.feature_selection.GenericUnivariateSelect.inverse_transform "sklearn.feature_selection.GenericUnivariateSelect.inverse_transform")(X) | Reverse the transformation operation. |
| [`set_params`](#sklearn.feature_selection.GenericUnivariateSelect.set_params "sklearn.feature_selection.GenericUnivariateSelect.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.feature_selection.GenericUnivariateSelect.transform "sklearn.feature_selection.GenericUnivariateSelect.transform")(X) | Reduce X to the selected features. |
fit(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_univariate_selection.py#L444)
Run score function on (X, y) and get the appropriate features.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The training input samples.
**y**array-like of shape (n\_samples,)
The target values (class labels in classification, real numbers in regression).
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L146)
Mask feature names according to selected features.
Parameters:
**input\_features**array-like of str or None, default=None
Input features.
* If `input_features` is `None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then the following input feature names are generated: `["x0", "x1", ..., "x(n_features_in_ - 1)"]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
get\_support(*indices=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L33)
Get a mask, or integer index, of the features selected.
Parameters:
**indices**bool, default=False
If True, the return value will be an array of integers, rather than a boolean mask.
Returns:
**support**array
An index that selects the retained features from a feature vector. If `indices` is False, this is a boolean array of shape [# input features], in which an element is True iff its corresponding feature is selected for retention. If `indices` is True, this is an integer array of shape [# output features] whose values are indices into the input feature vector.
inverse\_transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L106)
Reverse the transformation operation.
Parameters:
**X**array of shape [n\_samples, n\_selected\_features]
The input samples.
Returns:
**X\_r**array of shape [n\_samples, n\_original\_features]
`X` with columns of zeros inserted where features would have been removed by [`transform`](#sklearn.feature_selection.GenericUnivariateSelect.transform "sklearn.feature_selection.GenericUnivariateSelect.transform").
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L68)
Reduce X to the selected features.
Parameters:
**X**array of shape [n\_samples, n\_features]
The input samples.
Returns:
**X\_r**array of shape [n\_samples, n\_selected\_features]
The input samples with only the selected features.
scikit_learn sklearn.manifold.smacof sklearn.manifold.smacof
=======================
sklearn.manifold.smacof(*dissimilarities*, *\**, *metric=True*, *n\_components=2*, *init=None*, *n\_init=8*, *n\_jobs=None*, *max\_iter=300*, *verbose=0*, *eps=0.001*, *random\_state=None*, *return\_n\_iter=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_mds.py#L144)
Compute multidimensional scaling using the SMACOF algorithm.
The SMACOF (Scaling by MAjorizing a COmplicated Function) algorithm is a multidimensional scaling algorithm which minimizes an objective function (the *stress*) using a majorization technique. Stress majorization, also known as the Guttman Transform, guarantees a monotone convergence of stress, and is more powerful than traditional techniques such as gradient descent.
The SMACOF algorithm for metric MDS can be summarized by the following steps:
1. Set an initial start configuration, randomly or not.
2. Compute the stress
3. Compute the Guttman Transform
4. Iterate 2 and 3 until convergence.
The nonmetric algorithm adds a monotonic regression step before computing the stress.
Parameters:
**dissimilarities**ndarray of shape (n\_samples, n\_samples)
Pairwise dissimilarities between the points. Must be symmetric.
**metric**bool, default=True
Compute metric or nonmetric SMACOF algorithm. When `False` (i.e. non-metric MDS), dissimilarities with 0 are considered as missing values.
**n\_components**int, default=2
Number of dimensions in which to immerse the dissimilarities. If an `init` array is provided, this option is overridden and the shape of `init` is used to determine the dimensionality of the embedding space.
**init**ndarray of shape (n\_samples, n\_components), default=None
Starting configuration of the embedding to initialize the algorithm. By default, the algorithm is initialized with a randomly chosen array.
**n\_init**int, default=8
Number of times the SMACOF algorithm will be run with different initializations. The final results will be the best output of the runs, determined by the run with the smallest final stress. If `init` is provided, this option is overridden and a single run is performed.
**n\_jobs**int, default=None
The number of jobs to use for the computation. If multiple initializations are used (`n_init`), each run of the algorithm is computed in parallel.
`None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**max\_iter**int, default=300
Maximum number of iterations of the SMACOF algorithm for a single run.
**verbose**int, default=0
Level of verbosity.
**eps**float, default=1e-3
Relative tolerance with respect to stress at which to declare convergence.
**random\_state**int, RandomState instance or None, default=None
Determines the random number generator used to initialize the centers. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**return\_n\_iter**bool, default=False
Whether or not to return the number of iterations.
Returns:
**X**ndarray of shape (n\_samples, n\_components)
Coordinates of the points in a `n_components`-space.
**stress**float
The final value of the stress (sum of squared distance of the disparities and the distances for all constrained points).
**n\_iter**int
The number of iterations corresponding to the best stress. Returned only if `return_n_iter` is set to `True`.
#### Notes
“Modern Multidimensional Scaling - Theory and Applications” Borg, I.; Groenen P. Springer Series in Statistics (1997)
“Nonmetric multidimensional scaling: a numerical method” Kruskal, J. Psychometrika, 29 (1964)
“Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis” Kruskal, J. Psychometrika, 29, (1964)
scikit_learn sklearn.metrics.d2_pinball_score sklearn.metrics.d2\_pinball\_score
==================================
sklearn.metrics.d2\_pinball\_score(*y\_true*, *y\_pred*, *\**, *sample\_weight=None*, *alpha=0.5*, *multioutput='uniform\_average'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_regression.py#L1266)
\(D^2\) regression score function, fraction of pinball loss explained.
Best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A model that always uses the empirical alpha-quantile of `y_true` as constant prediction, disregarding the input features, gets a \(D^2\) score of 0.0.
Read more in the [User Guide](../model_evaluation#d2-score).
New in version 1.1.
Parameters:
**y\_true**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
Ground truth (correct) target values.
**y\_pred**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
Estimated target values.
**sample\_weight**array-like of shape (n\_samples,), optional
Sample weights.
**alpha**float, default=0.5
Slope of the pinball deviance. It determines the quantile level alpha for which the pinball deviance and also D2 are optimal. The default `alpha=0.5` is equivalent to `d2_absolute_error_score`.
**multioutput**{‘raw\_values’, ‘uniform\_average’} or array-like of shape (n\_outputs,), default=’uniform\_average’
Defines aggregating of multiple output values. Array-like value defines weights used to average scores.
‘raw\_values’ :
Returns a full set of errors in case of multioutput input.
‘uniform\_average’ :
Scores of all outputs are averaged with uniform weight.
Returns:
**score**float or ndarray of floats
The \(D^2\) score with a pinball deviance or ndarray of scores if `multioutput='raw_values'`.
#### Notes
Like \(R^2\), \(D^2\) score may be negative (it need not actually be the square of a quantity D).
This metric is not well-defined for a single point and will return a NaN value if n\_samples is less than two.
#### References
[1] Eq. (7) of [Koenker, Roger; Machado, José A. F. (1999). “Goodness of Fit and Related Inference Processes for Quantile Regression”](http://dx.doi.org/10.1080/01621459.1999.10473882)
[2] Eq. (3.11) of Hastie, Trevor J., Robert Tibshirani and Martin J. Wainwright. “Statistical Learning with Sparsity: The Lasso and Generalizations.” (2015). <https://hastie.su.domains/StatLearnSparsity/>
#### Examples
```
>>> from sklearn.metrics import d2_pinball_score
>>> y_true = [1, 2, 3]
>>> y_pred = [1, 3, 3]
>>> d2_pinball_score(y_true, y_pred)
0.5
>>> d2_pinball_score(y_true, y_pred, alpha=0.9)
0.772...
>>> d2_pinball_score(y_true, y_pred, alpha=0.1)
-1.045...
>>> d2_pinball_score(y_true, y_true, alpha=0.1)
1.0
```
scikit_learn sklearn.tree.ExtraTreeClassifier sklearn.tree.ExtraTreeClassifier
================================
*class*sklearn.tree.ExtraTreeClassifier(*\**, *criterion='gini'*, *splitter='random'*, *max\_depth=None*, *min\_samples\_split=2*, *min\_samples\_leaf=1*, *min\_weight\_fraction\_leaf=0.0*, *max\_features='sqrt'*, *random\_state=None*, *max\_leaf\_nodes=None*, *min\_impurity\_decrease=0.0*, *class\_weight=None*, *ccp\_alpha=0.0*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L1386)
An extremely randomized tree classifier.
Extra-trees differ from classic decision trees in the way they are built. When looking for the best split to separate the samples of a node into two groups, random splits are drawn for each of the `max_features` randomly selected features and the best split among those is chosen. When `max_features` is set 1, this amounts to building a totally random decision tree.
Warning: Extra-trees should only be used within ensemble methods.
Read more in the [User Guide](../tree#tree).
Parameters:
**criterion**{“gini”, “entropy”, “log\_loss”}, default=”gini”
The function to measure the quality of a split. Supported criteria are “gini” for the Gini impurity and “log\_loss” and “entropy” both for the Shannon information gain, see [Mathematical formulation](../tree#tree-mathematical-formulation).
**splitter**{“random”, “best”}, default=”random”
The strategy used to choose the split at each node. Supported strategies are “best” to choose the best split and “random” to choose the best random split.
**max\_depth**int, default=None
The maximum depth of the tree. If None, then nodes are expanded until all leaves are pure or until all leaves contain less than min\_samples\_split samples.
**min\_samples\_split**int or float, default=2
The minimum number of samples required to split an internal node:
* If int, then consider `min_samples_split` as the minimum number.
* If float, then `min_samples_split` is a fraction and `ceil(min_samples_split * n_samples)` are the minimum number of samples for each split.
Changed in version 0.18: Added float values for fractions.
**min\_samples\_leaf**int or float, default=1
The minimum number of samples required to be at a leaf node. A split point at any depth will only be considered if it leaves at least `min_samples_leaf` training samples in each of the left and right branches. This may have the effect of smoothing the model, especially in regression.
* If int, then consider `min_samples_leaf` as the minimum number.
* If float, then `min_samples_leaf` is a fraction and `ceil(min_samples_leaf * n_samples)` are the minimum number of samples for each node.
Changed in version 0.18: Added float values for fractions.
**min\_weight\_fraction\_leaf**float, default=0.0
The minimum weighted fraction of the sum total of weights (of all the input samples) required to be at a leaf node. Samples have equal weight when sample\_weight is not provided.
**max\_features**int, float, {“auto”, “sqrt”, “log2”} or None, default=”sqrt”
The number of features to consider when looking for the best split:
* If int, then consider `max_features` features at each split.
* If float, then `max_features` is a fraction and `max(1, int(max_features * n_features_in_))` features are considered at each split.
* If “auto”, then `max_features=sqrt(n_features)`.
* If “sqrt”, then `max_features=sqrt(n_features)`.
* If “log2”, then `max_features=log2(n_features)`.
* If None, then `max_features=n_features`.
Changed in version 1.1: The default of `max_features` changed from `"auto"` to `"sqrt"`.
Deprecated since version 1.1: The `"auto"` option was deprecated in 1.1 and will be removed in 1.3.
Note: the search for a split does not stop until at least one valid partition of the node samples is found, even if it requires to effectively inspect more than `max_features` features.
**random\_state**int, RandomState instance or None, default=None
Used to pick randomly the `max_features` used at each split. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state) for details.
**max\_leaf\_nodes**int, default=None
Grow a tree with `max_leaf_nodes` in best-first fashion. Best nodes are defined as relative reduction in impurity. If None then unlimited number of leaf nodes.
**min\_impurity\_decrease**float, default=0.0
A node will be split if this split induces a decrease of the impurity greater than or equal to this value.
The weighted impurity decrease equation is the following:
```
N_t / N * (impurity - N_t_R / N_t * right_impurity
- N_t_L / N_t * left_impurity)
```
where `N` is the total number of samples, `N_t` is the number of samples at the current node, `N_t_L` is the number of samples in the left child, and `N_t_R` is the number of samples in the right child.
`N`, `N_t`, `N_t_R` and `N_t_L` all refer to the weighted sum, if `sample_weight` is passed.
New in version 0.19.
**class\_weight**dict, list of dict or “balanced”, default=None
Weights associated with classes in the form `{class_label: weight}`. If None, all classes are supposed to have weight one. For multi-output problems, a list of dicts can be provided in the same order as the columns of y.
Note that for multioutput (including multilabel) weights should be defined for each class of every column in its own dict. For example, for four-class multilabel classification weights should be [{0: 1, 1: 1}, {0: 1, 1: 5}, {0: 1, 1: 1}, {0: 1, 1: 1}] instead of [{1:1}, {2:5}, {3:1}, {4:1}].
The “balanced” mode uses the values of y to automatically adjust weights inversely proportional to class frequencies in the input data as `n_samples / (n_classes * np.bincount(y))`
For multi-output, the weights of each column of y will be multiplied.
Note that these weights will be multiplied with sample\_weight (passed through the fit method) if sample\_weight is specified.
**ccp\_alpha**non-negative float, default=0.0
Complexity parameter used for Minimal Cost-Complexity Pruning. The subtree with the largest cost complexity that is smaller than `ccp_alpha` will be chosen. By default, no pruning is performed. See [Minimal Cost-Complexity Pruning](../tree#minimal-cost-complexity-pruning) for details.
New in version 0.22.
Attributes:
**classes\_**ndarray of shape (n\_classes,) or list of ndarray
The classes labels (single output problem), or a list of arrays of class labels (multi-output problem).
**max\_features\_**int
The inferred value of max\_features.
**n\_classes\_**int or list of int
The number of classes (for single output problems), or a list containing the number of classes for each output (for multi-output problems).
[`feature_importances_`](#sklearn.tree.ExtraTreeClassifier.feature_importances_ "sklearn.tree.ExtraTreeClassifier.feature_importances_")ndarray of shape (n\_features,)
Return the feature importances.
[`n_features_`](#sklearn.tree.ExtraTreeClassifier.n_features_ "sklearn.tree.ExtraTreeClassifier.n_features_")int
DEPRECATED: The attribute `n_features_` is deprecated in 1.0 and will be removed in 1.2.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_outputs\_**int
The number of outputs when `fit` is performed.
**tree\_**Tree instance
The underlying Tree object. Please refer to `help(sklearn.tree._tree.Tree)` for attributes of Tree object and [Understanding the decision tree structure](../../auto_examples/tree/plot_unveil_tree_structure#sphx-glr-auto-examples-tree-plot-unveil-tree-structure-py) for basic usage of these attributes.
See also
[`ExtraTreeRegressor`](sklearn.tree.extratreeregressor#sklearn.tree.ExtraTreeRegressor "sklearn.tree.ExtraTreeRegressor")
An extremely randomized tree regressor.
[`sklearn.ensemble.ExtraTreesClassifier`](sklearn.ensemble.extratreesclassifier#sklearn.ensemble.ExtraTreesClassifier "sklearn.ensemble.ExtraTreesClassifier")
An extra-trees classifier.
[`sklearn.ensemble.ExtraTreesRegressor`](sklearn.ensemble.extratreesregressor#sklearn.ensemble.ExtraTreesRegressor "sklearn.ensemble.ExtraTreesRegressor")
An extra-trees regressor.
[`sklearn.ensemble.RandomForestClassifier`](sklearn.ensemble.randomforestclassifier#sklearn.ensemble.RandomForestClassifier "sklearn.ensemble.RandomForestClassifier")
A random forest classifier.
[`sklearn.ensemble.RandomForestRegressor`](sklearn.ensemble.randomforestregressor#sklearn.ensemble.RandomForestRegressor "sklearn.ensemble.RandomForestRegressor")
A random forest regressor.
[`sklearn.ensemble.RandomTreesEmbedding`](sklearn.ensemble.randomtreesembedding#sklearn.ensemble.RandomTreesEmbedding "sklearn.ensemble.RandomTreesEmbedding")
An ensemble of totally random trees.
#### Notes
The default values for the parameters controlling the size of the trees (e.g. `max_depth`, `min_samples_leaf`, etc.) lead to fully grown and unpruned trees which can potentially be very large on some data sets. To reduce memory consumption, the complexity and size of the trees should be controlled by setting those parameter values.
#### References
[1] P. Geurts, D. Ernst., and L. Wehenkel, “Extremely randomized trees”, Machine Learning, 63(1), 3-42, 2006.
#### Examples
```
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.ensemble import BaggingClassifier
>>> from sklearn.tree import ExtraTreeClassifier
>>> X, y = load_iris(return_X_y=True)
>>> X_train, X_test, y_train, y_test = train_test_split(
... X, y, random_state=0)
>>> extra_tree = ExtraTreeClassifier(random_state=0)
>>> cls = BaggingClassifier(extra_tree, random_state=0).fit(
... X_train, y_train)
>>> cls.score(X_test, y_test)
0.8947...
```
#### Methods
| | |
| --- | --- |
| [`apply`](#sklearn.tree.ExtraTreeClassifier.apply "sklearn.tree.ExtraTreeClassifier.apply")(X[, check\_input]) | Return the index of the leaf that each sample is predicted as. |
| [`cost_complexity_pruning_path`](#sklearn.tree.ExtraTreeClassifier.cost_complexity_pruning_path "sklearn.tree.ExtraTreeClassifier.cost_complexity_pruning_path")(X, y[, ...]) | Compute the pruning path during Minimal Cost-Complexity Pruning. |
| [`decision_path`](#sklearn.tree.ExtraTreeClassifier.decision_path "sklearn.tree.ExtraTreeClassifier.decision_path")(X[, check\_input]) | Return the decision path in the tree. |
| [`fit`](#sklearn.tree.ExtraTreeClassifier.fit "sklearn.tree.ExtraTreeClassifier.fit")(X, y[, sample\_weight, check\_input]) | Build a decision tree classifier from the training set (X, y). |
| [`get_depth`](#sklearn.tree.ExtraTreeClassifier.get_depth "sklearn.tree.ExtraTreeClassifier.get_depth")() | Return the depth of the decision tree. |
| [`get_n_leaves`](#sklearn.tree.ExtraTreeClassifier.get_n_leaves "sklearn.tree.ExtraTreeClassifier.get_n_leaves")() | Return the number of leaves of the decision tree. |
| [`get_params`](#sklearn.tree.ExtraTreeClassifier.get_params "sklearn.tree.ExtraTreeClassifier.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.tree.ExtraTreeClassifier.predict "sklearn.tree.ExtraTreeClassifier.predict")(X[, check\_input]) | Predict class or regression value for X. |
| [`predict_log_proba`](#sklearn.tree.ExtraTreeClassifier.predict_log_proba "sklearn.tree.ExtraTreeClassifier.predict_log_proba")(X) | Predict class log-probabilities of the input samples X. |
| [`predict_proba`](#sklearn.tree.ExtraTreeClassifier.predict_proba "sklearn.tree.ExtraTreeClassifier.predict_proba")(X[, check\_input]) | Predict class probabilities of the input samples X. |
| [`score`](#sklearn.tree.ExtraTreeClassifier.score "sklearn.tree.ExtraTreeClassifier.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.tree.ExtraTreeClassifier.set_params "sklearn.tree.ExtraTreeClassifier.set_params")(\*\*params) | Set the parameters of this estimator. |
apply(*X*, *check\_input=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L532)
Return the index of the leaf that each sample is predicted as.
New in version 0.17.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
**check\_input**bool, default=True
Allow to bypass several input checking. Don’t use this parameter unless you know what you do.
Returns:
**X\_leaves**array-like of shape (n\_samples,)
For each datapoint x in X, return the index of the leaf x ends up in. Leaves are numbered within `[0; self.tree_.node_count)`, possibly with gaps in the numbering.
cost\_complexity\_pruning\_path(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L607)
Compute the pruning path during Minimal Cost-Complexity Pruning.
See [Minimal Cost-Complexity Pruning](../tree#minimal-cost-complexity-pruning) for details on the pruning process.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csc_matrix`.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
The target values (class labels) as integers or strings.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, then samples are equally weighted. Splits that would create child nodes with net zero or negative weight are ignored while searching for a split in each node. Splits are also ignored if they would result in any single class carrying a negative weight in either child node.
Returns:
**ccp\_path**[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
Dictionary-like object, with the following attributes.
ccp\_alphasndarray
Effective alphas of subtree during pruning.
impuritiesndarray
Sum of the impurities of the subtree leaves for the corresponding alpha value in `ccp_alphas`.
decision\_path(*X*, *check\_input=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L560)
Return the decision path in the tree.
New in version 0.18.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
**check\_input**bool, default=True
Allow to bypass several input checking. Don’t use this parameter unless you know what you do.
Returns:
**indicator**sparse matrix of shape (n\_samples, n\_nodes)
Return a node indicator CSR matrix where non zero elements indicates that the samples goes through the nodes.
*property*feature\_importances\_
Return the feature importances.
The importance of a feature is computed as the (normalized) total reduction of the criterion brought by that feature. It is also known as the Gini importance.
Warning: impurity-based feature importances can be misleading for high cardinality features (many unique values). See [`sklearn.inspection.permutation_importance`](sklearn.inspection.permutation_importance#sklearn.inspection.permutation_importance "sklearn.inspection.permutation_importance") as an alternative.
Returns:
**feature\_importances\_**ndarray of shape (n\_features,)
Normalized total reduction of criteria by feature (Gini importance).
fit(*X*, *y*, *sample\_weight=None*, *check\_input=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L939)
Build a decision tree classifier from the training set (X, y).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csc_matrix`.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
The target values (class labels) as integers or strings.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, then samples are equally weighted. Splits that would create child nodes with net zero or negative weight are ignored while searching for a split in each node. Splits are also ignored if they would result in any single class carrying a negative weight in either child node.
**check\_input**bool, default=True
Allow to bypass several input checking. Don’t use this parameter unless you know what you do.
Returns:
**self**DecisionTreeClassifier
Fitted estimator.
get\_depth()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L130)
Return the depth of the decision tree.
The depth of a tree is the maximum distance between the root and any leaf.
Returns:
**self.tree\_.max\_depth**int
The maximum depth of the tree.
get\_n\_leaves()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L144)
Return the number of leaves of the decision tree.
Returns:
**self.tree\_.n\_leaves**int
Number of leaves.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_features\_
DEPRECATED: The attribute `n_features_` is deprecated in 1.0 and will be removed in 1.2. Use `n_features_in_` instead.
predict(*X*, *check\_input=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L481)
Predict class or regression value for X.
For a classification model, the predicted class for each sample in X is returned. For a regression model, the predicted value based on X is returned.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
**check\_input**bool, default=True
Allow to bypass several input checking. Don’t use this parameter unless you know what you do.
Returns:
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
The predicted classes, or the predict values.
predict\_log\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L1025)
Predict class log-probabilities of the input samples X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
Returns:
**proba**ndarray of shape (n\_samples, n\_classes) or list of n\_outputs such arrays if n\_outputs > 1
The class log-probabilities of the input samples. The order of the classes corresponds to that in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
predict\_proba(*X*, *check\_input=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L977)
Predict class probabilities of the input samples X.
The predicted class probability is the fraction of samples of the same class in a leaf.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
**check\_input**bool, default=True
Allow to bypass several input checking. Don’t use this parameter unless you know what you do.
Returns:
**proba**ndarray of shape (n\_samples, n\_classes) or list of n\_outputs such arrays if n\_outputs > 1
The class probabilities of the input samples. The order of the classes corresponds to that in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
| programming_docs |
scikit_learn sklearn.preprocessing.power_transform sklearn.preprocessing.power\_transform
======================================
sklearn.preprocessing.power\_transform(*X*, *method='yeo-johnson'*, *\**, *standardize=True*, *copy=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L3326)
Parametric, monotonic transformation to make data more Gaussian-like.
Power transforms are a family of parametric, monotonic transformations that are applied to make data more Gaussian-like. This is useful for modeling issues related to heteroscedasticity (non-constant variance), or other situations where normality is desired.
Currently, power\_transform supports the Box-Cox transform and the Yeo-Johnson transform. The optimal parameter for stabilizing variance and minimizing skewness is estimated through maximum likelihood.
Box-Cox requires input data to be strictly positive, while Yeo-Johnson supports both positive or negative data.
By default, zero-mean, unit-variance normalization is applied to the transformed data.
Read more in the [User Guide](../preprocessing#preprocessing-transformer).
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The data to be transformed using a power transformation.
**method**{‘yeo-johnson’, ‘box-cox’}, default=’yeo-johnson’
The power transform method. Available methods are:
* ‘yeo-johnson’ [[1]](#r742a88cfa144-1), works with positive and negative values
* ‘box-cox’ [[2]](#r742a88cfa144-2), only works with strictly positive values
Changed in version 0.23: The default value of the `method` parameter changed from ‘box-cox’ to ‘yeo-johnson’ in 0.23.
**standardize**bool, default=True
Set to True to apply zero-mean, unit-variance normalization to the transformed output.
**copy**bool, default=True
Set to False to perform inplace computation during transformation.
Returns:
**X\_trans**ndarray of shape (n\_samples, n\_features)
The transformed data.
See also
[`PowerTransformer`](sklearn.preprocessing.powertransformer#sklearn.preprocessing.PowerTransformer "sklearn.preprocessing.PowerTransformer")
Equivalent transformation with the Transformer API (e.g. as part of a preprocessing [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")).
[`quantile_transform`](sklearn.preprocessing.quantile_transform#sklearn.preprocessing.quantile_transform "sklearn.preprocessing.quantile_transform")
Maps data to a standard normal distribution with the parameter `output_distribution='normal'`.
#### Notes
NaNs are treated as missing values: disregarded in `fit`, and maintained in `transform`.
For a comparison of the different scalers, transformers, and normalizers, see [examples/preprocessing/plot\_all\_scaling.py](../../auto_examples/preprocessing/plot_all_scaling#sphx-glr-auto-examples-preprocessing-plot-all-scaling-py).
#### References
[[1](#id1)] I.K. Yeo and R.A. Johnson, “A new family of power transformations to improve normality or symmetry.” Biometrika, 87(4), pp.954-959, (2000).
[[2](#id2)] G.E.P. Box and D.R. Cox, “An Analysis of Transformations”, Journal of the Royal Statistical Society B, 26, 211-252 (1964).
#### Examples
```
>>> import numpy as np
>>> from sklearn.preprocessing import power_transform
>>> data = [[1, 2], [3, 2], [4, 5]]
>>> print(power_transform(data, method='box-cox'))
[[-1.332... -0.707...]
[ 0.256... -0.707...]
[ 1.076... 1.414...]]
```
Warning
Risk of data leak. Do not use [`power_transform`](#sklearn.preprocessing.power_transform "sklearn.preprocessing.power_transform") unless you know what you are doing. A common mistake is to apply it to the entire data *before* splitting into training and test sets. This will bias the model evaluation because information would have leaked from the test set to the training set. In general, we recommend using [`PowerTransformer`](sklearn.preprocessing.powertransformer#sklearn.preprocessing.PowerTransformer "sklearn.preprocessing.PowerTransformer") within a [Pipeline](../compose#pipeline) in order to prevent most risks of data leaking, e.g.: `pipe = make_pipeline(PowerTransformer(),
LogisticRegression())`.
scikit_learn sklearn.metrics.adjusted_mutual_info_score sklearn.metrics.adjusted\_mutual\_info\_score
=============================================
sklearn.metrics.adjusted\_mutual\_info\_score(*labels\_true*, *labels\_pred*, *\**, *average\_method='arithmetic'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/cluster/_supervised.py#L824)
Adjusted Mutual Information between two clusterings.
Adjusted Mutual Information (AMI) is an adjustment of the Mutual Information (MI) score to account for chance. It accounts for the fact that the MI is generally higher for two clusterings with a larger number of clusters, regardless of whether there is actually more information shared. For two clusterings \(U\) and \(V\), the AMI is given as:
```
AMI(U, V) = [MI(U, V) - E(MI(U, V))] / [avg(H(U), H(V)) - E(MI(U, V))]
```
This metric is independent of the absolute values of the labels: a permutation of the class or cluster label values won’t change the score value in any way.
This metric is furthermore symmetric: switching \(U\) (`label_true`) with \(V\) (`labels_pred`) will return the same score value. This can be useful to measure the agreement of two independent label assignments strategies on the same dataset when the real ground truth is not known.
Be mindful that this function is an order of magnitude slower than other metrics, such as the Adjusted Rand Index.
Read more in the [User Guide](../clustering#mutual-info-score).
Parameters:
**labels\_true**int array, shape = [n\_samples]
A clustering of the data into disjoint subsets, called \(U\) in the above formula.
**labels\_pred**int array-like of shape (n\_samples,)
A clustering of the data into disjoint subsets, called \(V\) in the above formula.
**average\_method**str, default=’arithmetic’
How to compute the normalizer in the denominator. Possible options are ‘min’, ‘geometric’, ‘arithmetic’, and ‘max’.
New in version 0.20.
Changed in version 0.22: The default value of `average_method` changed from ‘max’ to ‘arithmetic’.
Returns:
ami: float (upperlimited by 1.0)
The AMI returns a value of 1 when the two partitions are identical (ie perfectly matched). Random partitions (independent labellings) have an expected AMI around 0 on average hence can be negative. The value is in adjusted nats (based on the natural logarithm).
See also
[`adjusted_rand_score`](sklearn.metrics.adjusted_rand_score#sklearn.metrics.adjusted_rand_score "sklearn.metrics.adjusted_rand_score")
Adjusted Rand Index.
[`mutual_info_score`](sklearn.metrics.mutual_info_score#sklearn.metrics.mutual_info_score "sklearn.metrics.mutual_info_score")
Mutual Information (not adjusted for chance).
#### References
[1] [Vinh, Epps, and Bailey, (2010). Information Theoretic Measures for Clusterings Comparison: Variants, Properties, Normalization and Correction for Chance, JMLR](http://jmlr.csail.mit.edu/papers/volume11/vinh10a/vinh10a.pdf)
[2] [Wikipedia entry for the Adjusted Mutual Information](https://en.wikipedia.org/wiki/Adjusted_Mutual_Information)
#### Examples
Perfect labelings are both homogeneous and complete, hence have score 1.0:
```
>>> from sklearn.metrics.cluster import adjusted_mutual_info_score
>>> adjusted_mutual_info_score([0, 0, 1, 1], [0, 0, 1, 1])
...
1.0
>>> adjusted_mutual_info_score([0, 0, 1, 1], [1, 1, 0, 0])
...
1.0
```
If classes members are completely split across different clusters, the assignment is totally in-complete, hence the AMI is null:
```
>>> adjusted_mutual_info_score([0, 0, 0, 0], [0, 1, 2, 3])
...
0.0
```
Examples using `sklearn.metrics.adjusted_mutual_info_score`
-----------------------------------------------------------
[A demo of K-Means clustering on the handwritten digits data](../../auto_examples/cluster/plot_kmeans_digits#sphx-glr-auto-examples-cluster-plot-kmeans-digits-py)
[Adjustment for chance in clustering performance evaluation](../../auto_examples/cluster/plot_adjusted_for_chance_measures#sphx-glr-auto-examples-cluster-plot-adjusted-for-chance-measures-py)
[Demo of DBSCAN clustering algorithm](../../auto_examples/cluster/plot_dbscan#sphx-glr-auto-examples-cluster-plot-dbscan-py)
[Demo of affinity propagation clustering algorithm](../../auto_examples/cluster/plot_affinity_propagation#sphx-glr-auto-examples-cluster-plot-affinity-propagation-py)
scikit_learn sklearn.linear_model.BayesianRidge sklearn.linear\_model.BayesianRidge
===================================
*class*sklearn.linear\_model.BayesianRidge(*\**, *n\_iter=300*, *tol=0.001*, *alpha\_1=1e-06*, *alpha\_2=1e-06*, *lambda\_1=1e-06*, *lambda\_2=1e-06*, *alpha\_init=None*, *lambda\_init=None*, *compute\_score=False*, *fit\_intercept=True*, *normalize='deprecated'*, *copy\_X=True*, *verbose=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_bayes.py#L24)
Bayesian ridge regression.
Fit a Bayesian ridge model. See the Notes section for details on this implementation and the optimization of the regularization parameters lambda (precision of the weights) and alpha (precision of the noise).
Read more in the [User Guide](../linear_model#bayesian-regression).
Parameters:
**n\_iter**int, default=300
Maximum number of iterations. Should be greater than or equal to 1.
**tol**float, default=1e-3
Stop the algorithm if w has converged.
**alpha\_1**float, default=1e-6
Hyper-parameter : shape parameter for the Gamma distribution prior over the alpha parameter.
**alpha\_2**float, default=1e-6
Hyper-parameter : inverse scale parameter (rate parameter) for the Gamma distribution prior over the alpha parameter.
**lambda\_1**float, default=1e-6
Hyper-parameter : shape parameter for the Gamma distribution prior over the lambda parameter.
**lambda\_2**float, default=1e-6
Hyper-parameter : inverse scale parameter (rate parameter) for the Gamma distribution prior over the lambda parameter.
**alpha\_init**float, default=None
Initial value for alpha (precision of the noise). If not set, alpha\_init is 1/Var(y).
New in version 0.22.
**lambda\_init**float, default=None
Initial value for lambda (precision of the weights). If not set, lambda\_init is 1.
New in version 0.22.
**compute\_score**bool, default=False
If True, compute the log marginal likelihood at each iteration of the optimization.
**fit\_intercept**bool, default=True
Whether to calculate the intercept for this model. The intercept is not treated as a probabilistic parameter and thus has no associated variance. If set to False, no intercept will be used in calculations (i.e. data is expected to be centered).
**normalize**bool, default=False
This parameter is ignored when `fit_intercept` is set to False. If True, the regressors X will be normalized before regression by subtracting the mean and dividing by the l2-norm. If you wish to standardize, please use [`StandardScaler`](sklearn.preprocessing.standardscaler#sklearn.preprocessing.StandardScaler "sklearn.preprocessing.StandardScaler") before calling `fit` on an estimator with `normalize=False`.
Deprecated since version 1.0: `normalize` was deprecated in version 1.0 and will be removed in 1.2.
**copy\_X**bool, default=True
If True, X will be copied; else, it may be overwritten.
**verbose**bool, default=False
Verbose mode when fitting the model.
Attributes:
**coef\_**array-like of shape (n\_features,)
Coefficients of the regression model (mean of distribution)
**intercept\_**float
Independent term in decision function. Set to 0.0 if `fit_intercept = False`.
**alpha\_**float
Estimated precision of the noise.
**lambda\_**float
Estimated precision of the weights.
**sigma\_**array-like of shape (n\_features, n\_features)
Estimated variance-covariance matrix of the weights
**scores\_**array-like of shape (n\_iter\_+1,)
If computed\_score is True, value of the log marginal likelihood (to be maximized) at each iteration of the optimization. The array starts with the value of the log marginal likelihood obtained for the initial values of alpha and lambda and ends with the value obtained for the estimated alpha and lambda.
**n\_iter\_**int
The actual number of iterations to reach the stopping criterion.
**X\_offset\_**float
If `normalize=True`, offset subtracted for centering data to a zero mean.
**X\_scale\_**float
If `normalize=True`, parameter used to scale data to a unit standard deviation.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`ARDRegression`](sklearn.linear_model.ardregression#sklearn.linear_model.ARDRegression "sklearn.linear_model.ARDRegression")
Bayesian ARD regression.
#### Notes
There exist several strategies to perform Bayesian ridge regression. This implementation is based on the algorithm described in Appendix A of (Tipping, 2001) where updates of the regularization parameters are done as suggested in (MacKay, 1992). Note that according to A New View of Automatic Relevance Determination (Wipf and Nagarajan, 2008) these update rules do not guarantee that the marginal likelihood is increasing between two consecutive iterations of the optimization.
#### References
D. J. C. MacKay, Bayesian Interpolation, Computation and Neural Systems, Vol. 4, No. 3, 1992.
M. E. Tipping, Sparse Bayesian Learning and the Relevance Vector Machine, Journal of Machine Learning Research, Vol. 1, 2001.
#### Examples
```
>>> from sklearn import linear_model
>>> clf = linear_model.BayesianRidge()
>>> clf.fit([[0,0], [1, 1], [2, 2]], [0, 1, 2])
BayesianRidge()
>>> clf.predict([[1, 1]])
array([1.])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.linear_model.BayesianRidge.fit "sklearn.linear_model.BayesianRidge.fit")(X, y[, sample\_weight]) | Fit the model. |
| [`get_params`](#sklearn.linear_model.BayesianRidge.get_params "sklearn.linear_model.BayesianRidge.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.linear_model.BayesianRidge.predict "sklearn.linear_model.BayesianRidge.predict")(X[, return\_std]) | Predict using the linear model. |
| [`score`](#sklearn.linear_model.BayesianRidge.score "sklearn.linear_model.BayesianRidge.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.linear_model.BayesianRidge.set_params "sklearn.linear_model.BayesianRidge.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_bayes.py#L208)
Fit the model.
Parameters:
**X**ndarray of shape (n\_samples, n\_features)
Training data.
**y**ndarray of shape (n\_samples,)
Target values. Will be cast to X’s dtype if necessary.
**sample\_weight**ndarray of shape (n\_samples,), default=None
Individual weights for each sample.
New in version 0.20: parameter *sample\_weight* support to BayesianRidge.
Returns:
**self**object
Returns the instance itself.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*, *return\_std=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_bayes.py#L340)
Predict using the linear model.
In addition to the mean of the predictive distribution, also its standard deviation can be returned.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Samples.
**return\_std**bool, default=False
Whether to return the standard deviation of posterior prediction.
Returns:
**y\_mean**array-like of shape (n\_samples,)
Mean of predictive distribution of query points.
**y\_std**array-like of shape (n\_samples,)
Standard deviation of predictive distribution of query points.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.linear_model.BayesianRidge`
---------------------------------------------------
[Feature agglomeration vs. univariate selection](../../auto_examples/cluster/plot_feature_agglomeration_vs_univariate_selection#sphx-glr-auto-examples-cluster-plot-feature-agglomeration-vs-univariate-selection-py)
[Comparing Linear Bayesian Regressors](../../auto_examples/linear_model/plot_ard#sphx-glr-auto-examples-linear-model-plot-ard-py)
[Curve Fitting with Bayesian Ridge Regression](../../auto_examples/linear_model/plot_bayesian_ridge_curvefit#sphx-glr-auto-examples-linear-model-plot-bayesian-ridge-curvefit-py)
[Imputing missing values with variants of IterativeImputer](../../auto_examples/impute/plot_iterative_imputer_variants_comparison#sphx-glr-auto-examples-impute-plot-iterative-imputer-variants-comparison-py)
| programming_docs |
scikit_learn sklearn.cluster.AgglomerativeClustering sklearn.cluster.AgglomerativeClustering
=======================================
*class*sklearn.cluster.AgglomerativeClustering(*n\_clusters=2*, *\**, *affinity='euclidean'*, *memory=None*, *connectivity=None*, *compute\_full\_tree='auto'*, *linkage='ward'*, *distance\_threshold=None*, *compute\_distances=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_agglomerative.py#L737)
Agglomerative Clustering.
Recursively merges pair of clusters of sample data; uses linkage distance.
Read more in the [User Guide](../clustering#hierarchical-clustering).
Parameters:
**n\_clusters**int or None, default=2
The number of clusters to find. It must be `None` if `distance_threshold` is not `None`.
**affinity**str or callable, default=’euclidean’
Metric used to compute the linkage. Can be “euclidean”, “l1”, “l2”, “manhattan”, “cosine”, or “precomputed”. If linkage is “ward”, only “euclidean” is accepted. If “precomputed”, a distance matrix (instead of a similarity matrix) is needed as input for the fit method.
**memory**str or object with the joblib.Memory interface, default=None
Used to cache the output of the computation of the tree. By default, no caching is done. If a string is given, it is the path to the caching directory.
**connectivity**array-like or callable, default=None
Connectivity matrix. Defines for each sample the neighboring samples following a given structure of the data. This can be a connectivity matrix itself or a callable that transforms the data into a connectivity matrix, such as derived from `kneighbors_graph`. Default is `None`, i.e, the hierarchical clustering algorithm is unstructured.
**compute\_full\_tree**‘auto’ or bool, default=’auto’
Stop early the construction of the tree at `n_clusters`. This is useful to decrease computation time if the number of clusters is not small compared to the number of samples. This option is useful only when specifying a connectivity matrix. Note also that when varying the number of clusters and using caching, it may be advantageous to compute the full tree. It must be `True` if `distance_threshold` is not `None`. By default `compute_full_tree` is “auto”, which is equivalent to `True` when `distance_threshold` is not `None` or that `n_clusters` is inferior to the maximum between 100 or `0.02 * n_samples`. Otherwise, “auto” is equivalent to `False`.
**linkage**{‘ward’, ‘complete’, ‘average’, ‘single’}, default=’ward’
Which linkage criterion to use. The linkage criterion determines which distance to use between sets of observation. The algorithm will merge the pairs of cluster that minimize this criterion.
* ‘ward’ minimizes the variance of the clusters being merged.
* ‘average’ uses the average of the distances of each observation of the two sets.
* ‘complete’ or ‘maximum’ linkage uses the maximum distances between all observations of the two sets.
* ‘single’ uses the minimum of the distances between all observations of the two sets.
New in version 0.20: Added the ‘single’ option
**distance\_threshold**float, default=None
The linkage distance threshold above which, clusters will not be merged. If not `None`, `n_clusters` must be `None` and `compute_full_tree` must be `True`.
New in version 0.21.
**compute\_distances**bool, default=False
Computes distances between clusters even if `distance_threshold` is not used. This can be used to make dendrogram visualization, but introduces a computational and memory overhead.
New in version 0.24.
Attributes:
**n\_clusters\_**int
The number of clusters found by the algorithm. If `distance_threshold=None`, it will be equal to the given `n_clusters`.
**labels\_**ndarray of shape (n\_samples)
Cluster labels for each point.
**n\_leaves\_**int
Number of leaves in the hierarchical tree.
**n\_connected\_components\_**int
The estimated number of connected components in the graph.
New in version 0.21: `n_connected_components_` was added to replace `n_components_`.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**children\_**array-like of shape (n\_samples-1, 2)
The children of each non-leaf node. Values less than `n_samples` correspond to leaves of the tree which are the original samples. A node `i` greater than or equal to `n_samples` is a non-leaf node and has children `children_[i - n_samples]`. Alternatively at the i-th iteration, children[i][0] and children[i][1] are merged to form node `n_samples + i`.
**distances\_**array-like of shape (n\_nodes-1,)
Distances between nodes in the corresponding place in `children_`. Only computed if `distance_threshold` is used or `compute_distances` is set to `True`.
See also
[`FeatureAgglomeration`](sklearn.cluster.featureagglomeration#sklearn.cluster.FeatureAgglomeration "sklearn.cluster.FeatureAgglomeration")
Agglomerative clustering but for features instead of samples.
[`ward_tree`](sklearn.cluster.ward_tree#sklearn.cluster.ward_tree "sklearn.cluster.ward_tree")
Hierarchical clustering with ward linkage.
#### Examples
```
>>> from sklearn.cluster import AgglomerativeClustering
>>> import numpy as np
>>> X = np.array([[1, 2], [1, 4], [1, 0],
... [4, 2], [4, 4], [4, 0]])
>>> clustering = AgglomerativeClustering().fit(X)
>>> clustering
AgglomerativeClustering()
>>> clustering.labels_
array([1, 1, 1, 0, 0, 0])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.cluster.AgglomerativeClustering.fit "sklearn.cluster.AgglomerativeClustering.fit")(X[, y]) | Fit the hierarchical clustering from features, or distance matrix. |
| [`fit_predict`](#sklearn.cluster.AgglomerativeClustering.fit_predict "sklearn.cluster.AgglomerativeClustering.fit_predict")(X[, y]) | Fit and return the result of each sample's clustering assignment. |
| [`get_params`](#sklearn.cluster.AgglomerativeClustering.get_params "sklearn.cluster.AgglomerativeClustering.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.cluster.AgglomerativeClustering.set_params "sklearn.cluster.AgglomerativeClustering.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_agglomerative.py#L896)
Fit the hierarchical clustering from features, or distance matrix.
Parameters:
**X**array-like, shape (n\_samples, n\_features) or (n\_samples, n\_samples)
Training instances to cluster, or distances between instances if `affinity='precomputed'`.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
**self**object
Returns the fitted instance.
fit\_predict(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_agglomerative.py#L1030)
Fit and return the result of each sample’s clustering assignment.
In addition to fitting, this method also return the result of the clustering assignment for each sample in the training set.
Parameters:
**X**array-like of shape (n\_samples, n\_features) or (n\_samples, n\_samples)
Training instances to cluster, or distances between instances if `affinity='precomputed'`.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
**labels**ndarray of shape (n\_samples,)
Cluster labels.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.cluster.AgglomerativeClustering`
--------------------------------------------------------
[A demo of structured Ward hierarchical clustering on an image of coins](../../auto_examples/cluster/plot_coin_ward_segmentation#sphx-glr-auto-examples-cluster-plot-coin-ward-segmentation-py)
[Agglomerative clustering with and without structure](../../auto_examples/cluster/plot_agglomerative_clustering#sphx-glr-auto-examples-cluster-plot-agglomerative-clustering-py)
[Agglomerative clustering with different metrics](../../auto_examples/cluster/plot_agglomerative_clustering_metrics#sphx-glr-auto-examples-cluster-plot-agglomerative-clustering-metrics-py)
[Comparing different clustering algorithms on toy datasets](../../auto_examples/cluster/plot_cluster_comparison#sphx-glr-auto-examples-cluster-plot-cluster-comparison-py)
[Comparing different hierarchical linkage methods on toy datasets](../../auto_examples/cluster/plot_linkage_comparison#sphx-glr-auto-examples-cluster-plot-linkage-comparison-py)
[Hierarchical clustering: structured vs unstructured ward](../../auto_examples/cluster/plot_ward_structured_vs_unstructured#sphx-glr-auto-examples-cluster-plot-ward-structured-vs-unstructured-py)
[Inductive Clustering](../../auto_examples/cluster/plot_inductive_clustering#sphx-glr-auto-examples-cluster-plot-inductive-clustering-py)
[Plot Hierarchical Clustering Dendrogram](../../auto_examples/cluster/plot_agglomerative_dendrogram#sphx-glr-auto-examples-cluster-plot-agglomerative-dendrogram-py)
[Various Agglomerative Clustering on a 2D embedding of digits](../../auto_examples/cluster/plot_digits_linkage#sphx-glr-auto-examples-cluster-plot-digits-linkage-py)
scikit_learn sklearn.manifold.SpectralEmbedding sklearn.manifold.SpectralEmbedding
==================================
*class*sklearn.manifold.SpectralEmbedding(*n\_components=2*, *\**, *affinity='nearest\_neighbors'*, *gamma=None*, *random\_state=None*, *eigen\_solver=None*, *n\_neighbors=None*, *n\_jobs=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_spectral_embedding.py#L391)
Spectral embedding for non-linear dimensionality reduction.
Forms an affinity matrix given by the specified function and applies spectral decomposition to the corresponding graph laplacian. The resulting transformation is given by the value of the eigenvectors for each data point.
Note : Laplacian Eigenmaps is the actual algorithm implemented here.
Read more in the [User Guide](../manifold#spectral-embedding).
Parameters:
**n\_components**int, default=2
The dimension of the projected subspace.
**affinity**{‘nearest\_neighbors’, ‘rbf’, ‘precomputed’, ‘precomputed\_nearest\_neighbors’} or callable, default=’nearest\_neighbors’
How to construct the affinity matrix.
* ‘nearest\_neighbors’ : construct the affinity matrix by computing a graph of nearest neighbors.
* ‘rbf’ : construct the affinity matrix by computing a radial basis function (RBF) kernel.
* ‘precomputed’ : interpret `X` as a precomputed affinity matrix.
* ‘precomputed\_nearest\_neighbors’ : interpret `X` as a sparse graph of precomputed nearest neighbors, and constructs the affinity matrix by selecting the `n_neighbors` nearest neighbors.
* callable : use passed in function as affinity the function takes in data matrix (n\_samples, n\_features) and return affinity matrix (n\_samples, n\_samples).
**gamma**float, default=None
Kernel coefficient for rbf kernel. If None, gamma will be set to 1/n\_features.
**random\_state**int, RandomState instance or None, default=None
A pseudo random number generator used for the initialization of the lobpcg eigen vectors decomposition when `eigen_solver ==
'amg'`, and for the K-Means initialization. Use an int to make the results deterministic across calls (See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state)).
Note
When using `eigen_solver == 'amg'`, it is necessary to also fix the global numpy seed with `np.random.seed(int)` to get deterministic results. See <https://github.com/pyamg/pyamg/issues/139> for further information.
**eigen\_solver**{‘arpack’, ‘lobpcg’, ‘amg’}, default=None
The eigenvalue decomposition strategy to use. AMG requires pyamg to be installed. It can be faster on very large, sparse problems. If None, then `'arpack'` is used.
**n\_neighbors**int, default=None
Number of nearest neighbors for nearest\_neighbors graph building. If None, n\_neighbors will be set to max(n\_samples/10, 1).
**n\_jobs**int, default=None
The number of parallel jobs to run. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
Attributes:
**embedding\_**ndarray of shape (n\_samples, n\_components)
Spectral embedding of the training matrix.
**affinity\_matrix\_**ndarray of shape (n\_samples, n\_samples)
Affinity\_matrix constructed from samples or precomputed.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_neighbors\_**int
Number of nearest neighbors effectively used.
See also
[`Isomap`](sklearn.manifold.isomap#sklearn.manifold.Isomap "sklearn.manifold.Isomap")
Non-linear dimensionality reduction through Isometric Mapping.
#### References
* [A Tutorial on Spectral Clustering, 2007 Ulrike von Luxburg](https://doi.org/10.1007/s11222-007-9033-z)
* On Spectral Clustering: Analysis and an algorithm, 2001 Andrew Y. Ng, Michael I. Jordan, Yair Weiss <http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.19.8100>
* [Normalized cuts and image segmentation, 2000 Jianbo Shi, Jitendra Malik](https://doi.org/10.1109/34.868688)
#### Examples
```
>>> from sklearn.datasets import load_digits
>>> from sklearn.manifold import SpectralEmbedding
>>> X, _ = load_digits(return_X_y=True)
>>> X.shape
(1797, 64)
>>> embedding = SpectralEmbedding(n_components=2)
>>> X_transformed = embedding.fit_transform(X[:100])
>>> X_transformed.shape
(100, 2)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.manifold.SpectralEmbedding.fit "sklearn.manifold.SpectralEmbedding.fit")(X[, y]) | Fit the model from data in X. |
| [`fit_transform`](#sklearn.manifold.SpectralEmbedding.fit_transform "sklearn.manifold.SpectralEmbedding.fit_transform")(X[, y]) | Fit the model from data in X and transform X. |
| [`get_params`](#sklearn.manifold.SpectralEmbedding.get_params "sklearn.manifold.SpectralEmbedding.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.manifold.SpectralEmbedding.set_params "sklearn.manifold.SpectralEmbedding.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_spectral_embedding.py#L594)
Fit the model from data in X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vector, where `n_samples` is the number of samples and `n_features` is the number of features.
If affinity is “precomputed” X : {array-like, sparse matrix}, shape (n\_samples, n\_samples), Interpret X as precomputed adjacency graph computed from samples.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_spectral_embedding.py#L648)
Fit the model from data in X and transform X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vector, where `n_samples` is the number of samples and `n_features` is the number of features.
If affinity is “precomputed” X : {array-like, sparse matrix} of shape (n\_samples, n\_samples), Interpret X as precomputed adjacency graph computed from samples.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**X\_new**array-like of shape (n\_samples, n\_components)
Spectral embedding of the training matrix.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.manifold.SpectralEmbedding`
---------------------------------------------------
[Various Agglomerative Clustering on a 2D embedding of digits](../../auto_examples/cluster/plot_digits_linkage#sphx-glr-auto-examples-cluster-plot-digits-linkage-py)
[Comparison of Manifold Learning methods](../../auto_examples/manifold/plot_compare_methods#sphx-glr-auto-examples-manifold-plot-compare-methods-py)
[Manifold Learning methods on a severed sphere](../../auto_examples/manifold/plot_manifold_sphere#sphx-glr-auto-examples-manifold-plot-manifold-sphere-py)
[Manifold learning on handwritten digits: Locally Linear Embedding, Isomap…](../../auto_examples/manifold/plot_lle_digits#sphx-glr-auto-examples-manifold-plot-lle-digits-py)
scikit_learn sklearn.metrics.mean_squared_error sklearn.metrics.mean\_squared\_error
====================================
sklearn.metrics.mean\_squared\_error(*y\_true*, *y\_pred*, *\**, *sample\_weight=None*, *multioutput='uniform\_average'*, *squared=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_regression.py#L382)
Mean squared error regression loss.
Read more in the [User Guide](../model_evaluation#mean-squared-error).
Parameters:
**y\_true**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
Ground truth (correct) target values.
**y\_pred**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
Estimated target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**multioutput**{‘raw\_values’, ‘uniform\_average’} or array-like of shape (n\_outputs,), default=’uniform\_average’
Defines aggregating of multiple output values. Array-like value defines weights used to average errors.
‘raw\_values’ :
Returns a full set of errors in case of multioutput input.
‘uniform\_average’ :
Errors of all outputs are averaged with uniform weight.
**squared**bool, default=True
If True returns MSE value, if False returns RMSE value.
Returns:
**loss**float or ndarray of floats
A non-negative floating point value (the best value is 0.0), or an array of floating point values, one for each individual target.
#### Examples
```
>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred)
0.375
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred, squared=False)
0.612...
>>> y_true = [[0.5, 1],[-1, 1],[7, -6]]
>>> y_pred = [[0, 2],[-1, 2],[8, -5]]
>>> mean_squared_error(y_true, y_pred)
0.708...
>>> mean_squared_error(y_true, y_pred, squared=False)
0.822...
>>> mean_squared_error(y_true, y_pred, multioutput='raw_values')
array([0.41666667, 1. ])
>>> mean_squared_error(y_true, y_pred, multioutput=[0.3, 0.7])
0.825...
```
Examples using `sklearn.metrics.mean_squared_error`
---------------------------------------------------
[Gradient Boosting regression](../../auto_examples/ensemble/plot_gradient_boosting_regression#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-regression-py)
[Prediction Intervals for Gradient Boosting Regression](../../auto_examples/ensemble/plot_gradient_boosting_quantile#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-quantile-py)
[Model Complexity Influence](../../auto_examples/applications/plot_model_complexity_influence#sphx-glr-auto-examples-applications-plot-model-complexity-influence-py)
[Linear Regression Example](../../auto_examples/linear_model/plot_ols#sphx-glr-auto-examples-linear-model-plot-ols-py)
[Plot Ridge coefficients as a function of the L2 regularization](../../auto_examples/linear_model/plot_ridge_coeffs#sphx-glr-auto-examples-linear-model-plot-ridge-coeffs-py)
[Poisson regression and non-normal loss](../../auto_examples/linear_model/plot_poisson_regression_non_normal_loss#sphx-glr-auto-examples-linear-model-plot-poisson-regression-non-normal-loss-py)
[Quantile regression](../../auto_examples/linear_model/plot_quantile_regression#sphx-glr-auto-examples-linear-model-plot-quantile-regression-py)
[Robust linear estimator fitting](../../auto_examples/linear_model/plot_robust_fit#sphx-glr-auto-examples-linear-model-plot-robust-fit-py)
[Tweedie regression on insurance claims](../../auto_examples/linear_model/plot_tweedie_regression_insurance_claims#sphx-glr-auto-examples-linear-model-plot-tweedie-regression-insurance-claims-py)
| programming_docs |
scikit_learn sklearn.base.ClassifierMixin sklearn.base.ClassifierMixin
============================
*class*sklearn.base.ClassifierMixin[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L635)
Mixin class for all classifiers in scikit-learn.
#### Methods
| | |
| --- | --- |
| [`score`](#sklearn.base.ClassifierMixin.score "sklearn.base.ClassifierMixin.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
scikit_learn sklearn.utils.graph.single_source_shortest_path_length sklearn.utils.graph.single\_source\_shortest\_path\_length
==========================================================
sklearn.utils.graph.single\_source\_shortest\_path\_length(*graph*, *source*, *\**, *cutoff=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/graph.py#L23)
Return the shortest path length from source to all reachable nodes.
Returns a dictionary of shortest path lengths keyed by target.
Parameters:
**graph**{sparse matrix, ndarray} of shape (n, n)
Adjacency matrix of the graph. Sparse matrix of format LIL is preferred.
**source**int
Starting node for path.
**cutoff**int, default=None
Depth to stop the search - only paths of length <= cutoff are returned.
#### Examples
```
>>> from sklearn.utils.graph import single_source_shortest_path_length
>>> import numpy as np
>>> graph = np.array([[ 0, 1, 0, 0],
... [ 1, 0, 1, 0],
... [ 0, 1, 0, 1],
... [ 0, 0, 1, 0]])
>>> list(sorted(single_source_shortest_path_length(graph, 0).items()))
[(0, 0), (1, 1), (2, 2), (3, 3)]
>>> graph = np.ones((6, 6))
>>> list(sorted(single_source_shortest_path_length(graph, 2).items()))
[(0, 1), (1, 1), (2, 0), (3, 1), (4, 1), (5, 1)]
```
scikit_learn sklearn.datasets.get_data_home sklearn.datasets.get\_data\_home
================================
sklearn.datasets.get\_data\_home(*data\_home=None*) → [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.10)")[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_base.py#L37)
Return the path of the scikit-learn data directory.
This folder is used by some large dataset loaders to avoid downloading the data several times.
By default the data directory is set to a folder named ‘scikit\_learn\_data’ in the user home folder.
Alternatively, it can be set by the ‘SCIKIT\_LEARN\_DATA’ environment variable or programmatically by giving an explicit folder path. The ‘~’ symbol is expanded to the user home folder.
If the folder does not already exist, it is automatically created.
Parameters:
**data\_home**str, default=None
The path to scikit-learn data directory. If `None`, the default path is `~/sklearn_learn_data`.
Returns:
data\_home: str
The path to scikit-learn data directory.
Examples using `sklearn.datasets.get_data_home`
-----------------------------------------------
[Out-of-core classification of text documents](../../auto_examples/applications/plot_out_of_core_classification#sphx-glr-auto-examples-applications-plot-out-of-core-classification-py)
scikit_learn sklearn.feature_extraction.DictVectorizer sklearn.feature\_extraction.DictVectorizer
==========================================
*class*sklearn.feature\_extraction.DictVectorizer(*\**, *dtype=<class 'numpy.float64'>*, *separator='='*, *sparse=True*, *sort=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/_dict_vectorizer.py#L26)
Transforms lists of feature-value mappings to vectors.
This transformer turns lists of mappings (dict-like objects) of feature names to feature values into Numpy arrays or scipy.sparse matrices for use with scikit-learn estimators.
When feature values are strings, this transformer will do a binary one-hot (aka one-of-K) coding: one boolean-valued feature is constructed for each of the possible string values that the feature can take on. For instance, a feature “f” that can take on the values “ham” and “spam” will become two features in the output, one signifying “f=ham”, the other “f=spam”.
If a feature value is a sequence or set of strings, this transformer will iterate over the values and will count the occurrences of each string value.
However, note that this transformer will only do a binary one-hot encoding when feature values are of type string. If categorical features are represented as numeric values such as int or iterables of strings, the DictVectorizer can be followed by [`OneHotEncoder`](sklearn.preprocessing.onehotencoder#sklearn.preprocessing.OneHotEncoder "sklearn.preprocessing.OneHotEncoder") to complete binary one-hot encoding.
Features that do not occur in a sample (mapping) will have a zero value in the resulting array/matrix.
Read more in the [User Guide](../feature_extraction#dict-feature-extraction).
Parameters:
**dtype**dtype, default=np.float64
The type of feature values. Passed to Numpy array/scipy.sparse matrix constructors as the dtype argument.
**separator**str, default=”=”
Separator string used when constructing new features for one-hot coding.
**sparse**bool, default=True
Whether transform should produce scipy.sparse matrices.
**sort**bool, default=True
Whether `feature_names_` and `vocabulary_` should be sorted when fitting.
Attributes:
**vocabulary\_**dict
A dictionary mapping feature names to feature indices.
**feature\_names\_**list
A list of length n\_features containing the feature names (e.g., “f=ham” and “f=spam”).
See also
[`FeatureHasher`](sklearn.feature_extraction.featurehasher#sklearn.feature_extraction.FeatureHasher "sklearn.feature_extraction.FeatureHasher")
Performs vectorization using only a hash function.
[`sklearn.preprocessing.OrdinalEncoder`](sklearn.preprocessing.ordinalencoder#sklearn.preprocessing.OrdinalEncoder "sklearn.preprocessing.OrdinalEncoder")
Handles nominal/categorical features encoded as columns of arbitrary data types.
#### Examples
```
>>> from sklearn.feature_extraction import DictVectorizer
>>> v = DictVectorizer(sparse=False)
>>> D = [{'foo': 1, 'bar': 2}, {'foo': 3, 'baz': 1}]
>>> X = v.fit_transform(D)
>>> X
array([[2., 0., 1.],
[0., 1., 3.]])
>>> v.inverse_transform(X) == [{'bar': 2.0, 'foo': 1.0},
... {'baz': 1.0, 'foo': 3.0}]
True
>>> v.transform({'foo': 4, 'unseen_feature': 3})
array([[0., 0., 4.]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.feature_extraction.DictVectorizer.fit "sklearn.feature_extraction.DictVectorizer.fit")(X[, y]) | Learn a list of feature name -> indices mappings. |
| [`fit_transform`](#sklearn.feature_extraction.DictVectorizer.fit_transform "sklearn.feature_extraction.DictVectorizer.fit_transform")(X[, y]) | Learn a list of feature name -> indices mappings and transform X. |
| [`get_feature_names`](#sklearn.feature_extraction.DictVectorizer.get_feature_names "sklearn.feature_extraction.DictVectorizer.get_feature_names")() | DEPRECATED: get\_feature\_names is deprecated in 1.0 and will be removed in 1.2. |
| [`get_feature_names_out`](#sklearn.feature_extraction.DictVectorizer.get_feature_names_out "sklearn.feature_extraction.DictVectorizer.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.feature_extraction.DictVectorizer.get_params "sklearn.feature_extraction.DictVectorizer.get_params")([deep]) | Get parameters for this estimator. |
| [`inverse_transform`](#sklearn.feature_extraction.DictVectorizer.inverse_transform "sklearn.feature_extraction.DictVectorizer.inverse_transform")(X[, dict\_type]) | Transform array or sparse matrix X back to feature mappings. |
| [`restrict`](#sklearn.feature_extraction.DictVectorizer.restrict "sklearn.feature_extraction.DictVectorizer.restrict")(support[, indices]) | Restrict the features to those in support using feature selection. |
| [`set_params`](#sklearn.feature_extraction.DictVectorizer.set_params "sklearn.feature_extraction.DictVectorizer.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.feature_extraction.DictVectorizer.transform "sklearn.feature_extraction.DictVectorizer.transform")(X) | Transform feature->value dicts to array or sparse matrix. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/_dict_vectorizer.py#L137)
Learn a list of feature name -> indices mappings.
Parameters:
**X**Mapping or iterable over Mappings
Dict(s) or Mapping(s) from feature names (arbitrary Python objects) to feature values (strings or convertible to dtype).
Changed in version 0.24: Accepts multiple string values for one categorical feature.
**y**(ignored)
Ignored parameter.
Returns:
**self**object
DictVectorizer class instance.
fit\_transform(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/_dict_vectorizer.py#L290)
Learn a list of feature name -> indices mappings and transform X.
Like fit(X) followed by transform(X), but does not require materializing X in memory.
Parameters:
**X**Mapping or iterable over Mappings
Dict(s) or Mapping(s) from feature names (arbitrary Python objects) to feature values (strings or convertible to dtype).
Changed in version 0.24: Accepts multiple string values for one categorical feature.
**y**(ignored)
Ignored parameter.
Returns:
**Xa**{array, sparse matrix}
Feature vectors; always 2-d.
get\_feature\_names()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/_dict_vectorizer.py#L375)
DEPRECATED: get\_feature\_names is deprecated in 1.0 and will be removed in 1.2. Please use get\_feature\_names\_out instead.
Return a list of feature names, ordered by their indices.
If one-of-K coding is applied to categorical features, this will include the constructed feature names but not the original ones.
Returns:
**feature\_names\_**list of length (n\_features,)
List containing the feature names (e.g., “f=ham” and “f=spam”).
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/_dict_vectorizer.py#L392)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Not used, present here for API consistency by convention.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
inverse\_transform(*X*, *dict\_type=<class 'dict'>*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/_dict_vectorizer.py#L315)
Transform array or sparse matrix X back to feature mappings.
X must have been produced by this DictVectorizer’s transform or fit\_transform method; it may only have passed through transformers that preserve the number of features and their order.
In the case of one-hot/one-of-K coding, the constructed feature names and values are returned rather than the original ones.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Sample matrix.
**dict\_type**type, default=dict
Constructor for feature mappings. Must conform to the collections.Mapping API.
Returns:
**D**list of dict\_type objects of shape (n\_samples,)
Feature mappings for the samples in X.
restrict(*support*, *indices=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/_dict_vectorizer.py#L411)
Restrict the features to those in support using feature selection.
This function modifies the estimator in-place.
Parameters:
**support**array-like
Boolean mask or list of indices (as returned by the get\_support member of feature selectors).
**indices**bool, default=False
Whether support is a list of indices.
Returns:
**self**object
DictVectorizer class instance.
#### Examples
```
>>> from sklearn.feature_extraction import DictVectorizer
>>> from sklearn.feature_selection import SelectKBest, chi2
>>> v = DictVectorizer()
>>> D = [{'foo': 1, 'bar': 2}, {'foo': 3, 'baz': 1}]
>>> X = v.fit_transform(D)
>>> support = SelectKBest(chi2, k=2).fit(X, [0, 1])
>>> v.get_feature_names_out()
array(['bar', 'baz', 'foo'], ...)
>>> v.restrict(support.get_support())
DictVectorizer()
>>> v.get_feature_names_out()
array(['bar', 'foo'], ...)
```
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/_dict_vectorizer.py#L356)
Transform feature->value dicts to array or sparse matrix.
Named features not encountered during fit or fit\_transform will be silently ignored.
Parameters:
**X**Mapping or iterable over Mappings of shape (n\_samples,)
Dict(s) or Mapping(s) from feature names (arbitrary Python objects) to feature values (strings or convertible to dtype).
Returns:
**Xa**{array, sparse matrix}
Feature vectors; always 2-d.
Examples using `sklearn.feature_extraction.DictVectorizer`
----------------------------------------------------------
[Column Transformer with Heterogeneous Data Sources](../../auto_examples/compose/plot_column_transformer#sphx-glr-auto-examples-compose-plot-column-transformer-py)
[FeatureHasher and DictVectorizer Comparison](../../auto_examples/text/plot_hashing_vs_dict_vectorizer#sphx-glr-auto-examples-text-plot-hashing-vs-dict-vectorizer-py)
scikit_learn sklearn.preprocessing.robust_scale sklearn.preprocessing.robust\_scale
===================================
sklearn.preprocessing.robust\_scale(*X*, *\**, *axis=0*, *with\_centering=True*, *with\_scaling=True*, *quantile\_range=(25.0, 75.0)*, *copy=True*, *unit\_variance=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L1601)
Standardize a dataset along any axis.
Center to the median and component wise scale according to the interquartile range.
Read more in the [User Guide](../preprocessing#preprocessing-scaler).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_sample, n\_features)
The data to center and scale.
**axis**int, default=0
Axis used to compute the medians and IQR along. If 0, independently scale each feature, otherwise (if 1) scale each sample.
**with\_centering**bool, default=True
If `True`, center the data before scaling.
**with\_scaling**bool, default=True
If `True`, scale the data to unit variance (or equivalently, unit standard deviation).
**quantile\_range**tuple (q\_min, q\_max), 0.0 < q\_min < q\_max < 100.0, default=(25.0, 75.0)
Quantile range used to calculate `scale_`. By default this is equal to the IQR, i.e., `q_min` is the first quantile and `q_max` is the third quantile.
New in version 0.18.
**copy**bool, default=True
Set to `False` to perform inplace row normalization and avoid a copy (if the input is already a numpy array or a scipy.sparse CSR matrix and if axis is 1).
**unit\_variance**bool, default=False
If `True`, scale data so that normally distributed features have a variance of 1. In general, if the difference between the x-values of `q_max` and `q_min` for a standard normal distribution is greater than 1, the dataset will be scaled down. If less than 1, the dataset will be scaled up.
New in version 0.24.
Returns:
**X\_tr**{ndarray, sparse matrix} of shape (n\_samples, n\_features)
The transformed data.
See also
[`RobustScaler`](sklearn.preprocessing.robustscaler#sklearn.preprocessing.RobustScaler "sklearn.preprocessing.RobustScaler")
Performs centering and scaling using the Transformer API (e.g. as part of a preprocessing [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")).
#### Notes
This implementation will refuse to center scipy.sparse matrices since it would make them non-sparse and would potentially crash the program with memory exhaustion problems.
Instead the caller is expected to either set explicitly `with_centering=False` (in that case, only variance scaling will be performed on the features of the CSR matrix) or to call `X.toarray()` if he/she expects the materialized dense array to fit in memory.
To avoid memory copy the caller should pass a CSR matrix.
For a comparison of the different scalers, transformers, and normalizers, see [examples/preprocessing/plot\_all\_scaling.py](../../auto_examples/preprocessing/plot_all_scaling#sphx-glr-auto-examples-preprocessing-plot-all-scaling-py).
Warning
Risk of data leak
Do not use [`robust_scale`](#sklearn.preprocessing.robust_scale "sklearn.preprocessing.robust_scale") unless you know what you are doing. A common mistake is to apply it to the entire data *before* splitting into training and test sets. This will bias the model evaluation because information would have leaked from the test set to the training set. In general, we recommend using [`RobustScaler`](sklearn.preprocessing.robustscaler#sklearn.preprocessing.RobustScaler "sklearn.preprocessing.RobustScaler") within a [Pipeline](../compose#pipeline) in order to prevent most risks of data leaking: `pipe = make_pipeline(RobustScaler(), LogisticRegression())`.
scikit_learn sklearn.linear_model.ElasticNetCV sklearn.linear\_model.ElasticNetCV
==================================
*class*sklearn.linear\_model.ElasticNetCV(*\**, *l1\_ratio=0.5*, *eps=0.001*, *n\_alphas=100*, *alphas=None*, *fit\_intercept=True*, *normalize='deprecated'*, *precompute='auto'*, *max\_iter=1000*, *tol=0.0001*, *cv=None*, *copy\_X=True*, *verbose=0*, *n\_jobs=None*, *positive=False*, *random\_state=None*, *selection='cyclic'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_coordinate_descent.py#L2016)
Elastic Net model with iterative fitting along a regularization path.
See glossary entry for [cross-validation estimator](https://scikit-learn.org/1.1/glossary.html#term-cross-validation-estimator).
Read more in the [User Guide](../linear_model#elastic-net).
Parameters:
**l1\_ratio**float or list of float, default=0.5
Float between 0 and 1 passed to ElasticNet (scaling between l1 and l2 penalties). For `l1_ratio = 0` the penalty is an L2 penalty. For `l1_ratio = 1` it is an L1 penalty. For `0 < l1_ratio < 1`, the penalty is a combination of L1 and L2 This parameter can be a list, in which case the different values are tested by cross-validation and the one giving the best prediction score is used. Note that a good choice of list of values for l1\_ratio is often to put more values close to 1 (i.e. Lasso) and less close to 0 (i.e. Ridge), as in `[.1, .5, .7,
.9, .95, .99, 1]`.
**eps**float, default=1e-3
Length of the path. `eps=1e-3` means that `alpha_min / alpha_max = 1e-3`.
**n\_alphas**int, default=100
Number of alphas along the regularization path, used for each l1\_ratio.
**alphas**ndarray, default=None
List of alphas where to compute the models. If None alphas are set automatically.
**fit\_intercept**bool, default=True
Whether to calculate the intercept for this model. If set to false, no intercept will be used in calculations (i.e. data is expected to be centered).
**normalize**bool, default=False
This parameter is ignored when `fit_intercept` is set to False. If True, the regressors X will be normalized before regression by subtracting the mean and dividing by the l2-norm. If you wish to standardize, please use [`StandardScaler`](sklearn.preprocessing.standardscaler#sklearn.preprocessing.StandardScaler "sklearn.preprocessing.StandardScaler") before calling `fit` on an estimator with `normalize=False`.
Deprecated since version 1.0: `normalize` was deprecated in version 1.0 and will be removed in 1.2.
**precompute**‘auto’, bool or array-like of shape (n\_features, n\_features), default=’auto’
Whether to use a precomputed Gram matrix to speed up calculations. If set to `'auto'` let us decide. The Gram matrix can also be passed as argument.
**max\_iter**int, default=1000
The maximum number of iterations.
**tol**float, default=1e-4
The tolerance for the optimization: if the updates are smaller than `tol`, the optimization code checks the dual gap for optimality and continues until it is smaller than `tol`.
**cv**int, cross-validation generator or iterable, default=None
Determines the cross-validation splitting strategy. Possible inputs for cv are:
* None, to use the default 5-fold cross-validation,
* int, to specify the number of folds.
* [CV splitter](https://scikit-learn.org/1.1/glossary.html#term-CV-splitter),
* An iterable yielding (train, test) splits as arrays of indices.
For int/None inputs, `KFold` is used.
Refer [User Guide](../cross_validation#cross-validation) for the various cross-validation strategies that can be used here.
Changed in version 0.22: `cv` default value if None changed from 3-fold to 5-fold.
**copy\_X**bool, default=True
If `True`, X will be copied; else, it may be overwritten.
**verbose**bool or int, default=0
Amount of verbosity.
**n\_jobs**int, default=None
Number of CPUs to use during the cross validation. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**positive**bool, default=False
When set to `True`, forces the coefficients to be positive.
**random\_state**int, RandomState instance, default=None
The seed of the pseudo random number generator that selects a random feature to update. Used when `selection` == ‘random’. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**selection**{‘cyclic’, ‘random’}, default=’cyclic’
If set to ‘random’, a random coefficient is updated every iteration rather than looping over features sequentially by default. This (setting to ‘random’) often leads to significantly faster convergence especially when tol is higher than 1e-4.
Attributes:
**alpha\_**float
The amount of penalization chosen by cross validation.
**l1\_ratio\_**float
The compromise between l1 and l2 penalization chosen by cross validation.
**coef\_**ndarray of shape (n\_features,) or (n\_targets, n\_features)
Parameter vector (w in the cost function formula).
**intercept\_**float or ndarray of shape (n\_targets, n\_features)
Independent term in the decision function.
**mse\_path\_**ndarray of shape (n\_l1\_ratio, n\_alpha, n\_folds)
Mean square error for the test set on each fold, varying l1\_ratio and alpha.
**alphas\_**ndarray of shape (n\_alphas,) or (n\_l1\_ratio, n\_alphas)
The grid of alphas used for fitting, for each l1\_ratio.
**dual\_gap\_**float
The dual gaps at the end of the optimization for the optimal alpha.
**n\_iter\_**int
Number of iterations run by the coordinate descent solver to reach the specified tolerance for the optimal alpha.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`enet_path`](sklearn.linear_model.enet_path#sklearn.linear_model.enet_path "sklearn.linear_model.enet_path")
Compute elastic net path with coordinate descent.
[`ElasticNet`](sklearn.linear_model.elasticnet#sklearn.linear_model.ElasticNet "sklearn.linear_model.ElasticNet")
Linear regression with combined L1 and L2 priors as regularizer.
#### Notes
In `fit`, once the best parameters `l1_ratio` and `alpha` are found through cross-validation, the model is fit again using the entire training set.
To avoid unnecessary memory duplication the `X` argument of the `fit` method should be directly passed as a Fortran-contiguous numpy array.
The parameter `l1_ratio` corresponds to alpha in the glmnet R package while alpha corresponds to the lambda parameter in glmnet. More specifically, the optimization objective is:
```
1 / (2 * n_samples) * ||y - Xw||^2_2
+ alpha * l1_ratio * ||w||_1
+ 0.5 * alpha * (1 - l1_ratio) * ||w||^2_2
```
If you are interested in controlling the L1 and L2 penalty separately, keep in mind that this is equivalent to:
```
a * L1 + b * L2
```
for:
```
alpha = a + b and l1_ratio = a / (a + b).
```
For an example, see [examples/linear\_model/plot\_lasso\_model\_selection.py](../../auto_examples/linear_model/plot_lasso_model_selection#sphx-glr-auto-examples-linear-model-plot-lasso-model-selection-py).
#### Examples
```
>>> from sklearn.linear_model import ElasticNetCV
>>> from sklearn.datasets import make_regression
```
```
>>> X, y = make_regression(n_features=2, random_state=0)
>>> regr = ElasticNetCV(cv=5, random_state=0)
>>> regr.fit(X, y)
ElasticNetCV(cv=5, random_state=0)
>>> print(regr.alpha_)
0.199...
>>> print(regr.intercept_)
0.398...
>>> print(regr.predict([[0, 0]]))
[0.398...]
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.linear_model.ElasticNetCV.fit "sklearn.linear_model.ElasticNetCV.fit")(X, y[, sample\_weight]) | Fit linear model with coordinate descent. |
| [`get_params`](#sklearn.linear_model.ElasticNetCV.get_params "sklearn.linear_model.ElasticNetCV.get_params")([deep]) | Get parameters for this estimator. |
| [`path`](#sklearn.linear_model.ElasticNetCV.path "sklearn.linear_model.ElasticNetCV.path")(X, y, \*[, l1\_ratio, eps, n\_alphas, ...]) | Compute elastic net path with coordinate descent. |
| [`predict`](#sklearn.linear_model.ElasticNetCV.predict "sklearn.linear_model.ElasticNetCV.predict")(X) | Predict using the linear model. |
| [`score`](#sklearn.linear_model.ElasticNetCV.score "sklearn.linear_model.ElasticNetCV.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.linear_model.ElasticNetCV.set_params "sklearn.linear_model.ElasticNetCV.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_coordinate_descent.py#L1521)
Fit linear model with coordinate descent.
Fit is on grid of alphas and best alpha estimated by cross-validation.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training data. Pass directly as Fortran-contiguous data to avoid unnecessary memory duplication. If y is mono-output, X can be sparse.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_targets)
Target values.
**sample\_weight**float or array-like of shape (n\_samples,), default=None
Sample weights used for fitting and evaluation of the weighted mean squared error of each cv-fold. Note that the cross validated MSE that is finally used to find the best model is the unweighted mean over the (weighted) MSEs of each test fold.
Returns:
**self**object
Returns an instance of fitted model.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*static*path(*X*, *y*, *\**, *l1\_ratio=0.5*, *eps=0.001*, *n\_alphas=100*, *alphas=None*, *precompute='auto'*, *Xy=None*, *copy\_X=True*, *coef\_init=None*, *verbose=False*, *return\_n\_iter=False*, *positive=False*, *check\_input=True*, *\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_coordinate_descent.py#L366)
Compute elastic net path with coordinate descent.
The elastic net optimization function varies for mono and multi-outputs.
For mono-output tasks it is:
```
1 / (2 * n_samples) * ||y - Xw||^2_2
+ alpha * l1_ratio * ||w||_1
+ 0.5 * alpha * (1 - l1_ratio) * ||w||^2_2
```
For multi-output tasks it is:
```
(1 / (2 * n_samples)) * ||Y - XW||_Fro^2
+ alpha * l1_ratio * ||W||_21
+ 0.5 * alpha * (1 - l1_ratio) * ||W||_Fro^2
```
Where:
```
||W||_21 = \sum_i \sqrt{\sum_j w_{ij}^2}
```
i.e. the sum of norm of each row.
Read more in the [User Guide](../linear_model#elastic-net).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training data. Pass directly as Fortran-contiguous data to avoid unnecessary memory duplication. If `y` is mono-output then `X` can be sparse.
**y**{array-like, sparse matrix} of shape (n\_samples,) or (n\_samples, n\_targets)
Target values.
**l1\_ratio**float, default=0.5
Number between 0 and 1 passed to elastic net (scaling between l1 and l2 penalties). `l1_ratio=1` corresponds to the Lasso.
**eps**float, default=1e-3
Length of the path. `eps=1e-3` means that `alpha_min / alpha_max = 1e-3`.
**n\_alphas**int, default=100
Number of alphas along the regularization path.
**alphas**ndarray, default=None
List of alphas where to compute the models. If None alphas are set automatically.
**precompute**‘auto’, bool or array-like of shape (n\_features, n\_features), default=’auto’
Whether to use a precomputed Gram matrix to speed up calculations. If set to `'auto'` let us decide. The Gram matrix can also be passed as argument.
**Xy**array-like of shape (n\_features,) or (n\_features, n\_targets), default=None
Xy = np.dot(X.T, y) that can be precomputed. It is useful only when the Gram matrix is precomputed.
**copy\_X**bool, default=True
If `True`, X will be copied; else, it may be overwritten.
**coef\_init**ndarray of shape (n\_features, ), default=None
The initial values of the coefficients.
**verbose**bool or int, default=False
Amount of verbosity.
**return\_n\_iter**bool, default=False
Whether to return the number of iterations or not.
**positive**bool, default=False
If set to True, forces coefficients to be positive. (Only allowed when `y.ndim == 1`).
**check\_input**bool, default=True
If set to False, the input validation checks are skipped (including the Gram matrix when provided). It is assumed that they are handled by the caller.
**\*\*params**kwargs
Keyword arguments passed to the coordinate descent solver.
Returns:
**alphas**ndarray of shape (n\_alphas,)
The alphas along the path where models are computed.
**coefs**ndarray of shape (n\_features, n\_alphas) or (n\_targets, n\_features, n\_alphas)
Coefficients along the path.
**dual\_gaps**ndarray of shape (n\_alphas,)
The dual gaps at the end of the optimization for each alpha.
**n\_iters**list of int
The number of iterations taken by the coordinate descent optimizer to reach the specified tolerance for each alpha. (Is returned when `return_n_iter` is set to True).
See also
[`MultiTaskElasticNet`](sklearn.linear_model.multitaskelasticnet#sklearn.linear_model.MultiTaskElasticNet "sklearn.linear_model.MultiTaskElasticNet")
Multi-task ElasticNet model trained with L1/L2 mixed-norm as regularizer.
[`MultiTaskElasticNetCV`](sklearn.linear_model.multitaskelasticnetcv#sklearn.linear_model.MultiTaskElasticNetCV "sklearn.linear_model.MultiTaskElasticNetCV")
Multi-task L1/L2 ElasticNet with built-in cross-validation.
[`ElasticNet`](sklearn.linear_model.elasticnet#sklearn.linear_model.ElasticNet "sklearn.linear_model.ElasticNet")
Linear regression with combined L1 and L2 priors as regularizer.
[`ElasticNetCV`](#sklearn.linear_model.ElasticNetCV "sklearn.linear_model.ElasticNetCV")
Elastic Net model with iterative fitting along a regularization path.
#### Notes
For an example, see [examples/linear\_model/plot\_lasso\_coordinate\_descent\_path.py](../../auto_examples/linear_model/plot_lasso_coordinate_descent_path#sphx-glr-auto-examples-linear-model-plot-lasso-coordinate-descent-path-py).
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L372)
Predict using the linear model.
Parameters:
**X**array-like or sparse matrix, shape (n\_samples, n\_features)
Samples.
Returns:
**C**array, shape (n\_samples,)
Returns predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
| programming_docs |
scikit_learn sklearn.exceptions.NotFittedError sklearn.exceptions.NotFittedError
=================================
*class*sklearn.exceptions.NotFittedError[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/exceptions.py#L19)
Exception class to raise if estimator is used before fitting.
This class inherits from both ValueError and AttributeError to help with exception handling and backward compatibility.
Attributes:
**args**
#### Examples
```
>>> from sklearn.svm import LinearSVC
>>> from sklearn.exceptions import NotFittedError
>>> try:
... LinearSVC().predict([[1, 2], [2, 3], [3, 4]])
... except NotFittedError as e:
... print(repr(e))
NotFittedError("This LinearSVC instance is not fitted yet. Call 'fit' with
appropriate arguments before using this estimator."...)
```
Changed in version 0.18: Moved from sklearn.utils.validation.
#### Methods
| | |
| --- | --- |
| [`with_traceback`](#sklearn.exceptions.NotFittedError.with_traceback "sklearn.exceptions.NotFittedError.with_traceback") | Exception.with\_traceback(tb) -- set self.\_\_traceback\_\_ to tb and return self. |
with\_traceback()
Exception.with\_traceback(tb) – set self.\_\_traceback\_\_ to tb and return self.
scikit_learn sklearn.show_versions sklearn.show\_versions
======================
sklearn.show\_versions()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/_show_versions.py#L96)
Print useful debugging information”
New in version 0.20.
scikit_learn sklearn.model_selection.StratifiedGroupKFold sklearn.model\_selection.StratifiedGroupKFold
=============================================
*class*sklearn.model\_selection.StratifiedGroupKFold(*n\_splits=5*, *shuffle=False*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L759)
Stratified K-Folds iterator variant with non-overlapping groups.
This cross-validation object is a variation of StratifiedKFold attempts to return stratified folds with non-overlapping groups. The folds are made by preserving the percentage of samples for each class.
Each group will appear exactly once in the test set across all folds (the number of distinct groups has to be at least equal to the number of folds).
The difference between [`GroupKFold`](sklearn.model_selection.groupkfold#sklearn.model_selection.GroupKFold "sklearn.model_selection.GroupKFold") and [`StratifiedGroupKFold`](#sklearn.model_selection.StratifiedGroupKFold "sklearn.model_selection.StratifiedGroupKFold") is that the former attempts to create balanced folds such that the number of distinct groups is approximately the same in each fold, whereas StratifiedGroupKFold attempts to create folds which preserve the percentage of samples for each class as much as possible given the constraint of non-overlapping groups between splits.
Read more in the [User Guide](../cross_validation#cross-validation).
Parameters:
**n\_splits**int, default=5
Number of folds. Must be at least 2.
**shuffle**bool, default=False
Whether to shuffle each class’s samples before splitting into batches. Note that the samples within each split will not be shuffled. This implementation can only shuffle groups that have approximately the same y distribution, no global shuffle will be performed.
**random\_state**int or RandomState instance, default=None
When `shuffle` is True, `random_state` affects the ordering of the indices, which controls the randomness of each fold for each class. Otherwise, leave `random_state` as `None`. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
See also
[`StratifiedKFold`](sklearn.model_selection.stratifiedkfold#sklearn.model_selection.StratifiedKFold "sklearn.model_selection.StratifiedKFold")
Takes class information into account to build folds which retain class distributions (for binary or multiclass classification tasks).
[`GroupKFold`](sklearn.model_selection.groupkfold#sklearn.model_selection.GroupKFold "sklearn.model_selection.GroupKFold")
K-fold iterator variant with non-overlapping groups.
#### Notes
The implementation is designed to:
* Mimic the behavior of StratifiedKFold as much as possible for trivial groups (e.g. when each group contains only one sample).
* Be invariant to class label: relabelling `y = ["Happy", "Sad"]` to `y = [1, 0]` should not change the indices generated.
* Stratify based on samples as much as possible while keeping non-overlapping groups constraint. That means that in some cases when there is a small number of groups containing a large number of samples the stratification will not be possible and the behavior will be close to GroupKFold.
#### Examples
```
>>> import numpy as np
>>> from sklearn.model_selection import StratifiedGroupKFold
>>> X = np.ones((17, 2))
>>> y = np.array([0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0])
>>> groups = np.array([1, 1, 2, 2, 3, 3, 3, 4, 5, 5, 5, 5, 6, 6, 7, 8, 8])
>>> cv = StratifiedGroupKFold(n_splits=3)
>>> for train_idxs, test_idxs in cv.split(X, y, groups):
... print("TRAIN:", groups[train_idxs])
... print(" ", y[train_idxs])
... print(" TEST:", groups[test_idxs])
... print(" ", y[test_idxs])
TRAIN: [1 1 2 2 4 5 5 5 5 8 8]
[0 0 1 1 1 0 0 0 0 0 0]
TEST: [3 3 3 6 6 7]
[1 1 1 0 0 0]
TRAIN: [3 3 3 4 5 5 5 5 6 6 7]
[1 1 1 1 0 0 0 0 0 0 0]
TEST: [1 1 2 2 8 8]
[0 0 1 1 0 0]
TRAIN: [1 1 2 2 3 3 3 6 6 7 8 8]
[0 0 1 1 1 1 1 0 0 0 0 0]
TEST: [4 5 5 5 5]
[1 0 0 0 0]
```
#### Methods
| | |
| --- | --- |
| [`get_n_splits`](#sklearn.model_selection.StratifiedGroupKFold.get_n_splits "sklearn.model_selection.StratifiedGroupKFold.get_n_splits")([X, y, groups]) | Returns the number of splitting iterations in the cross-validator |
| [`split`](#sklearn.model_selection.StratifiedGroupKFold.split "sklearn.model_selection.StratifiedGroupKFold.split")(X[, y, groups]) | Generate indices to split data into training and test set. |
get\_n\_splits(*X=None*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L343)
Returns the number of splitting iterations in the cross-validator
Parameters:
**X**object
Always ignored, exists for compatibility.
**y**object
Always ignored, exists for compatibility.
**groups**object
Always ignored, exists for compatibility.
Returns:
**n\_splits**int
Returns the number of splitting iterations in the cross-validator.
split(*X*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L306)
Generate indices to split data into training and test set.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,), default=None
The target variable for supervised learning problems.
**groups**array-like of shape (n\_samples,), default=None
Group labels for the samples used while splitting the dataset into train/test set.
Yields:
**train**ndarray
The training set indices for that split.
**test**ndarray
The testing set indices for that split.
Examples using `sklearn.model_selection.StratifiedGroupKFold`
-------------------------------------------------------------
[Visualizing cross-validation behavior in scikit-learn](../../auto_examples/model_selection/plot_cv_indices#sphx-glr-auto-examples-model-selection-plot-cv-indices-py)
scikit_learn sklearn.utils.class_weight.compute_sample_weight sklearn.utils.class\_weight.compute\_sample\_weight
===================================================
sklearn.utils.class\_weight.compute\_sample\_weight(*class\_weight*, *y*, *\**, *indices=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/class_weight.py#L79)
Estimate sample weights by class for unbalanced datasets.
Parameters:
**class\_weight**dict, list of dicts, “balanced”, or None
Weights associated with classes in the form `{class_label: weight}`. If not given, all classes are supposed to have weight one. For multi-output problems, a list of dicts can be provided in the same order as the columns of y.
Note that for multioutput (including multilabel) weights should be defined for each class of every column in its own dict. For example, for four-class multilabel classification weights should be [{0: 1, 1: 1}, {0: 1, 1: 5}, {0: 1, 1: 1}, {0: 1, 1: 1}] instead of [{1:1}, {2:5}, {3:1}, {4:1}].
The “balanced” mode uses the values of y to automatically adjust weights inversely proportional to class frequencies in the input data: `n_samples / (n_classes * np.bincount(y))`.
For multi-output, the weights of each column of y will be multiplied.
**y**{array-like, sparse matrix} of shape (n\_samples,) or (n\_samples, n\_outputs)
Array of original class labels per sample.
**indices**array-like of shape (n\_subsample,), default=None
Array of indices to be used in a subsample. Can be of length less than n\_samples in the case of a subsample, or equal to n\_samples in the case of a bootstrap subsample with repeated indices. If None, the sample weight will be calculated over the full sample. Only “balanced” is supported for class\_weight if this is provided.
Returns:
**sample\_weight\_vect**ndarray of shape (n\_samples,)
Array with sample weights as applied to the original y.
scikit_learn sklearn.compose.make_column_transformer sklearn.compose.make\_column\_transformer
=========================================
sklearn.compose.make\_column\_transformer(*\*transformers*, *remainder='drop'*, *sparse\_threshold=0.3*, *n\_jobs=None*, *verbose=False*, *verbose\_feature\_names\_out=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/compose/_column_transformer.py#L868)
Construct a ColumnTransformer from the given transformers.
This is a shorthand for the ColumnTransformer constructor; it does not require, and does not permit, naming the transformers. Instead, they will be given names automatically based on their types. It also does not allow weighting with `transformer_weights`.
Read more in the [User Guide](../compose#make-column-transformer).
Parameters:
**\*transformers**tuples
Tuples of the form (transformer, columns) specifying the transformer objects to be applied to subsets of the data.
transformer{‘drop’, ‘passthrough’} or estimator
Estimator must support [fit](https://scikit-learn.org/1.1/glossary.html#term-fit) and [transform](https://scikit-learn.org/1.1/glossary.html#term-transform). Special-cased strings ‘drop’ and ‘passthrough’ are accepted as well, to indicate to drop the columns or to pass them through untransformed, respectively.
columnsstr, array-like of str, int, array-like of int, slice, array-like of bool or callable
Indexes the data on its second axis. Integers are interpreted as positional columns, while strings can reference DataFrame columns by name. A scalar string or int should be used where `transformer` expects X to be a 1d array-like (vector), otherwise a 2d array will be passed to the transformer. A callable is passed the input data `X` and can return any of the above. To select multiple columns by name or dtype, you can use [`make_column_selector`](sklearn.compose.make_column_selector#sklearn.compose.make_column_selector "sklearn.compose.make_column_selector").
**remainder**{‘drop’, ‘passthrough’} or estimator, default=’drop’
By default, only the specified columns in `transformers` are transformed and combined in the output, and the non-specified columns are dropped. (default of `'drop'`). By specifying `remainder='passthrough'`, all remaining columns that were not specified in `transformers` will be automatically passed through. This subset of columns is concatenated with the output of the transformers. By setting `remainder` to be an estimator, the remaining non-specified columns will use the `remainder` estimator. The estimator must support [fit](https://scikit-learn.org/1.1/glossary.html#term-fit) and [transform](https://scikit-learn.org/1.1/glossary.html#term-transform).
**sparse\_threshold**float, default=0.3
If the transformed output consists of a mix of sparse and dense data, it will be stacked as a sparse matrix if the density is lower than this value. Use `sparse_threshold=0` to always return dense. When the transformed output consists of all sparse or all dense data, the stacked result will be sparse or dense, respectively, and this keyword will be ignored.
**n\_jobs**int, default=None
Number of jobs to run in parallel. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**verbose**bool, default=False
If True, the time elapsed while fitting each transformer will be printed as it is completed.
**verbose\_feature\_names\_out**bool, default=True
If True, `get_feature_names_out` will prefix all feature names with the name of the transformer that generated that feature. If False, `get_feature_names_out` will not prefix any feature names and will error if feature names are not unique.
New in version 1.0.
Returns:
**ct**ColumnTransformer
Returns a [`ColumnTransformer`](sklearn.compose.columntransformer#sklearn.compose.ColumnTransformer "sklearn.compose.ColumnTransformer") object.
See also
[`ColumnTransformer`](sklearn.compose.columntransformer#sklearn.compose.ColumnTransformer "sklearn.compose.ColumnTransformer")
Class that allows combining the outputs of multiple transformer objects used on column subsets of the data into a single feature space.
#### Examples
```
>>> from sklearn.preprocessing import StandardScaler, OneHotEncoder
>>> from sklearn.compose import make_column_transformer
>>> make_column_transformer(
... (StandardScaler(), ['numerical_column']),
... (OneHotEncoder(), ['categorical_column']))
ColumnTransformer(transformers=[('standardscaler', StandardScaler(...),
['numerical_column']),
('onehotencoder', OneHotEncoder(...),
['categorical_column'])])
```
Examples using `sklearn.compose.make_column_transformer`
--------------------------------------------------------
[Release Highlights for scikit-learn 0.23](../../auto_examples/release_highlights/plot_release_highlights_0_23_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-23-0-py)
[Categorical Feature Support in Gradient Boosting](../../auto_examples/ensemble/plot_gradient_boosting_categorical#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-categorical-py)
[Combine predictors using stacking](../../auto_examples/ensemble/plot_stack_predictors#sphx-glr-auto-examples-ensemble-plot-stack-predictors-py)
[Common pitfalls in the interpretation of coefficients of linear models](../../auto_examples/inspection/plot_linear_model_coefficient_interpretation#sphx-glr-auto-examples-inspection-plot-linear-model-coefficient-interpretation-py)
scikit_learn sklearn.datasets.make_biclusters sklearn.datasets.make\_biclusters
=================================
sklearn.datasets.make\_biclusters(*shape*, *n\_clusters*, *\**, *noise=0.0*, *minval=10*, *maxval=100*, *shuffle=True*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_samples_generator.py#L1708)
Generate a constant block diagonal structure array for biclustering.
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/sample_generators.html#sample-generators).
Parameters:
**shape**iterable of shape (n\_rows, n\_cols)
The shape of the result.
**n\_clusters**int
The number of biclusters.
**noise**float, default=0.0
The standard deviation of the gaussian noise.
**minval**int, default=10
Minimum value of a bicluster.
**maxval**int, default=100
Maximum value of a bicluster.
**shuffle**bool, default=True
Shuffle the samples.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for dataset creation. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Returns:
**X**ndarray of shape `shape`
The generated array.
**rows**ndarray of shape (n\_clusters, X.shape[0])
The indicators for cluster membership of each row.
**cols**ndarray of shape (n\_clusters, X.shape[1])
The indicators for cluster membership of each column.
See also
[`make_checkerboard`](sklearn.datasets.make_checkerboard#sklearn.datasets.make_checkerboard "sklearn.datasets.make_checkerboard")
Generate an array with block checkerboard structure for biclustering.
#### References
[1] Dhillon, I. S. (2001, August). Co-clustering documents and words using bipartite spectral graph partitioning. In Proceedings of the seventh ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 269-274). ACM.
Examples using `sklearn.datasets.make_biclusters`
-------------------------------------------------
[A demo of the Spectral Co-Clustering algorithm](../../auto_examples/bicluster/plot_spectral_coclustering#sphx-glr-auto-examples-bicluster-plot-spectral-coclustering-py)
scikit_learn sklearn.model_selection.GroupShuffleSplit sklearn.model\_selection.GroupShuffleSplit
==========================================
*class*sklearn.model\_selection.GroupShuffleSplit(*n\_splits=5*, *\**, *test\_size=None*, *train\_size=None*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L1746)
Shuffle-Group(s)-Out cross-validation iterator
Provides randomized train/test indices to split data according to a third-party provided group. This group information can be used to encode arbitrary domain specific stratifications of the samples as integers.
For instance the groups could be the year of collection of the samples and thus allow for cross-validation against time-based splits.
The difference between LeavePGroupsOut and GroupShuffleSplit is that the former generates splits using all subsets of size `p` unique groups, whereas GroupShuffleSplit generates a user-determined number of random test splits, each with a user-determined fraction of unique groups.
For example, a less computationally intensive alternative to `LeavePGroupsOut(p=10)` would be `GroupShuffleSplit(test_size=10, n_splits=100)`.
Note: The parameters `test_size` and `train_size` refer to groups, and not to samples, as in ShuffleSplit.
Read more in the [User Guide](../cross_validation#group-shuffle-split).
Parameters:
**n\_splits**int, default=5
Number of re-shuffling & splitting iterations.
**test\_size**float, int, default=0.2
If float, should be between 0.0 and 1.0 and represent the proportion of groups to include in the test split (rounded up). If int, represents the absolute number of test groups. If None, the value is set to the complement of the train size. The default will change in version 0.21. It will remain 0.2 only if `train_size` is unspecified, otherwise it will complement the specified `train_size`.
**train\_size**float or int, default=None
If float, should be between 0.0 and 1.0 and represent the proportion of the groups to include in the train split. If int, represents the absolute number of train groups. If None, the value is automatically set to the complement of the test size.
**random\_state**int, RandomState instance or None, default=None
Controls the randomness of the training and testing indices produced. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
See also
[`ShuffleSplit`](sklearn.model_selection.shufflesplit#sklearn.model_selection.ShuffleSplit "sklearn.model_selection.ShuffleSplit")
Shuffles samples to create independent test/train sets.
[`LeavePGroupsOut`](sklearn.model_selection.leavepgroupsout#sklearn.model_selection.LeavePGroupsOut "sklearn.model_selection.LeavePGroupsOut")
Train set leaves out all possible subsets of `p` groups.
#### Examples
```
>>> import numpy as np
>>> from sklearn.model_selection import GroupShuffleSplit
>>> X = np.ones(shape=(8, 2))
>>> y = np.ones(shape=(8, 1))
>>> groups = np.array([1, 1, 2, 2, 2, 3, 3, 3])
>>> print(groups.shape)
(8,)
>>> gss = GroupShuffleSplit(n_splits=2, train_size=.7, random_state=42)
>>> gss.get_n_splits()
2
>>> for train_idx, test_idx in gss.split(X, y, groups):
... print("TRAIN:", train_idx, "TEST:", test_idx)
TRAIN: [2 3 4 5 6 7] TEST: [0 1]
TRAIN: [0 1 5 6 7] TEST: [2 3 4]
```
#### Methods
| | |
| --- | --- |
| [`get_n_splits`](#sklearn.model_selection.GroupShuffleSplit.get_n_splits "sklearn.model_selection.GroupShuffleSplit.get_n_splits")([X, y, groups]) | Returns the number of splitting iterations in the cross-validator |
| [`split`](#sklearn.model_selection.GroupShuffleSplit.split "sklearn.model_selection.GroupShuffleSplit.split")(X[, y, groups]) | Generate indices to split data into training and test set. |
get\_n\_splits(*X=None*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L1629)
Returns the number of splitting iterations in the cross-validator
Parameters:
**X**object
Always ignored, exists for compatibility.
**y**object
Always ignored, exists for compatibility.
**groups**object
Always ignored, exists for compatibility.
Returns:
**n\_splits**int
Returns the number of splitting iterations in the cross-validator.
split(*X*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L1844)
Generate indices to split data into training and test set.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,), default=None
The target variable for supervised learning problems.
**groups**array-like of shape (n\_samples,)
Group labels for the samples used while splitting the dataset into train/test set.
Yields:
**train**ndarray
The training set indices for that split.
**test**ndarray
The testing set indices for that split.
#### Notes
Randomized CV splitters may return different results for each call of split. You can make the results identical by setting `random_state` to an integer.
Examples using `sklearn.model_selection.GroupShuffleSplit`
----------------------------------------------------------
[Visualizing cross-validation behavior in scikit-learn](../../auto_examples/model_selection/plot_cv_indices#sphx-glr-auto-examples-model-selection-plot-cv-indices-py)
| programming_docs |
scikit_learn sklearn.utils.class_weight.compute_class_weight sklearn.utils.class\_weight.compute\_class\_weight
==================================================
sklearn.utils.class\_weight.compute\_class\_weight(*class\_weight*, *\**, *classes*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/class_weight.py#L10)
Estimate class weights for unbalanced datasets.
Parameters:
**class\_weight**dict, ‘balanced’ or None
If ‘balanced’, class weights will be given by `n_samples / (n_classes * np.bincount(y))`. If a dictionary is given, keys are classes and values are corresponding class weights. If None is given, the class weights will be uniform.
**classes**ndarray
Array of the classes occurring in the data, as given by `np.unique(y_org)` with `y_org` the original class labels.
**y**array-like of shape (n\_samples,)
Array of original class labels per sample.
Returns:
**class\_weight\_vect**ndarray of shape (n\_classes,)
Array with class\_weight\_vect[i] the weight for i-th class.
#### References
The “balanced” heuristic is inspired by Logistic Regression in Rare Events Data, King, Zen, 2001.
scikit_learn sklearn.feature_extraction.text.TfidfTransformer sklearn.feature\_extraction.text.TfidfTransformer
=================================================
*class*sklearn.feature\_extraction.text.TfidfTransformer(*\**, *norm='l2'*, *use\_idf=True*, *smooth\_idf=True*, *sublinear\_tf=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L1469)
Transform a count matrix to a normalized tf or tf-idf representation.
Tf means term-frequency while tf-idf means term-frequency times inverse document-frequency. This is a common term weighting scheme in information retrieval, that has also found good use in document classification.
The goal of using tf-idf instead of the raw frequencies of occurrence of a token in a given document is to scale down the impact of tokens that occur very frequently in a given corpus and that are hence empirically less informative than features that occur in a small fraction of the training corpus.
The formula that is used to compute the tf-idf for a term t of a document d in a document set is tf-idf(t, d) = tf(t, d) \* idf(t), and the idf is computed as idf(t) = log [ n / df(t) ] + 1 (if `smooth_idf=False`), where n is the total number of documents in the document set and df(t) is the document frequency of t; the document frequency is the number of documents in the document set that contain the term t. The effect of adding “1” to the idf in the equation above is that terms with zero idf, i.e., terms that occur in all documents in a training set, will not be entirely ignored. (Note that the idf formula above differs from the standard textbook notation that defines the idf as idf(t) = log [ n / (df(t) + 1) ]).
If `smooth_idf=True` (the default), the constant “1” is added to the numerator and denominator of the idf as if an extra document was seen containing every term in the collection exactly once, which prevents zero divisions: idf(t) = log [ (1 + n) / (1 + df(t)) ] + 1.
Furthermore, the formulas used to compute tf and idf depend on parameter settings that correspond to the SMART notation used in IR as follows:
Tf is “n” (natural) by default, “l” (logarithmic) when `sublinear_tf=True`. Idf is “t” when use\_idf is given, “n” (none) otherwise. Normalization is “c” (cosine) when `norm='l2'`, “n” (none) when `norm=None`.
Read more in the [User Guide](../feature_extraction#text-feature-extraction).
Parameters:
**norm**{‘l1’, ‘l2’}, default=’l2’
Each output row will have unit norm, either:
* ‘l2’: Sum of squares of vector elements is 1. The cosine similarity between two vectors is their dot product when l2 norm has been applied.
* ‘l1’: Sum of absolute values of vector elements is 1. See `preprocessing.normalize`.
* None: No normalization.
**use\_idf**bool, default=True
Enable inverse-document-frequency reweighting. If False, idf(t) = 1.
**smooth\_idf**bool, default=True
Smooth idf weights by adding one to document frequencies, as if an extra document was seen containing every term in the collection exactly once. Prevents zero divisions.
**sublinear\_tf**bool, default=False
Apply sublinear tf scaling, i.e. replace tf with 1 + log(tf).
Attributes:
[`idf_`](#sklearn.feature_extraction.text.TfidfTransformer.idf_ "sklearn.feature_extraction.text.TfidfTransformer.idf_")array of shape (n\_features)
Inverse document frequency vector, only defined if `use_idf=True`.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 1.0.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`CountVectorizer`](sklearn.feature_extraction.text.countvectorizer#sklearn.feature_extraction.text.CountVectorizer "sklearn.feature_extraction.text.CountVectorizer")
Transforms text into a sparse matrix of n-gram counts.
[`TfidfVectorizer`](sklearn.feature_extraction.text.tfidfvectorizer#sklearn.feature_extraction.text.TfidfVectorizer "sklearn.feature_extraction.text.TfidfVectorizer")
Convert a collection of raw documents to a matrix of TF-IDF features.
[`HashingVectorizer`](sklearn.feature_extraction.text.hashingvectorizer#sklearn.feature_extraction.text.HashingVectorizer "sklearn.feature_extraction.text.HashingVectorizer")
Convert a collection of text documents to a matrix of token occurrences.
#### References
[Yates2011] R. Baeza-Yates and B. Ribeiro-Neto (2011). Modern Information Retrieval. Addison Wesley, pp. 68-74.
[MRS2008] C.D. Manning, P. Raghavan and H. Schütze (2008). Introduction to Information Retrieval. Cambridge University Press, pp. 118-120.
#### Examples
```
>>> from sklearn.feature_extraction.text import TfidfTransformer
>>> from sklearn.feature_extraction.text import CountVectorizer
>>> from sklearn.pipeline import Pipeline
>>> corpus = ['this is the first document',
... 'this document is the second document',
... 'and this is the third one',
... 'is this the first document']
>>> vocabulary = ['this', 'document', 'first', 'is', 'second', 'the',
... 'and', 'one']
>>> pipe = Pipeline([('count', CountVectorizer(vocabulary=vocabulary)),
... ('tfid', TfidfTransformer())]).fit(corpus)
>>> pipe['count'].transform(corpus).toarray()
array([[1, 1, 1, 1, 0, 1, 0, 0],
[1, 2, 0, 1, 1, 1, 0, 0],
[1, 0, 0, 1, 0, 1, 1, 1],
[1, 1, 1, 1, 0, 1, 0, 0]])
>>> pipe['tfid'].idf_
array([1. , 1.22314355, 1.51082562, 1. , 1.91629073,
1. , 1.91629073, 1.91629073])
>>> pipe.transform(corpus).shape
(4, 8)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.feature_extraction.text.TfidfTransformer.fit "sklearn.feature_extraction.text.TfidfTransformer.fit")(X[, y]) | Learn the idf vector (global term weights). |
| [`fit_transform`](#sklearn.feature_extraction.text.TfidfTransformer.fit_transform "sklearn.feature_extraction.text.TfidfTransformer.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.feature_extraction.text.TfidfTransformer.get_feature_names_out "sklearn.feature_extraction.text.TfidfTransformer.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.feature_extraction.text.TfidfTransformer.get_params "sklearn.feature_extraction.text.TfidfTransformer.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.feature_extraction.text.TfidfTransformer.set_params "sklearn.feature_extraction.text.TfidfTransformer.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.feature_extraction.text.TfidfTransformer.transform "sklearn.feature_extraction.text.TfidfTransformer.transform")(X[, copy]) | Transform a count matrix to a tf or tf-idf representation. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L1604)
Learn the idf vector (global term weights).
Parameters:
**X**sparse matrix of shape n\_samples, n\_features)
A matrix of term/token counts.
**y**None
This parameter is not needed to compute tf-idf.
Returns:
**self**object
Fitted transformer.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L880)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Input features.
* If `input_features` is `None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then the following input feature names are generated: `["x0", "x1", ..., "x(n_features_in_ - 1)"]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Same as input features.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*idf\_
Inverse document frequency vector, only defined if `use_idf=True`.
Returns:
ndarray of shape (n\_features,)
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*, *copy=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L1652)
Transform a count matrix to a tf or tf-idf representation.
Parameters:
**X**sparse matrix of (n\_samples, n\_features)
A matrix of term/token counts.
**copy**bool, default=True
Whether to copy X and operate on the copy or perform in-place operations.
Returns:
**vectors**sparse matrix of shape (n\_samples, n\_features)
Tf-idf-weighted document-term matrix.
Examples using `sklearn.feature_extraction.text.TfidfTransformer`
-----------------------------------------------------------------
[Sample pipeline for text feature extraction and evaluation](../../auto_examples/model_selection/grid_search_text_feature_extraction#sphx-glr-auto-examples-model-selection-grid-search-text-feature-extraction-py)
[Semi-supervised Classification on a Text Dataset](../../auto_examples/semi_supervised/plot_semi_supervised_newsgroups#sphx-glr-auto-examples-semi-supervised-plot-semi-supervised-newsgroups-py)
[Clustering text documents using k-means](../../auto_examples/text/plot_document_clustering#sphx-glr-auto-examples-text-plot-document-clustering-py)
[FeatureHasher and DictVectorizer Comparison](../../auto_examples/text/plot_hashing_vs_dict_vectorizer#sphx-glr-auto-examples-text-plot-hashing-vs-dict-vectorizer-py)
scikit_learn sklearn.set_config sklearn.set\_config
===================
sklearn.set\_config(*assume\_finite=None*, *working\_memory=None*, *print\_changed\_only=None*, *display=None*, *pairwise\_dist\_chunk\_size=None*, *enable\_cython\_pairwise\_dist=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/_config.py#L46)
Set global scikit-learn configuration
New in version 0.19.
Parameters:
**assume\_finite**bool, default=None
If True, validation for finiteness will be skipped, saving time, but leading to potential crashes. If False, validation for finiteness will be performed, avoiding error. Global default: False.
New in version 0.19.
**working\_memory**int, default=None
If set, scikit-learn will attempt to limit the size of temporary arrays to this number of MiB (per job when parallelised), often saving both computation time and memory on expensive operations that can be performed in chunks. Global default: 1024.
New in version 0.20.
**print\_changed\_only**bool, default=None
If True, only the parameters that were set to non-default values will be printed when printing an estimator. For example, `print(SVC())` while True will only print ‘SVC()’ while the default behaviour would be to print ‘SVC(C=1.0, cache\_size=200, …)’ with all the non-changed parameters.
New in version 0.21.
**display**{‘text’, ‘diagram’}, default=None
If ‘diagram’, estimators will be displayed as a diagram in a Jupyter lab or notebook context. If ‘text’, estimators will be displayed as text. Default is ‘diagram’.
New in version 0.23.
**pairwise\_dist\_chunk\_size**int, default=None
The number of row vectors per chunk for PairwiseDistancesReduction. Default is 256 (suitable for most of modern laptops’ caches and architectures).
Intended for easier benchmarking and testing of scikit-learn internals. End users are not expected to benefit from customizing this configuration setting.
New in version 1.1.
**enable\_cython\_pairwise\_dist**bool, default=None
Use PairwiseDistancesReduction when possible. Default is True.
Intended for easier benchmarking and testing of scikit-learn internals. End users are not expected to benefit from customizing this configuration setting.
New in version 1.1.
See also
[`config_context`](sklearn.config_context#sklearn.config_context "sklearn.config_context")
Context manager for global scikit-learn configuration.
[`get_config`](sklearn.get_config#sklearn.get_config "sklearn.get_config")
Retrieve current values of the global configuration.
Examples using `sklearn.set_config`
-----------------------------------
[Release Highlights for scikit-learn 0.23](../../auto_examples/release_highlights/plot_release_highlights_0_23_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-23-0-py)
[Compact estimator representations](../../auto_examples/miscellaneous/plot_changed_only_pprint_parameter#sphx-glr-auto-examples-miscellaneous-plot-changed-only-pprint-parameter-py)
[Displaying Pipelines](../../auto_examples/miscellaneous/plot_pipeline_display#sphx-glr-auto-examples-miscellaneous-plot-pipeline-display-py)
scikit_learn sklearn.datasets.load_sample_image sklearn.datasets.load\_sample\_image
====================================
sklearn.datasets.load\_sample\_image(*image\_name*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_base.py#L1417)
Load the numpy array of a single sample image.
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/loading_other_datasets.html#sample-images).
Parameters:
**image\_name**{`china.jpg`, `flower.jpg`}
The name of the sample image loaded.
Returns:
**img**3D array
The image as a numpy array: height x width x color.
#### Examples
```
>>> from sklearn.datasets import load_sample_image
>>> china = load_sample_image('china.jpg')
>>> china.dtype
dtype('uint8')
>>> china.shape
(427, 640, 3)
>>> flower = load_sample_image('flower.jpg')
>>> flower.dtype
dtype('uint8')
>>> flower.shape
(427, 640, 3)
```
Examples using `sklearn.datasets.load_sample_image`
---------------------------------------------------
[Color Quantization using K-Means](../../auto_examples/cluster/plot_color_quantization#sphx-glr-auto-examples-cluster-plot-color-quantization-py)
scikit_learn sklearn.feature_extraction.image.extract_patches_2d sklearn.feature\_extraction.image.extract\_patches\_2d
======================================================
sklearn.feature\_extraction.image.extract\_patches\_2d(*image*, *patch\_size*, *\**, *max\_patches=None*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/image.py#L323)
Reshape a 2D image into a collection of patches.
The resulting patches are allocated in a dedicated array.
Read more in the [User Guide](../feature_extraction#image-feature-extraction).
Parameters:
**image**ndarray of shape (image\_height, image\_width) or (image\_height, image\_width, n\_channels)
The original image data. For color images, the last dimension specifies the channel: a RGB image would have `n_channels=3`.
**patch\_size**tuple of int (patch\_height, patch\_width)
The dimensions of one patch.
**max\_patches**int or float, default=None
The maximum number of patches to extract. If `max_patches` is a float between 0 and 1, it is taken to be a proportion of the total number of patches.
**random\_state**int, RandomState instance, default=None
Determines the random number generator used for random sampling when `max_patches` is not None. Use an int to make the randomness deterministic. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Returns:
**patches**array of shape (n\_patches, patch\_height, patch\_width) or (n\_patches, patch\_height, patch\_width, n\_channels)
The collection of patches extracted from the image, where `n_patches` is either `max_patches` or the total number of patches that can be extracted.
#### Examples
```
>>> from sklearn.datasets import load_sample_image
>>> from sklearn.feature_extraction import image
>>> # Use the array data from the first image in this dataset:
>>> one_image = load_sample_image("china.jpg")
>>> print('Image shape: {}'.format(one_image.shape))
Image shape: (427, 640, 3)
>>> patches = image.extract_patches_2d(one_image, (2, 2))
>>> print('Patches shape: {}'.format(patches.shape))
Patches shape: (272214, 2, 2, 3)
>>> # Here are just two of these patches:
>>> print(patches[1])
[[[174 201 231]
[174 201 231]]
[[173 200 230]
[173 200 230]]]
>>> print(patches[800])
[[[187 214 243]
[188 215 244]]
[[187 214 243]
[188 215 244]]]
```
Examples using `sklearn.feature_extraction.image.extract_patches_2d`
--------------------------------------------------------------------
[Online learning of a dictionary of parts of faces](../../auto_examples/cluster/plot_dict_face_patches#sphx-glr-auto-examples-cluster-plot-dict-face-patches-py)
[Image denoising using dictionary learning](../../auto_examples/decomposition/plot_image_denoising#sphx-glr-auto-examples-decomposition-plot-image-denoising-py)
| programming_docs |
scikit_learn sklearn.metrics.log_loss sklearn.metrics.log\_loss
=========================
sklearn.metrics.log\_loss(*y\_true*, *y\_pred*, *\**, *eps=1e-15*, *normalize=True*, *sample\_weight=None*, *labels=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_classification.py#L2331)
Log loss, aka logistic loss or cross-entropy loss.
This is the loss function used in (multinomial) logistic regression and extensions of it such as neural networks, defined as the negative log-likelihood of a logistic model that returns `y_pred` probabilities for its training data `y_true`. The log loss is only defined for two or more labels. For a single sample with true label \(y \in \{0,1\}\) and a probability estimate \(p = \operatorname{Pr}(y = 1)\), the log loss is:
\[L\_{\log}(y, p) = -(y \log (p) + (1 - y) \log (1 - p))\] Read more in the [User Guide](../model_evaluation#log-loss).
Parameters:
**y\_true**array-like or label indicator matrix
Ground truth (correct) labels for n\_samples samples.
**y\_pred**array-like of float, shape = (n\_samples, n\_classes) or (n\_samples,)
Predicted probabilities, as returned by a classifier’s predict\_proba method. If `y_pred.shape = (n_samples,)` the probabilities provided are assumed to be that of the positive class. The labels in `y_pred` are assumed to be ordered alphabetically, as done by `preprocessing.LabelBinarizer`.
**eps**float, default=1e-15
Log loss is undefined for p=0 or p=1, so probabilities are clipped to max(eps, min(1 - eps, p)).
**normalize**bool, default=True
If true, return the mean loss per sample. Otherwise, return the sum of the per-sample losses.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**labels**array-like, default=None
If not provided, labels will be inferred from y\_true. If `labels` is `None` and `y_pred` has shape (n\_samples,) the labels are assumed to be binary and are inferred from `y_true`.
New in version 0.18.
Returns:
**loss**float
Log loss, aka logistic loss or cross-entropy loss.
#### Notes
The logarithm used is the natural logarithm (base-e).
#### References
C.M. Bishop (2006). Pattern Recognition and Machine Learning. Springer, p. 209.
#### Examples
```
>>> from sklearn.metrics import log_loss
>>> log_loss(["spam", "ham", "ham", "spam"],
... [[.1, .9], [.9, .1], [.8, .2], [.35, .65]])
0.21616...
```
Examples using `sklearn.metrics.log_loss`
-----------------------------------------
[Probability Calibration curves](../../auto_examples/calibration/plot_calibration_curve#sphx-glr-auto-examples-calibration-plot-calibration-curve-py)
[Probability Calibration for 3-class classification](../../auto_examples/calibration/plot_calibration_multiclass#sphx-glr-auto-examples-calibration-plot-calibration-multiclass-py)
[Probabilistic predictions with Gaussian process classification (GPC)](../../auto_examples/gaussian_process/plot_gpc#sphx-glr-auto-examples-gaussian-process-plot-gpc-py)
scikit_learn sklearn.linear_model.OrthogonalMatchingPursuit sklearn.linear\_model.OrthogonalMatchingPursuit
===============================================
*class*sklearn.linear\_model.OrthogonalMatchingPursuit(*\**, *n\_nonzero\_coefs=None*, *tol=None*, *fit\_intercept=True*, *normalize='deprecated'*, *precompute='auto'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_omp.py#L591)
Orthogonal Matching Pursuit model (OMP).
Read more in the [User Guide](../linear_model#omp).
Parameters:
**n\_nonzero\_coefs**int, default=None
Desired number of non-zero entries in the solution. If None (by default) this value is set to 10% of n\_features.
**tol**float, default=None
Maximum norm of the residual. If not None, overrides n\_nonzero\_coefs.
**fit\_intercept**bool, default=True
Whether to calculate the intercept for this model. If set to false, no intercept will be used in calculations (i.e. data is expected to be centered).
**normalize**bool, default=True
This parameter is ignored when `fit_intercept` is set to False. If True, the regressors X will be normalized before regression by subtracting the mean and dividing by the l2-norm. If you wish to standardize, please use [`StandardScaler`](sklearn.preprocessing.standardscaler#sklearn.preprocessing.StandardScaler "sklearn.preprocessing.StandardScaler") before calling `fit` on an estimator with `normalize=False`.
Deprecated since version 1.0: `normalize` was deprecated in version 1.0. It will default to False in 1.2 and be removed in 1.4.
**precompute**‘auto’ or bool, default=’auto’
Whether to use a precomputed Gram and Xy matrix to speed up calculations. Improves performance when [n\_targets](https://scikit-learn.org/1.1/glossary.html#term-n_targets) or [n\_samples](https://scikit-learn.org/1.1/glossary.html#term-n_samples) is very large. Note that if you already have such matrices, you can pass them directly to the fit method.
Attributes:
**coef\_**ndarray of shape (n\_features,) or (n\_targets, n\_features)
Parameter vector (w in the formula).
**intercept\_**float or ndarray of shape (n\_targets,)
Independent term in decision function.
**n\_iter\_**int or array-like
Number of active features across every target.
**n\_nonzero\_coefs\_**int
The number of non-zero coefficients in the solution. If `n_nonzero_coefs` is None and `tol` is None this value is either set to 10% of `n_features` or 1, whichever is greater.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`orthogonal_mp`](sklearn.linear_model.orthogonal_mp#sklearn.linear_model.orthogonal_mp "sklearn.linear_model.orthogonal_mp")
Solves n\_targets Orthogonal Matching Pursuit problems.
[`orthogonal_mp_gram`](sklearn.linear_model.orthogonal_mp_gram#sklearn.linear_model.orthogonal_mp_gram "sklearn.linear_model.orthogonal_mp_gram")
Solves n\_targets Orthogonal Matching Pursuit problems using only the Gram matrix X.T \* X and the product X.T \* y.
[`lars_path`](sklearn.linear_model.lars_path#sklearn.linear_model.lars_path "sklearn.linear_model.lars_path")
Compute Least Angle Regression or Lasso path using LARS algorithm.
[`Lars`](sklearn.linear_model.lars#sklearn.linear_model.Lars "sklearn.linear_model.Lars")
Least Angle Regression model a.k.a. LAR.
[`LassoLars`](sklearn.linear_model.lassolars#sklearn.linear_model.LassoLars "sklearn.linear_model.LassoLars")
Lasso model fit with Least Angle Regression a.k.a. Lars.
[`sklearn.decomposition.sparse_encode`](sklearn.decomposition.sparse_encode#sklearn.decomposition.sparse_encode "sklearn.decomposition.sparse_encode")
Generic sparse coding. Each column of the result is the solution to a Lasso problem.
[`OrthogonalMatchingPursuitCV`](sklearn.linear_model.orthogonalmatchingpursuitcv#sklearn.linear_model.OrthogonalMatchingPursuitCV "sklearn.linear_model.OrthogonalMatchingPursuitCV")
Cross-validated Orthogonal Matching Pursuit model (OMP).
#### Notes
Orthogonal matching pursuit was introduced in G. Mallat, Z. Zhang, Matching pursuits with time-frequency dictionaries, IEEE Transactions on Signal Processing, Vol. 41, No. 12. (December 1993), pp. 3397-3415. (<https://www.di.ens.fr/~mallat/papiers/MallatPursuit93.pdf>)
This implementation is based on Rubinstein, R., Zibulevsky, M. and Elad, M., Efficient Implementation of the K-SVD Algorithm using Batch Orthogonal Matching Pursuit Technical Report - CS Technion, April 2008. <https://www.cs.technion.ac.il/~ronrubin/Publications/KSVD-OMP-v2.pdf>
#### Examples
```
>>> from sklearn.linear_model import OrthogonalMatchingPursuit
>>> from sklearn.datasets import make_regression
>>> X, y = make_regression(noise=4, random_state=0)
>>> reg = OrthogonalMatchingPursuit(normalize=False).fit(X, y)
>>> reg.score(X, y)
0.9991...
>>> reg.predict(X[:1,])
array([-78.3854...])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.linear_model.OrthogonalMatchingPursuit.fit "sklearn.linear_model.OrthogonalMatchingPursuit.fit")(X, y) | Fit the model using X, y as training data. |
| [`get_params`](#sklearn.linear_model.OrthogonalMatchingPursuit.get_params "sklearn.linear_model.OrthogonalMatchingPursuit.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.linear_model.OrthogonalMatchingPursuit.predict "sklearn.linear_model.OrthogonalMatchingPursuit.predict")(X) | Predict using the linear model. |
| [`score`](#sklearn.linear_model.OrthogonalMatchingPursuit.score "sklearn.linear_model.OrthogonalMatchingPursuit.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.linear_model.OrthogonalMatchingPursuit.set_params "sklearn.linear_model.OrthogonalMatchingPursuit.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_omp.py#L707)
Fit the model using X, y as training data.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_targets)
Target values. Will be cast to X’s dtype if necessary.
Returns:
**self**object
Returns an instance of self.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L372)
Predict using the linear model.
Parameters:
**X**array-like or sparse matrix, shape (n\_samples, n\_features)
Samples.
Returns:
**C**array, shape (n\_samples,)
Returns predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.linear_model.OrthogonalMatchingPursuit`
---------------------------------------------------------------
[Orthogonal Matching Pursuit](../../auto_examples/linear_model/plot_omp#sphx-glr-auto-examples-linear-model-plot-omp-py)
scikit_learn sklearn.preprocessing.Binarizer sklearn.preprocessing.Binarizer
===============================
*class*sklearn.preprocessing.Binarizer(*\**, *threshold=0.0*, *copy=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L2003)
Binarize data (set feature values to 0 or 1) according to a threshold.
Values greater than the threshold map to 1, while values less than or equal to the threshold map to 0. With the default threshold of 0, only positive values map to 1.
Binarization is a common operation on text count data where the analyst can decide to only consider the presence or absence of a feature rather than a quantified number of occurrences for instance.
It can also be used as a pre-processing step for estimators that consider boolean random variables (e.g. modelled using the Bernoulli distribution in a Bayesian setting).
Read more in the [User Guide](../preprocessing#preprocessing-binarization).
Parameters:
**threshold**float, default=0.0
Feature values below or equal to this are replaced by 0, above it by 1. Threshold may not be less than 0 for operations on sparse matrices.
**copy**bool, default=True
Set to False to perform inplace binarization and avoid a copy (if the input is already a numpy array or a scipy.sparse CSR matrix).
Attributes:
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`binarize`](sklearn.preprocessing.binarize#sklearn.preprocessing.binarize "sklearn.preprocessing.binarize")
Equivalent function without the estimator API.
[`KBinsDiscretizer`](sklearn.preprocessing.kbinsdiscretizer#sklearn.preprocessing.KBinsDiscretizer "sklearn.preprocessing.KBinsDiscretizer")
Bin continuous data into intervals.
[`OneHotEncoder`](sklearn.preprocessing.onehotencoder#sklearn.preprocessing.OneHotEncoder "sklearn.preprocessing.OneHotEncoder")
Encode categorical features as a one-hot numeric array.
#### Notes
If the input is a sparse matrix, only the non-zero values are subject to update by the Binarizer class.
This estimator is stateless (besides constructor parameters), the fit method does nothing but is useful when used in a pipeline.
#### Examples
```
>>> from sklearn.preprocessing import Binarizer
>>> X = [[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]]
>>> transformer = Binarizer().fit(X) # fit does nothing.
>>> transformer
Binarizer()
>>> transformer.transform(X)
array([[1., 0., 1.],
[1., 0., 0.],
[0., 1., 0.]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.preprocessing.Binarizer.fit "sklearn.preprocessing.Binarizer.fit")(X[, y]) | Do nothing and return the estimator unchanged. |
| [`fit_transform`](#sklearn.preprocessing.Binarizer.fit_transform "sklearn.preprocessing.Binarizer.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.preprocessing.Binarizer.get_feature_names_out "sklearn.preprocessing.Binarizer.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.preprocessing.Binarizer.get_params "sklearn.preprocessing.Binarizer.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.preprocessing.Binarizer.set_params "sklearn.preprocessing.Binarizer.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.preprocessing.Binarizer.transform "sklearn.preprocessing.Binarizer.transform")(X[, copy]) | Binarize each element of X. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L2076)
Do nothing and return the estimator unchanged.
This method is just there to implement the usual API and hence work in pipelines.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data.
**y**None
Ignored.
Returns:
**self**object
Fitted transformer.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L880)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Input features.
* If `input_features` is `None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then the following input feature names are generated: `["x0", "x1", ..., "x(n_features_in_ - 1)"]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Same as input features.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*, *copy=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L2098)
Binarize each element of X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data to binarize, element by element. scipy.sparse matrices should be in CSR format to avoid an un-necessary copy.
**copy**bool
Copy the input X or not.
Returns:
**X\_tr**{ndarray, sparse matrix} of shape (n\_samples, n\_features)
Transformed array.
| programming_docs |
scikit_learn sklearn.linear_model.PoissonRegressor sklearn.linear\_model.PoissonRegressor
======================================
*class*sklearn.linear\_model.PoissonRegressor(*\**, *alpha=1.0*, *fit\_intercept=True*, *max\_iter=100*, *tol=0.0001*, *warm\_start=False*, *verbose=0*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_glm/glm.py#L463)
Generalized Linear Model with a Poisson distribution.
This regressor uses the ‘log’ link function.
Read more in the [User Guide](../linear_model#generalized-linear-regression).
New in version 0.23.
Parameters:
**alpha**float, default=1
Constant that multiplies the penalty term and thus determines the regularization strength. `alpha = 0` is equivalent to unpenalized GLMs. In this case, the design matrix `X` must have full column rank (no collinearities). Values must be in the range `[0.0, inf)`.
**fit\_intercept**bool, default=True
Specifies if a constant (a.k.a. bias or intercept) should be added to the linear predictor (X @ coef + intercept).
**max\_iter**int, default=100
The maximal number of iterations for the solver. Values must be in the range `[1, inf)`.
**tol**float, default=1e-4
Stopping criterion. For the lbfgs solver, the iteration will stop when `max{|g_j|, j = 1, ..., d} <= tol` where `g_j` is the j-th component of the gradient (derivative) of the objective function. Values must be in the range `(0.0, inf)`.
**warm\_start**bool, default=False
If set to `True`, reuse the solution of the previous call to `fit` as initialization for `coef_` and `intercept_` .
**verbose**int, default=0
For the lbfgs solver set verbose to any positive number for verbosity. Values must be in the range `[0, inf)`.
Attributes:
**coef\_**array of shape (n\_features,)
Estimated coefficients for the linear predictor (`X @ coef_ +
intercept_`) in the GLM.
**intercept\_**float
Intercept (a.k.a. bias) added to linear predictor.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_iter\_**int
Actual number of iterations used in the solver.
See also
[`TweedieRegressor`](sklearn.linear_model.tweedieregressor#sklearn.linear_model.TweedieRegressor "sklearn.linear_model.TweedieRegressor")
Generalized Linear Model with a Tweedie distribution.
#### Examples
```
>>> from sklearn import linear_model
>>> clf = linear_model.PoissonRegressor()
>>> X = [[1, 2], [2, 3], [3, 4], [4, 3]]
>>> y = [12, 17, 22, 21]
>>> clf.fit(X, y)
PoissonRegressor()
>>> clf.score(X, y)
0.990...
>>> clf.coef_
array([0.121..., 0.158...])
>>> clf.intercept_
2.088...
>>> clf.predict([[1, 1], [3, 4]])
array([10.676..., 21.875...])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.linear_model.PoissonRegressor.fit "sklearn.linear_model.PoissonRegressor.fit")(X, y[, sample\_weight]) | Fit a Generalized Linear Model. |
| [`get_params`](#sklearn.linear_model.PoissonRegressor.get_params "sklearn.linear_model.PoissonRegressor.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.linear_model.PoissonRegressor.predict "sklearn.linear_model.PoissonRegressor.predict")(X) | Predict using GLM with feature matrix X. |
| [`score`](#sklearn.linear_model.PoissonRegressor.score "sklearn.linear_model.PoissonRegressor.score")(X, y[, sample\_weight]) | Compute D^2, the percentage of deviance explained. |
| [`set_params`](#sklearn.linear_model.PoissonRegressor.set_params "sklearn.linear_model.PoissonRegressor.set_params")(\*\*params) | Set the parameters of this estimator. |
*property*family
DEPRECATED: Attribute `family` was deprecated in version 1.1 and will be removed in 1.3.
Ensure backward compatibility for the time of deprecation.
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_glm/glm.py#L144)
Fit a Generalized Linear Model.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training data.
**y**array-like of shape (n\_samples,)
Target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**self**object
Fitted model.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_glm/glm.py#L333)
Predict using GLM with feature matrix X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Samples.
Returns:
**y\_pred**array of shape (n\_samples,)
Returns predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_glm/glm.py#L351)
Compute D^2, the percentage of deviance explained.
D^2 is a generalization of the coefficient of determination R^2. R^2 uses squared error and D^2 uses the deviance of this GLM, see the [User Guide](../model_evaluation#regression-metrics).
D^2 is defined as \(D^2 = 1-\frac{D(y\_{true},y\_{pred})}{D\_{null}}\), \(D\_{null}\) is the null deviance, i.e. the deviance of a model with intercept alone, which corresponds to \(y\_{pred} = \bar{y}\). The mean \(\bar{y}\) is averaged by sample\_weight. Best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,)
True values of target.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
D^2 of self.predict(X) w.r.t. y.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.linear_model.PoissonRegressor`
------------------------------------------------------
[Release Highlights for scikit-learn 0.23](../../auto_examples/release_highlights/plot_release_highlights_0_23_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-23-0-py)
[Poisson regression and non-normal loss](../../auto_examples/linear_model/plot_poisson_regression_non_normal_loss#sphx-glr-auto-examples-linear-model-plot-poisson-regression-non-normal-loss-py)
[Tweedie regression on insurance claims](../../auto_examples/linear_model/plot_tweedie_regression_insurance_claims#sphx-glr-auto-examples-linear-model-plot-tweedie-regression-insurance-claims-py)
scikit_learn sklearn.manifold.Isomap sklearn.manifold.Isomap
=======================
*class*sklearn.manifold.Isomap(*\**, *n\_neighbors=5*, *radius=None*, *n\_components=2*, *eigen\_solver='auto'*, *tol=0*, *max\_iter=None*, *path\_method='auto'*, *neighbors\_algorithm='auto'*, *n\_jobs=None*, *metric='minkowski'*, *p=2*, *metric\_params=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_isomap.py#L22)
Isomap Embedding.
Non-linear dimensionality reduction through Isometric Mapping
Read more in the [User Guide](../manifold#isomap).
Parameters:
**n\_neighbors**int or None, default=5
Number of neighbors to consider for each point. If `n_neighbors` is an int, then `radius` must be `None`.
**radius**float or None, default=None
Limiting distance of neighbors to return. If `radius` is a float, then `n_neighbors` must be set to `None`.
New in version 1.1.
**n\_components**int, default=2
Number of coordinates for the manifold.
**eigen\_solver**{‘auto’, ‘arpack’, ‘dense’}, default=’auto’
‘auto’ : Attempt to choose the most efficient solver for the given problem.
‘arpack’ : Use Arnoldi decomposition to find the eigenvalues and eigenvectors.
‘dense’ : Use a direct solver (i.e. LAPACK) for the eigenvalue decomposition.
**tol**float, default=0
Convergence tolerance passed to arpack or lobpcg. not used if eigen\_solver == ‘dense’.
**max\_iter**int, default=None
Maximum number of iterations for the arpack solver. not used if eigen\_solver == ‘dense’.
**path\_method**{‘auto’, ‘FW’, ‘D’}, default=’auto’
Method to use in finding shortest path.
‘auto’ : attempt to choose the best algorithm automatically.
‘FW’ : Floyd-Warshall algorithm.
‘D’ : Dijkstra’s algorithm.
**neighbors\_algorithm**{‘auto’, ‘brute’, ‘kd\_tree’, ‘ball\_tree’}, default=’auto’
Algorithm to use for nearest neighbors search, passed to neighbors.NearestNeighbors instance.
**n\_jobs**int or None, default=None
The number of parallel jobs to run. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**metric**str, or callable, default=”minkowski”
The metric to use when calculating distance between instances in a feature array. If metric is a string or callable, it must be one of the options allowed by [`sklearn.metrics.pairwise_distances`](sklearn.metrics.pairwise_distances#sklearn.metrics.pairwise_distances "sklearn.metrics.pairwise_distances") for its metric parameter. If metric is “precomputed”, X is assumed to be a distance matrix and must be square. X may be a [Glossary](https://scikit-learn.org/1.1/glossary.html#term-sparse-graph).
New in version 0.22.
**p**int, default=2
Parameter for the Minkowski metric from sklearn.metrics.pairwise.pairwise\_distances. When p = 1, this is equivalent to using manhattan\_distance (l1), and euclidean\_distance (l2) for p = 2. For arbitrary p, minkowski\_distance (l\_p) is used.
New in version 0.22.
**metric\_params**dict, default=None
Additional keyword arguments for the metric function.
New in version 0.22.
Attributes:
**embedding\_**array-like, shape (n\_samples, n\_components)
Stores the embedding vectors.
**kernel\_pca\_**object
[`KernelPCA`](sklearn.decomposition.kernelpca#sklearn.decomposition.KernelPCA "sklearn.decomposition.KernelPCA") object used to implement the embedding.
**nbrs\_**sklearn.neighbors.NearestNeighbors instance
Stores nearest neighbors instance, including BallTree or KDtree if applicable.
**dist\_matrix\_**array-like, shape (n\_samples, n\_samples)
Stores the geodesic distance matrix of training data.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`sklearn.decomposition.PCA`](sklearn.decomposition.pca#sklearn.decomposition.PCA "sklearn.decomposition.PCA")
Principal component analysis that is a linear dimensionality reduction method.
[`sklearn.decomposition.KernelPCA`](sklearn.decomposition.kernelpca#sklearn.decomposition.KernelPCA "sklearn.decomposition.KernelPCA")
Non-linear dimensionality reduction using kernels and PCA.
[`MDS`](sklearn.manifold.mds#sklearn.manifold.MDS "sklearn.manifold.MDS")
Manifold learning using multidimensional scaling.
[`TSNE`](sklearn.manifold.tsne#sklearn.manifold.TSNE "sklearn.manifold.TSNE")
T-distributed Stochastic Neighbor Embedding.
[`LocallyLinearEmbedding`](sklearn.manifold.locallylinearembedding#sklearn.manifold.LocallyLinearEmbedding "sklearn.manifold.LocallyLinearEmbedding")
Manifold learning using Locally Linear Embedding.
[`SpectralEmbedding`](sklearn.manifold.spectralembedding#sklearn.manifold.SpectralEmbedding "sklearn.manifold.SpectralEmbedding")
Spectral embedding for non-linear dimensionality.
#### References
[1] Tenenbaum, J.B.; De Silva, V.; & Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 290 (5500)
#### Examples
```
>>> from sklearn.datasets import load_digits
>>> from sklearn.manifold import Isomap
>>> X, _ = load_digits(return_X_y=True)
>>> X.shape
(1797, 64)
>>> embedding = Isomap(n_components=2)
>>> X_transformed = embedding.fit_transform(X[:100])
>>> X_transformed.shape
(100, 2)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.manifold.Isomap.fit "sklearn.manifold.Isomap.fit")(X[, y]) | Compute the embedding vectors for data X. |
| [`fit_transform`](#sklearn.manifold.Isomap.fit_transform "sklearn.manifold.Isomap.fit_transform")(X[, y]) | Fit the model from data in X and transform X. |
| [`get_feature_names_out`](#sklearn.manifold.Isomap.get_feature_names_out "sklearn.manifold.Isomap.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.manifold.Isomap.get_params "sklearn.manifold.Isomap.get_params")([deep]) | Get parameters for this estimator. |
| [`reconstruction_error`](#sklearn.manifold.Isomap.reconstruction_error "sklearn.manifold.Isomap.reconstruction_error")() | Compute the reconstruction error for the embedding. |
| [`set_params`](#sklearn.manifold.Isomap.set_params "sklearn.manifold.Isomap.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.manifold.Isomap.transform "sklearn.manifold.Isomap.transform")(X) | Transform X. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_isomap.py#L310)
Compute the embedding vectors for data X.
Parameters:
**X**{array-like, sparse graph, BallTree, KDTree, NearestNeighbors}
Sample data, shape = (n\_samples, n\_features), in the form of a numpy array, sparse graph, precomputed tree, or NearestNeighbors object.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**self**object
Returns a fitted instance of self.
fit\_transform(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_isomap.py#L331)
Fit the model from data in X and transform X.
Parameters:
**X**{array-like, sparse graph, BallTree, KDTree}
Training vector, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**X\_new**array-like, shape (n\_samples, n\_components)
X transformed in the new space.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.manifold.Isomap.fit "sklearn.manifold.Isomap.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
reconstruction\_error()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_isomap.py#L285)
Compute the reconstruction error for the embedding.
Returns:
**reconstruction\_error**float
Reconstruction error.
#### Notes
The cost function of an isomap embedding is
`E = frobenius_norm[K(D) - K(D_fit)] / n_samples`
Where D is the matrix of distances for the input data X, D\_fit is the matrix of distances for the output embedding X\_fit, and K is the isomap kernel:
`K(D) = -0.5 * (I - 1/n_samples) * D^2 * (I - 1/n_samples)`
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_isomap.py#L351)
Transform X.
This is implemented by linking the points X into the graph of geodesic distances of the training data. First the `n_neighbors` nearest neighbors of X are found in the training data, and from these the shortest geodesic distances from each point in X to each point in the training data are computed in order to construct the kernel. The embedding of X is the projection of this kernel onto the embedding vectors of the training set.
Parameters:
**X**array-like, shape (n\_queries, n\_features)
If neighbors\_algorithm=’precomputed’, X is assumed to be a distance matrix or a sparse graph of shape (n\_queries, n\_samples\_fit).
Returns:
**X\_new**array-like, shape (n\_queries, n\_components)
X transformed in the new space.
Examples using `sklearn.manifold.Isomap`
----------------------------------------
[Release Highlights for scikit-learn 0.22](../../auto_examples/release_highlights/plot_release_highlights_0_22_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-22-0-py)
[Comparison of Manifold Learning methods](../../auto_examples/manifold/plot_compare_methods#sphx-glr-auto-examples-manifold-plot-compare-methods-py)
[Manifold Learning methods on a severed sphere](../../auto_examples/manifold/plot_manifold_sphere#sphx-glr-auto-examples-manifold-plot-manifold-sphere-py)
[Manifold learning on handwritten digits: Locally Linear Embedding, Isomap…](../../auto_examples/manifold/plot_lle_digits#sphx-glr-auto-examples-manifold-plot-lle-digits-py)
scikit_learn sklearn.model_selection.cross_validate sklearn.model\_selection.cross\_validate
========================================
sklearn.model\_selection.cross\_validate(*estimator*, *X*, *y=None*, *\**, *groups=None*, *scoring=None*, *cv=None*, *n\_jobs=None*, *verbose=0*, *fit\_params=None*, *pre\_dispatch='2\*n\_jobs'*, *return\_train\_score=False*, *return\_estimator=False*, *error\_score=nan*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_validation.py#L49)
Evaluate metric(s) by cross-validation and also record fit/score times.
Read more in the [User Guide](../cross_validation#multimetric-cross-validation).
Parameters:
**estimator**estimator object implementing ‘fit’
The object to use to fit the data.
**X**array-like of shape (n\_samples, n\_features)
The data to fit. Can be for example a list, or an array.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
The target variable to try to predict in the case of supervised learning.
**groups**array-like of shape (n\_samples,), default=None
Group labels for the samples used while splitting the dataset into train/test set. Only used in conjunction with a “Group” [cv](https://scikit-learn.org/1.1/glossary.html#term-cv) instance (e.g., [`GroupKFold`](sklearn.model_selection.groupkfold#sklearn.model_selection.GroupKFold "sklearn.model_selection.GroupKFold")).
**scoring**str, callable, list, tuple, or dict, default=None
Strategy to evaluate the performance of the cross-validated model on the test set.
If `scoring` represents a single score, one can use:
* a single string (see [The scoring parameter: defining model evaluation rules](../model_evaluation#scoring-parameter));
* a callable (see [Defining your scoring strategy from metric functions](../model_evaluation#scoring)) that returns a single value.
If `scoring` represents multiple scores, one can use:
* a list or tuple of unique strings;
* a callable returning a dictionary where the keys are the metric names and the values are the metric scores;
* a dictionary with metric names as keys and callables a values.
See [Specifying multiple metrics for evaluation](../grid_search#multimetric-grid-search) for an example.
**cv**int, cross-validation generator or an iterable, default=None
Determines the cross-validation splitting strategy. Possible inputs for cv are:
* None, to use the default 5-fold cross validation,
* int, to specify the number of folds in a `(Stratified)KFold`,
* [CV splitter](https://scikit-learn.org/1.1/glossary.html#term-CV-splitter),
* An iterable yielding (train, test) splits as arrays of indices.
For int/None inputs, if the estimator is a classifier and `y` is either binary or multiclass, [`StratifiedKFold`](sklearn.model_selection.stratifiedkfold#sklearn.model_selection.StratifiedKFold "sklearn.model_selection.StratifiedKFold") is used. In all other cases, `Fold` is used. These splitters are instantiated with `shuffle=False` so the splits will be the same across calls.
Refer [User Guide](../cross_validation#cross-validation) for the various cross-validation strategies that can be used here.
Changed in version 0.22: `cv` default value if None changed from 3-fold to 5-fold.
**n\_jobs**int, default=None
Number of jobs to run in parallel. Training the estimator and computing the score are parallelized over the cross-validation splits. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**verbose**int, default=0
The verbosity level.
**fit\_params**dict, default=None
Parameters to pass to the fit method of the estimator.
**pre\_dispatch**int or str, default=’2\*n\_jobs’
Controls the number of jobs that get dispatched during parallel execution. Reducing this number can be useful to avoid an explosion of memory consumption when more jobs get dispatched than CPUs can process. This parameter can be:
* None, in which case all the jobs are immediately created and spawned. Use this for lightweight and fast-running jobs, to avoid delays due to on-demand spawning of the jobs
* An int, giving the exact number of total jobs that are spawned
* A str, giving an expression as a function of n\_jobs, as in ‘2\*n\_jobs’
**return\_train\_score**bool, default=False
Whether to include train scores. Computing training scores is used to get insights on how different parameter settings impact the overfitting/underfitting trade-off. However computing the scores on the training set can be computationally expensive and is not strictly required to select the parameters that yield the best generalization performance.
New in version 0.19.
Changed in version 0.21: Default value was changed from `True` to `False`
**return\_estimator**bool, default=False
Whether to return the estimators fitted on each split.
New in version 0.20.
**error\_score**‘raise’ or numeric, default=np.nan
Value to assign to the score if an error occurs in estimator fitting. If set to ‘raise’, the error is raised. If a numeric value is given, FitFailedWarning is raised.
New in version 0.20.
Returns:
**scores**dict of float arrays of shape (n\_splits,)
Array of scores of the estimator for each run of the cross validation.
A dict of arrays containing the score/time arrays for each scorer is returned. The possible keys for this `dict` are:
`test_score`
The score array for test scores on each cv split. Suffix `_score` in `test_score` changes to a specific metric like `test_r2` or `test_auc` if there are multiple scoring metrics in the scoring parameter.
`train_score`
The score array for train scores on each cv split. Suffix `_score` in `train_score` changes to a specific metric like `train_r2` or `train_auc` if there are multiple scoring metrics in the scoring parameter. This is available only if `return_train_score` parameter is `True`.
`fit_time`
The time for fitting the estimator on the train set for each cv split.
`score_time`
The time for scoring the estimator on the test set for each cv split. (Note time for scoring on the train set is not included even if `return_train_score` is set to `True`
`estimator`
The estimator objects for each cv split. This is available only if `return_estimator` parameter is set to `True`.
See also
[`cross_val_score`](sklearn.model_selection.cross_val_score#sklearn.model_selection.cross_val_score "sklearn.model_selection.cross_val_score")
Run cross-validation for single metric evaluation.
[`cross_val_predict`](sklearn.model_selection.cross_val_predict#sklearn.model_selection.cross_val_predict "sklearn.model_selection.cross_val_predict")
Get predictions from each split of cross-validation for diagnostic purposes.
[`sklearn.metrics.make_scorer`](sklearn.metrics.make_scorer#sklearn.metrics.make_scorer "sklearn.metrics.make_scorer")
Make a scorer from a performance metric or loss function.
#### Examples
```
>>> from sklearn import datasets, linear_model
>>> from sklearn.model_selection import cross_validate
>>> from sklearn.metrics import make_scorer
>>> from sklearn.metrics import confusion_matrix
>>> from sklearn.svm import LinearSVC
>>> diabetes = datasets.load_diabetes()
>>> X = diabetes.data[:150]
>>> y = diabetes.target[:150]
>>> lasso = linear_model.Lasso()
```
Single metric evaluation using `cross_validate`
```
>>> cv_results = cross_validate(lasso, X, y, cv=3)
>>> sorted(cv_results.keys())
['fit_time', 'score_time', 'test_score']
>>> cv_results['test_score']
array([0.3315057 , 0.08022103, 0.03531816])
```
Multiple metric evaluation using `cross_validate` (please refer the `scoring` parameter doc for more information)
```
>>> scores = cross_validate(lasso, X, y, cv=3,
... scoring=('r2', 'neg_mean_squared_error'),
... return_train_score=True)
>>> print(scores['test_neg_mean_squared_error'])
[-3635.5... -3573.3... -6114.7...]
>>> print(scores['train_r2'])
[0.28009951 0.3908844 0.22784907]
```
Examples using `sklearn.model_selection.cross_validate`
-------------------------------------------------------
[Categorical Feature Support in Gradient Boosting](../../auto_examples/ensemble/plot_gradient_boosting_categorical#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-categorical-py)
[Combine predictors using stacking](../../auto_examples/ensemble/plot_stack_predictors#sphx-glr-auto-examples-ensemble-plot-stack-predictors-py)
[Time-related feature engineering](../../auto_examples/applications/plot_cyclical_feature_engineering#sphx-glr-auto-examples-applications-plot-cyclical-feature-engineering-py)
[Quantile regression](../../auto_examples/linear_model/plot_quantile_regression#sphx-glr-auto-examples-linear-model-plot-quantile-regression-py)
[Common pitfalls in the interpretation of coefficients of linear models](../../auto_examples/inspection/plot_linear_model_coefficient_interpretation#sphx-glr-auto-examples-inspection-plot-linear-model-coefficient-interpretation-py)
| programming_docs |
scikit_learn sklearn.metrics.matthews_corrcoef sklearn.metrics.matthews\_corrcoef
==================================
sklearn.metrics.matthews\_corrcoef(*y\_true*, *y\_pred*, *\**, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_classification.py#L838)
Compute the Matthews correlation coefficient (MCC).
The Matthews correlation coefficient is used in machine learning as a measure of the quality of binary and multiclass classifications. It takes into account true and false positives and negatives and is generally regarded as a balanced measure which can be used even if the classes are of very different sizes. The MCC is in essence a correlation coefficient value between -1 and +1. A coefficient of +1 represents a perfect prediction, 0 an average random prediction and -1 an inverse prediction. The statistic is also known as the phi coefficient. [source: Wikipedia]
Binary and multiclass labels are supported. Only in the binary case does this relate to information about true and false positives and negatives. See references below.
Read more in the [User Guide](../model_evaluation#matthews-corrcoef).
Parameters:
**y\_true**array, shape = [n\_samples]
Ground truth (correct) target values.
**y\_pred**array, shape = [n\_samples]
Estimated targets as returned by a classifier.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
New in version 0.18.
Returns:
**mcc**float
The Matthews correlation coefficient (+1 represents a perfect prediction, 0 an average random prediction and -1 and inverse prediction).
#### References
[1] [Baldi, Brunak, Chauvin, Andersen and Nielsen, (2000). Assessing the accuracy of prediction algorithms for classification: an overview.](https://doi.org/10.1093/bioinformatics/16.5.412)
[2] [Wikipedia entry for the Matthews Correlation Coefficient](https://en.wikipedia.org/wiki/Matthews_correlation_coefficient).
[3] [Gorodkin, (2004). Comparing two K-category assignments by a K-category correlation coefficient](https://www.sciencedirect.com/science/article/pii/S1476927104000799).
[4] [Jurman, Riccadonna, Furlanello, (2012). A Comparison of MCC and CEN Error Measures in MultiClass Prediction](https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0041882).
#### Examples
```
>>> from sklearn.metrics import matthews_corrcoef
>>> y_true = [+1, +1, +1, -1]
>>> y_pred = [+1, -1, +1, +1]
>>> matthews_corrcoef(y_true, y_pred)
-0.33...
```
scikit_learn sklearn.metrics.explained_variance_score sklearn.metrics.explained\_variance\_score
==========================================
sklearn.metrics.explained\_variance\_score(*y\_true*, *y\_pred*, *\**, *sample\_weight=None*, *multioutput='uniform\_average'*, *force\_finite=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_regression.py#L659)
Explained variance regression score function.
Best possible score is 1.0, lower values are worse.
In the particular case when `y_true` is constant, the explained variance score is not finite: it is either `NaN` (perfect predictions) or `-Inf` (imperfect predictions). To prevent such non-finite numbers to pollute higher-level experiments such as a grid search cross-validation, by default these cases are replaced with 1.0 (perfect predictions) or 0.0 (imperfect predictions) respectively. If `force_finite` is set to `False`, this score falls back on the original \(R^2\) definition.
Note
The Explained Variance score is similar to the [`R^2 score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"), with the notable difference that it does not account for systematic offsets in the prediction. Most often the [`R^2 score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score") should be preferred.
Read more in the [User Guide](../model_evaluation#explained-variance-score).
Parameters:
**y\_true**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
Ground truth (correct) target values.
**y\_pred**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
Estimated target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**multioutput**{‘raw\_values’, ‘uniform\_average’, ‘variance\_weighted’} or array-like of shape (n\_outputs,), default=’uniform\_average’
Defines aggregating of multiple output scores. Array-like value defines weights used to average scores.
‘raw\_values’ :
Returns a full set of scores in case of multioutput input.
‘uniform\_average’ :
Scores of all outputs are averaged with uniform weight.
‘variance\_weighted’ :
Scores of all outputs are averaged, weighted by the variances of each individual output.
**force\_finite**bool, default=True
Flag indicating if `NaN` and `-Inf` scores resulting from constant data should be replaced with real numbers (`1.0` if prediction is perfect, `0.0` otherwise). Default is `True`, a convenient setting for hyperparameters’ search procedures (e.g. grid search cross-validation).
New in version 1.1.
Returns:
**score**float or ndarray of floats
The explained variance or ndarray if ‘multioutput’ is ‘raw\_values’.
See also
[`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score")
Similar metric, but accounting for systematic offsets in prediction.
#### Notes
This is not a symmetric function.
#### Examples
```
>>> from sklearn.metrics import explained_variance_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> explained_variance_score(y_true, y_pred)
0.957...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> explained_variance_score(y_true, y_pred, multioutput='uniform_average')
0.983...
>>> y_true = [-2, -2, -2]
>>> y_pred = [-2, -2, -2]
>>> explained_variance_score(y_true, y_pred)
1.0
>>> explained_variance_score(y_true, y_pred, force_finite=False)
nan
>>> y_true = [-2, -2, -2]
>>> y_pred = [-2, -2, -2 + 1e-8]
>>> explained_variance_score(y_true, y_pred)
0.0
>>> explained_variance_score(y_true, y_pred, force_finite=False)
-inf
```
scikit_learn sklearn.gaussian_process.kernels.RBF sklearn.gaussian\_process.kernels.RBF
=====================================
*class*sklearn.gaussian\_process.kernels.RBF(*length\_scale=1.0*, *length\_scale\_bounds=(1e-05, 100000.0)*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L1423)
Radial basis function kernel (aka squared-exponential kernel).
The RBF kernel is a stationary kernel. It is also known as the “squared exponential” kernel. It is parameterized by a length scale parameter \(l>0\), which can either be a scalar (isotropic variant of the kernel) or a vector with the same number of dimensions as the inputs X (anisotropic variant of the kernel). The kernel is given by:
\[k(x\_i, x\_j) = \exp\left(- \frac{d(x\_i, x\_j)^2}{2l^2} \right)\] where \(l\) is the length scale of the kernel and \(d(\cdot,\cdot)\) is the Euclidean distance. For advice on how to set the length scale parameter, see e.g. [[1]](#redc669bcbe98-1).
This kernel is infinitely differentiable, which implies that GPs with this kernel as covariance function have mean square derivatives of all orders, and are thus very smooth. See [[2]](#redc669bcbe98-2), Chapter 4, Section 4.2, for further details of the RBF kernel.
Read more in the [User Guide](../gaussian_process#gp-kernels).
New in version 0.18.
Parameters:
**length\_scale**float or ndarray of shape (n\_features,), default=1.0
The length scale of the kernel. If a float, an isotropic kernel is used. If an array, an anisotropic kernel is used where each dimension of l defines the length-scale of the respective feature dimension.
**length\_scale\_bounds**pair of floats >= 0 or “fixed”, default=(1e-5, 1e5)
The lower and upper bound on ‘length\_scale’. If set to “fixed”, ‘length\_scale’ cannot be changed during hyperparameter tuning.
Attributes:
**anisotropic**
[`bounds`](#sklearn.gaussian_process.kernels.RBF.bounds "sklearn.gaussian_process.kernels.RBF.bounds")
Returns the log-transformed bounds on the theta.
**hyperparameter\_length\_scale**
[`hyperparameters`](#sklearn.gaussian_process.kernels.RBF.hyperparameters "sklearn.gaussian_process.kernels.RBF.hyperparameters")
Returns a list of all hyperparameter specifications.
[`n_dims`](#sklearn.gaussian_process.kernels.RBF.n_dims "sklearn.gaussian_process.kernels.RBF.n_dims")
Returns the number of non-fixed hyperparameters of the kernel.
[`requires_vector_input`](#sklearn.gaussian_process.kernels.RBF.requires_vector_input "sklearn.gaussian_process.kernels.RBF.requires_vector_input")
Returns whether the kernel is defined on fixed-length feature vectors or generic objects.
[`theta`](#sklearn.gaussian_process.kernels.RBF.theta "sklearn.gaussian_process.kernels.RBF.theta")
Returns the (flattened, log-transformed) non-fixed hyperparameters.
#### References
[[1](#id1)] [David Duvenaud (2014). “The Kernel Cookbook: Advice on Covariance functions”.](https://www.cs.toronto.edu/~duvenaud/cookbook/)
[[2](#id2)] [Carl Edward Rasmussen, Christopher K. I. Williams (2006). “Gaussian Processes for Machine Learning”. The MIT Press.](http://www.gaussianprocess.org/gpml/)
#### Examples
```
>>> from sklearn.datasets import load_iris
>>> from sklearn.gaussian_process import GaussianProcessClassifier
>>> from sklearn.gaussian_process.kernels import RBF
>>> X, y = load_iris(return_X_y=True)
>>> kernel = 1.0 * RBF(1.0)
>>> gpc = GaussianProcessClassifier(kernel=kernel,
... random_state=0).fit(X, y)
>>> gpc.score(X, y)
0.9866...
>>> gpc.predict_proba(X[:2,:])
array([[0.8354..., 0.03228..., 0.1322...],
[0.7906..., 0.0652..., 0.1441...]])
```
#### Methods
| | |
| --- | --- |
| [`__call__`](#sklearn.gaussian_process.kernels.RBF.__call__ "sklearn.gaussian_process.kernels.RBF.__call__")(X[, Y, eval\_gradient]) | Return the kernel k(X, Y) and optionally its gradient. |
| [`clone_with_theta`](#sklearn.gaussian_process.kernels.RBF.clone_with_theta "sklearn.gaussian_process.kernels.RBF.clone_with_theta")(theta) | Returns a clone of self with given hyperparameters theta. |
| [`diag`](#sklearn.gaussian_process.kernels.RBF.diag "sklearn.gaussian_process.kernels.RBF.diag")(X) | Returns the diagonal of the kernel k(X, X). |
| [`get_params`](#sklearn.gaussian_process.kernels.RBF.get_params "sklearn.gaussian_process.kernels.RBF.get_params")([deep]) | Get parameters of this kernel. |
| [`is_stationary`](#sklearn.gaussian_process.kernels.RBF.is_stationary "sklearn.gaussian_process.kernels.RBF.is_stationary")() | Returns whether the kernel is stationary. |
| [`set_params`](#sklearn.gaussian_process.kernels.RBF.set_params "sklearn.gaussian_process.kernels.RBF.set_params")(\*\*params) | Set the parameters of this kernel. |
\_\_call\_\_(*X*, *Y=None*, *eval\_gradient=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L1505)
Return the kernel k(X, Y) and optionally its gradient.
Parameters:
**X**ndarray of shape (n\_samples\_X, n\_features)
Left argument of the returned kernel k(X, Y)
**Y**ndarray of shape (n\_samples\_Y, n\_features), default=None
Right argument of the returned kernel k(X, Y). If None, k(X, X) if evaluated instead.
**eval\_gradient**bool, default=False
Determines whether the gradient with respect to the log of the kernel hyperparameter is computed. Only supported when Y is None.
Returns:
**K**ndarray of shape (n\_samples\_X, n\_samples\_Y)
Kernel k(X, Y)
**K\_gradient**ndarray of shape (n\_samples\_X, n\_samples\_X, n\_dims), optional
The gradient of the kernel k(X, X) with respect to the log of the hyperparameter of the kernel. Only returned when `eval_gradient` is True.
*property*bounds
Returns the log-transformed bounds on the theta.
Returns:
**bounds**ndarray of shape (n\_dims, 2)
The log-transformed bounds on the kernel’s hyperparameters theta
clone\_with\_theta(*theta*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L238)
Returns a clone of self with given hyperparameters theta.
Parameters:
**theta**ndarray of shape (n\_dims,)
The hyperparameters
diag(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L448)
Returns the diagonal of the kernel k(X, X).
The result of this method is identical to np.diag(self(X)); however, it can be evaluated more efficiently since only the diagonal is evaluated.
Parameters:
**X**ndarray of shape (n\_samples\_X, n\_features)
Left argument of the returned kernel k(X, Y)
Returns:
**K\_diag**ndarray of shape (n\_samples\_X,)
Diagonal of kernel k(X, X)
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L158)
Get parameters of this kernel.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*hyperparameters
Returns a list of all hyperparameter specifications.
is\_stationary()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L474)
Returns whether the kernel is stationary.
*property*n\_dims
Returns the number of non-fixed hyperparameters of the kernel.
*property*requires\_vector\_input
Returns whether the kernel is defined on fixed-length feature vectors or generic objects. Defaults to True for backward compatibility.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L198)
Set the parameters of this kernel.
The method works on simple kernels as well as on nested kernels. The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Returns:
self
*property*theta
Returns the (flattened, log-transformed) non-fixed hyperparameters.
Note that theta are typically the log-transformed values of the kernel’s hyperparameters as this representation of the search space is more amenable for hyperparameter search, as hyperparameters like length-scales naturally live on a log-scale.
Returns:
**theta**ndarray of shape (n\_dims,)
The non-fixed, log-transformed hyperparameters of the kernel
Examples using `sklearn.gaussian_process.kernels.RBF`
-----------------------------------------------------
[Classifier comparison](../../auto_examples/classification/plot_classifier_comparison#sphx-glr-auto-examples-classification-plot-classifier-comparison-py)
[Plot classification probability](../../auto_examples/classification/plot_classification_probability#sphx-glr-auto-examples-classification-plot-classification-probability-py)
[Comparison of kernel ridge and Gaussian process regression](../../auto_examples/gaussian_process/plot_compare_gpr_krr#sphx-glr-auto-examples-gaussian-process-plot-compare-gpr-krr-py)
[Gaussian Processes regression: basic introductory example](../../auto_examples/gaussian_process/plot_gpr_noisy_targets#sphx-glr-auto-examples-gaussian-process-plot-gpr-noisy-targets-py)
[Gaussian process classification (GPC) on iris dataset](../../auto_examples/gaussian_process/plot_gpc_iris#sphx-glr-auto-examples-gaussian-process-plot-gpc-iris-py)
[Gaussian process regression (GPR) on Mauna Loa CO2 data](../../auto_examples/gaussian_process/plot_gpr_co2#sphx-glr-auto-examples-gaussian-process-plot-gpr-co2-py)
[Gaussian process regression (GPR) with noise-level estimation](../../auto_examples/gaussian_process/plot_gpr_noisy#sphx-glr-auto-examples-gaussian-process-plot-gpr-noisy-py)
[Illustration of Gaussian process classification (GPC) on the XOR dataset](../../auto_examples/gaussian_process/plot_gpc_xor#sphx-glr-auto-examples-gaussian-process-plot-gpc-xor-py)
[Illustration of prior and posterior Gaussian process for different kernels](../../auto_examples/gaussian_process/plot_gpr_prior_posterior#sphx-glr-auto-examples-gaussian-process-plot-gpr-prior-posterior-py)
[Probabilistic predictions with Gaussian process classification (GPC)](../../auto_examples/gaussian_process/plot_gpc#sphx-glr-auto-examples-gaussian-process-plot-gpc-py)
scikit_learn sklearn.ensemble.StackingClassifier sklearn.ensemble.StackingClassifier
===================================
*class*sklearn.ensemble.StackingClassifier(*estimators*, *final\_estimator=None*, *\**, *cv=None*, *stack\_method='auto'*, *n\_jobs=None*, *passthrough=False*, *verbose=0*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_stacking.py#L365)
Stack of estimators with a final classifier.
Stacked generalization consists in stacking the output of individual estimator and use a classifier to compute the final prediction. Stacking allows to use the strength of each individual estimator by using their output as input of a final estimator.
Note that `estimators_` are fitted on the full `X` while `final_estimator_` is trained using cross-validated predictions of the base estimators using `cross_val_predict`.
Read more in the [User Guide](../ensemble#stacking).
New in version 0.22.
Parameters:
**estimators**list of (str, estimator)
Base estimators which will be stacked together. Each element of the list is defined as a tuple of string (i.e. name) and an estimator instance. An estimator can be set to ‘drop’ using `set_params`.
**final\_estimator**estimator, default=None
A classifier which will be used to combine the base estimators. The default classifier is a [`LogisticRegression`](sklearn.linear_model.logisticregression#sklearn.linear_model.LogisticRegression "sklearn.linear_model.LogisticRegression").
**cv**int, cross-validation generator, iterable, or “prefit”, default=None
Determines the cross-validation splitting strategy used in `cross_val_predict` to train `final_estimator`. Possible inputs for cv are:
* None, to use the default 5-fold cross validation,
* integer, to specify the number of folds in a (Stratified) KFold,
* An object to be used as a cross-validation generator,
* An iterable yielding train, test splits,
* `"prefit"` to assume the `estimators` are prefit. In this case, the estimators will not be refitted.
For integer/None inputs, if the estimator is a classifier and y is either binary or multiclass, [`StratifiedKFold`](sklearn.model_selection.stratifiedkfold#sklearn.model_selection.StratifiedKFold "sklearn.model_selection.StratifiedKFold") is used. In all other cases, [`KFold`](sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold") is used. These splitters are instantiated with `shuffle=False` so the splits will be the same across calls.
Refer [User Guide](../cross_validation#cross-validation) for the various cross-validation strategies that can be used here.
If “prefit” is passed, it is assumed that all `estimators` have been fitted already. The `final_estimator_` is trained on the `estimators` predictions on the full training set and are **not** cross validated predictions. Please note that if the models have been trained on the same data to train the stacking model, there is a very high risk of overfitting.
New in version 1.1: The ‘prefit’ option was added in 1.1
Note
A larger number of split will provide no benefits if the number of training samples is large enough. Indeed, the training time will increase. `cv` is not used for model evaluation but for prediction.
**stack\_method**{‘auto’, ‘predict\_proba’, ‘decision\_function’, ‘predict’}, default=’auto’
Methods called for each base estimator. It can be:
* if ‘auto’, it will try to invoke, for each estimator, `'predict_proba'`, `'decision_function'` or `'predict'` in that order.
* otherwise, one of `'predict_proba'`, `'decision_function'` or `'predict'`. If the method is not implemented by the estimator, it will raise an error.
**n\_jobs**int, default=None
The number of jobs to run in parallel all `estimators` `fit`. `None` means 1 unless in a `joblib.parallel_backend` context. -1 means using all processors. See Glossary for more details.
**passthrough**bool, default=False
When False, only the predictions of estimators will be used as training data for `final_estimator`. When True, the `final_estimator` is trained on the predictions as well as the original training data.
**verbose**int, default=0
Verbosity level.
Attributes:
**classes\_**ndarray of shape (n\_classes,)
Class labels.
**estimators\_**list of estimators
The elements of the `estimators` parameter, having been fitted on the training data. If an estimator has been set to `'drop'`, it will not appear in `estimators_`. When `cv="prefit"`, `estimators_` is set to `estimators` and is not fitted again.
**named\_estimators\_**[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
Attribute to access any fitted sub-estimators by name.
[`n_features_in_`](#sklearn.ensemble.StackingClassifier.n_features_in_ "sklearn.ensemble.StackingClassifier.n_features_in_")int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Only defined if the underlying estimators expose such an attribute when fit. .. versionadded:: 1.0
**final\_estimator\_**estimator
The classifier which predicts given the output of `estimators_`.
**stack\_method\_**list of str
The method used by each base estimator.
See also
[`StackingRegressor`](sklearn.ensemble.stackingregressor#sklearn.ensemble.StackingRegressor "sklearn.ensemble.StackingRegressor")
Stack of estimators with a final regressor.
#### Notes
When `predict_proba` is used by each estimator (i.e. most of the time for `stack_method='auto'` or specifically for `stack_method='predict_proba'`), The first column predicted by each estimator will be dropped in the case of a binary classification problem. Indeed, both feature will be perfectly collinear.
#### References
[1] Wolpert, David H. “Stacked generalization.” Neural networks 5.2 (1992): 241-259.
#### Examples
```
>>> from sklearn.datasets import load_iris
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.svm import LinearSVC
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.preprocessing import StandardScaler
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.ensemble import StackingClassifier
>>> X, y = load_iris(return_X_y=True)
>>> estimators = [
... ('rf', RandomForestClassifier(n_estimators=10, random_state=42)),
... ('svr', make_pipeline(StandardScaler(),
... LinearSVC(random_state=42)))
... ]
>>> clf = StackingClassifier(
... estimators=estimators, final_estimator=LogisticRegression()
... )
>>> from sklearn.model_selection import train_test_split
>>> X_train, X_test, y_train, y_test = train_test_split(
... X, y, stratify=y, random_state=42
... )
>>> clf.fit(X_train, y_train).score(X_test, y_test)
0.9...
```
#### Methods
| | |
| --- | --- |
| [`decision_function`](#sklearn.ensemble.StackingClassifier.decision_function "sklearn.ensemble.StackingClassifier.decision_function")(X) | Decision function for samples in `X` using the final estimator. |
| [`fit`](#sklearn.ensemble.StackingClassifier.fit "sklearn.ensemble.StackingClassifier.fit")(X, y[, sample\_weight]) | Fit the estimators. |
| [`fit_transform`](#sklearn.ensemble.StackingClassifier.fit_transform "sklearn.ensemble.StackingClassifier.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.ensemble.StackingClassifier.get_feature_names_out "sklearn.ensemble.StackingClassifier.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.ensemble.StackingClassifier.get_params "sklearn.ensemble.StackingClassifier.get_params")([deep]) | Get the parameters of an estimator from the ensemble. |
| [`predict`](#sklearn.ensemble.StackingClassifier.predict "sklearn.ensemble.StackingClassifier.predict")(X, \*\*predict\_params) | Predict target for X. |
| [`predict_proba`](#sklearn.ensemble.StackingClassifier.predict_proba "sklearn.ensemble.StackingClassifier.predict_proba")(X) | Predict class probabilities for `X` using the final estimator. |
| [`score`](#sklearn.ensemble.StackingClassifier.score "sklearn.ensemble.StackingClassifier.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.ensemble.StackingClassifier.set_params "sklearn.ensemble.StackingClassifier.set_params")(\*\*params) | Set the parameters of an estimator from the ensemble. |
| [`transform`](#sklearn.ensemble.StackingClassifier.transform "sklearn.ensemble.StackingClassifier.transform")(X) | Return class labels or probabilities for X for each estimator. |
decision\_function(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_stacking.py#L629)
Decision function for samples in `X` using the final estimator.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vectors, where `n_samples` is the number of samples and `n_features` is the number of features.
Returns:
**decisions**ndarray of shape (n\_samples,), (n\_samples, n\_classes), or (n\_samples, n\_classes \* (n\_classes-1) / 2)
The decision function computed the final estimator.
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_stacking.py#L559)
Fit the estimators.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vectors, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,)
Target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, then samples are equally weighted. Note that this is supported only if all underlying estimators support sample weights.
Returns:
**self**object
Returns a fitted instance of estimator.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_stacking.py#L283)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Input features. The input feature names are only used when `passthrough` is `True`.
* If `input_features` is `None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then names are generated: `[x0, x1, ..., x(n_features_in_ - 1)]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
If `passthrough` is `False`, then only the names of `estimators` are used to generate the output feature names.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_base.py#L310)
Get the parameters of an estimator from the ensemble.
Returns the parameters given in the constructor as well as the estimators contained within the `estimators` parameter.
Parameters:
**deep**bool, default=True
Setting it to True gets the various estimators and the parameters of the estimators as well.
Returns:
**params**dict
Parameter and estimator names mapped to their values or parameter names mapped to their values.
*property*n\_features\_in\_
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
*property*named\_estimators
Dictionary to access any fitted sub-estimators by name.
Returns:
[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
predict(*X*, *\*\*predict\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_stacking.py#L586)
Predict target for X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vectors, where `n_samples` is the number of samples and `n_features` is the number of features.
**\*\*predict\_params**dict of str -> obj
Parameters to the `predict` called by the `final_estimator`. Note that this may be used to return uncertainties from some estimators with `return_std` or `return_cov`. Be aware that it will only accounts for uncertainty in the final estimator.
Returns:
**y\_pred**ndarray of shape (n\_samples,) or (n\_samples, n\_output)
Predicted targets.
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_stacking.py#L610)
Predict class probabilities for `X` using the final estimator.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vectors, where `n_samples` is the number of samples and `n_features` is the number of features.
Returns:
**probabilities**ndarray of shape (n\_samples, n\_classes) or list of ndarray of shape (n\_output,)
The class probabilities of the input samples.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_base.py#L285)
Set the parameters of an estimator from the ensemble.
Valid parameter keys can be listed with `get_params()`. Note that you can directly set the parameters of the estimators contained in `estimators`.
Parameters:
**\*\*params**keyword arguments
Specific parameters using e.g. `set_params(parameter_name=new_value)`. In addition, to setting the parameters of the estimator, the individual estimator of the estimators can also be set, or can be removed by setting them to ‘drop’.
Returns:
**self**object
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_stacking.py#L648)
Return class labels or probabilities for X for each estimator.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vectors, where `n_samples` is the number of samples and `n_features` is the number of features.
Returns:
**y\_preds**ndarray of shape (n\_samples, n\_estimators) or (n\_samples, n\_classes \* n\_estimators)
Prediction outputs for each estimator.
Examples using `sklearn.ensemble.StackingClassifier`
----------------------------------------------------
[Release Highlights for scikit-learn 0.22](../../auto_examples/release_highlights/plot_release_highlights_0_22_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-22-0-py)
| programming_docs |
scikit_learn sklearn.metrics.multilabel_confusion_matrix sklearn.metrics.multilabel\_confusion\_matrix
=============================================
sklearn.metrics.multilabel\_confusion\_matrix(*y\_true*, *y\_pred*, *\**, *sample\_weight=None*, *labels=None*, *samplewise=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_classification.py#L379)
Compute a confusion matrix for each class or sample.
New in version 0.21.
Compute class-wise (default) or sample-wise (samplewise=True) multilabel confusion matrix to evaluate the accuracy of a classification, and output confusion matrices for each class or sample.
In multilabel confusion matrix \(MCM\), the count of true negatives is \(MCM\_{:,0,0}\), false negatives is \(MCM\_{:,1,0}\), true positives is \(MCM\_{:,1,1}\) and false positives is \(MCM\_{:,0,1}\).
Multiclass data will be treated as if binarized under a one-vs-rest transformation. Returned confusion matrices will be in the order of sorted unique labels in the union of (y\_true, y\_pred).
Read more in the [User Guide](../model_evaluation#multilabel-confusion-matrix).
Parameters:
**y\_true**{array-like, sparse matrix} of shape (n\_samples, n\_outputs) or (n\_samples,)
Ground truth (correct) target values.
**y\_pred**{array-like, sparse matrix} of shape (n\_samples, n\_outputs) or (n\_samples,)
Estimated targets as returned by a classifier.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**labels**array-like of shape (n\_classes,), default=None
A list of classes or column indices to select some (or to force inclusion of classes absent from the data).
**samplewise**bool, default=False
In the multilabel case, this calculates a confusion matrix per sample.
Returns:
**multi\_confusion**ndarray of shape (n\_outputs, 2, 2)
A 2x2 confusion matrix corresponding to each output in the input. When calculating class-wise multi\_confusion (default), then n\_outputs = n\_labels; when calculating sample-wise multi\_confusion (samplewise=True), n\_outputs = n\_samples. If `labels` is defined, the results will be returned in the order specified in `labels`, otherwise the results will be returned in sorted order by default.
See also
[`confusion_matrix`](sklearn.metrics.confusion_matrix#sklearn.metrics.confusion_matrix "sklearn.metrics.confusion_matrix")
Compute confusion matrix to evaluate the accuracy of a classifier.
#### Notes
The `multilabel_confusion_matrix` calculates class-wise or sample-wise multilabel confusion matrices, and in multiclass tasks, labels are binarized under a one-vs-rest way; while [`confusion_matrix`](sklearn.metrics.confusion_matrix#sklearn.metrics.confusion_matrix "sklearn.metrics.confusion_matrix") calculates one confusion matrix for confusion between every two classes.
#### Examples
Multilabel-indicator case:
```
>>> import numpy as np
>>> from sklearn.metrics import multilabel_confusion_matrix
>>> y_true = np.array([[1, 0, 1],
... [0, 1, 0]])
>>> y_pred = np.array([[1, 0, 0],
... [0, 1, 1]])
>>> multilabel_confusion_matrix(y_true, y_pred)
array([[[1, 0],
[0, 1]],
[[1, 0],
[0, 1]],
[[0, 1],
[1, 0]]])
```
Multiclass case:
```
>>> y_true = ["cat", "ant", "cat", "cat", "ant", "bird"]
>>> y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"]
>>> multilabel_confusion_matrix(y_true, y_pred,
... labels=["ant", "bird", "cat"])
array([[[3, 1],
[0, 2]],
[[5, 0],
[1, 0]],
[[2, 1],
[1, 2]]])
```
scikit_learn sklearn.metrics.fowlkes_mallows_score sklearn.metrics.fowlkes\_mallows\_score
=======================================
sklearn.metrics.fowlkes\_mallows\_score(*labels\_true*, *labels\_pred*, *\**, *sparse=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/cluster/_supervised.py#L1059)
Measure the similarity of two clusterings of a set of points.
New in version 0.18.
The Fowlkes-Mallows index (FMI) is defined as the geometric mean between of the precision and recall:
```
FMI = TP / sqrt((TP + FP) * (TP + FN))
```
Where `TP` is the number of **True Positive** (i.e. the number of pair of points that belongs in the same clusters in both `labels_true` and `labels_pred`), `FP` is the number of **False Positive** (i.e. the number of pair of points that belongs in the same clusters in `labels_true` and not in `labels_pred`) and `FN` is the number of **False Negative** (i.e the number of pair of points that belongs in the same clusters in `labels_pred` and not in `labels_True`).
The score ranges from 0 to 1. A high value indicates a good similarity between two clusters.
Read more in the [User Guide](../clustering#fowlkes-mallows-scores).
Parameters:
**labels\_true**int array, shape = (`n_samples`,)
A clustering of the data into disjoint subsets.
**labels\_pred**array, shape = (`n_samples`, )
A clustering of the data into disjoint subsets.
**sparse**bool, default=False
Compute contingency matrix internally with sparse matrix.
Returns:
**score**float
The resulting Fowlkes-Mallows score.
#### References
[1] [E. B. Fowkles and C. L. Mallows, 1983. “A method for comparing two hierarchical clusterings”. Journal of the American Statistical Association](https://www.tandfonline.com/doi/abs/10.1080/01621459.1983.10478008)
[2] [Wikipedia entry for the Fowlkes-Mallows Index](https://en.wikipedia.org/wiki/Fowlkes-Mallows_index)
#### Examples
Perfect labelings are both homogeneous and complete, hence have score 1.0:
```
>>> from sklearn.metrics.cluster import fowlkes_mallows_score
>>> fowlkes_mallows_score([0, 0, 1, 1], [0, 0, 1, 1])
1.0
>>> fowlkes_mallows_score([0, 0, 1, 1], [1, 1, 0, 0])
1.0
```
If classes members are completely split across different clusters, the assignment is totally random, hence the FMI is null:
```
>>> fowlkes_mallows_score([0, 0, 0, 0], [0, 1, 2, 3])
0.0
```
scikit_learn sklearn.ensemble.VotingRegressor sklearn.ensemble.VotingRegressor
================================
*class*sklearn.ensemble.VotingRegressor(*estimators*, *\**, *weights=None*, *n\_jobs=None*, *verbose=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_voting.py#L482)
Prediction voting regressor for unfitted estimators.
A voting regressor is an ensemble meta-estimator that fits several base regressors, each on the whole dataset. Then it averages the individual predictions to form a final prediction.
Read more in the [User Guide](../ensemble#voting-regressor).
New in version 0.21.
Parameters:
**estimators**list of (str, estimator) tuples
Invoking the `fit` method on the `VotingRegressor` will fit clones of those original estimators that will be stored in the class attribute `self.estimators_`. An estimator can be set to `'drop'` using [`set_params`](#sklearn.ensemble.VotingRegressor.set_params "sklearn.ensemble.VotingRegressor.set_params").
Changed in version 0.21: `'drop'` is accepted. Using None was deprecated in 0.22 and support was removed in 0.24.
**weights**array-like of shape (n\_regressors,), default=None
Sequence of weights (`float` or `int`) to weight the occurrences of predicted values before averaging. Uses uniform weights if `None`.
**n\_jobs**int, default=None
The number of jobs to run in parallel for `fit`. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**verbose**bool, default=False
If True, the time elapsed while fitting will be printed as it is completed.
New in version 0.23.
Attributes:
**estimators\_**list of regressors
The collection of fitted sub-estimators as defined in `estimators` that are not ‘drop’.
**named\_estimators\_**[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
Attribute to access any fitted sub-estimators by name.
New in version 0.20.
[`n_features_in_`](#sklearn.ensemble.VotingRegressor.n_features_in_ "sklearn.ensemble.VotingRegressor.n_features_in_")int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Only defined if the underlying estimators expose such an attribute when fit. .. versionadded:: 1.0
See also
[`VotingClassifier`](sklearn.ensemble.votingclassifier#sklearn.ensemble.VotingClassifier "sklearn.ensemble.VotingClassifier")
Soft Voting/Majority Rule classifier.
#### Examples
```
>>> import numpy as np
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.ensemble import RandomForestRegressor
>>> from sklearn.ensemble import VotingRegressor
>>> from sklearn.neighbors import KNeighborsRegressor
>>> r1 = LinearRegression()
>>> r2 = RandomForestRegressor(n_estimators=10, random_state=1)
>>> r3 = KNeighborsRegressor()
>>> X = np.array([[1, 1], [2, 4], [3, 9], [4, 16], [5, 25], [6, 36]])
>>> y = np.array([2, 6, 12, 20, 30, 42])
>>> er = VotingRegressor([('lr', r1), ('rf', r2), ('r3', r3)])
>>> print(er.fit(X, y).predict(X))
[ 6.8... 8.4... 12.5... 17.8... 26... 34...]
```
In the following example, we drop the `'lr'` estimator with [`set_params`](#sklearn.ensemble.VotingRegressor.set_params "sklearn.ensemble.VotingRegressor.set_params") and fit the remaining two estimators:
```
>>> er = er.set_params(lr='drop')
>>> er = er.fit(X, y)
>>> len(er.estimators_)
2
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.ensemble.VotingRegressor.fit "sklearn.ensemble.VotingRegressor.fit")(X, y[, sample\_weight]) | Fit the estimators. |
| [`fit_transform`](#sklearn.ensemble.VotingRegressor.fit_transform "sklearn.ensemble.VotingRegressor.fit_transform")(X[, y]) | Return class labels or probabilities for each estimator. |
| [`get_feature_names_out`](#sklearn.ensemble.VotingRegressor.get_feature_names_out "sklearn.ensemble.VotingRegressor.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.ensemble.VotingRegressor.get_params "sklearn.ensemble.VotingRegressor.get_params")([deep]) | Get the parameters of an estimator from the ensemble. |
| [`predict`](#sklearn.ensemble.VotingRegressor.predict "sklearn.ensemble.VotingRegressor.predict")(X) | Predict regression target for X. |
| [`score`](#sklearn.ensemble.VotingRegressor.score "sklearn.ensemble.VotingRegressor.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.ensemble.VotingRegressor.set_params "sklearn.ensemble.VotingRegressor.set_params")(\*\*params) | Set the parameters of an estimator from the ensemble. |
| [`transform`](#sklearn.ensemble.VotingRegressor.transform "sklearn.ensemble.VotingRegressor.transform")(X) | Return predictions for X for each estimator. |
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_voting.py#L578)
Fit the estimators.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vectors, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,)
Target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, then samples are equally weighted. Note that this is supported only if all underlying estimators support sample weights.
Returns:
**self**object
Fitted estimator.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_voting.py#L109)
Return class labels or probabilities for each estimator.
Return predictions for X for each estimator.
Parameters:
**X**{array-like, sparse matrix, dataframe} of shape (n\_samples, n\_features)
Input samples.
**y**ndarray of shape (n\_samples,), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_voting.py#L638)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Not used, present here for API consistency by convention.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_base.py#L310)
Get the parameters of an estimator from the ensemble.
Returns the parameters given in the constructor as well as the estimators contained within the `estimators` parameter.
Parameters:
**deep**bool, default=True
Setting it to True gets the various estimators and the parameters of the estimators as well.
Returns:
**params**dict
Parameter and estimator names mapped to their values or parameter names mapped to their values.
*property*n\_features\_in\_
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
*property*named\_estimators
Dictionary to access any fitted sub-estimators by name.
Returns:
[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_voting.py#L603)
Predict regression target for X.
The predicted regression target of an input sample is computed as the mean predicted regression targets of the estimators in the ensemble.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples.
Returns:
**y**ndarray of shape (n\_samples,)
The predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_base.py#L285)
Set the parameters of an estimator from the ensemble.
Valid parameter keys can be listed with `get_params()`. Note that you can directly set the parameters of the estimators contained in `estimators`.
Parameters:
**\*\*params**keyword arguments
Specific parameters using e.g. `set_params(parameter_name=new_value)`. In addition, to setting the parameters of the estimator, the individual estimator of the estimators can also be set, or can be removed by setting them to ‘drop’.
Returns:
**self**object
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_voting.py#L622)
Return predictions for X for each estimator.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples.
Returns:
**predictions**ndarray of shape (n\_samples, n\_classifiers)
Values predicted by each regressor.
Examples using `sklearn.ensemble.VotingRegressor`
-------------------------------------------------
[Plot individual and voting regression predictions](../../auto_examples/ensemble/plot_voting_regressor#sphx-glr-auto-examples-ensemble-plot-voting-regressor-py)
scikit_learn sklearn.datasets.fetch_kddcup99 sklearn.datasets.fetch\_kddcup99
================================
sklearn.datasets.fetch\_kddcup99(*\**, *subset=None*, *data\_home=None*, *shuffle=False*, *random\_state=None*, *percent10=True*, *download\_if\_missing=True*, *return\_X\_y=False*, *as\_frame=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_kddcup99.py#L49)
Load the kddcup99 dataset (classification).
Download it if necessary.
| | |
| --- | --- |
| Classes | 23 |
| Samples total | 4898431 |
| Dimensionality | 41 |
| Features | discrete (int) or continuous (float) |
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/real_world.html#kddcup99-dataset).
New in version 0.18.
Parameters:
**subset**{‘SA’, ‘SF’, ‘http’, ‘smtp’}, default=None
To return the corresponding classical subsets of kddcup 99. If None, return the entire kddcup 99 dataset.
**data\_home**str, default=None
Specify another download and cache folder for the datasets. By default all scikit-learn data is stored in ‘~/scikit\_learn\_data’ subfolders. .. versionadded:: 0.19
**shuffle**bool, default=False
Whether to shuffle dataset.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for dataset shuffling and for selection of abnormal samples if `subset='SA'`. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**percent10**bool, default=True
Whether to load only 10 percent of the data.
**download\_if\_missing**bool, default=True
If False, raise a IOError if the data is not locally available instead of trying to download the data from the source site.
**return\_X\_y**bool, default=False
If True, returns `(data, target)` instead of a Bunch object. See below for more information about the `data` and `target` object.
New in version 0.20.
**as\_frame**bool, default=False
If `True`, returns a pandas Dataframe for the `data` and `target` objects in the `Bunch` returned object; `Bunch` return object will also have a `frame` member.
New in version 0.24.
Returns:
**data**[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
Dictionary-like object, with the following attributes.
data{ndarray, dataframe} of shape (494021, 41)
The data matrix to learn. If `as_frame=True`, `data` will be a pandas DataFrame.
target{ndarray, series} of shape (494021,)
The regression target for each sample. If `as_frame=True`, `target` will be a pandas Series.
framedataframe of shape (494021, 42)
Only present when `as_frame=True`. Contains `data` and `target`.
DESCRstr
The full description of the dataset.
feature\_nameslist
The names of the dataset columns
target\_names: list
The names of the target columns
**(data, target)**tuple if `return_X_y` is True
A tuple of two ndarray. The first containing a 2D array of shape (n\_samples, n\_features) with each row representing one sample and each column representing the features. The second ndarray of shape (n\_samples,) containing the target samples.
New in version 0.20.
Examples using `sklearn.datasets.fetch_kddcup99`
------------------------------------------------
[Evaluation of outlier detection estimators](../../auto_examples/miscellaneous/plot_outlier_detection_bench#sphx-glr-auto-examples-miscellaneous-plot-outlier-detection-bench-py)
| programming_docs |
scikit_learn sklearn.exceptions.DataConversionWarning sklearn.exceptions.DataConversionWarning
========================================
*class*sklearn.exceptions.DataConversionWarning[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/exceptions.py#L49)
Warning used to notify implicit data conversions happening in the code.
This warning occurs when some input data needs to be converted or interpreted in a way that may not match the user’s expectations.
For example, this warning may occur when the user
* passes an integer array to a function which expects float input and will convert the input
* requests a non-copying operation, but a copy is required to meet the implementation’s data-type expectations;
* passes an input whose shape can be interpreted ambiguously.
Changed in version 0.18: Moved from sklearn.utils.validation.
Attributes:
**args**
#### Methods
| | |
| --- | --- |
| [`with_traceback`](#sklearn.exceptions.DataConversionWarning.with_traceback "sklearn.exceptions.DataConversionWarning.with_traceback") | Exception.with\_traceback(tb) -- set self.\_\_traceback\_\_ to tb and return self. |
with\_traceback()
Exception.with\_traceback(tb) – set self.\_\_traceback\_\_ to tb and return self.
scikit_learn sklearn.cluster.affinity_propagation sklearn.cluster.affinity\_propagation
=====================================
sklearn.cluster.affinity\_propagation(*S*, *\**, *preference=None*, *convergence\_iter=15*, *max\_iter=200*, *damping=0.5*, *copy=True*, *verbose=False*, *return\_n\_iter=False*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_affinity_propagation.py#L37)
Perform Affinity Propagation Clustering of data.
Read more in the [User Guide](../clustering#affinity-propagation).
Parameters:
**S**array-like of shape (n\_samples, n\_samples)
Matrix of similarities between points.
**preference**array-like of shape (n\_samples,) or float, default=None
Preferences for each point - points with larger values of preferences are more likely to be chosen as exemplars. The number of exemplars, i.e. of clusters, is influenced by the input preferences value. If the preferences are not passed as arguments, they will be set to the median of the input similarities (resulting in a moderate number of clusters). For a smaller amount of clusters, this can be set to the minimum value of the similarities.
**convergence\_iter**int, default=15
Number of iterations with no change in the number of estimated clusters that stops the convergence.
**max\_iter**int, default=200
Maximum number of iterations.
**damping**float, default=0.5
Damping factor between 0.5 and 1.
**copy**bool, default=True
If copy is False, the affinity matrix is modified inplace by the algorithm, for memory efficiency.
**verbose**bool, default=False
The verbosity level.
**return\_n\_iter**bool, default=False
Whether or not to return the number of iterations.
**random\_state**int, RandomState instance or None, default=None
Pseudo-random number generator to control the starting state. Use an int for reproducible results across function calls. See the [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
New in version 0.23: this parameter was previously hardcoded as 0.
Returns:
**cluster\_centers\_indices**ndarray of shape (n\_clusters,)
Index of clusters centers.
**labels**ndarray of shape (n\_samples,)
Cluster labels for each point.
**n\_iter**int
Number of iterations run. Returned only if `return_n_iter` is set to True.
#### Notes
For an example, see [examples/cluster/plot\_affinity\_propagation.py](../../auto_examples/cluster/plot_affinity_propagation#sphx-glr-auto-examples-cluster-plot-affinity-propagation-py).
When the algorithm does not converge, it will still return a arrays of `cluster_center_indices` and labels if there are any exemplars/clusters, however they may be degenerate and should be used with caution.
When all training samples have equal similarities and equal preferences, the assignment of cluster centers and labels depends on the preference. If the preference is smaller than the similarities, a single cluster center and label `0` for every sample will be returned. Otherwise, every training sample becomes its own cluster center and is assigned a unique label.
#### References
Brendan J. Frey and Delbert Dueck, “Clustering by Passing Messages Between Data Points”, Science Feb. 2007
Examples using `sklearn.cluster.affinity_propagation`
-----------------------------------------------------
[Visualizing the stock market structure](../../auto_examples/applications/plot_stock_market#sphx-glr-auto-examples-applications-plot-stock-market-py)
scikit_learn sklearn.svm.SVR sklearn.svm.SVR
===============
*class*sklearn.svm.SVR(*\**, *kernel='rbf'*, *degree=3*, *gamma='scale'*, *coef0=0.0*, *tol=0.001*, *C=1.0*, *epsilon=0.1*, *shrinking=True*, *cache\_size=200*, *verbose=False*, *max\_iter=-1*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/svm/_classes.py#L1063)
Epsilon-Support Vector Regression.
The free parameters in the model are C and epsilon.
The implementation is based on libsvm. The fit time complexity is more than quadratic with the number of samples which makes it hard to scale to datasets with more than a couple of 10000 samples. For large datasets consider using [`LinearSVR`](sklearn.svm.linearsvr#sklearn.svm.LinearSVR "sklearn.svm.LinearSVR") or [`SGDRegressor`](sklearn.linear_model.sgdregressor#sklearn.linear_model.SGDRegressor "sklearn.linear_model.SGDRegressor") instead, possibly after a [`Nystroem`](sklearn.kernel_approximation.nystroem#sklearn.kernel_approximation.Nystroem "sklearn.kernel_approximation.Nystroem") transformer.
Read more in the [User Guide](../svm#svm-regression).
Parameters:
**kernel**{‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’} or callable, default=’rbf’
Specifies the kernel type to be used in the algorithm. If none is given, ‘rbf’ will be used. If a callable is given it is used to precompute the kernel matrix.
**degree**int, default=3
Degree of the polynomial kernel function (‘poly’). Ignored by all other kernels.
**gamma**{‘scale’, ‘auto’} or float, default=’scale’
Kernel coefficient for ‘rbf’, ‘poly’ and ‘sigmoid’.
* if `gamma='scale'` (default) is passed then it uses 1 / (n\_features \* X.var()) as value of gamma,
* if ‘auto’, uses 1 / n\_features.
Changed in version 0.22: The default value of `gamma` changed from ‘auto’ to ‘scale’.
**coef0**float, default=0.0
Independent term in kernel function. It is only significant in ‘poly’ and ‘sigmoid’.
**tol**float, default=1e-3
Tolerance for stopping criterion.
**C**float, default=1.0
Regularization parameter. The strength of the regularization is inversely proportional to C. Must be strictly positive. The penalty is a squared l2 penalty.
**epsilon**float, default=0.1
Epsilon in the epsilon-SVR model. It specifies the epsilon-tube within which no penalty is associated in the training loss function with points predicted within a distance epsilon from the actual value.
**shrinking**bool, default=True
Whether to use the shrinking heuristic. See the [User Guide](../svm#shrinking-svm).
**cache\_size**float, default=200
Specify the size of the kernel cache (in MB).
**verbose**bool, default=False
Enable verbose output. Note that this setting takes advantage of a per-process runtime setting in libsvm that, if enabled, may not work properly in a multithreaded context.
**max\_iter**int, default=-1
Hard limit on iterations within solver, or -1 for no limit.
Attributes:
**class\_weight\_**ndarray of shape (n\_classes,)
Multipliers of parameter C for each class. Computed based on the `class_weight` parameter.
[`coef_`](#sklearn.svm.SVR.coef_ "sklearn.svm.SVR.coef_")ndarray of shape (1, n\_features)
Weights assigned to the features when `kernel="linear"`.
**dual\_coef\_**ndarray of shape (1, n\_SV)
Coefficients of the support vector in the decision function.
**fit\_status\_**int
0 if correctly fitted, 1 otherwise (will raise warning)
**intercept\_**ndarray of shape (1,)
Constants in decision function.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_iter\_**int
Number of iterations run by the optimization routine to fit the model.
New in version 1.1.
[`n_support_`](#sklearn.svm.SVR.n_support_ "sklearn.svm.SVR.n_support_")ndarray of shape (1,), dtype=int32
Number of support vectors for each class.
**shape\_fit\_**tuple of int of shape (n\_dimensions\_of\_X,)
Array dimensions of training vector `X`.
**support\_**ndarray of shape (n\_SV,)
Indices of support vectors.
**support\_vectors\_**ndarray of shape (n\_SV, n\_features)
Support vectors.
See also
[`NuSVR`](sklearn.svm.nusvr#sklearn.svm.NuSVR "sklearn.svm.NuSVR")
Support Vector Machine for regression implemented using libsvm using a parameter to control the number of support vectors.
[`LinearSVR`](sklearn.svm.linearsvr#sklearn.svm.LinearSVR "sklearn.svm.LinearSVR")
Scalable Linear Support Vector Machine for regression implemented using liblinear.
#### References
[1] [LIBSVM: A Library for Support Vector Machines](http://www.csie.ntu.edu.tw/~cjlin/papers/libsvm.pdf)
[2] [Platt, John (1999). “Probabilistic outputs for support vector machines and comparison to regularizedlikelihood methods.”](http://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.41.1639)
#### Examples
```
>>> from sklearn.svm import SVR
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.preprocessing import StandardScaler
>>> import numpy as np
>>> n_samples, n_features = 10, 5
>>> rng = np.random.RandomState(0)
>>> y = rng.randn(n_samples)
>>> X = rng.randn(n_samples, n_features)
>>> regr = make_pipeline(StandardScaler(), SVR(C=1.0, epsilon=0.2))
>>> regr.fit(X, y)
Pipeline(steps=[('standardscaler', StandardScaler()),
('svr', SVR(epsilon=0.2))])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.svm.SVR.fit "sklearn.svm.SVR.fit")(X, y[, sample\_weight]) | Fit the SVM model according to the given training data. |
| [`get_params`](#sklearn.svm.SVR.get_params "sklearn.svm.SVR.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.svm.SVR.predict "sklearn.svm.SVR.predict")(X) | Perform regression on samples in X. |
| [`score`](#sklearn.svm.SVR.score "sklearn.svm.SVR.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.svm.SVR.set_params "sklearn.svm.SVR.set_params")(\*\*params) | Set the parameters of this estimator. |
*property*coef\_
Weights assigned to the features when `kernel="linear"`.
Returns:
ndarray of shape (n\_features, n\_classes)
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/svm/_base.py#L122)
Fit the SVM model according to the given training data.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features) or (n\_samples, n\_samples)
Training vectors, where `n_samples` is the number of samples and `n_features` is the number of features. For kernel=”precomputed”, the expected shape of X is (n\_samples, n\_samples).
**y**array-like of shape (n\_samples,)
Target values (class labels in classification, real numbers in regression).
**sample\_weight**array-like of shape (n\_samples,), default=None
Per-sample weights. Rescale C per sample. Higher weights force the classifier to put more emphasis on these points.
Returns:
**self**object
Fitted estimator.
#### Notes
If X and y are not C-ordered and contiguous arrays of np.float64 and X is not a scipy.sparse.csr\_matrix, X and/or y may be copied.
If X is a dense array, then the other methods will not support sparse matrices as input.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_support\_
Number of support vectors for each class.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/svm/_base.py#L417)
Perform regression on samples in X.
For an one-class model, +1 (inlier) or -1 (outlier) is returned.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
For kernel=”precomputed”, the expected shape of X is (n\_samples\_test, n\_samples\_train).
Returns:
**y\_pred**ndarray of shape (n\_samples,)
The predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.svm.SVR`
--------------------------------
[Prediction Latency](../../auto_examples/applications/plot_prediction_latency#sphx-glr-auto-examples-applications-plot-prediction-latency-py)
[Comparison of kernel ridge regression and SVR](../../auto_examples/miscellaneous/plot_kernel_ridge_regression#sphx-glr-auto-examples-miscellaneous-plot-kernel-ridge-regression-py)
[Support Vector Regression (SVR) using linear and non-linear kernels](../../auto_examples/svm/plot_svm_regression#sphx-glr-auto-examples-svm-plot-svm-regression-py)
scikit_learn sklearn.datasets.fetch_covtype sklearn.datasets.fetch\_covtype
===============================
sklearn.datasets.fetch\_covtype(*\**, *data\_home=None*, *download\_if\_missing=True*, *random\_state=None*, *shuffle=False*, *return\_X\_y=False*, *as\_frame=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_covtype.py#L65)
Load the covertype dataset (classification).
Download it if necessary.
| | |
| --- | --- |
| Classes | 7 |
| Samples total | 581012 |
| Dimensionality | 54 |
| Features | int |
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/real_world.html#covtype-dataset).
Parameters:
**data\_home**str, default=None
Specify another download and cache folder for the datasets. By default all scikit-learn data is stored in ‘~/scikit\_learn\_data’ subfolders.
**download\_if\_missing**bool, default=True
If False, raise a IOError if the data is not locally available instead of trying to download the data from the source site.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for dataset shuffling. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**shuffle**bool, default=False
Whether to shuffle dataset.
**return\_X\_y**bool, default=False
If True, returns `(data.data, data.target)` instead of a Bunch object.
New in version 0.20.
**as\_frame**bool, default=False
If True, the data is a pandas DataFrame including columns with appropriate dtypes (numeric). The target is a pandas DataFrame or Series depending on the number of target columns. If `return_X_y` is True, then (`data`, `target`) will be pandas DataFrames or Series as described below.
New in version 0.24.
Returns:
**dataset**[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
Dictionary-like object, with the following attributes.
datandarray of shape (581012, 54)
Each row corresponds to the 54 features in the dataset.
targetndarray of shape (581012,)
Each value corresponds to one of the 7 forest covertypes with values ranging between 1 to 7.
framedataframe of shape (581012, 55)
Only present when `as_frame=True`. Contains `data` and `target`.
DESCRstr
Description of the forest covertype dataset.
feature\_nameslist
The names of the dataset columns.
target\_names: list
The names of the target columns.
**(data, target)**tuple if `return_X_y` is True
A tuple of two ndarray. The first containing a 2D array of shape (n\_samples, n\_features) with each row representing one sample and each column representing the features. The second ndarray of shape (n\_samples,) containing the target samples.
New in version 0.20.
Examples using `sklearn.datasets.fetch_covtype`
-----------------------------------------------
[Release Highlights for scikit-learn 0.24](../../auto_examples/release_highlights/plot_release_highlights_0_24_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-24-0-py)
[Scalable learning with polynomial kernel approximation](../../auto_examples/kernel_approximation/plot_scalable_poly_kernels#sphx-glr-auto-examples-kernel-approximation-plot-scalable-poly-kernels-py)
[Evaluation of outlier detection estimators](../../auto_examples/miscellaneous/plot_outlier_detection_bench#sphx-glr-auto-examples-miscellaneous-plot-outlier-detection-bench-py)
scikit_learn sklearn.feature_selection.f_regression sklearn.feature\_selection.f\_regression
========================================
sklearn.feature\_selection.f\_regression(*X*, *y*, *\**, *center=True*, *force\_finite=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_univariate_selection.py#L323)
Univariate linear regression tests returning F-statistic and p-values.
Quick linear model for testing the effect of a single regressor, sequentially for many regressors.
This is done in 2 steps:
1. The cross correlation between each regressor and the target is computed using [`r_regression`](sklearn.feature_selection.r_regression#sklearn.feature_selection.r_regression "sklearn.feature_selection.r_regression") as:
```
E[(X[:, i] - mean(X[:, i])) * (y - mean(y))] / (std(X[:, i]) * std(y))
```
2. It is converted to an F score and then to a p-value.
[`f_regression`](#sklearn.feature_selection.f_regression "sklearn.feature_selection.f_regression") is derived from [`r_regression`](sklearn.feature_selection.r_regression#sklearn.feature_selection.r_regression "sklearn.feature_selection.r_regression") and will rank features in the same order if all the features are positively correlated with the target.
Note however that contrary to [`f_regression`](#sklearn.feature_selection.f_regression "sklearn.feature_selection.f_regression"), [`r_regression`](sklearn.feature_selection.r_regression#sklearn.feature_selection.r_regression "sklearn.feature_selection.r_regression") values lie in [-1, 1] and can thus be negative. [`f_regression`](#sklearn.feature_selection.f_regression "sklearn.feature_selection.f_regression") is therefore recommended as a feature selection criterion to identify potentially predictive feature for a downstream classifier, irrespective of the sign of the association with the target variable.
Furthermore [`f_regression`](#sklearn.feature_selection.f_regression "sklearn.feature_selection.f_regression") returns p-values while [`r_regression`](sklearn.feature_selection.r_regression#sklearn.feature_selection.r_regression "sklearn.feature_selection.r_regression") does not.
Read more in the [User Guide](../feature_selection#univariate-feature-selection).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data matrix.
**y**array-like of shape (n\_samples,)
The target vector.
**center**bool, default=True
Whether or not to center the data matrix `X` and the target vector `y`. By default, `X` and `y` will be centered.
**force\_finite**bool, default=True
Whether or not to force the F-statistics and associated p-values to be finite. There are two cases where the F-statistic is expected to not be finite:
* when the target `y` or some features in `X` are constant. In this case, the Pearson’s R correlation is not defined leading to obtain `np.nan` values in the F-statistic and p-value. When `force_finite=True`, the F-statistic is set to `0.0` and the associated p-value is set to `1.0`.
* when the a feature in `X` is perfectly correlated (or anti-correlated) with the target `y`. In this case, the F-statistic is expected to be `np.inf`. When `force_finite=True`, the F-statistic is set to `np.finfo(dtype).max` and the associated p-value is set to `0.0`.
New in version 1.1.
Returns:
**f\_statistic**ndarray of shape (n\_features,)
F-statistic for each feature.
**p\_values**ndarray of shape (n\_features,)
P-values associated with the F-statistic.
See also
[`r_regression`](sklearn.feature_selection.r_regression#sklearn.feature_selection.r_regression "sklearn.feature_selection.r_regression")
Pearson’s R between label/feature for regression tasks.
[`f_classif`](sklearn.feature_selection.f_classif#sklearn.feature_selection.f_classif "sklearn.feature_selection.f_classif")
ANOVA F-value between label/feature for classification tasks.
[`chi2`](sklearn.feature_selection.chi2#sklearn.feature_selection.chi2 "sklearn.feature_selection.chi2")
Chi-squared stats of non-negative features for classification tasks.
[`SelectKBest`](sklearn.feature_selection.selectkbest#sklearn.feature_selection.SelectKBest "sklearn.feature_selection.SelectKBest")
Select features based on the k highest scores.
[`SelectFpr`](sklearn.feature_selection.selectfpr#sklearn.feature_selection.SelectFpr "sklearn.feature_selection.SelectFpr")
Select features based on a false positive rate test.
[`SelectFdr`](sklearn.feature_selection.selectfdr#sklearn.feature_selection.SelectFdr "sklearn.feature_selection.SelectFdr")
Select features based on an estimated false discovery rate.
[`SelectFwe`](sklearn.feature_selection.selectfwe#sklearn.feature_selection.SelectFwe "sklearn.feature_selection.SelectFwe")
Select features based on family-wise error rate.
[`SelectPercentile`](sklearn.feature_selection.selectpercentile#sklearn.feature_selection.SelectPercentile "sklearn.feature_selection.SelectPercentile")
Select features based on percentile of the highest scores.
Examples using `sklearn.feature_selection.f_regression`
-------------------------------------------------------
[Feature agglomeration vs. univariate selection](../../auto_examples/cluster/plot_feature_agglomeration_vs_univariate_selection#sphx-glr-auto-examples-cluster-plot-feature-agglomeration-vs-univariate-selection-py)
[Comparison of F-test and mutual information](../../auto_examples/feature_selection/plot_f_test_vs_mi#sphx-glr-auto-examples-feature-selection-plot-f-test-vs-mi-py)
| programming_docs |
scikit_learn sklearn.metrics.zero_one_loss sklearn.metrics.zero\_one\_loss
===============================
sklearn.metrics.zero\_one\_loss(*y\_true*, *y\_pred*, *\**, *normalize=True*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_classification.py#L926)
Zero-one classification loss.
If normalize is `True`, return the fraction of misclassifications (float), else it returns the number of misclassifications (int). The best performance is 0.
Read more in the [User Guide](../model_evaluation#zero-one-loss).
Parameters:
**y\_true**1d array-like, or label indicator array / sparse matrix
Ground truth (correct) labels.
**y\_pred**1d array-like, or label indicator array / sparse matrix
Predicted labels, as returned by a classifier.
**normalize**bool, default=True
If `False`, return the number of misclassifications. Otherwise, return the fraction of misclassifications.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**loss**float or int,
If `normalize == True`, return the fraction of misclassifications (float), else it returns the number of misclassifications (int).
See also
[`accuracy_score`](sklearn.metrics.accuracy_score#sklearn.metrics.accuracy_score "sklearn.metrics.accuracy_score")
Compute the accuracy score. By default, the function will return the fraction of correct predictions divided by the total number of predictions.
[`hamming_loss`](sklearn.metrics.hamming_loss#sklearn.metrics.hamming_loss "sklearn.metrics.hamming_loss")
Compute the average Hamming loss or Hamming distance between two sets of samples.
[`jaccard_score`](sklearn.metrics.jaccard_score#sklearn.metrics.jaccard_score "sklearn.metrics.jaccard_score")
Compute the Jaccard similarity coefficient score.
#### Notes
In multilabel classification, the zero\_one\_loss function corresponds to the subset zero-one loss: for each sample, the entire set of labels must be correctly predicted, otherwise the loss for that sample is equal to one.
#### Examples
```
>>> from sklearn.metrics import zero_one_loss
>>> y_pred = [1, 2, 3, 4]
>>> y_true = [2, 2, 3, 4]
>>> zero_one_loss(y_true, y_pred)
0.25
>>> zero_one_loss(y_true, y_pred, normalize=False)
1
```
In the multilabel case with binary label indicators:
```
>>> import numpy as np
>>> zero_one_loss(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
0.5
```
Examples using `sklearn.metrics.zero_one_loss`
----------------------------------------------
[Discrete versus Real AdaBoost](../../auto_examples/ensemble/plot_adaboost_hastie_10_2#sphx-glr-auto-examples-ensemble-plot-adaboost-hastie-10-2-py)
scikit_learn sklearn.datasets.make_moons sklearn.datasets.make\_moons
============================
sklearn.datasets.make\_moons(*n\_samples=100*, *\**, *shuffle=True*, *noise=None*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_samples_generator.py#L724)
Make two interleaving half circles.
A simple toy dataset to visualize clustering and classification algorithms. Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/sample_generators.html#sample-generators).
Parameters:
**n\_samples**int or tuple of shape (2,), dtype=int, default=100
If int, the total number of points generated. If two-element tuple, number of points in each of two moons.
Changed in version 0.23: Added two-element tuple.
**shuffle**bool, default=True
Whether to shuffle the samples.
**noise**float, default=None
Standard deviation of Gaussian noise added to the data.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for dataset shuffling and noise. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Returns:
**X**ndarray of shape (n\_samples, 2)
The generated samples.
**y**ndarray of shape (n\_samples,)
The integer labels (0 or 1) for class membership of each sample.
Examples using `sklearn.datasets.make_moons`
--------------------------------------------
[Classifier comparison](../../auto_examples/classification/plot_classifier_comparison#sphx-glr-auto-examples-classification-plot-classifier-comparison-py)
[Comparing different clustering algorithms on toy datasets](../../auto_examples/cluster/plot_cluster_comparison#sphx-glr-auto-examples-cluster-plot-cluster-comparison-py)
[Comparing different hierarchical linkage methods on toy datasets](../../auto_examples/cluster/plot_linkage_comparison#sphx-glr-auto-examples-cluster-plot-linkage-comparison-py)
[Comparing anomaly detection algorithms for outlier detection on toy datasets](../../auto_examples/miscellaneous/plot_anomaly_comparison#sphx-glr-auto-examples-miscellaneous-plot-anomaly-comparison-py)
[Statistical comparison of models using grid search](../../auto_examples/model_selection/plot_grid_search_stats#sphx-glr-auto-examples-model-selection-plot-grid-search-stats-py)
[Compare Stochastic learning strategies for MLPClassifier](../../auto_examples/neural_networks/plot_mlp_training_curves#sphx-glr-auto-examples-neural-networks-plot-mlp-training-curves-py)
[Varying regularization in Multi-layer Perceptron](../../auto_examples/neural_networks/plot_mlp_alpha#sphx-glr-auto-examples-neural-networks-plot-mlp-alpha-py)
[Feature discretization](../../auto_examples/preprocessing/plot_discretization_classification#sphx-glr-auto-examples-preprocessing-plot-discretization-classification-py)
scikit_learn sklearn.datasets.make_classification sklearn.datasets.make\_classification
=====================================
sklearn.datasets.make\_classification(*n\_samples=100*, *n\_features=20*, *\**, *n\_informative=2*, *n\_redundant=2*, *n\_repeated=0*, *n\_classes=2*, *n\_clusters\_per\_class=2*, *weights=None*, *flip\_y=0.01*, *class\_sep=1.0*, *hypercube=True*, *shift=0.0*, *scale=1.0*, *shuffle=True*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_samples_generator.py#L40)
Generate a random n-class classification problem.
This initially creates clusters of points normally distributed (std=1) about vertices of an `n_informative`-dimensional hypercube with sides of length `2*class_sep` and assigns an equal number of clusters to each class. It introduces interdependence between these features and adds various types of further noise to the data.
Without shuffling, `X` horizontally stacks features in the following order: the primary `n_informative` features, followed by `n_redundant` linear combinations of the informative features, followed by `n_repeated` duplicates, drawn randomly with replacement from the informative and redundant features. The remaining features are filled with random noise. Thus, without shuffling, all useful features are contained in the columns `X[:, :n_informative + n_redundant + n_repeated]`.
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/sample_generators.html#sample-generators).
Parameters:
**n\_samples**int, default=100
The number of samples.
**n\_features**int, default=20
The total number of features. These comprise `n_informative` informative features, `n_redundant` redundant features, `n_repeated` duplicated features and `n_features-n_informative-n_redundant-n_repeated` useless features drawn at random.
**n\_informative**int, default=2
The number of informative features. Each class is composed of a number of gaussian clusters each located around the vertices of a hypercube in a subspace of dimension `n_informative`. For each cluster, informative features are drawn independently from N(0, 1) and then randomly linearly combined within each cluster in order to add covariance. The clusters are then placed on the vertices of the hypercube.
**n\_redundant**int, default=2
The number of redundant features. These features are generated as random linear combinations of the informative features.
**n\_repeated**int, default=0
The number of duplicated features, drawn randomly from the informative and the redundant features.
**n\_classes**int, default=2
The number of classes (or labels) of the classification problem.
**n\_clusters\_per\_class**int, default=2
The number of clusters per class.
**weights**array-like of shape (n\_classes,) or (n\_classes - 1,), default=None
The proportions of samples assigned to each class. If None, then classes are balanced. Note that if `len(weights) == n_classes - 1`, then the last class weight is automatically inferred. More than `n_samples` samples may be returned if the sum of `weights` exceeds 1. Note that the actual class proportions will not exactly match `weights` when `flip_y` isn’t 0.
**flip\_y**float, default=0.01
The fraction of samples whose class is assigned randomly. Larger values introduce noise in the labels and make the classification task harder. Note that the default setting flip\_y > 0 might lead to less than `n_classes` in y in some cases.
**class\_sep**float, default=1.0
The factor multiplying the hypercube size. Larger values spread out the clusters/classes and make the classification task easier.
**hypercube**bool, default=True
If True, the clusters are put on the vertices of a hypercube. If False, the clusters are put on the vertices of a random polytope.
**shift**float, ndarray of shape (n\_features,) or None, default=0.0
Shift features by the specified value. If None, then features are shifted by a random value drawn in [-class\_sep, class\_sep].
**scale**float, ndarray of shape (n\_features,) or None, default=1.0
Multiply features by the specified value. If None, then features are scaled by a random value drawn in [1, 100]. Note that scaling happens after shifting.
**shuffle**bool, default=True
Shuffle the samples and the features.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for dataset creation. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Returns:
**X**ndarray of shape (n\_samples, n\_features)
The generated samples.
**y**ndarray of shape (n\_samples,)
The integer labels for class membership of each sample.
See also
[`make_blobs`](sklearn.datasets.make_blobs#sklearn.datasets.make_blobs "sklearn.datasets.make_blobs")
Simplified variant.
[`make_multilabel_classification`](sklearn.datasets.make_multilabel_classification#sklearn.datasets.make_multilabel_classification "sklearn.datasets.make_multilabel_classification")
Unrelated generator for multilabel tasks.
#### Notes
The algorithm is adapted from Guyon [1] and was designed to generate the “Madelon” dataset.
#### References
[1] I. Guyon, “Design of experiments for the NIPS 2003 variable selection benchmark”, 2003.
Examples using `sklearn.datasets.make_classification`
-----------------------------------------------------
[Release Highlights for scikit-learn 0.24](../../auto_examples/release_highlights/plot_release_highlights_0_24_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-24-0-py)
[Release Highlights for scikit-learn 0.22](../../auto_examples/release_highlights/plot_release_highlights_0_22_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-22-0-py)
[Comparison of Calibration of Classifiers](../../auto_examples/calibration/plot_compare_calibration#sphx-glr-auto-examples-calibration-plot-compare-calibration-py)
[Probability Calibration curves](../../auto_examples/calibration/plot_calibration_curve#sphx-glr-auto-examples-calibration-plot-calibration-curve-py)
[Classifier comparison](../../auto_examples/classification/plot_classifier_comparison#sphx-glr-auto-examples-classification-plot-classifier-comparison-py)
[Plot randomly generated classification dataset](../../auto_examples/datasets/plot_random_dataset#sphx-glr-auto-examples-datasets-plot-random-dataset-py)
[Early stopping of Gradient Boosting](../../auto_examples/ensemble/plot_gradient_boosting_early_stopping#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-early-stopping-py)
[Feature importances with a forest of trees](../../auto_examples/ensemble/plot_forest_importances#sphx-glr-auto-examples-ensemble-plot-forest-importances-py)
[Feature transformations with ensembles of trees](../../auto_examples/ensemble/plot_feature_transformation#sphx-glr-auto-examples-ensemble-plot-feature-transformation-py)
[OOB Errors for Random Forests](../../auto_examples/ensemble/plot_ensemble_oob#sphx-glr-auto-examples-ensemble-plot-ensemble-oob-py)
[Pipeline ANOVA SVM](../../auto_examples/feature_selection/plot_feature_selection_pipeline#sphx-glr-auto-examples-feature-selection-plot-feature-selection-pipeline-py)
[Recursive feature elimination with cross-validation](../../auto_examples/feature_selection/plot_rfe_with_cross_validation#sphx-glr-auto-examples-feature-selection-plot-rfe-with-cross-validation-py)
[Comparison between grid search and successive halving](../../auto_examples/model_selection/plot_successive_halving_heatmap#sphx-glr-auto-examples-model-selection-plot-successive-halving-heatmap-py)
[Detection error tradeoff (DET) curve](../../auto_examples/model_selection/plot_det#sphx-glr-auto-examples-model-selection-plot-det-py)
[Successive Halving Iterations](../../auto_examples/model_selection/plot_successive_halving_iterations#sphx-glr-auto-examples-model-selection-plot-successive-halving-iterations-py)
[Neighborhood Components Analysis Illustration](../../auto_examples/neighbors/plot_nca_illustration#sphx-glr-auto-examples-neighbors-plot-nca-illustration-py)
[Varying regularization in Multi-layer Perceptron](../../auto_examples/neural_networks/plot_mlp_alpha#sphx-glr-auto-examples-neural-networks-plot-mlp-alpha-py)
[Feature discretization](../../auto_examples/preprocessing/plot_discretization_classification#sphx-glr-auto-examples-preprocessing-plot-discretization-classification-py)
[Scaling the regularization parameter for SVCs](../../auto_examples/svm/plot_svm_scale_c#sphx-glr-auto-examples-svm-plot-svm-scale-c-py)
scikit_learn sklearn.utils.estimator_checks.parametrize_with_checks sklearn.utils.estimator\_checks.parametrize\_with\_checks
=========================================================
sklearn.utils.estimator\_checks.parametrize\_with\_checks(*estimators*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/estimator_checks.py#L476)
Pytest specific decorator for parametrizing estimator checks.
The `id` of each check is set to be a pprint version of the estimator and the name of the check with its keyword arguments. This allows to use `pytest -k` to specify which tests to run:
```
pytest test_check_estimators.py -k check_estimators_fit_returns_self
```
Parameters:
**estimators**list of estimators instances
Estimators to generated checks for.
Changed in version 0.24: Passing a class was deprecated in version 0.23, and support for classes was removed in 0.24. Pass an instance instead.
New in version 0.24.
Returns:
**decorator**`pytest.mark.parametrize`
See also
[`check_estimator`](sklearn.utils.estimator_checks.check_estimator#sklearn.utils.estimator_checks.check_estimator "sklearn.utils.estimator_checks.check_estimator")
Check if estimator adheres to scikit-learn conventions.
#### Examples
```
>>> from sklearn.utils.estimator_checks import parametrize_with_checks
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.tree import DecisionTreeRegressor
```
```
>>> @parametrize_with_checks([LogisticRegression(),
... DecisionTreeRegressor()])
... def test_sklearn_compatible_estimator(estimator, check):
... check(estimator)
```
Examples using `sklearn.utils.estimator_checks.parametrize_with_checks`
-----------------------------------------------------------------------
[Release Highlights for scikit-learn 0.22](../../auto_examples/release_highlights/plot_release_highlights_0_22_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-22-0-py)
scikit_learn sklearn.utils.check_X_y sklearn.utils.check\_X\_y
=========================
sklearn.utils.check\_X\_y(*X*, *y*, *accept\_sparse=False*, *\**, *accept\_large\_sparse=True*, *dtype='numeric'*, *order=None*, *copy=False*, *force\_all\_finite=True*, *ensure\_2d=True*, *allow\_nd=False*, *multi\_output=False*, *ensure\_min\_samples=1*, *ensure\_min\_features=1*, *y\_numeric=False*, *estimator=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/validation.py#L949)
Input validation for standard estimators.
Checks X and y for consistent length, enforces X to be 2D and y 1D. By default, X is checked to be non-empty and containing only finite values. Standard input checks are also applied to y, such as checking that y does not have np.nan or np.inf targets. For multi-label y, set multi\_output=True to allow 2D and sparse y. If the dtype of X is object, attempt converting to float, raising on failure.
Parameters:
**X**{ndarray, list, sparse matrix}
Input data.
**y**{ndarray, list, sparse matrix}
Labels.
**accept\_sparse**str, bool or list of str, default=False
String[s] representing allowed sparse matrix formats, such as ‘csc’, ‘csr’, etc. If the input is sparse but not in the allowed format, it will be converted to the first listed format. True allows the input to be any format. False means that a sparse matrix input will raise an error.
**accept\_large\_sparse**bool, default=True
If a CSR, CSC, COO or BSR sparse matrix is supplied and accepted by accept\_sparse, accept\_large\_sparse will cause it to be accepted only if its indices are stored with a 32-bit dtype.
New in version 0.20.
**dtype**‘numeric’, type, list of type or None, default=’numeric’
Data type of result. If None, the dtype of the input is preserved. If “numeric”, dtype is preserved unless array.dtype is object. If dtype is a list of types, conversion on the first type is only performed if the dtype of the input is not in the list.
**order**{‘F’, ‘C’}, default=None
Whether an array will be forced to be fortran or c-style.
**copy**bool, default=False
Whether a forced copy will be triggered. If copy=False, a copy might be triggered by a conversion.
**force\_all\_finite**bool or ‘allow-nan’, default=True
Whether to raise an error on np.inf, np.nan, pd.NA in X. This parameter does not influence whether y can have np.inf, np.nan, pd.NA values. The possibilities are:
* True: Force all values of X to be finite.
* False: accepts np.inf, np.nan, pd.NA in X.
* ‘allow-nan’: accepts only np.nan or pd.NA values in X. Values cannot be infinite.
New in version 0.20: `force_all_finite` accepts the string `'allow-nan'`.
Changed in version 0.23: Accepts `pd.NA` and converts it into `np.nan`
**ensure\_2d**bool, default=True
Whether to raise a value error if X is not 2D.
**allow\_nd**bool, default=False
Whether to allow X.ndim > 2.
**multi\_output**bool, default=False
Whether to allow 2D y (array or sparse matrix). If false, y will be validated as a vector. y cannot have np.nan or np.inf values if multi\_output=True.
**ensure\_min\_samples**int, default=1
Make sure that X has a minimum number of samples in its first axis (rows for a 2D array).
**ensure\_min\_features**int, default=1
Make sure that the 2D array has some minimum number of features (columns). The default value of 1 rejects empty datasets. This check is only enforced when X has effectively 2 dimensions or is originally 1D and `ensure_2d` is True. Setting to 0 disables this check.
**y\_numeric**bool, default=False
Whether to ensure that y has a numeric type. If dtype of y is object, it is converted to float64. Should only be used for regression algorithms.
**estimator**str or estimator instance, default=None
If passed, include the name of the estimator in warning messages.
Returns:
**X\_converted**object
The converted and validated X.
**y\_converted**object
The converted and validated y.
| programming_docs |
scikit_learn sklearn.gaussian_process.kernels.Sum sklearn.gaussian\_process.kernels.Sum
=====================================
*class*sklearn.gaussian\_process.kernels.Sum(*k1*, *k2*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L774)
The `Sum` kernel takes two kernels \(k\_1\) and \(k\_2\) and combines them via
\[k\_{sum}(X, Y) = k\_1(X, Y) + k\_2(X, Y)\] Note that the `__add__` magic method is overridden, so `Sum(RBF(), RBF())` is equivalent to using the + operator with `RBF() + RBF()`.
Read more in the [User Guide](../gaussian_process#gp-kernels).
New in version 0.18.
Parameters:
**k1**Kernel
The first base-kernel of the sum-kernel
**k2**Kernel
The second base-kernel of the sum-kernel
Attributes:
[`bounds`](#sklearn.gaussian_process.kernels.Sum.bounds "sklearn.gaussian_process.kernels.Sum.bounds")
Returns the log-transformed bounds on the theta.
[`hyperparameters`](#sklearn.gaussian_process.kernels.Sum.hyperparameters "sklearn.gaussian_process.kernels.Sum.hyperparameters")
Returns a list of all hyperparameter.
[`n_dims`](#sklearn.gaussian_process.kernels.Sum.n_dims "sklearn.gaussian_process.kernels.Sum.n_dims")
Returns the number of non-fixed hyperparameters of the kernel.
[`requires_vector_input`](#sklearn.gaussian_process.kernels.Sum.requires_vector_input "sklearn.gaussian_process.kernels.Sum.requires_vector_input")
Returns whether the kernel is stationary.
[`theta`](#sklearn.gaussian_process.kernels.Sum.theta "sklearn.gaussian_process.kernels.Sum.theta")
Returns the (flattened, log-transformed) non-fixed hyperparameters.
#### Examples
```
>>> from sklearn.datasets import make_friedman2
>>> from sklearn.gaussian_process import GaussianProcessRegressor
>>> from sklearn.gaussian_process.kernels import RBF, Sum, ConstantKernel
>>> X, y = make_friedman2(n_samples=500, noise=0, random_state=0)
>>> kernel = Sum(ConstantKernel(2), RBF())
>>> gpr = GaussianProcessRegressor(kernel=kernel,
... random_state=0).fit(X, y)
>>> gpr.score(X, y)
1.0
>>> kernel
1.41**2 + RBF(length_scale=1)
```
#### Methods
| | |
| --- | --- |
| [`__call__`](#sklearn.gaussian_process.kernels.Sum.__call__ "sklearn.gaussian_process.kernels.Sum.__call__")(X[, Y, eval\_gradient]) | Return the kernel k(X, Y) and optionally its gradient. |
| [`clone_with_theta`](#sklearn.gaussian_process.kernels.Sum.clone_with_theta "sklearn.gaussian_process.kernels.Sum.clone_with_theta")(theta) | Returns a clone of self with given hyperparameters theta. |
| [`diag`](#sklearn.gaussian_process.kernels.Sum.diag "sklearn.gaussian_process.kernels.Sum.diag")(X) | Returns the diagonal of the kernel k(X, X). |
| [`get_params`](#sklearn.gaussian_process.kernels.Sum.get_params "sklearn.gaussian_process.kernels.Sum.get_params")([deep]) | Get parameters of this kernel. |
| [`is_stationary`](#sklearn.gaussian_process.kernels.Sum.is_stationary "sklearn.gaussian_process.kernels.Sum.is_stationary")() | Returns whether the kernel is stationary. |
| [`set_params`](#sklearn.gaussian_process.kernels.Sum.set_params "sklearn.gaussian_process.kernels.Sum.set_params")(\*\*params) | Set the parameters of this kernel. |
\_\_call\_\_(*X*, *Y=None*, *eval\_gradient=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L813)
Return the kernel k(X, Y) and optionally its gradient.
Parameters:
**X**array-like of shape (n\_samples\_X, n\_features) or list of object
Left argument of the returned kernel k(X, Y)
**Y**array-like of shape (n\_samples\_X, n\_features) or list of object, default=None
Right argument of the returned kernel k(X, Y). If None, k(X, X) is evaluated instead.
**eval\_gradient**bool, default=False
Determines whether the gradient with respect to the log of the kernel hyperparameter is computed.
Returns:
**K**ndarray of shape (n\_samples\_X, n\_samples\_Y)
Kernel k(X, Y)
**K\_gradient**ndarray of shape (n\_samples\_X, n\_samples\_X, n\_dims), optional
The gradient of the kernel k(X, X) with respect to the log of the hyperparameter of the kernel. Only returned when `eval_gradient` is True.
*property*bounds
Returns the log-transformed bounds on the theta.
Returns:
**bounds**ndarray of shape (n\_dims, 2)
The log-transformed bounds on the kernel’s hyperparameters theta
clone\_with\_theta(*theta*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L238)
Returns a clone of self with given hyperparameters theta.
Parameters:
**theta**ndarray of shape (n\_dims,)
The hyperparameters
diag(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L848)
Returns the diagonal of the kernel k(X, X).
The result of this method is identical to `np.diag(self(X))`; however, it can be evaluated more efficiently since only the diagonal is evaluated.
Parameters:
**X**array-like of shape (n\_samples\_X, n\_features) or list of object
Argument to the kernel.
Returns:
**K\_diag**ndarray of shape (n\_samples\_X,)
Diagonal of kernel k(X, X)
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L666)
Get parameters of this kernel.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*hyperparameters
Returns a list of all hyperparameter.
is\_stationary()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L764)
Returns whether the kernel is stationary.
*property*n\_dims
Returns the number of non-fixed hyperparameters of the kernel.
*property*requires\_vector\_input
Returns whether the kernel is stationary.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L198)
Set the parameters of this kernel.
The method works on simple kernels as well as on nested kernels. The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Returns:
self
*property*theta
Returns the (flattened, log-transformed) non-fixed hyperparameters.
Note that theta are typically the log-transformed values of the kernel’s hyperparameters as this representation of the search space is more amenable for hyperparameter search, as hyperparameters like length-scales naturally live on a log-scale.
Returns:
**theta**ndarray of shape (n\_dims,)
The non-fixed, log-transformed hyperparameters of the kernel
scikit_learn sklearn.metrics.accuracy_score sklearn.metrics.accuracy\_score
===============================
sklearn.metrics.accuracy\_score(*y\_true*, *y\_pred*, *\**, *normalize=True*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_classification.py#L144)
Accuracy classification score.
In multilabel classification, this function computes subset accuracy: the set of labels predicted for a sample must *exactly* match the corresponding set of labels in y\_true.
Read more in the [User Guide](../model_evaluation#accuracy-score).
Parameters:
**y\_true**1d array-like, or label indicator array / sparse matrix
Ground truth (correct) labels.
**y\_pred**1d array-like, or label indicator array / sparse matrix
Predicted labels, as returned by a classifier.
**normalize**bool, default=True
If `False`, return the number of correctly classified samples. Otherwise, return the fraction of correctly classified samples.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
If `normalize == True`, return the fraction of correctly classified samples (float), else returns the number of correctly classified samples (int).
The best performance is 1 with `normalize == True` and the number of samples with `normalize == False`.
See also
[`balanced_accuracy_score`](sklearn.metrics.balanced_accuracy_score#sklearn.metrics.balanced_accuracy_score "sklearn.metrics.balanced_accuracy_score")
Compute the balanced accuracy to deal with imbalanced datasets.
[`jaccard_score`](sklearn.metrics.jaccard_score#sklearn.metrics.jaccard_score "sklearn.metrics.jaccard_score")
Compute the Jaccard similarity coefficient score.
[`hamming_loss`](sklearn.metrics.hamming_loss#sklearn.metrics.hamming_loss "sklearn.metrics.hamming_loss")
Compute the average Hamming loss or Hamming distance between two sets of samples.
[`zero_one_loss`](sklearn.metrics.zero_one_loss#sklearn.metrics.zero_one_loss "sklearn.metrics.zero_one_loss")
Compute the Zero-one classification loss. By default, the function will return the percentage of imperfectly predicted subsets.
#### Notes
In binary classification, this function is equal to the `jaccard_score` function.
#### Examples
```
>>> from sklearn.metrics import accuracy_score
>>> y_pred = [0, 2, 1, 3]
>>> y_true = [0, 1, 2, 3]
>>> accuracy_score(y_true, y_pred)
0.5
>>> accuracy_score(y_true, y_pred, normalize=False)
2
```
In the multilabel case with binary label indicators:
```
>>> import numpy as np
>>> accuracy_score(np.array([[0, 1], [1, 1]]), np.ones((2, 2)))
0.5
```
Examples using `sklearn.metrics.accuracy_score`
-----------------------------------------------
[Plot classification probability](../../auto_examples/classification/plot_classification_probability#sphx-glr-auto-examples-classification-plot-classification-probability-py)
[Multi-class AdaBoosted Decision Trees](../../auto_examples/ensemble/plot_adaboost_multiclass#sphx-glr-auto-examples-ensemble-plot-adaboost-multiclass-py)
[Probabilistic predictions with Gaussian process classification (GPC)](../../auto_examples/gaussian_process/plot_gpc#sphx-glr-auto-examples-gaussian-process-plot-gpc-py)
[Demonstration of multi-metric evaluation on cross\_val\_score and GridSearchCV](../../auto_examples/model_selection/plot_multi_metric_evaluation#sphx-glr-auto-examples-model-selection-plot-multi-metric-evaluation-py)
[Importance of Feature Scaling](../../auto_examples/preprocessing/plot_scaling_importance#sphx-glr-auto-examples-preprocessing-plot-scaling-importance-py)
[Effect of varying threshold for self-training](../../auto_examples/semi_supervised/plot_self_training_varying_threshold#sphx-glr-auto-examples-semi-supervised-plot-self-training-varying-threshold-py)
[Classification of text documents using sparse features](../../auto_examples/text/plot_document_classification_20newsgroups#sphx-glr-auto-examples-text-plot-document-classification-20newsgroups-py)
scikit_learn sklearn.metrics.plot_roc_curve sklearn.metrics.plot\_roc\_curve
================================
sklearn.metrics.plot\_roc\_curve(*estimator*, *X*, *y*, *\**, *sample\_weight=None*, *drop\_intermediate=True*, *response\_method='auto'*, *name=None*, *ax=None*, *pos\_label=None*, *\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_plot/roc_curve.py#L352)
DEPRECATED: Function [`plot_roc_curve`](#sklearn.metrics.plot_roc_curve "sklearn.metrics.plot_roc_curve") is deprecated in 1.0 and will be removed in 1.2. Use one of the class methods: [`sklearn.metrics.RocCurveDisplay.from_predictions`](sklearn.metrics.roccurvedisplay#sklearn.metrics.RocCurveDisplay.from_predictions "sklearn.metrics.RocCurveDisplay.from_predictions") or [`sklearn.metrics.RocCurveDisplay.from_estimator`](sklearn.metrics.roccurvedisplay#sklearn.metrics.RocCurveDisplay.from_estimator "sklearn.metrics.RocCurveDisplay.from_estimator").
Plot Receiver operating characteristic (ROC) curve.
Extra keyword arguments will be passed to matplotlib’s `plot`.
Read more in the [User Guide](https://scikit-learn.org/1.1/visualizations.html#visualizations).
Parameters:
**estimator**estimator instance
Fitted classifier or a fitted [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline") in which the last estimator is a classifier.
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Input values.
**y**array-like of shape (n\_samples,)
Target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**drop\_intermediate**bool, default=True
Whether to drop some suboptimal thresholds which would not appear on a plotted ROC curve. This is useful in order to create lighter ROC curves.
**response\_method**{‘predict\_proba’, ‘decision\_function’, ‘auto’} default=’auto’
Specifies whether to use [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) or [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) as the target response. If set to ‘auto’, [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) is tried first and if it does not exist [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) is tried next.
**name**str, default=None
Name of ROC Curve for labeling. If `None`, use the name of the estimator.
**ax**matplotlib axes, default=None
Axes object to plot on. If `None`, a new figure and axes is created.
**pos\_label**str or int, default=None
The class considered as the positive class when computing the roc auc metrics. By default, `estimators.classes_[1]` is considered as the positive class.
**\*\*kwargs**dict
Additional keywords arguments passed to matplotlib `plot` function.
New in version 0.24.
Returns:
**display**[`RocCurveDisplay`](sklearn.metrics.roccurvedisplay#sklearn.metrics.RocCurveDisplay "sklearn.metrics.RocCurveDisplay")
Object that stores computed values.
See also
[`roc_curve`](sklearn.metrics.roc_curve#sklearn.metrics.roc_curve "sklearn.metrics.roc_curve")
Compute Receiver operating characteristic (ROC) curve.
[`RocCurveDisplay.from_estimator`](sklearn.metrics.roccurvedisplay#sklearn.metrics.RocCurveDisplay.from_estimator "sklearn.metrics.RocCurveDisplay.from_estimator")
ROC Curve visualization given an estimator and some data.
[`RocCurveDisplay.from_predictions`](sklearn.metrics.roccurvedisplay#sklearn.metrics.RocCurveDisplay.from_predictions "sklearn.metrics.RocCurveDisplay.from_predictions")
ROC Curve visualisation given the true and predicted values.
[`roc_auc_score`](sklearn.metrics.roc_auc_score#sklearn.metrics.roc_auc_score "sklearn.metrics.roc_auc_score")
Compute the area under the ROC curve.
#### Examples
```
>>> import matplotlib.pyplot as plt
>>> from sklearn import datasets, metrics, model_selection, svm
>>> X, y = datasets.make_classification(random_state=0)
>>> X_train, X_test, y_train, y_test = model_selection.train_test_split(
... X, y, random_state=0)
>>> clf = svm.SVC(random_state=0)
>>> clf.fit(X_train, y_train)
SVC(random_state=0)
>>> metrics.plot_roc_curve(clf, X_test, y_test)
<...>
>>> plt.show()
```
Examples using `sklearn.metrics.plot_roc_curve`
-----------------------------------------------
[Release Highlights for scikit-learn 0.22](../../auto_examples/release_highlights/plot_release_highlights_0_22_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-22-0-py)
scikit_learn sklearn.model_selection.HalvingGridSearchCV sklearn.model\_selection.HalvingGridSearchCV
============================================
*class*sklearn.model\_selection.HalvingGridSearchCV(*estimator*, *param\_grid*, *\**, *factor=3*, *resource='n\_samples'*, *max\_resources='auto'*, *min\_resources='exhaust'*, *aggressive\_elimination=False*, *cv=5*, *scoring=None*, *refit=True*, *error\_score=nan*, *return\_train\_score=True*, *random\_state=None*, *n\_jobs=None*, *verbose=0*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_search_successive_halving.py#L395)
Search over specified parameter values with successive halving.
The search strategy starts evaluating all the candidates with a small amount of resources and iteratively selects the best candidates, using more and more resources.
Read more in the [User guide](../grid_search#successive-halving-user-guide).
Note
This estimator is still **experimental** for now: the predictions and the API might change without any deprecation cycle. To use it, you need to explicitly import `enable_halving_search_cv`:
```
>>> # explicitly require this experimental feature
>>> from sklearn.experimental import enable_halving_search_cv # noqa
>>> # now you can import normally from model_selection
>>> from sklearn.model_selection import HalvingGridSearchCV
```
Parameters:
**estimator**estimator object
This is assumed to implement the scikit-learn estimator interface. Either estimator needs to provide a `score` function, or `scoring` must be passed.
**param\_grid**dict or list of dictionaries
Dictionary with parameters names (string) as keys and lists of parameter settings to try as values, or a list of such dictionaries, in which case the grids spanned by each dictionary in the list are explored. This enables searching over any sequence of parameter settings.
**factor**int or float, default=3
The ‘halving’ parameter, which determines the proportion of candidates that are selected for each subsequent iteration. For example, `factor=3` means that only one third of the candidates are selected.
**resource**`'n_samples'` or str, default=’n\_samples’
Defines the resource that increases with each iteration. By default, the resource is the number of samples. It can also be set to any parameter of the base estimator that accepts positive integer values, e.g. ‘n\_iterations’ or ‘n\_estimators’ for a gradient boosting estimator. In this case `max_resources` cannot be ‘auto’ and must be set explicitly.
**max\_resources**int, default=’auto’
The maximum amount of resource that any candidate is allowed to use for a given iteration. By default, this is set to `n_samples` when `resource='n_samples'` (default), else an error is raised.
**min\_resources**{‘exhaust’, ‘smallest’} or int, default=’exhaust’
The minimum amount of resource that any candidate is allowed to use for a given iteration. Equivalently, this defines the amount of resources `r0` that are allocated for each candidate at the first iteration.
* ‘smallest’ is a heuristic that sets `r0` to a small value:
+ `n_splits * 2` when `resource='n_samples'` for a regression problem
+ `n_classes * n_splits * 2` when `resource='n_samples'` for a classification problem
+ `1` when `resource != 'n_samples'`
* ‘exhaust’ will set `r0` such that the **last** iteration uses as much resources as possible. Namely, the last iteration will use the highest value smaller than `max_resources` that is a multiple of both `min_resources` and `factor`. In general, using ‘exhaust’ leads to a more accurate estimator, but is slightly more time consuming.
Note that the amount of resources used at each iteration is always a multiple of `min_resources`.
**aggressive\_elimination**bool, default=False
This is only relevant in cases where there isn’t enough resources to reduce the remaining candidates to at most `factor` after the last iteration. If `True`, then the search process will ‘replay’ the first iteration for as long as needed until the number of candidates is small enough. This is `False` by default, which means that the last iteration may evaluate more than `factor` candidates. See [Aggressive elimination of candidates](../grid_search#aggressive-elimination) for more details.
**cv**int, cross-validation generator or iterable, default=5
Determines the cross-validation splitting strategy. Possible inputs for cv are:
* integer, to specify the number of folds in a `(Stratified)KFold`,
* [CV splitter](https://scikit-learn.org/1.1/glossary.html#term-CV-splitter),
* An iterable yielding (train, test) splits as arrays of indices.
For integer/None inputs, if the estimator is a classifier and `y` is either binary or multiclass, [`StratifiedKFold`](sklearn.model_selection.stratifiedkfold#sklearn.model_selection.StratifiedKFold "sklearn.model_selection.StratifiedKFold") is used. In all other cases, [`KFold`](sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold") is used. These splitters are instantiated with `shuffle=False` so the splits will be the same across calls.
Refer [User Guide](../cross_validation#cross-validation) for the various cross-validation strategies that can be used here.
Note
Due to implementation details, the folds produced by `cv` must be the same across multiple calls to `cv.split()`. For built-in `scikit-learn` iterators, this can be achieved by deactivating shuffling (`shuffle=False`), or by setting the `cv`’s `random_state` parameter to an integer.
**scoring**str, callable, or None, default=None
A single string (see [The scoring parameter: defining model evaluation rules](../model_evaluation#scoring-parameter)) or a callable (see [Defining your scoring strategy from metric functions](../model_evaluation#scoring)) to evaluate the predictions on the test set. If None, the estimator’s score method is used.
**refit**bool, default=True
If True, refit an estimator using the best found parameters on the whole dataset.
The refitted estimator is made available at the `best_estimator_` attribute and permits using `predict` directly on this `HalvingGridSearchCV` instance.
**error\_score**‘raise’ or numeric
Value to assign to the score if an error occurs in estimator fitting. If set to ‘raise’, the error is raised. If a numeric value is given, FitFailedWarning is raised. This parameter does not affect the refit step, which will always raise the error. Default is `np.nan`.
**return\_train\_score**bool, default=False
If `False`, the `cv_results_` attribute will not include training scores. Computing training scores is used to get insights on how different parameter settings impact the overfitting/underfitting trade-off. However computing the scores on the training set can be computationally expensive and is not strictly required to select the parameters that yield the best generalization performance.
**random\_state**int, RandomState instance or None, default=None
Pseudo random number generator state used for subsampling the dataset when `resources != 'n_samples'`. Ignored otherwise. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**n\_jobs**int or None, default=None
Number of jobs to run in parallel. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**verbose**int
Controls the verbosity: the higher, the more messages.
Attributes:
**n\_resources\_**list of int
The amount of resources used at each iteration.
**n\_candidates\_**list of int
The number of candidate parameters that were evaluated at each iteration.
**n\_remaining\_candidates\_**int
The number of candidate parameters that are left after the last iteration. It corresponds to `ceil(n_candidates[-1] / factor)`
**max\_resources\_**int
The maximum number of resources that any candidate is allowed to use for a given iteration. Note that since the number of resources used at each iteration must be a multiple of `min_resources_`, the actual number of resources used at the last iteration may be smaller than `max_resources_`.
**min\_resources\_**int
The amount of resources that are allocated for each candidate at the first iteration.
**n\_iterations\_**int
The actual number of iterations that were run. This is equal to `n_required_iterations_` if `aggressive_elimination` is `True`. Else, this is equal to `min(n_possible_iterations_,
n_required_iterations_)`.
**n\_possible\_iterations\_**int
The number of iterations that are possible starting with `min_resources_` resources and without exceeding `max_resources_`.
**n\_required\_iterations\_**int
The number of iterations that are required to end up with less than `factor` candidates at the last iteration, starting with `min_resources_` resources. This will be smaller than `n_possible_iterations_` when there isn’t enough resources.
**cv\_results\_**dict of numpy (masked) ndarrays
A dict with keys as column headers and values as columns, that can be imported into a pandas `DataFrame`. It contains lots of information for analysing the results of a search. Please refer to the [User guide](../grid_search#successive-halving-cv-results) for details.
**best\_estimator\_**estimator or dict
Estimator that was chosen by the search, i.e. estimator which gave highest score (or smallest loss if specified) on the left out data. Not available if `refit=False`.
**best\_score\_**float
Mean cross-validated score of the best\_estimator.
**best\_params\_**dict
Parameter setting that gave the best results on the hold out data.
**best\_index\_**int
The index (of the `cv_results_` arrays) which corresponds to the best candidate parameter setting.
The dict at `search.cv_results_['params'][search.best_index_]` gives the parameter setting for the best model, that gives the highest mean score (`search.best_score_`).
**scorer\_**function or a dict
Scorer function used on the held out data to choose the best parameters for the model.
**n\_splits\_**int
The number of cross-validation splits (folds/iterations).
**refit\_time\_**float
Seconds used for refitting the best model on the whole dataset.
This is present only if `refit` is not False.
**multimetric\_**bool
Whether or not the scorers compute several metrics.
[`classes_`](#sklearn.model_selection.HalvingGridSearchCV.classes_ "sklearn.model_selection.HalvingGridSearchCV.classes_")ndarray of shape (n\_classes,)
Class labels.
[`n_features_in_`](#sklearn.model_selection.HalvingGridSearchCV.n_features_in_ "sklearn.model_selection.HalvingGridSearchCV.n_features_in_")int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Only defined if `best_estimator_` is defined (see the documentation for the `refit` parameter for more details) and that `best_estimator_` exposes `feature_names_in_` when fit.
New in version 1.0.
See also
[`HalvingRandomSearchCV`](sklearn.model_selection.halvingrandomsearchcv#sklearn.model_selection.HalvingRandomSearchCV "sklearn.model_selection.HalvingRandomSearchCV")
Random search over a set of parameters using successive halving.
#### Notes
The parameters selected are those that maximize the score of the held-out data, according to the scoring parameter.
#### Examples
```
>>> from sklearn.datasets import load_iris
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.experimental import enable_halving_search_cv # noqa
>>> from sklearn.model_selection import HalvingGridSearchCV
...
>>> X, y = load_iris(return_X_y=True)
>>> clf = RandomForestClassifier(random_state=0)
...
>>> param_grid = {"max_depth": [3, None],
... "min_samples_split": [5, 10]}
>>> search = HalvingGridSearchCV(clf, param_grid, resource='n_estimators',
... max_resources=10,
... random_state=0).fit(X, y)
>>> search.best_params_
{'max_depth': None, 'min_samples_split': 10, 'n_estimators': 9}
```
#### Methods
| | |
| --- | --- |
| [`decision_function`](#sklearn.model_selection.HalvingGridSearchCV.decision_function "sklearn.model_selection.HalvingGridSearchCV.decision_function")(X) | Call decision\_function on the estimator with the best found parameters. |
| [`fit`](#sklearn.model_selection.HalvingGridSearchCV.fit "sklearn.model_selection.HalvingGridSearchCV.fit")(X[, y, groups]) | Run fit with all sets of parameters. |
| [`get_params`](#sklearn.model_selection.HalvingGridSearchCV.get_params "sklearn.model_selection.HalvingGridSearchCV.get_params")([deep]) | Get parameters for this estimator. |
| [`inverse_transform`](#sklearn.model_selection.HalvingGridSearchCV.inverse_transform "sklearn.model_selection.HalvingGridSearchCV.inverse_transform")(Xt) | Call inverse\_transform on the estimator with the best found params. |
| [`predict`](#sklearn.model_selection.HalvingGridSearchCV.predict "sklearn.model_selection.HalvingGridSearchCV.predict")(X) | Call predict on the estimator with the best found parameters. |
| [`predict_log_proba`](#sklearn.model_selection.HalvingGridSearchCV.predict_log_proba "sklearn.model_selection.HalvingGridSearchCV.predict_log_proba")(X) | Call predict\_log\_proba on the estimator with the best found parameters. |
| [`predict_proba`](#sklearn.model_selection.HalvingGridSearchCV.predict_proba "sklearn.model_selection.HalvingGridSearchCV.predict_proba")(X) | Call predict\_proba on the estimator with the best found parameters. |
| [`score`](#sklearn.model_selection.HalvingGridSearchCV.score "sklearn.model_selection.HalvingGridSearchCV.score")(X[, y]) | Return the score on the given data, if the estimator has been refit. |
| [`score_samples`](#sklearn.model_selection.HalvingGridSearchCV.score_samples "sklearn.model_selection.HalvingGridSearchCV.score_samples")(X) | Call score\_samples on the estimator with the best found parameters. |
| [`set_params`](#sklearn.model_selection.HalvingGridSearchCV.set_params "sklearn.model_selection.HalvingGridSearchCV.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.model_selection.HalvingGridSearchCV.transform "sklearn.model_selection.HalvingGridSearchCV.transform")(X) | Call transform on the estimator with the best found parameters. |
*property*classes\_
Class labels.
Only available when `refit=True` and the estimator is a classifier.
decision\_function(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_search.py#L548)
Call decision\_function on the estimator with the best found parameters.
Only available if `refit=True` and the underlying estimator supports `decision_function`.
Parameters:
**X**indexable, length n\_samples
Must fulfill the input assumptions of the underlying estimator.
Returns:
**y\_score**ndarray of shape (n\_samples,) or (n\_samples, n\_classes) or (n\_samples, n\_classes \* (n\_classes-1) / 2)
Result of the decision function for `X` based on the estimator with the best found parameters.
fit(*X*, *y=None*, *groups=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_search_successive_halving.py#L222)
Run fit with all sets of parameters.
Parameters:
**X**array-like, shape (n\_samples, n\_features)
Training vector, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like, shape (n\_samples,) or (n\_samples, n\_output), optional
Target relative to X for classification or regression; None for unsupervised learning.
**groups**array-like of shape (n\_samples,), default=None
Group labels for the samples used while splitting the dataset into train/test set. Only used in conjunction with a “Group” [cv](https://scikit-learn.org/1.1/glossary.html#term-cv) instance (e.g., [`GroupKFold`](sklearn.model_selection.groupkfold#sklearn.model_selection.GroupKFold "sklearn.model_selection.GroupKFold")).
**\*\*fit\_params**dict of string -> object
Parameters passed to the `fit` method of the estimator.
Returns:
**self**object
Instance of fitted estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
inverse\_transform(*Xt*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_search.py#L593)
Call inverse\_transform on the estimator with the best found params.
Only available if the underlying estimator implements `inverse_transform` and `refit=True`.
Parameters:
**Xt**indexable, length n\_samples
Must fulfill the input assumptions of the underlying estimator.
Returns:
**X**{ndarray, sparse matrix} of shape (n\_samples, n\_features)
Result of the `inverse_transform` function for `Xt` based on the estimator with the best found parameters.
*property*n\_features\_in\_
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
Only available when `refit=True`.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_search.py#L480)
Call predict on the estimator with the best found parameters.
Only available if `refit=True` and the underlying estimator supports `predict`.
Parameters:
**X**indexable, length n\_samples
Must fulfill the input assumptions of the underlying estimator.
Returns:
**y\_pred**ndarray of shape (n\_samples,)
The predicted labels or values for `X` based on the estimator with the best found parameters.
predict\_log\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_search.py#L525)
Call predict\_log\_proba on the estimator with the best found parameters.
Only available if `refit=True` and the underlying estimator supports `predict_log_proba`.
Parameters:
**X**indexable, length n\_samples
Must fulfill the input assumptions of the underlying estimator.
Returns:
**y\_pred**ndarray of shape (n\_samples,) or (n\_samples, n\_classes)
Predicted class log-probabilities for `X` based on the estimator with the best found parameters. The order of the classes corresponds to that in the fitted attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_search.py#L502)
Call predict\_proba on the estimator with the best found parameters.
Only available if `refit=True` and the underlying estimator supports `predict_proba`.
Parameters:
**X**indexable, length n\_samples
Must fulfill the input assumptions of the underlying estimator.
Returns:
**y\_pred**ndarray of shape (n\_samples,) or (n\_samples, n\_classes)
Predicted class probabilities for `X` based on the estimator with the best found parameters. The order of the classes corresponds to that in the fitted attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
score(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_search.py#L413)
Return the score on the given data, if the estimator has been refit.
This uses the score defined by `scoring` where provided, and the `best_estimator_.score` method otherwise.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples, n\_output) or (n\_samples,), default=None
Target relative to X for classification or regression; None for unsupervised learning.
Returns:
**score**float
The score defined by `scoring` if provided, and the `best_estimator_.score` method otherwise.
score\_samples(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_search.py#L457)
Call score\_samples on the estimator with the best found parameters.
Only available if `refit=True` and the underlying estimator supports `score_samples`.
New in version 0.24.
Parameters:
**X**iterable
Data to predict on. Must fulfill input requirements of the underlying estimator.
Returns:
**y\_score**ndarray of shape (n\_samples,)
The `best_estimator_.score_samples` method.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_search.py#L571)
Call transform on the estimator with the best found parameters.
Only available if the underlying estimator supports `transform` and `refit=True`.
Parameters:
**X**indexable, length n\_samples
Must fulfill the input assumptions of the underlying estimator.
Returns:
**Xt**{ndarray, sparse matrix} of shape (n\_samples, n\_features)
`X` transformed in the new space based on the estimator with the best found parameters.
Examples using `sklearn.model_selection.HalvingGridSearchCV`
------------------------------------------------------------
[Release Highlights for scikit-learn 0.24](../../auto_examples/release_highlights/plot_release_highlights_0_24_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-24-0-py)
[Comparison between grid search and successive halving](../../auto_examples/model_selection/plot_successive_halving_heatmap#sphx-glr-auto-examples-model-selection-plot-successive-halving-heatmap-py)
[Successive Halving Iterations](../../auto_examples/model_selection/plot_successive_halving_iterations#sphx-glr-auto-examples-model-selection-plot-successive-halving-iterations-py)
| programming_docs |
scikit_learn sklearn.cluster.cluster_optics_dbscan sklearn.cluster.cluster\_optics\_dbscan
=======================================
sklearn.cluster.cluster\_optics\_dbscan(*\**, *reachability*, *core\_distances*, *ordering*, *eps*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_optics.py#L623)
Perform DBSCAN extraction for an arbitrary epsilon.
Extracting the clusters runs in linear time. Note that this results in `labels_` which are close to a [`DBSCAN`](sklearn.cluster.dbscan#sklearn.cluster.DBSCAN "sklearn.cluster.DBSCAN") with similar settings and `eps`, only if `eps` is close to `max_eps`.
Parameters:
**reachability**array of shape (n\_samples,)
Reachability distances calculated by OPTICS (`reachability_`).
**core\_distances**array of shape (n\_samples,)
Distances at which points become core (`core_distances_`).
**ordering**array of shape (n\_samples,)
OPTICS ordered point indices (`ordering_`).
**eps**float
DBSCAN `eps` parameter. Must be set to < `max_eps`. Results will be close to DBSCAN algorithm if `eps` and `max_eps` are close to one another.
Returns:
**labels\_**array of shape (n\_samples,)
The estimated labels.
Examples using `sklearn.cluster.cluster_optics_dbscan`
------------------------------------------------------
[Demo of OPTICS clustering algorithm](../../auto_examples/cluster/plot_optics#sphx-glr-auto-examples-cluster-plot-optics-py)
scikit_learn sklearn.base.RegressorMixin sklearn.base.RegressorMixin
===========================
*class*sklearn.base.RegressorMixin[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L672)
Mixin class for all regression estimators in scikit-learn.
#### Methods
| | |
| --- | --- |
| [`score`](#sklearn.base.RegressorMixin.score "sklearn.base.RegressorMixin.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
scikit_learn sklearn.neighbors.radius_neighbors_graph sklearn.neighbors.radius\_neighbors\_graph
==========================================
sklearn.neighbors.radius\_neighbors\_graph(*X*, *radius*, *\**, *mode='connectivity'*, *metric='minkowski'*, *p=2*, *metric\_params=None*, *include\_self=False*, *n\_jobs=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_graph.py#L130)
Compute the (weighted) graph of Neighbors for points in X.
Neighborhoods are restricted the points at a distance lower than radius.
Read more in the [User Guide](../neighbors#unsupervised-neighbors).
Parameters:
**X**array-like of shape (n\_samples, n\_features) or BallTree
Sample data, in the form of a numpy array or a precomputed [`BallTree`](sklearn.neighbors.balltree#sklearn.neighbors.BallTree "sklearn.neighbors.BallTree").
**radius**float
Radius of neighborhoods.
**mode**{‘connectivity’, ‘distance’}, default=’connectivity’
Type of returned matrix: ‘connectivity’ will return the connectivity matrix with ones and zeros, and ‘distance’ will return the distances between neighbors according to the given metric.
**metric**str, default=’minkowski’
Metric to use for distance computation. Default is “minkowski”, which results in the standard Euclidean distance when p = 2. See the documentation of [scipy.spatial.distance](https://docs.scipy.org/doc/scipy/reference/spatial.distance.html) and the metrics listed in [`distance_metrics`](sklearn.metrics.pairwise.distance_metrics#sklearn.metrics.pairwise.distance_metrics "sklearn.metrics.pairwise.distance_metrics") for valid metric values.
**p**int, default=2
Power parameter for the Minkowski metric. When p = 1, this is equivalent to using manhattan\_distance (l1), and euclidean\_distance (l2) for p = 2. For arbitrary p, minkowski\_distance (l\_p) is used.
**metric\_params**dict, default=None
Additional keyword arguments for the metric function.
**include\_self**bool or ‘auto’, default=False
Whether or not to mark each sample as the first nearest neighbor to itself. If ‘auto’, then True is used for mode=’connectivity’ and False for mode=’distance’.
**n\_jobs**int, default=None
The number of parallel jobs to run for neighbors search. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
Returns:
**A**sparse matrix of shape (n\_samples, n\_samples)
Graph where A[i, j] is assigned the weight of edge that connects i to j. The matrix is of CSR format.
See also
[`kneighbors_graph`](sklearn.neighbors.kneighbors_graph#sklearn.neighbors.kneighbors_graph "sklearn.neighbors.kneighbors_graph")
Compute the weighted graph of k-neighbors for points in X.
#### Examples
```
>>> X = [[0], [3], [1]]
>>> from sklearn.neighbors import radius_neighbors_graph
>>> A = radius_neighbors_graph(X, 1.5, mode='connectivity',
... include_self=True)
>>> A.toarray()
array([[1., 0., 1.],
[0., 1., 0.],
[1., 0., 1.]])
```
scikit_learn sklearn.metrics.pairwise.nan_euclidean_distances sklearn.metrics.pairwise.nan\_euclidean\_distances
==================================================
sklearn.metrics.pairwise.nan\_euclidean\_distances(*X*, *Y=None*, *\**, *squared=False*, *missing\_values=nan*, *copy=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/pairwise.py#L382)
Calculate the euclidean distances in the presence of missing values.
Compute the euclidean distance between each pair of samples in X and Y, where Y=X is assumed if Y=None. When calculating the distance between a pair of samples, this formulation ignores feature coordinates with a missing value in either sample and scales up the weight of the remaining coordinates:
dist(x,y) = sqrt(weight \* sq. distance from present coordinates) where, weight = Total # of coordinates / # of present coordinates
For example, the distance between `[3, na, na, 6]` and `[1, na, 4, 5]` is:
\[\sqrt{\frac{4}{2}((3-1)^2 + (6-5)^2)}\] If all the coordinates are missing or if there are no common present coordinates then NaN is returned for that pair.
Read more in the [User Guide](../metrics#metrics).
New in version 0.22.
Parameters:
**X**array-like of shape (n\_samples\_X, n\_features)
An array where each row is a sample and each column is a feature.
**Y**array-like of shape (n\_samples\_Y, n\_features), default=None
An array where each row is a sample and each column is a feature. If `None`, method uses `Y=X`.
**squared**bool, default=False
Return squared Euclidean distances.
**missing\_values**np.nan or int, default=np.nan
Representation of missing value.
**copy**bool, default=True
Make and use a deep copy of X and Y (if Y exists).
Returns:
**distances**ndarray of shape (n\_samples\_X, n\_samples\_Y)
Returns the distances between the row vectors of `X` and the row vectors of `Y`.
See also
[`paired_distances`](sklearn.metrics.pairwise.paired_distances#sklearn.metrics.pairwise.paired_distances "sklearn.metrics.pairwise.paired_distances")
Distances between pairs of elements of X and Y.
#### References
* John K. Dixon, “Pattern Recognition with Partly Missing Data”, IEEE Transactions on Systems, Man, and Cybernetics, Volume: 9, Issue: 10, pp. 617 - 621, Oct. 1979. <http://ieeexplore.ieee.org/abstract/document/4310090/>
#### Examples
```
>>> from sklearn.metrics.pairwise import nan_euclidean_distances
>>> nan = float("NaN")
>>> X = [[0, 1], [1, nan]]
>>> nan_euclidean_distances(X, X) # distance between rows of X
array([[0. , 1.41421356],
[1.41421356, 0. ]])
```
```
>>> # get distance to origin
>>> nan_euclidean_distances(X, [[0, 0]])
array([[1. ],
[1.41421356]])
```
scikit_learn sklearn.utils.estimator_checks.check_estimator sklearn.utils.estimator\_checks.check\_estimator
================================================
sklearn.utils.estimator\_checks.check\_estimator(*estimator=None*, *generate\_only=False*, *Estimator='deprecated'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/estimator_checks.py#L538)
Check if estimator adheres to scikit-learn conventions.
This function will run an extensive test-suite for input validation, shapes, etc, making sure that the estimator complies with `scikit-learn` conventions as detailed in [Rolling your own estimator](https://scikit-learn.org/1.1/developers/develop.html#rolling-your-own-estimator). Additional tests for classifiers, regressors, clustering or transformers will be run if the Estimator class inherits from the corresponding mixin from sklearn.base.
Setting `generate_only=True` returns a generator that yields (estimator, check) tuples where the check can be called independently from each other, i.e. `check(estimator)`. This allows all checks to be run independently and report the checks that are failing.
scikit-learn provides a pytest specific decorator, `parametrize_with_checks`, making it easier to test multiple estimators.
Parameters:
**estimator**estimator object
Estimator instance to check.
New in version 1.1: Passing a class was deprecated in version 0.23, and support for classes was removed in 0.24.
**generate\_only**bool, default=False
When `False`, checks are evaluated when `check_estimator` is called. When `True`, `check_estimator` returns a generator that yields (estimator, check) tuples. The check is run by calling `check(estimator)`.
New in version 0.22.
**Estimator**estimator object
Estimator instance to check.
Deprecated since version 1.1: `Estimator` was deprecated in favor of `estimator` in version 1.1 and will be removed in version 1.3.
Returns:
**checks\_generator**generator
Generator that yields (estimator, check) tuples. Returned when `generate_only=True`.
See also
[`parametrize_with_checks`](sklearn.utils.estimator_checks.parametrize_with_checks#sklearn.utils.estimator_checks.parametrize_with_checks "sklearn.utils.estimator_checks.parametrize_with_checks")
Pytest specific decorator for parametrizing estimator checks.
scikit_learn sklearn.base.clone sklearn.base.clone
==================
sklearn.base.clone(*estimator*, *\**, *safe=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L32)
Construct a new unfitted estimator with the same parameters.
Clone does a deep copy of the model in an estimator without actually copying attached data. It returns a new estimator with the same parameters that has not been fitted on any data.
Parameters:
**estimator**{list, tuple, set} of estimator instance or a single estimator instance
The estimator or group of estimators to be cloned.
**safe**bool, default=True
If safe is False, clone will fall back to a deep copy on objects that are not estimators.
Returns:
**estimator**object
The deep copy of the input, an estimator if input is an estimator.
#### Notes
If the estimator’s `random_state` parameter is an integer (or if the estimator doesn’t have a `random_state` parameter), an *exact clone* is returned: the clone and the original estimator will give the exact same results. Otherwise, *statistical clone* is returned: the clone might return different results from the original estimator. More details can be found in [Controlling randomness](https://scikit-learn.org/1.1/common_pitfalls.html#randomness).
scikit_learn sklearn.preprocessing.Normalizer sklearn.preprocessing.Normalizer
================================
*class*sklearn.preprocessing.Normalizer(*norm='l2'*, *\**, *copy=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L1832)
Normalize samples individually to unit norm.
Each sample (i.e. each row of the data matrix) with at least one non zero component is rescaled independently of other samples so that its norm (l1, l2 or inf) equals one.
This transformer is able to work both with dense numpy arrays and scipy.sparse matrix (use CSR format if you want to avoid the burden of a copy / conversion).
Scaling inputs to unit norms is a common operation for text classification or clustering for instance. For instance the dot product of two l2-normalized TF-IDF vectors is the cosine similarity of the vectors and is the base similarity metric for the Vector Space Model commonly used by the Information Retrieval community.
Read more in the [User Guide](../preprocessing#preprocessing-normalization).
Parameters:
**norm**{‘l1’, ‘l2’, ‘max’}, default=’l2’
The norm to use to normalize each non zero sample. If norm=’max’ is used, values will be rescaled by the maximum of the absolute values.
**copy**bool, default=True
Set to False to perform inplace row normalization and avoid a copy (if the input is already a numpy array or a scipy.sparse CSR matrix).
Attributes:
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`normalize`](sklearn.preprocessing.normalize#sklearn.preprocessing.normalize "sklearn.preprocessing.normalize")
Equivalent function without the estimator API.
#### Notes
This estimator is stateless (besides constructor parameters), the fit method does nothing but is useful when used in a pipeline.
For a comparison of the different scalers, transformers, and normalizers, see [examples/preprocessing/plot\_all\_scaling.py](../../auto_examples/preprocessing/plot_all_scaling#sphx-glr-auto-examples-preprocessing-plot-all-scaling-py).
#### Examples
```
>>> from sklearn.preprocessing import Normalizer
>>> X = [[4, 1, 2, 2],
... [1, 3, 9, 3],
... [5, 7, 5, 1]]
>>> transformer = Normalizer().fit(X) # fit does nothing.
>>> transformer
Normalizer()
>>> transformer.transform(X)
array([[0.8, 0.2, 0.4, 0.4],
[0.1, 0.3, 0.9, 0.3],
[0.5, 0.7, 0.5, 0.1]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.preprocessing.Normalizer.fit "sklearn.preprocessing.Normalizer.fit")(X[, y]) | Do nothing and return the estimator unchanged. |
| [`fit_transform`](#sklearn.preprocessing.Normalizer.fit_transform "sklearn.preprocessing.Normalizer.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.preprocessing.Normalizer.get_feature_names_out "sklearn.preprocessing.Normalizer.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.preprocessing.Normalizer.get_params "sklearn.preprocessing.Normalizer.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.preprocessing.Normalizer.set_params "sklearn.preprocessing.Normalizer.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.preprocessing.Normalizer.transform "sklearn.preprocessing.Normalizer.transform")(X[, copy]) | Scale each non zero row of X to unit norm. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L1908)
Do nothing and return the estimator unchanged.
This method is just there to implement the usual API and hence work in pipelines.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data to estimate the normalization parameters.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
**self**object
Fitted transformer.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L880)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Input features.
* If `input_features` is `None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then the following input feature names are generated: `["x0", "x1", ..., "x(n_features_in_ - 1)"]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Same as input features.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*, *copy=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L1930)
Scale each non zero row of X to unit norm.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data to normalize, row by row. scipy.sparse matrices should be in CSR format to avoid an un-necessary copy.
**copy**bool, default=None
Copy the input X or not.
Returns:
**X\_tr**{ndarray, sparse matrix} of shape (n\_samples, n\_features)
Transformed array.
Examples using `sklearn.preprocessing.Normalizer`
-------------------------------------------------
[Scalable learning with polynomial kernel approximation](../../auto_examples/kernel_approximation/plot_scalable_poly_kernels#sphx-glr-auto-examples-kernel-approximation-plot-scalable-poly-kernels-py)
[Compare the effect of different scalers on data with outliers](../../auto_examples/preprocessing/plot_all_scaling#sphx-glr-auto-examples-preprocessing-plot-all-scaling-py)
[Clustering text documents using k-means](../../auto_examples/text/plot_document_clustering#sphx-glr-auto-examples-text-plot-document-clustering-py)
| programming_docs |
scikit_learn sklearn.utils.resample sklearn.utils.resample
======================
sklearn.utils.resample(*\*arrays*, *replace=True*, *n\_samples=None*, *random\_state=None*, *stratify=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/__init__.py#L435)
Resample arrays or sparse matrices in a consistent way.
The default strategy implements one step of the bootstrapping procedure.
Parameters:
**\*arrays**sequence of array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
Indexable data-structures can be arrays, lists, dataframes or scipy sparse matrices with consistent first dimension.
**replace**bool, default=True
Implements resampling with replacement. If False, this will implement (sliced) random permutations.
**n\_samples**int, default=None
Number of samples to generate. If left to None this is automatically set to the first dimension of the arrays. If replace is False it should not be larger than the length of arrays.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for shuffling the data. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**stratify**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
If not None, data is split in a stratified fashion, using this as the class labels.
Returns:
**resampled\_arrays**sequence of array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
Sequence of resampled copies of the collections. The original arrays are not impacted.
See also
[`shuffle`](sklearn.utils.shuffle#sklearn.utils.shuffle "sklearn.utils.shuffle")
Shuffle arrays or sparse matrices in a consistent way.
#### Examples
It is possible to mix sparse and dense arrays in the same run:
```
>>> import numpy as np
>>> X = np.array([[1., 0.], [2., 1.], [0., 0.]])
>>> y = np.array([0, 1, 2])
>>> from scipy.sparse import coo_matrix
>>> X_sparse = coo_matrix(X)
>>> from sklearn.utils import resample
>>> X, X_sparse, y = resample(X, X_sparse, y, random_state=0)
>>> X
array([[1., 0.],
[2., 1.],
[1., 0.]])
>>> X_sparse
<3x2 sparse matrix of type '<... 'numpy.float64'>'
with 4 stored elements in Compressed Sparse Row format>
>>> X_sparse.toarray()
array([[1., 0.],
[2., 1.],
[1., 0.]])
>>> y
array([0, 1, 0])
>>> resample(y, n_samples=2, random_state=0)
array([0, 1])
```
Example using stratification:
```
>>> y = [0, 0, 1, 1, 1, 1, 1, 1, 1]
>>> resample(y, n_samples=5, replace=False, stratify=y,
... random_state=0)
[1, 1, 1, 0, 1]
```
scikit_learn sklearn.metrics.get_scorer_names sklearn.metrics.get\_scorer\_names
==================================
sklearn.metrics.get\_scorer\_names()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_scorer.py#L811)
Get the names of all available scorers.
These names can be passed to [`get_scorer`](sklearn.metrics.get_scorer#sklearn.metrics.get_scorer "sklearn.metrics.get_scorer") to retrieve the scorer object.
Returns:
list of str
Names of all available scorers.
scikit_learn sklearn.cluster.MiniBatchKMeans sklearn.cluster.MiniBatchKMeans
===============================
*class*sklearn.cluster.MiniBatchKMeans(*n\_clusters=8*, *\**, *init='k-means++'*, *max\_iter=100*, *batch\_size=1024*, *verbose=0*, *compute\_labels=True*, *random\_state=None*, *tol=0.0*, *max\_no\_improvement=10*, *init\_size=None*, *n\_init=3*, *reassignment\_ratio=0.01*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_kmeans.py#L1589)
Mini-Batch K-Means clustering.
Read more in the [User Guide](../clustering#mini-batch-kmeans).
Parameters:
**n\_clusters**int, default=8
The number of clusters to form as well as the number of centroids to generate.
**init**{‘k-means++’, ‘random’}, callable or array-like of shape (n\_clusters, n\_features), default=’k-means++’
Method for initialization:
‘k-means++’ : selects initial cluster centroids using sampling based on an empirical probability distribution of the points’ contribution to the overall inertia. This technique speeds up convergence, and is theoretically proven to be \(\mathcal{O}(\log k)\)-optimal. See the description of `n_init` for more details.
‘random’: choose `n_clusters` observations (rows) at random from data for the initial centroids.
If an array is passed, it should be of shape (n\_clusters, n\_features) and gives the initial centers.
If a callable is passed, it should take arguments X, n\_clusters and a random state and return an initialization.
**max\_iter**int, default=100
Maximum number of iterations over the complete dataset before stopping independently of any early stopping criterion heuristics.
**batch\_size**int, default=1024
Size of the mini batches. For faster computations, you can set the `batch_size` greater than 256 \* number of cores to enable parallelism on all cores.
Changed in version 1.0: `batch_size` default changed from 100 to 1024.
**verbose**int, default=0
Verbosity mode.
**compute\_labels**bool, default=True
Compute label assignment and inertia for the complete dataset once the minibatch optimization has converged in fit.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for centroid initialization and random reassignment. Use an int to make the randomness deterministic. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**tol**float, default=0.0
Control early stopping based on the relative center changes as measured by a smoothed, variance-normalized of the mean center squared position changes. This early stopping heuristics is closer to the one used for the batch variant of the algorithms but induces a slight computational and memory overhead over the inertia heuristic.
To disable convergence detection based on normalized center change, set tol to 0.0 (default).
**max\_no\_improvement**int, default=10
Control early stopping based on the consecutive number of mini batches that does not yield an improvement on the smoothed inertia.
To disable convergence detection based on inertia, set max\_no\_improvement to None.
**init\_size**int, default=None
Number of samples to randomly sample for speeding up the initialization (sometimes at the expense of accuracy): the only algorithm is initialized by running a batch KMeans on a random subset of the data. This needs to be larger than n\_clusters.
If `None`, the heuristic is `init_size = 3 * batch_size` if `3 * batch_size < n_clusters`, else `init_size = 3 * n_clusters`.
**n\_init**int, default=3
Number of random initializations that are tried. In contrast to KMeans, the algorithm is only run once, using the best of the `n_init` initializations as measured by inertia. Several runs are recommended for sparse high-dimensional problems (see [Clustering sparse data with k-means](../../auto_examples/text/plot_document_clustering#kmeans-sparse-high-dim)).
**reassignment\_ratio**float, default=0.01
Control the fraction of the maximum number of counts for a center to be reassigned. A higher value means that low count centers are more easily reassigned, which means that the model will take longer to converge, but should converge in a better clustering. However, too high a value may cause convergence issues, especially with a small batch size.
Attributes:
**cluster\_centers\_**ndarray of shape (n\_clusters, n\_features)
Coordinates of cluster centers.
**labels\_**ndarray of shape (n\_samples,)
Labels of each point (if compute\_labels is set to True).
**inertia\_**float
The value of the inertia criterion associated with the chosen partition if compute\_labels is set to True. If compute\_labels is set to False, it’s an approximation of the inertia based on an exponentially weighted average of the batch inertiae. The inertia is defined as the sum of square distances of samples to their cluster center, weighted by the sample weights if provided.
**n\_iter\_**int
Number of iterations over the full dataset.
**n\_steps\_**int
Number of minibatches processed.
New in version 1.0.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`KMeans`](sklearn.cluster.kmeans#sklearn.cluster.KMeans "sklearn.cluster.KMeans")
The classic implementation of the clustering method based on the Lloyd’s algorithm. It consumes the whole set of input data at each iteration.
#### Notes
See <https://www.eecs.tufts.edu/~dsculley/papers/fastkmeans.pdf>
When there are too few points in the dataset, some centers may be duplicated, which means that a proper clustering in terms of the number of requesting clusters and the number of returned clusters will not always match. One solution is to set `reassignment_ratio=0`, which prevents reassignments of clusters that are too small.
#### Examples
```
>>> from sklearn.cluster import MiniBatchKMeans
>>> import numpy as np
>>> X = np.array([[1, 2], [1, 4], [1, 0],
... [4, 2], [4, 0], [4, 4],
... [4, 5], [0, 1], [2, 2],
... [3, 2], [5, 5], [1, -1]])
>>> # manually fit on batches
>>> kmeans = MiniBatchKMeans(n_clusters=2,
... random_state=0,
... batch_size=6)
>>> kmeans = kmeans.partial_fit(X[0:6,:])
>>> kmeans = kmeans.partial_fit(X[6:12,:])
>>> kmeans.cluster_centers_
array([[2. , 1. ],
[3.5, 4.5]])
>>> kmeans.predict([[0, 0], [4, 4]])
array([0, 1], dtype=int32)
>>> # fit on the whole data
>>> kmeans = MiniBatchKMeans(n_clusters=2,
... random_state=0,
... batch_size=6,
... max_iter=10).fit(X)
>>> kmeans.cluster_centers_
array([[1.19..., 1.22...],
[4.03..., 2.46...]])
>>> kmeans.predict([[0, 0], [4, 4]])
array([0, 1], dtype=int32)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.cluster.MiniBatchKMeans.fit "sklearn.cluster.MiniBatchKMeans.fit")(X[, y, sample\_weight]) | Compute the centroids on X by chunking it into mini-batches. |
| [`fit_predict`](#sklearn.cluster.MiniBatchKMeans.fit_predict "sklearn.cluster.MiniBatchKMeans.fit_predict")(X[, y, sample\_weight]) | Compute cluster centers and predict cluster index for each sample. |
| [`fit_transform`](#sklearn.cluster.MiniBatchKMeans.fit_transform "sklearn.cluster.MiniBatchKMeans.fit_transform")(X[, y, sample\_weight]) | Compute clustering and transform X to cluster-distance space. |
| [`get_feature_names_out`](#sklearn.cluster.MiniBatchKMeans.get_feature_names_out "sklearn.cluster.MiniBatchKMeans.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.cluster.MiniBatchKMeans.get_params "sklearn.cluster.MiniBatchKMeans.get_params")([deep]) | Get parameters for this estimator. |
| [`partial_fit`](#sklearn.cluster.MiniBatchKMeans.partial_fit "sklearn.cluster.MiniBatchKMeans.partial_fit")(X[, y, sample\_weight]) | Update k means estimate on a single mini-batch X. |
| [`predict`](#sklearn.cluster.MiniBatchKMeans.predict "sklearn.cluster.MiniBatchKMeans.predict")(X[, sample\_weight]) | Predict the closest cluster each sample in X belongs to. |
| [`score`](#sklearn.cluster.MiniBatchKMeans.score "sklearn.cluster.MiniBatchKMeans.score")(X[, y, sample\_weight]) | Opposite of the value of X on the K-means objective. |
| [`set_params`](#sklearn.cluster.MiniBatchKMeans.set_params "sklearn.cluster.MiniBatchKMeans.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.cluster.MiniBatchKMeans.transform "sklearn.cluster.MiniBatchKMeans.transform")(X) | Transform X to a cluster-distance space. |
fit(*X*, *y=None*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_kmeans.py#L1938)
Compute the centroids on X by chunking it into mini-batches.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training instances to cluster. It must be noted that the data will be converted to C ordering, which will cause a memory copy if the given data is not C-contiguous. If a sparse matrix is passed, a copy will be made if it’s not in CSR format.
**y**Ignored
Not used, present here for API consistency by convention.
**sample\_weight**array-like of shape (n\_samples,), default=None
The weights for each observation in X. If None, all observations are assigned equal weight.
New in version 0.20.
Returns:
**self**object
Fitted estimator.
fit\_predict(*X*, *y=None*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_kmeans.py#L973)
Compute cluster centers and predict cluster index for each sample.
Convenience method; equivalent to calling fit(X) followed by predict(X).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
New data to transform.
**y**Ignored
Not used, present here for API consistency by convention.
**sample\_weight**array-like of shape (n\_samples,), default=None
The weights for each observation in X. If None, all observations are assigned equal weight.
Returns:
**labels**ndarray of shape (n\_samples,)
Index of the cluster each sample belongs to.
fit\_transform(*X*, *y=None*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_kmeans.py#L1035)
Compute clustering and transform X to cluster-distance space.
Equivalent to fit(X).transform(X), but more efficiently implemented.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
New data to transform.
**y**Ignored
Not used, present here for API consistency by convention.
**sample\_weight**array-like of shape (n\_samples,), default=None
The weights for each observation in X. If None, all observations are assigned equal weight.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_clusters)
X transformed in the new space.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.cluster.MiniBatchKMeans.fit "sklearn.cluster.MiniBatchKMeans.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
partial\_fit(*X*, *y=None*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_kmeans.py#L2095)
Update k means estimate on a single mini-batch X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training instances to cluster. It must be noted that the data will be converted to C ordering, which will cause a memory copy if the given data is not C-contiguous. If a sparse matrix is passed, a copy will be made if it’s not in CSR format.
**y**Ignored
Not used, present here for API consistency by convention.
**sample\_weight**array-like of shape (n\_samples,), default=None
The weights for each observation in X. If None, all observations are assigned equal weight.
Returns:
**self**object
Return updated estimator.
predict(*X*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_kmeans.py#L998)
Predict the closest cluster each sample in X belongs to.
In the vector quantization literature, `cluster_centers_` is called the code book and each value returned by `predict` is the index of the closest code in the code book.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
New data to predict.
**sample\_weight**array-like of shape (n\_samples,), default=None
The weights for each observation in X. If None, all observations are assigned equal weight.
Returns:
**labels**ndarray of shape (n\_samples,)
Index of the cluster each sample belongs to.
score(*X*, *y=None*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_kmeans.py#L1085)
Opposite of the value of X on the K-means objective.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
New data.
**y**Ignored
Not used, present here for API consistency by convention.
**sample\_weight**array-like of shape (n\_samples,), default=None
The weights for each observation in X. If None, all observations are assigned equal weight.
Returns:
**score**float
Opposite of the value of X on the K-means objective.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_kmeans.py#L1059)
Transform X to a cluster-distance space.
In the new space, each dimension is the distance to the cluster centers. Note that even if X is sparse, the array returned by `transform` will typically be dense.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
New data to transform.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_clusters)
X transformed in the new space.
Examples using `sklearn.cluster.MiniBatchKMeans`
------------------------------------------------
[Biclustering documents with the Spectral Co-clustering algorithm](../../auto_examples/bicluster/plot_bicluster_newsgroups#sphx-glr-auto-examples-bicluster-plot-bicluster-newsgroups-py)
[Compare BIRCH and MiniBatchKMeans](../../auto_examples/cluster/plot_birch_vs_minibatchkmeans#sphx-glr-auto-examples-cluster-plot-birch-vs-minibatchkmeans-py)
[Comparing different clustering algorithms on toy datasets](../../auto_examples/cluster/plot_cluster_comparison#sphx-glr-auto-examples-cluster-plot-cluster-comparison-py)
[Comparison of the K-Means and MiniBatchKMeans clustering algorithms](../../auto_examples/cluster/plot_mini_batch_kmeans#sphx-glr-auto-examples-cluster-plot-mini-batch-kmeans-py)
[Empirical evaluation of the impact of k-means initialization](../../auto_examples/cluster/plot_kmeans_stability_low_dim_dense#sphx-glr-auto-examples-cluster-plot-kmeans-stability-low-dim-dense-py)
[Online learning of a dictionary of parts of faces](../../auto_examples/cluster/plot_dict_face_patches#sphx-glr-auto-examples-cluster-plot-dict-face-patches-py)
[Faces dataset decompositions](../../auto_examples/decomposition/plot_faces_decomposition#sphx-glr-auto-examples-decomposition-plot-faces-decomposition-py)
[Clustering text documents using k-means](../../auto_examples/text/plot_document_clustering#sphx-glr-auto-examples-text-plot-document-clustering-py)
| programming_docs |
scikit_learn sklearn.decomposition.PCA sklearn.decomposition.PCA
=========================
*class*sklearn.decomposition.PCA(*n\_components=None*, *\**, *copy=True*, *whiten=False*, *svd\_solver='auto'*, *tol=0.0*, *iterated\_power='auto'*, *n\_oversamples=10*, *power\_iteration\_normalizer='auto'*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_pca.py#L116)
Principal component analysis (PCA).
Linear dimensionality reduction using Singular Value Decomposition of the data to project it to a lower dimensional space. The input data is centered but not scaled for each feature before applying the SVD.
It uses the LAPACK implementation of the full SVD or a randomized truncated SVD by the method of Halko et al. 2009, depending on the shape of the input data and the number of components to extract.
It can also use the scipy.sparse.linalg ARPACK implementation of the truncated SVD.
Notice that this class does not support sparse input. See [`TruncatedSVD`](sklearn.decomposition.truncatedsvd#sklearn.decomposition.TruncatedSVD "sklearn.decomposition.TruncatedSVD") for an alternative with sparse data.
Read more in the [User Guide](../decomposition#pca).
Parameters:
**n\_components**int, float or ‘mle’, default=None
Number of components to keep. if n\_components is not set all components are kept:
```
n_components == min(n_samples, n_features)
```
If `n_components == 'mle'` and `svd_solver == 'full'`, Minka’s MLE is used to guess the dimension. Use of `n_components == 'mle'` will interpret `svd_solver == 'auto'` as `svd_solver == 'full'`.
If `0 < n_components < 1` and `svd_solver == 'full'`, select the number of components such that the amount of variance that needs to be explained is greater than the percentage specified by n\_components.
If `svd_solver == 'arpack'`, the number of components must be strictly less than the minimum of n\_features and n\_samples.
Hence, the None case results in:
```
n_components == min(n_samples, n_features) - 1
```
**copy**bool, default=True
If False, data passed to fit are overwritten and running fit(X).transform(X) will not yield the expected results, use fit\_transform(X) instead.
**whiten**bool, default=False
When True (False by default) the `components_` vectors are multiplied by the square root of n\_samples and then divided by the singular values to ensure uncorrelated outputs with unit component-wise variances.
Whitening will remove some information from the transformed signal (the relative variance scales of the components) but can sometime improve the predictive accuracy of the downstream estimators by making their data respect some hard-wired assumptions.
**svd\_solver**{‘auto’, ‘full’, ‘arpack’, ‘randomized’}, default=’auto’
If auto :
The solver is selected by a default policy based on `X.shape` and `n_components`: if the input data is larger than 500x500 and the number of components to extract is lower than 80% of the smallest dimension of the data, then the more efficient ‘randomized’ method is enabled. Otherwise the exact full SVD is computed and optionally truncated afterwards.
If full :
run exact full SVD calling the standard LAPACK solver via `scipy.linalg.svd` and select the components by postprocessing
If arpack :
run SVD truncated to n\_components calling ARPACK solver via `scipy.sparse.linalg.svds`. It requires strictly 0 < n\_components < min(X.shape)
If randomized :
run randomized SVD by the method of Halko et al.
New in version 0.18.0.
**tol**float, default=0.0
Tolerance for singular values computed by svd\_solver == ‘arpack’. Must be of range [0.0, infinity).
New in version 0.18.0.
**iterated\_power**int or ‘auto’, default=’auto’
Number of iterations for the power method computed by svd\_solver == ‘randomized’. Must be of range [0, infinity).
New in version 0.18.0.
**n\_oversamples**int, default=10
This parameter is only relevant when `svd_solver="randomized"`. It corresponds to the additional number of random vectors to sample the range of `X` so as to ensure proper conditioning. See [`randomized_svd`](sklearn.utils.extmath.randomized_svd#sklearn.utils.extmath.randomized_svd "sklearn.utils.extmath.randomized_svd") for more details.
New in version 1.1.
**power\_iteration\_normalizer**{‘auto’, ‘QR’, ‘LU’, ‘none’}, default=’auto’
Power iteration normalizer for randomized SVD solver. Not used by ARPACK. See [`randomized_svd`](sklearn.utils.extmath.randomized_svd#sklearn.utils.extmath.randomized_svd "sklearn.utils.extmath.randomized_svd") for more details.
New in version 1.1.
**random\_state**int, RandomState instance or None, default=None
Used when the ‘arpack’ or ‘randomized’ solvers are used. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
New in version 0.18.0.
Attributes:
**components\_**ndarray of shape (n\_components, n\_features)
Principal axes in feature space, representing the directions of maximum variance in the data. Equivalently, the right singular vectors of the centered input data, parallel to its eigenvectors. The components are sorted by `explained_variance_`.
**explained\_variance\_**ndarray of shape (n\_components,)
The amount of variance explained by each of the selected components. The variance estimation uses `n_samples - 1` degrees of freedom.
Equal to n\_components largest eigenvalues of the covariance matrix of X.
New in version 0.18.
**explained\_variance\_ratio\_**ndarray of shape (n\_components,)
Percentage of variance explained by each of the selected components.
If `n_components` is not set then all components are stored and the sum of the ratios is equal to 1.0.
**singular\_values\_**ndarray of shape (n\_components,)
The singular values corresponding to each of the selected components. The singular values are equal to the 2-norms of the `n_components` variables in the lower-dimensional space.
New in version 0.19.
**mean\_**ndarray of shape (n\_features,)
Per-feature empirical mean, estimated from the training set.
Equal to `X.mean(axis=0)`.
**n\_components\_**int
The estimated number of components. When n\_components is set to ‘mle’ or a number between 0 and 1 (with svd\_solver == ‘full’) this number is estimated from input data. Otherwise it equals the parameter n\_components, or the lesser value of n\_features and n\_samples if n\_components is None.
**n\_features\_**int
Number of features in the training data.
**n\_samples\_**int
Number of samples in the training data.
**noise\_variance\_**float
The estimated noise covariance following the Probabilistic PCA model from Tipping and Bishop 1999. See “Pattern Recognition and Machine Learning” by C. Bishop, 12.2.1 p. 574 or <http://www.miketipping.com/papers/met-mppca.pdf>. It is required to compute the estimated data covariance and score samples.
Equal to the average of (min(n\_features, n\_samples) - n\_components) smallest eigenvalues of the covariance matrix of X.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`KernelPCA`](sklearn.decomposition.kernelpca#sklearn.decomposition.KernelPCA "sklearn.decomposition.KernelPCA")
Kernel Principal Component Analysis.
[`SparsePCA`](sklearn.decomposition.sparsepca#sklearn.decomposition.SparsePCA "sklearn.decomposition.SparsePCA")
Sparse Principal Component Analysis.
[`TruncatedSVD`](sklearn.decomposition.truncatedsvd#sklearn.decomposition.TruncatedSVD "sklearn.decomposition.TruncatedSVD")
Dimensionality reduction using truncated SVD.
[`IncrementalPCA`](sklearn.decomposition.incrementalpca#sklearn.decomposition.IncrementalPCA "sklearn.decomposition.IncrementalPCA")
Incremental Principal Component Analysis.
#### References
For n\_components == ‘mle’, this class uses the method from: [Minka, T. P.. “Automatic choice of dimensionality for PCA”. In NIPS, pp. 598-604](https://tminka.github.io/papers/pca/minka-pca.pdf)
Implements the probabilistic PCA model from: [Tipping, M. E., and Bishop, C. M. (1999). “Probabilistic principal component analysis”. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 61(3), 611-622.](http://www.miketipping.com/papers/met-mppca.pdf) via the score and score\_samples methods.
For svd\_solver == ‘arpack’, refer to `scipy.sparse.linalg.svds`.
For svd\_solver == ‘randomized’, see: [Halko, N., Martinsson, P. G., and Tropp, J. A. (2011). “Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions”. SIAM review, 53(2), 217-288.](https://doi.org/10.1137/090771806) and also [Martinsson, P. G., Rokhlin, V., and Tygert, M. (2011). “A randomized algorithm for the decomposition of matrices”. Applied and Computational Harmonic Analysis, 30(1), 47-68.](https://doi.org/10.1016/j.acha.2010.02.003)
#### Examples
```
>>> import numpy as np
>>> from sklearn.decomposition import PCA
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> pca = PCA(n_components=2)
>>> pca.fit(X)
PCA(n_components=2)
>>> print(pca.explained_variance_ratio_)
[0.9924... 0.0075...]
>>> print(pca.singular_values_)
[6.30061... 0.54980...]
```
```
>>> pca = PCA(n_components=2, svd_solver='full')
>>> pca.fit(X)
PCA(n_components=2, svd_solver='full')
>>> print(pca.explained_variance_ratio_)
[0.9924... 0.00755...]
>>> print(pca.singular_values_)
[6.30061... 0.54980...]
```
```
>>> pca = PCA(n_components=1, svd_solver='arpack')
>>> pca.fit(X)
PCA(n_components=1, svd_solver='arpack')
>>> print(pca.explained_variance_ratio_)
[0.99244...]
>>> print(pca.singular_values_)
[6.30061...]
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.decomposition.PCA.fit "sklearn.decomposition.PCA.fit")(X[, y]) | Fit the model with X. |
| [`fit_transform`](#sklearn.decomposition.PCA.fit_transform "sklearn.decomposition.PCA.fit_transform")(X[, y]) | Fit the model with X and apply the dimensionality reduction on X. |
| [`get_covariance`](#sklearn.decomposition.PCA.get_covariance "sklearn.decomposition.PCA.get_covariance")() | Compute data covariance with the generative model. |
| [`get_feature_names_out`](#sklearn.decomposition.PCA.get_feature_names_out "sklearn.decomposition.PCA.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.decomposition.PCA.get_params "sklearn.decomposition.PCA.get_params")([deep]) | Get parameters for this estimator. |
| [`get_precision`](#sklearn.decomposition.PCA.get_precision "sklearn.decomposition.PCA.get_precision")() | Compute data precision matrix with the generative model. |
| [`inverse_transform`](#sklearn.decomposition.PCA.inverse_transform "sklearn.decomposition.PCA.inverse_transform")(X) | Transform data back to its original space. |
| [`score`](#sklearn.decomposition.PCA.score "sklearn.decomposition.PCA.score")(X[, y]) | Return the average log-likelihood of all samples. |
| [`score_samples`](#sklearn.decomposition.PCA.score_samples "sklearn.decomposition.PCA.score_samples")(X) | Return the log-likelihood of each sample. |
| [`set_params`](#sklearn.decomposition.PCA.set_params "sklearn.decomposition.PCA.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.decomposition.PCA.transform "sklearn.decomposition.PCA.transform")(X) | Apply dimensionality reduction to X. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_pca.py#L384)
Fit the model with X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Ignored.
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_pca.py#L411)
Fit the model with X and apply the dimensionality reduction on X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Ignored.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_components)
Transformed values.
#### Notes
This method returns a Fortran-ordered array. To convert it to a C-ordered array, use ‘np.ascontiguousarray’.
get\_covariance()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_base.py#L28)
Compute data covariance with the generative model.
`cov = components_.T * S**2 * components_ + sigma2 * eye(n_features)` where S\*\*2 contains the explained variances, and sigma2 contains the noise variances.
Returns:
**cov**array of shape=(n\_features, n\_features)
Estimated covariance of data.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.decomposition.PCA.fit "sklearn.decomposition.PCA.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
get\_precision()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_base.py#L49)
Compute data precision matrix with the generative model.
Equals the inverse of the covariance but computed with the matrix inversion lemma for efficiency.
Returns:
**precision**array, shape=(n\_features, n\_features)
Estimated precision of data.
inverse\_transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_base.py#L128)
Transform data back to its original space.
In other words, return an input `X_original` whose transform would be X.
Parameters:
**X**array-like of shape (n\_samples, n\_components)
New data, where `n_samples` is the number of samples and `n_components` is the number of components.
Returns:
X\_original array-like of shape (n\_samples, n\_features)
Original data, where `n_samples` is the number of samples and `n_features` is the number of features.
#### Notes
If whitening is enabled, inverse\_transform will compute the exact inverse operation, which includes reversing whitening.
score(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_pca.py#L668)
Return the average log-likelihood of all samples.
See. “Pattern Recognition and Machine Learning” by C. Bishop, 12.2.1 p. 574 or <http://www.miketipping.com/papers/met-mppca.pdf>
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The data.
**y**Ignored
Ignored.
Returns:
**ll**float
Average log-likelihood of the samples under the current model.
score\_samples(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_pca.py#L641)
Return the log-likelihood of each sample.
See. “Pattern Recognition and Machine Learning” by C. Bishop, 12.2.1 p. 574 or <http://www.miketipping.com/papers/met-mppca.pdf>
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The data.
Returns:
**ll**ndarray of shape (n\_samples,)
Log-likelihood of each sample under the current model.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_base.py#L100)
Apply dimensionality reduction to X.
X is projected on the first principal components previously extracted from a training set.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
New data, where `n_samples` is the number of samples and `n_features` is the number of features.
Returns:
**X\_new**array-like of shape (n\_samples, n\_components)
Projection of X in the first principal components, where `n_samples` is the number of samples and `n_components` is the number of the components.
Examples using `sklearn.decomposition.PCA`
------------------------------------------
[A demo of K-Means clustering on the handwritten digits data](../../auto_examples/cluster/plot_kmeans_digits#sphx-glr-auto-examples-cluster-plot-kmeans-digits-py)
[Principal Component Regression vs Partial Least Squares Regression](../../auto_examples/cross_decomposition/plot_pcr_vs_pls#sphx-glr-auto-examples-cross-decomposition-plot-pcr-vs-pls-py)
[The Iris Dataset](../../auto_examples/datasets/plot_iris_dataset#sphx-glr-auto-examples-datasets-plot-iris-dataset-py)
[Blind source separation using FastICA](../../auto_examples/decomposition/plot_ica_blind_source_separation#sphx-glr-auto-examples-decomposition-plot-ica-blind-source-separation-py)
[Comparison of LDA and PCA 2D projection of Iris dataset](../../auto_examples/decomposition/plot_pca_vs_lda#sphx-glr-auto-examples-decomposition-plot-pca-vs-lda-py)
[Faces dataset decompositions](../../auto_examples/decomposition/plot_faces_decomposition#sphx-glr-auto-examples-decomposition-plot-faces-decomposition-py)
[Factor Analysis (with rotation) to visualize patterns](../../auto_examples/decomposition/plot_varimax_fa#sphx-glr-auto-examples-decomposition-plot-varimax-fa-py)
[FastICA on 2D point clouds](../../auto_examples/decomposition/plot_ica_vs_pca#sphx-glr-auto-examples-decomposition-plot-ica-vs-pca-py)
[Incremental PCA](../../auto_examples/decomposition/plot_incremental_pca#sphx-glr-auto-examples-decomposition-plot-incremental-pca-py)
[Kernel PCA](../../auto_examples/decomposition/plot_kernel_pca#sphx-glr-auto-examples-decomposition-plot-kernel-pca-py)
[Model selection with Probabilistic PCA and Factor Analysis (FA)](../../auto_examples/decomposition/plot_pca_vs_fa_model_selection#sphx-glr-auto-examples-decomposition-plot-pca-vs-fa-model-selection-py)
[PCA example with Iris Data-set](../../auto_examples/decomposition/plot_pca_iris#sphx-glr-auto-examples-decomposition-plot-pca-iris-py)
[Principal components analysis (PCA)](../../auto_examples/decomposition/plot_pca_3d#sphx-glr-auto-examples-decomposition-plot-pca-3d-py)
[Faces recognition example using eigenfaces and SVMs](../../auto_examples/applications/plot_face_recognition#sphx-glr-auto-examples-applications-plot-face-recognition-py)
[Image denoising using kernel PCA](../../auto_examples/applications/plot_digits_denoising#sphx-glr-auto-examples-applications-plot-digits-denoising-py)
[Multi-dimensional scaling](../../auto_examples/manifold/plot_mds#sphx-glr-auto-examples-manifold-plot-mds-py)
[Displaying Pipelines](../../auto_examples/miscellaneous/plot_pipeline_display#sphx-glr-auto-examples-miscellaneous-plot-pipeline-display-py)
[Explicit feature map approximation for RBF kernels](../../auto_examples/miscellaneous/plot_kernel_approximation#sphx-glr-auto-examples-miscellaneous-plot-kernel-approximation-py)
[Multilabel classification](../../auto_examples/miscellaneous/plot_multilabel#sphx-glr-auto-examples-miscellaneous-plot-multilabel-py)
[Balance model complexity and cross-validated score](../../auto_examples/model_selection/plot_grid_search_refit_callable#sphx-glr-auto-examples-model-selection-plot-grid-search-refit-callable-py)
[Dimensionality Reduction with Neighborhood Components Analysis](../../auto_examples/neighbors/plot_nca_dim_reduction#sphx-glr-auto-examples-neighbors-plot-nca-dim-reduction-py)
[Kernel Density Estimation](../../auto_examples/neighbors/plot_digits_kde_sampling#sphx-glr-auto-examples-neighbors-plot-digits-kde-sampling-py)
[Concatenating multiple feature extraction methods](../../auto_examples/compose/plot_feature_union#sphx-glr-auto-examples-compose-plot-feature-union-py)
[Pipelining: chaining a PCA and a logistic regression](../../auto_examples/compose/plot_digits_pipe#sphx-glr-auto-examples-compose-plot-digits-pipe-py)
[Selecting dimensionality reduction with Pipeline and GridSearchCV](../../auto_examples/compose/plot_compare_reduction#sphx-glr-auto-examples-compose-plot-compare-reduction-py)
[Importance of Feature Scaling](../../auto_examples/preprocessing/plot_scaling_importance#sphx-glr-auto-examples-preprocessing-plot-scaling-importance-py)
| programming_docs |
scikit_learn sklearn.metrics.brier_score_loss sklearn.metrics.brier\_score\_loss
==================================
sklearn.metrics.brier\_score\_loss(*y\_true*, *y\_prob*, *\**, *sample\_weight=None*, *pos\_label=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_classification.py#L2614)
Compute the Brier score loss.
The smaller the Brier score loss, the better, hence the naming with “loss”. The Brier score measures the mean squared difference between the predicted probability and the actual outcome. The Brier score always takes on a value between zero and one, since this is the largest possible difference between a predicted probability (which must be between zero and one) and the actual outcome (which can take on values of only 0 and 1). It can be decomposed is the sum of refinement loss and calibration loss.
The Brier score is appropriate for binary and categorical outcomes that can be structured as true or false, but is inappropriate for ordinal variables which can take on three or more values (this is because the Brier score assumes that all possible outcomes are equivalently “distant” from one another). Which label is considered to be the positive label is controlled via the parameter `pos_label`, which defaults to the greater label unless `y_true` is all 0 or all -1, in which case `pos_label` defaults to 1.
Read more in the [User Guide](../model_evaluation#brier-score-loss).
Parameters:
**y\_true**array of shape (n\_samples,)
True targets.
**y\_prob**array of shape (n\_samples,)
Probabilities of the positive class.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**pos\_label**int or str, default=None
Label of the positive class. `pos_label` will be inferred in the following manner:
* if `y_true` in {-1, 1} or {0, 1}, `pos_label` defaults to 1;
* else if `y_true` contains string, an error will be raised and `pos_label` should be explicitly specified;
* otherwise, `pos_label` defaults to the greater label, i.e. `np.unique(y_true)[-1]`.
Returns:
**score**float
Brier score loss.
#### References
[1] [Wikipedia entry for the Brier score](https://en.wikipedia.org/wiki/Brier_score).
#### Examples
```
>>> import numpy as np
>>> from sklearn.metrics import brier_score_loss
>>> y_true = np.array([0, 1, 1, 0])
>>> y_true_categorical = np.array(["spam", "ham", "ham", "spam"])
>>> y_prob = np.array([0.1, 0.9, 0.8, 0.3])
>>> brier_score_loss(y_true, y_prob)
0.037...
>>> brier_score_loss(y_true, 1-y_prob, pos_label=0)
0.037...
>>> brier_score_loss(y_true_categorical, y_prob, pos_label="ham")
0.037...
>>> brier_score_loss(y_true, np.array(y_prob) > 0.5)
0.0
```
Examples using `sklearn.metrics.brier_score_loss`
-------------------------------------------------
[Probability Calibration curves](../../auto_examples/calibration/plot_calibration_curve#sphx-glr-auto-examples-calibration-plot-calibration-curve-py)
[Probability calibration of classifiers](../../auto_examples/calibration/plot_calibration#sphx-glr-auto-examples-calibration-plot-calibration-py)
scikit_learn sklearn.metrics.precision_recall_fscore_support sklearn.metrics.precision\_recall\_fscore\_support
==================================================
sklearn.metrics.precision\_recall\_fscore\_support(*y\_true*, *y\_pred*, *\**, *beta=1.0*, *labels=None*, *pos\_label=1*, *average=None*, *warn\_for=('precision', 'recall', 'f-score')*, *sample\_weight=None*, *zero\_division='warn'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_classification.py#L1396)
Compute precision, recall, F-measure and support for each class.
The precision is the ratio `tp / (tp + fp)` where `tp` is the number of true positives and `fp` the number of false positives. The precision is intuitively the ability of the classifier not to label a negative sample as positive.
The recall is the ratio `tp / (tp + fn)` where `tp` is the number of true positives and `fn` the number of false negatives. The recall is intuitively the ability of the classifier to find all the positive samples.
The F-beta score can be interpreted as a weighted harmonic mean of the precision and recall, where an F-beta score reaches its best value at 1 and worst score at 0.
The F-beta score weights recall more than precision by a factor of `beta`. `beta == 1.0` means recall and precision are equally important.
The support is the number of occurrences of each class in `y_true`.
If `pos_label is None` and in binary classification, this function returns the average precision, recall and F-measure if `average` is one of `'micro'`, `'macro'`, `'weighted'` or `'samples'`.
Read more in the [User Guide](../model_evaluation#precision-recall-f-measure-metrics).
Parameters:
**y\_true**1d array-like, or label indicator array / sparse matrix
Ground truth (correct) target values.
**y\_pred**1d array-like, or label indicator array / sparse matrix
Estimated targets as returned by a classifier.
**beta**float, default=1.0
The strength of recall versus precision in the F-score.
**labels**array-like, default=None
The set of labels to include when `average != 'binary'`, and their order if `average is None`. Labels present in the data can be excluded, for example to calculate a multiclass average ignoring a majority negative class, while labels not present in the data will result in 0 components in a macro average. For multilabel targets, labels are column indices. By default, all labels in `y_true` and `y_pred` are used in sorted order.
**pos\_label**str or int, default=1
The class to report if `average='binary'` and the data is binary. If the data are multiclass or multilabel, this will be ignored; setting `labels=[pos_label]` and `average != 'binary'` will report scores for that label only.
**average**{‘binary’, ‘micro’, ‘macro’, ‘samples’, ‘weighted’}, default=None
If `None`, the scores for each class are returned. Otherwise, this determines the type of averaging performed on the data:
`'binary'`:
Only report results for the class specified by `pos_label`. This is applicable only if targets (`y_{true,pred}`) are binary.
`'micro'`:
Calculate metrics globally by counting the total true positives, false negatives and false positives.
`'macro'`:
Calculate metrics for each label, and find their unweighted mean. This does not take label imbalance into account.
`'weighted'`:
Calculate metrics for each label, and find their average weighted by support (the number of true instances for each label). This alters ‘macro’ to account for label imbalance; it can result in an F-score that is not between precision and recall.
`'samples'`:
Calculate metrics for each instance, and find their average (only meaningful for multilabel classification where this differs from [`accuracy_score`](sklearn.metrics.accuracy_score#sklearn.metrics.accuracy_score "sklearn.metrics.accuracy_score")).
**warn\_for**tuple or set, for internal use
This determines which warnings will be made in the case that this function is being used to return only one of its metrics.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**zero\_division**“warn”, 0 or 1, default=”warn”
Sets the value to return when there is a zero division:
* recall: when there are no positive labels
* precision: when there are no positive predictions
* f-score: both
If set to “warn”, this acts as 0, but warnings are also raised.
Returns:
**precision**float (if average is not None) or array of float, shape = [n\_unique\_labels]
Precision score.
**recall**float (if average is not None) or array of float, shape = [n\_unique\_labels]
Recall score.
**fbeta\_score**float (if average is not None) or array of float, shape = [n\_unique\_labels]
F-beta score.
**support**None (if average is not None) or array of int, shape = [n\_unique\_labels]
The number of occurrences of each label in `y_true`.
#### Notes
When `true positive + false positive == 0`, precision is undefined. When `true positive + false negative == 0`, recall is undefined. In such cases, by default the metric will be set to 0, as will f-score, and `UndefinedMetricWarning` will be raised. This behavior can be modified with `zero_division`.
#### References
[1] [Wikipedia entry for the Precision and recall](https://en.wikipedia.org/wiki/Precision_and_recall).
[2] [Wikipedia entry for the F1-score](https://en.wikipedia.org/wiki/F1_score).
[3] [Discriminative Methods for Multi-labeled Classification Advances in Knowledge Discovery and Data Mining (2004), pp. 22-30 by Shantanu Godbole, Sunita Sarawagi](http://www.godbole.net/shantanu/pubs/multilabelsvm-pakdd04.pdf).
#### Examples
```
>>> import numpy as np
>>> from sklearn.metrics import precision_recall_fscore_support
>>> y_true = np.array(['cat', 'dog', 'pig', 'cat', 'dog', 'pig'])
>>> y_pred = np.array(['cat', 'pig', 'dog', 'cat', 'cat', 'dog'])
>>> precision_recall_fscore_support(y_true, y_pred, average='macro')
(0.22..., 0.33..., 0.26..., None)
>>> precision_recall_fscore_support(y_true, y_pred, average='micro')
(0.33..., 0.33..., 0.33..., None)
>>> precision_recall_fscore_support(y_true, y_pred, average='weighted')
(0.22..., 0.33..., 0.26..., None)
```
It is possible to compute per-label precisions, recalls, F1-scores and supports instead of averaging:
```
>>> precision_recall_fscore_support(y_true, y_pred, average=None,
... labels=['pig', 'dog', 'cat'])
(array([0. , 0. , 0.66...]),
array([0., 0., 1.]), array([0. , 0. , 0.8]),
array([2, 2, 2]))
```
scikit_learn sklearn.metrics.homogeneity_completeness_v_measure sklearn.metrics.homogeneity\_completeness\_v\_measure
=====================================================
sklearn.metrics.homogeneity\_completeness\_v\_measure(*labels\_true*, *labels\_pred*, *\**, *beta=1.0*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/cluster/_supervised.py#L401)
Compute the homogeneity and completeness and V-Measure scores at once.
Those metrics are based on normalized conditional entropy measures of the clustering labeling to evaluate given the knowledge of a Ground Truth class labels of the same samples.
A clustering result satisfies homogeneity if all of its clusters contain only data points which are members of a single class.
A clustering result satisfies completeness if all the data points that are members of a given class are elements of the same cluster.
Both scores have positive values between 0.0 and 1.0, larger values being desirable.
Those 3 metrics are independent of the absolute values of the labels: a permutation of the class or cluster label values won’t change the score values in any way.
V-Measure is furthermore symmetric: swapping `labels_true` and `label_pred` will give the same score. This does not hold for homogeneity and completeness. V-Measure is identical to [`normalized_mutual_info_score`](sklearn.metrics.normalized_mutual_info_score#sklearn.metrics.normalized_mutual_info_score "sklearn.metrics.normalized_mutual_info_score") with the arithmetic averaging method.
Read more in the [User Guide](../clustering#homogeneity-completeness).
Parameters:
**labels\_true**int array, shape = [n\_samples]
Ground truth class labels to be used as a reference.
**labels\_pred**array-like of shape (n\_samples,)
Gluster labels to evaluate.
**beta**float, default=1.0
Ratio of weight attributed to `homogeneity` vs `completeness`. If `beta` is greater than 1, `completeness` is weighted more strongly in the calculation. If `beta` is less than 1, `homogeneity` is weighted more strongly.
Returns:
**homogeneity**float
Score between 0.0 and 1.0. 1.0 stands for perfectly homogeneous labeling.
**completeness**float
Score between 0.0 and 1.0. 1.0 stands for perfectly complete labeling.
**v\_measure**float
Harmonic mean of the first two.
See also
[`homogeneity_score`](sklearn.metrics.homogeneity_score#sklearn.metrics.homogeneity_score "sklearn.metrics.homogeneity_score")
Homogeneity metric of cluster labeling.
[`completeness_score`](sklearn.metrics.completeness_score#sklearn.metrics.completeness_score "sklearn.metrics.completeness_score")
Completeness metric of cluster labeling.
[`v_measure_score`](sklearn.metrics.v_measure_score#sklearn.metrics.v_measure_score "sklearn.metrics.v_measure_score")
V-Measure (NMI with arithmetic mean option).
scikit_learn sklearn.datasets.load_files sklearn.datasets.load\_files
============================
sklearn.datasets.load\_files(*container\_path*, *\**, *description=None*, *categories=None*, *load\_content=True*, *shuffle=True*, *encoding=None*, *decode\_error='strict'*, *random\_state=0*, *allowed\_extensions=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_base.py#L101)
Load text files with categories as subfolder names.
Individual samples are assumed to be files stored a two levels folder structure such as the following:
container\_folder/
category\_1\_folder/
file\_1.txt file\_2.txt … file\_42.txt
category\_2\_folder/
file\_43.txt file\_44.txt …
The folder names are used as supervised signal label names. The individual file names are not important.
This function does not try to extract features into a numpy array or scipy sparse matrix. In addition, if load\_content is false it does not try to load the files in memory.
To use text files in a scikit-learn classification or clustering algorithm, you will need to use the :mod`~sklearn.feature\_extraction.text` module to build a feature extraction transformer that suits your problem.
If you set load\_content=True, you should also specify the encoding of the text using the ‘encoding’ parameter. For many modern text files, ‘utf-8’ will be the correct encoding. If you leave encoding equal to None, then the content will be made of bytes instead of Unicode, and you will not be able to use most functions in [`text`](../classes#module-sklearn.feature_extraction.text "sklearn.feature_extraction.text").
Similar feature extractors should be built for other kind of unstructured data input such as images, audio, video, …
If you want files with a specific file extension (e.g. `.txt`) then you can pass a list of those file extensions to `allowed_extensions`.
Read more in the [User Guide](../../datasets#datasets).
Parameters:
**container\_path**str
Path to the main folder holding one subfolder per category.
**description**str, default=None
A paragraph describing the characteristic of the dataset: its source, reference, etc.
**categories**list of str, default=None
If None (default), load all the categories. If not None, list of category names to load (other categories ignored).
**load\_content**bool, default=True
Whether to load or not the content of the different files. If true a ‘data’ attribute containing the text information is present in the data structure returned. If not, a filenames attribute gives the path to the files.
**shuffle**bool, default=True
Whether or not to shuffle the data: might be important for models that make the assumption that the samples are independent and identically distributed (i.i.d.), such as stochastic gradient descent.
**encoding**str, default=None
If None, do not try to decode the content of the files (e.g. for images or other non-text content). If not None, encoding to use to decode text files to Unicode if load\_content is True.
**decode\_error**{‘strict’, ‘ignore’, ‘replace’}, default=’strict’
Instruction on what to do if a byte sequence is given to analyze that contains characters not of the given `encoding`. Passed as keyword argument ‘errors’ to bytes.decode.
**random\_state**int, RandomState instance or None, default=0
Determines random number generation for dataset shuffling. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**allowed\_extensions**list of str, default=None
List of desired file extensions to filter the files to be loaded.
Returns:
**data**[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
Dictionary-like object, with the following attributes.
datalist of str
Only present when `load_content=True`. The raw text data to learn.
targetndarray
The target labels (integer index).
target\_nameslist
The names of target classes.
DESCRstr
The full description of the dataset.
filenames: ndarray
The filenames holding the dataset.
scikit_learn sklearn.metrics.consensus_score sklearn.metrics.consensus\_score
================================
sklearn.metrics.consensus\_score(*a*, *b*, *\**, *similarity='jaccard'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/cluster/_bicluster.py#L51)
The similarity of two sets of biclusters.
Similarity between individual biclusters is computed. Then the best matching between sets is found using the Hungarian algorithm. The final score is the sum of similarities divided by the size of the larger set.
Read more in the [User Guide](../biclustering#biclustering).
Parameters:
**a**(rows, columns)
Tuple of row and column indicators for a set of biclusters.
**b**(rows, columns)
Another set of biclusters like `a`.
**similarity**‘jaccard’ or callable, default=’jaccard’
May be the string “jaccard” to use the Jaccard coefficient, or any function that takes four arguments, each of which is a 1d indicator vector: (a\_rows, a\_columns, b\_rows, b\_columns).
#### References
* Hochreiter, Bodenhofer, et. al., 2010. [FABIA: factor analysis for bicluster acquisition](https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2881408/).
Examples using `sklearn.metrics.consensus_score`
------------------------------------------------
[A demo of the Spectral Biclustering algorithm](../../auto_examples/bicluster/plot_spectral_biclustering#sphx-glr-auto-examples-bicluster-plot-spectral-biclustering-py)
[A demo of the Spectral Co-Clustering algorithm](../../auto_examples/bicluster/plot_spectral_coclustering#sphx-glr-auto-examples-bicluster-plot-spectral-coclustering-py)
scikit_learn sklearn.metrics.mean_absolute_percentage_error sklearn.metrics.mean\_absolute\_percentage\_error
=================================================
sklearn.metrics.mean\_absolute\_percentage\_error(*y\_true*, *y\_pred*, *\**, *sample\_weight=None*, *multioutput='uniform\_average'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_regression.py#L296)
Mean absolute percentage error (MAPE) regression loss.
Note here that the output is not a percentage in the range [0, 100] and a value of 100 does not mean 100% but 1e2. Furthermore, the output can be arbitrarily high when `y_true` is small (which is specific to the metric) or when `abs(y_true - y_pred)` is large (which is common for most regression metrics). Read more in the [User Guide](../model_evaluation#mean-absolute-percentage-error).
New in version 0.24.
Parameters:
**y\_true**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
Ground truth (correct) target values.
**y\_pred**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
Estimated target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**multioutput**{‘raw\_values’, ‘uniform\_average’} or array-like
Defines aggregating of multiple output values. Array-like value defines weights used to average errors. If input is list then the shape must be (n\_outputs,).
‘raw\_values’ :
Returns a full set of errors in case of multioutput input.
‘uniform\_average’ :
Errors of all outputs are averaged with uniform weight.
Returns:
**loss**float or ndarray of floats
If multioutput is ‘raw\_values’, then mean absolute percentage error is returned for each output separately. If multioutput is ‘uniform\_average’ or an ndarray of weights, then the weighted average of all output errors is returned.
MAPE output is non-negative floating point. The best value is 0.0. But note that bad predictions can lead to arbitrarily large MAPE values, especially if some `y_true` values are very close to zero. Note that we return a large value instead of `inf` when `y_true` is zero.
#### Examples
```
>>> from sklearn.metrics import mean_absolute_percentage_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_absolute_percentage_error(y_true, y_pred)
0.3273...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> mean_absolute_percentage_error(y_true, y_pred)
0.5515...
>>> mean_absolute_percentage_error(y_true, y_pred, multioutput=[0.3, 0.7])
0.6198...
>>> # the value when some element of the y_true is zero is arbitrarily high because
>>> # of the division by epsilon
>>> y_true = [1., 0., 2.4, 7.]
>>> y_pred = [1.2, 0.1, 2.4, 8.]
>>> mean_absolute_percentage_error(y_true, y_pred)
112589990684262.48
```
| programming_docs |
scikit_learn sklearn.datasets.make_spd_matrix sklearn.datasets.make\_spd\_matrix
==================================
sklearn.datasets.make\_spd\_matrix(*n\_dim*, *\**, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_samples_generator.py#L1386)
Generate a random symmetric, positive-definite matrix.
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/sample_generators.html#sample-generators).
Parameters:
**n\_dim**int
The matrix dimension.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for dataset creation. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Returns:
**X**ndarray of shape (n\_dim, n\_dim)
The random symmetric, positive-definite matrix.
See also
[`make_sparse_spd_matrix`](sklearn.datasets.make_sparse_spd_matrix#sklearn.datasets.make_sparse_spd_matrix "sklearn.datasets.make_sparse_spd_matrix")
Generate a sparse symmetric definite positive matrix.
scikit_learn sklearn.linear_model.PassiveAggressiveClassifier sklearn.linear\_model.PassiveAggressiveClassifier
=================================================
*class*sklearn.linear\_model.PassiveAggressiveClassifier(*\**, *C=1.0*, *fit\_intercept=True*, *max\_iter=1000*, *tol=0.001*, *early\_stopping=False*, *validation\_fraction=0.1*, *n\_iter\_no\_change=5*, *shuffle=True*, *verbose=0*, *loss='hinge'*, *n\_jobs=None*, *random\_state=None*, *warm\_start=False*, *class\_weight=None*, *average=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_passive_aggressive.py#L9)
Passive Aggressive Classifier.
Read more in the [User Guide](../linear_model#passive-aggressive).
Parameters:
**C**float, default=1.0
Maximum step size (regularization). Defaults to 1.0.
**fit\_intercept**bool, default=True
Whether the intercept should be estimated or not. If False, the data is assumed to be already centered.
**max\_iter**int, default=1000
The maximum number of passes over the training data (aka epochs). It only impacts the behavior in the `fit` method, and not the [`partial_fit`](#sklearn.linear_model.PassiveAggressiveClassifier.partial_fit "sklearn.linear_model.PassiveAggressiveClassifier.partial_fit") method.
New in version 0.19.
**tol**float or None, default=1e-3
The stopping criterion. If it is not None, the iterations will stop when (loss > previous\_loss - tol).
New in version 0.19.
**early\_stopping**bool, default=False
Whether to use early stopping to terminate training when validation. score is not improving. If set to True, it will automatically set aside a stratified fraction of training data as validation and terminate training when validation score is not improving by at least tol for n\_iter\_no\_change consecutive epochs.
New in version 0.20.
**validation\_fraction**float, default=0.1
The proportion of training data to set aside as validation set for early stopping. Must be between 0 and 1. Only used if early\_stopping is True.
New in version 0.20.
**n\_iter\_no\_change**int, default=5
Number of iterations with no improvement to wait before early stopping.
New in version 0.20.
**shuffle**bool, default=True
Whether or not the training data should be shuffled after each epoch.
**verbose**int, default=0
The verbosity level.
**loss**str, default=”hinge”
The loss function to be used: hinge: equivalent to PA-I in the reference paper. squared\_hinge: equivalent to PA-II in the reference paper.
**n\_jobs**int or None, default=None
The number of CPUs to use to do the OVA (One Versus All, for multi-class problems) computation. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**random\_state**int, RandomState instance, default=None
Used to shuffle the training data, when `shuffle` is set to `True`. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**warm\_start**bool, default=False
When set to True, reuse the solution of the previous call to fit as initialization, otherwise, just erase the previous solution. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
Repeatedly calling fit or partial\_fit when warm\_start is True can result in a different solution than when calling fit a single time because of the way the data is shuffled.
**class\_weight**dict, {class\_label: weight} or “balanced” or None, default=None
Preset for the class\_weight fit parameter.
Weights associated with classes. If not given, all classes are supposed to have weight one.
The “balanced” mode uses the values of y to automatically adjust weights inversely proportional to class frequencies in the input data as `n_samples / (n_classes * np.bincount(y))`.
New in version 0.17: parameter *class\_weight* to automatically weight samples.
**average**bool or int, default=False
When set to True, computes the averaged SGD weights and stores the result in the `coef_` attribute. If set to an int greater than 1, averaging will begin once the total number of samples seen reaches average. So average=10 will begin averaging after seeing 10 samples.
New in version 0.19: parameter *average* to use weights averaging in SGD.
Attributes:
**coef\_**ndarray of shape (1, n\_features) if n\_classes == 2 else (n\_classes, n\_features)
Weights assigned to the features.
**intercept\_**ndarray of shape (1,) if n\_classes == 2 else (n\_classes,)
Constants in decision function.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_iter\_**int
The actual number of iterations to reach the stopping criterion. For multiclass fits, it is the maximum over every binary fit.
**classes\_**ndarray of shape (n\_classes,)
The unique classes labels.
**t\_**int
Number of weight updates performed during training. Same as `(n_iter_ * n_samples)`.
**loss\_function\_**callable
Loss function used by the algorithm.
See also
[`SGDClassifier`](sklearn.linear_model.sgdclassifier#sklearn.linear_model.SGDClassifier "sklearn.linear_model.SGDClassifier")
Incrementally trained logistic regression.
[`Perceptron`](sklearn.linear_model.perceptron#sklearn.linear_model.Perceptron "sklearn.linear_model.Perceptron")
Linear perceptron classifier.
#### References
Online Passive-Aggressive Algorithms <<http://jmlr.csail.mit.edu/papers/volume7/crammer06a/crammer06a.pdf>> K. Crammer, O. Dekel, J. Keshat, S. Shalev-Shwartz, Y. Singer - JMLR (2006)
#### Examples
```
>>> from sklearn.linear_model import PassiveAggressiveClassifier
>>> from sklearn.datasets import make_classification
>>> X, y = make_classification(n_features=4, random_state=0)
>>> clf = PassiveAggressiveClassifier(max_iter=1000, random_state=0,
... tol=1e-3)
>>> clf.fit(X, y)
PassiveAggressiveClassifier(random_state=0)
>>> print(clf.coef_)
[[0.26642044 0.45070924 0.67251877 0.64185414]]
>>> print(clf.intercept_)
[1.84127814]
>>> print(clf.predict([[0, 0, 0, 0]]))
[1]
```
#### Methods
| | |
| --- | --- |
| [`decision_function`](#sklearn.linear_model.PassiveAggressiveClassifier.decision_function "sklearn.linear_model.PassiveAggressiveClassifier.decision_function")(X) | Predict confidence scores for samples. |
| [`densify`](#sklearn.linear_model.PassiveAggressiveClassifier.densify "sklearn.linear_model.PassiveAggressiveClassifier.densify")() | Convert coefficient matrix to dense array format. |
| [`fit`](#sklearn.linear_model.PassiveAggressiveClassifier.fit "sklearn.linear_model.PassiveAggressiveClassifier.fit")(X, y[, coef\_init, intercept\_init]) | Fit linear model with Passive Aggressive algorithm. |
| [`get_params`](#sklearn.linear_model.PassiveAggressiveClassifier.get_params "sklearn.linear_model.PassiveAggressiveClassifier.get_params")([deep]) | Get parameters for this estimator. |
| [`partial_fit`](#sklearn.linear_model.PassiveAggressiveClassifier.partial_fit "sklearn.linear_model.PassiveAggressiveClassifier.partial_fit")(X, y[, classes]) | Fit linear model with Passive Aggressive algorithm. |
| [`predict`](#sklearn.linear_model.PassiveAggressiveClassifier.predict "sklearn.linear_model.PassiveAggressiveClassifier.predict")(X) | Predict class labels for samples in X. |
| [`score`](#sklearn.linear_model.PassiveAggressiveClassifier.score "sklearn.linear_model.PassiveAggressiveClassifier.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.linear_model.PassiveAggressiveClassifier.set_params "sklearn.linear_model.PassiveAggressiveClassifier.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`sparsify`](#sklearn.linear_model.PassiveAggressiveClassifier.sparsify "sklearn.linear_model.PassiveAggressiveClassifier.sparsify")() | Convert coefficient matrix to sparse format. |
decision\_function(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L408)
Predict confidence scores for samples.
The confidence score for a sample is proportional to the signed distance of that sample to the hyperplane.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data matrix for which we want to get the confidence scores.
Returns:
**scores**ndarray of shape (n\_samples,) or (n\_samples, n\_classes)
Confidence scores per `(n_samples, n_classes)` combination. In the binary case, confidence score for `self.classes_[1]` where >0 means this class would be predicted.
densify()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L477)
Convert coefficient matrix to dense array format.
Converts the `coef_` member (back) to a numpy.ndarray. This is the default format of `coef_` and is required for fitting, so calling this method is only required on models that have previously been sparsified; otherwise, it is a no-op.
Returns:
self
Fitted estimator.
fit(*X*, *y*, *coef\_init=None*, *intercept\_init=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_passive_aggressive.py#L267)
Fit linear model with Passive Aggressive algorithm.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training data.
**y**array-like of shape (n\_samples,)
Target values.
**coef\_init**ndarray of shape (n\_classes, n\_features)
The initial coefficients to warm-start the optimization.
**intercept\_init**ndarray of shape (n\_classes,)
The initial intercept to warm-start the optimization.
Returns:
**self**object
Fitted estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
partial\_fit(*X*, *y*, *classes=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_passive_aggressive.py#L215)
Fit linear model with Passive Aggressive algorithm.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Subset of the training data.
**y**array-like of shape (n\_samples,)
Subset of the target values.
**classes**ndarray of shape (n\_classes,)
Classes across all calls to partial\_fit. Can be obtained by via `np.unique(y_all)`, where y\_all is the target vector of the entire dataset. This argument is required for the first call to partial\_fit and can be omitted in the subsequent calls. Note that y doesn’t need to contain all labels in `classes`.
Returns:
**self**object
Fitted estimator.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L433)
Predict class labels for samples in X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data matrix for which we want to get the predictions.
Returns:
**y\_pred**ndarray of shape (n\_samples,)
Vector containing the class labels for each sample.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
sparsify()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L497)
Convert coefficient matrix to sparse format.
Converts the `coef_` member to a scipy.sparse matrix, which for L1-regularized models can be much more memory- and storage-efficient than the usual numpy.ndarray representation.
The `intercept_` member is not converted.
Returns:
self
Fitted estimator.
#### Notes
For non-sparse models, i.e. when there are not many zeros in `coef_`, this may actually *increase* memory usage, so use this method with care. A rule of thumb is that the number of zero elements, which can be computed with `(coef_ == 0).sum()`, must be more than 50% for this to provide significant benefits.
After calling this method, further fitting with the partial\_fit method (if any) will not work until you call densify.
Examples using `sklearn.linear_model.PassiveAggressiveClassifier`
-----------------------------------------------------------------
[Out-of-core classification of text documents](../../auto_examples/applications/plot_out_of_core_classification#sphx-glr-auto-examples-applications-plot-out-of-core-classification-py)
[Comparing various online solvers](../../auto_examples/linear_model/plot_sgd_comparison#sphx-glr-auto-examples-linear-model-plot-sgd-comparison-py)
scikit_learn sklearn.utils.validation.check_memory sklearn.utils.validation.check\_memory
======================================
sklearn.utils.validation.check\_memory(*memory*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/validation.py#L339)
Check that `memory` is joblib.Memory-like.
joblib.Memory-like means that `memory` can be converted into a joblib.Memory instance (typically a str denoting the `location`) or has the same interface (has a `cache` method).
Parameters:
**memory**None, str or object with the joblib.Memory interface
* If string, the location where to create the `joblib.Memory` interface.
* If None, no caching is done and the Memory object is completely transparent.
Returns:
**memory**object with the joblib.Memory interface
A correct joblib.Memory object.
Raises:
ValueError
If `memory` is not joblib.Memory-like.
scikit_learn sklearn.linear_model.MultiTaskLasso sklearn.linear\_model.MultiTaskLasso
====================================
*class*sklearn.linear\_model.MultiTaskLasso(*alpha=1.0*, *\**, *fit\_intercept=True*, *normalize='deprecated'*, *copy\_X=True*, *max\_iter=1000*, *tol=0.0001*, *warm\_start=False*, *random\_state=None*, *selection='cyclic'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_coordinate_descent.py#L2528)
Multi-task Lasso model trained with L1/L2 mixed-norm as regularizer.
The optimization objective for Lasso is:
```
(1 / (2 * n_samples)) * ||Y - XW||^2_Fro + alpha * ||W||_21
```
Where:
```
||W||_21 = \sum_i \sqrt{\sum_j w_{ij}^2}
```
i.e. the sum of norm of each row.
Read more in the [User Guide](../linear_model#multi-task-lasso).
Parameters:
**alpha**float, default=1.0
Constant that multiplies the L1/L2 term. Defaults to 1.0.
**fit\_intercept**bool, default=True
Whether to calculate the intercept for this model. If set to false, no intercept will be used in calculations (i.e. data is expected to be centered).
**normalize**bool, default=False
This parameter is ignored when `fit_intercept` is set to False. If True, the regressors X will be normalized before regression by subtracting the mean and dividing by the l2-norm. If you wish to standardize, please use [`StandardScaler`](sklearn.preprocessing.standardscaler#sklearn.preprocessing.StandardScaler "sklearn.preprocessing.StandardScaler") before calling `fit` on an estimator with `normalize=False`.
Deprecated since version 1.0: `normalize` was deprecated in version 1.0 and will be removed in 1.2.
**copy\_X**bool, default=True
If `True`, X will be copied; else, it may be overwritten.
**max\_iter**int, default=1000
The maximum number of iterations.
**tol**float, default=1e-4
The tolerance for the optimization: if the updates are smaller than `tol`, the optimization code checks the dual gap for optimality and continues until it is smaller than `tol`.
**warm\_start**bool, default=False
When set to `True`, reuse the solution of the previous call to fit as initialization, otherwise, just erase the previous solution. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
**random\_state**int, RandomState instance, default=None
The seed of the pseudo random number generator that selects a random feature to update. Used when `selection` == ‘random’. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**selection**{‘cyclic’, ‘random’}, default=’cyclic’
If set to ‘random’, a random coefficient is updated every iteration rather than looping over features sequentially by default. This (setting to ‘random’) often leads to significantly faster convergence especially when tol is higher than 1e-4.
Attributes:
**coef\_**ndarray of shape (n\_targets, n\_features)
Parameter vector (W in the cost function formula). Note that `coef_` stores the transpose of `W`, `W.T`.
**intercept\_**ndarray of shape (n\_targets,)
Independent term in decision function.
**n\_iter\_**int
Number of iterations run by the coordinate descent solver to reach the specified tolerance.
**dual\_gap\_**ndarray of shape (n\_alphas,)
The dual gaps at the end of the optimization for each alpha.
**eps\_**float
The tolerance scaled scaled by the variance of the target `y`.
[`sparse_coef_`](#sklearn.linear_model.MultiTaskLasso.sparse_coef_ "sklearn.linear_model.MultiTaskLasso.sparse_coef_")sparse matrix of shape (n\_features,) or (n\_targets, n\_features)
Sparse representation of the fitted `coef_`.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`Lasso`](sklearn.linear_model.lasso#sklearn.linear_model.Lasso "sklearn.linear_model.Lasso")
Linear Model trained with L1 prior as regularizer (aka the Lasso).
[`MultiTaskLasso`](#sklearn.linear_model.MultiTaskLasso "sklearn.linear_model.MultiTaskLasso")
Multi-task L1/L2 Lasso with built-in cross-validation.
[`MultiTaskElasticNet`](sklearn.linear_model.multitaskelasticnet#sklearn.linear_model.MultiTaskElasticNet "sklearn.linear_model.MultiTaskElasticNet")
Multi-task L1/L2 ElasticNet with built-in cross-validation.
#### Notes
The algorithm used to fit the model is coordinate descent.
To avoid unnecessary memory duplication the X and y arguments of the fit method should be directly passed as Fortran-contiguous numpy arrays.
#### Examples
```
>>> from sklearn import linear_model
>>> clf = linear_model.MultiTaskLasso(alpha=0.1)
>>> clf.fit([[0, 1], [1, 2], [2, 4]], [[0, 0], [1, 1], [2, 3]])
MultiTaskLasso(alpha=0.1)
>>> print(clf.coef_)
[[0. 0.60809415]
[0. 0.94592424]]
>>> print(clf.intercept_)
[-0.41888636 -0.87382323]
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.linear_model.MultiTaskLasso.fit "sklearn.linear_model.MultiTaskLasso.fit")(X, y) | Fit MultiTaskElasticNet model with coordinate descent. |
| [`get_params`](#sklearn.linear_model.MultiTaskLasso.get_params "sklearn.linear_model.MultiTaskLasso.get_params")([deep]) | Get parameters for this estimator. |
| [`path`](#sklearn.linear_model.MultiTaskLasso.path "sklearn.linear_model.MultiTaskLasso.path")(X, y, \*[, l1\_ratio, eps, n\_alphas, ...]) | Compute elastic net path with coordinate descent. |
| [`predict`](#sklearn.linear_model.MultiTaskLasso.predict "sklearn.linear_model.MultiTaskLasso.predict")(X) | Predict using the linear model. |
| [`score`](#sklearn.linear_model.MultiTaskLasso.score "sklearn.linear_model.MultiTaskLasso.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.linear_model.MultiTaskLasso.set_params "sklearn.linear_model.MultiTaskLasso.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_coordinate_descent.py#L2429)
Fit MultiTaskElasticNet model with coordinate descent.
Parameters:
**X**ndarray of shape (n\_samples, n\_features)
Data.
**y**ndarray of shape (n\_samples, n\_targets)
Target. Will be cast to X’s dtype if necessary.
Returns:
**self**object
Fitted estimator.
#### Notes
Coordinate descent is an algorithm that considers each column of data at a time hence it will automatically convert the X input as a Fortran-contiguous numpy array if necessary.
To avoid memory re-allocation it is advised to allocate the initial data in memory directly using that format.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*static*path(*X*, *y*, *\**, *l1\_ratio=0.5*, *eps=0.001*, *n\_alphas=100*, *alphas=None*, *precompute='auto'*, *Xy=None*, *copy\_X=True*, *coef\_init=None*, *verbose=False*, *return\_n\_iter=False*, *positive=False*, *check\_input=True*, *\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_coordinate_descent.py#L366)
Compute elastic net path with coordinate descent.
The elastic net optimization function varies for mono and multi-outputs.
For mono-output tasks it is:
```
1 / (2 * n_samples) * ||y - Xw||^2_2
+ alpha * l1_ratio * ||w||_1
+ 0.5 * alpha * (1 - l1_ratio) * ||w||^2_2
```
For multi-output tasks it is:
```
(1 / (2 * n_samples)) * ||Y - XW||_Fro^2
+ alpha * l1_ratio * ||W||_21
+ 0.5 * alpha * (1 - l1_ratio) * ||W||_Fro^2
```
Where:
```
||W||_21 = \sum_i \sqrt{\sum_j w_{ij}^2}
```
i.e. the sum of norm of each row.
Read more in the [User Guide](../linear_model#elastic-net).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training data. Pass directly as Fortran-contiguous data to avoid unnecessary memory duplication. If `y` is mono-output then `X` can be sparse.
**y**{array-like, sparse matrix} of shape (n\_samples,) or (n\_samples, n\_targets)
Target values.
**l1\_ratio**float, default=0.5
Number between 0 and 1 passed to elastic net (scaling between l1 and l2 penalties). `l1_ratio=1` corresponds to the Lasso.
**eps**float, default=1e-3
Length of the path. `eps=1e-3` means that `alpha_min / alpha_max = 1e-3`.
**n\_alphas**int, default=100
Number of alphas along the regularization path.
**alphas**ndarray, default=None
List of alphas where to compute the models. If None alphas are set automatically.
**precompute**‘auto’, bool or array-like of shape (n\_features, n\_features), default=’auto’
Whether to use a precomputed Gram matrix to speed up calculations. If set to `'auto'` let us decide. The Gram matrix can also be passed as argument.
**Xy**array-like of shape (n\_features,) or (n\_features, n\_targets), default=None
Xy = np.dot(X.T, y) that can be precomputed. It is useful only when the Gram matrix is precomputed.
**copy\_X**bool, default=True
If `True`, X will be copied; else, it may be overwritten.
**coef\_init**ndarray of shape (n\_features, ), default=None
The initial values of the coefficients.
**verbose**bool or int, default=False
Amount of verbosity.
**return\_n\_iter**bool, default=False
Whether to return the number of iterations or not.
**positive**bool, default=False
If set to True, forces coefficients to be positive. (Only allowed when `y.ndim == 1`).
**check\_input**bool, default=True
If set to False, the input validation checks are skipped (including the Gram matrix when provided). It is assumed that they are handled by the caller.
**\*\*params**kwargs
Keyword arguments passed to the coordinate descent solver.
Returns:
**alphas**ndarray of shape (n\_alphas,)
The alphas along the path where models are computed.
**coefs**ndarray of shape (n\_features, n\_alphas) or (n\_targets, n\_features, n\_alphas)
Coefficients along the path.
**dual\_gaps**ndarray of shape (n\_alphas,)
The dual gaps at the end of the optimization for each alpha.
**n\_iters**list of int
The number of iterations taken by the coordinate descent optimizer to reach the specified tolerance for each alpha. (Is returned when `return_n_iter` is set to True).
See also
[`MultiTaskElasticNet`](sklearn.linear_model.multitaskelasticnet#sklearn.linear_model.MultiTaskElasticNet "sklearn.linear_model.MultiTaskElasticNet")
Multi-task ElasticNet model trained with L1/L2 mixed-norm as regularizer.
[`MultiTaskElasticNetCV`](sklearn.linear_model.multitaskelasticnetcv#sklearn.linear_model.MultiTaskElasticNetCV "sklearn.linear_model.MultiTaskElasticNetCV")
Multi-task L1/L2 ElasticNet with built-in cross-validation.
[`ElasticNet`](sklearn.linear_model.elasticnet#sklearn.linear_model.ElasticNet "sklearn.linear_model.ElasticNet")
Linear regression with combined L1 and L2 priors as regularizer.
[`ElasticNetCV`](sklearn.linear_model.elasticnetcv#sklearn.linear_model.ElasticNetCV "sklearn.linear_model.ElasticNetCV")
Elastic Net model with iterative fitting along a regularization path.
#### Notes
For an example, see [examples/linear\_model/plot\_lasso\_coordinate\_descent\_path.py](../../auto_examples/linear_model/plot_lasso_coordinate_descent_path#sphx-glr-auto-examples-linear-model-plot-lasso-coordinate-descent-path-py).
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L372)
Predict using the linear model.
Parameters:
**X**array-like or sparse matrix, shape (n\_samples, n\_features)
Samples.
Returns:
**C**array, shape (n\_samples,)
Returns predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
*property*sparse\_coef\_
Sparse representation of the fitted `coef_`.
Examples using `sklearn.linear_model.MultiTaskLasso`
----------------------------------------------------
[Joint feature selection with multi-task Lasso](../../auto_examples/linear_model/plot_multi_task_lasso_support#sphx-glr-auto-examples-linear-model-plot-multi-task-lasso-support-py)
| programming_docs |
scikit_learn sklearn.cluster.AffinityPropagation sklearn.cluster.AffinityPropagation
===================================
*class*sklearn.cluster.AffinityPropagation(*\**, *damping=0.5*, *max\_iter=200*, *convergence\_iter=15*, *copy=True*, *preference=None*, *affinity='euclidean'*, *verbose=False*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_affinity_propagation.py#L273)
Perform Affinity Propagation Clustering of data.
Read more in the [User Guide](../clustering#affinity-propagation).
Parameters:
**damping**float, default=0.5
Damping factor in the range `[0.5, 1.0)` is the extent to which the current value is maintained relative to incoming values (weighted 1 - damping). This in order to avoid numerical oscillations when updating these values (messages).
**max\_iter**int, default=200
Maximum number of iterations.
**convergence\_iter**int, default=15
Number of iterations with no change in the number of estimated clusters that stops the convergence.
**copy**bool, default=True
Make a copy of input data.
**preference**array-like of shape (n\_samples,) or float, default=None
Preferences for each point - points with larger values of preferences are more likely to be chosen as exemplars. The number of exemplars, ie of clusters, is influenced by the input preferences value. If the preferences are not passed as arguments, they will be set to the median of the input similarities.
**affinity**{‘euclidean’, ‘precomputed’}, default=’euclidean’
Which affinity to use. At the moment ‘precomputed’ and `euclidean` are supported. ‘euclidean’ uses the negative squared euclidean distance between points.
**verbose**bool, default=False
Whether to be verbose.
**random\_state**int, RandomState instance or None, default=None
Pseudo-random number generator to control the starting state. Use an int for reproducible results across function calls. See the [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
New in version 0.23: this parameter was previously hardcoded as 0.
Attributes:
**cluster\_centers\_indices\_**ndarray of shape (n\_clusters,)
Indices of cluster centers.
**cluster\_centers\_**ndarray of shape (n\_clusters, n\_features)
Cluster centers (if affinity != `precomputed`).
**labels\_**ndarray of shape (n\_samples,)
Labels of each point.
**affinity\_matrix\_**ndarray of shape (n\_samples, n\_samples)
Stores the affinity matrix used in `fit`.
**n\_iter\_**int
Number of iterations taken to converge.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`AgglomerativeClustering`](sklearn.cluster.agglomerativeclustering#sklearn.cluster.AgglomerativeClustering "sklearn.cluster.AgglomerativeClustering")
Recursively merges the pair of clusters that minimally increases a given linkage distance.
[`FeatureAgglomeration`](sklearn.cluster.featureagglomeration#sklearn.cluster.FeatureAgglomeration "sklearn.cluster.FeatureAgglomeration")
Similar to AgglomerativeClustering, but recursively merges features instead of samples.
[`KMeans`](sklearn.cluster.kmeans#sklearn.cluster.KMeans "sklearn.cluster.KMeans")
K-Means clustering.
[`MiniBatchKMeans`](sklearn.cluster.minibatchkmeans#sklearn.cluster.MiniBatchKMeans "sklearn.cluster.MiniBatchKMeans")
Mini-Batch K-Means clustering.
[`MeanShift`](sklearn.cluster.meanshift#sklearn.cluster.MeanShift "sklearn.cluster.MeanShift")
Mean shift clustering using a flat kernel.
[`SpectralClustering`](sklearn.cluster.spectralclustering#sklearn.cluster.SpectralClustering "sklearn.cluster.SpectralClustering")
Apply clustering to a projection of the normalized Laplacian.
#### Notes
For an example, see [examples/cluster/plot\_affinity\_propagation.py](../../auto_examples/cluster/plot_affinity_propagation#sphx-glr-auto-examples-cluster-plot-affinity-propagation-py).
The algorithmic complexity of affinity propagation is quadratic in the number of points.
When the algorithm does not converge, it will still return a arrays of `cluster_center_indices` and labels if there are any exemplars/clusters, however they may be degenerate and should be used with caution.
When `fit` does not converge, `cluster_centers_` is still populated however it may be degenerate. In such a case, proceed with caution. If `fit` does not converge and fails to produce any `cluster_centers_` then `predict` will label every sample as `-1`.
When all training samples have equal similarities and equal preferences, the assignment of cluster centers and labels depends on the preference. If the preference is smaller than the similarities, `fit` will result in a single cluster center and label `0` for every sample. Otherwise, every training sample becomes its own cluster center and is assigned a unique label.
#### References
Brendan J. Frey and Delbert Dueck, “Clustering by Passing Messages Between Data Points”, Science Feb. 2007
#### Examples
```
>>> from sklearn.cluster import AffinityPropagation
>>> import numpy as np
>>> X = np.array([[1, 2], [1, 4], [1, 0],
... [4, 2], [4, 4], [4, 0]])
>>> clustering = AffinityPropagation(random_state=5).fit(X)
>>> clustering
AffinityPropagation(random_state=5)
>>> clustering.labels_
array([0, 0, 0, 1, 1, 1])
>>> clustering.predict([[0, 0], [4, 4]])
array([0, 1])
>>> clustering.cluster_centers_
array([[1, 2],
[4, 2]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.cluster.AffinityPropagation.fit "sklearn.cluster.AffinityPropagation.fit")(X[, y]) | Fit the clustering from features, or affinity matrix. |
| [`fit_predict`](#sklearn.cluster.AffinityPropagation.fit_predict "sklearn.cluster.AffinityPropagation.fit_predict")(X[, y]) | Fit clustering from features/affinity matrix; return cluster labels. |
| [`get_params`](#sklearn.cluster.AffinityPropagation.get_params "sklearn.cluster.AffinityPropagation.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.cluster.AffinityPropagation.predict "sklearn.cluster.AffinityPropagation.predict")(X) | Predict the closest cluster each sample in X belongs to. |
| [`set_params`](#sklearn.cluster.AffinityPropagation.set_params "sklearn.cluster.AffinityPropagation.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_affinity_propagation.py#L433)
Fit the clustering from features, or affinity matrix.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features), or array-like of shape (n\_samples, n\_samples)
Training instances to cluster, or similarities / affinities between instances if `affinity='precomputed'`. If a sparse feature matrix is provided, it will be converted into a sparse `csr_matrix`.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
self
Returns the instance itself.
fit\_predict(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_affinity_propagation.py#L537)
Fit clustering from features/affinity matrix; return cluster labels.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features), or array-like of shape (n\_samples, n\_samples)
Training instances to cluster, or similarities / affinities between instances if `affinity='precomputed'`. If a sparse feature matrix is provided, it will be converted into a sparse `csr_matrix`.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
**labels**ndarray of shape (n\_samples,)
Cluster labels.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_affinity_propagation.py#L504)
Predict the closest cluster each sample in X belongs to.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
New data to predict. If a sparse matrix is provided, it will be converted into a sparse `csr_matrix`.
Returns:
**labels**ndarray of shape (n\_samples,)
Cluster labels.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.cluster.AffinityPropagation`
----------------------------------------------------
[Comparing different clustering algorithms on toy datasets](../../auto_examples/cluster/plot_cluster_comparison#sphx-glr-auto-examples-cluster-plot-cluster-comparison-py)
[Demo of affinity propagation clustering algorithm](../../auto_examples/cluster/plot_affinity_propagation#sphx-glr-auto-examples-cluster-plot-affinity-propagation-py)
scikit_learn sklearn.datasets.make_friedman2 sklearn.datasets.make\_friedman2
================================
sklearn.datasets.make\_friedman2(*n\_samples=100*, *\**, *noise=0.0*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_samples_generator.py#L1030)
Generate the “Friedman #2” regression problem.
This dataset is described in Friedman [1] and Breiman [2].
Inputs `X` are 4 independent features uniformly distributed on the intervals:
```
0 <= X[:, 0] <= 100,
40 * pi <= X[:, 1] <= 560 * pi,
0 <= X[:, 2] <= 1,
1 <= X[:, 3] <= 11.
```
The output `y` is created according to the formula:
```
y(X) = (X[:, 0] ** 2 + (X[:, 1] * X[:, 2] - 1 / (X[:, 1] * X[:, 3])) ** 2) ** 0.5 + noise * N(0, 1).
```
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/sample_generators.html#sample-generators).
Parameters:
**n\_samples**int, default=100
The number of samples.
**noise**float, default=0.0
The standard deviation of the gaussian noise applied to the output.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for dataset noise. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Returns:
**X**ndarray of shape (n\_samples, 4)
The input samples.
**y**ndarray of shape (n\_samples,)
The output values.
#### References
[1] J. Friedman, “Multivariate adaptive regression splines”, The Annals of Statistics 19 (1), pages 1-67, 1991.
[2] L. Breiman, “Bagging predictors”, Machine Learning 24, pages 123-140, 1996.
scikit_learn sklearn.neighbors.NearestCentroid sklearn.neighbors.NearestCentroid
=================================
*class*sklearn.neighbors.NearestCentroid(*metric='euclidean'*, *\**, *shrink\_threshold=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_nearest_centroid.py#L22)
Nearest centroid classifier.
Each class is represented by its centroid, with test samples classified to the class with the nearest centroid.
Read more in the [User Guide](../neighbors#nearest-centroid-classifier).
Parameters:
**metric**str or callable, default=”euclidean”
Metric to use for distance computation. Default is “minkowski”, which results in the standard Euclidean distance when p = 2. See the documentation of [scipy.spatial.distance](https://docs.scipy.org/doc/scipy/reference/spatial.distance.html) and the metrics listed in [`distance_metrics`](sklearn.metrics.pairwise.distance_metrics#sklearn.metrics.pairwise.distance_metrics "sklearn.metrics.pairwise.distance_metrics") for valid metric values. Note that “wminkowski”, “seuclidean” and “mahalanobis” are not supported.
The centroids for the samples corresponding to each class is the point from which the sum of the distances (according to the metric) of all samples that belong to that particular class are minimized. If the `"manhattan"` metric is provided, this centroid is the median and for all other metrics, the centroid is now set to be the mean.
Changed in version 0.19: `metric='precomputed'` was deprecated and now raises an error
**shrink\_threshold**float, default=None
Threshold for shrinking centroids to remove features.
Attributes:
**centroids\_**array-like of shape (n\_classes, n\_features)
Centroid of each class.
**classes\_**array of shape (n\_classes,)
The unique classes labels.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`KNeighborsClassifier`](sklearn.neighbors.kneighborsclassifier#sklearn.neighbors.KNeighborsClassifier "sklearn.neighbors.KNeighborsClassifier")
Nearest neighbors classifier.
#### Notes
When used for text classification with tf-idf vectors, this classifier is also known as the Rocchio classifier.
#### References
Tibshirani, R., Hastie, T., Narasimhan, B., & Chu, G. (2002). Diagnosis of multiple cancer types by shrunken centroids of gene expression. Proceedings of the National Academy of Sciences of the United States of America, 99(10), 6567-6572. The National Academy of Sciences.
#### Examples
```
>>> from sklearn.neighbors import NearestCentroid
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> y = np.array([1, 1, 1, 2, 2, 2])
>>> clf = NearestCentroid()
>>> clf.fit(X, y)
NearestCentroid()
>>> print(clf.predict([[-0.8, -1]]))
[1]
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.neighbors.NearestCentroid.fit "sklearn.neighbors.NearestCentroid.fit")(X, y) | Fit the NearestCentroid model according to the given training data. |
| [`get_params`](#sklearn.neighbors.NearestCentroid.get_params "sklearn.neighbors.NearestCentroid.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.neighbors.NearestCentroid.predict "sklearn.neighbors.NearestCentroid.predict")(X) | Perform classification on an array of test vectors `X`. |
| [`score`](#sklearn.neighbors.NearestCentroid.score "sklearn.neighbors.NearestCentroid.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.neighbors.NearestCentroid.set_params "sklearn.neighbors.NearestCentroid.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_nearest_centroid.py#L106)
Fit the NearestCentroid model according to the given training data.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vector, where `n_samples` is the number of samples and `n_features` is the number of features. Note that centroid shrinking cannot be used with sparse matrices.
**y**array-like of shape (n\_samples,)
Target values.
Returns:
**self**object
Fitted estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_nearest_centroid.py#L201)
Perform classification on an array of test vectors `X`.
The predicted class `C` for each sample in `X` is returned.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Test samples.
Returns:
**C**ndarray of shape (n\_samples,)
The predicted classes.
#### Notes
If the metric constructor parameter is `"precomputed"`, `X` is assumed to be the distance matrix between the data to be predicted and `self.centroids_`.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.neighbors.NearestCentroid`
--------------------------------------------------
[Nearest Centroid Classification](../../auto_examples/neighbors/plot_nearest_centroid#sphx-glr-auto-examples-neighbors-plot-nearest-centroid-py)
[Classification of text documents using sparse features](../../auto_examples/text/plot_document_classification_20newsgroups#sphx-glr-auto-examples-text-plot-document-classification-20newsgroups-py)
scikit_learn sklearn.datasets.make_friedman3 sklearn.datasets.make\_friedman3
================================
sklearn.datasets.make\_friedman3(*n\_samples=100*, *\**, *noise=0.0*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_samples_generator.py#L1095)
Generate the “Friedman #3” regression problem.
This dataset is described in Friedman [1] and Breiman [2].
Inputs `X` are 4 independent features uniformly distributed on the intervals:
```
0 <= X[:, 0] <= 100,
40 * pi <= X[:, 1] <= 560 * pi,
0 <= X[:, 2] <= 1,
1 <= X[:, 3] <= 11.
```
The output `y` is created according to the formula:
```
y(X) = arctan((X[:, 1] * X[:, 2] - 1 / (X[:, 1] * X[:, 3])) / X[:, 0]) + noise * N(0, 1).
```
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/sample_generators.html#sample-generators).
Parameters:
**n\_samples**int, default=100
The number of samples.
**noise**float, default=0.0
The standard deviation of the gaussian noise applied to the output.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for dataset noise. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Returns:
**X**ndarray of shape (n\_samples, 4)
The input samples.
**y**ndarray of shape (n\_samples,)
The output values.
#### References
[1] J. Friedman, “Multivariate adaptive regression splines”, The Annals of Statistics 19 (1), pages 1-67, 1991.
[2] L. Breiman, “Bagging predictors”, Machine Learning 24, pages 123-140, 1996.
| programming_docs |
scikit_learn sklearn.neighbors.NearestNeighbors sklearn.neighbors.NearestNeighbors
==================================
*class*sklearn.neighbors.NearestNeighbors(*\**, *n\_neighbors=5*, *radius=1.0*, *algorithm='auto'*, *leaf\_size=30*, *metric='minkowski'*, *p=2*, *metric\_params=None*, *n\_jobs=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_unsupervised.py#L7)
Unsupervised learner for implementing neighbor searches.
Read more in the [User Guide](../neighbors#unsupervised-neighbors).
New in version 0.9.
Parameters:
**n\_neighbors**int, default=5
Number of neighbors to use by default for [`kneighbors`](#sklearn.neighbors.NearestNeighbors.kneighbors "sklearn.neighbors.NearestNeighbors.kneighbors") queries.
**radius**float, default=1.0
Range of parameter space to use by default for [`radius_neighbors`](#sklearn.neighbors.NearestNeighbors.radius_neighbors "sklearn.neighbors.NearestNeighbors.radius_neighbors") queries.
**algorithm**{‘auto’, ‘ball\_tree’, ‘kd\_tree’, ‘brute’}, default=’auto’
Algorithm used to compute the nearest neighbors:
* ‘ball\_tree’ will use [`BallTree`](sklearn.neighbors.balltree#sklearn.neighbors.BallTree "sklearn.neighbors.BallTree")
* ‘kd\_tree’ will use [`KDTree`](sklearn.neighbors.kdtree#sklearn.neighbors.KDTree "sklearn.neighbors.KDTree")
* ‘brute’ will use a brute-force search.
* ‘auto’ will attempt to decide the most appropriate algorithm based on the values passed to [`fit`](#sklearn.neighbors.NearestNeighbors.fit "sklearn.neighbors.NearestNeighbors.fit") method.
Note: fitting on sparse input will override the setting of this parameter, using brute force.
**leaf\_size**int, default=30
Leaf size passed to BallTree or KDTree. This can affect the speed of the construction and query, as well as the memory required to store the tree. The optimal value depends on the nature of the problem.
**metric**str or callable, default=’minkowski’
Metric to use for distance computation. Default is “minkowski”, which results in the standard Euclidean distance when p = 2. See the documentation of [scipy.spatial.distance](https://docs.scipy.org/doc/scipy/reference/spatial.distance.html) and the metrics listed in [`distance_metrics`](sklearn.metrics.pairwise.distance_metrics#sklearn.metrics.pairwise.distance_metrics "sklearn.metrics.pairwise.distance_metrics") for valid metric values.
If metric is “precomputed”, X is assumed to be a distance matrix and must be square during fit. X may be a [sparse graph](https://scikit-learn.org/1.1/glossary.html#term-sparse-graph), in which case only “nonzero” elements may be considered neighbors.
If metric is a callable function, it takes two arrays representing 1D vectors as inputs and must return one value indicating the distance between those vectors. This works for Scipy’s metrics, but is less efficient than passing the metric name as a string.
**p**int, default=2
Parameter for the Minkowski metric from sklearn.metrics.pairwise.pairwise\_distances. When p = 1, this is equivalent to using manhattan\_distance (l1), and euclidean\_distance (l2) for p = 2. For arbitrary p, minkowski\_distance (l\_p) is used.
**metric\_params**dict, default=None
Additional keyword arguments for the metric function.
**n\_jobs**int, default=None
The number of parallel jobs to run for neighbors search. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
Attributes:
**effective\_metric\_**str
Metric used to compute distances to neighbors.
**effective\_metric\_params\_**dict
Parameters for the metric used to compute distances to neighbors.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_samples\_fit\_**int
Number of samples in the fitted data.
See also
[`KNeighborsClassifier`](sklearn.neighbors.kneighborsclassifier#sklearn.neighbors.KNeighborsClassifier "sklearn.neighbors.KNeighborsClassifier")
Classifier implementing the k-nearest neighbors vote.
[`RadiusNeighborsClassifier`](sklearn.neighbors.radiusneighborsclassifier#sklearn.neighbors.RadiusNeighborsClassifier "sklearn.neighbors.RadiusNeighborsClassifier")
Classifier implementing a vote among neighbors within a given radius.
[`KNeighborsRegressor`](sklearn.neighbors.kneighborsregressor#sklearn.neighbors.KNeighborsRegressor "sklearn.neighbors.KNeighborsRegressor")
Regression based on k-nearest neighbors.
[`RadiusNeighborsRegressor`](sklearn.neighbors.radiusneighborsregressor#sklearn.neighbors.RadiusNeighborsRegressor "sklearn.neighbors.RadiusNeighborsRegressor")
Regression based on neighbors within a fixed radius.
[`BallTree`](sklearn.neighbors.balltree#sklearn.neighbors.BallTree "sklearn.neighbors.BallTree")
Space partitioning data structure for organizing points in a multi-dimensional space, used for nearest neighbor search.
#### Notes
See [Nearest Neighbors](../neighbors#neighbors) in the online documentation for a discussion of the choice of `algorithm` and `leaf_size`.
<https://en.wikipedia.org/wiki/K-nearest_neighbors_algorithm>
#### Examples
```
>>> import numpy as np
>>> from sklearn.neighbors import NearestNeighbors
>>> samples = [[0, 0, 2], [1, 0, 0], [0, 0, 1]]
```
```
>>> neigh = NearestNeighbors(n_neighbors=2, radius=0.4)
>>> neigh.fit(samples)
NearestNeighbors(...)
```
```
>>> neigh.kneighbors([[0, 0, 1.3]], 2, return_distance=False)
array([[2, 0]]...)
```
```
>>> nbrs = neigh.radius_neighbors(
... [[0, 0, 1.3]], 0.4, return_distance=False
... )
>>> np.asarray(nbrs[0][0])
array(2)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.neighbors.NearestNeighbors.fit "sklearn.neighbors.NearestNeighbors.fit")(X[, y]) | Fit the nearest neighbors estimator from the training dataset. |
| [`get_params`](#sklearn.neighbors.NearestNeighbors.get_params "sklearn.neighbors.NearestNeighbors.get_params")([deep]) | Get parameters for this estimator. |
| [`kneighbors`](#sklearn.neighbors.NearestNeighbors.kneighbors "sklearn.neighbors.NearestNeighbors.kneighbors")([X, n\_neighbors, return\_distance]) | Find the K-neighbors of a point. |
| [`kneighbors_graph`](#sklearn.neighbors.NearestNeighbors.kneighbors_graph "sklearn.neighbors.NearestNeighbors.kneighbors_graph")([X, n\_neighbors, mode]) | Compute the (weighted) graph of k-Neighbors for points in X. |
| [`radius_neighbors`](#sklearn.neighbors.NearestNeighbors.radius_neighbors "sklearn.neighbors.NearestNeighbors.radius_neighbors")([X, radius, ...]) | Find the neighbors within a given radius of a point or points. |
| [`radius_neighbors_graph`](#sklearn.neighbors.NearestNeighbors.radius_neighbors_graph "sklearn.neighbors.NearestNeighbors.radius_neighbors_graph")([X, radius, mode, ...]) | Compute the (weighted) graph of Neighbors for points in X. |
| [`set_params`](#sklearn.neighbors.NearestNeighbors.set_params "sklearn.neighbors.NearestNeighbors.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_unsupervised.py#L158)
Fit the nearest neighbors estimator from the training dataset.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features) or (n\_samples, n\_samples) if metric=’precomputed’
Training data.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**self**NearestNeighbors
The fitted nearest neighbors estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
kneighbors(*X=None*, *n\_neighbors=None*, *return\_distance=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_base.py#L670)
Find the K-neighbors of a point.
Returns indices of and distances to the neighbors of each point.
Parameters:
**X**array-like, shape (n\_queries, n\_features), or (n\_queries, n\_indexed) if metric == ‘precomputed’, default=None
The query point or points. If not provided, neighbors of each indexed point are returned. In this case, the query point is not considered its own neighbor.
**n\_neighbors**int, default=None
Number of neighbors required for each sample. The default is the value passed to the constructor.
**return\_distance**bool, default=True
Whether or not to return the distances.
Returns:
**neigh\_dist**ndarray of shape (n\_queries, n\_neighbors)
Array representing the lengths to points, only present if return\_distance=True.
**neigh\_ind**ndarray of shape (n\_queries, n\_neighbors)
Indices of the nearest points in the population matrix.
#### Examples
In the following example, we construct a NearestNeighbors class from an array representing our data set and ask who’s the closest point to [1,1,1]
```
>>> samples = [[0., 0., 0.], [0., .5, 0.], [1., 1., .5]]
>>> from sklearn.neighbors import NearestNeighbors
>>> neigh = NearestNeighbors(n_neighbors=1)
>>> neigh.fit(samples)
NearestNeighbors(n_neighbors=1)
>>> print(neigh.kneighbors([[1., 1., 1.]]))
(array([[0.5]]), array([[2]]))
```
As you can see, it returns [[0.5]], and [[2]], which means that the element is at distance 0.5 and is the third element of samples (indexes start at 0). You can also query for multiple points:
```
>>> X = [[0., 1., 0.], [1., 0., 1.]]
>>> neigh.kneighbors(X, return_distance=False)
array([[1],
[2]]...)
```
kneighbors\_graph(*X=None*, *n\_neighbors=None*, *mode='connectivity'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_base.py#L860)
Compute the (weighted) graph of k-Neighbors for points in X.
Parameters:
**X**array-like of shape (n\_queries, n\_features), or (n\_queries, n\_indexed) if metric == ‘precomputed’, default=None
The query point or points. If not provided, neighbors of each indexed point are returned. In this case, the query point is not considered its own neighbor. For `metric='precomputed'` the shape should be (n\_queries, n\_indexed). Otherwise the shape should be (n\_queries, n\_features).
**n\_neighbors**int, default=None
Number of neighbors for each sample. The default is the value passed to the constructor.
**mode**{‘connectivity’, ‘distance’}, default=’connectivity’
Type of returned matrix: ‘connectivity’ will return the connectivity matrix with ones and zeros, in ‘distance’ the edges are distances between points, type of distance depends on the selected metric parameter in NearestNeighbors class.
Returns:
**A**sparse-matrix of shape (n\_queries, n\_samples\_fit)
`n_samples_fit` is the number of samples in the fitted data. `A[i, j]` gives the weight of the edge connecting `i` to `j`. The matrix is of CSR format.
See also
[`NearestNeighbors.radius_neighbors_graph`](#sklearn.neighbors.NearestNeighbors.radius_neighbors_graph "sklearn.neighbors.NearestNeighbors.radius_neighbors_graph")
Compute the (weighted) graph of Neighbors for points in X.
#### Examples
```
>>> X = [[0], [3], [1]]
>>> from sklearn.neighbors import NearestNeighbors
>>> neigh = NearestNeighbors(n_neighbors=2)
>>> neigh.fit(X)
NearestNeighbors(n_neighbors=2)
>>> A = neigh.kneighbors_graph(X)
>>> A.toarray()
array([[1., 0., 1.],
[0., 1., 1.],
[1., 0., 1.]])
```
radius\_neighbors(*X=None*, *radius=None*, *return\_distance=True*, *sort\_results=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_base.py#L996)
Find the neighbors within a given radius of a point or points.
Return the indices and distances of each point from the dataset lying in a ball with size `radius` around the points of the query array. Points lying on the boundary are included in the results.
The result points are *not* necessarily sorted by distance to their query point.
Parameters:
**X**array-like of (n\_samples, n\_features), default=None
The query point or points. If not provided, neighbors of each indexed point are returned. In this case, the query point is not considered its own neighbor.
**radius**float, default=None
Limiting distance of neighbors to return. The default is the value passed to the constructor.
**return\_distance**bool, default=True
Whether or not to return the distances.
**sort\_results**bool, default=False
If True, the distances and indices will be sorted by increasing distances before being returned. If False, the results may not be sorted. If `return_distance=False`, setting `sort_results=True` will result in an error.
New in version 0.22.
Returns:
**neigh\_dist**ndarray of shape (n\_samples,) of arrays
Array representing the distances to each point, only present if `return_distance=True`. The distance values are computed according to the `metric` constructor parameter.
**neigh\_ind**ndarray of shape (n\_samples,) of arrays
An array of arrays of indices of the approximate nearest points from the population matrix that lie within a ball of size `radius` around the query points.
#### Notes
Because the number of neighbors of each point is not necessarily equal, the results for multiple query points cannot be fit in a standard data array. For efficiency, `radius_neighbors` returns arrays of objects, where each object is a 1D array of indices or distances.
#### Examples
In the following example, we construct a NeighborsClassifier class from an array representing our data set and ask who’s the closest point to [1, 1, 1]:
```
>>> import numpy as np
>>> samples = [[0., 0., 0.], [0., .5, 0.], [1., 1., .5]]
>>> from sklearn.neighbors import NearestNeighbors
>>> neigh = NearestNeighbors(radius=1.6)
>>> neigh.fit(samples)
NearestNeighbors(radius=1.6)
>>> rng = neigh.radius_neighbors([[1., 1., 1.]])
>>> print(np.asarray(rng[0][0]))
[1.5 0.5]
>>> print(np.asarray(rng[1][0]))
[1 2]
```
The first array returned contains the distances to all points which are closer than 1.6, while the second array returned contains their indices. In general, multiple points can be queried at the same time.
radius\_neighbors\_graph(*X=None*, *radius=None*, *mode='connectivity'*, *sort\_results=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_base.py#L1205)
Compute the (weighted) graph of Neighbors for points in X.
Neighborhoods are restricted the points at a distance lower than radius.
Parameters:
**X**array-like of shape (n\_samples, n\_features), default=None
The query point or points. If not provided, neighbors of each indexed point are returned. In this case, the query point is not considered its own neighbor.
**radius**float, default=None
Radius of neighborhoods. The default is the value passed to the constructor.
**mode**{‘connectivity’, ‘distance’}, default=’connectivity’
Type of returned matrix: ‘connectivity’ will return the connectivity matrix with ones and zeros, in ‘distance’ the edges are distances between points, type of distance depends on the selected metric parameter in NearestNeighbors class.
**sort\_results**bool, default=False
If True, in each row of the result, the non-zero entries will be sorted by increasing distances. If False, the non-zero entries may not be sorted. Only used with mode=’distance’.
New in version 0.22.
Returns:
**A**sparse-matrix of shape (n\_queries, n\_samples\_fit)
`n_samples_fit` is the number of samples in the fitted data. `A[i, j]` gives the weight of the edge connecting `i` to `j`. The matrix is of CSR format.
See also
[`kneighbors_graph`](sklearn.neighbors.kneighbors_graph#sklearn.neighbors.kneighbors_graph "sklearn.neighbors.kneighbors_graph")
Compute the (weighted) graph of k-Neighbors for points in X.
#### Examples
```
>>> X = [[0], [3], [1]]
>>> from sklearn.neighbors import NearestNeighbors
>>> neigh = NearestNeighbors(radius=1.5)
>>> neigh.fit(X)
NearestNeighbors(radius=1.5)
>>> A = neigh.radius_neighbors_graph(X)
>>> A.toarray()
array([[1., 0., 1.],
[0., 1., 0.],
[1., 0., 1.]])
```
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
scikit_learn sklearn.utils.register_parallel_backend sklearn.utils.register\_parallel\_backend
=========================================
sklearn.utils.register\_parallel\_backend(*name*, *factory*, *make\_default=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/../../../../mambaforge/envs/testenv/lib/python3.9/site-packages/joblib/parallel.py#L363)
Register a new Parallel backend factory.
The new backend can then be selected by passing its name as the backend argument to the Parallel class. Moreover, the default backend can be overwritten globally by setting make\_default=True.
The factory can be any callable that takes no argument and return an instance of `ParallelBackendBase`.
Warning: this function is experimental and subject to change in a future version of joblib.
New in version 0.10.
scikit_learn sklearn.cross_decomposition.PLSSVD sklearn.cross\_decomposition.PLSSVD
===================================
*class*sklearn.cross\_decomposition.PLSSVD(*n\_components=2*, *\**, *scale=True*, *copy=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cross_decomposition/_pls.py#L896)
Partial Least Square SVD.
This transformer simply performs a SVD on the cross-covariance matrix `X'Y`. It is able to project both the training data `X` and the targets `Y`. The training data `X` is projected on the left singular vectors, while the targets are projected on the right singular vectors.
Read more in the [User Guide](../cross_decomposition#cross-decomposition).
New in version 0.8.
Parameters:
**n\_components**int, default=2
The number of components to keep. Should be in `[1,
min(n_samples, n_features, n_targets)]`.
**scale**bool, default=True
Whether to scale `X` and `Y`.
**copy**bool, default=True
Whether to copy `X` and `Y` in fit before applying centering, and potentially scaling. If `False`, these operations will be done inplace, modifying both arrays.
Attributes:
**x\_weights\_**ndarray of shape (n\_features, n\_components)
The left singular vectors of the SVD of the cross-covariance matrix. Used to project `X` in [`transform`](#sklearn.cross_decomposition.PLSSVD.transform "sklearn.cross_decomposition.PLSSVD.transform").
**y\_weights\_**ndarray of (n\_targets, n\_components)
The right singular vectors of the SVD of the cross-covariance matrix. Used to project `X` in [`transform`](#sklearn.cross_decomposition.PLSSVD.transform "sklearn.cross_decomposition.PLSSVD.transform").
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`PLSCanonical`](sklearn.cross_decomposition.plscanonical#sklearn.cross_decomposition.PLSCanonical "sklearn.cross_decomposition.PLSCanonical")
Partial Least Squares transformer and regressor.
[`CCA`](sklearn.cross_decomposition.cca#sklearn.cross_decomposition.CCA "sklearn.cross_decomposition.CCA")
Canonical Correlation Analysis.
#### Examples
```
>>> import numpy as np
>>> from sklearn.cross_decomposition import PLSSVD
>>> X = np.array([[0., 0., 1.],
... [1., 0., 0.],
... [2., 2., 2.],
... [2., 5., 4.]])
>>> Y = np.array([[0.1, -0.2],
... [0.9, 1.1],
... [6.2, 5.9],
... [11.9, 12.3]])
>>> pls = PLSSVD(n_components=2).fit(X, Y)
>>> X_c, Y_c = pls.transform(X, Y)
>>> X_c.shape, Y_c.shape
((4, 2), (4, 2))
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.cross_decomposition.PLSSVD.fit "sklearn.cross_decomposition.PLSSVD.fit")(X, Y) | Fit model to data. |
| [`fit_transform`](#sklearn.cross_decomposition.PLSSVD.fit_transform "sklearn.cross_decomposition.PLSSVD.fit_transform")(X[, y]) | Learn and apply the dimensionality reduction. |
| [`get_feature_names_out`](#sklearn.cross_decomposition.PLSSVD.get_feature_names_out "sklearn.cross_decomposition.PLSSVD.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.cross_decomposition.PLSSVD.get_params "sklearn.cross_decomposition.PLSSVD.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.cross_decomposition.PLSSVD.set_params "sklearn.cross_decomposition.PLSSVD.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.cross_decomposition.PLSSVD.transform "sklearn.cross_decomposition.PLSSVD.transform")(X[, Y]) | Apply the dimensionality reduction. |
fit(*X*, *Y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cross_decomposition/_pls.py#L969)
Fit model to data.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training samples.
**Y**array-like of shape (n\_samples,) or (n\_samples, n\_targets)
Targets.
Returns:
**self**object
Fitted estimator.
fit\_transform(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cross_decomposition/_pls.py#L1057)
Learn and apply the dimensionality reduction.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_targets), default=None
Targets.
Returns:
**out**array-like or tuple of array-like
The transformed data `X_transformed` if `Y is not None`, `(X_transformed, Y_transformed)` otherwise.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.cross_decomposition.PLSSVD.fit "sklearn.cross_decomposition.PLSSVD.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*, *Y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cross_decomposition/_pls.py#L1025)
Apply the dimensionality reduction.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Samples to be transformed.
**Y**array-like of shape (n\_samples,) or (n\_samples, n\_targets), default=None
Targets.
Returns:
**x\_scores**array-like or tuple of array-like
The transformed data `X_transformed` if `Y is not None`, `(X_transformed, Y_transformed)` otherwise.
| programming_docs |
scikit_learn sklearn.metrics.hinge_loss sklearn.metrics.hinge\_loss
===========================
sklearn.metrics.hinge\_loss(*y\_true*, *pred\_decision*, *\**, *labels=None*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_classification.py#L2470)
Average hinge loss (non-regularized).
In binary class case, assuming labels in y\_true are encoded with +1 and -1, when a prediction mistake is made, `margin = y_true * pred_decision` is always negative (since the signs disagree), implying `1 - margin` is always greater than 1. The cumulated hinge loss is therefore an upper bound of the number of mistakes made by the classifier.
In multiclass case, the function expects that either all the labels are included in y\_true or an optional labels argument is provided which contains all the labels. The multilabel margin is calculated according to Crammer-Singer’s method. As in the binary case, the cumulated hinge loss is an upper bound of the number of mistakes made by the classifier.
Read more in the [User Guide](../model_evaluation#hinge-loss).
Parameters:
**y\_true**array of shape (n\_samples,)
True target, consisting of integers of two values. The positive label must be greater than the negative label.
**pred\_decision**array of shape (n\_samples,) or (n\_samples, n\_classes)
Predicted decisions, as output by decision\_function (floats).
**labels**array-like, default=None
Contains all the labels for the problem. Used in multiclass hinge loss.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**loss**float
Average hinge loss.
#### References
[1] [Wikipedia entry on the Hinge loss](https://en.wikipedia.org/wiki/Hinge_loss).
[2] Koby Crammer, Yoram Singer. On the Algorithmic Implementation of Multiclass Kernel-based Vector Machines. Journal of Machine Learning Research 2, (2001), 265-292.
[3] [L1 AND L2 Regularization for Multiclass Hinge Loss Models by Robert C. Moore, John DeNero](https://storage.googleapis.com/pub-tools-public-publication-data/pdf/37362.pdf).
#### Examples
```
>>> from sklearn import svm
>>> from sklearn.metrics import hinge_loss
>>> X = [[0], [1]]
>>> y = [-1, 1]
>>> est = svm.LinearSVC(random_state=0)
>>> est.fit(X, y)
LinearSVC(random_state=0)
>>> pred_decision = est.decision_function([[-2], [3], [0.5]])
>>> pred_decision
array([-2.18..., 2.36..., 0.09...])
>>> hinge_loss([-1, 1, 1], pred_decision)
0.30...
```
In the multiclass case:
```
>>> import numpy as np
>>> X = np.array([[0], [1], [2], [3]])
>>> Y = np.array([0, 1, 2, 3])
>>> labels = np.array([0, 1, 2, 3])
>>> est = svm.LinearSVC()
>>> est.fit(X, Y)
LinearSVC()
>>> pred_decision = est.decision_function([[-1], [2], [3]])
>>> y_true = [0, 2, 3]
>>> hinge_loss(y_true, pred_decision, labels=labels)
0.56...
```
scikit_learn sklearn.neighbors.KernelDensity sklearn.neighbors.KernelDensity
===============================
*class*sklearn.neighbors.KernelDensity(*\**, *bandwidth=1.0*, *algorithm='auto'*, *kernel='gaussian'*, *metric='euclidean'*, *atol=0*, *rtol=0*, *breadth\_first=True*, *leaf\_size=40*, *metric\_params=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_kde.py#L32)
Kernel Density Estimation.
Read more in the [User Guide](../density#kernel-density).
Parameters:
**bandwidth**float, default=1.0
The bandwidth of the kernel.
**algorithm**{‘kd\_tree’, ‘ball\_tree’, ‘auto’}, default=’auto’
The tree algorithm to use.
**kernel**{‘gaussian’, ‘tophat’, ‘epanechnikov’, ‘exponential’, ‘linear’, ‘cosine’}, default=’gaussian’
The kernel to use.
**metric**str, default=’euclidean’
Metric to use for distance computation. See the documentation of [scipy.spatial.distance](https://docs.scipy.org/doc/scipy/reference/spatial.distance.html) and the metrics listed in [`distance_metrics`](sklearn.metrics.pairwise.distance_metrics#sklearn.metrics.pairwise.distance_metrics "sklearn.metrics.pairwise.distance_metrics") for valid metric values.
Not all metrics are valid with all algorithms: refer to the documentation of [`BallTree`](sklearn.neighbors.balltree#sklearn.neighbors.BallTree "sklearn.neighbors.BallTree") and [`KDTree`](sklearn.neighbors.kdtree#sklearn.neighbors.KDTree "sklearn.neighbors.KDTree"). Note that the normalization of the density output is correct only for the Euclidean distance metric.
**atol**float, default=0
The desired absolute tolerance of the result. A larger tolerance will generally lead to faster execution.
**rtol**float, default=0
The desired relative tolerance of the result. A larger tolerance will generally lead to faster execution.
**breadth\_first**bool, default=True
If true (default), use a breadth-first approach to the problem. Otherwise use a depth-first approach.
**leaf\_size**int, default=40
Specify the leaf size of the underlying tree. See [`BallTree`](sklearn.neighbors.balltree#sklearn.neighbors.BallTree "sklearn.neighbors.BallTree") or [`KDTree`](sklearn.neighbors.kdtree#sklearn.neighbors.KDTree "sklearn.neighbors.KDTree") for details.
**metric\_params**dict, default=None
Additional parameters to be passed to the tree for use with the metric. For more information, see the documentation of [`BallTree`](sklearn.neighbors.balltree#sklearn.neighbors.BallTree "sklearn.neighbors.BallTree") or [`KDTree`](sklearn.neighbors.kdtree#sklearn.neighbors.KDTree "sklearn.neighbors.KDTree").
Attributes:
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**tree\_**`BinaryTree` instance
The tree algorithm for fast generalized N-point problems.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`sklearn.neighbors.KDTree`](sklearn.neighbors.kdtree#sklearn.neighbors.KDTree "sklearn.neighbors.KDTree")
K-dimensional tree for fast generalized N-point problems.
[`sklearn.neighbors.BallTree`](sklearn.neighbors.balltree#sklearn.neighbors.BallTree "sklearn.neighbors.BallTree")
Ball tree for fast generalized N-point problems.
#### Examples
Compute a gaussian kernel density estimate with a fixed bandwidth.
```
>>> from sklearn.neighbors import KernelDensity
>>> import numpy as np
>>> rng = np.random.RandomState(42)
>>> X = rng.random_sample((100, 3))
>>> kde = KernelDensity(kernel='gaussian', bandwidth=0.5).fit(X)
>>> log_density = kde.score_samples(X[:3])
>>> log_density
array([-1.52955942, -1.51462041, -1.60244657])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.neighbors.KernelDensity.fit "sklearn.neighbors.KernelDensity.fit")(X[, y, sample\_weight]) | Fit the Kernel Density model on the data. |
| [`get_params`](#sklearn.neighbors.KernelDensity.get_params "sklearn.neighbors.KernelDensity.get_params")([deep]) | Get parameters for this estimator. |
| [`sample`](#sklearn.neighbors.KernelDensity.sample "sklearn.neighbors.KernelDensity.sample")([n\_samples, random\_state]) | Generate random samples from the model. |
| [`score`](#sklearn.neighbors.KernelDensity.score "sklearn.neighbors.KernelDensity.score")(X[, y]) | Compute the total log-likelihood under the model. |
| [`score_samples`](#sklearn.neighbors.KernelDensity.score_samples "sklearn.neighbors.KernelDensity.score_samples")(X) | Compute the log-likelihood of each sample under the model. |
| [`set_params`](#sklearn.neighbors.KernelDensity.set_params "sklearn.neighbors.KernelDensity.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y=None*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_kde.py#L163)
Fit the Kernel Density model on the data.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
List of n\_features-dimensional data points. Each row corresponds to a single data point.
**y**None
Ignored. This parameter exists only for compatibility with [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline").
**sample\_weight**array-like of shape (n\_samples,), default=None
List of sample weights attached to the data X.
New in version 0.20.
Returns:
**self**object
Returns the instance itself.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
sample(*n\_samples=1*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_kde.py#L273)
Generate random samples from the model.
Currently, this is implemented only for gaussian and tophat kernels.
Parameters:
**n\_samples**int, default=1
Number of samples to generate.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation used to generate random samples. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Returns:
**X**array-like of shape (n\_samples, n\_features)
List of samples.
score(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_kde.py#L251)
Compute the total log-likelihood under the model.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
List of n\_features-dimensional data points. Each row corresponds to a single data point.
**y**None
Ignored. This parameter exists only for compatibility with [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline").
Returns:
**logprob**float
Total log-likelihood of the data in X. This is normalized to be a probability density, so the value will be low for high-dimensional data.
score\_samples(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_kde.py#L213)
Compute the log-likelihood of each sample under the model.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
An array of points to query. Last dimension should match dimension of training data (n\_features).
Returns:
**density**ndarray of shape (n\_samples,)
Log-likelihood of each sample in `X`. These are normalized to be probability densities, so values will be low for high-dimensional data.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.neighbors.KernelDensity`
------------------------------------------------
[Kernel Density Estimate of Species Distributions](../../auto_examples/neighbors/plot_species_kde#sphx-glr-auto-examples-neighbors-plot-species-kde-py)
[Kernel Density Estimation](../../auto_examples/neighbors/plot_digits_kde_sampling#sphx-glr-auto-examples-neighbors-plot-digits-kde-sampling-py)
[Simple 1D Kernel Density Estimation](../../auto_examples/neighbors/plot_kde_1d#sphx-glr-auto-examples-neighbors-plot-kde-1d-py)
scikit_learn sklearn.preprocessing.OneHotEncoder sklearn.preprocessing.OneHotEncoder
===================================
*class*sklearn.preprocessing.OneHotEncoder(*\**, *categories='auto'*, *drop=None*, *sparse=True*, *dtype=<class 'numpy.float64'>*, *handle\_unknown='error'*, *min\_frequency=None*, *max\_categories=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_encoders.py#L201)
Encode categorical features as a one-hot numeric array.
The input to this transformer should be an array-like of integers or strings, denoting the values taken on by categorical (discrete) features. The features are encoded using a one-hot (aka ‘one-of-K’ or ‘dummy’) encoding scheme. This creates a binary column for each category and returns a sparse matrix or dense array (depending on the `sparse` parameter)
By default, the encoder derives the categories based on the unique values in each feature. Alternatively, you can also specify the `categories` manually.
This encoding is needed for feeding categorical data to many scikit-learn estimators, notably linear models and SVMs with the standard kernels.
Note: a one-hot encoding of y labels should use a LabelBinarizer instead.
Read more in the [User Guide](../preprocessing#preprocessing-categorical-features).
Parameters:
**categories**‘auto’ or a list of array-like, default=’auto’
Categories (unique values) per feature:
* ‘auto’ : Determine categories automatically from the training data.
* list : `categories[i]` holds the categories expected in the ith column. The passed categories should not mix strings and numeric values within a single feature, and should be sorted in case of numeric values.
The used categories can be found in the `categories_` attribute.
New in version 0.20.
**drop**{‘first’, ‘if\_binary’} or an array-like of shape (n\_features,), default=None
Specifies a methodology to use to drop one of the categories per feature. This is useful in situations where perfectly collinear features cause problems, such as when feeding the resulting data into an unregularized linear regression model.
However, dropping one category breaks the symmetry of the original representation and can therefore induce a bias in downstream models, for instance for penalized linear classification or regression models.
* None : retain all features (the default).
* ‘first’ : drop the first category in each feature. If only one category is present, the feature will be dropped entirely.
* ‘if\_binary’ : drop the first category in each feature with two categories. Features with 1 or more than 2 categories are left intact.
* array : `drop[i]` is the category in feature `X[:, i]` that should be dropped.
New in version 0.21: The parameter `drop` was added in 0.21.
Changed in version 0.23: The option `drop='if_binary'` was added in 0.23.
Changed in version 1.1: Support for dropping infrequent categories.
**sparse**bool, default=True
Will return sparse matrix if set True else will return an array.
**dtype**number type, default=float
Desired dtype of output.
**handle\_unknown**{‘error’, ‘ignore’, ‘infrequent\_if\_exist’}, default=’error’
Specifies the way unknown categories are handled during [`transform`](#sklearn.preprocessing.OneHotEncoder.transform "sklearn.preprocessing.OneHotEncoder.transform").
* ‘error’ : Raise an error if an unknown category is present during transform.
* ‘ignore’ : When an unknown category is encountered during transform, the resulting one-hot encoded columns for this feature will be all zeros. In the inverse transform, an unknown category will be denoted as None.
* ‘infrequent\_if\_exist’ : When an unknown category is encountered during transform, the resulting one-hot encoded columns for this feature will map to the infrequent category if it exists. The infrequent category will be mapped to the last position in the encoding. During inverse transform, an unknown category will be mapped to the category denoted `'infrequent'` if it exists. If the `'infrequent'` category does not exist, then [`transform`](#sklearn.preprocessing.OneHotEncoder.transform "sklearn.preprocessing.OneHotEncoder.transform") and [`inverse_transform`](#sklearn.preprocessing.OneHotEncoder.inverse_transform "sklearn.preprocessing.OneHotEncoder.inverse_transform") will handle an unknown category as with `handle_unknown='ignore'`. Infrequent categories exist based on `min_frequency` and `max_categories`. Read more in the [User Guide](../preprocessing#one-hot-encoder-infrequent-categories).
Changed in version 1.1: `'infrequent_if_exist'` was added to automatically handle unknown categories and infrequent categories.
**min\_frequency**int or float, default=None
Specifies the minimum frequency below which a category will be considered infrequent.
* If `int`, categories with a smaller cardinality will be considered infrequent.
* If `float`, categories with a smaller cardinality than `min_frequency * n_samples` will be considered infrequent.
New in version 1.1: Read more in the [User Guide](../preprocessing#one-hot-encoder-infrequent-categories).
**max\_categories**int, default=None
Specifies an upper limit to the number of output features for each input feature when considering infrequent categories. If there are infrequent categories, `max_categories` includes the category representing the infrequent categories along with the frequent categories. If `None`, there is no limit to the number of output features.
New in version 1.1: Read more in the [User Guide](../preprocessing#one-hot-encoder-infrequent-categories).
Attributes:
**categories\_**list of arrays
The categories of each feature determined during fitting (in order of the features in X and corresponding with the output of `transform`). This includes the category specified in `drop` (if any).
**drop\_idx\_**array of shape (n\_features,)
* `drop_idx_[i]` is the index in `categories_[i]` of the category to be dropped for each feature.
* `drop_idx_[i] = None` if no category is to be dropped from the feature with index `i`, e.g. when `drop='if_binary'` and the feature isn’t binary.
* `drop_idx_ = None` if all the transformed features will be retained.
If infrequent categories are enabled by setting `min_frequency` or `max_categories` to a non-default value and `drop_idx[i]` corresponds to a infrequent category, then the entire infrequent category is dropped.
Changed in version 0.23: Added the possibility to contain `None` values.
[`infrequent_categories_`](#sklearn.preprocessing.OneHotEncoder.infrequent_categories_ "sklearn.preprocessing.OneHotEncoder.infrequent_categories_")list of ndarray
Infrequent categories for each feature.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 1.0.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`OrdinalEncoder`](sklearn.preprocessing.ordinalencoder#sklearn.preprocessing.OrdinalEncoder "sklearn.preprocessing.OrdinalEncoder")
Performs an ordinal (integer) encoding of the categorical features.
[`sklearn.feature_extraction.DictVectorizer`](sklearn.feature_extraction.dictvectorizer#sklearn.feature_extraction.DictVectorizer "sklearn.feature_extraction.DictVectorizer")
Performs a one-hot encoding of dictionary items (also handles string-valued features).
[`sklearn.feature_extraction.FeatureHasher`](sklearn.feature_extraction.featurehasher#sklearn.feature_extraction.FeatureHasher "sklearn.feature_extraction.FeatureHasher")
Performs an approximate one-hot encoding of dictionary items or strings.
[`LabelBinarizer`](sklearn.preprocessing.labelbinarizer#sklearn.preprocessing.LabelBinarizer "sklearn.preprocessing.LabelBinarizer")
Binarizes labels in a one-vs-all fashion.
[`MultiLabelBinarizer`](sklearn.preprocessing.multilabelbinarizer#sklearn.preprocessing.MultiLabelBinarizer "sklearn.preprocessing.MultiLabelBinarizer")
Transforms between iterable of iterables and a multilabel format, e.g. a (samples x classes) binary matrix indicating the presence of a class label.
#### Examples
Given a dataset with two features, we let the encoder find the unique values per feature and transform the data to a binary one-hot encoding.
```
>>> from sklearn.preprocessing import OneHotEncoder
```
One can discard categories not seen during `fit`:
```
>>> enc = OneHotEncoder(handle_unknown='ignore')
>>> X = [['Male', 1], ['Female', 3], ['Female', 2]]
>>> enc.fit(X)
OneHotEncoder(handle_unknown='ignore')
>>> enc.categories_
[array(['Female', 'Male'], dtype=object), array([1, 2, 3], dtype=object)]
>>> enc.transform([['Female', 1], ['Male', 4]]).toarray()
array([[1., 0., 1., 0., 0.],
[0., 1., 0., 0., 0.]])
>>> enc.inverse_transform([[0, 1, 1, 0, 0], [0, 0, 0, 1, 0]])
array([['Male', 1],
[None, 2]], dtype=object)
>>> enc.get_feature_names_out(['gender', 'group'])
array(['gender_Female', 'gender_Male', 'group_1', 'group_2', 'group_3'], ...)
```
One can always drop the first column for each feature:
```
>>> drop_enc = OneHotEncoder(drop='first').fit(X)
>>> drop_enc.categories_
[array(['Female', 'Male'], dtype=object), array([1, 2, 3], dtype=object)]
>>> drop_enc.transform([['Female', 1], ['Male', 2]]).toarray()
array([[0., 0., 0.],
[1., 1., 0.]])
```
Or drop a column for feature only having 2 categories:
```
>>> drop_binary_enc = OneHotEncoder(drop='if_binary').fit(X)
>>> drop_binary_enc.transform([['Female', 1], ['Male', 2]]).toarray()
array([[0., 1., 0., 0.],
[1., 0., 1., 0.]])
```
Infrequent categories are enabled by setting `max_categories` or `min_frequency`.
```
>>> import numpy as np
>>> X = np.array([["a"] * 5 + ["b"] * 20 + ["c"] * 10 + ["d"] * 3], dtype=object).T
>>> ohe = OneHotEncoder(max_categories=3, sparse=False).fit(X)
>>> ohe.infrequent_categories_
[array(['a', 'd'], dtype=object)]
>>> ohe.transform([["a"], ["b"]])
array([[0., 0., 1.],
[1., 0., 0.]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.preprocessing.OneHotEncoder.fit "sklearn.preprocessing.OneHotEncoder.fit")(X[, y]) | Fit OneHotEncoder to X. |
| [`fit_transform`](#sklearn.preprocessing.OneHotEncoder.fit_transform "sklearn.preprocessing.OneHotEncoder.fit_transform")(X[, y]) | Fit OneHotEncoder to X, then transform X. |
| [`get_feature_names`](#sklearn.preprocessing.OneHotEncoder.get_feature_names "sklearn.preprocessing.OneHotEncoder.get_feature_names")([input\_features]) | DEPRECATED: get\_feature\_names is deprecated in 1.0 and will be removed in 1.2. |
| [`get_feature_names_out`](#sklearn.preprocessing.OneHotEncoder.get_feature_names_out "sklearn.preprocessing.OneHotEncoder.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.preprocessing.OneHotEncoder.get_params "sklearn.preprocessing.OneHotEncoder.get_params")([deep]) | Get parameters for this estimator. |
| [`inverse_transform`](#sklearn.preprocessing.OneHotEncoder.inverse_transform "sklearn.preprocessing.OneHotEncoder.inverse_transform")(X) | Convert the data back to the original representation. |
| [`set_params`](#sklearn.preprocessing.OneHotEncoder.set_params "sklearn.preprocessing.OneHotEncoder.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.preprocessing.OneHotEncoder.transform "sklearn.preprocessing.OneHotEncoder.transform")(X) | Transform X using one-hot encoding. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_encoders.py#L799)
Fit OneHotEncoder to X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The data to determine the categories of each feature.
**y**None
Ignored. This parameter exists only for compatibility with [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline").
Returns:
self
Fitted encoder.
fit\_transform(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_encoders.py#L832)
Fit OneHotEncoder to X, then transform X.
Equivalent to fit(X).transform(X) but more convenient.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The data to encode.
**y**None
Ignored. This parameter exists only for compatibility with [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline").
Returns:
**X\_out**{ndarray, sparse matrix} of shape (n\_samples, n\_encoded\_features)
Transformed input. If `sparse=True`, a sparse matrix will be returned.
get\_feature\_names(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_encoders.py#L1041)
DEPRECATED: get\_feature\_names is deprecated in 1.0 and will be removed in 1.2. Please use get\_feature\_names\_out instead.
Return feature names for output features.
For a given input feature, if there is an infrequent category, the most ‘infrequent\_sklearn’ will be used as a feature name.
Parameters:
**input\_features**list of str of shape (n\_features,)
String names for input features if available. By default, “x0”, “x1”, … “xn\_features” is used.
Returns:
**output\_feature\_names**ndarray of shape (n\_output\_features,)
Array of feature names.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_encoders.py#L1082)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Input features.
* If `input_features` is `None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then the following input feature names are generated: `["x0", "x1", ..., "x(n_features_in_ - 1)"]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*infrequent\_categories\_
Infrequent categories for each feature.
inverse\_transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_encoders.py#L927)
Convert the data back to the original representation.
When unknown categories are encountered (all zeros in the one-hot encoding), `None` is used to represent this category. If the feature with the unknown category has a dropped category, the dropped category will be its inverse.
For a given input feature, if there is an infrequent category, ‘infrequent\_sklearn’ will be used to represent the infrequent category.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_encoded\_features)
The transformed data.
Returns:
**X\_tr**ndarray of shape (n\_samples, n\_features)
Inverse transformed array.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_encoders.py#L857)
Transform X using one-hot encoding.
If there are infrequent categories for a feature, the infrequent categories will be grouped into a single category.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The data to encode.
Returns:
**X\_out**{ndarray, sparse matrix} of shape (n\_samples, n\_encoded\_features)
Transformed input. If `sparse=True`, a sparse matrix will be returned.
Examples using `sklearn.preprocessing.OneHotEncoder`
----------------------------------------------------
[Release Highlights for scikit-learn 1.1](../../auto_examples/release_highlights/plot_release_highlights_1_1_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-1-1-0-py)
[Release Highlights for scikit-learn 1.0](../../auto_examples/release_highlights/plot_release_highlights_1_0_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-1-0-0-py)
[Release Highlights for scikit-learn 0.23](../../auto_examples/release_highlights/plot_release_highlights_0_23_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-23-0-py)
[Categorical Feature Support in Gradient Boosting](../../auto_examples/ensemble/plot_gradient_boosting_categorical#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-categorical-py)
[Combine predictors using stacking](../../auto_examples/ensemble/plot_stack_predictors#sphx-glr-auto-examples-ensemble-plot-stack-predictors-py)
[Feature transformations with ensembles of trees](../../auto_examples/ensemble/plot_feature_transformation#sphx-glr-auto-examples-ensemble-plot-feature-transformation-py)
[Time-related feature engineering](../../auto_examples/applications/plot_cyclical_feature_engineering#sphx-glr-auto-examples-applications-plot-cyclical-feature-engineering-py)
[Poisson regression and non-normal loss](../../auto_examples/linear_model/plot_poisson_regression_non_normal_loss#sphx-glr-auto-examples-linear-model-plot-poisson-regression-non-normal-loss-py)
[Tweedie regression on insurance claims](../../auto_examples/linear_model/plot_tweedie_regression_insurance_claims#sphx-glr-auto-examples-linear-model-plot-tweedie-regression-insurance-claims-py)
[Common pitfalls in the interpretation of coefficients of linear models](../../auto_examples/inspection/plot_linear_model_coefficient_interpretation#sphx-glr-auto-examples-inspection-plot-linear-model-coefficient-interpretation-py)
[Displaying Pipelines](../../auto_examples/miscellaneous/plot_pipeline_display#sphx-glr-auto-examples-miscellaneous-plot-pipeline-display-py)
[Column Transformer with Mixed Types](../../auto_examples/compose/plot_column_transformer_mixed_types#sphx-glr-auto-examples-compose-plot-column-transformer-mixed-types-py)
| programming_docs |
scikit_learn sklearn.naive_bayes.GaussianNB sklearn.naive\_bayes.GaussianNB
===============================
*class*sklearn.naive\_bayes.GaussianNB(*\**, *priors=None*, *var\_smoothing=1e-09*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/naive_bayes.py#L126)
Gaussian Naive Bayes (GaussianNB).
Can perform online updates to model parameters via [`partial_fit`](#sklearn.naive_bayes.GaussianNB.partial_fit "sklearn.naive_bayes.GaussianNB.partial_fit"). For details on algorithm used to update feature means and variance online, see Stanford CS tech report STAN-CS-79-773 by Chan, Golub, and LeVeque:
<http://i.stanford.edu/pub/cstr/reports/cs/tr/79/773/CS-TR-79-773.pdf>
Read more in the [User Guide](../naive_bayes#gaussian-naive-bayes).
Parameters:
**priors**array-like of shape (n\_classes,)
Prior probabilities of the classes. If specified, the priors are not adjusted according to the data.
**var\_smoothing**float, default=1e-9
Portion of the largest variance of all features that is added to variances for calculation stability.
New in version 0.20.
Attributes:
**class\_count\_**ndarray of shape (n\_classes,)
number of training samples observed in each class.
**class\_prior\_**ndarray of shape (n\_classes,)
probability of each class.
**classes\_**ndarray of shape (n\_classes,)
class labels known to the classifier.
**epsilon\_**float
absolute additive value to variances.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
[`sigma_`](#sklearn.naive_bayes.GaussianNB.sigma_ "sklearn.naive_bayes.GaussianNB.sigma_")ndarray of shape (n\_classes, n\_features)
DEPRECATED: Attribute `sigma_` was deprecated in 1.0 and will be removed in1.2.
**var\_**ndarray of shape (n\_classes, n\_features)
Variance of each feature per class.
New in version 1.0.
**theta\_**ndarray of shape (n\_classes, n\_features)
mean of each feature per class.
See also
[`BernoulliNB`](sklearn.naive_bayes.bernoullinb#sklearn.naive_bayes.BernoulliNB "sklearn.naive_bayes.BernoulliNB")
Naive Bayes classifier for multivariate Bernoulli models.
[`CategoricalNB`](sklearn.naive_bayes.categoricalnb#sklearn.naive_bayes.CategoricalNB "sklearn.naive_bayes.CategoricalNB")
Naive Bayes classifier for categorical features.
[`ComplementNB`](sklearn.naive_bayes.complementnb#sklearn.naive_bayes.ComplementNB "sklearn.naive_bayes.ComplementNB")
Complement Naive Bayes classifier.
[`MultinomialNB`](sklearn.naive_bayes.multinomialnb#sklearn.naive_bayes.MultinomialNB "sklearn.naive_bayes.MultinomialNB")
Naive Bayes classifier for multinomial models.
#### Examples
```
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> Y = np.array([1, 1, 1, 2, 2, 2])
>>> from sklearn.naive_bayes import GaussianNB
>>> clf = GaussianNB()
>>> clf.fit(X, Y)
GaussianNB()
>>> print(clf.predict([[-0.8, -1]]))
[1]
>>> clf_pf = GaussianNB()
>>> clf_pf.partial_fit(X, Y, np.unique(Y))
GaussianNB()
>>> print(clf_pf.predict([[-0.8, -1]]))
[1]
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.naive_bayes.GaussianNB.fit "sklearn.naive_bayes.GaussianNB.fit")(X, y[, sample\_weight]) | Fit Gaussian Naive Bayes according to X, y. |
| [`get_params`](#sklearn.naive_bayes.GaussianNB.get_params "sklearn.naive_bayes.GaussianNB.get_params")([deep]) | Get parameters for this estimator. |
| [`partial_fit`](#sklearn.naive_bayes.GaussianNB.partial_fit "sklearn.naive_bayes.GaussianNB.partial_fit")(X, y[, classes, sample\_weight]) | Incremental fit on a batch of samples. |
| [`predict`](#sklearn.naive_bayes.GaussianNB.predict "sklearn.naive_bayes.GaussianNB.predict")(X) | Perform classification on an array of test vectors X. |
| [`predict_log_proba`](#sklearn.naive_bayes.GaussianNB.predict_log_proba "sklearn.naive_bayes.GaussianNB.predict_log_proba")(X) | Return log-probability estimates for the test vector X. |
| [`predict_proba`](#sklearn.naive_bayes.GaussianNB.predict_proba "sklearn.naive_bayes.GaussianNB.predict_proba")(X) | Return probability estimates for the test vector X. |
| [`score`](#sklearn.naive_bayes.GaussianNB.score "sklearn.naive_bayes.GaussianNB.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.naive_bayes.GaussianNB.set_params "sklearn.naive_bayes.GaussianNB.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/naive_bayes.py#L219)
Fit Gaussian Naive Bayes according to X, y.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training vectors, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,)
Target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Weights applied to individual samples (1. for unweighted).
New in version 0.17: Gaussian Naive Bayes supports fitting with *sample\_weight*.
Returns:
**self**object
Returns the instance itself.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
partial\_fit(*X*, *y*, *classes=None*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/naive_bayes.py#L323)
Incremental fit on a batch of samples.
This method is expected to be called several times consecutively on different chunks of a dataset so as to implement out-of-core or online learning.
This is especially useful when the whole dataset is too big to fit in memory at once.
This method has some performance and numerical stability overhead, hence it is better to call partial\_fit on chunks of data that are as large as possible (as long as fitting in the memory budget) to hide the overhead.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training vectors, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,)
Target values.
**classes**array-like of shape (n\_classes,), default=None
List of all the classes that can possibly appear in the y vector.
Must be provided at the first call to partial\_fit, can be omitted in subsequent calls.
**sample\_weight**array-like of shape (n\_samples,), default=None
Weights applied to individual samples (1. for unweighted).
New in version 0.17.
Returns:
**self**object
Returns the instance itself.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/naive_bayes.py#L65)
Perform classification on an array of test vectors X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The input samples.
Returns:
**C**ndarray of shape (n\_samples,)
Predicted target values for X.
predict\_log\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/naive_bayes.py#L84)
Return log-probability estimates for the test vector X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The input samples.
Returns:
**C**array-like of shape (n\_samples, n\_classes)
Returns the log-probability of the samples for each class in the model. The columns correspond to the classes in sorted order, as they appear in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/naive_bayes.py#L107)
Return probability estimates for the test vector X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The input samples.
Returns:
**C**array-like of shape (n\_samples, n\_classes)
Returns the probability of the samples for each class in the model. The columns correspond to the classes in sorted order, as they appear in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
*property*sigma\_
DEPRECATED: Attribute `sigma_` was deprecated in 1.0 and will be removed in1.2. Use `var_` instead.
Examples using `sklearn.naive_bayes.GaussianNB`
-----------------------------------------------
[Comparison of Calibration of Classifiers](../../auto_examples/calibration/plot_compare_calibration#sphx-glr-auto-examples-calibration-plot-compare-calibration-py)
[Probability Calibration curves](../../auto_examples/calibration/plot_calibration_curve#sphx-glr-auto-examples-calibration-plot-calibration-curve-py)
[Probability calibration of classifiers](../../auto_examples/calibration/plot_calibration#sphx-glr-auto-examples-calibration-plot-calibration-py)
[Classifier comparison](../../auto_examples/classification/plot_classifier_comparison#sphx-glr-auto-examples-classification-plot-classifier-comparison-py)
[Plot class probabilities calculated by the VotingClassifier](../../auto_examples/ensemble/plot_voting_probas#sphx-glr-auto-examples-ensemble-plot-voting-probas-py)
[Plotting Learning Curves](../../auto_examples/model_selection/plot_learning_curve#sphx-glr-auto-examples-model-selection-plot-learning-curve-py)
[Importance of Feature Scaling](../../auto_examples/preprocessing/plot_scaling_importance#sphx-glr-auto-examples-preprocessing-plot-scaling-importance-py)
scikit_learn sklearn.metrics.mean_poisson_deviance sklearn.metrics.mean\_poisson\_deviance
=======================================
sklearn.metrics.mean\_poisson\_deviance(*y\_true*, *y\_pred*, *\**, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_regression.py#L1095)
Mean Poisson deviance regression loss.
Poisson deviance is equivalent to the Tweedie deviance with the power parameter `power=1`.
Read more in the [User Guide](../model_evaluation#mean-tweedie-deviance).
Parameters:
**y\_true**array-like of shape (n\_samples,)
Ground truth (correct) target values. Requires y\_true >= 0.
**y\_pred**array-like of shape (n\_samples,)
Estimated target values. Requires y\_pred > 0.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**loss**float
A non-negative floating point value (the best value is 0.0).
#### Examples
```
>>> from sklearn.metrics import mean_poisson_deviance
>>> y_true = [2, 0, 1, 4]
>>> y_pred = [0.5, 0.5, 2., 2.]
>>> mean_poisson_deviance(y_true, y_pred)
1.4260...
```
Examples using `sklearn.metrics.mean_poisson_deviance`
------------------------------------------------------
[Poisson regression and non-normal loss](../../auto_examples/linear_model/plot_poisson_regression_non_normal_loss#sphx-glr-auto-examples-linear-model-plot-poisson-regression-non-normal-loss-py)
scikit_learn sklearn.gaussian_process.GaussianProcessClassifier sklearn.gaussian\_process.GaussianProcessClassifier
===================================================
*class*sklearn.gaussian\_process.GaussianProcessClassifier(*kernel=None*, *\**, *optimizer='fmin\_l\_bfgs\_b'*, *n\_restarts\_optimizer=0*, *max\_iter\_predict=100*, *warm\_start=False*, *copy\_X\_train=True*, *random\_state=None*, *multi\_class='one\_vs\_rest'*, *n\_jobs=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/_gpc.py#L482)
Gaussian process classification (GPC) based on Laplace approximation.
The implementation is based on Algorithm 3.1, 3.2, and 5.1 of Gaussian Processes for Machine Learning (GPML) by Rasmussen and Williams.
Internally, the Laplace approximation is used for approximating the non-Gaussian posterior by a Gaussian.
Currently, the implementation is restricted to using the logistic link function. For multi-class classification, several binary one-versus rest classifiers are fitted. Note that this class thus does not implement a true multi-class Laplace approximation.
Read more in the [User Guide](../gaussian_process#gaussian-process).
New in version 0.18.
Parameters:
**kernel**kernel instance, default=None
The kernel specifying the covariance function of the GP. If None is passed, the kernel “1.0 \* RBF(1.0)” is used as default. Note that the kernel’s hyperparameters are optimized during fitting. Also kernel cannot be a `CompoundKernel`.
**optimizer**‘fmin\_l\_bfgs\_b’ or callable, default=’fmin\_l\_bfgs\_b’
Can either be one of the internally supported optimizers for optimizing the kernel’s parameters, specified by a string, or an externally defined optimizer passed as a callable. If a callable is passed, it must have the signature:
```
def optimizer(obj_func, initial_theta, bounds):
# * 'obj_func' is the objective function to be maximized, which
# takes the hyperparameters theta as parameter and an
# optional flag eval_gradient, which determines if the
# gradient is returned additionally to the function value
# * 'initial_theta': the initial value for theta, which can be
# used by local optimizers
# * 'bounds': the bounds on the values of theta
....
# Returned are the best found hyperparameters theta and
# the corresponding value of the target function.
return theta_opt, func_min
```
Per default, the ‘L-BFGS-B’ algorithm from scipy.optimize.minimize is used. If None is passed, the kernel’s parameters are kept fixed. Available internal optimizers are:
```
'fmin_l_bfgs_b'
```
**n\_restarts\_optimizer**int, default=0
The number of restarts of the optimizer for finding the kernel’s parameters which maximize the log-marginal likelihood. The first run of the optimizer is performed from the kernel’s initial parameters, the remaining ones (if any) from thetas sampled log-uniform randomly from the space of allowed theta-values. If greater than 0, all bounds must be finite. Note that n\_restarts\_optimizer=0 implies that one run is performed.
**max\_iter\_predict**int, default=100
The maximum number of iterations in Newton’s method for approximating the posterior during predict. Smaller values will reduce computation time at the cost of worse results.
**warm\_start**bool, default=False
If warm-starts are enabled, the solution of the last Newton iteration on the Laplace approximation of the posterior mode is used as initialization for the next call of \_posterior\_mode(). This can speed up convergence when \_posterior\_mode is called several times on similar problems as in hyperparameter optimization. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
**copy\_X\_train**bool, default=True
If True, a persistent copy of the training data is stored in the object. Otherwise, just a reference to the training data is stored, which might cause predictions to change if the data is modified externally.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation used to initialize the centers. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**multi\_class**{‘one\_vs\_rest’, ‘one\_vs\_one’}, default=’one\_vs\_rest’
Specifies how multi-class classification problems are handled. Supported are ‘one\_vs\_rest’ and ‘one\_vs\_one’. In ‘one\_vs\_rest’, one binary Gaussian process classifier is fitted for each class, which is trained to separate this class from the rest. In ‘one\_vs\_one’, one binary Gaussian process classifier is fitted for each pair of classes, which is trained to separate these two classes. The predictions of these binary predictors are combined into multi-class predictions. Note that ‘one\_vs\_one’ does not support predicting probability estimates.
**n\_jobs**int, default=None
The number of jobs to use for the computation: the specified multiclass problems are computed in parallel. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
Attributes:
**base\_estimator\_**`Estimator` instance
The estimator instance that defines the likelihood function using the observed data.
[`kernel_`](#sklearn.gaussian_process.GaussianProcessClassifier.kernel_ "sklearn.gaussian_process.GaussianProcessClassifier.kernel_")kernel instance
Return the kernel of the base estimator.
**log\_marginal\_likelihood\_value\_**float
The log-marginal-likelihood of `self.kernel_.theta`
**classes\_**array-like of shape (n\_classes,)
Unique class labels.
**n\_classes\_**int
The number of classes in the training data
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`GaussianProcessRegressor`](sklearn.gaussian_process.gaussianprocessregressor#sklearn.gaussian_process.GaussianProcessRegressor "sklearn.gaussian_process.GaussianProcessRegressor")
Gaussian process regression (GPR).
#### Examples
```
>>> from sklearn.datasets import load_iris
>>> from sklearn.gaussian_process import GaussianProcessClassifier
>>> from sklearn.gaussian_process.kernels import RBF
>>> X, y = load_iris(return_X_y=True)
>>> kernel = 1.0 * RBF(1.0)
>>> gpc = GaussianProcessClassifier(kernel=kernel,
... random_state=0).fit(X, y)
>>> gpc.score(X, y)
0.9866...
>>> gpc.predict_proba(X[:2,:])
array([[0.83548752, 0.03228706, 0.13222543],
[0.79064206, 0.06525643, 0.14410151]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.gaussian_process.GaussianProcessClassifier.fit "sklearn.gaussian_process.GaussianProcessClassifier.fit")(X, y) | Fit Gaussian process classification model. |
| [`get_params`](#sklearn.gaussian_process.GaussianProcessClassifier.get_params "sklearn.gaussian_process.GaussianProcessClassifier.get_params")([deep]) | Get parameters for this estimator. |
| [`log_marginal_likelihood`](#sklearn.gaussian_process.GaussianProcessClassifier.log_marginal_likelihood "sklearn.gaussian_process.GaussianProcessClassifier.log_marginal_likelihood")([theta, ...]) | Return log-marginal likelihood of theta for training data. |
| [`predict`](#sklearn.gaussian_process.GaussianProcessClassifier.predict "sklearn.gaussian_process.GaussianProcessClassifier.predict")(X) | Perform classification on an array of test vectors X. |
| [`predict_proba`](#sklearn.gaussian_process.GaussianProcessClassifier.predict_proba "sklearn.gaussian_process.GaussianProcessClassifier.predict_proba")(X) | Return probability estimates for the test vector X. |
| [`score`](#sklearn.gaussian_process.GaussianProcessClassifier.score "sklearn.gaussian_process.GaussianProcessClassifier.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.gaussian_process.GaussianProcessClassifier.set_params "sklearn.gaussian_process.GaussianProcessClassifier.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/_gpc.py#L661)
Fit Gaussian process classification model.
Parameters:
**X**array-like of shape (n\_samples, n\_features) or list of object
Feature vectors or other representations of training data.
**y**array-like of shape (n\_samples,)
Target values, must be binary.
Returns:
**self**object
Returns an instance of self.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*kernel\_
Return the kernel of the base estimator.
log\_marginal\_likelihood(*theta=None*, *eval\_gradient=False*, *clone\_kernel=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/_gpc.py#L797)
Return log-marginal likelihood of theta for training data.
In the case of multi-class classification, the mean log-marginal likelihood of the one-versus-rest classifiers are returned.
Parameters:
**theta**array-like of shape (n\_kernel\_params,), default=None
Kernel hyperparameters for which the log-marginal likelihood is evaluated. In the case of multi-class classification, theta may be the hyperparameters of the compound kernel or of an individual kernel. In the latter case, all individual kernel get assigned the same theta values. If None, the precomputed log\_marginal\_likelihood of `self.kernel_.theta` is returned.
**eval\_gradient**bool, default=False
If True, the gradient of the log-marginal likelihood with respect to the kernel hyperparameters at position theta is returned additionally. Note that gradient computation is not supported for non-binary classification. If True, theta must not be None.
**clone\_kernel**bool, default=True
If True, the kernel attribute is copied. If False, the kernel attribute is modified, but may result in a performance improvement.
Returns:
**log\_likelihood**float
Log-marginal likelihood of theta for training data.
**log\_likelihood\_gradient**ndarray of shape (n\_kernel\_params,), optional
Gradient of the log-marginal likelihood with respect to the kernel hyperparameters at position theta. Only returned when `eval_gradient` is True.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/_gpc.py#L735)
Perform classification on an array of test vectors X.
Parameters:
**X**array-like of shape (n\_samples, n\_features) or list of object
Query points where the GP is evaluated for classification.
Returns:
**C**ndarray of shape (n\_samples,)
Predicted target values for X, values are from `classes_`.
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/_gpc.py#L757)
Return probability estimates for the test vector X.
Parameters:
**X**array-like of shape (n\_samples, n\_features) or list of object
Query points where the GP is evaluated for classification.
Returns:
**C**array-like of shape (n\_samples, n\_classes)
Returns the probability of the samples for each class in the model. The columns correspond to the classes in sorted order, as they appear in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.gaussian_process.GaussianProcessClassifier`
-------------------------------------------------------------------
[Classifier comparison](../../auto_examples/classification/plot_classifier_comparison#sphx-glr-auto-examples-classification-plot-classifier-comparison-py)
[Plot classification probability](../../auto_examples/classification/plot_classification_probability#sphx-glr-auto-examples-classification-plot-classification-probability-py)
[Gaussian process classification (GPC) on iris dataset](../../auto_examples/gaussian_process/plot_gpc_iris#sphx-glr-auto-examples-gaussian-process-plot-gpc-iris-py)
[Gaussian processes on discrete data structures](../../auto_examples/gaussian_process/plot_gpr_on_structured_data#sphx-glr-auto-examples-gaussian-process-plot-gpr-on-structured-data-py)
[Illustration of Gaussian process classification (GPC) on the XOR dataset](../../auto_examples/gaussian_process/plot_gpc_xor#sphx-glr-auto-examples-gaussian-process-plot-gpc-xor-py)
[Iso-probability lines for Gaussian Processes classification (GPC)](../../auto_examples/gaussian_process/plot_gpc_isoprobability#sphx-glr-auto-examples-gaussian-process-plot-gpc-isoprobability-py)
[Probabilistic predictions with Gaussian process classification (GPC)](../../auto_examples/gaussian_process/plot_gpc#sphx-glr-auto-examples-gaussian-process-plot-gpc-py)
| programming_docs |
scikit_learn sklearn.metrics.pairwise.rbf_kernel sklearn.metrics.pairwise.rbf\_kernel
====================================
sklearn.metrics.pairwise.rbf\_kernel(*X*, *Y=None*, *gamma=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/pairwise.py#L1269)
Compute the rbf (gaussian) kernel between X and Y.
K(x, y) = exp(-gamma ||x-y||^2)
for each pair of rows x in X and y in Y.
Read more in the [User Guide](../metrics#rbf-kernel).
Parameters:
**X**ndarray of shape (n\_samples\_X, n\_features)
A feature array.
**Y**ndarray of shape (n\_samples\_Y, n\_features), default=None
An optional second feature array. If `None`, uses `Y=X`.
**gamma**float, default=None
If None, defaults to 1.0 / n\_features.
Returns:
**kernel\_matrix**ndarray of shape (n\_samples\_X, n\_samples\_Y)
The RBF kernel.
scikit_learn sklearn.decomposition.KernelPCA sklearn.decomposition.KernelPCA
===============================
*class*sklearn.decomposition.KernelPCA(*n\_components=None*, *\**, *kernel='linear'*, *gamma=None*, *degree=3*, *coef0=1*, *kernel\_params=None*, *alpha=1.0*, *fit\_inverse\_transform=False*, *eigen\_solver='auto'*, *tol=0*, *max\_iter=None*, *iterated\_power='auto'*, *remove\_zero\_eig=False*, *random\_state=None*, *copy\_X=True*, *n\_jobs=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_kernel_pca.py#L26)
Kernel Principal component analysis (KPCA) [[1]](#r396fc7d924b8-1).
Non-linear dimensionality reduction through the use of kernels (see [Pairwise metrics, Affinities and Kernels](../metrics#metrics)).
It uses the [`scipy.linalg.eigh`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.linalg.eigh.html#scipy.linalg.eigh "(in SciPy v1.9.3)") LAPACK implementation of the full SVD or the [`scipy.sparse.linalg.eigsh`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.linalg.eigsh.html#scipy.sparse.linalg.eigsh "(in SciPy v1.9.3)") ARPACK implementation of the truncated SVD, depending on the shape of the input data and the number of components to extract. It can also use a randomized truncated SVD by the method proposed in [[3]](#r396fc7d924b8-3), see `eigen_solver`.
Read more in the [User Guide](../decomposition#kernel-pca).
Parameters:
**n\_components**int, default=None
Number of components. If None, all non-zero components are kept.
**kernel**{‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘cosine’, ‘precomputed’}, default=’linear’
Kernel used for PCA.
**gamma**float, default=None
Kernel coefficient for rbf, poly and sigmoid kernels. Ignored by other kernels. If `gamma` is `None`, then it is set to `1/n_features`.
**degree**int, default=3
Degree for poly kernels. Ignored by other kernels.
**coef0**float, default=1
Independent term in poly and sigmoid kernels. Ignored by other kernels.
**kernel\_params**dict, default=None
Parameters (keyword arguments) and values for kernel passed as callable object. Ignored by other kernels.
**alpha**float, default=1.0
Hyperparameter of the ridge regression that learns the inverse transform (when fit\_inverse\_transform=True).
**fit\_inverse\_transform**bool, default=False
Learn the inverse transform for non-precomputed kernels (i.e. learn to find the pre-image of a point). This method is based on [[2]](#r396fc7d924b8-2).
**eigen\_solver**{‘auto’, ‘dense’, ‘arpack’, ‘randomized’}, default=’auto’
Select eigensolver to use. If `n_components` is much less than the number of training samples, randomized (or arpack to a smaller extent) may be more efficient than the dense eigensolver. Randomized SVD is performed according to the method of Halko et al [[3]](#r396fc7d924b8-3).
auto :
the solver is selected by a default policy based on n\_samples (the number of training samples) and `n_components`: if the number of components to extract is less than 10 (strict) and the number of samples is more than 200 (strict), the ‘arpack’ method is enabled. Otherwise the exact full eigenvalue decomposition is computed and optionally truncated afterwards (‘dense’ method).
dense :
run exact full eigenvalue decomposition calling the standard LAPACK solver via `scipy.linalg.eigh`, and select the components by postprocessing
arpack :
run SVD truncated to n\_components calling ARPACK solver using `scipy.sparse.linalg.eigsh`. It requires strictly 0 < n\_components < n\_samples
randomized :
run randomized SVD by the method of Halko et al. [[3]](#r396fc7d924b8-3). The current implementation selects eigenvalues based on their module; therefore using this method can lead to unexpected results if the kernel is not positive semi-definite. See also [[4]](#r396fc7d924b8-4).
Changed in version 1.0: `'randomized'` was added.
**tol**float, default=0
Convergence tolerance for arpack. If 0, optimal value will be chosen by arpack.
**max\_iter**int, default=None
Maximum number of iterations for arpack. If None, optimal value will be chosen by arpack.
**iterated\_power**int >= 0, or ‘auto’, default=’auto’
Number of iterations for the power method computed by svd\_solver == ‘randomized’. When ‘auto’, it is set to 7 when `n_components < 0.1 * min(X.shape)`, other it is set to 4.
New in version 1.0.
**remove\_zero\_eig**bool, default=False
If True, then all components with zero eigenvalues are removed, so that the number of components in the output may be < n\_components (and sometimes even zero due to numerical instability). When n\_components is None, this parameter is ignored and components with zero eigenvalues are removed regardless.
**random\_state**int, RandomState instance or None, default=None
Used when `eigen_solver` == ‘arpack’ or ‘randomized’. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
New in version 0.18.
**copy\_X**bool, default=True
If True, input X is copied and stored by the model in the `X_fit_` attribute. If no further changes will be done to X, setting `copy_X=False` saves memory by storing a reference.
New in version 0.18.
**n\_jobs**int, default=None
The number of parallel jobs to run. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
New in version 0.18.
Attributes:
**eigenvalues\_**ndarray of shape (n\_components,)
Eigenvalues of the centered kernel matrix in decreasing order. If `n_components` and `remove_zero_eig` are not set, then all values are stored.
[`lambdas_`](#sklearn.decomposition.KernelPCA.lambdas_ "sklearn.decomposition.KernelPCA.lambdas_")ndarray of shape (n\_components,)
DEPRECATED: Attribute `lambdas_` was deprecated in version 1.0 and will be removed in 1.2.
**eigenvectors\_**ndarray of shape (n\_samples, n\_components)
Eigenvectors of the centered kernel matrix. If `n_components` and `remove_zero_eig` are not set, then all components are stored.
[`alphas_`](#sklearn.decomposition.KernelPCA.alphas_ "sklearn.decomposition.KernelPCA.alphas_")ndarray of shape (n\_samples, n\_components)
DEPRECATED: Attribute `alphas_` was deprecated in version 1.0 and will be removed in 1.2.
**dual\_coef\_**ndarray of shape (n\_samples, n\_features)
Inverse transform matrix. Only available when `fit_inverse_transform` is True.
**X\_transformed\_fit\_**ndarray of shape (n\_samples, n\_components)
Projection of the fitted data on the kernel principal components. Only available when `fit_inverse_transform` is True.
**X\_fit\_**ndarray of shape (n\_samples, n\_features)
The data used to fit the model. If `copy_X=False`, then `X_fit_` is a reference. This attribute is used for the calls to transform.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`FastICA`](sklearn.decomposition.fastica#sklearn.decomposition.FastICA "sklearn.decomposition.FastICA")
A fast algorithm for Independent Component Analysis.
[`IncrementalPCA`](sklearn.decomposition.incrementalpca#sklearn.decomposition.IncrementalPCA "sklearn.decomposition.IncrementalPCA")
Incremental Principal Component Analysis.
[`NMF`](sklearn.decomposition.nmf#sklearn.decomposition.NMF "sklearn.decomposition.NMF")
Non-Negative Matrix Factorization.
[`PCA`](sklearn.decomposition.pca#sklearn.decomposition.PCA "sklearn.decomposition.PCA")
Principal Component Analysis.
[`SparsePCA`](sklearn.decomposition.sparsepca#sklearn.decomposition.SparsePCA "sklearn.decomposition.SparsePCA")
Sparse Principal Component Analysis.
[`TruncatedSVD`](sklearn.decomposition.truncatedsvd#sklearn.decomposition.TruncatedSVD "sklearn.decomposition.TruncatedSVD")
Dimensionality reduction using truncated SVD.
#### References
[[1](#id1)] [Schölkopf, Bernhard, Alexander Smola, and Klaus-Robert Müller. “Kernel principal component analysis.” International conference on artificial neural networks. Springer, Berlin, Heidelberg, 1997.](https://people.eecs.berkeley.edu/~wainwrig/stat241b/scholkopf_kernel.pdf)
[[2](#id3)] [Bakır, Gökhan H., Jason Weston, and Bernhard Schölkopf. “Learning to find pre-images.” Advances in neural information processing systems 16 (2004): 449-456.](https://papers.nips.cc/paper/2003/file/ac1ad983e08ad3304a97e147f522747e-Paper.pdf)
[3] ([1](#id2),[2](#id4),[3](#id5)) [Halko, Nathan, Per-Gunnar Martinsson, and Joel A. Tropp. “Finding structure with randomness: Probabilistic algorithms for constructing approximate matrix decompositions.” SIAM review 53.2 (2011): 217-288.](https://arxiv.org/abs/0909.4061)
[[4](#id6)] [Martinsson, Per-Gunnar, Vladimir Rokhlin, and Mark Tygert. “A randomized algorithm for the decomposition of matrices.” Applied and Computational Harmonic Analysis 30.1 (2011): 47-68.](https://www.sciencedirect.com/science/article/pii/S1063520310000242)
#### Examples
```
>>> from sklearn.datasets import load_digits
>>> from sklearn.decomposition import KernelPCA
>>> X, _ = load_digits(return_X_y=True)
>>> transformer = KernelPCA(n_components=7, kernel='linear')
>>> X_transformed = transformer.fit_transform(X)
>>> X_transformed.shape
(1797, 7)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.decomposition.KernelPCA.fit "sklearn.decomposition.KernelPCA.fit")(X[, y]) | Fit the model from data in X. |
| [`fit_transform`](#sklearn.decomposition.KernelPCA.fit_transform "sklearn.decomposition.KernelPCA.fit_transform")(X[, y]) | Fit the model from data in X and transform X. |
| [`get_feature_names_out`](#sklearn.decomposition.KernelPCA.get_feature_names_out "sklearn.decomposition.KernelPCA.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.decomposition.KernelPCA.get_params "sklearn.decomposition.KernelPCA.get_params")([deep]) | Get parameters for this estimator. |
| [`inverse_transform`](#sklearn.decomposition.KernelPCA.inverse_transform "sklearn.decomposition.KernelPCA.inverse_transform")(X) | Transform X back to original space. |
| [`set_params`](#sklearn.decomposition.KernelPCA.set_params "sklearn.decomposition.KernelPCA.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.decomposition.KernelPCA.transform "sklearn.decomposition.KernelPCA.transform")(X) | Transform X. |
*property*alphas\_
DEPRECATED: Attribute `alphas_` was deprecated in version 1.0 and will be removed in 1.2. Use `eigenvectors_` instead.
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_kernel_pca.py#L402)
Fit the model from data in X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vector, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*, *\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_kernel_pca.py#L435)
Fit the model from data in X and transform X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vector, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Not used, present for API consistency by convention.
**\*\*params**kwargs
Parameters (keyword arguments) and values passed to the fit\_transform instance.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_components)
Returns the instance itself.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.decomposition.KernelPCA.fit "sklearn.decomposition.KernelPCA.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
inverse\_transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_kernel_pca.py#L496)
Transform X back to original space.
`inverse_transform` approximates the inverse transformation using a learned pre-image. The pre-image is learned by kernel ridge regression of the original data on their low-dimensional representation vectors.
Note
When users want to compute inverse transformation for ‘linear’ kernel, it is recommended that they use [`PCA`](sklearn.decomposition.pca#sklearn.decomposition.PCA "sklearn.decomposition.PCA") instead. Unlike [`PCA`](sklearn.decomposition.pca#sklearn.decomposition.PCA "sklearn.decomposition.PCA"), [`KernelPCA`](#sklearn.decomposition.KernelPCA "sklearn.decomposition.KernelPCA")’s `inverse_transform` does not reconstruct the mean of data when ‘linear’ kernel is used due to the use of centered kernel.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_components)
Training vector, where `n_samples` is the number of samples and `n_features` is the number of features.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_features)
Returns the instance itself.
#### References
[Bakır, Gökhan H., Jason Weston, and Bernhard Schölkopf. “Learning to find pre-images.” Advances in neural information processing systems 16 (2004): 449-456.](https://papers.nips.cc/paper/2003/file/ac1ad983e08ad3304a97e147f522747e-Paper.pdf)
*property*lambdas\_
DEPRECATED: Attribute `lambdas_` was deprecated in version 1.0 and will be removed in 1.2. Use `eigenvalues_` instead.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_kernel_pca.py#L466)
Transform X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vector, where `n_samples` is the number of samples and `n_features` is the number of features.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_components)
Returns the instance itself.
Examples using `sklearn.decomposition.KernelPCA`
------------------------------------------------
[Kernel PCA](../../auto_examples/decomposition/plot_kernel_pca#sphx-glr-auto-examples-decomposition-plot-kernel-pca-py)
[Image denoising using kernel PCA](../../auto_examples/applications/plot_digits_denoising#sphx-glr-auto-examples-applications-plot-digits-denoising-py)
scikit_learn sklearn.calibration.CalibratedClassifierCV sklearn.calibration.CalibratedClassifierCV
==========================================
*class*sklearn.calibration.CalibratedClassifierCV(*base\_estimator=None*, *\**, *method='sigmoid'*, *cv=None*, *n\_jobs=None*, *ensemble=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/calibration.py#L54)
Probability calibration with isotonic regression or logistic regression.
This class uses cross-validation to both estimate the parameters of a classifier and subsequently calibrate a classifier. With default `ensemble=True`, for each cv split it fits a copy of the base estimator to the training subset, and calibrates it using the testing subset. For prediction, predicted probabilities are averaged across these individual calibrated classifiers. When `ensemble=False`, cross-validation is used to obtain unbiased predictions, via [`cross_val_predict`](sklearn.model_selection.cross_val_predict#sklearn.model_selection.cross_val_predict "sklearn.model_selection.cross_val_predict"), which are then used for calibration. For prediction, the base estimator, trained using all the data, is used. This is the method implemented when `probabilities=True` for [`sklearn.svm`](../classes#module-sklearn.svm "sklearn.svm") estimators.
Already fitted classifiers can be calibrated via the parameter `cv="prefit"`. In this case, no cross-validation is used and all provided data is used for calibration. The user has to take care manually that data for model fitting and calibration are disjoint.
The calibration is based on the [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) method of the `base_estimator` if it exists, else on [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba).
Read more in the [User Guide](../calibration#calibration).
Parameters:
**base\_estimator**estimator instance, default=None
The classifier whose output need to be calibrated to provide more accurate `predict_proba` outputs. The default classifier is a [`LinearSVC`](sklearn.svm.linearsvc#sklearn.svm.LinearSVC "sklearn.svm.LinearSVC").
**method**{‘sigmoid’, ‘isotonic’}, default=’sigmoid’
The method to use for calibration. Can be ‘sigmoid’ which corresponds to Platt’s method (i.e. a logistic regression model) or ‘isotonic’ which is a non-parametric approach. It is not advised to use isotonic calibration with too few calibration samples `(<<1000)` since it tends to overfit.
**cv**int, cross-validation generator, iterable or “prefit”, default=None
Determines the cross-validation splitting strategy. Possible inputs for cv are:
* None, to use the default 5-fold cross-validation,
* integer, to specify the number of folds.
* [CV splitter](https://scikit-learn.org/1.1/glossary.html#term-CV-splitter),
* An iterable yielding (train, test) splits as arrays of indices.
For integer/None inputs, if `y` is binary or multiclass, [`StratifiedKFold`](sklearn.model_selection.stratifiedkfold#sklearn.model_selection.StratifiedKFold "sklearn.model_selection.StratifiedKFold") is used. If `y` is neither binary nor multiclass, [`KFold`](sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold") is used.
Refer to the [User Guide](../cross_validation#cross-validation) for the various cross-validation strategies that can be used here.
If “prefit” is passed, it is assumed that `base_estimator` has been fitted already and all data is used for calibration.
Changed in version 0.22: `cv` default value if None changed from 3-fold to 5-fold.
**n\_jobs**int, default=None
Number of jobs to run in parallel. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors.
Base estimator clones are fitted in parallel across cross-validation iterations. Therefore parallelism happens only when `cv != "prefit"`.
See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
New in version 0.24.
**ensemble**bool, default=True
Determines how the calibrator is fitted when `cv` is not `'prefit'`. Ignored if `cv='prefit'`.
If `True`, the `base_estimator` is fitted using training data, and calibrated using testing data, for each `cv` fold. The final estimator is an ensemble of `n_cv` fitted classifier and calibrator pairs, where `n_cv` is the number of cross-validation folds. The output is the average predicted probabilities of all pairs.
If `False`, `cv` is used to compute unbiased predictions, via [`cross_val_predict`](sklearn.model_selection.cross_val_predict#sklearn.model_selection.cross_val_predict "sklearn.model_selection.cross_val_predict"), which are then used for calibration. At prediction time, the classifier used is the `base_estimator` trained on all the data. Note that this method is also internally implemented in [`sklearn.svm`](../classes#module-sklearn.svm "sklearn.svm") estimators with the `probabilities=True` parameter.
New in version 0.24.
Attributes:
**classes\_**ndarray of shape (n\_classes,)
The class labels.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Only defined if the underlying base\_estimator exposes such an attribute when fit.
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Only defined if the underlying base\_estimator exposes such an attribute when fit.
New in version 1.0.
**calibrated\_classifiers\_**list (len() equal to cv or 1 if `cv="prefit"` or `ensemble=False`)
The list of classifier and calibrator pairs.
* When `cv="prefit"`, the fitted `base_estimator` and fitted calibrator.
* When `cv` is not “prefit” and `ensemble=True`, `n_cv` fitted `base_estimator` and calibrator pairs. `n_cv` is the number of cross-validation folds.
* When `cv` is not “prefit” and `ensemble=False`, the `base_estimator`, fitted on all the data, and fitted calibrator.
Changed in version 0.24: Single calibrated classifier case when `ensemble=False`.
See also
[`calibration_curve`](sklearn.calibration.calibration_curve#sklearn.calibration.calibration_curve "sklearn.calibration.calibration_curve")
Compute true and predicted probabilities for a calibration curve.
#### References
[1] Obtaining calibrated probability estimates from decision trees and naive Bayesian classifiers, B. Zadrozny & C. Elkan, ICML 2001
[2] Transforming Classifier Scores into Accurate Multiclass Probability Estimates, B. Zadrozny & C. Elkan, (KDD 2002)
[3] Probabilistic Outputs for Support Vector Machines and Comparisons to Regularized Likelihood Methods, J. Platt, (1999)
[4] Predicting Good Probabilities with Supervised Learning, A. Niculescu-Mizil & R. Caruana, ICML 2005
#### Examples
```
>>> from sklearn.datasets import make_classification
>>> from sklearn.naive_bayes import GaussianNB
>>> from sklearn.calibration import CalibratedClassifierCV
>>> X, y = make_classification(n_samples=100, n_features=2,
... n_redundant=0, random_state=42)
>>> base_clf = GaussianNB()
>>> calibrated_clf = CalibratedClassifierCV(base_estimator=base_clf, cv=3)
>>> calibrated_clf.fit(X, y)
CalibratedClassifierCV(base_estimator=GaussianNB(), cv=3)
>>> len(calibrated_clf.calibrated_classifiers_)
3
>>> calibrated_clf.predict_proba(X)[:5, :]
array([[0.110..., 0.889...],
[0.072..., 0.927...],
[0.928..., 0.071...],
[0.928..., 0.071...],
[0.071..., 0.928...]])
>>> from sklearn.model_selection import train_test_split
>>> X, y = make_classification(n_samples=100, n_features=2,
... n_redundant=0, random_state=42)
>>> X_train, X_calib, y_train, y_calib = train_test_split(
... X, y, random_state=42
... )
>>> base_clf = GaussianNB()
>>> base_clf.fit(X_train, y_train)
GaussianNB()
>>> calibrated_clf = CalibratedClassifierCV(
... base_estimator=base_clf,
... cv="prefit"
... )
>>> calibrated_clf.fit(X_calib, y_calib)
CalibratedClassifierCV(base_estimator=GaussianNB(), cv='prefit')
>>> len(calibrated_clf.calibrated_classifiers_)
1
>>> calibrated_clf.predict_proba([[-0.5, 0.5]])
array([[0.936..., 0.063...]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.calibration.CalibratedClassifierCV.fit "sklearn.calibration.CalibratedClassifierCV.fit")(X, y[, sample\_weight]) | Fit the calibrated model. |
| [`get_params`](#sklearn.calibration.CalibratedClassifierCV.get_params "sklearn.calibration.CalibratedClassifierCV.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.calibration.CalibratedClassifierCV.predict "sklearn.calibration.CalibratedClassifierCV.predict")(X) | Predict the target of new samples. |
| [`predict_proba`](#sklearn.calibration.CalibratedClassifierCV.predict_proba "sklearn.calibration.CalibratedClassifierCV.predict_proba")(X) | Calibrated probabilities of classification. |
| [`score`](#sklearn.calibration.CalibratedClassifierCV.score "sklearn.calibration.CalibratedClassifierCV.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.calibration.CalibratedClassifierCV.set_params "sklearn.calibration.CalibratedClassifierCV.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*, *sample\_weight=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/calibration.py#L254)
Fit the calibrated model.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data.
**y**array-like of shape (n\_samples,)
Target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, then samples are equally weighted.
**\*\*fit\_params**dict
Parameters to pass to the `fit` method of the underlying classifier.
Returns:
**self**object
Returns an instance of self.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/calibration.py#L440)
Predict the target of new samples.
The predicted class is the class that has the highest probability, and can thus be different from the prediction of the uncalibrated classifier.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The samples, as accepted by `base_estimator.predict`.
Returns:
**C**ndarray of shape (n\_samples,)
The predicted class.
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/calibration.py#L412)
Calibrated probabilities of classification.
This function returns calibrated probabilities of classification according to each class on an array of test vectors X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The samples, as accepted by `base_estimator.predict_proba`.
Returns:
**C**ndarray of shape (n\_samples, n\_classes)
The predicted probas.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.calibration.CalibratedClassifierCV`
-----------------------------------------------------------
[Probability Calibration curves](../../auto_examples/calibration/plot_calibration_curve#sphx-glr-auto-examples-calibration-plot-calibration-curve-py)
[Probability Calibration for 3-class classification](../../auto_examples/calibration/plot_calibration_multiclass#sphx-glr-auto-examples-calibration-plot-calibration-multiclass-py)
[Probability calibration of classifiers](../../auto_examples/calibration/plot_calibration#sphx-glr-auto-examples-calibration-plot-calibration-py)
| programming_docs |
scikit_learn sklearn.exceptions.DataDimensionalityWarning sklearn.exceptions.DataDimensionalityWarning
============================================
*class*sklearn.exceptions.DataDimensionalityWarning[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/exceptions.py#L67)
Custom warning to notify potential issues with data dimensionality.
For example, in random projection, this warning is raised when the number of components, which quantifies the dimensionality of the target projection space, is higher than the number of features, which quantifies the dimensionality of the original source space, to imply that the dimensionality of the problem will not be reduced.
Changed in version 0.18: Moved from sklearn.utils.
Attributes:
**args**
#### Methods
| | |
| --- | --- |
| [`with_traceback`](#sklearn.exceptions.DataDimensionalityWarning.with_traceback "sklearn.exceptions.DataDimensionalityWarning.with_traceback") | Exception.with\_traceback(tb) -- set self.\_\_traceback\_\_ to tb and return self. |
with\_traceback()
Exception.with\_traceback(tb) – set self.\_\_traceback\_\_ to tb and return self.
scikit_learn sklearn.metrics.pairwise.pairwise_kernels sklearn.metrics.pairwise.pairwise\_kernels
==========================================
sklearn.metrics.pairwise.pairwise\_kernels(*X*, *Y=None*, *metric='linear'*, *\**, *filter\_params=False*, *n\_jobs=None*, *\*\*kwds*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/pairwise.py#L2099)
Compute the kernel between arrays X and optional array Y.
This method takes either a vector array or a kernel matrix, and returns a kernel matrix. If the input is a vector array, the kernels are computed. If the input is a kernel matrix, it is returned instead.
This method provides a safe way to take a kernel matrix as input, while preserving compatibility with many other algorithms that take a vector array.
If Y is given (default is None), then the returned matrix is the pairwise kernel between the arrays from both X and Y.
Valid values for metric are:
[‘additive\_chi2’, ‘chi2’, ‘linear’, ‘poly’, ‘polynomial’, ‘rbf’, ‘laplacian’, ‘sigmoid’, ‘cosine’]
Read more in the [User Guide](../metrics#metrics).
Parameters:
**X**ndarray of shape (n\_samples\_X, n\_samples\_X) or (n\_samples\_X, n\_features)
Array of pairwise kernels between samples, or a feature array. The shape of the array should be (n\_samples\_X, n\_samples\_X) if metric == “precomputed” and (n\_samples\_X, n\_features) otherwise.
**Y**ndarray of shape (n\_samples\_Y, n\_features), default=None
A second feature array only if X has shape (n\_samples\_X, n\_features).
**metric**str or callable, default=”linear”
The metric to use when calculating kernel between instances in a feature array. If metric is a string, it must be one of the metrics in pairwise.PAIRWISE\_KERNEL\_FUNCTIONS. If metric is “precomputed”, X is assumed to be a kernel matrix. Alternatively, if metric is a callable function, it is called on each pair of instances (rows) and the resulting value recorded. The callable should take two rows from X as input and return the corresponding kernel value as a single number. This means that callables from [`sklearn.metrics.pairwise`](../classes#module-sklearn.metrics.pairwise "sklearn.metrics.pairwise") are not allowed, as they operate on matrices, not single samples. Use the string identifying the kernel instead.
**filter\_params**bool, default=False
Whether to filter invalid parameters or not.
**n\_jobs**int, default=None
The number of jobs to use for the computation. This works by breaking down the pairwise matrix into n\_jobs even slices and computing them in parallel.
`None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**\*\*kwds**optional keyword parameters
Any further parameters are passed directly to the kernel function.
Returns:
**K**ndarray of shape (n\_samples\_X, n\_samples\_X) or (n\_samples\_X, n\_samples\_Y)
A kernel matrix K such that K\_{i, j} is the kernel between the ith and jth vectors of the given matrix X, if Y is None. If Y is not None, then K\_{i, j} is the kernel between the ith array from X and the jth array from Y.
#### Notes
If metric is ‘precomputed’, Y is ignored and X is returned.
scikit_learn sklearn.manifold.MDS sklearn.manifold.MDS
====================
*class*sklearn.manifold.MDS(*n\_components=2*, *\**, *metric=True*, *n\_init=4*, *max\_iter=300*, *verbose=0*, *eps=0.001*, *n\_jobs=None*, *random\_state=None*, *dissimilarity='euclidean'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_mds.py#L313)
Multidimensional scaling.
Read more in the [User Guide](../manifold#multidimensional-scaling).
Parameters:
**n\_components**int, default=2
Number of dimensions in which to immerse the dissimilarities.
**metric**bool, default=True
If `True`, perform metric MDS; otherwise, perform nonmetric MDS. When `False` (i.e. non-metric MDS), dissimilarities with 0 are considered as missing values.
**n\_init**int, default=4
Number of times the SMACOF algorithm will be run with different initializations. The final results will be the best output of the runs, determined by the run with the smallest final stress.
**max\_iter**int, default=300
Maximum number of iterations of the SMACOF algorithm for a single run.
**verbose**int, default=0
Level of verbosity.
**eps**float, default=1e-3
Relative tolerance with respect to stress at which to declare convergence.
**n\_jobs**int, default=None
The number of jobs to use for the computation. If multiple initializations are used (`n_init`), each run of the algorithm is computed in parallel.
`None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**random\_state**int, RandomState instance or None, default=None
Determines the random number generator used to initialize the centers. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**dissimilarity**{‘euclidean’, ‘precomputed’}, default=’euclidean’
Dissimilarity measure to use:
* ‘euclidean’:
Pairwise Euclidean distances between points in the dataset.
* ‘precomputed’:
Pre-computed dissimilarities are passed directly to `fit` and `fit_transform`.
Attributes:
**embedding\_**ndarray of shape (n\_samples, n\_components)
Stores the position of the dataset in the embedding space.
**stress\_**float
The final value of the stress (sum of squared distance of the disparities and the distances for all constrained points).
**dissimilarity\_matrix\_**ndarray of shape (n\_samples, n\_samples)
Pairwise dissimilarities between the points. Symmetric matrix that:
* either uses a custom dissimilarity matrix by setting `dissimilarity` to ‘precomputed’;
* or constructs a dissimilarity matrix from data using Euclidean distances.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_iter\_**int
The number of iterations corresponding to the best stress.
See also
[`sklearn.decomposition.PCA`](sklearn.decomposition.pca#sklearn.decomposition.PCA "sklearn.decomposition.PCA")
Principal component analysis that is a linear dimensionality reduction method.
[`sklearn.decomposition.KernelPCA`](sklearn.decomposition.kernelpca#sklearn.decomposition.KernelPCA "sklearn.decomposition.KernelPCA")
Non-linear dimensionality reduction using kernels and PCA.
[`TSNE`](sklearn.manifold.tsne#sklearn.manifold.TSNE "sklearn.manifold.TSNE")
T-distributed Stochastic Neighbor Embedding.
[`Isomap`](sklearn.manifold.isomap#sklearn.manifold.Isomap "sklearn.manifold.Isomap")
Manifold learning based on Isometric Mapping.
[`LocallyLinearEmbedding`](sklearn.manifold.locallylinearembedding#sklearn.manifold.LocallyLinearEmbedding "sklearn.manifold.LocallyLinearEmbedding")
Manifold learning using Locally Linear Embedding.
[`SpectralEmbedding`](sklearn.manifold.spectralembedding#sklearn.manifold.SpectralEmbedding "sklearn.manifold.SpectralEmbedding")
Spectral embedding for non-linear dimensionality.
#### References
“Modern Multidimensional Scaling - Theory and Applications” Borg, I.; Groenen P. Springer Series in Statistics (1997)
“Nonmetric multidimensional scaling: a numerical method” Kruskal, J. Psychometrika, 29 (1964)
“Multidimensional scaling by optimizing goodness of fit to a nonmetric hypothesis” Kruskal, J. Psychometrika, 29, (1964)
#### Examples
```
>>> from sklearn.datasets import load_digits
>>> from sklearn.manifold import MDS
>>> X, _ = load_digits(return_X_y=True)
>>> X.shape
(1797, 64)
>>> embedding = MDS(n_components=2)
>>> X_transformed = embedding.fit_transform(X[:100])
>>> X_transformed.shape
(100, 2)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.manifold.MDS.fit "sklearn.manifold.MDS.fit")(X[, y, init]) | Compute the position of the points in the embedding space. |
| [`fit_transform`](#sklearn.manifold.MDS.fit_transform "sklearn.manifold.MDS.fit_transform")(X[, y, init]) | Fit the data from `X`, and returns the embedded coordinates. |
| [`get_params`](#sklearn.manifold.MDS.get_params "sklearn.manifold.MDS.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.manifold.MDS.set_params "sklearn.manifold.MDS.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y=None*, *init=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_mds.py#L459)
Compute the position of the points in the embedding space.
Parameters:
**X**array-like of shape (n\_samples, n\_features) or (n\_samples, n\_samples)
Input data. If `dissimilarity=='precomputed'`, the input should be the dissimilarity matrix.
**y**Ignored
Not used, present for API consistency by convention.
**init**ndarray of shape (n\_samples,), default=None
Starting configuration of the embedding to initialize the SMACOF algorithm. By default, the algorithm is initialized with a randomly chosen array.
Returns:
**self**object
Fitted estimator.
fit\_transform(*X*, *y=None*, *init=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_mds.py#L486)
Fit the data from `X`, and returns the embedded coordinates.
Parameters:
**X**array-like of shape (n\_samples, n\_features) or (n\_samples, n\_samples)
Input data. If `dissimilarity=='precomputed'`, the input should be the dissimilarity matrix.
**y**Ignored
Not used, present for API consistency by convention.
**init**ndarray of shape (n\_samples, n\_components), default=None
Starting configuration of the embedding to initialize the SMACOF algorithm. By default, the algorithm is initialized with a randomly chosen array.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_components)
X transformed in the new space.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.manifold.MDS`
-------------------------------------
[Comparison of Manifold Learning methods](../../auto_examples/manifold/plot_compare_methods#sphx-glr-auto-examples-manifold-plot-compare-methods-py)
[Manifold Learning methods on a severed sphere](../../auto_examples/manifold/plot_manifold_sphere#sphx-glr-auto-examples-manifold-plot-manifold-sphere-py)
[Manifold learning on handwritten digits: Locally Linear Embedding, Isomap…](../../auto_examples/manifold/plot_lle_digits#sphx-glr-auto-examples-manifold-plot-lle-digits-py)
[Multi-dimensional scaling](../../auto_examples/manifold/plot_mds#sphx-glr-auto-examples-manifold-plot-mds-py)
scikit_learn sklearn.datasets.make_swiss_roll sklearn.datasets.make\_swiss\_roll
==================================
sklearn.datasets.make\_swiss\_roll(*n\_samples=100*, *\**, *noise=0.0*, *random\_state=None*, *hole=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_samples_generator.py#L1499)
Generate a swiss roll dataset.
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/sample_generators.html#sample-generators).
Parameters:
**n\_samples**int, default=100
The number of sample points on the Swiss Roll.
**noise**float, default=0.0
The standard deviation of the gaussian noise.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for dataset creation. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**hole**bool, default=False
If True generates the swiss roll with hole dataset.
Returns:
**X**ndarray of shape (n\_samples, 3)
The points.
**t**ndarray of shape (n\_samples,)
The univariate position of the sample according to the main dimension of the points in the manifold.
#### Notes
The algorithm is from Marsland [1].
#### References
[1] S. Marsland, “Machine Learning: An Algorithmic Perspective”, 2nd edition, Chapter 6, 2014. <https://homepages.ecs.vuw.ac.nz/~marslast/Code/Ch6/lle.py>
Examples using `sklearn.datasets.make_swiss_roll`
-------------------------------------------------
[Hierarchical clustering: structured vs unstructured ward](../../auto_examples/cluster/plot_ward_structured_vs_unstructured#sphx-glr-auto-examples-cluster-plot-ward-structured-vs-unstructured-py)
[Swiss Roll And Swiss-Hole Reduction](../../auto_examples/manifold/plot_swissroll#sphx-glr-auto-examples-manifold-plot-swissroll-py)
scikit_learn sklearn.metrics.cluster.contingency_matrix sklearn.metrics.cluster.contingency\_matrix
===========================================
sklearn.metrics.cluster.contingency\_matrix(*labels\_true*, *labels\_pred*, *\**, *eps=None*, *sparse=False*, *dtype=<class 'numpy.int64'>*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/cluster/_supervised.py#L92)
Build a contingency matrix describing the relationship between labels.
Parameters:
**labels\_true**int array, shape = [n\_samples]
Ground truth class labels to be used as a reference.
**labels\_pred**array-like of shape (n\_samples,)
Cluster labels to evaluate.
**eps**float, default=None
If a float, that value is added to all values in the contingency matrix. This helps to stop NaN propagation. If `None`, nothing is adjusted.
**sparse**bool, default=False
If `True`, return a sparse CSR continency matrix. If `eps` is not `None` and `sparse` is `True` will raise ValueError.
New in version 0.18.
**dtype**numeric type, default=np.int64
Output dtype. Ignored if `eps` is not `None`.
New in version 0.24.
Returns:
**contingency**{array-like, sparse}, shape=[n\_classes\_true, n\_classes\_pred]
Matrix \(C\) such that \(C\_{i, j}\) is the number of samples in true class \(i\) and in predicted class \(j\). If `eps is None`, the dtype of this array will be integer unless set otherwise with the `dtype` argument. If `eps` is given, the dtype will be float. Will be a `sklearn.sparse.csr_matrix` if `sparse=True`.
scikit_learn sklearn.model_selection.StratifiedKFold sklearn.model\_selection.StratifiedKFold
========================================
*class*sklearn.model\_selection.StratifiedKFold(*n\_splits=5*, *\**, *shuffle=False*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L581)
Stratified K-Folds cross-validator.
Provides train/test indices to split data in train/test sets.
This cross-validation object is a variation of KFold that returns stratified folds. The folds are made by preserving the percentage of samples for each class.
Read more in the [User Guide](../cross_validation#stratified-k-fold).
Parameters:
**n\_splits**int, default=5
Number of folds. Must be at least 2.
Changed in version 0.22: `n_splits` default value changed from 3 to 5.
**shuffle**bool, default=False
Whether to shuffle each class’s samples before splitting into batches. Note that the samples within each split will not be shuffled.
**random\_state**int, RandomState instance or None, default=None
When `shuffle` is True, `random_state` affects the ordering of the indices, which controls the randomness of each fold for each class. Otherwise, leave `random_state` as `None`. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
See also
[`RepeatedStratifiedKFold`](sklearn.model_selection.repeatedstratifiedkfold#sklearn.model_selection.RepeatedStratifiedKFold "sklearn.model_selection.RepeatedStratifiedKFold")
Repeats Stratified K-Fold n times.
#### Notes
The implementation is designed to:
* Generate test sets such that all contain the same distribution of classes, or as close as possible.
* Be invariant to class label: relabelling `y = ["Happy", "Sad"]` to `y = [1, 0]` should not change the indices generated.
* Preserve order dependencies in the dataset ordering, when `shuffle=False`: all samples from class k in some test set were contiguous in y, or separated in y by samples from classes other than k.
* Generate test sets where the smallest and largest differ by at most one sample.
Changed in version 0.22: The previous implementation did not follow the last constraint.
#### Examples
```
>>> import numpy as np
>>> from sklearn.model_selection import StratifiedKFold
>>> X = np.array([[1, 2], [3, 4], [1, 2], [3, 4]])
>>> y = np.array([0, 0, 1, 1])
>>> skf = StratifiedKFold(n_splits=2)
>>> skf.get_n_splits(X, y)
2
>>> print(skf)
StratifiedKFold(n_splits=2, random_state=None, shuffle=False)
>>> for train_index, test_index in skf.split(X, y):
... print("TRAIN:", train_index, "TEST:", test_index)
... X_train, X_test = X[train_index], X[test_index]
... y_train, y_test = y[train_index], y[test_index]
TRAIN: [1 3] TEST: [0 2]
TRAIN: [0 2] TEST: [1 3]
```
#### Methods
| | |
| --- | --- |
| [`get_n_splits`](#sklearn.model_selection.StratifiedKFold.get_n_splits "sklearn.model_selection.StratifiedKFold.get_n_splits")([X, y, groups]) | Returns the number of splitting iterations in the cross-validator |
| [`split`](#sklearn.model_selection.StratifiedKFold.split "sklearn.model_selection.StratifiedKFold.split")(X, y[, groups]) | Generate indices to split data into training and test set. |
get\_n\_splits(*X=None*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L343)
Returns the number of splitting iterations in the cross-validator
Parameters:
**X**object
Always ignored, exists for compatibility.
**y**object
Always ignored, exists for compatibility.
**groups**object
Always ignored, exists for compatibility.
Returns:
**n\_splits**int
Returns the number of splitting iterations in the cross-validator.
split(*X*, *y*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L721)
Generate indices to split data into training and test set.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
Note that providing `y` is sufficient to generate the splits and hence `np.zeros(n_samples)` may be used as a placeholder for `X` instead of actual training data.
**y**array-like of shape (n\_samples,)
The target variable for supervised learning problems. Stratification is done based on the y labels.
**groups**object
Always ignored, exists for compatibility.
Yields:
**train**ndarray
The training set indices for that split.
**test**ndarray
The testing set indices for that split.
#### Notes
Randomized CV splitters may return different results for each call of split. You can make the results identical by setting `random_state` to an integer.
Examples using `sklearn.model_selection.StratifiedKFold`
--------------------------------------------------------
[Recursive feature elimination with cross-validation](../../auto_examples/feature_selection/plot_rfe_with_cross_validation#sphx-glr-auto-examples-feature-selection-plot-rfe-with-cross-validation-py)
[GMM covariances](../../auto_examples/mixture/plot_gmm_covariances#sphx-glr-auto-examples-mixture-plot-gmm-covariances-py)
[Receiver Operating Characteristic (ROC) with cross validation](../../auto_examples/model_selection/plot_roc_crossval#sphx-glr-auto-examples-model-selection-plot-roc-crossval-py)
[Test with permutations the significance of a classification score](../../auto_examples/model_selection/plot_permutation_tests_for_classification#sphx-glr-auto-examples-model-selection-plot-permutation-tests-for-classification-py)
[Visualizing cross-validation behavior in scikit-learn](../../auto_examples/model_selection/plot_cv_indices#sphx-glr-auto-examples-model-selection-plot-cv-indices-py)
[Effect of varying threshold for self-training](../../auto_examples/semi_supervised/plot_self_training_varying_threshold#sphx-glr-auto-examples-semi-supervised-plot-self-training-varying-threshold-py)
| programming_docs |
scikit_learn sklearn.metrics.classification_report sklearn.metrics.classification\_report
======================================
sklearn.metrics.classification\_report(*y\_true*, *y\_pred*, *\**, *labels=None*, *target\_names=None*, *sample\_weight=None*, *digits=2*, *output\_dict=False*, *zero\_division='warn'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_classification.py#L2017)
Build a text report showing the main classification metrics.
Read more in the [User Guide](../model_evaluation#classification-report).
Parameters:
**y\_true**1d array-like, or label indicator array / sparse matrix
Ground truth (correct) target values.
**y\_pred**1d array-like, or label indicator array / sparse matrix
Estimated targets as returned by a classifier.
**labels**array-like of shape (n\_labels,), default=None
Optional list of label indices to include in the report.
**target\_names**list of str of shape (n\_labels,), default=None
Optional display names matching the labels (same order).
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**digits**int, default=2
Number of digits for formatting output floating point values. When `output_dict` is `True`, this will be ignored and the returned values will not be rounded.
**output\_dict**bool, default=False
If True, return output as dict.
New in version 0.20.
**zero\_division**“warn”, 0 or 1, default=”warn”
Sets the value to return when there is a zero division. If set to “warn”, this acts as 0, but warnings are also raised.
Returns:
**report**str or dict
Text summary of the precision, recall, F1 score for each class. Dictionary returned if output\_dict is True. Dictionary has the following structure:
```
{'label 1': {'precision':0.5,
'recall':1.0,
'f1-score':0.67,
'support':1},
'label 2': { ... },
...
}
```
The reported averages include macro average (averaging the unweighted mean per label), weighted average (averaging the support-weighted mean per label), and sample average (only for multilabel classification). Micro average (averaging the total true positives, false negatives and false positives) is only shown for multi-label or multi-class with a subset of classes, because it corresponds to accuracy otherwise and would be the same for all metrics. See also [`precision_recall_fscore_support`](sklearn.metrics.precision_recall_fscore_support#sklearn.metrics.precision_recall_fscore_support "sklearn.metrics.precision_recall_fscore_support") for more details on averages.
Note that in binary classification, recall of the positive class is also known as “sensitivity”; recall of the negative class is “specificity”.
See also
[`precision_recall_fscore_support`](sklearn.metrics.precision_recall_fscore_support#sklearn.metrics.precision_recall_fscore_support "sklearn.metrics.precision_recall_fscore_support")
Compute precision, recall, F-measure and support for each class.
[`confusion_matrix`](sklearn.metrics.confusion_matrix#sklearn.metrics.confusion_matrix "sklearn.metrics.confusion_matrix")
Compute confusion matrix to evaluate the accuracy of a classification.
[`multilabel_confusion_matrix`](sklearn.metrics.multilabel_confusion_matrix#sklearn.metrics.multilabel_confusion_matrix "sklearn.metrics.multilabel_confusion_matrix")
Compute a confusion matrix for each class or sample.
#### Examples
```
>>> from sklearn.metrics import classification_report
>>> y_true = [0, 1, 2, 2, 2]
>>> y_pred = [0, 0, 2, 2, 1]
>>> target_names = ['class 0', 'class 1', 'class 2']
>>> print(classification_report(y_true, y_pred, target_names=target_names))
precision recall f1-score support
class 0 0.50 1.00 0.67 1
class 1 0.00 0.00 0.00 1
class 2 1.00 0.67 0.80 3
accuracy 0.60 5
macro avg 0.50 0.56 0.49 5
weighted avg 0.70 0.60 0.61 5
>>> y_pred = [1, 1, 0]
>>> y_true = [1, 1, 1]
>>> print(classification_report(y_true, y_pred, labels=[1, 2, 3]))
precision recall f1-score support
1 1.00 0.67 0.80 3
2 0.00 0.00 0.00 0
3 0.00 0.00 0.00 0
micro avg 1.00 0.67 0.80 3
macro avg 0.33 0.22 0.27 3
weighted avg 1.00 0.67 0.80 3
```
Examples using `sklearn.metrics.classification_report`
------------------------------------------------------
[Recognizing hand-written digits](../../auto_examples/classification/plot_digits_classification#sphx-glr-auto-examples-classification-plot-digits-classification-py)
[Faces recognition example using eigenfaces and SVMs](../../auto_examples/applications/plot_face_recognition#sphx-glr-auto-examples-applications-plot-face-recognition-py)
[Pipeline ANOVA SVM](../../auto_examples/feature_selection/plot_feature_selection_pipeline#sphx-glr-auto-examples-feature-selection-plot-feature-selection-pipeline-py)
[Custom refit strategy of a grid search with cross-validation](../../auto_examples/model_selection/plot_grid_search_digits#sphx-glr-auto-examples-model-selection-plot-grid-search-digits-py)
[Restricted Boltzmann Machine features for digit classification](../../auto_examples/neural_networks/plot_rbm_logistic_classification#sphx-glr-auto-examples-neural-networks-plot-rbm-logistic-classification-py)
[Column Transformer with Heterogeneous Data Sources](../../auto_examples/compose/plot_column_transformer#sphx-glr-auto-examples-compose-plot-column-transformer-py)
[Label Propagation digits active learning](../../auto_examples/semi_supervised/plot_label_propagation_digits_active_learning#sphx-glr-auto-examples-semi-supervised-plot-label-propagation-digits-active-learning-py)
[Label Propagation digits: Demonstrating performance](../../auto_examples/semi_supervised/plot_label_propagation_digits#sphx-glr-auto-examples-semi-supervised-plot-label-propagation-digits-py)
scikit_learn sklearn.kernel_approximation.PolynomialCountSketch sklearn.kernel\_approximation.PolynomialCountSketch
===================================================
*class*sklearn.kernel\_approximation.PolynomialCountSketch(*\**, *gamma=1.0*, *degree=2*, *coef0=0*, *n\_components=100*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/kernel_approximation.py#L33)
Polynomial kernel approximation via Tensor Sketch.
Implements Tensor Sketch, which approximates the feature map of the polynomial kernel:
```
K(X, Y) = (gamma * <X, Y> + coef0)^degree
```
by efficiently computing a Count Sketch of the outer product of a vector with itself using Fast Fourier Transforms (FFT). Read more in the [User Guide](../kernel_approximation#polynomial-kernel-approx).
New in version 0.24.
Parameters:
**gamma**float, default=1.0
Parameter of the polynomial kernel whose feature map will be approximated.
**degree**int, default=2
Degree of the polynomial kernel whose feature map will be approximated.
**coef0**int, default=0
Constant term of the polynomial kernel whose feature map will be approximated.
**n\_components**int, default=100
Dimensionality of the output feature space. Usually, `n_components` should be greater than the number of features in input samples in order to achieve good performance. The optimal score / run time balance is typically achieved around `n_components` = 10 \* `n_features`, but this depends on the specific dataset being used.
**random\_state**int, RandomState instance, default=None
Determines random number generation for indexHash and bitHash initialization. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Attributes:
**indexHash\_**ndarray of shape (degree, n\_features), dtype=int64
Array of indexes in range [0, n\_components) used to represent the 2-wise independent hash functions for Count Sketch computation.
**bitHash\_**ndarray of shape (degree, n\_features), dtype=float32
Array with random entries in {+1, -1}, used to represent the 2-wise independent hash functions for Count Sketch computation.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`AdditiveChi2Sampler`](sklearn.kernel_approximation.additivechi2sampler#sklearn.kernel_approximation.AdditiveChi2Sampler "sklearn.kernel_approximation.AdditiveChi2Sampler")
Approximate feature map for additive chi2 kernel.
[`Nystroem`](sklearn.kernel_approximation.nystroem#sklearn.kernel_approximation.Nystroem "sklearn.kernel_approximation.Nystroem")
Approximate a kernel map using a subset of the training data.
[`RBFSampler`](sklearn.kernel_approximation.rbfsampler#sklearn.kernel_approximation.RBFSampler "sklearn.kernel_approximation.RBFSampler")
Approximate a RBF kernel feature map using random Fourier features.
[`SkewedChi2Sampler`](sklearn.kernel_approximation.skewedchi2sampler#sklearn.kernel_approximation.SkewedChi2Sampler "sklearn.kernel_approximation.SkewedChi2Sampler")
Approximate feature map for “skewed chi-squared” kernel.
[`sklearn.metrics.pairwise.kernel_metrics`](sklearn.metrics.pairwise.kernel_metrics#sklearn.metrics.pairwise.kernel_metrics "sklearn.metrics.pairwise.kernel_metrics")
List of built-in kernels.
#### Examples
```
>>> from sklearn.kernel_approximation import PolynomialCountSketch
>>> from sklearn.linear_model import SGDClassifier
>>> X = [[0, 0], [1, 1], [1, 0], [0, 1]]
>>> y = [0, 0, 1, 1]
>>> ps = PolynomialCountSketch(degree=3, random_state=1)
>>> X_features = ps.fit_transform(X)
>>> clf = SGDClassifier(max_iter=10, tol=1e-3)
>>> clf.fit(X_features, y)
SGDClassifier(max_iter=10)
>>> clf.score(X_features, y)
1.0
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.kernel_approximation.PolynomialCountSketch.fit "sklearn.kernel_approximation.PolynomialCountSketch.fit")(X[, y]) | Fit the model with X. |
| [`fit_transform`](#sklearn.kernel_approximation.PolynomialCountSketch.fit_transform "sklearn.kernel_approximation.PolynomialCountSketch.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.kernel_approximation.PolynomialCountSketch.get_feature_names_out "sklearn.kernel_approximation.PolynomialCountSketch.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.kernel_approximation.PolynomialCountSketch.get_params "sklearn.kernel_approximation.PolynomialCountSketch.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.kernel_approximation.PolynomialCountSketch.set_params "sklearn.kernel_approximation.PolynomialCountSketch.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.kernel_approximation.PolynomialCountSketch.transform "sklearn.kernel_approximation.PolynomialCountSketch.transform")(X) | Generate the feature map approximation for X. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/kernel_approximation.py#L129)
Fit the model with X.
Initializes the internal variables. The method needs no information about the distribution of data, so we only care about n\_features in X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.kernel_approximation.PolynomialCountSketch.fit "sklearn.kernel_approximation.PolynomialCountSketch.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/kernel_approximation.py#L168)
Generate the feature map approximation for X.
Parameters:
**X**{array-like}, shape (n\_samples, n\_features)
New data, where `n_samples` is the number of samples and `n_features` is the number of features.
Returns:
**X\_new**array-like, shape (n\_samples, n\_components)
Returns the instance itself.
Examples using `sklearn.kernel_approximation.PolynomialCountSketch`
-------------------------------------------------------------------
[Release Highlights for scikit-learn 0.24](../../auto_examples/release_highlights/plot_release_highlights_0_24_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-24-0-py)
[Scalable learning with polynomial kernel approximation](../../auto_examples/kernel_approximation/plot_scalable_poly_kernels#sphx-glr-auto-examples-kernel-approximation-plot-scalable-poly-kernels-py)
scikit_learn sklearn.kernel_ridge.KernelRidge sklearn.kernel\_ridge.KernelRidge
=================================
*class*sklearn.kernel\_ridge.KernelRidge(*alpha=1*, *\**, *kernel='linear'*, *gamma=None*, *degree=3*, *coef0=1*, *kernel\_params=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/kernel_ridge.py#L15)
Kernel ridge regression.
Kernel ridge regression (KRR) combines ridge regression (linear least squares with l2-norm regularization) with the kernel trick. It thus learns a linear function in the space induced by the respective kernel and the data. For non-linear kernels, this corresponds to a non-linear function in the original space.
The form of the model learned by KRR is identical to support vector regression (SVR). However, different loss functions are used: KRR uses squared error loss while support vector regression uses epsilon-insensitive loss, both combined with l2 regularization. In contrast to SVR, fitting a KRR model can be done in closed-form and is typically faster for medium-sized datasets. On the other hand, the learned model is non-sparse and thus slower than SVR, which learns a sparse model for epsilon > 0, at prediction-time.
This estimator has built-in support for multi-variate regression (i.e., when y is a 2d-array of shape [n\_samples, n\_targets]).
Read more in the [User Guide](../kernel_ridge#kernel-ridge).
Parameters:
**alpha**float or array-like of shape (n\_targets,), default=1.0
Regularization strength; must be a positive float. Regularization improves the conditioning of the problem and reduces the variance of the estimates. Larger values specify stronger regularization. Alpha corresponds to `1 / (2C)` in other linear models such as [`LogisticRegression`](sklearn.linear_model.logisticregression#sklearn.linear_model.LogisticRegression "sklearn.linear_model.LogisticRegression") or [`LinearSVC`](sklearn.svm.linearsvc#sklearn.svm.LinearSVC "sklearn.svm.LinearSVC"). If an array is passed, penalties are assumed to be specific to the targets. Hence they must correspond in number. See [Ridge regression and classification](../linear_model#ridge-regression) for formula.
**kernel**str or callable, default=”linear”
Kernel mapping used internally. This parameter is directly passed to `pairwise_kernel`. If `kernel` is a string, it must be one of the metrics in `pairwise.PAIRWISE_KERNEL_FUNCTIONS` or “precomputed”. If `kernel` is “precomputed”, X is assumed to be a kernel matrix. Alternatively, if `kernel` is a callable function, it is called on each pair of instances (rows) and the resulting value recorded. The callable should take two rows from X as input and return the corresponding kernel value as a single number. This means that callables from [`sklearn.metrics.pairwise`](../classes#module-sklearn.metrics.pairwise "sklearn.metrics.pairwise") are not allowed, as they operate on matrices, not single samples. Use the string identifying the kernel instead.
**gamma**float, default=None
Gamma parameter for the RBF, laplacian, polynomial, exponential chi2 and sigmoid kernels. Interpretation of the default value is left to the kernel; see the documentation for sklearn.metrics.pairwise. Ignored by other kernels.
**degree**float, default=3
Degree of the polynomial kernel. Ignored by other kernels.
**coef0**float, default=1
Zero coefficient for polynomial and sigmoid kernels. Ignored by other kernels.
**kernel\_params**mapping of str to any, default=None
Additional parameters (keyword arguments) for kernel function passed as callable object.
Attributes:
**dual\_coef\_**ndarray of shape (n\_samples,) or (n\_samples, n\_targets)
Representation of weight vector(s) in kernel space
**X\_fit\_**{ndarray, sparse matrix} of shape (n\_samples, n\_features)
Training data, which is also required for prediction. If kernel == “precomputed” this is instead the precomputed training matrix, of shape (n\_samples, n\_samples).
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`sklearn.gaussian_process.GaussianProcessRegressor`](sklearn.gaussian_process.gaussianprocessregressor#sklearn.gaussian_process.GaussianProcessRegressor "sklearn.gaussian_process.GaussianProcessRegressor")
Gaussian Process regressor providing automatic kernel hyperparameters tuning and predictions uncertainty.
[`sklearn.linear_model.Ridge`](sklearn.linear_model.ridge#sklearn.linear_model.Ridge "sklearn.linear_model.Ridge")
Linear ridge regression.
[`sklearn.linear_model.RidgeCV`](sklearn.linear_model.ridgecv#sklearn.linear_model.RidgeCV "sklearn.linear_model.RidgeCV")
Ridge regression with built-in cross-validation.
[`sklearn.svm.SVR`](sklearn.svm.svr#sklearn.svm.SVR "sklearn.svm.SVR")
Support Vector Regression accepting a large variety of kernels.
#### References
* Kevin P. Murphy “Machine Learning: A Probabilistic Perspective”, The MIT Press chapter 14.4.3, pp. 492-493
#### Examples
```
>>> from sklearn.kernel_ridge import KernelRidge
>>> import numpy as np
>>> n_samples, n_features = 10, 5
>>> rng = np.random.RandomState(0)
>>> y = rng.randn(n_samples)
>>> X = rng.randn(n_samples, n_features)
>>> krr = KernelRidge(alpha=1.0)
>>> krr.fit(X, y)
KernelRidge(alpha=1.0)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.kernel_ridge.KernelRidge.fit "sklearn.kernel_ridge.KernelRidge.fit")(X, y[, sample\_weight]) | Fit Kernel Ridge regression model. |
| [`get_params`](#sklearn.kernel_ridge.KernelRidge.get_params "sklearn.kernel_ridge.KernelRidge.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.kernel_ridge.KernelRidge.predict "sklearn.kernel_ridge.KernelRidge.predict")(X) | Predict using the kernel ridge model. |
| [`score`](#sklearn.kernel_ridge.KernelRidge.score "sklearn.kernel_ridge.KernelRidge.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.kernel_ridge.KernelRidge.set_params "sklearn.kernel_ridge.KernelRidge.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/kernel_ridge.py#L159)
Fit Kernel Ridge regression model.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training data. If kernel == “precomputed” this is instead a precomputed kernel matrix, of shape (n\_samples, n\_samples).
**y**array-like of shape (n\_samples,) or (n\_samples, n\_targets)
Target values.
**sample\_weight**float or array-like of shape (n\_samples,), default=None
Individual weights for each sample, ignored if None is passed.
Returns:
**self**object
Returns the instance itself.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/kernel_ridge.py#L203)
Predict using the kernel ridge model.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Samples. If kernel == “precomputed” this is instead a precomputed kernel matrix, shape = [n\_samples, n\_samples\_fitted], where n\_samples\_fitted is the number of samples used in the fitting for this estimator.
Returns:
**C**ndarray of shape (n\_samples,) or (n\_samples, n\_targets)
Returns predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.kernel_ridge.KernelRidge`
-------------------------------------------------
[Kernel PCA](../../auto_examples/decomposition/plot_kernel_pca#sphx-glr-auto-examples-decomposition-plot-kernel-pca-py)
[Comparison of kernel ridge and Gaussian process regression](../../auto_examples/gaussian_process/plot_compare_gpr_krr#sphx-glr-auto-examples-gaussian-process-plot-compare-gpr-krr-py)
[Comparison of kernel ridge regression and SVR](../../auto_examples/miscellaneous/plot_kernel_ridge_regression#sphx-glr-auto-examples-miscellaneous-plot-kernel-ridge-regression-py)
| programming_docs |
scikit_learn sklearn.decomposition.LatentDirichletAllocation sklearn.decomposition.LatentDirichletAllocation
===============================================
*class*sklearn.decomposition.LatentDirichletAllocation(*n\_components=10*, *\**, *doc\_topic\_prior=None*, *topic\_word\_prior=None*, *learning\_method='batch'*, *learning\_decay=0.7*, *learning\_offset=10.0*, *max\_iter=10*, *batch\_size=128*, *evaluate\_every=-1*, *total\_samples=1000000.0*, *perp\_tol=0.1*, *mean\_change\_tol=0.001*, *max\_doc\_update\_iter=100*, *n\_jobs=None*, *verbose=0*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_lda.py#L141)
Latent Dirichlet Allocation with online variational Bayes algorithm.
The implementation is based on [[1]](#re25e5648fc37-1) and [[2]](#re25e5648fc37-2).
New in version 0.17.
Read more in the [User Guide](../decomposition#latentdirichletallocation).
Parameters:
**n\_components**int, default=10
Number of topics.
Changed in version 0.19: `n_topics` was renamed to `n_components`
**doc\_topic\_prior**float, default=None
Prior of document topic distribution `theta`. If the value is None, defaults to `1 / n_components`. In [[1]](#re25e5648fc37-1), this is called `alpha`.
**topic\_word\_prior**float, default=None
Prior of topic word distribution `beta`. If the value is None, defaults to `1 / n_components`. In [[1]](#re25e5648fc37-1), this is called `eta`.
**learning\_method**{‘batch’, ‘online’}, default=’batch’
Method used to update `_component`. Only used in [`fit`](#sklearn.decomposition.LatentDirichletAllocation.fit "sklearn.decomposition.LatentDirichletAllocation.fit") method. In general, if the data size is large, the online update will be much faster than the batch update.
Valid options:
```
'batch': Batch variational Bayes method. Use all training data in
each EM update.
Old `components_` will be overwritten in each iteration.
'online': Online variational Bayes method. In each EM update, use
mini-batch of training data to update the ``components_``
variable incrementally. The learning rate is controlled by the
``learning_decay`` and the ``learning_offset`` parameters.
```
Changed in version 0.20: The default learning method is now `"batch"`.
**learning\_decay**float, default=0.7
It is a parameter that control learning rate in the online learning method. The value should be set between (0.5, 1.0] to guarantee asymptotic convergence. When the value is 0.0 and batch\_size is `n_samples`, the update method is same as batch learning. In the literature, this is called kappa.
**learning\_offset**float, default=10.0
A (positive) parameter that downweights early iterations in online learning. It should be greater than 1.0. In the literature, this is called tau\_0.
**max\_iter**int, default=10
The maximum number of passes over the training data (aka epochs). It only impacts the behavior in the [`fit`](#sklearn.decomposition.LatentDirichletAllocation.fit "sklearn.decomposition.LatentDirichletAllocation.fit") method, and not the [`partial_fit`](#sklearn.decomposition.LatentDirichletAllocation.partial_fit "sklearn.decomposition.LatentDirichletAllocation.partial_fit") method.
**batch\_size**int, default=128
Number of documents to use in each EM iteration. Only used in online learning.
**evaluate\_every**int, default=-1
How often to evaluate perplexity. Only used in `fit` method. set it to 0 or negative number to not evaluate perplexity in training at all. Evaluating perplexity can help you check convergence in training process, but it will also increase total training time. Evaluating perplexity in every iteration might increase training time up to two-fold.
**total\_samples**int, default=1e6
Total number of documents. Only used in the [`partial_fit`](#sklearn.decomposition.LatentDirichletAllocation.partial_fit "sklearn.decomposition.LatentDirichletAllocation.partial_fit") method.
**perp\_tol**float, default=1e-1
Perplexity tolerance in batch learning. Only used when `evaluate_every` is greater than 0.
**mean\_change\_tol**float, default=1e-3
Stopping tolerance for updating document topic distribution in E-step.
**max\_doc\_update\_iter**int, default=100
Max number of iterations for updating document topic distribution in the E-step.
**n\_jobs**int, default=None
The number of jobs to use in the E-step. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**verbose**int, default=0
Verbosity level.
**random\_state**int, RandomState instance or None, default=None
Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Attributes:
**components\_**ndarray of shape (n\_components, n\_features)
Variational parameters for topic word distribution. Since the complete conditional for topic word distribution is a Dirichlet, `components_[i, j]` can be viewed as pseudocount that represents the number of times word `j` was assigned to topic `i`. It can also be viewed as distribution over the words for each topic after normalization: `model.components_ / model.components_.sum(axis=1)[:, np.newaxis]`.
**exp\_dirichlet\_component\_**ndarray of shape (n\_components, n\_features)
Exponential value of expectation of log topic word distribution. In the literature, this is `exp(E[log(beta)])`.
**n\_batch\_iter\_**int
Number of iterations of the EM step.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_iter\_**int
Number of passes over the dataset.
**bound\_**float
Final perplexity score on training set.
**doc\_topic\_prior\_**float
Prior of document topic distribution `theta`. If the value is None, it is `1 / n_components`.
**random\_state\_**RandomState instance
RandomState instance that is generated either from a seed, the random number generator or by `np.random`.
**topic\_word\_prior\_**float
Prior of topic word distribution `beta`. If the value is None, it is `1 / n_components`.
See also
[`sklearn.discriminant_analysis.LinearDiscriminantAnalysis`](sklearn.discriminant_analysis.lineardiscriminantanalysis#sklearn.discriminant_analysis.LinearDiscriminantAnalysis "sklearn.discriminant_analysis.LinearDiscriminantAnalysis")
A classifier with a linear decision boundary, generated by fitting class conditional densities to the data and using Bayes’ rule.
#### References
[1] ([1](#id1),[2](#id3),[3](#id4)) “Online Learning for Latent Dirichlet Allocation”, Matthew D. Hoffman, David M. Blei, Francis Bach, 2010 <https://github.com/blei-lab/onlineldavb>
[[2](#id2)] “Stochastic Variational Inference”, Matthew D. Hoffman, David M. Blei, Chong Wang, John Paisley, 2013
#### Examples
```
>>> from sklearn.decomposition import LatentDirichletAllocation
>>> from sklearn.datasets import make_multilabel_classification
>>> # This produces a feature matrix of token counts, similar to what
>>> # CountVectorizer would produce on text.
>>> X, _ = make_multilabel_classification(random_state=0)
>>> lda = LatentDirichletAllocation(n_components=5,
... random_state=0)
>>> lda.fit(X)
LatentDirichletAllocation(...)
>>> # get topics for some given samples:
>>> lda.transform(X[-2:])
array([[0.00360392, 0.25499205, 0.0036211 , 0.64236448, 0.09541846],
[0.15297572, 0.00362644, 0.44412786, 0.39568399, 0.003586 ]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.decomposition.LatentDirichletAllocation.fit "sklearn.decomposition.LatentDirichletAllocation.fit")(X[, y]) | Learn model for the data X with variational Bayes method. |
| [`fit_transform`](#sklearn.decomposition.LatentDirichletAllocation.fit_transform "sklearn.decomposition.LatentDirichletAllocation.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.decomposition.LatentDirichletAllocation.get_feature_names_out "sklearn.decomposition.LatentDirichletAllocation.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.decomposition.LatentDirichletAllocation.get_params "sklearn.decomposition.LatentDirichletAllocation.get_params")([deep]) | Get parameters for this estimator. |
| [`partial_fit`](#sklearn.decomposition.LatentDirichletAllocation.partial_fit "sklearn.decomposition.LatentDirichletAllocation.partial_fit")(X[, y]) | Online VB with Mini-Batch update. |
| [`perplexity`](#sklearn.decomposition.LatentDirichletAllocation.perplexity "sklearn.decomposition.LatentDirichletAllocation.perplexity")(X[, sub\_sampling]) | Calculate approximate perplexity for data X. |
| [`score`](#sklearn.decomposition.LatentDirichletAllocation.score "sklearn.decomposition.LatentDirichletAllocation.score")(X[, y]) | Calculate approximate log-likelihood as score. |
| [`set_params`](#sklearn.decomposition.LatentDirichletAllocation.set_params "sklearn.decomposition.LatentDirichletAllocation.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.decomposition.LatentDirichletAllocation.transform "sklearn.decomposition.LatentDirichletAllocation.transform")(X) | Transform data X according to the fitted model. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_lda.py#L593)
Learn model for the data X with variational Bayes method.
When `learning_method` is ‘online’, use mini-batch update. Otherwise, use batch update.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Document word matrix.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
self
Fitted estimator.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.decomposition.LatentDirichletAllocation.fit "sklearn.decomposition.LatentDirichletAllocation.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
partial\_fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_lda.py#L546)
Online VB with Mini-Batch update.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Document word matrix.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
self
Partially fitted estimator.
perplexity(*X*, *sub\_sampling=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_lda.py#L865)
Calculate approximate perplexity for data X.
Perplexity is defined as exp(-1. \* log-likelihood per word)
Changed in version 0.19: *doc\_topic\_distr* argument has been deprecated and is ignored because user no longer has access to unnormalized distribution
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Document word matrix.
**sub\_sampling**bool
Do sub-sampling or not.
Returns:
**score**float
Perplexity score.
score(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_lda.py#L796)
Calculate approximate log-likelihood as score.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Document word matrix.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
**score**float
Use approximate bound as score.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_lda.py#L693)
Transform data X according to the fitted model.
Changed in version 0.18: *doc\_topic\_distr* is now normalized
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Document word matrix.
Returns:
**doc\_topic\_distr**ndarray of shape (n\_samples, n\_components)
Document topic distribution for X.
Examples using `sklearn.decomposition.LatentDirichletAllocation`
----------------------------------------------------------------
[Topic extraction with Non-negative Matrix Factorization and Latent Dirichlet Allocation](../../auto_examples/applications/plot_topics_extraction_with_nmf_lda#sphx-glr-auto-examples-applications-plot-topics-extraction-with-nmf-lda-py)
scikit_learn sklearn.metrics.mean_squared_log_error sklearn.metrics.mean\_squared\_log\_error
=========================================
sklearn.metrics.mean\_squared\_log\_error(*y\_true*, *y\_pred*, *\**, *sample\_weight=None*, *multioutput='uniform\_average'*, *squared=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_regression.py#L461)
Mean squared logarithmic error regression loss.
Read more in the [User Guide](../model_evaluation#mean-squared-log-error).
Parameters:
**y\_true**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
Ground truth (correct) target values.
**y\_pred**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
Estimated target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**multioutput**{‘raw\_values’, ‘uniform\_average’} or array-like of shape (n\_outputs,), default=’uniform\_average’
Defines aggregating of multiple output values. Array-like value defines weights used to average errors.
‘raw\_values’ :
Returns a full set of errors when the input is of multioutput format.
‘uniform\_average’ :
Errors of all outputs are averaged with uniform weight.
**squared**bool, default=True
If True returns MSLE (mean squared log error) value. If False returns RMSLE (root mean squared log error) value.
Returns:
**loss**float or ndarray of floats
A non-negative floating point value (the best value is 0.0), or an array of floating point values, one for each individual target.
#### Examples
```
>>> from sklearn.metrics import mean_squared_log_error
>>> y_true = [3, 5, 2.5, 7]
>>> y_pred = [2.5, 5, 4, 8]
>>> mean_squared_log_error(y_true, y_pred)
0.039...
>>> mean_squared_log_error(y_true, y_pred, squared=False)
0.199...
>>> y_true = [[0.5, 1], [1, 2], [7, 6]]
>>> y_pred = [[0.5, 2], [1, 2.5], [8, 8]]
>>> mean_squared_log_error(y_true, y_pred)
0.044...
>>> mean_squared_log_error(y_true, y_pred, multioutput='raw_values')
array([0.00462428, 0.08377444])
>>> mean_squared_log_error(y_true, y_pred, multioutput=[0.3, 0.7])
0.060...
```
scikit_learn sklearn.metrics.adjusted_rand_score sklearn.metrics.adjusted\_rand\_score
=====================================
sklearn.metrics.adjusted\_rand\_score(*labels\_true*, *labels\_pred*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/cluster/_supervised.py#L309)
Rand index adjusted for chance.
The Rand Index computes a similarity measure between two clusterings by considering all pairs of samples and counting pairs that are assigned in the same or different clusters in the predicted and true clusterings.
The raw RI score is then “adjusted for chance” into the ARI score using the following scheme:
```
ARI = (RI - Expected_RI) / (max(RI) - Expected_RI)
```
The adjusted Rand index is thus ensured to have a value close to 0.0 for random labeling independently of the number of clusters and samples and exactly 1.0 when the clusterings are identical (up to a permutation).
ARI is a symmetric measure:
```
adjusted_rand_score(a, b) == adjusted_rand_score(b, a)
```
Read more in the [User Guide](../clustering#adjusted-rand-score).
Parameters:
**labels\_true**int array, shape = [n\_samples]
Ground truth class labels to be used as a reference
**labels\_pred**array-like of shape (n\_samples,)
Cluster labels to evaluate
Returns:
**ARI**float
Similarity score between -1.0 and 1.0. Random labelings have an ARI close to 0.0. 1.0 stands for perfect match.
See also
[`adjusted_mutual_info_score`](sklearn.metrics.adjusted_mutual_info_score#sklearn.metrics.adjusted_mutual_info_score "sklearn.metrics.adjusted_mutual_info_score")
Adjusted Mutual Information.
#### References
[Hubert1985] L. Hubert and P. Arabie, Comparing Partitions, Journal of Classification 1985 <https://link.springer.com/article/10.1007%2FBF01908075>
[Steinley2004] D. Steinley, Properties of the Hubert-Arabie adjusted Rand index, Psychological Methods 2004
[wk] <https://en.wikipedia.org/wiki/Rand_index#Adjusted_Rand_index>
#### Examples
Perfectly matching labelings have a score of 1 even
```
>>> from sklearn.metrics.cluster import adjusted_rand_score
>>> adjusted_rand_score([0, 0, 1, 1], [0, 0, 1, 1])
1.0
>>> adjusted_rand_score([0, 0, 1, 1], [1, 1, 0, 0])
1.0
```
Labelings that assign all classes members to the same clusters are complete but may not always be pure, hence penalized:
```
>>> adjusted_rand_score([0, 0, 1, 2], [0, 0, 1, 1])
0.57...
```
ARI is symmetric, so labelings that have pure clusters with members coming from the same classes but unnecessary splits are penalized:
```
>>> adjusted_rand_score([0, 0, 1, 1], [0, 0, 1, 2])
0.57...
```
If classes members are completely split across different clusters, the assignment is totally incomplete, hence the ARI is very low:
```
>>> adjusted_rand_score([0, 0, 0, 0], [0, 1, 2, 3])
0.0
```
Examples using `sklearn.metrics.adjusted_rand_score`
----------------------------------------------------
[A demo of K-Means clustering on the handwritten digits data](../../auto_examples/cluster/plot_kmeans_digits#sphx-glr-auto-examples-cluster-plot-kmeans-digits-py)
[Adjustment for chance in clustering performance evaluation](../../auto_examples/cluster/plot_adjusted_for_chance_measures#sphx-glr-auto-examples-cluster-plot-adjusted-for-chance-measures-py)
[Demo of DBSCAN clustering algorithm](../../auto_examples/cluster/plot_dbscan#sphx-glr-auto-examples-cluster-plot-dbscan-py)
[Demo of affinity propagation clustering algorithm](../../auto_examples/cluster/plot_affinity_propagation#sphx-glr-auto-examples-cluster-plot-affinity-propagation-py)
[Clustering text documents using k-means](../../auto_examples/text/plot_document_clustering#sphx-glr-auto-examples-text-plot-document-clustering-py)
| programming_docs |
scikit_learn sklearn.cluster.SpectralCoclustering sklearn.cluster.SpectralCoclustering
====================================
*class*sklearn.cluster.SpectralCoclustering(*n\_clusters=3*, *\**, *svd\_method='randomized'*, *n\_svd\_vecs=None*, *mini\_batch=False*, *init='k-means++'*, *n\_init=10*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_bicluster.py#L209)
Spectral Co-Clustering algorithm (Dhillon, 2001).
Clusters rows and columns of an array `X` to solve the relaxed normalized cut of the bipartite graph created from `X` as follows: the edge between row vertex `i` and column vertex `j` has weight `X[i, j]`.
The resulting bicluster structure is block-diagonal, since each row and each column belongs to exactly one bicluster.
Supports sparse matrices, as long as they are nonnegative.
Read more in the [User Guide](../biclustering#spectral-coclustering).
Parameters:
**n\_clusters**int, default=3
The number of biclusters to find.
**svd\_method**{‘randomized’, ‘arpack’}, default=’randomized’
Selects the algorithm for finding singular vectors. May be ‘randomized’ or ‘arpack’. If ‘randomized’, use [`sklearn.utils.extmath.randomized_svd`](sklearn.utils.extmath.randomized_svd#sklearn.utils.extmath.randomized_svd "sklearn.utils.extmath.randomized_svd"), which may be faster for large matrices. If ‘arpack’, use [`scipy.sparse.linalg.svds`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.sparse.linalg.svds.html#scipy.sparse.linalg.svds "(in SciPy v1.9.3)"), which is more accurate, but possibly slower in some cases.
**n\_svd\_vecs**int, default=None
Number of vectors to use in calculating the SVD. Corresponds to `ncv` when `svd_method=arpack` and `n_oversamples` when `svd_method` is ‘randomized`.
**mini\_batch**bool, default=False
Whether to use mini-batch k-means, which is faster but may get different results.
**init**{‘k-means++’, ‘random’, or ndarray of shape (n\_clusters, n\_features), default=’k-means++’
Method for initialization of k-means algorithm; defaults to ‘k-means++’.
**n\_init**int, default=10
Number of random initializations that are tried with the k-means algorithm.
If mini-batch k-means is used, the best initialization is chosen and the algorithm runs once. Otherwise, the algorithm is run for each initialization and the best solution chosen.
**random\_state**int, RandomState instance, default=None
Used for randomizing the singular value decomposition and the k-means initialization. Use an int to make the randomness deterministic. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Attributes:
**rows\_**array-like of shape (n\_row\_clusters, n\_rows)
Results of the clustering. `rows[i, r]` is True if cluster `i` contains row `r`. Available only after calling `fit`.
**columns\_**array-like of shape (n\_column\_clusters, n\_columns)
Results of the clustering, like `rows`.
**row\_labels\_**array-like of shape (n\_rows,)
The bicluster label of each row.
**column\_labels\_**array-like of shape (n\_cols,)
The bicluster label of each column.
[`biclusters_`](#sklearn.cluster.SpectralCoclustering.biclusters_ "sklearn.cluster.SpectralCoclustering.biclusters_")tuple of two ndarrays
Convenient way to get row and column indicators together.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`SpectralBiclustering`](sklearn.cluster.spectralbiclustering#sklearn.cluster.SpectralBiclustering "sklearn.cluster.SpectralBiclustering")
Partitions rows and columns under the assumption that the data has an underlying checkerboard structure.
#### References
* [Dhillon, Inderjit S, 2001. Co-clustering documents and words using bipartite spectral graph partitioning.](https://doi.org/10.1145/502512.502550)
#### Examples
```
>>> from sklearn.cluster import SpectralCoclustering
>>> import numpy as np
>>> X = np.array([[1, 1], [2, 1], [1, 0],
... [4, 7], [3, 5], [3, 6]])
>>> clustering = SpectralCoclustering(n_clusters=2, random_state=0).fit(X)
>>> clustering.row_labels_
array([0, 1, 1, 0, 0, 0], dtype=int32)
>>> clustering.column_labels_
array([0, 0], dtype=int32)
>>> clustering
SpectralCoclustering(n_clusters=2, random_state=0)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.cluster.SpectralCoclustering.fit "sklearn.cluster.SpectralCoclustering.fit")(X[, y]) | Create a biclustering for X. |
| [`get_indices`](#sklearn.cluster.SpectralCoclustering.get_indices "sklearn.cluster.SpectralCoclustering.get_indices")(i) | Row and column indices of the `i`'th bicluster. |
| [`get_params`](#sklearn.cluster.SpectralCoclustering.get_params "sklearn.cluster.SpectralCoclustering.get_params")([deep]) | Get parameters for this estimator. |
| [`get_shape`](#sklearn.cluster.SpectralCoclustering.get_shape "sklearn.cluster.SpectralCoclustering.get_shape")(i) | Shape of the `i`'th bicluster. |
| [`get_submatrix`](#sklearn.cluster.SpectralCoclustering.get_submatrix "sklearn.cluster.SpectralCoclustering.get_submatrix")(i, data) | Return the submatrix corresponding to bicluster `i`. |
| [`set_params`](#sklearn.cluster.SpectralCoclustering.set_params "sklearn.cluster.SpectralCoclustering.set_params")(\*\*params) | Set the parameters of this estimator. |
*property*biclusters\_
Convenient way to get row and column indicators together.
Returns the `rows_` and `columns_` members.
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_bicluster.py#L117)
Create a biclustering for X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**self**object
SpectralBiclustering instance.
get\_indices(*i*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L769)
Row and column indices of the `i`’th bicluster.
Only works if `rows_` and `columns_` attributes exist.
Parameters:
**i**int
The index of the cluster.
Returns:
**row\_ind**ndarray, dtype=np.intp
Indices of rows in the dataset that belong to the bicluster.
**col\_ind**ndarray, dtype=np.intp
Indices of columns in the dataset that belong to the bicluster.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
get\_shape(*i*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L790)
Shape of the `i`’th bicluster.
Parameters:
**i**int
The index of the cluster.
Returns:
**n\_rows**int
Number of rows in the bicluster.
**n\_cols**int
Number of columns in the bicluster.
get\_submatrix(*i*, *data*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L809)
Return the submatrix corresponding to bicluster `i`.
Parameters:
**i**int
The index of the cluster.
**data**array-like of shape (n\_samples, n\_features)
The data.
Returns:
**submatrix**ndarray of shape (n\_rows, n\_cols)
The submatrix corresponding to bicluster `i`.
#### Notes
Works with sparse matrices. Only works if `rows_` and `columns_` attributes exist.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.cluster.SpectralCoclustering`
-----------------------------------------------------
[A demo of the Spectral Co-Clustering algorithm](../../auto_examples/bicluster/plot_spectral_coclustering#sphx-glr-auto-examples-bicluster-plot-spectral-coclustering-py)
[Biclustering documents with the Spectral Co-clustering algorithm](../../auto_examples/bicluster/plot_bicluster_newsgroups#sphx-glr-auto-examples-bicluster-plot-bicluster-newsgroups-py)
scikit_learn sklearn.metrics.median_absolute_error sklearn.metrics.median\_absolute\_error
=======================================
sklearn.metrics.median\_absolute\_error(*y\_true*, *y\_pred*, *\**, *multioutput='uniform\_average'*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_regression.py#L539)
Median absolute error regression loss.
Median absolute error output is non-negative floating point. The best value is 0.0. Read more in the [User Guide](../model_evaluation#median-absolute-error).
Parameters:
**y\_true**array-like of shape = (n\_samples) or (n\_samples, n\_outputs)
Ground truth (correct) target values.
**y\_pred**array-like of shape = (n\_samples) or (n\_samples, n\_outputs)
Estimated target values.
**multioutput**{‘raw\_values’, ‘uniform\_average’} or array-like of shape (n\_outputs,), default=’uniform\_average’
Defines aggregating of multiple output values. Array-like value defines weights used to average errors.
‘raw\_values’ :
Returns a full set of errors in case of multioutput input.
‘uniform\_average’ :
Errors of all outputs are averaged with uniform weight.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
New in version 0.24.
Returns:
**loss**float or ndarray of floats
If multioutput is ‘raw\_values’, then mean absolute error is returned for each output separately. If multioutput is ‘uniform\_average’ or an ndarray of weights, then the weighted average of all output errors is returned.
#### Examples
```
>>> from sklearn.metrics import median_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> median_absolute_error(y_true, y_pred)
0.5
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> median_absolute_error(y_true, y_pred)
0.75
>>> median_absolute_error(y_true, y_pred, multioutput='raw_values')
array([0.5, 1. ])
>>> median_absolute_error(y_true, y_pred, multioutput=[0.3, 0.7])
0.85
```
Examples using `sklearn.metrics.median_absolute_error`
------------------------------------------------------
[Common pitfalls in the interpretation of coefficients of linear models](../../auto_examples/inspection/plot_linear_model_coefficient_interpretation#sphx-glr-auto-examples-inspection-plot-linear-model-coefficient-interpretation-py)
[Effect of transforming the targets in regression model](../../auto_examples/compose/plot_transformed_target#sphx-glr-auto-examples-compose-plot-transformed-target-py)
scikit_learn sklearn.feature_selection.RFE sklearn.feature\_selection.RFE
==============================
*class*sklearn.feature\_selection.RFE(*estimator*, *\**, *n\_features\_to\_select=None*, *step=1*, *verbose=0*, *importance\_getter='auto'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_rfe.py#L59)
Feature ranking with recursive feature elimination.
Given an external estimator that assigns weights to features (e.g., the coefficients of a linear model), the goal of recursive feature elimination (RFE) is to select features by recursively considering smaller and smaller sets of features. First, the estimator is trained on the initial set of features and the importance of each feature is obtained either through any specific attribute or callable. Then, the least important features are pruned from current set of features. That procedure is recursively repeated on the pruned set until the desired number of features to select is eventually reached.
Read more in the [User Guide](../feature_selection#rfe).
Parameters:
**estimator**`Estimator` instance
A supervised learning estimator with a `fit` method that provides information about feature importance (e.g. `coef_`, `feature_importances_`).
**n\_features\_to\_select**int or float, default=None
The number of features to select. If `None`, half of the features are selected. If integer, the parameter is the absolute number of features to select. If float between 0 and 1, it is the fraction of features to select.
Changed in version 0.24: Added float values for fractions.
**step**int or float, default=1
If greater than or equal to 1, then `step` corresponds to the (integer) number of features to remove at each iteration. If within (0.0, 1.0), then `step` corresponds to the percentage (rounded down) of features to remove at each iteration.
**verbose**int, default=0
Controls verbosity of output.
**importance\_getter**str or callable, default=’auto’
If ‘auto’, uses the feature importance either through a `coef_` or `feature_importances_` attributes of estimator.
Also accepts a string that specifies an attribute name/path for extracting feature importance (implemented with `attrgetter`). For example, give `regressor_.coef_` in case of [`TransformedTargetRegressor`](sklearn.compose.transformedtargetregressor#sklearn.compose.TransformedTargetRegressor "sklearn.compose.TransformedTargetRegressor") or `named_steps.clf.feature_importances_` in case of class:`~sklearn.pipeline.Pipeline` with its last step named `clf`.
If `callable`, overrides the default feature importance getter. The callable is passed with the fitted estimator and it should return importance for each feature.
New in version 0.24.
Attributes:
[`classes_`](#sklearn.feature_selection.RFE.classes_ "sklearn.feature_selection.RFE.classes_")ndarray of shape (n\_classes,)
Classes labels available when `estimator` is a classifier.
**estimator\_**`Estimator` instance
The fitted estimator used to select features.
**n\_features\_**int
The number of selected features.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Only defined if the underlying estimator exposes such an attribute when fit.
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**ranking\_**ndarray of shape (n\_features,)
The feature ranking, such that `ranking_[i]` corresponds to the ranking position of the i-th feature. Selected (i.e., estimated best) features are assigned rank 1.
**support\_**ndarray of shape (n\_features,)
The mask of selected features.
See also
[`RFECV`](sklearn.feature_selection.rfecv#sklearn.feature_selection.RFECV "sklearn.feature_selection.RFECV")
Recursive feature elimination with built-in cross-validated selection of the best number of features.
[`SelectFromModel`](sklearn.feature_selection.selectfrommodel#sklearn.feature_selection.SelectFromModel "sklearn.feature_selection.SelectFromModel")
Feature selection based on thresholds of importance weights.
[`SequentialFeatureSelector`](sklearn.feature_selection.sequentialfeatureselector#sklearn.feature_selection.SequentialFeatureSelector "sklearn.feature_selection.SequentialFeatureSelector")
Sequential cross-validation based feature selection. Does not rely on importance weights.
#### Notes
Allows NaN/Inf in the input if the underlying estimator does as well.
#### References
[1] Guyon, I., Weston, J., Barnhill, S., & Vapnik, V., “Gene selection for cancer classification using support vector machines”, Mach. Learn., 46(1-3), 389–422, 2002.
#### Examples
The following example shows how to retrieve the 5 most informative features in the Friedman #1 dataset.
```
>>> from sklearn.datasets import make_friedman1
>>> from sklearn.feature_selection import RFE
>>> from sklearn.svm import SVR
>>> X, y = make_friedman1(n_samples=50, n_features=10, random_state=0)
>>> estimator = SVR(kernel="linear")
>>> selector = RFE(estimator, n_features_to_select=5, step=1)
>>> selector = selector.fit(X, y)
>>> selector.support_
array([ True, True, True, True, True, False, False, False, False,
False])
>>> selector.ranking_
array([1, 1, 1, 1, 1, 6, 4, 3, 2, 5])
```
#### Methods
| | |
| --- | --- |
| [`decision_function`](#sklearn.feature_selection.RFE.decision_function "sklearn.feature_selection.RFE.decision_function")(X) | Compute the decision function of `X`. |
| [`fit`](#sklearn.feature_selection.RFE.fit "sklearn.feature_selection.RFE.fit")(X, y, \*\*fit\_params) | Fit the RFE model and then the underlying estimator on the selected features. |
| [`fit_transform`](#sklearn.feature_selection.RFE.fit_transform "sklearn.feature_selection.RFE.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.feature_selection.RFE.get_feature_names_out "sklearn.feature_selection.RFE.get_feature_names_out")([input\_features]) | Mask feature names according to selected features. |
| [`get_params`](#sklearn.feature_selection.RFE.get_params "sklearn.feature_selection.RFE.get_params")([deep]) | Get parameters for this estimator. |
| [`get_support`](#sklearn.feature_selection.RFE.get_support "sklearn.feature_selection.RFE.get_support")([indices]) | Get a mask, or integer index, of the features selected. |
| [`inverse_transform`](#sklearn.feature_selection.RFE.inverse_transform "sklearn.feature_selection.RFE.inverse_transform")(X) | Reverse the transformation operation. |
| [`predict`](#sklearn.feature_selection.RFE.predict "sklearn.feature_selection.RFE.predict")(X) | Reduce X to the selected features and predict using the estimator. |
| [`predict_log_proba`](#sklearn.feature_selection.RFE.predict_log_proba "sklearn.feature_selection.RFE.predict_log_proba")(X) | Predict class log-probabilities for X. |
| [`predict_proba`](#sklearn.feature_selection.RFE.predict_proba "sklearn.feature_selection.RFE.predict_proba")(X) | Predict class probabilities for X. |
| [`score`](#sklearn.feature_selection.RFE.score "sklearn.feature_selection.RFE.score")(X, y, \*\*fit\_params) | Reduce X to the selected features and return the score of the estimator. |
| [`set_params`](#sklearn.feature_selection.RFE.set_params "sklearn.feature_selection.RFE.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.feature_selection.RFE.transform "sklearn.feature_selection.RFE.transform")(X) | Reduce X to the selected features. |
*property*classes\_
Classes labels available when `estimator` is a classifier.
Returns:
ndarray of shape (n\_classes,)
decision\_function(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_rfe.py#L382)
Compute the decision function of `X`.
Parameters:
**X**{array-like or sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
Returns:
**score**array, shape = [n\_samples, n\_classes] or [n\_samples]
The decision function of the input samples. The order of the classes corresponds to that in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_). Regression and binary classification produce an array of shape [n\_samples].
fit(*X*, *y*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_rfe.py#L215)
Fit the RFE model and then the underlying estimator on the selected features.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples.
**y**array-like of shape (n\_samples,)
The target values.
**\*\*fit\_params**dict
Additional parameters passed to the `fit` method of the underlying estimator.
Returns:
**self**object
Fitted estimator.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L146)
Mask feature names according to selected features.
Parameters:
**input\_features**array-like of str or None, default=None
Input features.
* If `input_features` is `None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then the following input feature names are generated: `["x0", "x1", ..., "x(n_features_in_ - 1)"]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
get\_support(*indices=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L33)
Get a mask, or integer index, of the features selected.
Parameters:
**indices**bool, default=False
If True, the return value will be an array of integers, rather than a boolean mask.
Returns:
**support**array
An index that selects the retained features from a feature vector. If `indices` is False, this is a boolean array of shape [# input features], in which an element is True iff its corresponding feature is selected for retention. If `indices` is True, this is an integer array of shape [# output features] whose values are indices into the input feature vector.
inverse\_transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L106)
Reverse the transformation operation.
Parameters:
**X**array of shape [n\_samples, n\_selected\_features]
The input samples.
Returns:
**X\_r**array of shape [n\_samples, n\_original\_features]
`X` with columns of zeros inserted where features would have been removed by [`transform`](#sklearn.feature_selection.RFE.transform "sklearn.feature_selection.RFE.transform").
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_rfe.py#L334)
Reduce X to the selected features and predict using the estimator.
Parameters:
**X**array of shape [n\_samples, n\_features]
The input samples.
Returns:
**y**array of shape [n\_samples]
The predicted target values.
predict\_log\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_rfe.py#L424)
Predict class log-probabilities for X.
Parameters:
**X**array of shape [n\_samples, n\_features]
The input samples.
Returns:
**p**array of shape (n\_samples, n\_classes)
The class log-probabilities of the input samples. The order of the classes corresponds to that in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_rfe.py#L404)
Predict class probabilities for X.
Parameters:
**X**{array-like or sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
Returns:
**p**array of shape (n\_samples, n\_classes)
The class probabilities of the input samples. The order of the classes corresponds to that in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
score(*X*, *y*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_rfe.py#L351)
Reduce X to the selected features and return the score of the estimator.
Parameters:
**X**array of shape [n\_samples, n\_features]
The input samples.
**y**array of shape [n\_samples]
The target values.
**\*\*fit\_params**dict
Parameters to pass to the `score` method of the underlying estimator.
New in version 1.0.
Returns:
**score**float
Score of the underlying base estimator computed with the selected features returned by `rfe.transform(X)` and `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L68)
Reduce X to the selected features.
Parameters:
**X**array of shape [n\_samples, n\_features]
The input samples.
Returns:
**X\_r**array of shape [n\_samples, n\_selected\_features]
The input samples with only the selected features.
Examples using `sklearn.feature_selection.RFE`
----------------------------------------------
[Recursive feature elimination](../../auto_examples/feature_selection/plot_rfe_digits#sphx-glr-auto-examples-feature-selection-plot-rfe-digits-py)
| programming_docs |
scikit_learn sklearn.kernel_approximation.SkewedChi2Sampler sklearn.kernel\_approximation.SkewedChi2Sampler
===============================================
*class*sklearn.kernel\_approximation.SkewedChi2Sampler(*\**, *skewedness=1.0*, *n\_components=100*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/kernel_approximation.py#L372)
Approximate feature map for “skewed chi-squared” kernel.
Read more in the [User Guide](../kernel_approximation#skewed-chi-kernel-approx).
Parameters:
**skewedness**float, default=1.0
“skewedness” parameter of the kernel. Needs to be cross-validated.
**n\_components**int, default=100
Number of Monte Carlo samples per original feature. Equals the dimensionality of the computed feature space.
**random\_state**int, RandomState instance or None, default=None
Pseudo-random number generator to control the generation of the random weights and random offset when fitting the training data. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Attributes:
**random\_weights\_**ndarray of shape (n\_features, n\_components)
Weight array, sampled from a secant hyperbolic distribution, which will be used to linearly transform the log of the data.
**random\_offset\_**ndarray of shape (n\_features, n\_components)
Bias term, which will be added to the data. It is uniformly distributed between 0 and 2\*pi.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`AdditiveChi2Sampler`](sklearn.kernel_approximation.additivechi2sampler#sklearn.kernel_approximation.AdditiveChi2Sampler "sklearn.kernel_approximation.AdditiveChi2Sampler")
Approximate feature map for additive chi2 kernel.
[`Nystroem`](sklearn.kernel_approximation.nystroem#sklearn.kernel_approximation.Nystroem "sklearn.kernel_approximation.Nystroem")
Approximate a kernel map using a subset of the training data.
[`RBFSampler`](sklearn.kernel_approximation.rbfsampler#sklearn.kernel_approximation.RBFSampler "sklearn.kernel_approximation.RBFSampler")
Approximate a RBF kernel feature map using random Fourier features.
[`SkewedChi2Sampler`](#sklearn.kernel_approximation.SkewedChi2Sampler "sklearn.kernel_approximation.SkewedChi2Sampler")
Approximate feature map for “skewed chi-squared” kernel.
[`sklearn.metrics.pairwise.chi2_kernel`](sklearn.metrics.pairwise.chi2_kernel#sklearn.metrics.pairwise.chi2_kernel "sklearn.metrics.pairwise.chi2_kernel")
The exact chi squared kernel.
[`sklearn.metrics.pairwise.kernel_metrics`](sklearn.metrics.pairwise.kernel_metrics#sklearn.metrics.pairwise.kernel_metrics "sklearn.metrics.pairwise.kernel_metrics")
List of built-in kernels.
#### References
See “Random Fourier Approximations for Skewed Multiplicative Histogram Kernels” by Fuxin Li, Catalin Ionescu and Cristian Sminchisescu.
#### Examples
```
>>> from sklearn.kernel_approximation import SkewedChi2Sampler
>>> from sklearn.linear_model import SGDClassifier
>>> X = [[0, 0], [1, 1], [1, 0], [0, 1]]
>>> y = [0, 0, 1, 1]
>>> chi2_feature = SkewedChi2Sampler(skewedness=.01,
... n_components=10,
... random_state=0)
>>> X_features = chi2_feature.fit_transform(X, y)
>>> clf = SGDClassifier(max_iter=10, tol=1e-3)
>>> clf.fit(X_features, y)
SGDClassifier(max_iter=10)
>>> clf.score(X_features, y)
1.0
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.kernel_approximation.SkewedChi2Sampler.fit "sklearn.kernel_approximation.SkewedChi2Sampler.fit")(X[, y]) | Fit the model with X. |
| [`fit_transform`](#sklearn.kernel_approximation.SkewedChi2Sampler.fit_transform "sklearn.kernel_approximation.SkewedChi2Sampler.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.kernel_approximation.SkewedChi2Sampler.get_feature_names_out "sklearn.kernel_approximation.SkewedChi2Sampler.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.kernel_approximation.SkewedChi2Sampler.get_params "sklearn.kernel_approximation.SkewedChi2Sampler.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.kernel_approximation.SkewedChi2Sampler.set_params "sklearn.kernel_approximation.SkewedChi2Sampler.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.kernel_approximation.SkewedChi2Sampler.transform "sklearn.kernel_approximation.SkewedChi2Sampler.transform")(X) | Apply the approximate feature map to X. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/kernel_approximation.py#L452)
Fit the model with X.
Samples random projection according to n\_features.
Parameters:
**X**array-like, shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like, shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.kernel_approximation.SkewedChi2Sampler.fit "sklearn.kernel_approximation.SkewedChi2Sampler.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/kernel_approximation.py#L483)
Apply the approximate feature map to X.
Parameters:
**X**array-like, shape (n\_samples, n\_features)
New data, where `n_samples` is the number of samples and `n_features` is the number of features. All values of X must be strictly greater than “-skewedness”.
Returns:
**X\_new**array-like, shape (n\_samples, n\_components)
Returns the instance itself.
scikit_learn sklearn.metrics.DetCurveDisplay sklearn.metrics.DetCurveDisplay
===============================
*class*sklearn.metrics.DetCurveDisplay(*\**, *fpr*, *fnr*, *estimator\_name=None*, *pos\_label=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_plot/det_curve.py#L12)
DET curve visualization.
It is recommend to use [`from_estimator`](#sklearn.metrics.DetCurveDisplay.from_estimator "sklearn.metrics.DetCurveDisplay.from_estimator") or [`from_predictions`](#sklearn.metrics.DetCurveDisplay.from_predictions "sklearn.metrics.DetCurveDisplay.from_predictions") to create a visualizer. All parameters are stored as attributes.
Read more in the [User Guide](https://scikit-learn.org/1.1/visualizations.html#visualizations).
New in version 0.24.
Parameters:
**fpr**ndarray
False positive rate.
**fnr**ndarray
False negative rate.
**estimator\_name**str, default=None
Name of estimator. If None, the estimator name is not shown.
**pos\_label**str or int, default=None
The label of the positive class.
Attributes:
**line\_**matplotlib Artist
DET Curve.
**ax\_**matplotlib Axes
Axes with DET Curve.
**figure\_**matplotlib Figure
Figure containing the curve.
See also
[`det_curve`](sklearn.metrics.det_curve#sklearn.metrics.det_curve "sklearn.metrics.det_curve")
Compute error rates for different probability thresholds.
[`DetCurveDisplay.from_estimator`](#sklearn.metrics.DetCurveDisplay.from_estimator "sklearn.metrics.DetCurveDisplay.from_estimator")
Plot DET curve given an estimator and some data.
[`DetCurveDisplay.from_predictions`](#sklearn.metrics.DetCurveDisplay.from_predictions "sklearn.metrics.DetCurveDisplay.from_predictions")
Plot DET curve given the true and predicted labels.
#### Examples
```
>>> import matplotlib.pyplot as plt
>>> from sklearn.datasets import make_classification
>>> from sklearn.metrics import det_curve, DetCurveDisplay
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.svm import SVC
>>> X, y = make_classification(n_samples=1000, random_state=0)
>>> X_train, X_test, y_train, y_test = train_test_split(
... X, y, test_size=0.4, random_state=0)
>>> clf = SVC(random_state=0).fit(X_train, y_train)
>>> y_pred = clf.decision_function(X_test)
>>> fpr, fnr, _ = det_curve(y_test, y_pred)
>>> display = DetCurveDisplay(
... fpr=fpr, fnr=fnr, estimator_name="SVC"
... )
>>> display.plot()
<...>
>>> plt.show()
```
#### Methods
| | |
| --- | --- |
| [`from_estimator`](#sklearn.metrics.DetCurveDisplay.from_estimator "sklearn.metrics.DetCurveDisplay.from_estimator")(estimator, X, y, \*[, ...]) | Plot DET curve given an estimator and data. |
| [`from_predictions`](#sklearn.metrics.DetCurveDisplay.from_predictions "sklearn.metrics.DetCurveDisplay.from_predictions")(y\_true, y\_pred, \*[, ...]) | Plot DET curve given the true and predicted labels. |
| [`plot`](#sklearn.metrics.DetCurveDisplay.plot "sklearn.metrics.DetCurveDisplay.plot")([ax, name]) | Plot visualization. |
*classmethod*from\_estimator(*estimator*, *X*, *y*, *\**, *sample\_weight=None*, *response\_method='auto'*, *pos\_label=None*, *name=None*, *ax=None*, *\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_plot/det_curve.py#L83)
Plot DET curve given an estimator and data.
Read more in the [User Guide](https://scikit-learn.org/1.1/visualizations.html#visualizations).
New in version 1.0.
Parameters:
**estimator**estimator instance
Fitted classifier or a fitted [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline") in which the last estimator is a classifier.
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Input values.
**y**array-like of shape (n\_samples,)
Target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**response\_method**{‘predict\_proba’, ‘decision\_function’, ‘auto’} default=’auto’
Specifies whether to use [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) or [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) as the predicted target response. If set to ‘auto’, [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) is tried first and if it does not exist [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) is tried next.
**pos\_label**str or int, default=None
The label of the positive class. When `pos_label=None`, if `y_true` is in {-1, 1} or {0, 1}, `pos_label` is set to 1, otherwise an error will be raised.
**name**str, default=None
Name of DET curve for labeling. If `None`, use the name of the estimator.
**ax**matplotlib axes, default=None
Axes object to plot on. If `None`, a new figure and axes is created.
**\*\*kwargs**dict
Additional keywords arguments passed to matplotlib `plot` function.
Returns:
**display**[`DetCurveDisplay`](#sklearn.metrics.DetCurveDisplay "sklearn.metrics.DetCurveDisplay")
Object that stores computed values.
See also
[`det_curve`](sklearn.metrics.det_curve#sklearn.metrics.det_curve "sklearn.metrics.det_curve")
Compute error rates for different probability thresholds.
[`DetCurveDisplay.from_predictions`](#sklearn.metrics.DetCurveDisplay.from_predictions "sklearn.metrics.DetCurveDisplay.from_predictions")
Plot DET curve given the true and predicted labels.
[`plot_roc_curve`](sklearn.metrics.plot_roc_curve#sklearn.metrics.plot_roc_curve "sklearn.metrics.plot_roc_curve")
Plot Receiver operating characteristic (ROC) curve.
#### Examples
```
>>> import matplotlib.pyplot as plt
>>> from sklearn.datasets import make_classification
>>> from sklearn.metrics import DetCurveDisplay
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.svm import SVC
>>> X, y = make_classification(n_samples=1000, random_state=0)
>>> X_train, X_test, y_train, y_test = train_test_split(
... X, y, test_size=0.4, random_state=0)
>>> clf = SVC(random_state=0).fit(X_train, y_train)
>>> DetCurveDisplay.from_estimator(
... clf, X_test, y_test)
<...>
>>> plt.show()
```
*classmethod*from\_predictions(*y\_true*, *y\_pred*, *\**, *sample\_weight=None*, *pos\_label=None*, *name=None*, *ax=None*, *\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_plot/det_curve.py#L190)
Plot DET curve given the true and predicted labels.
Read more in the [User Guide](https://scikit-learn.org/1.1/visualizations.html#visualizations).
New in version 1.0.
Parameters:
**y\_true**array-like of shape (n\_samples,)
True labels.
**y\_pred**array-like of shape (n\_samples,)
Target scores, can either be probability estimates of the positive class, confidence values, or non-thresholded measure of decisions (as returned by `decision_function` on some classifiers).
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**pos\_label**str or int, default=None
The label of the positive class. When `pos_label=None`, if `y_true` is in {-1, 1} or {0, 1}, `pos_label` is set to 1, otherwise an error will be raised.
**name**str, default=None
Name of DET curve for labeling. If `None`, name will be set to `"Classifier"`.
**ax**matplotlib axes, default=None
Axes object to plot on. If `None`, a new figure and axes is created.
**\*\*kwargs**dict
Additional keywords arguments passed to matplotlib `plot` function.
Returns:
**display**[`DetCurveDisplay`](#sklearn.metrics.DetCurveDisplay "sklearn.metrics.DetCurveDisplay")
Object that stores computed values.
See also
[`det_curve`](sklearn.metrics.det_curve#sklearn.metrics.det_curve "sklearn.metrics.det_curve")
Compute error rates for different probability thresholds.
[`DetCurveDisplay.from_estimator`](#sklearn.metrics.DetCurveDisplay.from_estimator "sklearn.metrics.DetCurveDisplay.from_estimator")
Plot DET curve given an estimator and some data.
[`plot_roc_curve`](sklearn.metrics.plot_roc_curve#sklearn.metrics.plot_roc_curve "sklearn.metrics.plot_roc_curve")
Plot Receiver operating characteristic (ROC) curve.
#### Examples
```
>>> import matplotlib.pyplot as plt
>>> from sklearn.datasets import make_classification
>>> from sklearn.metrics import DetCurveDisplay
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.svm import SVC
>>> X, y = make_classification(n_samples=1000, random_state=0)
>>> X_train, X_test, y_train, y_test = train_test_split(
... X, y, test_size=0.4, random_state=0)
>>> clf = SVC(random_state=0).fit(X_train, y_train)
>>> y_pred = clf.decision_function(X_test)
>>> DetCurveDisplay.from_predictions(
... y_test, y_pred)
<...>
>>> plt.show()
```
plot(*ax=None*, *\**, *name=None*, *\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_plot/det_curve.py#L287)
Plot visualization.
Parameters:
**ax**matplotlib axes, default=None
Axes object to plot on. If `None`, a new figure and axes is created.
**name**str, default=None
Name of DET curve for labeling. If `None`, use `estimator_name` if it is not `None`, otherwise no labeling is shown.
**\*\*kwargs**dict
Additional keywords arguments passed to matplotlib `plot` function.
Returns:
**display**`DetCurveDisplay`
Object that stores computed values.
scikit_learn sklearn.feature_selection.SequentialFeatureSelector sklearn.feature\_selection.SequentialFeatureSelector
====================================================
*class*sklearn.feature\_selection.SequentialFeatureSelector(*estimator*, *\**, *n\_features\_to\_select='warn'*, *tol=None*, *direction='forward'*, *scoring=None*, *cv=5*, *n\_jobs=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_sequential.py#L17)
Transformer that performs Sequential Feature Selection.
This Sequential Feature Selector adds (forward selection) or removes (backward selection) features to form a feature subset in a greedy fashion. At each stage, this estimator chooses the best feature to add or remove based on the cross-validation score of an estimator. In the case of unsupervised learning, this Sequential Feature Selector looks only at the features (X), not the desired outputs (y).
Read more in the [User Guide](../feature_selection#sequential-feature-selection).
New in version 0.24.
Parameters:
**estimator**estimator instance
An unfitted estimator.
**n\_features\_to\_select**“auto”, int or float, default=’warn’
If `"auto"`, the behaviour depends on the `tol` parameter:
* if `tol` is not `None`, then features are selected until the score improvement does not exceed `tol`.
* otherwise, half of the features are selected.
If integer, the parameter is the absolute number of features to select. If float between 0 and 1, it is the fraction of features to select.
New in version 1.1: The option `"auto"` was added in version 1.1.
Deprecated since version 1.1: The default changed from `None` to `"warn"` in 1.1 and will become `"auto"` in 1.3. `None` and `'warn'` will be removed in 1.3. To keep the same behaviour as `None`, set `n_features_to_select="auto" and `tol=None`.
**tol**float, default=None
If the score is not incremented by at least `tol` between two consecutive feature additions or removals, stop adding or removing. `tol` is enabled only when `n_features_to_select` is `"auto"`.
New in version 1.1.
**direction**{‘forward’, ‘backward’}, default=’forward’
Whether to perform forward selection or backward selection.
**scoring**str, callable, list/tuple or dict, default=None
A single str (see [The scoring parameter: defining model evaluation rules](../model_evaluation#scoring-parameter)) or a callable (see [Defining your scoring strategy from metric functions](../model_evaluation#scoring)) to evaluate the predictions on the test set.
NOTE that when using custom scorers, each scorer should return a single value. Metric functions returning a list/array of values can be wrapped into multiple scorers that return one value each.
If None, the estimator’s score method is used.
**cv**int, cross-validation generator or an iterable, default=None
Determines the cross-validation splitting strategy. Possible inputs for cv are:
* None, to use the default 5-fold cross validation,
* integer, to specify the number of folds in a `(Stratified)KFold`,
* [CV splitter](https://scikit-learn.org/1.1/glossary.html#term-CV-splitter),
* An iterable yielding (train, test) splits as arrays of indices.
For integer/None inputs, if the estimator is a classifier and `y` is either binary or multiclass, `StratifiedKFold` is used. In all other cases, `KFold` is used. These splitters are instantiated with `shuffle=False` so the splits will be the same across calls.
Refer [User Guide](../cross_validation#cross-validation) for the various cross-validation strategies that can be used here.
**n\_jobs**int, default=None
Number of jobs to run in parallel. When evaluating a new feature to add or remove, the cross-validation procedure is parallel over the folds. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
Attributes:
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Only defined if the underlying estimator exposes such an attribute when fit.
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_features\_to\_select\_**int
The number of features that were selected.
**support\_**ndarray of shape (n\_features,), dtype=bool
The mask of selected features.
See also
[`GenericUnivariateSelect`](sklearn.feature_selection.genericunivariateselect#sklearn.feature_selection.GenericUnivariateSelect "sklearn.feature_selection.GenericUnivariateSelect")
Univariate feature selector with configurable strategy.
[`RFE`](sklearn.feature_selection.rfe#sklearn.feature_selection.RFE "sklearn.feature_selection.RFE")
Recursive feature elimination based on importance weights.
[`RFECV`](sklearn.feature_selection.rfecv#sklearn.feature_selection.RFECV "sklearn.feature_selection.RFECV")
Recursive feature elimination based on importance weights, with automatic selection of the number of features.
[`SelectFromModel`](sklearn.feature_selection.selectfrommodel#sklearn.feature_selection.SelectFromModel "sklearn.feature_selection.SelectFromModel")
Feature selection based on thresholds of importance weights.
#### Examples
```
>>> from sklearn.feature_selection import SequentialFeatureSelector
>>> from sklearn.neighbors import KNeighborsClassifier
>>> from sklearn.datasets import load_iris
>>> X, y = load_iris(return_X_y=True)
>>> knn = KNeighborsClassifier(n_neighbors=3)
>>> sfs = SequentialFeatureSelector(knn, n_features_to_select=3)
>>> sfs.fit(X, y)
SequentialFeatureSelector(estimator=KNeighborsClassifier(n_neighbors=3),
n_features_to_select=3)
>>> sfs.get_support()
array([ True, False, True, True])
>>> sfs.transform(X).shape
(150, 3)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.feature_selection.SequentialFeatureSelector.fit "sklearn.feature_selection.SequentialFeatureSelector.fit")(X[, y]) | Learn the features to select from X. |
| [`fit_transform`](#sklearn.feature_selection.SequentialFeatureSelector.fit_transform "sklearn.feature_selection.SequentialFeatureSelector.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.feature_selection.SequentialFeatureSelector.get_feature_names_out "sklearn.feature_selection.SequentialFeatureSelector.get_feature_names_out")([input\_features]) | Mask feature names according to selected features. |
| [`get_params`](#sklearn.feature_selection.SequentialFeatureSelector.get_params "sklearn.feature_selection.SequentialFeatureSelector.get_params")([deep]) | Get parameters for this estimator. |
| [`get_support`](#sklearn.feature_selection.SequentialFeatureSelector.get_support "sklearn.feature_selection.SequentialFeatureSelector.get_support")([indices]) | Get a mask, or integer index, of the features selected. |
| [`inverse_transform`](#sklearn.feature_selection.SequentialFeatureSelector.inverse_transform "sklearn.feature_selection.SequentialFeatureSelector.inverse_transform")(X) | Reverse the transformation operation. |
| [`set_params`](#sklearn.feature_selection.SequentialFeatureSelector.set_params "sklearn.feature_selection.SequentialFeatureSelector.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.feature_selection.SequentialFeatureSelector.transform "sklearn.feature_selection.SequentialFeatureSelector.transform")(X) | Reduce X to the selected features. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_sequential.py#L167)
Learn the features to select from X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training vectors, where `n_samples` is the number of samples and `n_features` is the number of predictors.
**y**array-like of shape (n\_samples,), default=None
Target values. This parameter may be ignored for unsupervised learning.
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L146)
Mask feature names according to selected features.
Parameters:
**input\_features**array-like of str or None, default=None
Input features.
* If `input_features` is `None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then the following input feature names are generated: `["x0", "x1", ..., "x(n_features_in_ - 1)"]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
get\_support(*indices=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L33)
Get a mask, or integer index, of the features selected.
Parameters:
**indices**bool, default=False
If True, the return value will be an array of integers, rather than a boolean mask.
Returns:
**support**array
An index that selects the retained features from a feature vector. If `indices` is False, this is a boolean array of shape [# input features], in which an element is True iff its corresponding feature is selected for retention. If `indices` is True, this is an integer array of shape [# output features] whose values are indices into the input feature vector.
inverse\_transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L106)
Reverse the transformation operation.
Parameters:
**X**array of shape [n\_samples, n\_selected\_features]
The input samples.
Returns:
**X\_r**array of shape [n\_samples, n\_original\_features]
`X` with columns of zeros inserted where features would have been removed by [`transform`](#sklearn.feature_selection.SequentialFeatureSelector.transform "sklearn.feature_selection.SequentialFeatureSelector.transform").
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L68)
Reduce X to the selected features.
Parameters:
**X**array of shape [n\_samples, n\_features]
The input samples.
Returns:
**X\_r**array of shape [n\_samples, n\_selected\_features]
The input samples with only the selected features.
Examples using `sklearn.feature_selection.SequentialFeatureSelector`
--------------------------------------------------------------------
[Release Highlights for scikit-learn 0.24](../../auto_examples/release_highlights/plot_release_highlights_0_24_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-24-0-py)
[Model-based and sequential feature selection](../../auto_examples/feature_selection/plot_select_from_model_diabetes#sphx-glr-auto-examples-feature-selection-plot-select-from-model-diabetes-py)
| programming_docs |
scikit_learn sklearn.preprocessing.binarize sklearn.preprocessing.binarize
==============================
sklearn.preprocessing.binarize(*X*, *\**, *threshold=0.0*, *copy=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L1955)
Boolean thresholding of array-like or scipy.sparse matrix.
Read more in the [User Guide](../preprocessing#preprocessing-binarization).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data to binarize, element by element. scipy.sparse matrices should be in CSR or CSC format to avoid an un-necessary copy.
**threshold**float, default=0.0
Feature values below or equal to this are replaced by 0, above it by 1. Threshold may not be less than 0 for operations on sparse matrices.
**copy**bool, default=True
Set to False to perform inplace binarization and avoid a copy (if the input is already a numpy array or a scipy.sparse CSR / CSC matrix and if axis is 1).
Returns:
**X\_tr**{ndarray, sparse matrix} of shape (n\_samples, n\_features)
The transformed data.
See also
[`Binarizer`](sklearn.preprocessing.binarizer#sklearn.preprocessing.Binarizer "sklearn.preprocessing.Binarizer")
Performs binarization using the Transformer API (e.g. as part of a preprocessing [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")).
scikit_learn sklearn.utils.sparsefuncs.inplace_row_scale sklearn.utils.sparsefuncs.inplace\_row\_scale
=============================================
sklearn.utils.sparsefuncs.inplace\_row\_scale(*X*, *scale*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/sparsefuncs.py#L246)
Inplace row scaling of a CSR or CSC matrix.
Scale each row of the data matrix by multiplying with specific scale provided by the caller assuming a (n\_samples, n\_features) shape.
Parameters:
**X**sparse matrix of shape (n\_samples, n\_features)
Matrix to be scaled. It should be of CSR or CSC format.
**scale**ndarray of shape (n\_features,), dtype={np.float32, np.float64}
Array of precomputed sample-wise values to use for scaling.
scikit_learn sklearn.manifold.TSNE sklearn.manifold.TSNE
=====================
*class*sklearn.manifold.TSNE(*n\_components=2*, *\**, *perplexity=30.0*, *early\_exaggeration=12.0*, *learning\_rate='warn'*, *n\_iter=1000*, *n\_iter\_without\_progress=300*, *min\_grad\_norm=1e-07*, *metric='euclidean'*, *metric\_params=None*, *init='warn'*, *verbose=0*, *random\_state=None*, *method='barnes\_hut'*, *angle=0.5*, *n\_jobs=None*, *square\_distances='deprecated'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_t_sne.py#L538)
T-distributed Stochastic Neighbor Embedding.
t-SNE [1] is a tool to visualize high-dimensional data. It converts similarities between data points to joint probabilities and tries to minimize the Kullback-Leibler divergence between the joint probabilities of the low-dimensional embedding and the high-dimensional data. t-SNE has a cost function that is not convex, i.e. with different initializations we can get different results.
It is highly recommended to use another dimensionality reduction method (e.g. PCA for dense data or TruncatedSVD for sparse data) to reduce the number of dimensions to a reasonable amount (e.g. 50) if the number of features is very high. This will suppress some noise and speed up the computation of pairwise distances between samples. For more tips see Laurens van der Maaten’s FAQ [2].
Read more in the [User Guide](../manifold#t-sne).
Parameters:
**n\_components**int, default=2
Dimension of the embedded space.
**perplexity**float, default=30.0
The perplexity is related to the number of nearest neighbors that is used in other manifold learning algorithms. Larger datasets usually require a larger perplexity. Consider selecting a value between 5 and 50. Different values can result in significantly different results. The perplexity must be less that the number of samples.
**early\_exaggeration**float, default=12.0
Controls how tight natural clusters in the original space are in the embedded space and how much space will be between them. For larger values, the space between natural clusters will be larger in the embedded space. Again, the choice of this parameter is not very critical. If the cost function increases during initial optimization, the early exaggeration factor or the learning rate might be too high.
**learning\_rate**float or ‘auto’, default=200.0
The learning rate for t-SNE is usually in the range [10.0, 1000.0]. If the learning rate is too high, the data may look like a ‘ball’ with any point approximately equidistant from its nearest neighbours. If the learning rate is too low, most points may look compressed in a dense cloud with few outliers. If the cost function gets stuck in a bad local minimum increasing the learning rate may help. Note that many other t-SNE implementations (bhtsne, FIt-SNE, openTSNE, etc.) use a definition of learning\_rate that is 4 times smaller than ours. So our learning\_rate=200 corresponds to learning\_rate=800 in those other implementations. The ‘auto’ option sets the learning\_rate to `max(N / early_exaggeration / 4, 50)` where N is the sample size, following [4] and [5]. This will become default in 1.2.
**n\_iter**int, default=1000
Maximum number of iterations for the optimization. Should be at least 250.
**n\_iter\_without\_progress**int, default=300
Maximum number of iterations without progress before we abort the optimization, used after 250 initial iterations with early exaggeration. Note that progress is only checked every 50 iterations so this value is rounded to the next multiple of 50.
New in version 0.17: parameter *n\_iter\_without\_progress* to control stopping criteria.
**min\_grad\_norm**float, default=1e-7
If the gradient norm is below this threshold, the optimization will be stopped.
**metric**str or callable, default=’euclidean’
The metric to use when calculating distance between instances in a feature array. If metric is a string, it must be one of the options allowed by scipy.spatial.distance.pdist for its metric parameter, or a metric listed in pairwise.PAIRWISE\_DISTANCE\_FUNCTIONS. If metric is “precomputed”, X is assumed to be a distance matrix. Alternatively, if metric is a callable function, it is called on each pair of instances (rows) and the resulting value recorded. The callable should take two arrays from X as input and return a value indicating the distance between them. The default is “euclidean” which is interpreted as squared euclidean distance.
**metric\_params**dict, default=None
Additional keyword arguments for the metric function.
New in version 1.1.
**init**{‘random’, ‘pca’} or ndarray of shape (n\_samples, n\_components), default=’random’
Initialization of embedding. Possible options are ‘random’, ‘pca’, and a numpy array of shape (n\_samples, n\_components). PCA initialization cannot be used with precomputed distances and is usually more globally stable than random initialization. `init='pca'` will become default in 1.2.
**verbose**int, default=0
Verbosity level.
**random\_state**int, RandomState instance or None, default=None
Determines the random number generator. Pass an int for reproducible results across multiple function calls. Note that different initializations might result in different local minima of the cost function. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**method**str, default=’barnes\_hut’
By default the gradient calculation algorithm uses Barnes-Hut approximation running in O(NlogN) time. method=’exact’ will run on the slower, but exact, algorithm in O(N^2) time. The exact algorithm should be used when nearest-neighbor errors need to be better than 3%. However, the exact method cannot scale to millions of examples.
New in version 0.17: Approximate optimization *method* via the Barnes-Hut.
**angle**float, default=0.5
Only used if method=’barnes\_hut’ This is the trade-off between speed and accuracy for Barnes-Hut T-SNE. ‘angle’ is the angular size (referred to as theta in [3]) of a distant node as measured from a point. If this size is below ‘angle’ then it is used as a summary node of all points contained within it. This method is not very sensitive to changes in this parameter in the range of 0.2 - 0.8. Angle less than 0.2 has quickly increasing computation time and angle greater 0.8 has quickly increasing error.
**n\_jobs**int, default=None
The number of parallel jobs to run for neighbors search. This parameter has no impact when `metric="precomputed"` or (`metric="euclidean"` and `method="exact"`). `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
New in version 0.22.
**square\_distances**True, default=’deprecated’
This parameter has no effect since distance values are always squared since 1.1.
Deprecated since version 1.1: `square_distances` has no effect from 1.1 and will be removed in 1.3.
Attributes:
**embedding\_**array-like of shape (n\_samples, n\_components)
Stores the embedding vectors.
**kl\_divergence\_**float
Kullback-Leibler divergence after optimization.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_iter\_**int
Number of iterations run.
See also
[`sklearn.decomposition.PCA`](sklearn.decomposition.pca#sklearn.decomposition.PCA "sklearn.decomposition.PCA")
Principal component analysis that is a linear dimensionality reduction method.
[`sklearn.decomposition.KernelPCA`](sklearn.decomposition.kernelpca#sklearn.decomposition.KernelPCA "sklearn.decomposition.KernelPCA")
Non-linear dimensionality reduction using kernels and PCA.
[`MDS`](sklearn.manifold.mds#sklearn.manifold.MDS "sklearn.manifold.MDS")
Manifold learning using multidimensional scaling.
[`Isomap`](sklearn.manifold.isomap#sklearn.manifold.Isomap "sklearn.manifold.Isomap")
Manifold learning based on Isometric Mapping.
[`LocallyLinearEmbedding`](sklearn.manifold.locallylinearembedding#sklearn.manifold.LocallyLinearEmbedding "sklearn.manifold.LocallyLinearEmbedding")
Manifold learning using Locally Linear Embedding.
[`SpectralEmbedding`](sklearn.manifold.spectralembedding#sklearn.manifold.SpectralEmbedding "sklearn.manifold.SpectralEmbedding")
Spectral embedding for non-linear dimensionality.
#### References
[1] van der Maaten, L.J.P.; Hinton, G.E. Visualizing High-Dimensional Data
Using t-SNE. Journal of Machine Learning Research 9:2579-2605, 2008.
[2] van der Maaten, L.J.P. t-Distributed Stochastic Neighbor Embedding
<https://lvdmaaten.github.io/tsne/>
[3] L.J.P. van der Maaten. Accelerating t-SNE using Tree-Based Algorithms.
Journal of Machine Learning Research 15(Oct):3221-3245, 2014. <https://lvdmaaten.github.io/publications/papers/JMLR_2014.pdf>
[4] Belkina, A. C., Ciccolella, C. O., Anno, R., Halpert, R., Spidlen, J.,
& Snyder-Cappione, J. E. (2019). Automated optimized parameters for T-distributed stochastic neighbor embedding improve visualization and analysis of large datasets. Nature Communications, 10(1), 1-12.
[5] Kobak, D., & Berens, P. (2019). The art of using t-SNE for single-cell
transcriptomics. Nature Communications, 10(1), 1-14.
#### Examples
```
>>> import numpy as np
>>> from sklearn.manifold import TSNE
>>> X = np.array([[0, 0, 0], [0, 1, 1], [1, 0, 1], [1, 1, 1]])
>>> X_embedded = TSNE(n_components=2, learning_rate='auto',
... init='random', perplexity=3).fit_transform(X)
>>> X_embedded.shape
(4, 2)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.manifold.TSNE.fit "sklearn.manifold.TSNE.fit")(X[, y]) | Fit X into an embedded space. |
| [`fit_transform`](#sklearn.manifold.TSNE.fit_transform "sklearn.manifold.TSNE.fit_transform")(X[, y]) | Fit X into an embedded space and return that transformed output. |
| [`get_params`](#sklearn.manifold.TSNE.get_params "sklearn.manifold.TSNE.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.manifold.TSNE.set_params "sklearn.manifold.TSNE.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_t_sne.py#L1127)
Fit X into an embedded space.
Parameters:
**X**ndarray of shape (n\_samples, n\_features) or (n\_samples, n\_samples)
If the metric is ‘precomputed’ X must be a square distance matrix. Otherwise it contains a sample per row. If the method is ‘exact’, X may be a sparse matrix of type ‘csr’, ‘csc’ or ‘coo’. If the method is ‘barnes\_hut’ and the metric is ‘precomputed’, X may be a precomputed sparse graph.
**y**None
Ignored.
Returns:
**X\_new**array of shape (n\_samples, n\_components)
Embedding of the training data in low-dimensional space.
fit\_transform(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_t_sne.py#L1102)
Fit X into an embedded space and return that transformed output.
Parameters:
**X**ndarray of shape (n\_samples, n\_features) or (n\_samples, n\_samples)
If the metric is ‘precomputed’ X must be a square distance matrix. Otherwise it contains a sample per row. If the method is ‘exact’, X may be a sparse matrix of type ‘csr’, ‘csc’ or ‘coo’. If the method is ‘barnes\_hut’ and the metric is ‘precomputed’, X may be a precomputed sparse graph.
**y**None
Ignored.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_components)
Embedding of the training data in low-dimensional space.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.manifold.TSNE`
--------------------------------------
[Comparison of Manifold Learning methods](../../auto_examples/manifold/plot_compare_methods#sphx-glr-auto-examples-manifold-plot-compare-methods-py)
[Manifold Learning methods on a severed sphere](../../auto_examples/manifold/plot_manifold_sphere#sphx-glr-auto-examples-manifold-plot-manifold-sphere-py)
[Manifold learning on handwritten digits: Locally Linear Embedding, Isomap…](../../auto_examples/manifold/plot_lle_digits#sphx-glr-auto-examples-manifold-plot-lle-digits-py)
[Swiss Roll And Swiss-Hole Reduction](../../auto_examples/manifold/plot_swissroll#sphx-glr-auto-examples-manifold-plot-swissroll-py)
[t-SNE: The effect of various perplexity values on the shape](../../auto_examples/manifold/plot_t_sne_perplexity#sphx-glr-auto-examples-manifold-plot-t-sne-perplexity-py)
[Approximate nearest neighbors in TSNE](../../auto_examples/neighbors/approximate_nearest_neighbors#sphx-glr-auto-examples-neighbors-approximate-nearest-neighbors-py)
scikit_learn sklearn.covariance.GraphicalLassoCV sklearn.covariance.GraphicalLassoCV
===================================
*class*sklearn.covariance.GraphicalLassoCV(*\**, *alphas=4*, *n\_refinements=4*, *cv=None*, *tol=0.0001*, *enet\_tol=0.0001*, *max\_iter=100*, *mode='cd'*, *n\_jobs=None*, *verbose=False*, *assume\_centered=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_graph_lasso.py#L609)
Sparse inverse covariance w/ cross-validated choice of the l1 penalty.
See glossary entry for [cross-validation estimator](https://scikit-learn.org/1.1/glossary.html#term-cross-validation-estimator).
Read more in the [User Guide](../covariance#sparse-inverse-covariance).
Changed in version v0.20: GraphLassoCV has been renamed to GraphicalLassoCV
Parameters:
**alphas**int or array-like of shape (n\_alphas,), dtype=float, default=4
If an integer is given, it fixes the number of points on the grids of alpha to be used. If a list is given, it gives the grid to be used. See the notes in the class docstring for more details. Range is (0, inf] when floats given.
**n\_refinements**int, default=4
The number of times the grid is refined. Not used if explicit values of alphas are passed. Range is [1, inf).
**cv**int, cross-validation generator or iterable, default=None
Determines the cross-validation splitting strategy. Possible inputs for cv are:
* None, to use the default 5-fold cross-validation,
* integer, to specify the number of folds.
* [CV splitter](https://scikit-learn.org/1.1/glossary.html#term-CV-splitter),
* An iterable yielding (train, test) splits as arrays of indices.
For integer/None inputs `KFold` is used.
Refer [User Guide](../cross_validation#cross-validation) for the various cross-validation strategies that can be used here.
Changed in version 0.20: `cv` default value if None changed from 3-fold to 5-fold.
**tol**float, default=1e-4
The tolerance to declare convergence: if the dual gap goes below this value, iterations are stopped. Range is (0, inf].
**enet\_tol**float, default=1e-4
The tolerance for the elastic net solver used to calculate the descent direction. This parameter controls the accuracy of the search direction for a given column update, not of the overall parameter estimate. Only used for mode=’cd’. Range is (0, inf].
**max\_iter**int, default=100
Maximum number of iterations.
**mode**{‘cd’, ‘lars’}, default=’cd’
The Lasso solver to use: coordinate descent or LARS. Use LARS for very sparse underlying graphs, where number of features is greater than number of samples. Elsewhere prefer cd which is more numerically stable.
**n\_jobs**int, default=None
Number of jobs to run in parallel. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
Changed in version v0.20: `n_jobs` default changed from 1 to None
**verbose**bool, default=False
If verbose is True, the objective function and duality gap are printed at each iteration.
**assume\_centered**bool, default=False
If True, data are not centered before computation. Useful when working with data whose mean is almost, but not exactly zero. If False, data are centered before computation.
Attributes:
**location\_**ndarray of shape (n\_features,)
Estimated location, i.e. the estimated mean.
**covariance\_**ndarray of shape (n\_features, n\_features)
Estimated covariance matrix.
**precision\_**ndarray of shape (n\_features, n\_features)
Estimated precision matrix (inverse covariance).
**alpha\_**float
Penalization parameter selected.
**cv\_results\_**dict of ndarrays
A dict with keys:
alphasndarray of shape (n\_alphas,)
All penalization parameters explored.
split(k)\_test\_scorendarray of shape (n\_alphas,)
Log-likelihood score on left-out data across (k)th fold.
New in version 1.0.
mean\_test\_scorendarray of shape (n\_alphas,)
Mean of scores over the folds.
New in version 1.0.
std\_test\_scorendarray of shape (n\_alphas,)
Standard deviation of scores over the folds.
New in version 1.0.
split(k)\_scorendarray of shape (n\_alphas,)
Log-likelihood score on left-out data across (k)th fold.
Deprecated since version 1.0: `split(k)_score` is deprecated in 1.0 and will be removed in 1.2. Use `split(k)_test_score` instead.
mean\_scorendarray of shape (n\_alphas,)
Mean of scores over the folds.
Deprecated since version 1.0: `mean_score` is deprecated in 1.0 and will be removed in 1.2. Use `mean_test_score` instead.
std\_scorendarray of shape (n\_alphas,)
Standard deviation of scores over the folds.
Deprecated since version 1.0: `std_score` is deprecated in 1.0 and will be removed in 1.2. Use `std_test_score` instead.
New in version 0.24.
**n\_iter\_**int
Number of iterations run for the optimal alpha.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`graphical_lasso`](sklearn.covariance.graphical_lasso#sklearn.covariance.graphical_lasso "sklearn.covariance.graphical_lasso")
L1-penalized covariance estimator.
[`GraphicalLasso`](sklearn.covariance.graphicallasso#sklearn.covariance.GraphicalLasso "sklearn.covariance.GraphicalLasso")
Sparse inverse covariance estimation with an l1-penalized estimator.
#### Notes
The search for the optimal penalization parameter (`alpha`) is done on an iteratively refined grid: first the cross-validated scores on a grid are computed, then a new refined grid is centered around the maximum, and so on.
One of the challenges which is faced here is that the solvers can fail to converge to a well-conditioned estimate. The corresponding values of `alpha` then come out as missing values, but the optimum may be close to these missing values.
In `fit`, once the best parameter `alpha` is found through cross-validation, the model is fit again using the entire training set.
#### Examples
```
>>> import numpy as np
>>> from sklearn.covariance import GraphicalLassoCV
>>> true_cov = np.array([[0.8, 0.0, 0.2, 0.0],
... [0.0, 0.4, 0.0, 0.0],
... [0.2, 0.0, 0.3, 0.1],
... [0.0, 0.0, 0.1, 0.7]])
>>> np.random.seed(0)
>>> X = np.random.multivariate_normal(mean=[0, 0, 0, 0],
... cov=true_cov,
... size=200)
>>> cov = GraphicalLassoCV().fit(X)
>>> np.around(cov.covariance_, decimals=3)
array([[0.816, 0.051, 0.22 , 0.017],
[0.051, 0.364, 0.018, 0.036],
[0.22 , 0.018, 0.322, 0.094],
[0.017, 0.036, 0.094, 0.69 ]])
>>> np.around(cov.location_, decimals=3)
array([0.073, 0.04 , 0.038, 0.143])
```
#### Methods
| | |
| --- | --- |
| [`error_norm`](#sklearn.covariance.GraphicalLassoCV.error_norm "sklearn.covariance.GraphicalLassoCV.error_norm")(comp\_cov[, norm, scaling, squared]) | Compute the Mean Squared Error between two covariance estimators. |
| [`fit`](#sklearn.covariance.GraphicalLassoCV.fit "sklearn.covariance.GraphicalLassoCV.fit")(X[, y]) | Fit the GraphicalLasso covariance model to X. |
| [`get_params`](#sklearn.covariance.GraphicalLassoCV.get_params "sklearn.covariance.GraphicalLassoCV.get_params")([deep]) | Get parameters for this estimator. |
| [`get_precision`](#sklearn.covariance.GraphicalLassoCV.get_precision "sklearn.covariance.GraphicalLassoCV.get_precision")() | Getter for the precision matrix. |
| [`mahalanobis`](#sklearn.covariance.GraphicalLassoCV.mahalanobis "sklearn.covariance.GraphicalLassoCV.mahalanobis")(X) | Compute the squared Mahalanobis distances of given observations. |
| [`score`](#sklearn.covariance.GraphicalLassoCV.score "sklearn.covariance.GraphicalLassoCV.score")(X\_test[, y]) | Compute the log-likelihood of `X_test` under the estimated Gaussian model. |
| [`set_params`](#sklearn.covariance.GraphicalLassoCV.set_params "sklearn.covariance.GraphicalLassoCV.set_params")(\*\*params) | Set the parameters of this estimator. |
error\_norm(*comp\_cov*, *norm='frobenius'*, *scaling=True*, *squared=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_empirical_covariance.py#L267)
Compute the Mean Squared Error between two covariance estimators.
Parameters:
**comp\_cov**array-like of shape (n\_features, n\_features)
The covariance to compare with.
**norm**{“frobenius”, “spectral”}, default=”frobenius”
The type of norm used to compute the error. Available error types: - ‘frobenius’ (default): sqrt(tr(A^t.A)) - ‘spectral’: sqrt(max(eigenvalues(A^t.A)) where A is the error `(comp_cov - self.covariance_)`.
**scaling**bool, default=True
If True (default), the squared error norm is divided by n\_features. If False, the squared error norm is not rescaled.
**squared**bool, default=True
Whether to compute the squared error norm or the error norm. If True (default), the squared error norm is returned. If False, the error norm is returned.
Returns:
**result**float
The Mean Squared Error (in the sense of the Frobenius norm) between `self` and `comp_cov` covariance estimators.
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_graph_lasso.py#L828)
Fit the GraphicalLasso covariance model to X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Data from which to compute the covariance estimate.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**self**object
Returns the instance itself.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
get\_precision()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_empirical_covariance.py#L195)
Getter for the precision matrix.
Returns:
**precision\_**array-like of shape (n\_features, n\_features)
The precision matrix associated to the current covariance object.
mahalanobis(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_empirical_covariance.py#L318)
Compute the squared Mahalanobis distances of given observations.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The observations, the Mahalanobis distances of the which we compute. Observations are assumed to be drawn from the same distribution than the data used in fit.
Returns:
**dist**ndarray of shape (n\_samples,)
Squared Mahalanobis distances of the observations.
score(*X\_test*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_empirical_covariance.py#L236)
Compute the log-likelihood of `X_test` under the estimated Gaussian model.
The Gaussian model is defined by its mean and covariance matrix which are represented respectively by `self.location_` and `self.covariance_`.
Parameters:
**X\_test**array-like of shape (n\_samples, n\_features)
Test data of which we compute the likelihood, where `n_samples` is the number of samples and `n_features` is the number of features. `X_test` is assumed to be drawn from the same distribution than the data used in fit (including centering).
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**res**float
The log-likelihood of `X_test` with `self.location_` and `self.covariance_` as estimators of the Gaussian model mean and covariance matrix respectively.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.covariance.GraphicalLassoCV`
----------------------------------------------------
[Sparse inverse covariance estimation](../../auto_examples/covariance/plot_sparse_cov#sphx-glr-auto-examples-covariance-plot-sparse-cov-py)
[Visualizing the stock market structure](../../auto_examples/applications/plot_stock_market#sphx-glr-auto-examples-applications-plot-stock-market-py)
| programming_docs |
scikit_learn sklearn.utils.shuffle sklearn.utils.shuffle
=====================
sklearn.utils.shuffle(*\*arrays*, *random\_state=None*, *n\_samples=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/__init__.py#L585)
Shuffle arrays or sparse matrices in a consistent way.
This is a convenience alias to `resample(*arrays, replace=False)` to do random permutations of the collections.
Parameters:
**\*arrays**sequence of indexable data-structures
Indexable data-structures can be arrays, lists, dataframes or scipy sparse matrices with consistent first dimension.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for shuffling the data. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**n\_samples**int, default=None
Number of samples to generate. If left to None this is automatically set to the first dimension of the arrays. It should not be larger than the length of arrays.
Returns:
**shuffled\_arrays**sequence of indexable data-structures
Sequence of shuffled copies of the collections. The original arrays are not impacted.
See also
[`resample`](sklearn.utils.resample#sklearn.utils.resample "sklearn.utils.resample")
#### Examples
It is possible to mix sparse and dense arrays in the same run:
```
>>> import numpy as np
>>> X = np.array([[1., 0.], [2., 1.], [0., 0.]])
>>> y = np.array([0, 1, 2])
>>> from scipy.sparse import coo_matrix
>>> X_sparse = coo_matrix(X)
>>> from sklearn.utils import shuffle
>>> X, X_sparse, y = shuffle(X, X_sparse, y, random_state=0)
>>> X
array([[0., 0.],
[2., 1.],
[1., 0.]])
>>> X_sparse
<3x2 sparse matrix of type '<... 'numpy.float64'>'
with 3 stored elements in Compressed Sparse Row format>
>>> X_sparse.toarray()
array([[0., 0.],
[2., 1.],
[1., 0.]])
>>> y
array([2, 1, 0])
>>> shuffle(y, n_samples=2, random_state=0)
array([0, 1])
```
Examples using `sklearn.utils.shuffle`
--------------------------------------
[Color Quantization using K-Means](../../auto_examples/cluster/plot_color_quantization#sphx-glr-auto-examples-cluster-plot-color-quantization-py)
[Empirical evaluation of the impact of k-means initialization](../../auto_examples/cluster/plot_kmeans_stability_low_dim_dense#sphx-glr-auto-examples-cluster-plot-kmeans-stability-low-dim-dense-py)
[Combine predictors using stacking](../../auto_examples/ensemble/plot_stack_predictors#sphx-glr-auto-examples-ensemble-plot-stack-predictors-py)
[Prediction Latency](../../auto_examples/applications/plot_prediction_latency#sphx-glr-auto-examples-applications-plot-prediction-latency-py)
[Early stopping of Stochastic Gradient Descent](../../auto_examples/linear_model/plot_sgd_early_stopping#sphx-glr-auto-examples-linear-model-plot-sgd-early-stopping-py)
[Approximate nearest neighbors in TSNE](../../auto_examples/neighbors/approximate_nearest_neighbors#sphx-glr-auto-examples-neighbors-approximate-nearest-neighbors-py)
[Effect of varying threshold for self-training](../../auto_examples/semi_supervised/plot_self_training_varying_threshold#sphx-glr-auto-examples-semi-supervised-plot-self-training-varying-threshold-py)
scikit_learn sklearn.utils.parallel_backend sklearn.utils.parallel\_backend
===============================
sklearn.utils.parallel\_backend(*backend*, *n\_jobs=-1*, *inner\_max\_num\_threads=None*, *\*\*backend\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/../../../../mambaforge/envs/testenv/lib/python3.9/site-packages/joblib/parallel.py#L122)
Change the default backend used by Parallel inside a with block.
If `backend` is a string it must match a previously registered implementation using the `register_parallel_backend` function.
By default the following backends are available:
* ‘loky’: single-host, process-based parallelism (used by default),
* ‘threading’: single-host, thread-based parallelism,
* ‘multiprocessing’: legacy single-host, process-based parallelism.
‘loky’ is recommended to run functions that manipulate Python objects. ‘threading’ is a low-overhead alternative that is most efficient for functions that release the Global Interpreter Lock: e.g. I/O-bound code or CPU-bound code in a few calls to native code that explicitly releases the GIL.
In addition, if the `dask` and `distributed` Python packages are installed, it is possible to use the ‘dask’ backend for better scheduling of nested parallel calls without over-subscription and potentially distribute parallel calls over a networked cluster of several hosts.
It is also possible to use the distributed ‘ray’ backend for distributing the workload to a cluster of nodes. To use the ‘ray’ joblib backend add the following lines:
```
>>> from ray.util.joblib import register_ray
>>> register_ray()
>>> with parallel_backend("ray"):
... print(Parallel()(delayed(neg)(i + 1) for i in range(5)))
[-1, -2, -3, -4, -5]
```
Alternatively the backend can be passed directly as an instance.
By default all available workers will be used (`n_jobs=-1`) unless the caller passes an explicit value for the `n_jobs` parameter.
This is an alternative to passing a `backend='backend_name'` argument to the `Parallel` class constructor. It is particularly useful when calling into library code that uses joblib internally but does not expose the backend argument in its own API.
```
>>> from operator import neg
>>> with parallel_backend('threading'):
... print(Parallel()(delayed(neg)(i + 1) for i in range(5)))
...
[-1, -2, -3, -4, -5]
```
Warning: this function is experimental and subject to change in a future version of joblib.
Joblib also tries to limit the oversubscription by limiting the number of threads usable in some third-party library threadpools like OpenBLAS, MKL or OpenMP. The default limit in each worker is set to `max(cpu_count() // effective_n_jobs, 1)` but this limit can be overwritten with the `inner_max_num_threads` argument which will be used to set this limit in the child processes.
New in version 0.10.
scikit_learn sklearn.preprocessing.FunctionTransformer sklearn.preprocessing.FunctionTransformer
=========================================
*class*sklearn.preprocessing.FunctionTransformer(*func=None*, *inverse\_func=None*, *\**, *validate=False*, *accept\_sparse=False*, *check\_inverse=True*, *feature\_names\_out=None*, *kw\_args=None*, *inv\_kw\_args=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_function_transformer.py#L19)
Constructs a transformer from an arbitrary callable.
A FunctionTransformer forwards its X (and optionally y) arguments to a user-defined function or function object and returns the result of this function. This is useful for stateless transformations such as taking the log of frequencies, doing custom scaling, etc.
Note: If a lambda is used as the function, then the resulting transformer will not be pickleable.
New in version 0.17.
Read more in the [User Guide](../preprocessing#function-transformer).
Parameters:
**func**callable, default=None
The callable to use for the transformation. This will be passed the same arguments as transform, with args and kwargs forwarded. If func is None, then func will be the identity function.
**inverse\_func**callable, default=None
The callable to use for the inverse transformation. This will be passed the same arguments as inverse transform, with args and kwargs forwarded. If inverse\_func is None, then inverse\_func will be the identity function.
**validate**bool, default=False
Indicate that the input X array should be checked before calling `func`. The possibilities are:
* If False, there is no input validation.
* If True, then X will be converted to a 2-dimensional NumPy array or sparse matrix. If the conversion is not possible an exception is raised.
Changed in version 0.22: The default of `validate` changed from True to False.
**accept\_sparse**bool, default=False
Indicate that func accepts a sparse matrix as input. If validate is False, this has no effect. Otherwise, if accept\_sparse is false, sparse matrix inputs will cause an exception to be raised.
**check\_inverse**bool, default=True
Whether to check that or `func` followed by `inverse_func` leads to the original inputs. It can be used for a sanity check, raising a warning when the condition is not fulfilled.
New in version 0.20.
**feature\_names\_out**callable, ‘one-to-one’ or None, default=None
Determines the list of feature names that will be returned by the `get_feature_names_out` method. If it is ‘one-to-one’, then the output feature names will be equal to the input feature names. If it is a callable, then it must take two positional arguments: this `FunctionTransformer` (`self`) and an array-like of input feature names (`input_features`). It must return an array-like of output feature names. The `get_feature_names_out` method is only defined if `feature_names_out` is not None.
See `get_feature_names_out` for more details.
New in version 1.1.
**kw\_args**dict, default=None
Dictionary of additional keyword arguments to pass to func.
New in version 0.18.
**inv\_kw\_args**dict, default=None
Dictionary of additional keyword arguments to pass to inverse\_func.
New in version 0.18.
Attributes:
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `validate=True`.
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `validate=True` and `X` has feature names that are all strings.
New in version 1.0.
See also
[`MaxAbsScaler`](sklearn.preprocessing.maxabsscaler#sklearn.preprocessing.MaxAbsScaler "sklearn.preprocessing.MaxAbsScaler")
Scale each feature by its maximum absolute value.
[`StandardScaler`](sklearn.preprocessing.standardscaler#sklearn.preprocessing.StandardScaler "sklearn.preprocessing.StandardScaler")
Standardize features by removing the mean and scaling to unit variance.
[`LabelBinarizer`](sklearn.preprocessing.labelbinarizer#sklearn.preprocessing.LabelBinarizer "sklearn.preprocessing.LabelBinarizer")
Binarize labels in a one-vs-all fashion.
[`MultiLabelBinarizer`](sklearn.preprocessing.multilabelbinarizer#sklearn.preprocessing.MultiLabelBinarizer "sklearn.preprocessing.MultiLabelBinarizer")
Transform between iterable of iterables and a multilabel format.
#### Examples
```
>>> import numpy as np
>>> from sklearn.preprocessing import FunctionTransformer
>>> transformer = FunctionTransformer(np.log1p)
>>> X = np.array([[0, 1], [2, 3]])
>>> transformer.transform(X)
array([[0. , 0.6931...],
[1.0986..., 1.3862...]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.preprocessing.FunctionTransformer.fit "sklearn.preprocessing.FunctionTransformer.fit")(X[, y]) | Fit transformer by checking X. |
| [`fit_transform`](#sklearn.preprocessing.FunctionTransformer.fit_transform "sklearn.preprocessing.FunctionTransformer.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.preprocessing.FunctionTransformer.get_feature_names_out "sklearn.preprocessing.FunctionTransformer.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.preprocessing.FunctionTransformer.get_params "sklearn.preprocessing.FunctionTransformer.get_params")([deep]) | Get parameters for this estimator. |
| [`inverse_transform`](#sklearn.preprocessing.FunctionTransformer.inverse_transform "sklearn.preprocessing.FunctionTransformer.inverse_transform")(X) | Transform X using the inverse function. |
| [`set_params`](#sklearn.preprocessing.FunctionTransformer.set_params "sklearn.preprocessing.FunctionTransformer.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.preprocessing.FunctionTransformer.transform "sklearn.preprocessing.FunctionTransformer.transform")(X) | Transform X using the forward function. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_function_transformer.py#L175)
Fit transformer by checking X.
If `validate` is `True`, `X` will be checked.
Parameters:
**X**array-like, shape (n\_samples, n\_features)
Input array.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
**self**object
FunctionTransformer class instance.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_function_transformer.py#L231)
Get output feature names for transformation.
This method is only defined if `feature_names_out` is not None.
Parameters:
**input\_features**array-like of str or None, default=None
Input feature names.
* If `input_features` is None, then `feature_names_in_` is used as the input feature names. If `feature_names_in_` is not defined, then names are generated: `[x0, x1, ..., x(n_features_in_ - 1)]`.
* If `input_features` is array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
* If `feature_names_out` is ‘one-to-one’, the input feature names are returned (see `input_features` above). This requires `feature_names_in_` and/or `n_features_in_` to be defined, which is done automatically if `validate=True`. Alternatively, you can set them in `func`.
* If `feature_names_out` is a callable, then it is called with two arguments, `self` and `input_features`, and its return value is returned by this method.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
inverse\_transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_function_transformer.py#L214)
Transform X using the inverse function.
Parameters:
**X**array-like, shape (n\_samples, n\_features)
Input array.
Returns:
**X\_out**array-like, shape (n\_samples, n\_features)
Transformed input.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_function_transformer.py#L198)
Transform X using the forward function.
Parameters:
**X**array-like, shape (n\_samples, n\_features)
Input array.
Returns:
**X\_out**array-like, shape (n\_samples, n\_features)
Transformed input.
Examples using `sklearn.preprocessing.FunctionTransformer`
----------------------------------------------------------
[Feature transformations with ensembles of trees](../../auto_examples/ensemble/plot_feature_transformation#sphx-glr-auto-examples-ensemble-plot-feature-transformation-py)
[Time-related feature engineering](../../auto_examples/applications/plot_cyclical_feature_engineering#sphx-glr-auto-examples-applications-plot-cyclical-feature-engineering-py)
[Poisson regression and non-normal loss](../../auto_examples/linear_model/plot_poisson_regression_non_normal_loss#sphx-glr-auto-examples-linear-model-plot-poisson-regression-non-normal-loss-py)
[Tweedie regression on insurance claims](../../auto_examples/linear_model/plot_tweedie_regression_insurance_claims#sphx-glr-auto-examples-linear-model-plot-tweedie-regression-insurance-claims-py)
[Column Transformer with Heterogeneous Data Sources](../../auto_examples/compose/plot_column_transformer#sphx-glr-auto-examples-compose-plot-column-transformer-py)
[Semi-supervised Classification on a Text Dataset](../../auto_examples/semi_supervised/plot_semi_supervised_newsgroups#sphx-glr-auto-examples-semi-supervised-plot-semi-supervised-newsgroups-py)
scikit_learn sklearn.inspection.plot_partial_dependence sklearn.inspection.plot\_partial\_dependence
============================================
sklearn.inspection.plot\_partial\_dependence(*estimator*, *X*, *features*, *\**, *feature\_names=None*, *target=None*, *response\_method='auto'*, *n\_cols=3*, *grid\_resolution=100*, *percentiles=(0.05, 0.95)*, *method='auto'*, *n\_jobs=None*, *verbose=0*, *line\_kw=None*, *ice\_lines\_kw=None*, *pd\_line\_kw=None*, *contour\_kw=None*, *ax=None*, *kind='average'*, *subsample=1000*, *random\_state=None*, *centered=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/inspection/_plot/partial_dependence.py#L22)
DEPRECATED: Function `plot_partial_dependence` is deprecated in 1.0 and will be removed in 1.2. Use PartialDependenceDisplay.from\_estimator instead
Partial dependence (PD) and individual conditional expectation (ICE) plots.
Partial dependence plots, individual conditional expectation plots or an overlay of both of them can be plotted by setting the `kind` parameter.
The ICE and PD plots can be centered with the parameter `centered`.
The `len(features)` plots are arranged in a grid with `n_cols` columns. Two-way partial dependence plots are plotted as contour plots. The deciles of the feature values will be shown with tick marks on the x-axes for one-way plots, and on both axes for two-way plots.
Read more in the [User Guide](../partial_dependence#partial-dependence).
Note
[`plot_partial_dependence`](#sklearn.inspection.plot_partial_dependence "sklearn.inspection.plot_partial_dependence") does not support using the same axes with multiple calls. To plot the partial dependence for multiple estimators, please pass the axes created by the first call to the second call:
```
>>> from sklearn.inspection import plot_partial_dependence
>>> from sklearn.datasets import make_friedman1
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.ensemble import RandomForestRegressor
>>> X, y = make_friedman1()
>>> est1 = LinearRegression().fit(X, y)
>>> est2 = RandomForestRegressor().fit(X, y)
>>> disp1 = plot_partial_dependence(est1, X,
... [1, 2])
>>> disp2 = plot_partial_dependence(est2, X, [1, 2],
... ax=disp1.axes_)
```
Warning
For [`GradientBoostingClassifier`](sklearn.ensemble.gradientboostingclassifier#sklearn.ensemble.GradientBoostingClassifier "sklearn.ensemble.GradientBoostingClassifier") and [`GradientBoostingRegressor`](sklearn.ensemble.gradientboostingregressor#sklearn.ensemble.GradientBoostingRegressor "sklearn.ensemble.GradientBoostingRegressor"), the `'recursion'` method (used by default) will not account for the `init` predictor of the boosting process. In practice, this will produce the same values as `'brute'` up to a constant offset in the target response, provided that `init` is a constant estimator (which is the default). However, if `init` is not a constant estimator, the partial dependence values are incorrect for `'recursion'` because the offset will be sample-dependent. It is preferable to use the `'brute'` method. Note that this only applies to [`GradientBoostingClassifier`](sklearn.ensemble.gradientboostingclassifier#sklearn.ensemble.GradientBoostingClassifier "sklearn.ensemble.GradientBoostingClassifier") and [`GradientBoostingRegressor`](sklearn.ensemble.gradientboostingregressor#sklearn.ensemble.GradientBoostingRegressor "sklearn.ensemble.GradientBoostingRegressor"), not to [`HistGradientBoostingClassifier`](sklearn.ensemble.histgradientboostingclassifier#sklearn.ensemble.HistGradientBoostingClassifier "sklearn.ensemble.HistGradientBoostingClassifier") and [`HistGradientBoostingRegressor`](sklearn.ensemble.histgradientboostingregressor#sklearn.ensemble.HistGradientBoostingRegressor "sklearn.ensemble.HistGradientBoostingRegressor").
Deprecated since version 1.0: `plot_partial_dependence` is deprecated in 1.0 and will be removed in 1.2. Please use the class method: `from_estimator`.
Parameters:
**estimator**BaseEstimator
A fitted estimator object implementing [predict](https://scikit-learn.org/1.1/glossary.html#term-predict), [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba), or [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function). Multioutput-multiclass classifiers are not supported.
**X**{array-like, dataframe} of shape (n\_samples, n\_features)
`X` is used to generate a grid of values for the target `features` (where the partial dependence will be evaluated), and also to generate values for the complement features when the `method` is `'brute'`.
**features**list of {int, str, pair of int, pair of str}
The target features for which to create the PDPs. If `features[i]` is an integer or a string, a one-way PDP is created; if `features[i]` is a tuple, a two-way PDP is created (only supported with `kind='average'`). Each tuple must be of size 2. if any entry is a string, then it must be in `feature_names`.
**feature\_names**array-like of shape (n\_features,), dtype=str, default=None
Name of each feature; `feature_names[i]` holds the name of the feature with index `i`. By default, the name of the feature corresponds to their numerical index for NumPy array and their column name for pandas dataframe.
**target**int, default=None
* In a multiclass setting, specifies the class for which the PDPs should be computed. Note that for binary classification, the positive class (index 1) is always used.
* In a multioutput setting, specifies the task for which the PDPs should be computed.
Ignored in binary classification or classical regression settings.
**response\_method**{‘auto’, ‘predict\_proba’, ‘decision\_function’}, default=’auto’
Specifies whether to use [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) or [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) as the target response. For regressors this parameter is ignored and the response is always the output of [predict](https://scikit-learn.org/1.1/glossary.html#term-predict). By default, [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) is tried first and we revert to [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) if it doesn’t exist. If `method` is `'recursion'`, the response is always the output of [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function).
**n\_cols**int, default=3
The maximum number of columns in the grid plot. Only active when `ax` is a single axis or `None`.
**grid\_resolution**int, default=100
The number of equally spaced points on the axes of the plots, for each target feature.
**percentiles**tuple of float, default=(0.05, 0.95)
The lower and upper percentile used to create the extreme values for the PDP axes. Must be in [0, 1].
**method**str, default=’auto’
The method used to calculate the averaged predictions:
* `'recursion'` is only supported for some tree-based estimators (namely [`GradientBoostingClassifier`](sklearn.ensemble.gradientboostingclassifier#sklearn.ensemble.GradientBoostingClassifier "sklearn.ensemble.GradientBoostingClassifier"), [`GradientBoostingRegressor`](sklearn.ensemble.gradientboostingregressor#sklearn.ensemble.GradientBoostingRegressor "sklearn.ensemble.GradientBoostingRegressor"), [`HistGradientBoostingClassifier`](sklearn.ensemble.histgradientboostingclassifier#sklearn.ensemble.HistGradientBoostingClassifier "sklearn.ensemble.HistGradientBoostingClassifier"), [`HistGradientBoostingRegressor`](sklearn.ensemble.histgradientboostingregressor#sklearn.ensemble.HistGradientBoostingRegressor "sklearn.ensemble.HistGradientBoostingRegressor"), [`DecisionTreeRegressor`](sklearn.tree.decisiontreeregressor#sklearn.tree.DecisionTreeRegressor "sklearn.tree.DecisionTreeRegressor"), [`RandomForestRegressor`](sklearn.ensemble.randomforestregressor#sklearn.ensemble.RandomForestRegressor "sklearn.ensemble.RandomForestRegressor") but is more efficient in terms of speed. With this method, the target response of a classifier is always the decision function, not the predicted probabilities. Since the `'recursion'` method implicitly computes the average of the ICEs by design, it is not compatible with ICE and thus `kind` must be `'average'`.
* `'brute'` is supported for any estimator, but is more computationally intensive.
* `'auto'`: the `'recursion'` is used for estimators that support it, and `'brute'` is used otherwise.
Please see [this note](../partial_dependence#pdp-method-differences) for differences between the `'brute'` and `'recursion'` method.
**n\_jobs**int, default=None
The number of CPUs to use to compute the partial dependences. Computation is parallelized over features specified by the `features` parameter.
`None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**verbose**int, default=0
Verbose output during PD computations.
**line\_kw**dict, default=None
Dict with keywords passed to the `matplotlib.pyplot.plot` call. For one-way partial dependence plots. It can be used to define common properties for both `ice_lines_kw` and `pdp_line_kw`.
**ice\_lines\_kw**dict, default=None
Dictionary with keywords passed to the `matplotlib.pyplot.plot` call. For ICE lines in the one-way partial dependence plots. The key value pairs defined in `ice_lines_kw` takes priority over `line_kw`.
New in version 1.0.
**pd\_line\_kw**dict, default=None
Dictionary with keywords passed to the `matplotlib.pyplot.plot` call. For partial dependence in one-way partial dependence plots. The key value pairs defined in `pd_line_kw` takes priority over `line_kw`.
New in version 1.0.
**contour\_kw**dict, default=None
Dict with keywords passed to the `matplotlib.pyplot.contourf` call. For two-way partial dependence plots.
**ax**Matplotlib axes or array-like of Matplotlib axes, default=None
* If a single axis is passed in, it is treated as a bounding axes and a grid of partial dependence plots will be drawn within these bounds. The `n_cols` parameter controls the number of columns in the grid.
* If an array-like of axes are passed in, the partial dependence plots will be drawn directly into these axes.
* If `None`, a figure and a bounding axes is created and treated as the single axes case.
New in version 0.22.
**kind**{‘average’, ‘individual’, ‘both’} or list of such str, default=’average’
Whether to plot the partial dependence averaged across all the samples in the dataset or one line per sample or both.
* `kind='average'` results in the traditional PD plot;
* `kind='individual'` results in the ICE plot;
* `kind='both'` results in plotting both the ICE and PD on the same plot.
A list of such strings can be provided to specify `kind` on a per-plot basis. The length of the list should be the same as the number of interaction requested in `features`.
Note
ICE (‘individual’ or ‘both’) is not a valid option for 2-ways interactions plot. As a result, an error will be raised. 2-ways interaction plots should always be configured to use the ‘average’ kind instead.
Note
The fast `method='recursion'` option is only available for `kind='average'`. Plotting individual dependencies requires using the slower `method='brute'` option.
New in version 0.24: Add `kind` parameter with `'average'`, `'individual'`, and `'both'` options.
New in version 1.1: Add the possibility to pass a list of string specifying `kind` for each plot.
**subsample**float, int or None, default=1000
Sampling for ICE curves when `kind` is ‘individual’ or ‘both’. If `float`, should be between 0.0 and 1.0 and represent the proportion of the dataset to be used to plot ICE curves. If `int`, represents the absolute number samples to use.
Note that the full dataset is still used to calculate averaged partial dependence when `kind='both'`.
New in version 0.24.
**random\_state**int, RandomState instance or None, default=None
Controls the randomness of the selected samples when subsamples is not `None` and `kind` is either `'both'` or `'individual'`. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state) for details.
New in version 0.24.
**centered**bool, default=False
If `True`, the ICE and PD lines will start at the origin of the y-axis. By default, no centering is done.
New in version 1.1.
Returns:
**display**[`PartialDependenceDisplay`](sklearn.inspection.partialdependencedisplay#sklearn.inspection.PartialDependenceDisplay "sklearn.inspection.PartialDependenceDisplay")
See also
[`partial_dependence`](sklearn.inspection.partial_dependence#sklearn.inspection.partial_dependence "sklearn.inspection.partial_dependence")
Compute Partial Dependence values.
[`PartialDependenceDisplay`](sklearn.inspection.partialdependencedisplay#sklearn.inspection.PartialDependenceDisplay "sklearn.inspection.PartialDependenceDisplay")
Partial Dependence visualization.
[`PartialDependenceDisplay.from_estimator`](sklearn.inspection.partialdependencedisplay#sklearn.inspection.PartialDependenceDisplay.from_estimator "sklearn.inspection.PartialDependenceDisplay.from_estimator")
Plot Partial Dependence.
#### Examples
```
>>> import matplotlib.pyplot as plt
>>> from sklearn.datasets import make_friedman1
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> from sklearn.inspection import plot_partial_dependence
>>> X, y = make_friedman1()
>>> clf = GradientBoostingRegressor(n_estimators=10).fit(X, y)
>>> plot_partial_dependence(clf, X, [0, (0, 1)])
<...>
>>> plt.show()
```
Examples using `sklearn.inspection.plot_partial_dependence`
-----------------------------------------------------------
[Release Highlights for scikit-learn 0.24](../../auto_examples/release_highlights/plot_release_highlights_0_24_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-24-0-py)
[Release Highlights for scikit-learn 0.23](../../auto_examples/release_highlights/plot_release_highlights_0_23_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-23-0-py)
[Advanced Plotting With Partial Dependence](../../auto_examples/miscellaneous/plot_partial_dependence_visualization_api#sphx-glr-auto-examples-miscellaneous-plot-partial-dependence-visualization-api-py)
| programming_docs |
scikit_learn sklearn.random_projection.GaussianRandomProjection sklearn.random\_projection.GaussianRandomProjection
===================================================
*class*sklearn.random\_projection.GaussianRandomProjection(*n\_components='auto'*, *\**, *eps=0.1*, *compute\_inverse\_components=False*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/random_projection.py#L453)
Reduce dimensionality through Gaussian random projection.
The components of the random matrix are drawn from N(0, 1 / n\_components).
Read more in the [User Guide](../random_projection#gaussian-random-matrix).
New in version 0.13.
Parameters:
**n\_components**int or ‘auto’, default=’auto’
Dimensionality of the target projection space.
n\_components can be automatically adjusted according to the number of samples in the dataset and the bound given by the Johnson-Lindenstrauss lemma. In that case the quality of the embedding is controlled by the `eps` parameter.
It should be noted that Johnson-Lindenstrauss lemma can yield very conservative estimated of the required number of components as it makes no assumption on the structure of the dataset.
**eps**float, default=0.1
Parameter to control the quality of the embedding according to the Johnson-Lindenstrauss lemma when `n_components` is set to ‘auto’. The value should be strictly positive.
Smaller values lead to better embedding and higher number of dimensions (n\_components) in the target projection space.
**compute\_inverse\_components**bool, default=False
Learn the inverse transform by computing the pseudo-inverse of the components during fit. Note that computing the pseudo-inverse does not scale well to large matrices.
**random\_state**int, RandomState instance or None, default=None
Controls the pseudo random number generator used to generate the projection matrix at fit time. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Attributes:
**n\_components\_**int
Concrete number of components computed when n\_components=”auto”.
**components\_**ndarray of shape (n\_components, n\_features)
Random matrix used for the projection.
**inverse\_components\_**ndarray of shape (n\_features, n\_components)
Pseudo-inverse of the components, only computed if `compute_inverse_components` is True.
New in version 1.1.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`SparseRandomProjection`](sklearn.random_projection.sparserandomprojection#sklearn.random_projection.SparseRandomProjection "sklearn.random_projection.SparseRandomProjection")
Reduce dimensionality through sparse random projection.
#### Examples
```
>>> import numpy as np
>>> from sklearn.random_projection import GaussianRandomProjection
>>> rng = np.random.RandomState(42)
>>> X = rng.rand(25, 3000)
>>> transformer = GaussianRandomProjection(random_state=rng)
>>> X_new = transformer.fit_transform(X)
>>> X_new.shape
(25, 2759)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.random_projection.GaussianRandomProjection.fit "sklearn.random_projection.GaussianRandomProjection.fit")(X[, y]) | Generate a sparse random projection matrix. |
| [`fit_transform`](#sklearn.random_projection.GaussianRandomProjection.fit_transform "sklearn.random_projection.GaussianRandomProjection.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.random_projection.GaussianRandomProjection.get_feature_names_out "sklearn.random_projection.GaussianRandomProjection.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.random_projection.GaussianRandomProjection.get_params "sklearn.random_projection.GaussianRandomProjection.get_params")([deep]) | Get parameters for this estimator. |
| [`inverse_transform`](#sklearn.random_projection.GaussianRandomProjection.inverse_transform "sklearn.random_projection.GaussianRandomProjection.inverse_transform")(X) | Project data back to its original space. |
| [`set_params`](#sklearn.random_projection.GaussianRandomProjection.set_params "sklearn.random_projection.GaussianRandomProjection.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.random_projection.GaussianRandomProjection.transform "sklearn.random_projection.GaussianRandomProjection.transform")(X) | Project the data by using matrix product with the random matrix. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/random_projection.py#L341)
Generate a sparse random projection matrix.
Parameters:
**X**{ndarray, sparse matrix} of shape (n\_samples, n\_features)
Training set: only the shape is used to find optimal random matrix dimensions based on the theory referenced in the afore mentioned papers.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
**self**object
BaseRandomProjection class instance.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.random_projection.GaussianRandomProjection.fit "sklearn.random_projection.GaussianRandomProjection.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
inverse\_transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/random_projection.py#L418)
Project data back to its original space.
Returns an array X\_original whose transform would be X. Note that even if X is sparse, X\_original is dense: this may use a lot of RAM.
If `compute_inverse_components` is False, the inverse of the components is computed during each call to `inverse_transform` which can be costly.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_components)
Data to be transformed back.
Returns:
**X\_original**ndarray of shape (n\_samples, n\_features)
Reconstructed data.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/random_projection.py#L573)
Project the data by using matrix product with the random matrix.
Parameters:
**X**{ndarray, sparse matrix} of shape (n\_samples, n\_features)
The input data to project into a smaller dimensional space.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_components)
Projected array.
scikit_learn sklearn.base.BiclusterMixin sklearn.base.BiclusterMixin
===========================
*class*sklearn.base.BiclusterMixin[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L758)
Mixin class for all bicluster estimators in scikit-learn.
Attributes:
[`biclusters_`](#sklearn.base.BiclusterMixin.biclusters_ "sklearn.base.BiclusterMixin.biclusters_")
Convenient way to get row and column indicators together.
#### Methods
| | |
| --- | --- |
| [`get_indices`](#sklearn.base.BiclusterMixin.get_indices "sklearn.base.BiclusterMixin.get_indices")(i) | Row and column indices of the `i`'th bicluster. |
| [`get_shape`](#sklearn.base.BiclusterMixin.get_shape "sklearn.base.BiclusterMixin.get_shape")(i) | Shape of the `i`'th bicluster. |
| [`get_submatrix`](#sklearn.base.BiclusterMixin.get_submatrix "sklearn.base.BiclusterMixin.get_submatrix")(i, data) | Return the submatrix corresponding to bicluster `i`. |
*property*biclusters\_
Convenient way to get row and column indicators together.
Returns the `rows_` and `columns_` members.
get\_indices(*i*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L769)
Row and column indices of the `i`’th bicluster.
Only works if `rows_` and `columns_` attributes exist.
Parameters:
**i**int
The index of the cluster.
Returns:
**row\_ind**ndarray, dtype=np.intp
Indices of rows in the dataset that belong to the bicluster.
**col\_ind**ndarray, dtype=np.intp
Indices of columns in the dataset that belong to the bicluster.
get\_shape(*i*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L790)
Shape of the `i`’th bicluster.
Parameters:
**i**int
The index of the cluster.
Returns:
**n\_rows**int
Number of rows in the bicluster.
**n\_cols**int
Number of columns in the bicluster.
get\_submatrix(*i*, *data*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L809)
Return the submatrix corresponding to bicluster `i`.
Parameters:
**i**int
The index of the cluster.
**data**array-like of shape (n\_samples, n\_features)
The data.
Returns:
**submatrix**ndarray of shape (n\_rows, n\_cols)
The submatrix corresponding to bicluster `i`.
#### Notes
Works with sparse matrices. Only works if `rows_` and `columns_` attributes exist.
scikit_learn sklearn.ensemble.AdaBoostRegressor sklearn.ensemble.AdaBoostRegressor
==================================
*class*sklearn.ensemble.AdaBoostRegressor(*base\_estimator=None*, *\**, *n\_estimators=50*, *learning\_rate=1.0*, *loss='linear'*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_weight_boosting.py#L933)
An AdaBoost regressor.
An AdaBoost [1] regressor is a meta-estimator that begins by fitting a regressor on the original dataset and then fits additional copies of the regressor on the same dataset but where the weights of instances are adjusted according to the error of the current prediction. As such, subsequent regressors focus more on difficult cases.
This class implements the algorithm known as AdaBoost.R2 [2].
Read more in the [User Guide](../ensemble#adaboost).
New in version 0.14.
Parameters:
**base\_estimator**object, default=None
The base estimator from which the boosted ensemble is built. If `None`, then the base estimator is [`DecisionTreeRegressor`](sklearn.tree.decisiontreeregressor#sklearn.tree.DecisionTreeRegressor "sklearn.tree.DecisionTreeRegressor") initialized with `max_depth=3`.
**n\_estimators**int, default=50
The maximum number of estimators at which boosting is terminated. In case of perfect fit, the learning procedure is stopped early. Values must be in the range `[1, inf)`.
**learning\_rate**float, default=1.0
Weight applied to each regressor at each boosting iteration. A higher learning rate increases the contribution of each regressor. There is a trade-off between the `learning_rate` and `n_estimators` parameters. Values must be in the range `(0.0, inf)`.
**loss**{‘linear’, ‘square’, ‘exponential’}, default=’linear’
The loss function to use when updating the weights after each boosting iteration.
**random\_state**int, RandomState instance or None, default=None
Controls the random seed given at each `base_estimator` at each boosting iteration. Thus, it is only used when `base_estimator` exposes a `random_state`. In addition, it controls the bootstrap of the weights used to train the `base_estimator` at each boosting iteration. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Attributes:
**base\_estimator\_**estimator
The base estimator from which the ensemble is grown.
**estimators\_**list of regressors
The collection of fitted sub-estimators.
**estimator\_weights\_**ndarray of floats
Weights for each estimator in the boosted ensemble.
**estimator\_errors\_**ndarray of floats
Regression error for each estimator in the boosted ensemble.
[`feature_importances_`](#sklearn.ensemble.AdaBoostRegressor.feature_importances_ "sklearn.ensemble.AdaBoostRegressor.feature_importances_")ndarray of shape (n\_features,)
The impurity-based feature importances.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`AdaBoostClassifier`](sklearn.ensemble.adaboostclassifier#sklearn.ensemble.AdaBoostClassifier "sklearn.ensemble.AdaBoostClassifier")
An AdaBoost classifier.
[`GradientBoostingRegressor`](sklearn.ensemble.gradientboostingregressor#sklearn.ensemble.GradientBoostingRegressor "sklearn.ensemble.GradientBoostingRegressor")
Gradient Boosting Classification Tree.
[`sklearn.tree.DecisionTreeRegressor`](sklearn.tree.decisiontreeregressor#sklearn.tree.DecisionTreeRegressor "sklearn.tree.DecisionTreeRegressor")
A decision tree regressor.
#### References
[1] Y. Freund, R. Schapire, “A Decision-Theoretic Generalization of on-Line Learning and an Application to Boosting”, 1995.
[2] 8. Drucker, “Improving Regressors using Boosting Techniques”, 1997.
#### Examples
```
>>> from sklearn.ensemble import AdaBoostRegressor
>>> from sklearn.datasets import make_regression
>>> X, y = make_regression(n_features=4, n_informative=2,
... random_state=0, shuffle=False)
>>> regr = AdaBoostRegressor(random_state=0, n_estimators=100)
>>> regr.fit(X, y)
AdaBoostRegressor(n_estimators=100, random_state=0)
>>> regr.predict([[0, 0, 0, 0]])
array([4.7972...])
>>> regr.score(X, y)
0.9771...
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.ensemble.AdaBoostRegressor.fit "sklearn.ensemble.AdaBoostRegressor.fit")(X, y[, sample\_weight]) | Build a boosted regressor from the training set (X, y). |
| [`get_params`](#sklearn.ensemble.AdaBoostRegressor.get_params "sklearn.ensemble.AdaBoostRegressor.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.ensemble.AdaBoostRegressor.predict "sklearn.ensemble.AdaBoostRegressor.predict")(X) | Predict regression value for X. |
| [`score`](#sklearn.ensemble.AdaBoostRegressor.score "sklearn.ensemble.AdaBoostRegressor.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.ensemble.AdaBoostRegressor.set_params "sklearn.ensemble.AdaBoostRegressor.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`staged_predict`](#sklearn.ensemble.AdaBoostRegressor.staged_predict "sklearn.ensemble.AdaBoostRegressor.staged_predict")(X) | Return staged predictions for X. |
| [`staged_score`](#sklearn.ensemble.AdaBoostRegressor.staged_score "sklearn.ensemble.AdaBoostRegressor.staged_score")(X, y[, sample\_weight]) | Return staged scores for X, y. |
*property*feature\_importances\_
The impurity-based feature importances.
The higher, the more important the feature. The importance of a feature is computed as the (normalized) total reduction of the criterion brought by that feature. It is also known as the Gini importance.
Warning: impurity-based feature importances can be misleading for high cardinality features (many unique values). See [`sklearn.inspection.permutation_importance`](sklearn.inspection.permutation_importance#sklearn.inspection.permutation_importance "sklearn.inspection.permutation_importance") as an alternative.
Returns:
**feature\_importances\_**ndarray of shape (n\_features,)
The feature importances.
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_weight_boosting.py#L1061)
Build a boosted regressor from the training set (X, y).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Sparse matrix can be CSC, CSR, COO, DOK, or LIL. COO, DOK, and LIL are converted to CSR.
**y**array-like of shape (n\_samples,)
The target values (real numbers).
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, the sample weights are initialized to 1 / n\_samples.
Returns:
**self**object
Fitted AdaBoostRegressor estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_weight_boosting.py#L1211)
Predict regression value for X.
The predicted regression value of an input sample is computed as the weighted median prediction of the regressors in the ensemble.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Sparse matrix can be CSC, CSR, COO, DOK, or LIL. COO, DOK, and LIL are converted to CSR.
Returns:
**y**ndarray of shape (n\_samples,)
The predicted regression values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
staged\_predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_weight_boosting.py#L1233)
Return staged predictions for X.
The predicted regression value of an input sample is computed as the weighted median prediction of the regressors in the ensemble.
This generator method yields the ensemble prediction after each iteration of boosting and therefore allows monitoring, such as to determine the prediction on a test set after each boost.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples.
Yields:
**y**generator of ndarray of shape (n\_samples,)
The predicted regression values.
staged\_score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_weight_boosting.py#L235)
Return staged scores for X, y.
This generator method yields the ensemble score after each iteration of boosting and therefore allows monitoring, such as to determine the score on a test set after each boost.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Sparse matrix can be CSC, CSR, COO, DOK, or LIL. COO, DOK, and LIL are converted to CSR.
**y**array-like of shape (n\_samples,)
Labels for X.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Yields:
**z**float
Examples using `sklearn.ensemble.AdaBoostRegressor`
---------------------------------------------------
[Decision Tree Regression with AdaBoost](../../auto_examples/ensemble/plot_adaboost_regression#sphx-glr-auto-examples-ensemble-plot-adaboost-regression-py)
| programming_docs |
scikit_learn sklearn.feature_extraction.image.img_to_graph sklearn.feature\_extraction.image.img\_to\_graph
================================================
sklearn.feature\_extraction.image.img\_to\_graph(*img*, *\**, *mask=None*, *return\_as=<class 'scipy.sparse.\_coo.coo\_matrix'>*, *dtype=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/image.py#L141)
Graph of the pixel-to-pixel gradient connections.
Edges are weighted with the gradient values.
Read more in the [User Guide](../feature_extraction#image-feature-extraction).
Parameters:
**img**ndarray of shape (height, width) or (height, width, channel)
2D or 3D image.
**mask**ndarray of shape (height, width) or (height, width, channel), dtype=bool, default=None
An optional mask of the image, to consider only part of the pixels.
**return\_as**np.ndarray or a sparse matrix class, default=sparse.coo\_matrix
The class to use to build the returned adjacency matrix.
**dtype**dtype, default=None
The data of the returned sparse matrix. By default it is the dtype of img.
Returns:
**graph**ndarray or a sparse matrix class
The computed adjacency matrix.
#### Notes
For scikit-learn versions 0.14.1 and prior, return\_as=np.ndarray was handled by returning a dense np.matrix instance. Going forward, np.ndarray returns an np.ndarray, as expected.
For compatibility, user code relying on this method should wrap its calls in `np.asarray` to avoid type issues.
scikit_learn sklearn.utils.extmath.randomized_range_finder sklearn.utils.extmath.randomized\_range\_finder
===============================================
sklearn.utils.extmath.randomized\_range\_finder(*A*, *\**, *size*, *n\_iter*, *power\_iteration\_normalizer='auto'*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/extmath.py#L164)
Compute an orthonormal matrix whose range approximates the range of A.
Parameters:
**A**2D array
The input data matrix.
**size**int
Size of the return array.
**n\_iter**int
Number of power iterations used to stabilize the result.
**power\_iteration\_normalizer**{‘auto’, ‘QR’, ‘LU’, ‘none’}, default=’auto’
Whether the power iterations are normalized with step-by-step QR factorization (the slowest but most accurate), ‘none’ (the fastest but numerically unstable when `n_iter` is large, e.g. typically 5 or larger), or ‘LU’ factorization (numerically stable but can lose slightly in accuracy). The ‘auto’ mode applies no normalization if `n_iter` <= 2 and switches to LU otherwise.
New in version 0.18.
**random\_state**int, RandomState instance or None, default=None
The seed of the pseudo random number generator to use when shuffling the data, i.e. getting the random vectors to initialize the algorithm. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Returns:
**Q**ndarray
A (size x size) projection matrix, the range of which approximates well the range of the input matrix A.
#### Notes
Follows Algorithm 4.3 of [“Finding structure with randomness: Stochastic algorithms for constructing approximate matrix decompositions”](https://arxiv.org/abs/0909.4061) Halko, et al. (2009)
An implementation of a randomized algorithm for principal component analysis A. Szlam et al. 2014
scikit_learn sklearn.metrics.check_scoring sklearn.metrics.check\_scoring
==============================
sklearn.metrics.check\_scoring(*estimator*, *scoring=None*, *\**, *allow\_none=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_scorer.py#L432)
Determine scorer from user options.
A TypeError will be thrown if the estimator cannot be scored.
Parameters:
**estimator**estimator object implementing ‘fit’
The object to use to fit the data.
**scoring**str or callable, default=None
A string (see model evaluation documentation) or a scorer callable object / function with signature `scorer(estimator, X, y)`. If None, the provided estimator object’s `score` method is used.
**allow\_none**bool, default=False
If no scoring is specified and the estimator has no score function, we can either return None or raise an exception.
Returns:
**scoring**callable
A scorer callable object / function with signature `scorer(estimator, X, y)`.
scikit_learn sklearn.impute.MissingIndicator sklearn.impute.MissingIndicator
===============================
*class*sklearn.impute.MissingIndicator(*\**, *missing\_values=nan*, *features='missing-only'*, *sparse='auto'*, *error\_on\_new=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/impute/_base.py#L682)
Binary indicators for missing values.
Note that this component typically should not be used in a vanilla `Pipeline` consisting of transformers and a classifier, but rather could be added using a `FeatureUnion` or `ColumnTransformer`.
Read more in the [User Guide](../impute#impute).
New in version 0.20.
Parameters:
**missing\_values**int, float, str, np.nan or None, default=np.nan
The placeholder for the missing values. All occurrences of `missing_values` will be imputed. For pandas’ dataframes with nullable integer dtypes with missing values, `missing_values` should be set to `np.nan`, since `pd.NA` will be converted to `np.nan`.
**features**{‘missing-only’, ‘all’}, default=’missing-only’
Whether the imputer mask should represent all or a subset of features.
* If `'missing-only'` (default), the imputer mask will only represent features containing missing values during fit time.
* If `'all'`, the imputer mask will represent all features.
**sparse**bool or ‘auto’, default=’auto’
Whether the imputer mask format should be sparse or dense.
* If `'auto'` (default), the imputer mask will be of same type as input.
* If `True`, the imputer mask will be a sparse matrix.
* If `False`, the imputer mask will be a numpy array.
**error\_on\_new**bool, default=True
If `True`, [`transform`](#sklearn.impute.MissingIndicator.transform "sklearn.impute.MissingIndicator.transform") will raise an error when there are features with missing values that have no missing values in [`fit`](#sklearn.impute.MissingIndicator.fit "sklearn.impute.MissingIndicator.fit"). This is applicable only when `features='missing-only'`.
Attributes:
**features\_**ndarray of shape (n\_missing\_features,) or (n\_features,)
The features indices which will be returned when calling [`transform`](#sklearn.impute.MissingIndicator.transform "sklearn.impute.MissingIndicator.transform"). They are computed during [`fit`](#sklearn.impute.MissingIndicator.fit "sklearn.impute.MissingIndicator.fit"). If `features='all'`, `features_` is equal to `range(n_features)`.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`SimpleImputer`](sklearn.impute.simpleimputer#sklearn.impute.SimpleImputer "sklearn.impute.SimpleImputer")
Univariate imputation of missing values.
[`IterativeImputer`](sklearn.impute.iterativeimputer#sklearn.impute.IterativeImputer "sklearn.impute.IterativeImputer")
Multivariate imputation of missing values.
#### Examples
```
>>> import numpy as np
>>> from sklearn.impute import MissingIndicator
>>> X1 = np.array([[np.nan, 1, 3],
... [4, 0, np.nan],
... [8, 1, 0]])
>>> X2 = np.array([[5, 1, np.nan],
... [np.nan, 2, 3],
... [2, 4, 0]])
>>> indicator = MissingIndicator()
>>> indicator.fit(X1)
MissingIndicator()
>>> X2_tr = indicator.transform(X2)
>>> X2_tr
array([[False, True],
[ True, False],
[False, False]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.impute.MissingIndicator.fit "sklearn.impute.MissingIndicator.fit")(X[, y]) | Fit the transformer on `X`. |
| [`fit_transform`](#sklearn.impute.MissingIndicator.fit_transform "sklearn.impute.MissingIndicator.fit_transform")(X[, y]) | Generate missing values indicator for `X`. |
| [`get_feature_names_out`](#sklearn.impute.MissingIndicator.get_feature_names_out "sklearn.impute.MissingIndicator.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.impute.MissingIndicator.get_params "sklearn.impute.MissingIndicator.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.impute.MissingIndicator.set_params "sklearn.impute.MissingIndicator.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.impute.MissingIndicator.transform "sklearn.impute.MissingIndicator.transform")(X) | Generate missing values indicator for `X`. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/impute/_base.py#L920)
Fit the transformer on `X`.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Input data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**self**object
Fitted estimator.
fit\_transform(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/impute/_base.py#L982)
Generate missing values indicator for `X`.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input data to complete.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**Xt**{ndarray, sparse matrix} of shape (n\_samples, n\_features) or (n\_samples, n\_features\_with\_missing)
The missing indicator for input data. The data type of `Xt` will be boolean.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/impute/_base.py#L1007)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Input features.
* If `input_features` is `None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then the following input feature names are generated: `["x0", "x1", ..., "x(n_features_in_ - 1)"]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/impute/_base.py#L941)
Generate missing values indicator for `X`.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input data to complete.
Returns:
**Xt**{ndarray, sparse matrix} of shape (n\_samples, n\_features) or (n\_samples, n\_features\_with\_missing)
The missing indicator for input data. The data type of `Xt` will be boolean.
scikit_learn sklearn.feature_selection.SelectFromModel sklearn.feature\_selection.SelectFromModel
==========================================
*class*sklearn.feature\_selection.SelectFromModel(*estimator*, *\**, *threshold=None*, *prefit=False*, *norm\_order=1*, *max\_features=None*, *importance\_getter='auto'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_from_model.py#L82)
Meta-transformer for selecting features based on importance weights.
New in version 0.17.
Read more in the [User Guide](../feature_selection#select-from-model).
Parameters:
**estimator**object
The base estimator from which the transformer is built. This can be both a fitted (if `prefit` is set to True) or a non-fitted estimator. The estimator should have a `feature_importances_` or `coef_` attribute after fitting. Otherwise, the `importance_getter` parameter should be used.
**threshold**str or float, default=None
The threshold value to use for feature selection. Features whose absolute importance value is greater or equal are kept while the others are discarded. If “median” (resp. “mean”), then the `threshold` value is the median (resp. the mean) of the feature importances. A scaling factor (e.g., “1.25\*mean”) may also be used. If None and if the estimator has a parameter penalty set to l1, either explicitly or implicitly (e.g, Lasso), the threshold used is 1e-5. Otherwise, “mean” is used by default.
**prefit**bool, default=False
Whether a prefit model is expected to be passed into the constructor directly or not. If `True`, `estimator` must be a fitted estimator. If `False`, `estimator` is fitted and updated by calling `fit` and `partial_fit`, respectively.
**norm\_order**non-zero int, inf, -inf, default=1
Order of the norm used to filter the vectors of coefficients below `threshold` in the case where the `coef_` attribute of the estimator is of dimension 2.
**max\_features**int, callable, default=None
The maximum number of features to select.
* If an integer, then it specifies the maximum number of features to allow.
* If a callable, then it specifies how to calculate the maximum number of features allowed by using the output of `max_feaures(X)`.
* If `None`, then all features are kept.
To only select based on `max_features`, set `threshold=-np.inf`.
New in version 0.20.
Changed in version 1.1: `max_features` accepts a callable.
**importance\_getter**str or callable, default=’auto’
If ‘auto’, uses the feature importance either through a `coef_` attribute or `feature_importances_` attribute of estimator.
Also accepts a string that specifies an attribute name/path for extracting feature importance (implemented with `attrgetter`). For example, give `regressor_.coef_` in case of [`TransformedTargetRegressor`](sklearn.compose.transformedtargetregressor#sklearn.compose.TransformedTargetRegressor "sklearn.compose.TransformedTargetRegressor") or `named_steps.clf.feature_importances_` in case of [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline") with its last step named `clf`.
If `callable`, overrides the default feature importance getter. The callable is passed with the fitted estimator and it should return importance for each feature.
New in version 0.24.
Attributes:
**estimator\_**estimator
The base estimator from which the transformer is built. This attribute exist only when `fit` has been called.
* If `prefit=True`, it is a deep copy of `estimator`.
* If `prefit=False`, it is a clone of `estimator` and fit on the data passed to `fit` or `partial_fit`.
[`n_features_in_`](#sklearn.feature_selection.SelectFromModel.n_features_in_ "sklearn.feature_selection.SelectFromModel.n_features_in_")int
Number of features seen during `fit`.
**max\_features\_**int
Maximum number of features calculated during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Only defined if the `max_features` is not `None`.
* If `max_features` is an `int`, then `max_features_ = max_features`.
* If `max_features` is a callable, then `max_features_ = max_features(X)`.
New in version 1.1.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
[`threshold_`](#sklearn.feature_selection.SelectFromModel.threshold_ "sklearn.feature_selection.SelectFromModel.threshold_")float
Threshold value used for feature selection.
See also
[`RFE`](sklearn.feature_selection.rfe#sklearn.feature_selection.RFE "sklearn.feature_selection.RFE")
Recursive feature elimination based on importance weights.
[`RFECV`](sklearn.feature_selection.rfecv#sklearn.feature_selection.RFECV "sklearn.feature_selection.RFECV")
Recursive feature elimination with built-in cross-validated selection of the best number of features.
[`SequentialFeatureSelector`](sklearn.feature_selection.sequentialfeatureselector#sklearn.feature_selection.SequentialFeatureSelector "sklearn.feature_selection.SequentialFeatureSelector")
Sequential cross-validation based feature selection. Does not rely on importance weights.
#### Notes
Allows NaN/Inf in the input if the underlying estimator does as well.
#### Examples
```
>>> from sklearn.feature_selection import SelectFromModel
>>> from sklearn.linear_model import LogisticRegression
>>> X = [[ 0.87, -1.34, 0.31 ],
... [-2.79, -0.02, -0.85 ],
... [-1.34, -0.48, -2.55 ],
... [ 1.92, 1.48, 0.65 ]]
>>> y = [0, 1, 0, 1]
>>> selector = SelectFromModel(estimator=LogisticRegression()).fit(X, y)
>>> selector.estimator_.coef_
array([[-0.3252302 , 0.83462377, 0.49750423]])
>>> selector.threshold_
0.55245...
>>> selector.get_support()
array([False, True, False])
>>> selector.transform(X)
array([[-1.34],
[-0.02],
[-0.48],
[ 1.48]])
```
Using a callable to create a selector that can use no more than half of the input features.
```
>>> def half_callable(X):
... return round(len(X[0]) / 2)
>>> half_selector = SelectFromModel(estimator=LogisticRegression(),
... max_features=half_callable)
>>> _ = half_selector.fit(X, y)
>>> half_selector.max_features_
2
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.feature_selection.SelectFromModel.fit "sklearn.feature_selection.SelectFromModel.fit")(X[, y]) | Fit the SelectFromModel meta-transformer. |
| [`fit_transform`](#sklearn.feature_selection.SelectFromModel.fit_transform "sklearn.feature_selection.SelectFromModel.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.feature_selection.SelectFromModel.get_feature_names_out "sklearn.feature_selection.SelectFromModel.get_feature_names_out")([input\_features]) | Mask feature names according to selected features. |
| [`get_params`](#sklearn.feature_selection.SelectFromModel.get_params "sklearn.feature_selection.SelectFromModel.get_params")([deep]) | Get parameters for this estimator. |
| [`get_support`](#sklearn.feature_selection.SelectFromModel.get_support "sklearn.feature_selection.SelectFromModel.get_support")([indices]) | Get a mask, or integer index, of the features selected. |
| [`inverse_transform`](#sklearn.feature_selection.SelectFromModel.inverse_transform "sklearn.feature_selection.SelectFromModel.inverse_transform")(X) | Reverse the transformation operation. |
| [`partial_fit`](#sklearn.feature_selection.SelectFromModel.partial_fit "sklearn.feature_selection.SelectFromModel.partial_fit")(X[, y]) | Fit the SelectFromModel meta-transformer only once. |
| [`set_params`](#sklearn.feature_selection.SelectFromModel.set_params "sklearn.feature_selection.SelectFromModel.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.feature_selection.SelectFromModel.transform "sklearn.feature_selection.SelectFromModel.transform")(X) | Reduce X to the selected features. |
fit(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_from_model.py#L322)
Fit the SelectFromModel meta-transformer.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The training input samples.
**y**array-like of shape (n\_samples,), default=None
The target values (integers that correspond to classes in classification, real numbers in regression).
**\*\*fit\_params**dict
Other estimator specific parameters.
Returns:
**self**object
Fitted estimator.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L146)
Mask feature names according to selected features.
Parameters:
**input\_features**array-like of str or None, default=None
Input features.
* If `input_features` is `None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then the following input feature names are generated: `["x0", "x1", ..., "x(n_features_in_ - 1)"]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
get\_support(*indices=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L33)
Get a mask, or integer index, of the features selected.
Parameters:
**indices**bool, default=False
If True, the return value will be an array of integers, rather than a boolean mask.
Returns:
**support**array
An index that selects the retained features from a feature vector. If `indices` is False, this is a boolean array of shape [# input features], in which an element is True iff its corresponding feature is selected for retention. If `indices` is True, this is an integer array of shape [# output features] whose values are indices into the input feature vector.
inverse\_transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L106)
Reverse the transformation operation.
Parameters:
**X**array of shape [n\_samples, n\_selected\_features]
The input samples.
Returns:
**X\_r**array of shape [n\_samples, n\_original\_features]
`X` with columns of zeros inserted where features would have been removed by [`transform`](#sklearn.feature_selection.SelectFromModel.transform "sklearn.feature_selection.SelectFromModel.transform").
*property*n\_features\_in\_
Number of features seen during `fit`.
partial\_fit(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_from_model.py#L375)
Fit the SelectFromModel meta-transformer only once.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The training input samples.
**y**array-like of shape (n\_samples,), default=None
The target values (integers that correspond to classes in classification, real numbers in regression).
**\*\*fit\_params**dict
Other estimator specific parameters.
Returns:
**self**object
Fitted estimator.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
*property*threshold\_
Threshold value used for feature selection.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L68)
Reduce X to the selected features.
Parameters:
**X**array of shape [n\_samples, n\_features]
The input samples.
Returns:
**X\_r**array of shape [n\_samples, n\_selected\_features]
The input samples with only the selected features.
Examples using `sklearn.feature_selection.SelectFromModel`
----------------------------------------------------------
[Model-based and sequential feature selection](../../auto_examples/feature_selection/plot_select_from_model_diabetes#sphx-glr-auto-examples-feature-selection-plot-select-from-model-diabetes-py)
| programming_docs |
scikit_learn sklearn.metrics.recall_score sklearn.metrics.recall\_score
=============================
sklearn.metrics.recall\_score(*y\_true*, *y\_pred*, *\**, *labels=None*, *pos\_label=1*, *average='binary'*, *sample\_weight=None*, *zero\_division='warn'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_classification.py#L1789)
Compute the recall.
The recall is the ratio `tp / (tp + fn)` where `tp` is the number of true positives and `fn` the number of false negatives. The recall is intuitively the ability of the classifier to find all the positive samples.
The best value is 1 and the worst value is 0.
Read more in the [User Guide](../model_evaluation#precision-recall-f-measure-metrics).
Parameters:
**y\_true**1d array-like, or label indicator array / sparse matrix
Ground truth (correct) target values.
**y\_pred**1d array-like, or label indicator array / sparse matrix
Estimated targets as returned by a classifier.
**labels**array-like, default=None
The set of labels to include when `average != 'binary'`, and their order if `average is None`. Labels present in the data can be excluded, for example to calculate a multiclass average ignoring a majority negative class, while labels not present in the data will result in 0 components in a macro average. For multilabel targets, labels are column indices. By default, all labels in `y_true` and `y_pred` are used in sorted order.
Changed in version 0.17: Parameter `labels` improved for multiclass problem.
**pos\_label**str or int, default=1
The class to report if `average='binary'` and the data is binary. If the data are multiclass or multilabel, this will be ignored; setting `labels=[pos_label]` and `average != 'binary'` will report scores for that label only.
**average**{‘micro’, ‘macro’, ‘samples’, ‘weighted’, ‘binary’} or None, default=’binary’
This parameter is required for multiclass/multilabel targets. If `None`, the scores for each class are returned. Otherwise, this determines the type of averaging performed on the data:
`'binary'`:
Only report results for the class specified by `pos_label`. This is applicable only if targets (`y_{true,pred}`) are binary.
`'micro'`:
Calculate metrics globally by counting the total true positives, false negatives and false positives.
`'macro'`:
Calculate metrics for each label, and find their unweighted mean. This does not take label imbalance into account.
`'weighted'`:
Calculate metrics for each label, and find their average weighted by support (the number of true instances for each label). This alters ‘macro’ to account for label imbalance; it can result in an F-score that is not between precision and recall. Weighted recall is equal to accuracy.
`'samples'`:
Calculate metrics for each instance, and find their average (only meaningful for multilabel classification where this differs from [`accuracy_score`](sklearn.metrics.accuracy_score#sklearn.metrics.accuracy_score "sklearn.metrics.accuracy_score")).
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**zero\_division**“warn”, 0 or 1, default=”warn”
Sets the value to return when there is a zero division. If set to “warn”, this acts as 0, but warnings are also raised.
Returns:
**recall**float (if average is not None) or array of float of shape (n\_unique\_labels,)
Recall of the positive class in binary classification or weighted average of the recall of each class for the multiclass task.
See also
[`precision_recall_fscore_support`](sklearn.metrics.precision_recall_fscore_support#sklearn.metrics.precision_recall_fscore_support "sklearn.metrics.precision_recall_fscore_support")
Compute precision, recall, F-measure and support for each class.
[`precision_score`](sklearn.metrics.precision_score#sklearn.metrics.precision_score "sklearn.metrics.precision_score")
Compute the ratio `tp / (tp + fp)` where `tp` is the number of true positives and `fp` the number of false positives.
[`balanced_accuracy_score`](sklearn.metrics.balanced_accuracy_score#sklearn.metrics.balanced_accuracy_score "sklearn.metrics.balanced_accuracy_score")
Compute balanced accuracy to deal with imbalanced datasets.
[`multilabel_confusion_matrix`](sklearn.metrics.multilabel_confusion_matrix#sklearn.metrics.multilabel_confusion_matrix "sklearn.metrics.multilabel_confusion_matrix")
Compute a confusion matrix for each class or sample.
[`PrecisionRecallDisplay.from_estimator`](sklearn.metrics.precisionrecalldisplay#sklearn.metrics.PrecisionRecallDisplay.from_estimator "sklearn.metrics.PrecisionRecallDisplay.from_estimator")
Plot precision-recall curve given an estimator and some data.
[`PrecisionRecallDisplay.from_predictions`](sklearn.metrics.precisionrecalldisplay#sklearn.metrics.PrecisionRecallDisplay.from_predictions "sklearn.metrics.PrecisionRecallDisplay.from_predictions")
Plot precision-recall curve given binary class predictions.
#### Notes
When `true positive + false negative == 0`, recall returns 0 and raises `UndefinedMetricWarning`. This behavior can be modified with `zero_division`.
#### Examples
```
>>> from sklearn.metrics import recall_score
>>> y_true = [0, 1, 2, 0, 1, 2]
>>> y_pred = [0, 2, 1, 0, 0, 1]
>>> recall_score(y_true, y_pred, average='macro')
0.33...
>>> recall_score(y_true, y_pred, average='micro')
0.33...
>>> recall_score(y_true, y_pred, average='weighted')
0.33...
>>> recall_score(y_true, y_pred, average=None)
array([1., 0., 0.])
>>> y_true = [0, 0, 0, 0, 0, 0]
>>> recall_score(y_true, y_pred, average=None)
array([0.5, 0. , 0. ])
>>> recall_score(y_true, y_pred, average=None, zero_division=1)
array([0.5, 1. , 1. ])
>>> # multilabel classification
>>> y_true = [[0, 0, 0], [1, 1, 1], [0, 1, 1]]
>>> y_pred = [[0, 0, 0], [1, 1, 1], [1, 1, 0]]
>>> recall_score(y_true, y_pred, average=None)
array([1. , 1. , 0.5])
```
Examples using `sklearn.metrics.recall_score`
---------------------------------------------
[Probability Calibration curves](../../auto_examples/calibration/plot_calibration_curve#sphx-glr-auto-examples-calibration-plot-calibration-curve-py)
[Precision-Recall](../../auto_examples/model_selection/plot_precision_recall#sphx-glr-auto-examples-model-selection-plot-precision-recall-py)
scikit_learn sklearn.covariance.graphical_lasso sklearn.covariance.graphical\_lasso
===================================
sklearn.covariance.graphical\_lasso(*emp\_cov*, *alpha*, *\**, *cov\_init=None*, *mode='cd'*, *tol=0.0001*, *enet\_tol=0.0001*, *max\_iter=100*, *verbose=False*, *return\_costs=False*, *eps=2.220446049250313e-16*, *return\_n\_iter=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_graph_lasso.py#L99)
L1-penalized covariance estimator.
Read more in the [User Guide](../covariance#sparse-inverse-covariance).
Changed in version v0.20: graph\_lasso has been renamed to graphical\_lasso
Parameters:
**emp\_cov**ndarray of shape (n\_features, n\_features)
Empirical covariance from which to compute the covariance estimate.
**alpha**float
The regularization parameter: the higher alpha, the more regularization, the sparser the inverse covariance. Range is (0, inf].
**cov\_init**array of shape (n\_features, n\_features), default=None
The initial guess for the covariance. If None, then the empirical covariance is used.
**mode**{‘cd’, ‘lars’}, default=’cd’
The Lasso solver to use: coordinate descent or LARS. Use LARS for very sparse underlying graphs, where p > n. Elsewhere prefer cd which is more numerically stable.
**tol**float, default=1e-4
The tolerance to declare convergence: if the dual gap goes below this value, iterations are stopped. Range is (0, inf].
**enet\_tol**float, default=1e-4
The tolerance for the elastic net solver used to calculate the descent direction. This parameter controls the accuracy of the search direction for a given column update, not of the overall parameter estimate. Only used for mode=’cd’. Range is (0, inf].
**max\_iter**int, default=100
The maximum number of iterations.
**verbose**bool, default=False
If verbose is True, the objective function and dual gap are printed at each iteration.
**return\_costs**bool, default=Flase
If return\_costs is True, the objective function and dual gap at each iteration are returned.
**eps**float, default=eps
The machine-precision regularization in the computation of the Cholesky diagonal factors. Increase this for very ill-conditioned systems. Default is `np.finfo(np.float64).eps`.
**return\_n\_iter**bool, default=False
Whether or not to return the number of iterations.
Returns:
**covariance**ndarray of shape (n\_features, n\_features)
The estimated covariance matrix.
**precision**ndarray of shape (n\_features, n\_features)
The estimated (sparse) precision matrix.
**costs**list of (objective, dual\_gap) pairs
The list of values of the objective function and the dual gap at each iteration. Returned only if return\_costs is True.
**n\_iter**int
Number of iterations. Returned only if `return_n_iter` is set to True.
See also
[`GraphicalLasso`](sklearn.covariance.graphicallasso#sklearn.covariance.GraphicalLasso "sklearn.covariance.GraphicalLasso")
Sparse inverse covariance estimation with an l1-penalized estimator.
[`GraphicalLassoCV`](sklearn.covariance.graphicallassocv#sklearn.covariance.GraphicalLassoCV "sklearn.covariance.GraphicalLassoCV")
Sparse inverse covariance with cross-validated choice of the l1 penalty.
#### Notes
The algorithm employed to solve this problem is the GLasso algorithm, from the Friedman 2008 Biostatistics paper. It is the same algorithm as in the R `glasso` package.
One possible difference with the `glasso` R package is that the diagonal coefficients are not penalized.
scikit_learn sklearn.utils.validation.check_symmetric sklearn.utils.validation.check\_symmetric
=========================================
sklearn.utils.validation.check\_symmetric(*array*, *\**, *tol=1e-10*, *raise\_warning=True*, *raise\_exception=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/validation.py#L1215)
Make sure that array is 2D, square and symmetric.
If the array is not symmetric, then a symmetrized version is returned. Optionally, a warning or exception is raised if the matrix is not symmetric.
Parameters:
**array**{ndarray, sparse matrix}
Input object to check / convert. Must be two-dimensional and square, otherwise a ValueError will be raised.
**tol**float, default=1e-10
Absolute tolerance for equivalence of arrays. Default = 1E-10.
**raise\_warning**bool, default=True
If True then raise a warning if conversion is required.
**raise\_exception**bool, default=False
If True then raise an exception if array is not symmetric.
Returns:
**array\_sym**{ndarray, sparse matrix}
Symmetrized version of the input array, i.e. the average of array and array.transpose(). If sparse, then duplicate entries are first summed and zeros are eliminated.
scikit_learn sklearn.neighbors.KDTree sklearn.neighbors.KDTree
========================
*class*sklearn.neighbors.KDTree(*X*, *leaf\_size=40*, *metric='minkowski'*, *\*\*kwargs*)
KDTree for fast generalized N-point problems
Read more in the [User Guide](../neighbors#unsupervised-neighbors).
Parameters:
**X**array-like of shape (n\_samples, n\_features)
n\_samples is the number of points in the data set, and n\_features is the dimension of the parameter space. Note: if X is a C-contiguous array of doubles then data will not be copied. Otherwise, an internal copy will be made.
**leaf\_size**positive int, default=40
Number of points at which to switch to brute-force. Changing leaf\_size will not affect the results of a query, but can significantly impact the speed of a query and the memory required to store the constructed tree. The amount of memory needed to store the tree scales as approximately n\_samples / leaf\_size. For a specified `leaf_size`, a leaf node is guaranteed to satisfy `leaf_size <= n_points <= 2 * leaf_size`, except in the case that `n_samples < leaf_size`.
**metric**str or DistanceMetric object, default=’minkowski’
Metric to use for distance computation. Default is “minkowski”, which results in the standard Euclidean distance when p = 2. kd\_tree.valid\_metrics gives a list of the metrics which are valid for KDTree. See the documentation of [scipy.spatial.distance](https://docs.scipy.org/doc/scipy/reference/spatial.distance.html) and the metrics listed in [`distance_metrics`](sklearn.metrics.pairwise.distance_metrics#sklearn.metrics.pairwise.distance_metrics "sklearn.metrics.pairwise.distance_metrics") for more information.
**Additional keywords are passed to the distance metric class.**
**Note: Callable functions in the metric parameter are NOT supported for KDTree**
**and Ball Tree. Function call overhead will result in very poor performance.**
Attributes:
**data**memory view
The training data
#### Examples
Query for k-nearest neighbors
```
>>> import numpy as np
>>> from sklearn.neighbors import KDTree
>>> rng = np.random.RandomState(0)
>>> X = rng.random_sample((10, 3)) # 10 points in 3 dimensions
>>> tree = KDTree(X, leaf_size=2)
>>> dist, ind = tree.query(X[:1], k=3)
>>> print(ind) # indices of 3 closest neighbors
[0 3 1]
>>> print(dist) # distances to 3 closest neighbors
[ 0. 0.19662693 0.29473397]
```
Pickle and Unpickle a tree. Note that the state of the tree is saved in the pickle operation: the tree needs not be rebuilt upon unpickling.
```
>>> import numpy as np
>>> import pickle
>>> rng = np.random.RandomState(0)
>>> X = rng.random_sample((10, 3)) # 10 points in 3 dimensions
>>> tree = KDTree(X, leaf_size=2)
>>> s = pickle.dumps(tree)
>>> tree_copy = pickle.loads(s)
>>> dist, ind = tree_copy.query(X[:1], k=3)
>>> print(ind) # indices of 3 closest neighbors
[0 3 1]
>>> print(dist) # distances to 3 closest neighbors
[ 0. 0.19662693 0.29473397]
```
Query for neighbors within a given radius
```
>>> import numpy as np
>>> rng = np.random.RandomState(0)
>>> X = rng.random_sample((10, 3)) # 10 points in 3 dimensions
>>> tree = KDTree(X, leaf_size=2)
>>> print(tree.query_radius(X[:1], r=0.3, count_only=True))
3
>>> ind = tree.query_radius(X[:1], r=0.3)
>>> print(ind) # indices of neighbors within distance 0.3
[3 0 1]
```
Compute a gaussian kernel density estimate:
```
>>> import numpy as np
>>> rng = np.random.RandomState(42)
>>> X = rng.random_sample((100, 3))
>>> tree = KDTree(X)
>>> tree.kernel_density(X[:3], h=0.1, kernel='gaussian')
array([ 6.94114649, 7.83281226, 7.2071716 ])
```
Compute a two-point auto-correlation function
```
>>> import numpy as np
>>> rng = np.random.RandomState(0)
>>> X = rng.random_sample((30, 3))
>>> r = np.linspace(0, 1, 5)
>>> tree = KDTree(X)
>>> tree.two_point_correlation(X, r)
array([ 30, 62, 278, 580, 820])
```
#### Methods
| | |
| --- | --- |
| [`get_arrays`](#sklearn.neighbors.KDTree.get_arrays "sklearn.neighbors.KDTree.get_arrays")() | Get data and node arrays. |
| [`get_n_calls`](#sklearn.neighbors.KDTree.get_n_calls "sklearn.neighbors.KDTree.get_n_calls")() | Get number of calls. |
| [`get_tree_stats`](#sklearn.neighbors.KDTree.get_tree_stats "sklearn.neighbors.KDTree.get_tree_stats")() | Get tree status. |
| [`kernel_density`](#sklearn.neighbors.KDTree.kernel_density "sklearn.neighbors.KDTree.kernel_density")(X, h[, kernel, atol, rtol, ...]) | Compute the kernel density estimate at points X with the given kernel, using the distance metric specified at tree creation. |
| [`query`](#sklearn.neighbors.KDTree.query "sklearn.neighbors.KDTree.query")(X[, k, return\_distance, dualtree, ...]) | query the tree for the k nearest neighbors |
| [`query_radius`](#sklearn.neighbors.KDTree.query_radius "sklearn.neighbors.KDTree.query_radius")(X, r[, return\_distance, ...]) | query the tree for neighbors within a radius r |
| [`reset_n_calls`](#sklearn.neighbors.KDTree.reset_n_calls "sklearn.neighbors.KDTree.reset_n_calls")() | Reset number of calls to 0. |
| [`two_point_correlation`](#sklearn.neighbors.KDTree.two_point_correlation "sklearn.neighbors.KDTree.two_point_correlation")(X, r[, dualtree]) | Compute the two-point correlation function |
get\_arrays()
Get data and node arrays.
Returns:
arrays: tuple of array
Arrays for storing tree data, index, node data and node bounds.
get\_n\_calls()
Get number of calls.
Returns:
n\_calls: int
number of distance computation calls
get\_tree\_stats()
Get tree status.
Returns:
tree\_stats: tuple of int
(number of trims, number of leaves, number of splits)
kernel\_density(*X*, *h*, *kernel='gaussian'*, *atol=0*, *rtol=1E-8*, *breadth\_first=True*, *return\_log=False*)
Compute the kernel density estimate at points X with the given kernel, using the distance metric specified at tree creation.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
An array of points to query. Last dimension should match dimension of training data.
**h**float
the bandwidth of the kernel
**kernel**str, default=”gaussian”
specify the kernel to use. Options are - ‘gaussian’ - ‘tophat’ - ‘epanechnikov’ - ‘exponential’ - ‘linear’ - ‘cosine’ Default is kernel = ‘gaussian’
**atol**float, default=0
Specify the desired absolute tolerance of the result. If the true result is `K_true`, then the returned result `K_ret` satisfies `abs(K_true - K_ret) < atol + rtol * K_ret` The default is zero (i.e. machine precision).
**rtol**float, default=1e-8
Specify the desired relative tolerance of the result. If the true result is `K_true`, then the returned result `K_ret` satisfies `abs(K_true - K_ret) < atol + rtol * K_ret` The default is `1e-8` (i.e. machine precision).
**breadth\_first**bool, default=False
If True, use a breadth-first search. If False (default) use a depth-first search. Breadth-first is generally faster for compact kernels and/or high tolerances.
**return\_log**bool, default=False
Return the logarithm of the result. This can be more accurate than returning the result itself for narrow kernels.
Returns:
**density**ndarray of shape X.shape[:-1]
The array of (log)-density evaluations
query(*X*, *k=1*, *return\_distance=True*, *dualtree=False*, *breadth\_first=False*)
query the tree for the k nearest neighbors
Parameters:
**X**array-like of shape (n\_samples, n\_features)
An array of points to query
**k**int, default=1
The number of nearest neighbors to return
**return\_distance**bool, default=True
if True, return a tuple (d, i) of distances and indices if False, return array i
**dualtree**bool, default=False
if True, use the dual tree formalism for the query: a tree is built for the query points, and the pair of trees is used to efficiently search this space. This can lead to better performance as the number of points grows large.
**breadth\_first**bool, default=False
if True, then query the nodes in a breadth-first manner. Otherwise, query the nodes in a depth-first manner.
**sort\_results**bool, default=True
if True, then distances and indices of each point are sorted on return, so that the first column contains the closest points. Otherwise, neighbors are returned in an arbitrary order.
Returns:
**i**if return\_distance == False
**(d,i)**if return\_distance == True
**d**ndarray of shape X.shape[:-1] + (k,), dtype=double
Each entry gives the list of distances to the neighbors of the corresponding point.
**i**ndarray of shape X.shape[:-1] + (k,), dtype=int
Each entry gives the list of indices of neighbors of the corresponding point.
query\_radius(*X*, *r*, *return\_distance=False*, *count\_only=False*, *sort\_results=False*)
query the tree for neighbors within a radius r
Parameters:
**X**array-like of shape (n\_samples, n\_features)
An array of points to query
**r**distance within which neighbors are returned
r can be a single value, or an array of values of shape x.shape[:-1] if different radii are desired for each point.
**return\_distance**bool, default=False
if True, return distances to neighbors of each point if False, return only neighbors Note that unlike the query() method, setting return\_distance=True here adds to the computation time. Not all distances need to be calculated explicitly for return\_distance=False. Results are not sorted by default: see `sort_results` keyword.
**count\_only**bool, default=False
if True, return only the count of points within distance r if False, return the indices of all points within distance r If return\_distance==True, setting count\_only=True will result in an error.
**sort\_results**bool, default=False
if True, the distances and indices will be sorted before being returned. If False, the results will not be sorted. If return\_distance == False, setting sort\_results = True will result in an error.
Returns:
**count**if count\_only == True
**ind**if count\_only == False and return\_distance == False
**(ind, dist)**if count\_only == False and return\_distance == True
**count**ndarray of shape X.shape[:-1], dtype=int
Each entry gives the number of neighbors within a distance r of the corresponding point.
**ind**ndarray of shape X.shape[:-1], dtype=object
Each element is a numpy integer array listing the indices of neighbors of the corresponding point. Note that unlike the results of a k-neighbors query, the returned neighbors are not sorted by distance by default.
**dist**ndarray of shape X.shape[:-1], dtype=object
Each element is a numpy double array listing the distances corresponding to indices in i.
reset\_n\_calls()
Reset number of calls to 0.
two\_point\_correlation(*X*, *r*, *dualtree=False*)
Compute the two-point correlation function
Parameters:
**X**array-like of shape (n\_samples, n\_features)
An array of points to query. Last dimension should match dimension of training data.
**r**array-like
A one-dimensional array of distances
**dualtree**bool, default=False
If True, use a dualtree algorithm. Otherwise, use a single-tree algorithm. Dual tree algorithms can have better scaling for large N.
Returns:
**counts**ndarray
counts[i] contains the number of pairs of points with distance less than or equal to r[i]
| programming_docs |
scikit_learn sklearn.multiclass.OneVsOneClassifier sklearn.multiclass.OneVsOneClassifier
=====================================
*class*sklearn.multiclass.OneVsOneClassifier(*estimator*, *\**, *n\_jobs=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/multiclass.py#L566)
One-vs-one multiclass strategy.
This strategy consists in fitting one classifier per class pair. At prediction time, the class which received the most votes is selected. Since it requires to fit `n_classes * (n_classes - 1) / 2` classifiers, this method is usually slower than one-vs-the-rest, due to its O(n\_classes^2) complexity. However, this method may be advantageous for algorithms such as kernel algorithms which don’t scale well with `n_samples`. This is because each individual learning problem only involves a small subset of the data whereas, with one-vs-the-rest, the complete dataset is used `n_classes` times.
Read more in the [User Guide](../multiclass#ovo-classification).
Parameters:
**estimator**estimator object
An estimator object implementing [fit](https://scikit-learn.org/1.1/glossary.html#term-fit) and one of [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) or [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba).
**n\_jobs**int, default=None
The number of jobs to use for the computation: the `n_classes * (
n_classes - 1) / 2` OVO problems are computed in parallel.
`None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
Attributes:
**estimators\_**list of `n_classes * (n_classes - 1) / 2` estimators
Estimators used for predictions.
**classes\_**numpy array of shape [n\_classes]
Array containing labels.
[`n_classes_`](#sklearn.multiclass.OneVsOneClassifier.n_classes_ "sklearn.multiclass.OneVsOneClassifier.n_classes_")int
Number of classes.
**pairwise\_indices\_**list, length = `len(estimators_)`, or `None`
Indices of samples used when training the estimators. `None` when `estimator`’s `pairwise` tag is False.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`OneVsRestClassifier`](sklearn.multiclass.onevsrestclassifier#sklearn.multiclass.OneVsRestClassifier "sklearn.multiclass.OneVsRestClassifier")
One-vs-all multiclass strategy.
#### Examples
```
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.multiclass import OneVsOneClassifier
>>> from sklearn.svm import LinearSVC
>>> X, y = load_iris(return_X_y=True)
>>> X_train, X_test, y_train, y_test = train_test_split(
... X, y, test_size=0.33, shuffle=True, random_state=0)
>>> clf = OneVsOneClassifier(
... LinearSVC(random_state=0)).fit(X_train, y_train)
>>> clf.predict(X_test[:10])
array([2, 1, 0, 2, 0, 2, 0, 1, 1, 1])
```
#### Methods
| | |
| --- | --- |
| [`decision_function`](#sklearn.multiclass.OneVsOneClassifier.decision_function "sklearn.multiclass.OneVsOneClassifier.decision_function")(X) | Decision function for the OneVsOneClassifier. |
| [`fit`](#sklearn.multiclass.OneVsOneClassifier.fit "sklearn.multiclass.OneVsOneClassifier.fit")(X, y) | Fit underlying estimators. |
| [`get_params`](#sklearn.multiclass.OneVsOneClassifier.get_params "sklearn.multiclass.OneVsOneClassifier.get_params")([deep]) | Get parameters for this estimator. |
| [`partial_fit`](#sklearn.multiclass.OneVsOneClassifier.partial_fit "sklearn.multiclass.OneVsOneClassifier.partial_fit")(X, y[, classes]) | Partially fit underlying estimators. |
| [`predict`](#sklearn.multiclass.OneVsOneClassifier.predict "sklearn.multiclass.OneVsOneClassifier.predict")(X) | Estimate the best class label for each sample in X. |
| [`score`](#sklearn.multiclass.OneVsOneClassifier.score "sklearn.multiclass.OneVsOneClassifier.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.multiclass.OneVsOneClassifier.set_params "sklearn.multiclass.OneVsOneClassifier.set_params")(\*\*params) | Set the parameters of this estimator. |
decision\_function(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/multiclass.py#L781)
Decision function for the OneVsOneClassifier.
The decision values for the samples are computed by adding the normalized sum of pair-wise classification confidence levels to the votes in order to disambiguate between the decision values when the votes for all the classes are equal leading to a tie.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input data.
Returns:
**Y**array-like of shape (n\_samples, n\_classes) or (n\_samples,)
Result of calling `decision_function` on the final estimator.
Changed in version 0.19: output shape changed to `(n_samples,)` to conform to scikit-learn conventions for binary classification.
fit(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/multiclass.py#L644)
Fit underlying estimators.
Parameters:
**X**(sparse) array-like of shape (n\_samples, n\_features)
Data.
**y**array-like of shape (n\_samples,)
Multi-class targets.
Returns:
**self**object
The fitted underlying estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_classes\_
Number of classes.
partial\_fit(*X*, *y*, *classes=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/multiclass.py#L693)
Partially fit underlying estimators.
Should be used when memory is inefficient to train all data. Chunks of data can be passed in several iteration, where the first call should have an array of all target variables.
Parameters:
**X**(sparse) array-like of shape (n\_samples, n\_features)
Data.
**y**array-like of shape (n\_samples,)
Multi-class targets.
**classes**array, shape (n\_classes, )
Classes across all calls to partial\_fit. Can be obtained via `np.unique(y_all)`, where y\_all is the target vector of the entire dataset. This argument is only required in the first call of partial\_fit and can be omitted in the subsequent calls.
Returns:
**self**object
The partially fitted underlying estimator.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/multiclass.py#L758)
Estimate the best class label for each sample in X.
This is implemented as `argmax(decision_function(X), axis=1)` which will return the label of the class with most votes by estimators predicting the outcome of a decision for each possible class pair.
Parameters:
**X**(sparse) array-like of shape (n\_samples, n\_features)
Data.
Returns:
**y**numpy array of shape [n\_samples]
Predicted multi-class targets.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
scikit_learn sklearn.mixture.GaussianMixture sklearn.mixture.GaussianMixture
===============================
*class*sklearn.mixture.GaussianMixture(*n\_components=1*, *\**, *covariance\_type='full'*, *tol=0.001*, *reg\_covar=1e-06*, *max\_iter=100*, *n\_init=1*, *init\_params='kmeans'*, *weights\_init=None*, *means\_init=None*, *precisions\_init=None*, *random\_state=None*, *warm\_start=False*, *verbose=0*, *verbose\_interval=10*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/mixture/_gaussian_mixture.py#L456)
Gaussian Mixture.
Representation of a Gaussian mixture model probability distribution. This class allows to estimate the parameters of a Gaussian mixture distribution.
Read more in the [User Guide](../mixture#gmm).
New in version 0.18.
Parameters:
**n\_components**int, default=1
The number of mixture components.
**covariance\_type**{‘full’, ‘tied’, ‘diag’, ‘spherical’}, default=’full’
String describing the type of covariance parameters to use. Must be one of:
* ‘full’: each component has its own general covariance matrix.
* ‘tied’: all components share the same general covariance matrix.
* ‘diag’: each component has its own diagonal covariance matrix.
* ‘spherical’: each component has its own single variance.
**tol**float, default=1e-3
The convergence threshold. EM iterations will stop when the lower bound average gain is below this threshold.
**reg\_covar**float, default=1e-6
Non-negative regularization added to the diagonal of covariance. Allows to assure that the covariance matrices are all positive.
**max\_iter**int, default=100
The number of EM iterations to perform.
**n\_init**int, default=1
The number of initializations to perform. The best results are kept.
**init\_params**{‘kmeans’, ‘k-means++’, ‘random’, ‘random\_from\_data’}, default=’kmeans’
The method used to initialize the weights, the means and the precisions. String must be one of:
* ‘kmeans’ : responsibilities are initialized using kmeans.
* ‘k-means++’ : use the k-means++ method to initialize.
* ‘random’ : responsibilities are initialized randomly.
* ‘random\_from\_data’ : initial means are randomly selected data points.
Changed in version v1.1: `init_params` now accepts ‘random\_from\_data’ and ‘k-means++’ as initialization methods.
**weights\_init**array-like of shape (n\_components, ), default=None
The user-provided initial weights. If it is None, weights are initialized using the `init_params` method.
**means\_init**array-like of shape (n\_components, n\_features), default=None
The user-provided initial means, If it is None, means are initialized using the `init_params` method.
**precisions\_init**array-like, default=None
The user-provided initial precisions (inverse of the covariance matrices). If it is None, precisions are initialized using the ‘init\_params’ method. The shape depends on ‘covariance\_type’:
```
(n_components,) if 'spherical',
(n_features, n_features) if 'tied',
(n_components, n_features) if 'diag',
(n_components, n_features, n_features) if 'full'
```
**random\_state**int, RandomState instance or None, default=None
Controls the random seed given to the method chosen to initialize the parameters (see `init_params`). In addition, it controls the generation of random samples from the fitted distribution (see the method `sample`). Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**warm\_start**bool, default=False
If ‘warm\_start’ is True, the solution of the last fitting is used as initialization for the next call of fit(). This can speed up convergence when fit is called several times on similar problems. In that case, ‘n\_init’ is ignored and only a single initialization occurs upon the first call. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
**verbose**int, default=0
Enable verbose output. If 1 then it prints the current initialization and each iteration step. If greater than 1 then it prints also the log probability and the time needed for each step.
**verbose\_interval**int, default=10
Number of iteration done before the next print.
Attributes:
**weights\_**array-like of shape (n\_components,)
The weights of each mixture components.
**means\_**array-like of shape (n\_components, n\_features)
The mean of each mixture component.
**covariances\_**array-like
The covariance of each mixture component. The shape depends on `covariance_type`:
```
(n_components,) if 'spherical',
(n_features, n_features) if 'tied',
(n_components, n_features) if 'diag',
(n_components, n_features, n_features) if 'full'
```
**precisions\_**array-like
The precision matrices for each component in the mixture. A precision matrix is the inverse of a covariance matrix. A covariance matrix is symmetric positive definite so the mixture of Gaussian can be equivalently parameterized by the precision matrices. Storing the precision matrices instead of the covariance matrices makes it more efficient to compute the log-likelihood of new samples at test time. The shape depends on `covariance_type`:
```
(n_components,) if 'spherical',
(n_features, n_features) if 'tied',
(n_components, n_features) if 'diag',
(n_components, n_features, n_features) if 'full'
```
**precisions\_cholesky\_**array-like
The cholesky decomposition of the precision matrices of each mixture component. A precision matrix is the inverse of a covariance matrix. A covariance matrix is symmetric positive definite so the mixture of Gaussian can be equivalently parameterized by the precision matrices. Storing the precision matrices instead of the covariance matrices makes it more efficient to compute the log-likelihood of new samples at test time. The shape depends on `covariance_type`:
```
(n_components,) if 'spherical',
(n_features, n_features) if 'tied',
(n_components, n_features) if 'diag',
(n_components, n_features, n_features) if 'full'
```
**converged\_**bool
True when convergence was reached in fit(), False otherwise.
**n\_iter\_**int
Number of step used by the best fit of EM to reach the convergence.
**lower\_bound\_**float
Lower bound value on the log-likelihood (of the training data with respect to the model) of the best fit of EM.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`BayesianGaussianMixture`](sklearn.mixture.bayesiangaussianmixture#sklearn.mixture.BayesianGaussianMixture "sklearn.mixture.BayesianGaussianMixture")
Gaussian mixture model fit with a variational inference.
#### Examples
```
>>> import numpy as np
>>> from sklearn.mixture import GaussianMixture
>>> X = np.array([[1, 2], [1, 4], [1, 0], [10, 2], [10, 4], [10, 0]])
>>> gm = GaussianMixture(n_components=2, random_state=0).fit(X)
>>> gm.means_
array([[10., 2.],
[ 1., 2.]])
>>> gm.predict([[0, 0], [12, 3]])
array([1, 0])
```
#### Methods
| | |
| --- | --- |
| [`aic`](#sklearn.mixture.GaussianMixture.aic "sklearn.mixture.GaussianMixture.aic")(X) | Akaike information criterion for the current model on the input X. |
| [`bic`](#sklearn.mixture.GaussianMixture.bic "sklearn.mixture.GaussianMixture.bic")(X) | Bayesian information criterion for the current model on the input X. |
| [`fit`](#sklearn.mixture.GaussianMixture.fit "sklearn.mixture.GaussianMixture.fit")(X[, y]) | Estimate model parameters with the EM algorithm. |
| [`fit_predict`](#sklearn.mixture.GaussianMixture.fit_predict "sklearn.mixture.GaussianMixture.fit_predict")(X[, y]) | Estimate model parameters using X and predict the labels for X. |
| [`get_params`](#sklearn.mixture.GaussianMixture.get_params "sklearn.mixture.GaussianMixture.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.mixture.GaussianMixture.predict "sklearn.mixture.GaussianMixture.predict")(X) | Predict the labels for the data samples in X using trained model. |
| [`predict_proba`](#sklearn.mixture.GaussianMixture.predict_proba "sklearn.mixture.GaussianMixture.predict_proba")(X) | Evaluate the components' density for each sample. |
| [`sample`](#sklearn.mixture.GaussianMixture.sample "sklearn.mixture.GaussianMixture.sample")([n\_samples]) | Generate random samples from the fitted Gaussian distribution. |
| [`score`](#sklearn.mixture.GaussianMixture.score "sklearn.mixture.GaussianMixture.score")(X[, y]) | Compute the per-sample average log-likelihood of the given data X. |
| [`score_samples`](#sklearn.mixture.GaussianMixture.score_samples "sklearn.mixture.GaussianMixture.score_samples")(X) | Compute the log-likelihood of each sample. |
| [`set_params`](#sklearn.mixture.GaussianMixture.set_params "sklearn.mixture.GaussianMixture.set_params")(\*\*params) | Set the parameters of this estimator. |
aic(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/mixture/_gaussian_mixture.py#L835)
Akaike information criterion for the current model on the input X.
You can refer to this [mathematical section](../linear_model#aic-bic) for more details regarding the formulation of the AIC used.
Parameters:
**X**array of shape (n\_samples, n\_dimensions)
The input samples.
Returns:
**aic**float
The lower the better.
bic(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/mixture/_gaussian_mixture.py#L815)
Bayesian information criterion for the current model on the input X.
You can refer to this [mathematical section](../linear_model#aic-bic) for more details regarding the formulation of the BIC used.
Parameters:
**X**array of shape (n\_samples, n\_dimensions)
The input samples.
Returns:
**bic**float
The lower the better.
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/mixture/_base.py#L174)
Estimate model parameters with the EM algorithm.
The method fits the model `n_init` times and sets the parameters with which the model has the largest likelihood or lower bound. Within each trial, the method iterates between E-step and M-step for `max_iter` times until the change of likelihood or lower bound is less than `tol`, otherwise, a `ConvergenceWarning` is raised. If `warm_start` is `True`, then `n_init` is ignored and a single initialization is performed upon the first call. Upon consecutive calls, training starts where it left off.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
List of n\_features-dimensional data points. Each row corresponds to a single data point.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**self**object
The fitted mixture.
fit\_predict(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/mixture/_base.py#L203)
Estimate model parameters using X and predict the labels for X.
The method fits the model n\_init times and sets the parameters with which the model has the largest likelihood or lower bound. Within each trial, the method iterates between E-step and M-step for `max_iter` times until the change of likelihood or lower bound is less than `tol`, otherwise, a [`ConvergenceWarning`](sklearn.exceptions.convergencewarning#sklearn.exceptions.ConvergenceWarning "sklearn.exceptions.ConvergenceWarning") is raised. After fitting, it predicts the most probable label for the input data points.
New in version 0.20.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
List of n\_features-dimensional data points. Each row corresponds to a single data point.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**labels**array, shape (n\_samples,)
Component labels.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/mixture/_base.py#L384)
Predict the labels for the data samples in X using trained model.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
List of n\_features-dimensional data points. Each row corresponds to a single data point.
Returns:
**labels**array, shape (n\_samples,)
Component labels.
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/mixture/_base.py#L402)
Evaluate the components’ density for each sample.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
List of n\_features-dimensional data points. Each row corresponds to a single data point.
Returns:
**resp**array, shape (n\_samples, n\_components)
Density of each Gaussian component for each sample in X.
sample(*n\_samples=1*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/mixture/_base.py#L421)
Generate random samples from the fitted Gaussian distribution.
Parameters:
**n\_samples**int, default=1
Number of samples to generate.
Returns:
**X**array, shape (n\_samples, n\_features)
Randomly generated sample.
**y**array, shape (nsamples,)
Component labels.
score(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/mixture/_base.py#L365)
Compute the per-sample average log-likelihood of the given data X.
Parameters:
**X**array-like of shape (n\_samples, n\_dimensions)
List of n\_features-dimensional data points. Each row corresponds to a single data point.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**log\_likelihood**float
Log-likelihood of `X` under the Gaussian mixture model.
score\_samples(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/mixture/_base.py#L346)
Compute the log-likelihood of each sample.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
List of n\_features-dimensional data points. Each row corresponds to a single data point.
Returns:
**log\_prob**array, shape (n\_samples,)
Log-likelihood of each sample in `X` under the current model.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.mixture.GaussianMixture`
------------------------------------------------
[Comparing different clustering algorithms on toy datasets](../../auto_examples/cluster/plot_cluster_comparison#sphx-glr-auto-examples-cluster-plot-cluster-comparison-py)
[Density Estimation for a Gaussian mixture](../../auto_examples/mixture/plot_gmm_pdf#sphx-glr-auto-examples-mixture-plot-gmm-pdf-py)
[GMM Initialization Methods](../../auto_examples/mixture/plot_gmm_init#sphx-glr-auto-examples-mixture-plot-gmm-init-py)
[GMM covariances](../../auto_examples/mixture/plot_gmm_covariances#sphx-glr-auto-examples-mixture-plot-gmm-covariances-py)
[Gaussian Mixture Model Ellipsoids](../../auto_examples/mixture/plot_gmm#sphx-glr-auto-examples-mixture-plot-gmm-py)
[Gaussian Mixture Model Selection](../../auto_examples/mixture/plot_gmm_selection#sphx-glr-auto-examples-mixture-plot-gmm-selection-py)
[Gaussian Mixture Model Sine Curve](../../auto_examples/mixture/plot_gmm_sin#sphx-glr-auto-examples-mixture-plot-gmm-sin-py)
| programming_docs |
scikit_learn sklearn.utils.indexable sklearn.utils.indexable
=======================
sklearn.utils.indexable(*\*iterables*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/validation.py#L413)
Make arrays indexable for cross-validation.
Checks consistent length, passes through None, and ensures that everything can be indexed by converting sparse matrices to csr and converting non-interable objects to arrays.
Parameters:
**\*iterables**{lists, dataframes, ndarrays, sparse matrices}
List of objects to ensure sliceability.
Returns:
**result**list of {ndarray, sparse matrix, dataframe} or None
Returns a list containing indexable arrays (i.e. NumPy array, sparse matrix, or dataframe) or `None`.
scikit_learn sklearn.datasets.load_iris sklearn.datasets.load\_iris
===========================
sklearn.datasets.load\_iris(*\**, *return\_X\_y=False*, *as\_frame=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_base.py#L549)
Load and return the iris dataset (classification).
The iris dataset is a classic and very easy multi-class classification dataset.
| | |
| --- | --- |
| Classes | 3 |
| Samples per class | 50 |
| Samples total | 150 |
| Dimensionality | 4 |
| Features | real, positive |
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/toy_dataset.html#iris-dataset).
Parameters:
**return\_X\_y**bool, default=False
If True, returns `(data, target)` instead of a Bunch object. See below for more information about the `data` and `target` object.
New in version 0.18.
**as\_frame**bool, default=False
If True, the data is a pandas DataFrame including columns with appropriate dtypes (numeric). The target is a pandas DataFrame or Series depending on the number of target columns. If `return_X_y` is True, then (`data`, `target`) will be pandas DataFrames or Series as described below.
New in version 0.23.
Returns:
**data**[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
Dictionary-like object, with the following attributes.
data{ndarray, dataframe} of shape (150, 4)
The data matrix. If `as_frame=True`, `data` will be a pandas DataFrame.
target: {ndarray, Series} of shape (150,)
The classification target. If `as_frame=True`, `target` will be a pandas Series.
feature\_names: list
The names of the dataset columns.
target\_names: list
The names of target classes.
frame: DataFrame of shape (150, 5)
Only present when `as_frame=True`. DataFrame with `data` and `target`.
New in version 0.23.
DESCR: str
The full description of the dataset.
filename: str
The path to the location of the data.
New in version 0.20.
**(data, target)**tuple if `return_X_y` is True
A tuple of two ndarray. The first containing a 2D array of shape (n\_samples, n\_features) with each row representing one sample and each column representing the features. The second ndarray of shape (n\_samples,) containing the target samples.
New in version 0.18.
#### Notes
Changed in version 0.20: Fixed two wrong data points according to Fisher’s paper. The new version is the same as in R, but not as in the UCI Machine Learning Repository.
#### Examples
Let’s say you are interested in the samples 10, 25, and 50, and want to know their class name.
```
>>> from sklearn.datasets import load_iris
>>> data = load_iris()
>>> data.target[[10, 25, 50]]
array([0, 0, 1])
>>> list(data.target_names)
['setosa', 'versicolor', 'virginica']
```
Examples using `sklearn.datasets.load_iris`
-------------------------------------------
[Release Highlights for scikit-learn 0.24](../../auto_examples/release_highlights/plot_release_highlights_0_24_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-24-0-py)
[Release Highlights for scikit-learn 0.22](../../auto_examples/release_highlights/plot_release_highlights_0_22_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-22-0-py)
[Plot classification probability](../../auto_examples/classification/plot_classification_probability#sphx-glr-auto-examples-classification-plot-classification-probability-py)
[K-means Clustering](../../auto_examples/cluster/plot_cluster_iris#sphx-glr-auto-examples-cluster-plot-cluster-iris-py)
[Plot Hierarchical Clustering Dendrogram](../../auto_examples/cluster/plot_agglomerative_dendrogram#sphx-glr-auto-examples-cluster-plot-agglomerative-dendrogram-py)
[The Iris Dataset](../../auto_examples/datasets/plot_iris_dataset#sphx-glr-auto-examples-datasets-plot-iris-dataset-py)
[Plot the decision surface of decision trees trained on the iris dataset](../../auto_examples/tree/plot_iris_dtc#sphx-glr-auto-examples-tree-plot-iris-dtc-py)
[Understanding the decision tree structure](../../auto_examples/tree/plot_unveil_tree_structure#sphx-glr-auto-examples-tree-plot-unveil-tree-structure-py)
[Comparison of LDA and PCA 2D projection of Iris dataset](../../auto_examples/decomposition/plot_pca_vs_lda#sphx-glr-auto-examples-decomposition-plot-pca-vs-lda-py)
[Factor Analysis (with rotation) to visualize patterns](../../auto_examples/decomposition/plot_varimax_fa#sphx-glr-auto-examples-decomposition-plot-varimax-fa-py)
[Incremental PCA](../../auto_examples/decomposition/plot_incremental_pca#sphx-glr-auto-examples-decomposition-plot-incremental-pca-py)
[PCA example with Iris Data-set](../../auto_examples/decomposition/plot_pca_iris#sphx-glr-auto-examples-decomposition-plot-pca-iris-py)
[Early stopping of Gradient Boosting](../../auto_examples/ensemble/plot_gradient_boosting_early_stopping#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-early-stopping-py)
[Plot the decision boundaries of a VotingClassifier](../../auto_examples/ensemble/plot_voting_decision_regions#sphx-glr-auto-examples-ensemble-plot-voting-decision-regions-py)
[Plot the decision surfaces of ensembles of trees on the iris dataset](../../auto_examples/ensemble/plot_forest_iris#sphx-glr-auto-examples-ensemble-plot-forest-iris-py)
[Univariate Feature Selection](../../auto_examples/feature_selection/plot_feature_selection#sphx-glr-auto-examples-feature-selection-plot-feature-selection-py)
[GMM covariances](../../auto_examples/mixture/plot_gmm_covariances#sphx-glr-auto-examples-mixture-plot-gmm-covariances-py)
[Gaussian process classification (GPC) on iris dataset](../../auto_examples/gaussian_process/plot_gpc_iris#sphx-glr-auto-examples-gaussian-process-plot-gpc-iris-py)
[Logistic Regression 3-class Classifier](../../auto_examples/linear_model/plot_iris_logistic#sphx-glr-auto-examples-linear-model-plot-iris-logistic-py)
[Plot multi-class SGD on the iris dataset](../../auto_examples/linear_model/plot_sgd_iris#sphx-glr-auto-examples-linear-model-plot-sgd-iris-py)
[Regularization path of L1- Logistic Regression](../../auto_examples/linear_model/plot_logistic_path#sphx-glr-auto-examples-linear-model-plot-logistic-path-py)
[Confusion matrix](../../auto_examples/model_selection/plot_confusion_matrix#sphx-glr-auto-examples-model-selection-plot-confusion-matrix-py)
[Nested versus non-nested cross-validation](../../auto_examples/model_selection/plot_nested_cross_validation_iris#sphx-glr-auto-examples-model-selection-plot-nested-cross-validation-iris-py)
[Precision-Recall](../../auto_examples/model_selection/plot_precision_recall#sphx-glr-auto-examples-model-selection-plot-precision-recall-py)
[Receiver Operating Characteristic (ROC)](../../auto_examples/model_selection/plot_roc#sphx-glr-auto-examples-model-selection-plot-roc-py)
[Receiver Operating Characteristic (ROC) with cross validation](../../auto_examples/model_selection/plot_roc_crossval#sphx-glr-auto-examples-model-selection-plot-roc-crossval-py)
[Test with permutations the significance of a classification score](../../auto_examples/model_selection/plot_permutation_tests_for_classification#sphx-glr-auto-examples-model-selection-plot-permutation-tests-for-classification-py)
[Comparing Nearest Neighbors with and without Neighborhood Components Analysis](../../auto_examples/neighbors/plot_nca_classification#sphx-glr-auto-examples-neighbors-plot-nca-classification-py)
[Nearest Centroid Classification](../../auto_examples/neighbors/plot_nearest_centroid#sphx-glr-auto-examples-neighbors-plot-nearest-centroid-py)
[Nearest Neighbors Classification](../../auto_examples/neighbors/plot_classification#sphx-glr-auto-examples-neighbors-plot-classification-py)
[Compare Stochastic learning strategies for MLPClassifier](../../auto_examples/neural_networks/plot_mlp_training_curves#sphx-glr-auto-examples-neural-networks-plot-mlp-training-curves-py)
[Concatenating multiple feature extraction methods](../../auto_examples/compose/plot_feature_union#sphx-glr-auto-examples-compose-plot-feature-union-py)
[Decision boundary of semi-supervised classifiers versus SVM on the Iris dataset](../../auto_examples/semi_supervised/plot_semi_supervised_versus_svm_iris#sphx-glr-auto-examples-semi-supervised-plot-semi-supervised-versus-svm-iris-py)
[Plot different SVM classifiers in the iris dataset](../../auto_examples/svm/plot_iris_svc#sphx-glr-auto-examples-svm-plot-iris-svc-py)
[RBF SVM parameters](../../auto_examples/svm/plot_rbf_parameters#sphx-glr-auto-examples-svm-plot-rbf-parameters-py)
[SVM with custom kernel](../../auto_examples/svm/plot_custom_kernel#sphx-glr-auto-examples-svm-plot-custom-kernel-py)
[SVM-Anova: SVM with univariate feature selection](../../auto_examples/svm/plot_svm_anova#sphx-glr-auto-examples-svm-plot-svm-anova-py)
[SVM Exercise](../../auto_examples/exercises/plot_iris_exercise#sphx-glr-auto-examples-exercises-plot-iris-exercise-py)
scikit_learn sklearn.ensemble.BaggingRegressor sklearn.ensemble.BaggingRegressor
=================================
*class*sklearn.ensemble.BaggingRegressor(*base\_estimator=None*, *n\_estimators=10*, *\**, *max\_samples=1.0*, *max\_features=1.0*, *bootstrap=True*, *bootstrap\_features=False*, *oob\_score=False*, *warm\_start=False*, *n\_jobs=None*, *random\_state=None*, *verbose=0*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_bagging.py#L949)
A Bagging regressor.
A Bagging regressor is an ensemble meta-estimator that fits base regressors each on random subsets of the original dataset and then aggregate their individual predictions (either by voting or by averaging) to form a final prediction. Such a meta-estimator can typically be used as a way to reduce the variance of a black-box estimator (e.g., a decision tree), by introducing randomization into its construction procedure and then making an ensemble out of it.
This algorithm encompasses several works from the literature. When random subsets of the dataset are drawn as random subsets of the samples, then this algorithm is known as Pasting [[1]](#r4d113ba76fc0-1). If samples are drawn with replacement, then the method is known as Bagging [[2]](#r4d113ba76fc0-2). When random subsets of the dataset are drawn as random subsets of the features, then the method is known as Random Subspaces [[3]](#r4d113ba76fc0-3). Finally, when base estimators are built on subsets of both samples and features, then the method is known as Random Patches [[4]](#r4d113ba76fc0-4).
Read more in the [User Guide](../ensemble#bagging).
New in version 0.15.
Parameters:
**base\_estimator**object, default=None
The base estimator to fit on random subsets of the dataset. If None, then the base estimator is a [`DecisionTreeRegressor`](sklearn.tree.decisiontreeregressor#sklearn.tree.DecisionTreeRegressor "sklearn.tree.DecisionTreeRegressor").
**n\_estimators**int, default=10
The number of base estimators in the ensemble.
**max\_samples**int or float, default=1.0
The number of samples to draw from X to train each base estimator (with replacement by default, see `bootstrap` for more details).
* If int, then draw `max_samples` samples.
* If float, then draw `max_samples * X.shape[0]` samples.
**max\_features**int or float, default=1.0
The number of features to draw from X to train each base estimator ( without replacement by default, see `bootstrap_features` for more details).
* If int, then draw `max_features` features.
* If float, then draw `max(1, int(max_features * n_features_in_))` features.
**bootstrap**bool, default=True
Whether samples are drawn with replacement. If False, sampling without replacement is performed.
**bootstrap\_features**bool, default=False
Whether features are drawn with replacement.
**oob\_score**bool, default=False
Whether to use out-of-bag samples to estimate the generalization error. Only available if bootstrap=True.
**warm\_start**bool, default=False
When set to True, reuse the solution of the previous call to fit and add more estimators to the ensemble, otherwise, just fit a whole new ensemble. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
**n\_jobs**int, default=None
The number of jobs to run in parallel for both [`fit`](#sklearn.ensemble.BaggingRegressor.fit "sklearn.ensemble.BaggingRegressor.fit") and [`predict`](#sklearn.ensemble.BaggingRegressor.predict "sklearn.ensemble.BaggingRegressor.predict"). `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**random\_state**int, RandomState instance or None, default=None
Controls the random resampling of the original dataset (sample wise and feature wise). If the base estimator accepts a `random_state` attribute, a different seed is generated for each instance in the ensemble. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**verbose**int, default=0
Controls the verbosity when fitting and predicting.
Attributes:
**base\_estimator\_**estimator
The base estimator from which the ensemble is grown.
[`n_features_`](#sklearn.ensemble.BaggingRegressor.n_features_ "sklearn.ensemble.BaggingRegressor.n_features_")int
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**estimators\_**list of estimators
The collection of fitted sub-estimators.
[`estimators_samples_`](#sklearn.ensemble.BaggingRegressor.estimators_samples_ "sklearn.ensemble.BaggingRegressor.estimators_samples_")list of arrays
The subset of drawn samples for each base estimator.
**estimators\_features\_**list of arrays
The subset of drawn features for each base estimator.
**oob\_score\_**float
Score of the training dataset obtained using an out-of-bag estimate. This attribute exists only when `oob_score` is True.
**oob\_prediction\_**ndarray of shape (n\_samples,)
Prediction computed with out-of-bag estimate on the training set. If n\_estimators is small it might be possible that a data point was never left out during the bootstrap. In this case, `oob_prediction_` might contain NaN. This attribute exists only when `oob_score` is True.
See also
[`BaggingClassifier`](sklearn.ensemble.baggingclassifier#sklearn.ensemble.BaggingClassifier "sklearn.ensemble.BaggingClassifier")
A Bagging classifier.
#### References
[[1](#id1)] L. Breiman, “Pasting small votes for classification in large databases and on-line”, Machine Learning, 36(1), 85-103, 1999.
[[2](#id2)] L. Breiman, “Bagging predictors”, Machine Learning, 24(2), 123-140, 1996.
[[3](#id3)] T. Ho, “The random subspace method for constructing decision forests”, Pattern Analysis and Machine Intelligence, 20(8), 832-844, 1998.
[[4](#id4)] G. Louppe and P. Geurts, “Ensembles on Random Patches”, Machine Learning and Knowledge Discovery in Databases, 346-361, 2012.
#### Examples
```
>>> from sklearn.svm import SVR
>>> from sklearn.ensemble import BaggingRegressor
>>> from sklearn.datasets import make_regression
>>> X, y = make_regression(n_samples=100, n_features=4,
... n_informative=2, n_targets=1,
... random_state=0, shuffle=False)
>>> regr = BaggingRegressor(base_estimator=SVR(),
... n_estimators=10, random_state=0).fit(X, y)
>>> regr.predict([[0, 0, 0, 0]])
array([-2.8720...])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.ensemble.BaggingRegressor.fit "sklearn.ensemble.BaggingRegressor.fit")(X, y[, sample\_weight]) | Build a Bagging ensemble of estimators from the training set (X, y). |
| [`get_params`](#sklearn.ensemble.BaggingRegressor.get_params "sklearn.ensemble.BaggingRegressor.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.ensemble.BaggingRegressor.predict "sklearn.ensemble.BaggingRegressor.predict")(X) | Predict regression target for X. |
| [`score`](#sklearn.ensemble.BaggingRegressor.score "sklearn.ensemble.BaggingRegressor.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.ensemble.BaggingRegressor.set_params "sklearn.ensemble.BaggingRegressor.set_params")(\*\*params) | Set the parameters of this estimator. |
*property*estimators\_samples\_
The subset of drawn samples for each base estimator.
Returns a dynamically generated list of indices identifying the samples used for fitting each member of the ensemble, i.e., the in-bag samples.
Note: the list is re-created at each call to the property in order to reduce the object memory footprint by not storing the sampling data. Thus fetching the property may be slower than expected.
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_bagging.py#L265)
Build a Bagging ensemble of estimators from the training set (X, y).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Sparse matrices are accepted only if they are supported by the base estimator.
**y**array-like of shape (n\_samples,)
The target values (class labels in classification, real numbers in regression).
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, then samples are equally weighted. Note that this is supported only if the base estimator supports sample weighting.
Returns:
**self**object
Fitted estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_features\_
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2. Use `n_features_in_` instead.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_bagging.py#L1138)
Predict regression target for X.
The predicted regression target of an input sample is computed as the mean predicted regression targets of the estimators in the ensemble.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Sparse matrices are accepted only if they are supported by the base estimator.
Returns:
**y**ndarray of shape (n\_samples,)
The predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.ensemble.BaggingRegressor`
--------------------------------------------------
[Single estimator versus bagging: bias-variance decomposition](../../auto_examples/ensemble/plot_bias_variance#sphx-glr-auto-examples-ensemble-plot-bias-variance-py)
| programming_docs |
scikit_learn sklearn.metrics.pairwise.manhattan_distances sklearn.metrics.pairwise.manhattan\_distances
=============================================
sklearn.metrics.pairwise.manhattan\_distances(*X*, *Y=None*, *\**, *sum\_over\_features=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/pairwise.py#L874)
Compute the L1 distances between the vectors in X and Y.
With sum\_over\_features equal to False it returns the componentwise distances.
Read more in the [User Guide](../metrics#metrics).
Parameters:
**X**array-like of shape (n\_samples\_X, n\_features)
An array where each row is a sample and each column is a feature.
**Y**array-like of shape (n\_samples\_Y, n\_features), default=None
An array where each row is a sample and each column is a feature. If `None`, method uses `Y=X`.
**sum\_over\_features**bool, default=True
If True the function returns the pairwise distance matrix else it returns the componentwise L1 pairwise-distances. Not supported for sparse matrix inputs.
Returns:
**D**ndarray of shape (n\_samples\_X \* n\_samples\_Y, n\_features) or (n\_samples\_X, n\_samples\_Y)
If sum\_over\_features is False shape is (n\_samples\_X \* n\_samples\_Y, n\_features) and D contains the componentwise L1 pairwise-distances (ie. absolute difference), else shape is (n\_samples\_X, n\_samples\_Y) and D contains the pairwise L1 distances.
#### Notes
When X and/or Y are CSR sparse matrices and they are not already in canonical format, this function modifies them in-place to make them canonical.
#### Examples
```
>>> from sklearn.metrics.pairwise import manhattan_distances
>>> manhattan_distances([[3]], [[3]])
array([[0.]])
>>> manhattan_distances([[3]], [[2]])
array([[1.]])
>>> manhattan_distances([[2]], [[3]])
array([[1.]])
>>> manhattan_distances([[1, 2], [3, 4]], [[1, 2], [0, 3]])
array([[0., 2.],
[4., 4.]])
>>> import numpy as np
>>> X = np.ones((1, 2))
>>> y = np.full((2, 2), 2.)
>>> manhattan_distances(X, y, sum_over_features=False)
array([[1., 1.],
[1., 1.]])
```
scikit_learn sklearn.neural_network.MLPClassifier sklearn.neural\_network.MLPClassifier
=====================================
*class*sklearn.neural\_network.MLPClassifier(*hidden\_layer\_sizes=(100,)*, *activation='relu'*, *\**, *solver='adam'*, *alpha=0.0001*, *batch\_size='auto'*, *learning\_rate='constant'*, *learning\_rate\_init=0.001*, *power\_t=0.5*, *max\_iter=200*, *shuffle=True*, *random\_state=None*, *tol=0.0001*, *verbose=False*, *warm\_start=False*, *momentum=0.9*, *nesterovs\_momentum=True*, *early\_stopping=False*, *validation\_fraction=0.1*, *beta\_1=0.9*, *beta\_2=0.999*, *epsilon=1e-08*, *n\_iter\_no\_change=10*, *max\_fun=15000*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neural_network/_multilayer_perceptron.py#L793)
Multi-layer Perceptron classifier.
This model optimizes the log-loss function using LBFGS or stochastic gradient descent.
New in version 0.18.
Parameters:
**hidden\_layer\_sizes**tuple, length = n\_layers - 2, default=(100,)
The ith element represents the number of neurons in the ith hidden layer.
**activation**{‘identity’, ‘logistic’, ‘tanh’, ‘relu’}, default=’relu’
Activation function for the hidden layer.
* ‘identity’, no-op activation, useful to implement linear bottleneck, returns f(x) = x
* ‘logistic’, the logistic sigmoid function, returns f(x) = 1 / (1 + exp(-x)).
* ‘tanh’, the hyperbolic tan function, returns f(x) = tanh(x).
* ‘relu’, the rectified linear unit function, returns f(x) = max(0, x)
**solver**{‘lbfgs’, ‘sgd’, ‘adam’}, default=’adam’
The solver for weight optimization.
* ‘lbfgs’ is an optimizer in the family of quasi-Newton methods.
* ‘sgd’ refers to stochastic gradient descent.
* ‘adam’ refers to a stochastic gradient-based optimizer proposed by Kingma, Diederik, and Jimmy Ba
Note: The default solver ‘adam’ works pretty well on relatively large datasets (with thousands of training samples or more) in terms of both training time and validation score. For small datasets, however, ‘lbfgs’ can converge faster and perform better.
**alpha**float, default=0.0001
Strength of the L2 regularization term. The L2 regularization term is divided by the sample size when added to the loss.
**batch\_size**int, default=’auto’
Size of minibatches for stochastic optimizers. If the solver is ‘lbfgs’, the classifier will not use minibatch. When set to “auto”, `batch_size=min(200, n_samples)`.
**learning\_rate**{‘constant’, ‘invscaling’, ‘adaptive’}, default=’constant’
Learning rate schedule for weight updates.
* ‘constant’ is a constant learning rate given by ‘learning\_rate\_init’.
* ‘invscaling’ gradually decreases the learning rate at each time step ‘t’ using an inverse scaling exponent of ‘power\_t’. effective\_learning\_rate = learning\_rate\_init / pow(t, power\_t)
* ‘adaptive’ keeps the learning rate constant to ‘learning\_rate\_init’ as long as training loss keeps decreasing. Each time two consecutive epochs fail to decrease training loss by at least tol, or fail to increase validation score by at least tol if ‘early\_stopping’ is on, the current learning rate is divided by 5.
Only used when `solver='sgd'`.
**learning\_rate\_init**float, default=0.001
The initial learning rate used. It controls the step-size in updating the weights. Only used when solver=’sgd’ or ‘adam’.
**power\_t**float, default=0.5
The exponent for inverse scaling learning rate. It is used in updating effective learning rate when the learning\_rate is set to ‘invscaling’. Only used when solver=’sgd’.
**max\_iter**int, default=200
Maximum number of iterations. The solver iterates until convergence (determined by ‘tol’) or this number of iterations. For stochastic solvers (‘sgd’, ‘adam’), note that this determines the number of epochs (how many times each data point will be used), not the number of gradient steps.
**shuffle**bool, default=True
Whether to shuffle samples in each iteration. Only used when solver=’sgd’ or ‘adam’.
**random\_state**int, RandomState instance, default=None
Determines random number generation for weights and bias initialization, train-test split if early stopping is used, and batch sampling when solver=’sgd’ or ‘adam’. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**tol**float, default=1e-4
Tolerance for the optimization. When the loss or score is not improving by at least `tol` for `n_iter_no_change` consecutive iterations, unless `learning_rate` is set to ‘adaptive’, convergence is considered to be reached and training stops.
**verbose**bool, default=False
Whether to print progress messages to stdout.
**warm\_start**bool, default=False
When set to True, reuse the solution of the previous call to fit as initialization, otherwise, just erase the previous solution. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
**momentum**float, default=0.9
Momentum for gradient descent update. Should be between 0 and 1. Only used when solver=’sgd’.
**nesterovs\_momentum**bool, default=True
Whether to use Nesterov’s momentum. Only used when solver=’sgd’ and momentum > 0.
**early\_stopping**bool, default=False
Whether to use early stopping to terminate training when validation score is not improving. If set to true, it will automatically set aside 10% of training data as validation and terminate training when validation score is not improving by at least tol for `n_iter_no_change` consecutive epochs. The split is stratified, except in a multilabel setting. If early stopping is False, then the training stops when the training loss does not improve by more than tol for n\_iter\_no\_change consecutive passes over the training set. Only effective when solver=’sgd’ or ‘adam’.
**validation\_fraction**float, default=0.1
The proportion of training data to set aside as validation set for early stopping. Must be between 0 and 1. Only used if early\_stopping is True.
**beta\_1**float, default=0.9
Exponential decay rate for estimates of first moment vector in adam, should be in [0, 1). Only used when solver=’adam’.
**beta\_2**float, default=0.999
Exponential decay rate for estimates of second moment vector in adam, should be in [0, 1). Only used when solver=’adam’.
**epsilon**float, default=1e-8
Value for numerical stability in adam. Only used when solver=’adam’.
**n\_iter\_no\_change**int, default=10
Maximum number of epochs to not meet `tol` improvement. Only effective when solver=’sgd’ or ‘adam’.
New in version 0.20.
**max\_fun**int, default=15000
Only used when solver=’lbfgs’. Maximum number of loss function calls. The solver iterates until convergence (determined by ‘tol’), number of iterations reaches max\_iter, or this number of loss function calls. Note that number of loss function calls will be greater than or equal to the number of iterations for the `MLPClassifier`.
New in version 0.22.
Attributes:
**classes\_**ndarray or list of ndarray of shape (n\_classes,)
Class labels for each output.
**loss\_**float
The current loss computed with the loss function.
**best\_loss\_**float
The minimum loss reached by the solver throughout fitting.
**loss\_curve\_**list of shape (`n_iter_`,)
The ith element in the list represents the loss at the ith iteration.
**t\_**int
The number of training samples seen by the solver during fitting.
**coefs\_**list of shape (n\_layers - 1,)
The ith element in the list represents the weight matrix corresponding to layer i.
**intercepts\_**list of shape (n\_layers - 1,)
The ith element in the list represents the bias vector corresponding to layer i + 1.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_iter\_**int
The number of iterations the solver has run.
**n\_layers\_**int
Number of layers.
**n\_outputs\_**int
Number of outputs.
**out\_activation\_**str
Name of the output activation function.
See also
[`MLPRegressor`](sklearn.neural_network.mlpregressor#sklearn.neural_network.MLPRegressor "sklearn.neural_network.MLPRegressor")
Multi-layer Perceptron regressor.
[`BernoulliRBM`](sklearn.neural_network.bernoullirbm#sklearn.neural_network.BernoulliRBM "sklearn.neural_network.BernoulliRBM")
Bernoulli Restricted Boltzmann Machine (RBM).
#### Notes
MLPClassifier trains iteratively since at each time step the partial derivatives of the loss function with respect to the model parameters are computed to update the parameters.
It can also have a regularization term added to the loss function that shrinks model parameters to prevent overfitting.
This implementation works with data represented as dense numpy arrays or sparse scipy arrays of floating point values.
#### References
Hinton, Geoffrey E. “Connectionist learning procedures.” Artificial intelligence 40.1 (1989): 185-234.
Glorot, Xavier, and Yoshua Bengio. “Understanding the difficulty of training deep feedforward neural networks.” International Conference on Artificial Intelligence and Statistics. 2010.
[He, Kaiming, et al (2015). “Delving deep into rectifiers: Surpassing human-level performance on imagenet classification.”](https://arxiv.org/abs/1502.01852)
[Kingma, Diederik, and Jimmy Ba (2014) “Adam: A method for stochastic optimization.”](https://arxiv.org/abs/1412.6980)
#### Examples
```
>>> from sklearn.neural_network import MLPClassifier
>>> from sklearn.datasets import make_classification
>>> from sklearn.model_selection import train_test_split
>>> X, y = make_classification(n_samples=100, random_state=1)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y,
... random_state=1)
>>> clf = MLPClassifier(random_state=1, max_iter=300).fit(X_train, y_train)
>>> clf.predict_proba(X_test[:1])
array([[0.038..., 0.961...]])
>>> clf.predict(X_test[:5, :])
array([1, 0, 1, 0, 1])
>>> clf.score(X_test, y_test)
0.8...
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.neural_network.MLPClassifier.fit "sklearn.neural_network.MLPClassifier.fit")(X, y) | Fit the model to data matrix X and target(s) y. |
| [`get_params`](#sklearn.neural_network.MLPClassifier.get_params "sklearn.neural_network.MLPClassifier.get_params")([deep]) | Get parameters for this estimator. |
| [`partial_fit`](#sklearn.neural_network.MLPClassifier.partial_fit "sklearn.neural_network.MLPClassifier.partial_fit")(X, y[, classes]) | Update the model with a single iteration over the given data. |
| [`predict`](#sklearn.neural_network.MLPClassifier.predict "sklearn.neural_network.MLPClassifier.predict")(X) | Predict using the multi-layer perceptron classifier. |
| [`predict_log_proba`](#sklearn.neural_network.MLPClassifier.predict_log_proba "sklearn.neural_network.MLPClassifier.predict_log_proba")(X) | Return the log of probability estimates. |
| [`predict_proba`](#sklearn.neural_network.MLPClassifier.predict_proba "sklearn.neural_network.MLPClassifier.predict_proba")(X) | Probability estimates. |
| [`score`](#sklearn.neural_network.MLPClassifier.score "sklearn.neural_network.MLPClassifier.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.neural_network.MLPClassifier.set_params "sklearn.neural_network.MLPClassifier.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neural_network/_multilayer_perceptron.py#L745)
Fit the model to data matrix X and target(s) y.
Parameters:
**X**ndarray or sparse matrix of shape (n\_samples, n\_features)
The input data.
**y**ndarray of shape (n\_samples,) or (n\_samples, n\_outputs)
The target values (class labels in classification, real numbers in regression).
Returns:
**self**object
Returns a trained MLP model.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
partial\_fit(*X*, *y*, *classes=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neural_network/_multilayer_perceptron.py#L1183)
Update the model with a single iteration over the given data.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input data.
**y**array-like of shape (n\_samples,)
The target values.
**classes**array of shape (n\_classes,), default=None
Classes across all calls to partial\_fit. Can be obtained via `np.unique(y_all)`, where y\_all is the target vector of the entire dataset. This argument is required for the first call to partial\_fit and can be omitted in the subsequent calls. Note that y doesn’t need to contain all labels in `classes`.
Returns:
**self**object
Trained MLP model.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neural_network/_multilayer_perceptron.py#L1162)
Predict using the multi-layer perceptron classifier.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input data.
Returns:
**y**ndarray, shape (n\_samples,) or (n\_samples, n\_classes)
The predicted classes.
predict\_log\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neural_network/_multilayer_perceptron.py#L1219)
Return the log of probability estimates.
Parameters:
**X**ndarray of shape (n\_samples, n\_features)
The input data.
Returns:
**log\_y\_prob**ndarray of shape (n\_samples, n\_classes)
The predicted log-probability of the sample for each class in the model, where classes are ordered as they are in `self.classes_`. Equivalent to `log(predict_proba(X))`.
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neural_network/_multilayer_perceptron.py#L1237)
Probability estimates.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input data.
Returns:
**y\_prob**ndarray of shape (n\_samples, n\_classes)
The predicted probability of the sample for each class in the model, where classes are ordered as they are in `self.classes_`.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.neural_network.MLPClassifier`
-----------------------------------------------------
[Classifier comparison](../../auto_examples/classification/plot_classifier_comparison#sphx-glr-auto-examples-classification-plot-classifier-comparison-py)
[Compare Stochastic learning strategies for MLPClassifier](../../auto_examples/neural_networks/plot_mlp_training_curves#sphx-glr-auto-examples-neural-networks-plot-mlp-training-curves-py)
[Varying regularization in Multi-layer Perceptron](../../auto_examples/neural_networks/plot_mlp_alpha#sphx-glr-auto-examples-neural-networks-plot-mlp-alpha-py)
[Visualization of MLP weights on MNIST](../../auto_examples/neural_networks/plot_mnist_filters#sphx-glr-auto-examples-neural-networks-plot-mnist-filters-py)
scikit_learn sklearn.preprocessing.KBinsDiscretizer sklearn.preprocessing.KBinsDiscretizer
======================================
*class*sklearn.preprocessing.KBinsDiscretizer(*n\_bins=5*, *\**, *encode='onehot'*, *strategy='quantile'*, *dtype=None*, *subsample='warn'*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_discretization.py#L22)
Bin continuous data into intervals.
Read more in the [User Guide](../preprocessing#preprocessing-discretization).
New in version 0.20.
Parameters:
**n\_bins**int or array-like of shape (n\_features,), default=5
The number of bins to produce. Raises ValueError if `n_bins < 2`.
**encode**{‘onehot’, ‘onehot-dense’, ‘ordinal’}, default=’onehot’
Method used to encode the transformed result.
* ‘onehot’: Encode the transformed result with one-hot encoding and return a sparse matrix. Ignored features are always stacked to the right.
* ‘onehot-dense’: Encode the transformed result with one-hot encoding and return a dense array. Ignored features are always stacked to the right.
* ‘ordinal’: Return the bin identifier encoded as an integer value.
**strategy**{‘uniform’, ‘quantile’, ‘kmeans’}, default=’quantile’
Strategy used to define the widths of the bins.
* ‘uniform’: All bins in each feature have identical widths.
* ‘quantile’: All bins in each feature have the same number of points.
* ‘kmeans’: Values in each bin have the same nearest center of a 1D k-means cluster.
**dtype**{np.float32, np.float64}, default=None
The desired data-type for the output. If None, output dtype is consistent with input dtype. Only np.float32 and np.float64 are supported.
New in version 0.24.
**subsample**int or None (default=’warn’)
Maximum number of samples, used to fit the model, for computational efficiency. Used when `strategy="quantile"`. `subsample=None` means that all the training samples are used when computing the quantiles that determine the binning thresholds. Since quantile computation relies on sorting each column of `X` and that sorting has an `n log(n)` time complexity, it is recommended to use subsampling on datasets with a very large number of samples.
Deprecated since version 1.1: In version 1.3 and onwards, `subsample=2e5` will be the default.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for subsampling. Pass an int for reproducible results across multiple function calls. See the `subsample` parameter for more details. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
New in version 1.1.
Attributes:
**bin\_edges\_**ndarray of ndarray of shape (n\_features,)
The edges of each bin. Contain arrays of varying shapes `(n_bins_, )` Ignored features will have empty arrays.
**n\_bins\_**ndarray of shape (n\_features,), dtype=np.int\_
Number of bins per feature. Bins whose width are too small (i.e., <= 1e-8) are removed with a warning.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`Binarizer`](sklearn.preprocessing.binarizer#sklearn.preprocessing.Binarizer "sklearn.preprocessing.Binarizer")
Class used to bin values as `0` or `1` based on a parameter `threshold`.
#### Notes
In bin edges for feature `i`, the first and last values are used only for `inverse_transform`. During transform, bin edges are extended to:
```
np.concatenate([-np.inf, bin_edges_[i][1:-1], np.inf])
```
You can combine `KBinsDiscretizer` with [`ColumnTransformer`](sklearn.compose.columntransformer#sklearn.compose.ColumnTransformer "sklearn.compose.ColumnTransformer") if you only want to preprocess part of the features.
`KBinsDiscretizer` might produce constant features (e.g., when `encode = 'onehot'` and certain bins do not contain any data). These features can be removed with feature selection algorithms (e.g., [`VarianceThreshold`](sklearn.feature_selection.variancethreshold#sklearn.feature_selection.VarianceThreshold "sklearn.feature_selection.VarianceThreshold")).
#### Examples
```
>>> from sklearn.preprocessing import KBinsDiscretizer
>>> X = [[-2, 1, -4, -1],
... [-1, 2, -3, -0.5],
... [ 0, 3, -2, 0.5],
... [ 1, 4, -1, 2]]
>>> est = KBinsDiscretizer(n_bins=3, encode='ordinal', strategy='uniform')
>>> est.fit(X)
KBinsDiscretizer(...)
>>> Xt = est.transform(X)
>>> Xt
array([[ 0., 0., 0., 0.],
[ 1., 1., 1., 0.],
[ 2., 2., 2., 1.],
[ 2., 2., 2., 2.]])
```
Sometimes it may be useful to convert the data back into the original feature space. The `inverse_transform` function converts the binned data into the original feature space. Each value will be equal to the mean of the two bin edges.
```
>>> est.bin_edges_[0]
array([-2., -1., 0., 1.])
>>> est.inverse_transform(Xt)
array([[-1.5, 1.5, -3.5, -0.5],
[-0.5, 2.5, -2.5, -0.5],
[ 0.5, 3.5, -1.5, 0.5],
[ 0.5, 3.5, -1.5, 1.5]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.preprocessing.KBinsDiscretizer.fit "sklearn.preprocessing.KBinsDiscretizer.fit")(X[, y]) | Fit the estimator. |
| [`fit_transform`](#sklearn.preprocessing.KBinsDiscretizer.fit_transform "sklearn.preprocessing.KBinsDiscretizer.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.preprocessing.KBinsDiscretizer.get_feature_names_out "sklearn.preprocessing.KBinsDiscretizer.get_feature_names_out")([input\_features]) | Get output feature names. |
| [`get_params`](#sklearn.preprocessing.KBinsDiscretizer.get_params "sklearn.preprocessing.KBinsDiscretizer.get_params")([deep]) | Get parameters for this estimator. |
| [`inverse_transform`](#sklearn.preprocessing.KBinsDiscretizer.inverse_transform "sklearn.preprocessing.KBinsDiscretizer.inverse_transform")(Xt) | Transform discretized data back to original feature space. |
| [`set_params`](#sklearn.preprocessing.KBinsDiscretizer.set_params "sklearn.preprocessing.KBinsDiscretizer.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.preprocessing.KBinsDiscretizer.transform "sklearn.preprocessing.KBinsDiscretizer.transform")(X) | Discretize the data. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_discretization.py#L172)
Fit the estimator.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Data to be discretized.
**y**None
Ignored. This parameter exists only for compatibility with [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline").
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_discretization.py#L429)
Get output feature names.
Parameters:
**input\_features**array-like of str or None, default=None
Input features.
* If `input_features` is `None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then the following input feature names are generated: `["x0", "x1", ..., "x(n_features_in_ - 1)"]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
inverse\_transform(*Xt*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_discretization.py#L391)
Transform discretized data back to original feature space.
Note that this function does not regenerate the original data due to discretization rounding.
Parameters:
**Xt**array-like of shape (n\_samples, n\_features)
Transformed data in the binned space.
Returns:
**Xinv**ndarray, dtype={np.float32, np.float64}
Data in the original feature space.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_discretization.py#L352)
Discretize the data.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Data to be discretized.
Returns:
**Xt**{ndarray, sparse matrix}, dtype={np.float32, np.float64}
Data in the binned space. Will be a sparse matrix if `self.encode='onehot'` and ndarray otherwise.
Examples using `sklearn.preprocessing.KBinsDiscretizer`
-------------------------------------------------------
[Time-related feature engineering](../../auto_examples/applications/plot_cyclical_feature_engineering#sphx-glr-auto-examples-applications-plot-cyclical-feature-engineering-py)
[Poisson regression and non-normal loss](../../auto_examples/linear_model/plot_poisson_regression_non_normal_loss#sphx-glr-auto-examples-linear-model-plot-poisson-regression-non-normal-loss-py)
[Tweedie regression on insurance claims](../../auto_examples/linear_model/plot_tweedie_regression_insurance_claims#sphx-glr-auto-examples-linear-model-plot-tweedie-regression-insurance-claims-py)
[Demonstrating the different strategies of KBinsDiscretizer](../../auto_examples/preprocessing/plot_discretization_strategies#sphx-glr-auto-examples-preprocessing-plot-discretization-strategies-py)
[Feature discretization](../../auto_examples/preprocessing/plot_discretization_classification#sphx-glr-auto-examples-preprocessing-plot-discretization-classification-py)
[Using KBinsDiscretizer to discretize continuous features](../../auto_examples/preprocessing/plot_discretization#sphx-glr-auto-examples-preprocessing-plot-discretization-py)
| programming_docs |
scikit_learn sklearn.feature_selection.mutual_info_classif sklearn.feature\_selection.mutual\_info\_classif
================================================
sklearn.feature\_selection.mutual\_info\_classif(*X*, *y*, *\**, *discrete\_features='auto'*, *n\_neighbors=3*, *copy=True*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_mutual_info.py#L392)
Estimate mutual information for a discrete target variable.
Mutual information (MI) [[1]](#r50b872b699c4-1) between two random variables is a non-negative value, which measures the dependency between the variables. It is equal to zero if and only if two random variables are independent, and higher values mean higher dependency.
The function relies on nonparametric methods based on entropy estimation from k-nearest neighbors distances as described in [[2]](#r50b872b699c4-2) and [[3]](#r50b872b699c4-3). Both methods are based on the idea originally proposed in [[4]](#r50b872b699c4-4).
It can be used for univariate features selection, read more in the [User Guide](../feature_selection#univariate-feature-selection).
Parameters:
**X**array-like or sparse matrix, shape (n\_samples, n\_features)
Feature matrix.
**y**array-like of shape (n\_samples,)
Target vector.
**discrete\_features**{‘auto’, bool, array-like}, default=’auto’
If bool, then determines whether to consider all features discrete or continuous. If array, then it should be either a boolean mask with shape (n\_features,) or array with indices of discrete features. If ‘auto’, it is assigned to False for dense `X` and to True for sparse `X`.
**n\_neighbors**int, default=3
Number of neighbors to use for MI estimation for continuous variables, see [[2]](#r50b872b699c4-2) and [[3]](#r50b872b699c4-3). Higher values reduce variance of the estimation, but could introduce a bias.
**copy**bool, default=True
Whether to make a copy of the given data. If set to False, the initial data will be overwritten.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for adding small noise to continuous variables in order to remove repeated values. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Returns:
**mi**ndarray, shape (n\_features,)
Estimated mutual information between each feature and the target.
#### Notes
1. The term “discrete features” is used instead of naming them “categorical”, because it describes the essence more accurately. For example, pixel intensities of an image are discrete features (but hardly categorical) and you will get better results if mark them as such. Also note, that treating a continuous variable as discrete and vice versa will usually give incorrect results, so be attentive about that.
2. True mutual information can’t be negative. If its estimate turns out to be negative, it is replaced by zero.
#### References
[[1](#id1)] [Mutual Information](https://en.wikipedia.org/wiki/Mutual_information) on Wikipedia.
[2] ([1](#id2),[2](#id5)) A. Kraskov, H. Stogbauer and P. Grassberger, “Estimating mutual information”. Phys. Rev. E 69, 2004.
[3] ([1](#id3),[2](#id6)) B. C. Ross “Mutual Information between Discrete and Continuous Data Sets”. PLoS ONE 9(2), 2014.
[[4](#id4)] L. F. Kozachenko, N. N. Leonenko, “Sample Estimate of the Entropy of a Random Vector:, Probl. Peredachi Inf., 23:2 (1987), 9-16
scikit_learn sklearn.cluster.compute_optics_graph sklearn.cluster.compute\_optics\_graph
======================================
sklearn.cluster.compute\_optics\_graph(*X*, *\**, *min\_samples*, *max\_eps*, *metric*, *p*, *metric\_params*, *algorithm*, *leaf\_size*, *n\_jobs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_optics.py#L398)
Compute the OPTICS reachability graph.
Read more in the [User Guide](../clustering#optics).
Parameters:
**X**ndarray of shape (n\_samples, n\_features), or (n\_samples, n\_samples) if metric=’precomputed’
A feature array, or array of distances between samples if metric=’precomputed’.
**min\_samples**int > 1 or float between 0 and 1
The number of samples in a neighborhood for a point to be considered as a core point. Expressed as an absolute number or a fraction of the number of samples (rounded to be at least 2).
**max\_eps**float, default=np.inf
The maximum distance between two samples for one to be considered as in the neighborhood of the other. Default value of `np.inf` will identify clusters across all scales; reducing `max_eps` will result in shorter run times.
**metric**str or callable, default=’minkowski’
Metric to use for distance computation. Any metric from scikit-learn or scipy.spatial.distance can be used.
If metric is a callable function, it is called on each pair of instances (rows) and the resulting value recorded. The callable should take two arrays as input and return one value indicating the distance between them. This works for Scipy’s metrics, but is less efficient than passing the metric name as a string. If metric is “precomputed”, X is assumed to be a distance matrix and must be square.
Valid values for metric are:
* from scikit-learn: [‘cityblock’, ‘cosine’, ‘euclidean’, ‘l1’, ‘l2’, ‘manhattan’]
* from scipy.spatial.distance: [‘braycurtis’, ‘canberra’, ‘chebyshev’, ‘correlation’, ‘dice’, ‘hamming’, ‘jaccard’, ‘kulsinski’, ‘mahalanobis’, ‘minkowski’, ‘rogerstanimoto’, ‘russellrao’, ‘seuclidean’, ‘sokalmichener’, ‘sokalsneath’, ‘sqeuclidean’, ‘yule’]
See the documentation for scipy.spatial.distance for details on these metrics.
**p**int, default=2
Parameter for the Minkowski metric from [`pairwise_distances`](sklearn.metrics.pairwise_distances#sklearn.metrics.pairwise_distances "sklearn.metrics.pairwise_distances"). When p = 1, this is equivalent to using manhattan\_distance (l1), and euclidean\_distance (l2) for p = 2. For arbitrary p, minkowski\_distance (l\_p) is used.
**metric\_params**dict, default=None
Additional keyword arguments for the metric function.
**algorithm**{‘auto’, ‘ball\_tree’, ‘kd\_tree’, ‘brute’}, default=’auto’
Algorithm used to compute the nearest neighbors:
* ‘ball\_tree’ will use `BallTree`.
* ‘kd\_tree’ will use `KDTree`.
* ‘brute’ will use a brute-force search.
* ‘auto’ will attempt to decide the most appropriate algorithm based on the values passed to `fit` method. (default)
Note: fitting on sparse input will override the setting of this parameter, using brute force.
**leaf\_size**int, default=30
Leaf size passed to `BallTree` or `KDTree`. This can affect the speed of the construction and query, as well as the memory required to store the tree. The optimal value depends on the nature of the problem.
**n\_jobs**int, default=None
The number of parallel jobs to run for neighbors search. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
Returns:
**ordering\_**array of shape (n\_samples,)
The cluster ordered list of sample indices.
**core\_distances\_**array of shape (n\_samples,)
Distance at which each sample becomes a core point, indexed by object order. Points which will never be core have a distance of inf. Use `clust.core_distances_[clust.ordering_]` to access in cluster order.
**reachability\_**array of shape (n\_samples,)
Reachability distances per sample, indexed by object order. Use `clust.reachability_[clust.ordering_]` to access in cluster order.
**predecessor\_**array of shape (n\_samples,)
Point that a sample was reached from, indexed by object order. Seed points have a predecessor of -1.
#### References
[1] Ankerst, Mihael, Markus M. Breunig, Hans-Peter Kriegel, and Jörg Sander. “OPTICS: ordering points to identify the clustering structure.” ACM SIGMOD Record 28, no. 2 (1999): 49-60.
scikit_learn sklearn.inspection.partial_dependence sklearn.inspection.partial\_dependence
======================================
sklearn.inspection.partial\_dependence(*estimator*, *X*, *features*, *\**, *response\_method='auto'*, *percentiles=(0.05, 0.95)*, *grid\_resolution=100*, *method='auto'*, *kind='average'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/inspection/_partial_dependence.py#L207)
Partial dependence of `features`.
Partial dependence of a feature (or a set of features) corresponds to the average response of an estimator for each possible value of the feature.
Read more in the [User Guide](../partial_dependence#partial-dependence).
Warning
For [`GradientBoostingClassifier`](sklearn.ensemble.gradientboostingclassifier#sklearn.ensemble.GradientBoostingClassifier "sklearn.ensemble.GradientBoostingClassifier") and [`GradientBoostingRegressor`](sklearn.ensemble.gradientboostingregressor#sklearn.ensemble.GradientBoostingRegressor "sklearn.ensemble.GradientBoostingRegressor"), the `'recursion'` method (used by default) will not account for the `init` predictor of the boosting process. In practice, this will produce the same values as `'brute'` up to a constant offset in the target response, provided that `init` is a constant estimator (which is the default). However, if `init` is not a constant estimator, the partial dependence values are incorrect for `'recursion'` because the offset will be sample-dependent. It is preferable to use the `'brute'` method. Note that this only applies to [`GradientBoostingClassifier`](sklearn.ensemble.gradientboostingclassifier#sklearn.ensemble.GradientBoostingClassifier "sklearn.ensemble.GradientBoostingClassifier") and [`GradientBoostingRegressor`](sklearn.ensemble.gradientboostingregressor#sklearn.ensemble.GradientBoostingRegressor "sklearn.ensemble.GradientBoostingRegressor"), not to [`HistGradientBoostingClassifier`](sklearn.ensemble.histgradientboostingclassifier#sklearn.ensemble.HistGradientBoostingClassifier "sklearn.ensemble.HistGradientBoostingClassifier") and [`HistGradientBoostingRegressor`](sklearn.ensemble.histgradientboostingregressor#sklearn.ensemble.HistGradientBoostingRegressor "sklearn.ensemble.HistGradientBoostingRegressor").
Parameters:
**estimator**BaseEstimator
A fitted estimator object implementing [predict](https://scikit-learn.org/1.1/glossary.html#term-predict), [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba), or [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function). Multioutput-multiclass classifiers are not supported.
**X**{array-like or dataframe} of shape (n\_samples, n\_features)
`X` is used to generate a grid of values for the target `features` (where the partial dependence will be evaluated), and also to generate values for the complement features when the `method` is ‘brute’.
**features**array-like of {int, str}
The feature (e.g. `[0]`) or pair of interacting features (e.g. `[(0, 1)]`) for which the partial dependency should be computed.
**response\_method**{‘auto’, ‘predict\_proba’, ‘decision\_function’}, default=’auto’
Specifies whether to use [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) or [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) as the target response. For regressors this parameter is ignored and the response is always the output of [predict](https://scikit-learn.org/1.1/glossary.html#term-predict). By default, [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) is tried first and we revert to [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) if it doesn’t exist. If `method` is ‘recursion’, the response is always the output of [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function).
**percentiles**tuple of float, default=(0.05, 0.95)
The lower and upper percentile used to create the extreme values for the grid. Must be in [0, 1].
**grid\_resolution**int, default=100
The number of equally spaced points on the grid, for each target feature.
**method**{‘auto’, ‘recursion’, ‘brute’}, default=’auto’
The method used to calculate the averaged predictions:
* `'recursion'` is only supported for some tree-based estimators (namely [`GradientBoostingClassifier`](sklearn.ensemble.gradientboostingclassifier#sklearn.ensemble.GradientBoostingClassifier "sklearn.ensemble.GradientBoostingClassifier"), [`GradientBoostingRegressor`](sklearn.ensemble.gradientboostingregressor#sklearn.ensemble.GradientBoostingRegressor "sklearn.ensemble.GradientBoostingRegressor"), [`HistGradientBoostingClassifier`](sklearn.ensemble.histgradientboostingclassifier#sklearn.ensemble.HistGradientBoostingClassifier "sklearn.ensemble.HistGradientBoostingClassifier"), [`HistGradientBoostingRegressor`](sklearn.ensemble.histgradientboostingregressor#sklearn.ensemble.HistGradientBoostingRegressor "sklearn.ensemble.HistGradientBoostingRegressor"), [`DecisionTreeRegressor`](sklearn.tree.decisiontreeregressor#sklearn.tree.DecisionTreeRegressor "sklearn.tree.DecisionTreeRegressor"), [`RandomForestRegressor`](sklearn.ensemble.randomforestregressor#sklearn.ensemble.RandomForestRegressor "sklearn.ensemble.RandomForestRegressor"), ) when `kind='average'`. This is more efficient in terms of speed. With this method, the target response of a classifier is always the decision function, not the predicted probabilities. Since the `'recursion'` method implicitly computes the average of the Individual Conditional Expectation (ICE) by design, it is not compatible with ICE and thus `kind` must be `'average'`.
* `'brute'` is supported for any estimator, but is more computationally intensive.
* `'auto'`: the `'recursion'` is used for estimators that support it, and `'brute'` is used otherwise.
Please see [this note](../partial_dependence#pdp-method-differences) for differences between the `'brute'` and `'recursion'` method.
**kind**{‘average’, ‘individual’, ‘both’}, default=’average’
Whether to return the partial dependence averaged across all the samples in the dataset or one line per sample or both. See Returns below.
Note that the fast `method='recursion'` option is only available for `kind='average'`. Plotting individual dependencies requires using the slower `method='brute'` option.
New in version 0.24.
Returns:
**predictions**[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
Dictionary-like object, with the following attributes.
individualndarray of shape (n\_outputs, n\_instances, len(values[0]), len(values[1]), …)
The predictions for all the points in the grid for all samples in X. This is also known as Individual Conditional Expectation (ICE)
averagendarray of shape (n\_outputs, len(values[0]), len(values[1]), …)
The predictions for all the points in the grid, averaged over all samples in X (or over the training data if `method` is ‘recursion’). Only available when `kind='both'`.
valuesseq of 1d ndarrays
The values with which the grid has been created. The generated grid is a cartesian product of the arrays in `values`. `len(values) == len(features)`. The size of each array `values[j]` is either `grid_resolution`, or the number of unique values in `X[:, j]`, whichever is smaller.
`n_outputs` corresponds to the number of classes in a multi-class setting, or to the number of tasks for multi-output regression. For classical regression and binary classification `n_outputs==1`. `n_values_feature_j` corresponds to the size `values[j]`.
See also
[`PartialDependenceDisplay.from_estimator`](sklearn.inspection.partialdependencedisplay#sklearn.inspection.PartialDependenceDisplay.from_estimator "sklearn.inspection.PartialDependenceDisplay.from_estimator")
Plot Partial Dependence.
[`PartialDependenceDisplay`](sklearn.inspection.partialdependencedisplay#sklearn.inspection.PartialDependenceDisplay "sklearn.inspection.PartialDependenceDisplay")
Partial Dependence visualization.
#### Examples
```
>>> X = [[0, 0, 2], [1, 0, 0]]
>>> y = [0, 1]
>>> from sklearn.ensemble import GradientBoostingClassifier
>>> gb = GradientBoostingClassifier(random_state=0).fit(X, y)
>>> partial_dependence(gb, features=[0], X=X, percentiles=(0, 1),
... grid_resolution=2)
(array([[-4.52..., 4.52...]]), [array([ 0., 1.])])
```
Examples using `sklearn.inspection.partial_dependence`
------------------------------------------------------
[Partial Dependence and Individual Conditional Expectation Plots](../../auto_examples/inspection/plot_partial_dependence#sphx-glr-auto-examples-inspection-plot-partial-dependence-py)
scikit_learn sklearn.linear_model.ElasticNet sklearn.linear\_model.ElasticNet
================================
*class*sklearn.linear\_model.ElasticNet(*alpha=1.0*, *\**, *l1\_ratio=0.5*, *fit\_intercept=True*, *normalize='deprecated'*, *precompute=False*, *max\_iter=1000*, *copy\_X=True*, *tol=0.0001*, *warm\_start=False*, *positive=False*, *random\_state=None*, *selection='cyclic'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_coordinate_descent.py#L680)
Linear regression with combined L1 and L2 priors as regularizer.
Minimizes the objective function:
```
1 / (2 * n_samples) * ||y - Xw||^2_2
+ alpha * l1_ratio * ||w||_1
+ 0.5 * alpha * (1 - l1_ratio) * ||w||^2_2
```
If you are interested in controlling the L1 and L2 penalty separately, keep in mind that this is equivalent to:
```
a * ||w||_1 + 0.5 * b * ||w||_2^2
```
where:
```
alpha = a + b and l1_ratio = a / (a + b)
```
The parameter l1\_ratio corresponds to alpha in the glmnet R package while alpha corresponds to the lambda parameter in glmnet. Specifically, l1\_ratio = 1 is the lasso penalty. Currently, l1\_ratio <= 0.01 is not reliable, unless you supply your own sequence of alpha.
Read more in the [User Guide](../linear_model#elastic-net).
Parameters:
**alpha**float, default=1.0
Constant that multiplies the penalty terms. Defaults to 1.0. See the notes for the exact mathematical meaning of this parameter. `alpha = 0` is equivalent to an ordinary least square, solved by the [`LinearRegression`](sklearn.linear_model.linearregression#sklearn.linear_model.LinearRegression "sklearn.linear_model.LinearRegression") object. For numerical reasons, using `alpha = 0` with the `Lasso` object is not advised. Given this, you should use the [`LinearRegression`](sklearn.linear_model.linearregression#sklearn.linear_model.LinearRegression "sklearn.linear_model.LinearRegression") object.
**l1\_ratio**float, default=0.5
The ElasticNet mixing parameter, with `0 <= l1_ratio <= 1`. For `l1_ratio = 0` the penalty is an L2 penalty. `For l1_ratio = 1` it is an L1 penalty. For `0 < l1_ratio < 1`, the penalty is a combination of L1 and L2.
**fit\_intercept**bool, default=True
Whether the intercept should be estimated or not. If `False`, the data is assumed to be already centered.
**normalize**bool, default=False
This parameter is ignored when `fit_intercept` is set to False. If True, the regressors X will be normalized before regression by subtracting the mean and dividing by the l2-norm. If you wish to standardize, please use [`StandardScaler`](sklearn.preprocessing.standardscaler#sklearn.preprocessing.StandardScaler "sklearn.preprocessing.StandardScaler") before calling `fit` on an estimator with `normalize=False`.
Deprecated since version 1.0: `normalize` was deprecated in version 1.0 and will be removed in 1.2.
**precompute**bool or array-like of shape (n\_features, n\_features), default=False
Whether to use a precomputed Gram matrix to speed up calculations. The Gram matrix can also be passed as argument. For sparse input this option is always `False` to preserve sparsity.
**max\_iter**int, default=1000
The maximum number of iterations.
**copy\_X**bool, default=True
If `True`, X will be copied; else, it may be overwritten.
**tol**float, default=1e-4
The tolerance for the optimization: if the updates are smaller than `tol`, the optimization code checks the dual gap for optimality and continues until it is smaller than `tol`, see Notes below.
**warm\_start**bool, default=False
When set to `True`, reuse the solution of the previous call to fit as initialization, otherwise, just erase the previous solution. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
**positive**bool, default=False
When set to `True`, forces the coefficients to be positive.
**random\_state**int, RandomState instance, default=None
The seed of the pseudo random number generator that selects a random feature to update. Used when `selection` == ‘random’. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**selection**{‘cyclic’, ‘random’}, default=’cyclic’
If set to ‘random’, a random coefficient is updated every iteration rather than looping over features sequentially by default. This (setting to ‘random’) often leads to significantly faster convergence especially when tol is higher than 1e-4.
Attributes:
**coef\_**ndarray of shape (n\_features,) or (n\_targets, n\_features)
Parameter vector (w in the cost function formula).
[`sparse_coef_`](#sklearn.linear_model.ElasticNet.sparse_coef_ "sklearn.linear_model.ElasticNet.sparse_coef_")sparse matrix of shape (n\_features,) or (n\_targets, n\_features)
Sparse representation of the fitted `coef_`.
**intercept\_**float or ndarray of shape (n\_targets,)
Independent term in decision function.
**n\_iter\_**list of int
Number of iterations run by the coordinate descent solver to reach the specified tolerance.
**dual\_gap\_**float or ndarray of shape (n\_targets,)
Given param alpha, the dual gaps at the end of the optimization, same shape as each observation of y.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`ElasticNetCV`](sklearn.linear_model.elasticnetcv#sklearn.linear_model.ElasticNetCV "sklearn.linear_model.ElasticNetCV")
Elastic net model with best model selection by cross-validation.
[`SGDRegressor`](sklearn.linear_model.sgdregressor#sklearn.linear_model.SGDRegressor "sklearn.linear_model.SGDRegressor")
Implements elastic net regression with incremental training.
[`SGDClassifier`](sklearn.linear_model.sgdclassifier#sklearn.linear_model.SGDClassifier "sklearn.linear_model.SGDClassifier")
Implements logistic regression with elastic net penalty (`SGDClassifier(loss="log_loss", penalty="elasticnet")`).
#### Notes
To avoid unnecessary memory duplication the X argument of the fit method should be directly passed as a Fortran-contiguous numpy array.
The precise stopping criteria based on `tol` are the following: First, check that that maximum coordinate update, i.e. \(\max\_j |w\_j^{new} - w\_j^{old}|\) is smaller than `tol` times the maximum absolute coefficient, \(\max\_j |w\_j|\). If so, then additionally check whether the dual gap is smaller than `tol` times \(||y||\_2^2 / n\_{ ext{samples}}\).
#### Examples
```
>>> from sklearn.linear_model import ElasticNet
>>> from sklearn.datasets import make_regression
```
```
>>> X, y = make_regression(n_features=2, random_state=0)
>>> regr = ElasticNet(random_state=0)
>>> regr.fit(X, y)
ElasticNet(random_state=0)
>>> print(regr.coef_)
[18.83816048 64.55968825]
>>> print(regr.intercept_)
1.451...
>>> print(regr.predict([[0, 0]]))
[1.451...]
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.linear_model.ElasticNet.fit "sklearn.linear_model.ElasticNet.fit")(X, y[, sample\_weight, check\_input]) | Fit model with coordinate descent. |
| [`get_params`](#sklearn.linear_model.ElasticNet.get_params "sklearn.linear_model.ElasticNet.get_params")([deep]) | Get parameters for this estimator. |
| [`path`](#sklearn.linear_model.ElasticNet.path "sklearn.linear_model.ElasticNet.path")(X, y, \*[, l1\_ratio, eps, n\_alphas, ...]) | Compute elastic net path with coordinate descent. |
| [`predict`](#sklearn.linear_model.ElasticNet.predict "sklearn.linear_model.ElasticNet.predict")(X) | Predict using the linear model. |
| [`score`](#sklearn.linear_model.ElasticNet.score "sklearn.linear_model.ElasticNet.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.linear_model.ElasticNet.set_params "sklearn.linear_model.ElasticNet.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*, *sample\_weight=None*, *check\_input=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_coordinate_descent.py#L873)
Fit model with coordinate descent.
Parameters:
**X**{ndarray, sparse matrix} of (n\_samples, n\_features)
Data.
**y**{ndarray, sparse matrix} of shape (n\_samples,) or (n\_samples, n\_targets)
Target. Will be cast to X’s dtype if necessary.
**sample\_weight**float or array-like of shape (n\_samples,), default=None
Sample weights. Internally, the `sample_weight` vector will be rescaled to sum to `n_samples`.
New in version 0.23.
**check\_input**bool, default=True
Allow to bypass several input checking. Don’t use this parameter unless you know what you do.
Returns:
**self**object
Fitted estimator.
#### Notes
Coordinate descent is an algorithm that considers each column of data at a time hence it will automatically convert the X input as a Fortran-contiguous numpy array if necessary.
To avoid memory re-allocation it is advised to allocate the initial data in memory directly using that format.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*static*path(*X*, *y*, *\**, *l1\_ratio=0.5*, *eps=0.001*, *n\_alphas=100*, *alphas=None*, *precompute='auto'*, *Xy=None*, *copy\_X=True*, *coef\_init=None*, *verbose=False*, *return\_n\_iter=False*, *positive=False*, *check\_input=True*, *\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_coordinate_descent.py#L366)
Compute elastic net path with coordinate descent.
The elastic net optimization function varies for mono and multi-outputs.
For mono-output tasks it is:
```
1 / (2 * n_samples) * ||y - Xw||^2_2
+ alpha * l1_ratio * ||w||_1
+ 0.5 * alpha * (1 - l1_ratio) * ||w||^2_2
```
For multi-output tasks it is:
```
(1 / (2 * n_samples)) * ||Y - XW||_Fro^2
+ alpha * l1_ratio * ||W||_21
+ 0.5 * alpha * (1 - l1_ratio) * ||W||_Fro^2
```
Where:
```
||W||_21 = \sum_i \sqrt{\sum_j w_{ij}^2}
```
i.e. the sum of norm of each row.
Read more in the [User Guide](../linear_model#elastic-net).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training data. Pass directly as Fortran-contiguous data to avoid unnecessary memory duplication. If `y` is mono-output then `X` can be sparse.
**y**{array-like, sparse matrix} of shape (n\_samples,) or (n\_samples, n\_targets)
Target values.
**l1\_ratio**float, default=0.5
Number between 0 and 1 passed to elastic net (scaling between l1 and l2 penalties). `l1_ratio=1` corresponds to the Lasso.
**eps**float, default=1e-3
Length of the path. `eps=1e-3` means that `alpha_min / alpha_max = 1e-3`.
**n\_alphas**int, default=100
Number of alphas along the regularization path.
**alphas**ndarray, default=None
List of alphas where to compute the models. If None alphas are set automatically.
**precompute**‘auto’, bool or array-like of shape (n\_features, n\_features), default=’auto’
Whether to use a precomputed Gram matrix to speed up calculations. If set to `'auto'` let us decide. The Gram matrix can also be passed as argument.
**Xy**array-like of shape (n\_features,) or (n\_features, n\_targets), default=None
Xy = np.dot(X.T, y) that can be precomputed. It is useful only when the Gram matrix is precomputed.
**copy\_X**bool, default=True
If `True`, X will be copied; else, it may be overwritten.
**coef\_init**ndarray of shape (n\_features, ), default=None
The initial values of the coefficients.
**verbose**bool or int, default=False
Amount of verbosity.
**return\_n\_iter**bool, default=False
Whether to return the number of iterations or not.
**positive**bool, default=False
If set to True, forces coefficients to be positive. (Only allowed when `y.ndim == 1`).
**check\_input**bool, default=True
If set to False, the input validation checks are skipped (including the Gram matrix when provided). It is assumed that they are handled by the caller.
**\*\*params**kwargs
Keyword arguments passed to the coordinate descent solver.
Returns:
**alphas**ndarray of shape (n\_alphas,)
The alphas along the path where models are computed.
**coefs**ndarray of shape (n\_features, n\_alphas) or (n\_targets, n\_features, n\_alphas)
Coefficients along the path.
**dual\_gaps**ndarray of shape (n\_alphas,)
The dual gaps at the end of the optimization for each alpha.
**n\_iters**list of int
The number of iterations taken by the coordinate descent optimizer to reach the specified tolerance for each alpha. (Is returned when `return_n_iter` is set to True).
See also
[`MultiTaskElasticNet`](sklearn.linear_model.multitaskelasticnet#sklearn.linear_model.MultiTaskElasticNet "sklearn.linear_model.MultiTaskElasticNet")
Multi-task ElasticNet model trained with L1/L2 mixed-norm as regularizer.
[`MultiTaskElasticNetCV`](sklearn.linear_model.multitaskelasticnetcv#sklearn.linear_model.MultiTaskElasticNetCV "sklearn.linear_model.MultiTaskElasticNetCV")
Multi-task L1/L2 ElasticNet with built-in cross-validation.
[`ElasticNet`](#sklearn.linear_model.ElasticNet "sklearn.linear_model.ElasticNet")
Linear regression with combined L1 and L2 priors as regularizer.
[`ElasticNetCV`](sklearn.linear_model.elasticnetcv#sklearn.linear_model.ElasticNetCV "sklearn.linear_model.ElasticNetCV")
Elastic Net model with iterative fitting along a regularization path.
#### Notes
For an example, see [examples/linear\_model/plot\_lasso\_coordinate\_descent\_path.py](../../auto_examples/linear_model/plot_lasso_coordinate_descent_path#sphx-glr-auto-examples-linear-model-plot-lasso-coordinate-descent-path-py).
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L372)
Predict using the linear model.
Parameters:
**X**array-like or sparse matrix, shape (n\_samples, n\_features)
Samples.
Returns:
**C**array, shape (n\_samples,)
Returns predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
*property*sparse\_coef\_
Sparse representation of the fitted `coef_`.
Examples using `sklearn.linear_model.ElasticNet`
------------------------------------------------
[Release Highlights for scikit-learn 0.23](../../auto_examples/release_highlights/plot_release_highlights_0_23_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-23-0-py)
[Fitting an Elastic Net with a precomputed Gram Matrix and Weighted Samples](../../auto_examples/linear_model/plot_elastic_net_precomputed_gram_matrix_with_weighted_samples#sphx-glr-auto-examples-linear-model-plot-elastic-net-precomputed-gram-matrix-with-weighted-samples-py)
[Lasso and Elastic Net for Sparse Signals](../../auto_examples/linear_model/plot_lasso_and_elasticnet#sphx-glr-auto-examples-linear-model-plot-lasso-and-elasticnet-py)
[Train error vs Test error](../../auto_examples/model_selection/plot_train_error_vs_test_error#sphx-glr-auto-examples-model-selection-plot-train-error-vs-test-error-py)
| programming_docs |
scikit_learn sklearn.neural_network.MLPRegressor sklearn.neural\_network.MLPRegressor
====================================
*class*sklearn.neural\_network.MLPRegressor(*hidden\_layer\_sizes=(100,)*, *activation='relu'*, *\**, *solver='adam'*, *alpha=0.0001*, *batch\_size='auto'*, *learning\_rate='constant'*, *learning\_rate\_init=0.001*, *power\_t=0.5*, *max\_iter=200*, *shuffle=True*, *random\_state=None*, *tol=0.0001*, *verbose=False*, *warm\_start=False*, *momentum=0.9*, *nesterovs\_momentum=True*, *early\_stopping=False*, *validation\_fraction=0.1*, *beta\_1=0.9*, *beta\_2=0.999*, *epsilon=1e-08*, *n\_iter\_no\_change=10*, *max\_fun=15000*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neural_network/_multilayer_perceptron.py#L1266)
Multi-layer Perceptron regressor.
This model optimizes the squared error using LBFGS or stochastic gradient descent.
New in version 0.18.
Parameters:
**hidden\_layer\_sizes**tuple, length = n\_layers - 2, default=(100,)
The ith element represents the number of neurons in the ith hidden layer.
**activation**{‘identity’, ‘logistic’, ‘tanh’, ‘relu’}, default=’relu’
Activation function for the hidden layer.
* ‘identity’, no-op activation, useful to implement linear bottleneck, returns f(x) = x
* ‘logistic’, the logistic sigmoid function, returns f(x) = 1 / (1 + exp(-x)).
* ‘tanh’, the hyperbolic tan function, returns f(x) = tanh(x).
* ‘relu’, the rectified linear unit function, returns f(x) = max(0, x)
**solver**{‘lbfgs’, ‘sgd’, ‘adam’}, default=’adam’
The solver for weight optimization.
* ‘lbfgs’ is an optimizer in the family of quasi-Newton methods.
* ‘sgd’ refers to stochastic gradient descent.
* ‘adam’ refers to a stochastic gradient-based optimizer proposed by Kingma, Diederik, and Jimmy Ba
Note: The default solver ‘adam’ works pretty well on relatively large datasets (with thousands of training samples or more) in terms of both training time and validation score. For small datasets, however, ‘lbfgs’ can converge faster and perform better.
**alpha**float, default=0.0001
Strength of the L2 regularization term. The L2 regularization term is divided by the sample size when added to the loss.
**batch\_size**int, default=’auto’
Size of minibatches for stochastic optimizers. If the solver is ‘lbfgs’, the classifier will not use minibatch. When set to “auto”, `batch_size=min(200, n_samples)`.
**learning\_rate**{‘constant’, ‘invscaling’, ‘adaptive’}, default=’constant’
Learning rate schedule for weight updates.
* ‘constant’ is a constant learning rate given by ‘learning\_rate\_init’.
* ‘invscaling’ gradually decreases the learning rate `learning_rate_` at each time step ‘t’ using an inverse scaling exponent of ‘power\_t’. effective\_learning\_rate = learning\_rate\_init / pow(t, power\_t)
* ‘adaptive’ keeps the learning rate constant to ‘learning\_rate\_init’ as long as training loss keeps decreasing. Each time two consecutive epochs fail to decrease training loss by at least tol, or fail to increase validation score by at least tol if ‘early\_stopping’ is on, the current learning rate is divided by 5.
Only used when solver=’sgd’.
**learning\_rate\_init**float, default=0.001
The initial learning rate used. It controls the step-size in updating the weights. Only used when solver=’sgd’ or ‘adam’.
**power\_t**float, default=0.5
The exponent for inverse scaling learning rate. It is used in updating effective learning rate when the learning\_rate is set to ‘invscaling’. Only used when solver=’sgd’.
**max\_iter**int, default=200
Maximum number of iterations. The solver iterates until convergence (determined by ‘tol’) or this number of iterations. For stochastic solvers (‘sgd’, ‘adam’), note that this determines the number of epochs (how many times each data point will be used), not the number of gradient steps.
**shuffle**bool, default=True
Whether to shuffle samples in each iteration. Only used when solver=’sgd’ or ‘adam’.
**random\_state**int, RandomState instance, default=None
Determines random number generation for weights and bias initialization, train-test split if early stopping is used, and batch sampling when solver=’sgd’ or ‘adam’. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**tol**float, default=1e-4
Tolerance for the optimization. When the loss or score is not improving by at least `tol` for `n_iter_no_change` consecutive iterations, unless `learning_rate` is set to ‘adaptive’, convergence is considered to be reached and training stops.
**verbose**bool, default=False
Whether to print progress messages to stdout.
**warm\_start**bool, default=False
When set to True, reuse the solution of the previous call to fit as initialization, otherwise, just erase the previous solution. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
**momentum**float, default=0.9
Momentum for gradient descent update. Should be between 0 and 1. Only used when solver=’sgd’.
**nesterovs\_momentum**bool, default=True
Whether to use Nesterov’s momentum. Only used when solver=’sgd’ and momentum > 0.
**early\_stopping**bool, default=False
Whether to use early stopping to terminate training when validation score is not improving. If set to true, it will automatically set aside 10% of training data as validation and terminate training when validation score is not improving by at least `tol` for `n_iter_no_change` consecutive epochs. Only effective when solver=’sgd’ or ‘adam’.
**validation\_fraction**float, default=0.1
The proportion of training data to set aside as validation set for early stopping. Must be between 0 and 1. Only used if early\_stopping is True.
**beta\_1**float, default=0.9
Exponential decay rate for estimates of first moment vector in adam, should be in [0, 1). Only used when solver=’adam’.
**beta\_2**float, default=0.999
Exponential decay rate for estimates of second moment vector in adam, should be in [0, 1). Only used when solver=’adam’.
**epsilon**float, default=1e-8
Value for numerical stability in adam. Only used when solver=’adam’.
**n\_iter\_no\_change**int, default=10
Maximum number of epochs to not meet `tol` improvement. Only effective when solver=’sgd’ or ‘adam’.
New in version 0.20.
**max\_fun**int, default=15000
Only used when solver=’lbfgs’. Maximum number of function calls. The solver iterates until convergence (determined by ‘tol’), number of iterations reaches max\_iter, or this number of function calls. Note that number of function calls will be greater than or equal to the number of iterations for the MLPRegressor.
New in version 0.22.
Attributes:
**loss\_**float
The current loss computed with the loss function.
**best\_loss\_**float
The minimum loss reached by the solver throughout fitting.
**loss\_curve\_**list of shape (`n_iter_`,)
Loss value evaluated at the end of each training step. The ith element in the list represents the loss at the ith iteration.
**t\_**int
The number of training samples seen by the solver during fitting. Mathematically equals `n_iters * X.shape[0]`, it means `time_step` and it is used by optimizer’s learning rate scheduler.
**coefs\_**list of shape (n\_layers - 1,)
The ith element in the list represents the weight matrix corresponding to layer i.
**intercepts\_**list of shape (n\_layers - 1,)
The ith element in the list represents the bias vector corresponding to layer i + 1.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_iter\_**int
The number of iterations the solver has run.
**n\_layers\_**int
Number of layers.
**n\_outputs\_**int
Number of outputs.
**out\_activation\_**str
Name of the output activation function.
See also
[`BernoulliRBM`](sklearn.neural_network.bernoullirbm#sklearn.neural_network.BernoulliRBM "sklearn.neural_network.BernoulliRBM")
Bernoulli Restricted Boltzmann Machine (RBM).
[`MLPClassifier`](sklearn.neural_network.mlpclassifier#sklearn.neural_network.MLPClassifier "sklearn.neural_network.MLPClassifier")
Multi-layer Perceptron classifier.
[`sklearn.linear_model.SGDRegressor`](sklearn.linear_model.sgdregressor#sklearn.linear_model.SGDRegressor "sklearn.linear_model.SGDRegressor")
Linear model fitted by minimizing a regularized empirical loss with SGD.
#### Notes
MLPRegressor trains iteratively since at each time step the partial derivatives of the loss function with respect to the model parameters are computed to update the parameters.
It can also have a regularization term added to the loss function that shrinks model parameters to prevent overfitting.
This implementation works with data represented as dense and sparse numpy arrays of floating point values.
#### References
Hinton, Geoffrey E. “Connectionist learning procedures.” Artificial intelligence 40.1 (1989): 185-234.
Glorot, Xavier, and Yoshua Bengio. “Understanding the difficulty of training deep feedforward neural networks.” International Conference on Artificial Intelligence and Statistics. 2010.
[He, Kaiming, et al (2015). “Delving deep into rectifiers: Surpassing human-level performance on imagenet classification.”](https://arxiv.org/abs/1502.01852)
[Kingma, Diederik, and Jimmy Ba (2014) “Adam: A method for stochastic optimization.”](https://arxiv.org/abs/1412.6980)
#### Examples
```
>>> from sklearn.neural_network import MLPRegressor
>>> from sklearn.datasets import make_regression
>>> from sklearn.model_selection import train_test_split
>>> X, y = make_regression(n_samples=200, random_state=1)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y,
... random_state=1)
>>> regr = MLPRegressor(random_state=1, max_iter=500).fit(X_train, y_train)
>>> regr.predict(X_test[:2])
array([-0.9..., -7.1...])
>>> regr.score(X_test, y_test)
0.4...
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.neural_network.MLPRegressor.fit "sklearn.neural_network.MLPRegressor.fit")(X, y) | Fit the model to data matrix X and target(s) y. |
| [`get_params`](#sklearn.neural_network.MLPRegressor.get_params "sklearn.neural_network.MLPRegressor.get_params")([deep]) | Get parameters for this estimator. |
| [`partial_fit`](#sklearn.neural_network.MLPRegressor.partial_fit "sklearn.neural_network.MLPRegressor.partial_fit")(X, y) | Update the model with a single iteration over the given data. |
| [`predict`](#sklearn.neural_network.MLPRegressor.predict "sklearn.neural_network.MLPRegressor.predict")(X) | Predict using the multi-layer perceptron model. |
| [`score`](#sklearn.neural_network.MLPRegressor.score "sklearn.neural_network.MLPRegressor.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.neural_network.MLPRegressor.set_params "sklearn.neural_network.MLPRegressor.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neural_network/_multilayer_perceptron.py#L745)
Fit the model to data matrix X and target(s) y.
Parameters:
**X**ndarray or sparse matrix of shape (n\_samples, n\_features)
The input data.
**y**ndarray of shape (n\_samples,) or (n\_samples, n\_outputs)
The target values (class labels in classification, real numbers in regression).
Returns:
**self**object
Returns a trained MLP model.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
partial\_fit(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neural_network/_multilayer_perceptron.py#L773)
Update the model with a single iteration over the given data.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input data.
**y**ndarray of shape (n\_samples,)
The target values.
Returns:
**self**object
Trained MLP model.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neural_network/_multilayer_perceptron.py#L1577)
Predict using the multi-layer perceptron model.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input data.
Returns:
**y**ndarray of shape (n\_samples, n\_outputs)
The predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.neural_network.MLPRegressor`
----------------------------------------------------
[Time-related feature engineering](../../auto_examples/applications/plot_cyclical_feature_engineering#sphx-glr-auto-examples-applications-plot-cyclical-feature-engineering-py)
[Partial Dependence and Individual Conditional Expectation Plots](../../auto_examples/inspection/plot_partial_dependence#sphx-glr-auto-examples-inspection-plot-partial-dependence-py)
[Advanced Plotting With Partial Dependence](../../auto_examples/miscellaneous/plot_partial_dependence_visualization_api#sphx-glr-auto-examples-miscellaneous-plot-partial-dependence-visualization-api-py)
scikit_learn sklearn.inspection.DecisionBoundaryDisplay sklearn.inspection.DecisionBoundaryDisplay
==========================================
*class*sklearn.inspection.DecisionBoundaryDisplay(*\**, *xx0*, *xx1*, *response*, *xlabel=None*, *ylabel=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/inspection/_plot/decision_boundary.py#L60)
Decisions boundary visualization.
It is recommended to use [`from_estimator`](#sklearn.inspection.DecisionBoundaryDisplay.from_estimator "sklearn.inspection.DecisionBoundaryDisplay.from_estimator") to create a [`DecisionBoundaryDisplay`](#sklearn.inspection.DecisionBoundaryDisplay "sklearn.inspection.DecisionBoundaryDisplay"). All parameters are stored as attributes.
Read more in the [User Guide](https://scikit-learn.org/1.1/visualizations.html#visualizations).
New in version 1.1.
Parameters:
**xx0**ndarray of shape (grid\_resolution, grid\_resolution)
First output of [`meshgrid`](https://numpy.org/doc/stable/reference/generated/numpy.meshgrid.html#numpy.meshgrid "(in NumPy v1.23)").
**xx1**ndarray of shape (grid\_resolution, grid\_resolution)
Second output of [`meshgrid`](https://numpy.org/doc/stable/reference/generated/numpy.meshgrid.html#numpy.meshgrid "(in NumPy v1.23)").
**response**ndarray of shape (grid\_resolution, grid\_resolution)
Values of the response function.
**xlabel**str, default=None
Default label to place on x axis.
**ylabel**str, default=None
Default label to place on y axis.
Attributes:
**surface\_**matplotlib `QuadContourSet` or `QuadMesh`
If `plot_method` is ‘contour’ or ‘contourf’, `surface_` is a [`QuadContourSet`](https://matplotlib.org/stable/api/contour_api.html#matplotlib.contour.QuadContourSet "(in Matplotlib v3.6.0)"). If `plot_method is `pcolormesh`, `surface_` is a [`QuadMesh`](https://matplotlib.org/stable/api/collections_api.html#matplotlib.collections.QuadMesh "(in Matplotlib v3.6.0)").
**ax\_**matplotlib Axes
Axes with confusion matrix.
**figure\_**matplotlib Figure
Figure containing the confusion matrix.
#### Methods
| | |
| --- | --- |
| [`from_estimator`](#sklearn.inspection.DecisionBoundaryDisplay.from_estimator "sklearn.inspection.DecisionBoundaryDisplay.from_estimator")(estimator, X, \*[, ...]) | Plot decision boundary given an estimator. |
| [`plot`](#sklearn.inspection.DecisionBoundaryDisplay.plot "sklearn.inspection.DecisionBoundaryDisplay.plot")([plot\_method, ax, xlabel, ylabel]) | Plot visualization. |
*classmethod*from\_estimator(*estimator*, *X*, *\**, *grid\_resolution=100*, *eps=1.0*, *plot\_method='contourf'*, *response\_method='auto'*, *xlabel=None*, *ylabel=None*, *ax=None*, *\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/inspection/_plot/decision_boundary.py#L165)
Plot decision boundary given an estimator.
Read more in the [User Guide](https://scikit-learn.org/1.1/visualizations.html#visualizations).
Parameters:
**estimator**object
Trained estimator used to plot the decision boundary.
**X**{array-like, sparse matrix, dataframe} of shape (n\_samples, 2)
Input data that should be only 2-dimensional.
**grid\_resolution**int, default=100
Number of grid points to use for plotting decision boundary. Higher values will make the plot look nicer but be slower to render.
**eps**float, default=1.0
Extends the minimum and maximum values of X for evaluating the response function.
**plot\_method**{‘contourf’, ‘contour’, ‘pcolormesh’}, default=’contourf’
Plotting method to call when plotting the response. Please refer to the following matplotlib documentation for details: [`contourf`](https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.contourf.html#matplotlib.pyplot.contourf "(in Matplotlib v3.6.0)"), [`contour`](https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.contour.html#matplotlib.pyplot.contour "(in Matplotlib v3.6.0)"), `pcolomesh`.
**response\_method**{‘auto’, ‘predict\_proba’, ‘decision\_function’, ‘predict’}, default=’auto’
Specifies whether to use [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba), [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function), [predict](https://scikit-learn.org/1.1/glossary.html#term-predict) as the target response. If set to ‘auto’, the response method is tried in the following order: [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function), [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba), [predict](https://scikit-learn.org/1.1/glossary.html#term-predict). For multiclass problems, [predict](https://scikit-learn.org/1.1/glossary.html#term-predict) is selected when `response_method="auto"`.
**xlabel**str, default=None
The label used for the x-axis. If `None`, an attempt is made to extract a label from `X` if it is a dataframe, otherwise an empty string is used.
**ylabel**str, default=None
The label used for the y-axis. If `None`, an attempt is made to extract a label from `X` if it is a dataframe, otherwise an empty string is used.
**ax**Matplotlib axes, default=None
Axes object to plot on. If `None`, a new figure and axes is created.
**\*\*kwargs**dict
Additional keyword arguments to be passed to the `plot_method`.
Returns:
**display**[`DecisionBoundaryDisplay`](#sklearn.inspection.DecisionBoundaryDisplay "sklearn.inspection.DecisionBoundaryDisplay")
Object that stores the result.
See also
[`DecisionBoundaryDisplay`](#sklearn.inspection.DecisionBoundaryDisplay "sklearn.inspection.DecisionBoundaryDisplay")
Decision boundary visualization.
`ConfusionMatrixDisplay.from_estimator`
Plot the confusion matrix given an estimator, the data, and the label.
`ConfusionMatrixDisplay.from_predictions`
Plot the confusion matrix given the true and predicted labels.
#### Examples
```
>>> import matplotlib.pyplot as plt
>>> from sklearn.datasets import load_iris
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.inspection import DecisionBoundaryDisplay
>>> iris = load_iris()
>>> X = iris.data[:, :2]
>>> classifier = LogisticRegression().fit(X, iris.target)
>>> disp = DecisionBoundaryDisplay.from_estimator(
... classifier, X, response_method="predict",
... xlabel=iris.feature_names[0], ylabel=iris.feature_names[1],
... alpha=0.5,
... )
>>> disp.ax_.scatter(X[:, 0], X[:, 1], c=iris.target, edgecolor="k")
<...>
>>> plt.show()
```
plot(*plot\_method='contourf'*, *ax=None*, *xlabel=None*, *ylabel=None*, *\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/inspection/_plot/decision_boundary.py#L111)
Plot visualization.
Parameters:
**plot\_method**{‘contourf’, ‘contour’, ‘pcolormesh’}, default=’contourf’
Plotting method to call when plotting the response. Please refer to the following matplotlib documentation for details: [`contourf`](https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.contourf.html#matplotlib.pyplot.contourf "(in Matplotlib v3.6.0)"), [`contour`](https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.contour.html#matplotlib.pyplot.contour "(in Matplotlib v3.6.0)"), `pcolomesh`.
**ax**Matplotlib axes, default=None
Axes object to plot on. If `None`, a new figure and axes is created.
**xlabel**str, default=None
Overwrite the x-axis label.
**ylabel**str, default=None
Overwrite the y-axis label.
**\*\*kwargs**dict
Additional keyword arguments to be passed to the `plot_method`.
Returns:
**display:**class:`~sklearn.inspection.DecisionBoundaryDisplay`
| programming_docs |
scikit_learn sklearn.semi_supervised.SelfTrainingClassifier sklearn.semi\_supervised.SelfTrainingClassifier
===============================================
*class*sklearn.semi\_supervised.SelfTrainingClassifier(*base\_estimator*, *threshold=0.75*, *criterion='threshold'*, *k\_best=10*, *max\_iter=10*, *verbose=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/semi_supervised/_self_training.py#L26)
Self-training classifier.
This class allows a given supervised classifier to function as a semi-supervised classifier, allowing it to learn from unlabeled data. It does this by iteratively predicting pseudo-labels for the unlabeled data and adding them to the training set.
The classifier will continue iterating until either max\_iter is reached, or no pseudo-labels were added to the training set in the previous iteration.
Read more in the [User Guide](../semi_supervised#self-training).
Parameters:
**base\_estimator**estimator object
An estimator object implementing `fit` and `predict_proba`. Invoking the `fit` method will fit a clone of the passed estimator, which will be stored in the `base_estimator_` attribute.
**threshold**float, default=0.75
The decision threshold for use with `criterion='threshold'`. Should be in [0, 1). When using the `'threshold'` criterion, a [well calibrated classifier](../calibration#calibration) should be used.
**criterion**{‘threshold’, ‘k\_best’}, default=’threshold’
The selection criterion used to select which labels to add to the training set. If `'threshold'`, pseudo-labels with prediction probabilities above `threshold` are added to the dataset. If `'k_best'`, the `k_best` pseudo-labels with highest prediction probabilities are added to the dataset. When using the ‘threshold’ criterion, a [well calibrated classifier](../calibration#calibration) should be used.
**k\_best**int, default=10
The amount of samples to add in each iteration. Only used when `criterion='k_best'`.
**max\_iter**int or None, default=10
Maximum number of iterations allowed. Should be greater than or equal to 0. If it is `None`, the classifier will continue to predict labels until no new pseudo-labels are added, or all unlabeled samples have been labeled.
**verbose**bool, default=False
Enable verbose output.
Attributes:
**base\_estimator\_**estimator object
The fitted estimator.
**classes\_**ndarray or list of ndarray of shape (n\_classes,)
Class labels for each output. (Taken from the trained `base_estimator_`).
**transduction\_**ndarray of shape (n\_samples,)
The labels used for the final fit of the classifier, including pseudo-labels added during fit.
**labeled\_iter\_**ndarray of shape (n\_samples,)
The iteration in which each sample was labeled. When a sample has iteration 0, the sample was already labeled in the original dataset. When a sample has iteration -1, the sample was not labeled in any iteration.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_iter\_**int
The number of rounds of self-training, that is the number of times the base estimator is fitted on relabeled variants of the training set.
**termination\_condition\_**{‘max\_iter’, ‘no\_change’, ‘all\_labeled’}
The reason that fitting was stopped.
* `'max_iter'`: `n_iter_` reached `max_iter`.
* `'no_change'`: no new labels were predicted.
* `'all_labeled'`: all unlabeled samples were labeled before `max_iter` was reached.
See also
[`LabelPropagation`](sklearn.semi_supervised.labelpropagation#sklearn.semi_supervised.LabelPropagation "sklearn.semi_supervised.LabelPropagation")
Label propagation classifier.
[`LabelSpreading`](sklearn.semi_supervised.labelspreading#sklearn.semi_supervised.LabelSpreading "sklearn.semi_supervised.LabelSpreading")
Label spreading model for semi-supervised learning.
#### References
[David Yarowsky. 1995. Unsupervised word sense disambiguation rivaling supervised methods. In Proceedings of the 33rd annual meeting on Association for Computational Linguistics (ACL ‘95). Association for Computational Linguistics, Stroudsburg, PA, USA, 189-196.](https://doi.org/10.3115/981658.981684)
#### Examples
```
>>> import numpy as np
>>> from sklearn import datasets
>>> from sklearn.semi_supervised import SelfTrainingClassifier
>>> from sklearn.svm import SVC
>>> rng = np.random.RandomState(42)
>>> iris = datasets.load_iris()
>>> random_unlabeled_points = rng.rand(iris.target.shape[0]) < 0.3
>>> iris.target[random_unlabeled_points] = -1
>>> svc = SVC(probability=True, gamma="auto")
>>> self_training_model = SelfTrainingClassifier(svc)
>>> self_training_model.fit(iris.data, iris.target)
SelfTrainingClassifier(...)
```
#### Methods
| | |
| --- | --- |
| [`decision_function`](#sklearn.semi_supervised.SelfTrainingClassifier.decision_function "sklearn.semi_supervised.SelfTrainingClassifier.decision_function")(X) | Call decision function of the `base_estimator`. |
| [`fit`](#sklearn.semi_supervised.SelfTrainingClassifier.fit "sklearn.semi_supervised.SelfTrainingClassifier.fit")(X, y) | Fit self-training classifier using `X`, `y` as training data. |
| [`get_params`](#sklearn.semi_supervised.SelfTrainingClassifier.get_params "sklearn.semi_supervised.SelfTrainingClassifier.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.semi_supervised.SelfTrainingClassifier.predict "sklearn.semi_supervised.SelfTrainingClassifier.predict")(X) | Predict the classes of `X`. |
| [`predict_log_proba`](#sklearn.semi_supervised.SelfTrainingClassifier.predict_log_proba "sklearn.semi_supervised.SelfTrainingClassifier.predict_log_proba")(X) | Predict log probability for each possible outcome. |
| [`predict_proba`](#sklearn.semi_supervised.SelfTrainingClassifier.predict_proba "sklearn.semi_supervised.SelfTrainingClassifier.predict_proba")(X) | Predict probability for each possible outcome. |
| [`score`](#sklearn.semi_supervised.SelfTrainingClassifier.score "sklearn.semi_supervised.SelfTrainingClassifier.score")(X, y) | Call score on the `base_estimator`. |
| [`set_params`](#sklearn.semi_supervised.SelfTrainingClassifier.set_params "sklearn.semi_supervised.SelfTrainingClassifier.set_params")(\*\*params) | Set the parameters of this estimator. |
decision\_function(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/semi_supervised/_self_training.py#L330)
Call decision function of the `base_estimator`.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Array representing the data.
Returns:
**y**ndarray of shape (n\_samples, n\_features)
Result of the decision function of the `base_estimator`.
fit(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/semi_supervised/_self_training.py#L161)
Fit self-training classifier using `X`, `y` as training data.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Array representing the data.
**y**{array-like, sparse matrix} of shape (n\_samples,)
Array representing the labels. Unlabeled samples should have the label -1.
Returns:
**self**object
Fitted estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/semi_supervised/_self_training.py#L284)
Predict the classes of `X`.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Array representing the data.
Returns:
**y**ndarray of shape (n\_samples,)
Array with predicted labels.
predict\_log\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/semi_supervised/_self_training.py#L353)
Predict log probability for each possible outcome.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Array representing the data.
Returns:
**y**ndarray of shape (n\_samples, n\_features)
Array with log prediction probabilities.
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/semi_supervised/_self_training.py#L307)
Predict probability for each possible outcome.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Array representing the data.
Returns:
**y**ndarray of shape (n\_samples, n\_features)
Array with prediction probabilities.
score(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/semi_supervised/_self_training.py#L376)
Call score on the `base_estimator`.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Array representing the data.
**y**array-like of shape (n\_samples,)
Array representing the labels.
Returns:
**score**float
Result of calling score on the `base_estimator`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.semi_supervised.SelfTrainingClassifier`
---------------------------------------------------------------
[Release Highlights for scikit-learn 0.24](../../auto_examples/release_highlights/plot_release_highlights_0_24_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-24-0-py)
[Decision boundary of semi-supervised classifiers versus SVM on the Iris dataset](../../auto_examples/semi_supervised/plot_semi_supervised_versus_svm_iris#sphx-glr-auto-examples-semi-supervised-plot-semi-supervised-versus-svm-iris-py)
[Effect of varying threshold for self-training](../../auto_examples/semi_supervised/plot_self_training_varying_threshold#sphx-glr-auto-examples-semi-supervised-plot-self-training-varying-threshold-py)
[Semi-supervised Classification on a Text Dataset](../../auto_examples/semi_supervised/plot_semi_supervised_newsgroups#sphx-glr-auto-examples-semi-supervised-plot-semi-supervised-newsgroups-py)
scikit_learn sklearn.preprocessing.LabelBinarizer sklearn.preprocessing.LabelBinarizer
====================================
*class*sklearn.preprocessing.LabelBinarizer(*\**, *neg\_label=0*, *pos\_label=1*, *sparse\_output=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_label.py#L169)
Binarize labels in a one-vs-all fashion.
Several regression and binary classification algorithms are available in scikit-learn. A simple way to extend these algorithms to the multi-class classification case is to use the so-called one-vs-all scheme.
At learning time, this simply consists in learning one regressor or binary classifier per class. In doing so, one needs to convert multi-class labels to binary labels (belong or does not belong to the class). LabelBinarizer makes this process easy with the transform method.
At prediction time, one assigns the class for which the corresponding model gave the greatest confidence. LabelBinarizer makes this easy with the inverse\_transform method.
Read more in the [User Guide](../preprocessing_targets#preprocessing-targets).
Parameters:
**neg\_label**int, default=0
Value with which negative labels must be encoded.
**pos\_label**int, default=1
Value with which positive labels must be encoded.
**sparse\_output**bool, default=False
True if the returned array from transform is desired to be in sparse CSR format.
Attributes:
**classes\_**ndarray of shape (n\_classes,)
Holds the label for each class.
**y\_type\_**str
Represents the type of the target data as evaluated by utils.multiclass.type\_of\_target. Possible type are ‘continuous’, ‘continuous-multioutput’, ‘binary’, ‘multiclass’, ‘multiclass-multioutput’, ‘multilabel-indicator’, and ‘unknown’.
**sparse\_input\_**bool
True if the input data to transform is given as a sparse matrix, False otherwise.
See also
[`label_binarize`](sklearn.preprocessing.label_binarize#sklearn.preprocessing.label_binarize "sklearn.preprocessing.label_binarize")
Function to perform the transform operation of LabelBinarizer with fixed classes.
[`OneHotEncoder`](sklearn.preprocessing.onehotencoder#sklearn.preprocessing.OneHotEncoder "sklearn.preprocessing.OneHotEncoder")
Encode categorical features using a one-hot aka one-of-K scheme.
#### Examples
```
>>> from sklearn import preprocessing
>>> lb = preprocessing.LabelBinarizer()
>>> lb.fit([1, 2, 6, 4, 2])
LabelBinarizer()
>>> lb.classes_
array([1, 2, 4, 6])
>>> lb.transform([1, 6])
array([[1, 0, 0, 0],
[0, 0, 0, 1]])
```
Binary targets transform to a column vector
```
>>> lb = preprocessing.LabelBinarizer()
>>> lb.fit_transform(['yes', 'no', 'no', 'yes'])
array([[1],
[0],
[0],
[1]])
```
Passing a 2D matrix for multilabel classification
```
>>> import numpy as np
>>> lb.fit(np.array([[0, 1, 1], [1, 0, 0]]))
LabelBinarizer()
>>> lb.classes_
array([0, 1, 2])
>>> lb.transform([0, 1, 2, 1])
array([[1, 0, 0],
[0, 1, 0],
[0, 0, 1],
[0, 1, 0]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.preprocessing.LabelBinarizer.fit "sklearn.preprocessing.LabelBinarizer.fit")(y) | Fit label binarizer. |
| [`fit_transform`](#sklearn.preprocessing.LabelBinarizer.fit_transform "sklearn.preprocessing.LabelBinarizer.fit_transform")(y) | Fit label binarizer/transform multi-class labels to binary labels. |
| [`get_params`](#sklearn.preprocessing.LabelBinarizer.get_params "sklearn.preprocessing.LabelBinarizer.get_params")([deep]) | Get parameters for this estimator. |
| [`inverse_transform`](#sklearn.preprocessing.LabelBinarizer.inverse_transform "sklearn.preprocessing.LabelBinarizer.inverse_transform")(Y[, threshold]) | Transform binary labels back to multi-class labels. |
| [`set_params`](#sklearn.preprocessing.LabelBinarizer.set_params "sklearn.preprocessing.LabelBinarizer.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.preprocessing.LabelBinarizer.transform "sklearn.preprocessing.LabelBinarizer.transform")(y) | Transform multi-class labels to binary labels. |
fit(*y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_label.py#L264)
Fit label binarizer.
Parameters:
**y**ndarray of shape (n\_samples,) or (n\_samples, n\_classes)
Target values. The 2-d matrix should only contain 0 and 1, represents multilabel classification.
Returns:
**self**object
Returns the instance itself.
fit\_transform(*y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_label.py#L305)
Fit label binarizer/transform multi-class labels to binary labels.
The output of transform is sometimes referred to as the 1-of-K coding scheme.
Parameters:
**y**{ndarray, sparse matrix} of shape (n\_samples,) or (n\_samples, n\_classes)
Target values. The 2-d matrix should only contain 0 and 1, represents multilabel classification. Sparse matrix can be CSR, CSC, COO, DOK, or LIL.
Returns:
**Y**{ndarray, sparse matrix} of shape (n\_samples, n\_classes)
Shape will be (n\_samples, 1) for binary problems. Sparse matrix will be of CSR format.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
inverse\_transform(*Y*, *threshold=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_label.py#L361)
Transform binary labels back to multi-class labels.
Parameters:
**Y**{ndarray, sparse matrix} of shape (n\_samples, n\_classes)
Target values. All sparse matrices are converted to CSR before inverse transformation.
**threshold**float, default=None
Threshold used in the binary and multi-label cases.
Use 0 when `Y` contains the output of decision\_function (classifier). Use 0.5 when `Y` contains the output of predict\_proba.
If None, the threshold is assumed to be half way between neg\_label and pos\_label.
Returns:
**y**{ndarray, sparse matrix} of shape (n\_samples,)
Target values. Sparse matrix will be of CSR format.
#### Notes
In the case when the binary labels are fractional (probabilistic), inverse\_transform chooses the class with the greatest value. Typically, this allows to use the output of a linear model’s decision\_function method directly as the input of inverse\_transform.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_label.py#L327)
Transform multi-class labels to binary labels.
The output of transform is sometimes referred to by some authors as the 1-of-K coding scheme.
Parameters:
**y**{array, sparse matrix} of shape (n\_samples,) or (n\_samples, n\_classes)
Target values. The 2-d matrix should only contain 0 and 1, represents multilabel classification. Sparse matrix can be CSR, CSC, COO, DOK, or LIL.
Returns:
**Y**{ndarray, sparse matrix} of shape (n\_samples, n\_classes)
Shape will be (n\_samples, 1) for binary problems. Sparse matrix will be of CSR format.
Examples using `sklearn.preprocessing.LabelBinarizer`
-----------------------------------------------------
[Evaluation of outlier detection estimators](../../auto_examples/miscellaneous/plot_outlier_detection_bench#sphx-glr-auto-examples-miscellaneous-plot-outlier-detection-bench-py)
scikit_learn sklearn.compose.make_column_selector sklearn.compose.make\_column\_selector
======================================
sklearn.compose.make\_column\_selector(*pattern=None*, *\**, *dtype\_include=None*, *dtype\_exclude=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/compose/_column_transformer.py#L981)
Create a callable to select columns to be used with [`ColumnTransformer`](sklearn.compose.columntransformer#sklearn.compose.ColumnTransformer "sklearn.compose.ColumnTransformer").
[`make_column_selector`](#sklearn.compose.make_column_selector "sklearn.compose.make_column_selector") can select columns based on datatype or the columns name with a regex. When using multiple selection criteria, **all** criteria must match for a column to be selected.
Parameters:
**pattern**str, default=None
Name of columns containing this regex pattern will be included. If None, column selection will not be selected based on pattern.
**dtype\_include**column dtype or list of column dtypes, default=None
A selection of dtypes to include. For more details, see [`pandas.DataFrame.select_dtypes`](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.select_dtypes.html#pandas.DataFrame.select_dtypes "(in pandas v1.5.1)").
**dtype\_exclude**column dtype or list of column dtypes, default=None
A selection of dtypes to exclude. For more details, see [`pandas.DataFrame.select_dtypes`](https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.select_dtypes.html#pandas.DataFrame.select_dtypes "(in pandas v1.5.1)").
Returns:
**selector**callable
Callable for column selection to be used by a [`ColumnTransformer`](sklearn.compose.columntransformer#sklearn.compose.ColumnTransformer "sklearn.compose.ColumnTransformer").
See also
[`ColumnTransformer`](sklearn.compose.columntransformer#sklearn.compose.ColumnTransformer "sklearn.compose.ColumnTransformer")
Class that allows combining the outputs of multiple transformer objects used on column subsets of the data into a single feature space.
#### Examples
```
>>> from sklearn.preprocessing import StandardScaler, OneHotEncoder
>>> from sklearn.compose import make_column_transformer
>>> from sklearn.compose import make_column_selector
>>> import numpy as np
>>> import pandas as pd
>>> X = pd.DataFrame({'city': ['London', 'London', 'Paris', 'Sallisaw'],
... 'rating': [5, 3, 4, 5]})
>>> ct = make_column_transformer(
... (StandardScaler(),
... make_column_selector(dtype_include=np.number)), # rating
... (OneHotEncoder(),
... make_column_selector(dtype_include=object))) # city
>>> ct.fit_transform(X)
array([[ 0.90453403, 1. , 0. , 0. ],
[-1.50755672, 1. , 0. , 0. ],
[-0.30151134, 0. , 1. , 0. ],
[ 0.90453403, 0. , 0. , 1. ]])
```
Examples using `sklearn.compose.make_column_selector`
-----------------------------------------------------
[Categorical Feature Support in Gradient Boosting](../../auto_examples/ensemble/plot_gradient_boosting_categorical#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-categorical-py)
[Combine predictors using stacking](../../auto_examples/ensemble/plot_stack_predictors#sphx-glr-auto-examples-ensemble-plot-stack-predictors-py)
[Column Transformer with Mixed Types](../../auto_examples/compose/plot_column_transformer_mixed_types#sphx-glr-auto-examples-compose-plot-column-transformer-mixed-types-py)
| programming_docs |
scikit_learn sklearn.metrics.pairwise.cosine_similarity sklearn.metrics.pairwise.cosine\_similarity
===========================================
sklearn.metrics.pairwise.cosine\_similarity(*X*, *Y=None*, *dense\_output=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/pairwise.py#L1341)
Compute cosine similarity between samples in X and Y.
Cosine similarity, or the cosine kernel, computes similarity as the normalized dot product of X and Y:
K(X, Y) = <X, Y> / (||X||\*||Y||)
On L2-normalized data, this function is equivalent to linear\_kernel.
Read more in the [User Guide](../metrics#cosine-similarity).
Parameters:
**X**{ndarray, sparse matrix} of shape (n\_samples\_X, n\_features)
Input data.
**Y**{ndarray, sparse matrix} of shape (n\_samples\_Y, n\_features), default=None
Input data. If `None`, the output will be the pairwise similarities between all samples in `X`.
**dense\_output**bool, default=True
Whether to return dense output even when the input is sparse. If `False`, the output is sparse if both input arrays are sparse.
New in version 0.17: parameter `dense_output` for dense output.
Returns:
**kernel matrix**ndarray of shape (n\_samples\_X, n\_samples\_Y)
Returns the cosine similarity between samples in X and Y.
scikit_learn sklearn.tree.export_graphviz sklearn.tree.export\_graphviz
=============================
sklearn.tree.export\_graphviz(*decision\_tree*, *out\_file=None*, *\**, *max\_depth=None*, *feature\_names=None*, *class\_names=None*, *label='all'*, *filled=False*, *leaves\_parallel=False*, *impurity=True*, *node\_ids=False*, *proportion=False*, *rotate=False*, *rounded=False*, *special\_characters=False*, *precision=3*, *fontname='helvetica'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_export.py#L741)
Export a decision tree in DOT format.
This function generates a GraphViz representation of the decision tree, which is then written into `out_file`. Once exported, graphical renderings can be generated using, for example:
```
$ dot -Tps tree.dot -o tree.ps (PostScript format)
$ dot -Tpng tree.dot -o tree.png (PNG format)
```
The sample counts that are shown are weighted with any sample\_weights that might be present.
Read more in the [User Guide](../tree#tree).
Parameters:
**decision\_tree**decision tree classifier
The decision tree to be exported to GraphViz.
**out\_file**object or str, default=None
Handle or name of the output file. If `None`, the result is returned as a string.
Changed in version 0.20: Default of out\_file changed from “tree.dot” to None.
**max\_depth**int, default=None
The maximum depth of the representation. If None, the tree is fully generated.
**feature\_names**list of str, default=None
Names of each of the features. If None generic names will be used (“feature\_0”, “feature\_1”, …).
**class\_names**list of str or bool, default=None
Names of each of the target classes in ascending numerical order. Only relevant for classification and not supported for multi-output. If `True`, shows a symbolic representation of the class name.
**label**{‘all’, ‘root’, ‘none’}, default=’all’
Whether to show informative labels for impurity, etc. Options include ‘all’ to show at every node, ‘root’ to show only at the top root node, or ‘none’ to not show at any node.
**filled**bool, default=False
When set to `True`, paint nodes to indicate majority class for classification, extremity of values for regression, or purity of node for multi-output.
**leaves\_parallel**bool, default=False
When set to `True`, draw all leaf nodes at the bottom of the tree.
**impurity**bool, default=True
When set to `True`, show the impurity at each node.
**node\_ids**bool, default=False
When set to `True`, show the ID number on each node.
**proportion**bool, default=False
When set to `True`, change the display of ‘values’ and/or ‘samples’ to be proportions and percentages respectively.
**rotate**bool, default=False
When set to `True`, orient tree left to right rather than top-down.
**rounded**bool, default=False
When set to `True`, draw node boxes with rounded corners.
**special\_characters**bool, default=False
When set to `False`, ignore special characters for PostScript compatibility.
**precision**int, default=3
Number of digits of precision for floating point in the values of impurity, threshold and value attributes of each node.
**fontname**str, default=’helvetica’
Name of font used to render text.
Returns:
**dot\_data**str
String representation of the input tree in GraphViz dot format. Only returned if `out_file` is None.
New in version 0.18.
#### Examples
```
>>> from sklearn.datasets import load_iris
>>> from sklearn import tree
```
```
>>> clf = tree.DecisionTreeClassifier()
>>> iris = load_iris()
```
```
>>> clf = clf.fit(iris.data, iris.target)
>>> tree.export_graphviz(clf)
'digraph Tree {...
```
scikit_learn sklearn.datasets.make_checkerboard sklearn.datasets.make\_checkerboard
===================================
sklearn.datasets.make\_checkerboard(*shape*, *n\_clusters*, *\**, *noise=0.0*, *minval=10*, *maxval=100*, *shuffle=True*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_samples_generator.py#L1805)
Generate an array with block checkerboard structure for biclustering.
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/sample_generators.html#sample-generators).
Parameters:
**shape**tuple of shape (n\_rows, n\_cols)
The shape of the result.
**n\_clusters**int or array-like or shape (n\_row\_clusters, n\_column\_clusters)
The number of row and column clusters.
**noise**float, default=0.0
The standard deviation of the gaussian noise.
**minval**int, default=10
Minimum value of a bicluster.
**maxval**int, default=100
Maximum value of a bicluster.
**shuffle**bool, default=True
Shuffle the samples.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for dataset creation. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Returns:
**X**ndarray of shape `shape`
The generated array.
**rows**ndarray of shape (n\_clusters, X.shape[0])
The indicators for cluster membership of each row.
**cols**ndarray of shape (n\_clusters, X.shape[1])
The indicators for cluster membership of each column.
See also
[`make_biclusters`](sklearn.datasets.make_biclusters#sklearn.datasets.make_biclusters "sklearn.datasets.make_biclusters")
Generate an array with constant block diagonal structure for biclustering.
#### References
[1] Kluger, Y., Basri, R., Chang, J. T., & Gerstein, M. (2003). Spectral biclustering of microarray data: coclustering genes and conditions. Genome research, 13(4), 703-716.
Examples using `sklearn.datasets.make_checkerboard`
---------------------------------------------------
[A demo of the Spectral Biclustering algorithm](../../auto_examples/bicluster/plot_spectral_biclustering#sphx-glr-auto-examples-bicluster-plot-spectral-biclustering-py)
scikit_learn sklearn.datasets.make_sparse_coded_signal sklearn.datasets.make\_sparse\_coded\_signal
============================================
sklearn.datasets.make\_sparse\_coded\_signal(*n\_samples*, *\**, *n\_components*, *n\_features*, *n\_nonzero\_coefs*, *random\_state=None*, *data\_transposed='warn'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_samples_generator.py#L1244)
Generate a signal as a sparse combination of dictionary elements.
Returns a matrix Y = DX, such that D is (n\_features, n\_components), X is (n\_components, n\_samples) and each column of X has exactly n\_nonzero\_coefs non-zero elements.
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/sample_generators.html#sample-generators).
Parameters:
**n\_samples**int
Number of samples to generate.
**n\_components**int
Number of components in the dictionary.
**n\_features**int
Number of features of the dataset to generate.
**n\_nonzero\_coefs**int
Number of active (non-zero) coefficients in each sample.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for dataset creation. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**data\_transposed**bool, default=True
By default, Y, D and X are transposed.
New in version 1.1.
Returns:
**data**ndarray of shape (n\_features, n\_samples) or (n\_samples, n\_features)
The encoded signal (Y). The shape is `(n_samples, n_features)` if `data_transposed` is False, otherwise it’s `(n_features, n_samples)`.
**dictionary**ndarray of shape (n\_features, n\_components) or (n\_components, n\_features)
The dictionary with normalized components (D). The shape is `(n_components, n_features)` if `data_transposed` is False, otherwise it’s `(n_features, n_components)`.
**code**ndarray of shape (n\_components, n\_samples) or (n\_samples, n\_components)
The sparse code such that each column of this matrix has exactly n\_nonzero\_coefs non-zero items (X). The shape is `(n_samples, n_components)` if `data_transposed` is False, otherwise it’s `(n_components, n_samples)`.
Examples using `sklearn.datasets.make_sparse_coded_signal`
----------------------------------------------------------
[Orthogonal Matching Pursuit](../../auto_examples/linear_model/plot_omp#sphx-glr-auto-examples-linear-model-plot-omp-py)
scikit_learn sklearn.linear_model.enet_path sklearn.linear\_model.enet\_path
================================
sklearn.linear\_model.enet\_path(*X*, *y*, *\**, *l1\_ratio=0.5*, *eps=0.001*, *n\_alphas=100*, *alphas=None*, *precompute='auto'*, *Xy=None*, *copy\_X=True*, *coef\_init=None*, *verbose=False*, *return\_n\_iter=False*, *positive=False*, *check\_input=True*, *\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_coordinate_descent.py#L366)
Compute elastic net path with coordinate descent.
The elastic net optimization function varies for mono and multi-outputs.
For mono-output tasks it is:
```
1 / (2 * n_samples) * ||y - Xw||^2_2
+ alpha * l1_ratio * ||w||_1
+ 0.5 * alpha * (1 - l1_ratio) * ||w||^2_2
```
For multi-output tasks it is:
```
(1 / (2 * n_samples)) * ||Y - XW||_Fro^2
+ alpha * l1_ratio * ||W||_21
+ 0.5 * alpha * (1 - l1_ratio) * ||W||_Fro^2
```
Where:
```
||W||_21 = \sum_i \sqrt{\sum_j w_{ij}^2}
```
i.e. the sum of norm of each row.
Read more in the [User Guide](../linear_model#elastic-net).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training data. Pass directly as Fortran-contiguous data to avoid unnecessary memory duplication. If `y` is mono-output then `X` can be sparse.
**y**{array-like, sparse matrix} of shape (n\_samples,) or (n\_samples, n\_targets)
Target values.
**l1\_ratio**float, default=0.5
Number between 0 and 1 passed to elastic net (scaling between l1 and l2 penalties). `l1_ratio=1` corresponds to the Lasso.
**eps**float, default=1e-3
Length of the path. `eps=1e-3` means that `alpha_min / alpha_max = 1e-3`.
**n\_alphas**int, default=100
Number of alphas along the regularization path.
**alphas**ndarray, default=None
List of alphas where to compute the models. If None alphas are set automatically.
**precompute**‘auto’, bool or array-like of shape (n\_features, n\_features), default=’auto’
Whether to use a precomputed Gram matrix to speed up calculations. If set to `'auto'` let us decide. The Gram matrix can also be passed as argument.
**Xy**array-like of shape (n\_features,) or (n\_features, n\_targets), default=None
Xy = np.dot(X.T, y) that can be precomputed. It is useful only when the Gram matrix is precomputed.
**copy\_X**bool, default=True
If `True`, X will be copied; else, it may be overwritten.
**coef\_init**ndarray of shape (n\_features, ), default=None
The initial values of the coefficients.
**verbose**bool or int, default=False
Amount of verbosity.
**return\_n\_iter**bool, default=False
Whether to return the number of iterations or not.
**positive**bool, default=False
If set to True, forces coefficients to be positive. (Only allowed when `y.ndim == 1`).
**check\_input**bool, default=True
If set to False, the input validation checks are skipped (including the Gram matrix when provided). It is assumed that they are handled by the caller.
**\*\*params**kwargs
Keyword arguments passed to the coordinate descent solver.
Returns:
**alphas**ndarray of shape (n\_alphas,)
The alphas along the path where models are computed.
**coefs**ndarray of shape (n\_features, n\_alphas) or (n\_targets, n\_features, n\_alphas)
Coefficients along the path.
**dual\_gaps**ndarray of shape (n\_alphas,)
The dual gaps at the end of the optimization for each alpha.
**n\_iters**list of int
The number of iterations taken by the coordinate descent optimizer to reach the specified tolerance for each alpha. (Is returned when `return_n_iter` is set to True).
See also
[`MultiTaskElasticNet`](sklearn.linear_model.multitaskelasticnet#sklearn.linear_model.MultiTaskElasticNet "sklearn.linear_model.MultiTaskElasticNet")
Multi-task ElasticNet model trained with L1/L2 mixed-norm as regularizer.
[`MultiTaskElasticNetCV`](sklearn.linear_model.multitaskelasticnetcv#sklearn.linear_model.MultiTaskElasticNetCV "sklearn.linear_model.MultiTaskElasticNetCV")
Multi-task L1/L2 ElasticNet with built-in cross-validation.
[`ElasticNet`](sklearn.linear_model.elasticnet#sklearn.linear_model.ElasticNet "sklearn.linear_model.ElasticNet")
Linear regression with combined L1 and L2 priors as regularizer.
[`ElasticNetCV`](sklearn.linear_model.elasticnetcv#sklearn.linear_model.ElasticNetCV "sklearn.linear_model.ElasticNetCV")
Elastic Net model with iterative fitting along a regularization path.
#### Notes
For an example, see [examples/linear\_model/plot\_lasso\_coordinate\_descent\_path.py](../../auto_examples/linear_model/plot_lasso_coordinate_descent_path#sphx-glr-auto-examples-linear-model-plot-lasso-coordinate-descent-path-py).
Examples using `sklearn.linear_model.enet_path`
-----------------------------------------------
[Lasso and Elastic Net](../../auto_examples/linear_model/plot_lasso_coordinate_descent_path#sphx-glr-auto-examples-linear-model-plot-lasso-coordinate-descent-path-py)
scikit_learn sklearn.neighbors.BallTree sklearn.neighbors.BallTree
==========================
*class*sklearn.neighbors.BallTree(*X*, *leaf\_size=40*, *metric='minkowski'*, *\*\*kwargs*)
BallTree for fast generalized N-point problems
Read more in the [User Guide](../neighbors#unsupervised-neighbors).
Parameters:
**X**array-like of shape (n\_samples, n\_features)
n\_samples is the number of points in the data set, and n\_features is the dimension of the parameter space. Note: if X is a C-contiguous array of doubles then data will not be copied. Otherwise, an internal copy will be made.
**leaf\_size**positive int, default=40
Number of points at which to switch to brute-force. Changing leaf\_size will not affect the results of a query, but can significantly impact the speed of a query and the memory required to store the constructed tree. The amount of memory needed to store the tree scales as approximately n\_samples / leaf\_size. For a specified `leaf_size`, a leaf node is guaranteed to satisfy `leaf_size <= n_points <= 2 * leaf_size`, except in the case that `n_samples < leaf_size`.
**metric**str or DistanceMetric object, default=’minkowski’
Metric to use for distance computation. Default is “minkowski”, which results in the standard Euclidean distance when p = 2. ball\_tree.valid\_metrics gives a list of the metrics which are valid for BallTree. See the documentation of [scipy.spatial.distance](https://docs.scipy.org/doc/scipy/reference/spatial.distance.html) and the metrics listed in [`distance_metrics`](sklearn.metrics.pairwise.distance_metrics#sklearn.metrics.pairwise.distance_metrics "sklearn.metrics.pairwise.distance_metrics") for more information.
**Additional keywords are passed to the distance metric class.**
**Note: Callable functions in the metric parameter are NOT supported for KDTree**
**and Ball Tree. Function call overhead will result in very poor performance.**
Attributes:
**data**memory view
The training data
#### Examples
Query for k-nearest neighbors
```
>>> import numpy as np
>>> from sklearn.neighbors import BallTree
>>> rng = np.random.RandomState(0)
>>> X = rng.random_sample((10, 3)) # 10 points in 3 dimensions
>>> tree = BallTree(X, leaf_size=2)
>>> dist, ind = tree.query(X[:1], k=3)
>>> print(ind) # indices of 3 closest neighbors
[0 3 1]
>>> print(dist) # distances to 3 closest neighbors
[ 0. 0.19662693 0.29473397]
```
Pickle and Unpickle a tree. Note that the state of the tree is saved in the pickle operation: the tree needs not be rebuilt upon unpickling.
```
>>> import numpy as np
>>> import pickle
>>> rng = np.random.RandomState(0)
>>> X = rng.random_sample((10, 3)) # 10 points in 3 dimensions
>>> tree = BallTree(X, leaf_size=2)
>>> s = pickle.dumps(tree)
>>> tree_copy = pickle.loads(s)
>>> dist, ind = tree_copy.query(X[:1], k=3)
>>> print(ind) # indices of 3 closest neighbors
[0 3 1]
>>> print(dist) # distances to 3 closest neighbors
[ 0. 0.19662693 0.29473397]
```
Query for neighbors within a given radius
```
>>> import numpy as np
>>> rng = np.random.RandomState(0)
>>> X = rng.random_sample((10, 3)) # 10 points in 3 dimensions
>>> tree = BallTree(X, leaf_size=2)
>>> print(tree.query_radius(X[:1], r=0.3, count_only=True))
3
>>> ind = tree.query_radius(X[:1], r=0.3)
>>> print(ind) # indices of neighbors within distance 0.3
[3 0 1]
```
Compute a gaussian kernel density estimate:
```
>>> import numpy as np
>>> rng = np.random.RandomState(42)
>>> X = rng.random_sample((100, 3))
>>> tree = BallTree(X)
>>> tree.kernel_density(X[:3], h=0.1, kernel='gaussian')
array([ 6.94114649, 7.83281226, 7.2071716 ])
```
Compute a two-point auto-correlation function
```
>>> import numpy as np
>>> rng = np.random.RandomState(0)
>>> X = rng.random_sample((30, 3))
>>> r = np.linspace(0, 1, 5)
>>> tree = BallTree(X)
>>> tree.two_point_correlation(X, r)
array([ 30, 62, 278, 580, 820])
```
#### Methods
| | |
| --- | --- |
| [`get_arrays`](#sklearn.neighbors.BallTree.get_arrays "sklearn.neighbors.BallTree.get_arrays")() | Get data and node arrays. |
| [`get_n_calls`](#sklearn.neighbors.BallTree.get_n_calls "sklearn.neighbors.BallTree.get_n_calls")() | Get number of calls. |
| [`get_tree_stats`](#sklearn.neighbors.BallTree.get_tree_stats "sklearn.neighbors.BallTree.get_tree_stats")() | Get tree status. |
| [`kernel_density`](#sklearn.neighbors.BallTree.kernel_density "sklearn.neighbors.BallTree.kernel_density")(X, h[, kernel, atol, rtol, ...]) | Compute the kernel density estimate at points X with the given kernel, using the distance metric specified at tree creation. |
| [`query`](#sklearn.neighbors.BallTree.query "sklearn.neighbors.BallTree.query")(X[, k, return\_distance, dualtree, ...]) | query the tree for the k nearest neighbors |
| [`query_radius`](#sklearn.neighbors.BallTree.query_radius "sklearn.neighbors.BallTree.query_radius")(X, r[, return\_distance, ...]) | query the tree for neighbors within a radius r |
| [`reset_n_calls`](#sklearn.neighbors.BallTree.reset_n_calls "sklearn.neighbors.BallTree.reset_n_calls")() | Reset number of calls to 0. |
| [`two_point_correlation`](#sklearn.neighbors.BallTree.two_point_correlation "sklearn.neighbors.BallTree.two_point_correlation")(X, r[, dualtree]) | Compute the two-point correlation function |
get\_arrays()
Get data and node arrays.
Returns:
arrays: tuple of array
Arrays for storing tree data, index, node data and node bounds.
get\_n\_calls()
Get number of calls.
Returns:
n\_calls: int
number of distance computation calls
get\_tree\_stats()
Get tree status.
Returns:
tree\_stats: tuple of int
(number of trims, number of leaves, number of splits)
kernel\_density(*X*, *h*, *kernel='gaussian'*, *atol=0*, *rtol=1E-8*, *breadth\_first=True*, *return\_log=False*)
Compute the kernel density estimate at points X with the given kernel, using the distance metric specified at tree creation.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
An array of points to query. Last dimension should match dimension of training data.
**h**float
the bandwidth of the kernel
**kernel**str, default=”gaussian”
specify the kernel to use. Options are - ‘gaussian’ - ‘tophat’ - ‘epanechnikov’ - ‘exponential’ - ‘linear’ - ‘cosine’ Default is kernel = ‘gaussian’
**atol**float, default=0
Specify the desired absolute tolerance of the result. If the true result is `K_true`, then the returned result `K_ret` satisfies `abs(K_true - K_ret) < atol + rtol * K_ret` The default is zero (i.e. machine precision).
**rtol**float, default=1e-8
Specify the desired relative tolerance of the result. If the true result is `K_true`, then the returned result `K_ret` satisfies `abs(K_true - K_ret) < atol + rtol * K_ret` The default is `1e-8` (i.e. machine precision).
**breadth\_first**bool, default=False
If True, use a breadth-first search. If False (default) use a depth-first search. Breadth-first is generally faster for compact kernels and/or high tolerances.
**return\_log**bool, default=False
Return the logarithm of the result. This can be more accurate than returning the result itself for narrow kernels.
Returns:
**density**ndarray of shape X.shape[:-1]
The array of (log)-density evaluations
query(*X*, *k=1*, *return\_distance=True*, *dualtree=False*, *breadth\_first=False*)
query the tree for the k nearest neighbors
Parameters:
**X**array-like of shape (n\_samples, n\_features)
An array of points to query
**k**int, default=1
The number of nearest neighbors to return
**return\_distance**bool, default=True
if True, return a tuple (d, i) of distances and indices if False, return array i
**dualtree**bool, default=False
if True, use the dual tree formalism for the query: a tree is built for the query points, and the pair of trees is used to efficiently search this space. This can lead to better performance as the number of points grows large.
**breadth\_first**bool, default=False
if True, then query the nodes in a breadth-first manner. Otherwise, query the nodes in a depth-first manner.
**sort\_results**bool, default=True
if True, then distances and indices of each point are sorted on return, so that the first column contains the closest points. Otherwise, neighbors are returned in an arbitrary order.
Returns:
**i**if return\_distance == False
**(d,i)**if return\_distance == True
**d**ndarray of shape X.shape[:-1] + (k,), dtype=double
Each entry gives the list of distances to the neighbors of the corresponding point.
**i**ndarray of shape X.shape[:-1] + (k,), dtype=int
Each entry gives the list of indices of neighbors of the corresponding point.
query\_radius(*X*, *r*, *return\_distance=False*, *count\_only=False*, *sort\_results=False*)
query the tree for neighbors within a radius r
Parameters:
**X**array-like of shape (n\_samples, n\_features)
An array of points to query
**r**distance within which neighbors are returned
r can be a single value, or an array of values of shape x.shape[:-1] if different radii are desired for each point.
**return\_distance**bool, default=False
if True, return distances to neighbors of each point if False, return only neighbors Note that unlike the query() method, setting return\_distance=True here adds to the computation time. Not all distances need to be calculated explicitly for return\_distance=False. Results are not sorted by default: see `sort_results` keyword.
**count\_only**bool, default=False
if True, return only the count of points within distance r if False, return the indices of all points within distance r If return\_distance==True, setting count\_only=True will result in an error.
**sort\_results**bool, default=False
if True, the distances and indices will be sorted before being returned. If False, the results will not be sorted. If return\_distance == False, setting sort\_results = True will result in an error.
Returns:
**count**if count\_only == True
**ind**if count\_only == False and return\_distance == False
**(ind, dist)**if count\_only == False and return\_distance == True
**count**ndarray of shape X.shape[:-1], dtype=int
Each entry gives the number of neighbors within a distance r of the corresponding point.
**ind**ndarray of shape X.shape[:-1], dtype=object
Each element is a numpy integer array listing the indices of neighbors of the corresponding point. Note that unlike the results of a k-neighbors query, the returned neighbors are not sorted by distance by default.
**dist**ndarray of shape X.shape[:-1], dtype=object
Each element is a numpy double array listing the distances corresponding to indices in i.
reset\_n\_calls()
Reset number of calls to 0.
two\_point\_correlation(*X*, *r*, *dualtree=False*)
Compute the two-point correlation function
Parameters:
**X**array-like of shape (n\_samples, n\_features)
An array of points to query. Last dimension should match dimension of training data.
**r**array-like
A one-dimensional array of distances
**dualtree**bool, default=False
If True, use a dualtree algorithm. Otherwise, use a single-tree algorithm. Dual tree algorithms can have better scaling for large N.
Returns:
**counts**ndarray
counts[i] contains the number of pairs of points with distance less than or equal to r[i]
| programming_docs |
scikit_learn sklearn.metrics.pairwise.paired_distances sklearn.metrics.pairwise.paired\_distances
==========================================
sklearn.metrics.pairwise.paired\_distances(*X*, *Y*, *\**, *metric='euclidean'*, *\*\*kwds*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/pairwise.py#L1099)
Compute the paired distances between X and Y.
Compute the distances between (X[0], Y[0]), (X[1], Y[1]), etc…
Read more in the [User Guide](../metrics#metrics).
Parameters:
**X**ndarray of shape (n\_samples, n\_features)
Array 1 for distance computation.
**Y**ndarray of shape (n\_samples, n\_features)
Array 2 for distance computation.
**metric**str or callable, default=”euclidean”
The metric to use when calculating distance between instances in a feature array. If metric is a string, it must be one of the options specified in PAIRED\_DISTANCES, including “euclidean”, “manhattan”, or “cosine”. Alternatively, if metric is a callable function, it is called on each pair of instances (rows) and the resulting value recorded. The callable should take two arrays from `X` as input and return a value indicating the distance between them.
**\*\*kwds**dict
Unused parameters.
Returns:
**distances**ndarray of shape (n\_samples,)
Returns the distances between the row vectors of `X` and the row vectors of `Y`.
See also
`pairwise_distances`
Computes the distance between every pair of samples.
#### Examples
```
>>> from sklearn.metrics.pairwise import paired_distances
>>> X = [[0, 1], [1, 1]]
>>> Y = [[0, 1], [2, 1]]
>>> paired_distances(X, Y)
array([0., 1.])
```
scikit_learn sklearn.multioutput.MultiOutputRegressor sklearn.multioutput.MultiOutputRegressor
========================================
*class*sklearn.multioutput.MultiOutputRegressor(*estimator*, *\**, *n\_jobs=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/multioutput.py#L244)
Multi target regression.
This strategy consists of fitting one regressor per target. This is a simple strategy for extending regressors that do not natively support multi-target regression.
New in version 0.18.
Parameters:
**estimator**estimator object
An estimator object implementing [fit](https://scikit-learn.org/1.1/glossary.html#term-fit) and [predict](https://scikit-learn.org/1.1/glossary.html#term-predict).
**n\_jobs**int or None, optional (default=None)
The number of jobs to run in parallel. [`fit`](#sklearn.multioutput.MultiOutputRegressor.fit "sklearn.multioutput.MultiOutputRegressor.fit"), [`predict`](#sklearn.multioutput.MultiOutputRegressor.predict "sklearn.multioutput.MultiOutputRegressor.predict") and [`partial_fit`](#sklearn.multioutput.MultiOutputRegressor.partial_fit "sklearn.multioutput.MultiOutputRegressor.partial_fit") (if supported by the passed estimator) will be parallelized for each target.
When individual estimators are fast to train or predict, using `n_jobs > 1` can result in slower performance due to the parallelism overhead.
`None` means `1` unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all available processes / threads. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
Changed in version 0.20: `n_jobs` default changed from `1` to `None`.
Attributes:
**estimators\_**list of `n_output` estimators
Estimators used for predictions.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Only defined if the underlying `estimator` exposes such an attribute when fit.
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Only defined if the underlying estimators expose such an attribute when fit.
New in version 1.0.
See also
[`RegressorChain`](sklearn.multioutput.regressorchain#sklearn.multioutput.RegressorChain "sklearn.multioutput.RegressorChain")
A multi-label model that arranges regressions into a chain.
[`MultiOutputClassifier`](sklearn.multioutput.multioutputclassifier#sklearn.multioutput.MultiOutputClassifier "sklearn.multioutput.MultiOutputClassifier")
Classifies each output independently rather than chaining.
#### Examples
```
>>> import numpy as np
>>> from sklearn.datasets import load_linnerud
>>> from sklearn.multioutput import MultiOutputRegressor
>>> from sklearn.linear_model import Ridge
>>> X, y = load_linnerud(return_X_y=True)
>>> regr = MultiOutputRegressor(Ridge(random_state=123)).fit(X, y)
>>> regr.predict(X[[0]])
array([[176..., 35..., 57...]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.multioutput.MultiOutputRegressor.fit "sklearn.multioutput.MultiOutputRegressor.fit")(X, y[, sample\_weight]) | Fit the model to data, separately for each output variable. |
| [`get_params`](#sklearn.multioutput.MultiOutputRegressor.get_params "sklearn.multioutput.MultiOutputRegressor.get_params")([deep]) | Get parameters for this estimator. |
| [`partial_fit`](#sklearn.multioutput.MultiOutputRegressor.partial_fit "sklearn.multioutput.MultiOutputRegressor.partial_fit")(X, y[, sample\_weight]) | Incrementally fit the model to data, for each output variable. |
| [`predict`](#sklearn.multioutput.MultiOutputRegressor.predict "sklearn.multioutput.MultiOutputRegressor.predict")(X) | Predict multi-output variable using model for each target variable. |
| [`score`](#sklearn.multioutput.MultiOutputRegressor.score "sklearn.multioutput.MultiOutputRegressor.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.multioutput.MultiOutputRegressor.set_params "sklearn.multioutput.MultiOutputRegressor.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*, *sample\_weight=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/multioutput.py#L153)
Fit the model to data, separately for each output variable.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input data.
**y**{array-like, sparse matrix} of shape (n\_samples, n\_outputs)
Multi-output targets. An indicator matrix turns on multilabel estimation.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If `None`, then samples are equally weighted. Only supported if the underlying regressor supports sample weights.
**\*\*fit\_params**dict of string -> object
Parameters passed to the `estimator.fit` method of each step.
New in version 0.23.
Returns:
**self**object
Returns a fitted instance.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
partial\_fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/multioutput.py#L313)
Incrementally fit the model to data, for each output variable.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input data.
**y**{array-like, sparse matrix} of shape (n\_samples, n\_outputs)
Multi-output targets.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If `None`, then samples are equally weighted. Only supported if the underlying regressor supports sample weights.
Returns:
**self**object
Returns a fitted instance.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/multioutput.py#L216)
Predict multi-output variable using model for each target variable.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input data.
Returns:
**y**{array-like, sparse matrix} of shape (n\_samples, n\_outputs)
Multi-output targets predicted across multiple predictors. Note: Separate models are generated for each predictor.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.multioutput.MultiOutputRegressor`
---------------------------------------------------------
[Comparing random forests and the multi-output meta estimator](../../auto_examples/ensemble/plot_random_forest_regression_multioutput#sphx-glr-auto-examples-ensemble-plot-random-forest-regression-multioutput-py)
scikit_learn sklearn.naive_bayes.CategoricalNB sklearn.naive\_bayes.CategoricalNB
==================================
*class*sklearn.naive\_bayes.CategoricalNB(*\**, *alpha=1.0*, *fit\_prior=True*, *class\_prior=None*, *min\_categories=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/naive_bayes.py#L1155)
Naive Bayes classifier for categorical features.
The categorical Naive Bayes classifier is suitable for classification with discrete features that are categorically distributed. The categories of each feature are drawn from a categorical distribution.
Read more in the [User Guide](../naive_bayes#categorical-naive-bayes).
Parameters:
**alpha**float, default=1.0
Additive (Laplace/Lidstone) smoothing parameter (0 for no smoothing).
**fit\_prior**bool, default=True
Whether to learn class prior probabilities or not. If false, a uniform prior will be used.
**class\_prior**array-like of shape (n\_classes,), default=None
Prior probabilities of the classes. If specified, the priors are not adjusted according to the data.
**min\_categories**int or array-like of shape (n\_features,), default=None
Minimum number of categories per feature.
* integer: Sets the minimum number of categories per feature to `n_categories` for each features.
* array-like: shape (n\_features,) where `n_categories[i]` holds the minimum number of categories for the ith column of the input.
* None (default): Determines the number of categories automatically from the training data.
New in version 0.24.
Attributes:
**category\_count\_**list of arrays of shape (n\_features,)
Holds arrays of shape (n\_classes, n\_categories of respective feature) for each feature. Each array provides the number of samples encountered for each class and category of the specific feature.
**class\_count\_**ndarray of shape (n\_classes,)
Number of samples encountered for each class during fitting. This value is weighted by the sample weight when provided.
**class\_log\_prior\_**ndarray of shape (n\_classes,)
Smoothed empirical log probability for each class.
**classes\_**ndarray of shape (n\_classes,)
Class labels known to the classifier
**feature\_log\_prob\_**list of arrays of shape (n\_features,)
Holds arrays of shape (n\_classes, n\_categories of respective feature) for each feature. Each array provides the empirical log probability of categories given the respective feature and class, `P(x_i|y)`.
[`n_features_`](#sklearn.naive_bayes.CategoricalNB.n_features_ "sklearn.naive_bayes.CategoricalNB.n_features_")int
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_categories\_**ndarray of shape (n\_features,), dtype=np.int64
Number of categories for each feature. This value is inferred from the data or set by the minimum number of categories.
New in version 0.24.
See also
[`BernoulliNB`](sklearn.naive_bayes.bernoullinb#sklearn.naive_bayes.BernoulliNB "sklearn.naive_bayes.BernoulliNB")
Naive Bayes classifier for multivariate Bernoulli models.
[`ComplementNB`](sklearn.naive_bayes.complementnb#sklearn.naive_bayes.ComplementNB "sklearn.naive_bayes.ComplementNB")
Complement Naive Bayes classifier.
[`GaussianNB`](sklearn.naive_bayes.gaussiannb#sklearn.naive_bayes.GaussianNB "sklearn.naive_bayes.GaussianNB")
Gaussian Naive Bayes.
[`MultinomialNB`](sklearn.naive_bayes.multinomialnb#sklearn.naive_bayes.MultinomialNB "sklearn.naive_bayes.MultinomialNB")
Naive Bayes classifier for multinomial models.
#### Examples
```
>>> import numpy as np
>>> rng = np.random.RandomState(1)
>>> X = rng.randint(5, size=(6, 100))
>>> y = np.array([1, 2, 3, 4, 5, 6])
>>> from sklearn.naive_bayes import CategoricalNB
>>> clf = CategoricalNB()
>>> clf.fit(X, y)
CategoricalNB()
>>> print(clf.predict(X[2:3]))
[3]
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.naive_bayes.CategoricalNB.fit "sklearn.naive_bayes.CategoricalNB.fit")(X, y[, sample\_weight]) | Fit Naive Bayes classifier according to X, y. |
| [`get_params`](#sklearn.naive_bayes.CategoricalNB.get_params "sklearn.naive_bayes.CategoricalNB.get_params")([deep]) | Get parameters for this estimator. |
| [`partial_fit`](#sklearn.naive_bayes.CategoricalNB.partial_fit "sklearn.naive_bayes.CategoricalNB.partial_fit")(X, y[, classes, sample\_weight]) | Incremental fit on a batch of samples. |
| [`predict`](#sklearn.naive_bayes.CategoricalNB.predict "sklearn.naive_bayes.CategoricalNB.predict")(X) | Perform classification on an array of test vectors X. |
| [`predict_log_proba`](#sklearn.naive_bayes.CategoricalNB.predict_log_proba "sklearn.naive_bayes.CategoricalNB.predict_log_proba")(X) | Return log-probability estimates for the test vector X. |
| [`predict_proba`](#sklearn.naive_bayes.CategoricalNB.predict_proba "sklearn.naive_bayes.CategoricalNB.predict_proba")(X) | Return probability estimates for the test vector X. |
| [`score`](#sklearn.naive_bayes.CategoricalNB.score "sklearn.naive_bayes.CategoricalNB.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.naive_bayes.CategoricalNB.set_params "sklearn.naive_bayes.CategoricalNB.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/naive_bayes.py#L1265)
Fit Naive Bayes classifier according to X, y.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vectors, where `n_samples` is the number of samples and `n_features` is the number of features. Here, each feature of X is assumed to be from a different categorical distribution. It is further assumed that all categories of each feature are represented by the numbers 0, …, n - 1, where n refers to the total number of categories for the given feature. This can, for instance, be achieved with the help of OrdinalEncoder.
**y**array-like of shape (n\_samples,)
Target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Weights applied to individual samples (1. for unweighted).
Returns:
**self**object
Returns the instance itself.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_features\_
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2. Use `n_features_in_` instead.
partial\_fit(*X*, *y*, *classes=None*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/naive_bayes.py#L1292)
Incremental fit on a batch of samples.
This method is expected to be called several times consecutively on different chunks of a dataset so as to implement out-of-core or online learning.
This is especially useful when the whole dataset is too big to fit in memory at once.
This method has some performance overhead hence it is better to call partial\_fit on chunks of data that are as large as possible (as long as fitting in the memory budget) to hide the overhead.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vectors, where `n_samples` is the number of samples and `n_features` is the number of features. Here, each feature of X is assumed to be from a different categorical distribution. It is further assumed that all categories of each feature are represented by the numbers 0, …, n - 1, where n refers to the total number of categories for the given feature. This can, for instance, be achieved with the help of OrdinalEncoder.
**y**array-like of shape (n\_samples,)
Target values.
**classes**array-like of shape (n\_classes,), default=None
List of all the classes that can possibly appear in the y vector.
Must be provided at the first call to partial\_fit, can be omitted in subsequent calls.
**sample\_weight**array-like of shape (n\_samples,), default=None
Weights applied to individual samples (1. for unweighted).
Returns:
**self**object
Returns the instance itself.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/naive_bayes.py#L65)
Perform classification on an array of test vectors X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The input samples.
Returns:
**C**ndarray of shape (n\_samples,)
Predicted target values for X.
predict\_log\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/naive_bayes.py#L84)
Return log-probability estimates for the test vector X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The input samples.
Returns:
**C**array-like of shape (n\_samples, n\_classes)
Returns the log-probability of the samples for each class in the model. The columns correspond to the classes in sorted order, as they appear in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/naive_bayes.py#L107)
Return probability estimates for the test vector X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The input samples.
Returns:
**C**array-like of shape (n\_samples, n\_classes)
Returns the probability of the samples for each class in the model. The columns correspond to the classes in sorted order, as they appear in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
| programming_docs |
scikit_learn sklearn.gaussian_process.kernels.CompoundKernel sklearn.gaussian\_process.kernels.CompoundKernel
================================================
*class*sklearn.gaussian\_process.kernels.CompoundKernel(*kernels*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L492)
Kernel which is composed of a set of other kernels.
New in version 0.18.
Parameters:
**kernels**list of Kernels
The other kernels
Attributes:
[`bounds`](#sklearn.gaussian_process.kernels.CompoundKernel.bounds "sklearn.gaussian_process.kernels.CompoundKernel.bounds")
Returns the log-transformed bounds on the theta.
[`hyperparameters`](#sklearn.gaussian_process.kernels.CompoundKernel.hyperparameters "sklearn.gaussian_process.kernels.CompoundKernel.hyperparameters")
Returns a list of all hyperparameter specifications.
[`n_dims`](#sklearn.gaussian_process.kernels.CompoundKernel.n_dims "sklearn.gaussian_process.kernels.CompoundKernel.n_dims")
Returns the number of non-fixed hyperparameters of the kernel.
[`requires_vector_input`](#sklearn.gaussian_process.kernels.CompoundKernel.requires_vector_input "sklearn.gaussian_process.kernels.CompoundKernel.requires_vector_input")
Returns whether the kernel is defined on discrete structures.
[`theta`](#sklearn.gaussian_process.kernels.CompoundKernel.theta "sklearn.gaussian_process.kernels.CompoundKernel.theta")
Returns the (flattened, log-transformed) non-fixed hyperparameters.
#### Examples
```
>>> from sklearn.gaussian_process.kernels import WhiteKernel
>>> from sklearn.gaussian_process.kernels import RBF
>>> from sklearn.gaussian_process.kernels import CompoundKernel
>>> kernel = CompoundKernel(
... [WhiteKernel(noise_level=3.0), RBF(length_scale=2.0)])
>>> print(kernel.bounds)
[[-11.51292546 11.51292546]
[-11.51292546 11.51292546]]
>>> print(kernel.n_dims)
2
>>> print(kernel.theta)
[1.09861229 0.69314718]
```
#### Methods
| | |
| --- | --- |
| [`__call__`](#sklearn.gaussian_process.kernels.CompoundKernel.__call__ "sklearn.gaussian_process.kernels.CompoundKernel.__call__")(X[, Y, eval\_gradient]) | Return the kernel k(X, Y) and optionally its gradient. |
| [`clone_with_theta`](#sklearn.gaussian_process.kernels.CompoundKernel.clone_with_theta "sklearn.gaussian_process.kernels.CompoundKernel.clone_with_theta")(theta) | Returns a clone of self with given hyperparameters theta. |
| [`diag`](#sklearn.gaussian_process.kernels.CompoundKernel.diag "sklearn.gaussian_process.kernels.CompoundKernel.diag")(X) | Returns the diagonal of the kernel k(X, X). |
| [`get_params`](#sklearn.gaussian_process.kernels.CompoundKernel.get_params "sklearn.gaussian_process.kernels.CompoundKernel.get_params")([deep]) | Get parameters of this kernel. |
| [`is_stationary`](#sklearn.gaussian_process.kernels.CompoundKernel.is_stationary "sklearn.gaussian_process.kernels.CompoundKernel.is_stationary")() | Returns whether the kernel is stationary. |
| [`set_params`](#sklearn.gaussian_process.kernels.CompoundKernel.set_params "sklearn.gaussian_process.kernels.CompoundKernel.set_params")(\*\*params) | Set the parameters of this kernel. |
\_\_call\_\_(*X*, *Y=None*, *eval\_gradient=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L577)
Return the kernel k(X, Y) and optionally its gradient.
Note that this compound kernel returns the results of all simple kernel stacked along an additional axis.
Parameters:
**X**array-like of shape (n\_samples\_X, n\_features) or list of object, default=None
Left argument of the returned kernel k(X, Y)
**Y**array-like of shape (n\_samples\_X, n\_features) or list of object, default=None
Right argument of the returned kernel k(X, Y). If None, k(X, X) is evaluated instead.
**eval\_gradient**bool, default=False
Determines whether the gradient with respect to the log of the kernel hyperparameter is computed.
Returns:
**K**ndarray of shape (n\_samples\_X, n\_samples\_Y, n\_kernels)
Kernel k(X, Y)
**K\_gradient**ndarray of shape (n\_samples\_X, n\_samples\_X, n\_dims, n\_kernels), optional
The gradient of the kernel k(X, X) with respect to the log of the hyperparameter of the kernel. Only returned when `eval_gradient` is True.
*property*bounds
Returns the log-transformed bounds on the theta.
Returns:
**bounds**array of shape (n\_dims, 2)
The log-transformed bounds on the kernel’s hyperparameters theta
clone\_with\_theta(*theta*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L238)
Returns a clone of self with given hyperparameters theta.
Parameters:
**theta**ndarray of shape (n\_dims,)
The hyperparameters
diag(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L636)
Returns the diagonal of the kernel k(X, X).
The result of this method is identical to `np.diag(self(X))`; however, it can be evaluated more efficiently since only the diagonal is evaluated.
Parameters:
**X**array-like of shape (n\_samples\_X, n\_features) or list of object
Argument to the kernel.
Returns:
**K\_diag**ndarray of shape (n\_samples\_X, n\_kernels)
Diagonal of kernel k(X, X)
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L521)
Get parameters of this kernel.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*hyperparameters
Returns a list of all hyperparameter specifications.
is\_stationary()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L627)
Returns whether the kernel is stationary.
*property*n\_dims
Returns the number of non-fixed hyperparameters of the kernel.
*property*requires\_vector\_input
Returns whether the kernel is defined on discrete structures.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L198)
Set the parameters of this kernel.
The method works on simple kernels as well as on nested kernels. The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Returns:
self
*property*theta
Returns the (flattened, log-transformed) non-fixed hyperparameters.
Note that theta are typically the log-transformed values of the kernel’s hyperparameters as this representation of the search space is more amenable for hyperparameter search, as hyperparameters like length-scales naturally live on a log-scale.
Returns:
**theta**ndarray of shape (n\_dims,)
The non-fixed, log-transformed hyperparameters of the kernel
scikit_learn sklearn.pipeline.make_union sklearn.pipeline.make\_union
============================
sklearn.pipeline.make\_union(*\*transformers*, *n\_jobs=None*, *verbose=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/pipeline.py#L1246)
Construct a FeatureUnion from the given transformers.
This is a shorthand for the FeatureUnion constructor; it does not require, and does not permit, naming the transformers. Instead, they will be given names automatically based on their types. It also does not allow weighting.
Parameters:
**\*transformers**list of estimators
One or more estimators.
**n\_jobs**int, default=None
Number of jobs to run in parallel. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
Changed in version v0.20: `n_jobs` default changed from 1 to None.
**verbose**bool, default=False
If True, the time elapsed while fitting each transformer will be printed as it is completed.
Returns:
**f**FeatureUnion
A [`FeatureUnion`](sklearn.pipeline.featureunion#sklearn.pipeline.FeatureUnion "sklearn.pipeline.FeatureUnion") object for concatenating the results of multiple transformer objects.
See also
[`FeatureUnion`](sklearn.pipeline.featureunion#sklearn.pipeline.FeatureUnion "sklearn.pipeline.FeatureUnion")
Class for concatenating the results of multiple transformer objects.
#### Examples
```
>>> from sklearn.decomposition import PCA, TruncatedSVD
>>> from sklearn.pipeline import make_union
>>> make_union(PCA(), TruncatedSVD())
FeatureUnion(transformer_list=[('pca', PCA()),
('truncatedsvd', TruncatedSVD())])
```
scikit_learn sklearn.feature_extraction.text.CountVectorizer sklearn.feature\_extraction.text.CountVectorizer
================================================
*class*sklearn.feature\_extraction.text.CountVectorizer(*\**, *input='content'*, *encoding='utf-8'*, *decode\_error='strict'*, *strip\_accents=None*, *lowercase=True*, *preprocessor=None*, *tokenizer=None*, *stop\_words=None*, *token\_pattern='(?u)\\b\\w\\w+\\b'*, *ngram\_range=(1*, *1)*, *analyzer='word'*, *max\_df=1.0*, *min\_df=1*, *max\_features=None*, *vocabulary=None*, *binary=False*, *dtype=<class 'numpy.int64'>*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L892)
Convert a collection of text documents to a matrix of token counts.
This implementation produces a sparse representation of the counts using scipy.sparse.csr\_matrix.
If you do not provide an a-priori dictionary and you do not use an analyzer that does some kind of feature selection then the number of features will be equal to the vocabulary size found by analyzing the data.
Read more in the [User Guide](../feature_extraction#text-feature-extraction).
Parameters:
**input**{‘filename’, ‘file’, ‘content’}, default=’content’
* If `'filename'`, the sequence passed as an argument to fit is expected to be a list of filenames that need reading to fetch the raw content to analyze.
* If `'file'`, the sequence items must have a ‘read’ method (file-like object) that is called to fetch the bytes in memory.
* If `'content'`, the input is expected to be a sequence of items that can be of type string or byte.
**encoding**str, default=’utf-8’
If bytes or files are given to analyze, this encoding is used to decode.
**decode\_error**{‘strict’, ‘ignore’, ‘replace’}, default=’strict’
Instruction on what to do if a byte sequence is given to analyze that contains characters not of the given `encoding`. By default, it is ‘strict’, meaning that a UnicodeDecodeError will be raised. Other values are ‘ignore’ and ‘replace’.
**strip\_accents**{‘ascii’, ‘unicode’}, default=None
Remove accents and perform other character normalization during the preprocessing step. ‘ascii’ is a fast method that only works on characters that have an direct ASCII mapping. ‘unicode’ is a slightly slower method that works on any characters. None (default) does nothing.
Both ‘ascii’ and ‘unicode’ use NFKD normalization from [`unicodedata.normalize`](https://docs.python.org/3/library/unicodedata.html#unicodedata.normalize "(in Python v3.10)").
**lowercase**bool, default=True
Convert all characters to lowercase before tokenizing.
**preprocessor**callable, default=None
Override the preprocessing (strip\_accents and lowercase) stage while preserving the tokenizing and n-grams generation steps. Only applies if `analyzer` is not callable.
**tokenizer**callable, default=None
Override the string tokenization step while preserving the preprocessing and n-grams generation steps. Only applies if `analyzer == 'word'`.
**stop\_words**{‘english’}, list, default=None
If ‘english’, a built-in stop word list for English is used. There are several known issues with ‘english’ and you should consider an alternative (see [Using stop words](../feature_extraction#stop-words)).
If a list, that list is assumed to contain stop words, all of which will be removed from the resulting tokens. Only applies if `analyzer == 'word'`.
If None, no stop words will be used. max\_df can be set to a value in the range [0.7, 1.0) to automatically detect and filter stop words based on intra corpus document frequency of terms.
**token\_pattern**str, default=r”(?u)\b\w\w+\b”
Regular expression denoting what constitutes a “token”, only used if `analyzer == 'word'`. The default regexp select tokens of 2 or more alphanumeric characters (punctuation is completely ignored and always treated as a token separator).
If there is a capturing group in token\_pattern then the captured group content, not the entire match, becomes the token. At most one capturing group is permitted.
**ngram\_range**tuple (min\_n, max\_n), default=(1, 1)
The lower and upper boundary of the range of n-values for different word n-grams or char n-grams to be extracted. All values of n such such that min\_n <= n <= max\_n will be used. For example an `ngram_range` of `(1, 1)` means only unigrams, `(1, 2)` means unigrams and bigrams, and `(2, 2)` means only bigrams. Only applies if `analyzer` is not callable.
**analyzer**{‘word’, ‘char’, ‘char\_wb’} or callable, default=’word’
Whether the feature should be made of word n-gram or character n-grams. Option ‘char\_wb’ creates character n-grams only from text inside word boundaries; n-grams at the edges of words are padded with space.
If a callable is passed it is used to extract the sequence of features out of the raw, unprocessed input.
Changed in version 0.21.
Since v0.21, if `input` is `filename` or `file`, the data is first read from the file and then passed to the given callable analyzer.
**max\_df**float in range [0.0, 1.0] or int, default=1.0
When building the vocabulary ignore terms that have a document frequency strictly higher than the given threshold (corpus-specific stop words). If float, the parameter represents a proportion of documents, integer absolute counts. This parameter is ignored if vocabulary is not None.
**min\_df**float in range [0.0, 1.0] or int, default=1
When building the vocabulary ignore terms that have a document frequency strictly lower than the given threshold. This value is also called cut-off in the literature. If float, the parameter represents a proportion of documents, integer absolute counts. This parameter is ignored if vocabulary is not None.
**max\_features**int, default=None
If not None, build a vocabulary that only consider the top max\_features ordered by term frequency across the corpus.
This parameter is ignored if vocabulary is not None.
**vocabulary**Mapping or iterable, default=None
Either a Mapping (e.g., a dict) where keys are terms and values are indices in the feature matrix, or an iterable over terms. If not given, a vocabulary is determined from the input documents. Indices in the mapping should not be repeated and should not have any gap between 0 and the largest index.
**binary**bool, default=False
If True, all non zero counts are set to 1. This is useful for discrete probabilistic models that model binary events rather than integer counts.
**dtype**type, default=np.int64
Type of the matrix returned by fit\_transform() or transform().
Attributes:
**vocabulary\_**dict
A mapping of terms to feature indices.
**fixed\_vocabulary\_**bool
True if a fixed vocabulary of term to indices mapping is provided by the user.
**stop\_words\_**set
Terms that were ignored because they either:
* occurred in too many documents (`max_df`)
* occurred in too few documents (`min_df`)
* were cut off by feature selection (`max_features`).
This is only available if no vocabulary was given.
See also
[`HashingVectorizer`](sklearn.feature_extraction.text.hashingvectorizer#sklearn.feature_extraction.text.HashingVectorizer "sklearn.feature_extraction.text.HashingVectorizer")
Convert a collection of text documents to a matrix of token counts.
[`TfidfVectorizer`](sklearn.feature_extraction.text.tfidfvectorizer#sklearn.feature_extraction.text.TfidfVectorizer "sklearn.feature_extraction.text.TfidfVectorizer")
Convert a collection of raw documents to a matrix of TF-IDF features.
#### Notes
The `stop_words_` attribute can get large and increase the model size when pickling. This attribute is provided only for introspection and can be safely removed using delattr or set to None before pickling.
#### Examples
```
>>> from sklearn.feature_extraction.text import CountVectorizer
>>> corpus = [
... 'This is the first document.',
... 'This document is the second document.',
... 'And this is the third one.',
... 'Is this the first document?',
... ]
>>> vectorizer = CountVectorizer()
>>> X = vectorizer.fit_transform(corpus)
>>> vectorizer.get_feature_names_out()
array(['and', 'document', 'first', 'is', 'one', 'second', 'the', 'third',
'this'], ...)
>>> print(X.toarray())
[[0 1 1 1 0 0 1 0 1]
[0 2 0 1 0 1 1 0 1]
[1 0 0 1 1 0 1 1 1]
[0 1 1 1 0 0 1 0 1]]
>>> vectorizer2 = CountVectorizer(analyzer='word', ngram_range=(2, 2))
>>> X2 = vectorizer2.fit_transform(corpus)
>>> vectorizer2.get_feature_names_out()
array(['and this', 'document is', 'first document', 'is the', 'is this',
'second document', 'the first', 'the second', 'the third', 'third one',
'this document', 'this is', 'this the'], ...)
>>> print(X2.toarray())
[[0 0 1 1 0 0 1 0 0 0 0 1 0]
[0 1 0 1 0 1 0 1 0 0 1 0 0]
[1 0 0 1 0 0 0 0 1 1 0 1 0]
[0 0 1 0 1 0 1 0 0 0 0 0 1]]
```
#### Methods
| | |
| --- | --- |
| [`build_analyzer`](#sklearn.feature_extraction.text.CountVectorizer.build_analyzer "sklearn.feature_extraction.text.CountVectorizer.build_analyzer")() | Return a callable to process input data. |
| [`build_preprocessor`](#sklearn.feature_extraction.text.CountVectorizer.build_preprocessor "sklearn.feature_extraction.text.CountVectorizer.build_preprocessor")() | Return a function to preprocess the text before tokenization. |
| [`build_tokenizer`](#sklearn.feature_extraction.text.CountVectorizer.build_tokenizer "sklearn.feature_extraction.text.CountVectorizer.build_tokenizer")() | Return a function that splits a string into a sequence of tokens. |
| [`decode`](#sklearn.feature_extraction.text.CountVectorizer.decode "sklearn.feature_extraction.text.CountVectorizer.decode")(doc) | Decode the input into a string of unicode symbols. |
| [`fit`](#sklearn.feature_extraction.text.CountVectorizer.fit "sklearn.feature_extraction.text.CountVectorizer.fit")(raw\_documents[, y]) | Learn a vocabulary dictionary of all tokens in the raw documents. |
| [`fit_transform`](#sklearn.feature_extraction.text.CountVectorizer.fit_transform "sklearn.feature_extraction.text.CountVectorizer.fit_transform")(raw\_documents[, y]) | Learn the vocabulary dictionary and return document-term matrix. |
| [`get_feature_names`](#sklearn.feature_extraction.text.CountVectorizer.get_feature_names "sklearn.feature_extraction.text.CountVectorizer.get_feature_names")() | DEPRECATED: get\_feature\_names is deprecated in 1.0 and will be removed in 1.2. |
| [`get_feature_names_out`](#sklearn.feature_extraction.text.CountVectorizer.get_feature_names_out "sklearn.feature_extraction.text.CountVectorizer.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.feature_extraction.text.CountVectorizer.get_params "sklearn.feature_extraction.text.CountVectorizer.get_params")([deep]) | Get parameters for this estimator. |
| [`get_stop_words`](#sklearn.feature_extraction.text.CountVectorizer.get_stop_words "sklearn.feature_extraction.text.CountVectorizer.get_stop_words")() | Build or fetch the effective stop words list. |
| [`inverse_transform`](#sklearn.feature_extraction.text.CountVectorizer.inverse_transform "sklearn.feature_extraction.text.CountVectorizer.inverse_transform")(X) | Return terms per document with nonzero entries in X. |
| [`set_params`](#sklearn.feature_extraction.text.CountVectorizer.set_params "sklearn.feature_extraction.text.CountVectorizer.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.feature_extraction.text.CountVectorizer.transform "sklearn.feature_extraction.text.CountVectorizer.transform")(raw\_documents) | Transform documents to document-term matrix. |
build\_analyzer()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L418)
Return a callable to process input data.
The callable handles that handles preprocessing, tokenization, and n-grams generation.
Returns:
analyzer: callable
A function to handle preprocessing, tokenization and n-grams generation.
build\_preprocessor()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L321)
Return a function to preprocess the text before tokenization.
Returns:
preprocessor: callable
A function to preprocess the text before tokenization.
build\_tokenizer()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L348)
Return a function that splits a string into a sequence of tokens.
Returns:
tokenizer: callable
A function to split a string into a sequence of tokens.
decode(*doc*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L208)
Decode the input into a string of unicode symbols.
The decoding strategy depends on the vectorizer parameters.
Parameters:
**doc**bytes or str
The string to decode.
Returns:
doc: str
A string of unicode symbols.
fit(*raw\_documents*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L1274)
Learn a vocabulary dictionary of all tokens in the raw documents.
Parameters:
**raw\_documents**iterable
An iterable which generates either str, unicode or file objects.
**y**None
This parameter is ignored.
Returns:
**self**object
Fitted vectorizer.
fit\_transform(*raw\_documents*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L1294)
Learn the vocabulary dictionary and return document-term matrix.
This is equivalent to fit followed by transform, but more efficiently implemented.
Parameters:
**raw\_documents**iterable
An iterable which generates either str, unicode or file objects.
**y**None
This parameter is ignored.
Returns:
**X**array of shape (n\_samples, n\_features)
Document-term matrix.
get\_feature\_names()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L1425)
DEPRECATED: get\_feature\_names is deprecated in 1.0 and will be removed in 1.2. Please use get\_feature\_names\_out instead.
Array mapping from feature integer indices to feature name.
Returns:
**feature\_names**list
A list of feature names.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L1441)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Not used, present here for API consistency by convention.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
get\_stop\_words()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L368)
Build or fetch the effective stop words list.
Returns:
stop\_words: list or None
A list of stop words.
inverse\_transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L1392)
Return terms per document with nonzero entries in X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Document-term matrix.
Returns:
**X\_inv**list of arrays of shape (n\_samples,)
List of arrays of terms.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*raw\_documents*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L1364)
Transform documents to document-term matrix.
Extract token counts out of raw text documents using the vocabulary fitted with fit or the one provided to the constructor.
Parameters:
**raw\_documents**iterable
An iterable which generates either str, unicode or file objects.
Returns:
**X**sparse matrix of shape (n\_samples, n\_features)
Document-term matrix.
Examples using `sklearn.feature_extraction.text.CountVectorizer`
----------------------------------------------------------------
[Topic extraction with Non-negative Matrix Factorization and Latent Dirichlet Allocation](../../auto_examples/applications/plot_topics_extraction_with_nmf_lda#sphx-glr-auto-examples-applications-plot-topics-extraction-with-nmf-lda-py)
[Sample pipeline for text feature extraction and evaluation](../../auto_examples/model_selection/grid_search_text_feature_extraction#sphx-glr-auto-examples-model-selection-grid-search-text-feature-extraction-py)
[Semi-supervised Classification on a Text Dataset](../../auto_examples/semi_supervised/plot_semi_supervised_newsgroups#sphx-glr-auto-examples-semi-supervised-plot-semi-supervised-newsgroups-py)
[FeatureHasher and DictVectorizer Comparison](../../auto_examples/text/plot_hashing_vs_dict_vectorizer#sphx-glr-auto-examples-text-plot-hashing-vs-dict-vectorizer-py)
| programming_docs |
scikit_learn sklearn.impute.IterativeImputer sklearn.impute.IterativeImputer
===============================
*class*sklearn.impute.IterativeImputer(*estimator=None*, *\**, *missing\_values=nan*, *sample\_posterior=False*, *max\_iter=10*, *tol=0.001*, *n\_nearest\_features=None*, *initial\_strategy='mean'*, *imputation\_order='ascending'*, *skip\_complete=False*, *min\_value=-inf*, *max\_value=inf*, *verbose=0*, *random\_state=None*, *add\_indicator=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/impute/_iterative.py#L26)
Multivariate imputer that estimates each feature from all the others.
A strategy for imputing missing values by modeling each feature with missing values as a function of other features in a round-robin fashion.
Read more in the [User Guide](../impute#iterative-imputer).
New in version 0.21.
Note
This estimator is still **experimental** for now: the predictions and the API might change without any deprecation cycle. To use it, you need to explicitly import `enable_iterative_imputer`:
```
>>> # explicitly require this experimental feature
>>> from sklearn.experimental import enable_iterative_imputer # noqa
>>> # now you can import normally from sklearn.impute
>>> from sklearn.impute import IterativeImputer
```
Parameters:
**estimator**estimator object, default=BayesianRidge()
The estimator to use at each step of the round-robin imputation. If `sample_posterior=True`, the estimator must support `return_std` in its `predict` method.
**missing\_values**int or np.nan, default=np.nan
The placeholder for the missing values. All occurrences of `missing_values` will be imputed. For pandas’ dataframes with nullable integer dtypes with missing values, `missing_values` should be set to `np.nan`, since `pd.NA` will be converted to `np.nan`.
**sample\_posterior**bool, default=False
Whether to sample from the (Gaussian) predictive posterior of the fitted estimator for each imputation. Estimator must support `return_std` in its `predict` method if set to `True`. Set to `True` if using `IterativeImputer` for multiple imputations.
**max\_iter**int, default=10
Maximum number of imputation rounds to perform before returning the imputations computed during the final round. A round is a single imputation of each feature with missing values. The stopping criterion is met once `max(abs(X_t - X_{t-1}))/max(abs(X[known_vals])) < tol`, where `X_t` is `X` at iteration `t`. Note that early stopping is only applied if `sample_posterior=False`.
**tol**float, default=1e-3
Tolerance of the stopping condition.
**n\_nearest\_features**int, default=None
Number of other features to use to estimate the missing values of each feature column. Nearness between features is measured using the absolute correlation coefficient between each feature pair (after initial imputation). To ensure coverage of features throughout the imputation process, the neighbor features are not necessarily nearest, but are drawn with probability proportional to correlation for each imputed target feature. Can provide significant speed-up when the number of features is huge. If `None`, all features will be used.
**initial\_strategy**{‘mean’, ‘median’, ‘most\_frequent’, ‘constant’}, default=’mean’
Which strategy to use to initialize the missing values. Same as the `strategy` parameter in [`SimpleImputer`](sklearn.impute.simpleimputer#sklearn.impute.SimpleImputer "sklearn.impute.SimpleImputer").
**imputation\_order**{‘ascending’, ‘descending’, ‘roman’, ‘arabic’, ‘random’}, default=’ascending’
The order in which the features will be imputed. Possible values:
* `'ascending'`: From features with fewest missing values to most.
* `'descending'`: From features with most missing values to fewest.
* `'roman'`: Left to right.
* `'arabic'`: Right to left.
* `'random'`: A random order for each round.
**skip\_complete**bool, default=False
If `True` then features with missing values during [`transform`](#sklearn.impute.IterativeImputer.transform "sklearn.impute.IterativeImputer.transform") which did not have any missing values during [`fit`](#sklearn.impute.IterativeImputer.fit "sklearn.impute.IterativeImputer.fit") will be imputed with the initial imputation method only. Set to `True` if you have many features with no missing values at both [`fit`](#sklearn.impute.IterativeImputer.fit "sklearn.impute.IterativeImputer.fit") and [`transform`](#sklearn.impute.IterativeImputer.transform "sklearn.impute.IterativeImputer.transform") time to save compute.
**min\_value**float or array-like of shape (n\_features,), default=-np.inf
Minimum possible imputed value. Broadcast to shape `(n_features,)` if scalar. If array-like, expects shape `(n_features,)`, one min value for each feature. The default is `-np.inf`.
Changed in version 0.23: Added support for array-like.
**max\_value**float or array-like of shape (n\_features,), default=np.inf
Maximum possible imputed value. Broadcast to shape `(n_features,)` if scalar. If array-like, expects shape `(n_features,)`, one max value for each feature. The default is `np.inf`.
Changed in version 0.23: Added support for array-like.
**verbose**int, default=0
Verbosity flag, controls the debug messages that are issued as functions are evaluated. The higher, the more verbose. Can be 0, 1, or 2.
**random\_state**int, RandomState instance or None, default=None
The seed of the pseudo random number generator to use. Randomizes selection of estimator features if `n_nearest_features` is not `None`, the `imputation_order` if `random`, and the sampling from posterior if `sample_posterior=True`. Use an integer for determinism. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**add\_indicator**bool, default=False
If `True`, a [`MissingIndicator`](sklearn.impute.missingindicator#sklearn.impute.MissingIndicator "sklearn.impute.MissingIndicator") transform will stack onto output of the imputer’s transform. This allows a predictive estimator to account for missingness despite imputation. If a feature has no missing values at fit/train time, the feature won’t appear on the missing indicator even if there are missing values at transform/test time.
Attributes:
**initial\_imputer\_**object of type [`SimpleImputer`](sklearn.impute.simpleimputer#sklearn.impute.SimpleImputer "sklearn.impute.SimpleImputer")
Imputer used to initialize the missing values.
**imputation\_sequence\_**list of tuples
Each tuple has `(feat_idx, neighbor_feat_idx, estimator)`, where `feat_idx` is the current feature to be imputed, `neighbor_feat_idx` is the array of other features used to impute the current feature, and `estimator` is the trained estimator used for the imputation. Length is `self.n_features_with_missing_ *
self.n_iter_`.
**n\_iter\_**int
Number of iteration rounds that occurred. Will be less than `self.max_iter` if early stopping criterion was reached.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_features\_with\_missing\_**int
Number of features with missing values.
**indicator\_**[`MissingIndicator`](sklearn.impute.missingindicator#sklearn.impute.MissingIndicator "sklearn.impute.MissingIndicator")
Indicator used to add binary indicators for missing values. `None` if `add_indicator=False`.
**random\_state\_**RandomState instance
RandomState instance that is generated either from a seed, the random number generator or by `np.random`.
See also
[`SimpleImputer`](sklearn.impute.simpleimputer#sklearn.impute.SimpleImputer "sklearn.impute.SimpleImputer")
Univariate imputer for completing missing values with simple strategies.
[`KNNImputer`](sklearn.impute.knnimputer#sklearn.impute.KNNImputer "sklearn.impute.KNNImputer")
Multivariate imputer that estimates missing features using nearest samples.
#### Notes
To support imputation in inductive mode we store each feature’s estimator during the [`fit`](#sklearn.impute.IterativeImputer.fit "sklearn.impute.IterativeImputer.fit") phase, and predict without refitting (in order) during the [`transform`](#sklearn.impute.IterativeImputer.transform "sklearn.impute.IterativeImputer.transform") phase.
Features which contain all missing values at [`fit`](#sklearn.impute.IterativeImputer.fit "sklearn.impute.IterativeImputer.fit") are discarded upon [`transform`](#sklearn.impute.IterativeImputer.transform "sklearn.impute.IterativeImputer.transform").
Using defaults, the imputer scales in \(\mathcal{O}(knp^3\min(n,p))\) where \(k\) = `max_iter`, \(n\) the number of samples and \(p\) the number of features. It thus becomes prohibitively costly when the number of features increases. Setting `n_nearest_features << n_features`, `skip_complete=True` or increasing `tol` can help to reduce its computational cost.
Depending on the nature of missing values, simple imputers can be preferable in a prediction context.
#### References
[1] [Stef van Buuren, Karin Groothuis-Oudshoorn (2011). “mice: Multivariate Imputation by Chained Equations in R”. Journal of Statistical Software 45: 1-67.](https://www.jstatsoft.org/article/view/v045i03)
[2] [S. F. Buck, (1960). “A Method of Estimation of Missing Values in Multivariate Data Suitable for use with an Electronic Computer”. Journal of the Royal Statistical Society 22(2): 302-306.](https://www.jstor.org/stable/2984099)
#### Examples
```
>>> import numpy as np
>>> from sklearn.experimental import enable_iterative_imputer
>>> from sklearn.impute import IterativeImputer
>>> imp_mean = IterativeImputer(random_state=0)
>>> imp_mean.fit([[7, 2, 3], [4, np.nan, 6], [10, 5, 9]])
IterativeImputer(random_state=0)
>>> X = [[np.nan, 2, 3], [4, np.nan, 6], [10, np.nan, 9]]
>>> imp_mean.transform(X)
array([[ 6.9584..., 2. , 3. ],
[ 4. , 2.6000..., 6. ],
[10. , 4.9999..., 9. ]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.impute.IterativeImputer.fit "sklearn.impute.IterativeImputer.fit")(X[, y]) | Fit the imputer on `X` and return self. |
| [`fit_transform`](#sklearn.impute.IterativeImputer.fit_transform "sklearn.impute.IterativeImputer.fit_transform")(X[, y]) | Fit the imputer on `X` and return the transformed `X`. |
| [`get_feature_names_out`](#sklearn.impute.IterativeImputer.get_feature_names_out "sklearn.impute.IterativeImputer.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.impute.IterativeImputer.get_params "sklearn.impute.IterativeImputer.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.impute.IterativeImputer.set_params "sklearn.impute.IterativeImputer.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.impute.IterativeImputer.transform "sklearn.impute.IterativeImputer.transform")(X) | Impute all missing values in `X`. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/impute/_iterative.py#L772)
Fit the imputer on `X` and return self.
Parameters:
**X**array-like, shape (n\_samples, n\_features)
Input data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**self**object
Fitted estimator.
fit\_transform(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/impute/_iterative.py#L588)
Fit the imputer on `X` and return the transformed `X`.
Parameters:
**X**array-like, shape (n\_samples, n\_features)
Input data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**Xt**array-like, shape (n\_samples, n\_features)
The imputed input data.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/impute/_iterative.py#L792)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Input features.
* If `input_features` is `None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then the following input feature names are generated: `["x0", "x1", ..., "x(n_features_in_ - 1)"]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/impute/_iterative.py#L720)
Impute all missing values in `X`.
Note that this is stochastic, and that if `random_state` is not fixed, repeated calls, or permuted input, results will differ.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The input data to complete.
Returns:
**Xt**array-like, shape (n\_samples, n\_features)
The imputed input data.
Examples using `sklearn.impute.IterativeImputer`
------------------------------------------------
[Imputing missing values before building an estimator](../../auto_examples/impute/plot_missing_values#sphx-glr-auto-examples-impute-plot-missing-values-py)
[Imputing missing values with variants of IterativeImputer](../../auto_examples/impute/plot_iterative_imputer_variants_comparison#sphx-glr-auto-examples-impute-plot-iterative-imputer-variants-comparison-py)
scikit_learn sklearn.metrics.pairwise_distances_argmin_min sklearn.metrics.pairwise\_distances\_argmin\_min
================================================
sklearn.metrics.pairwise\_distances\_argmin\_min(*X*, *Y*, *\**, *axis=1*, *metric='euclidean'*, *metric\_kwargs=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/pairwise.py#L593)
Compute minimum distances between one point and a set of points.
This function computes for each row in X, the index of the row of Y which is closest (according to the specified distance). The minimal distances are also returned.
This is mostly equivalent to calling:
(pairwise\_distances(X, Y=Y, metric=metric).argmin(axis=axis),
pairwise\_distances(X, Y=Y, metric=metric).min(axis=axis))
but uses much less memory, and is faster for large arrays.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples\_X, n\_features)
Array containing points.
**Y**{array-like, sparse matrix} of shape (n\_samples\_Y, n\_features)
Array containing points.
**axis**int, default=1
Axis along which the argmin and distances are to be computed.
**metric**str or callable, default=’euclidean’
Metric to use for distance computation. Any metric from scikit-learn or scipy.spatial.distance can be used.
If metric is a callable function, it is called on each pair of instances (rows) and the resulting value recorded. The callable should take two arrays as input and return one value indicating the distance between them. This works for Scipy’s metrics, but is less efficient than passing the metric name as a string.
Distance matrices are not supported.
Valid values for metric are:
* from scikit-learn: [‘cityblock’, ‘cosine’, ‘euclidean’, ‘l1’, ‘l2’, ‘manhattan’]
* from scipy.spatial.distance: [‘braycurtis’, ‘canberra’, ‘chebyshev’, ‘correlation’, ‘dice’, ‘hamming’, ‘jaccard’, ‘kulsinski’, ‘mahalanobis’, ‘minkowski’, ‘rogerstanimoto’, ‘russellrao’, ‘seuclidean’, ‘sokalmichener’, ‘sokalsneath’, ‘sqeuclidean’, ‘yule’]
See the documentation for scipy.spatial.distance for details on these metrics.
**metric\_kwargs**dict, default=None
Keyword arguments to pass to specified metric function.
Returns:
**argmin**ndarray
Y[argmin[i], :] is the row in Y that is closest to X[i, :].
**distances**ndarray
The array of minimum distances. `distances[i]` is the distance between the i-th row in X and the argmin[i]-th row in Y.
See also
[`pairwise_distances`](sklearn.metrics.pairwise_distances#sklearn.metrics.pairwise_distances "sklearn.metrics.pairwise_distances")
Distances between every pair of samples of X and Y.
[`pairwise_distances_argmin`](sklearn.metrics.pairwise_distances_argmin#sklearn.metrics.pairwise_distances_argmin "sklearn.metrics.pairwise_distances_argmin")
Same as `pairwise_distances_argmin_min` but only returns the argmins.
scikit_learn sklearn.svm.NuSVR sklearn.svm.NuSVR
=================
*class*sklearn.svm.NuSVR(*\**, *nu=0.5*, *C=1.0*, *kernel='rbf'*, *degree=3*, *gamma='scale'*, *coef0=0.0*, *shrinking=True*, *tol=0.001*, *cache\_size=200*, *verbose=False*, *max\_iter=-1*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/svm/_classes.py#L1261)
Nu Support Vector Regression.
Similar to NuSVC, for regression, uses a parameter nu to control the number of support vectors. However, unlike NuSVC, where nu replaces C, here nu replaces the parameter epsilon of epsilon-SVR.
The implementation is based on libsvm.
Read more in the [User Guide](../svm#svm-regression).
Parameters:
**nu**float, default=0.5
An upper bound on the fraction of training errors and a lower bound of the fraction of support vectors. Should be in the interval (0, 1]. By default 0.5 will be taken.
**C**float, default=1.0
Penalty parameter C of the error term.
**kernel**{‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’} or callable, default=’rbf’
Specifies the kernel type to be used in the algorithm. If none is given, ‘rbf’ will be used. If a callable is given it is used to precompute the kernel matrix.
**degree**int, default=3
Degree of the polynomial kernel function (‘poly’). Ignored by all other kernels.
**gamma**{‘scale’, ‘auto’} or float, default=’scale’
Kernel coefficient for ‘rbf’, ‘poly’ and ‘sigmoid’.
* if `gamma='scale'` (default) is passed then it uses 1 / (n\_features \* X.var()) as value of gamma,
* if ‘auto’, uses 1 / n\_features.
Changed in version 0.22: The default value of `gamma` changed from ‘auto’ to ‘scale’.
**coef0**float, default=0.0
Independent term in kernel function. It is only significant in ‘poly’ and ‘sigmoid’.
**shrinking**bool, default=True
Whether to use the shrinking heuristic. See the [User Guide](../svm#shrinking-svm).
**tol**float, default=1e-3
Tolerance for stopping criterion.
**cache\_size**float, default=200
Specify the size of the kernel cache (in MB).
**verbose**bool, default=False
Enable verbose output. Note that this setting takes advantage of a per-process runtime setting in libsvm that, if enabled, may not work properly in a multithreaded context.
**max\_iter**int, default=-1
Hard limit on iterations within solver, or -1 for no limit.
Attributes:
**class\_weight\_**ndarray of shape (n\_classes,)
Multipliers of parameter C for each class. Computed based on the `class_weight` parameter.
[`coef_`](#sklearn.svm.NuSVR.coef_ "sklearn.svm.NuSVR.coef_")ndarray of shape (1, n\_features)
Weights assigned to the features when `kernel="linear"`.
**dual\_coef\_**ndarray of shape (1, n\_SV)
Coefficients of the support vector in the decision function.
**fit\_status\_**int
0 if correctly fitted, 1 otherwise (will raise warning)
**intercept\_**ndarray of shape (1,)
Constants in decision function.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_iter\_**int
Number of iterations run by the optimization routine to fit the model.
New in version 1.1.
[`n_support_`](#sklearn.svm.NuSVR.n_support_ "sklearn.svm.NuSVR.n_support_")ndarray of shape (1,), dtype=int32
Number of support vectors for each class.
**shape\_fit\_**tuple of int of shape (n\_dimensions\_of\_X,)
Array dimensions of training vector `X`.
**support\_**ndarray of shape (n\_SV,)
Indices of support vectors.
**support\_vectors\_**ndarray of shape (n\_SV, n\_features)
Support vectors.
See also
[`NuSVC`](sklearn.svm.nusvc#sklearn.svm.NuSVC "sklearn.svm.NuSVC")
Support Vector Machine for classification implemented with libsvm with a parameter to control the number of support vectors.
[`SVR`](sklearn.svm.svr#sklearn.svm.SVR "sklearn.svm.SVR")
Epsilon Support Vector Machine for regression implemented with libsvm.
#### References
[1] [LIBSVM: A Library for Support Vector Machines](http://www.csie.ntu.edu.tw/~cjlin/papers/libsvm.pdf)
[2] [Platt, John (1999). “Probabilistic outputs for support vector machines and comparison to regularizedlikelihood methods.”](http://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.41.1639)
#### Examples
```
>>> from sklearn.svm import NuSVR
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.preprocessing import StandardScaler
>>> import numpy as np
>>> n_samples, n_features = 10, 5
>>> np.random.seed(0)
>>> y = np.random.randn(n_samples)
>>> X = np.random.randn(n_samples, n_features)
>>> regr = make_pipeline(StandardScaler(), NuSVR(C=1.0, nu=0.1))
>>> regr.fit(X, y)
Pipeline(steps=[('standardscaler', StandardScaler()),
('nusvr', NuSVR(nu=0.1))])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.svm.NuSVR.fit "sklearn.svm.NuSVR.fit")(X, y[, sample\_weight]) | Fit the SVM model according to the given training data. |
| [`get_params`](#sklearn.svm.NuSVR.get_params "sklearn.svm.NuSVR.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.svm.NuSVR.predict "sklearn.svm.NuSVR.predict")(X) | Perform regression on samples in X. |
| [`score`](#sklearn.svm.NuSVR.score "sklearn.svm.NuSVR.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.svm.NuSVR.set_params "sklearn.svm.NuSVR.set_params")(\*\*params) | Set the parameters of this estimator. |
*property*coef\_
Weights assigned to the features when `kernel="linear"`.
Returns:
ndarray of shape (n\_features, n\_classes)
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/svm/_base.py#L122)
Fit the SVM model according to the given training data.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features) or (n\_samples, n\_samples)
Training vectors, where `n_samples` is the number of samples and `n_features` is the number of features. For kernel=”precomputed”, the expected shape of X is (n\_samples, n\_samples).
**y**array-like of shape (n\_samples,)
Target values (class labels in classification, real numbers in regression).
**sample\_weight**array-like of shape (n\_samples,), default=None
Per-sample weights. Rescale C per sample. Higher weights force the classifier to put more emphasis on these points.
Returns:
**self**object
Fitted estimator.
#### Notes
If X and y are not C-ordered and contiguous arrays of np.float64 and X is not a scipy.sparse.csr\_matrix, X and/or y may be copied.
If X is a dense array, then the other methods will not support sparse matrices as input.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_support\_
Number of support vectors for each class.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/svm/_base.py#L417)
Perform regression on samples in X.
For an one-class model, +1 (inlier) or -1 (outlier) is returned.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
For kernel=”precomputed”, the expected shape of X is (n\_samples\_test, n\_samples\_train).
Returns:
**y\_pred**ndarray of shape (n\_samples,)
The predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.svm.NuSVR`
----------------------------------
[Model Complexity Influence](../../auto_examples/applications/plot_model_complexity_influence#sphx-glr-auto-examples-applications-plot-model-complexity-influence-py)
| programming_docs |
scikit_learn sklearn.metrics.pairwise.polynomial_kernel sklearn.metrics.pairwise.polynomial\_kernel
===========================================
sklearn.metrics.pairwise.polynomial\_kernel(*X*, *Y=None*, *degree=3*, *gamma=None*, *coef0=1*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/pairwise.py#L1191)
Compute the polynomial kernel between X and Y.
\(K(X, Y) = (gamma <X, Y> + coef0)^degree\)
Read more in the [User Guide](../metrics#polynomial-kernel).
Parameters:
**X**ndarray of shape (n\_samples\_X, n\_features)
A feature array.
**Y**ndarray of shape (n\_samples\_Y, n\_features), default=None
An optional second feature array. If `None`, uses `Y=X`.
**degree**int, default=3
Kernel degree.
**gamma**float, default=None
Coefficient of the vector inner product. If None, defaults to 1.0 / n\_features.
**coef0**float, default=1
Constant offset added to scaled inner product.
Returns:
**Gram matrix**ndarray of shape (n\_samples\_X, n\_samples\_Y)
The polynomial kernel.
scikit_learn sklearn.feature_extraction.text.TfidfVectorizer sklearn.feature\_extraction.text.TfidfVectorizer
================================================
*class*sklearn.feature\_extraction.text.TfidfVectorizer(*\**, *input='content'*, *encoding='utf-8'*, *decode\_error='strict'*, *strip\_accents=None*, *lowercase=True*, *preprocessor=None*, *tokenizer=None*, *analyzer='word'*, *stop\_words=None*, *token\_pattern='(?u)\\b\\w\\w+\\b'*, *ngram\_range=(1*, *1)*, *max\_df=1.0*, *min\_df=1*, *max\_features=None*, *vocabulary=None*, *binary=False*, *dtype=<class 'numpy.float64'>*, *norm='l2'*, *use\_idf=True*, *smooth\_idf=True*, *sublinear\_tf=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L1717)
Convert a collection of raw documents to a matrix of TF-IDF features.
Equivalent to [`CountVectorizer`](sklearn.feature_extraction.text.countvectorizer#sklearn.feature_extraction.text.CountVectorizer "sklearn.feature_extraction.text.CountVectorizer") followed by [`TfidfTransformer`](sklearn.feature_extraction.text.tfidftransformer#sklearn.feature_extraction.text.TfidfTransformer "sklearn.feature_extraction.text.TfidfTransformer").
Read more in the [User Guide](../feature_extraction#text-feature-extraction).
Parameters:
**input**{‘filename’, ‘file’, ‘content’}, default=’content’
* If `'filename'`, the sequence passed as an argument to fit is expected to be a list of filenames that need reading to fetch the raw content to analyze.
* If `'file'`, the sequence items must have a ‘read’ method (file-like object) that is called to fetch the bytes in memory.
* If `'content'`, the input is expected to be a sequence of items that can be of type string or byte.
**encoding**str, default=’utf-8’
If bytes or files are given to analyze, this encoding is used to decode.
**decode\_error**{‘strict’, ‘ignore’, ‘replace’}, default=’strict’
Instruction on what to do if a byte sequence is given to analyze that contains characters not of the given `encoding`. By default, it is ‘strict’, meaning that a UnicodeDecodeError will be raised. Other values are ‘ignore’ and ‘replace’.
**strip\_accents**{‘ascii’, ‘unicode’}, default=None
Remove accents and perform other character normalization during the preprocessing step. ‘ascii’ is a fast method that only works on characters that have an direct ASCII mapping. ‘unicode’ is a slightly slower method that works on any characters. None (default) does nothing.
Both ‘ascii’ and ‘unicode’ use NFKD normalization from [`unicodedata.normalize`](https://docs.python.org/3/library/unicodedata.html#unicodedata.normalize "(in Python v3.10)").
**lowercase**bool, default=True
Convert all characters to lowercase before tokenizing.
**preprocessor**callable, default=None
Override the preprocessing (string transformation) stage while preserving the tokenizing and n-grams generation steps. Only applies if `analyzer` is not callable.
**tokenizer**callable, default=None
Override the string tokenization step while preserving the preprocessing and n-grams generation steps. Only applies if `analyzer == 'word'`.
**analyzer**{‘word’, ‘char’, ‘char\_wb’} or callable, default=’word’
Whether the feature should be made of word or character n-grams. Option ‘char\_wb’ creates character n-grams only from text inside word boundaries; n-grams at the edges of words are padded with space.
If a callable is passed it is used to extract the sequence of features out of the raw, unprocessed input.
Changed in version 0.21: Since v0.21, if `input` is `'filename'` or `'file'`, the data is first read from the file and then passed to the given callable analyzer.
**stop\_words**{‘english’}, list, default=None
If a string, it is passed to \_check\_stop\_list and the appropriate stop list is returned. ‘english’ is currently the only supported string value. There are several known issues with ‘english’ and you should consider an alternative (see [Using stop words](../feature_extraction#stop-words)).
If a list, that list is assumed to contain stop words, all of which will be removed from the resulting tokens. Only applies if `analyzer == 'word'`.
If None, no stop words will be used. max\_df can be set to a value in the range [0.7, 1.0) to automatically detect and filter stop words based on intra corpus document frequency of terms.
**token\_pattern**str, default=r”(?u)\b\w\w+\b”
Regular expression denoting what constitutes a “token”, only used if `analyzer == 'word'`. The default regexp selects tokens of 2 or more alphanumeric characters (punctuation is completely ignored and always treated as a token separator).
If there is a capturing group in token\_pattern then the captured group content, not the entire match, becomes the token. At most one capturing group is permitted.
**ngram\_range**tuple (min\_n, max\_n), default=(1, 1)
The lower and upper boundary of the range of n-values for different n-grams to be extracted. All values of n such that min\_n <= n <= max\_n will be used. For example an `ngram_range` of `(1, 1)` means only unigrams, `(1, 2)` means unigrams and bigrams, and `(2, 2)` means only bigrams. Only applies if `analyzer` is not callable.
**max\_df**float or int, default=1.0
When building the vocabulary ignore terms that have a document frequency strictly higher than the given threshold (corpus-specific stop words). If float in range [0.0, 1.0], the parameter represents a proportion of documents, integer absolute counts. This parameter is ignored if vocabulary is not None.
**min\_df**float or int, default=1
When building the vocabulary ignore terms that have a document frequency strictly lower than the given threshold. This value is also called cut-off in the literature. If float in range of [0.0, 1.0], the parameter represents a proportion of documents, integer absolute counts. This parameter is ignored if vocabulary is not None.
**max\_features**int, default=None
If not None, build a vocabulary that only consider the top max\_features ordered by term frequency across the corpus.
This parameter is ignored if vocabulary is not None.
**vocabulary**Mapping or iterable, default=None
Either a Mapping (e.g., a dict) where keys are terms and values are indices in the feature matrix, or an iterable over terms. If not given, a vocabulary is determined from the input documents.
**binary**bool, default=False
If True, all non-zero term counts are set to 1. This does not mean outputs will have only 0/1 values, only that the tf term in tf-idf is binary. (Set idf and normalization to False to get 0/1 outputs).
**dtype**dtype, default=float64
Type of the matrix returned by fit\_transform() or transform().
**norm**{‘l1’, ‘l2’}, default=’l2’
Each output row will have unit norm, either:
* ‘l2’: Sum of squares of vector elements is 1. The cosine similarity between two vectors is their dot product when l2 norm has been applied.
* ‘l1’: Sum of absolute values of vector elements is 1. See `preprocessing.normalize`.
**use\_idf**bool, default=True
Enable inverse-document-frequency reweighting. If False, idf(t) = 1.
**smooth\_idf**bool, default=True
Smooth idf weights by adding one to document frequencies, as if an extra document was seen containing every term in the collection exactly once. Prevents zero divisions.
**sublinear\_tf**bool, default=False
Apply sublinear tf scaling, i.e. replace tf with 1 + log(tf).
Attributes:
**vocabulary\_**dict
A mapping of terms to feature indices.
**fixed\_vocabulary\_**bool
True if a fixed vocabulary of term to indices mapping is provided by the user.
[`idf_`](#sklearn.feature_extraction.text.TfidfVectorizer.idf_ "sklearn.feature_extraction.text.TfidfVectorizer.idf_")array of shape (n\_features,)
Inverse document frequency vector, only defined if `use_idf=True`.
**stop\_words\_**set
Terms that were ignored because they either:
* occurred in too many documents (`max_df`)
* occurred in too few documents (`min_df`)
* were cut off by feature selection (`max_features`).
This is only available if no vocabulary was given.
See also
[`CountVectorizer`](sklearn.feature_extraction.text.countvectorizer#sklearn.feature_extraction.text.CountVectorizer "sklearn.feature_extraction.text.CountVectorizer")
Transforms text into a sparse matrix of n-gram counts.
[`TfidfTransformer`](sklearn.feature_extraction.text.tfidftransformer#sklearn.feature_extraction.text.TfidfTransformer "sklearn.feature_extraction.text.TfidfTransformer")
Performs the TF-IDF transformation from a provided matrix of counts.
#### Notes
The `stop_words_` attribute can get large and increase the model size when pickling. This attribute is provided only for introspection and can be safely removed using delattr or set to None before pickling.
#### Examples
```
>>> from sklearn.feature_extraction.text import TfidfVectorizer
>>> corpus = [
... 'This is the first document.',
... 'This document is the second document.',
... 'And this is the third one.',
... 'Is this the first document?',
... ]
>>> vectorizer = TfidfVectorizer()
>>> X = vectorizer.fit_transform(corpus)
>>> vectorizer.get_feature_names_out()
array(['and', 'document', 'first', 'is', 'one', 'second', 'the', 'third',
'this'], ...)
>>> print(X.shape)
(4, 9)
```
#### Methods
| | |
| --- | --- |
| [`build_analyzer`](#sklearn.feature_extraction.text.TfidfVectorizer.build_analyzer "sklearn.feature_extraction.text.TfidfVectorizer.build_analyzer")() | Return a callable to process input data. |
| [`build_preprocessor`](#sklearn.feature_extraction.text.TfidfVectorizer.build_preprocessor "sklearn.feature_extraction.text.TfidfVectorizer.build_preprocessor")() | Return a function to preprocess the text before tokenization. |
| [`build_tokenizer`](#sklearn.feature_extraction.text.TfidfVectorizer.build_tokenizer "sklearn.feature_extraction.text.TfidfVectorizer.build_tokenizer")() | Return a function that splits a string into a sequence of tokens. |
| [`decode`](#sklearn.feature_extraction.text.TfidfVectorizer.decode "sklearn.feature_extraction.text.TfidfVectorizer.decode")(doc) | Decode the input into a string of unicode symbols. |
| [`fit`](#sklearn.feature_extraction.text.TfidfVectorizer.fit "sklearn.feature_extraction.text.TfidfVectorizer.fit")(raw\_documents[, y]) | Learn vocabulary and idf from training set. |
| [`fit_transform`](#sklearn.feature_extraction.text.TfidfVectorizer.fit_transform "sklearn.feature_extraction.text.TfidfVectorizer.fit_transform")(raw\_documents[, y]) | Learn vocabulary and idf, return document-term matrix. |
| [`get_feature_names`](#sklearn.feature_extraction.text.TfidfVectorizer.get_feature_names "sklearn.feature_extraction.text.TfidfVectorizer.get_feature_names")() | DEPRECATED: get\_feature\_names is deprecated in 1.0 and will be removed in 1.2. |
| [`get_feature_names_out`](#sklearn.feature_extraction.text.TfidfVectorizer.get_feature_names_out "sklearn.feature_extraction.text.TfidfVectorizer.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.feature_extraction.text.TfidfVectorizer.get_params "sklearn.feature_extraction.text.TfidfVectorizer.get_params")([deep]) | Get parameters for this estimator. |
| [`get_stop_words`](#sklearn.feature_extraction.text.TfidfVectorizer.get_stop_words "sklearn.feature_extraction.text.TfidfVectorizer.get_stop_words")() | Build or fetch the effective stop words list. |
| [`inverse_transform`](#sklearn.feature_extraction.text.TfidfVectorizer.inverse_transform "sklearn.feature_extraction.text.TfidfVectorizer.inverse_transform")(X) | Return terms per document with nonzero entries in X. |
| [`set_params`](#sklearn.feature_extraction.text.TfidfVectorizer.set_params "sklearn.feature_extraction.text.TfidfVectorizer.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.feature_extraction.text.TfidfVectorizer.transform "sklearn.feature_extraction.text.TfidfVectorizer.transform")(raw\_documents) | Transform documents to document-term matrix. |
build\_analyzer()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L418)
Return a callable to process input data.
The callable handles that handles preprocessing, tokenization, and n-grams generation.
Returns:
analyzer: callable
A function to handle preprocessing, tokenization and n-grams generation.
build\_preprocessor()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L321)
Return a function to preprocess the text before tokenization.
Returns:
preprocessor: callable
A function to preprocess the text before tokenization.
build\_tokenizer()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L348)
Return a function that splits a string into a sequence of tokens.
Returns:
tokenizer: callable
A function to split a string into a sequence of tokens.
decode(*doc*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L208)
Decode the input into a string of unicode symbols.
The decoding strategy depends on the vectorizer parameters.
Parameters:
**doc**bytes or str
The string to decode.
Returns:
doc: str
A string of unicode symbols.
fit(*raw\_documents*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L2025)
Learn vocabulary and idf from training set.
Parameters:
**raw\_documents**iterable
An iterable which generates either str, unicode or file objects.
**y**None
This parameter is not needed to compute tfidf.
Returns:
**self**object
Fitted vectorizer.
fit\_transform(*raw\_documents*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L2053)
Learn vocabulary and idf, return document-term matrix.
This is equivalent to fit followed by transform, but more efficiently implemented.
Parameters:
**raw\_documents**iterable
An iterable which generates either str, unicode or file objects.
**y**None
This parameter is ignored.
Returns:
**X**sparse matrix of (n\_samples, n\_features)
Tf-idf-weighted document-term matrix.
get\_feature\_names()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L1425)
DEPRECATED: get\_feature\_names is deprecated in 1.0 and will be removed in 1.2. Please use get\_feature\_names\_out instead.
Array mapping from feature integer indices to feature name.
Returns:
**feature\_names**list
A list of feature names.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L1441)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Not used, present here for API consistency by convention.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
get\_stop\_words()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L368)
Build or fetch the effective stop words list.
Returns:
stop\_words: list or None
A list of stop words.
*property*idf\_
Inverse document frequency vector, only defined if `use_idf=True`.
Returns:
ndarray of shape (n\_features,)
inverse\_transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L1392)
Return terms per document with nonzero entries in X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Document-term matrix.
Returns:
**X\_inv**list of arrays of shape (n\_samples,)
List of arrays of terms.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*raw\_documents*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/text.py#L2085)
Transform documents to document-term matrix.
Uses the vocabulary and document frequencies (df) learned by fit (or fit\_transform).
Parameters:
**raw\_documents**iterable
An iterable which generates either str, unicode or file objects.
Returns:
**X**sparse matrix of (n\_samples, n\_features)
Tf-idf-weighted document-term matrix.
Examples using `sklearn.feature_extraction.text.TfidfVectorizer`
----------------------------------------------------------------
[Biclustering documents with the Spectral Co-clustering algorithm](../../auto_examples/bicluster/plot_bicluster_newsgroups#sphx-glr-auto-examples-bicluster-plot-bicluster-newsgroups-py)
[Topic extraction with Non-negative Matrix Factorization and Latent Dirichlet Allocation](../../auto_examples/applications/plot_topics_extraction_with_nmf_lda#sphx-glr-auto-examples-applications-plot-topics-extraction-with-nmf-lda-py)
[Column Transformer with Heterogeneous Data Sources](../../auto_examples/compose/plot_column_transformer#sphx-glr-auto-examples-compose-plot-column-transformer-py)
[Classification of text documents using sparse features](../../auto_examples/text/plot_document_classification_20newsgroups#sphx-glr-auto-examples-text-plot-document-classification-20newsgroups-py)
[Clustering text documents using k-means](../../auto_examples/text/plot_document_clustering#sphx-glr-auto-examples-text-plot-document-clustering-py)
[FeatureHasher and DictVectorizer Comparison](../../auto_examples/text/plot_hashing_vs_dict_vectorizer#sphx-glr-auto-examples-text-plot-hashing-vs-dict-vectorizer-py)
| programming_docs |
scikit_learn sklearn.model_selection.validation_curve sklearn.model\_selection.validation\_curve
==========================================
sklearn.model\_selection.validation\_curve(*estimator*, *X*, *y*, *\**, *param\_name*, *param\_range*, *groups=None*, *cv=None*, *scoring=None*, *n\_jobs=None*, *pre\_dispatch='all'*, *verbose=0*, *error\_score=nan*, *fit\_params=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_validation.py#L1715)
Validation curve.
Determine training and test scores for varying parameter values.
Compute scores for an estimator with different values of a specified parameter. This is similar to grid search with one parameter. However, this will also compute training scores and is merely a utility for plotting the results.
Read more in the [User Guide](../learning_curve#validation-curve).
Parameters:
**estimator**object type that implements the “fit” and “predict” methods
An object of that type which is cloned for each validation.
**X**array-like of shape (n\_samples, n\_features)
Training vector, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs) or None
Target relative to X for classification or regression; None for unsupervised learning.
**param\_name**str
Name of the parameter that will be varied.
**param\_range**array-like of shape (n\_values,)
The values of the parameter that will be evaluated.
**groups**array-like of shape (n\_samples,), default=None
Group labels for the samples used while splitting the dataset into train/test set. Only used in conjunction with a “Group” [cv](https://scikit-learn.org/1.1/glossary.html#term-cv) instance (e.g., [`GroupKFold`](sklearn.model_selection.groupkfold#sklearn.model_selection.GroupKFold "sklearn.model_selection.GroupKFold")).
**cv**int, cross-validation generator or an iterable, default=None
Determines the cross-validation splitting strategy. Possible inputs for cv are:
* None, to use the default 5-fold cross validation,
* int, to specify the number of folds in a `(Stratified)KFold`,
* [CV splitter](https://scikit-learn.org/1.1/glossary.html#term-CV-splitter),
* An iterable yielding (train, test) splits as arrays of indices.
For int/None inputs, if the estimator is a classifier and `y` is either binary or multiclass, [`StratifiedKFold`](sklearn.model_selection.stratifiedkfold#sklearn.model_selection.StratifiedKFold "sklearn.model_selection.StratifiedKFold") is used. In all other cases, [`KFold`](sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold") is used. These splitters are instantiated with `shuffle=False` so the splits will be the same across calls.
Refer [User Guide](../cross_validation#cross-validation) for the various cross-validation strategies that can be used here.
Changed in version 0.22: `cv` default value if None changed from 3-fold to 5-fold.
**scoring**str or callable, default=None
A str (see model evaluation documentation) or a scorer callable object / function with signature `scorer(estimator, X, y)`.
**n\_jobs**int, default=None
Number of jobs to run in parallel. Training the estimator and computing the score are parallelized over the combinations of each parameter value and each cross-validation split. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**pre\_dispatch**int or str, default=’all’
Number of predispatched jobs for parallel execution (default is all). The option can reduce the allocated memory. The str can be an expression like ‘2\*n\_jobs’.
**verbose**int, default=0
Controls the verbosity: the higher, the more messages.
**error\_score**‘raise’ or numeric, default=np.nan
Value to assign to the score if an error occurs in estimator fitting. If set to ‘raise’, the error is raised. If a numeric value is given, FitFailedWarning is raised.
New in version 0.20.
**fit\_params**dict, default=None
Parameters to pass to the fit method of the estimator.
New in version 0.24.
Returns:
**train\_scores**array of shape (n\_ticks, n\_cv\_folds)
Scores on training sets.
**test\_scores**array of shape (n\_ticks, n\_cv\_folds)
Scores on test set.
#### Notes
See [Plotting Validation Curves](../../auto_examples/model_selection/plot_validation_curve#sphx-glr-auto-examples-model-selection-plot-validation-curve-py)
Examples using `sklearn.model_selection.validation_curve`
---------------------------------------------------------
[Plotting Validation Curves](../../auto_examples/model_selection/plot_validation_curve#sphx-glr-auto-examples-model-selection-plot-validation-curve-py)
scikit_learn sklearn.utils.gen_even_slices sklearn.utils.gen\_even\_slices
===============================
sklearn.utils.gen\_even\_slices(*n*, *n\_packs*, *\**, *n\_samples=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/__init__.py#L748)
Generator to create n\_packs slices going up to n.
Parameters:
**n**int
**n\_packs**int
Number of slices to generate.
**n\_samples**int, default=None
Number of samples. Pass n\_samples when the slices are to be used for sparse matrix indexing; slicing off-the-end raises an exception, while it works for NumPy arrays.
Yields:
slice
See also
[`gen_batches`](sklearn.utils.gen_batches#sklearn.utils.gen_batches "sklearn.utils.gen_batches")
Generator to create slices containing batch\_size elements from 0 to n.
#### Examples
```
>>> from sklearn.utils import gen_even_slices
>>> list(gen_even_slices(10, 1))
[slice(0, 10, None)]
>>> list(gen_even_slices(10, 10))
[slice(0, 1, None), slice(1, 2, None), ..., slice(9, 10, None)]
>>> list(gen_even_slices(10, 5))
[slice(0, 2, None), slice(2, 4, None), ..., slice(8, 10, None)]
>>> list(gen_even_slices(10, 3))
[slice(0, 4, None), slice(4, 7, None), slice(7, 10, None)]
```
Examples using `sklearn.utils.gen_even_slices`
----------------------------------------------
[Poisson regression and non-normal loss](../../auto_examples/linear_model/plot_poisson_regression_non_normal_loss#sphx-glr-auto-examples-linear-model-plot-poisson-regression-non-normal-loss-py)
scikit_learn sklearn.naive_bayes.BernoulliNB sklearn.naive\_bayes.BernoulliNB
================================
*class*sklearn.naive\_bayes.BernoulliNB(*\**, *alpha=1.0*, *binarize=0.0*, *fit\_prior=True*, *class\_prior=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/naive_bayes.py#L1003)
Naive Bayes classifier for multivariate Bernoulli models.
Like MultinomialNB, this classifier is suitable for discrete data. The difference is that while MultinomialNB works with occurrence counts, BernoulliNB is designed for binary/boolean features.
Read more in the [User Guide](../naive_bayes#bernoulli-naive-bayes).
Parameters:
**alpha**float, default=1.0
Additive (Laplace/Lidstone) smoothing parameter (0 for no smoothing).
**binarize**float or None, default=0.0
Threshold for binarizing (mapping to booleans) of sample features. If None, input is presumed to already consist of binary vectors.
**fit\_prior**bool, default=True
Whether to learn class prior probabilities or not. If false, a uniform prior will be used.
**class\_prior**array-like of shape (n\_classes,), default=None
Prior probabilities of the classes. If specified, the priors are not adjusted according to the data.
Attributes:
**class\_count\_**ndarray of shape (n\_classes,)
Number of samples encountered for each class during fitting. This value is weighted by the sample weight when provided.
**class\_log\_prior\_**ndarray of shape (n\_classes,)
Log probability of each class (smoothed).
**classes\_**ndarray of shape (n\_classes,)
Class labels known to the classifier
**feature\_count\_**ndarray of shape (n\_classes, n\_features)
Number of samples encountered for each (class, feature) during fitting. This value is weighted by the sample weight when provided.
**feature\_log\_prob\_**ndarray of shape (n\_classes, n\_features)
Empirical log probability of features given a class, P(x\_i|y).
[`n_features_`](#sklearn.naive_bayes.BernoulliNB.n_features_ "sklearn.naive_bayes.BernoulliNB.n_features_")int
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`CategoricalNB`](sklearn.naive_bayes.categoricalnb#sklearn.naive_bayes.CategoricalNB "sklearn.naive_bayes.CategoricalNB")
Naive Bayes classifier for categorical features.
[`ComplementNB`](sklearn.naive_bayes.complementnb#sklearn.naive_bayes.ComplementNB "sklearn.naive_bayes.ComplementNB")
The Complement Naive Bayes classifier described in Rennie et al. (2003).
[`GaussianNB`](sklearn.naive_bayes.gaussiannb#sklearn.naive_bayes.GaussianNB "sklearn.naive_bayes.GaussianNB")
Gaussian Naive Bayes (GaussianNB).
[`MultinomialNB`](sklearn.naive_bayes.multinomialnb#sklearn.naive_bayes.MultinomialNB "sklearn.naive_bayes.MultinomialNB")
Naive Bayes classifier for multinomial models.
#### References
C.D. Manning, P. Raghavan and H. Schuetze (2008). Introduction to Information Retrieval. Cambridge University Press, pp. 234-265. <https://nlp.stanford.edu/IR-book/html/htmledition/the-bernoulli-model-1.html>
A. McCallum and K. Nigam (1998). A comparison of event models for naive Bayes text classification. Proc. AAAI/ICML-98 Workshop on Learning for Text Categorization, pp. 41-48.
V. Metsis, I. Androutsopoulos and G. Paliouras (2006). Spam filtering with naive Bayes – Which naive Bayes? 3rd Conf. on Email and Anti-Spam (CEAS).
#### Examples
```
>>> import numpy as np
>>> rng = np.random.RandomState(1)
>>> X = rng.randint(5, size=(6, 100))
>>> Y = np.array([1, 2, 3, 4, 4, 5])
>>> from sklearn.naive_bayes import BernoulliNB
>>> clf = BernoulliNB()
>>> clf.fit(X, Y)
BernoulliNB()
>>> print(clf.predict(X[2:3]))
[3]
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.naive_bayes.BernoulliNB.fit "sklearn.naive_bayes.BernoulliNB.fit")(X, y[, sample\_weight]) | Fit Naive Bayes classifier according to X, y. |
| [`get_params`](#sklearn.naive_bayes.BernoulliNB.get_params "sklearn.naive_bayes.BernoulliNB.get_params")([deep]) | Get parameters for this estimator. |
| [`partial_fit`](#sklearn.naive_bayes.BernoulliNB.partial_fit "sklearn.naive_bayes.BernoulliNB.partial_fit")(X, y[, classes, sample\_weight]) | Incremental fit on a batch of samples. |
| [`predict`](#sklearn.naive_bayes.BernoulliNB.predict "sklearn.naive_bayes.BernoulliNB.predict")(X) | Perform classification on an array of test vectors X. |
| [`predict_log_proba`](#sklearn.naive_bayes.BernoulliNB.predict_log_proba "sklearn.naive_bayes.BernoulliNB.predict_log_proba")(X) | Return log-probability estimates for the test vector X. |
| [`predict_proba`](#sklearn.naive_bayes.BernoulliNB.predict_proba "sklearn.naive_bayes.BernoulliNB.predict_proba")(X) | Return probability estimates for the test vector X. |
| [`score`](#sklearn.naive_bayes.BernoulliNB.score "sklearn.naive_bayes.BernoulliNB.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.naive_bayes.BernoulliNB.set_params "sklearn.naive_bayes.BernoulliNB.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/naive_bayes.py#L679)
Fit Naive Bayes classifier according to X, y.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vectors, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,)
Target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Weights applied to individual samples (1. for unweighted).
Returns:
**self**object
Returns the instance itself.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_features\_
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2. Use `n_features_in_` instead.
partial\_fit(*X*, *y*, *classes=None*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/naive_bayes.py#L598)
Incremental fit on a batch of samples.
This method is expected to be called several times consecutively on different chunks of a dataset so as to implement out-of-core or online learning.
This is especially useful when the whole dataset is too big to fit in memory at once.
This method has some performance overhead hence it is better to call partial\_fit on chunks of data that are as large as possible (as long as fitting in the memory budget) to hide the overhead.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vectors, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,)
Target values.
**classes**array-like of shape (n\_classes,), default=None
List of all the classes that can possibly appear in the y vector.
Must be provided at the first call to partial\_fit, can be omitted in subsequent calls.
**sample\_weight**array-like of shape (n\_samples,), default=None
Weights applied to individual samples (1. for unweighted).
Returns:
**self**object
Returns the instance itself.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/naive_bayes.py#L65)
Perform classification on an array of test vectors X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The input samples.
Returns:
**C**ndarray of shape (n\_samples,)
Predicted target values for X.
predict\_log\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/naive_bayes.py#L84)
Return log-probability estimates for the test vector X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The input samples.
Returns:
**C**array-like of shape (n\_samples, n\_classes)
Returns the log-probability of the samples for each class in the model. The columns correspond to the classes in sorted order, as they appear in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/naive_bayes.py#L107)
Return probability estimates for the test vector X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The input samples.
Returns:
**C**array-like of shape (n\_samples, n\_classes)
Returns the probability of the samples for each class in the model. The columns correspond to the classes in sorted order, as they appear in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.naive_bayes.BernoulliNB`
------------------------------------------------
[Hashing feature transformation using Totally Random Trees](../../auto_examples/ensemble/plot_random_forest_embedding#sphx-glr-auto-examples-ensemble-plot-random-forest-embedding-py)
scikit_learn sklearn.exceptions.EfficiencyWarning sklearn.exceptions.EfficiencyWarning
====================================
*class*sklearn.exceptions.EfficiencyWarning[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/exceptions.py#L81)
Warning used to notify the user of inefficient computation.
This warning notifies the user that the efficiency may not be optimal due to some reason which may be included as a part of the warning message. This may be subclassed into a more specific Warning class.
New in version 0.18.
Attributes:
**args**
#### Methods
| | |
| --- | --- |
| [`with_traceback`](#sklearn.exceptions.EfficiencyWarning.with_traceback "sklearn.exceptions.EfficiencyWarning.with_traceback") | Exception.with\_traceback(tb) -- set self.\_\_traceback\_\_ to tb and return self. |
with\_traceback()
Exception.with\_traceback(tb) – set self.\_\_traceback\_\_ to tb and return self.
scikit_learn sklearn.metrics.calinski_harabasz_score sklearn.metrics.calinski\_harabasz\_score
=========================================
sklearn.metrics.calinski\_harabasz\_score(*X*, *labels*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/cluster/_unsupervised.py#L253)
Compute the Calinski and Harabasz score.
It is also known as the Variance Ratio Criterion.
The score is defined as ratio of the sum of between-cluster dispersion and of within-cluster dispersion.
Read more in the [User Guide](../clustering#calinski-harabasz-index).
Parameters:
**X**array-like of shape (n\_samples, n\_features)
A list of `n_features`-dimensional data points. Each row corresponds to a single data point.
**labels**array-like of shape (n\_samples,)
Predicted labels for each sample.
Returns:
**score**float
The resulting Calinski-Harabasz score.
#### References
[1] [T. Calinski and J. Harabasz, 1974. “A dendrite method for cluster analysis”. Communications in Statistics](https://www.tandfonline.com/doi/abs/10.1080/03610927408827101)
scikit_learn sklearn.gaussian_process.kernels.Product sklearn.gaussian\_process.kernels.Product
=========================================
*class*sklearn.gaussian\_process.kernels.Product(*k1*, *k2*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L871)
The `Product` kernel takes two kernels \(k\_1\) and \(k\_2\) and combines them via
\[k\_{prod}(X, Y) = k\_1(X, Y) \* k\_2(X, Y)\] Note that the `__mul__` magic method is overridden, so `Product(RBF(), RBF())` is equivalent to using the \* operator with `RBF() * RBF()`.
Read more in the [User Guide](../gaussian_process#gp-kernels).
New in version 0.18.
Parameters:
**k1**Kernel
The first base-kernel of the product-kernel
**k2**Kernel
The second base-kernel of the product-kernel
Attributes:
[`bounds`](#sklearn.gaussian_process.kernels.Product.bounds "sklearn.gaussian_process.kernels.Product.bounds")
Returns the log-transformed bounds on the theta.
[`hyperparameters`](#sklearn.gaussian_process.kernels.Product.hyperparameters "sklearn.gaussian_process.kernels.Product.hyperparameters")
Returns a list of all hyperparameter.
[`n_dims`](#sklearn.gaussian_process.kernels.Product.n_dims "sklearn.gaussian_process.kernels.Product.n_dims")
Returns the number of non-fixed hyperparameters of the kernel.
[`requires_vector_input`](#sklearn.gaussian_process.kernels.Product.requires_vector_input "sklearn.gaussian_process.kernels.Product.requires_vector_input")
Returns whether the kernel is stationary.
[`theta`](#sklearn.gaussian_process.kernels.Product.theta "sklearn.gaussian_process.kernels.Product.theta")
Returns the (flattened, log-transformed) non-fixed hyperparameters.
#### Examples
```
>>> from sklearn.datasets import make_friedman2
>>> from sklearn.gaussian_process import GaussianProcessRegressor
>>> from sklearn.gaussian_process.kernels import (RBF, Product,
... ConstantKernel)
>>> X, y = make_friedman2(n_samples=500, noise=0, random_state=0)
>>> kernel = Product(ConstantKernel(2), RBF())
>>> gpr = GaussianProcessRegressor(kernel=kernel,
... random_state=0).fit(X, y)
>>> gpr.score(X, y)
1.0
>>> kernel
1.41**2 * RBF(length_scale=1)
```
#### Methods
| | |
| --- | --- |
| [`__call__`](#sklearn.gaussian_process.kernels.Product.__call__ "sklearn.gaussian_process.kernels.Product.__call__")(X[, Y, eval\_gradient]) | Return the kernel k(X, Y) and optionally its gradient. |
| [`clone_with_theta`](#sklearn.gaussian_process.kernels.Product.clone_with_theta "sklearn.gaussian_process.kernels.Product.clone_with_theta")(theta) | Returns a clone of self with given hyperparameters theta. |
| [`diag`](#sklearn.gaussian_process.kernels.Product.diag "sklearn.gaussian_process.kernels.Product.diag")(X) | Returns the diagonal of the kernel k(X, X). |
| [`get_params`](#sklearn.gaussian_process.kernels.Product.get_params "sklearn.gaussian_process.kernels.Product.get_params")([deep]) | Get parameters of this kernel. |
| [`is_stationary`](#sklearn.gaussian_process.kernels.Product.is_stationary "sklearn.gaussian_process.kernels.Product.is_stationary")() | Returns whether the kernel is stationary. |
| [`set_params`](#sklearn.gaussian_process.kernels.Product.set_params "sklearn.gaussian_process.kernels.Product.set_params")(\*\*params) | Set the parameters of this kernel. |
\_\_call\_\_(*X*, *Y=None*, *eval\_gradient=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L911)
Return the kernel k(X, Y) and optionally its gradient.
Parameters:
**X**array-like of shape (n\_samples\_X, n\_features) or list of object
Left argument of the returned kernel k(X, Y)
**Y**array-like of shape (n\_samples\_Y, n\_features) or list of object, default=None
Right argument of the returned kernel k(X, Y). If None, k(X, X) is evaluated instead.
**eval\_gradient**bool, default=False
Determines whether the gradient with respect to the log of the kernel hyperparameter is computed.
Returns:
**K**ndarray of shape (n\_samples\_X, n\_samples\_Y)
Kernel k(X, Y)
**K\_gradient**ndarray of shape (n\_samples\_X, n\_samples\_X, n\_dims), optional
The gradient of the kernel k(X, X) with respect to the log of the hyperparameter of the kernel. Only returned when `eval_gradient` is True.
*property*bounds
Returns the log-transformed bounds on the theta.
Returns:
**bounds**ndarray of shape (n\_dims, 2)
The log-transformed bounds on the kernel’s hyperparameters theta
clone\_with\_theta(*theta*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L238)
Returns a clone of self with given hyperparameters theta.
Parameters:
**theta**ndarray of shape (n\_dims,)
The hyperparameters
diag(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L948)
Returns the diagonal of the kernel k(X, X).
The result of this method is identical to np.diag(self(X)); however, it can be evaluated more efficiently since only the diagonal is evaluated.
Parameters:
**X**array-like of shape (n\_samples\_X, n\_features) or list of object
Argument to the kernel.
Returns:
**K\_diag**ndarray of shape (n\_samples\_X,)
Diagonal of kernel k(X, X)
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L666)
Get parameters of this kernel.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*hyperparameters
Returns a list of all hyperparameter.
is\_stationary()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L764)
Returns whether the kernel is stationary.
*property*n\_dims
Returns the number of non-fixed hyperparameters of the kernel.
*property*requires\_vector\_input
Returns whether the kernel is stationary.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L198)
Set the parameters of this kernel.
The method works on simple kernels as well as on nested kernels. The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Returns:
self
*property*theta
Returns the (flattened, log-transformed) non-fixed hyperparameters.
Note that theta are typically the log-transformed values of the kernel’s hyperparameters as this representation of the search space is more amenable for hyperparameter search, as hyperparameters like length-scales naturally live on a log-scale.
Returns:
**theta**ndarray of shape (n\_dims,)
The non-fixed, log-transformed hyperparameters of the kernel
| programming_docs |
scikit_learn sklearn.utils.sparsefuncs.mean_variance_axis sklearn.utils.sparsefuncs.mean\_variance\_axis
==============================================
sklearn.utils.sparsefuncs.mean\_variance\_axis(*X*, *axis*, *weights=None*, *return\_sum\_weights=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/sparsefuncs.py#L68)
Compute mean and variance along an axis on a CSR or CSC matrix.
Parameters:
**X**sparse matrix of shape (n\_samples, n\_features)
Input data. It can be of CSR or CSC format.
**axis**{0, 1}
Axis along which the axis should be computed.
**weights**ndarray of shape (n\_samples,) or (n\_features,), default=None
if axis is set to 0 shape is (n\_samples,) or if axis is set to 1 shape is (n\_features,). If it is set to None, then samples are equally weighted.
New in version 0.24.
**return\_sum\_weights**bool, default=False
If True, returns the sum of weights seen for each feature if `axis=0` or each sample if `axis=1`.
New in version 0.24.
Returns:
**means**ndarray of shape (n\_features,), dtype=floating
Feature-wise means.
**variances**ndarray of shape (n\_features,), dtype=floating
Feature-wise variances.
**sum\_weights**ndarray of shape (n\_features,), dtype=floating
Returned if `return_sum_weights` is `True`.
scikit_learn sklearn.model_selection.TimeSeriesSplit sklearn.model\_selection.TimeSeriesSplit
========================================
*class*sklearn.model\_selection.TimeSeriesSplit(*n\_splits=5*, *\**, *max\_train\_size=None*, *test\_size=None*, *gap=0*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L953)
Time Series cross-validator
Provides train/test indices to split time series data samples that are observed at fixed time intervals, in train/test sets. In each split, test indices must be higher than before, and thus shuffling in cross validator is inappropriate.
This cross-validation object is a variation of [`KFold`](sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold"). In the kth split, it returns first k folds as train set and the (k+1)th fold as test set.
Note that unlike standard cross-validation methods, successive training sets are supersets of those that come before them.
Read more in the [User Guide](../cross_validation#time-series-split).
New in version 0.18.
Parameters:
**n\_splits**int, default=5
Number of splits. Must be at least 2.
Changed in version 0.22: `n_splits` default value changed from 3 to 5.
**max\_train\_size**int, default=None
Maximum size for a single training set.
**test\_size**int, default=None
Used to limit the size of the test set. Defaults to `n_samples // (n_splits + 1)`, which is the maximum allowed value with `gap=0`.
New in version 0.24.
**gap**int, default=0
Number of samples to exclude from the end of each train set before the test set.
New in version 0.24.
#### Notes
The training set has size `i * n_samples // (n_splits + 1)
+ n_samples % (n_splits + 1)` in the `i` th split, with a test set of size `n_samples//(n_splits + 1)` by default, where `n_samples` is the number of samples.
#### Examples
```
>>> import numpy as np
>>> from sklearn.model_selection import TimeSeriesSplit
>>> X = np.array([[1, 2], [3, 4], [1, 2], [3, 4], [1, 2], [3, 4]])
>>> y = np.array([1, 2, 3, 4, 5, 6])
>>> tscv = TimeSeriesSplit()
>>> print(tscv)
TimeSeriesSplit(gap=0, max_train_size=None, n_splits=5, test_size=None)
>>> for train_index, test_index in tscv.split(X):
... print("TRAIN:", train_index, "TEST:", test_index)
... X_train, X_test = X[train_index], X[test_index]
... y_train, y_test = y[train_index], y[test_index]
TRAIN: [0] TEST: [1]
TRAIN: [0 1] TEST: [2]
TRAIN: [0 1 2] TEST: [3]
TRAIN: [0 1 2 3] TEST: [4]
TRAIN: [0 1 2 3 4] TEST: [5]
>>> # Fix test_size to 2 with 12 samples
>>> X = np.random.randn(12, 2)
>>> y = np.random.randint(0, 2, 12)
>>> tscv = TimeSeriesSplit(n_splits=3, test_size=2)
>>> for train_index, test_index in tscv.split(X):
... print("TRAIN:", train_index, "TEST:", test_index)
... X_train, X_test = X[train_index], X[test_index]
... y_train, y_test = y[train_index], y[test_index]
TRAIN: [0 1 2 3 4 5] TEST: [6 7]
TRAIN: [0 1 2 3 4 5 6 7] TEST: [8 9]
TRAIN: [0 1 2 3 4 5 6 7 8 9] TEST: [10 11]
>>> # Add in a 2 period gap
>>> tscv = TimeSeriesSplit(n_splits=3, test_size=2, gap=2)
>>> for train_index, test_index in tscv.split(X):
... print("TRAIN:", train_index, "TEST:", test_index)
... X_train, X_test = X[train_index], X[test_index]
... y_train, y_test = y[train_index], y[test_index]
TRAIN: [0 1 2 3] TEST: [6 7]
TRAIN: [0 1 2 3 4 5] TEST: [8 9]
TRAIN: [0 1 2 3 4 5 6 7] TEST: [10 11]
```
#### Methods
| | |
| --- | --- |
| [`get_n_splits`](#sklearn.model_selection.TimeSeriesSplit.get_n_splits "sklearn.model_selection.TimeSeriesSplit.get_n_splits")([X, y, groups]) | Returns the number of splitting iterations in the cross-validator |
| [`split`](#sklearn.model_selection.TimeSeriesSplit.split "sklearn.model_selection.TimeSeriesSplit.split")(X[, y, groups]) | Generate indices to split data into training and test set. |
get\_n\_splits(*X=None*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L343)
Returns the number of splitting iterations in the cross-validator
Parameters:
**X**object
Always ignored, exists for compatibility.
**y**object
Always ignored, exists for compatibility.
**groups**object
Always ignored, exists for compatibility.
Returns:
**n\_splits**int
Returns the number of splitting iterations in the cross-validator.
split(*X*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L1049)
Generate indices to split data into training and test set.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,)
Always ignored, exists for compatibility.
**groups**array-like of shape (n\_samples,)
Always ignored, exists for compatibility.
Yields:
**train**ndarray
The training set indices for that split.
**test**ndarray
The testing set indices for that split.
Examples using `sklearn.model_selection.TimeSeriesSplit`
--------------------------------------------------------
[Time-related feature engineering](../../auto_examples/applications/plot_cyclical_feature_engineering#sphx-glr-auto-examples-applications-plot-cyclical-feature-engineering-py)
[Visualizing cross-validation behavior in scikit-learn](../../auto_examples/model_selection/plot_cv_indices#sphx-glr-auto-examples-model-selection-plot-cv-indices-py)
scikit_learn sklearn.tree.DecisionTreeRegressor sklearn.tree.DecisionTreeRegressor
==================================
*class*sklearn.tree.DecisionTreeRegressor(*\**, *criterion='squared\_error'*, *splitter='best'*, *max\_depth=None*, *min\_samples\_split=2*, *min\_samples\_leaf=1*, *min\_weight\_fraction\_leaf=0.0*, *max\_features=None*, *random\_state=None*, *max\_leaf\_nodes=None*, *min\_impurity\_decrease=0.0*, *ccp\_alpha=0.0*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L1065)
A decision tree regressor.
Read more in the [User Guide](../tree#tree).
Parameters:
**criterion**{“squared\_error”, “friedman\_mse”, “absolute\_error”, “poisson”}, default=”squared\_error”
The function to measure the quality of a split. Supported criteria are “squared\_error” for the mean squared error, which is equal to variance reduction as feature selection criterion and minimizes the L2 loss using the mean of each terminal node, “friedman\_mse”, which uses mean squared error with Friedman’s improvement score for potential splits, “absolute\_error” for the mean absolute error, which minimizes the L1 loss using the median of each terminal node, and “poisson” which uses reduction in Poisson deviance to find splits.
New in version 0.18: Mean Absolute Error (MAE) criterion.
New in version 0.24: Poisson deviance criterion.
Deprecated since version 1.0: Criterion “mse” was deprecated in v1.0 and will be removed in version 1.2. Use `criterion="squared_error"` which is equivalent.
Deprecated since version 1.0: Criterion “mae” was deprecated in v1.0 and will be removed in version 1.2. Use `criterion="absolute_error"` which is equivalent.
**splitter**{“best”, “random”}, default=”best”
The strategy used to choose the split at each node. Supported strategies are “best” to choose the best split and “random” to choose the best random split.
**max\_depth**int, default=None
The maximum depth of the tree. If None, then nodes are expanded until all leaves are pure or until all leaves contain less than min\_samples\_split samples.
**min\_samples\_split**int or float, default=2
The minimum number of samples required to split an internal node:
* If int, then consider `min_samples_split` as the minimum number.
* If float, then `min_samples_split` is a fraction and `ceil(min_samples_split * n_samples)` are the minimum number of samples for each split.
Changed in version 0.18: Added float values for fractions.
**min\_samples\_leaf**int or float, default=1
The minimum number of samples required to be at a leaf node. A split point at any depth will only be considered if it leaves at least `min_samples_leaf` training samples in each of the left and right branches. This may have the effect of smoothing the model, especially in regression.
* If int, then consider `min_samples_leaf` as the minimum number.
* If float, then `min_samples_leaf` is a fraction and `ceil(min_samples_leaf * n_samples)` are the minimum number of samples for each node.
Changed in version 0.18: Added float values for fractions.
**min\_weight\_fraction\_leaf**float, default=0.0
The minimum weighted fraction of the sum total of weights (of all the input samples) required to be at a leaf node. Samples have equal weight when sample\_weight is not provided.
**max\_features**int, float or {“auto”, “sqrt”, “log2”}, default=None
The number of features to consider when looking for the best split:
* If int, then consider `max_features` features at each split.
* If float, then `max_features` is a fraction and `max(1, int(max_features * n_features_in_))` features are considered at each split.
* If “auto”, then `max_features=n_features`.
* If “sqrt”, then `max_features=sqrt(n_features)`.
* If “log2”, then `max_features=log2(n_features)`.
* If None, then `max_features=n_features`.
Deprecated since version 1.1: The `"auto"` option was deprecated in 1.1 and will be removed in 1.3.
Note: the search for a split does not stop until at least one valid partition of the node samples is found, even if it requires to effectively inspect more than `max_features` features.
**random\_state**int, RandomState instance or None, default=None
Controls the randomness of the estimator. The features are always randomly permuted at each split, even if `splitter` is set to `"best"`. When `max_features < n_features`, the algorithm will select `max_features` at random at each split before finding the best split among them. But the best found split may vary across different runs, even if `max_features=n_features`. That is the case, if the improvement of the criterion is identical for several splits and one split has to be selected at random. To obtain a deterministic behaviour during fitting, `random_state` has to be fixed to an integer. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state) for details.
**max\_leaf\_nodes**int, default=None
Grow a tree with `max_leaf_nodes` in best-first fashion. Best nodes are defined as relative reduction in impurity. If None then unlimited number of leaf nodes.
**min\_impurity\_decrease**float, default=0.0
A node will be split if this split induces a decrease of the impurity greater than or equal to this value.
The weighted impurity decrease equation is the following:
```
N_t / N * (impurity - N_t_R / N_t * right_impurity
- N_t_L / N_t * left_impurity)
```
where `N` is the total number of samples, `N_t` is the number of samples at the current node, `N_t_L` is the number of samples in the left child, and `N_t_R` is the number of samples in the right child.
`N`, `N_t`, `N_t_R` and `N_t_L` all refer to the weighted sum, if `sample_weight` is passed.
New in version 0.19.
**ccp\_alpha**non-negative float, default=0.0
Complexity parameter used for Minimal Cost-Complexity Pruning. The subtree with the largest cost complexity that is smaller than `ccp_alpha` will be chosen. By default, no pruning is performed. See [Minimal Cost-Complexity Pruning](../tree#minimal-cost-complexity-pruning) for details.
New in version 0.22.
Attributes:
[`feature_importances_`](#sklearn.tree.DecisionTreeRegressor.feature_importances_ "sklearn.tree.DecisionTreeRegressor.feature_importances_")ndarray of shape (n\_features,)
Return the feature importances.
**max\_features\_**int
The inferred value of max\_features.
[`n_features_`](#sklearn.tree.DecisionTreeRegressor.n_features_ "sklearn.tree.DecisionTreeRegressor.n_features_")int
DEPRECATED: The attribute `n_features_` is deprecated in 1.0 and will be removed in 1.2.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_outputs\_**int
The number of outputs when `fit` is performed.
**tree\_**Tree instance
The underlying Tree object. Please refer to `help(sklearn.tree._tree.Tree)` for attributes of Tree object and [Understanding the decision tree structure](../../auto_examples/tree/plot_unveil_tree_structure#sphx-glr-auto-examples-tree-plot-unveil-tree-structure-py) for basic usage of these attributes.
See also
[`DecisionTreeClassifier`](sklearn.tree.decisiontreeclassifier#sklearn.tree.DecisionTreeClassifier "sklearn.tree.DecisionTreeClassifier")
A decision tree classifier.
#### Notes
The default values for the parameters controlling the size of the trees (e.g. `max_depth`, `min_samples_leaf`, etc.) lead to fully grown and unpruned trees which can potentially be very large on some data sets. To reduce memory consumption, the complexity and size of the trees should be controlled by setting those parameter values.
#### References
[1] <https://en.wikipedia.org/wiki/Decision_tree_learning>
[2] L. Breiman, J. Friedman, R. Olshen, and C. Stone, “Classification and Regression Trees”, Wadsworth, Belmont, CA, 1984.
[3] T. Hastie, R. Tibshirani and J. Friedman. “Elements of Statistical Learning”, Springer, 2009.
[4] L. Breiman, and A. Cutler, “Random Forests”, <https://www.stat.berkeley.edu/~breiman/RandomForests/cc_home.htm>
#### Examples
```
>>> from sklearn.datasets import load_diabetes
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.tree import DecisionTreeRegressor
>>> X, y = load_diabetes(return_X_y=True)
>>> regressor = DecisionTreeRegressor(random_state=0)
>>> cross_val_score(regressor, X, y, cv=10)
...
...
array([-0.39..., -0.46..., 0.02..., 0.06..., -0.50...,
0.16..., 0.11..., -0.73..., -0.30..., -0.00...])
```
#### Methods
| | |
| --- | --- |
| [`apply`](#sklearn.tree.DecisionTreeRegressor.apply "sklearn.tree.DecisionTreeRegressor.apply")(X[, check\_input]) | Return the index of the leaf that each sample is predicted as. |
| [`cost_complexity_pruning_path`](#sklearn.tree.DecisionTreeRegressor.cost_complexity_pruning_path "sklearn.tree.DecisionTreeRegressor.cost_complexity_pruning_path")(X, y[, ...]) | Compute the pruning path during Minimal Cost-Complexity Pruning. |
| [`decision_path`](#sklearn.tree.DecisionTreeRegressor.decision_path "sklearn.tree.DecisionTreeRegressor.decision_path")(X[, check\_input]) | Return the decision path in the tree. |
| [`fit`](#sklearn.tree.DecisionTreeRegressor.fit "sklearn.tree.DecisionTreeRegressor.fit")(X, y[, sample\_weight, check\_input]) | Build a decision tree regressor from the training set (X, y). |
| [`get_depth`](#sklearn.tree.DecisionTreeRegressor.get_depth "sklearn.tree.DecisionTreeRegressor.get_depth")() | Return the depth of the decision tree. |
| [`get_n_leaves`](#sklearn.tree.DecisionTreeRegressor.get_n_leaves "sklearn.tree.DecisionTreeRegressor.get_n_leaves")() | Return the number of leaves of the decision tree. |
| [`get_params`](#sklearn.tree.DecisionTreeRegressor.get_params "sklearn.tree.DecisionTreeRegressor.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.tree.DecisionTreeRegressor.predict "sklearn.tree.DecisionTreeRegressor.predict")(X[, check\_input]) | Predict class or regression value for X. |
| [`score`](#sklearn.tree.DecisionTreeRegressor.score "sklearn.tree.DecisionTreeRegressor.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.tree.DecisionTreeRegressor.set_params "sklearn.tree.DecisionTreeRegressor.set_params")(\*\*params) | Set the parameters of this estimator. |
apply(*X*, *check\_input=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L532)
Return the index of the leaf that each sample is predicted as.
New in version 0.17.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
**check\_input**bool, default=True
Allow to bypass several input checking. Don’t use this parameter unless you know what you do.
Returns:
**X\_leaves**array-like of shape (n\_samples,)
For each datapoint x in X, return the index of the leaf x ends up in. Leaves are numbered within `[0; self.tree_.node_count)`, possibly with gaps in the numbering.
cost\_complexity\_pruning\_path(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L607)
Compute the pruning path during Minimal Cost-Complexity Pruning.
See [Minimal Cost-Complexity Pruning](../tree#minimal-cost-complexity-pruning) for details on the pruning process.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csc_matrix`.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
The target values (class labels) as integers or strings.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, then samples are equally weighted. Splits that would create child nodes with net zero or negative weight are ignored while searching for a split in each node. Splits are also ignored if they would result in any single class carrying a negative weight in either child node.
Returns:
**ccp\_path**[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
Dictionary-like object, with the following attributes.
ccp\_alphasndarray
Effective alphas of subtree during pruning.
impuritiesndarray
Sum of the impurities of the subtree leaves for the corresponding alpha value in `ccp_alphas`.
decision\_path(*X*, *check\_input=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L560)
Return the decision path in the tree.
New in version 0.18.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
**check\_input**bool, default=True
Allow to bypass several input checking. Don’t use this parameter unless you know what you do.
Returns:
**indicator**sparse matrix of shape (n\_samples, n\_nodes)
Return a node indicator CSR matrix where non zero elements indicates that the samples goes through the nodes.
*property*feature\_importances\_
Return the feature importances.
The importance of a feature is computed as the (normalized) total reduction of the criterion brought by that feature. It is also known as the Gini importance.
Warning: impurity-based feature importances can be misleading for high cardinality features (many unique values). See [`sklearn.inspection.permutation_importance`](sklearn.inspection.permutation_importance#sklearn.inspection.permutation_importance "sklearn.inspection.permutation_importance") as an alternative.
Returns:
**feature\_importances\_**ndarray of shape (n\_features,)
Normalized total reduction of criteria by feature (Gini importance).
fit(*X*, *y*, *sample\_weight=None*, *check\_input=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L1313)
Build a decision tree regressor from the training set (X, y).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csc_matrix`.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
The target values (real numbers). Use `dtype=np.float64` and `order='C'` for maximum efficiency.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, then samples are equally weighted. Splits that would create child nodes with net zero or negative weight are ignored while searching for a split in each node.
**check\_input**bool, default=True
Allow to bypass several input checking. Don’t use this parameter unless you know what you do.
Returns:
**self**DecisionTreeRegressor
Fitted estimator.
get\_depth()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L130)
Return the depth of the decision tree.
The depth of a tree is the maximum distance between the root and any leaf.
Returns:
**self.tree\_.max\_depth**int
The maximum depth of the tree.
get\_n\_leaves()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L144)
Return the number of leaves of the decision tree.
Returns:
**self.tree\_.n\_leaves**int
Number of leaves.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_features\_
DEPRECATED: The attribute `n_features_` is deprecated in 1.0 and will be removed in 1.2. Use `n_features_in_` instead.
predict(*X*, *check\_input=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L481)
Predict class or regression value for X.
For a classification model, the predicted class for each sample in X is returned. For a regression model, the predicted value based on X is returned.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
**check\_input**bool, default=True
Allow to bypass several input checking. Don’t use this parameter unless you know what you do.
Returns:
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
The predicted classes, or the predict values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.tree.DecisionTreeRegressor`
---------------------------------------------------
[Release Highlights for scikit-learn 0.24](../../auto_examples/release_highlights/plot_release_highlights_0_24_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-24-0-py)
[Release Highlights for scikit-learn 0.22](../../auto_examples/release_highlights/plot_release_highlights_0_22_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-22-0-py)
[Decision Tree Regression](../../auto_examples/tree/plot_tree_regression#sphx-glr-auto-examples-tree-plot-tree-regression-py)
[Multi-output Decision Tree Regression](../../auto_examples/tree/plot_tree_regression_multioutput#sphx-glr-auto-examples-tree-plot-tree-regression-multioutput-py)
[Decision Tree Regression with AdaBoost](../../auto_examples/ensemble/plot_adaboost_regression#sphx-glr-auto-examples-ensemble-plot-adaboost-regression-py)
[Single estimator versus bagging: bias-variance decomposition](../../auto_examples/ensemble/plot_bias_variance#sphx-glr-auto-examples-ensemble-plot-bias-variance-py)
[Advanced Plotting With Partial Dependence](../../auto_examples/miscellaneous/plot_partial_dependence_visualization_api#sphx-glr-auto-examples-miscellaneous-plot-partial-dependence-visualization-api-py)
[Using KBinsDiscretizer to discretize continuous features](../../auto_examples/preprocessing/plot_discretization#sphx-glr-auto-examples-preprocessing-plot-discretization-py)
| programming_docs |
scikit_learn sklearn.linear_model.lars_path sklearn.linear\_model.lars\_path
================================
sklearn.linear\_model.lars\_path(*X*, *y*, *Xy=None*, *\**, *Gram=None*, *max\_iter=500*, *alpha\_min=0*, *method='lar'*, *copy\_X=True*, *eps=2.220446049250313e-16*, *copy\_Gram=True*, *verbose=0*, *return\_path=True*, *return\_n\_iter=False*, *positive=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_least_angle.py#L34)
Compute Least Angle Regression or Lasso path using LARS algorithm [1].
The optimization objective for the case method=’lasso’ is:
```
(1 / (2 * n_samples)) * ||y - Xw||^2_2 + alpha * ||w||_1
```
in the case of method=’lars’, the objective function is only known in the form of an implicit equation (see discussion in [1])
Read more in the [User Guide](../linear_model#least-angle-regression).
Parameters:
**X**None or array-like of shape (n\_samples, n\_features)
Input data. Note that if X is None then the Gram matrix must be specified, i.e., cannot be None or False.
**y**None or array-like of shape (n\_samples,)
Input targets.
**Xy**array-like of shape (n\_samples,) or (n\_samples, n\_targets), default=None
Xy = np.dot(X.T, y) that can be precomputed. It is useful only when the Gram matrix is precomputed.
**Gram**None, ‘auto’, array-like of shape (n\_features, n\_features), default=None
Precomputed Gram matrix (X’ \* X), if `'auto'`, the Gram matrix is precomputed from the given X, if there are more samples than features.
**max\_iter**int, default=500
Maximum number of iterations to perform, set to infinity for no limit.
**alpha\_min**float, default=0
Minimum correlation along the path. It corresponds to the regularization parameter alpha parameter in the Lasso.
**method**{‘lar’, ‘lasso’}, default=’lar’
Specifies the returned model. Select `'lar'` for Least Angle Regression, `'lasso'` for the Lasso.
**copy\_X**bool, default=True
If `False`, `X` is overwritten.
**eps**float, default=np.finfo(float).eps
The machine-precision regularization in the computation of the Cholesky diagonal factors. Increase this for very ill-conditioned systems. Unlike the `tol` parameter in some iterative optimization-based algorithms, this parameter does not control the tolerance of the optimization.
**copy\_Gram**bool, default=True
If `False`, `Gram` is overwritten.
**verbose**int, default=0
Controls output verbosity.
**return\_path**bool, default=True
If `return_path==True` returns the entire path, else returns only the last point of the path.
**return\_n\_iter**bool, default=False
Whether to return the number of iterations.
**positive**bool, default=False
Restrict coefficients to be >= 0. This option is only allowed with method ‘lasso’. Note that the model coefficients will not converge to the ordinary-least-squares solution for small values of alpha. Only coefficients up to the smallest alpha value (`alphas_[alphas_ > 0.].min()` when fit\_path=True) reached by the stepwise Lars-Lasso algorithm are typically in congruence with the solution of the coordinate descent lasso\_path function.
Returns:
**alphas**array-like of shape (n\_alphas + 1,)
Maximum of covariances (in absolute value) at each iteration. `n_alphas` is either `max_iter`, `n_features` or the number of nodes in the path with `alpha >= alpha_min`, whichever is smaller.
**active**array-like of shape (n\_alphas,)
Indices of active variables at the end of the path.
**coefs**array-like of shape (n\_features, n\_alphas + 1)
Coefficients along the path.
**n\_iter**int
Number of iterations run. Returned only if return\_n\_iter is set to True.
See also
[`lars_path_gram`](sklearn.linear_model.lars_path_gram#sklearn.linear_model.lars_path_gram "sklearn.linear_model.lars_path_gram")
Compute LARS path in the sufficient stats mode.
[`lasso_path`](sklearn.linear_model.lasso_path#sklearn.linear_model.lasso_path "sklearn.linear_model.lasso_path")
Compute Lasso path with coordinate descent.
[`LassoLars`](sklearn.linear_model.lassolars#sklearn.linear_model.LassoLars "sklearn.linear_model.LassoLars")
Lasso model fit with Least Angle Regression a.k.a. Lars.
[`Lars`](sklearn.linear_model.lars#sklearn.linear_model.Lars "sklearn.linear_model.Lars")
Least Angle Regression model a.k.a. LAR.
[`LassoLarsCV`](sklearn.linear_model.lassolarscv#sklearn.linear_model.LassoLarsCV "sklearn.linear_model.LassoLarsCV")
Cross-validated Lasso, using the LARS algorithm.
[`LarsCV`](sklearn.linear_model.larscv#sklearn.linear_model.LarsCV "sklearn.linear_model.LarsCV")
Cross-validated Least Angle Regression model.
[`sklearn.decomposition.sparse_encode`](sklearn.decomposition.sparse_encode#sklearn.decomposition.sparse_encode "sklearn.decomposition.sparse_encode")
Sparse coding.
#### References
[1] “Least Angle Regression”, Efron et al. <http://statweb.stanford.edu/~tibs/ftp/lars.pdf>
[2] [Wikipedia entry on the Least-angle regression](https://en.wikipedia.org/wiki/Least-angle_regression)
[3] [Wikipedia entry on the Lasso](https://en.wikipedia.org/wiki/Lasso_(statistics))
Examples using `sklearn.linear_model.lars_path`
-----------------------------------------------
[Lasso path using LARS](../../auto_examples/linear_model/plot_lasso_lars#sphx-glr-auto-examples-linear-model-plot-lasso-lars-py)
scikit_learn sklearn.metrics.plot_confusion_matrix sklearn.metrics.plot\_confusion\_matrix
=======================================
sklearn.metrics.plot\_confusion\_matrix(*estimator*, *X*, *y\_true*, *\**, *labels=None*, *sample\_weight=None*, *normalize=None*, *display\_labels=None*, *include\_values=True*, *xticks\_rotation='horizontal'*, *values\_format=None*, *cmap='viridis'*, *ax=None*, *colorbar=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_plot/confusion_matrix.py#L462)
DEPRECATED: Function `plot_confusion_matrix` is deprecated in 1.0 and will be removed in 1.2. Use one of the class methods: ConfusionMatrixDisplay.from\_predictions or ConfusionMatrixDisplay.from\_estimator.
Plot Confusion Matrix.
`plot_confusion_matrix` is deprecated in 1.0 and will be removed in 1.2. Use one of the following class methods: [`from_predictions`](sklearn.metrics.confusionmatrixdisplay#sklearn.metrics.ConfusionMatrixDisplay.from_predictions "sklearn.metrics.ConfusionMatrixDisplay.from_predictions") or [`from_estimator`](sklearn.metrics.confusionmatrixdisplay#sklearn.metrics.ConfusionMatrixDisplay.from_estimator "sklearn.metrics.ConfusionMatrixDisplay.from_estimator").
Read more in the [User Guide](../model_evaluation#confusion-matrix).
Parameters:
**estimator**estimator instance
Fitted classifier or a fitted [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline") in which the last estimator is a classifier.
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Input values.
**y\_true**array-like of shape (n\_samples,)
Target values.
**labels**array-like of shape (n\_classes,), default=None
List of labels to index the matrix. This may be used to reorder or select a subset of labels. If `None` is given, those that appear at least once in `y_true` or `y_pred` are used in sorted order.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**normalize**{‘true’, ‘pred’, ‘all’}, default=None
Either to normalize the counts display in the matrix:
* if `'true'`, the confusion matrix is normalized over the true conditions (e.g. rows);
* if `'pred'`, the confusion matrix is normalized over the predicted conditions (e.g. columns);
* if `'all'`, the confusion matrix is normalized by the total number of samples;
* if `None` (default), the confusion matrix will not be normalized.
**display\_labels**array-like of shape (n\_classes,), default=None
Target names used for plotting. By default, `labels` will be used if it is defined, otherwise the unique labels of `y_true` and `y_pred` will be used.
**include\_values**bool, default=True
Includes values in confusion matrix.
**xticks\_rotation**{‘vertical’, ‘horizontal’} or float, default=’horizontal’
Rotation of xtick labels.
**values\_format**str, default=None
Format specification for values in confusion matrix. If `None`, the format specification is ‘d’ or ‘.2g’ whichever is shorter.
**cmap**str or matplotlib Colormap, default=’viridis’
Colormap recognized by matplotlib.
**ax**matplotlib Axes, default=None
Axes object to plot on. If `None`, a new figure and axes is created.
**colorbar**bool, default=True
Whether or not to add a colorbar to the plot.
New in version 0.24.
Returns:
**display**[`ConfusionMatrixDisplay`](sklearn.metrics.confusionmatrixdisplay#sklearn.metrics.ConfusionMatrixDisplay "sklearn.metrics.ConfusionMatrixDisplay")
Object that stores computed values.
See also
[`confusion_matrix`](sklearn.metrics.confusion_matrix#sklearn.metrics.confusion_matrix "sklearn.metrics.confusion_matrix")
Compute Confusion Matrix to evaluate the accuracy of a classification.
[`ConfusionMatrixDisplay`](sklearn.metrics.confusionmatrixdisplay#sklearn.metrics.ConfusionMatrixDisplay "sklearn.metrics.ConfusionMatrixDisplay")
Confusion Matrix visualization.
#### Examples
```
>>> import matplotlib.pyplot as plt
>>> from sklearn.datasets import make_classification
>>> from sklearn.metrics import plot_confusion_matrix
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.svm import SVC
>>> X, y = make_classification(random_state=0)
>>> X_train, X_test, y_train, y_test = train_test_split(
... X, y, random_state=0)
>>> clf = SVC(random_state=0)
>>> clf.fit(X_train, y_train)
SVC(random_state=0)
>>> plot_confusion_matrix(clf, X_test, y_test)
>>> plt.show()
```
scikit_learn sklearn.model_selection.train_test_split sklearn.model\_selection.train\_test\_split
===========================================
sklearn.model\_selection.train\_test\_split(*\*arrays*, *test\_size=None*, *train\_size=None*, *random\_state=None*, *shuffle=True*, *stratify=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L2349)
Split arrays or matrices into random train and test subsets.
Quick utility that wraps input validation and `next(ShuffleSplit().split(X, y))` and application to input data into a single call for splitting (and optionally subsampling) data in a oneliner.
Read more in the [User Guide](../cross_validation#cross-validation).
Parameters:
**\*arrays**sequence of indexables with same length / shape[0]
Allowed inputs are lists, numpy arrays, scipy-sparse matrices or pandas dataframes.
**test\_size**float or int, default=None
If float, should be between 0.0 and 1.0 and represent the proportion of the dataset to include in the test split. If int, represents the absolute number of test samples. If None, the value is set to the complement of the train size. If `train_size` is also None, it will be set to 0.25.
**train\_size**float or int, default=None
If float, should be between 0.0 and 1.0 and represent the proportion of the dataset to include in the train split. If int, represents the absolute number of train samples. If None, the value is automatically set to the complement of the test size.
**random\_state**int, RandomState instance or None, default=None
Controls the shuffling applied to the data before applying the split. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**shuffle**bool, default=True
Whether or not to shuffle the data before splitting. If shuffle=False then stratify must be None.
**stratify**array-like, default=None
If not None, data is split in a stratified fashion, using this as the class labels. Read more in the [User Guide](../cross_validation#stratification).
Returns:
**splitting**list, length=2 \* len(arrays)
List containing train-test split of inputs.
New in version 0.16: If the input is sparse, the output will be a `scipy.sparse.csr_matrix`. Else, output type is the same as the input type.
#### Examples
```
>>> import numpy as np
>>> from sklearn.model_selection import train_test_split
>>> X, y = np.arange(10).reshape((5, 2)), range(5)
>>> X
array([[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9]])
>>> list(y)
[0, 1, 2, 3, 4]
```
```
>>> X_train, X_test, y_train, y_test = train_test_split(
... X, y, test_size=0.33, random_state=42)
...
>>> X_train
array([[4, 5],
[0, 1],
[6, 7]])
>>> y_train
[2, 0, 3]
>>> X_test
array([[2, 3],
[8, 9]])
>>> y_test
[1, 4]
```
```
>>> train_test_split(y, shuffle=False)
[[0, 1, 2], [3, 4]]
```
Examples using `sklearn.model_selection.train_test_split`
---------------------------------------------------------
[Release Highlights for scikit-learn 0.24](../../auto_examples/release_highlights/plot_release_highlights_0_24_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-24-0-py)
[Release Highlights for scikit-learn 0.23](../../auto_examples/release_highlights/plot_release_highlights_0_23_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-23-0-py)
[Release Highlights for scikit-learn 0.22](../../auto_examples/release_highlights/plot_release_highlights_0_22_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-22-0-py)
[Comparison of Calibration of Classifiers](../../auto_examples/calibration/plot_compare_calibration#sphx-glr-auto-examples-calibration-plot-compare-calibration-py)
[Probability Calibration curves](../../auto_examples/calibration/plot_calibration_curve#sphx-glr-auto-examples-calibration-plot-calibration-curve-py)
[Probability calibration of classifiers](../../auto_examples/calibration/plot_calibration#sphx-glr-auto-examples-calibration-plot-calibration-py)
[Classifier comparison](../../auto_examples/classification/plot_classifier_comparison#sphx-glr-auto-examples-classification-plot-classifier-comparison-py)
[Recognizing hand-written digits](../../auto_examples/classification/plot_digits_classification#sphx-glr-auto-examples-classification-plot-digits-classification-py)
[Principal Component Regression vs Partial Least Squares Regression](../../auto_examples/cross_decomposition/plot_pcr_vs_pls#sphx-glr-auto-examples-cross-decomposition-plot-pcr-vs-pls-py)
[Post pruning decision trees with cost complexity pruning](../../auto_examples/tree/plot_cost_complexity_pruning#sphx-glr-auto-examples-tree-plot-cost-complexity-pruning-py)
[Understanding the decision tree structure](../../auto_examples/tree/plot_unveil_tree_structure#sphx-glr-auto-examples-tree-plot-unveil-tree-structure-py)
[Kernel PCA](../../auto_examples/decomposition/plot_kernel_pca#sphx-glr-auto-examples-decomposition-plot-kernel-pca-py)
[Comparing random forests and the multi-output meta estimator](../../auto_examples/ensemble/plot_random_forest_regression_multioutput#sphx-glr-auto-examples-ensemble-plot-random-forest-regression-multioutput-py)
[Discrete versus Real AdaBoost](../../auto_examples/ensemble/plot_adaboost_hastie_10_2#sphx-glr-auto-examples-ensemble-plot-adaboost-hastie-10-2-py)
[Early stopping of Gradient Boosting](../../auto_examples/ensemble/plot_gradient_boosting_early_stopping#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-early-stopping-py)
[Feature importances with a forest of trees](../../auto_examples/ensemble/plot_forest_importances#sphx-glr-auto-examples-ensemble-plot-forest-importances-py)
[Feature transformations with ensembles of trees](../../auto_examples/ensemble/plot_feature_transformation#sphx-glr-auto-examples-ensemble-plot-feature-transformation-py)
[Gradient Boosting Out-of-Bag estimates](../../auto_examples/ensemble/plot_gradient_boosting_oob#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-oob-py)
[Gradient Boosting regression](../../auto_examples/ensemble/plot_gradient_boosting_regression#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-regression-py)
[Gradient Boosting regularization](../../auto_examples/ensemble/plot_gradient_boosting_regularization#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-regularization-py)
[Prediction Intervals for Gradient Boosting Regression](../../auto_examples/ensemble/plot_gradient_boosting_quantile#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-quantile-py)
[Faces recognition example using eigenfaces and SVMs](../../auto_examples/applications/plot_face_recognition#sphx-glr-auto-examples-applications-plot-face-recognition-py)
[Image denoising using kernel PCA](../../auto_examples/applications/plot_digits_denoising#sphx-glr-auto-examples-applications-plot-digits-denoising-py)
[Model Complexity Influence](../../auto_examples/applications/plot_model_complexity_influence#sphx-glr-auto-examples-applications-plot-model-complexity-influence-py)
[Prediction Latency](../../auto_examples/applications/plot_prediction_latency#sphx-glr-auto-examples-applications-plot-prediction-latency-py)
[Pipeline ANOVA SVM](../../auto_examples/feature_selection/plot_feature_selection_pipeline#sphx-glr-auto-examples-feature-selection-plot-feature-selection-pipeline-py)
[Univariate Feature Selection](../../auto_examples/feature_selection/plot_feature_selection#sphx-glr-auto-examples-feature-selection-plot-feature-selection-py)
[Comparing various online solvers](../../auto_examples/linear_model/plot_sgd_comparison#sphx-glr-auto-examples-linear-model-plot-sgd-comparison-py)
[Early stopping of Stochastic Gradient Descent](../../auto_examples/linear_model/plot_sgd_early_stopping#sphx-glr-auto-examples-linear-model-plot-sgd-early-stopping-py)
[MNIST classification using multinomial logistic + L1](../../auto_examples/linear_model/plot_sparse_logistic_regression_mnist#sphx-glr-auto-examples-linear-model-plot-sparse-logistic-regression-mnist-py)
[Multiclass sparse logistic regression on 20newgroups](../../auto_examples/linear_model/plot_sparse_logistic_regression_20newsgroups#sphx-glr-auto-examples-linear-model-plot-sparse-logistic-regression-20newsgroups-py)
[Non-negative least squares](../../auto_examples/linear_model/plot_nnls#sphx-glr-auto-examples-linear-model-plot-nnls-py)
[Poisson regression and non-normal loss](../../auto_examples/linear_model/plot_poisson_regression_non_normal_loss#sphx-glr-auto-examples-linear-model-plot-poisson-regression-non-normal-loss-py)
[Tweedie regression on insurance claims](../../auto_examples/linear_model/plot_tweedie_regression_insurance_claims#sphx-glr-auto-examples-linear-model-plot-tweedie-regression-insurance-claims-py)
[Common pitfalls in the interpretation of coefficients of linear models](../../auto_examples/inspection/plot_linear_model_coefficient_interpretation#sphx-glr-auto-examples-inspection-plot-linear-model-coefficient-interpretation-py)
[Partial Dependence and Individual Conditional Expectation Plots](../../auto_examples/inspection/plot_partial_dependence#sphx-glr-auto-examples-inspection-plot-partial-dependence-py)
[Permutation Importance vs Random Forest Feature Importance (MDI)](../../auto_examples/inspection/plot_permutation_importance#sphx-glr-auto-examples-inspection-plot-permutation-importance-py)
[Permutation Importance with Multicollinear or Correlated Features](../../auto_examples/inspection/plot_permutation_importance_multicollinear#sphx-glr-auto-examples-inspection-plot-permutation-importance-multicollinear-py)
[Scalable learning with polynomial kernel approximation](../../auto_examples/kernel_approximation/plot_scalable_poly_kernels#sphx-glr-auto-examples-kernel-approximation-plot-scalable-poly-kernels-py)
[ROC Curve with Visualization API](../../auto_examples/miscellaneous/plot_roc_curve_visualization_api#sphx-glr-auto-examples-miscellaneous-plot-roc-curve-visualization-api-py)
[Visualizations with Display Objects](../../auto_examples/miscellaneous/plot_display_object_visualization#sphx-glr-auto-examples-miscellaneous-plot-display-object-visualization-py)
[Confusion matrix](../../auto_examples/model_selection/plot_confusion_matrix#sphx-glr-auto-examples-model-selection-plot-confusion-matrix-py)
[Custom refit strategy of a grid search with cross-validation](../../auto_examples/model_selection/plot_grid_search_digits#sphx-glr-auto-examples-model-selection-plot-grid-search-digits-py)
[Detection error tradeoff (DET) curve](../../auto_examples/model_selection/plot_det#sphx-glr-auto-examples-model-selection-plot-det-py)
[Precision-Recall](../../auto_examples/model_selection/plot_precision_recall#sphx-glr-auto-examples-model-selection-plot-precision-recall-py)
[Receiver Operating Characteristic (ROC)](../../auto_examples/model_selection/plot_roc#sphx-glr-auto-examples-model-selection-plot-roc-py)
[Train error vs Test error](../../auto_examples/model_selection/plot_train_error_vs_test_error#sphx-glr-auto-examples-model-selection-plot-train-error-vs-test-error-py)
[Classifier Chain](../../auto_examples/multioutput/plot_classifier_chain_yeast#sphx-glr-auto-examples-multioutput-plot-classifier-chain-yeast-py)
[Comparing Nearest Neighbors with and without Neighborhood Components Analysis](../../auto_examples/neighbors/plot_nca_classification#sphx-glr-auto-examples-neighbors-plot-nca-classification-py)
[Dimensionality Reduction with Neighborhood Components Analysis](../../auto_examples/neighbors/plot_nca_dim_reduction#sphx-glr-auto-examples-neighbors-plot-nca-dim-reduction-py)
[Restricted Boltzmann Machine features for digit classification](../../auto_examples/neural_networks/plot_rbm_logistic_classification#sphx-glr-auto-examples-neural-networks-plot-rbm-logistic-classification-py)
[Varying regularization in Multi-layer Perceptron](../../auto_examples/neural_networks/plot_mlp_alpha#sphx-glr-auto-examples-neural-networks-plot-mlp-alpha-py)
[Visualization of MLP weights on MNIST](../../auto_examples/neural_networks/plot_mnist_filters#sphx-glr-auto-examples-neural-networks-plot-mnist-filters-py)
[Column Transformer with Mixed Types](../../auto_examples/compose/plot_column_transformer_mixed_types#sphx-glr-auto-examples-compose-plot-column-transformer-mixed-types-py)
[Effect of transforming the targets in regression model](../../auto_examples/compose/plot_transformed_target#sphx-glr-auto-examples-compose-plot-transformed-target-py)
[Feature discretization](../../auto_examples/preprocessing/plot_discretization_classification#sphx-glr-auto-examples-preprocessing-plot-discretization-classification-py)
[Importance of Feature Scaling](../../auto_examples/preprocessing/plot_scaling_importance#sphx-glr-auto-examples-preprocessing-plot-scaling-importance-py)
[Map data to a normal distribution](../../auto_examples/preprocessing/plot_map_data_to_normal#sphx-glr-auto-examples-preprocessing-plot-map-data-to-normal-py)
[Semi-supervised Classification on a Text Dataset](../../auto_examples/semi_supervised/plot_semi_supervised_newsgroups#sphx-glr-auto-examples-semi-supervised-plot-semi-supervised-newsgroups-py)
| programming_docs |
scikit_learn sklearn.utils.Bunch sklearn.utils.Bunch
===================
*class*sklearn.utils.Bunch(*\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/_bunch.py#L1)
Container object exposing keys as attributes.
Bunch objects are sometimes used as an output for functions and methods. They extend dictionaries by enabling values to be accessed by key, `bunch["value_key"]`, or by an attribute, `bunch.value_key`.
#### Examples
```
>>> from sklearn.utils import Bunch
>>> b = Bunch(a=1, b=2)
>>> b['b']
2
>>> b.b
2
>>> b.a = 3
>>> b['a']
3
>>> b.c = 6
>>> b['c']
6
```
#### Methods
| | |
| --- | --- |
| [`clear`](#sklearn.utils.Bunch.clear "sklearn.utils.Bunch.clear")() | |
| [`copy`](#sklearn.utils.Bunch.copy "sklearn.utils.Bunch.copy")() | |
| [`fromkeys`](#sklearn.utils.Bunch.fromkeys "sklearn.utils.Bunch.fromkeys")(iterable[, value]) | Create a new dictionary with keys from iterable and values set to value. |
| [`get`](#sklearn.utils.Bunch.get "sklearn.utils.Bunch.get")(key[, default]) | Return the value for key if key is in the dictionary, else default. |
| [`items`](#sklearn.utils.Bunch.items "sklearn.utils.Bunch.items")() | |
| [`keys`](#sklearn.utils.Bunch.keys "sklearn.utils.Bunch.keys")() | |
| [`pop`](#sklearn.utils.Bunch.pop "sklearn.utils.Bunch.pop")(key[, default]) | If key is not found, default is returned if given, otherwise KeyError is raised |
| [`popitem`](#sklearn.utils.Bunch.popitem "sklearn.utils.Bunch.popitem")(/) | Remove and return a (key, value) pair as a 2-tuple. |
| [`setdefault`](#sklearn.utils.Bunch.setdefault "sklearn.utils.Bunch.setdefault")(key[, default]) | Insert key with a value of default if key is not in the dictionary. |
| [`update`](#sklearn.utils.Bunch.update "sklearn.utils.Bunch.update")([E, ]\*\*F) | If E is present and has a .keys() method, then does: for k in E: D[k] = E[k] If E is present and lacks a .keys() method, then does: for k, v in E: D[k] = v In either case, this is followed by: for k in F: D[k] = F[k] |
| [`values`](#sklearn.utils.Bunch.values "sklearn.utils.Bunch.values")() | |
clear() → None. Remove all items from D.
copy() → a shallow copy of D
fromkeys(*iterable*, *value=None*, */*)
Create a new dictionary with keys from iterable and values set to value.
get(*key*, *default=None*, */*)
Return the value for key if key is in the dictionary, else default.
items() → a set-like object providing a view on D's items
keys() → a set-like object providing a view on D's keys
pop(*key*, *default=<unrepresentable>*, */*)
If key is not found, default is returned if given, otherwise KeyError is raised
popitem(*/*)
Remove and return a (key, value) pair as a 2-tuple.
Pairs are returned in LIFO (last-in, first-out) order. Raises KeyError if the dict is empty.
setdefault(*key*, *default=None*, */*)
Insert key with a value of default if key is not in the dictionary.
Return the value for key if key is in the dictionary, else default.
update([*E*, ]*\*\*F*) → None. Update D from dict/iterable E and F.
If E is present and has a .keys() method, then does: for k in E: D[k] = E[k] If E is present and lacks a .keys() method, then does: for k, v in E: D[k] = v In either case, this is followed by: for k in F: D[k] = F[k]
values() → an object providing a view on D's values
Examples using `sklearn.utils.Bunch`
------------------------------------
[Species distribution modeling](../../auto_examples/applications/plot_species_distribution_modeling#sphx-glr-auto-examples-applications-plot-species-distribution-modeling-py)
scikit_learn sklearn.linear_model.PassiveAggressiveRegressor sklearn.linear\_model.PassiveAggressiveRegressor
================================================
sklearn.linear\_model.PassiveAggressiveRegressor(*\**, *C=1.0*, *fit\_intercept=True*, *max\_iter=1000*, *tol=0.001*, *early\_stopping=False*, *validation\_fraction=0.1*, *n\_iter\_no\_change=5*, *shuffle=True*, *verbose=0*, *loss='epsilon\_insensitive'*, *epsilon=0.1*, *random\_state=None*, *warm\_start=False*, *average=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_passive_aggressive.py#L303)
Passive Aggressive Regressor.
Read more in the [User Guide](../linear_model#passive-aggressive).
Parameters:
**C**float, default=1.0
Maximum step size (regularization). Defaults to 1.0.
**fit\_intercept**bool, default=True
Whether the intercept should be estimated or not. If False, the data is assumed to be already centered. Defaults to True.
**max\_iter**int, default=1000
The maximum number of passes over the training data (aka epochs). It only impacts the behavior in the `fit` method, and not the `partial_fit` method.
New in version 0.19.
**tol**float or None, default=1e-3
The stopping criterion. If it is not None, the iterations will stop when (loss > previous\_loss - tol).
New in version 0.19.
**early\_stopping**bool, default=False
Whether to use early stopping to terminate training when validation. score is not improving. If set to True, it will automatically set aside a fraction of training data as validation and terminate training when validation score is not improving by at least tol for n\_iter\_no\_change consecutive epochs.
New in version 0.20.
**validation\_fraction**float, default=0.1
The proportion of training data to set aside as validation set for early stopping. Must be between 0 and 1. Only used if early\_stopping is True.
New in version 0.20.
**n\_iter\_no\_change**int, default=5
Number of iterations with no improvement to wait before early stopping.
New in version 0.20.
**shuffle**bool, default=True
Whether or not the training data should be shuffled after each epoch.
**verbose**int, default=0
The verbosity level.
**loss**str, default=”epsilon\_insensitive”
The loss function to be used: epsilon\_insensitive: equivalent to PA-I in the reference paper. squared\_epsilon\_insensitive: equivalent to PA-II in the reference paper.
**epsilon**float, default=0.1
If the difference between the current prediction and the correct label is below this threshold, the model is not updated.
**random\_state**int, RandomState instance, default=None
Used to shuffle the training data, when `shuffle` is set to `True`. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**warm\_start**bool, default=False
When set to True, reuse the solution of the previous call to fit as initialization, otherwise, just erase the previous solution. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
Repeatedly calling fit or partial\_fit when warm\_start is True can result in a different solution than when calling fit a single time because of the way the data is shuffled.
**average**bool or int, default=False
When set to True, computes the averaged SGD weights and stores the result in the `coef_` attribute. If set to an int greater than 1, averaging will begin once the total number of samples seen reaches average. So average=10 will begin averaging after seeing 10 samples.
New in version 0.19: parameter *average* to use weights averaging in SGD.
Attributes:
**coef\_**array, shape = [1, n\_features] if n\_classes == 2 else [n\_classes, n\_features]
Weights assigned to the features.
**intercept\_**array, shape = [1] if n\_classes == 2 else [n\_classes]
Constants in decision function.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_iter\_**int
The actual number of iterations to reach the stopping criterion.
**t\_**int
Number of weight updates performed during training. Same as `(n_iter_ * n_samples)`.
See also
[`SGDRegressor`](sklearn.linear_model.sgdregressor#sklearn.linear_model.SGDRegressor "sklearn.linear_model.SGDRegressor")
Linear model fitted by minimizing a regularized empirical loss with SGD.
#### References
Online Passive-Aggressive Algorithms <<http://jmlr.csail.mit.edu/papers/volume7/crammer06a/crammer06a.pdf>> K. Crammer, O. Dekel, J. Keshat, S. Shalev-Shwartz, Y. Singer - JMLR (2006).
#### Examples
```
>>> from sklearn.linear_model import PassiveAggressiveRegressor
>>> from sklearn.datasets import make_regression
```
```
>>> X, y = make_regression(n_features=4, random_state=0)
>>> regr = PassiveAggressiveRegressor(max_iter=100, random_state=0,
... tol=1e-3)
>>> regr.fit(X, y)
PassiveAggressiveRegressor(max_iter=100, random_state=0)
>>> print(regr.coef_)
[20.48736655 34.18818427 67.59122734 87.94731329]
>>> print(regr.intercept_)
[-0.02306214]
>>> print(regr.predict([[0, 0, 0, 0]]))
[-0.02306214]
```
scikit_learn sklearn.preprocessing.MaxAbsScaler sklearn.preprocessing.MaxAbsScaler
==================================
*class*sklearn.preprocessing.MaxAbsScaler(*\**, *copy=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L1044)
Scale each feature by its maximum absolute value.
This estimator scales and translates each feature individually such that the maximal absolute value of each feature in the training set will be 1.0. It does not shift/center the data, and thus does not destroy any sparsity.
This scaler can also be applied to sparse CSR or CSC matrices.
New in version 0.17.
Parameters:
**copy**bool, default=True
Set to False to perform inplace scaling and avoid a copy (if the input is already a numpy array).
Attributes:
**scale\_**ndarray of shape (n\_features,)
Per feature relative scaling of the data.
New in version 0.17: *scale\_* attribute.
**max\_abs\_**ndarray of shape (n\_features,)
Per feature maximum absolute value.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_samples\_seen\_**int
The number of samples processed by the estimator. Will be reset on new calls to fit, but increments across `partial_fit` calls.
See also
[`maxabs_scale`](sklearn.preprocessing.maxabs_scale#sklearn.preprocessing.maxabs_scale "sklearn.preprocessing.maxabs_scale")
Equivalent function without the estimator API.
#### Notes
NaNs are treated as missing values: disregarded in fit, and maintained in transform.
For a comparison of the different scalers, transformers, and normalizers, see [examples/preprocessing/plot\_all\_scaling.py](../../auto_examples/preprocessing/plot_all_scaling#sphx-glr-auto-examples-preprocessing-plot-all-scaling-py).
#### Examples
```
>>> from sklearn.preprocessing import MaxAbsScaler
>>> X = [[ 1., -1., 2.],
... [ 2., 0., 0.],
... [ 0., 1., -1.]]
>>> transformer = MaxAbsScaler().fit(X)
>>> transformer
MaxAbsScaler()
>>> transformer.transform(X)
array([[ 0.5, -1. , 1. ],
[ 1. , 0. , 0. ],
[ 0. , 1. , -0.5]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.preprocessing.MaxAbsScaler.fit "sklearn.preprocessing.MaxAbsScaler.fit")(X[, y]) | Compute the maximum absolute value to be used for later scaling. |
| [`fit_transform`](#sklearn.preprocessing.MaxAbsScaler.fit_transform "sklearn.preprocessing.MaxAbsScaler.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.preprocessing.MaxAbsScaler.get_feature_names_out "sklearn.preprocessing.MaxAbsScaler.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.preprocessing.MaxAbsScaler.get_params "sklearn.preprocessing.MaxAbsScaler.get_params")([deep]) | Get parameters for this estimator. |
| [`inverse_transform`](#sklearn.preprocessing.MaxAbsScaler.inverse_transform "sklearn.preprocessing.MaxAbsScaler.inverse_transform")(X) | Scale back the data to the original representation. |
| [`partial_fit`](#sklearn.preprocessing.MaxAbsScaler.partial_fit "sklearn.preprocessing.MaxAbsScaler.partial_fit")(X[, y]) | Online computation of max absolute value of X for later scaling. |
| [`set_params`](#sklearn.preprocessing.MaxAbsScaler.set_params "sklearn.preprocessing.MaxAbsScaler.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.preprocessing.MaxAbsScaler.transform "sklearn.preprocessing.MaxAbsScaler.transform")(X) | Scale the data. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L1131)
Compute the maximum absolute value to be used for later scaling.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data used to compute the per-feature minimum and maximum used for later scaling along the features axis.
**y**None
Ignored.
Returns:
**self**object
Fitted scaler.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L880)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Input features.
* If `input_features` is `None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then the following input feature names are generated: `["x0", "x1", ..., "x(n_features_in_ - 1)"]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Same as input features.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
inverse\_transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L1227)
Scale back the data to the original representation.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data that should be transformed back.
Returns:
**X\_tr**{ndarray, sparse matrix} of shape (n\_samples, n\_features)
Transformed array.
partial\_fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L1152)
Online computation of max absolute value of X for later scaling.
All of X is processed as a single batch. This is intended for cases when [`fit`](#sklearn.preprocessing.MaxAbsScaler.fit "sklearn.preprocessing.MaxAbsScaler.fit") is not feasible due to very large number of `n_samples` or because X is read from a continuous stream.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data used to compute the mean and standard deviation used for later scaling along the features axis.
**y**None
Ignored.
Returns:
**self**object
Fitted scaler.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L1198)
Scale the data.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data that should be scaled.
Returns:
**X\_tr**{ndarray, sparse matrix} of shape (n\_samples, n\_features)
Transformed array.
Examples using `sklearn.preprocessing.MaxAbsScaler`
---------------------------------------------------
[Compare the effect of different scalers on data with outliers](../../auto_examples/preprocessing/plot_all_scaling#sphx-glr-auto-examples-preprocessing-plot-all-scaling-py)
scikit_learn sklearn.datasets.make_low_rank_matrix sklearn.datasets.make\_low\_rank\_matrix
========================================
sklearn.datasets.make\_low\_rank\_matrix(*n\_samples=100*, *n\_features=100*, *\**, *effective\_rank=10*, *tail\_strength=0.5*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_samples_generator.py#L1160)
Generate a mostly low rank matrix with bell-shaped singular values.
Most of the variance can be explained by a bell-shaped curve of width effective\_rank: the low rank part of the singular values profile is:
```
(1 - tail_strength) * exp(-1.0 * (i / effective_rank) ** 2)
```
The remaining singular values’ tail is fat, decreasing as:
```
tail_strength * exp(-0.1 * i / effective_rank).
```
The low rank part of the profile can be considered the structured signal part of the data while the tail can be considered the noisy part of the data that cannot be summarized by a low number of linear components (singular vectors).
This kind of singular profiles is often seen in practice, for instance:
* gray level pictures of faces
* TF-IDF vectors of text documents crawled from the web
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/sample_generators.html#sample-generators).
Parameters:
**n\_samples**int, default=100
The number of samples.
**n\_features**int, default=100
The number of features.
**effective\_rank**int, default=10
The approximate number of singular vectors required to explain most of the data by linear combinations.
**tail\_strength**float, default=0.5
The relative importance of the fat noisy tail of the singular values profile. The value should be between 0 and 1.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for dataset creation. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Returns:
**X**ndarray of shape (n\_samples, n\_features)
The matrix.
scikit_learn sklearn.metrics.pairwise_distances sklearn.metrics.pairwise\_distances
===================================
sklearn.metrics.pairwise\_distances(*X*, *Y=None*, *metric='euclidean'*, *\**, *n\_jobs=None*, *force\_all\_finite=True*, *\*\*kwds*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/pairwise.py#L1864)
Compute the distance matrix from a vector array X and optional Y.
This method takes either a vector array or a distance matrix, and returns a distance matrix. If the input is a vector array, the distances are computed. If the input is a distances matrix, it is returned instead.
This method provides a safe way to take a distance matrix as input, while preserving compatibility with many other algorithms that take a vector array.
If Y is given (default is None), then the returned matrix is the pairwise distance between the arrays from both X and Y.
Valid values for metric are:
* From scikit-learn: [‘cityblock’, ‘cosine’, ‘euclidean’, ‘l1’, ‘l2’, ‘manhattan’]. These metrics support sparse matrix inputs. [‘nan\_euclidean’] but it does not yet support sparse matrices.
* From scipy.spatial.distance: [‘braycurtis’, ‘canberra’, ‘chebyshev’, ‘correlation’, ‘dice’, ‘hamming’, ‘jaccard’, ‘kulsinski’, ‘mahalanobis’, ‘minkowski’, ‘rogerstanimoto’, ‘russellrao’, ‘seuclidean’, ‘sokalmichener’, ‘sokalsneath’, ‘sqeuclidean’, ‘yule’] See the documentation for scipy.spatial.distance for details on these metrics. These metrics do not support sparse matrix inputs.
Note that in the case of ‘cityblock’, ‘cosine’ and ‘euclidean’ (which are valid scipy.spatial.distance metrics), the scikit-learn implementation will be used, which is faster and has support for sparse matrices (except for ‘cityblock’). For a verbose description of the metrics from scikit-learn, see [`sklearn.metrics.pairwise.distance_metrics`](sklearn.metrics.pairwise.distance_metrics#sklearn.metrics.pairwise.distance_metrics "sklearn.metrics.pairwise.distance_metrics") function.
Read more in the [User Guide](../metrics#metrics).
Parameters:
**X**ndarray of shape (n\_samples\_X, n\_samples\_X) or (n\_samples\_X, n\_features)
Array of pairwise distances between samples, or a feature array. The shape of the array should be (n\_samples\_X, n\_samples\_X) if metric == “precomputed” and (n\_samples\_X, n\_features) otherwise.
**Y**ndarray of shape (n\_samples\_Y, n\_features), default=None
An optional second feature array. Only allowed if metric != “precomputed”.
**metric**str or callable, default=’euclidean’
The metric to use when calculating distance between instances in a feature array. If metric is a string, it must be one of the options allowed by scipy.spatial.distance.pdist for its metric parameter, or a metric listed in `pairwise.PAIRWISE_DISTANCE_FUNCTIONS`. If metric is “precomputed”, X is assumed to be a distance matrix. Alternatively, if metric is a callable function, it is called on each pair of instances (rows) and the resulting value recorded. The callable should take two arrays from X as input and return a value indicating the distance between them.
**n\_jobs**int, default=None
The number of jobs to use for the computation. This works by breaking down the pairwise matrix into n\_jobs even slices and computing them in parallel.
`None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**force\_all\_finite**bool or ‘allow-nan’, default=True
Whether to raise an error on np.inf, np.nan, pd.NA in array. Ignored for a metric listed in `pairwise.PAIRWISE_DISTANCE_FUNCTIONS`. The possibilities are:
* True: Force all values of array to be finite.
* False: accepts np.inf, np.nan, pd.NA in array.
* ‘allow-nan’: accepts only np.nan and pd.NA values in array. Values cannot be infinite.
New in version 0.22: `force_all_finite` accepts the string `'allow-nan'`.
Changed in version 0.23: Accepts `pd.NA` and converts it into `np.nan`.
**\*\*kwds**optional keyword parameters
Any further parameters are passed directly to the distance function. If using a scipy.spatial.distance metric, the parameters are still metric dependent. See the scipy docs for usage examples.
Returns:
**D**ndarray of shape (n\_samples\_X, n\_samples\_X) or (n\_samples\_X, n\_samples\_Y)
A distance matrix D such that D\_{i, j} is the distance between the ith and jth vectors of the given matrix X, if Y is None. If Y is not None, then D\_{i, j} is the distance between the ith array from X and the jth array from Y.
See also
[`pairwise_distances_chunked`](sklearn.metrics.pairwise_distances_chunked#sklearn.metrics.pairwise_distances_chunked "sklearn.metrics.pairwise_distances_chunked")
Performs the same calculation as this function, but returns a generator of chunks of the distance matrix, in order to limit memory usage.
`paired_distances`
Computes the distances between corresponding elements of two arrays.
Examples using `sklearn.metrics.pairwise_distances`
---------------------------------------------------
[Agglomerative clustering with different metrics](../../auto_examples/cluster/plot_agglomerative_clustering_metrics#sphx-glr-auto-examples-cluster-plot-agglomerative-clustering-metrics-py)
| programming_docs |
scikit_learn sklearn.cluster.dbscan sklearn.cluster.dbscan
======================
sklearn.cluster.dbscan(*X*, *eps=0.5*, *\**, *min\_samples=5*, *metric='minkowski'*, *metric\_params=None*, *algorithm='auto'*, *leaf\_size=30*, *p=2*, *sample\_weight=None*, *n\_jobs=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_dbscan.py#L24)
Perform DBSCAN clustering from vector array or distance matrix.
Read more in the [User Guide](../clustering#dbscan).
Parameters:
**X**{array-like, sparse (CSR) matrix} of shape (n\_samples, n\_features) or (n\_samples, n\_samples)
A feature array, or array of distances between samples if `metric='precomputed'`.
**eps**float, default=0.5
The maximum distance between two samples for one to be considered as in the neighborhood of the other. This is not a maximum bound on the distances of points within a cluster. This is the most important DBSCAN parameter to choose appropriately for your data set and distance function.
**min\_samples**int, default=5
The number of samples (or total weight) in a neighborhood for a point to be considered as a core point. This includes the point itself.
**metric**str or callable, default=’minkowski’
The metric to use when calculating distance between instances in a feature array. If metric is a string or callable, it must be one of the options allowed by [`sklearn.metrics.pairwise_distances`](sklearn.metrics.pairwise_distances#sklearn.metrics.pairwise_distances "sklearn.metrics.pairwise_distances") for its metric parameter. If metric is “precomputed”, X is assumed to be a distance matrix and must be square during fit. X may be a [sparse graph](https://scikit-learn.org/1.1/glossary.html#term-sparse-graph), in which case only “nonzero” elements may be considered neighbors.
**metric\_params**dict, default=None
Additional keyword arguments for the metric function.
New in version 0.19.
**algorithm**{‘auto’, ‘ball\_tree’, ‘kd\_tree’, ‘brute’}, default=’auto’
The algorithm to be used by the NearestNeighbors module to compute pointwise distances and find nearest neighbors. See NearestNeighbors module documentation for details.
**leaf\_size**int, default=30
Leaf size passed to BallTree or cKDTree. This can affect the speed of the construction and query, as well as the memory required to store the tree. The optimal value depends on the nature of the problem.
**p**float, default=2
The power of the Minkowski metric to be used to calculate distance between points.
**sample\_weight**array-like of shape (n\_samples,), default=None
Weight of each sample, such that a sample with a weight of at least `min_samples` is by itself a core sample; a sample with negative weight may inhibit its eps-neighbor from being core. Note that weights are absolute, and default to 1.
**n\_jobs**int, default=None
The number of parallel jobs to run for neighbors search. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details. If precomputed distance are used, parallel execution is not available and thus n\_jobs will have no effect.
Returns:
**core\_samples**ndarray of shape (n\_core\_samples,)
Indices of core samples.
**labels**ndarray of shape (n\_samples,)
Cluster labels for each point. Noisy samples are given the label -1.
See also
[`DBSCAN`](sklearn.cluster.dbscan#sklearn.cluster.DBSCAN "sklearn.cluster.DBSCAN")
An estimator interface for this clustering algorithm.
[`OPTICS`](sklearn.cluster.optics#sklearn.cluster.OPTICS "sklearn.cluster.OPTICS")
A similar estimator interface clustering at multiple values of eps. Our implementation is optimized for memory usage.
#### Notes
For an example, see [examples/cluster/plot\_dbscan.py](../../auto_examples/cluster/plot_dbscan#sphx-glr-auto-examples-cluster-plot-dbscan-py).
This implementation bulk-computes all neighborhood queries, which increases the memory complexity to O(n.d) where d is the average number of neighbors, while original DBSCAN had memory complexity O(n). It may attract a higher memory complexity when querying these nearest neighborhoods, depending on the `algorithm`.
One way to avoid the query complexity is to pre-compute sparse neighborhoods in chunks using [`NearestNeighbors.radius_neighbors_graph`](sklearn.neighbors.nearestneighbors#sklearn.neighbors.NearestNeighbors.radius_neighbors_graph "sklearn.neighbors.NearestNeighbors.radius_neighbors_graph") with `mode='distance'`, then using `metric='precomputed'` here.
Another way to reduce memory and computation time is to remove (near-)duplicate points and use `sample_weight` instead.
`cluster.optics` provides a similar clustering with lower memory usage.
#### References
Ester, M., H. P. Kriegel, J. Sander, and X. Xu, “A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise”. In: Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, Portland, OR, AAAI Press, pp. 226-231. 1996
Schubert, E., Sander, J., Ester, M., Kriegel, H. P., & Xu, X. (2017). DBSCAN revisited, revisited: why and how you should (still) use DBSCAN. ACM Transactions on Database Systems (TODS), 42(3), 19.
scikit_learn sklearn.model_selection.PredefinedSplit sklearn.model\_selection.PredefinedSplit
========================================
*class*sklearn.model\_selection.PredefinedSplit(*test\_fold*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L2135)
Predefined split cross-validator
Provides train/test indices to split data into train/test sets using a predefined scheme specified by the user with the `test_fold` parameter.
Read more in the [User Guide](../cross_validation#predefined-split).
New in version 0.16.
Parameters:
**test\_fold**array-like of shape (n\_samples,)
The entry `test_fold[i]` represents the index of the test set that sample `i` belongs to. It is possible to exclude sample `i` from any test set (i.e. include sample `i` in every training set) by setting `test_fold[i]` equal to -1.
#### Examples
```
>>> import numpy as np
>>> from sklearn.model_selection import PredefinedSplit
>>> X = np.array([[1, 2], [3, 4], [1, 2], [3, 4]])
>>> y = np.array([0, 0, 1, 1])
>>> test_fold = [0, 1, -1, 1]
>>> ps = PredefinedSplit(test_fold)
>>> ps.get_n_splits()
2
>>> print(ps)
PredefinedSplit(test_fold=array([ 0, 1, -1, 1]))
>>> for train_index, test_index in ps.split():
... print("TRAIN:", train_index, "TEST:", test_index)
... X_train, X_test = X[train_index], X[test_index]
... y_train, y_test = y[train_index], y[test_index]
TRAIN: [1 2 3] TEST: [0]
TRAIN: [0 2] TEST: [1 3]
```
#### Methods
| | |
| --- | --- |
| [`get_n_splits`](#sklearn.model_selection.PredefinedSplit.get_n_splits "sklearn.model_selection.PredefinedSplit.get_n_splits")([X, y, groups]) | Returns the number of splitting iterations in the cross-validator |
| [`split`](#sklearn.model_selection.PredefinedSplit.split "sklearn.model_selection.PredefinedSplit.split")([X, y, groups]) | Generate indices to split data into training and test set. |
get\_n\_splits(*X=None*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L2215)
Returns the number of splitting iterations in the cross-validator
Parameters:
**X**object
Always ignored, exists for compatibility.
**y**object
Always ignored, exists for compatibility.
**groups**object
Always ignored, exists for compatibility.
Returns:
**n\_splits**int
Returns the number of splitting iterations in the cross-validator.
split(*X=None*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L2179)
Generate indices to split data into training and test set.
Parameters:
**X**object
Always ignored, exists for compatibility.
**y**object
Always ignored, exists for compatibility.
**groups**object
Always ignored, exists for compatibility.
Yields:
**train**ndarray
The training set indices for that split.
**test**ndarray
The testing set indices for that split.
scikit_learn sklearn.ensemble.HistGradientBoostingRegressor sklearn.ensemble.HistGradientBoostingRegressor
==============================================
*class*sklearn.ensemble.HistGradientBoostingRegressor(*loss='squared\_error'*, *\**, *quantile=None*, *learning\_rate=0.1*, *max\_iter=100*, *max\_leaf\_nodes=31*, *max\_depth=None*, *min\_samples\_leaf=20*, *l2\_regularization=0.0*, *max\_bins=255*, *categorical\_features=None*, *monotonic\_cst=None*, *warm\_start=False*, *early\_stopping='auto'*, *scoring='loss'*, *validation\_fraction=0.1*, *n\_iter\_no\_change=10*, *tol=1e-07*, *verbose=0*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_hist_gradient_boosting/gradient_boosting.py#L1099)
Histogram-based Gradient Boosting Regression Tree.
This estimator is much faster than [`GradientBoostingRegressor`](sklearn.ensemble.gradientboostingregressor#sklearn.ensemble.GradientBoostingRegressor "sklearn.ensemble.GradientBoostingRegressor") for big datasets (n\_samples >= 10 000).
This estimator has native support for missing values (NaNs). During training, the tree grower learns at each split point whether samples with missing values should go to the left or right child, based on the potential gain. When predicting, samples with missing values are assigned to the left or right child consequently. If no missing values were encountered for a given feature during training, then samples with missing values are mapped to whichever child has the most samples.
This implementation is inspired by [LightGBM](https://github.com/Microsoft/LightGBM).
Read more in the [User Guide](../ensemble#histogram-based-gradient-boosting).
New in version 0.21.
Parameters:
**loss**{‘squared\_error’, ‘absolute\_error’, ‘poisson’, ‘quantile’}, default=’squared\_error’
The loss function to use in the boosting process. Note that the “squared error” and “poisson” losses actually implement “half least squares loss” and “half poisson deviance” to simplify the computation of the gradient. Furthermore, “poisson” loss internally uses a log-link and requires `y >= 0`. “quantile” uses the pinball loss.
Changed in version 0.23: Added option ‘poisson’.
Changed in version 1.1: Added option ‘quantile’.
Deprecated since version 1.0: The loss ‘least\_squares’ was deprecated in v1.0 and will be removed in version 1.2. Use `loss='squared_error'` which is equivalent.
Deprecated since version 1.0: The loss ‘least\_absolute\_deviation’ was deprecated in v1.0 and will be removed in version 1.2. Use `loss='absolute_error'` which is equivalent.
**quantile**float, default=None
If loss is “quantile”, this parameter specifies which quantile to be estimated and must be between 0 and 1.
**learning\_rate**float, default=0.1
The learning rate, also known as *shrinkage*. This is used as a multiplicative factor for the leaves values. Use `1` for no shrinkage.
**max\_iter**int, default=100
The maximum number of iterations of the boosting process, i.e. the maximum number of trees.
**max\_leaf\_nodes**int or None, default=31
The maximum number of leaves for each tree. Must be strictly greater than 1. If None, there is no maximum limit.
**max\_depth**int or None, default=None
The maximum depth of each tree. The depth of a tree is the number of edges to go from the root to the deepest leaf. Depth isn’t constrained by default.
**min\_samples\_leaf**int, default=20
The minimum number of samples per leaf. For small datasets with less than a few hundred samples, it is recommended to lower this value since only very shallow trees would be built.
**l2\_regularization**float, default=0
The L2 regularization parameter. Use `0` for no regularization (default).
**max\_bins**int, default=255
The maximum number of bins to use for non-missing values. Before training, each feature of the input array `X` is binned into integer-valued bins, which allows for a much faster training stage. Features with a small number of unique values may use less than `max_bins` bins. In addition to the `max_bins` bins, one more bin is always reserved for missing values. Must be no larger than 255.
**categorical\_features**array-like of {bool, int} of shape (n\_features) or shape (n\_categorical\_features,), default=None
Indicates the categorical features.
* None : no feature will be considered categorical.
* boolean array-like : boolean mask indicating categorical features.
* integer array-like : integer indices indicating categorical features.
For each categorical feature, there must be at most `max_bins` unique categories, and each categorical value must be in [0, max\_bins -1].
Read more in the [User Guide](../ensemble#categorical-support-gbdt).
New in version 0.24.
**monotonic\_cst**array-like of int of shape (n\_features), default=None
Indicates the monotonic constraint to enforce on each feature. -1, 1 and 0 respectively correspond to a negative constraint, positive constraint and no constraint. Read more in the [User Guide](../ensemble#monotonic-cst-gbdt).
New in version 0.23.
**warm\_start**bool, default=False
When set to `True`, reuse the solution of the previous call to fit and add more estimators to the ensemble. For results to be valid, the estimator should be re-trained on the same data only. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
**early\_stopping**‘auto’ or bool, default=’auto’
If ‘auto’, early stopping is enabled if the sample size is larger than 10000. If True, early stopping is enabled, otherwise early stopping is disabled.
New in version 0.23.
**scoring**str or callable or None, default=’loss’
Scoring parameter to use for early stopping. It can be a single string (see [The scoring parameter: defining model evaluation rules](../model_evaluation#scoring-parameter)) or a callable (see [Defining your scoring strategy from metric functions](../model_evaluation#scoring)). If None, the estimator’s default scorer is used. If `scoring='loss'`, early stopping is checked w.r.t the loss value. Only used if early stopping is performed.
**validation\_fraction**int or float or None, default=0.1
Proportion (or absolute size) of training data to set aside as validation data for early stopping. If None, early stopping is done on the training data. Only used if early stopping is performed.
**n\_iter\_no\_change**int, default=10
Used to determine when to “early stop”. The fitting process is stopped when none of the last `n_iter_no_change` scores are better than the `n_iter_no_change - 1` -th-to-last one, up to some tolerance. Only used if early stopping is performed.
**tol**float, default=1e-7
The absolute tolerance to use when comparing scores during early stopping. The higher the tolerance, the more likely we are to early stop: higher tolerance means that it will be harder for subsequent iterations to be considered an improvement upon the reference score.
**verbose**int, default=0
The verbosity level. If not zero, print some information about the fitting process.
**random\_state**int, RandomState instance or None, default=None
Pseudo-random number generator to control the subsampling in the binning process, and the train/validation data split if early stopping is enabled. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Attributes:
**do\_early\_stopping\_**bool
Indicates whether early stopping is used during training.
[`n_iter_`](#sklearn.ensemble.HistGradientBoostingRegressor.n_iter_ "sklearn.ensemble.HistGradientBoostingRegressor.n_iter_")int
Number of iterations of the boosting process.
**n\_trees\_per\_iteration\_**int
The number of tree that are built at each iteration. For regressors, this is always 1.
**train\_score\_**ndarray, shape (n\_iter\_+1,)
The scores at each iteration on the training data. The first entry is the score of the ensemble before the first iteration. Scores are computed according to the `scoring` parameter. If `scoring` is not ‘loss’, scores are computed on a subset of at most 10 000 samples. Empty if no early stopping.
**validation\_score\_**ndarray, shape (n\_iter\_+1,)
The scores at each iteration on the held-out validation data. The first entry is the score of the ensemble before the first iteration. Scores are computed according to the `scoring` parameter. Empty if no early stopping or if `validation_fraction` is None.
**is\_categorical\_**ndarray, shape (n\_features, ) or None
Boolean mask for the categorical features. `None` if there are no categorical features.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`GradientBoostingRegressor`](sklearn.ensemble.gradientboostingregressor#sklearn.ensemble.GradientBoostingRegressor "sklearn.ensemble.GradientBoostingRegressor")
Exact gradient boosting method that does not scale as good on datasets with a large number of samples.
[`sklearn.tree.DecisionTreeRegressor`](sklearn.tree.decisiontreeregressor#sklearn.tree.DecisionTreeRegressor "sklearn.tree.DecisionTreeRegressor")
A decision tree regressor.
[`RandomForestRegressor`](sklearn.ensemble.randomforestregressor#sklearn.ensemble.RandomForestRegressor "sklearn.ensemble.RandomForestRegressor")
A meta-estimator that fits a number of decision tree regressors on various sub-samples of the dataset and uses averaging to improve the statistical performance and control over-fitting.
[`AdaBoostRegressor`](sklearn.ensemble.adaboostregressor#sklearn.ensemble.AdaBoostRegressor "sklearn.ensemble.AdaBoostRegressor")
A meta-estimator that begins by fitting a regressor on the original dataset and then fits additional copies of the regressor on the same dataset but where the weights of instances are adjusted according to the error of the current prediction. As such, subsequent regressors focus more on difficult cases.
#### Examples
```
>>> from sklearn.ensemble import HistGradientBoostingRegressor
>>> from sklearn.datasets import load_diabetes
>>> X, y = load_diabetes(return_X_y=True)
>>> est = HistGradientBoostingRegressor().fit(X, y)
>>> est.score(X, y)
0.92...
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.ensemble.HistGradientBoostingRegressor.fit "sklearn.ensemble.HistGradientBoostingRegressor.fit")(X, y[, sample\_weight]) | Fit the gradient boosting model. |
| [`get_params`](#sklearn.ensemble.HistGradientBoostingRegressor.get_params "sklearn.ensemble.HistGradientBoostingRegressor.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.ensemble.HistGradientBoostingRegressor.predict "sklearn.ensemble.HistGradientBoostingRegressor.predict")(X) | Predict values for X. |
| [`score`](#sklearn.ensemble.HistGradientBoostingRegressor.score "sklearn.ensemble.HistGradientBoostingRegressor.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.ensemble.HistGradientBoostingRegressor.set_params "sklearn.ensemble.HistGradientBoostingRegressor.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`staged_predict`](#sklearn.ensemble.HistGradientBoostingRegressor.staged_predict "sklearn.ensemble.HistGradientBoostingRegressor.staged_predict")(X) | Predict regression target for each iteration. |
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_hist_gradient_boosting/gradient_boosting.py#L260)
Fit the gradient boosting model.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The input samples.
**y**array-like of shape (n\_samples,)
Target values.
**sample\_weight**array-like of shape (n\_samples,) default=None
Weights of training data.
New in version 0.23.
Returns:
**self**object
Fitted estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_iter\_
Number of iterations of the boosting process.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_hist_gradient_boosting/gradient_boosting.py#L1358)
Predict values for X.
Parameters:
**X**array-like, shape (n\_samples, n\_features)
The input samples.
Returns:
**y**ndarray, shape (n\_samples,)
The predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
staged\_predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_hist_gradient_boosting/gradient_boosting.py#L1376)
Predict regression target for each iteration.
This method allows monitoring (i.e. determine error on testing set) after each stage.
New in version 0.24.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The input samples.
Yields:
**y**generator of ndarray of shape (n\_samples,)
The predicted values of the input samples, for each iteration.
Examples using `sklearn.ensemble.HistGradientBoostingRegressor`
---------------------------------------------------------------
[Release Highlights for scikit-learn 1.1](../../auto_examples/release_highlights/plot_release_highlights_1_1_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-1-1-0-py)
[Release Highlights for scikit-learn 1.0](../../auto_examples/release_highlights/plot_release_highlights_1_0_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-1-0-0-py)
[Release Highlights for scikit-learn 0.24](../../auto_examples/release_highlights/plot_release_highlights_0_24_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-24-0-py)
[Release Highlights for scikit-learn 0.23](../../auto_examples/release_highlights/plot_release_highlights_0_23_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-23-0-py)
[Categorical Feature Support in Gradient Boosting](../../auto_examples/ensemble/plot_gradient_boosting_categorical#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-categorical-py)
[Combine predictors using stacking](../../auto_examples/ensemble/plot_stack_predictors#sphx-glr-auto-examples-ensemble-plot-stack-predictors-py)
[Gradient Boosting regression](../../auto_examples/ensemble/plot_gradient_boosting_regression#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-regression-py)
[Monotonic Constraints](../../auto_examples/ensemble/plot_monotonic_constraints#sphx-glr-auto-examples-ensemble-plot-monotonic-constraints-py)
[Prediction Intervals for Gradient Boosting Regression](../../auto_examples/ensemble/plot_gradient_boosting_quantile#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-quantile-py)
[Model Complexity Influence](../../auto_examples/applications/plot_model_complexity_influence#sphx-glr-auto-examples-applications-plot-model-complexity-influence-py)
[Time-related feature engineering](../../auto_examples/applications/plot_cyclical_feature_engineering#sphx-glr-auto-examples-applications-plot-cyclical-feature-engineering-py)
[Poisson regression and non-normal loss](../../auto_examples/linear_model/plot_poisson_regression_non_normal_loss#sphx-glr-auto-examples-linear-model-plot-poisson-regression-non-normal-loss-py)
[Partial Dependence and Individual Conditional Expectation Plots](../../auto_examples/inspection/plot_partial_dependence#sphx-glr-auto-examples-inspection-plot-partial-dependence-py)
| programming_docs |
scikit_learn sklearn.manifold.spectral_embedding sklearn.manifold.spectral\_embedding
====================================
sklearn.manifold.spectral\_embedding(*adjacency*, *\**, *n\_components=8*, *eigen\_solver=None*, *random\_state=None*, *eigen\_tol=0.0*, *norm\_laplacian=True*, *drop\_first=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_spectral_embedding.py#L142)
Project the sample on the first eigenvectors of the graph Laplacian.
The adjacency matrix is used to compute a normalized graph Laplacian whose spectrum (especially the eigenvectors associated to the smallest eigenvalues) has an interpretation in terms of minimal number of cuts necessary to split the graph into comparably sized components.
This embedding can also ‘work’ even if the `adjacency` variable is not strictly the adjacency matrix of a graph but more generally an affinity or similarity matrix between samples (for instance the heat kernel of a euclidean distance matrix or a k-NN matrix).
However care must taken to always make the affinity matrix symmetric so that the eigenvector decomposition works as expected.
Note : Laplacian Eigenmaps is the actual algorithm implemented here.
Read more in the [User Guide](../manifold#spectral-embedding).
Parameters:
**adjacency**{array-like, sparse graph} of shape (n\_samples, n\_samples)
The adjacency matrix of the graph to embed.
**n\_components**int, default=8
The dimension of the projection subspace.
**eigen\_solver**{‘arpack’, ‘lobpcg’, ‘amg’}, default=None
The eigenvalue decomposition strategy to use. AMG requires pyamg to be installed. It can be faster on very large, sparse problems, but may also lead to instabilities. If None, then `'arpack'` is used.
**random\_state**int, RandomState instance or None, default=None
A pseudo random number generator used for the initialization of the lobpcg eigen vectors decomposition when `eigen_solver ==
'amg'`, and for the K-Means initialization. Use an int to make the results deterministic across calls (See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state)).
Note
When using `eigen_solver == 'amg'`, it is necessary to also fix the global numpy seed with `np.random.seed(int)` to get deterministic results. See <https://github.com/pyamg/pyamg/issues/139> for further information.
**eigen\_tol**float, default=0.0
Stopping criterion for eigendecomposition of the Laplacian matrix when using arpack eigen\_solver.
**norm\_laplacian**bool, default=True
If True, then compute symmetric normalized Laplacian.
**drop\_first**bool, default=True
Whether to drop the first eigenvector. For spectral embedding, this should be True as the first eigenvector should be constant vector for connected graph, but for spectral clustering, this should be kept as False to retain the first eigenvector.
Returns:
**embedding**ndarray of shape (n\_samples, n\_components)
The reduced samples.
#### Notes
Spectral Embedding (Laplacian Eigenmaps) is most useful when the graph has one connected component. If there graph has many components, the first few eigenvectors will simply uncover the connected components of the graph.
#### References
* <https://en.wikipedia.org/wiki/LOBPCG>
* [“Toward the Optimal Preconditioned Eigensolver: Locally Optimal Block Preconditioned Conjugate Gradient Method”, Andrew V. Knyazev](https://doi.org/10.1137/S1064827500366124)
scikit_learn sklearn.covariance.ledoit_wolf sklearn.covariance.ledoit\_wolf
===============================
sklearn.covariance.ledoit\_wolf(*X*, *\**, *assume\_centered=False*, *block\_size=1000*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_shrunk_covariance.py#L283)
Estimate the shrunk Ledoit-Wolf covariance matrix.
Read more in the [User Guide](../covariance#shrunk-covariance).
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Data from which to compute the covariance estimate.
**assume\_centered**bool, default=False
If True, data will not be centered before computation. Useful to work with data whose mean is significantly equal to zero but is not exactly zero. If False, data will be centered before computation.
**block\_size**int, default=1000
Size of blocks into which the covariance matrix will be split. This is purely a memory optimization and does not affect results.
Returns:
**shrunk\_cov**ndarray of shape (n\_features, n\_features)
Shrunk covariance.
**shrinkage**float
Coefficient in the convex combination used for the computation of the shrunk estimate.
#### Notes
The regularized (shrunk) covariance is:
(1 - shrinkage) \* cov + shrinkage \* mu \* np.identity(n\_features)
where mu = trace(cov) / n\_features
Examples using `sklearn.covariance.ledoit_wolf`
-----------------------------------------------
[Sparse inverse covariance estimation](../../auto_examples/covariance/plot_sparse_cov#sphx-glr-auto-examples-covariance-plot-sparse-cov-py)
scikit_learn sklearn.linear_model.LogisticRegression sklearn.linear\_model.LogisticRegression
========================================
*class*sklearn.linear\_model.LogisticRegression(*penalty='l2'*, *\**, *dual=False*, *tol=0.0001*, *C=1.0*, *fit\_intercept=True*, *intercept\_scaling=1*, *class\_weight=None*, *random\_state=None*, *solver='lbfgs'*, *max\_iter=100*, *multi\_class='auto'*, *verbose=0*, *warm\_start=False*, *n\_jobs=None*, *l1\_ratio=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_logistic.py#L754)
Logistic Regression (aka logit, MaxEnt) classifier.
In the multiclass case, the training algorithm uses the one-vs-rest (OvR) scheme if the ‘multi\_class’ option is set to ‘ovr’, and uses the cross-entropy loss if the ‘multi\_class’ option is set to ‘multinomial’. (Currently the ‘multinomial’ option is supported only by the ‘lbfgs’, ‘sag’, ‘saga’ and ‘newton-cg’ solvers.)
This class implements regularized logistic regression using the ‘liblinear’ library, ‘newton-cg’, ‘sag’, ‘saga’ and ‘lbfgs’ solvers. **Note that regularization is applied by default**. It can handle both dense and sparse input. Use C-ordered arrays or CSR matrices containing 64-bit floats for optimal performance; any other input format will be converted (and copied).
The ‘newton-cg’, ‘sag’, and ‘lbfgs’ solvers support only L2 regularization with primal formulation, or no regularization. The ‘liblinear’ solver supports both L1 and L2 regularization, with a dual formulation only for the L2 penalty. The Elastic-Net regularization is only supported by the ‘saga’ solver.
Read more in the [User Guide](../linear_model#logistic-regression).
Parameters:
**penalty**{‘l1’, ‘l2’, ‘elasticnet’, ‘none’}, default=’l2’
Specify the norm of the penalty:
* `'none'`: no penalty is added;
* `'l2'`: add a L2 penalty term and it is the default choice;
* `'l1'`: add a L1 penalty term;
* `'elasticnet'`: both L1 and L2 penalty terms are added.
Warning
Some penalties may not work with some solvers. See the parameter `solver` below, to know the compatibility between the penalty and solver.
New in version 0.19: l1 penalty with SAGA solver (allowing ‘multinomial’ + L1)
**dual**bool, default=False
Dual or primal formulation. Dual formulation is only implemented for l2 penalty with liblinear solver. Prefer dual=False when n\_samples > n\_features.
**tol**float, default=1e-4
Tolerance for stopping criteria.
**C**float, default=1.0
Inverse of regularization strength; must be a positive float. Like in support vector machines, smaller values specify stronger regularization.
**fit\_intercept**bool, default=True
Specifies if a constant (a.k.a. bias or intercept) should be added to the decision function.
**intercept\_scaling**float, default=1
Useful only when the solver ‘liblinear’ is used and self.fit\_intercept is set to True. In this case, x becomes [x, self.intercept\_scaling], i.e. a “synthetic” feature with constant value equal to intercept\_scaling is appended to the instance vector. The intercept becomes `intercept_scaling * synthetic_feature_weight`.
Note! the synthetic feature weight is subject to l1/l2 regularization as all other features. To lessen the effect of regularization on synthetic feature weight (and therefore on the intercept) intercept\_scaling has to be increased.
**class\_weight**dict or ‘balanced’, default=None
Weights associated with classes in the form `{class_label: weight}`. If not given, all classes are supposed to have weight one.
The “balanced” mode uses the values of y to automatically adjust weights inversely proportional to class frequencies in the input data as `n_samples / (n_classes * np.bincount(y))`.
Note that these weights will be multiplied with sample\_weight (passed through the fit method) if sample\_weight is specified.
New in version 0.17: *class\_weight=’balanced’*
**random\_state**int, RandomState instance, default=None
Used when `solver` == ‘sag’, ‘saga’ or ‘liblinear’ to shuffle the data. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state) for details.
**solver**{‘newton-cg’, ‘lbfgs’, ‘liblinear’, ‘sag’, ‘saga’}, default=’lbfgs’
Algorithm to use in the optimization problem. Default is ‘lbfgs’. To choose a solver, you might want to consider the following aspects:
* For small datasets, ‘liblinear’ is a good choice, whereas ‘sag’ and ‘saga’ are faster for large ones;
* For multiclass problems, only ‘newton-cg’, ‘sag’, ‘saga’ and ‘lbfgs’ handle multinomial loss;
* ‘liblinear’ is limited to one-versus-rest schemes.
Warning
The choice of the algorithm depends on the penalty chosen: Supported penalties by solver:
* ‘newton-cg’ - [‘l2’, ‘none’]
* ‘lbfgs’ - [‘l2’, ‘none’]
* ‘liblinear’ - [‘l1’, ‘l2’]
* ‘sag’ - [‘l2’, ‘none’]
* ‘saga’ - [‘elasticnet’, ‘l1’, ‘l2’, ‘none’]
Note
‘sag’ and ‘saga’ fast convergence is only guaranteed on features with approximately the same scale. You can preprocess the data with a scaler from [`sklearn.preprocessing`](../classes#module-sklearn.preprocessing "sklearn.preprocessing").
See also
Refer to the User Guide for more information regarding [`LogisticRegression`](#sklearn.linear_model.LogisticRegression "sklearn.linear_model.LogisticRegression") and more specifically the [Table](../linear_model#logistic-regression) summarizing solver/penalty supports.
New in version 0.17: Stochastic Average Gradient descent solver.
New in version 0.19: SAGA solver.
Changed in version 0.22: The default solver changed from ‘liblinear’ to ‘lbfgs’ in 0.22.
**max\_iter**int, default=100
Maximum number of iterations taken for the solvers to converge.
**multi\_class**{‘auto’, ‘ovr’, ‘multinomial’}, default=’auto’
If the option chosen is ‘ovr’, then a binary problem is fit for each label. For ‘multinomial’ the loss minimised is the multinomial loss fit across the entire probability distribution, *even when the data is binary*. ‘multinomial’ is unavailable when solver=’liblinear’. ‘auto’ selects ‘ovr’ if the data is binary, or if solver=’liblinear’, and otherwise selects ‘multinomial’.
New in version 0.18: Stochastic Average Gradient descent solver for ‘multinomial’ case.
Changed in version 0.22: Default changed from ‘ovr’ to ‘auto’ in 0.22.
**verbose**int, default=0
For the liblinear and lbfgs solvers set verbose to any positive number for verbosity.
**warm\_start**bool, default=False
When set to True, reuse the solution of the previous call to fit as initialization, otherwise, just erase the previous solution. Useless for liblinear solver. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
New in version 0.17: *warm\_start* to support *lbfgs*, *newton-cg*, *sag*, *saga* solvers.
**n\_jobs**int, default=None
Number of CPU cores used when parallelizing over classes if multi\_class=’ovr’”. This parameter is ignored when the `solver` is set to ‘liblinear’ regardless of whether ‘multi\_class’ is specified or not. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**l1\_ratio**float, default=None
The Elastic-Net mixing parameter, with `0 <= l1_ratio <= 1`. Only used if `penalty='elasticnet'`. Setting `l1_ratio=0` is equivalent to using `penalty='l2'`, while setting `l1_ratio=1` is equivalent to using `penalty='l1'`. For `0 < l1_ratio <1`, the penalty is a combination of L1 and L2.
Attributes:
**classes\_**ndarray of shape (n\_classes, )
A list of class labels known to the classifier.
**coef\_**ndarray of shape (1, n\_features) or (n\_classes, n\_features)
Coefficient of the features in the decision function.
`coef_` is of shape (1, n\_features) when the given problem is binary. In particular, when `multi_class='multinomial'`, `coef_` corresponds to outcome 1 (True) and `-coef_` corresponds to outcome 0 (False).
**intercept\_**ndarray of shape (1,) or (n\_classes,)
Intercept (a.k.a. bias) added to the decision function.
If `fit_intercept` is set to False, the intercept is set to zero. `intercept_` is of shape (1,) when the given problem is binary. In particular, when `multi_class='multinomial'`, `intercept_` corresponds to outcome 1 (True) and `-intercept_` corresponds to outcome 0 (False).
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_iter\_**ndarray of shape (n\_classes,) or (1, )
Actual number of iterations for all classes. If binary or multinomial, it returns only 1 element. For liblinear solver, only the maximum number of iteration across all classes is given.
Changed in version 0.20: In SciPy <= 1.0.0 the number of lbfgs iterations may exceed `max_iter`. `n_iter_` will now report at most `max_iter`.
See also
[`SGDClassifier`](sklearn.linear_model.sgdclassifier#sklearn.linear_model.SGDClassifier "sklearn.linear_model.SGDClassifier")
Incrementally trained logistic regression (when given the parameter `loss="log"`).
[`LogisticRegressionCV`](sklearn.linear_model.logisticregressioncv#sklearn.linear_model.LogisticRegressionCV "sklearn.linear_model.LogisticRegressionCV")
Logistic regression with built-in cross validation.
#### Notes
The underlying C implementation uses a random number generator to select features when fitting the model. It is thus not uncommon, to have slightly different results for the same input data. If that happens, try with a smaller tol parameter.
Predict output may not match that of standalone liblinear in certain cases. See [differences from liblinear](../linear_model#liblinear-differences) in the narrative documentation.
#### References
L-BFGS-B – Software for Large-scale Bound-constrained Optimization
Ciyou Zhu, Richard Byrd, Jorge Nocedal and Jose Luis Morales. <http://users.iems.northwestern.edu/~nocedal/lbfgsb.html>
LIBLINEAR – A Library for Large Linear Classification
<https://www.csie.ntu.edu.tw/~cjlin/liblinear/>
SAG – Mark Schmidt, Nicolas Le Roux, and Francis Bach
Minimizing Finite Sums with the Stochastic Average Gradient <https://hal.inria.fr/hal-00860051/document>
SAGA – Defazio, A., Bach F. & Lacoste-Julien S. (2014).
[“SAGA: A Fast Incremental Gradient Method With Support for Non-Strongly Convex Composite Objectives”](https://arxiv.org/abs/1407.0202)
Hsiang-Fu Yu, Fang-Lan Huang, Chih-Jen Lin (2011). Dual coordinate descent
methods for logistic regression and maximum entropy models. Machine Learning 85(1-2):41-75. <https://www.csie.ntu.edu.tw/~cjlin/papers/maxent_dual.pdf>
#### Examples
```
>>> from sklearn.datasets import load_iris
>>> from sklearn.linear_model import LogisticRegression
>>> X, y = load_iris(return_X_y=True)
>>> clf = LogisticRegression(random_state=0).fit(X, y)
>>> clf.predict(X[:2, :])
array([0, 0])
>>> clf.predict_proba(X[:2, :])
array([[9.8...e-01, 1.8...e-02, 1.4...e-08],
[9.7...e-01, 2.8...e-02, ...e-08]])
>>> clf.score(X, y)
0.97...
```
#### Methods
| | |
| --- | --- |
| [`decision_function`](#sklearn.linear_model.LogisticRegression.decision_function "sklearn.linear_model.LogisticRegression.decision_function")(X) | Predict confidence scores for samples. |
| [`densify`](#sklearn.linear_model.LogisticRegression.densify "sklearn.linear_model.LogisticRegression.densify")() | Convert coefficient matrix to dense array format. |
| [`fit`](#sklearn.linear_model.LogisticRegression.fit "sklearn.linear_model.LogisticRegression.fit")(X, y[, sample\_weight]) | Fit the model according to the given training data. |
| [`get_params`](#sklearn.linear_model.LogisticRegression.get_params "sklearn.linear_model.LogisticRegression.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.linear_model.LogisticRegression.predict "sklearn.linear_model.LogisticRegression.predict")(X) | Predict class labels for samples in X. |
| [`predict_log_proba`](#sklearn.linear_model.LogisticRegression.predict_log_proba "sklearn.linear_model.LogisticRegression.predict_log_proba")(X) | Predict logarithm of probability estimates. |
| [`predict_proba`](#sklearn.linear_model.LogisticRegression.predict_proba "sklearn.linear_model.LogisticRegression.predict_proba")(X) | Probability estimates. |
| [`score`](#sklearn.linear_model.LogisticRegression.score "sklearn.linear_model.LogisticRegression.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.linear_model.LogisticRegression.set_params "sklearn.linear_model.LogisticRegression.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`sparsify`](#sklearn.linear_model.LogisticRegression.sparsify "sklearn.linear_model.LogisticRegression.sparsify")() | Convert coefficient matrix to sparse format. |
decision\_function(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L408)
Predict confidence scores for samples.
The confidence score for a sample is proportional to the signed distance of that sample to the hyperplane.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data matrix for which we want to get the confidence scores.
Returns:
**scores**ndarray of shape (n\_samples,) or (n\_samples, n\_classes)
Confidence scores per `(n_samples, n_classes)` combination. In the binary case, confidence score for `self.classes_[1]` where >0 means this class would be predicted.
densify()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L477)
Convert coefficient matrix to dense array format.
Converts the `coef_` member (back) to a numpy.ndarray. This is the default format of `coef_` and is required for fitting, so calling this method is only required on models that have previously been sparsified; otherwise, it is a no-op.
Returns:
self
Fitted estimator.
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_logistic.py#L1062)
Fit the model according to the given training data.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vector, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,)
Target vector relative to X.
**sample\_weight**array-like of shape (n\_samples,) default=None
Array of weights that are assigned to individual samples. If not provided, then each sample is given unit weight.
New in version 0.17: *sample\_weight* support to LogisticRegression.
Returns:
self
Fitted estimator.
#### Notes
The SAGA solver supports both float64 and float32 bit arrays.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L433)
Predict class labels for samples in X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data matrix for which we want to get the predictions.
Returns:
**y\_pred**ndarray of shape (n\_samples,)
Vector containing the class labels for each sample.
predict\_log\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_logistic.py#L1322)
Predict logarithm of probability estimates.
The returned estimates for all classes are ordered by the label of classes.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Vector to be scored, where `n_samples` is the number of samples and `n_features` is the number of features.
Returns:
**T**array-like of shape (n\_samples, n\_classes)
Returns the log-probability of the sample for each class in the model, where classes are ordered as they are in `self.classes_`.
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_logistic.py#L1278)
Probability estimates.
The returned estimates for all classes are ordered by the label of classes.
For a multi\_class problem, if multi\_class is set to be “multinomial” the softmax function is used to find the predicted probability of each class. Else use a one-vs-rest approach, i.e calculate the probability of each class assuming it to be positive using the logistic function. and normalize these values across all the classes.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Vector to be scored, where `n_samples` is the number of samples and `n_features` is the number of features.
Returns:
**T**array-like of shape (n\_samples, n\_classes)
Returns the probability of the sample for each class in the model, where classes are ordered as they are in `self.classes_`.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
sparsify()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L497)
Convert coefficient matrix to sparse format.
Converts the `coef_` member to a scipy.sparse matrix, which for L1-regularized models can be much more memory- and storage-efficient than the usual numpy.ndarray representation.
The `intercept_` member is not converted.
Returns:
self
Fitted estimator.
#### Notes
For non-sparse models, i.e. when there are not many zeros in `coef_`, this may actually *increase* memory usage, so use this method with care. A rule of thumb is that the number of zero elements, which can be computed with `(coef_ == 0).sum()`, must be more than 50% for this to provide significant benefits.
After calling this method, further fitting with the partial\_fit method (if any) will not work until you call densify.
Examples using `sklearn.linear_model.LogisticRegression`
--------------------------------------------------------
[Release Highlights for scikit-learn 1.1](../../auto_examples/release_highlights/plot_release_highlights_1_1_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-1-1-0-py)
[Release Highlights for scikit-learn 1.0](../../auto_examples/release_highlights/plot_release_highlights_1_0_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-1-0-0-py)
[Release Highlights for scikit-learn 0.24](../../auto_examples/release_highlights/plot_release_highlights_0_24_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-24-0-py)
[Release Highlights for scikit-learn 0.23](../../auto_examples/release_highlights/plot_release_highlights_0_23_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-23-0-py)
[Release Highlights for scikit-learn 0.22](../../auto_examples/release_highlights/plot_release_highlights_0_22_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-22-0-py)
[Comparison of Calibration of Classifiers](../../auto_examples/calibration/plot_compare_calibration#sphx-glr-auto-examples-calibration-plot-compare-calibration-py)
[Probability Calibration curves](../../auto_examples/calibration/plot_calibration_curve#sphx-glr-auto-examples-calibration-plot-calibration-curve-py)
[Plot classification probability](../../auto_examples/classification/plot_classification_probability#sphx-glr-auto-examples-classification-plot-classification-probability-py)
[Feature transformations with ensembles of trees](../../auto_examples/ensemble/plot_feature_transformation#sphx-glr-auto-examples-ensemble-plot-feature-transformation-py)
[Plot class probabilities calculated by the VotingClassifier](../../auto_examples/ensemble/plot_voting_probas#sphx-glr-auto-examples-ensemble-plot-voting-probas-py)
[Comparing various online solvers](../../auto_examples/linear_model/plot_sgd_comparison#sphx-glr-auto-examples-linear-model-plot-sgd-comparison-py)
[L1 Penalty and Sparsity in Logistic Regression](../../auto_examples/linear_model/plot_logistic_l1_l2_sparsity#sphx-glr-auto-examples-linear-model-plot-logistic-l1-l2-sparsity-py)
[Logistic Regression 3-class Classifier](../../auto_examples/linear_model/plot_iris_logistic#sphx-glr-auto-examples-linear-model-plot-iris-logistic-py)
[Logistic function](../../auto_examples/linear_model/plot_logistic#sphx-glr-auto-examples-linear-model-plot-logistic-py)
[MNIST classification using multinomial logistic + L1](../../auto_examples/linear_model/plot_sparse_logistic_regression_mnist#sphx-glr-auto-examples-linear-model-plot-sparse-logistic-regression-mnist-py)
[Multiclass sparse logistic regression on 20newgroups](../../auto_examples/linear_model/plot_sparse_logistic_regression_20newsgroups#sphx-glr-auto-examples-linear-model-plot-sparse-logistic-regression-20newsgroups-py)
[Plot multinomial and One-vs-Rest Logistic Regression](../../auto_examples/linear_model/plot_logistic_multinomial#sphx-glr-auto-examples-linear-model-plot-logistic-multinomial-py)
[Regularization path of L1- Logistic Regression](../../auto_examples/linear_model/plot_logistic_path#sphx-glr-auto-examples-linear-model-plot-logistic-path-py)
[Compact estimator representations](../../auto_examples/miscellaneous/plot_changed_only_pprint_parameter#sphx-glr-auto-examples-miscellaneous-plot-changed-only-pprint-parameter-py)
[Displaying Pipelines](../../auto_examples/miscellaneous/plot_pipeline_display#sphx-glr-auto-examples-miscellaneous-plot-pipeline-display-py)
[Visualizations with Display Objects](../../auto_examples/miscellaneous/plot_display_object_visualization#sphx-glr-auto-examples-miscellaneous-plot-display-object-visualization-py)
[Classifier Chain](../../auto_examples/multioutput/plot_classifier_chain_yeast#sphx-glr-auto-examples-multioutput-plot-classifier-chain-yeast-py)
[Restricted Boltzmann Machine features for digit classification](../../auto_examples/neural_networks/plot_rbm_logistic_classification#sphx-glr-auto-examples-neural-networks-plot-rbm-logistic-classification-py)
[Column Transformer with Mixed Types](../../auto_examples/compose/plot_column_transformer_mixed_types#sphx-glr-auto-examples-compose-plot-column-transformer-mixed-types-py)
[Pipelining: chaining a PCA and a logistic regression](../../auto_examples/compose/plot_digits_pipe#sphx-glr-auto-examples-compose-plot-digits-pipe-py)
[Feature discretization](../../auto_examples/preprocessing/plot_discretization_classification#sphx-glr-auto-examples-preprocessing-plot-discretization-classification-py)
[Digits Classification Exercise](../../auto_examples/exercises/plot_digits_classification_exercise#sphx-glr-auto-examples-exercises-plot-digits-classification-exercise-py)
[Classification of text documents using sparse features](../../auto_examples/text/plot_document_classification_20newsgroups#sphx-glr-auto-examples-text-plot-document-classification-20newsgroups-py)
| programming_docs |
scikit_learn sklearn.preprocessing.minmax_scale sklearn.preprocessing.minmax\_scale
===================================
sklearn.preprocessing.minmax\_scale(*X*, *feature\_range=(0, 1)*, *\**, *axis=0*, *copy=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L540)
Transform features by scaling each feature to a given range.
This estimator scales and translates each feature individually such that it is in the given range on the training set, i.e. between zero and one.
The transformation is given by (when `axis=0`):
```
X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
X_scaled = X_std * (max - min) + min
```
where min, max = feature\_range.
The transformation is calculated as (when `axis=0`):
```
X_scaled = scale * X + min - X.min(axis=0) * scale
where scale = (max - min) / (X.max(axis=0) - X.min(axis=0))
```
This transformation is often used as an alternative to zero mean, unit variance scaling.
Read more in the [User Guide](../preprocessing#preprocessing-scaler).
New in version 0.17: *minmax\_scale* function interface to [`MinMaxScaler`](sklearn.preprocessing.minmaxscaler#sklearn.preprocessing.MinMaxScaler "sklearn.preprocessing.MinMaxScaler").
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The data.
**feature\_range**tuple (min, max), default=(0, 1)
Desired range of transformed data.
**axis**int, default=0
Axis used to scale along. If 0, independently scale each feature, otherwise (if 1) scale each sample.
**copy**bool, default=True
Set to False to perform inplace scaling and avoid a copy (if the input is already a numpy array).
Returns:
**X\_tr**ndarray of shape (n\_samples, n\_features)
The transformed data.
Warning
Risk of data leak Do not use [`minmax_scale`](#sklearn.preprocessing.minmax_scale "sklearn.preprocessing.minmax_scale") unless you know what you are doing. A common mistake is to apply it to the entire data *before* splitting into training and test sets. This will bias the model evaluation because information would have leaked from the test set to the training set. In general, we recommend using [`MinMaxScaler`](sklearn.preprocessing.minmaxscaler#sklearn.preprocessing.MinMaxScaler "sklearn.preprocessing.MinMaxScaler") within a [Pipeline](../compose#pipeline) in order to prevent most risks of data leaking: `pipe = make_pipeline(MinMaxScaler(), LogisticRegression())`.
See also
[`MinMaxScaler`](sklearn.preprocessing.minmaxscaler#sklearn.preprocessing.MinMaxScaler "sklearn.preprocessing.MinMaxScaler")
Performs scaling to a given range using the Transformer API (e.g. as part of a preprocessing [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")).
#### Notes
For a comparison of the different scalers, transformers, and normalizers, see [examples/preprocessing/plot\_all\_scaling.py](../../auto_examples/preprocessing/plot_all_scaling#sphx-glr-auto-examples-preprocessing-plot-all-scaling-py).
Examples using `sklearn.preprocessing.minmax_scale`
---------------------------------------------------
[Restricted Boltzmann Machine features for digit classification](../../auto_examples/neural_networks/plot_rbm_logistic_classification#sphx-glr-auto-examples-neural-networks-plot-rbm-logistic-classification-py)
[Compare the effect of different scalers on data with outliers](../../auto_examples/preprocessing/plot_all_scaling#sphx-glr-auto-examples-preprocessing-plot-all-scaling-py)
scikit_learn sklearn.metrics.plot_det_curve sklearn.metrics.plot\_det\_curve
================================
sklearn.metrics.plot\_det\_curve(*estimator*, *X*, *y*, *\**, *sample\_weight=None*, *response\_method='auto'*, *name=None*, *ax=None*, *pos\_label=None*, *\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_plot/det_curve.py#L353)
DEPRECATED: Function plot\_det\_curve is deprecated in 1.0 and will be removed in 1.2. Use one of the class methods: DetCurveDisplay.from\_predictions or DetCurveDisplay.from\_estimator.
Plot detection error tradeoff (DET) curve.
Extra keyword arguments will be passed to matplotlib’s `plot`.
Read more in the [User Guide](https://scikit-learn.org/1.1/visualizations.html#visualizations).
New in version 0.24.
Deprecated since version 1.0: `plot_det_curve` is deprecated in 1.0 and will be removed in 1.2. Use one of the following class methods: [`from_predictions`](sklearn.metrics.detcurvedisplay#sklearn.metrics.DetCurveDisplay.from_predictions "sklearn.metrics.DetCurveDisplay.from_predictions") or [`from_estimator`](sklearn.metrics.detcurvedisplay#sklearn.metrics.DetCurveDisplay.from_estimator "sklearn.metrics.DetCurveDisplay.from_estimator").
Parameters:
**estimator**estimator instance
Fitted classifier or a fitted [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline") in which the last estimator is a classifier.
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Input values.
**y**array-like of shape (n\_samples,)
Target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**response\_method**{‘predict\_proba’, ‘decision\_function’, ‘auto’} default=’auto’
Specifies whether to use [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) or [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) as the predicted target response. If set to ‘auto’, [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) is tried first and if it does not exist [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) is tried next.
**name**str, default=None
Name of DET curve for labeling. If `None`, use the name of the estimator.
**ax**matplotlib axes, default=None
Axes object to plot on. If `None`, a new figure and axes is created.
**pos\_label**str or int, default=None
The label of the positive class. When `pos_label=None`, if `y_true` is in {-1, 1} or {0, 1}, `pos_label` is set to 1, otherwise an error will be raised.
**\*\*kwargs**dict
Additional keywords arguments passed to matplotlib `plot` function.
Returns:
**display**[`DetCurveDisplay`](sklearn.metrics.detcurvedisplay#sklearn.metrics.DetCurveDisplay "sklearn.metrics.DetCurveDisplay")
Object that stores computed values.
See also
[`det_curve`](sklearn.metrics.det_curve#sklearn.metrics.det_curve "sklearn.metrics.det_curve")
Compute error rates for different probability thresholds.
[`DetCurveDisplay`](sklearn.metrics.detcurvedisplay#sklearn.metrics.DetCurveDisplay "sklearn.metrics.DetCurveDisplay")
DET curve visualization.
[`DetCurveDisplay.from_estimator`](sklearn.metrics.detcurvedisplay#sklearn.metrics.DetCurveDisplay.from_estimator "sklearn.metrics.DetCurveDisplay.from_estimator")
Plot DET curve given an estimator and some data.
[`DetCurveDisplay.from_predictions`](sklearn.metrics.detcurvedisplay#sklearn.metrics.DetCurveDisplay.from_predictions "sklearn.metrics.DetCurveDisplay.from_predictions")
Plot DET curve given the true and predicted labels.
[`RocCurveDisplay.from_estimator`](sklearn.metrics.roccurvedisplay#sklearn.metrics.RocCurveDisplay.from_estimator "sklearn.metrics.RocCurveDisplay.from_estimator")
Plot Receiver Operating Characteristic (ROC) curve given an estimator and some data.
[`RocCurveDisplay.from_predictions`](sklearn.metrics.roccurvedisplay#sklearn.metrics.RocCurveDisplay.from_predictions "sklearn.metrics.RocCurveDisplay.from_predictions")
Plot Receiver Operating Characteristic (ROC) curve given the true and predicted values.
#### Examples
```
>>> import matplotlib.pyplot as plt
>>> from sklearn.datasets import make_classification
>>> from sklearn.metrics import plot_det_curve
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.svm import SVC
>>> X, y = make_classification(n_samples=1000, random_state=0)
>>> X_train, X_test, y_train, y_test = train_test_split(
... X, y, test_size=0.4, random_state=0)
>>> clf = SVC(random_state=0).fit(X_train, y_train)
>>> plot_det_curve(clf, X_test, y_test)
<...>
>>> plt.show()
```
scikit_learn sklearn.model_selection.ParameterSampler sklearn.model\_selection.ParameterSampler
=========================================
*class*sklearn.model\_selection.ParameterSampler(*param\_distributions*, *n\_iter*, *\**, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_search.py#L202)
Generator on parameters sampled from given distributions.
Non-deterministic iterable over random candidate combinations for hyper- parameter search. If all parameters are presented as a list, sampling without replacement is performed. If at least one parameter is given as a distribution, sampling with replacement is used. It is highly recommended to use continuous distributions for continuous parameters.
Read more in the [User Guide](../grid_search#grid-search).
Parameters:
**param\_distributions**dict
Dictionary with parameters names (`str`) as keys and distributions or lists of parameters to try. Distributions must provide a `rvs` method for sampling (such as those from scipy.stats.distributions). If a list is given, it is sampled uniformly. If a list of dicts is given, first a dict is sampled uniformly, and then a parameter is sampled using that dict as above.
**n\_iter**int
Number of parameter settings that are produced.
**random\_state**int, RandomState instance or None, default=None
Pseudo random number generator state used for random uniform sampling from lists of possible values instead of scipy.stats distributions. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Returns:
**params**dict of str to any
**Yields** dictionaries mapping each estimator parameter to as sampled value.
#### Examples
```
>>> from sklearn.model_selection import ParameterSampler
>>> from scipy.stats.distributions import expon
>>> import numpy as np
>>> rng = np.random.RandomState(0)
>>> param_grid = {'a':[1, 2], 'b': expon()}
>>> param_list = list(ParameterSampler(param_grid, n_iter=4,
... random_state=rng))
>>> rounded_list = [dict((k, round(v, 6)) for (k, v) in d.items())
... for d in param_list]
>>> rounded_list == [{'b': 0.89856, 'a': 1},
... {'b': 0.923223, 'a': 1},
... {'b': 1.878964, 'a': 2},
... {'b': 1.038159, 'a': 2}]
True
```
scikit_learn sklearn.inspection.PartialDependenceDisplay sklearn.inspection.PartialDependenceDisplay
===========================================
*class*sklearn.inspection.PartialDependenceDisplay(*pd\_results*, *\**, *features*, *feature\_names*, *target\_idx*, *deciles*, *pdp\_lim='deprecated'*, *kind='average'*, *subsample=1000*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/inspection/_plot/partial_dependence.py#L551)
Partial Dependence Plot (PDP).
This can also display individual partial dependencies which are often referred to as: Individual Condition Expectation (ICE).
It is recommended to use [`from_estimator`](#sklearn.inspection.PartialDependenceDisplay.from_estimator "sklearn.inspection.PartialDependenceDisplay.from_estimator") to create a [`PartialDependenceDisplay`](#sklearn.inspection.PartialDependenceDisplay "sklearn.inspection.PartialDependenceDisplay"). All parameters are stored as attributes.
Read more in [Advanced Plotting With Partial Dependence](../../auto_examples/miscellaneous/plot_partial_dependence_visualization_api#sphx-glr-auto-examples-miscellaneous-plot-partial-dependence-visualization-api-py) and the [User Guide](../partial_dependence#partial-dependence).
New in version 0.22.
Parameters:
**pd\_results**list of Bunch
Results of [`partial_dependence`](sklearn.inspection.partial_dependence#sklearn.inspection.partial_dependence "sklearn.inspection.partial_dependence") for `features`.
**features**list of (int,) or list of (int, int)
Indices of features for a given plot. A tuple of one integer will plot a partial dependence curve of one feature. A tuple of two integers will plot a two-way partial dependence curve as a contour plot.
**feature\_names**list of str
Feature names corresponding to the indices in `features`.
**target\_idx**int
* In a multiclass setting, specifies the class for which the PDPs should be computed. Note that for binary classification, the positive class (index 1) is always used.
* In a multioutput setting, specifies the task for which the PDPs should be computed.
Ignored in binary classification or classical regression settings.
**deciles**dict
Deciles for feature indices in `features`.
**pdp\_lim**dict or None
Global min and max average predictions, such that all plots will have the same scale and y limits. `pdp_lim[1]` is the global min and max for single partial dependence curves. `pdp_lim[2]` is the global min and max for two-way partial dependence curves. If `None`, the limit will be inferred from the global minimum and maximum of all predictions.
Deprecated since version 1.1: Pass the parameter `pdp_lim` to [`plot`](#sklearn.inspection.PartialDependenceDisplay.plot "sklearn.inspection.PartialDependenceDisplay.plot") instead. It will be removed in 1.3.
**kind**{‘average’, ‘individual’, ‘both’} or list of such str, default=’average’
Whether to plot the partial dependence averaged across all the samples in the dataset or one line per sample or both.
* `kind='average'` results in the traditional PD plot;
* `kind='individual'` results in the ICE plot;
* `kind='both'` results in plotting both the ICE and PD on the same plot.
A list of such strings can be provided to specify `kind` on a per-plot basis. The length of the list should be the same as the number of interaction requested in `features`.
Note
ICE (‘individual’ or ‘both’) is not a valid option for 2-ways interactions plot. As a result, an error will be raised. 2-ways interaction plots should always be configured to use the ‘average’ kind instead.
Note
The fast `method='recursion'` option is only available for `kind='average'`. Plotting individual dependencies requires using the slower `method='brute'` option.
New in version 0.24: Add `kind` parameter with `'average'`, `'individual'`, and `'both'` options.
New in version 1.1: Add the possibility to pass a list of string specifying `kind` for each plot.
**subsample**float, int or None, default=1000
Sampling for ICE curves when `kind` is ‘individual’ or ‘both’. If float, should be between 0.0 and 1.0 and represent the proportion of the dataset to be used to plot ICE curves. If int, represents the maximum absolute number of samples to use.
Note that the full dataset is still used to calculate partial dependence when `kind='both'`.
New in version 0.24.
**random\_state**int, RandomState instance or None, default=None
Controls the randomness of the selected samples when subsamples is not `None`. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state) for details.
New in version 0.24.
Attributes:
**bounding\_ax\_**matplotlib Axes or None
If `ax` is an axes or None, the `bounding_ax_` is the axes where the grid of partial dependence plots are drawn. If `ax` is a list of axes or a numpy array of axes, `bounding_ax_` is None.
**axes\_**ndarray of matplotlib Axes
If `ax` is an axes or None, `axes_[i, j]` is the axes on the i-th row and j-th column. If `ax` is a list of axes, `axes_[i]` is the i-th item in `ax`. Elements that are None correspond to a nonexisting axes in that position.
**lines\_**ndarray of matplotlib Artists
If `ax` is an axes or None, `lines_[i, j]` is the partial dependence curve on the i-th row and j-th column. If `ax` is a list of axes, `lines_[i]` is the partial dependence curve corresponding to the i-th item in `ax`. Elements that are None correspond to a nonexisting axes or an axes that does not include a line plot.
**deciles\_vlines\_**ndarray of matplotlib LineCollection
If `ax` is an axes or None, `vlines_[i, j]` is the line collection representing the x axis deciles of the i-th row and j-th column. If `ax` is a list of axes, `vlines_[i]` corresponds to the i-th item in `ax`. Elements that are None correspond to a nonexisting axes or an axes that does not include a PDP plot.
New in version 0.23.
**deciles\_hlines\_**ndarray of matplotlib LineCollection
If `ax` is an axes or None, `vlines_[i, j]` is the line collection representing the y axis deciles of the i-th row and j-th column. If `ax` is a list of axes, `vlines_[i]` corresponds to the i-th item in `ax`. Elements that are None correspond to a nonexisting axes or an axes that does not include a 2-way plot.
New in version 0.23.
**contours\_**ndarray of matplotlib Artists
If `ax` is an axes or None, `contours_[i, j]` is the partial dependence plot on the i-th row and j-th column. If `ax` is a list of axes, `contours_[i]` is the partial dependence plot corresponding to the i-th item in `ax`. Elements that are None correspond to a nonexisting axes or an axes that does not include a contour plot.
**figure\_**matplotlib Figure
Figure containing partial dependence plots.
See also
[`partial_dependence`](sklearn.inspection.partial_dependence#sklearn.inspection.partial_dependence "sklearn.inspection.partial_dependence")
Compute Partial Dependence values.
[`PartialDependenceDisplay.from_estimator`](#sklearn.inspection.PartialDependenceDisplay.from_estimator "sklearn.inspection.PartialDependenceDisplay.from_estimator")
Plot Partial Dependence.
#### Methods
| | |
| --- | --- |
| [`from_estimator`](#sklearn.inspection.PartialDependenceDisplay.from_estimator "sklearn.inspection.PartialDependenceDisplay.from_estimator")(estimator, X, features, \*[, ...]) | Partial dependence (PD) and individual conditional expectation (ICE) plots. |
| [`plot`](#sklearn.inspection.PartialDependenceDisplay.plot "sklearn.inspection.PartialDependenceDisplay.plot")(\*[, ax, n\_cols, line\_kw, ice\_lines\_kw, ...]) | Plot partial dependence plots. |
*classmethod*from\_estimator(*estimator*, *X*, *features*, *\**, *feature\_names=None*, *target=None*, *response\_method='auto'*, *n\_cols=3*, *grid\_resolution=100*, *percentiles=(0.05, 0.95)*, *method='auto'*, *n\_jobs=None*, *verbose=0*, *line\_kw=None*, *ice\_lines\_kw=None*, *pd\_line\_kw=None*, *contour\_kw=None*, *ax=None*, *kind='average'*, *centered=False*, *subsample=1000*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/inspection/_plot/partial_dependence.py#L734)
Partial dependence (PD) and individual conditional expectation (ICE) plots.
Partial dependence plots, individual conditional expectation plots or an overlay of both of them can be plotted by setting the `kind` parameter. The `len(features)` plots are arranged in a grid with `n_cols` columns. Two-way partial dependence plots are plotted as contour plots. The deciles of the feature values will be shown with tick marks on the x-axes for one-way plots, and on both axes for two-way plots.
Read more in the [User Guide](../partial_dependence#partial-dependence).
Note
[`PartialDependenceDisplay.from_estimator`](#sklearn.inspection.PartialDependenceDisplay.from_estimator "sklearn.inspection.PartialDependenceDisplay.from_estimator") does not support using the same axes with multiple calls. To plot the partial dependence for multiple estimators, please pass the axes created by the first call to the second call:
```
>>> from sklearn.inspection import PartialDependenceDisplay
>>> from sklearn.datasets import make_friedman1
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.ensemble import RandomForestRegressor
>>> X, y = make_friedman1()
>>> est1 = LinearRegression().fit(X, y)
>>> est2 = RandomForestRegressor().fit(X, y)
>>> disp1 = PartialDependenceDisplay.from_estimator(est1, X,
... [1, 2])
>>> disp2 = PartialDependenceDisplay.from_estimator(est2, X, [1, 2],
... ax=disp1.axes_)
```
Warning
For [`GradientBoostingClassifier`](sklearn.ensemble.gradientboostingclassifier#sklearn.ensemble.GradientBoostingClassifier "sklearn.ensemble.GradientBoostingClassifier") and [`GradientBoostingRegressor`](sklearn.ensemble.gradientboostingregressor#sklearn.ensemble.GradientBoostingRegressor "sklearn.ensemble.GradientBoostingRegressor"), the `'recursion'` method (used by default) will not account for the `init` predictor of the boosting process. In practice, this will produce the same values as `'brute'` up to a constant offset in the target response, provided that `init` is a constant estimator (which is the default). However, if `init` is not a constant estimator, the partial dependence values are incorrect for `'recursion'` because the offset will be sample-dependent. It is preferable to use the `'brute'` method. Note that this only applies to [`GradientBoostingClassifier`](sklearn.ensemble.gradientboostingclassifier#sklearn.ensemble.GradientBoostingClassifier "sklearn.ensemble.GradientBoostingClassifier") and [`GradientBoostingRegressor`](sklearn.ensemble.gradientboostingregressor#sklearn.ensemble.GradientBoostingRegressor "sklearn.ensemble.GradientBoostingRegressor"), not to [`HistGradientBoostingClassifier`](sklearn.ensemble.histgradientboostingclassifier#sklearn.ensemble.HistGradientBoostingClassifier "sklearn.ensemble.HistGradientBoostingClassifier") and [`HistGradientBoostingRegressor`](sklearn.ensemble.histgradientboostingregressor#sklearn.ensemble.HistGradientBoostingRegressor "sklearn.ensemble.HistGradientBoostingRegressor").
New in version 1.0.
Parameters:
**estimator**BaseEstimator
A fitted estimator object implementing [predict](https://scikit-learn.org/1.1/glossary.html#term-predict), [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba), or [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function). Multioutput-multiclass classifiers are not supported.
**X**{array-like, dataframe} of shape (n\_samples, n\_features)
`X` is used to generate a grid of values for the target `features` (where the partial dependence will be evaluated), and also to generate values for the complement features when the `method` is `'brute'`.
**features**list of {int, str, pair of int, pair of str}
The target features for which to create the PDPs. If `features[i]` is an integer or a string, a one-way PDP is created; if `features[i]` is a tuple, a two-way PDP is created (only supported with `kind='average'`). Each tuple must be of size 2. if any entry is a string, then it must be in `feature_names`.
**feature\_names**array-like of shape (n\_features,), dtype=str, default=None
Name of each feature; `feature_names[i]` holds the name of the feature with index `i`. By default, the name of the feature corresponds to their numerical index for NumPy array and their column name for pandas dataframe.
**target**int, default=None
* In a multiclass setting, specifies the class for which the PDPs should be computed. Note that for binary classification, the positive class (index 1) is always used.
* In a multioutput setting, specifies the task for which the PDPs should be computed.
Ignored in binary classification or classical regression settings.
**response\_method**{‘auto’, ‘predict\_proba’, ‘decision\_function’}, default=’auto’
Specifies whether to use [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) or [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) as the target response. For regressors this parameter is ignored and the response is always the output of [predict](https://scikit-learn.org/1.1/glossary.html#term-predict). By default, [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) is tried first and we revert to [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) if it doesn’t exist. If `method` is `'recursion'`, the response is always the output of [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function).
**n\_cols**int, default=3
The maximum number of columns in the grid plot. Only active when `ax` is a single axis or `None`.
**grid\_resolution**int, default=100
The number of equally spaced points on the axes of the plots, for each target feature.
**percentiles**tuple of float, default=(0.05, 0.95)
The lower and upper percentile used to create the extreme values for the PDP axes. Must be in [0, 1].
**method**str, default=’auto’
The method used to calculate the averaged predictions:
* `'recursion'` is only supported for some tree-based estimators (namely [`GradientBoostingClassifier`](sklearn.ensemble.gradientboostingclassifier#sklearn.ensemble.GradientBoostingClassifier "sklearn.ensemble.GradientBoostingClassifier"), [`GradientBoostingRegressor`](sklearn.ensemble.gradientboostingregressor#sklearn.ensemble.GradientBoostingRegressor "sklearn.ensemble.GradientBoostingRegressor"), [`HistGradientBoostingClassifier`](sklearn.ensemble.histgradientboostingclassifier#sklearn.ensemble.HistGradientBoostingClassifier "sklearn.ensemble.HistGradientBoostingClassifier"), [`HistGradientBoostingRegressor`](sklearn.ensemble.histgradientboostingregressor#sklearn.ensemble.HistGradientBoostingRegressor "sklearn.ensemble.HistGradientBoostingRegressor"), [`DecisionTreeRegressor`](sklearn.tree.decisiontreeregressor#sklearn.tree.DecisionTreeRegressor "sklearn.tree.DecisionTreeRegressor"), [`RandomForestRegressor`](sklearn.ensemble.randomforestregressor#sklearn.ensemble.RandomForestRegressor "sklearn.ensemble.RandomForestRegressor") but is more efficient in terms of speed. With this method, the target response of a classifier is always the decision function, not the predicted probabilities. Since the `'recursion'` method implicitly computes the average of the ICEs by design, it is not compatible with ICE and thus `kind` must be `'average'`.
* `'brute'` is supported for any estimator, but is more computationally intensive.
* `'auto'`: the `'recursion'` is used for estimators that support it, and `'brute'` is used otherwise.
Please see [this note](../partial_dependence#pdp-method-differences) for differences between the `'brute'` and `'recursion'` method.
**n\_jobs**int, default=None
The number of CPUs to use to compute the partial dependences. Computation is parallelized over features specified by the `features` parameter.
`None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**verbose**int, default=0
Verbose output during PD computations.
**line\_kw**dict, default=None
Dict with keywords passed to the `matplotlib.pyplot.plot` call. For one-way partial dependence plots. It can be used to define common properties for both `ice_lines_kw` and `pdp_line_kw`.
**ice\_lines\_kw**dict, default=None
Dictionary with keywords passed to the `matplotlib.pyplot.plot` call. For ICE lines in the one-way partial dependence plots. The key value pairs defined in `ice_lines_kw` takes priority over `line_kw`.
**pd\_line\_kw**dict, default=None
Dictionary with keywords passed to the `matplotlib.pyplot.plot` call. For partial dependence in one-way partial dependence plots. The key value pairs defined in `pd_line_kw` takes priority over `line_kw`.
**contour\_kw**dict, default=None
Dict with keywords passed to the `matplotlib.pyplot.contourf` call. For two-way partial dependence plots.
**ax**Matplotlib axes or array-like of Matplotlib axes, default=None
* If a single axis is passed in, it is treated as a bounding axes and a grid of partial dependence plots will be drawn within these bounds. The `n_cols` parameter controls the number of columns in the grid.
* If an array-like of axes are passed in, the partial dependence plots will be drawn directly into these axes.
* If `None`, a figure and a bounding axes is created and treated as the single axes case.
**kind**{‘average’, ‘individual’, ‘both’}, default=’average’
Whether to plot the partial dependence averaged across all the samples in the dataset or one line per sample or both.
* `kind='average'` results in the traditional PD plot;
* `kind='individual'` results in the ICE plot.
Note that the fast `method='recursion'` option is only available for `kind='average'`. Plotting individual dependencies requires using the slower `method='brute'` option.
**centered**bool, default=False
If `True`, the ICE and PD lines will start at the origin of the y-axis. By default, no centering is done.
New in version 1.1.
**subsample**float, int or None, default=1000
Sampling for ICE curves when `kind` is ‘individual’ or ‘both’. If `float`, should be between 0.0 and 1.0 and represent the proportion of the dataset to be used to plot ICE curves. If `int`, represents the absolute number samples to use.
Note that the full dataset is still used to calculate averaged partial dependence when `kind='both'`.
**random\_state**int, RandomState instance or None, default=None
Controls the randomness of the selected samples when subsamples is not `None` and `kind` is either `'both'` or `'individual'`. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state) for details.
Returns:
**display**[`PartialDependenceDisplay`](#sklearn.inspection.PartialDependenceDisplay "sklearn.inspection.PartialDependenceDisplay")
See also
[`partial_dependence`](sklearn.inspection.partial_dependence#sklearn.inspection.partial_dependence "sklearn.inspection.partial_dependence")
Compute Partial Dependence values.
#### Examples
```
>>> import matplotlib.pyplot as plt
>>> from sklearn.datasets import make_friedman1
>>> from sklearn.ensemble import GradientBoostingRegressor
>>> from sklearn.inspection import PartialDependenceDisplay
>>> X, y = make_friedman1()
>>> clf = GradientBoostingRegressor(n_estimators=10).fit(X, y)
>>> PartialDependenceDisplay.from_estimator(clf, X, [0, (0, 1)])
<...>
>>> plt.show()
```
plot(*\**, *ax=None*, *n\_cols=3*, *line\_kw=None*, *ice\_lines\_kw=None*, *pd\_line\_kw=None*, *contour\_kw=None*, *pdp\_lim=None*, *centered=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/inspection/_plot/partial_dependence.py#L1291)
Plot partial dependence plots.
Parameters:
**ax**Matplotlib axes or array-like of Matplotlib axes, default=None
* If a single axis is passed in, it is treated as a bounding axes
and a grid of partial dependence plots will be drawn within these bounds. The `n_cols` parameter controls the number of columns in the grid.
* If an array-like of axes are passed in, the partial dependence
plots will be drawn directly into these axes.
* If `None`, a figure and a bounding axes is created and treated
as the single axes case.
**n\_cols**int, default=3
The maximum number of columns in the grid plot. Only active when `ax` is a single axes or `None`.
**line\_kw**dict, default=None
Dict with keywords passed to the `matplotlib.pyplot.plot` call. For one-way partial dependence plots.
**ice\_lines\_kw**dict, default=None
Dictionary with keywords passed to the `matplotlib.pyplot.plot` call. For ICE lines in the one-way partial dependence plots. The key value pairs defined in `ice_lines_kw` takes priority over `line_kw`.
New in version 1.0.
**pd\_line\_kw**dict, default=None
Dictionary with keywords passed to the `matplotlib.pyplot.plot` call. For partial dependence in one-way partial dependence plots. The key value pairs defined in `pd_line_kw` takes priority over `line_kw`.
New in version 1.0.
**contour\_kw**dict, default=None
Dict with keywords passed to the `matplotlib.pyplot.contourf` call for two-way partial dependence plots.
**pdp\_lim**dict, default=None
Global min and max average predictions, such that all plots will have the same scale and y limits. `pdp_lim[1]` is the global min and max for single partial dependence curves. `pdp_lim[2]` is the global min and max for two-way partial dependence curves. If `None` (default), the limit will be inferred from the global minimum and maximum of all predictions.
New in version 1.1.
**centered**bool, default=False
If `True`, the ICE and PD lines will start at the origin of the y-axis. By default, no centering is done.
New in version 1.1.
Returns:
**display**[`PartialDependenceDisplay`](#sklearn.inspection.PartialDependenceDisplay "sklearn.inspection.PartialDependenceDisplay")
Examples using `sklearn.inspection.PartialDependenceDisplay`
------------------------------------------------------------
[Advanced Plotting With Partial Dependence](../../auto_examples/miscellaneous/plot_partial_dependence_visualization_api#sphx-glr-auto-examples-miscellaneous-plot-partial-dependence-visualization-api-py)
| programming_docs |
scikit_learn sklearn.gaussian_process.kernels.Hyperparameter sklearn.gaussian\_process.kernels.Hyperparameter
================================================
*class*sklearn.gaussian\_process.kernels.Hyperparameter(*name*, *value\_type*, *bounds*, *n\_elements=1*, *fixed=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L51)
A kernel hyperparameter’s specification in form of a namedtuple.
New in version 0.18.
Attributes:
**name**str
The name of the hyperparameter. Note that a kernel using a hyperparameter with name “x” must have the attributes self.x and self.x\_bounds
**value\_type**str
The type of the hyperparameter. Currently, only “numeric” hyperparameters are supported.
**bounds**pair of floats >= 0 or “fixed”
The lower and upper bound on the parameter. If n\_elements>1, a pair of 1d array with n\_elements each may be given alternatively. If the string “fixed” is passed as bounds, the hyperparameter’s value cannot be changed.
**n\_elements**int, default=1
The number of elements of the hyperparameter value. Defaults to 1, which corresponds to a scalar hyperparameter. n\_elements > 1 corresponds to a hyperparameter which is vector-valued, such as, e.g., anisotropic length-scales.
**fixed**bool, default=None
Whether the value of this hyperparameter is fixed, i.e., cannot be changed during hyperparameter tuning. If None is passed, the “fixed” is derived based on the given bounds.
#### Examples
```
>>> from sklearn.gaussian_process.kernels import ConstantKernel
>>> from sklearn.datasets import make_friedman2
>>> from sklearn.gaussian_process import GaussianProcessRegressor
>>> from sklearn.gaussian_process.kernels import Hyperparameter
>>> X, y = make_friedman2(n_samples=50, noise=0, random_state=0)
>>> kernel = ConstantKernel(constant_value=1.0,
... constant_value_bounds=(0.0, 10.0))
```
We can access each hyperparameter:
```
>>> for hyperparameter in kernel.hyperparameters:
... print(hyperparameter)
Hyperparameter(name='constant_value', value_type='numeric',
bounds=array([[ 0., 10.]]), n_elements=1, fixed=False)
```
```
>>> params = kernel.get_params()
>>> for key in sorted(params): print(f"{key} : {params[key]}")
constant_value : 1.0
constant_value_bounds : (0.0, 10.0)
```
#### Methods
| | |
| --- | --- |
| [`count`](#sklearn.gaussian_process.kernels.Hyperparameter.count "sklearn.gaussian_process.kernels.Hyperparameter.count")(value, /) | Return number of occurrences of value. |
| [`index`](#sklearn.gaussian_process.kernels.Hyperparameter.index "sklearn.gaussian_process.kernels.Hyperparameter.index")(value[, start, stop]) | Return first index of value. |
\_\_call\_\_(*\*args*, *\*\*kwargs*)
Call self as a function.
bounds
Alias for field number 2
count(*value*, */*)
Return number of occurrences of value.
fixed
Alias for field number 4
index(*value*, *start=0*, *stop=sys.maxsize*, */*)
Return first index of value.
Raises ValueError if the value is not present.
n\_elements
Alias for field number 3
name
Alias for field number 0
value\_type
Alias for field number 1
Examples using `sklearn.gaussian_process.kernels.Hyperparameter`
----------------------------------------------------------------
[Gaussian processes on discrete data structures](../../auto_examples/gaussian_process/plot_gpr_on_structured_data#sphx-glr-auto-examples-gaussian-process-plot-gpr-on-structured-data-py)
scikit_learn sklearn.utils.murmurhash3_32 sklearn.utils.murmurhash3\_32
=============================
sklearn.utils.murmurhash3\_32()
Compute the 32bit murmurhash3 of key at seed.
The underlying implementation is MurmurHash3\_x86\_32 generating low latency 32bits hash suitable for implementing lookup tables, Bloom filters, count min sketch or feature hashing.
Parameters:
**key**np.int32, bytes, unicode or ndarray of dtype=np.int32
The physical object to hash.
**seed**int, default=0
Integer seed for the hashing algorithm.
**positive**bool, default=False
True: the results is casted to an unsigned int
from 0 to 2 \*\* 32 - 1
False: the results is casted to a signed int
from -(2 \*\* 31) to 2 \*\* 31 - 1
scikit_learn sklearn.kernel_approximation.Nystroem sklearn.kernel\_approximation.Nystroem
======================================
*class*sklearn.kernel\_approximation.Nystroem(*kernel='rbf'*, *\**, *gamma=None*, *coef0=None*, *degree=None*, *kernel\_params=None*, *n\_components=100*, *random\_state=None*, *n\_jobs=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/kernel_approximation.py#L754)
Approximate a kernel map using a subset of the training data.
Constructs an approximate feature map for an arbitrary kernel using a subset of the data as basis.
Read more in the [User Guide](../kernel_approximation#nystroem-kernel-approx).
New in version 0.13.
Parameters:
**kernel**str or callable, default=’rbf’
Kernel map to be approximated. A callable should accept two arguments and the keyword arguments passed to this object as `kernel_params`, and should return a floating point number.
**gamma**float, default=None
Gamma parameter for the RBF, laplacian, polynomial, exponential chi2 and sigmoid kernels. Interpretation of the default value is left to the kernel; see the documentation for sklearn.metrics.pairwise. Ignored by other kernels.
**coef0**float, default=None
Zero coefficient for polynomial and sigmoid kernels. Ignored by other kernels.
**degree**float, default=None
Degree of the polynomial kernel. Ignored by other kernels.
**kernel\_params**dict, default=None
Additional parameters (keyword arguments) for kernel function passed as callable object.
**n\_components**int, default=100
Number of features to construct. How many data points will be used to construct the mapping.
**random\_state**int, RandomState instance or None, default=None
Pseudo-random number generator to control the uniform sampling without replacement of `n_components` of the training data to construct the basis kernel. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**n\_jobs**int, default=None
The number of jobs to use for the computation. This works by breaking down the kernel matrix into `n_jobs` even slices and computing them in parallel.
`None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
New in version 0.24.
Attributes:
**components\_**ndarray of shape (n\_components, n\_features)
Subset of training points used to construct the feature map.
**component\_indices\_**ndarray of shape (n\_components)
Indices of `components_` in the training set.
**normalization\_**ndarray of shape (n\_components, n\_components)
Normalization matrix needed for embedding. Square root of the kernel matrix on `components_`.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`AdditiveChi2Sampler`](sklearn.kernel_approximation.additivechi2sampler#sklearn.kernel_approximation.AdditiveChi2Sampler "sklearn.kernel_approximation.AdditiveChi2Sampler")
Approximate feature map for additive chi2 kernel.
[`PolynomialCountSketch`](sklearn.kernel_approximation.polynomialcountsketch#sklearn.kernel_approximation.PolynomialCountSketch "sklearn.kernel_approximation.PolynomialCountSketch")
Polynomial kernel approximation via Tensor Sketch.
[`RBFSampler`](sklearn.kernel_approximation.rbfsampler#sklearn.kernel_approximation.RBFSampler "sklearn.kernel_approximation.RBFSampler")
Approximate a RBF kernel feature map using random Fourier features.
[`SkewedChi2Sampler`](sklearn.kernel_approximation.skewedchi2sampler#sklearn.kernel_approximation.SkewedChi2Sampler "sklearn.kernel_approximation.SkewedChi2Sampler")
Approximate feature map for “skewed chi-squared” kernel.
[`sklearn.metrics.pairwise.kernel_metrics`](sklearn.metrics.pairwise.kernel_metrics#sklearn.metrics.pairwise.kernel_metrics "sklearn.metrics.pairwise.kernel_metrics")
List of built-in kernels.
#### References
* Williams, C.K.I. and Seeger, M. “Using the Nystroem method to speed up kernel machines”, Advances in neural information processing systems 2001
* T. Yang, Y. Li, M. Mahdavi, R. Jin and Z. Zhou “Nystroem Method vs Random Fourier Features: A Theoretical and Empirical Comparison”, Advances in Neural Information Processing Systems 2012
#### Examples
```
>>> from sklearn import datasets, svm
>>> from sklearn.kernel_approximation import Nystroem
>>> X, y = datasets.load_digits(n_class=9, return_X_y=True)
>>> data = X / 16.
>>> clf = svm.LinearSVC()
>>> feature_map_nystroem = Nystroem(gamma=.2,
... random_state=1,
... n_components=300)
>>> data_transformed = feature_map_nystroem.fit_transform(data)
>>> clf.fit(data_transformed, y)
LinearSVC()
>>> clf.score(data_transformed, y)
0.9987...
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.kernel_approximation.Nystroem.fit "sklearn.kernel_approximation.Nystroem.fit")(X[, y]) | Fit estimator to data. |
| [`fit_transform`](#sklearn.kernel_approximation.Nystroem.fit_transform "sklearn.kernel_approximation.Nystroem.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.kernel_approximation.Nystroem.get_feature_names_out "sklearn.kernel_approximation.Nystroem.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.kernel_approximation.Nystroem.get_params "sklearn.kernel_approximation.Nystroem.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.kernel_approximation.Nystroem.set_params "sklearn.kernel_approximation.Nystroem.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.kernel_approximation.Nystroem.transform "sklearn.kernel_approximation.Nystroem.transform")(X) | Apply feature map to X. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/kernel_approximation.py#L892)
Fit estimator to data.
Samples a subset of training points, computes kernel on these and computes normalization matrix.
Parameters:
**X**array-like, shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like, shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.kernel_approximation.Nystroem.fit "sklearn.kernel_approximation.Nystroem.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/kernel_approximation.py#L951)
Apply feature map to X.
Computes an approximate feature map using the kernel between some training points and X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Data to transform.
Returns:
**X\_transformed**ndarray of shape (n\_samples, n\_components)
Transformed data.
Examples using `sklearn.kernel_approximation.Nystroem`
------------------------------------------------------
[Time-related feature engineering](../../auto_examples/applications/plot_cyclical_feature_engineering#sphx-glr-auto-examples-applications-plot-cyclical-feature-engineering-py)
[One-Class SVM versus One-Class SVM using Stochastic Gradient Descent](../../auto_examples/linear_model/plot_sgdocsvm_vs_ocsvm#sphx-glr-auto-examples-linear-model-plot-sgdocsvm-vs-ocsvm-py)
[Comparing anomaly detection algorithms for outlier detection on toy datasets](../../auto_examples/miscellaneous/plot_anomaly_comparison#sphx-glr-auto-examples-miscellaneous-plot-anomaly-comparison-py)
[Explicit feature map approximation for RBF kernels](../../auto_examples/miscellaneous/plot_kernel_approximation#sphx-glr-auto-examples-miscellaneous-plot-kernel-approximation-py)
[Imputing missing values with variants of IterativeImputer](../../auto_examples/impute/plot_iterative_imputer_variants_comparison#sphx-glr-auto-examples-impute-plot-iterative-imputer-variants-comparison-py)
scikit_learn sklearn.linear_model.MultiTaskLassoCV sklearn.linear\_model.MultiTaskLassoCV
======================================
*class*sklearn.linear\_model.MultiTaskLassoCV(*\**, *eps=0.001*, *n\_alphas=100*, *alphas=None*, *fit\_intercept=True*, *normalize='deprecated'*, *max\_iter=1000*, *tol=0.0001*, *copy\_X=True*, *cv=None*, *verbose=False*, *n\_jobs=None*, *random\_state=None*, *selection='cyclic'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_coordinate_descent.py#L2931)
Multi-task Lasso model trained with L1/L2 mixed-norm as regularizer.
See glossary entry for [cross-validation estimator](https://scikit-learn.org/1.1/glossary.html#term-cross-validation-estimator).
The optimization objective for MultiTaskLasso is:
```
(1 / (2 * n_samples)) * ||Y - XW||^Fro_2 + alpha * ||W||_21
```
Where:
```
||W||_21 = \sum_i \sqrt{\sum_j w_{ij}^2}
```
i.e. the sum of norm of each row.
Read more in the [User Guide](../linear_model#multi-task-lasso).
New in version 0.15.
Parameters:
**eps**float, default=1e-3
Length of the path. `eps=1e-3` means that `alpha_min / alpha_max = 1e-3`.
**n\_alphas**int, default=100
Number of alphas along the regularization path.
**alphas**array-like, default=None
List of alphas where to compute the models. If not provided, set automatically.
**fit\_intercept**bool, default=True
Whether to calculate the intercept for this model. If set to false, no intercept will be used in calculations (i.e. data is expected to be centered).
**normalize**bool, default=False
This parameter is ignored when `fit_intercept` is set to False. If True, the regressors X will be normalized before regression by subtracting the mean and dividing by the l2-norm. If you wish to standardize, please use [`StandardScaler`](sklearn.preprocessing.standardscaler#sklearn.preprocessing.StandardScaler "sklearn.preprocessing.StandardScaler") before calling `fit` on an estimator with `normalize=False`.
Deprecated since version 1.0: `normalize` was deprecated in version 1.0 and will be removed in 1.2.
**max\_iter**int, default=1000
The maximum number of iterations.
**tol**float, default=1e-4
The tolerance for the optimization: if the updates are smaller than `tol`, the optimization code checks the dual gap for optimality and continues until it is smaller than `tol`.
**copy\_X**bool, default=True
If `True`, X will be copied; else, it may be overwritten.
**cv**int, cross-validation generator or iterable, default=None
Determines the cross-validation splitting strategy. Possible inputs for cv are:
* None, to use the default 5-fold cross-validation,
* int, to specify the number of folds.
* [CV splitter](https://scikit-learn.org/1.1/glossary.html#term-CV-splitter),
* An iterable yielding (train, test) splits as arrays of indices.
For int/None inputs, `KFold` is used.
Refer [User Guide](../cross_validation#cross-validation) for the various cross-validation strategies that can be used here.
Changed in version 0.22: `cv` default value if None changed from 3-fold to 5-fold.
**verbose**bool or int, default=False
Amount of verbosity.
**n\_jobs**int, default=None
Number of CPUs to use during the cross validation. Note that this is used only if multiple values for l1\_ratio are given. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**random\_state**int, RandomState instance, default=None
The seed of the pseudo random number generator that selects a random feature to update. Used when `selection` == ‘random’. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**selection**{‘cyclic’, ‘random’}, default=’cyclic’
If set to ‘random’, a random coefficient is updated every iteration rather than looping over features sequentially by default. This (setting to ‘random’) often leads to significantly faster convergence especially when tol is higher than 1e-4.
Attributes:
**intercept\_**ndarray of shape (n\_targets,)
Independent term in decision function.
**coef\_**ndarray of shape (n\_targets, n\_features)
Parameter vector (W in the cost function formula). Note that `coef_` stores the transpose of `W`, `W.T`.
**alpha\_**float
The amount of penalization chosen by cross validation.
**mse\_path\_**ndarray of shape (n\_alphas, n\_folds)
Mean square error for the test set on each fold, varying alpha.
**alphas\_**ndarray of shape (n\_alphas,)
The grid of alphas used for fitting.
**n\_iter\_**int
Number of iterations run by the coordinate descent solver to reach the specified tolerance for the optimal alpha.
**dual\_gap\_**float
The dual gap at the end of the optimization for the optimal alpha.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`MultiTaskElasticNet`](sklearn.linear_model.multitaskelasticnet#sklearn.linear_model.MultiTaskElasticNet "sklearn.linear_model.MultiTaskElasticNet")
Multi-task ElasticNet model trained with L1/L2 mixed-norm as regularizer.
[`ElasticNetCV`](sklearn.linear_model.elasticnetcv#sklearn.linear_model.ElasticNetCV "sklearn.linear_model.ElasticNetCV")
Elastic net model with best model selection by cross-validation.
[`MultiTaskElasticNetCV`](sklearn.linear_model.multitaskelasticnetcv#sklearn.linear_model.MultiTaskElasticNetCV "sklearn.linear_model.MultiTaskElasticNetCV")
Multi-task L1/L2 ElasticNet with built-in cross-validation.
#### Notes
The algorithm used to fit the model is coordinate descent.
In `fit`, once the best parameter `alpha` is found through cross-validation, the model is fit again using the entire training set.
To avoid unnecessary memory duplication the `X` and `y` arguments of the `fit` method should be directly passed as Fortran-contiguous numpy arrays.
#### Examples
```
>>> from sklearn.linear_model import MultiTaskLassoCV
>>> from sklearn.datasets import make_regression
>>> from sklearn.metrics import r2_score
>>> X, y = make_regression(n_targets=2, noise=4, random_state=0)
>>> reg = MultiTaskLassoCV(cv=5, random_state=0).fit(X, y)
>>> r2_score(y, reg.predict(X))
0.9994...
>>> reg.alpha_
0.5713...
>>> reg.predict(X[:1,])
array([[153.7971..., 94.9015...]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.linear_model.MultiTaskLassoCV.fit "sklearn.linear_model.MultiTaskLassoCV.fit")(X, y) | Fit MultiTaskLasso model with coordinate descent. |
| [`get_params`](#sklearn.linear_model.MultiTaskLassoCV.get_params "sklearn.linear_model.MultiTaskLassoCV.get_params")([deep]) | Get parameters for this estimator. |
| [`path`](#sklearn.linear_model.MultiTaskLassoCV.path "sklearn.linear_model.MultiTaskLassoCV.path")(X, y, \*[, eps, n\_alphas, alphas, ...]) | Compute Lasso path with coordinate descent. |
| [`predict`](#sklearn.linear_model.MultiTaskLassoCV.predict "sklearn.linear_model.MultiTaskLassoCV.predict")(X) | Predict using the linear model. |
| [`score`](#sklearn.linear_model.MultiTaskLassoCV.score "sklearn.linear_model.MultiTaskLassoCV.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.linear_model.MultiTaskLassoCV.set_params "sklearn.linear_model.MultiTaskLassoCV.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_coordinate_descent.py#L3147)
Fit MultiTaskLasso model with coordinate descent.
Fit is on grid of alphas and best alpha estimated by cross-validation.
Parameters:
**X**ndarray of shape (n\_samples, n\_features)
Data.
**y**ndarray of shape (n\_samples, n\_targets)
Target. Will be cast to X’s dtype if necessary.
Returns:
**self**object
Returns an instance of fitted model.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*static*path(*X*, *y*, *\**, *eps=0.001*, *n\_alphas=100*, *alphas=None*, *precompute='auto'*, *Xy=None*, *copy\_X=True*, *coef\_init=None*, *verbose=False*, *return\_n\_iter=False*, *positive=False*, *\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_coordinate_descent.py#L192)
Compute Lasso path with coordinate descent.
The Lasso optimization function varies for mono and multi-outputs.
For mono-output tasks it is:
```
(1 / (2 * n_samples)) * ||y - Xw||^2_2 + alpha * ||w||_1
```
For multi-output tasks it is:
```
(1 / (2 * n_samples)) * ||Y - XW||^2_Fro + alpha * ||W||_21
```
Where:
```
||W||_21 = \sum_i \sqrt{\sum_j w_{ij}^2}
```
i.e. the sum of norm of each row.
Read more in the [User Guide](../linear_model#lasso).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training data. Pass directly as Fortran-contiguous data to avoid unnecessary memory duplication. If `y` is mono-output then `X` can be sparse.
**y**{array-like, sparse matrix} of shape (n\_samples,) or (n\_samples, n\_targets)
Target values.
**eps**float, default=1e-3
Length of the path. `eps=1e-3` means that `alpha_min / alpha_max = 1e-3`.
**n\_alphas**int, default=100
Number of alphas along the regularization path.
**alphas**ndarray, default=None
List of alphas where to compute the models. If `None` alphas are set automatically.
**precompute**‘auto’, bool or array-like of shape (n\_features, n\_features), default=’auto’
Whether to use a precomputed Gram matrix to speed up calculations. If set to `'auto'` let us decide. The Gram matrix can also be passed as argument.
**Xy**array-like of shape (n\_features,) or (n\_features, n\_targets), default=None
Xy = np.dot(X.T, y) that can be precomputed. It is useful only when the Gram matrix is precomputed.
**copy\_X**bool, default=True
If `True`, X will be copied; else, it may be overwritten.
**coef\_init**ndarray of shape (n\_features, ), default=None
The initial values of the coefficients.
**verbose**bool or int, default=False
Amount of verbosity.
**return\_n\_iter**bool, default=False
Whether to return the number of iterations or not.
**positive**bool, default=False
If set to True, forces coefficients to be positive. (Only allowed when `y.ndim == 1`).
**\*\*params**kwargs
Keyword arguments passed to the coordinate descent solver.
Returns:
**alphas**ndarray of shape (n\_alphas,)
The alphas along the path where models are computed.
**coefs**ndarray of shape (n\_features, n\_alphas) or (n\_targets, n\_features, n\_alphas)
Coefficients along the path.
**dual\_gaps**ndarray of shape (n\_alphas,)
The dual gaps at the end of the optimization for each alpha.
**n\_iters**list of int
The number of iterations taken by the coordinate descent optimizer to reach the specified tolerance for each alpha.
See also
[`lars_path`](sklearn.linear_model.lars_path#sklearn.linear_model.lars_path "sklearn.linear_model.lars_path")
Compute Least Angle Regression or Lasso path using LARS algorithm.
[`Lasso`](sklearn.linear_model.lasso#sklearn.linear_model.Lasso "sklearn.linear_model.Lasso")
The Lasso is a linear model that estimates sparse coefficients.
[`LassoLars`](sklearn.linear_model.lassolars#sklearn.linear_model.LassoLars "sklearn.linear_model.LassoLars")
Lasso model fit with Least Angle Regression a.k.a. Lars.
[`LassoCV`](sklearn.linear_model.lassocv#sklearn.linear_model.LassoCV "sklearn.linear_model.LassoCV")
Lasso linear model with iterative fitting along a regularization path.
[`LassoLarsCV`](sklearn.linear_model.lassolarscv#sklearn.linear_model.LassoLarsCV "sklearn.linear_model.LassoLarsCV")
Cross-validated Lasso using the LARS algorithm.
[`sklearn.decomposition.sparse_encode`](sklearn.decomposition.sparse_encode#sklearn.decomposition.sparse_encode "sklearn.decomposition.sparse_encode")
Estimator that can be used to transform signals into sparse linear combination of atoms from a fixed.
#### Notes
For an example, see [examples/linear\_model/plot\_lasso\_coordinate\_descent\_path.py](../../auto_examples/linear_model/plot_lasso_coordinate_descent_path#sphx-glr-auto-examples-linear-model-plot-lasso-coordinate-descent-path-py).
To avoid unnecessary memory duplication the X argument of the fit method should be directly passed as a Fortran-contiguous numpy array.
Note that in certain cases, the Lars solver may be significantly faster to implement this functionality. In particular, linear interpolation can be used to retrieve model coefficients between the values output by lars\_path
#### Examples
Comparing lasso\_path and lars\_path with interpolation:
```
>>> import numpy as np
>>> from sklearn.linear_model import lasso_path
>>> X = np.array([[1, 2, 3.1], [2.3, 5.4, 4.3]]).T
>>> y = np.array([1, 2, 3.1])
>>> # Use lasso_path to compute a coefficient path
>>> _, coef_path, _ = lasso_path(X, y, alphas=[5., 1., .5])
>>> print(coef_path)
[[0. 0. 0.46874778]
[0.2159048 0.4425765 0.23689075]]
```
```
>>> # Now use lars_path and 1D linear interpolation to compute the
>>> # same path
>>> from sklearn.linear_model import lars_path
>>> alphas, active, coef_path_lars = lars_path(X, y, method='lasso')
>>> from scipy import interpolate
>>> coef_path_continuous = interpolate.interp1d(alphas[::-1],
... coef_path_lars[:, ::-1])
>>> print(coef_path_continuous([5., 1., .5]))
[[0. 0. 0.46915237]
[0.2159048 0.4425765 0.23668876]]
```
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L372)
Predict using the linear model.
Parameters:
**X**array-like or sparse matrix, shape (n\_samples, n\_features)
Samples.
Returns:
**C**array, shape (n\_samples,)
Returns predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
| programming_docs |
scikit_learn sklearn.exceptions.FitFailedWarning sklearn.exceptions.FitFailedWarning
===================================
*class*sklearn.exceptions.FitFailedWarning[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/exceptions.py#L92)
Warning class used if there is an error while fitting the estimator.
This Warning is used in meta estimators GridSearchCV and RandomizedSearchCV and the cross-validation helper function cross\_val\_score to warn when there is an error while fitting the estimator.
Changed in version 0.18: Moved from sklearn.cross\_validation.
Attributes:
**args**
#### Methods
| | |
| --- | --- |
| [`with_traceback`](#sklearn.exceptions.FitFailedWarning.with_traceback "sklearn.exceptions.FitFailedWarning.with_traceback") | Exception.with\_traceback(tb) -- set self.\_\_traceback\_\_ to tb and return self. |
with\_traceback()
Exception.with\_traceback(tb) – set self.\_\_traceback\_\_ to tb and return self.
scikit_learn sklearn.feature_selection.SelectFpr sklearn.feature\_selection.SelectFpr
====================================
*class*sklearn.feature\_selection.SelectFpr(*score\_func=<function f\_classif>*, *\**, *alpha=0.05*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_univariate_selection.py#L690)
Filter: Select the pvalues below alpha based on a FPR test.
FPR test stands for False Positive Rate test. It controls the total amount of false detections.
Read more in the [User Guide](../feature_selection#univariate-feature-selection).
Parameters:
**score\_func**callable, default=f\_classif
Function taking two arrays X and y, and returning a pair of arrays (scores, pvalues). Default is f\_classif (see below “See Also”). The default function only works with classification tasks.
**alpha**float, default=5e-2
Features with p-values less than `alpha` are selected.
Attributes:
**scores\_**array-like of shape (n\_features,)
Scores of features.
**pvalues\_**array-like of shape (n\_features,)
p-values of feature scores.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`f_classif`](sklearn.feature_selection.f_classif#sklearn.feature_selection.f_classif "sklearn.feature_selection.f_classif")
ANOVA F-value between label/feature for classification tasks.
[`chi2`](sklearn.feature_selection.chi2#sklearn.feature_selection.chi2 "sklearn.feature_selection.chi2")
Chi-squared stats of non-negative features for classification tasks.
[`mutual_info_classif`](sklearn.feature_selection.mutual_info_classif#sklearn.feature_selection.mutual_info_classif "sklearn.feature_selection.mutual_info_classif")
Mutual information for a discrete target.
[`f_regression`](sklearn.feature_selection.f_regression#sklearn.feature_selection.f_regression "sklearn.feature_selection.f_regression")
F-value between label/feature for regression tasks.
[`mutual_info_regression`](sklearn.feature_selection.mutual_info_regression#sklearn.feature_selection.mutual_info_regression "sklearn.feature_selection.mutual_info_regression")
Mutual information for a continuous target.
[`SelectPercentile`](sklearn.feature_selection.selectpercentile#sklearn.feature_selection.SelectPercentile "sklearn.feature_selection.SelectPercentile")
Select features based on percentile of the highest scores.
[`SelectKBest`](sklearn.feature_selection.selectkbest#sklearn.feature_selection.SelectKBest "sklearn.feature_selection.SelectKBest")
Select features based on the k highest scores.
[`SelectFdr`](sklearn.feature_selection.selectfdr#sklearn.feature_selection.SelectFdr "sklearn.feature_selection.SelectFdr")
Select features based on an estimated false discovery rate.
[`SelectFwe`](sklearn.feature_selection.selectfwe#sklearn.feature_selection.SelectFwe "sklearn.feature_selection.SelectFwe")
Select features based on family-wise error rate.
[`GenericUnivariateSelect`](sklearn.feature_selection.genericunivariateselect#sklearn.feature_selection.GenericUnivariateSelect "sklearn.feature_selection.GenericUnivariateSelect")
Univariate feature selector with configurable mode.
#### Examples
```
>>> from sklearn.datasets import load_breast_cancer
>>> from sklearn.feature_selection import SelectFpr, chi2
>>> X, y = load_breast_cancer(return_X_y=True)
>>> X.shape
(569, 30)
>>> X_new = SelectFpr(chi2, alpha=0.01).fit_transform(X, y)
>>> X_new.shape
(569, 16)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.feature_selection.SelectFpr.fit "sklearn.feature_selection.SelectFpr.fit")(X, y) | Run score function on (X, y) and get the appropriate features. |
| [`fit_transform`](#sklearn.feature_selection.SelectFpr.fit_transform "sklearn.feature_selection.SelectFpr.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.feature_selection.SelectFpr.get_feature_names_out "sklearn.feature_selection.SelectFpr.get_feature_names_out")([input\_features]) | Mask feature names according to selected features. |
| [`get_params`](#sklearn.feature_selection.SelectFpr.get_params "sklearn.feature_selection.SelectFpr.get_params")([deep]) | Get parameters for this estimator. |
| [`get_support`](#sklearn.feature_selection.SelectFpr.get_support "sklearn.feature_selection.SelectFpr.get_support")([indices]) | Get a mask, or integer index, of the features selected. |
| [`inverse_transform`](#sklearn.feature_selection.SelectFpr.inverse_transform "sklearn.feature_selection.SelectFpr.inverse_transform")(X) | Reverse the transformation operation. |
| [`set_params`](#sklearn.feature_selection.SelectFpr.set_params "sklearn.feature_selection.SelectFpr.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.feature_selection.SelectFpr.transform "sklearn.feature_selection.SelectFpr.transform")(X) | Reduce X to the selected features. |
fit(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_univariate_selection.py#L444)
Run score function on (X, y) and get the appropriate features.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The training input samples.
**y**array-like of shape (n\_samples,)
The target values (class labels in classification, real numbers in regression).
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L146)
Mask feature names according to selected features.
Parameters:
**input\_features**array-like of str or None, default=None
Input features.
* If `input_features` is `None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then the following input feature names are generated: `["x0", "x1", ..., "x(n_features_in_ - 1)"]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
get\_support(*indices=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L33)
Get a mask, or integer index, of the features selected.
Parameters:
**indices**bool, default=False
If True, the return value will be an array of integers, rather than a boolean mask.
Returns:
**support**array
An index that selects the retained features from a feature vector. If `indices` is False, this is a boolean array of shape [# input features], in which an element is True iff its corresponding feature is selected for retention. If `indices` is True, this is an integer array of shape [# output features] whose values are indices into the input feature vector.
inverse\_transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L106)
Reverse the transformation operation.
Parameters:
**X**array of shape [n\_samples, n\_selected\_features]
The input samples.
Returns:
**X\_r**array of shape [n\_samples, n\_original\_features]
`X` with columns of zeros inserted where features would have been removed by [`transform`](#sklearn.feature_selection.SelectFpr.transform "sklearn.feature_selection.SelectFpr.transform").
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L68)
Reduce X to the selected features.
Parameters:
**X**array of shape [n\_samples, n\_features]
The input samples.
Returns:
**X\_r**array of shape [n\_samples, n\_selected\_features]
The input samples with only the selected features.
scikit_learn sklearn.tree.DecisionTreeClassifier sklearn.tree.DecisionTreeClassifier
===================================
*class*sklearn.tree.DecisionTreeClassifier(*\**, *criterion='gini'*, *splitter='best'*, *max\_depth=None*, *min\_samples\_split=2*, *min\_samples\_leaf=1*, *min\_weight\_fraction\_leaf=0.0*, *max\_features=None*, *random\_state=None*, *max\_leaf\_nodes=None*, *min\_impurity\_decrease=0.0*, *class\_weight=None*, *ccp\_alpha=0.0*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L674)
A decision tree classifier.
Read more in the [User Guide](../tree#tree).
Parameters:
**criterion**{“gini”, “entropy”, “log\_loss”}, default=”gini”
The function to measure the quality of a split. Supported criteria are “gini” for the Gini impurity and “log\_loss” and “entropy” both for the Shannon information gain, see [Mathematical formulation](../tree#tree-mathematical-formulation).
**splitter**{“best”, “random”}, default=”best”
The strategy used to choose the split at each node. Supported strategies are “best” to choose the best split and “random” to choose the best random split.
**max\_depth**int, default=None
The maximum depth of the tree. If None, then nodes are expanded until all leaves are pure or until all leaves contain less than min\_samples\_split samples.
**min\_samples\_split**int or float, default=2
The minimum number of samples required to split an internal node:
* If int, then consider `min_samples_split` as the minimum number.
* If float, then `min_samples_split` is a fraction and `ceil(min_samples_split * n_samples)` are the minimum number of samples for each split.
Changed in version 0.18: Added float values for fractions.
**min\_samples\_leaf**int or float, default=1
The minimum number of samples required to be at a leaf node. A split point at any depth will only be considered if it leaves at least `min_samples_leaf` training samples in each of the left and right branches. This may have the effect of smoothing the model, especially in regression.
* If int, then consider `min_samples_leaf` as the minimum number.
* If float, then `min_samples_leaf` is a fraction and `ceil(min_samples_leaf * n_samples)` are the minimum number of samples for each node.
Changed in version 0.18: Added float values for fractions.
**min\_weight\_fraction\_leaf**float, default=0.0
The minimum weighted fraction of the sum total of weights (of all the input samples) required to be at a leaf node. Samples have equal weight when sample\_weight is not provided.
**max\_features**int, float or {“auto”, “sqrt”, “log2”}, default=None
The number of features to consider when looking for the best split:
* If int, then consider `max_features` features at each split.
* If float, then `max_features` is a fraction and `max(1, int(max_features * n_features_in_))` features are considered at each split.
* If “auto”, then `max_features=sqrt(n_features)`.
* If “sqrt”, then `max_features=sqrt(n_features)`.
* If “log2”, then `max_features=log2(n_features)`.
* If None, then `max_features=n_features`.
Deprecated since version 1.1: The `"auto"` option was deprecated in 1.1 and will be removed in 1.3.
Note: the search for a split does not stop until at least one valid partition of the node samples is found, even if it requires to effectively inspect more than `max_features` features.
**random\_state**int, RandomState instance or None, default=None
Controls the randomness of the estimator. The features are always randomly permuted at each split, even if `splitter` is set to `"best"`. When `max_features < n_features`, the algorithm will select `max_features` at random at each split before finding the best split among them. But the best found split may vary across different runs, even if `max_features=n_features`. That is the case, if the improvement of the criterion is identical for several splits and one split has to be selected at random. To obtain a deterministic behaviour during fitting, `random_state` has to be fixed to an integer. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state) for details.
**max\_leaf\_nodes**int, default=None
Grow a tree with `max_leaf_nodes` in best-first fashion. Best nodes are defined as relative reduction in impurity. If None then unlimited number of leaf nodes.
**min\_impurity\_decrease**float, default=0.0
A node will be split if this split induces a decrease of the impurity greater than or equal to this value.
The weighted impurity decrease equation is the following:
```
N_t / N * (impurity - N_t_R / N_t * right_impurity
- N_t_L / N_t * left_impurity)
```
where `N` is the total number of samples, `N_t` is the number of samples at the current node, `N_t_L` is the number of samples in the left child, and `N_t_R` is the number of samples in the right child.
`N`, `N_t`, `N_t_R` and `N_t_L` all refer to the weighted sum, if `sample_weight` is passed.
New in version 0.19.
**class\_weight**dict, list of dict or “balanced”, default=None
Weights associated with classes in the form `{class_label: weight}`. If None, all classes are supposed to have weight one. For multi-output problems, a list of dicts can be provided in the same order as the columns of y.
Note that for multioutput (including multilabel) weights should be defined for each class of every column in its own dict. For example, for four-class multilabel classification weights should be [{0: 1, 1: 1}, {0: 1, 1: 5}, {0: 1, 1: 1}, {0: 1, 1: 1}] instead of [{1:1}, {2:5}, {3:1}, {4:1}].
The “balanced” mode uses the values of y to automatically adjust weights inversely proportional to class frequencies in the input data as `n_samples / (n_classes * np.bincount(y))`
For multi-output, the weights of each column of y will be multiplied.
Note that these weights will be multiplied with sample\_weight (passed through the fit method) if sample\_weight is specified.
**ccp\_alpha**non-negative float, default=0.0
Complexity parameter used for Minimal Cost-Complexity Pruning. The subtree with the largest cost complexity that is smaller than `ccp_alpha` will be chosen. By default, no pruning is performed. See [Minimal Cost-Complexity Pruning](../tree#minimal-cost-complexity-pruning) for details.
New in version 0.22.
Attributes:
**classes\_**ndarray of shape (n\_classes,) or list of ndarray
The classes labels (single output problem), or a list of arrays of class labels (multi-output problem).
[`feature_importances_`](#sklearn.tree.DecisionTreeClassifier.feature_importances_ "sklearn.tree.DecisionTreeClassifier.feature_importances_")ndarray of shape (n\_features,)
Return the feature importances.
**max\_features\_**int
The inferred value of max\_features.
**n\_classes\_**int or list of int
The number of classes (for single output problems), or a list containing the number of classes for each output (for multi-output problems).
[`n_features_`](#sklearn.tree.DecisionTreeClassifier.n_features_ "sklearn.tree.DecisionTreeClassifier.n_features_")int
DEPRECATED: The attribute `n_features_` is deprecated in 1.0 and will be removed in 1.2.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_outputs\_**int
The number of outputs when `fit` is performed.
**tree\_**Tree instance
The underlying Tree object. Please refer to `help(sklearn.tree._tree.Tree)` for attributes of Tree object and [Understanding the decision tree structure](../../auto_examples/tree/plot_unveil_tree_structure#sphx-glr-auto-examples-tree-plot-unveil-tree-structure-py) for basic usage of these attributes.
See also
[`DecisionTreeRegressor`](sklearn.tree.decisiontreeregressor#sklearn.tree.DecisionTreeRegressor "sklearn.tree.DecisionTreeRegressor")
A decision tree regressor.
#### Notes
The default values for the parameters controlling the size of the trees (e.g. `max_depth`, `min_samples_leaf`, etc.) lead to fully grown and unpruned trees which can potentially be very large on some data sets. To reduce memory consumption, the complexity and size of the trees should be controlled by setting those parameter values.
The [`predict`](#sklearn.tree.DecisionTreeClassifier.predict "sklearn.tree.DecisionTreeClassifier.predict") method operates using the [`numpy.argmax`](https://numpy.org/doc/stable/reference/generated/numpy.argmax.html#numpy.argmax "(in NumPy v1.23)") function on the outputs of [`predict_proba`](#sklearn.tree.DecisionTreeClassifier.predict_proba "sklearn.tree.DecisionTreeClassifier.predict_proba"). This means that in case the highest predicted probabilities are tied, the classifier will predict the tied class with the lowest index in [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
#### References
[1] <https://en.wikipedia.org/wiki/Decision_tree_learning>
[2] L. Breiman, J. Friedman, R. Olshen, and C. Stone, “Classification and Regression Trees”, Wadsworth, Belmont, CA, 1984.
[3] T. Hastie, R. Tibshirani and J. Friedman. “Elements of Statistical Learning”, Springer, 2009.
[4] L. Breiman, and A. Cutler, “Random Forests”, <https://www.stat.berkeley.edu/~breiman/RandomForests/cc_home.htm>
#### Examples
```
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import cross_val_score
>>> from sklearn.tree import DecisionTreeClassifier
>>> clf = DecisionTreeClassifier(random_state=0)
>>> iris = load_iris()
>>> cross_val_score(clf, iris.data, iris.target, cv=10)
...
...
array([ 1. , 0.93..., 0.86..., 0.93..., 0.93...,
0.93..., 0.93..., 1. , 0.93..., 1. ])
```
#### Methods
| | |
| --- | --- |
| [`apply`](#sklearn.tree.DecisionTreeClassifier.apply "sklearn.tree.DecisionTreeClassifier.apply")(X[, check\_input]) | Return the index of the leaf that each sample is predicted as. |
| [`cost_complexity_pruning_path`](#sklearn.tree.DecisionTreeClassifier.cost_complexity_pruning_path "sklearn.tree.DecisionTreeClassifier.cost_complexity_pruning_path")(X, y[, ...]) | Compute the pruning path during Minimal Cost-Complexity Pruning. |
| [`decision_path`](#sklearn.tree.DecisionTreeClassifier.decision_path "sklearn.tree.DecisionTreeClassifier.decision_path")(X[, check\_input]) | Return the decision path in the tree. |
| [`fit`](#sklearn.tree.DecisionTreeClassifier.fit "sklearn.tree.DecisionTreeClassifier.fit")(X, y[, sample\_weight, check\_input]) | Build a decision tree classifier from the training set (X, y). |
| [`get_depth`](#sklearn.tree.DecisionTreeClassifier.get_depth "sklearn.tree.DecisionTreeClassifier.get_depth")() | Return the depth of the decision tree. |
| [`get_n_leaves`](#sklearn.tree.DecisionTreeClassifier.get_n_leaves "sklearn.tree.DecisionTreeClassifier.get_n_leaves")() | Return the number of leaves of the decision tree. |
| [`get_params`](#sklearn.tree.DecisionTreeClassifier.get_params "sklearn.tree.DecisionTreeClassifier.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.tree.DecisionTreeClassifier.predict "sklearn.tree.DecisionTreeClassifier.predict")(X[, check\_input]) | Predict class or regression value for X. |
| [`predict_log_proba`](#sklearn.tree.DecisionTreeClassifier.predict_log_proba "sklearn.tree.DecisionTreeClassifier.predict_log_proba")(X) | Predict class log-probabilities of the input samples X. |
| [`predict_proba`](#sklearn.tree.DecisionTreeClassifier.predict_proba "sklearn.tree.DecisionTreeClassifier.predict_proba")(X[, check\_input]) | Predict class probabilities of the input samples X. |
| [`score`](#sklearn.tree.DecisionTreeClassifier.score "sklearn.tree.DecisionTreeClassifier.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.tree.DecisionTreeClassifier.set_params "sklearn.tree.DecisionTreeClassifier.set_params")(\*\*params) | Set the parameters of this estimator. |
apply(*X*, *check\_input=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L532)
Return the index of the leaf that each sample is predicted as.
New in version 0.17.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
**check\_input**bool, default=True
Allow to bypass several input checking. Don’t use this parameter unless you know what you do.
Returns:
**X\_leaves**array-like of shape (n\_samples,)
For each datapoint x in X, return the index of the leaf x ends up in. Leaves are numbered within `[0; self.tree_.node_count)`, possibly with gaps in the numbering.
cost\_complexity\_pruning\_path(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L607)
Compute the pruning path during Minimal Cost-Complexity Pruning.
See [Minimal Cost-Complexity Pruning](../tree#minimal-cost-complexity-pruning) for details on the pruning process.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csc_matrix`.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
The target values (class labels) as integers or strings.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, then samples are equally weighted. Splits that would create child nodes with net zero or negative weight are ignored while searching for a split in each node. Splits are also ignored if they would result in any single class carrying a negative weight in either child node.
Returns:
**ccp\_path**[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
Dictionary-like object, with the following attributes.
ccp\_alphasndarray
Effective alphas of subtree during pruning.
impuritiesndarray
Sum of the impurities of the subtree leaves for the corresponding alpha value in `ccp_alphas`.
decision\_path(*X*, *check\_input=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L560)
Return the decision path in the tree.
New in version 0.18.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
**check\_input**bool, default=True
Allow to bypass several input checking. Don’t use this parameter unless you know what you do.
Returns:
**indicator**sparse matrix of shape (n\_samples, n\_nodes)
Return a node indicator CSR matrix where non zero elements indicates that the samples goes through the nodes.
*property*feature\_importances\_
Return the feature importances.
The importance of a feature is computed as the (normalized) total reduction of the criterion brought by that feature. It is also known as the Gini importance.
Warning: impurity-based feature importances can be misleading for high cardinality features (many unique values). See [`sklearn.inspection.permutation_importance`](sklearn.inspection.permutation_importance#sklearn.inspection.permutation_importance "sklearn.inspection.permutation_importance") as an alternative.
Returns:
**feature\_importances\_**ndarray of shape (n\_features,)
Normalized total reduction of criteria by feature (Gini importance).
fit(*X*, *y*, *sample\_weight=None*, *check\_input=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L939)
Build a decision tree classifier from the training set (X, y).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csc_matrix`.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
The target values (class labels) as integers or strings.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, then samples are equally weighted. Splits that would create child nodes with net zero or negative weight are ignored while searching for a split in each node. Splits are also ignored if they would result in any single class carrying a negative weight in either child node.
**check\_input**bool, default=True
Allow to bypass several input checking. Don’t use this parameter unless you know what you do.
Returns:
**self**DecisionTreeClassifier
Fitted estimator.
get\_depth()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L130)
Return the depth of the decision tree.
The depth of a tree is the maximum distance between the root and any leaf.
Returns:
**self.tree\_.max\_depth**int
The maximum depth of the tree.
get\_n\_leaves()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L144)
Return the number of leaves of the decision tree.
Returns:
**self.tree\_.n\_leaves**int
Number of leaves.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_features\_
DEPRECATED: The attribute `n_features_` is deprecated in 1.0 and will be removed in 1.2. Use `n_features_in_` instead.
predict(*X*, *check\_input=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L481)
Predict class or regression value for X.
For a classification model, the predicted class for each sample in X is returned. For a regression model, the predicted value based on X is returned.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
**check\_input**bool, default=True
Allow to bypass several input checking. Don’t use this parameter unless you know what you do.
Returns:
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
The predicted classes, or the predict values.
predict\_log\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L1025)
Predict class log-probabilities of the input samples X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
Returns:
**proba**ndarray of shape (n\_samples, n\_classes) or list of n\_outputs such arrays if n\_outputs > 1
The class log-probabilities of the input samples. The order of the classes corresponds to that in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
predict\_proba(*X*, *check\_input=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/tree/_classes.py#L977)
Predict class probabilities of the input samples X.
The predicted class probability is the fraction of samples of the same class in a leaf.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
**check\_input**bool, default=True
Allow to bypass several input checking. Don’t use this parameter unless you know what you do.
Returns:
**proba**ndarray of shape (n\_samples, n\_classes) or list of n\_outputs such arrays if n\_outputs > 1
The class probabilities of the input samples. The order of the classes corresponds to that in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.tree.DecisionTreeClassifier`
----------------------------------------------------
[Classifier comparison](../../auto_examples/classification/plot_classifier_comparison#sphx-glr-auto-examples-classification-plot-classifier-comparison-py)
[Plot the decision surface of decision trees trained on the iris dataset](../../auto_examples/tree/plot_iris_dtc#sphx-glr-auto-examples-tree-plot-iris-dtc-py)
[Post pruning decision trees with cost complexity pruning](../../auto_examples/tree/plot_cost_complexity_pruning#sphx-glr-auto-examples-tree-plot-cost-complexity-pruning-py)
[Understanding the decision tree structure](../../auto_examples/tree/plot_unveil_tree_structure#sphx-glr-auto-examples-tree-plot-unveil-tree-structure-py)
[Discrete versus Real AdaBoost](../../auto_examples/ensemble/plot_adaboost_hastie_10_2#sphx-glr-auto-examples-ensemble-plot-adaboost-hastie-10-2-py)
[Multi-class AdaBoosted Decision Trees](../../auto_examples/ensemble/plot_adaboost_multiclass#sphx-glr-auto-examples-ensemble-plot-adaboost-multiclass-py)
[Plot the decision boundaries of a VotingClassifier](../../auto_examples/ensemble/plot_voting_decision_regions#sphx-glr-auto-examples-ensemble-plot-voting-decision-regions-py)
[Plot the decision surfaces of ensembles of trees on the iris dataset](../../auto_examples/ensemble/plot_forest_iris#sphx-glr-auto-examples-ensemble-plot-forest-iris-py)
[Two-class AdaBoost](../../auto_examples/ensemble/plot_adaboost_twoclass#sphx-glr-auto-examples-ensemble-plot-adaboost-twoclass-py)
[Demonstration of multi-metric evaluation on cross\_val\_score and GridSearchCV](../../auto_examples/model_selection/plot_multi_metric_evaluation#sphx-glr-auto-examples-model-selection-plot-multi-metric-evaluation-py)
| programming_docs |
scikit_learn sklearn.neighbors.NeighborhoodComponentsAnalysis sklearn.neighbors.NeighborhoodComponentsAnalysis
================================================
*class*sklearn.neighbors.NeighborhoodComponentsAnalysis(*n\_components=None*, *\**, *init='auto'*, *warm\_start=False*, *max\_iter=50*, *tol=1e-05*, *callback=None*, *verbose=0*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_nca.py#L26)
Neighborhood Components Analysis.
Neighborhood Component Analysis (NCA) is a machine learning algorithm for metric learning. It learns a linear transformation in a supervised fashion to improve the classification accuracy of a stochastic nearest neighbors rule in the transformed space.
Read more in the [User Guide](../neighbors#nca).
Parameters:
**n\_components**int, default=None
Preferred dimensionality of the projected space. If None it will be set to `n_features`.
**init**{‘auto’, ‘pca’, ‘lda’, ‘identity’, ‘random’} or ndarray of shape (n\_features\_a, n\_features\_b), default=’auto’
Initialization of the linear transformation. Possible options are `'auto'`, `'pca'`, `'lda'`, `'identity'`, `'random'`, and a numpy array of shape `(n_features_a, n_features_b)`.
* `'auto'`
Depending on `n_components`, the most reasonable initialization will be chosen. If `n_components <= n_classes` we use `'lda'`, as it uses labels information. If not, but `n_components < min(n_features, n_samples)`, we use `'pca'`, as it projects data in meaningful directions (those of higher variance). Otherwise, we just use `'identity'`.
* `'pca'`
`n_components` principal components of the inputs passed to [`fit`](#sklearn.neighbors.NeighborhoodComponentsAnalysis.fit "sklearn.neighbors.NeighborhoodComponentsAnalysis.fit") will be used to initialize the transformation. (See [`PCA`](sklearn.decomposition.pca#sklearn.decomposition.PCA "sklearn.decomposition.PCA"))
* `'lda'`
`min(n_components, n_classes)` most discriminative components of the inputs passed to [`fit`](#sklearn.neighbors.NeighborhoodComponentsAnalysis.fit "sklearn.neighbors.NeighborhoodComponentsAnalysis.fit") will be used to initialize the transformation. (If `n_components > n_classes`, the rest of the components will be zero.) (See [`LinearDiscriminantAnalysis`](sklearn.discriminant_analysis.lineardiscriminantanalysis#sklearn.discriminant_analysis.LinearDiscriminantAnalysis "sklearn.discriminant_analysis.LinearDiscriminantAnalysis"))
* `'identity'`
If `n_components` is strictly smaller than the dimensionality of the inputs passed to [`fit`](#sklearn.neighbors.NeighborhoodComponentsAnalysis.fit "sklearn.neighbors.NeighborhoodComponentsAnalysis.fit"), the identity matrix will be truncated to the first `n_components` rows.
* `'random'`
The initial transformation will be a random array of shape `(n_components, n_features)`. Each value is sampled from the standard normal distribution.
* numpy array
`n_features_b` must match the dimensionality of the inputs passed to [`fit`](#sklearn.neighbors.NeighborhoodComponentsAnalysis.fit "sklearn.neighbors.NeighborhoodComponentsAnalysis.fit") and n\_features\_a must be less than or equal to that. If `n_components` is not `None`, `n_features_a` must match it.
**warm\_start**bool, default=False
If `True` and [`fit`](#sklearn.neighbors.NeighborhoodComponentsAnalysis.fit "sklearn.neighbors.NeighborhoodComponentsAnalysis.fit") has been called before, the solution of the previous call to [`fit`](#sklearn.neighbors.NeighborhoodComponentsAnalysis.fit "sklearn.neighbors.NeighborhoodComponentsAnalysis.fit") is used as the initial linear transformation (`n_components` and `init` will be ignored).
**max\_iter**int, default=50
Maximum number of iterations in the optimization.
**tol**float, default=1e-5
Convergence tolerance for the optimization.
**callback**callable, default=None
If not `None`, this function is called after every iteration of the optimizer, taking as arguments the current solution (flattened transformation matrix) and the number of iterations. This might be useful in case one wants to examine or store the transformation found after each iteration.
**verbose**int, default=0
If 0, no progress messages will be printed. If 1, progress messages will be printed to stdout. If > 1, progress messages will be printed and the `disp` parameter of [`scipy.optimize.minimize`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html#scipy.optimize.minimize "(in SciPy v1.9.3)") will be set to `verbose - 2`.
**random\_state**int or numpy.RandomState, default=None
A pseudo random number generator object or a seed for it if int. If `init='random'`, `random_state` is used to initialize the random transformation. If `init='pca'`, `random_state` is passed as an argument to PCA when initializing the transformation. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Attributes:
**components\_**ndarray of shape (n\_components, n\_features)
The linear transformation learned during fitting.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**n\_iter\_**int
Counts the number of iterations performed by the optimizer.
**random\_state\_**numpy.RandomState
Pseudo random number generator object used during initialization.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`sklearn.discriminant_analysis.LinearDiscriminantAnalysis`](sklearn.discriminant_analysis.lineardiscriminantanalysis#sklearn.discriminant_analysis.LinearDiscriminantAnalysis "sklearn.discriminant_analysis.LinearDiscriminantAnalysis")
Linear Discriminant Analysis.
[`sklearn.decomposition.PCA`](sklearn.decomposition.pca#sklearn.decomposition.PCA "sklearn.decomposition.PCA")
Principal component analysis (PCA).
#### References
[1] J. Goldberger, G. Hinton, S. Roweis, R. Salakhutdinov. “Neighbourhood Components Analysis”. Advances in Neural Information Processing Systems. 17, 513-520, 2005. <http://www.cs.nyu.edu/~roweis/papers/ncanips.pdf>
[2] Wikipedia entry on Neighborhood Components Analysis <https://en.wikipedia.org/wiki/Neighbourhood_components_analysis>
#### Examples
```
>>> from sklearn.neighbors import NeighborhoodComponentsAnalysis
>>> from sklearn.neighbors import KNeighborsClassifier
>>> from sklearn.datasets import load_iris
>>> from sklearn.model_selection import train_test_split
>>> X, y = load_iris(return_X_y=True)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y,
... stratify=y, test_size=0.7, random_state=42)
>>> nca = NeighborhoodComponentsAnalysis(random_state=42)
>>> nca.fit(X_train, y_train)
NeighborhoodComponentsAnalysis(...)
>>> knn = KNeighborsClassifier(n_neighbors=3)
>>> knn.fit(X_train, y_train)
KNeighborsClassifier(...)
>>> print(knn.score(X_test, y_test))
0.933333...
>>> knn.fit(nca.transform(X_train), y_train)
KNeighborsClassifier(...)
>>> print(knn.score(nca.transform(X_test), y_test))
0.961904...
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.neighbors.NeighborhoodComponentsAnalysis.fit "sklearn.neighbors.NeighborhoodComponentsAnalysis.fit")(X, y) | Fit the model according to the given training data. |
| [`fit_transform`](#sklearn.neighbors.NeighborhoodComponentsAnalysis.fit_transform "sklearn.neighbors.NeighborhoodComponentsAnalysis.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.neighbors.NeighborhoodComponentsAnalysis.get_feature_names_out "sklearn.neighbors.NeighborhoodComponentsAnalysis.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.neighbors.NeighborhoodComponentsAnalysis.get_params "sklearn.neighbors.NeighborhoodComponentsAnalysis.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.neighbors.NeighborhoodComponentsAnalysis.set_params "sklearn.neighbors.NeighborhoodComponentsAnalysis.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.neighbors.NeighborhoodComponentsAnalysis.transform "sklearn.neighbors.NeighborhoodComponentsAnalysis.transform")(X) | Apply the learned transformation to the given data. |
fit(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_nca.py#L200)
Fit the model according to the given training data.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The training samples.
**y**array-like of shape (n\_samples,)
The corresponding training labels.
Returns:
**self**object
Fitted estimator.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.neighbors.NeighborhoodComponentsAnalysis.fit "sklearn.neighbors.NeighborhoodComponentsAnalysis.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_nca.py#L273)
Apply the learned transformation to the given data.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Data samples.
Returns:
X\_embedded: ndarray of shape (n\_samples, n\_components)
The data samples transformed.
Raises:
NotFittedError
If [`fit`](#sklearn.neighbors.NeighborhoodComponentsAnalysis.fit "sklearn.neighbors.NeighborhoodComponentsAnalysis.fit") has not been called before.
Examples using `sklearn.neighbors.NeighborhoodComponentsAnalysis`
-----------------------------------------------------------------
[Manifold learning on handwritten digits: Locally Linear Embedding, Isomap…](../../auto_examples/manifold/plot_lle_digits#sphx-glr-auto-examples-manifold-plot-lle-digits-py)
[Comparing Nearest Neighbors with and without Neighborhood Components Analysis](../../auto_examples/neighbors/plot_nca_classification#sphx-glr-auto-examples-neighbors-plot-nca-classification-py)
[Dimensionality Reduction with Neighborhood Components Analysis](../../auto_examples/neighbors/plot_nca_dim_reduction#sphx-glr-auto-examples-neighbors-plot-nca-dim-reduction-py)
[Neighborhood Components Analysis Illustration](../../auto_examples/neighbors/plot_nca_illustration#sphx-glr-auto-examples-neighbors-plot-nca-illustration-py)
scikit_learn sklearn.model_selection.ShuffleSplit sklearn.model\_selection.ShuffleSplit
=====================================
*class*sklearn.model\_selection.ShuffleSplit(*n\_splits=10*, *\**, *test\_size=None*, *train\_size=None*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L1654)
Random permutation cross-validator
Yields indices to split data into training and test sets.
Note: contrary to other cross-validation strategies, random splits do not guarantee that all folds will be different, although this is still very likely for sizeable datasets.
Read more in the [User Guide](../cross_validation#shufflesplit).
Parameters:
**n\_splits**int, default=10
Number of re-shuffling & splitting iterations.
**test\_size**float or int, default=None
If float, should be between 0.0 and 1.0 and represent the proportion of the dataset to include in the test split. If int, represents the absolute number of test samples. If None, the value is set to the complement of the train size. If `train_size` is also None, it will be set to 0.1.
**train\_size**float or int, default=None
If float, should be between 0.0 and 1.0 and represent the proportion of the dataset to include in the train split. If int, represents the absolute number of train samples. If None, the value is automatically set to the complement of the test size.
**random\_state**int, RandomState instance or None, default=None
Controls the randomness of the training and testing indices produced. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
#### Examples
```
>>> import numpy as np
>>> from sklearn.model_selection import ShuffleSplit
>>> X = np.array([[1, 2], [3, 4], [5, 6], [7, 8], [3, 4], [5, 6]])
>>> y = np.array([1, 2, 1, 2, 1, 2])
>>> rs = ShuffleSplit(n_splits=5, test_size=.25, random_state=0)
>>> rs.get_n_splits(X)
5
>>> print(rs)
ShuffleSplit(n_splits=5, random_state=0, test_size=0.25, train_size=None)
>>> for train_index, test_index in rs.split(X):
... print("TRAIN:", train_index, "TEST:", test_index)
TRAIN: [1 3 0 4] TEST: [5 2]
TRAIN: [4 0 2 5] TEST: [1 3]
TRAIN: [1 2 4 0] TEST: [3 5]
TRAIN: [3 4 1 0] TEST: [5 2]
TRAIN: [3 5 1 0] TEST: [2 4]
>>> rs = ShuffleSplit(n_splits=5, train_size=0.5, test_size=.25,
... random_state=0)
>>> for train_index, test_index in rs.split(X):
... print("TRAIN:", train_index, "TEST:", test_index)
TRAIN: [1 3 0] TEST: [5 2]
TRAIN: [4 0 2] TEST: [1 3]
TRAIN: [1 2 4] TEST: [3 5]
TRAIN: [3 4 1] TEST: [5 2]
TRAIN: [3 5 1] TEST: [2 4]
```
#### Methods
| | |
| --- | --- |
| [`get_n_splits`](#sklearn.model_selection.ShuffleSplit.get_n_splits "sklearn.model_selection.ShuffleSplit.get_n_splits")([X, y, groups]) | Returns the number of splitting iterations in the cross-validator |
| [`split`](#sklearn.model_selection.ShuffleSplit.split "sklearn.model_selection.ShuffleSplit.split")(X[, y, groups]) | Generate indices to split data into training and test set. |
get\_n\_splits(*X=None*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L1629)
Returns the number of splitting iterations in the cross-validator
Parameters:
**X**object
Always ignored, exists for compatibility.
**y**object
Always ignored, exists for compatibility.
**groups**object
Always ignored, exists for compatibility.
Returns:
**n\_splits**int
Returns the number of splitting iterations in the cross-validator.
split(*X*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L1591)
Generate indices to split data into training and test set.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,)
The target variable for supervised learning problems.
**groups**array-like of shape (n\_samples,), default=None
Group labels for the samples used while splitting the dataset into train/test set.
Yields:
**train**ndarray
The training set indices for that split.
**test**ndarray
The testing set indices for that split.
#### Notes
Randomized CV splitters may return different results for each call of split. You can make the results identical by setting `random_state` to an integer.
Examples using `sklearn.model_selection.ShuffleSplit`
-----------------------------------------------------
[Plotting Learning Curves](../../auto_examples/model_selection/plot_learning_curve#sphx-glr-auto-examples-model-selection-plot-learning-curve-py)
[Visualizing cross-validation behavior in scikit-learn](../../auto_examples/model_selection/plot_cv_indices#sphx-glr-auto-examples-model-selection-plot-cv-indices-py)
[Scaling the regularization parameter for SVCs](../../auto_examples/svm/plot_svm_scale_c#sphx-glr-auto-examples-svm-plot-svm-scale-c-py)
scikit_learn sklearn.metrics.make_scorer sklearn.metrics.make\_scorer
============================
sklearn.metrics.make\_scorer(*score\_func*, *\**, *greater\_is\_better=True*, *needs\_proba=False*, *needs\_threshold=False*, *\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_scorer.py#L589)
Make a scorer from a performance metric or loss function.
This factory function wraps scoring functions for use in [`GridSearchCV`](sklearn.model_selection.gridsearchcv#sklearn.model_selection.GridSearchCV "sklearn.model_selection.GridSearchCV") and [`cross_val_score`](sklearn.model_selection.cross_val_score#sklearn.model_selection.cross_val_score "sklearn.model_selection.cross_val_score"). It takes a score function, such as [`accuracy_score`](sklearn.metrics.accuracy_score#sklearn.metrics.accuracy_score "sklearn.metrics.accuracy_score"), [`mean_squared_error`](sklearn.metrics.mean_squared_error#sklearn.metrics.mean_squared_error "sklearn.metrics.mean_squared_error"), [`adjusted_rand_score`](sklearn.metrics.adjusted_rand_score#sklearn.metrics.adjusted_rand_score "sklearn.metrics.adjusted_rand_score") or [`average_precision_score`](sklearn.metrics.average_precision_score#sklearn.metrics.average_precision_score "sklearn.metrics.average_precision_score") and returns a callable that scores an estimator’s output. The signature of the call is `(estimator, X, y)` where `estimator` is the model to be evaluated, `X` is the data and `y` is the ground truth labeling (or `None` in the case of unsupervised models).
Read more in the [User Guide](../model_evaluation#scoring).
Parameters:
**score\_func**callable
Score function (or loss function) with signature `score_func(y, y_pred, **kwargs)`.
**greater\_is\_better**bool, default=True
Whether `score_func` is a score function (default), meaning high is good, or a loss function, meaning low is good. In the latter case, the scorer object will sign-flip the outcome of the `score_func`.
**needs\_proba**bool, default=False
Whether `score_func` requires `predict_proba` to get probability estimates out of a classifier.
If True, for binary `y_true`, the score function is supposed to accept a 1D `y_pred` (i.e., probability of the positive class, shape `(n_samples,)`).
**needs\_threshold**bool, default=False
Whether `score_func` takes a continuous decision certainty. This only works for binary classification using estimators that have either a `decision_function` or `predict_proba` method.
If True, for binary `y_true`, the score function is supposed to accept a 1D `y_pred` (i.e., probability of the positive class or the decision function, shape `(n_samples,)`).
For example `average_precision` or the area under the roc curve can not be computed using discrete predictions alone.
**\*\*kwargs**additional arguments
Additional parameters to be passed to `score_func`.
Returns:
**scorer**callable
Callable object that returns a scalar score; greater is better.
#### Notes
If `needs_proba=False` and `needs_threshold=False`, the score function is supposed to accept the output of [predict](https://scikit-learn.org/1.1/glossary.html#term-predict). If `needs_proba=True`, the score function is supposed to accept the output of [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) (For binary `y_true`, the score function is supposed to accept probability of the positive class). If `needs_threshold=True`, the score function is supposed to accept the output of [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) or [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) when [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) is not present.
#### Examples
```
>>> from sklearn.metrics import fbeta_score, make_scorer
>>> ftwo_scorer = make_scorer(fbeta_score, beta=2)
>>> ftwo_scorer
make_scorer(fbeta_score, beta=2)
>>> from sklearn.model_selection import GridSearchCV
>>> from sklearn.svm import LinearSVC
>>> grid = GridSearchCV(LinearSVC(), param_grid={'C': [1, 10]},
... scoring=ftwo_scorer)
```
Examples using `sklearn.metrics.make_scorer`
--------------------------------------------
[Prediction Intervals for Gradient Boosting Regression](../../auto_examples/ensemble/plot_gradient_boosting_quantile#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-quantile-py)
[Demonstration of multi-metric evaluation on cross\_val\_score and GridSearchCV](../../auto_examples/model_selection/plot_multi_metric_evaluation#sphx-glr-auto-examples-model-selection-plot-multi-metric-evaluation-py)
| programming_docs |
scikit_learn sklearn.metrics.pairwise.paired_cosine_distances sklearn.metrics.pairwise.paired\_cosine\_distances
==================================================
sklearn.metrics.pairwise.paired\_cosine\_distances(*X*, *Y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/pairwise.py#L1059)
Compute the paired cosine distances between X and Y.
Read more in the [User Guide](../metrics#metrics).
Parameters:
**X**array-like of shape (n\_samples, n\_features)
An array where each row is a sample and each column is a feature.
**Y**array-like of shape (n\_samples, n\_features)
An array where each row is a sample and each column is a feature.
Returns:
**distances**ndarray of shape (n\_samples,)
Returns the distances between the row vectors of `X` and the row vectors of `Y`, where `distances[i]` is the distance between `X[i]` and `Y[i]`.
#### Notes
The cosine distance is equivalent to the half the squared euclidean distance if each sample is normalized to unit norm.
scikit_learn sklearn.gaussian_process.kernels.Kernel sklearn.gaussian\_process.kernels.Kernel
========================================
*class*sklearn.gaussian\_process.kernels.Kernel[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L152)
Base class for all kernels.
New in version 0.18.
Attributes:
[`bounds`](#sklearn.gaussian_process.kernels.Kernel.bounds "sklearn.gaussian_process.kernels.Kernel.bounds")
Returns the log-transformed bounds on the theta.
[`hyperparameters`](#sklearn.gaussian_process.kernels.Kernel.hyperparameters "sklearn.gaussian_process.kernels.Kernel.hyperparameters")
Returns a list of all hyperparameter specifications.
[`n_dims`](#sklearn.gaussian_process.kernels.Kernel.n_dims "sklearn.gaussian_process.kernels.Kernel.n_dims")
Returns the number of non-fixed hyperparameters of the kernel.
[`requires_vector_input`](#sklearn.gaussian_process.kernels.Kernel.requires_vector_input "sklearn.gaussian_process.kernels.Kernel.requires_vector_input")
Returns whether the kernel is defined on fixed-length feature vectors or generic objects.
[`theta`](#sklearn.gaussian_process.kernels.Kernel.theta "sklearn.gaussian_process.kernels.Kernel.theta")
Returns the (flattened, log-transformed) non-fixed hyperparameters.
#### Methods
| | |
| --- | --- |
| [`__call__`](#sklearn.gaussian_process.kernels.Kernel.__call__ "sklearn.gaussian_process.kernels.Kernel.__call__")(X[, Y, eval\_gradient]) | Evaluate the kernel. |
| [`clone_with_theta`](#sklearn.gaussian_process.kernels.Kernel.clone_with_theta "sklearn.gaussian_process.kernels.Kernel.clone_with_theta")(theta) | Returns a clone of self with given hyperparameters theta. |
| [`diag`](#sklearn.gaussian_process.kernels.Kernel.diag "sklearn.gaussian_process.kernels.Kernel.diag")(X) | Returns the diagonal of the kernel k(X, X). |
| [`get_params`](#sklearn.gaussian_process.kernels.Kernel.get_params "sklearn.gaussian_process.kernels.Kernel.get_params")([deep]) | Get parameters of this kernel. |
| [`is_stationary`](#sklearn.gaussian_process.kernels.Kernel.is_stationary "sklearn.gaussian_process.kernels.Kernel.is_stationary")() | Returns whether the kernel is stationary. |
| [`set_params`](#sklearn.gaussian_process.kernels.Kernel.set_params "sklearn.gaussian_process.kernels.Kernel.set_params")(\*\*params) | Set the parameters of this kernel. |
*abstract*\_\_call\_\_(*X*, *Y=None*, *eval\_gradient=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L377)
Evaluate the kernel.
*property*bounds
Returns the log-transformed bounds on the theta.
Returns:
**bounds**ndarray of shape (n\_dims, 2)
The log-transformed bounds on the kernel’s hyperparameters theta
clone\_with\_theta(*theta*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L238)
Returns a clone of self with given hyperparameters theta.
Parameters:
**theta**ndarray of shape (n\_dims,)
The hyperparameters
*abstract*diag(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L381)
Returns the diagonal of the kernel k(X, X).
The result of this method is identical to np.diag(self(X)); however, it can be evaluated more efficiently since only the diagonal is evaluated.
Parameters:
**X**array-like of shape (n\_samples,)
Left argument of the returned kernel k(X, Y)
Returns:
**K\_diag**ndarray of shape (n\_samples\_X,)
Diagonal of kernel k(X, X)
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L158)
Get parameters of this kernel.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*hyperparameters
Returns a list of all hyperparameter specifications.
*abstract*is\_stationary()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L400)
Returns whether the kernel is stationary.
*property*n\_dims
Returns the number of non-fixed hyperparameters of the kernel.
*property*requires\_vector\_input
Returns whether the kernel is defined on fixed-length feature vectors or generic objects. Defaults to True for backward compatibility.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L198)
Set the parameters of this kernel.
The method works on simple kernels as well as on nested kernels. The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Returns:
self
*property*theta
Returns the (flattened, log-transformed) non-fixed hyperparameters.
Note that theta are typically the log-transformed values of the kernel’s hyperparameters as this representation of the search space is more amenable for hyperparameter search, as hyperparameters like length-scales naturally live on a log-scale.
Returns:
**theta**ndarray of shape (n\_dims,)
The non-fixed, log-transformed hyperparameters of the kernel
Examples using `sklearn.gaussian_process.kernels.Kernel`
--------------------------------------------------------
[Gaussian processes on discrete data structures](../../auto_examples/gaussian_process/plot_gpr_on_structured_data#sphx-glr-auto-examples-gaussian-process-plot-gpr-on-structured-data-py)
scikit_learn sklearn.linear_model.LassoLarsIC sklearn.linear\_model.LassoLarsIC
=================================
*class*sklearn.linear\_model.LassoLarsIC(*criterion='aic'*, *\**, *fit\_intercept=True*, *verbose=False*, *normalize='deprecated'*, *precompute='auto'*, *max\_iter=500*, *eps=2.220446049250313e-16*, *copy\_X=True*, *positive=False*, *noise\_variance=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_least_angle.py#L1965)
Lasso model fit with Lars using BIC or AIC for model selection.
The optimization objective for Lasso is:
```
(1 / (2 * n_samples)) * ||y - Xw||^2_2 + alpha * ||w||_1
```
AIC is the Akaike information criterion [[2]](#rde9cc43d0d41-2) and BIC is the Bayes Information criterion [[3]](#rde9cc43d0d41-3). Such criteria are useful to select the value of the regularization parameter by making a trade-off between the goodness of fit and the complexity of the model. A good model should explain well the data while being simple.
Read more in the [User Guide](../linear_model#lasso-lars-ic).
Parameters:
**criterion**{‘aic’, ‘bic’}, default=’aic’
The type of criterion to use.
**fit\_intercept**bool, default=True
Whether to calculate the intercept for this model. If set to false, no intercept will be used in calculations (i.e. data is expected to be centered).
**verbose**bool or int, default=False
Sets the verbosity amount.
**normalize**bool, default=True
This parameter is ignored when `fit_intercept` is set to False. If True, the regressors X will be normalized before regression by subtracting the mean and dividing by the l2-norm. If you wish to standardize, please use [`StandardScaler`](sklearn.preprocessing.standardscaler#sklearn.preprocessing.StandardScaler "sklearn.preprocessing.StandardScaler") before calling `fit` on an estimator with `normalize=False`.
Deprecated since version 1.0: `normalize` was deprecated in version 1.0. It will default to False in 1.2 and be removed in 1.4.
**precompute**bool, ‘auto’ or array-like, default=’auto’
Whether to use a precomputed Gram matrix to speed up calculations. If set to `'auto'` let us decide. The Gram matrix can also be passed as argument.
**max\_iter**int, default=500
Maximum number of iterations to perform. Can be used for early stopping.
**eps**float, default=np.finfo(float).eps
The machine-precision regularization in the computation of the Cholesky diagonal factors. Increase this for very ill-conditioned systems. Unlike the `tol` parameter in some iterative optimization-based algorithms, this parameter does not control the tolerance of the optimization.
**copy\_X**bool, default=True
If True, X will be copied; else, it may be overwritten.
**positive**bool, default=False
Restrict coefficients to be >= 0. Be aware that you might want to remove fit\_intercept which is set True by default. Under the positive restriction the model coefficients do not converge to the ordinary-least-squares solution for small values of alpha. Only coefficients up to the smallest alpha value (`alphas_[alphas_ >
0.].min()` when fit\_path=True) reached by the stepwise Lars-Lasso algorithm are typically in congruence with the solution of the coordinate descent Lasso estimator. As a consequence using LassoLarsIC only makes sense for problems where a sparse solution is expected and/or reached.
**noise\_variance**float, default=None
The estimated noise variance of the data. If `None`, an unbiased estimate is computed by an OLS model. However, it is only possible in the case where `n_samples > n_features + fit_intercept`.
New in version 1.1.
Attributes:
**coef\_**array-like of shape (n\_features,)
parameter vector (w in the formulation formula)
**intercept\_**float
independent term in decision function.
**alpha\_**float
the alpha parameter chosen by the information criterion
**alphas\_**array-like of shape (n\_alphas + 1,) or list of such arrays
Maximum of covariances (in absolute value) at each iteration. `n_alphas` is either `max_iter`, `n_features` or the number of nodes in the path with `alpha >= alpha_min`, whichever is smaller. If a list, it will be of length `n_targets`.
**n\_iter\_**int
number of iterations run by lars\_path to find the grid of alphas.
**criterion\_**array-like of shape (n\_alphas,)
The value of the information criteria (‘aic’, ‘bic’) across all alphas. The alpha which has the smallest information criterion is chosen, as specified in [[1]](#rde9cc43d0d41-1).
**noise\_variance\_**float
The estimated noise variance from the data used to compute the criterion.
New in version 1.1.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`lars_path`](sklearn.linear_model.lars_path#sklearn.linear_model.lars_path "sklearn.linear_model.lars_path")
Compute Least Angle Regression or Lasso path using LARS algorithm.
[`lasso_path`](sklearn.linear_model.lasso_path#sklearn.linear_model.lasso_path "sklearn.linear_model.lasso_path")
Compute Lasso path with coordinate descent.
[`Lasso`](sklearn.linear_model.lasso#sklearn.linear_model.Lasso "sklearn.linear_model.Lasso")
Linear Model trained with L1 prior as regularizer (aka the Lasso).
[`LassoCV`](sklearn.linear_model.lassocv#sklearn.linear_model.LassoCV "sklearn.linear_model.LassoCV")
Lasso linear model with iterative fitting along a regularization path.
[`LassoLars`](sklearn.linear_model.lassolars#sklearn.linear_model.LassoLars "sklearn.linear_model.LassoLars")
Lasso model fit with Least Angle Regression a.k.a. Lars.
[`LassoLarsCV`](sklearn.linear_model.lassolarscv#sklearn.linear_model.LassoLarsCV "sklearn.linear_model.LassoLarsCV")
Cross-validated Lasso, using the LARS algorithm.
[`sklearn.decomposition.sparse_encode`](sklearn.decomposition.sparse_encode#sklearn.decomposition.sparse_encode "sklearn.decomposition.sparse_encode")
Sparse coding.
#### Notes
The number of degrees of freedom is computed as in [[1]](#rde9cc43d0d41-1).
To have more details regarding the mathematical formulation of the AIC and BIC criteria, please refer to [User Guide](../linear_model#lasso-lars-ic).
#### References
[1] ([1](#id3),[2](#id4)) [Zou, Hui, Trevor Hastie, and Robert Tibshirani. “On the degrees of freedom of the lasso.” The Annals of Statistics 35.5 (2007): 2173-2192.](https://arxiv.org/abs/0712.0881)
[[2](#id1)] [Wikipedia entry on the Akaike information criterion](https://en.wikipedia.org/wiki/Akaike_information_criterion)
[[3](#id2)] [Wikipedia entry on the Bayesian information criterion](https://en.wikipedia.org/wiki/Bayesian_information_criterion)
#### Examples
```
>>> from sklearn import linear_model
>>> reg = linear_model.LassoLarsIC(criterion='bic', normalize=False)
>>> X = [[-2, 2], [-1, 1], [0, 0], [1, 1], [2, 2]]
>>> y = [-2.2222, -1.1111, 0, -1.1111, -2.2222]
>>> reg.fit(X, y)
LassoLarsIC(criterion='bic', normalize=False)
>>> print(reg.coef_)
[ 0. -1.11...]
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.linear_model.LassoLarsIC.fit "sklearn.linear_model.LassoLarsIC.fit")(X, y[, copy\_X]) | Fit the model using X, y as training data. |
| [`get_params`](#sklearn.linear_model.LassoLarsIC.get_params "sklearn.linear_model.LassoLarsIC.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.linear_model.LassoLarsIC.predict "sklearn.linear_model.LassoLarsIC.predict")(X) | Predict using the linear model. |
| [`score`](#sklearn.linear_model.LassoLarsIC.score "sklearn.linear_model.LassoLarsIC.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.linear_model.LassoLarsIC.set_params "sklearn.linear_model.LassoLarsIC.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*, *copy\_X=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_least_angle.py#L2160)
Fit the model using X, y as training data.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data.
**y**array-like of shape (n\_samples,)
Target values. Will be cast to X’s dtype if necessary.
**copy\_X**bool, default=None
If provided, this parameter will override the choice of copy\_X made at instance creation. If `True`, X will be copied; else, it may be overwritten.
Returns:
**self**object
Returns an instance of self.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L372)
Predict using the linear model.
Parameters:
**X**array-like or sparse matrix, shape (n\_samples, n\_features)
Samples.
Returns:
**C**array, shape (n\_samples,)
Returns predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.linear_model.LassoLarsIC`
-------------------------------------------------
[Lasso model selection via information criteria](../../auto_examples/linear_model/plot_lasso_lars_ic#sphx-glr-auto-examples-linear-model-plot-lasso-lars-ic-py)
[Lasso model selection: AIC-BIC / cross-validation](../../auto_examples/linear_model/plot_lasso_model_selection#sphx-glr-auto-examples-linear-model-plot-lasso-model-selection-py)
scikit_learn sklearn.impute.KNNImputer sklearn.impute.KNNImputer
=========================
*class*sklearn.impute.KNNImputer(*\**, *missing\_values=nan*, *n\_neighbors=5*, *weights='uniform'*, *metric='nan\_euclidean'*, *copy=True*, *add\_indicator=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/impute/_knn.py#L19)
Imputation for completing missing values using k-Nearest Neighbors.
Each sample’s missing values are imputed using the mean value from `n_neighbors` nearest neighbors found in the training set. Two samples are close if the features that neither is missing are close.
Read more in the [User Guide](../impute#knnimpute).
New in version 0.22.
Parameters:
**missing\_values**int, float, str, np.nan or None, default=np.nan
The placeholder for the missing values. All occurrences of `missing_values` will be imputed. For pandas’ dataframes with nullable integer dtypes with missing values, `missing_values` should be set to np.nan, since `pd.NA` will be converted to np.nan.
**n\_neighbors**int, default=5
Number of neighboring samples to use for imputation.
**weights**{‘uniform’, ‘distance’} or callable, default=’uniform’
Weight function used in prediction. Possible values:
* ‘uniform’ : uniform weights. All points in each neighborhood are weighted equally.
* ‘distance’ : weight points by the inverse of their distance. in this case, closer neighbors of a query point will have a greater influence than neighbors which are further away.
* callable : a user-defined function which accepts an array of distances, and returns an array of the same shape containing the weights.
**metric**{‘nan\_euclidean’} or callable, default=’nan\_euclidean’
Distance metric for searching neighbors. Possible values:
* ‘nan\_euclidean’
* callable : a user-defined function which conforms to the definition of `_pairwise_callable(X, Y, metric, **kwds)`. The function accepts two arrays, X and Y, and a `missing_values` keyword in `kwds` and returns a scalar distance value.
**copy**bool, default=True
If True, a copy of X will be created. If False, imputation will be done in-place whenever possible.
**add\_indicator**bool, default=False
If True, a [`MissingIndicator`](sklearn.impute.missingindicator#sklearn.impute.MissingIndicator "sklearn.impute.MissingIndicator") transform will stack onto the output of the imputer’s transform. This allows a predictive estimator to account for missingness despite imputation. If a feature has no missing values at fit/train time, the feature won’t appear on the missing indicator even if there are missing values at transform/test time.
Attributes:
**indicator\_**[`MissingIndicator`](sklearn.impute.missingindicator#sklearn.impute.MissingIndicator "sklearn.impute.MissingIndicator")
Indicator used to add binary indicators for missing values. `None` if add\_indicator is False.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`SimpleImputer`](sklearn.impute.simpleimputer#sklearn.impute.SimpleImputer "sklearn.impute.SimpleImputer")
Univariate imputer for completing missing values with simple strategies.
[`IterativeImputer`](sklearn.impute.iterativeimputer#sklearn.impute.IterativeImputer "sklearn.impute.IterativeImputer")
Multivariate imputer that estimates values to impute for each feature with missing values from all the others.
#### References
* Olga Troyanskaya, Michael Cantor, Gavin Sherlock, Pat Brown, Trevor Hastie, Robert Tibshirani, David Botstein and Russ B. Altman, Missing value estimation methods for DNA microarrays, BIOINFORMATICS Vol. 17 no. 6, 2001 Pages 520-525.
#### Examples
```
>>> import numpy as np
>>> from sklearn.impute import KNNImputer
>>> X = [[1, 2, np.nan], [3, 4, 3], [np.nan, 6, 5], [8, 8, 7]]
>>> imputer = KNNImputer(n_neighbors=2)
>>> imputer.fit_transform(X)
array([[1. , 2. , 4. ],
[3. , 4. , 3. ],
[5.5, 6. , 5. ],
[8. , 8. , 7. ]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.impute.KNNImputer.fit "sklearn.impute.KNNImputer.fit")(X[, y]) | Fit the imputer on X. |
| [`fit_transform`](#sklearn.impute.KNNImputer.fit_transform "sklearn.impute.KNNImputer.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.impute.KNNImputer.get_feature_names_out "sklearn.impute.KNNImputer.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.impute.KNNImputer.get_params "sklearn.impute.KNNImputer.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.impute.KNNImputer.set_params "sklearn.impute.KNNImputer.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.impute.KNNImputer.transform "sklearn.impute.KNNImputer.transform")(X) | Impute all missing values in X. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/impute/_knn.py#L181)
Fit the imputer on X.
Parameters:
**X**array-like shape of (n\_samples, n\_features)
Input data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
**self**object
The fitted `KNNImputer` class instance.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/impute/_knn.py#L344)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Input features.
* If `input_features` is `None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then the following input feature names are generated: `["x0", "x1", ..., "x(n_features_in_ - 1)"]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/impute/_knn.py#L227)
Impute all missing values in X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The input data to complete.
Returns:
**X**array-like of shape (n\_samples, n\_output\_features)
The imputed dataset. `n_output_features` is the number of features that is not always missing during `fit`.
Examples using `sklearn.impute.KNNImputer`
------------------------------------------
[Release Highlights for scikit-learn 0.22](../../auto_examples/release_highlights/plot_release_highlights_0_22_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-22-0-py)
[Imputing missing values before building an estimator](../../auto_examples/impute/plot_missing_values#sphx-glr-auto-examples-impute-plot-missing-values-py)
| programming_docs |
scikit_learn sklearn.ensemble.RandomForestClassifier sklearn.ensemble.RandomForestClassifier
=======================================
*class*sklearn.ensemble.RandomForestClassifier(*n\_estimators=100*, *\**, *criterion='gini'*, *max\_depth=None*, *min\_samples\_split=2*, *min\_samples\_leaf=1*, *min\_weight\_fraction\_leaf=0.0*, *max\_features='sqrt'*, *max\_leaf\_nodes=None*, *min\_impurity\_decrease=0.0*, *bootstrap=True*, *oob\_score=False*, *n\_jobs=None*, *random\_state=None*, *verbose=0*, *warm\_start=False*, *class\_weight=None*, *ccp\_alpha=0.0*, *max\_samples=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L1091)
A random forest classifier.
A random forest is a meta estimator that fits a number of decision tree classifiers on various sub-samples of the dataset and uses averaging to improve the predictive accuracy and control over-fitting. The sub-sample size is controlled with the `max_samples` parameter if `bootstrap=True` (default), otherwise the whole dataset is used to build each tree.
Read more in the [User Guide](../ensemble#forest).
Parameters:
**n\_estimators**int, default=100
The number of trees in the forest.
Changed in version 0.22: The default value of `n_estimators` changed from 10 to 100 in 0.22.
**criterion**{“gini”, “entropy”, “log\_loss”}, default=”gini”
The function to measure the quality of a split. Supported criteria are “gini” for the Gini impurity and “log\_loss” and “entropy” both for the Shannon information gain, see [Mathematical formulation](../tree#tree-mathematical-formulation). Note: This parameter is tree-specific.
**max\_depth**int, default=None
The maximum depth of the tree. If None, then nodes are expanded until all leaves are pure or until all leaves contain less than min\_samples\_split samples.
**min\_samples\_split**int or float, default=2
The minimum number of samples required to split an internal node:
* If int, then consider `min_samples_split` as the minimum number.
* If float, then `min_samples_split` is a fraction and `ceil(min_samples_split * n_samples)` are the minimum number of samples for each split.
Changed in version 0.18: Added float values for fractions.
**min\_samples\_leaf**int or float, default=1
The minimum number of samples required to be at a leaf node. A split point at any depth will only be considered if it leaves at least `min_samples_leaf` training samples in each of the left and right branches. This may have the effect of smoothing the model, especially in regression.
* If int, then consider `min_samples_leaf` as the minimum number.
* If float, then `min_samples_leaf` is a fraction and `ceil(min_samples_leaf * n_samples)` are the minimum number of samples for each node.
Changed in version 0.18: Added float values for fractions.
**min\_weight\_fraction\_leaf**float, default=0.0
The minimum weighted fraction of the sum total of weights (of all the input samples) required to be at a leaf node. Samples have equal weight when sample\_weight is not provided.
**max\_features**{“sqrt”, “log2”, None}, int or float, default=”sqrt”
The number of features to consider when looking for the best split:
* If int, then consider `max_features` features at each split.
* If float, then `max_features` is a fraction and `max(1, int(max_features * n_features_in_))` features are considered at each split.
* If “auto”, then `max_features=sqrt(n_features)`.
* If “sqrt”, then `max_features=sqrt(n_features)`.
* If “log2”, then `max_features=log2(n_features)`.
* If None, then `max_features=n_features`.
Changed in version 1.1: The default of `max_features` changed from `"auto"` to `"sqrt"`.
Deprecated since version 1.1: The `"auto"` option was deprecated in 1.1 and will be removed in 1.3.
Note: the search for a split does not stop until at least one valid partition of the node samples is found, even if it requires to effectively inspect more than `max_features` features.
**max\_leaf\_nodes**int, default=None
Grow trees with `max_leaf_nodes` in best-first fashion. Best nodes are defined as relative reduction in impurity. If None then unlimited number of leaf nodes.
**min\_impurity\_decrease**float, default=0.0
A node will be split if this split induces a decrease of the impurity greater than or equal to this value.
The weighted impurity decrease equation is the following:
```
N_t / N * (impurity - N_t_R / N_t * right_impurity
- N_t_L / N_t * left_impurity)
```
where `N` is the total number of samples, `N_t` is the number of samples at the current node, `N_t_L` is the number of samples in the left child, and `N_t_R` is the number of samples in the right child.
`N`, `N_t`, `N_t_R` and `N_t_L` all refer to the weighted sum, if `sample_weight` is passed.
New in version 0.19.
**bootstrap**bool, default=True
Whether bootstrap samples are used when building trees. If False, the whole dataset is used to build each tree.
**oob\_score**bool, default=False
Whether to use out-of-bag samples to estimate the generalization score. Only available if bootstrap=True.
**n\_jobs**int, default=None
The number of jobs to run in parallel. [`fit`](#sklearn.ensemble.RandomForestClassifier.fit "sklearn.ensemble.RandomForestClassifier.fit"), [`predict`](#sklearn.ensemble.RandomForestClassifier.predict "sklearn.ensemble.RandomForestClassifier.predict"), [`decision_path`](#sklearn.ensemble.RandomForestClassifier.decision_path "sklearn.ensemble.RandomForestClassifier.decision_path") and [`apply`](#sklearn.ensemble.RandomForestClassifier.apply "sklearn.ensemble.RandomForestClassifier.apply") are all parallelized over the trees. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**random\_state**int, RandomState instance or None, default=None
Controls both the randomness of the bootstrapping of the samples used when building trees (if `bootstrap=True`) and the sampling of the features to consider when looking for the best split at each node (if `max_features < n_features`). See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state) for details.
**verbose**int, default=0
Controls the verbosity when fitting and predicting.
**warm\_start**bool, default=False
When set to `True`, reuse the solution of the previous call to fit and add more estimators to the ensemble, otherwise, just fit a whole new forest. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
**class\_weight**{“balanced”, “balanced\_subsample”}, dict or list of dicts, default=None
Weights associated with classes in the form `{class_label: weight}`. If not given, all classes are supposed to have weight one. For multi-output problems, a list of dicts can be provided in the same order as the columns of y.
Note that for multioutput (including multilabel) weights should be defined for each class of every column in its own dict. For example, for four-class multilabel classification weights should be [{0: 1, 1: 1}, {0: 1, 1: 5}, {0: 1, 1: 1}, {0: 1, 1: 1}] instead of [{1:1}, {2:5}, {3:1}, {4:1}].
The “balanced” mode uses the values of y to automatically adjust weights inversely proportional to class frequencies in the input data as `n_samples / (n_classes * np.bincount(y))`
The “balanced\_subsample” mode is the same as “balanced” except that weights are computed based on the bootstrap sample for every tree grown.
For multi-output, the weights of each column of y will be multiplied.
Note that these weights will be multiplied with sample\_weight (passed through the fit method) if sample\_weight is specified.
**ccp\_alpha**non-negative float, default=0.0
Complexity parameter used for Minimal Cost-Complexity Pruning. The subtree with the largest cost complexity that is smaller than `ccp_alpha` will be chosen. By default, no pruning is performed. See [Minimal Cost-Complexity Pruning](../tree#minimal-cost-complexity-pruning) for details.
New in version 0.22.
**max\_samples**int or float, default=None
If bootstrap is True, the number of samples to draw from X to train each base estimator.
* If None (default), then draw `X.shape[0]` samples.
* If int, then draw `max_samples` samples.
* If float, then draw `max_samples * X.shape[0]` samples. Thus, `max_samples` should be in the interval `(0.0, 1.0]`.
New in version 0.22.
Attributes:
**base\_estimator\_**DecisionTreeClassifier
The child estimator template used to create the collection of fitted sub-estimators.
**estimators\_**list of DecisionTreeClassifier
The collection of fitted sub-estimators.
**classes\_**ndarray of shape (n\_classes,) or a list of such arrays
The classes labels (single output problem), or a list of arrays of class labels (multi-output problem).
**n\_classes\_**int or list
The number of classes (single output problem), or a list containing the number of classes for each output (multi-output problem).
[`n_features_`](#sklearn.ensemble.RandomForestClassifier.n_features_ "sklearn.ensemble.RandomForestClassifier.n_features_")int
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_outputs\_**int
The number of outputs when `fit` is performed.
[`feature_importances_`](#sklearn.ensemble.RandomForestClassifier.feature_importances_ "sklearn.ensemble.RandomForestClassifier.feature_importances_")ndarray of shape (n\_features,)
The impurity-based feature importances.
**oob\_score\_**float
Score of the training dataset obtained using an out-of-bag estimate. This attribute exists only when `oob_score` is True.
**oob\_decision\_function\_**ndarray of shape (n\_samples, n\_classes) or (n\_samples, n\_classes, n\_outputs)
Decision function computed with out-of-bag estimate on the training set. If n\_estimators is small it might be possible that a data point was never left out during the bootstrap. In this case, `oob_decision_function_` might contain NaN. This attribute exists only when `oob_score` is True.
See also
[`sklearn.tree.DecisionTreeClassifier`](sklearn.tree.decisiontreeclassifier#sklearn.tree.DecisionTreeClassifier "sklearn.tree.DecisionTreeClassifier")
A decision tree classifier.
[`sklearn.ensemble.ExtraTreesClassifier`](sklearn.ensemble.extratreesclassifier#sklearn.ensemble.ExtraTreesClassifier "sklearn.ensemble.ExtraTreesClassifier")
Ensemble of extremely randomized tree classifiers.
#### Notes
The default values for the parameters controlling the size of the trees (e.g. `max_depth`, `min_samples_leaf`, etc.) lead to fully grown and unpruned trees which can potentially be very large on some data sets. To reduce memory consumption, the complexity and size of the trees should be controlled by setting those parameter values.
The features are always randomly permuted at each split. Therefore, the best found split may vary, even with the same training data, `max_features=n_features` and `bootstrap=False`, if the improvement of the criterion is identical for several splits enumerated during the search of the best split. To obtain a deterministic behaviour during fitting, `random_state` has to be fixed.
#### References
[1] 12. Breiman, “Random Forests”, Machine Learning, 45(1), 5-32, 2001.
#### Examples
```
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.datasets import make_classification
>>> X, y = make_classification(n_samples=1000, n_features=4,
... n_informative=2, n_redundant=0,
... random_state=0, shuffle=False)
>>> clf = RandomForestClassifier(max_depth=2, random_state=0)
>>> clf.fit(X, y)
RandomForestClassifier(...)
>>> print(clf.predict([[0, 0, 0, 0]]))
[1]
```
#### Methods
| | |
| --- | --- |
| [`apply`](#sklearn.ensemble.RandomForestClassifier.apply "sklearn.ensemble.RandomForestClassifier.apply")(X) | Apply trees in the forest to X, return leaf indices. |
| [`decision_path`](#sklearn.ensemble.RandomForestClassifier.decision_path "sklearn.ensemble.RandomForestClassifier.decision_path")(X) | Return the decision path in the forest. |
| [`fit`](#sklearn.ensemble.RandomForestClassifier.fit "sklearn.ensemble.RandomForestClassifier.fit")(X, y[, sample\_weight]) | Build a forest of trees from the training set (X, y). |
| [`get_params`](#sklearn.ensemble.RandomForestClassifier.get_params "sklearn.ensemble.RandomForestClassifier.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.ensemble.RandomForestClassifier.predict "sklearn.ensemble.RandomForestClassifier.predict")(X) | Predict class for X. |
| [`predict_log_proba`](#sklearn.ensemble.RandomForestClassifier.predict_log_proba "sklearn.ensemble.RandomForestClassifier.predict_log_proba")(X) | Predict class log-probabilities for X. |
| [`predict_proba`](#sklearn.ensemble.RandomForestClassifier.predict_proba "sklearn.ensemble.RandomForestClassifier.predict_proba")(X) | Predict class probabilities for X. |
| [`score`](#sklearn.ensemble.RandomForestClassifier.score "sklearn.ensemble.RandomForestClassifier.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.ensemble.RandomForestClassifier.set_params "sklearn.ensemble.RandomForestClassifier.set_params")(\*\*params) | Set the parameters of this estimator. |
apply(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L235)
Apply trees in the forest to X, return leaf indices.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, its dtype will be converted to `dtype=np.float32`. If a sparse matrix is provided, it will be converted into a sparse `csr_matrix`.
Returns:
**X\_leaves**ndarray of shape (n\_samples, n\_estimators)
For each datapoint x in X and for each tree in the forest, return the index of the leaf x ends up in.
decision\_path(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L261)
Return the decision path in the forest.
New in version 0.18.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, its dtype will be converted to `dtype=np.float32`. If a sparse matrix is provided, it will be converted into a sparse `csr_matrix`.
Returns:
**indicator**sparse matrix of shape (n\_samples, n\_nodes)
Return a node indicator matrix where non zero elements indicates that the samples goes through the nodes. The matrix is of CSR format.
**n\_nodes\_ptr**ndarray of shape (n\_estimators + 1,)
The columns from indicator[n\_nodes\_ptr[i]:n\_nodes\_ptr[i+1]] gives the indicator value for the i-th estimator.
*property*feature\_importances\_
The impurity-based feature importances.
The higher, the more important the feature. The importance of a feature is computed as the (normalized) total reduction of the criterion brought by that feature. It is also known as the Gini importance.
Warning: impurity-based feature importances can be misleading for high cardinality features (many unique values). See [`sklearn.inspection.permutation_importance`](sklearn.inspection.permutation_importance#sklearn.inspection.permutation_importance "sklearn.inspection.permutation_importance") as an alternative.
Returns:
**feature\_importances\_**ndarray of shape (n\_features,)
The values of this array sum to 1, unless all trees are single node trees consisting of only the root node, in which case it will be an array of zeros.
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L301)
Build a forest of trees from the training set (X, y).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Internally, its dtype will be converted to `dtype=np.float32`. If a sparse matrix is provided, it will be converted into a sparse `csc_matrix`.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
The target values (class labels in classification, real numbers in regression).
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, then samples are equally weighted. Splits that would create child nodes with net zero or negative weight are ignored while searching for a split in each node. In the case of classification, splits are also ignored if they would result in any single class carrying a negative weight in either child node.
Returns:
**self**object
Fitted estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_features\_
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2. Use `n_features_in_` instead.
Number of features when fitting the estimator.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L811)
Predict class for X.
The predicted class of an input sample is a vote by the trees in the forest, weighted by their probability estimates. That is, the predicted class is the one with highest mean probability estimate across the trees.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, its dtype will be converted to `dtype=np.float32`. If a sparse matrix is provided, it will be converted into a sparse `csr_matrix`.
Returns:
**y**ndarray of shape (n\_samples,) or (n\_samples, n\_outputs)
The predicted classes.
predict\_log\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L898)
Predict class log-probabilities for X.
The predicted class log-probabilities of an input sample is computed as the log of the mean predicted class probabilities of the trees in the forest.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, its dtype will be converted to `dtype=np.float32`. If a sparse matrix is provided, it will be converted into a sparse `csr_matrix`.
Returns:
**p**ndarray of shape (n\_samples, n\_classes), or a list of such arrays
The class probabilities of the input samples. The order of the classes corresponds to that in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L850)
Predict class probabilities for X.
The predicted class probabilities of an input sample are computed as the mean predicted class probabilities of the trees in the forest. The class probability of a single tree is the fraction of samples of the same class in a leaf.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, its dtype will be converted to `dtype=np.float32`. If a sparse matrix is provided, it will be converted into a sparse `csr_matrix`.
Returns:
**p**ndarray of shape (n\_samples, n\_classes), or a list of such arrays
The class probabilities of the input samples. The order of the classes corresponds to that in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.ensemble.RandomForestClassifier`
--------------------------------------------------------
[Release Highlights for scikit-learn 0.24](../../auto_examples/release_highlights/plot_release_highlights_0_24_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-24-0-py)
[Release Highlights for scikit-learn 0.22](../../auto_examples/release_highlights/plot_release_highlights_0_22_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-22-0-py)
[Comparison of Calibration of Classifiers](../../auto_examples/calibration/plot_compare_calibration#sphx-glr-auto-examples-calibration-plot-compare-calibration-py)
[Probability Calibration for 3-class classification](../../auto_examples/calibration/plot_calibration_multiclass#sphx-glr-auto-examples-calibration-plot-calibration-multiclass-py)
[Classifier comparison](../../auto_examples/classification/plot_classifier_comparison#sphx-glr-auto-examples-classification-plot-classifier-comparison-py)
[Inductive Clustering](../../auto_examples/cluster/plot_inductive_clustering#sphx-glr-auto-examples-cluster-plot-inductive-clustering-py)
[Feature importances with a forest of trees](../../auto_examples/ensemble/plot_forest_importances#sphx-glr-auto-examples-ensemble-plot-forest-importances-py)
[Feature transformations with ensembles of trees](../../auto_examples/ensemble/plot_feature_transformation#sphx-glr-auto-examples-ensemble-plot-feature-transformation-py)
[OOB Errors for Random Forests](../../auto_examples/ensemble/plot_ensemble_oob#sphx-glr-auto-examples-ensemble-plot-ensemble-oob-py)
[Pixel importances with a parallel forest of trees](../../auto_examples/ensemble/plot_forest_importances_faces#sphx-glr-auto-examples-ensemble-plot-forest-importances-faces-py)
[Plot class probabilities calculated by the VotingClassifier](../../auto_examples/ensemble/plot_voting_probas#sphx-glr-auto-examples-ensemble-plot-voting-probas-py)
[Plot the decision surfaces of ensembles of trees on the iris dataset](../../auto_examples/ensemble/plot_forest_iris#sphx-glr-auto-examples-ensemble-plot-forest-iris-py)
[Permutation Importance vs Random Forest Feature Importance (MDI)](../../auto_examples/inspection/plot_permutation_importance#sphx-glr-auto-examples-inspection-plot-permutation-importance-py)
[Permutation Importance with Multicollinear or Correlated Features](../../auto_examples/inspection/plot_permutation_importance_multicollinear#sphx-glr-auto-examples-inspection-plot-permutation-importance-multicollinear-py)
[Displaying Pipelines](../../auto_examples/miscellaneous/plot_pipeline_display#sphx-glr-auto-examples-miscellaneous-plot-pipeline-display-py)
[ROC Curve with Visualization API](../../auto_examples/miscellaneous/plot_roc_curve_visualization_api#sphx-glr-auto-examples-miscellaneous-plot-roc-curve-visualization-api-py)
[Detection error tradeoff (DET) curve](../../auto_examples/model_selection/plot_det#sphx-glr-auto-examples-model-selection-plot-det-py)
[Successive Halving Iterations](../../auto_examples/model_selection/plot_successive_halving_iterations#sphx-glr-auto-examples-model-selection-plot-successive-halving-iterations-py)
[Classification of text documents using sparse features](../../auto_examples/text/plot_document_classification_20newsgroups#sphx-glr-auto-examples-text-plot-document-classification-20newsgroups-py)
| programming_docs |
scikit_learn sklearn.decomposition.MiniBatchNMF sklearn.decomposition.MiniBatchNMF
==================================
*class*sklearn.decomposition.MiniBatchNMF(*n\_components=None*, *\**, *init=None*, *batch\_size=1024*, *beta\_loss='frobenius'*, *tol=0.0001*, *max\_no\_improvement=10*, *max\_iter=200*, *alpha\_W=0.0*, *alpha\_H='same'*, *l1\_ratio=0.0*, *forget\_factor=0.7*, *fresh\_restarts=False*, *fresh\_restarts\_max\_iter=30*, *transform\_max\_iter=None*, *random\_state=None*, *verbose=0*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_nmf.py#L1773)
Mini-Batch Non-Negative Matrix Factorization (NMF).
New in version 1.1.
Find two non-negative matrices, i.e. matrices with all non-negative elements, (`W`, `H`) whose product approximates the non-negative matrix `X`. This factorization can be used for example for dimensionality reduction, source separation or topic extraction.
The objective function is:
\[ \begin{align}\begin{aligned}L(W, H) &= 0.5 \* ||X - WH||\_{loss}^2\\&+ alpha\\_W \* l1\\_ratio \* n\\_features \* ||vec(W)||\_1\\&+ alpha\\_H \* l1\\_ratio \* n\\_samples \* ||vec(H)||\_1\\&+ 0.5 \* alpha\\_W \* (1 - l1\\_ratio) \* n\\_features \* ||W||\_{Fro}^2\\&+ 0.5 \* alpha\\_H \* (1 - l1\\_ratio) \* n\\_samples \* ||H||\_{Fro}^2\end{aligned}\end{align} \] Where:
\(||A||\_{Fro}^2 = \sum\_{i,j} A\_{ij}^2\) (Frobenius norm)
\(||vec(A)||\_1 = \sum\_{i,j} abs(A\_{ij})\) (Elementwise L1 norm)
The generic norm \(||X - WH||\_{loss}^2\) may represent the Frobenius norm or another supported beta-divergence loss. The choice between options is controlled by the `beta_loss` parameter.
The objective function is minimized with an alternating minimization of `W` and `H`.
Note that the transformed data is named `W` and the components matrix is named `H`. In the NMF literature, the naming convention is usually the opposite since the data matrix `X` is transposed.
Read more in the [User Guide](../decomposition#minibatchnmf).
Parameters:
**n\_components**int, default=None
Number of components, if `n_components` is not set all features are kept.
**init**{‘random’, ‘nndsvd’, ‘nndsvda’, ‘nndsvdar’, ‘custom’}, default=None
Method used to initialize the procedure. Valid options:
* `None`: ‘nndsvda’ if `n_components <= min(n_samples, n_features)`, otherwise random.
* `'random'`: non-negative random matrices, scaled with: `sqrt(X.mean() / n_components)`
* `'nndsvd'`: Nonnegative Double Singular Value Decomposition (NNDSVD) initialization (better for sparseness).
* `'nndsvda'`: NNDSVD with zeros filled with the average of X (better when sparsity is not desired).
* `'nndsvdar'` NNDSVD with zeros filled with small random values (generally faster, less accurate alternative to NNDSVDa for when sparsity is not desired).
* `'custom'`: use custom matrices `W` and `H`
**batch\_size**int, default=1024
Number of samples in each mini-batch. Large batch sizes give better long-term convergence at the cost of a slower start.
**beta\_loss**float or {‘frobenius’, ‘kullback-leibler’, ‘itakura-saito’}, default=’frobenius’
Beta divergence to be minimized, measuring the distance between `X` and the dot product `WH`. Note that values different from ‘frobenius’ (or 2) and ‘kullback-leibler’ (or 1) lead to significantly slower fits. Note that for `beta_loss <= 0` (or ‘itakura-saito’), the input matrix `X` cannot contain zeros.
**tol**float, default=1e-4
Control early stopping based on the norm of the differences in `H` between 2 steps. To disable early stopping based on changes in `H`, set `tol` to 0.0.
**max\_no\_improvement**int, default=10
Control early stopping based on the consecutive number of mini batches that does not yield an improvement on the smoothed cost function. To disable convergence detection based on cost function, set `max_no_improvement` to None.
**max\_iter**int, default=200
Maximum number of iterations over the complete dataset before timing out.
**alpha\_W**float, default=0.0
Constant that multiplies the regularization terms of `W`. Set it to zero (default) to have no regularization on `W`.
**alpha\_H**float or “same”, default=”same”
Constant that multiplies the regularization terms of `H`. Set it to zero to have no regularization on `H`. If “same” (default), it takes the same value as `alpha_W`.
**l1\_ratio**float, default=0.0
The regularization mixing parameter, with 0 <= l1\_ratio <= 1. For l1\_ratio = 0 the penalty is an elementwise L2 penalty (aka Frobenius Norm). For l1\_ratio = 1 it is an elementwise L1 penalty. For 0 < l1\_ratio < 1, the penalty is a combination of L1 and L2.
**forget\_factor**float, default=0.7
Amount of rescaling of past information. Its value could be 1 with finite datasets. Choosing values < 1 is recommended with online learning as more recent batches will weight more than past batches.
**fresh\_restarts**bool, default=False
Whether to completely solve for W at each step. Doing fresh restarts will likely lead to a better solution for a same number of iterations but it is much slower.
**fresh\_restarts\_max\_iter**int, default=30
Maximum number of iterations when solving for W at each step. Only used when doing fresh restarts. These iterations may be stopped early based on a small change of W controlled by `tol`.
**transform\_max\_iter**int, default=None
Maximum number of iterations when solving for W at transform time. If None, it defaults to `max_iter`.
**random\_state**int, RandomState instance or None, default=None
Used for initialisation (when `init` == ‘nndsvdar’ or ‘random’), and in Coordinate Descent. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**verbose**bool, default=False
Whether to be verbose.
Attributes:
**components\_**ndarray of shape (n\_components, n\_features)
Factorization matrix, sometimes called ‘dictionary’.
**n\_components\_**int
The number of components. It is same as the `n_components` parameter if it was given. Otherwise, it will be same as the number of features.
**reconstruction\_err\_**float
Frobenius norm of the matrix difference, or beta-divergence, between the training data `X` and the reconstructed data `WH` from the fitted model.
**n\_iter\_**int
Actual number of started iterations over the whole dataset.
**n\_steps\_**int
Number of mini-batches processed.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
See also
[`NMF`](sklearn.decomposition.nmf#sklearn.decomposition.NMF "sklearn.decomposition.NMF")
Non-negative matrix factorization.
[`MiniBatchDictionaryLearning`](sklearn.decomposition.minibatchdictionarylearning#sklearn.decomposition.MiniBatchDictionaryLearning "sklearn.decomposition.MiniBatchDictionaryLearning")
Finds a dictionary that can best be used to represent data using a sparse code.
#### References
[1] [“Fast local algorithms for large scale nonnegative matrix and tensor factorizations”](https://doi.org/10.1587/transfun.E92.A.708) Cichocki, Andrzej, and P. H. A. N. Anh-Huy. IEICE transactions on fundamentals of electronics, communications and computer sciences 92.3: 708-721, 2009.
[2] [“Algorithms for nonnegative matrix factorization with the beta-divergence”](https://doi.org/10.1162/NECO_a_00168) Fevotte, C., & Idier, J. (2011). Neural Computation, 23(9).
[3] [“Online algorithms for nonnegative matrix factorization with the Itakura-Saito divergence”](https://doi.org/10.1109/ASPAA.2011.6082314) Lefevre, A., Bach, F., Fevotte, C. (2011). WASPA.
#### Examples
```
>>> import numpy as np
>>> X = np.array([[1, 1], [2, 1], [3, 1.2], [4, 1], [5, 0.8], [6, 1]])
>>> from sklearn.decomposition import MiniBatchNMF
>>> model = MiniBatchNMF(n_components=2, init='random', random_state=0)
>>> W = model.fit_transform(X)
>>> H = model.components_
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.decomposition.MiniBatchNMF.fit "sklearn.decomposition.MiniBatchNMF.fit")(X[, y]) | Learn a NMF model for the data X. |
| [`fit_transform`](#sklearn.decomposition.MiniBatchNMF.fit_transform "sklearn.decomposition.MiniBatchNMF.fit_transform")(X[, y, W, H]) | Learn a NMF model for the data X and returns the transformed data. |
| [`get_feature_names_out`](#sklearn.decomposition.MiniBatchNMF.get_feature_names_out "sklearn.decomposition.MiniBatchNMF.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.decomposition.MiniBatchNMF.get_params "sklearn.decomposition.MiniBatchNMF.get_params")([deep]) | Get parameters for this estimator. |
| [`inverse_transform`](#sklearn.decomposition.MiniBatchNMF.inverse_transform "sklearn.decomposition.MiniBatchNMF.inverse_transform")(W) | Transform data back to its original space. |
| [`partial_fit`](#sklearn.decomposition.MiniBatchNMF.partial_fit "sklearn.decomposition.MiniBatchNMF.partial_fit")(X[, y, W, H]) | Update the model using the data in `X` as a mini-batch. |
| [`set_params`](#sklearn.decomposition.MiniBatchNMF.set_params "sklearn.decomposition.MiniBatchNMF.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.decomposition.MiniBatchNMF.transform "sklearn.decomposition.MiniBatchNMF.transform")(X) | Transform the data X according to the fitted MiniBatchNMF model. |
fit(*X*, *y=None*, *\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_nmf.py#L1701)
Learn a NMF model for the data X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vector, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Not used, present for API consistency by convention.
**\*\*params**kwargs
Parameters (keyword arguments) and values passed to the fit\_transform instance.
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*, *W=None*, *H=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_nmf.py#L2183)
Learn a NMF model for the data X and returns the transformed data.
This is more efficient than calling fit followed by transform.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Data matrix to be decomposed.
**y**Ignored
Not used, present here for API consistency by convention.
**W**array-like of shape (n\_samples, n\_components), default=None
If `init='custom'`, it is used as initial guess for the solution.
**H**array-like of shape (n\_components, n\_features), default=None
If `init='custom'`, it is used as initial guess for the solution.
Returns:
**W**ndarray of shape (n\_samples, n\_components)
Transformed data.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.decomposition.MiniBatchNMF.fit "sklearn.decomposition.MiniBatchNMF.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
inverse\_transform(*W*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_nmf.py#L1749)
Transform data back to its original space.
New in version 0.18.
Parameters:
**W**{ndarray, sparse matrix} of shape (n\_samples, n\_components)
Transformed data matrix.
Returns:
**X**{ndarray, sparse matrix} of shape (n\_samples, n\_features)
Returns a data matrix of the original shape.
partial\_fit(*X*, *y=None*, *W=None*, *H=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_nmf.py#L2338)
Update the model using the data in `X` as a mini-batch.
This method is expected to be called several times consecutively on different chunks of a dataset so as to implement out-of-core or online learning.
This is especially useful when the whole dataset is too big to fit in memory at once (see [Strategies to scale computationally: bigger data](https://scikit-learn.org/1.1/computing/scaling_strategies.html#scaling-strategies)).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Data matrix to be decomposed.
**y**Ignored
Not used, present here for API consistency by convention.
**W**array-like of shape (n\_samples, n\_components), default=None
If `init='custom'`, it is used as initial guess for the solution. Only used for the first call to `partial_fit`.
**H**array-like of shape (n\_components, n\_features), default=None
If `init='custom'`, it is used as initial guess for the solution. Only used for the first call to `partial_fit`.
Returns:
self
Returns the instance itself.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_nmf.py#L2316)
Transform the data X according to the fitted MiniBatchNMF model.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Data matrix to be transformed by the model.
Returns:
**W**ndarray of shape (n\_samples, n\_components)
Transformed data.
Examples using `sklearn.decomposition.MiniBatchNMF`
---------------------------------------------------
[Release Highlights for scikit-learn 1.1](../../auto_examples/release_highlights/plot_release_highlights_1_1_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-1-1-0-py)
[Topic extraction with Non-negative Matrix Factorization and Latent Dirichlet Allocation](../../auto_examples/applications/plot_topics_extraction_with_nmf_lda#sphx-glr-auto-examples-applications-plot-topics-extraction-with-nmf-lda-py)
scikit_learn sklearn.utils.safe_mask sklearn.utils.safe\_mask
========================
sklearn.utils.safe\_mask(*X*, *mask*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/__init__.py#L119)
Return a mask which is safe to use on X.
Parameters:
**X**{array-like, sparse matrix}
Data on which to apply mask.
**mask**ndarray
Mask to be used on X.
Returns:
mask
scikit_learn sklearn.utils.arrayfuncs.min_pos sklearn.utils.arrayfuncs.min\_pos
=================================
sklearn.utils.arrayfuncs.min\_pos()
Find the minimum value of an array over positive values
Returns the maximum representable value of the input dtype if none of the values are positive.
scikit_learn sklearn.metrics.pairwise.paired_manhattan_distances sklearn.metrics.pairwise.paired\_manhattan\_distances
=====================================================
sklearn.metrics.pairwise.paired\_manhattan\_distances(*X*, *Y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/pairwise.py#L1019)
Compute the paired L1 distances between X and Y.
Distances are calculated between (X[0], Y[0]), (X[1], Y[1]), …, (X[n\_samples], Y[n\_samples]).
Read more in the [User Guide](../metrics#metrics).
Parameters:
**X**array-like of shape (n\_samples, n\_features)
An array-like where each row is a sample and each column is a feature.
**Y**array-like of shape (n\_samples, n\_features)
An array-like where each row is a sample and each column is a feature.
Returns:
**distances**ndarray of shape (n\_samples,)
L1 paired distances between the row vectors of `X` and the row vectors of `Y`.
#### Examples
```
>>> from sklearn.metrics.pairwise import paired_manhattan_distances
>>> import numpy as np
>>> X = np.array([[1, 1, 0], [0, 1, 0], [0, 0, 1]])
>>> Y = np.array([[0, 1, 0], [0, 0, 1], [0, 0, 0]])
>>> paired_manhattan_distances(X, Y)
array([1., 2., 1.])
```
scikit_learn sklearn.preprocessing.add_dummy_feature sklearn.preprocessing.add\_dummy\_feature
=========================================
sklearn.preprocessing.add\_dummy\_feature(*X*, *value=1.0*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L2278)
Augment dataset with an additional dummy feature.
This is useful for fitting an intercept term with implementations which cannot otherwise fit it directly.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Data.
**value**float
Value to use for the dummy feature.
Returns:
**X**{ndarray, sparse matrix} of shape (n\_samples, n\_features + 1)
Same data with dummy feature added as first column.
#### Examples
```
>>> from sklearn.preprocessing import add_dummy_feature
>>> add_dummy_feature([[0, 1], [1, 0]])
array([[1., 0., 1.],
[1., 1., 0.]])
```
scikit_learn sklearn.datasets.fetch_lfw_pairs sklearn.datasets.fetch\_lfw\_pairs
==================================
sklearn.datasets.fetch\_lfw\_pairs(*\**, *subset='train'*, *data\_home=None*, *funneled=True*, *resize=0.5*, *color=False*, *slice\_=(slice(70, 195, None), slice(78, 172, None))*, *download\_if\_missing=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_lfw.py#L410)
Load the Labeled Faces in the Wild (LFW) pairs dataset (classification).
Download it if necessary.
| | |
| --- | --- |
| Classes | 2 |
| Samples total | 13233 |
| Dimensionality | 5828 |
| Features | real, between 0 and 255 |
In the official [README.txt](http://vis-www.cs.umass.edu/lfw/README.txt) this task is described as the “Restricted” task. As I am not sure as to implement the “Unrestricted” variant correctly, I left it as unsupported for now.
The original images are 250 x 250 pixels, but the default slice and resize arguments reduce them to 62 x 47.
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/real_world.html#labeled-faces-in-the-wild-dataset).
Parameters:
**subset**{‘train’, ‘test’, ‘10\_folds’}, default=’train’
Select the dataset to load: ‘train’ for the development training set, ‘test’ for the development test set, and ‘10\_folds’ for the official evaluation set that is meant to be used with a 10-folds cross validation.
**data\_home**str, default=None
Specify another download and cache folder for the datasets. By default all scikit-learn data is stored in ‘~/scikit\_learn\_data’ subfolders.
**funneled**bool, default=True
Download and use the funneled variant of the dataset.
**resize**float, default=0.5
Ratio used to resize the each face picture.
**color**bool, default=False
Keep the 3 RGB channels instead of averaging them to a single gray level channel. If color is True the shape of the data has one more dimension than the shape with color = False.
**slice\_**tuple of slice, default=(slice(70, 195), slice(78, 172))
Provide a custom 2D slice (height, width) to extract the ‘interesting’ part of the jpeg files and avoid use statistical correlation from the background.
**download\_if\_missing**bool, default=True
If False, raise a IOError if the data is not locally available instead of trying to download the data from the source site.
Returns:
**data**[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
Dictionary-like object, with the following attributes.
datandarray of shape (2200, 5828). Shape depends on `subset`.
Each row corresponds to 2 ravel’d face images of original size 62 x 47 pixels. Changing the `slice_`, `resize` or `subset` parameters will change the shape of the output.
pairsndarray of shape (2200, 2, 62, 47). Shape depends on `subset`
Each row has 2 face images corresponding to same or different person from the dataset containing 5749 people. Changing the `slice_`, `resize` or `subset` parameters will change the shape of the output.
targetnumpy array of shape (2200,). Shape depends on `subset`.
Labels associated to each pair of images. The two label values being different persons or the same person.
target\_namesnumpy array of shape (2,)
Explains the target values of the target array. 0 corresponds to “Different person”, 1 corresponds to “same person”.
DESCRstr
Description of the Labeled Faces in the Wild (LFW) dataset.
| programming_docs |
scikit_learn sklearn.metrics.plot_precision_recall_curve sklearn.metrics.plot\_precision\_recall\_curve
==============================================
sklearn.metrics.plot\_precision\_recall\_curve(*estimator*, *X*, *y*, *\**, *sample\_weight=None*, *response\_method='auto'*, *name=None*, *ax=None*, *pos\_label=None*, *\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_plot/precision_recall_curve.py#L396)
DEPRECATED: Function `plot_precision_recall_curve` is deprecated in 1.0 and will be removed in 1.2. Use one of the class methods: PrecisionRecallDisplay.from\_predictions or PrecisionRecallDisplay.from\_estimator.
Plot Precision Recall Curve for binary classifiers.
Extra keyword arguments will be passed to matplotlib’s `plot`.
Read more in the [User Guide](../model_evaluation#precision-recall-f-measure-metrics).
Deprecated since version 1.0: `plot_precision_recall_curve` is deprecated in 1.0 and will be removed in 1.2. Use one of the following class methods: [`from_predictions`](sklearn.metrics.precisionrecalldisplay#sklearn.metrics.PrecisionRecallDisplay.from_predictions "sklearn.metrics.PrecisionRecallDisplay.from_predictions") or [`from_estimator`](sklearn.metrics.precisionrecalldisplay#sklearn.metrics.PrecisionRecallDisplay.from_estimator "sklearn.metrics.PrecisionRecallDisplay.from_estimator").
Parameters:
**estimator**estimator instance
Fitted classifier or a fitted [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline") in which the last estimator is a classifier.
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Input values.
**y**array-like of shape (n\_samples,)
Binary target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**response\_method**{‘predict\_proba’, ‘decision\_function’, ‘auto’}, default=’auto’
Specifies whether to use [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) or [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) as the target response. If set to ‘auto’, [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) is tried first and if it does not exist [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) is tried next.
**name**str, default=None
Name for labeling curve. If `None`, the name of the estimator is used.
**ax**matplotlib axes, default=None
Axes object to plot on. If `None`, a new figure and axes is created.
**pos\_label**str or int, default=None
The class considered as the positive class when computing the precision and recall metrics. By default, `estimators.classes_[1]` is considered as the positive class.
New in version 0.24.
**\*\*kwargs**dict
Keyword arguments to be passed to matplotlib’s `plot`.
Returns:
**display**[`PrecisionRecallDisplay`](sklearn.metrics.precisionrecalldisplay#sklearn.metrics.PrecisionRecallDisplay "sklearn.metrics.PrecisionRecallDisplay")
Object that stores computed values.
See also
[`precision_recall_curve`](sklearn.metrics.precision_recall_curve#sklearn.metrics.precision_recall_curve "sklearn.metrics.precision_recall_curve")
Compute precision-recall pairs for different probability thresholds.
[`PrecisionRecallDisplay`](sklearn.metrics.precisionrecalldisplay#sklearn.metrics.PrecisionRecallDisplay "sklearn.metrics.PrecisionRecallDisplay")
Precision Recall visualization.
scikit_learn sklearn.cluster.Birch sklearn.cluster.Birch
=====================
*class*sklearn.cluster.Birch(*\**, *threshold=0.5*, *branching\_factor=50*, *n\_clusters=3*, *compute\_labels=True*, *copy=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_birch.py#L355)
Implements the BIRCH clustering algorithm.
It is a memory-efficient, online-learning algorithm provided as an alternative to [`MiniBatchKMeans`](sklearn.cluster.minibatchkmeans#sklearn.cluster.MiniBatchKMeans "sklearn.cluster.MiniBatchKMeans"). It constructs a tree data structure with the cluster centroids being read off the leaf. These can be either the final cluster centroids or can be provided as input to another clustering algorithm such as [`AgglomerativeClustering`](sklearn.cluster.agglomerativeclustering#sklearn.cluster.AgglomerativeClustering "sklearn.cluster.AgglomerativeClustering").
Read more in the [User Guide](../clustering#birch).
New in version 0.16.
Parameters:
**threshold**float, default=0.5
The radius of the subcluster obtained by merging a new sample and the closest subcluster should be lesser than the threshold. Otherwise a new subcluster is started. Setting this value to be very low promotes splitting and vice-versa.
**branching\_factor**int, default=50
Maximum number of CF subclusters in each node. If a new samples enters such that the number of subclusters exceed the branching\_factor then that node is split into two nodes with the subclusters redistributed in each. The parent subcluster of that node is removed and two new subclusters are added as parents of the 2 split nodes.
**n\_clusters**int, instance of sklearn.cluster model, default=3
Number of clusters after the final clustering step, which treats the subclusters from the leaves as new samples.
* `None` : the final clustering step is not performed and the subclusters are returned as they are.
* [`sklearn.cluster`](../classes#module-sklearn.cluster "sklearn.cluster") Estimator : If a model is provided, the model is fit treating the subclusters as new samples and the initial data is mapped to the label of the closest subcluster.
* `int` : the model fit is [`AgglomerativeClustering`](sklearn.cluster.agglomerativeclustering#sklearn.cluster.AgglomerativeClustering "sklearn.cluster.AgglomerativeClustering") with `n_clusters` set to be equal to the int.
**compute\_labels**bool, default=True
Whether or not to compute labels for each fit.
**copy**bool, default=True
Whether or not to make a copy of the given data. If set to False, the initial data will be overwritten.
Attributes:
**root\_**\_CFNode
Root of the CFTree.
**dummy\_leaf\_**\_CFNode
Start pointer to all the leaves.
**subcluster\_centers\_**ndarray
Centroids of all subclusters read directly from the leaves.
**subcluster\_labels\_**ndarray
Labels assigned to the centroids of the subclusters after they are clustered globally.
**labels\_**ndarray of shape (n\_samples,)
Array of labels assigned to the input data. if partial\_fit is used instead of fit, they are assigned to the last batch of data.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`MiniBatchKMeans`](sklearn.cluster.minibatchkmeans#sklearn.cluster.MiniBatchKMeans "sklearn.cluster.MiniBatchKMeans")
Alternative implementation that does incremental updates of the centers’ positions using mini-batches.
#### Notes
The tree data structure consists of nodes with each node consisting of a number of subclusters. The maximum number of subclusters in a node is determined by the branching factor. Each subcluster maintains a linear sum, squared sum and the number of samples in that subcluster. In addition, each subcluster can also have a node as its child, if the subcluster is not a member of a leaf node.
For a new point entering the root, it is merged with the subcluster closest to it and the linear sum, squared sum and the number of samples of that subcluster are updated. This is done recursively till the properties of the leaf node are updated.
#### References
* Tian Zhang, Raghu Ramakrishnan, Maron Livny BIRCH: An efficient data clustering method for large databases. <https://www.cs.sfu.ca/CourseCentral/459/han/papers/zhang96.pdf>
* Roberto Perdisci JBirch - Java implementation of BIRCH clustering algorithm <https://code.google.com/archive/p/jbirch>
#### Examples
```
>>> from sklearn.cluster import Birch
>>> X = [[0, 1], [0.3, 1], [-0.3, 1], [0, -1], [0.3, -1], [-0.3, -1]]
>>> brc = Birch(n_clusters=None)
>>> brc.fit(X)
Birch(n_clusters=None)
>>> brc.predict(X)
array([0, 0, 0, 1, 1, 1])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.cluster.Birch.fit "sklearn.cluster.Birch.fit")(X[, y]) | Build a CF Tree for the input data. |
| [`fit_predict`](#sklearn.cluster.Birch.fit_predict "sklearn.cluster.Birch.fit_predict")(X[, y]) | Perform clustering on `X` and returns cluster labels. |
| [`fit_transform`](#sklearn.cluster.Birch.fit_transform "sklearn.cluster.Birch.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.cluster.Birch.get_feature_names_out "sklearn.cluster.Birch.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.cluster.Birch.get_params "sklearn.cluster.Birch.get_params")([deep]) | Get parameters for this estimator. |
| [`partial_fit`](#sklearn.cluster.Birch.partial_fit "sklearn.cluster.Birch.partial_fit")([X, y]) | Online learning. |
| [`predict`](#sklearn.cluster.Birch.predict "sklearn.cluster.Birch.predict")(X) | Predict data using the `centroids_` of subclusters. |
| [`set_params`](#sklearn.cluster.Birch.set_params "sklearn.cluster.Birch.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.cluster.Birch.transform "sklearn.cluster.Birch.transform")(X) | Transform X into subcluster centroids dimension. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_birch.py#L510)
Build a CF Tree for the input data.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Input data.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
self
Fitted estimator.
*property*fit\_
DEPRECATED: `fit_` is deprecated in 1.0 and will be removed in 1.2.
fit\_predict(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L732)
Perform clustering on `X` and returns cluster labels.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input data.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**labels**ndarray of shape (n\_samples,), dtype=np.int64
Cluster labels.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.cluster.Birch.fit "sklearn.cluster.Birch.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
partial\_fit(*X=None*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_birch.py#L635)
Online learning. Prevents rebuilding of CFTree from scratch.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features), default=None
Input data. If X is not provided, only the global clustering step is done.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
self
Fitted estimator.
*property*partial\_fit\_
DEPRECATED: `partial_fit_` is deprecated in 1.0 and will be removed in 1.2.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_birch.py#L674)
Predict data using the `centroids_` of subclusters.
Avoid computation of the row norms of X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Input data.
Returns:
**labels**ndarray of shape(n\_samples,)
Labelled data.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_birch.py#L704)
Transform X into subcluster centroids dimension.
Each dimension represents the distance from the sample point to each cluster centroid.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Input data.
Returns:
**X\_trans**{array-like, sparse matrix} of shape (n\_samples, n\_clusters)
Transformed data.
Examples using `sklearn.cluster.Birch`
--------------------------------------
[Compare BIRCH and MiniBatchKMeans](../../auto_examples/cluster/plot_birch_vs_minibatchkmeans#sphx-glr-auto-examples-cluster-plot-birch-vs-minibatchkmeans-py)
[Comparing different clustering algorithms on toy datasets](../../auto_examples/cluster/plot_cluster_comparison#sphx-glr-auto-examples-cluster-plot-cluster-comparison-py)
scikit_learn sklearn.ensemble.GradientBoostingClassifier sklearn.ensemble.GradientBoostingClassifier
===========================================
*class*sklearn.ensemble.GradientBoostingClassifier(*\**, *loss='log\_loss'*, *learning\_rate=0.1*, *n\_estimators=100*, *subsample=1.0*, *criterion='friedman\_mse'*, *min\_samples\_split=2*, *min\_samples\_leaf=1*, *min\_weight\_fraction\_leaf=0.0*, *max\_depth=3*, *min\_impurity\_decrease=0.0*, *init=None*, *random\_state=None*, *max\_features=None*, *verbose=0*, *max\_leaf\_nodes=None*, *warm\_start=False*, *validation\_fraction=0.1*, *n\_iter\_no\_change=None*, *tol=0.0001*, *ccp\_alpha=0.0*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_gb.py#L991)
Gradient Boosting for classification.
This algorithm builds an additive model in a forward stage-wise fashion; it allows for the optimization of arbitrary differentiable loss functions. In each stage `n_classes_` regression trees are fit on the negative gradient of the loss function, e.g. binary or multiclass log loss. Binary classification is a special case where only a single regression tree is induced.
[`sklearn.ensemble.HistGradientBoostingClassifier`](sklearn.ensemble.histgradientboostingclassifier#sklearn.ensemble.HistGradientBoostingClassifier "sklearn.ensemble.HistGradientBoostingClassifier") is a much faster variant of this algorithm for intermediate datasets (`n_samples >= 10_000`).
Read more in the [User Guide](../ensemble#gradient-boosting).
Parameters:
**loss**{‘log\_loss’, ‘deviance’, ‘exponential’}, default=’log\_loss’
The loss function to be optimized. ‘log\_loss’ refers to binomial and multinomial deviance, the same as used in logistic regression. It is a good choice for classification with probabilistic outputs. For loss ‘exponential’, gradient boosting recovers the AdaBoost algorithm.
Deprecated since version 1.1: The loss ‘deviance’ was deprecated in v1.1 and will be removed in version 1.3. Use `loss='log_loss'` which is equivalent.
**learning\_rate**float, default=0.1
Learning rate shrinks the contribution of each tree by `learning_rate`. There is a trade-off between learning\_rate and n\_estimators. Values must be in the range `(0.0, inf)`.
**n\_estimators**int, default=100
The number of boosting stages to perform. Gradient boosting is fairly robust to over-fitting so a large number usually results in better performance. Values must be in the range `[1, inf)`.
**subsample**float, default=1.0
The fraction of samples to be used for fitting the individual base learners. If smaller than 1.0 this results in Stochastic Gradient Boosting. `subsample` interacts with the parameter `n_estimators`. Choosing `subsample < 1.0` leads to a reduction of variance and an increase in bias. Values must be in the range `(0.0, 1.0]`.
**criterion**{‘friedman\_mse’, ‘squared\_error’, ‘mse’}, default=’friedman\_mse’
The function to measure the quality of a split. Supported criteria are ‘friedman\_mse’ for the mean squared error with improvement score by Friedman, ‘squared\_error’ for mean squared error. The default value of ‘friedman\_mse’ is generally the best as it can provide a better approximation in some cases.
New in version 0.18.
Deprecated since version 1.0: Criterion ‘mse’ was deprecated in v1.0 and will be removed in version 1.2. Use `criterion='squared_error'` which is equivalent.
**min\_samples\_split**int or float, default=2
The minimum number of samples required to split an internal node:
* If int, values must be in the range `[2, inf)`.
* If float, values must be in the range `(0.0, 1.0]` and `min_samples_split` will be `ceil(min_samples_split * n_samples)`.
Changed in version 0.18: Added float values for fractions.
**min\_samples\_leaf**int or float, default=1
The minimum number of samples required to be at a leaf node. A split point at any depth will only be considered if it leaves at least `min_samples_leaf` training samples in each of the left and right branches. This may have the effect of smoothing the model, especially in regression.
* If int, values must be in the range `[1, inf)`.
* If float, values must be in the range `(0.0, 1.0]` and `min_samples_leaf` will be `ceil(min_samples_leaf * n_samples)`.
Changed in version 0.18: Added float values for fractions.
**min\_weight\_fraction\_leaf**float, default=0.0
The minimum weighted fraction of the sum total of weights (of all the input samples) required to be at a leaf node. Samples have equal weight when sample\_weight is not provided. Values must be in the range `[0.0, 0.5]`.
**max\_depth**int, default=3
The maximum depth of the individual regression estimators. The maximum depth limits the number of nodes in the tree. Tune this parameter for best performance; the best value depends on the interaction of the input variables. Values must be in the range `[1, inf)`.
**min\_impurity\_decrease**float, default=0.0
A node will be split if this split induces a decrease of the impurity greater than or equal to this value. Values must be in the range `[0.0, inf)`.
The weighted impurity decrease equation is the following:
```
N_t / N * (impurity - N_t_R / N_t * right_impurity
- N_t_L / N_t * left_impurity)
```
where `N` is the total number of samples, `N_t` is the number of samples at the current node, `N_t_L` is the number of samples in the left child, and `N_t_R` is the number of samples in the right child.
`N`, `N_t`, `N_t_R` and `N_t_L` all refer to the weighted sum, if `sample_weight` is passed.
New in version 0.19.
**init**estimator or ‘zero’, default=None
An estimator object that is used to compute the initial predictions. `init` has to provide [`fit`](#sklearn.ensemble.GradientBoostingClassifier.fit "sklearn.ensemble.GradientBoostingClassifier.fit") and [`predict_proba`](#sklearn.ensemble.GradientBoostingClassifier.predict_proba "sklearn.ensemble.GradientBoostingClassifier.predict_proba"). If ‘zero’, the initial raw predictions are set to zero. By default, a `DummyEstimator` predicting the classes priors is used.
**random\_state**int, RandomState instance or None, default=None
Controls the random seed given to each Tree estimator at each boosting iteration. In addition, it controls the random permutation of the features at each split (see Notes for more details). It also controls the random splitting of the training data to obtain a validation set if `n_iter_no_change` is not None. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**max\_features**{‘auto’, ‘sqrt’, ‘log2’}, int or float, default=None
The number of features to consider when looking for the best split:
* If int, values must be in the range `[1, inf)`.
* If float, values must be in the range `(0.0, 1.0]` and the features considered at each split will be `max(1, int(max_features * n_features_in_))`.
* If ‘auto’, then `max_features=sqrt(n_features)`.
* If ‘sqrt’, then `max_features=sqrt(n_features)`.
* If ‘log2’, then `max_features=log2(n_features)`.
* If None, then `max_features=n_features`.
Choosing `max_features < n_features` leads to a reduction of variance and an increase in bias.
Note: the search for a split does not stop until at least one valid partition of the node samples is found, even if it requires to effectively inspect more than `max_features` features.
**verbose**int, default=0
Enable verbose output. If 1 then it prints progress and performance once in a while (the more trees the lower the frequency). If greater than 1 then it prints progress and performance for every tree. Values must be in the range `[0, inf)`.
**max\_leaf\_nodes**int, default=None
Grow trees with `max_leaf_nodes` in best-first fashion. Best nodes are defined as relative reduction in impurity. Values must be in the range `[2, inf)`. If `None`, then unlimited number of leaf nodes.
**warm\_start**bool, default=False
When set to `True`, reuse the solution of the previous call to fit and add more estimators to the ensemble, otherwise, just erase the previous solution. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
**validation\_fraction**float, default=0.1
The proportion of training data to set aside as validation set for early stopping. Values must be in the range `(0.0, 1.0)`. Only used if `n_iter_no_change` is set to an integer.
New in version 0.20.
**n\_iter\_no\_change**int, default=None
`n_iter_no_change` is used to decide if early stopping will be used to terminate training when validation score is not improving. By default it is set to None to disable early stopping. If set to a number, it will set aside `validation_fraction` size of the training data as validation and terminate training when validation score is not improving in all of the previous `n_iter_no_change` numbers of iterations. The split is stratified. Values must be in the range `[1, inf)`.
New in version 0.20.
**tol**float, default=1e-4
Tolerance for the early stopping. When the loss is not improving by at least tol for `n_iter_no_change` iterations (if set to a number), the training stops. Values must be in the range `(0.0, inf)`.
New in version 0.20.
**ccp\_alpha**non-negative float, default=0.0
Complexity parameter used for Minimal Cost-Complexity Pruning. The subtree with the largest cost complexity that is smaller than `ccp_alpha` will be chosen. By default, no pruning is performed. Values must be in the range `[0.0, inf)`. See [Minimal Cost-Complexity Pruning](../tree#minimal-cost-complexity-pruning) for details.
New in version 0.22.
Attributes:
**n\_estimators\_**int
The number of estimators as selected by early stopping (if `n_iter_no_change` is specified). Otherwise it is set to `n_estimators`.
New in version 0.20.
[`feature_importances_`](#sklearn.ensemble.GradientBoostingClassifier.feature_importances_ "sklearn.ensemble.GradientBoostingClassifier.feature_importances_")ndarray of shape (n\_features,)
The impurity-based feature importances.
**oob\_improvement\_**ndarray of shape (n\_estimators,)
The improvement in loss (= deviance) on the out-of-bag samples relative to the previous iteration. `oob_improvement_[0]` is the improvement in loss of the first stage over the `init` estimator. Only available if `subsample < 1.0`
**train\_score\_**ndarray of shape (n\_estimators,)
The i-th score `train_score_[i]` is the deviance (= loss) of the model at iteration `i` on the in-bag sample. If `subsample == 1` this is the deviance on the training data.
[`loss_`](#sklearn.ensemble.GradientBoostingClassifier.loss_ "sklearn.ensemble.GradientBoostingClassifier.loss_")LossFunction
DEPRECATED: Attribute `loss_` was deprecated in version 1.1 and will be removed in 1.3.
**init\_**estimator
The estimator that provides the initial predictions. Set via the `init` argument or `loss.init_estimator`.
**estimators\_**ndarray of DecisionTreeRegressor of shape (n\_estimators, `loss_.K`)
The collection of fitted sub-estimators. `loss_.K` is 1 for binary classification, otherwise n\_classes.
**classes\_**ndarray of shape (n\_classes,)
The classes labels.
[`n_features_`](#sklearn.ensemble.GradientBoostingClassifier.n_features_ "sklearn.ensemble.GradientBoostingClassifier.n_features_")int
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_classes\_**int
The number of classes.
**max\_features\_**int
The inferred value of max\_features.
See also
[`HistGradientBoostingClassifier`](sklearn.ensemble.histgradientboostingclassifier#sklearn.ensemble.HistGradientBoostingClassifier "sklearn.ensemble.HistGradientBoostingClassifier")
Histogram-based Gradient Boosting Classification Tree.
[`sklearn.tree.DecisionTreeClassifier`](sklearn.tree.decisiontreeclassifier#sklearn.tree.DecisionTreeClassifier "sklearn.tree.DecisionTreeClassifier")
A decision tree classifier.
[`RandomForestClassifier`](sklearn.ensemble.randomforestclassifier#sklearn.ensemble.RandomForestClassifier "sklearn.ensemble.RandomForestClassifier")
A meta-estimator that fits a number of decision tree classifiers on various sub-samples of the dataset and uses averaging to improve the predictive accuracy and control over-fitting.
[`AdaBoostClassifier`](sklearn.ensemble.adaboostclassifier#sklearn.ensemble.AdaBoostClassifier "sklearn.ensemble.AdaBoostClassifier")
A meta-estimator that begins by fitting a classifier on the original dataset and then fits additional copies of the classifier on the same dataset where the weights of incorrectly classified instances are adjusted such that subsequent classifiers focus more on difficult cases.
#### Notes
The features are always randomly permuted at each split. Therefore, the best found split may vary, even with the same training data and `max_features=n_features`, if the improvement of the criterion is identical for several splits enumerated during the search of the best split. To obtain a deterministic behaviour during fitting, `random_state` has to be fixed.
#### References
J. Friedman, Greedy Function Approximation: A Gradient Boosting Machine, The Annals of Statistics, Vol. 29, No. 5, 2001.
10. Friedman, Stochastic Gradient Boosting, 1999
T. Hastie, R. Tibshirani and J. Friedman. Elements of Statistical Learning Ed. 2, Springer, 2009.
#### Examples
The following example shows how to fit a gradient boosting classifier with 100 decision stumps as weak learners.
```
>>> from sklearn.datasets import make_hastie_10_2
>>> from sklearn.ensemble import GradientBoostingClassifier
```
```
>>> X, y = make_hastie_10_2(random_state=0)
>>> X_train, X_test = X[:2000], X[2000:]
>>> y_train, y_test = y[:2000], y[2000:]
```
```
>>> clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0,
... max_depth=1, random_state=0).fit(X_train, y_train)
>>> clf.score(X_test, y_test)
0.913...
```
#### Methods
| | |
| --- | --- |
| [`apply`](#sklearn.ensemble.GradientBoostingClassifier.apply "sklearn.ensemble.GradientBoostingClassifier.apply")(X) | Apply trees in the ensemble to X, return leaf indices. |
| [`decision_function`](#sklearn.ensemble.GradientBoostingClassifier.decision_function "sklearn.ensemble.GradientBoostingClassifier.decision_function")(X) | Compute the decision function of `X`. |
| [`fit`](#sklearn.ensemble.GradientBoostingClassifier.fit "sklearn.ensemble.GradientBoostingClassifier.fit")(X, y[, sample\_weight, monitor]) | Fit the gradient boosting model. |
| [`get_params`](#sklearn.ensemble.GradientBoostingClassifier.get_params "sklearn.ensemble.GradientBoostingClassifier.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.ensemble.GradientBoostingClassifier.predict "sklearn.ensemble.GradientBoostingClassifier.predict")(X) | Predict class for X. |
| [`predict_log_proba`](#sklearn.ensemble.GradientBoostingClassifier.predict_log_proba "sklearn.ensemble.GradientBoostingClassifier.predict_log_proba")(X) | Predict class log-probabilities for X. |
| [`predict_proba`](#sklearn.ensemble.GradientBoostingClassifier.predict_proba "sklearn.ensemble.GradientBoostingClassifier.predict_proba")(X) | Predict class probabilities for X. |
| [`score`](#sklearn.ensemble.GradientBoostingClassifier.score "sklearn.ensemble.GradientBoostingClassifier.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.ensemble.GradientBoostingClassifier.set_params "sklearn.ensemble.GradientBoostingClassifier.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`staged_decision_function`](#sklearn.ensemble.GradientBoostingClassifier.staged_decision_function "sklearn.ensemble.GradientBoostingClassifier.staged_decision_function")(X) | Compute decision function of `X` for each iteration. |
| [`staged_predict`](#sklearn.ensemble.GradientBoostingClassifier.staged_predict "sklearn.ensemble.GradientBoostingClassifier.staged_predict")(X) | Predict class at each stage for X. |
| [`staged_predict_proba`](#sklearn.ensemble.GradientBoostingClassifier.staged_predict_proba "sklearn.ensemble.GradientBoostingClassifier.staged_predict_proba")(X) | Predict class probabilities at each stage for X. |
apply(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_gb.py#L936)
Apply trees in the ensemble to X, return leaf indices.
New in version 0.17.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, its dtype will be converted to `dtype=np.float32`. If a sparse matrix is provided, it will be converted to a sparse `csr_matrix`.
Returns:
**X\_leaves**array-like of shape (n\_samples, n\_estimators, n\_classes)
For each datapoint x in X and for each tree in the ensemble, return the index of the leaf x ends up in each estimator. In the case of binary classification n\_classes is 1.
decision\_function(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_gb.py#L1386)
Compute the decision function of `X`.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
Returns:
**score**ndarray of shape (n\_samples, n\_classes) or (n\_samples,)
The decision function of the input samples, which corresponds to the raw values predicted from the trees of the ensemble . The order of the classes corresponds to that in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_). Regression and binary classification produce an array of shape (n\_samples,).
*property*feature\_importances\_
The impurity-based feature importances.
The higher, the more important the feature. The importance of a feature is computed as the (normalized) total reduction of the criterion brought by that feature. It is also known as the Gini importance.
Warning: impurity-based feature importances can be misleading for high cardinality features (many unique values). See [`sklearn.inspection.permutation_importance`](sklearn.inspection.permutation_importance#sklearn.inspection.permutation_importance "sklearn.inspection.permutation_importance") as an alternative.
Returns:
**feature\_importances\_**ndarray of shape (n\_features,)
The values of this array sum to 1, unless all trees are single node trees consisting of only the root node, in which case it will be an array of zeros.
fit(*X*, *y*, *sample\_weight=None*, *monitor=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_gb.py#L495)
Fit the gradient boosting model.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
**y**array-like of shape (n\_samples,)
Target values (strings or integers in classification, real numbers in regression) For classification, labels must correspond to classes.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, then samples are equally weighted. Splits that would create child nodes with net zero or negative weight are ignored while searching for a split in each node. In the case of classification, splits are also ignored if they would result in any single class carrying a negative weight in either child node.
**monitor**callable, default=None
The monitor is called after each iteration with the current iteration, a reference to the estimator and the local variables of `_fit_stages` as keyword arguments `callable(i, self,
locals())`. If the callable returns `True` the fitting procedure is stopped. The monitor can be used for various things such as computing held-out estimates, early stopping, model introspect, and snapshoting.
Returns:
**self**object
Fitted estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*loss\_
DEPRECATED: Attribute `loss_` was deprecated in version 1.1 and will be removed in 1.3.
*property*n\_features\_
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2. Use `n_features_in_` instead.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_gb.py#L1437)
Predict class for X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
Returns:
**y**ndarray of shape (n\_samples,)
The predicted values.
predict\_log\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_gb.py#L1509)
Predict class log-probabilities for X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
Returns:
**p**ndarray of shape (n\_samples, n\_classes)
The class log-probabilities of the input samples. The order of the classes corresponds to that in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
Raises:
AttributeError
If the `loss` does not support probabilities.
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_gb.py#L1478)
Predict class probabilities for X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
Returns:
**p**ndarray of shape (n\_samples, n\_classes)
The class probabilities of the input samples. The order of the classes corresponds to that in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
Raises:
AttributeError
If the `loss` does not support probabilities.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
staged\_decision\_function(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_gb.py#L1413)
Compute decision function of `X` for each iteration.
This method allows monitoring (i.e. determine error on testing set) after each stage.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
Yields:
**score**generator of ndarray of shape (n\_samples, k)
The decision function of the input samples, which corresponds to the raw values predicted from the trees of the ensemble . The classes corresponds to that in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_). Regression and binary classification are special cases with `k == 1`, otherwise `k==n_classes`.
staged\_predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_gb.py#L1456)
Predict class at each stage for X.
This method allows monitoring (i.e. determine error on testing set) after each stage.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
Yields:
**y**generator of ndarray of shape (n\_samples,)
The predicted value of the input samples.
staged\_predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_gb.py#L1533)
Predict class probabilities at each stage for X.
This method allows monitoring (i.e. determine error on testing set) after each stage.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
Yields:
**y**generator of ndarray of shape (n\_samples,)
The predicted value of the input samples.
Examples using `sklearn.ensemble.GradientBoostingClassifier`
------------------------------------------------------------
[Early stopping of Gradient Boosting](../../auto_examples/ensemble/plot_gradient_boosting_early_stopping#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-early-stopping-py)
[Feature transformations with ensembles of trees](../../auto_examples/ensemble/plot_feature_transformation#sphx-glr-auto-examples-ensemble-plot-feature-transformation-py)
[Gradient Boosting Out-of-Bag estimates](../../auto_examples/ensemble/plot_gradient_boosting_oob#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-oob-py)
[Gradient Boosting regularization](../../auto_examples/ensemble/plot_gradient_boosting_regularization#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-regularization-py)
[Feature discretization](../../auto_examples/preprocessing/plot_discretization_classification#sphx-glr-auto-examples-preprocessing-plot-discretization-classification-py)
| programming_docs |
scikit_learn sklearn.utils.metaestimators.available_if sklearn.utils.metaestimators.available\_if
==========================================
sklearn.utils.metaestimators.available\_if(*check*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/metaestimators.py#L143)
An attribute that is available only if check returns a truthy value
Parameters:
**check**callable
When passed the object with the decorated method, this should return a truthy value if the attribute is available, and either return False or raise an AttributeError if not available.
#### Examples
```
>>> from sklearn.utils.metaestimators import available_if
>>> class HelloIfEven:
... def __init__(self, x):
... self.x = x
...
... def _x_is_even(self):
... return self.x % 2 == 0
...
... @available_if(_x_is_even)
... def say_hello(self):
... print("Hello")
...
>>> obj = HelloIfEven(1)
>>> hasattr(obj, "say_hello")
False
>>> obj.x = 2
>>> hasattr(obj, "say_hello")
True
>>> obj.say_hello()
Hello
```
Examples using `sklearn.utils.metaestimators.available_if`
----------------------------------------------------------
[Inductive Clustering](../../auto_examples/cluster/plot_inductive_clustering#sphx-glr-auto-examples-cluster-plot-inductive-clustering-py)
scikit_learn sklearn.model_selection.KFold sklearn.model\_selection.KFold
==============================
*class*sklearn.model\_selection.KFold(*n\_splits=5*, *\**, *shuffle=False*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L365)
K-Folds cross-validator
Provides train/test indices to split data in train/test sets. Split dataset into k consecutive folds (without shuffling by default).
Each fold is then used once as a validation while the k - 1 remaining folds form the training set.
Read more in the [User Guide](../cross_validation#k-fold).
Parameters:
**n\_splits**int, default=5
Number of folds. Must be at least 2.
Changed in version 0.22: `n_splits` default value changed from 3 to 5.
**shuffle**bool, default=False
Whether to shuffle the data before splitting into batches. Note that the samples within each split will not be shuffled.
**random\_state**int, RandomState instance or None, default=None
When `shuffle` is True, `random_state` affects the ordering of the indices, which controls the randomness of each fold. Otherwise, this parameter has no effect. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
See also
[`StratifiedKFold`](sklearn.model_selection.stratifiedkfold#sklearn.model_selection.StratifiedKFold "sklearn.model_selection.StratifiedKFold")
Takes class information into account to avoid building folds with imbalanced class distributions (for binary or multiclass classification tasks).
[`GroupKFold`](sklearn.model_selection.groupkfold#sklearn.model_selection.GroupKFold "sklearn.model_selection.GroupKFold")
K-fold iterator variant with non-overlapping groups.
[`RepeatedKFold`](sklearn.model_selection.repeatedkfold#sklearn.model_selection.RepeatedKFold "sklearn.model_selection.RepeatedKFold")
Repeats K-Fold n times.
#### Notes
The first `n_samples % n_splits` folds have size `n_samples // n_splits + 1`, other folds have size `n_samples // n_splits`, where `n_samples` is the number of samples.
Randomized CV splitters may return different results for each call of split. You can make the results identical by setting `random_state` to an integer.
#### Examples
```
>>> import numpy as np
>>> from sklearn.model_selection import KFold
>>> X = np.array([[1, 2], [3, 4], [1, 2], [3, 4]])
>>> y = np.array([1, 2, 3, 4])
>>> kf = KFold(n_splits=2)
>>> kf.get_n_splits(X)
2
>>> print(kf)
KFold(n_splits=2, random_state=None, shuffle=False)
>>> for train_index, test_index in kf.split(X):
... print("TRAIN:", train_index, "TEST:", test_index)
... X_train, X_test = X[train_index], X[test_index]
... y_train, y_test = y[train_index], y[test_index]
TRAIN: [2 3] TEST: [0 1]
TRAIN: [0 1] TEST: [2 3]
```
#### Methods
| | |
| --- | --- |
| [`get_n_splits`](#sklearn.model_selection.KFold.get_n_splits "sklearn.model_selection.KFold.get_n_splits")([X, y, groups]) | Returns the number of splitting iterations in the cross-validator |
| [`split`](#sklearn.model_selection.KFold.split "sklearn.model_selection.KFold.split")(X[, y, groups]) | Generate indices to split data into training and test set. |
get\_n\_splits(*X=None*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L343)
Returns the number of splitting iterations in the cross-validator
Parameters:
**X**object
Always ignored, exists for compatibility.
**y**object
Always ignored, exists for compatibility.
**groups**object
Always ignored, exists for compatibility.
Returns:
**n\_splits**int
Returns the number of splitting iterations in the cross-validator.
split(*X*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L306)
Generate indices to split data into training and test set.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,), default=None
The target variable for supervised learning problems.
**groups**array-like of shape (n\_samples,), default=None
Group labels for the samples used while splitting the dataset into train/test set.
Yields:
**train**ndarray
The training set indices for that split.
**test**ndarray
The testing set indices for that split.
Examples using `sklearn.model_selection.KFold`
----------------------------------------------
[Feature agglomeration vs. univariate selection](../../auto_examples/cluster/plot_feature_agglomeration_vs_univariate_selection#sphx-glr-auto-examples-cluster-plot-feature-agglomeration-vs-univariate-selection-py)
[Gradient Boosting Out-of-Bag estimates](../../auto_examples/ensemble/plot_gradient_boosting_oob#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-oob-py)
[Nested versus non-nested cross-validation](../../auto_examples/model_selection/plot_nested_cross_validation_iris#sphx-glr-auto-examples-model-selection-plot-nested-cross-validation-iris-py)
[Visualizing cross-validation behavior in scikit-learn](../../auto_examples/model_selection/plot_cv_indices#sphx-glr-auto-examples-model-selection-plot-cv-indices-py)
[Cross-validation on diabetes Dataset Exercise](../../auto_examples/exercises/plot_cv_diabetes#sphx-glr-auto-examples-exercises-plot-cv-diabetes-py)
scikit_learn sklearn.utils.as_float_array sklearn.utils.as\_float\_array
==============================
sklearn.utils.as\_float\_array(*X*, *\**, *copy=True*, *force\_all\_finite=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/validation.py#L188)
Convert an array-like to an array of floats.
The new dtype will be np.float32 or np.float64, depending on the original type. The function can create a copy or modify the argument depending on the argument copy.
Parameters:
**X**{array-like, sparse matrix}
The input data.
**copy**bool, default=True
If True, a copy of X will be created. If False, a copy may still be returned if X’s dtype is not a floating point type.
**force\_all\_finite**bool or ‘allow-nan’, default=True
Whether to raise an error on np.inf, np.nan, pd.NA in X. The possibilities are:
* True: Force all values of X to be finite.
* False: accepts np.inf, np.nan, pd.NA in X.
* ‘allow-nan’: accepts only np.nan and pd.NA values in X. Values cannot be infinite.
New in version 0.20: `force_all_finite` accepts the string `'allow-nan'`.
Changed in version 0.23: Accepts `pd.NA` and converts it into `np.nan`
Returns:
**XT**{ndarray, sparse matrix}
An array of type float.
scikit_learn sklearn.linear_model.MultiTaskElasticNetCV sklearn.linear\_model.MultiTaskElasticNetCV
===========================================
*class*sklearn.linear\_model.MultiTaskElasticNetCV(*\**, *l1\_ratio=0.5*, *eps=0.001*, *n\_alphas=100*, *alphas=None*, *fit\_intercept=True*, *normalize='deprecated'*, *max\_iter=1000*, *tol=0.0001*, *cv=None*, *copy\_X=True*, *verbose=0*, *n\_jobs=None*, *random\_state=None*, *selection='cyclic'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_coordinate_descent.py#L2679)
Multi-task L1/L2 ElasticNet with built-in cross-validation.
See glossary entry for [cross-validation estimator](https://scikit-learn.org/1.1/glossary.html#term-cross-validation-estimator).
The optimization objective for MultiTaskElasticNet is:
```
(1 / (2 * n_samples)) * ||Y - XW||^Fro_2
+ alpha * l1_ratio * ||W||_21
+ 0.5 * alpha * (1 - l1_ratio) * ||W||_Fro^2
```
Where:
```
||W||_21 = \sum_i \sqrt{\sum_j w_{ij}^2}
```
i.e. the sum of norm of each row.
Read more in the [User Guide](../linear_model#multi-task-elastic-net).
New in version 0.15.
Parameters:
**l1\_ratio**float or list of float, default=0.5
The ElasticNet mixing parameter, with 0 < l1\_ratio <= 1. For l1\_ratio = 1 the penalty is an L1/L2 penalty. For l1\_ratio = 0 it is an L2 penalty. For `0 < l1_ratio < 1`, the penalty is a combination of L1/L2 and L2. This parameter can be a list, in which case the different values are tested by cross-validation and the one giving the best prediction score is used. Note that a good choice of list of values for l1\_ratio is often to put more values close to 1 (i.e. Lasso) and less close to 0 (i.e. Ridge), as in `[.1, .5, .7,
.9, .95, .99, 1]`.
**eps**float, default=1e-3
Length of the path. `eps=1e-3` means that `alpha_min / alpha_max = 1e-3`.
**n\_alphas**int, default=100
Number of alphas along the regularization path.
**alphas**array-like, default=None
List of alphas where to compute the models. If not provided, set automatically.
**fit\_intercept**bool, default=True
Whether to calculate the intercept for this model. If set to false, no intercept will be used in calculations (i.e. data is expected to be centered).
**normalize**bool, default=False
This parameter is ignored when `fit_intercept` is set to False. If True, the regressors X will be normalized before regression by subtracting the mean and dividing by the l2-norm. If you wish to standardize, please use [`StandardScaler`](sklearn.preprocessing.standardscaler#sklearn.preprocessing.StandardScaler "sklearn.preprocessing.StandardScaler") before calling `fit` on an estimator with `normalize=False`.
Deprecated since version 1.0: `normalize` was deprecated in version 1.0 and will be removed in 1.2.
**max\_iter**int, default=1000
The maximum number of iterations.
**tol**float, default=1e-4
The tolerance for the optimization: if the updates are smaller than `tol`, the optimization code checks the dual gap for optimality and continues until it is smaller than `tol`.
**cv**int, cross-validation generator or iterable, default=None
Determines the cross-validation splitting strategy. Possible inputs for cv are:
* None, to use the default 5-fold cross-validation,
* int, to specify the number of folds.
* [CV splitter](https://scikit-learn.org/1.1/glossary.html#term-CV-splitter),
* An iterable yielding (train, test) splits as arrays of indices.
For int/None inputs, `KFold` is used.
Refer [User Guide](../cross_validation#cross-validation) for the various cross-validation strategies that can be used here.
Changed in version 0.22: `cv` default value if None changed from 3-fold to 5-fold.
**copy\_X**bool, default=True
If `True`, X will be copied; else, it may be overwritten.
**verbose**bool or int, default=0
Amount of verbosity.
**n\_jobs**int, default=None
Number of CPUs to use during the cross validation. Note that this is used only if multiple values for l1\_ratio are given. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**random\_state**int, RandomState instance, default=None
The seed of the pseudo random number generator that selects a random feature to update. Used when `selection` == ‘random’. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**selection**{‘cyclic’, ‘random’}, default=’cyclic’
If set to ‘random’, a random coefficient is updated every iteration rather than looping over features sequentially by default. This (setting to ‘random’) often leads to significantly faster convergence especially when tol is higher than 1e-4.
Attributes:
**intercept\_**ndarray of shape (n\_targets,)
Independent term in decision function.
**coef\_**ndarray of shape (n\_targets, n\_features)
Parameter vector (W in the cost function formula). Note that `coef_` stores the transpose of `W`, `W.T`.
**alpha\_**float
The amount of penalization chosen by cross validation.
**mse\_path\_**ndarray of shape (n\_alphas, n\_folds) or (n\_l1\_ratio, n\_alphas, n\_folds)
Mean square error for the test set on each fold, varying alpha.
**alphas\_**ndarray of shape (n\_alphas,) or (n\_l1\_ratio, n\_alphas)
The grid of alphas used for fitting, for each l1\_ratio.
**l1\_ratio\_**float
Best l1\_ratio obtained by cross-validation.
**n\_iter\_**int
Number of iterations run by the coordinate descent solver to reach the specified tolerance for the optimal alpha.
**dual\_gap\_**float
The dual gap at the end of the optimization for the optimal alpha.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`MultiTaskElasticNet`](sklearn.linear_model.multitaskelasticnet#sklearn.linear_model.MultiTaskElasticNet "sklearn.linear_model.MultiTaskElasticNet")
Multi-task L1/L2 ElasticNet with built-in cross-validation.
[`ElasticNetCV`](sklearn.linear_model.elasticnetcv#sklearn.linear_model.ElasticNetCV "sklearn.linear_model.ElasticNetCV")
Elastic net model with best model selection by cross-validation.
[`MultiTaskLassoCV`](sklearn.linear_model.multitasklassocv#sklearn.linear_model.MultiTaskLassoCV "sklearn.linear_model.MultiTaskLassoCV")
Multi-task Lasso model trained with L1/L2 mixed-norm as regularizer.
#### Notes
The algorithm used to fit the model is coordinate descent.
In `fit`, once the best parameters `l1_ratio` and `alpha` are found through cross-validation, the model is fit again using the entire training set.
To avoid unnecessary memory duplication the `X` and `y` arguments of the `fit` method should be directly passed as Fortran-contiguous numpy arrays.
#### Examples
```
>>> from sklearn import linear_model
>>> clf = linear_model.MultiTaskElasticNetCV(cv=3)
>>> clf.fit([[0,0], [1, 1], [2, 2]],
... [[0, 0], [1, 1], [2, 2]])
MultiTaskElasticNetCV(cv=3)
>>> print(clf.coef_)
[[0.52875032 0.46958558]
[0.52875032 0.46958558]]
>>> print(clf.intercept_)
[0.00166409 0.00166409]
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.linear_model.MultiTaskElasticNetCV.fit "sklearn.linear_model.MultiTaskElasticNetCV.fit")(X, y) | Fit MultiTaskElasticNet model with coordinate descent. |
| [`get_params`](#sklearn.linear_model.MultiTaskElasticNetCV.get_params "sklearn.linear_model.MultiTaskElasticNetCV.get_params")([deep]) | Get parameters for this estimator. |
| [`path`](#sklearn.linear_model.MultiTaskElasticNetCV.path "sklearn.linear_model.MultiTaskElasticNetCV.path")(X, y, \*[, l1\_ratio, eps, n\_alphas, ...]) | Compute elastic net path with coordinate descent. |
| [`predict`](#sklearn.linear_model.MultiTaskElasticNetCV.predict "sklearn.linear_model.MultiTaskElasticNetCV.predict")(X) | Predict using the linear model. |
| [`score`](#sklearn.linear_model.MultiTaskElasticNetCV.score "sklearn.linear_model.MultiTaskElasticNetCV.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.linear_model.MultiTaskElasticNetCV.set_params "sklearn.linear_model.MultiTaskElasticNetCV.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_coordinate_descent.py#L2911)
Fit MultiTaskElasticNet model with coordinate descent.
Fit is on grid of alphas and best alpha estimated by cross-validation.
Parameters:
**X**ndarray of shape (n\_samples, n\_features)
Training data.
**y**ndarray of shape (n\_samples, n\_targets)
Training target variable. Will be cast to X’s dtype if necessary.
Returns:
**self**object
Returns MultiTaskElasticNet instance.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*static*path(*X*, *y*, *\**, *l1\_ratio=0.5*, *eps=0.001*, *n\_alphas=100*, *alphas=None*, *precompute='auto'*, *Xy=None*, *copy\_X=True*, *coef\_init=None*, *verbose=False*, *return\_n\_iter=False*, *positive=False*, *check\_input=True*, *\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_coordinate_descent.py#L366)
Compute elastic net path with coordinate descent.
The elastic net optimization function varies for mono and multi-outputs.
For mono-output tasks it is:
```
1 / (2 * n_samples) * ||y - Xw||^2_2
+ alpha * l1_ratio * ||w||_1
+ 0.5 * alpha * (1 - l1_ratio) * ||w||^2_2
```
For multi-output tasks it is:
```
(1 / (2 * n_samples)) * ||Y - XW||_Fro^2
+ alpha * l1_ratio * ||W||_21
+ 0.5 * alpha * (1 - l1_ratio) * ||W||_Fro^2
```
Where:
```
||W||_21 = \sum_i \sqrt{\sum_j w_{ij}^2}
```
i.e. the sum of norm of each row.
Read more in the [User Guide](../linear_model#elastic-net).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training data. Pass directly as Fortran-contiguous data to avoid unnecessary memory duplication. If `y` is mono-output then `X` can be sparse.
**y**{array-like, sparse matrix} of shape (n\_samples,) or (n\_samples, n\_targets)
Target values.
**l1\_ratio**float, default=0.5
Number between 0 and 1 passed to elastic net (scaling between l1 and l2 penalties). `l1_ratio=1` corresponds to the Lasso.
**eps**float, default=1e-3
Length of the path. `eps=1e-3` means that `alpha_min / alpha_max = 1e-3`.
**n\_alphas**int, default=100
Number of alphas along the regularization path.
**alphas**ndarray, default=None
List of alphas where to compute the models. If None alphas are set automatically.
**precompute**‘auto’, bool or array-like of shape (n\_features, n\_features), default=’auto’
Whether to use a precomputed Gram matrix to speed up calculations. If set to `'auto'` let us decide. The Gram matrix can also be passed as argument.
**Xy**array-like of shape (n\_features,) or (n\_features, n\_targets), default=None
Xy = np.dot(X.T, y) that can be precomputed. It is useful only when the Gram matrix is precomputed.
**copy\_X**bool, default=True
If `True`, X will be copied; else, it may be overwritten.
**coef\_init**ndarray of shape (n\_features, ), default=None
The initial values of the coefficients.
**verbose**bool or int, default=False
Amount of verbosity.
**return\_n\_iter**bool, default=False
Whether to return the number of iterations or not.
**positive**bool, default=False
If set to True, forces coefficients to be positive. (Only allowed when `y.ndim == 1`).
**check\_input**bool, default=True
If set to False, the input validation checks are skipped (including the Gram matrix when provided). It is assumed that they are handled by the caller.
**\*\*params**kwargs
Keyword arguments passed to the coordinate descent solver.
Returns:
**alphas**ndarray of shape (n\_alphas,)
The alphas along the path where models are computed.
**coefs**ndarray of shape (n\_features, n\_alphas) or (n\_targets, n\_features, n\_alphas)
Coefficients along the path.
**dual\_gaps**ndarray of shape (n\_alphas,)
The dual gaps at the end of the optimization for each alpha.
**n\_iters**list of int
The number of iterations taken by the coordinate descent optimizer to reach the specified tolerance for each alpha. (Is returned when `return_n_iter` is set to True).
See also
[`MultiTaskElasticNet`](sklearn.linear_model.multitaskelasticnet#sklearn.linear_model.MultiTaskElasticNet "sklearn.linear_model.MultiTaskElasticNet")
Multi-task ElasticNet model trained with L1/L2 mixed-norm as regularizer.
[`MultiTaskElasticNetCV`](#sklearn.linear_model.MultiTaskElasticNetCV "sklearn.linear_model.MultiTaskElasticNetCV")
Multi-task L1/L2 ElasticNet with built-in cross-validation.
[`ElasticNet`](sklearn.linear_model.elasticnet#sklearn.linear_model.ElasticNet "sklearn.linear_model.ElasticNet")
Linear regression with combined L1 and L2 priors as regularizer.
[`ElasticNetCV`](sklearn.linear_model.elasticnetcv#sklearn.linear_model.ElasticNetCV "sklearn.linear_model.ElasticNetCV")
Elastic Net model with iterative fitting along a regularization path.
#### Notes
For an example, see [examples/linear\_model/plot\_lasso\_coordinate\_descent\_path.py](../../auto_examples/linear_model/plot_lasso_coordinate_descent_path#sphx-glr-auto-examples-linear-model-plot-lasso-coordinate-descent-path-py).
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L372)
Predict using the linear model.
Parameters:
**X**array-like or sparse matrix, shape (n\_samples, n\_features)
Samples.
Returns:
**C**array, shape (n\_samples,)
Returns predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
| programming_docs |
scikit_learn sklearn.metrics.max_error sklearn.metrics.max\_error
==========================
sklearn.metrics.max\_error(*y\_true*, *y\_pred*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_regression.py#L941)
The max\_error metric calculates the maximum residual error.
Read more in the [User Guide](../model_evaluation#max-error).
Parameters:
**y\_true**array-like of shape (n\_samples,)
Ground truth (correct) target values.
**y\_pred**array-like of shape (n\_samples,)
Estimated target values.
Returns:
**max\_error**float
A positive floating point value (the best value is 0.0).
#### Examples
```
>>> from sklearn.metrics import max_error
>>> y_true = [3, 2, 7, 1]
>>> y_pred = [4, 2, 7, 1]
>>> max_error(y_true, y_pred)
1
```
scikit_learn sklearn.ensemble.IsolationForest sklearn.ensemble.IsolationForest
================================
*class*sklearn.ensemble.IsolationForest(*\**, *n\_estimators=100*, *max\_samples='auto'*, *contamination='auto'*, *max\_features=1.0*, *bootstrap=False*, *n\_jobs=None*, *random\_state=None*, *verbose=0*, *warm\_start=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_iforest.py#L25)
Isolation Forest Algorithm.
Return the anomaly score of each sample using the IsolationForest algorithm
The IsolationForest ‘isolates’ observations by randomly selecting a feature and then randomly selecting a split value between the maximum and minimum values of the selected feature.
Since recursive partitioning can be represented by a tree structure, the number of splittings required to isolate a sample is equivalent to the path length from the root node to the terminating node.
This path length, averaged over a forest of such random trees, is a measure of normality and our decision function.
Random partitioning produces noticeably shorter paths for anomalies. Hence, when a forest of random trees collectively produce shorter path lengths for particular samples, they are highly likely to be anomalies.
Read more in the [User Guide](../outlier_detection#isolation-forest).
New in version 0.18.
Parameters:
**n\_estimators**int, default=100
The number of base estimators in the ensemble.
**max\_samples**“auto”, int or float, default=”auto”
The number of samples to draw from X to train each base estimator.
* If int, then draw `max_samples` samples.
* If float, then draw `max_samples * X.shape[0]` samples.
* If “auto”, then `max_samples=min(256, n_samples)`.
If max\_samples is larger than the number of samples provided, all samples will be used for all trees (no sampling).
**contamination**‘auto’ or float, default=’auto’
The amount of contamination of the data set, i.e. the proportion of outliers in the data set. Used when fitting to define the threshold on the scores of the samples.
* If ‘auto’, the threshold is determined as in the original paper.
* If float, the contamination should be in the range (0, 0.5].
Changed in version 0.22: The default value of `contamination` changed from 0.1 to `'auto'`.
**max\_features**int or float, default=1.0
The number of features to draw from X to train each base estimator.
* If int, then draw `max_features` features.
* If float, then draw `max(1, int(max_features * n_features_in_))` features.
**bootstrap**bool, default=False
If True, individual trees are fit on random subsets of the training data sampled with replacement. If False, sampling without replacement is performed.
**n\_jobs**int, default=None
The number of jobs to run in parallel for both [`fit`](#sklearn.ensemble.IsolationForest.fit "sklearn.ensemble.IsolationForest.fit") and [`predict`](#sklearn.ensemble.IsolationForest.predict "sklearn.ensemble.IsolationForest.predict"). `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**random\_state**int, RandomState instance or None, default=None
Controls the pseudo-randomness of the selection of the feature and split values for each branching step and each tree in the forest.
Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**verbose**int, default=0
Controls the verbosity of the tree building process.
**warm\_start**bool, default=False
When set to `True`, reuse the solution of the previous call to fit and add more estimators to the ensemble, otherwise, just fit a whole new forest. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
New in version 0.21.
Attributes:
**base\_estimator\_**ExtraTreeRegressor instance
The child estimator template used to create the collection of fitted sub-estimators.
**estimators\_**list of ExtraTreeRegressor instances
The collection of fitted sub-estimators.
**estimators\_features\_**list of ndarray
The subset of drawn features for each base estimator.
[`estimators_samples_`](#sklearn.ensemble.IsolationForest.estimators_samples_ "sklearn.ensemble.IsolationForest.estimators_samples_")list of ndarray
The subset of drawn samples for each base estimator.
**max\_samples\_**int
The actual number of samples.
**offset\_**float
Offset used to define the decision function from the raw scores. We have the relation: `decision_function = score_samples - offset_`. `offset_` is defined as follows. When the contamination parameter is set to “auto”, the offset is equal to -0.5 as the scores of inliers are close to 0 and the scores of outliers are close to -1. When a contamination parameter different than “auto” is provided, the offset is defined in such a way we obtain the expected number of outliers (samples with decision function < 0) in training.
New in version 0.20.
[`n_features_`](#sklearn.ensemble.IsolationForest.n_features_ "sklearn.ensemble.IsolationForest.n_features_")int
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`sklearn.covariance.EllipticEnvelope`](sklearn.covariance.ellipticenvelope#sklearn.covariance.EllipticEnvelope "sklearn.covariance.EllipticEnvelope")
An object for detecting outliers in a Gaussian distributed dataset.
[`sklearn.svm.OneClassSVM`](sklearn.svm.oneclasssvm#sklearn.svm.OneClassSVM "sklearn.svm.OneClassSVM")
Unsupervised Outlier Detection. Estimate the support of a high-dimensional distribution. The implementation is based on libsvm.
[`sklearn.neighbors.LocalOutlierFactor`](sklearn.neighbors.localoutlierfactor#sklearn.neighbors.LocalOutlierFactor "sklearn.neighbors.LocalOutlierFactor")
Unsupervised Outlier Detection using Local Outlier Factor (LOF).
#### Notes
The implementation is based on an ensemble of ExtraTreeRegressor. The maximum depth of each tree is set to `ceil(log_2(n))` where \(n\) is the number of samples used to build the tree (see (Liu et al., 2008) for more details).
#### References
[1] Liu, Fei Tony, Ting, Kai Ming and Zhou, Zhi-Hua. “Isolation forest.” Data Mining, 2008. ICDM’08. Eighth IEEE International Conference on.
[2] Liu, Fei Tony, Ting, Kai Ming and Zhou, Zhi-Hua. “Isolation-based anomaly detection.” ACM Transactions on Knowledge Discovery from Data (TKDD) 6.1 (2012): 3.
#### Examples
```
>>> from sklearn.ensemble import IsolationForest
>>> X = [[-1.1], [0.3], [0.5], [100]]
>>> clf = IsolationForest(random_state=0).fit(X)
>>> clf.predict([[0.1], [0], [90]])
array([ 1, 1, -1])
```
#### Methods
| | |
| --- | --- |
| [`decision_function`](#sklearn.ensemble.IsolationForest.decision_function "sklearn.ensemble.IsolationForest.decision_function")(X) | Average anomaly score of X of the base classifiers. |
| [`fit`](#sklearn.ensemble.IsolationForest.fit "sklearn.ensemble.IsolationForest.fit")(X[, y, sample\_weight]) | Fit estimator. |
| [`fit_predict`](#sklearn.ensemble.IsolationForest.fit_predict "sklearn.ensemble.IsolationForest.fit_predict")(X[, y]) | Perform fit on X and returns labels for X. |
| [`get_params`](#sklearn.ensemble.IsolationForest.get_params "sklearn.ensemble.IsolationForest.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.ensemble.IsolationForest.predict "sklearn.ensemble.IsolationForest.predict")(X) | Predict if a particular sample is an outlier or not. |
| [`score_samples`](#sklearn.ensemble.IsolationForest.score_samples "sklearn.ensemble.IsolationForest.score_samples")(X) | Opposite of the anomaly score defined in the original paper. |
| [`set_params`](#sklearn.ensemble.IsolationForest.set_params "sklearn.ensemble.IsolationForest.set_params")(\*\*params) | Set the parameters of this estimator. |
decision\_function(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_iforest.py#L349)
Average anomaly score of X of the base classifiers.
The anomaly score of an input sample is computed as the mean anomaly score of the trees in the forest.
The measure of normality of an observation given a tree is the depth of the leaf containing this observation, which is equivalent to the number of splittings required to isolate this point. In case of several observations n\_left in the leaf, the average path length of a n\_left samples isolation tree is added.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
Returns:
**scores**ndarray of shape (n\_samples,)
The anomaly score of the input samples. The lower, the more abnormal. Negative scores represent outliers, positive scores represent inliers.
*property*estimators\_samples\_
The subset of drawn samples for each base estimator.
Returns a dynamically generated list of indices identifying the samples used for fitting each member of the ensemble, i.e., the in-bag samples.
Note: the list is re-created at each call to the property in order to reduce the object memory footprint by not storing the sampling data. Thus fetching the property may be slower than expected.
fit(*X*, *y=None*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_iforest.py#L235)
Fit estimator.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Use `dtype=np.float32` for maximum efficiency. Sparse matrices are also supported, use sparse `csc_matrix` for maximum efficiency.
**y**Ignored
Not used, present for API consistency by convention.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, then samples are equally weighted.
Returns:
**self**object
Fitted estimator.
fit\_predict(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L956)
Perform fit on X and returns labels for X.
Returns -1 for outliers and 1 for inliers.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**y**ndarray of shape (n\_samples,)
1 for inliers, -1 for outliers.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_features\_
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2. Use `n_features_in_` instead.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_iforest.py#L326)
Predict if a particular sample is an outlier or not.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, it will be converted to `dtype=np.float32` and if a sparse matrix is provided to a sparse `csr_matrix`.
Returns:
**is\_inlier**ndarray of shape (n\_samples,)
For each observation, tells whether or not (+1 or -1) it should be considered as an inlier according to the fitted model.
score\_samples(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_iforest.py#L381)
Opposite of the anomaly score defined in the original paper.
The anomaly score of an input sample is computed as the mean anomaly score of the trees in the forest.
The measure of normality of an observation given a tree is the depth of the leaf containing this observation, which is equivalent to the number of splittings required to isolate this point. In case of several observations n\_left in the leaf, the average path length of a n\_left samples isolation tree is added.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples.
Returns:
**scores**ndarray of shape (n\_samples,)
The anomaly score of the input samples. The lower, the more abnormal.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.ensemble.IsolationForest`
-------------------------------------------------
[IsolationForest example](../../auto_examples/ensemble/plot_isolation_forest#sphx-glr-auto-examples-ensemble-plot-isolation-forest-py)
[Comparing anomaly detection algorithms for outlier detection on toy datasets](../../auto_examples/miscellaneous/plot_anomaly_comparison#sphx-glr-auto-examples-miscellaneous-plot-anomaly-comparison-py)
[Evaluation of outlier detection estimators](../../auto_examples/miscellaneous/plot_outlier_detection_bench#sphx-glr-auto-examples-miscellaneous-plot-outlier-detection-bench-py)
scikit_learn sklearn.preprocessing.PolynomialFeatures sklearn.preprocessing.PolynomialFeatures
========================================
*class*sklearn.preprocessing.PolynomialFeatures(*degree=2*, *\**, *interaction\_only=False*, *include\_bias=True*, *order='C'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_polynomial.py#L30)
Generate polynomial and interaction features.
Generate a new feature matrix consisting of all polynomial combinations of the features with degree less than or equal to the specified degree. For example, if an input sample is two dimensional and of the form [a, b], the degree-2 polynomial features are [1, a, b, a^2, ab, b^2].
Read more in the [User Guide](../preprocessing#polynomial-features).
Parameters:
**degree**int or tuple (min\_degree, max\_degree), default=2
If a single int is given, it specifies the maximal degree of the polynomial features. If a tuple `(min_degree, max_degree)` is passed, then `min_degree` is the minimum and `max_degree` is the maximum polynomial degree of the generated features. Note that `min_degree=0` and `min_degree=1` are equivalent as outputting the degree zero term is determined by `include_bias`.
**interaction\_only**bool, default=False
If `True`, only interaction features are produced: features that are products of at most `degree` *distinct* input features, i.e. terms with power of 2 or higher of the same input feature are excluded:
* included: `x[0]`, `x[1]`, `x[0] * x[1]`, etc.
* excluded: `x[0] ** 2`, `x[0] ** 2 * x[1]`, etc.
**include\_bias**bool, default=True
If `True` (default), then include a bias column, the feature in which all polynomial powers are zero (i.e. a column of ones - acts as an intercept term in a linear model).
**order**{‘C’, ‘F’}, default=’C’
Order of output array in the dense case. `'F'` order is faster to compute, but may slow down subsequent estimators.
New in version 0.21.
Attributes:
[`powers_`](#sklearn.preprocessing.PolynomialFeatures.powers_ "sklearn.preprocessing.PolynomialFeatures.powers_")ndarray of shape (`n_output_features_`, `n_features_in_`)
Exponent for each of the inputs in the output.
[`n_input_features_`](#sklearn.preprocessing.PolynomialFeatures.n_input_features_ "sklearn.preprocessing.PolynomialFeatures.n_input_features_")int
DEPRECATED: The attribute `n_input_features_` was deprecated in version 1.0 and will be removed in 1.2.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_output\_features\_**int
The total number of polynomial output features. The number of output features is computed by iterating over all suitably sized combinations of input features.
See also
[`SplineTransformer`](sklearn.preprocessing.splinetransformer#sklearn.preprocessing.SplineTransformer "sklearn.preprocessing.SplineTransformer")
Transformer that generates univariate B-spline bases for features.
#### Notes
Be aware that the number of features in the output array scales polynomially in the number of features of the input array, and exponentially in the degree. High degrees can cause overfitting.
See [examples/linear\_model/plot\_polynomial\_interpolation.py](../../auto_examples/linear_model/plot_polynomial_interpolation#sphx-glr-auto-examples-linear-model-plot-polynomial-interpolation-py)
#### Examples
```
>>> import numpy as np
>>> from sklearn.preprocessing import PolynomialFeatures
>>> X = np.arange(6).reshape(3, 2)
>>> X
array([[0, 1],
[2, 3],
[4, 5]])
>>> poly = PolynomialFeatures(2)
>>> poly.fit_transform(X)
array([[ 1., 0., 1., 0., 0., 1.],
[ 1., 2., 3., 4., 6., 9.],
[ 1., 4., 5., 16., 20., 25.]])
>>> poly = PolynomialFeatures(interaction_only=True)
>>> poly.fit_transform(X)
array([[ 1., 0., 1., 0.],
[ 1., 2., 3., 6.],
[ 1., 4., 5., 20.]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.preprocessing.PolynomialFeatures.fit "sklearn.preprocessing.PolynomialFeatures.fit")(X[, y]) | Compute number of output features. |
| [`fit_transform`](#sklearn.preprocessing.PolynomialFeatures.fit_transform "sklearn.preprocessing.PolynomialFeatures.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names`](#sklearn.preprocessing.PolynomialFeatures.get_feature_names "sklearn.preprocessing.PolynomialFeatures.get_feature_names")([input\_features]) | DEPRECATED: get\_feature\_names is deprecated in 1.0 and will be removed in 1.2. |
| [`get_feature_names_out`](#sklearn.preprocessing.PolynomialFeatures.get_feature_names_out "sklearn.preprocessing.PolynomialFeatures.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.preprocessing.PolynomialFeatures.get_params "sklearn.preprocessing.PolynomialFeatures.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.preprocessing.PolynomialFeatures.set_params "sklearn.preprocessing.PolynomialFeatures.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.preprocessing.PolynomialFeatures.transform "sklearn.preprocessing.PolynomialFeatures.transform")(X) | Transform data to polynomial features. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_polynomial.py#L270)
Compute number of output features.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
**self**object
Fitted transformer.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_polynomial.py#L197)
DEPRECATED: get\_feature\_names is deprecated in 1.0 and will be removed in 1.2. Please use get\_feature\_names\_out instead.
Return feature names for output features.
Parameters:
**input\_features**list of str of shape (n\_features,), default=None
String names for input features if available. By default, “x0”, “x1”, … “xn\_features” is used.
Returns:
**output\_feature\_names**list of str of shape (n\_output\_features,)
Transformed feature names.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_polynomial.py#L233)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Input features.
* If `input_features is None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then the following input feature names are generated: `["x0", "x1", ..., "x(n_features_in_ - 1)"]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_input\_features\_
DEPRECATED: The attribute `n_input_features_` was deprecated in version 1.0 and will be removed in 1.2.
*property*powers\_
Exponent for each of the inputs in the output.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_polynomial.py#L349)
Transform data to polynomial features.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data to transform, row by row.
Prefer CSR over CSC for sparse input (for speed), but CSC is required if the degree is 4 or higher. If the degree is less than 4 and the input format is CSC, it will be converted to CSR, have its polynomial features generated, then converted back to CSC.
If the degree is 2 or 3, the method described in “Leveraging Sparsity to Speed Up Polynomial Feature Expansions of CSR Matrices Using K-Simplex Numbers” by Andrew Nystrom and John Hughes is used, which is much faster than the method used on CSC input. For this reason, a CSC input will be converted to CSR, and the output will be converted back to CSC prior to being returned, hence the preference of CSR.
Returns:
**XP**{ndarray, sparse matrix} of shape (n\_samples, NP)
The matrix of features, where `NP` is the number of polynomial features generated from the combination of inputs. If a sparse matrix is provided, it will be converted into a sparse `csr_matrix`.
Examples using `sklearn.preprocessing.PolynomialFeatures`
---------------------------------------------------------
[Release Highlights for scikit-learn 0.24](../../auto_examples/release_highlights/plot_release_highlights_0_24_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-24-0-py)
[Time-related feature engineering](../../auto_examples/applications/plot_cyclical_feature_engineering#sphx-glr-auto-examples-applications-plot-cyclical-feature-engineering-py)
[Comparing Linear Bayesian Regressors](../../auto_examples/linear_model/plot_ard#sphx-glr-auto-examples-linear-model-plot-ard-py)
[Poisson regression and non-normal loss](../../auto_examples/linear_model/plot_poisson_regression_non_normal_loss#sphx-glr-auto-examples-linear-model-plot-poisson-regression-non-normal-loss-py)
[Polynomial and Spline interpolation](../../auto_examples/linear_model/plot_polynomial_interpolation#sphx-glr-auto-examples-linear-model-plot-polynomial-interpolation-py)
[Robust linear estimator fitting](../../auto_examples/linear_model/plot_robust_fit#sphx-glr-auto-examples-linear-model-plot-robust-fit-py)
[Displaying Pipelines](../../auto_examples/miscellaneous/plot_pipeline_display#sphx-glr-auto-examples-miscellaneous-plot-pipeline-display-py)
[Underfitting vs. Overfitting](../../auto_examples/model_selection/plot_underfitting_overfitting#sphx-glr-auto-examples-model-selection-plot-underfitting-overfitting-py)
| programming_docs |
scikit_learn sklearn.metrics.DistanceMetric sklearn.metrics.DistanceMetric
==============================
*class*sklearn.metrics.DistanceMetric
DistanceMetric class
This class provides a uniform interface to fast distance metric functions. The various metrics can be accessed via the [`get_metric`](#sklearn.metrics.DistanceMetric.get_metric "sklearn.metrics.DistanceMetric.get_metric") class method and the metric string identifier (see below).
#### Examples
```
>>> from sklearn.metrics import DistanceMetric
>>> dist = DistanceMetric.get_metric('euclidean')
>>> X = [[0, 1, 2],
[3, 4, 5]]
>>> dist.pairwise(X)
array([[ 0. , 5.19615242],
[ 5.19615242, 0. ]])
```
Available Metrics
The following lists the string metric identifiers and the associated distance metric classes:
**Metrics intended for real-valued vector spaces:**
| | | | |
| --- | --- | --- | --- |
| identifier | class name | args | distance function |
| “euclidean” | EuclideanDistance | *
| `sqrt(sum((x - y)^2))` |
| “manhattan” | ManhattanDistance | *
| `sum(|x - y|)` |
| “chebyshev” | ChebyshevDistance | *
| `max(|x - y|)` |
| “minkowski” | MinkowskiDistance | p, w | `sum(w * |x - y|^p)^(1/p)` |
| “wminkowski” | WMinkowskiDistance | p, w | `sum(|w * (x - y)|^p)^(1/p)` |
| “seuclidean” | SEuclideanDistance | V | `sqrt(sum((x - y)^2 / V))` |
| “mahalanobis” | MahalanobisDistance | V or VI | `sqrt((x - y)' V^-1 (x - y))` |
Deprecated since version 1.1: `WMinkowskiDistance` is deprecated in version 1.1 and will be removed in version 1.3. Use `MinkowskiDistance` instead. Note that in `MinkowskiDistance`, the weights are applied to the absolute differences already raised to the p power. This is different from `WMinkowskiDistance` where weights are applied to the absolute differences before raising to the p power. The deprecation aims to remain consistent with SciPy 1.8 convention.
**Metrics intended for two-dimensional vector spaces:** Note that the haversine distance metric requires data in the form of [latitude, longitude] and both inputs and outputs are in units of radians.
| | | |
| --- | --- | --- |
| identifier | class name | distance function |
| “haversine” | HaversineDistance | `2 arcsin(sqrt(sin^2(0.5*dx) + cos(x1)cos(x2)sin^2(0.5*dy)))` |
**Metrics intended for integer-valued vector spaces:** Though intended for integer-valued vectors, these are also valid metrics in the case of real-valued vectors.
| | | |
| --- | --- | --- |
| identifier | class name | distance function |
| “hamming” | HammingDistance | `N_unequal(x, y) / N_tot` |
| “canberra” | CanberraDistance | `sum(|x - y| / (|x| + |y|))` |
| “braycurtis” | BrayCurtisDistance | `sum(|x - y|) / (sum(|x|) + sum(|y|))` |
**Metrics intended for boolean-valued vector spaces:** Any nonzero entry is evaluated to “True”. In the listings below, the following abbreviations are used:
* N : number of dimensions
* NTT : number of dims in which both values are True
* NTF : number of dims in which the first value is True, second is False
* NFT : number of dims in which the first value is False, second is True
* NFF : number of dims in which both values are False
* NNEQ : number of non-equal dimensions, NNEQ = NTF + NFT
* NNZ : number of nonzero dimensions, NNZ = NTF + NFT + NTT
| | | |
| --- | --- | --- |
| identifier | class name | distance function |
| “jaccard” | JaccardDistance | NNEQ / NNZ |
| “matching” | MatchingDistance | NNEQ / N |
| “dice” | DiceDistance | NNEQ / (NTT + NNZ) |
| “kulsinski” | KulsinskiDistance | (NNEQ + N - NTT) / (NNEQ + N) |
| “rogerstanimoto” | RogersTanimotoDistance | 2 \* NNEQ / (N + NNEQ) |
| “russellrao” | RussellRaoDistance | (N - NTT) / N |
| “sokalmichener” | SokalMichenerDistance | 2 \* NNEQ / (N + NNEQ) |
| “sokalsneath” | SokalSneathDistance | NNEQ / (NNEQ + 0.5 \* NTT) |
**User-defined distance:**
| | | |
| --- | --- | --- |
| identifier | class name | args |
| “pyfunc” | PyFuncDistance | func |
Here `func` is a function which takes two one-dimensional numpy arrays, and returns a distance. Note that in order to be used within the BallTree, the distance must be a true metric: i.e. it must satisfy the following properties
1. Non-negativity: d(x, y) >= 0
2. Identity: d(x, y) = 0 if and only if x == y
3. Symmetry: d(x, y) = d(y, x)
4. Triangle Inequality: d(x, y) + d(y, z) >= d(x, z)
Because of the Python object overhead involved in calling the python function, this will be fairly slow, but it will have the same scaling as other distances.
#### Methods
| | |
| --- | --- |
| [`dist_to_rdist`](#sklearn.metrics.DistanceMetric.dist_to_rdist "sklearn.metrics.DistanceMetric.dist_to_rdist") | Convert the true distance to the rank-preserving surrogate distance. |
| [`get_metric`](#sklearn.metrics.DistanceMetric.get_metric "sklearn.metrics.DistanceMetric.get_metric") | Get the given distance metric from the string identifier. |
| [`pairwise`](#sklearn.metrics.DistanceMetric.pairwise "sklearn.metrics.DistanceMetric.pairwise") | Compute the pairwise distances between X and Y |
| [`rdist_to_dist`](#sklearn.metrics.DistanceMetric.rdist_to_dist "sklearn.metrics.DistanceMetric.rdist_to_dist") | Convert the rank-preserving surrogate distance to the distance. |
dist\_to\_rdist()
Convert the true distance to the rank-preserving surrogate distance.
The surrogate distance is any measure that yields the same rank as the distance, but is more efficient to compute. For example, the rank-preserving surrogate distance of the Euclidean metric is the squared-euclidean distance.
Parameters:
**dist**double
True distance.
Returns:
double
Surrogate distance.
get\_metric()
Get the given distance metric from the string identifier.
See the docstring of DistanceMetric for a list of available metrics.
Parameters:
**metric**str or class name
The distance metric to use
**\*\*kwargs**
additional arguments will be passed to the requested metric
pairwise()
Compute the pairwise distances between X and Y
This is a convenience routine for the sake of testing. For many metrics, the utilities in scipy.spatial.distance.cdist and scipy.spatial.distance.pdist will be faster.
Parameters:
**X**array-like
Array of shape (Nx, D), representing Nx points in D dimensions.
**Y**array-like (optional)
Array of shape (Ny, D), representing Ny points in D dimensions. If not specified, then Y=X.
Returns:
**dist**ndarray
The shape (Nx, Ny) array of pairwise distances between points in X and Y.
rdist\_to\_dist()
Convert the rank-preserving surrogate distance to the distance.
The surrogate distance is any measure that yields the same rank as the distance, but is more efficient to compute. For example, the rank-preserving surrogate distance of the Euclidean metric is the squared-euclidean distance.
Parameters:
**rdist**double
Surrogate distance.
Returns:
double
True distance.
scikit_learn sklearn.multioutput.ClassifierChain sklearn.multioutput.ClassifierChain
===================================
*class*sklearn.multioutput.ClassifierChain(*base\_estimator*, *\**, *order=None*, *cv=None*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/multioutput.py#L641)
A multi-label model that arranges binary classifiers into a chain.
Each model makes a prediction in the order specified by the chain using all of the available features provided to the model plus the predictions of models that are earlier in the chain.
Read more in the [User Guide](../multiclass#classifierchain).
New in version 0.19.
Parameters:
**base\_estimator**estimator
The base estimator from which the classifier chain is built.
**order**array-like of shape (n\_outputs,) or ‘random’, default=None
If `None`, the order will be determined by the order of columns in the label matrix Y.:
```
order = [0, 1, 2, ..., Y.shape[1] - 1]
```
The order of the chain can be explicitly set by providing a list of integers. For example, for a chain of length 5.:
```
order = [1, 3, 2, 4, 0]
```
means that the first model in the chain will make predictions for column 1 in the Y matrix, the second model will make predictions for column 3, etc.
If order is `random` a random ordering will be used.
**cv**int, cross-validation generator or an iterable, default=None
Determines whether to use cross validated predictions or true labels for the results of previous estimators in the chain. Possible inputs for cv are:
* None, to use true labels when fitting,
* integer, to specify the number of folds in a (Stratified)KFold,
* [CV splitter](https://scikit-learn.org/1.1/glossary.html#term-CV-splitter),
* An iterable yielding (train, test) splits as arrays of indices.
**random\_state**int, RandomState instance or None, optional (default=None)
If `order='random'`, determines random number generation for the chain order. In addition, it controls the random seed given at each `base_estimator` at each chaining iteration. Thus, it is only used when `base_estimator` exposes a `random_state`. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Attributes:
**classes\_**list
A list of arrays of length `len(estimators_)` containing the class labels for each estimator in the chain.
**estimators\_**list
A list of clones of base\_estimator.
**order\_**list
The order of labels in the classifier chain.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Only defined if the underlying `base_estimator` exposes such an attribute when fit.
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`RegressorChain`](sklearn.multioutput.regressorchain#sklearn.multioutput.RegressorChain "sklearn.multioutput.RegressorChain")
Equivalent for regression.
`MultioutputClassifier`
Classifies each output independently rather than chaining.
#### References
Jesse Read, Bernhard Pfahringer, Geoff Holmes, Eibe Frank, “Classifier Chains for Multi-label Classification”, 2009.
#### Examples
```
>>> from sklearn.datasets import make_multilabel_classification
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.multioutput import ClassifierChain
>>> X, Y = make_multilabel_classification(
... n_samples=12, n_classes=3, random_state=0
... )
>>> X_train, X_test, Y_train, Y_test = train_test_split(
... X, Y, random_state=0
... )
>>> base_lr = LogisticRegression(solver='lbfgs', random_state=0)
>>> chain = ClassifierChain(base_lr, order='random', random_state=0)
>>> chain.fit(X_train, Y_train).predict(X_test)
array([[1., 1., 0.],
[1., 0., 0.],
[0., 1., 0.]])
>>> chain.predict_proba(X_test)
array([[0.8387..., 0.9431..., 0.4576...],
[0.8878..., 0.3684..., 0.2640...],
[0.0321..., 0.9935..., 0.0625...]])
```
#### Methods
| | |
| --- | --- |
| [`decision_function`](#sklearn.multioutput.ClassifierChain.decision_function "sklearn.multioutput.ClassifierChain.decision_function")(X) | Evaluate the decision\_function of the models in the chain. |
| [`fit`](#sklearn.multioutput.ClassifierChain.fit "sklearn.multioutput.ClassifierChain.fit")(X, Y) | Fit the model to data matrix X and targets Y. |
| [`get_params`](#sklearn.multioutput.ClassifierChain.get_params "sklearn.multioutput.ClassifierChain.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.multioutput.ClassifierChain.predict "sklearn.multioutput.ClassifierChain.predict")(X) | Predict on the data matrix X using the ClassifierChain model. |
| [`predict_proba`](#sklearn.multioutput.ClassifierChain.predict_proba "sklearn.multioutput.ClassifierChain.predict_proba")(X) | Predict probability estimates. |
| [`score`](#sklearn.multioutput.ClassifierChain.score "sklearn.multioutput.ClassifierChain.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.multioutput.ClassifierChain.set_params "sklearn.multioutput.ClassifierChain.set_params")(\*\*params) | Set the parameters of this estimator. |
decision\_function(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/multioutput.py#L805)
Evaluate the decision\_function of the models in the chain.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The input data.
Returns:
**Y\_decision**array-like of shape (n\_samples, n\_classes)
Returns the decision function of the sample for each model in the chain.
fit(*X*, *Y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/multioutput.py#L752)
Fit the model to data matrix X and targets Y.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input data.
**Y**array-like of shape (n\_samples, n\_classes)
The target values.
Returns:
**self**object
Class instance.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/multioutput.py#L607)
Predict on the data matrix X using the ClassifierChain model.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input data.
Returns:
**Y\_pred**array-like of shape (n\_samples, n\_classes)
The predicted values.
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/multioutput.py#L774)
Predict probability estimates.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input data.
Returns:
**Y\_prob**array-like of shape (n\_samples, n\_classes)
The predicted probabilities.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.multioutput.ClassifierChain`
----------------------------------------------------
[Classifier Chain](../../auto_examples/multioutput/plot_classifier_chain_yeast#sphx-glr-auto-examples-multioutput-plot-classifier-chain-yeast-py)
scikit_learn sklearn.decomposition.DictionaryLearning sklearn.decomposition.DictionaryLearning
========================================
*class*sklearn.decomposition.DictionaryLearning(*n\_components=None*, *\**, *alpha=1*, *max\_iter=1000*, *tol=1e-08*, *fit\_algorithm='lars'*, *transform\_algorithm='omp'*, *transform\_n\_nonzero\_coefs=None*, *transform\_alpha=None*, *n\_jobs=None*, *code\_init=None*, *dict\_init=None*, *verbose=False*, *split\_sign=False*, *random\_state=None*, *positive\_code=False*, *positive\_dict=False*, *transform\_max\_iter=1000*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_dict_learning.py#L1448)
Dictionary learning.
Finds a dictionary (a set of atoms) that performs well at sparsely encoding the fitted data.
Solves the optimization problem:
```
(U^*,V^*) = argmin 0.5 || X - U V ||_Fro^2 + alpha * || U ||_1,1
(U,V)
with || V_k ||_2 <= 1 for all 0 <= k < n_components
```
||.||\_Fro stands for the Frobenius norm and ||.||\_1,1 stands for the entry-wise matrix norm which is the sum of the absolute values of all the entries in the matrix.
Read more in the [User Guide](../decomposition#dictionarylearning).
Parameters:
**n\_components**int, default=None
Number of dictionary elements to extract. If None, then `n_components` is set to `n_features`.
**alpha**float, default=1.0
Sparsity controlling parameter.
**max\_iter**int, default=1000
Maximum number of iterations to perform.
**tol**float, default=1e-8
Tolerance for numerical error.
**fit\_algorithm**{‘lars’, ‘cd’}, default=’lars’
* `'lars'`: uses the least angle regression method to solve the lasso problem ([`lars_path`](sklearn.linear_model.lars_path#sklearn.linear_model.lars_path "sklearn.linear_model.lars_path"));
* `'cd'`: uses the coordinate descent method to compute the Lasso solution ([`Lasso`](sklearn.linear_model.lasso#sklearn.linear_model.Lasso "sklearn.linear_model.Lasso")). Lars will be faster if the estimated components are sparse.
New in version 0.17: *cd* coordinate descent method to improve speed.
**transform\_algorithm**{‘lasso\_lars’, ‘lasso\_cd’, ‘lars’, ‘omp’, ‘threshold’}, default=’omp’
Algorithm used to transform the data:
* `'lars'`: uses the least angle regression method ([`lars_path`](sklearn.linear_model.lars_path#sklearn.linear_model.lars_path "sklearn.linear_model.lars_path"));
* `'lasso_lars'`: uses Lars to compute the Lasso solution.
* `'lasso_cd'`: uses the coordinate descent method to compute the Lasso solution ([`Lasso`](sklearn.linear_model.lasso#sklearn.linear_model.Lasso "sklearn.linear_model.Lasso")). `'lasso_lars'` will be faster if the estimated components are sparse.
* `'omp'`: uses orthogonal matching pursuit to estimate the sparse solution.
* `'threshold'`: squashes to zero all coefficients less than alpha from the projection `dictionary * X'`.
New in version 0.17: *lasso\_cd* coordinate descent method to improve speed.
**transform\_n\_nonzero\_coefs**int, default=None
Number of nonzero coefficients to target in each column of the solution. This is only used by `algorithm='lars'` and `algorithm='omp'`. If `None`, then `transform_n_nonzero_coefs=int(n_features / 10)`.
**transform\_alpha**float, default=None
If `algorithm='lasso_lars'` or `algorithm='lasso_cd'`, `alpha` is the penalty applied to the L1 norm. If `algorithm='threshold'`, `alpha` is the absolute value of the threshold below which coefficients will be squashed to zero. If `None`, defaults to `alpha`.
**n\_jobs**int or None, default=None
Number of parallel jobs to run. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**code\_init**ndarray of shape (n\_samples, n\_components), default=None
Initial value for the code, for warm restart. Only used if `code_init` and `dict_init` are not None.
**dict\_init**ndarray of shape (n\_components, n\_features), default=None
Initial values for the dictionary, for warm restart. Only used if `code_init` and `dict_init` are not None.
**verbose**bool, default=False
To control the verbosity of the procedure.
**split\_sign**bool, default=False
Whether to split the sparse feature vector into the concatenation of its negative part and its positive part. This can improve the performance of downstream classifiers.
**random\_state**int, RandomState instance or None, default=None
Used for initializing the dictionary when `dict_init` is not specified, randomly shuffling the data when `shuffle` is set to `True`, and updating the dictionary. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**positive\_code**bool, default=False
Whether to enforce positivity when finding the code.
New in version 0.20.
**positive\_dict**bool, default=False
Whether to enforce positivity when finding the dictionary.
New in version 0.20.
**transform\_max\_iter**int, default=1000
Maximum number of iterations to perform if `algorithm='lasso_cd'` or `'lasso_lars'`.
New in version 0.22.
Attributes:
**components\_**ndarray of shape (n\_components, n\_features)
dictionary atoms extracted from the data
**error\_**array
vector of errors at each iteration
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_iter\_**int
Number of iterations run.
See also
[`MiniBatchDictionaryLearning`](sklearn.decomposition.minibatchdictionarylearning#sklearn.decomposition.MiniBatchDictionaryLearning "sklearn.decomposition.MiniBatchDictionaryLearning")
A faster, less accurate, version of the dictionary learning algorithm.
[`MiniBatchSparsePCA`](sklearn.decomposition.minibatchsparsepca#sklearn.decomposition.MiniBatchSparsePCA "sklearn.decomposition.MiniBatchSparsePCA")
Mini-batch Sparse Principal Components Analysis.
[`SparseCoder`](sklearn.decomposition.sparsecoder#sklearn.decomposition.SparseCoder "sklearn.decomposition.SparseCoder")
Find a sparse representation of data from a fixed, precomputed dictionary.
[`SparsePCA`](sklearn.decomposition.sparsepca#sklearn.decomposition.SparsePCA "sklearn.decomposition.SparsePCA")
Sparse Principal Components Analysis.
#### References
J. Mairal, F. Bach, J. Ponce, G. Sapiro, 2009: Online dictionary learning for sparse coding (<https://www.di.ens.fr/sierra/pdfs/icml09.pdf>)
#### Examples
```
>>> import numpy as np
>>> from sklearn.datasets import make_sparse_coded_signal
>>> from sklearn.decomposition import DictionaryLearning
>>> X, dictionary, code = make_sparse_coded_signal(
... n_samples=100, n_components=15, n_features=20, n_nonzero_coefs=10,
... random_state=42, data_transposed=False
... )
>>> dict_learner = DictionaryLearning(
... n_components=15, transform_algorithm='lasso_lars', transform_alpha=0.1,
... random_state=42,
... )
>>> X_transformed = dict_learner.fit_transform(X)
```
We can check the level of sparsity of `X_transformed`:
```
>>> np.mean(X_transformed == 0)
0.41...
```
We can compare the average squared euclidean norm of the reconstruction error of the sparse coded signal relative to the squared euclidean norm of the original signal:
```
>>> X_hat = X_transformed @ dict_learner.components_
>>> np.mean(np.sum((X_hat - X) ** 2, axis=1) / np.sum(X ** 2, axis=1))
0.07...
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.decomposition.DictionaryLearning.fit "sklearn.decomposition.DictionaryLearning.fit")(X[, y]) | Fit the model from data in X. |
| [`fit_transform`](#sklearn.decomposition.DictionaryLearning.fit_transform "sklearn.decomposition.DictionaryLearning.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.decomposition.DictionaryLearning.get_feature_names_out "sklearn.decomposition.DictionaryLearning.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.decomposition.DictionaryLearning.get_params "sklearn.decomposition.DictionaryLearning.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.decomposition.DictionaryLearning.set_params "sklearn.decomposition.DictionaryLearning.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.decomposition.DictionaryLearning.transform "sklearn.decomposition.DictionaryLearning.transform")(X) | Encode the data as a sparse combination of the dictionary atoms. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_dict_learning.py#L1675)
Fit the model from data in X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training vector, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.decomposition.DictionaryLearning.fit "sklearn.decomposition.DictionaryLearning.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_dict_learning.py#L1217)
Encode the data as a sparse combination of the dictionary atoms.
Coding method is determined by the object parameter `transform_algorithm`.
Parameters:
**X**ndarray of shape (n\_samples, n\_features)
Test data to be transformed, must have the same number of features as the data used to train the model.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_components)
Transformed data.
| programming_docs |
scikit_learn sklearn.compose.TransformedTargetRegressor sklearn.compose.TransformedTargetRegressor
==========================================
*class*sklearn.compose.TransformedTargetRegressor(*regressor=None*, *\**, *transformer=None*, *func=None*, *inverse\_func=None*, *check\_inverse=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/compose/_target.py#L19)
Meta-estimator to regress on a transformed target.
Useful for applying a non-linear transformation to the target `y` in regression problems. This transformation can be given as a Transformer such as the [`QuantileTransformer`](sklearn.preprocessing.quantiletransformer#sklearn.preprocessing.QuantileTransformer "sklearn.preprocessing.QuantileTransformer") or as a function and its inverse such as `np.log` and `np.exp`.
The computation during [`fit`](#sklearn.compose.TransformedTargetRegressor.fit "sklearn.compose.TransformedTargetRegressor.fit") is:
```
regressor.fit(X, func(y))
```
or:
```
regressor.fit(X, transformer.transform(y))
```
The computation during [`predict`](#sklearn.compose.TransformedTargetRegressor.predict "sklearn.compose.TransformedTargetRegressor.predict") is:
```
inverse_func(regressor.predict(X))
```
or:
```
transformer.inverse_transform(regressor.predict(X))
```
Read more in the [User Guide](../compose#transformed-target-regressor).
New in version 0.20.
Parameters:
**regressor**object, default=None
Regressor object such as derived from [`RegressorMixin`](sklearn.base.regressormixin#sklearn.base.RegressorMixin "sklearn.base.RegressorMixin"). This regressor will automatically be cloned each time prior to fitting. If `regressor is
None`, [`LinearRegression`](sklearn.linear_model.linearregression#sklearn.linear_model.LinearRegression "sklearn.linear_model.LinearRegression") is created and used.
**transformer**object, default=None
Estimator object such as derived from [`TransformerMixin`](sklearn.base.transformermixin#sklearn.base.TransformerMixin "sklearn.base.TransformerMixin"). Cannot be set at the same time as `func` and `inverse_func`. If `transformer is None` as well as `func` and `inverse_func`, the transformer will be an identity transformer. Note that the transformer will be cloned during fitting. Also, the transformer is restricting `y` to be a numpy array.
**func**function, default=None
Function to apply to `y` before passing to [`fit`](#sklearn.compose.TransformedTargetRegressor.fit "sklearn.compose.TransformedTargetRegressor.fit"). Cannot be set at the same time as `transformer`. The function needs to return a 2-dimensional array. If `func is None`, the function used will be the identity function.
**inverse\_func**function, default=None
Function to apply to the prediction of the regressor. Cannot be set at the same time as `transformer`. The function needs to return a 2-dimensional array. The inverse function is used to return predictions to the same space of the original training labels.
**check\_inverse**bool, default=True
Whether to check that `transform` followed by `inverse_transform` or `func` followed by `inverse_func` leads to the original targets.
Attributes:
**regressor\_**object
Fitted regressor.
**transformer\_**object
Transformer used in [`fit`](#sklearn.compose.TransformedTargetRegressor.fit "sklearn.compose.TransformedTargetRegressor.fit") and [`predict`](#sklearn.compose.TransformedTargetRegressor.predict "sklearn.compose.TransformedTargetRegressor.predict").
[`n_features_in_`](#sklearn.compose.TransformedTargetRegressor.n_features_in_ "sklearn.compose.TransformedTargetRegressor.n_features_in_")int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`sklearn.preprocessing.FunctionTransformer`](sklearn.preprocessing.functiontransformer#sklearn.preprocessing.FunctionTransformer "sklearn.preprocessing.FunctionTransformer")
Construct a transformer from an arbitrary callable.
#### Notes
Internally, the target `y` is always converted into a 2-dimensional array to be used by scikit-learn transformers. At the time of prediction, the output will be reshaped to a have the same number of dimensions as `y`.
See [examples/compose/plot\_transformed\_target.py](../../auto_examples/compose/plot_transformed_target#sphx-glr-auto-examples-compose-plot-transformed-target-py).
#### Examples
```
>>> import numpy as np
>>> from sklearn.linear_model import LinearRegression
>>> from sklearn.compose import TransformedTargetRegressor
>>> tt = TransformedTargetRegressor(regressor=LinearRegression(),
... func=np.log, inverse_func=np.exp)
>>> X = np.arange(4).reshape(-1, 1)
>>> y = np.exp(2 * X).ravel()
>>> tt.fit(X, y)
TransformedTargetRegressor(...)
>>> tt.score(X, y)
1.0
>>> tt.regressor_.coef_
array([2.])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.compose.TransformedTargetRegressor.fit "sklearn.compose.TransformedTargetRegressor.fit")(X, y, \*\*fit\_params) | Fit the model according to the given training data. |
| [`get_params`](#sklearn.compose.TransformedTargetRegressor.get_params "sklearn.compose.TransformedTargetRegressor.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.compose.TransformedTargetRegressor.predict "sklearn.compose.TransformedTargetRegressor.predict")(X, \*\*predict\_params) | Predict using the base regressor, applying inverse. |
| [`score`](#sklearn.compose.TransformedTargetRegressor.score "sklearn.compose.TransformedTargetRegressor.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.compose.TransformedTargetRegressor.set_params "sklearn.compose.TransformedTargetRegressor.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/compose/_target.py#L189)
Fit the model according to the given training data.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vector, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,)
Target values.
**\*\*fit\_params**dict
Parameters passed to the `fit` method of the underlying regressor.
Returns:
**self**object
Fitted estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_features\_in\_
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
predict(*X*, *\*\*predict\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/compose/_target.py#L259)
Predict using the base regressor, applying inverse.
The regressor is used to predict and the `inverse_func` or `inverse_transform` is applied before returning the prediction.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Samples.
**\*\*predict\_params**dict of str -> object
Parameters passed to the `predict` method of the underlying regressor.
Returns:
**y\_hat**ndarray of shape (n\_samples,)
Predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.compose.TransformedTargetRegressor`
-----------------------------------------------------------
[Poisson regression and non-normal loss](../../auto_examples/linear_model/plot_poisson_regression_non_normal_loss#sphx-glr-auto-examples-linear-model-plot-poisson-regression-non-normal-loss-py)
[Common pitfalls in the interpretation of coefficients of linear models](../../auto_examples/inspection/plot_linear_model_coefficient_interpretation#sphx-glr-auto-examples-inspection-plot-linear-model-coefficient-interpretation-py)
[Effect of transforming the targets in regression model](../../auto_examples/compose/plot_transformed_target#sphx-glr-auto-examples-compose-plot-transformed-target-py)
scikit_learn sklearn.decomposition.FactorAnalysis sklearn.decomposition.FactorAnalysis
====================================
*class*sklearn.decomposition.FactorAnalysis(*n\_components=None*, *\**, *tol=0.01*, *copy=True*, *max\_iter=1000*, *noise\_variance\_init=None*, *svd\_method='randomized'*, *iterated\_power=3*, *rotation=None*, *random\_state=0*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_factor_analysis.py#L35)
Factor Analysis (FA).
A simple linear generative model with Gaussian latent variables.
The observations are assumed to be caused by a linear transformation of lower dimensional latent factors and added Gaussian noise. Without loss of generality the factors are distributed according to a Gaussian with zero mean and unit covariance. The noise is also zero mean and has an arbitrary diagonal covariance matrix.
If we would restrict the model further, by assuming that the Gaussian noise is even isotropic (all diagonal entries are the same) we would obtain [`PCA`](sklearn.decomposition.pca#sklearn.decomposition.PCA "sklearn.decomposition.PCA").
FactorAnalysis performs a maximum likelihood estimate of the so-called `loading` matrix, the transformation of the latent variables to the observed ones, using SVD based approach.
Read more in the [User Guide](../decomposition#fa).
New in version 0.13.
Parameters:
**n\_components**int, default=None
Dimensionality of latent space, the number of components of `X` that are obtained after `transform`. If None, n\_components is set to the number of features.
**tol**float, default=1e-2
Stopping tolerance for log-likelihood increase.
**copy**bool, default=True
Whether to make a copy of X. If `False`, the input X gets overwritten during fitting.
**max\_iter**int, default=1000
Maximum number of iterations.
**noise\_variance\_init**ndarray of shape (n\_features,), default=None
The initial guess of the noise variance for each feature. If None, it defaults to np.ones(n\_features).
**svd\_method**{‘lapack’, ‘randomized’}, default=’randomized’
Which SVD method to use. If ‘lapack’ use standard SVD from scipy.linalg, if ‘randomized’ use fast `randomized_svd` function. Defaults to ‘randomized’. For most applications ‘randomized’ will be sufficiently precise while providing significant speed gains. Accuracy can also be improved by setting higher values for `iterated_power`. If this is not sufficient, for maximum precision you should choose ‘lapack’.
**iterated\_power**int, default=3
Number of iterations for the power method. 3 by default. Only used if `svd_method` equals ‘randomized’.
**rotation**{‘varimax’, ‘quartimax’}, default=None
If not None, apply the indicated rotation. Currently, varimax and quartimax are implemented. See [“The varimax criterion for analytic rotation in factor analysis”](https://link.springer.com/article/10.1007%2FBF02289233) H. F. Kaiser, 1958.
New in version 0.24.
**random\_state**int or RandomState instance, default=0
Only used when `svd_method` equals ‘randomized’. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Attributes:
**components\_**ndarray of shape (n\_components, n\_features)
Components with maximum variance.
**loglike\_**list of shape (n\_iterations,)
The log likelihood at each iteration.
**noise\_variance\_**ndarray of shape (n\_features,)
The estimated noise variance for each feature.
**n\_iter\_**int
Number of iterations run.
**mean\_**ndarray of shape (n\_features,)
Per-feature empirical mean, estimated from the training set.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`PCA`](sklearn.decomposition.pca#sklearn.decomposition.PCA "sklearn.decomposition.PCA")
Principal component analysis is also a latent linear variable model which however assumes equal noise variance for each feature. This extra assumption makes probabilistic PCA faster as it can be computed in closed form.
[`FastICA`](sklearn.decomposition.fastica#sklearn.decomposition.FastICA "sklearn.decomposition.FastICA")
Independent component analysis, a latent variable model with non-Gaussian latent variables.
#### References
* David Barber, Bayesian Reasoning and Machine Learning, Algorithm 21.1.
* Christopher M. Bishop: Pattern Recognition and Machine Learning, Chapter 12.2.4.
#### Examples
```
>>> from sklearn.datasets import load_digits
>>> from sklearn.decomposition import FactorAnalysis
>>> X, _ = load_digits(return_X_y=True)
>>> transformer = FactorAnalysis(n_components=7, random_state=0)
>>> X_transformed = transformer.fit_transform(X)
>>> X_transformed.shape
(1797, 7)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.decomposition.FactorAnalysis.fit "sklearn.decomposition.FactorAnalysis.fit")(X[, y]) | Fit the FactorAnalysis model to X using SVD based approach. |
| [`fit_transform`](#sklearn.decomposition.FactorAnalysis.fit_transform "sklearn.decomposition.FactorAnalysis.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_covariance`](#sklearn.decomposition.FactorAnalysis.get_covariance "sklearn.decomposition.FactorAnalysis.get_covariance")() | Compute data covariance with the FactorAnalysis model. |
| [`get_feature_names_out`](#sklearn.decomposition.FactorAnalysis.get_feature_names_out "sklearn.decomposition.FactorAnalysis.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.decomposition.FactorAnalysis.get_params "sklearn.decomposition.FactorAnalysis.get_params")([deep]) | Get parameters for this estimator. |
| [`get_precision`](#sklearn.decomposition.FactorAnalysis.get_precision "sklearn.decomposition.FactorAnalysis.get_precision")() | Compute data precision matrix with the FactorAnalysis model. |
| [`score`](#sklearn.decomposition.FactorAnalysis.score "sklearn.decomposition.FactorAnalysis.score")(X[, y]) | Compute the average log-likelihood of the samples. |
| [`score_samples`](#sklearn.decomposition.FactorAnalysis.score_samples "sklearn.decomposition.FactorAnalysis.score_samples")(X) | Compute the log-likelihood of each sample. |
| [`set_params`](#sklearn.decomposition.FactorAnalysis.set_params "sklearn.decomposition.FactorAnalysis.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.decomposition.FactorAnalysis.transform "sklearn.decomposition.FactorAnalysis.transform")(X) | Apply dimensionality reduction to X using the model. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_factor_analysis.py#L186)
Fit the FactorAnalysis model to X using SVD based approach.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data.
**y**Ignored
Ignored parameter.
Returns:
**self**object
FactorAnalysis class instance.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_covariance()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_factor_analysis.py#L335)
Compute data covariance with the FactorAnalysis model.
`cov = components_.T * components_ + diag(noise_variance)`
Returns:
**cov**ndarray of shape (n\_features, n\_features)
Estimated covariance of data.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.decomposition.FactorAnalysis.fit "sklearn.decomposition.FactorAnalysis.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
get\_precision()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_factor_analysis.py#L351)
Compute data precision matrix with the FactorAnalysis model.
Returns:
**precision**ndarray of shape (n\_features, n\_features)
Estimated precision of data.
score(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_factor_analysis.py#L401)
Compute the average log-likelihood of the samples.
Parameters:
**X**ndarray of shape (n\_samples, n\_features)
The data.
**y**Ignored
Ignored parameter.
Returns:
**ll**float
Average log-likelihood of the samples under the current model.
score\_samples(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_factor_analysis.py#L379)
Compute the log-likelihood of each sample.
Parameters:
**X**ndarray of shape (n\_samples, n\_features)
The data.
Returns:
**ll**ndarray of shape (n\_samples,)
Log-likelihood of each sample under the current model.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_factor_analysis.py#L305)
Apply dimensionality reduction to X using the model.
Compute the expected mean of the latent variables. See Barber, 21.2.33 (or Bishop, 12.66).
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_components)
The latent variables of X.
Examples using `sklearn.decomposition.FactorAnalysis`
-----------------------------------------------------
[Faces dataset decompositions](../../auto_examples/decomposition/plot_faces_decomposition#sphx-glr-auto-examples-decomposition-plot-faces-decomposition-py)
[Factor Analysis (with rotation) to visualize patterns](../../auto_examples/decomposition/plot_varimax_fa#sphx-glr-auto-examples-decomposition-plot-varimax-fa-py)
[Model selection with Probabilistic PCA and Factor Analysis (FA)](../../auto_examples/decomposition/plot_pca_vs_fa_model_selection#sphx-glr-auto-examples-decomposition-plot-pca-vs-fa-model-selection-py)
| programming_docs |
scikit_learn sklearn.cluster.SpectralBiclustering sklearn.cluster.SpectralBiclustering
====================================
*class*sklearn.cluster.SpectralBiclustering(*n\_clusters=3*, *\**, *method='bistochastic'*, *n\_components=6*, *n\_best=3*, *svd\_method='randomized'*, *n\_svd\_vecs=None*, *mini\_batch=False*, *init='k-means++'*, *n\_init=10*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_bicluster.py#L362)
Spectral biclustering (Kluger, 2003).
Partitions rows and columns under the assumption that the data has an underlying checkerboard structure. For instance, if there are two row partitions and three column partitions, each row will belong to three biclusters, and each column will belong to two biclusters. The outer product of the corresponding row and column label vectors gives this checkerboard structure.
Read more in the [User Guide](../biclustering#spectral-biclustering).
Parameters:
**n\_clusters**int or tuple (n\_row\_clusters, n\_column\_clusters), default=3
The number of row and column clusters in the checkerboard structure.
**method**{‘bistochastic’, ‘scale’, ‘log’}, default=’bistochastic’
Method of normalizing and converting singular vectors into biclusters. May be one of ‘scale’, ‘bistochastic’, or ‘log’. The authors recommend using ‘log’. If the data is sparse, however, log normalization will not work, which is why the default is ‘bistochastic’.
Warning
if `method='log'`, the data must not be sparse.
**n\_components**int, default=6
Number of singular vectors to check.
**n\_best**int, default=3
Number of best singular vectors to which to project the data for clustering.
**svd\_method**{‘randomized’, ‘arpack’}, default=’randomized’
Selects the algorithm for finding singular vectors. May be ‘randomized’ or ‘arpack’. If ‘randomized’, uses [`randomized_svd`](sklearn.utils.extmath.randomized_svd#sklearn.utils.extmath.randomized_svd "sklearn.utils.extmath.randomized_svd"), which may be faster for large matrices. If ‘arpack’, uses `scipy.sparse.linalg.svds`, which is more accurate, but possibly slower in some cases.
**n\_svd\_vecs**int, default=None
Number of vectors to use in calculating the SVD. Corresponds to `ncv` when `svd_method=arpack` and `n_oversamples` when `svd_method` is ‘randomized`.
**mini\_batch**bool, default=False
Whether to use mini-batch k-means, which is faster but may get different results.
**init**{‘k-means++’, ‘random’} or ndarray of (n\_clusters, n\_features), default=’k-means++’
Method for initialization of k-means algorithm; defaults to ‘k-means++’.
**n\_init**int, default=10
Number of random initializations that are tried with the k-means algorithm.
If mini-batch k-means is used, the best initialization is chosen and the algorithm runs once. Otherwise, the algorithm is run for each initialization and the best solution chosen.
**random\_state**int, RandomState instance, default=None
Used for randomizing the singular value decomposition and the k-means initialization. Use an int to make the randomness deterministic. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Attributes:
**rows\_**array-like of shape (n\_row\_clusters, n\_rows)
Results of the clustering. `rows[i, r]` is True if cluster `i` contains row `r`. Available only after calling `fit`.
**columns\_**array-like of shape (n\_column\_clusters, n\_columns)
Results of the clustering, like `rows`.
**row\_labels\_**array-like of shape (n\_rows,)
Row partition labels.
**column\_labels\_**array-like of shape (n\_cols,)
Column partition labels.
[`biclusters_`](#sklearn.cluster.SpectralBiclustering.biclusters_ "sklearn.cluster.SpectralBiclustering.biclusters_")tuple of two ndarrays
Convenient way to get row and column indicators together.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`SpectralCoclustering`](sklearn.cluster.spectralcoclustering#sklearn.cluster.SpectralCoclustering "sklearn.cluster.SpectralCoclustering")
Spectral Co-Clustering algorithm (Dhillon, 2001).
#### References
* [Kluger, Yuval, et. al., 2003. Spectral biclustering of microarray data: coclustering genes and conditions.](https://doi.org/10.1101/gr.648603)
#### Examples
```
>>> from sklearn.cluster import SpectralBiclustering
>>> import numpy as np
>>> X = np.array([[1, 1], [2, 1], [1, 0],
... [4, 7], [3, 5], [3, 6]])
>>> clustering = SpectralBiclustering(n_clusters=2, random_state=0).fit(X)
>>> clustering.row_labels_
array([1, 1, 1, 0, 0, 0], dtype=int32)
>>> clustering.column_labels_
array([0, 1], dtype=int32)
>>> clustering
SpectralBiclustering(n_clusters=2, random_state=0)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.cluster.SpectralBiclustering.fit "sklearn.cluster.SpectralBiclustering.fit")(X[, y]) | Create a biclustering for X. |
| [`get_indices`](#sklearn.cluster.SpectralBiclustering.get_indices "sklearn.cluster.SpectralBiclustering.get_indices")(i) | Row and column indices of the `i`'th bicluster. |
| [`get_params`](#sklearn.cluster.SpectralBiclustering.get_params "sklearn.cluster.SpectralBiclustering.get_params")([deep]) | Get parameters for this estimator. |
| [`get_shape`](#sklearn.cluster.SpectralBiclustering.get_shape "sklearn.cluster.SpectralBiclustering.get_shape")(i) | Shape of the `i`'th bicluster. |
| [`get_submatrix`](#sklearn.cluster.SpectralBiclustering.get_submatrix "sklearn.cluster.SpectralBiclustering.get_submatrix")(i, data) | Return the submatrix corresponding to bicluster `i`. |
| [`set_params`](#sklearn.cluster.SpectralBiclustering.set_params "sklearn.cluster.SpectralBiclustering.set_params")(\*\*params) | Set the parameters of this estimator. |
*property*biclusters\_
Convenient way to get row and column indicators together.
Returns the `rows_` and `columns_` members.
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_bicluster.py#L117)
Create a biclustering for X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**self**object
SpectralBiclustering instance.
get\_indices(*i*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L769)
Row and column indices of the `i`’th bicluster.
Only works if `rows_` and `columns_` attributes exist.
Parameters:
**i**int
The index of the cluster.
Returns:
**row\_ind**ndarray, dtype=np.intp
Indices of rows in the dataset that belong to the bicluster.
**col\_ind**ndarray, dtype=np.intp
Indices of columns in the dataset that belong to the bicluster.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
get\_shape(*i*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L790)
Shape of the `i`’th bicluster.
Parameters:
**i**int
The index of the cluster.
Returns:
**n\_rows**int
Number of rows in the bicluster.
**n\_cols**int
Number of columns in the bicluster.
get\_submatrix(*i*, *data*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L809)
Return the submatrix corresponding to bicluster `i`.
Parameters:
**i**int
The index of the cluster.
**data**array-like of shape (n\_samples, n\_features)
The data.
Returns:
**submatrix**ndarray of shape (n\_rows, n\_cols)
The submatrix corresponding to bicluster `i`.
#### Notes
Works with sparse matrices. Only works if `rows_` and `columns_` attributes exist.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.cluster.SpectralBiclustering`
-----------------------------------------------------
[A demo of the Spectral Biclustering algorithm](../../auto_examples/bicluster/plot_spectral_biclustering#sphx-glr-auto-examples-bicluster-plot-spectral-biclustering-py)
scikit_learn sklearn.decomposition.TruncatedSVD sklearn.decomposition.TruncatedSVD
==================================
*class*sklearn.decomposition.TruncatedSVD(*n\_components=2*, *\**, *algorithm='randomized'*, *n\_iter=5*, *n\_oversamples=10*, *power\_iteration\_normalizer='auto'*, *random\_state=None*, *tol=0.0*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_truncated_svd.py#L24)
Dimensionality reduction using truncated SVD (aka LSA).
This transformer performs linear dimensionality reduction by means of truncated singular value decomposition (SVD). Contrary to PCA, this estimator does not center the data before computing the singular value decomposition. This means it can work with sparse matrices efficiently.
In particular, truncated SVD works on term count/tf-idf matrices as returned by the vectorizers in [`sklearn.feature_extraction.text`](../classes#module-sklearn.feature_extraction.text "sklearn.feature_extraction.text"). In that context, it is known as latent semantic analysis (LSA).
This estimator supports two algorithms: a fast randomized SVD solver, and a “naive” algorithm that uses ARPACK as an eigensolver on `X * X.T` or `X.T * X`, whichever is more efficient.
Read more in the [User Guide](../decomposition#lsa).
Parameters:
**n\_components**int, default=2
Desired dimensionality of output data. If algorithm=’arpack’, must be strictly less than the number of features. If algorithm=’randomized’, must be less than or equal to the number of features. The default value is useful for visualisation. For LSA, a value of 100 is recommended.
**algorithm**{‘arpack’, ‘randomized’}, default=’randomized’
SVD solver to use. Either “arpack” for the ARPACK wrapper in SciPy (scipy.sparse.linalg.svds), or “randomized” for the randomized algorithm due to Halko (2009).
**n\_iter**int, default=5
Number of iterations for randomized SVD solver. Not used by ARPACK. The default is larger than the default in [`randomized_svd`](sklearn.utils.extmath.randomized_svd#sklearn.utils.extmath.randomized_svd "sklearn.utils.extmath.randomized_svd") to handle sparse matrices that may have large slowly decaying spectrum.
**n\_oversamples**int, default=10
Number of oversamples for randomized SVD solver. Not used by ARPACK. See [`randomized_svd`](sklearn.utils.extmath.randomized_svd#sklearn.utils.extmath.randomized_svd "sklearn.utils.extmath.randomized_svd") for a complete description.
New in version 1.1.
**power\_iteration\_normalizer**{‘auto’, ‘QR’, ‘LU’, ‘none’}, default=’auto’
Power iteration normalizer for randomized SVD solver. Not used by ARPACK. See [`randomized_svd`](sklearn.utils.extmath.randomized_svd#sklearn.utils.extmath.randomized_svd "sklearn.utils.extmath.randomized_svd") for more details.
New in version 1.1.
**random\_state**int, RandomState instance or None, default=None
Used during randomized svd. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**tol**float, default=0.0
Tolerance for ARPACK. 0 means machine precision. Ignored by randomized SVD solver.
Attributes:
**components\_**ndarray of shape (n\_components, n\_features)
The right singular vectors of the input data.
**explained\_variance\_**ndarray of shape (n\_components,)
The variance of the training samples transformed by a projection to each component.
**explained\_variance\_ratio\_**ndarray of shape (n\_components,)
Percentage of variance explained by each of the selected components.
**singular\_values\_**ndarray of shape (n\_components,)
The singular values corresponding to each of the selected components. The singular values are equal to the 2-norms of the `n_components` variables in the lower-dimensional space.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`DictionaryLearning`](sklearn.decomposition.dictionarylearning#sklearn.decomposition.DictionaryLearning "sklearn.decomposition.DictionaryLearning")
Find a dictionary that sparsely encodes data.
[`FactorAnalysis`](sklearn.decomposition.factoranalysis#sklearn.decomposition.FactorAnalysis "sklearn.decomposition.FactorAnalysis")
A simple linear generative model with Gaussian latent variables.
[`IncrementalPCA`](sklearn.decomposition.incrementalpca#sklearn.decomposition.IncrementalPCA "sklearn.decomposition.IncrementalPCA")
Incremental principal components analysis.
[`KernelPCA`](sklearn.decomposition.kernelpca#sklearn.decomposition.KernelPCA "sklearn.decomposition.KernelPCA")
Kernel Principal component analysis.
[`NMF`](sklearn.decomposition.nmf#sklearn.decomposition.NMF "sklearn.decomposition.NMF")
Non-Negative Matrix Factorization.
[`PCA`](sklearn.decomposition.pca#sklearn.decomposition.PCA "sklearn.decomposition.PCA")
Principal component analysis.
#### Notes
SVD suffers from a problem called “sign indeterminacy”, which means the sign of the `components_` and the output from transform depend on the algorithm and random state. To work around this, fit instances of this class to data once, then keep the instance around to do transformations.
#### References
[Halko, et al. (2009). “Finding structure with randomness: Stochastic algorithms for constructing approximate matrix decompositions”](https://arxiv.org/abs/0909.4061)
#### Examples
```
>>> from sklearn.decomposition import TruncatedSVD
>>> from scipy.sparse import csr_matrix
>>> import numpy as np
>>> np.random.seed(0)
>>> X_dense = np.random.rand(100, 100)
>>> X_dense[:, 2 * np.arange(50)] = 0
>>> X = csr_matrix(X_dense)
>>> svd = TruncatedSVD(n_components=5, n_iter=7, random_state=42)
>>> svd.fit(X)
TruncatedSVD(n_components=5, n_iter=7, random_state=42)
>>> print(svd.explained_variance_ratio_)
[0.0157... 0.0512... 0.0499... 0.0479... 0.0453...]
>>> print(svd.explained_variance_ratio_.sum())
0.2102...
>>> print(svd.singular_values_)
[35.2410... 4.5981... 4.5420... 4.4486... 4.3288...]
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.decomposition.TruncatedSVD.fit "sklearn.decomposition.TruncatedSVD.fit")(X[, y]) | Fit model on training data X. |
| [`fit_transform`](#sklearn.decomposition.TruncatedSVD.fit_transform "sklearn.decomposition.TruncatedSVD.fit_transform")(X[, y]) | Fit model to X and perform dimensionality reduction on X. |
| [`get_feature_names_out`](#sklearn.decomposition.TruncatedSVD.get_feature_names_out "sklearn.decomposition.TruncatedSVD.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.decomposition.TruncatedSVD.get_params "sklearn.decomposition.TruncatedSVD.get_params")([deep]) | Get parameters for this estimator. |
| [`inverse_transform`](#sklearn.decomposition.TruncatedSVD.inverse_transform "sklearn.decomposition.TruncatedSVD.inverse_transform")(X) | Transform X back to its original space. |
| [`set_params`](#sklearn.decomposition.TruncatedSVD.set_params "sklearn.decomposition.TruncatedSVD.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.decomposition.TruncatedSVD.transform "sklearn.decomposition.TruncatedSVD.transform")(X) | Perform dimensionality reduction on X. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_truncated_svd.py#L176)
Fit model on training data X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training data.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
**self**object
Returns the transformer object.
fit\_transform(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_truncated_svd.py#L195)
Fit model to X and perform dimensionality reduction on X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training data.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_components)
Reduced version of X. This will always be a dense array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.decomposition.TruncatedSVD.fit "sklearn.decomposition.TruncatedSVD.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
inverse\_transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_truncated_svd.py#L290)
Transform X back to its original space.
Returns an array X\_original whose transform would be X.
Parameters:
**X**array-like of shape (n\_samples, n\_components)
New data.
Returns:
**X\_original**ndarray of shape (n\_samples, n\_features)
Note that this is always a dense array.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_truncated_svd.py#L273)
Perform dimensionality reduction on X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
New data.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_components)
Reduced version of X. This will always be a dense array.
Examples using `sklearn.decomposition.TruncatedSVD`
---------------------------------------------------
[Hashing feature transformation using Totally Random Trees](../../auto_examples/ensemble/plot_random_forest_embedding#sphx-glr-auto-examples-ensemble-plot-random-forest-embedding-py)
[Manifold learning on handwritten digits: Locally Linear Embedding, Isomap…](../../auto_examples/manifold/plot_lle_digits#sphx-glr-auto-examples-manifold-plot-lle-digits-py)
[Column Transformer with Heterogeneous Data Sources](../../auto_examples/compose/plot_column_transformer#sphx-glr-auto-examples-compose-plot-column-transformer-py)
[Clustering text documents using k-means](../../auto_examples/text/plot_document_clustering#sphx-glr-auto-examples-text-plot-document-clustering-py)
| programming_docs |
scikit_learn sklearn.metrics.get_scorer sklearn.metrics.get\_scorer
===========================
sklearn.metrics.get\_scorer(*scoring*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_scorer.py#L390)
Get a scorer from string.
Read more in the [User Guide](../model_evaluation#scoring-parameter). [`get_scorer_names`](sklearn.metrics.get_scorer_names#sklearn.metrics.get_scorer_names "sklearn.metrics.get_scorer_names") can be used to retrieve the names of all available scorers.
Parameters:
**scoring**str or callable
Scoring method as string. If callable it is returned as is.
Returns:
**scorer**callable
The scorer.
#### Notes
When passed a string, this function always returns a copy of the scorer object. Calling `get_scorer` twice for the same scorer results in two separate scorer objects.
scikit_learn sklearn.ensemble.RandomTreesEmbedding sklearn.ensemble.RandomTreesEmbedding
=====================================
*class*sklearn.ensemble.RandomTreesEmbedding(*n\_estimators=100*, *\**, *max\_depth=5*, *min\_samples\_split=2*, *min\_samples\_leaf=1*, *min\_weight\_fraction\_leaf=0.0*, *max\_leaf\_nodes=None*, *min\_impurity\_decrease=0.0*, *sparse\_output=True*, *n\_jobs=None*, *random\_state=None*, *verbose=0*, *warm\_start=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L2416)
An ensemble of totally random trees.
An unsupervised transformation of a dataset to a high-dimensional sparse representation. A datapoint is coded according to which leaf of each tree it is sorted into. Using a one-hot encoding of the leaves, this leads to a binary coding with as many ones as there are trees in the forest.
The dimensionality of the resulting representation is `n_out <= n_estimators * max_leaf_nodes`. If `max_leaf_nodes == None`, the number of leaf nodes is at most `n_estimators * 2 ** max_depth`.
Read more in the [User Guide](../ensemble#random-trees-embedding).
Parameters:
**n\_estimators**int, default=100
Number of trees in the forest.
Changed in version 0.22: The default value of `n_estimators` changed from 10 to 100 in 0.22.
**max\_depth**int, default=5
The maximum depth of each tree. If None, then nodes are expanded until all leaves are pure or until all leaves contain less than min\_samples\_split samples.
**min\_samples\_split**int or float, default=2
The minimum number of samples required to split an internal node:
* If int, then consider `min_samples_split` as the minimum number.
* If float, then `min_samples_split` is a fraction and `ceil(min_samples_split * n_samples)` is the minimum number of samples for each split.
Changed in version 0.18: Added float values for fractions.
**min\_samples\_leaf**int or float, default=1
The minimum number of samples required to be at a leaf node. A split point at any depth will only be considered if it leaves at least `min_samples_leaf` training samples in each of the left and right branches. This may have the effect of smoothing the model, especially in regression.
* If int, then consider `min_samples_leaf` as the minimum number.
* If float, then `min_samples_leaf` is a fraction and `ceil(min_samples_leaf * n_samples)` is the minimum number of samples for each node.
Changed in version 0.18: Added float values for fractions.
**min\_weight\_fraction\_leaf**float, default=0.0
The minimum weighted fraction of the sum total of weights (of all the input samples) required to be at a leaf node. Samples have equal weight when sample\_weight is not provided.
**max\_leaf\_nodes**int, default=None
Grow trees with `max_leaf_nodes` in best-first fashion. Best nodes are defined as relative reduction in impurity. If None then unlimited number of leaf nodes.
**min\_impurity\_decrease**float, default=0.0
A node will be split if this split induces a decrease of the impurity greater than or equal to this value.
The weighted impurity decrease equation is the following:
```
N_t / N * (impurity - N_t_R / N_t * right_impurity
- N_t_L / N_t * left_impurity)
```
where `N` is the total number of samples, `N_t` is the number of samples at the current node, `N_t_L` is the number of samples in the left child, and `N_t_R` is the number of samples in the right child.
`N`, `N_t`, `N_t_R` and `N_t_L` all refer to the weighted sum, if `sample_weight` is passed.
New in version 0.19.
**sparse\_output**bool, default=True
Whether or not to return a sparse CSR matrix, as default behavior, or to return a dense array compatible with dense pipeline operators.
**n\_jobs**int, default=None
The number of jobs to run in parallel. [`fit`](#sklearn.ensemble.RandomTreesEmbedding.fit "sklearn.ensemble.RandomTreesEmbedding.fit"), [`transform`](#sklearn.ensemble.RandomTreesEmbedding.transform "sklearn.ensemble.RandomTreesEmbedding.transform"), [`decision_path`](#sklearn.ensemble.RandomTreesEmbedding.decision_path "sklearn.ensemble.RandomTreesEmbedding.decision_path") and [`apply`](#sklearn.ensemble.RandomTreesEmbedding.apply "sklearn.ensemble.RandomTreesEmbedding.apply") are all parallelized over the trees. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**random\_state**int, RandomState instance or None, default=None
Controls the generation of the random `y` used to fit the trees and the draw of the splits for each feature at the trees’ nodes. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state) for details.
**verbose**int, default=0
Controls the verbosity when fitting and predicting.
**warm\_start**bool, default=False
When set to `True`, reuse the solution of the previous call to fit and add more estimators to the ensemble, otherwise, just fit a whole new forest. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
Attributes:
**base\_estimator\_**[`ExtraTreeClassifier`](sklearn.tree.extratreeclassifier#sklearn.tree.ExtraTreeClassifier "sklearn.tree.ExtraTreeClassifier") instance
The child estimator template used to create the collection of fitted sub-estimators.
**estimators\_**list of [`ExtraTreeClassifier`](sklearn.tree.extratreeclassifier#sklearn.tree.ExtraTreeClassifier "sklearn.tree.ExtraTreeClassifier") instances
The collection of fitted sub-estimators.
[`feature_importances_`](#sklearn.ensemble.RandomTreesEmbedding.feature_importances_ "sklearn.ensemble.RandomTreesEmbedding.feature_importances_")ndarray of shape (n\_features,)
The impurity-based feature importances.
[`n_features_`](#sklearn.ensemble.RandomTreesEmbedding.n_features_ "sklearn.ensemble.RandomTreesEmbedding.n_features_")int
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_outputs\_**int
The number of outputs when `fit` is performed.
**one\_hot\_encoder\_**OneHotEncoder instance
One-hot encoder used to create the sparse embedding.
See also
[`ExtraTreesClassifier`](sklearn.ensemble.extratreesclassifier#sklearn.ensemble.ExtraTreesClassifier "sklearn.ensemble.ExtraTreesClassifier")
An extra-trees classifier.
[`ExtraTreesRegressor`](sklearn.ensemble.extratreesregressor#sklearn.ensemble.ExtraTreesRegressor "sklearn.ensemble.ExtraTreesRegressor")
An extra-trees regressor.
[`RandomForestClassifier`](sklearn.ensemble.randomforestclassifier#sklearn.ensemble.RandomForestClassifier "sklearn.ensemble.RandomForestClassifier")
A random forest classifier.
[`RandomForestRegressor`](sklearn.ensemble.randomforestregressor#sklearn.ensemble.RandomForestRegressor "sklearn.ensemble.RandomForestRegressor")
A random forest regressor.
[`sklearn.tree.ExtraTreeClassifier`](sklearn.tree.extratreeclassifier#sklearn.tree.ExtraTreeClassifier "sklearn.tree.ExtraTreeClassifier")
An extremely randomized tree classifier.
[`sklearn.tree.ExtraTreeRegressor`](sklearn.tree.extratreeregressor#sklearn.tree.ExtraTreeRegressor "sklearn.tree.ExtraTreeRegressor")
An extremely randomized tree regressor.
#### References
[1] P. Geurts, D. Ernst., and L. Wehenkel, “Extremely randomized trees”, Machine Learning, 63(1), 3-42, 2006.
[2] Moosmann, F. and Triggs, B. and Jurie, F. “Fast discriminative visual codebooks using randomized clustering forests” NIPS 2007
#### Examples
```
>>> from sklearn.ensemble import RandomTreesEmbedding
>>> X = [[0,0], [1,0], [0,1], [-1,0], [0,-1]]
>>> random_trees = RandomTreesEmbedding(
... n_estimators=5, random_state=0, max_depth=1).fit(X)
>>> X_sparse_embedding = random_trees.transform(X)
>>> X_sparse_embedding.toarray()
array([[0., 1., 1., 0., 1., 0., 0., 1., 1., 0.],
[0., 1., 1., 0., 1., 0., 0., 1., 1., 0.],
[0., 1., 0., 1., 0., 1., 0., 1., 0., 1.],
[1., 0., 1., 0., 1., 0., 1., 0., 1., 0.],
[0., 1., 1., 0., 1., 0., 0., 1., 1., 0.]])
```
#### Methods
| | |
| --- | --- |
| [`apply`](#sklearn.ensemble.RandomTreesEmbedding.apply "sklearn.ensemble.RandomTreesEmbedding.apply")(X) | Apply trees in the forest to X, return leaf indices. |
| [`decision_path`](#sklearn.ensemble.RandomTreesEmbedding.decision_path "sklearn.ensemble.RandomTreesEmbedding.decision_path")(X) | Return the decision path in the forest. |
| [`fit`](#sklearn.ensemble.RandomTreesEmbedding.fit "sklearn.ensemble.RandomTreesEmbedding.fit")(X[, y, sample\_weight]) | Fit estimator. |
| [`fit_transform`](#sklearn.ensemble.RandomTreesEmbedding.fit_transform "sklearn.ensemble.RandomTreesEmbedding.fit_transform")(X[, y, sample\_weight]) | Fit estimator and transform dataset. |
| [`get_feature_names_out`](#sklearn.ensemble.RandomTreesEmbedding.get_feature_names_out "sklearn.ensemble.RandomTreesEmbedding.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.ensemble.RandomTreesEmbedding.get_params "sklearn.ensemble.RandomTreesEmbedding.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.ensemble.RandomTreesEmbedding.set_params "sklearn.ensemble.RandomTreesEmbedding.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.ensemble.RandomTreesEmbedding.transform "sklearn.ensemble.RandomTreesEmbedding.transform")(X) | Transform dataset. |
apply(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L235)
Apply trees in the forest to X, return leaf indices.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, its dtype will be converted to `dtype=np.float32`. If a sparse matrix is provided, it will be converted into a sparse `csr_matrix`.
Returns:
**X\_leaves**ndarray of shape (n\_samples, n\_estimators)
For each datapoint x in X and for each tree in the forest, return the index of the leaf x ends up in.
decision\_path(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L261)
Return the decision path in the forest.
New in version 0.18.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, its dtype will be converted to `dtype=np.float32`. If a sparse matrix is provided, it will be converted into a sparse `csr_matrix`.
Returns:
**indicator**sparse matrix of shape (n\_samples, n\_nodes)
Return a node indicator matrix where non zero elements indicates that the samples goes through the nodes. The matrix is of CSR format.
**n\_nodes\_ptr**ndarray of shape (n\_estimators + 1,)
The columns from indicator[n\_nodes\_ptr[i]:n\_nodes\_ptr[i+1]] gives the indicator value for the i-th estimator.
*property*feature\_importances\_
The impurity-based feature importances.
The higher, the more important the feature. The importance of a feature is computed as the (normalized) total reduction of the criterion brought by that feature. It is also known as the Gini importance.
Warning: impurity-based feature importances can be misleading for high cardinality features (many unique values). See [`sklearn.inspection.permutation_importance`](sklearn.inspection.permutation_importance#sklearn.inspection.permutation_importance "sklearn.inspection.permutation_importance") as an alternative.
Returns:
**feature\_importances\_**ndarray of shape (n\_features,)
The values of this array sum to 1, unless all trees are single node trees consisting of only the root node, in which case it will be an array of zeros.
fit(*X*, *y=None*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L2647)
Fit estimator.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Use `dtype=np.float32` for maximum efficiency. Sparse matrices are also supported, use sparse `csc_matrix` for maximum efficiency.
**y**Ignored
Not used, present for API consistency by convention.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, then samples are equally weighted. Splits that would create child nodes with net zero or negative weight are ignored while searching for a split in each node. In the case of classification, splits are also ignored if they would result in any single class carrying a negative weight in either child node.
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L2676)
Fit estimator and transform dataset.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Input data used to build forests. Use `dtype=np.float32` for maximum efficiency.
**y**Ignored
Not used, present for API consistency by convention.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, then samples are equally weighted. Splits that would create child nodes with net zero or negative weight are ignored while searching for a split in each node. In the case of classification, splits are also ignored if they would result in any single class carrying a negative weight in either child node.
Returns:
**X\_transformed**sparse matrix of shape (n\_samples, n\_out)
Transformed dataset.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L2710)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.ensemble.RandomTreesEmbedding.fit "sklearn.ensemble.RandomTreesEmbedding.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names, in the format of `randomtreesembedding_{tree}_{leaf}`, where `tree` is the tree used to generate the leaf and `leaf` is the index of a leaf node in that tree. Note that the node indexing scheme is used to index both nodes with children (split nodes) and leaf nodes. Only the latter can be present as output features. As a consequence, there are missing indices in the output feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_features\_
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2. Use `n_features_in_` instead.
Number of features when fitting the estimator.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L2742)
Transform dataset.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Input data to be transformed. Use `dtype=np.float32` for maximum efficiency. Sparse matrices are also supported, use sparse `csr_matrix` for maximum efficiency.
Returns:
**X\_transformed**sparse matrix of shape (n\_samples, n\_out)
Transformed dataset.
Examples using `sklearn.ensemble.RandomTreesEmbedding`
------------------------------------------------------
[Feature transformations with ensembles of trees](../../auto_examples/ensemble/plot_feature_transformation#sphx-glr-auto-examples-ensemble-plot-feature-transformation-py)
[Hashing feature transformation using Totally Random Trees](../../auto_examples/ensemble/plot_random_forest_embedding#sphx-glr-auto-examples-ensemble-plot-random-forest-embedding-py)
[Manifold learning on handwritten digits: Locally Linear Embedding, Isomap…](../../auto_examples/manifold/plot_lle_digits#sphx-glr-auto-examples-manifold-plot-lle-digits-py)
scikit_learn sklearn.multiclass.OutputCodeClassifier sklearn.multiclass.OutputCodeClassifier
=======================================
*class*sklearn.multiclass.OutputCodeClassifier(*estimator*, *\**, *code\_size=1.5*, *random\_state=None*, *n\_jobs=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/multiclass.py#L838)
(Error-Correcting) Output-Code multiclass strategy.
Output-code based strategies consist in representing each class with a binary code (an array of 0s and 1s). At fitting time, one binary classifier per bit in the code book is fitted. At prediction time, the classifiers are used to project new points in the class space and the class closest to the points is chosen. The main advantage of these strategies is that the number of classifiers used can be controlled by the user, either for compressing the model (0 < code\_size < 1) or for making the model more robust to errors (code\_size > 1). See the documentation for more details.
Read more in the [User Guide](../multiclass#ecoc).
Parameters:
**estimator**estimator object
An estimator object implementing [fit](https://scikit-learn.org/1.1/glossary.html#term-fit) and one of [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) or [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba).
**code\_size**float, default=1.5
Percentage of the number of classes to be used to create the code book. A number between 0 and 1 will require fewer classifiers than one-vs-the-rest. A number greater than 1 will require more classifiers than one-vs-the-rest.
**random\_state**int, RandomState instance, default=None
The generator used to initialize the codebook. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**n\_jobs**int, default=None
The number of jobs to use for the computation: the multiclass problems are computed in parallel.
`None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
Attributes:
**estimators\_**list of `int(n_classes * code_size)` estimators
Estimators used for predictions.
**classes\_**ndarray of shape (n\_classes,)
Array containing labels.
**code\_book\_**ndarray of shape (n\_classes, code\_size)
Binary array containing the code of each class.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Only defined if the underlying estimator exposes such an attribute when fit.
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Only defined if the underlying estimator exposes such an attribute when fit.
New in version 1.0.
See also
[`OneVsRestClassifier`](sklearn.multiclass.onevsrestclassifier#sklearn.multiclass.OneVsRestClassifier "sklearn.multiclass.OneVsRestClassifier")
One-vs-all multiclass strategy.
[`OneVsOneClassifier`](sklearn.multiclass.onevsoneclassifier#sklearn.multiclass.OneVsOneClassifier "sklearn.multiclass.OneVsOneClassifier")
One-vs-one multiclass strategy.
#### References
[1] “Solving multiclass learning problems via error-correcting output codes”, Dietterich T., Bakiri G., Journal of Artificial Intelligence Research 2, 1995.
[2] “The error coding method and PICTs”, James G., Hastie T., Journal of Computational and Graphical statistics 7, 1998.
[3] “The Elements of Statistical Learning”, Hastie T., Tibshirani R., Friedman J., page 606 (second-edition) 2008.
#### Examples
```
>>> from sklearn.multiclass import OutputCodeClassifier
>>> from sklearn.ensemble import RandomForestClassifier
>>> from sklearn.datasets import make_classification
>>> X, y = make_classification(n_samples=100, n_features=4,
... n_informative=2, n_redundant=0,
... random_state=0, shuffle=False)
>>> clf = OutputCodeClassifier(
... estimator=RandomForestClassifier(random_state=0),
... random_state=0).fit(X, y)
>>> clf.predict([[0, 0, 0, 0]])
array([1])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.multiclass.OutputCodeClassifier.fit "sklearn.multiclass.OutputCodeClassifier.fit")(X, y) | Fit underlying estimators. |
| [`get_params`](#sklearn.multiclass.OutputCodeClassifier.get_params "sklearn.multiclass.OutputCodeClassifier.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.multiclass.OutputCodeClassifier.predict "sklearn.multiclass.OutputCodeClassifier.predict")(X) | Predict multi-class targets using underlying estimators. |
| [`score`](#sklearn.multiclass.OutputCodeClassifier.score "sklearn.multiclass.OutputCodeClassifier.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.multiclass.OutputCodeClassifier.set_params "sklearn.multiclass.OutputCodeClassifier.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/multiclass.py#L944)
Fit underlying estimators.
Parameters:
**X**(sparse) array-like of shape (n\_samples, n\_features)
Data.
**y**array-like of shape (n\_samples,)
Multi-class targets.
Returns:
**self**object
Returns a fitted instance of self.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/multiclass.py#L1007)
Predict multi-class targets using underlying estimators.
Parameters:
**X**(sparse) array-like of shape (n\_samples, n\_features)
Data.
Returns:
**y**ndarray of shape (n\_samples,)
Predicted multi-class targets.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
| programming_docs |
scikit_learn sklearn.linear_model.QuantileRegressor sklearn.linear\_model.QuantileRegressor
=======================================
*class*sklearn.linear\_model.QuantileRegressor(*\**, *quantile=0.5*, *alpha=1.0*, *fit\_intercept=True*, *solver='interior-point'*, *solver\_options=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_quantile.py#L18)
Linear regression model that predicts conditional quantiles.
The linear [`QuantileRegressor`](#sklearn.linear_model.QuantileRegressor "sklearn.linear_model.QuantileRegressor") optimizes the pinball loss for a desired `quantile` and is robust to outliers.
This model uses an L1 regularization like [`Lasso`](sklearn.linear_model.lasso#sklearn.linear_model.Lasso "sklearn.linear_model.Lasso").
Read more in the [User Guide](../linear_model#quantile-regression).
New in version 1.0.
Parameters:
**quantile**float, default=0.5
The quantile that the model tries to predict. It must be strictly between 0 and 1. If 0.5 (default), the model predicts the 50% quantile, i.e. the median.
**alpha**float, default=1.0
Regularization constant that multiplies the L1 penalty term.
**fit\_intercept**bool, default=True
Whether or not to fit the intercept.
**solver**{‘highs-ds’, ‘highs-ipm’, ‘highs’, ‘interior-point’, ‘revised simplex’}, default=’interior-point’
Method used by [`scipy.optimize.linprog`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.linprog.html#scipy.optimize.linprog "(in SciPy v1.9.3)") to solve the linear programming formulation. Note that the highs methods are recommended for usage with `scipy>=1.6.0` because they are the fastest ones. Solvers “highs-ds”, “highs-ipm” and “highs” support sparse input data and, in fact, always convert to sparse csc.
**solver\_options**dict, default=None
Additional parameters passed to [`scipy.optimize.linprog`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.linprog.html#scipy.optimize.linprog "(in SciPy v1.9.3)") as options. If `None` and if `solver='interior-point'`, then `{"lstsq": True}` is passed to [`scipy.optimize.linprog`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.linprog.html#scipy.optimize.linprog "(in SciPy v1.9.3)") for the sake of stability.
Attributes:
**coef\_**array of shape (n\_features,)
Estimated coefficients for the features.
**intercept\_**float
The intercept of the model, aka bias term.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_iter\_**int
The actual number of iterations performed by the solver.
See also
[`Lasso`](sklearn.linear_model.lasso#sklearn.linear_model.Lasso "sklearn.linear_model.Lasso")
The Lasso is a linear model that estimates sparse coefficients with l1 regularization.
[`HuberRegressor`](sklearn.linear_model.huberregressor#sklearn.linear_model.HuberRegressor "sklearn.linear_model.HuberRegressor")
Linear regression model that is robust to outliers.
#### Examples
```
>>> from sklearn.linear_model import QuantileRegressor
>>> import numpy as np
>>> n_samples, n_features = 10, 2
>>> rng = np.random.RandomState(0)
>>> y = rng.randn(n_samples)
>>> X = rng.randn(n_samples, n_features)
>>> reg = QuantileRegressor(quantile=0.8).fit(X, y)
>>> np.mean(y <= reg.predict(X))
0.8
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.linear_model.QuantileRegressor.fit "sklearn.linear_model.QuantileRegressor.fit")(X, y[, sample\_weight]) | Fit the model according to the given training data. |
| [`get_params`](#sklearn.linear_model.QuantileRegressor.get_params "sklearn.linear_model.QuantileRegressor.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.linear_model.QuantileRegressor.predict "sklearn.linear_model.QuantileRegressor.predict")(X) | Predict using the linear model. |
| [`score`](#sklearn.linear_model.QuantileRegressor.score "sklearn.linear_model.QuantileRegressor.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.linear_model.QuantileRegressor.set_params "sklearn.linear_model.QuantileRegressor.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_quantile.py#L114)
Fit the model according to the given training data.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training data.
**y**array-like of shape (n\_samples,)
Target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**self**object
Returns self.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L372)
Predict using the linear model.
Parameters:
**X**array-like or sparse matrix, shape (n\_samples, n\_features)
Samples.
Returns:
**C**array, shape (n\_samples,)
Returns predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.linear_model.QuantileRegressor`
-------------------------------------------------------
[Quantile regression](../../auto_examples/linear_model/plot_quantile_regression#sphx-glr-auto-examples-linear-model-plot-quantile-regression-py)
scikit_learn sklearn.model_selection.LeaveOneOut sklearn.model\_selection.LeaveOneOut
====================================
*class*sklearn.model\_selection.LeaveOneOut[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L115)
Leave-One-Out cross-validator
Provides train/test indices to split data in train/test sets. Each sample is used once as a test set (singleton) while the remaining samples form the training set.
Note: `LeaveOneOut()` is equivalent to `KFold(n_splits=n)` and `LeavePOut(p=1)` where `n` is the number of samples.
Due to the high number of test sets (which is the same as the number of samples) this cross-validation method can be very costly. For large datasets one should favor [`KFold`](sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold"), [`ShuffleSplit`](sklearn.model_selection.shufflesplit#sklearn.model_selection.ShuffleSplit "sklearn.model_selection.ShuffleSplit") or [`StratifiedKFold`](sklearn.model_selection.stratifiedkfold#sklearn.model_selection.StratifiedKFold "sklearn.model_selection.StratifiedKFold").
Read more in the [User Guide](../cross_validation#leave-one-out).
See also
[`LeaveOneGroupOut`](sklearn.model_selection.leaveonegroupout#sklearn.model_selection.LeaveOneGroupOut "sklearn.model_selection.LeaveOneGroupOut")
For splitting the data according to explicit, domain-specific stratification of the dataset.
[`GroupKFold`](sklearn.model_selection.groupkfold#sklearn.model_selection.GroupKFold "sklearn.model_selection.GroupKFold")
K-fold iterator variant with non-overlapping groups.
#### Examples
```
>>> import numpy as np
>>> from sklearn.model_selection import LeaveOneOut
>>> X = np.array([[1, 2], [3, 4]])
>>> y = np.array([1, 2])
>>> loo = LeaveOneOut()
>>> loo.get_n_splits(X)
2
>>> print(loo)
LeaveOneOut()
>>> for train_index, test_index in loo.split(X):
... print("TRAIN:", train_index, "TEST:", test_index)
... X_train, X_test = X[train_index], X[test_index]
... y_train, y_test = y[train_index], y[test_index]
... print(X_train, X_test, y_train, y_test)
TRAIN: [1] TEST: [0]
[[3 4]] [[1 2]] [2] [1]
TRAIN: [0] TEST: [1]
[[1 2]] [[3 4]] [1] [2]
```
#### Methods
| | |
| --- | --- |
| [`get_n_splits`](#sklearn.model_selection.LeaveOneOut.get_n_splits "sklearn.model_selection.LeaveOneOut.get_n_splits")(X[, y, groups]) | Returns the number of splitting iterations in the cross-validator |
| [`split`](#sklearn.model_selection.LeaveOneOut.split "sklearn.model_selection.LeaveOneOut.split")(X[, y, groups]) | Generate indices to split data into training and test set. |
get\_n\_splits(*X*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L168)
Returns the number of splitting iterations in the cross-validator
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**object
Always ignored, exists for compatibility.
**groups**object
Always ignored, exists for compatibility.
Returns:
**n\_splits**int
Returns the number of splitting iterations in the cross-validator.
split(*X*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L60)
Generate indices to split data into training and test set.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,)
The target variable for supervised learning problems.
**groups**array-like of shape (n\_samples,), default=None
Group labels for the samples used while splitting the dataset into train/test set.
Yields:
**train**ndarray
The training set indices for that split.
**test**ndarray
The testing set indices for that split.
scikit_learn sklearn.ensemble.RandomForestRegressor sklearn.ensemble.RandomForestRegressor
======================================
*class*sklearn.ensemble.RandomForestRegressor(*n\_estimators=100*, *\**, *criterion='squared\_error'*, *max\_depth=None*, *min\_samples\_split=2*, *min\_samples\_leaf=1*, *min\_weight\_fraction\_leaf=0.0*, *max\_features=1.0*, *max\_leaf\_nodes=None*, *min\_impurity\_decrease=0.0*, *bootstrap=True*, *oob\_score=False*, *n\_jobs=None*, *random\_state=None*, *verbose=0*, *warm\_start=False*, *ccp\_alpha=0.0*, *max\_samples=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L1434)
A random forest regressor.
A random forest is a meta estimator that fits a number of classifying decision trees on various sub-samples of the dataset and uses averaging to improve the predictive accuracy and control over-fitting. The sub-sample size is controlled with the `max_samples` parameter if `bootstrap=True` (default), otherwise the whole dataset is used to build each tree.
Read more in the [User Guide](../ensemble#forest).
Parameters:
**n\_estimators**int, default=100
The number of trees in the forest.
Changed in version 0.22: The default value of `n_estimators` changed from 10 to 100 in 0.22.
**criterion**{“squared\_error”, “absolute\_error”, “poisson”}, default=”squared\_error”
The function to measure the quality of a split. Supported criteria are “squared\_error” for the mean squared error, which is equal to variance reduction as feature selection criterion, “absolute\_error” for the mean absolute error, and “poisson” which uses reduction in Poisson deviance to find splits. Training using “absolute\_error” is significantly slower than when using “squared\_error”.
New in version 0.18: Mean Absolute Error (MAE) criterion.
New in version 1.0: Poisson criterion.
Deprecated since version 1.0: Criterion “mse” was deprecated in v1.0 and will be removed in version 1.2. Use `criterion="squared_error"` which is equivalent.
Deprecated since version 1.0: Criterion “mae” was deprecated in v1.0 and will be removed in version 1.2. Use `criterion="absolute_error"` which is equivalent.
**max\_depth**int, default=None
The maximum depth of the tree. If None, then nodes are expanded until all leaves are pure or until all leaves contain less than min\_samples\_split samples.
**min\_samples\_split**int or float, default=2
The minimum number of samples required to split an internal node:
* If int, then consider `min_samples_split` as the minimum number.
* If float, then `min_samples_split` is a fraction and `ceil(min_samples_split * n_samples)` are the minimum number of samples for each split.
Changed in version 0.18: Added float values for fractions.
**min\_samples\_leaf**int or float, default=1
The minimum number of samples required to be at a leaf node. A split point at any depth will only be considered if it leaves at least `min_samples_leaf` training samples in each of the left and right branches. This may have the effect of smoothing the model, especially in regression.
* If int, then consider `min_samples_leaf` as the minimum number.
* If float, then `min_samples_leaf` is a fraction and `ceil(min_samples_leaf * n_samples)` are the minimum number of samples for each node.
Changed in version 0.18: Added float values for fractions.
**min\_weight\_fraction\_leaf**float, default=0.0
The minimum weighted fraction of the sum total of weights (of all the input samples) required to be at a leaf node. Samples have equal weight when sample\_weight is not provided.
**max\_features**{“sqrt”, “log2”, None}, int or float, default=1.0
The number of features to consider when looking for the best split:
* If int, then consider `max_features` features at each split.
* If float, then `max_features` is a fraction and `max(1, int(max_features * n_features_in_))` features are considered at each split.
* If “auto”, then `max_features=n_features`.
* If “sqrt”, then `max_features=sqrt(n_features)`.
* If “log2”, then `max_features=log2(n_features)`.
* If None or 1.0, then `max_features=n_features`.
Note
The default of 1.0 is equivalent to bagged trees and more randomness can be achieved by setting smaller values, e.g. 0.3.
Changed in version 1.1: The default of `max_features` changed from `"auto"` to 1.0.
Deprecated since version 1.1: The `"auto"` option was deprecated in 1.1 and will be removed in 1.3.
Note: the search for a split does not stop until at least one valid partition of the node samples is found, even if it requires to effectively inspect more than `max_features` features.
**max\_leaf\_nodes**int, default=None
Grow trees with `max_leaf_nodes` in best-first fashion. Best nodes are defined as relative reduction in impurity. If None then unlimited number of leaf nodes.
**min\_impurity\_decrease**float, default=0.0
A node will be split if this split induces a decrease of the impurity greater than or equal to this value.
The weighted impurity decrease equation is the following:
```
N_t / N * (impurity - N_t_R / N_t * right_impurity
- N_t_L / N_t * left_impurity)
```
where `N` is the total number of samples, `N_t` is the number of samples at the current node, `N_t_L` is the number of samples in the left child, and `N_t_R` is the number of samples in the right child.
`N`, `N_t`, `N_t_R` and `N_t_L` all refer to the weighted sum, if `sample_weight` is passed.
New in version 0.19.
**bootstrap**bool, default=True
Whether bootstrap samples are used when building trees. If False, the whole dataset is used to build each tree.
**oob\_score**bool, default=False
Whether to use out-of-bag samples to estimate the generalization score. Only available if bootstrap=True.
**n\_jobs**int, default=None
The number of jobs to run in parallel. [`fit`](#sklearn.ensemble.RandomForestRegressor.fit "sklearn.ensemble.RandomForestRegressor.fit"), [`predict`](#sklearn.ensemble.RandomForestRegressor.predict "sklearn.ensemble.RandomForestRegressor.predict"), [`decision_path`](#sklearn.ensemble.RandomForestRegressor.decision_path "sklearn.ensemble.RandomForestRegressor.decision_path") and [`apply`](#sklearn.ensemble.RandomForestRegressor.apply "sklearn.ensemble.RandomForestRegressor.apply") are all parallelized over the trees. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**random\_state**int, RandomState instance or None, default=None
Controls both the randomness of the bootstrapping of the samples used when building trees (if `bootstrap=True`) and the sampling of the features to consider when looking for the best split at each node (if `max_features < n_features`). See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state) for details.
**verbose**int, default=0
Controls the verbosity when fitting and predicting.
**warm\_start**bool, default=False
When set to `True`, reuse the solution of the previous call to fit and add more estimators to the ensemble, otherwise, just fit a whole new forest. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
**ccp\_alpha**non-negative float, default=0.0
Complexity parameter used for Minimal Cost-Complexity Pruning. The subtree with the largest cost complexity that is smaller than `ccp_alpha` will be chosen. By default, no pruning is performed. See [Minimal Cost-Complexity Pruning](../tree#minimal-cost-complexity-pruning) for details.
New in version 0.22.
**max\_samples**int or float, default=None
If bootstrap is True, the number of samples to draw from X to train each base estimator.
* If None (default), then draw `X.shape[0]` samples.
* If int, then draw `max_samples` samples.
* If float, then draw `max_samples * X.shape[0]` samples. Thus, `max_samples` should be in the interval `(0.0, 1.0]`.
New in version 0.22.
Attributes:
**base\_estimator\_**DecisionTreeRegressor
The child estimator template used to create the collection of fitted sub-estimators.
**estimators\_**list of DecisionTreeRegressor
The collection of fitted sub-estimators.
[`feature_importances_`](#sklearn.ensemble.RandomForestRegressor.feature_importances_ "sklearn.ensemble.RandomForestRegressor.feature_importances_")ndarray of shape (n\_features,)
The impurity-based feature importances.
[`n_features_`](#sklearn.ensemble.RandomForestRegressor.n_features_ "sklearn.ensemble.RandomForestRegressor.n_features_")int
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_outputs\_**int
The number of outputs when `fit` is performed.
**oob\_score\_**float
Score of the training dataset obtained using an out-of-bag estimate. This attribute exists only when `oob_score` is True.
**oob\_prediction\_**ndarray of shape (n\_samples,) or (n\_samples, n\_outputs)
Prediction computed with out-of-bag estimate on the training set. This attribute exists only when `oob_score` is True.
See also
[`sklearn.tree.DecisionTreeRegressor`](sklearn.tree.decisiontreeregressor#sklearn.tree.DecisionTreeRegressor "sklearn.tree.DecisionTreeRegressor")
A decision tree regressor.
[`sklearn.ensemble.ExtraTreesRegressor`](sklearn.ensemble.extratreesregressor#sklearn.ensemble.ExtraTreesRegressor "sklearn.ensemble.ExtraTreesRegressor")
Ensemble of extremely randomized tree regressors.
#### Notes
The default values for the parameters controlling the size of the trees (e.g. `max_depth`, `min_samples_leaf`, etc.) lead to fully grown and unpruned trees which can potentially be very large on some data sets. To reduce memory consumption, the complexity and size of the trees should be controlled by setting those parameter values.
The features are always randomly permuted at each split. Therefore, the best found split may vary, even with the same training data, `max_features=n_features` and `bootstrap=False`, if the improvement of the criterion is identical for several splits enumerated during the search of the best split. To obtain a deterministic behaviour during fitting, `random_state` has to be fixed.
The default value `max_features="auto"` uses `n_features` rather than `n_features / 3`. The latter was originally suggested in [1], whereas the former was more recently justified empirically in [2].
#### References
[1] 12. Breiman, “Random Forests”, Machine Learning, 45(1), 5-32, 2001.
[2] P. Geurts, D. Ernst., and L. Wehenkel, “Extremely randomized trees”, Machine Learning, 63(1), 3-42, 2006.
#### Examples
```
>>> from sklearn.ensemble import RandomForestRegressor
>>> from sklearn.datasets import make_regression
>>> X, y = make_regression(n_features=4, n_informative=2,
... random_state=0, shuffle=False)
>>> regr = RandomForestRegressor(max_depth=2, random_state=0)
>>> regr.fit(X, y)
RandomForestRegressor(...)
>>> print(regr.predict([[0, 0, 0, 0]]))
[-8.32987858]
```
#### Methods
| | |
| --- | --- |
| [`apply`](#sklearn.ensemble.RandomForestRegressor.apply "sklearn.ensemble.RandomForestRegressor.apply")(X) | Apply trees in the forest to X, return leaf indices. |
| [`decision_path`](#sklearn.ensemble.RandomForestRegressor.decision_path "sklearn.ensemble.RandomForestRegressor.decision_path")(X) | Return the decision path in the forest. |
| [`fit`](#sklearn.ensemble.RandomForestRegressor.fit "sklearn.ensemble.RandomForestRegressor.fit")(X, y[, sample\_weight]) | Build a forest of trees from the training set (X, y). |
| [`get_params`](#sklearn.ensemble.RandomForestRegressor.get_params "sklearn.ensemble.RandomForestRegressor.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.ensemble.RandomForestRegressor.predict "sklearn.ensemble.RandomForestRegressor.predict")(X) | Predict regression target for X. |
| [`score`](#sklearn.ensemble.RandomForestRegressor.score "sklearn.ensemble.RandomForestRegressor.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.ensemble.RandomForestRegressor.set_params "sklearn.ensemble.RandomForestRegressor.set_params")(\*\*params) | Set the parameters of this estimator. |
apply(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L235)
Apply trees in the forest to X, return leaf indices.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, its dtype will be converted to `dtype=np.float32`. If a sparse matrix is provided, it will be converted into a sparse `csr_matrix`.
Returns:
**X\_leaves**ndarray of shape (n\_samples, n\_estimators)
For each datapoint x in X and for each tree in the forest, return the index of the leaf x ends up in.
decision\_path(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L261)
Return the decision path in the forest.
New in version 0.18.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, its dtype will be converted to `dtype=np.float32`. If a sparse matrix is provided, it will be converted into a sparse `csr_matrix`.
Returns:
**indicator**sparse matrix of shape (n\_samples, n\_nodes)
Return a node indicator matrix where non zero elements indicates that the samples goes through the nodes. The matrix is of CSR format.
**n\_nodes\_ptr**ndarray of shape (n\_estimators + 1,)
The columns from indicator[n\_nodes\_ptr[i]:n\_nodes\_ptr[i+1]] gives the indicator value for the i-th estimator.
*property*feature\_importances\_
The impurity-based feature importances.
The higher, the more important the feature. The importance of a feature is computed as the (normalized) total reduction of the criterion brought by that feature. It is also known as the Gini importance.
Warning: impurity-based feature importances can be misleading for high cardinality features (many unique values). See [`sklearn.inspection.permutation_importance`](sklearn.inspection.permutation_importance#sklearn.inspection.permutation_importance "sklearn.inspection.permutation_importance") as an alternative.
Returns:
**feature\_importances\_**ndarray of shape (n\_features,)
The values of this array sum to 1, unless all trees are single node trees consisting of only the root node, in which case it will be an array of zeros.
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L301)
Build a forest of trees from the training set (X, y).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Internally, its dtype will be converted to `dtype=np.float32`. If a sparse matrix is provided, it will be converted into a sparse `csc_matrix`.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
The target values (class labels in classification, real numbers in regression).
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, then samples are equally weighted. Splits that would create child nodes with net zero or negative weight are ignored while searching for a split in each node. In the case of classification, splits are also ignored if they would result in any single class carrying a negative weight in either child node.
Returns:
**self**object
Fitted estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_features\_
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2. Use `n_features_in_` instead.
Number of features when fitting the estimator.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_forest.py#L970)
Predict regression target for X.
The predicted regression target of an input sample is computed as the mean predicted regression targets of the trees in the forest.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples. Internally, its dtype will be converted to `dtype=np.float32`. If a sparse matrix is provided, it will be converted into a sparse `csr_matrix`.
Returns:
**y**ndarray of shape (n\_samples,) or (n\_samples, n\_outputs)
The predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.ensemble.RandomForestRegressor`
-------------------------------------------------------
[Release Highlights for scikit-learn 0.24](../../auto_examples/release_highlights/plot_release_highlights_0_24_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-24-0-py)
[Combine predictors using stacking](../../auto_examples/ensemble/plot_stack_predictors#sphx-glr-auto-examples-ensemble-plot-stack-predictors-py)
[Comparing random forests and the multi-output meta estimator](../../auto_examples/ensemble/plot_random_forest_regression_multioutput#sphx-glr-auto-examples-ensemble-plot-random-forest-regression-multioutput-py)
[Plot individual and voting regression predictions](../../auto_examples/ensemble/plot_voting_regressor#sphx-glr-auto-examples-ensemble-plot-voting-regressor-py)
[Prediction Latency](../../auto_examples/applications/plot_prediction_latency#sphx-glr-auto-examples-applications-plot-prediction-latency-py)
[Imputing missing values before building an estimator](../../auto_examples/impute/plot_missing_values#sphx-glr-auto-examples-impute-plot-missing-values-py)
[Imputing missing values with variants of IterativeImputer](../../auto_examples/impute/plot_iterative_imputer_variants_comparison#sphx-glr-auto-examples-impute-plot-iterative-imputer-variants-comparison-py)
| programming_docs |
scikit_learn sklearn.decomposition.IncrementalPCA sklearn.decomposition.IncrementalPCA
====================================
*class*sklearn.decomposition.IncrementalPCA(*n\_components=None*, *\**, *whiten=False*, *copy=True*, *batch\_size=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_incremental_pca.py#L15)
Incremental principal components analysis (IPCA).
Linear dimensionality reduction using Singular Value Decomposition of the data, keeping only the most significant singular vectors to project the data to a lower dimensional space. The input data is centered but not scaled for each feature before applying the SVD.
Depending on the size of the input data, this algorithm can be much more memory efficient than a PCA, and allows sparse input.
This algorithm has constant memory complexity, on the order of `batch_size * n_features`, enabling use of np.memmap files without loading the entire file into memory. For sparse matrices, the input is converted to dense in batches (in order to be able to subtract the mean) which avoids storing the entire dense matrix at any one time.
The computational overhead of each SVD is `O(batch_size * n_features ** 2)`, but only 2 \* batch\_size samples remain in memory at a time. There will be `n_samples / batch_size` SVD computations to get the principal components, versus 1 large SVD of complexity `O(n_samples * n_features ** 2)` for PCA.
Read more in the [User Guide](../decomposition#incrementalpca).
New in version 0.16.
Parameters:
**n\_components**int, default=None
Number of components to keep. If `n_components` is `None`, then `n_components` is set to `min(n_samples, n_features)`.
**whiten**bool, default=False
When True (False by default) the `components_` vectors are divided by `n_samples` times `components_` to ensure uncorrelated outputs with unit component-wise variances.
Whitening will remove some information from the transformed signal (the relative variance scales of the components) but can sometimes improve the predictive accuracy of the downstream estimators by making data respect some hard-wired assumptions.
**copy**bool, default=True
If False, X will be overwritten. `copy=False` can be used to save memory but is unsafe for general use.
**batch\_size**int, default=None
The number of samples to use for each batch. Only used when calling `fit`. If `batch_size` is `None`, then `batch_size` is inferred from the data and set to `5 * n_features`, to provide a balance between approximation accuracy and memory consumption.
Attributes:
**components\_**ndarray of shape (n\_components, n\_features)
Principal axes in feature space, representing the directions of maximum variance in the data. Equivalently, the right singular vectors of the centered input data, parallel to its eigenvectors. The components are sorted by `explained_variance_`.
**explained\_variance\_**ndarray of shape (n\_components,)
Variance explained by each of the selected components.
**explained\_variance\_ratio\_**ndarray of shape (n\_components,)
Percentage of variance explained by each of the selected components. If all components are stored, the sum of explained variances is equal to 1.0.
**singular\_values\_**ndarray of shape (n\_components,)
The singular values corresponding to each of the selected components. The singular values are equal to the 2-norms of the `n_components` variables in the lower-dimensional space.
**mean\_**ndarray of shape (n\_features,)
Per-feature empirical mean, aggregate over calls to `partial_fit`.
**var\_**ndarray of shape (n\_features,)
Per-feature empirical variance, aggregate over calls to `partial_fit`.
**noise\_variance\_**float
The estimated noise covariance following the Probabilistic PCA model from Tipping and Bishop 1999. See “Pattern Recognition and Machine Learning” by C. Bishop, 12.2.1 p. 574 or <http://www.miketipping.com/papers/met-mppca.pdf>.
**n\_components\_**int
The estimated number of components. Relevant when `n_components=None`.
**n\_samples\_seen\_**int
The number of samples processed by the estimator. Will be reset on new calls to fit, but increments across `partial_fit` calls.
**batch\_size\_**int
Inferred batch size from `batch_size`.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`PCA`](sklearn.decomposition.pca#sklearn.decomposition.PCA "sklearn.decomposition.PCA")
Principal component analysis (PCA).
[`KernelPCA`](sklearn.decomposition.kernelpca#sklearn.decomposition.KernelPCA "sklearn.decomposition.KernelPCA")
Kernel Principal component analysis (KPCA).
[`SparsePCA`](sklearn.decomposition.sparsepca#sklearn.decomposition.SparsePCA "sklearn.decomposition.SparsePCA")
Sparse Principal Components Analysis (SparsePCA).
[`TruncatedSVD`](sklearn.decomposition.truncatedsvd#sklearn.decomposition.TruncatedSVD "sklearn.decomposition.TruncatedSVD")
Dimensionality reduction using truncated SVD.
#### Notes
Implements the incremental PCA model from: *D. Ross, J. Lim, R. Lin, M. Yang, Incremental Learning for Robust Visual Tracking, International Journal of Computer Vision, Volume 77, Issue 1-3, pp. 125-141, May 2008.* See <https://www.cs.toronto.edu/~dross/ivt/RossLimLinYang_ijcv.pdf>
This model is an extension of the Sequential Karhunen-Loeve Transform from: [A. Levy and M. Lindenbaum, Sequential Karhunen-Loeve Basis Extraction and its Application to Images, IEEE Transactions on Image Processing, Volume 9, Number 8, pp. 1371-1374, August 2000.](https://doi.org/10.1109/83.855432)
We have specifically abstained from an optimization used by authors of both papers, a QR decomposition used in specific situations to reduce the algorithmic complexity of the SVD. The source for this technique is *Matrix Computations, Third Edition, G. Holub and C. Van Loan, Chapter 5, section 5.4.4, pp 252-253.*. This technique has been omitted because it is advantageous only when decomposing a matrix with `n_samples` (rows) >= 5/3 \* `n_features` (columns), and hurts the readability of the implemented algorithm. This would be a good opportunity for future optimization, if it is deemed necessary.
#### References
D. Ross, J. Lim, R. Lin, M. Yang. Incremental Learning for Robust Visual Tracking, International Journal of Computer Vision, Volume 77, Issue 1-3, pp. 125-141, May 2008.
G. Golub and C. Van Loan. Matrix Computations, Third Edition, Chapter 5, Section 5.4.4, pp. 252-253.
#### Examples
```
>>> from sklearn.datasets import load_digits
>>> from sklearn.decomposition import IncrementalPCA
>>> from scipy import sparse
>>> X, _ = load_digits(return_X_y=True)
>>> transformer = IncrementalPCA(n_components=7, batch_size=200)
>>> # either partially fit on smaller batches of data
>>> transformer.partial_fit(X[:100, :])
IncrementalPCA(batch_size=200, n_components=7)
>>> # or let the fit function itself divide the data into batches
>>> X_sparse = sparse.csr_matrix(X)
>>> X_transformed = transformer.fit_transform(X_sparse)
>>> X_transformed.shape
(1797, 7)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.decomposition.IncrementalPCA.fit "sklearn.decomposition.IncrementalPCA.fit")(X[, y]) | Fit the model with X, using minibatches of size batch\_size. |
| [`fit_transform`](#sklearn.decomposition.IncrementalPCA.fit_transform "sklearn.decomposition.IncrementalPCA.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_covariance`](#sklearn.decomposition.IncrementalPCA.get_covariance "sklearn.decomposition.IncrementalPCA.get_covariance")() | Compute data covariance with the generative model. |
| [`get_feature_names_out`](#sklearn.decomposition.IncrementalPCA.get_feature_names_out "sklearn.decomposition.IncrementalPCA.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.decomposition.IncrementalPCA.get_params "sklearn.decomposition.IncrementalPCA.get_params")([deep]) | Get parameters for this estimator. |
| [`get_precision`](#sklearn.decomposition.IncrementalPCA.get_precision "sklearn.decomposition.IncrementalPCA.get_precision")() | Compute data precision matrix with the generative model. |
| [`inverse_transform`](#sklearn.decomposition.IncrementalPCA.inverse_transform "sklearn.decomposition.IncrementalPCA.inverse_transform")(X) | Transform data back to its original space. |
| [`partial_fit`](#sklearn.decomposition.IncrementalPCA.partial_fit "sklearn.decomposition.IncrementalPCA.partial_fit")(X[, y, check\_input]) | Incremental fit with X. |
| [`set_params`](#sklearn.decomposition.IncrementalPCA.set_params "sklearn.decomposition.IncrementalPCA.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.decomposition.IncrementalPCA.transform "sklearn.decomposition.IncrementalPCA.transform")(X) | Apply dimensionality reduction to X. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_incremental_pca.py#L186)
Fit the model with X, using minibatches of size batch\_size.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_covariance()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_base.py#L28)
Compute data covariance with the generative model.
`cov = components_.T * S**2 * components_ + sigma2 * eye(n_features)` where S\*\*2 contains the explained variances, and sigma2 contains the noise variances.
Returns:
**cov**array of shape=(n\_features, n\_features)
Estimated covariance of data.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.decomposition.IncrementalPCA.fit "sklearn.decomposition.IncrementalPCA.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
get\_precision()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_base.py#L49)
Compute data precision matrix with the generative model.
Equals the inverse of the covariance but computed with the matrix inversion lemma for efficiency.
Returns:
**precision**array, shape=(n\_features, n\_features)
Estimated precision of data.
inverse\_transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_base.py#L128)
Transform data back to its original space.
In other words, return an input `X_original` whose transform would be X.
Parameters:
**X**array-like of shape (n\_samples, n\_components)
New data, where `n_samples` is the number of samples and `n_components` is the number of components.
Returns:
X\_original array-like of shape (n\_samples, n\_features)
Original data, where `n_samples` is the number of samples and `n_features` is the number of features.
#### Notes
If whitening is enabled, inverse\_transform will compute the exact inverse operation, which includes reversing whitening.
partial\_fit(*X*, *y=None*, *check\_input=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_incremental_pca.py#L235)
Incremental fit with X. All of X is processed as a single batch.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Not used, present for API consistency by convention.
**check\_input**bool, default=True
Run check\_array on X.
Returns:
**self**object
Returns the instance itself.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_incremental_pca.py#L353)
Apply dimensionality reduction to X.
X is projected on the first principal components previously extracted from a training set, using minibatches of size batch\_size if X is sparse.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
New data, where `n_samples` is the number of samples and `n_features` is the number of features.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_components)
Projection of X in the first principal components.
#### Examples
```
>>> import numpy as np
>>> from sklearn.decomposition import IncrementalPCA
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2],
... [1, 1], [2, 1], [3, 2]])
>>> ipca = IncrementalPCA(n_components=2, batch_size=3)
>>> ipca.fit(X)
IncrementalPCA(batch_size=3, n_components=2)
>>> ipca.transform(X)
```
Examples using `sklearn.decomposition.IncrementalPCA`
-----------------------------------------------------
[Incremental PCA](../../auto_examples/decomposition/plot_incremental_pca#sphx-glr-auto-examples-decomposition-plot-incremental-pca-py)
scikit_learn sklearn.linear_model.lars_path_gram sklearn.linear\_model.lars\_path\_gram
======================================
sklearn.linear\_model.lars\_path\_gram(*Xy*, *Gram*, *\**, *n\_samples*, *max\_iter=500*, *alpha\_min=0*, *method='lar'*, *copy\_X=True*, *eps=2.220446049250313e-16*, *copy\_Gram=True*, *verbose=0*, *return\_path=True*, *return\_n\_iter=False*, *positive=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_least_angle.py#L188)
lars\_path in the sufficient stats mode [1]
The optimization objective for the case method=’lasso’ is:
```
(1 / (2 * n_samples)) * ||y - Xw||^2_2 + alpha * ||w||_1
```
in the case of method=’lars’, the objective function is only known in the form of an implicit equation (see discussion in [1])
Read more in the [User Guide](../linear_model#least-angle-regression).
Parameters:
**Xy**array-like of shape (n\_samples,) or (n\_samples, n\_targets)
Xy = np.dot(X.T, y).
**Gram**array-like of shape (n\_features, n\_features)
Gram = np.dot(X.T \* X).
**n\_samples**int or float
Equivalent size of sample.
**max\_iter**int, default=500
Maximum number of iterations to perform, set to infinity for no limit.
**alpha\_min**float, default=0
Minimum correlation along the path. It corresponds to the regularization parameter alpha parameter in the Lasso.
**method**{‘lar’, ‘lasso’}, default=’lar’
Specifies the returned model. Select `'lar'` for Least Angle Regression, `'lasso'` for the Lasso.
**copy\_X**bool, default=True
If `False`, `X` is overwritten.
**eps**float, default=np.finfo(float).eps
The machine-precision regularization in the computation of the Cholesky diagonal factors. Increase this for very ill-conditioned systems. Unlike the `tol` parameter in some iterative optimization-based algorithms, this parameter does not control the tolerance of the optimization.
**copy\_Gram**bool, default=True
If `False`, `Gram` is overwritten.
**verbose**int, default=0
Controls output verbosity.
**return\_path**bool, default=True
If `return_path==True` returns the entire path, else returns only the last point of the path.
**return\_n\_iter**bool, default=False
Whether to return the number of iterations.
**positive**bool, default=False
Restrict coefficients to be >= 0. This option is only allowed with method ‘lasso’. Note that the model coefficients will not converge to the ordinary-least-squares solution for small values of alpha. Only coefficients up to the smallest alpha value (`alphas_[alphas_ > 0.].min()` when fit\_path=True) reached by the stepwise Lars-Lasso algorithm are typically in congruence with the solution of the coordinate descent lasso\_path function.
Returns:
**alphas**array-like of shape (n\_alphas + 1,)
Maximum of covariances (in absolute value) at each iteration. `n_alphas` is either `max_iter`, `n_features` or the number of nodes in the path with `alpha >= alpha_min`, whichever is smaller.
**active**array-like of shape (n\_alphas,)
Indices of active variables at the end of the path.
**coefs**array-like of shape (n\_features, n\_alphas + 1)
Coefficients along the path
**n\_iter**int
Number of iterations run. Returned only if return\_n\_iter is set to True.
See also
[`lars_path`](sklearn.linear_model.lars_path#sklearn.linear_model.lars_path "sklearn.linear_model.lars_path")
[`lasso_path`](sklearn.linear_model.lasso_path#sklearn.linear_model.lasso_path "sklearn.linear_model.lasso_path")
`lasso_path_gram`
[`LassoLars`](sklearn.linear_model.lassolars#sklearn.linear_model.LassoLars "sklearn.linear_model.LassoLars")
[`Lars`](sklearn.linear_model.lars#sklearn.linear_model.Lars "sklearn.linear_model.Lars")
[`LassoLarsCV`](sklearn.linear_model.lassolarscv#sklearn.linear_model.LassoLarsCV "sklearn.linear_model.LassoLarsCV")
[`LarsCV`](sklearn.linear_model.larscv#sklearn.linear_model.LarsCV "sklearn.linear_model.LarsCV")
[`sklearn.decomposition.sparse_encode`](sklearn.decomposition.sparse_encode#sklearn.decomposition.sparse_encode "sklearn.decomposition.sparse_encode")
#### References
[1] “Least Angle Regression”, Efron et al. <http://statweb.stanford.edu/~tibs/ftp/lars.pdf>
[2] [Wikipedia entry on the Least-angle regression](https://en.wikipedia.org/wiki/Least-angle_regression)
[3] [Wikipedia entry on the Lasso](https://en.wikipedia.org/wiki/Lasso_(statistics))
scikit_learn sklearn.cluster.spectral_clustering sklearn.cluster.spectral\_clustering
====================================
sklearn.cluster.spectral\_clustering(*affinity*, *\**, *n\_clusters=8*, *n\_components=None*, *eigen\_solver=None*, *random\_state=None*, *n\_init=10*, *eigen\_tol=0.0*, *assign\_labels='kmeans'*, *verbose=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_spectral.py#L193)
Apply clustering to a projection of the normalized Laplacian.
In practice Spectral Clustering is very useful when the structure of the individual clusters is highly non-convex or more generally when a measure of the center and spread of the cluster is not a suitable description of the complete cluster. For instance, when clusters are nested circles on the 2D plane.
If affinity is the adjacency matrix of a graph, this method can be used to find normalized graph cuts [[1]](#r89dec4780971-1), [[2]](#r89dec4780971-2).
Read more in the [User Guide](../clustering#spectral-clustering).
Parameters:
**affinity**{array-like, sparse matrix} of shape (n\_samples, n\_samples)
The affinity matrix describing the relationship of the samples to embed. **Must be symmetric**.
Possible examples:
* adjacency matrix of a graph,
* heat kernel of the pairwise distance matrix of the samples,
* symmetric k-nearest neighbours connectivity matrix of the samples.
**n\_clusters**int, default=None
Number of clusters to extract.
**n\_components**int, default=n\_clusters
Number of eigenvectors to use for the spectral embedding.
**eigen\_solver**{None, ‘arpack’, ‘lobpcg’, or ‘amg’}
The eigenvalue decomposition method. If None then `'arpack'` is used. See [[4]](#r89dec4780971-4) for more details regarding `'lobpcg'`. Eigensolver `'amg'` runs `'lobpcg'` with optional Algebraic MultiGrid preconditioning and requires pyamg to be installed. It can be faster on very large sparse problems [[6]](#r89dec4780971-6) and [[7]](#r89dec4780971-7).
**random\_state**int, RandomState instance, default=None
A pseudo random number generator used for the initialization of the lobpcg eigenvectors decomposition when `eigen_solver ==
'amg'`, and for the K-Means initialization. Use an int to make the results deterministic across calls (See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state)).
Note
When using `eigen_solver == 'amg'`, it is necessary to also fix the global numpy seed with `np.random.seed(int)` to get deterministic results. See <https://github.com/pyamg/pyamg/issues/139> for further information.
**n\_init**int, default=10
Number of time the k-means algorithm will be run with different centroid seeds. The final results will be the best output of n\_init consecutive runs in terms of inertia. Only used if `assign_labels='kmeans'`.
**eigen\_tol**float, default=0.0
Stopping criterion for eigendecomposition of the Laplacian matrix when using arpack eigen\_solver.
**assign\_labels**{‘kmeans’, ‘discretize’, ‘cluster\_qr’}, default=’kmeans’
The strategy to use to assign labels in the embedding space. There are three ways to assign labels after the Laplacian embedding. k-means can be applied and is a popular choice. But it can also be sensitive to initialization. Discretization is another approach which is less sensitive to random initialization [[3]](#r89dec4780971-3). The cluster\_qr method [[5]](#r89dec4780971-5) directly extracts clusters from eigenvectors in spectral clustering. In contrast to k-means and discretization, cluster\_qr has no tuning parameters and is not an iterative method, yet may outperform k-means and discretization in terms of both quality and speed.
Changed in version 1.1: Added new labeling method ‘cluster\_qr’.
**verbose**bool, default=False
Verbosity mode.
New in version 0.24.
Returns:
**labels**array of integers, shape: n\_samples
The labels of the clusters.
#### Notes
The graph should contain only one connected component, elsewhere the results make little sense.
This algorithm solves the normalized cut for `k=2`: it is a normalized spectral clustering.
#### References
[[1](#id1)] [Normalized cuts and image segmentation, 2000 Jianbo Shi, Jitendra Malik](https://doi.org/10.1109/34.868688)
[[2](#id2)] [A Tutorial on Spectral Clustering, 2007 Ulrike von Luxburg](https://doi.org/10.1007/s11222-007-9033-z)
[[3](#id6)] [Multiclass spectral clustering, 2003 Stella X. Yu, Jianbo Shi](https://www1.icsi.berkeley.edu/~stellayu/publication/doc/2003kwayICCV.pdf)
[[4](#id3)] [Toward the Optimal Preconditioned Eigensolver: Locally Optimal Block Preconditioned Conjugate Gradient Method, 2001 A. V. Knyazev SIAM Journal on Scientific Computing 23, no. 2, pp. 517-541.](https://doi.org/10.1137/S1064827500366124)
[[5](#id7)] [Simple, direct, and efficient multi-way spectral clustering, 2019 Anil Damle, Victor Minden, Lexing Ying](https://doi.org/10.1093/imaiai/iay008)
[[6](#id4)] [Multiscale Spectral Image Segmentation Multiscale preconditioning for computing eigenvalues of graph Laplacians in image segmentation, 2006 Andrew Knyazev](https://doi.org/10.13140/RG.2.2.35280.02565)
[[7](#id5)] [Preconditioned spectral clustering for stochastic block partition streaming graph challenge (Preliminary version at arXiv.) David Zhuzhunashvili, Andrew Knyazev](https://doi.org/10.1109/HPEC.2017.8091045)
Examples using `sklearn.cluster.spectral_clustering`
----------------------------------------------------
[Segmenting the picture of greek coins in regions](../../auto_examples/cluster/plot_coin_segmentation#sphx-glr-auto-examples-cluster-plot-coin-segmentation-py)
[Spectral clustering for image segmentation](../../auto_examples/cluster/plot_segmentation_toy#sphx-glr-auto-examples-cluster-plot-segmentation-toy-py)
| programming_docs |
scikit_learn sklearn.base.is_regressor sklearn.base.is\_regressor
==========================
sklearn.base.is\_regressor(*estimator*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L1017)
Return True if the given estimator is (probably) a regressor.
Parameters:
**estimator**estimator instance
Estimator object to test.
Returns:
**out**bool
True if estimator is a regressor and False otherwise.
scikit_learn sklearn.utils.extmath.randomized_svd sklearn.utils.extmath.randomized\_svd
=====================================
sklearn.utils.extmath.randomized\_svd(*M*, *n\_components*, *\**, *n\_oversamples=10*, *n\_iter='auto'*, *power\_iteration\_normalizer='auto'*, *transpose='auto'*, *flip\_sign=True*, *random\_state='warn'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/extmath.py#L250)
Computes a truncated randomized SVD.
This method solves the fixed-rank approximation problem described in the Halko et al paper (problem (1.5), p5).
Parameters:
**M**{ndarray, sparse matrix}
Matrix to decompose.
**n\_components**int
Number of singular values and vectors to extract.
**n\_oversamples**int, default=10
Additional number of random vectors to sample the range of M so as to ensure proper conditioning. The total number of random vectors used to find the range of M is n\_components + n\_oversamples. Smaller number can improve speed but can negatively impact the quality of approximation of singular vectors and singular values. Users might wish to increase this parameter up to `2*k - n_components` where k is the effective rank, for large matrices, noisy problems, matrices with slowly decaying spectrums, or to increase precision accuracy. See Halko et al (pages 5, 23 and 26).
**n\_iter**int or ‘auto’, default=’auto’
Number of power iterations. It can be used to deal with very noisy problems. When ‘auto’, it is set to 4, unless `n_components` is small (< .1 \* min(X.shape)) in which case `n_iter` is set to 7. This improves precision with few components. Note that in general users should rather increase `n_oversamples` before increasing `n_iter` as the principle of the randomized method is to avoid usage of these more costly power iterations steps. When `n_components` is equal or greater to the effective matrix rank and the spectrum does not present a slow decay, `n_iter=0` or `1` should even work fine in theory (see Halko et al paper, page 9).
Changed in version 0.18.
**power\_iteration\_normalizer**{‘auto’, ‘QR’, ‘LU’, ‘none’}, default=’auto’
Whether the power iterations are normalized with step-by-step QR factorization (the slowest but most accurate), ‘none’ (the fastest but numerically unstable when `n_iter` is large, e.g. typically 5 or larger), or ‘LU’ factorization (numerically stable but can lose slightly in accuracy). The ‘auto’ mode applies no normalization if `n_iter` <= 2 and switches to LU otherwise.
New in version 0.18.
**transpose**bool or ‘auto’, default=’auto’
Whether the algorithm should be applied to M.T instead of M. The result should approximately be the same. The ‘auto’ mode will trigger the transposition if M.shape[1] > M.shape[0] since this implementation of randomized SVD tend to be a little faster in that case.
Changed in version 0.18.
**flip\_sign**bool, default=True
The output of a singular value decomposition is only unique up to a permutation of the signs of the singular vectors. If `flip_sign` is set to `True`, the sign ambiguity is resolved by making the largest loadings for each component in the left singular vectors positive.
**random\_state**int, RandomState instance or None, default=’warn’
The seed of the pseudo random number generator to use when shuffling the data, i.e. getting the random vectors to initialize the algorithm. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Changed in version 1.2: The previous behavior (`random_state=0`) is deprecated, and from v1.2 the default value will be `random_state=None`. Set the value of `random_state` explicitly to suppress the deprecation warning.
#### Notes
This algorithm finds a (usually very good) approximate truncated singular value decomposition using randomization to speed up the computations. It is particularly fast on large matrices on which you wish to extract only a small number of components. In order to obtain further speed up, `n_iter` can be set <=2 (at the cost of loss of precision). To increase the precision it is recommended to increase `n_oversamples`, up to `2*k-n_components` where k is the effective rank. Usually, `n_components` is chosen to be greater than k so increasing `n_oversamples` up to `n_components` should be enough.
#### References
* [“Finding structure with randomness: Stochastic algorithms for constructing approximate matrix decompositions”](https://arxiv.org/abs/0909.4061) Halko, et al. (2009)
* A randomized algorithm for the decomposition of matrices Per-Gunnar Martinsson, Vladimir Rokhlin and Mark Tygert
* An implementation of a randomized algorithm for principal component analysis A. Szlam et al. 2014
scikit_learn sklearn.datasets.load_wine sklearn.datasets.load\_wine
===========================
sklearn.datasets.load\_wine(*\**, *return\_X\_y=False*, *as\_frame=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_base.py#L429)
Load and return the wine dataset (classification).
New in version 0.18.
The wine dataset is a classic and very easy multi-class classification dataset.
| | |
| --- | --- |
| Classes | 3 |
| Samples per class | [59,71,48] |
| Samples total | 178 |
| Dimensionality | 13 |
| Features | real, positive |
The copy of UCI ML Wine Data Set dataset is downloaded and modified to fit standard format from: <https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data>
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/toy_dataset.html#wine-dataset).
Parameters:
**return\_X\_y**bool, default=False
If True, returns `(data, target)` instead of a Bunch object. See below for more information about the `data` and `target` object.
**as\_frame**bool, default=False
If True, the data is a pandas DataFrame including columns with appropriate dtypes (numeric). The target is a pandas DataFrame or Series depending on the number of target columns. If `return_X_y` is True, then (`data`, `target`) will be pandas DataFrames or Series as described below.
New in version 0.23.
Returns:
**data**[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
Dictionary-like object, with the following attributes.
data{ndarray, dataframe} of shape (178, 13)
The data matrix. If `as_frame=True`, `data` will be a pandas DataFrame.
target: {ndarray, Series} of shape (178,)
The classification target. If `as_frame=True`, `target` will be a pandas Series.
feature\_names: list
The names of the dataset columns.
target\_names: list
The names of target classes.
frame: DataFrame of shape (178, 14)
Only present when `as_frame=True`. DataFrame with `data` and `target`.
New in version 0.23.
DESCR: str
The full description of the dataset.
**(data, target)**tuple if `return_X_y` is True
A tuple of two ndarrays by default. The first contains a 2D array of shape (178, 13) with each row representing one sample and each column representing the features. The second array of shape (178,) contains the target samples.
#### Examples
Let’s say you are interested in the samples 10, 80, and 140, and want to know their class name.
```
>>> from sklearn.datasets import load_wine
>>> data = load_wine()
>>> data.target[[10, 80, 140]]
array([0, 1, 2])
>>> list(data.target_names)
['class_0', 'class_1', 'class_2']
```
Examples using `sklearn.datasets.load_wine`
-------------------------------------------
[Outlier detection on a real data set](../../auto_examples/applications/plot_outlier_detection_wine#sphx-glr-auto-examples-applications-plot-outlier-detection-wine-py)
[ROC Curve with Visualization API](../../auto_examples/miscellaneous/plot_roc_curve_visualization_api#sphx-glr-auto-examples-miscellaneous-plot-roc-curve-visualization-api-py)
[Importance of Feature Scaling](../../auto_examples/preprocessing/plot_scaling_importance#sphx-glr-auto-examples-preprocessing-plot-scaling-importance-py)
scikit_learn sklearn.datasets.load_svmlight_files sklearn.datasets.load\_svmlight\_files
======================================
sklearn.datasets.load\_svmlight\_files(*files*, *\**, *n\_features=None*, *dtype=<class 'numpy.float64'>*, *multilabel=False*, *zero\_based='auto'*, *query\_id=False*, *offset=0*, *length=-1*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_svmlight_format_io.py#L219)
Load dataset from multiple files in SVMlight format
This function is equivalent to mapping load\_svmlight\_file over a list of files, except that the results are concatenated into a single, flat list and the samples vectors are constrained to all have the same number of features.
In case the file contains a pairwise preference constraint (known as “qid” in the svmlight format) these are ignored unless the query\_id parameter is set to True. These pairwise preference constraints can be used to constraint the combination of samples when using pairwise loss functions (as is the case in some learning to rank problems) so that only pairs with the same query\_id value are considered.
Parameters:
**files**array-like, dtype=str, file-like or int
(Paths of) files to load. If a path ends in “.gz” or “.bz2”, it will be uncompressed on the fly. If an integer is passed, it is assumed to be a file descriptor. File-likes and file descriptors will not be closed by this function. File-like objects must be opened in binary mode.
**n\_features**int, default=None
The number of features to use. If None, it will be inferred from the maximum column index occurring in any of the files.
This can be set to a higher value than the actual number of features in any of the input files, but setting it to a lower value will cause an exception to be raised.
**dtype**numpy data type, default=np.float64
Data type of dataset to be loaded. This will be the data type of the output numpy arrays `X` and `y`.
**multilabel**bool, default=False
Samples may have several labels each (see <https://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/multilabel.html>)
**zero\_based**bool or “auto”, default=”auto”
Whether column indices in f are zero-based (True) or one-based (False). If column indices are one-based, they are transformed to zero-based to match Python/NumPy conventions. If set to “auto”, a heuristic check is applied to determine this from the file contents. Both kinds of files occur “in the wild”, but they are unfortunately not self-identifying. Using “auto” or True should always be safe when no offset or length is passed. If offset or length are passed, the “auto” mode falls back to zero\_based=True to avoid having the heuristic check yield inconsistent results on different segments of the file.
**query\_id**bool, default=False
If True, will return the query\_id array for each file.
**offset**int, default=0
Ignore the offset first bytes by seeking forward, then discarding the following bytes up until the next new line character.
**length**int, default=-1
If strictly positive, stop reading any new line of data once the position in the file has reached the (offset + length) bytes threshold.
Returns:
[X1, y1, …, Xn, yn]
where each (Xi, yi) pair is the result from load\_svmlight\_file(files[i]).
If query\_id is set to True, this will return instead [X1, y1, q1,
…, Xn, yn, qn] where (Xi, yi, qi) is the result from
load\_svmlight\_file(files[i])
See also
[`load_svmlight_file`](sklearn.datasets.load_svmlight_file#sklearn.datasets.load_svmlight_file "sklearn.datasets.load_svmlight_file")
#### Notes
When fitting a model to a matrix X\_train and evaluating it against a matrix X\_test, it is essential that X\_train and X\_test have the same number of features (X\_train.shape[1] == X\_test.shape[1]). This may not be the case if you load the files individually with load\_svmlight\_file.
scikit_learn sklearn.model_selection.learning_curve sklearn.model\_selection.learning\_curve
========================================
sklearn.model\_selection.learning\_curve(*estimator*, *X*, *y*, *\**, *groups=None*, *train\_sizes=array([0.1, 0.33, 0.55, 0.78, 1.])*, *cv=None*, *scoring=None*, *exploit\_incremental\_learning=False*, *n\_jobs=None*, *pre\_dispatch='all'*, *verbose=0*, *shuffle=False*, *random\_state=None*, *error\_score=nan*, *return\_times=False*, *fit\_params=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_validation.py#L1350)
Learning curve.
Determines cross-validated training and test scores for different training set sizes.
A cross-validation generator splits the whole dataset k times in training and test data. Subsets of the training set with varying sizes will be used to train the estimator and a score for each training subset size and the test set will be computed. Afterwards, the scores will be averaged over all k runs for each training subset size.
Read more in the [User Guide](../learning_curve#learning-curve).
Parameters:
**estimator**object type that implements the “fit” and “predict” methods
An object of that type which is cloned for each validation.
**X**array-like of shape (n\_samples, n\_features)
Training vector, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
Target relative to X for classification or regression; None for unsupervised learning.
**groups**array-like of shape (n\_samples,), default=None
Group labels for the samples used while splitting the dataset into train/test set. Only used in conjunction with a “Group” [cv](https://scikit-learn.org/1.1/glossary.html#term-cv) instance (e.g., [`GroupKFold`](sklearn.model_selection.groupkfold#sklearn.model_selection.GroupKFold "sklearn.model_selection.GroupKFold")).
**train\_sizes**array-like of shape (n\_ticks,), default=np.linspace(0.1, 1.0, 5)
Relative or absolute numbers of training examples that will be used to generate the learning curve. If the dtype is float, it is regarded as a fraction of the maximum size of the training set (that is determined by the selected validation method), i.e. it has to be within (0, 1]. Otherwise it is interpreted as absolute sizes of the training sets. Note that for classification the number of samples usually have to be big enough to contain at least one sample from each class.
**cv**int, cross-validation generator or an iterable, default=None
Determines the cross-validation splitting strategy. Possible inputs for cv are:
* None, to use the default 5-fold cross validation,
* int, to specify the number of folds in a `(Stratified)KFold`,
* [CV splitter](https://scikit-learn.org/1.1/glossary.html#term-CV-splitter),
* An iterable yielding (train, test) splits as arrays of indices.
For int/None inputs, if the estimator is a classifier and `y` is either binary or multiclass, [`StratifiedKFold`](sklearn.model_selection.stratifiedkfold#sklearn.model_selection.StratifiedKFold "sklearn.model_selection.StratifiedKFold") is used. In all other cases, [`KFold`](sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold") is used. These splitters are instantiated with `shuffle=False` so the splits will be the same across calls.
Refer [User Guide](../cross_validation#cross-validation) for the various cross-validation strategies that can be used here.
Changed in version 0.22: `cv` default value if None changed from 3-fold to 5-fold.
**scoring**str or callable, default=None
A str (see model evaluation documentation) or a scorer callable object / function with signature `scorer(estimator, X, y)`.
**exploit\_incremental\_learning**bool, default=False
If the estimator supports incremental learning, this will be used to speed up fitting for different training set sizes.
**n\_jobs**int, default=None
Number of jobs to run in parallel. Training the estimator and computing the score are parallelized over the different training and test sets. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**pre\_dispatch**int or str, default=’all’
Number of predispatched jobs for parallel execution (default is all). The option can reduce the allocated memory. The str can be an expression like ‘2\*n\_jobs’.
**verbose**int, default=0
Controls the verbosity: the higher, the more messages.
**shuffle**bool, default=False
Whether to shuffle training data before taking prefixes of it based on``train\_sizes``.
**random\_state**int, RandomState instance or None, default=None
Used when `shuffle` is True. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**error\_score**‘raise’ or numeric, default=np.nan
Value to assign to the score if an error occurs in estimator fitting. If set to ‘raise’, the error is raised. If a numeric value is given, FitFailedWarning is raised.
New in version 0.20.
**return\_times**bool, default=False
Whether to return the fit and score times.
**fit\_params**dict, default=None
Parameters to pass to the fit method of the estimator.
New in version 0.24.
Returns:
**train\_sizes\_abs**array of shape (n\_unique\_ticks,)
Numbers of training examples that has been used to generate the learning curve. Note that the number of ticks might be less than n\_ticks because duplicate entries will be removed.
**train\_scores**array of shape (n\_ticks, n\_cv\_folds)
Scores on training sets.
**test\_scores**array of shape (n\_ticks, n\_cv\_folds)
Scores on test set.
**fit\_times**array of shape (n\_ticks, n\_cv\_folds)
Times spent for fitting in seconds. Only present if `return_times` is True.
**score\_times**array of shape (n\_ticks, n\_cv\_folds)
Times spent for scoring in seconds. Only present if `return_times` is True.
#### Notes
See [examples/model\_selection/plot\_learning\_curve.py](../../auto_examples/model_selection/plot_learning_curve#sphx-glr-auto-examples-model-selection-plot-learning-curve-py)
Examples using `sklearn.model_selection.learning_curve`
-------------------------------------------------------
[Comparison of kernel ridge regression and SVR](../../auto_examples/miscellaneous/plot_kernel_ridge_regression#sphx-glr-auto-examples-miscellaneous-plot-kernel-ridge-regression-py)
[Plotting Learning Curves](../../auto_examples/model_selection/plot_learning_curve#sphx-glr-auto-examples-model-selection-plot-learning-curve-py)
scikit_learn sklearn.utils.assert_all_finite sklearn.utils.assert\_all\_finite
=================================
sklearn.utils.assert\_all\_finite(*X*, *\**, *allow\_nan=False*, *estimator\_name=None*, *input\_name=''*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/validation.py#L154)
Throw a ValueError if X contains NaN or infinity.
Parameters:
**X**{ndarray, sparse matrix}
The input data.
**allow\_nan**bool, default=False
If True, do not throw error when `X` contains NaN.
**estimator\_name**str, default=None
The estimator name, used to construct the error message.
**input\_name**str, default=””
The data name used to construct the error message. In particular if `input_name` is “X” and the data has NaN values and allow\_nan is False, the error message will link to the imputer documentation.
| programming_docs |
scikit_learn sklearn.linear_model.LinearRegression sklearn.linear\_model.LinearRegression
======================================
*class*sklearn.linear\_model.LinearRegression(*\**, *fit\_intercept=True*, *normalize='deprecated'*, *copy\_X=True*, *n\_jobs=None*, *positive=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L529)
Ordinary least squares Linear Regression.
LinearRegression fits a linear model with coefficients w = (w1, …, wp) to minimize the residual sum of squares between the observed targets in the dataset, and the targets predicted by the linear approximation.
Parameters:
**fit\_intercept**bool, default=True
Whether to calculate the intercept for this model. If set to False, no intercept will be used in calculations (i.e. data is expected to be centered).
**normalize**bool, default=False
This parameter is ignored when `fit_intercept` is set to False. If True, the regressors X will be normalized before regression by subtracting the mean and dividing by the l2-norm. If you wish to standardize, please use [`StandardScaler`](sklearn.preprocessing.standardscaler#sklearn.preprocessing.StandardScaler "sklearn.preprocessing.StandardScaler") before calling `fit` on an estimator with `normalize=False`.
Deprecated since version 1.0: `normalize` was deprecated in version 1.0 and will be removed in 1.2.
**copy\_X**bool, default=True
If True, X will be copied; else, it may be overwritten.
**n\_jobs**int, default=None
The number of jobs to use for the computation. This will only provide speedup in case of sufficiently large problems, that is if firstly `n_targets > 1` and secondly `X` is sparse or if `positive` is set to `True`. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**positive**bool, default=False
When set to `True`, forces the coefficients to be positive. This option is only supported for dense arrays.
New in version 0.24.
Attributes:
**coef\_**array of shape (n\_features, ) or (n\_targets, n\_features)
Estimated coefficients for the linear regression problem. If multiple targets are passed during the fit (y 2D), this is a 2D array of shape (n\_targets, n\_features), while if only one target is passed, this is a 1D array of length n\_features.
**rank\_**int
Rank of matrix `X`. Only available when `X` is dense.
**singular\_**array of shape (min(X, y),)
Singular values of `X`. Only available when `X` is dense.
**intercept\_**float or array of shape (n\_targets,)
Independent term in the linear model. Set to 0.0 if `fit_intercept = False`.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`Ridge`](sklearn.linear_model.ridge#sklearn.linear_model.Ridge "sklearn.linear_model.Ridge")
Ridge regression addresses some of the problems of Ordinary Least Squares by imposing a penalty on the size of the coefficients with l2 regularization.
[`Lasso`](sklearn.linear_model.lasso#sklearn.linear_model.Lasso "sklearn.linear_model.Lasso")
The Lasso is a linear model that estimates sparse coefficients with l1 regularization.
[`ElasticNet`](sklearn.linear_model.elasticnet#sklearn.linear_model.ElasticNet "sklearn.linear_model.ElasticNet")
Elastic-Net is a linear regression model trained with both l1 and l2 -norm regularization of the coefficients.
#### Notes
From the implementation point of view, this is just plain Ordinary Least Squares (scipy.linalg.lstsq) or Non Negative Least Squares (scipy.optimize.nnls) wrapped as a predictor object.
#### Examples
```
>>> import numpy as np
>>> from sklearn.linear_model import LinearRegression
>>> X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
>>> # y = 1 * x_0 + 2 * x_1 + 3
>>> y = np.dot(X, np.array([1, 2])) + 3
>>> reg = LinearRegression().fit(X, y)
>>> reg.score(X, y)
1.0
>>> reg.coef_
array([1., 2.])
>>> reg.intercept_
3.0...
>>> reg.predict(np.array([[3, 5]]))
array([16.])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.linear_model.LinearRegression.fit "sklearn.linear_model.LinearRegression.fit")(X, y[, sample\_weight]) | Fit linear model. |
| [`get_params`](#sklearn.linear_model.LinearRegression.get_params "sklearn.linear_model.LinearRegression.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.linear_model.LinearRegression.predict "sklearn.linear_model.LinearRegression.predict")(X) | Predict using the linear model. |
| [`score`](#sklearn.linear_model.LinearRegression.score "sklearn.linear_model.LinearRegression.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.linear_model.LinearRegression.set_params "sklearn.linear_model.LinearRegression.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L652)
Fit linear model.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training data.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_targets)
Target values. Will be cast to X’s dtype if necessary.
**sample\_weight**array-like of shape (n\_samples,), default=None
Individual weights for each sample.
New in version 0.17: parameter *sample\_weight* support to LinearRegression.
Returns:
**self**object
Fitted Estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L372)
Predict using the linear model.
Parameters:
**X**array-like or sparse matrix, shape (n\_samples, n\_features)
Samples.
Returns:
**C**array, shape (n\_samples,)
Returns predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.linear_model.LinearRegression`
------------------------------------------------------
[Principal Component Regression vs Partial Least Squares Regression](../../auto_examples/cross_decomposition/plot_pcr_vs_pls#sphx-glr-auto-examples-cross-decomposition-plot-pcr-vs-pls-py)
[Plot individual and voting regression predictions](../../auto_examples/ensemble/plot_voting_regressor#sphx-glr-auto-examples-ensemble-plot-voting-regressor-py)
[Comparing Linear Bayesian Regressors](../../auto_examples/linear_model/plot_ard#sphx-glr-auto-examples-linear-model-plot-ard-py)
[Linear Regression Example](../../auto_examples/linear_model/plot_ols#sphx-glr-auto-examples-linear-model-plot-ols-py)
[Logistic function](../../auto_examples/linear_model/plot_logistic#sphx-glr-auto-examples-linear-model-plot-logistic-py)
[Non-negative least squares](../../auto_examples/linear_model/plot_nnls#sphx-glr-auto-examples-linear-model-plot-nnls-py)
[Ordinary Least Squares and Ridge Regression Variance](../../auto_examples/linear_model/plot_ols_ridge_variance#sphx-glr-auto-examples-linear-model-plot-ols-ridge-variance-py)
[Quantile regression](../../auto_examples/linear_model/plot_quantile_regression#sphx-glr-auto-examples-linear-model-plot-quantile-regression-py)
[Robust linear estimator fitting](../../auto_examples/linear_model/plot_robust_fit#sphx-glr-auto-examples-linear-model-plot-robust-fit-py)
[Robust linear model estimation using RANSAC](../../auto_examples/linear_model/plot_ransac#sphx-glr-auto-examples-linear-model-plot-ransac-py)
[Sparsity Example: Fitting only features 1 and 2](../../auto_examples/linear_model/plot_ols_3d#sphx-glr-auto-examples-linear-model-plot-ols-3d-py)
[Theil-Sen Regression](../../auto_examples/linear_model/plot_theilsen#sphx-glr-auto-examples-linear-model-plot-theilsen-py)
[Face completion with a multi-output estimators](../../auto_examples/miscellaneous/plot_multioutput_face_completion#sphx-glr-auto-examples-miscellaneous-plot-multioutput-face-completion-py)
[Isotonic Regression](../../auto_examples/miscellaneous/plot_isotonic_regression#sphx-glr-auto-examples-miscellaneous-plot-isotonic-regression-py)
[Plotting Cross-Validated Predictions](../../auto_examples/model_selection/plot_cv_predict#sphx-glr-auto-examples-model-selection-plot-cv-predict-py)
[Underfitting vs. Overfitting](../../auto_examples/model_selection/plot_underfitting_overfitting#sphx-glr-auto-examples-model-selection-plot-underfitting-overfitting-py)
[Using KBinsDiscretizer to discretize continuous features](../../auto_examples/preprocessing/plot_discretization#sphx-glr-auto-examples-preprocessing-plot-discretization-py)
scikit_learn sklearn.preprocessing.quantile_transform sklearn.preprocessing.quantile\_transform
=========================================
sklearn.preprocessing.quantile\_transform(*X*, *\**, *axis=0*, *n\_quantiles=1000*, *output\_distribution='uniform'*, *ignore\_implicit\_zeros=False*, *subsample=100000*, *random\_state=None*, *copy=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L2776)
Transform features using quantiles information.
This method transforms the features to follow a uniform or a normal distribution. Therefore, for a given feature, this transformation tends to spread out the most frequent values. It also reduces the impact of (marginal) outliers: this is therefore a robust preprocessing scheme.
The transformation is applied on each feature independently. First an estimate of the cumulative distribution function of a feature is used to map the original values to a uniform distribution. The obtained values are then mapped to the desired output distribution using the associated quantile function. Features values of new/unseen data that fall below or above the fitted range will be mapped to the bounds of the output distribution. Note that this transform is non-linear. It may distort linear correlations between variables measured at the same scale but renders variables measured at different scales more directly comparable.
Read more in the [User Guide](../preprocessing#preprocessing-transformer).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data to transform.
**axis**int, default=0
Axis used to compute the means and standard deviations along. If 0, transform each feature, otherwise (if 1) transform each sample.
**n\_quantiles**int, default=1000 or n\_samples
Number of quantiles to be computed. It corresponds to the number of landmarks used to discretize the cumulative distribution function. If n\_quantiles is larger than the number of samples, n\_quantiles is set to the number of samples as a larger number of quantiles does not give a better approximation of the cumulative distribution function estimator.
**output\_distribution**{‘uniform’, ‘normal’}, default=’uniform’
Marginal distribution for the transformed data. The choices are ‘uniform’ (default) or ‘normal’.
**ignore\_implicit\_zeros**bool, default=False
Only applies to sparse matrices. If True, the sparse entries of the matrix are discarded to compute the quantile statistics. If False, these entries are treated as zeros.
**subsample**int, default=1e5
Maximum number of samples used to estimate the quantiles for computational efficiency. Note that the subsampling procedure may differ for value-identical sparse and dense matrices.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for subsampling and smoothing noise. Please see `subsample` for more details. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**copy**bool, default=True
Set to False to perform inplace transformation and avoid a copy (if the input is already a numpy array). If True, a copy of `X` is transformed, leaving the original `X` unchanged
..versionchanged:: 0.23
The default value of `copy` changed from False to True in 0.23.
Returns:
**Xt**{ndarray, sparse matrix} of shape (n\_samples, n\_features)
The transformed data.
See also
[`QuantileTransformer`](sklearn.preprocessing.quantiletransformer#sklearn.preprocessing.QuantileTransformer "sklearn.preprocessing.QuantileTransformer")
Performs quantile-based scaling using the Transformer API (e.g. as part of a preprocessing [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")).
[`power_transform`](sklearn.preprocessing.power_transform#sklearn.preprocessing.power_transform "sklearn.preprocessing.power_transform")
Maps data to a normal distribution using a power transformation.
[`scale`](sklearn.preprocessing.scale#sklearn.preprocessing.scale "sklearn.preprocessing.scale")
Performs standardization that is faster, but less robust to outliers.
[`robust_scale`](sklearn.preprocessing.robust_scale#sklearn.preprocessing.robust_scale "sklearn.preprocessing.robust_scale")
Performs robust standardization that removes the influence of outliers but does not put outliers and inliers on the same scale.
#### Notes
NaNs are treated as missing values: disregarded in fit, and maintained in transform.
Warning
Risk of data leak
Do not use [`quantile_transform`](#sklearn.preprocessing.quantile_transform "sklearn.preprocessing.quantile_transform") unless you know what you are doing. A common mistake is to apply it to the entire data *before* splitting into training and test sets. This will bias the model evaluation because information would have leaked from the test set to the training set. In general, we recommend using [`QuantileTransformer`](sklearn.preprocessing.quantiletransformer#sklearn.preprocessing.QuantileTransformer "sklearn.preprocessing.QuantileTransformer") within a [Pipeline](../compose#pipeline) in order to prevent most risks of data leaking:`pipe = make_pipeline(QuantileTransformer(),
LogisticRegression())`.
For a comparison of the different scalers, transformers, and normalizers, see [examples/preprocessing/plot\_all\_scaling.py](../../auto_examples/preprocessing/plot_all_scaling#sphx-glr-auto-examples-preprocessing-plot-all-scaling-py).
#### Examples
```
>>> import numpy as np
>>> from sklearn.preprocessing import quantile_transform
>>> rng = np.random.RandomState(0)
>>> X = np.sort(rng.normal(loc=0.5, scale=0.25, size=(25, 1)), axis=0)
>>> quantile_transform(X, n_quantiles=10, random_state=0, copy=True)
array([...])
```
Examples using `sklearn.preprocessing.quantile_transform`
---------------------------------------------------------
[Effect of transforming the targets in regression model](../../auto_examples/compose/plot_transformed_target#sphx-glr-auto-examples-compose-plot-transformed-target-py)
scikit_learn sklearn.utils.extmath.safe_sparse_dot sklearn.utils.extmath.safe\_sparse\_dot
=======================================
sklearn.utils.extmath.safe\_sparse\_dot(*a*, *b*, *\**, *dense\_output=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/extmath.py#L119)
Dot product that handle the sparse matrix case correctly.
Parameters:
**a**{ndarray, sparse matrix}
**b**{ndarray, sparse matrix}
**dense\_output**bool, default=False
When False, `a` and `b` both being sparse will yield sparse output. When True, output will always be a dense array.
Returns:
**dot\_product**{ndarray, sparse matrix}
Sparse if `a` and `b` are sparse and `dense_output=False`.
scikit_learn sklearn.model_selection.LeaveOneGroupOut sklearn.model\_selection.LeaveOneGroupOut
=========================================
*class*sklearn.model\_selection.LeaveOneGroupOut[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L1110)
Leave One Group Out cross-validator
Provides train/test indices to split data according to a third-party provided group. This group information can be used to encode arbitrary domain specific stratifications of the samples as integers.
For instance the groups could be the year of collection of the samples and thus allow for cross-validation against time-based splits.
Read more in the [User Guide](../cross_validation#leave-one-group-out).
See also
[`GroupKFold`](sklearn.model_selection.groupkfold#sklearn.model_selection.GroupKFold "sklearn.model_selection.GroupKFold")
K-fold iterator variant with non-overlapping groups.
#### Notes
Splits are ordered according to the index of the group left out. The first split has training set consting of the group whose index in `groups` is lowest, and so on.
#### Examples
```
>>> import numpy as np
>>> from sklearn.model_selection import LeaveOneGroupOut
>>> X = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
>>> y = np.array([1, 2, 1, 2])
>>> groups = np.array([1, 1, 2, 2])
>>> logo = LeaveOneGroupOut()
>>> logo.get_n_splits(X, y, groups)
2
>>> logo.get_n_splits(groups=groups) # 'groups' is always required
2
>>> print(logo)
LeaveOneGroupOut()
>>> for train_index, test_index in logo.split(X, y, groups):
... print("TRAIN:", train_index, "TEST:", test_index)
... X_train, X_test = X[train_index], X[test_index]
... y_train, y_test = y[train_index], y[test_index]
... print(X_train, X_test, y_train, y_test)
TRAIN: [2 3] TEST: [0 1]
[[5 6]
[7 8]] [[1 2]
[3 4]] [1 2] [1 2]
TRAIN: [0 1] TEST: [2 3]
[[1 2]
[3 4]] [[5 6]
[7 8]] [1 2] [1 2]
```
#### Methods
| | |
| --- | --- |
| [`get_n_splits`](#sklearn.model_selection.LeaveOneGroupOut.get_n_splits "sklearn.model_selection.LeaveOneGroupOut.get_n_splits")([X, y, groups]) | Returns the number of splitting iterations in the cross-validator |
| [`split`](#sklearn.model_selection.LeaveOneGroupOut.split "sklearn.model_selection.LeaveOneGroupOut.split")(X[, y, groups]) | Generate indices to split data into training and test set. |
get\_n\_splits(*X=None*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L1177)
Returns the number of splitting iterations in the cross-validator
Parameters:
**X**object
Always ignored, exists for compatibility.
**y**object
Always ignored, exists for compatibility.
**groups**array-like of shape (n\_samples,)
Group labels for the samples used while splitting the dataset into train/test set. This ‘groups’ parameter must always be specified to calculate the number of splits, though the other parameters can be omitted.
Returns:
**n\_splits**int
Returns the number of splitting iterations in the cross-validator.
split(*X*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L1204)
Generate indices to split data into training and test set.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,), default=None
The target variable for supervised learning problems.
**groups**array-like of shape (n\_samples,)
Group labels for the samples used while splitting the dataset into train/test set.
Yields:
**train**ndarray
The training set indices for that split.
**test**ndarray
The testing set indices for that split.
| programming_docs |
scikit_learn sklearn.cluster.FeatureAgglomeration sklearn.cluster.FeatureAgglomeration
====================================
*class*sklearn.cluster.FeatureAgglomeration(*n\_clusters=2*, *\**, *affinity='euclidean'*, *memory=None*, *connectivity=None*, *compute\_full\_tree='auto'*, *linkage='ward'*, *pooling\_func=<function mean>*, *distance\_threshold=None*, *compute\_distances=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_agglomerative.py#L1054)
Agglomerate features.
Recursively merges pair of clusters of features.
Read more in the [User Guide](../clustering#hierarchical-clustering).
Parameters:
**n\_clusters**int, default=2
The number of clusters to find. It must be `None` if `distance_threshold` is not `None`.
**affinity**str or callable, default=’euclidean’
Metric used to compute the linkage. Can be “euclidean”, “l1”, “l2”, “manhattan”, “cosine”, or ‘precomputed’. If linkage is “ward”, only “euclidean” is accepted.
**memory**str or object with the joblib.Memory interface, default=None
Used to cache the output of the computation of the tree. By default, no caching is done. If a string is given, it is the path to the caching directory.
**connectivity**array-like or callable, default=None
Connectivity matrix. Defines for each feature the neighboring features following a given structure of the data. This can be a connectivity matrix itself or a callable that transforms the data into a connectivity matrix, such as derived from `kneighbors_graph`. Default is `None`, i.e, the hierarchical clustering algorithm is unstructured.
**compute\_full\_tree**‘auto’ or bool, default=’auto’
Stop early the construction of the tree at `n_clusters`. This is useful to decrease computation time if the number of clusters is not small compared to the number of features. This option is useful only when specifying a connectivity matrix. Note also that when varying the number of clusters and using caching, it may be advantageous to compute the full tree. It must be `True` if `distance_threshold` is not `None`. By default `compute_full_tree` is “auto”, which is equivalent to `True` when `distance_threshold` is not `None` or that `n_clusters` is inferior to the maximum between 100 or `0.02 * n_samples`. Otherwise, “auto” is equivalent to `False`.
**linkage**{“ward”, “complete”, “average”, “single”}, default=”ward”
Which linkage criterion to use. The linkage criterion determines which distance to use between sets of features. The algorithm will merge the pairs of cluster that minimize this criterion.
* “ward” minimizes the variance of the clusters being merged.
* “complete” or maximum linkage uses the maximum distances between all features of the two sets.
* “average” uses the average of the distances of each feature of the two sets.
* “single” uses the minimum of the distances between all features of the two sets.
**pooling\_func**callable, default=np.mean
This combines the values of agglomerated features into a single value, and should accept an array of shape [M, N] and the keyword argument `axis=1`, and reduce it to an array of size [M].
**distance\_threshold**float, default=None
The linkage distance threshold above which, clusters will not be merged. If not `None`, `n_clusters` must be `None` and `compute_full_tree` must be `True`.
New in version 0.21.
**compute\_distances**bool, default=False
Computes distances between clusters even if `distance_threshold` is not used. This can be used to make dendrogram visualization, but introduces a computational and memory overhead.
New in version 0.24.
Attributes:
**n\_clusters\_**int
The number of clusters found by the algorithm. If `distance_threshold=None`, it will be equal to the given `n_clusters`.
**labels\_**array-like of (n\_features,)
Cluster labels for each feature.
**n\_leaves\_**int
Number of leaves in the hierarchical tree.
**n\_connected\_components\_**int
The estimated number of connected components in the graph.
New in version 0.21: `n_connected_components_` was added to replace `n_components_`.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**children\_**array-like of shape (n\_nodes-1, 2)
The children of each non-leaf node. Values less than `n_features` correspond to leaves of the tree which are the original samples. A node `i` greater than or equal to `n_features` is a non-leaf node and has children `children_[i - n_features]`. Alternatively at the i-th iteration, children[i][0] and children[i][1] are merged to form node `n_features + i`.
**distances\_**array-like of shape (n\_nodes-1,)
Distances between nodes in the corresponding place in `children_`. Only computed if `distance_threshold` is used or `compute_distances` is set to `True`.
See also
[`AgglomerativeClustering`](sklearn.cluster.agglomerativeclustering#sklearn.cluster.AgglomerativeClustering "sklearn.cluster.AgglomerativeClustering")
Agglomerative clustering samples instead of features.
[`ward_tree`](sklearn.cluster.ward_tree#sklearn.cluster.ward_tree "sklearn.cluster.ward_tree")
Hierarchical clustering with ward linkage.
#### Examples
```
>>> import numpy as np
>>> from sklearn import datasets, cluster
>>> digits = datasets.load_digits()
>>> images = digits.images
>>> X = np.reshape(images, (len(images), -1))
>>> agglo = cluster.FeatureAgglomeration(n_clusters=32)
>>> agglo.fit(X)
FeatureAgglomeration(n_clusters=32)
>>> X_reduced = agglo.transform(X)
>>> X_reduced.shape
(1797, 32)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.cluster.FeatureAgglomeration.fit "sklearn.cluster.FeatureAgglomeration.fit")(X[, y]) | Fit the hierarchical clustering on the data. |
| [`fit_transform`](#sklearn.cluster.FeatureAgglomeration.fit_transform "sklearn.cluster.FeatureAgglomeration.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.cluster.FeatureAgglomeration.get_feature_names_out "sklearn.cluster.FeatureAgglomeration.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.cluster.FeatureAgglomeration.get_params "sklearn.cluster.FeatureAgglomeration.get_params")([deep]) | Get parameters for this estimator. |
| [`inverse_transform`](#sklearn.cluster.FeatureAgglomeration.inverse_transform "sklearn.cluster.FeatureAgglomeration.inverse_transform")(Xred) | Inverse the transformation and return a vector of size `n_features`. |
| [`set_params`](#sklearn.cluster.FeatureAgglomeration.set_params "sklearn.cluster.FeatureAgglomeration.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.cluster.FeatureAgglomeration.transform "sklearn.cluster.FeatureAgglomeration.transform")(X) | Transform a new matrix using the built clustering. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_agglomerative.py#L1220)
Fit the hierarchical clustering on the data.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The data.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
**self**object
Returns the transformer.
*property*fit\_predict
Fit and return the result of each sample’s clustering assignment.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.cluster.FeatureAgglomeration.fit "sklearn.cluster.FeatureAgglomeration.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
inverse\_transform(*Xred*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_feature_agglomeration.py#L57)
Inverse the transformation and return a vector of size `n_features`.
Parameters:
**Xred**array-like of shape (n\_samples, n\_clusters) or (n\_clusters,)
The values to be assigned to each cluster of samples.
Returns:
**X**ndarray of shape (n\_samples, n\_features) or (n\_features,)
A vector of size `n_samples` with the values of `Xred` assigned to each of the cluster of samples.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/cluster/_feature_agglomeration.py#L23)
Transform a new matrix using the built clustering.
Parameters:
**X**array-like of shape (n\_samples, n\_features) or (n\_samples, n\_samples)
A M by N array of M observations in N dimensions or a length M array of M one-dimensional observations.
Returns:
**Y**ndarray of shape (n\_samples, n\_clusters) or (n\_clusters,)
The pooled values for each feature cluster.
Examples using `sklearn.cluster.FeatureAgglomeration`
-----------------------------------------------------
[Feature agglomeration](../../auto_examples/cluster/plot_digits_agglomeration#sphx-glr-auto-examples-cluster-plot-digits-agglomeration-py)
[Feature agglomeration vs. univariate selection](../../auto_examples/cluster/plot_feature_agglomeration_vs_univariate_selection#sphx-glr-auto-examples-cluster-plot-feature-agglomeration-vs-univariate-selection-py)
scikit_learn sklearn.datasets.fetch_lfw_people sklearn.datasets.fetch\_lfw\_people
===================================
sklearn.datasets.fetch\_lfw\_people(*\**, *data\_home=None*, *funneled=True*, *resize=0.5*, *min\_faces\_per\_person=0*, *color=False*, *slice\_=(slice(70, 195, None), slice(78, 172, None))*, *download\_if\_missing=True*, *return\_X\_y=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_lfw.py#L232)
Load the Labeled Faces in the Wild (LFW) people dataset (classification).
Download it if necessary.
| | |
| --- | --- |
| Classes | 5749 |
| Samples total | 13233 |
| Dimensionality | 5828 |
| Features | real, between 0 and 255 |
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/real_world.html#labeled-faces-in-the-wild-dataset).
Parameters:
**data\_home**str, default=None
Specify another download and cache folder for the datasets. By default all scikit-learn data is stored in ‘~/scikit\_learn\_data’ subfolders.
**funneled**bool, default=True
Download and use the funneled variant of the dataset.
**resize**float, default=0.5
Ratio used to resize the each face picture.
**min\_faces\_per\_person**int, default=None
The extracted dataset will only retain pictures of people that have at least `min_faces_per_person` different pictures.
**color**bool, default=False
Keep the 3 RGB channels instead of averaging them to a single gray level channel. If color is True the shape of the data has one more dimension than the shape with color = False.
**slice\_**tuple of slice, default=(slice(70, 195), slice(78, 172))
Provide a custom 2D slice (height, width) to extract the ‘interesting’ part of the jpeg files and avoid use statistical correlation from the background
**download\_if\_missing**bool, default=True
If False, raise a IOError if the data is not locally available instead of trying to download the data from the source site.
**return\_X\_y**bool, default=False
If True, returns `(dataset.data, dataset.target)` instead of a Bunch object. See below for more information about the `dataset.data` and `dataset.target` object.
New in version 0.20.
Returns:
**dataset**[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
Dictionary-like object, with the following attributes.
datanumpy array of shape (13233, 2914)
Each row corresponds to a ravelled face image of original size 62 x 47 pixels. Changing the `slice_` or resize parameters will change the shape of the output.
imagesnumpy array of shape (13233, 62, 47)
Each row is a face image corresponding to one of the 5749 people in the dataset. Changing the `slice_` or resize parameters will change the shape of the output.
targetnumpy array of shape (13233,)
Labels associated to each face image. Those labels range from 0-5748 and correspond to the person IDs.
target\_namesnumpy array of shape (5749,)
Names of all persons in the dataset. Position in array corresponds to the person ID in the target array.
DESCRstr
Description of the Labeled Faces in the Wild (LFW) dataset.
**(data, target)**tuple if `return_X_y` is True
New in version 0.20.
Examples using `sklearn.datasets.fetch_lfw_people`
--------------------------------------------------
[Faces recognition example using eigenfaces and SVMs](../../auto_examples/applications/plot_face_recognition#sphx-glr-auto-examples-applications-plot-face-recognition-py)
scikit_learn sklearn.metrics.top_k_accuracy_score sklearn.metrics.top\_k\_accuracy\_score
=======================================
sklearn.metrics.top\_k\_accuracy\_score(*y\_true*, *y\_score*, *\**, *k=2*, *normalize=True*, *sample\_weight=None*, *labels=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_ranking.py#L1644)
Top-k Accuracy classification score.
This metric computes the number of times where the correct label is among the top `k` labels predicted (ranked by predicted scores). Note that the multilabel case isn’t covered here.
Read more in the [User Guide](../model_evaluation#top-k-accuracy-score)
Parameters:
**y\_true**array-like of shape (n\_samples,)
True labels.
**y\_score**array-like of shape (n\_samples,) or (n\_samples, n\_classes)
Target scores. These can be either probability estimates or non-thresholded decision values (as returned by [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) on some classifiers). The binary case expects scores with shape (n\_samples,) while the multiclass case expects scores with shape (n\_samples, n\_classes). In the multiclass case, the order of the class scores must correspond to the order of `labels`, if provided, or else to the numerical or lexicographical order of the labels in `y_true`. If `y_true` does not contain all the labels, `labels` must be provided.
**k**int, default=2
Number of most likely outcomes considered to find the correct label.
**normalize**bool, default=True
If `True`, return the fraction of correctly classified samples. Otherwise, return the number of correctly classified samples.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If `None`, all samples are given the same weight.
**labels**array-like of shape (n\_classes,), default=None
Multiclass only. List of labels that index the classes in `y_score`. If `None`, the numerical or lexicographical order of the labels in `y_true` is used. If `y_true` does not contain all the labels, `labels` must be provided.
Returns:
**score**float
The top-k accuracy score. The best performance is 1 with `normalize == True` and the number of samples with `normalize == False`.
See also
[`accuracy_score`](sklearn.metrics.accuracy_score#sklearn.metrics.accuracy_score "sklearn.metrics.accuracy_score")
#### Notes
In cases where two or more labels are assigned equal predicted scores, the labels with the highest indices will be chosen first. This might impact the result if the correct label falls after the threshold because of that.
#### Examples
```
>>> import numpy as np
>>> from sklearn.metrics import top_k_accuracy_score
>>> y_true = np.array([0, 1, 2, 2])
>>> y_score = np.array([[0.5, 0.2, 0.2], # 0 is in top 2
... [0.3, 0.4, 0.2], # 1 is in top 2
... [0.2, 0.4, 0.3], # 2 is in top 2
... [0.7, 0.2, 0.1]]) # 2 isn't in top 2
>>> top_k_accuracy_score(y_true, y_score, k=2)
0.75
>>> # Not normalizing gives the number of "correctly" classified samples
>>> top_k_accuracy_score(y_true, y_score, k=2, normalize=False)
3
```
scikit_learn sklearn.metrics.davies_bouldin_score sklearn.metrics.davies\_bouldin\_score
======================================
sklearn.metrics.davies\_bouldin\_score(*X*, *labels*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/cluster/_unsupervised.py#L307)
Compute the Davies-Bouldin score.
The score is defined as the average similarity measure of each cluster with its most similar cluster, where similarity is the ratio of within-cluster distances to between-cluster distances. Thus, clusters which are farther apart and less dispersed will result in a better score.
The minimum score is zero, with lower values indicating better clustering.
Read more in the [User Guide](../clustering#davies-bouldin-index).
New in version 0.20.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
A list of `n_features`-dimensional data points. Each row corresponds to a single data point.
**labels**array-like of shape (n\_samples,)
Predicted labels for each sample.
Returns:
score: float
The resulting Davies-Bouldin score.
#### References
[1] Davies, David L.; Bouldin, Donald W. (1979). [“A Cluster Separation Measure”](https://ieeexplore.ieee.org/document/4766909). IEEE Transactions on Pattern Analysis and Machine Intelligence. PAMI-1 (2): 224-227
scikit_learn sklearn.linear_model.orthogonal_mp_gram sklearn.linear\_model.orthogonal\_mp\_gram
==========================================
sklearn.linear\_model.orthogonal\_mp\_gram(*Gram*, *Xy*, *\**, *n\_nonzero\_coefs=None*, *tol=None*, *norms\_squared=None*, *copy\_Gram=True*, *copy\_Xy=True*, *return\_path=False*, *return\_n\_iter=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_omp.py#L440)
Gram Orthogonal Matching Pursuit (OMP).
Solves n\_targets Orthogonal Matching Pursuit problems using only the Gram matrix X.T \* X and the product X.T \* y.
Read more in the [User Guide](../linear_model#omp).
Parameters:
**Gram**ndarray of shape (n\_features, n\_features)
Gram matrix of the input data: X.T \* X.
**Xy**ndarray of shape (n\_features,) or (n\_features, n\_targets)
Input targets multiplied by X: X.T \* y.
**n\_nonzero\_coefs**int, default=None
Desired number of non-zero entries in the solution. If None (by default) this value is set to 10% of n\_features.
**tol**float, default=None
Maximum norm of the residual. If not None, overrides n\_nonzero\_coefs.
**norms\_squared**array-like of shape (n\_targets,), default=None
Squared L2 norms of the lines of y. Required if tol is not None.
**copy\_Gram**bool, default=True
Whether the gram matrix must be copied by the algorithm. A false value is only helpful if it is already Fortran-ordered, otherwise a copy is made anyway.
**copy\_Xy**bool, default=True
Whether the covariance vector Xy must be copied by the algorithm. If False, it may be overwritten.
**return\_path**bool, default=False
Whether to return every value of the nonzero coefficients along the forward path. Useful for cross-validation.
**return\_n\_iter**bool, default=False
Whether or not to return the number of iterations.
Returns:
**coef**ndarray of shape (n\_features,) or (n\_features, n\_targets)
Coefficients of the OMP solution. If `return_path=True`, this contains the whole coefficient path. In this case its shape is (n\_features, n\_features) or (n\_features, n\_targets, n\_features) and iterating over the last axis yields coefficients in increasing order of active features.
**n\_iters**array-like or int
Number of active features across every target. Returned only if `return_n_iter` is set to True.
See also
[`OrthogonalMatchingPursuit`](sklearn.linear_model.orthogonalmatchingpursuit#sklearn.linear_model.OrthogonalMatchingPursuit "sklearn.linear_model.OrthogonalMatchingPursuit")
[`orthogonal_mp`](sklearn.linear_model.orthogonal_mp#sklearn.linear_model.orthogonal_mp "sklearn.linear_model.orthogonal_mp")
[`lars_path`](sklearn.linear_model.lars_path#sklearn.linear_model.lars_path "sklearn.linear_model.lars_path")
[`sklearn.decomposition.sparse_encode`](sklearn.decomposition.sparse_encode#sklearn.decomposition.sparse_encode "sklearn.decomposition.sparse_encode")
#### Notes
Orthogonal matching pursuit was introduced in G. Mallat, Z. Zhang, Matching pursuits with time-frequency dictionaries, IEEE Transactions on Signal Processing, Vol. 41, No. 12. (December 1993), pp. 3397-3415. (<https://www.di.ens.fr/~mallat/papiers/MallatPursuit93.pdf>)
This implementation is based on Rubinstein, R., Zibulevsky, M. and Elad, M., Efficient Implementation of the K-SVD Algorithm using Batch Orthogonal Matching Pursuit Technical Report - CS Technion, April 2008. <https://www.cs.technion.ac.il/~ronrubin/Publications/KSVD-OMP-v2.pdf>
| programming_docs |
scikit_learn sklearn.metrics.ndcg_score sklearn.metrics.ndcg\_score
===========================
sklearn.metrics.ndcg\_score(*y\_true*, *y\_score*, *\**, *k=None*, *sample\_weight=None*, *ignore\_ties=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_ranking.py#L1543)
Compute Normalized Discounted Cumulative Gain.
Sum the true scores ranked in the order induced by the predicted scores, after applying a logarithmic discount. Then divide by the best possible score (Ideal DCG, obtained for a perfect ranking) to obtain a score between 0 and 1.
This ranking metric returns a high value if true labels are ranked high by `y_score`.
Parameters:
**y\_true**ndarray of shape (n\_samples, n\_labels)
True targets of multilabel classification, or true scores of entities to be ranked.
**y\_score**ndarray of shape (n\_samples, n\_labels)
Target scores, can either be probability estimates, confidence values, or non-thresholded measure of decisions (as returned by “decision\_function” on some classifiers).
**k**int, default=None
Only consider the highest k scores in the ranking. If `None`, use all outputs.
**sample\_weight**ndarray of shape (n\_samples,), default=None
Sample weights. If `None`, all samples are given the same weight.
**ignore\_ties**bool, default=False
Assume that there are no ties in y\_score (which is likely to be the case if y\_score is continuous) for efficiency gains.
Returns:
**normalized\_discounted\_cumulative\_gain**float in [0., 1.]
The averaged NDCG scores for all samples.
See also
[`dcg_score`](sklearn.metrics.dcg_score#sklearn.metrics.dcg_score "sklearn.metrics.dcg_score")
Discounted Cumulative Gain (not normalized).
#### References
[Wikipedia entry for Discounted Cumulative Gain](https://en.wikipedia.org/wiki/Discounted_cumulative_gain)
Jarvelin, K., & Kekalainen, J. (2002). Cumulated gain-based evaluation of IR techniques. ACM Transactions on Information Systems (TOIS), 20(4), 422-446.
Wang, Y., Wang, L., Li, Y., He, D., Chen, W., & Liu, T. Y. (2013, May). A theoretical analysis of NDCG ranking measures. In Proceedings of the 26th Annual Conference on Learning Theory (COLT 2013)
McSherry, F., & Najork, M. (2008, March). Computing information retrieval performance measures efficiently in the presence of tied scores. In European conference on information retrieval (pp. 414-421). Springer, Berlin, Heidelberg.
#### Examples
```
>>> import numpy as np
>>> from sklearn.metrics import ndcg_score
>>> # we have groud-truth relevance of some answers to a query:
>>> true_relevance = np.asarray([[10, 0, 0, 1, 5]])
>>> # we predict some scores (relevance) for the answers
>>> scores = np.asarray([[.1, .2, .3, 4, 70]])
>>> ndcg_score(true_relevance, scores)
0.69...
>>> scores = np.asarray([[.05, 1.1, 1., .5, .0]])
>>> ndcg_score(true_relevance, scores)
0.49...
>>> # we can set k to truncate the sum; only top k answers contribute.
>>> ndcg_score(true_relevance, scores, k=4)
0.35...
>>> # the normalization takes k into account so a perfect answer
>>> # would still get 1.0
>>> ndcg_score(true_relevance, true_relevance, k=4)
1.0...
>>> # now we have some ties in our prediction
>>> scores = np.asarray([[1, 0, 0, 0, 1]])
>>> # by default ties are averaged, so here we get the average (normalized)
>>> # true relevance of our top predictions: (10 / 10 + 5 / 10) / 2 = .75
>>> ndcg_score(true_relevance, scores, k=1)
0.75...
>>> # we can choose to ignore ties for faster results, but only
>>> # if we know there aren't ties in our scores, otherwise we get
>>> # wrong results:
>>> ndcg_score(true_relevance,
... scores, k=1, ignore_ties=True)
0.5...
```
scikit_learn sklearn.neighbors.kneighbors_graph sklearn.neighbors.kneighbors\_graph
===================================
sklearn.neighbors.kneighbors\_graph(*X*, *n\_neighbors*, *\**, *mode='connectivity'*, *metric='minkowski'*, *p=2*, *metric\_params=None*, *include\_self=False*, *n\_jobs=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_graph.py#L38)
Compute the (weighted) graph of k-Neighbors for points in X.
Read more in the [User Guide](../neighbors#unsupervised-neighbors).
Parameters:
**X**array-like of shape (n\_samples, n\_features) or BallTree
Sample data, in the form of a numpy array or a precomputed [`BallTree`](sklearn.neighbors.balltree#sklearn.neighbors.BallTree "sklearn.neighbors.BallTree").
**n\_neighbors**int
Number of neighbors for each sample.
**mode**{‘connectivity’, ‘distance’}, default=’connectivity’
Type of returned matrix: ‘connectivity’ will return the connectivity matrix with ones and zeros, and ‘distance’ will return the distances between neighbors according to the given metric.
**metric**str, default=’minkowski’
Metric to use for distance computation. Default is “minkowski”, which results in the standard Euclidean distance when p = 2. See the documentation of [scipy.spatial.distance](https://docs.scipy.org/doc/scipy/reference/spatial.distance.html) and the metrics listed in [`distance_metrics`](sklearn.metrics.pairwise.distance_metrics#sklearn.metrics.pairwise.distance_metrics "sklearn.metrics.pairwise.distance_metrics") for valid metric values.
**p**int, default=2
Power parameter for the Minkowski metric. When p = 1, this is equivalent to using manhattan\_distance (l1), and euclidean\_distance (l2) for p = 2. For arbitrary p, minkowski\_distance (l\_p) is used.
**metric\_params**dict, default=None
Additional keyword arguments for the metric function.
**include\_self**bool or ‘auto’, default=False
Whether or not to mark each sample as the first nearest neighbor to itself. If ‘auto’, then True is used for mode=’connectivity’ and False for mode=’distance’.
**n\_jobs**int, default=None
The number of parallel jobs to run for neighbors search. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
Returns:
**A**sparse matrix of shape (n\_samples, n\_samples)
Graph where A[i, j] is assigned the weight of edge that connects i to j. The matrix is of CSR format.
See also
[`radius_neighbors_graph`](sklearn.neighbors.radius_neighbors_graph#sklearn.neighbors.radius_neighbors_graph "sklearn.neighbors.radius_neighbors_graph")
Compute the (weighted) graph of Neighbors for points in X.
#### Examples
```
>>> X = [[0], [3], [1]]
>>> from sklearn.neighbors import kneighbors_graph
>>> A = kneighbors_graph(X, 2, mode='connectivity', include_self=True)
>>> A.toarray()
array([[1., 0., 1.],
[0., 1., 1.],
[1., 0., 1.]])
```
Examples using `sklearn.neighbors.kneighbors_graph`
---------------------------------------------------
[Agglomerative clustering with and without structure](../../auto_examples/cluster/plot_agglomerative_clustering#sphx-glr-auto-examples-cluster-plot-agglomerative-clustering-py)
[Comparing different clustering algorithms on toy datasets](../../auto_examples/cluster/plot_cluster_comparison#sphx-glr-auto-examples-cluster-plot-cluster-comparison-py)
[Hierarchical clustering: structured vs unstructured ward](../../auto_examples/cluster/plot_ward_structured_vs_unstructured#sphx-glr-auto-examples-cluster-plot-ward-structured-vs-unstructured-py)
scikit_learn sklearn.manifold.LocallyLinearEmbedding sklearn.manifold.LocallyLinearEmbedding
=======================================
*class*sklearn.manifold.LocallyLinearEmbedding(*\**, *n\_neighbors=5*, *n\_components=2*, *reg=0.001*, *eigen\_solver='auto'*, *tol=1e-06*, *max\_iter=100*, *method='standard'*, *hessian\_tol=0.0001*, *modified\_tol=1e-12*, *neighbors\_algorithm='auto'*, *random\_state=None*, *n\_jobs=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_locally_linear.py#L550)
Locally Linear Embedding.
Read more in the [User Guide](../manifold#locally-linear-embedding).
Parameters:
**n\_neighbors**int, default=5
Number of neighbors to consider for each point.
**n\_components**int, default=2
Number of coordinates for the manifold.
**reg**float, default=1e-3
Regularization constant, multiplies the trace of the local covariance matrix of the distances.
**eigen\_solver**{‘auto’, ‘arpack’, ‘dense’}, default=’auto’
The solver used to compute the eigenvectors. The available options are:
* `'auto'` : algorithm will attempt to choose the best method for input data.
* `'arpack'` : use arnoldi iteration in shift-invert mode. For this method, M may be a dense matrix, sparse matrix, or general linear operator.
* `'dense'` : use standard dense matrix operations for the eigenvalue decomposition. For this method, M must be an array or matrix type. This method should be avoided for large problems.
Warning
ARPACK can be unstable for some problems. It is best to try several random seeds in order to check results.
**tol**float, default=1e-6
Tolerance for ‘arpack’ method Not used if eigen\_solver==’dense’.
**max\_iter**int, default=100
Maximum number of iterations for the arpack solver. Not used if eigen\_solver==’dense’.
**method**{‘standard’, ‘hessian’, ‘modified’, ‘ltsa’}, default=’standard’
* `standard`: use the standard locally linear embedding algorithm. see reference [[1]](#r62e36dd1b056-1)
* `hessian`: use the Hessian eigenmap method. This method requires `n_neighbors > n_components * (1 + (n_components + 1) / 2`. see reference [[2]](#r62e36dd1b056-2)
* `modified`: use the modified locally linear embedding algorithm. see reference [[3]](#r62e36dd1b056-3)
* `ltsa`: use local tangent space alignment algorithm. see reference [[4]](#r62e36dd1b056-4)
**hessian\_tol**float, default=1e-4
Tolerance for Hessian eigenmapping method. Only used if `method == 'hessian'`.
**modified\_tol**float, default=1e-12
Tolerance for modified LLE method. Only used if `method == 'modified'`.
**neighbors\_algorithm**{‘auto’, ‘brute’, ‘kd\_tree’, ‘ball\_tree’}, default=’auto’
Algorithm to use for nearest neighbors search, passed to [`NearestNeighbors`](sklearn.neighbors.nearestneighbors#sklearn.neighbors.NearestNeighbors "sklearn.neighbors.NearestNeighbors") instance.
**random\_state**int, RandomState instance, default=None
Determines the random number generator when `eigen_solver` == ‘arpack’. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**n\_jobs**int or None, default=None
The number of parallel jobs to run. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
Attributes:
**embedding\_**array-like, shape [n\_samples, n\_components]
Stores the embedding vectors
**reconstruction\_error\_**float
Reconstruction error associated with `embedding_`
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**nbrs\_**NearestNeighbors object
Stores nearest neighbors instance, including BallTree or KDtree if applicable.
See also
[`SpectralEmbedding`](sklearn.manifold.spectralembedding#sklearn.manifold.SpectralEmbedding "sklearn.manifold.SpectralEmbedding")
Spectral embedding for non-linear dimensionality reduction.
[`TSNE`](sklearn.manifold.tsne#sklearn.manifold.TSNE "sklearn.manifold.TSNE")
Distributed Stochastic Neighbor Embedding.
#### References
[[1](#id1)] Roweis, S. & Saul, L. Nonlinear dimensionality reduction by locally linear embedding. Science 290:2323 (2000).
[[2](#id2)] Donoho, D. & Grimes, C. Hessian eigenmaps: Locally linear embedding techniques for high-dimensional data. Proc Natl Acad Sci U S A. 100:5591 (2003).
[[3](#id3)] Zhang, Z. & Wang, J. MLLE: Modified Locally Linear Embedding Using Multiple Weights. <http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.70.382>
[[4](#id4)] Zhang, Z. & Zha, H. Principal manifolds and nonlinear dimensionality reduction via tangent space alignment. Journal of Shanghai Univ. 8:406 (2004)
#### Examples
```
>>> from sklearn.datasets import load_digits
>>> from sklearn.manifold import LocallyLinearEmbedding
>>> X, _ = load_digits(return_X_y=True)
>>> X.shape
(1797, 64)
>>> embedding = LocallyLinearEmbedding(n_components=2)
>>> X_transformed = embedding.fit_transform(X[:100])
>>> X_transformed.shape
(100, 2)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.manifold.LocallyLinearEmbedding.fit "sklearn.manifold.LocallyLinearEmbedding.fit")(X[, y]) | Compute the embedding vectors for data X. |
| [`fit_transform`](#sklearn.manifold.LocallyLinearEmbedding.fit_transform "sklearn.manifold.LocallyLinearEmbedding.fit_transform")(X[, y]) | Compute the embedding vectors for data X and transform X. |
| [`get_feature_names_out`](#sklearn.manifold.LocallyLinearEmbedding.get_feature_names_out "sklearn.manifold.LocallyLinearEmbedding.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.manifold.LocallyLinearEmbedding.get_params "sklearn.manifold.LocallyLinearEmbedding.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.manifold.LocallyLinearEmbedding.set_params "sklearn.manifold.LocallyLinearEmbedding.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.manifold.LocallyLinearEmbedding.transform "sklearn.manifold.LocallyLinearEmbedding.transform")(X) | Transform new points into embedding space. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_locally_linear.py#L743)
Compute the embedding vectors for data X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training set.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
**self**object
Fitted `LocallyLinearEmbedding` class instance.
fit\_transform(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_locally_linear.py#L762)
Compute the embedding vectors for data X and transform X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training set.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
**X\_new**array-like, shape (n\_samples, n\_components)
Returns the instance itself.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.manifold.LocallyLinearEmbedding.fit "sklearn.manifold.LocallyLinearEmbedding.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/manifold/_locally_linear.py#L781)
Transform new points into embedding space.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training set.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_components)
Returns the instance itself.
#### Notes
Because of scaling performed by this method, it is discouraged to use it together with methods that are not scale-invariant (like SVMs).
Examples using `sklearn.manifold.LocallyLinearEmbedding`
--------------------------------------------------------
[Visualizing the stock market structure](../../auto_examples/applications/plot_stock_market#sphx-glr-auto-examples-applications-plot-stock-market-py)
[Comparison of Manifold Learning methods](../../auto_examples/manifold/plot_compare_methods#sphx-glr-auto-examples-manifold-plot-compare-methods-py)
[Manifold Learning methods on a severed sphere](../../auto_examples/manifold/plot_manifold_sphere#sphx-glr-auto-examples-manifold-plot-manifold-sphere-py)
[Manifold learning on handwritten digits: Locally Linear Embedding, Isomap…](../../auto_examples/manifold/plot_lle_digits#sphx-glr-auto-examples-manifold-plot-lle-digits-py)
scikit_learn sklearn.datasets.fetch_20newsgroups sklearn.datasets.fetch\_20newsgroups
====================================
sklearn.datasets.fetch\_20newsgroups(*\**, *data\_home=None*, *subset='train'*, *categories=None*, *shuffle=True*, *random\_state=42*, *remove=()*, *download\_if\_missing=True*, *return\_X\_y=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_twenty_newsgroups.py#L152)
Load the filenames and data from the 20 newsgroups dataset (classification).
Download it if necessary.
| | |
| --- | --- |
| Classes | 20 |
| Samples total | 18846 |
| Dimensionality | 1 |
| Features | text |
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/real_world.html#newsgroups-dataset).
Parameters:
**data\_home**str, default=None
Specify a download and cache folder for the datasets. If None, all scikit-learn data is stored in ‘~/scikit\_learn\_data’ subfolders.
**subset**{‘train’, ‘test’, ‘all’}, default=’train’
Select the dataset to load: ‘train’ for the training set, ‘test’ for the test set, ‘all’ for both, with shuffled ordering.
**categories**array-like, dtype=str, default=None
If None (default), load all the categories. If not None, list of category names to load (other categories ignored).
**shuffle**bool, default=True
Whether or not to shuffle the data: might be important for models that make the assumption that the samples are independent and identically distributed (i.i.d.), such as stochastic gradient descent.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for dataset shuffling. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**remove**tuple, default=()
May contain any subset of (‘headers’, ‘footers’, ‘quotes’). Each of these are kinds of text that will be detected and removed from the newsgroup posts, preventing classifiers from overfitting on metadata.
‘headers’ removes newsgroup headers, ‘footers’ removes blocks at the ends of posts that look like signatures, and ‘quotes’ removes lines that appear to be quoting another post.
‘headers’ follows an exact standard; the other filters are not always correct.
**download\_if\_missing**bool, default=True
If False, raise an IOError if the data is not locally available instead of trying to download the data from the source site.
**return\_X\_y**bool, default=False
If True, returns `(data.data, data.target)` instead of a Bunch object.
New in version 0.22.
Returns:
**bunch**[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
Dictionary-like object, with the following attributes.
datalist of shape (n\_samples,)
The data list to learn.
target: ndarray of shape (n\_samples,)
The target labels.
filenames: list of shape (n\_samples,)
The path to the location of the data.
DESCR: str
The full description of the dataset.
target\_names: list of shape (n\_classes,)
The names of target classes.
**(data, target)**tuple if `return_X_y=True`
A tuple of two ndarrays. The first contains a 2D array of shape (n\_samples, n\_classes) with each row representing one sample and each column representing the features. The second array of shape (n\_samples,) contains the target samples.
New in version 0.22.
Examples using `sklearn.datasets.fetch_20newsgroups`
----------------------------------------------------
[Biclustering documents with the Spectral Co-clustering algorithm](../../auto_examples/bicluster/plot_bicluster_newsgroups#sphx-glr-auto-examples-bicluster-plot-bicluster-newsgroups-py)
[Topic extraction with Non-negative Matrix Factorization and Latent Dirichlet Allocation](../../auto_examples/applications/plot_topics_extraction_with_nmf_lda#sphx-glr-auto-examples-applications-plot-topics-extraction-with-nmf-lda-py)
[Sample pipeline for text feature extraction and evaluation](../../auto_examples/model_selection/grid_search_text_feature_extraction#sphx-glr-auto-examples-model-selection-grid-search-text-feature-extraction-py)
[Column Transformer with Heterogeneous Data Sources](../../auto_examples/compose/plot_column_transformer#sphx-glr-auto-examples-compose-plot-column-transformer-py)
[Semi-supervised Classification on a Text Dataset](../../auto_examples/semi_supervised/plot_semi_supervised_newsgroups#sphx-glr-auto-examples-semi-supervised-plot-semi-supervised-newsgroups-py)
[Classification of text documents using sparse features](../../auto_examples/text/plot_document_classification_20newsgroups#sphx-glr-auto-examples-text-plot-document-classification-20newsgroups-py)
[Clustering text documents using k-means](../../auto_examples/text/plot_document_clustering#sphx-glr-auto-examples-text-plot-document-clustering-py)
[FeatureHasher and DictVectorizer Comparison](../../auto_examples/text/plot_hashing_vs_dict_vectorizer#sphx-glr-auto-examples-text-plot-hashing-vs-dict-vectorizer-py)
| programming_docs |
scikit_learn sklearn.linear_model.SGDRegressor sklearn.linear\_model.SGDRegressor
==================================
*class*sklearn.linear\_model.SGDRegressor(*loss='squared\_error'*, *\**, *penalty='l2'*, *alpha=0.0001*, *l1\_ratio=0.15*, *fit\_intercept=True*, *max\_iter=1000*, *tol=0.001*, *shuffle=True*, *verbose=0*, *epsilon=0.1*, *random\_state=None*, *learning\_rate='invscaling'*, *eta0=0.01*, *power\_t=0.25*, *early\_stopping=False*, *validation\_fraction=0.1*, *n\_iter\_no\_change=5*, *warm\_start=False*, *average=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_stochastic_gradient.py#L1694)
Linear model fitted by minimizing a regularized empirical loss with SGD.
SGD stands for Stochastic Gradient Descent: the gradient of the loss is estimated each sample at a time and the model is updated along the way with a decreasing strength schedule (aka learning rate).
The regularizer is a penalty added to the loss function that shrinks model parameters towards the zero vector using either the squared euclidean norm L2 or the absolute norm L1 or a combination of both (Elastic Net). If the parameter update crosses the 0.0 value because of the regularizer, the update is truncated to 0.0 to allow for learning sparse models and achieve online feature selection.
This implementation works with data represented as dense numpy arrays of floating point values for the features.
Read more in the [User Guide](../sgd#sgd).
Parameters:
**loss**str, default=’squared\_error’
The loss function to be used. The possible values are ‘squared\_error’, ‘huber’, ‘epsilon\_insensitive’, or ‘squared\_epsilon\_insensitive’
The ‘squared\_error’ refers to the ordinary least squares fit. ‘huber’ modifies ‘squared\_error’ to focus less on getting outliers correct by switching from squared to linear loss past a distance of epsilon. ‘epsilon\_insensitive’ ignores errors less than epsilon and is linear past that; this is the loss function used in SVR. ‘squared\_epsilon\_insensitive’ is the same but becomes squared loss past a tolerance of epsilon.
More details about the losses formulas can be found in the [User Guide](../sgd#sgd-mathematical-formulation).
Deprecated since version 1.0: The loss ‘squared\_loss’ was deprecated in v1.0 and will be removed in version 1.2. Use `loss='squared_error'` which is equivalent.
**penalty**{‘l2’, ‘l1’, ‘elasticnet’}, default=’l2’
The penalty (aka regularization term) to be used. Defaults to ‘l2’ which is the standard regularizer for linear SVM models. ‘l1’ and ‘elasticnet’ might bring sparsity to the model (feature selection) not achievable with ‘l2’.
**alpha**float, default=0.0001
Constant that multiplies the regularization term. The higher the value, the stronger the regularization. Also used to compute the learning rate when set to `learning_rate` is set to ‘optimal’.
**l1\_ratio**float, default=0.15
The Elastic Net mixing parameter, with 0 <= l1\_ratio <= 1. l1\_ratio=0 corresponds to L2 penalty, l1\_ratio=1 to L1. Only used if `penalty` is ‘elasticnet’.
**fit\_intercept**bool, default=True
Whether the intercept should be estimated or not. If False, the data is assumed to be already centered.
**max\_iter**int, default=1000
The maximum number of passes over the training data (aka epochs). It only impacts the behavior in the `fit` method, and not the [`partial_fit`](#sklearn.linear_model.SGDRegressor.partial_fit "sklearn.linear_model.SGDRegressor.partial_fit") method.
New in version 0.19.
**tol**float, default=1e-3
The stopping criterion. If it is not None, training will stop when (loss > best\_loss - tol) for `n_iter_no_change` consecutive epochs. Convergence is checked against the training loss or the validation loss depending on the `early_stopping` parameter.
New in version 0.19.
**shuffle**bool, default=True
Whether or not the training data should be shuffled after each epoch.
**verbose**int, default=0
The verbosity level.
**epsilon**float, default=0.1
Epsilon in the epsilon-insensitive loss functions; only if `loss` is ‘huber’, ‘epsilon\_insensitive’, or ‘squared\_epsilon\_insensitive’. For ‘huber’, determines the threshold at which it becomes less important to get the prediction exactly right. For epsilon-insensitive, any differences between the current prediction and the correct label are ignored if they are less than this threshold.
**random\_state**int, RandomState instance, default=None
Used for shuffling the data, when `shuffle` is set to `True`. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**learning\_rate**str, default=’invscaling’
The learning rate schedule:
* ‘constant’: `eta = eta0`
* ‘optimal’: `eta = 1.0 / (alpha * (t + t0))` where t0 is chosen by a heuristic proposed by Leon Bottou.
* ‘invscaling’: `eta = eta0 / pow(t, power_t)`
* ‘adaptive’: eta = eta0, as long as the training keeps decreasing. Each time n\_iter\_no\_change consecutive epochs fail to decrease the training loss by tol or fail to increase validation score by tol if early\_stopping is True, the current learning rate is divided by 5.
New in version 0.20: Added ‘adaptive’ option
**eta0**float, default=0.01
The initial learning rate for the ‘constant’, ‘invscaling’ or ‘adaptive’ schedules. The default value is 0.01.
**power\_t**float, default=0.25
The exponent for inverse scaling learning rate.
**early\_stopping**bool, default=False
Whether to use early stopping to terminate training when validation score is not improving. If set to True, it will automatically set aside a fraction of training data as validation and terminate training when validation score returned by the `score` method is not improving by at least `tol` for `n_iter_no_change` consecutive epochs.
New in version 0.20: Added ‘early\_stopping’ option
**validation\_fraction**float, default=0.1
The proportion of training data to set aside as validation set for early stopping. Must be between 0 and 1. Only used if `early_stopping` is True.
New in version 0.20: Added ‘validation\_fraction’ option
**n\_iter\_no\_change**int, default=5
Number of iterations with no improvement to wait before stopping fitting. Convergence is checked against the training loss or the validation loss depending on the `early_stopping` parameter.
New in version 0.20: Added ‘n\_iter\_no\_change’ option
**warm\_start**bool, default=False
When set to True, reuse the solution of the previous call to fit as initialization, otherwise, just erase the previous solution. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
Repeatedly calling fit or partial\_fit when warm\_start is True can result in a different solution than when calling fit a single time because of the way the data is shuffled. If a dynamic learning rate is used, the learning rate is adapted depending on the number of samples already seen. Calling `fit` resets this counter, while `partial_fit` will result in increasing the existing counter.
**average**bool or int, default=False
When set to True, computes the averaged SGD weights across all updates and stores the result in the `coef_` attribute. If set to an int greater than 1, averaging will begin once the total number of samples seen reaches `average`. So `average=10` will begin averaging after seeing 10 samples.
Attributes:
**coef\_**ndarray of shape (n\_features,)
Weights assigned to the features.
**intercept\_**ndarray of shape (1,)
The intercept term.
**n\_iter\_**int
The actual number of iterations before reaching the stopping criterion.
**t\_**int
Number of weight updates performed during training. Same as `(n_iter_ * n_samples)`.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`HuberRegressor`](sklearn.linear_model.huberregressor#sklearn.linear_model.HuberRegressor "sklearn.linear_model.HuberRegressor")
Linear regression model that is robust to outliers.
[`Lars`](sklearn.linear_model.lars#sklearn.linear_model.Lars "sklearn.linear_model.Lars")
Least Angle Regression model.
[`Lasso`](sklearn.linear_model.lasso#sklearn.linear_model.Lasso "sklearn.linear_model.Lasso")
Linear Model trained with L1 prior as regularizer.
[`RANSACRegressor`](sklearn.linear_model.ransacregressor#sklearn.linear_model.RANSACRegressor "sklearn.linear_model.RANSACRegressor")
RANSAC (RANdom SAmple Consensus) algorithm.
[`Ridge`](sklearn.linear_model.ridge#sklearn.linear_model.Ridge "sklearn.linear_model.Ridge")
Linear least squares with l2 regularization.
[`sklearn.svm.SVR`](sklearn.svm.svr#sklearn.svm.SVR "sklearn.svm.SVR")
Epsilon-Support Vector Regression.
[`TheilSenRegressor`](sklearn.linear_model.theilsenregressor#sklearn.linear_model.TheilSenRegressor "sklearn.linear_model.TheilSenRegressor")
Theil-Sen Estimator robust multivariate regression model.
#### Examples
```
>>> import numpy as np
>>> from sklearn.linear_model import SGDRegressor
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.preprocessing import StandardScaler
>>> n_samples, n_features = 10, 5
>>> rng = np.random.RandomState(0)
>>> y = rng.randn(n_samples)
>>> X = rng.randn(n_samples, n_features)
>>> # Always scale the input. The most convenient way is to use a pipeline.
>>> reg = make_pipeline(StandardScaler(),
... SGDRegressor(max_iter=1000, tol=1e-3))
>>> reg.fit(X, y)
Pipeline(steps=[('standardscaler', StandardScaler()),
('sgdregressor', SGDRegressor())])
```
#### Methods
| | |
| --- | --- |
| [`densify`](#sklearn.linear_model.SGDRegressor.densify "sklearn.linear_model.SGDRegressor.densify")() | Convert coefficient matrix to dense array format. |
| [`fit`](#sklearn.linear_model.SGDRegressor.fit "sklearn.linear_model.SGDRegressor.fit")(X, y[, coef\_init, intercept\_init, ...]) | Fit linear model with Stochastic Gradient Descent. |
| [`get_params`](#sklearn.linear_model.SGDRegressor.get_params "sklearn.linear_model.SGDRegressor.get_params")([deep]) | Get parameters for this estimator. |
| [`partial_fit`](#sklearn.linear_model.SGDRegressor.partial_fit "sklearn.linear_model.SGDRegressor.partial_fit")(X, y[, sample\_weight]) | Perform one epoch of stochastic gradient descent on given samples. |
| [`predict`](#sklearn.linear_model.SGDRegressor.predict "sklearn.linear_model.SGDRegressor.predict")(X) | Predict using the linear model. |
| [`score`](#sklearn.linear_model.SGDRegressor.score "sklearn.linear_model.SGDRegressor.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.linear_model.SGDRegressor.set_params "sklearn.linear_model.SGDRegressor.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`sparsify`](#sklearn.linear_model.SGDRegressor.sparsify "sklearn.linear_model.SGDRegressor.sparsify")() | Convert coefficient matrix to sparse format. |
densify()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L477)
Convert coefficient matrix to dense array format.
Converts the `coef_` member (back) to a numpy.ndarray. This is the default format of `coef_` and is required for fitting, so calling this method is only required on models that have previously been sparsified; otherwise, it is a no-op.
Returns:
self
Fitted estimator.
fit(*X*, *y*, *coef\_init=None*, *intercept\_init=None*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_stochastic_gradient.py#L1536)
Fit linear model with Stochastic Gradient Descent.
Parameters:
**X**{array-like, sparse matrix}, shape (n\_samples, n\_features)
Training data.
**y**ndarray of shape (n\_samples,)
Target values.
**coef\_init**ndarray of shape (n\_features,), default=None
The initial coefficients to warm-start the optimization.
**intercept\_init**ndarray of shape (1,), default=None
The initial intercept to warm-start the optimization.
**sample\_weight**array-like, shape (n\_samples,), default=None
Weights applied to individual samples (1. for unweighted).
Returns:
**self**object
Fitted `SGDRegressor` estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
partial\_fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_stochastic_gradient.py#L1445)
Perform one epoch of stochastic gradient descent on given samples.
Internally, this method uses `max_iter = 1`. Therefore, it is not guaranteed that a minimum of the cost function is reached after calling it once. Matters such as objective convergence and early stopping should be handled by the user.
Parameters:
**X**{array-like, sparse matrix}, shape (n\_samples, n\_features)
Subset of training data.
**y**numpy array of shape (n\_samples,)
Subset of target values.
**sample\_weight**array-like, shape (n\_samples,), default=None
Weights applied to individual samples. If not provided, uniform weights are assumed.
Returns:
**self**object
Returns an instance of self.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_stochastic_gradient.py#L1592)
Predict using the linear model.
Parameters:
**X**{array-like, sparse matrix}, shape (n\_samples, n\_features)
Input data.
Returns:
ndarray of shape (n\_samples,)
Predicted target values per element in X.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
sparsify()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L497)
Convert coefficient matrix to sparse format.
Converts the `coef_` member to a scipy.sparse matrix, which for L1-regularized models can be much more memory- and storage-efficient than the usual numpy.ndarray representation.
The `intercept_` member is not converted.
Returns:
self
Fitted estimator.
#### Notes
For non-sparse models, i.e. when there are not many zeros in `coef_`, this may actually *increase* memory usage, so use this method with care. A rule of thumb is that the number of zero elements, which can be computed with `(coef_ == 0).sum()`, must be more than 50% for this to provide significant benefits.
After calling this method, further fitting with the partial\_fit method (if any) will not work until you call densify.
Examples using `sklearn.linear_model.SGDRegressor`
--------------------------------------------------
[Prediction Latency](../../auto_examples/applications/plot_prediction_latency#sphx-glr-auto-examples-applications-plot-prediction-latency-py)
[SGD: Penalties](../../auto_examples/linear_model/plot_sgd_penalties#sphx-glr-auto-examples-linear-model-plot-sgd-penalties-py)
scikit_learn sklearn.metrics.auc sklearn.metrics.auc
===================
sklearn.metrics.auc(*x*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_ranking.py#L47)
Compute Area Under the Curve (AUC) using the trapezoidal rule.
This is a general function, given points on a curve. For computing the area under the ROC-curve, see [`roc_auc_score`](sklearn.metrics.roc_auc_score#sklearn.metrics.roc_auc_score "sklearn.metrics.roc_auc_score"). For an alternative way to summarize a precision-recall curve, see [`average_precision_score`](sklearn.metrics.average_precision_score#sklearn.metrics.average_precision_score "sklearn.metrics.average_precision_score").
Parameters:
**x**ndarray of shape (n,)
X coordinates. These must be either monotonic increasing or monotonic decreasing.
**y**ndarray of shape, (n,)
Y coordinates.
Returns:
**auc**float
Area Under the Curve.
See also
[`roc_auc_score`](sklearn.metrics.roc_auc_score#sklearn.metrics.roc_auc_score "sklearn.metrics.roc_auc_score")
Compute the area under the ROC curve.
[`average_precision_score`](sklearn.metrics.average_precision_score#sklearn.metrics.average_precision_score "sklearn.metrics.average_precision_score")
Compute average precision from prediction scores.
[`precision_recall_curve`](sklearn.metrics.precision_recall_curve#sklearn.metrics.precision_recall_curve "sklearn.metrics.precision_recall_curve")
Compute precision-recall pairs for different probability thresholds.
#### Examples
```
>>> import numpy as np
>>> from sklearn import metrics
>>> y = np.array([1, 1, 2, 2])
>>> pred = np.array([0.1, 0.4, 0.35, 0.8])
>>> fpr, tpr, thresholds = metrics.roc_curve(y, pred, pos_label=2)
>>> metrics.auc(fpr, tpr)
0.75
```
Examples using `sklearn.metrics.auc`
------------------------------------
[Species distribution modeling](../../auto_examples/applications/plot_species_distribution_modeling#sphx-glr-auto-examples-applications-plot-species-distribution-modeling-py)
[Poisson regression and non-normal loss](../../auto_examples/linear_model/plot_poisson_regression_non_normal_loss#sphx-glr-auto-examples-linear-model-plot-poisson-regression-non-normal-loss-py)
[Tweedie regression on insurance claims](../../auto_examples/linear_model/plot_tweedie_regression_insurance_claims#sphx-glr-auto-examples-linear-model-plot-tweedie-regression-insurance-claims-py)
[Precision-Recall](../../auto_examples/model_selection/plot_precision_recall#sphx-glr-auto-examples-model-selection-plot-precision-recall-py)
[Receiver Operating Characteristic (ROC)](../../auto_examples/model_selection/plot_roc#sphx-glr-auto-examples-model-selection-plot-roc-py)
[Receiver Operating Characteristic (ROC) with cross validation](../../auto_examples/model_selection/plot_roc_crossval#sphx-glr-auto-examples-model-selection-plot-roc-crossval-py)
| programming_docs |
scikit_learn sklearn.feature_selection.r_regression sklearn.feature\_selection.r\_regression
========================================
sklearn.feature\_selection.r\_regression(*X*, *y*, *\**, *center=True*, *force\_finite=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_univariate_selection.py#L240)
Compute Pearson’s r for each features and the target.
Pearson’s r is also known as the Pearson correlation coefficient.
Linear model for testing the individual effect of each of many regressors. This is a scoring function to be used in a feature selection procedure, not a free standing feature selection procedure.
The cross correlation between each regressor and the target is computed as:
```
E[(X[:, i] - mean(X[:, i])) * (y - mean(y))] / (std(X[:, i]) * std(y))
```
For more on usage see the [User Guide](../feature_selection#univariate-feature-selection).
New in version 1.0.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data matrix.
**y**array-like of shape (n\_samples,)
The target vector.
**center**bool, default=True
Whether or not to center the data matrix `X` and the target vector `y`. By default, `X` and `y` will be centered.
**force\_finite**bool, default=True
Whether or not to force the Pearson’s R correlation to be finite. In the particular case where some features in `X` or the target `y` are constant, the Pearson’s R correlation is not defined. When `force_finite=False`, a correlation of `np.nan` is returned to acknowledge this case. When `force_finite=True`, this value will be forced to a minimal correlation of `0.0`.
New in version 1.1.
Returns:
**correlation\_coefficient**ndarray of shape (n\_features,)
Pearson’s R correlation coefficients of features.
See also
[`f_regression`](sklearn.feature_selection.f_regression#sklearn.feature_selection.f_regression "sklearn.feature_selection.f_regression")
Univariate linear regression tests returning f-statistic and p-values.
[`mutual_info_regression`](sklearn.feature_selection.mutual_info_regression#sklearn.feature_selection.mutual_info_regression "sklearn.feature_selection.mutual_info_regression")
Mutual information for a continuous target.
[`f_classif`](sklearn.feature_selection.f_classif#sklearn.feature_selection.f_classif "sklearn.feature_selection.f_classif")
ANOVA F-value between label/feature for classification tasks.
[`chi2`](sklearn.feature_selection.chi2#sklearn.feature_selection.chi2 "sklearn.feature_selection.chi2")
Chi-squared stats of non-negative features for classification tasks.
scikit_learn sklearn.svm.LinearSVR sklearn.svm.LinearSVR
=====================
*class*sklearn.svm.LinearSVR(*\**, *epsilon=0.0*, *tol=0.0001*, *C=1.0*, *loss='epsilon\_insensitive'*, *fit\_intercept=True*, *intercept\_scaling=1.0*, *dual=True*, *verbose=0*, *random\_state=None*, *max\_iter=1000*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/svm/_classes.py#L298)
Linear Support Vector Regression.
Similar to SVR with parameter kernel=’linear’, but implemented in terms of liblinear rather than libsvm, so it has more flexibility in the choice of penalties and loss functions and should scale better to large numbers of samples.
This class supports both dense and sparse input.
Read more in the [User Guide](../svm#svm-regression).
New in version 0.16.
Parameters:
**epsilon**float, default=0.0
Epsilon parameter in the epsilon-insensitive loss function. Note that the value of this parameter depends on the scale of the target variable y. If unsure, set `epsilon=0`.
**tol**float, default=1e-4
Tolerance for stopping criteria.
**C**float, default=1.0
Regularization parameter. The strength of the regularization is inversely proportional to C. Must be strictly positive.
**loss**{‘epsilon\_insensitive’, ‘squared\_epsilon\_insensitive’}, default=’epsilon\_insensitive’
Specifies the loss function. The epsilon-insensitive loss (standard SVR) is the L1 loss, while the squared epsilon-insensitive loss (‘squared\_epsilon\_insensitive’) is the L2 loss.
**fit\_intercept**bool, default=True
Whether to calculate the intercept for this model. If set to false, no intercept will be used in calculations (i.e. data is expected to be already centered).
**intercept\_scaling**float, default=1.0
When self.fit\_intercept is True, instance vector x becomes [x, self.intercept\_scaling], i.e. a “synthetic” feature with constant value equals to intercept\_scaling is appended to the instance vector. The intercept becomes intercept\_scaling \* synthetic feature weight Note! the synthetic feature weight is subject to l1/l2 regularization as all other features. To lessen the effect of regularization on synthetic feature weight (and therefore on the intercept) intercept\_scaling has to be increased.
**dual**bool, default=True
Select the algorithm to either solve the dual or primal optimization problem. Prefer dual=False when n\_samples > n\_features.
**verbose**int, default=0
Enable verbose output. Note that this setting takes advantage of a per-process runtime setting in liblinear that, if enabled, may not work properly in a multithreaded context.
**random\_state**int, RandomState instance or None, default=None
Controls the pseudo random number generation for shuffling the data. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**max\_iter**int, default=1000
The maximum number of iterations to be run.
Attributes:
**coef\_**ndarray of shape (n\_features) if n\_classes == 2 else (n\_classes, n\_features)
Weights assigned to the features (coefficients in the primal problem).
`coef_` is a readonly property derived from `raw_coef_` that follows the internal memory layout of liblinear.
**intercept\_**ndarray of shape (1) if n\_classes == 2 else (n\_classes)
Constants in decision function.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_iter\_**int
Maximum number of iterations run across all classes.
See also
[`LinearSVC`](sklearn.svm.linearsvc#sklearn.svm.LinearSVC "sklearn.svm.LinearSVC")
Implementation of Support Vector Machine classifier using the same library as this class (liblinear).
[`SVR`](sklearn.svm.svr#sklearn.svm.SVR "sklearn.svm.SVR")
Implementation of Support Vector Machine regression using libsvm: the kernel can be non-linear but its SMO algorithm does not scale to large number of samples as LinearSVC does.
[`sklearn.linear_model.SGDRegressor`](sklearn.linear_model.sgdregressor#sklearn.linear_model.SGDRegressor "sklearn.linear_model.SGDRegressor")
SGDRegressor can optimize the same cost function as LinearSVR by adjusting the penalty and loss parameters. In addition it requires less memory, allows incremental (online) learning, and implements various loss functions and regularization regimes.
#### Examples
```
>>> from sklearn.svm import LinearSVR
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.preprocessing import StandardScaler
>>> from sklearn.datasets import make_regression
>>> X, y = make_regression(n_features=4, random_state=0)
>>> regr = make_pipeline(StandardScaler(),
... LinearSVR(random_state=0, tol=1e-5))
>>> regr.fit(X, y)
Pipeline(steps=[('standardscaler', StandardScaler()),
('linearsvr', LinearSVR(random_state=0, tol=1e-05))])
```
```
>>> print(regr.named_steps['linearsvr'].coef_)
[18.582... 27.023... 44.357... 64.522...]
>>> print(regr.named_steps['linearsvr'].intercept_)
[-4...]
>>> print(regr.predict([[0, 0, 0, 0]]))
[-2.384...]
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.svm.LinearSVR.fit "sklearn.svm.LinearSVR.fit")(X, y[, sample\_weight]) | Fit the model according to the given training data. |
| [`get_params`](#sklearn.svm.LinearSVR.get_params "sklearn.svm.LinearSVR.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.svm.LinearSVR.predict "sklearn.svm.LinearSVR.predict")(X) | Predict using the linear model. |
| [`score`](#sklearn.svm.LinearSVR.score "sklearn.svm.LinearSVR.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.svm.LinearSVR.set_params "sklearn.svm.LinearSVR.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/svm/_classes.py#L453)
Fit the model according to the given training data.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vector, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,)
Target vector relative to X.
**sample\_weight**array-like of shape (n\_samples,), default=None
Array of weights that are assigned to individual samples. If not provided, then each sample is given unit weight.
New in version 0.18.
Returns:
**self**object
An instance of the estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L372)
Predict using the linear model.
Parameters:
**X**array-like or sparse matrix, shape (n\_samples, n\_features)
Samples.
Returns:
**C**array, shape (n\_samples,)
Returns predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
scikit_learn sklearn.datasets.make_blobs sklearn.datasets.make\_blobs
============================
sklearn.datasets.make\_blobs(*n\_samples=100*, *n\_features=2*, *\**, *centers=None*, *cluster\_std=1.0*, *center\_box=(-10.0, 10.0)*, *shuffle=True*, *random\_state=None*, *return\_centers=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_samples_generator.py#L793)
Generate isotropic Gaussian blobs for clustering.
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/sample_generators.html#sample-generators).
Parameters:
**n\_samples**int or array-like, default=100
If int, it is the total number of points equally divided among clusters. If array-like, each element of the sequence indicates the number of samples per cluster.
Changed in version v0.20: one can now pass an array-like to the `n_samples` parameter
**n\_features**int, default=2
The number of features for each sample.
**centers**int or ndarray of shape (n\_centers, n\_features), default=None
The number of centers to generate, or the fixed center locations. If n\_samples is an int and centers is None, 3 centers are generated. If n\_samples is array-like, centers must be either None or an array of length equal to the length of n\_samples.
**cluster\_std**float or array-like of float, default=1.0
The standard deviation of the clusters.
**center\_box**tuple of float (min, max), default=(-10.0, 10.0)
The bounding box for each cluster center when centers are generated at random.
**shuffle**bool, default=True
Shuffle the samples.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for dataset creation. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**return\_centers**bool, default=False
If True, then return the centers of each cluster.
New in version 0.23.
Returns:
**X**ndarray of shape (n\_samples, n\_features)
The generated samples.
**y**ndarray of shape (n\_samples,)
The integer labels for cluster membership of each sample.
**centers**ndarray of shape (n\_centers, n\_features)
The centers of each cluster. Only returned if `return_centers=True`.
See also
[`make_classification`](sklearn.datasets.make_classification#sklearn.datasets.make_classification "sklearn.datasets.make_classification")
A more intricate variant.
#### Examples
```
>>> from sklearn.datasets import make_blobs
>>> X, y = make_blobs(n_samples=10, centers=3, n_features=2,
... random_state=0)
>>> print(X.shape)
(10, 2)
>>> y
array([0, 0, 1, 0, 2, 2, 2, 1, 1, 0])
>>> X, y = make_blobs(n_samples=[3, 3, 4], centers=None, n_features=2,
... random_state=0)
>>> print(X.shape)
(10, 2)
>>> y
array([0, 1, 2, 0, 2, 2, 2, 1, 1, 0])
```
Examples using `sklearn.datasets.make_blobs`
--------------------------------------------
[Release Highlights for scikit-learn 1.1](../../auto_examples/release_highlights/plot_release_highlights_1_1_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-1-1-0-py)
[Release Highlights for scikit-learn 0.23](../../auto_examples/release_highlights/plot_release_highlights_0_23_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-23-0-py)
[Probability Calibration for 3-class classification](../../auto_examples/calibration/plot_calibration_multiclass#sphx-glr-auto-examples-calibration-plot-calibration-multiclass-py)
[Probability calibration of classifiers](../../auto_examples/calibration/plot_calibration#sphx-glr-auto-examples-calibration-plot-calibration-py)
[Normal, Ledoit-Wolf and OAS Linear Discriminant Analysis for classification](../../auto_examples/classification/plot_lda#sphx-glr-auto-examples-classification-plot-lda-py)
[A demo of the mean-shift clustering algorithm](../../auto_examples/cluster/plot_mean_shift#sphx-glr-auto-examples-cluster-plot-mean-shift-py)
[An example of K-Means++ initialization](../../auto_examples/cluster/plot_kmeans_plusplus#sphx-glr-auto-examples-cluster-plot-kmeans-plusplus-py)
[Bisecting K-Means and Regular K-Means Performance Comparison](../../auto_examples/cluster/plot_bisect_kmeans#sphx-glr-auto-examples-cluster-plot-bisect-kmeans-py)
[Compare BIRCH and MiniBatchKMeans](../../auto_examples/cluster/plot_birch_vs_minibatchkmeans#sphx-glr-auto-examples-cluster-plot-birch-vs-minibatchkmeans-py)
[Comparing different clustering algorithms on toy datasets](../../auto_examples/cluster/plot_cluster_comparison#sphx-glr-auto-examples-cluster-plot-cluster-comparison-py)
[Comparing different hierarchical linkage methods on toy datasets](../../auto_examples/cluster/plot_linkage_comparison#sphx-glr-auto-examples-cluster-plot-linkage-comparison-py)
[Comparison of the K-Means and MiniBatchKMeans clustering algorithms](../../auto_examples/cluster/plot_mini_batch_kmeans#sphx-glr-auto-examples-cluster-plot-mini-batch-kmeans-py)
[Demo of DBSCAN clustering algorithm](../../auto_examples/cluster/plot_dbscan#sphx-glr-auto-examples-cluster-plot-dbscan-py)
[Demo of affinity propagation clustering algorithm](../../auto_examples/cluster/plot_affinity_propagation#sphx-glr-auto-examples-cluster-plot-affinity-propagation-py)
[Demonstration of k-means assumptions](../../auto_examples/cluster/plot_kmeans_assumptions#sphx-glr-auto-examples-cluster-plot-kmeans-assumptions-py)
[Inductive Clustering](../../auto_examples/cluster/plot_inductive_clustering#sphx-glr-auto-examples-cluster-plot-inductive-clustering-py)
[Selecting the number of clusters with silhouette analysis on KMeans clustering](../../auto_examples/cluster/plot_kmeans_silhouette_analysis#sphx-glr-auto-examples-cluster-plot-kmeans-silhouette-analysis-py)
[Plot randomly generated classification dataset](../../auto_examples/datasets/plot_random_dataset#sphx-glr-auto-examples-datasets-plot-random-dataset-py)
[GMM Initialization Methods](../../auto_examples/mixture/plot_gmm_init#sphx-glr-auto-examples-mixture-plot-gmm-init-py)
[Plot multinomial and One-vs-Rest Logistic Regression](../../auto_examples/linear_model/plot_logistic_multinomial#sphx-glr-auto-examples-linear-model-plot-logistic-multinomial-py)
[SGD: Maximum margin separating hyperplane](../../auto_examples/linear_model/plot_sgd_separating_hyperplane#sphx-glr-auto-examples-linear-model-plot-sgd-separating-hyperplane-py)
[Comparing anomaly detection algorithms for outlier detection on toy datasets](../../auto_examples/miscellaneous/plot_anomaly_comparison#sphx-glr-auto-examples-miscellaneous-plot-anomaly-comparison-py)
[Demonstrating the different strategies of KBinsDiscretizer](../../auto_examples/preprocessing/plot_discretization_strategies#sphx-glr-auto-examples-preprocessing-plot-discretization-strategies-py)
[Plot the support vectors in LinearSVC](../../auto_examples/svm/plot_linearsvc_support_vectors#sphx-glr-auto-examples-svm-plot-linearsvc-support-vectors-py)
[SVM Tie Breaking Example](../../auto_examples/svm/plot_svm_tie_breaking#sphx-glr-auto-examples-svm-plot-svm-tie-breaking-py)
[SVM: Maximum margin separating hyperplane](../../auto_examples/svm/plot_separating_hyperplane#sphx-glr-auto-examples-svm-plot-separating-hyperplane-py)
[SVM: Separating hyperplane for unbalanced classes](../../auto_examples/svm/plot_separating_hyperplane_unbalanced#sphx-glr-auto-examples-svm-plot-separating-hyperplane-unbalanced-py)
| programming_docs |
scikit_learn sklearn.linear_model.ARDRegression sklearn.linear\_model.ARDRegression
===================================
*class*sklearn.linear\_model.ARDRegression(*\**, *n\_iter=300*, *tol=0.001*, *alpha\_1=1e-06*, *alpha\_2=1e-06*, *lambda\_1=1e-06*, *lambda\_2=1e-06*, *compute\_score=False*, *threshold\_lambda=10000.0*, *fit\_intercept=True*, *normalize='deprecated'*, *copy\_X=True*, *verbose=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_bayes.py#L432)
Bayesian ARD regression.
Fit the weights of a regression model, using an ARD prior. The weights of the regression model are assumed to be in Gaussian distributions. Also estimate the parameters lambda (precisions of the distributions of the weights) and alpha (precision of the distribution of the noise). The estimation is done by an iterative procedures (Evidence Maximization)
Read more in the [User Guide](../linear_model#bayesian-regression).
Parameters:
**n\_iter**int, default=300
Maximum number of iterations.
**tol**float, default=1e-3
Stop the algorithm if w has converged.
**alpha\_1**float, default=1e-6
Hyper-parameter : shape parameter for the Gamma distribution prior over the alpha parameter.
**alpha\_2**float, default=1e-6
Hyper-parameter : inverse scale parameter (rate parameter) for the Gamma distribution prior over the alpha parameter.
**lambda\_1**float, default=1e-6
Hyper-parameter : shape parameter for the Gamma distribution prior over the lambda parameter.
**lambda\_2**float, default=1e-6
Hyper-parameter : inverse scale parameter (rate parameter) for the Gamma distribution prior over the lambda parameter.
**compute\_score**bool, default=False
If True, compute the objective function at each step of the model.
**threshold\_lambda**float, default=10 000
Threshold for removing (pruning) weights with high precision from the computation.
**fit\_intercept**bool, default=True
Whether to calculate the intercept for this model. If set to false, no intercept will be used in calculations (i.e. data is expected to be centered).
**normalize**bool, default=False
This parameter is ignored when `fit_intercept` is set to False. If True, the regressors X will be normalized before regression by subtracting the mean and dividing by the l2-norm. If you wish to standardize, please use [`StandardScaler`](sklearn.preprocessing.standardscaler#sklearn.preprocessing.StandardScaler "sklearn.preprocessing.StandardScaler") before calling `fit` on an estimator with `normalize=False`.
Deprecated since version 1.0: `normalize` was deprecated in version 1.0 and will be removed in 1.2.
**copy\_X**bool, default=True
If True, X will be copied; else, it may be overwritten.
**verbose**bool, default=False
Verbose mode when fitting the model.
Attributes:
**coef\_**array-like of shape (n\_features,)
Coefficients of the regression model (mean of distribution)
**alpha\_**float
estimated precision of the noise.
**lambda\_**array-like of shape (n\_features,)
estimated precisions of the weights.
**sigma\_**array-like of shape (n\_features, n\_features)
estimated variance-covariance matrix of the weights
**scores\_**float
if computed, value of the objective function (to be maximized)
**intercept\_**float
Independent term in decision function. Set to 0.0 if `fit_intercept = False`.
**X\_offset\_**float
If `normalize=True`, offset subtracted for centering data to a zero mean.
**X\_scale\_**float
If `normalize=True`, parameter used to scale data to a unit standard deviation.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`BayesianRidge`](sklearn.linear_model.bayesianridge#sklearn.linear_model.BayesianRidge "sklearn.linear_model.BayesianRidge")
Bayesian ridge regression.
#### Notes
For an example, see [examples/linear\_model/plot\_ard.py](../../auto_examples/linear_model/plot_ard#sphx-glr-auto-examples-linear-model-plot-ard-py).
#### References
D. J. C. MacKay, Bayesian nonlinear modeling for the prediction competition, ASHRAE Transactions, 1994.
R. Salakhutdinov, Lecture notes on Statistical Machine Learning, <http://www.utstat.toronto.edu/~rsalakhu/sta4273/notes/Lecture2.pdf#page=15> Their beta is our `self.alpha_` Their alpha is our `self.lambda_` ARD is a little different than the slide: only dimensions/features for which `self.lambda_ < self.threshold_lambda` are kept and the rest are discarded.
#### Examples
```
>>> from sklearn import linear_model
>>> clf = linear_model.ARDRegression()
>>> clf.fit([[0,0], [1, 1], [2, 2]], [0, 1, 2])
ARDRegression()
>>> clf.predict([[1, 1]])
array([1.])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.linear_model.ARDRegression.fit "sklearn.linear_model.ARDRegression.fit")(X, y) | Fit the model according to the given training data and parameters. |
| [`get_params`](#sklearn.linear_model.ARDRegression.get_params "sklearn.linear_model.ARDRegression.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.linear_model.ARDRegression.predict "sklearn.linear_model.ARDRegression.predict")(X[, return\_std]) | Predict using the linear model. |
| [`score`](#sklearn.linear_model.ARDRegression.score "sklearn.linear_model.ARDRegression.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.linear_model.ARDRegression.set_params "sklearn.linear_model.ARDRegression.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_bayes.py#L598)
Fit the model according to the given training data and parameters.
Iterative procedure to maximize the evidence
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training vector, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,)
Target values (integers). Will be cast to X’s dtype if necessary.
Returns:
**self**object
Fitted estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*, *return\_std=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_bayes.py#L748)
Predict using the linear model.
In addition to the mean of the predictive distribution, also its standard deviation can be returned.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Samples.
**return\_std**bool, default=False
Whether to return the standard deviation of posterior prediction.
Returns:
**y\_mean**array-like of shape (n\_samples,)
Mean of predictive distribution of query points.
**y\_std**array-like of shape (n\_samples,)
Standard deviation of predictive distribution of query points.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.linear_model.ARDRegression`
---------------------------------------------------
[Comparing Linear Bayesian Regressors](../../auto_examples/linear_model/plot_ard#sphx-glr-auto-examples-linear-model-plot-ard-py)
scikit_learn sklearn.gaussian_process.kernels.ConstantKernel sklearn.gaussian\_process.kernels.ConstantKernel
================================================
*class*sklearn.gaussian\_process.kernels.ConstantKernel(*constant\_value=1.0*, *constant\_value\_bounds=(1e-05, 100000.0)*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L1162)
Constant kernel.
Can be used as part of a product-kernel where it scales the magnitude of the other factor (kernel) or as part of a sum-kernel, where it modifies the mean of the Gaussian process.
\[k(x\_1, x\_2) = constant\\_value \;\forall\; x\_1, x\_2\] Adding a constant kernel is equivalent to adding a constant:
```
kernel = RBF() + ConstantKernel(constant_value=2)
```
is the same as:
```
kernel = RBF() + 2
```
Read more in the [User Guide](../gaussian_process#gp-kernels).
New in version 0.18.
Parameters:
**constant\_value**float, default=1.0
The constant value which defines the covariance: k(x\_1, x\_2) = constant\_value
**constant\_value\_bounds**pair of floats >= 0 or “fixed”, default=(1e-5, 1e5)
The lower and upper bound on `constant_value`. If set to “fixed”, `constant_value` cannot be changed during hyperparameter tuning.
Attributes:
[`bounds`](#sklearn.gaussian_process.kernels.ConstantKernel.bounds "sklearn.gaussian_process.kernels.ConstantKernel.bounds")
Returns the log-transformed bounds on the theta.
**hyperparameter\_constant\_value**
[`hyperparameters`](#sklearn.gaussian_process.kernels.ConstantKernel.hyperparameters "sklearn.gaussian_process.kernels.ConstantKernel.hyperparameters")
Returns a list of all hyperparameter specifications.
[`n_dims`](#sklearn.gaussian_process.kernels.ConstantKernel.n_dims "sklearn.gaussian_process.kernels.ConstantKernel.n_dims")
Returns the number of non-fixed hyperparameters of the kernel.
[`requires_vector_input`](#sklearn.gaussian_process.kernels.ConstantKernel.requires_vector_input "sklearn.gaussian_process.kernels.ConstantKernel.requires_vector_input")
Whether the kernel works only on fixed-length feature vectors.
[`theta`](#sklearn.gaussian_process.kernels.ConstantKernel.theta "sklearn.gaussian_process.kernels.ConstantKernel.theta")
Returns the (flattened, log-transformed) non-fixed hyperparameters.
#### Examples
```
>>> from sklearn.datasets import make_friedman2
>>> from sklearn.gaussian_process import GaussianProcessRegressor
>>> from sklearn.gaussian_process.kernels import RBF, ConstantKernel
>>> X, y = make_friedman2(n_samples=500, noise=0, random_state=0)
>>> kernel = RBF() + ConstantKernel(constant_value=2)
>>> gpr = GaussianProcessRegressor(kernel=kernel, alpha=5,
... random_state=0).fit(X, y)
>>> gpr.score(X, y)
0.3696...
>>> gpr.predict(X[:1,:], return_std=True)
(array([606.1...]), array([0.24...]))
```
#### Methods
| | |
| --- | --- |
| [`__call__`](#sklearn.gaussian_process.kernels.ConstantKernel.__call__ "sklearn.gaussian_process.kernels.ConstantKernel.__call__")(X[, Y, eval\_gradient]) | Return the kernel k(X, Y) and optionally its gradient. |
| [`clone_with_theta`](#sklearn.gaussian_process.kernels.ConstantKernel.clone_with_theta "sklearn.gaussian_process.kernels.ConstantKernel.clone_with_theta")(theta) | Returns a clone of self with given hyperparameters theta. |
| [`diag`](#sklearn.gaussian_process.kernels.ConstantKernel.diag "sklearn.gaussian_process.kernels.ConstantKernel.diag")(X) | Returns the diagonal of the kernel k(X, X). |
| [`get_params`](#sklearn.gaussian_process.kernels.ConstantKernel.get_params "sklearn.gaussian_process.kernels.ConstantKernel.get_params")([deep]) | Get parameters of this kernel. |
| [`is_stationary`](#sklearn.gaussian_process.kernels.ConstantKernel.is_stationary "sklearn.gaussian_process.kernels.ConstantKernel.is_stationary")() | Returns whether the kernel is stationary. |
| [`set_params`](#sklearn.gaussian_process.kernels.ConstantKernel.set_params "sklearn.gaussian_process.kernels.ConstantKernel.set_params")(\*\*params) | Set the parameters of this kernel. |
\_\_call\_\_(*X*, *Y=None*, *eval\_gradient=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L1219)
Return the kernel k(X, Y) and optionally its gradient.
Parameters:
**X**array-like of shape (n\_samples\_X, n\_features) or list of object
Left argument of the returned kernel k(X, Y)
**Y**array-like of shape (n\_samples\_X, n\_features) or list of object, default=None
Right argument of the returned kernel k(X, Y). If None, k(X, X) is evaluated instead.
**eval\_gradient**bool, default=False
Determines whether the gradient with respect to the log of the kernel hyperparameter is computed. Only supported when Y is None.
Returns:
**K**ndarray of shape (n\_samples\_X, n\_samples\_Y)
Kernel k(X, Y)
**K\_gradient**ndarray of shape (n\_samples\_X, n\_samples\_X, n\_dims), optional
The gradient of the kernel k(X, X) with respect to the log of the hyperparameter of the kernel. Only returned when eval\_gradient is True.
*property*bounds
Returns the log-transformed bounds on the theta.
Returns:
**bounds**ndarray of shape (n\_dims, 2)
The log-transformed bounds on the kernel’s hyperparameters theta
clone\_with\_theta(*theta*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L238)
Returns a clone of self with given hyperparameters theta.
Parameters:
**theta**ndarray of shape (n\_dims,)
The hyperparameters
diag(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L1273)
Returns the diagonal of the kernel k(X, X).
The result of this method is identical to np.diag(self(X)); however, it can be evaluated more efficiently since only the diagonal is evaluated.
Parameters:
**X**array-like of shape (n\_samples\_X, n\_features) or list of object
Argument to the kernel.
Returns:
**K\_diag**ndarray of shape (n\_samples\_X,)
Diagonal of kernel k(X, X)
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L158)
Get parameters of this kernel.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*hyperparameters
Returns a list of all hyperparameter specifications.
is\_stationary()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L474)
Returns whether the kernel is stationary.
*property*n\_dims
Returns the number of non-fixed hyperparameters of the kernel.
*property*requires\_vector\_input
Whether the kernel works only on fixed-length feature vectors.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/gaussian_process/kernels.py#L198)
Set the parameters of this kernel.
The method works on simple kernels as well as on nested kernels. The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Returns:
self
*property*theta
Returns the (flattened, log-transformed) non-fixed hyperparameters.
Note that theta are typically the log-transformed values of the kernel’s hyperparameters as this representation of the search space is more amenable for hyperparameter search, as hyperparameters like length-scales naturally live on a log-scale.
Returns:
**theta**ndarray of shape (n\_dims,)
The non-fixed, log-transformed hyperparameters of the kernel
Examples using `sklearn.gaussian_process.kernels.ConstantKernel`
----------------------------------------------------------------
[Illustration of prior and posterior Gaussian process for different kernels](../../auto_examples/gaussian_process/plot_gpr_prior_posterior#sphx-glr-auto-examples-gaussian-process-plot-gpr-prior-posterior-py)
[Iso-probability lines for Gaussian Processes classification (GPC)](../../auto_examples/gaussian_process/plot_gpc_isoprobability#sphx-glr-auto-examples-gaussian-process-plot-gpc-isoprobability-py)
scikit_learn sklearn.metrics.roc_auc_score sklearn.metrics.roc\_auc\_score
===============================
sklearn.metrics.roc\_auc\_score(*y\_true*, *y\_score*, *\**, *average='macro'*, *sample\_weight=None*, *max\_fpr=None*, *multi\_class='raise'*, *labels=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_ranking.py#L365)
Compute Area Under the Receiver Operating Characteristic Curve (ROC AUC) from prediction scores.
Note: this implementation can be used with binary, multiclass and multilabel classification, but some restrictions apply (see Parameters).
Read more in the [User Guide](../model_evaluation#roc-metrics).
Parameters:
**y\_true**array-like of shape (n\_samples,) or (n\_samples, n\_classes)
True labels or binary label indicators. The binary and multiclass cases expect labels with shape (n\_samples,) while the multilabel case expects binary label indicators with shape (n\_samples, n\_classes).
**y\_score**array-like of shape (n\_samples,) or (n\_samples, n\_classes)
Target scores.
* In the binary case, it corresponds to an array of shape `(n_samples,)`. Both probability estimates and non-thresholded decision values can be provided. The probability estimates correspond to the **probability of the class with the greater label**, i.e. `estimator.classes_[1]` and thus `estimator.predict_proba(X, y)[:, 1]`. The decision values corresponds to the output of `estimator.decision_function(X, y)`. See more information in the [User guide](../model_evaluation#roc-auc-binary);
* In the multiclass case, it corresponds to an array of shape `(n_samples, n_classes)` of probability estimates provided by the `predict_proba` method. The probability estimates **must** sum to 1 across the possible classes. In addition, the order of the class scores must correspond to the order of `labels`, if provided, or else to the numerical or lexicographical order of the labels in `y_true`. See more information in the [User guide](../model_evaluation#roc-auc-multiclass);
* In the multilabel case, it corresponds to an array of shape `(n_samples, n_classes)`. Probability estimates are provided by the `predict_proba` method and the non-thresholded decision values by the `decision_function` method. The probability estimates correspond to the **probability of the class with the greater label for each output** of the classifier. See more information in the [User guide](../model_evaluation#roc-auc-multilabel).
**average**{‘micro’, ‘macro’, ‘samples’, ‘weighted’} or None, default=’macro’
If `None`, the scores for each class are returned. Otherwise, this determines the type of averaging performed on the data. Note: multiclass ROC AUC currently only handles the ‘macro’ and ‘weighted’ averages. For multiclass targets, `average=None` is only implemented for `multi_class='ovo'`.
`'micro'`:
Calculate metrics globally by considering each element of the label indicator matrix as a label.
`'macro'`:
Calculate metrics for each label, and find their unweighted mean. This does not take label imbalance into account.
`'weighted'`:
Calculate metrics for each label, and find their average, weighted by support (the number of true instances for each label).
`'samples'`:
Calculate metrics for each instance, and find their average.
Will be ignored when `y_true` is binary.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**max\_fpr**float > 0 and <= 1, default=None
If not `None`, the standardized partial AUC [[2]](#r4bb7c4558997-2) over the range [0, max\_fpr] is returned. For the multiclass case, `max_fpr`, should be either equal to `None` or `1.0` as AUC ROC partial computation currently is not supported for multiclass.
**multi\_class**{‘raise’, ‘ovr’, ‘ovo’}, default=’raise’
Only used for multiclass targets. Determines the type of configuration to use. The default value raises an error, so either `'ovr'` or `'ovo'` must be passed explicitly.
`'ovr'`:
Stands for One-vs-rest. Computes the AUC of each class against the rest [[3]](#r4bb7c4558997-3) [[4]](#r4bb7c4558997-4). This treats the multiclass case in the same way as the multilabel case. Sensitive to class imbalance even when `average == 'macro'`, because class imbalance affects the composition of each of the ‘rest’ groupings.
`'ovo'`:
Stands for One-vs-one. Computes the average AUC of all possible pairwise combinations of classes [[5]](#r4bb7c4558997-5). Insensitive to class imbalance when `average == 'macro'`.
**labels**array-like of shape (n\_classes,), default=None
Only used for multiclass targets. List of labels that index the classes in `y_score`. If `None`, the numerical or lexicographical order of the labels in `y_true` is used.
Returns:
**auc**float
Area Under the Curve score.
See also
[`average_precision_score`](sklearn.metrics.average_precision_score#sklearn.metrics.average_precision_score "sklearn.metrics.average_precision_score")
Area under the precision-recall curve.
[`roc_curve`](sklearn.metrics.roc_curve#sklearn.metrics.roc_curve "sklearn.metrics.roc_curve")
Compute Receiver operating characteristic (ROC) curve.
[`RocCurveDisplay.from_estimator`](sklearn.metrics.roccurvedisplay#sklearn.metrics.RocCurveDisplay.from_estimator "sklearn.metrics.RocCurveDisplay.from_estimator")
Plot Receiver Operating Characteristic (ROC) curve given an estimator and some data.
[`RocCurveDisplay.from_predictions`](sklearn.metrics.roccurvedisplay#sklearn.metrics.RocCurveDisplay.from_predictions "sklearn.metrics.RocCurveDisplay.from_predictions")
Plot Receiver Operating Characteristic (ROC) curve given the true and predicted values.
#### References
[1] [Wikipedia entry for the Receiver operating characteristic](https://en.wikipedia.org/wiki/Receiver_operating_characteristic)
[[2](#id1)] [Analyzing a portion of the ROC curve. McClish, 1989](https://www.ncbi.nlm.nih.gov/pubmed/2668680)
[[3](#id2)] Provost, F., Domingos, P. (2000). Well-trained PETs: Improving probability estimation trees (Section 6.2), CeDER Working Paper #IS-00-04, Stern School of Business, New York University.
[[4](#id3)] [Fawcett, T. (2006). An introduction to ROC analysis. Pattern Recognition Letters, 27(8), 861-874.](https://www.sciencedirect.com/science/article/pii/S016786550500303X)
[[5](#id4)] [Hand, D.J., Till, R.J. (2001). A Simple Generalisation of the Area Under the ROC Curve for Multiple Class Classification Problems. Machine Learning, 45(2), 171-186.](http://link.springer.com/article/10.1023/A:1010920819831)
#### Examples
Binary case:
```
>>> from sklearn.datasets import load_breast_cancer
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.metrics import roc_auc_score
>>> X, y = load_breast_cancer(return_X_y=True)
>>> clf = LogisticRegression(solver="liblinear", random_state=0).fit(X, y)
>>> roc_auc_score(y, clf.predict_proba(X)[:, 1])
0.99...
>>> roc_auc_score(y, clf.decision_function(X))
0.99...
```
Multiclass case:
```
>>> from sklearn.datasets import load_iris
>>> X, y = load_iris(return_X_y=True)
>>> clf = LogisticRegression(solver="liblinear").fit(X, y)
>>> roc_auc_score(y, clf.predict_proba(X), multi_class='ovr')
0.99...
```
Multilabel case:
```
>>> import numpy as np
>>> from sklearn.datasets import make_multilabel_classification
>>> from sklearn.multioutput import MultiOutputClassifier
>>> X, y = make_multilabel_classification(random_state=0)
>>> clf = MultiOutputClassifier(clf).fit(X, y)
>>> # get a list of n_output containing probability arrays of shape
>>> # (n_samples, n_classes)
>>> y_pred = clf.predict_proba(X)
>>> # extract the positive columns for each output
>>> y_pred = np.transpose([pred[:, 1] for pred in y_pred])
>>> roc_auc_score(y, y_pred, average=None)
array([0.82..., 0.86..., 0.94..., 0.85... , 0.94...])
>>> from sklearn.linear_model import RidgeClassifierCV
>>> clf = RidgeClassifierCV().fit(X, y)
>>> roc_auc_score(y, clf.decision_function(X), average=None)
array([0.81..., 0.84... , 0.93..., 0.87..., 0.94...])
```
Examples using `sklearn.metrics.roc_auc_score`
----------------------------------------------
[Release Highlights for scikit-learn 0.22](../../auto_examples/release_highlights/plot_release_highlights_0_22_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-22-0-py)
[Probability Calibration curves](../../auto_examples/calibration/plot_calibration_curve#sphx-glr-auto-examples-calibration-plot-calibration-curve-py)
[Receiver Operating Characteristic (ROC)](../../auto_examples/model_selection/plot_roc#sphx-glr-auto-examples-model-selection-plot-roc-py)
[Receiver Operating Characteristic (ROC) with cross validation](../../auto_examples/model_selection/plot_roc_crossval#sphx-glr-auto-examples-model-selection-plot-roc-crossval-py)
[Statistical comparison of models using grid search](../../auto_examples/model_selection/plot_grid_search_stats#sphx-glr-auto-examples-model-selection-plot-grid-search-stats-py)
| programming_docs |
scikit_learn sklearn.datasets.make_multilabel_classification sklearn.datasets.make\_multilabel\_classification
=================================================
sklearn.datasets.make\_multilabel\_classification(*n\_samples=100*, *n\_features=20*, *\**, *n\_classes=5*, *n\_labels=2*, *length=50*, *allow\_unlabeled=True*, *sparse=False*, *return\_indicator='dense'*, *return\_distributions=False*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_samples_generator.py#L291)
Generate a random multilabel classification problem.
For each sample, the generative process is:
* pick the number of labels: n ~ Poisson(n\_labels)
* n times, choose a class c: c ~ Multinomial(theta)
* pick the document length: k ~ Poisson(length)
* k times, choose a word: w ~ Multinomial(theta\_c)
In the above process, rejection sampling is used to make sure that n is never zero or more than `n_classes`, and that the document length is never zero. Likewise, we reject classes which have already been chosen.
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/sample_generators.html#sample-generators).
Parameters:
**n\_samples**int, default=100
The number of samples.
**n\_features**int, default=20
The total number of features.
**n\_classes**int, default=5
The number of classes of the classification problem.
**n\_labels**int, default=2
The average number of labels per instance. More precisely, the number of labels per sample is drawn from a Poisson distribution with `n_labels` as its expected value, but samples are bounded (using rejection sampling) by `n_classes`, and must be nonzero if `allow_unlabeled` is False.
**length**int, default=50
The sum of the features (number of words if documents) is drawn from a Poisson distribution with this expected value.
**allow\_unlabeled**bool, default=True
If `True`, some instances might not belong to any class.
**sparse**bool, default=False
If `True`, return a sparse feature matrix.
New in version 0.17: parameter to allow *sparse* output.
**return\_indicator**{‘dense’, ‘sparse’} or False, default=’dense’
If `'dense'` return `Y` in the dense binary indicator format. If `'sparse'` return `Y` in the sparse binary indicator format. `False` returns a list of lists of labels.
**return\_distributions**bool, default=False
If `True`, return the prior class probability and conditional probabilities of features given classes, from which the data was drawn.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for dataset creation. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Returns:
**X**ndarray of shape (n\_samples, n\_features)
The generated samples.
**Y**{ndarray, sparse matrix} of shape (n\_samples, n\_classes)
The label sets. Sparse matrix should be of CSR format.
**p\_c**ndarray of shape (n\_classes,)
The probability of each class being drawn. Only returned if `return_distributions=True`.
**p\_w\_c**ndarray of shape (n\_features, n\_classes)
The probability of each feature being drawn given each class. Only returned if `return_distributions=True`.
Examples using `sklearn.datasets.make_multilabel_classification`
----------------------------------------------------------------
[Plot randomly generated multilabel dataset](../../auto_examples/datasets/plot_random_multilabel_dataset#sphx-glr-auto-examples-datasets-plot-random-multilabel-dataset-py)
[Multilabel classification](../../auto_examples/miscellaneous/plot_multilabel#sphx-glr-auto-examples-miscellaneous-plot-multilabel-py)
scikit_learn sklearn.base.ClusterMixin sklearn.base.ClusterMixin
=========================
*class*sklearn.base.ClusterMixin[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L727)
Mixin class for all cluster estimators in scikit-learn.
#### Methods
| | |
| --- | --- |
| [`fit_predict`](#sklearn.base.ClusterMixin.fit_predict "sklearn.base.ClusterMixin.fit_predict")(X[, y]) | Perform clustering on `X` and returns cluster labels. |
fit\_predict(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L732)
Perform clustering on `X` and returns cluster labels.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input data.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**labels**ndarray of shape (n\_samples,), dtype=np.int64
Cluster labels.
scikit_learn sklearn.covariance.MinCovDet sklearn.covariance.MinCovDet
============================
*class*sklearn.covariance.MinCovDet(*\**, *store\_precision=True*, *assume\_centered=False*, *support\_fraction=None*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_robust_covariance.py#L576)
Minimum Covariance Determinant (MCD): robust estimator of covariance.
The Minimum Covariance Determinant covariance estimator is to be applied on Gaussian-distributed data, but could still be relevant on data drawn from a unimodal, symmetric distribution. It is not meant to be used with multi-modal data (the algorithm used to fit a MinCovDet object is likely to fail in such a case). One should consider projection pursuit methods to deal with multi-modal datasets.
Read more in the [User Guide](../covariance#robust-covariance).
Parameters:
**store\_precision**bool, default=True
Specify if the estimated precision is stored.
**assume\_centered**bool, default=False
If True, the support of the robust location and the covariance estimates is computed, and a covariance estimate is recomputed from it, without centering the data. Useful to work with data whose mean is significantly equal to zero but is not exactly zero. If False, the robust location and covariance are directly computed with the FastMCD algorithm without additional treatment.
**support\_fraction**float, default=None
The proportion of points to be included in the support of the raw MCD estimate. Default is None, which implies that the minimum value of support\_fraction will be used within the algorithm: `(n_sample + n_features + 1) / 2`. The parameter must be in the range (0, 1).
**random\_state**int, RandomState instance or None, default=None
Determines the pseudo random number generator for shuffling the data. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Attributes:
**raw\_location\_**ndarray of shape (n\_features,)
The raw robust estimated location before correction and re-weighting.
**raw\_covariance\_**ndarray of shape (n\_features, n\_features)
The raw robust estimated covariance before correction and re-weighting.
**raw\_support\_**ndarray of shape (n\_samples,)
A mask of the observations that have been used to compute the raw robust estimates of location and shape, before correction and re-weighting.
**location\_**ndarray of shape (n\_features,)
Estimated robust location.
**covariance\_**ndarray of shape (n\_features, n\_features)
Estimated robust covariance matrix.
**precision\_**ndarray of shape (n\_features, n\_features)
Estimated pseudo inverse matrix. (stored only if store\_precision is True)
**support\_**ndarray of shape (n\_samples,)
A mask of the observations that have been used to compute the robust estimates of location and shape.
**dist\_**ndarray of shape (n\_samples,)
Mahalanobis distances of the training set (on which [`fit`](#sklearn.covariance.MinCovDet.fit "sklearn.covariance.MinCovDet.fit") is called) observations.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`EllipticEnvelope`](sklearn.covariance.ellipticenvelope#sklearn.covariance.EllipticEnvelope "sklearn.covariance.EllipticEnvelope")
An object for detecting outliers in a Gaussian distributed dataset.
[`EmpiricalCovariance`](sklearn.covariance.empiricalcovariance#sklearn.covariance.EmpiricalCovariance "sklearn.covariance.EmpiricalCovariance")
Maximum likelihood covariance estimator.
[`GraphicalLasso`](sklearn.covariance.graphicallasso#sklearn.covariance.GraphicalLasso "sklearn.covariance.GraphicalLasso")
Sparse inverse covariance estimation with an l1-penalized estimator.
[`GraphicalLassoCV`](sklearn.covariance.graphicallassocv#sklearn.covariance.GraphicalLassoCV "sklearn.covariance.GraphicalLassoCV")
Sparse inverse covariance with cross-validated choice of the l1 penalty.
[`LedoitWolf`](sklearn.covariance.ledoitwolf#sklearn.covariance.LedoitWolf "sklearn.covariance.LedoitWolf")
LedoitWolf Estimator.
[`OAS`](sklearn.covariance.oas#sklearn.covariance.OAS "sklearn.covariance.OAS")
Oracle Approximating Shrinkage Estimator.
[`ShrunkCovariance`](sklearn.covariance.shrunkcovariance#sklearn.covariance.ShrunkCovariance "sklearn.covariance.ShrunkCovariance")
Covariance estimator with shrinkage.
#### References
[Rouseeuw1984] P. J. Rousseeuw. Least median of squares regression. J. Am Stat Ass, 79:871, 1984.
[Rousseeuw] A Fast Algorithm for the Minimum Covariance Determinant Estimator, 1999, American Statistical Association and the American Society for Quality, TECHNOMETRICS
[ButlerDavies] R. W. Butler, P. L. Davies and M. Jhun, Asymptotics For The Minimum Covariance Determinant Estimator, The Annals of Statistics, 1993, Vol. 21, No. 3, 1385-1400
#### Examples
```
>>> import numpy as np
>>> from sklearn.covariance import MinCovDet
>>> from sklearn.datasets import make_gaussian_quantiles
>>> real_cov = np.array([[.8, .3],
... [.3, .4]])
>>> rng = np.random.RandomState(0)
>>> X = rng.multivariate_normal(mean=[0, 0],
... cov=real_cov,
... size=500)
>>> cov = MinCovDet(random_state=0).fit(X)
>>> cov.covariance_
array([[0.7411..., 0.2535...],
[0.2535..., 0.3053...]])
>>> cov.location_
array([0.0813... , 0.0427...])
```
#### Methods
| | |
| --- | --- |
| [`correct_covariance`](#sklearn.covariance.MinCovDet.correct_covariance "sklearn.covariance.MinCovDet.correct_covariance")(data) | Apply a correction to raw Minimum Covariance Determinant estimates. |
| [`error_norm`](#sklearn.covariance.MinCovDet.error_norm "sklearn.covariance.MinCovDet.error_norm")(comp\_cov[, norm, scaling, squared]) | Compute the Mean Squared Error between two covariance estimators. |
| [`fit`](#sklearn.covariance.MinCovDet.fit "sklearn.covariance.MinCovDet.fit")(X[, y]) | Fit a Minimum Covariance Determinant with the FastMCD algorithm. |
| [`get_params`](#sklearn.covariance.MinCovDet.get_params "sklearn.covariance.MinCovDet.get_params")([deep]) | Get parameters for this estimator. |
| [`get_precision`](#sklearn.covariance.MinCovDet.get_precision "sklearn.covariance.MinCovDet.get_precision")() | Getter for the precision matrix. |
| [`mahalanobis`](#sklearn.covariance.MinCovDet.mahalanobis "sklearn.covariance.MinCovDet.mahalanobis")(X) | Compute the squared Mahalanobis distances of given observations. |
| [`reweight_covariance`](#sklearn.covariance.MinCovDet.reweight_covariance "sklearn.covariance.MinCovDet.reweight_covariance")(data) | Re-weight raw Minimum Covariance Determinant estimates. |
| [`score`](#sklearn.covariance.MinCovDet.score "sklearn.covariance.MinCovDet.score")(X\_test[, y]) | Compute the log-likelihood of `X_test` under the estimated Gaussian model. |
| [`set_params`](#sklearn.covariance.MinCovDet.set_params "sklearn.covariance.MinCovDet.set_params")(\*\*params) | Set the parameters of this estimator. |
correct\_covariance(*data*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_robust_covariance.py#L769)
Apply a correction to raw Minimum Covariance Determinant estimates.
Correction using the empirical correction factor suggested by Rousseeuw and Van Driessen in [[RVD]](#r491365aeaa84-rvd).
Parameters:
**data**array-like of shape (n\_samples, n\_features)
The data matrix, with p features and n samples. The data set must be the one which was used to compute the raw estimates.
Returns:
**covariance\_corrected**ndarray of shape (n\_features, n\_features)
Corrected robust covariance estimate.
#### References
[[RVD](#id4)] A Fast Algorithm for the Minimum Covariance Determinant Estimator, 1999, American Statistical Association and the American Society for Quality, TECHNOMETRICS
error\_norm(*comp\_cov*, *norm='frobenius'*, *scaling=True*, *squared=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_empirical_covariance.py#L267)
Compute the Mean Squared Error between two covariance estimators.
Parameters:
**comp\_cov**array-like of shape (n\_features, n\_features)
The covariance to compare with.
**norm**{“frobenius”, “spectral”}, default=”frobenius”
The type of norm used to compute the error. Available error types: - ‘frobenius’ (default): sqrt(tr(A^t.A)) - ‘spectral’: sqrt(max(eigenvalues(A^t.A)) where A is the error `(comp_cov - self.covariance_)`.
**scaling**bool, default=True
If True (default), the squared error norm is divided by n\_features. If False, the squared error norm is not rescaled.
**squared**bool, default=True
Whether to compute the squared error norm or the error norm. If True (default), the squared error norm is returned. If False, the error norm is returned.
Returns:
**result**float
The Mean Squared Error (in the sense of the Frobenius norm) between `self` and `comp_cov` covariance estimators.
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_robust_covariance.py#L716)
Fit a Minimum Covariance Determinant with the FastMCD algorithm.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**self**object
Returns the instance itself.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
get\_precision()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_empirical_covariance.py#L195)
Getter for the precision matrix.
Returns:
**precision\_**array-like of shape (n\_features, n\_features)
The precision matrix associated to the current covariance object.
mahalanobis(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_empirical_covariance.py#L318)
Compute the squared Mahalanobis distances of given observations.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The observations, the Mahalanobis distances of the which we compute. Observations are assumed to be drawn from the same distribution than the data used in fit.
Returns:
**dist**ndarray of shape (n\_samples,)
Squared Mahalanobis distances of the observations.
reweight\_covariance(*data*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_robust_covariance.py#L809)
Re-weight raw Minimum Covariance Determinant estimates.
Re-weight observations using Rousseeuw’s method (equivalent to deleting outlying observations from the data set before computing location and covariance estimates) described in [[RVDriessen]](#r9465bad4668c-rvdriessen).
Parameters:
**data**array-like of shape (n\_samples, n\_features)
The data matrix, with p features and n samples. The data set must be the one which was used to compute the raw estimates.
Returns:
**location\_reweighted**ndarray of shape (n\_features,)
Re-weighted robust location estimate.
**covariance\_reweighted**ndarray of shape (n\_features, n\_features)
Re-weighted robust covariance estimate.
**support\_reweighted**ndarray of shape (n\_samples,), dtype=bool
A mask of the observations that have been used to compute the re-weighted robust location and covariance estimates.
#### References
[[RVDriessen](#id6)] A Fast Algorithm for the Minimum Covariance Determinant Estimator, 1999, American Statistical Association and the American Society for Quality, TECHNOMETRICS
score(*X\_test*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_empirical_covariance.py#L236)
Compute the log-likelihood of `X_test` under the estimated Gaussian model.
The Gaussian model is defined by its mean and covariance matrix which are represented respectively by `self.location_` and `self.covariance_`.
Parameters:
**X\_test**array-like of shape (n\_samples, n\_features)
Test data of which we compute the likelihood, where `n_samples` is the number of samples and `n_features` is the number of features. `X_test` is assumed to be drawn from the same distribution than the data used in fit (including centering).
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**res**float
The log-likelihood of `X_test` with `self.location_` and `self.covariance_` as estimators of the Gaussian model mean and covariance matrix respectively.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.covariance.MinCovDet`
---------------------------------------------
[Robust covariance estimation and Mahalanobis distances relevance](../../auto_examples/covariance/plot_mahalanobis_distances#sphx-glr-auto-examples-covariance-plot-mahalanobis-distances-py)
[Robust vs Empirical covariance estimate](../../auto_examples/covariance/plot_robust_vs_empirical_covariance#sphx-glr-auto-examples-covariance-plot-robust-vs-empirical-covariance-py)
scikit_learn sklearn.ensemble.BaggingClassifier sklearn.ensemble.BaggingClassifier
==================================
*class*sklearn.ensemble.BaggingClassifier(*base\_estimator=None*, *n\_estimators=10*, *\**, *max\_samples=1.0*, *max\_features=1.0*, *bootstrap=True*, *bootstrap\_features=False*, *oob\_score=False*, *warm\_start=False*, *n\_jobs=None*, *random\_state=None*, *verbose=0*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_bagging.py#L517)
A Bagging classifier.
A Bagging classifier is an ensemble meta-estimator that fits base classifiers each on random subsets of the original dataset and then aggregate their individual predictions (either by voting or by averaging) to form a final prediction. Such a meta-estimator can typically be used as a way to reduce the variance of a black-box estimator (e.g., a decision tree), by introducing randomization into its construction procedure and then making an ensemble out of it.
This algorithm encompasses several works from the literature. When random subsets of the dataset are drawn as random subsets of the samples, then this algorithm is known as Pasting [[1]](#rb1846455d0e5-1). If samples are drawn with replacement, then the method is known as Bagging [[2]](#rb1846455d0e5-2). When random subsets of the dataset are drawn as random subsets of the features, then the method is known as Random Subspaces [[3]](#rb1846455d0e5-3). Finally, when base estimators are built on subsets of both samples and features, then the method is known as Random Patches [[4]](#rb1846455d0e5-4).
Read more in the [User Guide](../ensemble#bagging).
New in version 0.15.
Parameters:
**base\_estimator**object, default=None
The base estimator to fit on random subsets of the dataset. If None, then the base estimator is a [`DecisionTreeClassifier`](sklearn.tree.decisiontreeclassifier#sklearn.tree.DecisionTreeClassifier "sklearn.tree.DecisionTreeClassifier").
**n\_estimators**int, default=10
The number of base estimators in the ensemble.
**max\_samples**int or float, default=1.0
The number of samples to draw from X to train each base estimator (with replacement by default, see `bootstrap` for more details).
* If int, then draw `max_samples` samples.
* If float, then draw `max_samples * X.shape[0]` samples.
**max\_features**int or float, default=1.0
The number of features to draw from X to train each base estimator ( without replacement by default, see `bootstrap_features` for more details).
* If int, then draw `max_features` features.
* If float, then draw `max(1, int(max_features * n_features_in_))` features.
**bootstrap**bool, default=True
Whether samples are drawn with replacement. If False, sampling without replacement is performed.
**bootstrap\_features**bool, default=False
Whether features are drawn with replacement.
**oob\_score**bool, default=False
Whether to use out-of-bag samples to estimate the generalization error. Only available if bootstrap=True.
**warm\_start**bool, default=False
When set to True, reuse the solution of the previous call to fit and add more estimators to the ensemble, otherwise, just fit a whole new ensemble. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
New in version 0.17: *warm\_start* constructor parameter.
**n\_jobs**int, default=None
The number of jobs to run in parallel for both [`fit`](#sklearn.ensemble.BaggingClassifier.fit "sklearn.ensemble.BaggingClassifier.fit") and [`predict`](#sklearn.ensemble.BaggingClassifier.predict "sklearn.ensemble.BaggingClassifier.predict"). `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**random\_state**int, RandomState instance or None, default=None
Controls the random resampling of the original dataset (sample wise and feature wise). If the base estimator accepts a `random_state` attribute, a different seed is generated for each instance in the ensemble. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**verbose**int, default=0
Controls the verbosity when fitting and predicting.
Attributes:
**base\_estimator\_**estimator
The base estimator from which the ensemble is grown.
[`n_features_`](#sklearn.ensemble.BaggingClassifier.n_features_ "sklearn.ensemble.BaggingClassifier.n_features_")int
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**estimators\_**list of estimators
The collection of fitted base estimators.
[`estimators_samples_`](#sklearn.ensemble.BaggingClassifier.estimators_samples_ "sklearn.ensemble.BaggingClassifier.estimators_samples_")list of arrays
The subset of drawn samples for each base estimator.
**estimators\_features\_**list of arrays
The subset of drawn features for each base estimator.
**classes\_**ndarray of shape (n\_classes,)
The classes labels.
**n\_classes\_**int or list
The number of classes.
**oob\_score\_**float
Score of the training dataset obtained using an out-of-bag estimate. This attribute exists only when `oob_score` is True.
**oob\_decision\_function\_**ndarray of shape (n\_samples, n\_classes)
Decision function computed with out-of-bag estimate on the training set. If n\_estimators is small it might be possible that a data point was never left out during the bootstrap. In this case, `oob_decision_function_` might contain NaN. This attribute exists only when `oob_score` is True.
See also
[`BaggingRegressor`](sklearn.ensemble.baggingregressor#sklearn.ensemble.BaggingRegressor "sklearn.ensemble.BaggingRegressor")
A Bagging regressor.
#### References
[[1](#id1)] L. Breiman, “Pasting small votes for classification in large databases and on-line”, Machine Learning, 36(1), 85-103, 1999.
[[2](#id2)] L. Breiman, “Bagging predictors”, Machine Learning, 24(2), 123-140, 1996.
[[3](#id3)] T. Ho, “The random subspace method for constructing decision forests”, Pattern Analysis and Machine Intelligence, 20(8), 832-844, 1998.
[[4](#id4)] G. Louppe and P. Geurts, “Ensembles on Random Patches”, Machine Learning and Knowledge Discovery in Databases, 346-361, 2012.
#### Examples
```
>>> from sklearn.svm import SVC
>>> from sklearn.ensemble import BaggingClassifier
>>> from sklearn.datasets import make_classification
>>> X, y = make_classification(n_samples=100, n_features=4,
... n_informative=2, n_redundant=0,
... random_state=0, shuffle=False)
>>> clf = BaggingClassifier(base_estimator=SVC(),
... n_estimators=10, random_state=0).fit(X, y)
>>> clf.predict([[0, 0, 0, 0]])
array([1])
```
#### Methods
| | |
| --- | --- |
| [`decision_function`](#sklearn.ensemble.BaggingClassifier.decision_function "sklearn.ensemble.BaggingClassifier.decision_function")(X) | Average of the decision functions of the base classifiers. |
| [`fit`](#sklearn.ensemble.BaggingClassifier.fit "sklearn.ensemble.BaggingClassifier.fit")(X, y[, sample\_weight]) | Build a Bagging ensemble of estimators from the training set (X, y). |
| [`get_params`](#sklearn.ensemble.BaggingClassifier.get_params "sklearn.ensemble.BaggingClassifier.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.ensemble.BaggingClassifier.predict "sklearn.ensemble.BaggingClassifier.predict")(X) | Predict class for X. |
| [`predict_log_proba`](#sklearn.ensemble.BaggingClassifier.predict_log_proba "sklearn.ensemble.BaggingClassifier.predict_log_proba")(X) | Predict class log-probabilities for X. |
| [`predict_proba`](#sklearn.ensemble.BaggingClassifier.predict_proba "sklearn.ensemble.BaggingClassifier.predict_proba")(X) | Predict class probabilities for X. |
| [`score`](#sklearn.ensemble.BaggingClassifier.score "sklearn.ensemble.BaggingClassifier.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.ensemble.BaggingClassifier.set_params "sklearn.ensemble.BaggingClassifier.set_params")(\*\*params) | Set the parameters of this estimator. |
decision\_function(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_bagging.py#L900)
Average of the decision functions of the base classifiers.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Sparse matrices are accepted only if they are supported by the base estimator.
Returns:
**score**ndarray of shape (n\_samples, k)
The decision function of the input samples. The columns correspond to the classes in sorted order, as they appear in the attribute `classes_`. Regression and binary classification are special cases with `k == 1`, otherwise `k==n_classes`.
*property*estimators\_samples\_
The subset of drawn samples for each base estimator.
Returns a dynamically generated list of indices identifying the samples used for fitting each member of the ensemble, i.e., the in-bag samples.
Note: the list is re-created at each call to the property in order to reduce the object memory footprint by not storing the sampling data. Thus fetching the property may be slower than expected.
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_bagging.py#L265)
Build a Bagging ensemble of estimators from the training set (X, y).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Sparse matrices are accepted only if they are supported by the base estimator.
**y**array-like of shape (n\_samples,)
The target values (class labels in classification, real numbers in regression).
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, then samples are equally weighted. Note that this is supported only if the base estimator supports sample weighting.
Returns:
**self**object
Fitted estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_features\_
DEPRECATED: Attribute `n_features_` was deprecated in version 1.0 and will be removed in 1.2. Use `n_features_in_` instead.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_bagging.py#L767)
Predict class for X.
The predicted class of an input sample is computed as the class with the highest mean predicted probability. If base estimators do not implement a `predict_proba` method, then it resorts to voting.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Sparse matrices are accepted only if they are supported by the base estimator.
Returns:
**y**ndarray of shape (n\_samples,)
The predicted classes.
predict\_log\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_bagging.py#L842)
Predict class log-probabilities for X.
The predicted class log-probabilities of an input sample is computed as the log of the mean predicted class probabilities of the base estimators in the ensemble.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Sparse matrices are accepted only if they are supported by the base estimator.
Returns:
**p**ndarray of shape (n\_samples, n\_classes)
The class log-probabilities of the input samples. The order of the classes corresponds to that in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_bagging.py#L788)
Predict class probabilities for X.
The predicted class probabilities of an input sample is computed as the mean predicted class probabilities of the base estimators in the ensemble. If base estimators do not implement a `predict_proba` method, then it resorts to voting and the predicted class probabilities of an input sample represents the proportion of estimators predicting each class.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Sparse matrices are accepted only if they are supported by the base estimator.
Returns:
**p**ndarray of shape (n\_samples, n\_classes)
The class probabilities of the input samples. The order of the classes corresponds to that in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
| programming_docs |
scikit_learn sklearn.decomposition.SparsePCA sklearn.decomposition.SparsePCA
===============================
*class*sklearn.decomposition.SparsePCA(*n\_components=None*, *\**, *alpha=1*, *ridge\_alpha=0.01*, *max\_iter=1000*, *tol=1e-08*, *method='lars'*, *n\_jobs=None*, *U\_init=None*, *V\_init=None*, *verbose=False*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_sparse_pca.py#L16)
Sparse Principal Components Analysis (SparsePCA).
Finds the set of sparse components that can optimally reconstruct the data. The amount of sparseness is controllable by the coefficient of the L1 penalty, given by the parameter alpha.
Read more in the [User Guide](../decomposition#sparsepca).
Parameters:
**n\_components**int, default=None
Number of sparse atoms to extract. If None, then `n_components` is set to `n_features`.
**alpha**float, default=1
Sparsity controlling parameter. Higher values lead to sparser components.
**ridge\_alpha**float, default=0.01
Amount of ridge shrinkage to apply in order to improve conditioning when calling the transform method.
**max\_iter**int, default=1000
Maximum number of iterations to perform.
**tol**float, default=1e-8
Tolerance for the stopping condition.
**method**{‘lars’, ‘cd’}, default=’lars’
Method to be used for optimization. lars: uses the least angle regression method to solve the lasso problem (linear\_model.lars\_path) cd: uses the coordinate descent method to compute the Lasso solution (linear\_model.Lasso). Lars will be faster if the estimated components are sparse.
**n\_jobs**int, default=None
Number of parallel jobs to run. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**U\_init**ndarray of shape (n\_samples, n\_components), default=None
Initial values for the loadings for warm restart scenarios. Only used if `U_init` and `V_init` are not None.
**V\_init**ndarray of shape (n\_components, n\_features), default=None
Initial values for the components for warm restart scenarios. Only used if `U_init` and `V_init` are not None.
**verbose**int or bool, default=False
Controls the verbosity; the higher, the more messages. Defaults to 0.
**random\_state**int, RandomState instance or None, default=None
Used during dictionary learning. Pass an int for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Attributes:
**components\_**ndarray of shape (n\_components, n\_features)
Sparse components extracted from the data.
**error\_**ndarray
Vector of errors at each iteration.
**n\_components\_**int
Estimated number of components.
New in version 0.23.
**n\_iter\_**int
Number of iterations run.
**mean\_**ndarray of shape (n\_features,)
Per-feature empirical mean, estimated from the training set. Equal to `X.mean(axis=0)`.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`PCA`](sklearn.decomposition.pca#sklearn.decomposition.PCA "sklearn.decomposition.PCA")
Principal Component Analysis implementation.
[`MiniBatchSparsePCA`](sklearn.decomposition.minibatchsparsepca#sklearn.decomposition.MiniBatchSparsePCA "sklearn.decomposition.MiniBatchSparsePCA")
Mini batch variant of `SparsePCA` that is faster but less accurate.
[`DictionaryLearning`](sklearn.decomposition.dictionarylearning#sklearn.decomposition.DictionaryLearning "sklearn.decomposition.DictionaryLearning")
Generic dictionary learning problem using a sparse code.
#### Examples
```
>>> import numpy as np
>>> from sklearn.datasets import make_friedman1
>>> from sklearn.decomposition import SparsePCA
>>> X, _ = make_friedman1(n_samples=200, n_features=30, random_state=0)
>>> transformer = SparsePCA(n_components=5, random_state=0)
>>> transformer.fit(X)
SparsePCA(...)
>>> X_transformed = transformer.transform(X)
>>> X_transformed.shape
(200, 5)
>>> # most values in the components_ are zero (sparsity)
>>> np.mean(transformer.components_ == 0)
0.9666...
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.decomposition.SparsePCA.fit "sklearn.decomposition.SparsePCA.fit")(X[, y]) | Fit the model from data in X. |
| [`fit_transform`](#sklearn.decomposition.SparsePCA.fit_transform "sklearn.decomposition.SparsePCA.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.decomposition.SparsePCA.get_feature_names_out "sklearn.decomposition.SparsePCA.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.decomposition.SparsePCA.get_params "sklearn.decomposition.SparsePCA.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.decomposition.SparsePCA.set_params "sklearn.decomposition.SparsePCA.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.decomposition.SparsePCA.transform "sklearn.decomposition.SparsePCA.transform")(X) | Least Squares projection of the data onto the sparse components. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_sparse_pca.py#L157)
Fit the model from data in X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training vector, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.decomposition.SparsePCA.fit "sklearn.decomposition.SparsePCA.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_sparse_pca.py#L209)
Least Squares projection of the data onto the sparse components.
To avoid instability issues in case the system is under-determined, regularization can be applied (Ridge regression) via the `ridge_alpha` parameter.
Note that Sparse PCA components orthogonality is not enforced as in PCA hence one cannot use a simple linear projection.
Parameters:
**X**ndarray of shape (n\_samples, n\_features)
Test data to be transformed, must have the same number of features as the data used to train the model.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_components)
Transformed data.
scikit_learn sklearn.feature_selection.SelectPercentile sklearn.feature\_selection.SelectPercentile
===========================================
*class*sklearn.feature\_selection.SelectPercentile(*score\_func=<function f\_classif>*, *\**, *percentile=10*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_univariate_selection.py#L494)
Select features according to a percentile of the highest scores.
Read more in the [User Guide](../feature_selection#univariate-feature-selection).
Parameters:
**score\_func**callable, default=f\_classif
Function taking two arrays X and y, and returning a pair of arrays (scores, pvalues) or a single array with scores. Default is f\_classif (see below “See Also”). The default function only works with classification tasks.
New in version 0.18.
**percentile**int, default=10
Percent of features to keep.
Attributes:
**scores\_**array-like of shape (n\_features,)
Scores of features.
**pvalues\_**array-like of shape (n\_features,)
p-values of feature scores, None if `score_func` returned only scores.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`f_classif`](sklearn.feature_selection.f_classif#sklearn.feature_selection.f_classif "sklearn.feature_selection.f_classif")
ANOVA F-value between label/feature for classification tasks.
[`mutual_info_classif`](sklearn.feature_selection.mutual_info_classif#sklearn.feature_selection.mutual_info_classif "sklearn.feature_selection.mutual_info_classif")
Mutual information for a discrete target.
[`chi2`](sklearn.feature_selection.chi2#sklearn.feature_selection.chi2 "sklearn.feature_selection.chi2")
Chi-squared stats of non-negative features for classification tasks.
[`f_regression`](sklearn.feature_selection.f_regression#sklearn.feature_selection.f_regression "sklearn.feature_selection.f_regression")
F-value between label/feature for regression tasks.
[`mutual_info_regression`](sklearn.feature_selection.mutual_info_regression#sklearn.feature_selection.mutual_info_regression "sklearn.feature_selection.mutual_info_regression")
Mutual information for a continuous target.
[`SelectKBest`](sklearn.feature_selection.selectkbest#sklearn.feature_selection.SelectKBest "sklearn.feature_selection.SelectKBest")
Select features based on the k highest scores.
[`SelectFpr`](sklearn.feature_selection.selectfpr#sklearn.feature_selection.SelectFpr "sklearn.feature_selection.SelectFpr")
Select features based on a false positive rate test.
[`SelectFdr`](sklearn.feature_selection.selectfdr#sklearn.feature_selection.SelectFdr "sklearn.feature_selection.SelectFdr")
Select features based on an estimated false discovery rate.
[`SelectFwe`](sklearn.feature_selection.selectfwe#sklearn.feature_selection.SelectFwe "sklearn.feature_selection.SelectFwe")
Select features based on family-wise error rate.
[`GenericUnivariateSelect`](sklearn.feature_selection.genericunivariateselect#sklearn.feature_selection.GenericUnivariateSelect "sklearn.feature_selection.GenericUnivariateSelect")
Univariate feature selector with configurable mode.
#### Notes
Ties between features with equal scores will be broken in an unspecified way.
#### Examples
```
>>> from sklearn.datasets import load_digits
>>> from sklearn.feature_selection import SelectPercentile, chi2
>>> X, y = load_digits(return_X_y=True)
>>> X.shape
(1797, 64)
>>> X_new = SelectPercentile(chi2, percentile=10).fit_transform(X, y)
>>> X_new.shape
(1797, 7)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.feature_selection.SelectPercentile.fit "sklearn.feature_selection.SelectPercentile.fit")(X, y) | Run score function on (X, y) and get the appropriate features. |
| [`fit_transform`](#sklearn.feature_selection.SelectPercentile.fit_transform "sklearn.feature_selection.SelectPercentile.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.feature_selection.SelectPercentile.get_feature_names_out "sklearn.feature_selection.SelectPercentile.get_feature_names_out")([input\_features]) | Mask feature names according to selected features. |
| [`get_params`](#sklearn.feature_selection.SelectPercentile.get_params "sklearn.feature_selection.SelectPercentile.get_params")([deep]) | Get parameters for this estimator. |
| [`get_support`](#sklearn.feature_selection.SelectPercentile.get_support "sklearn.feature_selection.SelectPercentile.get_support")([indices]) | Get a mask, or integer index, of the features selected. |
| [`inverse_transform`](#sklearn.feature_selection.SelectPercentile.inverse_transform "sklearn.feature_selection.SelectPercentile.inverse_transform")(X) | Reverse the transformation operation. |
| [`set_params`](#sklearn.feature_selection.SelectPercentile.set_params "sklearn.feature_selection.SelectPercentile.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.feature_selection.SelectPercentile.transform "sklearn.feature_selection.SelectPercentile.transform")(X) | Reduce X to the selected features. |
fit(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_univariate_selection.py#L444)
Run score function on (X, y) and get the appropriate features.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The training input samples.
**y**array-like of shape (n\_samples,)
The target values (class labels in classification, real numbers in regression).
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L146)
Mask feature names according to selected features.
Parameters:
**input\_features**array-like of str or None, default=None
Input features.
* If `input_features` is `None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then the following input feature names are generated: `["x0", "x1", ..., "x(n_features_in_ - 1)"]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
get\_support(*indices=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L33)
Get a mask, or integer index, of the features selected.
Parameters:
**indices**bool, default=False
If True, the return value will be an array of integers, rather than a boolean mask.
Returns:
**support**array
An index that selects the retained features from a feature vector. If `indices` is False, this is a boolean array of shape [# input features], in which an element is True iff its corresponding feature is selected for retention. If `indices` is True, this is an integer array of shape [# output features] whose values are indices into the input feature vector.
inverse\_transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L106)
Reverse the transformation operation.
Parameters:
**X**array of shape [n\_samples, n\_selected\_features]
The input samples.
Returns:
**X\_r**array of shape [n\_samples, n\_original\_features]
`X` with columns of zeros inserted where features would have been removed by [`transform`](#sklearn.feature_selection.SelectPercentile.transform "sklearn.feature_selection.SelectPercentile.transform").
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_selection/_base.py#L68)
Reduce X to the selected features.
Parameters:
**X**array of shape [n\_samples, n\_features]
The input samples.
Returns:
**X\_r**array of shape [n\_samples, n\_selected\_features]
The input samples with only the selected features.
Examples using `sklearn.feature_selection.SelectPercentile`
-----------------------------------------------------------
[Feature agglomeration vs. univariate selection](../../auto_examples/cluster/plot_feature_agglomeration_vs_univariate_selection#sphx-glr-auto-examples-cluster-plot-feature-agglomeration-vs-univariate-selection-py)
[SVM-Anova: SVM with univariate feature selection](../../auto_examples/svm/plot_svm_anova#sphx-glr-auto-examples-svm-plot-svm-anova-py)
scikit_learn sklearn.ensemble.AdaBoostClassifier sklearn.ensemble.AdaBoostClassifier
===================================
*class*sklearn.ensemble.AdaBoostClassifier(*base\_estimator=None*, *\**, *n\_estimators=50*, *learning\_rate=1.0*, *algorithm='SAMME.R'*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_weight_boosting.py#L328)
An AdaBoost classifier.
An AdaBoost [1] classifier is a meta-estimator that begins by fitting a classifier on the original dataset and then fits additional copies of the classifier on the same dataset but where the weights of incorrectly classified instances are adjusted such that subsequent classifiers focus more on difficult cases.
This class implements the algorithm known as AdaBoost-SAMME [2].
Read more in the [User Guide](../ensemble#adaboost).
New in version 0.14.
Parameters:
**base\_estimator**object, default=None
The base estimator from which the boosted ensemble is built. Support for sample weighting is required, as well as proper `classes_` and `n_classes_` attributes. If `None`, then the base estimator is [`DecisionTreeClassifier`](sklearn.tree.decisiontreeclassifier#sklearn.tree.DecisionTreeClassifier "sklearn.tree.DecisionTreeClassifier") initialized with `max_depth=1`.
**n\_estimators**int, default=50
The maximum number of estimators at which boosting is terminated. In case of perfect fit, the learning procedure is stopped early. Values must be in the range `[1, inf)`.
**learning\_rate**float, default=1.0
Weight applied to each classifier at each boosting iteration. A higher learning rate increases the contribution of each classifier. There is a trade-off between the `learning_rate` and `n_estimators` parameters. Values must be in the range `(0.0, inf)`.
**algorithm**{‘SAMME’, ‘SAMME.R’}, default=’SAMME.R’
If ‘SAMME.R’ then use the SAMME.R real boosting algorithm. `base_estimator` must support calculation of class probabilities. If ‘SAMME’ then use the SAMME discrete boosting algorithm. The SAMME.R algorithm typically converges faster than SAMME, achieving a lower test error with fewer boosting iterations.
**random\_state**int, RandomState instance or None, default=None
Controls the random seed given at each `base_estimator` at each boosting iteration. Thus, it is only used when `base_estimator` exposes a `random_state`. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Attributes:
**base\_estimator\_**estimator
The base estimator from which the ensemble is grown.
**estimators\_**list of classifiers
The collection of fitted sub-estimators.
**classes\_**ndarray of shape (n\_classes,)
The classes labels.
**n\_classes\_**int
The number of classes.
**estimator\_weights\_**ndarray of floats
Weights for each estimator in the boosted ensemble.
**estimator\_errors\_**ndarray of floats
Classification error for each estimator in the boosted ensemble.
[`feature_importances_`](#sklearn.ensemble.AdaBoostClassifier.feature_importances_ "sklearn.ensemble.AdaBoostClassifier.feature_importances_")ndarray of shape (n\_features,)
The impurity-based feature importances.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`AdaBoostRegressor`](sklearn.ensemble.adaboostregressor#sklearn.ensemble.AdaBoostRegressor "sklearn.ensemble.AdaBoostRegressor")
An AdaBoost regressor that begins by fitting a regressor on the original dataset and then fits additional copies of the regressor on the same dataset but where the weights of instances are adjusted according to the error of the current prediction.
[`GradientBoostingClassifier`](sklearn.ensemble.gradientboostingclassifier#sklearn.ensemble.GradientBoostingClassifier "sklearn.ensemble.GradientBoostingClassifier")
GB builds an additive model in a forward stage-wise fashion. Regression trees are fit on the negative gradient of the binomial or multinomial deviance loss function. Binary classification is a special case where only a single regression tree is induced.
[`sklearn.tree.DecisionTreeClassifier`](sklearn.tree.decisiontreeclassifier#sklearn.tree.DecisionTreeClassifier "sklearn.tree.DecisionTreeClassifier")
A non-parametric supervised learning method used for classification. Creates a model that predicts the value of a target variable by learning simple decision rules inferred from the data features.
#### References
[1] Y. Freund, R. Schapire, “A Decision-Theoretic Generalization of on-Line Learning and an Application to Boosting”, 1995.
[2] 10. Zhu, H. Zou, S. Rosset, T. Hastie, “Multi-class AdaBoost”, 2009.
#### Examples
```
>>> from sklearn.ensemble import AdaBoostClassifier
>>> from sklearn.datasets import make_classification
>>> X, y = make_classification(n_samples=1000, n_features=4,
... n_informative=2, n_redundant=0,
... random_state=0, shuffle=False)
>>> clf = AdaBoostClassifier(n_estimators=100, random_state=0)
>>> clf.fit(X, y)
AdaBoostClassifier(n_estimators=100, random_state=0)
>>> clf.predict([[0, 0, 0, 0]])
array([1])
>>> clf.score(X, y)
0.983...
```
#### Methods
| | |
| --- | --- |
| [`decision_function`](#sklearn.ensemble.AdaBoostClassifier.decision_function "sklearn.ensemble.AdaBoostClassifier.decision_function")(X) | Compute the decision function of `X`. |
| [`fit`](#sklearn.ensemble.AdaBoostClassifier.fit "sklearn.ensemble.AdaBoostClassifier.fit")(X, y[, sample\_weight]) | Build a boosted classifier from the training set (X, y). |
| [`get_params`](#sklearn.ensemble.AdaBoostClassifier.get_params "sklearn.ensemble.AdaBoostClassifier.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.ensemble.AdaBoostClassifier.predict "sklearn.ensemble.AdaBoostClassifier.predict")(X) | Predict classes for X. |
| [`predict_log_proba`](#sklearn.ensemble.AdaBoostClassifier.predict_log_proba "sklearn.ensemble.AdaBoostClassifier.predict_log_proba")(X) | Predict class log-probabilities for X. |
| [`predict_proba`](#sklearn.ensemble.AdaBoostClassifier.predict_proba "sklearn.ensemble.AdaBoostClassifier.predict_proba")(X) | Predict class probabilities for X. |
| [`score`](#sklearn.ensemble.AdaBoostClassifier.score "sklearn.ensemble.AdaBoostClassifier.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.ensemble.AdaBoostClassifier.set_params "sklearn.ensemble.AdaBoostClassifier.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`staged_decision_function`](#sklearn.ensemble.AdaBoostClassifier.staged_decision_function "sklearn.ensemble.AdaBoostClassifier.staged_decision_function")(X) | Compute decision function of `X` for each boosting iteration. |
| [`staged_predict`](#sklearn.ensemble.AdaBoostClassifier.staged_predict "sklearn.ensemble.AdaBoostClassifier.staged_predict")(X) | Return staged predictions for X. |
| [`staged_predict_proba`](#sklearn.ensemble.AdaBoostClassifier.staged_predict_proba "sklearn.ensemble.AdaBoostClassifier.staged_predict_proba")(X) | Predict class probabilities for X. |
| [`staged_score`](#sklearn.ensemble.AdaBoostClassifier.staged_score "sklearn.ensemble.AdaBoostClassifier.staged_score")(X, y[, sample\_weight]) | Return staged scores for X, y. |
decision\_function(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_weight_boosting.py#L740)
Compute the decision function of `X`.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Sparse matrix can be CSC, CSR, COO, DOK, or LIL. COO, DOK, and LIL are converted to CSR.
Returns:
**score**ndarray of shape of (n\_samples, k)
The decision function of the input samples. The order of outputs is the same of that of the [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_) attribute. Binary classification is a special cases with `k == 1`, otherwise `k==n_classes`. For binary classification, values closer to -1 or 1 mean more like the first or second class in `classes_`, respectively.
*property*feature\_importances\_
The impurity-based feature importances.
The higher, the more important the feature. The importance of a feature is computed as the (normalized) total reduction of the criterion brought by that feature. It is also known as the Gini importance.
Warning: impurity-based feature importances can be misleading for high cardinality features (many unique values). See [`sklearn.inspection.permutation_importance`](sklearn.inspection.permutation_importance#sklearn.inspection.permutation_importance "sklearn.inspection.permutation_importance") as an alternative.
Returns:
**feature\_importances\_**ndarray of shape (n\_features,)
The feature importances.
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_weight_boosting.py#L477)
Build a boosted classifier from the training set (X, y).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Sparse matrix can be CSC, CSR, COO, DOK, or LIL. COO, DOK, and LIL are converted to CSR.
**y**array-like of shape (n\_samples,)
The target values (class labels).
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, the sample weights are initialized to `1 / n_samples`.
Returns:
**self**object
Fitted estimator.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_weight_boosting.py#L682)
Predict classes for X.
The predicted class of an input sample is computed as the weighted mean prediction of the classifiers in the ensemble.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Sparse matrix can be CSC, CSR, COO, DOK, or LIL. COO, DOK, and LIL are converted to CSR.
Returns:
**y**ndarray of shape (n\_samples,)
The predicted classes.
predict\_log\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_weight_boosting.py#L911)
Predict class log-probabilities for X.
The predicted class log-probabilities of an input sample is computed as the weighted mean predicted class log-probabilities of the classifiers in the ensemble.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Sparse matrix can be CSC, CSR, COO, DOK, or LIL. COO, DOK, and LIL are converted to CSR.
Returns:
**p**ndarray of shape (n\_samples, n\_classes)
The class probabilities of the input samples. The order of outputs is the same of that of the [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_) attribute.
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_weight_boosting.py#L853)
Predict class probabilities for X.
The predicted class probabilities of an input sample is computed as the weighted mean predicted class probabilities of the classifiers in the ensemble.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Sparse matrix can be CSC, CSR, COO, DOK, or LIL. COO, DOK, and LIL are converted to CSR.
Returns:
**p**ndarray of shape (n\_samples, n\_classes)
The class probabilities of the input samples. The order of outputs is the same of that of the [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_) attribute.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
staged\_decision\_function(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_weight_boosting.py#L782)
Compute decision function of `X` for each boosting iteration.
This method allows monitoring (i.e. determine error on testing set) after each boosting iteration.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Sparse matrix can be CSC, CSR, COO, DOK, or LIL. COO, DOK, and LIL are converted to CSR.
Yields:
**score**generator of ndarray of shape (n\_samples, k)
The decision function of the input samples. The order of outputs is the same of that of the [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_) attribute. Binary classification is a special cases with `k == 1`, otherwise `k==n_classes`. For binary classification, values closer to -1 or 1 mean more like the first or second class in `classes_`, respectively.
staged\_predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_weight_boosting.py#L706)
Return staged predictions for X.
The predicted class of an input sample is computed as the weighted mean prediction of the classifiers in the ensemble.
This generator method yields the ensemble prediction after each iteration of boosting and therefore allows monitoring, such as to determine the prediction on a test set after each boost.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The input samples. Sparse matrix can be CSC, CSR, COO, DOK, or LIL. COO, DOK, and LIL are converted to CSR.
Yields:
**y**generator of ndarray of shape (n\_samples,)
The predicted classes.
staged\_predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_weight_boosting.py#L881)
Predict class probabilities for X.
The predicted class probabilities of an input sample is computed as the weighted mean predicted class probabilities of the classifiers in the ensemble.
This generator method yields the ensemble predicted class probabilities after each iteration of boosting and therefore allows monitoring, such as to determine the predicted class probabilities on a test set after each boost.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Sparse matrix can be CSC, CSR, COO, DOK, or LIL. COO, DOK, and LIL are converted to CSR.
Yields:
**p**generator of ndarray of shape (n\_samples,)
The class probabilities of the input samples. The order of outputs is the same of that of the [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_) attribute.
staged\_score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_weight_boosting.py#L235)
Return staged scores for X, y.
This generator method yields the ensemble score after each iteration of boosting and therefore allows monitoring, such as to determine the score on a test set after each boost.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The training input samples. Sparse matrix can be CSC, CSR, COO, DOK, or LIL. COO, DOK, and LIL are converted to CSR.
**y**array-like of shape (n\_samples,)
Labels for X.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Yields:
**z**float
Examples using `sklearn.ensemble.AdaBoostClassifier`
----------------------------------------------------
[Classifier comparison](../../auto_examples/classification/plot_classifier_comparison#sphx-glr-auto-examples-classification-plot-classifier-comparison-py)
[Discrete versus Real AdaBoost](../../auto_examples/ensemble/plot_adaboost_hastie_10_2#sphx-glr-auto-examples-ensemble-plot-adaboost-hastie-10-2-py)
[Multi-class AdaBoosted Decision Trees](../../auto_examples/ensemble/plot_adaboost_multiclass#sphx-glr-auto-examples-ensemble-plot-adaboost-multiclass-py)
[Plot the decision surfaces of ensembles of trees on the iris dataset](../../auto_examples/ensemble/plot_forest_iris#sphx-glr-auto-examples-ensemble-plot-forest-iris-py)
[Two-class AdaBoost](../../auto_examples/ensemble/plot_adaboost_twoclass#sphx-glr-auto-examples-ensemble-plot-adaboost-twoclass-py)
| programming_docs |
scikit_learn sklearn.metrics.fbeta_score sklearn.metrics.fbeta\_score
============================
sklearn.metrics.fbeta\_score(*y\_true*, *y\_pred*, *\**, *beta*, *labels=None*, *pos\_label=1*, *average='binary'*, *sample\_weight=None*, *zero\_division='warn'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_classification.py#L1148)
Compute the F-beta score.
The F-beta score is the weighted harmonic mean of precision and recall, reaching its optimal value at 1 and its worst value at 0.
The `beta` parameter determines the weight of recall in the combined score. `beta < 1` lends more weight to precision, while `beta > 1` favors recall (`beta -> 0` considers only precision, `beta -> +inf` only recall).
Read more in the [User Guide](../model_evaluation#precision-recall-f-measure-metrics).
Parameters:
**y\_true**1d array-like, or label indicator array / sparse matrix
Ground truth (correct) target values.
**y\_pred**1d array-like, or label indicator array / sparse matrix
Estimated targets as returned by a classifier.
**beta**float
Determines the weight of recall in the combined score.
**labels**array-like, default=None
The set of labels to include when `average != 'binary'`, and their order if `average is None`. Labels present in the data can be excluded, for example to calculate a multiclass average ignoring a majority negative class, while labels not present in the data will result in 0 components in a macro average. For multilabel targets, labels are column indices. By default, all labels in `y_true` and `y_pred` are used in sorted order.
Changed in version 0.17: Parameter `labels` improved for multiclass problem.
**pos\_label**str or int, default=1
The class to report if `average='binary'` and the data is binary. If the data are multiclass or multilabel, this will be ignored; setting `labels=[pos_label]` and `average != 'binary'` will report scores for that label only.
**average**{‘micro’, ‘macro’, ‘samples’, ‘weighted’, ‘binary’} or None, default=’binary’
This parameter is required for multiclass/multilabel targets. If `None`, the scores for each class are returned. Otherwise, this determines the type of averaging performed on the data:
`'binary'`:
Only report results for the class specified by `pos_label`. This is applicable only if targets (`y_{true,pred}`) are binary.
`'micro'`:
Calculate metrics globally by counting the total true positives, false negatives and false positives.
`'macro'`:
Calculate metrics for each label, and find their unweighted mean. This does not take label imbalance into account.
`'weighted'`:
Calculate metrics for each label, and find their average weighted by support (the number of true instances for each label). This alters ‘macro’ to account for label imbalance; it can result in an F-score that is not between precision and recall.
`'samples'`:
Calculate metrics for each instance, and find their average (only meaningful for multilabel classification where this differs from [`accuracy_score`](sklearn.metrics.accuracy_score#sklearn.metrics.accuracy_score "sklearn.metrics.accuracy_score")).
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**zero\_division**“warn”, 0 or 1, default=”warn”
Sets the value to return when there is a zero division, i.e. when all predictions and labels are negative. If set to “warn”, this acts as 0, but warnings are also raised.
Returns:
**fbeta\_score**float (if average is not None) or array of float, shape = [n\_unique\_labels]
F-beta score of the positive class in binary classification or weighted average of the F-beta score of each class for the multiclass task.
See also
[`precision_recall_fscore_support`](sklearn.metrics.precision_recall_fscore_support#sklearn.metrics.precision_recall_fscore_support "sklearn.metrics.precision_recall_fscore_support")
Compute the precision, recall, F-score, and support.
[`multilabel_confusion_matrix`](sklearn.metrics.multilabel_confusion_matrix#sklearn.metrics.multilabel_confusion_matrix "sklearn.metrics.multilabel_confusion_matrix")
Compute a confusion matrix for each class or sample.
#### Notes
When `true positive + false positive == 0` or `true positive + false negative == 0`, f-score returns 0 and raises `UndefinedMetricWarning`. This behavior can be modified with `zero_division`.
#### References
[1] R. Baeza-Yates and B. Ribeiro-Neto (2011). Modern Information Retrieval. Addison Wesley, pp. 327-328.
[2] [Wikipedia entry for the F1-score](https://en.wikipedia.org/wiki/F1_score).
#### Examples
```
>>> from sklearn.metrics import fbeta_score
>>> y_true = [0, 1, 2, 0, 1, 2]
>>> y_pred = [0, 2, 1, 0, 0, 1]
>>> fbeta_score(y_true, y_pred, average='macro', beta=0.5)
0.23...
>>> fbeta_score(y_true, y_pred, average='micro', beta=0.5)
0.33...
>>> fbeta_score(y_true, y_pred, average='weighted', beta=0.5)
0.23...
>>> fbeta_score(y_true, y_pred, average=None, beta=0.5)
array([0.71..., 0. , 0. ])
```
scikit_learn sklearn.metrics.mean_pinball_loss sklearn.metrics.mean\_pinball\_loss
===================================
sklearn.metrics.mean\_pinball\_loss(*y\_true*, *y\_pred*, *\**, *sample\_weight=None*, *alpha=0.5*, *multioutput='uniform\_average'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_regression.py#L211)
Pinball loss for quantile regression.
Read more in the [User Guide](../model_evaluation#pinball-loss).
Parameters:
**y\_true**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
Ground truth (correct) target values.
**y\_pred**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
Estimated target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**alpha: float, slope of the pinball loss, default=0.5,**
this loss is equivalent to [Mean absolute error](../model_evaluation#mean-absolute-error) when `alpha=0.5`, `alpha=0.95` is minimized by estimators of the 95th percentile.
**multioutput**{‘raw\_values’, ‘uniform\_average’} or array-like of shape (n\_outputs,), default=’uniform\_average’
Defines aggregating of multiple output values. Array-like value defines weights used to average errors.
‘raw\_values’ :
Returns a full set of errors in case of multioutput input.
‘uniform\_average’ :
Errors of all outputs are averaged with uniform weight.
Returns:
**loss**float or ndarray of floats
If multioutput is ‘raw\_values’, then mean absolute error is returned for each output separately. If multioutput is ‘uniform\_average’ or an ndarray of weights, then the weighted average of all output errors is returned.
The pinball loss output is a non-negative floating point. The best value is 0.0.
#### Examples
```
>>> from sklearn.metrics import mean_pinball_loss
>>> y_true = [1, 2, 3]
>>> mean_pinball_loss(y_true, [0, 2, 3], alpha=0.1)
0.03...
>>> mean_pinball_loss(y_true, [1, 2, 4], alpha=0.1)
0.3...
>>> mean_pinball_loss(y_true, [0, 2, 3], alpha=0.9)
0.3...
>>> mean_pinball_loss(y_true, [1, 2, 4], alpha=0.9)
0.03...
>>> mean_pinball_loss(y_true, y_true, alpha=0.1)
0.0
>>> mean_pinball_loss(y_true, y_true, alpha=0.9)
0.0
```
Examples using `sklearn.metrics.mean_pinball_loss`
--------------------------------------------------
[Release Highlights for scikit-learn 1.0](../../auto_examples/release_highlights/plot_release_highlights_1_0_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-1-0-0-py)
[Prediction Intervals for Gradient Boosting Regression](../../auto_examples/ensemble/plot_gradient_boosting_quantile#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-quantile-py)
scikit_learn sklearn.model_selection.RepeatedStratifiedKFold sklearn.model\_selection.RepeatedStratifiedKFold
================================================
*class*sklearn.model\_selection.RepeatedStratifiedKFold(*\**, *n\_splits=5*, *n\_repeats=10*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L1520)
Repeated Stratified K-Fold cross validator.
Repeats Stratified K-Fold n times with different randomization in each repetition.
Read more in the [User Guide](../cross_validation#repeated-k-fold).
Parameters:
**n\_splits**int, default=5
Number of folds. Must be at least 2.
**n\_repeats**int, default=10
Number of times cross-validator needs to be repeated.
**random\_state**int, RandomState instance or None, default=None
Controls the generation of the random states for each repetition. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
See also
[`RepeatedKFold`](sklearn.model_selection.repeatedkfold#sklearn.model_selection.RepeatedKFold "sklearn.model_selection.RepeatedKFold")
Repeats K-Fold n times.
#### Notes
Randomized CV splitters may return different results for each call of split. You can make the results identical by setting `random_state` to an integer.
#### Examples
```
>>> import numpy as np
>>> from sklearn.model_selection import RepeatedStratifiedKFold
>>> X = np.array([[1, 2], [3, 4], [1, 2], [3, 4]])
>>> y = np.array([0, 0, 1, 1])
>>> rskf = RepeatedStratifiedKFold(n_splits=2, n_repeats=2,
... random_state=36851234)
>>> for train_index, test_index in rskf.split(X, y):
... print("TRAIN:", train_index, "TEST:", test_index)
... X_train, X_test = X[train_index], X[test_index]
... y_train, y_test = y[train_index], y[test_index]
...
TRAIN: [1 2] TEST: [0 3]
TRAIN: [0 3] TEST: [1 2]
TRAIN: [1 3] TEST: [0 2]
TRAIN: [0 2] TEST: [1 3]
```
#### Methods
| | |
| --- | --- |
| [`get_n_splits`](#sklearn.model_selection.RepeatedStratifiedKFold.get_n_splits "sklearn.model_selection.RepeatedStratifiedKFold.get_n_splits")([X, y, groups]) | Returns the number of splitting iterations in the cross-validator |
| [`split`](#sklearn.model_selection.RepeatedStratifiedKFold.split "sklearn.model_selection.RepeatedStratifiedKFold.split")(X[, y, groups]) | Generates indices to split data into training and test set. |
get\_n\_splits(*X=None*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L1436)
Returns the number of splitting iterations in the cross-validator
Parameters:
**X**object
Always ignored, exists for compatibility. `np.zeros(n_samples)` may be used as a placeholder.
**y**object
Always ignored, exists for compatibility. `np.zeros(n_samples)` may be used as a placeholder.
**groups**array-like of shape (n\_samples,), default=None
Group labels for the samples used while splitting the dataset into train/test set.
Returns:
**n\_splits**int
Returns the number of splitting iterations in the cross-validator.
split(*X*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L1404)
Generates indices to split data into training and test set.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,)
The target variable for supervised learning problems.
**groups**array-like of shape (n\_samples,), default=None
Group labels for the samples used while splitting the dataset into train/test set.
Yields:
**train**ndarray
The training set indices for that split.
**test**ndarray
The testing set indices for that split.
Examples using `sklearn.model_selection.RepeatedStratifiedKFold`
----------------------------------------------------------------
[Statistical comparison of models using grid search](../../auto_examples/model_selection/plot_grid_search_stats#sphx-glr-auto-examples-model-selection-plot-grid-search-stats-py)
scikit_learn sklearn.svm.SVC sklearn.svm.SVC
===============
*class*sklearn.svm.SVC(*\**, *C=1.0*, *kernel='rbf'*, *degree=3*, *gamma='scale'*, *coef0=0.0*, *shrinking=True*, *probability=False*, *tol=0.001*, *cache\_size=200*, *class\_weight=None*, *verbose=False*, *max\_iter=-1*, *decision\_function\_shape='ovr'*, *break\_ties=False*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/svm/_classes.py#L525)
C-Support Vector Classification.
The implementation is based on libsvm. The fit time scales at least quadratically with the number of samples and may be impractical beyond tens of thousands of samples. For large datasets consider using [`LinearSVC`](sklearn.svm.linearsvc#sklearn.svm.LinearSVC "sklearn.svm.LinearSVC") or [`SGDClassifier`](sklearn.linear_model.sgdclassifier#sklearn.linear_model.SGDClassifier "sklearn.linear_model.SGDClassifier") instead, possibly after a [`Nystroem`](sklearn.kernel_approximation.nystroem#sklearn.kernel_approximation.Nystroem "sklearn.kernel_approximation.Nystroem") transformer.
The multiclass support is handled according to a one-vs-one scheme.
For details on the precise mathematical formulation of the provided kernel functions and how `gamma`, `coef0` and `degree` affect each other, see the corresponding section in the narrative documentation: [Kernel functions](../svm#svm-kernels).
Read more in the [User Guide](../svm#svm-classification).
Parameters:
**C**float, default=1.0
Regularization parameter. The strength of the regularization is inversely proportional to C. Must be strictly positive. The penalty is a squared l2 penalty.
**kernel**{‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’} or callable, default=’rbf’
Specifies the kernel type to be used in the algorithm. If none is given, ‘rbf’ will be used. If a callable is given it is used to pre-compute the kernel matrix from data matrices; that matrix should be an array of shape `(n_samples, n_samples)`.
**degree**int, default=3
Degree of the polynomial kernel function (‘poly’). Ignored by all other kernels.
**gamma**{‘scale’, ‘auto’} or float, default=’scale’
Kernel coefficient for ‘rbf’, ‘poly’ and ‘sigmoid’.
* if `gamma='scale'` (default) is passed then it uses 1 / (n\_features \* X.var()) as value of gamma,
* if ‘auto’, uses 1 / n\_features.
Changed in version 0.22: The default value of `gamma` changed from ‘auto’ to ‘scale’.
**coef0**float, default=0.0
Independent term in kernel function. It is only significant in ‘poly’ and ‘sigmoid’.
**shrinking**bool, default=True
Whether to use the shrinking heuristic. See the [User Guide](../svm#shrinking-svm).
**probability**bool, default=False
Whether to enable probability estimates. This must be enabled prior to calling `fit`, will slow down that method as it internally uses 5-fold cross-validation, and `predict_proba` may be inconsistent with `predict`. Read more in the [User Guide](../svm#scores-probabilities).
**tol**float, default=1e-3
Tolerance for stopping criterion.
**cache\_size**float, default=200
Specify the size of the kernel cache (in MB).
**class\_weight**dict or ‘balanced’, default=None
Set the parameter C of class i to class\_weight[i]\*C for SVC. If not given, all classes are supposed to have weight one. The “balanced” mode uses the values of y to automatically adjust weights inversely proportional to class frequencies in the input data as `n_samples / (n_classes * np.bincount(y))`.
**verbose**bool, default=False
Enable verbose output. Note that this setting takes advantage of a per-process runtime setting in libsvm that, if enabled, may not work properly in a multithreaded context.
**max\_iter**int, default=-1
Hard limit on iterations within solver, or -1 for no limit.
**decision\_function\_shape**{‘ovo’, ‘ovr’}, default=’ovr’
Whether to return a one-vs-rest (‘ovr’) decision function of shape (n\_samples, n\_classes) as all other classifiers, or the original one-vs-one (‘ovo’) decision function of libsvm which has shape (n\_samples, n\_classes \* (n\_classes - 1) / 2). However, note that internally, one-vs-one (‘ovo’) is always used as a multi-class strategy to train models; an ovr matrix is only constructed from the ovo matrix. The parameter is ignored for binary classification.
Changed in version 0.19: decision\_function\_shape is ‘ovr’ by default.
New in version 0.17: *decision\_function\_shape=’ovr’* is recommended.
Changed in version 0.17: Deprecated *decision\_function\_shape=’ovo’ and None*.
**break\_ties**bool, default=False
If true, `decision_function_shape='ovr'`, and number of classes > 2, [predict](https://scikit-learn.org/1.1/glossary.html#term-predict) will break ties according to the confidence values of [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function); otherwise the first class among the tied classes is returned. Please note that breaking ties comes at a relatively high computational cost compared to a simple predict.
New in version 0.22.
**random\_state**int, RandomState instance or None, default=None
Controls the pseudo random number generation for shuffling the data for probability estimates. Ignored when `probability` is False. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Attributes:
**class\_weight\_**ndarray of shape (n\_classes,)
Multipliers of parameter C for each class. Computed based on the `class_weight` parameter.
**classes\_**ndarray of shape (n\_classes,)
The classes labels.
[`coef_`](#sklearn.svm.SVC.coef_ "sklearn.svm.SVC.coef_")ndarray of shape (n\_classes \* (n\_classes - 1) / 2, n\_features)
Weights assigned to the features when `kernel="linear"`.
**dual\_coef\_**ndarray of shape (n\_classes -1, n\_SV)
Dual coefficients of the support vector in the decision function (see [Mathematical formulation](../sgd#sgd-mathematical-formulation)), multiplied by their targets. For multiclass, coefficient for all 1-vs-1 classifiers. The layout of the coefficients in the multiclass case is somewhat non-trivial. See the [multi-class section of the User Guide](../svm#svm-multi-class) for details.
**fit\_status\_**int
0 if correctly fitted, 1 otherwise (will raise warning)
**intercept\_**ndarray of shape (n\_classes \* (n\_classes - 1) / 2,)
Constants in decision function.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_iter\_**ndarray of shape (n\_classes \* (n\_classes - 1) // 2,)
Number of iterations run by the optimization routine to fit the model. The shape of this attribute depends on the number of models optimized which in turn depends on the number of classes.
New in version 1.1.
**support\_**ndarray of shape (n\_SV)
Indices of support vectors.
**support\_vectors\_**ndarray of shape (n\_SV, n\_features)
Support vectors.
[`n_support_`](#sklearn.svm.SVC.n_support_ "sklearn.svm.SVC.n_support_")ndarray of shape (n\_classes,), dtype=int32
Number of support vectors for each class.
[`probA_`](#sklearn.svm.SVC.probA_ "sklearn.svm.SVC.probA_")ndarray of shape (n\_classes \* (n\_classes - 1) / 2)
Parameter learned in Platt scaling when `probability=True`.
[`probB_`](#sklearn.svm.SVC.probB_ "sklearn.svm.SVC.probB_")ndarray of shape (n\_classes \* (n\_classes - 1) / 2)
Parameter learned in Platt scaling when `probability=True`.
**shape\_fit\_**tuple of int of shape (n\_dimensions\_of\_X,)
Array dimensions of training vector `X`.
See also
[`SVR`](sklearn.svm.svr#sklearn.svm.SVR "sklearn.svm.SVR")
Support Vector Machine for Regression implemented using libsvm.
[`LinearSVC`](sklearn.svm.linearsvc#sklearn.svm.LinearSVC "sklearn.svm.LinearSVC")
Scalable Linear Support Vector Machine for classification implemented using liblinear. Check the See Also section of LinearSVC for more comparison element.
#### References
[1] [LIBSVM: A Library for Support Vector Machines](http://www.csie.ntu.edu.tw/~cjlin/papers/libsvm.pdf)
[2] [Platt, John (1999). “Probabilistic outputs for support vector machines and comparison to regularizedlikelihood methods.”](http://citeseer.ist.psu.edu/viewdoc/summary?doi=10.1.1.41.1639)
#### Examples
```
>>> import numpy as np
>>> from sklearn.pipeline import make_pipeline
>>> from sklearn.preprocessing import StandardScaler
>>> X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
>>> y = np.array([1, 1, 2, 2])
>>> from sklearn.svm import SVC
>>> clf = make_pipeline(StandardScaler(), SVC(gamma='auto'))
>>> clf.fit(X, y)
Pipeline(steps=[('standardscaler', StandardScaler()),
('svc', SVC(gamma='auto'))])
```
```
>>> print(clf.predict([[-0.8, -1]]))
[1]
```
#### Methods
| | |
| --- | --- |
| [`decision_function`](#sklearn.svm.SVC.decision_function "sklearn.svm.SVC.decision_function")(X) | Evaluate the decision function for the samples in X. |
| [`fit`](#sklearn.svm.SVC.fit "sklearn.svm.SVC.fit")(X, y[, sample\_weight]) | Fit the SVM model according to the given training data. |
| [`get_params`](#sklearn.svm.SVC.get_params "sklearn.svm.SVC.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.svm.SVC.predict "sklearn.svm.SVC.predict")(X) | Perform classification on samples in X. |
| [`predict_log_proba`](#sklearn.svm.SVC.predict_log_proba "sklearn.svm.SVC.predict_log_proba")(X) | Compute log probabilities of possible outcomes for samples in X. |
| [`predict_proba`](#sklearn.svm.SVC.predict_proba "sklearn.svm.SVC.predict_proba")(X) | Compute probabilities of possible outcomes for samples in X. |
| [`score`](#sklearn.svm.SVC.score "sklearn.svm.SVC.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.svm.SVC.set_params "sklearn.svm.SVC.set_params")(\*\*params) | Set the parameters of this estimator. |
*property*coef\_
Weights assigned to the features when `kernel="linear"`.
Returns:
ndarray of shape (n\_features, n\_classes)
decision\_function(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/svm/_base.py#L748)
Evaluate the decision function for the samples in X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The input samples.
Returns:
**X**ndarray of shape (n\_samples, n\_classes \* (n\_classes-1) / 2)
Returns the decision function of the sample for each class in the model. If decision\_function\_shape=’ovr’, the shape is (n\_samples, n\_classes).
#### Notes
If decision\_function\_shape=’ovo’, the function values are proportional to the distance of the samples X to the separating hyperplane. If the exact distances are required, divide the function values by the norm of the weight vector (`coef_`). See also [this question](https://stats.stackexchange.com/questions/14876/interpreting-distance-from-hyperplane-in-svm) for further details. If decision\_function\_shape=’ovr’, the decision function is a monotonic transformation of ovo decision function.
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/svm/_base.py#L122)
Fit the SVM model according to the given training data.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features) or (n\_samples, n\_samples)
Training vectors, where `n_samples` is the number of samples and `n_features` is the number of features. For kernel=”precomputed”, the expected shape of X is (n\_samples, n\_samples).
**y**array-like of shape (n\_samples,)
Target values (class labels in classification, real numbers in regression).
**sample\_weight**array-like of shape (n\_samples,), default=None
Per-sample weights. Rescale C per sample. Higher weights force the classifier to put more emphasis on these points.
Returns:
**self**object
Fitted estimator.
#### Notes
If X and y are not C-ordered and contiguous arrays of np.float64 and X is not a scipy.sparse.csr\_matrix, X and/or y may be copied.
If X is a dense array, then the other methods will not support sparse matrices as input.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_support\_
Number of support vectors for each class.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/svm/_base.py#L780)
Perform classification on samples in X.
For an one-class model, +1 or -1 is returned.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features) or (n\_samples\_test, n\_samples\_train)
For kernel=”precomputed”, the expected shape of X is (n\_samples\_test, n\_samples\_train).
Returns:
**y\_pred**ndarray of shape (n\_samples,)
Class labels for samples in X.
predict\_log\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/svm/_base.py#L863)
Compute log probabilities of possible outcomes for samples in X.
The model need to have probability information computed at training time: fit with attribute `probability` set to True.
Parameters:
**X**array-like of shape (n\_samples, n\_features) or (n\_samples\_test, n\_samples\_train)
For kernel=”precomputed”, the expected shape of X is (n\_samples\_test, n\_samples\_train).
Returns:
**T**ndarray of shape (n\_samples, n\_classes)
Returns the log-probabilities of the sample for each class in the model. The columns correspond to the classes in sorted order, as they appear in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
#### Notes
The probability model is created using cross validation, so the results can be slightly different than those obtained by predict. Also, it will produce meaningless results on very small datasets.
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/svm/_base.py#L826)
Compute probabilities of possible outcomes for samples in X.
The model need to have probability information computed at training time: fit with attribute `probability` set to True.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
For kernel=”precomputed”, the expected shape of X is (n\_samples\_test, n\_samples\_train).
Returns:
**T**ndarray of shape (n\_samples, n\_classes)
Returns the probability of the sample for each class in the model. The columns correspond to the classes in sorted order, as they appear in the attribute [classes\_](https://scikit-learn.org/1.1/glossary.html#term-classes_).
#### Notes
The probability model is created using cross validation, so the results can be slightly different than those obtained by predict. Also, it will produce meaningless results on very small datasets.
*property*probA\_
Parameter learned in Platt scaling when `probability=True`.
Returns:
ndarray of shape (n\_classes \* (n\_classes - 1) / 2)
*property*probB\_
Parameter learned in Platt scaling when `probability=True`.
Returns:
ndarray of shape (n\_classes \* (n\_classes - 1) / 2)
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.svm.SVC`
--------------------------------
[Release Highlights for scikit-learn 0.24](../../auto_examples/release_highlights/plot_release_highlights_0_24_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-24-0-py)
[Release Highlights for scikit-learn 0.22](../../auto_examples/release_highlights/plot_release_highlights_0_22_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-22-0-py)
[Classifier comparison](../../auto_examples/classification/plot_classifier_comparison#sphx-glr-auto-examples-classification-plot-classifier-comparison-py)
[Plot classification probability](../../auto_examples/classification/plot_classification_probability#sphx-glr-auto-examples-classification-plot-classification-probability-py)
[Recognizing hand-written digits](../../auto_examples/classification/plot_digits_classification#sphx-glr-auto-examples-classification-plot-digits-classification-py)
[Plot the decision boundaries of a VotingClassifier](../../auto_examples/ensemble/plot_voting_decision_regions#sphx-glr-auto-examples-ensemble-plot-voting-decision-regions-py)
[Faces recognition example using eigenfaces and SVMs](../../auto_examples/applications/plot_face_recognition#sphx-glr-auto-examples-applications-plot-face-recognition-py)
[Libsvm GUI](../../auto_examples/applications/svm_gui#sphx-glr-auto-examples-applications-svm-gui-py)
[Recursive feature elimination](../../auto_examples/feature_selection/plot_rfe_digits#sphx-glr-auto-examples-feature-selection-plot-rfe-digits-py)
[Recursive feature elimination with cross-validation](../../auto_examples/feature_selection/plot_rfe_with_cross_validation#sphx-glr-auto-examples-feature-selection-plot-rfe-with-cross-validation-py)
[Scalable learning with polynomial kernel approximation](../../auto_examples/kernel_approximation/plot_scalable_poly_kernels#sphx-glr-auto-examples-kernel-approximation-plot-scalable-poly-kernels-py)
[Displaying Pipelines](../../auto_examples/miscellaneous/plot_pipeline_display#sphx-glr-auto-examples-miscellaneous-plot-pipeline-display-py)
[Explicit feature map approximation for RBF kernels](../../auto_examples/miscellaneous/plot_kernel_approximation#sphx-glr-auto-examples-miscellaneous-plot-kernel-approximation-py)
[Multilabel classification](../../auto_examples/miscellaneous/plot_multilabel#sphx-glr-auto-examples-miscellaneous-plot-multilabel-py)
[ROC Curve with Visualization API](../../auto_examples/miscellaneous/plot_roc_curve_visualization_api#sphx-glr-auto-examples-miscellaneous-plot-roc-curve-visualization-api-py)
[Comparison between grid search and successive halving](../../auto_examples/model_selection/plot_successive_halving_heatmap#sphx-glr-auto-examples-model-selection-plot-successive-halving-heatmap-py)
[Confusion matrix](../../auto_examples/model_selection/plot_confusion_matrix#sphx-glr-auto-examples-model-selection-plot-confusion-matrix-py)
[Custom refit strategy of a grid search with cross-validation](../../auto_examples/model_selection/plot_grid_search_digits#sphx-glr-auto-examples-model-selection-plot-grid-search-digits-py)
[Nested versus non-nested cross-validation](../../auto_examples/model_selection/plot_nested_cross_validation_iris#sphx-glr-auto-examples-model-selection-plot-nested-cross-validation-iris-py)
[Plotting Learning Curves](../../auto_examples/model_selection/plot_learning_curve#sphx-glr-auto-examples-model-selection-plot-learning-curve-py)
[Plotting Validation Curves](../../auto_examples/model_selection/plot_validation_curve#sphx-glr-auto-examples-model-selection-plot-validation-curve-py)
[Receiver Operating Characteristic (ROC)](../../auto_examples/model_selection/plot_roc#sphx-glr-auto-examples-model-selection-plot-roc-py)
[Receiver Operating Characteristic (ROC) with cross validation](../../auto_examples/model_selection/plot_roc_crossval#sphx-glr-auto-examples-model-selection-plot-roc-crossval-py)
[Statistical comparison of models using grid search](../../auto_examples/model_selection/plot_grid_search_stats#sphx-glr-auto-examples-model-selection-plot-grid-search-stats-py)
[Test with permutations the significance of a classification score](../../auto_examples/model_selection/plot_permutation_tests_for_classification#sphx-glr-auto-examples-model-selection-plot-permutation-tests-for-classification-py)
[Concatenating multiple feature extraction methods](../../auto_examples/compose/plot_feature_union#sphx-glr-auto-examples-compose-plot-feature-union-py)
[Feature discretization](../../auto_examples/preprocessing/plot_discretization_classification#sphx-glr-auto-examples-preprocessing-plot-discretization-classification-py)
[Decision boundary of semi-supervised classifiers versus SVM on the Iris dataset](../../auto_examples/semi_supervised/plot_semi_supervised_versus_svm_iris#sphx-glr-auto-examples-semi-supervised-plot-semi-supervised-versus-svm-iris-py)
[Effect of varying threshold for self-training](../../auto_examples/semi_supervised/plot_self_training_varying_threshold#sphx-glr-auto-examples-semi-supervised-plot-self-training-varying-threshold-py)
[Plot different SVM classifiers in the iris dataset](../../auto_examples/svm/plot_iris_svc#sphx-glr-auto-examples-svm-plot-iris-svc-py)
[RBF SVM parameters](../../auto_examples/svm/plot_rbf_parameters#sphx-glr-auto-examples-svm-plot-rbf-parameters-py)
[SVM Margins Example](../../auto_examples/svm/plot_svm_margin#sphx-glr-auto-examples-svm-plot-svm-margin-py)
[SVM Tie Breaking Example](../../auto_examples/svm/plot_svm_tie_breaking#sphx-glr-auto-examples-svm-plot-svm-tie-breaking-py)
[SVM with custom kernel](../../auto_examples/svm/plot_custom_kernel#sphx-glr-auto-examples-svm-plot-custom-kernel-py)
[SVM-Anova: SVM with univariate feature selection](../../auto_examples/svm/plot_svm_anova#sphx-glr-auto-examples-svm-plot-svm-anova-py)
[SVM-Kernels](../../auto_examples/svm/plot_svm_kernels#sphx-glr-auto-examples-svm-plot-svm-kernels-py)
[SVM: Maximum margin separating hyperplane](../../auto_examples/svm/plot_separating_hyperplane#sphx-glr-auto-examples-svm-plot-separating-hyperplane-py)
[SVM: Separating hyperplane for unbalanced classes](../../auto_examples/svm/plot_separating_hyperplane_unbalanced#sphx-glr-auto-examples-svm-plot-separating-hyperplane-unbalanced-py)
[SVM: Weighted samples](../../auto_examples/svm/plot_weighted_samples#sphx-glr-auto-examples-svm-plot-weighted-samples-py)
[Cross-validation on Digits Dataset Exercise](../../auto_examples/exercises/plot_cv_digits#sphx-glr-auto-examples-exercises-plot-cv-digits-py)
[SVM Exercise](../../auto_examples/exercises/plot_iris_exercise#sphx-glr-auto-examples-exercises-plot-iris-exercise-py)
| programming_docs |
scikit_learn sklearn.base.TransformerMixin sklearn.base.TransformerMixin
=============================
*class*sklearn.base.TransformerMixin[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L836)
Mixin class for all transformers in scikit-learn.
#### Methods
| | |
| --- | --- |
| [`fit_transform`](#sklearn.base.TransformerMixin.fit_transform "sklearn.base.TransformerMixin.fit_transform")(X[, y]) | Fit to data, then transform it. |
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
Examples using `sklearn.base.TransformerMixin`
----------------------------------------------
[Approximate nearest neighbors in TSNE](../../auto_examples/neighbors/approximate_nearest_neighbors#sphx-glr-auto-examples-neighbors-approximate-nearest-neighbors-py)
scikit_learn sklearn.preprocessing.normalize sklearn.preprocessing.normalize
===============================
sklearn.preprocessing.normalize(*X*, *norm='l2'*, *\**, *axis=1*, *copy=True*, *return\_norm=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L1727)
Scale input vectors individually to unit norm (vector length).
Read more in the [User Guide](../preprocessing#preprocessing-normalization).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data to normalize, element by element. scipy.sparse matrices should be in CSR format to avoid an un-necessary copy.
**norm**{‘l1’, ‘l2’, ‘max’}, default=’l2’
The norm to use to normalize each non zero sample (or each non-zero feature if axis is 0).
**axis**{0, 1}, default=1
Define axis used to normalize the data along. If 1, independently normalize each sample, otherwise (if 0) normalize each feature.
**copy**bool, default=True
Set to False to perform inplace row normalization and avoid a copy (if the input is already a numpy array or a scipy.sparse CSR matrix and if axis is 1).
**return\_norm**bool, default=False
Whether to return the computed norms.
Returns:
**X**{ndarray, sparse matrix} of shape (n\_samples, n\_features)
Normalized input X.
**norms**ndarray of shape (n\_samples, ) if axis=1 else (n\_features, )
An array of norms along given axis for X. When X is sparse, a NotImplementedError will be raised for norm ‘l1’ or ‘l2’.
See also
[`Normalizer`](sklearn.preprocessing.normalizer#sklearn.preprocessing.Normalizer "sklearn.preprocessing.Normalizer")
Performs normalization using the Transformer API (e.g. as part of a preprocessing [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")).
#### Notes
For a comparison of the different scalers, transformers, and normalizers, see [examples/preprocessing/plot\_all\_scaling.py](../../auto_examples/preprocessing/plot_all_scaling#sphx-glr-auto-examples-preprocessing-plot-all-scaling-py).
scikit_learn sklearn.covariance.GraphicalLasso sklearn.covariance.GraphicalLasso
=================================
*class*sklearn.covariance.GraphicalLasso(*alpha=0.01*, *\**, *mode='cd'*, *tol=0.0001*, *enet\_tol=0.0001*, *max\_iter=100*, *verbose=False*, *assume\_centered=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_graph_lasso.py#L337)
Sparse inverse covariance estimation with an l1-penalized estimator.
Read more in the [User Guide](../covariance#sparse-inverse-covariance).
Changed in version v0.20: GraphLasso has been renamed to GraphicalLasso
Parameters:
**alpha**float, default=0.01
The regularization parameter: the higher alpha, the more regularization, the sparser the inverse covariance. Range is (0, inf].
**mode**{‘cd’, ‘lars’}, default=’cd’
The Lasso solver to use: coordinate descent or LARS. Use LARS for very sparse underlying graphs, where p > n. Elsewhere prefer cd which is more numerically stable.
**tol**float, default=1e-4
The tolerance to declare convergence: if the dual gap goes below this value, iterations are stopped. Range is (0, inf].
**enet\_tol**float, default=1e-4
The tolerance for the elastic net solver used to calculate the descent direction. This parameter controls the accuracy of the search direction for a given column update, not of the overall parameter estimate. Only used for mode=’cd’. Range is (0, inf].
**max\_iter**int, default=100
The maximum number of iterations.
**verbose**bool, default=False
If verbose is True, the objective function and dual gap are plotted at each iteration.
**assume\_centered**bool, default=False
If True, data are not centered before computation. Useful when working with data whose mean is almost, but not exactly zero. If False, data are centered before computation.
Attributes:
**location\_**ndarray of shape (n\_features,)
Estimated location, i.e. the estimated mean.
**covariance\_**ndarray of shape (n\_features, n\_features)
Estimated covariance matrix
**precision\_**ndarray of shape (n\_features, n\_features)
Estimated pseudo inverse matrix.
**n\_iter\_**int
Number of iterations run.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`graphical_lasso`](sklearn.covariance.graphical_lasso#sklearn.covariance.graphical_lasso "sklearn.covariance.graphical_lasso")
L1-penalized covariance estimator.
[`GraphicalLassoCV`](sklearn.covariance.graphicallassocv#sklearn.covariance.GraphicalLassoCV "sklearn.covariance.GraphicalLassoCV")
Sparse inverse covariance with cross-validated choice of the l1 penalty.
#### Examples
```
>>> import numpy as np
>>> from sklearn.covariance import GraphicalLasso
>>> true_cov = np.array([[0.8, 0.0, 0.2, 0.0],
... [0.0, 0.4, 0.0, 0.0],
... [0.2, 0.0, 0.3, 0.1],
... [0.0, 0.0, 0.1, 0.7]])
>>> np.random.seed(0)
>>> X = np.random.multivariate_normal(mean=[0, 0, 0, 0],
... cov=true_cov,
... size=200)
>>> cov = GraphicalLasso().fit(X)
>>> np.around(cov.covariance_, decimals=3)
array([[0.816, 0.049, 0.218, 0.019],
[0.049, 0.364, 0.017, 0.034],
[0.218, 0.017, 0.322, 0.093],
[0.019, 0.034, 0.093, 0.69 ]])
>>> np.around(cov.location_, decimals=3)
array([0.073, 0.04 , 0.038, 0.143])
```
#### Methods
| | |
| --- | --- |
| [`error_norm`](#sklearn.covariance.GraphicalLasso.error_norm "sklearn.covariance.GraphicalLasso.error_norm")(comp\_cov[, norm, scaling, squared]) | Compute the Mean Squared Error between two covariance estimators. |
| [`fit`](#sklearn.covariance.GraphicalLasso.fit "sklearn.covariance.GraphicalLasso.fit")(X[, y]) | Fit the GraphicalLasso model to X. |
| [`get_params`](#sklearn.covariance.GraphicalLasso.get_params "sklearn.covariance.GraphicalLasso.get_params")([deep]) | Get parameters for this estimator. |
| [`get_precision`](#sklearn.covariance.GraphicalLasso.get_precision "sklearn.covariance.GraphicalLasso.get_precision")() | Getter for the precision matrix. |
| [`mahalanobis`](#sklearn.covariance.GraphicalLasso.mahalanobis "sklearn.covariance.GraphicalLasso.mahalanobis")(X) | Compute the squared Mahalanobis distances of given observations. |
| [`score`](#sklearn.covariance.GraphicalLasso.score "sklearn.covariance.GraphicalLasso.score")(X\_test[, y]) | Compute the log-likelihood of `X_test` under the estimated Gaussian model. |
| [`set_params`](#sklearn.covariance.GraphicalLasso.set_params "sklearn.covariance.GraphicalLasso.set_params")(\*\*params) | Set the parameters of this estimator. |
error\_norm(*comp\_cov*, *norm='frobenius'*, *scaling=True*, *squared=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_empirical_covariance.py#L267)
Compute the Mean Squared Error between two covariance estimators.
Parameters:
**comp\_cov**array-like of shape (n\_features, n\_features)
The covariance to compare with.
**norm**{“frobenius”, “spectral”}, default=”frobenius”
The type of norm used to compute the error. Available error types: - ‘frobenius’ (default): sqrt(tr(A^t.A)) - ‘spectral’: sqrt(max(eigenvalues(A^t.A)) where A is the error `(comp_cov - self.covariance_)`.
**scaling**bool, default=True
If True (default), the squared error norm is divided by n\_features. If False, the squared error norm is not rescaled.
**squared**bool, default=True
Whether to compute the squared error norm or the error norm. If True (default), the squared error norm is returned. If False, the error norm is returned.
Returns:
**result**float
The Mean Squared Error (in the sense of the Frobenius norm) between `self` and `comp_cov` covariance estimators.
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_graph_lasso.py#L452)
Fit the GraphicalLasso model to X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Data from which to compute the covariance estimate.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**self**object
Returns the instance itself.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
get\_precision()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_empirical_covariance.py#L195)
Getter for the precision matrix.
Returns:
**precision\_**array-like of shape (n\_features, n\_features)
The precision matrix associated to the current covariance object.
mahalanobis(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_empirical_covariance.py#L318)
Compute the squared Mahalanobis distances of given observations.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The observations, the Mahalanobis distances of the which we compute. Observations are assumed to be drawn from the same distribution than the data used in fit.
Returns:
**dist**ndarray of shape (n\_samples,)
Squared Mahalanobis distances of the observations.
score(*X\_test*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_empirical_covariance.py#L236)
Compute the log-likelihood of `X_test` under the estimated Gaussian model.
The Gaussian model is defined by its mean and covariance matrix which are represented respectively by `self.location_` and `self.covariance_`.
Parameters:
**X\_test**array-like of shape (n\_samples, n\_features)
Test data of which we compute the likelihood, where `n_samples` is the number of samples and `n_features` is the number of features. `X_test` is assumed to be drawn from the same distribution than the data used in fit (including centering).
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**res**float
The log-likelihood of `X_test` with `self.location_` and `self.covariance_` as estimators of the Gaussian model mean and covariance matrix respectively.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
scikit_learn sklearn.isotonic.IsotonicRegression sklearn.isotonic.IsotonicRegression
===================================
*class*sklearn.isotonic.IsotonicRegression(*\**, *y\_min=None*, *y\_max=None*, *increasing=True*, *out\_of\_bounds='nan'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/isotonic.py#L135)
Isotonic regression model.
Read more in the [User Guide](../isotonic#isotonic).
New in version 0.13.
Parameters:
**y\_min**float, default=None
Lower bound on the lowest predicted value (the minimum value may still be higher). If not set, defaults to -inf.
**y\_max**float, default=None
Upper bound on the highest predicted value (the maximum may still be lower). If not set, defaults to +inf.
**increasing**bool or ‘auto’, default=True
Determines whether the predictions should be constrained to increase or decrease with `X`. ‘auto’ will decide based on the Spearman correlation estimate’s sign.
**out\_of\_bounds**{‘nan’, ‘clip’, ‘raise’}, default=’nan’
Handles how `X` values outside of the training domain are handled during prediction.
* ‘nan’, predictions will be NaN.
* ‘clip’, predictions will be set to the value corresponding to the nearest train interval endpoint.
* ‘raise’, a `ValueError` is raised.
Attributes:
**X\_min\_**float
Minimum value of input array `X_` for left bound.
**X\_max\_**float
Maximum value of input array `X_` for right bound.
**X\_thresholds\_**ndarray of shape (n\_thresholds,)
Unique ascending `X` values used to interpolate the y = f(X) monotonic function.
New in version 0.24.
**y\_thresholds\_**ndarray of shape (n\_thresholds,)
De-duplicated `y` values suitable to interpolate the y = f(X) monotonic function.
New in version 0.24.
**f\_**function
The stepwise interpolating function that covers the input domain `X`.
**increasing\_**bool
Inferred value for `increasing`.
See also
[`sklearn.linear_model.LinearRegression`](sklearn.linear_model.linearregression#sklearn.linear_model.LinearRegression "sklearn.linear_model.LinearRegression")
Ordinary least squares Linear Regression.
[`sklearn.ensemble.HistGradientBoostingRegressor`](sklearn.ensemble.histgradientboostingregressor#sklearn.ensemble.HistGradientBoostingRegressor "sklearn.ensemble.HistGradientBoostingRegressor")
Gradient boosting that is a non-parametric model accepting monotonicity constraints.
[`isotonic_regression`](sklearn.isotonic.isotonic_regression#sklearn.isotonic.isotonic_regression "sklearn.isotonic.isotonic_regression")
Function to solve the isotonic regression model.
#### Notes
Ties are broken using the secondary method from de Leeuw, 1977.
#### References
Isotonic Median Regression: A Linear Programming Approach Nilotpal Chakravarti Mathematics of Operations Research Vol. 14, No. 2 (May, 1989), pp. 303-308
Isotone Optimization in R : Pool-Adjacent-Violators Algorithm (PAVA) and Active Set Methods de Leeuw, Hornik, Mair Journal of Statistical Software 2009
Correctness of Kruskal’s algorithms for monotone regression with ties de Leeuw, Psychometrica, 1977
#### Examples
```
>>> from sklearn.datasets import make_regression
>>> from sklearn.isotonic import IsotonicRegression
>>> X, y = make_regression(n_samples=10, n_features=1, random_state=41)
>>> iso_reg = IsotonicRegression().fit(X, y)
>>> iso_reg.predict([.1, .2])
array([1.8628..., 3.7256...])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.isotonic.IsotonicRegression.fit "sklearn.isotonic.IsotonicRegression.fit")(X, y[, sample\_weight]) | Fit the model using X, y as training data. |
| [`fit_transform`](#sklearn.isotonic.IsotonicRegression.fit_transform "sklearn.isotonic.IsotonicRegression.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.isotonic.IsotonicRegression.get_feature_names_out "sklearn.isotonic.IsotonicRegression.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.isotonic.IsotonicRegression.get_params "sklearn.isotonic.IsotonicRegression.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.isotonic.IsotonicRegression.predict "sklearn.isotonic.IsotonicRegression.predict")(T) | Predict new data by linear interpolation. |
| [`score`](#sklearn.isotonic.IsotonicRegression.score "sklearn.isotonic.IsotonicRegression.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.isotonic.IsotonicRegression.set_params "sklearn.isotonic.IsotonicRegression.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.isotonic.IsotonicRegression.transform "sklearn.isotonic.IsotonicRegression.transform")(T) | Transform new data by linear interpolation. |
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/isotonic.py#L311)
Fit the model using X, y as training data.
Parameters:
**X**array-like of shape (n\_samples,) or (n\_samples, 1)
Training data.
Changed in version 0.24: Also accepts 2d array with 1 feature.
**y**array-like of shape (n\_samples,)
Training target.
**sample\_weight**array-like of shape (n\_samples,), default=None
Weights. If set to None, all weights will be set to 1 (equal weights).
Returns:
**self**object
Returns an instance of self.
#### Notes
X is stored for future use, as [`transform`](#sklearn.isotonic.IsotonicRegression.transform "sklearn.isotonic.IsotonicRegression.transform") needs X to interpolate new input data.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/isotonic.py#L423)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Ignored.
Returns:
**feature\_names\_out**ndarray of str objects
An ndarray with one string i.e. [“isotonicregression0”].
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*T*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/isotonic.py#L404)
Predict new data by linear interpolation.
Parameters:
**T**array-like of shape (n\_samples,) or (n\_samples, 1)
Data to transform.
Returns:
**y\_pred**ndarray of shape (n\_samples,)
Transformed data.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*T*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/isotonic.py#L360)
Transform new data by linear interpolation.
Parameters:
**T**array-like of shape (n\_samples,) or (n\_samples, 1)
Data to transform.
Changed in version 0.24: Also accepts 2d array with 1 feature.
Returns:
**y\_pred**ndarray of shape (n\_samples,)
The transformed data.
Examples using `sklearn.isotonic.IsotonicRegression`
----------------------------------------------------
[Isotonic Regression](../../auto_examples/miscellaneous/plot_isotonic_regression#sphx-glr-auto-examples-miscellaneous-plot-isotonic-regression-py)
| programming_docs |
scikit_learn sklearn.datasets.make_circles sklearn.datasets.make\_circles
==============================
sklearn.datasets.make\_circles(*n\_samples=100*, *\**, *shuffle=True*, *noise=None*, *random\_state=None*, *factor=0.8*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_samples_generator.py#L641)
Make a large circle containing a smaller circle in 2d.
A simple toy dataset to visualize clustering and classification algorithms.
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/sample_generators.html#sample-generators).
Parameters:
**n\_samples**int or tuple of shape (2,), dtype=int, default=100
If int, it is the total number of points generated. For odd numbers, the inner circle will have one point more than the outer circle. If two-element tuple, number of points in outer circle and inner circle.
Changed in version 0.23: Added two-element tuple.
**shuffle**bool, default=True
Whether to shuffle the samples.
**noise**float, default=None
Standard deviation of Gaussian noise added to the data.
**random\_state**int, RandomState instance or None, default=None
Determines random number generation for dataset shuffling and noise. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**factor**float, default=.8
Scale factor between inner and outer circle in the range `(0, 1)`.
Returns:
**X**ndarray of shape (n\_samples, 2)
The generated samples.
**y**ndarray of shape (n\_samples,)
The integer labels (0 or 1) for class membership of each sample.
Examples using `sklearn.datasets.make_circles`
----------------------------------------------
[Classifier comparison](../../auto_examples/classification/plot_classifier_comparison#sphx-glr-auto-examples-classification-plot-classifier-comparison-py)
[Comparing different clustering algorithms on toy datasets](../../auto_examples/cluster/plot_cluster_comparison#sphx-glr-auto-examples-cluster-plot-cluster-comparison-py)
[Comparing different hierarchical linkage methods on toy datasets](../../auto_examples/cluster/plot_linkage_comparison#sphx-glr-auto-examples-cluster-plot-linkage-comparison-py)
[Kernel PCA](../../auto_examples/decomposition/plot_kernel_pca#sphx-glr-auto-examples-decomposition-plot-kernel-pca-py)
[Hashing feature transformation using Totally Random Trees](../../auto_examples/ensemble/plot_random_forest_embedding#sphx-glr-auto-examples-ensemble-plot-random-forest-embedding-py)
[t-SNE: The effect of various perplexity values on the shape](../../auto_examples/manifold/plot_t_sne_perplexity#sphx-glr-auto-examples-manifold-plot-t-sne-perplexity-py)
[Compare Stochastic learning strategies for MLPClassifier](../../auto_examples/neural_networks/plot_mlp_training_curves#sphx-glr-auto-examples-neural-networks-plot-mlp-training-curves-py)
[Varying regularization in Multi-layer Perceptron](../../auto_examples/neural_networks/plot_mlp_alpha#sphx-glr-auto-examples-neural-networks-plot-mlp-alpha-py)
[Feature discretization](../../auto_examples/preprocessing/plot_discretization_classification#sphx-glr-auto-examples-preprocessing-plot-discretization-classification-py)
[Label Propagation learning a complex structure](../../auto_examples/semi_supervised/plot_label_propagation_structure#sphx-glr-auto-examples-semi-supervised-plot-label-propagation-structure-py)
scikit_learn sklearn.linear_model.GammaRegressor sklearn.linear\_model.GammaRegressor
====================================
*class*sklearn.linear\_model.GammaRegressor(*\**, *alpha=1.0*, *fit\_intercept=True*, *max\_iter=100*, *tol=0.0001*, *warm\_start=False*, *verbose=0*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_glm/glm.py#L572)
Generalized Linear Model with a Gamma distribution.
This regressor uses the ‘log’ link function.
Read more in the [User Guide](../linear_model#generalized-linear-regression).
New in version 0.23.
Parameters:
**alpha**float, default=1
Constant that multiplies the penalty term and thus determines the regularization strength. `alpha = 0` is equivalent to unpenalized GLMs. In this case, the design matrix `X` must have full column rank (no collinearities). Values must be in the range `[0.0, inf)`.
**fit\_intercept**bool, default=True
Specifies if a constant (a.k.a. bias or intercept) should be added to the linear predictor (X @ coef + intercept).
**max\_iter**int, default=100
The maximal number of iterations for the solver. Values must be in the range `[1, inf)`.
**tol**float, default=1e-4
Stopping criterion. For the lbfgs solver, the iteration will stop when `max{|g_j|, j = 1, ..., d} <= tol` where `g_j` is the j-th component of the gradient (derivative) of the objective function. Values must be in the range `(0.0, inf)`.
**warm\_start**bool, default=False
If set to `True`, reuse the solution of the previous call to `fit` as initialization for `coef_` and `intercept_` .
**verbose**int, default=0
For the lbfgs solver set verbose to any positive number for verbosity. Values must be in the range `[0, inf)`.
Attributes:
**coef\_**array of shape (n\_features,)
Estimated coefficients for the linear predictor (`X * coef_ +
intercept_`) in the GLM.
**intercept\_**float
Intercept (a.k.a. bias) added to linear predictor.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**n\_iter\_**int
Actual number of iterations used in the solver.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`PoissonRegressor`](sklearn.linear_model.poissonregressor#sklearn.linear_model.PoissonRegressor "sklearn.linear_model.PoissonRegressor")
Generalized Linear Model with a Poisson distribution.
[`TweedieRegressor`](sklearn.linear_model.tweedieregressor#sklearn.linear_model.TweedieRegressor "sklearn.linear_model.TweedieRegressor")
Generalized Linear Model with a Tweedie distribution.
#### Examples
```
>>> from sklearn import linear_model
>>> clf = linear_model.GammaRegressor()
>>> X = [[1, 2], [2, 3], [3, 4], [4, 3]]
>>> y = [19, 26, 33, 30]
>>> clf.fit(X, y)
GammaRegressor()
>>> clf.score(X, y)
0.773...
>>> clf.coef_
array([0.072..., 0.066...])
>>> clf.intercept_
2.896...
>>> clf.predict([[1, 0], [2, 8]])
array([19.483..., 35.795...])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.linear_model.GammaRegressor.fit "sklearn.linear_model.GammaRegressor.fit")(X, y[, sample\_weight]) | Fit a Generalized Linear Model. |
| [`get_params`](#sklearn.linear_model.GammaRegressor.get_params "sklearn.linear_model.GammaRegressor.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.linear_model.GammaRegressor.predict "sklearn.linear_model.GammaRegressor.predict")(X) | Predict using GLM with feature matrix X. |
| [`score`](#sklearn.linear_model.GammaRegressor.score "sklearn.linear_model.GammaRegressor.score")(X, y[, sample\_weight]) | Compute D^2, the percentage of deviance explained. |
| [`set_params`](#sklearn.linear_model.GammaRegressor.set_params "sklearn.linear_model.GammaRegressor.set_params")(\*\*params) | Set the parameters of this estimator. |
*property*family
DEPRECATED: Attribute `family` was deprecated in version 1.1 and will be removed in 1.3.
Ensure backward compatibility for the time of deprecation.
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_glm/glm.py#L144)
Fit a Generalized Linear Model.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training data.
**y**array-like of shape (n\_samples,)
Target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**self**object
Fitted model.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_glm/glm.py#L333)
Predict using GLM with feature matrix X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Samples.
Returns:
**y\_pred**array of shape (n\_samples,)
Returns predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_glm/glm.py#L351)
Compute D^2, the percentage of deviance explained.
D^2 is a generalization of the coefficient of determination R^2. R^2 uses squared error and D^2 uses the deviance of this GLM, see the [User Guide](../model_evaluation#regression-metrics).
D^2 is defined as \(D^2 = 1-\frac{D(y\_{true},y\_{pred})}{D\_{null}}\), \(D\_{null}\) is the null deviance, i.e. the deviance of a model with intercept alone, which corresponds to \(y\_{pred} = \bar{y}\). The mean \(\bar{y}\) is averaged by sample\_weight. Best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse).
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,)
True values of target.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
D^2 of self.predict(X) w.r.t. y.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.linear_model.GammaRegressor`
----------------------------------------------------
[Release Highlights for scikit-learn 0.23](../../auto_examples/release_highlights/plot_release_highlights_0_23_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-23-0-py)
[Tweedie regression on insurance claims](../../auto_examples/linear_model/plot_tweedie_regression_insurance_claims#sphx-glr-auto-examples-linear-model-plot-tweedie-regression-insurance-claims-py)
scikit_learn sklearn.metrics.PrecisionRecallDisplay sklearn.metrics.PrecisionRecallDisplay
======================================
*class*sklearn.metrics.PrecisionRecallDisplay(*precision*, *recall*, *\**, *average\_precision=None*, *estimator\_name=None*, *pos\_label=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_plot/precision_recall_curve.py#L12)
Precision Recall visualization.
It is recommend to use [`from_estimator`](#sklearn.metrics.PrecisionRecallDisplay.from_estimator "sklearn.metrics.PrecisionRecallDisplay.from_estimator") or [`from_predictions`](#sklearn.metrics.PrecisionRecallDisplay.from_predictions "sklearn.metrics.PrecisionRecallDisplay.from_predictions") to create a `PredictionRecallDisplay`. All parameters are stored as attributes.
Read more in the [User Guide](https://scikit-learn.org/1.1/visualizations.html#visualizations).
Parameters:
**precision**ndarray
Precision values.
**recall**ndarray
Recall values.
**average\_precision**float, default=None
Average precision. If None, the average precision is not shown.
**estimator\_name**str, default=None
Name of estimator. If None, then the estimator name is not shown.
**pos\_label**str or int, default=None
The class considered as the positive class. If None, the class will not be shown in the legend.
New in version 0.24.
Attributes:
**line\_**matplotlib Artist
Precision recall curve.
**ax\_**matplotlib Axes
Axes with precision recall curve.
**figure\_**matplotlib Figure
Figure containing the curve.
See also
[`precision_recall_curve`](sklearn.metrics.precision_recall_curve#sklearn.metrics.precision_recall_curve "sklearn.metrics.precision_recall_curve")
Compute precision-recall pairs for different probability thresholds.
[`PrecisionRecallDisplay.from_estimator`](#sklearn.metrics.PrecisionRecallDisplay.from_estimator "sklearn.metrics.PrecisionRecallDisplay.from_estimator")
Plot Precision Recall Curve given a binary classifier.
[`PrecisionRecallDisplay.from_predictions`](#sklearn.metrics.PrecisionRecallDisplay.from_predictions "sklearn.metrics.PrecisionRecallDisplay.from_predictions")
Plot Precision Recall Curve using predictions from a binary classifier.
#### Notes
The average precision (cf. `average_precision`) in scikit-learn is computed without any interpolation. To be consistent with this metric, the precision-recall curve is plotted without any interpolation as well (step-wise style).
You can change this style by passing the keyword argument `drawstyle="default"` in [`plot`](#sklearn.metrics.PrecisionRecallDisplay.plot "sklearn.metrics.PrecisionRecallDisplay.plot"), [`from_estimator`](#sklearn.metrics.PrecisionRecallDisplay.from_estimator "sklearn.metrics.PrecisionRecallDisplay.from_estimator"), or [`from_predictions`](#sklearn.metrics.PrecisionRecallDisplay.from_predictions "sklearn.metrics.PrecisionRecallDisplay.from_predictions"). However, the curve will not be strictly consistent with the reported average precision.
#### Examples
```
>>> import matplotlib.pyplot as plt
>>> from sklearn.datasets import make_classification
>>> from sklearn.metrics import (precision_recall_curve,
... PrecisionRecallDisplay)
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.svm import SVC
>>> X, y = make_classification(random_state=0)
>>> X_train, X_test, y_train, y_test = train_test_split(X, y,
... random_state=0)
>>> clf = SVC(random_state=0)
>>> clf.fit(X_train, y_train)
SVC(random_state=0)
>>> predictions = clf.predict(X_test)
>>> precision, recall, _ = precision_recall_curve(y_test, predictions)
>>> disp = PrecisionRecallDisplay(precision=precision, recall=recall)
>>> disp.plot()
<...>
>>> plt.show()
```
#### Methods
| | |
| --- | --- |
| [`from_estimator`](#sklearn.metrics.PrecisionRecallDisplay.from_estimator "sklearn.metrics.PrecisionRecallDisplay.from_estimator")(estimator, X, y, \*[, ...]) | Plot precision-recall curve given an estimator and some data. |
| [`from_predictions`](#sklearn.metrics.PrecisionRecallDisplay.from_predictions "sklearn.metrics.PrecisionRecallDisplay.from_predictions")(y\_true, y\_pred, \*[, ...]) | Plot precision-recall curve given binary class predictions. |
| [`plot`](#sklearn.metrics.PrecisionRecallDisplay.plot "sklearn.metrics.PrecisionRecallDisplay.plot")([ax, name]) | Plot visualization. |
*classmethod*from\_estimator(*estimator*, *X*, *y*, *\**, *sample\_weight=None*, *pos\_label=None*, *response\_method='auto'*, *name=None*, *ax=None*, *\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_plot/precision_recall_curve.py#L180)
Plot precision-recall curve given an estimator and some data.
Parameters:
**estimator**estimator instance
Fitted classifier or a fitted [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline") in which the last estimator is a classifier.
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Input values.
**y**array-like of shape (n\_samples,)
Target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**pos\_label**str or int, default=None
The class considered as the positive class when computing the precision and recall metrics. By default, `estimators.classes_[1]` is considered as the positive class.
**response\_method**{‘predict\_proba’, ‘decision\_function’, ‘auto’}, default=’auto’
Specifies whether to use [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) or [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) as the target response. If set to ‘auto’, [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) is tried first and if it does not exist [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) is tried next.
**name**str, default=None
Name for labeling curve. If `None`, no name is used.
**ax**matplotlib axes, default=None
Axes object to plot on. If `None`, a new figure and axes is created.
**\*\*kwargs**dict
Keyword arguments to be passed to matplotlib’s `plot`.
Returns:
**display**[`PrecisionRecallDisplay`](#sklearn.metrics.PrecisionRecallDisplay "sklearn.metrics.PrecisionRecallDisplay")
See also
[`PrecisionRecallDisplay.from_predictions`](#sklearn.metrics.PrecisionRecallDisplay.from_predictions "sklearn.metrics.PrecisionRecallDisplay.from_predictions")
Plot precision-recall curve using estimated probabilities or output of decision function.
#### Notes
The average precision (cf. `average_precision`) in scikit-learn is computed without any interpolation. To be consistent with this metric, the precision-recall curve is plotted without any interpolation as well (step-wise style).
You can change this style by passing the keyword argument `drawstyle="default"`. However, the curve will not be strictly consistent with the reported average precision.
#### Examples
```
>>> import matplotlib.pyplot as plt
>>> from sklearn.datasets import make_classification
>>> from sklearn.metrics import PrecisionRecallDisplay
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.linear_model import LogisticRegression
>>> X, y = make_classification(random_state=0)
>>> X_train, X_test, y_train, y_test = train_test_split(
... X, y, random_state=0)
>>> clf = LogisticRegression()
>>> clf.fit(X_train, y_train)
LogisticRegression()
>>> PrecisionRecallDisplay.from_estimator(
... clf, X_test, y_test)
<...>
>>> plt.show()
```
*classmethod*from\_predictions(*y\_true*, *y\_pred*, *\**, *sample\_weight=None*, *pos\_label=None*, *name=None*, *ax=None*, *\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_plot/precision_recall_curve.py#L293)
Plot precision-recall curve given binary class predictions.
Parameters:
**y\_true**array-like of shape (n\_samples,)
True binary labels.
**y\_pred**array-like of shape (n\_samples,)
Estimated probabilities or output of decision function.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**pos\_label**str or int, default=None
The class considered as the positive class when computing the precision and recall metrics.
**name**str, default=None
Name for labeling curve. If `None`, name will be set to `"Classifier"`.
**ax**matplotlib axes, default=None
Axes object to plot on. If `None`, a new figure and axes is created.
**\*\*kwargs**dict
Keyword arguments to be passed to matplotlib’s `plot`.
Returns:
**display**[`PrecisionRecallDisplay`](#sklearn.metrics.PrecisionRecallDisplay "sklearn.metrics.PrecisionRecallDisplay")
See also
[`PrecisionRecallDisplay.from_estimator`](#sklearn.metrics.PrecisionRecallDisplay.from_estimator "sklearn.metrics.PrecisionRecallDisplay.from_estimator")
Plot precision-recall curve using an estimator.
#### Notes
The average precision (cf. `average_precision`) in scikit-learn is computed without any interpolation. To be consistent with this metric, the precision-recall curve is plotted without any interpolation as well (step-wise style).
You can change this style by passing the keyword argument `drawstyle="default"`. However, the curve will not be strictly consistent with the reported average precision.
#### Examples
```
>>> import matplotlib.pyplot as plt
>>> from sklearn.datasets import make_classification
>>> from sklearn.metrics import PrecisionRecallDisplay
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.linear_model import LogisticRegression
>>> X, y = make_classification(random_state=0)
>>> X_train, X_test, y_train, y_test = train_test_split(
... X, y, random_state=0)
>>> clf = LogisticRegression()
>>> clf.fit(X_train, y_train)
LogisticRegression()
>>> y_pred = clf.predict_proba(X_test)[:, 1]
>>> PrecisionRecallDisplay.from_predictions(
... y_test, y_pred)
<...>
>>> plt.show()
```
plot(*ax=None*, *\**, *name=None*, *\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_plot/precision_recall_curve.py#L112)
Plot visualization.
Extra keyword arguments will be passed to matplotlib’s `plot`.
Parameters:
**ax**Matplotlib Axes, default=None
Axes object to plot on. If `None`, a new figure and axes is created.
**name**str, default=None
Name of precision recall curve for labeling. If `None`, use `estimator_name` if not `None`, otherwise no labeling is shown.
**\*\*kwargs**dict
Keyword arguments to be passed to matplotlib’s `plot`.
Returns:
**display**[`PrecisionRecallDisplay`](#sklearn.metrics.PrecisionRecallDisplay "sklearn.metrics.PrecisionRecallDisplay")
Object that stores computed values.
#### Notes
The average precision (cf. `average_precision`) in scikit-learn is computed without any interpolation. To be consistent with this metric, the precision-recall curve is plotted without any interpolation as well (step-wise style).
You can change this style by passing the keyword argument `drawstyle="default"`. However, the curve will not be strictly consistent with the reported average precision.
Examples using `sklearn.metrics.PrecisionRecallDisplay`
-------------------------------------------------------
[Visualizations with Display Objects](../../auto_examples/miscellaneous/plot_display_object_visualization#sphx-glr-auto-examples-miscellaneous-plot-display-object-visualization-py)
[Precision-Recall](../../auto_examples/model_selection/plot_precision_recall#sphx-glr-auto-examples-model-selection-plot-precision-recall-py)
| programming_docs |
scikit_learn sklearn.utils.multiclass.is_multilabel sklearn.utils.multiclass.is\_multilabel
=======================================
sklearn.utils.multiclass.is\_multilabel(*y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/multiclass.py#L118)
Check if `y` is in a multilabel format.
Parameters:
**y**ndarray of shape (n\_samples,)
Target values.
Returns:
**out**bool
Return `True`, if `y` is in a multilabel format, else ``False`.
#### Examples
```
>>> import numpy as np
>>> from sklearn.utils.multiclass import is_multilabel
>>> is_multilabel([0, 1, 0, 1])
False
>>> is_multilabel([[1], [0, 2], []])
False
>>> is_multilabel(np.array([[1, 0], [0, 0]]))
True
>>> is_multilabel(np.array([[1], [0], [0]]))
False
>>> is_multilabel(np.array([[1, 0, 0]]))
True
```
scikit_learn sklearn.impute.SimpleImputer sklearn.impute.SimpleImputer
============================
*class*sklearn.impute.SimpleImputer(*\**, *missing\_values=nan*, *strategy='mean'*, *fill\_value=None*, *verbose='deprecated'*, *copy=True*, *add\_indicator=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/impute/_base.py#L132)
Univariate imputer for completing missing values with simple strategies.
Replace missing values using a descriptive statistic (e.g. mean, median, or most frequent) along each column, or using a constant value.
Read more in the [User Guide](../impute#impute).
New in version 0.20: `SimpleImputer` replaces the previous `sklearn.preprocessing.Imputer` estimator which is now removed.
Parameters:
**missing\_values**int, float, str, np.nan, None or pandas.NA, default=np.nan
The placeholder for the missing values. All occurrences of `missing_values` will be imputed. For pandas’ dataframes with nullable integer dtypes with missing values, `missing_values` can be set to either `np.nan` or `pd.NA`.
**strategy**str, default=’mean’
The imputation strategy.
* If “mean”, then replace missing values using the mean along each column. Can only be used with numeric data.
* If “median”, then replace missing values using the median along each column. Can only be used with numeric data.
* If “most\_frequent”, then replace missing using the most frequent value along each column. Can be used with strings or numeric data. If there is more than one such value, only the smallest is returned.
* If “constant”, then replace missing values with fill\_value. Can be used with strings or numeric data.
New in version 0.20: strategy=”constant” for fixed value imputation.
**fill\_value**str or numerical value, default=None
When strategy == “constant”, fill\_value is used to replace all occurrences of missing\_values. If left to the default, fill\_value will be 0 when imputing numerical data and “missing\_value” for strings or object data types.
**verbose**int, default=0
Controls the verbosity of the imputer.
Deprecated since version 1.1: The ‘verbose’ parameter was deprecated in version 1.1 and will be removed in 1.3. A warning will always be raised upon the removal of empty columns in the future version.
**copy**bool, default=True
If True, a copy of X will be created. If False, imputation will be done in-place whenever possible. Note that, in the following cases, a new copy will always be made, even if `copy=False`:
* If `X` is not an array of floating values;
* If `X` is encoded as a CSR matrix;
* If `add_indicator=True`.
**add\_indicator**bool, default=False
If True, a [`MissingIndicator`](sklearn.impute.missingindicator#sklearn.impute.MissingIndicator "sklearn.impute.MissingIndicator") transform will stack onto output of the imputer’s transform. This allows a predictive estimator to account for missingness despite imputation. If a feature has no missing values at fit/train time, the feature won’t appear on the missing indicator even if there are missing values at transform/test time.
Attributes:
**statistics\_**array of shape (n\_features,)
The imputation fill value for each feature. Computing statistics can result in `np.nan` values. During [`transform`](#sklearn.impute.SimpleImputer.transform "sklearn.impute.SimpleImputer.transform"), features corresponding to `np.nan` statistics will be discarded.
**indicator\_**[`MissingIndicator`](sklearn.impute.missingindicator#sklearn.impute.MissingIndicator "sklearn.impute.MissingIndicator")
Indicator used to add binary indicators for missing values. `None` if `add_indicator=False`.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`IterativeImputer`](sklearn.impute.iterativeimputer#sklearn.impute.IterativeImputer "sklearn.impute.IterativeImputer")
Multivariate imputer that estimates values to impute for each feature with missing values from all the others.
[`KNNImputer`](sklearn.impute.knnimputer#sklearn.impute.KNNImputer "sklearn.impute.KNNImputer")
Multivariate imputer that estimates missing features using nearest samples.
#### Notes
Columns which only contained missing values at [`fit`](#sklearn.impute.SimpleImputer.fit "sklearn.impute.SimpleImputer.fit") are discarded upon [`transform`](#sklearn.impute.SimpleImputer.transform "sklearn.impute.SimpleImputer.transform") if strategy is not `"constant"`.
In a prediction context, simple imputation usually performs poorly when associated with a weak learner. However, with a powerful learner, it can lead to as good or better performance than complex imputation such as [`IterativeImputer`](sklearn.impute.iterativeimputer#sklearn.impute.IterativeImputer "sklearn.impute.IterativeImputer") or [`KNNImputer`](sklearn.impute.knnimputer#sklearn.impute.KNNImputer "sklearn.impute.KNNImputer").
#### Examples
```
>>> import numpy as np
>>> from sklearn.impute import SimpleImputer
>>> imp_mean = SimpleImputer(missing_values=np.nan, strategy='mean')
>>> imp_mean.fit([[7, 2, 3], [4, np.nan, 6], [10, 5, 9]])
SimpleImputer()
>>> X = [[np.nan, 2, 3], [4, np.nan, 6], [10, np.nan, 9]]
>>> print(imp_mean.transform(X))
[[ 7. 2. 3. ]
[ 4. 3.5 6. ]
[10. 3.5 9. ]]
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.impute.SimpleImputer.fit "sklearn.impute.SimpleImputer.fit")(X[, y]) | Fit the imputer on `X`. |
| [`fit_transform`](#sklearn.impute.SimpleImputer.fit_transform "sklearn.impute.SimpleImputer.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.impute.SimpleImputer.get_feature_names_out "sklearn.impute.SimpleImputer.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.impute.SimpleImputer.get_params "sklearn.impute.SimpleImputer.get_params")([deep]) | Get parameters for this estimator. |
| [`inverse_transform`](#sklearn.impute.SimpleImputer.inverse_transform "sklearn.impute.SimpleImputer.inverse_transform")(X) | Convert the data back to the original representation. |
| [`set_params`](#sklearn.impute.SimpleImputer.set_params "sklearn.impute.SimpleImputer.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.impute.SimpleImputer.transform "sklearn.impute.SimpleImputer.transform")(X) | Impute all missing values in `X`. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/impute/_base.py#L338)
Fit the imputer on `X`.
Parameters:
**X**{array-like, sparse matrix}, shape (n\_samples, n\_features)
Input data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Not used, present here for API consistency by convention.
Returns:
**self**object
Fitted estimator.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/impute/_base.py#L656)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Input features.
* If `input_features` is `None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then the following input feature names are generated: `["x0", "x1", ..., "x(n_features_in_ - 1)"]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
inverse\_transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/impute/_base.py#L587)
Convert the data back to the original representation.
Inverts the `transform` operation performed on an array. This operation can only be performed after [`SimpleImputer`](#sklearn.impute.SimpleImputer "sklearn.impute.SimpleImputer") is instantiated with `add_indicator=True`.
Note that `inverse_transform` can only invert the transform in features that have binary indicators for missing values. If a feature has no missing values at `fit` time, the feature won’t have a binary indicator, and the imputation done at `transform` time won’t be inverted.
New in version 0.24.
Parameters:
**X**array-like of shape (n\_samples, n\_features + n\_features\_missing\_indicator)
The imputed data to be reverted to original data. It has to be an augmented array of imputed data and the missing indicator mask.
Returns:
**X\_original**ndarray of shape (n\_samples, n\_features)
The original `X` with missing values as it was prior to imputation.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/impute/_base.py#L499)
Impute all missing values in `X`.
Parameters:
**X**{array-like, sparse matrix}, shape (n\_samples, n\_features)
The input data to complete.
Returns:
**X\_imputed**{ndarray, sparse matrix} of shape (n\_samples, n\_features\_out)
`X` with imputed values.
Examples using `sklearn.impute.SimpleImputer`
---------------------------------------------
[Release Highlights for scikit-learn 1.1](../../auto_examples/release_highlights/plot_release_highlights_1_1_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-1-1-0-py)
[Release Highlights for scikit-learn 0.23](../../auto_examples/release_highlights/plot_release_highlights_0_23_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-23-0-py)
[Combine predictors using stacking](../../auto_examples/ensemble/plot_stack_predictors#sphx-glr-auto-examples-ensemble-plot-stack-predictors-py)
[Permutation Importance vs Random Forest Feature Importance (MDI)](../../auto_examples/inspection/plot_permutation_importance#sphx-glr-auto-examples-inspection-plot-permutation-importance-py)
[Displaying Pipelines](../../auto_examples/miscellaneous/plot_pipeline_display#sphx-glr-auto-examples-miscellaneous-plot-pipeline-display-py)
[Imputing missing values before building an estimator](../../auto_examples/impute/plot_missing_values#sphx-glr-auto-examples-impute-plot-missing-values-py)
[Imputing missing values with variants of IterativeImputer](../../auto_examples/impute/plot_iterative_imputer_variants_comparison#sphx-glr-auto-examples-impute-plot-iterative-imputer-variants-comparison-py)
[Column Transformer with Mixed Types](../../auto_examples/compose/plot_column_transformer_mixed_types#sphx-glr-auto-examples-compose-plot-column-transformer-mixed-types-py)
scikit_learn sklearn.metrics.RocCurveDisplay sklearn.metrics.RocCurveDisplay
===============================
*class*sklearn.metrics.RocCurveDisplay(*\**, *fpr*, *tpr*, *roc\_auc=None*, *estimator\_name=None*, *pos\_label=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_plot/roc_curve.py#L10)
ROC Curve visualization.
It is recommend to use [`from_estimator`](#sklearn.metrics.RocCurveDisplay.from_estimator "sklearn.metrics.RocCurveDisplay.from_estimator") or [`from_predictions`](#sklearn.metrics.RocCurveDisplay.from_predictions "sklearn.metrics.RocCurveDisplay.from_predictions") to create a [`RocCurveDisplay`](#sklearn.metrics.RocCurveDisplay "sklearn.metrics.RocCurveDisplay"). All parameters are stored as attributes.
Read more in the [User Guide](https://scikit-learn.org/1.1/visualizations.html#visualizations).
Parameters:
**fpr**ndarray
False positive rate.
**tpr**ndarray
True positive rate.
**roc\_auc**float, default=None
Area under ROC curve. If None, the roc\_auc score is not shown.
**estimator\_name**str, default=None
Name of estimator. If None, the estimator name is not shown.
**pos\_label**str or int, default=None
The class considered as the positive class when computing the roc auc metrics. By default, `estimators.classes_[1]` is considered as the positive class.
New in version 0.24.
Attributes:
**line\_**matplotlib Artist
ROC Curve.
**ax\_**matplotlib Axes
Axes with ROC Curve.
**figure\_**matplotlib Figure
Figure containing the curve.
See also
[`roc_curve`](sklearn.metrics.roc_curve#sklearn.metrics.roc_curve "sklearn.metrics.roc_curve")
Compute Receiver operating characteristic (ROC) curve.
[`RocCurveDisplay.from_estimator`](#sklearn.metrics.RocCurveDisplay.from_estimator "sklearn.metrics.RocCurveDisplay.from_estimator")
Plot Receiver Operating Characteristic (ROC) curve given an estimator and some data.
[`RocCurveDisplay.from_predictions`](#sklearn.metrics.RocCurveDisplay.from_predictions "sklearn.metrics.RocCurveDisplay.from_predictions")
Plot Receiver Operating Characteristic (ROC) curve given the true and predicted values.
[`roc_auc_score`](sklearn.metrics.roc_auc_score#sklearn.metrics.roc_auc_score "sklearn.metrics.roc_auc_score")
Compute the area under the ROC curve.
#### Examples
```
>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> from sklearn import metrics
>>> y = np.array([0, 0, 1, 1])
>>> pred = np.array([0.1, 0.4, 0.35, 0.8])
>>> fpr, tpr, thresholds = metrics.roc_curve(y, pred)
>>> roc_auc = metrics.auc(fpr, tpr)
>>> display = metrics.RocCurveDisplay(fpr=fpr, tpr=tpr, roc_auc=roc_auc,
... estimator_name='example estimator')
>>> display.plot()
<...>
>>> plt.show()
```
#### Methods
| | |
| --- | --- |
| [`from_estimator`](#sklearn.metrics.RocCurveDisplay.from_estimator "sklearn.metrics.RocCurveDisplay.from_estimator")(estimator, X, y, \*[, ...]) | Create a ROC Curve display from an estimator. |
| [`from_predictions`](#sklearn.metrics.RocCurveDisplay.from_predictions "sklearn.metrics.RocCurveDisplay.from_predictions")(y\_true, y\_pred, \*[, ...]) | Plot ROC curve given the true and predicted values. |
| [`plot`](#sklearn.metrics.RocCurveDisplay.plot "sklearn.metrics.RocCurveDisplay.plot")([ax, name]) | Plot visualization |
*classmethod*from\_estimator(*estimator*, *X*, *y*, *\**, *sample\_weight=None*, *drop\_intermediate=True*, *response\_method='auto'*, *pos\_label=None*, *name=None*, *ax=None*, *\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_plot/roc_curve.py#L140)
Create a ROC Curve display from an estimator.
Parameters:
**estimator**estimator instance
Fitted classifier or a fitted [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline") in which the last estimator is a classifier.
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Input values.
**y**array-like of shape (n\_samples,)
Target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**drop\_intermediate**bool, default=True
Whether to drop some suboptimal thresholds which would not appear on a plotted ROC curve. This is useful in order to create lighter ROC curves.
**response\_method**{‘predict\_proba’, ‘decision\_function’, ‘auto’} default=’auto’
Specifies whether to use [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) or [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) as the target response. If set to ‘auto’, [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) is tried first and if it does not exist [decision\_function](https://scikit-learn.org/1.1/glossary.html#term-decision_function) is tried next.
**pos\_label**str or int, default=None
The class considered as the positive class when computing the roc auc metrics. By default, `estimators.classes_[1]` is considered as the positive class.
**name**str, default=None
Name of ROC Curve for labeling. If `None`, use the name of the estimator.
**ax**matplotlib axes, default=None
Axes object to plot on. If `None`, a new figure and axes is created.
**\*\*kwargs**dict
Keyword arguments to be passed to matplotlib’s `plot`.
Returns:
**display**`RocCurveDisplay`
The ROC Curve display.
See also
[`roc_curve`](sklearn.metrics.roc_curve#sklearn.metrics.roc_curve "sklearn.metrics.roc_curve")
Compute Receiver operating characteristic (ROC) curve.
[`RocCurveDisplay.from_predictions`](#sklearn.metrics.RocCurveDisplay.from_predictions "sklearn.metrics.RocCurveDisplay.from_predictions")
ROC Curve visualization given the probabilities of scores of a classifier.
[`roc_auc_score`](sklearn.metrics.roc_auc_score#sklearn.metrics.roc_auc_score "sklearn.metrics.roc_auc_score")
Compute the area under the ROC curve.
#### Examples
```
>>> import matplotlib.pyplot as plt
>>> from sklearn.datasets import make_classification
>>> from sklearn.metrics import RocCurveDisplay
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.svm import SVC
>>> X, y = make_classification(random_state=0)
>>> X_train, X_test, y_train, y_test = train_test_split(
... X, y, random_state=0)
>>> clf = SVC(random_state=0).fit(X_train, y_train)
>>> RocCurveDisplay.from_estimator(
... clf, X_test, y_test)
<...>
>>> plt.show()
```
*classmethod*from\_predictions(*y\_true*, *y\_pred*, *\**, *sample\_weight=None*, *drop\_intermediate=True*, *pos\_label=None*, *name=None*, *ax=None*, *\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_plot/roc_curve.py#L249)
Plot ROC curve given the true and predicted values.
Read more in the [User Guide](https://scikit-learn.org/1.1/visualizations.html#visualizations).
New in version 1.0.
Parameters:
**y\_true**array-like of shape (n\_samples,)
True labels.
**y\_pred**array-like of shape (n\_samples,)
Target scores, can either be probability estimates of the positive class, confidence values, or non-thresholded measure of decisions (as returned by “decision\_function” on some classifiers).
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**drop\_intermediate**bool, default=True
Whether to drop some suboptimal thresholds which would not appear on a plotted ROC curve. This is useful in order to create lighter ROC curves.
**pos\_label**str or int, default=None
The label of the positive class. When `pos_label=None`, if `y_true` is in {-1, 1} or {0, 1}, `pos_label` is set to 1, otherwise an error will be raised.
**name**str, default=None
Name of ROC curve for labeling. If `None`, name will be set to `"Classifier"`.
**ax**matplotlib axes, default=None
Axes object to plot on. If `None`, a new figure and axes is created.
**\*\*kwargs**dict
Additional keywords arguments passed to matplotlib `plot` function.
Returns:
**display**[`RocCurveDisplay`](#sklearn.metrics.RocCurveDisplay "sklearn.metrics.RocCurveDisplay")
Object that stores computed values.
See also
[`roc_curve`](sklearn.metrics.roc_curve#sklearn.metrics.roc_curve "sklearn.metrics.roc_curve")
Compute Receiver operating characteristic (ROC) curve.
[`RocCurveDisplay.from_estimator`](#sklearn.metrics.RocCurveDisplay.from_estimator "sklearn.metrics.RocCurveDisplay.from_estimator")
ROC Curve visualization given an estimator and some data.
[`roc_auc_score`](sklearn.metrics.roc_auc_score#sklearn.metrics.roc_auc_score "sklearn.metrics.roc_auc_score")
Compute the area under the ROC curve.
#### Examples
```
>>> import matplotlib.pyplot as plt
>>> from sklearn.datasets import make_classification
>>> from sklearn.metrics import RocCurveDisplay
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.svm import SVC
>>> X, y = make_classification(random_state=0)
>>> X_train, X_test, y_train, y_test = train_test_split(
... X, y, random_state=0)
>>> clf = SVC(random_state=0).fit(X_train, y_train)
>>> y_pred = clf.decision_function(X_test)
>>> RocCurveDisplay.from_predictions(
... y_test, y_pred)
<...>
>>> plt.show()
```
plot(*ax=None*, *\**, *name=None*, *\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_plot/roc_curve.py#L85)
Plot visualization
Extra keyword arguments will be passed to matplotlib’s `plot`.
Parameters:
**ax**matplotlib axes, default=None
Axes object to plot on. If `None`, a new figure and axes is created.
**name**str, default=None
Name of ROC Curve for labeling. If `None`, use `estimator_name` if not `None`, otherwise no labeling is shown.
Returns:
**display**`RocCurveDisplay`
Object that stores computed values.
Examples using `sklearn.metrics.RocCurveDisplay`
------------------------------------------------
[Evaluation of outlier detection estimators](../../auto_examples/miscellaneous/plot_outlier_detection_bench#sphx-glr-auto-examples-miscellaneous-plot-outlier-detection-bench-py)
[Visualizations with Display Objects](../../auto_examples/miscellaneous/plot_display_object_visualization#sphx-glr-auto-examples-miscellaneous-plot-display-object-visualization-py)
| programming_docs |
scikit_learn sklearn.model_selection.LeavePOut sklearn.model\_selection.LeavePOut
==================================
*class*sklearn.model\_selection.LeavePOut(*p*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L193)
Leave-P-Out cross-validator
Provides train/test indices to split data in train/test sets. This results in testing on all distinct samples of size p, while the remaining n - p samples form the training set in each iteration.
Note: `LeavePOut(p)` is NOT equivalent to `KFold(n_splits=n_samples // p)` which creates non-overlapping test sets.
Due to the high number of iterations which grows combinatorically with the number of samples this cross-validation method can be very costly. For large datasets one should favor [`KFold`](sklearn.model_selection.kfold#sklearn.model_selection.KFold "sklearn.model_selection.KFold"), [`StratifiedKFold`](sklearn.model_selection.stratifiedkfold#sklearn.model_selection.StratifiedKFold "sklearn.model_selection.StratifiedKFold") or [`ShuffleSplit`](sklearn.model_selection.shufflesplit#sklearn.model_selection.ShuffleSplit "sklearn.model_selection.ShuffleSplit").
Read more in the [User Guide](../cross_validation#leave-p-out).
Parameters:
**p**int
Size of the test sets. Must be strictly less than the number of samples.
#### Examples
```
>>> import numpy as np
>>> from sklearn.model_selection import LeavePOut
>>> X = np.array([[1, 2], [3, 4], [5, 6], [7, 8]])
>>> y = np.array([1, 2, 3, 4])
>>> lpo = LeavePOut(2)
>>> lpo.get_n_splits(X)
6
>>> print(lpo)
LeavePOut(p=2)
>>> for train_index, test_index in lpo.split(X):
... print("TRAIN:", train_index, "TEST:", test_index)
... X_train, X_test = X[train_index], X[test_index]
... y_train, y_test = y[train_index], y[test_index]
TRAIN: [2 3] TEST: [0 1]
TRAIN: [1 3] TEST: [0 2]
TRAIN: [1 2] TEST: [0 3]
TRAIN: [0 3] TEST: [1 2]
TRAIN: [0 2] TEST: [1 3]
TRAIN: [0 1] TEST: [2 3]
```
#### Methods
| | |
| --- | --- |
| [`get_n_splits`](#sklearn.model_selection.LeavePOut.get_n_splits "sklearn.model_selection.LeavePOut.get_n_splits")(X[, y, groups]) | Returns the number of splitting iterations in the cross-validator |
| [`split`](#sklearn.model_selection.LeavePOut.split "sklearn.model_selection.LeavePOut.split")(X[, y, groups]) | Generate indices to split data into training and test set. |
get\_n\_splits(*X*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L253)
Returns the number of splitting iterations in the cross-validator
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**object
Always ignored, exists for compatibility.
**groups**object
Always ignored, exists for compatibility.
split(*X*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L60)
Generate indices to split data into training and test set.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,)
The target variable for supervised learning problems.
**groups**array-like of shape (n\_samples,), default=None
Group labels for the samples used while splitting the dataset into train/test set.
Yields:
**train**ndarray
The training set indices for that split.
**test**ndarray
The testing set indices for that split.
scikit_learn sklearn.neighbors.RadiusNeighborsTransformer sklearn.neighbors.RadiusNeighborsTransformer
============================================
*class*sklearn.neighbors.RadiusNeighborsTransformer(*\**, *mode='distance'*, *radius=1.0*, *algorithm='auto'*, *leaf\_size=30*, *metric='minkowski'*, *p=2*, *metric\_params=None*, *n\_jobs=1*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_graph.py#L442)
Transform X into a (weighted) graph of neighbors nearer than a radius.
The transformed data is a sparse graph as returned by `radius_neighbors_graph`.
Read more in the [User Guide](../neighbors#neighbors-transformer).
New in version 0.22.
Parameters:
**mode**{‘distance’, ‘connectivity’}, default=’distance’
Type of returned matrix: ‘connectivity’ will return the connectivity matrix with ones and zeros, and ‘distance’ will return the distances between neighbors according to the given metric.
**radius**float, default=1.0
Radius of neighborhood in the transformed sparse graph.
**algorithm**{‘auto’, ‘ball\_tree’, ‘kd\_tree’, ‘brute’}, default=’auto’
Algorithm used to compute the nearest neighbors:
* ‘ball\_tree’ will use [`BallTree`](sklearn.neighbors.balltree#sklearn.neighbors.BallTree "sklearn.neighbors.BallTree")
* ‘kd\_tree’ will use [`KDTree`](sklearn.neighbors.kdtree#sklearn.neighbors.KDTree "sklearn.neighbors.KDTree")
* ‘brute’ will use a brute-force search.
* ‘auto’ will attempt to decide the most appropriate algorithm based on the values passed to [`fit`](#sklearn.neighbors.RadiusNeighborsTransformer.fit "sklearn.neighbors.RadiusNeighborsTransformer.fit") method.
Note: fitting on sparse input will override the setting of this parameter, using brute force.
**leaf\_size**int, default=30
Leaf size passed to BallTree or KDTree. This can affect the speed of the construction and query, as well as the memory required to store the tree. The optimal value depends on the nature of the problem.
**metric**str or callable, default=’minkowski’
Metric to use for distance computation. Default is “minkowski”, which results in the standard Euclidean distance when p = 2. See the documentation of [scipy.spatial.distance](https://docs.scipy.org/doc/scipy/reference/spatial.distance.html) and the metrics listed in [`distance_metrics`](sklearn.metrics.pairwise.distance_metrics#sklearn.metrics.pairwise.distance_metrics "sklearn.metrics.pairwise.distance_metrics") for valid metric values.
If metric is a callable function, it takes two arrays representing 1D vectors as inputs and must return one value indicating the distance between those vectors. This works for Scipy’s metrics, but is less efficient than passing the metric name as a string.
Distance matrices are not supported.
**p**int, default=2
Parameter for the Minkowski metric from sklearn.metrics.pairwise.pairwise\_distances. When p = 1, this is equivalent to using manhattan\_distance (l1), and euclidean\_distance (l2) for p = 2. For arbitrary p, minkowski\_distance (l\_p) is used.
**metric\_params**dict, default=None
Additional keyword arguments for the metric function.
**n\_jobs**int, default=1
The number of parallel jobs to run for neighbors search. If `-1`, then the number of jobs is set to the number of CPU cores.
Attributes:
**effective\_metric\_**str or callable
The distance metric used. It will be same as the `metric` parameter or a synonym of it, e.g. ‘euclidean’ if the `metric` parameter set to ‘minkowski’ and `p` parameter set to 2.
**effective\_metric\_params\_**dict
Additional keyword arguments for the metric function. For most metrics will be same with `metric_params` parameter, but may also contain the `p` parameter value if the `effective_metric_` attribute is set to ‘minkowski’.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_samples\_fit\_**int
Number of samples in the fitted data.
See also
[`kneighbors_graph`](sklearn.neighbors.kneighbors_graph#sklearn.neighbors.kneighbors_graph "sklearn.neighbors.kneighbors_graph")
Compute the weighted graph of k-neighbors for points in X.
[`KNeighborsTransformer`](sklearn.neighbors.kneighborstransformer#sklearn.neighbors.KNeighborsTransformer "sklearn.neighbors.KNeighborsTransformer")
Transform X into a weighted graph of k nearest neighbors.
#### Examples
```
>>> import numpy as np
>>> from sklearn.datasets import load_wine
>>> from sklearn.cluster import DBSCAN
>>> from sklearn.neighbors import RadiusNeighborsTransformer
>>> from sklearn.pipeline import make_pipeline
>>> X, _ = load_wine(return_X_y=True)
>>> estimator = make_pipeline(
... RadiusNeighborsTransformer(radius=42.0, mode='distance'),
... DBSCAN(eps=25.0, metric='precomputed'))
>>> X_clustered = estimator.fit_predict(X)
>>> clusters, counts = np.unique(X_clustered, return_counts=True)
>>> print(counts)
[ 29 15 111 11 12]
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.neighbors.RadiusNeighborsTransformer.fit "sklearn.neighbors.RadiusNeighborsTransformer.fit")(X[, y]) | Fit the radius neighbors transformer from the training dataset. |
| [`fit_transform`](#sklearn.neighbors.RadiusNeighborsTransformer.fit_transform "sklearn.neighbors.RadiusNeighborsTransformer.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.neighbors.RadiusNeighborsTransformer.get_feature_names_out "sklearn.neighbors.RadiusNeighborsTransformer.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.neighbors.RadiusNeighborsTransformer.get_params "sklearn.neighbors.RadiusNeighborsTransformer.get_params")([deep]) | Get parameters for this estimator. |
| [`radius_neighbors`](#sklearn.neighbors.RadiusNeighborsTransformer.radius_neighbors "sklearn.neighbors.RadiusNeighborsTransformer.radius_neighbors")([X, radius, ...]) | Find the neighbors within a given radius of a point or points. |
| [`radius_neighbors_graph`](#sklearn.neighbors.RadiusNeighborsTransformer.radius_neighbors_graph "sklearn.neighbors.RadiusNeighborsTransformer.radius_neighbors_graph")([X, radius, mode, ...]) | Compute the (weighted) graph of Neighbors for points in X. |
| [`set_params`](#sklearn.neighbors.RadiusNeighborsTransformer.set_params "sklearn.neighbors.RadiusNeighborsTransformer.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.neighbors.RadiusNeighborsTransformer.transform "sklearn.neighbors.RadiusNeighborsTransformer.transform")(X) | Compute the (weighted) graph of Neighbors for points in X. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_graph.py#L589)
Fit the radius neighbors transformer from the training dataset.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features) or (n\_samples, n\_samples) if metric=’precomputed’
Training data.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**self**RadiusNeighborsTransformer
The fitted radius neighbors transformer.
fit\_transform(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_graph.py#L629)
Fit to data, then transform it.
Fits transformer to X and y with optional parameters fit\_params and returns a transformed version of X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training set.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**Xt**sparse matrix of shape (n\_samples, n\_samples)
Xt[i, j] is assigned the weight of edge that connects i to j. Only the neighbors have an explicit value. The diagonal is always explicit. The matrix is of CSR format.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.neighbors.RadiusNeighborsTransformer.fit "sklearn.neighbors.RadiusNeighborsTransformer.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
radius\_neighbors(*X=None*, *radius=None*, *return\_distance=True*, *sort\_results=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_base.py#L996)
Find the neighbors within a given radius of a point or points.
Return the indices and distances of each point from the dataset lying in a ball with size `radius` around the points of the query array. Points lying on the boundary are included in the results.
The result points are *not* necessarily sorted by distance to their query point.
Parameters:
**X**array-like of (n\_samples, n\_features), default=None
The query point or points. If not provided, neighbors of each indexed point are returned. In this case, the query point is not considered its own neighbor.
**radius**float, default=None
Limiting distance of neighbors to return. The default is the value passed to the constructor.
**return\_distance**bool, default=True
Whether or not to return the distances.
**sort\_results**bool, default=False
If True, the distances and indices will be sorted by increasing distances before being returned. If False, the results may not be sorted. If `return_distance=False`, setting `sort_results=True` will result in an error.
New in version 0.22.
Returns:
**neigh\_dist**ndarray of shape (n\_samples,) of arrays
Array representing the distances to each point, only present if `return_distance=True`. The distance values are computed according to the `metric` constructor parameter.
**neigh\_ind**ndarray of shape (n\_samples,) of arrays
An array of arrays of indices of the approximate nearest points from the population matrix that lie within a ball of size `radius` around the query points.
#### Notes
Because the number of neighbors of each point is not necessarily equal, the results for multiple query points cannot be fit in a standard data array. For efficiency, `radius_neighbors` returns arrays of objects, where each object is a 1D array of indices or distances.
#### Examples
In the following example, we construct a NeighborsClassifier class from an array representing our data set and ask who’s the closest point to [1, 1, 1]:
```
>>> import numpy as np
>>> samples = [[0., 0., 0.], [0., .5, 0.], [1., 1., .5]]
>>> from sklearn.neighbors import NearestNeighbors
>>> neigh = NearestNeighbors(radius=1.6)
>>> neigh.fit(samples)
NearestNeighbors(radius=1.6)
>>> rng = neigh.radius_neighbors([[1., 1., 1.]])
>>> print(np.asarray(rng[0][0]))
[1.5 0.5]
>>> print(np.asarray(rng[1][0]))
[1 2]
```
The first array returned contains the distances to all points which are closer than 1.6, while the second array returned contains their indices. In general, multiple points can be queried at the same time.
radius\_neighbors\_graph(*X=None*, *radius=None*, *mode='connectivity'*, *sort\_results=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_base.py#L1205)
Compute the (weighted) graph of Neighbors for points in X.
Neighborhoods are restricted the points at a distance lower than radius.
Parameters:
**X**array-like of shape (n\_samples, n\_features), default=None
The query point or points. If not provided, neighbors of each indexed point are returned. In this case, the query point is not considered its own neighbor.
**radius**float, default=None
Radius of neighborhoods. The default is the value passed to the constructor.
**mode**{‘connectivity’, ‘distance’}, default=’connectivity’
Type of returned matrix: ‘connectivity’ will return the connectivity matrix with ones and zeros, in ‘distance’ the edges are distances between points, type of distance depends on the selected metric parameter in NearestNeighbors class.
**sort\_results**bool, default=False
If True, in each row of the result, the non-zero entries will be sorted by increasing distances. If False, the non-zero entries may not be sorted. Only used with mode=’distance’.
New in version 0.22.
Returns:
**A**sparse-matrix of shape (n\_queries, n\_samples\_fit)
`n_samples_fit` is the number of samples in the fitted data. `A[i, j]` gives the weight of the edge connecting `i` to `j`. The matrix is of CSR format.
See also
[`kneighbors_graph`](sklearn.neighbors.kneighbors_graph#sklearn.neighbors.kneighbors_graph "sklearn.neighbors.kneighbors_graph")
Compute the (weighted) graph of k-Neighbors for points in X.
#### Examples
```
>>> X = [[0], [3], [1]]
>>> from sklearn.neighbors import NearestNeighbors
>>> neigh = NearestNeighbors(radius=1.5)
>>> neigh.fit(X)
NearestNeighbors(radius=1.5)
>>> A = neigh.radius_neighbors_graph(X)
>>> A.toarray()
array([[1., 0., 1.],
[0., 1., 0.],
[1., 0., 1.]])
```
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/neighbors/_graph.py#L610)
Compute the (weighted) graph of Neighbors for points in X.
Parameters:
**X**array-like of shape (n\_samples\_transform, n\_features)
Sample data.
Returns:
**Xt**sparse matrix of shape (n\_samples\_transform, n\_samples\_fit)
Xt[i, j] is assigned the weight of edge that connects i to j. Only the neighbors have an explicit value. The diagonal is always explicit. The matrix is of CSR format.
scikit_learn sklearn.preprocessing.SplineTransformer sklearn.preprocessing.SplineTransformer
=======================================
*class*sklearn.preprocessing.SplineTransformer(*n\_knots=5*, *degree=3*, *\**, *knots='uniform'*, *extrapolation='constant'*, *include\_bias=True*, *order='C'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_polynomial.py#L516)
Generate univariate B-spline bases for features.
Generate a new feature matrix consisting of `n_splines=n_knots + degree - 1` (`n_knots - 1` for `extrapolation="periodic"`) spline basis functions (B-splines) of polynomial order=`degree` for each feature.
Read more in the [User Guide](../preprocessing#spline-transformer).
New in version 1.0.
Parameters:
**n\_knots**int, default=5
Number of knots of the splines if `knots` equals one of {‘uniform’, ‘quantile’}. Must be larger or equal 2. Ignored if `knots` is array-like.
**degree**int, default=3
The polynomial degree of the spline basis. Must be a non-negative integer.
**knots**{‘uniform’, ‘quantile’} or array-like of shape (n\_knots, n\_features), default=’uniform’
Set knot positions such that first knot <= features <= last knot.
* If ‘uniform’, `n_knots` number of knots are distributed uniformly from min to max values of the features.
* If ‘quantile’, they are distributed uniformly along the quantiles of the features.
* If an array-like is given, it directly specifies the sorted knot positions including the boundary knots. Note that, internally, `degree` number of knots are added before the first knot, the same after the last knot.
**extrapolation**{‘error’, ‘constant’, ‘linear’, ‘continue’, ‘periodic’}, default=’constant’
If ‘error’, values outside the min and max values of the training features raises a `ValueError`. If ‘constant’, the value of the splines at minimum and maximum value of the features is used as constant extrapolation. If ‘linear’, a linear extrapolation is used. If ‘continue’, the splines are extrapolated as is, i.e. option `extrapolate=True` in [`scipy.interpolate.BSpline`](https://docs.scipy.org/doc/scipy/reference/generated/scipy.interpolate.BSpline.html#scipy.interpolate.BSpline "(in SciPy v1.9.3)"). If ‘periodic’, periodic splines with a periodicity equal to the distance between the first and last knot are used. Periodic splines enforce equal function values and derivatives at the first and last knot. For example, this makes it possible to avoid introducing an arbitrary jump between Dec 31st and Jan 1st in spline features derived from a naturally periodic “day-of-year” input feature. In this case it is recommended to manually set the knot values to control the period.
**include\_bias**bool, default=True
If True (default), then the last spline element inside the data range of a feature is dropped. As B-splines sum to one over the spline basis functions for each data point, they implicitly include a bias term, i.e. a column of ones. It acts as an intercept term in a linear models.
**order**{‘C’, ‘F’}, default=’C’
Order of output array. ‘F’ order is faster to compute, but may slow down subsequent estimators.
Attributes:
**bsplines\_**list of shape (n\_features,)
List of BSplines objects, one for each feature.
**n\_features\_in\_**int
The total number of input features.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_features\_out\_**int
The total number of output features, which is computed as `n_features * n_splines`, where `n_splines` is the number of bases elements of the B-splines, `n_knots + degree - 1` for non-periodic splines and `n_knots - 1` for periodic ones. If `include_bias=False`, then it is only `n_features * (n_splines - 1)`.
See also
[`KBinsDiscretizer`](sklearn.preprocessing.kbinsdiscretizer#sklearn.preprocessing.KBinsDiscretizer "sklearn.preprocessing.KBinsDiscretizer")
Transformer that bins continuous data into intervals.
[`PolynomialFeatures`](sklearn.preprocessing.polynomialfeatures#sklearn.preprocessing.PolynomialFeatures "sklearn.preprocessing.PolynomialFeatures")
Transformer that generates polynomial and interaction features.
#### Notes
High degrees and a high number of knots can cause overfitting.
See [examples/linear\_model/plot\_polynomial\_interpolation.py](../../auto_examples/linear_model/plot_polynomial_interpolation#sphx-glr-auto-examples-linear-model-plot-polynomial-interpolation-py).
#### Examples
```
>>> import numpy as np
>>> from sklearn.preprocessing import SplineTransformer
>>> X = np.arange(6).reshape(6, 1)
>>> spline = SplineTransformer(degree=2, n_knots=3)
>>> spline.fit_transform(X)
array([[0.5 , 0.5 , 0. , 0. ],
[0.18, 0.74, 0.08, 0. ],
[0.02, 0.66, 0.32, 0. ],
[0. , 0.32, 0.66, 0.02],
[0. , 0.08, 0.74, 0.18],
[0. , 0. , 0.5 , 0.5 ]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.preprocessing.SplineTransformer.fit "sklearn.preprocessing.SplineTransformer.fit")(X[, y, sample\_weight]) | Compute knot positions of splines. |
| [`fit_transform`](#sklearn.preprocessing.SplineTransformer.fit_transform "sklearn.preprocessing.SplineTransformer.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names`](#sklearn.preprocessing.SplineTransformer.get_feature_names "sklearn.preprocessing.SplineTransformer.get_feature_names")([input\_features]) | DEPRECATED: get\_feature\_names is deprecated in 1.0 and will be removed in 1.2. |
| [`get_feature_names_out`](#sklearn.preprocessing.SplineTransformer.get_feature_names_out "sklearn.preprocessing.SplineTransformer.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.preprocessing.SplineTransformer.get_params "sklearn.preprocessing.SplineTransformer.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.preprocessing.SplineTransformer.set_params "sklearn.preprocessing.SplineTransformer.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.preprocessing.SplineTransformer.transform "sklearn.preprocessing.SplineTransformer.transform")(X) | Transform each feature data to B-splines. |
fit(*X*, *y=None*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_polynomial.py#L749)
Compute knot positions of splines.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The data.
**y**None
Ignored.
**sample\_weight**array-like of shape (n\_samples,), default = None
Individual weights for each sample. Used to calculate quantiles if `knots="quantile"`. For `knots="uniform"`, zero weighted observations are ignored for finding the min and max of `X`.
Returns:
**self**object
Fitted transformer.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_polynomial.py#L694)
DEPRECATED: get\_feature\_names is deprecated in 1.0 and will be removed in 1.2. Please use get\_feature\_names\_out instead.
Return feature names for output features.
Parameters:
**input\_features**list of str of shape (n\_features,), default=None
String names for input features if available. By default, “x0”, “x1”, … “xn\_features” is used.
Returns:
**output\_feature\_names**list of str of shape (n\_output\_features,)
Transformed feature names.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_polynomial.py#L721)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Input features.
* If `input_features` is `None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then the following input feature names are generated: `["x0", "x1", ..., "x(n_features_in_ - 1)"]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_polynomial.py#L904)
Transform each feature data to B-splines.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The data to transform.
Returns:
**XBS**ndarray of shape (n\_samples, n\_features \* n\_splines)
The matrix of features, where n\_splines is the number of bases elements of the B-splines, n\_knots + degree - 1.
Examples using `sklearn.preprocessing.SplineTransformer`
--------------------------------------------------------
[Release Highlights for scikit-learn 1.0](../../auto_examples/release_highlights/plot_release_highlights_1_0_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-1-0-0-py)
[Time-related feature engineering](../../auto_examples/applications/plot_cyclical_feature_engineering#sphx-glr-auto-examples-applications-plot-cyclical-feature-engineering-py)
[Polynomial and Spline interpolation](../../auto_examples/linear_model/plot_polynomial_interpolation#sphx-glr-auto-examples-linear-model-plot-polynomial-interpolation-py)
| programming_docs |
scikit_learn sklearn.preprocessing.MinMaxScaler sklearn.preprocessing.MinMaxScaler
==================================
*class*sklearn.preprocessing.MinMaxScaler(*feature\_range=(0, 1)*, *\**, *copy=True*, *clip=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L269)
Transform features by scaling each feature to a given range.
This estimator scales and translates each feature individually such that it is in the given range on the training set, e.g. between zero and one.
The transformation is given by:
```
X_std = (X - X.min(axis=0)) / (X.max(axis=0) - X.min(axis=0))
X_scaled = X_std * (max - min) + min
```
where min, max = feature\_range.
This transformation is often used as an alternative to zero mean, unit variance scaling.
Read more in the [User Guide](../preprocessing#preprocessing-scaler).
Parameters:
**feature\_range**tuple (min, max), default=(0, 1)
Desired range of transformed data.
**copy**bool, default=True
Set to False to perform inplace row normalization and avoid a copy (if the input is already a numpy array).
**clip**bool, default=False
Set to True to clip transformed values of held-out data to provided `feature range`.
New in version 0.24.
Attributes:
**min\_**ndarray of shape (n\_features,)
Per feature adjustment for minimum. Equivalent to `min - X.min(axis=0) * self.scale_`
**scale\_**ndarray of shape (n\_features,)
Per feature relative scaling of the data. Equivalent to `(max - min) / (X.max(axis=0) - X.min(axis=0))`
New in version 0.17: *scale\_* attribute.
**data\_min\_**ndarray of shape (n\_features,)
Per feature minimum seen in the data
New in version 0.17: *data\_min\_*
**data\_max\_**ndarray of shape (n\_features,)
Per feature maximum seen in the data
New in version 0.17: *data\_max\_*
**data\_range\_**ndarray of shape (n\_features,)
Per feature range `(data_max_ - data_min_)` seen in the data
New in version 0.17: *data\_range\_*
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**n\_samples\_seen\_**int
The number of samples processed by the estimator. It will be reset on new calls to fit, but increments across `partial_fit` calls.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`minmax_scale`](sklearn.preprocessing.minmax_scale#sklearn.preprocessing.minmax_scale "sklearn.preprocessing.minmax_scale")
Equivalent function without the estimator API.
#### Notes
NaNs are treated as missing values: disregarded in fit, and maintained in transform.
For a comparison of the different scalers, transformers, and normalizers, see [examples/preprocessing/plot\_all\_scaling.py](../../auto_examples/preprocessing/plot_all_scaling#sphx-glr-auto-examples-preprocessing-plot-all-scaling-py).
#### Examples
```
>>> from sklearn.preprocessing import MinMaxScaler
>>> data = [[-1, 2], [-0.5, 6], [0, 10], [1, 18]]
>>> scaler = MinMaxScaler()
>>> print(scaler.fit(data))
MinMaxScaler()
>>> print(scaler.data_max_)
[ 1. 18.]
>>> print(scaler.transform(data))
[[0. 0. ]
[0.25 0.25]
[0.5 0.5 ]
[1. 1. ]]
>>> print(scaler.transform([[2, 2]]))
[[1.5 0. ]]
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.preprocessing.MinMaxScaler.fit "sklearn.preprocessing.MinMaxScaler.fit")(X[, y]) | Compute the minimum and maximum to be used for later scaling. |
| [`fit_transform`](#sklearn.preprocessing.MinMaxScaler.fit_transform "sklearn.preprocessing.MinMaxScaler.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.preprocessing.MinMaxScaler.get_feature_names_out "sklearn.preprocessing.MinMaxScaler.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.preprocessing.MinMaxScaler.get_params "sklearn.preprocessing.MinMaxScaler.get_params")([deep]) | Get parameters for this estimator. |
| [`inverse_transform`](#sklearn.preprocessing.MinMaxScaler.inverse_transform "sklearn.preprocessing.MinMaxScaler.inverse_transform")(X) | Undo the scaling of X according to feature\_range. |
| [`partial_fit`](#sklearn.preprocessing.MinMaxScaler.partial_fit "sklearn.preprocessing.MinMaxScaler.partial_fit")(X[, y]) | Online computation of min and max on X for later scaling. |
| [`set_params`](#sklearn.preprocessing.MinMaxScaler.set_params "sklearn.preprocessing.MinMaxScaler.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.preprocessing.MinMaxScaler.transform "sklearn.preprocessing.MinMaxScaler.transform")(X) | Scale features of X according to feature\_range. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L401)
Compute the minimum and maximum to be used for later scaling.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The data used to compute the per-feature minimum and maximum used for later scaling along the features axis.
**y**None
Ignored.
Returns:
**self**object
Fitted scaler.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L880)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Input features.
* If `input_features` is `None`, then `feature_names_in_` is used as feature names in. If `feature_names_in_` is not defined, then the following input feature names are generated: `["x0", "x1", ..., "x(n_features_in_ - 1)"]`.
* If `input_features` is an array-like, then `input_features` must match `feature_names_in_` if `feature_names_in_` is defined.
Returns:
**feature\_names\_out**ndarray of str objects
Same as input features.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
inverse\_transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L513)
Undo the scaling of X according to feature\_range.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input data that will be transformed. It cannot be sparse.
Returns:
**Xt**ndarray of shape (n\_samples, n\_features)
Transformed data.
partial\_fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L422)
Online computation of min and max on X for later scaling.
All of X is processed as a single batch. This is intended for cases when [`fit`](#sklearn.preprocessing.MinMaxScaler.fit "sklearn.preprocessing.MinMaxScaler.fit") is not feasible due to very large number of `n_samples` or because X is read from a continuous stream.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The data used to compute the mean and standard deviation used for later scaling along the features axis.
**y**None
Ignored.
Returns:
**self**object
Fitted scaler.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/preprocessing/_data.py#L484)
Scale features of X according to feature\_range.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input data that will be transformed.
Returns:
**Xt**ndarray of shape (n\_samples, n\_features)
Transformed data.
Examples using `sklearn.preprocessing.MinMaxScaler`
---------------------------------------------------
[Release Highlights for scikit-learn 0.24](../../auto_examples/release_highlights/plot_release_highlights_0_24_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-24-0-py)
[Image denoising using kernel PCA](../../auto_examples/applications/plot_digits_denoising#sphx-glr-auto-examples-applications-plot-digits-denoising-py)
[Time-related feature engineering](../../auto_examples/applications/plot_cyclical_feature_engineering#sphx-glr-auto-examples-applications-plot-cyclical-feature-engineering-py)
[Univariate Feature Selection](../../auto_examples/feature_selection/plot_feature_selection#sphx-glr-auto-examples-feature-selection-plot-feature-selection-py)
[Scalable learning with polynomial kernel approximation](../../auto_examples/kernel_approximation/plot_scalable_poly_kernels#sphx-glr-auto-examples-kernel-approximation-plot-scalable-poly-kernels-py)
[Manifold learning on handwritten digits: Locally Linear Embedding, Isomap…](../../auto_examples/manifold/plot_lle_digits#sphx-glr-auto-examples-manifold-plot-lle-digits-py)
[Compare Stochastic learning strategies for MLPClassifier](../../auto_examples/neural_networks/plot_mlp_training_curves#sphx-glr-auto-examples-neural-networks-plot-mlp-training-curves-py)
[Compare the effect of different scalers on data with outliers](../../auto_examples/preprocessing/plot_all_scaling#sphx-glr-auto-examples-preprocessing-plot-all-scaling-py)
scikit_learn sklearn.model_selection.StratifiedShuffleSplit sklearn.model\_selection.StratifiedShuffleSplit
===============================================
*class*sklearn.model\_selection.StratifiedShuffleSplit(*n\_splits=10*, *\**, *test\_size=None*, *train\_size=None*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L1877)
Stratified ShuffleSplit cross-validator
Provides train/test indices to split data in train/test sets.
This cross-validation object is a merge of StratifiedKFold and ShuffleSplit, which returns stratified randomized folds. The folds are made by preserving the percentage of samples for each class.
Note: like the ShuffleSplit strategy, stratified random splits do not guarantee that all folds will be different, although this is still very likely for sizeable datasets.
Read more in the [User Guide](../cross_validation#stratified-shuffle-split).
Parameters:
**n\_splits**int, default=10
Number of re-shuffling & splitting iterations.
**test\_size**float or int, default=None
If float, should be between 0.0 and 1.0 and represent the proportion of the dataset to include in the test split. If int, represents the absolute number of test samples. If None, the value is set to the complement of the train size. If `train_size` is also None, it will be set to 0.1.
**train\_size**float or int, default=None
If float, should be between 0.0 and 1.0 and represent the proportion of the dataset to include in the train split. If int, represents the absolute number of train samples. If None, the value is automatically set to the complement of the test size.
**random\_state**int, RandomState instance or None, default=None
Controls the randomness of the training and testing indices produced. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
#### Examples
```
>>> import numpy as np
>>> from sklearn.model_selection import StratifiedShuffleSplit
>>> X = np.array([[1, 2], [3, 4], [1, 2], [3, 4], [1, 2], [3, 4]])
>>> y = np.array([0, 0, 0, 1, 1, 1])
>>> sss = StratifiedShuffleSplit(n_splits=5, test_size=0.5, random_state=0)
>>> sss.get_n_splits(X, y)
5
>>> print(sss)
StratifiedShuffleSplit(n_splits=5, random_state=0, ...)
>>> for train_index, test_index in sss.split(X, y):
... print("TRAIN:", train_index, "TEST:", test_index)
... X_train, X_test = X[train_index], X[test_index]
... y_train, y_test = y[train_index], y[test_index]
TRAIN: [5 2 3] TEST: [4 1 0]
TRAIN: [5 1 4] TEST: [0 2 3]
TRAIN: [5 0 2] TEST: [4 3 1]
TRAIN: [4 1 0] TEST: [2 3 5]
TRAIN: [0 5 1] TEST: [3 4 2]
```
#### Methods
| | |
| --- | --- |
| [`get_n_splits`](#sklearn.model_selection.StratifiedShuffleSplit.get_n_splits "sklearn.model_selection.StratifiedShuffleSplit.get_n_splits")([X, y, groups]) | Returns the number of splitting iterations in the cross-validator |
| [`split`](#sklearn.model_selection.StratifiedShuffleSplit.split "sklearn.model_selection.StratifiedShuffleSplit.split")(X, y[, groups]) | Generate indices to split data into training and test set. |
get\_n\_splits(*X=None*, *y=None*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L1629)
Returns the number of splitting iterations in the cross-validator
Parameters:
**X**object
Always ignored, exists for compatibility.
**y**object
Always ignored, exists for compatibility.
**groups**object
Always ignored, exists for compatibility.
Returns:
**n\_splits**int
Returns the number of splitting iterations in the cross-validator.
split(*X*, *y*, *groups=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/model_selection/_split.py#L2016)
Generate indices to split data into training and test set.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
Note that providing `y` is sufficient to generate the splits and hence `np.zeros(n_samples)` may be used as a placeholder for `X` instead of actual training data.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_labels)
The target variable for supervised learning problems. Stratification is done based on the y labels.
**groups**object
Always ignored, exists for compatibility.
Yields:
**train**ndarray
The training set indices for that split.
**test**ndarray
The testing set indices for that split.
#### Notes
Randomized CV splitters may return different results for each call of split. You can make the results identical by setting `random_state` to an integer.
Examples using `sklearn.model_selection.StratifiedShuffleSplit`
---------------------------------------------------------------
[Visualizing cross-validation behavior in scikit-learn](../../auto_examples/model_selection/plot_cv_indices#sphx-glr-auto-examples-model-selection-plot-cv-indices-py)
[RBF SVM parameters](../../auto_examples/svm/plot_rbf_parameters#sphx-glr-auto-examples-svm-plot-rbf-parameters-py)
scikit_learn sklearn.metrics.f1_score sklearn.metrics.f1\_score
=========================
sklearn.metrics.f1\_score(*y\_true*, *y\_pred*, *\**, *labels=None*, *pos\_label=1*, *average='binary'*, *sample\_weight=None*, *zero\_division='warn'*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_classification.py#L1001)
Compute the F1 score, also known as balanced F-score or F-measure.
The F1 score can be interpreted as a harmonic mean of the precision and recall, where an F1 score reaches its best value at 1 and worst score at 0. The relative contribution of precision and recall to the F1 score are equal. The formula for the F1 score is:
```
F1 = 2 * (precision * recall) / (precision + recall)
```
In the multi-class and multi-label case, this is the average of the F1 score of each class with weighting depending on the `average` parameter.
Read more in the [User Guide](../model_evaluation#precision-recall-f-measure-metrics).
Parameters:
**y\_true**1d array-like, or label indicator array / sparse matrix
Ground truth (correct) target values.
**y\_pred**1d array-like, or label indicator array / sparse matrix
Estimated targets as returned by a classifier.
**labels**array-like, default=None
The set of labels to include when `average != 'binary'`, and their order if `average is None`. Labels present in the data can be excluded, for example to calculate a multiclass average ignoring a majority negative class, while labels not present in the data will result in 0 components in a macro average. For multilabel targets, labels are column indices. By default, all labels in `y_true` and `y_pred` are used in sorted order.
Changed in version 0.17: Parameter `labels` improved for multiclass problem.
**pos\_label**str or int, default=1
The class to report if `average='binary'` and the data is binary. If the data are multiclass or multilabel, this will be ignored; setting `labels=[pos_label]` and `average != 'binary'` will report scores for that label only.
**average**{‘micro’, ‘macro’, ‘samples’, ‘weighted’, ‘binary’} or None, default=’binary’
This parameter is required for multiclass/multilabel targets. If `None`, the scores for each class are returned. Otherwise, this determines the type of averaging performed on the data:
`'binary'`:
Only report results for the class specified by `pos_label`. This is applicable only if targets (`y_{true,pred}`) are binary.
`'micro'`:
Calculate metrics globally by counting the total true positives, false negatives and false positives.
`'macro'`:
Calculate metrics for each label, and find their unweighted mean. This does not take label imbalance into account.
`'weighted'`:
Calculate metrics for each label, and find their average weighted by support (the number of true instances for each label). This alters ‘macro’ to account for label imbalance; it can result in an F-score that is not between precision and recall.
`'samples'`:
Calculate metrics for each instance, and find their average (only meaningful for multilabel classification where this differs from [`accuracy_score`](sklearn.metrics.accuracy_score#sklearn.metrics.accuracy_score "sklearn.metrics.accuracy_score")).
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
**zero\_division**“warn”, 0 or 1, default=”warn”
Sets the value to return when there is a zero division, i.e. when all predictions and labels are negative. If set to “warn”, this acts as 0, but warnings are also raised.
Returns:
**f1\_score**float or array of float, shape = [n\_unique\_labels]
F1 score of the positive class in binary classification or weighted average of the F1 scores of each class for the multiclass task.
See also
[`fbeta_score`](sklearn.metrics.fbeta_score#sklearn.metrics.fbeta_score "sklearn.metrics.fbeta_score")
Compute the F-beta score.
[`precision_recall_fscore_support`](sklearn.metrics.precision_recall_fscore_support#sklearn.metrics.precision_recall_fscore_support "sklearn.metrics.precision_recall_fscore_support")
Compute the precision, recall, F-score, and support.
[`jaccard_score`](sklearn.metrics.jaccard_score#sklearn.metrics.jaccard_score "sklearn.metrics.jaccard_score")
Compute the Jaccard similarity coefficient score.
[`multilabel_confusion_matrix`](sklearn.metrics.multilabel_confusion_matrix#sklearn.metrics.multilabel_confusion_matrix "sklearn.metrics.multilabel_confusion_matrix")
Compute a confusion matrix for each class or sample.
#### Notes
When `true positive + false positive == 0`, precision is undefined. When `true positive + false negative == 0`, recall is undefined. In such cases, by default the metric will be set to 0, as will f-score, and `UndefinedMetricWarning` will be raised. This behavior can be modified with `zero_division`.
#### References
[1] [Wikipedia entry for the F1-score](https://en.wikipedia.org/wiki/F1_score).
#### Examples
```
>>> from sklearn.metrics import f1_score
>>> y_true = [0, 1, 2, 0, 1, 2]
>>> y_pred = [0, 2, 1, 0, 0, 1]
>>> f1_score(y_true, y_pred, average='macro')
0.26...
>>> f1_score(y_true, y_pred, average='micro')
0.33...
>>> f1_score(y_true, y_pred, average='weighted')
0.26...
>>> f1_score(y_true, y_pred, average=None)
array([0.8, 0. , 0. ])
>>> y_true = [0, 0, 0, 0, 0, 0]
>>> y_pred = [0, 0, 0, 0, 0, 0]
>>> f1_score(y_true, y_pred, zero_division=1)
1.0...
>>> # multilabel classification
>>> y_true = [[0, 0, 0], [1, 1, 1], [0, 1, 1]]
>>> y_pred = [[0, 0, 0], [1, 1, 1], [1, 1, 0]]
>>> f1_score(y_true, y_pred, average=None)
array([0.66666667, 1. , 0.66666667])
```
Examples using `sklearn.metrics.f1_score`
-----------------------------------------
[Probability Calibration curves](../../auto_examples/calibration/plot_calibration_curve#sphx-glr-auto-examples-calibration-plot-calibration-curve-py)
[Precision-Recall](../../auto_examples/model_selection/plot_precision_recall#sphx-glr-auto-examples-model-selection-plot-precision-recall-py)
[Semi-supervised Classification on a Text Dataset](../../auto_examples/semi_supervised/plot_semi_supervised_newsgroups#sphx-glr-auto-examples-semi-supervised-plot-semi-supervised-newsgroups-py)
| programming_docs |
scikit_learn sklearn.base.BaseEstimator sklearn.base.BaseEstimator
==========================
*class*sklearn.base.BaseEstimator[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L153)
Base class for all estimators in scikit-learn.
#### Notes
All estimators should specify all the parameters that can be set at the class level in their `__init__` as explicit keyword arguments (no `*args` or `**kwargs`).
#### Methods
| | |
| --- | --- |
| [`get_params`](#sklearn.base.BaseEstimator.get_params "sklearn.base.BaseEstimator.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.base.BaseEstimator.set_params "sklearn.base.BaseEstimator.set_params")(\*\*params) | Set the parameters of this estimator. |
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.base.BaseEstimator`
-------------------------------------------
[Inductive Clustering](../../auto_examples/cluster/plot_inductive_clustering#sphx-glr-auto-examples-cluster-plot-inductive-clustering-py)
[Approximate nearest neighbors in TSNE](../../auto_examples/neighbors/approximate_nearest_neighbors#sphx-glr-auto-examples-neighbors-approximate-nearest-neighbors-py)
scikit_learn sklearn.covariance.LedoitWolf sklearn.covariance.LedoitWolf
=============================
*class*sklearn.covariance.LedoitWolf(*\**, *store\_precision=True*, *assume\_centered=False*, *block\_size=1000*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_shrunk_covariance.py#L347)
LedoitWolf Estimator.
Ledoit-Wolf is a particular form of shrinkage, where the shrinkage coefficient is computed using O. Ledoit and M. Wolf’s formula as described in “A Well-Conditioned Estimator for Large-Dimensional Covariance Matrices”, Ledoit and Wolf, Journal of Multivariate Analysis, Volume 88, Issue 2, February 2004, pages 365-411.
Read more in the [User Guide](../covariance#shrunk-covariance).
Parameters:
**store\_precision**bool, default=True
Specify if the estimated precision is stored.
**assume\_centered**bool, default=False
If True, data will not be centered before computation. Useful when working with data whose mean is almost, but not exactly zero. If False (default), data will be centered before computation.
**block\_size**int, default=1000
Size of blocks into which the covariance matrix will be split during its Ledoit-Wolf estimation. This is purely a memory optimization and does not affect results.
Attributes:
**covariance\_**ndarray of shape (n\_features, n\_features)
Estimated covariance matrix.
**location\_**ndarray of shape (n\_features,)
Estimated location, i.e. the estimated mean.
**precision\_**ndarray of shape (n\_features, n\_features)
Estimated pseudo inverse matrix. (stored only if store\_precision is True)
**shrinkage\_**float
Coefficient in the convex combination used for the computation of the shrunk estimate. Range is [0, 1].
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`EllipticEnvelope`](sklearn.covariance.ellipticenvelope#sklearn.covariance.EllipticEnvelope "sklearn.covariance.EllipticEnvelope")
An object for detecting outliers in a Gaussian distributed dataset.
[`EmpiricalCovariance`](sklearn.covariance.empiricalcovariance#sklearn.covariance.EmpiricalCovariance "sklearn.covariance.EmpiricalCovariance")
Maximum likelihood covariance estimator.
[`GraphicalLasso`](sklearn.covariance.graphicallasso#sklearn.covariance.GraphicalLasso "sklearn.covariance.GraphicalLasso")
Sparse inverse covariance estimation with an l1-penalized estimator.
[`GraphicalLassoCV`](sklearn.covariance.graphicallassocv#sklearn.covariance.GraphicalLassoCV "sklearn.covariance.GraphicalLassoCV")
Sparse inverse covariance with cross-validated choice of the l1 penalty.
[`MinCovDet`](sklearn.covariance.mincovdet#sklearn.covariance.MinCovDet "sklearn.covariance.MinCovDet")
Minimum Covariance Determinant (robust estimator of covariance).
[`OAS`](sklearn.covariance.oas#sklearn.covariance.OAS "sklearn.covariance.OAS")
Oracle Approximating Shrinkage Estimator.
[`ShrunkCovariance`](sklearn.covariance.shrunkcovariance#sklearn.covariance.ShrunkCovariance "sklearn.covariance.ShrunkCovariance")
Covariance estimator with shrinkage.
#### Notes
The regularised covariance is:
(1 - shrinkage) \* cov + shrinkage \* mu \* np.identity(n\_features)
where mu = trace(cov) / n\_features and shrinkage is given by the Ledoit and Wolf formula (see References)
#### References
“A Well-Conditioned Estimator for Large-Dimensional Covariance Matrices”, Ledoit and Wolf, Journal of Multivariate Analysis, Volume 88, Issue 2, February 2004, pages 365-411.
#### Examples
```
>>> import numpy as np
>>> from sklearn.covariance import LedoitWolf
>>> real_cov = np.array([[.4, .2],
... [.2, .8]])
>>> np.random.seed(0)
>>> X = np.random.multivariate_normal(mean=[0, 0],
... cov=real_cov,
... size=50)
>>> cov = LedoitWolf().fit(X)
>>> cov.covariance_
array([[0.4406..., 0.1616...],
[0.1616..., 0.8022...]])
>>> cov.location_
array([ 0.0595... , -0.0075...])
```
#### Methods
| | |
| --- | --- |
| [`error_norm`](#sklearn.covariance.LedoitWolf.error_norm "sklearn.covariance.LedoitWolf.error_norm")(comp\_cov[, norm, scaling, squared]) | Compute the Mean Squared Error between two covariance estimators. |
| [`fit`](#sklearn.covariance.LedoitWolf.fit "sklearn.covariance.LedoitWolf.fit")(X[, y]) | Fit the Ledoit-Wolf shrunk covariance model to X. |
| [`get_params`](#sklearn.covariance.LedoitWolf.get_params "sklearn.covariance.LedoitWolf.get_params")([deep]) | Get parameters for this estimator. |
| [`get_precision`](#sklearn.covariance.LedoitWolf.get_precision "sklearn.covariance.LedoitWolf.get_precision")() | Getter for the precision matrix. |
| [`mahalanobis`](#sklearn.covariance.LedoitWolf.mahalanobis "sklearn.covariance.LedoitWolf.mahalanobis")(X) | Compute the squared Mahalanobis distances of given observations. |
| [`score`](#sklearn.covariance.LedoitWolf.score "sklearn.covariance.LedoitWolf.score")(X\_test[, y]) | Compute the log-likelihood of `X_test` under the estimated Gaussian model. |
| [`set_params`](#sklearn.covariance.LedoitWolf.set_params "sklearn.covariance.LedoitWolf.set_params")(\*\*params) | Set the parameters of this estimator. |
error\_norm(*comp\_cov*, *norm='frobenius'*, *scaling=True*, *squared=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_empirical_covariance.py#L267)
Compute the Mean Squared Error between two covariance estimators.
Parameters:
**comp\_cov**array-like of shape (n\_features, n\_features)
The covariance to compare with.
**norm**{“frobenius”, “spectral”}, default=”frobenius”
The type of norm used to compute the error. Available error types: - ‘frobenius’ (default): sqrt(tr(A^t.A)) - ‘spectral’: sqrt(max(eigenvalues(A^t.A)) where A is the error `(comp_cov - self.covariance_)`.
**scaling**bool, default=True
If True (default), the squared error norm is divided by n\_features. If False, the squared error norm is not rescaled.
**squared**bool, default=True
Whether to compute the squared error norm or the error norm. If True (default), the squared error norm is returned. If False, the error norm is returned.
Returns:
**result**float
The Mean Squared Error (in the sense of the Frobenius norm) between `self` and `comp_cov` covariance estimators.
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_shrunk_covariance.py#L454)
Fit the Ledoit-Wolf shrunk covariance model to X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**self**object
Returns the instance itself.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
get\_precision()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_empirical_covariance.py#L195)
Getter for the precision matrix.
Returns:
**precision\_**array-like of shape (n\_features, n\_features)
The precision matrix associated to the current covariance object.
mahalanobis(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_empirical_covariance.py#L318)
Compute the squared Mahalanobis distances of given observations.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
The observations, the Mahalanobis distances of the which we compute. Observations are assumed to be drawn from the same distribution than the data used in fit.
Returns:
**dist**ndarray of shape (n\_samples,)
Squared Mahalanobis distances of the observations.
score(*X\_test*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/covariance/_empirical_covariance.py#L236)
Compute the log-likelihood of `X_test` under the estimated Gaussian model.
The Gaussian model is defined by its mean and covariance matrix which are represented respectively by `self.location_` and `self.covariance_`.
Parameters:
**X\_test**array-like of shape (n\_samples, n\_features)
Test data of which we compute the likelihood, where `n_samples` is the number of samples and `n_features` is the number of features. `X_test` is assumed to be drawn from the same distribution than the data used in fit (including centering).
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**res**float
The log-likelihood of `X_test` with `self.location_` and `self.covariance_` as estimators of the Gaussian model mean and covariance matrix respectively.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.covariance.LedoitWolf`
----------------------------------------------
[Ledoit-Wolf vs OAS estimation](../../auto_examples/covariance/plot_lw_vs_oas#sphx-glr-auto-examples-covariance-plot-lw-vs-oas-py)
[Shrinkage covariance estimation: LedoitWolf vs OAS and max-likelihood](../../auto_examples/covariance/plot_covariance_estimation#sphx-glr-auto-examples-covariance-plot-covariance-estimation-py)
[Model selection with Probabilistic PCA and Factor Analysis (FA)](../../auto_examples/decomposition/plot_pca_vs_fa_model_selection#sphx-glr-auto-examples-decomposition-plot-pca-vs-fa-model-selection-py)
scikit_learn sklearn.decomposition.SparseCoder sklearn.decomposition.SparseCoder
=================================
*class*sklearn.decomposition.SparseCoder(*dictionary*, *\**, *transform\_algorithm='omp'*, *transform\_n\_nonzero\_coefs=None*, *transform\_alpha=None*, *split\_sign=False*, *n\_jobs=None*, *positive\_code=False*, *transform\_max\_iter=1000*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_dict_learning.py#L1238)
Sparse coding.
Finds a sparse representation of data against a fixed, precomputed dictionary.
Each row of the result is the solution to a sparse coding problem. The goal is to find a sparse array `code` such that:
```
X ~= code * dictionary
```
Read more in the [User Guide](../decomposition#sparsecoder).
Parameters:
**dictionary**ndarray of shape (n\_components, n\_features)
The dictionary atoms used for sparse coding. Lines are assumed to be normalized to unit norm.
**transform\_algorithm**{‘lasso\_lars’, ‘lasso\_cd’, ‘lars’, ‘omp’, ‘threshold’}, default=’omp’
Algorithm used to transform the data:
* `'lars'`: uses the least angle regression method (`linear_model.lars_path`);
* `'lasso_lars'`: uses Lars to compute the Lasso solution;
* `'lasso_cd'`: uses the coordinate descent method to compute the Lasso solution (linear\_model.Lasso). `'lasso_lars'` will be faster if the estimated components are sparse;
* `'omp'`: uses orthogonal matching pursuit to estimate the sparse solution;
* `'threshold'`: squashes to zero all coefficients less than alpha from the projection `dictionary * X'`.
**transform\_n\_nonzero\_coefs**int, default=None
Number of nonzero coefficients to target in each column of the solution. This is only used by `algorithm='lars'` and `algorithm='omp'` and is overridden by `alpha` in the `omp` case. If `None`, then `transform_n_nonzero_coefs=int(n_features / 10)`.
**transform\_alpha**float, default=None
If `algorithm='lasso_lars'` or `algorithm='lasso_cd'`, `alpha` is the penalty applied to the L1 norm. If `algorithm='threshold'`, `alpha` is the absolute value of the threshold below which coefficients will be squashed to zero. If `algorithm='omp'`, `alpha` is the tolerance parameter: the value of the reconstruction error targeted. In this case, it overrides `n_nonzero_coefs`. If `None`, default to 1.
**split\_sign**bool, default=False
Whether to split the sparse feature vector into the concatenation of its negative part and its positive part. This can improve the performance of downstream classifiers.
**n\_jobs**int, default=None
Number of parallel jobs to run. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**positive\_code**bool, default=False
Whether to enforce positivity when finding the code.
New in version 0.20.
**transform\_max\_iter**int, default=1000
Maximum number of iterations to perform if `algorithm='lasso_cd'` or `lasso_lars`.
New in version 0.22.
Attributes:
[`n_components_`](#sklearn.decomposition.SparseCoder.n_components_ "sklearn.decomposition.SparseCoder.n_components_")int
Number of atoms.
[`n_features_in_`](#sklearn.decomposition.SparseCoder.n_features_in_ "sklearn.decomposition.SparseCoder.n_features_in_")int
Number of features seen during `fit`.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`DictionaryLearning`](sklearn.decomposition.dictionarylearning#sklearn.decomposition.DictionaryLearning "sklearn.decomposition.DictionaryLearning")
Find a dictionary that sparsely encodes data.
[`MiniBatchDictionaryLearning`](sklearn.decomposition.minibatchdictionarylearning#sklearn.decomposition.MiniBatchDictionaryLearning "sklearn.decomposition.MiniBatchDictionaryLearning")
A faster, less accurate, version of the dictionary learning algorithm.
[`MiniBatchSparsePCA`](sklearn.decomposition.minibatchsparsepca#sklearn.decomposition.MiniBatchSparsePCA "sklearn.decomposition.MiniBatchSparsePCA")
Mini-batch Sparse Principal Components Analysis.
[`SparsePCA`](sklearn.decomposition.sparsepca#sklearn.decomposition.SparsePCA "sklearn.decomposition.SparsePCA")
Mini-batch Sparse Principal Components Analysis.
[`sparse_encode`](sklearn.decomposition.sparse_encode#sklearn.decomposition.sparse_encode "sklearn.decomposition.sparse_encode")
Sparse coding where each row of the result is the solution to a sparse coding problem.
#### Examples
```
>>> import numpy as np
>>> from sklearn.decomposition import SparseCoder
>>> X = np.array([[-1, -1, -1], [0, 0, 3]])
>>> dictionary = np.array(
... [[0, 1, 0],
... [-1, -1, 2],
... [1, 1, 1],
... [0, 1, 1],
... [0, 2, 1]],
... dtype=np.float64
... )
>>> coder = SparseCoder(
... dictionary=dictionary, transform_algorithm='lasso_lars',
... transform_alpha=1e-10,
... )
>>> coder.transform(X)
array([[ 0., 0., -1., 0., 0.],
[ 0., 1., 1., 0., 0.]])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.decomposition.SparseCoder.fit "sklearn.decomposition.SparseCoder.fit")(X[, y]) | Do nothing and return the estimator unchanged. |
| [`fit_transform`](#sklearn.decomposition.SparseCoder.fit_transform "sklearn.decomposition.SparseCoder.fit_transform")(X[, y]) | Fit to data, then transform it. |
| [`get_feature_names_out`](#sklearn.decomposition.SparseCoder.get_feature_names_out "sklearn.decomposition.SparseCoder.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.decomposition.SparseCoder.get_params "sklearn.decomposition.SparseCoder.get_params")([deep]) | Get parameters for this estimator. |
| [`set_params`](#sklearn.decomposition.SparseCoder.set_params "sklearn.decomposition.SparseCoder.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.decomposition.SparseCoder.transform "sklearn.decomposition.SparseCoder.transform")(X[, y]) | Encode the data as a sparse combination of the dictionary atoms. |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_dict_learning.py#L1383)
Do nothing and return the estimator unchanged.
This method is just there to implement the usual API and hence work in pipelines.
Parameters:
**X**Ignored
Not used, present for API consistency by convention.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L839)
Fit to data, then transform it.
Fits transformer to `X` and `y` with optional parameters `fit_params` and returns a transformed version of `X`.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Input samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.decomposition.SparseCoder.fit "sklearn.decomposition.SparseCoder.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
*property*n\_components\_
Number of atoms.
*property*n\_features\_in\_
Number of features seen during `fit`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_dict_learning.py#L1404)
Encode the data as a sparse combination of the dictionary atoms.
Coding method is determined by the object parameter `transform_algorithm`.
Parameters:
**X**ndarray of shape (n\_samples, n\_features)
Training vector, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_components)
Transformed data.
Examples using `sklearn.decomposition.SparseCoder`
--------------------------------------------------
[Sparse coding with a precomputed dictionary](../../auto_examples/decomposition/plot_sparse_coding#sphx-glr-auto-examples-decomposition-plot-sparse-coding-py)
| programming_docs |
scikit_learn sklearn.metrics.completeness_score sklearn.metrics.completeness\_score
===================================
sklearn.metrics.completeness\_score(*labels\_true*, *labels\_pred*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/cluster/_supervised.py#L556)
Compute completeness metric of a cluster labeling given a ground truth.
A clustering result satisfies completeness if all the data points that are members of a given class are elements of the same cluster.
This metric is independent of the absolute values of the labels: a permutation of the class or cluster label values won’t change the score value in any way.
This metric is not symmetric: switching `label_true` with `label_pred` will return the [`homogeneity_score`](sklearn.metrics.homogeneity_score#sklearn.metrics.homogeneity_score "sklearn.metrics.homogeneity_score") which will be different in general.
Read more in the [User Guide](../clustering#homogeneity-completeness).
Parameters:
**labels\_true**int array, shape = [n\_samples]
Ground truth class labels to be used as a reference.
**labels\_pred**array-like of shape (n\_samples,)
Cluster labels to evaluate.
Returns:
**completeness**float
Score between 0.0 and 1.0. 1.0 stands for perfectly complete labeling.
See also
[`homogeneity_score`](sklearn.metrics.homogeneity_score#sklearn.metrics.homogeneity_score "sklearn.metrics.homogeneity_score")
Homogeneity metric of cluster labeling.
[`v_measure_score`](sklearn.metrics.v_measure_score#sklearn.metrics.v_measure_score "sklearn.metrics.v_measure_score")
V-Measure (NMI with arithmetic mean option).
#### References
[1] [Andrew Rosenberg and Julia Hirschberg, 2007. V-Measure: A conditional entropy-based external cluster evaluation measure](https://aclweb.org/anthology/D/D07/D07-1043.pdf)
#### Examples
Perfect labelings are complete:
```
>>> from sklearn.metrics.cluster import completeness_score
>>> completeness_score([0, 0, 1, 1], [1, 1, 0, 0])
1.0
```
Non-perfect labelings that assign all classes members to the same clusters are still complete:
```
>>> print(completeness_score([0, 0, 1, 1], [0, 0, 0, 0]))
1.0
>>> print(completeness_score([0, 1, 2, 3], [0, 0, 1, 1]))
0.999...
```
If classes members are split across different clusters, the assignment cannot be complete:
```
>>> print(completeness_score([0, 0, 1, 1], [0, 1, 0, 1]))
0.0
>>> print(completeness_score([0, 0, 0, 0], [0, 1, 2, 3]))
0.0
```
Examples using `sklearn.metrics.completeness_score`
---------------------------------------------------
[Release Highlights for scikit-learn 0.23](../../auto_examples/release_highlights/plot_release_highlights_0_23_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-23-0-py)
[A demo of K-Means clustering on the handwritten digits data](../../auto_examples/cluster/plot_kmeans_digits#sphx-glr-auto-examples-cluster-plot-kmeans-digits-py)
[Demo of DBSCAN clustering algorithm](../../auto_examples/cluster/plot_dbscan#sphx-glr-auto-examples-cluster-plot-dbscan-py)
[Demo of affinity propagation clustering algorithm](../../auto_examples/cluster/plot_affinity_propagation#sphx-glr-auto-examples-cluster-plot-affinity-propagation-py)
[Clustering text documents using k-means](../../auto_examples/text/plot_document_clustering#sphx-glr-auto-examples-text-plot-document-clustering-py)
scikit_learn sklearn.datasets.load_diabetes sklearn.datasets.load\_diabetes
===============================
sklearn.datasets.load\_diabetes(*\**, *return\_X\_y=False*, *as\_frame=False*, *scaled=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_base.py#L954)
Load and return the diabetes dataset (regression).
| | |
| --- | --- |
| Samples total | 442 |
| Dimensionality | 10 |
| Features | real, -.2 < x < .2 |
| Targets | integer 25 - 346 |
Note
The meaning of each feature (i.e. `feature_names`) might be unclear (especially for `ltg`) as the documentation of the original dataset is not explicit. We provide information that seems correct in regard with the scientific literature in this field of research.
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/toy_dataset.html#diabetes-dataset).
Parameters:
**return\_X\_y**bool, default=False
If True, returns `(data, target)` instead of a Bunch object. See below for more information about the `data` and `target` object.
New in version 0.18.
**as\_frame**bool, default=False
If True, the data is a pandas DataFrame including columns with appropriate dtypes (numeric). The target is a pandas DataFrame or Series depending on the number of target columns. If `return_X_y` is True, then (`data`, `target`) will be pandas DataFrames or Series as described below.
New in version 0.23.
**scaled**bool, default=True
If True, the feature variables are mean centered and scaled by the standard deviation times the square root of `n_samples`. If False, raw data is returned for the feature variables.
New in version 1.1.
Returns:
**data**[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
Dictionary-like object, with the following attributes.
data{ndarray, dataframe} of shape (442, 10)
The data matrix. If `as_frame=True`, `data` will be a pandas DataFrame.
target: {ndarray, Series} of shape (442,)
The regression target. If `as_frame=True`, `target` will be a pandas Series.
feature\_names: list
The names of the dataset columns.
frame: DataFrame of shape (442, 11)
Only present when `as_frame=True`. DataFrame with `data` and `target`.
New in version 0.23.
DESCR: str
The full description of the dataset.
data\_filename: str
The path to the location of the data.
target\_filename: str
The path to the location of the target.
**(data, target)**tuple if `return_X_y` is True
Returns a tuple of two ndarray of shape (n\_samples, n\_features) A 2D array with each row representing one sample and each column representing the features and/or target of a given sample.
New in version 0.18.
Examples using `sklearn.datasets.load_diabetes`
-----------------------------------------------
[Gradient Boosting regression](../../auto_examples/ensemble/plot_gradient_boosting_regression#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-regression-py)
[Plot individual and voting regression predictions](../../auto_examples/ensemble/plot_voting_regressor#sphx-glr-auto-examples-ensemble-plot-voting-regressor-py)
[Model Complexity Influence](../../auto_examples/applications/plot_model_complexity_influence#sphx-glr-auto-examples-applications-plot-model-complexity-influence-py)
[Model-based and sequential feature selection](../../auto_examples/feature_selection/plot_select_from_model_diabetes#sphx-glr-auto-examples-feature-selection-plot-select-from-model-diabetes-py)
[Lasso and Elastic Net](../../auto_examples/linear_model/plot_lasso_coordinate_descent_path#sphx-glr-auto-examples-linear-model-plot-lasso-coordinate-descent-path-py)
[Lasso model selection via information criteria](../../auto_examples/linear_model/plot_lasso_lars_ic#sphx-glr-auto-examples-linear-model-plot-lasso-lars-ic-py)
[Lasso model selection: AIC-BIC / cross-validation](../../auto_examples/linear_model/plot_lasso_model_selection#sphx-glr-auto-examples-linear-model-plot-lasso-model-selection-py)
[Lasso path using LARS](../../auto_examples/linear_model/plot_lasso_lars#sphx-glr-auto-examples-linear-model-plot-lasso-lars-py)
[Linear Regression Example](../../auto_examples/linear_model/plot_ols#sphx-glr-auto-examples-linear-model-plot-ols-py)
[Sparsity Example: Fitting only features 1 and 2](../../auto_examples/linear_model/plot_ols_3d#sphx-glr-auto-examples-linear-model-plot-ols-3d-py)
[Advanced Plotting With Partial Dependence](../../auto_examples/miscellaneous/plot_partial_dependence_visualization_api#sphx-glr-auto-examples-miscellaneous-plot-partial-dependence-visualization-api-py)
[Imputing missing values before building an estimator](../../auto_examples/impute/plot_missing_values#sphx-glr-auto-examples-impute-plot-missing-values-py)
[Plotting Cross-Validated Predictions](../../auto_examples/model_selection/plot_cv_predict#sphx-glr-auto-examples-model-selection-plot-cv-predict-py)
[Cross-validation on diabetes Dataset Exercise](../../auto_examples/exercises/plot_cv_diabetes#sphx-glr-auto-examples-exercises-plot-cv-diabetes-py)
scikit_learn sklearn.utils.estimator_html_repr sklearn.utils.estimator\_html\_repr
===================================
sklearn.utils.estimator\_html\_repr(*estimator*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/_estimator_html_repr.py#L373)
Build a HTML representation of an estimator.
Read more in the [User Guide](../compose#visualizing-composite-estimators).
Parameters:
**estimator**estimator object
The estimator to visualize.
Returns:
html: str
HTML representation of estimator.
scikit_learn sklearn.metrics.pairwise.distance_metrics sklearn.metrics.pairwise.distance\_metrics
==========================================
sklearn.metrics.pairwise.distance\_metrics()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/pairwise.py#L1517)
Valid metrics for pairwise\_distances.
This function simply returns the valid pairwise distance metrics. It exists to allow for a description of the mapping for each of the valid strings.
The valid distance metrics, and the function they map to, are:
| metric | Function |
| --- | --- |
| ‘cityblock’ | metrics.pairwise.manhattan\_distances |
| ‘cosine’ | metrics.pairwise.cosine\_distances |
| ‘euclidean’ | metrics.pairwise.euclidean\_distances |
| ‘haversine’ | metrics.pairwise.haversine\_distances |
| ‘l1’ | metrics.pairwise.manhattan\_distances |
| ‘l2’ | metrics.pairwise.euclidean\_distances |
| ‘manhattan’ | metrics.pairwise.manhattan\_distances |
| ‘nan\_euclidean’ | metrics.pairwise.nan\_euclidean\_distances |
Read more in the [User Guide](../metrics#metrics).
Returns:
**distance\_metrics**dict
Returns valid metrics for pairwise\_distances.
scikit_learn sklearn.linear_model.LassoLarsCV sklearn.linear\_model.LassoLarsCV
=================================
*class*sklearn.linear\_model.LassoLarsCV(*\**, *fit\_intercept=True*, *verbose=False*, *max\_iter=500*, *normalize='deprecated'*, *precompute='auto'*, *cv=None*, *max\_n\_alphas=1000*, *n\_jobs=None*, *eps=2.220446049250313e-16*, *copy\_X=True*, *positive=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_least_angle.py#L1758)
Cross-validated Lasso, using the LARS algorithm.
See glossary entry for [cross-validation estimator](https://scikit-learn.org/1.1/glossary.html#term-cross-validation-estimator).
The optimization objective for Lasso is:
```
(1 / (2 * n_samples)) * ||y - Xw||^2_2 + alpha * ||w||_1
```
Read more in the [User Guide](../linear_model#least-angle-regression).
Parameters:
**fit\_intercept**bool, default=True
Whether to calculate the intercept for this model. If set to false, no intercept will be used in calculations (i.e. data is expected to be centered).
**verbose**bool or int, default=False
Sets the verbosity amount.
**max\_iter**int, default=500
Maximum number of iterations to perform.
**normalize**bool, default=True
This parameter is ignored when `fit_intercept` is set to False. If True, the regressors X will be normalized before regression by subtracting the mean and dividing by the l2-norm. If you wish to standardize, please use [`StandardScaler`](sklearn.preprocessing.standardscaler#sklearn.preprocessing.StandardScaler "sklearn.preprocessing.StandardScaler") before calling `fit` on an estimator with `normalize=False`.
Deprecated since version 1.0: `normalize` was deprecated in version 1.0. It will default to False in 1.2 and be removed in 1.4.
**precompute**bool or ‘auto’ , default=’auto’
Whether to use a precomputed Gram matrix to speed up calculations. If set to `'auto'` let us decide. The Gram matrix cannot be passed as argument since we will use only subsets of X.
**cv**int, cross-validation generator or an iterable, default=None
Determines the cross-validation splitting strategy. Possible inputs for cv are:
* None, to use the default 5-fold cross-validation,
* integer, to specify the number of folds.
* [CV splitter](https://scikit-learn.org/1.1/glossary.html#term-CV-splitter),
* An iterable yielding (train, test) splits as arrays of indices.
For integer/None inputs, `KFold` is used.
Refer [User Guide](../cross_validation#cross-validation) for the various cross-validation strategies that can be used here.
Changed in version 0.22: `cv` default value if None changed from 3-fold to 5-fold.
**max\_n\_alphas**int, default=1000
The maximum number of points on the path used to compute the residuals in the cross-validation.
**n\_jobs**int or None, default=None
Number of CPUs to use during the cross validation. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**eps**float, default=np.finfo(float).eps
The machine-precision regularization in the computation of the Cholesky diagonal factors. Increase this for very ill-conditioned systems. Unlike the `tol` parameter in some iterative optimization-based algorithms, this parameter does not control the tolerance of the optimization.
**copy\_X**bool, default=True
If True, X will be copied; else, it may be overwritten.
**positive**bool, default=False
Restrict coefficients to be >= 0. Be aware that you might want to remove fit\_intercept which is set True by default. Under the positive restriction the model coefficients do not converge to the ordinary-least-squares solution for small values of alpha. Only coefficients up to the smallest alpha value (`alphas_[alphas_ >
0.].min()` when fit\_path=True) reached by the stepwise Lars-Lasso algorithm are typically in congruence with the solution of the coordinate descent Lasso estimator. As a consequence using LassoLarsCV only makes sense for problems where a sparse solution is expected and/or reached.
Attributes:
**coef\_**array-like of shape (n\_features,)
parameter vector (w in the formulation formula)
**intercept\_**float
independent term in decision function.
**coef\_path\_**array-like of shape (n\_features, n\_alphas)
the varying values of the coefficients along the path
**alpha\_**float
the estimated regularization parameter alpha
**alphas\_**array-like of shape (n\_alphas,)
the different values of alpha along the path
**cv\_alphas\_**array-like of shape (n\_cv\_alphas,)
all the values of alpha along the path for the different folds
**mse\_path\_**array-like of shape (n\_folds, n\_cv\_alphas)
the mean square error on left-out for each fold along the path (alpha values given by `cv_alphas`)
**n\_iter\_**array-like or int
the number of iterations run by Lars with the optimal alpha.
**active\_**list of int
Indices of active variables at the end of the path.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
See also
[`lars_path`](sklearn.linear_model.lars_path#sklearn.linear_model.lars_path "sklearn.linear_model.lars_path")
Compute Least Angle Regression or Lasso path using LARS algorithm.
[`lasso_path`](sklearn.linear_model.lasso_path#sklearn.linear_model.lasso_path "sklearn.linear_model.lasso_path")
Compute Lasso path with coordinate descent.
[`Lasso`](sklearn.linear_model.lasso#sklearn.linear_model.Lasso "sklearn.linear_model.Lasso")
Linear Model trained with L1 prior as regularizer (aka the Lasso).
[`LassoCV`](sklearn.linear_model.lassocv#sklearn.linear_model.LassoCV "sklearn.linear_model.LassoCV")
Lasso linear model with iterative fitting along a regularization path.
[`LassoLars`](sklearn.linear_model.lassolars#sklearn.linear_model.LassoLars "sklearn.linear_model.LassoLars")
Lasso model fit with Least Angle Regression a.k.a. Lars.
[`LassoLarsIC`](sklearn.linear_model.lassolarsic#sklearn.linear_model.LassoLarsIC "sklearn.linear_model.LassoLarsIC")
Lasso model fit with Lars using BIC or AIC for model selection.
[`sklearn.decomposition.sparse_encode`](sklearn.decomposition.sparse_encode#sklearn.decomposition.sparse_encode "sklearn.decomposition.sparse_encode")
Sparse coding.
#### Notes
The object solves the same problem as the [`LassoCV`](sklearn.linear_model.lassocv#sklearn.linear_model.LassoCV "sklearn.linear_model.LassoCV") object. However, unlike the [`LassoCV`](sklearn.linear_model.lassocv#sklearn.linear_model.LassoCV "sklearn.linear_model.LassoCV"), it find the relevant alphas values by itself. In general, because of this property, it will be more stable. However, it is more fragile to heavily multicollinear datasets.
It is more efficient than the [`LassoCV`](sklearn.linear_model.lassocv#sklearn.linear_model.LassoCV "sklearn.linear_model.LassoCV") if only a small number of features are selected compared to the total number, for instance if there are very few samples compared to the number of features.
In `fit`, once the best parameter `alpha` is found through cross-validation, the model is fit again using the entire training set.
#### Examples
```
>>> from sklearn.linear_model import LassoLarsCV
>>> from sklearn.datasets import make_regression
>>> X, y = make_regression(noise=4.0, random_state=0)
>>> reg = LassoLarsCV(cv=5, normalize=False).fit(X, y)
>>> reg.score(X, y)
0.9993...
>>> reg.alpha_
0.3972...
>>> reg.predict(X[:1,])
array([-78.4831...])
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.linear_model.LassoLarsCV.fit "sklearn.linear_model.LassoLarsCV.fit")(X, y) | Fit the model using X, y as training data. |
| [`get_params`](#sklearn.linear_model.LassoLarsCV.get_params "sklearn.linear_model.LassoLarsCV.get_params")([deep]) | Get parameters for this estimator. |
| [`predict`](#sklearn.linear_model.LassoLarsCV.predict "sklearn.linear_model.LassoLarsCV.predict")(X) | Predict using the linear model. |
| [`score`](#sklearn.linear_model.LassoLarsCV.score "sklearn.linear_model.LassoLarsCV.score")(X, y[, sample\_weight]) | Return the coefficient of determination of the prediction. |
| [`set_params`](#sklearn.linear_model.LassoLarsCV.set_params "sklearn.linear_model.LassoLarsCV.set_params")(\*\*params) | Set the parameters of this estimator. |
fit(*X*, *y*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_least_angle.py#L1655)
Fit the model using X, y as training data.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data.
**y**array-like of shape (n\_samples,)
Target values.
Returns:
**self**object
Returns an instance of self.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L372)
Predict using the linear model.
Parameters:
**X**array-like or sparse matrix, shape (n\_samples, n\_features)
Samples.
Returns:
**C**array, shape (n\_samples,)
Returns predicted values.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L677)
Return the coefficient of determination of the prediction.
The coefficient of determination \(R^2\) is defined as \((1 - \frac{u}{v})\), where \(u\) is the residual sum of squares `((y_true - y_pred)** 2).sum()` and \(v\) is the total sum of squares `((y_true - y_true.mean()) ** 2).sum()`. The best possible score is 1.0 and it can be negative (because the model can be arbitrarily worse). A constant model that always predicts the expected value of `y`, disregarding the input features, would get a \(R^2\) score of 0.0.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples. For some estimators this may be a precomputed kernel matrix or a list of generic objects instead with shape `(n_samples, n_samples_fitted)`, where `n_samples_fitted` is the number of samples used in the fitting for the estimator.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True values for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
\(R^2\) of `self.predict(X)` wrt. `y`.
#### Notes
The \(R^2\) score used when calling `score` on a regressor uses `multioutput='uniform_average'` from version 0.23 to keep consistent with default value of [`r2_score`](sklearn.metrics.r2_score#sklearn.metrics.r2_score "sklearn.metrics.r2_score"). This influences the `score` method of all the multioutput regressors (except for [`MultiOutputRegressor`](sklearn.multioutput.multioutputregressor#sklearn.multioutput.MultiOutputRegressor "sklearn.multioutput.MultiOutputRegressor")).
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
Examples using `sklearn.linear_model.LassoLarsCV`
-------------------------------------------------
[Lasso model selection: AIC-BIC / cross-validation](../../auto_examples/linear_model/plot_lasso_model_selection#sphx-glr-auto-examples-linear-model-plot-lasso-model-selection-py)
| programming_docs |
scikit_learn sklearn.datasets.fetch_openml sklearn.datasets.fetch\_openml
==============================
sklearn.datasets.fetch\_openml(*name:[Optional](https://docs.python.org/3/library/typing.html#typing.Optional "(in Python v3.10)")[[str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.10)")]=None*, *\**, *version:[Union](https://docs.python.org/3/library/typing.html#typing.Union "(in Python v3.10)")[[str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.10)"),[int](https://docs.python.org/3/library/functions.html#int "(in Python v3.10)")]='active'*, *data\_id:[Optional](https://docs.python.org/3/library/typing.html#typing.Optional "(in Python v3.10)")[[int](https://docs.python.org/3/library/functions.html#int "(in Python v3.10)")]=None*, *data\_home:[Optional](https://docs.python.org/3/library/typing.html#typing.Optional "(in Python v3.10)")[[str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.10)")]=None*, *target\_column:[Optional](https://docs.python.org/3/library/typing.html#typing.Optional "(in Python v3.10)")[[Union](https://docs.python.org/3/library/typing.html#typing.Union "(in Python v3.10)")[[str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.10)"),[List](https://docs.python.org/3/library/typing.html#typing.List "(in Python v3.10)")]]='default-target'*, *cache:[bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.10)")=True*, *return\_X\_y:[bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.10)")=False*, *as\_frame:[Union](https://docs.python.org/3/library/typing.html#typing.Union "(in Python v3.10)")[[str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.10)"),[bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.10)")]='auto'*, *n\_retries:[int](https://docs.python.org/3/library/functions.html#int "(in Python v3.10)")=3*, *delay:[float](https://docs.python.org/3/library/functions.html#float "(in Python v3.10)")=1.0*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/datasets/_openml.py#L590)
Fetch dataset from openml by name or dataset id.
Datasets are uniquely identified by either an integer ID or by a combination of name and version (i.e. there might be multiple versions of the ‘iris’ dataset). Please give either name or data\_id (not both). In case a name is given, a version can also be provided.
Read more in the [User Guide](https://scikit-learn.org/1.1/datasets/loading_other_datasets.html#openml).
New in version 0.20.
Note
EXPERIMENTAL
The API is experimental (particularly the return value structure), and might have small backward-incompatible changes without notice or warning in future releases.
Parameters:
**name**str, default=None
String identifier of the dataset. Note that OpenML can have multiple datasets with the same name.
**version**int or ‘active’, default=’active’
Version of the dataset. Can only be provided if also `name` is given. If ‘active’ the oldest version that’s still active is used. Since there may be more than one active version of a dataset, and those versions may fundamentally be different from one another, setting an exact version is highly recommended.
**data\_id**int, default=None
OpenML ID of the dataset. The most specific way of retrieving a dataset. If data\_id is not given, name (and potential version) are used to obtain a dataset.
**data\_home**str, default=None
Specify another download and cache folder for the data sets. By default all scikit-learn data is stored in ‘~/scikit\_learn\_data’ subfolders.
**target\_column**str, list or None, default=’default-target’
Specify the column name in the data to use as target. If ‘default-target’, the standard target column a stored on the server is used. If `None`, all columns are returned as data and the target is `None`. If list (of strings), all columns with these names are returned as multi-target (Note: not all scikit-learn classifiers can handle all types of multi-output combinations).
**cache**bool, default=True
Whether to cache the downloaded datasets into `data_home`.
**return\_X\_y**bool, default=False
If True, returns `(data, target)` instead of a Bunch object. See below for more information about the `data` and `target` objects.
**as\_frame**bool or ‘auto’, default=’auto’
If True, the data is a pandas DataFrame including columns with appropriate dtypes (numeric, string or categorical). The target is a pandas DataFrame or Series depending on the number of target\_columns. The Bunch will contain a `frame` attribute with the target and the data. If `return_X_y` is True, then `(data, target)` will be pandas DataFrames or Series as describe above.
If as\_frame is ‘auto’, the data and target will be converted to DataFrame or Series as if as\_frame is set to True, unless the dataset is stored in sparse format.
Changed in version 0.24: The default value of `as_frame` changed from `False` to `'auto'` in 0.24.
**n\_retries**int, default=3
Number of retries when HTTP errors or network timeouts are encountered. Error with status code 412 won’t be retried as they represent OpenML generic errors.
**delay**float, default=1.0
Number of seconds between retries.
Returns:
**data**[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
Dictionary-like object, with the following attributes.
datanp.array, scipy.sparse.csr\_matrix of floats, or pandas DataFrame
The feature matrix. Categorical features are encoded as ordinals.
targetnp.array, pandas Series or DataFrame
The regression target or classification labels, if applicable. Dtype is float if numeric, and object if categorical. If `as_frame` is True, `target` is a pandas object.
DESCRstr
The full description of the dataset.
feature\_nameslist
The names of the dataset columns.
target\_names: list
The names of the target columns.
New in version 0.22.
categoriesdict or None
Maps each categorical feature name to a list of values, such that the value encoded as i is ith in the list. If `as_frame` is True, this is None.
detailsdict
More metadata from OpenML.
framepandas DataFrame
Only present when `as_frame=True`. DataFrame with `data` and `target`.
**(data, target)**tuple if `return_X_y` is True
Note
EXPERIMENTAL
This interface is **experimental** and subsequent releases may change attributes without notice (although there should only be minor changes to `data` and `target`).
Missing values in the ‘data’ are represented as NaN’s. Missing values in ‘target’ are represented as NaN’s (numerical target) or None (categorical target).
Examples using `sklearn.datasets.fetch_openml`
----------------------------------------------
[Release Highlights for scikit-learn 1.1](../../auto_examples/release_highlights/plot_release_highlights_1_1_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-1-1-0-py)
[Release Highlights for scikit-learn 0.22](../../auto_examples/release_highlights/plot_release_highlights_0_22_0#sphx-glr-auto-examples-release-highlights-plot-release-highlights-0-22-0-py)
[Categorical Feature Support in Gradient Boosting](../../auto_examples/ensemble/plot_gradient_boosting_categorical#sphx-glr-auto-examples-ensemble-plot-gradient-boosting-categorical-py)
[Combine predictors using stacking](../../auto_examples/ensemble/plot_stack_predictors#sphx-glr-auto-examples-ensemble-plot-stack-predictors-py)
[Image denoising using kernel PCA](../../auto_examples/applications/plot_digits_denoising#sphx-glr-auto-examples-applications-plot-digits-denoising-py)
[Time-related feature engineering](../../auto_examples/applications/plot_cyclical_feature_engineering#sphx-glr-auto-examples-applications-plot-cyclical-feature-engineering-py)
[Gaussian process regression (GPR) on Mauna Loa CO2 data](../../auto_examples/gaussian_process/plot_gpr_co2#sphx-glr-auto-examples-gaussian-process-plot-gpr-co2-py)
[Early stopping of Stochastic Gradient Descent](../../auto_examples/linear_model/plot_sgd_early_stopping#sphx-glr-auto-examples-linear-model-plot-sgd-early-stopping-py)
[MNIST classification using multinomial logistic + L1](../../auto_examples/linear_model/plot_sparse_logistic_regression_mnist#sphx-glr-auto-examples-linear-model-plot-sparse-logistic-regression-mnist-py)
[Poisson regression and non-normal loss](../../auto_examples/linear_model/plot_poisson_regression_non_normal_loss#sphx-glr-auto-examples-linear-model-plot-poisson-regression-non-normal-loss-py)
[Tweedie regression on insurance claims](../../auto_examples/linear_model/plot_tweedie_regression_insurance_claims#sphx-glr-auto-examples-linear-model-plot-tweedie-regression-insurance-claims-py)
[Common pitfalls in the interpretation of coefficients of linear models](../../auto_examples/inspection/plot_linear_model_coefficient_interpretation#sphx-glr-auto-examples-inspection-plot-linear-model-coefficient-interpretation-py)
[Permutation Importance vs Random Forest Feature Importance (MDI)](../../auto_examples/inspection/plot_permutation_importance#sphx-glr-auto-examples-inspection-plot-permutation-importance-py)
[Evaluation of outlier detection estimators](../../auto_examples/miscellaneous/plot_outlier_detection_bench#sphx-glr-auto-examples-miscellaneous-plot-outlier-detection-bench-py)
[Visualizations with Display Objects](../../auto_examples/miscellaneous/plot_display_object_visualization#sphx-glr-auto-examples-miscellaneous-plot-display-object-visualization-py)
[Classifier Chain](../../auto_examples/multioutput/plot_classifier_chain_yeast#sphx-glr-auto-examples-multioutput-plot-classifier-chain-yeast-py)
[Approximate nearest neighbors in TSNE](../../auto_examples/neighbors/approximate_nearest_neighbors#sphx-glr-auto-examples-neighbors-approximate-nearest-neighbors-py)
[Visualization of MLP weights on MNIST](../../auto_examples/neural_networks/plot_mnist_filters#sphx-glr-auto-examples-neural-networks-plot-mnist-filters-py)
[Column Transformer with Mixed Types](../../auto_examples/compose/plot_column_transformer_mixed_types#sphx-glr-auto-examples-compose-plot-column-transformer-mixed-types-py)
[Effect of transforming the targets in regression model](../../auto_examples/compose/plot_transformed_target#sphx-glr-auto-examples-compose-plot-transformed-target-py)
scikit_learn sklearn.calibration.CalibrationDisplay sklearn.calibration.CalibrationDisplay
======================================
*class*sklearn.calibration.CalibrationDisplay(*prob\_true*, *prob\_pred*, *y\_prob*, *\**, *estimator\_name=None*, *pos\_label=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/calibration.py#L1009)
Calibration curve (also known as reliability diagram) visualization.
It is recommended to use [`from_estimator`](#sklearn.calibration.CalibrationDisplay.from_estimator "sklearn.calibration.CalibrationDisplay.from_estimator") or [`from_predictions`](#sklearn.calibration.CalibrationDisplay.from_predictions "sklearn.calibration.CalibrationDisplay.from_predictions") to create a `CalibrationDisplay`. All parameters are stored as attributes.
Read more about calibration in the [User Guide](../calibration#calibration) and more about the scikit-learn visualization API in [Visualizations](https://scikit-learn.org/1.1/visualizations.html#visualizations).
New in version 1.0.
Parameters:
**prob\_true**ndarray of shape (n\_bins,)
The proportion of samples whose class is the positive class (fraction of positives), in each bin.
**prob\_pred**ndarray of shape (n\_bins,)
The mean predicted probability in each bin.
**y\_prob**ndarray of shape (n\_samples,)
Probability estimates for the positive class, for each sample.
**estimator\_name**str, default=None
Name of estimator. If None, the estimator name is not shown.
**pos\_label**str or int, default=None
The positive class when computing the calibration curve. By default, `estimators.classes_[1]` is considered as the positive class.
New in version 1.1.
Attributes:
**line\_**matplotlib Artist
Calibration curve.
**ax\_**matplotlib Axes
Axes with calibration curve.
**figure\_**matplotlib Figure
Figure containing the curve.
See also
[`calibration_curve`](sklearn.calibration.calibration_curve#sklearn.calibration.calibration_curve "sklearn.calibration.calibration_curve")
Compute true and predicted probabilities for a calibration curve.
[`CalibrationDisplay.from_predictions`](#sklearn.calibration.CalibrationDisplay.from_predictions "sklearn.calibration.CalibrationDisplay.from_predictions")
Plot calibration curve using true and predicted labels.
[`CalibrationDisplay.from_estimator`](#sklearn.calibration.CalibrationDisplay.from_estimator "sklearn.calibration.CalibrationDisplay.from_estimator")
Plot calibration curve using an estimator and data.
#### Examples
```
>>> from sklearn.datasets import make_classification
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.calibration import calibration_curve, CalibrationDisplay
>>> X, y = make_classification(random_state=0)
>>> X_train, X_test, y_train, y_test = train_test_split(
... X, y, random_state=0)
>>> clf = LogisticRegression(random_state=0)
>>> clf.fit(X_train, y_train)
LogisticRegression(random_state=0)
>>> y_prob = clf.predict_proba(X_test)[:, 1]
>>> prob_true, prob_pred = calibration_curve(y_test, y_prob, n_bins=10)
>>> disp = CalibrationDisplay(prob_true, prob_pred, y_prob)
>>> disp.plot()
<...>
```
#### Methods
| | |
| --- | --- |
| [`from_estimator`](#sklearn.calibration.CalibrationDisplay.from_estimator "sklearn.calibration.CalibrationDisplay.from_estimator")(estimator, X, y, \*[, n\_bins, ...]) | Plot calibration curve using a binary classifier and data. |
| [`from_predictions`](#sklearn.calibration.CalibrationDisplay.from_predictions "sklearn.calibration.CalibrationDisplay.from_predictions")(y\_true, y\_prob, \*[, ...]) | Plot calibration curve using true labels and predicted probabilities. |
| [`plot`](#sklearn.calibration.CalibrationDisplay.plot "sklearn.calibration.CalibrationDisplay.plot")(\*[, ax, name, ref\_line]) | Plot visualization. |
*classmethod*from\_estimator(*estimator*, *X*, *y*, *\**, *n\_bins=5*, *strategy='uniform'*, *pos\_label=None*, *name=None*, *ref\_line=True*, *ax=None*, *\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/calibration.py#L1153)
Plot calibration curve using a binary classifier and data.
A calibration curve, also known as a reliability diagram, uses inputs from a binary classifier and plots the average predicted probability for each bin against the fraction of positive classes, on the y-axis.
Extra keyword arguments will be passed to [`matplotlib.pyplot.plot`](https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.plot.html#matplotlib.pyplot.plot "(in Matplotlib v3.6.0)").
Read more about calibration in the [User Guide](../calibration#calibration) and more about the scikit-learn visualization API in [Visualizations](https://scikit-learn.org/1.1/visualizations.html#visualizations).
New in version 1.0.
Parameters:
**estimator**estimator instance
Fitted classifier or a fitted [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline") in which the last estimator is a classifier. The classifier must have a [predict\_proba](https://scikit-learn.org/1.1/glossary.html#term-predict_proba) method.
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Input values.
**y**array-like of shape (n\_samples,)
Binary target values.
**n\_bins**int, default=5
Number of bins to discretize the [0, 1] interval into when calculating the calibration curve. A bigger number requires more data.
**strategy**{‘uniform’, ‘quantile’}, default=’uniform’
Strategy used to define the widths of the bins.
* `'uniform'`: The bins have identical widths.
* `'quantile'`: The bins have the same number of samples and depend on predicted probabilities.
**pos\_label**str or int, default=None
The positive class when computing the calibration curve. By default, `estimators.classes_[1]` is considered as the positive class.
New in version 1.1.
**name**str, default=None
Name for labeling curve. If `None`, the name of the estimator is used.
**ref\_line**bool, default=True
If `True`, plots a reference line representing a perfectly calibrated classifier.
**ax**matplotlib axes, default=None
Axes object to plot on. If `None`, a new figure and axes is created.
**\*\*kwargs**dict
Keyword arguments to be passed to [`matplotlib.pyplot.plot`](https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.plot.html#matplotlib.pyplot.plot "(in Matplotlib v3.6.0)").
Returns:
**display**[`CalibrationDisplay`](#sklearn.calibration.CalibrationDisplay "sklearn.calibration.CalibrationDisplay").
Object that stores computed values.
See also
[`CalibrationDisplay.from_predictions`](#sklearn.calibration.CalibrationDisplay.from_predictions "sklearn.calibration.CalibrationDisplay.from_predictions")
Plot calibration curve using true and predicted labels.
#### Examples
```
>>> import matplotlib.pyplot as plt
>>> from sklearn.datasets import make_classification
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.calibration import CalibrationDisplay
>>> X, y = make_classification(random_state=0)
>>> X_train, X_test, y_train, y_test = train_test_split(
... X, y, random_state=0)
>>> clf = LogisticRegression(random_state=0)
>>> clf.fit(X_train, y_train)
LogisticRegression(random_state=0)
>>> disp = CalibrationDisplay.from_estimator(clf, X_test, y_test)
>>> plt.show()
```
*classmethod*from\_predictions(*y\_true*, *y\_prob*, *\**, *n\_bins=5*, *strategy='uniform'*, *pos\_label=None*, *name=None*, *ref\_line=True*, *ax=None*, *\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/calibration.py#L1279)
Plot calibration curve using true labels and predicted probabilities.
Calibration curve, also known as reliability diagram, uses inputs from a binary classifier and plots the average predicted probability for each bin against the fraction of positive classes, on the y-axis.
Extra keyword arguments will be passed to [`matplotlib.pyplot.plot`](https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.plot.html#matplotlib.pyplot.plot "(in Matplotlib v3.6.0)").
Read more about calibration in the [User Guide](../calibration#calibration) and more about the scikit-learn visualization API in [Visualizations](https://scikit-learn.org/1.1/visualizations.html#visualizations).
New in version 1.0.
Parameters:
**y\_true**array-like of shape (n\_samples,)
True labels.
**y\_prob**array-like of shape (n\_samples,)
The predicted probabilities of the positive class.
**n\_bins**int, default=5
Number of bins to discretize the [0, 1] interval into when calculating the calibration curve. A bigger number requires more data.
**strategy**{‘uniform’, ‘quantile’}, default=’uniform’
Strategy used to define the widths of the bins.
* `'uniform'`: The bins have identical widths.
* `'quantile'`: The bins have the same number of samples and depend on predicted probabilities.
**pos\_label**str or int, default=None
The positive class when computing the calibration curve. By default, `estimators.classes_[1]` is considered as the positive class.
New in version 1.1.
**name**str, default=None
Name for labeling curve.
**ref\_line**bool, default=True
If `True`, plots a reference line representing a perfectly calibrated classifier.
**ax**matplotlib axes, default=None
Axes object to plot on. If `None`, a new figure and axes is created.
**\*\*kwargs**dict
Keyword arguments to be passed to [`matplotlib.pyplot.plot`](https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.plot.html#matplotlib.pyplot.plot "(in Matplotlib v3.6.0)").
Returns:
**display**[`CalibrationDisplay`](#sklearn.calibration.CalibrationDisplay "sklearn.calibration.CalibrationDisplay").
Object that stores computed values.
See also
[`CalibrationDisplay.from_estimator`](#sklearn.calibration.CalibrationDisplay.from_estimator "sklearn.calibration.CalibrationDisplay.from_estimator")
Plot calibration curve using an estimator and data.
#### Examples
```
>>> import matplotlib.pyplot as plt
>>> from sklearn.datasets import make_classification
>>> from sklearn.model_selection import train_test_split
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.calibration import CalibrationDisplay
>>> X, y = make_classification(random_state=0)
>>> X_train, X_test, y_train, y_test = train_test_split(
... X, y, random_state=0)
>>> clf = LogisticRegression(random_state=0)
>>> clf.fit(X_train, y_train)
LogisticRegression(random_state=0)
>>> y_prob = clf.predict_proba(X_test)[:, 1]
>>> disp = CalibrationDisplay.from_predictions(y_test, y_prob)
>>> plt.show()
```
plot(*\**, *ax=None*, *name=None*, *ref\_line=True*, *\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/calibration.py#L1092)
Plot visualization.
Extra keyword arguments will be passed to [`matplotlib.pyplot.plot`](https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.plot.html#matplotlib.pyplot.plot "(in Matplotlib v3.6.0)").
Parameters:
**ax**Matplotlib Axes, default=None
Axes object to plot on. If `None`, a new figure and axes is created.
**name**str, default=None
Name for labeling curve. If `None`, use `estimator_name` if not `None`, otherwise no labeling is shown.
**ref\_line**bool, default=True
If `True`, plots a reference line representing a perfectly calibrated classifier.
**\*\*kwargs**dict
Keyword arguments to be passed to [`matplotlib.pyplot.plot`](https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.plot.html#matplotlib.pyplot.plot "(in Matplotlib v3.6.0)").
Returns:
**display**[`CalibrationDisplay`](#sklearn.calibration.CalibrationDisplay "sklearn.calibration.CalibrationDisplay")
Object that stores computed values.
| programming_docs |
scikit_learn sklearn.linear_model.Perceptron sklearn.linear\_model.Perceptron
================================
*class*sklearn.linear\_model.Perceptron(*\**, *penalty=None*, *alpha=0.0001*, *l1\_ratio=0.15*, *fit\_intercept=True*, *max\_iter=1000*, *tol=0.001*, *shuffle=True*, *verbose=0*, *eta0=1.0*, *n\_jobs=None*, *random\_state=0*, *early\_stopping=False*, *validation\_fraction=0.1*, *n\_iter\_no\_change=5*, *class\_weight=None*, *warm\_start=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_perceptron.py#L7)
Linear perceptron classifier.
Read more in the [User Guide](../linear_model#perceptron).
Parameters:
**penalty**{‘l2’,’l1’,’elasticnet’}, default=None
The penalty (aka regularization term) to be used.
**alpha**float, default=0.0001
Constant that multiplies the regularization term if regularization is used.
**l1\_ratio**float, default=0.15
The Elastic Net mixing parameter, with `0 <= l1_ratio <= 1`. `l1_ratio=0` corresponds to L2 penalty, `l1_ratio=1` to L1. Only used if `penalty='elasticnet'`.
New in version 0.24.
**fit\_intercept**bool, default=True
Whether the intercept should be estimated or not. If False, the data is assumed to be already centered.
**max\_iter**int, default=1000
The maximum number of passes over the training data (aka epochs). It only impacts the behavior in the `fit` method, and not the [`partial_fit`](#sklearn.linear_model.Perceptron.partial_fit "sklearn.linear_model.Perceptron.partial_fit") method.
New in version 0.19.
**tol**float, default=1e-3
The stopping criterion. If it is not None, the iterations will stop when (loss > previous\_loss - tol).
New in version 0.19.
**shuffle**bool, default=True
Whether or not the training data should be shuffled after each epoch.
**verbose**int, default=0
The verbosity level.
**eta0**float, default=1
Constant by which the updates are multiplied.
**n\_jobs**int, default=None
The number of CPUs to use to do the OVA (One Versus All, for multi-class problems) computation. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
**random\_state**int, RandomState instance or None, default=0
Used to shuffle the training data, when `shuffle` is set to `True`. Pass an int for reproducible output across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
**early\_stopping**bool, default=False
Whether to use early stopping to terminate training when validation. score is not improving. If set to True, it will automatically set aside a stratified fraction of training data as validation and terminate training when validation score is not improving by at least tol for n\_iter\_no\_change consecutive epochs.
New in version 0.20.
**validation\_fraction**float, default=0.1
The proportion of training data to set aside as validation set for early stopping. Must be between 0 and 1. Only used if early\_stopping is True.
New in version 0.20.
**n\_iter\_no\_change**int, default=5
Number of iterations with no improvement to wait before early stopping.
New in version 0.20.
**class\_weight**dict, {class\_label: weight} or “balanced”, default=None
Preset for the class\_weight fit parameter.
Weights associated with classes. If not given, all classes are supposed to have weight one.
The “balanced” mode uses the values of y to automatically adjust weights inversely proportional to class frequencies in the input data as `n_samples / (n_classes * np.bincount(y))`.
**warm\_start**bool, default=False
When set to True, reuse the solution of the previous call to fit as initialization, otherwise, just erase the previous solution. See [the Glossary](https://scikit-learn.org/1.1/glossary.html#term-warm_start).
Attributes:
**classes\_**ndarray of shape (n\_classes,)
The unique classes labels.
**coef\_**ndarray of shape (1, n\_features) if n\_classes == 2 else (n\_classes, n\_features)
Weights assigned to the features.
**intercept\_**ndarray of shape (1,) if n\_classes == 2 else (n\_classes,)
Constants in decision function.
**loss\_function\_**concrete LossFunction
The function that determines the loss, or difference between the output of the algorithm and the target values.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_iter\_**int
The actual number of iterations to reach the stopping criterion. For multiclass fits, it is the maximum over every binary fit.
**t\_**int
Number of weight updates performed during training. Same as `(n_iter_ * n_samples)`.
See also
[`sklearn.linear_model.SGDClassifier`](sklearn.linear_model.sgdclassifier#sklearn.linear_model.SGDClassifier "sklearn.linear_model.SGDClassifier")
Linear classifiers (SVM, logistic regression, etc.) with SGD training.
#### Notes
`Perceptron` is a classification algorithm which shares the same underlying implementation with `SGDClassifier`. In fact, `Perceptron()` is equivalent to `SGDClassifier(loss="perceptron",
eta0=1, learning_rate="constant", penalty=None)`.
#### References
<https://en.wikipedia.org/wiki/Perceptron> and references therein.
#### Examples
```
>>> from sklearn.datasets import load_digits
>>> from sklearn.linear_model import Perceptron
>>> X, y = load_digits(return_X_y=True)
>>> clf = Perceptron(tol=1e-3, random_state=0)
>>> clf.fit(X, y)
Perceptron()
>>> clf.score(X, y)
0.939...
```
#### Methods
| | |
| --- | --- |
| [`decision_function`](#sklearn.linear_model.Perceptron.decision_function "sklearn.linear_model.Perceptron.decision_function")(X) | Predict confidence scores for samples. |
| [`densify`](#sklearn.linear_model.Perceptron.densify "sklearn.linear_model.Perceptron.densify")() | Convert coefficient matrix to dense array format. |
| [`fit`](#sklearn.linear_model.Perceptron.fit "sklearn.linear_model.Perceptron.fit")(X, y[, coef\_init, intercept\_init, ...]) | Fit linear model with Stochastic Gradient Descent. |
| [`get_params`](#sklearn.linear_model.Perceptron.get_params "sklearn.linear_model.Perceptron.get_params")([deep]) | Get parameters for this estimator. |
| [`partial_fit`](#sklearn.linear_model.Perceptron.partial_fit "sklearn.linear_model.Perceptron.partial_fit")(X, y[, classes, sample\_weight]) | Perform one epoch of stochastic gradient descent on given samples. |
| [`predict`](#sklearn.linear_model.Perceptron.predict "sklearn.linear_model.Perceptron.predict")(X) | Predict class labels for samples in X. |
| [`score`](#sklearn.linear_model.Perceptron.score "sklearn.linear_model.Perceptron.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.linear_model.Perceptron.set_params "sklearn.linear_model.Perceptron.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`sparsify`](#sklearn.linear_model.Perceptron.sparsify "sklearn.linear_model.Perceptron.sparsify")() | Convert coefficient matrix to sparse format. |
decision\_function(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L408)
Predict confidence scores for samples.
The confidence score for a sample is proportional to the signed distance of that sample to the hyperplane.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data matrix for which we want to get the confidence scores.
Returns:
**scores**ndarray of shape (n\_samples,) or (n\_samples, n\_classes)
Confidence scores per `(n_samples, n_classes)` combination. In the binary case, confidence score for `self.classes_[1]` where >0 means this class would be predicted.
densify()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L477)
Convert coefficient matrix to dense array format.
Converts the `coef_` member (back) to a numpy.ndarray. This is the default format of `coef_` and is required for fitting, so calling this method is only required on models that have previously been sparsified; otherwise, it is a no-op.
Returns:
self
Fitted estimator.
fit(*X*, *y*, *coef\_init=None*, *intercept\_init=None*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_stochastic_gradient.py#L862)
Fit linear model with Stochastic Gradient Descent.
Parameters:
**X**{array-like, sparse matrix}, shape (n\_samples, n\_features)
Training data.
**y**ndarray of shape (n\_samples,)
Target values.
**coef\_init**ndarray of shape (n\_classes, n\_features), default=None
The initial coefficients to warm-start the optimization.
**intercept\_init**ndarray of shape (n\_classes,), default=None
The initial intercept to warm-start the optimization.
**sample\_weight**array-like, shape (n\_samples,), default=None
Weights applied to individual samples. If not provided, uniform weights are assumed. These weights will be multiplied with class\_weight (passed through the constructor) if class\_weight is specified.
Returns:
**self**object
Returns an instance of self.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
partial\_fit(*X*, *y*, *classes=None*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_stochastic_gradient.py#L802)
Perform one epoch of stochastic gradient descent on given samples.
Internally, this method uses `max_iter = 1`. Therefore, it is not guaranteed that a minimum of the cost function is reached after calling it once. Matters such as objective convergence, early stopping, and learning rate adjustments should be handled by the user.
Parameters:
**X**{array-like, sparse matrix}, shape (n\_samples, n\_features)
Subset of the training data.
**y**ndarray of shape (n\_samples,)
Subset of the target values.
**classes**ndarray of shape (n\_classes,), default=None
Classes across all calls to partial\_fit. Can be obtained by via `np.unique(y_all)`, where y\_all is the target vector of the entire dataset. This argument is required for the first call to partial\_fit and can be omitted in the subsequent calls. Note that y doesn’t need to contain all labels in `classes`.
**sample\_weight**array-like, shape (n\_samples,), default=None
Weights applied to individual samples. If not provided, uniform weights are assumed.
Returns:
**self**object
Returns an instance of self.
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L433)
Predict class labels for samples in X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The data matrix for which we want to get the predictions.
Returns:
**y\_pred**ndarray of shape (n\_samples,)
Vector containing the class labels for each sample.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
sparsify()[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/linear_model/_base.py#L497)
Convert coefficient matrix to sparse format.
Converts the `coef_` member to a scipy.sparse matrix, which for L1-regularized models can be much more memory- and storage-efficient than the usual numpy.ndarray representation.
The `intercept_` member is not converted.
Returns:
self
Fitted estimator.
#### Notes
For non-sparse models, i.e. when there are not many zeros in `coef_`, this may actually *increase* memory usage, so use this method with care. A rule of thumb is that the number of zero elements, which can be computed with `(coef_ == 0).sum()`, must be more than 50% for this to provide significant benefits.
After calling this method, further fitting with the partial\_fit method (if any) will not work until you call densify.
Examples using `sklearn.linear_model.Perceptron`
------------------------------------------------
[Out-of-core classification of text documents](../../auto_examples/applications/plot_out_of_core_classification#sphx-glr-auto-examples-applications-plot-out-of-core-classification-py)
[Comparing various online solvers](../../auto_examples/linear_model/plot_sgd_comparison#sphx-glr-auto-examples-linear-model-plot-sgd-comparison-py)
scikit_learn sklearn.ensemble.VotingClassifier sklearn.ensemble.VotingClassifier
=================================
*class*sklearn.ensemble.VotingClassifier(*estimators*, *\**, *voting='hard'*, *weights=None*, *n\_jobs=None*, *flatten\_transform=True*, *verbose=False*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_voting.py#L157)
Soft Voting/Majority Rule classifier for unfitted estimators.
Read more in the [User Guide](../ensemble#voting-classifier).
New in version 0.17.
Parameters:
**estimators**list of (str, estimator) tuples
Invoking the `fit` method on the `VotingClassifier` will fit clones of those original estimators that will be stored in the class attribute `self.estimators_`. An estimator can be set to `'drop'` using [`set_params`](#sklearn.ensemble.VotingClassifier.set_params "sklearn.ensemble.VotingClassifier.set_params").
Changed in version 0.21: `'drop'` is accepted. Using None was deprecated in 0.22 and support was removed in 0.24.
**voting**{‘hard’, ‘soft’}, default=’hard’
If ‘hard’, uses predicted class labels for majority rule voting. Else if ‘soft’, predicts the class label based on the argmax of the sums of the predicted probabilities, which is recommended for an ensemble of well-calibrated classifiers.
**weights**array-like of shape (n\_classifiers,), default=None
Sequence of weights (`float` or `int`) to weight the occurrences of predicted class labels (`hard` voting) or class probabilities before averaging (`soft` voting). Uses uniform weights if `None`.
**n\_jobs**int, default=None
The number of jobs to run in parallel for `fit`. `None` means 1 unless in a [`joblib.parallel_backend`](https://joblib.readthedocs.io/en/latest/parallel.html#joblib.parallel_backend "(in joblib v1.3.0.dev0)") context. `-1` means using all processors. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-n_jobs) for more details.
New in version 0.18.
**flatten\_transform**bool, default=True
Affects shape of transform output only when voting=’soft’ If voting=’soft’ and flatten\_transform=True, transform method returns matrix with shape (n\_samples, n\_classifiers \* n\_classes). If flatten\_transform=False, it returns (n\_classifiers, n\_samples, n\_classes).
**verbose**bool, default=False
If True, the time elapsed while fitting will be printed as it is completed.
New in version 0.23.
Attributes:
**estimators\_**list of classifiers
The collection of fitted sub-estimators as defined in `estimators` that are not ‘drop’.
**named\_estimators\_**[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
Attribute to access any fitted sub-estimators by name.
New in version 0.20.
**le\_**[`LabelEncoder`](sklearn.preprocessing.labelencoder#sklearn.preprocessing.LabelEncoder "sklearn.preprocessing.LabelEncoder")
Transformer used to encode the labels during fit and decode during prediction.
**classes\_**ndarray of shape (n\_classes,)
The classes labels.
[`n_features_in_`](#sklearn.ensemble.VotingClassifier.n_features_in_ "sklearn.ensemble.VotingClassifier.n_features_in_")int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Only defined if the underlying estimators expose such an attribute when fit. .. versionadded:: 1.0
See also
[`VotingRegressor`](sklearn.ensemble.votingregressor#sklearn.ensemble.VotingRegressor "sklearn.ensemble.VotingRegressor")
Prediction voting regressor.
#### Examples
```
>>> import numpy as np
>>> from sklearn.linear_model import LogisticRegression
>>> from sklearn.naive_bayes import GaussianNB
>>> from sklearn.ensemble import RandomForestClassifier, VotingClassifier
>>> clf1 = LogisticRegression(multi_class='multinomial', random_state=1)
>>> clf2 = RandomForestClassifier(n_estimators=50, random_state=1)
>>> clf3 = GaussianNB()
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> y = np.array([1, 1, 1, 2, 2, 2])
>>> eclf1 = VotingClassifier(estimators=[
... ('lr', clf1), ('rf', clf2), ('gnb', clf3)], voting='hard')
>>> eclf1 = eclf1.fit(X, y)
>>> print(eclf1.predict(X))
[1 1 1 2 2 2]
>>> np.array_equal(eclf1.named_estimators_.lr.predict(X),
... eclf1.named_estimators_['lr'].predict(X))
True
>>> eclf2 = VotingClassifier(estimators=[
... ('lr', clf1), ('rf', clf2), ('gnb', clf3)],
... voting='soft')
>>> eclf2 = eclf2.fit(X, y)
>>> print(eclf2.predict(X))
[1 1 1 2 2 2]
```
To drop an estimator, [`set_params`](#sklearn.ensemble.VotingClassifier.set_params "sklearn.ensemble.VotingClassifier.set_params") can be used to remove it. Here we dropped one of the estimators, resulting in 2 fitted estimators:
```
>>> eclf2 = eclf2.set_params(lr='drop')
>>> eclf2 = eclf2.fit(X, y)
>>> len(eclf2.estimators_)
2
```
Setting `flatten_transform=True` with `voting='soft'` flattens output shape of `transform`:
```
>>> eclf3 = VotingClassifier(estimators=[
... ('lr', clf1), ('rf', clf2), ('gnb', clf3)],
... voting='soft', weights=[2,1,1],
... flatten_transform=True)
>>> eclf3 = eclf3.fit(X, y)
>>> print(eclf3.predict(X))
[1 1 1 2 2 2]
>>> print(eclf3.transform(X).shape)
(6, 6)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.ensemble.VotingClassifier.fit "sklearn.ensemble.VotingClassifier.fit")(X, y[, sample\_weight]) | Fit the estimators. |
| [`fit_transform`](#sklearn.ensemble.VotingClassifier.fit_transform "sklearn.ensemble.VotingClassifier.fit_transform")(X[, y]) | Return class labels or probabilities for each estimator. |
| [`get_feature_names_out`](#sklearn.ensemble.VotingClassifier.get_feature_names_out "sklearn.ensemble.VotingClassifier.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.ensemble.VotingClassifier.get_params "sklearn.ensemble.VotingClassifier.get_params")([deep]) | Get the parameters of an estimator from the ensemble. |
| [`predict`](#sklearn.ensemble.VotingClassifier.predict "sklearn.ensemble.VotingClassifier.predict")(X) | Predict class labels for X. |
| [`predict_proba`](#sklearn.ensemble.VotingClassifier.predict_proba "sklearn.ensemble.VotingClassifier.predict_proba")(X) | Compute probabilities of possible outcomes for samples in X. |
| [`score`](#sklearn.ensemble.VotingClassifier.score "sklearn.ensemble.VotingClassifier.score")(X, y[, sample\_weight]) | Return the mean accuracy on the given test data and labels. |
| [`set_params`](#sklearn.ensemble.VotingClassifier.set_params "sklearn.ensemble.VotingClassifier.set_params")(\*\*params) | Set the parameters of an estimator from the ensemble. |
| [`transform`](#sklearn.ensemble.VotingClassifier.transform "sklearn.ensemble.VotingClassifier.transform")(X) | Return class labels or probabilities for X for each estimator. |
fit(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_voting.py#L306)
Fit the estimators.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vectors, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**array-like of shape (n\_samples,)
Target values.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights. If None, then samples are equally weighted. Note that this is supported only if all underlying estimators support sample weights.
New in version 0.18.
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*, *\*\*fit\_params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_voting.py#L109)
Return class labels or probabilities for each estimator.
Return predictions for X for each estimator.
Parameters:
**X**{array-like, sparse matrix, dataframe} of shape (n\_samples, n\_features)
Input samples.
**y**ndarray of shape (n\_samples,), default=None
Target values (None for unsupervised transformations).
**\*\*fit\_params**dict
Additional fit parameters.
Returns:
**X\_new**ndarray array of shape (n\_samples, n\_features\_new)
Transformed array.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_voting.py#L445)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Not used, present here for API consistency by convention.
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_base.py#L310)
Get the parameters of an estimator from the ensemble.
Returns the parameters given in the constructor as well as the estimators contained within the `estimators` parameter.
Parameters:
**deep**bool, default=True
Setting it to True gets the various estimators and the parameters of the estimators as well.
Returns:
**params**dict
Parameter and estimator names mapped to their values or parameter names mapped to their values.
*property*n\_features\_in\_
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
*property*named\_estimators
Dictionary to access any fitted sub-estimators by name.
Returns:
[`Bunch`](sklearn.utils.bunch#sklearn.utils.Bunch "sklearn.utils.Bunch")
predict(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_voting.py#L353)
Predict class labels for X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples.
Returns:
**maj**array-like of shape (n\_samples,)
Predicted class labels.
predict\_proba(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_voting.py#L393)
Compute probabilities of possible outcomes for samples in X.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
The input samples.
Returns:
**avg**array-like of shape (n\_samples, n\_classes)
Weighted average probability for each class per sample.
score(*X*, *y*, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L640)
Return the mean accuracy on the given test data and labels.
In multi-label classification, this is the subset accuracy which is a harsh metric since you require for each sample that each label set be correctly predicted.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Test samples.
**y**array-like of shape (n\_samples,) or (n\_samples, n\_outputs)
True labels for `X`.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**score**float
Mean accuracy of `self.predict(X)` wrt. `y`.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_base.py#L285)
Set the parameters of an estimator from the ensemble.
Valid parameter keys can be listed with `get_params()`. Note that you can directly set the parameters of the estimators contained in `estimators`.
Parameters:
**\*\*params**keyword arguments
Specific parameters using e.g. `set_params(parameter_name=new_value)`. In addition, to setting the parameters of the estimator, the individual estimator of the estimators can also be set, or can be removed by setting them to ‘drop’.
Returns:
**self**object
Estimator instance.
transform(*X*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/ensemble/_voting.py#L413)
Return class labels or probabilities for X for each estimator.
Parameters:
**X**{array-like, sparse matrix} of shape (n\_samples, n\_features)
Training vectors, where `n_samples` is the number of samples and `n_features` is the number of features.
Returns:
probabilities\_or\_labels
If `voting='soft'` and `flatten_transform=True`:
returns ndarray of shape (n\_samples, n\_classifiers \* n\_classes), being class probabilities calculated by each classifier.
If `voting='soft' and `flatten_transform=False`:
ndarray of shape (n\_classifiers, n\_samples, n\_classes)
If `voting='hard'`:
ndarray of shape (n\_samples, n\_classifiers), being class labels predicted by each classifier.
Examples using `sklearn.ensemble.VotingClassifier`
--------------------------------------------------
[Plot class probabilities calculated by the VotingClassifier](../../auto_examples/ensemble/plot_voting_probas#sphx-glr-auto-examples-ensemble-plot-voting-probas-py)
[Plot the decision boundaries of a VotingClassifier](../../auto_examples/ensemble/plot_voting_decision_regions#sphx-glr-auto-examples-ensemble-plot-voting-decision-regions-py)
| programming_docs |
scikit_learn sklearn.metrics.coverage_error sklearn.metrics.coverage\_error
===============================
sklearn.metrics.coverage\_error(*y\_true*, *y\_score*, *\**, *sample\_weight=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_ranking.py#L1118)
Coverage error measure.
Compute how far we need to go through the ranked scores to cover all true labels. The best value is equal to the average number of labels in `y_true` per sample.
Ties in `y_scores` are broken by giving maximal rank that would have been assigned to all tied values.
Note: Our implementation’s score is 1 greater than the one given in Tsoumakas et al., 2010. This extends it to handle the degenerate case in which an instance has 0 true labels.
Read more in the [User Guide](../model_evaluation#coverage-error).
Parameters:
**y\_true**ndarray of shape (n\_samples, n\_labels)
True binary labels in binary indicator format.
**y\_score**ndarray of shape (n\_samples, n\_labels)
Target scores, can either be probability estimates of the positive class, confidence values, or non-thresholded measure of decisions (as returned by “decision\_function” on some classifiers).
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
Returns:
**coverage\_error**float
#### References
[1] Tsoumakas, G., Katakis, I., & Vlahavas, I. (2010). Mining multi-label data. In Data mining and knowledge discovery handbook (pp. 667-685). Springer US.
scikit_learn sklearn.decomposition.FastICA sklearn.decomposition.FastICA
=============================
*class*sklearn.decomposition.FastICA(*n\_components=None*, *\**, *algorithm='parallel'*, *whiten='warn'*, *fun='logcosh'*, *fun\_args=None*, *max\_iter=200*, *tol=0.0001*, *w\_init=None*, *random\_state=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_fastica.py#L323)
FastICA: a fast algorithm for Independent Component Analysis.
The implementation is based on [[1]](#r44c805292efc-1).
Read more in the [User Guide](../decomposition#ica).
Parameters:
**n\_components**int, default=None
Number of components to use. If None is passed, all are used.
**algorithm**{‘parallel’, ‘deflation’}, default=’parallel’
Specify which algorithm to use for FastICA.
**whiten**str or bool, default=”warn”
Specify the whitening strategy to use.
* If ‘arbitrary-variance’ (default), a whitening with variance arbitrary is used.
* If ‘unit-variance’, the whitening matrix is rescaled to ensure that each recovered source has unit variance.
* If False, the data is already considered to be whitened, and no whitening is performed.
Deprecated since version 1.1: Starting in v1.3, `whiten='unit-variance'` will be used by default. `whiten=True` is deprecated from 1.1 and will raise ValueError in 1.3. Use `whiten=arbitrary-variance` instead.
**fun**{‘logcosh’, ‘exp’, ‘cube’} or callable, default=’logcosh’
The functional form of the G function used in the approximation to neg-entropy. Could be either ‘logcosh’, ‘exp’, or ‘cube’. You can also provide your own function. It should return a tuple containing the value of the function, and of its derivative, in the point. The derivative should be averaged along its last dimension. Example:
```
def my_g(x):
return x ** 3, (3 * x ** 2).mean(axis=-1)
```
**fun\_args**dict, default=None
Arguments to send to the functional form. If empty or None and if fun=’logcosh’, fun\_args will take value {‘alpha’ : 1.0}.
**max\_iter**int, default=200
Maximum number of iterations during fit.
**tol**float, default=1e-4
A positive scalar giving the tolerance at which the un-mixing matrix is considered to have converged.
**w\_init**ndarray of shape (n\_components, n\_components), default=None
Initial un-mixing array. If `w_init=None`, then an array of values drawn from a normal distribution is used.
**random\_state**int, RandomState instance or None, default=None
Used to initialize `w_init` when not specified, with a normal distribution. Pass an int, for reproducible results across multiple function calls. See [Glossary](https://scikit-learn.org/1.1/glossary.html#term-random_state).
Attributes:
**components\_**ndarray of shape (n\_components, n\_features)
The linear operator to apply to the data to get the independent sources. This is equal to the unmixing matrix when `whiten` is False, and equal to `np.dot(unmixing_matrix, self.whitening_)` when `whiten` is True.
**mixing\_**ndarray of shape (n\_features, n\_components)
The pseudo-inverse of `components_`. It is the linear operator that maps independent sources to the data.
**mean\_**ndarray of shape(n\_features,)
The mean over features. Only set if `self.whiten` is True.
**n\_features\_in\_**int
Number of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit).
New in version 0.24.
**feature\_names\_in\_**ndarray of shape (`n_features_in_`,)
Names of features seen during [fit](https://scikit-learn.org/1.1/glossary.html#term-fit). Defined only when `X` has feature names that are all strings.
New in version 1.0.
**n\_iter\_**int
If the algorithm is “deflation”, n\_iter is the maximum number of iterations run across all components. Else they are just the number of iterations taken to converge.
**whitening\_**ndarray of shape (n\_components, n\_features)
Only set if whiten is ‘True’. This is the pre-whitening matrix that projects data onto the first `n_components` principal components.
See also
[`PCA`](sklearn.decomposition.pca#sklearn.decomposition.PCA "sklearn.decomposition.PCA")
Principal component analysis (PCA).
[`IncrementalPCA`](sklearn.decomposition.incrementalpca#sklearn.decomposition.IncrementalPCA "sklearn.decomposition.IncrementalPCA")
Incremental principal components analysis (IPCA).
[`KernelPCA`](sklearn.decomposition.kernelpca#sklearn.decomposition.KernelPCA "sklearn.decomposition.KernelPCA")
Kernel Principal component analysis (KPCA).
[`MiniBatchSparsePCA`](sklearn.decomposition.minibatchsparsepca#sklearn.decomposition.MiniBatchSparsePCA "sklearn.decomposition.MiniBatchSparsePCA")
Mini-batch Sparse Principal Components Analysis.
[`SparsePCA`](sklearn.decomposition.sparsepca#sklearn.decomposition.SparsePCA "sklearn.decomposition.SparsePCA")
Sparse Principal Components Analysis (SparsePCA).
#### References
[[1](#id1)] A. Hyvarinen and E. Oja, Independent Component Analysis: Algorithms and Applications, Neural Networks, 13(4-5), 2000, pp. 411-430.
#### Examples
```
>>> from sklearn.datasets import load_digits
>>> from sklearn.decomposition import FastICA
>>> X, _ = load_digits(return_X_y=True)
>>> transformer = FastICA(n_components=7,
... random_state=0,
... whiten='unit-variance')
>>> X_transformed = transformer.fit_transform(X)
>>> X_transformed.shape
(1797, 7)
```
#### Methods
| | |
| --- | --- |
| [`fit`](#sklearn.decomposition.FastICA.fit "sklearn.decomposition.FastICA.fit")(X[, y]) | Fit the model to X. |
| [`fit_transform`](#sklearn.decomposition.FastICA.fit_transform "sklearn.decomposition.FastICA.fit_transform")(X[, y]) | Fit the model and recover the sources from X. |
| [`get_feature_names_out`](#sklearn.decomposition.FastICA.get_feature_names_out "sklearn.decomposition.FastICA.get_feature_names_out")([input\_features]) | Get output feature names for transformation. |
| [`get_params`](#sklearn.decomposition.FastICA.get_params "sklearn.decomposition.FastICA.get_params")([deep]) | Get parameters for this estimator. |
| [`inverse_transform`](#sklearn.decomposition.FastICA.inverse_transform "sklearn.decomposition.FastICA.inverse_transform")(X[, copy]) | Transform the sources back to the mixed data (apply mixing matrix). |
| [`set_params`](#sklearn.decomposition.FastICA.set_params "sklearn.decomposition.FastICA.set_params")(\*\*params) | Set the parameters of this estimator. |
| [`transform`](#sklearn.decomposition.FastICA.transform "sklearn.decomposition.FastICA.transform")(X[, copy]) | Recover the sources from X (apply the unmixing matrix). |
fit(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_fastica.py#L662)
Fit the model to X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**self**object
Returns the instance itself.
fit\_transform(*X*, *y=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_fastica.py#L642)
Fit the model and recover the sources from X.
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Training data, where `n_samples` is the number of samples and `n_features` is the number of features.
**y**Ignored
Not used, present for API consistency by convention.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_components)
Estimated sources obtained by transforming the data with the estimated unmixing matrix.
get\_feature\_names\_out(*input\_features=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L909)
Get output feature names for transformation.
Parameters:
**input\_features**array-like of str or None, default=None
Only used to validate feature names with the names seen in [`fit`](#sklearn.decomposition.FastICA.fit "sklearn.decomposition.FastICA.fit").
Returns:
**feature\_names\_out**ndarray of str objects
Transformed feature names.
get\_params(*deep=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L194)
Get parameters for this estimator.
Parameters:
**deep**bool, default=True
If True, will return the parameters for this estimator and contained subobjects that are estimators.
Returns:
**params**dict
Parameter names mapped to their values.
inverse\_transform(*X*, *copy=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_fastica.py#L710)
Transform the sources back to the mixed data (apply mixing matrix).
Parameters:
**X**array-like of shape (n\_samples, n\_components)
Sources, where `n_samples` is the number of samples and `n_components` is the number of components.
**copy**bool, default=True
If False, data passed to fit are overwritten. Defaults to True.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_features)
Reconstructed data obtained with the mixing matrix.
set\_params(*\*\*params*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/base.py#L218)
Set the parameters of this estimator.
The method works on simple estimators as well as on nested objects (such as [`Pipeline`](sklearn.pipeline.pipeline#sklearn.pipeline.Pipeline "sklearn.pipeline.Pipeline")). The latter have parameters of the form `<component>__<parameter>` so that it’s possible to update each component of a nested object.
Parameters:
**\*\*params**dict
Estimator parameters.
Returns:
**self**estimator instance
Estimator instance.
transform(*X*, *copy=True*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/decomposition/_fastica.py#L682)
Recover the sources from X (apply the unmixing matrix).
Parameters:
**X**array-like of shape (n\_samples, n\_features)
Data to transform, where `n_samples` is the number of samples and `n_features` is the number of features.
**copy**bool, default=True
If False, data passed to fit can be overwritten. Defaults to True.
Returns:
**X\_new**ndarray of shape (n\_samples, n\_components)
Estimated sources obtained by transforming the data with the estimated unmixing matrix.
Examples using `sklearn.decomposition.FastICA`
----------------------------------------------
[Blind source separation using FastICA](../../auto_examples/decomposition/plot_ica_blind_source_separation#sphx-glr-auto-examples-decomposition-plot-ica-blind-source-separation-py)
[Faces dataset decompositions](../../auto_examples/decomposition/plot_faces_decomposition#sphx-glr-auto-examples-decomposition-plot-faces-decomposition-py)
[FastICA on 2D point clouds](../../auto_examples/decomposition/plot_ica_vs_pca#sphx-glr-auto-examples-decomposition-plot-ica-vs-pca-py)
scikit_learn sklearn.utils.extmath.density sklearn.utils.extmath.density
=============================
sklearn.utils.extmath.density(*w*, *\*\*kwargs*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/extmath.py#L99)
Compute density of a sparse vector.
Parameters:
**w**array-like
The sparse vector.
Returns:
float
The density of w, between 0 and 1.
Examples using `sklearn.utils.extmath.density`
----------------------------------------------
[Classification of text documents using sparse features](../../auto_examples/text/plot_document_classification_20newsgroups#sphx-glr-auto-examples-text-plot-document-classification-20newsgroups-py)
scikit_learn sklearn.utils.sparsefuncs.incr_mean_variance_axis sklearn.utils.sparsefuncs.incr\_mean\_variance\_axis
====================================================
sklearn.utils.sparsefuncs.incr\_mean\_variance\_axis(*X*, *\**, *axis*, *last\_mean*, *last\_var*, *last\_n*, *weights=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/utils/sparsefuncs.py#L128)
Compute incremental mean and variance along an axis on a CSR or CSC matrix.
last\_mean, last\_var are the statistics computed at the last step by this function. Both must be initialized to 0-arrays of the proper size, i.e. the number of features in X. last\_n is the number of samples encountered until now.
Parameters:
**X**CSR or CSC sparse matrix of shape (n\_samples, n\_features)
Input data.
**axis**{0, 1}
Axis along which the axis should be computed.
**last\_mean**ndarray of shape (n\_features,) or (n\_samples,), dtype=floating
Array of means to update with the new data X. Should be of shape (n\_features,) if axis=0 or (n\_samples,) if axis=1.
**last\_var**ndarray of shape (n\_features,) or (n\_samples,), dtype=floating
Array of variances to update with the new data X. Should be of shape (n\_features,) if axis=0 or (n\_samples,) if axis=1.
**last\_n**float or ndarray of shape (n\_features,) or (n\_samples,), dtype=floating
Sum of the weights seen so far, excluding the current weights If not float, it should be of shape (n\_samples,) if axis=0 or (n\_features,) if axis=1. If float it corresponds to having same weights for all samples (or features).
**weights**ndarray of shape (n\_samples,) or (n\_features,), default=None
If axis is set to 0 shape is (n\_samples,) or if axis is set to 1 shape is (n\_features,). If it is set to None, then samples are equally weighted.
New in version 0.24.
Returns:
**means**ndarray of shape (n\_features,) or (n\_samples,), dtype=floating
Updated feature-wise means if axis = 0 or sample-wise means if axis = 1.
**variances**ndarray of shape (n\_features,) or (n\_samples,), dtype=floating
Updated feature-wise variances if axis = 0 or sample-wise variances if axis = 1.
**n**ndarray of shape (n\_features,) or (n\_samples,), dtype=integral
Updated number of seen samples per feature if axis=0 or number of seen features per sample if axis=1.
If weights is not None, n is a sum of the weights of the seen samples or features instead of the actual number of seen samples or features.
#### Notes
NaNs are ignored in the algorithm.
scikit_learn sklearn.feature_extraction.image.grid_to_graph sklearn.feature\_extraction.image.grid\_to\_graph
=================================================
sklearn.feature\_extraction.image.grid\_to\_graph(*n\_x*, *n\_y*, *n\_z=1*, *\**, *mask=None*, *return\_as=<class 'scipy.sparse.\_coo.coo\_matrix'>*, *dtype=<class 'int'>*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/feature_extraction/image.py#L182)
Graph of the pixel-to-pixel connections.
Edges exist if 2 voxels are connected.
Parameters:
**n\_x**int
Dimension in x axis.
**n\_y**int
Dimension in y axis.
**n\_z**int, default=1
Dimension in z axis.
**mask**ndarray of shape (n\_x, n\_y, n\_z), dtype=bool, default=None
An optional mask of the image, to consider only part of the pixels.
**return\_as**np.ndarray or a sparse matrix class, default=sparse.coo\_matrix
The class to use to build the returned adjacency matrix.
**dtype**dtype, default=int
The data of the returned sparse matrix. By default it is int.
Returns:
**graph**np.ndarray or a sparse matrix class
The computed adjacency matrix.
#### Notes
For scikit-learn versions 0.14.1 and prior, return\_as=np.ndarray was handled by returning a dense np.matrix instance. Going forward, np.ndarray returns an np.ndarray, as expected.
For compatibility, user code relying on this method should wrap its calls in `np.asarray` to avoid type issues.
scikit_learn sklearn.metrics.confusion_matrix sklearn.metrics.confusion\_matrix
=================================
sklearn.metrics.confusion\_matrix(*y\_true*, *y\_pred*, *\**, *labels=None*, *sample\_weight=None*, *normalize=None*)[[source]](https://github.com/scikit-learn/scikit-learn/blob/f3f51f9b6/sklearn/metrics/_classification.py#L222)
Compute confusion matrix to evaluate the accuracy of a classification.
By definition a confusion matrix \(C\) is such that \(C\_{i, j}\) is equal to the number of observations known to be in group \(i\) and predicted to be in group \(j\).
Thus in binary classification, the count of true negatives is \(C\_{0,0}\), false negatives is \(C\_{1,0}\), true positives is \(C\_{1,1}\) and false positives is \(C\_{0,1}\).
Read more in the [User Guide](../model_evaluation#confusion-matrix).
Parameters:
**y\_true**array-like of shape (n\_samples,)
Ground truth (correct) target values.
**y\_pred**array-like of shape (n\_samples,)
Estimated targets as returned by a classifier.
**labels**array-like of shape (n\_classes), default=None
List of labels to index the matrix. This may be used to reorder or select a subset of labels. If `None` is given, those that appear at least once in `y_true` or `y_pred` are used in sorted order.
**sample\_weight**array-like of shape (n\_samples,), default=None
Sample weights.
New in version 0.18.
**normalize**{‘true’, ‘pred’, ‘all’}, default=None
Normalizes confusion matrix over the true (rows), predicted (columns) conditions or all the population. If None, confusion matrix will not be normalized.
Returns:
**C**ndarray of shape (n\_classes, n\_classes)
Confusion matrix whose i-th row and j-th column entry indicates the number of samples with true label being i-th class and predicted label being j-th class.
See also
[`ConfusionMatrixDisplay.from_estimator`](sklearn.metrics.confusionmatrixdisplay#sklearn.metrics.ConfusionMatrixDisplay.from_estimator "sklearn.metrics.ConfusionMatrixDisplay.from_estimator")
Plot the confusion matrix given an estimator, the data, and the label.
[`ConfusionMatrixDisplay.from_predictions`](sklearn.metrics.confusionmatrixdisplay#sklearn.metrics.ConfusionMatrixDisplay.from_predictions "sklearn.metrics.ConfusionMatrixDisplay.from_predictions")
Plot the confusion matrix given the true and predicted labels.
[`ConfusionMatrixDisplay`](sklearn.metrics.confusionmatrixdisplay#sklearn.metrics.ConfusionMatrixDisplay "sklearn.metrics.ConfusionMatrixDisplay")
Confusion Matrix visualization.
#### References
[1] [Wikipedia entry for the Confusion matrix](https://en.wikipedia.org/wiki/Confusion_matrix) (Wikipedia and other references may use a different convention for axes).
#### Examples
```
>>> from sklearn.metrics import confusion_matrix
>>> y_true = [2, 0, 2, 2, 0, 1]
>>> y_pred = [0, 0, 2, 2, 0, 2]
>>> confusion_matrix(y_true, y_pred)
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
```
```
>>> y_true = ["cat", "ant", "cat", "cat", "ant", "bird"]
>>> y_pred = ["ant", "ant", "cat", "cat", "ant", "cat"]
>>> confusion_matrix(y_true, y_pred, labels=["ant", "bird", "cat"])
array([[2, 0, 0],
[0, 0, 1],
[1, 0, 2]])
```
In the binary case, we can extract true positives, etc as follows:
```
>>> tn, fp, fn, tp = confusion_matrix([0, 1, 0, 1], [1, 1, 1, 0]).ravel()
>>> (tn, fp, fn, tp)
(0, 2, 1, 1)
```
Examples using `sklearn.metrics.confusion_matrix`
-------------------------------------------------
[Visualizations with Display Objects](../../auto_examples/miscellaneous/plot_display_object_visualization#sphx-glr-auto-examples-miscellaneous-plot-display-object-visualization-py)
[Label Propagation digits active learning](../../auto_examples/semi_supervised/plot_label_propagation_digits_active_learning#sphx-glr-auto-examples-semi-supervised-plot-label-propagation-digits-active-learning-py)
| programming_docs |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.