Datasets:

vikp
/

clean_notebooks

Dataset card Data Studio Files Files and versions Community

Split (1)

train · 1.01M rows

code stringlengths 2.5k 150k	kind stringclasses 1 value
statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.cov_params_oim statsmodels.regression.recursive\_ls.RecursiveLSResults.cov\_params\_oim ======================================================================== `RecursiveLSResults.cov_params_oim()` (array) The variance / covariance matrix. Computed using the method from Harvey (1989). statsmodels statsmodels.regression.linear_model.OLSResults.compare_f_test statsmodels.regression.linear\_model.OLSResults.compare\_f\_test ================================================================ `OLSResults.compare_f_test(restricted)` use F test to test whether restricted model is correct \| Parameters: \| restricted (Result instance) – The restricted model is assumed to be nested in the current model. The result instance of the restricted model is required to have two attributes, residual sum of squares, `ssr`, residual degrees of freedom, `df_resid`. \| \| Returns: \| * f\_value (float) – test statistic, F distributed * p\_value (float) – p-value of the test statistic * df\_diff (int) – degrees of freedom of the restriction, i.e. difference in df between models \| #### Notes See mailing list discussion October 17, This test compares the residual sum of squares of the two models. This is not a valid test, if there is unspecified heteroscedasticity or correlation. This method will issue a warning if this is detected but still return the results under the assumption of homoscedasticity and no autocorrelation (sphericity). statsmodels statsmodels.graphics.gofplots.qqline statsmodels.graphics.gofplots.qqline ==================================== `statsmodels.graphics.gofplots.qqline(ax, line, x=None, y=None, dist=None, fmt='r-')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/graphics/gofplots.html#qqline) Plot a reference line for a qqplot. \| Parameters: \| * ax (matplotlib axes instance) – The axes on which to plot the line * line (str {'45','r','s','q'}) – Options for the reference line to which the data is compared.: + ‘45’ - 45-degree line + ’s‘ - standardized line, the expected order statistics are scaled by the standard deviation of the given sample and have the mean added to them + ’r’ - A regression line is fit + ’q’ - A line is fit through the quartiles. + None - By default no reference line is added to the plot. * x (array) – X data for plot. Not needed if line is ‘45’. * y (array) – Y data for plot. Not needed if line is ‘45’. * dist (scipy.stats.distribution) – A scipy.stats distribution, needed if line is ‘q’. \| #### Notes There is no return value. The line is plotted on the given `ax`. statsmodels statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.vb_elbo_base statsmodels.genmod.bayes\_mixed\_glm.PoissonBayesMixedGLM.vb\_elbo\_base ======================================================================== `PoissonBayesMixedGLM.vb_elbo_base(h, tm, fep_mean, vcp_mean, vc_mean, fep_sd, vcp_sd, vc_sd)` Returns the evidence lower bound (ELBO) for the model. This function calculates the family-specific ELBO function based on information provided from a subclass. \| Parameters: \| h (function mapping 1d vector to 1d vector) – The contribution of the model to the ELBO function can be expressed as y\_i\lp\_i + Eh\_i(z), where y\_i and lp\_i are the response and linear predictor for observation i, and z is a standard normal rangom variable. This formulation can be achieved for any GLM with a canonical link function. \| statsmodels statsmodels.emplike.descriptive.DescStatMV.mv_mean_contour statsmodels.emplike.descriptive.DescStatMV.mv\_mean\_contour ============================================================ `DescStatMV.mv_mean_contour(mu1_low, mu1_upp, mu2_low, mu2_upp, step1, step2, levs=(0.001, 0.01, 0.05, 0.1, 0.2), var1_name=None, var2_name=None, plot_dta=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/emplike/descriptive.html#DescStatMV.mv_mean_contour) Creates a confidence region plot for the mean of bivariate data \| Parameters: \| m1\_low (float) – Minimum value of the mean for variable 1 * m1\_upp (float) – Maximum value of the mean for variable 1 * mu2\_low (float) – Minimum value of the mean for variable 2 * mu2\_upp (float) – Maximum value of the mean for variable 2 * step1 (float) – Increment of evaluations for variable 1 * step2 (float) – Increment of evaluations for variable 2 * levs (list) – Levels to be drawn on the contour plot. Default = (.001, .01, .05, .1, .2) * plot\_dta (bool) – If True, makes a scatter plot of the data on top of the contour plot. Defaultis False. * var1\_name (str) – Name of variable 1 to be plotted on the x-axis * var2\_name (str) – Name of variable 2 to be plotted on the y-axis \| #### Notes The smaller the step size, the more accurate the intervals will be If the function returns optimization failed, consider narrowing the boundaries of the plot #### Examples ``` >>> import statsmodels.api as sm >>> two_rvs = np.random.standard_normal((20,2)) >>> el_analysis = sm.emplike.DescStat(two_rvs) >>> contourp = el_analysis.mv_mean_contour(-2, 2, -2, 2, .1, .1) >>> contourp.show() ``` statsmodels statsmodels.tsa.statespace.mlemodel.MLEResults.simulate statsmodels.tsa.statespace.mlemodel.MLEResults.simulate ======================================================= `MLEResults.simulate(nsimulations, measurement_shocks=None, state_shocks=None, initial_state=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/mlemodel.html#MLEResults.simulate) Simulate a new time series following the state space model \| Parameters: \| * nsimulations (int) – The number of observations to simulate. If the model is time-invariant this can be any number. If the model is time-varying, then this number must be less than or equal to the number * measurement\_shocks (array\_like, optional) – If specified, these are the shocks to the measurement equation, $\varepsilon\_t$. If unspecified, these are automatically generated using a pseudo-random number generator. If specified, must be shaped `nsimulations` x `k_endog`, where `k_endog` is the same as in the state space model. * state\_shocks (array\_like, optional) – If specified, these are the shocks to the state equation, $\eta\_t$. If unspecified, these are automatically generated using a pseudo-random number generator. If specified, must be shaped `nsimulations` x `k_posdef` where `k_posdef` is the same as in the state space model. * initial\_state (array\_like, optional) – If specified, this is the state vector at time zero, which should be shaped (`k_states` x 1), where `k_states` is the same as in the state space model. If unspecified, but the model has been initialized, then that initialization is used. If unspecified and the model has not been initialized, then a vector of zeros is used. Note that this is not included in the returned `simulated_states` array. \| \| Returns: \| simulated\_obs – An (nsimulations x k\_endog) array of simulated observations. \| \| Return type: \| array \| statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.forecast statsmodels.tsa.vector\_ar.var\_model.VARResults.forecast ========================================================= `VARResults.forecast(y, steps, exog_future=None)` Produce linear minimum MSE forecasts for desired number of steps ahead, using prior values y \| Parameters: \| * y (ndarray (p x k)) – * steps (int) – \| \| Returns: \| forecasts \| \| Return type: \| ndarray (steps x neqs) \| #### Notes Lütkepohl pp 37-38 statsmodels statsmodels.tsa.regime_switching.markov_regression.MarkovRegression.score statsmodels.tsa.regime\_switching.markov\_regression.MarkovRegression.score =========================================================================== `MarkovRegression.score(params, transformed=True)` Compute the score function at params. \| Parameters: \| * params (array\_like) – Array of parameters at which to evaluate the score function. * transformed (boolean, optional) – Whether or not `params` is already transformed. Default is True. \| statsmodels statsmodels.sandbox.distributions.transformed.TransfTwo_gen.moment statsmodels.sandbox.distributions.transformed.TransfTwo\_gen.moment =================================================================== `TransfTwo_gen.moment(n, args, kwds)` n-th order non-central moment of distribution. \| Parameters: \| n (int, n >= 1) – Order of moment. * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information). * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| statsmodels statsmodels.sandbox.distributions.extras.SkewNorm_gen.logsf statsmodels.sandbox.distributions.extras.SkewNorm\_gen.logsf ============================================================ `SkewNorm_gen.logsf(x, args, kwds)` Log of the survival function of the given RV. Returns the log of the “survival function,” defined as (1 - `cdf`), evaluated at `x`. \| Parameters: \| x (array\_like) – quantiles * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| logsf – Log of the survival function evaluated at `x`. \| \| Return type: \| ndarray \| statsmodels statsmodels.tsa.arima_model.ARMAResults.tvalues statsmodels.tsa.arima\_model.ARMAResults.tvalues ================================================ `ARMAResults.tvalues()` Return the t-statistic for a given parameter estimate. statsmodels statsmodels.genmod.generalized_linear_model.GLMResults.normalized_cov_params statsmodels.genmod.generalized\_linear\_model.GLMResults.normalized\_cov\_params ================================================================================ `GLMResults.normalized_cov_params()` statsmodels statsmodels.genmod.families.links.CDFLink.deriv2 statsmodels.genmod.families.links.CDFLink.deriv2 ================================================ `CDFLink.deriv2(p)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#CDFLink.deriv2) Second derivative of the link function g’‘(p) implemented through numerical differentiation statsmodels statsmodels.sandbox.distributions.extras.NormExpan_gen.stats statsmodels.sandbox.distributions.extras.NormExpan\_gen.stats ============================================================= `NormExpan_gen.stats(args, kwds)` Some statistics of the given RV. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional (continuous RVs only)) – scale parameter (default=1) * moments (str, optional) – composed of letters [‘mvsk’] defining which moments to compute: ‘m’ = mean, ‘v’ = variance, ‘s’ = (Fisher’s) skew, ‘k’ = (Fisher’s) kurtosis. (default is ‘mv’) \| \| Returns: \| stats – of requested moments. \| \| Return type: \| sequence \| statsmodels statsmodels.tsa.holtwinters.ExponentialSmoothing.from_formula statsmodels.tsa.holtwinters.ExponentialSmoothing.from\_formula ============================================================== `classmethod ExponentialSmoothing.from_formula(formula, data, subset=None, drop_cols=None, args, kwargs)` Create a Model from a formula and dataframe. \| Parameters: \| formula (str or generic Formula object) – The formula specifying the model * data (array-like) – The data for the model. See Notes. * subset (array-like) – An array-like object of booleans, integers, or index values that indicate the subset of df to use in the model. Assumes df is a `pandas.DataFrame` * drop\_cols (array-like) – Columns to drop from the design matrix. Cannot be used to drop terms involving categoricals. * args (extra arguments) – These are passed to the model * kwargs (extra keyword arguments) – These are passed to the model with one exception. The `eval_env` keyword is passed to patsy. It can be either a [`patsy.EvalEnvironment`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.EvalEnvironment "(in patsy v0.5.0+dev)") object or an integer indicating the depth of the namespace to use. For example, the default `eval_env=0` uses the calling namespace. If you wish to use a “clean” environment set `eval_env=-1`. \| \| Returns: \| model \| \| Return type: \| Model instance \| #### Notes data must define \_\_getitem\_\_ with the keys in the formula terms args and kwargs are passed on to the model instantiation. E.g., a numpy structured or rec array, a dictionary, or a pandas DataFrame. statsmodels statsmodels.miscmodels.count.PoissonZiGMLE.score statsmodels.miscmodels.count.PoissonZiGMLE.score ================================================ `PoissonZiGMLE.score(params)` Gradient of log-likelihood evaluated at params statsmodels statsmodels.tsa.statespace.structural.UnobservedComponents.score statsmodels.tsa.statespace.structural.UnobservedComponents.score ================================================================ `UnobservedComponents.score(params, args, kwargs)` Compute the score function at params. \| Parameters: \| params (array\_like) – Array of parameters at which to evaluate the score. * args – Additional positional arguments to the `loglike` method. * kwargs – Additional keyword arguments to the `loglike` method. \| \| Returns: \| score – Score, evaluated at `params`. \| \| Return type: \| array \| #### Notes This is a numerical approximation, calculated using first-order complex step differentiation on the `loglike` method. Both \args and \\kwargs are necessary because the optimizer from `fit` must call this function and only supports passing arguments via \args (for example `scipy.optimize.fmin_l_bfgs`). statsmodels statsmodels.tsa.vector_ar.dynamic.DynamicVAR.equations statsmodels.tsa.vector\_ar.dynamic.DynamicVAR.equations ======================================================= `DynamicVAR.equations()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/dynamic.html#DynamicVAR.equations) statsmodels statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.from_formula statsmodels.discrete.count\_model.ZeroInflatedNegativeBinomialP.from\_formula ============================================================================= `classmethod ZeroInflatedNegativeBinomialP.from_formula(formula, data, subset=None, drop_cols=None, args, kwargs)` Create a Model from a formula and dataframe. \| Parameters: \| formula (str or generic Formula object) – The formula specifying the model * data (array-like) – The data for the model. See Notes. * subset (array-like) – An array-like object of booleans, integers, or index values that indicate the subset of df to use in the model. Assumes df is a `pandas.DataFrame` * drop\_cols (array-like) – Columns to drop from the design matrix. Cannot be used to drop terms involving categoricals. * args (extra arguments) – These are passed to the model * kwargs (extra keyword arguments) – These are passed to the model with one exception. The `eval_env` keyword is passed to patsy. It can be either a [`patsy.EvalEnvironment`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.EvalEnvironment "(in patsy v0.5.0+dev)") object or an integer indicating the depth of the namespace to use. For example, the default `eval_env=0` uses the calling namespace. If you wish to use a “clean” environment set `eval_env=-1`. \| \| Returns: \| model \| \| Return type: \| Model instance \| #### Notes data must define \_\_getitem\_\_ with the keys in the formula terms args and kwargs are passed on to the model instantiation. E.g., a numpy structured or rec array, a dictionary, or a pandas DataFrame. statsmodels statsmodels.genmod.families.family.NegativeBinomial.loglike statsmodels.genmod.families.family.NegativeBinomial.loglike =========================================================== `NegativeBinomial.loglike(endog, mu, var_weights=1.0, freq_weights=1.0, scale=1.0)` The log-likelihood function in terms of the fitted mean response. \| Parameters: \| * endog (array) – Usually the endogenous response variable. * mu (array) – Usually but not always the fitted mean response variable. * var\_weights (array-like) – 1d array of variance (analytic) weights. The default is 1. * freq\_weights (array-like) – 1d array of frequency weights. The default is 1. * scale (float) – The scale parameter. The default is 1. \| \| Returns: \| ll – The value of the loglikelihood evaluated at (endog, mu, var\_weights, freq\_weights, scale) as defined below. \| \| Return type: \| float \| #### Notes Where $ll\_i$ is the by-observation log-likelihood: \[ll = \sum(ll\_i \* freq\\_weights\_i)\] `ll_i` is defined for each family. endog and mu are not restricted to `endog` and `mu` respectively. For instance, you could call both `loglike(endog, endog)` and `loglike(endog, mu)` to get the log-likelihood ratio. statsmodels statsmodels.sandbox.stats.runs.runstest_2samp statsmodels.sandbox.stats.runs.runstest\_2samp ============================================== `statsmodels.sandbox.stats.runs.runstest_2samp(x, y=None, groups=None, correction=True)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/stats/runs.html#runstest_2samp) Wald-Wolfowitz runstest for two samples This tests whether two samples come from the same distribution. \| Parameters: \| * x (array\_like) – data, numeric, contains either one group, if y is also given, or both groups, if additionally a group indicator is provided * y (array\_like (optional)) – data, numeric * groups (array\_like) – group labels or indicator the data for both groups is given in a single 1-dimensional array, x. If group labels are not [0,1], then * correction (bool) – Following the SAS manual, for samplesize below 50, the test statistic is corrected by 0.5. This can be turned off with correction=False, and was included to match R, tseries, which does not use any correction. \| \| Returns: \| * z\_stat (float) – test statistic, asymptotically normally distributed * p-value (float) – p-value, reject the null hypothesis if it is below an type 1 error level, alpha . \| #### Notes Wald-Wolfowitz runs test. If there are ties, then then the test statistic and p-value that is reported, is based on the higher p-value between sorting all tied observations of the same group This test is intended for continuous distributions SAS has treatment for ties, but not clear, and sounds more complicated (minimum and maximum possible runs prevent use of argsort) (maybe it’s not so difficult, idea: add small positive noise to first one, run test, then to the other, run test, take max(?) p-value - DONE This gives not the minimum and maximum of the number of runs, but should be close. Not true, this is close to minimum but far away from maximum. maximum number of runs would use alternating groups in the ties.) Maybe adding random noise would be the better approach. SAS has exact distribution for sample size <=30, doesn’t look standard but should be easy to add. currently two-sided test only This has not been verified against a reference implementation. In a short Monte Carlo simulation where both samples are normally distribute, the test seems to be correctly sized for larger number of observations (30 or larger), but conservative (i.e. reject less often than nominal) with a sample size of 10 in each group. See also `runs_test_1samp`, [`Runs`](statsmodels.sandbox.stats.runs.runs#statsmodels.sandbox.stats.runs.Runs "statsmodels.sandbox.stats.runs.Runs"), `RunsProb`	programming_docs
statsmodels statsmodels.sandbox.tsa.fftarma.ArmaFft.acf2spdfreq statsmodels.sandbox.tsa.fftarma.ArmaFft.acf2spdfreq =================================================== `ArmaFft.acf2spdfreq(acovf, nfreq=100, w=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/tsa/fftarma.html#ArmaFft.acf2spdfreq) not really a method just for comparison, not efficient for large n or long acf this is also similarly use in tsa.stattools.periodogram with window statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.get_prediction statsmodels.tsa.statespace.dynamic\_factor.DynamicFactorResults.get\_prediction =============================================================================== `DynamicFactorResults.get_prediction(start=None, end=None, dynamic=False, index=None, exog=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/dynamic_factor.html#DynamicFactorResults.get_prediction) In-sample prediction and out-of-sample forecasting \| Parameters: \| start (int, str, or datetime, optional) – Zero-indexed observation number at which to start forecasting, ie., the first forecast is start. Can also be a date string to parse or a datetime type. Default is the the zeroth observation. * end (int, str, or datetime, optional) – Zero-indexed observation number at which to end forecasting, ie., the first forecast is start. Can also be a date string to parse or a datetime type. However, if the dates index does not have a fixed frequency, end must be an integer index if you want out of sample prediction. Default is the last observation in the sample. * exog (array\_like, optional) – If the model includes exogenous regressors, you must provide exactly enough out-of-sample values for the exogenous variables if end is beyond the last observation in the sample. * dynamic (boolean, int, str, or datetime, optional) – Integer offset relative to `start` at which to begin dynamic prediction. Can also be an absolute date string to parse or a datetime type (these are not interpreted as offsets). Prior to this observation, true endogenous values will be used for prediction; starting with this observation and continuing through the end of prediction, forecasted endogenous values will be used instead. * *\\kwargs* – Additional arguments may required for forecasting beyond the end of the sample. See `FilterResults.predict` for more details. \| \| Returns: \| forecast – Array of out of sample forecasts. \| \| Return type: \| array \| statsmodels statsmodels.tsa.vector_ar.vecm.CointRankResults statsmodels.tsa.vector\_ar.vecm.CointRankResults ================================================ `class statsmodels.tsa.vector_ar.vecm.CointRankResults(rank, neqs, test_stats, crit_vals, method='trace', signif=0.05)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/vecm.html#CointRankResults) A class for holding the results from testing the cointegration rank. \| Parameters: \| * rank (int (0 <= `rank` <= `neqs`)) – The rank to choose according to the Johansen cointegration rank test. * neqs (int) – Number of variables in the time series. * test\_stats (array-like (`rank` + 1 if `rank` < `neqs` else `rank`)) – A one-dimensional array-like object containing the test statistics of the conducted tests. * crit\_vals (array-like (`rank` +1 if `rank` < `neqs` else `rank`)) – A one-dimensional array-like object containing the critical values corresponding to the entries in the `test_stats` argument. * method (str, {`"trace"`, `"maxeig"`}, default: `"trace"`) – If `"trace"`, the trace test statistic is used. If `"maxeig"`, the maximum eigenvalue test statistic is used. * signif (float, {0.1, 0.05, 0.01}, default: 0.05) – The test’s significance level. \| #### Methods \| \| \| \| --- \| --- \| \| [`summary`](statsmodels.tsa.vector_ar.vecm.cointrankresults.summary#statsmodels.tsa.vector_ar.vecm.CointRankResults.summary "statsmodels.tsa.vector_ar.vecm.CointRankResults.summary")() \| \| statsmodels statsmodels.discrete.discrete_model.ProbitResults.resid_pearson statsmodels.discrete.discrete\_model.ProbitResults.resid\_pearson ================================================================= `ProbitResults.resid_pearson()` Pearson residuals #### Notes Pearson residuals are defined to be \[r\_j = \frac{(y - M\_jp\_j)}{\sqrt{M\_jp\_j(1-p\_j)}}\] where $p\_j=cdf(X\beta)$ and $M\_j$ is the total number of observations sharing the covariate pattern $j$. For now $M\_j$ is always set to 1. statsmodels statsmodels.regression.linear_model.OLSResults.bse statsmodels.regression.linear\_model.OLSResults.bse =================================================== `OLSResults.bse()` statsmodels statsmodels.discrete.discrete_model.NegativeBinomialP.loglikeobs statsmodels.discrete.discrete\_model.NegativeBinomialP.loglikeobs ================================================================= `NegativeBinomialP.loglikeobs(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#NegativeBinomialP.loglikeobs) Loglikelihood for observations of Generalized Negative Binomial (NB-P) model \| Parameters: \| params (array-like) – The parameters of the model. \| \| Returns: \| loglike – The log likelihood for each observation of the model evaluated at `params`. See Notes \| \| Return type: \| ndarray \| statsmodels statsmodels.genmod.generalized_linear_model.GLMResults.conf_int statsmodels.genmod.generalized\_linear\_model.GLMResults.conf\_int ================================================================== `GLMResults.conf_int(alpha=0.05, cols=None, method='default')` Returns the confidence interval of the fitted parameters. \| Parameters: \| * alpha (float, optional) – The significance level for the confidence interval. ie., The default `alpha` = .05 returns a 95% confidence interval. * cols (array-like, optional) – `cols` specifies which confidence intervals to return * method (string) – Not Implemented Yet Method to estimate the confidence\_interval. “Default” : uses self.bse which is based on inverse Hessian for MLE “hjjh” : “jac” : “boot-bse” “boot\_quant” “profile” \| \| Returns: \| conf\_int – Each row contains [lower, upper] limits of the confidence interval for the corresponding parameter. The first column contains all lower, the second column contains all upper limits. \| \| Return type: \| array \| #### Examples ``` >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> results.conf_int() array([[-5496529.48322745, -1467987.78596704], [ -177.02903529, 207.15277984], [ -0.1115811 , 0.03994274], [ -3.12506664, -0.91539297], [ -1.5179487 , -0.54850503], [ -0.56251721, 0.460309 ], [ 798.7875153 , 2859.51541392]]) ``` ``` >>> results.conf_int(cols=(2,3)) array([[-0.1115811 , 0.03994274], [-3.12506664, -0.91539297]]) ``` #### Notes The confidence interval is based on the standard normal distribution. Models wish to use a different distribution should overwrite this method. statsmodels statsmodels.discrete.count_model.ZeroInflatedPoissonResults.summary statsmodels.discrete.count\_model.ZeroInflatedPoissonResults.summary ==================================================================== `ZeroInflatedPoissonResults.summary(yname=None, xname=None, title=None, alpha=0.05, yname_list=None)` Summarize the Regression Results \| Parameters: \| * yname (string, optional) – Default is `y` * xname (list of strings, optional) – Default is `var_##` for ## in p the number of regressors * title (string, optional) – Title for the top table. If not None, then this replaces the default title * alpha (float) – significance level for the confidence intervals \| \| Returns: \| smry – this holds the summary tables and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary.Summary`](statsmodels.iolib.summary.summary#statsmodels.iolib.summary.Summary "statsmodels.iolib.summary.Summary") class to hold summary results statsmodels statsmodels.tsa.arima_model.ARIMAResults.fittedvalues statsmodels.tsa.arima\_model.ARIMAResults.fittedvalues ====================================================== `ARIMAResults.fittedvalues()` statsmodels statsmodels.tsa.holtwinters.Holt.score statsmodels.tsa.holtwinters.Holt.score ====================================== `Holt.score(params)` Score vector of model. The gradient of logL with respect to each parameter. statsmodels statsmodels.tsa.vector_ar.vecm.VECMResults.cov_params_default statsmodels.tsa.vector\_ar.vecm.VECMResults.cov\_params\_default ================================================================ `VECMResults.cov_params_default()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/vecm.html#VECMResults.cov_params_default) statsmodels statsmodels.discrete.discrete_model.Logit.fit_regularized statsmodels.discrete.discrete\_model.Logit.fit\_regularized =========================================================== `Logit.fit_regularized(start_params=None, method='l1', maxiter='defined_by_method', full_output=1, disp=1, callback=None, alpha=0, trim_mode='auto', auto_trim_tol=0.01, size_trim_tol=0.0001, qc_tol=0.03, *kwargs)` Fit the model using a regularized maximum likelihood. The regularization method AND the solver used is determined by the argument method. \| Parameters: \| start\_params (array-like, optional) – Initial guess of the solution for the loglikelihood maximization. The default is an array of zeros. * method ('l1' or 'l1\_cvxopt\_cp') – See notes for details. * maxiter (Integer or 'defined\_by\_method') – Maximum number of iterations to perform. If ‘defined\_by\_method’, then use method defaults (see notes). * full\_output (bool) – Set to True to have all available output in the Results object’s mle\_retvals attribute. The output is dependent on the solver. See LikelihoodModelResults notes section for more information. * disp (bool) – Set to True to print convergence messages. * fargs (tuple) – Extra arguments passed to the likelihood function, i.e., loglike(x,\args) callback (callable callback(xk)) – Called after each iteration, as callback(xk), where xk is the current parameter vector. * retall (bool) – Set to True to return list of solutions at each iteration. Available in Results object’s mle\_retvals attribute. * alpha (non-negative scalar or numpy array (same size as parameters)) – The weight multiplying the l1 penalty term * trim\_mode ('auto, 'size', or 'off') – If not ‘off’, trim (set to zero) parameters that would have been zero if the solver reached the theoretical minimum. If ‘auto’, trim params using the Theory above. If ‘size’, trim params if they have very small absolute value * size\_trim\_tol (float or 'auto' (default = 'auto')) – For use when trim\_mode == ‘size’ * auto\_trim\_tol (float) – For sue when trim\_mode == ‘auto’. Use * qc\_tol (float) – Print warning and don’t allow auto trim when (ii) (above) is violated by this much. * qc\_verbose (Boolean) – If true, print out a full QC report upon failure \| #### Notes Extra parameters are not penalized if alpha is given as a scalar. An example is the shape parameter in NegativeBinomial `nb1` and `nb2`. Optional arguments for the solvers (available in Results.mle\_settings): ``` 'l1' acc : float (default 1e-6) Requested accuracy as used by slsqp 'l1_cvxopt_cp' abstol : float absolute accuracy (default: 1e-7). reltol : float relative accuracy (default: 1e-6). feastol : float tolerance for feasibility conditions (default: 1e-7). refinement : int number of iterative refinement steps when solving KKT equations (default: 1). ``` Optimization methodology With $L$ the negative log likelihood, we solve the convex but non-smooth problem \[\min\_\beta L(\beta) + \sum\_k\alpha\_k \|\beta\_k\|\] via the transformation to the smooth, convex, constrained problem in twice as many variables (adding the “added variables” $u\_k$) \[\min\_{\beta,u} L(\beta) + \sum\_k\alpha\_k u\_k,\] subject to \[-u\_k \leq \beta\_k \leq u\_k.\] With $\partial\_k L$ the derivative of $L$ in the $k^{th}$ parameter direction, theory dictates that, at the minimum, exactly one of two conditions holds: 1. $\|\partial\_k L\| = \alpha\_k$ and $\beta\_k \neq 0$ 2. $\|\partial\_k L\| \leq \alpha\_k$ and $\beta\_k = 0$ statsmodels statsmodels.genmod.cov_struct.Autoregressive.summary statsmodels.genmod.cov\_struct.Autoregressive.summary ===================================================== `Autoregressive.summary()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/cov_struct.html#Autoregressive.summary) Returns a text summary of the current estimate of the dependence structure. statsmodels statsmodels.tsa.statespace.sarimax.SARIMAXResults.forecast statsmodels.tsa.statespace.sarimax.SARIMAXResults.forecast ========================================================== `SARIMAXResults.forecast(steps=1, *kwargs)` Out-of-sample forecasts \| Parameters: \| steps (int, str, or datetime, optional) – If an integer, the number of steps to forecast from the end of the sample. Can also be a date string to parse or a datetime type. However, if the dates index does not have a fixed frequency, steps must be an integer. Default * *\\kwargs* – Additional arguments may required for forecasting beyond the end of the sample. See `FilterResults.predict` for more details. \| \| Returns: \| forecast – Array of out of sample forecasts. A (steps x k\_endog) array. \| \| Return type: \| array \| statsmodels statsmodels.stats.proportion.power_ztost_prop statsmodels.stats.proportion.power\_ztost\_prop =============================================== `statsmodels.stats.proportion.power_ztost_prop(low, upp, nobs, p_alt, alpha=0.05, dist='norm', variance_prop=None, discrete=True, continuity=0, critval_continuity=0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/proportion.html#power_ztost_prop) Power of proportions equivalence test based on normal distribution \| Parameters: \| * upp (low,) – lower and upper limit of equivalence region * nobs (int) – number of observations * p\_alt (float in (0,1)) – proportion under the alternative * alpha (float in (0,1)) – significance level of the test * dist (string in ['norm', 'binom']) – This defines the distribution to evalute the power of the test. The critical values of the TOST test are always based on the normal approximation, but the distribution for the power can be either the normal (default) or the binomial (exact) distribution. * variance\_prop (None or float in (0,1)) – If this is None, then the variances for the two one sided tests are based on the proportions equal to the equivalence limits. If variance\_prop is given, then it is used to calculate the variance for the TOST statistics. If this is based on an sample, then the estimated proportion can be used. * discrete (bool) – If true, then the critical values of the rejection region are converted to integers. If dist is “binom”, this is automatically assumed. If discrete is false, then the TOST critical values are used as floating point numbers, and the power is calculated based on the rejection region that is not discretized. * continuity (bool or float) – adjust the rejection region for the normal power probability. This has and effect only if `dist='norm'` * critval\_continuity (bool or float) – If this is non-zero, then the critical values of the tost rejection region are adjusted before converting to integers. This affects both distributions, `dist='norm'` and `dist='binom'`. \| \| Returns: \| * power (float) – statistical power of the equivalence test. * (k\_low, k\_upp, z\_low, z\_upp) (tuple of floats) – critical limits in intermediate steps temporary return, will be changed \| #### Notes In small samples the power for the `discrete` version, has a sawtooth pattern as a function of the number of observations. As a consequence, small changes in the number of observations or in the normal approximation can have a large effect on the power. `continuity` and `critval_continuity` are added to match some results of PASS, and are mainly to investigate the sensitivity of the ztost power to small changes in the rejection region. From my interpretation of the equations in the SAS manual, both are zero in SAS. works vectorized verification: The `dist='binom'` results match PASS, The `dist='norm'` results look reasonable, but no benchmark is available. #### References SAS Manual: Chapter 68: The Power Procedure, Computational Resources PASS Chapter 110: Equivalence Tests for One Proportion. statsmodels statsmodels.iolib.foreign.StataReader.variables statsmodels.iolib.foreign.StataReader.variables =============================================== `StataReader.variables()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/iolib/foreign.html#StataReader.variables) Returns a list of the dataset’s StataVariables objects. statsmodels statsmodels.nonparametric.kernel_density.KDEMultivariate.cdf statsmodels.nonparametric.kernel\_density.KDEMultivariate.cdf ============================================================= `KDEMultivariate.cdf(data_predict=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/nonparametric/kernel_density.html#KDEMultivariate.cdf) Evaluate the cumulative distribution function. \| Parameters: \| data\_predict (array\_like, optional) – Points to evaluate at. If unspecified, the training data is used. \| \| Returns: \| cdf\_est – The estimate of the cdf. \| \| Return type: \| array\_like \| #### Notes See <http://en.wikipedia.org/wiki/Cumulative_distribution_function> For more details on the estimation see Ref. [5] in module docstring. The multivariate CDF for mixed data (continuous and ordered/unordered discrete) is estimated by: \[F(x^{c},x^{d})=n^{-1}\sum\_{i=1}^{n}\left[G(\frac{x^{c}-X\_{i}}{h})\sum\_{u\leq x^{d}}L(X\_{i}^{d},x\_{i}^{d}, \lambda)\right]\] where G() is the product kernel CDF estimator for the continuous and L() for the discrete variables. Used bandwidth is `self.bw`. statsmodels statsmodels.discrete.discrete_model.NegativeBinomialP.cov_params_func_l1 statsmodels.discrete.discrete\_model.NegativeBinomialP.cov\_params\_func\_l1 ============================================================================ `NegativeBinomialP.cov_params_func_l1(likelihood_model, xopt, retvals)` Computes cov\_params on a reduced parameter space corresponding to the nonzero parameters resulting from the l1 regularized fit. Returns a full cov\_params matrix, with entries corresponding to zero’d values set to np.nan. statsmodels statsmodels.iolib.foreign.StataReader.dataset statsmodels.iolib.foreign.StataReader.dataset ============================================= `StataReader.dataset(as_dict=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/iolib/foreign.html#StataReader.dataset) Returns a Python generator object for iterating over the dataset. \| Parameters: \| as\_dict (bool, optional) – If as\_dict is True, yield each row of observations as a dict. If False, yields each row of observations as a list. \| \| Returns: \| * Generator object for iterating over the dataset. Yields each row of * observations as a list by default. \| #### Notes If missing\_values is True during instantiation of StataReader then observations with \_StataMissingValue(s) are not filtered and should be handled by your applcation.	programming_docs
statsmodels statsmodels.graphics.tsaplots.plot_acf statsmodels.graphics.tsaplots.plot\_acf ======================================= `statsmodels.graphics.tsaplots.plot_acf(x, ax=None, lags=None, alpha=0.05, use_vlines=True, unbiased=False, fft=False, title='Autocorrelation', zero=True, vlines_kwargs=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/graphics/tsaplots.html#plot_acf) Plot the autocorrelation function Plots lags on the horizontal and the correlations on vertical axis. \| Parameters: \| x (array\_like) – Array of time-series values * ax (Matplotlib AxesSubplot instance, optional) – If given, this subplot is used to plot in instead of a new figure being created. * lags (int or array\_like, optional) – int or Array of lag values, used on horizontal axis. Uses np.arange(lags) when lags is an int. If not provided, `lags=np.arange(len(corr))` is used. * alpha (scalar, optional) – If a number is given, the confidence intervals for the given level are returned. For instance if alpha=.05, 95 % confidence intervals are returned where the standard deviation is computed according to Bartlett’s formula. If None, no confidence intervals are plotted. * use\_vlines (bool, optional) – If True, vertical lines and markers are plotted. If False, only markers are plotted. The default marker is ‘o’; it can be overridden with a `marker` kwarg. * unbiased (bool) – If True, then denominators for autocovariance are n-k, otherwise n * fft (bool, optional) – If True, computes the ACF via FFT. * title (str, optional) – Title to place on plot. Default is ‘Autocorrelation’ * zero (bool, optional) – Flag indicating whether to include the 0-lag autocorrelation. Default is True. * vlines\_kwargs ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)"), optional) – Optional dictionary of keyword arguments that are passed to vlines. * *\\kwargs* (kwargs, optional) – Optional keyword arguments that are directly passed on to the Matplotlib `plot` and `axhline` functions. \| \| Returns: \| fig – If `ax` is None, the created figure. Otherwise the figure to which `ax` is connected. \| \| Return type: \| Matplotlib figure instance \| See also `matplotlib.pyplot.xcorr`, `matplotlib.pyplot.acorr`, `mpl_examples` #### Notes Adapted from matplotlib’s `xcorr`. Data are plotted as `plot(lags, corr, *kwargs)` kwargs is used to pass matplotlib optional arguments to both the line tracing the autocorrelations and for the horizontal line at 0. These options must be valid for a Line2D object. vlines\_kwargs is used to pass additional optional arguments to the vertical lines connecting each autocorrelation to the axis. These options must be valid for a LineCollection object. statsmodels statsmodels.tsa.statespace.sarimax.SARIMAXResults.cov_params_robust statsmodels.tsa.statespace.sarimax.SARIMAXResults.cov\_params\_robust ===================================================================== `SARIMAXResults.cov_params_robust()` (array) The QMLE variance / covariance matrix. Alias for `cov_params_robust_oim` statsmodels statsmodels.tsa.statespace.sarimax.SARIMAX.from_formula statsmodels.tsa.statespace.sarimax.SARIMAX.from\_formula ======================================================== `classmethod SARIMAX.from_formula(formula, data, subset=None)` Not implemented for state space models statsmodels statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.initialize_known statsmodels.tsa.regime\_switching.markov\_autoregression.MarkovAutoregression.initialize\_known =============================================================================================== `MarkovAutoregression.initialize_known(probabilities, tol=1e-08)` Set initialization of regime probabilities to use known values statsmodels statsmodels.sandbox.regression.gmm.IVGMM.fititer statsmodels.sandbox.regression.gmm.IVGMM.fititer ================================================ `IVGMM.fititer(start, maxiter=2, start_invweights=None, weights_method='cov', wargs=(), optim_method='bfgs', optim_args=None)` iterative estimation with updating of optimal weighting matrix stopping criteria are maxiter or change in parameter estimate less than self.epsilon\_iter, with default 1e-6. \| Parameters: \| start (array) – starting value for parameters * maxiter (int) – maximum number of iterations * start\_weights (array (nmoms, nmoms)) – initial weighting matrix; if None, then the identity matrix is used * weights\_method ({'cov', ..}) – method to use to estimate the optimal weighting matrix, see calc\_weightmatrix for details \| \| Returns: \| * params (array) – estimated parameters * weights (array) – optimal weighting matrix calculated with final parameter estimates \| #### Notes statsmodels statsmodels.robust.norms.RobustNorm.rho statsmodels.robust.norms.RobustNorm.rho ======================================= `RobustNorm.rho(z)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/norms.html#RobustNorm.rho) The robust criterion estimator function. Abstract method: -2 loglike used in M-estimator statsmodels statsmodels.tsa.ar_model.ARResults.initialize statsmodels.tsa.ar\_model.ARResults.initialize ============================================== `ARResults.initialize(model, params, *kwd)` statsmodels statsmodels.stats.moment_helpers.mnc2mvsk statsmodels.stats.moment\_helpers.mnc2mvsk ========================================== `statsmodels.stats.moment_helpers.mnc2mvsk(args)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/moment_helpers.html#mnc2mvsk) convert central moments to mean, variance, skew, kurtosis statsmodels statsmodels.sandbox.regression.gmm.IVGMM.score statsmodels.sandbox.regression.gmm.IVGMM.score ============================================== `IVGMM.score(params, weights, epsilon=None, centered=True)` statsmodels statsmodels.tools.tools.add_constant statsmodels.tools.tools.add\_constant ===================================== `statsmodels.tools.tools.add_constant(data, prepend=True, has_constant='skip')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tools/tools.html#add_constant) Adds a column of ones to an array \| Parameters: \| data (array-like) – `data` is the column-ordered design matrix * prepend (bool) – If true, the constant is in the first column. Else the constant is appended (last column). * has\_constant (str {'raise', 'add', 'skip'}) – Behavior if `data` already has a constant. The default will return data without adding another constant. If ‘raise’, will raise an error if a constant is present. Using ‘add’ will duplicate the constant, if one is present. \| \| Returns: \| data – The original values with a constant (column of ones) as the first or last column. Returned value depends on input type. \| \| Return type: \| array, recarray or DataFrame \| #### Notes When the input is recarray or a pandas Series or DataFrame, the added column’s name is ‘const’. statsmodels statsmodels.genmod.families.links.identity.deriv statsmodels.genmod.families.links.identity.deriv ================================================ `identity.deriv(p)` Derivative of the power transform \| Parameters: \| p (array-like) – Mean parameters \| \| Returns: \| g’(p) – Derivative of power transform of `p` \| \| Return type: \| array \| #### Notes g’(`p`) = `power` \* `p`*(`power` - 1) statsmodels statsmodels.graphics.functional.rainbowplot statsmodels.graphics.functional.rainbowplot =========================================== `statsmodels.graphics.functional.rainbowplot(data, xdata=None, depth=None, method='MBD', ax=None, cmap=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/graphics/functional.html#rainbowplot) 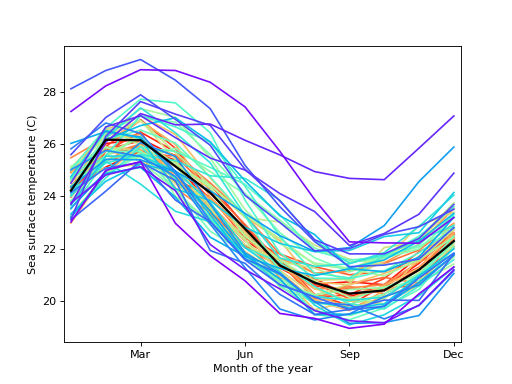Create a rainbow plot for a set of curves. A rainbow plot contains line plots of all curves in the dataset, colored in order of functional depth. The median curve is shown in black. \| Parameters: \| data (sequence of ndarrays or 2-D ndarray) – The vectors of functions to create a functional boxplot from. If a sequence of 1-D arrays, these should all be the same size. The first axis is the function index, the second axis the one along which the function is defined. So `data[0, :]` is the first functional curve. * xdata (ndarray, optional) – The independent variable for the data. If not given, it is assumed to be an array of integers 0..N-1 with N the length of the vectors in `data`. * depth (ndarray, optional) – A 1-D array of band depths for `data`, or equivalent order statistic. If not given, it will be calculated through `banddepth`. * method ({'MBD', 'BD2'}, optional) – The method to use to calculate the band depth. Default is ‘MBD’. * ax (Matplotlib AxesSubplot instance, optional) – If given, this subplot is used to plot in instead of a new figure being created. * cmap (Matplotlib LinearSegmentedColormap instance, optional) – The colormap used to color curves with. Default is a rainbow colormap, with red used for the most central and purple for the least central curves. \| \| Returns: \| fig – If `ax` is None, the created figure. Otherwise the figure to which `ax` is connected. \| \| Return type: \| Matplotlib figure instance \| See also [`banddepth`](statsmodels.graphics.functional.banddepth#statsmodels.graphics.functional.banddepth "statsmodels.graphics.functional.banddepth"), [`fboxplot`](statsmodels.graphics.functional.fboxplot#statsmodels.graphics.functional.fboxplot "statsmodels.graphics.functional.fboxplot") #### References [1] R.J. Hyndman and H.L. Shang, “Rainbow Plots, Bagplots, and Boxplots for Functional Data”, vol. 19, pp. 29-25, 2010. #### Examples Load the El Nino dataset. Consists of 60 years worth of Pacific Ocean sea surface temperature data. ``` >>> import matplotlib.pyplot as plt >>> import statsmodels.api as sm >>> data = sm.datasets.elnino.load() ``` Create a rainbow plot: ``` >>> fig = plt.figure() >>> ax = fig.add_subplot(111) >>> res = sm.graphics.rainbowplot(data.raw_data[:, 1:], ax=ax) ``` ``` >>> ax.set_xlabel("Month of the year") >>> ax.set_ylabel("Sea surface temperature (C)") >>> ax.set_xticks(np.arange(13, step=3) - 1) >>> ax.set_xticklabels(["", "Mar", "Jun", "Sep", "Dec"]) >>> ax.set_xlim([-0.2, 11.2]) >>> plt.show() ``` ([Source code](../plots/graphics_functional_rainbowplot.py), [png](../plots/graphics_functional_rainbowplot.png), [hires.png](../plots/graphics_functional_rainbowplot.hires.png), [pdf](../plots/graphics_functional_rainbowplot.pdf)) ![../_images/graphics_functional_rainbowplot.png](http://www.statsmodels.org/stable/_images/graphics_functional_rainbowplot.png) statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.zvalues statsmodels.regression.recursive\_ls.RecursiveLSResults.zvalues =============================================================== `RecursiveLSResults.zvalues()` (array) The z-statistics for the coefficients. statsmodels statsmodels.genmod.generalized_linear_model.GLMResults.null_deviance statsmodels.genmod.generalized\_linear\_model.GLMResults.null\_deviance ======================================================================= `GLMResults.null_deviance()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_linear_model.html#GLMResults.null_deviance) statsmodels statsmodels.tsa.ar_model.AR.score statsmodels.tsa.ar\_model.AR.score ================================== `AR.score(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/ar_model.html#AR.score) Return the gradient of the loglikelihood at params. \| Parameters: \| params (array-like) – The parameter values at which to evaluate the score function. \| #### Notes Returns numerical gradient. statsmodels statsmodels.tsa.vector_ar.vecm.VECMResults.conf_int_beta statsmodels.tsa.vector\_ar.vecm.VECMResults.conf\_int\_beta =========================================================== `VECMResults.conf_int_beta(alpha=0.05)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/vecm.html#VECMResults.conf_int_beta) statsmodels statsmodels.regression.linear_model.OLSResults.predict statsmodels.regression.linear\_model.OLSResults.predict ======================================================= `OLSResults.predict(exog=None, transform=True, args, kwargs)` Call self.model.predict with self.params as the first argument. \| Parameters: \| exog (array-like, optional) – The values for which you want to predict. see Notes below. * transform (bool, optional) – If the model was fit via a formula, do you want to pass exog through the formula. Default is True. E.g., if you fit a model y ~ log(x1) + log(x2), and transform is True, then you can pass a data structure that contains x1 and x2 in their original form. Otherwise, you’d need to log the data first. * kwargs (args,) – Some models can take additional arguments or keywords, see the predict method of the model for the details. \| \| Returns: \| prediction – See self.model.predict \| \| Return type: \| ndarray, [pandas.Series](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.html#pandas.Series "(in pandas v0.22.0)") or [pandas.DataFrame](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html#pandas.DataFrame "(in pandas v0.22.0)") \| #### Notes The types of exog that are supported depends on whether a formula was used in the specification of the model. If a formula was used, then exog is processed in the same way as the original data. This transformation needs to have key access to the same variable names, and can be a pandas DataFrame or a dict like object. If no formula was used, then the provided exog needs to have the same number of columns as the original exog in the model. No transformation of the data is performed except converting it to a numpy array. Row indices as in pandas data frames are supported, and added to the returned prediction. statsmodels statsmodels.discrete.discrete_model.BinaryResults.conf_int statsmodels.discrete.discrete\_model.BinaryResults.conf\_int ============================================================ `BinaryResults.conf_int(alpha=0.05, cols=None, method='default')` Returns the confidence interval of the fitted parameters. \| Parameters: \| * alpha (float, optional) – The significance level for the confidence interval. ie., The default `alpha` = .05 returns a 95% confidence interval. * cols (array-like, optional) – `cols` specifies which confidence intervals to return * method (string) – Not Implemented Yet Method to estimate the confidence\_interval. “Default” : uses self.bse which is based on inverse Hessian for MLE “hjjh” : “jac” : “boot-bse” “boot\_quant” “profile” \| \| Returns: \| conf\_int – Each row contains [lower, upper] limits of the confidence interval for the corresponding parameter. The first column contains all lower, the second column contains all upper limits. \| \| Return type: \| array \| #### Examples ``` >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> results.conf_int() array([[-5496529.48322745, -1467987.78596704], [ -177.02903529, 207.15277984], [ -0.1115811 , 0.03994274], [ -3.12506664, -0.91539297], [ -1.5179487 , -0.54850503], [ -0.56251721, 0.460309 ], [ 798.7875153 , 2859.51541392]]) ``` ``` >>> results.conf_int(cols=(2,3)) array([[-0.1115811 , 0.03994274], [-3.12506664, -0.91539297]]) ``` #### Notes The confidence interval is based on the standard normal distribution. Models wish to use a different distribution should overwrite this method. statsmodels statsmodels.sandbox.distributions.extras.ACSkewT_gen.fit statsmodels.sandbox.distributions.extras.ACSkewT\_gen.fit ========================================================= `ACSkewT_gen.fit(data, args, kwds)` Return MLEs for shape (if applicable), location, and scale parameters from data. MLE stands for Maximum Likelihood Estimate. Starting estimates for the fit are given by input arguments; for any arguments not provided with starting estimates, `self._fitstart(data)` is called to generate such. One can hold some parameters fixed to specific values by passing in keyword arguments `f0`, `f1`, …, `fn` (for shape parameters) and `floc` and `fscale` (for location and scale parameters, respectively). \| Parameters: \| data (array\_like) – Data to use in calculating the MLEs. * args (floats, optional) – Starting value(s) for any shape-characterizing arguments (those not provided will be determined by a call to `_fitstart(data)`). No default value. * kwds (floats, optional) – Starting values for the location and scale parameters; no default. Special keyword arguments are recognized as holding certain parameters fixed: + f0…fn : hold respective shape parameters fixed. Alternatively, shape parameters to fix can be specified by name. For example, if `self.shapes == "a, b"`, `fa``and ``fix_a` are equivalent to `f0`, and `fb` and `fix_b` are equivalent to `f1`. + floc : hold location parameter fixed to specified value. + fscale : hold scale parameter fixed to specified value. + optimizer : The optimizer to use. The optimizer must take `func`, and starting position as the first two arguments, plus `args` (for extra arguments to pass to the function to be optimized) and `disp=0` to suppress output as keyword arguments. \| \| Returns: \| mle\_tuple – MLEs for any shape parameters (if applicable), followed by those for location and scale. For most random variables, shape statistics will be returned, but there are exceptions (e.g. `norm`). \| \| Return type: \| tuple of floats \| #### Notes This fit is computed by maximizing a log-likelihood function, with penalty applied for samples outside of range of the distribution. The returned answer is not guaranteed to be the globally optimal MLE, it may only be locally optimal, or the optimization may fail altogether. #### Examples Generate some data to fit: draw random variates from the `beta` distribution ``` >>> from scipy.stats import beta >>> a, b = 1., 2. >>> x = beta.rvs(a, b, size=1000) ``` Now we can fit all four parameters (`a`, `b`, `loc` and `scale`): ``` >>> a1, b1, loc1, scale1 = beta.fit(x) ``` We can also use some prior knowledge about the dataset: let’s keep `loc` and `scale` fixed: ``` >>> a1, b1, loc1, scale1 = beta.fit(x, floc=0, fscale=1) >>> loc1, scale1 (0, 1) ``` We can also keep shape parameters fixed by using `f`-keywords. To keep the zero-th shape parameter `a` equal 1, use `f0=1` or, equivalently, `fa=1`: ``` >>> a1, b1, loc1, scale1 = beta.fit(x, fa=1, floc=0, fscale=1) >>> a1 1 ``` Not all distributions return estimates for the shape parameters. `norm` for example just returns estimates for location and scale: ``` >>> from scipy.stats import norm >>> x = norm.rvs(a, b, size=1000, random_state=123) >>> loc1, scale1 = norm.fit(x) >>> loc1, scale1 (0.92087172783841631, 2.0015750750324668) ``` statsmodels statsmodels.tsa.statespace.varmax.VARMAX.score statsmodels.tsa.statespace.varmax.VARMAX.score ============================================== `VARMAX.score(params, args, kwargs)` Compute the score function at params. \| Parameters: \| params (array\_like) – Array of parameters at which to evaluate the score. * args – Additional positional arguments to the `loglike` method. * kwargs – Additional keyword arguments to the `loglike` method. \| \| Returns: \| score – Score, evaluated at `params`. \| \| Return type: \| array \| #### Notes This is a numerical approximation, calculated using first-order complex step differentiation on the `loglike` method. Both \args and \\kwargs are necessary because the optimizer from `fit` must call this function and only supports passing arguments via \args (for example `scipy.optimize.fmin_l_bfgs`).	programming_docs
statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults statsmodels.tsa.statespace.dynamic\_factor.DynamicFactorResults =============================================================== `class statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults(model, params, filter_results, cov_type='opg', kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/dynamic_factor.html#DynamicFactorResults) Class to hold results from fitting an DynamicFactor model. \| Parameters: \| model** (DynamicFactor instance) – The fitted model instance \| `specification` dictionary – Dictionary including all attributes from the DynamicFactor model instance. `coefficient_matrices_var` array – Array containing autoregressive lag polynomial coefficient matrices, ordered from lowest degree to highest. See also [`statsmodels.tsa.statespace.kalman_filter.FilterResults`](statsmodels.tsa.statespace.kalman_filter.filterresults#statsmodels.tsa.statespace.kalman_filter.FilterResults "statsmodels.tsa.statespace.kalman_filter.FilterResults"), [`statsmodels.tsa.statespace.mlemodel.MLEResults`](statsmodels.tsa.statespace.mlemodel.mleresults#statsmodels.tsa.statespace.mlemodel.MLEResults "statsmodels.tsa.statespace.mlemodel.MLEResults") #### Methods \| \| \| \| --- \| --- \| \| [`aic`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.aic#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.aic "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.aic")() \| (float) Akaike Information Criterion \| \| [`bic`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.bic#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.bic "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.bic")() \| (float) Bayes Information Criterion \| \| [`bse`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.bse#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.bse "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.bse")() \| \| \| [`coefficients_of_determination`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.coefficients_of_determination#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.coefficients_of_determination "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.coefficients_of_determination")() \| Coefficients of determination ($R^2$) from regressions of individual estimated factors on endogenous variables. \| \| [`conf_int`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.conf_int#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.conf_int "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.conf_int")([alpha, cols, method]) \| Returns the confidence interval of the fitted parameters. \| \| [`cov_params`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.cov_params#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.cov_params "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.cov_params")([r\_matrix, column, scale, cov\_p, …]) \| Returns the variance/covariance matrix. \| \| [`cov_params_approx`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.cov_params_approx#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.cov_params_approx "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.cov_params_approx")() \| (array) The variance / covariance matrix. \| \| [`cov_params_oim`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.cov_params_oim#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.cov_params_oim "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.cov_params_oim")() \| (array) The variance / covariance matrix. \| \| [`cov_params_opg`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.cov_params_opg#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.cov_params_opg "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.cov_params_opg")() \| (array) The variance / covariance matrix. \| \| [`cov_params_robust`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.cov_params_robust#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.cov_params_robust "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.cov_params_robust")() \| (array) The QMLE variance / covariance matrix. \| \| [`cov_params_robust_approx`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.cov_params_robust_approx#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.cov_params_robust_approx "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.cov_params_robust_approx")() \| (array) The QMLE variance / covariance matrix. \| \| [`cov_params_robust_oim`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.cov_params_robust_oim#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.cov_params_robust_oim "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.cov_params_robust_oim")() \| (array) The QMLE variance / covariance matrix. \| \| [`f_test`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.f_test#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.f_test "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.f_test")(r\_matrix[, cov\_p, scale, invcov]) \| Compute the F-test for a joint linear hypothesis. \| \| [`fittedvalues`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.fittedvalues#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.fittedvalues "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.fittedvalues")() \| (array) The predicted values of the model. \| \| [`forecast`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.forecast#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.forecast "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.forecast")([steps]) \| Out-of-sample forecasts \| \| [`get_forecast`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.get_forecast#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.get_forecast "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.get_forecast")([steps]) \| Out-of-sample forecasts \| \| [`get_prediction`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.get_prediction#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.get_prediction "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.get_prediction")([start, end, dynamic, index, …]) \| In-sample prediction and out-of-sample forecasting \| \| [`hqic`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.hqic#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.hqic "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.hqic")() \| (float) Hannan-Quinn Information Criterion \| \| [`impulse_responses`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.impulse_responses#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.impulse_responses "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.impulse_responses")([steps, impulse, …]) \| Impulse response function \| \| [`info_criteria`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.info_criteria#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.info_criteria "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.info_criteria")(criteria[, method]) \| Information criteria \| \| [`initialize`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.initialize#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.initialize "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.initialize")(model, params, \\kwd) \| \| \| [`llf`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.llf#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.llf "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.llf")() \| (float) The value of the log-likelihood function evaluated at `params`. \| \| [`llf_obs`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.llf_obs#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.llf_obs "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.llf_obs")() \| (float) The value of the log-likelihood function evaluated at `params`. \| \| [`load`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.load#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.load "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.load")(fname) \| load a pickle, (class method) \| \| [`loglikelihood_burn`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.loglikelihood_burn#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.loglikelihood_burn "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.loglikelihood_burn")() \| (float) The number of observations during which the likelihood is not evaluated. \| \| [`normalized_cov_params`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.normalized_cov_params#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.normalized_cov_params "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.normalized_cov_params")() \| \| \| [`plot_coefficients_of_determination`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.plot_coefficients_of_determination#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.plot_coefficients_of_determination "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.plot_coefficients_of_determination")([…]) \| Plot the coefficients of determination \| \| [`plot_diagnostics`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.plot_diagnostics#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.plot_diagnostics "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.plot_diagnostics")([variable, lags, fig, figsize]) \| Diagnostic plots for standardized residuals of one endogenous variable \| \| [`predict`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.predict#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.predict "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.predict")([start, end, dynamic]) \| In-sample prediction and out-of-sample forecasting \| \| [`pvalues`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.pvalues#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.pvalues "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.pvalues")() \| (array) The p-values associated with the z-statistics of the coefficients. \| \| [`remove_data`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.remove_data#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.remove_data "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.remove_data")() \| remove data arrays, all nobs arrays from result and model \| \| [`resid`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.resid#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.resid "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.resid")() \| (array) The model residuals. \| \| [`save`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.save#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.save "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.save")(fname[, remove\_data]) \| save a pickle of this instance \| \| [`simulate`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.simulate#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.simulate "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.simulate")(nsimulations[, measurement\_shocks, …]) \| Simulate a new time series following the state space model \| \| [`summary`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.summary#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.summary "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.summary")([alpha, start, separate\_params]) \| Summarize the Model \| \| [`t_test`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.t_test#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.t_test "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.t_test")(r\_matrix[, cov\_p, scale, use\_t]) \| Compute a t-test for a each linear hypothesis of the form Rb = q \| \| [`t_test_pairwise`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.t_test_pairwise#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.t_test_pairwise "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.t_test_pairwise")(term\_name[, method, alpha, …]) \| perform pairwise t\_test with multiple testing corrected p-values \| \| [`test_heteroskedasticity`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.test_heteroskedasticity#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.test_heteroskedasticity "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.test_heteroskedasticity")(method[, …]) \| Test for heteroskedasticity of standardized residuals \| \| [`test_normality`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.test_normality#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.test_normality "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.test_normality")(method) \| Test for normality of standardized residuals. \| \| [`test_serial_correlation`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.test_serial_correlation#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.test_serial_correlation "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.test_serial_correlation")(method[, lags]) \| Ljung-box test for no serial correlation of standardized residuals \| \| [`tvalues`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.tvalues#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.tvalues "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.tvalues")() \| Return the t-statistic for a given parameter estimate. \| \| [`wald_test`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.wald_test#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.wald_test "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.wald_test")(r\_matrix[, cov\_p, scale, invcov, …]) \| Compute a Wald-test for a joint linear hypothesis. \| \| [`wald_test_terms`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.wald_test_terms#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.wald_test_terms "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.wald_test_terms")([skip\_single, …]) \| Compute a sequence of Wald tests for terms over multiple columns \| \| [`zvalues`](statsmodels.tsa.statespace.dynamic_factor.dynamicfactorresults.zvalues#statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.zvalues "statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.zvalues")() \| (array) The z-statistics for the coefficients. \| #### Attributes \| \| \| \| --- \| --- \| \| `factors` \| Estimates of unobserved factors :returns: out – Has the following attributes: \| \| `use_t` \| \| statsmodels statsmodels.regression.mixed_linear_model.MixedLMResults.predict statsmodels.regression.mixed\_linear\_model.MixedLMResults.predict ================================================================== `MixedLMResults.predict(exog=None, transform=True, args, kwargs)` Call self.model.predict with self.params as the first argument. \| Parameters: \| exog (array-like, optional) – The values for which you want to predict. see Notes below. * transform (bool, optional) – If the model was fit via a formula, do you want to pass exog through the formula. Default is True. E.g., if you fit a model y ~ log(x1) + log(x2), and transform is True, then you can pass a data structure that contains x1 and x2 in their original form. Otherwise, you’d need to log the data first. * kwargs (args,) – Some models can take additional arguments or keywords, see the predict method of the model for the details. \| \| Returns: \| prediction – See self.model.predict \| \| Return type: \| ndarray, [pandas.Series](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.html#pandas.Series "(in pandas v0.22.0)") or [pandas.DataFrame](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html#pandas.DataFrame "(in pandas v0.22.0)") \| #### Notes The types of exog that are supported depends on whether a formula was used in the specification of the model. If a formula was used, then exog is processed in the same way as the original data. This transformation needs to have key access to the same variable names, and can be a pandas DataFrame or a dict like object. If no formula was used, then the provided exog needs to have the same number of columns as the original exog in the model. No transformation of the data is performed except converting it to a numpy array. Row indices as in pandas data frames are supported, and added to the returned prediction. statsmodels statsmodels.tsa.ar_model.AR.fit statsmodels.tsa.ar\_model.AR.fit ================================ `AR.fit(maxlag=None, method='cmle', ic=None, trend='c', transparams=True, start_params=None, solver='lbfgs', maxiter=35, full_output=1, disp=1, callback=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/ar_model.html#AR.fit) Fit the unconditional maximum likelihood of an AR(p) process. \| Parameters: \| maxlag (int) – If `ic` is None, then maxlag is the lag length used in fit. If `ic` is specified then maxlag is the highest lag order used to select the correct lag order. If maxlag is None, the default is round(12\(nobs/100.)\\(1/4.)) method (str {'cmle', 'mle'}, optional) – cmle - Conditional maximum likelihood using OLS mle - Unconditional (exact) maximum likelihood. See `solver` and the Notes. * ic (str {'aic','bic','hic','t-stat'}) – Criterion used for selecting the optimal lag length. aic - Akaike Information Criterion bic - Bayes Information Criterion t-stat - Based on last lag hqic - Hannan-Quinn Information Criterion If any of the information criteria are selected, the lag length which results in the lowest value is selected. If t-stat, the model starts with maxlag and drops a lag until the highest lag has a t-stat that is significant at the 95 % level. * trend (str {'c','nc'}) – Whether to include a constant or not. ‘c’ - include constant. ‘nc’ - no constant. * below can be specified if method is 'mle' (The) – * transparams (bool, optional) – Whether or not to transform the parameters to ensure stationarity. Uses the transformation suggested in Jones (1980). * start\_params (array-like, optional) – A first guess on the parameters. Default is cmle estimates. * solver (str or None, optional) – Solver to be used if method is ‘mle’. The default is ‘lbfgs’ (limited memory Broyden-Fletcher-Goldfarb-Shanno). Other choices are ‘bfgs’, ‘newton’ (Newton-Raphson), ‘nm’ (Nelder-Mead), ‘cg’ - (conjugate gradient), ‘ncg’ (non-conjugate gradient), and ‘powell’. * maxiter (int, optional) – The maximum number of function evaluations. Default is 35. * tol (float) – The convergence tolerance. Default is 1e-08. * full\_output (bool, optional) – If True, all output from solver will be available in the Results object’s mle\_retvals attribute. Output is dependent on the solver. See Notes for more information. * disp (bool, optional) – If True, convergence information is output. * callback (function, optional) – Called after each iteration as callback(xk) where xk is the current parameter vector. * kwargs – See Notes for keyword arguments that can be passed to fit. \| #### References Jones, R.H. 1980 “Maximum likelihood fitting of ARMA models to time series with missing observations.” `Technometrics`. 22.3. 389-95. See also [`statsmodels.base.model.LikelihoodModel.fit`](http://www.statsmodels.org/stable/dev/generated/statsmodels.base.model.LikelihoodModel.fit.html#statsmodels.base.model.LikelihoodModel.fit "statsmodels.base.model.LikelihoodModel.fit")	programming_docs
statsmodels statsmodels.tools.tools.fullrank statsmodels.tools.tools.fullrank ================================ `statsmodels.tools.tools.fullrank(X, r=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tools/tools.html#fullrank) Return a matrix whose column span is the same as X. If the rank of X is known it can be specified as r – no check is made to ensure that this really is the rank of X. statsmodels statsmodels.regression.linear_model.WLS.initialize statsmodels.regression.linear\_model.WLS.initialize =================================================== `WLS.initialize()` Initialize (possibly re-initialize) a Model instance. For instance, the design matrix of a linear model may change and some things must be recomputed. statsmodels statsmodels.genmod.generalized_linear_model.GLM.fit_constrained statsmodels.genmod.generalized\_linear\_model.GLM.fit\_constrained ================================================================== `GLM.fit_constrained(constraints, start_params=None, *fit_kwds)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_linear_model.html#GLM.fit_constrained) fit the model subject to linear equality constraints The constraints are of the form `R params = q` where R is the constraint\_matrix and q is the vector of constraint\_values. The estimation creates a new model with transformed design matrix, exog, and converts the results back to the original parameterization. \| Parameters: \| constraints (formula expression or tuple) – If it is a tuple, then the constraint needs to be given by two arrays (constraint\_matrix, constraint\_value), i.e. (R, q). Otherwise, the constraints can be given as strings or list of strings. see t\_test for details * start\_params (None or array\_like) – starting values for the optimization. `start_params` needs to be given in the original parameter space and are internally transformed. * *\\fit\_kwds* (keyword arguments) – fit\_kwds are used in the optimization of the transformed model. \| \| Returns: \| results \| \| Return type: \| Results instance \| statsmodels statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM statsmodels.genmod.bayes\_mixed\_glm.PoissonBayesMixedGLM ========================================================= `class statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM(endog, exog, exog_vc, ident, vcp_p=1, fe_p=2, fep_names=None, vcp_names=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/bayes_mixed_glm.html#PoissonBayesMixedGLM) Fit a generalized linear mixed model using Bayesian methods. The class implements the Laplace approximation to the posterior distribution (`fit_map`) and a variational Bayes approximation to the posterior (`fit_vb`). See the two fit method docstrings for more information about the fitting approaches. \| Parameters: \| * endog (array-like) – Vector of response values. * exog (array-like) – Array of covariates for the fixed effects part of the mean structure. * exog\_vc (array-like) – Array of covariates for the random part of the model. A scipy.sparse array may be provided, or else the passed array will be converted to sparse internally. * ident (array-like) – Array of labels showing which random terms (columns of `exog_vc`) have a common variance. * vc\_p (float) – Prior standard deviation for variance component parameters (the prior standard deviation of log(s) is vc\_p, where s is the standard deviation of a random effect). * fe\_p (float) – Prior standard deviation for fixed effects parameters. * family (statsmodels.genmod.families instance) – The GLM family. * fep\_names (list of strings) – The names of the fixed effects parameters (corresponding to columns of exog). If None, default names are constructed. * vcp\_names (list of strings) – The names of the variance component parameters (corresponding to distinct labels in ident). If None, default names are constructed. * vc\_names (list of strings) – The names of the random effect realizations. \| \| Returns: \| \| \| Return type: \| MixedGLMResults object \| #### Notes There are three types of values in the posterior distribution: fixed effects parameters (fep), corresponding to the columns of `exog`, random effects realizations (vc), corresponding to the columns of `exog_vc`, and the standard deviations of the random effects realizations (vcp), corresponding to the unique labels in `ident`. All random effects are modeled as being independent Gaussian values (given the variance parameters). Every column of `exog_vc` has a distinct realized random effect that is used to form the linear predictors. The elements of `ident` determine the distinct random effect variance parameters. Two random effect realizations that have the same value in `ident` are constrained to have the same variance. When fitting with a formula, `ident` is constructed internally (each element of `vc_formulas` yields a distinct label in `ident`). The random effect standard deviation parameters (vcp) have log-normal prior distributions with mean 0 and standard deviation `vcp_p`. Note that for some families, e.g. Binomial, the posterior mode may be difficult to find numerically if `vcp_p` is set to too large of a value. Setting `vcp_p` to 0.5 seems to work well. The prior for the fixed effects parameters is Gaussian with mean 0 and standard deviation `fe_p`. #### Examples A Poisson random effects model with random intercepts for villages and random slopes for each year within each village: ``` >>> data['year_cen'] = data['Year'] - data.Year.mean() >>> random = ['0 + C(Village)', '0 + C(Village)year_cen'] >>> model = PoissonBayesMixedGLM.from_formula('y ~ year_cen', random, data) >>> result = model.fit() ``` #### References Introduction to generalized linear mixed models: <https://stats.idre.ucla.edu/other/mult-pkg/introduction-to-generalized-linear-mixed-models> SAS documentation: <https://support.sas.com/documentation/cdl/en/statug/63033/HTML/default/viewer.htm#statug_intromix_a0000000215.htm> An assessment of estimation methods for generalized linear mixed models with binary outcomes <https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3866838/> #### Methods \| \| \| \| --- \| --- \| \| [`fit`](statsmodels.genmod.bayes_mixed_glm.poissonbayesmixedglm.fit#statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.fit "statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.fit")() \| Fit a model to data. \| \| [`fit_map`](statsmodels.genmod.bayes_mixed_glm.poissonbayesmixedglm.fit_map#statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.fit_map "statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.fit_map")([method, minim\_opts]) \| Construct the Laplace approximation to the posterior distribution. \| \| [`fit_vb`](statsmodels.genmod.bayes_mixed_glm.poissonbayesmixedglm.fit_vb#statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.fit_vb "statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.fit_vb")([mean, sd, fit\_method, minim\_opts, …]) \| Fit a model using the variational Bayes mean field approximation. \| \| [`from_formula`](statsmodels.genmod.bayes_mixed_glm.poissonbayesmixedglm.from_formula#statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.from_formula "statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.from_formula")(formula, vc\_formulas, data[, …]) \| Fit a BayesMixedGLM using a formula. \| \| [`logposterior`](statsmodels.genmod.bayes_mixed_glm.poissonbayesmixedglm.logposterior#statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.logposterior "statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.logposterior")(params) \| The overall log-density: log p(y, fe, vc, vcp). \| \| [`logposterior_grad`](statsmodels.genmod.bayes_mixed_glm.poissonbayesmixedglm.logposterior_grad#statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.logposterior_grad "statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.logposterior_grad")(params) \| The gradient of the log posterior. \| \| [`predict`](statsmodels.genmod.bayes_mixed_glm.poissonbayesmixedglm.predict#statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.predict "statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.predict")(params[, exog]) \| After a model has been fit predict returns the fitted values. \| \| [`vb_elbo`](statsmodels.genmod.bayes_mixed_glm.poissonbayesmixedglm.vb_elbo#statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.vb_elbo "statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.vb_elbo")(vb\_mean, vb\_sd) \| Returns the evidence lower bound (ELBO) for the model. \| \| [`vb_elbo_base`](statsmodels.genmod.bayes_mixed_glm.poissonbayesmixedglm.vb_elbo_base#statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.vb_elbo_base "statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.vb_elbo_base")(h, tm, fep\_mean, vcp\_mean, …) \| Returns the evidence lower bound (ELBO) for the model. \| \| [`vb_elbo_grad`](statsmodels.genmod.bayes_mixed_glm.poissonbayesmixedglm.vb_elbo_grad#statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.vb_elbo_grad "statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.vb_elbo_grad")(vb\_mean, vb\_sd) \| Returns the gradient of the model’s evidence lower bound (ELBO). \| \| [`vb_elbo_grad_base`](statsmodels.genmod.bayes_mixed_glm.poissonbayesmixedglm.vb_elbo_grad_base#statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.vb_elbo_grad_base "statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.vb_elbo_grad_base")(h, tm, tv, fep\_mean, …) \| Return the gradient of the ELBO function. \| #### Attributes \| \| \| \| --- \| --- \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| Names of exogenous variables \| \| `rng` \| \| \| `verbose` \| \| statsmodels statsmodels.regression.mixed_linear_model.MixedLMResults.t_test_pairwise statsmodels.regression.mixed\_linear\_model.MixedLMResults.t\_test\_pairwise ============================================================================ `MixedLMResults.t_test_pairwise(term_name, method='hs', alpha=0.05, factor_labels=None)` perform pairwise t\_test with multiple testing corrected p-values This uses the formula design\_info encoding contrast matrix and should work for all encodings of a main effect. \| Parameters: \| result (result instance) – The results of an estimated model with a categorical main effect. * term\_name (str) – name of the term for which pairwise comparisons are computed. Term names for categorical effects are created by patsy and correspond to the main part of the exog names. * method (str or list of strings) – multiple testing p-value correction, default is ‘hs’, see stats.multipletesting * alpha (float) – significance level for multiple testing reject decision. * factor\_labels (None, list of str) – Labels for the factor levels used for pairwise labels. If not provided, then the labels from the formula design\_info are used. \| \| Returns: \| results – The results are stored as attributes, the main attributes are the following two. Other attributes are added for debugging purposes or as background information.* result\_frame : pandas DataFrame with t\_test results and multiple testing corrected p-values. * contrasts : matrix of constraints of the null hypothesis in the t\_test. \| \| Return type: \| instance of a simple Results class \| #### Notes Status: experimental. Currently only checked for treatment coding with and without specified reference level. Currently there are no multiple testing corrected confidence intervals available. #### Examples ``` >>> res = ols("np.log(Days+1) ~ C(Weight) + C(Duration)", data).fit() >>> pw = res.t_test_pairwise("C(Weight)") >>> pw.result_frame coef std err t P>\|t\| Conf. Int. Low 2-1 0.632315 0.230003 2.749157 8.028083e-03 0.171563 3-1 1.302555 0.230003 5.663201 5.331513e-07 0.841803 3-2 0.670240 0.230003 2.914044 5.119126e-03 0.209488 Conf. Int. Upp. pvalue-hs reject-hs 2-1 1.093067 0.010212 True 3-1 1.763307 0.000002 True 3-2 1.130992 0.010212 True ``` statsmodels statsmodels.sandbox.regression.gmm.NonlinearIVGMM.gmmobjective_cu statsmodels.sandbox.regression.gmm.NonlinearIVGMM.gmmobjective\_cu ================================================================== `NonlinearIVGMM.gmmobjective_cu(params, weights_method='cov', wargs=())` objective function for continuously updating GMM minimization \| Parameters: \| params (array) – parameter values at which objective is evaluated \| \| Returns: \| jval – value of objective function \| \| Return type: \| float \| statsmodels statsmodels.tsa.vector_ar.var_model.VARProcess.forecast_interval statsmodels.tsa.vector\_ar.var\_model.VARProcess.forecast\_interval =================================================================== `VARProcess.forecast_interval(y, steps, alpha=0.05, exog_future=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARProcess.forecast_interval) Construct forecast interval estimates assuming the y are Gaussian #### Notes Lütkepohl pp. 39-40 \| Returns: \| (mid, lower, upper) \| \| Return type: \| (ndarray, ndarray, ndarray) \| statsmodels statsmodels.robust.norms.LeastSquares.rho statsmodels.robust.norms.LeastSquares.rho ========================================= `LeastSquares.rho(z)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/norms.html#LeastSquares.rho) The least squares estimator rho function \| Parameters: \| z (array) – 1d array \| \| Returns: \| rho – rho(z) = (1/2.)\z\\2 \| \| Return type: \| array \| statsmodels statsmodels.tsa.vector_ar.var_model.LagOrderResults.summary statsmodels.tsa.vector\_ar.var\_model.LagOrderResults.summary ============================================================= `LagOrderResults.summary()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#LagOrderResults.summary) statsmodels statsmodels.discrete.discrete_model.Logit.from_formula statsmodels.discrete.discrete\_model.Logit.from\_formula ======================================================== `classmethod Logit.from_formula(formula, data, subset=None, drop_cols=None, args, *kwargs)` Create a Model from a formula and dataframe. \| Parameters: \| formula (str or generic Formula object) – The formula specifying the model * data (array-like) – The data for the model. See Notes. * subset (array-like) – An array-like object of booleans, integers, or index values that indicate the subset of df to use in the model. Assumes df is a `pandas.DataFrame` * drop\_cols (array-like) – Columns to drop from the design matrix. Cannot be used to drop terms involving categoricals. * args (extra arguments) – These are passed to the model * kwargs (extra keyword arguments) – These are passed to the model with one exception. The `eval_env` keyword is passed to patsy. It can be either a [`patsy.EvalEnvironment`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.EvalEnvironment "(in patsy v0.5.0+dev)") object or an integer indicating the depth of the namespace to use. For example, the default `eval_env=0` uses the calling namespace. If you wish to use a “clean” environment set `eval_env=-1`. \| \| Returns: \| model \| \| Return type: \| Model instance \| #### Notes data must define \_\_getitem\_\_ with the keys in the formula terms args and kwargs are passed on to the model instantiation. E.g., a numpy structured or rec array, a dictionary, or a pandas DataFrame. statsmodels statsmodels.regression.linear_model.RegressionResults.compare_lm_test statsmodels.regression.linear\_model.RegressionResults.compare\_lm\_test ======================================================================== `RegressionResults.compare_lm_test(restricted, demean=True, use_lr=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#RegressionResults.compare_lm_test) Use Lagrange Multiplier test to test whether restricted model is correct \| Parameters: \| * restricted (Result instance) – The restricted model is assumed to be nested in the current model. The result instance of the restricted model is required to have two attributes, residual sum of squares, `ssr`, residual degrees of freedom, `df_resid`. * demean (bool) – Flag indicating whether the demean the scores based on the residuals from the restricted model. If True, the covariance of the scores are used and the LM test is identical to the large sample version of the LR test. \| \| Returns: \| * lm\_value (float) – test statistic, chi2 distributed * p\_value (float) – p-value of the test statistic * df\_diff (int) – degrees of freedom of the restriction, i.e. difference in df between models \| #### Notes TODO: explain LM text statsmodels statsmodels.regression.linear_model.RegressionResults.centered_tss statsmodels.regression.linear\_model.RegressionResults.centered\_tss ==================================================================== `RegressionResults.centered_tss()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#RegressionResults.centered_tss) statsmodels statsmodels.tsa.statespace.structural.UnobservedComponents.simulate statsmodels.tsa.statespace.structural.UnobservedComponents.simulate =================================================================== `UnobservedComponents.simulate(params, nsimulations, measurement_shocks=None, state_shocks=None, initial_state=None)` Simulate a new time series following the state space model \| Parameters: \| * params (array\_like) – Array of model parameters. * nsimulations (int) – The number of observations to simulate. If the model is time-invariant this can be any number. If the model is time-varying, then this number must be less than or equal to the number * measurement\_shocks (array\_like, optional) – If specified, these are the shocks to the measurement equation, $\varepsilon\_t$. If unspecified, these are automatically generated using a pseudo-random number generator. If specified, must be shaped `nsimulations` x `k_endog`, where `k_endog` is the same as in the state space model. * state\_shocks (array\_like, optional) – If specified, these are the shocks to the state equation, $\eta\_t$. If unspecified, these are automatically generated using a pseudo-random number generator. If specified, must be shaped `nsimulations` x `k_posdef` where `k_posdef` is the same as in the state space model. * initial\_state (array\_like, optional) – If specified, this is the state vector at time zero, which should be shaped (`k_states` x 1), where `k_states` is the same as in the state space model. If unspecified, but the model has been initialized, then that initialization is used. If unspecified and the model has not been initialized, then a vector of zeros is used. Note that this is not included in the returned `simulated_states` array. \| \| Returns: \| simulated\_obs – An (nsimulations x k\_endog) array of simulated observations. \| \| Return type: \| array \| statsmodels statsmodels.tsa.arima_model.ARMAResults.load statsmodels.tsa.arima\_model.ARMAResults.load ============================================= `classmethod ARMAResults.load(fname)` load a pickle, (class method) \| Parameters: \| fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. \| \| Returns: \| \| \| Return type: \| unpickled instance \| statsmodels statsmodels.regression.linear_model.OLSResults.eigenvals statsmodels.regression.linear\_model.OLSResults.eigenvals ========================================================= `OLSResults.eigenvals()` Return eigenvalues sorted in decreasing order.	programming_docs
statsmodels statsmodels.tools.eval_measures.vare statsmodels.tools.eval\_measures.vare ===================================== `statsmodels.tools.eval_measures.vare(x1, x2, ddof=0, axis=0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tools/eval_measures.html#vare) variance of error \| Parameters: \| * x2 (x1,) – The performance measure depends on the difference between these two arrays. * axis (int) – axis along which the summary statistic is calculated \| \| Returns: \| vare – variance of difference along given axis. \| \| Return type: \| ndarray or float \| #### Notes If `x1` and `x2` have different shapes, then they need to broadcast. This uses `numpy.asanyarray` to convert the input. Whether this is the desired result or not depends on the array subclass. statsmodels statsmodels.genmod.generalized_linear_model.GLMResults.plot_partial_residuals statsmodels.genmod.generalized\_linear\_model.GLMResults.plot\_partial\_residuals ================================================================================= `GLMResults.plot_partial_residuals(focus_exog, ax=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_linear_model.html#GLMResults.plot_partial_residuals) Create a partial residual, or ‘component plus residual’ plot for a fited regression model. \| Parameters: \| * focus\_exog (int or string) – The column index of exog, or variable name, indicating the variable whose role in the regression is to be assessed. * ax (Axes instance) – Matplotlib Axes instance \| \| Returns: \| fig – A matplotlib figure instance. \| \| Return type: \| matplotlib Figure \| statsmodels statsmodels.sandbox.distributions.transformed.Transf_gen.isf statsmodels.sandbox.distributions.transformed.Transf\_gen.isf ============================================================= `Transf_gen.isf(q, args, kwds)` Inverse survival function (inverse of `sf`) at q of the given RV. \| Parameters: \| q (array\_like) – upper tail probability * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| x – Quantile corresponding to the upper tail probability q. \| \| Return type: \| ndarray or scalar \| statsmodels statsmodels.stats.moment_helpers.mnc2mc statsmodels.stats.moment\_helpers.mnc2mc ======================================== `statsmodels.stats.moment_helpers.mnc2mc(mnc, wmean=True)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/moment_helpers.html#mnc2mc) convert non-central to central moments, uses recursive formula optionally adjusts first moment to return mean statsmodels statsmodels.regression.linear_model.RegressionResults.conf_int statsmodels.regression.linear\_model.RegressionResults.conf\_int ================================================================ `RegressionResults.conf_int(alpha=0.05, cols=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#RegressionResults.conf_int) Returns the confidence interval of the fitted parameters. \| Parameters: \| * alpha (float, optional) – The `alpha` level for the confidence interval. ie., The default `alpha` = .05 returns a 95% confidence interval. * cols (array-like, optional) – `cols` specifies which confidence intervals to return \| #### Notes The confidence interval is based on Student’s t-distribution. statsmodels statsmodels.discrete.count_model.ZeroInflatedGeneralizedPoisson.predict statsmodels.discrete.count\_model.ZeroInflatedGeneralizedPoisson.predict ======================================================================== `ZeroInflatedGeneralizedPoisson.predict(params, exog=None, exog_infl=None, exposure=None, offset=None, which='mean')` Predict response variable of a count model given exogenous variables. \| Parameters: \| * params (array-like) – The parameters of the model * exog (array, optional) – A reference to the exogenous design. If not assigned, will be used exog from fitting. * exog\_infl (array, optional) – A reference to the zero-inflated exogenous design. If not assigned, will be used exog from fitting. * offset (array, optional) – Offset is added to the linear prediction with coefficient equal to 1. * exposure (array, optional) – Log(exposure) is added to the linear prediction with coefficient equal to 1. If exposure is specified, then it will be logged by the method. The user does not need to log it first. * which (string, optional) – Define values that will be predicted. ‘mean’, ‘mean-main’, ‘linear’, ‘mean-nonzero’, ‘prob-zero, ‘prob’, ‘prob-main’ Default is ‘mean’. \| #### Notes statsmodels statsmodels.regression.linear_model.OLSResults.bic statsmodels.regression.linear\_model.OLSResults.bic =================================================== `OLSResults.bic()` statsmodels statsmodels.discrete.discrete_model.MultinomialResults.remove_data statsmodels.discrete.discrete\_model.MultinomialResults.remove\_data ==================================================================== `MultinomialResults.remove_data()` remove data arrays, all nobs arrays from result and model This reduces the size of the instance, so it can be pickled with less memory. Currently tested for use with predict from an unpickled results and model instance. Warning Since data and some intermediate results have been removed calculating new statistics that require them will raise exceptions. The exception will occur the first time an attribute is accessed that has been set to None. Not fully tested for time series models, tsa, and might delete too much for prediction or not all that would be possible. The lists of arrays to delete are maintained as attributes of the result and model instance, except for cached values. These lists could be changed before calling remove\_data. The attributes to remove are named in: `model._data_attr : arrays attached to both the model instance` and the results instance with the same attribute name. `result.data_in_cache : arrays that may exist as values in` result.\_cache (TODO : should privatize name) `result._data_attr_model : arrays attached to the model` instance but not to the results instance statsmodels statsmodels.tsa.statespace.structural.UnobservedComponents.information statsmodels.tsa.statespace.structural.UnobservedComponents.information ====================================================================== `UnobservedComponents.information(params)` Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.duration.hazard_regression.PHRegResults.normalized_cov_params statsmodels.duration.hazard\_regression.PHRegResults.normalized\_cov\_params ============================================================================ `PHRegResults.normalized_cov_params()` statsmodels statsmodels.discrete.discrete_model.NegativeBinomialResults.llr_pvalue statsmodels.discrete.discrete\_model.NegativeBinomialResults.llr\_pvalue ======================================================================== `NegativeBinomialResults.llr_pvalue()` statsmodels statsmodels.genmod.generalized_estimating_equations.GEEResults.split_resid statsmodels.genmod.generalized\_estimating\_equations.GEEResults.split\_resid ============================================================================= `GEEResults.split_resid()` Returns the residuals, the endogeneous data minus the fitted values from the model. The residuals are returned as a list of arrays containing the residuals for each cluster. statsmodels statsmodels.regression.linear_model.RegressionResults.predict statsmodels.regression.linear\_model.RegressionResults.predict ============================================================== `RegressionResults.predict(exog=None, transform=True, args, kwargs)` Call self.model.predict with self.params as the first argument. \| Parameters: \| exog (array-like, optional) – The values for which you want to predict. see Notes below. * transform (bool, optional) – If the model was fit via a formula, do you want to pass exog through the formula. Default is True. E.g., if you fit a model y ~ log(x1) + log(x2), and transform is True, then you can pass a data structure that contains x1 and x2 in their original form. Otherwise, you’d need to log the data first. * kwargs (args,) – Some models can take additional arguments or keywords, see the predict method of the model for the details. \| \| Returns: \| prediction – See self.model.predict \| \| Return type: \| ndarray, [pandas.Series](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.html#pandas.Series "(in pandas v0.22.0)") or [pandas.DataFrame](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html#pandas.DataFrame "(in pandas v0.22.0)") \| #### Notes The types of exog that are supported depends on whether a formula was used in the specification of the model. If a formula was used, then exog is processed in the same way as the original data. This transformation needs to have key access to the same variable names, and can be a pandas DataFrame or a dict like object. If no formula was used, then the provided exog needs to have the same number of columns as the original exog in the model. No transformation of the data is performed except converting it to a numpy array. Row indices as in pandas data frames are supported, and added to the returned prediction. statsmodels statsmodels.tsa.statespace.structural.UnobservedComponentsResults.cov_params_robust_oim statsmodels.tsa.statespace.structural.UnobservedComponentsResults.cov\_params\_robust\_oim ========================================================================================== `UnobservedComponentsResults.cov_params_robust_oim()` (array) The QMLE variance / covariance matrix. Computed using the method from Harvey (1989) as the evaluated hessian. statsmodels statsmodels.tsa.statespace.structural.UnobservedComponentsResults.resid statsmodels.tsa.statespace.structural.UnobservedComponentsResults.resid ======================================================================= `UnobservedComponentsResults.resid()` (array) The model residuals. An (nobs x k\_endog) array. statsmodels statsmodels.stats.diagnostic.linear_harvey_collier statsmodels.stats.diagnostic.linear\_harvey\_collier ==================================================== `statsmodels.stats.diagnostic.linear_harvey_collier(res)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/stats/diagnostic.html#linear_harvey_collier) Harvey Collier test for linearity The Null hypothesis is that the regression is correctly modeled as linear. \| Parameters: \| res (Result instance) – \| \| Returns: \| * tvalue (float) – test statistic, based on ttest\_1sample * pvalue (float) – pvalue of the test \| #### Notes TODO: add sort\_by option This test is a t-test that the mean of the recursive ols residuals is zero. Calculating the recursive residuals might take some time for large samples. statsmodels statsmodels.regression.mixed_linear_model.MixedLMResults.fittedvalues statsmodels.regression.mixed\_linear\_model.MixedLMResults.fittedvalues ======================================================================= `MixedLMResults.fittedvalues()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/mixed_linear_model.html#MixedLMResults.fittedvalues) Returns the fitted values for the model. The fitted values reflect the mean structure specified by the fixed effects and the predicted random effects. statsmodels statsmodels.nonparametric.bandwidths.bw_scott statsmodels.nonparametric.bandwidths.bw\_scott ============================================== `statsmodels.nonparametric.bandwidths.bw_scott(x, kernel=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/nonparametric/bandwidths.html#bw_scott) Scott’s Rule of Thumb \| Parameters: \| * x (array-like) – Array for which to get the bandwidth * kernel (CustomKernel object) – Unused \| \| Returns: \| bw – The estimate of the bandwidth \| \| Return type: \| float \| #### Notes Returns 1.059 \* A \* n \\ (-1/5.) where ``` A = min(std(x, ddof=1), IQR/1.349) IQR = np.subtract.reduce(np.percentile(x, [75,25])) ``` #### References Scott, D.W. (1992) Multivariate Density Estimation: Theory, Practice, and Visualization. statsmodels statsmodels.sandbox.distributions.transformed.ExpTransf_gen.pdf statsmodels.sandbox.distributions.transformed.ExpTransf\_gen.pdf ================================================================ `ExpTransf_gen.pdf(x, args, kwds)` Probability density function at x of the given RV. \| Parameters: \| x (array\_like) – quantiles * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| pdf – Probability density function evaluated at x \| \| Return type: \| ndarray \| statsmodels statsmodels.stats.weightstats.DescrStatsW.ttost_mean statsmodels.stats.weightstats.DescrStatsW.ttost\_mean ===================================================== `DescrStatsW.ttost_mean(low, upp)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/weightstats.html#DescrStatsW.ttost_mean) test of (non-)equivalence of one sample TOST: two one-sided t tests null hypothesis: m < low or m > upp alternative hypothesis: low < m < upp where m is the expected value of the sample (mean of the population). If the pvalue is smaller than a threshold, say 0.05, then we reject the hypothesis that the expected value of the sample (mean of the population) is outside of the interval given by thresholds low and upp. \| Parameters: \| upp (low,) – equivalence interval low < mean < upp \| \| Returns: \| * pvalue (float) – pvalue of the non-equivalence test * t1, pv1, df1 (tuple) – test statistic, pvalue and degrees of freedom for lower threshold test * t2, pv2, df2 (tuple) – test statistic, pvalue and degrees of freedom for upper threshold test \| statsmodels statsmodels.genmod.bayes_mixed_glm.BayesMixedGLMResults.summary statsmodels.genmod.bayes\_mixed\_glm.BayesMixedGLMResults.summary ================================================================= `BayesMixedGLMResults.summary()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/bayes_mixed_glm.html#BayesMixedGLMResults.summary) statsmodels statsmodels.tsa.statespace.structural.UnobservedComponentsResults.t_test statsmodels.tsa.statespace.structural.UnobservedComponentsResults.t\_test ========================================================================= `UnobservedComponentsResults.t_test(r_matrix, cov_p=None, scale=None, use_t=None)` Compute a t-test for a each linear hypothesis of the form Rb = q \| Parameters: \| * r\_matrix (array-like, str, tuple) – + array : If an array is given, a p x k 2d array or length k 1d array specifying the linear restrictions. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q). If q is given, can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – An optional `scale` to use. Default is the scale specified by the model fit. * use\_t (bool, optional) – If use\_t is None, then the default of the model is used. If use\_t is True, then the p-values are based on the t distribution. If use\_t is False, then the p-values are based on the normal distribution. \| \| Returns: \| res – The results for the test are attributes of this results instance. The available results have the same elements as the parameter table in `summary()`. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> r = np.zeros_like(results.params) >>> r[5:] = [1,-1] >>> print(r) [ 0. 0. 0. 0. 0. 1. -1.] ``` r tests that the coefficients on the 5th and 6th independent variable are the same. ``` >>> T_test = results.t_test(r) >>> print(T_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 -1829.2026 455.391 -4.017 0.003 -2859.368 -799.037 ============================================================================== >>> T_test.effect -1829.2025687192481 >>> T_test.sd 455.39079425193762 >>> T_test.tvalue -4.0167754636411717 >>> T_test.pvalue 0.0015163772380899498 ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.formula.api import ols >>> dta = sm.datasets.longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = 'GNPDEFL = GNP, UNEMP = 2, YEAR/1829 = 1' >>> t_test = results.t_test(hypotheses) >>> print(t_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 15.0977 84.937 0.178 0.863 -177.042 207.238 c1 -2.0202 0.488 -8.231 0.000 -3.125 -0.915 c2 1.0001 0.249 0.000 1.000 0.437 1.563 ============================================================================== ``` See also [`tvalues`](statsmodels.tsa.statespace.structural.unobservedcomponentsresults.tvalues#statsmodels.tsa.statespace.structural.UnobservedComponentsResults.tvalues "statsmodels.tsa.statespace.structural.UnobservedComponentsResults.tvalues") individual t statistics [`f_test`](statsmodels.tsa.statespace.structural.unobservedcomponentsresults.f_test#statsmodels.tsa.statespace.structural.UnobservedComponentsResults.f_test "statsmodels.tsa.statespace.structural.UnobservedComponentsResults.f_test") for F tests [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") statsmodels statsmodels.sandbox.tsa.movstat.movvar statsmodels.sandbox.tsa.movstat.movvar ====================================== `statsmodels.sandbox.tsa.movstat.movvar(x, windowsize=3, lag='lagged')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/tsa/movstat.html#movvar) moving window variance \| Parameters: \| * x (array) – time series data * windsize (int) – window size * lag ('lagged', 'centered', or 'leading') – location of window relative to current position \| \| Returns: \| mk – moving variance, with same shape as x \| \| Return type: \| array \|	programming_docs
statsmodels statsmodels.robust.norms.RamsayE.weights statsmodels.robust.norms.RamsayE.weights ======================================== `RamsayE.weights(z)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/norms.html#RamsayE.weights) Ramsay’s Ea weighting function for the IRLS algorithm The psi function scaled by z \| Parameters: \| z (array-like) – 1d array \| \| Returns: \| weights – weights(z) = exp(-a\\|z\|) \| \| Return type: \| array \| statsmodels statsmodels.discrete.discrete_model.ProbitResults.t_test statsmodels.discrete.discrete\_model.ProbitResults.t\_test ========================================================== `ProbitResults.t_test(r_matrix, cov_p=None, scale=None, use_t=None)` Compute a t-test for a each linear hypothesis of the form Rb = q \| Parameters: \| r\_matrix (array-like, str, tuple) – + array : If an array is given, a p x k 2d array or length k 1d array specifying the linear restrictions. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q). If q is given, can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – An optional `scale` to use. Default is the scale specified by the model fit. * use\_t (bool, optional) – If use\_t is None, then the default of the model is used. If use\_t is True, then the p-values are based on the t distribution. If use\_t is False, then the p-values are based on the normal distribution. \| \| Returns: \| res – The results for the test are attributes of this results instance. The available results have the same elements as the parameter table in `summary()`. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> r = np.zeros_like(results.params) >>> r[5:] = [1,-1] >>> print(r) [ 0. 0. 0. 0. 0. 1. -1.] ``` r tests that the coefficients on the 5th and 6th independent variable are the same. ``` >>> T_test = results.t_test(r) >>> print(T_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 -1829.2026 455.391 -4.017 0.003 -2859.368 -799.037 ============================================================================== >>> T_test.effect -1829.2025687192481 >>> T_test.sd 455.39079425193762 >>> T_test.tvalue -4.0167754636411717 >>> T_test.pvalue 0.0015163772380899498 ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.formula.api import ols >>> dta = sm.datasets.longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = 'GNPDEFL = GNP, UNEMP = 2, YEAR/1829 = 1' >>> t_test = results.t_test(hypotheses) >>> print(t_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 15.0977 84.937 0.178 0.863 -177.042 207.238 c1 -2.0202 0.488 -8.231 0.000 -3.125 -0.915 c2 1.0001 0.249 0.000 1.000 0.437 1.563 ============================================================================== ``` See also [`tvalues`](statsmodels.discrete.discrete_model.probitresults.tvalues#statsmodels.discrete.discrete_model.ProbitResults.tvalues "statsmodels.discrete.discrete_model.ProbitResults.tvalues") individual t statistics [`f_test`](statsmodels.discrete.discrete_model.probitresults.f_test#statsmodels.discrete.discrete_model.ProbitResults.f_test "statsmodels.discrete.discrete_model.ProbitResults.f_test") for F tests [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") statsmodels statsmodels.regression.mixed_linear_model.MixedLMResults.df_modelwc statsmodels.regression.mixed\_linear\_model.MixedLMResults.df\_modelwc ====================================================================== `MixedLMResults.df_modelwc()` statsmodels statsmodels.tsa.statespace.sarimax.SARIMAXResults.summary statsmodels.tsa.statespace.sarimax.SARIMAXResults.summary ========================================================= `SARIMAXResults.summary(alpha=0.05, start=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/sarimax.html#SARIMAXResults.summary) Summarize the Model \| Parameters: \| * alpha (float, optional) – Significance level for the confidence intervals. Default is 0.05. * start (int, optional) – Integer of the start observation. Default is 0. * model\_name (string) – The name of the model used. Default is to use model class name. \| \| Returns: \| summary – This holds the summary table and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary.Summary`](statsmodels.iolib.summary.summary#statsmodels.iolib.summary.Summary "statsmodels.iolib.summary.Summary") statsmodels statsmodels.sandbox.distributions.extras.NormExpan_gen.fit statsmodels.sandbox.distributions.extras.NormExpan\_gen.fit =========================================================== `NormExpan_gen.fit(data, args, kwds)` Return MLEs for shape (if applicable), location, and scale parameters from data. MLE stands for Maximum Likelihood Estimate. Starting estimates for the fit are given by input arguments; for any arguments not provided with starting estimates, `self._fitstart(data)` is called to generate such. One can hold some parameters fixed to specific values by passing in keyword arguments `f0`, `f1`, …, `fn` (for shape parameters) and `floc` and `fscale` (for location and scale parameters, respectively). \| Parameters: \| data (array\_like) – Data to use in calculating the MLEs. * args (floats, optional) – Starting value(s) for any shape-characterizing arguments (those not provided will be determined by a call to `_fitstart(data)`). No default value. * kwds (floats, optional) – Starting values for the location and scale parameters; no default. Special keyword arguments are recognized as holding certain parameters fixed: + f0…fn : hold respective shape parameters fixed. Alternatively, shape parameters to fix can be specified by name. For example, if `self.shapes == "a, b"`, `fa``and ``fix_a` are equivalent to `f0`, and `fb` and `fix_b` are equivalent to `f1`. + floc : hold location parameter fixed to specified value. + fscale : hold scale parameter fixed to specified value. + optimizer : The optimizer to use. The optimizer must take `func`, and starting position as the first two arguments, plus `args` (for extra arguments to pass to the function to be optimized) and `disp=0` to suppress output as keyword arguments. \| \| Returns: \| mle\_tuple – MLEs for any shape parameters (if applicable), followed by those for location and scale. For most random variables, shape statistics will be returned, but there are exceptions (e.g. `norm`). \| \| Return type: \| tuple of floats \| #### Notes This fit is computed by maximizing a log-likelihood function, with penalty applied for samples outside of range of the distribution. The returned answer is not guaranteed to be the globally optimal MLE, it may only be locally optimal, or the optimization may fail altogether. #### Examples Generate some data to fit: draw random variates from the `beta` distribution ``` >>> from scipy.stats import beta >>> a, b = 1., 2. >>> x = beta.rvs(a, b, size=1000) ``` Now we can fit all four parameters (`a`, `b`, `loc` and `scale`): ``` >>> a1, b1, loc1, scale1 = beta.fit(x) ``` We can also use some prior knowledge about the dataset: let’s keep `loc` and `scale` fixed: ``` >>> a1, b1, loc1, scale1 = beta.fit(x, floc=0, fscale=1) >>> loc1, scale1 (0, 1) ``` We can also keep shape parameters fixed by using `f`-keywords. To keep the zero-th shape parameter `a` equal 1, use `f0=1` or, equivalently, `fa=1`: ``` >>> a1, b1, loc1, scale1 = beta.fit(x, fa=1, floc=0, fscale=1) >>> a1 1 ``` Not all distributions return estimates for the shape parameters. `norm` for example just returns estimates for location and scale: ``` >>> from scipy.stats import norm >>> x = norm.rvs(a, b, size=1000, random_state=123) >>> loc1, scale1 = norm.fit(x) >>> loc1, scale1 (0.92087172783841631, 2.0015750750324668) ``` statsmodels statsmodels.tsa.statespace.tools.unconstrain_stationary_univariate statsmodels.tsa.statespace.tools.unconstrain\_stationary\_univariate ==================================================================== `statsmodels.tsa.statespace.tools.unconstrain_stationary_univariate(constrained)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/tools.html#unconstrain_stationary_univariate) Transform constrained parameters used in likelihood evaluation to unconstrained parameters used by the optimizer \| Parameters: \| constrained (array) – Constrained parameters of, e.g., an autoregressive or moving average component, to be transformed to arbitrary parameters used by the optimizer. \| \| Returns: \| unconstrained – Unconstrained parameters used by the optimizer, to be transformed to stationary coefficients of, e.g., an autoregressive or moving average component. \| \| Return type: \| array \| #### References \| \| \| \| --- \| --- \| \| [\] \| Monahan, John F. 1984. “A Note on Enforcing Stationarity in Autoregressive-moving Average Models.” Biometrika 71 (2) (August 1): 403-404. \| statsmodels statsmodels.sandbox.distributions.extras.SkewNorm_gen.std statsmodels.sandbox.distributions.extras.SkewNorm\_gen.std ========================================================== `SkewNorm_gen.std(args, *kwds)` Standard deviation of the distribution. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| std – standard deviation of the distribution \| \| Return type: \| float \| statsmodels statsmodels.sandbox.distributions.extras.SkewNorm2_gen.pdf statsmodels.sandbox.distributions.extras.SkewNorm2\_gen.pdf =========================================================== `SkewNorm2_gen.pdf(x, args, kwds)` Probability density function at x of the given RV. \| Parameters: \| x (array\_like) – quantiles * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| pdf – Probability density function evaluated at x \| \| Return type: \| ndarray \| statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.remove_data statsmodels.regression.recursive\_ls.RecursiveLSResults.remove\_data ==================================================================== `RecursiveLSResults.remove_data()` remove data arrays, all nobs arrays from result and model This reduces the size of the instance, so it can be pickled with less memory. Currently tested for use with predict from an unpickled results and model instance. Warning Since data and some intermediate results have been removed calculating new statistics that require them will raise exceptions. The exception will occur the first time an attribute is accessed that has been set to None. Not fully tested for time series models, tsa, and might delete too much for prediction or not all that would be possible. The lists of arrays to delete are maintained as attributes of the result and model instance, except for cached values. These lists could be changed before calling remove\_data. The attributes to remove are named in: `model._data_attr : arrays attached to both the model instance` and the results instance with the same attribute name. `result.data_in_cache : arrays that may exist as values in` result.\_cache (TODO : should privatize name) `result._data_attr_model : arrays attached to the model` instance but not to the results instance statsmodels statsmodels.tsa.statespace.varmax.VARMAXResults.bic statsmodels.tsa.statespace.varmax.VARMAXResults.bic =================================================== `VARMAXResults.bic()` (float) Bayes Information Criterion statsmodels statsmodels.stats.correlation_tools.corr_nearest statsmodels.stats.correlation\_tools.corr\_nearest ================================================== `statsmodels.stats.correlation_tools.corr_nearest(corr, threshold=1e-15, n_fact=100)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/correlation_tools.html#corr_nearest) Find the nearest correlation matrix that is positive semi-definite. The function iteratively adjust the correlation matrix by clipping the eigenvalues of a difference matrix. The diagonal elements are set to one. \| Parameters: \| * corr (ndarray, (k, k)) – initial correlation matrix * threshold (float) – clipping threshold for smallest eigenvalue, see Notes * n\_fact (int or float) – factor to determine the maximum number of iterations. The maximum number of iterations is the integer part of the number of columns in the correlation matrix times n\_fact. \| \| Returns: \| corr\_new – corrected correlation matrix \| \| Return type: \| ndarray, (optional) \| #### Notes The smallest eigenvalue of the corrected correlation matrix is approximately equal to the `threshold`. If the threshold=0, then the smallest eigenvalue of the correlation matrix might be negative, but zero within a numerical error, for example in the range of -1e-16. Assumes input correlation matrix is symmetric. Stops after the first step if correlation matrix is already positive semi-definite or positive definite, so that smallest eigenvalue is above threshold. In this case, the returned array is not the original, but is equal to it within numerical precision. See also [`corr_clipped`](statsmodels.stats.correlation_tools.corr_clipped#statsmodels.stats.correlation_tools.corr_clipped "statsmodels.stats.correlation_tools.corr_clipped"), [`cov_nearest`](statsmodels.stats.correlation_tools.cov_nearest#statsmodels.stats.correlation_tools.cov_nearest "statsmodels.stats.correlation_tools.cov_nearest") statsmodels statsmodels.tsa.arima_model.ARIMAResults.t_test_pairwise statsmodels.tsa.arima\_model.ARIMAResults.t\_test\_pairwise =========================================================== `ARIMAResults.t_test_pairwise(term_name, method='hs', alpha=0.05, factor_labels=None)` perform pairwise t\_test with multiple testing corrected p-values This uses the formula design\_info encoding contrast matrix and should work for all encodings of a main effect. \| Parameters: \| * result (result instance) – The results of an estimated model with a categorical main effect. * term\_name (str) – name of the term for which pairwise comparisons are computed. Term names for categorical effects are created by patsy and correspond to the main part of the exog names. * method (str or list of strings) – multiple testing p-value correction, default is ‘hs’, see stats.multipletesting * alpha (float) – significance level for multiple testing reject decision. * factor\_labels (None, list of str) – Labels for the factor levels used for pairwise labels. If not provided, then the labels from the formula design\_info are used. \| \| Returns: \| results – The results are stored as attributes, the main attributes are the following two. Other attributes are added for debugging purposes or as background information.* result\_frame : pandas DataFrame with t\_test results and multiple testing corrected p-values. * contrasts : matrix of constraints of the null hypothesis in the t\_test. \| \| Return type: \| instance of a simple Results class \| #### Notes Status: experimental. Currently only checked for treatment coding with and without specified reference level. Currently there are no multiple testing corrected confidence intervals available. #### Examples ``` >>> res = ols("np.log(Days+1) ~ C(Weight) + C(Duration)", data).fit() >>> pw = res.t_test_pairwise("C(Weight)") >>> pw.result_frame coef std err t P>\|t\| Conf. Int. Low 2-1 0.632315 0.230003 2.749157 8.028083e-03 0.171563 3-1 1.302555 0.230003 5.663201 5.331513e-07 0.841803 3-2 0.670240 0.230003 2.914044 5.119126e-03 0.209488 Conf. Int. Upp. pvalue-hs reject-hs 2-1 1.093067 0.010212 True 3-1 1.763307 0.000002 True 3-2 1.130992 0.010212 True ``` statsmodels statsmodels.tsa.arima_model.ARMAResults.maroots statsmodels.tsa.arima\_model.ARMAResults.maroots ================================================ `ARMAResults.maroots()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_model.html#ARMAResults.maroots) statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.cov_params_approx statsmodels.tsa.statespace.dynamic\_factor.DynamicFactorResults.cov\_params\_approx =================================================================================== `DynamicFactorResults.cov_params_approx()` (array) The variance / covariance matrix. Computed using the numerical Hessian approximated by complex step or finite differences methods. statsmodels statsmodels.stats.weightstats.ztest statsmodels.stats.weightstats.ztest =================================== `statsmodels.stats.weightstats.ztest(x1, x2=None, value=0, alternative='two-sided', usevar='pooled', ddof=1.0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/weightstats.html#ztest) test for mean based on normal distribution, one or two samples In the case of two samples, the samples are assumed to be independent. \| Parameters: \| * x2 (x1,) – two independent samples * value (float) – In the one sample case, value is the mean of x1 under the Null hypothesis. In the two sample case, value is the difference between mean of x1 and mean of x2 under the Null hypothesis. The test statistic is `x1_mean - x2_mean - value`. * alternative (string) – The alternative hypothesis, H1, has to be one of the following ’two-sided’: H1: difference in means not equal to value (default) ‘larger’ : H1: difference in means larger than value ‘smaller’ : H1: difference in means smaller than value * usevar (string, 'pooled') – Currently, only ‘pooled’ is implemented. If `pooled`, then the standard deviation of the samples is assumed to be the same. see CompareMeans.ztest\_ind for different options. * ddof (int) – Degrees of freedom use in the calculation of the variance of the mean estimate. In the case of comparing means this is one, however it can be adjusted for testing other statistics (proportion, correlation) \| \| Returns: \| * tstat (float) – test statisic * pvalue (float) – pvalue of the t-test \| #### Notes usevar not implemented, is always pooled in two sample case use CompareMeans instead.	programming_docs
statsmodels statsmodels.stats.diagnostic.het_arch statsmodels.stats.diagnostic.het\_arch ====================================== `statsmodels.stats.diagnostic.het_arch(resid, maxlag=None, autolag=None, store=False, regresults=False, ddof=0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/stats/diagnostic.html#het_arch) Engle’s Test for Autoregressive Conditional Heteroscedasticity (ARCH) \| Parameters: \| * resid (ndarray) – residuals from an estimation, or time series * maxlag (int) – highest lag to use * autolag (None or string) – If None, then a fixed number of lags given by maxlag is used. * store (bool) – If true then the intermediate results are also returned * ddof (int) – Not Implemented Yet If the residuals are from a regression, or ARMA estimation, then there are recommendations to correct the degrees of freedom by the number of parameters that have been estimated, for example ddof=p+a for an ARMA(p,q) (need reference, based on discussion on R finance mailinglist) \| \| Returns: \| * lm (float) – Lagrange multiplier test statistic * lmpval (float) – p-value for Lagrange multiplier test * fval (float) – fstatistic for F test, alternative version of the same test based on F test for the parameter restriction * fpval (float) – pvalue for F test * resstore (instance (optional)) – a class instance that holds intermediate results. Only returned if store=True \| #### Notes verified agains R:FinTS::ArchTest statsmodels statsmodels.tsa.vector_ar.vecm.VECMResults.plot_forecast statsmodels.tsa.vector\_ar.vecm.VECMResults.plot\_forecast ========================================================== `VECMResults.plot_forecast(steps, alpha=0.05, plot_conf_int=True, n_last_obs=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/vecm.html#VECMResults.plot_forecast) Plot the forecast. \| Parameters: \| * steps (int) – Prediction horizon. * alpha (float, 0 < `alpha` < 1) – The confidence level. * plot\_conf\_int (bool, default: True) – If True, plot bounds of confidence intervals. * n\_last\_obs (int or None, default: None) – If int, restrict plotted history to n\_last\_obs observations. If None, include the whole history in the plot. \| statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.fittedvalues statsmodels.tsa.statespace.dynamic\_factor.DynamicFactorResults.fittedvalues ============================================================================ `DynamicFactorResults.fittedvalues()` (array) The predicted values of the model. An (nobs x k\_endog) array. statsmodels statsmodels.robust.norms.AndrewWave statsmodels.robust.norms.AndrewWave =================================== `class statsmodels.robust.norms.AndrewWave(a=1.339)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/norms.html#AndrewWave) Andrew’s wave for M estimation. \| Parameters: \| a (float, optional) – The tuning constant for Andrew’s Wave function. The default value is 1.339. \| See also [`statsmodels.robust.norms.RobustNorm`](statsmodels.robust.norms.robustnorm#statsmodels.robust.norms.RobustNorm "statsmodels.robust.norms.RobustNorm") #### Methods \| \| \| \| --- \| --- \| \| [`psi`](statsmodels.robust.norms.andrewwave.psi#statsmodels.robust.norms.AndrewWave.psi "statsmodels.robust.norms.AndrewWave.psi")(z) \| The psi function for Andrew’s wave \| \| [`psi_deriv`](statsmodels.robust.norms.andrewwave.psi_deriv#statsmodels.robust.norms.AndrewWave.psi_deriv "statsmodels.robust.norms.AndrewWave.psi_deriv")(z) \| The derivative of Andrew’s wave psi function \| \| [`rho`](statsmodels.robust.norms.andrewwave.rho#statsmodels.robust.norms.AndrewWave.rho "statsmodels.robust.norms.AndrewWave.rho")(z) \| The robust criterion function for Andrew’s wave. \| \| [`weights`](statsmodels.robust.norms.andrewwave.weights#statsmodels.robust.norms.AndrewWave.weights "statsmodels.robust.norms.AndrewWave.weights")(z) \| Andrew’s wave weighting function for the IRLS algorithm \| statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.summary statsmodels.tsa.vector\_ar.var\_model.VARResults.summary ======================================================== `VARResults.summary()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARResults.summary) Compute console output summary of estimates \| Returns: \| summary \| \| Return type: \| VARSummary \| statsmodels statsmodels.stats.multitest.RegressionFDR.threshold statsmodels.stats.multitest.RegressionFDR.threshold =================================================== `RegressionFDR.threshold(tfdr)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/_knockoff.html#RegressionFDR.threshold) Returns the threshold statistic for a given target FDR. statsmodels statsmodels.discrete.discrete_model.BinaryResults.get_margeff statsmodels.discrete.discrete\_model.BinaryResults.get\_margeff =============================================================== `BinaryResults.get_margeff(at='overall', method='dydx', atexog=None, dummy=False, count=False)` Get marginal effects of the fitted model. \| Parameters: \| * at (str, optional) – Options are: + ’overall’, The average of the marginal effects at each observation. + ’mean’, The marginal effects at the mean of each regressor. + ’median’, The marginal effects at the median of each regressor. + ’zero’, The marginal effects at zero for each regressor. + ’all’, The marginal effects at each observation. If `at` is all only margeff will be available from the returned object.Note that if `exog` is specified, then marginal effects for all variables not specified by `exog` are calculated using the `at` option. * method (str, optional) – Options are: + ’dydx’ - dy/dx - No transformation is made and marginal effects are returned. This is the default. + ’eyex’ - estimate elasticities of variables in `exog` – d(lny)/d(lnx) + ’dyex’ - estimate semielasticity – dy/d(lnx) + ’eydx’ - estimate semeilasticity – d(lny)/dxNote that tranformations are done after each observation is calculated. Semi-elasticities for binary variables are computed using the midpoint method. ‘dyex’ and ‘eyex’ do not make sense for discrete variables. * atexog (array-like, optional) – Optionally, you can provide the exogenous variables over which to get the marginal effects. This should be a dictionary with the key as the zero-indexed column number and the value of the dictionary. Default is None for all independent variables less the constant. * dummy (bool, optional) – If False, treats binary variables (if present) as continuous. This is the default. Else if True, treats binary variables as changing from 0 to 1. Note that any variable that is either 0 or 1 is treated as binary. Each binary variable is treated separately for now. * count (bool, optional) – If False, treats count variables (if present) as continuous. This is the default. Else if True, the marginal effect is the change in probabilities when each observation is increased by one. \| \| Returns: \| DiscreteMargins – Returns an object that holds the marginal effects, standard errors, confidence intervals, etc. See `statsmodels.discrete.discrete_margins.DiscreteMargins` for more information. \| \| Return type: \| marginal effects instance \| #### Notes When using after Poisson, returns the expected number of events per period, assuming that the model is loglinear. statsmodels statsmodels.tsa.vector_ar.vecm.VECMResults.irf statsmodels.tsa.vector\_ar.vecm.VECMResults.irf =============================================== `VECMResults.irf(periods=10)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/vecm.html#VECMResults.irf) statsmodels statsmodels.genmod.bayes_mixed_glm.BinomialBayesMixedGLM.predict statsmodels.genmod.bayes\_mixed\_glm.BinomialBayesMixedGLM.predict ================================================================== `BinomialBayesMixedGLM.predict(params, exog=None, args, kwargs)` After a model has been fit predict returns the fitted values. This is a placeholder intended to be overwritten by individual models. statsmodels statsmodels.tsa.filters.filtertools.fftconvolveinv statsmodels.tsa.filters.filtertools.fftconvolveinv ================================================== `statsmodels.tsa.filters.filtertools.fftconvolveinv(in1, in2, mode='full')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/filters/filtertools.html#fftconvolveinv) Convolve two N-dimensional arrays using FFT. See convolve. copied from scipy.signal.signaltools, but here used to try out inverse filter doesn’t work or I can’t get it to work 2010-10-23: looks ok to me for 1d, from results below with padded data array (fftp) but it doesn’t work for multidimensional inverse filter (fftn) original signal.fftconvolve also uses fftn statsmodels statsmodels.tsa.statespace.varmax.VARMAX.set_conserve_memory statsmodels.tsa.statespace.varmax.VARMAX.set\_conserve\_memory ============================================================== `VARMAX.set_conserve_memory(conserve_memory=None, kwargs)` Set the memory conservation method By default, the Kalman filter computes a number of intermediate matrices at each iteration. The memory conservation options control which of those matrices are stored. \| Parameters: \| conserve\_memory (integer, optional) – Bitmask value to set the memory conservation method to. See notes for details. * *\\kwargs* – Keyword arguments may be used to influence the memory conservation method by setting individual boolean flags. \| #### Notes This method is rarely used. See the corresponding function in the `KalmanFilter` class for details. statsmodels statsmodels.sandbox.regression.gmm.IVRegressionResults.cov_HC1 statsmodels.sandbox.regression.gmm.IVRegressionResults.cov\_HC1 =============================================================== `IVRegressionResults.cov_HC1()` See statsmodels.RegressionResults statsmodels statsmodels.sandbox.regression.gmm.IVRegressionResults.wald_test statsmodels.sandbox.regression.gmm.IVRegressionResults.wald\_test ================================================================= `IVRegressionResults.wald_test(r_matrix, cov_p=None, scale=1.0, invcov=None, use_f=None)` Compute a Wald-test for a joint linear hypothesis. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. * use\_f (bool) – If True, then the F-distribution is used. If False, then the asymptotic distribution, chisquare is used. If use\_f is None, then the F distribution is used if the model specifies that use\_t is True. The test statistic is proportionally adjusted for the distribution by the number of constraints in the hypothesis. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`f_test`](statsmodels.sandbox.regression.gmm.ivregressionresults.f_test#statsmodels.sandbox.regression.gmm.IVRegressionResults.f_test "statsmodels.sandbox.regression.gmm.IVRegressionResults.f_test"), [`t_test`](statsmodels.sandbox.regression.gmm.ivregressionresults.t_test#statsmodels.sandbox.regression.gmm.IVRegressionResults.t_test "statsmodels.sandbox.regression.gmm.IVRegressionResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.duration.hazard_regression.PHReg.baseline_cumulative_hazard statsmodels.duration.hazard\_regression.PHReg.baseline\_cumulative\_hazard ========================================================================== `PHReg.baseline_cumulative_hazard(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/duration/hazard_regression.html#PHReg.baseline_cumulative_hazard) Estimate the baseline cumulative hazard and survival functions. \| Parameters: \| params (ndarray) – The model parameters. \| \| Returns: \| * A list of triples (time, hazard, survival) containing the time * values and corresponding cumulative hazard and survival * function values for each stratum. \| #### Notes Uses the Nelson-Aalen estimator. statsmodels statsmodels.sandbox.regression.gmm.IV2SLS.loglike statsmodels.sandbox.regression.gmm.IV2SLS.loglike ================================================= `IV2SLS.loglike(params)` Log-likelihood of model. statsmodels statsmodels.tsa.vector_ar.var_model.VARProcess.mse statsmodels.tsa.vector\_ar.var\_model.VARProcess.mse ==================================================== `VARProcess.mse(steps)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARProcess.mse) Compute theoretical forecast error variance matrices \| Parameters: \| steps (int) – Number of steps ahead \| #### Notes \[\mathrm{MSE}(h) = \sum\_{i=0}^{h-1} \Phi \Sigma\_u \Phi^T\] \| Returns: \| forc\_covs \| \| Return type: \| ndarray (steps x neqs x neqs) \| statsmodels statsmodels.sandbox.distributions.extras.NormExpan_gen.interval statsmodels.sandbox.distributions.extras.NormExpan\_gen.interval ================================================================ `NormExpan_gen.interval(alpha, args, kwds)` Confidence interval with equal areas around the median. \| Parameters: \| alpha (array\_like of float) – Probability that an rv will be drawn from the returned range. Each value should be in the range [0, 1]. * arg2, .. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information). * loc (array\_like, optional) – location parameter, Default is 0. * scale (array\_like, optional) – scale parameter, Default is 1. \| \| Returns: \| a, b – end-points of range that contain `100 * alpha %` of the rv’s possible values. \| \| Return type: \| ndarray of float \| statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactor.initialize_stationary statsmodels.tsa.statespace.dynamic\_factor.DynamicFactor.initialize\_stationary =============================================================================== `DynamicFactor.initialize_stationary()` statsmodels statsmodels.discrete.discrete_model.GeneralizedPoissonResults.aic statsmodels.discrete.discrete\_model.GeneralizedPoissonResults.aic ================================================================== `GeneralizedPoissonResults.aic()` statsmodels statsmodels.tsa.statespace.varmax.VARMAXResults.forecast statsmodels.tsa.statespace.varmax.VARMAXResults.forecast ======================================================== `VARMAXResults.forecast(steps=1, *kwargs)` Out-of-sample forecasts \| Parameters: \| steps (int, str, or datetime, optional) – If an integer, the number of steps to forecast from the end of the sample. Can also be a date string to parse or a datetime type. However, if the dates index does not have a fixed frequency, steps must be an integer. Default * *\\kwargs* – Additional arguments may required for forecasting beyond the end of the sample. See `FilterResults.predict` for more details. \| \| Returns: \| forecast – Array of out of sample forecasts. A (steps x k\_endog) array. \| \| Return type: \| array \| statsmodels statsmodels.regression.quantile_regression.QuantRegResults.normalized_cov_params statsmodels.regression.quantile\_regression.QuantRegResults.normalized\_cov\_params =================================================================================== `QuantRegResults.normalized_cov_params()` statsmodels statsmodels.sandbox.distributions.extras.SkewNorm2_gen.interval statsmodels.sandbox.distributions.extras.SkewNorm2\_gen.interval ================================================================ `SkewNorm2_gen.interval(alpha, args, kwds)` Confidence interval with equal areas around the median. \| Parameters: \| alpha (array\_like of float) – Probability that an rv will be drawn from the returned range. Each value should be in the range [0, 1]. * arg2, .. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information). * loc (array\_like, optional) – location parameter, Default is 0. * scale (array\_like, optional) – scale parameter, Default is 1. \| \| Returns: \| a, b – end-points of range that contain `100 * alpha %` of the rv’s possible values. \| \| Return type: \| ndarray of float \| statsmodels statsmodels.sandbox.distributions.transformed.LogTransf_gen.freeze statsmodels.sandbox.distributions.transformed.LogTransf\_gen.freeze =================================================================== `LogTransf_gen.freeze(args, kwds)` Freeze the distribution for the given arguments. \| Parameters: \| arg2*, arg3,.. (arg1,) – The shape parameter(s) for the distribution. Should include all the non-optional arguments, may include `loc` and `scale`. \| \| Returns: \| rv\_frozen – The frozen distribution. \| \| Return type: \| rv\_frozen instance \| statsmodels statsmodels.stats.contingency_tables.Table2x2.log_oddsratio_se statsmodels.stats.contingency\_tables.Table2x2.log\_oddsratio\_se ================================================================= `Table2x2.log_oddsratio_se()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/contingency_tables.html#Table2x2.log_oddsratio_se) statsmodels statsmodels.sandbox.regression.gmm.NonlinearIVGMM.start_weights statsmodels.sandbox.regression.gmm.NonlinearIVGMM.start\_weights ================================================================ `NonlinearIVGMM.start_weights(inv=True)` statsmodels statsmodels.regression.linear_model.OLSResults.cov_HC0 statsmodels.regression.linear\_model.OLSResults.cov\_HC0 ======================================================== `OLSResults.cov_HC0()` See statsmodels.RegressionResults statsmodels statsmodels.discrete.discrete_model.NegativeBinomialResults.llf statsmodels.discrete.discrete\_model.NegativeBinomialResults.llf ================================================================ `NegativeBinomialResults.llf()` statsmodels statsmodels.multivariate.cancorr.CanCorr statsmodels.multivariate.cancorr.CanCorr ======================================== `class statsmodels.multivariate.cancorr.CanCorr(endog, exog, tolerance=1e-08, missing='none', hasconst=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/multivariate/cancorr.html#CanCorr) Canonical correlation analysis using singluar value decomposition For matrices exog=x and endog=y, find projections x\_cancoef and y\_cancoef such that: x1 = x \ x\_cancoef, x1’ \* x1 is identity matrix y1 = y \* y\_cancoef, y1’ \* y1 is identity matrix and the correlation between x1 and y1 is maximized. `endog` array – See Parameters. `exog` array – See Parameters. `cancorr` array – The canonical correlation values `y_cancoeff` array – The canonical coeefficients for endog `x_cancoeff` array – The canonical coefficients for exog #### References \| \| \| \| --- \| --- \| \| [\*] \| <http://numerical.recipes/whp/notes/CanonCorrBySVD.pdf> \| \| \| \| \| --- \| --- \| \| [†] \| <http://www.csun.edu/~ata20315/psy524/docs/Psy524%20Lecture%208%20CC.pdf> \| \| \| \| \| --- \| --- \| \| [‡] \| <http://www.mathematica-journal.com/2014/06/canonical-correlation-analysis/> \| #### Methods \| \| \| \| --- \| --- \| \| [`corr_test`](statsmodels.multivariate.cancorr.cancorr.corr_test#statsmodels.multivariate.cancorr.CanCorr.corr_test "statsmodels.multivariate.cancorr.CanCorr.corr_test")() \| Approximate F test Perform multivariate statistical tests of the hypothesis that there is no canonical correlation between endog and exog. \| \| [`fit`](statsmodels.multivariate.cancorr.cancorr.fit#statsmodels.multivariate.cancorr.CanCorr.fit "statsmodels.multivariate.cancorr.CanCorr.fit")() \| Fit a model to data. \| \| [`from_formula`](statsmodels.multivariate.cancorr.cancorr.from_formula#statsmodels.multivariate.cancorr.CanCorr.from_formula "statsmodels.multivariate.cancorr.CanCorr.from_formula")(formula, data[, subset, drop\_cols]) \| Create a Model from a formula and dataframe. \| \| [`predict`](statsmodels.multivariate.cancorr.cancorr.predict#statsmodels.multivariate.cancorr.CanCorr.predict "statsmodels.multivariate.cancorr.CanCorr.predict")(params[, exog]) \| After a model has been fit predict returns the fitted values. \| #### Attributes \| \| \| \| --- \| --- \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| Names of exogenous variables \|	programming_docs
statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.stderr_dt statsmodels.tsa.vector\_ar.var\_model.VARResults.stderr\_dt =========================================================== `VARResults.stderr_dt()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARResults.stderr_dt) statsmodels statsmodels.tsa.statespace.varmax.VARMAXResults.bse statsmodels.tsa.statespace.varmax.VARMAXResults.bse =================================================== `VARMAXResults.bse()` statsmodels statsmodels.multivariate.factor_rotation.procrustes statsmodels.multivariate.factor\_rotation.procrustes ==================================================== `statsmodels.multivariate.factor_rotation.procrustes(A, H)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/multivariate/factor_rotation/_analytic_rotation.html#procrustes) Analytically solves the following Procrustes problem: \[\phi(L) =\frac{1}{2}\\|AT-H\\|^2.\] (With no further conditions on $H$) Under the assumption that $A^\H$ has full rank, the analytical solution $T$ is given by: \[T = (A^\HH^\A)^{-\frac{1}{2}}A^\H,\] see Navarra, Simoncini (2010). \| Parameters: \| * A (numpy matrix) – non rotated factors * H (numpy matrix) – target matrix * full\_rank (boolean (default False)) – if set to true full rank is assumed \| \| Returns: \| \| \| Return type: \| The matrix $T$. \| #### References [1] Navarra, Simoncini (2010) - A guide to emprirical orthogonal functions for climate data analysis statsmodels statsmodels.nonparametric.smoothers_lowess.lowess statsmodels.nonparametric.smoothers\_lowess.lowess ================================================== `statsmodels.nonparametric.smoothers_lowess.lowess(endog, exog, frac=0.6666666666666666, it=3, delta=0.0, is_sorted=False, missing='drop', return_sorted=True)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/nonparametric/smoothers_lowess.html#lowess) LOWESS (Locally Weighted Scatterplot Smoothing) A lowess function that outs smoothed estimates of endog at the given exog values from points (exog, endog) \| Parameters: \| * endog (1-D numpy array) – The y-values of the observed points * exog (1-D numpy array) – The x-values of the observed points * frac (float) – Between 0 and 1. The fraction of the data used when estimating each y-value. * it (int) – The number of residual-based reweightings to perform. * delta (float) – Distance within which to use linear-interpolation instead of weighted regression. * is\_sorted (bool) – If False (default), then the data will be sorted by exog before calculating lowess. If True, then it is assumed that the data is already sorted by exog. * missing (str) – Available options are ‘none’, ‘drop’, and ‘raise’. If ‘none’, no nan checking is done. If ‘drop’, any observations with nans are dropped. If ‘raise’, an error is raised. Default is ‘drop’. * return\_sorted (bool) – If True (default), then the returned array is sorted by exog and has missing (nan or infinite) observations removed. If False, then the returned array is in the same length and the same sequence of observations as the input array. \| \| Returns: \| out – The returned array is two-dimensional if return\_sorted is True, and one dimensional if return\_sorted is False. If return\_sorted is True, then a numpy array with two columns. The first column contains the sorted x (exog) values and the second column the associated estimated y (endog) values. If return\_sorted is False, then only the fitted values are returned, and the observations will be in the same order as the input arrays. \| \| Return type: \| ndarray, float \| #### Notes This lowess function implements the algorithm given in the reference below using local linear estimates. Suppose the input data has N points. The algorithm works by estimating the `smooth` y\_i by taking the frac\N closest points to (x\_i,y\_i) based on their x values and estimating y\_i using a weighted linear regression. The weight for (x\_j,y\_j) is tricube function applied to abs(x\_i-x\_j). If it > 1, then further weighted local linear regressions are performed, where the weights are the same as above times the \_lowess\_bisquare function of the residuals. Each iteration takes approximately the same amount of time as the original fit, so these iterations are expensive. They are most useful when the noise has extremely heavy tails, such as Cauchy noise. Noise with less heavy-tails, such as t-distributions with df>2, are less problematic. The weights downgrade the influence of points with large residuals. In the extreme case, points whose residuals are larger than 6 times the median absolute residual are given weight 0. `delta` can be used to save computations. For each `x_i`, regressions are skipped for points closer than `delta`. The next regression is fit for the farthest point within delta of `x_i` and all points in between are estimated by linearly interpolating between the two regression fits. Judicious choice of delta can cut computation time considerably for large data (N > 5000). A good choice is `delta = 0.01 range(exog)`. Some experimentation is likely required to find a good choice of `frac` and `iter` for a particular dataset. #### References Cleveland, W.S. (1979) “Robust Locally Weighted Regression and Smoothing Scatterplots”. Journal of the American Statistical Association 74 (368): 829-836. #### Examples The below allows a comparison between how different the fits from lowess for different values of frac can be. ``` >>> import numpy as np >>> import statsmodels.api as sm >>> lowess = sm.nonparametric.lowess >>> x = np.random.uniform(low = -2np.pi, high = 2np.pi, size=500) >>> y = np.sin(x) + np.random.normal(size=len(x)) >>> z = lowess(y, x) >>> w = lowess(y, x, frac=1./3) ``` This gives a similar comparison for when it is 0 vs not. ``` >>> import numpy as np >>> import scipy.stats as stats >>> import statsmodels.api as sm >>> lowess = sm.nonparametric.lowess >>> x = np.random.uniform(low = -2np.pi, high = 2np.pi, size=500) >>> y = np.sin(x) + stats.cauchy.rvs(size=len(x)) >>> z = lowess(y, x, frac= 1./3, it=0) >>> w = lowess(y, x, frac=1./3) ``` statsmodels statsmodels.discrete.count_model.ZeroInflatedPoisson.predict statsmodels.discrete.count\_model.ZeroInflatedPoisson.predict ============================================================= `ZeroInflatedPoisson.predict(params, exog=None, exog_infl=None, exposure=None, offset=None, which='mean')` Predict response variable of a count model given exogenous variables. \| Parameters: \| * params (array-like) – The parameters of the model * exog (array, optional) – A reference to the exogenous design. If not assigned, will be used exog from fitting. * exog\_infl (array, optional) – A reference to the zero-inflated exogenous design. If not assigned, will be used exog from fitting. * offset (array, optional) – Offset is added to the linear prediction with coefficient equal to 1. * exposure (array, optional) – Log(exposure) is added to the linear prediction with coefficient equal to 1. If exposure is specified, then it will be logged by the method. The user does not need to log it first. * which (string, optional) – Define values that will be predicted. ‘mean’, ‘mean-main’, ‘linear’, ‘mean-nonzero’, ‘prob-zero, ‘prob’, ‘prob-main’ Default is ‘mean’. \| #### Notes statsmodels statsmodels.discrete.count_model.ZeroInflatedGeneralizedPoissonResults.save statsmodels.discrete.count\_model.ZeroInflatedGeneralizedPoissonResults.save ============================================================================ `ZeroInflatedGeneralizedPoissonResults.save(fname, remove_data=False)` save a pickle of this instance \| Parameters: \| * fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. * remove\_data (bool) – If False (default), then the instance is pickled without changes. If True, then all arrays with length nobs are set to None before pickling. See the remove\_data method. In some cases not all arrays will be set to None. \| #### Notes If remove\_data is true and the model result does not implement a remove\_data method then this will raise an exception. statsmodels statsmodels.tsa.arima_model.ARMAResults.mafreq statsmodels.tsa.arima\_model.ARMAResults.mafreq =============================================== `ARMAResults.mafreq()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_model.html#ARMAResults.mafreq) Returns the frequency of the MA roots. This is the solution, x, to z = abs(z)\exp(2j\np.pi\x) where z are the roots. statsmodels statsmodels.sandbox.distributions.extras.SkewNorm2_gen.var statsmodels.sandbox.distributions.extras.SkewNorm2\_gen.var =========================================================== `SkewNorm2_gen.var(args, *kwds)` Variance of the distribution. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| var – the variance of the distribution \| \| Return type: \| float \| statsmodels statsmodels.regression.linear_model.RegressionResults.nobs statsmodels.regression.linear\_model.RegressionResults.nobs =========================================================== `RegressionResults.nobs()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#RegressionResults.nobs) statsmodels statsmodels.stats.moment_helpers.mvsk2mc statsmodels.stats.moment\_helpers.mvsk2mc ========================================= `statsmodels.stats.moment_helpers.mvsk2mc(args)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/moment_helpers.html#mvsk2mc) convert mean, variance, skew, kurtosis to central moments statsmodels statsmodels.regression.linear_model.GLSAR.get_distribution statsmodels.regression.linear\_model.GLSAR.get\_distribution ============================================================ `GLSAR.get_distribution(params, scale, exog=None, dist_class=None)` Returns a random number generator for the predictive distribution. \| Parameters: \| * params (array-like) – The model parameters (regression coefficients). * scale (scalar) – The variance parameter. * exog (array-like) – The predictor variable matrix. * dist\_class (class) – A random number generator class. Must take ‘loc’ and ‘scale’ as arguments and return a random number generator implementing an `rvs` method for simulating random values. Defaults to Gaussian. \| \| Returns: \| Frozen random number generator object with mean and variance determined by the fitted linear model. Use the `rvs` method to generate random values. \| \| Return type: \| gen \| #### Notes Due to the behavior of `scipy.stats.distributions objects`, the returned random number generator must be called with `gen.rvs(n)` where `n` is the number of observations in the data set used to fit the model. If any other value is used for `n`, misleading results will be produced. statsmodels statsmodels.discrete.count_model.ZeroInflatedPoisson.loglikeobs statsmodels.discrete.count\_model.ZeroInflatedPoisson.loglikeobs ================================================================ `ZeroInflatedPoisson.loglikeobs(params)` Loglikelihood for observations of Generic Zero Inflated model \| Parameters: \| params (array-like) – The parameters of the model. \| \| Returns: \| loglike – The log likelihood for each observation of the model evaluated at `params`. See Notes \| \| Return type: \| ndarray \| #### Notes \[\ln L=\ln(w\_{i}+(1-w\_{i})\P\_{main\\_model})+ \ln(1-w\_{i})+L\_{main\\_model} where P - pdf of main model, L - loglike function of main model.\] for observations $i=1,...,n$ statsmodels statsmodels.sandbox.distributions.transformed.ExpTransf_gen.var statsmodels.sandbox.distributions.transformed.ExpTransf\_gen.var ================================================================ `ExpTransf_gen.var(args, *kwds)` Variance of the distribution. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| var – the variance of the distribution \| \| Return type: \| float \| statsmodels statsmodels.discrete.discrete_model.NegativeBinomialResults.prsquared statsmodels.discrete.discrete\_model.NegativeBinomialResults.prsquared ====================================================================== `NegativeBinomialResults.prsquared()` statsmodels statsmodels.regression.quantile_regression.QuantRegResults.t_test statsmodels.regression.quantile\_regression.QuantRegResults.t\_test =================================================================== `QuantRegResults.t_test(r_matrix, cov_p=None, scale=None, use_t=None)` Compute a t-test for a each linear hypothesis of the form Rb = q \| Parameters: \| * r\_matrix (array-like, str, tuple) – + array : If an array is given, a p x k 2d array or length k 1d array specifying the linear restrictions. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q). If q is given, can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – An optional `scale` to use. Default is the scale specified by the model fit. * use\_t (bool, optional) – If use\_t is None, then the default of the model is used. If use\_t is True, then the p-values are based on the t distribution. If use\_t is False, then the p-values are based on the normal distribution. \| \| Returns: \| res – The results for the test are attributes of this results instance. The available results have the same elements as the parameter table in `summary()`. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> r = np.zeros_like(results.params) >>> r[5:] = [1,-1] >>> print(r) [ 0. 0. 0. 0. 0. 1. -1.] ``` r tests that the coefficients on the 5th and 6th independent variable are the same. ``` >>> T_test = results.t_test(r) >>> print(T_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 -1829.2026 455.391 -4.017 0.003 -2859.368 -799.037 ============================================================================== >>> T_test.effect -1829.2025687192481 >>> T_test.sd 455.39079425193762 >>> T_test.tvalue -4.0167754636411717 >>> T_test.pvalue 0.0015163772380899498 ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.formula.api import ols >>> dta = sm.datasets.longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = 'GNPDEFL = GNP, UNEMP = 2, YEAR/1829 = 1' >>> t_test = results.t_test(hypotheses) >>> print(t_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 15.0977 84.937 0.178 0.863 -177.042 207.238 c1 -2.0202 0.488 -8.231 0.000 -3.125 -0.915 c2 1.0001 0.249 0.000 1.000 0.437 1.563 ============================================================================== ``` See also [`tvalues`](statsmodels.regression.quantile_regression.quantregresults.tvalues#statsmodels.regression.quantile_regression.QuantRegResults.tvalues "statsmodels.regression.quantile_regression.QuantRegResults.tvalues") individual t statistics [`f_test`](statsmodels.regression.quantile_regression.quantregresults.f_test#statsmodels.regression.quantile_regression.QuantRegResults.f_test "statsmodels.regression.quantile_regression.QuantRegResults.f_test") for F tests [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") statsmodels statsmodels.discrete.count_model.GenericZeroInflated.hessian statsmodels.discrete.count\_model.GenericZeroInflated.hessian ============================================================= `GenericZeroInflated.hessian(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/count_model.html#GenericZeroInflated.hessian) Generic Zero Inflated model Hessian matrix of the loglikelihood \| Parameters: \| params (array-like) – The parameters of the model \| \| Returns: \| hess – The Hessian, second derivative of loglikelihood function, evaluated at `params` \| \| Return type: \| ndarray, (k\_vars, k\_vars) \| #### Notes statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.save statsmodels.regression.recursive\_ls.RecursiveLSResults.save ============================================================ `RecursiveLSResults.save(fname, remove_data=False)` save a pickle of this instance \| Parameters: \| * fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. * remove\_data (bool) – If False (default), then the instance is pickled without changes. If True, then all arrays with length nobs are set to None before pickling. See the remove\_data method. In some cases not all arrays will be set to None. \| #### Notes If remove\_data is true and the model result does not implement a remove\_data method then this will raise an exception. statsmodels statsmodels.tsa.arima_model.ARIMA.predict statsmodels.tsa.arima\_model.ARIMA.predict ========================================== `ARIMA.predict(params, start=None, end=None, exog=None, typ='linear', dynamic=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_model.html#ARIMA.predict) ARIMA model in-sample and out-of-sample prediction \| Parameters: \| * params (array-like) – The fitted parameters of the model. * start (int, str, or datetime) – Zero-indexed observation number at which to start forecasting, ie., the first forecast is start. Can also be a date string to parse or a datetime type. * end (int, str, or datetime) – Zero-indexed observation number at which to end forecasting, ie., the first forecast is start. Can also be a date string to parse or a datetime type. However, if the dates index does not have a fixed frequency, end must be an integer index if you want out of sample prediction. * exog (array-like, optional) – If the model is an ARMAX and out-of-sample forecasting is requested, exog must be given. Note that you’ll need to pass `k_ar` additional lags for any exogenous variables. E.g., if you fit an ARMAX(2, q) model and want to predict 5 steps, you need 7 observations to do this. * dynamic (bool, optional) – The `dynamic` keyword affects in-sample prediction. If dynamic is False, then the in-sample lagged values are used for prediction. If `dynamic` is True, then in-sample forecasts are used in place of lagged dependent variables. The first forecasted value is `start`. * typ (str {'linear', 'levels'}) – + ‘linear’ : Linear prediction in terms of the differenced endogenous variables. + ’levels’ : Predict the levels of the original endogenous variables. \| \| Returns: \| predict – The predicted values. \| \| Return type: \| array \| #### Notes Use the results predict method instead.	programming_docs
statsmodels statsmodels.discrete.discrete_model.DiscreteResults.prsquared statsmodels.discrete.discrete\_model.DiscreteResults.prsquared ============================================================== `DiscreteResults.prsquared()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#DiscreteResults.prsquared) statsmodels statsmodels.regression.linear_model.OLS.fit_regularized statsmodels.regression.linear\_model.OLS.fit\_regularized ========================================================= `OLS.fit_regularized(method='elastic_net', alpha=0.0, L1_wt=1.0, start_params=None, profile_scale=False, refit=False, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#OLS.fit_regularized) Return a regularized fit to a linear regression model. \| Parameters: \| method (string) – Only the ‘elastic\_net’ approach is currently implemented. * alpha (scalar or array-like) – The penalty weight. If a scalar, the same penalty weight applies to all variables in the model. If a vector, it must have the same length as `params`, and contains a penalty weight for each coefficient. * L1\_wt (scalar) – The fraction of the penalty given to the L1 penalty term. Must be between 0 and 1 (inclusive). If 0, the fit is a ridge fit, if 1 it is a lasso fit. * start\_params (array-like) – Starting values for `params`. * profile\_scale (bool) – If True the penalized fit is computed using the profile (concentrated) log-likelihood for the Gaussian model. Otherwise the fit uses the residual sum of squares. * refit (bool) – If True, the model is refit using only the variables that have non-zero coefficients in the regularized fit. The refitted model is not regularized. * distributed (bool) – If True, the model uses distributed methods for fitting, will raise an error if True and partitions is None. * generator (function) – generator used to partition the model, allows for handling of out of memory/parallel computing. * partitions (scalar) – The number of partitions desired for the distributed estimation. * threshold (scalar or array-like) – The threshold below which coefficients are zeroed out, only used for distributed estimation \| \| Returns: \| \| \| Return type: \| A RegularizedResults instance. \| #### Notes The elastic net approach closely follows that implemented in the glmnet package in R. The penalty is a combination of L1 and L2 penalties. The function that is minimized is: \[0.5\RSS/n + alpha\((1-L1\\_wt)\\|params\|\_2^2/2 + L1\\_wt\\|params\|\_1)\] where RSS is the usual regression sum of squares, n is the sample size, and $\|\\|\_1$ and $\|\\|\_2$ are the L1 and L2 norms. For WLS and GLS, the RSS is calculated using the whitened endog and exog data. Post-estimation results are based on the same data used to select variables, hence may be subject to overfitting biases. The elastic\_net method uses the following keyword arguments: `maxiter : int` Maximum number of iterations `cnvrg_tol : float` Convergence threshold for line searches `zero_tol : float` Coefficients below this threshold are treated as zero. #### References Friedman, Hastie, Tibshirani (2008). Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software 33(1), 1-22 Feb 2010. statsmodels statsmodels.tools.tools.unsqueeze statsmodels.tools.tools.unsqueeze ================================= `statsmodels.tools.tools.unsqueeze(data, axis, oldshape)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tools/tools.html#unsqueeze) Unsqueeze a collapsed array ``` >>> from numpy import mean >>> from numpy.random import standard_normal >>> x = standard_normal((3,4,5)) >>> m = mean(x, axis=1) >>> m.shape (3, 5) >>> m = unsqueeze(m, 1, x.shape) >>> m.shape (3, 1, 5) >>> ``` statsmodels statsmodels.discrete.discrete_model.BinaryResults.load statsmodels.discrete.discrete\_model.BinaryResults.load ======================================================= `classmethod BinaryResults.load(fname)` load a pickle, (class method) \| Parameters: \| fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. \| \| Returns: \| \| \| Return type: \| unpickled instance \| statsmodels statsmodels.discrete.count_model.ZeroInflatedGeneralizedPoissonResults.aic statsmodels.discrete.count\_model.ZeroInflatedGeneralizedPoissonResults.aic =========================================================================== `ZeroInflatedGeneralizedPoissonResults.aic()` statsmodels statsmodels.stats.sandwich_covariance.cov_nw_panel statsmodels.stats.sandwich\_covariance.cov\_nw\_panel ===================================================== `statsmodels.stats.sandwich_covariance.cov_nw_panel(results, nlags, groupidx, weights_func=<function weights_bartlett>, use_correction='hac')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/sandwich_covariance.html#cov_nw_panel) Panel HAC robust covariance matrix Assumes we have a panel of time series with consecutive, equal spaced time periods. Data is assumed to be in long format with time series of each individual stacked into one array. Panel can be unbalanced. \| Parameters: \| * results (result instance) – result of a regression, uses results.model.exog and results.resid TODO: this should use wexog instead * nlags (int or None) – Highest lag to include in kernel window. Currently, no default because the optimal length will depend on the number of observations per cross-sectional unit. * groupidx (list of tuple) – each tuple should contain the start and end index for an individual. (groupidx might change in future). * weights\_func (callable) – weights\_func is called with nlags as argument to get the kernel weights. default are Bartlett weights * use\_correction ('cluster' or 'hac' or False) – If False, then no small sample correction is used. If ‘cluster’ (default), then the same correction as in cov\_cluster is used. If ‘hac’, then the same correction as in single time series, cov\_hac is used. \| \| Returns: \| cov – HAC robust covariance matrix for parameter estimates \| \| Return type: \| ndarray, (k\_vars, k\_vars) \| #### Notes For nlags=0, this is just White covariance, cov\_white. If kernel is uniform, `weights_uniform`, with nlags equal to the number of observations per unit in a balance panel, then cov\_cluster and cov\_hac\_panel are identical. Tested against STATA `newey` command with same defaults. Options might change when other kernels besides Bartlett and uniform are available. statsmodels statsmodels.imputation.mice.MICEData.plot_imputed_hist statsmodels.imputation.mice.MICEData.plot\_imputed\_hist ======================================================== `MICEData.plot_imputed_hist(col_name, ax=None, imp_hist_args=None, obs_hist_args=None, all_hist_args=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/imputation/mice.html#MICEData.plot_imputed_hist) Display imputed values for one variable as a histogram. \| Parameters: \| * col\_name (string) – The name of the variable to be plotted. * ax (matplotlib axes) – An axes on which to draw the histograms. If not provided, one is created. * imp\_hist\_args ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)")) – Keyword arguments to be passed to pyplot.hist when creating the histogram for imputed values. * obs\_hist\_args ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)")) – Keyword arguments to be passed to pyplot.hist when creating the histogram for observed values. * all\_hist\_args ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)")) – Keyword arguments to be passed to pyplot.hist when creating the histogram for all values. \| \| Returns: \| \| \| Return type: \| The matplotlib figure on which the histograms were drawn \| statsmodels statsmodels.regression.linear_model.GLS.get_distribution statsmodels.regression.linear\_model.GLS.get\_distribution ========================================================== `GLS.get_distribution(params, scale, exog=None, dist_class=None)` Returns a random number generator for the predictive distribution. \| Parameters: \| * params (array-like) – The model parameters (regression coefficients). * scale (scalar) – The variance parameter. * exog (array-like) – The predictor variable matrix. * dist\_class (class) – A random number generator class. Must take ‘loc’ and ‘scale’ as arguments and return a random number generator implementing an `rvs` method for simulating random values. Defaults to Gaussian. \| \| Returns: \| Frozen random number generator object with mean and variance determined by the fitted linear model. Use the `rvs` method to generate random values. \| \| Return type: \| gen \| #### Notes Due to the behavior of `scipy.stats.distributions objects`, the returned random number generator must be called with `gen.rvs(n)` where `n` is the number of observations in the data set used to fit the model. If any other value is used for `n`, misleading results will be produced. statsmodels statsmodels.sandbox.sysreg.SUR.fit statsmodels.sandbox.sysreg.SUR.fit ================================== `SUR.fit(igls=False, tol=1e-05, maxiter=100)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/sysreg.html#SUR.fit) `igls : bool` Iterate until estimates converge if sigma is None instead of two-step GLS, which is the default is sigma is None. tol : float maxiter : int #### Notes This ia naive implementation that does not exploit the block diagonal structure. It should work for ill-conditioned `sigma` but this is untested. statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactor.transform_params statsmodels.tsa.statespace.dynamic\_factor.DynamicFactor.transform\_params ========================================================================== `DynamicFactor.transform_params(unconstrained)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/dynamic_factor.html#DynamicFactor.transform_params) Transform unconstrained parameters used by the optimizer to constrained parameters used in likelihood evaluation \| Parameters: \| unconstrained (array\_like) – Array of unconstrained parameters used by the optimizer, to be transformed. \| \| Returns: \| constrained – Array of constrained parameters which may be used in likelihood evalation. \| \| Return type: \| array\_like \| #### Notes Constrains the factor transition to be stationary and variances to be positive. statsmodels statsmodels.discrete.discrete_model.BinaryResults.llr statsmodels.discrete.discrete\_model.BinaryResults.llr ====================================================== `BinaryResults.llr()` statsmodels statsmodels.regression.quantile_regression.QuantRegResults.tvalues statsmodels.regression.quantile\_regression.QuantRegResults.tvalues =================================================================== `QuantRegResults.tvalues()` Return the t-statistic for a given parameter estimate. statsmodels statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.impulse_responses statsmodels.tsa.statespace.kalman\_smoother.KalmanSmoother.impulse\_responses ============================================================================= `KalmanSmoother.impulse_responses(steps=10, impulse=0, orthogonalized=False, cumulative=False, *kwargs)` Impulse response function \| Parameters: \| steps (int, optional) – The number of steps for which impulse responses are calculated. Default is 10. Note that the initial impulse is not counted as a step, so if `steps=1`, the output will have 2 entries. * impulse (int or array\_like) – If an integer, the state innovation to pulse; must be between 0 and `k_posdef-1` where `k_posdef` is the same as in the state space model. Alternatively, a custom impulse vector may be provided; must be a column vector with shape `(k_posdef, 1)`. * orthogonalized (boolean, optional) – Whether or not to perform impulse using orthogonalized innovations. Note that this will also affect custum `impulse` vectors. Default is False. * cumulative (boolean, optional) – Whether or not to return cumulative impulse responses. Default is False. * *\\kwargs* – If the model is time-varying and `steps` is greater than the number of observations, any of the state space representation matrices that are time-varying must have updated values provided for the out-of-sample steps. For example, if `design` is a time-varying component, `nobs` is 10, and `steps` is 15, a (`k_endog` x `k_states` x 5) matrix must be provided with the new design matrix values. \| \| Returns: \| impulse\_responses – Responses for each endogenous variable due to the impulse given by the `impulse` argument. A (steps + 1 x k\_endog) array. \| \| Return type: \| array \| #### Notes Intercepts in the measurement and state equation are ignored when calculating impulse responses. statsmodels statsmodels.tsa.statespace.sarimax.SARIMAXResults.test_serial_correlation statsmodels.tsa.statespace.sarimax.SARIMAXResults.test\_serial\_correlation =========================================================================== `SARIMAXResults.test_serial_correlation(method, lags=None)` Ljung-box test for no serial correlation of standardized residuals Null hypothesis is no serial correlation. \| Parameters: \| * method (string {'ljungbox','boxpierece'} or None) – The statistical test for serial correlation. If None, an attempt is made to select an appropriate test. * lags (None, int or array\_like) – If lags is an integer then this is taken to be the largest lag that is included, the test result is reported for all smaller lag length. If lags is a list or array, then all lags are included up to the largest lag in the list, however only the tests for the lags in the list are reported. If lags is None, then the default maxlag is 12\(nobs/100)^{1/4} \| \| Returns: \| output* – An array with `(test_statistic, pvalue)` for each endogenous variable and each lag. The array is then sized `(k_endog, 2, lags)`. If the method is called as `ljungbox = res.test_serial_correlation()`, then `ljungbox[i]` holds the results of the Ljung-Box test (as would be returned by `statsmodels.stats.diagnostic.acorr_ljungbox`) for the `i` th endogenous variable. \| \| Return type: \| array \| #### Notes If the first `d` loglikelihood values were burned (i.e. in the specified model, `loglikelihood_burn=d`), then this test is calculated ignoring the first `d` residuals. Output is nan for any endogenous variable which has missing values. See also [`statsmodels.stats.diagnostic.acorr_ljungbox`](statsmodels.stats.diagnostic.acorr_ljungbox#statsmodels.stats.diagnostic.acorr_ljungbox "statsmodels.stats.diagnostic.acorr_ljungbox") statsmodels statsmodels.genmod.generalized_estimating_equations.GEEMargins statsmodels.genmod.generalized\_estimating\_equations.GEEMargins ================================================================ `class statsmodels.genmod.generalized_estimating_equations.GEEMargins(results, args, kwargs={})` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_estimating_equations.html#GEEMargins) Estimated marginal effects for a regression model fit with GEE. \| Parameters: \| * results (GEEResults instance) – The results instance of a fitted discrete choice model * args (tuple) – Args are passed to `get_margeff`. This is the same as results.get\_margeff. See there for more information. * kwargs ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)")) – Keyword args are passed to `get_margeff`. This is the same as results.get\_margeff. See there for more information. \| #### Methods \| \| \| \| --- \| --- \| \| [`conf_int`](statsmodels.genmod.generalized_estimating_equations.geemargins.conf_int#statsmodels.genmod.generalized_estimating_equations.GEEMargins.conf_int "statsmodels.genmod.generalized_estimating_equations.GEEMargins.conf_int")([alpha]) \| Returns the confidence intervals of the marginal effects \| \| [`get_margeff`](statsmodels.genmod.generalized_estimating_equations.geemargins.get_margeff#statsmodels.genmod.generalized_estimating_equations.GEEMargins.get_margeff "statsmodels.genmod.generalized_estimating_equations.GEEMargins.get_margeff")([at, method, atexog, dummy, count]) \| \| \| [`pvalues`](statsmodels.genmod.generalized_estimating_equations.geemargins.pvalues#statsmodels.genmod.generalized_estimating_equations.GEEMargins.pvalues "statsmodels.genmod.generalized_estimating_equations.GEEMargins.pvalues")() \| \| \| [`summary`](statsmodels.genmod.generalized_estimating_equations.geemargins.summary#statsmodels.genmod.generalized_estimating_equations.GEEMargins.summary "statsmodels.genmod.generalized_estimating_equations.GEEMargins.summary")([alpha]) \| Returns a summary table for marginal effects \| \| [`summary_frame`](statsmodels.genmod.generalized_estimating_equations.geemargins.summary_frame#statsmodels.genmod.generalized_estimating_equations.GEEMargins.summary_frame "statsmodels.genmod.generalized_estimating_equations.GEEMargins.summary_frame")([alpha]) \| Returns a DataFrame summarizing the marginal effects. \| \| [`tvalues`](statsmodels.genmod.generalized_estimating_equations.geemargins.tvalues#statsmodels.genmod.generalized_estimating_equations.GEEMargins.tvalues "statsmodels.genmod.generalized_estimating_equations.GEEMargins.tvalues")() \| \| statsmodels statsmodels.discrete.discrete_model.ProbitResults.summary statsmodels.discrete.discrete\_model.ProbitResults.summary ========================================================== `ProbitResults.summary(yname=None, xname=None, title=None, alpha=0.05, yname_list=None)` Summarize the Regression Results \| Parameters: \| * yname (string, optional) – Default is `y` * xname (list of strings, optional) – Default is `var_##` for ## in p the number of regressors * title (string, optional) – Title for the top table. If not None, then this replaces the default title * alpha (float) – significance level for the confidence intervals \| \| Returns: \| smry – this holds the summary tables and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary.Summary`](statsmodels.iolib.summary.summary#statsmodels.iolib.summary.Summary "statsmodels.iolib.summary.Summary") class to hold summary results statsmodels statsmodels.iolib.table.SimpleTable.extend statsmodels.iolib.table.SimpleTable.extend ========================================== `SimpleTable.extend(iterable) → None -- extend list by appending elements from the iterable` statsmodels statsmodels.sandbox.stats.multicomp.TukeyHSDResults.plot_simultaneous statsmodels.sandbox.stats.multicomp.TukeyHSDResults.plot\_simultaneous ====================================================================== `TukeyHSDResults.plot_simultaneous(comparison_name=None, ax=None, figsize=(10, 6), xlabel=None, ylabel=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/stats/multicomp.html#TukeyHSDResults.plot_simultaneous) Plot a universal confidence interval of each group mean Visiualize significant differences in a plot with one confidence interval per group instead of all pairwise confidence intervals. \| Parameters: \| * comparison\_name (string, optional) – if provided, plot\_intervals will color code all groups that are significantly different from the comparison\_name red, and will color code insignificant groups gray. Otherwise, all intervals will just be plotted in black. * ax (matplotlib axis, optional) – An axis handle on which to attach the plot. * figsize (tuple, optional) – tuple for the size of the figure generated * xlabel (string, optional) – Name to be displayed on x axis * ylabel (string, optional) – Name to be displayed on y axis \| \| Returns: \| fig – handle to figure object containing interval plots \| \| Return type: \| Matplotlib Figure object \| #### Notes Multiple comparison tests are nice, but lack a good way to be visualized. If you have, say, 6 groups, showing a graph of the means between each group will require 15 confidence intervals. Instead, we can visualize inter-group differences with a single interval for each group mean. Hochberg et al. [1] first proposed this idea and used Tukey’s Q critical value to compute the interval widths. Unlike plotting the differences in the means and their respective confidence intervals, any two pairs can be compared for significance by looking for overlap. #### References \| \| \| \| --- \| --- \| \| [\*] \| Hochberg, Y., and A. C. Tamhane. Multiple Comparison Procedures. Hoboken, NJ: John Wiley & Sons, 1987. \| #### Examples ``` >>> from statsmodels.examples.try_tukey_hsd import cylinders, cyl_labels >>> from statsmodels.stats.multicomp import MultiComparison >>> cardata = MultiComparison(cylinders, cyl_labels) >>> results = cardata.tukeyhsd() >>> results.plot_simultaneous() <matplotlib.figure.Figure at 0x...> ``` This example shows an example plot comparing significant differences in group means. Significant differences at the alpha=0.05 level can be identified by intervals that do not overlap (i.e. USA vs Japan, USA vs Germany). ``` >>> results.plot_simultaneous(comparison_name="USA") <matplotlib.figure.Figure at 0x...> ``` Optionally provide one of the group names to color code the plot to highlight group means different from comparison\_name.	programming_docs
statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.tvalues statsmodels.tsa.statespace.dynamic\_factor.DynamicFactorResults.tvalues ======================================================================= `DynamicFactorResults.tvalues()` Return the t-statistic for a given parameter estimate. statsmodels statsmodels.regression.recursive_ls.RecursiveLS.initialize statsmodels.regression.recursive\_ls.RecursiveLS.initialize =========================================================== `RecursiveLS.initialize()` Initialize (possibly re-initialize) a Model instance. For instance, the design matrix of a linear model may change and some things must be recomputed. statsmodels statsmodels.regression.linear_model.RegressionResults.cov_HC0 statsmodels.regression.linear\_model.RegressionResults.cov\_HC0 =============================================================== `RegressionResults.cov_HC0()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#RegressionResults.cov_HC0) See statsmodels.RegressionResults statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.impulse_responses statsmodels.tsa.statespace.dynamic\_factor.DynamicFactorResults.impulse\_responses ================================================================================== `DynamicFactorResults.impulse_responses(steps=1, impulse=0, orthogonalized=False, cumulative=False, *kwargs)` Impulse response function \| Parameters: \| steps (int, optional) – The number of steps for which impulse responses are calculated. Default is 1. Note that the initial impulse is not counted as a step, so if `steps=1`, the output will have 2 entries. * impulse (int or array\_like) – If an integer, the state innovation to pulse; must be between 0 and `k_posdef-1`. Alternatively, a custom impulse vector may be provided; must be shaped `k_posdef x 1`. * orthogonalized (boolean, optional) – Whether or not to perform impulse using orthogonalized innovations. Note that this will also affect custum `impulse` vectors. Default is False. * cumulative (boolean, optional) – Whether or not to return cumulative impulse responses. Default is False. * *\\kwargs* – If the model is time-varying and `steps` is greater than the number of observations, any of the state space representation matrices that are time-varying must have updated values provided for the out-of-sample steps. For example, if `design` is a time-varying component, `nobs` is 10, and `steps` is 15, a (`k_endog` x `k_states` x 5) matrix must be provided with the new design matrix values. \| \| Returns: \| impulse\_responses – Responses for each endogenous variable due to the impulse given by the `impulse` argument. A (steps + 1 x k\_endog) array. \| \| Return type: \| array \| #### Notes Intercepts in the measurement and state equation are ignored when calculating impulse responses. statsmodels statsmodels.duration.hazard_regression.PHRegResults.schoenfeld_residuals statsmodels.duration.hazard\_regression.PHRegResults.schoenfeld\_residuals ========================================================================== `PHRegResults.schoenfeld_residuals()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/duration/hazard_regression.html#PHRegResults.schoenfeld_residuals) A matrix containing the Schoenfeld residuals. #### Notes Schoenfeld residuals for censored observations are set to zero. statsmodels statsmodels.genmod.families.family.Binomial statsmodels.genmod.families.family.Binomial =========================================== `class statsmodels.genmod.families.family.Binomial(link=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/family.html#Binomial) Binomial exponential family distribution. \| Parameters: \| link (a link instance, optional) – The default link for the Binomial family is the logit link. Available links are logit, probit, cauchy, log, and cloglog. See statsmodels.genmod.families.links for more information. \| `link` a link instance – The link function of the Binomial instance `variance` varfunc instance – `variance` is an instance of statsmodels.genmod.families.varfuncs.binary See also [`statsmodels.genmod.families.family.Family`](statsmodels.genmod.families.family.family#statsmodels.genmod.families.family.Family "statsmodels.genmod.families.family.Family"), [Link Functions](../glm#links) #### Notes endog for Binomial can be specified in one of three ways. #### Methods \| \| \| \| --- \| --- \| \| [`deviance`](statsmodels.genmod.families.family.binomial.deviance#statsmodels.genmod.families.family.Binomial.deviance "statsmodels.genmod.families.family.Binomial.deviance")(endog, mu[, var\_weights, …]) \| The deviance function evaluated at (endog, mu, var\_weights, freq\_weights, scale) for the distribution. \| \| [`fitted`](statsmodels.genmod.families.family.binomial.fitted#statsmodels.genmod.families.family.Binomial.fitted "statsmodels.genmod.families.family.Binomial.fitted")(lin\_pred) \| Fitted values based on linear predictors lin\_pred. \| \| [`initialize`](statsmodels.genmod.families.family.binomial.initialize#statsmodels.genmod.families.family.Binomial.initialize "statsmodels.genmod.families.family.Binomial.initialize")(endog, freq\_weights) \| Initialize the response variable. \| \| [`loglike`](statsmodels.genmod.families.family.binomial.loglike#statsmodels.genmod.families.family.Binomial.loglike "statsmodels.genmod.families.family.Binomial.loglike")(endog, mu[, var\_weights, …]) \| The log-likelihood function in terms of the fitted mean response. \| \| [`loglike_obs`](statsmodels.genmod.families.family.binomial.loglike_obs#statsmodels.genmod.families.family.Binomial.loglike_obs "statsmodels.genmod.families.family.Binomial.loglike_obs")(endog, mu[, var\_weights, scale]) \| The log-likelihood function for each observation in terms of the fitted mean response for the Binomial distribution. \| \| [`predict`](statsmodels.genmod.families.family.binomial.predict#statsmodels.genmod.families.family.Binomial.predict "statsmodels.genmod.families.family.Binomial.predict")(mu) \| Linear predictors based on given mu values. \| \| [`resid_anscombe`](statsmodels.genmod.families.family.binomial.resid_anscombe#statsmodels.genmod.families.family.Binomial.resid_anscombe "statsmodels.genmod.families.family.Binomial.resid_anscombe")(endog, mu[, var\_weights, scale]) \| The Anscombe residuals \| \| [`resid_dev`](statsmodels.genmod.families.family.binomial.resid_dev#statsmodels.genmod.families.family.Binomial.resid_dev "statsmodels.genmod.families.family.Binomial.resid_dev")(endog, mu[, var\_weights, scale]) \| The deviance residuals \| \| [`starting_mu`](statsmodels.genmod.families.family.binomial.starting_mu#statsmodels.genmod.families.family.Binomial.starting_mu "statsmodels.genmod.families.family.Binomial.starting_mu")(y) \| The starting values for the IRLS algorithm for the Binomial family. \| \| [`weights`](statsmodels.genmod.families.family.binomial.weights#statsmodels.genmod.families.family.Binomial.weights "statsmodels.genmod.families.family.Binomial.weights")(mu) \| Weights for IRLS steps \| statsmodels statsmodels.discrete.discrete_model.MultinomialModel.cdf statsmodels.discrete.discrete\_model.MultinomialModel.cdf ========================================================= `MultinomialModel.cdf(X)` The cumulative distribution function of the model. statsmodels statsmodels.discrete.discrete_model.GeneralizedPoisson.pdf statsmodels.discrete.discrete\_model.GeneralizedPoisson.pdf =========================================================== `GeneralizedPoisson.pdf(X)` The probability density (mass) function of the model. statsmodels statsmodels.tsa.kalmanf.kalmanfilter.KalmanFilter statsmodels.tsa.kalmanf.kalmanfilter.KalmanFilter ================================================= `class statsmodels.tsa.kalmanf.kalmanfilter.KalmanFilter` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/kalmanf/kalmanfilter.html#KalmanFilter) Kalman Filter code intended for use with the ARMA model. #### Notes The notation for the state-space form follows Durbin and Koopman (2001). The observation equations is \[y\_{t} = Z\_{t}\alpha\_{t} + \epsilon\_{t}\] The state equation is \[\alpha\_{t+1} = T\_{t}\alpha\_{t} + R\_{t}\eta\_{t}\] For the present purposed epsilon\_{t} is assumed to always be zero. #### Methods \| \| \| \| --- \| --- \| \| [`R`](statsmodels.tsa.kalmanf.kalmanfilter.kalmanfilter.r#statsmodels.tsa.kalmanf.kalmanfilter.KalmanFilter.R "statsmodels.tsa.kalmanf.kalmanfilter.KalmanFilter.R")(params, r, k, q, p) \| The coefficient matrix for the state vector in the observation equation. \| \| [`T`](statsmodels.tsa.kalmanf.kalmanfilter.kalmanfilter.t#statsmodels.tsa.kalmanf.kalmanfilter.KalmanFilter.T "statsmodels.tsa.kalmanf.kalmanfilter.KalmanFilter.T")(params, r, k, p) \| The coefficient matrix for the state vector in the state equation. \| \| [`Z`](statsmodels.tsa.kalmanf.kalmanfilter.kalmanfilter.z#statsmodels.tsa.kalmanf.kalmanfilter.KalmanFilter.Z "statsmodels.tsa.kalmanf.kalmanfilter.KalmanFilter.Z")(r) \| Returns the Z selector matrix in the observation equation. \| \| [`geterrors`](statsmodels.tsa.kalmanf.kalmanfilter.kalmanfilter.geterrors#statsmodels.tsa.kalmanf.kalmanfilter.KalmanFilter.geterrors "statsmodels.tsa.kalmanf.kalmanfilter.KalmanFilter.geterrors")(y, k, k\_ar, k\_ma, k\_lags, nobs, …) \| Returns just the errors of the Kalman Filter \| \| [`loglike`](statsmodels.tsa.kalmanf.kalmanfilter.kalmanfilter.loglike#statsmodels.tsa.kalmanf.kalmanfilter.KalmanFilter.loglike "statsmodels.tsa.kalmanf.kalmanfilter.KalmanFilter.loglike")(params, arma\_model[, set\_sigma2]) \| The loglikelihood for an ARMA model using the Kalman Filter recursions. \| statsmodels statsmodels.discrete.discrete_model.NegativeBinomialP.convert_params statsmodels.discrete.discrete\_model.NegativeBinomialP.convert\_params ====================================================================== `NegativeBinomialP.convert_params(params, mu)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#NegativeBinomialP.convert_params) statsmodels statsmodels.sandbox.stats.runs.Runs.runs_test statsmodels.sandbox.stats.runs.Runs.runs\_test ============================================== `Runs.runs_test(correction=True)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/stats/runs.html#Runs.runs_test) basic version of runs test \| Parameters: \| * correction (bool) – Following the SAS manual, for samplesize below 50, the test statistic is corrected by 0.5. This can be turned off with correction=False, and was included to match R, tseries, which does not use any correction. * based on normal distribution, with integer correction (pvalue) – \| statsmodels statsmodels.genmod.families.links.Power.deriv2 statsmodels.genmod.families.links.Power.deriv2 ============================================== `Power.deriv2(p)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#Power.deriv2) Second derivative of the power transform \| Parameters: \| p (array-like) – Mean parameters \| \| Returns: \| g’‘(p) – Second derivative of the power transform of `p` \| \| Return type: \| array \| #### Notes g’‘(`p`) = `power` \* (`power` - 1) \* `p`*(`power` - 2) statsmodels statsmodels.nonparametric.kde.KDEUnivariate.cumhazard statsmodels.nonparametric.kde.KDEUnivariate.cumhazard ===================================================== `KDEUnivariate.cumhazard()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/nonparametric/kde.html#KDEUnivariate.cumhazard) Returns the hazard function evaluated at the support. #### Notes Will not work if fit has not been called. statsmodels statsmodels.stats.contingency_tables.Table2x2.log_oddsratio statsmodels.stats.contingency\_tables.Table2x2.log\_oddsratio ============================================================= `Table2x2.log_oddsratio()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/contingency_tables.html#Table2x2.log_oddsratio) statsmodels statsmodels.tsa.vector_ar.vecm.CointRankResults.summary statsmodels.tsa.vector\_ar.vecm.CointRankResults.summary ======================================================== `CointRankResults.summary()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/vecm.html#CointRankResults.summary) statsmodels statsmodels.duration.survfunc.SurvfuncRight.plot statsmodels.duration.survfunc.SurvfuncRight.plot ================================================ `SurvfuncRight.plot(ax=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/duration/survfunc.html#SurvfuncRight.plot) Plot the survival function. #### Examples Change the line color: ``` >>> import statsmodels.api as sm >>> data = sm.datasets.get_rdataset("flchain", "survival").data >>> df = data.loc[data.sex == "F", :] >>> sf = sm.SurvfuncRight(df["futime"], df["death"]) >>> fig = sf.plot() >>> ax = fig.get_axes()[0] >>> li = ax.get_lines() >>> li[0].set_color('purple') >>> li[1].set_color('purple') ``` Don’t show the censoring points: ``` >>> fig = sf.plot() >>> ax = fig.get_axes()[0] >>> li = ax.get_lines() >>> li[1].set_visible(False) ``` statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.aic statsmodels.tsa.statespace.dynamic\_factor.DynamicFactorResults.aic =================================================================== `DynamicFactorResults.aic()` (float) Akaike Information Criterion statsmodels statsmodels.genmod.cov_struct.Independence.summary statsmodels.genmod.cov\_struct.Independence.summary =================================================== `Independence.summary()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/cov_struct.html#Independence.summary) Returns a text summary of the current estimate of the dependence structure. statsmodels statsmodels.regression.quantile_regression.QuantRegResults.nobs statsmodels.regression.quantile\_regression.QuantRegResults.nobs ================================================================ `QuantRegResults.nobs()` statsmodels statsmodels.stats.weightstats.DescrStatsW.corrcoef statsmodels.stats.weightstats.DescrStatsW.corrcoef ================================================== `DescrStatsW.corrcoef()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/weightstats.html#DescrStatsW.corrcoef) weighted correlation with default ddof assumes variables in columns and observations in rows statsmodels statsmodels.sandbox.distributions.extras.NormExpan_gen.std statsmodels.sandbox.distributions.extras.NormExpan\_gen.std =========================================================== `NormExpan_gen.std(args, *kwds)` Standard deviation of the distribution. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| std – standard deviation of the distribution \| \| Return type: \| float \| statsmodels statsmodels.sandbox.stats.multicomp.varcorrection_pairs_unbalanced statsmodels.sandbox.stats.multicomp.varcorrection\_pairs\_unbalanced ==================================================================== `statsmodels.sandbox.stats.multicomp.varcorrection_pairs_unbalanced(nobs_all, srange=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/stats/multicomp.html#varcorrection_pairs_unbalanced) correction factor for variance with unequal sample sizes for all pairs this is just a harmonic mean \| Parameters: \| * nobs\_all (array\_like) – The number of observations for each sample * srange (bool) – if true, then the correction is divided by 2 for the variance of the studentized range statistic \| \| Returns: \| correction – Correction factor for variance. \| \| Return type: \| array \| #### Notes variance correction factor is 1/k \* sum\_i 1/n\_i where k is the number of samples and summation is over i=0,…,k-1. If all n\_i are the same, then the correction factor is 1. This needs to be multiplies by the joint variance estimate, means square error, MSE. To obtain the correction factor for the standard deviation, square root needs to be taken. For the studentized range statistic, the resulting factor has to be divided by 2. statsmodels statsmodels.tsa.statespace.mlemodel.MLEModel.from_formula statsmodels.tsa.statespace.mlemodel.MLEModel.from\_formula ========================================================== `classmethod MLEModel.from_formula(formula, data, subset=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/mlemodel.html#MLEModel.from_formula) Not implemented for state space models statsmodels statsmodels.genmod.families.links.NegativeBinomial statsmodels.genmod.families.links.NegativeBinomial ================================================== `class statsmodels.genmod.families.links.NegativeBinomial(alpha=1.0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#NegativeBinomial) The negative binomial link function \| Parameters: \| alpha (float, optional) – Alpha is the ancillary parameter of the Negative Binomial link function. It is assumed to be nonstochastic. The default value is 1. Permissible values are usually assumed to be in (.01, 2). \| #### Methods \| \| \| \| --- \| --- \| \| [`deriv`](statsmodels.genmod.families.links.negativebinomial.deriv#statsmodels.genmod.families.links.NegativeBinomial.deriv "statsmodels.genmod.families.links.NegativeBinomial.deriv")(p) \| Derivative of the negative binomial transform \| \| [`deriv2`](statsmodels.genmod.families.links.negativebinomial.deriv2#statsmodels.genmod.families.links.NegativeBinomial.deriv2 "statsmodels.genmod.families.links.NegativeBinomial.deriv2")(p) \| Second derivative of the negative binomial link function. \| \| [`inverse`](statsmodels.genmod.families.links.negativebinomial.inverse#statsmodels.genmod.families.links.NegativeBinomial.inverse "statsmodels.genmod.families.links.NegativeBinomial.inverse")(z) \| Inverse of the negative binomial transform \| \| [`inverse_deriv`](statsmodels.genmod.families.links.negativebinomial.inverse_deriv#statsmodels.genmod.families.links.NegativeBinomial.inverse_deriv "statsmodels.genmod.families.links.NegativeBinomial.inverse_deriv")(z) \| Derivative of the inverse of the negative binomial transform \| statsmodels statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.set_smoother_output statsmodels.tsa.statespace.kalman\_smoother.KalmanSmoother.set\_smoother\_output ================================================================================ `KalmanSmoother.set_smoother_output(smoother_output=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/kalman_smoother.html#KalmanSmoother.set_smoother_output) Set the smoother output The smoother can produce several types of results. The smoother output variable controls which are calculated and returned. \| Parameters: \| smoother\_output (integer, optional) – Bitmask value to set the smoother output to. See notes for details. * *\\kwargs* – Keyword arguments may be used to influence the smoother output by setting individual boolean flags. See notes for details. \| #### Notes The smoother output is defined by a collection of boolean flags, and is internally stored as a bitmask. The methods available are: SMOOTHER\_STATE = 0x01 Calculate and return the smoothed states. SMOOTHER\_STATE\_COV = 0x02 Calculate and return the smoothed state covariance matrices. SMOOTHER\_STATE\_AUTOCOV = 0x10 Calculate and return the smoothed state lag-one autocovariance matrices. SMOOTHER\_DISTURBANCE = 0x04 Calculate and return the smoothed state and observation disturbances. SMOOTHER\_DISTURBANCE\_COV = 0x08 Calculate and return the covariance matrices for the smoothed state and observation disturbances. SMOOTHER\_ALL Calculate and return all results. If the bitmask is set directly via the `smoother_output` argument, then the full method must be provided. If keyword arguments are used to set individual boolean flags, then the lowercase of the method must be used as an argument name, and the value is the desired value of the boolean flag (True or False). Note that the smoother output may also be specified by directly modifying the class attributes which are defined similarly to the keyword arguments. The default smoother output is SMOOTHER\_ALL. If performance is a concern, only those results which are needed should be specified as any results that are not specified will not be calculated. For example, if the smoother output is set to only include SMOOTHER\_STATE, the smoother operates much more quickly than if all output is required. #### Examples ``` >>> import statsmodels.tsa.statespace.kalman_smoother as ks >>> mod = ks.KalmanSmoother(1,1) >>> mod.smoother_output 15 >>> mod.set_smoother_output(smoother_output=0) >>> mod.smoother_state = True >>> mod.smoother_output 1 >>> mod.smoother_state True ```	programming_docs
statsmodels statsmodels.regression.linear_model.OLSResults.HC1_se statsmodels.regression.linear\_model.OLSResults.HC1\_se ======================================================= `OLSResults.HC1_se()` See statsmodels.RegressionResults statsmodels statsmodels.tsa.vector_ar.var_model.FEVD.plot statsmodels.tsa.vector\_ar.var\_model.FEVD.plot =============================================== `FEVD.plot(periods=None, figsize=(10, 10), plot_kwds)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#FEVD.plot) Plot graphical display of FEVD \| Parameters: \| periods** (int, default None) – Defaults to number originally specified. Can be at most that number \| statsmodels statsmodels.graphics.tsaplots.plot_pacf statsmodels.graphics.tsaplots.plot\_pacf ======================================== `statsmodels.graphics.tsaplots.plot_pacf(x, ax=None, lags=None, alpha=0.05, method='ywunbiased', use_vlines=True, title='Partial Autocorrelation', zero=True, vlines_kwargs=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/graphics/tsaplots.html#plot_pacf) Plot the partial autocorrelation function \| Parameters: \| x (array\_like) – Array of time-series values * ax (Matplotlib AxesSubplot instance, optional) – If given, this subplot is used to plot in instead of a new figure being created. * lags (int or array\_like, optional) – int or Array of lag values, used on horizontal axis. Uses np.arange(lags) when lags is an int. If not provided, `lags=np.arange(len(corr))` is used. * alpha (float, optional) – If a number is given, the confidence intervals for the given level are returned. For instance if alpha=.05, 95 % confidence intervals are returned where the standard deviation is computed according to 1/sqrt(len(x)) * method ({'ywunbiased', 'ywmle', 'ols'}) – Specifies which method for the calculations to use: + yw or ywunbiased : yule walker with bias correction in denominator for acovf. Default. + ywm or ywmle : yule walker without bias correction + ols - regression of time series on lags of it and on constant + ld or ldunbiased : Levinson-Durbin recursion with bias correction + ldb or ldbiased : Levinson-Durbin recursion without bias correction * use\_vlines (bool, optional) – If True, vertical lines and markers are plotted. If False, only markers are plotted. The default marker is ‘o’; it can be overridden with a `marker` kwarg. * title (str, optional) – Title to place on plot. Default is ‘Partial Autocorrelation’ * zero (bool, optional) – Flag indicating whether to include the 0-lag autocorrelation. Default is True. * vlines\_kwargs ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)"), optional) – Optional dictionary of keyword arguments that are passed to vlines. * *\\kwargs* (kwargs, optional) – Optional keyword arguments that are directly passed on to the Matplotlib `plot` and `axhline` functions. \| \| Returns: \| fig – If `ax` is None, the created figure. Otherwise the figure to which `ax` is connected. \| \| Return type: \| Matplotlib figure instance \| See also `matplotlib.pyplot.xcorr`, `matplotlib.pyplot.acorr`, `mpl_examples` #### Notes Plots lags on the horizontal and the correlations on vertical axis. Adapted from matplotlib’s `xcorr`. Data are plotted as `plot(lags, corr, kwargs)` kwargs is used to pass matplotlib optional arguments to both the line tracing the autocorrelations and for the horizontal line at 0. These options must be valid for a Line2D object. vlines\_kwargs is used to pass additional optional arguments to the vertical lines connecting each autocorrelation to the axis. These options must be valid for a LineCollection object. statsmodels statsmodels.discrete.discrete_model.MultinomialResults.bse statsmodels.discrete.discrete\_model.MultinomialResults.bse =========================================================== `MultinomialResults.bse()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#MultinomialResults.bse) statsmodels statsmodels.discrete.discrete_model.BinaryResults.pred_table statsmodels.discrete.discrete\_model.BinaryResults.pred\_table ============================================================== `BinaryResults.pred_table(threshold=0.5)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#BinaryResults.pred_table) Prediction table \| Parameters: \| threshold** (scalar) – Number between 0 and 1. Threshold above which a prediction is considered 1 and below which a prediction is considered 0. \| #### Notes pred\_table[i,j] refers to the number of times “i” was observed and the model predicted “j”. Correct predictions are along the diagonal. statsmodels statsmodels.tsa.arima_model.ARMAResults.cov_params statsmodels.tsa.arima\_model.ARMAResults.cov\_params ==================================================== `ARMAResults.cov_params()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_model.html#ARMAResults.cov_params) Returns the variance/covariance matrix. The variance/covariance matrix can be of a linear contrast of the estimates of params or all params multiplied by scale which will usually be an estimate of sigma^2. Scale is assumed to be a scalar. \| Parameters: \| * r\_matrix (array-like) – Can be 1d, or 2d. Can be used alone or with other. * column (array-like, optional) – Must be used on its own. Can be 0d or 1d see below. * scale (float, optional) – Can be specified or not. Default is None, which means that the scale argument is taken from the model. * other (array-like, optional) – Can be used when r\_matrix is specified. \| \| Returns: \| cov – covariance matrix of the parameter estimates or of linear combination of parameter estimates. See Notes. \| \| Return type: \| ndarray \| #### Notes (The below are assumed to be in matrix notation.) If no argument is specified returns the covariance matrix of a model `(scale)(X.T X)^(-1)` If contrast is specified it pre and post-multiplies as follows `(scale) r_matrix (X.T X)^(-1) r_matrix.T` If contrast and other are specified returns `(scale) * r_matrix (X.T X)^(-1) other.T` If column is specified returns `(scale) * (X.T X)^(-1)[column,column]` if column is 0d OR `(scale) * (X.T X)^(-1)[column][:,column]` if column is 1d statsmodels statsmodels.tsa.statespace.structural.UnobservedComponentsResults.conf_int statsmodels.tsa.statespace.structural.UnobservedComponentsResults.conf\_int =========================================================================== `UnobservedComponentsResults.conf_int(alpha=0.05, cols=None, method='default')` Returns the confidence interval of the fitted parameters. \| Parameters: \| * alpha (float, optional) – The significance level for the confidence interval. ie., The default `alpha` = .05 returns a 95% confidence interval. * cols (array-like, optional) – `cols` specifies which confidence intervals to return * method (string) – Not Implemented Yet Method to estimate the confidence\_interval. “Default” : uses self.bse which is based on inverse Hessian for MLE “hjjh” : “jac” : “boot-bse” “boot\_quant” “profile” \| \| Returns: \| conf\_int – Each row contains [lower, upper] limits of the confidence interval for the corresponding parameter. The first column contains all lower, the second column contains all upper limits. \| \| Return type: \| array \| #### Examples ``` >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> results.conf_int() array([[-5496529.48322745, -1467987.78596704], [ -177.02903529, 207.15277984], [ -0.1115811 , 0.03994274], [ -3.12506664, -0.91539297], [ -1.5179487 , -0.54850503], [ -0.56251721, 0.460309 ], [ 798.7875153 , 2859.51541392]]) ``` ``` >>> results.conf_int(cols=(2,3)) array([[-0.1115811 , 0.03994274], [-3.12506664, -0.91539297]]) ``` #### Notes The confidence interval is based on the standard normal distribution. Models wish to use a different distribution should overwrite this method. statsmodels statsmodels.sandbox.distributions.transformed.Transf_gen.moment statsmodels.sandbox.distributions.transformed.Transf\_gen.moment ================================================================ `Transf_gen.moment(n, args, kwds)` n-th order non-central moment of distribution. \| Parameters: \| n (int, n >= 1) – Order of moment. * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information). * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| statsmodels statsmodels.stats.proportion.proportion_effectsize statsmodels.stats.proportion.proportion\_effectsize =================================================== `statsmodels.stats.proportion.proportion_effectsize(prop1, prop2, method='normal')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/proportion.html#proportion_effectsize) effect size for a test comparing two proportions for use in power function \| Parameters: \| prop2 (prop1,) – \| \| Returns: \| es – effect size for (transformed) prop1 - prop2 \| \| Return type: \| float or ndarray \| #### Notes only method=’normal’ is implemented to match pwr.p2.test see <http://www.statmethods.net/stats/power.html> Effect size for `normal` is defined as ``` 2 * (arcsin(sqrt(prop1)) - arcsin(sqrt(prop2))) ``` I think other conversions to normality can be used, but I need to check. #### Examples ``` >>> import statsmodels.api as sm >>> sm.stats.proportion_effectsize(0.5, 0.4) 0.20135792079033088 >>> sm.stats.proportion_effectsize([0.3, 0.4, 0.5], 0.4) array([-0.21015893, 0. , 0.20135792]) ``` statsmodels statsmodels.tsa.arima_model.ARIMAResults.normalized_cov_params statsmodels.tsa.arima\_model.ARIMAResults.normalized\_cov\_params ================================================================= `ARIMAResults.normalized_cov_params()` statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.predict statsmodels.regression.recursive\_ls.RecursiveLSResults.predict =============================================================== `RecursiveLSResults.predict(start=None, end=None, dynamic=False, *kwargs)` In-sample prediction and out-of-sample forecasting \| Parameters: \| start (int, str, or datetime, optional) – Zero-indexed observation number at which to start forecasting, i.e., the first forecast is start. Can also be a date string to parse or a datetime type. Default is the the zeroth observation. * end (int, str, or datetime, optional) – Zero-indexed observation number at which to end forecasting, i.e., the last forecast is end. Can also be a date string to parse or a datetime type. However, if the dates index does not have a fixed frequency, end must be an integer index if you want out of sample prediction. Default is the last observation in the sample. * dynamic (boolean, int, str, or datetime, optional) – Integer offset relative to `start` at which to begin dynamic prediction. Can also be an absolute date string to parse or a datetime type (these are not interpreted as offsets). Prior to this observation, true endogenous values will be used for prediction; starting with this observation and continuing through the end of prediction, forecasted endogenous values will be used instead. * *\\kwargs* – Additional arguments may required for forecasting beyond the end of the sample. See `FilterResults.predict` for more details. \| \| Returns: \| forecast – Array of out of in-sample predictions and / or out-of-sample forecasts. An (npredict x k\_endog) array. \| \| Return type: \| array \| statsmodels statsmodels.sandbox.distributions.extras.SkewNorm_gen.fit statsmodels.sandbox.distributions.extras.SkewNorm\_gen.fit ========================================================== `SkewNorm_gen.fit(data, args, kwds)` Return MLEs for shape (if applicable), location, and scale parameters from data. MLE stands for Maximum Likelihood Estimate. Starting estimates for the fit are given by input arguments; for any arguments not provided with starting estimates, `self._fitstart(data)` is called to generate such. One can hold some parameters fixed to specific values by passing in keyword arguments `f0`, `f1`, …, `fn` (for shape parameters) and `floc` and `fscale` (for location and scale parameters, respectively). \| Parameters: \| data (array\_like) – Data to use in calculating the MLEs. * args (floats, optional) – Starting value(s) for any shape-characterizing arguments (those not provided will be determined by a call to `_fitstart(data)`). No default value. * kwds (floats, optional) – Starting values for the location and scale parameters; no default. Special keyword arguments are recognized as holding certain parameters fixed: + f0…fn : hold respective shape parameters fixed. Alternatively, shape parameters to fix can be specified by name. For example, if `self.shapes == "a, b"`, `fa``and ``fix_a` are equivalent to `f0`, and `fb` and `fix_b` are equivalent to `f1`. + floc : hold location parameter fixed to specified value. + fscale : hold scale parameter fixed to specified value. + optimizer : The optimizer to use. The optimizer must take `func`, and starting position as the first two arguments, plus `args` (for extra arguments to pass to the function to be optimized) and `disp=0` to suppress output as keyword arguments. \| \| Returns: \| mle\_tuple – MLEs for any shape parameters (if applicable), followed by those for location and scale. For most random variables, shape statistics will be returned, but there are exceptions (e.g. `norm`). \| \| Return type: \| tuple of floats \| #### Notes This fit is computed by maximizing a log-likelihood function, with penalty applied for samples outside of range of the distribution. The returned answer is not guaranteed to be the globally optimal MLE, it may only be locally optimal, or the optimization may fail altogether. #### Examples Generate some data to fit: draw random variates from the `beta` distribution ``` >>> from scipy.stats import beta >>> a, b = 1., 2. >>> x = beta.rvs(a, b, size=1000) ``` Now we can fit all four parameters (`a`, `b`, `loc` and `scale`): ``` >>> a1, b1, loc1, scale1 = beta.fit(x) ``` We can also use some prior knowledge about the dataset: let’s keep `loc` and `scale` fixed: ``` >>> a1, b1, loc1, scale1 = beta.fit(x, floc=0, fscale=1) >>> loc1, scale1 (0, 1) ``` We can also keep shape parameters fixed by using `f`-keywords. To keep the zero-th shape parameter `a` equal 1, use `f0=1` or, equivalently, `fa=1`: ``` >>> a1, b1, loc1, scale1 = beta.fit(x, fa=1, floc=0, fscale=1) >>> a1 1 ``` Not all distributions return estimates for the shape parameters. `norm` for example just returns estimates for location and scale: ``` >>> from scipy.stats import norm >>> x = norm.rvs(a, b, size=1000, random_state=123) >>> loc1, scale1 = norm.fit(x) >>> loc1, scale1 (0.92087172783841631, 2.0015750750324668) ``` statsmodels statsmodels.duration.hazard_regression.PHRegResults.cov_params statsmodels.duration.hazard\_regression.PHRegResults.cov\_params ================================================================ `PHRegResults.cov_params(r_matrix=None, column=None, scale=None, cov_p=None, other=None)` Returns the variance/covariance matrix. The variance/covariance matrix can be of a linear contrast of the estimates of params or all params multiplied by scale which will usually be an estimate of sigma^2. Scale is assumed to be a scalar. \| Parameters: \| * r\_matrix (array-like) – Can be 1d, or 2d. Can be used alone or with other. * column (array-like, optional) – Must be used on its own. Can be 0d or 1d see below. * scale (float, optional) – Can be specified or not. Default is None, which means that the scale argument is taken from the model. * other (array-like, optional) – Can be used when r\_matrix is specified. \| \| Returns: \| cov – covariance matrix of the parameter estimates or of linear combination of parameter estimates. See Notes. \| \| Return type: \| ndarray \| #### Notes (The below are assumed to be in matrix notation.) If no argument is specified returns the covariance matrix of a model `(scale)(X.T X)^(-1)` If contrast is specified it pre and post-multiplies as follows `(scale) r_matrix (X.T X)^(-1) r_matrix.T` If contrast and other are specified returns `(scale) * r_matrix (X.T X)^(-1) other.T` If column is specified returns `(scale) * (X.T X)^(-1)[column,column]` if column is 0d OR `(scale) * (X.T X)^(-1)[column][:,column]` if column is 1d statsmodels statsmodels.tsa.statespace.kalman_filter.PredictionResults statsmodels.tsa.statespace.kalman\_filter.PredictionResults =========================================================== `class statsmodels.tsa.statespace.kalman_filter.PredictionResults(results, start, end, nstatic, ndynamic, nforecast)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/kalman_filter.html#PredictionResults) Results of in-sample and out-of-sample prediction for state space models generally \| Parameters: \| * results ([FilterResults](statsmodels.tsa.statespace.kalman_filter.filterresults#statsmodels.tsa.statespace.kalman_filter.FilterResults "statsmodels.tsa.statespace.kalman_filter.FilterResults")) – Output from filtering, corresponding to the prediction desired * start (int) – Zero-indexed observation number at which to start forecasting, i.e., the first forecast will be at start. * end (int) – Zero-indexed observation number at which to end forecasting, i.e., the last forecast will be at end. * nstatic (int) – Number of in-sample static predictions (these are always the first elements of the prediction output). * ndynamic (int) – Number of in-sample dynamic predictions (these always follow the static predictions directly, and are directly followed by the forecasts). * nforecast (int) – Number of in-sample forecasts (these always follow the dynamic predictions directly). \| `npredictions` int – Number of observations in the predicted series; this is not necessarily the same as the number of observations in the original model from which prediction was performed. `start` int – Zero-indexed observation number at which to start prediction, i.e., the first predict will be at `start`; this is relative to the original model from which prediction was performed. `end` int – Zero-indexed observation number at which to end prediction, i.e., the last predict will be at `end`; this is relative to the original model from which prediction was performed. `nstatic` int – Number of in-sample static predictions. `ndynamic` int – Number of in-sample dynamic predictions. `nforecast` int – Number of in-sample forecasts. `endog` array – The observation vector. `design` array – The design matrix, $Z$. `obs_intercept` array – The intercept for the observation equation, $d$. `obs_cov` array – The covariance matrix for the observation equation $H$. `transition` array – The transition matrix, $T$. `state_intercept` array – The intercept for the transition equation, $c$. `selection` array – The selection matrix, $R$. `state_cov` array – The covariance matrix for the state equation $Q$. `filtered_state` array – The filtered state vector at each time period. `filtered_state_cov` array – The filtered state covariance matrix at each time period. `predicted_state` array – The predicted state vector at each time period. `predicted_state_cov` array – The predicted state covariance matrix at each time period. `forecasts` array – The one-step-ahead forecasts of observations at each time period. `forecasts_error` array – The forecast errors at each time period. `forecasts_error_cov` array – The forecast error covariance matrices at each time period. #### Notes The provided ranges must be conformable, meaning that it must be that `end - start == nstatic + ndynamic + nforecast`. This class is essentially a view to the FilterResults object, but returning the appropriate ranges for everything. #### Methods \| \| \| \| --- \| --- \| \| [`predict`](statsmodels.tsa.statespace.kalman_filter.predictionresults.predict#statsmodels.tsa.statespace.kalman_filter.PredictionResults.predict "statsmodels.tsa.statespace.kalman_filter.PredictionResults.predict")([start, end, dynamic]) \| In-sample and out-of-sample prediction for state space models generally \| \| [`update_filter`](statsmodels.tsa.statespace.kalman_filter.predictionresults.update_filter#statsmodels.tsa.statespace.kalman_filter.PredictionResults.update_filter "statsmodels.tsa.statespace.kalman_filter.PredictionResults.update_filter")(kalman\_filter) \| Update the filter results \| \| [`update_representation`](statsmodels.tsa.statespace.kalman_filter.predictionresults.update_representation#statsmodels.tsa.statespace.kalman_filter.PredictionResults.update_representation "statsmodels.tsa.statespace.kalman_filter.PredictionResults.update_representation")(model[, only\_options]) \| Update the results to match a given model \| #### Attributes \| \| \| \| --- \| --- \| \| `filter_attributes` \| \| \| `kalman_gain` \| Kalman gain matrices \| \| `representation_attributes` \| \| \| `standardized_forecasts_error` \| Standardized forecast errors \|	programming_docs
statsmodels statsmodels.tsa.arima_model.ARIMAResults.initialize statsmodels.tsa.arima\_model.ARIMAResults.initialize ==================================================== `ARIMAResults.initialize(model, params, kwd)` statsmodels statsmodels.genmod.families.links.inverse_squared.deriv statsmodels.genmod.families.links.inverse\_squared.deriv ======================================================== `inverse_squared.deriv(p)` Derivative of the power transform \| Parameters: \| p** (array-like) – Mean parameters \| \| Returns: \| g’(p) – Derivative of power transform of `p` \| \| Return type: \| array \| #### Notes g’(`p`) = `power` \* `p`*(`power` - 1) statsmodels statsmodels.discrete.discrete_model.GeneralizedPoisson.from_formula statsmodels.discrete.discrete\_model.GeneralizedPoisson.from\_formula ===================================================================== `classmethod GeneralizedPoisson.from_formula(formula, data, subset=None, drop_cols=None, args, *kwargs)` Create a Model from a formula and dataframe. \| Parameters: \| formula (str or generic Formula object) – The formula specifying the model * data (array-like) – The data for the model. See Notes. * subset (array-like) – An array-like object of booleans, integers, or index values that indicate the subset of df to use in the model. Assumes df is a `pandas.DataFrame` * drop\_cols (array-like) – Columns to drop from the design matrix. Cannot be used to drop terms involving categoricals. * args (extra arguments) – These are passed to the model * kwargs (extra keyword arguments) – These are passed to the model with one exception. The `eval_env` keyword is passed to patsy. It can be either a [`patsy.EvalEnvironment`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.EvalEnvironment "(in patsy v0.5.0+dev)") object or an integer indicating the depth of the namespace to use. For example, the default `eval_env=0` uses the calling namespace. If you wish to use a “clean” environment set `eval_env=-1`. \| \| Returns: \| model \| \| Return type: \| Model instance \| #### Notes data must define \_\_getitem\_\_ with the keys in the formula terms args and kwargs are passed on to the model instantiation. E.g., a numpy structured or rec array, a dictionary, or a pandas DataFrame. statsmodels statsmodels.genmod.generalized_estimating_equations.GEE.fit statsmodels.genmod.generalized\_estimating\_equations.GEE.fit ============================================================= `GEE.fit(maxiter=60, ctol=1e-06, start_params=None, params_niter=1, first_dep_update=0, cov_type='robust', ddof_scale=None, scaling_factor=1.0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_estimating_equations.html#GEE.fit) Fits a marginal regression model using generalized estimating equations (GEE). \| Parameters: \| * maxiter (integer) – The maximum number of iterations * ctol (float) – The convergence criterion for stopping the Gauss-Seidel iterations * start\_params (array-like) – A vector of starting values for the regression coefficients. If None, a default is chosen. * params\_niter (integer) – The number of Gauss-Seidel updates of the mean structure parameters that take place prior to each update of the dependence structure. * first\_dep\_update (integer) – No dependence structure updates occur before this iteration number. * cov\_type (string) – One of “robust”, “naive”, or “bias\_reduced”. * ddof\_scale (scalar or None) – The scale parameter is estimated as the sum of squared Pearson residuals divided by `N - ddof_scale`, where N is the total sample size. If `ddof_scale` is None, the number of covariates (including an intercept if present) is used. * scaling\_factor (scalar) – The estimated covariance of the parameter estimates is scaled by this value. Default is 1, Stata uses N / (N - g), where N is the total sample size and g is the average group size. \| \| Returns: \| \| \| Return type: \| An instance of the GEEResults class or subclass \| #### Notes If convergence difficulties occur, increase the values of `first_dep_update` and/or `params_niter`. Setting `first_dep_update` to a greater value (e.g. ~10-20) causes the algorithm to move close to the GLM solution before attempting to identify the dependence structure. For the Gaussian family, there is no benefit to setting `params_niter` to a value greater than 1, since the mean structure parameters converge in one step. statsmodels statsmodels.miscmodels.count.PoissonOffsetGMLE.reduceparams statsmodels.miscmodels.count.PoissonOffsetGMLE.reduceparams =========================================================== `PoissonOffsetGMLE.reduceparams(params)` statsmodels statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.information statsmodels.tsa.regime\_switching.markov\_autoregression.MarkovAutoregression.information ========================================================================================= `MarkovAutoregression.information(params)` Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.regression.linear_model.OLSResults.f_pvalue statsmodels.regression.linear\_model.OLSResults.f\_pvalue ========================================================= `OLSResults.f_pvalue()` statsmodels statsmodels.discrete.count_model.ZeroInflatedGeneralizedPoissonResults.predict statsmodels.discrete.count\_model.ZeroInflatedGeneralizedPoissonResults.predict =============================================================================== `ZeroInflatedGeneralizedPoissonResults.predict(exog=None, transform=True, args, kwargs)` Call self.model.predict with self.params as the first argument. \| Parameters: \| exog (array-like, optional) – The values for which you want to predict. see Notes below. * transform (bool, optional) – If the model was fit via a formula, do you want to pass exog through the formula. Default is True. E.g., if you fit a model y ~ log(x1) + log(x2), and transform is True, then you can pass a data structure that contains x1 and x2 in their original form. Otherwise, you’d need to log the data first. * kwargs (args,) – Some models can take additional arguments or keywords, see the predict method of the model for the details. \| \| Returns: \| prediction – See self.model.predict \| \| Return type: \| ndarray, [pandas.Series](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.html#pandas.Series "(in pandas v0.22.0)") or [pandas.DataFrame](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html#pandas.DataFrame "(in pandas v0.22.0)") \| #### Notes The types of exog that are supported depends on whether a formula was used in the specification of the model. If a formula was used, then exog is processed in the same way as the original data. This transformation needs to have key access to the same variable names, and can be a pandas DataFrame or a dict like object. If no formula was used, then the provided exog needs to have the same number of columns as the original exog in the model. No transformation of the data is performed except converting it to a numpy array. Row indices as in pandas data frames are supported, and added to the returned prediction. statsmodels statsmodels.stats.power.FTestPower statsmodels.stats.power.FTestPower ================================== `class statsmodels.stats.power.FTestPower(kwds)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/power.html#FTestPower) Statistical Power calculations for generic F-test #### Methods \| \| \| \| --- \| --- \| \| [`plot_power`](statsmodels.stats.power.ftestpower.plot_power#statsmodels.stats.power.FTestPower.plot_power "statsmodels.stats.power.FTestPower.plot_power")([dep\_var, nobs, effect\_size, …]) \| plot power with number of observations or effect size on x-axis \| \| [`power`](statsmodels.stats.power.ftestpower.power#statsmodels.stats.power.FTestPower.power "statsmodels.stats.power.FTestPower.power")(effect\_size, df\_num, df\_denom, alpha) \| Calculate the power of a F-test. \| \| [`solve_power`](statsmodels.stats.power.ftestpower.solve_power#statsmodels.stats.power.FTestPower.solve_power "statsmodels.stats.power.FTestPower.solve_power")([effect\_size, df\_num, df\_denom, …]) \| solve for any one parameter of the power of a F-test \| statsmodels statsmodels.tsa.statespace.sarimax.SARIMAX.set_stability_method statsmodels.tsa.statespace.sarimax.SARIMAX.set\_stability\_method ================================================================= `SARIMAX.set_stability_method(stability_method=None, kwargs)` Set the numerical stability method The Kalman filter is a recursive algorithm that may in some cases suffer issues with numerical stability. The stability method controls what, if any, measures are taken to promote stability. \| Parameters: \| * stability\_method (integer, optional) – Bitmask value to set the stability method to. See notes for details. * *\\kwargs* – Keyword arguments may be used to influence the stability method by setting individual boolean flags. See notes for details. \| #### Notes This method is rarely used. See the corresponding function in the `KalmanFilter` class for details. statsmodels statsmodels.tsa.statespace.mlemodel.MLEResults.f_test statsmodels.tsa.statespace.mlemodel.MLEResults.f\_test ====================================================== `MLEResults.f_test(r_matrix, cov_p=None, scale=1.0, invcov=None)` Compute the F-test for a joint linear hypothesis. This is a special case of `wald_test` that always uses the F distribution. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length k row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> A = np.identity(len(results.params)) >>> A = A[1:,:] ``` This tests that each coefficient is jointly statistically significantly different from zero. ``` >>> print(results.f_test(A)) <F test: F=array([[ 330.28533923]]), p=4.984030528700946e-10, df_denom=9, df_num=6> ``` Compare this to ``` >>> results.fvalue 330.2853392346658 >>> results.f_pvalue 4.98403096572e-10 ``` ``` >>> B = np.array(([0,0,1,-1,0,0,0],[0,0,0,0,0,1,-1])) ``` This tests that the coefficient on the 2nd and 3rd regressors are equal and jointly that the coefficient on the 5th and 6th regressors are equal. ``` >>> print(results.f_test(B)) <F test: F=array([[ 9.74046187]]), p=0.005605288531708235, df_denom=9, df_num=2> ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.datasets import longley >>> from statsmodels.formula.api import ols >>> dta = longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = '(GNPDEFL = GNP), (UNEMP = 2), (YEAR/1829 = 1)' >>> f_test = results.f_test(hypotheses) >>> print(f_test) <F test: F=array([[ 144.17976065]]), p=6.322026217355609e-08, df_denom=9, df_num=3> ``` See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`wald_test`](statsmodels.tsa.statespace.mlemodel.mleresults.wald_test#statsmodels.tsa.statespace.mlemodel.MLEResults.wald_test "statsmodels.tsa.statespace.mlemodel.MLEResults.wald_test"), [`t_test`](statsmodels.tsa.statespace.mlemodel.mleresults.t_test#statsmodels.tsa.statespace.mlemodel.MLEResults.t_test "statsmodels.tsa.statespace.mlemodel.MLEResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.discrete.count_model.GenericZeroInflated.cov_params_func_l1 statsmodels.discrete.count\_model.GenericZeroInflated.cov\_params\_func\_l1 =========================================================================== `GenericZeroInflated.cov_params_func_l1(likelihood_model, xopt, retvals)` Computes cov\_params on a reduced parameter space corresponding to the nonzero parameters resulting from the l1 regularized fit. Returns a full cov\_params matrix, with entries corresponding to zero’d values set to np.nan. statsmodels statsmodels.discrete.discrete_model.Poisson.fit_regularized statsmodels.discrete.discrete\_model.Poisson.fit\_regularized ============================================================= `Poisson.fit_regularized(start_params=None, method='l1', maxiter='defined_by_method', full_output=1, disp=1, callback=None, alpha=0, trim_mode='auto', auto_trim_tol=0.01, size_trim_tol=0.0001, qc_tol=0.03, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#Poisson.fit_regularized) Fit the model using a regularized maximum likelihood. The regularization method AND the solver used is determined by the argument method. \| Parameters: \| start\_params (array-like, optional) – Initial guess of the solution for the loglikelihood maximization. The default is an array of zeros. * method ('l1' or 'l1\_cvxopt\_cp') – See notes for details. * maxiter (Integer or 'defined\_by\_method') – Maximum number of iterations to perform. If ‘defined\_by\_method’, then use method defaults (see notes). * full\_output (bool) – Set to True to have all available output in the Results object’s mle\_retvals attribute. The output is dependent on the solver. See LikelihoodModelResults notes section for more information. * disp (bool) – Set to True to print convergence messages. * fargs (tuple) – Extra arguments passed to the likelihood function, i.e., loglike(x,\args) callback (callable callback(xk)) – Called after each iteration, as callback(xk), where xk is the current parameter vector. * retall (bool) – Set to True to return list of solutions at each iteration. Available in Results object’s mle\_retvals attribute. * alpha (non-negative scalar or numpy array (same size as parameters)) – The weight multiplying the l1 penalty term * trim\_mode ('auto, 'size', or 'off') – If not ‘off’, trim (set to zero) parameters that would have been zero if the solver reached the theoretical minimum. If ‘auto’, trim params using the Theory above. If ‘size’, trim params if they have very small absolute value * size\_trim\_tol (float or 'auto' (default = 'auto')) – For use when trim\_mode == ‘size’ * auto\_trim\_tol (float) – For sue when trim\_mode == ‘auto’. Use * qc\_tol (float) – Print warning and don’t allow auto trim when (ii) (above) is violated by this much. * qc\_verbose (Boolean) – If true, print out a full QC report upon failure \| #### Notes Extra parameters are not penalized if alpha is given as a scalar. An example is the shape parameter in NegativeBinomial `nb1` and `nb2`. Optional arguments for the solvers (available in Results.mle\_settings): ``` 'l1' acc : float (default 1e-6) Requested accuracy as used by slsqp 'l1_cvxopt_cp' abstol : float absolute accuracy (default: 1e-7). reltol : float relative accuracy (default: 1e-6). feastol : float tolerance for feasibility conditions (default: 1e-7). refinement : int number of iterative refinement steps when solving KKT equations (default: 1). ``` Optimization methodology With $L$ the negative log likelihood, we solve the convex but non-smooth problem \[\min\_\beta L(\beta) + \sum\_k\alpha\_k \|\beta\_k\|\] via the transformation to the smooth, convex, constrained problem in twice as many variables (adding the “added variables” $u\_k$) \[\min\_{\beta,u} L(\beta) + \sum\_k\alpha\_k u\_k,\] subject to \[-u\_k \leq \beta\_k \leq u\_k.\] With $\partial\_k L$ the derivative of $L$ in the $k^{th}$ parameter direction, theory dictates that, at the minimum, exactly one of two conditions holds: 1. $\|\partial\_k L\| = \alpha\_k$ and $\beta\_k \neq 0$ 2. $\|\partial\_k L\| \leq \alpha\_k$ and $\beta\_k = 0$ statsmodels statsmodels.tsa.vector_ar.vecm.VECM.initialize statsmodels.tsa.vector\_ar.vecm.VECM.initialize =============================================== `VECM.initialize()` Initialize (possibly re-initialize) a Model instance. For instance, the design matrix of a linear model may change and some things must be recomputed. statsmodels statsmodels.stats.contingency_tables.Table2x2.riskratio_pvalue statsmodels.stats.contingency\_tables.Table2x2.riskratio\_pvalue ================================================================ `Table2x2.riskratio_pvalue(null=1)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/contingency_tables.html#Table2x2.riskratio_pvalue) p-value for a hypothesis test about the risk ratio. \| Parameters: \| null (float) – The null value of the risk ratio. \| statsmodels statsmodels.sandbox.tsa.fftarma.ArmaFft.filter2 statsmodels.sandbox.tsa.fftarma.ArmaFft.filter2 =============================================== `ArmaFft.filter2(x, pad=0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/tsa/fftarma.html#ArmaFft.filter2) filter a time series using fftconvolve3 with ARMA filter padding of x currently works only if x is 1d in example it produces same observations at beginning as lfilter even without padding. TODO: this returns 1 additional observation at the end statsmodels statsmodels.discrete.discrete_model.DiscreteModel.loglike statsmodels.discrete.discrete\_model.DiscreteModel.loglike ========================================================== `DiscreteModel.loglike(params)` Log-likelihood of model. statsmodels statsmodels.tsa.ar_model.ARResults.llf statsmodels.tsa.ar\_model.ARResults.llf ======================================= `ARResults.llf()` statsmodels statsmodels.discrete.discrete_model.LogitResults.save statsmodels.discrete.discrete\_model.LogitResults.save ====================================================== `LogitResults.save(fname, remove_data=False)` save a pickle of this instance \| Parameters: \| * fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. * remove\_data (bool) – If False (default), then the instance is pickled without changes. If True, then all arrays with length nobs are set to None before pickling. See the remove\_data method. In some cases not all arrays will be set to None. \| #### Notes If remove\_data is true and the model result does not implement a remove\_data method then this will raise an exception.	programming_docs
statsmodels statsmodels.sandbox.distributions.extras.SkewNorm2_gen.stats statsmodels.sandbox.distributions.extras.SkewNorm2\_gen.stats ============================================================= `SkewNorm2_gen.stats(args, kwds)` Some statistics of the given RV. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional (continuous RVs only)) – scale parameter (default=1) * moments (str, optional) – composed of letters [‘mvsk’] defining which moments to compute: ‘m’ = mean, ‘v’ = variance, ‘s’ = (Fisher’s) skew, ‘k’ = (Fisher’s) kurtosis. (default is ‘mv’) \| \| Returns: \| stats – of requested moments. \| \| Return type: \| sequence \| statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.initialize statsmodels.tsa.statespace.dynamic\_factor.DynamicFactorResults.initialize ========================================================================== `DynamicFactorResults.initialize(model, params, kwd)` statsmodels statsmodels.discrete.count_model.ZeroInflatedPoissonResults.llnull statsmodels.discrete.count\_model.ZeroInflatedPoissonResults.llnull =================================================================== `ZeroInflatedPoissonResults.llnull()` statsmodels statsmodels.tsa.vector_ar.hypothesis_test_results.WhitenessTestResults.summary statsmodels.tsa.vector\_ar.hypothesis\_test\_results.WhitenessTestResults.summary ================================================================================= `WhitenessTestResults.summary()` statsmodels statsmodels.robust.robust_linear_model.RLMResults.tvalues statsmodels.robust.robust\_linear\_model.RLMResults.tvalues =========================================================== `RLMResults.tvalues()` Return the t-statistic for a given parameter estimate. statsmodels statsmodels.tsa.statespace.representation.Representation.bind statsmodels.tsa.statespace.representation.Representation.bind ============================================================= `Representation.bind(endog)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/representation.html#Representation.bind) Bind data to the statespace representation \| Parameters: \| endog** (array) – Endogenous data to bind to the model. Must be column-ordered ndarray with shape (`k_endog`, `nobs`) or row-ordered ndarray with shape (`nobs`, `k_endog`). \| #### Notes The strict requirements arise because the underlying statespace and Kalman filtering classes require Fortran-ordered arrays in the wide format (shaped (`k_endog`, `nobs`)), and this structure is setup to prevent copying arrays in memory. By default, numpy arrays are row (C)-ordered and most time series are represented in the long format (with time on the 0-th axis). In this case, no copying or re-ordering needs to be performed, instead the array can simply be transposed to get it in the right order and shape. Although this class (Representation) has stringent `bind` requirements, it is assumed that it will rarely be used directly. statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactor.set_filter_method statsmodels.tsa.statespace.dynamic\_factor.DynamicFactor.set\_filter\_method ============================================================================ `DynamicFactor.set_filter_method(filter_method=None, *kwargs)` Set the filtering method The filtering method controls aspects of which Kalman filtering approach will be used. \| Parameters: \| filter\_method (integer, optional) – Bitmask value to set the filter method to. See notes for details. * *\\kwargs* – Keyword arguments may be used to influence the filter method by setting individual boolean flags. See notes for details. \| #### Notes This method is rarely used. See the corresponding function in the `KalmanFilter` class for details. statsmodels statsmodels.sandbox.distributions.transformed.Transf_gen.mean statsmodels.sandbox.distributions.transformed.Transf\_gen.mean ============================================================== `Transf_gen.mean(args, kwds)` Mean of the distribution. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| mean – the mean of the distribution \| \| Return type: \| float \| statsmodels statsmodels.regression.linear_model.GLS.from_formula statsmodels.regression.linear\_model.GLS.from\_formula ====================================================== `classmethod GLS.from_formula(formula, data, subset=None, drop_cols=None, args, kwargs)` Create a Model from a formula and dataframe. \| Parameters: \| formula (str or generic Formula object) – The formula specifying the model * data (array-like) – The data for the model. See Notes. * subset (array-like) – An array-like object of booleans, integers, or index values that indicate the subset of df to use in the model. Assumes df is a `pandas.DataFrame` * drop\_cols (array-like) – Columns to drop from the design matrix. Cannot be used to drop terms involving categoricals. * args (extra arguments) – These are passed to the model * kwargs (extra keyword arguments) – These are passed to the model with one exception. The `eval_env` keyword is passed to patsy. It can be either a [`patsy.EvalEnvironment`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.EvalEnvironment "(in patsy v0.5.0+dev)") object or an integer indicating the depth of the namespace to use. For example, the default `eval_env=0` uses the calling namespace. If you wish to use a “clean” environment set `eval_env=-1`. \| \| Returns: \| model \| \| Return type: \| Model instance \| #### Notes data must define \_\_getitem\_\_ with the keys in the formula terms args and kwargs are passed on to the model instantiation. E.g., a numpy structured or rec array, a dictionary, or a pandas DataFrame. statsmodels statsmodels.discrete.discrete_model.CountModel.fit_regularized statsmodels.discrete.discrete\_model.CountModel.fit\_regularized ================================================================ `CountModel.fit_regularized(start_params=None, method='l1', maxiter='defined_by_method', full_output=1, disp=1, callback=None, alpha=0, trim_mode='auto', auto_trim_tol=0.01, size_trim_tol=0.0001, qc_tol=0.03, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#CountModel.fit_regularized) Fit the model using a regularized maximum likelihood. The regularization method AND the solver used is determined by the argument method. \| Parameters: \| start\_params (array-like, optional) – Initial guess of the solution for the loglikelihood maximization. The default is an array of zeros. * method ('l1' or 'l1\_cvxopt\_cp') – See notes for details. * maxiter (Integer or 'defined\_by\_method') – Maximum number of iterations to perform. If ‘defined\_by\_method’, then use method defaults (see notes). * full\_output (bool) – Set to True to have all available output in the Results object’s mle\_retvals attribute. The output is dependent on the solver. See LikelihoodModelResults notes section for more information. * disp (bool) – Set to True to print convergence messages. * fargs (tuple) – Extra arguments passed to the likelihood function, i.e., loglike(x,\args) callback (callable callback(xk)) – Called after each iteration, as callback(xk), where xk is the current parameter vector. * retall (bool) – Set to True to return list of solutions at each iteration. Available in Results object’s mle\_retvals attribute. * alpha (non-negative scalar or numpy array (same size as parameters)) – The weight multiplying the l1 penalty term * trim\_mode ('auto, 'size', or 'off') – If not ‘off’, trim (set to zero) parameters that would have been zero if the solver reached the theoretical minimum. If ‘auto’, trim params using the Theory above. If ‘size’, trim params if they have very small absolute value * size\_trim\_tol (float or 'auto' (default = 'auto')) – For use when trim\_mode == ‘size’ * auto\_trim\_tol (float) – For sue when trim\_mode == ‘auto’. Use * qc\_tol (float) – Print warning and don’t allow auto trim when (ii) (above) is violated by this much. * qc\_verbose (Boolean) – If true, print out a full QC report upon failure \| #### Notes Extra parameters are not penalized if alpha is given as a scalar. An example is the shape parameter in NegativeBinomial `nb1` and `nb2`. Optional arguments for the solvers (available in Results.mle\_settings): ``` 'l1' acc : float (default 1e-6) Requested accuracy as used by slsqp 'l1_cvxopt_cp' abstol : float absolute accuracy (default: 1e-7). reltol : float relative accuracy (default: 1e-6). feastol : float tolerance for feasibility conditions (default: 1e-7). refinement : int number of iterative refinement steps when solving KKT equations (default: 1). ``` Optimization methodology With $L$ the negative log likelihood, we solve the convex but non-smooth problem \[\min\_\beta L(\beta) + \sum\_k\alpha\_k \|\beta\_k\|\] via the transformation to the smooth, convex, constrained problem in twice as many variables (adding the “added variables” $u\_k$) \[\min\_{\beta,u} L(\beta) + \sum\_k\alpha\_k u\_k,\] subject to \[-u\_k \leq \beta\_k \leq u\_k.\] With $\partial\_k L$ the derivative of $L$ in the $k^{th}$ parameter direction, theory dictates that, at the minimum, exactly one of two conditions holds: 1. $\|\partial\_k L\| = \alpha\_k$ and $\beta\_k \neq 0$ 2. $\|\partial\_k L\| \leq \alpha\_k$ and $\beta\_k = 0$ statsmodels statsmodels.multivariate.multivariate_ols._MultivariateOLS.predict statsmodels.multivariate.multivariate\_ols.\_MultivariateOLS.predict ==================================================================== `_MultivariateOLS.predict(params, exog=None, args, kwargs)` After a model has been fit predict returns the fitted values. This is a placeholder intended to be overwritten by individual models. statsmodels statsmodels.stats.power.TTestPower.plot_power statsmodels.stats.power.TTestPower.plot\_power ============================================== `TTestPower.plot_power(dep_var='nobs', nobs=None, effect_size=None, alpha=0.05, ax=None, title=None, plt_kwds=None, kwds)` plot power with number of observations or effect size on x-axis \| Parameters: \| dep\_var (string in ['nobs', 'effect\_size', 'alpha']) – This specifies which variable is used for the horizontal axis. If dep\_var=’nobs’ (default), then one curve is created for each value of `effect_size`. If dep\_var=’effect\_size’ or alpha, then one curve is created for each value of `nobs`. * nobs (scalar or array\_like) – specifies the values of the number of observations in the plot * effect\_size (scalar or array\_like) – specifies the values of the effect\_size in the plot * alpha (float or array\_like) – The significance level (type I error) used in the power calculation. Can only be more than a scalar, if `dep_var='alpha'` * ax (None or axis instance) – If ax is None, than a matplotlib figure is created. If ax is a matplotlib axis instance, then it is reused, and the plot elements are created with it. * title (string) – title for the axis. Use an empty string, `''`, to avoid a title. * plt\_kwds (None or [dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)")) – not used yet * kwds (optional keywords for power function) – These remaining keyword arguments are used as arguments to the power function. Many power function support `alternative` as a keyword argument, two-sample test support `ratio`. \| \| Returns: \| fig \| \| Return type: \| matplotlib figure instance \| #### Notes This works only for classes where the `power` method has `effect_size`, `nobs` and `alpha` as the first three arguments. If the second argument is `nobs1`, then the number of observations in the plot are those for the first sample. TODO: fix this for FTestPower and GofChisquarePower TODO: maybe add line variable, if we want more than nobs and effectsize statsmodels statsmodels.sandbox.stats.runs.Runs statsmodels.sandbox.stats.runs.Runs =================================== `class statsmodels.sandbox.stats.runs.Runs(x)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/stats/runs.html#Runs) class for runs in a binary sequence \| Parameters: \| x (array\_like, 1d) – data array, \| #### Notes This was written as a more general class for runs. This has some redundant calculations when only the runs\_test is used. TODO: make it lazy The runs test could be generalized to more than 1d if there is a use case for it. This should be extended once I figure out what the distribution of runs of any length k is. The exact distribution for the runs test is also available but not yet verified. #### Methods \| \| \| \| --- \| --- \| \| [`runs_test`](statsmodels.sandbox.stats.runs.runs.runs_test#statsmodels.sandbox.stats.runs.Runs.runs_test "statsmodels.sandbox.stats.runs.Runs.runs_test")([correction]) \| basic version of runs test \| statsmodels statsmodels.tsa.statespace.mlemodel.MLEResults.info_criteria statsmodels.tsa.statespace.mlemodel.MLEResults.info\_criteria ============================================================= `MLEResults.info_criteria(criteria, method='standard')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/mlemodel.html#MLEResults.info_criteria) Information criteria \| Parameters: \| * criteria ({'aic', 'bic', 'hqic'}) – The information criteria to compute. * method ({'standard', 'lutkepohl'}) – The method for information criteria computation. Default is ‘standard’ method; ‘lutkepohl’ computes the information criteria as in Lütkepohl (2007). See Notes for formulas. \| #### Notes The `‘standard’` formulas are: \[\begin{split}AIC & = -2 \log L(Y\_n \| \hat \psi) + 2 k \\ BIC & = -2 \log L(Y\_n \| \hat \psi) + k \log n \\ HQIC & = -2 \log L(Y\_n \| \hat \psi) + 2 k \log \log n \\\end{split}\] where $\hat \psi$ are the maximum likelihood estimates of the parameters, $n$ is the number of observations, and `k` is the number of estimated parameters. Note that the `‘standard’` formulas are returned from the `aic`, `bic`, and `hqic` results attributes. The `‘lutkepohl’` formuals are (Lütkepohl, 2010): \[\begin{split}AIC\_L & = \log \| Q \| + \frac{2 k}{n} \\ BIC\_L & = \log \| Q \| + \frac{k \log n}{n} \\ HQIC\_L & = \log \| Q \| + \frac{2 k \log \log n}{n} \\\end{split}\] where $Q$ is the state covariance matrix. Note that the Lütkepohl definitions do not apply to all state space models, and should be used with care outside of SARIMAX and VARMAX models. #### References \| \| \| \| --- \| --- \| \| [\] \| Lütkepohl, Helmut. 2007. New Introduction to Multiple Time* Series Analysis. Berlin: Springer. \| statsmodels statsmodels.sandbox.distributions.transformed.TransfTwo_gen.logsf statsmodels.sandbox.distributions.transformed.TransfTwo\_gen.logsf ================================================================== `TransfTwo_gen.logsf(x, args, kwds)` Log of the survival function of the given RV. Returns the log of the “survival function,” defined as (1 - `cdf`), evaluated at `x`. \| Parameters: \| x (array\_like) – quantiles * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| logsf – Log of the survival function evaluated at `x`. \| \| Return type: \| ndarray \| statsmodels statsmodels.sandbox.distributions.extras.NormExpan_gen.freeze statsmodels.sandbox.distributions.extras.NormExpan\_gen.freeze ============================================================== `NormExpan_gen.freeze(args, kwds)` Freeze the distribution for the given arguments. \| Parameters: \| arg2*, arg3,.. (arg1,) – The shape parameter(s) for the distribution. Should include all the non-optional arguments, may include `loc` and `scale`. \| \| Returns: \| rv\_frozen – The frozen distribution. \| \| Return type: \| rv\_frozen instance \| statsmodels statsmodels.genmod.families.family.Poisson statsmodels.genmod.families.family.Poisson ========================================== `class statsmodels.genmod.families.family.Poisson(link=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/family.html#Poisson) Poisson exponential family. \| Parameters: \| link (a link instance, optional) – The default link for the Poisson family is the log link. Available links are log, identity, and sqrt. See statsmodels.families.links for more information. \| `link` a link instance – The link function of the Poisson instance. `variance` varfuncs instance – `variance` is an instance of statsmodels.genmod.families.varfuncs.mu See also [`statsmodels.genmod.families.family.Family`](statsmodels.genmod.families.family.family#statsmodels.genmod.families.family.Family "statsmodels.genmod.families.family.Family"), [Link Functions](../glm#links) #### Methods \| \| \| \| --- \| --- \| \| [`deviance`](statsmodels.genmod.families.family.poisson.deviance#statsmodels.genmod.families.family.Poisson.deviance "statsmodels.genmod.families.family.Poisson.deviance")(endog, mu[, var\_weights, …]) \| The deviance function evaluated at (endog, mu, var\_weights, freq\_weights, scale) for the distribution. \| \| [`fitted`](statsmodels.genmod.families.family.poisson.fitted#statsmodels.genmod.families.family.Poisson.fitted "statsmodels.genmod.families.family.Poisson.fitted")(lin\_pred) \| Fitted values based on linear predictors lin\_pred. \| \| [`loglike`](statsmodels.genmod.families.family.poisson.loglike#statsmodels.genmod.families.family.Poisson.loglike "statsmodels.genmod.families.family.Poisson.loglike")(endog, mu[, var\_weights, …]) \| The log-likelihood function in terms of the fitted mean response. \| \| [`loglike_obs`](statsmodels.genmod.families.family.poisson.loglike_obs#statsmodels.genmod.families.family.Poisson.loglike_obs "statsmodels.genmod.families.family.Poisson.loglike_obs")(endog, mu[, var\_weights, scale]) \| The log-likelihood function for each observation in terms of the fitted mean response for the Poisson distribution. \| \| [`predict`](statsmodels.genmod.families.family.poisson.predict#statsmodels.genmod.families.family.Poisson.predict "statsmodels.genmod.families.family.Poisson.predict")(mu) \| Linear predictors based on given mu values. \| \| [`resid_anscombe`](statsmodels.genmod.families.family.poisson.resid_anscombe#statsmodels.genmod.families.family.Poisson.resid_anscombe "statsmodels.genmod.families.family.Poisson.resid_anscombe")(endog, mu[, var\_weights, scale]) \| The Anscombe residuals \| \| [`resid_dev`](statsmodels.genmod.families.family.poisson.resid_dev#statsmodels.genmod.families.family.Poisson.resid_dev "statsmodels.genmod.families.family.Poisson.resid_dev")(endog, mu[, var\_weights, scale]) \| The deviance residuals \| \| [`starting_mu`](statsmodels.genmod.families.family.poisson.starting_mu#statsmodels.genmod.families.family.Poisson.starting_mu "statsmodels.genmod.families.family.Poisson.starting_mu")(y) \| Starting value for mu in the IRLS algorithm. \| \| [`weights`](statsmodels.genmod.families.family.poisson.weights#statsmodels.genmod.families.family.Poisson.weights "statsmodels.genmod.families.family.Poisson.weights")(mu) \| Weights for IRLS steps \|	programming_docs
statsmodels statsmodels.multivariate.factor.Factor.predict statsmodels.multivariate.factor.Factor.predict ============================================== `Factor.predict(params, exog=None, args, kwargs)` After a model has been fit predict returns the fitted values. This is a placeholder intended to be overwritten by individual models. statsmodels statsmodels.regression.mixed_linear_model.MixedLMResults.bsejhj statsmodels.regression.mixed\_linear\_model.MixedLMResults.bsejhj ================================================================= `MixedLMResults.bsejhj()` standard deviation of parameter estimates based on covHJH statsmodels statsmodels.discrete.count_model.ZeroInflatedPoissonResults.llr_pvalue statsmodels.discrete.count\_model.ZeroInflatedPoissonResults.llr\_pvalue ======================================================================== `ZeroInflatedPoissonResults.llr_pvalue()` statsmodels statsmodels.iolib.table.SimpleTable.pad statsmodels.iolib.table.SimpleTable.pad ======================================= `SimpleTable.pad(s, width, align)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/iolib/table.html#SimpleTable.pad) DEPRECATED: just use the pad function statsmodels statsmodels.discrete.discrete_model.ProbitResults.load statsmodels.discrete.discrete\_model.ProbitResults.load ======================================================= `classmethod ProbitResults.load(fname)` load a pickle, (class method) \| Parameters: \| fname* (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. \| \| Returns: \| \| \| Return type: \| unpickled instance \| statsmodels statsmodels.genmod.families.links.Log.deriv statsmodels.genmod.families.links.Log.deriv =========================================== `Log.deriv(p)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#Log.deriv) Derivative of log transform link function \| Parameters: \| p (array-like) – Mean parameters \| \| Returns: \| g’(p) – derivative of log transform of x \| \| Return type: \| array \| #### Notes g’(x) = 1/x statsmodels statsmodels.genmod.families.family.Binomial.weights statsmodels.genmod.families.family.Binomial.weights =================================================== `Binomial.weights(mu)` Weights for IRLS steps \| Parameters: \| mu (array-like) – The transformed mean response variable in the exponential family \| \| Returns: \| w – The weights for the IRLS steps \| \| Return type: \| array \| #### Notes \[w = 1 / (g'(\mu)^2 \* Var(\mu))\] statsmodels statsmodels.discrete.discrete_model.MultinomialResults.pred_table statsmodels.discrete.discrete\_model.MultinomialResults.pred\_table =================================================================== `MultinomialResults.pred_table()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#MultinomialResults.pred_table) Returns the J x J prediction table. #### Notes pred\_table[i,j] refers to the number of times “i” was observed and the model predicted “j”. Correct predictions are along the diagonal. statsmodels statsmodels.discrete.discrete_model.GeneralizedPoisson.score_obs statsmodels.discrete.discrete\_model.GeneralizedPoisson.score\_obs ================================================================== `GeneralizedPoisson.score_obs(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#GeneralizedPoisson.score_obs) statsmodels statsmodels.iolib.summary2.Summary.add_title statsmodels.iolib.summary2.Summary.add\_title ============================================= `Summary.add_title(title=None, results=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/iolib/summary2.html#Summary.add_title) Insert a title on top of the summary table. If a string is provided in the title argument, that string is printed. If no title string is provided but a results instance is provided, statsmodels attempts to construct a useful title automatically. statsmodels statsmodels.discrete.discrete_model.NegativeBinomialP.loglike statsmodels.discrete.discrete\_model.NegativeBinomialP.loglike ============================================================== `NegativeBinomialP.loglike(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#NegativeBinomialP.loglike) Loglikelihood of Generalized Negative Binomial (NB-P) model \| Parameters: \| params (array-like) – The parameters of the model. \| \| Returns: \| loglike – The log-likelihood function of the model evaluated at `params`. See notes. \| \| Return type: \| float \| statsmodels statsmodels.regression.linear_model.WLS.from_formula statsmodels.regression.linear\_model.WLS.from\_formula ====================================================== `classmethod WLS.from_formula(formula, data, subset=None, drop_cols=None, args, kwargs)` Create a Model from a formula and dataframe. \| Parameters: \| formula (str or generic Formula object) – The formula specifying the model * data (array-like) – The data for the model. See Notes. * subset (array-like) – An array-like object of booleans, integers, or index values that indicate the subset of df to use in the model. Assumes df is a `pandas.DataFrame` * drop\_cols (array-like) – Columns to drop from the design matrix. Cannot be used to drop terms involving categoricals. * args (extra arguments) – These are passed to the model * kwargs (extra keyword arguments) – These are passed to the model with one exception. The `eval_env` keyword is passed to patsy. It can be either a [`patsy.EvalEnvironment`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.EvalEnvironment "(in patsy v0.5.0+dev)") object or an integer indicating the depth of the namespace to use. For example, the default `eval_env=0` uses the calling namespace. If you wish to use a “clean” environment set `eval_env=-1`. \| \| Returns: \| model \| \| Return type: \| Model instance \| #### Notes data must define \_\_getitem\_\_ with the keys in the formula terms args and kwargs are passed on to the model instantiation. E.g., a numpy structured or rec array, a dictionary, or a pandas DataFrame. statsmodels statsmodels.discrete.discrete_model.MultinomialResults.bic statsmodels.discrete.discrete\_model.MultinomialResults.bic =========================================================== `MultinomialResults.bic()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#MultinomialResults.bic) statsmodels statsmodels.genmod.families.family.Gaussian.predict statsmodels.genmod.families.family.Gaussian.predict =================================================== `Gaussian.predict(mu)` Linear predictors based on given mu values. \| Parameters: \| mu (array) – The mean response variables \| \| Returns: \| lin\_pred – Linear predictors based on the mean response variables. The value of the link function at the given mu. \| \| Return type: \| array \| statsmodels statsmodels.genmod.generalized_linear_model.GLMResults.initialize statsmodels.genmod.generalized\_linear\_model.GLMResults.initialize =================================================================== `GLMResults.initialize(model, params, *kwd)` statsmodels statsmodels.discrete.discrete_model.CountResults.save statsmodels.discrete.discrete\_model.CountResults.save ====================================================== `CountResults.save(fname, remove_data=False)` save a pickle of this instance \| Parameters: \| fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. * remove\_data (bool) – If False (default), then the instance is pickled without changes. If True, then all arrays with length nobs are set to None before pickling. See the remove\_data method. In some cases not all arrays will be set to None. \| #### Notes If remove\_data is true and the model result does not implement a remove\_data method then this will raise an exception. statsmodels statsmodels.discrete.discrete_model.BinaryModel.score statsmodels.discrete.discrete\_model.BinaryModel.score ====================================================== `BinaryModel.score(params)` Score vector of model. The gradient of logL with respect to each parameter. statsmodels statsmodels.genmod.families.family.Binomial.deviance statsmodels.genmod.families.family.Binomial.deviance ==================================================== `Binomial.deviance(endog, mu, var_weights=1.0, freq_weights=1.0, scale=1.0)` The deviance function evaluated at (endog, mu, var\_weights, freq\_weights, scale) for the distribution. Deviance is usually defined as twice the loglikelihood ratio. \| Parameters: \| * endog (array-like) – The endogenous response variable * mu (array-like) – The inverse of the link function at the linear predicted values. * var\_weights (array-like) – 1d array of variance (analytic) weights. The default is 1. * freq\_weights (array-like) – 1d array of frequency weights. The default is 1. * scale (float, optional) – An optional scale argument. The default is 1. \| \| Returns: \| Deviance – The value of deviance function defined below. \| \| Return type: \| array \| #### Notes Deviance is defined \[D = 2\sum\_i (freq\\_weights\_i \* var\\_weights \* (llf(endog\_i, endog\_i) - llf(endog\_i, \mu\_i)))\] where y is the endogenous variable. The deviance functions are analytically defined for each family. Internally, we calculate deviance as: \[D = \sum\_i freq\\_weights\_i \* var\\_weights \* resid\\_dev\_i / scale\] statsmodels statsmodels.genmod.families.family.Gamma.loglike statsmodels.genmod.families.family.Gamma.loglike ================================================ `Gamma.loglike(endog, mu, var_weights=1.0, freq_weights=1.0, scale=1.0)` The log-likelihood function in terms of the fitted mean response. \| Parameters: \| * endog (array) – Usually the endogenous response variable. * mu (array) – Usually but not always the fitted mean response variable. * var\_weights (array-like) – 1d array of variance (analytic) weights. The default is 1. * freq\_weights (array-like) – 1d array of frequency weights. The default is 1. * scale (float) – The scale parameter. The default is 1. \| \| Returns: \| ll – The value of the loglikelihood evaluated at (endog, mu, var\_weights, freq\_weights, scale) as defined below. \| \| Return type: \| float \| #### Notes Where $ll\_i$ is the by-observation log-likelihood: \[ll = \sum(ll\_i \* freq\\_weights\_i)\] `ll_i` is defined for each family. endog and mu are not restricted to `endog` and `mu` respectively. For instance, you could call both `loglike(endog, endog)` and `loglike(endog, mu)` to get the log-likelihood ratio. statsmodels statsmodels.tsa.statespace.kalman_filter.FilterResults.update_representation statsmodels.tsa.statespace.kalman\_filter.FilterResults.update\_representation ============================================================================== `FilterResults.update_representation(model, only_options=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/kalman_filter.html#FilterResults.update_representation) Update the results to match a given model \| Parameters: \| * model ([Representation](statsmodels.tsa.statespace.representation.representation#statsmodels.tsa.statespace.representation.Representation "statsmodels.tsa.statespace.representation.Representation")) – The model object from which to take the updated values. * only\_options (boolean, optional) – If set to true, only the filter options are updated, and the state space representation is not updated. Default is False. \| #### Notes This method is rarely required except for internal usage. statsmodels statsmodels.discrete.discrete_model.NegativeBinomialResults.pvalues statsmodels.discrete.discrete\_model.NegativeBinomialResults.pvalues ==================================================================== `NegativeBinomialResults.pvalues()` statsmodels statsmodels.regression.recursive_ls.RecursiveLS.score_obs statsmodels.regression.recursive\_ls.RecursiveLS.score\_obs =========================================================== `RecursiveLS.score_obs(params, method='approx', transformed=True, approx_complex_step=None, approx_centered=False, *kwargs)` Compute the score per observation, evaluated at params \| Parameters: \| params (array\_like) – Array of parameters at which to evaluate the score. * kwargs – Additional arguments to the `loglike` method. \| \| Returns: \| score – Score per observation, evaluated at `params`. \| \| Return type: \| array \| #### Notes This is a numerical approximation, calculated using first-order complex step differentiation on the `loglikeobs` method. statsmodels statsmodels.stats.contingency_tables.Table2x2.test_ordinal_association statsmodels.stats.contingency\_tables.Table2x2.test\_ordinal\_association ========================================================================= `Table2x2.test_ordinal_association(row_scores=None, col_scores=None)` Assess independence between two ordinal variables. This is the ‘linear by linear’ association test, which uses weights or scores to target the test to have more power against ordered alternatives. \| Parameters: \| * row\_scores (array-like) – An array of numeric row scores * col\_scores (array-like) – An array of numeric column scores \| \| Returns: \| * A bunch with the following attributes * statistic (float) – The test statistic. * null\_mean (float) – The expected value of the test statistic under the null hypothesis. * null\_sd (float) – The standard deviation of the test statistic under the null hypothesis. * zscore (float) – The Z-score for the test statistic. * pvalue (float) – The p-value for the test. \| #### Notes The scores define the trend to which the test is most sensitive. Using the default row and column scores gives the Cochran-Armitage trend test. statsmodels statsmodels.tsa.arima_model.ARMAResults.arfreq statsmodels.tsa.arima\_model.ARMAResults.arfreq =============================================== `ARMAResults.arfreq()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_model.html#ARMAResults.arfreq) Returns the frequency of the AR roots. This is the solution, x, to z = abs(z)\exp(2j\np.pi\x) where z are the roots. statsmodels statsmodels.discrete.count_model.ZeroInflatedPoissonResults.summary2 statsmodels.discrete.count\_model.ZeroInflatedPoissonResults.summary2 ===================================================================== `ZeroInflatedPoissonResults.summary2(yname=None, xname=None, title=None, alpha=0.05, float_format='%.4f')` Experimental function to summarize regression results \| Parameters: \| xname (List of strings of length equal to the number of parameters) – Names of the independent variables (optional) * yname (string) – Name of the dependent variable (optional) * title (string, optional) – Title for the top table. If not None, then this replaces the default title * alpha (float) – significance level for the confidence intervals * float\_format (string) – print format for floats in parameters summary \| \| Returns: \| smry – this holds the summary tables and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary.Summary`](statsmodels.iolib.summary.summary#statsmodels.iolib.summary.Summary "statsmodels.iolib.summary.Summary") class to hold summary results statsmodels statsmodels.imputation.mice.MICE.combine statsmodels.imputation.mice.MICE.combine ======================================== `MICE.combine()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/imputation/mice.html#MICE.combine) Pools MICE imputation results. This method can only be used after the `run` method has been called. Returns estimates and standard errors of the analysis model parameters. Returns a MICEResults instance. statsmodels statsmodels.tsa.statespace.structural.UnobservedComponents.impulse_responses statsmodels.tsa.statespace.structural.UnobservedComponents.impulse\_responses ============================================================================= `UnobservedComponents.impulse_responses(params, steps=1, impulse=0, orthogonalized=False, cumulative=False, *kwargs)` Impulse response function \| Parameters: \| params (array\_like) – Array of model parameters. * steps (int, optional) – The number of steps for which impulse responses are calculated. Default is 1. Note that the initial impulse is not counted as a step, so if `steps=1`, the output will have 2 entries. * impulse (int or array\_like) – If an integer, the state innovation to pulse; must be between 0 and `k_posdef-1`. Alternatively, a custom impulse vector may be provided; must be shaped `k_posdef x 1`. * orthogonalized (boolean, optional) – Whether or not to perform impulse using orthogonalized innovations. Note that this will also affect custum `impulse` vectors. Default is False. * cumulative (boolean, optional) – Whether or not to return cumulative impulse responses. Default is False. * *\\kwargs* – If the model is time-varying and `steps` is greater than the number of observations, any of the state space representation matrices that are time-varying must have updated values provided for the out-of-sample steps. For example, if `design` is a time-varying component, `nobs` is 10, and `steps` is 15, a (`k_endog` x `k_states` x 5) matrix must be provided with the new design matrix values. \| \| Returns: \| impulse\_responses – Responses for each endogenous variable due to the impulse given by the `impulse` argument. A (steps + 1 x k\_endog) array. \| \| Return type: \| array \| #### Notes Intercepts in the measurement and state equation are ignored when calculating impulse responses. statsmodels statsmodels.tsa.arima_model.ARIMAResults.forecast statsmodels.tsa.arima\_model.ARIMAResults.forecast ================================================== `ARIMAResults.forecast(steps=1, exog=None, alpha=0.05)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_model.html#ARIMAResults.forecast) Out-of-sample forecasts \| Parameters: \| * steps (int) – The number of out of sample forecasts from the end of the sample. * exog (array) – If the model is an ARIMAX, you must provide out of sample values for the exogenous variables. This should not include the constant. * alpha (float) – The confidence intervals for the forecasts are (1 - alpha) % \| \| Returns: \| * forecast (array) – Array of out of sample forecasts * stderr (array) – Array of the standard error of the forecasts. * conf\_int (array) – 2d array of the confidence interval for the forecast \| #### Notes Prediction is done in the levels of the original endogenous variable. If you would like prediction of differences in levels use `predict`. statsmodels statsmodels.discrete.discrete_model.DiscreteResults.wald_test_terms statsmodels.discrete.discrete\_model.DiscreteResults.wald\_test\_terms ====================================================================== `DiscreteResults.wald_test_terms(skip_single=False, extra_constraints=None, combine_terms=None)` Compute a sequence of Wald tests for terms over multiple columns This computes joined Wald tests for the hypothesis that all coefficients corresponding to a `term` are zero. `Terms` are defined by the underlying formula or by string matching. \| Parameters: \| * skip\_single (boolean) – If true, then terms that consist only of a single column and, therefore, refers only to a single parameter is skipped. If false, then all terms are included. * extra\_constraints (ndarray) – not tested yet * combine\_terms (None or list of strings) – Each string in this list is matched to the name of the terms or the name of the exogenous variables. All columns whose name includes that string are combined in one joint test. \| \| Returns: \| test\_result – The result instance contains `table` which is a pandas DataFrame with the test results: test statistic, degrees of freedom and pvalues. \| \| Return type: \| result instance \| #### Examples ``` >>> res_ols = ols("np.log(Days+1) ~ C(Duration, Sum)C(Weight, Sum)", data).fit() >>> res_ols.wald_test_terms() <class 'statsmodels.stats.contrast.WaldTestResults'> F P>F df constraint df denom Intercept 279.754525 2.37985521351e-22 1 51 C(Duration, Sum) 5.367071 0.0245738436636 1 51 C(Weight, Sum) 12.432445 3.99943118767e-05 2 51 C(Duration, Sum):C(Weight, Sum) 0.176002 0.83912310946 2 51 ``` ``` >>> res_poi = Poisson.from_formula("Days ~ C(Weight) C(Duration)", data).fit(cov_type='HC0') >>> wt = res_poi.wald_test_terms(skip_single=False, combine_terms=['Duration', 'Weight']) >>> print(wt) chi2 P>chi2 df constraint Intercept 15.695625 7.43960374424e-05 1 C(Weight) 16.132616 0.000313940174705 2 C(Duration) 1.009147 0.315107378931 1 C(Weight):C(Duration) 0.216694 0.897315972824 2 Duration 11.187849 0.010752286833 3 Weight 30.263368 4.32586407145e-06 4 ```	programming_docs
statsmodels statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.hessian statsmodels.discrete.count\_model.ZeroInflatedNegativeBinomialP.hessian ======================================================================= `ZeroInflatedNegativeBinomialP.hessian(params)` Generic Zero Inflated model Hessian matrix of the loglikelihood \| Parameters: \| params (array-like) – The parameters of the model \| \| Returns: \| hess – The Hessian, second derivative of loglikelihood function, evaluated at `params` \| \| Return type: \| ndarray, (k\_vars, k\_vars) \| #### Notes statsmodels statsmodels.stats.weightstats.DescrStatsW.ztest_mean statsmodels.stats.weightstats.DescrStatsW.ztest\_mean ===================================================== `DescrStatsW.ztest_mean(value=0, alternative='two-sided')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/weightstats.html#DescrStatsW.ztest_mean) z-test of Null hypothesis that mean is equal to value. The alternative hypothesis H1 is defined by the following ‘two-sided’: H1: mean not equal to value ‘larger’ : H1: mean larger than value ‘smaller’ : H1: mean smaller than value \| Parameters: \| * value (float or array) – the hypothesized value for the mean * alternative (string) – The alternative hypothesis, H1, has to be one of the following ’two-sided’: H1: mean not equal to value (default) ‘larger’ : H1: mean larger than value ‘smaller’ : H1: mean smaller than value \| \| Returns: \| * tstat (float) – test statisic * pvalue (float) – pvalue of the t-test \| #### Notes This uses the same degrees of freedom correction as the t-test in the calculation of the standard error of the mean, i.e it uses `(sum_weights - 1)` instead of `sum_weights` in the denominator. See Examples below for the difference. #### Examples z-test on a proportion, with 20 observations, 15 of those are our event ``` >>> import statsmodels.api as sm >>> x1 = [0, 1] >>> w1 = [5, 15] >>> d1 = sm.stats.DescrStatsW(x1, w1) >>> d1.ztest_mean(0.5) (2.5166114784235836, 0.011848940928347452) ``` This differs from the proportions\_ztest because of the degrees of freedom correction: >>> sm.stats.proportions\_ztest(15, 20.0, value=0.5) (2.5819888974716112, 0.009823274507519247). We can replicate the results from `proportions_ztest` if we increase the weights to have artificially one more observation: ``` >>> sm.stats.DescrStatsW(x1, np.array(w1)21./20).ztest_mean(0.5) (2.5819888974716116, 0.0098232745075192366) ``` statsmodels statsmodels.genmod.bayes_mixed_glm.BinomialBayesMixedGLM.from_formula statsmodels.genmod.bayes\_mixed\_glm.BinomialBayesMixedGLM.from\_formula ======================================================================== `classmethod BinomialBayesMixedGLM.from_formula(formula, vc_formulas, data, vcp_p=1, fe_p=2)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/bayes_mixed_glm.html#BinomialBayesMixedGLM.from_formula) Fit a BayesMixedGLM using a formula. \| Parameters: \| formula (string) – Formula for the endog and fixed effects terms (use ~ to separate dependent and independent expressions). * vc\_formulas (dictionary) – vc\_formulas[name] is a one-sided formula that creates one collection of random effects with a common variance prameter. If using a categorical expression to produce variance components, note that generally `0 + …` should be used so that an intercept is not included. * data (data frame) – The data to which the formulas are applied. * family (genmod.families instance) – A GLM family. * vcp\_p (float) – The prior standard deviation for the logarithms of the standard deviations of the random effects. * fe\_p (float) – The prior standard deviation for the fixed effects parameters. \| statsmodels statsmodels.tsa.statespace.kalman_filter.PredictionResults.predict statsmodels.tsa.statespace.kalman\_filter.PredictionResults.predict =================================================================== `PredictionResults.predict(start=None, end=None, dynamic=None, *kwargs)` In-sample and out-of-sample prediction for state space models generally \| Parameters: \| start (int, optional) – Zero-indexed observation number at which to start forecasting, i.e., the first forecast will be at start. * end (int, optional) – Zero-indexed observation number at which to end forecasting, i.e., the last forecast will be at end. * dynamic (int, optional) – Offset relative to `start` at which to begin dynamic prediction. Prior to this observation, true endogenous values will be used for prediction; starting with this observation and continuing through the end of prediction, forecasted endogenous values will be used instead. * *\\kwargs* – If the prediction range is outside of the sample range, any of the state space representation matrices that are time-varying must have updated values provided for the out-of-sample range. For example, of `obs_intercept` is a time-varying component and the prediction range extends 10 periods beyond the end of the sample, a (`k_endog` x 10) matrix must be provided with the new intercept values. \| \| Returns: \| results – A PredictionResults object. \| \| Return type: \| [kalman\_filter.PredictionResults](statsmodels.tsa.statespace.kalman_filter.predictionresults#statsmodels.tsa.statespace.kalman_filter.PredictionResults "statsmodels.tsa.statespace.kalman_filter.PredictionResults") \| #### Notes All prediction is performed by applying the deterministic part of the measurement equation using the predicted state variables. Out-of-sample prediction first applies the Kalman filter to missing data for the number of periods desired to obtain the predicted states. statsmodels statsmodels.robust.norms.TukeyBiweight.weights statsmodels.robust.norms.TukeyBiweight.weights ============================================== `TukeyBiweight.weights(z)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/norms.html#TukeyBiweight.weights) Tukey’s biweight weighting function for the IRLS algorithm The psi function scaled by z \| Parameters: \| z (array-like) – 1d array \| \| Returns: \| weights – psi(z) = (1 - (z/c)\\2)\\2 for \|z\| <= Rpsi(z) = 0 for \|z\| > R \| \| Return type: \| array \| statsmodels statsmodels.regression.linear_model.OLSResults.load statsmodels.regression.linear\_model.OLSResults.load ==================================================== `classmethod OLSResults.load(fname)` load a pickle, (class method) \| Parameters: \| fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. \| \| Returns: \| \| \| Return type: \| unpickled instance \| statsmodels statsmodels.discrete.discrete_model.MultinomialModel.hessian statsmodels.discrete.discrete\_model.MultinomialModel.hessian ============================================================= `MultinomialModel.hessian(params)` The Hessian matrix of the model statsmodels statsmodels.discrete.discrete_model.Probit.fit statsmodels.discrete.discrete\_model.Probit.fit =============================================== `Probit.fit(start_params=None, method='newton', maxiter=35, full_output=1, disp=1, callback=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#Probit.fit) Fit the model using maximum likelihood. The rest of the docstring is from statsmodels.base.model.LikelihoodModel.fit Fit method for likelihood based models \| Parameters: \| start\_params (array-like, optional) – Initial guess of the solution for the loglikelihood maximization. The default is an array of zeros. * method (str, optional) – The `method` determines which solver from `scipy.optimize` is used, and it can be chosen from among the following strings: + ’newton’ for Newton-Raphson, ‘nm’ for Nelder-Mead + ’bfgs’ for Broyden-Fletcher-Goldfarb-Shanno (BFGS) + ’lbfgs’ for limited-memory BFGS with optional box constraints + ’powell’ for modified Powell’s method + ’cg’ for conjugate gradient + ’ncg’ for Newton-conjugate gradient + ’basinhopping’ for global basin-hopping solver + ’minimize’ for generic wrapper of scipy minimize (BFGS by default)The explicit arguments in `fit` are passed to the solver, with the exception of the basin-hopping solver. Each solver has several optional arguments that are not the same across solvers. See the notes section below (or scipy.optimize) for the available arguments and for the list of explicit arguments that the basin-hopping solver supports. * maxiter (int, optional) – The maximum number of iterations to perform. * full\_output (bool, optional) – Set to True to have all available output in the Results object’s mle\_retvals attribute. The output is dependent on the solver. See LikelihoodModelResults notes section for more information. * disp (bool, optional) – Set to True to print convergence messages. * fargs (tuple, optional) – Extra arguments passed to the likelihood function, i.e., loglike(x,\args) callback (callable callback(xk), optional) – Called after each iteration, as callback(xk), where xk is the current parameter vector. * retall (bool, optional) – Set to True to return list of solutions at each iteration. Available in Results object’s mle\_retvals attribute. * skip\_hessian (bool, optional) – If False (default), then the negative inverse hessian is calculated after the optimization. If True, then the hessian will not be calculated. However, it will be available in methods that use the hessian in the optimization (currently only with `“newton”`). * kwargs (keywords) – All kwargs are passed to the chosen solver with one exception. The following keyword controls what happens after the fit: ``` warn_convergence : bool, optional If True, checks the model for the converged flag. If the converged flag is False, a ConvergenceWarning is issued. ``` \| #### Notes The ‘basinhopping’ solver ignores `maxiter`, `retall`, `full_output` explicit arguments. Optional arguments for solvers (see returned Results.mle\_settings): ``` 'newton' tol : float Relative error in params acceptable for convergence. 'nm' -- Nelder Mead xtol : float Relative error in params acceptable for convergence ftol : float Relative error in loglike(params) acceptable for convergence maxfun : int Maximum number of function evaluations to make. 'bfgs' gtol : float Stop when norm of gradient is less than gtol. norm : float Order of norm (np.Inf is max, -np.Inf is min) epsilon If fprime is approximated, use this value for the step size. Only relevant if LikelihoodModel.score is None. 'lbfgs' m : int This many terms are used for the Hessian approximation. factr : float A stop condition that is a variant of relative error. pgtol : float A stop condition that uses the projected gradient. epsilon If fprime is approximated, use this value for the step size. Only relevant if LikelihoodModel.score is None. maxfun : int Maximum number of function evaluations to make. bounds : sequence (min, max) pairs for each element in x, defining the bounds on that parameter. Use None for one of min or max when there is no bound in that direction. 'cg' gtol : float Stop when norm of gradient is less than gtol. norm : float Order of norm (np.Inf is max, -np.Inf is min) epsilon : float If fprime is approximated, use this value for the step size. Can be scalar or vector. Only relevant if Likelihoodmodel.score is None. 'ncg' fhess_p : callable f'(x,args) Function which computes the Hessian of f times an arbitrary vector, p. Should only be supplied if LikelihoodModel.hessian is None. avextol : float Stop when the average relative error in the minimizer falls below this amount. epsilon : float or ndarray If fhess is approximated, use this value for the step size. Only relevant if Likelihoodmodel.hessian is None. 'powell' xtol : float Line-search error tolerance ftol : float Relative error in loglike(params) for acceptable for convergence. maxfun : int Maximum number of function evaluations to make. start_direc : ndarray Initial direction set. 'basinhopping' niter : integer The number of basin hopping iterations. niter_success : integer Stop the run if the global minimum candidate remains the same for this number of iterations. T : float The "temperature" parameter for the accept or reject criterion. Higher "temperatures" mean that larger jumps in function value will be accepted. For best results `T` should be comparable to the separation (in function value) between local minima. stepsize : float Initial step size for use in the random displacement. interval : integer The interval for how often to update the `stepsize`. minimizer : dict Extra keyword arguments to be passed to the minimizer `scipy.optimize.minimize()`, for example 'method' - the minimization method (e.g. 'L-BFGS-B'), or 'tol' - the tolerance for termination. Other arguments are mapped from explicit argument of `fit`: - `args` <- `fargs` - `jac` <- `score` - `hess` <- `hess` 'minimize' min_method : str, optional Name of minimization method to use. Any method specific arguments can be passed directly. For a list of methods and their arguments, see documentation of `scipy.optimize.minimize`. If no method is specified, then BFGS is used. ``` statsmodels statsmodels.multivariate.factor.FactorResults.plot_scree statsmodels.multivariate.factor.FactorResults.plot\_scree ========================================================= `FactorResults.plot_scree(ncomp=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/multivariate/factor.html#FactorResults.plot_scree) Plot of the ordered eigenvalues and variance explained for the loadings \| Parameters: \| ncomp* (int, optional) – Number of loadings to include in the plot. If None, will included the same as the number of maximum possible loadings \| \| Returns: \| fig – Handle to the figure \| \| Return type: \| figure \| statsmodels statsmodels.genmod.generalized_estimating_equations.GEEMargins.summary statsmodels.genmod.generalized\_estimating\_equations.GEEMargins.summary ======================================================================== `GEEMargins.summary(alpha=0.05)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_estimating_equations.html#GEEMargins.summary) Returns a summary table for marginal effects \| Parameters: \| alpha (float) – Number between 0 and 1. The confidence intervals have the probability 1-alpha. \| \| Returns: \| Summary – A SummaryTable instance \| \| Return type: \| SummaryTable \| statsmodels statsmodels.discrete.discrete_model.MultinomialResults.margeff statsmodels.discrete.discrete\_model.MultinomialResults.margeff =============================================================== `MultinomialResults.margeff()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#MultinomialResults.margeff) statsmodels statsmodels.tsa.vector_ar.vecm.VECMResults.cov_params_wo_det statsmodels.tsa.vector\_ar.vecm.VECMResults.cov\_params\_wo\_det ================================================================ `VECMResults.cov_params_wo_det()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/vecm.html#VECMResults.cov_params_wo_det) statsmodels statsmodels.robust.robust_linear_model.RLMResults.cov_params statsmodels.robust.robust\_linear\_model.RLMResults.cov\_params =============================================================== `RLMResults.cov_params(r_matrix=None, column=None, scale=None, cov_p=None, other=None)` Returns the variance/covariance matrix. The variance/covariance matrix can be of a linear contrast of the estimates of params or all params multiplied by scale which will usually be an estimate of sigma^2. Scale is assumed to be a scalar. \| Parameters: \| * r\_matrix (array-like) – Can be 1d, or 2d. Can be used alone or with other. * column (array-like, optional) – Must be used on its own. Can be 0d or 1d see below. * scale (float, optional) – Can be specified or not. Default is None, which means that the scale argument is taken from the model. * other (array-like, optional) – Can be used when r\_matrix is specified. \| \| Returns: \| cov – covariance matrix of the parameter estimates or of linear combination of parameter estimates. See Notes. \| \| Return type: \| ndarray \| #### Notes (The below are assumed to be in matrix notation.) If no argument is specified returns the covariance matrix of a model `(scale)(X.T X)^(-1)` If contrast is specified it pre and post-multiplies as follows `(scale) r_matrix (X.T X)^(-1) r_matrix.T` If contrast and other are specified returns `(scale) * r_matrix (X.T X)^(-1) other.T` If column is specified returns `(scale) * (X.T X)^(-1)[column,column]` if column is 0d OR `(scale) * (X.T X)^(-1)[column][:,column]` if column is 1d statsmodels statsmodels.tsa.statespace.structural.UnobservedComponents.untransform_params statsmodels.tsa.statespace.structural.UnobservedComponents.untransform\_params ============================================================================== `UnobservedComponents.untransform_params(constrained)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/structural.html#UnobservedComponents.untransform_params) Reverse the transformation statsmodels statsmodels.tsa.statespace.varmax.VARMAX.untransform_params statsmodels.tsa.statespace.varmax.VARMAX.untransform\_params ============================================================ `VARMAX.untransform_params(constrained)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/varmax.html#VARMAX.untransform_params) Transform constrained parameters used in likelihood evaluation to unconstrained parameters used by the optimizer. \| Parameters: \| constrained (array\_like) – Array of constrained parameters used in likelihood evalution, to be transformed. \| \| Returns: \| unconstrained – Array of unconstrained parameters used by the optimizer. \| \| Return type: \| array\_like \| statsmodels statsmodels.sandbox.regression.gmm.NonlinearIVGMM.from_formula statsmodels.sandbox.regression.gmm.NonlinearIVGMM.from\_formula =============================================================== `classmethod NonlinearIVGMM.from_formula(formula, data, subset=None, drop_cols=None, args, kwargs)` Create a Model from a formula and dataframe. \| Parameters: \| formula (str or generic Formula object) – The formula specifying the model * data (array-like) – The data for the model. See Notes. * subset (array-like) – An array-like object of booleans, integers, or index values that indicate the subset of df to use in the model. Assumes df is a `pandas.DataFrame` * drop\_cols (array-like) – Columns to drop from the design matrix. Cannot be used to drop terms involving categoricals. * args (extra arguments) – These are passed to the model * kwargs (extra keyword arguments) – These are passed to the model with one exception. The `eval_env` keyword is passed to patsy. It can be either a [`patsy.EvalEnvironment`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.EvalEnvironment "(in patsy v0.5.0+dev)") object or an integer indicating the depth of the namespace to use. For example, the default `eval_env=0` uses the calling namespace. If you wish to use a “clean” environment set `eval_env=-1`. \| \| Returns: \| model \| \| Return type: \| Model instance \| #### Notes data must define \_\_getitem\_\_ with the keys in the formula terms args and kwargs are passed on to the model instantiation. E.g., a numpy structured or rec array, a dictionary, or a pandas DataFrame.	programming_docs
statsmodels statsmodels.tsa.arima_model.ARMA.loglike statsmodels.tsa.arima\_model.ARMA.loglike ========================================= `ARMA.loglike(params, set_sigma2=True)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_model.html#ARMA.loglike) Compute the log-likelihood for ARMA(p,q) model #### Notes Likelihood used depends on the method set in fit statsmodels statsmodels.discrete.discrete_model.MultinomialResults.predict statsmodels.discrete.discrete\_model.MultinomialResults.predict =============================================================== `MultinomialResults.predict(exog=None, transform=True, args, kwargs)` Call self.model.predict with self.params as the first argument. \| Parameters: \| exog (array-like, optional) – The values for which you want to predict. see Notes below. * transform (bool, optional) – If the model was fit via a formula, do you want to pass exog through the formula. Default is True. E.g., if you fit a model y ~ log(x1) + log(x2), and transform is True, then you can pass a data structure that contains x1 and x2 in their original form. Otherwise, you’d need to log the data first. * kwargs (args,) – Some models can take additional arguments or keywords, see the predict method of the model for the details. \| \| Returns: \| prediction – See self.model.predict \| \| Return type: \| ndarray, [pandas.Series](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.html#pandas.Series "(in pandas v0.22.0)") or [pandas.DataFrame](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html#pandas.DataFrame "(in pandas v0.22.0)") \| #### Notes The types of exog that are supported depends on whether a formula was used in the specification of the model. If a formula was used, then exog is processed in the same way as the original data. This transformation needs to have key access to the same variable names, and can be a pandas DataFrame or a dict like object. If no formula was used, then the provided exog needs to have the same number of columns as the original exog in the model. No transformation of the data is performed except converting it to a numpy array. Row indices as in pandas data frames are supported, and added to the returned prediction. statsmodels statsmodels.discrete.discrete_model.NegativeBinomialP.initialize statsmodels.discrete.discrete\_model.NegativeBinomialP.initialize ================================================================= `NegativeBinomialP.initialize()` Initialize is called by statsmodels.model.LikelihoodModel.\_\_init\_\_ and should contain any preprocessing that needs to be done for a model. statsmodels statsmodels.tsa.vector_ar.var_model.VAR.select_order statsmodels.tsa.vector\_ar.var\_model.VAR.select\_order ======================================================= `VAR.select_order(maxlags=None, trend='c')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VAR.select_order) Compute lag order selections based on each of the available information criteria \| Parameters: \| * maxlags (int) – if None, defaults to 12 \* (nobs/100.)\\(1./4) * trend (str {"nc", "c", "ct", "ctt"}) – + “nc” - no deterministic terms + ”c” - constant term + ”ct” - constant and linear term + ”ctt” - constant, linear, and quadratic term \| \| Returns: \| selections \| \| Return type: \| [LagOrderResults](statsmodels.tsa.vector_ar.var_model.lagorderresults#statsmodels.tsa.vector_ar.var_model.LagOrderResults "statsmodels.tsa.vector_ar.var_model.LagOrderResults") \| statsmodels statsmodels.tsa.arima_model.ARMAResults.t_test statsmodels.tsa.arima\_model.ARMAResults.t\_test ================================================ `ARMAResults.t_test(r_matrix, cov_p=None, scale=None, use_t=None)` Compute a t-test for a each linear hypothesis of the form Rb = q \| Parameters: \| * r\_matrix (array-like, str, tuple) – + array : If an array is given, a p x k 2d array or length k 1d array specifying the linear restrictions. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q). If q is given, can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – An optional `scale` to use. Default is the scale specified by the model fit. * use\_t (bool, optional) – If use\_t is None, then the default of the model is used. If use\_t is True, then the p-values are based on the t distribution. If use\_t is False, then the p-values are based on the normal distribution. \| \| Returns: \| res – The results for the test are attributes of this results instance. The available results have the same elements as the parameter table in `summary()`. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> r = np.zeros_like(results.params) >>> r[5:] = [1,-1] >>> print(r) [ 0. 0. 0. 0. 0. 1. -1.] ``` r tests that the coefficients on the 5th and 6th independent variable are the same. ``` >>> T_test = results.t_test(r) >>> print(T_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 -1829.2026 455.391 -4.017 0.003 -2859.368 -799.037 ============================================================================== >>> T_test.effect -1829.2025687192481 >>> T_test.sd 455.39079425193762 >>> T_test.tvalue -4.0167754636411717 >>> T_test.pvalue 0.0015163772380899498 ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.formula.api import ols >>> dta = sm.datasets.longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = 'GNPDEFL = GNP, UNEMP = 2, YEAR/1829 = 1' >>> t_test = results.t_test(hypotheses) >>> print(t_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 15.0977 84.937 0.178 0.863 -177.042 207.238 c1 -2.0202 0.488 -8.231 0.000 -3.125 -0.915 c2 1.0001 0.249 0.000 1.000 0.437 1.563 ============================================================================== ``` See also [`tvalues`](statsmodels.tsa.arima_model.armaresults.tvalues#statsmodels.tsa.arima_model.ARMAResults.tvalues "statsmodels.tsa.arima_model.ARMAResults.tvalues") individual t statistics [`f_test`](statsmodels.tsa.arima_model.armaresults.f_test#statsmodels.tsa.arima_model.ARMAResults.f_test "statsmodels.tsa.arima_model.ARMAResults.f_test") for F tests [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") statsmodels statsmodels.graphics.gofplots.ProbPlot.sorted_data statsmodels.graphics.gofplots.ProbPlot.sorted\_data =================================================== `ProbPlot.sorted_data()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/graphics/gofplots.html#ProbPlot.sorted_data) statsmodels statsmodels.imputation.mice.MICEData.update_all statsmodels.imputation.mice.MICEData.update\_all ================================================ `MICEData.update_all(n_iter=1)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/imputation/mice.html#MICEData.update_all) Perform a specified number of MICE iterations. \| Parameters: \| n\_iter (int) – The number of updates to perform. Only the result of the final update will be available. \| #### Notes The imputed values are stored in the class attribute `self.data`. statsmodels statsmodels.sandbox.regression.gmm.GMM.fititer statsmodels.sandbox.regression.gmm.GMM.fititer ============================================== `GMM.fititer(start, maxiter=2, start_invweights=None, weights_method='cov', wargs=(), optim_method='bfgs', optim_args=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/regression/gmm.html#GMM.fititer) iterative estimation with updating of optimal weighting matrix stopping criteria are maxiter or change in parameter estimate less than self.epsilon\_iter, with default 1e-6. \| Parameters: \| * start (array) – starting value for parameters * maxiter (int) – maximum number of iterations * start\_weights (array (nmoms, nmoms)) – initial weighting matrix; if None, then the identity matrix is used * weights\_method ({'cov', ..}) – method to use to estimate the optimal weighting matrix, see calc\_weightmatrix for details \| \| Returns: \| * params (array) – estimated parameters * weights (array) – optimal weighting matrix calculated with final parameter estimates \| #### Notes statsmodels statsmodels.genmod.families.links.Link.inverse statsmodels.genmod.families.links.Link.inverse ============================================== `Link.inverse(z)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#Link.inverse) Inverse of the link function. Just a placeholder. \| Parameters: \| z (array-like) – `z` is usually the linear predictor of the transformed variable in the IRLS algorithm for GLM. \| \| Returns: \| g^(-1)(z) – The value of the inverse of the link function g^(-1)(z) = p \| \| Return type: \| array \| statsmodels statsmodels.tsa.statespace.structural.UnobservedComponentsResults.summary statsmodels.tsa.statespace.structural.UnobservedComponentsResults.summary ========================================================================= `UnobservedComponentsResults.summary(alpha=0.05, start=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/structural.html#UnobservedComponentsResults.summary) Summarize the Model \| Parameters: \| * alpha (float, optional) – Significance level for the confidence intervals. Default is 0.05. * start (int, optional) – Integer of the start observation. Default is 0. * model\_name (string) – The name of the model used. Default is to use model class name. \| \| Returns: \| summary – This holds the summary table and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary.Summary`](statsmodels.iolib.summary.summary#statsmodels.iolib.summary.Summary "statsmodels.iolib.summary.Summary") statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.hqic statsmodels.tsa.statespace.dynamic\_factor.DynamicFactorResults.hqic ==================================================================== `DynamicFactorResults.hqic()` (float) Hannan-Quinn Information Criterion statsmodels statsmodels.tsa.statespace.sarimax.SARIMAX.hessian statsmodels.tsa.statespace.sarimax.SARIMAX.hessian ================================================== `SARIMAX.hessian(params, args, kwargs)` Hessian matrix of the likelihood function, evaluated at the given parameters \| Parameters: \| params (array\_like) – Array of parameters at which to evaluate the hessian. * args – Additional positional arguments to the `loglike` method. * kwargs – Additional keyword arguments to the `loglike` method. \| \| Returns: \| hessian – Hessian matrix evaluated at `params` \| \| Return type: \| array \| #### Notes This is a numerical approximation. Both \args and \\kwargs are necessary because the optimizer from `fit` must call this function and only supports passing arguments via \args (for example `scipy.optimize.fmin_l_bfgs`). statsmodels statsmodels.discrete.count_model.ZeroInflatedPoisson.initialize statsmodels.discrete.count\_model.ZeroInflatedPoisson.initialize ================================================================ `ZeroInflatedPoisson.initialize()` Initialize is called by statsmodels.model.LikelihoodModel.\_\_init\_\_ and should contain any preprocessing that needs to be done for a model. statsmodels statsmodels.genmod.families.links.nbinom statsmodels.genmod.families.links.nbinom ======================================== `class statsmodels.genmod.families.links.nbinom(alpha=1.0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#nbinom) The negative binomial link function. #### Notes g(p) = log(p/(p + 1/alpha)) nbinom is an alias of NegativeBinomial. nbinom = NegativeBinomial(alpha=1.) #### Methods \| \| \| \| --- \| --- \| \| [`deriv`](statsmodels.genmod.families.links.nbinom.deriv#statsmodels.genmod.families.links.nbinom.deriv "statsmodels.genmod.families.links.nbinom.deriv")(p) \| Derivative of the negative binomial transform \| \| [`deriv2`](statsmodels.genmod.families.links.nbinom.deriv2#statsmodels.genmod.families.links.nbinom.deriv2 "statsmodels.genmod.families.links.nbinom.deriv2")(p) \| Second derivative of the negative binomial link function. \| \| [`inverse`](statsmodels.genmod.families.links.nbinom.inverse#statsmodels.genmod.families.links.nbinom.inverse "statsmodels.genmod.families.links.nbinom.inverse")(z) \| Inverse of the negative binomial transform \| \| [`inverse_deriv`](statsmodels.genmod.families.links.nbinom.inverse_deriv#statsmodels.genmod.families.links.nbinom.inverse_deriv "statsmodels.genmod.families.links.nbinom.inverse_deriv")(z) \| Derivative of the inverse of the negative binomial transform \| statsmodels statsmodels.sandbox.regression.gmm.IVGMMResults.f_test statsmodels.sandbox.regression.gmm.IVGMMResults.f\_test ======================================================= `IVGMMResults.f_test(r_matrix, cov_p=None, scale=1.0, invcov=None)` Compute the F-test for a joint linear hypothesis. This is a special case of `wald_test` that always uses the F distribution. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length k row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> A = np.identity(len(results.params)) >>> A = A[1:,:] ``` This tests that each coefficient is jointly statistically significantly different from zero. ``` >>> print(results.f_test(A)) <F test: F=array([[ 330.28533923]]), p=4.984030528700946e-10, df_denom=9, df_num=6> ``` Compare this to ``` >>> results.fvalue 330.2853392346658 >>> results.f_pvalue 4.98403096572e-10 ``` ``` >>> B = np.array(([0,0,1,-1,0,0,0],[0,0,0,0,0,1,-1])) ``` This tests that the coefficient on the 2nd and 3rd regressors are equal and jointly that the coefficient on the 5th and 6th regressors are equal. ``` >>> print(results.f_test(B)) <F test: F=array([[ 9.74046187]]), p=0.005605288531708235, df_denom=9, df_num=2> ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.datasets import longley >>> from statsmodels.formula.api import ols >>> dta = longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = '(GNPDEFL = GNP), (UNEMP = 2), (YEAR/1829 = 1)' >>> f_test = results.f_test(hypotheses) >>> print(f_test) <F test: F=array([[ 144.17976065]]), p=6.322026217355609e-08, df_denom=9, df_num=3> ``` See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`wald_test`](statsmodels.sandbox.regression.gmm.ivgmmresults.wald_test#statsmodels.sandbox.regression.gmm.IVGMMResults.wald_test "statsmodels.sandbox.regression.gmm.IVGMMResults.wald_test"), [`t_test`](statsmodels.sandbox.regression.gmm.ivgmmresults.t_test#statsmodels.sandbox.regression.gmm.IVGMMResults.t_test "statsmodels.sandbox.regression.gmm.IVGMMResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.regression.linear_model.RegressionResults.mse_resid statsmodels.regression.linear\_model.RegressionResults.mse\_resid ================================================================= `RegressionResults.mse_resid()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#RegressionResults.mse_resid) statsmodels statsmodels.stats.moment_helpers.corr2cov statsmodels.stats.moment\_helpers.corr2cov ========================================== `statsmodels.stats.moment_helpers.corr2cov(corr, std)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/moment_helpers.html#corr2cov) convert correlation matrix to covariance matrix given standard deviation \| Parameters: \| * corr (array\_like, 2d) – correlation matrix, see Notes * std (array\_like, 1d) – standard deviation \| \| Returns: \| cov – covariance matrix \| \| Return type: \| ndarray (subclass) \| #### Notes This function does not convert subclasses of ndarrays. This requires that multiplication is defined elementwise. np.ma.array are allowed, but not matrices. statsmodels statsmodels.regression.mixed_linear_model.MixedLM statsmodels.regression.mixed\_linear\_model.MixedLM =================================================== `class statsmodels.regression.mixed_linear_model.MixedLM(endog, exog, groups, exog_re=None, exog_vc=None, use_sqrt=True, missing='none', *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/mixed_linear_model.html#MixedLM) An object specifying a linear mixed effects model. Use the `fit` method to fit the model and obtain a results object. \| Parameters: \| endog (1d array-like) – The dependent variable * exog (2d array-like) – A matrix of covariates used to determine the mean structure (the “fixed effects” covariates). * groups (1d array-like) – A vector of labels determining the groups – data from different groups are independent * exog\_re (2d array-like) – A matrix of covariates used to determine the variance and covariance structure (the “random effects” covariates). If None, defaults to a random intercept for each group. * exog\_vc (dict-like) – A dictionary containing specifications of the variance component terms. See below for details. * use\_sqrt (bool) – If True, optimization is carried out using the lower triangle of the square root of the random effects covariance matrix, otherwise it is carried out using the lower triangle of the random effects covariance matrix. * missing (string) – The approach to missing data handling \| #### Notes `exog_vc` is a dictionary of dictionaries. Specifically, `exog_vc[a][g]` is a matrix whose columns are linearly combined using independent random coefficients. This random term then contributes to the variance structure of the data for group `g`. The random coefficients all have mean zero, and have the same variance. The matrix must be `m x k`, where `m` is the number of observations in group `g`. The number of columns may differ among the top-level groups. The covariates in `exog`, `exog_re` and `exog_vc` may (but need not) partially or wholly overlap. `use_sqrt` should almost always be set to True. The main use case for use\_sqrt=False is when complicated patterns of fixed values in the covariance structure are set (using the `free` argument to `fit`) that cannot be expressed in terms of the Cholesky factor L. #### Examples A basic mixed model with fixed effects for the columns of `exog` and a random intercept for each distinct value of `group`: ``` >>> model = sm.MixedLM(endog, exog, groups) >>> result = model.fit() ``` A mixed model with fixed effects for the columns of `exog` and correlated random coefficients for the columns of `exog_re`: ``` >>> model = sm.MixedLM(endog, exog, groups, exog_re=exog_re) >>> result = model.fit() ``` A mixed model with fixed effects for the columns of `exog` and independent random coefficients for the columns of `exog_re`: ``` >>> free = MixedLMParams.from_components( fe_params=np.ones(exog.shape[1]), cov_re=np.eye(exog_re.shape[1])) >>> model = sm.MixedLM(endog, exog, groups, exog_re=exog_re) >>> result = model.fit(free=free) ``` A different way to specify independent random coefficients for the columns of `exog_re`. In this example `groups` must be a Pandas Series with compatible indexing with `exog_re`, and `exog_re` has two columns. ``` >>> g = pd.groupby(groups, by=groups).groups >>> vc = {} >>> vc['1'] = {k : exog_re.loc[g[k], 0] for k in g} >>> vc['2'] = {k : exog_re.loc[g[k], 1] for k in g} >>> model = sm.MixedLM(endog, exog, groups, vcomp=vc) >>> result = model.fit() ``` #### Methods \| \| \| \| --- \| --- \| \| [`fit`](statsmodels.regression.mixed_linear_model.mixedlm.fit#statsmodels.regression.mixed_linear_model.MixedLM.fit "statsmodels.regression.mixed_linear_model.MixedLM.fit")([start\_params, reml, niter\_sa, do\_cg, …]) \| Fit a linear mixed model to the data. \| \| [`fit_regularized`](statsmodels.regression.mixed_linear_model.mixedlm.fit_regularized#statsmodels.regression.mixed_linear_model.MixedLM.fit_regularized "statsmodels.regression.mixed_linear_model.MixedLM.fit_regularized")([start\_params, method, …]) \| Fit a model in which the fixed effects parameters are penalized. \| \| [`from_formula`](statsmodels.regression.mixed_linear_model.mixedlm.from_formula#statsmodels.regression.mixed_linear_model.MixedLM.from_formula "statsmodels.regression.mixed_linear_model.MixedLM.from_formula")(formula, data[, re\_formula, …]) \| Create a Model from a formula and dataframe. \| \| [`get_fe_params`](statsmodels.regression.mixed_linear_model.mixedlm.get_fe_params#statsmodels.regression.mixed_linear_model.MixedLM.get_fe_params "statsmodels.regression.mixed_linear_model.MixedLM.get_fe_params")(cov\_re, vcomp) \| Use GLS to update the fixed effects parameter estimates. \| \| [`get_scale`](statsmodels.regression.mixed_linear_model.mixedlm.get_scale#statsmodels.regression.mixed_linear_model.MixedLM.get_scale "statsmodels.regression.mixed_linear_model.MixedLM.get_scale")(fe\_params, cov\_re, vcomp) \| Returns the estimated error variance based on given estimates of the slopes and random effects covariance matrix. \| \| [`group_list`](statsmodels.regression.mixed_linear_model.mixedlm.group_list#statsmodels.regression.mixed_linear_model.MixedLM.group_list "statsmodels.regression.mixed_linear_model.MixedLM.group_list")(array) \| Returns `array` split into subarrays corresponding to the grouping structure. \| \| [`hessian`](statsmodels.regression.mixed_linear_model.mixedlm.hessian#statsmodels.regression.mixed_linear_model.MixedLM.hessian "statsmodels.regression.mixed_linear_model.MixedLM.hessian")(params) \| Returns the model’s Hessian matrix. \| \| [`information`](statsmodels.regression.mixed_linear_model.mixedlm.information#statsmodels.regression.mixed_linear_model.MixedLM.information "statsmodels.regression.mixed_linear_model.MixedLM.information")(params) \| Fisher information matrix of model \| \| [`initialize`](statsmodels.regression.mixed_linear_model.mixedlm.initialize#statsmodels.regression.mixed_linear_model.MixedLM.initialize "statsmodels.regression.mixed_linear_model.MixedLM.initialize")() \| Initialize (possibly re-initialize) a Model instance. \| \| [`loglike`](statsmodels.regression.mixed_linear_model.mixedlm.loglike#statsmodels.regression.mixed_linear_model.MixedLM.loglike "statsmodels.regression.mixed_linear_model.MixedLM.loglike")(params[, profile\_fe]) \| Evaluate the (profile) log-likelihood of the linear mixed effects model. \| \| [`predict`](statsmodels.regression.mixed_linear_model.mixedlm.predict#statsmodels.regression.mixed_linear_model.MixedLM.predict "statsmodels.regression.mixed_linear_model.MixedLM.predict")(params[, exog]) \| Return predicted values from a design matrix. \| \| [`score`](statsmodels.regression.mixed_linear_model.mixedlm.score#statsmodels.regression.mixed_linear_model.MixedLM.score "statsmodels.regression.mixed_linear_model.MixedLM.score")(params[, profile\_fe]) \| Returns the score vector of the profile log-likelihood. \| \| [`score_full`](statsmodels.regression.mixed_linear_model.mixedlm.score_full#statsmodels.regression.mixed_linear_model.MixedLM.score_full "statsmodels.regression.mixed_linear_model.MixedLM.score_full")(params, calc\_fe) \| Returns the score with respect to untransformed parameters. \| \| [`score_sqrt`](statsmodels.regression.mixed_linear_model.mixedlm.score_sqrt#statsmodels.regression.mixed_linear_model.MixedLM.score_sqrt "statsmodels.regression.mixed_linear_model.MixedLM.score_sqrt")(params[, calc\_fe]) \| Returns the score with respect to transformed parameters. \| #### Attributes \| \| \| \| --- \| --- \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| Names of exogenous variables \|	programming_docs
statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.irf_resim statsmodels.tsa.vector\_ar.var\_model.VARResults.irf\_resim =========================================================== `VARResults.irf_resim(orth=False, repl=1000, T=10, seed=None, burn=100, cum=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARResults.irf_resim) Simulates impulse response function, returning an array of simulations. Used for Sims-Zha error band calculation. \| Parameters: \| * orth (bool, default False) – Compute orthoganalized impulse response error bands * repl (int) – number of Monte Carlo replications to perform * T (int, default 10) – number of impulse response periods * signif (float (0 < signif <1)) – Significance level for error bars, defaults to 95% CI * seed (int) – np.random.seed for replications * burn (int) – number of initial observations to discard for simulation * cum (bool, default False) – produce cumulative irf error bands \| #### Notes Sims, Christoper A., and Tao Zha. 1999. “Error Bands for Impulse Response.” Econometrica 67: 1113-1155. \| Returns: \| \| \| Return type: \| Array of simulated impulse response functions \| statsmodels statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.llf statsmodels.discrete.count\_model.ZeroInflatedNegativeBinomialResults.llf ========================================================================= `ZeroInflatedNegativeBinomialResults.llf()` statsmodels statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.remove_data statsmodels.discrete.count\_model.ZeroInflatedNegativeBinomialResults.remove\_data ================================================================================== `ZeroInflatedNegativeBinomialResults.remove_data()` remove data arrays, all nobs arrays from result and model This reduces the size of the instance, so it can be pickled with less memory. Currently tested for use with predict from an unpickled results and model instance. Warning Since data and some intermediate results have been removed calculating new statistics that require them will raise exceptions. The exception will occur the first time an attribute is accessed that has been set to None. Not fully tested for time series models, tsa, and might delete too much for prediction or not all that would be possible. The lists of arrays to delete are maintained as attributes of the result and model instance, except for cached values. These lists could be changed before calling remove\_data. The attributes to remove are named in: `model._data_attr : arrays attached to both the model instance` and the results instance with the same attribute name. `result.data_in_cache : arrays that may exist as values in` result.\_cache (TODO : should privatize name) `result._data_attr_model : arrays attached to the model` instance but not to the results instance statsmodels statsmodels.tsa.statespace.kalman_filter.KalmanFilter.loglike statsmodels.tsa.statespace.kalman\_filter.KalmanFilter.loglike ============================================================== `KalmanFilter.loglike(kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/kalman_filter.html#KalmanFilter.loglike) Calculate the loglikelihood associated with the statespace model. \| Parameters: \| \\kwargs – Additional keyword arguments to pass to the Kalman filter. See `KalmanFilter.filter` for more details. \| \| Returns: \| loglike** – The joint loglikelihood. \| \| Return type: \| float \| statsmodels statsmodels.imputation.mice.MICEData.plot_bivariate statsmodels.imputation.mice.MICEData.plot\_bivariate ==================================================== `MICEData.plot_bivariate(col1_name, col2_name, lowess_args=None, lowess_min_n=40, jitter=None, plot_points=True, ax=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/imputation/mice.html#MICEData.plot_bivariate) Plot observed and imputed values for two variables. Displays a scatterplot of one variable against another. The points are colored according to whether the values are observed or imputed. \| Parameters: \| * col1\_name (string) – The variable to be plotted on the horizontal axis. * col2\_name (string) – The variable to be plotted on the vertical axis. * lowess\_args (dictionary) – A dictionary of dictionaries, keys are ‘ii’, ‘io’, ‘oi’ and ‘oo’, where ‘o’ denotes ‘observed’ and ‘i’ denotes imputed. See Notes for details. * lowess\_min\_n (integer) – Minimum sample size to plot a lowess fit * jitter (float or tuple) – Standard deviation for jittering points in the plot. Either a single scalar applied to both axes, or a tuple containing x-axis jitter and y-axis jitter, respectively. * plot\_points (bool) – If True, the data points are plotted. * ax (matplotlib axes object) – Axes on which to plot, created if not provided. \| \| Returns: \| \| \| Return type: \| The matplotlib figure on which the plot id drawn. \| statsmodels statsmodels.regression.linear_model.RegressionResults.llf statsmodels.regression.linear\_model.RegressionResults.llf ========================================================== `RegressionResults.llf()` statsmodels statsmodels.genmod.generalized_estimating_equations.GEEResults.bse statsmodels.genmod.generalized\_estimating\_equations.GEEResults.bse ==================================================================== `GEEResults.bse()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_estimating_equations.html#GEEResults.bse) statsmodels statsmodels.duration.hazard_regression.PHReg.information statsmodels.duration.hazard\_regression.PHReg.information ========================================================= `PHReg.information(params)` Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.miscmodels.count.PoissonGMLE.score statsmodels.miscmodels.count.PoissonGMLE.score ============================================== `PoissonGMLE.score(params)` Gradient of log-likelihood evaluated at params statsmodels statsmodels.sandbox.distributions.extras.ACSkewT_gen statsmodels.sandbox.distributions.extras.ACSkewT\_gen ===================================================== `class statsmodels.sandbox.distributions.extras.ACSkewT_gen` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/distributions/extras.html#ACSkewT_gen) univariate Skew-T distribution of Azzalini class follows scipy.stats.distributions pattern but with \_\_init\_\_ #### Methods \| \| \| \| --- \| --- \| \| [`cdf`](statsmodels.sandbox.distributions.extras.acskewt_gen.cdf#statsmodels.sandbox.distributions.extras.ACSkewT_gen.cdf "statsmodels.sandbox.distributions.extras.ACSkewT_gen.cdf")(x, \args, \\kwds) \| Cumulative distribution function of the given RV. \| \| [`entropy`](statsmodels.sandbox.distributions.extras.acskewt_gen.entropy#statsmodels.sandbox.distributions.extras.ACSkewT_gen.entropy "statsmodels.sandbox.distributions.extras.ACSkewT_gen.entropy")(\args, \\kwds) \| Differential entropy of the RV. \| \| [`expect`](statsmodels.sandbox.distributions.extras.acskewt_gen.expect#statsmodels.sandbox.distributions.extras.ACSkewT_gen.expect "statsmodels.sandbox.distributions.extras.ACSkewT_gen.expect")([func, args, loc, scale, lb, ub, …]) \| Calculate expected value of a function with respect to the distribution. \| \| [`fit`](statsmodels.sandbox.distributions.extras.acskewt_gen.fit#statsmodels.sandbox.distributions.extras.ACSkewT_gen.fit "statsmodels.sandbox.distributions.extras.ACSkewT_gen.fit")(data, \args, \\kwds) \| Return MLEs for shape (if applicable), location, and scale parameters from data. \| \| [`fit_loc_scale`](statsmodels.sandbox.distributions.extras.acskewt_gen.fit_loc_scale#statsmodels.sandbox.distributions.extras.ACSkewT_gen.fit_loc_scale "statsmodels.sandbox.distributions.extras.ACSkewT_gen.fit_loc_scale")(data, \args) \| Estimate loc and scale parameters from data using 1st and 2nd moments. \| \| [`freeze`](statsmodels.sandbox.distributions.extras.acskewt_gen.freeze#statsmodels.sandbox.distributions.extras.ACSkewT_gen.freeze "statsmodels.sandbox.distributions.extras.ACSkewT_gen.freeze")(\args, \\kwds) \| Freeze the distribution for the given arguments. \| \| [`interval`](statsmodels.sandbox.distributions.extras.acskewt_gen.interval#statsmodels.sandbox.distributions.extras.ACSkewT_gen.interval "statsmodels.sandbox.distributions.extras.ACSkewT_gen.interval")(alpha, \args, \\kwds) \| Confidence interval with equal areas around the median. \| \| [`isf`](statsmodels.sandbox.distributions.extras.acskewt_gen.isf#statsmodels.sandbox.distributions.extras.ACSkewT_gen.isf "statsmodels.sandbox.distributions.extras.ACSkewT_gen.isf")(q, \args, \\kwds) \| Inverse survival function (inverse of `sf`) at q of the given RV. \| \| [`logcdf`](statsmodels.sandbox.distributions.extras.acskewt_gen.logcdf#statsmodels.sandbox.distributions.extras.ACSkewT_gen.logcdf "statsmodels.sandbox.distributions.extras.ACSkewT_gen.logcdf")(x, \args, \\kwds) \| Log of the cumulative distribution function at x of the given RV. \| \| [`logpdf`](statsmodels.sandbox.distributions.extras.acskewt_gen.logpdf#statsmodels.sandbox.distributions.extras.ACSkewT_gen.logpdf "statsmodels.sandbox.distributions.extras.ACSkewT_gen.logpdf")(x, \args, \\kwds) \| Log of the probability density function at x of the given RV. \| \| [`logsf`](statsmodels.sandbox.distributions.extras.acskewt_gen.logsf#statsmodels.sandbox.distributions.extras.ACSkewT_gen.logsf "statsmodels.sandbox.distributions.extras.ACSkewT_gen.logsf")(x, \args, \\kwds) \| Log of the survival function of the given RV. \| \| [`mean`](statsmodels.sandbox.distributions.extras.acskewt_gen.mean#statsmodels.sandbox.distributions.extras.ACSkewT_gen.mean "statsmodels.sandbox.distributions.extras.ACSkewT_gen.mean")(\args, \\kwds) \| Mean of the distribution. \| \| [`median`](statsmodels.sandbox.distributions.extras.acskewt_gen.median#statsmodels.sandbox.distributions.extras.ACSkewT_gen.median "statsmodels.sandbox.distributions.extras.ACSkewT_gen.median")(\args, \\kwds) \| Median of the distribution. \| \| [`moment`](statsmodels.sandbox.distributions.extras.acskewt_gen.moment#statsmodels.sandbox.distributions.extras.ACSkewT_gen.moment "statsmodels.sandbox.distributions.extras.ACSkewT_gen.moment")(n, \args, \\kwds) \| n-th order non-central moment of distribution. \| \| [`nnlf`](statsmodels.sandbox.distributions.extras.acskewt_gen.nnlf#statsmodels.sandbox.distributions.extras.ACSkewT_gen.nnlf "statsmodels.sandbox.distributions.extras.ACSkewT_gen.nnlf")(theta, x) \| Return negative loglikelihood function. \| \| [`pdf`](statsmodels.sandbox.distributions.extras.acskewt_gen.pdf#statsmodels.sandbox.distributions.extras.ACSkewT_gen.pdf "statsmodels.sandbox.distributions.extras.ACSkewT_gen.pdf")(x, \args, \\kwds) \| Probability density function at x of the given RV. \| \| [`ppf`](statsmodels.sandbox.distributions.extras.acskewt_gen.ppf#statsmodels.sandbox.distributions.extras.ACSkewT_gen.ppf "statsmodels.sandbox.distributions.extras.ACSkewT_gen.ppf")(q, \args, \\kwds) \| Percent point function (inverse of `cdf`) at q of the given RV. \| \| [`rvs`](statsmodels.sandbox.distributions.extras.acskewt_gen.rvs#statsmodels.sandbox.distributions.extras.ACSkewT_gen.rvs "statsmodels.sandbox.distributions.extras.ACSkewT_gen.rvs")(\args, \\kwds) \| Random variates of given type. \| \| [`sf`](statsmodels.sandbox.distributions.extras.acskewt_gen.sf#statsmodels.sandbox.distributions.extras.ACSkewT_gen.sf "statsmodels.sandbox.distributions.extras.ACSkewT_gen.sf")(x, \args, \\kwds) \| Survival function (1 - `cdf`) at x of the given RV. \| \| [`stats`](statsmodels.sandbox.distributions.extras.acskewt_gen.stats#statsmodels.sandbox.distributions.extras.ACSkewT_gen.stats "statsmodels.sandbox.distributions.extras.ACSkewT_gen.stats")(\args, \\kwds) \| Some statistics of the given RV. \| \| [`std`](statsmodels.sandbox.distributions.extras.acskewt_gen.std#statsmodels.sandbox.distributions.extras.ACSkewT_gen.std "statsmodels.sandbox.distributions.extras.ACSkewT_gen.std")(\args, \\kwds) \| Standard deviation of the distribution. \| \| [`var`](statsmodels.sandbox.distributions.extras.acskewt_gen.var#statsmodels.sandbox.distributions.extras.ACSkewT_gen.var "statsmodels.sandbox.distributions.extras.ACSkewT_gen.var")(\args, \\kwds) \| Variance of the distribution. \| #### Attributes \| \| \| \| --- \| --- \| \| `random_state` \| Get or set the RandomState object for generating random variates. \| statsmodels statsmodels.multivariate.factor.FactorResults.fitted_cov statsmodels.multivariate.factor.FactorResults.fitted\_cov ========================================================= `FactorResults.fitted_cov()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/multivariate/factor.html#FactorResults.fitted_cov) Returns the fitted covariance matrix. statsmodels statsmodels.discrete.count_model.ZeroInflatedPoissonResults.t_test_pairwise statsmodels.discrete.count\_model.ZeroInflatedPoissonResults.t\_test\_pairwise ============================================================================== `ZeroInflatedPoissonResults.t_test_pairwise(term_name, method='hs', alpha=0.05, factor_labels=None)` perform pairwise t\_test with multiple testing corrected p-values This uses the formula design\_info encoding contrast matrix and should work for all encodings of a main effect. \| Parameters: \| * result (result instance) – The results of an estimated model with a categorical main effect. * term\_name (str) – name of the term for which pairwise comparisons are computed. Term names for categorical effects are created by patsy and correspond to the main part of the exog names. * method (str or list of strings) – multiple testing p-value correction, default is ‘hs’, see stats.multipletesting * alpha (float) – significance level for multiple testing reject decision. * factor\_labels (None, list of str) – Labels for the factor levels used for pairwise labels. If not provided, then the labels from the formula design\_info are used. \| \| Returns: \| results – The results are stored as attributes, the main attributes are the following two. Other attributes are added for debugging purposes or as background information.* result\_frame : pandas DataFrame with t\_test results and multiple testing corrected p-values. * contrasts : matrix of constraints of the null hypothesis in the t\_test. \| \| Return type: \| instance of a simple Results class \| #### Notes Status: experimental. Currently only checked for treatment coding with and without specified reference level. Currently there are no multiple testing corrected confidence intervals available. #### Examples ``` >>> res = ols("np.log(Days+1) ~ C(Weight) + C(Duration)", data).fit() >>> pw = res.t_test_pairwise("C(Weight)") >>> pw.result_frame coef std err t P>\|t\| Conf. Int. Low 2-1 0.632315 0.230003 2.749157 8.028083e-03 0.171563 3-1 1.302555 0.230003 5.663201 5.331513e-07 0.841803 3-2 0.670240 0.230003 2.914044 5.119126e-03 0.209488 Conf. Int. Upp. pvalue-hs reject-hs 2-1 1.093067 0.010212 True 3-1 1.763307 0.000002 True 3-2 1.130992 0.010212 True ``` statsmodels statsmodels.stats.proportion.samplesize_confint_proportion statsmodels.stats.proportion.samplesize\_confint\_proportion ============================================================ `statsmodels.stats.proportion.samplesize_confint_proportion(proportion, half_length, alpha=0.05, method='normal')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/proportion.html#samplesize_confint_proportion) find sample size to get desired confidence interval length \| Parameters: \| * proportion (float in (0, 1)) – proportion or quantile * half\_length (float in (0, 1)) – desired half length of the confidence interval * alpha (float in (0, 1)) – significance level, default 0.05, coverage of the two-sided interval is (approximately) `1 - alpha` * method (string in ['normal']) – method to use for confidence interval, currently only normal approximation \| \| Returns: \| n – sample size to get the desired half length of the confidence interval \| \| Return type: \| float \| #### Notes this is mainly to store the formula. possible application: number of replications in bootstrap samples statsmodels statsmodels.graphics.regressionplots.abline_plot statsmodels.graphics.regressionplots.abline\_plot ================================================= `statsmodels.graphics.regressionplots.abline_plot(intercept=None, slope=None, horiz=None, vert=None, model_results=None, ax=None, kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/graphics/regressionplots.html#abline_plot) Plots a line given an intercept and slope. `intercept : float` The intercept of the line `slope : float` The slope of the line `horiz : float or array-like` Data for horizontal lines on the y-axis `vert : array-like` Data for verterical lines on the x-axis `model_results : statsmodels results instance` Any object that has a two-value `params` attribute. Assumed that it is (intercept, slope) `ax : axes, optional` Matplotlib axes instance kwargs Options passed to matplotlib.pyplot.plt \| Returns: \| fig** – The figure given by `ax.figure` or a new instance. \| \| Return type: \| Figure \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> np.random.seed(12345) >>> X = sm.add_constant(np.random.normal(0, 20, size=30)) >>> y = np.dot(X, [25, 3.5]) + np.random.normal(0, 30, size=30) >>> mod = sm.OLS(y,X).fit() >>> fig = sm.graphics.abline_plot(model_results=mod) >>> ax = fig.axes[0] >>> ax.scatter(X[:,1], y) >>> ax.margins(.1) >>> import matplotlib.pyplot as plt >>> plt.show() ``` statsmodels statsmodels.sandbox.distributions.transformed.ExpTransf_gen.freeze statsmodels.sandbox.distributions.transformed.ExpTransf\_gen.freeze =================================================================== `ExpTransf_gen.freeze(args, kwds)` Freeze the distribution for the given arguments. \| Parameters: \| arg2*, arg3,.. (arg1,) – The shape parameter(s) for the distribution. Should include all the non-optional arguments, may include `loc` and `scale`. \| \| Returns: \| rv\_frozen – The frozen distribution. \| \| Return type: \| rv\_frozen instance \| statsmodels statsmodels.sandbox.regression.gmm.IVGMMResults.conf_int statsmodels.sandbox.regression.gmm.IVGMMResults.conf\_int ========================================================= `IVGMMResults.conf_int(alpha=0.05, cols=None, method='default')` Returns the confidence interval of the fitted parameters. \| Parameters: \| * alpha (float, optional) – The significance level for the confidence interval. ie., The default `alpha` = .05 returns a 95% confidence interval. * cols (array-like, optional) – `cols` specifies which confidence intervals to return * method (string) – Not Implemented Yet Method to estimate the confidence\_interval. “Default” : uses self.bse which is based on inverse Hessian for MLE “hjjh” : “jac” : “boot-bse” “boot\_quant” “profile” \| \| Returns: \| conf\_int – Each row contains [lower, upper] limits of the confidence interval for the corresponding parameter. The first column contains all lower, the second column contains all upper limits. \| \| Return type: \| array \| #### Examples ``` >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> results.conf_int() array([[-5496529.48322745, -1467987.78596704], [ -177.02903529, 207.15277984], [ -0.1115811 , 0.03994274], [ -3.12506664, -0.91539297], [ -1.5179487 , -0.54850503], [ -0.56251721, 0.460309 ], [ 798.7875153 , 2859.51541392]]) ``` ``` >>> results.conf_int(cols=(2,3)) array([[-0.1115811 , 0.03994274], [-3.12506664, -0.91539297]]) ``` #### Notes The confidence interval is based on the standard normal distribution. Models wish to use a different distribution should overwrite this method.	programming_docs
statsmodels statsmodels.regression.quantile_regression.QuantRegResults.cov_HC3 statsmodels.regression.quantile\_regression.QuantRegResults.cov\_HC3 ==================================================================== `QuantRegResults.cov_HC3()` See statsmodels.RegressionResults statsmodels statsmodels.tsa.ar_model.ARResults.load statsmodels.tsa.ar\_model.ARResults.load ======================================== `classmethod ARResults.load(fname)` load a pickle, (class method) \| Parameters: \| fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. \| \| Returns: \| \| \| Return type: \| unpickled instance \| statsmodels statsmodels.stats.multitest.NullDistribution statsmodels.stats.multitest.NullDistribution ============================================ `class statsmodels.stats.multitest.NullDistribution(zscores, null_lb=-1, null_ub=1, estimate_mean=True, estimate_scale=True, estimate_null_proportion=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/multitest.html#NullDistribution) Estimate a Gaussian distribution for the null Z-scores. The observed Z-scores consist of both null and non-null values. The fitted distribution of null Z-scores is Gaussian, but may have non-zero mean and/or non-unit scale. \| Parameters: \| * zscores (array-like) – The observed Z-scores. * null\_lb (float) – Z-scores between `null_lb` and `null_ub` are all considered to be true null hypotheses. * null\_ub (float) – See `null_lb`. * estimate\_mean (bool) – If True, estimate the mean of the distribution. If False, the mean is fixed at zero. * estimate\_scale (bool) – If True, estimate the scale of the distribution. If False, the scale parameter is fixed at 1. * estimate\_null\_proportion (bool) – If True, estimate the proportion of true null hypotheses (i.e. the proportion of z-scores with expected value zero). If False, this parameter is fixed at 1. \| `mean` float – The estimated mean of the empirical null distribution `sd` float – The estimated standard deviation of the empirical null distribution `null_proportion` float – The estimated proportion of true null hypotheses among all hypotheses #### References B Efron (2008). Microarrays, Empirical Bayes, and the Two-Groups Model. Statistical Science 23:1, 1-22. #### Notes See also: <http://nipy.org/nipy/labs/enn.html#nipy.algorithms.statistics.empirical_pvalue.NormalEmpiricalNull.fdr> #### Methods \| \| \| \| --- \| --- \| \| [`pdf`](statsmodels.stats.multitest.nulldistribution.pdf#statsmodels.stats.multitest.NullDistribution.pdf "statsmodels.stats.multitest.NullDistribution.pdf")(zscores) \| Evaluates the fitted emirical null Z-score density. \| statsmodels statsmodels.sandbox.distributions.transformed.squarenormalg statsmodels.sandbox.distributions.transformed.squarenormalg =========================================================== `statsmodels.sandbox.distributions.transformed.squarenormalg = <statsmodels.sandbox.distributions.transformed.TransfTwo_gen object>` Distribution based on a non-monotonic (u- or hump-shaped transformation) the constructor can be called with a distribution class, and functions that define the non-linear transformation. and generates the distribution of the transformed random variable Note: the transformation, it’s inverse and derivatives need to be fully specified: func, funcinvplus, funcinvminus, derivplus, derivminus. Currently no numerical derivatives or inverse are calculated This can be used to generate distribution instances similar to the distributions in scipy.stats. statsmodels statsmodels.tools.eval_measures.aicc_sigma statsmodels.tools.eval\_measures.aicc\_sigma ============================================ `statsmodels.tools.eval_measures.aicc_sigma(sigma2, nobs, df_modelwc, islog=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tools/eval_measures.html#aicc_sigma) Akaike information criterion (AIC) with small sample correction \| Parameters: \| * sigma2 (float) – estimate of the residual variance or determinant of Sigma\_hat in the multivariate case. If islog is true, then it is assumed that sigma is already log-ed, for example logdetSigma. * nobs (int) – number of observations * df\_modelwc (int) – number of parameters including constant \| \| Returns: \| aicc – information criterion \| \| Return type: \| float \| #### Notes A constant has been dropped in comparison to the loglikelihood base information criteria. These should be used to compare for comparable models. #### References <http://en.wikipedia.org/wiki/Akaike_information_criterion#AICc> statsmodels statsmodels.tsa.stattools.adfuller statsmodels.tsa.stattools.adfuller ================================== `statsmodels.tsa.stattools.adfuller(x, maxlag=None, regression='c', autolag='AIC', store=False, regresults=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/stattools.html#adfuller) Augmented Dickey-Fuller unit root test The Augmented Dickey-Fuller test can be used to test for a unit root in a univariate process in the presence of serial correlation. \| Parameters: \| * x (array\_like, 1d) – data series * maxlag (int) – Maximum lag which is included in test, default 12\(nobs/100)^{1/4} regression ({'c','ct','ctt','nc'}) – Constant and trend order to include in regression + ’c’ : constant only (default) + ’ct’ : constant and trend + ’ctt’ : constant, and linear and quadratic trend + ’nc’ : no constant, no trend * autolag ({'AIC', 'BIC', 't-stat', None}) – + if None, then maxlag lags are used + if ‘AIC’ (default) or ‘BIC’, then the number of lags is chosen to minimize the corresponding information criterion + ’t-stat’ based choice of maxlag. Starts with maxlag and drops a lag until the t-statistic on the last lag length is significant using a 5%-sized test * store (bool) – If True, then a result instance is returned additionally to the adf statistic. Default is False * regresults (bool, optional) – If True, the full regression results are returned. Default is False \| \| Returns: \| * adf (float) – Test statistic * pvalue (float) – MacKinnon’s approximate p-value based on MacKinnon (1994, 2010) * usedlag (int) – Number of lags used * nobs (int) – Number of observations used for the ADF regression and calculation of the critical values * critical values (dict) – Critical values for the test statistic at the 1 %, 5 %, and 10 % levels. Based on MacKinnon (2010) * icbest (float) – The maximized information criterion if autolag is not None. * resstore (ResultStore, optional) – A dummy class with results attached as attributes \| #### Notes The null hypothesis of the Augmented Dickey-Fuller is that there is a unit root, with the alternative that there is no unit root. If the pvalue is above a critical size, then we cannot reject that there is a unit root. The p-values are obtained through regression surface approximation from MacKinnon 1994, but using the updated 2010 tables. If the p-value is close to significant, then the critical values should be used to judge whether to reject the null. The autolag option and maxlag for it are described in Greene. #### Examples See example notebook #### References \| \| \| \| --- \| --- \| \| [\] \| 23. Green. “Econometric Analysis,” 5th ed., Pearson, 2003. \| \| \| \| \| --- \| --- \| \| [†] \| Hamilton, J.D. “Time Series Analysis”. Princeton, 1994. \| \| \| \| \| --- \| --- \| \| [‡] \| MacKinnon, J.G. 1994. “Approximate asymptotic distribution functions for unit-root and cointegration tests. `Journal of Business and Economic Statistics` 12, 167-76. \| \| \| \| \| --- \| --- \| \| [§] \| MacKinnon, J.G. 2010. “Critical Values for Cointegration Tests.” Queen’s University, Dept of Economics, Working Papers. Available at <http://ideas.repec.org/p/qed/wpaper/1227.html> \| statsmodels statsmodels.regression.linear_model.OLSResults statsmodels.regression.linear\_model.OLSResults =============================================== `class statsmodels.regression.linear_model.OLSResults(model, params, normalized_cov_params=None, scale=1.0, cov_type='nonrobust', cov_kwds=None, use_t=None, kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#OLSResults) Results class for for an OLS model. Most of the methods and attributes are inherited from RegressionResults. The special methods that are only available for OLS are: get\_influence * outlier\_test * el\_test * conf\_int\_el See also [`RegressionResults`](statsmodels.regression.linear_model.regressionresults#statsmodels.regression.linear_model.RegressionResults "statsmodels.regression.linear_model.RegressionResults") #### Methods \| \| \| \| --- \| --- \| \| [`HC0_se`](statsmodels.regression.linear_model.olsresults.hc0_se#statsmodels.regression.linear_model.OLSResults.HC0_se "statsmodels.regression.linear_model.OLSResults.HC0_se")() \| See statsmodels.RegressionResults \| \| [`HC1_se`](statsmodels.regression.linear_model.olsresults.hc1_se#statsmodels.regression.linear_model.OLSResults.HC1_se "statsmodels.regression.linear_model.OLSResults.HC1_se")() \| See statsmodels.RegressionResults \| \| [`HC2_se`](statsmodels.regression.linear_model.olsresults.hc2_se#statsmodels.regression.linear_model.OLSResults.HC2_se "statsmodels.regression.linear_model.OLSResults.HC2_se")() \| See statsmodels.RegressionResults \| \| [`HC3_se`](statsmodels.regression.linear_model.olsresults.hc3_se#statsmodels.regression.linear_model.OLSResults.HC3_se "statsmodels.regression.linear_model.OLSResults.HC3_se")() \| See statsmodels.RegressionResults \| \| [`aic`](statsmodels.regression.linear_model.olsresults.aic#statsmodels.regression.linear_model.OLSResults.aic "statsmodels.regression.linear_model.OLSResults.aic")() \| \| \| [`bic`](statsmodels.regression.linear_model.olsresults.bic#statsmodels.regression.linear_model.OLSResults.bic "statsmodels.regression.linear_model.OLSResults.bic")() \| \| \| [`bse`](statsmodels.regression.linear_model.olsresults.bse#statsmodels.regression.linear_model.OLSResults.bse "statsmodels.regression.linear_model.OLSResults.bse")() \| \| \| [`centered_tss`](statsmodels.regression.linear_model.olsresults.centered_tss#statsmodels.regression.linear_model.OLSResults.centered_tss "statsmodels.regression.linear_model.OLSResults.centered_tss")() \| \| \| [`compare_f_test`](statsmodels.regression.linear_model.olsresults.compare_f_test#statsmodels.regression.linear_model.OLSResults.compare_f_test "statsmodels.regression.linear_model.OLSResults.compare_f_test")(restricted) \| use F test to test whether restricted model is correct \| \| [`compare_lm_test`](statsmodels.regression.linear_model.olsresults.compare_lm_test#statsmodels.regression.linear_model.OLSResults.compare_lm_test "statsmodels.regression.linear_model.OLSResults.compare_lm_test")(restricted[, demean, use\_lr]) \| Use Lagrange Multiplier test to test whether restricted model is correct \| \| [`compare_lr_test`](statsmodels.regression.linear_model.olsresults.compare_lr_test#statsmodels.regression.linear_model.OLSResults.compare_lr_test "statsmodels.regression.linear_model.OLSResults.compare_lr_test")(restricted[, large\_sample]) \| Likelihood ratio test to test whether restricted model is correct \| \| [`condition_number`](statsmodels.regression.linear_model.olsresults.condition_number#statsmodels.regression.linear_model.OLSResults.condition_number "statsmodels.regression.linear_model.OLSResults.condition_number")() \| Return condition number of exogenous matrix. \| \| [`conf_int`](statsmodels.regression.linear_model.olsresults.conf_int#statsmodels.regression.linear_model.OLSResults.conf_int "statsmodels.regression.linear_model.OLSResults.conf_int")([alpha, cols]) \| Returns the confidence interval of the fitted parameters. \| \| [`conf_int_el`](statsmodels.regression.linear_model.olsresults.conf_int_el#statsmodels.regression.linear_model.OLSResults.conf_int_el "statsmodels.regression.linear_model.OLSResults.conf_int_el")(param\_num[, sig, upper\_bound, …]) \| Computes the confidence interval for the parameter given by param\_num using Empirical Likelihood \| \| [`cov_HC0`](statsmodels.regression.linear_model.olsresults.cov_hc0#statsmodels.regression.linear_model.OLSResults.cov_HC0 "statsmodels.regression.linear_model.OLSResults.cov_HC0")() \| See statsmodels.RegressionResults \| \| [`cov_HC1`](statsmodels.regression.linear_model.olsresults.cov_hc1#statsmodels.regression.linear_model.OLSResults.cov_HC1 "statsmodels.regression.linear_model.OLSResults.cov_HC1")() \| See statsmodels.RegressionResults \| \| [`cov_HC2`](statsmodels.regression.linear_model.olsresults.cov_hc2#statsmodels.regression.linear_model.OLSResults.cov_HC2 "statsmodels.regression.linear_model.OLSResults.cov_HC2")() \| See statsmodels.RegressionResults \| \| [`cov_HC3`](statsmodels.regression.linear_model.olsresults.cov_hc3#statsmodels.regression.linear_model.OLSResults.cov_HC3 "statsmodels.regression.linear_model.OLSResults.cov_HC3")() \| See statsmodels.RegressionResults \| \| [`cov_params`](statsmodels.regression.linear_model.olsresults.cov_params#statsmodels.regression.linear_model.OLSResults.cov_params "statsmodels.regression.linear_model.OLSResults.cov_params")([r\_matrix, column, scale, cov\_p, …]) \| Returns the variance/covariance matrix. \| \| [`eigenvals`](statsmodels.regression.linear_model.olsresults.eigenvals#statsmodels.regression.linear_model.OLSResults.eigenvals "statsmodels.regression.linear_model.OLSResults.eigenvals")() \| Return eigenvalues sorted in decreasing order. \| \| [`el_test`](statsmodels.regression.linear_model.olsresults.el_test#statsmodels.regression.linear_model.OLSResults.el_test "statsmodels.regression.linear_model.OLSResults.el_test")(b0\_vals, param\_nums[, …]) \| Tests single or joint hypotheses of the regression parameters using Empirical Likelihood. \| \| [`ess`](statsmodels.regression.linear_model.olsresults.ess#statsmodels.regression.linear_model.OLSResults.ess "statsmodels.regression.linear_model.OLSResults.ess")() \| \| \| [`f_pvalue`](statsmodels.regression.linear_model.olsresults.f_pvalue#statsmodels.regression.linear_model.OLSResults.f_pvalue "statsmodels.regression.linear_model.OLSResults.f_pvalue")() \| \| \| [`f_test`](statsmodels.regression.linear_model.olsresults.f_test#statsmodels.regression.linear_model.OLSResults.f_test "statsmodels.regression.linear_model.OLSResults.f_test")(r\_matrix[, cov\_p, scale, invcov]) \| Compute the F-test for a joint linear hypothesis. \| \| [`fittedvalues`](statsmodels.regression.linear_model.olsresults.fittedvalues#statsmodels.regression.linear_model.OLSResults.fittedvalues "statsmodels.regression.linear_model.OLSResults.fittedvalues")() \| \| \| [`fvalue`](statsmodels.regression.linear_model.olsresults.fvalue#statsmodels.regression.linear_model.OLSResults.fvalue "statsmodels.regression.linear_model.OLSResults.fvalue")() \| \| \| [`get_influence`](statsmodels.regression.linear_model.olsresults.get_influence#statsmodels.regression.linear_model.OLSResults.get_influence "statsmodels.regression.linear_model.OLSResults.get_influence")() \| get an instance of Influence with influence and outlier measures \| \| [`get_prediction`](statsmodels.regression.linear_model.olsresults.get_prediction#statsmodels.regression.linear_model.OLSResults.get_prediction "statsmodels.regression.linear_model.OLSResults.get_prediction")([exog, transform, weights, …]) \| compute prediction results \| \| [`get_robustcov_results`](statsmodels.regression.linear_model.olsresults.get_robustcov_results#statsmodels.regression.linear_model.OLSResults.get_robustcov_results "statsmodels.regression.linear_model.OLSResults.get_robustcov_results")([cov\_type, use\_t]) \| create new results instance with robust covariance as default \| \| [`initialize`](statsmodels.regression.linear_model.olsresults.initialize#statsmodels.regression.linear_model.OLSResults.initialize "statsmodels.regression.linear_model.OLSResults.initialize")(model, params, \\kwd) \| \| \| [`llf`](statsmodels.regression.linear_model.olsresults.llf#statsmodels.regression.linear_model.OLSResults.llf "statsmodels.regression.linear_model.OLSResults.llf")() \| \| \| [`load`](statsmodels.regression.linear_model.olsresults.load#statsmodels.regression.linear_model.OLSResults.load "statsmodels.regression.linear_model.OLSResults.load")(fname) \| load a pickle, (class method) \| \| [`mse_model`](statsmodels.regression.linear_model.olsresults.mse_model#statsmodels.regression.linear_model.OLSResults.mse_model "statsmodels.regression.linear_model.OLSResults.mse_model")() \| \| \| [`mse_resid`](statsmodels.regression.linear_model.olsresults.mse_resid#statsmodels.regression.linear_model.OLSResults.mse_resid "statsmodels.regression.linear_model.OLSResults.mse_resid")() \| \| \| [`mse_total`](statsmodels.regression.linear_model.olsresults.mse_total#statsmodels.regression.linear_model.OLSResults.mse_total "statsmodels.regression.linear_model.OLSResults.mse_total")() \| \| \| [`nobs`](statsmodels.regression.linear_model.olsresults.nobs#statsmodels.regression.linear_model.OLSResults.nobs "statsmodels.regression.linear_model.OLSResults.nobs")() \| \| \| [`normalized_cov_params`](statsmodels.regression.linear_model.olsresults.normalized_cov_params#statsmodels.regression.linear_model.OLSResults.normalized_cov_params "statsmodels.regression.linear_model.OLSResults.normalized_cov_params")() \| \| \| [`outlier_test`](statsmodels.regression.linear_model.olsresults.outlier_test#statsmodels.regression.linear_model.OLSResults.outlier_test "statsmodels.regression.linear_model.OLSResults.outlier_test")([method, alpha, labels, order, …]) \| Test observations for outliers according to method \| \| [`predict`](statsmodels.regression.linear_model.olsresults.predict#statsmodels.regression.linear_model.OLSResults.predict "statsmodels.regression.linear_model.OLSResults.predict")([exog, transform]) \| Call self.model.predict with self.params as the first argument. \| \| [`pvalues`](statsmodels.regression.linear_model.olsresults.pvalues#statsmodels.regression.linear_model.OLSResults.pvalues "statsmodels.regression.linear_model.OLSResults.pvalues")() \| \| \| [`remove_data`](statsmodels.regression.linear_model.olsresults.remove_data#statsmodels.regression.linear_model.OLSResults.remove_data "statsmodels.regression.linear_model.OLSResults.remove_data")() \| remove data arrays, all nobs arrays from result and model \| \| [`resid`](statsmodels.regression.linear_model.olsresults.resid#statsmodels.regression.linear_model.OLSResults.resid "statsmodels.regression.linear_model.OLSResults.resid")() \| \| \| [`resid_pearson`](statsmodels.regression.linear_model.olsresults.resid_pearson#statsmodels.regression.linear_model.OLSResults.resid_pearson "statsmodels.regression.linear_model.OLSResults.resid_pearson")() \| Residuals, normalized to have unit variance. \| \| [`rsquared`](statsmodels.regression.linear_model.olsresults.rsquared#statsmodels.regression.linear_model.OLSResults.rsquared "statsmodels.regression.linear_model.OLSResults.rsquared")() \| \| \| [`rsquared_adj`](statsmodels.regression.linear_model.olsresults.rsquared_adj#statsmodels.regression.linear_model.OLSResults.rsquared_adj "statsmodels.regression.linear_model.OLSResults.rsquared_adj")() \| \| \| [`save`](statsmodels.regression.linear_model.olsresults.save#statsmodels.regression.linear_model.OLSResults.save "statsmodels.regression.linear_model.OLSResults.save")(fname[, remove\_data]) \| save a pickle of this instance \| \| [`scale`](statsmodels.regression.linear_model.olsresults.scale#statsmodels.regression.linear_model.OLSResults.scale "statsmodels.regression.linear_model.OLSResults.scale")() \| \| \| [`ssr`](statsmodels.regression.linear_model.olsresults.ssr#statsmodels.regression.linear_model.OLSResults.ssr "statsmodels.regression.linear_model.OLSResults.ssr")() \| \| \| [`summary`](statsmodels.regression.linear_model.olsresults.summary#statsmodels.regression.linear_model.OLSResults.summary "statsmodels.regression.linear_model.OLSResults.summary")([yname, xname, title, alpha]) \| Summarize the Regression Results \| \| [`summary2`](statsmodels.regression.linear_model.olsresults.summary2#statsmodels.regression.linear_model.OLSResults.summary2 "statsmodels.regression.linear_model.OLSResults.summary2")([yname, xname, title, alpha, …]) \| Experimental summary function to summarize the regression results \| \| [`t_test`](statsmodels.regression.linear_model.olsresults.t_test#statsmodels.regression.linear_model.OLSResults.t_test "statsmodels.regression.linear_model.OLSResults.t_test")(r\_matrix[, cov\_p, scale, use\_t]) \| Compute a t-test for a each linear hypothesis of the form Rb = q \| \| [`t_test_pairwise`](statsmodels.regression.linear_model.olsresults.t_test_pairwise#statsmodels.regression.linear_model.OLSResults.t_test_pairwise "statsmodels.regression.linear_model.OLSResults.t_test_pairwise")(term\_name[, method, alpha, …]) \| perform pairwise t\_test with multiple testing corrected p-values \| \| [`tvalues`](statsmodels.regression.linear_model.olsresults.tvalues#statsmodels.regression.linear_model.OLSResults.tvalues "statsmodels.regression.linear_model.OLSResults.tvalues")() \| Return the t-statistic for a given parameter estimate. \| \| [`uncentered_tss`](statsmodels.regression.linear_model.olsresults.uncentered_tss#statsmodels.regression.linear_model.OLSResults.uncentered_tss "statsmodels.regression.linear_model.OLSResults.uncentered_tss")() \| \| \| [`wald_test`](statsmodels.regression.linear_model.olsresults.wald_test#statsmodels.regression.linear_model.OLSResults.wald_test "statsmodels.regression.linear_model.OLSResults.wald_test")(r\_matrix[, cov\_p, scale, invcov, …]) \| Compute a Wald-test for a joint linear hypothesis. \| \| [`wald_test_terms`](statsmodels.regression.linear_model.olsresults.wald_test_terms#statsmodels.regression.linear_model.OLSResults.wald_test_terms "statsmodels.regression.linear_model.OLSResults.wald_test_terms")([skip\_single, …]) \| Compute a sequence of Wald tests for terms over multiple columns \| \| [`wresid`](statsmodels.regression.linear_model.olsresults.wresid#statsmodels.regression.linear_model.OLSResults.wresid "statsmodels.regression.linear_model.OLSResults.wresid")() \| \| #### Attributes \| \| \| \| --- \| --- \| \| `use_t` \| \|	programming_docs
statsmodels statsmodels.tools.tools.recipr0 statsmodels.tools.tools.recipr0 =============================== `statsmodels.tools.tools.recipr0(x)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tools/tools.html#recipr0) Return the reciprocal of an array, setting all entries equal to 0 as 0. It does not assume that X should be positive in general. statsmodels statsmodels.regression.linear_model.RegressionResults.t_test_pairwise statsmodels.regression.linear\_model.RegressionResults.t\_test\_pairwise ======================================================================== `RegressionResults.t_test_pairwise(term_name, method='hs', alpha=0.05, factor_labels=None)` perform pairwise t\_test with multiple testing corrected p-values This uses the formula design\_info encoding contrast matrix and should work for all encodings of a main effect. \| Parameters: \| * result (result instance) – The results of an estimated model with a categorical main effect. * term\_name (str) – name of the term for which pairwise comparisons are computed. Term names for categorical effects are created by patsy and correspond to the main part of the exog names. * method (str or list of strings) – multiple testing p-value correction, default is ‘hs’, see stats.multipletesting * alpha (float) – significance level for multiple testing reject decision. * factor\_labels (None, list of str) – Labels for the factor levels used for pairwise labels. If not provided, then the labels from the formula design\_info are used. \| \| Returns: \| results – The results are stored as attributes, the main attributes are the following two. Other attributes are added for debugging purposes or as background information.* result\_frame : pandas DataFrame with t\_test results and multiple testing corrected p-values. * contrasts : matrix of constraints of the null hypothesis in the t\_test. \| \| Return type: \| instance of a simple Results class \| #### Notes Status: experimental. Currently only checked for treatment coding with and without specified reference level. Currently there are no multiple testing corrected confidence intervals available. #### Examples ``` >>> res = ols("np.log(Days+1) ~ C(Weight) + C(Duration)", data).fit() >>> pw = res.t_test_pairwise("C(Weight)") >>> pw.result_frame coef std err t P>\|t\| Conf. Int. Low 2-1 0.632315 0.230003 2.749157 8.028083e-03 0.171563 3-1 1.302555 0.230003 5.663201 5.331513e-07 0.841803 3-2 0.670240 0.230003 2.914044 5.119126e-03 0.209488 Conf. Int. Upp. pvalue-hs reject-hs 2-1 1.093067 0.010212 True 3-1 1.763307 0.000002 True 3-2 1.130992 0.010212 True ``` statsmodels statsmodels.multivariate.factor.Factor statsmodels.multivariate.factor.Factor ====================================== `class statsmodels.multivariate.factor.Factor(endog=None, n_factor=1, corr=None, method='pa', smc=True, endog_names=None, nobs=None, missing='drop')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/multivariate/factor.html#Factor) Factor analysis \| Parameters: \| * endog (array-like) – Variables in columns, observations in rows. May be `None` if `corr` is not `None`. * n\_factor (int) – The number of factors to extract * corr (array-like) – Directly specify the correlation matrix instead of estimating it from `endog`. If provided, `endog` is not used for the factor analysis, it may be used in post-estimation. * method (str) – The method to extract factors, currently must be either ‘pa’ for principal axis factor analysis or ‘ml’ for maximum likelihood estimation. * smc (True or False) – Whether or not to apply squared multiple correlations (method=’pa’) * endog\_names (str) – Names of endogeous variables. If specified, it will be used instead of the column names in endog * nobs (int) – The number of observations, not used if endog is present. Needs to be provided for inference if endog is None. * missing ('none', 'drop', or 'raise') – Missing value handling for endog, default is row-wise deletion ‘drop’ If ‘none’, no nan checking is done. If ‘drop’, any observations with nans are dropped. If ‘raise’, an error is raised. \| #### Notes Experimental Supported rotations: ‘varimax’, ‘quartimax’, ‘biquartimax’, ‘equamax’, ‘oblimin’, ‘parsimax’, ‘parsimony’, ‘biquartimin’, ‘promax’ If method=’ml’, the factors are rotated to satisfy condition IC3 of Bai and Li (2012). This means that the scores have covariance I, so the model for the covariance matrix is L \* L’ + diag(U), where L are the loadings and U are the uniquenesses. In addition, L’ \* diag(U)^{-1} L must be diagonal. #### References \| \| \| \| --- \| --- \| \| [\] \| Hofacker, C. (2004). Exploratory Factor Analysis, Mathematical Marketing. <http://www.openaccesstexts.org/pdf/Quant_Chapter_11_efa.pdf> \| \| \| \| \| --- \| --- \| \| [†] \| J Bai, K Li (2012). Statistical analysis of factor models of high dimension. Annals of Statistics. <https://arxiv.org/pdf/1205.6617.pdf> \| #### Methods \| \| \| \| --- \| --- \| \| [`fit`](statsmodels.multivariate.factor.factor.fit#statsmodels.multivariate.factor.Factor.fit "statsmodels.multivariate.factor.Factor.fit")([maxiter, tol, start, opt\_method, opt, …]) \| Estimate factor model parameters. \| \| [`from_formula`](statsmodels.multivariate.factor.factor.from_formula#statsmodels.multivariate.factor.Factor.from_formula "statsmodels.multivariate.factor.Factor.from_formula")(formula, data[, subset, drop\_cols]) \| Create a Model from a formula and dataframe. \| \| [`loglike`](statsmodels.multivariate.factor.factor.loglike#statsmodels.multivariate.factor.Factor.loglike "statsmodels.multivariate.factor.Factor.loglike")(par) \| Evaluate the log-likelihood function. \| \| [`predict`](statsmodels.multivariate.factor.factor.predict#statsmodels.multivariate.factor.Factor.predict "statsmodels.multivariate.factor.Factor.predict")(params[, exog]) \| After a model has been fit predict returns the fitted values. \| \| [`score`](statsmodels.multivariate.factor.factor.score#statsmodels.multivariate.factor.Factor.score "statsmodels.multivariate.factor.Factor.score")(par) \| Evaluate the score function (first derivative of loglike). \| #### Attributes \| \| \| \| --- \| --- \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| Names of exogenous variables \| statsmodels statsmodels.multivariate.cancorr.CanCorr.from_formula statsmodels.multivariate.cancorr.CanCorr.from\_formula ====================================================== `classmethod CanCorr.from_formula(formula, data, subset=None, drop_cols=None, args, *kwargs)` Create a Model from a formula and dataframe. \| Parameters: \| formula (str or generic Formula object) – The formula specifying the model * data (array-like) – The data for the model. See Notes. * subset (array-like) – An array-like object of booleans, integers, or index values that indicate the subset of df to use in the model. Assumes df is a `pandas.DataFrame` * drop\_cols (array-like) – Columns to drop from the design matrix. Cannot be used to drop terms involving categoricals. * args (extra arguments) – These are passed to the model * kwargs (extra keyword arguments) – These are passed to the model with one exception. The `eval_env` keyword is passed to patsy. It can be either a [`patsy.EvalEnvironment`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.EvalEnvironment "(in patsy v0.5.0+dev)") object or an integer indicating the depth of the namespace to use. For example, the default `eval_env=0` uses the calling namespace. If you wish to use a “clean” environment set `eval_env=-1`. \| \| Returns: \| model \| \| Return type: \| Model instance \| #### Notes data must define \_\_getitem\_\_ with the keys in the formula terms args and kwargs are passed on to the model instantiation. E.g., a numpy structured or rec array, a dictionary, or a pandas DataFrame. statsmodels statsmodels.tsa.vector_ar.var_model.FEVD.summary statsmodels.tsa.vector\_ar.var\_model.FEVD.summary ================================================== `FEVD.summary()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#FEVD.summary) statsmodels statsmodels.discrete.count_model.ZeroInflatedGeneralizedPoissonResults.summary2 statsmodels.discrete.count\_model.ZeroInflatedGeneralizedPoissonResults.summary2 ================================================================================ `ZeroInflatedGeneralizedPoissonResults.summary2(yname=None, xname=None, title=None, alpha=0.05, float_format='%.4f')` Experimental function to summarize regression results \| Parameters: \| * xname (List of strings of length equal to the number of parameters) – Names of the independent variables (optional) * yname (string) – Name of the dependent variable (optional) * title (string, optional) – Title for the top table. If not None, then this replaces the default title * alpha (float) – significance level for the confidence intervals * float\_format (string) – print format for floats in parameters summary \| \| Returns: \| smry – this holds the summary tables and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary.Summary`](statsmodels.iolib.summary.summary#statsmodels.iolib.summary.Summary "statsmodels.iolib.summary.Summary") class to hold summary results statsmodels statsmodels.genmod.cov_struct.GlobalOddsRatio.update statsmodels.genmod.cov\_struct.GlobalOddsRatio.update ===================================================== `GlobalOddsRatio.update(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/cov_struct.html#GlobalOddsRatio.update) Updates the association parameter values based on the current regression coefficients. \| Parameters: \| params (array-like) – Working values for the regression parameters. \| statsmodels statsmodels.sandbox.regression.gmm.NonlinearIVGMM statsmodels.sandbox.regression.gmm.NonlinearIVGMM ================================================= `class statsmodels.sandbox.regression.gmm.NonlinearIVGMM(endog, exog, instrument, func, *kwds)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/regression/gmm.html#NonlinearIVGMM) Class for non-linear instrumental variables estimation wusing GMM The model is assumed to have the following moment condition E[ z \ (y - f(X, beta)] = 0 Where `y` is the dependent endogenous variable, `x` are the explanatory variables and `z` are the instruments. Variables in `x` that are exogenous need also be included in z. `f` is a nonlinear function. Notation Warning: our name `exog` stands for the explanatory variables, and includes both exogenous and explanatory variables that are endogenous, i.e. included endogenous variables \| Parameters: \| * endog (array\_like) – dependent endogenous variable * exog (array\_like) – explanatory, right hand side variables, including explanatory variables that are endogenous. * instruments (array\_like) – Instrumental variables, variables that are exogenous to the error in the linear model containing both included and excluded exogenous variables * func (callable) – function for the mean or conditional expectation of the endogenous variable. The function will be called with parameters and the array of explanatory, right hand side variables, `func(params, exog)` \| #### Notes This class uses numerical differences to obtain the derivative of the objective function. If the jacobian of the conditional mean function, `func` is available, then it can be used by subclassing this class and defining a method `jac_func`. TODO: check required signature of jac\_error and jac\_func #### Methods \| \| \| \| --- \| --- \| \| [`calc_weightmatrix`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.calc_weightmatrix#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.calc_weightmatrix "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.calc_weightmatrix")(moms[, weights\_method, …]) \| calculate omega or the weighting matrix \| \| [`fit`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.fit#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.fit "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.fit")([start\_params, maxiter, inv\_weights, …]) \| Estimate parameters using GMM and return GMMResults \| \| [`fitgmm`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.fitgmm#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.fitgmm "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.fitgmm")(start[, weights, optim\_method, …]) \| estimate parameters using GMM \| \| [`fitgmm_cu`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.fitgmm_cu#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.fitgmm_cu "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.fitgmm_cu")(start[, optim\_method, optim\_args]) \| estimate parameters using continuously updating GMM \| \| [`fititer`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.fititer#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.fititer "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.fititer")(start[, maxiter, start\_invweights, …]) \| iterative estimation with updating of optimal weighting matrix \| \| [`fitstart`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.fitstart#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.fitstart "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.fitstart")() \| \| \| [`from_formula`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.from_formula#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.from_formula "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.from_formula")(formula, data[, subset, drop\_cols]) \| Create a Model from a formula and dataframe. \| \| [`get_error`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.get_error#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.get_error "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.get_error")(params) \| \| \| [`gmmobjective`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.gmmobjective#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.gmmobjective "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.gmmobjective")(params, weights) \| objective function for GMM minimization \| \| [`gmmobjective_cu`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.gmmobjective_cu#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.gmmobjective_cu "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.gmmobjective_cu")(params[, weights\_method, wargs]) \| objective function for continuously updating GMM minimization \| \| [`gradient_momcond`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.gradient_momcond#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.gradient_momcond "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.gradient_momcond")(params[, epsilon, centered]) \| gradient of moment conditions \| \| [`jac_error`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.jac_error#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.jac_error "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.jac_error")(params, weights[, args, centered, …]) \| \| \| [`jac_func`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.jac_func#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.jac_func "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.jac_func")(params, weights[, args, centered, …]) \| \| \| [`momcond`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.momcond#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.momcond "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.momcond")(params) \| \| \| [`momcond_mean`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.momcond_mean#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.momcond_mean "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.momcond_mean")(params) \| mean of moment conditions, \| \| [`predict`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.predict#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.predict "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.predict")(params[, exog]) \| After a model has been fit predict returns the fitted values. \| \| [`score`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.score#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.score "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.score")(params, weights, \\kwds) \| \| \| [`score_cu`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.score_cu#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.score_cu "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.score_cu")(params[, epsilon, centered]) \| \| \| [`set_param_names`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.set_param_names#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.set_param_names "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.set_param_names")(param\_names[, k\_params]) \| set the parameter names in the model \| \| [`start_weights`](statsmodels.sandbox.regression.gmm.nonlinearivgmm.start_weights#statsmodels.sandbox.regression.gmm.NonlinearIVGMM.start_weights "statsmodels.sandbox.regression.gmm.NonlinearIVGMM.start_weights")([inv]) \| \| #### Attributes \| \| \| \| --- \| --- \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| Names of exogenous variables \| \| `results_class` \| \| statsmodels statsmodels.regression.linear_model.RegressionResults.scale statsmodels.regression.linear\_model.RegressionResults.scale ============================================================ `RegressionResults.scale()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#RegressionResults.scale) statsmodels statsmodels.tsa.vector_ar.vecm.VECMResults.test_granger_causality statsmodels.tsa.vector\_ar.vecm.VECMResults.test\_granger\_causality ==================================================================== `VECMResults.test_granger_causality(caused, causing=None, signif=0.05)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/vecm.html#VECMResults.test_granger_causality) Test for Granger-causality. The concept of Granger-causality is described in chapter 7.6.3 of [[1]](#id2). Test H0: “The variables in `causing` do not Granger-cause those in `caused`” against H1: “`causing` is Granger-causal for `caused`”. \| Parameters: \| * caused (int or str or sequence of int or str) – If int or str, test whether the variable specified via this index (int) or name (str) is Granger-caused by the variable(s) specified by `causing`. If a sequence of int or str, test whether the corresponding variables are Granger-caused by the variable(s) specified by `causing`. * causing (int or str or sequence of int or str or `None`, default: `None`) – If int or str, test whether the variable specified via this index (int) or name (str) is Granger-causing the variable(s) specified by `caused`. If a sequence of int or str, test whether the corresponding variables are Granger-causing the variable(s) specified by `caused`. If `None`, `causing` is assumed to be the complement of `caused` (the remaining variables of the system). * signif (float, 0 < `signif` < 1, default 5 %) – Significance level for computing critical values for test, defaulting to standard 0.05 level. \| \| Returns: \| results \| \| Return type: \| [`statsmodels.tsa.vector_ar.hypothesis_test_results.CausalityTestResults`](statsmodels.tsa.vector_ar.hypothesis_test_results.causalitytestresults#statsmodels.tsa.vector_ar.hypothesis_test_results.CausalityTestResults "statsmodels.tsa.vector_ar.hypothesis_test_results.CausalityTestResults") \| #### References \| \| \| \| --- \| --- \| \| [[1]](#id1) \| Lütkepohl, H. 2005. New Introduction to Multiple Time Series Analysis. Springer. \| statsmodels statsmodels.sandbox.regression.gmm.NonlinearIVGMM.fitstart statsmodels.sandbox.regression.gmm.NonlinearIVGMM.fitstart ========================================================== `NonlinearIVGMM.fitstart()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/regression/gmm.html#NonlinearIVGMM.fitstart)	programming_docs
statsmodels statsmodels.sandbox.regression.gmm.IVGMM.calc_weightmatrix statsmodels.sandbox.regression.gmm.IVGMM.calc\_weightmatrix =========================================================== `IVGMM.calc_weightmatrix(moms, weights_method='cov', wargs=(), params=None)` calculate omega or the weighting matrix \| Parameters: \| * moms (array) – moment conditions (nobs x nmoms) for all observations evaluated at a parameter value * weights\_method (string 'cov') – If method=’cov’ is cov then the matrix is calculated as simple covariance of the moment conditions. see fit method for available aoptions for the weight and covariance matrix * wargs (tuple or [dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)")) – parameters that are required by some kernel methods to estimate the long-run covariance. Not used yet. \| \| Returns: \| w – estimate for the weighting matrix or covariance of the moment condition \| \| Return type: \| array (nmoms, nmoms) \| #### Notes currently a constant cutoff window is used TODO: implement long-run cov estimators, kernel-based Newey-West Andrews Andrews-Moy???? #### References Greene Hansen, Bruce statsmodels statsmodels.stats.weightstats.zconfint statsmodels.stats.weightstats.zconfint ====================================== `statsmodels.stats.weightstats.zconfint(x1, x2=None, value=0, alpha=0.05, alternative='two-sided', usevar='pooled', ddof=1.0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/weightstats.html#zconfint) confidence interval based on normal distribution z-test \| Parameters: \| * x2 (x1,) – two independent samples, see notes for 2-D case * value (float) – In the one sample case, value is the mean of x1 under the Null hypothesis. In the two sample case, value is the difference between mean of x1 and mean of x2 under the Null hypothesis. The test statistic is `x1_mean - x2_mean - value`. * usevar (string, 'pooled') – Currently, only ‘pooled’ is implemented. If `pooled`, then the standard deviation of the samples is assumed to be the same. see CompareMeans.ztest\_ind for different options. * ddof (int) – Degrees of freedom use in the calculation of the variance of the mean estimate. In the case of comparing means this is one, however it can be adjusted for testing other statistics (proportion, correlation) \| #### Notes checked only for 1 sample case usevar not implemented, is always pooled in two sample case `value` shifts the confidence interval so it is centered at `x1_mean - x2_mean - value` See also [`ztest`](statsmodels.stats.weightstats.ztest#statsmodels.stats.weightstats.ztest "statsmodels.stats.weightstats.ztest"), [`CompareMeans`](statsmodels.stats.weightstats.comparemeans#statsmodels.stats.weightstats.CompareMeans "statsmodels.stats.weightstats.CompareMeans") statsmodels statsmodels.discrete.count_model.GenericZeroInflated.score statsmodels.discrete.count\_model.GenericZeroInflated.score =========================================================== `GenericZeroInflated.score(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/count_model.html#GenericZeroInflated.score) Score vector of model. The gradient of logL with respect to each parameter. statsmodels statsmodels.genmod.generalized_estimating_equations.GEEResults.t_test statsmodels.genmod.generalized\_estimating\_equations.GEEResults.t\_test ======================================================================== `GEEResults.t_test(r_matrix, cov_p=None, scale=None, use_t=None)` Compute a t-test for a each linear hypothesis of the form Rb = q \| Parameters: \| * r\_matrix (array-like, str, tuple) – + array : If an array is given, a p x k 2d array or length k 1d array specifying the linear restrictions. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q). If q is given, can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – An optional `scale` to use. Default is the scale specified by the model fit. * use\_t (bool, optional) – If use\_t is None, then the default of the model is used. If use\_t is True, then the p-values are based on the t distribution. If use\_t is False, then the p-values are based on the normal distribution. \| \| Returns: \| res – The results for the test are attributes of this results instance. The available results have the same elements as the parameter table in `summary()`. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> r = np.zeros_like(results.params) >>> r[5:] = [1,-1] >>> print(r) [ 0. 0. 0. 0. 0. 1. -1.] ``` r tests that the coefficients on the 5th and 6th independent variable are the same. ``` >>> T_test = results.t_test(r) >>> print(T_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 -1829.2026 455.391 -4.017 0.003 -2859.368 -799.037 ============================================================================== >>> T_test.effect -1829.2025687192481 >>> T_test.sd 455.39079425193762 >>> T_test.tvalue -4.0167754636411717 >>> T_test.pvalue 0.0015163772380899498 ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.formula.api import ols >>> dta = sm.datasets.longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = 'GNPDEFL = GNP, UNEMP = 2, YEAR/1829 = 1' >>> t_test = results.t_test(hypotheses) >>> print(t_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 15.0977 84.937 0.178 0.863 -177.042 207.238 c1 -2.0202 0.488 -8.231 0.000 -3.125 -0.915 c2 1.0001 0.249 0.000 1.000 0.437 1.563 ============================================================================== ``` See also [`tvalues`](statsmodels.genmod.generalized_estimating_equations.geeresults.tvalues#statsmodels.genmod.generalized_estimating_equations.GEEResults.tvalues "statsmodels.genmod.generalized_estimating_equations.GEEResults.tvalues") individual t statistics [`f_test`](statsmodels.genmod.generalized_estimating_equations.geeresults.f_test#statsmodels.genmod.generalized_estimating_equations.GEEResults.f_test "statsmodels.genmod.generalized_estimating_equations.GEEResults.f_test") for F tests [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") statsmodels statsmodels.multivariate.manova.MANOVA statsmodels.multivariate.manova.MANOVA ====================================== `class statsmodels.multivariate.manova.MANOVA(endog, exog, missing='none', hasconst=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/multivariate/manova.html#MANOVA) Multivariate analysis of variance The implementation of MANOVA is based on multivariate regression and does not assume that the explanatory variables are categorical. Any type of variables as in regression is allowed. \| Parameters: \| endog (array\_like) – Dependent variables. A nobs x k\_endog array where nobs is the number of observations and k\_endog is the number of dependent variables. * exog (array\_like) – Independent variables. A nobs x k\_exog array where nobs is the number of observations and k\_exog is the number of independent variables. An intercept is not included by default and should be added by the user. Models specified using a formula include an intercept by default. \| `endog` array – See Parameters. `exog` array – See Parameters. #### References \| \| \| \| --- \| --- \| \| [\] \| <ftp://public.dhe.ibm.com/software/analytics/spss/documentation/statistics/20.0/en/client/Manuals/IBM_SPSS_Statistics_Algorithms.pdf> \| #### Methods \| \| \| \| --- \| --- \| \| [`fit`](statsmodels.multivariate.manova.manova.fit#statsmodels.multivariate.manova.MANOVA.fit "statsmodels.multivariate.manova.MANOVA.fit")() \| Fit a model to data. \| \| [`from_formula`](statsmodels.multivariate.manova.manova.from_formula#statsmodels.multivariate.manova.MANOVA.from_formula "statsmodels.multivariate.manova.MANOVA.from_formula")(formula, data[, subset, drop\_cols]) \| Create a Model from a formula and dataframe. \| \| [`mv_test`](statsmodels.multivariate.manova.manova.mv_test#statsmodels.multivariate.manova.MANOVA.mv_test "statsmodels.multivariate.manova.MANOVA.mv_test")([hypotheses]) \| Linear hypotheses testing \| \| [`predict`](statsmodels.multivariate.manova.manova.predict#statsmodels.multivariate.manova.MANOVA.predict "statsmodels.multivariate.manova.MANOVA.predict")(params[, exog]) \| After a model has been fit predict returns the fitted values. \| #### Attributes \| \| \| \| --- \| --- \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| Names of exogenous variables \| statsmodels statsmodels.sandbox.distributions.extras.SkewNorm_gen.expect statsmodels.sandbox.distributions.extras.SkewNorm\_gen.expect ============================================================= `SkewNorm_gen.expect(func=None, args=(), loc=0, scale=1, lb=None, ub=None, conditional=False, kwds)` Calculate expected value of a function with respect to the distribution. The expected value of a function `f(x)` with respect to a distribution `dist` is defined as: ``` ubound E[x] = Integral(f(x) dist.pdf(x)) lbound ``` \| Parameters: \| * func (callable, optional) – Function for which integral is calculated. Takes only one argument. The default is the identity mapping f(x) = x. * args (tuple, optional) – Shape parameters of the distribution. * loc (float, optional) – Location parameter (default=0). * scale (float, optional) – Scale parameter (default=1). * ub (lb,) – Lower and upper bound for integration. Default is set to the support of the distribution. * conditional (bool, optional) – If True, the integral is corrected by the conditional probability of the integration interval. The return value is the expectation of the function, conditional on being in the given interval. Default is False. * keyword arguments are passed to the integration routine. (Additional) – \| \| Returns: \| expect – The calculated expected value. \| \| Return type: \| float \| #### Notes The integration behavior of this function is inherited from `integrate.quad`. statsmodels statsmodels.miscmodels.count.PoissonOffsetGMLE.loglike statsmodels.miscmodels.count.PoissonOffsetGMLE.loglike ====================================================== `PoissonOffsetGMLE.loglike(params)` Log-likelihood of model. statsmodels statsmodels.sandbox.regression.gmm.GMMResults.initialize statsmodels.sandbox.regression.gmm.GMMResults.initialize ======================================================== `GMMResults.initialize(model, params, kwd)` statsmodels statsmodels.robust.norms.AndrewWave.weights statsmodels.robust.norms.AndrewWave.weights =========================================== `AndrewWave.weights(z)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/norms.html#AndrewWave.weights) Andrew’s wave weighting function for the IRLS algorithm The psi function scaled by z \| Parameters: \| z** (array-like) – 1d array \| \| Returns: \| weights – weights(z) = sin(z/a)/(z/a) for \|z\| <= a\piweights(z) = 0 for \|z\| > a\pi \| \| Return type: \| array \| statsmodels statsmodels.tsa.stattools.acovf statsmodels.tsa.stattools.acovf =============================== `statsmodels.tsa.stattools.acovf(x, unbiased=False, demean=True, fft=False, missing='none')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/stattools.html#acovf) Autocovariance for 1D \| Parameters: \| * x (array) – Time series data. Must be 1d. * unbiased (bool) – If True, then denominators is n-k, otherwise n * demean (bool) – If True, then subtract the mean x from each element of x * fft (bool) – If True, use FFT convolution. This method should be preferred for long time series. * missing (str) – A string in [‘none’, ‘raise’, ‘conservative’, ‘drop’] specifying how the NaNs are to be treated. \| \| Returns: \| acovf – autocovariance function \| \| Return type: \| array \| #### References \| \| \| \| --- \| --- \| \| [\] \| Parzen, E., 1963. On spectral analysis with missing observations and amplitude modulation. Sankhya: The Indian Journal of Statistics, Series A, pp.383-392. \| statsmodels statsmodels.tsa.ar_model.AR.predict statsmodels.tsa.ar\_model.AR.predict ==================================== `AR.predict(params, start=None, end=None, dynamic=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/ar_model.html#AR.predict) Returns in-sample and out-of-sample prediction. \| Parameters: \| params (array) – The fitted model parameters. * start (int, str, or datetime) – Zero-indexed observation number at which to start forecasting, ie., the first forecast is start. Can also be a date string to parse or a datetime type. * end (int, str, or datetime) – Zero-indexed observation number at which to end forecasting, ie., the first forecast is start. Can also be a date string to parse or a datetime type. * dynamic (bool) – The `dynamic` keyword affects in-sample prediction. If dynamic is False, then the in-sample lagged values are used for prediction. If `dynamic` is True, then in-sample forecasts are used in place of lagged dependent variables. The first forecasted value is `start`. \| \| Returns: \| predicted values \| \| Return type: \| array \| #### Notes The linear Gaussian Kalman filter is used to return pre-sample fitted values. The exact initial Kalman Filter is used. See Durbin and Koopman in the references for more information. statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.wald_test_terms statsmodels.regression.recursive\_ls.RecursiveLSResults.wald\_test\_terms ========================================================================= `RecursiveLSResults.wald_test_terms(skip_single=False, extra_constraints=None, combine_terms=None)` Compute a sequence of Wald tests for terms over multiple columns This computes joined Wald tests for the hypothesis that all coefficients corresponding to a `term` are zero. `Terms` are defined by the underlying formula or by string matching. \| Parameters: \| * skip\_single (boolean) – If true, then terms that consist only of a single column and, therefore, refers only to a single parameter is skipped. If false, then all terms are included. * extra\_constraints (ndarray) – not tested yet * combine\_terms (None or list of strings) – Each string in this list is matched to the name of the terms or the name of the exogenous variables. All columns whose name includes that string are combined in one joint test. \| \| Returns: \| test\_result – The result instance contains `table` which is a pandas DataFrame with the test results: test statistic, degrees of freedom and pvalues. \| \| Return type: \| result instance \| #### Examples ``` >>> res_ols = ols("np.log(Days+1) ~ C(Duration, Sum)C(Weight, Sum)", data).fit() >>> res_ols.wald_test_terms() <class 'statsmodels.stats.contrast.WaldTestResults'> F P>F df constraint df denom Intercept 279.754525 2.37985521351e-22 1 51 C(Duration, Sum) 5.367071 0.0245738436636 1 51 C(Weight, Sum) 12.432445 3.99943118767e-05 2 51 C(Duration, Sum):C(Weight, Sum) 0.176002 0.83912310946 2 51 ``` ``` >>> res_poi = Poisson.from_formula("Days ~ C(Weight) C(Duration)", data).fit(cov_type='HC0') >>> wt = res_poi.wald_test_terms(skip_single=False, combine_terms=['Duration', 'Weight']) >>> print(wt) chi2 P>chi2 df constraint Intercept 15.695625 7.43960374424e-05 1 C(Weight) 16.132616 0.000313940174705 2 C(Duration) 1.009147 0.315107378931 1 C(Weight):C(Duration) 0.216694 0.897315972824 2 Duration 11.187849 0.010752286833 3 Weight 30.263368 4.32586407145e-06 4 ``` statsmodels statsmodels.miscmodels.count.PoissonZiGMLE.expandparams statsmodels.miscmodels.count.PoissonZiGMLE.expandparams ======================================================= `PoissonZiGMLE.expandparams(params)` expand to full parameter array when some parameters are fixed \| Parameters: \| params (array) – reduced parameter array \| \| Returns: \| paramsfull – expanded parameter array where fixed parameters are included \| \| Return type: \| array \| #### Notes Calling this requires that self.fixed\_params and self.fixed\_paramsmask are defined. developer notes: This can be used in the log-likelihood to … this could also be replaced by a more general parameter transformation. statsmodels statsmodels.discrete.discrete_model.CountModel.pdf statsmodels.discrete.discrete\_model.CountModel.pdf =================================================== `CountModel.pdf(X)` The probability density (mass) function of the model. statsmodels statsmodels.genmod.generalized_estimating_equations.GEEResults.resid_centered statsmodels.genmod.generalized\_estimating\_equations.GEEResults.resid\_centered ================================================================================ `GEEResults.resid_centered()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_estimating_equations.html#GEEResults.resid_centered) Returns the residuals centered within each group. statsmodels statsmodels.regression.recursive_ls.RecursiveLS.loglikeobs statsmodels.regression.recursive\_ls.RecursiveLS.loglikeobs =========================================================== `RecursiveLS.loglikeobs(params, transformed=True, complex_step=False, *kwargs)` Loglikelihood evaluation \| Parameters: \| params (array\_like) – Array of parameters at which to evaluate the loglikelihood function. * transformed (boolean, optional) – Whether or not `params` is already transformed. Default is True. * *\\kwargs* – Additional keyword arguments to pass to the Kalman filter. See `KalmanFilter.filter` for more details. \| #### Notes [[1]](#id2) recommend maximizing the average likelihood to avoid scale issues; this is done automatically by the base Model fit method. #### References \| \| \| \| --- \| --- \| \| [[1]](#id1) \| Koopman, Siem Jan, Neil Shephard, and Jurgen A. Doornik. 1999. Statistical Algorithms for Models in State Space Using SsfPack 2.2. Econometrics Journal 2 (1): 107-60. doi:10.1111/1368-423X.00023. \| See also [`update`](statsmodels.regression.recursive_ls.recursivels.update#statsmodels.regression.recursive_ls.RecursiveLS.update "statsmodels.regression.recursive_ls.RecursiveLS.update") modifies the internal state of the Model to reflect new params	programming_docs
statsmodels statsmodels.discrete.discrete_model.LogitResults.llf statsmodels.discrete.discrete\_model.LogitResults.llf ===================================================== `LogitResults.llf()` statsmodels statsmodels.sandbox.distributions.extras.ACSkewT_gen.std statsmodels.sandbox.distributions.extras.ACSkewT\_gen.std ========================================================= `ACSkewT_gen.std(args, kwds)` Standard deviation of the distribution. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| std – standard deviation of the distribution \| \| Return type: \| float \| statsmodels statsmodels.tsa.statespace.sarimax.SARIMAX.transform_params statsmodels.tsa.statespace.sarimax.SARIMAX.transform\_params ============================================================ `SARIMAX.transform_params(unconstrained)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/sarimax.html#SARIMAX.transform_params) Transform unconstrained parameters used by the optimizer to constrained parameters used in likelihood evaluation. Used primarily to enforce stationarity of the autoregressive lag polynomial, invertibility of the moving average lag polynomial, and positive variance parameters. \| Parameters: \| unconstrained (array\_like) – Unconstrained parameters used by the optimizer. \| \| Returns: \| constrained – Constrained parameters used in likelihood evaluation. \| \| Return type: \| array\_like \| #### Notes If the lag polynomial has non-consecutive powers (so that the coefficient is zero on some element of the polynomial), then the constraint function is not onto the entire space of invertible polynomials, although it only excludes a very small portion very close to the invertibility boundary. statsmodels statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.initialize_approximate_diffuse statsmodels.tsa.statespace.kalman\_smoother.KalmanSmoother.initialize\_approximate\_diffuse =========================================================================================== `KalmanSmoother.initialize_approximate_diffuse(variance=None)` Initialize the statespace model with approximate diffuse values. Rather than following the exact diffuse treatment (which is developed for the case that the variance becomes infinitely large), this assigns an arbitrary large number for the variance. \| Parameters: \| variance (float, optional) – The variance for approximating diffuse initial conditions. Default is 1e6. \| statsmodels statsmodels.stats.sandwich_covariance.cov_hac statsmodels.stats.sandwich\_covariance.cov\_hac =============================================== `statsmodels.stats.sandwich_covariance.cov_hac(results, nlags=None, weights_func=<function weights_bartlett>, use_correction=True)` heteroscedasticity and autocorrelation robust covariance matrix (Newey-West) Assumes we have a single time series with zero axis consecutive, equal spaced time periods \| Parameters: \| * results (result instance) – result of a regression, uses results.model.exog and results.resid TODO: this should use wexog instead * nlags (int or None) – highest lag to include in kernel window. If None, then nlags = floor[4(T/100)^(2/9)] is used. * weights\_func (callable) – weights\_func is called with nlags as argument to get the kernel weights. default are Bartlett weights \| \| Returns: \| cov – HAC robust covariance matrix for parameter estimates \| \| Return type: \| ndarray, (k\_vars, k\_vars) \| #### Notes verified only for nlags=0, which is just White just guessing on correction factor, need reference options might change when other kernels besides Bartlett are available. statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.test_normality statsmodels.tsa.statespace.dynamic\_factor.DynamicFactorResults.test\_normality =============================================================================== `DynamicFactorResults.test_normality(method)` Test for normality of standardized residuals. Null hypothesis is normality. \| Parameters: \| method (string {'jarquebera'} or None) – The statistical test for normality. Must be ‘jarquebera’ for Jarque-Bera normality test. If None, an attempt is made to select an appropriate test. \| #### Notes If the first `d` loglikelihood values were burned (i.e. in the specified model, `loglikelihood_burn=d`), then this test is calculated ignoring the first `d` residuals. In the case of missing data, the maintained hypothesis is that the data are missing completely at random. This test is then run on the standardized residuals excluding those corresponding to missing observations. See also [`statsmodels.stats.stattools.jarque_bera`](statsmodels.stats.stattools.jarque_bera#statsmodels.stats.stattools.jarque_bera "statsmodels.stats.stattools.jarque_bera") statsmodels statsmodels.discrete.count_model.ZeroInflatedGeneralizedPoissonResults.cov_params statsmodels.discrete.count\_model.ZeroInflatedGeneralizedPoissonResults.cov\_params =================================================================================== `ZeroInflatedGeneralizedPoissonResults.cov_params(r_matrix=None, column=None, scale=None, cov_p=None, other=None)` Returns the variance/covariance matrix. The variance/covariance matrix can be of a linear contrast of the estimates of params or all params multiplied by scale which will usually be an estimate of sigma^2. Scale is assumed to be a scalar. \| Parameters: \| * r\_matrix (array-like) – Can be 1d, or 2d. Can be used alone or with other. * column (array-like, optional) – Must be used on its own. Can be 0d or 1d see below. * scale (float, optional) – Can be specified or not. Default is None, which means that the scale argument is taken from the model. * other (array-like, optional) – Can be used when r\_matrix is specified. \| \| Returns: \| cov – covariance matrix of the parameter estimates or of linear combination of parameter estimates. See Notes. \| \| Return type: \| ndarray \| #### Notes (The below are assumed to be in matrix notation.) If no argument is specified returns the covariance matrix of a model `(scale)(X.T X)^(-1)` If contrast is specified it pre and post-multiplies as follows `(scale) r_matrix (X.T X)^(-1) r_matrix.T` If contrast and other are specified returns `(scale) * r_matrix (X.T X)^(-1) other.T` If column is specified returns `(scale) * (X.T X)^(-1)[column,column]` if column is 0d OR `(scale) * (X.T X)^(-1)[column][:,column]` if column is 1d statsmodels statsmodels.sandbox.regression.gmm.GMMResults.get_bse statsmodels.sandbox.regression.gmm.GMMResults.get\_bse ====================================================== `GMMResults.get_bse(kwds)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/regression/gmm.html#GMMResults.get_bse) standard error of the parameter estimates with options \| Parameters: \| kwds** (optional keywords) – options for calculating cov\_params \| \| Returns: \| bse – estimated standard error of parameter estimates \| \| Return type: \| ndarray \| statsmodels statsmodels.tsa.varma_process.VarmaPoly statsmodels.tsa.varma\_process.VarmaPoly ======================================== `class statsmodels.tsa.varma_process.VarmaPoly(ar, ma=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/varma_process.html#VarmaPoly) class to keep track of Varma polynomial format #### Examples ar23 = np.array([[[ 1. , 0. ], [ 0. , 1. ]], [[-0.6, 0. ], [ 0.2, -0.6]], [[-0.1, 0. ], [ 0.1, -0.1]]]) ma22 = np.array([[[ 1. , 0. ], [ 0. , 1. ]], [[ 0.4, 0. ], [ 0.2, 0.3]]]) #### Methods \| \| \| \| --- \| --- \| \| [`getisinvertible`](statsmodels.tsa.varma_process.varmapoly.getisinvertible#statsmodels.tsa.varma_process.VarmaPoly.getisinvertible "statsmodels.tsa.varma_process.VarmaPoly.getisinvertible")([a]) \| check whether the auto-regressive lag-polynomial is stationary \| \| [`getisstationary`](statsmodels.tsa.varma_process.varmapoly.getisstationary#statsmodels.tsa.varma_process.VarmaPoly.getisstationary "statsmodels.tsa.varma_process.VarmaPoly.getisstationary")([a]) \| check whether the auto-regressive lag-polynomial is stationary \| \| [`hstack`](statsmodels.tsa.varma_process.varmapoly.hstack#statsmodels.tsa.varma_process.VarmaPoly.hstack "statsmodels.tsa.varma_process.VarmaPoly.hstack")([a, name]) \| stack lagpolynomial horizontally in 2d array \| \| [`hstackarma_minus1`](statsmodels.tsa.varma_process.varmapoly.hstackarma_minus1#statsmodels.tsa.varma_process.VarmaPoly.hstackarma_minus1 "statsmodels.tsa.varma_process.VarmaPoly.hstackarma_minus1")() \| stack ar and lagpolynomial vertically in 2d array \| \| [`reduceform`](statsmodels.tsa.varma_process.varmapoly.reduceform#statsmodels.tsa.varma_process.VarmaPoly.reduceform "statsmodels.tsa.varma_process.VarmaPoly.reduceform")(apoly) \| this assumes no exog, todo \| \| [`stacksquare`](statsmodels.tsa.varma_process.varmapoly.stacksquare#statsmodels.tsa.varma_process.VarmaPoly.stacksquare "statsmodels.tsa.varma_process.VarmaPoly.stacksquare")([a, name, orientation]) \| stack lagpolynomial vertically in 2d square array with eye \| \| [`vstack`](statsmodels.tsa.varma_process.varmapoly.vstack#statsmodels.tsa.varma_process.VarmaPoly.vstack "statsmodels.tsa.varma_process.VarmaPoly.vstack")([a, name]) \| stack lagpolynomial vertically in 2d array \| \| [`vstackarma_minus1`](statsmodels.tsa.varma_process.varmapoly.vstackarma_minus1#statsmodels.tsa.varma_process.VarmaPoly.vstackarma_minus1 "statsmodels.tsa.varma_process.VarmaPoly.vstackarma_minus1")() \| stack ar and lagpolynomial vertically in 2d array \| statsmodels statsmodels.tsa.vector_ar.irf.IRAnalysis.cum_effect_stderr statsmodels.tsa.vector\_ar.irf.IRAnalysis.cum\_effect\_stderr ============================================================= `IRAnalysis.cum_effect_stderr(orth=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/irf.html#IRAnalysis.cum_effect_stderr) statsmodels statsmodels.stats.sandwich_covariance.cov_cluster statsmodels.stats.sandwich\_covariance.cov\_cluster =================================================== `statsmodels.stats.sandwich_covariance.cov_cluster(results, group, use_correction=True)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/sandwich_covariance.html#cov_cluster) cluster robust covariance matrix Calculates sandwich covariance matrix for a single cluster, i.e. grouped variables. \| Parameters: \| * results (result instance) – result of a regression, uses results.model.exog and results.resid TODO: this should use wexog instead * use\_correction (bool) – If true (default), then the small sample correction factor is used. \| \| Returns: \| cov – cluster robust covariance matrix for parameter estimates \| \| Return type: \| ndarray, (k\_vars, k\_vars) \| #### Notes same result as Stata in UCLA example and same as Peterson statsmodels statsmodels.sandbox.regression.gmm.LinearIVGMM.gmmobjective_cu statsmodels.sandbox.regression.gmm.LinearIVGMM.gmmobjective\_cu =============================================================== `LinearIVGMM.gmmobjective_cu(params, weights_method='cov', wargs=())` objective function for continuously updating GMM minimization \| Parameters: \| params (array) – parameter values at which objective is evaluated \| \| Returns: \| jval – value of objective function \| \| Return type: \| float \| statsmodels statsmodels.tsa.ar_model.ARResults.predict statsmodels.tsa.ar\_model.ARResults.predict =========================================== `ARResults.predict(start=None, end=None, dynamic=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/ar_model.html#ARResults.predict) Returns in-sample and out-of-sample prediction. \| Parameters: \| * start (int, str, or datetime) – Zero-indexed observation number at which to start forecasting, ie., the first forecast is start. Can also be a date string to parse or a datetime type. * end (int, str, or datetime) – Zero-indexed observation number at which to end forecasting, ie., the first forecast is start. Can also be a date string to parse or a datetime type. * dynamic (bool) – The `dynamic` keyword affects in-sample prediction. If dynamic is False, then the in-sample lagged values are used for prediction. If `dynamic` is True, then in-sample forecasts are used in place of lagged dependent variables. The first forecasted * confint (bool, float) – Whether to return confidence intervals. If `confint` == True, 95 % confidence intervals are returned. Else if `confint` is a float, then it is assumed to be the alpha value of the confidence interval. That is confint == .05 returns a 95% confidence interval, and .10 would return a 90% confidence interval. value is `start`. \| \| Returns: \| predicted values \| \| Return type: \| array \| #### Notes The linear Gaussian Kalman filter is used to return pre-sample fitted values. The exact initial Kalman Filter is used. See Durbin and Koopman in the references for more information. statsmodels statsmodels.regression.quantile_regression.QuantRegResults statsmodels.regression.quantile\_regression.QuantRegResults =========================================================== `class statsmodels.regression.quantile_regression.QuantRegResults(model, params, normalized_cov_params=None, scale=1.0, cov_type='nonrobust', cov_kwds=None, use_t=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/quantile_regression.html#QuantRegResults) Results instance for the QuantReg model #### Methods \| \| \| \| --- \| --- \| \| [`HC0_se`](statsmodels.regression.quantile_regression.quantregresults.hc0_se#statsmodels.regression.quantile_regression.QuantRegResults.HC0_se "statsmodels.regression.quantile_regression.QuantRegResults.HC0_se")() \| See statsmodels.RegressionResults \| \| [`HC1_se`](statsmodels.regression.quantile_regression.quantregresults.hc1_se#statsmodels.regression.quantile_regression.QuantRegResults.HC1_se "statsmodels.regression.quantile_regression.QuantRegResults.HC1_se")() \| See statsmodels.RegressionResults \| \| [`HC2_se`](statsmodels.regression.quantile_regression.quantregresults.hc2_se#statsmodels.regression.quantile_regression.QuantRegResults.HC2_se "statsmodels.regression.quantile_regression.QuantRegResults.HC2_se")() \| See statsmodels.RegressionResults \| \| [`HC3_se`](statsmodels.regression.quantile_regression.quantregresults.hc3_se#statsmodels.regression.quantile_regression.QuantRegResults.HC3_se "statsmodels.regression.quantile_regression.QuantRegResults.HC3_se")() \| See statsmodels.RegressionResults \| \| [`aic`](statsmodels.regression.quantile_regression.quantregresults.aic#statsmodels.regression.quantile_regression.QuantRegResults.aic "statsmodels.regression.quantile_regression.QuantRegResults.aic")() \| \| \| [`bic`](statsmodels.regression.quantile_regression.quantregresults.bic#statsmodels.regression.quantile_regression.QuantRegResults.bic "statsmodels.regression.quantile_regression.QuantRegResults.bic")() \| \| \| [`bse`](statsmodels.regression.quantile_regression.quantregresults.bse#statsmodels.regression.quantile_regression.QuantRegResults.bse "statsmodels.regression.quantile_regression.QuantRegResults.bse")() \| \| \| [`centered_tss`](statsmodels.regression.quantile_regression.quantregresults.centered_tss#statsmodels.regression.quantile_regression.QuantRegResults.centered_tss "statsmodels.regression.quantile_regression.QuantRegResults.centered_tss")() \| \| \| [`compare_f_test`](statsmodels.regression.quantile_regression.quantregresults.compare_f_test#statsmodels.regression.quantile_regression.QuantRegResults.compare_f_test "statsmodels.regression.quantile_regression.QuantRegResults.compare_f_test")(restricted) \| use F test to test whether restricted model is correct \| \| [`compare_lm_test`](statsmodels.regression.quantile_regression.quantregresults.compare_lm_test#statsmodels.regression.quantile_regression.QuantRegResults.compare_lm_test "statsmodels.regression.quantile_regression.QuantRegResults.compare_lm_test")(restricted[, demean, use\_lr]) \| Use Lagrange Multiplier test to test whether restricted model is correct \| \| [`compare_lr_test`](statsmodels.regression.quantile_regression.quantregresults.compare_lr_test#statsmodels.regression.quantile_regression.QuantRegResults.compare_lr_test "statsmodels.regression.quantile_regression.QuantRegResults.compare_lr_test")(restricted[, large\_sample]) \| Likelihood ratio test to test whether restricted model is correct \| \| [`condition_number`](statsmodels.regression.quantile_regression.quantregresults.condition_number#statsmodels.regression.quantile_regression.QuantRegResults.condition_number "statsmodels.regression.quantile_regression.QuantRegResults.condition_number")() \| Return condition number of exogenous matrix. \| \| [`conf_int`](statsmodels.regression.quantile_regression.quantregresults.conf_int#statsmodels.regression.quantile_regression.QuantRegResults.conf_int "statsmodels.regression.quantile_regression.QuantRegResults.conf_int")([alpha, cols]) \| Returns the confidence interval of the fitted parameters. \| \| [`cov_HC0`](statsmodels.regression.quantile_regression.quantregresults.cov_hc0#statsmodels.regression.quantile_regression.QuantRegResults.cov_HC0 "statsmodels.regression.quantile_regression.QuantRegResults.cov_HC0")() \| See statsmodels.RegressionResults \| \| [`cov_HC1`](statsmodels.regression.quantile_regression.quantregresults.cov_hc1#statsmodels.regression.quantile_regression.QuantRegResults.cov_HC1 "statsmodels.regression.quantile_regression.QuantRegResults.cov_HC1")() \| See statsmodels.RegressionResults \| \| [`cov_HC2`](statsmodels.regression.quantile_regression.quantregresults.cov_hc2#statsmodels.regression.quantile_regression.QuantRegResults.cov_HC2 "statsmodels.regression.quantile_regression.QuantRegResults.cov_HC2")() \| See statsmodels.RegressionResults \| \| [`cov_HC3`](statsmodels.regression.quantile_regression.quantregresults.cov_hc3#statsmodels.regression.quantile_regression.QuantRegResults.cov_HC3 "statsmodels.regression.quantile_regression.QuantRegResults.cov_HC3")() \| See statsmodels.RegressionResults \| \| [`cov_params`](statsmodels.regression.quantile_regression.quantregresults.cov_params#statsmodels.regression.quantile_regression.QuantRegResults.cov_params "statsmodels.regression.quantile_regression.QuantRegResults.cov_params")([r\_matrix, column, scale, cov\_p, …]) \| Returns the variance/covariance matrix. \| \| [`eigenvals`](statsmodels.regression.quantile_regression.quantregresults.eigenvals#statsmodels.regression.quantile_regression.QuantRegResults.eigenvals "statsmodels.regression.quantile_regression.QuantRegResults.eigenvals")() \| Return eigenvalues sorted in decreasing order. \| \| [`ess`](statsmodels.regression.quantile_regression.quantregresults.ess#statsmodels.regression.quantile_regression.QuantRegResults.ess "statsmodels.regression.quantile_regression.QuantRegResults.ess")() \| \| \| [`f_pvalue`](statsmodels.regression.quantile_regression.quantregresults.f_pvalue#statsmodels.regression.quantile_regression.QuantRegResults.f_pvalue "statsmodels.regression.quantile_regression.QuantRegResults.f_pvalue")() \| \| \| [`f_test`](statsmodels.regression.quantile_regression.quantregresults.f_test#statsmodels.regression.quantile_regression.QuantRegResults.f_test "statsmodels.regression.quantile_regression.QuantRegResults.f_test")(r\_matrix[, cov\_p, scale, invcov]) \| Compute the F-test for a joint linear hypothesis. \| \| [`fittedvalues`](statsmodels.regression.quantile_regression.quantregresults.fittedvalues#statsmodels.regression.quantile_regression.QuantRegResults.fittedvalues "statsmodels.regression.quantile_regression.QuantRegResults.fittedvalues")() \| \| \| [`fvalue`](statsmodels.regression.quantile_regression.quantregresults.fvalue#statsmodels.regression.quantile_regression.QuantRegResults.fvalue "statsmodels.regression.quantile_regression.QuantRegResults.fvalue")() \| \| \| [`get_prediction`](statsmodels.regression.quantile_regression.quantregresults.get_prediction#statsmodels.regression.quantile_regression.QuantRegResults.get_prediction "statsmodels.regression.quantile_regression.QuantRegResults.get_prediction")([exog, transform, weights, …]) \| compute prediction results \| \| [`get_robustcov_results`](statsmodels.regression.quantile_regression.quantregresults.get_robustcov_results#statsmodels.regression.quantile_regression.QuantRegResults.get_robustcov_results "statsmodels.regression.quantile_regression.QuantRegResults.get_robustcov_results")([cov\_type, use\_t]) \| create new results instance with robust covariance as default \| \| [`initialize`](statsmodels.regression.quantile_regression.quantregresults.initialize#statsmodels.regression.quantile_regression.QuantRegResults.initialize "statsmodels.regression.quantile_regression.QuantRegResults.initialize")(model, params, \\*kwd) \| \| \| [`llf`](statsmodels.regression.quantile_regression.quantregresults.llf#statsmodels.regression.quantile_regression.QuantRegResults.llf "statsmodels.regression.quantile_regression.QuantRegResults.llf")() \| \| \| [`load`](statsmodels.regression.quantile_regression.quantregresults.load#statsmodels.regression.quantile_regression.QuantRegResults.load "statsmodels.regression.quantile_regression.QuantRegResults.load")(fname) \| load a pickle, (class method) \| \| [`mse`](statsmodels.regression.quantile_regression.quantregresults.mse#statsmodels.regression.quantile_regression.QuantRegResults.mse "statsmodels.regression.quantile_regression.QuantRegResults.mse")() \| \| \| [`mse_model`](statsmodels.regression.quantile_regression.quantregresults.mse_model#statsmodels.regression.quantile_regression.QuantRegResults.mse_model "statsmodels.regression.quantile_regression.QuantRegResults.mse_model")() \| \| \| [`mse_resid`](statsmodels.regression.quantile_regression.quantregresults.mse_resid#statsmodels.regression.quantile_regression.QuantRegResults.mse_resid "statsmodels.regression.quantile_regression.QuantRegResults.mse_resid")() \| \| \| [`mse_total`](statsmodels.regression.quantile_regression.quantregresults.mse_total#statsmodels.regression.quantile_regression.QuantRegResults.mse_total "statsmodels.regression.quantile_regression.QuantRegResults.mse_total")() \| \| \| [`nobs`](statsmodels.regression.quantile_regression.quantregresults.nobs#statsmodels.regression.quantile_regression.QuantRegResults.nobs "statsmodels.regression.quantile_regression.QuantRegResults.nobs")() \| \| \| [`normalized_cov_params`](statsmodels.regression.quantile_regression.quantregresults.normalized_cov_params#statsmodels.regression.quantile_regression.QuantRegResults.normalized_cov_params "statsmodels.regression.quantile_regression.QuantRegResults.normalized_cov_params")() \| \| \| [`predict`](statsmodels.regression.quantile_regression.quantregresults.predict#statsmodels.regression.quantile_regression.QuantRegResults.predict "statsmodels.regression.quantile_regression.QuantRegResults.predict")([exog, transform]) \| Call self.model.predict with self.params as the first argument. \| \| [`prsquared`](statsmodels.regression.quantile_regression.quantregresults.prsquared#statsmodels.regression.quantile_regression.QuantRegResults.prsquared "statsmodels.regression.quantile_regression.QuantRegResults.prsquared")() \| \| \| [`pvalues`](statsmodels.regression.quantile_regression.quantregresults.pvalues#statsmodels.regression.quantile_regression.QuantRegResults.pvalues "statsmodels.regression.quantile_regression.QuantRegResults.pvalues")() \| \| \| [`remove_data`](statsmodels.regression.quantile_regression.quantregresults.remove_data#statsmodels.regression.quantile_regression.QuantRegResults.remove_data "statsmodels.regression.quantile_regression.QuantRegResults.remove_data")() \| remove data arrays, all nobs arrays from result and model \| \| [`resid`](statsmodels.regression.quantile_regression.quantregresults.resid#statsmodels.regression.quantile_regression.QuantRegResults.resid "statsmodels.regression.quantile_regression.QuantRegResults.resid")() \| \| \| [`resid_pearson`](statsmodels.regression.quantile_regression.quantregresults.resid_pearson#statsmodels.regression.quantile_regression.QuantRegResults.resid_pearson "statsmodels.regression.quantile_regression.QuantRegResults.resid_pearson")() \| Residuals, normalized to have unit variance. \| \| [`rsquared`](statsmodels.regression.quantile_regression.quantregresults.rsquared#statsmodels.regression.quantile_regression.QuantRegResults.rsquared "statsmodels.regression.quantile_regression.QuantRegResults.rsquared")() \| \| \| [`rsquared_adj`](statsmodels.regression.quantile_regression.quantregresults.rsquared_adj#statsmodels.regression.quantile_regression.QuantRegResults.rsquared_adj "statsmodels.regression.quantile_regression.QuantRegResults.rsquared_adj")() \| \| \| [`save`](statsmodels.regression.quantile_regression.quantregresults.save#statsmodels.regression.quantile_regression.QuantRegResults.save "statsmodels.regression.quantile_regression.QuantRegResults.save")(fname[, remove\_data]) \| save a pickle of this instance \| \| [`scale`](statsmodels.regression.quantile_regression.quantregresults.scale#statsmodels.regression.quantile_regression.QuantRegResults.scale "statsmodels.regression.quantile_regression.QuantRegResults.scale")() \| \| \| [`ssr`](statsmodels.regression.quantile_regression.quantregresults.ssr#statsmodels.regression.quantile_regression.QuantRegResults.ssr "statsmodels.regression.quantile_regression.QuantRegResults.ssr")() \| \| \| [`summary`](statsmodels.regression.quantile_regression.quantregresults.summary#statsmodels.regression.quantile_regression.QuantRegResults.summary "statsmodels.regression.quantile_regression.QuantRegResults.summary")([yname, xname, title, alpha]) \| Summarize the Regression Results \| \| [`summary2`](statsmodels.regression.quantile_regression.quantregresults.summary2#statsmodels.regression.quantile_regression.QuantRegResults.summary2 "statsmodels.regression.quantile_regression.QuantRegResults.summary2")([yname, xname, title, alpha, …]) \| Experimental summary function to summarize the regression results \| \| [`t_test`](statsmodels.regression.quantile_regression.quantregresults.t_test#statsmodels.regression.quantile_regression.QuantRegResults.t_test "statsmodels.regression.quantile_regression.QuantRegResults.t_test")(r\_matrix[, cov\_p, scale, use\_t]) \| Compute a t-test for a each linear hypothesis of the form Rb = q \| \| [`t_test_pairwise`](statsmodels.regression.quantile_regression.quantregresults.t_test_pairwise#statsmodels.regression.quantile_regression.QuantRegResults.t_test_pairwise "statsmodels.regression.quantile_regression.QuantRegResults.t_test_pairwise")(term\_name[, method, alpha, …]) \| perform pairwise t\_test with multiple testing corrected p-values \| \| [`tvalues`](statsmodels.regression.quantile_regression.quantregresults.tvalues#statsmodels.regression.quantile_regression.QuantRegResults.tvalues "statsmodels.regression.quantile_regression.QuantRegResults.tvalues")() \| Return the t-statistic for a given parameter estimate. \| \| [`uncentered_tss`](statsmodels.regression.quantile_regression.quantregresults.uncentered_tss#statsmodels.regression.quantile_regression.QuantRegResults.uncentered_tss "statsmodels.regression.quantile_regression.QuantRegResults.uncentered_tss")() \| \| \| [`wald_test`](statsmodels.regression.quantile_regression.quantregresults.wald_test#statsmodels.regression.quantile_regression.QuantRegResults.wald_test "statsmodels.regression.quantile_regression.QuantRegResults.wald_test")(r\_matrix[, cov\_p, scale, invcov, …]) \| Compute a Wald-test for a joint linear hypothesis. \| \| [`wald_test_terms`](statsmodels.regression.quantile_regression.quantregresults.wald_test_terms#statsmodels.regression.quantile_regression.QuantRegResults.wald_test_terms "statsmodels.regression.quantile_regression.QuantRegResults.wald_test_terms")([skip\_single, …]) \| Compute a sequence of Wald tests for terms over multiple columns \| \| [`wresid`](statsmodels.regression.quantile_regression.quantregresults.wresid#statsmodels.regression.quantile_regression.QuantRegResults.wresid "statsmodels.regression.quantile_regression.QuantRegResults.wresid")() \| \| #### Attributes \| \| \| \| --- \| --- \| \| `use_t` \| \|	programming_docs
statsmodels statsmodels.discrete.discrete_model.MNLogit.loglike_and_score statsmodels.discrete.discrete\_model.MNLogit.loglike\_and\_score ================================================================ `MNLogit.loglike_and_score(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#MNLogit.loglike_and_score) Returns log likelihood and score, efficiently reusing calculations. Note that both of these returned quantities will need to be negated before being minimized by the maximum likelihood fitting machinery. statsmodels statsmodels.discrete.discrete_model.GeneralizedPoissonResults.summary statsmodels.discrete.discrete\_model.GeneralizedPoissonResults.summary ====================================================================== `GeneralizedPoissonResults.summary(yname=None, xname=None, title=None, alpha=0.05, yname_list=None)` Summarize the Regression Results \| Parameters: \| * yname (string, optional) – Default is `y` * xname (list of strings, optional) – Default is `var_##` for ## in p the number of regressors * title (string, optional) – Title for the top table. If not None, then this replaces the default title * alpha (float) – significance level for the confidence intervals \| \| Returns: \| smry – this holds the summary tables and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary.Summary`](statsmodels.iolib.summary.summary#statsmodels.iolib.summary.Summary "statsmodels.iolib.summary.Summary") class to hold summary results statsmodels statsmodels.sandbox.regression.gmm.IVRegressionResults statsmodels.sandbox.regression.gmm.IVRegressionResults ====================================================== `class statsmodels.sandbox.regression.gmm.IVRegressionResults(model, params, normalized_cov_params=None, scale=1.0, cov_type='nonrobust', cov_kwds=None, use_t=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/regression/gmm.html#IVRegressionResults) Results class for for an OLS model. Most of the methods and attributes are inherited from RegressionResults. The special methods that are only available for OLS are: get\_influence * outlier\_test * el\_test * conf\_int\_el See also `RegressionResults` #### Methods \| \| \| \| --- \| --- \| \| [`HC0_se`](statsmodels.sandbox.regression.gmm.ivregressionresults.hc0_se#statsmodels.sandbox.regression.gmm.IVRegressionResults.HC0_se "statsmodels.sandbox.regression.gmm.IVRegressionResults.HC0_se")() \| See statsmodels.RegressionResults \| \| [`HC1_se`](statsmodels.sandbox.regression.gmm.ivregressionresults.hc1_se#statsmodels.sandbox.regression.gmm.IVRegressionResults.HC1_se "statsmodels.sandbox.regression.gmm.IVRegressionResults.HC1_se")() \| See statsmodels.RegressionResults \| \| [`HC2_se`](statsmodels.sandbox.regression.gmm.ivregressionresults.hc2_se#statsmodels.sandbox.regression.gmm.IVRegressionResults.HC2_se "statsmodels.sandbox.regression.gmm.IVRegressionResults.HC2_se")() \| See statsmodels.RegressionResults \| \| [`HC3_se`](statsmodels.sandbox.regression.gmm.ivregressionresults.hc3_se#statsmodels.sandbox.regression.gmm.IVRegressionResults.HC3_se "statsmodels.sandbox.regression.gmm.IVRegressionResults.HC3_se")() \| See statsmodels.RegressionResults \| \| [`aic`](statsmodels.sandbox.regression.gmm.ivregressionresults.aic#statsmodels.sandbox.regression.gmm.IVRegressionResults.aic "statsmodels.sandbox.regression.gmm.IVRegressionResults.aic")() \| \| \| [`bic`](statsmodels.sandbox.regression.gmm.ivregressionresults.bic#statsmodels.sandbox.regression.gmm.IVRegressionResults.bic "statsmodels.sandbox.regression.gmm.IVRegressionResults.bic")() \| \| \| [`bse`](statsmodels.sandbox.regression.gmm.ivregressionresults.bse#statsmodels.sandbox.regression.gmm.IVRegressionResults.bse "statsmodels.sandbox.regression.gmm.IVRegressionResults.bse")() \| \| \| [`centered_tss`](statsmodels.sandbox.regression.gmm.ivregressionresults.centered_tss#statsmodels.sandbox.regression.gmm.IVRegressionResults.centered_tss "statsmodels.sandbox.regression.gmm.IVRegressionResults.centered_tss")() \| \| \| [`compare_f_test`](statsmodels.sandbox.regression.gmm.ivregressionresults.compare_f_test#statsmodels.sandbox.regression.gmm.IVRegressionResults.compare_f_test "statsmodels.sandbox.regression.gmm.IVRegressionResults.compare_f_test")(restricted) \| use F test to test whether restricted model is correct \| \| [`compare_lm_test`](statsmodels.sandbox.regression.gmm.ivregressionresults.compare_lm_test#statsmodels.sandbox.regression.gmm.IVRegressionResults.compare_lm_test "statsmodels.sandbox.regression.gmm.IVRegressionResults.compare_lm_test")(restricted[, demean, use\_lr]) \| Use Lagrange Multiplier test to test whether restricted model is correct \| \| [`compare_lr_test`](statsmodels.sandbox.regression.gmm.ivregressionresults.compare_lr_test#statsmodels.sandbox.regression.gmm.IVRegressionResults.compare_lr_test "statsmodels.sandbox.regression.gmm.IVRegressionResults.compare_lr_test")(restricted[, large\_sample]) \| Likelihood ratio test to test whether restricted model is correct \| \| [`condition_number`](statsmodels.sandbox.regression.gmm.ivregressionresults.condition_number#statsmodels.sandbox.regression.gmm.IVRegressionResults.condition_number "statsmodels.sandbox.regression.gmm.IVRegressionResults.condition_number")() \| Return condition number of exogenous matrix. \| \| [`conf_int`](statsmodels.sandbox.regression.gmm.ivregressionresults.conf_int#statsmodels.sandbox.regression.gmm.IVRegressionResults.conf_int "statsmodels.sandbox.regression.gmm.IVRegressionResults.conf_int")([alpha, cols]) \| Returns the confidence interval of the fitted parameters. \| \| [`cov_HC0`](statsmodels.sandbox.regression.gmm.ivregressionresults.cov_hc0#statsmodels.sandbox.regression.gmm.IVRegressionResults.cov_HC0 "statsmodels.sandbox.regression.gmm.IVRegressionResults.cov_HC0")() \| See statsmodels.RegressionResults \| \| [`cov_HC1`](statsmodels.sandbox.regression.gmm.ivregressionresults.cov_hc1#statsmodels.sandbox.regression.gmm.IVRegressionResults.cov_HC1 "statsmodels.sandbox.regression.gmm.IVRegressionResults.cov_HC1")() \| See statsmodels.RegressionResults \| \| [`cov_HC2`](statsmodels.sandbox.regression.gmm.ivregressionresults.cov_hc2#statsmodels.sandbox.regression.gmm.IVRegressionResults.cov_HC2 "statsmodels.sandbox.regression.gmm.IVRegressionResults.cov_HC2")() \| See statsmodels.RegressionResults \| \| [`cov_HC3`](statsmodels.sandbox.regression.gmm.ivregressionresults.cov_hc3#statsmodels.sandbox.regression.gmm.IVRegressionResults.cov_HC3 "statsmodels.sandbox.regression.gmm.IVRegressionResults.cov_HC3")() \| See statsmodels.RegressionResults \| \| [`cov_params`](statsmodels.sandbox.regression.gmm.ivregressionresults.cov_params#statsmodels.sandbox.regression.gmm.IVRegressionResults.cov_params "statsmodels.sandbox.regression.gmm.IVRegressionResults.cov_params")([r\_matrix, column, scale, cov\_p, …]) \| Returns the variance/covariance matrix. \| \| [`eigenvals`](statsmodels.sandbox.regression.gmm.ivregressionresults.eigenvals#statsmodels.sandbox.regression.gmm.IVRegressionResults.eigenvals "statsmodels.sandbox.regression.gmm.IVRegressionResults.eigenvals")() \| Return eigenvalues sorted in decreasing order. \| \| [`ess`](statsmodels.sandbox.regression.gmm.ivregressionresults.ess#statsmodels.sandbox.regression.gmm.IVRegressionResults.ess "statsmodels.sandbox.regression.gmm.IVRegressionResults.ess")() \| \| \| [`f_pvalue`](statsmodels.sandbox.regression.gmm.ivregressionresults.f_pvalue#statsmodels.sandbox.regression.gmm.IVRegressionResults.f_pvalue "statsmodels.sandbox.regression.gmm.IVRegressionResults.f_pvalue")() \| \| \| [`f_test`](statsmodels.sandbox.regression.gmm.ivregressionresults.f_test#statsmodels.sandbox.regression.gmm.IVRegressionResults.f_test "statsmodels.sandbox.regression.gmm.IVRegressionResults.f_test")(r\_matrix[, cov\_p, scale, invcov]) \| Compute the F-test for a joint linear hypothesis. \| \| [`fittedvalues`](statsmodels.sandbox.regression.gmm.ivregressionresults.fittedvalues#statsmodels.sandbox.regression.gmm.IVRegressionResults.fittedvalues "statsmodels.sandbox.regression.gmm.IVRegressionResults.fittedvalues")() \| \| \| [`fvalue`](statsmodels.sandbox.regression.gmm.ivregressionresults.fvalue#statsmodels.sandbox.regression.gmm.IVRegressionResults.fvalue "statsmodels.sandbox.regression.gmm.IVRegressionResults.fvalue")() \| \| \| [`get_prediction`](statsmodels.sandbox.regression.gmm.ivregressionresults.get_prediction#statsmodels.sandbox.regression.gmm.IVRegressionResults.get_prediction "statsmodels.sandbox.regression.gmm.IVRegressionResults.get_prediction")([exog, transform, weights, …]) \| compute prediction results \| \| [`get_robustcov_results`](statsmodels.sandbox.regression.gmm.ivregressionresults.get_robustcov_results#statsmodels.sandbox.regression.gmm.IVRegressionResults.get_robustcov_results "statsmodels.sandbox.regression.gmm.IVRegressionResults.get_robustcov_results")([cov\_type, use\_t]) \| create new results instance with robust covariance as default \| \| [`initialize`](statsmodels.sandbox.regression.gmm.ivregressionresults.initialize#statsmodels.sandbox.regression.gmm.IVRegressionResults.initialize "statsmodels.sandbox.regression.gmm.IVRegressionResults.initialize")(model, params, \\kwd) \| \| \| [`llf`](statsmodels.sandbox.regression.gmm.ivregressionresults.llf#statsmodels.sandbox.regression.gmm.IVRegressionResults.llf "statsmodels.sandbox.regression.gmm.IVRegressionResults.llf")() \| \| \| [`load`](statsmodels.sandbox.regression.gmm.ivregressionresults.load#statsmodels.sandbox.regression.gmm.IVRegressionResults.load "statsmodels.sandbox.regression.gmm.IVRegressionResults.load")(fname) \| load a pickle, (class method) \| \| [`mse_model`](statsmodels.sandbox.regression.gmm.ivregressionresults.mse_model#statsmodels.sandbox.regression.gmm.IVRegressionResults.mse_model "statsmodels.sandbox.regression.gmm.IVRegressionResults.mse_model")() \| \| \| [`mse_resid`](statsmodels.sandbox.regression.gmm.ivregressionresults.mse_resid#statsmodels.sandbox.regression.gmm.IVRegressionResults.mse_resid "statsmodels.sandbox.regression.gmm.IVRegressionResults.mse_resid")() \| \| \| [`mse_total`](statsmodels.sandbox.regression.gmm.ivregressionresults.mse_total#statsmodels.sandbox.regression.gmm.IVRegressionResults.mse_total "statsmodels.sandbox.regression.gmm.IVRegressionResults.mse_total")() \| \| \| [`nobs`](statsmodels.sandbox.regression.gmm.ivregressionresults.nobs#statsmodels.sandbox.regression.gmm.IVRegressionResults.nobs "statsmodels.sandbox.regression.gmm.IVRegressionResults.nobs")() \| \| \| [`normalized_cov_params`](statsmodels.sandbox.regression.gmm.ivregressionresults.normalized_cov_params#statsmodels.sandbox.regression.gmm.IVRegressionResults.normalized_cov_params "statsmodels.sandbox.regression.gmm.IVRegressionResults.normalized_cov_params")() \| \| \| [`predict`](statsmodels.sandbox.regression.gmm.ivregressionresults.predict#statsmodels.sandbox.regression.gmm.IVRegressionResults.predict "statsmodels.sandbox.regression.gmm.IVRegressionResults.predict")([exog, transform]) \| Call self.model.predict with self.params as the first argument. \| \| [`pvalues`](statsmodels.sandbox.regression.gmm.ivregressionresults.pvalues#statsmodels.sandbox.regression.gmm.IVRegressionResults.pvalues "statsmodels.sandbox.regression.gmm.IVRegressionResults.pvalues")() \| \| \| [`remove_data`](statsmodels.sandbox.regression.gmm.ivregressionresults.remove_data#statsmodels.sandbox.regression.gmm.IVRegressionResults.remove_data "statsmodels.sandbox.regression.gmm.IVRegressionResults.remove_data")() \| remove data arrays, all nobs arrays from result and model \| \| [`resid`](statsmodels.sandbox.regression.gmm.ivregressionresults.resid#statsmodels.sandbox.regression.gmm.IVRegressionResults.resid "statsmodels.sandbox.regression.gmm.IVRegressionResults.resid")() \| \| \| [`resid_pearson`](statsmodels.sandbox.regression.gmm.ivregressionresults.resid_pearson#statsmodels.sandbox.regression.gmm.IVRegressionResults.resid_pearson "statsmodels.sandbox.regression.gmm.IVRegressionResults.resid_pearson")() \| Residuals, normalized to have unit variance. \| \| [`rsquared`](statsmodels.sandbox.regression.gmm.ivregressionresults.rsquared#statsmodels.sandbox.regression.gmm.IVRegressionResults.rsquared "statsmodels.sandbox.regression.gmm.IVRegressionResults.rsquared")() \| \| \| [`rsquared_adj`](statsmodels.sandbox.regression.gmm.ivregressionresults.rsquared_adj#statsmodels.sandbox.regression.gmm.IVRegressionResults.rsquared_adj "statsmodels.sandbox.regression.gmm.IVRegressionResults.rsquared_adj")() \| \| \| [`save`](statsmodels.sandbox.regression.gmm.ivregressionresults.save#statsmodels.sandbox.regression.gmm.IVRegressionResults.save "statsmodels.sandbox.regression.gmm.IVRegressionResults.save")(fname[, remove\_data]) \| save a pickle of this instance \| \| [`scale`](statsmodels.sandbox.regression.gmm.ivregressionresults.scale#statsmodels.sandbox.regression.gmm.IVRegressionResults.scale "statsmodels.sandbox.regression.gmm.IVRegressionResults.scale")() \| \| \| [`spec_hausman`](statsmodels.sandbox.regression.gmm.ivregressionresults.spec_hausman#statsmodels.sandbox.regression.gmm.IVRegressionResults.spec_hausman "statsmodels.sandbox.regression.gmm.IVRegressionResults.spec_hausman")([dof]) \| Hausman’s specification test \| \| [`ssr`](statsmodels.sandbox.regression.gmm.ivregressionresults.ssr#statsmodels.sandbox.regression.gmm.IVRegressionResults.ssr "statsmodels.sandbox.regression.gmm.IVRegressionResults.ssr")() \| \| \| [`summary`](statsmodels.sandbox.regression.gmm.ivregressionresults.summary#statsmodels.sandbox.regression.gmm.IVRegressionResults.summary "statsmodels.sandbox.regression.gmm.IVRegressionResults.summary")([yname, xname, title, alpha]) \| Summarize the Regression Results \| \| [`summary2`](statsmodels.sandbox.regression.gmm.ivregressionresults.summary2#statsmodels.sandbox.regression.gmm.IVRegressionResults.summary2 "statsmodels.sandbox.regression.gmm.IVRegressionResults.summary2")([yname, xname, title, alpha, …]) \| Experimental summary function to summarize the regression results \| \| [`t_test`](statsmodels.sandbox.regression.gmm.ivregressionresults.t_test#statsmodels.sandbox.regression.gmm.IVRegressionResults.t_test "statsmodels.sandbox.regression.gmm.IVRegressionResults.t_test")(r\_matrix[, cov\_p, scale, use\_t]) \| Compute a t-test for a each linear hypothesis of the form Rb = q \| \| [`t_test_pairwise`](statsmodels.sandbox.regression.gmm.ivregressionresults.t_test_pairwise#statsmodels.sandbox.regression.gmm.IVRegressionResults.t_test_pairwise "statsmodels.sandbox.regression.gmm.IVRegressionResults.t_test_pairwise")(term\_name[, method, alpha, …]) \| perform pairwise t\_test with multiple testing corrected p-values \| \| [`tvalues`](statsmodels.sandbox.regression.gmm.ivregressionresults.tvalues#statsmodels.sandbox.regression.gmm.IVRegressionResults.tvalues "statsmodels.sandbox.regression.gmm.IVRegressionResults.tvalues")() \| Return the t-statistic for a given parameter estimate. \| \| [`uncentered_tss`](statsmodels.sandbox.regression.gmm.ivregressionresults.uncentered_tss#statsmodels.sandbox.regression.gmm.IVRegressionResults.uncentered_tss "statsmodels.sandbox.regression.gmm.IVRegressionResults.uncentered_tss")() \| \| \| [`wald_test`](statsmodels.sandbox.regression.gmm.ivregressionresults.wald_test#statsmodels.sandbox.regression.gmm.IVRegressionResults.wald_test "statsmodels.sandbox.regression.gmm.IVRegressionResults.wald_test")(r\_matrix[, cov\_p, scale, invcov, …]) \| Compute a Wald-test for a joint linear hypothesis. \| \| [`wald_test_terms`](statsmodels.sandbox.regression.gmm.ivregressionresults.wald_test_terms#statsmodels.sandbox.regression.gmm.IVRegressionResults.wald_test_terms "statsmodels.sandbox.regression.gmm.IVRegressionResults.wald_test_terms")([skip\_single, …]) \| Compute a sequence of Wald tests for terms over multiple columns \| \| [`wresid`](statsmodels.sandbox.regression.gmm.ivregressionresults.wresid#statsmodels.sandbox.regression.gmm.IVRegressionResults.wresid "statsmodels.sandbox.regression.gmm.IVRegressionResults.wresid")() \| \| #### Attributes \| \| \| \| --- \| --- \| \| `use_t` \| \| statsmodels statsmodels.stats.moment_helpers.cov2corr statsmodels.stats.moment\_helpers.cov2corr ========================================== `statsmodels.stats.moment_helpers.cov2corr(cov, return_std=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/moment_helpers.html#cov2corr) convert covariance matrix to correlation matrix \| Parameters: \| cov (array\_like, 2d) – covariance matrix, see Notes \| \| Returns: \| * corr (ndarray (subclass)) – correlation matrix * return\_std (bool) – If this is true then the standard deviation is also returned. By default only the correlation matrix is returned. \| #### Notes This function does not convert subclasses of ndarrays. This requires that division is defined elementwise. np.ma.array and np.matrix are allowed. statsmodels statsmodels.tsa.vector_ar.dynamic.DynamicVAR.r2 statsmodels.tsa.vector\_ar.dynamic.DynamicVAR.r2 ================================================ `DynamicVAR.r2()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/dynamic.html#DynamicVAR.r2) Returns the r-squared values. statsmodels statsmodels.tsa.statespace.kalman_filter.KalmanFilter.initialize_stationary statsmodels.tsa.statespace.kalman\_filter.KalmanFilter.initialize\_stationary ============================================================================= `KalmanFilter.initialize_stationary()` Initialize the statespace model as stationary. statsmodels statsmodels.sandbox.distributions.transformed.LogTransf_gen.cdf statsmodels.sandbox.distributions.transformed.LogTransf\_gen.cdf ================================================================ `LogTransf_gen.cdf(x, args, kwds)` Cumulative distribution function of the given RV. \| Parameters: \| x (array\_like) – quantiles * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| cdf – Cumulative distribution function evaluated at `x` \| \| Return type: \| ndarray \| statsmodels statsmodels.tsa.x13.x13_arima_select_order statsmodels.tsa.x13.x13\_arima\_select\_order ============================================= `statsmodels.tsa.x13.x13_arima_select_order(endog, maxorder=(2, 1), maxdiff=(2, 1), diff=None, exog=None, log=None, outlier=True, trading=False, forecast_years=None, start=None, freq=None, print_stdout=False, x12path=None, prefer_x13=True)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/x13.html#x13_arima_select_order) Perform automatic seaonal ARIMA order identification using x12/x13 ARIMA. \| Parameters: \| * endog (array-like, [pandas.Series](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.html#pandas.Series "(in pandas v0.22.0)")) – The series to model. It is best to use a pandas object with a DatetimeIndex or PeriodIndex. However, you can pass an array-like object. If your object does not have a dates index then `start` and `freq` are not optional. * maxorder (tuple) – The maximum order of the regular and seasonal ARMA polynomials to examine during the model identification. The order for the regular polynomial must be greater than zero and no larger than 4. The order for the seaonal polynomial may be 1 or 2. * maxdiff (tuple) – The maximum orders for regular and seasonal differencing in the automatic differencing procedure. Acceptable inputs for regular differencing are 1 and 2. The maximum order for seasonal differencing is 1. If `diff` is specified then `maxdiff` should be None. Otherwise, `diff` will be ignored. See also `diff`. * diff (tuple) – Fixes the orders of differencing for the regular and seasonal differencing. Regular differencing may be 0, 1, or 2. Seasonal differencing may be 0 or 1. `maxdiff` must be None, otherwise `diff` is ignored. * exog (array-like) – Exogenous variables. * log (bool or None) – If None, it is automatically determined whether to log the series or not. If False, logs are not taken. If True, logs are taken. * outlier (bool) – Whether or not outliers are tested for and corrected, if detected. * trading (bool) – Whether or not trading day effects are tested for. * forecast\_years (int) – Number of forecasts produced. The default is one year. * start (str, datetime) – Must be given if `endog` does not have date information in its index. Anything accepted by pandas.DatetimeIndex for the start value. * freq (str) – Must be givein if `endog` does not have date information in its index. Anything accapted by pandas.DatetimeIndex for the freq value. * print\_stdout (bool) – The stdout from X12/X13 is suppressed. To print it out, set this to True. Default is False. * x12path (str or None) – The path to x12 or x13 binary. If None, the program will attempt to find x13as or x12a on the PATH or by looking at X13PATH or X12PATH depending on the value of prefer\_x13. * prefer\_x13 (bool) – If True, will look for x13as first and will fallback to the X13PATH environmental variable. If False, will look for x12a first and will fallback to the X12PATH environmental variable. If x12path points to the path for the X12/X13 binary, it does nothing. \| \| Returns: \| results – A bunch object that has the following attributes:* order : tuple The regular order * sorder : tuple The seasonal order * include\_mean : bool Whether to include a mean or not * results : str The full results from the X12/X13 analysis * stdout : str The captured stdout from the X12/X13 analysis \| \| Return type: \| Bunch \| #### Notes This works by creating a specification file, writing it to a temporary directory, invoking X12/X13 in a subprocess, and reading the output back in.	programming_docs
statsmodels statsmodels.tsa.arima_model.ARIMA.score statsmodels.tsa.arima\_model.ARIMA.score ======================================== `ARIMA.score(params)` Compute the score function at params. #### Notes This is a numerical approximation. statsmodels statsmodels.sandbox.regression.try_catdata.labelmeanfilter statsmodels.sandbox.regression.try\_catdata.labelmeanfilter =========================================================== `statsmodels.sandbox.regression.try_catdata.labelmeanfilter(y, x)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/regression/try_catdata.html#labelmeanfilter) statsmodels statsmodels.robust.norms.TukeyBiweight.psi statsmodels.robust.norms.TukeyBiweight.psi ========================================== `TukeyBiweight.psi(z)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/norms.html#TukeyBiweight.psi) The psi function for Tukey’s biweight estimator The analytic derivative of rho \| Parameters: \| z (array-like) – 1d array \| \| Returns: \| psi – psi(z) = z\(1 - (z/c)\\2)\\2 for \|z\| <= Rpsi(z) = 0 for \|z\| > R \| \| Return type: \| array \| statsmodels statsmodels.discrete.discrete_model.MultinomialResults.summary2 statsmodels.discrete.discrete\_model.MultinomialResults.summary2 ================================================================ `MultinomialResults.summary2(alpha=0.05, float_format='%.4f')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#MultinomialResults.summary2) Experimental function to summarize regression results \| Parameters: \| alpha (float) – significance level for the confidence intervals * float\_format (string) – print format for floats in parameters summary \| \| Returns: \| smry – this holds the summary tables and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary2.Summary`](statsmodels.iolib.summary2.summary#statsmodels.iolib.summary2.Summary "statsmodels.iolib.summary2.Summary") class to hold summary results statsmodels statsmodels.genmod.families.family.Gamma.starting_mu statsmodels.genmod.families.family.Gamma.starting\_mu ===================================================== `Gamma.starting_mu(y)` Starting value for mu in the IRLS algorithm. \| Parameters: \| y (array) – The untransformed response variable. \| \| Returns: \| mu\_0 – The first guess on the transformed response variable. \| \| Return type: \| array \| #### Notes \[\mu\_0 = (Y + \overline{Y})/2\] Only the Binomial family takes a different initial value. statsmodels statsmodels.miscmodels.tmodel.TLinearModel.reduceparams statsmodels.miscmodels.tmodel.TLinearModel.reduceparams ======================================================= `TLinearModel.reduceparams(params)` statsmodels statsmodels.tsa.statespace.varmax.VARMAXResults.save statsmodels.tsa.statespace.varmax.VARMAXResults.save ==================================================== `VARMAXResults.save(fname, remove_data=False)` save a pickle of this instance \| Parameters: \| * fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. * remove\_data (bool) – If False (default), then the instance is pickled without changes. If True, then all arrays with length nobs are set to None before pickling. See the remove\_data method. In some cases not all arrays will be set to None. \| #### Notes If remove\_data is true and the model result does not implement a remove\_data method then this will raise an exception. statsmodels statsmodels.sandbox.regression.gmm.GMM.fitgmm statsmodels.sandbox.regression.gmm.GMM.fitgmm ============================================= `GMM.fitgmm(start, weights=None, optim_method='bfgs', optim_args=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/regression/gmm.html#GMM.fitgmm) estimate parameters using GMM \| Parameters: \| * start (array\_like) – starting values for minimization * weights (array) – weighting matrix for moment conditions. If weights is None, then the identity matrix is used \| \| Returns: \| paramest – estimated parameters \| \| Return type: \| array \| #### Notes todo: add fixed parameter option, not here ??? uses scipy.optimize.fmin statsmodels statsmodels.discrete.discrete_model.DiscreteResults.llr_pvalue statsmodels.discrete.discrete\_model.DiscreteResults.llr\_pvalue ================================================================ `DiscreteResults.llr_pvalue()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#DiscreteResults.llr_pvalue) statsmodels statsmodels.genmod.generalized_linear_model.GLM.get_distribution statsmodels.genmod.generalized\_linear\_model.GLM.get\_distribution =================================================================== `GLM.get_distribution(params, scale=1, exog=None, exposure=None, offset=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_linear_model.html#GLM.get_distribution) Returns a random number generator for the predictive distribution. \| Parameters: \| * params (array-like) – The model parameters. * scale (scalar) – The scale parameter. * exog (array-like) – The predictor variable matrix. \| \| Returns: \| Frozen random number generator object. Use the `rvs` method to generate random values. \| \| Return type: \| gen \| #### Notes Due to the behavior of `scipy.stats.distributions objects`, the returned random number generator must be called with `gen.rvs(n)` where `n` is the number of observations in the data set used to fit the model. If any other value is used for `n`, misleading results will be produced. statsmodels statsmodels.miscmodels.count.PoissonGMLE.information statsmodels.miscmodels.count.PoissonGMLE.information ==================================================== `PoissonGMLE.information(params)` Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.stats.contingency_tables.Table.independence_probabilities statsmodels.stats.contingency\_tables.Table.independence\_probabilities ======================================================================= `Table.independence_probabilities()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/contingency_tables.html#Table.independence_probabilities) statsmodels statsmodels.nonparametric.kernel_density.KDEMultivariate.imse statsmodels.nonparametric.kernel\_density.KDEMultivariate.imse ============================================================== `KDEMultivariate.imse(bw)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/nonparametric/kernel_density.html#KDEMultivariate.imse) Returns the Integrated Mean Square Error for the unconditional KDE. \| Parameters: \| bw (array\_like) – The bandwidth parameter(s). \| \| Returns: \| CV – The cross-validation objective function. \| \| Return type: \| float \| #### Notes See p. 27 in [[1]](#id4) for details on how to handle the multivariate estimation with mixed data types see p.6 in [[2]](#id5). The formula for the cross-validation objective function is: \[CV=\frac{1}{n^{2}}\sum\_{i=1}^{n}\sum\_{j=1}^{N} \bar{K}\_{h}(X\_{i},X\_{j})-\frac{2}{n(n-1)}\sum\_{i=1}^{n} \sum\_{j=1,j\neq i}^{N}K\_{h}(X\_{i},X\_{j})\] Where $\bar{K}\_{h}$ is the multivariate product convolution kernel (consult [[2]](#id5) for mixed data types). #### References \| \| \| \| --- \| --- \| \| [[1]](#id1) \| Racine, J., Li, Q. Nonparametric econometrics: theory and practice. Princeton University Press. (2007) \| \| \| \| \| --- \| --- \| \| [2] \| ([1](#id2), [2](#id3)) Racine, J., Li, Q. “Nonparametric Estimation of Distributions with Categorical and Continuous Data.” Working Paper. (2000) \| statsmodels statsmodels.genmod.families.links.CDFLink.deriv statsmodels.genmod.families.links.CDFLink.deriv =============================================== `CDFLink.deriv(p)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#CDFLink.deriv) Derivative of CDF link \| Parameters: \| p (array-like) – mean parameters \| \| Returns: \| g’(p) – The derivative of CDF transform at `p` \| \| Return type: \| array \| #### Notes g’(`p`) = 1./ `dbn`.pdf(`dbn`.ppf(`p`)) statsmodels statsmodels.sandbox.stats.multicomp.varcorrection_unequal statsmodels.sandbox.stats.multicomp.varcorrection\_unequal ========================================================== `statsmodels.sandbox.stats.multicomp.varcorrection_unequal(var_all, nobs_all, df_all)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/stats/multicomp.html#varcorrection_unequal) return joint variance from samples with unequal variances and unequal sample sizes something is wrong \| Parameters: \| * var\_all (array\_like) – The variance for each sample * nobs\_all (array\_like) – The number of observations for each sample * df\_all (array\_like) – degrees of freedom for each sample \| \| Returns: \| * varjoint (float) – joint variance. * dfjoint (float) – joint Satterthwait’s degrees of freedom \| #### Notes (copy, paste not correct) variance is 1/k \* sum\_i 1/n\_i where k is the number of samples and summation is over i=0,…,k-1. If all n\_i are the same, then the correction factor is 1/n. This needs to be multiplies by the joint variance estimate, means square error, MSE. To obtain the correction factor for the standard deviation, square root needs to be taken. This is for variance of mean difference not of studentized range. statsmodels statsmodels.tsa.statespace.mlemodel.MLEResults statsmodels.tsa.statespace.mlemodel.MLEResults ============================================== `class statsmodels.tsa.statespace.mlemodel.MLEResults(model, params, results, cov_type='opg', cov_kwds=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/mlemodel.html#MLEResults) Class to hold results from fitting a state space model. \| Parameters: \| model (MLEModel instance) – The fitted model instance * params (array) – Fitted parameters * filter\_results (KalmanFilter instance) – The underlying state space model and Kalman filter output \| `model` Model instance – A reference to the model that was fit. `filter_results` KalmanFilter instance – The underlying state space model and Kalman filter output `nobs` float – The number of observations used to fit the model. `params` array – The parameters of the model. `scale` float – This is currently set to 1.0 and not used by the model or its results. See also [`MLEModel`](statsmodels.tsa.statespace.mlemodel.mlemodel#statsmodels.tsa.statespace.mlemodel.MLEModel "statsmodels.tsa.statespace.mlemodel.MLEModel"), [`statsmodels.tsa.statespace.kalman_filter.FilterResults`](statsmodels.tsa.statespace.kalman_filter.filterresults#statsmodels.tsa.statespace.kalman_filter.FilterResults "statsmodels.tsa.statespace.kalman_filter.FilterResults"), [`statsmodels.tsa.statespace.representation.FrozenRepresentation`](statsmodels.tsa.statespace.representation.frozenrepresentation#statsmodels.tsa.statespace.representation.FrozenRepresentation "statsmodels.tsa.statespace.representation.FrozenRepresentation") #### Methods \| \| \| \| --- \| --- \| \| [`aic`](statsmodels.tsa.statespace.mlemodel.mleresults.aic#statsmodels.tsa.statespace.mlemodel.MLEResults.aic "statsmodels.tsa.statespace.mlemodel.MLEResults.aic")() \| (float) Akaike Information Criterion \| \| [`bic`](statsmodels.tsa.statespace.mlemodel.mleresults.bic#statsmodels.tsa.statespace.mlemodel.MLEResults.bic "statsmodels.tsa.statespace.mlemodel.MLEResults.bic")() \| (float) Bayes Information Criterion \| \| [`bse`](statsmodels.tsa.statespace.mlemodel.mleresults.bse#statsmodels.tsa.statespace.mlemodel.MLEResults.bse "statsmodels.tsa.statespace.mlemodel.MLEResults.bse")() \| \| \| [`conf_int`](statsmodels.tsa.statespace.mlemodel.mleresults.conf_int#statsmodels.tsa.statespace.mlemodel.MLEResults.conf_int "statsmodels.tsa.statespace.mlemodel.MLEResults.conf_int")([alpha, cols, method]) \| Returns the confidence interval of the fitted parameters. \| \| [`cov_params`](statsmodels.tsa.statespace.mlemodel.mleresults.cov_params#statsmodels.tsa.statespace.mlemodel.MLEResults.cov_params "statsmodels.tsa.statespace.mlemodel.MLEResults.cov_params")([r\_matrix, column, scale, cov\_p, …]) \| Returns the variance/covariance matrix. \| \| [`cov_params_approx`](statsmodels.tsa.statespace.mlemodel.mleresults.cov_params_approx#statsmodels.tsa.statespace.mlemodel.MLEResults.cov_params_approx "statsmodels.tsa.statespace.mlemodel.MLEResults.cov_params_approx")() \| (array) The variance / covariance matrix. \| \| [`cov_params_oim`](statsmodels.tsa.statespace.mlemodel.mleresults.cov_params_oim#statsmodels.tsa.statespace.mlemodel.MLEResults.cov_params_oim "statsmodels.tsa.statespace.mlemodel.MLEResults.cov_params_oim")() \| (array) The variance / covariance matrix. \| \| [`cov_params_opg`](statsmodels.tsa.statespace.mlemodel.mleresults.cov_params_opg#statsmodels.tsa.statespace.mlemodel.MLEResults.cov_params_opg "statsmodels.tsa.statespace.mlemodel.MLEResults.cov_params_opg")() \| (array) The variance / covariance matrix. \| \| [`cov_params_robust`](statsmodels.tsa.statespace.mlemodel.mleresults.cov_params_robust#statsmodels.tsa.statespace.mlemodel.MLEResults.cov_params_robust "statsmodels.tsa.statespace.mlemodel.MLEResults.cov_params_robust")() \| (array) The QMLE variance / covariance matrix. \| \| [`cov_params_robust_approx`](statsmodels.tsa.statespace.mlemodel.mleresults.cov_params_robust_approx#statsmodels.tsa.statespace.mlemodel.MLEResults.cov_params_robust_approx "statsmodels.tsa.statespace.mlemodel.MLEResults.cov_params_robust_approx")() \| (array) The QMLE variance / covariance matrix. \| \| [`cov_params_robust_oim`](statsmodels.tsa.statespace.mlemodel.mleresults.cov_params_robust_oim#statsmodels.tsa.statespace.mlemodel.MLEResults.cov_params_robust_oim "statsmodels.tsa.statespace.mlemodel.MLEResults.cov_params_robust_oim")() \| (array) The QMLE variance / covariance matrix. \| \| [`f_test`](statsmodels.tsa.statespace.mlemodel.mleresults.f_test#statsmodels.tsa.statespace.mlemodel.MLEResults.f_test "statsmodels.tsa.statespace.mlemodel.MLEResults.f_test")(r\_matrix[, cov\_p, scale, invcov]) \| Compute the F-test for a joint linear hypothesis. \| \| [`fittedvalues`](statsmodels.tsa.statespace.mlemodel.mleresults.fittedvalues#statsmodels.tsa.statespace.mlemodel.MLEResults.fittedvalues "statsmodels.tsa.statespace.mlemodel.MLEResults.fittedvalues")() \| (array) The predicted values of the model. \| \| [`forecast`](statsmodels.tsa.statespace.mlemodel.mleresults.forecast#statsmodels.tsa.statespace.mlemodel.MLEResults.forecast "statsmodels.tsa.statespace.mlemodel.MLEResults.forecast")([steps]) \| Out-of-sample forecasts \| \| [`get_forecast`](statsmodels.tsa.statespace.mlemodel.mleresults.get_forecast#statsmodels.tsa.statespace.mlemodel.MLEResults.get_forecast "statsmodels.tsa.statespace.mlemodel.MLEResults.get_forecast")([steps]) \| Out-of-sample forecasts \| \| [`get_prediction`](statsmodels.tsa.statespace.mlemodel.mleresults.get_prediction#statsmodels.tsa.statespace.mlemodel.MLEResults.get_prediction "statsmodels.tsa.statespace.mlemodel.MLEResults.get_prediction")([start, end, dynamic, index]) \| In-sample prediction and out-of-sample forecasting \| \| [`hqic`](statsmodels.tsa.statespace.mlemodel.mleresults.hqic#statsmodels.tsa.statespace.mlemodel.MLEResults.hqic "statsmodels.tsa.statespace.mlemodel.MLEResults.hqic")() \| (float) Hannan-Quinn Information Criterion \| \| [`impulse_responses`](statsmodels.tsa.statespace.mlemodel.mleresults.impulse_responses#statsmodels.tsa.statespace.mlemodel.MLEResults.impulse_responses "statsmodels.tsa.statespace.mlemodel.MLEResults.impulse_responses")([steps, impulse, …]) \| Impulse response function \| \| [`info_criteria`](statsmodels.tsa.statespace.mlemodel.mleresults.info_criteria#statsmodels.tsa.statespace.mlemodel.MLEResults.info_criteria "statsmodels.tsa.statespace.mlemodel.MLEResults.info_criteria")(criteria[, method]) \| Information criteria \| \| [`initialize`](statsmodels.tsa.statespace.mlemodel.mleresults.initialize#statsmodels.tsa.statespace.mlemodel.MLEResults.initialize "statsmodels.tsa.statespace.mlemodel.MLEResults.initialize")(model, params, \\kwd) \| \| \| [`llf`](statsmodels.tsa.statespace.mlemodel.mleresults.llf#statsmodels.tsa.statespace.mlemodel.MLEResults.llf "statsmodels.tsa.statespace.mlemodel.MLEResults.llf")() \| (float) The value of the log-likelihood function evaluated at `params`. \| \| [`llf_obs`](statsmodels.tsa.statespace.mlemodel.mleresults.llf_obs#statsmodels.tsa.statespace.mlemodel.MLEResults.llf_obs "statsmodels.tsa.statespace.mlemodel.MLEResults.llf_obs")() \| (float) The value of the log-likelihood function evaluated at `params`. \| \| [`load`](statsmodels.tsa.statespace.mlemodel.mleresults.load#statsmodels.tsa.statespace.mlemodel.MLEResults.load "statsmodels.tsa.statespace.mlemodel.MLEResults.load")(fname) \| load a pickle, (class method) \| \| [`loglikelihood_burn`](statsmodels.tsa.statespace.mlemodel.mleresults.loglikelihood_burn#statsmodels.tsa.statespace.mlemodel.MLEResults.loglikelihood_burn "statsmodels.tsa.statespace.mlemodel.MLEResults.loglikelihood_burn")() \| (float) The number of observations during which the likelihood is not evaluated. \| \| [`normalized_cov_params`](statsmodels.tsa.statespace.mlemodel.mleresults.normalized_cov_params#statsmodels.tsa.statespace.mlemodel.MLEResults.normalized_cov_params "statsmodels.tsa.statespace.mlemodel.MLEResults.normalized_cov_params")() \| \| \| [`plot_diagnostics`](statsmodels.tsa.statespace.mlemodel.mleresults.plot_diagnostics#statsmodels.tsa.statespace.mlemodel.MLEResults.plot_diagnostics "statsmodels.tsa.statespace.mlemodel.MLEResults.plot_diagnostics")([variable, lags, fig, figsize]) \| Diagnostic plots for standardized residuals of one endogenous variable \| \| [`predict`](statsmodels.tsa.statespace.mlemodel.mleresults.predict#statsmodels.tsa.statespace.mlemodel.MLEResults.predict "statsmodels.tsa.statespace.mlemodel.MLEResults.predict")([start, end, dynamic]) \| In-sample prediction and out-of-sample forecasting \| \| [`pvalues`](statsmodels.tsa.statespace.mlemodel.mleresults.pvalues#statsmodels.tsa.statespace.mlemodel.MLEResults.pvalues "statsmodels.tsa.statespace.mlemodel.MLEResults.pvalues")() \| (array) The p-values associated with the z-statistics of the coefficients. \| \| [`remove_data`](statsmodels.tsa.statespace.mlemodel.mleresults.remove_data#statsmodels.tsa.statespace.mlemodel.MLEResults.remove_data "statsmodels.tsa.statespace.mlemodel.MLEResults.remove_data")() \| remove data arrays, all nobs arrays from result and model \| \| [`resid`](statsmodels.tsa.statespace.mlemodel.mleresults.resid#statsmodels.tsa.statespace.mlemodel.MLEResults.resid "statsmodels.tsa.statespace.mlemodel.MLEResults.resid")() \| (array) The model residuals. \| \| [`save`](statsmodels.tsa.statespace.mlemodel.mleresults.save#statsmodels.tsa.statespace.mlemodel.MLEResults.save "statsmodels.tsa.statespace.mlemodel.MLEResults.save")(fname[, remove\_data]) \| save a pickle of this instance \| \| [`simulate`](statsmodels.tsa.statespace.mlemodel.mleresults.simulate#statsmodels.tsa.statespace.mlemodel.MLEResults.simulate "statsmodels.tsa.statespace.mlemodel.MLEResults.simulate")(nsimulations[, measurement\_shocks, …]) \| Simulate a new time series following the state space model \| \| [`summary`](statsmodels.tsa.statespace.mlemodel.mleresults.summary#statsmodels.tsa.statespace.mlemodel.MLEResults.summary "statsmodels.tsa.statespace.mlemodel.MLEResults.summary")([alpha, start, title, model\_name, …]) \| Summarize the Model \| \| [`t_test`](statsmodels.tsa.statespace.mlemodel.mleresults.t_test#statsmodels.tsa.statespace.mlemodel.MLEResults.t_test "statsmodels.tsa.statespace.mlemodel.MLEResults.t_test")(r\_matrix[, cov\_p, scale, use\_t]) \| Compute a t-test for a each linear hypothesis of the form Rb = q \| \| [`t_test_pairwise`](statsmodels.tsa.statespace.mlemodel.mleresults.t_test_pairwise#statsmodels.tsa.statespace.mlemodel.MLEResults.t_test_pairwise "statsmodels.tsa.statespace.mlemodel.MLEResults.t_test_pairwise")(term\_name[, method, alpha, …]) \| perform pairwise t\_test with multiple testing corrected p-values \| \| [`test_heteroskedasticity`](statsmodels.tsa.statespace.mlemodel.mleresults.test_heteroskedasticity#statsmodels.tsa.statespace.mlemodel.MLEResults.test_heteroskedasticity "statsmodels.tsa.statespace.mlemodel.MLEResults.test_heteroskedasticity")(method[, …]) \| Test for heteroskedasticity of standardized residuals \| \| [`test_normality`](statsmodels.tsa.statespace.mlemodel.mleresults.test_normality#statsmodels.tsa.statespace.mlemodel.MLEResults.test_normality "statsmodels.tsa.statespace.mlemodel.MLEResults.test_normality")(method) \| Test for normality of standardized residuals. \| \| [`test_serial_correlation`](statsmodels.tsa.statespace.mlemodel.mleresults.test_serial_correlation#statsmodels.tsa.statespace.mlemodel.MLEResults.test_serial_correlation "statsmodels.tsa.statespace.mlemodel.MLEResults.test_serial_correlation")(method[, lags]) \| Ljung-box test for no serial correlation of standardized residuals \| \| [`tvalues`](statsmodels.tsa.statespace.mlemodel.mleresults.tvalues#statsmodels.tsa.statespace.mlemodel.MLEResults.tvalues "statsmodels.tsa.statespace.mlemodel.MLEResults.tvalues")() \| Return the t-statistic for a given parameter estimate. \| \| [`wald_test`](statsmodels.tsa.statespace.mlemodel.mleresults.wald_test#statsmodels.tsa.statespace.mlemodel.MLEResults.wald_test "statsmodels.tsa.statespace.mlemodel.MLEResults.wald_test")(r\_matrix[, cov\_p, scale, invcov, …]) \| Compute a Wald-test for a joint linear hypothesis. \| \| [`wald_test_terms`](statsmodels.tsa.statespace.mlemodel.mleresults.wald_test_terms#statsmodels.tsa.statespace.mlemodel.MLEResults.wald_test_terms "statsmodels.tsa.statespace.mlemodel.MLEResults.wald_test_terms")([skip\_single, …]) \| Compute a sequence of Wald tests for terms over multiple columns \| \| [`zvalues`](statsmodels.tsa.statespace.mlemodel.mleresults.zvalues#statsmodels.tsa.statespace.mlemodel.MLEResults.zvalues "statsmodels.tsa.statespace.mlemodel.MLEResults.zvalues")() \| (array) The z-statistics for the coefficients. \| #### Attributes \| \| \| \| --- \| --- \| \| `use_t` \| \|	programming_docs
statsmodels statsmodels.sandbox.regression.gmm.GMM.score_cu statsmodels.sandbox.regression.gmm.GMM.score\_cu ================================================ `GMM.score_cu(params, epsilon=None, centered=True)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/regression/gmm.html#GMM.score_cu) statsmodels statsmodels.sandbox.tsa.fftarma.ArmaFft.padarr statsmodels.sandbox.tsa.fftarma.ArmaFft.padarr ============================================== `ArmaFft.padarr(arr, maxlag, atend=True)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/tsa/fftarma.html#ArmaFft.padarr) pad 1d array with zeros at end to have length maxlag function that is a method, no self used \| Parameters: \| * arr (array\_like, 1d) – array that will be padded with zeros * maxlag (int) – length of array after padding * atend (boolean) – If True (default), then the zeros are added to the end, otherwise to the front of the array \| \| Returns: \| arrp – zero-padded array \| \| Return type: \| ndarray \| #### Notes This is mainly written to extend coefficient arrays for the lag-polynomials. It returns a copy. statsmodels statsmodels.sandbox.distributions.extras.SkewNorm_gen.logcdf statsmodels.sandbox.distributions.extras.SkewNorm\_gen.logcdf ============================================================= `SkewNorm_gen.logcdf(x, args, kwds)` Log of the cumulative distribution function at x of the given RV. \| Parameters: \| x (array\_like) – quantiles * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| logcdf – Log of the cumulative distribution function evaluated at x \| \| Return type: \| array\_like \| statsmodels statsmodels.stats.stattools.robust_skewness statsmodels.stats.stattools.robust\_skewness ============================================ `statsmodels.stats.stattools.robust_skewness(y, axis=0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/stattools.html#robust_skewness) Calculates the four skewness measures in Kim & White \| Parameters: \| * y (array-like) – * axis (int or None, optional) – Axis along which the skewness measures are computed. If `None`, the entire array is used. \| \| Returns: \| * sk1 (ndarray) – The standard skewness estimator. * sk2 (ndarray) – Skewness estimator based on quartiles. * sk3 (ndarray) – Skewness estimator based on mean-median difference, standardized by absolute deviation. * sk4 (ndarray) – Skewness estimator based on mean-median difference, standardized by standard deviation. \| #### Notes The robust skewness measures are defined \[SK\_{2}=\frac{\left(q\_{.75}-q\_{.5}\right) -\left(q\_{.5}-q\_{.25}\right)}{q\_{.75}-q\_{.25}}\] \[SK\_{3}=\frac{\mu-\hat{q}\_{0.5}} {\hat{E}\left[\left\|y-\hat{\mu}\right\|\right]}\] \[SK\_{4}=\frac{\mu-\hat{q}\_{0.5}}{\hat{\sigma}}\] \| \| \| \| --- \| --- \| \| [\] \| Tae-Hwan Kim and Halbert White, “On more robust estimation of skewness and kurtosis,” Finance Research Letters, vol. 1, pp. 56-73, March 2004. \| statsmodels statsmodels.robust.robust_linear_model.RLMResults.chisq statsmodels.robust.robust\_linear\_model.RLMResults.chisq ========================================================= `RLMResults.chisq()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/robust_linear_model.html#RLMResults.chisq) statsmodels statsmodels.discrete.discrete_model.Logit.score_obs statsmodels.discrete.discrete\_model.Logit.score\_obs ===================================================== `Logit.score_obs(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#Logit.score_obs) Logit model Jacobian of the log-likelihood for each observation \| Parameters: \| params* (array-like) – The parameters of the model \| \| Returns: \| jac – The derivative of the loglikelihood for each observation evaluated at `params`. \| \| Return type: \| array-like \| #### Notes \[\frac{\partial\ln L\_{i}}{\partial\beta}=\left(y\_{i}-\Lambda\_{i}\right)x\_{i}\] for observations $i=1,...,n$ statsmodels statsmodels.nonparametric.kernel_density.KDEMultivariateConditional statsmodels.nonparametric.kernel\_density.KDEMultivariateConditional ==================================================================== `class statsmodels.nonparametric.kernel_density.KDEMultivariateConditional(endog, exog, dep_type, indep_type, bw, defaults=<statsmodels.nonparametric._kernel_base.EstimatorSettings object>)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/nonparametric/kernel_density.html#KDEMultivariateConditional) Conditional multivariate kernel density estimator. Calculates `P(Y_1,Y_2,...Y_n \| X_1,X_2...X_m) = P(X_1, X_2,...X_n, Y_1, Y_2,..., Y_m)/P(X_1, X_2,..., X_m)`. The conditional density is by definition the ratio of the two densities, see [[1]](#id2). \| Parameters: \| * endog (list of ndarrays or 2-D ndarray) – The training data for the dependent variables, used to determine the bandwidth(s). If a 2-D array, should be of shape (num\_observations, num\_variables). If a list, each list element is a separate observation. * exog (list of ndarrays or 2-D ndarray) – The training data for the independent variable; same shape as `endog`. * dep\_type (str) – The type of the dependent variables: c : Continuous u : Unordered (Discrete) o : Ordered (Discrete) The string should contain a type specifier for each variable, so for example `dep_type='ccuo'`. * indep\_type (str) – The type of the independent variables; specifed like `dep_type`. * bw (array\_like or str, optional) – If an array, it is a fixed user-specified bandwidth. If a string, should be one of: + normal\_reference: normal reference rule of thumb (default) + cv\_ml: cross validation maximum likelihood + cv\_ls: cross validation least squares * defaults (Instance of class EstimatorSettings) – The default values for the efficient bandwidth estimation \| `bw` array\_like – The bandwidth parameters See also [`KDEMultivariate`](statsmodels.nonparametric.kernel_density.kdemultivariate#statsmodels.nonparametric.kernel_density.KDEMultivariate "statsmodels.nonparametric.kernel_density.KDEMultivariate") #### References \| \| \| \| --- \| --- \| \| [[1]](#id1) \| <http://en.wikipedia.org/wiki/Conditional_probability_distribution> \| #### Examples ``` >>> import statsmodels.api as sm >>> nobs = 300 >>> c1 = np.random.normal(size=(nobs,1)) >>> c2 = np.random.normal(2,1,size=(nobs,1)) ``` ``` >>> dens_c = sm.nonparametric.KDEMultivariateConditional(endog=[c1], ... exog=[c2], dep_type='c', indep_type='c', bw='normal_reference') >>> dens_c.bw # show computed bandwidth array([ 0.41223484, 0.40976931]) ``` #### Methods \| \| \| \| --- \| --- \| \| [`cdf`](statsmodels.nonparametric.kernel_density.kdemultivariateconditional.cdf#statsmodels.nonparametric.kernel_density.KDEMultivariateConditional.cdf "statsmodels.nonparametric.kernel_density.KDEMultivariateConditional.cdf")([endog\_predict, exog\_predict]) \| Cumulative distribution function for the conditional density. \| \| [`imse`](statsmodels.nonparametric.kernel_density.kdemultivariateconditional.imse#statsmodels.nonparametric.kernel_density.KDEMultivariateConditional.imse "statsmodels.nonparametric.kernel_density.KDEMultivariateConditional.imse")(bw) \| The integrated mean square error for the conditional KDE. \| \| [`loo_likelihood`](statsmodels.nonparametric.kernel_density.kdemultivariateconditional.loo_likelihood#statsmodels.nonparametric.kernel_density.KDEMultivariateConditional.loo_likelihood "statsmodels.nonparametric.kernel_density.KDEMultivariateConditional.loo_likelihood")(bw[, func]) \| Returns the leave-one-out conditional likelihood of the data. \| \| [`pdf`](statsmodels.nonparametric.kernel_density.kdemultivariateconditional.pdf#statsmodels.nonparametric.kernel_density.KDEMultivariateConditional.pdf "statsmodels.nonparametric.kernel_density.KDEMultivariateConditional.pdf")([endog\_predict, exog\_predict]) \| Evaluate the probability density function. \| statsmodels statsmodels.stats.weightstats.DescrStatsW.std_ddof statsmodels.stats.weightstats.DescrStatsW.std\_ddof =================================================== `DescrStatsW.std_ddof(ddof=0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/weightstats.html#DescrStatsW.std_ddof) standard deviation of data with given ddof \| Parameters: \| ddof (int, float) – degrees of freedom correction, independent of attribute ddof \| \| Returns: \| std – standard deviation with denominator `sum_weights - ddof` \| \| Return type: \| float, ndarray \| statsmodels statsmodels.discrete.discrete_model.LogitResults.fittedvalues statsmodels.discrete.discrete\_model.LogitResults.fittedvalues ============================================================== `LogitResults.fittedvalues()` statsmodels statsmodels.robust.robust_linear_model.RLMResults.bse statsmodels.robust.robust\_linear\_model.RLMResults.bse ======================================================= `RLMResults.bse()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/robust_linear_model.html#RLMResults.bse) statsmodels statsmodels.tsa.statespace.varmax.VARMAXResults.summary statsmodels.tsa.statespace.varmax.VARMAXResults.summary ======================================================= `VARMAXResults.summary(alpha=0.05, start=None, separate_params=True)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/varmax.html#VARMAXResults.summary) Summarize the Model \| Parameters: \| * alpha (float, optional) – Significance level for the confidence intervals. Default is 0.05. * start (int, optional) – Integer of the start observation. Default is 0. * model\_name (string) – The name of the model used. Default is to use model class name. \| \| Returns: \| summary – This holds the summary table and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary.Summary`](statsmodels.iolib.summary.summary#statsmodels.iolib.summary.Summary "statsmodels.iolib.summary.Summary") statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.get_forecast statsmodels.regression.recursive\_ls.RecursiveLSResults.get\_forecast ===================================================================== `RecursiveLSResults.get_forecast(steps=1, *kwargs)` Out-of-sample forecasts \| Parameters: \| steps (int, str, or datetime, optional) – If an integer, the number of steps to forecast from the end of the sample. Can also be a date string to parse or a datetime type. However, if the dates index does not have a fixed frequency, steps must be an integer. Default * *\\kwargs* – Additional arguments may required for forecasting beyond the end of the sample. See `FilterResults.predict` for more details. \| \| Returns: \| forecast – Array of out of sample forecasts. A (steps x k\_endog) array. \| \| Return type: \| array \| statsmodels statsmodels.tsa.vector_ar.var_model.VARProcess.mean statsmodels.tsa.vector\_ar.var\_model.VARProcess.mean ===================================================== `VARProcess.mean()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARProcess.mean) Long run intercept of stable VAR process Warning: trend and exog except for intercept are ignored for this. This might change in future versions. Lütkepohl eq. 2.1.23 \[\mu = (I - A\_1 - \dots - A\_p)^{-1} \alpha\] where alpha is the intercept (parameter of the constant) statsmodels statsmodels.genmod.generalized_linear_model.GLMResults.resid_anscombe statsmodels.genmod.generalized\_linear\_model.GLMResults.resid\_anscombe ======================================================================== `GLMResults.resid_anscombe()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_linear_model.html#GLMResults.resid_anscombe) statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.cusum_squares statsmodels.regression.recursive\_ls.RecursiveLSResults.cusum\_squares ====================================================================== `RecursiveLSResults.cusum_squares()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/recursive_ls.html#RecursiveLSResults.cusum_squares) Cumulative sum of squares of standardized recursive residuals statistics \| Returns: \| cusum\_squares – An array of length `nobs - k_exog` holding the CUSUM of squares statistics. \| \| Return type: \| array\_like \| #### Notes The CUSUM of squares statistic takes the form: \[s\_t = \left ( \sum\_{j=k+1}^t w\_j^2 \right ) \Bigg / \left ( \sum\_{j=k+1}^T w\_j^2 \right )\] where $w\_j$ is the recursive residual at time $j$. Excludes the first `k_exog` datapoints. #### References \| \| \| \| --- \| --- \| \| [\] \| Brown, R. L., J. Durbin, and J. M. Evans. 1975. “Techniques for Testing the Constancy of Regression Relationships over Time.” Journal of the Royal Statistical Society. Series B (Methodological) 37 (2): 149-92. \| statsmodels statsmodels.genmod.families.family.NegativeBinomial.resid_dev statsmodels.genmod.families.family.NegativeBinomial.resid\_dev ============================================================== `NegativeBinomial.resid_dev(endog, mu, var_weights=1.0, scale=1.0)` The deviance residuals \| Parameters: \| endog (array-like) – The endogenous response variable * mu (array-like) – The inverse of the link function at the linear predicted values. * var\_weights (array-like) – 1d array of variance (analytic) weights. The default is 1. * scale (float, optional) – An optional scale argument. The default is 1. \| \| Returns: \| resid\_dev – Deviance residuals as defined below. \| \| Return type: \| float \| #### Notes The deviance residuals are defined by the contribution D\_i of observation i to the deviance as \[resid\\_dev\_i = sign(y\_i-\mu\_i) \sqrt{D\_i}\] D\_i is calculated from the \_resid\_dev method in each family. Distribution-specific documentation of the calculation is available there. statsmodels statsmodels.regression.quantile_regression.QuantRegResults.initialize statsmodels.regression.quantile\_regression.QuantRegResults.initialize ====================================================================== `QuantRegResults.initialize(model, params, kwd)` statsmodels statsmodels.genmod.cov_struct.Nested.update statsmodels.genmod.cov\_struct.Nested.update ============================================ `Nested.update(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/cov_struct.html#Nested.update) Updates the association parameter values based on the current regression coefficients. \| Parameters: \| params** (array-like) – Working values for the regression parameters. \| statsmodels statsmodels.discrete.discrete_model.GeneralizedPoisson.hessian statsmodels.discrete.discrete\_model.GeneralizedPoisson.hessian =============================================================== `GeneralizedPoisson.hessian(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#GeneralizedPoisson.hessian) Generalized Poisson model Hessian matrix of the loglikelihood \| Parameters: \| params (array-like) – The parameters of the model \| \| Returns: \| hess – The Hessian, second derivative of loglikelihood function, evaluated at `params` \| \| Return type: \| ndarray, (k\_vars, k\_vars) \| statsmodels statsmodels.tsa.statespace.mlemodel.MLEModel.hessian statsmodels.tsa.statespace.mlemodel.MLEModel.hessian ==================================================== `MLEModel.hessian(params, args, kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/mlemodel.html#MLEModel.hessian) Hessian matrix of the likelihood function, evaluated at the given parameters \| Parameters: \| params (array\_like) – Array of parameters at which to evaluate the hessian. * args – Additional positional arguments to the `loglike` method. * kwargs – Additional keyword arguments to the `loglike` method. \| \| Returns: \| hessian – Hessian matrix evaluated at `params` \| \| Return type: \| array \| #### Notes This is a numerical approximation. Both \args and \\kwargs are necessary because the optimizer from `fit` must call this function and only supports passing arguments via \args (for example `scipy.optimize.fmin_l_bfgs`). statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.resid statsmodels.regression.recursive\_ls.RecursiveLSResults.resid ============================================================= `RecursiveLSResults.resid()` (array) The model residuals. An (nobs x k\_endog) array. statsmodels statsmodels.discrete.discrete_model.DiscreteModel.cov_params_func_l1 statsmodels.discrete.discrete\_model.DiscreteModel.cov\_params\_func\_l1 ======================================================================== `DiscreteModel.cov_params_func_l1(likelihood_model, xopt, retvals)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#DiscreteModel.cov_params_func_l1) Computes cov\_params on a reduced parameter space corresponding to the nonzero parameters resulting from the l1 regularized fit. Returns a full cov\_params matrix, with entries corresponding to zero’d values set to np.nan. statsmodels statsmodels.tsa.statespace.sarimax.SARIMAXResults.save statsmodels.tsa.statespace.sarimax.SARIMAXResults.save ====================================================== `SARIMAXResults.save(fname, remove_data=False)` save a pickle of this instance \| Parameters: \| * fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. * remove\_data (bool) – If False (default), then the instance is pickled without changes. If True, then all arrays with length nobs are set to None before pickling. See the remove\_data method. In some cases not all arrays will be set to None. \| #### Notes If remove\_data is true and the model result does not implement a remove\_data method then this will raise an exception. statsmodels statsmodels.imputation.mice.MICEData.next_sample statsmodels.imputation.mice.MICEData.next\_sample ================================================= `MICEData.next_sample()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/imputation/mice.html#MICEData.next_sample) Returns the next imputed dataset in the imputation process. \| Returns: \| data – An imputed dataset from the MICE chain. \| \| Return type: \| array-like \| #### Notes `MICEData` does not have a `skip` parameter. Consecutive values returned by `next_sample` are immediately consecutive in the imputation chain. The returned value is a reference to the data attribute of the class and should be copied before making any changes. statsmodels statsmodels.genmod.generalized_linear_model.GLM.score_factor statsmodels.genmod.generalized\_linear\_model.GLM.score\_factor =============================================================== `GLM.score_factor(params, scale=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_linear_model.html#GLM.score_factor) weights for score for each observation This can be considered as score residuals. \| Parameters: \| * params (ndarray) – parameter at which score is evaluated * scale (None or float) – If scale is None, then the default scale will be calculated. Default scale is defined by `self.scaletype` and set in fit. If scale is not None, then it is used as a fixed scale. \| \| Returns: \| score\_factor – A 1d weight vector used in the calculation of the score\_obs. The score\_obs are obtained by `score_factor[:, None] * exog` \| \| Return type: \| ndarray\_1d \|	programming_docs
statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.loglikelihood_burn statsmodels.tsa.statespace.dynamic\_factor.DynamicFactorResults.loglikelihood\_burn =================================================================================== `DynamicFactorResults.loglikelihood_burn()` (float) The number of observations during which the likelihood is not evaluated. statsmodels statsmodels.genmod.generalized_linear_model.GLMResults.mu statsmodels.genmod.generalized\_linear\_model.GLMResults.mu =========================================================== `GLMResults.mu()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_linear_model.html#GLMResults.mu) statsmodels statsmodels.stats.contingency_tables.Table2x2.oddsratio statsmodels.stats.contingency\_tables.Table2x2.oddsratio ======================================================== `Table2x2.oddsratio()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/contingency_tables.html#Table2x2.oddsratio) statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.cov_params_robust_approx statsmodels.regression.recursive\_ls.RecursiveLSResults.cov\_params\_robust\_approx =================================================================================== `RecursiveLSResults.cov_params_robust_approx()` (array) The QMLE variance / covariance matrix. Computed using the numerical Hessian as the evaluated hessian. statsmodels statsmodels.sandbox.distributions.extras.SkewNorm2_gen.isf statsmodels.sandbox.distributions.extras.SkewNorm2\_gen.isf =========================================================== `SkewNorm2_gen.isf(q, args, kwds)` Inverse survival function (inverse of `sf`) at q of the given RV. \| Parameters: \| q (array\_like) – upper tail probability * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| x – Quantile corresponding to the upper tail probability q. \| \| Return type: \| ndarray or scalar \| statsmodels statsmodels.discrete.count_model.ZeroInflatedPoissonResults.wald_test_terms statsmodels.discrete.count\_model.ZeroInflatedPoissonResults.wald\_test\_terms ============================================================================== `ZeroInflatedPoissonResults.wald_test_terms(skip_single=False, extra_constraints=None, combine_terms=None)` Compute a sequence of Wald tests for terms over multiple columns This computes joined Wald tests for the hypothesis that all coefficients corresponding to a `term` are zero. `Terms` are defined by the underlying formula or by string matching. \| Parameters: \| * skip\_single (boolean) – If true, then terms that consist only of a single column and, therefore, refers only to a single parameter is skipped. If false, then all terms are included. * extra\_constraints (ndarray) – not tested yet * combine\_terms (None or list of strings) – Each string in this list is matched to the name of the terms or the name of the exogenous variables. All columns whose name includes that string are combined in one joint test. \| \| Returns: \| test\_result – The result instance contains `table` which is a pandas DataFrame with the test results: test statistic, degrees of freedom and pvalues. \| \| Return type: \| result instance \| #### Examples ``` >>> res_ols = ols("np.log(Days+1) ~ C(Duration, Sum)C(Weight, Sum)", data).fit() >>> res_ols.wald_test_terms() <class 'statsmodels.stats.contrast.WaldTestResults'> F P>F df constraint df denom Intercept 279.754525 2.37985521351e-22 1 51 C(Duration, Sum) 5.367071 0.0245738436636 1 51 C(Weight, Sum) 12.432445 3.99943118767e-05 2 51 C(Duration, Sum):C(Weight, Sum) 0.176002 0.83912310946 2 51 ``` ``` >>> res_poi = Poisson.from_formula("Days ~ C(Weight) C(Duration)", data).fit(cov_type='HC0') >>> wt = res_poi.wald_test_terms(skip_single=False, combine_terms=['Duration', 'Weight']) >>> print(wt) chi2 P>chi2 df constraint Intercept 15.695625 7.43960374424e-05 1 C(Weight) 16.132616 0.000313940174705 2 C(Duration) 1.009147 0.315107378931 1 C(Weight):C(Duration) 0.216694 0.897315972824 2 Duration 11.187849 0.010752286833 3 Weight 30.263368 4.32586407145e-06 4 ``` statsmodels statsmodels.regression.quantile_regression.QuantReg.information statsmodels.regression.quantile\_regression.QuantReg.information ================================================================ `QuantReg.information(params)` Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.tsa.regime_switching.markov_regression.MarkovRegression.predict_conditional statsmodels.tsa.regime\_switching.markov\_regression.MarkovRegression.predict\_conditional ========================================================================================== `MarkovRegression.predict_conditional(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/regime_switching/markov_regression.html#MarkovRegression.predict_conditional) In-sample prediction, conditional on the current regime \| Parameters: \| params (array\_like) – Array of parameters at which to perform prediction. \| \| Returns: \| predict – Array of predictions conditional on current, and possibly past, regimes \| \| Return type: \| array\_like \| statsmodels statsmodels.genmod.cov_struct.GlobalOddsRatio statsmodels.genmod.cov\_struct.GlobalOddsRatio ============================================== `class statsmodels.genmod.cov_struct.GlobalOddsRatio(endog_type)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/cov_struct.html#GlobalOddsRatio) Estimate the global odds ratio for a GEE with ordinal or nominal data. #### References PJ Heagerty and S Zeger. “Marginal Regression Models for Clustered Ordinal Measurements”. Journal of the American Statistical Association Vol. 91, Issue 435 (1996). Thomas Lumley. Generalized Estimating Equations for Ordinal Data: A Note on Working Correlation Structures. Biometrics Vol. 52, No. 1 (Mar., 1996), pp. 354-361 <http://www.jstor.org/stable/2533173> #### Notes The following data structures are calculated in the class: ‘ibd’ is a list whose i^th element ibd[i] is a sequence of integer pairs (a,b), where endog\_li[i][a:b] is the subvector of binary indicators derived from the same ordinal value. `cpp` is a dictionary where cpp[group] is a map from cut-point pairs (c,c’) to the indices of all between-subject pairs derived from the given cut points. #### Methods \| \| \| \| --- \| --- \| \| [`covariance_matrix`](statsmodels.genmod.cov_struct.globaloddsratio.covariance_matrix#statsmodels.genmod.cov_struct.GlobalOddsRatio.covariance_matrix "statsmodels.genmod.cov_struct.GlobalOddsRatio.covariance_matrix")(expected\_value, index) \| Returns the working covariance or correlation matrix for a given cluster of data. \| \| [`covariance_matrix_solve`](statsmodels.genmod.cov_struct.globaloddsratio.covariance_matrix_solve#statsmodels.genmod.cov_struct.GlobalOddsRatio.covariance_matrix_solve "statsmodels.genmod.cov_struct.GlobalOddsRatio.covariance_matrix_solve")(expval, index, …) \| Solves matrix equations of the form `covmat * soln = rhs` and returns the values of `soln`, where `covmat` is the covariance matrix represented by this class. \| \| [`get_eyy`](statsmodels.genmod.cov_struct.globaloddsratio.get_eyy#statsmodels.genmod.cov_struct.GlobalOddsRatio.get_eyy "statsmodels.genmod.cov_struct.GlobalOddsRatio.get_eyy")(endog\_expval, index) \| Returns a matrix V such that V[i,j] is the joint probability that endog[i] = 1 and endog[j] = 1, based on the marginal probabilities of endog and the global odds ratio `current_or`. \| \| [`initialize`](statsmodels.genmod.cov_struct.globaloddsratio.initialize#statsmodels.genmod.cov_struct.GlobalOddsRatio.initialize "statsmodels.genmod.cov_struct.GlobalOddsRatio.initialize")(model) \| Called by GEE, used by implementations that need additional setup prior to running `fit`. \| \| [`observed_crude_oddsratio`](statsmodels.genmod.cov_struct.globaloddsratio.observed_crude_oddsratio#statsmodels.genmod.cov_struct.GlobalOddsRatio.observed_crude_oddsratio "statsmodels.genmod.cov_struct.GlobalOddsRatio.observed_crude_oddsratio")() \| To obtain the crude (global) odds ratio, first pool all binary indicators corresponding to a given pair of cut points (c,c’), then calculate the odds ratio for this 2x2 table. \| \| [`pooled_odds_ratio`](statsmodels.genmod.cov_struct.globaloddsratio.pooled_odds_ratio#statsmodels.genmod.cov_struct.GlobalOddsRatio.pooled_odds_ratio "statsmodels.genmod.cov_struct.GlobalOddsRatio.pooled_odds_ratio")(tables) \| Returns the pooled odds ratio for a list of 2x2 tables. \| \| [`summary`](statsmodels.genmod.cov_struct.globaloddsratio.summary#statsmodels.genmod.cov_struct.GlobalOddsRatio.summary "statsmodels.genmod.cov_struct.GlobalOddsRatio.summary")() \| Returns a text summary of the current estimate of the dependence structure. \| \| [`update`](statsmodels.genmod.cov_struct.globaloddsratio.update#statsmodels.genmod.cov_struct.GlobalOddsRatio.update "statsmodels.genmod.cov_struct.GlobalOddsRatio.update")(params) \| Updates the association parameter values based on the current regression coefficients. \| statsmodels statsmodels.discrete.discrete_model.MultinomialResults.llr_pvalue statsmodels.discrete.discrete\_model.MultinomialResults.llr\_pvalue =================================================================== `MultinomialResults.llr_pvalue()` statsmodels statsmodels.stats.proportion.binom_tost_reject_interval statsmodels.stats.proportion.binom\_tost\_reject\_interval ========================================================== `statsmodels.stats.proportion.binom_tost_reject_interval(low, upp, nobs, alpha=0.05)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/proportion.html#binom_tost_reject_interval) rejection region for binomial TOST The interval includes the end points, `reject` if and only if `r_low <= x <= r_upp`. The interval might be empty with `r_upp < r_low`. \| Parameters: \| * upp (low,) – lower and upper limit of equivalence region * nobs (integer) – the number of trials or observations. \| \| Returns: \| x\_low, x\_upp – lower and upper bound of rejection region \| \| Return type: \| float \| statsmodels statsmodels.tsa.ar_model.AR.loglike statsmodels.tsa.ar\_model.AR.loglike ==================================== `AR.loglike(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/ar_model.html#AR.loglike) The loglikelihood of an AR(p) process \| Parameters: \| params (array) – The fitted parameters of the AR model \| \| Returns: \| llf – The loglikelihood evaluated at `params` \| \| Return type: \| float \| #### Notes Contains constant term. If the model is fit by OLS then this returns the conditonal maximum likelihood. \[\frac{\left(n-p\right)}{2}\left(\log\left(2\pi\right)+\log\left(\sigma^{2}\right)\right)-\frac{1}{\sigma^{2}}\sum\_{i}\epsilon\_{i}^{2}\] If it is fit by MLE then the (exact) unconditional maximum likelihood is returned. \[-\frac{n}{2}log\left(2\pi\right)-\frac{n}{2}\log\left(\sigma^{2}\right)+\frac{1}{2}\left\|V\_{p}^{-1}\right\|-\frac{1}{2\sigma^{2}}\left(y\_{p}-\mu\_{p}\right)^{\prime}V\_{p}^{-1}\left(y\_{p}-\mu\_{p}\right)-\frac{1}{2\sigma^{2}}\sum\_{t=p+1}^{n}\epsilon\_{i}^{2}\] where $\mu\_{p}$ is a (`p` x 1) vector with each element equal to the mean of the AR process and $\sigma^{2}V\_{p}$ is the (`p` x `p`) variance-covariance matrix of the first `p` observations. statsmodels statsmodels.nonparametric.kernel_regression.KernelReg.aic_hurvich statsmodels.nonparametric.kernel\_regression.KernelReg.aic\_hurvich =================================================================== `KernelReg.aic_hurvich(bw, func=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/nonparametric/kernel_regression.html#KernelReg.aic_hurvich) Computes the AIC Hurvich criteria for the estimation of the bandwidth. \| Parameters: \| bw (str or array\_like) – See the `bw` parameter of `KernelReg` for details. \| \| Returns: \| * aic (ndarray) – The AIC Hurvich criteria, one element for each variable. * func (None) – Unused here, needed in signature because it’s used in `cv_loo`. \| #### References See ch.2 in [1] and p.35 in [2]. statsmodels statsmodels.discrete.discrete_model.LogitResults.cov_params statsmodels.discrete.discrete\_model.LogitResults.cov\_params ============================================================= `LogitResults.cov_params(r_matrix=None, column=None, scale=None, cov_p=None, other=None)` Returns the variance/covariance matrix. The variance/covariance matrix can be of a linear contrast of the estimates of params or all params multiplied by scale which will usually be an estimate of sigma^2. Scale is assumed to be a scalar. \| Parameters: \| * r\_matrix (array-like) – Can be 1d, or 2d. Can be used alone or with other. * column (array-like, optional) – Must be used on its own. Can be 0d or 1d see below. * scale (float, optional) – Can be specified or not. Default is None, which means that the scale argument is taken from the model. * other (array-like, optional) – Can be used when r\_matrix is specified. \| \| Returns: \| cov – covariance matrix of the parameter estimates or of linear combination of parameter estimates. See Notes. \| \| Return type: \| ndarray \| #### Notes (The below are assumed to be in matrix notation.) If no argument is specified returns the covariance matrix of a model `(scale)(X.T X)^(-1)` If contrast is specified it pre and post-multiplies as follows `(scale) r_matrix (X.T X)^(-1) r_matrix.T` If contrast and other are specified returns `(scale) * r_matrix (X.T X)^(-1) other.T` If column is specified returns `(scale) * (X.T X)^(-1)[column,column]` if column is 0d OR `(scale) * (X.T X)^(-1)[column][:,column]` if column is 1d statsmodels statsmodels.regression.linear_model.RegressionResults.wald_test_terms statsmodels.regression.linear\_model.RegressionResults.wald\_test\_terms ======================================================================== `RegressionResults.wald_test_terms(skip_single=False, extra_constraints=None, combine_terms=None)` Compute a sequence of Wald tests for terms over multiple columns This computes joined Wald tests for the hypothesis that all coefficients corresponding to a `term` are zero. `Terms` are defined by the underlying formula or by string matching. \| Parameters: \| * skip\_single (boolean) – If true, then terms that consist only of a single column and, therefore, refers only to a single parameter is skipped. If false, then all terms are included. * extra\_constraints (ndarray) – not tested yet * combine\_terms (None or list of strings) – Each string in this list is matched to the name of the terms or the name of the exogenous variables. All columns whose name includes that string are combined in one joint test. \| \| Returns: \| test\_result – The result instance contains `table` which is a pandas DataFrame with the test results: test statistic, degrees of freedom and pvalues. \| \| Return type: \| result instance \| #### Examples ``` >>> res_ols = ols("np.log(Days+1) ~ C(Duration, Sum)C(Weight, Sum)", data).fit() >>> res_ols.wald_test_terms() <class 'statsmodels.stats.contrast.WaldTestResults'> F P>F df constraint df denom Intercept 279.754525 2.37985521351e-22 1 51 C(Duration, Sum) 5.367071 0.0245738436636 1 51 C(Weight, Sum) 12.432445 3.99943118767e-05 2 51 C(Duration, Sum):C(Weight, Sum) 0.176002 0.83912310946 2 51 ``` ``` >>> res_poi = Poisson.from_formula("Days ~ C(Weight) C(Duration)", data).fit(cov_type='HC0') >>> wt = res_poi.wald_test_terms(skip_single=False, combine_terms=['Duration', 'Weight']) >>> print(wt) chi2 P>chi2 df constraint Intercept 15.695625 7.43960374424e-05 1 C(Weight) 16.132616 0.000313940174705 2 C(Duration) 1.009147 0.315107378931 1 C(Weight):C(Duration) 0.216694 0.897315972824 2 Duration 11.187849 0.010752286833 3 Weight 30.263368 4.32586407145e-06 4 ``` statsmodels statsmodels.stats.proportion.proportions_chisquare_allpairs statsmodels.stats.proportion.proportions\_chisquare\_allpairs ============================================================= `statsmodels.stats.proportion.proportions_chisquare_allpairs(count, nobs, multitest_method='hs')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/proportion.html#proportions_chisquare_allpairs) chisquare test of proportions for all pairs of k samples Performs a chisquare test for proportions for all pairwise comparisons. The alternative is two-sided \| Parameters: \| * count (integer or array\_like) – the number of successes in nobs trials. * nobs (integer) – the number of trials or observations. * prop (float, optional) – The probability of success under the null hypothesis, `0 <= prop <= 1`. The default value is `prop = 0.5` * multitest\_method (string) – This chooses the method for the multiple testing p-value correction, that is used as default in the results. It can be any method that is available in `multipletesting`. The default is Holm-Sidak ‘hs’. \| \| Returns: \| result – The returned results instance has several statistics, such as p-values, attached, and additional methods for using a non-default `multitest_method`. \| \| Return type: \| AllPairsResults instance \| #### Notes Yates continuity correction is not available. statsmodels statsmodels.multivariate.pca.PCA.plot_rsquare statsmodels.multivariate.pca.PCA.plot\_rsquare ============================================== `PCA.plot_rsquare(ncomp=None, ax=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/multivariate/pca.html#PCA.plot_rsquare) Box plots of the individual series R-square against the number of PCs \| Parameters: \| * ncomp (int, optional) – Number of components ot include in the plot. If None, will plot the minimum of 10 or the number of computed components * ax (Matplotlib axes instance, optional) – An axes on which to draw the graph. If omitted, new a figure is created \| \| Returns: \| fig – Handle to the figure \| \| Return type: \| figure \| statsmodels statsmodels.tsa.statespace.varmax.VARMAX.loglikeobs statsmodels.tsa.statespace.varmax.VARMAX.loglikeobs =================================================== `VARMAX.loglikeobs(params, transformed=True, complex_step=False, *kwargs)` Loglikelihood evaluation \| Parameters: \| params (array\_like) – Array of parameters at which to evaluate the loglikelihood function. * transformed (boolean, optional) – Whether or not `params` is already transformed. Default is True. * *\\kwargs* – Additional keyword arguments to pass to the Kalman filter. See `KalmanFilter.filter` for more details. \| #### Notes [[1]](#id2) recommend maximizing the average likelihood to avoid scale issues; this is done automatically by the base Model fit method. #### References \| \| \| \| --- \| --- \| \| [[1]](#id1) \| Koopman, Siem Jan, Neil Shephard, and Jurgen A. Doornik. 1999. Statistical Algorithms for Models in State Space Using SsfPack 2.2. Econometrics Journal 2 (1): 107-60. doi:10.1111/1368-423X.00023. \| See also [`update`](statsmodels.tsa.statespace.varmax.varmax.update#statsmodels.tsa.statespace.varmax.VARMAX.update "statsmodels.tsa.statespace.varmax.VARMAX.update") modifies the internal state of the Model to reflect new params	programming_docs
statsmodels statsmodels.tsa.arima_model.ARIMAResults statsmodels.tsa.arima\_model.ARIMAResults ========================================= `class statsmodels.tsa.arima_model.ARIMAResults(model, params, normalized_cov_params=None, scale=1.0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_model.html#ARIMAResults) #### Methods \| \| \| \| --- \| --- \| \| [`aic`](statsmodels.tsa.arima_model.arimaresults.aic#statsmodels.tsa.arima_model.ARIMAResults.aic "statsmodels.tsa.arima_model.ARIMAResults.aic")() \| \| \| [`arfreq`](statsmodels.tsa.arima_model.arimaresults.arfreq#statsmodels.tsa.arima_model.ARIMAResults.arfreq "statsmodels.tsa.arima_model.ARIMAResults.arfreq")() \| Returns the frequency of the AR roots. \| \| [`arparams`](statsmodels.tsa.arima_model.arimaresults.arparams#statsmodels.tsa.arima_model.ARIMAResults.arparams "statsmodels.tsa.arima_model.ARIMAResults.arparams")() \| \| \| [`arroots`](statsmodels.tsa.arima_model.arimaresults.arroots#statsmodels.tsa.arima_model.ARIMAResults.arroots "statsmodels.tsa.arima_model.ARIMAResults.arroots")() \| \| \| [`bic`](statsmodels.tsa.arima_model.arimaresults.bic#statsmodels.tsa.arima_model.ARIMAResults.bic "statsmodels.tsa.arima_model.ARIMAResults.bic")() \| \| \| [`bse`](statsmodels.tsa.arima_model.arimaresults.bse#statsmodels.tsa.arima_model.ARIMAResults.bse "statsmodels.tsa.arima_model.ARIMAResults.bse")() \| \| \| [`conf_int`](statsmodels.tsa.arima_model.arimaresults.conf_int#statsmodels.tsa.arima_model.ARIMAResults.conf_int "statsmodels.tsa.arima_model.ARIMAResults.conf_int")([alpha, cols, method]) \| Returns the confidence interval of the fitted parameters. \| \| [`cov_params`](statsmodels.tsa.arima_model.arimaresults.cov_params#statsmodels.tsa.arima_model.ARIMAResults.cov_params "statsmodels.tsa.arima_model.ARIMAResults.cov_params")() \| Returns the variance/covariance matrix. \| \| [`f_test`](statsmodels.tsa.arima_model.arimaresults.f_test#statsmodels.tsa.arima_model.ARIMAResults.f_test "statsmodels.tsa.arima_model.ARIMAResults.f_test")(r\_matrix[, cov\_p, scale, invcov]) \| Compute the F-test for a joint linear hypothesis. \| \| [`fittedvalues`](statsmodels.tsa.arima_model.arimaresults.fittedvalues#statsmodels.tsa.arima_model.ARIMAResults.fittedvalues "statsmodels.tsa.arima_model.ARIMAResults.fittedvalues")() \| \| \| [`forecast`](statsmodels.tsa.arima_model.arimaresults.forecast#statsmodels.tsa.arima_model.ARIMAResults.forecast "statsmodels.tsa.arima_model.ARIMAResults.forecast")([steps, exog, alpha]) \| Out-of-sample forecasts \| \| [`hqic`](statsmodels.tsa.arima_model.arimaresults.hqic#statsmodels.tsa.arima_model.ARIMAResults.hqic "statsmodels.tsa.arima_model.ARIMAResults.hqic")() \| \| \| [`initialize`](statsmodels.tsa.arima_model.arimaresults.initialize#statsmodels.tsa.arima_model.ARIMAResults.initialize "statsmodels.tsa.arima_model.ARIMAResults.initialize")(model, params, \\kwd) \| \| \| [`llf`](statsmodels.tsa.arima_model.arimaresults.llf#statsmodels.tsa.arima_model.ARIMAResults.llf "statsmodels.tsa.arima_model.ARIMAResults.llf")() \| \| \| [`load`](statsmodels.tsa.arima_model.arimaresults.load#statsmodels.tsa.arima_model.ARIMAResults.load "statsmodels.tsa.arima_model.ARIMAResults.load")(fname) \| load a pickle, (class method) \| \| [`mafreq`](statsmodels.tsa.arima_model.arimaresults.mafreq#statsmodels.tsa.arima_model.ARIMAResults.mafreq "statsmodels.tsa.arima_model.ARIMAResults.mafreq")() \| Returns the frequency of the MA roots. \| \| [`maparams`](statsmodels.tsa.arima_model.arimaresults.maparams#statsmodels.tsa.arima_model.ARIMAResults.maparams "statsmodels.tsa.arima_model.ARIMAResults.maparams")() \| \| \| [`maroots`](statsmodels.tsa.arima_model.arimaresults.maroots#statsmodels.tsa.arima_model.ARIMAResults.maroots "statsmodels.tsa.arima_model.ARIMAResults.maroots")() \| \| \| [`normalized_cov_params`](statsmodels.tsa.arima_model.arimaresults.normalized_cov_params#statsmodels.tsa.arima_model.ARIMAResults.normalized_cov_params "statsmodels.tsa.arima_model.ARIMAResults.normalized_cov_params")() \| \| \| [`plot_predict`](statsmodels.tsa.arima_model.arimaresults.plot_predict#statsmodels.tsa.arima_model.ARIMAResults.plot_predict "statsmodels.tsa.arima_model.ARIMAResults.plot_predict")([start, end, exog, dynamic, …]) \| Plot forecasts \| \| [`predict`](statsmodels.tsa.arima_model.arimaresults.predict#statsmodels.tsa.arima_model.ARIMAResults.predict "statsmodels.tsa.arima_model.ARIMAResults.predict")([start, end, exog, typ, dynamic]) \| ARIMA model in-sample and out-of-sample prediction \| \| [`pvalues`](statsmodels.tsa.arima_model.arimaresults.pvalues#statsmodels.tsa.arima_model.ARIMAResults.pvalues "statsmodels.tsa.arima_model.ARIMAResults.pvalues")() \| \| \| [`remove_data`](statsmodels.tsa.arima_model.arimaresults.remove_data#statsmodels.tsa.arima_model.ARIMAResults.remove_data "statsmodels.tsa.arima_model.ARIMAResults.remove_data")() \| remove data arrays, all nobs arrays from result and model \| \| [`resid`](statsmodels.tsa.arima_model.arimaresults.resid#statsmodels.tsa.arima_model.ARIMAResults.resid "statsmodels.tsa.arima_model.ARIMAResults.resid")() \| \| \| [`save`](statsmodels.tsa.arima_model.arimaresults.save#statsmodels.tsa.arima_model.ARIMAResults.save "statsmodels.tsa.arima_model.ARIMAResults.save")(fname[, remove\_data]) \| save a pickle of this instance \| \| [`summary`](statsmodels.tsa.arima_model.arimaresults.summary#statsmodels.tsa.arima_model.ARIMAResults.summary "statsmodels.tsa.arima_model.ARIMAResults.summary")([alpha]) \| Summarize the Model \| \| [`summary2`](statsmodels.tsa.arima_model.arimaresults.summary2#statsmodels.tsa.arima_model.ARIMAResults.summary2 "statsmodels.tsa.arima_model.ARIMAResults.summary2")([title, alpha, float\_format]) \| Experimental summary function for ARIMA Results \| \| [`t_test`](statsmodels.tsa.arima_model.arimaresults.t_test#statsmodels.tsa.arima_model.ARIMAResults.t_test "statsmodels.tsa.arima_model.ARIMAResults.t_test")(r\_matrix[, cov\_p, scale, use\_t]) \| Compute a t-test for a each linear hypothesis of the form Rb = q \| \| [`t_test_pairwise`](statsmodels.tsa.arima_model.arimaresults.t_test_pairwise#statsmodels.tsa.arima_model.ARIMAResults.t_test_pairwise "statsmodels.tsa.arima_model.ARIMAResults.t_test_pairwise")(term\_name[, method, alpha, …]) \| perform pairwise t\_test with multiple testing corrected p-values \| \| [`tvalues`](statsmodels.tsa.arima_model.arimaresults.tvalues#statsmodels.tsa.arima_model.ARIMAResults.tvalues "statsmodels.tsa.arima_model.ARIMAResults.tvalues")() \| Return the t-statistic for a given parameter estimate. \| \| [`wald_test`](statsmodels.tsa.arima_model.arimaresults.wald_test#statsmodels.tsa.arima_model.ARIMAResults.wald_test "statsmodels.tsa.arima_model.ARIMAResults.wald_test")(r\_matrix[, cov\_p, scale, invcov, …]) \| Compute a Wald-test for a joint linear hypothesis. \| \| [`wald_test_terms`](statsmodels.tsa.arima_model.arimaresults.wald_test_terms#statsmodels.tsa.arima_model.ARIMAResults.wald_test_terms "statsmodels.tsa.arima_model.ARIMAResults.wald_test_terms")([skip\_single, …]) \| Compute a sequence of Wald tests for terms over multiple columns \| #### Attributes \| \| \| \| --- \| --- \| \| `use_t` \| \| statsmodels statsmodels.graphics.regressionplots.plot_regress_exog statsmodels.graphics.regressionplots.plot\_regress\_exog ======================================================== `statsmodels.graphics.regressionplots.plot_regress_exog(results, exog_idx, fig=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/graphics/regressionplots.html#plot_regress_exog) Plot regression results against one regressor. This plots four graphs in a 2 by 2 figure: ‘endog versus exog’, ‘residuals versus exog’, ‘fitted versus exog’ and ‘fitted plus residual versus exog’ \| Parameters: \| * results (result instance) – result instance with resid, model.endog and model.exog as attributes * exog\_idx (int) – index of regressor in exog matrix * fig (Matplotlib figure instance, optional) – If given, this figure is simply returned. Otherwise a new figure is created. \| \| Returns: \| fig \| \| Return type: \| matplotlib figure instance \| statsmodels statsmodels.miscmodels.count.PoissonOffsetGMLE.predict statsmodels.miscmodels.count.PoissonOffsetGMLE.predict ====================================================== `PoissonOffsetGMLE.predict(params, exog=None, args, kwargs)` After a model has been fit predict returns the fitted values. This is a placeholder intended to be overwritten by individual models. statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.plot_sample_acorr statsmodels.tsa.vector\_ar.var\_model.VARResults.plot\_sample\_acorr ==================================================================== `VARResults.plot_sample_acorr(nlags=10, linewidth=8)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARResults.plot_sample_acorr) Plot theoretical autocorrelation function statsmodels statsmodels.stats.gof.gof_chisquare_discrete statsmodels.stats.gof.gof\_chisquare\_discrete ============================================== `statsmodels.stats.gof.gof_chisquare_discrete(distfn, arg, rvs, alpha, msg)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/gof.html#gof_chisquare_discrete) perform chisquare test for random sample of a discrete distribution \| Parameters: \| distname (string) – name of distribution function * arg (sequence) – parameters of distribution * alpha (float) – significance level, threshold for p-value \| \| Returns: \| result – 0 if test passes, 1 if test fails \| \| Return type: \| bool \| #### Notes originally written for scipy.stats test suite, still needs to be checked for standalone usage, insufficient input checking may not run yet (after copy/paste) refactor: maybe a class, check returns, or separate binning from test results statsmodels statsmodels.sandbox.regression.gmm.IV2SLS.score statsmodels.sandbox.regression.gmm.IV2SLS.score =============================================== `IV2SLS.score(params)` Score vector of model. The gradient of logL with respect to each parameter. statsmodels statsmodels.discrete.discrete_model.Poisson.pdf statsmodels.discrete.discrete\_model.Poisson.pdf ================================================ `Poisson.pdf(X)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#Poisson.pdf) Poisson model probability mass function \| Parameters: \| X (array-like) – `X` is the linear predictor of the model. See notes. \| \| Returns: \| pdf – The value of the Poisson probability mass function, PMF, for each point of X. \| \| Return type: \| ndarray \| #### Notes The PMF is defined as \[\frac{e^{-\lambda\_{i}}\lambda\_{i}^{y\_{i}}}{y\_{i}!}\] where $\lambda$ assumes the loglinear model. I.e., \[\ln\lambda\_{i}=x\_{i}\beta\] The parameter `X` is $x\_{i}\beta$ in the above formula. statsmodels statsmodels.robust.norms.RobustNorm.psi statsmodels.robust.norms.RobustNorm.psi ======================================= `RobustNorm.psi(z)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/norms.html#RobustNorm.psi) Derivative of rho. Sometimes referred to as the influence function. Abstract method: psi = rho’ statsmodels statsmodels.tsa.statespace.varmax.VARMAXResults.llf_obs statsmodels.tsa.statespace.varmax.VARMAXResults.llf\_obs ======================================================== `VARMAXResults.llf_obs()` (float) The value of the log-likelihood function evaluated at `params`. statsmodels statsmodels.discrete.count_model.ZeroInflatedPoissonResults.bse statsmodels.discrete.count\_model.ZeroInflatedPoissonResults.bse ================================================================ `ZeroInflatedPoissonResults.bse()` statsmodels statsmodels.iolib.table.SimpleTable.clear statsmodels.iolib.table.SimpleTable.clear ========================================= `SimpleTable.clear() → None -- remove all items from L` statsmodels statsmodels.duration.hazard_regression.PHRegResults.tvalues statsmodels.duration.hazard\_regression.PHRegResults.tvalues ============================================================ `PHRegResults.tvalues()` Return the t-statistic for a given parameter estimate. statsmodels statsmodels.discrete.discrete_model.MultinomialResults.get_margeff statsmodels.discrete.discrete\_model.MultinomialResults.get\_margeff ==================================================================== `MultinomialResults.get_margeff(at='overall', method='dydx', atexog=None, dummy=False, count=False)` Get marginal effects of the fitted model. \| Parameters: \| * at (str, optional) – Options are: + ’overall’, The average of the marginal effects at each observation. + ’mean’, The marginal effects at the mean of each regressor. + ’median’, The marginal effects at the median of each regressor. + ’zero’, The marginal effects at zero for each regressor. + ’all’, The marginal effects at each observation. If `at` is all only margeff will be available from the returned object.Note that if `exog` is specified, then marginal effects for all variables not specified by `exog` are calculated using the `at` option. * method (str, optional) – Options are: + ’dydx’ - dy/dx - No transformation is made and marginal effects are returned. This is the default. + ’eyex’ - estimate elasticities of variables in `exog` – d(lny)/d(lnx) + ’dyex’ - estimate semielasticity – dy/d(lnx) + ’eydx’ - estimate semeilasticity – d(lny)/dxNote that tranformations are done after each observation is calculated. Semi-elasticities for binary variables are computed using the midpoint method. ‘dyex’ and ‘eyex’ do not make sense for discrete variables. * atexog (array-like, optional) – Optionally, you can provide the exogenous variables over which to get the marginal effects. This should be a dictionary with the key as the zero-indexed column number and the value of the dictionary. Default is None for all independent variables less the constant. * dummy (bool, optional) – If False, treats binary variables (if present) as continuous. This is the default. Else if True, treats binary variables as changing from 0 to 1. Note that any variable that is either 0 or 1 is treated as binary. Each binary variable is treated separately for now. * count (bool, optional) – If False, treats count variables (if present) as continuous. This is the default. Else if True, the marginal effect is the change in probabilities when each observation is increased by one. \| \| Returns: \| DiscreteMargins – Returns an object that holds the marginal effects, standard errors, confidence intervals, etc. See `statsmodels.discrete.discrete_margins.DiscreteMargins` for more information. \| \| Return type: \| marginal effects instance \| #### Notes When using after Poisson, returns the expected number of events per period, assuming that the model is loglinear. statsmodels statsmodels.stats.correlation_tools.FactoredPSDMatrix.decorrelate statsmodels.stats.correlation\_tools.FactoredPSDMatrix.decorrelate ================================================================== `FactoredPSDMatrix.decorrelate(rhs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/correlation_tools.html#FactoredPSDMatrix.decorrelate) Decorrelate the columns of `rhs`. \| Parameters: \| rhs (array-like) – A 2 dimensional array with the same number of rows as the PSD matrix represented by the class instance. \| \| Returns: \| * C^{-1/2} \ rhs, where C is the covariance matrix represented* * by this class instance. \| #### Notes The returned matrix has the identity matrix as its row-wise population covariance matrix. This function exploits the factor structure for efficiency. statsmodels statsmodels.sandbox.distributions.transformed.ExpTransf_gen.isf statsmodels.sandbox.distributions.transformed.ExpTransf\_gen.isf ================================================================ `ExpTransf_gen.isf(q, args, kwds)` Inverse survival function (inverse of `sf`) at q of the given RV. \| Parameters: \| q (array\_like) – upper tail probability * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| x – Quantile corresponding to the upper tail probability q. \| \| Return type: \| ndarray or scalar \| statsmodels statsmodels.tsa.statespace.varmax.VARMAX.initialize_approximate_diffuse statsmodels.tsa.statespace.varmax.VARMAX.initialize\_approximate\_diffuse ========================================================================= `VARMAX.initialize_approximate_diffuse(variance=None)` statsmodels statsmodels.tools.eval_measures.bias statsmodels.tools.eval\_measures.bias ===================================== `statsmodels.tools.eval_measures.bias(x1, x2, axis=0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tools/eval_measures.html#bias) bias, mean error \| Parameters: \| * x2 (x1,) – The performance measure depends on the difference between these two arrays. * axis (int) – axis along which the summary statistic is calculated \| \| Returns: \| bias – bias, or mean difference along given axis. \| \| Return type: \| ndarray or float \| #### Notes If `x1` and `x2` have different shapes, then they need to broadcast. This uses `numpy.asanyarray` to convert the input. Whether this is the desired result or not depends on the array subclass. statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.t_test_pairwise statsmodels.regression.recursive\_ls.RecursiveLSResults.t\_test\_pairwise ========================================================================= `RecursiveLSResults.t_test_pairwise(term_name, method='hs', alpha=0.05, factor_labels=None)` perform pairwise t\_test with multiple testing corrected p-values This uses the formula design\_info encoding contrast matrix and should work for all encodings of a main effect. \| Parameters: \| * result (result instance) – The results of an estimated model with a categorical main effect. * term\_name (str) – name of the term for which pairwise comparisons are computed. Term names for categorical effects are created by patsy and correspond to the main part of the exog names. * method (str or list of strings) – multiple testing p-value correction, default is ‘hs’, see stats.multipletesting * alpha (float) – significance level for multiple testing reject decision. * factor\_labels (None, list of str) – Labels for the factor levels used for pairwise labels. If not provided, then the labels from the formula design\_info are used. \| \| Returns: \| results – The results are stored as attributes, the main attributes are the following two. Other attributes are added for debugging purposes or as background information.* result\_frame : pandas DataFrame with t\_test results and multiple testing corrected p-values. * contrasts : matrix of constraints of the null hypothesis in the t\_test. \| \| Return type: \| instance of a simple Results class \| #### Notes Status: experimental. Currently only checked for treatment coding with and without specified reference level. Currently there are no multiple testing corrected confidence intervals available. #### Examples ``` >>> res = ols("np.log(Days+1) ~ C(Weight) + C(Duration)", data).fit() >>> pw = res.t_test_pairwise("C(Weight)") >>> pw.result_frame coef std err t P>\|t\| Conf. Int. Low 2-1 0.632315 0.230003 2.749157 8.028083e-03 0.171563 3-1 1.302555 0.230003 5.663201 5.331513e-07 0.841803 3-2 0.670240 0.230003 2.914044 5.119126e-03 0.209488 Conf. Int. Upp. pvalue-hs reject-hs 2-1 1.093067 0.010212 True 3-1 1.763307 0.000002 True 3-2 1.130992 0.010212 True ```	programming_docs
statsmodels statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.initialize_known statsmodels.tsa.statespace.kalman\_smoother.KalmanSmoother.initialize\_known ============================================================================ `KalmanSmoother.initialize_known(initial_state, initial_state_cov)` Initialize the statespace model with known distribution for initial state. These values are assumed to be known with certainty or else filled with parameters during, for example, maximum likelihood estimation. \| Parameters: \| * initial\_state (array\_like) – Known mean of the initial state vector. * initial\_state\_cov (array\_like) – Known covariance matrix of the initial state vector. \| statsmodels statsmodels.sandbox.regression.gmm.NonlinearIVGMM.gradient_momcond statsmodels.sandbox.regression.gmm.NonlinearIVGMM.gradient\_momcond =================================================================== `NonlinearIVGMM.gradient_momcond(params, epsilon=0.0001, centered=True)` gradient of moment conditions \| Parameters: \| * params (ndarray) – parameter at which the moment conditions are evaluated * epsilon (float) – stepsize for finite difference calculation * centered (bool) – This refers to the finite difference calculation. If `centered` is true, then the centered finite difference calculation is used. Otherwise the one-sided forward differences are used. * TODO (looks like not used yet) – missing argument `weights` \| statsmodels statsmodels.genmod.families.links.Link.deriv2 statsmodels.genmod.families.links.Link.deriv2 ============================================= `Link.deriv2(p)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#Link.deriv2) Second derivative of the link function g’‘(p) implemented through numerical differentiation statsmodels statsmodels.tsa.ar_model.ARResults.pvalues statsmodels.tsa.ar\_model.ARResults.pvalues =========================================== `ARResults.pvalues()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/ar_model.html#ARResults.pvalues) statsmodels statsmodels.sandbox.distributions.transformed.LogTransf_gen.ppf statsmodels.sandbox.distributions.transformed.LogTransf\_gen.ppf ================================================================ `LogTransf_gen.ppf(q, args, kwds)` Percent point function (inverse of `cdf`) at q of the given RV. \| Parameters: \| q (array\_like) – lower tail probability * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| x – quantile corresponding to the lower tail probability q. \| \| Return type: \| array\_like \| statsmodels statsmodels.nonparametric.kde.KDEUnivariate.sf statsmodels.nonparametric.kde.KDEUnivariate.sf ============================================== `KDEUnivariate.sf()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/nonparametric/kde.html#KDEUnivariate.sf) Returns the survival function evaluated at the support. #### Notes Will not work if fit has not been called. statsmodels statsmodels.tsa.statespace.mlemodel.MLEResults.bic statsmodels.tsa.statespace.mlemodel.MLEResults.bic ================================================== `MLEResults.bic()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/mlemodel.html#MLEResults.bic) (float) Bayes Information Criterion statsmodels statsmodels.robust.norms.LeastSquares.psi statsmodels.robust.norms.LeastSquares.psi ========================================= `LeastSquares.psi(z)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/norms.html#LeastSquares.psi) The psi function for the least squares estimator The analytic derivative of rho \| Parameters: \| z (array-like) – 1d array \| \| Returns: \| psi – psi(z) = z \| \| Return type: \| array \| statsmodels statsmodels.sandbox.distributions.transformed.TransfTwo_gen.sf statsmodels.sandbox.distributions.transformed.TransfTwo\_gen.sf =============================================================== `TransfTwo_gen.sf(x, args, kwds)` Survival function (1 - `cdf`) at x of the given RV. \| Parameters: \| x (array\_like) – quantiles * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| sf – Survival function evaluated at x \| \| Return type: \| array\_like \| statsmodels statsmodels.miscmodels.tmodel.TLinearModel.nloglike statsmodels.miscmodels.tmodel.TLinearModel.nloglike =================================================== `TLinearModel.nloglike(params)` statsmodels statsmodels.regression.recursive_ls.RecursiveLS.transform_params statsmodels.regression.recursive\_ls.RecursiveLS.transform\_params ================================================================== `RecursiveLS.transform_params(unconstrained)` Transform unconstrained parameters used by the optimizer to constrained parameters used in likelihood evaluation \| Parameters: \| unconstrained (array\_like) – Array of unconstrained parameters used by the optimizer, to be transformed. \| \| Returns: \| constrained – Array of constrained parameters which may be used in likelihood evalation. \| \| Return type: \| array\_like \| #### Notes This is a noop in the base class, subclasses should override where appropriate. statsmodels statsmodels.genmod.families.family.Family.starting_mu statsmodels.genmod.families.family.Family.starting\_mu ====================================================== `Family.starting_mu(y)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/family.html#Family.starting_mu) Starting value for mu in the IRLS algorithm. \| Parameters: \| y (array) – The untransformed response variable. \| \| Returns: \| mu\_0 – The first guess on the transformed response variable. \| \| Return type: \| array \| #### Notes \[\mu\_0 = (Y + \overline{Y})/2\] Only the Binomial family takes a different initial value. statsmodels statsmodels.stats.contingency_tables.Table.chi2_contribs statsmodels.stats.contingency\_tables.Table.chi2\_contribs ========================================================== `Table.chi2_contribs()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/contingency_tables.html#Table.chi2_contribs) statsmodels statsmodels.discrete.discrete_model.LogitResults.resid_pearson statsmodels.discrete.discrete\_model.LogitResults.resid\_pearson ================================================================ `LogitResults.resid_pearson()` Pearson residuals #### Notes Pearson residuals are defined to be \[r\_j = \frac{(y - M\_jp\_j)}{\sqrt{M\_jp\_j(1-p\_j)}}\] where $p\_j=cdf(X\beta)$ and $M\_j$ is the total number of observations sharing the covariate pattern $j$. For now $M\_j$ is always set to 1. statsmodels statsmodels.sandbox.distributions.extras.ACSkewT_gen.sf statsmodels.sandbox.distributions.extras.ACSkewT\_gen.sf ======================================================== `ACSkewT_gen.sf(x, args, kwds)` Survival function (1 - `cdf`) at x of the given RV. \| Parameters: \| x (array\_like) – quantiles * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| sf – Survival function evaluated at x \| \| Return type: \| array\_like \| statsmodels statsmodels.multivariate.multivariate_ols._MultivariateOLSResults statsmodels.multivariate.multivariate\_ols.\_MultivariateOLSResults =================================================================== `class statsmodels.multivariate.multivariate_ols._MultivariateOLSResults(fitted_mv_ols)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/multivariate/multivariate_ols.html#_MultivariateOLSResults) \_MultivariateOLS results class #### Methods \| \| \| \| --- \| --- \| \| [`mv_test`](statsmodels.multivariate.multivariate_ols._multivariateolsresults.mv_test#statsmodels.multivariate.multivariate_ols._MultivariateOLSResults.mv_test "statsmodels.multivariate.multivariate_ols._MultivariateOLSResults.mv_test")([hypotheses]) \| Linear hypotheses testing \| \| [`summary`](statsmodels.multivariate.multivariate_ols._multivariateolsresults.summary#statsmodels.multivariate.multivariate_ols._MultivariateOLSResults.summary "statsmodels.multivariate.multivariate_ols._MultivariateOLSResults.summary")() \| \| statsmodels statsmodels.stats.inter_rater.to_table statsmodels.stats.inter\_rater.to\_table ======================================== `statsmodels.stats.inter_rater.to_table(data, bins=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/inter_rater.html#to_table) convert raw data with shape (subject, rater) to (rater1, rater2) brings data into correct format for cohens\_kappa \| Parameters: \| * data (array\_like, 2-Dim) – data containing category assignment with subjects in rows and raters in columns. * bins (None, int or tuple of array\_like) – If None, then the data is converted to integer categories, 0,1,2,…,n\_cat-1. Because of the relabeling only category levels with non-zero counts are included. If this is an integer, then the category levels in the data are already assumed to be in integers, 0,1,2,…,n\_cat-1. In this case, the returned array may contain columns with zero count, if no subject has been categorized with this level. If bins are a tuple of two array\_like, then the bins are directly used by `numpy.histogramdd`. This is useful if we want to merge categories. \| \| Returns: \| arr – Contingency table that contains counts of category level with rater1 in rows and rater2 in columns. \| \| Return type: \| nd\_array, (n\_cat, n\_cat) \| #### Notes no NaN handling, delete rows with missing values This works also for more than two raters. In that case the dimension of the resulting contingency table is the same as the number of raters instead of 2-dimensional. statsmodels statsmodels.tsa.statespace.tools.constrain_stationary_univariate statsmodels.tsa.statespace.tools.constrain\_stationary\_univariate ================================================================== `statsmodels.tsa.statespace.tools.constrain_stationary_univariate(unconstrained)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/tools.html#constrain_stationary_univariate) Transform unconstrained parameters used by the optimizer to constrained parameters used in likelihood evaluation \| Parameters: \| unconstrained (array) – Unconstrained parameters used by the optimizer, to be transformed to stationary coefficients of, e.g., an autoregressive or moving average component. \| \| Returns: \| constrained – Constrained parameters of, e.g., an autoregressive or moving average component, to be transformed to arbitrary parameters used by the optimizer. \| \| Return type: \| array \| #### References \| \| \| \| --- \| --- \| \| [\] \| Monahan, John F. 1984. “A Note on Enforcing Stationarity in Autoregressive-moving Average Models.” Biometrika 71 (2) (August 1): 403-404. \| statsmodels statsmodels.sandbox.distributions.transformed.LogTransf_gen.interval statsmodels.sandbox.distributions.transformed.LogTransf\_gen.interval ===================================================================== `LogTransf_gen.interval(alpha, args, *kwds)` Confidence interval with equal areas around the median. \| Parameters: \| alpha (array\_like of float) – Probability that an rv will be drawn from the returned range. Each value should be in the range [0, 1]. * arg2, .. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information). * loc (array\_like, optional) – location parameter, Default is 0. * scale (array\_like, optional) – scale parameter, Default is 1. \| \| Returns: \| a, b – end-points of range that contain `100 * alpha %` of the rv’s possible values. \| \| Return type: \| ndarray of float \| statsmodels statsmodels.discrete.count_model.ZeroInflatedPoissonResults.bic statsmodels.discrete.count\_model.ZeroInflatedPoissonResults.bic ================================================================ `ZeroInflatedPoissonResults.bic()` statsmodels statsmodels.tsa.statespace.varmax.VARMAXResults.simulate statsmodels.tsa.statespace.varmax.VARMAXResults.simulate ======================================================== `VARMAXResults.simulate(nsimulations, measurement_shocks=None, state_shocks=None, initial_state=None)` Simulate a new time series following the state space model \| Parameters: \| * nsimulations (int) – The number of observations to simulate. If the model is time-invariant this can be any number. If the model is time-varying, then this number must be less than or equal to the number * measurement\_shocks (array\_like, optional) – If specified, these are the shocks to the measurement equation, $\varepsilon\_t$. If unspecified, these are automatically generated using a pseudo-random number generator. If specified, must be shaped `nsimulations` x `k_endog`, where `k_endog` is the same as in the state space model. * state\_shocks (array\_like, optional) – If specified, these are the shocks to the state equation, $\eta\_t$. If unspecified, these are automatically generated using a pseudo-random number generator. If specified, must be shaped `nsimulations` x `k_posdef` where `k_posdef` is the same as in the state space model. * initial\_state (array\_like, optional) – If specified, this is the state vector at time zero, which should be shaped (`k_states` x 1), where `k_states` is the same as in the state space model. If unspecified, but the model has been initialized, then that initialization is used. If unspecified and the model has not been initialized, then a vector of zeros is used. Note that this is not included in the returned `simulated_states` array. \| \| Returns: \| simulated\_obs – An (nsimulations x k\_endog) array of simulated observations. \| \| Return type: \| array \| statsmodels statsmodels.graphics.gofplots.ProbPlot.ppplot statsmodels.graphics.gofplots.ProbPlot.ppplot ============================================= `ProbPlot.ppplot(xlabel=None, ylabel=None, line=None, other=None, ax=None, *plotkwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/graphics/gofplots.html#ProbPlot.ppplot) P-P plot of the percentiles (probabilities) of x versus the probabilities (percetiles) of a distribution. \| Parameters: \| ylabel (xlabel,) – User-provided lables for the x-axis and y-axis. If None (default), other values are used depending on the status of the kwarg `other`. * line (str {'45', 's', 'r', q'} or None, optional) – Options for the reference line to which the data is compared: + ‘45’ - 45-degree line + ’s‘ - standardized line, the expected order statistics are scaled by the standard deviation of the given sample and have the mean added to them + ’r’ - A regression line is fit + ’q’ - A line is fit through the quartiles. + None - by default no reference line is added to the plot. * other (`ProbPlot` instance, array-like, or None, optional) – If provided, the sample quantiles of this `ProbPlot` instance are plotted against the sample quantiles of the `other` `ProbPlot` instance. If an array-like object is provided, it will be turned into a `ProbPlot` instance using default parameters. If not provided (default), the theoretical quantiles are used. * ax (Matplotlib AxesSubplot instance, optional) – If given, this subplot is used to plot in instead of a new figure being created. * *\\plotkwargs* (additional matplotlib arguments to be passed to the) – `plot` command. \| \| Returns: \| fig – If `ax` is None, the created figure. Otherwise the figure to which `ax` is connected. \| \| Return type: \| Matplotlib figure instance \| statsmodels statsmodels.tsa.arima_model.ARMAResults.conf_int statsmodels.tsa.arima\_model.ARMAResults.conf\_int ================================================== `ARMAResults.conf_int(alpha=0.05, cols=None, method='default')` Returns the confidence interval of the fitted parameters. \| Parameters: \| * alpha (float, optional) – The significance level for the confidence interval. ie., The default `alpha` = .05 returns a 95% confidence interval. * cols (array-like, optional) – `cols` specifies which confidence intervals to return * method (string) – Not Implemented Yet Method to estimate the confidence\_interval. “Default” : uses self.bse which is based on inverse Hessian for MLE “hjjh” : “jac” : “boot-bse” “boot\_quant” “profile” \| \| Returns: \| conf\_int – Each row contains [lower, upper] limits of the confidence interval for the corresponding parameter. The first column contains all lower, the second column contains all upper limits. \| \| Return type: \| array \| #### Examples ``` >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> results.conf_int() array([[-5496529.48322745, -1467987.78596704], [ -177.02903529, 207.15277984], [ -0.1115811 , 0.03994274], [ -3.12506664, -0.91539297], [ -1.5179487 , -0.54850503], [ -0.56251721, 0.460309 ], [ 798.7875153 , 2859.51541392]]) ``` ``` >>> results.conf_int(cols=(2,3)) array([[-0.1115811 , 0.03994274], [-3.12506664, -0.91539297]]) ``` #### Notes The confidence interval is based on the standard normal distribution. Models wish to use a different distribution should overwrite this method. statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.plot_cusum statsmodels.regression.recursive\_ls.RecursiveLSResults.plot\_cusum =================================================================== `RecursiveLSResults.plot_cusum(alpha=0.05, legend_loc='upper left', fig=None, figsize=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/recursive_ls.html#RecursiveLSResults.plot_cusum) Plot the CUSUM statistic and significance bounds. \| Parameters: \| * alpha (float, optional) – The plotted significance bounds are alpha %. * legend\_loc (string, optional) – The location of the legend in the plot. Default is upper left. * fig (Matplotlib Figure instance, optional) – If given, subplots are created in this figure instead of in a new figure. Note that the grid will be created in the provided figure using `fig.add_subplot()`. * figsize (tuple, optional) – If a figure is created, this argument allows specifying a size. The tuple is (width, height). \| #### Notes Evidence of parameter instability may be found if the CUSUM statistic moves out of the significance bounds. #### References \| \| \| \| --- \| --- \| \| [\*] \| Brown, R. L., J. Durbin, and J. M. Evans. 1975. “Techniques for Testing the Constancy of Regression Relationships over Time.” Journal of the Royal Statistical Society. Series B (Methodological) 37 (2): 149-92. \|	programming_docs
statsmodels statsmodels.discrete.discrete_model.BinaryResults.llr_pvalue statsmodels.discrete.discrete\_model.BinaryResults.llr\_pvalue ============================================================== `BinaryResults.llr_pvalue()` statsmodels statsmodels.regression.quantile_regression.QuantReg statsmodels.regression.quantile\_regression.QuantReg ==================================================== `class statsmodels.regression.quantile_regression.QuantReg(endog, exog, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/quantile_regression.html#QuantReg) Quantile Regression Estimate a quantile regression model using iterative reweighted least squares. \| Parameters: \| endog (array or dataframe) – endogenous/response variable * exog (array or dataframe) – exogenous/explanatory variable(s) \| #### Notes The Least Absolute Deviation (LAD) estimator is a special case where quantile is set to 0.5 (q argument of the fit method). The asymptotic covariance matrix is estimated following the procedure in Greene (2008, p.407-408), using either the logistic or gaussian kernels (kernel argument of the fit method). #### References General: * Birkes, D. and Y. Dodge(1993). Alternative Methods of Regression, John Wiley and Sons. * Green,W. H. (2008). Econometric Analysis. Sixth Edition. International Student Edition. * Koenker, R. (2005). Quantile Regression. New York: Cambridge University Press. * LeSage, J. P.(1999). Applied Econometrics Using MATLAB, Kernels (used by the fit method): * Green (2008) Table 14.2 Bandwidth selection (used by the fit method): * Bofinger, E. (1975). Estimation of a density function using order statistics. Australian Journal of Statistics 17: 1-17. * Chamberlain, G. (1994). Quantile regression, censoring, and the structure of wages. In Advances in Econometrics, Vol. 1: Sixth World Congress, ed. C. A. Sims, 171-209. Cambridge: Cambridge University Press. * Hall, P., and S. Sheather. (1988). On the distribution of the Studentized quantile. Journal of the Royal Statistical Society, Series B 50: 381-391. Keywords: Least Absolute Deviation(LAD) Regression, Quantile Regression, Regression, Robust Estimation. #### Methods \| \| \| \| --- \| --- \| \| [`fit`](statsmodels.regression.quantile_regression.quantreg.fit#statsmodels.regression.quantile_regression.QuantReg.fit "statsmodels.regression.quantile_regression.QuantReg.fit")([q, vcov, kernel, bandwidth, max\_iter, …]) \| Solve by Iterative Weighted Least Squares \| \| [`from_formula`](statsmodels.regression.quantile_regression.quantreg.from_formula#statsmodels.regression.quantile_regression.QuantReg.from_formula "statsmodels.regression.quantile_regression.QuantReg.from_formula")(formula, data[, subset, drop\_cols]) \| Create a Model from a formula and dataframe. \| \| [`get_distribution`](statsmodels.regression.quantile_regression.quantreg.get_distribution#statsmodels.regression.quantile_regression.QuantReg.get_distribution "statsmodels.regression.quantile_regression.QuantReg.get_distribution")(params, scale[, exog, …]) \| Returns a random number generator for the predictive distribution. \| \| [`hessian`](statsmodels.regression.quantile_regression.quantreg.hessian#statsmodels.regression.quantile_regression.QuantReg.hessian "statsmodels.regression.quantile_regression.QuantReg.hessian")(params) \| The Hessian matrix of the model \| \| [`information`](statsmodels.regression.quantile_regression.quantreg.information#statsmodels.regression.quantile_regression.QuantReg.information "statsmodels.regression.quantile_regression.QuantReg.information")(params) \| Fisher information matrix of model \| \| [`initialize`](statsmodels.regression.quantile_regression.quantreg.initialize#statsmodels.regression.quantile_regression.QuantReg.initialize "statsmodels.regression.quantile_regression.QuantReg.initialize")() \| Initialize (possibly re-initialize) a Model instance. \| \| [`loglike`](statsmodels.regression.quantile_regression.quantreg.loglike#statsmodels.regression.quantile_regression.QuantReg.loglike "statsmodels.regression.quantile_regression.QuantReg.loglike")(params) \| Log-likelihood of model. \| \| [`predict`](statsmodels.regression.quantile_regression.quantreg.predict#statsmodels.regression.quantile_regression.QuantReg.predict "statsmodels.regression.quantile_regression.QuantReg.predict")(params[, exog]) \| Return linear predicted values from a design matrix. \| \| [`score`](statsmodels.regression.quantile_regression.quantreg.score#statsmodels.regression.quantile_regression.QuantReg.score "statsmodels.regression.quantile_regression.QuantReg.score")(params) \| Score vector of model. \| \| [`whiten`](statsmodels.regression.quantile_regression.quantreg.whiten#statsmodels.regression.quantile_regression.QuantReg.whiten "statsmodels.regression.quantile_regression.QuantReg.whiten")(data) \| QuantReg model whitener does nothing: returns data. \| #### Attributes \| \| \| \| --- \| --- \| \| `df_model` \| The model degree of freedom, defined as the rank of the regressor matrix minus 1 if a constant is included. \| \| `df_resid` \| The residual degree of freedom, defined as the number of observations minus the rank of the regressor matrix. \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| Names of exogenous variables \| statsmodels statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression statsmodels.tsa.regime\_switching.markov\_autoregression.MarkovAutoregression ============================================================================= `class statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression(endog, k_regimes, order, trend='c', exog=None, exog_tvtp=None, switching_ar=True, switching_trend=True, switching_exog=False, switching_variance=False, dates=None, freq=None, missing='none')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/regime_switching/markov_autoregression.html#MarkovAutoregression) Markov switching regression model \| Parameters: \| * endog (array\_like) – The endogenous variable. * k\_regimes (integer) – The number of regimes. * order (integer) – The order of the autoregressive lag polynomial. * trend ({'nc', 'c', 't', 'ct'}) – Whether or not to include a trend. To include an constant, time trend, or both, set `trend=’c’`, `trend=’t’`, or `trend=’ct’`. For no trend, set `trend=’nc’`. Default is a constant. * exog (array\_like, optional) – Array of exogenous regressors, shaped nobs x k. * exog\_tvtp (array\_like, optional) – Array of exogenous or lagged variables to use in calculating time-varying transition probabilities (TVTP). TVTP is only used if this variable is provided. If an intercept is desired, a column of ones must be explicitly included in this array. * switching\_ar (boolean or iterable, optional) – If a boolean, sets whether or not all autoregressive coefficients are switching across regimes. If an iterable, should be of length equal to `order`, where each element is a boolean describing whether the corresponding coefficient is switching. Default is True. * switching\_trend (boolean or iterable, optional) – If a boolean, sets whether or not all trend coefficients are switching across regimes. If an iterable, should be of length equal to the number of trend variables, where each element is a boolean describing whether the corresponding coefficient is switching. Default is True. * switching\_exog (boolean or iterable, optional) – If a boolean, sets whether or not all regression coefficients are switching across regimes. If an iterable, should be of length equal to the number of exogenous variables, where each element is a boolean describing whether the corresponding coefficient is switching. Default is True. * switching\_variance (boolean, optional) – Whether or not there is regime-specific heteroskedasticity, i.e. whether or not the error term has a switching variance. Default is False. \| #### Notes This model is new and API stability is not guaranteed, although changes will be made in a backwards compatible way if possible. The model can be written as: \[\begin{split}y\_t = a\_{S\_t} + x\_t' \beta\_{S\_t} + \phi\_{1, S\_t} (y\_{t-1} - a\_{S\_{t-1}} - x\_{t-1}' \beta\_{S\_{t-1}}) + \dots + \phi\_{p, S\_t} (y\_{t-p} - a\_{S\_{t-p}} - x\_{t-p}' \beta\_{S\_{t-p}}) + \varepsilon\_t \\ \varepsilon\_t \sim N(0, \sigma\_{S\_t}^2)\end{split}\] i.e. the model is an autoregression with where the autoregressive coefficients, the mean of the process (possibly including trend or regression effects) and the variance of the error term may be switching across regimes. The `trend` is accomodated by prepending columns to the `exog` array. Thus if `trend=’c’`, the passed `exog` array should not already have a column of ones. #### References Kim, Chang-Jin, and Charles R. Nelson. 1999. “State-Space Models with Regime Switching: Classical and Gibbs-Sampling Approaches with Applications”. MIT Press Books. The MIT Press. #### Methods \| \| \| \| --- \| --- \| \| [`filter`](statsmodels.tsa.regime_switching.markov_autoregression.markovautoregression.filter#statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.filter "statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.filter")(params[, transformed, cov\_type, …]) \| Apply the Hamilton filter \| \| [`fit`](statsmodels.tsa.regime_switching.markov_autoregression.markovautoregression.fit#statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.fit "statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.fit")([start\_params, transformed, cov\_type, …]) \| Fits the model by maximum likelihood via Hamilton filter. \| \| [`from_formula`](statsmodels.tsa.regime_switching.markov_autoregression.markovautoregression.from_formula#statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.from_formula "statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.from_formula")(formula, data[, subset, drop\_cols]) \| Create a Model from a formula and dataframe. \| \| [`hessian`](statsmodels.tsa.regime_switching.markov_autoregression.markovautoregression.hessian#statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.hessian "statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.hessian")(params[, transformed]) \| Hessian matrix of the likelihood function, evaluated at the given parameters \| \| [`information`](statsmodels.tsa.regime_switching.markov_autoregression.markovautoregression.information#statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.information "statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.information")(params) \| Fisher information matrix of model \| \| [`initial_probabilities`](statsmodels.tsa.regime_switching.markov_autoregression.markovautoregression.initial_probabilities#statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.initial_probabilities "statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.initial_probabilities")(params[, …]) \| Retrieve initial probabilities \| \| [`initialize`](statsmodels.tsa.regime_switching.markov_autoregression.markovautoregression.initialize#statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.initialize "statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.initialize")() \| Initialize (possibly re-initialize) a Model instance. \| \| [`initialize_known`](statsmodels.tsa.regime_switching.markov_autoregression.markovautoregression.initialize_known#statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.initialize_known "statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.initialize_known")(probabilities[, tol]) \| Set initialization of regime probabilities to use known values \| \| [`initialize_steady_state`](statsmodels.tsa.regime_switching.markov_autoregression.markovautoregression.initialize_steady_state#statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.initialize_steady_state "statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.initialize_steady_state")() \| Set initialization of regime probabilities to be steady-state values \| \| [`loglike`](statsmodels.tsa.regime_switching.markov_autoregression.markovautoregression.loglike#statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.loglike "statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.loglike")(params[, transformed]) \| Loglikelihood evaluation \| \| [`loglikeobs`](statsmodels.tsa.regime_switching.markov_autoregression.markovautoregression.loglikeobs#statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.loglikeobs "statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.loglikeobs")(params[, transformed]) \| Loglikelihood evaluation for each period \| \| [`predict`](statsmodels.tsa.regime_switching.markov_autoregression.markovautoregression.predict#statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.predict "statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.predict")(params[, start, end, probabilities, …]) \| In-sample prediction and out-of-sample forecasting \| \| [`predict_conditional`](statsmodels.tsa.regime_switching.markov_autoregression.markovautoregression.predict_conditional#statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.predict_conditional "statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.predict_conditional")(params) \| In-sample prediction, conditional on the current and previous regime \| \| [`regime_transition_matrix`](statsmodels.tsa.regime_switching.markov_autoregression.markovautoregression.regime_transition_matrix#statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.regime_transition_matrix "statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.regime_transition_matrix")(params[, exog\_tvtp]) \| Construct the left-stochastic transition matrix \| \| [`score`](statsmodels.tsa.regime_switching.markov_autoregression.markovautoregression.score#statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.score "statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.score")(params[, transformed]) \| Compute the score function at params. \| \| [`score_obs`](statsmodels.tsa.regime_switching.markov_autoregression.markovautoregression.score_obs#statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.score_obs "statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.score_obs")(params[, transformed]) \| Compute the score per observation, evaluated at params \| \| [`smooth`](statsmodels.tsa.regime_switching.markov_autoregression.markovautoregression.smooth#statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.smooth "statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.smooth")(params[, transformed, cov\_type, …]) \| Apply the Kim smoother and Hamilton filter \| \| [`transform_params`](statsmodels.tsa.regime_switching.markov_autoregression.markovautoregression.transform_params#statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.transform_params "statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.transform_params")(unconstrained) \| Transform unconstrained parameters used by the optimizer to constrained parameters used in likelihood evaluation \| \| [`untransform_params`](statsmodels.tsa.regime_switching.markov_autoregression.markovautoregression.untransform_params#statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.untransform_params "statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.untransform_params")(constrained) \| Transform constrained parameters used in likelihood evaluation to unconstrained parameters used by the optimizer \| #### Attributes \| \| \| \| --- \| --- \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| \| \| `k_params` \| (int) Number of parameters in the model \| \| `param_names` \| (list of str) List of human readable parameter names (for parameters actually included in the model). \| \| `start_params` \| (array) Starting parameters for maximum likelihood estimation. \| statsmodels statsmodels.genmod.generalized_linear_model.GLMResults.resid_deviance statsmodels.genmod.generalized\_linear\_model.GLMResults.resid\_deviance ======================================================================== `GLMResults.resid_deviance()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_linear_model.html#GLMResults.resid_deviance) statsmodels statsmodels.tools.numdiff.approx_hess1 statsmodels.tools.numdiff.approx\_hess1 ======================================= `statsmodels.tools.numdiff.approx_hess1(x, f, epsilon=None, args=(), kwargs={}, return_grad=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tools/numdiff.html#approx_hess1) Calculate Hessian with finite difference derivative approximation \| Parameters: \| * x (array\_like) – value at which function derivative is evaluated * f (function) – function of one array f(x, `args`, `kwargs`) epsilon (float or array-like, optional) – Stepsize used, if None, then stepsize is automatically chosen according to EPS\\(1/3)\x. args (tuple) – Arguments for function `f`. * kwargs ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)")) – Keyword arguments for function `f`. * return\_grad (bool) – Whether or not to also return the gradient \| \| Returns: \| * hess (ndarray) – array of partial second derivatives, Hessian * grad (nparray) – Gradient if return\_grad == True \| #### Notes Equation (7) in Ridout. Computes the Hessian as: ``` 1/(d_jd_k) ((f(x + d[j]e[j] + d[k]e[k]) - f(x + d[j]e[j]))) ``` where e[j] is a vector with element j == 1 and the rest are zero and d[i] is epsilon[i]. #### References Ridout, M.S. (2009) Statistical applications of the complex-step method of numerical differentiation. The American Statistician, 63, 66-74 statsmodels statsmodels.sandbox.regression.try_catdata.cat2dummy statsmodels.sandbox.regression.try\_catdata.cat2dummy ===================================================== `statsmodels.sandbox.regression.try_catdata.cat2dummy(y, nonseq=0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/regression/try_catdata.html#cat2dummy) statsmodels statsmodels.tsa.statespace.mlemodel.MLEModel.impulse_responses statsmodels.tsa.statespace.mlemodel.MLEModel.impulse\_responses =============================================================== `MLEModel.impulse_responses(params, steps=1, impulse=0, orthogonalized=False, cumulative=False, kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/mlemodel.html#MLEModel.impulse_responses) Impulse response function \| Parameters: \| params (array\_like) – Array of model parameters. * steps (int, optional) – The number of steps for which impulse responses are calculated. Default is 1. Note that the initial impulse is not counted as a step, so if `steps=1`, the output will have 2 entries. * impulse (int or array\_like) – If an integer, the state innovation to pulse; must be between 0 and `k_posdef-1`. Alternatively, a custom impulse vector may be provided; must be shaped `k_posdef x 1`. * orthogonalized (boolean, optional) – Whether or not to perform impulse using orthogonalized innovations. Note that this will also affect custum `impulse` vectors. Default is False. * cumulative (boolean, optional) – Whether or not to return cumulative impulse responses. Default is False. * *\\kwargs* – If the model is time-varying and `steps` is greater than the number of observations, any of the state space representation matrices that are time-varying must have updated values provided for the out-of-sample steps. For example, if `design` is a time-varying component, `nobs` is 10, and `steps` is 15, a (`k_endog` x `k_states` x 5) matrix must be provided with the new design matrix values. \| \| Returns: \| impulse\_responses – Responses for each endogenous variable due to the impulse given by the `impulse` argument. A (steps + 1 x k\_endog) array. \| \| Return type: \| array \| #### Notes Intercepts in the measurement and state equation are ignored when calculating impulse responses.	programming_docs
statsmodels statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP statsmodels.discrete.count\_model.ZeroInflatedNegativeBinomialP =============================================================== `class statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP(endog, exog, exog_infl=None, offset=None, exposure=None, inflation='logit', p=2, missing='none', *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/count_model.html#ZeroInflatedNegativeBinomialP) Zero Inflated Generalized Negative Binomial model for count data \| Parameters: \| endog (array-like) – 1-d endogenous response variable. The dependent variable. * exog (array-like) – A nobs x k array where `nobs` is the number of observations and `k` is the number of regressors. An intercept is not included by default and should be added by the user. See `statsmodels.tools.add_constant`. * exog\_infl (array\_like or None) – Explanatory variables for the binary inflation model, i.e. for mixing probability model. If None, then a constant is used. * offset (array\_like) – Offset is added to the linear prediction with coefficient equal to 1. * exposure (array\_like) – Log(exposure) is added to the linear prediction with coefficient equal to 1. * inflation (string, 'logit' or 'probit') – The model for the zero inflation, either Logit (default) or Probit * p (float) – dispersion power parameter for the NegativeBinomialP model. p=1 for ZINB-1 and p=2 for ZINM-2. Default is p=2 * missing (str) – Available options are ‘none’, ‘drop’, and ‘raise’. If ‘none’, no nan checking is done. If ‘drop’, any observations with nans are dropped. If ‘raise’, an error is raised. Default is ‘none.’ \| `endog` array – A reference to the endogenous response variable `exog` array – A reference to the exogenous design. `exog_infl` array – A reference to the zero-inflated exogenous design. `p` scalar – P denotes parametrizations for ZINB regression. p=1 for ZINB-1 and `p=2 for ZINB-2. Default is p=2` #### Methods \| \| \| \| --- \| --- \| \| [`cdf`](statsmodels.discrete.count_model.zeroinflatednegativebinomialp.cdf#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.cdf "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.cdf")(X) \| The cumulative distribution function of the model. \| \| [`cov_params_func_l1`](statsmodels.discrete.count_model.zeroinflatednegativebinomialp.cov_params_func_l1#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.cov_params_func_l1 "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.cov_params_func_l1")(likelihood\_model, xopt, …) \| Computes cov\_params on a reduced parameter space corresponding to the nonzero parameters resulting from the l1 regularized fit. \| \| [`fit`](statsmodels.discrete.count_model.zeroinflatednegativebinomialp.fit#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.fit "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.fit")([start\_params, method, maxiter, …]) \| Fit the model using maximum likelihood. \| \| [`fit_regularized`](statsmodels.discrete.count_model.zeroinflatednegativebinomialp.fit_regularized#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.fit_regularized "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.fit_regularized")([start\_params, method, …]) \| Fit the model using a regularized maximum likelihood. \| \| [`from_formula`](statsmodels.discrete.count_model.zeroinflatednegativebinomialp.from_formula#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.from_formula "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.from_formula")(formula, data[, subset, drop\_cols]) \| Create a Model from a formula and dataframe. \| \| [`hessian`](statsmodels.discrete.count_model.zeroinflatednegativebinomialp.hessian#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.hessian "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.hessian")(params) \| Generic Zero Inflated model Hessian matrix of the loglikelihood \| \| [`information`](statsmodels.discrete.count_model.zeroinflatednegativebinomialp.information#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.information "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.information")(params) \| Fisher information matrix of model \| \| [`initialize`](statsmodels.discrete.count_model.zeroinflatednegativebinomialp.initialize#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.initialize "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.initialize")() \| Initialize is called by statsmodels.model.LikelihoodModel.\_\_init\_\_ and should contain any preprocessing that needs to be done for a model. \| \| [`loglike`](statsmodels.discrete.count_model.zeroinflatednegativebinomialp.loglike#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.loglike "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.loglike")(params) \| Loglikelihood of Generic Zero Inflated model \| \| [`loglikeobs`](statsmodels.discrete.count_model.zeroinflatednegativebinomialp.loglikeobs#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.loglikeobs "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.loglikeobs")(params) \| Loglikelihood for observations of Generic Zero Inflated model \| \| [`pdf`](statsmodels.discrete.count_model.zeroinflatednegativebinomialp.pdf#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.pdf "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.pdf")(X) \| The probability density (mass) function of the model. \| \| [`predict`](statsmodels.discrete.count_model.zeroinflatednegativebinomialp.predict#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.predict "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.predict")(params[, exog, exog\_infl, exposure, …]) \| Predict response variable of a count model given exogenous variables. \| \| [`score`](statsmodels.discrete.count_model.zeroinflatednegativebinomialp.score#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.score "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.score")(params) \| Score vector of model. \| \| [`score_obs`](statsmodels.discrete.count_model.zeroinflatednegativebinomialp.score_obs#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.score_obs "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.score_obs")(params) \| Generic Zero Inflated model score (gradient) vector of the log-likelihood \| #### Attributes \| \| \| \| --- \| --- \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| Names of exogenous variables \| statsmodels statsmodels.stats.mediation.MediationResults statsmodels.stats.mediation.MediationResults ============================================ `class statsmodels.stats.mediation.MediationResults(indirect_effects, direct_effects)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/mediation.html#MediationResults) A class for holding the results of a mediation analysis. The following terms are used in the summary output: ACME : average causal mediated effect ADE : average direct effect #### Methods \| \| \| \| --- \| --- \| \| [`summary`](statsmodels.stats.mediation.mediationresults.summary#statsmodels.stats.mediation.MediationResults.summary "statsmodels.stats.mediation.MediationResults.summary")([alpha]) \| Provide a summary of a mediation analysis. \| statsmodels statsmodels.multivariate.multivariate_ols._MultivariateOLS.from_formula statsmodels.multivariate.multivariate\_ols.\_MultivariateOLS.from\_formula ========================================================================== `classmethod _MultivariateOLS.from_formula(formula, data, subset=None, drop_cols=None, args, kwargs)` Create a Model from a formula and dataframe. \| Parameters: \| formula (str or generic Formula object) – The formula specifying the model * data (array-like) – The data for the model. See Notes. * subset (array-like) – An array-like object of booleans, integers, or index values that indicate the subset of df to use in the model. Assumes df is a `pandas.DataFrame` * drop\_cols (array-like) – Columns to drop from the design matrix. Cannot be used to drop terms involving categoricals. * args (extra arguments) – These are passed to the model * kwargs (extra keyword arguments) – These are passed to the model with one exception. The `eval_env` keyword is passed to patsy. It can be either a [`patsy.EvalEnvironment`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.EvalEnvironment "(in patsy v0.5.0+dev)") object or an integer indicating the depth of the namespace to use. For example, the default `eval_env=0` uses the calling namespace. If you wish to use a “clean” environment set `eval_env=-1`. \| \| Returns: \| model \| \| Return type: \| Model instance \| #### Notes data must define \_\_getitem\_\_ with the keys in the formula terms args and kwargs are passed on to the model instantiation. E.g., a numpy structured or rec array, a dictionary, or a pandas DataFrame. statsmodels statsmodels.tsa.holtwinters.HoltWintersResults.summary statsmodels.tsa.holtwinters.HoltWintersResults.summary ====================================================== `HoltWintersResults.summary()` statsmodels statsmodels.regression.mixed_linear_model.MixedLMResults.load statsmodels.regression.mixed\_linear\_model.MixedLMResults.load =============================================================== `classmethod MixedLMResults.load(fname)` load a pickle, (class method) \| Parameters: \| fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. \| \| Returns: \| \| \| Return type: \| unpickled instance \| statsmodels statsmodels.genmod.families.family.InverseGaussian.resid_dev statsmodels.genmod.families.family.InverseGaussian.resid\_dev ============================================================= `InverseGaussian.resid_dev(endog, mu, var_weights=1.0, scale=1.0)` The deviance residuals \| Parameters: \| * endog (array-like) – The endogenous response variable * mu (array-like) – The inverse of the link function at the linear predicted values. * var\_weights (array-like) – 1d array of variance (analytic) weights. The default is 1. * scale (float, optional) – An optional scale argument. The default is 1. \| \| Returns: \| resid\_dev – Deviance residuals as defined below. \| \| Return type: \| float \| #### Notes The deviance residuals are defined by the contribution D\_i of observation i to the deviance as \[resid\\_dev\_i = sign(y\_i-\mu\_i) \sqrt{D\_i}\] D\_i is calculated from the \_resid\_dev method in each family. Distribution-specific documentation of the calculation is available there. statsmodels statsmodels.discrete.discrete_model.ProbitResults.cov_params statsmodels.discrete.discrete\_model.ProbitResults.cov\_params ============================================================== `ProbitResults.cov_params(r_matrix=None, column=None, scale=None, cov_p=None, other=None)` Returns the variance/covariance matrix. The variance/covariance matrix can be of a linear contrast of the estimates of params or all params multiplied by scale which will usually be an estimate of sigma^2. Scale is assumed to be a scalar. \| Parameters: \| * r\_matrix (array-like) – Can be 1d, or 2d. Can be used alone or with other. * column (array-like, optional) – Must be used on its own. Can be 0d or 1d see below. * scale (float, optional) – Can be specified or not. Default is None, which means that the scale argument is taken from the model. * other (array-like, optional) – Can be used when r\_matrix is specified. \| \| Returns: \| cov – covariance matrix of the parameter estimates or of linear combination of parameter estimates. See Notes. \| \| Return type: \| ndarray \| #### Notes (The below are assumed to be in matrix notation.) If no argument is specified returns the covariance matrix of a model `(scale)(X.T X)^(-1)` If contrast is specified it pre and post-multiplies as follows `(scale) r_matrix (X.T X)^(-1) r_matrix.T` If contrast and other are specified returns `(scale) * r_matrix (X.T X)^(-1) other.T` If column is specified returns `(scale) * (X.T X)^(-1)[column,column]` if column is 0d OR `(scale) * (X.T X)^(-1)[column][:,column]` if column is 1d statsmodels statsmodels.genmod.families.links.cauchy.inverse statsmodels.genmod.families.links.cauchy.inverse ================================================ `cauchy.inverse(z)` The inverse of the CDF link \| Parameters: \| z (array-like) – The value of the inverse of the link function at `p` \| \| Returns: \| p – Mean probabilities. The value of the inverse of CDF link of `z` \| \| Return type: \| array \| #### Notes g^(-1)(`z`) = `dbn`.cdf(`z`) statsmodels statsmodels.sandbox.sysreg.Sem2SLS.fit statsmodels.sandbox.sysreg.Sem2SLS.fit ====================================== `Sem2SLS.fit()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/sysreg.html#Sem2SLS.fit) statsmodels statsmodels.tsa.vector_ar.var_model.VARProcess.simulate_var statsmodels.tsa.vector\_ar.var\_model.VARProcess.simulate\_var ============================================================== `VARProcess.simulate_var(steps=None, offset=None, seed=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARProcess.simulate_var) simulate the VAR(p) process for the desired number of steps \| Parameters: \| * steps (None or int) – number of observations to simulate, this includes the initial observations to start the autoregressive process. If offset is not None, then exog of the model are used if they were provided in the model * offset (None or ndarray (steps, neqs)) – If not None, then offset is added as an observation specific intercept to the autoregression. If it is None and either trend (including intercept) or exog were used in the VAR model, then the linear predictor of those components will be used as offset. This should have the same number of rows as steps, and the same number of columns as endogenous variables (neqs). * seed (None or integer) – If seed is not None, then it will be used with for the random variables generated by numpy.random. \| \| Returns: \| endog\_simulated – Endog of the simulated VAR process \| \| Return type: \| nd\_array \| statsmodels statsmodels.stats.weightstats.DescrStatsW.ttest_mean statsmodels.stats.weightstats.DescrStatsW.ttest\_mean ===================================================== `DescrStatsW.ttest_mean(value=0, alternative='two-sided')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/weightstats.html#DescrStatsW.ttest_mean) ttest of Null hypothesis that mean is equal to value. The alternative hypothesis H1 is defined by the following ‘two-sided’: H1: mean not equal to value ‘larger’ : H1: mean larger than value ‘smaller’ : H1: mean smaller than value \| Parameters: \| * value (float or array) – the hypothesized value for the mean * alternative (string) – The alternative hypothesis, H1, has to be one of the following ’two-sided’: H1: mean not equal to value (default) ‘larger’ : H1: mean larger than value ‘smaller’ : H1: mean smaller than value \| \| Returns: \| * tstat (float) – test statisic * pvalue (float) – pvalue of the t-test * df (int or float) \| statsmodels statsmodels.stats.contingency_tables.StratifiedTable statsmodels.stats.contingency\_tables.StratifiedTable ===================================================== `class statsmodels.stats.contingency_tables.StratifiedTable(tables, shift_zeros=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/contingency_tables.html#StratifiedTable) Analyses for a collection of 2x2 contingency tables. Such a collection may arise by stratifying a single 2x2 table with respect to another factor. This class implements the ‘Cochran-Mantel-Haenszel’ and ‘Breslow-Day’ procedures for analyzing collections of 2x2 contingency tables. \| Parameters: \| tables (list or ndarray) – Either a list containing several 2x2 contingency tables, or a 2x2xk ndarray in which each slice along the third axis is a 2x2 contingency table. \| `logodds_pooled` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/contingency_tables.html#StratifiedTable.logodds_pooled) float – An estimate of the pooled log odds ratio. This is the Mantel-Haenszel estimate of an odds ratio that is common to all the tables. `log_oddsratio_se` float – The estimated standard error of the pooled log odds ratio, following Robins, Breslow and Greenland (Biometrics 42:311-323). `oddsratio_pooled` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/contingency_tables.html#StratifiedTable.oddsratio_pooled) float – An estimate of the pooled odds ratio. This is the Mantel-Haenszel estimate of an odds ratio that is common to all tables. `risk_pooled` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/contingency_tables.html#StratifiedTable.risk_pooled) float – An estimate of the pooled risk ratio. This is an estimate of a risk ratio that is common to all the tables. #### Notes This results are based on a sampling model in which the units are independent both within and between strata. #### Methods \| \| \| \| --- \| --- \| \| [`from_data`](statsmodels.stats.contingency_tables.stratifiedtable.from_data#statsmodels.stats.contingency_tables.StratifiedTable.from_data "statsmodels.stats.contingency_tables.StratifiedTable.from_data")(var1, var2, strata, data) \| Construct a StratifiedTable object from data. \| \| [`logodds_pooled`](statsmodels.stats.contingency_tables.stratifiedtable.logodds_pooled#statsmodels.stats.contingency_tables.StratifiedTable.logodds_pooled "statsmodels.stats.contingency_tables.StratifiedTable.logodds_pooled")() \| \| \| [`logodds_pooled_confint`](statsmodels.stats.contingency_tables.stratifiedtable.logodds_pooled_confint#statsmodels.stats.contingency_tables.StratifiedTable.logodds_pooled_confint "statsmodels.stats.contingency_tables.StratifiedTable.logodds_pooled_confint")([alpha, method]) \| A confidence interval for the pooled log odds ratio. \| \| [`logodds_pooled_se`](statsmodels.stats.contingency_tables.stratifiedtable.logodds_pooled_se#statsmodels.stats.contingency_tables.StratifiedTable.logodds_pooled_se "statsmodels.stats.contingency_tables.StratifiedTable.logodds_pooled_se")() \| \| \| [`oddsratio_pooled`](statsmodels.stats.contingency_tables.stratifiedtable.oddsratio_pooled#statsmodels.stats.contingency_tables.StratifiedTable.oddsratio_pooled "statsmodels.stats.contingency_tables.StratifiedTable.oddsratio_pooled")() \| \| \| [`oddsratio_pooled_confint`](statsmodels.stats.contingency_tables.stratifiedtable.oddsratio_pooled_confint#statsmodels.stats.contingency_tables.StratifiedTable.oddsratio_pooled_confint "statsmodels.stats.contingency_tables.StratifiedTable.oddsratio_pooled_confint")([alpha, method]) \| A confidence interval for the pooled odds ratio. \| \| [`risk_pooled`](statsmodels.stats.contingency_tables.stratifiedtable.risk_pooled#statsmodels.stats.contingency_tables.StratifiedTable.risk_pooled "statsmodels.stats.contingency_tables.StratifiedTable.risk_pooled")() \| \| \| [`summary`](statsmodels.stats.contingency_tables.stratifiedtable.summary#statsmodels.stats.contingency_tables.StratifiedTable.summary "statsmodels.stats.contingency_tables.StratifiedTable.summary")([alpha, float\_format, method]) \| A summary of all the main results. \| \| [`test_equal_odds`](statsmodels.stats.contingency_tables.stratifiedtable.test_equal_odds#statsmodels.stats.contingency_tables.StratifiedTable.test_equal_odds "statsmodels.stats.contingency_tables.StratifiedTable.test_equal_odds")([adjust]) \| Test that all odds ratios are identical. \| \| [`test_null_odds`](statsmodels.stats.contingency_tables.stratifiedtable.test_null_odds#statsmodels.stats.contingency_tables.StratifiedTable.test_null_odds "statsmodels.stats.contingency_tables.StratifiedTable.test_null_odds")([correction]) \| Test that all tables have odds ratio equal to 1. \|	programming_docs
statsmodels statsmodels.tsa.arima_process.ArmaProcess.pacf statsmodels.tsa.arima\_process.ArmaProcess.pacf =============================================== `ArmaProcess.pacf(lags=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_process.html#ArmaProcess.pacf) Partial autocorrelation function of an ARMA process \| Parameters: \| * ar (array\_like, 1d) – coefficient for autoregressive lag polynomial, including zero lag * ma (array\_like, 1d) – coefficient for moving-average lag polynomial, including zero lag * lags (int) – number of terms (lags plus zero lag) to include in returned pacf \| \| Returns: \| pacf – partial autocorrelation of ARMA process given by ar, ma \| \| Return type: \| array \| #### Notes solves yule-walker equation for each lag order up to nobs lags not tested/checked yet statsmodels statsmodels.regression.linear_model.OLSResults.rsquared_adj statsmodels.regression.linear\_model.OLSResults.rsquared\_adj ============================================================= `OLSResults.rsquared_adj()` statsmodels statsmodels.stats.proportion.binom_test_reject_interval statsmodels.stats.proportion.binom\_test\_reject\_interval ========================================================== `statsmodels.stats.proportion.binom_test_reject_interval(value, nobs, alpha=0.05, alternative='two-sided')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/proportion.html#binom_test_reject_interval) rejection region for binomial test for one sample proportion The interval includes the end points of the rejection region. \| Parameters: \| * value (float) – proportion under the Null hypothesis * nobs (integer) – the number of trials or observations. \| \| Returns: \| x\_low, x\_upp – lower and upper bound of rejection region \| \| Return type: \| float \| statsmodels statsmodels.discrete.discrete_model.NegativeBinomialResults.summary2 statsmodels.discrete.discrete\_model.NegativeBinomialResults.summary2 ===================================================================== `NegativeBinomialResults.summary2(yname=None, xname=None, title=None, alpha=0.05, float_format='%.4f')` Experimental function to summarize regression results \| Parameters: \| * xname (List of strings of length equal to the number of parameters) – Names of the independent variables (optional) * yname (string) – Name of the dependent variable (optional) * title (string, optional) – Title for the top table. If not None, then this replaces the default title * alpha (float) – significance level for the confidence intervals * float\_format (string) – print format for floats in parameters summary \| \| Returns: \| smry – this holds the summary tables and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary.Summary`](statsmodels.iolib.summary.summary#statsmodels.iolib.summary.Summary "statsmodels.iolib.summary.Summary") class to hold summary results statsmodels statsmodels.discrete.discrete_model.DiscreteModel.pdf statsmodels.discrete.discrete\_model.DiscreteModel.pdf ====================================================== `DiscreteModel.pdf(X)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#DiscreteModel.pdf) The probability density (mass) function of the model. statsmodels statsmodels.regression.linear_model.RegressionResults.eigenvals statsmodels.regression.linear\_model.RegressionResults.eigenvals ================================================================ `RegressionResults.eigenvals()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#RegressionResults.eigenvals) Return eigenvalues sorted in decreasing order. statsmodels statsmodels.tsa.statespace.mlemodel.MLEResults.bse statsmodels.tsa.statespace.mlemodel.MLEResults.bse ================================================== `MLEResults.bse()` statsmodels statsmodels.robust.robust_linear_model.RLM.information statsmodels.robust.robust\_linear\_model.RLM.information ======================================================== `RLM.information(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/robust_linear_model.html#RLM.information) Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.robust.robust_linear_model.RLM.initialize statsmodels.robust.robust\_linear\_model.RLM.initialize ======================================================= `RLM.initialize()` Initialize (possibly re-initialize) a Model instance. For instance, the design matrix of a linear model may change and some things must be recomputed. statsmodels statsmodels.discrete.count_model.GenericZeroInflated.pdf statsmodels.discrete.count\_model.GenericZeroInflated.pdf ========================================================= `GenericZeroInflated.pdf(X)` The probability density (mass) function of the model. statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.test_heteroskedasticity statsmodels.tsa.statespace.dynamic\_factor.DynamicFactorResults.test\_heteroskedasticity ======================================================================================== `DynamicFactorResults.test_heteroskedasticity(method, alternative='two-sided', use_f=True)` Test for heteroskedasticity of standardized residuals Tests whether the sum-of-squares in the first third of the sample is significantly different than the sum-of-squares in the last third of the sample. Analogous to a Goldfeld-Quandt test. The null hypothesis is of no heteroskedasticity. \| Parameters: \| * method (string {'breakvar'} or None) – The statistical test for heteroskedasticity. Must be ‘breakvar’ for test of a break in the variance. If None, an attempt is made to select an appropriate test. * alternative (string, 'increasing', 'decreasing' or 'two-sided') – This specifies the alternative for the p-value calculation. Default is two-sided. * use\_f (boolean, optional) – Whether or not to compare against the asymptotic distribution (chi-squared) or the approximate small-sample distribution (F). Default is True (i.e. default is to compare against an F distribution). \| \| Returns: \| output – An array with `(test_statistic, pvalue)` for each endogenous variable. The array is then sized `(k_endog, 2)`. If the method is called as `het = res.test_heteroskedasticity()`, then `het[0]` is an array of size 2 corresponding to the first endogenous variable, where `het[0][0]` is the test statistic, and `het[0][1]` is the p-value. \| \| Return type: \| array \| #### Notes The null hypothesis is of no heteroskedasticity. That means different things depending on which alternative is selected: * Increasing: Null hypothesis is that the variance is not increasing throughout the sample; that the sum-of-squares in the later subsample is not greater than the sum-of-squares in the earlier subsample. * Decreasing: Null hypothesis is that the variance is not decreasing throughout the sample; that the sum-of-squares in the earlier subsample is not greater than the sum-of-squares in the later subsample. * Two-sided: Null hypothesis is that the variance is not changing throughout the sample. Both that the sum-of-squares in the earlier subsample is not greater than the sum-of-squares in the later subsample and that the sum-of-squares in the later subsample is not greater than the sum-of-squares in the earlier subsample. For $h = [T/3]$, the test statistic is: \[H(h) = \sum\_{t=T-h+1}^T \tilde v\_t^2 \Bigg / \sum\_{t=d+1}^{d+1+h} \tilde v\_t^2\] where $d$ is the number of periods in which the loglikelihood was burned in the parent model (usually corresponding to diffuse initialization). This statistic can be tested against an $F(h,h)$ distribution. Alternatively, $h H(h)$ is asymptotically distributed according to $\chi\_h^2$; this second test can be applied by passing `asymptotic=True` as an argument. See section 5.4 of [[1]](#id2) for the above formula and discussion, as well as additional details. TODO * Allow specification of $h$ #### References \| \| \| \| --- \| --- \| \| [[1]](#id1) \| Harvey, Andrew C. 1990. Forecasting, Structural Time Series Models and the Kalman Filter. Cambridge University Press. \| statsmodels statsmodels.tsa.vector_ar.vecm.VECMResults.orth_ma_rep statsmodels.tsa.vector\_ar.vecm.VECMResults.orth\_ma\_rep ========================================================= `VECMResults.orth_ma_rep(maxn=10, P=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/vecm.html#VECMResults.orth_ma_rep) Compute orthogonalized MA coefficient matrices. For this purpose a matrix P is used which fulfills $\Sigma\_u = PP^\prime$. P defaults to the Cholesky decomposition of $\Sigma\_u$ \| Parameters: \| * maxn (int) – Number of coefficient matrices to compute * P (ndarray (neqs x neqs), optional) – Matrix such that $\Sigma\_u = PP'$. Defaults to Cholesky decomposition. \| \| Returns: \| coefs \| \| Return type: \| ndarray (maxn x neqs x neqs) \| statsmodels statsmodels.sandbox.tsa.fftarma.ArmaFft.impulse_response statsmodels.sandbox.tsa.fftarma.ArmaFft.impulse\_response ========================================================= `ArmaFft.impulse_response(leads=None)` Get the impulse response function (MA representation) for ARMA process \| Parameters: \| * ma (array\_like, 1d) – moving average lag polynomial * ar (array\_like, 1d) – auto regressive lag polynomial * leads (int) – number of observations to calculate \| \| Returns: \| ir – impulse response function with nobs elements \| \| Return type: \| array, 1d \| #### Notes This is the same as finding the MA representation of an ARMA(p,q). By reversing the role of ar and ma in the function arguments, the returned result is the AR representation of an ARMA(p,q), i.e ma\_representation = arma\_impulse\_response(ar, ma, leads=100) ar\_representation = arma\_impulse\_response(ma, ar, leads=100) Fully tested against matlab #### Examples AR(1) ``` >>> arma_impulse_response([1.0, -0.8], [1.], leads=10) array([ 1. , 0.8 , 0.64 , 0.512 , 0.4096 , 0.32768 , 0.262144 , 0.2097152 , 0.16777216, 0.13421773]) ``` this is the same as ``` >>> 0.8np.arange(10) array([ 1. , 0.8 , 0.64 , 0.512 , 0.4096 , 0.32768 , 0.262144 , 0.2097152 , 0.16777216, 0.13421773]) ``` MA(2) ``` >>> arma_impulse_response([1.0], [1., 0.5, 0.2], leads=10) array([ 1. , 0.5, 0.2, 0. , 0. , 0. , 0. , 0. , 0. , 0. ]) ``` ARMA(1,2) ``` >>> arma_impulse_response([1.0, -0.8], [1., 0.5, 0.2], leads=10) array([ 1. , 1.3 , 1.24 , 0.992 , 0.7936 , 0.63488 , 0.507904 , 0.4063232 , 0.32505856, 0.26004685]) ``` statsmodels statsmodels.tsa.vector_ar.vecm.VECMResults.tvalues_det_coef_coint statsmodels.tsa.vector\_ar.vecm.VECMResults.tvalues\_det\_coef\_coint ===================================================================== `VECMResults.tvalues_det_coef_coint()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/vecm.html#VECMResults.tvalues_det_coef_coint) statsmodels statsmodels.miscmodels.count.PoissonGMLE.expandparams statsmodels.miscmodels.count.PoissonGMLE.expandparams ===================================================== `PoissonGMLE.expandparams(params)` expand to full parameter array when some parameters are fixed \| Parameters: \| params** (array) – reduced parameter array \| \| Returns: \| paramsfull – expanded parameter array where fixed parameters are included \| \| Return type: \| array \| #### Notes Calling this requires that self.fixed\_params and self.fixed\_paramsmask are defined. developer notes: This can be used in the log-likelihood to … this could also be replaced by a more general parameter transformation. statsmodels statsmodels.genmod.generalized_linear_model.GLMResults.summary statsmodels.genmod.generalized\_linear\_model.GLMResults.summary ================================================================ `GLMResults.summary(yname=None, xname=None, title=None, alpha=0.05)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_linear_model.html#GLMResults.summary) Summarize the Regression Results \| Parameters: \| * yname (string, optional) – Default is `y` * xname (list of strings, optional) – Default is `var_##` for ## in p the number of regressors * title (string, optional) – Title for the top table. If not None, then this replaces the default title * alpha (float) – significance level for the confidence intervals \| \| Returns: \| smry – this holds the summary tables and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary.Summary`](statsmodels.iolib.summary.summary#statsmodels.iolib.summary.Summary "statsmodels.iolib.summary.Summary") class to hold summary results statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.tvalues_endog_lagged statsmodels.tsa.vector\_ar.var\_model.VARResults.tvalues\_endog\_lagged ======================================================================= `VARResults.tvalues_endog_lagged()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARResults.tvalues_endog_lagged) statsmodels statsmodels.tsa.arima_model.ARIMAResults.maroots statsmodels.tsa.arima\_model.ARIMAResults.maroots ================================================= `ARIMAResults.maroots()` statsmodels statsmodels.genmod.families.family.Gaussian.deviance statsmodels.genmod.families.family.Gaussian.deviance ==================================================== `Gaussian.deviance(endog, mu, var_weights=1.0, freq_weights=1.0, scale=1.0)` The deviance function evaluated at (endog, mu, var\_weights, freq\_weights, scale) for the distribution. Deviance is usually defined as twice the loglikelihood ratio. \| Parameters: \| * endog (array-like) – The endogenous response variable * mu (array-like) – The inverse of the link function at the linear predicted values. * var\_weights (array-like) – 1d array of variance (analytic) weights. The default is 1. * freq\_weights (array-like) – 1d array of frequency weights. The default is 1. * scale (float, optional) – An optional scale argument. The default is 1. \| \| Returns: \| Deviance – The value of deviance function defined below. \| \| Return type: \| array \| #### Notes Deviance is defined \[D = 2\sum\_i (freq\\_weights\_i \* var\\_weights \* (llf(endog\_i, endog\_i) - llf(endog\_i, \mu\_i)))\] where y is the endogenous variable. The deviance functions are analytically defined for each family. Internally, we calculate deviance as: \[D = \sum\_i freq\\_weights\_i \* var\\_weights \* resid\\_dev\_i / scale\] statsmodels statsmodels.stats.contingency_tables.SquareTable.cumulative_log_oddsratios statsmodels.stats.contingency\_tables.SquareTable.cumulative\_log\_oddsratios ============================================================================= `SquareTable.cumulative_log_oddsratios()` statsmodels statsmodels.sandbox.distributions.extras.SkewNorm2_gen.entropy statsmodels.sandbox.distributions.extras.SkewNorm2\_gen.entropy =============================================================== `SkewNorm2_gen.entropy(args, kwds)` Differential entropy of the RV. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information). * loc (array\_like, optional) – Location parameter (default=0). * scale (array\_like, optional (continuous distributions only)) – Scale parameter (default=1). \| #### Notes Entropy is defined base `e`: ``` >>> drv = rv_discrete(values=((0, 1), (0.5, 0.5))) >>> np.allclose(drv.entropy(), np.log(2.0)) True ``` statsmodels statsmodels.robust.norms.TukeyBiweight statsmodels.robust.norms.TukeyBiweight ====================================== `class statsmodels.robust.norms.TukeyBiweight(c=4.685)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/norms.html#TukeyBiweight) Tukey’s biweight function for M-estimation. \| Parameters: \| c (float, optional) – The tuning constant for Tukey’s Biweight. The default value is c = 4.685. \| #### Notes Tukey’s biweight is sometime’s called bisquare. #### Methods \| \| \| \| --- \| --- \| \| [`psi`](statsmodels.robust.norms.tukeybiweight.psi#statsmodels.robust.norms.TukeyBiweight.psi "statsmodels.robust.norms.TukeyBiweight.psi")(z) \| The psi function for Tukey’s biweight estimator \| \| [`psi_deriv`](statsmodels.robust.norms.tukeybiweight.psi_deriv#statsmodels.robust.norms.TukeyBiweight.psi_deriv "statsmodels.robust.norms.TukeyBiweight.psi_deriv")(z) \| The derivative of Tukey’s biweight psi function \| \| [`rho`](statsmodels.robust.norms.tukeybiweight.rho#statsmodels.robust.norms.TukeyBiweight.rho "statsmodels.robust.norms.TukeyBiweight.rho")(z) \| The robust criterion function for Tukey’s biweight estimator \| \| [`weights`](statsmodels.robust.norms.tukeybiweight.weights#statsmodels.robust.norms.TukeyBiweight.weights "statsmodels.robust.norms.TukeyBiweight.weights")(z) \| Tukey’s biweight weighting function for the IRLS algorithm \| statsmodels statsmodels.multivariate.factor.FactorResults.plot_loadings statsmodels.multivariate.factor.FactorResults.plot\_loadings ============================================================ `FactorResults.plot_loadings(loading_pairs=None, plot_prerotated=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/multivariate/factor.html#FactorResults.plot_loadings) Plot factor loadings in 2-d plots \| Parameters: \| * loading\_pairs (None or a list of tuples) – Specify plots. Each tuple (i, j) represent one figure, i and j is the loading number for x-axis and y-axis, respectively. If `None`, all combinations of the loadings will be plotted. * plot\_prerotated (True or False) – If True, the loadings before rotation applied will be plotted. If False, rotated loadings will be plotted. \| \| Returns: \| figs \| \| Return type: \| a list of figure handles \| statsmodels statsmodels.discrete.discrete_model.GeneralizedPoissonResults.llr statsmodels.discrete.discrete\_model.GeneralizedPoissonResults.llr ================================================================== `GeneralizedPoissonResults.llr()` statsmodels statsmodels.tsa.ar_model.ARResults.wald_test statsmodels.tsa.ar\_model.ARResults.wald\_test ============================================== `ARResults.wald_test(r_matrix, cov_p=None, scale=1.0, invcov=None, use_f=None)` Compute a Wald-test for a joint linear hypothesis. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. * use\_f (bool) – If True, then the F-distribution is used. If False, then the asymptotic distribution, chisquare is used. If use\_f is None, then the F distribution is used if the model specifies that use\_t is True. The test statistic is proportionally adjusted for the distribution by the number of constraints in the hypothesis. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`f_test`](statsmodels.tsa.ar_model.arresults.f_test#statsmodels.tsa.ar_model.ARResults.f_test "statsmodels.tsa.ar_model.ARResults.f_test"), [`t_test`](statsmodels.tsa.ar_model.arresults.t_test#statsmodels.tsa.ar_model.ARResults.t_test "statsmodels.tsa.ar_model.ARResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full.	programming_docs
statsmodels statsmodels.genmod.families.links.Power.inverse_deriv statsmodels.genmod.families.links.Power.inverse\_deriv ====================================================== `Power.inverse_deriv(z)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#Power.inverse_deriv) Derivative of the inverse of the power transform \| Parameters: \| z (array-like) – `z` is usually the linear predictor for a GLM or GEE model. \| \| Returns: \| * g^(-1)’(z) (array) – The value of the derivative of the inverse of the power transform * function \| statsmodels statsmodels.genmod.families.links.nbinom.deriv statsmodels.genmod.families.links.nbinom.deriv ============================================== `nbinom.deriv(p)` Derivative of the negative binomial transform \| Parameters: \| p (array-like) – Mean parameters \| \| Returns: \| g’(p) – The derivative of the negative binomial transform link function \| \| Return type: \| array \| #### Notes g’(x) = 1/(x+alpha\x^2) statsmodels statsmodels.sandbox.regression.gmm.IVRegressionResults.centered_tss statsmodels.sandbox.regression.gmm.IVRegressionResults.centered\_tss ==================================================================== `IVRegressionResults.centered_tss()` statsmodels statsmodels.discrete.discrete_model.MultinomialResults.pvalues statsmodels.discrete.discrete\_model.MultinomialResults.pvalues =============================================================== `MultinomialResults.pvalues()` statsmodels statsmodels.tsa.vector_ar.var_model.VAR.fit statsmodels.tsa.vector\_ar.var\_model.VAR.fit ============================================= `VAR.fit(maxlags=None, method='ols', ic=None, trend='c', verbose=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VAR.fit) Fit the VAR model \| Parameters: \| maxlags (int) – Maximum number of lags to check for order selection, defaults to 12 \* (nobs/100.)\\(1./4), see select\_order function * method ({'ols'}) – Estimation method to use * ic ({'aic', 'fpe', 'hqic', 'bic', None}) – Information criterion to use for VAR order selection. aic : Akaike fpe : Final prediction error hqic : Hannan-Quinn bic : Bayesian a.k.a. Schwarz * verbose (bool, default False) – Print order selection output to the screen * trend (str {"c", "ct", "ctt", "nc"}) – “c” - add constant “ct” - constant and trend “ctt” - constant, linear and quadratic trend “nc” - co constant, no trend Note that these are prepended to the columns of the dataset. \| #### Notes Lütkepohl pp. 146-153 \| Returns: \| est \| \| Return type: \| VARResultsWrapper \| statsmodels statsmodels.stats.outliers_influence.variance_inflation_factor statsmodels.stats.outliers\_influence.variance\_inflation\_factor ================================================================= `statsmodels.stats.outliers_influence.variance_inflation_factor(exog, exog_idx)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/outliers_influence.html#variance_inflation_factor) variance inflation factor, VIF, for one exogenous variable The variance inflation factor is a measure for the increase of the variance of the parameter estimates if an additional variable, given by exog\_idx is added to the linear regression. It is a measure for multicollinearity of the design matrix, exog. One recommendation is that if VIF is greater than 5, then the explanatory variable given by exog\_idx is highly collinear with the other explanatory variables, and the parameter estimates will have large standard errors because of this. \| Parameters: \| * exog (ndarray) – design matrix with all explanatory variables, as for example used in regression * exog\_idx (int) – index of the exogenous variable in the columns of exog \| \| Returns: \| vif – variance inflation factor \| \| Return type: \| float \| #### Notes This function does not save the auxiliary regression. See also `xxx` class for regression diagnostics TODO: doesn’t exist yet #### References <http://en.wikipedia.org/wiki/Variance_inflation_factor> statsmodels statsmodels.iolib.summary2.Summary.add_text statsmodels.iolib.summary2.Summary.add\_text ============================================ `Summary.add_text(string)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/iolib/summary2.html#Summary.add_text) Append a note to the bottom of the summary table. In ASCII tables, the note will be wrapped to table width. Notes are not indendented. statsmodels statsmodels.discrete.discrete_model.Logit.pdf statsmodels.discrete.discrete\_model.Logit.pdf ============================================== `Logit.pdf(X)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#Logit.pdf) The logistic probability density function \| Parameters: \| X (array-like) – `X` is the linear predictor of the logit model. See notes. \| \| Returns: \| pdf – The value of the Logit probability mass function, PMF, for each point of X. `np.exp(-x)/(1+np.exp(-X))*2` \| \| Return type: \| ndarray \| #### Notes In the logit model, \[\lambda\left(x^{\prime}\beta\right)=\frac{e^{-x^{\prime}\beta}}{\left(1+e^{-x^{\prime}\beta}\right)^{2}}\] statsmodels statsmodels.tsa.arima_model.ARMAResults.wald_test statsmodels.tsa.arima\_model.ARMAResults.wald\_test =================================================== `ARMAResults.wald_test(r_matrix, cov_p=None, scale=1.0, invcov=None, use_f=None)` Compute a Wald-test for a joint linear hypothesis. \| Parameters: \| r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. * use\_f (bool) – If True, then the F-distribution is used. If False, then the asymptotic distribution, chisquare is used. If use\_f is None, then the F distribution is used if the model specifies that use\_t is True. The test statistic is proportionally adjusted for the distribution by the number of constraints in the hypothesis. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`f_test`](statsmodels.tsa.arima_model.armaresults.f_test#statsmodels.tsa.arima_model.ARMAResults.f_test "statsmodels.tsa.arima_model.ARMAResults.f_test"), [`t_test`](statsmodels.tsa.arima_model.armaresults.t_test#statsmodels.tsa.arima_model.ARMAResults.t_test "statsmodels.tsa.arima_model.ARMAResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.discrete.discrete_model.ProbitResults.conf_int statsmodels.discrete.discrete\_model.ProbitResults.conf\_int ============================================================ `ProbitResults.conf_int(alpha=0.05, cols=None, method='default')` Returns the confidence interval of the fitted parameters. \| Parameters: \| * alpha (float, optional) – The significance level for the confidence interval. ie., The default `alpha` = .05 returns a 95% confidence interval. * cols (array-like, optional) – `cols` specifies which confidence intervals to return * method (string) – Not Implemented Yet Method to estimate the confidence\_interval. “Default” : uses self.bse which is based on inverse Hessian for MLE “hjjh” : “jac” : “boot-bse” “boot\_quant” “profile” \| \| Returns: \| conf\_int – Each row contains [lower, upper] limits of the confidence interval for the corresponding parameter. The first column contains all lower, the second column contains all upper limits. \| \| Return type: \| array \| #### Examples ``` >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> results.conf_int() array([[-5496529.48322745, -1467987.78596704], [ -177.02903529, 207.15277984], [ -0.1115811 , 0.03994274], [ -3.12506664, -0.91539297], [ -1.5179487 , -0.54850503], [ -0.56251721, 0.460309 ], [ 798.7875153 , 2859.51541392]]) ``` ``` >>> results.conf_int(cols=(2,3)) array([[-0.1115811 , 0.03994274], [-3.12506664, -0.91539297]]) ``` #### Notes The confidence interval is based on the standard normal distribution. Models wish to use a different distribution should overwrite this method. statsmodels statsmodels.discrete.discrete_model.NegativeBinomialP.score_obs statsmodels.discrete.discrete\_model.NegativeBinomialP.score\_obs ================================================================= `NegativeBinomialP.score_obs(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#NegativeBinomialP.score_obs) Generalized Negative Binomial (NB-P) model score (gradient) vector of the log-likelihood for each observations. \| Parameters: \| params (array-like) – The parameters of the model \| \| Returns: \| score – The score vector of the model, i.e. the first derivative of the loglikelihood function, evaluated at `params` \| \| Return type: \| ndarray, 1-D \| statsmodels statsmodels.discrete.discrete_model.DiscreteModel.predict statsmodels.discrete.discrete\_model.DiscreteModel.predict ========================================================== `DiscreteModel.predict(params, exog=None, linear=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#DiscreteModel.predict) Predict response variable of a model given exogenous variables. statsmodels statsmodels.sandbox.regression.gmm.IVGMMResults.bse statsmodels.sandbox.regression.gmm.IVGMMResults.bse =================================================== `IVGMMResults.bse()` statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.test_whiteness statsmodels.tsa.vector\_ar.var\_model.VARResults.test\_whiteness ================================================================ `VARResults.test_whiteness(nlags=10, signif=0.05, adjusted=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARResults.test_whiteness) Residual whiteness tests using Portmanteau test \| Parameters: \| * nlags (int > 0) – * signif (float, between 0 and 1) – * adjusted (bool, default False) – \| \| Returns: \| results \| \| Return type: \| [WhitenessTestResults](statsmodels.tsa.vector_ar.hypothesis_test_results.whitenesstestresults#statsmodels.tsa.vector_ar.hypothesis_test_results.WhitenessTestResults "statsmodels.tsa.vector_ar.hypothesis_test_results.WhitenessTestResults") \| #### Notes Test the whiteness of the residuals using the Portmanteau test as described in [[1]](#id2), chapter 4.4.3. #### References \| \| \| \| --- \| --- \| \| [[1]](#id1) \| Lütkepohl, H. 2005. New Introduction to Multiple Time Series Analysis. Springer. \| statsmodels statsmodels.regression.recursive_ls.RecursiveLS.initialize_approximate_diffuse statsmodels.regression.recursive\_ls.RecursiveLS.initialize\_approximate\_diffuse ================================================================================= `RecursiveLS.initialize_approximate_diffuse(variance=None)` statsmodels statsmodels.tsa.statespace.sarimax.SARIMAX.initialize_state statsmodels.tsa.statespace.sarimax.SARIMAX.initialize\_state ============================================================ `SARIMAX.initialize_state(variance=None, complex_step=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/sarimax.html#SARIMAX.initialize_state) Initialize state and state covariance arrays in preparation for the Kalman filter. \| Parameters: \| variance (float, optional) – The variance for approximating diffuse initial conditions. Default can be found in the Representation class documentation. \| #### Notes Initializes the ARMA component of the state space to the typical stationary values and the other components as approximate diffuse. Can be overridden be calling one of the other initialization methods before fitting the model. statsmodels statsmodels.tsa.statespace.varmax.VARMAX.impulse_responses statsmodels.tsa.statespace.varmax.VARMAX.impulse\_responses =========================================================== `VARMAX.impulse_responses(params, steps=1, impulse=0, orthogonalized=False, cumulative=False, *kwargs)` Impulse response function \| Parameters: \| params (array\_like) – Array of model parameters. * steps (int, optional) – The number of steps for which impulse responses are calculated. Default is 1. Note that the initial impulse is not counted as a step, so if `steps=1`, the output will have 2 entries. * impulse (int or array\_like) – If an integer, the state innovation to pulse; must be between 0 and `k_posdef-1`. Alternatively, a custom impulse vector may be provided; must be shaped `k_posdef x 1`. * orthogonalized (boolean, optional) – Whether or not to perform impulse using orthogonalized innovations. Note that this will also affect custum `impulse` vectors. Default is False. * cumulative (boolean, optional) – Whether or not to return cumulative impulse responses. Default is False. * *\\kwargs* – If the model is time-varying and `steps` is greater than the number of observations, any of the state space representation matrices that are time-varying must have updated values provided for the out-of-sample steps. For example, if `design` is a time-varying component, `nobs` is 10, and `steps` is 15, a (`k_endog` x `k_states` x 5) matrix must be provided with the new design matrix values. \| \| Returns: \| impulse\_responses – Responses for each endogenous variable due to the impulse given by the `impulse` argument. A (steps + 1 x k\_endog) array. \| \| Return type: \| array \| #### Notes Intercepts in the measurement and state equation are ignored when calculating impulse responses. statsmodels statsmodels.tsa.ar_model.AR.from_formula statsmodels.tsa.ar\_model.AR.from\_formula ========================================== `classmethod AR.from_formula(formula, data, subset=None, drop_cols=None, args, kwargs)` Create a Model from a formula and dataframe. \| Parameters: \| formula (str or generic Formula object) – The formula specifying the model * data (array-like) – The data for the model. See Notes. * subset (array-like) – An array-like object of booleans, integers, or index values that indicate the subset of df to use in the model. Assumes df is a `pandas.DataFrame` * drop\_cols (array-like) – Columns to drop from the design matrix. Cannot be used to drop terms involving categoricals. * args (extra arguments) – These are passed to the model * kwargs (extra keyword arguments) – These are passed to the model with one exception. The `eval_env` keyword is passed to patsy. It can be either a [`patsy.EvalEnvironment`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.EvalEnvironment "(in patsy v0.5.0+dev)") object or an integer indicating the depth of the namespace to use. For example, the default `eval_env=0` uses the calling namespace. If you wish to use a “clean” environment set `eval_env=-1`. \| \| Returns: \| model \| \| Return type: \| Model instance \| #### Notes data must define \_\_getitem\_\_ with the keys in the formula terms args and kwargs are passed on to the model instantiation. E.g., a numpy structured or rec array, a dictionary, or a pandas DataFrame. statsmodels statsmodels.duration.hazard_regression.PHReg.efron_loglike statsmodels.duration.hazard\_regression.PHReg.efron\_loglike ============================================================ `PHReg.efron_loglike(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/duration/hazard_regression.html#PHReg.efron_loglike) Returns the value of the log partial likelihood function evaluated at `params`, using the Efron method to handle tied times. statsmodels statsmodels.tsa.statespace.structural.UnobservedComponentsResults.llf_obs statsmodels.tsa.statespace.structural.UnobservedComponentsResults.llf\_obs ========================================================================== `UnobservedComponentsResults.llf_obs()` (float) The value of the log-likelihood function evaluated at `params`. statsmodels statsmodels.regression.quantile_regression.QuantRegResults.f_test statsmodels.regression.quantile\_regression.QuantRegResults.f\_test =================================================================== `QuantRegResults.f_test(r_matrix, cov_p=None, scale=1.0, invcov=None)` Compute the F-test for a joint linear hypothesis. This is a special case of `wald_test` that always uses the F distribution. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length k row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> A = np.identity(len(results.params)) >>> A = A[1:,:] ``` This tests that each coefficient is jointly statistically significantly different from zero. ``` >>> print(results.f_test(A)) <F test: F=array([[ 330.28533923]]), p=4.984030528700946e-10, df_denom=9, df_num=6> ``` Compare this to ``` >>> results.fvalue 330.2853392346658 >>> results.f_pvalue 4.98403096572e-10 ``` ``` >>> B = np.array(([0,0,1,-1,0,0,0],[0,0,0,0,0,1,-1])) ``` This tests that the coefficient on the 2nd and 3rd regressors are equal and jointly that the coefficient on the 5th and 6th regressors are equal. ``` >>> print(results.f_test(B)) <F test: F=array([[ 9.74046187]]), p=0.005605288531708235, df_denom=9, df_num=2> ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.datasets import longley >>> from statsmodels.formula.api import ols >>> dta = longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = '(GNPDEFL = GNP), (UNEMP = 2), (YEAR/1829 = 1)' >>> f_test = results.f_test(hypotheses) >>> print(f_test) <F test: F=array([[ 144.17976065]]), p=6.322026217355609e-08, df_denom=9, df_num=3> ``` See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`wald_test`](statsmodels.regression.quantile_regression.quantregresults.wald_test#statsmodels.regression.quantile_regression.QuantRegResults.wald_test "statsmodels.regression.quantile_regression.QuantRegResults.wald_test"), [`t_test`](statsmodels.regression.quantile_regression.quantregresults.t_test#statsmodels.regression.quantile_regression.QuantRegResults.t_test "statsmodels.regression.quantile_regression.QuantRegResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full.	programming_docs
statsmodels statsmodels.discrete.discrete_model.DiscreteModel.initialize statsmodels.discrete.discrete\_model.DiscreteModel.initialize ============================================================= `DiscreteModel.initialize()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#DiscreteModel.initialize) Initialize is called by statsmodels.model.LikelihoodModel.\_\_init\_\_ and should contain any preprocessing that needs to be done for a model. statsmodels statsmodels.stats.power.TTestIndPower.plot_power statsmodels.stats.power.TTestIndPower.plot\_power ================================================= `TTestIndPower.plot_power(dep_var='nobs', nobs=None, effect_size=None, alpha=0.05, ax=None, title=None, plt_kwds=None, *kwds)` plot power with number of observations or effect size on x-axis \| Parameters: \| dep\_var (string in ['nobs', 'effect\_size', 'alpha']) – This specifies which variable is used for the horizontal axis. If dep\_var=’nobs’ (default), then one curve is created for each value of `effect_size`. If dep\_var=’effect\_size’ or alpha, then one curve is created for each value of `nobs`. * nobs (scalar or array\_like) – specifies the values of the number of observations in the plot * effect\_size (scalar or array\_like) – specifies the values of the effect\_size in the plot * alpha (float or array\_like) – The significance level (type I error) used in the power calculation. Can only be more than a scalar, if `dep_var='alpha'` * ax (None or axis instance) – If ax is None, than a matplotlib figure is created. If ax is a matplotlib axis instance, then it is reused, and the plot elements are created with it. * title (string) – title for the axis. Use an empty string, `''`, to avoid a title. * plt\_kwds (None or [dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)")) – not used yet * kwds (optional keywords for power function) – These remaining keyword arguments are used as arguments to the power function. Many power function support `alternative` as a keyword argument, two-sample test support `ratio`. \| \| Returns: \| fig \| \| Return type: \| matplotlib figure instance \| #### Notes This works only for classes where the `power` method has `effect_size`, `nobs` and `alpha` as the first three arguments. If the second argument is `nobs1`, then the number of observations in the plot are those for the first sample. TODO: fix this for FTestPower and GofChisquarePower TODO: maybe add line variable, if we want more than nobs and effectsize statsmodels statsmodels.stats.diagnostic.lilliefors statsmodels.stats.diagnostic.lilliefors ======================================= `statsmodels.stats.diagnostic.lilliefors(x, dist='norm', pvalmethod='approx')` Lilliefors test for normality or an exponential distribution. Kolmogorov Smirnov test with estimated mean and variance \| Parameters: \| * x (array\_like, 1d) – data series, sample * dist ({'norm', 'exp'}, optional) – Distribution to test in set. * pvalmethod ({'approx', 'table'}, optional) – ‘approx’ is only valid for normality. if `dist = ‘exp’`, `table` is returned. ‘approx’ uses the approximation formula of Dalal and Wilkinson, valid for pvalues < 0.1. If the pvalue is larger than 0.1, then the result of `table` is returned For normality: ‘table’ uses the table from Dalal and Wilkinson, which is available for pvalues between 0.001 and 0.2, and the formula of Lilliefors for large n (n>900). Values in the table are linearly interpolated. Values outside the range will be returned as bounds, 0.2 for large and 0.001 for small pvalues. For exponential: ‘table’ uses the table from Lilliefors 1967, available for pvalues between 0.01 and 0.2. Values outside the range will be returned as bounds, 0.2 for large and 0.01 for small pvalues. \| \| Returns: \| * ksstat (float) – Kolmogorov-Smirnov test statistic with estimated mean and variance. * pvalue (float) – If the pvalue is lower than some threshold, e.g. 0.05, then we can reject the Null hypothesis that the sample comes from a normal distribution \| #### Notes Reported power to distinguish normal from some other distributions is lower than with the Anderson-Darling test. could be vectorized statsmodels statsmodels.genmod.cov_struct.Autoregressive.covariance_matrix statsmodels.genmod.cov\_struct.Autoregressive.covariance\_matrix ================================================================ `Autoregressive.covariance_matrix(endog_expval, index)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/cov_struct.html#Autoregressive.covariance_matrix) Returns the working covariance or correlation matrix for a given cluster of data. \| Parameters: \| * endog\_expval (array-like) – The expected values of endog for the cluster for which the covariance or correlation matrix will be returned * index (integer) – The index of the cluster for which the covariane or correlation matrix will be returned \| \| Returns: \| * M (matrix) – The covariance or correlation matrix of endog * is\_cor (bool) – True if M is a correlation matrix, False if M is a covariance matrix \| statsmodels statsmodels.sandbox.distributions.transformed.Transf_gen.var statsmodels.sandbox.distributions.transformed.Transf\_gen.var ============================================================= `Transf_gen.var(args, kwds)` Variance of the distribution. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| var – the variance of the distribution \| \| Return type: \| float \| statsmodels statsmodels.regression.linear_model.GLS.fit statsmodels.regression.linear\_model.GLS.fit ============================================ `GLS.fit(method='pinv', cov_type='nonrobust', cov_kwds=None, use_t=None, *kwargs)` Full fit of the model. The results include an estimate of covariance matrix, (whitened) residuals and an estimate of scale. \| Parameters: \| method (str, optional) – Can be “pinv”, “qr”. “pinv” uses the Moore-Penrose pseudoinverse to solve the least squares problem. “qr” uses the QR factorization. * cov\_type (str, optional) – See `regression.linear_model.RegressionResults` for a description of the available covariance estimators * cov\_kwds (list or None, optional) – See `linear_model.RegressionResults.get_robustcov_results` for a description required keywords for alternative covariance estimators * use\_t (bool, optional) – Flag indicating to use the Student’s t distribution when computing p-values. Default behavior depends on cov\_type. See `linear_model.RegressionResults.get_robustcov_results` for implementation details. \| \| Returns: \| \| \| Return type: \| A RegressionResults class instance. \| See also `regression.linear_model.RegressionResults`, `regression.linear_model.RegressionResults.get_robustcov_results` #### Notes The fit method uses the pseudoinverse of the design/exogenous variables to solve the least squares minimization. statsmodels statsmodels.regression.linear_model.GLSAR statsmodels.regression.linear\_model.GLSAR ========================================== `class statsmodels.regression.linear_model.GLSAR(endog, exog=None, rho=1, missing='none', *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#GLSAR) A regression model with an AR(p) covariance structure. \| Parameters: \| endog (array-like) – 1-d endogenous response variable. The dependent variable. * exog (array-like) – A nobs x k array where `nobs` is the number of observations and `k` is the number of regressors. An intercept is not included by default and should be added by the user. See `statsmodels.tools.add_constant`. * rho (int) – Order of the autoregressive covariance * missing (str) – Available options are ‘none’, ‘drop’, and ‘raise’. If ‘none’, no nan checking is done. If ‘drop’, any observations with nans are dropped. If ‘raise’, an error is raised. Default is ‘none.’ * hasconst (None or bool) – Indicates whether the RHS includes a user-supplied constant. If True, a constant is not checked for and k\_constant is set to 1 and all result statistics are calculated as if a constant is present. If False, a constant is not checked for and k\_constant is set to 0. \| #### Examples ``` >>> import statsmodels.api as sm >>> X = range(1,8) >>> X = sm.add_constant(X) >>> Y = [1,3,4,5,8,10,9] >>> model = sm.GLSAR(Y, X, rho=2) >>> for i in range(6): ... results = model.fit() ... print("AR coefficients: {0}".format(model.rho)) ... rho, sigma = sm.regression.yule_walker(results.resid, ... order=model.order) ... model = sm.GLSAR(Y, X, rho) ... AR coefficients: [ 0. 0.] AR coefficients: [-0.52571491 -0.84496178] AR coefficients: [-0.6104153 -0.86656458] AR coefficients: [-0.60439494 -0.857867 ] AR coefficients: [-0.6048218 -0.85846157] AR coefficients: [-0.60479146 -0.85841922] >>> results.params array([-0.66661205, 1.60850853]) >>> results.tvalues array([ -2.10304127, 21.8047269 ]) >>> print(results.t_test([1, 0])) <T test: effect=array([-0.66661205]), sd=array([[ 0.31697526]]), t=array([[-2.10304127]]), p=array([[ 0.06309969]]), df_denom=3> >>> print(results.f_test(np.identity(2))) <F test: F=array([[ 1815.23061844]]), p=[[ 0.00002372]], df_denom=3, df_num=2> ``` Or, equivalently ``` >>> model2 = sm.GLSAR(Y, X, rho=2) >>> res = model2.iterative_fit(maxiter=6) >>> model2.rho array([-0.60479146, -0.85841922]) ``` #### Notes GLSAR is considered to be experimental. The linear autoregressive process of order p–AR(p)–is defined as: TODO #### Methods \| \| \| \| --- \| --- \| \| [`fit`](statsmodels.regression.linear_model.glsar.fit#statsmodels.regression.linear_model.GLSAR.fit "statsmodels.regression.linear_model.GLSAR.fit")([method, cov\_type, cov\_kwds, use\_t]) \| Full fit of the model. \| \| [`fit_regularized`](statsmodels.regression.linear_model.glsar.fit_regularized#statsmodels.regression.linear_model.GLSAR.fit_regularized "statsmodels.regression.linear_model.GLSAR.fit_regularized")([method, alpha, L1\_wt, …]) \| Return a regularized fit to a linear regression model. \| \| [`from_formula`](statsmodels.regression.linear_model.glsar.from_formula#statsmodels.regression.linear_model.GLSAR.from_formula "statsmodels.regression.linear_model.GLSAR.from_formula")(formula, data[, subset, drop\_cols]) \| Create a Model from a formula and dataframe. \| \| [`get_distribution`](statsmodels.regression.linear_model.glsar.get_distribution#statsmodels.regression.linear_model.GLSAR.get_distribution "statsmodels.regression.linear_model.GLSAR.get_distribution")(params, scale[, exog, …]) \| Returns a random number generator for the predictive distribution. \| \| [`hessian`](statsmodels.regression.linear_model.glsar.hessian#statsmodels.regression.linear_model.GLSAR.hessian "statsmodels.regression.linear_model.GLSAR.hessian")(params) \| The Hessian matrix of the model \| \| [`hessian_factor`](statsmodels.regression.linear_model.glsar.hessian_factor#statsmodels.regression.linear_model.GLSAR.hessian_factor "statsmodels.regression.linear_model.GLSAR.hessian_factor")(params[, scale, observed]) \| Weights for calculating Hessian \| \| [`information`](statsmodels.regression.linear_model.glsar.information#statsmodels.regression.linear_model.GLSAR.information "statsmodels.regression.linear_model.GLSAR.information")(params) \| Fisher information matrix of model \| \| [`initialize`](statsmodels.regression.linear_model.glsar.initialize#statsmodels.regression.linear_model.GLSAR.initialize "statsmodels.regression.linear_model.GLSAR.initialize")() \| Initialize (possibly re-initialize) a Model instance. \| \| [`iterative_fit`](statsmodels.regression.linear_model.glsar.iterative_fit#statsmodels.regression.linear_model.GLSAR.iterative_fit "statsmodels.regression.linear_model.GLSAR.iterative_fit")([maxiter, rtol]) \| Perform an iterative two-stage procedure to estimate a GLS model. \| \| [`loglike`](statsmodels.regression.linear_model.glsar.loglike#statsmodels.regression.linear_model.GLSAR.loglike "statsmodels.regression.linear_model.GLSAR.loglike")(params) \| Returns the value of the Gaussian log-likelihood function at params. \| \| [`predict`](statsmodels.regression.linear_model.glsar.predict#statsmodels.regression.linear_model.GLSAR.predict "statsmodels.regression.linear_model.GLSAR.predict")(params[, exog]) \| Return linear predicted values from a design matrix. \| \| [`score`](statsmodels.regression.linear_model.glsar.score#statsmodels.regression.linear_model.GLSAR.score "statsmodels.regression.linear_model.GLSAR.score")(params) \| Score vector of model. \| \| [`whiten`](statsmodels.regression.linear_model.glsar.whiten#statsmodels.regression.linear_model.GLSAR.whiten "statsmodels.regression.linear_model.GLSAR.whiten")(X) \| Whiten a series of columns according to an AR(p) covariance structure. \| #### Attributes \| \| \| \| --- \| --- \| \| `df_model` \| The model degree of freedom, defined as the rank of the regressor matrix minus 1 if a constant is included. \| \| `df_resid` \| The residual degree of freedom, defined as the number of observations minus the rank of the regressor matrix. \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| Names of exogenous variables \| statsmodels statsmodels.discrete.discrete_model.NegativeBinomial.information statsmodels.discrete.discrete\_model.NegativeBinomial.information ================================================================= `NegativeBinomial.information(params)` Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.discrete.discrete_model.NegativeBinomialResults.predict statsmodels.discrete.discrete\_model.NegativeBinomialResults.predict ==================================================================== `NegativeBinomialResults.predict(exog=None, transform=True, args, kwargs)` Call self.model.predict with self.params as the first argument. \| Parameters: \| exog (array-like, optional) – The values for which you want to predict. see Notes below. * transform (bool, optional) – If the model was fit via a formula, do you want to pass exog through the formula. Default is True. E.g., if you fit a model y ~ log(x1) + log(x2), and transform is True, then you can pass a data structure that contains x1 and x2 in their original form. Otherwise, you’d need to log the data first. * kwargs (args,) – Some models can take additional arguments or keywords, see the predict method of the model for the details. \| \| Returns: \| prediction – See self.model.predict \| \| Return type: \| ndarray, [pandas.Series](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.html#pandas.Series "(in pandas v0.22.0)") or [pandas.DataFrame](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html#pandas.DataFrame "(in pandas v0.22.0)") \| #### Notes The types of exog that are supported depends on whether a formula was used in the specification of the model. If a formula was used, then exog is processed in the same way as the original data. This transformation needs to have key access to the same variable names, and can be a pandas DataFrame or a dict like object. If no formula was used, then the provided exog needs to have the same number of columns as the original exog in the model. No transformation of the data is performed except converting it to a numpy array. Row indices as in pandas data frames are supported, and added to the returned prediction. statsmodels statsmodels.multivariate.manova.MANOVA.predict statsmodels.multivariate.manova.MANOVA.predict ============================================== `MANOVA.predict(params, exog=None, args, kwargs)` After a model has been fit predict returns the fitted values. This is a placeholder intended to be overwritten by individual models. statsmodels statsmodels.sandbox.regression.gmm.IVGMM.get_error statsmodels.sandbox.regression.gmm.IVGMM.get\_error =================================================== `IVGMM.get_error(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/regression/gmm.html#IVGMM.get_error) statsmodels statsmodels.genmod.generalized_estimating_equations.GEEResults.resid_response statsmodels.genmod.generalized\_estimating\_equations.GEEResults.resid\_response ================================================================================ `GEEResults.resid_response()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_estimating_equations.html#GEEResults.resid_response) statsmodels statsmodels.stats.contingency_tables.Table2x2.oddsratio_pvalue statsmodels.stats.contingency\_tables.Table2x2.oddsratio\_pvalue ================================================================ `Table2x2.oddsratio_pvalue(null=1)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/contingency_tables.html#Table2x2.oddsratio_pvalue) P-value for a hypothesis test about the odds ratio. \| Parameters: \| null* (float) – The null value of the odds ratio. \| statsmodels statsmodels.tsa.statespace.sarimax.SARIMAXResults.cov_params_oim statsmodels.tsa.statespace.sarimax.SARIMAXResults.cov\_params\_oim ================================================================== `SARIMAXResults.cov_params_oim()` (array) The variance / covariance matrix. Computed using the method from Harvey (1989). statsmodels statsmodels.genmod.families.links.probit.deriv2 statsmodels.genmod.families.links.probit.deriv2 =============================================== `probit.deriv2(p)` Second derivative of the link function g’‘(p) implemented through numerical differentiation statsmodels statsmodels.genmod.cov_struct.Autoregressive.update statsmodels.genmod.cov\_struct.Autoregressive.update ==================================================== `Autoregressive.update(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/cov_struct.html#Autoregressive.update) Updates the association parameter values based on the current regression coefficients. \| Parameters: \| params (array-like) – Working values for the regression parameters. \| statsmodels statsmodels.tsa.statespace.sarimax.SARIMAX.score_obs statsmodels.tsa.statespace.sarimax.SARIMAX.score\_obs ===================================================== `SARIMAX.score_obs(params, method='approx', transformed=True, approx_complex_step=None, approx_centered=False, *kwargs)` Compute the score per observation, evaluated at params \| Parameters: \| params (array\_like) – Array of parameters at which to evaluate the score. * kwargs – Additional arguments to the `loglike` method. \| \| Returns: \| score – Score per observation, evaluated at `params`. \| \| Return type: \| array \| #### Notes This is a numerical approximation, calculated using first-order complex step differentiation on the `loglikeobs` method. statsmodels statsmodels.tsa.vector_ar.vecm.VECMResults.tvalues_beta statsmodels.tsa.vector\_ar.vecm.VECMResults.tvalues\_beta ========================================================= `VECMResults.tvalues_beta()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/vecm.html#VECMResults.tvalues_beta) statsmodels statsmodels.discrete.discrete_model.ProbitResults.f_test statsmodels.discrete.discrete\_model.ProbitResults.f\_test ========================================================== `ProbitResults.f_test(r_matrix, cov_p=None, scale=1.0, invcov=None)` Compute the F-test for a joint linear hypothesis. This is a special case of `wald_test` that always uses the F distribution. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length k row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> A = np.identity(len(results.params)) >>> A = A[1:,:] ``` This tests that each coefficient is jointly statistically significantly different from zero. ``` >>> print(results.f_test(A)) <F test: F=array([[ 330.28533923]]), p=4.984030528700946e-10, df_denom=9, df_num=6> ``` Compare this to ``` >>> results.fvalue 330.2853392346658 >>> results.f_pvalue 4.98403096572e-10 ``` ``` >>> B = np.array(([0,0,1,-1,0,0,0],[0,0,0,0,0,1,-1])) ``` This tests that the coefficient on the 2nd and 3rd regressors are equal and jointly that the coefficient on the 5th and 6th regressors are equal. ``` >>> print(results.f_test(B)) <F test: F=array([[ 9.74046187]]), p=0.005605288531708235, df_denom=9, df_num=2> ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.datasets import longley >>> from statsmodels.formula.api import ols >>> dta = longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = '(GNPDEFL = GNP), (UNEMP = 2), (YEAR/1829 = 1)' >>> f_test = results.f_test(hypotheses) >>> print(f_test) <F test: F=array([[ 144.17976065]]), p=6.322026217355609e-08, df_denom=9, df_num=3> ``` See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`wald_test`](statsmodels.discrete.discrete_model.probitresults.wald_test#statsmodels.discrete.discrete_model.ProbitResults.wald_test "statsmodels.discrete.discrete_model.ProbitResults.wald_test"), [`t_test`](statsmodels.discrete.discrete_model.probitresults.t_test#statsmodels.discrete.discrete_model.ProbitResults.t_test "statsmodels.discrete.discrete_model.ProbitResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full.	programming_docs
statsmodels statsmodels.tsa.statespace.sarimax.SARIMAXResults.simulate statsmodels.tsa.statespace.sarimax.SARIMAXResults.simulate ========================================================== `SARIMAXResults.simulate(nsimulations, measurement_shocks=None, state_shocks=None, initial_state=None)` Simulate a new time series following the state space model \| Parameters: \| * nsimulations (int) – The number of observations to simulate. If the model is time-invariant this can be any number. If the model is time-varying, then this number must be less than or equal to the number * measurement\_shocks (array\_like, optional) – If specified, these are the shocks to the measurement equation, $\varepsilon\_t$. If unspecified, these are automatically generated using a pseudo-random number generator. If specified, must be shaped `nsimulations` x `k_endog`, where `k_endog` is the same as in the state space model. * state\_shocks (array\_like, optional) – If specified, these are the shocks to the state equation, $\eta\_t$. If unspecified, these are automatically generated using a pseudo-random number generator. If specified, must be shaped `nsimulations` x `k_posdef` where `k_posdef` is the same as in the state space model. * initial\_state (array\_like, optional) – If specified, this is the state vector at time zero, which should be shaped (`k_states` x 1), where `k_states` is the same as in the state space model. If unspecified, but the model has been initialized, then that initialization is used. If unspecified and the model has not been initialized, then a vector of zeros is used. Note that this is not included in the returned `simulated_states` array. \| \| Returns: \| simulated\_obs – An (nsimulations x k\_endog) array of simulated observations. \| \| Return type: \| array \| statsmodels statsmodels.tsa.ar_model.ARResults statsmodels.tsa.ar\_model.ARResults =================================== `class statsmodels.tsa.ar_model.ARResults(model, params, normalized_cov_params=None, scale=1.0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/ar_model.html#ARResults) Class to hold results from fitting an AR model. \| Parameters: \| * model (AR Model instance) – Reference to the model that is fit. * params (array) – The fitted parameters from the AR Model. * normalized\_cov\_params (array) – inv(dot(X.T,X)) where X is the lagged values. * scale (float, optional) – An estimate of the scale of the model. \| \| Returns: \| * \\Attributes\\** * aic (float) – Akaike Information Criterion using Lutkephol’s definition. $log(sigma) + 2\(1 + k\_ar + k\_trend)/nobs$ bic (float) – Bayes Information Criterion $\log(\sigma) + (1 + k\_ar + k\_trend)\\log(nobs)/nobs$ bse (array) – The standard errors of the estimated parameters. If `method` is ‘cmle’, then the standard errors that are returned are the OLS standard errors of the coefficients. If the `method` is ‘mle’ then they are computed using the numerical Hessian. * fittedvalues (array) – The in-sample predicted values of the fitted AR model. The `k_ar` initial values are computed via the Kalman Filter if the model is fit by `mle`. * fpe (float) – Final prediction error using Lütkepohl’s definition ((n\_totobs+k\_trend)/(n\_totobs-k\_ar-k\_trend))\sigma hqic (float) – Hannan-Quinn Information Criterion. * k\_ar (float) – Lag length. Sometimes used as `p` in the docs. * k\_trend (float) – The number of trend terms included. ‘nc’=0, ‘c’=1. * llf (float) – The loglikelihood of the model evaluated at `params`. See `AR.loglike` * model (AR model instance) – A reference to the fitted AR model. * nobs (float) – The number of available observations `nobs` - `k_ar` * n\_totobs (float) – The number of total observations in `endog`. Sometimes `n` in the docs. * params (array) – The fitted parameters of the model. * pvalues (array) – The p values associated with the standard errors. * resid (array) – The residuals of the model. If the model is fit by ‘mle’ then the pre-sample residuals are calculated using fittedvalues from the Kalman Filter. * roots (array) – The roots of the AR process are the solution to (1 - arparams[0]\z - arparams[1]\z\\2 -…- arparams[p-1]\z\\k\_ar) = 0 Stability requires that the roots in modulus lie outside the unit circle. scale (float) – Same as sigma2 * sigma2 (float) – The variance of the innovations (residuals). * trendorder (int) – The polynomial order of the trend. ‘nc’ = None, ‘c’ or ‘t’ = 0, ‘ct’ = 1, etc. * tvalues (array) – The t-values associated with `params`. \| #### Methods \| \| \| \| --- \| --- \| \| [`aic`](statsmodels.tsa.ar_model.arresults.aic#statsmodels.tsa.ar_model.ARResults.aic "statsmodels.tsa.ar_model.ARResults.aic")() \| \| \| [`bic`](statsmodels.tsa.ar_model.arresults.bic#statsmodels.tsa.ar_model.ARResults.bic "statsmodels.tsa.ar_model.ARResults.bic")() \| \| \| [`bse`](statsmodels.tsa.ar_model.arresults.bse#statsmodels.tsa.ar_model.ARResults.bse "statsmodels.tsa.ar_model.ARResults.bse")() \| \| \| [`conf_int`](statsmodels.tsa.ar_model.arresults.conf_int#statsmodels.tsa.ar_model.ARResults.conf_int "statsmodels.tsa.ar_model.ARResults.conf_int")([alpha, cols, method]) \| Returns the confidence interval of the fitted parameters. \| \| [`cov_params`](statsmodels.tsa.ar_model.arresults.cov_params#statsmodels.tsa.ar_model.ARResults.cov_params "statsmodels.tsa.ar_model.ARResults.cov_params")([r\_matrix, column, scale, cov\_p, …]) \| Returns the variance/covariance matrix. \| \| [`f_test`](statsmodels.tsa.ar_model.arresults.f_test#statsmodels.tsa.ar_model.ARResults.f_test "statsmodels.tsa.ar_model.ARResults.f_test")(r\_matrix[, cov\_p, scale, invcov]) \| Compute the F-test for a joint linear hypothesis. \| \| [`fittedvalues`](statsmodels.tsa.ar_model.arresults.fittedvalues#statsmodels.tsa.ar_model.ARResults.fittedvalues "statsmodels.tsa.ar_model.ARResults.fittedvalues")() \| \| \| [`fpe`](statsmodels.tsa.ar_model.arresults.fpe#statsmodels.tsa.ar_model.ARResults.fpe "statsmodels.tsa.ar_model.ARResults.fpe")() \| \| \| [`hqic`](statsmodels.tsa.ar_model.arresults.hqic#statsmodels.tsa.ar_model.ARResults.hqic "statsmodels.tsa.ar_model.ARResults.hqic")() \| \| \| [`initialize`](statsmodels.tsa.ar_model.arresults.initialize#statsmodels.tsa.ar_model.ARResults.initialize "statsmodels.tsa.ar_model.ARResults.initialize")(model, params, \\kwd) \| \| \| [`llf`](statsmodels.tsa.ar_model.arresults.llf#statsmodels.tsa.ar_model.ARResults.llf "statsmodels.tsa.ar_model.ARResults.llf")() \| \| \| [`load`](statsmodels.tsa.ar_model.arresults.load#statsmodels.tsa.ar_model.ARResults.load "statsmodels.tsa.ar_model.ARResults.load")(fname) \| load a pickle, (class method) \| \| [`normalized_cov_params`](statsmodels.tsa.ar_model.arresults.normalized_cov_params#statsmodels.tsa.ar_model.ARResults.normalized_cov_params "statsmodels.tsa.ar_model.ARResults.normalized_cov_params")() \| \| \| [`predict`](statsmodels.tsa.ar_model.arresults.predict#statsmodels.tsa.ar_model.ARResults.predict "statsmodels.tsa.ar_model.ARResults.predict")([start, end, dynamic]) \| Returns in-sample and out-of-sample prediction. \| \| [`pvalues`](statsmodels.tsa.ar_model.arresults.pvalues#statsmodels.tsa.ar_model.ARResults.pvalues "statsmodels.tsa.ar_model.ARResults.pvalues")() \| \| \| [`remove_data`](statsmodels.tsa.ar_model.arresults.remove_data#statsmodels.tsa.ar_model.ARResults.remove_data "statsmodels.tsa.ar_model.ARResults.remove_data")() \| remove data arrays, all nobs arrays from result and model \| \| [`resid`](statsmodels.tsa.ar_model.arresults.resid#statsmodels.tsa.ar_model.ARResults.resid "statsmodels.tsa.ar_model.ARResults.resid")() \| \| \| [`roots`](statsmodels.tsa.ar_model.arresults.roots#statsmodels.tsa.ar_model.ARResults.roots "statsmodels.tsa.ar_model.ARResults.roots")() \| \| \| [`save`](statsmodels.tsa.ar_model.arresults.save#statsmodels.tsa.ar_model.ARResults.save "statsmodels.tsa.ar_model.ARResults.save")(fname[, remove\_data]) \| save a pickle of this instance \| \| [`scale`](statsmodels.tsa.ar_model.arresults.scale#statsmodels.tsa.ar_model.ARResults.scale "statsmodels.tsa.ar_model.ARResults.scale")() \| \| \| [`sigma2`](statsmodels.tsa.ar_model.arresults.sigma2#statsmodels.tsa.ar_model.ARResults.sigma2 "statsmodels.tsa.ar_model.ARResults.sigma2")() \| \| \| [`summary`](statsmodels.tsa.ar_model.arresults.summary#statsmodels.tsa.ar_model.ARResults.summary "statsmodels.tsa.ar_model.ARResults.summary")() \| \| \| [`t_test`](statsmodels.tsa.ar_model.arresults.t_test#statsmodels.tsa.ar_model.ARResults.t_test "statsmodels.tsa.ar_model.ARResults.t_test")(r\_matrix[, cov\_p, scale, use\_t]) \| Compute a t-test for a each linear hypothesis of the form Rb = q \| \| [`t_test_pairwise`](statsmodels.tsa.ar_model.arresults.t_test_pairwise#statsmodels.tsa.ar_model.ARResults.t_test_pairwise "statsmodels.tsa.ar_model.ARResults.t_test_pairwise")(term\_name[, method, alpha, …]) \| perform pairwise t\_test with multiple testing corrected p-values \| \| [`tvalues`](statsmodels.tsa.ar_model.arresults.tvalues#statsmodels.tsa.ar_model.ARResults.tvalues "statsmodels.tsa.ar_model.ARResults.tvalues")() \| Return the t-statistic for a given parameter estimate. \| \| [`wald_test`](statsmodels.tsa.ar_model.arresults.wald_test#statsmodels.tsa.ar_model.ARResults.wald_test "statsmodels.tsa.ar_model.ARResults.wald_test")(r\_matrix[, cov\_p, scale, invcov, …]) \| Compute a Wald-test for a joint linear hypothesis. \| \| [`wald_test_terms`](statsmodels.tsa.ar_model.arresults.wald_test_terms#statsmodels.tsa.ar_model.ARResults.wald_test_terms "statsmodels.tsa.ar_model.ARResults.wald_test_terms")([skip\_single, …]) \| Compute a sequence of Wald tests for terms over multiple columns \| #### Attributes \| \| \| \| --- \| --- \| \| `extra_doc` \| \| \| `preddoc` \| \| \| `use_t` \| \| statsmodels statsmodels.tsa.arima_model.ARMA.predict statsmodels.tsa.arima\_model.ARMA.predict ========================================= `ARMA.predict(params, start=None, end=None, exog=None, dynamic=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_model.html#ARMA.predict) ARMA model in-sample and out-of-sample prediction \| Parameters: \| * params (array-like) – The fitted parameters of the model. * start (int, str, or datetime) – Zero-indexed observation number at which to start forecasting, ie., the first forecast is start. Can also be a date string to parse or a datetime type. * end (int, str, or datetime) – Zero-indexed observation number at which to end forecasting, ie., the first forecast is start. Can also be a date string to parse or a datetime type. However, if the dates index does not have a fixed frequency, end must be an integer index if you want out of sample prediction. * exog (array-like, optional) – If the model is an ARMAX and out-of-sample forecasting is requested, exog must be given. Note that you’ll need to pass `k_ar` additional lags for any exogenous variables. E.g., if you fit an ARMAX(2, q) model and want to predict 5 steps, you need 7 observations to do this. * dynamic (bool, optional) – The `dynamic` keyword affects in-sample prediction. If dynamic is False, then the in-sample lagged values are used for prediction. If `dynamic` is True, then in-sample forecasts are used in place of lagged dependent variables. The first forecasted value is `start`. \| \| Returns: \| predict – The predicted values. \| \| Return type: \| array \| #### Notes Use the results predict method instead. statsmodels statsmodels.tsa.arima_model.ARIMAResults.tvalues statsmodels.tsa.arima\_model.ARIMAResults.tvalues ================================================= `ARIMAResults.tvalues()` Return the t-statistic for a given parameter estimate. statsmodels statsmodels.tsa.statespace.structural.UnobservedComponentsResults.f_test statsmodels.tsa.statespace.structural.UnobservedComponentsResults.f\_test ========================================================================= `UnobservedComponentsResults.f_test(r_matrix, cov_p=None, scale=1.0, invcov=None)` Compute the F-test for a joint linear hypothesis. This is a special case of `wald_test` that always uses the F distribution. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length k row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> A = np.identity(len(results.params)) >>> A = A[1:,:] ``` This tests that each coefficient is jointly statistically significantly different from zero. ``` >>> print(results.f_test(A)) <F test: F=array([[ 330.28533923]]), p=4.984030528700946e-10, df_denom=9, df_num=6> ``` Compare this to ``` >>> results.fvalue 330.2853392346658 >>> results.f_pvalue 4.98403096572e-10 ``` ``` >>> B = np.array(([0,0,1,-1,0,0,0],[0,0,0,0,0,1,-1])) ``` This tests that the coefficient on the 2nd and 3rd regressors are equal and jointly that the coefficient on the 5th and 6th regressors are equal. ``` >>> print(results.f_test(B)) <F test: F=array([[ 9.74046187]]), p=0.005605288531708235, df_denom=9, df_num=2> ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.datasets import longley >>> from statsmodels.formula.api import ols >>> dta = longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = '(GNPDEFL = GNP), (UNEMP = 2), (YEAR/1829 = 1)' >>> f_test = results.f_test(hypotheses) >>> print(f_test) <F test: F=array([[ 144.17976065]]), p=6.322026217355609e-08, df_denom=9, df_num=3> ``` See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`wald_test`](statsmodels.tsa.statespace.structural.unobservedcomponentsresults.wald_test#statsmodels.tsa.statespace.structural.UnobservedComponentsResults.wald_test "statsmodels.tsa.statespace.structural.UnobservedComponentsResults.wald_test"), [`t_test`](statsmodels.tsa.statespace.structural.unobservedcomponentsresults.t_test#statsmodels.tsa.statespace.structural.UnobservedComponentsResults.t_test "statsmodels.tsa.statespace.structural.UnobservedComponentsResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.discrete.discrete_model.CountResults.cov_params statsmodels.discrete.discrete\_model.CountResults.cov\_params ============================================================= `CountResults.cov_params(r_matrix=None, column=None, scale=None, cov_p=None, other=None)` Returns the variance/covariance matrix. The variance/covariance matrix can be of a linear contrast of the estimates of params or all params multiplied by scale which will usually be an estimate of sigma^2. Scale is assumed to be a scalar. \| Parameters: \| * r\_matrix (array-like) – Can be 1d, or 2d. Can be used alone or with other. * column (array-like, optional) – Must be used on its own. Can be 0d or 1d see below. * scale (float, optional) – Can be specified or not. Default is None, which means that the scale argument is taken from the model. * other (array-like, optional) – Can be used when r\_matrix is specified. \| \| Returns: \| cov – covariance matrix of the parameter estimates or of linear combination of parameter estimates. See Notes. \| \| Return type: \| ndarray \| #### Notes (The below are assumed to be in matrix notation.) If no argument is specified returns the covariance matrix of a model `(scale)(X.T X)^(-1)` If contrast is specified it pre and post-multiplies as follows `(scale) r_matrix (X.T X)^(-1) r_matrix.T` If contrast and other are specified returns `(scale) * r_matrix (X.T X)^(-1) other.T` If column is specified returns `(scale) * (X.T X)^(-1)[column,column]` if column is 0d OR `(scale) * (X.T X)^(-1)[column][:,column]` if column is 1d statsmodels statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.save statsmodels.discrete.count\_model.ZeroInflatedNegativeBinomialResults.save ========================================================================== `ZeroInflatedNegativeBinomialResults.save(fname, remove_data=False)` save a pickle of this instance \| Parameters: \| * fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. * remove\_data (bool) – If False (default), then the instance is pickled without changes. If True, then all arrays with length nobs are set to None before pickling. See the remove\_data method. In some cases not all arrays will be set to None. \| #### Notes If remove\_data is true and the model result does not implement a remove\_data method then this will raise an exception. statsmodels statsmodels.sandbox.stats.multicomp.GroupsStats.runbasic statsmodels.sandbox.stats.multicomp.GroupsStats.runbasic ======================================================== `GroupsStats.runbasic(useranks=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/stats/multicomp.html#GroupsStats.runbasic) statsmodels statsmodels.sandbox.stats.multicomp.set_partition statsmodels.sandbox.stats.multicomp.set\_partition ================================================== `statsmodels.sandbox.stats.multicomp.set_partition(ssli)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/stats/multicomp.html#set_partition) extract a partition from a list of tuples this should be correctly called select largest disjoint sets. Begun and Gabriel 1981 don’t seem to be bothered by sets of accepted hypothesis with joint elements, e.g. maximal\_accepted\_sets = { {1,2,3}, {2,3,4} } This creates a set partition from a list of sets given as tuples. It tries to find the partition with the largest sets. That is, sets are included after being sorted by length. If the list doesn’t include the singletons, then it will be only a partial partition. Missing items are singletons (I think). #### Examples ``` >>> li [(5, 6, 7, 8), (1, 2, 3), (4, 5), (0, 1)] >>> set_partition(li) ([(5, 6, 7, 8), (1, 2, 3)], [0, 4]) ``` statsmodels statsmodels.tsa.statespace.tools.is_invertible statsmodels.tsa.statespace.tools.is\_invertible =============================================== `statsmodels.tsa.statespace.tools.is_invertible(polynomial, threshold=0.9999999999)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/tools.html#is_invertible) Determine if a polynomial is invertible. Requires all roots of the polynomial lie inside the unit circle. \| Parameters: \| * polynomial (array\_like or tuple, list) – Coefficients of a polynomial, in order of increasing degree. For example, `polynomial=[1, -0.5]` corresponds to the polynomial $1 - 0.5x$ which has root $2$. If it is a matrix polynomial (in which case the coefficients are coefficient matrices), a tuple or list of matrices should be passed. * threshold (number) – Allowed threshold for `is_invertible` to return True. Default is 1. \| #### Notes If the coefficients provided are scalars $(c\_0, c\_1, \dots, c\_n)$, then the corresponding polynomial is $c\_0 + c\_1 L + \dots + c\_n L^n$. If the coefficients provided are matrices $(C\_0, C\_1, \dots, C\_n)$, then the corresponding polynomial is $C\_0 + C\_1 L + \dots + C\_n L^n$. There are three equivalent methods of determining if the polynomial represented by the coefficients is invertible: The first method factorizes the polynomial into: \[\begin{split}C(L) & = c\_0 + c\_1 L + \dots + c\_n L^n \\ & = constant (1 - \lambda\_1 L) (1 - \lambda\_2 L) \dots (1 - \lambda\_n L)\end{split}\] In order for $C(L)$ to be invertible, it must be that each factor $(1 - \lambda\_i L)$ is invertible; the condition is then that $\|\lambda\_i\| < 1$, where $\lambda\_i$ is a root of the polynomial. The second method factorizes the polynomial into: \[\begin{split}C(L) & = c\_0 + c\_1 L + \dots + c\_n L^n \\ & = constant (L - \zeta\_1) (L - \zeta\_2) \dots (L - \zeta\_3)\end{split}\] The condition is now $\|\zeta\_i\| > 1$, where $\zeta\_i$ is a root of the polynomial with reversed coefficients and $\lambda\_i = \frac{1}{\zeta\_i}$. Finally, a companion matrix can be formed using the coefficients of the polynomial. Then the eigenvalues of that matrix give the roots of the polynomial. This last method is the one actually used. See also [`companion_matrix`](statsmodels.tsa.statespace.tools.companion_matrix#statsmodels.tsa.statespace.tools.companion_matrix "statsmodels.tsa.statespace.tools.companion_matrix")	programming_docs
statsmodels statsmodels.stats.contingency_tables.SquareTable.marginal_probabilities statsmodels.stats.contingency\_tables.SquareTable.marginal\_probabilities ========================================================================= `SquareTable.marginal_probabilities()` statsmodels statsmodels.sandbox.tsa.fftarma.ArmaFft.acovf statsmodels.sandbox.tsa.fftarma.ArmaFft.acovf ============================================= `ArmaFft.acovf(nobs=None)` Theoretical autocovariance function of ARMA process \| Parameters: \| * ar (array\_like, 1d) – coefficient for autoregressive lag polynomial, including zero lag * ma (array\_like, 1d) – coefficient for moving-average lag polynomial, including zero lag * nobs (int) – number of terms (lags plus zero lag) to include in returned acovf \| \| Returns: \| acovf – autocovariance of ARMA process given by ar, ma \| \| Return type: \| array \| See also `arma_acf`, [`acovf`](#statsmodels.sandbox.tsa.fftarma.ArmaFft.acovf "statsmodels.sandbox.tsa.fftarma.ArmaFft.acovf") #### Notes Tries to do some crude numerical speed improvements for cases with high persistence. However, this algorithm is slow if the process is highly persistent and only a few autocovariances are desired. statsmodels statsmodels.discrete.discrete_model.BinaryResults.aic statsmodels.discrete.discrete\_model.BinaryResults.aic ====================================================== `BinaryResults.aic()` statsmodels statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.set_null_options statsmodels.discrete.count\_model.ZeroInflatedNegativeBinomialResults.set\_null\_options ======================================================================================== `ZeroInflatedNegativeBinomialResults.set_null_options(llnull=None, attach_results=True, *kwds)` set fit options for Null (constant-only) model This resets the cache for related attributes which is potentially fragile. This only sets the option, the null model is estimated when llnull is accessed, if llnull is not yet in cache. \| Parameters: \| llnull (None or float) – If llnull is not None, then the value will be directly assigned to the cached attribute “llnull”. * attach\_results (bool) – Sets an internal flag whether the results instance of the null model should be attached. By default without calling this method, thenull model results are not attached and only the loglikelihood value llnull is stored. * kwds (keyword arguments) – `kwds` are directly used as fit keyword arguments for the null model, overriding any provided defaults. \| \| Returns: \| \| \| Return type: \| no returns, modifies attributes of this instance \| statsmodels statsmodels.emplike.descriptive.DescStatMV statsmodels.emplike.descriptive.DescStatMV ========================================== `class statsmodels.emplike.descriptive.DescStatMV(endog)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/emplike/descriptive.html#DescStatMV) A class for conducting inference on multivariate means and correlation. \| Parameters: \| endog (ndarray) – Data to be analyzed \| `endog` ndarray – Data to be analyzed `nobs` float – Number of observations #### Methods \| \| \| \| --- \| --- \| \| [`ci_corr`](statsmodels.emplike.descriptive.descstatmv.ci_corr#statsmodels.emplike.descriptive.DescStatMV.ci_corr "statsmodels.emplike.descriptive.DescStatMV.ci_corr")([sig, upper\_bound, lower\_bound]) \| Returns the confidence intervals for the correlation coefficient \| \| [`mv_mean_contour`](statsmodels.emplike.descriptive.descstatmv.mv_mean_contour#statsmodels.emplike.descriptive.DescStatMV.mv_mean_contour "statsmodels.emplike.descriptive.DescStatMV.mv_mean_contour")(mu1\_low, mu1\_upp, mu2\_low, …) \| Creates a confidence region plot for the mean of bivariate data \| \| [`mv_test_mean`](statsmodels.emplike.descriptive.descstatmv.mv_test_mean#statsmodels.emplike.descriptive.DescStatMV.mv_test_mean "statsmodels.emplike.descriptive.DescStatMV.mv_test_mean")(mu\_array[, return\_weights]) \| Returns -2 x log likelihood and the p-value for a multivariate hypothesis test of the mean \| \| [`test_corr`](statsmodels.emplike.descriptive.descstatmv.test_corr#statsmodels.emplike.descriptive.DescStatMV.test_corr "statsmodels.emplike.descriptive.DescStatMV.test_corr")(corr0[, return\_weights]) \| Returns -2 x log-likelihood ratio and p-value for the correlation coefficient between 2 variables \| statsmodels statsmodels.discrete.count_model.ZeroInflatedGeneralizedPoissonResults.llr statsmodels.discrete.count\_model.ZeroInflatedGeneralizedPoissonResults.llr =========================================================================== `ZeroInflatedGeneralizedPoissonResults.llr()` statsmodels statsmodels.discrete.discrete_model.BinaryResults.remove_data statsmodels.discrete.discrete\_model.BinaryResults.remove\_data =============================================================== `BinaryResults.remove_data()` remove data arrays, all nobs arrays from result and model This reduces the size of the instance, so it can be pickled with less memory. Currently tested for use with predict from an unpickled results and model instance. Warning Since data and some intermediate results have been removed calculating new statistics that require them will raise exceptions. The exception will occur the first time an attribute is accessed that has been set to None. Not fully tested for time series models, tsa, and might delete too much for prediction or not all that would be possible. The lists of arrays to delete are maintained as attributes of the result and model instance, except for cached values. These lists could be changed before calling remove\_data. The attributes to remove are named in: `model._data_attr : arrays attached to both the model instance` and the results instance with the same attribute name. `result.data_in_cache : arrays that may exist as values in` result.\_cache (TODO : should privatize name) `result._data_attr_model : arrays attached to the model` instance but not to the results instance statsmodels statsmodels.genmod.cov_struct.Independence.update statsmodels.genmod.cov\_struct.Independence.update ================================================== `Independence.update(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/cov_struct.html#Independence.update) Updates the association parameter values based on the current regression coefficients. \| Parameters: \| params (array-like) – Working values for the regression parameters. \| statsmodels statsmodels.genmod.cov_struct.Independence.initialize statsmodels.genmod.cov\_struct.Independence.initialize ====================================================== `Independence.initialize(model)` Called by GEE, used by implementations that need additional setup prior to running `fit`. \| Parameters: \| model (GEE class) – A reference to the parent GEE class instance. \| statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactor.filter statsmodels.tsa.statespace.dynamic\_factor.DynamicFactor.filter =============================================================== `DynamicFactor.filter(params, transformed=True, complex_step=False, cov_type=None, cov_kwds=None, return_ssm=False, results_class=None, results_wrapper_class=None, *kwargs)` Kalman filtering \| Parameters: \| params (array\_like) – Array of parameters at which to evaluate the loglikelihood function. * transformed (boolean, optional) – Whether or not `params` is already transformed. Default is True. * return\_ssm (boolean,optional) – Whether or not to return only the state space output or a full results object. Default is to return a full results object. * cov\_type (str, optional) – See `MLEResults.fit` for a description of covariance matrix types for results object. * cov\_kwds ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)") or None, optional) – See `MLEResults.get_robustcov_results` for a description required keywords for alternative covariance estimators * *\\kwargs* – Additional keyword arguments to pass to the Kalman filter. See `KalmanFilter.filter` for more details. \| statsmodels statsmodels.genmod.families.family.Gamma.predict statsmodels.genmod.families.family.Gamma.predict ================================================ `Gamma.predict(mu)` Linear predictors based on given mu values. \| Parameters: \| mu (array) – The mean response variables \| \| Returns: \| lin\_pred – Linear predictors based on the mean response variables. The value of the link function at the given mu. \| \| Return type: \| array \| statsmodels statsmodels.tsa.kalmanf.kalmanfilter.KalmanFilter.geterrors statsmodels.tsa.kalmanf.kalmanfilter.KalmanFilter.geterrors =========================================================== `classmethod KalmanFilter.geterrors(y, k, k_ar, k_ma, k_lags, nobs, Z_mat, m, R_mat, T_mat, paramsdtype)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/kalmanf/kalmanfilter.html#KalmanFilter.geterrors) Returns just the errors of the Kalman Filter statsmodels statsmodels.discrete.discrete_model.BinaryModel.information statsmodels.discrete.discrete\_model.BinaryModel.information ============================================================ `BinaryModel.information(params)` Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.genmod.generalized_linear_model.GLMResults.pearson_chi2 statsmodels.genmod.generalized\_linear\_model.GLMResults.pearson\_chi2 ====================================================================== `GLMResults.pearson_chi2()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_linear_model.html#GLMResults.pearson_chi2) statsmodels statsmodels.stats.moment_helpers.se_cov statsmodels.stats.moment\_helpers.se\_cov ========================================= `statsmodels.stats.moment_helpers.se_cov(cov)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/moment_helpers.html#se_cov) get standard deviation from covariance matrix just a shorthand function np.sqrt(np.diag(cov)) \| Parameters: \| cov (array\_like, square) – covariance matrix \| \| Returns: \| std – standard deviation from diagonal of cov \| \| Return type: \| ndarray \| statsmodels statsmodels.sandbox.regression.gmm.LinearIVGMM.fitgmm_cu statsmodels.sandbox.regression.gmm.LinearIVGMM.fitgmm\_cu ========================================================= `LinearIVGMM.fitgmm_cu(start, optim_method='bfgs', optim_args=None)` estimate parameters using continuously updating GMM \| Parameters: \| start (array\_like) – starting values for minimization \| \| Returns: \| paramest – estimated parameters \| \| Return type: \| array \| #### Notes todo: add fixed parameter option, not here ??? uses scipy.optimize.fmin statsmodels statsmodels.tsa.x13.x13_arima_analysis statsmodels.tsa.x13.x13\_arima\_analysis ======================================== `statsmodels.tsa.x13.x13_arima_analysis(endog, maxorder=(2, 1), maxdiff=(2, 1), diff=None, exog=None, log=None, outlier=True, trading=False, forecast_years=None, retspec=False, speconly=False, start=None, freq=None, print_stdout=False, x12path=None, prefer_x13=True)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/x13.html#x13_arima_analysis) Perform x13-arima analysis for monthly or quarterly data. \| Parameters: \| * endog (array-like, [pandas.Series](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.html#pandas.Series "(in pandas v0.22.0)")) – The series to model. It is best to use a pandas object with a DatetimeIndex or PeriodIndex. However, you can pass an array-like object. If your object does not have a dates index then `start` and `freq` are not optional. * maxorder (tuple) – The maximum order of the regular and seasonal ARMA polynomials to examine during the model identification. The order for the regular polynomial must be greater than zero and no larger than 4. The order for the seaonal polynomial may be 1 or 2. * maxdiff (tuple) – The maximum orders for regular and seasonal differencing in the automatic differencing procedure. Acceptable inputs for regular differencing are 1 and 2. The maximum order for seasonal differencing is 1. If `diff` is specified then `maxdiff` should be None. Otherwise, `diff` will be ignored. See also `diff`. * diff (tuple) – Fixes the orders of differencing for the regular and seasonal differencing. Regular differencing may be 0, 1, or 2. Seasonal differencing may be 0 or 1. `maxdiff` must be None, otherwise `diff` is ignored. * exog (array-like) – Exogenous variables. * log (bool or None) – If None, it is automatically determined whether to log the series or not. If False, logs are not taken. If True, logs are taken. * outlier (bool) – Whether or not outliers are tested for and corrected, if detected. * trading (bool) – Whether or not trading day effects are tested for. * forecast\_years (int) – Number of forecasts produced. The default is one year. * retspec (bool) – Whether to return the created specification file. Can be useful for debugging. * speconly (bool) – Whether to create the specification file and then return it without performing the analysis. Can be useful for debugging. * start (str, datetime) – Must be given if `endog` does not have date information in its index. Anything accepted by pandas.DatetimeIndex for the start value. * freq (str) – Must be givein if `endog` does not have date information in its index. Anything accapted by pandas.DatetimeIndex for the freq value. * print\_stdout (bool) – The stdout from X12/X13 is suppressed. To print it out, set this to True. Default is False. * x12path (str or None) – The path to x12 or x13 binary. If None, the program will attempt to find x13as or x12a on the PATH or by looking at X13PATH or X12PATH depending on the value of prefer\_x13. * prefer\_x13 (bool) – If True, will look for x13as first and will fallback to the X13PATH environmental variable. If False, will look for x12a first and will fallback to the X12PATH environmental variable. If x12path points to the path for the X12/X13 binary, it does nothing. \| \| Returns: \| res – A bunch object with the following attributes:* results : str The full output from the X12/X13 run. * seasadj : pandas.Series The final seasonally adjusted `endog` * trend : pandas.Series The trend-cycle component of `endog` * irregular : pandas.Series The final irregular component of `endog` * stdout : str The captured stdout produced by x12/x13. * spec : str, optional Returned if `retspec` is True. The only thing returned if `speconly` is True. \| \| Return type: \| Bunch \| #### Notes This works by creating a specification file, writing it to a temporary directory, invoking X12/X13 in a subprocess, and reading the output directory, invoking exog12/X13 in a subprocess, and reading the output back in. statsmodels statsmodels.discrete.count_model.ZeroInflatedGeneralizedPoissonResults.pvalues statsmodels.discrete.count\_model.ZeroInflatedGeneralizedPoissonResults.pvalues =============================================================================== `ZeroInflatedGeneralizedPoissonResults.pvalues()` statsmodels statsmodels.iolib.smpickle.load_pickle statsmodels.iolib.smpickle.load\_pickle ======================================= `statsmodels.iolib.smpickle.load_pickle(fname)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/iolib/smpickle.html#load_pickle) Load a previously saved object from file \| Parameters: \| fname (str) – Filename to unpickle \| #### Notes This method can be used to load both models and results. statsmodels statsmodels.genmod.families.family.Gaussian.loglike statsmodels.genmod.families.family.Gaussian.loglike =================================================== `Gaussian.loglike(endog, mu, var_weights=1.0, freq_weights=1.0, scale=1.0)` The log-likelihood function in terms of the fitted mean response. \| Parameters: \| * endog (array) – Usually the endogenous response variable. * mu (array) – Usually but not always the fitted mean response variable. * var\_weights (array-like) – 1d array of variance (analytic) weights. The default is 1. * freq\_weights (array-like) – 1d array of frequency weights. The default is 1. * scale (float) – The scale parameter. The default is 1. \| \| Returns: \| ll – The value of the loglikelihood evaluated at (endog, mu, var\_weights, freq\_weights, scale) as defined below. \| \| Return type: \| float \| #### Notes Where $ll\_i$ is the by-observation log-likelihood: \[ll = \sum(ll\_i \* freq\\_weights\_i)\] `ll_i` is defined for each family. endog and mu are not restricted to `endog` and `mu` respectively. For instance, you could call both `loglike(endog, endog)` and `loglike(endog, mu)` to get the log-likelihood ratio. statsmodels statsmodels.discrete.discrete_model.NegativeBinomialP.predict statsmodels.discrete.discrete\_model.NegativeBinomialP.predict ============================================================== `NegativeBinomialP.predict(params, exog=None, exposure=None, offset=None, which='mean')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#NegativeBinomialP.predict) Predict response variable of a model given exogenous variables. \| Parameters: \| * params (array-like) – 2d array of fitted parameters of the model. Should be in the order returned from the model. * exog (array-like, optional) – 1d or 2d array of exogenous values. If not supplied, the whole exog attribute of the model is used. If a 1d array is given it assumed to be 1 row of exogenous variables. If you only have one regressor and would like to do prediction, you must provide a 2d array with shape[1] == 1. * linear (bool, optional) – If True, returns the linear predictor dot(exog,params). Else, returns the value of the cdf at the linear predictor. * offset (array\_like, optional) – Offset is added to the linear prediction with coefficient equal to 1. * exposure (array\_like, optional) – Log(exposure) is added to the linear prediction with coefficient * to 1. (equal) – * which ('mean', 'linear', 'prob', optional.) – ‘mean’ returns the exp of linear predictor exp(dot(exog,params)). ‘linear’ returns the linear predictor dot(exog,params). ‘prob’ return probabilities for counts from 0 to max(endog). Default is ‘mean’. \| #### Notes statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.fittedvalues statsmodels.regression.recursive\_ls.RecursiveLSResults.fittedvalues ==================================================================== `RecursiveLSResults.fittedvalues()` (array) The predicted values of the model. An (nobs x k\_endog) array. statsmodels statsmodels.tsa.statespace.mlemodel.MLEResults.forecast statsmodels.tsa.statespace.mlemodel.MLEResults.forecast ======================================================= `MLEResults.forecast(steps=1, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/mlemodel.html#MLEResults.forecast) Out-of-sample forecasts \| Parameters: \| steps (int, str, or datetime, optional) – If an integer, the number of steps to forecast from the end of the sample. Can also be a date string to parse or a datetime type. However, if the dates index does not have a fixed frequency, steps must be an integer. Default * *\\kwargs* – Additional arguments may required for forecasting beyond the end of the sample. See `FilterResults.predict` for more details. \| \| Returns: \| forecast – Array of out of sample forecasts. A (steps x k\_endog) array. \| \| Return type: \| array \|	programming_docs
statsmodels statsmodels.sandbox.distributions.transformed.Transf_gen.pdf statsmodels.sandbox.distributions.transformed.Transf\_gen.pdf ============================================================= `Transf_gen.pdf(x, args, kwds)` Probability density function at x of the given RV. \| Parameters: \| x (array\_like) – quantiles * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| pdf – Probability density function evaluated at x \| \| Return type: \| ndarray \| statsmodels statsmodels.sandbox.regression.gmm.IVGMM.from_formula statsmodels.sandbox.regression.gmm.IVGMM.from\_formula ====================================================== `classmethod IVGMM.from_formula(formula, data, subset=None, drop_cols=None, args, kwargs)` Create a Model from a formula and dataframe. \| Parameters: \| formula (str or generic Formula object) – The formula specifying the model * data (array-like) – The data for the model. See Notes. * subset (array-like) – An array-like object of booleans, integers, or index values that indicate the subset of df to use in the model. Assumes df is a `pandas.DataFrame` * drop\_cols (array-like) – Columns to drop from the design matrix. Cannot be used to drop terms involving categoricals. * args (extra arguments) – These are passed to the model * kwargs (extra keyword arguments) – These are passed to the model with one exception. The `eval_env` keyword is passed to patsy. It can be either a [`patsy.EvalEnvironment`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.EvalEnvironment "(in patsy v0.5.0+dev)") object or an integer indicating the depth of the namespace to use. For example, the default `eval_env=0` uses the calling namespace. If you wish to use a “clean” environment set `eval_env=-1`. \| \| Returns: \| model \| \| Return type: \| Model instance \| #### Notes data must define \_\_getitem\_\_ with the keys in the formula terms args and kwargs are passed on to the model instantiation. E.g., a numpy structured or rec array, a dictionary, or a pandas DataFrame. statsmodels statsmodels.tsa.vector_ar.vecm.VECMResults.stderr_params statsmodels.tsa.vector\_ar.vecm.VECMResults.stderr\_params ========================================================== `VECMResults.stderr_params()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/vecm.html#VECMResults.stderr_params) statsmodels statsmodels.tsa.vector_ar.vecm.VECMResults.test_inst_causality statsmodels.tsa.vector\_ar.vecm.VECMResults.test\_inst\_causality ================================================================= `VECMResults.test_inst_causality(causing, signif=0.05)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/vecm.html#VECMResults.test_inst_causality) Test for instantaneous causality. The concept of instantaneous causality is described in chapters 3.6.3 and 7.6.4 of [[1]](#id3). Test H0: “No instantaneous causality between the variables in `caused` and those in `causing`” against H1: “Instantaneous causality between `caused` and `causing` exists”. Note that instantaneous causality is a symmetric relation (i.e. if `causing` is “instantaneously causing” `caused`, then also `caused` is “instantaneously causing” `causing`), thus the naming of the parameters (which is chosen to be in accordance with [`test_granger_causality`](statsmodels.tsa.vector_ar.vecm.vecmresults.test_granger_causality#statsmodels.tsa.vector_ar.vecm.VECMResults.test_granger_causality "statsmodels.tsa.vector_ar.vecm.VECMResults.test_granger_causality")) may be misleading. \| Parameters: \| * causing (int or str or sequence of int or str) – If int or str, test whether the corresponding variable is causing the variable(s) specified in caused. If sequence of int or str, test whether the corresponding variables are causing the variable(s) specified in caused. * signif (float, 0 < `signif` < 1, default 5 %) – Significance level for computing critical values for test, defaulting to standard 0.05 level. \| \| Returns: \| results \| \| Return type: \| [`statsmodels.tsa.vector_ar.hypothesis_test_results.CausalityTestResults`](statsmodels.tsa.vector_ar.hypothesis_test_results.causalitytestresults#statsmodels.tsa.vector_ar.hypothesis_test_results.CausalityTestResults "statsmodels.tsa.vector_ar.hypothesis_test_results.CausalityTestResults") \| #### Notes This method is not returning the same result as `JMulTi`. This is because the test is based on a VAR(k\_ar) model in `statsmodels` (in accordance to pp. 104, 320-321 in [[1]](#id3)) whereas `JMulTi` seems to be using a VAR(k\_ar+1) model. Reducing the lag order by one in `JMulTi` leads to equal results in `statsmodels` and `JMulTi`. #### References \| \| \| \| --- \| --- \| \| [1] \| ([1](#id1), [2](#id2)) Lütkepohl, H. 2005. New Introduction to Multiple Time Series Analysis. Springer. \| statsmodels statsmodels.discrete.discrete_model.DiscreteResults.t_test_pairwise statsmodels.discrete.discrete\_model.DiscreteResults.t\_test\_pairwise ====================================================================== `DiscreteResults.t_test_pairwise(term_name, method='hs', alpha=0.05, factor_labels=None)` perform pairwise t\_test with multiple testing corrected p-values This uses the formula design\_info encoding contrast matrix and should work for all encodings of a main effect. \| Parameters: \| * result (result instance) – The results of an estimated model with a categorical main effect. * term\_name (str) – name of the term for which pairwise comparisons are computed. Term names for categorical effects are created by patsy and correspond to the main part of the exog names. * method (str or list of strings) – multiple testing p-value correction, default is ‘hs’, see stats.multipletesting * alpha (float) – significance level for multiple testing reject decision. * factor\_labels (None, list of str) – Labels for the factor levels used for pairwise labels. If not provided, then the labels from the formula design\_info are used. \| \| Returns: \| results – The results are stored as attributes, the main attributes are the following two. Other attributes are added for debugging purposes or as background information.* result\_frame : pandas DataFrame with t\_test results and multiple testing corrected p-values. * contrasts : matrix of constraints of the null hypothesis in the t\_test. \| \| Return type: \| instance of a simple Results class \| #### Notes Status: experimental. Currently only checked for treatment coding with and without specified reference level. Currently there are no multiple testing corrected confidence intervals available. #### Examples ``` >>> res = ols("np.log(Days+1) ~ C(Weight) + C(Duration)", data).fit() >>> pw = res.t_test_pairwise("C(Weight)") >>> pw.result_frame coef std err t P>\|t\| Conf. Int. Low 2-1 0.632315 0.230003 2.749157 8.028083e-03 0.171563 3-1 1.302555 0.230003 5.663201 5.331513e-07 0.841803 3-2 0.670240 0.230003 2.914044 5.119126e-03 0.209488 Conf. Int. Upp. pvalue-hs reject-hs 2-1 1.093067 0.010212 True 3-1 1.763307 0.000002 True 3-2 1.130992 0.010212 True ``` statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.pvalues statsmodels.regression.recursive\_ls.RecursiveLSResults.pvalues =============================================================== `RecursiveLSResults.pvalues()` (array) The p-values associated with the z-statistics of the coefficients. Note that the coefficients are assumed to have a Normal distribution. statsmodels statsmodels.tsa.arima_model.ARIMA.information statsmodels.tsa.arima\_model.ARIMA.information ============================================== `ARIMA.information(params)` Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.multivariate.factor.Factor.loglike statsmodels.multivariate.factor.Factor.loglike ============================================== `Factor.loglike(par)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/multivariate/factor.html#Factor.loglike) Evaluate the log-likelihood function. \| Parameters: \| par (ndarray or tuple of 2 ndarray's) – The model parameters, either a packed representation of the model parameters or a 2-tuple containing a `k_endog x n_factor` matrix of factor loadings and a `k_endog` vector of uniquenesses. \| \| Returns: \| loglike \| \| Return type: \| float \| statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.resid_acorr statsmodels.tsa.vector\_ar.var\_model.VARResults.resid\_acorr ============================================================= `VARResults.resid_acorr(nlags=1)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARResults.resid_acorr) Compute sample autocorrelation (including lag 0) \| Parameters: \| nlags (int) – \| statsmodels statsmodels.discrete.discrete_model.BinaryModel.fit statsmodels.discrete.discrete\_model.BinaryModel.fit ==================================================== `BinaryModel.fit(start_params=None, method='newton', maxiter=35, full_output=1, disp=1, callback=None, *kwargs)` Fit the model using maximum likelihood. The rest of the docstring is from statsmodels.base.model.LikelihoodModel.fit Fit method for likelihood based models \| Parameters: \| start\_params (array-like, optional) – Initial guess of the solution for the loglikelihood maximization. The default is an array of zeros. * method (str, optional) – The `method` determines which solver from `scipy.optimize` is used, and it can be chosen from among the following strings: + ’newton’ for Newton-Raphson, ‘nm’ for Nelder-Mead + ’bfgs’ for Broyden-Fletcher-Goldfarb-Shanno (BFGS) + ’lbfgs’ for limited-memory BFGS with optional box constraints + ’powell’ for modified Powell’s method + ’cg’ for conjugate gradient + ’ncg’ for Newton-conjugate gradient + ’basinhopping’ for global basin-hopping solver + ’minimize’ for generic wrapper of scipy minimize (BFGS by default)The explicit arguments in `fit` are passed to the solver, with the exception of the basin-hopping solver. Each solver has several optional arguments that are not the same across solvers. See the notes section below (or scipy.optimize) for the available arguments and for the list of explicit arguments that the basin-hopping solver supports. * maxiter (int, optional) – The maximum number of iterations to perform. * full\_output (bool, optional) – Set to True to have all available output in the Results object’s mle\_retvals attribute. The output is dependent on the solver. See LikelihoodModelResults notes section for more information. * disp (bool, optional) – Set to True to print convergence messages. * fargs (tuple, optional) – Extra arguments passed to the likelihood function, i.e., loglike(x,\args) callback (callable callback(xk), optional) – Called after each iteration, as callback(xk), where xk is the current parameter vector. * retall (bool, optional) – Set to True to return list of solutions at each iteration. Available in Results object’s mle\_retvals attribute. * skip\_hessian (bool, optional) – If False (default), then the negative inverse hessian is calculated after the optimization. If True, then the hessian will not be calculated. However, it will be available in methods that use the hessian in the optimization (currently only with `“newton”`). * kwargs (keywords) – All kwargs are passed to the chosen solver with one exception. The following keyword controls what happens after the fit: ``` warn_convergence : bool, optional If True, checks the model for the converged flag. If the converged flag is False, a ConvergenceWarning is issued. ``` \| #### Notes The ‘basinhopping’ solver ignores `maxiter`, `retall`, `full_output` explicit arguments. Optional arguments for solvers (see returned Results.mle\_settings): ``` 'newton' tol : float Relative error in params acceptable for convergence. 'nm' -- Nelder Mead xtol : float Relative error in params acceptable for convergence ftol : float Relative error in loglike(params) acceptable for convergence maxfun : int Maximum number of function evaluations to make. 'bfgs' gtol : float Stop when norm of gradient is less than gtol. norm : float Order of norm (np.Inf is max, -np.Inf is min) epsilon If fprime is approximated, use this value for the step size. Only relevant if LikelihoodModel.score is None. 'lbfgs' m : int This many terms are used for the Hessian approximation. factr : float A stop condition that is a variant of relative error. pgtol : float A stop condition that uses the projected gradient. epsilon If fprime is approximated, use this value for the step size. Only relevant if LikelihoodModel.score is None. maxfun : int Maximum number of function evaluations to make. bounds : sequence (min, max) pairs for each element in x, defining the bounds on that parameter. Use None for one of min or max when there is no bound in that direction. 'cg' gtol : float Stop when norm of gradient is less than gtol. norm : float Order of norm (np.Inf is max, -np.Inf is min) epsilon : float If fprime is approximated, use this value for the step size. Can be scalar or vector. Only relevant if Likelihoodmodel.score is None. 'ncg' fhess_p : callable f'(x,args) Function which computes the Hessian of f times an arbitrary vector, p. Should only be supplied if LikelihoodModel.hessian is None. avextol : float Stop when the average relative error in the minimizer falls below this amount. epsilon : float or ndarray If fhess is approximated, use this value for the step size. Only relevant if Likelihoodmodel.hessian is None. 'powell' xtol : float Line-search error tolerance ftol : float Relative error in loglike(params) for acceptable for convergence. maxfun : int Maximum number of function evaluations to make. start_direc : ndarray Initial direction set. 'basinhopping' niter : integer The number of basin hopping iterations. niter_success : integer Stop the run if the global minimum candidate remains the same for this number of iterations. T : float The "temperature" parameter for the accept or reject criterion. Higher "temperatures" mean that larger jumps in function value will be accepted. For best results `T` should be comparable to the separation (in function value) between local minima. stepsize : float Initial step size for use in the random displacement. interval : integer The interval for how often to update the `stepsize`. minimizer : dict Extra keyword arguments to be passed to the minimizer `scipy.optimize.minimize()`, for example 'method' - the minimization method (e.g. 'L-BFGS-B'), or 'tol' - the tolerance for termination. Other arguments are mapped from explicit argument of `fit`: - `args` <- `fargs` - `jac` <- `score` - `hess` <- `hess` 'minimize' min_method : str, optional Name of minimization method to use. Any method specific arguments can be passed directly. For a list of methods and their arguments, see documentation of `scipy.optimize.minimize`. If no method is specified, then BFGS is used. ``` statsmodels statsmodels.discrete.count_model.ZeroInflatedGeneralizedPoissonResults.llnull statsmodels.discrete.count\_model.ZeroInflatedGeneralizedPoissonResults.llnull ============================================================================== `ZeroInflatedGeneralizedPoissonResults.llnull()` statsmodels statsmodels.regression.recursive_ls.RecursiveLS.simulate statsmodels.regression.recursive\_ls.RecursiveLS.simulate ========================================================= `RecursiveLS.simulate(params, nsimulations, measurement_shocks=None, state_shocks=None, initial_state=None)` Simulate a new time series following the state space model \| Parameters: \| params (array\_like) – Array of model parameters. * nsimulations (int) – The number of observations to simulate. If the model is time-invariant this can be any number. If the model is time-varying, then this number must be less than or equal to the number * measurement\_shocks (array\_like, optional) – If specified, these are the shocks to the measurement equation, $\varepsilon\_t$. If unspecified, these are automatically generated using a pseudo-random number generator. If specified, must be shaped `nsimulations` x `k_endog`, where `k_endog` is the same as in the state space model. * state\_shocks (array\_like, optional) – If specified, these are the shocks to the state equation, $\eta\_t$. If unspecified, these are automatically generated using a pseudo-random number generator. If specified, must be shaped `nsimulations` x `k_posdef` where `k_posdef` is the same as in the state space model. * initial\_state (array\_like, optional) – If specified, this is the state vector at time zero, which should be shaped (`k_states` x 1), where `k_states` is the same as in the state space model. If unspecified, but the model has been initialized, then that initialization is used. If unspecified and the model has not been initialized, then a vector of zeros is used. Note that this is not included in the returned `simulated_states` array. \| \| Returns: \| simulated\_obs – An (nsimulations x k\_endog) array of simulated observations. \| \| Return type: \| array \| statsmodels statsmodels.genmod.cov_struct.CovStruct statsmodels.genmod.cov\_struct.CovStruct ======================================== `class statsmodels.genmod.cov_struct.CovStruct(cov_nearest_method='clipped')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/cov_struct.html#CovStruct) A base class for correlation and covariance structures of grouped data. Each implementation of this class takes the residuals from a regression model that has been fitted to grouped data, and uses them to estimate the within-group dependence structure of the random errors in the model. The state of the covariance structure is represented through the value of the class variable `dep_params`. The default state of a newly-created instance should correspond to the identity correlation matrix. #### Methods \| \| \| \| --- \| --- \| \| [`covariance_matrix`](statsmodels.genmod.cov_struct.covstruct.covariance_matrix#statsmodels.genmod.cov_struct.CovStruct.covariance_matrix "statsmodels.genmod.cov_struct.CovStruct.covariance_matrix")(endog\_expval, index) \| Returns the working covariance or correlation matrix for a given cluster of data. \| \| [`covariance_matrix_solve`](statsmodels.genmod.cov_struct.covstruct.covariance_matrix_solve#statsmodels.genmod.cov_struct.CovStruct.covariance_matrix_solve "statsmodels.genmod.cov_struct.CovStruct.covariance_matrix_solve")(expval, index, …) \| Solves matrix equations of the form `covmat * soln = rhs` and returns the values of `soln`, where `covmat` is the covariance matrix represented by this class. \| \| [`initialize`](statsmodels.genmod.cov_struct.covstruct.initialize#statsmodels.genmod.cov_struct.CovStruct.initialize "statsmodels.genmod.cov_struct.CovStruct.initialize")(model) \| Called by GEE, used by implementations that need additional setup prior to running `fit`. \| \| [`summary`](statsmodels.genmod.cov_struct.covstruct.summary#statsmodels.genmod.cov_struct.CovStruct.summary "statsmodels.genmod.cov_struct.CovStruct.summary")() \| Returns a text summary of the current estimate of the dependence structure. \| \| [`update`](statsmodels.genmod.cov_struct.covstruct.update#statsmodels.genmod.cov_struct.CovStruct.update "statsmodels.genmod.cov_struct.CovStruct.update")(params) \| Updates the association parameter values based on the current regression coefficients. \|	programming_docs
statsmodels statsmodels.tsa.statespace.kalman_filter.FilterResults.predict statsmodels.tsa.statespace.kalman\_filter.FilterResults.predict =============================================================== `FilterResults.predict(start=None, end=None, dynamic=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/kalman_filter.html#FilterResults.predict) In-sample and out-of-sample prediction for state space models generally \| Parameters: \| start (int, optional) – Zero-indexed observation number at which to start forecasting, i.e., the first forecast will be at start. * end (int, optional) – Zero-indexed observation number at which to end forecasting, i.e., the last forecast will be at end. * dynamic (int, optional) – Offset relative to `start` at which to begin dynamic prediction. Prior to this observation, true endogenous values will be used for prediction; starting with this observation and continuing through the end of prediction, forecasted endogenous values will be used instead. * *\\kwargs* – If the prediction range is outside of the sample range, any of the state space representation matrices that are time-varying must have updated values provided for the out-of-sample range. For example, of `obs_intercept` is a time-varying component and the prediction range extends 10 periods beyond the end of the sample, a (`k_endog` x 10) matrix must be provided with the new intercept values. \| \| Returns: \| results – A PredictionResults object. \| \| Return type: \| [kalman\_filter.PredictionResults](statsmodels.tsa.statespace.kalman_filter.predictionresults#statsmodels.tsa.statespace.kalman_filter.PredictionResults "statsmodels.tsa.statespace.kalman_filter.PredictionResults") \| #### Notes All prediction is performed by applying the deterministic part of the measurement equation using the predicted state variables. Out-of-sample prediction first applies the Kalman filter to missing data for the number of periods desired to obtain the predicted states. statsmodels statsmodels.sandbox.regression.gmm.IV2SLS.predict statsmodels.sandbox.regression.gmm.IV2SLS.predict ================================================= `IV2SLS.predict(params, exog=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/regression/gmm.html#IV2SLS.predict) Return linear predicted values from a design matrix. \| Parameters: \| * exog (array-like) – Design / exogenous data * params (array-like, optional after fit has been called) – Parameters of a linear model \| \| Returns: \| \| \| Return type: \| An array of fitted values \| #### Notes If the model as not yet been fit, params is not optional. statsmodels statsmodels.sandbox.distributions.transformed.TransfTwo_gen statsmodels.sandbox.distributions.transformed.TransfTwo\_gen ============================================================ `class statsmodels.sandbox.distributions.transformed.TransfTwo_gen(kls, func, funcinvplus, funcinvminus, derivplus, derivminus, args, kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/distributions/transformed.html#TransfTwo_gen) Distribution based on a non-monotonic (u- or hump-shaped transformation) the constructor can be called with a distribution class, and functions that define the non-linear transformation. and generates the distribution of the transformed random variable Note: the transformation, it’s inverse and derivatives need to be fully specified: func, funcinvplus, funcinvminus, derivplus, derivminus. Currently no numerical derivatives or inverse are calculated This can be used to generate distribution instances similar to the distributions in scipy.stats. #### Methods \| \| \| \| --- \| --- \| \| [`cdf`](statsmodels.sandbox.distributions.transformed.transftwo_gen.cdf#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.cdf "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.cdf")(x, \args, \\kwds) \| Cumulative distribution function of the given RV. \| \| [`entropy`](statsmodels.sandbox.distributions.transformed.transftwo_gen.entropy#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.entropy "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.entropy")(\args, \\kwds) \| Differential entropy of the RV. \| \| [`expect`](statsmodels.sandbox.distributions.transformed.transftwo_gen.expect#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.expect "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.expect")([func, args, loc, scale, lb, ub, …]) \| Calculate expected value of a function with respect to the distribution. \| \| [`fit`](statsmodels.sandbox.distributions.transformed.transftwo_gen.fit#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.fit "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.fit")(data, \args, \\kwds) \| Return MLEs for shape (if applicable), location, and scale parameters from data. \| \| [`fit_loc_scale`](statsmodels.sandbox.distributions.transformed.transftwo_gen.fit_loc_scale#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.fit_loc_scale "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.fit_loc_scale")(data, \args) \| Estimate loc and scale parameters from data using 1st and 2nd moments. \| \| [`freeze`](statsmodels.sandbox.distributions.transformed.transftwo_gen.freeze#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.freeze "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.freeze")(\args, \\kwds) \| Freeze the distribution for the given arguments. \| \| [`interval`](statsmodels.sandbox.distributions.transformed.transftwo_gen.interval#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.interval "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.interval")(alpha, \args, \\kwds) \| Confidence interval with equal areas around the median. \| \| [`isf`](statsmodels.sandbox.distributions.transformed.transftwo_gen.isf#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.isf "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.isf")(q, \args, \\kwds) \| Inverse survival function (inverse of `sf`) at q of the given RV. \| \| [`logcdf`](statsmodels.sandbox.distributions.transformed.transftwo_gen.logcdf#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.logcdf "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.logcdf")(x, \args, \\kwds) \| Log of the cumulative distribution function at x of the given RV. \| \| [`logpdf`](statsmodels.sandbox.distributions.transformed.transftwo_gen.logpdf#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.logpdf "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.logpdf")(x, \args, \\kwds) \| Log of the probability density function at x of the given RV. \| \| [`logsf`](statsmodels.sandbox.distributions.transformed.transftwo_gen.logsf#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.logsf "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.logsf")(x, \args, \\kwds) \| Log of the survival function of the given RV. \| \| [`mean`](statsmodels.sandbox.distributions.transformed.transftwo_gen.mean#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.mean "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.mean")(\args, \\kwds) \| Mean of the distribution. \| \| [`median`](statsmodels.sandbox.distributions.transformed.transftwo_gen.median#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.median "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.median")(\args, \\kwds) \| Median of the distribution. \| \| [`moment`](statsmodels.sandbox.distributions.transformed.transftwo_gen.moment#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.moment "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.moment")(n, \args, \\kwds) \| n-th order non-central moment of distribution. \| \| [`nnlf`](statsmodels.sandbox.distributions.transformed.transftwo_gen.nnlf#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.nnlf "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.nnlf")(theta, x) \| Return negative loglikelihood function. \| \| [`pdf`](statsmodels.sandbox.distributions.transformed.transftwo_gen.pdf#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.pdf "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.pdf")(x, \args, \\kwds) \| Probability density function at x of the given RV. \| \| [`ppf`](statsmodels.sandbox.distributions.transformed.transftwo_gen.ppf#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.ppf "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.ppf")(q, \args, \\kwds) \| Percent point function (inverse of `cdf`) at q of the given RV. \| \| [`rvs`](statsmodels.sandbox.distributions.transformed.transftwo_gen.rvs#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.rvs "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.rvs")(\args, \\kwds) \| Random variates of given type. \| \| [`sf`](statsmodels.sandbox.distributions.transformed.transftwo_gen.sf#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.sf "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.sf")(x, \args, \\kwds) \| Survival function (1 - `cdf`) at x of the given RV. \| \| [`stats`](statsmodels.sandbox.distributions.transformed.transftwo_gen.stats#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.stats "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.stats")(\args, \\kwds) \| Some statistics of the given RV. \| \| [`std`](statsmodels.sandbox.distributions.transformed.transftwo_gen.std#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.std "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.std")(\args, \\kwds) \| Standard deviation of the distribution. \| \| [`var`](statsmodels.sandbox.distributions.transformed.transftwo_gen.var#statsmodels.sandbox.distributions.transformed.TransfTwo_gen.var "statsmodels.sandbox.distributions.transformed.TransfTwo_gen.var")(\args, \\kwds) \| Variance of the distribution. \| #### Attributes \| \| \| \| --- \| --- \| \| `random_state` \| Get or set the RandomState object for generating random variates. \| statsmodels statsmodels.tsa.arima_model.ARIMAResults.wald_test_terms statsmodels.tsa.arima\_model.ARIMAResults.wald\_test\_terms =========================================================== `ARIMAResults.wald_test_terms(skip_single=False, extra_constraints=None, combine_terms=None)` Compute a sequence of Wald tests for terms over multiple columns This computes joined Wald tests for the hypothesis that all coefficients corresponding to a `term` are zero. `Terms` are defined by the underlying formula or by string matching. \| Parameters: \| skip\_single (boolean) – If true, then terms that consist only of a single column and, therefore, refers only to a single parameter is skipped. If false, then all terms are included. * extra\_constraints (ndarray) – not tested yet * combine\_terms (None or list of strings) – Each string in this list is matched to the name of the terms or the name of the exogenous variables. All columns whose name includes that string are combined in one joint test. \| \| Returns: \| test\_result – The result instance contains `table` which is a pandas DataFrame with the test results: test statistic, degrees of freedom and pvalues. \| \| Return type: \| result instance \| #### Examples ``` >>> res_ols = ols("np.log(Days+1) ~ C(Duration, Sum)C(Weight, Sum)", data).fit() >>> res_ols.wald_test_terms() <class 'statsmodels.stats.contrast.WaldTestResults'> F P>F df constraint df denom Intercept 279.754525 2.37985521351e-22 1 51 C(Duration, Sum) 5.367071 0.0245738436636 1 51 C(Weight, Sum) 12.432445 3.99943118767e-05 2 51 C(Duration, Sum):C(Weight, Sum) 0.176002 0.83912310946 2 51 ``` ``` >>> res_poi = Poisson.from_formula("Days ~ C(Weight) C(Duration)", data).fit(cov_type='HC0') >>> wt = res_poi.wald_test_terms(skip_single=False, combine_terms=['Duration', 'Weight']) >>> print(wt) chi2 P>chi2 df constraint Intercept 15.695625 7.43960374424e-05 1 C(Weight) 16.132616 0.000313940174705 2 C(Duration) 1.009147 0.315107378931 1 C(Weight):C(Duration) 0.216694 0.897315972824 2 Duration 11.187849 0.010752286833 3 Weight 30.263368 4.32586407145e-06 4 ``` statsmodels statsmodels.sandbox.regression.gmm.IVRegressionResults.remove_data statsmodels.sandbox.regression.gmm.IVRegressionResults.remove\_data =================================================================== `IVRegressionResults.remove_data()` remove data arrays, all nobs arrays from result and model This reduces the size of the instance, so it can be pickled with less memory. Currently tested for use with predict from an unpickled results and model instance. Warning Since data and some intermediate results have been removed calculating new statistics that require them will raise exceptions. The exception will occur the first time an attribute is accessed that has been set to None. Not fully tested for time series models, tsa, and might delete too much for prediction or not all that would be possible. The lists of arrays to delete are maintained as attributes of the result and model instance, except for cached values. These lists could be changed before calling remove\_data. The attributes to remove are named in: `model._data_attr : arrays attached to both the model instance` and the results instance with the same attribute name. `result.data_in_cache : arrays that may exist as values in` result.\_cache (TODO : should privatize name) `result._data_attr_model : arrays attached to the model` instance but not to the results instance statsmodels statsmodels.stats.contingency_tables.StratifiedTable.test_equal_odds statsmodels.stats.contingency\_tables.StratifiedTable.test\_equal\_odds ======================================================================= `StratifiedTable.test_equal_odds(adjust=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/contingency_tables.html#StratifiedTable.test_equal_odds) Test that all odds ratios are identical. This is the ‘Breslow-Day’ testing procedure. \| Parameters: \| adjust (boolean) – Use the ‘Tarone’ adjustment to achieve the chi^2 asymptotic distribution. \| \| Returns: \| * A bunch containing the following attributes * statistic (float) – The chi^2 test statistic. * p-value (float) – The p-value for the test. \| statsmodels statsmodels.sandbox.descstats.descstats statsmodels.sandbox.descstats.descstats ======================================= `statsmodels.sandbox.descstats.descstats(data, cols=None, axis=0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/descstats.html#descstats) Prints descriptive statistics for one or multiple variables. \| Parameters: \| * data (numpy array) – `x` is the data * v (list, optional) – A list of the column number or field names (for a recarray) of variables. Default is all columns. * axis (1 or 0) – axis order of data. Default is 0 for column-ordered data. \| #### Examples ``` >>> descstats(data.exog,v=['x_1','x_2','x_3']) ``` statsmodels statsmodels.sandbox.regression.gmm.IVRegressionResults.save statsmodels.sandbox.regression.gmm.IVRegressionResults.save =========================================================== `IVRegressionResults.save(fname, remove_data=False)` save a pickle of this instance \| Parameters: \| * fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. * remove\_data (bool) – If False (default), then the instance is pickled without changes. If True, then all arrays with length nobs are set to None before pickling. See the remove\_data method. In some cases not all arrays will be set to None. \| #### Notes If remove\_data is true and the model result does not implement a remove\_data method then this will raise an exception. statsmodels statsmodels.genmod.families.links.CLogLog statsmodels.genmod.families.links.CLogLog ========================================= `class statsmodels.genmod.families.links.CLogLog` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#CLogLog) The complementary log-log transform CLogLog inherits from Logit in order to have access to its \_clean method for the link and its derivative. #### Notes CLogLog is untested. #### Methods \| \| \| \| --- \| --- \| \| [`deriv`](statsmodels.genmod.families.links.cloglog.deriv#statsmodels.genmod.families.links.CLogLog.deriv "statsmodels.genmod.families.links.CLogLog.deriv")(p) \| Derivative of C-Log-Log transform link function \| \| [`deriv2`](statsmodels.genmod.families.links.cloglog.deriv2#statsmodels.genmod.families.links.CLogLog.deriv2 "statsmodels.genmod.families.links.CLogLog.deriv2")(p) \| Second derivative of the C-Log-Log ink function \| \| [`inverse`](statsmodels.genmod.families.links.cloglog.inverse#statsmodels.genmod.families.links.CLogLog.inverse "statsmodels.genmod.families.links.CLogLog.inverse")(z) \| Inverse of C-Log-Log transform link function \| \| [`inverse_deriv`](statsmodels.genmod.families.links.cloglog.inverse_deriv#statsmodels.genmod.families.links.CLogLog.inverse_deriv "statsmodels.genmod.families.links.CLogLog.inverse_deriv")(z) \| Derivative of the inverse of the C-Log-Log transform link function \| statsmodels statsmodels.robust.norms.Hampel statsmodels.robust.norms.Hampel =============================== `class statsmodels.robust.norms.Hampel(a=2.0, b=4.0, c=8.0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/norms.html#Hampel) Hampel function for M-estimation. \| Parameters: \| * a (float, optional) – * b (float, optional) – * c (float, optional) – The tuning constants for Hampel’s function. The default values are a,b,c = 2, 4, 8. \| See also [`statsmodels.robust.norms.RobustNorm`](statsmodels.robust.norms.robustnorm#statsmodels.robust.norms.RobustNorm "statsmodels.robust.norms.RobustNorm") #### Methods \| \| \| \| --- \| --- \| \| [`psi`](statsmodels.robust.norms.hampel.psi#statsmodels.robust.norms.Hampel.psi "statsmodels.robust.norms.Hampel.psi")(z) \| The psi function for Hampel’s estimator \| \| [`psi_deriv`](statsmodels.robust.norms.hampel.psi_deriv#statsmodels.robust.norms.Hampel.psi_deriv "statsmodels.robust.norms.Hampel.psi_deriv")(z) \| Deriative of psi. \| \| [`rho`](statsmodels.robust.norms.hampel.rho#statsmodels.robust.norms.Hampel.rho "statsmodels.robust.norms.Hampel.rho")(z) \| The robust criterion function for Hampel’s estimator \| \| [`weights`](statsmodels.robust.norms.hampel.weights#statsmodels.robust.norms.Hampel.weights "statsmodels.robust.norms.Hampel.weights")(z) \| Hampel weighting function for the IRLS algorithm \| statsmodels statsmodels.regression.linear_model.OLSResults.cov_params statsmodels.regression.linear\_model.OLSResults.cov\_params =========================================================== `OLSResults.cov_params(r_matrix=None, column=None, scale=None, cov_p=None, other=None)` Returns the variance/covariance matrix. The variance/covariance matrix can be of a linear contrast of the estimates of params or all params multiplied by scale which will usually be an estimate of sigma^2. Scale is assumed to be a scalar. \| Parameters: \| * r\_matrix (array-like) – Can be 1d, or 2d. Can be used alone or with other. * column (array-like, optional) – Must be used on its own. Can be 0d or 1d see below. * scale (float, optional) – Can be specified or not. Default is None, which means that the scale argument is taken from the model. * other (array-like, optional) – Can be used when r\_matrix is specified. \| \| Returns: \| cov – covariance matrix of the parameter estimates or of linear combination of parameter estimates. See Notes. \| \| Return type: \| ndarray \| #### Notes (The below are assumed to be in matrix notation.) If no argument is specified returns the covariance matrix of a model `(scale)(X.T X)^(-1)` If contrast is specified it pre and post-multiplies as follows `(scale) r_matrix (X.T X)^(-1) r_matrix.T` If contrast and other are specified returns `(scale) * r_matrix (X.T X)^(-1) other.T` If column is specified returns `(scale) * (X.T X)^(-1)[column,column]` if column is 0d OR `(scale) * (X.T X)^(-1)[column][:,column]` if column is 1d	programming_docs
statsmodels statsmodels.regression.linear_model.OLSResults.scale statsmodels.regression.linear\_model.OLSResults.scale ===================================================== `OLSResults.scale()` statsmodels statsmodels.stats.stattools.expected_robust_kurtosis statsmodels.stats.stattools.expected\_robust\_kurtosis ====================================================== `statsmodels.stats.stattools.expected_robust_kurtosis(ab=(5.0, 50.0), dg=(2.5, 25.0))` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/stattools.html#expected_robust_kurtosis) Calculates the expected value of the robust kurtosis measures in Kim and White assuming the data are normally distributed. \| Parameters: \| * ab (iterable, optional) – Contains 100\(alpha, beta) in the kr3 measure where alpha is the tail quantile cut-off for measuring the extreme tail and beta is the central quantile cutoff for the standardization of the measure db (iterable, optional) – Contains 100\(delta, gamma) in the kr4 measure where delta is the tail quantile for measuring extreme values and gamma is the central quantile used in the the standardization of the measure \| \| Returns: \| ekr* – Contains the expected values of the 4 robust kurtosis measures \| \| Return type: \| array, 4-element \| #### Notes See `robust_kurtosis` for definitions of the robust kurtosis measures statsmodels statsmodels.discrete.discrete_model.MNLogit.from_formula statsmodels.discrete.discrete\_model.MNLogit.from\_formula ========================================================== `classmethod MNLogit.from_formula(formula, data, subset=None, drop_cols=None, args, kwargs)` Create a Model from a formula and dataframe. \| Parameters: \| formula (str or generic Formula object) – The formula specifying the model * data (array-like) – The data for the model. See Notes. * subset (array-like) – An array-like object of booleans, integers, or index values that indicate the subset of df to use in the model. Assumes df is a `pandas.DataFrame` * drop\_cols (array-like) – Columns to drop from the design matrix. Cannot be used to drop terms involving categoricals. * args (extra arguments) – These are passed to the model * kwargs (extra keyword arguments) – These are passed to the model with one exception. The `eval_env` keyword is passed to patsy. It can be either a [`patsy.EvalEnvironment`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.EvalEnvironment "(in patsy v0.5.0+dev)") object or an integer indicating the depth of the namespace to use. For example, the default `eval_env=0` uses the calling namespace. If you wish to use a “clean” environment set `eval_env=-1`. \| \| Returns: \| model \| \| Return type: \| Model instance \| #### Notes data must define \_\_getitem\_\_ with the keys in the formula terms args and kwargs are passed on to the model instantiation. E.g., a numpy structured or rec array, a dictionary, or a pandas DataFrame. statsmodels statsmodels.stats.diagnostic.het_white statsmodels.stats.diagnostic.het\_white ======================================= `statsmodels.stats.diagnostic.het_white(resid, exog, retres=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/stats/diagnostic.html#het_white) White’s Lagrange Multiplier Test for Heteroscedasticity \| Parameters: \| * resid (array\_like) – residuals, square of it is used as endogenous variable * exog (array\_like) – possible explanatory variables for variance, squares and interaction terms are included in the auxilliary regression. * resstore (instance (optional)) – a class instance that holds intermediate results. Only returned if store=True \| \| Returns: \| * lm (float) – lagrange multiplier statistic * lm\_pvalue (float) – p-value of lagrange multiplier test * fvalue (float) – f-statistic of the hypothesis that the error variance does not depend on x. This is an alternative test variant not the original LM test. * f\_pvalue (float) – p-value for the f-statistic \| #### Notes assumes x contains constant (for counting dof) question: does f-statistic make sense? constant ? #### References Greene section 11.4.1 5th edition p. 222 now test statistic reproduces Greene 5th, example 11.3 statsmodels statsmodels.discrete.discrete_model.DiscreteResults.set_null_options statsmodels.discrete.discrete\_model.DiscreteResults.set\_null\_options ======================================================================= `DiscreteResults.set_null_options(llnull=None, attach_results=True, *kwds)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#DiscreteResults.set_null_options) set fit options for Null (constant-only) model This resets the cache for related attributes which is potentially fragile. This only sets the option, the null model is estimated when llnull is accessed, if llnull is not yet in cache. \| Parameters: \| llnull (None or float) – If llnull is not None, then the value will be directly assigned to the cached attribute “llnull”. * attach\_results (bool) – Sets an internal flag whether the results instance of the null model should be attached. By default without calling this method, thenull model results are not attached and only the loglikelihood value llnull is stored. * kwds (keyword arguments) – `kwds` are directly used as fit keyword arguments for the null model, overriding any provided defaults. \| \| Returns: \| \| \| Return type: \| no returns, modifies attributes of this instance \| statsmodels statsmodels.tsa.vector_ar.vecm.VECMResults.plot_data statsmodels.tsa.vector\_ar.vecm.VECMResults.plot\_data ====================================================== `VECMResults.plot_data(with_presample=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/vecm.html#VECMResults.plot_data) Plot the input time series. \| Parameters: \| with\_presample (bool, default: `False`) – If `False`, the pre-sample data (the first `k_ar` values) will not be plotted. \| statsmodels statsmodels.tsa.kalmanf.kalmanfilter.KalmanFilter.Z statsmodels.tsa.kalmanf.kalmanfilter.KalmanFilter.Z =================================================== `classmethod KalmanFilter.Z(r)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/kalmanf/kalmanfilter.html#KalmanFilter.Z) Returns the Z selector matrix in the observation equation. \| Parameters: \| r (int) – In the context of the ARMA model r is max(p,q+1) where p is the AR order and q is the MA order. \| #### Notes Currently only returns a 1 x r vector [1,0,0,…0]. Will need to be generalized when the Kalman Filter becomes more flexible. statsmodels statsmodels.sandbox.distributions.transformed.ExpTransf_gen.entropy statsmodels.sandbox.distributions.transformed.ExpTransf\_gen.entropy ==================================================================== `ExpTransf_gen.entropy(args, kwds)` Differential entropy of the RV. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information). * loc (array\_like, optional) – Location parameter (default=0). * scale (array\_like, optional (continuous distributions only)) – Scale parameter (default=1). \| #### Notes Entropy is defined base `e`: ``` >>> drv = rv_discrete(values=((0, 1), (0.5, 0.5))) >>> np.allclose(drv.entropy(), np.log(2.0)) True ``` statsmodels statsmodels.tsa.holtwinters.SimpleExpSmoothing.score statsmodels.tsa.holtwinters.SimpleExpSmoothing.score ==================================================== `SimpleExpSmoothing.score(params)` Score vector of model. The gradient of logL with respect to each parameter. statsmodels statsmodels.discrete.discrete_model.GeneralizedPoissonResults.llr_pvalue statsmodels.discrete.discrete\_model.GeneralizedPoissonResults.llr\_pvalue ========================================================================== `GeneralizedPoissonResults.llr_pvalue()` statsmodels statsmodels.sandbox.distributions.transformed.SquareFunc.inverseplus statsmodels.sandbox.distributions.transformed.SquareFunc.inverseplus ==================================================================== `SquareFunc.inverseplus(x)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/distributions/transformed.html#SquareFunc.inverseplus) statsmodels statsmodels.discrete.count_model.ZeroInflatedPoissonResults.normalized_cov_params statsmodels.discrete.count\_model.ZeroInflatedPoissonResults.normalized\_cov\_params ==================================================================================== `ZeroInflatedPoissonResults.normalized_cov_params()` statsmodels statsmodels.duration.hazard_regression.PHRegResults.standard_errors statsmodels.duration.hazard\_regression.PHRegResults.standard\_errors ===================================================================== `PHRegResults.standard_errors()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/duration/hazard_regression.html#PHRegResults.standard_errors) Returns the standard errors of the parameter estimates. statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.irf_errband_mc statsmodels.tsa.vector\_ar.var\_model.VARResults.irf\_errband\_mc ================================================================= `VARResults.irf_errband_mc(orth=False, repl=1000, T=10, signif=0.05, seed=None, burn=100, cum=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARResults.irf_errband_mc) Compute Monte Carlo integrated error bands assuming normally distributed for impulse response functions \| Parameters: \| * orth (bool, default False) – Compute orthoganalized impulse response error bands * repl (int) – number of Monte Carlo replications to perform * T (int, default 10) – number of impulse response periods * signif (float (0 < signif <1)) – Significance level for error bars, defaults to 95% CI * seed (int) – np.random.seed for replications * burn (int) – number of initial observations to discard for simulation * cum (bool, default False) – produce cumulative irf error bands \| #### Notes Lütkepohl (2005) Appendix D \| Returns: \| \| \| Return type: \| Tuple of lower and upper arrays of ma\_rep monte carlo standard errors \| statsmodels statsmodels.genmod.generalized_estimating_equations.GEE statsmodels.genmod.generalized\_estimating\_equations.GEE ========================================================= `class statsmodels.genmod.generalized_estimating_equations.GEE(endog, exog, groups, time=None, family=None, cov_struct=None, missing='none', offset=None, exposure=None, dep_data=None, constraint=None, update_dep=True, weights=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_estimating_equations.html#GEE) Estimation of marginal regression models using Generalized Estimating Equations (GEE). Marginal regression model fit using Generalized Estimating Equations. GEE can be used to fit Generalized Linear Models (GLMs) when the data have a grouped structure, and the observations are possibly correlated within groups but not between groups. \| Parameters: \| endog (array-like) – 1d array of endogenous values (i.e. responses, outcomes, dependent variables, or ‘Y’ values). * exog (array-like) – 2d array of exogeneous values (i.e. covariates, predictors, independent variables, regressors, or ‘X’ values). A `nobs x k` array where `nobs` is the number of observations and `k` is the number of regressors. An intercept is not included by default and should be added by the user. See `statsmodels.tools.add_constant`. * groups (array-like) – A 1d array of length `nobs` containing the group labels. * time (array-like) – A 2d array of time (or other index) values, used by some dependence structures to define similarity relationships among observations within a cluster. * family (family class instance) – The default is Gaussian. To specify the binomial distribution use `family=sm.families.Binomial()`. Each family can take a link instance as an argument. See statsmodels.genmod.families.family for more information. * cov\_struct (CovStruct class instance) – The default is Independence. To specify an exchangeable structure use cov\_struct = Exchangeable(). See statsmodels.genmod.cov\_struct.CovStruct for more information. * offset (array-like) – An offset to be included in the fit. If provided, must be an array whose length is the number of rows in exog. * dep\_data (array-like) – Additional data passed to the dependence structure. * constraint ((ndarray, ndarray)) – If provided, the constraint is a tuple (L, R) such that the model parameters are estimated under the constraint L \* param = R, where L is a q x p matrix and R is a q-dimensional vector. If constraint is provided, a score test is performed to compare the constrained model to the unconstrained model. * update\_dep (bool) – If true, the dependence parameters are optimized, otherwise they are held fixed at their starting values. * weights (array-like) – An array of weights to use in the analysis. The weights must be constant within each group. These correspond to probability weights (pweights) in Stata. * missing (str) – Available options are ‘none’, ‘drop’, and ‘raise’. If ‘none’, no nan checking is done. If ‘drop’, any observations with nans are dropped. If ‘raise’, an error is raised. Default is ‘none.’ \| See also [`statsmodels.genmod.families.family`](../glm#module-statsmodels.genmod.families.family "statsmodels.genmod.families.family"), [Families](../glm#families), [Link Functions](../glm#links) #### Notes Only the following combinations make sense for family and link ``` + ident log logit probit cloglog pow opow nbinom loglog logc Gaussian \| x x x inv Gaussian \| x x x binomial \| x x x x x x x x x Poission \| x x x neg binomial \| x x x x gamma \| x x x ``` Not all of these link functions are currently available. Endog and exog are references so that if the data they refer to are already arrays and these arrays are changed, endog and exog will change. The “robust” covariance type is the standard “sandwich estimator” (e.g. Liang and Zeger (1986)). It is the default here and in most other packages. The “naive” estimator gives smaller standard errors, but is only correct if the working correlation structure is correctly specified. The “bias reduced” estimator of Mancl and DeRouen (Biometrics, 2001) reduces the downard bias of the robust estimator. The robust covariance provided here follows Liang and Zeger (1986) and agrees with R’s gee implementation. To obtain the robust standard errors reported in Stata, multiply by sqrt(N / (N - g)), where N is the total sample size, and g is the average group size. #### Examples Logistic regression with autoregressive working dependence: ``` >>> import statsmodels.api as sm >>> family = sm.families.Binomial() >>> va = sm.cov_struct.Autoregressive() >>> model = sm.GEE(endog, exog, group, family=family, cov_struct=va) >>> result = model.fit() >>> print(result.summary()) ``` Use formulas to fit a Poisson GLM with independent working dependence: ``` >>> import statsmodels.api as sm >>> fam = sm.families.Poisson() >>> ind = sm.cov_struct.Independence() >>> model = sm.GEE.from_formula("y ~ age + trt + base", "subject", data, cov_struct=ind, family=fam) >>> result = model.fit() >>> print(result.summary()) ``` Equivalent, using the formula API: ``` >>> import statsmodels.api as sm >>> import statsmodels.formula.api as smf >>> fam = sm.families.Poisson() >>> ind = sm.cov_struct.Independence() >>> model = smf.gee("y ~ age + trt + base", "subject", data, cov_struct=ind, family=fam) >>> result = model.fit() >>> print(result.summary()) ``` #### Methods \| \| \| \| --- \| --- \| \| [`cluster_list`](statsmodels.genmod.generalized_estimating_equations.gee.cluster_list#statsmodels.genmod.generalized_estimating_equations.GEE.cluster_list "statsmodels.genmod.generalized_estimating_equations.GEE.cluster_list")(array) \| Returns `array` split into subarrays corresponding to the cluster structure. \| \| [`estimate_scale`](statsmodels.genmod.generalized_estimating_equations.gee.estimate_scale#statsmodels.genmod.generalized_estimating_equations.GEE.estimate_scale "statsmodels.genmod.generalized_estimating_equations.GEE.estimate_scale")() \| Returns an estimate of the scale parameter at the current parameter value. \| \| [`fit`](statsmodels.genmod.generalized_estimating_equations.gee.fit#statsmodels.genmod.generalized_estimating_equations.GEE.fit "statsmodels.genmod.generalized_estimating_equations.GEE.fit")([maxiter, ctol, start\_params, …]) \| Fits a marginal regression model using generalized estimating equations (GEE). \| \| [`from_formula`](statsmodels.genmod.generalized_estimating_equations.gee.from_formula#statsmodels.genmod.generalized_estimating_equations.GEE.from_formula "statsmodels.genmod.generalized_estimating_equations.GEE.from_formula")(formula, groups, data[, …]) \| Create a Model from a formula and dataframe. \| \| [`mean_deriv`](statsmodels.genmod.generalized_estimating_equations.gee.mean_deriv#statsmodels.genmod.generalized_estimating_equations.GEE.mean_deriv "statsmodels.genmod.generalized_estimating_equations.GEE.mean_deriv")(exog, lin\_pred) \| Derivative of the expected endog with respect to the parameters. \| \| [`mean_deriv_exog`](statsmodels.genmod.generalized_estimating_equations.gee.mean_deriv_exog#statsmodels.genmod.generalized_estimating_equations.GEE.mean_deriv_exog "statsmodels.genmod.generalized_estimating_equations.GEE.mean_deriv_exog")(exog, params[, offset\_exposure]) \| Derivative of the expected endog with respect to exog. \| \| [`predict`](statsmodels.genmod.generalized_estimating_equations.gee.predict#statsmodels.genmod.generalized_estimating_equations.GEE.predict "statsmodels.genmod.generalized_estimating_equations.GEE.predict")(params[, exog, offset, exposure, linear]) \| Return predicted values for a marginal regression model fit using GEE. \| \| [`update_cached_means`](statsmodels.genmod.generalized_estimating_equations.gee.update_cached_means#statsmodels.genmod.generalized_estimating_equations.GEE.update_cached_means "statsmodels.genmod.generalized_estimating_equations.GEE.update_cached_means")(mean\_params) \| cached\_means should always contain the most recent calculation of the group-wise mean vectors. \| #### Attributes \| \| \| \| --- \| --- \| \| `cached_means` \| \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| Names of exogenous variables \| statsmodels statsmodels.regression.recursive_ls.RecursiveLS statsmodels.regression.recursive\_ls.RecursiveLS ================================================ `class statsmodels.regression.recursive_ls.RecursiveLS(endog, exog, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/recursive_ls.html#RecursiveLS) Recursive least squares \| Parameters: \| endog (array\_like) – The observed time-series process $y$ * exog (array\_like) – Array of exogenous regressors, shaped nobs x k. \| #### Notes Recursive least squares (RLS) corresponds to expanding window ordinary least squares (OLS). This model applies the Kalman filter to compute recursive estimates of the coefficients and recursive residuals. #### References \| \| \| \| --- \| --- \| \| [\] \| Durbin, James, and Siem Jan Koopman. 2012. Time Series Analysis by State Space Methods: Second Edition. Oxford University Press. \| #### Methods \| \| \| \| --- \| --- \| \| [`filter`](statsmodels.regression.recursive_ls.recursivels.filter#statsmodels.regression.recursive_ls.RecursiveLS.filter "statsmodels.regression.recursive_ls.RecursiveLS.filter")([return\_ssm]) \| Kalman filtering \| \| [`fit`](statsmodels.regression.recursive_ls.recursivels.fit#statsmodels.regression.recursive_ls.RecursiveLS.fit "statsmodels.regression.recursive_ls.RecursiveLS.fit")() \| Fits the model by application of the Kalman filter \| \| [`from_formula`](statsmodels.regression.recursive_ls.recursivels.from_formula#statsmodels.regression.recursive_ls.RecursiveLS.from_formula "statsmodels.regression.recursive_ls.RecursiveLS.from_formula")(formula, data[, subset]) \| Not implemented for state space models \| \| [`hessian`](statsmodels.regression.recursive_ls.recursivels.hessian#statsmodels.regression.recursive_ls.RecursiveLS.hessian "statsmodels.regression.recursive_ls.RecursiveLS.hessian")(params, \args, \\kwargs) \| Hessian matrix of the likelihood function, evaluated at the given parameters \| \| [`impulse_responses`](statsmodels.regression.recursive_ls.recursivels.impulse_responses#statsmodels.regression.recursive_ls.RecursiveLS.impulse_responses "statsmodels.regression.recursive_ls.RecursiveLS.impulse_responses")(params[, steps, impulse, …]) \| Impulse response function \| \| [`information`](statsmodels.regression.recursive_ls.recursivels.information#statsmodels.regression.recursive_ls.RecursiveLS.information "statsmodels.regression.recursive_ls.RecursiveLS.information")(params) \| Fisher information matrix of model \| \| [`initialize`](statsmodels.regression.recursive_ls.recursivels.initialize#statsmodels.regression.recursive_ls.RecursiveLS.initialize "statsmodels.regression.recursive_ls.RecursiveLS.initialize")() \| Initialize (possibly re-initialize) a Model instance. \| \| [`initialize_approximate_diffuse`](statsmodels.regression.recursive_ls.recursivels.initialize_approximate_diffuse#statsmodels.regression.recursive_ls.RecursiveLS.initialize_approximate_diffuse "statsmodels.regression.recursive_ls.RecursiveLS.initialize_approximate_diffuse")([variance]) \| \| \| [`initialize_known`](statsmodels.regression.recursive_ls.recursivels.initialize_known#statsmodels.regression.recursive_ls.RecursiveLS.initialize_known "statsmodels.regression.recursive_ls.RecursiveLS.initialize_known")(initial\_state, …) \| \| \| [`initialize_statespace`](statsmodels.regression.recursive_ls.recursivels.initialize_statespace#statsmodels.regression.recursive_ls.RecursiveLS.initialize_statespace "statsmodels.regression.recursive_ls.RecursiveLS.initialize_statespace")(\\kwargs) \| Initialize the state space representation \| \| [`initialize_stationary`](statsmodels.regression.recursive_ls.recursivels.initialize_stationary#statsmodels.regression.recursive_ls.RecursiveLS.initialize_stationary "statsmodels.regression.recursive_ls.RecursiveLS.initialize_stationary")() \| \| \| [`loglike`](statsmodels.regression.recursive_ls.recursivels.loglike#statsmodels.regression.recursive_ls.RecursiveLS.loglike "statsmodels.regression.recursive_ls.RecursiveLS.loglike")(params, \args, \\kwargs) \| Loglikelihood evaluation \| \| [`loglikeobs`](statsmodels.regression.recursive_ls.recursivels.loglikeobs#statsmodels.regression.recursive_ls.RecursiveLS.loglikeobs "statsmodels.regression.recursive_ls.RecursiveLS.loglikeobs")(params[, transformed, complex\_step]) \| Loglikelihood evaluation \| \| [`observed_information_matrix`](statsmodels.regression.recursive_ls.recursivels.observed_information_matrix#statsmodels.regression.recursive_ls.RecursiveLS.observed_information_matrix "statsmodels.regression.recursive_ls.RecursiveLS.observed_information_matrix")(params[, …]) \| Observed information matrix \| \| [`opg_information_matrix`](statsmodels.regression.recursive_ls.recursivels.opg_information_matrix#statsmodels.regression.recursive_ls.RecursiveLS.opg_information_matrix "statsmodels.regression.recursive_ls.RecursiveLS.opg_information_matrix")(params[, …]) \| Outer product of gradients information matrix \| \| [`predict`](statsmodels.regression.recursive_ls.recursivels.predict#statsmodels.regression.recursive_ls.RecursiveLS.predict "statsmodels.regression.recursive_ls.RecursiveLS.predict")(params[, exog]) \| After a model has been fit predict returns the fitted values. \| \| [`prepare_data`](statsmodels.regression.recursive_ls.recursivels.prepare_data#statsmodels.regression.recursive_ls.RecursiveLS.prepare_data "statsmodels.regression.recursive_ls.RecursiveLS.prepare_data")() \| Prepare data for use in the state space representation \| \| [`score`](statsmodels.regression.recursive_ls.recursivels.score#statsmodels.regression.recursive_ls.RecursiveLS.score "statsmodels.regression.recursive_ls.RecursiveLS.score")(params, \args, \\kwargs) \| Compute the score function at params. \| \| [`score_obs`](statsmodels.regression.recursive_ls.recursivels.score_obs#statsmodels.regression.recursive_ls.RecursiveLS.score_obs "statsmodels.regression.recursive_ls.RecursiveLS.score_obs")(params[, method, transformed, …]) \| Compute the score per observation, evaluated at params \| \| [`set_conserve_memory`](statsmodels.regression.recursive_ls.recursivels.set_conserve_memory#statsmodels.regression.recursive_ls.RecursiveLS.set_conserve_memory "statsmodels.regression.recursive_ls.RecursiveLS.set_conserve_memory")([conserve\_memory]) \| Set the memory conservation method \| \| [`set_filter_method`](statsmodels.regression.recursive_ls.recursivels.set_filter_method#statsmodels.regression.recursive_ls.RecursiveLS.set_filter_method "statsmodels.regression.recursive_ls.RecursiveLS.set_filter_method")([filter\_method]) \| Set the filtering method \| \| [`set_inversion_method`](statsmodels.regression.recursive_ls.recursivels.set_inversion_method#statsmodels.regression.recursive_ls.RecursiveLS.set_inversion_method "statsmodels.regression.recursive_ls.RecursiveLS.set_inversion_method")([inversion\_method]) \| Set the inversion method \| \| [`set_smoother_output`](statsmodels.regression.recursive_ls.recursivels.set_smoother_output#statsmodels.regression.recursive_ls.RecursiveLS.set_smoother_output "statsmodels.regression.recursive_ls.RecursiveLS.set_smoother_output")([smoother\_output]) \| Set the smoother output \| \| [`set_stability_method`](statsmodels.regression.recursive_ls.recursivels.set_stability_method#statsmodels.regression.recursive_ls.RecursiveLS.set_stability_method "statsmodels.regression.recursive_ls.RecursiveLS.set_stability_method")([stability\_method]) \| Set the numerical stability method \| \| [`simulate`](statsmodels.regression.recursive_ls.recursivels.simulate#statsmodels.regression.recursive_ls.RecursiveLS.simulate "statsmodels.regression.recursive_ls.RecursiveLS.simulate")(params, nsimulations[, …]) \| Simulate a new time series following the state space model \| \| [`simulation_smoother`](statsmodels.regression.recursive_ls.recursivels.simulation_smoother#statsmodels.regression.recursive_ls.RecursiveLS.simulation_smoother "statsmodels.regression.recursive_ls.RecursiveLS.simulation_smoother")([simulation\_output]) \| Retrieve a simulation smoother for the state space model. \| \| [`smooth`](statsmodels.regression.recursive_ls.recursivels.smooth#statsmodels.regression.recursive_ls.RecursiveLS.smooth "statsmodels.regression.recursive_ls.RecursiveLS.smooth")([return\_ssm]) \| Kalman smoothing \| \| [`transform_jacobian`](statsmodels.regression.recursive_ls.recursivels.transform_jacobian#statsmodels.regression.recursive_ls.RecursiveLS.transform_jacobian "statsmodels.regression.recursive_ls.RecursiveLS.transform_jacobian")(unconstrained[, …]) \| Jacobian matrix for the parameter transformation function \| \| [`transform_params`](statsmodels.regression.recursive_ls.recursivels.transform_params#statsmodels.regression.recursive_ls.RecursiveLS.transform_params "statsmodels.regression.recursive_ls.RecursiveLS.transform_params")(unconstrained) \| Transform unconstrained parameters used by the optimizer to constrained parameters used in likelihood evaluation \| \| [`untransform_params`](statsmodels.regression.recursive_ls.recursivels.untransform_params#statsmodels.regression.recursive_ls.RecursiveLS.untransform_params "statsmodels.regression.recursive_ls.RecursiveLS.untransform_params")(constrained) \| Transform constrained parameters used in likelihood evaluation to unconstrained parameters used by the optimizer \| \| [`update`](statsmodels.regression.recursive_ls.recursivels.update#statsmodels.regression.recursive_ls.RecursiveLS.update "statsmodels.regression.recursive_ls.RecursiveLS.update")(params, \\kwargs) \| Update the parameters of the model \| #### Attributes \| \| \| \| --- \| --- \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| \| \| `initial_variance` \| \| \| `initialization` \| \| \| `loglikelihood_burn` \| \| \| `param_names` \| (list of str) List of human readable parameter names (for parameters actually included in the model). \| \| `start_params` \| (array) Starting parameters for maximum likelihood estimation. \| \| `tolerance` \| \|	programming_docs
statsmodels statsmodels.discrete.discrete_model.LogitResults.resid_generalized statsmodels.discrete.discrete\_model.LogitResults.resid\_generalized ==================================================================== `LogitResults.resid_generalized()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#LogitResults.resid_generalized) Generalized residuals #### Notes The generalized residuals for the Logit model are defined \[y - p\] where $p=cdf(X\beta)$. This is the same as the `resid_response` for the Logit model. statsmodels statsmodels.tsa.stattools.periodogram statsmodels.tsa.stattools.periodogram ===================================== `statsmodels.tsa.stattools.periodogram(X)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/stattools.html#periodogram) Returns the periodogram for the natural frequency of X \| Parameters: \| X (array-like) – Array for which the periodogram is desired. \| \| Returns: \| pgram – 1./len(X) \* np.abs(np.fft.fft(X))\\2 \| \| Return type: \| array \| #### References Brockwell and Davis. statsmodels statsmodels.sandbox.distributions.transformed.LogTransf_gen.entropy statsmodels.sandbox.distributions.transformed.LogTransf\_gen.entropy ==================================================================== `LogTransf_gen.entropy(args, kwds)` Differential entropy of the RV. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information). * loc (array\_like, optional) – Location parameter (default=0). * scale (array\_like, optional (continuous distributions only)) – Scale parameter (default=1). \| #### Notes Entropy is defined base `e`: ``` >>> drv = rv_discrete(values=((0, 1), (0.5, 0.5))) >>> np.allclose(drv.entropy(), np.log(2.0)) True ``` statsmodels statsmodels.tsa.vector_ar.var_model.VARProcess.acf statsmodels.tsa.vector\_ar.var\_model.VARProcess.acf ==================================================== `VARProcess.acf(nlags=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARProcess.acf) Compute theoretical autocovariance function \| Returns: \| acf \| \| Return type: \| ndarray (p x k x k) \| statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.bic statsmodels.regression.recursive\_ls.RecursiveLSResults.bic =========================================================== `RecursiveLSResults.bic()` (float) Bayes Information Criterion statsmodels statsmodels.duration.hazard_regression.PHReg statsmodels.duration.hazard\_regression.PHReg ============================================= `class statsmodels.duration.hazard_regression.PHReg(endog, exog, status=None, entry=None, strata=None, offset=None, ties='breslow', missing='drop', *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/duration/hazard_regression.html#PHReg) Fit the Cox proportional hazards regression model for right censored data. \| Parameters: \| endog (array-like) – The observed times (event or censoring) * exog (2D array-like) – The covariates or exogeneous variables * status (array-like) – The censoring status values; status=1 indicates that an event occured (e.g. failure or death), status=0 indicates that the observation was right censored. If None, defaults to status=1 for all cases. * entry (array-like) – The entry times, if left truncation occurs * strata (array-like) – Stratum labels. If None, all observations are taken to be in a single stratum. * ties (string) – The method used to handle tied times, must be either ‘breslow’ or ‘efron’. * offset (array-like) – Array of offset values * missing (string) – The method used to handle missing data \| #### Notes Proportional hazards regression models should not include an explicit or implicit intercept. The effect of an intercept is not identified using the partial likelihood approach. `endog`, `event`, `strata`, `entry`, and the first dimension of `exog` all must have the same length #### Methods \| \| \| \| --- \| --- \| \| [`baseline_cumulative_hazard`](statsmodels.duration.hazard_regression.phreg.baseline_cumulative_hazard#statsmodels.duration.hazard_regression.PHReg.baseline_cumulative_hazard "statsmodels.duration.hazard_regression.PHReg.baseline_cumulative_hazard")(params) \| Estimate the baseline cumulative hazard and survival functions. \| \| [`baseline_cumulative_hazard_function`](statsmodels.duration.hazard_regression.phreg.baseline_cumulative_hazard_function#statsmodels.duration.hazard_regression.PHReg.baseline_cumulative_hazard_function "statsmodels.duration.hazard_regression.PHReg.baseline_cumulative_hazard_function")(params) \| Returns a function that calculates the baseline cumulative hazard function for each stratum. \| \| [`breslow_gradient`](statsmodels.duration.hazard_regression.phreg.breslow_gradient#statsmodels.duration.hazard_regression.PHReg.breslow_gradient "statsmodels.duration.hazard_regression.PHReg.breslow_gradient")(params) \| Returns the gradient of the log partial likelihood, using the Breslow method to handle tied times. \| \| [`breslow_hessian`](statsmodels.duration.hazard_regression.phreg.breslow_hessian#statsmodels.duration.hazard_regression.PHReg.breslow_hessian "statsmodels.duration.hazard_regression.PHReg.breslow_hessian")(params) \| Returns the Hessian of the log partial likelihood evaluated at `params`, using the Breslow method to handle tied times. \| \| [`breslow_loglike`](statsmodels.duration.hazard_regression.phreg.breslow_loglike#statsmodels.duration.hazard_regression.PHReg.breslow_loglike "statsmodels.duration.hazard_regression.PHReg.breslow_loglike")(params) \| Returns the value of the log partial likelihood function evaluated at `params`, using the Breslow method to handle tied times. \| \| [`efron_gradient`](statsmodels.duration.hazard_regression.phreg.efron_gradient#statsmodels.duration.hazard_regression.PHReg.efron_gradient "statsmodels.duration.hazard_regression.PHReg.efron_gradient")(params) \| Returns the gradient of the log partial likelihood evaluated at `params`, using the Efron method to handle tied times. \| \| [`efron_hessian`](statsmodels.duration.hazard_regression.phreg.efron_hessian#statsmodels.duration.hazard_regression.PHReg.efron_hessian "statsmodels.duration.hazard_regression.PHReg.efron_hessian")(params) \| Returns the Hessian matrix of the partial log-likelihood evaluated at `params`, using the Efron method to handle tied times. \| \| [`efron_loglike`](statsmodels.duration.hazard_regression.phreg.efron_loglike#statsmodels.duration.hazard_regression.PHReg.efron_loglike "statsmodels.duration.hazard_regression.PHReg.efron_loglike")(params) \| Returns the value of the log partial likelihood function evaluated at `params`, using the Efron method to handle tied times. \| \| [`fit`](statsmodels.duration.hazard_regression.phreg.fit#statsmodels.duration.hazard_regression.PHReg.fit "statsmodels.duration.hazard_regression.PHReg.fit")([groups]) \| Fit a proportional hazards regression model. \| \| [`fit_regularized`](statsmodels.duration.hazard_regression.phreg.fit_regularized#statsmodels.duration.hazard_regression.PHReg.fit_regularized "statsmodels.duration.hazard_regression.PHReg.fit_regularized")([method, alpha, …]) \| Return a regularized fit to a linear regression model. \| \| [`from_formula`](statsmodels.duration.hazard_regression.phreg.from_formula#statsmodels.duration.hazard_regression.PHReg.from_formula "statsmodels.duration.hazard_regression.PHReg.from_formula")(formula, data[, status, entry, …]) \| Create a proportional hazards regression model from a formula and dataframe. \| \| [`get_distribution`](statsmodels.duration.hazard_regression.phreg.get_distribution#statsmodels.duration.hazard_regression.PHReg.get_distribution "statsmodels.duration.hazard_regression.PHReg.get_distribution")(params) \| Returns a scipy distribution object corresponding to the distribution of uncensored endog (duration) values for each case. \| \| [`hessian`](statsmodels.duration.hazard_regression.phreg.hessian#statsmodels.duration.hazard_regression.PHReg.hessian "statsmodels.duration.hazard_regression.PHReg.hessian")(params) \| Returns the Hessian matrix of the log partial likelihood function evaluated at `params`. \| \| [`information`](statsmodels.duration.hazard_regression.phreg.information#statsmodels.duration.hazard_regression.PHReg.information "statsmodels.duration.hazard_regression.PHReg.information")(params) \| Fisher information matrix of model \| \| [`initialize`](statsmodels.duration.hazard_regression.phreg.initialize#statsmodels.duration.hazard_regression.PHReg.initialize "statsmodels.duration.hazard_regression.PHReg.initialize")() \| Initialize (possibly re-initialize) a Model instance. \| \| [`loglike`](statsmodels.duration.hazard_regression.phreg.loglike#statsmodels.duration.hazard_regression.PHReg.loglike "statsmodels.duration.hazard_regression.PHReg.loglike")(params) \| Returns the log partial likelihood function evaluated at `params`. \| \| [`predict`](statsmodels.duration.hazard_regression.phreg.predict#statsmodels.duration.hazard_regression.PHReg.predict "statsmodels.duration.hazard_regression.PHReg.predict")(params[, exog, cov\_params, endog, …]) \| Returns predicted values from the proportional hazards regression model. \| \| [`robust_covariance`](statsmodels.duration.hazard_regression.phreg.robust_covariance#statsmodels.duration.hazard_regression.PHReg.robust_covariance "statsmodels.duration.hazard_regression.PHReg.robust_covariance")(params) \| Returns a covariance matrix for the proportional hazards model regresion coefficient estimates that is robust to certain forms of model misspecification. \| \| [`score`](statsmodels.duration.hazard_regression.phreg.score#statsmodels.duration.hazard_regression.PHReg.score "statsmodels.duration.hazard_regression.PHReg.score")(params) \| Returns the score function evaluated at `params`. \| \| [`score_residuals`](statsmodels.duration.hazard_regression.phreg.score_residuals#statsmodels.duration.hazard_regression.PHReg.score_residuals "statsmodels.duration.hazard_regression.PHReg.score_residuals")(params) \| Returns the score residuals calculated at a given vector of parameters. \| \| [`weighted_covariate_averages`](statsmodels.duration.hazard_regression.phreg.weighted_covariate_averages#statsmodels.duration.hazard_regression.PHReg.weighted_covariate_averages "statsmodels.duration.hazard_regression.PHReg.weighted_covariate_averages")(params) \| Returns the hazard-weighted average of covariate values for subjects who are at-risk at a particular time. \| #### Attributes \| \| \| \| --- \| --- \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| Names of exogenous variables \| statsmodels statsmodels.stats.contingency_tables.SquareTable.local_log_oddsratios statsmodels.stats.contingency\_tables.SquareTable.local\_log\_oddsratios ======================================================================== `SquareTable.local_log_oddsratios()` statsmodels statsmodels.tsa.arima_model.ARMAResults.f_test statsmodels.tsa.arima\_model.ARMAResults.f\_test ================================================ `ARMAResults.f_test(r_matrix, cov_p=None, scale=1.0, invcov=None)` Compute the F-test for a joint linear hypothesis. This is a special case of `wald_test` that always uses the F distribution. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length k row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> A = np.identity(len(results.params)) >>> A = A[1:,:] ``` This tests that each coefficient is jointly statistically significantly different from zero. ``` >>> print(results.f_test(A)) <F test: F=array([[ 330.28533923]]), p=4.984030528700946e-10, df_denom=9, df_num=6> ``` Compare this to ``` >>> results.fvalue 330.2853392346658 >>> results.f_pvalue 4.98403096572e-10 ``` ``` >>> B = np.array(([0,0,1,-1,0,0,0],[0,0,0,0,0,1,-1])) ``` This tests that the coefficient on the 2nd and 3rd regressors are equal and jointly that the coefficient on the 5th and 6th regressors are equal. ``` >>> print(results.f_test(B)) <F test: F=array([[ 9.74046187]]), p=0.005605288531708235, df_denom=9, df_num=2> ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.datasets import longley >>> from statsmodels.formula.api import ols >>> dta = longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = '(GNPDEFL = GNP), (UNEMP = 2), (YEAR/1829 = 1)' >>> f_test = results.f_test(hypotheses) >>> print(f_test) <F test: F=array([[ 144.17976065]]), p=6.322026217355609e-08, df_denom=9, df_num=3> ``` See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`wald_test`](statsmodels.tsa.arima_model.armaresults.wald_test#statsmodels.tsa.arima_model.ARMAResults.wald_test "statsmodels.tsa.arima_model.ARMAResults.wald_test"), [`t_test`](statsmodels.tsa.arima_model.armaresults.t_test#statsmodels.tsa.arima_model.ARMAResults.t_test "statsmodels.tsa.arima_model.ARMAResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.multivariate.factor.FactorResults.factor_score_params statsmodels.multivariate.factor.FactorResults.factor\_score\_params =================================================================== `FactorResults.factor_score_params(method='bartlett')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/multivariate/factor.html#FactorResults.factor_score_params) compute factor scoring coefficient matrix The coefficient matrix is not cached. \| Parameters: \| method ('bartlett' or 'regression') – Method to use for factor scoring. ‘regression’ can be abbreviated to `reg` \| \| Returns: \| coeff\_matrix – matrix s to compute factors f from a standardized endog ys. `f = ys dot s` \| \| Return type: \| ndarray \| #### Notes The `regression` method follows the Stata definition. Method bartlett and regression are verified against Stats. Two inofficial methods, ‘ols’ and ‘gls’, produce similar factor scores but are not verified. See also `factor_scoring` : compute factor scores using scoring matrix statsmodels statsmodels.iolib.summary.Summary statsmodels.iolib.summary.Summary ================================= `class statsmodels.iolib.summary.Summary` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/iolib/summary.html#Summary) class to hold tables for result summary presentation Construction does not take any parameters. Tables and text can be added with the `add_` methods. `tables` list of tables – Contains the list of SimpleTable instances, horizontally concatenated tables are not saved separately. `extra_txt` string – extra lines that are added to the text output, used for warnings and explanations. #### Methods \| \| \| \| --- \| --- \| \| [`add_extra_txt`](statsmodels.iolib.summary.summary.add_extra_txt#statsmodels.iolib.summary.Summary.add_extra_txt "statsmodels.iolib.summary.Summary.add_extra_txt")(etext) \| add additional text that will be added at the end in text format \| \| [`add_table_2cols`](statsmodels.iolib.summary.summary.add_table_2cols#statsmodels.iolib.summary.Summary.add_table_2cols "statsmodels.iolib.summary.Summary.add_table_2cols")(res[, title, gleft, gright, …]) \| add a double table, 2 tables with one column merged horizontally \| \| [`add_table_params`](statsmodels.iolib.summary.summary.add_table_params#statsmodels.iolib.summary.Summary.add_table_params "statsmodels.iolib.summary.Summary.add_table_params")(res[, yname, xname, alpha, …]) \| create and add a table for the parameter estimates \| \| [`as_csv`](statsmodels.iolib.summary.summary.as_csv#statsmodels.iolib.summary.Summary.as_csv "statsmodels.iolib.summary.Summary.as_csv")() \| return tables as string \| \| [`as_html`](statsmodels.iolib.summary.summary.as_html#statsmodels.iolib.summary.Summary.as_html "statsmodels.iolib.summary.Summary.as_html")() \| return tables as string \| \| [`as_latex`](statsmodels.iolib.summary.summary.as_latex#statsmodels.iolib.summary.Summary.as_latex "statsmodels.iolib.summary.Summary.as_latex")() \| return tables as string \| \| [`as_text`](statsmodels.iolib.summary.summary.as_text#statsmodels.iolib.summary.Summary.as_text "statsmodels.iolib.summary.Summary.as_text")() \| return tables as string \| statsmodels statsmodels.regression.linear_model.RegressionResults.compare_lr_test statsmodels.regression.linear\_model.RegressionResults.compare\_lr\_test ======================================================================== `RegressionResults.compare_lr_test(restricted, large_sample=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#RegressionResults.compare_lr_test) Likelihood ratio test to test whether restricted model is correct \| Parameters: \| * restricted (Result instance) – The restricted model is assumed to be nested in the current model. The result instance of the restricted model is required to have two attributes, residual sum of squares, `ssr`, residual degrees of freedom, `df_resid`. * large\_sample (bool) – Flag indicating whether to use a heteroskedasticity robust version of the LR test, which is a modified LM test. \| \| Returns: \| * lr\_stat (float) – likelihood ratio, chisquare distributed with df\_diff degrees of freedom * p\_value (float) – p-value of the test statistic * df\_diff (int) – degrees of freedom of the restriction, i.e. difference in df between models \| #### Notes The exact likelihood ratio is valid for homoskedastic data, and is defined as \[D=-2\log\left(\frac{\mathcal{L}\_{null}} {\mathcal{L}\_{alternative}}\right)\] where $\mathcal{L}$ is the likelihood of the model. With $D$ distributed as chisquare with df equal to difference in number of parameters or equivalently difference in residual degrees of freedom. The large sample version of the likelihood ratio is defined as \[D=n s^{\prime}S^{-1}s\] where $s=n^{-1}\sum\_{i=1}^{n} s\_{i}$ \[s\_{i} = x\_{i,alternative} \epsilon\_{i,null}\] is the average score of the model evaluated using the residuals from null model and the regressors from the alternative model and $S$ is the covariance of the scores, $s\_{i}$. The covariance of the scores is estimated using the same estimator as in the alternative model. This test compares the loglikelihood of the two models. This may not be a valid test, if there is unspecified heteroscedasticity or correlation. This method will issue a warning if this is detected but still return the results without taking unspecified heteroscedasticity or correlation into account. This test compares the loglikelihood of the two models. This may not be a valid test, if there is unspecified heteroscedasticity or correlation. This method will issue a warning if this is detected but still return the results without taking unspecified heteroscedasticity or correlation into account. is the average score of the model evaluated using the residuals from null model and the regressors from the alternative model and $S$ is the covariance of the scores, $s\_{i}$. The covariance of the scores is estimated using the same estimator as in the alternative model. TODO: put into separate function, needs tests	programming_docs
statsmodels statsmodels.genmod.generalized_estimating_equations.GEE.estimate_scale statsmodels.genmod.generalized\_estimating\_equations.GEE.estimate\_scale ========================================================================= `GEE.estimate_scale()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_estimating_equations.html#GEE.estimate_scale) Returns an estimate of the scale parameter at the current parameter value. statsmodels statsmodels.genmod.bayes_mixed_glm.BinomialBayesMixedGLM.vb_elbo_grad statsmodels.genmod.bayes\_mixed\_glm.BinomialBayesMixedGLM.vb\_elbo\_grad ========================================================================= `BinomialBayesMixedGLM.vb_elbo_grad(vb_mean, vb_sd)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/bayes_mixed_glm.html#BinomialBayesMixedGLM.vb_elbo_grad) Returns the gradient of the model’s evidence lower bound (ELBO). statsmodels statsmodels.discrete.discrete_model.NegativeBinomialP.from_formula statsmodels.discrete.discrete\_model.NegativeBinomialP.from\_formula ==================================================================== `classmethod NegativeBinomialP.from_formula(formula, data, subset=None, drop_cols=None, args, kwargs)` Create a Model from a formula and dataframe. \| Parameters: \| formula (str or generic Formula object) – The formula specifying the model * data (array-like) – The data for the model. See Notes. * subset (array-like) – An array-like object of booleans, integers, or index values that indicate the subset of df to use in the model. Assumes df is a `pandas.DataFrame` * drop\_cols (array-like) – Columns to drop from the design matrix. Cannot be used to drop terms involving categoricals. * args (extra arguments) – These are passed to the model * kwargs (extra keyword arguments) – These are passed to the model with one exception. The `eval_env` keyword is passed to patsy. It can be either a [`patsy.EvalEnvironment`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.EvalEnvironment "(in patsy v0.5.0+dev)") object or an integer indicating the depth of the namespace to use. For example, the default `eval_env=0` uses the calling namespace. If you wish to use a “clean” environment set `eval_env=-1`. \| \| Returns: \| model \| \| Return type: \| Model instance \| #### Notes data must define \_\_getitem\_\_ with the keys in the formula terms args and kwargs are passed on to the model instantiation. E.g., a numpy structured or rec array, a dictionary, or a pandas DataFrame. statsmodels statsmodels.regression.mixed_linear_model.MixedLMResults.covjhj statsmodels.regression.mixed\_linear\_model.MixedLMResults.covjhj ================================================================= `MixedLMResults.covjhj()` covariance of parameters based on HJJH dot product of Hessian, Jacobian, Jacobian, Hessian of likelihood name should be covhjh statsmodels statsmodels.genmod.generalized_linear_model.GLMResults statsmodels.genmod.generalized\_linear\_model.GLMResults ======================================================== `class statsmodels.genmod.generalized_linear_model.GLMResults(model, params, normalized_cov_params, scale, cov_type='nonrobust', cov_kwds=None, use_t=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_linear_model.html#GLMResults) Class to contain GLM results. GLMResults inherits from statsmodels.LikelihoodModelResults \| Parameters: \| statsmodels.LikelihoodModelReesults (See) – \| \| Returns: \| * \\Attributes\\** * aic (float) – Akaike Information Criterion -2 \* `llf` + 2\(`df_model` + 1) bic (float) – Bayes Information Criterion `deviance` - `df_resid` \* log(`nobs`) * deviance (float) – See statsmodels.families.family for the distribution-specific deviance functions. * df\_model (float) – See GLM.df\_model * df\_resid (float) – See GLM.df\_resid * fit\_history (dict) – Contains information about the iterations. Its keys are `iterations`, `deviance` and `params`. * fittedvalues (array) – Linear predicted values for the fitted model. dot(exog, params) * llf (float) – Value of the loglikelihood function evalued at params. See statsmodels.families.family for distribution-specific loglikelihoods. * model (class instance) – Pointer to GLM model instance that called fit. * mu (array) – See GLM docstring. * nobs (float) – The number of observations n. * normalized\_cov\_params (array) – See GLM docstring * null\_deviance (float) – The value of the deviance function for the model fit with a constant as the only regressor. * params (array) – The coefficients of the fitted model. Note that interpretation of the coefficients often depends on the distribution family and the data. * pearson\_chi2 (array) – Pearson’s Chi-Squared statistic is defined as the sum of the squares of the Pearson residuals. * pvalues (array) – The two-tailed p-values for the parameters. * resid\_anscombe (array) – Anscombe residuals. See statsmodels.families.family for distribution- specific Anscombe residuals. Currently, the unscaled residuals are provided. In a future version, the scaled residuals will be provided. * resid\_anscombe\_scaled (array) – Scaled Anscombe residuals. See statsmodels.families.family for distribution-specific Anscombe residuals. * resid\_anscombe\_unscaled (array) – Unscaled Anscombe residuals. See statsmodels.families.family for distribution-specific Anscombe residuals. * resid\_deviance (array) – Deviance residuals. See statsmodels.families.family for distribution- specific deviance residuals. * resid\_pearson (array) – Pearson residuals. The Pearson residuals are defined as (`endog` - `mu`)/sqrt(VAR(`mu`)) where VAR is the distribution specific variance function. See statsmodels.families.family and statsmodels.families.varfuncs for more information. * resid\_response (array) – Respnose residuals. The response residuals are defined as `endog` - `fittedvalues` * resid\_working (array) – Working residuals. The working residuals are defined as `resid_response`/link’(`mu`). See statsmodels.family.links for the derivatives of the link functions. They are defined analytically. * scale (float) – The estimate of the scale / dispersion for the model fit. See GLM.fit and GLM.estimate\_scale for more information. * stand\_errors (array) – The standard errors of the fitted GLM. #TODO still named bse \| See also [`statsmodels.base.model.LikelihoodModelResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.base.model.LikelihoodModelResults.html#statsmodels.base.model.LikelihoodModelResults "statsmodels.base.model.LikelihoodModelResults") #### Methods \| \| \| \| --- \| --- \| \| [`aic`](statsmodels.genmod.generalized_linear_model.glmresults.aic#statsmodels.genmod.generalized_linear_model.GLMResults.aic "statsmodels.genmod.generalized_linear_model.GLMResults.aic")() \| \| \| [`bic`](statsmodels.genmod.generalized_linear_model.glmresults.bic#statsmodels.genmod.generalized_linear_model.GLMResults.bic "statsmodels.genmod.generalized_linear_model.GLMResults.bic")() \| \| \| [`bse`](statsmodels.genmod.generalized_linear_model.glmresults.bse#statsmodels.genmod.generalized_linear_model.GLMResults.bse "statsmodels.genmod.generalized_linear_model.GLMResults.bse")() \| \| \| [`conf_int`](statsmodels.genmod.generalized_linear_model.glmresults.conf_int#statsmodels.genmod.generalized_linear_model.GLMResults.conf_int "statsmodels.genmod.generalized_linear_model.GLMResults.conf_int")([alpha, cols, method]) \| Returns the confidence interval of the fitted parameters. \| \| [`cov_params`](statsmodels.genmod.generalized_linear_model.glmresults.cov_params#statsmodels.genmod.generalized_linear_model.GLMResults.cov_params "statsmodels.genmod.generalized_linear_model.GLMResults.cov_params")([r\_matrix, column, scale, cov\_p, …]) \| Returns the variance/covariance matrix. \| \| [`deviance`](statsmodels.genmod.generalized_linear_model.glmresults.deviance#statsmodels.genmod.generalized_linear_model.GLMResults.deviance "statsmodels.genmod.generalized_linear_model.GLMResults.deviance")() \| \| \| [`f_test`](statsmodels.genmod.generalized_linear_model.glmresults.f_test#statsmodels.genmod.generalized_linear_model.GLMResults.f_test "statsmodels.genmod.generalized_linear_model.GLMResults.f_test")(r\_matrix[, cov\_p, scale, invcov]) \| Compute the F-test for a joint linear hypothesis. \| \| [`fittedvalues`](statsmodels.genmod.generalized_linear_model.glmresults.fittedvalues#statsmodels.genmod.generalized_linear_model.GLMResults.fittedvalues "statsmodels.genmod.generalized_linear_model.GLMResults.fittedvalues")() \| \| \| [`get_prediction`](statsmodels.genmod.generalized_linear_model.glmresults.get_prediction#statsmodels.genmod.generalized_linear_model.GLMResults.get_prediction "statsmodels.genmod.generalized_linear_model.GLMResults.get_prediction")([exog, exposure, offset, …]) \| compute prediction results \| \| [`initialize`](statsmodels.genmod.generalized_linear_model.glmresults.initialize#statsmodels.genmod.generalized_linear_model.GLMResults.initialize "statsmodels.genmod.generalized_linear_model.GLMResults.initialize")(model, params, \\kwd) \| \| \| [`llf`](statsmodels.genmod.generalized_linear_model.glmresults.llf#statsmodels.genmod.generalized_linear_model.GLMResults.llf "statsmodels.genmod.generalized_linear_model.GLMResults.llf")() \| \| \| [`llnull`](statsmodels.genmod.generalized_linear_model.glmresults.llnull#statsmodels.genmod.generalized_linear_model.GLMResults.llnull "statsmodels.genmod.generalized_linear_model.GLMResults.llnull")() \| \| \| [`load`](statsmodels.genmod.generalized_linear_model.glmresults.load#statsmodels.genmod.generalized_linear_model.GLMResults.load "statsmodels.genmod.generalized_linear_model.GLMResults.load")(fname) \| load a pickle, (class method) \| \| [`mu`](statsmodels.genmod.generalized_linear_model.glmresults.mu#statsmodels.genmod.generalized_linear_model.GLMResults.mu "statsmodels.genmod.generalized_linear_model.GLMResults.mu")() \| \| \| [`normalized_cov_params`](statsmodels.genmod.generalized_linear_model.glmresults.normalized_cov_params#statsmodels.genmod.generalized_linear_model.GLMResults.normalized_cov_params "statsmodels.genmod.generalized_linear_model.GLMResults.normalized_cov_params")() \| \| \| [`null`](statsmodels.genmod.generalized_linear_model.glmresults.null#statsmodels.genmod.generalized_linear_model.GLMResults.null "statsmodels.genmod.generalized_linear_model.GLMResults.null")() \| \| \| [`null_deviance`](statsmodels.genmod.generalized_linear_model.glmresults.null_deviance#statsmodels.genmod.generalized_linear_model.GLMResults.null_deviance "statsmodels.genmod.generalized_linear_model.GLMResults.null_deviance")() \| \| \| [`pearson_chi2`](statsmodels.genmod.generalized_linear_model.glmresults.pearson_chi2#statsmodels.genmod.generalized_linear_model.GLMResults.pearson_chi2 "statsmodels.genmod.generalized_linear_model.GLMResults.pearson_chi2")() \| \| \| [`plot_added_variable`](statsmodels.genmod.generalized_linear_model.glmresults.plot_added_variable#statsmodels.genmod.generalized_linear_model.GLMResults.plot_added_variable "statsmodels.genmod.generalized_linear_model.GLMResults.plot_added_variable")(focus\_exog[, …]) \| Create an added variable plot for a fitted regression model. \| \| [`plot_ceres_residuals`](statsmodels.genmod.generalized_linear_model.glmresults.plot_ceres_residuals#statsmodels.genmod.generalized_linear_model.GLMResults.plot_ceres_residuals "statsmodels.genmod.generalized_linear_model.GLMResults.plot_ceres_residuals")(focus\_exog[, frac, …]) \| Produces a CERES (Conditional Expectation Partial Residuals) plot for a fitted regression model. \| \| [`plot_partial_residuals`](statsmodels.genmod.generalized_linear_model.glmresults.plot_partial_residuals#statsmodels.genmod.generalized_linear_model.GLMResults.plot_partial_residuals "statsmodels.genmod.generalized_linear_model.GLMResults.plot_partial_residuals")(focus\_exog[, ax]) \| Create a partial residual, or ‘component plus residual’ plot for a fited regression model. \| \| [`predict`](statsmodels.genmod.generalized_linear_model.glmresults.predict#statsmodels.genmod.generalized_linear_model.GLMResults.predict "statsmodels.genmod.generalized_linear_model.GLMResults.predict")([exog, transform]) \| Call self.model.predict with self.params as the first argument. \| \| [`pvalues`](statsmodels.genmod.generalized_linear_model.glmresults.pvalues#statsmodels.genmod.generalized_linear_model.GLMResults.pvalues "statsmodels.genmod.generalized_linear_model.GLMResults.pvalues")() \| \| \| [`remove_data`](statsmodels.genmod.generalized_linear_model.glmresults.remove_data#statsmodels.genmod.generalized_linear_model.GLMResults.remove_data "statsmodels.genmod.generalized_linear_model.GLMResults.remove_data")() \| remove data arrays, all nobs arrays from result and model \| \| [`resid_anscombe`](statsmodels.genmod.generalized_linear_model.glmresults.resid_anscombe#statsmodels.genmod.generalized_linear_model.GLMResults.resid_anscombe "statsmodels.genmod.generalized_linear_model.GLMResults.resid_anscombe")() \| \| \| [`resid_anscombe_scaled`](statsmodels.genmod.generalized_linear_model.glmresults.resid_anscombe_scaled#statsmodels.genmod.generalized_linear_model.GLMResults.resid_anscombe_scaled "statsmodels.genmod.generalized_linear_model.GLMResults.resid_anscombe_scaled")() \| \| \| [`resid_anscombe_unscaled`](statsmodels.genmod.generalized_linear_model.glmresults.resid_anscombe_unscaled#statsmodels.genmod.generalized_linear_model.GLMResults.resid_anscombe_unscaled "statsmodels.genmod.generalized_linear_model.GLMResults.resid_anscombe_unscaled")() \| \| \| [`resid_deviance`](statsmodels.genmod.generalized_linear_model.glmresults.resid_deviance#statsmodels.genmod.generalized_linear_model.GLMResults.resid_deviance "statsmodels.genmod.generalized_linear_model.GLMResults.resid_deviance")() \| \| \| [`resid_pearson`](statsmodels.genmod.generalized_linear_model.glmresults.resid_pearson#statsmodels.genmod.generalized_linear_model.GLMResults.resid_pearson "statsmodels.genmod.generalized_linear_model.GLMResults.resid_pearson")() \| \| \| [`resid_response`](statsmodels.genmod.generalized_linear_model.glmresults.resid_response#statsmodels.genmod.generalized_linear_model.GLMResults.resid_response "statsmodels.genmod.generalized_linear_model.GLMResults.resid_response")() \| \| \| [`resid_working`](statsmodels.genmod.generalized_linear_model.glmresults.resid_working#statsmodels.genmod.generalized_linear_model.GLMResults.resid_working "statsmodels.genmod.generalized_linear_model.GLMResults.resid_working")() \| \| \| [`save`](statsmodels.genmod.generalized_linear_model.glmresults.save#statsmodels.genmod.generalized_linear_model.GLMResults.save "statsmodels.genmod.generalized_linear_model.GLMResults.save")(fname[, remove\_data]) \| save a pickle of this instance \| \| [`summary`](statsmodels.genmod.generalized_linear_model.glmresults.summary#statsmodels.genmod.generalized_linear_model.GLMResults.summary "statsmodels.genmod.generalized_linear_model.GLMResults.summary")([yname, xname, title, alpha]) \| Summarize the Regression Results \| \| [`summary2`](statsmodels.genmod.generalized_linear_model.glmresults.summary2#statsmodels.genmod.generalized_linear_model.GLMResults.summary2 "statsmodels.genmod.generalized_linear_model.GLMResults.summary2")([yname, xname, title, alpha, …]) \| Experimental summary for regression Results \| \| [`t_test`](statsmodels.genmod.generalized_linear_model.glmresults.t_test#statsmodels.genmod.generalized_linear_model.GLMResults.t_test "statsmodels.genmod.generalized_linear_model.GLMResults.t_test")(r\_matrix[, cov\_p, scale, use\_t]) \| Compute a t-test for a each linear hypothesis of the form Rb = q \| \| [`t_test_pairwise`](statsmodels.genmod.generalized_linear_model.glmresults.t_test_pairwise#statsmodels.genmod.generalized_linear_model.GLMResults.t_test_pairwise "statsmodels.genmod.generalized_linear_model.GLMResults.t_test_pairwise")(term\_name[, method, alpha, …]) \| perform pairwise t\_test with multiple testing corrected p-values \| \| [`tvalues`](statsmodels.genmod.generalized_linear_model.glmresults.tvalues#statsmodels.genmod.generalized_linear_model.GLMResults.tvalues "statsmodels.genmod.generalized_linear_model.GLMResults.tvalues")() \| Return the t-statistic for a given parameter estimate. \| \| [`wald_test`](statsmodels.genmod.generalized_linear_model.glmresults.wald_test#statsmodels.genmod.generalized_linear_model.GLMResults.wald_test "statsmodels.genmod.generalized_linear_model.GLMResults.wald_test")(r\_matrix[, cov\_p, scale, invcov, …]) \| Compute a Wald-test for a joint linear hypothesis. \| \| [`wald_test_terms`](statsmodels.genmod.generalized_linear_model.glmresults.wald_test_terms#statsmodels.genmod.generalized_linear_model.GLMResults.wald_test_terms "statsmodels.genmod.generalized_linear_model.GLMResults.wald_test_terms")([skip\_single, …]) \| Compute a sequence of Wald tests for terms over multiple columns \| #### Attributes \| \| \| \| --- \| --- \| \| `use_t` \| \| statsmodels statsmodels.stats.proportion.proportions_chisquare_pairscontrol statsmodels.stats.proportion.proportions\_chisquare\_pairscontrol ================================================================= `statsmodels.stats.proportion.proportions_chisquare_pairscontrol(count, nobs, value=None, multitest_method='hs', alternative='two-sided')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/proportion.html#proportions_chisquare_pairscontrol) chisquare test of proportions for pairs of k samples compared to control Performs a chisquare test for proportions for pairwise comparisons with a control (Dunnet’s test). The control is assumed to be the first element of `count` and `nobs`. The alternative is two-sided, larger or smaller. \| Parameters: \| * count (integer or array\_like) – the number of successes in nobs trials. * nobs (integer) – the number of trials or observations. * prop (float, optional) – The probability of success under the null hypothesis, `0 <= prop <= 1`. The default value is `prop = 0.5` * multitest\_method (string) – This chooses the method for the multiple testing p-value correction, that is used as default in the results. It can be any method that is available in `multipletesting`. The default is Holm-Sidak ‘hs’. * alternative (string in ['two-sided', 'smaller', 'larger']) – alternative hypothesis, which can be two-sided or either one of the one-sided tests. \| \| Returns: \| result – The returned results instance has several statistics, such as p-values, attached, and additional methods for using a non-default `multitest_method`. \| \| Return type: \| AllPairsResults instance \| #### Notes Yates continuity correction is not available. `value` and `alternative` options are not yet implemented. statsmodels statsmodels.sandbox.regression.gmm.IV2SLS.whiten statsmodels.sandbox.regression.gmm.IV2SLS.whiten ================================================ `IV2SLS.whiten(X)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/regression/gmm.html#IV2SLS.whiten) statsmodels statsmodels.sandbox.distributions.extras.ACSkewT_gen.logcdf statsmodels.sandbox.distributions.extras.ACSkewT\_gen.logcdf ============================================================ `ACSkewT_gen.logcdf(x, args, kwds)` Log of the cumulative distribution function at x of the given RV. \| Parameters: \| x (array\_like) – quantiles * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| logcdf – Log of the cumulative distribution function evaluated at x \| \| Return type: \| array\_like \|	programming_docs
statsmodels statsmodels.sandbox.regression.gmm.LinearIVGMM.fitstart statsmodels.sandbox.regression.gmm.LinearIVGMM.fitstart ======================================================= `LinearIVGMM.fitstart()` statsmodels statsmodels.emplike.descriptive.DescStatMV.mv_test_mean statsmodels.emplike.descriptive.DescStatMV.mv\_test\_mean ========================================================= `DescStatMV.mv_test_mean(mu_array, return_weights=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/emplike/descriptive.html#DescStatMV.mv_test_mean) Returns -2 x log likelihood and the p-value for a multivariate hypothesis test of the mean \| Parameters: \| * mu\_array (1d array) – Hypothesized values for the mean. Must have same number of elements as columns in endog * return\_weights (bool) – If True, returns the weights that maximize the likelihood of mu\_array. Default is False. \| \| Returns: \| test\_results – The log-likelihood ratio and p-value for mu\_array \| \| Return type: \| tuple \| statsmodels statsmodels.discrete.discrete_model.GeneralizedPoissonResults.fittedvalues statsmodels.discrete.discrete\_model.GeneralizedPoissonResults.fittedvalues =========================================================================== `GeneralizedPoissonResults.fittedvalues()` statsmodels statsmodels.tsa.statespace.structural.UnobservedComponents.setup statsmodels.tsa.statespace.structural.UnobservedComponents.setup ================================================================ `UnobservedComponents.setup()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/structural.html#UnobservedComponents.setup) Setup the structural time series representation statsmodels statsmodels.genmod.generalized_linear_model.GLMResults.plot_added_variable statsmodels.genmod.generalized\_linear\_model.GLMResults.plot\_added\_variable ============================================================================== `GLMResults.plot_added_variable(focus_exog, resid_type=None, use_glm_weights=True, fit_kwargs=None, ax=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_linear_model.html#GLMResults.plot_added_variable) Create an added variable plot for a fitted regression model. \| Parameters: \| * focus\_exog (int or string) – The column index of exog, or a variable name, indicating the variable whose role in the regression is to be assessed. * resid\_type (string) – The type of residuals to use for the dependent variable. If None, uses `resid_deviance` for GLM/GEE and `resid` otherwise. * use\_glm\_weights (bool) – Only used if the model is a GLM or GEE. If True, the residuals for the focus predictor are computed using WLS, with the weights obtained from the IRLS calculations for fitting the GLM. If False, unweighted regression is used. * fit\_kwargs ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)"), optional) – Keyword arguments to be passed to fit when refitting the model. * ax (Axes instance) – Matplotlib Axes instance \| \| Returns: \| fig – A matplotlib figure instance. \| \| Return type: \| matplotlib Figure \| statsmodels statsmodels.regression.linear_model.yule_walker statsmodels.regression.linear\_model.yule\_walker ================================================= `statsmodels.regression.linear_model.yule_walker(X, order=1, method='unbiased', df=None, inv=False, demean=True)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#yule_walker) Estimate AR(p) parameters from a sequence X using Yule-Walker equation. Unbiased or maximum-likelihood estimator (mle) See, for example: <http://en.wikipedia.org/wiki/Autoregressive_moving_average_model> \| Parameters: \| * X (array-like) – 1d array * order (integer, optional) – The order of the autoregressive process. Default is 1. * method (string, optional) – Method can be ‘unbiased’ or ‘mle’ and this determines denominator in estimate of autocorrelation function (ACF) at lag k. If ‘mle’, the denominator is n=X.shape[0], if ‘unbiased’ the denominator is n-k. The default is unbiased. * df (integer, optional) – Specifies the degrees of freedom. If `df` is supplied, then it is assumed the X has `df` degrees of freedom rather than `n`. Default is None. * inv (bool) – If inv is True the inverse of R is also returned. Default is False. * demean (bool) – True, the mean is subtracted from `X` before estimation. \| \| Returns: \| * rho – The autoregressive coefficients * sigma – TODO \| #### Examples ``` >>> import statsmodels.api as sm >>> from statsmodels.datasets.sunspots import load >>> data = load() >>> rho, sigma = sm.regression.yule_walker(data.endog, ... order=4, method="mle") ``` ``` >>> rho array([ 1.28310031, -0.45240924, -0.20770299, 0.04794365]) >>> sigma 16.808022730464351 ``` statsmodels statsmodels.miscmodels.count.PoissonZiGMLE.fit statsmodels.miscmodels.count.PoissonZiGMLE.fit ============================================== `PoissonZiGMLE.fit(start_params=None, method='nm', maxiter=500, full_output=1, disp=1, callback=None, retall=0, *kwargs)` Fit the model using maximum likelihood. The rest of the docstring is from statsmodels.LikelihoodModel.fit statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.pvalues_dt statsmodels.tsa.vector\_ar.var\_model.VARResults.pvalues\_dt ============================================================ `VARResults.pvalues_dt()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARResults.pvalues_dt) statsmodels statsmodels.tsa.statespace.tools.unconstrain_stationary_multivariate statsmodels.tsa.statespace.tools.unconstrain\_stationary\_multivariate ====================================================================== `statsmodels.tsa.statespace.tools.unconstrain_stationary_multivariate(constrained, error_variance)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/tools.html#unconstrain_stationary_multivariate) Transform constrained parameters used in likelihood evaluation to unconstrained parameters used by the optimizer \| Parameters: \| constrained (array or list) – Constrained parameters of, e.g., an autoregressive or moving average component, to be transformed to arbitrary parameters used by the optimizer. If a list, should be a list of length `order`, where each element is an array sized `k_endog` x `k_endog`. If an array, should be the coefficient matrices horizontally concatenated and sized `k_endog` x `k_endog * order`. * error\_variance (array) – The variance / covariance matrix of the error term. Should be sized `k_endog` x `k_endog`. This is used as input in the algorithm even if is not transformed by it (when `transform_variance` is False). \| \| Returns: \| unconstrained – Unconstrained parameters used by the optimizer, to be transformed to stationary coefficients of, e.g., an autoregressive or moving average component. Will match the type of the passed `constrained` variable (so if a list was passed, a list will be returned). \| \| Return type: \| array \| #### Notes Uses the list representation internally, even if an array is passed. #### References \| \| \| \| --- \| --- \| \| [\] \| Ansley, Craig F., and Robert Kohn. 1986. “A Note on Reparameterizing a Vector Autoregressive Moving Average Model to Enforce Stationarity.” Journal of Statistical Computation and Simulation 24 (2): 99-106. \| statsmodels statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.fit_map statsmodels.genmod.bayes\_mixed\_glm.PoissonBayesMixedGLM.fit\_map ================================================================== `PoissonBayesMixedGLM.fit_map(method='BFGS', minim_opts=None)` Construct the Laplace approximation to the posterior distribution. \| Parameters: \| method (string) – Optimization method for finding the posterior mode. * minim\_opts (dict-like) – Options passed to scipy.minimize. \| \| Returns: \| \| \| Return type: \| BayesMixedGLMResults instance. \| statsmodels statsmodels.tsa.statespace.structural.UnobservedComponentsResults.plot_components statsmodels.tsa.statespace.structural.UnobservedComponentsResults.plot\_components ================================================================================== `UnobservedComponentsResults.plot_components(which=None, alpha=0.05, observed=True, level=True, trend=True, seasonal=True, freq_seasonal=True, cycle=True, autoregressive=True, legend_loc='upper right', fig=None, figsize=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/structural.html#UnobservedComponentsResults.plot_components) Plot the estimated components of the model. \| Parameters: \| * which ({'filtered', 'smoothed'}, or None, optional) – Type of state estimate to plot. Default is ‘smoothed’ if smoothed results are available otherwise ‘filtered’. * alpha (float, optional) – The confidence intervals for the components are (1 - alpha) % * level (boolean, optional) – Whether or not to plot the level component, if applicable. Default is True. * trend (boolean, optional) – Whether or not to plot the trend component, if applicable. Default is True. * seasonal (boolean, optional) – Whether or not to plot the seasonal component, if applicable. Default is True. * freq\_seasonal (boolean, optional) – Whether or not to plot the frequency domain seasonal component(s), if applicable. Default is True. * cycle (boolean, optional) – Whether or not to plot the cyclical component, if applicable. Default is True. * autoregressive (boolean, optional) – Whether or not to plot the autoregressive state, if applicable. Default is True. * fig (Matplotlib Figure instance, optional) – If given, subplots are created in this figure instead of in a new figure. Note that the grid will be created in the provided figure using `fig.add_subplot()`. * figsize (tuple, optional) – If a figure is created, this argument allows specifying a size. The tuple is (width, height). \| #### Notes If all options are included in the model and selected, this produces a 6x1 plot grid with the following plots (ordered top-to-bottom): 0. Observed series against predicted series 1. Level 2. Trend 3. Seasonal 4. Freq Seasonal 5. Cycle 6. Autoregressive Specific subplots will be removed if the component is not present in the estimated model or if the corresponding keywork argument is set to False. All plots contain (1 - `alpha`) % confidence intervals. statsmodels statsmodels.genmod.generalized_linear_model.GLM.hessian_factor statsmodels.genmod.generalized\_linear\_model.GLM.hessian\_factor ================================================================= `GLM.hessian_factor(params, scale=None, observed=True)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_linear_model.html#GLM.hessian_factor) Weights for calculating Hessian \| Parameters: \| * params (ndarray) – parameter at which Hessian is evaluated * scale (None or float) – If scale is None, then the default scale will be calculated. Default scale is defined by `self.scaletype` and set in fit. If scale is not None, then it is used as a fixed scale. * observed (bool) – If True, then the observed Hessian is returned. If false then the expected information matrix is returned. \| \| Returns: \| hessian\_factor – A 1d weight vector used in the calculation of the Hessian. The hessian is obtained by `(exog.T * hessian_factor).dot(exog)` \| \| Return type: \| ndarray, 1d \| statsmodels statsmodels.regression.quantile_regression.QuantRegResults.aic statsmodels.regression.quantile\_regression.QuantRegResults.aic =============================================================== `QuantRegResults.aic()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/quantile_regression.html#QuantRegResults.aic) statsmodels statsmodels.tsa.statespace.varmax.VARMAXResults.cov_params_robust statsmodels.tsa.statespace.varmax.VARMAXResults.cov\_params\_robust =================================================================== `VARMAXResults.cov_params_robust()` (array) The QMLE variance / covariance matrix. Alias for `cov_params_robust_oim` statsmodels statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.from_formula statsmodels.tsa.regime\_switching.markov\_autoregression.MarkovAutoregression.from\_formula =========================================================================================== `classmethod MarkovAutoregression.from_formula(formula, data, subset=None, drop_cols=None, args, kwargs)` Create a Model from a formula and dataframe. \| Parameters: \| formula (str or generic Formula object) – The formula specifying the model * data (array-like) – The data for the model. See Notes. * subset (array-like) – An array-like object of booleans, integers, or index values that indicate the subset of df to use in the model. Assumes df is a `pandas.DataFrame` * drop\_cols (array-like) – Columns to drop from the design matrix. Cannot be used to drop terms involving categoricals. * args (extra arguments) – These are passed to the model * kwargs (extra keyword arguments) – These are passed to the model with one exception. The `eval_env` keyword is passed to patsy. It can be either a [`patsy.EvalEnvironment`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.EvalEnvironment "(in patsy v0.5.0+dev)") object or an integer indicating the depth of the namespace to use. For example, the default `eval_env=0` uses the calling namespace. If you wish to use a “clean” environment set `eval_env=-1`. \| \| Returns: \| model \| \| Return type: \| Model instance \| #### Notes data must define \_\_getitem\_\_ with the keys in the formula terms args and kwargs are passed on to the model instantiation. E.g., a numpy structured or rec array, a dictionary, or a pandas DataFrame. statsmodels statsmodels.regression.mixed_linear_model.MixedLMResults.cov_params statsmodels.regression.mixed\_linear\_model.MixedLMResults.cov\_params ====================================================================== `MixedLMResults.cov_params(r_matrix=None, column=None, scale=None, cov_p=None, other=None)` Returns the variance/covariance matrix. The variance/covariance matrix can be of a linear contrast of the estimates of params or all params multiplied by scale which will usually be an estimate of sigma^2. Scale is assumed to be a scalar. \| Parameters: \| * r\_matrix (array-like) – Can be 1d, or 2d. Can be used alone or with other. * column (array-like, optional) – Must be used on its own. Can be 0d or 1d see below. * scale (float, optional) – Can be specified or not. Default is None, which means that the scale argument is taken from the model. * other (array-like, optional) – Can be used when r\_matrix is specified. \| \| Returns: \| cov – covariance matrix of the parameter estimates or of linear combination of parameter estimates. See Notes. \| \| Return type: \| ndarray \| #### Notes (The below are assumed to be in matrix notation.) If no argument is specified returns the covariance matrix of a model `(scale)(X.T X)^(-1)` If contrast is specified it pre and post-multiplies as follows `(scale) r_matrix (X.T X)^(-1) r_matrix.T` If contrast and other are specified returns `(scale) * r_matrix (X.T X)^(-1) other.T` If column is specified returns `(scale) * (X.T X)^(-1)[column,column]` if column is 0d OR `(scale) * (X.T X)^(-1)[column][:,column]` if column is 1d statsmodels statsmodels.regression.linear_model.GLS.hessian statsmodels.regression.linear\_model.GLS.hessian ================================================ `GLS.hessian(params)` The Hessian matrix of the model statsmodels statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother statsmodels.tsa.statespace.kalman\_smoother.KalmanSmoother ========================================================== `class statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother(k_endog, k_states, k_posdef=None, results_class=None, kalman_smoother_classes=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/kalman_smoother.html#KalmanSmoother) State space representation of a time series process, with Kalman filter and smoother. \| Parameters: \| k\_endog (array\_like or integer) – The observed time-series process $y$ if array like or the number of variables in the process if an integer. * k\_states (int) – The dimension of the unobserved state process. * k\_posdef (int, optional) – The dimension of a guaranteed positive definite covariance matrix describing the shocks in the measurement equation. Must be less than or equal to `k_states`. Default is `k_states`. * results\_class (class, optional) – Default results class to use to save filtering output. Default is `SmootherResults`. If specified, class must extend from `SmootherResults`. * *\\kwargs* – Keyword arguments may be used to provide default values for state space matrices, for Kalman filtering options, or for Kalman smoothing options. See `Representation` for more details. \| #### Methods \| \| \| \| --- \| --- \| \| [`bind`](statsmodels.tsa.statespace.kalman_smoother.kalmansmoother.bind#statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.bind "statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.bind")(endog) \| Bind data to the statespace representation \| \| [`filter`](statsmodels.tsa.statespace.kalman_smoother.kalmansmoother.filter#statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.filter "statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.filter")([filter\_method, inversion\_method, …]) \| Apply the Kalman filter to the statespace model. \| \| [`impulse_responses`](statsmodels.tsa.statespace.kalman_smoother.kalmansmoother.impulse_responses#statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.impulse_responses "statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.impulse_responses")([steps, impulse, …]) \| Impulse response function \| \| [`initialize_approximate_diffuse`](statsmodels.tsa.statespace.kalman_smoother.kalmansmoother.initialize_approximate_diffuse#statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.initialize_approximate_diffuse "statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.initialize_approximate_diffuse")([variance]) \| Initialize the statespace model with approximate diffuse values. \| \| [`initialize_known`](statsmodels.tsa.statespace.kalman_smoother.kalmansmoother.initialize_known#statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.initialize_known "statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.initialize_known")(initial\_state, …) \| Initialize the statespace model with known distribution for initial state. \| \| [`initialize_stationary`](statsmodels.tsa.statespace.kalman_smoother.kalmansmoother.initialize_stationary#statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.initialize_stationary "statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.initialize_stationary")() \| Initialize the statespace model as stationary. \| \| [`loglike`](statsmodels.tsa.statespace.kalman_smoother.kalmansmoother.loglike#statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.loglike "statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.loglike")(\\kwargs) \| Calculate the loglikelihood associated with the statespace model. \| \| [`loglikeobs`](statsmodels.tsa.statespace.kalman_smoother.kalmansmoother.loglikeobs#statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.loglikeobs "statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.loglikeobs")(\\kwargs) \| Calculate the loglikelihood for each observation associated with the statespace model. \| \| [`set_conserve_memory`](statsmodels.tsa.statespace.kalman_smoother.kalmansmoother.set_conserve_memory#statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.set_conserve_memory "statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.set_conserve_memory")([conserve\_memory]) \| Set the memory conservation method \| \| [`set_filter_method`](statsmodels.tsa.statespace.kalman_smoother.kalmansmoother.set_filter_method#statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.set_filter_method "statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.set_filter_method")([filter\_method]) \| Set the filtering method \| \| [`set_filter_timing`](statsmodels.tsa.statespace.kalman_smoother.kalmansmoother.set_filter_timing#statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.set_filter_timing "statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.set_filter_timing")([alternate\_timing]) \| Set the filter timing convention \| \| [`set_inversion_method`](statsmodels.tsa.statespace.kalman_smoother.kalmansmoother.set_inversion_method#statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.set_inversion_method "statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.set_inversion_method")([inversion\_method]) \| Set the inversion method \| \| [`set_smooth_method`](statsmodels.tsa.statespace.kalman_smoother.kalmansmoother.set_smooth_method#statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.set_smooth_method "statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.set_smooth_method")([smooth\_method]) \| Set the smoothing method \| \| [`set_smoother_output`](statsmodels.tsa.statespace.kalman_smoother.kalmansmoother.set_smoother_output#statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.set_smoother_output "statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.set_smoother_output")([smoother\_output]) \| Set the smoother output \| \| [`set_stability_method`](statsmodels.tsa.statespace.kalman_smoother.kalmansmoother.set_stability_method#statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.set_stability_method "statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.set_stability_method")([stability\_method]) \| Set the numerical stability method \| \| [`simulate`](statsmodels.tsa.statespace.kalman_smoother.kalmansmoother.simulate#statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.simulate "statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.simulate")(nsimulations[, measurement\_shocks, …]) \| Simulate a new time series following the state space model \| \| [`smooth`](statsmodels.tsa.statespace.kalman_smoother.kalmansmoother.smooth#statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.smooth "statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.smooth")([smoother\_output, smooth\_method, …]) \| Apply the Kalman smoother to the statespace model. \| #### Attributes \| \| \| \| --- \| --- \| \| `conserve_memory` \| \| \| `design` \| \| \| `dtype` \| (dtype) Datatype of currently active representation matrices \| \| `endog` \| \| \| `filter_augmented` \| \| \| `filter_collapsed` \| \| \| `filter_conventional` \| \| \| `filter_exact_initial` \| \| \| `filter_extended` \| \| \| `filter_method` \| \| \| `filter_methods` \| \| \| `filter_square_root` \| \| \| `filter_timing` \| \| \| `filter_univariate` \| \| \| `filter_unscented` \| \| \| `inversion_method` \| \| \| `inversion_methods` \| \| \| `invert_cholesky` \| \| \| `invert_lu` \| \| \| `invert_univariate` \| \| \| `memory_conserve` \| \| \| `memory_no_filtered` \| \| \| `memory_no_forecast` \| \| \| `memory_no_gain` \| \| \| `memory_no_likelihood` \| \| \| `memory_no_predicted` \| \| \| `memory_no_smoothing` \| \| \| `memory_no_std_forecast` \| \| \| `memory_options` \| \| \| `memory_store_all` \| \| \| `obs` \| (array) Observation vector – $y~(k\\_endog \times nobs)$ \| \| `obs_cov` \| \| \| `obs_intercept` \| \| \| `prefix` \| (str) BLAS prefix of currently active representation matrices \| \| `selection` \| \| \| `smooth_alternative` \| (bool) Flag for alternative (modified Bryson-Frazier) smoothing. \| \| `smooth_classical` \| (bool) Flag for classical (see e.g. \| \| `smooth_conventional` \| (bool) Flag for conventional (Durbin and Koopman, 2012) Kalman smoothing. \| \| `smooth_method` \| \| \| `smooth_methods` \| \| \| `smooth_univariate` \| (bool) Flag for univariate smoothing (uses modified Bryson-Frazier timing). \| \| `smoother_all` \| \| \| `smoother_disturbance` \| \| \| `smoother_disturbance_cov` \| \| \| `smoother_output` \| \| \| `smoother_outputs` \| \| \| `smoother_state` \| \| \| `smoother_state_autocov` \| \| \| `smoother_state_cov` \| \| \| `solve_cholesky` \| \| \| `solve_lu` \| \| \| `stability_force_symmetry` \| \| \| `stability_method` \| \| \| `stability_methods` \| \| \| `state_cov` \| \| \| `state_intercept` \| \| \| `time_invariant` \| (bool) Whether or not currently active representation matrices are time-invariant \| \| `timing_init_filtered` \| \| \| `timing_init_predicted` \| \| \| `timing_options` \| \| \| `transition` \| \|	programming_docs
statsmodels statsmodels.iolib.table.csv2st statsmodels.iolib.table.csv2st ============================== `statsmodels.iolib.table.csv2st(csvfile, headers=False, stubs=False, title=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/iolib/table.html#csv2st) Return SimpleTable instance, created from the data in `csvfile`, which is in comma separated values format. The first row may contain headers: set headers=True. The first column may contain stubs: set stubs=True. Can also supply headers and stubs as tuples of strings. statsmodels statsmodels.discrete.discrete_model.CountResults.summary2 statsmodels.discrete.discrete\_model.CountResults.summary2 ========================================================== `CountResults.summary2(yname=None, xname=None, title=None, alpha=0.05, float_format='%.4f')` Experimental function to summarize regression results \| Parameters: \| * xname (List of strings of length equal to the number of parameters) – Names of the independent variables (optional) * yname (string) – Name of the dependent variable (optional) * title (string, optional) – Title for the top table. If not None, then this replaces the default title * alpha (float) – significance level for the confidence intervals * float\_format (string) – print format for floats in parameters summary \| \| Returns: \| smry – this holds the summary tables and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary.Summary`](statsmodels.iolib.summary.summary#statsmodels.iolib.summary.Summary "statsmodels.iolib.summary.Summary") class to hold summary results statsmodels statsmodels.stats.contingency_tables.SquareTable.local_oddsratios statsmodels.stats.contingency\_tables.SquareTable.local\_oddsratios =================================================================== `SquareTable.local_oddsratios()` statsmodels statsmodels.tsa.vector_ar.irf.IRAnalysis.err_band_sz3 statsmodels.tsa.vector\_ar.irf.IRAnalysis.err\_band\_sz3 ======================================================== `IRAnalysis.err_band_sz3(orth=False, svar=False, repl=1000, signif=0.05, seed=None, burn=100, component=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/irf.html#IRAnalysis.err_band_sz3) IRF Sims-Zha error band method 3. Does not assume symmetric error bands around mean. \| Parameters: \| * orth (bool, default False) – Compute orthogonalized impulse responses * repl (int, default 1000) – Number of MC replications * signif (float (0 < signif < 1)) – Significance level for error bars, defaults to 95% CI * seed (int, default None) – np.random seed * burn (int, default 100) – Number of initial simulated obs to discard * component (vector length neqs, default to largest for each) – Index of column of eigenvector/value to use for each error band Note: period of impulse (t=0) is not included when computing principle component \| #### References Sims, Christopher A., and Tao Zha. 1999. “Error Bands for Impulse Response”. Econometrica 67: 1113-1155. statsmodels statsmodels.discrete.discrete_model.NegativeBinomialP statsmodels.discrete.discrete\_model.NegativeBinomialP ====================================================== `class statsmodels.discrete.discrete_model.NegativeBinomialP(endog, exog, p=2, offset=None, exposure=None, missing='none', *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#NegativeBinomialP) Generalized Negative Binomial (NB-P) model for count data \| Parameters: \| endog (array-like) – 1-d endogenous response variable. The dependent variable. * exog (array-like) – A nobs x k array where `nobs` is the number of observations and `k` is the number of regressors. An intercept is not included by default and should be added by the user. See `statsmodels.tools.add_constant`. * p (scalar) – P denotes parameterizations for NB regression. p=1 for NB-1 and p=2 for NB-2. Default is p=2. * offset (array\_like) – Offset is added to the linear prediction with coefficient equal to 1. * exposure (array\_like) – Log(exposure) is added to the linear prediction with coefficient equal to 1. * missing (str) – Available options are ‘none’, ‘drop’, and ‘raise’. If ‘none’, no nan checking is done. If ‘drop’, any observations with nans are dropped. If ‘raise’, an error is raised. Default is ‘none.’ \| `endog` array – A reference to the endogenous response variable `exog` array – A reference to the exogenous design. `p` scalar – P denotes parameterizations for NB-P regression. p=1 for NB-1 and p=2 for NB-2. Default is p=1. #### Methods \| \| \| \| --- \| --- \| \| [`cdf`](statsmodels.discrete.discrete_model.negativebinomialp.cdf#statsmodels.discrete.discrete_model.NegativeBinomialP.cdf "statsmodels.discrete.discrete_model.NegativeBinomialP.cdf")(X) \| The cumulative distribution function of the model. \| \| [`convert_params`](statsmodels.discrete.discrete_model.negativebinomialp.convert_params#statsmodels.discrete.discrete_model.NegativeBinomialP.convert_params "statsmodels.discrete.discrete_model.NegativeBinomialP.convert_params")(params, mu) \| \| \| [`cov_params_func_l1`](statsmodels.discrete.discrete_model.negativebinomialp.cov_params_func_l1#statsmodels.discrete.discrete_model.NegativeBinomialP.cov_params_func_l1 "statsmodels.discrete.discrete_model.NegativeBinomialP.cov_params_func_l1")(likelihood\_model, xopt, …) \| Computes cov\_params on a reduced parameter space corresponding to the nonzero parameters resulting from the l1 regularized fit. \| \| [`fit`](statsmodels.discrete.discrete_model.negativebinomialp.fit#statsmodels.discrete.discrete_model.NegativeBinomialP.fit "statsmodels.discrete.discrete_model.NegativeBinomialP.fit")([start\_params, method, maxiter, …]) \| \| param use\_transparams: \| \| \| This parameter enable internal transformation to impose non-negativity. \| \| \| [`fit_regularized`](statsmodels.discrete.discrete_model.negativebinomialp.fit_regularized#statsmodels.discrete.discrete_model.NegativeBinomialP.fit_regularized "statsmodels.discrete.discrete_model.NegativeBinomialP.fit_regularized")([start\_params, method, …]) \| Fit the model using a regularized maximum likelihood. \| \| [`from_formula`](statsmodels.discrete.discrete_model.negativebinomialp.from_formula#statsmodels.discrete.discrete_model.NegativeBinomialP.from_formula "statsmodels.discrete.discrete_model.NegativeBinomialP.from_formula")(formula, data[, subset, drop\_cols]) \| Create a Model from a formula and dataframe. \| \| [`hessian`](statsmodels.discrete.discrete_model.negativebinomialp.hessian#statsmodels.discrete.discrete_model.NegativeBinomialP.hessian "statsmodels.discrete.discrete_model.NegativeBinomialP.hessian")(params) \| Generalized Negative Binomial (NB-P) model hessian maxtrix of the log-likelihood \| \| [`information`](statsmodels.discrete.discrete_model.negativebinomialp.information#statsmodels.discrete.discrete_model.NegativeBinomialP.information "statsmodels.discrete.discrete_model.NegativeBinomialP.information")(params) \| Fisher information matrix of model \| \| [`initialize`](statsmodels.discrete.discrete_model.negativebinomialp.initialize#statsmodels.discrete.discrete_model.NegativeBinomialP.initialize "statsmodels.discrete.discrete_model.NegativeBinomialP.initialize")() \| Initialize is called by statsmodels.model.LikelihoodModel.\_\_init\_\_ and should contain any preprocessing that needs to be done for a model. \| \| [`loglike`](statsmodels.discrete.discrete_model.negativebinomialp.loglike#statsmodels.discrete.discrete_model.NegativeBinomialP.loglike "statsmodels.discrete.discrete_model.NegativeBinomialP.loglike")(params) \| Loglikelihood of Generalized Negative Binomial (NB-P) model \| \| [`loglikeobs`](statsmodels.discrete.discrete_model.negativebinomialp.loglikeobs#statsmodels.discrete.discrete_model.NegativeBinomialP.loglikeobs "statsmodels.discrete.discrete_model.NegativeBinomialP.loglikeobs")(params) \| Loglikelihood for observations of Generalized Negative Binomial (NB-P) model \| \| [`pdf`](statsmodels.discrete.discrete_model.negativebinomialp.pdf#statsmodels.discrete.discrete_model.NegativeBinomialP.pdf "statsmodels.discrete.discrete_model.NegativeBinomialP.pdf")(X) \| The probability density (mass) function of the model. \| \| [`predict`](statsmodels.discrete.discrete_model.negativebinomialp.predict#statsmodels.discrete.discrete_model.NegativeBinomialP.predict "statsmodels.discrete.discrete_model.NegativeBinomialP.predict")(params[, exog, exposure, offset, which]) \| Predict response variable of a model given exogenous variables. \| \| [`score`](statsmodels.discrete.discrete_model.negativebinomialp.score#statsmodels.discrete.discrete_model.NegativeBinomialP.score "statsmodels.discrete.discrete_model.NegativeBinomialP.score")(params) \| Generalized Negative Binomial (NB-P) model score (gradient) vector of the log-likelihood \| \| [`score_obs`](statsmodels.discrete.discrete_model.negativebinomialp.score_obs#statsmodels.discrete.discrete_model.NegativeBinomialP.score_obs "statsmodels.discrete.discrete_model.NegativeBinomialP.score_obs")(params) \| Generalized Negative Binomial (NB-P) model score (gradient) vector of the log-likelihood for each observations. \| #### Attributes \| \| \| \| --- \| --- \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| Names of exogenous variables \| statsmodels statsmodels.stats.contingency_tables.Table2x2.resid_pearson statsmodels.stats.contingency\_tables.Table2x2.resid\_pearson ============================================================= `Table2x2.resid_pearson()` statsmodels statsmodels.multivariate.manova.MANOVA.fit statsmodels.multivariate.manova.MANOVA.fit ========================================== `MANOVA.fit()` Fit a model to data. statsmodels statsmodels.discrete.discrete_model.NegativeBinomialResults.lnalpha statsmodels.discrete.discrete\_model.NegativeBinomialResults.lnalpha ==================================================================== `NegativeBinomialResults.lnalpha()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#NegativeBinomialResults.lnalpha) statsmodels statsmodels.discrete.count_model.ZeroInflatedPoisson.cov_params_func_l1 statsmodels.discrete.count\_model.ZeroInflatedPoisson.cov\_params\_func\_l1 =========================================================================== `ZeroInflatedPoisson.cov_params_func_l1(likelihood_model, xopt, retvals)` Computes cov\_params on a reduced parameter space corresponding to the nonzero parameters resulting from the l1 regularized fit. Returns a full cov\_params matrix, with entries corresponding to zero’d values set to np.nan. statsmodels statsmodels.iolib.summary2.Summary.add_df statsmodels.iolib.summary2.Summary.add\_df ========================================== `Summary.add_df(df, index=True, header=True, float_format='%.4f', align='r')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/iolib/summary2.html#Summary.add_df) Add the contents of a DataFrame to summary table \| Parameters: \| * df (DataFrame) – * header (bool) – Reproduce the DataFrame column labels in summary table * index (bool) – Reproduce the DataFrame row labels in summary table * float\_format (string) – Formatting to float data columns * align (string) – Data alignment (l/c/r) \| statsmodels statsmodels.regression.linear_model.OLSResults.HC3_se statsmodels.regression.linear\_model.OLSResults.HC3\_se ======================================================= `OLSResults.HC3_se()` See statsmodels.RegressionResults statsmodels statsmodels.discrete.discrete_model.CountResults.llf statsmodels.discrete.discrete\_model.CountResults.llf ===================================================== `CountResults.llf()` statsmodels statsmodels.stats.descriptivestats.sign_test statsmodels.stats.descriptivestats.sign\_test ============================================= `statsmodels.stats.descriptivestats.sign_test(samp, mu0=0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/descriptivestats.html#sign_test) Signs test. \| Parameters: \| * samp (array-like) – 1d array. The sample for which you want to perform the signs test. * mu0 (float) – See Notes for the definition of the sign test. mu0 is 0 by default, but it is common to set it to the median. \| \| Returns: \| \| \| Return type: \| M, p-value \| #### Notes The signs test returns M = (N(+) - N(-))/2 where N(+) is the number of values above `mu0`, N(-) is the number of values below. Values equal to `mu0` are discarded. The p-value for M is calculated using the binomial distrubution and can be intrepreted the same as for a t-test. The test-statistic is distributed Binom(min(N(+), N(-)), n\_trials, .5) where n\_trials equals N(+) + N(-). See also `scipy.stats.wilcoxon` statsmodels statsmodels.discrete.discrete_model.CountResults statsmodels.discrete.discrete\_model.CountResults ================================================= `class statsmodels.discrete.discrete_model.CountResults(model, mlefit, cov_type='nonrobust', cov_kwds=None, use_t=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#CountResults) A results class for count data \| Parameters: \| * model (A DiscreteModel instance) – * params (array-like) – The parameters of a fitted model. * hessian (array-like) – The hessian of the fitted model. * scale (float) – A scale parameter for the covariance matrix. \| \| Returns: \| * \Attributes\** * aic (float) – Akaike information criterion. `-2(llf - p)` where `p` is the number of regressors including the intercept. bic (float) – Bayesian information criterion. `-2llf + ln(nobs)p` where `p` is the number of regressors including the intercept. * bse (array) – The standard errors of the coefficients. * df\_resid (float) – See model definition. * df\_model (float) – See model definition. * fitted\_values (array) – Linear predictor XB. * llf (float) – Value of the loglikelihood * llnull (float) – Value of the constant-only loglikelihood * llr (float) – Likelihood ratio chi-squared statistic; `-2(llnull - llf)` llr\_pvalue (float) – The chi-squared probability of getting a log-likelihood ratio statistic greater than llr. llr has a chi-squared distribution with degrees of freedom `df_model`. * prsquared (float) – McFadden’s pseudo-R-squared. `1 - (llf / llnull)` \| #### Methods \| \| \| \| --- \| --- \| \| [`aic`](statsmodels.discrete.discrete_model.countresults.aic#statsmodels.discrete.discrete_model.CountResults.aic "statsmodels.discrete.discrete_model.CountResults.aic")() \| \| \| [`bic`](statsmodels.discrete.discrete_model.countresults.bic#statsmodels.discrete.discrete_model.CountResults.bic "statsmodels.discrete.discrete_model.CountResults.bic")() \| \| \| [`bse`](statsmodels.discrete.discrete_model.countresults.bse#statsmodels.discrete.discrete_model.CountResults.bse "statsmodels.discrete.discrete_model.CountResults.bse")() \| \| \| [`conf_int`](statsmodels.discrete.discrete_model.countresults.conf_int#statsmodels.discrete.discrete_model.CountResults.conf_int "statsmodels.discrete.discrete_model.CountResults.conf_int")([alpha, cols, method]) \| Returns the confidence interval of the fitted parameters. \| \| [`cov_params`](statsmodels.discrete.discrete_model.countresults.cov_params#statsmodels.discrete.discrete_model.CountResults.cov_params "statsmodels.discrete.discrete_model.CountResults.cov_params")([r\_matrix, column, scale, cov\_p, …]) \| Returns the variance/covariance matrix. \| \| [`f_test`](statsmodels.discrete.discrete_model.countresults.f_test#statsmodels.discrete.discrete_model.CountResults.f_test "statsmodels.discrete.discrete_model.CountResults.f_test")(r\_matrix[, cov\_p, scale, invcov]) \| Compute the F-test for a joint linear hypothesis. \| \| [`fittedvalues`](statsmodels.discrete.discrete_model.countresults.fittedvalues#statsmodels.discrete.discrete_model.CountResults.fittedvalues "statsmodels.discrete.discrete_model.CountResults.fittedvalues")() \| \| \| [`get_margeff`](statsmodels.discrete.discrete_model.countresults.get_margeff#statsmodels.discrete.discrete_model.CountResults.get_margeff "statsmodels.discrete.discrete_model.CountResults.get_margeff")([at, method, atexog, dummy, count]) \| Get marginal effects of the fitted model. \| \| [`initialize`](statsmodels.discrete.discrete_model.countresults.initialize#statsmodels.discrete.discrete_model.CountResults.initialize "statsmodels.discrete.discrete_model.CountResults.initialize")(model, params, \\kwd) \| \| \| [`llf`](statsmodels.discrete.discrete_model.countresults.llf#statsmodels.discrete.discrete_model.CountResults.llf "statsmodels.discrete.discrete_model.CountResults.llf")() \| \| \| [`llnull`](statsmodels.discrete.discrete_model.countresults.llnull#statsmodels.discrete.discrete_model.CountResults.llnull "statsmodels.discrete.discrete_model.CountResults.llnull")() \| \| \| [`llr`](statsmodels.discrete.discrete_model.countresults.llr#statsmodels.discrete.discrete_model.CountResults.llr "statsmodels.discrete.discrete_model.CountResults.llr")() \| \| \| [`llr_pvalue`](statsmodels.discrete.discrete_model.countresults.llr_pvalue#statsmodels.discrete.discrete_model.CountResults.llr_pvalue "statsmodels.discrete.discrete_model.CountResults.llr_pvalue")() \| \| \| [`load`](statsmodels.discrete.discrete_model.countresults.load#statsmodels.discrete.discrete_model.CountResults.load "statsmodels.discrete.discrete_model.CountResults.load")(fname) \| load a pickle, (class method) \| \| [`normalized_cov_params`](statsmodels.discrete.discrete_model.countresults.normalized_cov_params#statsmodels.discrete.discrete_model.CountResults.normalized_cov_params "statsmodels.discrete.discrete_model.CountResults.normalized_cov_params")() \| \| \| [`predict`](statsmodels.discrete.discrete_model.countresults.predict#statsmodels.discrete.discrete_model.CountResults.predict "statsmodels.discrete.discrete_model.CountResults.predict")([exog, transform]) \| Call self.model.predict with self.params as the first argument. \| \| [`prsquared`](statsmodels.discrete.discrete_model.countresults.prsquared#statsmodels.discrete.discrete_model.CountResults.prsquared "statsmodels.discrete.discrete_model.CountResults.prsquared")() \| \| \| [`pvalues`](statsmodels.discrete.discrete_model.countresults.pvalues#statsmodels.discrete.discrete_model.CountResults.pvalues "statsmodels.discrete.discrete_model.CountResults.pvalues")() \| \| \| [`remove_data`](statsmodels.discrete.discrete_model.countresults.remove_data#statsmodels.discrete.discrete_model.CountResults.remove_data "statsmodels.discrete.discrete_model.CountResults.remove_data")() \| remove data arrays, all nobs arrays from result and model \| \| [`resid`](statsmodels.discrete.discrete_model.countresults.resid#statsmodels.discrete.discrete_model.CountResults.resid "statsmodels.discrete.discrete_model.CountResults.resid")() \| Residuals \| \| [`save`](statsmodels.discrete.discrete_model.countresults.save#statsmodels.discrete.discrete_model.CountResults.save "statsmodels.discrete.discrete_model.CountResults.save")(fname[, remove\_data]) \| save a pickle of this instance \| \| [`set_null_options`](statsmodels.discrete.discrete_model.countresults.set_null_options#statsmodels.discrete.discrete_model.CountResults.set_null_options "statsmodels.discrete.discrete_model.CountResults.set_null_options")([llnull, attach\_results]) \| set fit options for Null (constant-only) model \| \| [`summary`](statsmodels.discrete.discrete_model.countresults.summary#statsmodels.discrete.discrete_model.CountResults.summary "statsmodels.discrete.discrete_model.CountResults.summary")([yname, xname, title, alpha, yname\_list]) \| Summarize the Regression Results \| \| [`summary2`](statsmodels.discrete.discrete_model.countresults.summary2#statsmodels.discrete.discrete_model.CountResults.summary2 "statsmodels.discrete.discrete_model.CountResults.summary2")([yname, xname, title, alpha, …]) \| Experimental function to summarize regression results \| \| [`t_test`](statsmodels.discrete.discrete_model.countresults.t_test#statsmodels.discrete.discrete_model.CountResults.t_test "statsmodels.discrete.discrete_model.CountResults.t_test")(r\_matrix[, cov\_p, scale, use\_t]) \| Compute a t-test for a each linear hypothesis of the form Rb = q \| \| [`t_test_pairwise`](statsmodels.discrete.discrete_model.countresults.t_test_pairwise#statsmodels.discrete.discrete_model.CountResults.t_test_pairwise "statsmodels.discrete.discrete_model.CountResults.t_test_pairwise")(term\_name[, method, alpha, …]) \| perform pairwise t\_test with multiple testing corrected p-values \| \| [`tvalues`](statsmodels.discrete.discrete_model.countresults.tvalues#statsmodels.discrete.discrete_model.CountResults.tvalues "statsmodels.discrete.discrete_model.CountResults.tvalues")() \| Return the t-statistic for a given parameter estimate. \| \| [`wald_test`](statsmodels.discrete.discrete_model.countresults.wald_test#statsmodels.discrete.discrete_model.CountResults.wald_test "statsmodels.discrete.discrete_model.CountResults.wald_test")(r\_matrix[, cov\_p, scale, invcov, …]) \| Compute a Wald-test for a joint linear hypothesis. \| \| [`wald_test_terms`](statsmodels.discrete.discrete_model.countresults.wald_test_terms#statsmodels.discrete.discrete_model.CountResults.wald_test_terms "statsmodels.discrete.discrete_model.CountResults.wald_test_terms")([skip\_single, …]) \| Compute a sequence of Wald tests for terms over multiple columns \| #### Attributes \| \| \| \| --- \| --- \| \| `use_t` \| \|	programming_docs
statsmodels statsmodels.tsa.statespace.varmax.VARMAX.initialize statsmodels.tsa.statespace.varmax.VARMAX.initialize =================================================== `VARMAX.initialize()` Initialize (possibly re-initialize) a Model instance. For instance, the design matrix of a linear model may change and some things must be recomputed. statsmodels statsmodels.regression.mixed_linear_model.MixedLM.from_formula statsmodels.regression.mixed\_linear\_model.MixedLM.from\_formula ================================================================= `classmethod MixedLM.from_formula(formula, data, re_formula=None, vc_formula=None, subset=None, use_sparse=False, missing='none', args, kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/mixed_linear_model.html#MixedLM.from_formula) Create a Model from a formula and dataframe. \| Parameters: \| formula (str or generic Formula object) – The formula specifying the model * data (array-like) – The data for the model. See Notes. * re\_formula (string) – A one-sided formula defining the variance structure of the model. The default gives a random intercept for each group. * vc\_formula (dict-like) – Formulas describing variance components. `vc_formula[vc]` is the formula for the component with variance parameter named `vc`. The formula is processed into a matrix, and the columns of this matrix are linearly combined with independent random coefficients having mean zero and a common variance. * subset (array-like) – An array-like object of booleans, integers, or index values that indicate the subset of df to use in the model. Assumes df is a `pandas.DataFrame` * missing (string) – Either ‘none’ or ‘drop’ * args (extra arguments) – These are passed to the model * kwargs (extra keyword arguments) – These are passed to the model with one exception. The `eval_env` keyword is passed to patsy. It can be either a [`patsy.EvalEnvironment`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.EvalEnvironment "(in patsy v0.5.0+dev)") object or an integer indicating the depth of the namespace to use. For example, the default `eval_env=0` uses the calling namespace. If you wish to use a “clean” environment set `eval_env=-1`. \| \| Returns: \| model \| \| Return type: \| Model instance \| #### Notes `data` must define \_\_getitem\_\_ with the keys in the formula terms args and kwargs are passed on to the model instantiation. E.g., a numpy structured or rec array, a dictionary, or a pandas DataFrame. If the variance component is intended to produce random intercepts for disjoint subsets of a group, specified by string labels or a categorical data value, always use ‘0 +’ in the formula so that no overall intercept is included. If the variance components specify random slopes and you do not also want a random group-level intercept in the model, then use ‘0 +’ in the formula to exclude the intercept. The variance components formulas are processed separately for each group. If a variable is categorical the results will not be affected by whether the group labels are distinct or re-used over the top-level groups. #### Examples Suppose we have data from an educational study with students nested in classrooms nested in schools. The students take a test, and we want to relate the test scores to the students’ ages, while accounting for the effects of classrooms and schools. The school will be the top-level group, and the classroom is a nested group that is specified as a variance component. Note that the schools may have different number of classrooms, and the classroom labels may (but need not be) different across the schools. ``` >>> vc = {'classroom': '0 + C(classroom)'} >>> MixedLM.from_formula('test_score ~ age', vc_formula=vc, re_formula='1', groups='school', data=data) ``` Now suppose we also have a previous test score called ‘pretest’. If we want the relationship between pretest scores and the current test to vary by classroom, we can specify a random slope for the pretest score ``` >>> vc = {'classroom': '0 + C(classroom)', 'pretest': '0 + pretest'} >>> MixedLM.from_formula('test_score ~ age + pretest', vc_formula=vc, re_formula='1', groups='school', data=data) ``` The following model is almost equivalent to the previous one, but here the classroom random intercept and pretest slope may be correlated. ``` >>> vc = {'classroom': '0 + C(classroom)'} >>> MixedLM.from_formula('test_score ~ age + pretest', vc_formula=vc, re_formula='1 + pretest', groups='school', data=data) ``` statsmodels statsmodels.tsa.arima_process.arma2ar statsmodels.tsa.arima\_process.arma2ar ====================================== `statsmodels.tsa.arima_process.arma2ar(ar, ma, lags=100, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_process.html#arma2ar) Get the AR representation of an ARMA process \| Parameters: \| ar (array\_like, 1d) – auto regressive lag polynomial * ma (array\_like, 1d) – moving average lag polynomial * lags (int) – number of coefficients to calculate \| \| Returns: \| ar – coefficients of AR lag polynomial with nobs elements \| \| Return type: \| array, 1d \| #### Notes Equivalent to `arma_impulse_response(ma, ar, leads=100)` #### Examples statsmodels statsmodels.sandbox.distributions.extras.ACSkewT_gen.expect statsmodels.sandbox.distributions.extras.ACSkewT\_gen.expect ============================================================ `ACSkewT_gen.expect(func=None, args=(), loc=0, scale=1, lb=None, ub=None, conditional=False, *kwds)` Calculate expected value of a function with respect to the distribution. The expected value of a function `f(x)` with respect to a distribution `dist` is defined as: ``` ubound E[x] = Integral(f(x) dist.pdf(x)) lbound ``` \| Parameters: \| * func (callable, optional) – Function for which integral is calculated. Takes only one argument. The default is the identity mapping f(x) = x. * args (tuple, optional) – Shape parameters of the distribution. * loc (float, optional) – Location parameter (default=0). * scale (float, optional) – Scale parameter (default=1). * ub (lb,) – Lower and upper bound for integration. Default is set to the support of the distribution. * conditional (bool, optional) – If True, the integral is corrected by the conditional probability of the integration interval. The return value is the expectation of the function, conditional on being in the given interval. Default is False. * keyword arguments are passed to the integration routine. (Additional) – \| \| Returns: \| expect – The calculated expected value. \| \| Return type: \| float \| #### Notes The integration behavior of this function is inherited from `integrate.quad`. statsmodels statsmodels.tsa.arima_model.ARIMA.loglike statsmodels.tsa.arima\_model.ARIMA.loglike ========================================== `ARIMA.loglike(params, set_sigma2=True)` Compute the log-likelihood for ARMA(p,q) model #### Notes Likelihood used depends on the method set in fit statsmodels statsmodels.tsa.vector_ar.vecm.VECMResults.predict statsmodels.tsa.vector\_ar.vecm.VECMResults.predict =================================================== `VECMResults.predict(steps=5, alpha=None, exog_fc=None, exog_coint_fc=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/vecm.html#VECMResults.predict) Calculate future values of the time series. \| Parameters: \| * steps (int) – Prediction horizon. * alpha (float, 0 < `alpha` < 1 or None) – If None, compute point forecast only. If float, compute confidence intervals too. In this case the argument stands for the confidence level. * exog (ndarray (steps x self.exog.shape[1])) – If self.exog is not None, then information about the future values of exog have to be passed via this parameter. The ndarray may be larger in it’s first dimension. In this case only the first steps rows will be considered. \| \| Returns: \| In case of a point forecast: each row of the returned ndarray represents the forecast of the neqs variables for a specific period. The first row (index [0]) is the forecast for the next period, the last row (index [steps-1]) is the steps-periods-ahead- forecast. \| \| Return type: \| forecast - ndarray (steps x neqs) or three ndarrays \| statsmodels statsmodels.duration.survfunc.SurvfuncRight.quantile statsmodels.duration.survfunc.SurvfuncRight.quantile ==================================================== `SurvfuncRight.quantile(p)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/duration/survfunc.html#SurvfuncRight.quantile) Estimated quantile of a survival distribution. \| Parameters: \| * p (float) – The probability point at which the quantile is determined. * the estimated quantile. (Returns) – \| statsmodels statsmodels.stats.contingency_tables.SquareTable.symmetry statsmodels.stats.contingency\_tables.SquareTable.symmetry ========================================================== `SquareTable.symmetry(method='bowker')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/contingency_tables.html#SquareTable.symmetry) Test for symmetry of a joint distribution. This procedure tests the null hypothesis that the joint distribution is symmetric around the main diagonal, that is \[\] p\_{i, j} = p\_{j, i} for all i, j \| Returns: \| * A bunch with attributes * statistic (float) – chisquare test statistic * p-value (float) – p-value of the test statistic based on chisquare distribution * df (int) – degrees of freedom of the chisquare distribution \| #### Notes The implementation is based on the SAS documentation. R includes it in `mcnemar.test` if the table is not 2 by 2. However a more direct generalization of the McNemar test to larger tables is provided by the homogeneity test (TableSymmetry.homogeneity). The p-value is based on the chi-square distribution which requires that the sample size is not very small to be a good approximation of the true distribution. For 2x2 contingency tables the exact distribution can be obtained with `mcnemar` See also [`mcnemar`](statsmodels.stats.contingency_tables.mcnemar#statsmodels.stats.contingency_tables.mcnemar "statsmodels.stats.contingency_tables.mcnemar"), [`homogeneity`](statsmodels.stats.contingency_tables.squaretable.homogeneity#statsmodels.stats.contingency_tables.SquareTable.homogeneity "statsmodels.stats.contingency_tables.SquareTable.homogeneity") statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.cov_params_robust_approx statsmodels.tsa.statespace.dynamic\_factor.DynamicFactorResults.cov\_params\_robust\_approx =========================================================================================== `DynamicFactorResults.cov_params_robust_approx()` (array) The QMLE variance / covariance matrix. Computed using the numerical Hessian as the evaluated hessian. statsmodels statsmodels.tsa.statespace.mlemodel.MLEResults.t_test statsmodels.tsa.statespace.mlemodel.MLEResults.t\_test ====================================================== `MLEResults.t_test(r_matrix, cov_p=None, scale=None, use_t=None)` Compute a t-test for a each linear hypothesis of the form Rb = q \| Parameters: \| * r\_matrix (array-like, str, tuple) – + array : If an array is given, a p x k 2d array or length k 1d array specifying the linear restrictions. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q). If q is given, can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – An optional `scale` to use. Default is the scale specified by the model fit. * use\_t (bool, optional) – If use\_t is None, then the default of the model is used. If use\_t is True, then the p-values are based on the t distribution. If use\_t is False, then the p-values are based on the normal distribution. \| \| Returns: \| res – The results for the test are attributes of this results instance. The available results have the same elements as the parameter table in `summary()`. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> r = np.zeros_like(results.params) >>> r[5:] = [1,-1] >>> print(r) [ 0. 0. 0. 0. 0. 1. -1.] ``` r tests that the coefficients on the 5th and 6th independent variable are the same. ``` >>> T_test = results.t_test(r) >>> print(T_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 -1829.2026 455.391 -4.017 0.003 -2859.368 -799.037 ============================================================================== >>> T_test.effect -1829.2025687192481 >>> T_test.sd 455.39079425193762 >>> T_test.tvalue -4.0167754636411717 >>> T_test.pvalue 0.0015163772380899498 ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.formula.api import ols >>> dta = sm.datasets.longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = 'GNPDEFL = GNP, UNEMP = 2, YEAR/1829 = 1' >>> t_test = results.t_test(hypotheses) >>> print(t_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 15.0977 84.937 0.178 0.863 -177.042 207.238 c1 -2.0202 0.488 -8.231 0.000 -3.125 -0.915 c2 1.0001 0.249 0.000 1.000 0.437 1.563 ============================================================================== ``` See also [`tvalues`](statsmodels.tsa.statespace.mlemodel.mleresults.tvalues#statsmodels.tsa.statespace.mlemodel.MLEResults.tvalues "statsmodels.tsa.statespace.mlemodel.MLEResults.tvalues") individual t statistics [`f_test`](statsmodels.tsa.statespace.mlemodel.mleresults.f_test#statsmodels.tsa.statespace.mlemodel.MLEResults.f_test "statsmodels.tsa.statespace.mlemodel.MLEResults.f_test") for F tests [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") statsmodels statsmodels.regression.mixed_linear_model.MixedLMResults.get_nlfun statsmodels.regression.mixed\_linear\_model.MixedLMResults.get\_nlfun ===================================================================== `MixedLMResults.get_nlfun(fun)` statsmodels statsmodels.robust.norms.HuberT.psi_deriv statsmodels.robust.norms.HuberT.psi\_deriv ========================================== `HuberT.psi_deriv(z)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/norms.html#HuberT.psi_deriv) The derivative of Huber’s t psi function #### Notes Used to estimate the robust covariance matrix. statsmodels statsmodels.sandbox.regression.gmm.IVGMMResults.initialize statsmodels.sandbox.regression.gmm.IVGMMResults.initialize ========================================================== `IVGMMResults.initialize(model, params, *kwd)` statsmodels statsmodels.sandbox.regression.gmm.GMM.calc_weightmatrix statsmodels.sandbox.regression.gmm.GMM.calc\_weightmatrix ========================================================= `GMM.calc_weightmatrix(moms, weights_method='cov', wargs=(), params=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/regression/gmm.html#GMM.calc_weightmatrix) calculate omega or the weighting matrix \| Parameters: \| moms (array) – moment conditions (nobs x nmoms) for all observations evaluated at a parameter value * weights\_method (string 'cov') – If method=’cov’ is cov then the matrix is calculated as simple covariance of the moment conditions. see fit method for available aoptions for the weight and covariance matrix * wargs (tuple or [dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)")) – parameters that are required by some kernel methods to estimate the long-run covariance. Not used yet. \| \| Returns: \| w – estimate for the weighting matrix or covariance of the moment condition \| \| Return type: \| array (nmoms, nmoms) \| #### Notes currently a constant cutoff window is used TODO: implement long-run cov estimators, kernel-based Newey-West Andrews Andrews-Moy???? #### References Greene Hansen, Bruce statsmodels statsmodels.graphics.gofplots.ProbPlot.sample_quantiles statsmodels.graphics.gofplots.ProbPlot.sample\_quantiles ======================================================== `ProbPlot.sample_quantiles()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/graphics/gofplots.html#ProbPlot.sample_quantiles) statsmodels statsmodels.tsa.statespace.sarimax.SARIMAXResults.llf_obs statsmodels.tsa.statespace.sarimax.SARIMAXResults.llf\_obs ========================================================== `SARIMAXResults.llf_obs()` (float) The value of the log-likelihood function evaluated at `params`. statsmodels statsmodels.regression.quantile_regression.QuantRegResults.mse statsmodels.regression.quantile\_regression.QuantRegResults.mse =============================================================== `QuantRegResults.mse()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/quantile_regression.html#QuantRegResults.mse) statsmodels statsmodels.tsa.vector_ar.irf.IRAnalysis.cum_errband_mc statsmodels.tsa.vector\_ar.irf.IRAnalysis.cum\_errband\_mc ========================================================== `IRAnalysis.cum_errband_mc(orth=False, repl=1000, signif=0.05, seed=None, burn=100)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/irf.html#IRAnalysis.cum_errband_mc) IRF Monte Carlo integrated error bands of cumulative effect statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.bse statsmodels.regression.recursive\_ls.RecursiveLSResults.bse =========================================================== `RecursiveLSResults.bse()` statsmodels statsmodels.robust.norms.estimate_location statsmodels.robust.norms.estimate\_location =========================================== `statsmodels.robust.norms.estimate_location(a, scale, norm=None, axis=0, initial=None, maxiter=30, tol=1e-06)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/norms.html#estimate_location) M-estimator of location using self.norm and a current estimator of scale. This iteratively finds a solution to norm.psi((a-mu)/scale).sum() == 0 \| Parameters: \| * a (array) – Array over which the location parameter is to be estimated * scale (array) – Scale parameter to be used in M-estimator * norm ([RobustNorm](statsmodels.robust.norms.robustnorm#statsmodels.robust.norms.RobustNorm "statsmodels.robust.norms.RobustNorm"), optional) – Robust norm used in the M-estimator. The default is HuberT(). * axis (int, optional) – Axis along which to estimate the location parameter. The default is 0. * initial (array, optional) – Initial condition for the location parameter. Default is None, which uses the median of a. * niter (int, optional) – Maximum number of iterations. The default is 30. * tol (float, optional) – Toleration for convergence. The default is 1e-06. \| \| Returns: \| mu – Estimate of location \| \| Return type: \| array \|	programming_docs
statsmodels statsmodels.regression.mixed_linear_model.MixedLMResults.remove_data statsmodels.regression.mixed\_linear\_model.MixedLMResults.remove\_data ======================================================================= `MixedLMResults.remove_data()` remove data arrays, all nobs arrays from result and model This reduces the size of the instance, so it can be pickled with less memory. Currently tested for use with predict from an unpickled results and model instance. Warning Since data and some intermediate results have been removed calculating new statistics that require them will raise exceptions. The exception will occur the first time an attribute is accessed that has been set to None. Not fully tested for time series models, tsa, and might delete too much for prediction or not all that would be possible. The lists of arrays to delete are maintained as attributes of the result and model instance, except for cached values. These lists could be changed before calling remove\_data. The attributes to remove are named in: `model._data_attr : arrays attached to both the model instance` and the results instance with the same attribute name. `result.data_in_cache : arrays that may exist as values in` result.\_cache (TODO : should privatize name) `result._data_attr_model : arrays attached to the model` instance but not to the results instance statsmodels statsmodels.tsa.arima_model.ARIMA statsmodels.tsa.arima\_model.ARIMA ================================== `class statsmodels.tsa.arima_model.ARIMA(endog, order, exog=None, dates=None, freq=None, missing='none')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_model.html#ARIMA) Autoregressive Integrated Moving Average ARIMA(p,d,q) Model \| Parameters: \| * endog (array-like) – The endogenous variable. * order (iterable) – The (p,d,q) order of the model for the number of AR parameters, differences, and MA parameters to use. * exog (array-like, optional) – An optional array of exogenous variables. This should not include a constant or trend. You can specify this in the `fit` method. * dates (array-like of datetime, optional) – An array-like object of datetime objects. If a pandas object is given for endog or exog, it is assumed to have a DateIndex. * freq (str, optional) – The frequency of the time-series. A Pandas offset or ‘B’, ‘D’, ‘W’, ‘M’, ‘A’, or ‘Q’. This is optional if dates are given. \| #### Notes If exogenous variables are given, then the model that is fit is \[\phi(L)(y\_t - X\_t\beta) = \theta(L)\epsilon\_t\] where $\phi$ and $\theta$ are polynomials in the lag operator, $L$. This is the regression model with ARMA errors, or ARMAX model. This specification is used, whether or not the model is fit using conditional sum of square or maximum-likelihood, using the `method` argument in [`statsmodels.tsa.arima_model.ARIMA.fit`](statsmodels.tsa.arima_model.arima.fit#statsmodels.tsa.arima_model.ARIMA.fit "statsmodels.tsa.arima_model.ARIMA.fit"). Therefore, for now, `css` and `mle` refer to estimation methods only. This may change for the case of the `css` model in future versions. #### Methods \| \| \| \| --- \| --- \| \| [`fit`](statsmodels.tsa.arima_model.arima.fit#statsmodels.tsa.arima_model.ARIMA.fit "statsmodels.tsa.arima_model.ARIMA.fit")([start\_params, trend, method, …]) \| Fits ARIMA(p,d,q) model by exact maximum likelihood via Kalman filter. \| \| [`from_formula`](statsmodels.tsa.arima_model.arima.from_formula#statsmodels.tsa.arima_model.ARIMA.from_formula "statsmodels.tsa.arima_model.ARIMA.from_formula")(formula, data[, subset, drop\_cols]) \| Create a Model from a formula and dataframe. \| \| [`geterrors`](statsmodels.tsa.arima_model.arima.geterrors#statsmodels.tsa.arima_model.ARIMA.geterrors "statsmodels.tsa.arima_model.ARIMA.geterrors")(params) \| Get the errors of the ARMA process. \| \| [`hessian`](statsmodels.tsa.arima_model.arima.hessian#statsmodels.tsa.arima_model.ARIMA.hessian "statsmodels.tsa.arima_model.ARIMA.hessian")(params) \| Compute the Hessian at params, \| \| [`information`](statsmodels.tsa.arima_model.arima.information#statsmodels.tsa.arima_model.ARIMA.information "statsmodels.tsa.arima_model.ARIMA.information")(params) \| Fisher information matrix of model \| \| [`initialize`](statsmodels.tsa.arima_model.arima.initialize#statsmodels.tsa.arima_model.ARIMA.initialize "statsmodels.tsa.arima_model.ARIMA.initialize")() \| Initialize (possibly re-initialize) a Model instance. \| \| [`loglike`](statsmodels.tsa.arima_model.arima.loglike#statsmodels.tsa.arima_model.ARIMA.loglike "statsmodels.tsa.arima_model.ARIMA.loglike")(params[, set\_sigma2]) \| Compute the log-likelihood for ARMA(p,q) model \| \| [`loglike_css`](statsmodels.tsa.arima_model.arima.loglike_css#statsmodels.tsa.arima_model.ARIMA.loglike_css "statsmodels.tsa.arima_model.ARIMA.loglike_css")(params[, set\_sigma2]) \| Conditional Sum of Squares likelihood function. \| \| [`loglike_kalman`](statsmodels.tsa.arima_model.arima.loglike_kalman#statsmodels.tsa.arima_model.ARIMA.loglike_kalman "statsmodels.tsa.arima_model.ARIMA.loglike_kalman")(params[, set\_sigma2]) \| Compute exact loglikelihood for ARMA(p,q) model by the Kalman Filter. \| \| [`predict`](statsmodels.tsa.arima_model.arima.predict#statsmodels.tsa.arima_model.ARIMA.predict "statsmodels.tsa.arima_model.ARIMA.predict")(params[, start, end, exog, typ, dynamic]) \| ARIMA model in-sample and out-of-sample prediction \| \| [`score`](statsmodels.tsa.arima_model.arima.score#statsmodels.tsa.arima_model.ARIMA.score "statsmodels.tsa.arima_model.ARIMA.score")(params) \| Compute the score function at params. \| #### Attributes \| \| \| \| --- \| --- \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| \| statsmodels statsmodels.duration.hazard_regression.PHReg.fit_regularized statsmodels.duration.hazard\_regression.PHReg.fit\_regularized ============================================================== `PHReg.fit_regularized(method='elastic_net', alpha=0.0, start_params=None, refit=False, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/duration/hazard_regression.html#PHReg.fit_regularized) Return a regularized fit to a linear regression model. \| Parameters: \| method – Only the `elastic_net` approach is currently implemented. * alpha (scalar or array-like) – The penalty weight. If a scalar, the same penalty weight applies to all variables in the model. If a vector, it must have the same length as `params`, and contains a penalty weight for each coefficient. * start\_params (array-like) – Starting values for `params`. * refit (bool) – If True, the model is refit using only the variables that have non-zero coefficients in the regularized fit. The refitted model is not regularized. \| \| Returns: \| \| \| Return type: \| A results object. \| #### Notes The penalty is the `elastic net` penalty, which is a combination of L1 and L2 penalties. The function that is minimized is: \[-loglike/n + alpha\((1-L1\\_wt)\\|params\|\_2^2/2 + L1\\_wt\\|params\|\_1)\] where $\|\\|\_1$ and $\|\\|\_2$ are the L1 and L2 norms. Post-estimation results are based on the same data used to select variables, hence may be subject to overfitting biases. The elastic\_net method uses the following keyword arguments: `maxiter : int` Maximum number of iterations `L1_wt : float` Must be in [0, 1]. The L1 penalty has weight L1\_wt and the L2 penalty has weight 1 - L1\_wt. `cnvrg_tol : float` Convergence threshold for line searches `zero_tol : float` Coefficients below this threshold are treated as zero. statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.cov_params_opg statsmodels.tsa.statespace.dynamic\_factor.DynamicFactorResults.cov\_params\_opg ================================================================================ `DynamicFactorResults.cov_params_opg()` (array) The variance / covariance matrix. Computed using the outer product of gradients method. statsmodels statsmodels.discrete.count_model.ZeroInflatedPoisson.loglike statsmodels.discrete.count\_model.ZeroInflatedPoisson.loglike ============================================================= `ZeroInflatedPoisson.loglike(params)` Loglikelihood of Generic Zero Inflated model \| Parameters: \| params* (array-like) – The parameters of the model. \| \| Returns: \| loglike – The log-likelihood function of the model evaluated at `params`. See notes. \| \| Return type: \| float \| #### Notes \[\ln L=\sum\_{y\_{i}=0}\ln(w\_{i}+(1-w\_{i})\P\_{main\\_model})+ \sum\_{y\_{i}>0}(\ln(1-w\_{i})+L\_{main\\_model}) where P - pdf of main model, L - loglike function of main model.\] statsmodels statsmodels.genmod.families.links.cauchy statsmodels.genmod.families.links.cauchy ======================================== `class statsmodels.genmod.families.links.cauchy` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#cauchy) The Cauchy (standard Cauchy CDF) transform #### Notes g(p) = scipy.stats.cauchy.ppf(p) cauchy is an alias of CDFLink with dbn=scipy.stats.cauchy #### Methods \| \| \| \| --- \| --- \| \| [`deriv`](statsmodels.genmod.families.links.cauchy.deriv#statsmodels.genmod.families.links.cauchy.deriv "statsmodels.genmod.families.links.cauchy.deriv")(p) \| Derivative of CDF link \| \| [`deriv2`](statsmodels.genmod.families.links.cauchy.deriv2#statsmodels.genmod.families.links.cauchy.deriv2 "statsmodels.genmod.families.links.cauchy.deriv2")(p) \| Second derivative of the Cauchy link function. \| \| [`inverse`](statsmodels.genmod.families.links.cauchy.inverse#statsmodels.genmod.families.links.cauchy.inverse "statsmodels.genmod.families.links.cauchy.inverse")(z) \| The inverse of the CDF link \| \| [`inverse_deriv`](statsmodels.genmod.families.links.cauchy.inverse_deriv#statsmodels.genmod.families.links.cauchy.inverse_deriv "statsmodels.genmod.families.links.cauchy.inverse_deriv")(z) \| Derivative of the inverse of the CDF transformation link function \| statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactor.smooth statsmodels.tsa.statespace.dynamic\_factor.DynamicFactor.smooth =============================================================== `DynamicFactor.smooth(params, transformed=True, complex_step=False, cov_type=None, cov_kwds=None, return_ssm=False, results_class=None, results_wrapper_class=None, kwargs)` Kalman smoothing \| Parameters: \| params (array\_like) – Array of parameters at which to evaluate the loglikelihood function. * transformed (boolean, optional) – Whether or not `params` is already transformed. Default is True. * return\_ssm (boolean,optional) – Whether or not to return only the state space output or a full results object. Default is to return a full results object. * cov\_type (str, optional) – See `MLEResults.fit` for a description of covariance matrix types for results object. * cov\_kwds ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)") or None, optional) – See `MLEResults.get_robustcov_results` for a description required keywords for alternative covariance estimators * *\\kwargs* – Additional keyword arguments to pass to the Kalman filter. See `KalmanFilter.filter` for more details. \| statsmodels statsmodels.genmod.families.links.CLogLog.deriv statsmodels.genmod.families.links.CLogLog.deriv =============================================== `CLogLog.deriv(p)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#CLogLog.deriv) Derivative of C-Log-Log transform link function \| Parameters: \| p (array-like) – Mean parameters \| \| Returns: \| g’(p) – The derivative of the CLogLog transform link function \| \| Return type: \| array \| #### Notes g’(p) = - 1 / ((p-1)\log(1-p)) statsmodels statsmodels.discrete.discrete_model.DiscreteResults.summary statsmodels.discrete.discrete\_model.DiscreteResults.summary ============================================================ `DiscreteResults.summary(yname=None, xname=None, title=None, alpha=0.05, yname_list=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#DiscreteResults.summary) Summarize the Regression Results \| Parameters: \| yname (string, optional) – Default is `y` * xname (list of strings, optional) – Default is `var_##` for ## in p the number of regressors * title (string, optional) – Title for the top table. If not None, then this replaces the default title * alpha (float) – significance level for the confidence intervals \| \| Returns: \| smry – this holds the summary tables and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary.Summary`](statsmodels.iolib.summary.summary#statsmodels.iolib.summary.Summary "statsmodels.iolib.summary.Summary") class to hold summary results statsmodels statsmodels.stats.weightstats.DescrStatsW.sum_weights statsmodels.stats.weightstats.DescrStatsW.sum\_weights ====================================================== `DescrStatsW.sum_weights()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/weightstats.html#DescrStatsW.sum_weights) statsmodels statsmodels.tsa.statespace.varmax.VARMAXResults.normalized_cov_params statsmodels.tsa.statespace.varmax.VARMAXResults.normalized\_cov\_params ======================================================================= `VARMAXResults.normalized_cov_params()` statsmodels statsmodels.stats.outliers_influence.OLSInfluence statsmodels.stats.outliers\_influence.OLSInfluence ================================================== `class statsmodels.stats.outliers_influence.OLSInfluence(results)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/outliers_influence.html#OLSInfluence) class to calculate outlier and influence measures for OLS result \| Parameters: \| results (Regression Results instance) – currently assumes the results are from an OLS regression \| #### Notes One part of the results can be calculated without any auxiliary regression (some of which have the `_internal` postfix in the name. Other statistics require leave-one-observation-out (LOOO) auxiliary regression, and will be slower (mainly results with `_external` postfix in the name). The auxiliary LOOO regression only the required results are stored. Using the LOO measures is currently only recommended if the data set is not too large. One possible approach for LOOO measures would be to identify possible problem observations with the \_internal measures, and then run the leave-one-observation-out only with observations that are possible outliers. (However, this is not yet available in an automized way.) This should be extended to general least squares. The leave-one-variable-out (LOVO) auxiliary regression are currently not used. #### Methods \| \| \| \| --- \| --- \| \| [`cooks_distance`](statsmodels.stats.outliers_influence.olsinfluence.cooks_distance#statsmodels.stats.outliers_influence.OLSInfluence.cooks_distance "statsmodels.stats.outliers_influence.OLSInfluence.cooks_distance")() \| (cached attribute) Cooks distance \| \| [`cov_ratio`](statsmodels.stats.outliers_influence.olsinfluence.cov_ratio#statsmodels.stats.outliers_influence.OLSInfluence.cov_ratio "statsmodels.stats.outliers_influence.OLSInfluence.cov_ratio")() \| (cached attribute) covariance ratio between LOOO and original \| \| [`det_cov_params_not_obsi`](statsmodels.stats.outliers_influence.olsinfluence.det_cov_params_not_obsi#statsmodels.stats.outliers_influence.OLSInfluence.det_cov_params_not_obsi "statsmodels.stats.outliers_influence.OLSInfluence.det_cov_params_not_obsi")() \| (cached attribute) determinant of cov\_params of all LOOO regressions \| \| [`dfbetas`](statsmodels.stats.outliers_influence.olsinfluence.dfbetas#statsmodels.stats.outliers_influence.OLSInfluence.dfbetas "statsmodels.stats.outliers_influence.OLSInfluence.dfbetas")() \| (cached attribute) dfbetas \| \| [`dffits`](statsmodels.stats.outliers_influence.olsinfluence.dffits#statsmodels.stats.outliers_influence.OLSInfluence.dffits "statsmodels.stats.outliers_influence.OLSInfluence.dffits")() \| (cached attribute) dffits measure for influence of an observation \| \| [`dffits_internal`](statsmodels.stats.outliers_influence.olsinfluence.dffits_internal#statsmodels.stats.outliers_influence.OLSInfluence.dffits_internal "statsmodels.stats.outliers_influence.OLSInfluence.dffits_internal")() \| (cached attribute) dffits measure for influence of an observation \| \| [`ess_press`](statsmodels.stats.outliers_influence.olsinfluence.ess_press#statsmodels.stats.outliers_influence.OLSInfluence.ess_press "statsmodels.stats.outliers_influence.OLSInfluence.ess_press")() \| (cached attribute) error sum of squares of PRESS residuals \| \| [`get_resid_studentized_external`](statsmodels.stats.outliers_influence.olsinfluence.get_resid_studentized_external#statsmodels.stats.outliers_influence.OLSInfluence.get_resid_studentized_external "statsmodels.stats.outliers_influence.OLSInfluence.get_resid_studentized_external")([sigma]) \| calculate studentized residuals \| \| [`hat_diag_factor`](statsmodels.stats.outliers_influence.olsinfluence.hat_diag_factor#statsmodels.stats.outliers_influence.OLSInfluence.hat_diag_factor "statsmodels.stats.outliers_influence.OLSInfluence.hat_diag_factor")() \| (cached attribute) factor of diagonal of hat\_matrix used in influence \| \| [`hat_matrix_diag`](statsmodels.stats.outliers_influence.olsinfluence.hat_matrix_diag#statsmodels.stats.outliers_influence.OLSInfluence.hat_matrix_diag "statsmodels.stats.outliers_influence.OLSInfluence.hat_matrix_diag")() \| (cached attribute) diagonal of the hat\_matrix for OLS \| \| [`influence`](statsmodels.stats.outliers_influence.olsinfluence.influence#statsmodels.stats.outliers_influence.OLSInfluence.influence "statsmodels.stats.outliers_influence.OLSInfluence.influence")() \| (cached attribute) influence measure \| \| [`params_not_obsi`](statsmodels.stats.outliers_influence.olsinfluence.params_not_obsi#statsmodels.stats.outliers_influence.OLSInfluence.params_not_obsi "statsmodels.stats.outliers_influence.OLSInfluence.params_not_obsi")() \| (cached attribute) parameter estimates for all LOOO regressions \| \| [`resid_press`](statsmodels.stats.outliers_influence.olsinfluence.resid_press#statsmodels.stats.outliers_influence.OLSInfluence.resid_press "statsmodels.stats.outliers_influence.OLSInfluence.resid_press")() \| (cached attribute) PRESS residuals \| \| [`resid_std`](statsmodels.stats.outliers_influence.olsinfluence.resid_std#statsmodels.stats.outliers_influence.OLSInfluence.resid_std "statsmodels.stats.outliers_influence.OLSInfluence.resid_std")() \| (cached attribute) estimate of standard deviation of the residuals \| \| [`resid_studentized_external`](statsmodels.stats.outliers_influence.olsinfluence.resid_studentized_external#statsmodels.stats.outliers_influence.OLSInfluence.resid_studentized_external "statsmodels.stats.outliers_influence.OLSInfluence.resid_studentized_external")() \| (cached attribute) studentized residuals using LOOO variance \| \| [`resid_studentized_internal`](statsmodels.stats.outliers_influence.olsinfluence.resid_studentized_internal#statsmodels.stats.outliers_influence.OLSInfluence.resid_studentized_internal "statsmodels.stats.outliers_influence.OLSInfluence.resid_studentized_internal")() \| (cached attribute) studentized residuals using variance from OLS \| \| [`resid_var`](statsmodels.stats.outliers_influence.olsinfluence.resid_var#statsmodels.stats.outliers_influence.OLSInfluence.resid_var "statsmodels.stats.outliers_influence.OLSInfluence.resid_var")() \| (cached attribute) estimate of variance of the residuals \| \| [`sigma2_not_obsi`](statsmodels.stats.outliers_influence.olsinfluence.sigma2_not_obsi#statsmodels.stats.outliers_influence.OLSInfluence.sigma2_not_obsi "statsmodels.stats.outliers_influence.OLSInfluence.sigma2_not_obsi")() \| (cached attribute) error variance for all LOOO regressions \| \| [`summary_frame`](statsmodels.stats.outliers_influence.olsinfluence.summary_frame#statsmodels.stats.outliers_influence.OLSInfluence.summary_frame "statsmodels.stats.outliers_influence.OLSInfluence.summary_frame")() \| Creates a DataFrame with all available influence results. \| \| [`summary_table`](statsmodels.stats.outliers_influence.olsinfluence.summary_table#statsmodels.stats.outliers_influence.OLSInfluence.summary_table "statsmodels.stats.outliers_influence.OLSInfluence.summary_table")([float\_fmt]) \| create a summary table with all influence and outlier measures \|	programming_docs
statsmodels statsmodels.tsa.statespace.sarimax.SARIMAX.simulation_smoother statsmodels.tsa.statespace.sarimax.SARIMAX.simulation\_smoother =============================================================== `SARIMAX.simulation_smoother(simulation_output=None, *kwargs)` Retrieve a simulation smoother for the state space model. \| Parameters: \| simulation\_output (int, optional) – Determines which simulation smoother output is calculated. Default is all (including state and disturbances). * *\\kwargs* – Additional keyword arguments, used to set the simulation output. See `set_simulation_output` for more details. \| \| Returns: \| \| \| Return type: \| SimulationSmoothResults \| statsmodels statsmodels.sandbox.regression.gmm.IVRegressionResults.mse_total statsmodels.sandbox.regression.gmm.IVRegressionResults.mse\_total ================================================================= `IVRegressionResults.mse_total()` statsmodels statsmodels.stats.weightstats.DescrStatsW.ztost_mean statsmodels.stats.weightstats.DescrStatsW.ztost\_mean ===================================================== `DescrStatsW.ztost_mean(low, upp)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/weightstats.html#DescrStatsW.ztost_mean) test of (non-)equivalence of one sample, based on z-test TOST: two one-sided z-tests null hypothesis: m < low or m > upp alternative hypothesis: low < m < upp where m is the expected value of the sample (mean of the population). If the pvalue is smaller than a threshold, say 0.05, then we reject the hypothesis that the expected value of the sample (mean of the population) is outside of the interval given by thresholds low and upp. \| Parameters: \| upp (low,) – equivalence interval low < mean < upp \| \| Returns: \| * pvalue (float) – pvalue of the non-equivalence test * t1, pv1 (tuple) – test statistic and p-value for lower threshold test * t2, pv2 (tuple) – test statistic and p-value for upper threshold test \| statsmodels statsmodels.tsa.vector_ar.var_model.VAR.hessian statsmodels.tsa.vector\_ar.var\_model.VAR.hessian ================================================= `VAR.hessian(params)` The Hessian matrix of the model statsmodels statsmodels.tsa.statespace.mlemodel.MLEModel.opg_information_matrix statsmodels.tsa.statespace.mlemodel.MLEModel.opg\_information\_matrix ===================================================================== `MLEModel.opg_information_matrix(params, transformed=True, approx_complex_step=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/mlemodel.html#MLEModel.opg_information_matrix) Outer product of gradients information matrix \| Parameters: \| params (array\_like, optional) – Array of parameters at which to evaluate the loglikelihood function. * *\\kwargs* – Additional arguments to the `loglikeobs` method. \| #### References Berndt, Ernst R., Bronwyn Hall, Robert Hall, and Jerry Hausman. 1974. Estimation and Inference in Nonlinear Structural Models. NBER Chapters. National Bureau of Economic Research, Inc. statsmodels statsmodels.regression.quantile_regression.QuantRegResults.summary2 statsmodels.regression.quantile\_regression.QuantRegResults.summary2 ==================================================================== `QuantRegResults.summary2(yname=None, xname=None, title=None, alpha=0.05, float_format='%.4f')` Experimental summary function to summarize the regression results \| Parameters: \| * xname (List of strings of length equal to the number of parameters) – Names of the independent variables (optional) * yname (string) – Name of the dependent variable (optional) * title (string, optional) – Title for the top table. If not None, then this replaces the default title * alpha (float) – significance level for the confidence intervals * float\_format (string) – print format for floats in parameters summary \| \| Returns: \| smry – this holds the summary tables and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary.Summary`](statsmodels.iolib.summary.summary#statsmodels.iolib.summary.Summary "statsmodels.iolib.summary.Summary") class to hold summary results statsmodels statsmodels.nonparametric.kernel_regression.KernelCensoredReg.fit statsmodels.nonparametric.kernel\_regression.KernelCensoredReg.fit ================================================================== `KernelCensoredReg.fit(data_predict=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/nonparametric/kernel_regression.html#KernelCensoredReg.fit) Returns the marginal effects at the data\_predict points. statsmodels statsmodels.regression.linear_model.RegressionResults.pvalues statsmodels.regression.linear\_model.RegressionResults.pvalues ============================================================== `RegressionResults.pvalues()` statsmodels statsmodels.regression.linear_model.OLSResults.mse_resid statsmodels.regression.linear\_model.OLSResults.mse\_resid ========================================================== `OLSResults.mse_resid()` statsmodels statsmodels.imputation.mice.MICEData.get_fitting_data statsmodels.imputation.mice.MICEData.get\_fitting\_data ======================================================= `MICEData.get_fitting_data(vname)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/imputation/mice.html#MICEData.get_fitting_data) Return the data needed to fit a model for imputation. The data is used to impute variable `vname`, and therefore only includes cases for which `vname` is observed. Values of type `PatsyFormula` in `init_kwds` or `fit_kwds` are processed through Patsy and subset to align with the model’s endog and exog. \| Parameters: \| vname (string) – The variable for which the fitting data is returned. \| \| Returns: \| * endog (DataFrame) – Observed values of `vname`. * exog (DataFrame) – Regression design matrix for imputing `vname`. * init\_kwds (dict-like) – The init keyword arguments for `vname`, processed through Patsy as required. * fit\_kwds (dict-like) – The fit keyword arguments for `vname`, processed through Patsy as required. \| statsmodels statsmodels.tools.eval_measures.aic_sigma statsmodels.tools.eval\_measures.aic\_sigma =========================================== `statsmodels.tools.eval_measures.aic_sigma(sigma2, nobs, df_modelwc, islog=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tools/eval_measures.html#aic_sigma) Akaike information criterion \| Parameters: \| * sigma2 (float) – estimate of the residual variance or determinant of Sigma\_hat in the multivariate case. If islog is true, then it is assumed that sigma is already log-ed, for example logdetSigma. * nobs (int) – number of observations * df\_modelwc (int) – number of parameters including constant \| \| Returns: \| aic – information criterion \| \| Return type: \| float \| #### Notes A constant has been dropped in comparison to the loglikelihood base information criteria. The information criteria should be used to compare only comparable models. For example, AIC is defined in terms of the loglikelihood as $-2 llf + 2 k$ in terms of $\hat{\sigma}^2$ $log(\hat{\sigma}^2) + 2 k / n$ in terms of the determinant of $\hat{\Sigma}$ $log(\\|\hat{\Sigma}\\|) + 2 k / n$ Note: In our definition we do not divide by n in the log-likelihood version. TODO: Latex math reference for example lecture notes by Herman Bierens #### References <http://en.wikipedia.org/wiki/Akaike_information_criterion> statsmodels statsmodels.tsa.statespace.structural.UnobservedComponentsResults.aic statsmodels.tsa.statespace.structural.UnobservedComponentsResults.aic ===================================================================== `UnobservedComponentsResults.aic()` (float) Akaike Information Criterion statsmodels statsmodels.tsa.arima_model.ARMAResults.arparams statsmodels.tsa.arima\_model.ARMAResults.arparams ================================================= `ARMAResults.arparams()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_model.html#ARMAResults.arparams) statsmodels statsmodels.tsa.vector_ar.vecm.VECM statsmodels.tsa.vector\_ar.vecm.VECM ==================================== `class statsmodels.tsa.vector_ar.vecm.VECM(endog, exog=None, exog_coint=None, dates=None, freq=None, missing='none', k_ar_diff=1, coint_rank=1, deterministic='nc', seasons=0, first_season=0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/vecm.html#VECM) Class representing a Vector Error Correction Model (VECM). A VECM($k\_{ar}-1$) has the following form \[\Delta y\_t = \Pi y\_{t-1} + \Gamma\_1 \Delta y\_{t-1} + \ldots + \Gamma\_{k\_{ar}-1} \Delta y\_{t-k\_{ar}+1} + u\_t\] where \[\Pi = \alpha \beta'\] as described in chapter 7 of [[1]](#id3). \| Parameters: \| * endog (array-like (nobs\_tot x neqs)) – 2-d endogenous response variable. * exog (ndarray (nobs\_tot x neqs) or None) – Deterministic terms outside the cointegration relation. * exog\_coint (ndarray (nobs\_tot x neqs) or None) – Deterministic terms inside the cointegration relation. * dates (array-like of datetime, optional) – See `statsmodels.tsa.base.tsa_model.TimeSeriesModel` for more information. * freq (str, optional) – See `statsmodels.tsa.base.tsa_model.TimeSeriesModel` for more information. * missing (str, optional) – See [`statsmodels.base.model.Model`](http://www.statsmodels.org/stable/dev/generated/statsmodels.base.model.Model.html#statsmodels.base.model.Model "statsmodels.base.model.Model") for more information. * k\_ar\_diff (int) – Number of lagged differences in the model. Equals $k\_{ar} - 1$ in the formula above. * coint\_rank (int) – Cointegration rank, equals the rank of the matrix $\Pi$ and the number of columns of $\alpha$ and $\beta$. * deterministic (str {`"nc"`, `"co"`, `"ci"`, `"lo"`, `"li"`}) – + `"nc"` - no deterministic terms + `"co"` - constant outside the cointegration relation + `"ci"` - constant within the cointegration relation + `"lo"` - linear trend outside the cointegration relation + `"li"` - linear trend within the cointegration relationCombinations of these are possible (e.g. `"cili"` or `"colo"` for linear trend with intercept). When using a constant term you have to choose whether you want to restrict it to the cointegration relation (i.e. `"ci"`) or leave it unrestricted (i.e. `"co"`). Don’t use both `"ci"` and `"co"`. The same applies for `"li"` and `"lo"` when using a linear term. See the Notes-section for more information. * seasons (int, default: 0) – Number of periods in a seasonal cycle. 0 means no seasons. * first\_season (int, default: 0) – Season of the first observation. \| #### Notes A VECM($k\_{ar} - 1$) with deterministic terms has the form \[\begin{split}\Delta y\_t = \alpha \begin{pmatrix}\beta' & \eta'\end{pmatrix} \begin{pmatrix}y\_{t-1}\\D^{co}\_{t-1}\end{pmatrix} + \Gamma\_1 \Delta y\_{t-1} + \dots + \Gamma\_{k\_{ar}-1} \Delta y\_{t-k\_{ar}+1} + C D\_t + u\_t.\end{split}\] In $D^{co}\_{t-1}$ we have the deterministic terms which are inside the cointegration relation (or restricted to the cointegration relation). $\eta$ is the corresponding estimator. To pass a deterministic term inside the cointegration relation, we can use the `exog_coint` argument. For the two special cases of an intercept and a linear trend there exists a simpler way to declare these terms: we can pass `"ci"` and `"li"` respectively to the `deterministic` argument. So for an intercept inside the cointegration relation we can either pass `"ci"` as `deterministic` or `np.ones(len(data))` as `exog_coint` if `data` is passed as the `endog` argument. This ensures that $D\_{t-1}^{co} = 1$ for all $t$. We can also use deterministic terms outside the cointegration relation. These are defined in $D\_t$ in the formula above with the corresponding estimators in the matrix $C$. We specify such terms by passing them to the `exog` argument. For an intercept and/or linear trend we again have the possibility to use `deterministic` alternatively. For an intercept we pass `"co"` and for a linear trend we pass `"lo"` where the `o` stands for `outside`. The following table shows the five cases considered in [[2]](#id4). The last column indicates which string to pass to the `deterministic` argument for each of these cases. \| Case \| Intercept \| Slope of the linear trend \| `deterministic` \| \| --- \| --- \| --- \| --- \| \| I \| 0 \| 0 \| `"nc"` \| \| II \| $- \alpha \beta^T \mu$ \| 0 \| `"ci"` \| \| III \| $\neq 0$ \| 0 \| `"co"` \| \| IV \| $\neq 0$ \| $- \alpha \beta^T \gamma$ \| `"coli"` \| \| V \| $\neq 0$ \| $\neq 0$ \| `"colo"` \| #### References \| \| \| \| --- \| --- \| \| [[1]](#id1) \| Lütkepohl, H. 2005. New Introduction to Multiple Time Series Analysis. Springer. \| \| \| \| \| --- \| --- \| \| [[2]](#id2) \| Johansen, S. 1995. Likelihood-Based Inference in Cointegrated \ \Vector Autoregressive Models. Oxford University Press. \| #### Methods \| \| \| \| --- \| --- \| \| [`fit`](statsmodels.tsa.vector_ar.vecm.vecm.fit#statsmodels.tsa.vector_ar.vecm.VECM.fit "statsmodels.tsa.vector_ar.vecm.VECM.fit")([method]) \| Estimates the parameters of a VECM. \| \| [`from_formula`](statsmodels.tsa.vector_ar.vecm.vecm.from_formula#statsmodels.tsa.vector_ar.vecm.VECM.from_formula "statsmodels.tsa.vector_ar.vecm.VECM.from_formula")(formula, data[, subset, drop\_cols]) \| Create a Model from a formula and dataframe. \| \| [`hessian`](statsmodels.tsa.vector_ar.vecm.vecm.hessian#statsmodels.tsa.vector_ar.vecm.VECM.hessian "statsmodels.tsa.vector_ar.vecm.VECM.hessian")(params) \| The Hessian matrix of the model \| \| [`information`](statsmodels.tsa.vector_ar.vecm.vecm.information#statsmodels.tsa.vector_ar.vecm.VECM.information "statsmodels.tsa.vector_ar.vecm.VECM.information")(params) \| Fisher information matrix of model \| \| [`initialize`](statsmodels.tsa.vector_ar.vecm.vecm.initialize#statsmodels.tsa.vector_ar.vecm.VECM.initialize "statsmodels.tsa.vector_ar.vecm.VECM.initialize")() \| Initialize (possibly re-initialize) a Model instance. \| \| [`loglike`](statsmodels.tsa.vector_ar.vecm.vecm.loglike#statsmodels.tsa.vector_ar.vecm.VECM.loglike "statsmodels.tsa.vector_ar.vecm.VECM.loglike")(params) \| Log-likelihood of model. \| \| [`predict`](statsmodels.tsa.vector_ar.vecm.vecm.predict#statsmodels.tsa.vector_ar.vecm.VECM.predict "statsmodels.tsa.vector_ar.vecm.VECM.predict")(params[, exog]) \| After a model has been fit predict returns the fitted values. \| \| [`score`](statsmodels.tsa.vector_ar.vecm.vecm.score#statsmodels.tsa.vector_ar.vecm.VECM.score "statsmodels.tsa.vector_ar.vecm.VECM.score")(params) \| Score vector of model. \| #### Attributes \| \| \| \| --- \| --- \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| \| statsmodels statsmodels.robust.norms.TukeyBiweight.rho statsmodels.robust.norms.TukeyBiweight.rho ========================================== `TukeyBiweight.rho(z)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/norms.html#TukeyBiweight.rho) The robust criterion function for Tukey’s biweight estimator \| Parameters: \| z (array-like) – 1d array \| \| Returns: \| rho – rho(z) = -(1 - (z/c)\\2)\\3 \* c\\2/6. for \|z\| <= Rrho(z) = 0 for \|z\| > R \| \| Return type: \| array \| statsmodels statsmodels.robust.robust_linear_model.RLMResults.bcov_unscaled statsmodels.robust.robust\_linear\_model.RLMResults.bcov\_unscaled ================================================================== `RLMResults.bcov_unscaled()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/robust_linear_model.html#RLMResults.bcov_unscaled) statsmodels statsmodels.robust.norms.HuberT.weights statsmodels.robust.norms.HuberT.weights ======================================= `HuberT.weights(z)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/norms.html#HuberT.weights) Huber’s t weighting function for the IRLS algorithm The psi function scaled by z \| Parameters: \| z (array-like) – 1d array \| \| Returns: \| weights – weights(z) = 1 for \|z\| <= tweights(z) = t/\|z\| for \|z\| > t \| \| Return type: \| array \| statsmodels statsmodels.tsa.holtwinters.SimpleExpSmoothing.hessian statsmodels.tsa.holtwinters.SimpleExpSmoothing.hessian ====================================================== `SimpleExpSmoothing.hessian(params)` The Hessian matrix of the model statsmodels statsmodels.emplike.descriptive.DescStatUV.ci_var statsmodels.emplike.descriptive.DescStatUV.ci\_var ================================================== `DescStatUV.ci_var(lower_bound=None, upper_bound=None, sig=0.05)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/emplike/descriptive.html#DescStatUV.ci_var) Returns the confidence interval for the variance. \| Parameters: \| * lower\_bound (float) – The minimum value the lower confidence interval can take. The p-value from test\_var(lower\_bound) must be lower than 1 - significance level. Default is .99 confidence limit assuming normality * upper\_bound (float) – The maximum value the upper confidence interval can take. The p-value from test\_var(upper\_bound) must be lower than 1 - significance level. Default is .99 confidence limit assuming normality * sig (float) – The significance level. Default is .05 \| \| Returns: \| Interval – Confidence interval for the variance \| \| Return type: \| tuple \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> random_numbers = np.random.standard_normal(100) >>> el_analysis = sm.emplike.DescStat(random_numbers) >>> el_analysis.ci_var() (0.7539322567470305, 1.229998852496268) >>> el_analysis.ci_var(.5, 2) (0.7539322567469926, 1.2299988524962664) ``` #### Notes If the function returns the error f(a) and f(b) must have different signs, consider lowering lower\_bound and raising upper\_bound. statsmodels statsmodels.sandbox.regression.gmm.IVRegressionResults.bse statsmodels.sandbox.regression.gmm.IVRegressionResults.bse ========================================================== `IVRegressionResults.bse()` statsmodels statsmodels.genmod.families.family.NegativeBinomial.predict statsmodels.genmod.families.family.NegativeBinomial.predict =========================================================== `NegativeBinomial.predict(mu)` Linear predictors based on given mu values. \| Parameters: \| mu (array) – The mean response variables \| \| Returns: \| lin\_pred – Linear predictors based on the mean response variables. The value of the link function at the given mu. \| \| Return type: \| array \| statsmodels statsmodels.sandbox.sysreg.SUR.predict statsmodels.sandbox.sysreg.SUR.predict ====================================== `SUR.predict(design)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/sysreg.html#SUR.predict) statsmodels statsmodels.regression.mixed_linear_model.MixedLMResults.pvalues statsmodels.regression.mixed\_linear\_model.MixedLMResults.pvalues ================================================================== `MixedLMResults.pvalues()` statsmodels statsmodels.tsa.arima_model.ARIMAResults.aic statsmodels.tsa.arima\_model.ARIMAResults.aic ============================================= `ARIMAResults.aic()` statsmodels statsmodels.discrete.discrete_model.BinaryResults.llnull statsmodels.discrete.discrete\_model.BinaryResults.llnull ========================================================= `BinaryResults.llnull()`	programming_docs
statsmodels statsmodels.tsa.statespace.kalman_filter.KalmanFilter.set_filter_timing statsmodels.tsa.statespace.kalman\_filter.KalmanFilter.set\_filter\_timing ========================================================================== `KalmanFilter.set_filter_timing(alternate_timing=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/kalman_filter.html#KalmanFilter.set_filter_timing) Set the filter timing convention By default, the Kalman filter follows Durbin and Koopman, 2012, in initializing the filter with predicted values. Kim and Nelson, 1999, instead initialize the filter with filtered values, which is essentially just a different timing convention. \| Parameters: \| alternate\_timing (integer, optional) – Whether or not to use the alternate timing convention. Default is unspecified. * *\\kwargs* – Keyword arguments may be used to influence the memory conservation method by setting individual boolean flags. See notes for details. \| statsmodels statsmodels.regression.linear_model.OLSResults.pvalues statsmodels.regression.linear\_model.OLSResults.pvalues ======================================================= `OLSResults.pvalues()` statsmodels statsmodels.tsa.statespace.varmax.VARMAX.from_formula statsmodels.tsa.statespace.varmax.VARMAX.from\_formula ====================================================== `classmethod VARMAX.from_formula(formula, data, subset=None)` Not implemented for state space models statsmodels statsmodels.discrete.discrete_model.NegativeBinomialResults.wald_test statsmodels.discrete.discrete\_model.NegativeBinomialResults.wald\_test ======================================================================= `NegativeBinomialResults.wald_test(r_matrix, cov_p=None, scale=1.0, invcov=None, use_f=None)` Compute a Wald-test for a joint linear hypothesis. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. * use\_f (bool) – If True, then the F-distribution is used. If False, then the asymptotic distribution, chisquare is used. If use\_f is None, then the F distribution is used if the model specifies that use\_t is True. The test statistic is proportionally adjusted for the distribution by the number of constraints in the hypothesis. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`f_test`](statsmodels.discrete.discrete_model.negativebinomialresults.f_test#statsmodels.discrete.discrete_model.NegativeBinomialResults.f_test "statsmodels.discrete.discrete_model.NegativeBinomialResults.f_test"), [`t_test`](statsmodels.discrete.discrete_model.negativebinomialresults.t_test#statsmodels.discrete.discrete_model.NegativeBinomialResults.t_test "statsmodels.discrete.discrete_model.NegativeBinomialResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactor.fit statsmodels.tsa.statespace.dynamic\_factor.DynamicFactor.fit ============================================================ `DynamicFactor.fit(start_params=None, transformed=True, cov_type='opg', cov_kwds=None, method='lbfgs', maxiter=50, full_output=1, disp=5, callback=None, return_params=False, optim_score=None, optim_complex_step=None, optim_hessian=None, flags=None, *kwargs)` Fits the model by maximum likelihood via Kalman filter. \| Parameters: \| start\_params (array\_like, optional) – Initial guess of the solution for the loglikelihood maximization. If None, the default is given by Model.start\_params. * transformed (boolean, optional) – Whether or not `start_params` is already transformed. Default is True. * cov\_type (str, optional) – The `cov_type` keyword governs the method for calculating the covariance matrix of parameter estimates. Can be one of: + ’opg’ for the outer product of gradient estimator + ’oim’ for the observed information matrix estimator, calculated using the method of Harvey (1989) + ’approx’ for the observed information matrix estimator, calculated using a numerical approximation of the Hessian matrix. + ’robust’ for an approximate (quasi-maximum likelihood) covariance matrix that may be valid even in the presense of some misspecifications. Intermediate calculations use the ‘oim’ method. + ’robust\_approx’ is the same as ‘robust’ except that the intermediate calculations use the ‘approx’ method. + ’none’ for no covariance matrix calculation. * cov\_kwds ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)") or None, optional) – A dictionary of arguments affecting covariance matrix computation. opg, oim, approx, robust, robust\_approx + ’approx\_complex\_step’ : boolean, optional - If True, numerical approximations are computed using complex-step methods. If False, numerical approximations are computed using finite difference methods. Default is True. + ’approx\_centered’ : boolean, optional - If True, numerical approximations computed using finite difference methods use a centered approximation. Default is False. * method (str, optional) – The `method` determines which solver from `scipy.optimize` is used, and it can be chosen from among the following strings: + ’newton’ for Newton-Raphson, ‘nm’ for Nelder-Mead + ’bfgs’ for Broyden-Fletcher-Goldfarb-Shanno (BFGS) + ’lbfgs’ for limited-memory BFGS with optional box constraints + ’powell’ for modified Powell’s method + ’cg’ for conjugate gradient + ’ncg’ for Newton-conjugate gradient + ’basinhopping’ for global basin-hopping solverThe explicit arguments in `fit` are passed to the solver, with the exception of the basin-hopping solver. Each solver has several optional arguments that are not the same across solvers. See the notes section below (or scipy.optimize) for the available arguments and for the list of explicit arguments that the basin-hopping solver supports. * maxiter (int, optional) – The maximum number of iterations to perform. * full\_output (boolean, optional) – Set to True to have all available output in the Results object’s mle\_retvals attribute. The output is dependent on the solver. See LikelihoodModelResults notes section for more information. * disp (boolean, optional) – Set to True to print convergence messages. * callback (callable callback(xk), optional) – Called after each iteration, as callback(xk), where xk is the current parameter vector. * return\_params (boolean, optional) – Whether or not to return only the array of maximizing parameters. Default is False. * optim\_score ({'harvey', 'approx'} or None, optional) – The method by which the score vector is calculated. ‘harvey’ uses the method from Harvey (1989), ‘approx’ uses either finite difference or complex step differentiation depending upon the value of `optim_complex_step`, and None uses the built-in gradient approximation of the optimizer. Default is None. This keyword is only relevant if the optimization method uses the score. * optim\_complex\_step (bool, optional) – Whether or not to use complex step differentiation when approximating the score; if False, finite difference approximation is used. Default is True. This keyword is only relevant if `optim_score` is set to ‘harvey’ or ‘approx’. * optim\_hessian ({'opg','oim','approx'}, optional) – The method by which the Hessian is numerically approximated. ‘opg’ uses outer product of gradients, ‘oim’ uses the information matrix formula from Harvey (1989), and ‘approx’ uses numerical approximation. This keyword is only relevant if the optimization method uses the Hessian matrix. * *\\kwargs* – Additional keyword arguments to pass to the optimizer. \| \| Returns: \| \| \| Return type: \| [MLEResults](statsmodels.tsa.statespace.mlemodel.mleresults#statsmodels.tsa.statespace.mlemodel.MLEResults "statsmodels.tsa.statespace.mlemodel.MLEResults") \| See also [`statsmodels.base.model.LikelihoodModel.fit`](http://www.statsmodels.org/stable/dev/generated/statsmodels.base.model.LikelihoodModel.fit.html#statsmodels.base.model.LikelihoodModel.fit "statsmodels.base.model.LikelihoodModel.fit"), `MLEResults` statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.get_forecast statsmodels.tsa.statespace.dynamic\_factor.DynamicFactorResults.get\_forecast ============================================================================= `DynamicFactorResults.get_forecast(steps=1, *kwargs)` Out-of-sample forecasts \| Parameters: \| steps (int, str, or datetime, optional) – If an integer, the number of steps to forecast from the end of the sample. Can also be a date string to parse or a datetime type. However, if the dates index does not have a fixed frequency, steps must be an integer. Default * *\\kwargs* – Additional arguments may required for forecasting beyond the end of the sample. See `FilterResults.predict` for more details. \| \| Returns: \| forecast – Array of out of sample forecasts. A (steps x k\_endog) array. \| \| Return type: \| array \| statsmodels statsmodels.discrete.discrete_model.DiscreteResults.wald_test statsmodels.discrete.discrete\_model.DiscreteResults.wald\_test =============================================================== `DiscreteResults.wald_test(r_matrix, cov_p=None, scale=1.0, invcov=None, use_f=None)` Compute a Wald-test for a joint linear hypothesis. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. * use\_f (bool) – If True, then the F-distribution is used. If False, then the asymptotic distribution, chisquare is used. If use\_f is None, then the F distribution is used if the model specifies that use\_t is True. The test statistic is proportionally adjusted for the distribution by the number of constraints in the hypothesis. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`f_test`](statsmodels.discrete.discrete_model.discreteresults.f_test#statsmodels.discrete.discrete_model.DiscreteResults.f_test "statsmodels.discrete.discrete_model.DiscreteResults.f_test"), [`t_test`](statsmodels.discrete.discrete_model.discreteresults.t_test#statsmodels.discrete.discrete_model.DiscreteResults.t_test "statsmodels.discrete.discrete_model.DiscreteResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.regression.mixed_linear_model.MixedLMResults.llf statsmodels.regression.mixed\_linear\_model.MixedLMResults.llf ============================================================== `MixedLMResults.llf()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/mixed_linear_model.html#MixedLMResults.llf) statsmodels statsmodels.genmod.families.links.inverse_squared statsmodels.genmod.families.links.inverse\_squared ================================================== `class statsmodels.genmod.families.links.inverse_squared` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#inverse_squared) The inverse squared transform #### Notes g(`p`) = 1/(`p`\\2) Alias of statsmodels.family.links.Power(power=2.) #### Methods \| \| \| \| --- \| --- \| \| [`deriv`](statsmodels.genmod.families.links.inverse_squared.deriv#statsmodels.genmod.families.links.inverse_squared.deriv "statsmodels.genmod.families.links.inverse_squared.deriv")(p) \| Derivative of the power transform \| \| [`deriv2`](statsmodels.genmod.families.links.inverse_squared.deriv2#statsmodels.genmod.families.links.inverse_squared.deriv2 "statsmodels.genmod.families.links.inverse_squared.deriv2")(p) \| Second derivative of the power transform \| \| [`inverse`](statsmodels.genmod.families.links.inverse_squared.inverse#statsmodels.genmod.families.links.inverse_squared.inverse "statsmodels.genmod.families.links.inverse_squared.inverse")(z) \| Inverse of the power transform link function \| \| [`inverse_deriv`](statsmodels.genmod.families.links.inverse_squared.inverse_deriv#statsmodels.genmod.families.links.inverse_squared.inverse_deriv "statsmodels.genmod.families.links.inverse_squared.inverse_deriv")(z) \| Derivative of the inverse of the power transform \| statsmodels statsmodels.tsa.vector_ar.hypothesis_test_results.HypothesisTestResults statsmodels.tsa.vector\_ar.hypothesis\_test\_results.HypothesisTestResults ========================================================================== `class statsmodels.tsa.vector_ar.hypothesis_test_results.HypothesisTestResults(test_statistic, crit_value, pvalue, df, signif, method, title, h0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/hypothesis_test_results.html#HypothesisTestResults) Results class for hypothesis tests. \| Parameters: \| * test\_statistic (float) – * crit\_value (float) – * pvalue (float, 0 <= `pvalue` <= 1) – * df (int) – Degrees of freedom. * signif (float, 0 < `signif` < 1) – Significance level. * method (str) – The kind of test (e.g. `"f"` for F-test, `"wald"` for Wald-test). * title (str) – A title describing the test. It will be part of the summary. * h0 (str) – A string describing the null hypothesis. It will be used in the summary. \| #### Methods \| \| \| \| --- \| --- \| \| [`summary`](statsmodels.tsa.vector_ar.hypothesis_test_results.hypothesistestresults.summary#statsmodels.tsa.vector_ar.hypothesis_test_results.HypothesisTestResults.summary "statsmodels.tsa.vector_ar.hypothesis_test_results.HypothesisTestResults.summary")() \| \| statsmodels statsmodels.nonparametric.bandwidths.bw_silverman statsmodels.nonparametric.bandwidths.bw\_silverman ================================================== `statsmodels.nonparametric.bandwidths.bw_silverman(x, kernel=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/nonparametric/bandwidths.html#bw_silverman) Silverman’s Rule of Thumb \| Parameters: \| * x (array-like) – Array for which to get the bandwidth * kernel (CustomKernel object) – Unused \| \| Returns: \| bw – The estimate of the bandwidth \| \| Return type: \| float \| #### Notes Returns .9 \* A \* n \\ (-1/5.) where ``` A = min(std(x, ddof=1), IQR/1.349) IQR = np.subtract.reduce(np.percentile(x, [75,25])) ``` #### References Silverman, B.W. (1986) `Density Estimation.` statsmodels statsmodels.regression.linear_model.OLS.hessian statsmodels.regression.linear\_model.OLS.hessian ================================================ `OLS.hessian(params, scale=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#OLS.hessian) Evaluate the Hessian function at a given point. \| Parameters: \| * params (array-like) – The parameter vector at which the Hessian is computed. * scale (float or None) – If None, return the profile (concentrated) log likelihood (profiled over the scale parameter), else return the log-likelihood using the given scale value. \| \| Returns: \| \| \| Return type: \| The Hessian matrix. \| statsmodels statsmodels.sandbox.distributions.extras.SkewNorm2_gen.moment statsmodels.sandbox.distributions.extras.SkewNorm2\_gen.moment ============================================================== `SkewNorm2_gen.moment(n, args, kwds)` n-th order non-central moment of distribution. \| Parameters: \| n (int, n >= 1) – Order of moment. * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information). * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| statsmodels statsmodels.tsa.statespace.varmax.VARMAX.transform_params statsmodels.tsa.statespace.varmax.VARMAX.transform\_params ========================================================== `VARMAX.transform_params(unconstrained)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/varmax.html#VARMAX.transform_params) Transform unconstrained parameters used by the optimizer to constrained parameters used in likelihood evaluation \| Parameters: \| unconstrained (array\_like) – Array of unconstrained parameters used by the optimizer, to be transformed. \| \| Returns: \| constrained – Array of constrained parameters which may be used in likelihood evalation. \| \| Return type: \| array\_like \| #### Notes Constrains the factor transition to be stationary and variances to be positive. statsmodels statsmodels.regression.linear_model.OLS.initialize statsmodels.regression.linear\_model.OLS.initialize =================================================== `OLS.initialize()` Initialize (possibly re-initialize) a Model instance. For instance, the design matrix of a linear model may change and some things must be recomputed. statsmodels statsmodels.tsa.arima_model.ARIMA.from_formula statsmodels.tsa.arima\_model.ARIMA.from\_formula ================================================ `classmethod ARIMA.from_formula(formula, data, subset=None, drop_cols=None, args, kwargs)` Create a Model from a formula and dataframe. \| Parameters: \| formula (str or generic Formula object) – The formula specifying the model * data (array-like) – The data for the model. See Notes. * subset (array-like) – An array-like object of booleans, integers, or index values that indicate the subset of df to use in the model. Assumes df is a `pandas.DataFrame` * drop\_cols (array-like) – Columns to drop from the design matrix. Cannot be used to drop terms involving categoricals. * args (extra arguments) – These are passed to the model * kwargs (extra keyword arguments) – These are passed to the model with one exception. The `eval_env` keyword is passed to patsy. It can be either a [`patsy.EvalEnvironment`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.EvalEnvironment "(in patsy v0.5.0+dev)") object or an integer indicating the depth of the namespace to use. For example, the default `eval_env=0` uses the calling namespace. If you wish to use a “clean” environment set `eval_env=-1`. \| \| Returns: \| model \| \| Return type: \| Model instance \| #### Notes data must define \_\_getitem\_\_ with the keys in the formula terms args and kwargs are passed on to the model instantiation. E.g., a numpy structured or rec array, a dictionary, or a pandas DataFrame.	programming_docs
statsmodels statsmodels.tsa.statespace.structural.UnobservedComponents.simulation_smoother statsmodels.tsa.statespace.structural.UnobservedComponents.simulation\_smoother =============================================================================== `UnobservedComponents.simulation_smoother(simulation_output=None, *kwargs)` Retrieve a simulation smoother for the state space model. \| Parameters: \| simulation\_output (int, optional) – Determines which simulation smoother output is calculated. Default is all (including state and disturbances). * *\\kwargs* – Additional keyword arguments, used to set the simulation output. See `set_simulation_output` for more details. \| \| Returns: \| \| \| Return type: \| SimulationSmoothResults \| statsmodels statsmodels.genmod.cov_struct.Exchangeable.update statsmodels.genmod.cov\_struct.Exchangeable.update ================================================== `Exchangeable.update(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/cov_struct.html#Exchangeable.update) Updates the association parameter values based on the current regression coefficients. \| Parameters: \| params (array-like) – Working values for the regression parameters. \| statsmodels statsmodels.sandbox.regression.try_catdata.groupsstats_dummy statsmodels.sandbox.regression.try\_catdata.groupsstats\_dummy ============================================================== `statsmodels.sandbox.regression.try_catdata.groupsstats_dummy(y, x, nonseq=0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/regression/try_catdata.html#groupsstats_dummy) statsmodels statsmodels.tsa.statespace.representation.Representation.initialize_approximate_diffuse statsmodels.tsa.statespace.representation.Representation.initialize\_approximate\_diffuse ========================================================================================= `Representation.initialize_approximate_diffuse(variance=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/representation.html#Representation.initialize_approximate_diffuse) Initialize the statespace model with approximate diffuse values. Rather than following the exact diffuse treatment (which is developed for the case that the variance becomes infinitely large), this assigns an arbitrary large number for the variance. \| Parameters: \| variance (float, optional) – The variance for approximating diffuse initial conditions. Default is 1e6. \| statsmodels statsmodels.sandbox.regression.gmm.IVRegressionResults.bic statsmodels.sandbox.regression.gmm.IVRegressionResults.bic ========================================================== `IVRegressionResults.bic()` statsmodels statsmodels.discrete.discrete_model.NegativeBinomialP.fit_regularized statsmodels.discrete.discrete\_model.NegativeBinomialP.fit\_regularized ======================================================================= `NegativeBinomialP.fit_regularized(start_params=None, method='l1', maxiter='defined_by_method', full_output=1, disp=1, callback=None, alpha=0, trim_mode='auto', auto_trim_tol=0.01, size_trim_tol=0.0001, qc_tol=0.03, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#NegativeBinomialP.fit_regularized) Fit the model using a regularized maximum likelihood. The regularization method AND the solver used is determined by the argument method. \| Parameters: \| start\_params (array-like, optional) – Initial guess of the solution for the loglikelihood maximization. The default is an array of zeros. * method ('l1' or 'l1\_cvxopt\_cp') – See notes for details. * maxiter (Integer or 'defined\_by\_method') – Maximum number of iterations to perform. If ‘defined\_by\_method’, then use method defaults (see notes). * full\_output (bool) – Set to True to have all available output in the Results object’s mle\_retvals attribute. The output is dependent on the solver. See LikelihoodModelResults notes section for more information. * disp (bool) – Set to True to print convergence messages. * fargs (tuple) – Extra arguments passed to the likelihood function, i.e., loglike(x,\args) callback (callable callback(xk)) – Called after each iteration, as callback(xk), where xk is the current parameter vector. * retall (bool) – Set to True to return list of solutions at each iteration. Available in Results object’s mle\_retvals attribute. * alpha (non-negative scalar or numpy array (same size as parameters)) – The weight multiplying the l1 penalty term * trim\_mode ('auto, 'size', or 'off') – If not ‘off’, trim (set to zero) parameters that would have been zero if the solver reached the theoretical minimum. If ‘auto’, trim params using the Theory above. If ‘size’, trim params if they have very small absolute value * size\_trim\_tol (float or 'auto' (default = 'auto')) – For use when trim\_mode == ‘size’ * auto\_trim\_tol (float) – For sue when trim\_mode == ‘auto’. Use * qc\_tol (float) – Print warning and don’t allow auto trim when (ii) (above) is violated by this much. * qc\_verbose (Boolean) – If true, print out a full QC report upon failure \| #### Notes Extra parameters are not penalized if alpha is given as a scalar. An example is the shape parameter in NegativeBinomial `nb1` and `nb2`. Optional arguments for the solvers (available in Results.mle\_settings): ``` 'l1' acc : float (default 1e-6) Requested accuracy as used by slsqp 'l1_cvxopt_cp' abstol : float absolute accuracy (default: 1e-7). reltol : float relative accuracy (default: 1e-6). feastol : float tolerance for feasibility conditions (default: 1e-7). refinement : int number of iterative refinement steps when solving KKT equations (default: 1). ``` Optimization methodology With $L$ the negative log likelihood, we solve the convex but non-smooth problem \[\min\_\beta L(\beta) + \sum\_k\alpha\_k \|\beta\_k\|\] via the transformation to the smooth, convex, constrained problem in twice as many variables (adding the “added variables” $u\_k$) \[\min\_{\beta,u} L(\beta) + \sum\_k\alpha\_k u\_k,\] subject to \[-u\_k \leq \beta\_k \leq u\_k.\] With $\partial\_k L$ the derivative of $L$ in the $k^{th}$ parameter direction, theory dictates that, at the minimum, exactly one of two conditions holds: 1. $\|\partial\_k L\| = \alpha\_k$ and $\beta\_k \neq 0$ 2. $\|\partial\_k L\| \leq \alpha\_k$ and $\beta\_k = 0$ statsmodels statsmodels.discrete.discrete_model.MNLogit.pdf statsmodels.discrete.discrete\_model.MNLogit.pdf ================================================ `MNLogit.pdf(eXB)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#MNLogit.pdf) NotImplemented statsmodels statsmodels.discrete.discrete_model.GeneralizedPoisson.fit_regularized statsmodels.discrete.discrete\_model.GeneralizedPoisson.fit\_regularized ======================================================================== `GeneralizedPoisson.fit_regularized(start_params=None, method='l1', maxiter='defined_by_method', full_output=1, disp=1, callback=None, alpha=0, trim_mode='auto', auto_trim_tol=0.01, size_trim_tol=0.0001, qc_tol=0.03, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#GeneralizedPoisson.fit_regularized) Fit the model using a regularized maximum likelihood. The regularization method AND the solver used is determined by the argument method. \| Parameters: \| start\_params (array-like, optional) – Initial guess of the solution for the loglikelihood maximization. The default is an array of zeros. * method ('l1' or 'l1\_cvxopt\_cp') – See notes for details. * maxiter (Integer or 'defined\_by\_method') – Maximum number of iterations to perform. If ‘defined\_by\_method’, then use method defaults (see notes). * full\_output (bool) – Set to True to have all available output in the Results object’s mle\_retvals attribute. The output is dependent on the solver. See LikelihoodModelResults notes section for more information. * disp (bool) – Set to True to print convergence messages. * fargs (tuple) – Extra arguments passed to the likelihood function, i.e., loglike(x,\args) callback (callable callback(xk)) – Called after each iteration, as callback(xk), where xk is the current parameter vector. * retall (bool) – Set to True to return list of solutions at each iteration. Available in Results object’s mle\_retvals attribute. * alpha (non-negative scalar or numpy array (same size as parameters)) – The weight multiplying the l1 penalty term * trim\_mode ('auto, 'size', or 'off') – If not ‘off’, trim (set to zero) parameters that would have been zero if the solver reached the theoretical minimum. If ‘auto’, trim params using the Theory above. If ‘size’, trim params if they have very small absolute value * size\_trim\_tol (float or 'auto' (default = 'auto')) – For use when trim\_mode == ‘size’ * auto\_trim\_tol (float) – For sue when trim\_mode == ‘auto’. Use * qc\_tol (float) – Print warning and don’t allow auto trim when (ii) (above) is violated by this much. * qc\_verbose (Boolean) – If true, print out a full QC report upon failure \| #### Notes Extra parameters are not penalized if alpha is given as a scalar. An example is the shape parameter in NegativeBinomial `nb1` and `nb2`. Optional arguments for the solvers (available in Results.mle\_settings): ``` 'l1' acc : float (default 1e-6) Requested accuracy as used by slsqp 'l1_cvxopt_cp' abstol : float absolute accuracy (default: 1e-7). reltol : float relative accuracy (default: 1e-6). feastol : float tolerance for feasibility conditions (default: 1e-7). refinement : int number of iterative refinement steps when solving KKT equations (default: 1). ``` Optimization methodology With $L$ the negative log likelihood, we solve the convex but non-smooth problem \[\min\_\beta L(\beta) + \sum\_k\alpha\_k \|\beta\_k\|\] via the transformation to the smooth, convex, constrained problem in twice as many variables (adding the “added variables” $u\_k$) \[\min\_{\beta,u} L(\beta) + \sum\_k\alpha\_k u\_k,\] subject to \[-u\_k \leq \beta\_k \leq u\_k.\] With $\partial\_k L$ the derivative of $L$ in the $k^{th}$ parameter direction, theory dictates that, at the minimum, exactly one of two conditions holds: 1. $\|\partial\_k L\| = \alpha\_k$ and $\beta\_k \neq 0$ 2. $\|\partial\_k L\| \leq \alpha\_k$ and $\beta\_k = 0$ statsmodels statsmodels.sandbox.distributions.transformed.SquareFunc.derivminus statsmodels.sandbox.distributions.transformed.SquareFunc.derivminus =================================================================== `SquareFunc.derivminus(x)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/distributions/transformed.html#SquareFunc.derivminus) statsmodels statsmodels.genmod.cov_struct.GlobalOddsRatio.get_eyy statsmodels.genmod.cov\_struct.GlobalOddsRatio.get\_eyy ======================================================= `GlobalOddsRatio.get_eyy(endog_expval, index)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/cov_struct.html#GlobalOddsRatio.get_eyy) Returns a matrix V such that V[i,j] is the joint probability that endog[i] = 1 and endog[j] = 1, based on the marginal probabilities of endog and the global odds ratio `current_or`. statsmodels statsmodels.regression.mixed_linear_model.MixedLMResults.wald_test_terms statsmodels.regression.mixed\_linear\_model.MixedLMResults.wald\_test\_terms ============================================================================ `MixedLMResults.wald_test_terms(skip_single=False, extra_constraints=None, combine_terms=None)` Compute a sequence of Wald tests for terms over multiple columns This computes joined Wald tests for the hypothesis that all coefficients corresponding to a `term` are zero. `Terms` are defined by the underlying formula or by string matching. \| Parameters: \| * skip\_single (boolean) – If true, then terms that consist only of a single column and, therefore, refers only to a single parameter is skipped. If false, then all terms are included. * extra\_constraints (ndarray) – not tested yet * combine\_terms (None or list of strings) – Each string in this list is matched to the name of the terms or the name of the exogenous variables. All columns whose name includes that string are combined in one joint test. \| \| Returns: \| test\_result – The result instance contains `table` which is a pandas DataFrame with the test results: test statistic, degrees of freedom and pvalues. \| \| Return type: \| result instance \| #### Examples ``` >>> res_ols = ols("np.log(Days+1) ~ C(Duration, Sum)C(Weight, Sum)", data).fit() >>> res_ols.wald_test_terms() <class 'statsmodels.stats.contrast.WaldTestResults'> F P>F df constraint df denom Intercept 279.754525 2.37985521351e-22 1 51 C(Duration, Sum) 5.367071 0.0245738436636 1 51 C(Weight, Sum) 12.432445 3.99943118767e-05 2 51 C(Duration, Sum):C(Weight, Sum) 0.176002 0.83912310946 2 51 ``` ``` >>> res_poi = Poisson.from_formula("Days ~ C(Weight) C(Duration)", data).fit(cov_type='HC0') >>> wt = res_poi.wald_test_terms(skip_single=False, combine_terms=['Duration', 'Weight']) >>> print(wt) chi2 P>chi2 df constraint Intercept 15.695625 7.43960374424e-05 1 C(Weight) 16.132616 0.000313940174705 2 C(Duration) 1.009147 0.315107378931 1 C(Weight):C(Duration) 0.216694 0.897315972824 2 Duration 11.187849 0.010752286833 3 Weight 30.263368 4.32586407145e-06 4 ``` statsmodels statsmodels.regression.linear_model.OLSResults.fvalue statsmodels.regression.linear\_model.OLSResults.fvalue ====================================================== `OLSResults.fvalue()` statsmodels statsmodels.sandbox.regression.gmm.IVGMMResults.t_test statsmodels.sandbox.regression.gmm.IVGMMResults.t\_test ======================================================= `IVGMMResults.t_test(r_matrix, cov_p=None, scale=None, use_t=None)` Compute a t-test for a each linear hypothesis of the form Rb = q \| Parameters: \| * r\_matrix (array-like, str, tuple) – + array : If an array is given, a p x k 2d array or length k 1d array specifying the linear restrictions. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q). If q is given, can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – An optional `scale` to use. Default is the scale specified by the model fit. * use\_t (bool, optional) – If use\_t is None, then the default of the model is used. If use\_t is True, then the p-values are based on the t distribution. If use\_t is False, then the p-values are based on the normal distribution. \| \| Returns: \| res – The results for the test are attributes of this results instance. The available results have the same elements as the parameter table in `summary()`. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> r = np.zeros_like(results.params) >>> r[5:] = [1,-1] >>> print(r) [ 0. 0. 0. 0. 0. 1. -1.] ``` r tests that the coefficients on the 5th and 6th independent variable are the same. ``` >>> T_test = results.t_test(r) >>> print(T_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 -1829.2026 455.391 -4.017 0.003 -2859.368 -799.037 ============================================================================== >>> T_test.effect -1829.2025687192481 >>> T_test.sd 455.39079425193762 >>> T_test.tvalue -4.0167754636411717 >>> T_test.pvalue 0.0015163772380899498 ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.formula.api import ols >>> dta = sm.datasets.longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = 'GNPDEFL = GNP, UNEMP = 2, YEAR/1829 = 1' >>> t_test = results.t_test(hypotheses) >>> print(t_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 15.0977 84.937 0.178 0.863 -177.042 207.238 c1 -2.0202 0.488 -8.231 0.000 -3.125 -0.915 c2 1.0001 0.249 0.000 1.000 0.437 1.563 ============================================================================== ``` See also [`tvalues`](statsmodels.sandbox.regression.gmm.ivgmmresults.tvalues#statsmodels.sandbox.regression.gmm.IVGMMResults.tvalues "statsmodels.sandbox.regression.gmm.IVGMMResults.tvalues") individual t statistics [`f_test`](statsmodels.sandbox.regression.gmm.ivgmmresults.f_test#statsmodels.sandbox.regression.gmm.IVGMMResults.f_test "statsmodels.sandbox.regression.gmm.IVGMMResults.f_test") for F tests [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") statsmodels statsmodels.tsa.arima_process.ArmaProcess.acovf statsmodels.tsa.arima\_process.ArmaProcess.acovf ================================================ `ArmaProcess.acovf(nobs=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_process.html#ArmaProcess.acovf) Theoretical autocovariance function of ARMA process \| Parameters: \| * ar (array\_like, 1d) – coefficient for autoregressive lag polynomial, including zero lag * ma (array\_like, 1d) – coefficient for moving-average lag polynomial, including zero lag * nobs (int) – number of terms (lags plus zero lag) to include in returned acovf \| \| Returns: \| acovf – autocovariance of ARMA process given by ar, ma \| \| Return type: \| array \| See also [`arma_acf`](statsmodels.tsa.arima_process.arma_acf#statsmodels.tsa.arima_process.arma_acf "statsmodels.tsa.arima_process.arma_acf"), [`acovf`](#statsmodels.tsa.arima_process.ArmaProcess.acovf "statsmodels.tsa.arima_process.ArmaProcess.acovf") #### Notes Tries to do some crude numerical speed improvements for cases with high persistence. However, this algorithm is slow if the process is highly persistent and only a few autocovariances are desired.	programming_docs
statsmodels statsmodels.genmod.generalized_linear_model.GLM.information statsmodels.genmod.generalized\_linear\_model.GLM.information ============================================================= `GLM.information(params, scale=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_linear_model.html#GLM.information) Fisher information matrix. statsmodels statsmodels.discrete.count_model.ZeroInflatedGeneralizedPoisson.loglike statsmodels.discrete.count\_model.ZeroInflatedGeneralizedPoisson.loglike ======================================================================== `ZeroInflatedGeneralizedPoisson.loglike(params)` Loglikelihood of Generic Zero Inflated model \| Parameters: \| params (array-like) – The parameters of the model. \| \| Returns: \| loglike – The log-likelihood function of the model evaluated at `params`. See notes. \| \| Return type: \| float \| #### Notes \[\ln L=\sum\_{y\_{i}=0}\ln(w\_{i}+(1-w\_{i})\P\_{main\\_model})+ \sum\_{y\_{i}>0}(\ln(1-w\_{i})+L\_{main\\_model}) where P - pdf of main model, L - loglike function of main model.\] statsmodels statsmodels.discrete.discrete_model.GeneralizedPoissonResults.save statsmodels.discrete.discrete\_model.GeneralizedPoissonResults.save =================================================================== `GeneralizedPoissonResults.save(fname, remove_data=False)` save a pickle of this instance \| Parameters: \| fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. * remove\_data (bool) – If False (default), then the instance is pickled without changes. If True, then all arrays with length nobs are set to None before pickling. See the remove\_data method. In some cases not all arrays will be set to None. \| #### Notes If remove\_data is true and the model result does not implement a remove\_data method then this will raise an exception. statsmodels statsmodels.robust.robust_linear_model.RLM.fit statsmodels.robust.robust\_linear\_model.RLM.fit ================================================ `RLM.fit(maxiter=50, tol=1e-08, scale_est='mad', init=None, cov='H1', update_scale=True, conv='dev')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/robust_linear_model.html#RLM.fit) Fits the model using iteratively reweighted least squares. The IRLS routine runs until the specified objective converges to `tol` or `maxiter` has been reached. \| Parameters: \| * conv (string) – Indicates the convergence criteria. Available options are “coefs” (the coefficients), “weights” (the weights in the iteration), “sresid” (the standardized residuals), and “dev” (the un-normalized log-likelihood for the M estimator). The default is “dev”. * cov (string, optional) – ‘H1’, ‘H2’, or ‘H3’ Indicates how the covariance matrix is estimated. Default is ‘H1’. See rlm.RLMResults for more information. * init (string) – Specifies method for the initial estimates of the parameters. Default is None, which means that the least squares estimate is used. Currently it is the only available choice. * maxiter (int) – The maximum number of iterations to try. Default is 50. * scale\_est (string or [HuberScale](statsmodels.robust.scale.huberscale#statsmodels.robust.scale.HuberScale "statsmodels.robust.scale.HuberScale")()) – ‘mad’ or HuberScale() Indicates the estimate to use for scaling the weights in the IRLS. The default is ‘mad’ (median absolute deviation. Other options are ‘HuberScale’ for Huber’s proposal 2. Huber’s proposal 2 has optional keyword arguments d, tol, and maxiter for specifying the tuning constant, the convergence tolerance, and the maximum number of iterations. See statsmodels.robust.scale for more information. * tol (float) – The convergence tolerance of the estimate. Default is 1e-8. * update\_scale (Bool) – If `update_scale` is False then the scale estimate for the weights is held constant over the iteration. Otherwise, it is updated for each fit in the iteration. Default is True. \| \| Returns: \| results – statsmodels.rlm.RLMresults \| \| Return type: \| object \| statsmodels statsmodels.stats.outliers_influence.OLSInfluence.influence statsmodels.stats.outliers\_influence.OLSInfluence.influence ============================================================ `OLSInfluence.influence()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/outliers_influence.html#OLSInfluence.influence) (cached attribute) influence measure matches the influence measure that gretl reports u \* h / (1 - h) where u are the residuals and h is the diagonal of the hat\_matrix statsmodels statsmodels.robust.norms.Hampel.weights statsmodels.robust.norms.Hampel.weights ======================================= `Hampel.weights(z)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/norms.html#Hampel.weights) Hampel weighting function for the IRLS algorithm The psi function scaled by z \| Parameters: \| z (array-like) – 1d array \| \| Returns: \| weights – weights(z) = 1 for \|z\| <= aweights(z) = a/\|z\| for a < \|z\| <= b weights(z) = a\(c - \|z\|)/(\|z\|\(c-b)) for b < \|z\| <= c weights(z) = 0 for \|z\| > c \| \| Return type: \| array \| statsmodels statsmodels.stats.outliers_influence.OLSInfluence.get_resid_studentized_external statsmodels.stats.outliers\_influence.OLSInfluence.get\_resid\_studentized\_external ==================================================================================== `OLSInfluence.get_resid_studentized_external(sigma=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/outliers_influence.html#OLSInfluence.get_resid_studentized_external) calculate studentized residuals \| Parameters: \| sigma (None or float) – estimate of the standard deviation of the residuals. If None, then the estimate from the regression results is used. \| \| Returns: \| stzd\_resid – studentized residuals \| \| Return type: \| ndarray \| #### Notes studentized residuals are defined as ``` resid / sigma / np.sqrt(1 - hii) ``` where resid are the residuals from the regression, sigma is an estimate of the standard deviation of the residuals, and hii is the diagonal of the hat\_matrix. statsmodels statsmodels.tsa.vector_ar.vecm.VECMResults.var_rep statsmodels.tsa.vector\_ar.vecm.VECMResults.var\_rep ==================================================== `VECMResults.var_rep()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/vecm.html#VECMResults.var_rep) statsmodels statsmodels.sandbox.tsa.fftarma.ArmaFft.spdpoly statsmodels.sandbox.tsa.fftarma.ArmaFft.spdpoly =============================================== `ArmaFft.spdpoly(w, nma=50)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/tsa/fftarma.html#ArmaFft.spdpoly) spectral density from MA polynomial representation for ARMA process #### References Cochrane, section 8.3.3 statsmodels statsmodels.sandbox.distributions.extras.mvnormcdf statsmodels.sandbox.distributions.extras.mvnormcdf ================================================== `statsmodels.sandbox.distributions.extras.mvnormcdf(upper, mu, cov, lower=None, *kwds)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/distributions/extras.html#mvnormcdf) multivariate normal cumulative distribution function This is a wrapper for scipy.stats.kde.mvn.mvndst which calculates a rectangular integral over a multivariate normal distribution. \| Parameters: \| upper (lower,) – lower and upper integration limits with length equal to the number of dimensions of the multivariate normal distribution. It can contain -np.inf or np.inf for open integration intervals * mu (array\_lik, 1d) – list or array of means * cov (array\_like, 2d) – specifies covariance matrix * keyword parameters to influence integration (optional) – + `maxpts : int, maximum number of function values allowed. This` parameter can be used to limit the time. A sensible strategy is to start with `maxpts` = 1000\N, and then increase `maxpts` if ERROR is too large. + abseps : float absolute error tolerance. + releps : float relative error tolerance. \| \| Returns: \| cdfvalue* – value of the integral \| \| Return type: \| float \| #### Notes This function normalizes the location and scale of the multivariate normal distribution and then uses `mvstdnormcdf` to call the integration. See also [`mvstdnormcdf`](statsmodels.sandbox.distributions.extras.mvstdnormcdf#statsmodels.sandbox.distributions.extras.mvstdnormcdf "statsmodels.sandbox.distributions.extras.mvstdnormcdf") location and scale standardized multivariate normal cdf statsmodels statsmodels.miscmodels.count.PoissonOffsetGMLE.nloglike statsmodels.miscmodels.count.PoissonOffsetGMLE.nloglike ======================================================= `PoissonOffsetGMLE.nloglike(params)` statsmodels statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.score_obs statsmodels.discrete.count\_model.ZeroInflatedNegativeBinomialP.score\_obs ========================================================================== `ZeroInflatedNegativeBinomialP.score_obs(params)` Generic Zero Inflated model score (gradient) vector of the log-likelihood \| Parameters: \| params (array-like) – The parameters of the model \| \| Returns: \| score – The score vector of the model, i.e. the first derivative of the loglikelihood function, evaluated at `params` \| \| Return type: \| ndarray, 1-D \| statsmodels statsmodels.tsa.arima_process.arma_pacf statsmodels.tsa.arima\_process.arma\_pacf ========================================= `statsmodels.tsa.arima_process.arma_pacf(ar, ma, lags=10, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_process.html#arma_pacf) Partial autocorrelation function of an ARMA process \| Parameters: \| ar (array\_like, 1d) – coefficient for autoregressive lag polynomial, including zero lag * ma (array\_like, 1d) – coefficient for moving-average lag polynomial, including zero lag * lags (int) – number of terms (lags plus zero lag) to include in returned pacf \| \| Returns: \| pacf – partial autocorrelation of ARMA process given by ar, ma \| \| Return type: \| array \| #### Notes solves yule-walker equation for each lag order up to nobs lags not tested/checked yet statsmodels statsmodels.stats.correlation_tools.cov_nearest statsmodels.stats.correlation\_tools.cov\_nearest ================================================= `statsmodels.stats.correlation_tools.cov_nearest(cov, method='clipped', threshold=1e-15, n_fact=100, return_all=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/correlation_tools.html#cov_nearest) Find the nearest covariance matrix that is postive (semi-) definite This leaves the diagonal, i.e. the variance, unchanged \| Parameters: \| * cov (ndarray, (k,k)) – initial covariance matrix * method (string) – if “clipped”, then the faster but less accurate `corr_clipped` is used. if “nearest”, then `corr_nearest` is used * threshold (float) – clipping threshold for smallest eigen value, see Notes * nfact (int or float) – factor to determine the maximum number of iterations in `corr_nearest`. See its doc string * return\_all (bool) – if False (default), then only the covariance matrix is returned. If True, then correlation matrix and standard deviation are additionally returned. \| \| Returns: \| * cov\_ (ndarray) – corrected covariance matrix * corr\_ (ndarray, (optional)) – corrected correlation matrix * std\_ (ndarray, (optional)) – standard deviation \| #### Notes This converts the covariance matrix to a correlation matrix. Then, finds the nearest correlation matrix that is positive semidefinite and converts it back to a covariance matrix using the initial standard deviation. The smallest eigenvalue of the intermediate correlation matrix is approximately equal to the `threshold`. If the threshold=0, then the smallest eigenvalue of the correlation matrix might be negative, but zero within a numerical error, for example in the range of -1e-16. Assumes input covariance matrix is symmetric. See also [`corr_nearest`](statsmodels.stats.correlation_tools.corr_nearest#statsmodels.stats.correlation_tools.corr_nearest "statsmodels.stats.correlation_tools.corr_nearest"), [`corr_clipped`](statsmodels.stats.correlation_tools.corr_clipped#statsmodels.stats.correlation_tools.corr_clipped "statsmodels.stats.correlation_tools.corr_clipped") statsmodels statsmodels.genmod.generalized_estimating_equations.GEEResults.f_test statsmodels.genmod.generalized\_estimating\_equations.GEEResults.f\_test ======================================================================== `GEEResults.f_test(r_matrix, cov_p=None, scale=1.0, invcov=None)` Compute the F-test for a joint linear hypothesis. This is a special case of `wald_test` that always uses the F distribution. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length k row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> A = np.identity(len(results.params)) >>> A = A[1:,:] ``` This tests that each coefficient is jointly statistically significantly different from zero. ``` >>> print(results.f_test(A)) <F test: F=array([[ 330.28533923]]), p=4.984030528700946e-10, df_denom=9, df_num=6> ``` Compare this to ``` >>> results.fvalue 330.2853392346658 >>> results.f_pvalue 4.98403096572e-10 ``` ``` >>> B = np.array(([0,0,1,-1,0,0,0],[0,0,0,0,0,1,-1])) ``` This tests that the coefficient on the 2nd and 3rd regressors are equal and jointly that the coefficient on the 5th and 6th regressors are equal. ``` >>> print(results.f_test(B)) <F test: F=array([[ 9.74046187]]), p=0.005605288531708235, df_denom=9, df_num=2> ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.datasets import longley >>> from statsmodels.formula.api import ols >>> dta = longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = '(GNPDEFL = GNP), (UNEMP = 2), (YEAR/1829 = 1)' >>> f_test = results.f_test(hypotheses) >>> print(f_test) <F test: F=array([[ 144.17976065]]), p=6.322026217355609e-08, df_denom=9, df_num=3> ``` See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`wald_test`](statsmodels.genmod.generalized_estimating_equations.geeresults.wald_test#statsmodels.genmod.generalized_estimating_equations.GEEResults.wald_test "statsmodels.genmod.generalized_estimating_equations.GEEResults.wald_test"), [`t_test`](statsmodels.genmod.generalized_estimating_equations.geeresults.t_test#statsmodels.genmod.generalized_estimating_equations.GEEResults.t_test "statsmodels.genmod.generalized_estimating_equations.GEEResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.sandbox.distributions.transformed.LogTransf_gen.rvs statsmodels.sandbox.distributions.transformed.LogTransf\_gen.rvs ================================================================ `LogTransf_gen.rvs(args, kwds)` Random variates of given type. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information). * loc (array\_like, optional) – Location parameter (default=0). * scale (array\_like, optional) – Scale parameter (default=1). * size (int or tuple of ints, optional) – Defining number of random variates (default is 1). * random\_state (None or int or `np.random.RandomState` instance, optional) – If int or RandomState, use it for drawing the random variates. If None, rely on `self.random_state`. Default is None. \| \| Returns: \| rvs – Random variates of given `size`. \| \| Return type: \| ndarray or scalar \| statsmodels statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.get_margeff statsmodels.discrete.count\_model.ZeroInflatedNegativeBinomialResults.get\_margeff ================================================================================== `ZeroInflatedNegativeBinomialResults.get_margeff(at='overall', method='dydx', atexog=None, dummy=False, count=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/count_model.html#ZeroInflatedNegativeBinomialResults.get_margeff) Get marginal effects of the fitted model. Not yet implemented for Zero Inflated Models statsmodels statsmodels.stats.sandwich_covariance.cov_hc3 statsmodels.stats.sandwich\_covariance.cov\_hc3 =============================================== `statsmodels.stats.sandwich_covariance.cov_hc3(results)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/sandwich_covariance.html#cov_hc3) See statsmodels.RegressionResults statsmodels statsmodels.sandbox.regression.gmm.IVRegressionResults.mse_model statsmodels.sandbox.regression.gmm.IVRegressionResults.mse\_model ================================================================= `IVRegressionResults.mse_model()` statsmodels statsmodels.miscmodels.count.PoissonZiGMLE.information statsmodels.miscmodels.count.PoissonZiGMLE.information ====================================================== `PoissonZiGMLE.information(params)` Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.sandbox.distributions.extras.mvstdnormcdf statsmodels.sandbox.distributions.extras.mvstdnormcdf ===================================================== `statsmodels.sandbox.distributions.extras.mvstdnormcdf(lower, upper, corrcoef, *kwds)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/distributions/extras.html#mvstdnormcdf) standardized multivariate normal cumulative distribution function This is a wrapper for scipy.stats.kde.mvn.mvndst which calculates a rectangular integral over a standardized multivariate normal distribution. This function assumes standardized scale, that is the variance in each dimension is one, but correlation can be arbitrary, covariance = correlation matrix \| Parameters: \| upper (lower,) – lower and upper integration limits with length equal to the number of dimensions of the multivariate normal distribution. It can contain -np.inf or np.inf for open integration intervals * corrcoef (float or array\_like) – specifies correlation matrix in one of three ways, see notes * keyword parameters to influence integration (optional) – + `maxpts : int, maximum number of function values allowed. This` parameter can be used to limit the time. A sensible strategy is to start with `maxpts` = 1000\N, and then increase `maxpts` if ERROR is too large. + abseps : float absolute error tolerance. + releps : float relative error tolerance. \| \| Returns: \| cdfvalue* – value of the integral \| \| Return type: \| float \| #### Notes The correlation matrix corrcoef can be given in 3 different ways If the multivariate normal is two-dimensional than only the correlation coefficient needs to be provided. For general dimension the correlation matrix can be provided either as a one-dimensional array of the upper triangular correlation coefficients stacked by rows, or as full square correlation matrix See also [`mvnormcdf`](statsmodels.sandbox.distributions.extras.mvnormcdf#statsmodels.sandbox.distributions.extras.mvnormcdf "statsmodels.sandbox.distributions.extras.mvnormcdf") cdf of multivariate normal distribution without standardization #### Examples ``` >>> print(mvstdnormcdf([-np.inf,-np.inf], [0.0,np.inf], 0.5)) 0.5 >>> corr = [[1.0, 0, 0.5],[0,1,0],[0.5,0,1]] >>> print(mvstdnormcdf([-np.inf,-np.inf,-100.0], [0.0,0.0,0.0], corr, abseps=1e-6)) 0.166666399198 >>> print(mvstdnormcdf([-np.inf,-np.inf,-100.0],[0.0,0.0,0.0],corr, abseps=1e-8)) something wrong completion with ERROR > EPS and MAXPTS function values used; increase MAXPTS to decrease ERROR; 1.048330348e-006 0.166666546218 >>> print(mvstdnormcdf([-np.inf,-np.inf,-100.0],[0.0,0.0,0.0], corr, maxpts=100000, abseps=1e-8)) 0.166666588293 ```	programming_docs
statsmodels statsmodels.tsa.vector_ar.dynamic.DynamicVAR.plot_forecast statsmodels.tsa.vector\_ar.dynamic.DynamicVAR.plot\_forecast ============================================================ `DynamicVAR.plot_forecast(steps=1, figsize=(10, 10))` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/dynamic.html#DynamicVAR.plot_forecast) Plot h-step ahead forecasts against actual realizations of time series. Note that forecasts are lined up with their respective realizations. \| Parameters: \| steps – \| statsmodels statsmodels.tsa.stattools.pacf_yw statsmodels.tsa.stattools.pacf\_yw ================================== `statsmodels.tsa.stattools.pacf_yw(x, nlags=40, method='unbiased')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/stattools.html#pacf_yw) Partial autocorrelation estimated with non-recursive yule\_walker \| Parameters: \| * x (1d array) – observations of time series for which pacf is calculated * nlags (int) – largest lag for which pacf is returned * method ('unbiased' (default) or 'mle') – method for the autocovariance calculations in yule walker \| \| Returns: \| pacf – partial autocorrelations, maxlag+1 elements \| \| Return type: \| 1d array \| #### Notes This solves yule\_walker for each desired lag and contains currently duplicate calculations. statsmodels statsmodels.nonparametric.kernel_regression.KernelReg statsmodels.nonparametric.kernel\_regression.KernelReg ====================================================== `class statsmodels.nonparametric.kernel_regression.KernelReg(endog, exog, var_type, reg_type='ll', bw='cv_ls', defaults=<statsmodels.nonparametric._kernel_base.EstimatorSettings object>)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/nonparametric/kernel_regression.html#KernelReg) Nonparametric kernel regression class. Calculates the conditional mean `E[y\|X]` where `y = g(X) + e`. Note that the “local constant” type of regression provided here is also known as Nadaraya-Watson kernel regression; “local linear” is an extension of that which suffers less from bias issues at the edge of the support. \| Parameters: \| * endog (list with one element which is array\_like) – This is the dependent variable. * exog (list) – The training data for the independent variable(s) Each element in the list is a separate variable * var\_type (str) – The type of the variables, one character per variable: + c: continuous + u: unordered (discrete) + o: ordered (discrete) * reg\_type ({'lc', 'll'}, optional) – Type of regression estimator. ‘lc’ means local constant and ‘ll’ local Linear estimator. Default is ‘ll’ * bw (str or array\_like, optional) – Either a user-specified bandwidth or the method for bandwidth selection. If a string, valid values are ‘cv\_ls’ (least-squares cross-validation) and ‘aic’ (AIC Hurvich bandwidth estimation). Default is ‘cv\_ls’. * defaults (EstimatorSettings instance, optional) – The default values for the efficient bandwidth estimation. \| `bw` array\_like – The bandwidth parameters. #### Methods \| \| \| \| --- \| --- \| \| [`aic_hurvich`](statsmodels.nonparametric.kernel_regression.kernelreg.aic_hurvich#statsmodels.nonparametric.kernel_regression.KernelReg.aic_hurvich "statsmodels.nonparametric.kernel_regression.KernelReg.aic_hurvich")(bw[, func]) \| Computes the AIC Hurvich criteria for the estimation of the bandwidth. \| \| [`cv_loo`](statsmodels.nonparametric.kernel_regression.kernelreg.cv_loo#statsmodels.nonparametric.kernel_regression.KernelReg.cv_loo "statsmodels.nonparametric.kernel_regression.KernelReg.cv_loo")(bw, func) \| The cross-validation function with leave-one-out estimator. \| \| [`fit`](statsmodels.nonparametric.kernel_regression.kernelreg.fit#statsmodels.nonparametric.kernel_regression.KernelReg.fit "statsmodels.nonparametric.kernel_regression.KernelReg.fit")([data\_predict]) \| Returns the mean and marginal effects at the `data_predict` points. \| \| [`loo_likelihood`](statsmodels.nonparametric.kernel_regression.kernelreg.loo_likelihood#statsmodels.nonparametric.kernel_regression.KernelReg.loo_likelihood "statsmodels.nonparametric.kernel_regression.KernelReg.loo_likelihood")() \| \| \| [`r_squared`](statsmodels.nonparametric.kernel_regression.kernelreg.r_squared#statsmodels.nonparametric.kernel_regression.KernelReg.r_squared "statsmodels.nonparametric.kernel_regression.KernelReg.r_squared")() \| Returns the R-Squared for the nonparametric regression. \| \| [`sig_test`](statsmodels.nonparametric.kernel_regression.kernelreg.sig_test#statsmodels.nonparametric.kernel_regression.KernelReg.sig_test "statsmodels.nonparametric.kernel_regression.KernelReg.sig_test")(var\_pos[, nboot, nested\_res, pivot]) \| Significance test for the variables in the regression. \| statsmodels statsmodels.robust.robust_linear_model.RLMResults.wald_test statsmodels.robust.robust\_linear\_model.RLMResults.wald\_test ============================================================== `RLMResults.wald_test(r_matrix, cov_p=None, scale=1.0, invcov=None, use_f=None)` Compute a Wald-test for a joint linear hypothesis. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. * use\_f (bool) – If True, then the F-distribution is used. If False, then the asymptotic distribution, chisquare is used. If use\_f is None, then the F distribution is used if the model specifies that use\_t is True. The test statistic is proportionally adjusted for the distribution by the number of constraints in the hypothesis. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`f_test`](statsmodels.robust.robust_linear_model.rlmresults.f_test#statsmodels.robust.robust_linear_model.RLMResults.f_test "statsmodels.robust.robust_linear_model.RLMResults.f_test"), [`t_test`](statsmodels.robust.robust_linear_model.rlmresults.t_test#statsmodels.robust.robust_linear_model.RLMResults.t_test "statsmodels.robust.robust_linear_model.RLMResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.sandbox.regression.gmm.IVRegressionResults.summary2 statsmodels.sandbox.regression.gmm.IVRegressionResults.summary2 =============================================================== `IVRegressionResults.summary2(yname=None, xname=None, title=None, alpha=0.05, float_format='%.4f')` Experimental summary function to summarize the regression results \| Parameters: \| * xname (List of strings of length equal to the number of parameters) – Names of the independent variables (optional) * yname (string) – Name of the dependent variable (optional) * title (string, optional) – Title for the top table. If not None, then this replaces the default title * alpha (float) – significance level for the confidence intervals * float\_format (string) – print format for floats in parameters summary \| \| Returns: \| smry – this holds the summary tables and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary.Summary`](statsmodels.iolib.summary.summary#statsmodels.iolib.summary.Summary "statsmodels.iolib.summary.Summary") class to hold summary results statsmodels statsmodels.tsa.statespace.structural.UnobservedComponents.transform_jacobian statsmodels.tsa.statespace.structural.UnobservedComponents.transform\_jacobian ============================================================================== `UnobservedComponents.transform_jacobian(unconstrained, approx_centered=False)` Jacobian matrix for the parameter transformation function \| Parameters: \| unconstrained (array\_like) – Array of unconstrained parameters used by the optimizer. \| \| Returns: \| jacobian – Jacobian matrix of the transformation, evaluated at `unconstrained` \| \| Return type: \| array \| #### Notes This is a numerical approximation using finite differences. Note that in general complex step methods cannot be used because it is not guaranteed that the `transform_params` method is a real function (e.g. if Cholesky decomposition is used). See also [`transform_params`](statsmodels.tsa.statespace.structural.unobservedcomponents.transform_params#statsmodels.tsa.statespace.structural.UnobservedComponents.transform_params "statsmodels.tsa.statespace.structural.UnobservedComponents.transform_params") statsmodels statsmodels.genmod.families.links.Logit statsmodels.genmod.families.links.Logit ======================================= `class statsmodels.genmod.families.links.Logit` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#Logit) The logit transform #### Notes call and derivative use a private method \_clean to make trim p by machine epsilon so that p is in (0,1) Alias of Logit: logit = Logit() #### Methods \| \| \| \| --- \| --- \| \| [`deriv`](statsmodels.genmod.families.links.logit.deriv#statsmodels.genmod.families.links.Logit.deriv "statsmodels.genmod.families.links.Logit.deriv")(p) \| Derivative of the logit transform \| \| [`deriv2`](statsmodels.genmod.families.links.logit.deriv2#statsmodels.genmod.families.links.Logit.deriv2 "statsmodels.genmod.families.links.Logit.deriv2")(p) \| Second derivative of the logit function. \| \| [`inverse`](statsmodels.genmod.families.links.logit.inverse#statsmodels.genmod.families.links.Logit.inverse "statsmodels.genmod.families.links.Logit.inverse")(z) \| Inverse of the logit transform \| \| [`inverse_deriv`](statsmodels.genmod.families.links.logit.inverse_deriv#statsmodels.genmod.families.links.Logit.inverse_deriv "statsmodels.genmod.families.links.Logit.inverse_deriv")(z) \| Derivative of the inverse of the logit transform \| statsmodels statsmodels.tsa.statespace.varmax.VARMAX.transform_jacobian statsmodels.tsa.statespace.varmax.VARMAX.transform\_jacobian ============================================================ `VARMAX.transform_jacobian(unconstrained, approx_centered=False)` Jacobian matrix for the parameter transformation function \| Parameters: \| unconstrained (array\_like) – Array of unconstrained parameters used by the optimizer. \| \| Returns: \| jacobian – Jacobian matrix of the transformation, evaluated at `unconstrained` \| \| Return type: \| array \| #### Notes This is a numerical approximation using finite differences. Note that in general complex step methods cannot be used because it is not guaranteed that the `transform_params` method is a real function (e.g. if Cholesky decomposition is used). See also [`transform_params`](statsmodels.tsa.statespace.varmax.varmax.transform_params#statsmodels.tsa.statespace.varmax.VARMAX.transform_params "statsmodels.tsa.statespace.varmax.VARMAX.transform_params") statsmodels statsmodels.sandbox.regression.gmm.IVGMMResults.tvalues statsmodels.sandbox.regression.gmm.IVGMMResults.tvalues ======================================================= `IVGMMResults.tvalues()` Return the t-statistic for a given parameter estimate. statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.tvalues_dt statsmodels.tsa.vector\_ar.var\_model.VARResults.tvalues\_dt ============================================================ `VARResults.tvalues_dt()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARResults.tvalues_dt) statsmodels statsmodels.discrete.count_model.ZeroInflatedGeneralizedPoisson.cov_params_func_l1 statsmodels.discrete.count\_model.ZeroInflatedGeneralizedPoisson.cov\_params\_func\_l1 ====================================================================================== `ZeroInflatedGeneralizedPoisson.cov_params_func_l1(likelihood_model, xopt, retvals)` Computes cov\_params on a reduced parameter space corresponding to the nonzero parameters resulting from the l1 regularized fit. Returns a full cov\_params matrix, with entries corresponding to zero’d values set to np.nan. statsmodels statsmodels.stats.contingency_tables.Table2x2.marginal_probabilities statsmodels.stats.contingency\_tables.Table2x2.marginal\_probabilities ====================================================================== `Table2x2.marginal_probabilities()` statsmodels statsmodels.regression.recursive_ls.RecursiveLS.update statsmodels.regression.recursive\_ls.RecursiveLS.update ======================================================= `RecursiveLS.update(params, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/recursive_ls.html#RecursiveLS.update) Update the parameters of the model Updates the representation matrices to fill in the new parameter values. \| Parameters: \| params (array\_like) – Array of new parameters. * transformed (boolean, optional) – Whether or not `params` is already transformed. If set to False, `transform_params` is called. Default is True.. \| \| Returns: \| params – Array of parameters. \| \| Return type: \| array\_like \| statsmodels statsmodels.tsa.statespace.sarimax.SARIMAXResults.maroots statsmodels.tsa.statespace.sarimax.SARIMAXResults.maroots ========================================================= `SARIMAXResults.maroots()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/sarimax.html#SARIMAXResults.maroots) (array) Roots of the reduced form moving average lag polynomial statsmodels statsmodels.tsa.vector_ar.irf.IRAnalysis.plot statsmodels.tsa.vector\_ar.irf.IRAnalysis.plot ============================================== `IRAnalysis.plot(orth=False, impulse=None, response=None, signif=0.05, plot_params=None, subplot_params=None, plot_stderr=True, stderr_type='asym', repl=1000, seed=None, component=None)` Plot impulse responses \| Parameters: \| * orth (bool, default False) – Compute orthogonalized impulse responses * impulse (string or int) – variable providing the impulse * response (string or int) – variable affected by the impulse * signif (float (0 < signif < 1)) – Significance level for error bars, defaults to 95% CI * subplot\_params ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)")) – To pass to subplot plotting funcions. Example: if fonts are too big, pass {‘fontsize’ : 8} or some number to your taste. * plot\_params ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)")) – * plot\_stderr (bool, default True) – Plot standard impulse response error bands * stderr\_type (string) – ‘asym’: default, computes asymptotic standard errors ‘mc’: monte carlo standard errors (use rpl) * repl (int, default 1000) – Number of replications for Monte Carlo and Sims-Zha standard errors * seed (int) – np.random.seed for Monte Carlo replications * component (array or vector of principal component indices) – \| statsmodels statsmodels.genmod.families.family.Binomial.fitted statsmodels.genmod.families.family.Binomial.fitted ================================================== `Binomial.fitted(lin_pred)` Fitted values based on linear predictors lin\_pred. \| Parameters: \| lin\_pred (array) – Values of the linear predictor of the model. $X \cdot \beta$ in a classical linear model. \| \| Returns: \| mu – The mean response variables given by the inverse of the link function. \| \| Return type: \| array \| statsmodels statsmodels.tsa.vector_ar.var_model.VARProcess.long_run_effects statsmodels.tsa.vector\_ar.var\_model.VARProcess.long\_run\_effects =================================================================== `VARProcess.long_run_effects()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARProcess.long_run_effects) Compute long-run effect of unit impulse \[\Psi\_\infty = \sum\_{i=0}^\infty \Phi\_i\] statsmodels statsmodels.discrete.discrete_model.LogitResults.t_test_pairwise statsmodels.discrete.discrete\_model.LogitResults.t\_test\_pairwise =================================================================== `LogitResults.t_test_pairwise(term_name, method='hs', alpha=0.05, factor_labels=None)` perform pairwise t\_test with multiple testing corrected p-values This uses the formula design\_info encoding contrast matrix and should work for all encodings of a main effect. \| Parameters: \| * result (result instance) – The results of an estimated model with a categorical main effect. * term\_name (str) – name of the term for which pairwise comparisons are computed. Term names for categorical effects are created by patsy and correspond to the main part of the exog names. * method (str or list of strings) – multiple testing p-value correction, default is ‘hs’, see stats.multipletesting * alpha (float) – significance level for multiple testing reject decision. * factor\_labels (None, list of str) – Labels for the factor levels used for pairwise labels. If not provided, then the labels from the formula design\_info are used. \| \| Returns: \| results – The results are stored as attributes, the main attributes are the following two. Other attributes are added for debugging purposes or as background information.* result\_frame : pandas DataFrame with t\_test results and multiple testing corrected p-values. * contrasts : matrix of constraints of the null hypothesis in the t\_test. \| \| Return type: \| instance of a simple Results class \| #### Notes Status: experimental. Currently only checked for treatment coding with and without specified reference level. Currently there are no multiple testing corrected confidence intervals available. #### Examples ``` >>> res = ols("np.log(Days+1) ~ C(Weight) + C(Duration)", data).fit() >>> pw = res.t_test_pairwise("C(Weight)") >>> pw.result_frame coef std err t P>\|t\| Conf. Int. Low 2-1 0.632315 0.230003 2.749157 8.028083e-03 0.171563 3-1 1.302555 0.230003 5.663201 5.331513e-07 0.841803 3-2 0.670240 0.230003 2.914044 5.119126e-03 0.209488 Conf. Int. Upp. pvalue-hs reject-hs 2-1 1.093067 0.010212 True 3-1 1.763307 0.000002 True 3-2 1.130992 0.010212 True ``` statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.test_normality statsmodels.tsa.vector\_ar.var\_model.VARResults.test\_normality ================================================================ `VARResults.test_normality(signif=0.05)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARResults.test_normality) Test assumption of normal-distributed errors using Jarque-Bera-style omnibus Chi^2 test. \| Parameters: \| signif (float) – Test significance level. \| \| Returns: \| result \| \| Return type: \| [NormalityTestResults](statsmodels.tsa.vector_ar.hypothesis_test_results.normalitytestresults#statsmodels.tsa.vector_ar.hypothesis_test_results.NormalityTestResults "statsmodels.tsa.vector_ar.hypothesis_test_results.NormalityTestResults") \| #### Notes H0 (null) : data are generated by a Gaussian-distributed process	programming_docs
statsmodels statsmodels.sandbox.distributions.transformed.Transf_gen.fit_loc_scale statsmodels.sandbox.distributions.transformed.Transf\_gen.fit\_loc\_scale ========================================================================= `Transf_gen.fit_loc_scale(data, args)` Estimate loc and scale parameters from data using 1st and 2nd moments. \| Parameters: \| data (array\_like) – Data to fit. * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information). \| \| Returns: \| * Lhat (float) – Estimated location parameter for the data. * Shat (float) – Estimated scale parameter for the data. \| statsmodels statsmodels.tsa.statespace.kalman_filter.KalmanFilter.set_conserve_memory statsmodels.tsa.statespace.kalman\_filter.KalmanFilter.set\_conserve\_memory ============================================================================ `KalmanFilter.set_conserve_memory(conserve_memory=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/kalman_filter.html#KalmanFilter.set_conserve_memory) Set the memory conservation method By default, the Kalman filter computes a number of intermediate matrices at each iteration. The memory conservation options control which of those matrices are stored. \| Parameters: \| conserve\_memory (integer, optional) – Bitmask value to set the memory conservation method to. See notes for details. * *\\kwargs* – Keyword arguments may be used to influence the memory conservation method by setting individual boolean flags. See notes for details. \| #### Notes The memory conservation method is defined by a collection of boolean flags, and is internally stored as a bitmask. The methods available are: MEMORY\_STORE\_ALL = 0 Store all intermediate matrices. This is the default value. MEMORY\_NO\_FORECAST = 0x01 Do not store the forecast, forecast error, or forecast error covariance matrices. If this option is used, the `predict` method from the results class is unavailable. MEMORY\_NO\_PREDICTED = 0x02 Do not store the predicted state or predicted state covariance matrices. MEMORY\_NO\_FILTERED = 0x04 Do not store the filtered state or filtered state covariance matrices. MEMORY\_NO\_LIKELIHOOD = 0x08 Do not store the vector of loglikelihood values for each observation. Only the sum of the loglikelihood values is stored. MEMORY\_NO\_GAIN = 0x10 Do not store the Kalman gain matrices. MEMORY\_NO\_SMOOTHING = 0x20 Do not store temporary variables related to Klaman smoothing. If this option is used, smoothing is unavailable. MEMORY\_NO\_SMOOTHING = 0x20 Do not store standardized forecast errors. MEMORY\_CONSERVE Do not store any intermediate matrices. Note that if using a Scipy version less than 0.16, the options MEMORY\_NO\_GAIN, MEMORY\_NO\_SMOOTHING, and MEMORY\_NO\_STD\_FORECAST have no effect. If the bitmask is set directly via the `conserve_memory` argument, then the full method must be provided. If keyword arguments are used to set individual boolean flags, then the lowercase of the method must be used as an argument name, and the value is the desired value of the boolean flag (True or False). Note that the memory conservation method may also be specified by directly modifying the class attributes which are defined similarly to the keyword arguments. The default memory conservation method is `MEMORY_STORE_ALL`, so that all intermediate matrices are stored. #### Examples ``` >>> mod = sm.tsa.statespace.SARIMAX(range(10)) >>> mod.ssm..conserve_memory 0 >>> mod.ssm.memory_no_predicted False >>> mod.ssm.memory_no_predicted = True >>> mod.ssm.conserve_memory 2 >>> mod.ssm.set_conserve_memory(memory_no_filtered=True, ... memory_no_forecast=True) >>> mod.ssm.conserve_memory 7 ``` statsmodels statsmodels.imputation.mice.MICE.next_sample statsmodels.imputation.mice.MICE.next\_sample ============================================= `MICE.next_sample()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/imputation/mice.html#MICE.next_sample) Perform one complete MICE iteration. A single MICE iteration updates all missing values using their respective imputation models, then fits the analysis model to the imputed data. \| Returns: \| params – The model parameters for the analysis model. \| \| Return type: \| array-like \| #### Notes This function fits the analysis model and returns its parameter estimate. The parameter vector is not stored by the class and is not used in any subsequent calls to `combine`. Use `fit` to run all MICE steps together and obtain summary results. The complete cycle of missing value imputation followed by fitting the analysis model is repeated `n_skip + 1` times and the analysis model parameters from the final fit are returned. statsmodels statsmodels.discrete.count_model.ZeroInflatedPoisson.pdf statsmodels.discrete.count\_model.ZeroInflatedPoisson.pdf ========================================================= `ZeroInflatedPoisson.pdf(X)` The probability density (mass) function of the model. statsmodels statsmodels.regression.linear_model.GLS.fit_regularized statsmodels.regression.linear\_model.GLS.fit\_regularized ========================================================= `GLS.fit_regularized(method='elastic_net', alpha=0.0, L1_wt=1.0, start_params=None, profile_scale=False, refit=False, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#GLS.fit_regularized) Return a regularized fit to a linear regression model. \| Parameters: \| method (string) – Only the ‘elastic\_net’ approach is currently implemented. * alpha (scalar or array-like) – The penalty weight. If a scalar, the same penalty weight applies to all variables in the model. If a vector, it must have the same length as `params`, and contains a penalty weight for each coefficient. * L1\_wt (scalar) – The fraction of the penalty given to the L1 penalty term. Must be between 0 and 1 (inclusive). If 0, the fit is a ridge fit, if 1 it is a lasso fit. * start\_params (array-like) – Starting values for `params`. * profile\_scale (bool) – If True the penalized fit is computed using the profile (concentrated) log-likelihood for the Gaussian model. Otherwise the fit uses the residual sum of squares. * refit (bool) – If True, the model is refit using only the variables that have non-zero coefficients in the regularized fit. The refitted model is not regularized. * distributed (bool) – If True, the model uses distributed methods for fitting, will raise an error if True and partitions is None. * generator (function) – generator used to partition the model, allows for handling of out of memory/parallel computing. * partitions (scalar) – The number of partitions desired for the distributed estimation. * threshold (scalar or array-like) – The threshold below which coefficients are zeroed out, only used for distributed estimation \| \| Returns: \| \| \| Return type: \| A RegularizedResults instance. \| #### Notes The elastic net approach closely follows that implemented in the glmnet package in R. The penalty is a combination of L1 and L2 penalties. The function that is minimized is: \[0.5\RSS/n + alpha\((1-L1\\_wt)\\|params\|\_2^2/2 + L1\\_wt\\|params\|\_1)\] where RSS is the usual regression sum of squares, n is the sample size, and $\|\\|\_1$ and $\|\\|\_2$ are the L1 and L2 norms. For WLS and GLS, the RSS is calculated using the whitened endog and exog data. Post-estimation results are based on the same data used to select variables, hence may be subject to overfitting biases. The elastic\_net method uses the following keyword arguments: `maxiter : int` Maximum number of iterations `cnvrg_tol : float` Convergence threshold for line searches `zero_tol : float` Coefficients below this threshold are treated as zero. #### References Friedman, Hastie, Tibshirani (2008). Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software 33(1), 1-22 Feb 2010. statsmodels statsmodels.tsa.statespace.sarimax.SARIMAXResults.f_test statsmodels.tsa.statespace.sarimax.SARIMAXResults.f\_test ========================================================= `SARIMAXResults.f_test(r_matrix, cov_p=None, scale=1.0, invcov=None)` Compute the F-test for a joint linear hypothesis. This is a special case of `wald_test` that always uses the F distribution. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length k row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> A = np.identity(len(results.params)) >>> A = A[1:,:] ``` This tests that each coefficient is jointly statistically significantly different from zero. ``` >>> print(results.f_test(A)) <F test: F=array([[ 330.28533923]]), p=4.984030528700946e-10, df_denom=9, df_num=6> ``` Compare this to ``` >>> results.fvalue 330.2853392346658 >>> results.f_pvalue 4.98403096572e-10 ``` ``` >>> B = np.array(([0,0,1,-1,0,0,0],[0,0,0,0,0,1,-1])) ``` This tests that the coefficient on the 2nd and 3rd regressors are equal and jointly that the coefficient on the 5th and 6th regressors are equal. ``` >>> print(results.f_test(B)) <F test: F=array([[ 9.74046187]]), p=0.005605288531708235, df_denom=9, df_num=2> ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.datasets import longley >>> from statsmodels.formula.api import ols >>> dta = longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = '(GNPDEFL = GNP), (UNEMP = 2), (YEAR/1829 = 1)' >>> f_test = results.f_test(hypotheses) >>> print(f_test) <F test: F=array([[ 144.17976065]]), p=6.322026217355609e-08, df_denom=9, df_num=3> ``` See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`wald_test`](statsmodels.tsa.statespace.sarimax.sarimaxresults.wald_test#statsmodels.tsa.statespace.sarimax.SARIMAXResults.wald_test "statsmodels.tsa.statespace.sarimax.SARIMAXResults.wald_test"), [`t_test`](statsmodels.tsa.statespace.sarimax.sarimaxresults.t_test#statsmodels.tsa.statespace.sarimax.SARIMAXResults.t_test "statsmodels.tsa.statespace.sarimax.SARIMAXResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.regression.linear_model.PredictionResults statsmodels.regression.linear\_model.PredictionResults ====================================================== `class statsmodels.regression.linear_model.PredictionResults(predicted_mean, var_pred_mean, var_resid, df=None, dist=None, row_labels=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/_prediction.html#PredictionResults) #### Methods \| \| \| \| --- \| --- \| \| [`conf_int`](statsmodels.regression.linear_model.predictionresults.conf_int#statsmodels.regression.linear_model.PredictionResults.conf_int "statsmodels.regression.linear_model.PredictionResults.conf_int")([obs, alpha]) \| Returns the confidence interval of the value, `effect` of the constraint. \| \| [`summary_frame`](statsmodels.regression.linear_model.predictionresults.summary_frame#statsmodels.regression.linear_model.PredictionResults.summary_frame "statsmodels.regression.linear_model.PredictionResults.summary_frame")([what, alpha]) \| \| #### Attributes \| \| \| \| --- \| --- \| \| `se_mean` \| \| \| `se_obs` \| \| statsmodels statsmodels.genmod.generalized_estimating_equations.GEE.mean_deriv_exog statsmodels.genmod.generalized\_estimating\_equations.GEE.mean\_deriv\_exog =========================================================================== `GEE.mean_deriv_exog(exog, params, offset_exposure=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_estimating_equations.html#GEE.mean_deriv_exog) Derivative of the expected endog with respect to exog. \| Parameters: \| * exog (array-like) – Values of the independent variables at which the derivative is calculated. * params (array-like) – Parameter values at which the derivative is calculated. * offset\_exposure (array-like, optional) – Combined offset and exposure. \| \| Returns: \| \| \| Return type: \| The derivative of the expected endog with respect to exog. \| statsmodels statsmodels.regression.recursive_ls.RecursiveLS.set_inversion_method statsmodels.regression.recursive\_ls.RecursiveLS.set\_inversion\_method ======================================================================= `RecursiveLS.set_inversion_method(inversion_method=None, *kwargs)` Set the inversion method The Kalman filter may contain one matrix inversion: that of the forecast error covariance matrix. The inversion method controls how and if that inverse is performed. \| Parameters: \| inversion\_method (integer, optional) – Bitmask value to set the inversion method to. See notes for details. * *\\kwargs* – Keyword arguments may be used to influence the inversion method by setting individual boolean flags. See notes for details. \| #### Notes This method is rarely used. See the corresponding function in the `KalmanFilter` class for details. statsmodels statsmodels.genmod.generalized_linear_model.GLMResults.fittedvalues statsmodels.genmod.generalized\_linear\_model.GLMResults.fittedvalues ===================================================================== `GLMResults.fittedvalues()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_linear_model.html#GLMResults.fittedvalues) statsmodels statsmodels.tsa.filters.filtertools.fftconvolve3 statsmodels.tsa.filters.filtertools.fftconvolve3 ================================================ `statsmodels.tsa.filters.filtertools.fftconvolve3(in1, in2=None, in3=None, mode='full')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/filters/filtertools.html#fftconvolve3) Convolve two N-dimensional arrays using FFT. See convolve. for use with arma (old version: in1=num in2=den in3=data * better for consistency with other functions in1=data in2=num in3=den * note in2 and in3 need to have consistent dimension/shape since I’m using max of in2, in3 shapes and not the sum copied from scipy.signal.signaltools, but here used to try out inverse filter doesn’t work or I can’t get it to work 2010-10-23 looks ok to me for 1d, from results below with padded data array (fftp) but it doesn’t work for multidimensional inverse filter (fftn) original signal.fftconvolve also uses fftn statsmodels statsmodels.tsa.statespace.sarimax.SARIMAX.predict statsmodels.tsa.statespace.sarimax.SARIMAX.predict ================================================== `SARIMAX.predict(params, exog=None, args, kwargs)` After a model has been fit predict returns the fitted values. This is a placeholder intended to be overwritten by individual models. statsmodels statsmodels.genmod.families.family.Poisson.fitted statsmodels.genmod.families.family.Poisson.fitted ================================================= `Poisson.fitted(lin_pred)` Fitted values based on linear predictors lin\_pred. \| Parameters: \| lin\_pred* (array) – Values of the linear predictor of the model. $X \cdot \beta$ in a classical linear model. \| \| Returns: \| mu – The mean response variables given by the inverse of the link function. \| \| Return type: \| array \| statsmodels statsmodels.discrete.count_model.ZeroInflatedPoissonResults.tvalues statsmodels.discrete.count\_model.ZeroInflatedPoissonResults.tvalues ==================================================================== `ZeroInflatedPoissonResults.tvalues()` Return the t-statistic for a given parameter estimate. statsmodels statsmodels.sandbox.regression.gmm.IVGMM.fitgmm statsmodels.sandbox.regression.gmm.IVGMM.fitgmm =============================================== `IVGMM.fitgmm(start, weights=None, optim_method='bfgs', optim_args=None)` estimate parameters using GMM \| Parameters: \| * start (array\_like) – starting values for minimization * weights (array) – weighting matrix for moment conditions. If weights is None, then the identity matrix is used \| \| Returns: \| paramest – estimated parameters \| \| Return type: \| array \| #### Notes todo: add fixed parameter option, not here ??? uses scipy.optimize.fmin statsmodels statsmodels.stats.sandwich_covariance.cov_hc2 statsmodels.stats.sandwich\_covariance.cov\_hc2 =============================================== `statsmodels.stats.sandwich_covariance.cov_hc2(results)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/sandwich_covariance.html#cov_hc2) See statsmodels.RegressionResults statsmodels statsmodels.stats.multitest.RegressionFDR statsmodels.stats.multitest.RegressionFDR ========================================= `class statsmodels.stats.multitest.RegressionFDR(endog, exog, regeffects, method='knockoff', *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/_knockoff.html#RegressionFDR) Control FDR in a regression procedure. \| Parameters: \| endog (array-like) – The dependent variable of the regression * exog (array-like) – The independent variables of the regression * regeffects (RegressionEffects instance) – An instance of a RegressionEffects class that can compute effect sizes for the regression coefficients. * method (string) – The approach used to asssess and control FDR, currently must be ‘knockoff’. \| \| Returns: \| * Returns an instance of the RegressionFDR class. The `fdr` attribute * holds the estimated false discovery rates. \| #### Notes This class Implements the knockoff method of Barber and Candes. This is an approach for controlling the FDR of a variety of regression estimation procedures, including correlation coefficients, OLS regression, OLS with forward selection, and LASSO regression. For other approaches to FDR control in regression, see the statsmodels.stats.multitest module. Methods provided in that module use Z-scores or p-values, and therefore require standard errors for the coefficient estimates to be available. The default method for constructing the augmented design matrix is the ‘equivariant’ approach, set `design_method=’sdp’` to use an alternative approach involving semidefinite programming. See Barber and Candes for more information about both approaches. The sdp approach requires that cvxopt be installed. #### Methods \| \| \| \| --- \| --- \| \| [`threshold`](statsmodels.stats.multitest.regressionfdr.threshold#statsmodels.stats.multitest.RegressionFDR.threshold "statsmodels.stats.multitest.RegressionFDR.threshold")(tfdr) \| Returns the threshold statistic for a given target FDR. \|	programming_docs
statsmodels statsmodels.tsa.statespace.sarimax.SARIMAXResults.get_prediction statsmodels.tsa.statespace.sarimax.SARIMAXResults.get\_prediction ================================================================= `SARIMAXResults.get_prediction(start=None, end=None, dynamic=False, index=None, exog=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/sarimax.html#SARIMAXResults.get_prediction) In-sample prediction and out-of-sample forecasting \| Parameters: \| start (int, str, or datetime, optional) – Zero-indexed observation number at which to start forecasting, ie., the first forecast is start. Can also be a date string to parse or a datetime type. Default is the the zeroth observation. * end (int, str, or datetime, optional) – Zero-indexed observation number at which to end forecasting, ie., the first forecast is start. Can also be a date string to parse or a datetime type. However, if the dates index does not have a fixed frequency, end must be an integer index if you want out of sample prediction. Default is the last observation in the sample. * exog (array\_like, optional) – If the model includes exogenous regressors, you must provide exactly enough out-of-sample values for the exogenous variables if end is beyond the last observation in the sample. * dynamic (boolean, int, str, or datetime, optional) – Integer offset relative to `start` at which to begin dynamic prediction. Can also be an absolute date string to parse or a datetime type (these are not interpreted as offsets). Prior to this observation, true endogenous values will be used for prediction; starting with this observation and continuing through the end of prediction, forecasted endogenous values will be used instead. * full\_results (boolean, optional) – If True, returns a FilterResults instance; if False returns a tuple with forecasts, the forecast errors, and the forecast error covariance matrices. Default is False. * *\\kwargs* – Additional arguments may required for forecasting beyond the end of the sample. See `FilterResults.predict` for more details. \| \| Returns: \| forecast – Array of out of sample forecasts. \| \| Return type: \| array \| statsmodels statsmodels.sandbox.regression.gmm.GMM.predict statsmodels.sandbox.regression.gmm.GMM.predict ============================================== `GMM.predict(params, exog=None, args, kwargs)` After a model has been fit predict returns the fitted values. This is a placeholder intended to be overwritten by individual models. statsmodels statsmodels.stats.power.NormalIndPower statsmodels.stats.power.NormalIndPower ====================================== `class statsmodels.stats.power.NormalIndPower(ddof=0, kwds)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/power.html#NormalIndPower) Statistical Power calculations for z-test for two independent samples. currently only uses pooled variance #### Methods \| \| \| \| --- \| --- \| \| [`plot_power`](statsmodels.stats.power.normalindpower.plot_power#statsmodels.stats.power.NormalIndPower.plot_power "statsmodels.stats.power.NormalIndPower.plot_power")([dep\_var, nobs, effect\_size, …]) \| plot power with number of observations or effect size on x-axis \| \| [`power`](statsmodels.stats.power.normalindpower.power#statsmodels.stats.power.NormalIndPower.power "statsmodels.stats.power.NormalIndPower.power")(effect\_size, nobs1, alpha[, ratio, …]) \| Calculate the power of a z-test for two independent sample \| \| [`solve_power`](statsmodels.stats.power.normalindpower.solve_power#statsmodels.stats.power.NormalIndPower.solve_power "statsmodels.stats.power.NormalIndPower.solve_power")([effect\_size, nobs1, alpha, …]) \| solve for any one parameter of the power of a two sample z-test \| statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactor.initialize_approximate_diffuse statsmodels.tsa.statespace.dynamic\_factor.DynamicFactor.initialize\_approximate\_diffuse ========================================================================================= `DynamicFactor.initialize_approximate_diffuse(variance=None)` statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.acorr statsmodels.tsa.vector\_ar.var\_model.VARResults.acorr ====================================================== `VARResults.acorr(nlags=None)` Compute theoretical autocorrelation function \| Returns: \| acorr* \| \| Return type: \| ndarray (p x k x k) \| statsmodels statsmodels.sandbox.stats.multicomp.mcfdr statsmodels.sandbox.stats.multicomp.mcfdr ========================================= `statsmodels.sandbox.stats.multicomp.mcfdr(nrepl=100, nobs=50, ntests=10, ntrue=6, mu=0.5, alpha=0.05, rho=0.0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/stats/multicomp.html#mcfdr) MonteCarlo to test fdrcorrection statsmodels statsmodels.discrete.discrete_model.Poisson statsmodels.discrete.discrete\_model.Poisson ============================================ `class statsmodels.discrete.discrete_model.Poisson(endog, exog, offset=None, exposure=None, missing='none', *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#Poisson) Poisson model for count data \| Parameters: \| endog (array-like) – 1-d endogenous response variable. The dependent variable. * exog (array-like) – A nobs x k array where `nobs` is the number of observations and `k` is the number of regressors. An intercept is not included by default and should be added by the user. See `statsmodels.tools.add_constant`. * offset (array\_like) – Offset is added to the linear prediction with coefficient equal to 1. * exposure (array\_like) – Log(exposure) is added to the linear prediction with coefficient equal to 1. * missing (str) – Available options are ‘none’, ‘drop’, and ‘raise’. If ‘none’, no nan checking is done. If ‘drop’, any observations with nans are dropped. If ‘raise’, an error is raised. Default is ‘none.’ \| `endog` array – A reference to the endogenous response variable `exog` array – A reference to the exogenous design. #### Methods \| \| \| \| --- \| --- \| \| [`cdf`](statsmodels.discrete.discrete_model.poisson.cdf#statsmodels.discrete.discrete_model.Poisson.cdf "statsmodels.discrete.discrete_model.Poisson.cdf")(X) \| Poisson model cumulative distribution function \| \| [`cov_params_func_l1`](statsmodels.discrete.discrete_model.poisson.cov_params_func_l1#statsmodels.discrete.discrete_model.Poisson.cov_params_func_l1 "statsmodels.discrete.discrete_model.Poisson.cov_params_func_l1")(likelihood\_model, xopt, …) \| Computes cov\_params on a reduced parameter space corresponding to the nonzero parameters resulting from the l1 regularized fit. \| \| [`fit`](statsmodels.discrete.discrete_model.poisson.fit#statsmodels.discrete.discrete_model.Poisson.fit "statsmodels.discrete.discrete_model.Poisson.fit")([start\_params, method, maxiter, …]) \| Fit the model using maximum likelihood. \| \| [`fit_constrained`](statsmodels.discrete.discrete_model.poisson.fit_constrained#statsmodels.discrete.discrete_model.Poisson.fit_constrained "statsmodels.discrete.discrete_model.Poisson.fit_constrained")(constraints[, start\_params]) \| fit the model subject to linear equality constraints \| \| [`fit_regularized`](statsmodels.discrete.discrete_model.poisson.fit_regularized#statsmodels.discrete.discrete_model.Poisson.fit_regularized "statsmodels.discrete.discrete_model.Poisson.fit_regularized")([start\_params, method, …]) \| Fit the model using a regularized maximum likelihood. \| \| [`from_formula`](statsmodels.discrete.discrete_model.poisson.from_formula#statsmodels.discrete.discrete_model.Poisson.from_formula "statsmodels.discrete.discrete_model.Poisson.from_formula")(formula, data[, subset, drop\_cols]) \| Create a Model from a formula and dataframe. \| \| [`hessian`](statsmodels.discrete.discrete_model.poisson.hessian#statsmodels.discrete.discrete_model.Poisson.hessian "statsmodels.discrete.discrete_model.Poisson.hessian")(params) \| Poisson model Hessian matrix of the loglikelihood \| \| [`information`](statsmodels.discrete.discrete_model.poisson.information#statsmodels.discrete.discrete_model.Poisson.information "statsmodels.discrete.discrete_model.Poisson.information")(params) \| Fisher information matrix of model \| \| [`initialize`](statsmodels.discrete.discrete_model.poisson.initialize#statsmodels.discrete.discrete_model.Poisson.initialize "statsmodels.discrete.discrete_model.Poisson.initialize")() \| Initialize is called by statsmodels.model.LikelihoodModel.\_\_init\_\_ and should contain any preprocessing that needs to be done for a model. \| \| [`loglike`](statsmodels.discrete.discrete_model.poisson.loglike#statsmodels.discrete.discrete_model.Poisson.loglike "statsmodels.discrete.discrete_model.Poisson.loglike")(params) \| Loglikelihood of Poisson model \| \| [`loglikeobs`](statsmodels.discrete.discrete_model.poisson.loglikeobs#statsmodels.discrete.discrete_model.Poisson.loglikeobs "statsmodels.discrete.discrete_model.Poisson.loglikeobs")(params) \| Loglikelihood for observations of Poisson model \| \| [`pdf`](statsmodels.discrete.discrete_model.poisson.pdf#statsmodels.discrete.discrete_model.Poisson.pdf "statsmodels.discrete.discrete_model.Poisson.pdf")(X) \| Poisson model probability mass function \| \| [`predict`](statsmodels.discrete.discrete_model.poisson.predict#statsmodels.discrete.discrete_model.Poisson.predict "statsmodels.discrete.discrete_model.Poisson.predict")(params[, exog, exposure, offset, linear]) \| Predict response variable of a count model given exogenous variables. \| \| [`score`](statsmodels.discrete.discrete_model.poisson.score#statsmodels.discrete.discrete_model.Poisson.score "statsmodels.discrete.discrete_model.Poisson.score")(params) \| Poisson model score (gradient) vector of the log-likelihood \| \| [`score_obs`](statsmodels.discrete.discrete_model.poisson.score_obs#statsmodels.discrete.discrete_model.Poisson.score_obs "statsmodels.discrete.discrete_model.Poisson.score_obs")(params) \| Poisson model Jacobian of the log-likelihood for each observation \| #### Attributes \| \| \| \| --- \| --- \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| Names of exogenous variables \| statsmodels statsmodels.tools.eval_measures.iqr statsmodels.tools.eval\_measures.iqr ==================================== `statsmodels.tools.eval_measures.iqr(x1, x2, axis=0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tools/eval_measures.html#iqr) interquartile range of error rounded index, no interpolations this could use newer numpy function instead \| Parameters: \| * x2 (x1,) – The performance measure depends on the difference between these two arrays. * axis (int) – axis along which the summary statistic is calculated \| \| Returns: \| mse – mean squared error along given axis. \| \| Return type: \| ndarray or float \| #### Notes If `x1` and `x2` have different shapes, then they need to broadcast. This uses `numpy.asarray` to convert the input, in contrast to the other functions in this category. statsmodels statsmodels.tsa.statespace.structural.UnobservedComponents.set_inversion_method statsmodels.tsa.statespace.structural.UnobservedComponents.set\_inversion\_method ================================================================================= `UnobservedComponents.set_inversion_method(inversion_method=None, *kwargs)` Set the inversion method The Kalman filter may contain one matrix inversion: that of the forecast error covariance matrix. The inversion method controls how and if that inverse is performed. \| Parameters: \| inversion\_method (integer, optional) – Bitmask value to set the inversion method to. See notes for details. * *\\kwargs* – Keyword arguments may be used to influence the inversion method by setting individual boolean flags. See notes for details. \| #### Notes This method is rarely used. See the corresponding function in the `KalmanFilter` class for details. statsmodels statsmodels.regression.linear_model.RegressionResults.summary2 statsmodels.regression.linear\_model.RegressionResults.summary2 =============================================================== `RegressionResults.summary2(yname=None, xname=None, title=None, alpha=0.05, float_format='%.4f')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#RegressionResults.summary2) Experimental summary function to summarize the regression results \| Parameters: \| * xname (List of strings of length equal to the number of parameters) – Names of the independent variables (optional) * yname (string) – Name of the dependent variable (optional) * title (string, optional) – Title for the top table. If not None, then this replaces the default title * alpha (float) – significance level for the confidence intervals * float\_format (string) – print format for floats in parameters summary \| \| Returns: \| smry – this holds the summary tables and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary.Summary`](statsmodels.iolib.summary.summary#statsmodels.iolib.summary.Summary "statsmodels.iolib.summary.Summary") class to hold summary results statsmodels statsmodels.stats.diagnostic.CompareCox statsmodels.stats.diagnostic.CompareCox ======================================= `class statsmodels.stats.diagnostic.CompareCox` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/stats/diagnostic.html#CompareCox) Cox Test for non-nested models \| Parameters: \| * results\_x (Result instance) – result instance of first model * results\_z (Result instance) – result instance of second model * attach (bool) – \| Formulas from Greene, section 8.3.4 translated to code produces correct results for Example 8.3, Greene #### Methods \| \| \| \| --- \| --- \| \| [`run`](statsmodels.stats.diagnostic.comparecox.run#statsmodels.stats.diagnostic.CompareCox.run "statsmodels.stats.diagnostic.CompareCox.run")(results\_x, results\_z[, attach]) \| run Cox test for non-nested models \| statsmodels statsmodels.miscmodels.count.PoissonZiGMLE.nloglike statsmodels.miscmodels.count.PoissonZiGMLE.nloglike =================================================== `PoissonZiGMLE.nloglike(params)` statsmodels statsmodels.sandbox.regression.gmm.IVRegressionResults.pvalues statsmodels.sandbox.regression.gmm.IVRegressionResults.pvalues ============================================================== `IVRegressionResults.pvalues()` statsmodels statsmodels.genmod.families.family.NegativeBinomial.starting_mu statsmodels.genmod.families.family.NegativeBinomial.starting\_mu ================================================================ `NegativeBinomial.starting_mu(y)` Starting value for mu in the IRLS algorithm. \| Parameters: \| y (array) – The untransformed response variable. \| \| Returns: \| mu\_0 – The first guess on the transformed response variable. \| \| Return type: \| array \| #### Notes \[\mu\_0 = (Y + \overline{Y})/2\] Only the Binomial family takes a different initial value. statsmodels statsmodels.imputation.mice.MICEData.plot_missing_pattern statsmodels.imputation.mice.MICEData.plot\_missing\_pattern =========================================================== `MICEData.plot_missing_pattern(ax=None, row_order='pattern', column_order='pattern', hide_complete_rows=False, hide_complete_columns=False, color_row_patterns=True)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/imputation/mice.html#MICEData.plot_missing_pattern) Generate an image showing the missing data pattern. \| Parameters: \| * ax (matplotlib axes) – Axes on which to draw the plot. * row\_order (string) – The method for ordering the rows. Must be one of ‘pattern’, ‘proportion’, or ‘raw’. * column\_order (string) – The method for ordering the columns. Must be one of ‘pattern’, ‘proportion’, or ‘raw’. * hide\_complete\_rows (boolean) – If True, rows with no missing values are not drawn. * hide\_complete\_columns (boolean) – If True, columns with no missing values are not drawn. * color\_row\_patterns (boolean) – If True, color the unique row patterns, otherwise use grey and white as colors. \| \| Returns: \| \| \| Return type: \| A figure containing a plot of the missing data pattern. \| statsmodels statsmodels.tsa.vector_ar.vecm.VECM.information statsmodels.tsa.vector\_ar.vecm.VECM.information ================================================ `VECM.information(params)` Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.discrete.discrete_model.BinaryResults.resid_dev statsmodels.discrete.discrete\_model.BinaryResults.resid\_dev ============================================================= `BinaryResults.resid_dev()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#BinaryResults.resid_dev) Deviance residuals #### Notes Deviance residuals are defined \[d\_j = \pm\left(2\left[Y\_j\ln\left(\frac{Y\_j}{M\_jp\_j}\right) + (M\_j - Y\_j\ln\left(\frac{M\_j-Y\_j}{M\_j(1-p\_j)} \right) \right] \right)^{1/2}\] where $p\_j = cdf(X\beta)$ and $M\_j$ is the total number of observations sharing the covariate pattern $j$. For now $M\_j$ is always set to 1. statsmodels statsmodels.distributions.empirical_distribution.StepFunction statsmodels.distributions.empirical\_distribution.StepFunction ============================================================== `class statsmodels.distributions.empirical_distribution.StepFunction(x, y, ival=0.0, sorted=False, side='left')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/distributions/empirical_distribution.html#StepFunction) A basic step function. Values at the ends are handled in the simplest way possible: everything to the left of x[0] is set to ival; everything to the right of x[-1] is set to y[-1]. \| Parameters: \| * x (array-like) – * y (array-like) – * ival (float) – ival is the value given to the values to the left of x[0]. Default is 0. * sorted (bool) – Default is False. * side ({'left', 'right'}, optional) – Default is ‘left’. Defines the shape of the intervals constituting the steps. ‘right’ correspond to [a, b) intervals and ‘left’ to (a, b]. \| #### Examples ``` >>> import numpy as np >>> from statsmodels.distributions.empirical_distribution import StepFunction >>> >>> x = np.arange(20) >>> y = np.arange(20) >>> f = StepFunction(x, y) >>> >>> print(f(3.2)) 3.0 >>> print(f([[3.2,4.5],[24,-3.1]])) [[ 3. 4.] [ 19. 0.]] >>> f2 = StepFunction(x, y, side='right') >>> >>> print(f(3.0)) 2.0 >>> print(f2(3.0)) 3.0 ``` #### Methods statsmodels statsmodels.discrete.discrete_model.ProbitResults.get_margeff statsmodels.discrete.discrete\_model.ProbitResults.get\_margeff =============================================================== `ProbitResults.get_margeff(at='overall', method='dydx', atexog=None, dummy=False, count=False)` Get marginal effects of the fitted model. \| Parameters: \| * at (str, optional) – Options are: + ’overall’, The average of the marginal effects at each observation. + ’mean’, The marginal effects at the mean of each regressor. + ’median’, The marginal effects at the median of each regressor. + ’zero’, The marginal effects at zero for each regressor. + ’all’, The marginal effects at each observation. If `at` is all only margeff will be available from the returned object.Note that if `exog` is specified, then marginal effects for all variables not specified by `exog` are calculated using the `at` option. * method (str, optional) – Options are: + ’dydx’ - dy/dx - No transformation is made and marginal effects are returned. This is the default. + ’eyex’ - estimate elasticities of variables in `exog` – d(lny)/d(lnx) + ’dyex’ - estimate semielasticity – dy/d(lnx) + ’eydx’ - estimate semeilasticity – d(lny)/dxNote that tranformations are done after each observation is calculated. Semi-elasticities for binary variables are computed using the midpoint method. ‘dyex’ and ‘eyex’ do not make sense for discrete variables. * atexog (array-like, optional) – Optionally, you can provide the exogenous variables over which to get the marginal effects. This should be a dictionary with the key as the zero-indexed column number and the value of the dictionary. Default is None for all independent variables less the constant. * dummy (bool, optional) – If False, treats binary variables (if present) as continuous. This is the default. Else if True, treats binary variables as changing from 0 to 1. Note that any variable that is either 0 or 1 is treated as binary. Each binary variable is treated separately for now. * count (bool, optional) – If False, treats count variables (if present) as continuous. This is the default. Else if True, the marginal effect is the change in probabilities when each observation is increased by one. \| \| Returns: \| DiscreteMargins – Returns an object that holds the marginal effects, standard errors, confidence intervals, etc. See `statsmodels.discrete.discrete_margins.DiscreteMargins` for more information. \| \| Return type: \| marginal effects instance \| #### Notes When using after Poisson, returns the expected number of events per period, assuming that the model is loglinear.	programming_docs
statsmodels statsmodels.tsa.ar_model.AR.hessian statsmodels.tsa.ar\_model.AR.hessian ==================================== `AR.hessian(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/ar_model.html#AR.hessian) Returns numerical hessian for now. statsmodels statsmodels.sandbox.regression.gmm.IV2SLS.initialize statsmodels.sandbox.regression.gmm.IV2SLS.initialize ==================================================== `IV2SLS.initialize()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/regression/gmm.html#IV2SLS.initialize) Initialize (possibly re-initialize) a Model instance. For instance, the design matrix of a linear model may change and some things must be recomputed. statsmodels statsmodels.tsa.arima_model.ARIMA.loglike_kalman statsmodels.tsa.arima\_model.ARIMA.loglike\_kalman ================================================== `ARIMA.loglike_kalman(params, set_sigma2=True)` Compute exact loglikelihood for ARMA(p,q) model by the Kalman Filter. statsmodels statsmodels.tsa.ar_model.ARResults.aic statsmodels.tsa.ar\_model.ARResults.aic ======================================= `ARResults.aic()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/ar_model.html#ARResults.aic) statsmodels statsmodels.tsa.vector_ar.dynamic.DynamicVAR.forecast statsmodels.tsa.vector\_ar.dynamic.DynamicVAR.forecast ====================================================== `DynamicVAR.forecast(steps=1)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/dynamic.html#DynamicVAR.forecast) Produce dynamic forecast \| Parameters: \| steps – \| \| Returns: \| forecasts \| \| Return type: \| [pandas.DataFrame](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html#pandas.DataFrame "(in pandas v0.22.0)") \| statsmodels statsmodels.regression.linear_model.WLS.information statsmodels.regression.linear\_model.WLS.information ==================================================== `WLS.information(params)` Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.stats.contingency_tables.Table.cumulative_oddsratios statsmodels.stats.contingency\_tables.Table.cumulative\_oddsratios ================================================================== `Table.cumulative_oddsratios()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/contingency_tables.html#Table.cumulative_oddsratios) statsmodels statsmodels.tsa.statespace.mlemodel.MLEModel.loglike statsmodels.tsa.statespace.mlemodel.MLEModel.loglike ==================================================== `MLEModel.loglike(params, args, kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/mlemodel.html#MLEModel.loglike) Loglikelihood evaluation \| Parameters: \| params (array\_like) – Array of parameters at which to evaluate the loglikelihood function. * transformed (boolean, optional) – Whether or not `params` is already transformed. Default is True. * kwargs – Additional keyword arguments to pass to the Kalman filter. See `KalmanFilter.filter` for more details. \| #### Notes [[1]](#id2) recommend maximizing the average likelihood to avoid scale issues; this is done automatically by the base Model fit method. #### References \| \| \| \| --- \| --- \| \| [[1]](#id1) \| Koopman, Siem Jan, Neil Shephard, and Jurgen A. Doornik. 1999. Statistical Algorithms for Models in State Space Using SsfPack 2.2. Econometrics Journal 2 (1): 107-60. doi:10.1111/1368-423X.00023. \| See also [`update`](statsmodels.tsa.statespace.mlemodel.mlemodel.update#statsmodels.tsa.statespace.mlemodel.MLEModel.update "statsmodels.tsa.statespace.mlemodel.MLEModel.update") modifies the internal state of the state space model to reflect new params statsmodels statsmodels.discrete.discrete_model.GeneralizedPoisson.loglike statsmodels.discrete.discrete\_model.GeneralizedPoisson.loglike =============================================================== `GeneralizedPoisson.loglike(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#GeneralizedPoisson.loglike) Loglikelihood of Generalized Poisson model \| Parameters: \| params (array-like) – The parameters of the model. \| \| Returns: \| loglike – The log-likelihood function of the model evaluated at `params`. See notes. \| \| Return type: \| float \| #### Notes \[\ln L=\sum\_{i=1}^{n}\left[\mu\_{i}+(y\_{i}-1)\ln(\mu\_{i}+ \alpha\\mu\_{i}^{p-1}\y\_{i})-y\_{i}\ln(1+\alpha\\mu\_{i}^{p-1})- ln(y\_{i}!)-\frac{\mu\_{i}+\alpha\\mu\_{i}^{p-1}\y\_{i}}{1+\alpha\ \mu\_{i}^{p-1}}\right]\] statsmodels statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.cov_params statsmodels.discrete.count\_model.ZeroInflatedNegativeBinomialResults.cov\_params ================================================================================= `ZeroInflatedNegativeBinomialResults.cov_params(r_matrix=None, column=None, scale=None, cov_p=None, other=None)` Returns the variance/covariance matrix. The variance/covariance matrix can be of a linear contrast of the estimates of params or all params multiplied by scale which will usually be an estimate of sigma^2. Scale is assumed to be a scalar. \| Parameters: \| * r\_matrix (array-like) – Can be 1d, or 2d. Can be used alone or with other. * column (array-like, optional) – Must be used on its own. Can be 0d or 1d see below. * scale (float, optional) – Can be specified or not. Default is None, which means that the scale argument is taken from the model. * other (array-like, optional) – Can be used when r\_matrix is specified. \| \| Returns: \| cov – covariance matrix of the parameter estimates or of linear combination of parameter estimates. See Notes. \| \| Return type: \| ndarray \| #### Notes (The below are assumed to be in matrix notation.) If no argument is specified returns the covariance matrix of a model `(scale)(X.T X)^(-1)` If contrast is specified it pre and post-multiplies as follows `(scale) r_matrix (X.T X)^(-1) r_matrix.T` If contrast and other are specified returns `(scale) * r_matrix (X.T X)^(-1) other.T` If column is specified returns `(scale) * (X.T X)^(-1)[column,column]` if column is 0d OR `(scale) * (X.T X)^(-1)[column][:,column]` if column is 1d statsmodels statsmodels.discrete.discrete_model.GeneralizedPoissonResults.t_test statsmodels.discrete.discrete\_model.GeneralizedPoissonResults.t\_test ====================================================================== `GeneralizedPoissonResults.t_test(r_matrix, cov_p=None, scale=None, use_t=None)` Compute a t-test for a each linear hypothesis of the form Rb = q \| Parameters: \| * r\_matrix (array-like, str, tuple) – + array : If an array is given, a p x k 2d array or length k 1d array specifying the linear restrictions. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q). If q is given, can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – An optional `scale` to use. Default is the scale specified by the model fit. * use\_t (bool, optional) – If use\_t is None, then the default of the model is used. If use\_t is True, then the p-values are based on the t distribution. If use\_t is False, then the p-values are based on the normal distribution. \| \| Returns: \| res – The results for the test are attributes of this results instance. The available results have the same elements as the parameter table in `summary()`. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> r = np.zeros_like(results.params) >>> r[5:] = [1,-1] >>> print(r) [ 0. 0. 0. 0. 0. 1. -1.] ``` r tests that the coefficients on the 5th and 6th independent variable are the same. ``` >>> T_test = results.t_test(r) >>> print(T_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 -1829.2026 455.391 -4.017 0.003 -2859.368 -799.037 ============================================================================== >>> T_test.effect -1829.2025687192481 >>> T_test.sd 455.39079425193762 >>> T_test.tvalue -4.0167754636411717 >>> T_test.pvalue 0.0015163772380899498 ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.formula.api import ols >>> dta = sm.datasets.longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = 'GNPDEFL = GNP, UNEMP = 2, YEAR/1829 = 1' >>> t_test = results.t_test(hypotheses) >>> print(t_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 15.0977 84.937 0.178 0.863 -177.042 207.238 c1 -2.0202 0.488 -8.231 0.000 -3.125 -0.915 c2 1.0001 0.249 0.000 1.000 0.437 1.563 ============================================================================== ``` See also [`tvalues`](statsmodels.discrete.discrete_model.generalizedpoissonresults.tvalues#statsmodels.discrete.discrete_model.GeneralizedPoissonResults.tvalues "statsmodels.discrete.discrete_model.GeneralizedPoissonResults.tvalues") individual t statistics [`f_test`](statsmodels.discrete.discrete_model.generalizedpoissonresults.f_test#statsmodels.discrete.discrete_model.GeneralizedPoissonResults.f_test "statsmodels.discrete.discrete_model.GeneralizedPoissonResults.f_test") for F tests [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") statsmodels statsmodels.tsa.statespace.varmax.VARMAXResults.cov_params_robust_oim statsmodels.tsa.statespace.varmax.VARMAXResults.cov\_params\_robust\_oim ======================================================================== `VARMAXResults.cov_params_robust_oim()` (array) The QMLE variance / covariance matrix. Computed using the method from Harvey (1989) as the evaluated hessian. statsmodels statsmodels.tsa.statespace.structural.UnobservedComponents.smooth statsmodels.tsa.statespace.structural.UnobservedComponents.smooth ================================================================= `UnobservedComponents.smooth(params, transformed=True, complex_step=False, cov_type=None, cov_kwds=None, return_ssm=False, results_class=None, results_wrapper_class=None, *kwargs)` Kalman smoothing \| Parameters: \| params (array\_like) – Array of parameters at which to evaluate the loglikelihood function. * transformed (boolean, optional) – Whether or not `params` is already transformed. Default is True. * return\_ssm (boolean,optional) – Whether or not to return only the state space output or a full results object. Default is to return a full results object. * cov\_type (str, optional) – See `MLEResults.fit` for a description of covariance matrix types for results object. * cov\_kwds ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)") or None, optional) – See `MLEResults.get_robustcov_results` for a description required keywords for alternative covariance estimators * *\\kwargs* – Additional keyword arguments to pass to the Kalman filter. See `KalmanFilter.filter` for more details. \| statsmodels statsmodels.genmod.families.links.Link.inverse_deriv statsmodels.genmod.families.links.Link.inverse\_deriv ===================================================== `Link.inverse_deriv(z)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#Link.inverse_deriv) Derivative of the inverse link function g^(-1)(z). \| Parameters: \| z (array-like) – `z` is usually the linear predictor for a GLM or GEE model. \| \| Returns: \| g’^(-1)(z) – The value of the derivative of the inverse of the link function \| \| Return type: \| array \| #### Notes This reference implementation gives the correct result but is inefficient, so it can be overriden in subclasses. statsmodels statsmodels.tsa.arima_model.ARMAResults.summary statsmodels.tsa.arima\_model.ARMAResults.summary ================================================ `ARMAResults.summary(alpha=0.05)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_model.html#ARMAResults.summary) Summarize the Model \| Parameters: \| alpha (float, optional) – Significance level for the confidence intervals. \| \| Returns: \| smry – This holds the summary table and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary.Summary`](statsmodels.iolib.summary.summary#statsmodels.iolib.summary.Summary "statsmodels.iolib.summary.Summary") statsmodels statsmodels.sandbox.distributions.transformed.ExpTransf_gen.mean statsmodels.sandbox.distributions.transformed.ExpTransf\_gen.mean ================================================================= `ExpTransf_gen.mean(args, kwds)` Mean of the distribution. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| mean – the mean of the distribution \| \| Return type: \| float \| statsmodels statsmodels.regression.quantile_regression.QuantRegResults.centered_tss statsmodels.regression.quantile\_regression.QuantRegResults.centered\_tss ========================================================================= `QuantRegResults.centered_tss()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/quantile_regression.html#QuantRegResults.centered_tss) statsmodels statsmodels.discrete.count_model.ZeroInflatedPoissonResults.wald_test statsmodels.discrete.count\_model.ZeroInflatedPoissonResults.wald\_test ======================================================================= `ZeroInflatedPoissonResults.wald_test(r_matrix, cov_p=None, scale=1.0, invcov=None, use_f=None)` Compute a Wald-test for a joint linear hypothesis. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. * use\_f (bool) – If True, then the F-distribution is used. If False, then the asymptotic distribution, chisquare is used. If use\_f is None, then the F distribution is used if the model specifies that use\_t is True. The test statistic is proportionally adjusted for the distribution by the number of constraints in the hypothesis. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`f_test`](statsmodels.discrete.count_model.zeroinflatedpoissonresults.f_test#statsmodels.discrete.count_model.ZeroInflatedPoissonResults.f_test "statsmodels.discrete.count_model.ZeroInflatedPoissonResults.f_test"), [`t_test`](statsmodels.discrete.count_model.zeroinflatedpoissonresults.t_test#statsmodels.discrete.count_model.ZeroInflatedPoissonResults.t_test "statsmodels.discrete.count_model.ZeroInflatedPoissonResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.tsa.statespace.mlemodel.MLEResults.test_heteroskedasticity statsmodels.tsa.statespace.mlemodel.MLEResults.test\_heteroskedasticity ======================================================================= `MLEResults.test_heteroskedasticity(method, alternative='two-sided', use_f=True)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/mlemodel.html#MLEResults.test_heteroskedasticity) Test for heteroskedasticity of standardized residuals Tests whether the sum-of-squares in the first third of the sample is significantly different than the sum-of-squares in the last third of the sample. Analogous to a Goldfeld-Quandt test. The null hypothesis is of no heteroskedasticity. \| Parameters: \| * method (string {'breakvar'} or None) – The statistical test for heteroskedasticity. Must be ‘breakvar’ for test of a break in the variance. If None, an attempt is made to select an appropriate test. * alternative (string, 'increasing', 'decreasing' or 'two-sided') – This specifies the alternative for the p-value calculation. Default is two-sided. * use\_f (boolean, optional) – Whether or not to compare against the asymptotic distribution (chi-squared) or the approximate small-sample distribution (F). Default is True (i.e. default is to compare against an F distribution). \| \| Returns: \| output – An array with `(test_statistic, pvalue)` for each endogenous variable. The array is then sized `(k_endog, 2)`. If the method is called as `het = res.test_heteroskedasticity()`, then `het[0]` is an array of size 2 corresponding to the first endogenous variable, where `het[0][0]` is the test statistic, and `het[0][1]` is the p-value. \| \| Return type: \| array \| #### Notes The null hypothesis is of no heteroskedasticity. That means different things depending on which alternative is selected: * Increasing: Null hypothesis is that the variance is not increasing throughout the sample; that the sum-of-squares in the later subsample is not greater than the sum-of-squares in the earlier subsample. * Decreasing: Null hypothesis is that the variance is not decreasing throughout the sample; that the sum-of-squares in the earlier subsample is not greater than the sum-of-squares in the later subsample. * Two-sided: Null hypothesis is that the variance is not changing throughout the sample. Both that the sum-of-squares in the earlier subsample is not greater than the sum-of-squares in the later subsample and that the sum-of-squares in the later subsample is not greater than the sum-of-squares in the earlier subsample. For $h = [T/3]$, the test statistic is: \[H(h) = \sum\_{t=T-h+1}^T \tilde v\_t^2 \Bigg / \sum\_{t=d+1}^{d+1+h} \tilde v\_t^2\] where $d$ is the number of periods in which the loglikelihood was burned in the parent model (usually corresponding to diffuse initialization). This statistic can be tested against an $F(h,h)$ distribution. Alternatively, $h H(h)$ is asymptotically distributed according to $\chi\_h^2$; this second test can be applied by passing `asymptotic=True` as an argument. See section 5.4 of [[1]](#id2) for the above formula and discussion, as well as additional details. TODO * Allow specification of $h$ #### References \| \| \| \| --- \| --- \| \| [[1]](#id1) \| Harvey, Andrew C. 1990. Forecasting, Structural Time Series Models and the Kalman Filter. Cambridge University Press. \|	programming_docs
statsmodels statsmodels.stats.contingency_tables.StratifiedTable.logodds_pooled_se statsmodels.stats.contingency\_tables.StratifiedTable.logodds\_pooled\_se ========================================================================= `StratifiedTable.logodds_pooled_se()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/contingency_tables.html#StratifiedTable.logodds_pooled_se) statsmodels statsmodels.tsa.vector_ar.var_model.VAR.initialize statsmodels.tsa.vector\_ar.var\_model.VAR.initialize ==================================================== `VAR.initialize()` Initialize (possibly re-initialize) a Model instance. For instance, the design matrix of a linear model may change and some things must be recomputed. statsmodels statsmodels.tsa.statespace.structural.UnobservedComponentsResults.t_test_pairwise statsmodels.tsa.statespace.structural.UnobservedComponentsResults.t\_test\_pairwise =================================================================================== `UnobservedComponentsResults.t_test_pairwise(term_name, method='hs', alpha=0.05, factor_labels=None)` perform pairwise t\_test with multiple testing corrected p-values This uses the formula design\_info encoding contrast matrix and should work for all encodings of a main effect. \| Parameters: \| * result (result instance) – The results of an estimated model with a categorical main effect. * term\_name (str) – name of the term for which pairwise comparisons are computed. Term names for categorical effects are created by patsy and correspond to the main part of the exog names. * method (str or list of strings) – multiple testing p-value correction, default is ‘hs’, see stats.multipletesting * alpha (float) – significance level for multiple testing reject decision. * factor\_labels (None, list of str) – Labels for the factor levels used for pairwise labels. If not provided, then the labels from the formula design\_info are used. \| \| Returns: \| results – The results are stored as attributes, the main attributes are the following two. Other attributes are added for debugging purposes or as background information.* result\_frame : pandas DataFrame with t\_test results and multiple testing corrected p-values. * contrasts : matrix of constraints of the null hypothesis in the t\_test. \| \| Return type: \| instance of a simple Results class \| #### Notes Status: experimental. Currently only checked for treatment coding with and without specified reference level. Currently there are no multiple testing corrected confidence intervals available. #### Examples ``` >>> res = ols("np.log(Days+1) ~ C(Weight) + C(Duration)", data).fit() >>> pw = res.t_test_pairwise("C(Weight)") >>> pw.result_frame coef std err t P>\|t\| Conf. Int. Low 2-1 0.632315 0.230003 2.749157 8.028083e-03 0.171563 3-1 1.302555 0.230003 5.663201 5.331513e-07 0.841803 3-2 0.670240 0.230003 2.914044 5.119126e-03 0.209488 Conf. Int. Upp. pvalue-hs reject-hs 2-1 1.093067 0.010212 True 3-1 1.763307 0.000002 True 3-2 1.130992 0.010212 True ``` statsmodels statsmodels.sandbox.distributions.extras.NormExpan_gen.logcdf statsmodels.sandbox.distributions.extras.NormExpan\_gen.logcdf ============================================================== `NormExpan_gen.logcdf(x, args, kwds)` Log of the cumulative distribution function at x of the given RV. \| Parameters: \| x (array\_like) – quantiles * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| logcdf – Log of the cumulative distribution function evaluated at x \| \| Return type: \| array\_like \| statsmodels statsmodels.tsa.arima_model.ARIMAResults.mafreq statsmodels.tsa.arima\_model.ARIMAResults.mafreq ================================================ `ARIMAResults.mafreq()` Returns the frequency of the MA roots. This is the solution, x, to z = abs(z)\exp(2j\np.pi\x) where z are the roots. statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.f_test statsmodels.regression.recursive\_ls.RecursiveLSResults.f\_test =============================================================== `RecursiveLSResults.f_test(r_matrix, cov_p=None, scale=1.0, invcov=None)` Compute the F-test for a joint linear hypothesis. This is a special case of `wald_test` that always uses the F distribution. \| Parameters: \| r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length k row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> A = np.identity(len(results.params)) >>> A = A[1:,:] ``` This tests that each coefficient is jointly statistically significantly different from zero. ``` >>> print(results.f_test(A)) <F test: F=array([[ 330.28533923]]), p=4.984030528700946e-10, df_denom=9, df_num=6> ``` Compare this to ``` >>> results.fvalue 330.2853392346658 >>> results.f_pvalue 4.98403096572e-10 ``` ``` >>> B = np.array(([0,0,1,-1,0,0,0],[0,0,0,0,0,1,-1])) ``` This tests that the coefficient on the 2nd and 3rd regressors are equal and jointly that the coefficient on the 5th and 6th regressors are equal. ``` >>> print(results.f_test(B)) <F test: F=array([[ 9.74046187]]), p=0.005605288531708235, df_denom=9, df_num=2> ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.datasets import longley >>> from statsmodels.formula.api import ols >>> dta = longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = '(GNPDEFL = GNP), (UNEMP = 2), (YEAR/1829 = 1)' >>> f_test = results.f_test(hypotheses) >>> print(f_test) <F test: F=array([[ 144.17976065]]), p=6.322026217355609e-08, df_denom=9, df_num=3> ``` See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`wald_test`](statsmodels.regression.recursive_ls.recursivelsresults.wald_test#statsmodels.regression.recursive_ls.RecursiveLSResults.wald_test "statsmodels.regression.recursive_ls.RecursiveLSResults.wald_test"), [`t_test`](statsmodels.regression.recursive_ls.recursivelsresults.t_test#statsmodels.regression.recursive_ls.RecursiveLSResults.t_test "statsmodels.regression.recursive_ls.RecursiveLSResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.tsa.vector_ar.dynamic.DynamicVAR statsmodels.tsa.vector\_ar.dynamic.DynamicVAR ============================================= `class statsmodels.tsa.vector_ar.dynamic.DynamicVAR(data, lag_order=1, window=None, window_type='expanding', trend='c', min_periods=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/dynamic.html#DynamicVAR) Estimates time-varying vector autoregression (VAR(p)) using equation-by-equation least squares \| Parameters: \| * data ([pandas.DataFrame](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html#pandas.DataFrame "(in pandas v0.22.0)")) – * lag\_order (int, default 1) – * window (int) – * window\_type ({'expanding', 'rolling'}) – * min\_periods (int or None) – Minimum number of observations to require in window, defaults to window size if None specified * trend ({'c', 'nc', 'ct', 'ctt'}) – TODO \| \| Returns: \| * \\Attributes\\** * coefs (Panel) – items : coefficient names major\_axis : dates minor\_axis : VAR equation names \| #### Methods \| \| \| \| --- \| --- \| \| [`T`](statsmodels.tsa.vector_ar.dynamic.dynamicvar.t#statsmodels.tsa.vector_ar.dynamic.DynamicVAR.T "statsmodels.tsa.vector_ar.dynamic.DynamicVAR.T")() \| Number of time periods in results \| \| [`coefs`](statsmodels.tsa.vector_ar.dynamic.dynamicvar.coefs#statsmodels.tsa.vector_ar.dynamic.DynamicVAR.coefs "statsmodels.tsa.vector_ar.dynamic.DynamicVAR.coefs")() \| Return dynamic regression coefficients as Panel \| \| [`equations`](statsmodels.tsa.vector_ar.dynamic.dynamicvar.equations#statsmodels.tsa.vector_ar.dynamic.DynamicVAR.equations "statsmodels.tsa.vector_ar.dynamic.DynamicVAR.equations")() \| \| \| [`forecast`](statsmodels.tsa.vector_ar.dynamic.dynamicvar.forecast#statsmodels.tsa.vector_ar.dynamic.DynamicVAR.forecast "statsmodels.tsa.vector_ar.dynamic.DynamicVAR.forecast")([steps]) \| Produce dynamic forecast \| \| [`plot_forecast`](statsmodels.tsa.vector_ar.dynamic.dynamicvar.plot_forecast#statsmodels.tsa.vector_ar.dynamic.DynamicVAR.plot_forecast "statsmodels.tsa.vector_ar.dynamic.DynamicVAR.plot_forecast")([steps, figsize]) \| Plot h-step ahead forecasts against actual realizations of time series. \| \| [`r2`](statsmodels.tsa.vector_ar.dynamic.dynamicvar.r2#statsmodels.tsa.vector_ar.dynamic.DynamicVAR.r2 "statsmodels.tsa.vector_ar.dynamic.DynamicVAR.r2")() \| Returns the r-squared values. \| \| [`resid`](statsmodels.tsa.vector_ar.dynamic.dynamicvar.resid#statsmodels.tsa.vector_ar.dynamic.DynamicVAR.resid "statsmodels.tsa.vector_ar.dynamic.DynamicVAR.resid")() \| \| #### Attributes \| \| \| \| --- \| --- \| \| `nobs` \| \| \| `result_index` \| \| statsmodels statsmodels.discrete.discrete_model.ProbitResults.wald_test_terms statsmodels.discrete.discrete\_model.ProbitResults.wald\_test\_terms ==================================================================== `ProbitResults.wald_test_terms(skip_single=False, extra_constraints=None, combine_terms=None)` Compute a sequence of Wald tests for terms over multiple columns This computes joined Wald tests for the hypothesis that all coefficients corresponding to a `term` are zero. `Terms` are defined by the underlying formula or by string matching. \| Parameters: \| * skip\_single (boolean) – If true, then terms that consist only of a single column and, therefore, refers only to a single parameter is skipped. If false, then all terms are included. * extra\_constraints (ndarray) – not tested yet * combine\_terms (None or list of strings) – Each string in this list is matched to the name of the terms or the name of the exogenous variables. All columns whose name includes that string are combined in one joint test. \| \| Returns: \| test\_result – The result instance contains `table` which is a pandas DataFrame with the test results: test statistic, degrees of freedom and pvalues. \| \| Return type: \| result instance \| #### Examples ``` >>> res_ols = ols("np.log(Days+1) ~ C(Duration, Sum)C(Weight, Sum)", data).fit() >>> res_ols.wald_test_terms() <class 'statsmodels.stats.contrast.WaldTestResults'> F P>F df constraint df denom Intercept 279.754525 2.37985521351e-22 1 51 C(Duration, Sum) 5.367071 0.0245738436636 1 51 C(Weight, Sum) 12.432445 3.99943118767e-05 2 51 C(Duration, Sum):C(Weight, Sum) 0.176002 0.83912310946 2 51 ``` ``` >>> res_poi = Poisson.from_formula("Days ~ C(Weight) C(Duration)", data).fit(cov_type='HC0') >>> wt = res_poi.wald_test_terms(skip_single=False, combine_terms=['Duration', 'Weight']) >>> print(wt) chi2 P>chi2 df constraint Intercept 15.695625 7.43960374424e-05 1 C(Weight) 16.132616 0.000313940174705 2 C(Duration) 1.009147 0.315107378931 1 C(Weight):C(Duration) 0.216694 0.897315972824 2 Duration 11.187849 0.010752286833 3 Weight 30.263368 4.32586407145e-06 4 ``` statsmodels statsmodels.discrete.discrete_model.BinaryResults.summary2 statsmodels.discrete.discrete\_model.BinaryResults.summary2 =========================================================== `BinaryResults.summary2(yname=None, xname=None, title=None, alpha=0.05, float_format='%.4f')` Experimental function to summarize regression results \| Parameters: \| * xname (List of strings of length equal to the number of parameters) – Names of the independent variables (optional) * yname (string) – Name of the dependent variable (optional) * title (string, optional) – Title for the top table. If not None, then this replaces the default title * alpha (float) – significance level for the confidence intervals * float\_format (string) – print format for floats in parameters summary \| \| Returns: \| smry – this holds the summary tables and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary.Summary`](statsmodels.iolib.summary.summary#statsmodels.iolib.summary.Summary "statsmodels.iolib.summary.Summary") class to hold summary results statsmodels statsmodels.tsa.holtwinters.SimpleExpSmoothing.fit statsmodels.tsa.holtwinters.SimpleExpSmoothing.fit ================================================== `SimpleExpSmoothing.fit(smoothing_level=None, optimized=True)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/holtwinters.html#SimpleExpSmoothing.fit) fit Simple Exponential Smoothing wrapper(…) \| Parameters: \| * smoothing\_level (float, optional) – The smoothing\_level value of the simple exponential smoothing, if the value is set then this value will be used as the value. * optimized (bool) – Should the values that have not been set above be optimized automatically? \| \| Returns: \| results – See statsmodels.tsa.holtwinters.HoltWintersResults \| \| Return type: \| HoltWintersResults class \| #### Notes This is a full implementation of the simple exponential smoothing as per [1]. #### References [1] Hyndman, Rob J., and George Athanasopoulos. Forecasting: principles and practice. OTexts, 2014. statsmodels statsmodels.genmod.families.family.InverseGaussian.predict statsmodels.genmod.families.family.InverseGaussian.predict ========================================================== `InverseGaussian.predict(mu)` Linear predictors based on given mu values. \| Parameters: \| mu (array) – The mean response variables \| \| Returns: \| lin\_pred – Linear predictors based on the mean response variables. The value of the link function at the given mu. \| \| Return type: \| array \| statsmodels statsmodels.genmod.generalized_linear_model.GLMResults.summary2 statsmodels.genmod.generalized\_linear\_model.GLMResults.summary2 ================================================================= `GLMResults.summary2(yname=None, xname=None, title=None, alpha=0.05, float_format='%.4f')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_linear_model.html#GLMResults.summary2) Experimental summary for regression Results \| Parameters: \| * yname (string) – Name of the dependent variable (optional) * xname (List of strings of length equal to the number of parameters) – Names of the independent variables (optional) * title (string, optional) – Title for the top table. If not None, then this replaces the default title * alpha (float) – significance level for the confidence intervals * float\_format (string) – print format for floats in parameters summary \| \| Returns: \| smry – this holds the summary tables and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary2.Summary`](statsmodels.iolib.summary2.summary#statsmodels.iolib.summary2.Summary "statsmodels.iolib.summary2.Summary") class to hold summary results statsmodels statsmodels.regression.quantile_regression.QuantRegResults.compare_lm_test statsmodels.regression.quantile\_regression.QuantRegResults.compare\_lm\_test ============================================================================= `QuantRegResults.compare_lm_test(restricted, demean=True, use_lr=False)` Use Lagrange Multiplier test to test whether restricted model is correct \| Parameters: \| * restricted (Result instance) – The restricted model is assumed to be nested in the current model. The result instance of the restricted model is required to have two attributes, residual sum of squares, `ssr`, residual degrees of freedom, `df_resid`. * demean (bool) – Flag indicating whether the demean the scores based on the residuals from the restricted model. If True, the covariance of the scores are used and the LM test is identical to the large sample version of the LR test. \| \| Returns: \| * lm\_value (float) – test statistic, chi2 distributed * p\_value (float) – p-value of the test statistic * df\_diff (int) – degrees of freedom of the restriction, i.e. difference in df between models \| #### Notes TODO: explain LM text statsmodels statsmodels.genmod.cov_struct.Exchangeable.summary statsmodels.genmod.cov\_struct.Exchangeable.summary =================================================== `Exchangeable.summary()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/cov_struct.html#Exchangeable.summary) Returns a text summary of the current estimate of the dependence structure. statsmodels statsmodels.tsa.statespace.structural.UnobservedComponents statsmodels.tsa.statespace.structural.UnobservedComponents ========================================================== `class statsmodels.tsa.statespace.structural.UnobservedComponents(endog, level=False, trend=False, seasonal=None, freq_seasonal=None, cycle=False, autoregressive=None, exog=None, irregular=False, stochastic_level=False, stochastic_trend=False, stochastic_seasonal=True, stochastic_freq_seasonal=None, stochastic_cycle=False, damped_cycle=False, cycle_period_bounds=None, mle_regression=True, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/structural.html#UnobservedComponents) Univariate unobserved components time series model These are also known as structural time series models, and decompose a (univariate) time series into trend, seasonal, cyclical, and irregular components. \| Parameters: \| level (bool or string, optional) – Whether or not to include a level component. Default is False. Can also be a string specification of the level / trend component; see Notes for available model specification strings. * trend (bool, optional) – Whether or not to include a trend component. Default is False. If True, `level` must also be True. * seasonal (int or None, optional) – The period of the seasonal component, if any. Default is None. * freq\_seasonal (list of dicts or None, optional.) – Whether (and how) to model seasonal component(s) with trig. functions. If specified, there is one dictionary for each frequency-domain seasonal component. Each dictionary must have the key, value pair for ‘period’ – integer and may have a key, value pair for ‘harmonics’ – integer. If ‘harmonics’ is not specified in any of the dictionaries, it defaults to the floor of period/2. * cycle (bool, optional) – Whether or not to include a cycle component. Default is False. * ar (int or None, optional) – The order of the autoregressive component. Default is None. * exog (array\_like or None, optional) – Exogenous variables. * irregular (bool, optional) – Whether or not to include an irregular component. Default is False. * stochastic\_level (bool, optional) – Whether or not any level component is stochastic. Default is False. * stochastic\_trend (bool, optional) – Whether or not any trend component is stochastic. Default is False. * stochastic\_seasonal (bool, optional) – Whether or not any seasonal component is stochastic. Default is True. * stochastic\_freq\_seasonal (list of bools, optional) – Whether or not each seasonal component(s) is (are) stochastic. Default is True for each component. The list should be of the same length as freq\_seasonal. * stochastic\_cycle (bool, optional) – Whether or not any cycle component is stochastic. Default is False. * damped\_cycle (bool, optional) – Whether or not the cycle component is damped. Default is False. * cycle\_period\_bounds (tuple, optional) – A tuple with lower and upper allowed bounds for the period of the cycle. If not provided, the following default bounds are used: (1) if no date / time information is provided, the frequency is constrained to be between zero and $\pi$, so the period is constrained to be in [0.5, infinity]. (2) If the date / time information is provided, the default bounds allow the cyclical component to be between 1.5 and 12 years; depending on the frequency of the endogenous variable, this will imply different specific bounds. \| #### Notes These models take the general form (see [[1]](#id2) Chapter 3.2 for all details) \[y\_t = \mu\_t + \gamma\_t + c\_t + \varepsilon\_t\] where $y\_t$ refers to the observation vector at time $t$, $\mu\_t$ refers to the trend component, $\gamma\_t$ refers to the seasonal component, $c\_t$ refers to the cycle, and $\varepsilon\_t$ is the irregular. The modeling details of these components are given below. Trend The trend component is a dynamic extension of a regression model that includes an intercept and linear time-trend. It can be written: \[\begin{split}\mu\_t = \mu\_{t-1} + \beta\_{t-1} + \eta\_{t-1} \\ \beta\_t = \beta\_{t-1} + \zeta\_{t-1}\end{split}\] where the level is a generalization of the intercept term that can dynamically vary across time, and the trend is a generalization of the time-trend such that the slope can dynamically vary across time. Here $\eta\_t \sim N(0, \sigma\_\eta^2)$ and $\zeta\_t \sim N(0, \sigma\_\zeta^2)$. For both elements (level and trend), we can consider models in which: * The element is included vs excluded (if the trend is included, there must also be a level included). * The element is deterministic vs stochastic (i.e. whether or not the variance on the error term is confined to be zero or not) The only additional parameters to be estimated via MLE are the variances of any included stochastic components. The level/trend components can be specified using the boolean keyword arguments `level`, `stochastic_level`, `trend`, etc., or all at once as a string argument to `level`. The following table shows the available model specifications: \| Model name \| Full string syntax \| Abbreviated syntax \| Model \| \| --- \| --- \| --- \| --- \| \| No trend \| `‘irregular’` \| `‘ntrend’` \| \[y\_t &= \varepsilon\_t\] \| \| Fixed intercept \| `‘fixed intercept’` \| \| \[y\_t &= \mu\] \| \| Deterministic constant \| `‘deterministic constant’` \| `‘dconstant’` \| \[y\_t &= \mu + \varepsilon\_t\] \| \| Local level \| `‘local level’` \| `‘llevel’` \| \[\begin{split}y\_t &= \mu\_t + \varepsilon\_t \\ \mu\_t &= \mu\_{t-1} + \eta\_t\end{split}\] \| \| Random walk \| `‘random walk’` \| `‘rwalk’` \| \[\begin{split}y\_t &= \mu\_t \\ \mu\_t &= \mu\_{t-1} + \eta\_t\end{split}\] \| \| Fixed slope \| `‘fixed slope’` \| \| \[\begin{split}y\_t &= \mu\_t \\ \mu\_t &= \mu\_{t-1} + \beta\end{split}\] \| \| Deterministic trend \| `‘deterministic trend’` \| `‘dtrend’` \| \[\begin{split}y\_t &= \mu\_t + \varepsilon\_t \\ \mu\_t &= \mu\_{t-1} + \beta\end{split}\] \| \| Local linear deterministic trend \| `‘local linear deterministic trend’` \| `‘lldtrend’` \| \[\begin{split}y\_t &= \mu\_t + \varepsilon\_t \\ \mu\_t &= \mu\_{t-1} + \beta + \eta\_t\end{split}\] \| \| Random walk with drift \| `‘random walk with drift’` \| `‘rwdrift’` \| \[\begin{split}y\_t &= \mu\_t \\ \mu\_t &= \mu\_{t-1} + \beta + \eta\_t\end{split}\] \| \| Local linear trend \| `‘local linear trend’` \| `‘lltrend’` \| \[\begin{split}y\_t &= \mu\_t + \varepsilon\_t \\ \mu\_t &= \mu\_{t-1} + \beta\_{t-1} + \eta\_t \\ \beta\_t &= \beta\_{t-1} + \zeta\_t\end{split}\] \| \| Smooth trend \| `‘smooth trend’` \| `‘strend’` \| \[\begin{split}y\_t &= \mu\_t + \varepsilon\_t \\ \mu\_t &= \mu\_{t-1} + \beta\_{t-1} \\ \beta\_t &= \beta\_{t-1} + \zeta\_t\end{split}\] \| \| Random trend \| `‘random trend’` \| `‘rtrend’` \| \[\begin{split}y\_t &= \mu\_t \\ \mu\_t &= \mu\_{t-1} + \beta\_{t-1} \\ \beta\_t &= \beta\_{t-1} + \zeta\_t\end{split}\] \| Following the fitting of the model, the unobserved level and trend component time series are available in the results class in the `level` and `trend` attributes, respectively. Seasonal (Time-domain) The seasonal component is modeled as: \[\begin{split}\gamma\_t = - \sum\_{j=1}^{s-1} \gamma\_{t+1-j} + \omega\_t \\ \omega\_t \sim N(0, \sigma\_\omega^2)\end{split}\] The periodicity (number of seasons) is s, and the defining character is that (without the error term), the seasonal components sum to zero across one complete cycle. The inclusion of an error term allows the seasonal effects to vary over time (if this is not desired, $\sigma\_\omega^2$ can be set to zero using the `stochastic_seasonal=False` keyword argument). This component results in one parameter to be selected via maximum likelihood: $\sigma\_\omega^2$, and one parameter to be chosen, the number of seasons `s`. Following the fitting of the model, the unobserved seasonal component time series is available in the results class in the `seasonal` attribute. \\ Frequency-domain Seasonal\\ Each frequency-domain seasonal component is modeled as: \[\begin{split}\gamma\_t & = \sum\_{j=1}^h \gamma\_{j, t} \\ \gamma\_{j, t+1} & = \gamma\_{j, t}\cos(\lambda\_j) + \gamma^{\}\_{j, t}\sin(\lambda\_j) + \omega\_{j,t} \\ \gamma^{\}\_{j, t+1} & = -\gamma^{(1)}\_{j, t}\sin(\lambda\_j) + \gamma^{\}\_{j, t}\cos(\lambda\_j) + \omega^{\}\_{j, t}, \\ \omega^{\}\_{j, t}, \omega\_{j, t} & \sim N(0, \sigma\_{\omega^2}) \\ \lambda\_j & = \frac{2 \pi j}{s}\end{split}\] where j ranges from 1 to h. The periodicity (number of “seasons” in a “year”) is s and the number of harmonics is h. Note that h is configurable to be less than s/2, but s/2 harmonics is sufficient to fully model all seasonal variations of periodicity s. Like the time domain seasonal term (cf. Seasonal section, above), the inclusion of the error terms allows for the seasonal effects to vary over time. The argument stochastic\_freq\_seasonal can be used to set one or more of the seasonal components of this type to be non-random, meaning they will not vary over time. This component results in one parameter to be fitted using maximum likelihood: $\sigma\_{\omega^2}$, and up to two parameters to be chosen, the number of seasons s and optionally the number of harmonics h, with $1 \leq h \leq \floor(s/2)$. After fitting the model, each unobserved seasonal component modeled in the frequency domain is available in the results class in the `freq_seasonal` attribute. Cycle* The cyclical component is intended to capture cyclical effects at time frames much longer than captured by the seasonal component. For example, in economics the cyclical term is often intended to capture the business cycle, and is then expected to have a period between “1.5 and 12 years” (see Durbin and Koopman). \[\begin{split}c\_{t+1} & = \rho\_c (\tilde c\_t \cos \lambda\_c t + \tilde c\_t^\* \sin \lambda\_c) + \tilde \omega\_t \\ c\_{t+1}^\* & = \rho\_c (- \tilde c\_t \sin \lambda\_c t + \tilde c\_t^\* \cos \lambda\_c) + \tilde \omega\_t^\* \\\end{split}\] where $\omega\_t, \tilde \omega\_t iid N(0, \sigma\_{\tilde \omega}^2)$ The parameter $\lambda\_c$ (the frequency of the cycle) is an additional parameter to be estimated by MLE. If the cyclical effect is stochastic (`stochastic_cycle=True`), then there is another parameter to estimate (the variance of the error term - note that both of the error terms here share the same variance, but are assumed to have independent draws). If the cycle is damped (`damped_cycle=True`), then there is a third parameter to estimate, $\rho\_c$. In order to achieve cycles with the appropriate frequencies, bounds are imposed on the parameter $\lambda\_c$ in estimation. These can be controlled via the keyword argument `cycle_period_bounds`, which, if specified, must be a tuple of bounds on the period `(lower, upper)`. The bounds on the frequency are then calculated from those bounds. The default bounds, if none are provided, are selected in the following way: 1. If no date / time information is provided, the frequency is constrained to be between zero and $\pi$, so the period is constrained to be in $[0.5, \infty]$. 2. If the date / time information is provided, the default bounds allow the cyclical component to be between 1.5 and 12 years; depending on the frequency of the endogenous variable, this will imply different specific bounds. Following the fitting of the model, the unobserved cyclical component time series is available in the results class in the `cycle` attribute. Irregular The irregular components are independent and identically distributed (iid): \[\varepsilon\_t \sim N(0, \sigma\_\varepsilon^2)\] Autoregressive Irregular An autoregressive component (often used as a replacement for the white noise irregular term) can be specified as: \[\begin{split}\varepsilon\_t = \rho(L) \varepsilon\_{t-1} + \epsilon\_t \\ \epsilon\_t \sim N(0, \sigma\_\epsilon^2)\end{split}\] In this case, the AR order is specified via the `autoregressive` keyword, and the autoregressive coefficients are estimated. Following the fitting of the model, the unobserved autoregressive component time series is available in the results class in the `autoregressive` attribute. Regression effects Exogenous regressors can be pass to the `exog` argument. The regression coefficients will be estimated by maximum likelihood unless `mle_regression=False`, in which case the regression coefficients will be included in the state vector where they are essentially estimated via recursive OLS. If the regression\_coefficients are included in the state vector, the recursive estimates are available in the results class in the `regression_coefficients` attribute. #### References \| \| \| \| --- \| --- \| \| [[1]](#id1) \| Durbin, James, and Siem Jan Koopman. 2012. Time Series Analysis by State Space Methods: Second Edition. Oxford University Press. \| #### Methods \| \| \| \| --- \| --- \| \| [`filter`](statsmodels.tsa.statespace.structural.unobservedcomponents.filter#statsmodels.tsa.statespace.structural.UnobservedComponents.filter "statsmodels.tsa.statespace.structural.UnobservedComponents.filter")(params[, transformed, complex\_step, …]) \| Kalman filtering \| \| [`fit`](statsmodels.tsa.statespace.structural.unobservedcomponents.fit#statsmodels.tsa.statespace.structural.UnobservedComponents.fit "statsmodels.tsa.statespace.structural.UnobservedComponents.fit")([start\_params, transformed, cov\_type, …]) \| Fits the model by maximum likelihood via Kalman filter. \| \| [`from_formula`](statsmodels.tsa.statespace.structural.unobservedcomponents.from_formula#statsmodels.tsa.statespace.structural.UnobservedComponents.from_formula "statsmodels.tsa.statespace.structural.UnobservedComponents.from_formula")(formula, data[, subset]) \| Not implemented for state space models \| \| [`hessian`](statsmodels.tsa.statespace.structural.unobservedcomponents.hessian#statsmodels.tsa.statespace.structural.UnobservedComponents.hessian "statsmodels.tsa.statespace.structural.UnobservedComponents.hessian")(params, \args, \\kwargs) \| Hessian matrix of the likelihood function, evaluated at the given parameters \| \| [`impulse_responses`](statsmodels.tsa.statespace.structural.unobservedcomponents.impulse_responses#statsmodels.tsa.statespace.structural.UnobservedComponents.impulse_responses "statsmodels.tsa.statespace.structural.UnobservedComponents.impulse_responses")(params[, steps, impulse, …]) \| Impulse response function \| \| [`information`](statsmodels.tsa.statespace.structural.unobservedcomponents.information#statsmodels.tsa.statespace.structural.UnobservedComponents.information "statsmodels.tsa.statespace.structural.UnobservedComponents.information")(params) \| Fisher information matrix of model \| \| [`initialize`](statsmodels.tsa.statespace.structural.unobservedcomponents.initialize#statsmodels.tsa.statespace.structural.UnobservedComponents.initialize "statsmodels.tsa.statespace.structural.UnobservedComponents.initialize")() \| Initialize (possibly re-initialize) a Model instance. \| \| [`initialize_approximate_diffuse`](statsmodels.tsa.statespace.structural.unobservedcomponents.initialize_approximate_diffuse#statsmodels.tsa.statespace.structural.UnobservedComponents.initialize_approximate_diffuse "statsmodels.tsa.statespace.structural.UnobservedComponents.initialize_approximate_diffuse")([variance]) \| \| \| [`initialize_known`](statsmodels.tsa.statespace.structural.unobservedcomponents.initialize_known#statsmodels.tsa.statespace.structural.UnobservedComponents.initialize_known "statsmodels.tsa.statespace.structural.UnobservedComponents.initialize_known")(initial\_state, …) \| \| \| [`initialize_state`](statsmodels.tsa.statespace.structural.unobservedcomponents.initialize_state#statsmodels.tsa.statespace.structural.UnobservedComponents.initialize_state "statsmodels.tsa.statespace.structural.UnobservedComponents.initialize_state")() \| \| \| [`initialize_statespace`](statsmodels.tsa.statespace.structural.unobservedcomponents.initialize_statespace#statsmodels.tsa.statespace.structural.UnobservedComponents.initialize_statespace "statsmodels.tsa.statespace.structural.UnobservedComponents.initialize_statespace")(\\kwargs) \| Initialize the state space representation \| \| [`initialize_stationary`](statsmodels.tsa.statespace.structural.unobservedcomponents.initialize_stationary#statsmodels.tsa.statespace.structural.UnobservedComponents.initialize_stationary "statsmodels.tsa.statespace.structural.UnobservedComponents.initialize_stationary")() \| \| \| [`loglike`](statsmodels.tsa.statespace.structural.unobservedcomponents.loglike#statsmodels.tsa.statespace.structural.UnobservedComponents.loglike "statsmodels.tsa.statespace.structural.UnobservedComponents.loglike")(params, \args, \\kwargs) \| Loglikelihood evaluation \| \| [`loglikeobs`](statsmodels.tsa.statespace.structural.unobservedcomponents.loglikeobs#statsmodels.tsa.statespace.structural.UnobservedComponents.loglikeobs "statsmodels.tsa.statespace.structural.UnobservedComponents.loglikeobs")(params[, transformed, complex\_step]) \| Loglikelihood evaluation \| \| [`observed_information_matrix`](statsmodels.tsa.statespace.structural.unobservedcomponents.observed_information_matrix#statsmodels.tsa.statespace.structural.UnobservedComponents.observed_information_matrix "statsmodels.tsa.statespace.structural.UnobservedComponents.observed_information_matrix")(params[, …]) \| Observed information matrix \| \| [`opg_information_matrix`](statsmodels.tsa.statespace.structural.unobservedcomponents.opg_information_matrix#statsmodels.tsa.statespace.structural.UnobservedComponents.opg_information_matrix "statsmodels.tsa.statespace.structural.UnobservedComponents.opg_information_matrix")(params[, …]) \| Outer product of gradients information matrix \| \| [`predict`](statsmodels.tsa.statespace.structural.unobservedcomponents.predict#statsmodels.tsa.statespace.structural.UnobservedComponents.predict "statsmodels.tsa.statespace.structural.UnobservedComponents.predict")(params[, exog]) \| After a model has been fit predict returns the fitted values. \| \| [`prepare_data`](statsmodels.tsa.statespace.structural.unobservedcomponents.prepare_data#statsmodels.tsa.statespace.structural.UnobservedComponents.prepare_data "statsmodels.tsa.statespace.structural.UnobservedComponents.prepare_data")() \| Prepare data for use in the state space representation \| \| [`score`](statsmodels.tsa.statespace.structural.unobservedcomponents.score#statsmodels.tsa.statespace.structural.UnobservedComponents.score "statsmodels.tsa.statespace.structural.UnobservedComponents.score")(params, \args, \\kwargs) \| Compute the score function at params. \| \| [`score_obs`](statsmodels.tsa.statespace.structural.unobservedcomponents.score_obs#statsmodels.tsa.statespace.structural.UnobservedComponents.score_obs "statsmodels.tsa.statespace.structural.UnobservedComponents.score_obs")(params[, method, transformed, …]) \| Compute the score per observation, evaluated at params \| \| [`set_conserve_memory`](statsmodels.tsa.statespace.structural.unobservedcomponents.set_conserve_memory#statsmodels.tsa.statespace.structural.UnobservedComponents.set_conserve_memory "statsmodels.tsa.statespace.structural.UnobservedComponents.set_conserve_memory")([conserve\_memory]) \| Set the memory conservation method \| \| [`set_filter_method`](statsmodels.tsa.statespace.structural.unobservedcomponents.set_filter_method#statsmodels.tsa.statespace.structural.UnobservedComponents.set_filter_method "statsmodels.tsa.statespace.structural.UnobservedComponents.set_filter_method")([filter\_method]) \| Set the filtering method \| \| [`set_inversion_method`](statsmodels.tsa.statespace.structural.unobservedcomponents.set_inversion_method#statsmodels.tsa.statespace.structural.UnobservedComponents.set_inversion_method "statsmodels.tsa.statespace.structural.UnobservedComponents.set_inversion_method")([inversion\_method]) \| Set the inversion method \| \| [`set_smoother_output`](statsmodels.tsa.statespace.structural.unobservedcomponents.set_smoother_output#statsmodels.tsa.statespace.structural.UnobservedComponents.set_smoother_output "statsmodels.tsa.statespace.structural.UnobservedComponents.set_smoother_output")([smoother\_output]) \| Set the smoother output \| \| [`set_stability_method`](statsmodels.tsa.statespace.structural.unobservedcomponents.set_stability_method#statsmodels.tsa.statespace.structural.UnobservedComponents.set_stability_method "statsmodels.tsa.statespace.structural.UnobservedComponents.set_stability_method")([stability\_method]) \| Set the numerical stability method \| \| [`setup`](statsmodels.tsa.statespace.structural.unobservedcomponents.setup#statsmodels.tsa.statespace.structural.UnobservedComponents.setup "statsmodels.tsa.statespace.structural.UnobservedComponents.setup")() \| Setup the structural time series representation \| \| [`simulate`](statsmodels.tsa.statespace.structural.unobservedcomponents.simulate#statsmodels.tsa.statespace.structural.UnobservedComponents.simulate "statsmodels.tsa.statespace.structural.UnobservedComponents.simulate")(params, nsimulations[, …]) \| Simulate a new time series following the state space model \| \| [`simulation_smoother`](statsmodels.tsa.statespace.structural.unobservedcomponents.simulation_smoother#statsmodels.tsa.statespace.structural.UnobservedComponents.simulation_smoother "statsmodels.tsa.statespace.structural.UnobservedComponents.simulation_smoother")([simulation\_output]) \| Retrieve a simulation smoother for the state space model. \| \| [`smooth`](statsmodels.tsa.statespace.structural.unobservedcomponents.smooth#statsmodels.tsa.statespace.structural.UnobservedComponents.smooth "statsmodels.tsa.statespace.structural.UnobservedComponents.smooth")(params[, transformed, complex\_step, …]) \| Kalman smoothing \| \| [`transform_jacobian`](statsmodels.tsa.statespace.structural.unobservedcomponents.transform_jacobian#statsmodels.tsa.statespace.structural.UnobservedComponents.transform_jacobian "statsmodels.tsa.statespace.structural.UnobservedComponents.transform_jacobian")(unconstrained[, …]) \| Jacobian matrix for the parameter transformation function \| \| [`transform_params`](statsmodels.tsa.statespace.structural.unobservedcomponents.transform_params#statsmodels.tsa.statespace.structural.UnobservedComponents.transform_params "statsmodels.tsa.statespace.structural.UnobservedComponents.transform_params")(unconstrained) \| Transform unconstrained parameters used by the optimizer to constrained parameters used in likelihood evaluation \| \| [`untransform_params`](statsmodels.tsa.statespace.structural.unobservedcomponents.untransform_params#statsmodels.tsa.statespace.structural.UnobservedComponents.untransform_params "statsmodels.tsa.statespace.structural.UnobservedComponents.untransform_params")(constrained) \| Reverse the transformation \| \| [`update`](statsmodels.tsa.statespace.structural.unobservedcomponents.update#statsmodels.tsa.statespace.structural.UnobservedComponents.update "statsmodels.tsa.statespace.structural.UnobservedComponents.update")(params, \\*kwargs) \| Update the parameters of the model \| #### Attributes \| \| \| \| --- \| --- \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| \| \| `initial_variance` \| \| \| `initialization` \| \| \| `loglikelihood_burn` \| \| \| `param_names` \| (list of str) List of human readable parameter names (for parameters actually included in the model). \| \| `start_params` \| (array) Starting parameters for maximum likelihood estimation. \| \| `tolerance` \| \|	programming_docs
statsmodels statsmodels.stats.diagnostic.breaks_hansen statsmodels.stats.diagnostic.breaks\_hansen =========================================== `statsmodels.stats.diagnostic.breaks_hansen(olsresults)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/stats/diagnostic.html#breaks_hansen) test for model stability, breaks in parameters for ols, Hansen 1992 \| Parameters: \| olsresults (instance of RegressionResults) – uses only endog and exog \| \| Returns: \| * teststat (float) – Hansen’s test statistic * crit (structured array) – critical values at alpha=0.95 for different nvars * pvalue Not yet * ft, s (arrays) – temporary return for debugging, will be removed \| #### Notes looks good in example, maybe not very powerful for small changes in parameters According to Greene, distribution of test statistics depends on nvar but not on nobs. Test statistic is verified against R:strucchange #### References Greene section 7.5.1, notation follows Greene statsmodels statsmodels.duration.hazard_regression.PHReg.breslow_gradient statsmodels.duration.hazard\_regression.PHReg.breslow\_gradient =============================================================== `PHReg.breslow_gradient(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/duration/hazard_regression.html#PHReg.breslow_gradient) Returns the gradient of the log partial likelihood, using the Breslow method to handle tied times. statsmodels statsmodels.tsa.stattools.bds statsmodels.tsa.stattools.bds ============================= `statsmodels.tsa.stattools.bds(x, max_dim=2, epsilon=None, distance=1.5)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/_bds.html#bds) Calculate the BDS test statistic for independence of a time series \| Parameters: \| * x (1d array) – observations of time series for which bds statistics is calculated * max\_dim (integer) – maximum embedding dimension * epsilon (scalar, optional) – the threshold distance to use in calculating the correlation sum * distance (scalar, optional) – if epsilon is omitted, specifies the distance multiplier to use when computing it \| \| Returns: \| * bds\_stat (float) – The BDS statistic * pvalue (float) – The p-values associated with the BDS statistic \| #### Notes The null hypothesis of the test statistic is for an independent and identically distributed (i.i.d.) time series, and an unspecified alternative hypothesis. This test is often used as a residual diagnostic. The calculation involves matrices of size (nobs, nobs), so this test will not work with very long datasets. Implementation conditions on the first m-1 initial values, which are required to calculate the m-histories: x\_t^m = (x\_t, x\_{t-1}, … x\_{t-(m-1)}) statsmodels statsmodels.tsa.arima_model.ARMAResults statsmodels.tsa.arima\_model.ARMAResults ======================================== `class statsmodels.tsa.arima_model.ARMAResults(model, params, normalized_cov_params=None, scale=1.0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_model.html#ARMAResults) Class to hold results from fitting an ARMA model. \| Parameters: \| * model (ARMA instance) – The fitted model instance * params (array) – Fitted parameters * normalized\_cov\_params (array, optional) – The normalized variance covariance matrix * scale (float, optional) – Optional argument to scale the variance covariance matrix. \| \| Returns: \| * \\Attributes\\** * aic (float) – Akaike Information Criterion $-2\llf+2\ df\_model$ where `df_model` includes all AR parameters, MA parameters, constant terms parameters on constant terms and the variance. * arparams (array) – The parameters associated with the AR coefficients in the model. * arroots (array) – The roots of the AR coefficients are the solution to (1 - arparams[0]\z - arparams[1]\z\\2 -…- arparams[p-1]\z\\k\_ar) = 0 Stability requires that the roots in modulus lie outside the unit circle. bic (float) – Bayes Information Criterion -2\llf + log(nobs)\df\_model Where if the model is fit using conditional sum of squares, the number of observations `nobs` does not include the `p` pre-sample observations. * bse (array) – The standard errors of the parameters. These are computed using the numerical Hessian. * df\_model (array) – The model degrees of freedom = `k_exog` + `k_trend` + `k_ar` + `k_ma` * df\_resid (array) – The residual degrees of freedom = `nobs` - `df_model` * fittedvalues (array) – The predicted values of the model. * hqic (float) – Hannan-Quinn Information Criterion -2\llf + 2\(`df_model`)\log(log(nobs)) Like `bic` if the model is fit using conditional sum of squares then the `k_ar` pre-sample observations are not counted in `nobs`. k\_ar (int) – The number of AR coefficients in the model. * k\_exog (int) – The number of exogenous variables included in the model. Does not include the constant. * k\_ma (int) – The number of MA coefficients. * k\_trend (int) – This is 0 for no constant or 1 if a constant is included. * llf (float) – The value of the log-likelihood function evaluated at `params`. * maparams (array) – The value of the moving average coefficients. * maroots (array) – The roots of the MA coefficients are the solution to (1 + maparams[0]\z + maparams[1]\z\\2 + … + maparams[q-1]\z\\q) = 0 Stability requires that the roots in modules lie outside the unit circle. model (ARMA instance) – A reference to the model that was fit. * nobs (float) – The number of observations used to fit the model. If the model is fit using exact maximum likelihood this is equal to the total number of observations, `n_totobs`. If the model is fit using conditional maximum likelihood this is equal to `n_totobs` - `k_ar`. * n\_totobs (float) – The total number of observations for `endog`. This includes all observations, even pre-sample values if the model is fit using `css`. * params (array) – The parameters of the model. The order of variables is the trend coefficients and the `k_exog` exognous coefficients, then the `k_ar` AR coefficients, and finally the `k_ma` MA coefficients. * pvalues (array) – The p-values associated with the t-values of the coefficients. Note that the coefficients are assumed to have a Student’s T distribution. * resid (array) – The model residuals. If the model is fit using ‘mle’ then the residuals are created via the Kalman Filter. If the model is fit using ‘css’ then the residuals are obtained via `scipy.signal.lfilter` adjusted such that the first `k_ma` residuals are zero. These zero residuals are not returned. * scale (float) – This is currently set to 1.0 and not used by the model or its results. * sigma2 (float) – The variance of the residuals. If the model is fit by ‘css’, sigma2 = ssr/nobs, where ssr is the sum of squared residuals. If the model is fit by ‘mle’, then sigma2 = 1/nobs \* sum(v\\2 / F) where v is the one-step forecast error and F is the forecast error variance. See `nobs` for the difference in definitions depending on the fit. \| #### Methods \| \| \| \| --- \| --- \| \| [`aic`](statsmodels.tsa.arima_model.armaresults.aic#statsmodels.tsa.arima_model.ARMAResults.aic "statsmodels.tsa.arima_model.ARMAResults.aic")() \| \| \| [`arfreq`](statsmodels.tsa.arima_model.armaresults.arfreq#statsmodels.tsa.arima_model.ARMAResults.arfreq "statsmodels.tsa.arima_model.ARMAResults.arfreq")() \| Returns the frequency of the AR roots. \| \| [`arparams`](statsmodels.tsa.arima_model.armaresults.arparams#statsmodels.tsa.arima_model.ARMAResults.arparams "statsmodels.tsa.arima_model.ARMAResults.arparams")() \| \| \| [`arroots`](statsmodels.tsa.arima_model.armaresults.arroots#statsmodels.tsa.arima_model.ARMAResults.arroots "statsmodels.tsa.arima_model.ARMAResults.arroots")() \| \| \| [`bic`](statsmodels.tsa.arima_model.armaresults.bic#statsmodels.tsa.arima_model.ARMAResults.bic "statsmodels.tsa.arima_model.ARMAResults.bic")() \| \| \| [`bse`](statsmodels.tsa.arima_model.armaresults.bse#statsmodels.tsa.arima_model.ARMAResults.bse "statsmodels.tsa.arima_model.ARMAResults.bse")() \| \| \| [`conf_int`](statsmodels.tsa.arima_model.armaresults.conf_int#statsmodels.tsa.arima_model.ARMAResults.conf_int "statsmodels.tsa.arima_model.ARMAResults.conf_int")([alpha, cols, method]) \| Returns the confidence interval of the fitted parameters. \| \| [`cov_params`](statsmodels.tsa.arima_model.armaresults.cov_params#statsmodels.tsa.arima_model.ARMAResults.cov_params "statsmodels.tsa.arima_model.ARMAResults.cov_params")() \| Returns the variance/covariance matrix. \| \| [`f_test`](statsmodels.tsa.arima_model.armaresults.f_test#statsmodels.tsa.arima_model.ARMAResults.f_test "statsmodels.tsa.arima_model.ARMAResults.f_test")(r\_matrix[, cov\_p, scale, invcov]) \| Compute the F-test for a joint linear hypothesis. \| \| [`fittedvalues`](statsmodels.tsa.arima_model.armaresults.fittedvalues#statsmodels.tsa.arima_model.ARMAResults.fittedvalues "statsmodels.tsa.arima_model.ARMAResults.fittedvalues")() \| \| \| [`forecast`](statsmodels.tsa.arima_model.armaresults.forecast#statsmodels.tsa.arima_model.ARMAResults.forecast "statsmodels.tsa.arima_model.ARMAResults.forecast")([steps, exog, alpha]) \| Out-of-sample forecasts \| \| [`hqic`](statsmodels.tsa.arima_model.armaresults.hqic#statsmodels.tsa.arima_model.ARMAResults.hqic "statsmodels.tsa.arima_model.ARMAResults.hqic")() \| \| \| [`initialize`](statsmodels.tsa.arima_model.armaresults.initialize#statsmodels.tsa.arima_model.ARMAResults.initialize "statsmodels.tsa.arima_model.ARMAResults.initialize")(model, params, \\kwd) \| \| \| [`llf`](statsmodels.tsa.arima_model.armaresults.llf#statsmodels.tsa.arima_model.ARMAResults.llf "statsmodels.tsa.arima_model.ARMAResults.llf")() \| \| \| [`load`](statsmodels.tsa.arima_model.armaresults.load#statsmodels.tsa.arima_model.ARMAResults.load "statsmodels.tsa.arima_model.ARMAResults.load")(fname) \| load a pickle, (class method) \| \| [`mafreq`](statsmodels.tsa.arima_model.armaresults.mafreq#statsmodels.tsa.arima_model.ARMAResults.mafreq "statsmodels.tsa.arima_model.ARMAResults.mafreq")() \| Returns the frequency of the MA roots. \| \| [`maparams`](statsmodels.tsa.arima_model.armaresults.maparams#statsmodels.tsa.arima_model.ARMAResults.maparams "statsmodels.tsa.arima_model.ARMAResults.maparams")() \| \| \| [`maroots`](statsmodels.tsa.arima_model.armaresults.maroots#statsmodels.tsa.arima_model.ARMAResults.maroots "statsmodels.tsa.arima_model.ARMAResults.maroots")() \| \| \| [`normalized_cov_params`](statsmodels.tsa.arima_model.armaresults.normalized_cov_params#statsmodels.tsa.arima_model.ARMAResults.normalized_cov_params "statsmodels.tsa.arima_model.ARMAResults.normalized_cov_params")() \| \| \| [`plot_predict`](statsmodels.tsa.arima_model.armaresults.plot_predict#statsmodels.tsa.arima_model.ARMAResults.plot_predict "statsmodels.tsa.arima_model.ARMAResults.plot_predict")([start, end, exog, dynamic, …]) \| Plot forecasts \| \| [`predict`](statsmodels.tsa.arima_model.armaresults.predict#statsmodels.tsa.arima_model.ARMAResults.predict "statsmodels.tsa.arima_model.ARMAResults.predict")([start, end, exog, dynamic]) \| ARMA model in-sample and out-of-sample prediction \| \| [`pvalues`](statsmodels.tsa.arima_model.armaresults.pvalues#statsmodels.tsa.arima_model.ARMAResults.pvalues "statsmodels.tsa.arima_model.ARMAResults.pvalues")() \| \| \| [`remove_data`](statsmodels.tsa.arima_model.armaresults.remove_data#statsmodels.tsa.arima_model.ARMAResults.remove_data "statsmodels.tsa.arima_model.ARMAResults.remove_data")() \| remove data arrays, all nobs arrays from result and model \| \| [`resid`](statsmodels.tsa.arima_model.armaresults.resid#statsmodels.tsa.arima_model.ARMAResults.resid "statsmodels.tsa.arima_model.ARMAResults.resid")() \| \| \| [`save`](statsmodels.tsa.arima_model.armaresults.save#statsmodels.tsa.arima_model.ARMAResults.save "statsmodels.tsa.arima_model.ARMAResults.save")(fname[, remove\_data]) \| save a pickle of this instance \| \| [`summary`](statsmodels.tsa.arima_model.armaresults.summary#statsmodels.tsa.arima_model.ARMAResults.summary "statsmodels.tsa.arima_model.ARMAResults.summary")([alpha]) \| Summarize the Model \| \| [`summary2`](statsmodels.tsa.arima_model.armaresults.summary2#statsmodels.tsa.arima_model.ARMAResults.summary2 "statsmodels.tsa.arima_model.ARMAResults.summary2")([title, alpha, float\_format]) \| Experimental summary function for ARIMA Results \| \| [`t_test`](statsmodels.tsa.arima_model.armaresults.t_test#statsmodels.tsa.arima_model.ARMAResults.t_test "statsmodels.tsa.arima_model.ARMAResults.t_test")(r\_matrix[, cov\_p, scale, use\_t]) \| Compute a t-test for a each linear hypothesis of the form Rb = q \| \| [`t_test_pairwise`](statsmodels.tsa.arima_model.armaresults.t_test_pairwise#statsmodels.tsa.arima_model.ARMAResults.t_test_pairwise "statsmodels.tsa.arima_model.ARMAResults.t_test_pairwise")(term\_name[, method, alpha, …]) \| perform pairwise t\_test with multiple testing corrected p-values \| \| [`tvalues`](statsmodels.tsa.arima_model.armaresults.tvalues#statsmodels.tsa.arima_model.ARMAResults.tvalues "statsmodels.tsa.arima_model.ARMAResults.tvalues")() \| Return the t-statistic for a given parameter estimate. \| \| [`wald_test`](statsmodels.tsa.arima_model.armaresults.wald_test#statsmodels.tsa.arima_model.ARMAResults.wald_test "statsmodels.tsa.arima_model.ARMAResults.wald_test")(r\_matrix[, cov\_p, scale, invcov, …]) \| Compute a Wald-test for a joint linear hypothesis. \| \| [`wald_test_terms`](statsmodels.tsa.arima_model.armaresults.wald_test_terms#statsmodels.tsa.arima_model.ARMAResults.wald_test_terms "statsmodels.tsa.arima_model.ARMAResults.wald_test_terms")([skip\_single, …]) \| Compute a sequence of Wald tests for terms over multiple columns \| #### Attributes \| \| \| \| --- \| --- \| \| `use_t` \| \| statsmodels statsmodels.tsa.statespace.sarimax.SARIMAX.initialize statsmodels.tsa.statespace.sarimax.SARIMAX.initialize ===================================================== `SARIMAX.initialize()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/sarimax.html#SARIMAX.initialize) Initialize the SARIMAX model. #### Notes These initialization steps must occur following the parent class \_\_init\_\_ function calls. statsmodels statsmodels.sandbox.distributions.extras.ACSkewT_gen.ppf statsmodels.sandbox.distributions.extras.ACSkewT\_gen.ppf ========================================================= `ACSkewT_gen.ppf(q, args, kwds)` Percent point function (inverse of `cdf`) at q of the given RV. \| Parameters: \| q (array\_like) – lower tail probability * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| x – quantile corresponding to the lower tail probability q. \| \| Return type: \| array\_like \| statsmodels statsmodels.sandbox.regression.gmm.IVRegressionResults.ess statsmodels.sandbox.regression.gmm.IVRegressionResults.ess ========================================================== `IVRegressionResults.ess()` statsmodels statsmodels.tsa.arima_process.ArmaProcess.generate_sample statsmodels.tsa.arima\_process.ArmaProcess.generate\_sample =========================================================== `ArmaProcess.generate_sample(nsample=100, scale=1.0, distrvs=None, axis=0, burnin=0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_process.html#ArmaProcess.generate_sample) Simulate an ARMA \| Parameters: \| * nsample (int or tuple of ints) – If nsample is an integer, then this creates a 1d timeseries of length size. If nsample is a tuple, creates a len(nsample) dimensional time series where time is indexed along the input variable `axis`. All series are unless `distrvs` generates dependent data. * scale (float) – standard deviation of noise * distrvs (function, random number generator) – function that generates the random numbers, and takes sample size as argument default: np.random.randn TODO: change to size argument * burnin (integer (default: 0)) – to reduce the effect of initial conditions, burnin observations at the beginning of the sample are dropped * axis (int) – See nsample. \| \| Returns: \| rvs – random sample(s) of arma process \| \| Return type: \| ndarray \| #### Notes Should work for n-dimensional with time series along axis, but not tested yet. Processes are sampled independently. statsmodels statsmodels.genmod.generalized_linear_model.GLM.fit statsmodels.genmod.generalized\_linear\_model.GLM.fit ===================================================== `GLM.fit(start_params=None, maxiter=100, method='IRLS', tol=1e-08, scale=None, cov_type='nonrobust', cov_kwds=None, use_t=None, full_output=True, disp=False, max_start_irls=3, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_linear_model.html#GLM.fit) Fits a generalized linear model for a given family. \| Parameters: \| start\_params (array-like, optional) – Initial guess of the solution for the loglikelihood maximization. The default is family-specific and is given by the `family.starting_mu(endog)`. If start\_params is given then the initial mean will be calculated as `np.dot(exog, start_params)`. * maxiter (int, optional) – Default is 100. * method (string) – Default is ‘IRLS’ for iteratively reweighted least squares. Otherwise gradient optimization is used. * tol (float) – Convergence tolerance. Default is 1e-8. * scale (string or float, optional) – `scale` can be ‘X2’, ‘dev’, or a float The default value is None, which uses `X2` for Gamma, Gaussian, and Inverse Gaussian. `X2` is Pearson’s chi-square divided by `df_resid`. The default is 1 for the Binomial and Poisson families. `dev` is the deviance divided by df\_resid * cov\_type (string) – The type of parameter estimate covariance matrix to compute. * cov\_kwds (dict-like) – Extra arguments for calculating the covariance of the parameter estimates. * use\_t (bool) – If True, the Student t-distribution is used for inference. * full\_output (bool, optional) – Set to True to have all available output in the Results object’s mle\_retvals attribute. The output is dependent on the solver. See LikelihoodModelResults notes section for more information. Not used if methhod is IRLS. * disp (bool, optional) – Set to True to print convergence messages. Not used if method is IRLS. * max\_start\_irls (int) – The number of IRLS iterations used to obtain starting values for gradient optimization. Only relevant if `method` is set to something other than ‘IRLS’. * IRLS fitting used, the following additional parameters are (If) – * available – * atol (float, optional) – The absolute tolerance criterion that must be satisfied. Defaults to `tol`. Convergence is attained when: $rtol \* prior + atol > abs(current - prior)$ * rtol (float, optional) – The relative tolerance criterion that must be satisfied. Defaults to 0 which means `rtol` is not used. Convergence is attained when: $rtol \* prior + atol > abs(current - prior)$ * tol\_criterion (str, optional) – Defaults to `'deviance'`. Can optionally be `'params'`. * wls\_method (str, optional) – options are ‘lstsq’, ‘pinv’ and ‘qr’ specifies which linear algebra function to use for the irls optimization. Default is `lstsq` which uses the same underlying svd based approach as ‘pinv’, but is faster during iterations. ‘lstsq’ and ‘pinv’ regularize the estimate in singular and near-singular cases by truncating small singular values based on `rcond` of the respective numpy.linalg function. ‘qr’ is only valied for cases that are not singular nor near-singular. * a scipy optimizer is used, the following additional parameter is (If) – * available – * optim\_hessian ({'eim', 'oim'}, optional) – When ‘oim’, the default, the observed Hessian is used in fitting. ‘eim’ is the expected Hessian. This may provide more stable fits, but adds assumption that the Hessian is correctly specified. \| #### Notes If method is ‘IRLS’, then an additional keyword ‘attach\_wls’ is available. This is currently for internal use only and might change in future versions. If attach\_wls’ is true, then the final WLS instance of the IRLS iteration is attached to the results instance as `results_wls` attribute.	programming_docs
statsmodels statsmodels.discrete.discrete_model.Probit.loglikeobs statsmodels.discrete.discrete\_model.Probit.loglikeobs ====================================================== `Probit.loglikeobs(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#Probit.loglikeobs) Log-likelihood of probit model for each observation \| Parameters: \| params (array-like) – The parameters of the model. \| \| Returns: \| loglike – The log likelihood for each observation of the model evaluated at `params`. See Notes \| \| Return type: \| array-like \| #### Notes \[\ln L\_{i}=\ln\Phi\left(q\_{i}x\_{i}^{\prime}\beta\right)\] for observations $i=1,...,n$ where $q=2y-1$. This simplification comes from the fact that the normal distribution is symmetric. statsmodels statsmodels.sandbox.regression.gmm.IVRegressionResults.resid statsmodels.sandbox.regression.gmm.IVRegressionResults.resid ============================================================ `IVRegressionResults.resid()` statsmodels statsmodels.tsa.statespace.mlemodel.MLEModel.initialize statsmodels.tsa.statespace.mlemodel.MLEModel.initialize ======================================================= `MLEModel.initialize()` Initialize (possibly re-initialize) a Model instance. For instance, the design matrix of a linear model may change and some things must be recomputed. statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.sample_acorr statsmodels.tsa.vector\_ar.var\_model.VARResults.sample\_acorr ============================================================== `VARResults.sample_acorr(nlags=1)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARResults.sample_acorr) statsmodels statsmodels.discrete.discrete_model.CountResults.llr statsmodels.discrete.discrete\_model.CountResults.llr ===================================================== `CountResults.llr()` statsmodels statsmodels.genmod.families.family.Poisson.starting_mu statsmodels.genmod.families.family.Poisson.starting\_mu ======================================================= `Poisson.starting_mu(y)` Starting value for mu in the IRLS algorithm. \| Parameters: \| y (array) – The untransformed response variable. \| \| Returns: \| mu\_0 – The first guess on the transformed response variable. \| \| Return type: \| array \| #### Notes \[\mu\_0 = (Y + \overline{Y})/2\] Only the Binomial family takes a different initial value. statsmodels statsmodels.tsa.arima_model.ARMAResults.maparams statsmodels.tsa.arima\_model.ARMAResults.maparams ================================================= `ARMAResults.maparams()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_model.html#ARMAResults.maparams) statsmodels statsmodels.genmod.bayes_mixed_glm.PoissonBayesMixedGLM.logposterior_grad statsmodels.genmod.bayes\_mixed\_glm.PoissonBayesMixedGLM.logposterior\_grad ============================================================================ `PoissonBayesMixedGLM.logposterior_grad(params)` The gradient of the log posterior. statsmodels statsmodels.tsa.vector_ar.var_model.FEVD statsmodels.tsa.vector\_ar.var\_model.FEVD ========================================== `class statsmodels.tsa.vector_ar.var_model.FEVD(model, P=None, periods=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#FEVD) Compute and plot Forecast error variance decomposition and asymptotic standard errors #### Methods \| \| \| \| --- \| --- \| \| [`cov`](statsmodels.tsa.vector_ar.var_model.fevd.cov#statsmodels.tsa.vector_ar.var_model.FEVD.cov "statsmodels.tsa.vector_ar.var_model.FEVD.cov")() \| Compute asymptotic standard errors \| \| [`plot`](statsmodels.tsa.vector_ar.var_model.fevd.plot#statsmodels.tsa.vector_ar.var_model.FEVD.plot "statsmodels.tsa.vector_ar.var_model.FEVD.plot")([periods, figsize]) \| Plot graphical display of FEVD \| \| [`summary`](statsmodels.tsa.vector_ar.var_model.fevd.summary#statsmodels.tsa.vector_ar.var_model.FEVD.summary "statsmodels.tsa.vector_ar.var_model.FEVD.summary")() \| \| statsmodels statsmodels.sandbox.distributions.extras.NormExpan_gen.expect statsmodels.sandbox.distributions.extras.NormExpan\_gen.expect ============================================================== `NormExpan_gen.expect(func=None, args=(), loc=0, scale=1, lb=None, ub=None, conditional=False, *kwds)` Calculate expected value of a function with respect to the distribution. The expected value of a function `f(x)` with respect to a distribution `dist` is defined as: ``` ubound E[x] = Integral(f(x) dist.pdf(x)) lbound ``` \| Parameters: \| * func (callable, optional) – Function for which integral is calculated. Takes only one argument. The default is the identity mapping f(x) = x. * args (tuple, optional) – Shape parameters of the distribution. * loc (float, optional) – Location parameter (default=0). * scale (float, optional) – Scale parameter (default=1). * ub (lb,) – Lower and upper bound for integration. Default is set to the support of the distribution. * conditional (bool, optional) – If True, the integral is corrected by the conditional probability of the integration interval. The return value is the expectation of the function, conditional on being in the given interval. Default is False. * keyword arguments are passed to the integration routine. (Additional) – \| \| Returns: \| expect – The calculated expected value. \| \| Return type: \| float \| #### Notes The integration behavior of this function is inherited from `integrate.quad`. statsmodels statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.predict statsmodels.discrete.count\_model.ZeroInflatedNegativeBinomialResults.predict ============================================================================= `ZeroInflatedNegativeBinomialResults.predict(exog=None, transform=True, args, kwargs)` Call self.model.predict with self.params as the first argument. \| Parameters: \| exog (array-like, optional) – The values for which you want to predict. see Notes below. * transform (bool, optional) – If the model was fit via a formula, do you want to pass exog through the formula. Default is True. E.g., if you fit a model y ~ log(x1) + log(x2), and transform is True, then you can pass a data structure that contains x1 and x2 in their original form. Otherwise, you’d need to log the data first. * kwargs (args,) – Some models can take additional arguments or keywords, see the predict method of the model for the details. \| \| Returns: \| prediction – See self.model.predict \| \| Return type: \| ndarray, [pandas.Series](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.html#pandas.Series "(in pandas v0.22.0)") or [pandas.DataFrame](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html#pandas.DataFrame "(in pandas v0.22.0)") \| #### Notes The types of exog that are supported depends on whether a formula was used in the specification of the model. If a formula was used, then exog is processed in the same way as the original data. This transformation needs to have key access to the same variable names, and can be a pandas DataFrame or a dict like object. If no formula was used, then the provided exog needs to have the same number of columns as the original exog in the model. No transformation of the data is performed except converting it to a numpy array. Row indices as in pandas data frames are supported, and added to the returned prediction. statsmodels statsmodels.regression.recursive_ls.RecursiveLS.transform_jacobian statsmodels.regression.recursive\_ls.RecursiveLS.transform\_jacobian ==================================================================== `RecursiveLS.transform_jacobian(unconstrained, approx_centered=False)` Jacobian matrix for the parameter transformation function \| Parameters: \| unconstrained (array\_like) – Array of unconstrained parameters used by the optimizer. \| \| Returns: \| jacobian – Jacobian matrix of the transformation, evaluated at `unconstrained` \| \| Return type: \| array \| #### Notes This is a numerical approximation using finite differences. Note that in general complex step methods cannot be used because it is not guaranteed that the `transform_params` method is a real function (e.g. if Cholesky decomposition is used). See also [`transform_params`](statsmodels.regression.recursive_ls.recursivels.transform_params#statsmodels.regression.recursive_ls.RecursiveLS.transform_params "statsmodels.regression.recursive_ls.RecursiveLS.transform_params") statsmodels statsmodels.tsa.statespace.varmax.VARMAXResults.test_heteroskedasticity statsmodels.tsa.statespace.varmax.VARMAXResults.test\_heteroskedasticity ======================================================================== `VARMAXResults.test_heteroskedasticity(method, alternative='two-sided', use_f=True)` Test for heteroskedasticity of standardized residuals Tests whether the sum-of-squares in the first third of the sample is significantly different than the sum-of-squares in the last third of the sample. Analogous to a Goldfeld-Quandt test. The null hypothesis is of no heteroskedasticity. \| Parameters: \| * method (string {'breakvar'} or None) – The statistical test for heteroskedasticity. Must be ‘breakvar’ for test of a break in the variance. If None, an attempt is made to select an appropriate test. * alternative (string, 'increasing', 'decreasing' or 'two-sided') – This specifies the alternative for the p-value calculation. Default is two-sided. * use\_f (boolean, optional) – Whether or not to compare against the asymptotic distribution (chi-squared) or the approximate small-sample distribution (F). Default is True (i.e. default is to compare against an F distribution). \| \| Returns: \| output – An array with `(test_statistic, pvalue)` for each endogenous variable. The array is then sized `(k_endog, 2)`. If the method is called as `het = res.test_heteroskedasticity()`, then `het[0]` is an array of size 2 corresponding to the first endogenous variable, where `het[0][0]` is the test statistic, and `het[0][1]` is the p-value. \| \| Return type: \| array \| #### Notes The null hypothesis is of no heteroskedasticity. That means different things depending on which alternative is selected: * Increasing: Null hypothesis is that the variance is not increasing throughout the sample; that the sum-of-squares in the later subsample is not greater than the sum-of-squares in the earlier subsample. * Decreasing: Null hypothesis is that the variance is not decreasing throughout the sample; that the sum-of-squares in the earlier subsample is not greater than the sum-of-squares in the later subsample. * Two-sided: Null hypothesis is that the variance is not changing throughout the sample. Both that the sum-of-squares in the earlier subsample is not greater than the sum-of-squares in the later subsample and that the sum-of-squares in the later subsample is not greater than the sum-of-squares in the earlier subsample. For $h = [T/3]$, the test statistic is: \[H(h) = \sum\_{t=T-h+1}^T \tilde v\_t^2 \Bigg / \sum\_{t=d+1}^{d+1+h} \tilde v\_t^2\] where $d$ is the number of periods in which the loglikelihood was burned in the parent model (usually corresponding to diffuse initialization). This statistic can be tested against an $F(h,h)$ distribution. Alternatively, $h H(h)$ is asymptotically distributed according to $\chi\_h^2$; this second test can be applied by passing `asymptotic=True` as an argument. See section 5.4 of [[1]](#id2) for the above formula and discussion, as well as additional details. TODO * Allow specification of $h$ #### References \| \| \| \| --- \| --- \| \| [[1]](#id1) \| Harvey, Andrew C. 1990. Forecasting, Structural Time Series Models and the Kalman Filter. Cambridge University Press. \| statsmodels statsmodels.tsa.statespace.varmax.VARMAX.initialize_statespace statsmodels.tsa.statespace.varmax.VARMAX.initialize\_statespace =============================================================== `VARMAX.initialize_statespace(kwargs)` Initialize the state space representation \| Parameters: \| \\kwargs – Additional keyword arguments to pass to the state space class constructor. \| statsmodels statsmodels.discrete.discrete_model.CountModel.cov_params_func_l1 statsmodels.discrete.discrete\_model.CountModel.cov\_params\_func\_l1 ===================================================================== `CountModel.cov_params_func_l1(likelihood_model, xopt, retvals)` Computes cov\_params on a reduced parameter space corresponding to the nonzero parameters resulting from the l1 regularized fit. Returns a full cov\_params matrix, with entries corresponding to zero’d values set to np.nan. statsmodels statsmodels.discrete.count_model.ZeroInflatedPoissonResults.load statsmodels.discrete.count\_model.ZeroInflatedPoissonResults.load ================================================================= `classmethod ZeroInflatedPoissonResults.load(fname)` load a pickle, (class method) \| Parameters: \| fname** (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. \| \| Returns: \| \| \| Return type: \| unpickled instance \| statsmodels statsmodels.discrete.discrete_model.BinaryResults.wald_test statsmodels.discrete.discrete\_model.BinaryResults.wald\_test ============================================================= `BinaryResults.wald_test(r_matrix, cov_p=None, scale=1.0, invcov=None, use_f=None)` Compute a Wald-test for a joint linear hypothesis. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. * use\_f (bool) – If True, then the F-distribution is used. If False, then the asymptotic distribution, chisquare is used. If use\_f is None, then the F distribution is used if the model specifies that use\_t is True. The test statistic is proportionally adjusted for the distribution by the number of constraints in the hypothesis. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`f_test`](statsmodels.discrete.discrete_model.binaryresults.f_test#statsmodels.discrete.discrete_model.BinaryResults.f_test "statsmodels.discrete.discrete_model.BinaryResults.f_test"), [`t_test`](statsmodels.discrete.discrete_model.binaryresults.t_test#statsmodels.discrete.discrete_model.BinaryResults.t_test "statsmodels.discrete.discrete_model.BinaryResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.fit statsmodels.tsa.regime\_switching.markov\_autoregression.MarkovAutoregression.fit ================================================================================= `MarkovAutoregression.fit(start_params=None, transformed=True, cov_type='approx', cov_kwds=None, method='bfgs', maxiter=100, full_output=1, disp=0, callback=None, return_params=False, em_iter=5, search_reps=0, search_iter=5, search_scale=1.0, *kwargs)` Fits the model by maximum likelihood via Hamilton filter. \| Parameters: \| start\_params (array\_like, optional) – Initial guess of the solution for the loglikelihood maximization. If None, the default is given by Model.start\_params. * transformed (boolean, optional) – Whether or not `start_params` is already transformed. Default is True. * cov\_type (str, optional) – The type of covariance matrix estimator to use. Can be one of ‘approx’, ‘opg’, ‘robust’, or ‘none’. Default is ‘approx’. * cov\_kwds ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)") or None, optional) – Keywords for alternative covariance estimators * method (str, optional) – The `method` determines which solver from `scipy.optimize` is used, and it can be chosen from among the following strings: + ’newton’ for Newton-Raphson, ‘nm’ for Nelder-Mead + ’bfgs’ for Broyden-Fletcher-Goldfarb-Shanno (BFGS) + ’lbfgs’ for limited-memory BFGS with optional box constraints + ’powell’ for modified Powell’s method + ’cg’ for conjugate gradient + ’ncg’ for Newton-conjugate gradient + ’basinhopping’ for global basin-hopping solverThe explicit arguments in `fit` are passed to the solver, with the exception of the basin-hopping solver. Each solver has several optional arguments that are not the same across solvers. See the notes section below (or scipy.optimize) for the available arguments and for the list of explicit arguments that the basin-hopping solver supports. * maxiter (int, optional) – The maximum number of iterations to perform. * full\_output (boolean, optional) – Set to True to have all available output in the Results object’s mle\_retvals attribute. The output is dependent on the solver. See LikelihoodModelResults notes section for more information. * disp (boolean, optional) – Set to True to print convergence messages. * callback (callable callback(xk), optional) – Called after each iteration, as callback(xk), where xk is the current parameter vector. * return\_params (boolean, optional) – Whether or not to return only the array of maximizing parameters. Default is False. * em\_iter (int, optional) – Number of initial EM iteration steps used to improve starting parameters. * search\_reps (int, optional) – Number of randomly drawn search parameters that are drawn around `start_params` to try and improve starting parameters. Default is 0. * search\_iter (int, optional) – Number of initial EM iteration steps used to improve each of the search parameter repetitions. * search\_scale (float or array, optional.) – Scale of variates for random start parameter search. * *\\kwargs* – Additional keyword arguments to pass to the optimizer. \| \| Returns: \| \| \| Return type: \| MarkovSwitchingResults \| statsmodels statsmodels.sandbox.tsa.fftarma.ArmaFft.arma2ar statsmodels.sandbox.tsa.fftarma.ArmaFft.arma2ar =============================================== `ArmaFft.arma2ar(lags=None)` statsmodels statsmodels.duration.hazard_regression.PHReg.efron_gradient statsmodels.duration.hazard\_regression.PHReg.efron\_gradient ============================================================= `PHReg.efron_gradient(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/duration/hazard_regression.html#PHReg.efron_gradient) Returns the gradient of the log partial likelihood evaluated at `params`, using the Efron method to handle tied times.	programming_docs
statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.forecast statsmodels.tsa.statespace.dynamic\_factor.DynamicFactorResults.forecast ======================================================================== `DynamicFactorResults.forecast(steps=1, *kwargs)` Out-of-sample forecasts \| Parameters: \| steps (int, str, or datetime, optional) – If an integer, the number of steps to forecast from the end of the sample. Can also be a date string to parse or a datetime type. However, if the dates index does not have a fixed frequency, steps must be an integer. Default * *\\kwargs* – Additional arguments may required for forecasting beyond the end of the sample. See `FilterResults.predict` for more details. \| \| Returns: \| forecast – Array of out of sample forecasts. A (steps x k\_endog) array. \| \| Return type: \| array \| statsmodels statsmodels.genmod.families.family.Family.loglike statsmodels.genmod.families.family.Family.loglike ================================================= `Family.loglike(endog, mu, var_weights=1.0, freq_weights=1.0, scale=1.0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/family.html#Family.loglike) The log-likelihood function in terms of the fitted mean response. \| Parameters: \| * endog (array) – Usually the endogenous response variable. * mu (array) – Usually but not always the fitted mean response variable. * var\_weights (array-like) – 1d array of variance (analytic) weights. The default is 1. * freq\_weights (array-like) – 1d array of frequency weights. The default is 1. * scale (float) – The scale parameter. The default is 1. \| \| Returns: \| ll – The value of the loglikelihood evaluated at (endog, mu, var\_weights, freq\_weights, scale) as defined below. \| \| Return type: \| float \| #### Notes Where $ll\_i$ is the by-observation log-likelihood: \[ll = \sum(ll\_i \* freq\\_weights\_i)\] `ll_i` is defined for each family. endog and mu are not restricted to `endog` and `mu` respectively. For instance, you could call both `loglike(endog, endog)` and `loglike(endog, mu)` to get the log-likelihood ratio. statsmodels statsmodels.discrete.count_model.ZeroInflatedGeneralizedPoissonResults.normalized_cov_params statsmodels.discrete.count\_model.ZeroInflatedGeneralizedPoissonResults.normalized\_cov\_params =============================================================================================== `ZeroInflatedGeneralizedPoissonResults.normalized_cov_params()` statsmodels statsmodels.sandbox.regression.gmm.NonlinearIVGMM.set_param_names statsmodels.sandbox.regression.gmm.NonlinearIVGMM.set\_param\_names =================================================================== `NonlinearIVGMM.set_param_names(param_names, k_params=None)` set the parameter names in the model \| Parameters: \| * param\_names (list of strings) – param\_names should have the same length as the number of params * k\_params (None or int) – If k\_params is None, then the k\_params attribute is used, unless it is None. If k\_params is not None, then it will also set the k\_params attribute. \| statsmodels statsmodels.tools.eval_measures.hqic statsmodels.tools.eval\_measures.hqic ===================================== `statsmodels.tools.eval_measures.hqic(llf, nobs, df_modelwc)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tools/eval_measures.html#hqic) Hannan-Quinn information criterion (HQC) \| Parameters: \| * llf (float) – value of the loglikelihood * nobs (int) – number of observations * df\_modelwc (int) – number of parameters including constant \| \| Returns: \| hqic – information criterion \| \| Return type: \| float \| #### References Wikipedia doesn’t say much statsmodels statsmodels.discrete.count_model.ZeroInflatedPoisson.from_formula statsmodels.discrete.count\_model.ZeroInflatedPoisson.from\_formula =================================================================== `classmethod ZeroInflatedPoisson.from_formula(formula, data, subset=None, drop_cols=None, args, kwargs)` Create a Model from a formula and dataframe. \| Parameters: \| formula (str or generic Formula object) – The formula specifying the model * data (array-like) – The data for the model. See Notes. * subset (array-like) – An array-like object of booleans, integers, or index values that indicate the subset of df to use in the model. Assumes df is a `pandas.DataFrame` * drop\_cols (array-like) – Columns to drop from the design matrix. Cannot be used to drop terms involving categoricals. * args (extra arguments) – These are passed to the model * kwargs (extra keyword arguments) – These are passed to the model with one exception. The `eval_env` keyword is passed to patsy. It can be either a [`patsy.EvalEnvironment`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.EvalEnvironment "(in patsy v0.5.0+dev)") object or an integer indicating the depth of the namespace to use. For example, the default `eval_env=0` uses the calling namespace. If you wish to use a “clean” environment set `eval_env=-1`. \| \| Returns: \| model \| \| Return type: \| Model instance \| #### Notes data must define \_\_getitem\_\_ with the keys in the formula terms args and kwargs are passed on to the model instantiation. E.g., a numpy structured or rec array, a dictionary, or a pandas DataFrame. statsmodels statsmodels.genmod.families.links.probit statsmodels.genmod.families.links.probit ======================================== `class statsmodels.genmod.families.links.probit(dbn=<scipy.stats._continuous_distns.norm_gen object>)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#probit) The probit (standard normal CDF) transform #### Notes g(p) = scipy.stats.norm.ppf(p) probit is an alias of CDFLink. #### Methods \| \| \| \| --- \| --- \| \| [`deriv`](statsmodels.genmod.families.links.probit.deriv#statsmodels.genmod.families.links.probit.deriv "statsmodels.genmod.families.links.probit.deriv")(p) \| Derivative of CDF link \| \| [`deriv2`](statsmodels.genmod.families.links.probit.deriv2#statsmodels.genmod.families.links.probit.deriv2 "statsmodels.genmod.families.links.probit.deriv2")(p) \| Second derivative of the link function g’‘(p) \| \| [`inverse`](statsmodels.genmod.families.links.probit.inverse#statsmodels.genmod.families.links.probit.inverse "statsmodels.genmod.families.links.probit.inverse")(z) \| The inverse of the CDF link \| \| [`inverse_deriv`](statsmodels.genmod.families.links.probit.inverse_deriv#statsmodels.genmod.families.links.probit.inverse_deriv "statsmodels.genmod.families.links.probit.inverse_deriv")(z) \| Derivative of the inverse of the CDF transformation link function \| statsmodels statsmodels.tsa.arima_model.ARMA.initialize statsmodels.tsa.arima\_model.ARMA.initialize ============================================ `ARMA.initialize()` Initialize (possibly re-initialize) a Model instance. For instance, the design matrix of a linear model may change and some things must be recomputed. statsmodels statsmodels.sandbox.regression.gmm.GMMResults.predict statsmodels.sandbox.regression.gmm.GMMResults.predict ===================================================== `GMMResults.predict(exog=None, transform=True, args, kwargs)` Call self.model.predict with self.params as the first argument. \| Parameters: \| exog (array-like, optional) – The values for which you want to predict. see Notes below. * transform (bool, optional) – If the model was fit via a formula, do you want to pass exog through the formula. Default is True. E.g., if you fit a model y ~ log(x1) + log(x2), and transform is True, then you can pass a data structure that contains x1 and x2 in their original form. Otherwise, you’d need to log the data first. * kwargs (args,) – Some models can take additional arguments or keywords, see the predict method of the model for the details. \| \| Returns: \| prediction – See self.model.predict \| \| Return type: \| ndarray, [pandas.Series](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.html#pandas.Series "(in pandas v0.22.0)") or [pandas.DataFrame](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html#pandas.DataFrame "(in pandas v0.22.0)") \| #### Notes The types of exog that are supported depends on whether a formula was used in the specification of the model. If a formula was used, then exog is processed in the same way as the original data. This transformation needs to have key access to the same variable names, and can be a pandas DataFrame or a dict like object. If no formula was used, then the provided exog needs to have the same number of columns as the original exog in the model. No transformation of the data is performed except converting it to a numpy array. Row indices as in pandas data frames are supported, and added to the returned prediction. statsmodels statsmodels.regression.linear_model.OLSResults.HC2_se statsmodels.regression.linear\_model.OLSResults.HC2\_se ======================================================= `OLSResults.HC2_se()` See statsmodels.RegressionResults statsmodels statsmodels.genmod.families.family.Tweedie statsmodels.genmod.families.family.Tweedie ========================================== `class statsmodels.genmod.families.family.Tweedie(link=None, var_power=1.0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/family.html#Tweedie) Tweedie family. \| Parameters: \| * link (a link instance, optional) – The default link for the Tweedie family is the log link. Available links are log and Power. See statsmodels.genmod.families.links for more information. * var\_power (float, optional) – The variance power. The default is 1. \| `link` a link instance – The link function of the Tweedie instance `variance` varfunc instance – `variance` is an instance of statsmodels.genmod.families.varfuncs.Power `var_power` float – The power of the variance function. See also [`statsmodels.genmod.families.family.Family`](statsmodels.genmod.families.family.family#statsmodels.genmod.families.family.Family "statsmodels.genmod.families.family.Family"), [Link Functions](../glm#links) #### Notes Logliklihood function not implemented because of the complexity of calculating an infinite series of summations. The variance power can be estimated using the `estimate_tweedie_power` function that is part of the statsmodels.genmod.generalized\_linear\_model.GLM class. #### Methods \| \| \| \| --- \| --- \| \| [`deviance`](statsmodels.genmod.families.family.tweedie.deviance#statsmodels.genmod.families.family.Tweedie.deviance "statsmodels.genmod.families.family.Tweedie.deviance")(endog, mu[, var\_weights, …]) \| The deviance function evaluated at (endog, mu, var\_weights, freq\_weights, scale) for the distribution. \| \| [`fitted`](statsmodels.genmod.families.family.tweedie.fitted#statsmodels.genmod.families.family.Tweedie.fitted "statsmodels.genmod.families.family.Tweedie.fitted")(lin\_pred) \| Fitted values based on linear predictors lin\_pred. \| \| [`loglike`](statsmodels.genmod.families.family.tweedie.loglike#statsmodels.genmod.families.family.Tweedie.loglike "statsmodels.genmod.families.family.Tweedie.loglike")(endog, mu[, var\_weights, …]) \| The log-likelihood function in terms of the fitted mean response. \| \| [`loglike_obs`](statsmodels.genmod.families.family.tweedie.loglike_obs#statsmodels.genmod.families.family.Tweedie.loglike_obs "statsmodels.genmod.families.family.Tweedie.loglike_obs")(endog, mu[, var\_weights, scale]) \| The log-likelihood function for each observation in terms of the fitted mean response for the Tweedie distribution. \| \| [`predict`](statsmodels.genmod.families.family.tweedie.predict#statsmodels.genmod.families.family.Tweedie.predict "statsmodels.genmod.families.family.Tweedie.predict")(mu) \| Linear predictors based on given mu values. \| \| [`resid_anscombe`](statsmodels.genmod.families.family.tweedie.resid_anscombe#statsmodels.genmod.families.family.Tweedie.resid_anscombe "statsmodels.genmod.families.family.Tweedie.resid_anscombe")(endog, mu[, var\_weights, scale]) \| The Anscombe residuals \| \| [`resid_dev`](statsmodels.genmod.families.family.tweedie.resid_dev#statsmodels.genmod.families.family.Tweedie.resid_dev "statsmodels.genmod.families.family.Tweedie.resid_dev")(endog, mu[, var\_weights, scale]) \| The deviance residuals \| \| [`starting_mu`](statsmodels.genmod.families.family.tweedie.starting_mu#statsmodels.genmod.families.family.Tweedie.starting_mu "statsmodels.genmod.families.family.Tweedie.starting_mu")(y) \| Starting value for mu in the IRLS algorithm. \| \| [`weights`](statsmodels.genmod.families.family.tweedie.weights#statsmodels.genmod.families.family.Tweedie.weights "statsmodels.genmod.families.family.Tweedie.weights")(mu) \| Weights for IRLS steps \| statsmodels statsmodels.sandbox.distributions.extras.pdf_mvsk statsmodels.sandbox.distributions.extras.pdf\_mvsk ================================================== `statsmodels.sandbox.distributions.extras.pdf_mvsk(mvsk)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/distributions/extras.html#pdf_mvsk) Return the Gaussian expanded pdf function given the list of 1st, 2nd moment and skew and Fisher (excess) kurtosis. \| Parameters: \| mvsk (list of mu, mc2, skew, kurt) – distribution is matched to these four moments \| \| Returns: \| pdffunc – function that evaluates the pdf(x), where x is the non-standardized random variable. \| \| Return type: \| function \| #### Notes Changed so it works only if four arguments are given. Uses explicit formula, not loop. This implements a Gram-Charlier expansion of the normal distribution where the first 2 moments coincide with those of the normal distribution but skew and kurtosis can deviate from it. In the Gram-Charlier distribution it is possible that the density becomes negative. This is the case when the deviation from the normal distribution is too large. #### References <http://en.wikipedia.org/wiki/Edgeworth_series> Johnson N.L., S. Kotz, N. Balakrishnan: Continuous Univariate Distributions, Volume 1, 2nd ed., p.30 statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactor.opg_information_matrix statsmodels.tsa.statespace.dynamic\_factor.DynamicFactor.opg\_information\_matrix ================================================================================= `DynamicFactor.opg_information_matrix(params, transformed=True, approx_complex_step=None, *kwargs)` Outer product of gradients information matrix \| Parameters: \| params (array\_like, optional) – Array of parameters at which to evaluate the loglikelihood function. * *\\kwargs* – Additional arguments to the `loglikeobs` method. \| #### References Berndt, Ernst R., Bronwyn Hall, Robert Hall, and Jerry Hausman. 1974. Estimation and Inference in Nonlinear Structural Models. NBER Chapters. National Bureau of Economic Research, Inc. statsmodels statsmodels.stats.weightstats.DescrStatsW.var statsmodels.stats.weightstats.DescrStatsW.var ============================================= `DescrStatsW.var()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/weightstats.html#DescrStatsW.var) variance with default degrees of freedom correction statsmodels statsmodels.sandbox.regression.gmm.IVRegressionResults.ssr statsmodels.sandbox.regression.gmm.IVRegressionResults.ssr ========================================================== `IVRegressionResults.ssr()` statsmodels statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.f_test statsmodels.discrete.count\_model.ZeroInflatedNegativeBinomialResults.f\_test ============================================================================= `ZeroInflatedNegativeBinomialResults.f_test(r_matrix, cov_p=None, scale=1.0, invcov=None)` Compute the F-test for a joint linear hypothesis. This is a special case of `wald_test` that always uses the F distribution. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length k row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> A = np.identity(len(results.params)) >>> A = A[1:,:] ``` This tests that each coefficient is jointly statistically significantly different from zero. ``` >>> print(results.f_test(A)) <F test: F=array([[ 330.28533923]]), p=4.984030528700946e-10, df_denom=9, df_num=6> ``` Compare this to ``` >>> results.fvalue 330.2853392346658 >>> results.f_pvalue 4.98403096572e-10 ``` ``` >>> B = np.array(([0,0,1,-1,0,0,0],[0,0,0,0,0,1,-1])) ``` This tests that the coefficient on the 2nd and 3rd regressors are equal and jointly that the coefficient on the 5th and 6th regressors are equal. ``` >>> print(results.f_test(B)) <F test: F=array([[ 9.74046187]]), p=0.005605288531708235, df_denom=9, df_num=2> ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.datasets import longley >>> from statsmodels.formula.api import ols >>> dta = longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = '(GNPDEFL = GNP), (UNEMP = 2), (YEAR/1829 = 1)' >>> f_test = results.f_test(hypotheses) >>> print(f_test) <F test: F=array([[ 144.17976065]]), p=6.322026217355609e-08, df_denom=9, df_num=3> ``` See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`wald_test`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.wald_test#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.wald_test "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.wald_test"), [`t_test`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.t_test#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.t_test "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.genmod.families.family.Gamma statsmodels.genmod.families.family.Gamma ======================================== `class statsmodels.genmod.families.family.Gamma(link=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/family.html#Gamma) Gamma exponential family distribution. \| Parameters: \| link (a link instance, optional) – The default link for the Gamma family is the inverse link. Available links are log, identity, and inverse. See statsmodels.genmod.families.links for more information. \| `link` a link instance – The link function of the Gamma instance `variance` varfunc instance – `variance` is an instance of statsmodels.genmod.family.varfuncs.mu\_squared See also [`statsmodels.genmod.families.family.Family`](statsmodels.genmod.families.family.family#statsmodels.genmod.families.family.Family "statsmodels.genmod.families.family.Family"), [Link Functions](../glm#links) #### Methods \| \| \| \| --- \| --- \| \| [`deviance`](statsmodels.genmod.families.family.gamma.deviance#statsmodels.genmod.families.family.Gamma.deviance "statsmodels.genmod.families.family.Gamma.deviance")(endog, mu[, var\_weights, …]) \| The deviance function evaluated at (endog, mu, var\_weights, freq\_weights, scale) for the distribution. \| \| [`fitted`](statsmodels.genmod.families.family.gamma.fitted#statsmodels.genmod.families.family.Gamma.fitted "statsmodels.genmod.families.family.Gamma.fitted")(lin\_pred) \| Fitted values based on linear predictors lin\_pred. \| \| [`loglike`](statsmodels.genmod.families.family.gamma.loglike#statsmodels.genmod.families.family.Gamma.loglike "statsmodels.genmod.families.family.Gamma.loglike")(endog, mu[, var\_weights, …]) \| The log-likelihood function in terms of the fitted mean response. \| \| [`loglike_obs`](statsmodels.genmod.families.family.gamma.loglike_obs#statsmodels.genmod.families.family.Gamma.loglike_obs "statsmodels.genmod.families.family.Gamma.loglike_obs")(endog, mu[, var\_weights, scale]) \| The log-likelihood function for each observation in terms of the fitted mean response for the Gamma distribution. \| \| [`predict`](statsmodels.genmod.families.family.gamma.predict#statsmodels.genmod.families.family.Gamma.predict "statsmodels.genmod.families.family.Gamma.predict")(mu) \| Linear predictors based on given mu values. \| \| [`resid_anscombe`](statsmodels.genmod.families.family.gamma.resid_anscombe#statsmodels.genmod.families.family.Gamma.resid_anscombe "statsmodels.genmod.families.family.Gamma.resid_anscombe")(endog, mu[, var\_weights, scale]) \| The Anscombe residuals \| \| [`resid_dev`](statsmodels.genmod.families.family.gamma.resid_dev#statsmodels.genmod.families.family.Gamma.resid_dev "statsmodels.genmod.families.family.Gamma.resid_dev")(endog, mu[, var\_weights, scale]) \| The deviance residuals \| \| [`starting_mu`](statsmodels.genmod.families.family.gamma.starting_mu#statsmodels.genmod.families.family.Gamma.starting_mu "statsmodels.genmod.families.family.Gamma.starting_mu")(y) \| Starting value for mu in the IRLS algorithm. \| \| [`weights`](statsmodels.genmod.families.family.gamma.weights#statsmodels.genmod.families.family.Gamma.weights "statsmodels.genmod.families.family.Gamma.weights")(mu) \| Weights for IRLS steps \|	programming_docs
statsmodels statsmodels.genmod.generalized_linear_model.GLMResults.save statsmodels.genmod.generalized\_linear\_model.GLMResults.save ============================================================= `GLMResults.save(fname, remove_data=False)` save a pickle of this instance \| Parameters: \| * fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. * remove\_data (bool) – If False (default), then the instance is pickled without changes. If True, then all arrays with length nobs are set to None before pickling. See the remove\_data method. In some cases not all arrays will be set to None. \| #### Notes If remove\_data is true and the model result does not implement a remove\_data method then this will raise an exception. statsmodels statsmodels.genmod.families.family.Tweedie.resid_anscombe statsmodels.genmod.families.family.Tweedie.resid\_anscombe ========================================================== `Tweedie.resid_anscombe(endog, mu, var_weights=1.0, scale=1.0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/family.html#Tweedie.resid_anscombe) The Anscombe residuals \| Parameters: \| * endog (array) – The endogenous response variable * mu (array) – The inverse of the link function at the linear predicted values. * var\_weights (array-like) – 1d array of variance (analytic) weights. The default is 1. * scale (float, optional) – An optional argument to divide the residuals by sqrt(scale). The default is 1. \| \| Returns: \| resid\_anscombe – The Anscombe residuals as defined below. \| \| Return type: \| array \| #### Notes When $p = 3$, then \[resid\\_anscombe\_i = \log(endog\_i / \mu\_i) / \sqrt{\mu\_i \* scale} \* \sqrt(var\\_weights)\] Otherwise, \[c = (3 - p) / 3\] \[resid\\_anscombe\_i = (1 / c) \* (endog\_i^c - \mu\_i^c) / \mu\_i^{p / 6} / \sqrt{scale} \* \sqrt(var\\_weights)\] statsmodels statsmodels.iolib.summary2.Summary.add_base statsmodels.iolib.summary2.Summary.add\_base ============================================ `Summary.add_base(results, alpha=0.05, float_format='%.4f', title=None, xname=None, yname=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/iolib/summary2.html#Summary.add_base) Try to construct a basic summary instance. \| Parameters: \| * results (Model results instance) – * alpha (float) – significance level for the confidence intervals (optional) * float\_formatting (string) – Float formatting for summary of parameters (optional) * title (string) – Title of the summary table (optional) * xname (List of strings of length equal to the number of parameters) – Names of the independent variables (optional) * yname (string) – Name of the dependent variable (optional) \| statsmodels statsmodels.stats.weightstats.CompareMeans.ttest_ind statsmodels.stats.weightstats.CompareMeans.ttest\_ind ===================================================== `CompareMeans.ttest_ind(alternative='two-sided', usevar='pooled', value=0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/weightstats.html#CompareMeans.ttest_ind) ttest for the null hypothesis of identical means this should also be the same as onewaygls, except for ddof differences \| Parameters: \| * x2 (x1,) – two independent samples, see notes for 2-D case * alternative (string) – The alternative hypothesis, H1, has to be one of the following ‘two-sided’: H1: difference in means not equal to value (default) ‘larger’ : H1: difference in means larger than value ‘smaller’ : H1: difference in means smaller than value * usevar (string, 'pooled' or 'unequal') – If `pooled`, then the standard deviation of the samples is assumed to be the same. If `unequal`, then Welsh ttest with Satterthwait degrees of freedom is used * value (float) – difference between the means under the Null hypothesis. \| \| Returns: \| * tstat (float) – test statisic * pvalue (float) – pvalue of the t-test * df (int or float) – degrees of freedom used in the t-test \| #### Notes The result is independent of the user specified ddof. statsmodels statsmodels.tsa.stattools.kpss statsmodels.tsa.stattools.kpss ============================== `statsmodels.tsa.stattools.kpss(x, regression='c', lags=None, store=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/stattools.html#kpss) Kwiatkowski-Phillips-Schmidt-Shin test for stationarity. Computes the Kwiatkowski-Phillips-Schmidt-Shin (KPSS) test for the null hypothesis that x is level or trend stationary. \| Parameters: \| * x (array\_like, 1d) – Data series * regression (str{'c', 'ct'}) – Indicates the null hypothesis for the KPSS test \* ‘c’ : The data is stationary around a constant (default) \* ‘ct’ : The data is stationary around a trend * lags (int) – Indicates the number of lags to be used. If None (default), lags is set to int(12 \* (n / 100)\\(1 / 4)), as outlined in Schwert (1989). * store (bool) – If True, then a result instance is returned additionally to the KPSS statistic (default is False). \| \| Returns: \| * kpss\_stat (float) – The KPSS test statistic * p\_value (float) – The p-value of the test. The p-value is interpolated from Table 1 in Kwiatkowski et al. (1992), and a boundary point is returned if the test statistic is outside the table of critical values, that is, if the p-value is outside the interval (0.01, 0.1). * lags (int) – The truncation lag parameter * crit (dict) – The critical values at 10%, 5%, 2.5% and 1%. Based on Kwiatkowski et al. (1992). * resstore ((optional) instance of ResultStore) – An instance of a dummy class with results attached as attributes \| #### Notes To estimate sigma^2 the Newey-West estimator is used. If lags is None, the truncation lag parameter is set to int(12 \* (n / 100) \\ (1 / 4)), as outlined in Schwert (1989). The p-values are interpolated from Table 1 of Kwiatkowski et al. (1992). If the computed statistic is outside the table of critical values, then a warning message is generated. Missing values are not handled. #### References D. Kwiatkowski, P. C. B. Phillips, P. Schmidt, and Y. Shin (1992): Testing the Null Hypothesis of Stationarity against the Alternative of a Unit Root. `Journal of Econometrics` 54, 159-178. statsmodels statsmodels.stats.contingency_tables.Table2x2.riskratio_confint statsmodels.stats.contingency\_tables.Table2x2.riskratio\_confint ================================================================= `Table2x2.riskratio_confint(alpha=0.05, method='normal')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/contingency_tables.html#Table2x2.riskratio_confint) A confidence interval for the risk ratio. \| Parameters: \| * alpha (float) – `1 - alpha` is the nominal coverage probability of the confidence interval. * method (string) – The method for producing the confidence interval. Currently must be ‘normal’ which uses the normal approximation. \| statsmodels statsmodels.genmod.families.links.cauchy.deriv statsmodels.genmod.families.links.cauchy.deriv ============================================== `cauchy.deriv(p)` Derivative of CDF link \| Parameters: \| p (array-like) – mean parameters \| \| Returns: \| g’(p) – The derivative of CDF transform at `p` \| \| Return type: \| array \| #### Notes g’(`p`) = 1./ `dbn`.pdf(`dbn`.ppf(`p`)) statsmodels statsmodels.tsa.statespace.sarimax.SARIMAX.initialize_stationary statsmodels.tsa.statespace.sarimax.SARIMAX.initialize\_stationary ================================================================= `SARIMAX.initialize_stationary()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/sarimax.html#SARIMAX.initialize_stationary) Initialize the statespace model as stationary. statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.tvalues statsmodels.tsa.vector\_ar.var\_model.VARResults.tvalues ======================================================== `VARResults.tvalues()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARResults.tvalues) Compute t-statistics. Use Student-t(T - Kp - 1) = t(df\_resid) to test significance. statsmodels statsmodels.stats.correlation_tools.corr_nearest_factor statsmodels.stats.correlation\_tools.corr\_nearest\_factor ========================================================== `statsmodels.stats.correlation_tools.corr_nearest_factor(corr, rank, ctol=1e-06, lam_min=1e-30, lam_max=1e+30, maxiter=1000)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/correlation_tools.html#corr_nearest_factor) Find the nearest correlation matrix with factor structure to a given square matrix. \| Parameters: \| * corr (square array) – The target matrix (to which the nearest correlation matrix is sought). Must be square, but need not be positive semidefinite. * rank (positive integer) – The rank of the factor structure of the solution, i.e., the number of linearly independent columns of X. * ctol (positive real) – Convergence criterion. * lam\_min (float) – Tuning parameter for spectral projected gradient optimization (smallest allowed step in the search direction). * lam\_max (float) – Tuning parameter for spectral projected gradient optimization (largest allowed step in the search direction). * maxiter (integer) – Maximum number of iterations in spectral projected gradient optimization. \| \| Returns: \| rslt – rslt.corr is a FactoredPSDMatrix defining the estimated correlation structure. Other fields of `rslt` contain returned values from spg\_optim. \| \| Return type: \| Bunch \| #### Notes A correlation matrix has factor structure if it can be written in the form I + XX’ - diag(XX’), where X is n x k with linearly independent columns, and with each row having sum of squares at most equal to 1. The approximation is made in terms of the Frobenius norm. This routine is useful when one has an approximate correlation matrix that is not positive semidefinite, and there is need to estimate the inverse, square root, or inverse square root of the population correlation matrix. The factor structure allows these tasks to be done without constructing any n x n matrices. This is a non-convex problem with no known gauranteed globally convergent algorithm for computing the solution. Borsdof, Higham and Raydan (2010) compared several methods for this problem and found the spectral projected gradient (SPG) method (used here) to perform best. The input matrix `corr` can be a dense numpy array or any scipy sparse matrix. The latter is useful if the input matrix is obtained by thresholding a very large sample correlation matrix. If `corr` is sparse, the calculations are optimized to save memory, so no working matrix with more than 10^6 elements is constructed. #### References R Borsdof, N Higham, M Raydan (2010). Computing a nearest correlation matrix with factor structure. SIAM J Matrix Anal Appl, 31:5, 2603-2622. <http://eprints.ma.man.ac.uk/1523/01/covered/MIMS_ep2009_87.pdf> #### Examples Hard thresholding a correlation matrix may result in a matrix that is not positive semidefinite. We can approximate a hard thresholded correlation matrix with a PSD matrix as follows, where `corr` is the input correlation matrix. ``` >>> import numpy as np >>> from statsmodels.stats.correlation_tools import corr_nearest_factor >>> np.random.seed(1234) >>> b = 1.5 - np.random.rand(10, 1) >>> x = np.random.randn(100,1).dot(b.T) + np.random.randn(100,10) >>> corr = np.corrcoef(x.T) >>> corr = corr * (np.abs(corr) >= 0.3) >>> rslt = corr_nearest_factor(corr, 3) ``` statsmodels statsmodels.regression.quantile_regression.QuantRegResults.condition_number statsmodels.regression.quantile\_regression.QuantRegResults.condition\_number ============================================================================= `QuantRegResults.condition_number()` Return condition number of exogenous matrix. Calculated as ratio of largest to smallest eigenvalue. statsmodels statsmodels.sandbox.tsa.fftarma.ArmaFft.spdmapoly statsmodels.sandbox.tsa.fftarma.ArmaFft.spdmapoly ================================================= `ArmaFft.spdmapoly(w, twosided=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/tsa/fftarma.html#ArmaFft.spdmapoly) ma only, need division for ar, use LagPolynomial statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.wald_test statsmodels.regression.recursive\_ls.RecursiveLSResults.wald\_test ================================================================== `RecursiveLSResults.wald_test(r_matrix, cov_p=None, scale=1.0, invcov=None, use_f=None)` Compute a Wald-test for a joint linear hypothesis. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. * use\_f (bool) – If True, then the F-distribution is used. If False, then the asymptotic distribution, chisquare is used. If use\_f is None, then the F distribution is used if the model specifies that use\_t is True. The test statistic is proportionally adjusted for the distribution by the number of constraints in the hypothesis. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`f_test`](statsmodels.regression.recursive_ls.recursivelsresults.f_test#statsmodels.regression.recursive_ls.RecursiveLSResults.f_test "statsmodels.regression.recursive_ls.RecursiveLSResults.f_test"), [`t_test`](statsmodels.regression.recursive_ls.recursivelsresults.t_test#statsmodels.regression.recursive_ls.RecursiveLSResults.t_test "statsmodels.regression.recursive_ls.RecursiveLSResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.aic statsmodels.discrete.count\_model.ZeroInflatedNegativeBinomialResults.aic ========================================================================= `ZeroInflatedNegativeBinomialResults.aic()` statsmodels statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults statsmodels.discrete.count\_model.ZeroInflatedNegativeBinomialResults ===================================================================== `class statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults(model, mlefit, cov_type='nonrobust', cov_kwds=None, use_t=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/count_model.html#ZeroInflatedNegativeBinomialResults) A results class for Zero Inflated Genaralized Negative Binomial \| Parameters: \| * model (A DiscreteModel instance) – * params (array-like) – The parameters of a fitted model. * hessian (array-like) – The hessian of the fitted model. * scale (float) – A scale parameter for the covariance matrix. \| \| Returns: \| * \Attributes\** * aic (float) – Akaike information criterion. `-2(llf - p)` where `p` is the number of regressors including the intercept. bic (float) – Bayesian information criterion. `-2llf + ln(nobs)p` where `p` is the number of regressors including the intercept. * bse (array) – The standard errors of the coefficients. * df\_resid (float) – See model definition. * df\_model (float) – See model definition. * fitted\_values (array) – Linear predictor XB. * llf (float) – Value of the loglikelihood * llnull (float) – Value of the constant-only loglikelihood * llr (float) – Likelihood ratio chi-squared statistic; `-2(llnull - llf)` llr\_pvalue (float) – The chi-squared probability of getting a log-likelihood ratio statistic greater than llr. llr has a chi-squared distribution with degrees of freedom `df_model`. * prsquared (float) – McFadden’s pseudo-R-squared. `1 - (llf / llnull)` \| #### Methods \| \| \| \| --- \| --- \| \| [`aic`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.aic#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.aic "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.aic")() \| \| \| [`bic`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.bic#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.bic "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.bic")() \| \| \| [`bse`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.bse#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.bse "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.bse")() \| \| \| [`conf_int`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.conf_int#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.conf_int "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.conf_int")([alpha, cols, method]) \| Returns the confidence interval of the fitted parameters. \| \| [`cov_params`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.cov_params#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.cov_params "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.cov_params")([r\_matrix, column, scale, cov\_p, …]) \| Returns the variance/covariance matrix. \| \| [`f_test`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.f_test#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.f_test "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.f_test")(r\_matrix[, cov\_p, scale, invcov]) \| Compute the F-test for a joint linear hypothesis. \| \| [`fittedvalues`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.fittedvalues#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.fittedvalues "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.fittedvalues")() \| \| \| [`get_margeff`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.get_margeff#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.get_margeff "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.get_margeff")([at, method, atexog, dummy, count]) \| Get marginal effects of the fitted model. \| \| [`initialize`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.initialize#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.initialize "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.initialize")(model, params, \\kwd) \| \| \| [`llf`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.llf#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.llf "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.llf")() \| \| \| [`llnull`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.llnull#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.llnull "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.llnull")() \| \| \| [`llr`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.llr#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.llr "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.llr")() \| \| \| [`llr_pvalue`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.llr_pvalue#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.llr_pvalue "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.llr_pvalue")() \| \| \| [`load`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.load#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.load "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.load")(fname) \| load a pickle, (class method) \| \| [`normalized_cov_params`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.normalized_cov_params#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.normalized_cov_params "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.normalized_cov_params")() \| \| \| [`predict`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.predict#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.predict "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.predict")([exog, transform]) \| Call self.model.predict with self.params as the first argument. \| \| [`prsquared`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.prsquared#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.prsquared "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.prsquared")() \| \| \| [`pvalues`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.pvalues#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.pvalues "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.pvalues")() \| \| \| [`remove_data`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.remove_data#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.remove_data "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.remove_data")() \| remove data arrays, all nobs arrays from result and model \| \| [`resid`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.resid#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.resid "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.resid")() \| Residuals \| \| [`save`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.save#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.save "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.save")(fname[, remove\_data]) \| save a pickle of this instance \| \| [`set_null_options`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.set_null_options#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.set_null_options "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.set_null_options")([llnull, attach\_results]) \| set fit options for Null (constant-only) model \| \| [`summary`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.summary#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.summary "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.summary")([yname, xname, title, alpha, yname\_list]) \| Summarize the Regression Results \| \| [`summary2`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.summary2#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.summary2 "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.summary2")([yname, xname, title, alpha, …]) \| Experimental function to summarize regression results \| \| [`t_test`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.t_test#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.t_test "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.t_test")(r\_matrix[, cov\_p, scale, use\_t]) \| Compute a t-test for a each linear hypothesis of the form Rb = q \| \| [`t_test_pairwise`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.t_test_pairwise#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.t_test_pairwise "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.t_test_pairwise")(term\_name[, method, alpha, …]) \| perform pairwise t\_test with multiple testing corrected p-values \| \| [`tvalues`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.tvalues#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.tvalues "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.tvalues")() \| Return the t-statistic for a given parameter estimate. \| \| [`wald_test`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.wald_test#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.wald_test "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.wald_test")(r\_matrix[, cov\_p, scale, invcov, …]) \| Compute a Wald-test for a joint linear hypothesis. \| \| [`wald_test_terms`](statsmodels.discrete.count_model.zeroinflatednegativebinomialresults.wald_test_terms#statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.wald_test_terms "statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.wald_test_terms")([skip\_single, …]) \| Compute a sequence of Wald tests for terms over multiple columns \| #### Attributes \| \| \| \| --- \| --- \| \| `use_t` \| \|	programming_docs
statsmodels statsmodels.stats.moment_helpers.mc2mvsk statsmodels.stats.moment\_helpers.mc2mvsk ========================================= `statsmodels.stats.moment_helpers.mc2mvsk(args)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/moment_helpers.html#mc2mvsk) convert central moments to mean, variance, skew, kurtosis statsmodels statsmodels.regression.linear_model.OLS.from_formula statsmodels.regression.linear\_model.OLS.from\_formula ====================================================== `classmethod OLS.from_formula(formula, data, subset=None, drop_cols=None, args, kwargs)` Create a Model from a formula and dataframe. \| Parameters: \| formula (str or generic Formula object) – The formula specifying the model * data (array-like) – The data for the model. See Notes. * subset (array-like) – An array-like object of booleans, integers, or index values that indicate the subset of df to use in the model. Assumes df is a `pandas.DataFrame` * drop\_cols (array-like) – Columns to drop from the design matrix. Cannot be used to drop terms involving categoricals. * args (extra arguments) – These are passed to the model * kwargs (extra keyword arguments) – These are passed to the model with one exception. The `eval_env` keyword is passed to patsy. It can be either a [`patsy.EvalEnvironment`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.EvalEnvironment "(in patsy v0.5.0+dev)") object or an integer indicating the depth of the namespace to use. For example, the default `eval_env=0` uses the calling namespace. If you wish to use a “clean” environment set `eval_env=-1`. \| \| Returns: \| model \| \| Return type: \| Model instance \| #### Notes data must define \_\_getitem\_\_ with the keys in the formula terms args and kwargs are passed on to the model instantiation. E.g., a numpy structured or rec array, a dictionary, or a pandas DataFrame. statsmodels statsmodels.stats.weightstats.DescrStatsW.sum statsmodels.stats.weightstats.DescrStatsW.sum ============================================= `DescrStatsW.sum()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/weightstats.html#DescrStatsW.sum) weighted sum of data statsmodels statsmodels.regression.linear_model.RegressionResults.aic statsmodels.regression.linear\_model.RegressionResults.aic ========================================================== `RegressionResults.aic()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#RegressionResults.aic) statsmodels statsmodels.sandbox.distributions.extras.SkewNorm_gen.freeze statsmodels.sandbox.distributions.extras.SkewNorm\_gen.freeze ============================================================= `SkewNorm_gen.freeze(args, kwds)` Freeze the distribution for the given arguments. \| Parameters: \| arg2*, arg3,.. (arg1,) – The shape parameter(s) for the distribution. Should include all the non-optional arguments, may include `loc` and `scale`. \| \| Returns: \| rv\_frozen – The frozen distribution. \| \| Return type: \| rv\_frozen instance \| statsmodels statsmodels.sandbox.distributions.extras.NormExpan_gen.ppf statsmodels.sandbox.distributions.extras.NormExpan\_gen.ppf =========================================================== `NormExpan_gen.ppf(q, args, kwds)` Percent point function (inverse of `cdf`) at q of the given RV. \| Parameters: \| q (array\_like) – lower tail probability * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| x – quantile corresponding to the lower tail probability q. \| \| Return type: \| array\_like \| statsmodels statsmodels.sandbox.distributions.extras.ACSkewT_gen.mean statsmodels.sandbox.distributions.extras.ACSkewT\_gen.mean ========================================================== `ACSkewT_gen.mean(args, kwds)` Mean of the distribution. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| mean – the mean of the distribution \| \| Return type: \| float \| statsmodels statsmodels.nonparametric.kernel_density.KDEMultivariateConditional.cdf statsmodels.nonparametric.kernel\_density.KDEMultivariateConditional.cdf ======================================================================== `KDEMultivariateConditional.cdf(endog_predict=None, exog_predict=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/nonparametric/kernel_density.html#KDEMultivariateConditional.cdf) Cumulative distribution function for the conditional density. \| Parameters: \| * endog\_predict (array\_like, optional) – The evaluation dependent variables at which the cdf is estimated. If not specified the training dependent variables are used. * exog\_predict (array\_like, optional) – The evaluation independent variables at which the cdf is estimated. If not specified the training independent variables are used. \| \| Returns: \| cdf\_est – The estimate of the cdf. \| \| Return type: \| array\_like \| #### Notes For more details on the estimation see [[2]](#id4), and p.181 in [[1]](#id3). The multivariate conditional CDF for mixed data (continuous and ordered/unordered discrete) is estimated by: \[F(y\|x)=\frac{n^{-1}\sum\_{i=1}^{n}G(\frac{y-Y\_{i}}{h\_{0}}) W\_{h}(X\_{i},x)}{\widehat{\mu}(x)}\] where G() is the product kernel CDF estimator for the dependent (y) variable(s) and W() is the product kernel CDF estimator for the independent variable(s). #### References \| \| \| \| --- \| --- \| \| [[1]](#id2) \| Racine, J., Li, Q. Nonparametric econometrics: theory and practice. Princeton University Press. (2007) \| \| \| \| \| --- \| --- \| \| [[2]](#id1) \| Liu, R., Yang, L. “Kernel estimation of multivariate cumulative distribution function.” Journal of Nonparametric Statistics (2008) \| statsmodels statsmodels.discrete.discrete_model.DiscreteResults.bse statsmodels.discrete.discrete\_model.DiscreteResults.bse ======================================================== `DiscreteResults.bse()` statsmodels statsmodels.tsa.vector_ar.var_model.VARProcess.orth_ma_rep statsmodels.tsa.vector\_ar.var\_model.VARProcess.orth\_ma\_rep ============================================================== `VARProcess.orth_ma_rep(maxn=10, P=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARProcess.orth_ma_rep) Compute orthogonalized MA coefficient matrices using P matrix such that $\Sigma\_u = PP^\prime$. P defaults to the Cholesky decomposition of $\Sigma\_u$ \| Parameters: \| * maxn (int) – Number of coefficient matrices to compute * P (ndarray (k x k), optional) – Matrix such that Sigma\_u = PP’, defaults to Cholesky descomp \| \| Returns: \| coefs \| \| Return type: \| ndarray (maxn x k x k) \| statsmodels statsmodels.tsa.statespace.mlemodel.MLEResults.resid statsmodels.tsa.statespace.mlemodel.MLEResults.resid ==================================================== `MLEResults.resid()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/mlemodel.html#MLEResults.resid) (array) The model residuals. An (nobs x k\_endog) array. statsmodels statsmodels.discrete.discrete_model.NegativeBinomialP.information statsmodels.discrete.discrete\_model.NegativeBinomialP.information ================================================================== `NegativeBinomialP.information(params)` Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.genmod.bayes_mixed_glm.BayesMixedGLMResults statsmodels.genmod.bayes\_mixed\_glm.BayesMixedGLMResults ========================================================= `class statsmodels.genmod.bayes_mixed_glm.BayesMixedGLMResults(model, params, cov_params, optim_retvals=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/bayes_mixed_glm.html#BayesMixedGLMResults) `fe_mean` array-like – Posterior mean of the fixed effects coefficients. `fe_sd` array-like – Posterior standard deviation of the fixed effects coefficients `vcp_mean` array-like – Posterior mean of the logged variance component standard deviations. `vcp_sd` array-like – Posterior standard deviation of the logged variance component standard deviations. `vc_mean` array-like – Posterior mean of the random coefficients `vc_sd` array-like – Posterior standard deviation of the random coefficients #### Methods \| \| \| \| --- \| --- \| \| [`random_effects`](statsmodels.genmod.bayes_mixed_glm.bayesmixedglmresults.random_effects#statsmodels.genmod.bayes_mixed_glm.BayesMixedGLMResults.random_effects "statsmodels.genmod.bayes_mixed_glm.BayesMixedGLMResults.random_effects")([term]) \| Posterior mean and standard deviation of random effects. \| \| [`summary`](statsmodels.genmod.bayes_mixed_glm.bayesmixedglmresults.summary#statsmodels.genmod.bayes_mixed_glm.BayesMixedGLMResults.summary "statsmodels.genmod.bayes_mixed_glm.BayesMixedGLMResults.summary")() \| \| statsmodels statsmodels.regression.linear_model.OLS.fit statsmodels.regression.linear\_model.OLS.fit ============================================ `OLS.fit(method='pinv', cov_type='nonrobust', cov_kwds=None, use_t=None, *kwargs)` Full fit of the model. The results include an estimate of covariance matrix, (whitened) residuals and an estimate of scale. \| Parameters: \| method (str, optional) – Can be “pinv”, “qr”. “pinv” uses the Moore-Penrose pseudoinverse to solve the least squares problem. “qr” uses the QR factorization. * cov\_type (str, optional) – See `regression.linear_model.RegressionResults` for a description of the available covariance estimators * cov\_kwds (list or None, optional) – See `linear_model.RegressionResults.get_robustcov_results` for a description required keywords for alternative covariance estimators * use\_t (bool, optional) – Flag indicating to use the Student’s t distribution when computing p-values. Default behavior depends on cov\_type. See `linear_model.RegressionResults.get_robustcov_results` for implementation details. \| \| Returns: \| \| \| Return type: \| A RegressionResults class instance. \| See also `regression.linear_model.RegressionResults`, `regression.linear_model.RegressionResults.get_robustcov_results` #### Notes The fit method uses the pseudoinverse of the design/exogenous variables to solve the least squares minimization. statsmodels statsmodels.discrete.discrete_model.GeneralizedPoisson.information statsmodels.discrete.discrete\_model.GeneralizedPoisson.information =================================================================== `GeneralizedPoisson.information(params)` Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.sandbox.regression.gmm.GMMResults.t_test_pairwise statsmodels.sandbox.regression.gmm.GMMResults.t\_test\_pairwise =============================================================== `GMMResults.t_test_pairwise(term_name, method='hs', alpha=0.05, factor_labels=None)` perform pairwise t\_test with multiple testing corrected p-values This uses the formula design\_info encoding contrast matrix and should work for all encodings of a main effect. \| Parameters: \| * result (result instance) – The results of an estimated model with a categorical main effect. * term\_name (str) – name of the term for which pairwise comparisons are computed. Term names for categorical effects are created by patsy and correspond to the main part of the exog names. * method (str or list of strings) – multiple testing p-value correction, default is ‘hs’, see stats.multipletesting * alpha (float) – significance level for multiple testing reject decision. * factor\_labels (None, list of str) – Labels for the factor levels used for pairwise labels. If not provided, then the labels from the formula design\_info are used. \| \| Returns: \| results – The results are stored as attributes, the main attributes are the following two. Other attributes are added for debugging purposes or as background information.* result\_frame : pandas DataFrame with t\_test results and multiple testing corrected p-values. * contrasts : matrix of constraints of the null hypothesis in the t\_test. \| \| Return type: \| instance of a simple Results class \| #### Notes Status: experimental. Currently only checked for treatment coding with and without specified reference level. Currently there are no multiple testing corrected confidence intervals available. #### Examples ``` >>> res = ols("np.log(Days+1) ~ C(Weight) + C(Duration)", data).fit() >>> pw = res.t_test_pairwise("C(Weight)") >>> pw.result_frame coef std err t P>\|t\| Conf. Int. Low 2-1 0.632315 0.230003 2.749157 8.028083e-03 0.171563 3-1 1.302555 0.230003 5.663201 5.331513e-07 0.841803 3-2 0.670240 0.230003 2.914044 5.119126e-03 0.209488 Conf. Int. Upp. pvalue-hs reject-hs 2-1 1.093067 0.010212 True 3-1 1.763307 0.000002 True 3-2 1.130992 0.010212 True ``` statsmodels statsmodels.sandbox.regression.gmm.GMMResults.llf statsmodels.sandbox.regression.gmm.GMMResults.llf ================================================= `GMMResults.llf()` statsmodels statsmodels.tsa.statespace.mlemodel.MLEModel.simulate statsmodels.tsa.statespace.mlemodel.MLEModel.simulate ===================================================== `MLEModel.simulate(params, nsimulations, measurement_shocks=None, state_shocks=None, initial_state=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/mlemodel.html#MLEModel.simulate) Simulate a new time series following the state space model \| Parameters: \| * params (array\_like) – Array of model parameters. * nsimulations (int) – The number of observations to simulate. If the model is time-invariant this can be any number. If the model is time-varying, then this number must be less than or equal to the number * measurement\_shocks (array\_like, optional) – If specified, these are the shocks to the measurement equation, $\varepsilon\_t$. If unspecified, these are automatically generated using a pseudo-random number generator. If specified, must be shaped `nsimulations` x `k_endog`, where `k_endog` is the same as in the state space model. * state\_shocks (array\_like, optional) – If specified, these are the shocks to the state equation, $\eta\_t$. If unspecified, these are automatically generated using a pseudo-random number generator. If specified, must be shaped `nsimulations` x `k_posdef` where `k_posdef` is the same as in the state space model. * initial\_state (array\_like, optional) – If specified, this is the state vector at time zero, which should be shaped (`k_states` x 1), where `k_states` is the same as in the state space model. If unspecified, but the model has been initialized, then that initialization is used. If unspecified and the model has not been initialized, then a vector of zeros is used. Note that this is not included in the returned `simulated_states` array. \| \| Returns: \| simulated\_obs – An (nsimulations x k\_endog) array of simulated observations. \| \| Return type: \| array \| statsmodels statsmodels.tsa.statespace.sarimax.SARIMAX.opg_information_matrix statsmodels.tsa.statespace.sarimax.SARIMAX.opg\_information\_matrix =================================================================== `SARIMAX.opg_information_matrix(params, transformed=True, approx_complex_step=None, *kwargs)` Outer product of gradients information matrix \| Parameters: \| params (array\_like, optional) – Array of parameters at which to evaluate the loglikelihood function. * *\\kwargs* – Additional arguments to the `loglikeobs` method. \| #### References Berndt, Ernst R., Bronwyn Hall, Robert Hall, and Jerry Hausman. 1974. Estimation and Inference in Nonlinear Structural Models. NBER Chapters. National Bureau of Economic Research, Inc. statsmodels statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialResults.fittedvalues statsmodels.discrete.count\_model.ZeroInflatedNegativeBinomialResults.fittedvalues ================================================================================== `ZeroInflatedNegativeBinomialResults.fittedvalues()` statsmodels statsmodels.tsa.statespace.structural.UnobservedComponentsResults.cov_params statsmodels.tsa.statespace.structural.UnobservedComponentsResults.cov\_params ============================================================================= `UnobservedComponentsResults.cov_params(r_matrix=None, column=None, scale=None, cov_p=None, other=None)` Returns the variance/covariance matrix. The variance/covariance matrix can be of a linear contrast of the estimates of params or all params multiplied by scale which will usually be an estimate of sigma^2. Scale is assumed to be a scalar. \| Parameters: \| * r\_matrix (array-like) – Can be 1d, or 2d. Can be used alone or with other. * column (array-like, optional) – Must be used on its own. Can be 0d or 1d see below. * scale (float, optional) – Can be specified or not. Default is None, which means that the scale argument is taken from the model. * other (array-like, optional) – Can be used when r\_matrix is specified. \| \| Returns: \| cov – covariance matrix of the parameter estimates or of linear combination of parameter estimates. See Notes. \| \| Return type: \| ndarray \| #### Notes (The below are assumed to be in matrix notation.) If no argument is specified returns the covariance matrix of a model `(scale)(X.T X)^(-1)` If contrast is specified it pre and post-multiplies as follows `(scale) r_matrix (X.T X)^(-1) r_matrix.T` If contrast and other are specified returns `(scale) * r_matrix (X.T X)^(-1) other.T` If column is specified returns `(scale) * (X.T X)^(-1)[column,column]` if column is 0d OR `(scale) * (X.T X)^(-1)[column][:,column]` if column is 1d statsmodels statsmodels.tsa.vector_ar.dynamic.DynamicVAR.resid statsmodels.tsa.vector\_ar.dynamic.DynamicVAR.resid =================================================== `DynamicVAR.resid()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/dynamic.html#DynamicVAR.resid) statsmodels statsmodels.tsa.statespace.sarimax.SARIMAXResults.tvalues statsmodels.tsa.statespace.sarimax.SARIMAXResults.tvalues ========================================================= `SARIMAXResults.tvalues()` Return the t-statistic for a given parameter estimate. statsmodels statsmodels.discrete.discrete_model.Poisson.cov_params_func_l1 statsmodels.discrete.discrete\_model.Poisson.cov\_params\_func\_l1 ================================================================== `Poisson.cov_params_func_l1(likelihood_model, xopt, retvals)` Computes cov\_params on a reduced parameter space corresponding to the nonzero parameters resulting from the l1 regularized fit. Returns a full cov\_params matrix, with entries corresponding to zero’d values set to np.nan. statsmodels statsmodels.nonparametric.kernel_density.KDEMultivariateConditional.loo_likelihood statsmodels.nonparametric.kernel\_density.KDEMultivariateConditional.loo\_likelihood ==================================================================================== `KDEMultivariateConditional.loo_likelihood(bw, func=<function KDEMultivariateConditional.<lambda>>)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/nonparametric/kernel_density.html#KDEMultivariateConditional.loo_likelihood) Returns the leave-one-out conditional likelihood of the data. If `func` is not equal to the default, what’s calculated is a function of the leave-one-out conditional likelihood. \| Parameters: \| * bw (array\_like) – The bandwidth parameter(s). * func (callable, optional) – Function to transform the likelihood values (before summing); for the log likelihood, use `func=np.log`. Default is `f(x) = x`. \| \| Returns: \| L – The value of the leave-one-out function for the data. \| \| Return type: \| float \| #### Notes Similar to `KDE.loo_likelihood`, but substitute ``f(y\|x)=f(x,y)/f(x)` for `f(x)`.	programming_docs
statsmodels statsmodels.duration.hazard_regression.PHReg.efron_hessian statsmodels.duration.hazard\_regression.PHReg.efron\_hessian ============================================================ `PHReg.efron_hessian(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/duration/hazard_regression.html#PHReg.efron_hessian) Returns the Hessian matrix of the partial log-likelihood evaluated at `params`, using the Efron method to handle tied times. statsmodels statsmodels.sandbox.distributions.transformed.ExpTransf_gen.expect statsmodels.sandbox.distributions.transformed.ExpTransf\_gen.expect =================================================================== `ExpTransf_gen.expect(func=None, args=(), loc=0, scale=1, lb=None, ub=None, conditional=False, *kwds)` Calculate expected value of a function with respect to the distribution. The expected value of a function `f(x)` with respect to a distribution `dist` is defined as: ``` ubound E[x] = Integral(f(x) dist.pdf(x)) lbound ``` \| Parameters: \| * func (callable, optional) – Function for which integral is calculated. Takes only one argument. The default is the identity mapping f(x) = x. * args (tuple, optional) – Shape parameters of the distribution. * loc (float, optional) – Location parameter (default=0). * scale (float, optional) – Scale parameter (default=1). * ub (lb,) – Lower and upper bound for integration. Default is set to the support of the distribution. * conditional (bool, optional) – If True, the integral is corrected by the conditional probability of the integration interval. The return value is the expectation of the function, conditional on being in the given interval. Default is False. * keyword arguments are passed to the integration routine. (Additional) – \| \| Returns: \| expect – The calculated expected value. \| \| Return type: \| float \| #### Notes The integration behavior of this function is inherited from `integrate.quad`. statsmodels statsmodels.sandbox.distributions.transformed.LogTransf_gen.logsf statsmodels.sandbox.distributions.transformed.LogTransf\_gen.logsf ================================================================== `LogTransf_gen.logsf(x, args, kwds)` Log of the survival function of the given RV. Returns the log of the “survival function,” defined as (1 - `cdf`), evaluated at `x`. \| Parameters: \| x (array\_like) – quantiles * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| logsf – Log of the survival function evaluated at `x`. \| \| Return type: \| ndarray \| statsmodels statsmodels.sandbox.regression.gmm.GMMResults.remove_data statsmodels.sandbox.regression.gmm.GMMResults.remove\_data ========================================================== `GMMResults.remove_data()` remove data arrays, all nobs arrays from result and model This reduces the size of the instance, so it can be pickled with less memory. Currently tested for use with predict from an unpickled results and model instance. Warning Since data and some intermediate results have been removed calculating new statistics that require them will raise exceptions. The exception will occur the first time an attribute is accessed that has been set to None. Not fully tested for time series models, tsa, and might delete too much for prediction or not all that would be possible. The lists of arrays to delete are maintained as attributes of the result and model instance, except for cached values. These lists could be changed before calling remove\_data. The attributes to remove are named in: `model._data_attr : arrays attached to both the model instance` and the results instance with the same attribute name. `result.data_in_cache : arrays that may exist as values in` result.\_cache (TODO : should privatize name) `result._data_attr_model : arrays attached to the model` instance but not to the results instance statsmodels statsmodels.discrete.count_model.GenericZeroInflated.fit_regularized statsmodels.discrete.count\_model.GenericZeroInflated.fit\_regularized ====================================================================== `GenericZeroInflated.fit_regularized(start_params=None, method='l1', maxiter='defined_by_method', full_output=1, disp=1, callback=None, alpha=0, trim_mode='auto', auto_trim_tol=0.01, size_trim_tol=0.0001, qc_tol=0.03, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/count_model.html#GenericZeroInflated.fit_regularized) Fit the model using a regularized maximum likelihood. The regularization method AND the solver used is determined by the argument method. \| Parameters: \| start\_params (array-like, optional) – Initial guess of the solution for the loglikelihood maximization. The default is an array of zeros. * method ('l1' or 'l1\_cvxopt\_cp') – See notes for details. * maxiter (Integer or 'defined\_by\_method') – Maximum number of iterations to perform. If ‘defined\_by\_method’, then use method defaults (see notes). * full\_output (bool) – Set to True to have all available output in the Results object’s mle\_retvals attribute. The output is dependent on the solver. See LikelihoodModelResults notes section for more information. * disp (bool) – Set to True to print convergence messages. * fargs (tuple) – Extra arguments passed to the likelihood function, i.e., loglike(x,\args) callback (callable callback(xk)) – Called after each iteration, as callback(xk), where xk is the current parameter vector. * retall (bool) – Set to True to return list of solutions at each iteration. Available in Results object’s mle\_retvals attribute. * alpha (non-negative scalar or numpy array (same size as parameters)) – The weight multiplying the l1 penalty term * trim\_mode ('auto, 'size', or 'off') – If not ‘off’, trim (set to zero) parameters that would have been zero if the solver reached the theoretical minimum. If ‘auto’, trim params using the Theory above. If ‘size’, trim params if they have very small absolute value * size\_trim\_tol (float or 'auto' (default = 'auto')) – For use when trim\_mode == ‘size’ * auto\_trim\_tol (float) – For sue when trim\_mode == ‘auto’. Use * qc\_tol (float) – Print warning and don’t allow auto trim when (ii) (above) is violated by this much. * qc\_verbose (Boolean) – If true, print out a full QC report upon failure \| #### Notes Extra parameters are not penalized if alpha is given as a scalar. An example is the shape parameter in NegativeBinomial `nb1` and `nb2`. Optional arguments for the solvers (available in Results.mle\_settings): ``` 'l1' acc : float (default 1e-6) Requested accuracy as used by slsqp 'l1_cvxopt_cp' abstol : float absolute accuracy (default: 1e-7). reltol : float relative accuracy (default: 1e-6). feastol : float tolerance for feasibility conditions (default: 1e-7). refinement : int number of iterative refinement steps when solving KKT equations (default: 1). ``` Optimization methodology With $L$ the negative log likelihood, we solve the convex but non-smooth problem \[\min\_\beta L(\beta) + \sum\_k\alpha\_k \|\beta\_k\|\] via the transformation to the smooth, convex, constrained problem in twice as many variables (adding the “added variables” $u\_k$) \[\min\_{\beta,u} L(\beta) + \sum\_k\alpha\_k u\_k,\] subject to \[-u\_k \leq \beta\_k \leq u\_k.\] With $\partial\_k L$ the derivative of $L$ in the $k^{th}$ parameter direction, theory dictates that, at the minimum, exactly one of two conditions holds: 1. $\|\partial\_k L\| = \alpha\_k$ and $\beta\_k \neq 0$ 2. $\|\partial\_k L\| \leq \alpha\_k$ and $\beta\_k = 0$ statsmodels statsmodels.tsa.varma_process.VarmaPoly.reduceform statsmodels.tsa.varma\_process.VarmaPoly.reduceform =================================================== `VarmaPoly.reduceform(apoly)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/varma_process.html#VarmaPoly.reduceform) this assumes no exog, todo statsmodels statsmodels.tsa.tsatools.lagmat statsmodels.tsa.tsatools.lagmat =============================== `statsmodels.tsa.tsatools.lagmat(x, maxlag, trim='forward', original='ex', use_pandas=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/tsatools.html#lagmat) Create 2d array of lags \| Parameters: \| * x (array\_like, 1d or 2d) – data; if 2d, observation in rows and variables in columns * maxlag (int) – all lags from zero to maxlag are included * trim (str {'forward', 'backward', 'both', 'none'} or None) – + ‘forward’ : trim invalid observations in front + ’backward’ : trim invalid initial observations + ’both’ : trim invalid observations on both sides + ’none’, None : no trimming of observations * original (str {'ex','sep','in'}) – + ‘ex’ : drops the original array returning only the lagged values. + ’in’ : returns the original array and the lagged values as a single array. + `’sep’ : returns a tuple (original array, lagged values). The original` array is truncated to have the same number of rows as the returned lagmat. * use\_pandas (bool, optional) – If true, returns a DataFrame when the input is a pandas Series or DataFrame. If false, return numpy ndarrays. \| \| Returns: \| * lagmat (2d array) – array with lagged observations * y (2d array, optional) – Only returned if original == ‘sep’ \| #### Examples ``` >>> from statsmodels.tsa.tsatools import lagmat >>> import numpy as np >>> X = np.arange(1,7).reshape(-1,2) >>> lagmat(X, maxlag=2, trim="forward", original='in') array([[ 1., 2., 0., 0., 0., 0.], [ 3., 4., 1., 2., 0., 0.], [ 5., 6., 3., 4., 1., 2.]]) ``` ``` >>> lagmat(X, maxlag=2, trim="backward", original='in') array([[ 5., 6., 3., 4., 1., 2.], [ 0., 0., 5., 6., 3., 4.], [ 0., 0., 0., 0., 5., 6.]]) ``` ``` >>> lagmat(X, maxlag=2, trim="both", original='in') array([[ 5., 6., 3., 4., 1., 2.]]) ``` ``` >>> lagmat(X, maxlag=2, trim="none", original='in') array([[ 1., 2., 0., 0., 0., 0.], [ 3., 4., 1., 2., 0., 0.], [ 5., 6., 3., 4., 1., 2.], [ 0., 0., 5., 6., 3., 4.], [ 0., 0., 0., 0., 5., 6.]]) ``` #### Notes When using a pandas DataFrame or Series with use\_pandas=True, trim can only be ‘forward’ or ‘both’ since it is not possible to consistently extend index values. statsmodels statsmodels.miscmodels.tmodel.TLinearModel.hessian_factor statsmodels.miscmodels.tmodel.TLinearModel.hessian\_factor ========================================================== `TLinearModel.hessian_factor(params, scale=None, observed=True)` Weights for calculating Hessian \| Parameters: \| * params (ndarray) – parameter at which Hessian is evaluated * scale (None or float) – If scale is None, then the default scale will be calculated. Default scale is defined by `self.scaletype` and set in fit. If scale is not None, then it is used as a fixed scale. * observed (bool) – If True, then the observed Hessian is returned. If false then the expected information matrix is returned. \| \| Returns: \| hessian\_factor – A 1d weight vector used in the calculation of the Hessian. The hessian is obtained by `(exog.T * hessian_factor).dot(exog)` \| \| Return type: \| ndarray, 1d \| statsmodels statsmodels.tsa.vector_ar.irf.IRAnalysis.err_band_sz2 statsmodels.tsa.vector\_ar.irf.IRAnalysis.err\_band\_sz2 ======================================================== `IRAnalysis.err_band_sz2(orth=False, svar=False, repl=1000, signif=0.05, seed=None, burn=100, component=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/irf.html#IRAnalysis.err_band_sz2) IRF Sims-Zha error band method 2. This method Does not assume symmetric error bands around mean. \| Parameters: \| * orth (bool, default False) – Compute orthogonalized impulse responses * repl (int, default 1000) – Number of MC replications * signif (float (0 < signif < 1)) – Significance level for error bars, defaults to 95% CI * seed (int, default None) – np.random seed * burn (int, default 100) – Number of initial simulated obs to discard * component (neqs x neqs array, default to largest for each) – Index of column of eigenvector/value to use for each error band Note: period of impulse (t=0) is not included when computing principle component \| #### References Sims, Christopher A., and Tao Zha. 1999. “Error Bands for Impulse Response”. Econometrica 67: 1113-1155. statsmodels statsmodels.tsa.ar_model.ARResults.wald_test_terms statsmodels.tsa.ar\_model.ARResults.wald\_test\_terms ===================================================== `ARResults.wald_test_terms(skip_single=False, extra_constraints=None, combine_terms=None)` Compute a sequence of Wald tests for terms over multiple columns This computes joined Wald tests for the hypothesis that all coefficients corresponding to a `term` are zero. `Terms` are defined by the underlying formula or by string matching. \| Parameters: \| * skip\_single (boolean) – If true, then terms that consist only of a single column and, therefore, refers only to a single parameter is skipped. If false, then all terms are included. * extra\_constraints (ndarray) – not tested yet * combine\_terms (None or list of strings) – Each string in this list is matched to the name of the terms or the name of the exogenous variables. All columns whose name includes that string are combined in one joint test. \| \| Returns: \| test\_result – The result instance contains `table` which is a pandas DataFrame with the test results: test statistic, degrees of freedom and pvalues. \| \| Return type: \| result instance \| #### Examples ``` >>> res_ols = ols("np.log(Days+1) ~ C(Duration, Sum)C(Weight, Sum)", data).fit() >>> res_ols.wald_test_terms() <class 'statsmodels.stats.contrast.WaldTestResults'> F P>F df constraint df denom Intercept 279.754525 2.37985521351e-22 1 51 C(Duration, Sum) 5.367071 0.0245738436636 1 51 C(Weight, Sum) 12.432445 3.99943118767e-05 2 51 C(Duration, Sum):C(Weight, Sum) 0.176002 0.83912310946 2 51 ``` ``` >>> res_poi = Poisson.from_formula("Days ~ C(Weight) C(Duration)", data).fit(cov_type='HC0') >>> wt = res_poi.wald_test_terms(skip_single=False, combine_terms=['Duration', 'Weight']) >>> print(wt) chi2 P>chi2 df constraint Intercept 15.695625 7.43960374424e-05 1 C(Weight) 16.132616 0.000313940174705 2 C(Duration) 1.009147 0.315107378931 1 C(Weight):C(Duration) 0.216694 0.897315972824 2 Duration 11.187849 0.010752286833 3 Weight 30.263368 4.32586407145e-06 4 ``` statsmodels statsmodels.tsa.statespace.sarimax.SARIMAXResults.loglikelihood_burn statsmodels.tsa.statespace.sarimax.SARIMAXResults.loglikelihood\_burn ===================================================================== `SARIMAXResults.loglikelihood_burn()` (float) The number of observations during which the likelihood is not evaluated. statsmodels statsmodels.regression.quantile_regression.QuantRegResults.summary statsmodels.regression.quantile\_regression.QuantRegResults.summary =================================================================== `QuantRegResults.summary(yname=None, xname=None, title=None, alpha=0.05)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/quantile_regression.html#QuantRegResults.summary) Summarize the Regression Results \| Parameters: \| * yname (string, optional) – Default is `y` * xname (list of strings, optional) – Default is `var_##` for ## in p the number of regressors * title (string, optional) – Title for the top table. If not None, then this replaces the default title * alpha (float) – significance level for the confidence intervals \| \| Returns: \| smry – this holds the summary tables and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary.Summary`](statsmodels.iolib.summary.summary#statsmodels.iolib.summary.Summary "statsmodels.iolib.summary.Summary") class to hold summary results statsmodels statsmodels.stats.inter_rater.cohens_kappa statsmodels.stats.inter\_rater.cohens\_kappa ============================================ `statsmodels.stats.inter_rater.cohens_kappa(table, weights=None, return_results=True, wt=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/inter_rater.html#cohens_kappa) Compute Cohen’s kappa with variance and equal-zero test \| Parameters: \| * table (array\_like, 2-Dim) – square array with results of two raters, one rater in rows, second rater in columns * weights (array\_like) – The interpretation of weights depends on the wt argument. If both are None, then the simple kappa is computed. see wt for the case when wt is not None If weights is two dimensional, then it is directly used as a weight matrix. For computing the variance of kappa, the maximum of the weights is assumed to be smaller or equal to one. TODO: fix conflicting definitions in the 2-Dim case for * wt (None or string) – If wt and weights are None, then the simple kappa is computed. If wt is given, but weights is None, then the weights are set to be [0, 1, 2, …, k]. If weights is a one-dimensional array, then it is used to construct the weight matrix given the following options. `wt in [‘linear’, ‘ca’ or None] : use linear weights, Cicchetti-Allison` actual weights are linear in the score “weights” difference `wt in [‘quadratic’, ‘fc’] : use linear weights, Fleiss-Cohen` actual weights are squared in the score “weights” difference `wt = ‘toeplitz’ : weight matrix is constructed as a toeplitz matrix` from the one dimensional weights. * return\_results (bool) – If True (default), then an instance of KappaResults is returned. If False, then only kappa is computed and returned. \| \| Returns: \| If return\_results is True (default), then a results instance with all statistics is returned If return\_results is False, then only kappa is calculated and returned. \| \| Return type: \| results or kappa \| #### Notes There are two conflicting definitions of the weight matrix, Wikipedia versus SAS manual. However, the computation are invariant to rescaling of the weights matrix, so there is no difference in the results. Weights for ‘linear’ and ‘quadratic’ are interpreted as scores for the categories, the weights in the computation are based on the pairwise difference between the scores. Weights for ‘toeplitz’ are a interpreted as weighted distance. The distance only depends on how many levels apart two entries in the table are but not on the levels themselves. example: weights = ‘0, 1, 2, 3’ and wt is either linear or toeplitz means that the weighting only depends on the simple distance of levels. weights = ‘0, 0, 1, 1’ and wt = ‘linear’ means that the first two levels are zero distance apart and the same for the last two levels. This is the sampe as forming two aggregated levels by merging the first two and the last two levels, respectively. weights = [0, 1, 2, 3] and wt = ‘quadratic’ is the same as squaring these weights and using wt = ‘toeplitz’. #### References Wikipedia SAS Manual	programming_docs
statsmodels statsmodels.sandbox.distributions.extras.SkewNorm_gen.rvs statsmodels.sandbox.distributions.extras.SkewNorm\_gen.rvs ========================================================== `SkewNorm_gen.rvs(args, kwds)` Random variates of given type. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information). * loc (array\_like, optional) – Location parameter (default=0). * scale (array\_like, optional) – Scale parameter (default=1). * size (int or tuple of ints, optional) – Defining number of random variates (default is 1). * random\_state (None or int or `np.random.RandomState` instance, optional) – If int or RandomState, use it for drawing the random variates. If None, rely on `self.random_state`. Default is None. \| \| Returns: \| rvs – Random variates of given `size`. \| \| Return type: \| ndarray or scalar \| statsmodels statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.information statsmodels.discrete.count\_model.ZeroInflatedNegativeBinomialP.information =========================================================================== `ZeroInflatedNegativeBinomialP.information(params)` Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.discrete.discrete_model.LogitResults.aic statsmodels.discrete.discrete\_model.LogitResults.aic ===================================================== `LogitResults.aic()` statsmodels statsmodels.discrete.discrete_model.ProbitResults.tvalues statsmodels.discrete.discrete\_model.ProbitResults.tvalues ========================================================== `ProbitResults.tvalues()` Return the t-statistic for a given parameter estimate. statsmodels statsmodels.stats.weightstats.DescrStatsW.asrepeats statsmodels.stats.weightstats.DescrStatsW.asrepeats =================================================== `DescrStatsW.asrepeats()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/weightstats.html#DescrStatsW.asrepeats) get array that has repeats given by floor(weights) observations with weight=0 are dropped statsmodels statsmodels.regression.linear_model.OLSResults.wresid statsmodels.regression.linear\_model.OLSResults.wresid ====================================================== `OLSResults.wresid()` statsmodels statsmodels.discrete.discrete_model.LogitResults.pvalues statsmodels.discrete.discrete\_model.LogitResults.pvalues ========================================================= `LogitResults.pvalues()` statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.summary statsmodels.tsa.statespace.dynamic\_factor.DynamicFactorResults.summary ======================================================================= `DynamicFactorResults.summary(alpha=0.05, start=None, separate_params=True)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/dynamic_factor.html#DynamicFactorResults.summary) Summarize the Model \| Parameters: \| * alpha (float, optional) – Significance level for the confidence intervals. Default is 0.05. * start (int, optional) – Integer of the start observation. Default is 0. * model\_name (string) – The name of the model used. Default is to use model class name. \| \| Returns: \| summary – This holds the summary table and text, which can be printed or converted to various output formats. \| \| Return type: \| Summary instance \| See also [`statsmodels.iolib.summary.Summary`](statsmodels.iolib.summary.summary#statsmodels.iolib.summary.Summary "statsmodels.iolib.summary.Summary") statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.pvalues_endog_lagged statsmodels.tsa.vector\_ar.var\_model.VARResults.pvalues\_endog\_lagged ======================================================================= `VARResults.pvalues_endog_lagged()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARResults.pvalues_endog_lagged) statsmodels statsmodels.sandbox.distributions.extras.SkewNorm_gen.nnlf statsmodels.sandbox.distributions.extras.SkewNorm\_gen.nnlf =========================================================== `SkewNorm_gen.nnlf(theta, x)` Return negative loglikelihood function. #### Notes This is `-sum(log pdf(x, theta), axis=0)` where `theta` are the parameters (including loc and scale). statsmodels statsmodels.miscmodels.count.PoissonGMLE.initialize statsmodels.miscmodels.count.PoissonGMLE.initialize =================================================== `PoissonGMLE.initialize()` Initialize (possibly re-initialize) a Model instance. For instance, the design matrix of a linear model may change and some things must be recomputed. statsmodels statsmodels.sandbox.tsa.fftarma.ArmaFft.from_coeffs statsmodels.sandbox.tsa.fftarma.ArmaFft.from\_coeffs ==================================================== `classmethod ArmaFft.from_coeffs(arcoefs=None, macoefs=None, nobs=100)` Convenience function to create ArmaProcess from ARMA representation \| Parameters: \| * arcoefs (array-like, optional) – Coefficient for autoregressive lag polynomial, not including zero lag. The sign is inverted to conform to the usual time series representation of an ARMA process in statistics. See the class docstring for more information. * macoefs (array-like, optional) – Coefficient for moving-average lag polynomial, excluding zero lag * nobs (int, optional) – Length of simulated time series. Used, for example, if a sample is generated. \| #### Examples ``` >>> arparams = [.75, -.25] >>> maparams = [.65, .35] >>> arma_process = sm.tsa.ArmaProcess.from_coeffs(ar, ma) >>> arma_process.isstationary True >>> arma_process.isinvertible True ``` statsmodels statsmodels.discrete.discrete_model.DiscreteResults.bic statsmodels.discrete.discrete\_model.DiscreteResults.bic ======================================================== `DiscreteResults.bic()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#DiscreteResults.bic) statsmodels statsmodels.sandbox.stats.multicomp.set_remove_subs statsmodels.sandbox.stats.multicomp.set\_remove\_subs ===================================================== `statsmodels.sandbox.stats.multicomp.set_remove_subs(ssli)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/stats/multicomp.html#set_remove_subs) remove sets that are subsets of another set from a list of tuples \| Parameters: \| ssli (list of tuples) – each tuple is considered as a set \| \| Returns: \| part – new list with subset tuples removed, it is sorted by set-length of tuples. The list contains original tuples, duplicate elements are not removed. \| \| Return type: \| list of tuples \| #### Examples ``` >>> set_remove_subs([(0, 1), (1, 2), (1, 2, 3), (0,)]) [(1, 2, 3), (0, 1)] >>> set_remove_subs([(0, 1), (1, 2), (1,1, 1, 2, 3), (0,)]) [(1, 1, 1, 2, 3), (0, 1)] ``` statsmodels statsmodels.regression.mixed_linear_model.MixedLMResults.bse_re statsmodels.regression.mixed\_linear\_model.MixedLMResults.bse\_re ================================================================== `MixedLMResults.bse_re()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/mixed_linear_model.html#MixedLMResults.bse_re) Returns the standard errors of the variance parameters. The first `k_re x (k_re + 1)` elements of the returned array are the standard errors of the lower triangle of `cov_re`. The remaining elements are the standard errors of the variance components. Note that the sampling distribution of variance parameters is strongly skewed unless the sample size is large, so these standard errors may not give meaningful confidence intervals or p-values if used in the usual way. statsmodels statsmodels.genmod.families.family.Tweedie.resid_dev statsmodels.genmod.families.family.Tweedie.resid\_dev ===================================================== `Tweedie.resid_dev(endog, mu, var_weights=1.0, scale=1.0)` The deviance residuals \| Parameters: \| * endog (array-like) – The endogenous response variable * mu (array-like) – The inverse of the link function at the linear predicted values. * var\_weights (array-like) – 1d array of variance (analytic) weights. The default is 1. * scale (float, optional) – An optional scale argument. The default is 1. \| \| Returns: \| resid\_dev – Deviance residuals as defined below. \| \| Return type: \| float \| #### Notes The deviance residuals are defined by the contribution D\_i of observation i to the deviance as \[resid\\_dev\_i = sign(y\_i-\mu\_i) \sqrt{D\_i}\] D\_i is calculated from the \_resid\_dev method in each family. Distribution-specific documentation of the calculation is available there. statsmodels statsmodels.genmod.cov_struct.Nested.covariance_matrix_solve statsmodels.genmod.cov\_struct.Nested.covariance\_matrix\_solve =============================================================== `Nested.covariance_matrix_solve(expval, index, stdev, rhs)` Solves matrix equations of the form `covmat * soln = rhs` and returns the values of `soln`, where `covmat` is the covariance matrix represented by this class. \| Parameters: \| * expval (array-like) – The expected value of endog for each observed value in the group. * index (integer) – The group index. * stdev (array-like) – The standard deviation of endog for each observation in the group. * rhs (list/tuple of array-like) – A set of right-hand sides; each defines a matrix equation to be solved. \| \| Returns: \| soln – The solutions to the matrix equations. \| \| Return type: \| list/tuple of array-like \| #### Notes Returns None if the solver fails. Some dependence structures do not use `expval` and/or `index` to determine the correlation matrix. Some families (e.g. binomial) do not use the `stdev` parameter when forming the covariance matrix. If the covariance matrix is singular or not SPD, it is projected to the nearest such matrix. These projection events are recorded in the fit\_history member of the GEE model. Systems of linear equations with the covariance matrix as the left hand side (LHS) are solved for different right hand sides (RHS); the LHS is only factorized once to save time. This is a default implementation, it can be reimplemented in subclasses to optimize the linear algebra according to the struture of the covariance matrix. statsmodels statsmodels.tsa.holtwinters.SimpleExpSmoothing statsmodels.tsa.holtwinters.SimpleExpSmoothing ============================================== `class statsmodels.tsa.holtwinters.SimpleExpSmoothing(endog)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/holtwinters.html#SimpleExpSmoothing) Simple Exponential Smoothing wrapper(…) \| Parameters: \| endog (array-like) – Time series \| \| Returns: \| results \| \| Return type: \| SimpleExpSmoothing class \| #### Notes This is a full implementation of the simple exponential smoothing as per [1]. See also `Exponential`, [`Holt`](statsmodels.tsa.holtwinters.holt#statsmodels.tsa.holtwinters.Holt "statsmodels.tsa.holtwinters.Holt") #### References [1] Hyndman, Rob J., and George Athanasopoulos. Forecasting: principles and practice. OTexts, 2014. #### Methods \| \| \| \| --- \| --- \| \| [`fit`](statsmodels.tsa.holtwinters.simpleexpsmoothing.fit#statsmodels.tsa.holtwinters.SimpleExpSmoothing.fit "statsmodels.tsa.holtwinters.SimpleExpSmoothing.fit")([smoothing\_level, optimized]) \| fit Simple Exponential Smoothing wrapper(…) \| \| [`from_formula`](statsmodels.tsa.holtwinters.simpleexpsmoothing.from_formula#statsmodels.tsa.holtwinters.SimpleExpSmoothing.from_formula "statsmodels.tsa.holtwinters.SimpleExpSmoothing.from_formula")(formula, data[, subset, drop\_cols]) \| Create a Model from a formula and dataframe. \| \| [`hessian`](statsmodels.tsa.holtwinters.simpleexpsmoothing.hessian#statsmodels.tsa.holtwinters.SimpleExpSmoothing.hessian "statsmodels.tsa.holtwinters.SimpleExpSmoothing.hessian")(params) \| The Hessian matrix of the model \| \| [`information`](statsmodels.tsa.holtwinters.simpleexpsmoothing.information#statsmodels.tsa.holtwinters.SimpleExpSmoothing.information "statsmodels.tsa.holtwinters.SimpleExpSmoothing.information")(params) \| Fisher information matrix of model \| \| [`initialize`](statsmodels.tsa.holtwinters.simpleexpsmoothing.initialize#statsmodels.tsa.holtwinters.SimpleExpSmoothing.initialize "statsmodels.tsa.holtwinters.SimpleExpSmoothing.initialize")() \| Initialize (possibly re-initialize) a Model instance. \| \| [`loglike`](statsmodels.tsa.holtwinters.simpleexpsmoothing.loglike#statsmodels.tsa.holtwinters.SimpleExpSmoothing.loglike "statsmodels.tsa.holtwinters.SimpleExpSmoothing.loglike")(params) \| Log-likelihood of model. \| \| [`predict`](statsmodels.tsa.holtwinters.simpleexpsmoothing.predict#statsmodels.tsa.holtwinters.SimpleExpSmoothing.predict "statsmodels.tsa.holtwinters.SimpleExpSmoothing.predict")(params[, start, end]) \| Returns in-sample and out-of-sample prediction. \| \| [`score`](statsmodels.tsa.holtwinters.simpleexpsmoothing.score#statsmodels.tsa.holtwinters.SimpleExpSmoothing.score "statsmodels.tsa.holtwinters.SimpleExpSmoothing.score")(params) \| Score vector of model. \| #### Attributes \| \| \| \| --- \| --- \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| \| statsmodels statsmodels.tsa.statespace.mlemodel.MLEResults.pvalues statsmodels.tsa.statespace.mlemodel.MLEResults.pvalues ====================================================== `MLEResults.pvalues()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/mlemodel.html#MLEResults.pvalues) (array) The p-values associated with the z-statistics of the coefficients. Note that the coefficients are assumed to have a Normal distribution. statsmodels statsmodels.sandbox.stats.multicomp.GroupsStats.groupvarwithin statsmodels.sandbox.stats.multicomp.GroupsStats.groupvarwithin ============================================================== `GroupsStats.groupvarwithin()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/stats/multicomp.html#GroupsStats.groupvarwithin) statsmodels statsmodels.tsa.holtwinters.ExponentialSmoothing statsmodels.tsa.holtwinters.ExponentialSmoothing ================================================ `class statsmodels.tsa.holtwinters.ExponentialSmoothing(endog, trend=None, damped=False, seasonal=None, seasonal_periods=None, dates=None, freq=None, missing='none')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/holtwinters.html#ExponentialSmoothing) Holt Winter’s Exponential Smoothing \| Parameters: \| * endog (array-like) – Time series * trend ({"add", "mul", "additive", "multiplicative", None}, optional) – Type of trend component. * damped (bool, optional) – Should the trend component be damped. * seasonal ({"add", "mul", "additive", "multiplicative", None}, optional) – Type of seasonal component. * seasonal\_periods (int, optional) – The number of seasons to consider for the holt winters. \| \| Returns: \| results \| \| Return type: \| ExponentialSmoothing class \| #### Notes This is a full implementation of the holt winters exponential smoothing as per [1]. This includes all the unstable methods as well as the stable methods. The implementation of the library covers the functionality of the R library as much as possible whilst still being pythonic. #### References [1] Hyndman, Rob J., and George Athanasopoulos. Forecasting: principles and practice. OTexts, 2014. #### Methods \| \| \| \| --- \| --- \| \| [`fit`](statsmodels.tsa.holtwinters.exponentialsmoothing.fit#statsmodels.tsa.holtwinters.ExponentialSmoothing.fit "statsmodels.tsa.holtwinters.ExponentialSmoothing.fit")([smoothing\_level, smoothing\_slope, …]) \| fit Holt Winter’s Exponential Smoothing \| \| [`from_formula`](statsmodels.tsa.holtwinters.exponentialsmoothing.from_formula#statsmodels.tsa.holtwinters.ExponentialSmoothing.from_formula "statsmodels.tsa.holtwinters.ExponentialSmoothing.from_formula")(formula, data[, subset, drop\_cols]) \| Create a Model from a formula and dataframe. \| \| [`hessian`](statsmodels.tsa.holtwinters.exponentialsmoothing.hessian#statsmodels.tsa.holtwinters.ExponentialSmoothing.hessian "statsmodels.tsa.holtwinters.ExponentialSmoothing.hessian")(params) \| The Hessian matrix of the model \| \| [`information`](statsmodels.tsa.holtwinters.exponentialsmoothing.information#statsmodels.tsa.holtwinters.ExponentialSmoothing.information "statsmodels.tsa.holtwinters.ExponentialSmoothing.information")(params) \| Fisher information matrix of model \| \| [`initialize`](statsmodels.tsa.holtwinters.exponentialsmoothing.initialize#statsmodels.tsa.holtwinters.ExponentialSmoothing.initialize "statsmodels.tsa.holtwinters.ExponentialSmoothing.initialize")() \| Initialize (possibly re-initialize) a Model instance. \| \| [`loglike`](statsmodels.tsa.holtwinters.exponentialsmoothing.loglike#statsmodels.tsa.holtwinters.ExponentialSmoothing.loglike "statsmodels.tsa.holtwinters.ExponentialSmoothing.loglike")(params) \| Log-likelihood of model. \| \| [`predict`](statsmodels.tsa.holtwinters.exponentialsmoothing.predict#statsmodels.tsa.holtwinters.ExponentialSmoothing.predict "statsmodels.tsa.holtwinters.ExponentialSmoothing.predict")(params[, start, end]) \| Returns in-sample and out-of-sample prediction. \| \| [`score`](statsmodels.tsa.holtwinters.exponentialsmoothing.score#statsmodels.tsa.holtwinters.ExponentialSmoothing.score "statsmodels.tsa.holtwinters.ExponentialSmoothing.score")(params) \| Score vector of model. \| #### Attributes \| \| \| \| --- \| --- \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| \| statsmodels statsmodels.regression.linear_model.WLS.score statsmodels.regression.linear\_model.WLS.score ============================================== `WLS.score(params)` Score vector of model. The gradient of logL with respect to each parameter. statsmodels statsmodels.discrete.discrete_model.LogitResults statsmodels.discrete.discrete\_model.LogitResults ================================================= `class statsmodels.discrete.discrete_model.LogitResults(model, mlefit, cov_type='nonrobust', cov_kwds=None, use_t=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#LogitResults) A results class for Logit Model \| Parameters: \| * model (A DiscreteModel instance) – * params (array-like) – The parameters of a fitted model. * hessian (array-like) – The hessian of the fitted model. * scale (float) – A scale parameter for the covariance matrix. \| \| Returns: \| * \Attributes\** * aic (float) – Akaike information criterion. `-2(llf - p)` where `p` is the number of regressors including the intercept. bic (float) – Bayesian information criterion. `-2llf + ln(nobs)p` where `p` is the number of regressors including the intercept. * bse (array) – The standard errors of the coefficients. * df\_resid (float) – See model definition. * df\_model (float) – See model definition. * fitted\_values (array) – Linear predictor XB. * llf (float) – Value of the loglikelihood * llnull (float) – Value of the constant-only loglikelihood * llr (float) – Likelihood ratio chi-squared statistic; `-2(llnull - llf)` llr\_pvalue (float) – The chi-squared probability of getting a log-likelihood ratio statistic greater than llr. llr has a chi-squared distribution with degrees of freedom `df_model`. * prsquared (float) – McFadden’s pseudo-R-squared. `1 - (llf / llnull)` \| #### Methods \| \| \| \| --- \| --- \| \| [`aic`](statsmodels.discrete.discrete_model.logitresults.aic#statsmodels.discrete.discrete_model.LogitResults.aic "statsmodels.discrete.discrete_model.LogitResults.aic")() \| \| \| [`bic`](statsmodels.discrete.discrete_model.logitresults.bic#statsmodels.discrete.discrete_model.LogitResults.bic "statsmodels.discrete.discrete_model.LogitResults.bic")() \| \| \| [`bse`](statsmodels.discrete.discrete_model.logitresults.bse#statsmodels.discrete.discrete_model.LogitResults.bse "statsmodels.discrete.discrete_model.LogitResults.bse")() \| \| \| [`conf_int`](statsmodels.discrete.discrete_model.logitresults.conf_int#statsmodels.discrete.discrete_model.LogitResults.conf_int "statsmodels.discrete.discrete_model.LogitResults.conf_int")([alpha, cols, method]) \| Returns the confidence interval of the fitted parameters. \| \| [`cov_params`](statsmodels.discrete.discrete_model.logitresults.cov_params#statsmodels.discrete.discrete_model.LogitResults.cov_params "statsmodels.discrete.discrete_model.LogitResults.cov_params")([r\_matrix, column, scale, cov\_p, …]) \| Returns the variance/covariance matrix. \| \| [`f_test`](statsmodels.discrete.discrete_model.logitresults.f_test#statsmodels.discrete.discrete_model.LogitResults.f_test "statsmodels.discrete.discrete_model.LogitResults.f_test")(r\_matrix[, cov\_p, scale, invcov]) \| Compute the F-test for a joint linear hypothesis. \| \| [`fittedvalues`](statsmodels.discrete.discrete_model.logitresults.fittedvalues#statsmodels.discrete.discrete_model.LogitResults.fittedvalues "statsmodels.discrete.discrete_model.LogitResults.fittedvalues")() \| \| \| [`get_margeff`](statsmodels.discrete.discrete_model.logitresults.get_margeff#statsmodels.discrete.discrete_model.LogitResults.get_margeff "statsmodels.discrete.discrete_model.LogitResults.get_margeff")([at, method, atexog, dummy, count]) \| Get marginal effects of the fitted model. \| \| [`initialize`](statsmodels.discrete.discrete_model.logitresults.initialize#statsmodels.discrete.discrete_model.LogitResults.initialize "statsmodels.discrete.discrete_model.LogitResults.initialize")(model, params, \\kwd) \| \| \| [`llf`](statsmodels.discrete.discrete_model.logitresults.llf#statsmodels.discrete.discrete_model.LogitResults.llf "statsmodels.discrete.discrete_model.LogitResults.llf")() \| \| \| [`llnull`](statsmodels.discrete.discrete_model.logitresults.llnull#statsmodels.discrete.discrete_model.LogitResults.llnull "statsmodels.discrete.discrete_model.LogitResults.llnull")() \| \| \| [`llr`](statsmodels.discrete.discrete_model.logitresults.llr#statsmodels.discrete.discrete_model.LogitResults.llr "statsmodels.discrete.discrete_model.LogitResults.llr")() \| \| \| [`llr_pvalue`](statsmodels.discrete.discrete_model.logitresults.llr_pvalue#statsmodels.discrete.discrete_model.LogitResults.llr_pvalue "statsmodels.discrete.discrete_model.LogitResults.llr_pvalue")() \| \| \| [`load`](statsmodels.discrete.discrete_model.logitresults.load#statsmodels.discrete.discrete_model.LogitResults.load "statsmodels.discrete.discrete_model.LogitResults.load")(fname) \| load a pickle, (class method) \| \| [`normalized_cov_params`](statsmodels.discrete.discrete_model.logitresults.normalized_cov_params#statsmodels.discrete.discrete_model.LogitResults.normalized_cov_params "statsmodels.discrete.discrete_model.LogitResults.normalized_cov_params")() \| \| \| [`pred_table`](statsmodels.discrete.discrete_model.logitresults.pred_table#statsmodels.discrete.discrete_model.LogitResults.pred_table "statsmodels.discrete.discrete_model.LogitResults.pred_table")([threshold]) \| Prediction table \| \| [`predict`](statsmodels.discrete.discrete_model.logitresults.predict#statsmodels.discrete.discrete_model.LogitResults.predict "statsmodels.discrete.discrete_model.LogitResults.predict")([exog, transform]) \| Call self.model.predict with self.params as the first argument. \| \| [`prsquared`](statsmodels.discrete.discrete_model.logitresults.prsquared#statsmodels.discrete.discrete_model.LogitResults.prsquared "statsmodels.discrete.discrete_model.LogitResults.prsquared")() \| \| \| [`pvalues`](statsmodels.discrete.discrete_model.logitresults.pvalues#statsmodels.discrete.discrete_model.LogitResults.pvalues "statsmodels.discrete.discrete_model.LogitResults.pvalues")() \| \| \| [`remove_data`](statsmodels.discrete.discrete_model.logitresults.remove_data#statsmodels.discrete.discrete_model.LogitResults.remove_data "statsmodels.discrete.discrete_model.LogitResults.remove_data")() \| remove data arrays, all nobs arrays from result and model \| \| [`resid_dev`](statsmodels.discrete.discrete_model.logitresults.resid_dev#statsmodels.discrete.discrete_model.LogitResults.resid_dev "statsmodels.discrete.discrete_model.LogitResults.resid_dev")() \| Deviance residuals \| \| [`resid_generalized`](statsmodels.discrete.discrete_model.logitresults.resid_generalized#statsmodels.discrete.discrete_model.LogitResults.resid_generalized "statsmodels.discrete.discrete_model.LogitResults.resid_generalized")() \| Generalized residuals \| \| [`resid_pearson`](statsmodels.discrete.discrete_model.logitresults.resid_pearson#statsmodels.discrete.discrete_model.LogitResults.resid_pearson "statsmodels.discrete.discrete_model.LogitResults.resid_pearson")() \| Pearson residuals \| \| [`resid_response`](statsmodels.discrete.discrete_model.logitresults.resid_response#statsmodels.discrete.discrete_model.LogitResults.resid_response "statsmodels.discrete.discrete_model.LogitResults.resid_response")() \| The response residuals \| \| [`save`](statsmodels.discrete.discrete_model.logitresults.save#statsmodels.discrete.discrete_model.LogitResults.save "statsmodels.discrete.discrete_model.LogitResults.save")(fname[, remove\_data]) \| save a pickle of this instance \| \| [`set_null_options`](statsmodels.discrete.discrete_model.logitresults.set_null_options#statsmodels.discrete.discrete_model.LogitResults.set_null_options "statsmodels.discrete.discrete_model.LogitResults.set_null_options")([llnull, attach\_results]) \| set fit options for Null (constant-only) model \| \| [`summary`](statsmodels.discrete.discrete_model.logitresults.summary#statsmodels.discrete.discrete_model.LogitResults.summary "statsmodels.discrete.discrete_model.LogitResults.summary")([yname, xname, title, alpha, yname\_list]) \| Summarize the Regression Results \| \| [`summary2`](statsmodels.discrete.discrete_model.logitresults.summary2#statsmodels.discrete.discrete_model.LogitResults.summary2 "statsmodels.discrete.discrete_model.LogitResults.summary2")([yname, xname, title, alpha, …]) \| Experimental function to summarize regression results \| \| [`t_test`](statsmodels.discrete.discrete_model.logitresults.t_test#statsmodels.discrete.discrete_model.LogitResults.t_test "statsmodels.discrete.discrete_model.LogitResults.t_test")(r\_matrix[, cov\_p, scale, use\_t]) \| Compute a t-test for a each linear hypothesis of the form Rb = q \| \| [`t_test_pairwise`](statsmodels.discrete.discrete_model.logitresults.t_test_pairwise#statsmodels.discrete.discrete_model.LogitResults.t_test_pairwise "statsmodels.discrete.discrete_model.LogitResults.t_test_pairwise")(term\_name[, method, alpha, …]) \| perform pairwise t\_test with multiple testing corrected p-values \| \| [`tvalues`](statsmodels.discrete.discrete_model.logitresults.tvalues#statsmodels.discrete.discrete_model.LogitResults.tvalues "statsmodels.discrete.discrete_model.LogitResults.tvalues")() \| Return the t-statistic for a given parameter estimate. \| \| [`wald_test`](statsmodels.discrete.discrete_model.logitresults.wald_test#statsmodels.discrete.discrete_model.LogitResults.wald_test "statsmodels.discrete.discrete_model.LogitResults.wald_test")(r\_matrix[, cov\_p, scale, invcov, …]) \| Compute a Wald-test for a joint linear hypothesis. \| \| [`wald_test_terms`](statsmodels.discrete.discrete_model.logitresults.wald_test_terms#statsmodels.discrete.discrete_model.LogitResults.wald_test_terms "statsmodels.discrete.discrete_model.LogitResults.wald_test_terms")([skip\_single, …]) \| Compute a sequence of Wald tests for terms over multiple columns \| #### Attributes \| \| \| \| --- \| --- \| \| `use_t` \| \|	programming_docs
statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.plot_recursive_coefficient statsmodels.regression.recursive\_ls.RecursiveLSResults.plot\_recursive\_coefficient ==================================================================================== `RecursiveLSResults.plot_recursive_coefficient(variables=0, alpha=0.05, legend_loc='upper left', fig=None, figsize=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/recursive_ls.html#RecursiveLSResults.plot_recursive_coefficient) Plot the recursively estimated coefficients on a given variable \| Parameters: \| * variables (int or str or iterable of int or string, optional) – Integer index or string name of the variable whose coefficient will be plotted. Can also be an iterable of integers or strings. Default is the first variable. * alpha (float, optional) – The confidence intervals for the coefficient are (1 - alpha) % * legend\_loc (string, optional) – The location of the legend in the plot. Default is upper left. * fig (Matplotlib Figure instance, optional) – If given, subplots are created in this figure instead of in a new figure. Note that the grid will be created in the provided figure using `fig.add_subplot()`. * figsize (tuple, optional) – If a figure is created, this argument allows specifying a size. The tuple is (width, height). \| #### Notes All plots contain (1 - `alpha`) % confidence intervals. statsmodels statsmodels.tsa.statespace.varmax.VARMAX.simulate statsmodels.tsa.statespace.varmax.VARMAX.simulate ================================================= `VARMAX.simulate(params, nsimulations, measurement_shocks=None, state_shocks=None, initial_state=None)` Simulate a new time series following the state space model \| Parameters: \| * params (array\_like) – Array of model parameters. * nsimulations (int) – The number of observations to simulate. If the model is time-invariant this can be any number. If the model is time-varying, then this number must be less than or equal to the number * measurement\_shocks (array\_like, optional) – If specified, these are the shocks to the measurement equation, $\varepsilon\_t$. If unspecified, these are automatically generated using a pseudo-random number generator. If specified, must be shaped `nsimulations` x `k_endog`, where `k_endog` is the same as in the state space model. * state\_shocks (array\_like, optional) – If specified, these are the shocks to the state equation, $\eta\_t$. If unspecified, these are automatically generated using a pseudo-random number generator. If specified, must be shaped `nsimulations` x `k_posdef` where `k_posdef` is the same as in the state space model. * initial\_state (array\_like, optional) – If specified, this is the state vector at time zero, which should be shaped (`k_states` x 1), where `k_states` is the same as in the state space model. If unspecified, but the model has been initialized, then that initialization is used. If unspecified and the model has not been initialized, then a vector of zeros is used. Note that this is not included in the returned `simulated_states` array. \| \| Returns: \| simulated\_obs – An (nsimulations x k\_endog) array of simulated observations. \| \| Return type: \| array \| statsmodels statsmodels.discrete.discrete_model.NegativeBinomialResults.initialize statsmodels.discrete.discrete\_model.NegativeBinomialResults.initialize ======================================================================= `NegativeBinomialResults.initialize(model, params, *kwd)` statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.stderr statsmodels.tsa.vector\_ar.var\_model.VARResults.stderr ======================================================= `VARResults.stderr()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARResults.stderr) Standard errors of coefficients, reshaped to match in size statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.test_heteroskedasticity statsmodels.regression.recursive\_ls.RecursiveLSResults.test\_heteroskedasticity ================================================================================ `RecursiveLSResults.test_heteroskedasticity(method, alternative='two-sided', use_f=True)` Test for heteroskedasticity of standardized residuals Tests whether the sum-of-squares in the first third of the sample is significantly different than the sum-of-squares in the last third of the sample. Analogous to a Goldfeld-Quandt test. The null hypothesis is of no heteroskedasticity. \| Parameters: \| method (string {'breakvar'} or None) – The statistical test for heteroskedasticity. Must be ‘breakvar’ for test of a break in the variance. If None, an attempt is made to select an appropriate test. * alternative (string, 'increasing', 'decreasing' or 'two-sided') – This specifies the alternative for the p-value calculation. Default is two-sided. * use\_f (boolean, optional) – Whether or not to compare against the asymptotic distribution (chi-squared) or the approximate small-sample distribution (F). Default is True (i.e. default is to compare against an F distribution). \| \| Returns: \| output – An array with `(test_statistic, pvalue)` for each endogenous variable. The array is then sized `(k_endog, 2)`. If the method is called as `het = res.test_heteroskedasticity()`, then `het[0]` is an array of size 2 corresponding to the first endogenous variable, where `het[0][0]` is the test statistic, and `het[0][1]` is the p-value. \| \| Return type: \| array \| #### Notes The null hypothesis is of no heteroskedasticity. That means different things depending on which alternative is selected: * Increasing: Null hypothesis is that the variance is not increasing throughout the sample; that the sum-of-squares in the later subsample is not greater than the sum-of-squares in the earlier subsample. * Decreasing: Null hypothesis is that the variance is not decreasing throughout the sample; that the sum-of-squares in the earlier subsample is not greater than the sum-of-squares in the later subsample. * Two-sided: Null hypothesis is that the variance is not changing throughout the sample. Both that the sum-of-squares in the earlier subsample is not greater than the sum-of-squares in the later subsample and that the sum-of-squares in the later subsample is not greater than the sum-of-squares in the earlier subsample. For $h = [T/3]$, the test statistic is: \[H(h) = \sum\_{t=T-h+1}^T \tilde v\_t^2 \Bigg / \sum\_{t=d+1}^{d+1+h} \tilde v\_t^2\] where $d$ is the number of periods in which the loglikelihood was burned in the parent model (usually corresponding to diffuse initialization). This statistic can be tested against an $F(h,h)$ distribution. Alternatively, $h H(h)$ is asymptotically distributed according to $\chi\_h^2$; this second test can be applied by passing `asymptotic=True` as an argument. See section 5.4 of [[1]](#id2) for the above formula and discussion, as well as additional details. TODO * Allow specification of $h$ #### References \| \| \| \| --- \| --- \| \| [[1]](#id1) \| Harvey, Andrew C. 1990. Forecasting, Structural Time Series Models and the Kalman Filter. Cambridge University Press. \| statsmodels statsmodels.discrete.discrete_model.MultinomialModel.cov_params_func_l1 statsmodels.discrete.discrete\_model.MultinomialModel.cov\_params\_func\_l1 =========================================================================== `MultinomialModel.cov_params_func_l1(likelihood_model, xopt, retvals)` Computes cov\_params on a reduced parameter space corresponding to the nonzero parameters resulting from the l1 regularized fit. Returns a full cov\_params matrix, with entries corresponding to zero’d values set to np.nan. statsmodels statsmodels.genmod.generalized_linear_model.GLMResults.f_test statsmodels.genmod.generalized\_linear\_model.GLMResults.f\_test ================================================================ `GLMResults.f_test(r_matrix, cov_p=None, scale=1.0, invcov=None)` Compute the F-test for a joint linear hypothesis. This is a special case of `wald_test` that always uses the F distribution. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length k row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> A = np.identity(len(results.params)) >>> A = A[1:,:] ``` This tests that each coefficient is jointly statistically significantly different from zero. ``` >>> print(results.f_test(A)) <F test: F=array([[ 330.28533923]]), p=4.984030528700946e-10, df_denom=9, df_num=6> ``` Compare this to ``` >>> results.fvalue 330.2853392346658 >>> results.f_pvalue 4.98403096572e-10 ``` ``` >>> B = np.array(([0,0,1,-1,0,0,0],[0,0,0,0,0,1,-1])) ``` This tests that the coefficient on the 2nd and 3rd regressors are equal and jointly that the coefficient on the 5th and 6th regressors are equal. ``` >>> print(results.f_test(B)) <F test: F=array([[ 9.74046187]]), p=0.005605288531708235, df_denom=9, df_num=2> ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.datasets import longley >>> from statsmodels.formula.api import ols >>> dta = longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = '(GNPDEFL = GNP), (UNEMP = 2), (YEAR/1829 = 1)' >>> f_test = results.f_test(hypotheses) >>> print(f_test) <F test: F=array([[ 144.17976065]]), p=6.322026217355609e-08, df_denom=9, df_num=3> ``` See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`wald_test`](statsmodels.genmod.generalized_linear_model.glmresults.wald_test#statsmodels.genmod.generalized_linear_model.GLMResults.wald_test "statsmodels.genmod.generalized_linear_model.GLMResults.wald_test"), [`t_test`](statsmodels.genmod.generalized_linear_model.glmresults.t_test#statsmodels.genmod.generalized_linear_model.GLMResults.t_test "statsmodels.genmod.generalized_linear_model.GLMResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.tsa.arima_model.ARIMAResults.remove_data statsmodels.tsa.arima\_model.ARIMAResults.remove\_data ====================================================== `ARIMAResults.remove_data()` remove data arrays, all nobs arrays from result and model This reduces the size of the instance, so it can be pickled with less memory. Currently tested for use with predict from an unpickled results and model instance. Warning Since data and some intermediate results have been removed calculating new statistics that require them will raise exceptions. The exception will occur the first time an attribute is accessed that has been set to None. Not fully tested for time series models, tsa, and might delete too much for prediction or not all that would be possible. The lists of arrays to delete are maintained as attributes of the result and model instance, except for cached values. These lists could be changed before calling remove\_data. The attributes to remove are named in: `model._data_attr : arrays attached to both the model instance` and the results instance with the same attribute name. `result.data_in_cache : arrays that may exist as values in` result.\_cache (TODO : should privatize name) `result._data_attr_model : arrays attached to the model` instance but not to the results instance statsmodels statsmodels.stats.weightstats.DescrStatsW.mean statsmodels.stats.weightstats.DescrStatsW.mean ============================================== `DescrStatsW.mean()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/weightstats.html#DescrStatsW.mean) weighted mean of data statsmodels statsmodels.discrete.discrete_model.NegativeBinomialP.score statsmodels.discrete.discrete\_model.NegativeBinomialP.score ============================================================ `NegativeBinomialP.score(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#NegativeBinomialP.score) Generalized Negative Binomial (NB-P) model score (gradient) vector of the log-likelihood \| Parameters: \| params (array-like) – The parameters of the model \| \| Returns: \| score – The score vector of the model, i.e. the first derivative of the loglikelihood function, evaluated at `params` \| \| Return type: \| ndarray, 1-D \| statsmodels statsmodels.sandbox.distributions.transformed.LogTransf_gen statsmodels.sandbox.distributions.transformed.LogTransf\_gen ============================================================ `class statsmodels.sandbox.distributions.transformed.LogTransf_gen(kls, args, kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/distributions/transformed.html#LogTransf_gen) Distribution based on log/exp transformation the constructor can be called with a distribution class and generates the distribution of the transformed random variable #### Methods \| \| \| \| --- \| --- \| \| [`cdf`](statsmodels.sandbox.distributions.transformed.logtransf_gen.cdf#statsmodels.sandbox.distributions.transformed.LogTransf_gen.cdf "statsmodels.sandbox.distributions.transformed.LogTransf_gen.cdf")(x, \args, \\kwds) \| Cumulative distribution function of the given RV. \| \| [`entropy`](statsmodels.sandbox.distributions.transformed.logtransf_gen.entropy#statsmodels.sandbox.distributions.transformed.LogTransf_gen.entropy "statsmodels.sandbox.distributions.transformed.LogTransf_gen.entropy")(\args, \\kwds) \| Differential entropy of the RV. \| \| [`expect`](statsmodels.sandbox.distributions.transformed.logtransf_gen.expect#statsmodels.sandbox.distributions.transformed.LogTransf_gen.expect "statsmodels.sandbox.distributions.transformed.LogTransf_gen.expect")([func, args, loc, scale, lb, ub, …]) \| Calculate expected value of a function with respect to the distribution. \| \| [`fit`](statsmodels.sandbox.distributions.transformed.logtransf_gen.fit#statsmodels.sandbox.distributions.transformed.LogTransf_gen.fit "statsmodels.sandbox.distributions.transformed.LogTransf_gen.fit")(data, \args, \\kwds) \| Return MLEs for shape (if applicable), location, and scale parameters from data. \| \| [`fit_loc_scale`](statsmodels.sandbox.distributions.transformed.logtransf_gen.fit_loc_scale#statsmodels.sandbox.distributions.transformed.LogTransf_gen.fit_loc_scale "statsmodels.sandbox.distributions.transformed.LogTransf_gen.fit_loc_scale")(data, \args) \| Estimate loc and scale parameters from data using 1st and 2nd moments. \| \| [`freeze`](statsmodels.sandbox.distributions.transformed.logtransf_gen.freeze#statsmodels.sandbox.distributions.transformed.LogTransf_gen.freeze "statsmodels.sandbox.distributions.transformed.LogTransf_gen.freeze")(\args, \\kwds) \| Freeze the distribution for the given arguments. \| \| [`interval`](statsmodels.sandbox.distributions.transformed.logtransf_gen.interval#statsmodels.sandbox.distributions.transformed.LogTransf_gen.interval "statsmodels.sandbox.distributions.transformed.LogTransf_gen.interval")(alpha, \args, \\kwds) \| Confidence interval with equal areas around the median. \| \| [`isf`](statsmodels.sandbox.distributions.transformed.logtransf_gen.isf#statsmodels.sandbox.distributions.transformed.LogTransf_gen.isf "statsmodels.sandbox.distributions.transformed.LogTransf_gen.isf")(q, \args, \\kwds) \| Inverse survival function (inverse of `sf`) at q of the given RV. \| \| [`logcdf`](statsmodels.sandbox.distributions.transformed.logtransf_gen.logcdf#statsmodels.sandbox.distributions.transformed.LogTransf_gen.logcdf "statsmodels.sandbox.distributions.transformed.LogTransf_gen.logcdf")(x, \args, \\kwds) \| Log of the cumulative distribution function at x of the given RV. \| \| [`logpdf`](statsmodels.sandbox.distributions.transformed.logtransf_gen.logpdf#statsmodels.sandbox.distributions.transformed.LogTransf_gen.logpdf "statsmodels.sandbox.distributions.transformed.LogTransf_gen.logpdf")(x, \args, \\kwds) \| Log of the probability density function at x of the given RV. \| \| [`logsf`](statsmodels.sandbox.distributions.transformed.logtransf_gen.logsf#statsmodels.sandbox.distributions.transformed.LogTransf_gen.logsf "statsmodels.sandbox.distributions.transformed.LogTransf_gen.logsf")(x, \args, \\kwds) \| Log of the survival function of the given RV. \| \| [`mean`](statsmodels.sandbox.distributions.transformed.logtransf_gen.mean#statsmodels.sandbox.distributions.transformed.LogTransf_gen.mean "statsmodels.sandbox.distributions.transformed.LogTransf_gen.mean")(\args, \\kwds) \| Mean of the distribution. \| \| [`median`](statsmodels.sandbox.distributions.transformed.logtransf_gen.median#statsmodels.sandbox.distributions.transformed.LogTransf_gen.median "statsmodels.sandbox.distributions.transformed.LogTransf_gen.median")(\args, \\kwds) \| Median of the distribution. \| \| [`moment`](statsmodels.sandbox.distributions.transformed.logtransf_gen.moment#statsmodels.sandbox.distributions.transformed.LogTransf_gen.moment "statsmodels.sandbox.distributions.transformed.LogTransf_gen.moment")(n, \args, \\kwds) \| n-th order non-central moment of distribution. \| \| [`nnlf`](statsmodels.sandbox.distributions.transformed.logtransf_gen.nnlf#statsmodels.sandbox.distributions.transformed.LogTransf_gen.nnlf "statsmodels.sandbox.distributions.transformed.LogTransf_gen.nnlf")(theta, x) \| Return negative loglikelihood function. \| \| [`pdf`](statsmodels.sandbox.distributions.transformed.logtransf_gen.pdf#statsmodels.sandbox.distributions.transformed.LogTransf_gen.pdf "statsmodels.sandbox.distributions.transformed.LogTransf_gen.pdf")(x, \args, \\kwds) \| Probability density function at x of the given RV. \| \| [`ppf`](statsmodels.sandbox.distributions.transformed.logtransf_gen.ppf#statsmodels.sandbox.distributions.transformed.LogTransf_gen.ppf "statsmodels.sandbox.distributions.transformed.LogTransf_gen.ppf")(q, \args, \\kwds) \| Percent point function (inverse of `cdf`) at q of the given RV. \| \| [`rvs`](statsmodels.sandbox.distributions.transformed.logtransf_gen.rvs#statsmodels.sandbox.distributions.transformed.LogTransf_gen.rvs "statsmodels.sandbox.distributions.transformed.LogTransf_gen.rvs")(\args, \\kwds) \| Random variates of given type. \| \| [`sf`](statsmodels.sandbox.distributions.transformed.logtransf_gen.sf#statsmodels.sandbox.distributions.transformed.LogTransf_gen.sf "statsmodels.sandbox.distributions.transformed.LogTransf_gen.sf")(x, \args, \\kwds) \| Survival function (1 - `cdf`) at x of the given RV. \| \| [`stats`](statsmodels.sandbox.distributions.transformed.logtransf_gen.stats#statsmodels.sandbox.distributions.transformed.LogTransf_gen.stats "statsmodels.sandbox.distributions.transformed.LogTransf_gen.stats")(\args, \\kwds) \| Some statistics of the given RV. \| \| [`std`](statsmodels.sandbox.distributions.transformed.logtransf_gen.std#statsmodels.sandbox.distributions.transformed.LogTransf_gen.std "statsmodels.sandbox.distributions.transformed.LogTransf_gen.std")(\args, \\kwds) \| Standard deviation of the distribution. \| \| [`var`](statsmodels.sandbox.distributions.transformed.logtransf_gen.var#statsmodels.sandbox.distributions.transformed.LogTransf_gen.var "statsmodels.sandbox.distributions.transformed.LogTransf_gen.var")(\args, \\*kwds) \| Variance of the distribution. \| #### Attributes \| \| \| \| --- \| --- \| \| `random_state` \| Get or set the RandomState object for generating random variates. \|	programming_docs
statsmodels statsmodels.tsa.statespace.sarimax.SARIMAX.prepare_data statsmodels.tsa.statespace.sarimax.SARIMAX.prepare\_data ======================================================== `SARIMAX.prepare_data()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/sarimax.html#SARIMAX.prepare_data) Prepare data for use in the state space representation statsmodels statsmodels.sandbox.distributions.transformed.ExpTransf_gen.logcdf statsmodels.sandbox.distributions.transformed.ExpTransf\_gen.logcdf =================================================================== `ExpTransf_gen.logcdf(x, args, kwds)` Log of the cumulative distribution function at x of the given RV. \| Parameters: \| x (array\_like) – quantiles * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| logcdf – Log of the cumulative distribution function evaluated at x \| \| Return type: \| array\_like \| statsmodels statsmodels.stats.weightstats.DescrStatsW.demeaned statsmodels.stats.weightstats.DescrStatsW.demeaned ================================================== `DescrStatsW.demeaned()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/weightstats.html#DescrStatsW.demeaned) data with weighted mean subtracted statsmodels statsmodels.tsa.holtwinters.HoltWintersResults.forecast statsmodels.tsa.holtwinters.HoltWintersResults.forecast ======================================================= `HoltWintersResults.forecast(steps=1)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/holtwinters.html#HoltWintersResults.forecast) Out-of-sample forecasts \| Parameters: \| steps (int) – The number of out of sample forecasts from the end of the sample. \| \| Returns: \| forecast – Array of out of sample forecasts \| \| Return type: \| array \| statsmodels statsmodels.graphics.boxplots.violinplot statsmodels.graphics.boxplots.violinplot ======================================== `statsmodels.graphics.boxplots.violinplot(data, ax=None, labels=None, positions=None, side='both', show_boxplot=True, plot_opts={})` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/graphics/boxplots.html#violinplot) Make a violin plot of each dataset in the `data` sequence. A violin plot is a boxplot combined with a kernel density estimate of the probability density function per point. \| Parameters: \| * data (sequence of ndarrays) – Data arrays, one array per value in `positions`. * ax (Matplotlib AxesSubplot instance, optional) – If given, this subplot is used to plot in instead of a new figure being created. * labels (list of str, optional) – Tick labels for the horizontal axis. If not given, integers `1..len(data)` are used. * positions (array\_like, optional) – Position array, used as the horizontal axis of the plot. If not given, spacing of the violins will be equidistant. * side ({'both', 'left', 'right'}, optional) – How to plot the violin. Default is ‘both’. The ‘left’, ‘right’ options can be used to create asymmetric violin plots. * show\_boxplot (bool, optional) – Whether or not to show normal box plots on top of the violins. Default is True. * plot\_opts ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)"), optional) – A dictionary with plotting options. Any of the following can be provided, if not present in `plot_opts` the defaults will be used: ``` - 'violin_fc', MPL color. Fill color for violins. Default is 'y'. - 'violin_ec', MPL color. Edge color for violins. Default is 'k'. - 'violin_lw', scalar. Edge linewidth for violins. Default is 1. - 'violin_alpha', float. Transparancy of violins. Default is 0.5. - 'cutoff', bool. If True, limit violin range to data range. Default is False. - 'cutoff_val', scalar. Where to cut off violins if `cutoff` is True. Default is 1.5 standard deviations. - 'cutoff_type', {'std', 'abs'}. Whether cutoff value is absolute, or in standard deviations. Default is 'std'. - 'violin_width' : float. Relative width of violins. Max available space is 1, default is 0.8. - 'label_fontsize', MPL fontsize. Adjusts fontsize only if given. - 'label_rotation', scalar. Adjusts label rotation only if given. Specify in degrees. - 'bw_factor', Adjusts the scipy gaussian_kde kernel. default: None. Options for scalar or callable. ``` \| \| Returns: \| fig – If `ax` is None, the created figure. Otherwise the figure to which `ax` is connected. \| \| Return type: \| Matplotlib figure instance \| See also [`beanplot`](statsmodels.graphics.boxplots.beanplot#statsmodels.graphics.boxplots.beanplot "statsmodels.graphics.boxplots.beanplot") Bean plot, builds on `violinplot`. `matplotlib.pyplot.boxplot` Standard boxplot. #### Notes The appearance of violins can be customized with `plot_opts`. If customization of boxplot elements is required, set `show_boxplot` to False and plot it on top of the violins by calling the Matplotlib `boxplot` function directly. For example: ``` violinplot(data, ax=ax, show_boxplot=False) ax.boxplot(data, sym='cv', whis=2.5) ``` It can happen that the axis labels or tick labels fall outside the plot area, especially with rotated labels on the horizontal axis. With Matplotlib 1.1 or higher, this can easily be fixed by calling `ax.tight_layout()`. With older Matplotlib one has to use `plt.rc` or `plt.rcParams` to fix this, for example: ``` plt.rc('figure.subplot', bottom=0.25) violinplot(data, ax=ax) ``` #### References J.L. Hintze and R.D. Nelson, “Violin Plots: A Box Plot-Density Trace Synergism”, The American Statistician, Vol. 52, pp.181-84, 1998. #### Examples We use the American National Election Survey 1996 dataset, which has Party Identification of respondents as independent variable and (among other data) age as dependent variable. ``` >>> data = sm.datasets.anes96.load_pandas() >>> party_ID = np.arange(7) >>> labels = ["Strong Democrat", "Weak Democrat", "Independent-Democrat", ... "Independent-Indpendent", "Independent-Republican", ... "Weak Republican", "Strong Republican"] ``` Group age by party ID, and create a violin plot with it: ``` >>> plt.rcParams['figure.subplot.bottom'] = 0.23 # keep labels visible >>> age = [data.exog['age'][data.endog == id] for id in party_ID] >>> fig = plt.figure() >>> ax = fig.add_subplot(111) >>> sm.graphics.violinplot(age, ax=ax, labels=labels, ... plot_opts={'cutoff_val':5, 'cutoff_type':'abs', ... 'label_fontsize':'small', ... 'label_rotation':30}) >>> ax.set_xlabel("Party identification of respondent.") >>> ax.set_ylabel("Age") >>> plt.show() ``` ([Source code](../plots/graphics_boxplot_violinplot.py), [png](../plots/graphics_boxplot_violinplot.png), [hires.png](../plots/graphics_boxplot_violinplot.hires.png), [pdf](../plots/graphics_boxplot_violinplot.pdf)) statsmodels statsmodels.discrete.count_model.ZeroInflatedNegativeBinomialP.predict statsmodels.discrete.count\_model.ZeroInflatedNegativeBinomialP.predict ======================================================================= `ZeroInflatedNegativeBinomialP.predict(params, exog=None, exog_infl=None, exposure=None, offset=None, which='mean')` Predict response variable of a count model given exogenous variables. \| Parameters: \| * params (array-like) – The parameters of the model * exog (array, optional) – A reference to the exogenous design. If not assigned, will be used exog from fitting. * exog\_infl (array, optional) – A reference to the zero-inflated exogenous design. If not assigned, will be used exog from fitting. * offset (array, optional) – Offset is added to the linear prediction with coefficient equal to 1. * exposure (array, optional) – Log(exposure) is added to the linear prediction with coefficient equal to 1. If exposure is specified, then it will be logged by the method. The user does not need to log it first. * which (string, optional) – Define values that will be predicted. ‘mean’, ‘mean-main’, ‘linear’, ‘mean-nonzero’, ‘prob-zero, ‘prob’, ‘prob-main’ Default is ‘mean’. \| #### Notes statsmodels statsmodels.sandbox.distributions.transformed.Transf_gen.median statsmodels.sandbox.distributions.transformed.Transf\_gen.median ================================================================ `Transf_gen.median(args, kwds)` Median of the distribution. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – Location parameter, Default is 0. * scale (array\_like, optional) – Scale parameter, Default is 1. \| \| Returns: \| median – The median of the distribution. \| \| Return type: \| float \| See also `stats.distributions.rv_discrete.ppf` Inverse of the CDF statsmodels statsmodels.sandbox.distributions.transformed.Transf_gen.interval statsmodels.sandbox.distributions.transformed.Transf\_gen.interval ================================================================== `Transf_gen.interval(alpha, args, kwds)` Confidence interval with equal areas around the median. \| Parameters: \| alpha (array\_like of float) – Probability that an rv will be drawn from the returned range. Each value should be in the range [0, 1]. * arg2, .. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information). * loc (array\_like, optional) – location parameter, Default is 0. * scale (array\_like, optional) – scale parameter, Default is 1. \| \| Returns: \| a, b – end-points of range that contain `100 * alpha %` of the rv’s possible values. \| \| Return type: \| ndarray of float \| statsmodels statsmodels.discrete.discrete_model.BinaryModel.cdf statsmodels.discrete.discrete\_model.BinaryModel.cdf ==================================================== `BinaryModel.cdf(X)` The cumulative distribution function of the model. statsmodels statsmodels.discrete.discrete_model.MultinomialResults.f_test statsmodels.discrete.discrete\_model.MultinomialResults.f\_test =============================================================== `MultinomialResults.f_test(r_matrix, cov_p=None, scale=1.0, invcov=None)` Compute the F-test for a joint linear hypothesis. This is a special case of `wald_test` that always uses the F distribution. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length k row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> A = np.identity(len(results.params)) >>> A = A[1:,:] ``` This tests that each coefficient is jointly statistically significantly different from zero. ``` >>> print(results.f_test(A)) <F test: F=array([[ 330.28533923]]), p=4.984030528700946e-10, df_denom=9, df_num=6> ``` Compare this to ``` >>> results.fvalue 330.2853392346658 >>> results.f_pvalue 4.98403096572e-10 ``` ``` >>> B = np.array(([0,0,1,-1,0,0,0],[0,0,0,0,0,1,-1])) ``` This tests that the coefficient on the 2nd and 3rd regressors are equal and jointly that the coefficient on the 5th and 6th regressors are equal. ``` >>> print(results.f_test(B)) <F test: F=array([[ 9.74046187]]), p=0.005605288531708235, df_denom=9, df_num=2> ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.datasets import longley >>> from statsmodels.formula.api import ols >>> dta = longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = '(GNPDEFL = GNP), (UNEMP = 2), (YEAR/1829 = 1)' >>> f_test = results.f_test(hypotheses) >>> print(f_test) <F test: F=array([[ 144.17976065]]), p=6.322026217355609e-08, df_denom=9, df_num=3> ``` See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`wald_test`](statsmodels.discrete.discrete_model.multinomialresults.wald_test#statsmodels.discrete.discrete_model.MultinomialResults.wald_test "statsmodels.discrete.discrete_model.MultinomialResults.wald_test"), [`t_test`](statsmodels.discrete.discrete_model.multinomialresults.t_test#statsmodels.discrete.discrete_model.MultinomialResults.t_test "statsmodels.discrete.discrete_model.MultinomialResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.stats.weightstats.CompareMeans.std_meandiff_pooledvar statsmodels.stats.weightstats.CompareMeans.std\_meandiff\_pooledvar =================================================================== `CompareMeans.std_meandiff_pooledvar()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/weightstats.html#CompareMeans.std_meandiff_pooledvar) variance assuming equal variance in both data sets statsmodels statsmodels.sandbox.regression.gmm.GMM.fitgmm_cu statsmodels.sandbox.regression.gmm.GMM.fitgmm\_cu ================================================= `GMM.fitgmm_cu(start, optim_method='bfgs', optim_args=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/regression/gmm.html#GMM.fitgmm_cu) estimate parameters using continuously updating GMM \| Parameters: \| start (array\_like) – starting values for minimization \| \| Returns: \| paramest – estimated parameters \| \| Return type: \| array \| #### Notes todo: add fixed parameter option, not here ??? uses scipy.optimize.fmin statsmodels statsmodels.genmod.families.family.Poisson.weights statsmodels.genmod.families.family.Poisson.weights ================================================== `Poisson.weights(mu)` Weights for IRLS steps \| Parameters: \| mu (array-like) – The transformed mean response variable in the exponential family \| \| Returns: \| w – The weights for the IRLS steps \| \| Return type: \| array \| #### Notes \[w = 1 / (g'(\mu)^2 \* Var(\mu))\] statsmodels statsmodels.discrete.discrete_model.MultinomialModel.predict statsmodels.discrete.discrete\_model.MultinomialModel.predict ============================================================= `MultinomialModel.predict(params, exog=None, linear=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#MultinomialModel.predict) Predict response variable of a model given exogenous variables. \| Parameters: \| * params (array-like) – 2d array of fitted parameters of the model. Should be in the order returned from the model. * exog (array-like) – 1d or 2d array of exogenous values. If not supplied, the whole exog attribute of the model is used. If a 1d array is given it assumed to be 1 row of exogenous variables. If you only have one regressor and would like to do prediction, you must provide a 2d array with shape[1] == 1. * linear (bool, optional) – If True, returns the linear predictor dot(exog,params). Else, returns the value of the cdf at the linear predictor. \| #### Notes Column 0 is the base case, the rest conform to the rows of params shifted up one for the base case. statsmodels statsmodels.discrete.discrete_model.NegativeBinomial.pdf statsmodels.discrete.discrete\_model.NegativeBinomial.pdf ========================================================= `NegativeBinomial.pdf(X)` The probability density (mass) function of the model. statsmodels statsmodels.sandbox.distributions.transformed.ExpTransf_gen.stats statsmodels.sandbox.distributions.transformed.ExpTransf\_gen.stats ================================================================== `ExpTransf_gen.stats(args, kwds)` Some statistics of the given RV. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional (continuous RVs only)) – scale parameter (default=1) * moments (str, optional) – composed of letters [‘mvsk’] defining which moments to compute: ‘m’ = mean, ‘v’ = variance, ‘s’ = (Fisher’s) skew, ‘k’ = (Fisher’s) kurtosis. (default is ‘mv’) \| \| Returns: \| stats – of requested moments. \| \| Return type: \| sequence \| statsmodels statsmodels.discrete.discrete_model.DiscreteResults.save statsmodels.discrete.discrete\_model.DiscreteResults.save ========================================================= `DiscreteResults.save(fname, remove_data=False)` save a pickle of this instance \| Parameters: \| * fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. * remove\_data (bool) – If False (default), then the instance is pickled without changes. If True, then all arrays with length nobs are set to None before pickling. See the remove\_data method. In some cases not all arrays will be set to None. \| #### Notes If remove\_data is true and the model result does not implement a remove\_data method then this will raise an exception. statsmodels statsmodels.tsa.statespace.sarimax.SARIMAX.loglikeobs statsmodels.tsa.statespace.sarimax.SARIMAX.loglikeobs ===================================================== `SARIMAX.loglikeobs(params, transformed=True, complex_step=False, *kwargs)` Loglikelihood evaluation \| Parameters: \| params (array\_like) – Array of parameters at which to evaluate the loglikelihood function. * transformed (boolean, optional) – Whether or not `params` is already transformed. Default is True. * *\\kwargs* – Additional keyword arguments to pass to the Kalman filter. See `KalmanFilter.filter` for more details. \| #### Notes [[1]](#id2) recommend maximizing the average likelihood to avoid scale issues; this is done automatically by the base Model fit method. #### References \| \| \| \| --- \| --- \| \| [[1]](#id1) \| Koopman, Siem Jan, Neil Shephard, and Jurgen A. Doornik. 1999. Statistical Algorithms for Models in State Space Using SsfPack 2.2. Econometrics Journal 2 (1): 107-60. doi:10.1111/1368-423X.00023. \| See also [`update`](statsmodels.tsa.statespace.sarimax.sarimax.update#statsmodels.tsa.statespace.sarimax.SARIMAX.update "statsmodels.tsa.statespace.sarimax.SARIMAX.update") modifies the internal state of the Model to reflect new params	programming_docs
statsmodels statsmodels.discrete.discrete_model.Poisson.from_formula statsmodels.discrete.discrete\_model.Poisson.from\_formula ========================================================== `classmethod Poisson.from_formula(formula, data, subset=None, drop_cols=None, args, kwargs)` Create a Model from a formula and dataframe. \| Parameters: \| formula (str or generic Formula object) – The formula specifying the model * data (array-like) – The data for the model. See Notes. * subset (array-like) – An array-like object of booleans, integers, or index values that indicate the subset of df to use in the model. Assumes df is a `pandas.DataFrame` * drop\_cols (array-like) – Columns to drop from the design matrix. Cannot be used to drop terms involving categoricals. * args (extra arguments) – These are passed to the model * kwargs (extra keyword arguments) – These are passed to the model with one exception. The `eval_env` keyword is passed to patsy. It can be either a [`patsy.EvalEnvironment`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.EvalEnvironment "(in patsy v0.5.0+dev)") object or an integer indicating the depth of the namespace to use. For example, the default `eval_env=0` uses the calling namespace. If you wish to use a “clean” environment set `eval_env=-1`. \| \| Returns: \| model \| \| Return type: \| Model instance \| #### Notes data must define \_\_getitem\_\_ with the keys in the formula terms args and kwargs are passed on to the model instantiation. E.g., a numpy structured or rec array, a dictionary, or a pandas DataFrame. statsmodels statsmodels.tsa.ar_model.ARResults.scale statsmodels.tsa.ar\_model.ARResults.scale ========================================= `ARResults.scale()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/ar_model.html#ARResults.scale) statsmodels statsmodels.discrete.discrete_model.CountResults.pvalues statsmodels.discrete.discrete\_model.CountResults.pvalues ========================================================= `CountResults.pvalues()` statsmodels statsmodels.tsa.statespace.varmax.VARMAXResults.wald_test statsmodels.tsa.statespace.varmax.VARMAXResults.wald\_test ========================================================== `VARMAXResults.wald_test(r_matrix, cov_p=None, scale=1.0, invcov=None, use_f=None)` Compute a Wald-test for a joint linear hypothesis. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. * use\_f (bool) – If True, then the F-distribution is used. If False, then the asymptotic distribution, chisquare is used. If use\_f is None, then the F distribution is used if the model specifies that use\_t is True. The test statistic is proportionally adjusted for the distribution by the number of constraints in the hypothesis. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`f_test`](statsmodels.tsa.statespace.varmax.varmaxresults.f_test#statsmodels.tsa.statespace.varmax.VARMAXResults.f_test "statsmodels.tsa.statespace.varmax.VARMAXResults.f_test"), [`t_test`](statsmodels.tsa.statespace.varmax.varmaxresults.t_test#statsmodels.tsa.statespace.varmax.VARMAXResults.t_test "statsmodels.tsa.statespace.varmax.VARMAXResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.tsa.vector_ar.hypothesis_test_results.WhitenessTestResults statsmodels.tsa.vector\_ar.hypothesis\_test\_results.WhitenessTestResults ========================================================================= `class statsmodels.tsa.vector_ar.hypothesis_test_results.WhitenessTestResults(test_statistic, crit_value, pvalue, df, signif, nlags, adjusted)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/hypothesis_test_results.html#WhitenessTestResults) Results class for the Portmanteau-test for residual autocorrelation. \| Parameters: \| * test\_statistic (float) – The test’s test statistic. * crit\_value (float) – The test’s critical value. * pvalue (float) – The test’s p-value. * df (int) – Degrees of freedom. * signif (float) – Significance level. * nlags (int) – Number of lags tested. \| #### Methods \| \| \| \| --- \| --- \| \| [`summary`](statsmodels.tsa.vector_ar.hypothesis_test_results.whitenesstestresults.summary#statsmodels.tsa.vector_ar.hypothesis_test_results.WhitenessTestResults.summary "statsmodels.tsa.vector_ar.hypothesis_test_results.WhitenessTestResults.summary")() \| \| statsmodels statsmodels.sandbox.distributions.extras.SkewNorm_gen.ppf statsmodels.sandbox.distributions.extras.SkewNorm\_gen.ppf ========================================================== `SkewNorm_gen.ppf(q, args, kwds)` Percent point function (inverse of `cdf`) at q of the given RV. \| Parameters: \| q (array\_like) – lower tail probability * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| x – quantile corresponding to the lower tail probability q. \| \| Return type: \| array\_like \| statsmodels statsmodels.tsa.statespace.mlemodel.MLEModel.loglikeobs statsmodels.tsa.statespace.mlemodel.MLEModel.loglikeobs ======================================================= `MLEModel.loglikeobs(params, transformed=True, complex_step=False, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/mlemodel.html#MLEModel.loglikeobs) Loglikelihood evaluation \| Parameters: \| params (array\_like) – Array of parameters at which to evaluate the loglikelihood function. * transformed (boolean, optional) – Whether or not `params` is already transformed. Default is True. * *\\kwargs* – Additional keyword arguments to pass to the Kalman filter. See `KalmanFilter.filter` for more details. \| #### Notes [[1]](#id2) recommend maximizing the average likelihood to avoid scale issues; this is done automatically by the base Model fit method. #### References \| \| \| \| --- \| --- \| \| [[1]](#id1) \| Koopman, Siem Jan, Neil Shephard, and Jurgen A. Doornik. 1999. Statistical Algorithms for Models in State Space Using SsfPack 2.2. Econometrics Journal 2 (1): 107-60. doi:10.1111/1368-423X.00023. \| See also [`update`](statsmodels.tsa.statespace.mlemodel.mlemodel.update#statsmodels.tsa.statespace.mlemodel.MLEModel.update "statsmodels.tsa.statespace.mlemodel.MLEModel.update") modifies the internal state of the Model to reflect new params statsmodels statsmodels.discrete.discrete_model.Probit.initialize statsmodels.discrete.discrete\_model.Probit.initialize ====================================================== `Probit.initialize()` Initialize is called by statsmodels.model.LikelihoodModel.\_\_init\_\_ and should contain any preprocessing that needs to be done for a model. statsmodels statsmodels.tsa.statespace.kalman_filter.KalmanFilter.impulse_responses statsmodels.tsa.statespace.kalman\_filter.KalmanFilter.impulse\_responses ========================================================================= `KalmanFilter.impulse_responses(steps=10, impulse=0, orthogonalized=False, cumulative=False, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/kalman_filter.html#KalmanFilter.impulse_responses) Impulse response function \| Parameters: \| steps (int, optional) – The number of steps for which impulse responses are calculated. Default is 10. Note that the initial impulse is not counted as a step, so if `steps=1`, the output will have 2 entries. * impulse (int or array\_like) – If an integer, the state innovation to pulse; must be between 0 and `k_posdef-1` where `k_posdef` is the same as in the state space model. Alternatively, a custom impulse vector may be provided; must be a column vector with shape `(k_posdef, 1)`. * orthogonalized (boolean, optional) – Whether or not to perform impulse using orthogonalized innovations. Note that this will also affect custum `impulse` vectors. Default is False. * cumulative (boolean, optional) – Whether or not to return cumulative impulse responses. Default is False. * *\\kwargs* – If the model is time-varying and `steps` is greater than the number of observations, any of the state space representation matrices that are time-varying must have updated values provided for the out-of-sample steps. For example, if `design` is a time-varying component, `nobs` is 10, and `steps` is 15, a (`k_endog` x `k_states` x 5) matrix must be provided with the new design matrix values. \| \| Returns: \| impulse\_responses – Responses for each endogenous variable due to the impulse given by the `impulse` argument. A (steps + 1 x k\_endog) array. \| \| Return type: \| array \| #### Notes Intercepts in the measurement and state equation are ignored when calculating impulse responses. statsmodels statsmodels.robust.robust_linear_model.RLMResults.summary statsmodels.robust.robust\_linear\_model.RLMResults.summary =========================================================== `RLMResults.summary(yname=None, xname=None, title=0, alpha=0.05, return_fmt='text')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/robust_linear_model.html#RLMResults.summary) This is for testing the new summary setup statsmodels statsmodels.genmod.families.family.Tweedie.starting_mu statsmodels.genmod.families.family.Tweedie.starting\_mu ======================================================= `Tweedie.starting_mu(y)` Starting value for mu in the IRLS algorithm. \| Parameters: \| y (array) – The untransformed response variable. \| \| Returns: \| mu\_0 – The first guess on the transformed response variable. \| \| Return type: \| array \| #### Notes \[\mu\_0 = (Y + \overline{Y})/2\] Only the Binomial family takes a different initial value. statsmodels statsmodels.genmod.cov_struct.Nested.covariance_matrix statsmodels.genmod.cov\_struct.Nested.covariance\_matrix ======================================================== `Nested.covariance_matrix(expval, index)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/cov_struct.html#Nested.covariance_matrix) Returns the working covariance or correlation matrix for a given cluster of data. \| Parameters: \| * endog\_expval (array-like) – The expected values of endog for the cluster for which the covariance or correlation matrix will be returned * index (integer) – The index of the cluster for which the covariane or correlation matrix will be returned \| \| Returns: \| * M (matrix) – The covariance or correlation matrix of endog * is\_cor (bool) – True if M is a correlation matrix, False if M is a covariance matrix \| statsmodels statsmodels.duration.hazard_regression.PHRegResults statsmodels.duration.hazard\_regression.PHRegResults ==================================================== `class statsmodels.duration.hazard_regression.PHRegResults(model, params, cov_params, scale=1.0, covariance_type='naive')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/duration/hazard_regression.html#PHRegResults) Class to contain results of fitting a Cox proportional hazards survival model. PHregResults inherits from statsmodels.LikelihoodModelResults \| Parameters: \| statsmodels.LikelihoodModelResults (See) – \| \| Returns: \| * \\Attributes\\** * model (class instance) – PHreg model instance that called fit. * normalized\_cov\_params (array) – The sampling covariance matrix of the estimates * params (array) – The coefficients of the fitted model. Each coefficient is the log hazard ratio corresponding to a 1 unit difference in a single covariate while holding the other covariates fixed. * bse (array) – The standard errors of the fitted parameters. \| See also `statsmodels.LikelihoodModelResults` #### Methods \| \| \| \| --- \| --- \| \| [`baseline_cumulative_hazard`](statsmodels.duration.hazard_regression.phregresults.baseline_cumulative_hazard#statsmodels.duration.hazard_regression.PHRegResults.baseline_cumulative_hazard "statsmodels.duration.hazard_regression.PHRegResults.baseline_cumulative_hazard")() \| A list (corresponding to the strata) containing the baseline cumulative hazard function evaluated at the event points. \| \| [`baseline_cumulative_hazard_function`](statsmodels.duration.hazard_regression.phregresults.baseline_cumulative_hazard_function#statsmodels.duration.hazard_regression.PHRegResults.baseline_cumulative_hazard_function "statsmodels.duration.hazard_regression.PHRegResults.baseline_cumulative_hazard_function")() \| A list (corresponding to the strata) containing function objects that calculate the cumulative hazard function. \| \| [`bse`](statsmodels.duration.hazard_regression.phregresults.bse#statsmodels.duration.hazard_regression.PHRegResults.bse "statsmodels.duration.hazard_regression.PHRegResults.bse")() \| Returns the standard errors of the parameter estimates. \| \| [`conf_int`](statsmodels.duration.hazard_regression.phregresults.conf_int#statsmodels.duration.hazard_regression.PHRegResults.conf_int "statsmodels.duration.hazard_regression.PHRegResults.conf_int")([alpha, cols, method]) \| Returns the confidence interval of the fitted parameters. \| \| [`cov_params`](statsmodels.duration.hazard_regression.phregresults.cov_params#statsmodels.duration.hazard_regression.PHRegResults.cov_params "statsmodels.duration.hazard_regression.PHRegResults.cov_params")([r\_matrix, column, scale, cov\_p, …]) \| Returns the variance/covariance matrix. \| \| [`f_test`](statsmodels.duration.hazard_regression.phregresults.f_test#statsmodels.duration.hazard_regression.PHRegResults.f_test "statsmodels.duration.hazard_regression.PHRegResults.f_test")(r\_matrix[, cov\_p, scale, invcov]) \| Compute the F-test for a joint linear hypothesis. \| \| [`get_distribution`](statsmodels.duration.hazard_regression.phregresults.get_distribution#statsmodels.duration.hazard_regression.PHRegResults.get_distribution "statsmodels.duration.hazard_regression.PHRegResults.get_distribution")() \| Returns a scipy distribution object corresponding to the distribution of uncensored endog (duration) values for each case. \| \| [`initialize`](statsmodels.duration.hazard_regression.phregresults.initialize#statsmodels.duration.hazard_regression.PHRegResults.initialize "statsmodels.duration.hazard_regression.PHRegResults.initialize")(model, params, \\kwd) \| \| \| [`llf`](statsmodels.duration.hazard_regression.phregresults.llf#statsmodels.duration.hazard_regression.PHRegResults.llf "statsmodels.duration.hazard_regression.PHRegResults.llf")() \| \| \| [`load`](statsmodels.duration.hazard_regression.phregresults.load#statsmodels.duration.hazard_regression.PHRegResults.load "statsmodels.duration.hazard_regression.PHRegResults.load")(fname) \| load a pickle, (class method) \| \| [`martingale_residuals`](statsmodels.duration.hazard_regression.phregresults.martingale_residuals#statsmodels.duration.hazard_regression.PHRegResults.martingale_residuals "statsmodels.duration.hazard_regression.PHRegResults.martingale_residuals")() \| The martingale residuals. \| \| [`normalized_cov_params`](statsmodels.duration.hazard_regression.phregresults.normalized_cov_params#statsmodels.duration.hazard_regression.PHRegResults.normalized_cov_params "statsmodels.duration.hazard_regression.PHRegResults.normalized_cov_params")() \| \| \| [`predict`](statsmodels.duration.hazard_regression.phregresults.predict#statsmodels.duration.hazard_regression.PHRegResults.predict "statsmodels.duration.hazard_regression.PHRegResults.predict")([endog, exog, strata, offset, …]) \| Returns predicted values from the proportional hazards regression model. \| \| [`pvalues`](statsmodels.duration.hazard_regression.phregresults.pvalues#statsmodels.duration.hazard_regression.PHRegResults.pvalues "statsmodels.duration.hazard_regression.PHRegResults.pvalues")() \| \| \| [`remove_data`](statsmodels.duration.hazard_regression.phregresults.remove_data#statsmodels.duration.hazard_regression.PHRegResults.remove_data "statsmodels.duration.hazard_regression.PHRegResults.remove_data")() \| remove data arrays, all nobs arrays from result and model \| \| [`save`](statsmodels.duration.hazard_regression.phregresults.save#statsmodels.duration.hazard_regression.PHRegResults.save "statsmodels.duration.hazard_regression.PHRegResults.save")(fname[, remove\_data]) \| save a pickle of this instance \| \| [`schoenfeld_residuals`](statsmodels.duration.hazard_regression.phregresults.schoenfeld_residuals#statsmodels.duration.hazard_regression.PHRegResults.schoenfeld_residuals "statsmodels.duration.hazard_regression.PHRegResults.schoenfeld_residuals")() \| A matrix containing the Schoenfeld residuals. \| \| [`score_residuals`](statsmodels.duration.hazard_regression.phregresults.score_residuals#statsmodels.duration.hazard_regression.PHRegResults.score_residuals "statsmodels.duration.hazard_regression.PHRegResults.score_residuals")() \| A matrix containing the score residuals. \| \| [`standard_errors`](statsmodels.duration.hazard_regression.phregresults.standard_errors#statsmodels.duration.hazard_regression.PHRegResults.standard_errors "statsmodels.duration.hazard_regression.PHRegResults.standard_errors")() \| Returns the standard errors of the parameter estimates. \| \| [`summary`](statsmodels.duration.hazard_regression.phregresults.summary#statsmodels.duration.hazard_regression.PHRegResults.summary "statsmodels.duration.hazard_regression.PHRegResults.summary")([yname, xname, title, alpha]) \| Summarize the proportional hazards regression results. \| \| [`t_test`](statsmodels.duration.hazard_regression.phregresults.t_test#statsmodels.duration.hazard_regression.PHRegResults.t_test "statsmodels.duration.hazard_regression.PHRegResults.t_test")(r\_matrix[, cov\_p, scale, use\_t]) \| Compute a t-test for a each linear hypothesis of the form Rb = q \| \| [`t_test_pairwise`](statsmodels.duration.hazard_regression.phregresults.t_test_pairwise#statsmodels.duration.hazard_regression.PHRegResults.t_test_pairwise "statsmodels.duration.hazard_regression.PHRegResults.t_test_pairwise")(term\_name[, method, alpha, …]) \| perform pairwise t\_test with multiple testing corrected p-values \| \| [`tvalues`](statsmodels.duration.hazard_regression.phregresults.tvalues#statsmodels.duration.hazard_regression.PHRegResults.tvalues "statsmodels.duration.hazard_regression.PHRegResults.tvalues")() \| Return the t-statistic for a given parameter estimate. \| \| [`wald_test`](statsmodels.duration.hazard_regression.phregresults.wald_test#statsmodels.duration.hazard_regression.PHRegResults.wald_test "statsmodels.duration.hazard_regression.PHRegResults.wald_test")(r\_matrix[, cov\_p, scale, invcov, …]) \| Compute a Wald-test for a joint linear hypothesis. \| \| [`wald_test_terms`](statsmodels.duration.hazard_regression.phregresults.wald_test_terms#statsmodels.duration.hazard_regression.PHRegResults.wald_test_terms "statsmodels.duration.hazard_regression.PHRegResults.wald_test_terms")([skip\_single, …]) \| Compute a sequence of Wald tests for terms over multiple columns \| \| [`weighted_covariate_averages`](statsmodels.duration.hazard_regression.phregresults.weighted_covariate_averages#statsmodels.duration.hazard_regression.PHRegResults.weighted_covariate_averages "statsmodels.duration.hazard_regression.PHRegResults.weighted_covariate_averages")() \| The average covariate values within the at-risk set at each event time point, weighted by hazard. \| #### Attributes \| \| \| \| --- \| --- \| \| `use_t` \| \|	programming_docs
statsmodels statsmodels.tsa.statespace.sarimax.SARIMAXResults.get_forecast statsmodels.tsa.statespace.sarimax.SARIMAXResults.get\_forecast =============================================================== `SARIMAXResults.get_forecast(steps=1, *kwargs)` Out-of-sample forecasts \| Parameters: \| steps (int, str, or datetime, optional) – If an integer, the number of steps to forecast from the end of the sample. Can also be a date string to parse or a datetime type. However, if the dates index does not have a fixed frequency, steps must be an integer. Default * *\\kwargs* – Additional arguments may required for forecasting beyond the end of the sample. See `FilterResults.predict` for more details. \| \| Returns: \| forecast – Array of out of sample forecasts. A (steps x k\_endog) array. \| \| Return type: \| array \| statsmodels statsmodels.tsa.statespace.kalman_filter.KalmanFilter.set_stability_method statsmodels.tsa.statespace.kalman\_filter.KalmanFilter.set\_stability\_method ============================================================================= `KalmanFilter.set_stability_method(stability_method=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/kalman_filter.html#KalmanFilter.set_stability_method) Set the numerical stability method The Kalman filter is a recursive algorithm that may in some cases suffer issues with numerical stability. The stability method controls what, if any, measures are taken to promote stability. \| Parameters: \| stability\_method (integer, optional) – Bitmask value to set the stability method to. See notes for details. * *\\kwargs* – Keyword arguments may be used to influence the stability method by setting individual boolean flags. See notes for details. \| #### Notes The stability method is defined by a collection of boolean flags, and is internally stored as a bitmask. The methods available are: STABILITY\_FORCE\_SYMMETRY = 0x01 If this flag is set, symmetry of the predicted state covariance matrix is enforced at each iteration of the filter, where each element is set to the average of the corresponding elements in the upper and lower triangle. If the bitmask is set directly via the `stability_method` argument, then the full method must be provided. If keyword arguments are used to set individual boolean flags, then the lowercase of the method must be used as an argument name, and the value is the desired value of the boolean flag (True or False). Note that the stability method may also be specified by directly modifying the class attributes which are defined similarly to the keyword arguments. The default stability method is `STABILITY_FORCE_SYMMETRY` #### Examples ``` >>> mod = sm.tsa.statespace.SARIMAX(range(10)) >>> mod.ssm.stability_method 1 >>> mod.ssm.stability_force_symmetry True >>> mod.ssm.stability_force_symmetry = False >>> mod.ssm.stability_method 0 ``` statsmodels statsmodels.genmod.families.family.Gamma.resid_anscombe statsmodels.genmod.families.family.Gamma.resid\_anscombe ======================================================== `Gamma.resid_anscombe(endog, mu, var_weights=1.0, scale=1.0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/family.html#Gamma.resid_anscombe) The Anscombe residuals \| Parameters: \| * endog (array) – The endogenous response variable * mu (array) – The inverse of the link function at the linear predicted values. * var\_weights (array-like) – 1d array of variance (analytic) weights. The default is 1. * scale (float, optional) – An optional argument to divide the residuals by sqrt(scale). The default is 1. \| \| Returns: \| resid\_anscombe – The Anscombe residuals for the Gamma family defined below \| \| Return type: \| array \| #### Notes \[resid\\_anscombe\_i = 3 \* (endog\_i^{1/3} - \mu\_i^{1/3}) / \mu\_i^{1/3} / \sqrt{scale} \* \sqrt(var\\_weights)\] statsmodels statsmodels.tsa.arima_model.ARIMA.fit statsmodels.tsa.arima\_model.ARIMA.fit ====================================== `ARIMA.fit(start_params=None, trend='c', method='css-mle', transparams=True, solver='lbfgs', maxiter=500, full_output=1, disp=5, callback=None, start_ar_lags=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_model.html#ARIMA.fit) Fits ARIMA(p,d,q) model by exact maximum likelihood via Kalman filter. \| Parameters: \| start\_params (array-like, optional) – Starting parameters for ARMA(p,q). If None, the default is given by ARMA.\_fit\_start\_params. See there for more information. * transparams (bool, optional) – Whehter or not to transform the parameters to ensure stationarity. Uses the transformation suggested in Jones (1980). If False, no checking for stationarity or invertibility is done. * method (str {'css-mle','mle','css'}) – This is the loglikelihood to maximize. If “css-mle”, the conditional sum of squares likelihood is maximized and its values are used as starting values for the computation of the exact likelihood via the Kalman filter. If “mle”, the exact likelihood is maximized via the Kalman Filter. If “css” the conditional sum of squares likelihood is maximized. All three methods use `start_params` as starting parameters. See above for more information. * trend (str {'c','nc'}) – Whether to include a constant or not. ‘c’ includes constant, ‘nc’ no constant. * solver (str or None, optional) – Solver to be used. The default is ‘lbfgs’ (limited memory Broyden-Fletcher-Goldfarb-Shanno). Other choices are ‘bfgs’, ‘newton’ (Newton-Raphson), ‘nm’ (Nelder-Mead), ‘cg’ - (conjugate gradient), ‘ncg’ (non-conjugate gradient), and ‘powell’. By default, the limited memory BFGS uses m=12 to approximate the Hessian, projected gradient tolerance of 1e-8 and factr = 1e2. You can change these by using kwargs. * maxiter (int, optional) – The maximum number of function evaluations. Default is 500. * tol (float) – The convergence tolerance. Default is 1e-08. * full\_output (bool, optional) – If True, all output from solver will be available in the Results object’s mle\_retvals attribute. Output is dependent on the solver. See Notes for more information. * disp (int, optional) – If True, convergence information is printed. For the default l\_bfgs\_b solver, disp controls the frequency of the output during the iterations. disp < 0 means no output in this case. * callback (function, optional) – Called after each iteration as callback(xk) where xk is the current parameter vector. * start\_ar\_lags (int, optional) – Parameter for fitting start\_params. When fitting start\_params, residuals are obtained from an AR fit, then an ARMA(p,q) model is fit via OLS using these residuals. If start\_ar\_lags is None, fit an AR process according to best BIC. If start\_ar\_lags is not None, fits an AR process with a lag length equal to start\_ar\_lags. See ARMA.\_fit\_start\_params\_hr for more information. * kwargs – See Notes for keyword arguments that can be passed to fit. \| \| Returns: \| \| \| Return type: \| `statsmodels.tsa.arima.ARIMAResults` class \| See also [`statsmodels.base.model.LikelihoodModel.fit`](http://www.statsmodels.org/stable/dev/generated/statsmodels.base.model.LikelihoodModel.fit.html#statsmodels.base.model.LikelihoodModel.fit "statsmodels.base.model.LikelihoodModel.fit") for more information on using the solvers. [`ARIMAResults`](statsmodels.tsa.arima_model.arimaresults#statsmodels.tsa.arima_model.ARIMAResults "statsmodels.tsa.arima_model.ARIMAResults") results class returned by fit #### Notes If fit by ‘mle’, it is assumed for the Kalman Filter that the initial unkown state is zero, and that the inital variance is P = dot(inv(identity(m\\2)-kron(T,T)),dot(R,R.T).ravel(‘F’)).reshape(r, r, order = ‘F’) statsmodels statsmodels.tsa.seasonal.seasonal_decompose statsmodels.tsa.seasonal.seasonal\_decompose ============================================ `statsmodels.tsa.seasonal.seasonal_decompose(x, model='additive', filt=None, freq=None, two_sided=True, extrapolate_trend=0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/seasonal.html#seasonal_decompose) Seasonal decomposition using moving averages \| Parameters: \| * x (array-like) – Time series. If 2d, individual series are in columns. * model (str {"additive", "multiplicative"}) – Type of seasonal component. Abbreviations are accepted. * filt (array-like) – The filter coefficients for filtering out the seasonal component. The concrete moving average method used in filtering is determined by two\_sided. * freq (int, optional) – Frequency of the series. Must be used if x is not a pandas object. Overrides default periodicity of x if x is a pandas object with a timeseries index. * two\_sided (bool) – The moving average method used in filtering. If True (default), a centered moving average is computed using the filt. If False, the filter coefficients are for past values only. * extrapolate\_trend (int or 'freq', optional) – If set to > 0, the trend resulting from the convolution is linear least-squares extrapolated on both ends (or the single one if two\_sided is False) considering this many (+1) closest points. If set to ‘freq’, use `freq` closest points. Setting this parameter results in no NaN values in trend or resid components. \| \| Returns: \| results – A object with seasonal, trend, and resid attributes. \| \| Return type: \| obj \| #### Notes This is a naive decomposition. More sophisticated methods should be preferred. The additive model is Y[t] = T[t] + S[t] + e[t] The multiplicative model is Y[t] = T[t] \* S[t] \* e[t] The seasonal component is first removed by applying a convolution filter to the data. The average of this smoothed series for each period is the returned seasonal component. See also [`statsmodels.tsa.filters.bk_filter.bkfilter`](statsmodels.tsa.filters.bk_filter.bkfilter#statsmodels.tsa.filters.bk_filter.bkfilter "statsmodels.tsa.filters.bk_filter.bkfilter"), `statsmodels.tsa.filters.cf_filter.xffilter`, [`statsmodels.tsa.filters.hp_filter.hpfilter`](statsmodels.tsa.filters.hp_filter.hpfilter#statsmodels.tsa.filters.hp_filter.hpfilter "statsmodels.tsa.filters.hp_filter.hpfilter"), `statsmodels.tsa.filters.convolution_filter` statsmodels statsmodels.tsa.statespace.structural.UnobservedComponentsResults.get_forecast statsmodels.tsa.statespace.structural.UnobservedComponentsResults.get\_forecast =============================================================================== `UnobservedComponentsResults.get_forecast(steps=1, *kwargs)` Out-of-sample forecasts \| Parameters: \| steps (int, str, or datetime, optional) – If an integer, the number of steps to forecast from the end of the sample. Can also be a date string to parse or a datetime type. However, if the dates index does not have a fixed frequency, steps must be an integer. Default * *\\kwargs* – Additional arguments may required for forecasting beyond the end of the sample. See `FilterResults.predict` for more details. \| \| Returns: \| forecast – Array of out of sample forecasts. A (steps x k\_endog) array. \| \| Return type: \| array \| statsmodels statsmodels.genmod.generalized_linear_model.GLM.initialize statsmodels.genmod.generalized\_linear\_model.GLM.initialize ============================================================ `GLM.initialize()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_linear_model.html#GLM.initialize) Initialize a generalized linear model. statsmodels statsmodels.discrete.discrete_model.DiscreteModel.information statsmodels.discrete.discrete\_model.DiscreteModel.information ============================================================== `DiscreteModel.information(params)` Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.discrete.discrete_model.NegativeBinomialResults.t_test statsmodels.discrete.discrete\_model.NegativeBinomialResults.t\_test ==================================================================== `NegativeBinomialResults.t_test(r_matrix, cov_p=None, scale=None, use_t=None)` Compute a t-test for a each linear hypothesis of the form Rb = q \| Parameters: \| * r\_matrix (array-like, str, tuple) – + array : If an array is given, a p x k 2d array or length k 1d array specifying the linear restrictions. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q). If q is given, can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – An optional `scale` to use. Default is the scale specified by the model fit. * use\_t (bool, optional) – If use\_t is None, then the default of the model is used. If use\_t is True, then the p-values are based on the t distribution. If use\_t is False, then the p-values are based on the normal distribution. \| \| Returns: \| res – The results for the test are attributes of this results instance. The available results have the same elements as the parameter table in `summary()`. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> r = np.zeros_like(results.params) >>> r[5:] = [1,-1] >>> print(r) [ 0. 0. 0. 0. 0. 1. -1.] ``` r tests that the coefficients on the 5th and 6th independent variable are the same. ``` >>> T_test = results.t_test(r) >>> print(T_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 -1829.2026 455.391 -4.017 0.003 -2859.368 -799.037 ============================================================================== >>> T_test.effect -1829.2025687192481 >>> T_test.sd 455.39079425193762 >>> T_test.tvalue -4.0167754636411717 >>> T_test.pvalue 0.0015163772380899498 ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.formula.api import ols >>> dta = sm.datasets.longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = 'GNPDEFL = GNP, UNEMP = 2, YEAR/1829 = 1' >>> t_test = results.t_test(hypotheses) >>> print(t_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 15.0977 84.937 0.178 0.863 -177.042 207.238 c1 -2.0202 0.488 -8.231 0.000 -3.125 -0.915 c2 1.0001 0.249 0.000 1.000 0.437 1.563 ============================================================================== ``` See also [`tvalues`](statsmodels.discrete.discrete_model.negativebinomialresults.tvalues#statsmodels.discrete.discrete_model.NegativeBinomialResults.tvalues "statsmodels.discrete.discrete_model.NegativeBinomialResults.tvalues") individual t statistics [`f_test`](statsmodels.discrete.discrete_model.negativebinomialresults.f_test#statsmodels.discrete.discrete_model.NegativeBinomialResults.f_test "statsmodels.discrete.discrete_model.NegativeBinomialResults.f_test") for F tests [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") statsmodels statsmodels.robust.robust_linear_model.RLMResults.save statsmodels.robust.robust\_linear\_model.RLMResults.save ======================================================== `RLMResults.save(fname, remove_data=False)` save a pickle of this instance \| Parameters: \| * fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. * remove\_data (bool) – If False (default), then the instance is pickled without changes. If True, then all arrays with length nobs are set to None before pickling. See the remove\_data method. In some cases not all arrays will be set to None. \| #### Notes If remove\_data is true and the model result does not implement a remove\_data method then this will raise an exception. statsmodels statsmodels.duration.hazard_regression.PHReg.score_residuals statsmodels.duration.hazard\_regression.PHReg.score\_residuals ============================================================== `PHReg.score_residuals(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/duration/hazard_regression.html#PHReg.score_residuals) Returns the score residuals calculated at a given vector of parameters. \| Parameters: \| params (ndarray) – The parameter vector at which the score residuals are calculated. \| \| Returns: \| * The score residuals, returned as a ndarray having the same * shape as `exog`. \| #### Notes Observations in a stratum with no observed events have undefined score residuals, and contain NaN in the returned matrix. statsmodels statsmodels.genmod.families.links.Link.deriv statsmodels.genmod.families.links.Link.deriv ============================================ `Link.deriv(p)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#Link.deriv) Derivative of the link function g’(p). Just a placeholder. \| Parameters: \| p (array-like) – \| \| Returns: \| g’(p) – The value of the derivative of the link function g’(p) \| \| Return type: \| array \| statsmodels statsmodels.tsa.statespace.varmax.VARMAXResults.impulse_responses statsmodels.tsa.statespace.varmax.VARMAXResults.impulse\_responses ================================================================== `VARMAXResults.impulse_responses(steps=1, impulse=0, orthogonalized=False, cumulative=False, *kwargs)` Impulse response function \| Parameters: \| steps (int, optional) – The number of steps for which impulse responses are calculated. Default is 1. Note that the initial impulse is not counted as a step, so if `steps=1`, the output will have 2 entries. * impulse (int or array\_like) – If an integer, the state innovation to pulse; must be between 0 and `k_posdef-1`. Alternatively, a custom impulse vector may be provided; must be shaped `k_posdef x 1`. * orthogonalized (boolean, optional) – Whether or not to perform impulse using orthogonalized innovations. Note that this will also affect custum `impulse` vectors. Default is False. * cumulative (boolean, optional) – Whether or not to return cumulative impulse responses. Default is False. * *\\kwargs* – If the model is time-varying and `steps` is greater than the number of observations, any of the state space representation matrices that are time-varying must have updated values provided for the out-of-sample steps. For example, if `design` is a time-varying component, `nobs` is 10, and `steps` is 15, a (`k_endog` x `k_states` x 5) matrix must be provided with the new design matrix values. \| \| Returns: \| impulse\_responses – Responses for each endogenous variable due to the impulse given by the `impulse` argument. A (steps + 1 x k\_endog) array. \| \| Return type: \| array \| #### Notes Intercepts in the measurement and state equation are ignored when calculating impulse responses.	programming_docs
statsmodels statsmodels.sandbox.tsa.fftarma.ArmaFft.from_estimation statsmodels.sandbox.tsa.fftarma.ArmaFft.from\_estimation ======================================================== `classmethod ArmaFft.from_estimation(model_results, nobs=None)` Convenience function to create an ArmaProcess from the results of an ARMA estimation \| Parameters: \| * model\_results (ARMAResults instance) – A fitted model * nobs (int, optional) – If None, nobs is taken from the results \| statsmodels statsmodels.stats.anova.AnovaRM statsmodels.stats.anova.AnovaRM =============================== `class statsmodels.stats.anova.AnovaRM(data, depvar, subject, within=None, between=None, aggregate_func=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/anova.html#AnovaRM) Repeated measures Anova using least squares regression The full model regression residual sum of squares is used to compare with the reduced model for calculating the within-subject effect sum of squares [1]. Currently, only fully balanced within-subject designs are supported. Calculation of between-subject effects and corrections for violation of sphericity are not yet implemented. \| Parameters: \| * data (DataFrame) – * depvar (string) – The dependent variable in `data` * subject (string) – Specify the subject id * within (a list of string(s)) – The within-subject factors * between (a list of string(s)) – The between-subject factors, this is not yet implemented * aggregate\_func (None, 'mean', or function) – If the data set contains more than a single observation per subject and cell of the specified model, this function will be used to aggregate the data before running the Anova. `None` (the default) will not perform any aggregation; ‘mean’ is s shortcut to `numpy.mean`. An exception will be raised if aggregation is required, but no aggregation function was specified. \| \| Returns: \| results \| \| Return type: \| AnovaResults instance \| \| Raises: \| [`ValueError`](https://docs.python.org/3.2/library/exceptions.html#ValueError "(in Python v3.2)") – If the data need to be aggregated, but `aggregate_func` was not specified. \| #### Notes This implementation currently only supports fully balanced designs. If the data contain more than one observation per subject and cell of the design, these observations need to be aggregated into a single observation before the Anova is calculated, either manually or by passing an aggregation function via the `aggregate_func` keyword argument. Note that if the input data set was not balanced before performing the aggregation, the implied heteroscedasticity of the data is ignored. #### References \| \| \| \| --- \| --- \| \| [\] \| Rutherford, Andrew. Anova and ANCOVA: a GLM approach. John Wiley & Sons, 2011. \| #### Methods \| \| \| \| --- \| --- \| \| [`fit`](statsmodels.stats.anova.anovarm.fit#statsmodels.stats.anova.AnovaRM.fit "statsmodels.stats.anova.AnovaRM.fit")() \| estimate the model and compute the Anova table \| statsmodels statsmodels.sandbox.regression.gmm.IVGMM.predict statsmodels.sandbox.regression.gmm.IVGMM.predict ================================================ `IVGMM.predict(params, exog=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/regression/gmm.html#IVGMM.predict) After a model has been fit predict returns the fitted values. This is a placeholder intended to be overwritten by individual models. statsmodels statsmodels.tsa.filters.filtertools.miso_lfilter statsmodels.tsa.filters.filtertools.miso\_lfilter ================================================= `statsmodels.tsa.filters.filtertools.miso_lfilter(ar, ma, x, useic=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/filters/filtertools.html#miso_lfilter) use nd convolution to merge inputs, then use lfilter to produce output arguments for column variables return currently 1d \| Parameters: \| ar (array\_like, 1d, float) – autoregressive lag polynomial including lag zero, ar(L)y\_t * ma (array\_like, same ndim as x, currently 2d) – moving average lag polynomial ma(L)x\_t * x (array\_like, 2d) – input data series, time in rows, variables in columns \| \| Returns: \| * y (array, 1d) – filtered output series * inp (array, 1d) – combined input series \| #### Notes currently for 2d inputs only, no choice of axis Use of signal.lfilter requires that ar lag polynomial contains floating point numbers does not cut off invalid starting and final values miso\_lfilter find array y such that: ``` ar(L)y_t = ma(L)x_t ``` with shapes y (nobs,), x (nobs,nvars), ar (narlags,), ma (narlags,nvars) statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactor.simulation_smoother statsmodels.tsa.statespace.dynamic\_factor.DynamicFactor.simulation\_smoother ============================================================================= `DynamicFactor.simulation_smoother(simulation_output=None, *kwargs)` Retrieve a simulation smoother for the state space model. \| Parameters: \| simulation\_output (int, optional) – Determines which simulation smoother output is calculated. Default is all (including state and disturbances). * *\\kwargs* – Additional keyword arguments, used to set the simulation output. See `set_simulation_output` for more details. \| \| Returns: \| \| \| Return type: \| SimulationSmoothResults \| statsmodels statsmodels.discrete.count_model.ZeroInflatedPoissonResults.conf_int statsmodels.discrete.count\_model.ZeroInflatedPoissonResults.conf\_int ====================================================================== `ZeroInflatedPoissonResults.conf_int(alpha=0.05, cols=None, method='default')` Returns the confidence interval of the fitted parameters. \| Parameters: \| * alpha (float, optional) – The significance level for the confidence interval. ie., The default `alpha` = .05 returns a 95% confidence interval. * cols (array-like, optional) – `cols` specifies which confidence intervals to return * method (string) – Not Implemented Yet Method to estimate the confidence\_interval. “Default” : uses self.bse which is based on inverse Hessian for MLE “hjjh” : “jac” : “boot-bse” “boot\_quant” “profile” \| \| Returns: \| conf\_int – Each row contains [lower, upper] limits of the confidence interval for the corresponding parameter. The first column contains all lower, the second column contains all upper limits. \| \| Return type: \| array \| #### Examples ``` >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> results.conf_int() array([[-5496529.48322745, -1467987.78596704], [ -177.02903529, 207.15277984], [ -0.1115811 , 0.03994274], [ -3.12506664, -0.91539297], [ -1.5179487 , -0.54850503], [ -0.56251721, 0.460309 ], [ 798.7875153 , 2859.51541392]]) ``` ``` >>> results.conf_int(cols=(2,3)) array([[-0.1115811 , 0.03994274], [-3.12506664, -0.91539297]]) ``` #### Notes The confidence interval is based on the standard normal distribution. Models wish to use a different distribution should overwrite this method. statsmodels statsmodels.regression.linear_model.RegressionResults.uncentered_tss statsmodels.regression.linear\_model.RegressionResults.uncentered\_tss ====================================================================== `RegressionResults.uncentered_tss()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#RegressionResults.uncentered_tss) statsmodels statsmodels.regression.mixed_linear_model.MixedLMResults.covjac statsmodels.regression.mixed\_linear\_model.MixedLMResults.covjac ================================================================= `MixedLMResults.covjac()` covariance of parameters based on outer product of jacobian of log-likelihood statsmodels statsmodels.nonparametric.kernel_regression.KernelCensoredReg.loo_likelihood statsmodels.nonparametric.kernel\_regression.KernelCensoredReg.loo\_likelihood ============================================================================== `KernelCensoredReg.loo_likelihood()` statsmodels statsmodels.genmod.families.family.Family.resid_dev statsmodels.genmod.families.family.Family.resid\_dev ==================================================== `Family.resid_dev(endog, mu, var_weights=1.0, scale=1.0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/family.html#Family.resid_dev) The deviance residuals \| Parameters: \| * endog (array-like) – The endogenous response variable * mu (array-like) – The inverse of the link function at the linear predicted values. * var\_weights (array-like) – 1d array of variance (analytic) weights. The default is 1. * scale (float, optional) – An optional scale argument. The default is 1. \| \| Returns: \| resid\_dev – Deviance residuals as defined below. \| \| Return type: \| float \| #### Notes The deviance residuals are defined by the contribution D\_i of observation i to the deviance as \[resid\\_dev\_i = sign(y\_i-\mu\_i) \sqrt{D\_i}\] D\_i is calculated from the \_resid\_dev method in each family. Distribution-specific documentation of the calculation is available there. statsmodels statsmodels.tsa.vector_ar.var_model.VAR.score statsmodels.tsa.vector\_ar.var\_model.VAR.score =============================================== `VAR.score(params)` Score vector of model. The gradient of logL with respect to each parameter. statsmodels statsmodels.emplike.descriptive.DescStatUV.test_kurt statsmodels.emplike.descriptive.DescStatUV.test\_kurt ===================================================== `DescStatUV.test_kurt(kurt0, return_weights=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/emplike/descriptive.html#DescStatUV.test_kurt) Returns -2 x log-likelihood and the p-value for the hypothesized kurtosis. \| Parameters: \| * kurt0 (float) – Kurtosis value to be tested * return\_weights (bool) – If True, function also returns the weights that maximize the likelihood ratio. Default is False. \| \| Returns: \| test\_results – The log-likelihood ratio and p-value of kurt0 \| \| Return type: \| tuple \| statsmodels statsmodels.sandbox.distributions.extras.NormExpan_gen.sf statsmodels.sandbox.distributions.extras.NormExpan\_gen.sf ========================================================== `NormExpan_gen.sf(x, args, kwds)` Survival function (1 - `cdf`) at x of the given RV. \| Parameters: \| x (array\_like) – quantiles * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| sf – Survival function evaluated at x \| \| Return type: \| array\_like \| statsmodels statsmodels.tsa.holtwinters.Holt.initialize statsmodels.tsa.holtwinters.Holt.initialize =========================================== `Holt.initialize()` Initialize (possibly re-initialize) a Model instance. For instance, the design matrix of a linear model may change and some things must be recomputed. statsmodels statsmodels.tsa.statespace.mlemodel.MLEModel.transform_jacobian statsmodels.tsa.statespace.mlemodel.MLEModel.transform\_jacobian ================================================================ `MLEModel.transform_jacobian(unconstrained, approx_centered=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/mlemodel.html#MLEModel.transform_jacobian) Jacobian matrix for the parameter transformation function \| Parameters: \| unconstrained (array\_like) – Array of unconstrained parameters used by the optimizer. \| \| Returns: \| jacobian – Jacobian matrix of the transformation, evaluated at `unconstrained` \| \| Return type: \| array \| #### Notes This is a numerical approximation using finite differences. Note that in general complex step methods cannot be used because it is not guaranteed that the `transform_params` method is a real function (e.g. if Cholesky decomposition is used). See also [`transform_params`](statsmodels.tsa.statespace.mlemodel.mlemodel.transform_params#statsmodels.tsa.statespace.mlemodel.MLEModel.transform_params "statsmodels.tsa.statespace.mlemodel.MLEModel.transform_params") statsmodels statsmodels.discrete.discrete_model.DiscreteResults.initialize statsmodels.discrete.discrete\_model.DiscreteResults.initialize =============================================================== `DiscreteResults.initialize(model, params, *kwd)` statsmodels statsmodels.discrete.count_model.GenericZeroInflated.predict statsmodels.discrete.count\_model.GenericZeroInflated.predict ============================================================= `GenericZeroInflated.predict(params, exog=None, exog_infl=None, exposure=None, offset=None, which='mean')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/count_model.html#GenericZeroInflated.predict) Predict response variable of a count model given exogenous variables. \| Parameters: \| params (array-like) – The parameters of the model * exog (array, optional) – A reference to the exogenous design. If not assigned, will be used exog from fitting. * exog\_infl (array, optional) – A reference to the zero-inflated exogenous design. If not assigned, will be used exog from fitting. * offset (array, optional) – Offset is added to the linear prediction with coefficient equal to 1. * exposure (array, optional) – Log(exposure) is added to the linear prediction with coefficient equal to 1. If exposure is specified, then it will be logged by the method. The user does not need to log it first. * which (string, optional) – Define values that will be predicted. ‘mean’, ‘mean-main’, ‘linear’, ‘mean-nonzero’, ‘prob-zero, ‘prob’, ‘prob-main’ Default is ‘mean’. \| #### Notes statsmodels statsmodels.tsa.arima_model.ARIMA.hessian statsmodels.tsa.arima\_model.ARIMA.hessian ========================================== `ARIMA.hessian(params)` Compute the Hessian at params, #### Notes This is a numerical approximation. statsmodels statsmodels.regression.quantile_regression.QuantRegResults.save statsmodels.regression.quantile\_regression.QuantRegResults.save ================================================================ `QuantRegResults.save(fname, remove_data=False)` save a pickle of this instance \| Parameters: \| * fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. * remove\_data (bool) – If False (default), then the instance is pickled without changes. If True, then all arrays with length nobs are set to None before pickling. See the remove\_data method. In some cases not all arrays will be set to None. \| #### Notes If remove\_data is true and the model result does not implement a remove\_data method then this will raise an exception. statsmodels statsmodels.stats.multitest.multipletests statsmodels.stats.multitest.multipletests ========================================= `statsmodels.stats.multitest.multipletests(pvals, alpha=0.05, method='hs', is_sorted=False, returnsorted=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/multitest.html#multipletests) Test results and p-value correction for multiple tests \| Parameters: \| * pvals (array\_like, 1-d) – uncorrected p-values. Must be 1-dimensional. * alpha (float) – FWER, family-wise error rate, e.g. 0.1 * method (string) – Method used for testing and adjustment of pvalues. Can be either the full name or initial letters. Available methods are: + `bonferroni` : one-step correction + `sidak` : one-step correction + `holm-sidak` : step down method using Sidak adjustments + `holm` : step-down method using Bonferroni adjustments + `simes-hochberg` : step-up method (independent) + `hommel` : closed method based on Simes tests (non-negative) + `fdr_bh` : Benjamini/Hochberg (non-negative) + `fdr_by` : Benjamini/Yekutieli (negative) + `fdr_tsbh` : two stage fdr correction (non-negative) + `fdr_tsbky` : two stage fdr correction (non-negative) * is\_sorted (bool) – If False (default), the p\_values will be sorted, but the corrected pvalues are in the original order. If True, then it assumed that the pvalues are already sorted in ascending order. * returnsorted (bool) – not tested, return sorted p-values instead of original sequence \| \| Returns: \| * reject (array, boolean) – true for hypothesis that can be rejected for given alpha * pvals\_corrected (array) – p-values corrected for multiple tests * alphacSidak (float) – corrected alpha for Sidak method * alphacBonf (float) – corrected alpha for Bonferroni method \| #### Notes There may be API changes for this function in the future. Except for ‘fdr\_twostage’, the p-value correction is independent of the alpha specified as argument. In these cases the corrected p-values can also be compared with a different alpha. In the case of ‘fdr\_twostage’, the corrected p-values are specific to the given alpha, see `fdrcorrection_twostage`. The ‘fdr\_gbs’ procedure is not verified against another package, p-values are derived from scratch and are not derived in the reference. In Monte Carlo experiments the method worked correctly and maintained the false discovery rate. All procedures that are included, control FWER or FDR in the independent case, and most are robust in the positively correlated case. `fdr_gbs`: high power, fdr control for independent case and only small violation in positively correlated case Timing: Most of the time with large arrays is spent in `argsort`. When we want to calculate the p-value for several methods, then it is more efficient to presort the pvalues, and put the results back into the original order outside of the function. Method=’hommel’ is very slow for large arrays, since it requires the evaluation of n partitions, where n is the number of p-values. statsmodels statsmodels.sandbox.regression.gmm.GMMResults.load statsmodels.sandbox.regression.gmm.GMMResults.load ================================================== `classmethod GMMResults.load(fname)` load a pickle, (class method) \| Parameters: \| fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. \| \| Returns: \| \| \| Return type: \| unpickled instance \| statsmodels statsmodels.robust.robust_linear_model.RLMResults.fittedvalues statsmodels.robust.robust\_linear\_model.RLMResults.fittedvalues ================================================================ `RLMResults.fittedvalues()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/robust_linear_model.html#RLMResults.fittedvalues) statsmodels statsmodels.tsa.arima_process.ArmaProcess.from_coeffs statsmodels.tsa.arima\_process.ArmaProcess.from\_coeffs ======================================================= `classmethod ArmaProcess.from_coeffs(arcoefs=None, macoefs=None, nobs=100)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_process.html#ArmaProcess.from_coeffs) Convenience function to create ArmaProcess from ARMA representation \| Parameters: \| * arcoefs (array-like, optional) – Coefficient for autoregressive lag polynomial, not including zero lag. The sign is inverted to conform to the usual time series representation of an ARMA process in statistics. See the class docstring for more information. * macoefs (array-like, optional) – Coefficient for moving-average lag polynomial, excluding zero lag * nobs (int, optional) – Length of simulated time series. Used, for example, if a sample is generated. \| #### Examples ``` >>> arparams = [.75, -.25] >>> maparams = [.65, .35] >>> arma_process = sm.tsa.ArmaProcess.from_coeffs(ar, ma) >>> arma_process.isstationary True >>> arma_process.isinvertible True ```	programming_docs
statsmodels statsmodels.tsa.statespace.sarimax.SARIMAX.information statsmodels.tsa.statespace.sarimax.SARIMAX.information ====================================================== `SARIMAX.information(params)` Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.genmod.generalized_estimating_equations.GEEMargins.tvalues statsmodels.genmod.generalized\_estimating\_equations.GEEMargins.tvalues ======================================================================== `GEEMargins.tvalues()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_estimating_equations.html#GEEMargins.tvalues) statsmodels statsmodels.sandbox.distributions.extras.SkewNorm2_gen.logpdf statsmodels.sandbox.distributions.extras.SkewNorm2\_gen.logpdf ============================================================== `SkewNorm2_gen.logpdf(x, args, kwds)` Log of the probability density function at x of the given RV. This uses a more numerically accurate calculation if available. \| Parameters: \| x (array\_like) – quantiles * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| logpdf – Log of the probability density function evaluated at x \| \| Return type: \| array\_like \| statsmodels statsmodels.genmod.families.family.Gaussian.starting_mu statsmodels.genmod.families.family.Gaussian.starting\_mu ======================================================== `Gaussian.starting_mu(y)` Starting value for mu in the IRLS algorithm. \| Parameters: \| y (array) – The untransformed response variable. \| \| Returns: \| mu\_0 – The first guess on the transformed response variable. \| \| Return type: \| array \| #### Notes \[\mu\_0 = (Y + \overline{Y})/2\] Only the Binomial family takes a different initial value. statsmodels statsmodels.discrete.count_model.ZeroInflatedPoisson.hessian statsmodels.discrete.count\_model.ZeroInflatedPoisson.hessian ============================================================= `ZeroInflatedPoisson.hessian(params)` Generic Zero Inflated model Hessian matrix of the loglikelihood \| Parameters: \| params (array-like) – The parameters of the model \| \| Returns: \| hess – The Hessian, second derivative of loglikelihood function, evaluated at `params` \| \| Return type: \| ndarray, (k\_vars, k\_vars) \| #### Notes statsmodels statsmodels.sandbox.distributions.extras.NormExpan_gen.rvs statsmodels.sandbox.distributions.extras.NormExpan\_gen.rvs =========================================================== `NormExpan_gen.rvs(args, kwds)` Random variates of given type. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information). * loc (array\_like, optional) – Location parameter (default=0). * scale (array\_like, optional) – Scale parameter (default=1). * size (int or tuple of ints, optional) – Defining number of random variates (default is 1). * random\_state (None or int or `np.random.RandomState` instance, optional) – If int or RandomState, use it for drawing the random variates. If None, rely on `self.random_state`. Default is None. \| \| Returns: \| rvs – Random variates of given `size`. \| \| Return type: \| ndarray or scalar \| statsmodels statsmodels.graphics.regressionplots.plot_leverage_resid2 statsmodels.graphics.regressionplots.plot\_leverage\_resid2 =========================================================== `statsmodels.graphics.regressionplots.plot_leverage_resid2(results, alpha=0.05, ax=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/graphics/regressionplots.html#plot_leverage_resid2) Plots leverage statistics vs. normalized residuals squared \| Parameters: \| results (results instance) – A regression results instance * alpha (float) – Specifies the cut-off for large-standardized residuals. Residuals are assumed to be distributed N(0, 1) with alpha=alpha. * ax (Axes instance) – Matplotlib Axes instance \| \| Returns: \| fig – A matplotlib figure instance. \| \| Return type: \| matplotlib Figure \| statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.simulate statsmodels.regression.recursive\_ls.RecursiveLSResults.simulate ================================================================ `RecursiveLSResults.simulate(nsimulations, measurement_shocks=None, state_shocks=None, initial_state=None)` Simulate a new time series following the state space model \| Parameters: \| * nsimulations (int) – The number of observations to simulate. If the model is time-invariant this can be any number. If the model is time-varying, then this number must be less than or equal to the number * measurement\_shocks (array\_like, optional) – If specified, these are the shocks to the measurement equation, $\varepsilon\_t$. If unspecified, these are automatically generated using a pseudo-random number generator. If specified, must be shaped `nsimulations` x `k_endog`, where `k_endog` is the same as in the state space model. * state\_shocks (array\_like, optional) – If specified, these are the shocks to the state equation, $\eta\_t$. If unspecified, these are automatically generated using a pseudo-random number generator. If specified, must be shaped `nsimulations` x `k_posdef` where `k_posdef` is the same as in the state space model. * initial\_state (array\_like, optional) – If specified, this is the state vector at time zero, which should be shaped (`k_states` x 1), where `k_states` is the same as in the state space model. If unspecified, but the model has been initialized, then that initialization is used. If unspecified and the model has not been initialized, then a vector of zeros is used. Note that this is not included in the returned `simulated_states` array. \| \| Returns: \| simulated\_obs – An (nsimulations x k\_endog) array of simulated observations. \| \| Return type: \| array \| statsmodels statsmodels.tsa.statespace.structural.UnobservedComponentsResults.tvalues statsmodels.tsa.statespace.structural.UnobservedComponentsResults.tvalues ========================================================================= `UnobservedComponentsResults.tvalues()` Return the t-statistic for a given parameter estimate. statsmodels statsmodels.stats.diagnostic.linear_rainbow statsmodels.stats.diagnostic.linear\_rainbow ============================================ `statsmodels.stats.diagnostic.linear_rainbow(res, frac=0.5)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/stats/diagnostic.html#linear_rainbow) Rainbow test for linearity The Null hypothesis is that the regression is correctly modelled as linear. The alternative for which the power might be large are convex, check \| Parameters: \| res (Result instance) – \| \| Returns: \| * fstat (float) – test statistic based of F test * pvalue (float) – pvalue of the test \| statsmodels statsmodels.discrete.discrete_model.LogitResults.f_test statsmodels.discrete.discrete\_model.LogitResults.f\_test ========================================================= `LogitResults.f_test(r_matrix, cov_p=None, scale=1.0, invcov=None)` Compute the F-test for a joint linear hypothesis. This is a special case of `wald_test` that always uses the F distribution. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length k row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> A = np.identity(len(results.params)) >>> A = A[1:,:] ``` This tests that each coefficient is jointly statistically significantly different from zero. ``` >>> print(results.f_test(A)) <F test: F=array([[ 330.28533923]]), p=4.984030528700946e-10, df_denom=9, df_num=6> ``` Compare this to ``` >>> results.fvalue 330.2853392346658 >>> results.f_pvalue 4.98403096572e-10 ``` ``` >>> B = np.array(([0,0,1,-1,0,0,0],[0,0,0,0,0,1,-1])) ``` This tests that the coefficient on the 2nd and 3rd regressors are equal and jointly that the coefficient on the 5th and 6th regressors are equal. ``` >>> print(results.f_test(B)) <F test: F=array([[ 9.74046187]]), p=0.005605288531708235, df_denom=9, df_num=2> ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.datasets import longley >>> from statsmodels.formula.api import ols >>> dta = longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = '(GNPDEFL = GNP), (UNEMP = 2), (YEAR/1829 = 1)' >>> f_test = results.f_test(hypotheses) >>> print(f_test) <F test: F=array([[ 144.17976065]]), p=6.322026217355609e-08, df_denom=9, df_num=3> ``` See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`wald_test`](statsmodels.discrete.discrete_model.logitresults.wald_test#statsmodels.discrete.discrete_model.LogitResults.wald_test "statsmodels.discrete.discrete_model.LogitResults.wald_test"), [`t_test`](statsmodels.discrete.discrete_model.logitresults.t_test#statsmodels.discrete.discrete_model.LogitResults.t_test "statsmodels.discrete.discrete_model.LogitResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.sandbox.distributions.transformed.lognormalg statsmodels.sandbox.distributions.transformed.lognormalg ======================================================== `statsmodels.sandbox.distributions.transformed.lognormalg = <statsmodels.sandbox.distributions.transformed.Transf_gen object>` a class for non-linear monotonic transformation of a continuous random variable statsmodels statsmodels.sandbox.distributions.extras.pdf_moments_st statsmodels.sandbox.distributions.extras.pdf\_moments\_st ========================================================= `statsmodels.sandbox.distributions.extras.pdf_moments_st(cnt)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/distributions/extras.html#pdf_moments_st) Return the Gaussian expanded pdf function given the list of central moments (first one is mean). version of scipy.stats, any changes ? the scipy.stats version has a bug and returns normal distribution statsmodels statsmodels.genmod.generalized_estimating_equations.GEEResults.conf_int statsmodels.genmod.generalized\_estimating\_equations.GEEResults.conf\_int ========================================================================== `GEEResults.conf_int(alpha=0.05, cols=None, cov_type=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_estimating_equations.html#GEEResults.conf_int) Returns confidence intervals for the fitted parameters. \| Parameters: \| * alpha (float, optional) – The `alpha` level for the confidence interval. i.e., The default `alpha` = .05 returns a 95% confidence interval. * cols (array-like, optional) – `cols` specifies which confidence intervals to return * cov\_type (string) – The covariance type used for computing standard errors; must be one of ‘robust’, ‘naive’, and ‘bias reduced’. See `GEE` for details. \| #### Notes The confidence interval is based on the Gaussian distribution. statsmodels statsmodels.discrete.discrete_model.GeneralizedPoissonResults.remove_data statsmodels.discrete.discrete\_model.GeneralizedPoissonResults.remove\_data =========================================================================== `GeneralizedPoissonResults.remove_data()` remove data arrays, all nobs arrays from result and model This reduces the size of the instance, so it can be pickled with less memory. Currently tested for use with predict from an unpickled results and model instance. Warning Since data and some intermediate results have been removed calculating new statistics that require them will raise exceptions. The exception will occur the first time an attribute is accessed that has been set to None. Not fully tested for time series models, tsa, and might delete too much for prediction or not all that would be possible. The lists of arrays to delete are maintained as attributes of the result and model instance, except for cached values. These lists could be changed before calling remove\_data. The attributes to remove are named in: `model._data_attr : arrays attached to both the model instance` and the results instance with the same attribute name. `result.data_in_cache : arrays that may exist as values in` result.\_cache (TODO : should privatize name) `result._data_attr_model : arrays attached to the model` instance but not to the results instance statsmodels statsmodels.tsa.statespace.varmax.VARMAXResults.cov_params_approx statsmodels.tsa.statespace.varmax.VARMAXResults.cov\_params\_approx =================================================================== `VARMAXResults.cov_params_approx()` (array) The variance / covariance matrix. Computed using the numerical Hessian approximated by complex step or finite differences methods. statsmodels statsmodels.nonparametric.kernel_regression.KernelCensoredReg.r_squared statsmodels.nonparametric.kernel\_regression.KernelCensoredReg.r\_squared ========================================================================= `KernelCensoredReg.r_squared()` Returns the R-Squared for the nonparametric regression. #### Notes For more details see p.45 in [2] The R-Squared is calculated by: \[R^{2}=\frac{\left[\sum\_{i=1}^{n} (Y\_{i}-\bar{y})(\hat{Y\_{i}}-\bar{y}\right]^{2}}{\sum\_{i=1}^{n} (Y\_{i}-\bar{y})^{2}\sum\_{i=1}^{n}(\hat{Y\_{i}}-\bar{y})^{2}},\] where $\hat{Y\_{i}}$ is the mean calculated in `fit` at the exog points. statsmodels statsmodels.regression.linear_model.GLS.loglike statsmodels.regression.linear\_model.GLS.loglike ================================================ `GLS.loglike(params)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#GLS.loglike) Returns the value of the Gaussian log-likelihood function at params. Given the whitened design matrix, the log-likelihood is evaluated at the parameter vector `params` for the dependent variable `endog`. \| Parameters: \| params (array-like) – The parameter estimates \| \| Returns: \| loglike – The value of the log-likelihood function for a GLS Model. \| \| Return type: \| float \| #### Notes The log-likelihood function for the normal distribution is \[-\frac{n}{2}\log\left(\left(Y-\hat{Y}\right)^{\prime}\left(Y-\hat{Y}\right)\right)-\frac{n}{2}\left(1+\log\left(\frac{2\pi}{n}\right)\right)-\frac{1}{2}\log\left(\left\|\Sigma\right\|\right)\] Y and Y-hat are whitened. statsmodels statsmodels.genmod.families.links.CDFLink.inverse statsmodels.genmod.families.links.CDFLink.inverse ================================================= `CDFLink.inverse(z)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#CDFLink.inverse) The inverse of the CDF link \| Parameters: \| z (array-like) – The value of the inverse of the link function at `p` \| \| Returns: \| p – Mean probabilities. The value of the inverse of CDF link of `z` \| \| Return type: \| array \| #### Notes g^(-1)(`z`) = `dbn`.cdf(`z`) statsmodels statsmodels.regression.linear_model.OLSResults.fittedvalues statsmodels.regression.linear\_model.OLSResults.fittedvalues ============================================================ `OLSResults.fittedvalues()` statsmodels statsmodels.tools.eval_measures.maxabs statsmodels.tools.eval\_measures.maxabs ======================================= `statsmodels.tools.eval_measures.maxabs(x1, x2, axis=0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tools/eval_measures.html#maxabs) maximum absolute error \| Parameters: \| * x2 (x1,) – The performance measure depends on the difference between these two arrays. * axis (int) – axis along which the summary statistic is calculated \| \| Returns: \| maxabs – maximum absolute difference along given axis. \| \| Return type: \| ndarray or float \| #### Notes If `x1` and `x2` have different shapes, then they need to broadcast. This uses `numpy.asanyarray` to convert the input. Whether this is the desired result or not depends on the array subclass. statsmodels statsmodels.stats.power.FTestAnovaPower.solve_power statsmodels.stats.power.FTestAnovaPower.solve\_power ==================================================== `FTestAnovaPower.solve_power(effect_size=None, nobs=None, alpha=None, power=None, k_groups=2)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/power.html#FTestAnovaPower.solve_power) solve for any one parameter of the power of a F-test for the one sample F-test the keywords are: effect\_size, nobs, alpha, power Exactly one needs to be `None`, all others need numeric values. \| Parameters: \| * effect\_size (float) – standardized effect size, mean divided by the standard deviation. effect size has to be positive. * nobs (int or float) – sample size, number of observations. * alpha (float in interval (0,1)) – significance level, e.g. 0.05, is the probability of a type I error, that is wrong rejections if the Null Hypothesis is true. * power (float in interval (0,1)) – power of the test, e.g. 0.8, is one minus the probability of a type II error. Power is the probability that the test correctly rejects the Null Hypothesis if the Alternative Hypothesis is true. \| \| Returns: \| value – The value of the parameter that was set to None in the call. The value solves the power equation given the remainding parameters. \| \| Return type: \| float \| #### Notes The function uses scipy.optimize for finding the value that satisfies the power equation. It first uses `brentq` with a prior search for bounds. If this fails to find a root, `fsolve` is used. If `fsolve` also fails, then, for `alpha`, `power` and `effect_size`, `brentq` with fixed bounds is used. However, there can still be cases where this fails.	programming_docs
statsmodels statsmodels.stats.weightstats.ztost statsmodels.stats.weightstats.ztost =================================== `statsmodels.stats.weightstats.ztost(x1, low, upp, x2=None, usevar='pooled', ddof=1.0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/weightstats.html#ztost) Equivalence test based on normal distribution \| Parameters: \| * x1 (array\_like or None) – one sample or first sample for 2 independent samples * upp (low,) – equivalence interval low < m1 - m2 < upp * x1 – second sample for 2 independent samples test. If None, then a one-sample test is performed. * usevar (string, 'pooled') – If `pooled`, then the standard deviation of the samples is assumed to be the same. Only `pooled` is currently implemented. \| \| Returns: \| * pvalue (float) – pvalue of the non-equivalence test * t1, pv1 (tuple of floats) – test statistic and pvalue for lower threshold test * t2, pv2 (tuple of floats) – test statistic and pvalue for upper threshold test \| #### Notes checked only for 1 sample case statsmodels statsmodels.discrete.discrete_model.CountResults.set_null_options statsmodels.discrete.discrete\_model.CountResults.set\_null\_options ==================================================================== `CountResults.set_null_options(llnull=None, attach_results=True, *kwds)` set fit options for Null (constant-only) model This resets the cache for related attributes which is potentially fragile. This only sets the option, the null model is estimated when llnull is accessed, if llnull is not yet in cache. \| Parameters: \| llnull (None or float) – If llnull is not None, then the value will be directly assigned to the cached attribute “llnull”. * attach\_results (bool) – Sets an internal flag whether the results instance of the null model should be attached. By default without calling this method, thenull model results are not attached and only the loglikelihood value llnull is stored. * kwds (keyword arguments) – `kwds` are directly used as fit keyword arguments for the null model, overriding any provided defaults. \| \| Returns: \| \| \| Return type: \| no returns, modifies attributes of this instance \| statsmodels statsmodels.stats.contingency_tables.StratifiedTable.test_null_odds statsmodels.stats.contingency\_tables.StratifiedTable.test\_null\_odds ====================================================================== `StratifiedTable.test_null_odds(correction=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/contingency_tables.html#StratifiedTable.test_null_odds) Test that all tables have odds ratio equal to 1. This is the ‘Mantel-Haenszel’ test. \| Parameters: \| correction (boolean) – If True, use the continuity correction when calculating the test statistic. \| \| Returns: \| \| \| Return type: \| A bunch containing the chi^2 test statistic and p-value. \| statsmodels statsmodels.discrete.discrete_model.ProbitResults statsmodels.discrete.discrete\_model.ProbitResults ================================================== `class statsmodels.discrete.discrete_model.ProbitResults(model, mlefit, cov_type='nonrobust', cov_kwds=None, use_t=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#ProbitResults) A results class for Probit Model \| Parameters: \| * model (A DiscreteModel instance) – * params (array-like) – The parameters of a fitted model. * hessian (array-like) – The hessian of the fitted model. * scale (float) – A scale parameter for the covariance matrix. \| \| Returns: \| * \Attributes\** * aic (float) – Akaike information criterion. `-2(llf - p)` where `p` is the number of regressors including the intercept. bic (float) – Bayesian information criterion. `-2llf + ln(nobs)p` where `p` is the number of regressors including the intercept. * bse (array) – The standard errors of the coefficients. * df\_resid (float) – See model definition. * df\_model (float) – See model definition. * fitted\_values (array) – Linear predictor XB. * llf (float) – Value of the loglikelihood * llnull (float) – Value of the constant-only loglikelihood * llr (float) – Likelihood ratio chi-squared statistic; `-2(llnull - llf)` llr\_pvalue (float) – The chi-squared probability of getting a log-likelihood ratio statistic greater than llr. llr has a chi-squared distribution with degrees of freedom `df_model`. * prsquared (float) – McFadden’s pseudo-R-squared. `1 - (llf / llnull)` \| #### Methods \| \| \| \| --- \| --- \| \| [`aic`](statsmodels.discrete.discrete_model.probitresults.aic#statsmodels.discrete.discrete_model.ProbitResults.aic "statsmodels.discrete.discrete_model.ProbitResults.aic")() \| \| \| [`bic`](statsmodels.discrete.discrete_model.probitresults.bic#statsmodels.discrete.discrete_model.ProbitResults.bic "statsmodels.discrete.discrete_model.ProbitResults.bic")() \| \| \| [`bse`](statsmodels.discrete.discrete_model.probitresults.bse#statsmodels.discrete.discrete_model.ProbitResults.bse "statsmodels.discrete.discrete_model.ProbitResults.bse")() \| \| \| [`conf_int`](statsmodels.discrete.discrete_model.probitresults.conf_int#statsmodels.discrete.discrete_model.ProbitResults.conf_int "statsmodels.discrete.discrete_model.ProbitResults.conf_int")([alpha, cols, method]) \| Returns the confidence interval of the fitted parameters. \| \| [`cov_params`](statsmodels.discrete.discrete_model.probitresults.cov_params#statsmodels.discrete.discrete_model.ProbitResults.cov_params "statsmodels.discrete.discrete_model.ProbitResults.cov_params")([r\_matrix, column, scale, cov\_p, …]) \| Returns the variance/covariance matrix. \| \| [`f_test`](statsmodels.discrete.discrete_model.probitresults.f_test#statsmodels.discrete.discrete_model.ProbitResults.f_test "statsmodels.discrete.discrete_model.ProbitResults.f_test")(r\_matrix[, cov\_p, scale, invcov]) \| Compute the F-test for a joint linear hypothesis. \| \| [`fittedvalues`](statsmodels.discrete.discrete_model.probitresults.fittedvalues#statsmodels.discrete.discrete_model.ProbitResults.fittedvalues "statsmodels.discrete.discrete_model.ProbitResults.fittedvalues")() \| \| \| [`get_margeff`](statsmodels.discrete.discrete_model.probitresults.get_margeff#statsmodels.discrete.discrete_model.ProbitResults.get_margeff "statsmodels.discrete.discrete_model.ProbitResults.get_margeff")([at, method, atexog, dummy, count]) \| Get marginal effects of the fitted model. \| \| [`initialize`](statsmodels.discrete.discrete_model.probitresults.initialize#statsmodels.discrete.discrete_model.ProbitResults.initialize "statsmodels.discrete.discrete_model.ProbitResults.initialize")(model, params, \\kwd) \| \| \| [`llf`](statsmodels.discrete.discrete_model.probitresults.llf#statsmodels.discrete.discrete_model.ProbitResults.llf "statsmodels.discrete.discrete_model.ProbitResults.llf")() \| \| \| [`llnull`](statsmodels.discrete.discrete_model.probitresults.llnull#statsmodels.discrete.discrete_model.ProbitResults.llnull "statsmodels.discrete.discrete_model.ProbitResults.llnull")() \| \| \| [`llr`](statsmodels.discrete.discrete_model.probitresults.llr#statsmodels.discrete.discrete_model.ProbitResults.llr "statsmodels.discrete.discrete_model.ProbitResults.llr")() \| \| \| [`llr_pvalue`](statsmodels.discrete.discrete_model.probitresults.llr_pvalue#statsmodels.discrete.discrete_model.ProbitResults.llr_pvalue "statsmodels.discrete.discrete_model.ProbitResults.llr_pvalue")() \| \| \| [`load`](statsmodels.discrete.discrete_model.probitresults.load#statsmodels.discrete.discrete_model.ProbitResults.load "statsmodels.discrete.discrete_model.ProbitResults.load")(fname) \| load a pickle, (class method) \| \| [`normalized_cov_params`](statsmodels.discrete.discrete_model.probitresults.normalized_cov_params#statsmodels.discrete.discrete_model.ProbitResults.normalized_cov_params "statsmodels.discrete.discrete_model.ProbitResults.normalized_cov_params")() \| \| \| [`pred_table`](statsmodels.discrete.discrete_model.probitresults.pred_table#statsmodels.discrete.discrete_model.ProbitResults.pred_table "statsmodels.discrete.discrete_model.ProbitResults.pred_table")([threshold]) \| Prediction table \| \| [`predict`](statsmodels.discrete.discrete_model.probitresults.predict#statsmodels.discrete.discrete_model.ProbitResults.predict "statsmodels.discrete.discrete_model.ProbitResults.predict")([exog, transform]) \| Call self.model.predict with self.params as the first argument. \| \| [`prsquared`](statsmodels.discrete.discrete_model.probitresults.prsquared#statsmodels.discrete.discrete_model.ProbitResults.prsquared "statsmodels.discrete.discrete_model.ProbitResults.prsquared")() \| \| \| [`pvalues`](statsmodels.discrete.discrete_model.probitresults.pvalues#statsmodels.discrete.discrete_model.ProbitResults.pvalues "statsmodels.discrete.discrete_model.ProbitResults.pvalues")() \| \| \| [`remove_data`](statsmodels.discrete.discrete_model.probitresults.remove_data#statsmodels.discrete.discrete_model.ProbitResults.remove_data "statsmodels.discrete.discrete_model.ProbitResults.remove_data")() \| remove data arrays, all nobs arrays from result and model \| \| [`resid_dev`](statsmodels.discrete.discrete_model.probitresults.resid_dev#statsmodels.discrete.discrete_model.ProbitResults.resid_dev "statsmodels.discrete.discrete_model.ProbitResults.resid_dev")() \| Deviance residuals \| \| [`resid_generalized`](statsmodels.discrete.discrete_model.probitresults.resid_generalized#statsmodels.discrete.discrete_model.ProbitResults.resid_generalized "statsmodels.discrete.discrete_model.ProbitResults.resid_generalized")() \| Generalized residuals \| \| [`resid_pearson`](statsmodels.discrete.discrete_model.probitresults.resid_pearson#statsmodels.discrete.discrete_model.ProbitResults.resid_pearson "statsmodels.discrete.discrete_model.ProbitResults.resid_pearson")() \| Pearson residuals \| \| [`resid_response`](statsmodels.discrete.discrete_model.probitresults.resid_response#statsmodels.discrete.discrete_model.ProbitResults.resid_response "statsmodels.discrete.discrete_model.ProbitResults.resid_response")() \| The response residuals \| \| [`save`](statsmodels.discrete.discrete_model.probitresults.save#statsmodels.discrete.discrete_model.ProbitResults.save "statsmodels.discrete.discrete_model.ProbitResults.save")(fname[, remove\_data]) \| save a pickle of this instance \| \| [`set_null_options`](statsmodels.discrete.discrete_model.probitresults.set_null_options#statsmodels.discrete.discrete_model.ProbitResults.set_null_options "statsmodels.discrete.discrete_model.ProbitResults.set_null_options")([llnull, attach\_results]) \| set fit options for Null (constant-only) model \| \| [`summary`](statsmodels.discrete.discrete_model.probitresults.summary#statsmodels.discrete.discrete_model.ProbitResults.summary "statsmodels.discrete.discrete_model.ProbitResults.summary")([yname, xname, title, alpha, yname\_list]) \| Summarize the Regression Results \| \| [`summary2`](statsmodels.discrete.discrete_model.probitresults.summary2#statsmodels.discrete.discrete_model.ProbitResults.summary2 "statsmodels.discrete.discrete_model.ProbitResults.summary2")([yname, xname, title, alpha, …]) \| Experimental function to summarize regression results \| \| [`t_test`](statsmodels.discrete.discrete_model.probitresults.t_test#statsmodels.discrete.discrete_model.ProbitResults.t_test "statsmodels.discrete.discrete_model.ProbitResults.t_test")(r\_matrix[, cov\_p, scale, use\_t]) \| Compute a t-test for a each linear hypothesis of the form Rb = q \| \| [`t_test_pairwise`](statsmodels.discrete.discrete_model.probitresults.t_test_pairwise#statsmodels.discrete.discrete_model.ProbitResults.t_test_pairwise "statsmodels.discrete.discrete_model.ProbitResults.t_test_pairwise")(term\_name[, method, alpha, …]) \| perform pairwise t\_test with multiple testing corrected p-values \| \| [`tvalues`](statsmodels.discrete.discrete_model.probitresults.tvalues#statsmodels.discrete.discrete_model.ProbitResults.tvalues "statsmodels.discrete.discrete_model.ProbitResults.tvalues")() \| Return the t-statistic for a given parameter estimate. \| \| [`wald_test`](statsmodels.discrete.discrete_model.probitresults.wald_test#statsmodels.discrete.discrete_model.ProbitResults.wald_test "statsmodels.discrete.discrete_model.ProbitResults.wald_test")(r\_matrix[, cov\_p, scale, invcov, …]) \| Compute a Wald-test for a joint linear hypothesis. \| \| [`wald_test_terms`](statsmodels.discrete.discrete_model.probitresults.wald_test_terms#statsmodels.discrete.discrete_model.ProbitResults.wald_test_terms "statsmodels.discrete.discrete_model.ProbitResults.wald_test_terms")([skip\_single, …]) \| Compute a sequence of Wald tests for terms over multiple columns \| #### Attributes \| \| \| \| --- \| --- \| \| `use_t` \| \| statsmodels statsmodels.sandbox.regression.gmm.IVGMMResults.ssr statsmodels.sandbox.regression.gmm.IVGMMResults.ssr =================================================== `IVGMMResults.ssr()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/regression/gmm.html#IVGMMResults.ssr) statsmodels statsmodels.regression.linear_model.RegressionResults.save statsmodels.regression.linear\_model.RegressionResults.save =========================================================== `RegressionResults.save(fname, remove_data=False)` save a pickle of this instance \| Parameters: \| * fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. * remove\_data (bool) – If False (default), then the instance is pickled without changes. If True, then all arrays with length nobs are set to None before pickling. See the remove\_data method. In some cases not all arrays will be set to None. \| #### Notes If remove\_data is true and the model result does not implement a remove\_data method then this will raise an exception. statsmodels statsmodels.robust.scale.Huber statsmodels.robust.scale.Huber ============================== `class statsmodels.robust.scale.Huber(c=1.5, tol=1e-08, maxiter=30, norm=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/scale.html#Huber) Huber’s proposal 2 for estimating location and scale jointly. \| Parameters: \| * c (float, optional) – Threshold used in threshold for chi=psi\\2. Default value is 1.5. * tol (float, optional) – Tolerance for convergence. Default value is 1e-08. * maxiter (int, optional0) – Maximum number of iterations. Default value is 30. * norm ([statsmodels.robust.norms.RobustNorm](statsmodels.robust.norms.robustnorm#statsmodels.robust.norms.RobustNorm "statsmodels.robust.norms.RobustNorm"), optional) – A robust norm used in M estimator of location. If None, the location estimator defaults to a one-step fixed point version of the M-estimator using Huber’s T. * call – Return joint estimates of Huber’s scale and location. \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> chem_data = np.array([2.20, 2.20, 2.4, 2.4, 2.5, 2.7, 2.8, 2.9, 3.03, ... 3.03, 3.10, 3.37, 3.4, 3.4, 3.4, 3.5, 3.6, 3.7, 3.7, 3.7, 3.7, ... 3.77, 5.28, 28.95]) >>> sm.robust.scale.huber(chem_data) (array(3.2054980819923693), array(0.67365260010478967)) ``` #### Methods statsmodels statsmodels.tsa.arima_model.ARIMA.loglike_css statsmodels.tsa.arima\_model.ARIMA.loglike\_css =============================================== `ARIMA.loglike_css(params, set_sigma2=True)` Conditional Sum of Squares likelihood function. statsmodels statsmodels.sandbox.distributions.extras.NormExpan_gen.nnlf statsmodels.sandbox.distributions.extras.NormExpan\_gen.nnlf ============================================================ `NormExpan_gen.nnlf(theta, x)` Return negative loglikelihood function. #### Notes This is `-sum(log pdf(x, theta), axis=0)` where `theta` are the parameters (including loc and scale). statsmodels statsmodels.sandbox.sysreg.SUR.whiten statsmodels.sandbox.sysreg.SUR.whiten ===================================== `SUR.whiten(X)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/sysreg.html#SUR.whiten) SUR whiten method. \| Parameters: \| X (list of arrays) – Data to be whitened. \| \| Returns: \| * If X is the exogenous RHS of the system. * `np.dot(np.kron(cholsigmainv,np.eye(M)),np.diag(X))` * If X is the endogenous LHS of the system. \| statsmodels statsmodels.sandbox.regression.gmm.GMMResults.normalized_cov_params statsmodels.sandbox.regression.gmm.GMMResults.normalized\_cov\_params ===================================================================== `GMMResults.normalized_cov_params()` statsmodels statsmodels.regression.quantile_regression.QuantRegResults.wald_test statsmodels.regression.quantile\_regression.QuantRegResults.wald\_test ====================================================================== `QuantRegResults.wald_test(r_matrix, cov_p=None, scale=1.0, invcov=None, use_f=None)` Compute a Wald-test for a joint linear hypothesis. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. * use\_f (bool) – If True, then the F-distribution is used. If False, then the asymptotic distribution, chisquare is used. If use\_f is None, then the F distribution is used if the model specifies that use\_t is True. The test statistic is proportionally adjusted for the distribution by the number of constraints in the hypothesis. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`f_test`](statsmodels.regression.quantile_regression.quantregresults.f_test#statsmodels.regression.quantile_regression.QuantRegResults.f_test "statsmodels.regression.quantile_regression.QuantRegResults.f_test"), [`t_test`](statsmodels.regression.quantile_regression.quantregresults.t_test#statsmodels.regression.quantile_regression.QuantRegResults.t_test "statsmodels.regression.quantile_regression.QuantRegResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.tsa.arima_process.arma_generate_sample statsmodels.tsa.arima\_process.arma\_generate\_sample ===================================================== `statsmodels.tsa.arima_process.arma_generate_sample(ar, ma, nsample, sigma=1, distrvs=<built-in method randn of mtrand.RandomState object>, burnin=0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/arima_process.html#arma_generate_sample) Generate a random sample of an ARMA process \| Parameters: \| * ar (array\_like, 1d) – coefficient for autoregressive lag polynomial, including zero lag * ma (array\_like, 1d) – coefficient for moving-average lag polynomial, including zero lag * nsample (int) – length of simulated time series * sigma (float) – standard deviation of noise * distrvs (function, random number generator) – function that generates the random numbers, and takes sample size as argument default: np.random.randn TODO: change to size argument * burnin (integer) – Burn in observations at the generated and dropped from the beginning of the sample \| \| Returns: \| sample – sample of ARMA process given by ar, ma of length nsample \| \| Return type: \| array \| #### Notes As mentioned above, both the AR and MA components should include the coefficient on the zero-lag. This is typically 1. Further, due to the conventions used in signal processing used in signal.lfilter vs. conventions in statistics for ARMA processes, the AR parameters should have the opposite sign of what you might expect. See the examples below. #### Examples ``` >>> import numpy as np >>> np.random.seed(12345) >>> arparams = np.array([.75, -.25]) >>> maparams = np.array([.65, .35]) >>> ar = np.r_[1, -arparams] # add zero-lag and negate >>> ma = np.r_[1, maparams] # add zero-lag >>> y = sm.tsa.arma_generate_sample(ar, ma, 250) >>> model = sm.tsa.ARMA(y, (2, 2)).fit(trend='nc', disp=0) >>> model.params array([ 0.79044189, -0.23140636, 0.70072904, 0.40608028]) ```	programming_docs
statsmodels statsmodels.discrete.count_model.ZeroInflatedGeneralizedPoissonResults.set_null_options statsmodels.discrete.count\_model.ZeroInflatedGeneralizedPoissonResults.set\_null\_options ========================================================================================== `ZeroInflatedGeneralizedPoissonResults.set_null_options(llnull=None, attach_results=True, *kwds)` set fit options for Null (constant-only) model This resets the cache for related attributes which is potentially fragile. This only sets the option, the null model is estimated when llnull is accessed, if llnull is not yet in cache. \| Parameters: \| llnull (None or float) – If llnull is not None, then the value will be directly assigned to the cached attribute “llnull”. * attach\_results (bool) – Sets an internal flag whether the results instance of the null model should be attached. By default without calling this method, thenull model results are not attached and only the loglikelihood value llnull is stored. * kwds (keyword arguments) – `kwds` are directly used as fit keyword arguments for the null model, overriding any provided defaults. \| \| Returns: \| \| \| Return type: \| no returns, modifies attributes of this instance \| statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.resid_corr statsmodels.tsa.vector\_ar.var\_model.VARResults.resid\_corr ============================================================ `VARResults.resid_corr()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARResults.resid_corr) Centered residual correlation matrix statsmodels statsmodels.discrete.discrete_model.MultinomialResults.conf_int statsmodels.discrete.discrete\_model.MultinomialResults.conf\_int ================================================================= `MultinomialResults.conf_int(alpha=0.05, cols=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#MultinomialResults.conf_int) Returns the confidence interval of the fitted parameters. \| Parameters: \| * alpha (float, optional) – The significance level for the confidence interval. ie., The default `alpha` = .05 returns a 95% confidence interval. * cols (array-like, optional) – `cols` specifies which confidence intervals to return * method (string) – Not Implemented Yet Method to estimate the confidence\_interval. “Default” : uses self.bse which is based on inverse Hessian for MLE “hjjh” : “jac” : “boot-bse” “boot\_quant” “profile” \| \| Returns: \| conf\_int – Each row contains [lower, upper] limits of the confidence interval for the corresponding parameter. The first column contains all lower, the second column contains all upper limits. \| \| Return type: \| array \| #### Examples ``` >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> results.conf_int() array([[-5496529.48322745, -1467987.78596704], [ -177.02903529, 207.15277984], [ -0.1115811 , 0.03994274], [ -3.12506664, -0.91539297], [ -1.5179487 , -0.54850503], [ -0.56251721, 0.460309 ], [ 798.7875153 , 2859.51541392]]) ``` ``` >>> results.conf_int(cols=(2,3)) array([[-0.1115811 , 0.03994274], [-3.12506664, -0.91539297]]) ``` #### Notes The confidence interval is based on the standard normal distribution. Models wish to use a different distribution should overwrite this method. statsmodels statsmodels.tsa.statespace.structural.UnobservedComponents.filter statsmodels.tsa.statespace.structural.UnobservedComponents.filter ================================================================= `UnobservedComponents.filter(params, transformed=True, complex_step=False, cov_type=None, cov_kwds=None, return_ssm=False, results_class=None, results_wrapper_class=None, *kwargs)` Kalman filtering \| Parameters: \| params (array\_like) – Array of parameters at which to evaluate the loglikelihood function. * transformed (boolean, optional) – Whether or not `params` is already transformed. Default is True. * return\_ssm (boolean,optional) – Whether or not to return only the state space output or a full results object. Default is to return a full results object. * cov\_type (str, optional) – See `MLEResults.fit` for a description of covariance matrix types for results object. * cov\_kwds ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)") or None, optional) – See `MLEResults.get_robustcov_results` for a description required keywords for alternative covariance estimators * *\\kwargs* – Additional keyword arguments to pass to the Kalman filter. See `KalmanFilter.filter` for more details. \| statsmodels statsmodels.genmod.generalized_estimating_equations.GEEMargins.get_margeff statsmodels.genmod.generalized\_estimating\_equations.GEEMargins.get\_margeff ============================================================================= `GEEMargins.get_margeff(at='overall', method='dydx', atexog=None, dummy=False, count=False)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_estimating_equations.html#GEEMargins.get_margeff) statsmodels statsmodels.tsa.filters.cf_filter.cffilter statsmodels.tsa.filters.cf\_filter.cffilter =========================================== `statsmodels.tsa.filters.cf_filter.cffilter(X, low=6, high=32, drift=True)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/filters/cf_filter.html#cffilter) Christiano Fitzgerald asymmetric, random walk filter \| Parameters: \| * X (array-like) – 1 or 2d array to filter. If 2d, variables are assumed to be in columns. * low (float) – Minimum period of oscillations. Features below low periodicity are filtered out. Default is 6 for quarterly data, giving a 1.5 year periodicity. * high (float) – Maximum period of oscillations. Features above high periodicity are filtered out. Default is 32 for quarterly data, giving an 8 year periodicity. * drift (bool) – Whether or not to remove a trend from the data. The trend is estimated as np.arange(nobs)\(X[-1] - X[0])/(len(X)-1) \| \| Returns: \| cycle (array) – The features of `X` between periodicities given by low and high * trend (array) – The trend in the data with the cycles removed. \| #### Examples ``` >>> import statsmodels.api as sm >>> import pandas as pd >>> dta = sm.datasets.macrodata.load_pandas().data >>> index = pd.DatetimeIndex(start='1959Q1', end='2009Q4', freq='Q') >>> dta.set_index(index, inplace=True) ``` ``` >>> cf_cycles, cf_trend = sm.tsa.filters.cffilter(dta[["infl", "unemp"]]) ``` ``` >>> import matplotlib.pyplot as plt >>> fig, ax = plt.subplots() >>> cf_cycles.plot(ax=ax, style=['r--', 'b-']) >>> plt.show() ``` ([Source code](../plots/cff_plot.py), [png](../plots/cff_plot.png), [hires.png](../plots/cff_plot.hires.png), [pdf](../plots/cff_plot.pdf)) See also [`statsmodels.tsa.filters.bk_filter.bkfilter`](statsmodels.tsa.filters.bk_filter.bkfilter#statsmodels.tsa.filters.bk_filter.bkfilter "statsmodels.tsa.filters.bk_filter.bkfilter"), [`statsmodels.tsa.filters.hp_filter.hpfilter`](statsmodels.tsa.filters.hp_filter.hpfilter#statsmodels.tsa.filters.hp_filter.hpfilter "statsmodels.tsa.filters.hp_filter.hpfilter"), [`statsmodels.tsa.seasonal.seasonal_decompose`](statsmodels.tsa.seasonal.seasonal_decompose#statsmodels.tsa.seasonal.seasonal_decompose "statsmodels.tsa.seasonal.seasonal_decompose") statsmodels statsmodels.tsa.arima_model.ARIMAResults.t_test statsmodels.tsa.arima\_model.ARIMAResults.t\_test ================================================= `ARIMAResults.t_test(r_matrix, cov_p=None, scale=None, use_t=None)` Compute a t-test for a each linear hypothesis of the form Rb = q \| Parameters: \| * r\_matrix (array-like, str, tuple) – + array : If an array is given, a p x k 2d array or length k 1d array specifying the linear restrictions. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q). If q is given, can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – An optional `scale` to use. Default is the scale specified by the model fit. * use\_t (bool, optional) – If use\_t is None, then the default of the model is used. If use\_t is True, then the p-values are based on the t distribution. If use\_t is False, then the p-values are based on the normal distribution. \| \| Returns: \| res – The results for the test are attributes of this results instance. The available results have the same elements as the parameter table in `summary()`. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> r = np.zeros_like(results.params) >>> r[5:] = [1,-1] >>> print(r) [ 0. 0. 0. 0. 0. 1. -1.] ``` r tests that the coefficients on the 5th and 6th independent variable are the same. ``` >>> T_test = results.t_test(r) >>> print(T_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 -1829.2026 455.391 -4.017 0.003 -2859.368 -799.037 ============================================================================== >>> T_test.effect -1829.2025687192481 >>> T_test.sd 455.39079425193762 >>> T_test.tvalue -4.0167754636411717 >>> T_test.pvalue 0.0015163772380899498 ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.formula.api import ols >>> dta = sm.datasets.longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = 'GNPDEFL = GNP, UNEMP = 2, YEAR/1829 = 1' >>> t_test = results.t_test(hypotheses) >>> print(t_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 15.0977 84.937 0.178 0.863 -177.042 207.238 c1 -2.0202 0.488 -8.231 0.000 -3.125 -0.915 c2 1.0001 0.249 0.000 1.000 0.437 1.563 ============================================================================== ``` See also [`tvalues`](statsmodels.tsa.arima_model.arimaresults.tvalues#statsmodels.tsa.arima_model.ARIMAResults.tvalues "statsmodels.tsa.arima_model.ARIMAResults.tvalues") individual t statistics [`f_test`](statsmodels.tsa.arima_model.arimaresults.f_test#statsmodels.tsa.arima_model.ARIMAResults.f_test "statsmodels.tsa.arima_model.ARIMAResults.f_test") for F tests [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") statsmodels statsmodels.sandbox.regression.try_catdata.groupsstats_1d statsmodels.sandbox.regression.try\_catdata.groupsstats\_1d =========================================================== `statsmodels.sandbox.regression.try_catdata.groupsstats_1d(y, x, labelsunique)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/regression/try_catdata.html#groupsstats_1d) use ndimage to get fast mean and variance statsmodels statsmodels.genmod.families.family.Gamma.deviance statsmodels.genmod.families.family.Gamma.deviance ================================================= `Gamma.deviance(endog, mu, var_weights=1.0, freq_weights=1.0, scale=1.0)` The deviance function evaluated at (endog, mu, var\_weights, freq\_weights, scale) for the distribution. Deviance is usually defined as twice the loglikelihood ratio. \| Parameters: \| * endog (array-like) – The endogenous response variable * mu (array-like) – The inverse of the link function at the linear predicted values. * var\_weights (array-like) – 1d array of variance (analytic) weights. The default is 1. * freq\_weights (array-like) – 1d array of frequency weights. The default is 1. * scale (float, optional) – An optional scale argument. The default is 1. \| \| Returns: \| Deviance – The value of deviance function defined below. \| \| Return type: \| array \| #### Notes Deviance is defined \[D = 2\sum\_i (freq\\_weights\_i \* var\\_weights \* (llf(endog\_i, endog\_i) - llf(endog\_i, \mu\_i)))\] where y is the endogenous variable. The deviance functions are analytically defined for each family. Internally, we calculate deviance as: \[D = \sum\_i freq\\_weights\_i \* var\\_weights \* resid\\_dev\_i / scale\] statsmodels statsmodels.sandbox.sysreg.Sem2SLS statsmodels.sandbox.sysreg.Sem2SLS ================================== `class statsmodels.sandbox.sysreg.Sem2SLS(sys, indep_endog=None, instruments=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/sysreg.html#Sem2SLS) Two-Stage Least Squares for Simultaneous equations \| Parameters: \| * sys (list) – [endog1, exog1, endog2, exog2,…] It will be of length 2 x M, where M is the number of equations endog = exog. * indep\_endog ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)")) – A dictionary mapping the equation to the column numbers of the the independent endogenous regressors in each equation. It is assumed that the system is inputed as broken up into LHS and RHS. For now, the values of the dict have to be sequences. Note that the keys for the equations should be zero-indexed. * instruments (array) – Array of the exogenous independent variables. \| #### Notes This is unfinished, and the design should be refactored. Estimation is done by brute force and there is no exploitation of the structure of the system. #### Methods \| \| \| \| --- \| --- \| \| [`fit`](statsmodels.sandbox.sysreg.sem2sls.fit#statsmodels.sandbox.sysreg.Sem2SLS.fit "statsmodels.sandbox.sysreg.Sem2SLS.fit")() \| \| \| [`whiten`](statsmodels.sandbox.sysreg.sem2sls.whiten#statsmodels.sandbox.sysreg.Sem2SLS.whiten "statsmodels.sandbox.sysreg.Sem2SLS.whiten")(Y) \| Runs the first stage of the 2SLS. \| statsmodels statsmodels.tsa.statespace.kalman_smoother.KalmanSmoother.set_stability_method statsmodels.tsa.statespace.kalman\_smoother.KalmanSmoother.set\_stability\_method ================================================================================= `KalmanSmoother.set_stability_method(stability_method=None, *kwargs)` Set the numerical stability method The Kalman filter is a recursive algorithm that may in some cases suffer issues with numerical stability. The stability method controls what, if any, measures are taken to promote stability. \| Parameters: \| stability\_method (integer, optional) – Bitmask value to set the stability method to. See notes for details. * *\\kwargs* – Keyword arguments may be used to influence the stability method by setting individual boolean flags. See notes for details. \| #### Notes The stability method is defined by a collection of boolean flags, and is internally stored as a bitmask. The methods available are: STABILITY\_FORCE\_SYMMETRY = 0x01 If this flag is set, symmetry of the predicted state covariance matrix is enforced at each iteration of the filter, where each element is set to the average of the corresponding elements in the upper and lower triangle. If the bitmask is set directly via the `stability_method` argument, then the full method must be provided. If keyword arguments are used to set individual boolean flags, then the lowercase of the method must be used as an argument name, and the value is the desired value of the boolean flag (True or False). Note that the stability method may also be specified by directly modifying the class attributes which are defined similarly to the keyword arguments. The default stability method is `STABILITY_FORCE_SYMMETRY` #### Examples ``` >>> mod = sm.tsa.statespace.SARIMAX(range(10)) >>> mod.ssm.stability_method 1 >>> mod.ssm.stability_force_symmetry True >>> mod.ssm.stability_force_symmetry = False >>> mod.ssm.stability_method 0 ``` statsmodels statsmodels.miscmodels.count.PoissonOffsetGMLE.information statsmodels.miscmodels.count.PoissonOffsetGMLE.information ========================================================== `PoissonOffsetGMLE.information(params)` Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.sandbox.distributions.extras.ACSkewT_gen.rvs statsmodels.sandbox.distributions.extras.ACSkewT\_gen.rvs ========================================================= `ACSkewT_gen.rvs(args, kwds)` Random variates of given type. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information). * loc (array\_like, optional) – Location parameter (default=0). * scale (array\_like, optional) – Scale parameter (default=1). * size (int or tuple of ints, optional) – Defining number of random variates (default is 1). * random\_state (None or int or `np.random.RandomState` instance, optional) – If int or RandomState, use it for drawing the random variates. If None, rely on `self.random_state`. Default is None. \| \| Returns: \| rvs – Random variates of given `size`. \| \| Return type: \| ndarray or scalar \| statsmodels statsmodels.stats.contingency_tables.Table2x2.log_oddsratio_confint statsmodels.stats.contingency\_tables.Table2x2.log\_oddsratio\_confint ====================================================================== `Table2x2.log_oddsratio_confint(alpha=0.05, method='normal')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/contingency_tables.html#Table2x2.log_oddsratio_confint) A confidence level for the log odds ratio. \| Parameters: \| * alpha (float) – `1 - alpha` is the nominal coverage probability of the confidence interval. * method (string) – The method for producing the confidence interval. Currently must be ‘normal’ which uses the normal approximation. \| statsmodels statsmodels.genmod.generalized_linear_model.PredictionResults.t_test statsmodels.genmod.generalized\_linear\_model.PredictionResults.t\_test ======================================================================= `PredictionResults.t_test(value=0, alternative='two-sided')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/_prediction.html#PredictionResults.t_test) z- or t-test for hypothesis that mean is equal to value \| Parameters: \| * value (array\_like) – value under the null hypothesis * alternative (string) – ‘two-sided’, ‘larger’, ‘smaller’ \| \| Returns: \| * stat (ndarray) – test statistic * pvalue (ndarray) – p-value of the hypothesis test, the distribution is given by the attribute of the instance, specified in `__init__`. Default if not specified is the normal distribution. \|	programming_docs
statsmodels statsmodels.tsa.vector_ar.var_model.VAR.information statsmodels.tsa.vector\_ar.var\_model.VAR.information ===================================================== `VAR.information(params)` Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.regression.linear_model.OLS.get_distribution statsmodels.regression.linear\_model.OLS.get\_distribution ========================================================== `OLS.get_distribution(params, scale, exog=None, dist_class=None)` Returns a random number generator for the predictive distribution. \| Parameters: \| * params (array-like) – The model parameters (regression coefficients). * scale (scalar) – The variance parameter. * exog (array-like) – The predictor variable matrix. * dist\_class (class) – A random number generator class. Must take ‘loc’ and ‘scale’ as arguments and return a random number generator implementing an `rvs` method for simulating random values. Defaults to Gaussian. \| \| Returns: \| Frozen random number generator object with mean and variance determined by the fitted linear model. Use the `rvs` method to generate random values. \| \| Return type: \| gen \| #### Notes Due to the behavior of `scipy.stats.distributions objects`, the returned random number generator must be called with `gen.rvs(n)` where `n` is the number of observations in the data set used to fit the model. If any other value is used for `n`, misleading results will be produced. statsmodels statsmodels.sandbox.distributions.transformed.LogTransf_gen.expect statsmodels.sandbox.distributions.transformed.LogTransf\_gen.expect =================================================================== `LogTransf_gen.expect(func=None, args=(), loc=0, scale=1, lb=None, ub=None, conditional=False, *kwds)` Calculate expected value of a function with respect to the distribution. The expected value of a function `f(x)` with respect to a distribution `dist` is defined as: ``` ubound E[x] = Integral(f(x) dist.pdf(x)) lbound ``` \| Parameters: \| * func (callable, optional) – Function for which integral is calculated. Takes only one argument. The default is the identity mapping f(x) = x. * args (tuple, optional) – Shape parameters of the distribution. * loc (float, optional) – Location parameter (default=0). * scale (float, optional) – Scale parameter (default=1). * ub (lb,) – Lower and upper bound for integration. Default is set to the support of the distribution. * conditional (bool, optional) – If True, the integral is corrected by the conditional probability of the integration interval. The return value is the expectation of the function, conditional on being in the given interval. Default is False. * keyword arguments are passed to the integration routine. (Additional) – \| \| Returns: \| expect – The calculated expected value. \| \| Return type: \| float \| #### Notes The integration behavior of this function is inherited from `integrate.quad`. statsmodels statsmodels.regression.linear_model.OLS.score statsmodels.regression.linear\_model.OLS.score ============================================== `OLS.score(params, scale=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#OLS.score) Evaluate the score function at a given point. The score corresponds to the profile (concentrated) log-likelihood in which the scale parameter has been profiled out. \| Parameters: \| * params (array-like) – The parameter vector at which the score function is computed. * scale (float or None) – If None, return the profile (concentrated) log likelihood (profiled over the scale parameter), else return the log-likelihood using the given scale value. \| \| Returns: \| \| \| Return type: \| The score vector. \| statsmodels statsmodels.sandbox.distributions.transformed.SquareFunc statsmodels.sandbox.distributions.transformed.SquareFunc ======================================================== `class statsmodels.sandbox.distributions.transformed.SquareFunc` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/distributions/transformed.html#SquareFunc) class to hold quadratic function with inverse function and derivative using instance methods instead of class methods, if we want extension to parameterized function #### Methods \| \| \| \| --- \| --- \| \| [`derivminus`](statsmodels.sandbox.distributions.transformed.squarefunc.derivminus#statsmodels.sandbox.distributions.transformed.SquareFunc.derivminus "statsmodels.sandbox.distributions.transformed.SquareFunc.derivminus")(x) \| \| \| [`derivplus`](statsmodels.sandbox.distributions.transformed.squarefunc.derivplus#statsmodels.sandbox.distributions.transformed.SquareFunc.derivplus "statsmodels.sandbox.distributions.transformed.SquareFunc.derivplus")(x) \| \| \| [`inverseminus`](statsmodels.sandbox.distributions.transformed.squarefunc.inverseminus#statsmodels.sandbox.distributions.transformed.SquareFunc.inverseminus "statsmodels.sandbox.distributions.transformed.SquareFunc.inverseminus")(x) \| \| \| [`inverseplus`](statsmodels.sandbox.distributions.transformed.squarefunc.inverseplus#statsmodels.sandbox.distributions.transformed.SquareFunc.inverseplus "statsmodels.sandbox.distributions.transformed.SquareFunc.inverseplus")(x) \| \| \| [`squarefunc`](statsmodels.sandbox.distributions.transformed.squarefunc.squarefunc#statsmodels.sandbox.distributions.transformed.SquareFunc.squarefunc "statsmodels.sandbox.distributions.transformed.SquareFunc.squarefunc")(x) \| \| statsmodels statsmodels.discrete.discrete_model.BinaryResults.wald_test_terms statsmodels.discrete.discrete\_model.BinaryResults.wald\_test\_terms ==================================================================== `BinaryResults.wald_test_terms(skip_single=False, extra_constraints=None, combine_terms=None)` Compute a sequence of Wald tests for terms over multiple columns This computes joined Wald tests for the hypothesis that all coefficients corresponding to a `term` are zero. `Terms` are defined by the underlying formula or by string matching. \| Parameters: \| * skip\_single (boolean) – If true, then terms that consist only of a single column and, therefore, refers only to a single parameter is skipped. If false, then all terms are included. * extra\_constraints (ndarray) – not tested yet * combine\_terms (None or list of strings) – Each string in this list is matched to the name of the terms or the name of the exogenous variables. All columns whose name includes that string are combined in one joint test. \| \| Returns: \| test\_result – The result instance contains `table` which is a pandas DataFrame with the test results: test statistic, degrees of freedom and pvalues. \| \| Return type: \| result instance \| #### Examples ``` >>> res_ols = ols("np.log(Days+1) ~ C(Duration, Sum)C(Weight, Sum)", data).fit() >>> res_ols.wald_test_terms() <class 'statsmodels.stats.contrast.WaldTestResults'> F P>F df constraint df denom Intercept 279.754525 2.37985521351e-22 1 51 C(Duration, Sum) 5.367071 0.0245738436636 1 51 C(Weight, Sum) 12.432445 3.99943118767e-05 2 51 C(Duration, Sum):C(Weight, Sum) 0.176002 0.83912310946 2 51 ``` ``` >>> res_poi = Poisson.from_formula("Days ~ C(Weight) C(Duration)", data).fit(cov_type='HC0') >>> wt = res_poi.wald_test_terms(skip_single=False, combine_terms=['Duration', 'Weight']) >>> print(wt) chi2 P>chi2 df constraint Intercept 15.695625 7.43960374424e-05 1 C(Weight) 16.132616 0.000313940174705 2 C(Duration) 1.009147 0.315107378931 1 C(Weight):C(Duration) 0.216694 0.897315972824 2 Duration 11.187849 0.010752286833 3 Weight 30.263368 4.32586407145e-06 4 ``` statsmodels statsmodels.discrete.discrete_model.MultinomialResults statsmodels.discrete.discrete\_model.MultinomialResults ======================================================= `class statsmodels.discrete.discrete_model.MultinomialResults(model, mlefit, cov_type='nonrobust', cov_kwds=None, use_t=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#MultinomialResults) A results class for multinomial data \| Parameters: \| * model (A DiscreteModel instance) – * params (array-like) – The parameters of a fitted model. * hessian (array-like) – The hessian of the fitted model. * scale (float) – A scale parameter for the covariance matrix. \| \| Returns: \| * \Attributes\** * aic (float) – Akaike information criterion. `-2(llf - p)` where `p` is the number of regressors including the intercept. bic (float) – Bayesian information criterion. `-2llf + ln(nobs)p` where `p` is the number of regressors including the intercept. * bse (array) – The standard errors of the coefficients. * df\_resid (float) – See model definition. * df\_model (float) – See model definition. * fitted\_values (array) – Linear predictor XB. * llf (float) – Value of the loglikelihood * llnull (float) – Value of the constant-only loglikelihood * llr (float) – Likelihood ratio chi-squared statistic; `-2(llnull - llf)` llr\_pvalue (float) – The chi-squared probability of getting a log-likelihood ratio statistic greater than llr. llr has a chi-squared distribution with degrees of freedom `df_model`. * prsquared (float) – McFadden’s pseudo-R-squared. `1 - (llf / llnull)` \| #### Methods \| \| \| \| --- \| --- \| \| [`aic`](statsmodels.discrete.discrete_model.multinomialresults.aic#statsmodels.discrete.discrete_model.MultinomialResults.aic "statsmodels.discrete.discrete_model.MultinomialResults.aic")() \| \| \| [`bic`](statsmodels.discrete.discrete_model.multinomialresults.bic#statsmodels.discrete.discrete_model.MultinomialResults.bic "statsmodels.discrete.discrete_model.MultinomialResults.bic")() \| \| \| [`bse`](statsmodels.discrete.discrete_model.multinomialresults.bse#statsmodels.discrete.discrete_model.MultinomialResults.bse "statsmodels.discrete.discrete_model.MultinomialResults.bse")() \| \| \| [`conf_int`](statsmodels.discrete.discrete_model.multinomialresults.conf_int#statsmodels.discrete.discrete_model.MultinomialResults.conf_int "statsmodels.discrete.discrete_model.MultinomialResults.conf_int")([alpha, cols]) \| Returns the confidence interval of the fitted parameters. \| \| [`cov_params`](statsmodels.discrete.discrete_model.multinomialresults.cov_params#statsmodels.discrete.discrete_model.MultinomialResults.cov_params "statsmodels.discrete.discrete_model.MultinomialResults.cov_params")([r\_matrix, column, scale, cov\_p, …]) \| Returns the variance/covariance matrix. \| \| [`f_test`](statsmodels.discrete.discrete_model.multinomialresults.f_test#statsmodels.discrete.discrete_model.MultinomialResults.f_test "statsmodels.discrete.discrete_model.MultinomialResults.f_test")(r\_matrix[, cov\_p, scale, invcov]) \| Compute the F-test for a joint linear hypothesis. \| \| [`fittedvalues`](statsmodels.discrete.discrete_model.multinomialresults.fittedvalues#statsmodels.discrete.discrete_model.MultinomialResults.fittedvalues "statsmodels.discrete.discrete_model.MultinomialResults.fittedvalues")() \| \| \| [`get_margeff`](statsmodels.discrete.discrete_model.multinomialresults.get_margeff#statsmodels.discrete.discrete_model.MultinomialResults.get_margeff "statsmodels.discrete.discrete_model.MultinomialResults.get_margeff")([at, method, atexog, dummy, count]) \| Get marginal effects of the fitted model. \| \| [`initialize`](statsmodels.discrete.discrete_model.multinomialresults.initialize#statsmodels.discrete.discrete_model.MultinomialResults.initialize "statsmodels.discrete.discrete_model.MultinomialResults.initialize")(model, params, \\kwd) \| \| \| [`llf`](statsmodels.discrete.discrete_model.multinomialresults.llf#statsmodels.discrete.discrete_model.MultinomialResults.llf "statsmodels.discrete.discrete_model.MultinomialResults.llf")() \| \| \| [`llnull`](statsmodels.discrete.discrete_model.multinomialresults.llnull#statsmodels.discrete.discrete_model.MultinomialResults.llnull "statsmodels.discrete.discrete_model.MultinomialResults.llnull")() \| \| \| [`llr`](statsmodels.discrete.discrete_model.multinomialresults.llr#statsmodels.discrete.discrete_model.MultinomialResults.llr "statsmodels.discrete.discrete_model.MultinomialResults.llr")() \| \| \| [`llr_pvalue`](statsmodels.discrete.discrete_model.multinomialresults.llr_pvalue#statsmodels.discrete.discrete_model.MultinomialResults.llr_pvalue "statsmodels.discrete.discrete_model.MultinomialResults.llr_pvalue")() \| \| \| [`load`](statsmodels.discrete.discrete_model.multinomialresults.load#statsmodels.discrete.discrete_model.MultinomialResults.load "statsmodels.discrete.discrete_model.MultinomialResults.load")(fname) \| load a pickle, (class method) \| \| [`margeff`](statsmodels.discrete.discrete_model.multinomialresults.margeff#statsmodels.discrete.discrete_model.MultinomialResults.margeff "statsmodels.discrete.discrete_model.MultinomialResults.margeff")() \| \| \| [`normalized_cov_params`](statsmodels.discrete.discrete_model.multinomialresults.normalized_cov_params#statsmodels.discrete.discrete_model.MultinomialResults.normalized_cov_params "statsmodels.discrete.discrete_model.MultinomialResults.normalized_cov_params")() \| \| \| [`pred_table`](statsmodels.discrete.discrete_model.multinomialresults.pred_table#statsmodels.discrete.discrete_model.MultinomialResults.pred_table "statsmodels.discrete.discrete_model.MultinomialResults.pred_table")() \| Returns the J x J prediction table. \| \| [`predict`](statsmodels.discrete.discrete_model.multinomialresults.predict#statsmodels.discrete.discrete_model.MultinomialResults.predict "statsmodels.discrete.discrete_model.MultinomialResults.predict")([exog, transform]) \| Call self.model.predict with self.params as the first argument. \| \| [`prsquared`](statsmodels.discrete.discrete_model.multinomialresults.prsquared#statsmodels.discrete.discrete_model.MultinomialResults.prsquared "statsmodels.discrete.discrete_model.MultinomialResults.prsquared")() \| \| \| [`pvalues`](statsmodels.discrete.discrete_model.multinomialresults.pvalues#statsmodels.discrete.discrete_model.MultinomialResults.pvalues "statsmodels.discrete.discrete_model.MultinomialResults.pvalues")() \| \| \| [`remove_data`](statsmodels.discrete.discrete_model.multinomialresults.remove_data#statsmodels.discrete.discrete_model.MultinomialResults.remove_data "statsmodels.discrete.discrete_model.MultinomialResults.remove_data")() \| remove data arrays, all nobs arrays from result and model \| \| [`resid_misclassified`](statsmodels.discrete.discrete_model.multinomialresults.resid_misclassified#statsmodels.discrete.discrete_model.MultinomialResults.resid_misclassified "statsmodels.discrete.discrete_model.MultinomialResults.resid_misclassified")() \| Residuals indicating which observations are misclassified. \| \| [`save`](statsmodels.discrete.discrete_model.multinomialresults.save#statsmodels.discrete.discrete_model.MultinomialResults.save "statsmodels.discrete.discrete_model.MultinomialResults.save")(fname[, remove\_data]) \| save a pickle of this instance \| \| [`set_null_options`](statsmodels.discrete.discrete_model.multinomialresults.set_null_options#statsmodels.discrete.discrete_model.MultinomialResults.set_null_options "statsmodels.discrete.discrete_model.MultinomialResults.set_null_options")([llnull, attach\_results]) \| set fit options for Null (constant-only) model \| \| [`summary`](statsmodels.discrete.discrete_model.multinomialresults.summary#statsmodels.discrete.discrete_model.MultinomialResults.summary "statsmodels.discrete.discrete_model.MultinomialResults.summary")([yname, xname, title, alpha, yname\_list]) \| Summarize the Regression Results \| \| [`summary2`](statsmodels.discrete.discrete_model.multinomialresults.summary2#statsmodels.discrete.discrete_model.MultinomialResults.summary2 "statsmodels.discrete.discrete_model.MultinomialResults.summary2")([alpha, float\_format]) \| Experimental function to summarize regression results \| \| [`t_test`](statsmodels.discrete.discrete_model.multinomialresults.t_test#statsmodels.discrete.discrete_model.MultinomialResults.t_test "statsmodels.discrete.discrete_model.MultinomialResults.t_test")(r\_matrix[, cov\_p, scale, use\_t]) \| Compute a t-test for a each linear hypothesis of the form Rb = q \| \| [`t_test_pairwise`](statsmodels.discrete.discrete_model.multinomialresults.t_test_pairwise#statsmodels.discrete.discrete_model.MultinomialResults.t_test_pairwise "statsmodels.discrete.discrete_model.MultinomialResults.t_test_pairwise")(term\_name[, method, alpha, …]) \| perform pairwise t\_test with multiple testing corrected p-values \| \| [`tvalues`](statsmodels.discrete.discrete_model.multinomialresults.tvalues#statsmodels.discrete.discrete_model.MultinomialResults.tvalues "statsmodels.discrete.discrete_model.MultinomialResults.tvalues")() \| Return the t-statistic for a given parameter estimate. \| \| [`wald_test`](statsmodels.discrete.discrete_model.multinomialresults.wald_test#statsmodels.discrete.discrete_model.MultinomialResults.wald_test "statsmodels.discrete.discrete_model.MultinomialResults.wald_test")(r\_matrix[, cov\_p, scale, invcov, …]) \| Compute a Wald-test for a joint linear hypothesis. \| \| [`wald_test_terms`](statsmodels.discrete.discrete_model.multinomialresults.wald_test_terms#statsmodels.discrete.discrete_model.MultinomialResults.wald_test_terms "statsmodels.discrete.discrete_model.MultinomialResults.wald_test_terms")([skip\_single, …]) \| Compute a sequence of Wald tests for terms over multiple columns \| #### Attributes \| \| \| \| --- \| --- \| \| `use_t` \| \| statsmodels statsmodels.miscmodels.count.PoissonGMLE.loglikeobs statsmodels.miscmodels.count.PoissonGMLE.loglikeobs =================================================== `PoissonGMLE.loglikeobs(params)` statsmodels statsmodels.regression.linear_model.OLS.loglike statsmodels.regression.linear\_model.OLS.loglike ================================================ `OLS.loglike(params, scale=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#OLS.loglike) The likelihood function for the OLS model. \| Parameters: \| * params (array-like) – The coefficients with which to estimate the log-likelihood. * scale (float or None) – If None, return the profile (concentrated) log likelihood (profiled over the scale parameter), else return the log-likelihood using the given scale value. \| \| Returns: \| \| \| Return type: \| The likelihood function evaluated at params. \| statsmodels statsmodels.nonparametric.kernel_regression.KernelReg.cv_loo statsmodels.nonparametric.kernel\_regression.KernelReg.cv\_loo ============================================================== `KernelReg.cv_loo(bw, func)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/nonparametric/kernel_regression.html#KernelReg.cv_loo) The cross-validation function with leave-one-out estimator. \| Parameters: \| * bw (array\_like) – Vector of bandwidth values. * func (callable function) – Returns the estimator of g(x). Can be either `_est_loc_constant` (local constant) or `_est_loc_linear` (local\_linear). \| \| Returns: \| L – The value of the CV function. \| \| Return type: \| float \| #### Notes Calculates the cross-validation least-squares function. This function is minimized by compute\_bw to calculate the optimal value of `bw`. For details see p.35 in [2] \[CV(h)=n^{-1}\sum\_{i=1}^{n}(Y\_{i}-g\_{-i}(X\_{i}))^{2}\] where $g\_{-i}(X\_{i})$ is the leave-one-out estimator of g(X) and $h$ is the vector of bandwidths	programming_docs
statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.irf statsmodels.tsa.vector\_ar.var\_model.VARResults.irf ==================================================== `VARResults.irf(periods=10, var_decomp=None, var_order=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARResults.irf) Analyze impulse responses to shocks in system \| Parameters: \| * periods (int) – * var\_decomp (ndarray (k x k), lower triangular) – Must satisfy Omega = P P’, where P is the passed matrix. Defaults to Cholesky decomposition of Omega * var\_order (sequence) – Alternate variable order for Cholesky decomposition \| \| Returns: \| irf \| \| Return type: \| [IRAnalysis](statsmodels.tsa.vector_ar.irf.iranalysis#statsmodels.tsa.vector_ar.irf.IRAnalysis "statsmodels.tsa.vector_ar.irf.IRAnalysis") \| statsmodels statsmodels.tsa.statespace.mlemodel.MLEModel statsmodels.tsa.statespace.mlemodel.MLEModel ============================================ `class statsmodels.tsa.statespace.mlemodel.MLEModel(endog, k_states, exog=None, dates=None, freq=None, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/mlemodel.html#MLEModel) State space model for maximum likelihood estimation \| Parameters: \| endog (array\_like) – The observed time-series process $y$ * k\_states (int) – The dimension of the unobserved state process. * exog (array\_like, optional) – Array of exogenous regressors, shaped nobs x k. Default is no exogenous regressors. * dates (array-like of datetime, optional) – An array-like object of datetime objects. If a Pandas object is given for endog, it is assumed to have a DateIndex. * freq (str, optional) – The frequency of the time-series. A Pandas offset or ‘B’, ‘D’, ‘W’, ‘M’, ‘A’, or ‘Q’. This is optional if dates are given. * *\\kwargs* – Keyword arguments may be used to provide default values for state space matrices or for Kalman filtering options. See `Representation`, and `KalmanFilter` for more details. \| `ssm` KalmanFilter – Underlying state space representation. #### Notes This class wraps the state space model with Kalman filtering to add in functionality for maximum likelihood estimation. In particular, it adds the concept of updating the state space representation based on a defined set of parameters, through the `update` method or `updater` attribute (see below for more details on which to use when), and it adds a `fit` method which uses a numerical optimizer to select the parameters that maximize the likelihood of the model. The `start_params` `update` method must be overridden in the child class (and the `transform` and `untransform` methods, if needed). See also [`MLEResults`](statsmodels.tsa.statespace.mlemodel.mleresults#statsmodels.tsa.statespace.mlemodel.MLEResults "statsmodels.tsa.statespace.mlemodel.MLEResults"), [`statsmodels.tsa.statespace.kalman_filter.KalmanFilter`](statsmodels.tsa.statespace.kalman_filter.kalmanfilter#statsmodels.tsa.statespace.kalman_filter.KalmanFilter "statsmodels.tsa.statespace.kalman_filter.KalmanFilter"), [`statsmodels.tsa.statespace.representation.Representation`](statsmodels.tsa.statespace.representation.representation#statsmodels.tsa.statespace.representation.Representation "statsmodels.tsa.statespace.representation.Representation") #### Methods \| \| \| \| --- \| --- \| \| [`filter`](statsmodels.tsa.statespace.mlemodel.mlemodel.filter#statsmodels.tsa.statespace.mlemodel.MLEModel.filter "statsmodels.tsa.statespace.mlemodel.MLEModel.filter")(params[, transformed, complex\_step, …]) \| Kalman filtering \| \| [`fit`](statsmodels.tsa.statespace.mlemodel.mlemodel.fit#statsmodels.tsa.statespace.mlemodel.MLEModel.fit "statsmodels.tsa.statespace.mlemodel.MLEModel.fit")([start\_params, transformed, cov\_type, …]) \| Fits the model by maximum likelihood via Kalman filter. \| \| [`from_formula`](statsmodels.tsa.statespace.mlemodel.mlemodel.from_formula#statsmodels.tsa.statespace.mlemodel.MLEModel.from_formula "statsmodels.tsa.statespace.mlemodel.MLEModel.from_formula")(formula, data[, subset]) \| Not implemented for state space models \| \| [`hessian`](statsmodels.tsa.statespace.mlemodel.mlemodel.hessian#statsmodels.tsa.statespace.mlemodel.MLEModel.hessian "statsmodels.tsa.statespace.mlemodel.MLEModel.hessian")(params, \args, \\kwargs) \| Hessian matrix of the likelihood function, evaluated at the given parameters \| \| [`impulse_responses`](statsmodels.tsa.statespace.mlemodel.mlemodel.impulse_responses#statsmodels.tsa.statespace.mlemodel.MLEModel.impulse_responses "statsmodels.tsa.statespace.mlemodel.MLEModel.impulse_responses")(params[, steps, impulse, …]) \| Impulse response function \| \| [`information`](statsmodels.tsa.statespace.mlemodel.mlemodel.information#statsmodels.tsa.statespace.mlemodel.MLEModel.information "statsmodels.tsa.statespace.mlemodel.MLEModel.information")(params) \| Fisher information matrix of model \| \| [`initialize`](statsmodels.tsa.statespace.mlemodel.mlemodel.initialize#statsmodels.tsa.statespace.mlemodel.MLEModel.initialize "statsmodels.tsa.statespace.mlemodel.MLEModel.initialize")() \| Initialize (possibly re-initialize) a Model instance. \| \| [`initialize_approximate_diffuse`](statsmodels.tsa.statespace.mlemodel.mlemodel.initialize_approximate_diffuse#statsmodels.tsa.statespace.mlemodel.MLEModel.initialize_approximate_diffuse "statsmodels.tsa.statespace.mlemodel.MLEModel.initialize_approximate_diffuse")([variance]) \| \| \| [`initialize_known`](statsmodels.tsa.statespace.mlemodel.mlemodel.initialize_known#statsmodels.tsa.statespace.mlemodel.MLEModel.initialize_known "statsmodels.tsa.statespace.mlemodel.MLEModel.initialize_known")(initial\_state, …) \| \| \| [`initialize_statespace`](statsmodels.tsa.statespace.mlemodel.mlemodel.initialize_statespace#statsmodels.tsa.statespace.mlemodel.MLEModel.initialize_statespace "statsmodels.tsa.statespace.mlemodel.MLEModel.initialize_statespace")(\\kwargs) \| Initialize the state space representation \| \| [`initialize_stationary`](statsmodels.tsa.statespace.mlemodel.mlemodel.initialize_stationary#statsmodels.tsa.statespace.mlemodel.MLEModel.initialize_stationary "statsmodels.tsa.statespace.mlemodel.MLEModel.initialize_stationary")() \| \| \| [`loglike`](statsmodels.tsa.statespace.mlemodel.mlemodel.loglike#statsmodels.tsa.statespace.mlemodel.MLEModel.loglike "statsmodels.tsa.statespace.mlemodel.MLEModel.loglike")(params, \args, \\kwargs) \| Loglikelihood evaluation \| \| [`loglikeobs`](statsmodels.tsa.statespace.mlemodel.mlemodel.loglikeobs#statsmodels.tsa.statespace.mlemodel.MLEModel.loglikeobs "statsmodels.tsa.statespace.mlemodel.MLEModel.loglikeobs")(params[, transformed, complex\_step]) \| Loglikelihood evaluation \| \| [`observed_information_matrix`](statsmodels.tsa.statespace.mlemodel.mlemodel.observed_information_matrix#statsmodels.tsa.statespace.mlemodel.MLEModel.observed_information_matrix "statsmodels.tsa.statespace.mlemodel.MLEModel.observed_information_matrix")(params[, …]) \| Observed information matrix \| \| [`opg_information_matrix`](statsmodels.tsa.statespace.mlemodel.mlemodel.opg_information_matrix#statsmodels.tsa.statespace.mlemodel.MLEModel.opg_information_matrix "statsmodels.tsa.statespace.mlemodel.MLEModel.opg_information_matrix")(params[, …]) \| Outer product of gradients information matrix \| \| [`predict`](statsmodels.tsa.statespace.mlemodel.mlemodel.predict#statsmodels.tsa.statespace.mlemodel.MLEModel.predict "statsmodels.tsa.statespace.mlemodel.MLEModel.predict")(params[, exog]) \| After a model has been fit predict returns the fitted values. \| \| [`prepare_data`](statsmodels.tsa.statespace.mlemodel.mlemodel.prepare_data#statsmodels.tsa.statespace.mlemodel.MLEModel.prepare_data "statsmodels.tsa.statespace.mlemodel.MLEModel.prepare_data")() \| Prepare data for use in the state space representation \| \| [`score`](statsmodels.tsa.statespace.mlemodel.mlemodel.score#statsmodels.tsa.statespace.mlemodel.MLEModel.score "statsmodels.tsa.statespace.mlemodel.MLEModel.score")(params, \args, \\kwargs) \| Compute the score function at params. \| \| [`score_obs`](statsmodels.tsa.statespace.mlemodel.mlemodel.score_obs#statsmodels.tsa.statespace.mlemodel.MLEModel.score_obs "statsmodels.tsa.statespace.mlemodel.MLEModel.score_obs")(params[, method, transformed, …]) \| Compute the score per observation, evaluated at params \| \| [`set_conserve_memory`](statsmodels.tsa.statespace.mlemodel.mlemodel.set_conserve_memory#statsmodels.tsa.statespace.mlemodel.MLEModel.set_conserve_memory "statsmodels.tsa.statespace.mlemodel.MLEModel.set_conserve_memory")([conserve\_memory]) \| Set the memory conservation method \| \| [`set_filter_method`](statsmodels.tsa.statespace.mlemodel.mlemodel.set_filter_method#statsmodels.tsa.statespace.mlemodel.MLEModel.set_filter_method "statsmodels.tsa.statespace.mlemodel.MLEModel.set_filter_method")([filter\_method]) \| Set the filtering method \| \| [`set_inversion_method`](statsmodels.tsa.statespace.mlemodel.mlemodel.set_inversion_method#statsmodels.tsa.statespace.mlemodel.MLEModel.set_inversion_method "statsmodels.tsa.statespace.mlemodel.MLEModel.set_inversion_method")([inversion\_method]) \| Set the inversion method \| \| [`set_smoother_output`](statsmodels.tsa.statespace.mlemodel.mlemodel.set_smoother_output#statsmodels.tsa.statespace.mlemodel.MLEModel.set_smoother_output "statsmodels.tsa.statespace.mlemodel.MLEModel.set_smoother_output")([smoother\_output]) \| Set the smoother output \| \| [`set_stability_method`](statsmodels.tsa.statespace.mlemodel.mlemodel.set_stability_method#statsmodels.tsa.statespace.mlemodel.MLEModel.set_stability_method "statsmodels.tsa.statespace.mlemodel.MLEModel.set_stability_method")([stability\_method]) \| Set the numerical stability method \| \| [`simulate`](statsmodels.tsa.statespace.mlemodel.mlemodel.simulate#statsmodels.tsa.statespace.mlemodel.MLEModel.simulate "statsmodels.tsa.statespace.mlemodel.MLEModel.simulate")(params, nsimulations[, …]) \| Simulate a new time series following the state space model \| \| [`simulation_smoother`](statsmodels.tsa.statespace.mlemodel.mlemodel.simulation_smoother#statsmodels.tsa.statespace.mlemodel.MLEModel.simulation_smoother "statsmodels.tsa.statespace.mlemodel.MLEModel.simulation_smoother")([simulation\_output]) \| Retrieve a simulation smoother for the state space model. \| \| [`smooth`](statsmodels.tsa.statespace.mlemodel.mlemodel.smooth#statsmodels.tsa.statespace.mlemodel.MLEModel.smooth "statsmodels.tsa.statespace.mlemodel.MLEModel.smooth")(params[, transformed, complex\_step, …]) \| Kalman smoothing \| \| [`transform_jacobian`](statsmodels.tsa.statespace.mlemodel.mlemodel.transform_jacobian#statsmodels.tsa.statespace.mlemodel.MLEModel.transform_jacobian "statsmodels.tsa.statespace.mlemodel.MLEModel.transform_jacobian")(unconstrained[, …]) \| Jacobian matrix for the parameter transformation function \| \| [`transform_params`](statsmodels.tsa.statespace.mlemodel.mlemodel.transform_params#statsmodels.tsa.statespace.mlemodel.MLEModel.transform_params "statsmodels.tsa.statespace.mlemodel.MLEModel.transform_params")(unconstrained) \| Transform unconstrained parameters used by the optimizer to constrained parameters used in likelihood evaluation \| \| [`untransform_params`](statsmodels.tsa.statespace.mlemodel.mlemodel.untransform_params#statsmodels.tsa.statespace.mlemodel.MLEModel.untransform_params "statsmodels.tsa.statespace.mlemodel.MLEModel.untransform_params")(constrained) \| Transform constrained parameters used in likelihood evaluation to unconstrained parameters used by the optimizer \| \| [`update`](statsmodels.tsa.statespace.mlemodel.mlemodel.update#statsmodels.tsa.statespace.mlemodel.MLEModel.update "statsmodels.tsa.statespace.mlemodel.MLEModel.update")(params[, transformed, complex\_step]) \| Update the parameters of the model \| #### Attributes \| \| \| \| --- \| --- \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| \| \| `initial_variance` \| \| \| `initialization` \| \| \| `loglikelihood_burn` \| \| \| `param_names` \| (list of str) List of human readable parameter names (for parameters actually included in the model). \| \| `start_params` \| (array) Starting parameters for maximum likelihood estimation. \| \| `tolerance` \| \| statsmodels statsmodels.sandbox.regression.gmm.IVRegressionResults.uncentered_tss statsmodels.sandbox.regression.gmm.IVRegressionResults.uncentered\_tss ====================================================================== `IVRegressionResults.uncentered_tss()` statsmodels statsmodels.tsa.vector_ar.var_model.VAR.loglike statsmodels.tsa.vector\_ar.var\_model.VAR.loglike ================================================= `VAR.loglike(params)` Log-likelihood of model. statsmodels statsmodels.tsa.arima_model.ARIMAResults.arfreq statsmodels.tsa.arima\_model.ARIMAResults.arfreq ================================================ `ARIMAResults.arfreq()` Returns the frequency of the AR roots. This is the solution, x, to z = abs(z)\exp(2j\np.pi\x) where z are the roots. statsmodels statsmodels.tsa.statespace.mlemodel.MLEModel.prepare_data statsmodels.tsa.statespace.mlemodel.MLEModel.prepare\_data ========================================================== `MLEModel.prepare_data()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/statespace/mlemodel.html#MLEModel.prepare_data) Prepare data for use in the state space representation statsmodels statsmodels.genmod.families.family.InverseGaussian.loglike_obs statsmodels.genmod.families.family.InverseGaussian.loglike\_obs =============================================================== `InverseGaussian.loglike_obs(endog, mu, var_weights=1.0, scale=1.0)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/family.html#InverseGaussian.loglike_obs) The log-likelihood function for each observation in terms of the fitted mean response for the Inverse Gaussian distribution. \| Parameters: \| * endog (array) – Usually the endogenous response variable. * mu (array) – Usually but not always the fitted mean response variable. * var\_weights (array-like) – 1d array of variance (analytic) weights. The default is 1. * scale (float) – The scale parameter. The default is 1. \| \| Returns: \| ll\_i – The value of the loglikelihood evaluated at (endog, mu, var\_weights, scale) as defined below. \| \| Return type: \| float \| #### Notes \[ll\_i = -1/2 \* (var\\_weights\_i \* (endog\_i - \mu\_i)^2 / (scale \* endog\_i \* \mu\_i^2) + \ln(scale \* \endog\_i^3 / var\\_weights\_i) - \ln(2 \* \pi))\] statsmodels statsmodels.discrete.discrete_model.Probit statsmodels.discrete.discrete\_model.Probit =========================================== `class statsmodels.discrete.discrete_model.Probit(endog, exog, *kwargs)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#Probit) Binary choice Probit model \| Parameters: \| endog (array-like) – 1-d endogenous response variable. The dependent variable. * exog (array-like) – A nobs x k array where `nobs` is the number of observations and `k` is the number of regressors. An intercept is not included by default and should be added by the user. See `statsmodels.tools.add_constant`. * missing (str) – Available options are ‘none’, ‘drop’, and ‘raise’. If ‘none’, no nan checking is done. If ‘drop’, any observations with nans are dropped. If ‘raise’, an error is raised. Default is ‘none.’ \| `endog` array – A reference to the endogenous response variable `exog` array – A reference to the exogenous design. #### Methods \| \| \| \| --- \| --- \| \| [`cdf`](statsmodels.discrete.discrete_model.probit.cdf#statsmodels.discrete.discrete_model.Probit.cdf "statsmodels.discrete.discrete_model.Probit.cdf")(X) \| Probit (Normal) cumulative distribution function \| \| [`cov_params_func_l1`](statsmodels.discrete.discrete_model.probit.cov_params_func_l1#statsmodels.discrete.discrete_model.Probit.cov_params_func_l1 "statsmodels.discrete.discrete_model.Probit.cov_params_func_l1")(likelihood\_model, xopt, …) \| Computes cov\_params on a reduced parameter space corresponding to the nonzero parameters resulting from the l1 regularized fit. \| \| [`fit`](statsmodels.discrete.discrete_model.probit.fit#statsmodels.discrete.discrete_model.Probit.fit "statsmodels.discrete.discrete_model.Probit.fit")([start\_params, method, maxiter, …]) \| Fit the model using maximum likelihood. \| \| [`fit_regularized`](statsmodels.discrete.discrete_model.probit.fit_regularized#statsmodels.discrete.discrete_model.Probit.fit_regularized "statsmodels.discrete.discrete_model.Probit.fit_regularized")([start\_params, method, …]) \| Fit the model using a regularized maximum likelihood. \| \| [`from_formula`](statsmodels.discrete.discrete_model.probit.from_formula#statsmodels.discrete.discrete_model.Probit.from_formula "statsmodels.discrete.discrete_model.Probit.from_formula")(formula, data[, subset, drop\_cols]) \| Create a Model from a formula and dataframe. \| \| [`hessian`](statsmodels.discrete.discrete_model.probit.hessian#statsmodels.discrete.discrete_model.Probit.hessian "statsmodels.discrete.discrete_model.Probit.hessian")(params) \| Probit model Hessian matrix of the log-likelihood \| \| [`information`](statsmodels.discrete.discrete_model.probit.information#statsmodels.discrete.discrete_model.Probit.information "statsmodels.discrete.discrete_model.Probit.information")(params) \| Fisher information matrix of model \| \| [`initialize`](statsmodels.discrete.discrete_model.probit.initialize#statsmodels.discrete.discrete_model.Probit.initialize "statsmodels.discrete.discrete_model.Probit.initialize")() \| Initialize is called by statsmodels.model.LikelihoodModel.\_\_init\_\_ and should contain any preprocessing that needs to be done for a model. \| \| [`loglike`](statsmodels.discrete.discrete_model.probit.loglike#statsmodels.discrete.discrete_model.Probit.loglike "statsmodels.discrete.discrete_model.Probit.loglike")(params) \| Log-likelihood of probit model (i.e., the normal distribution). \| \| [`loglikeobs`](statsmodels.discrete.discrete_model.probit.loglikeobs#statsmodels.discrete.discrete_model.Probit.loglikeobs "statsmodels.discrete.discrete_model.Probit.loglikeobs")(params) \| Log-likelihood of probit model for each observation \| \| [`pdf`](statsmodels.discrete.discrete_model.probit.pdf#statsmodels.discrete.discrete_model.Probit.pdf "statsmodels.discrete.discrete_model.Probit.pdf")(X) \| Probit (Normal) probability density function \| \| [`predict`](statsmodels.discrete.discrete_model.probit.predict#statsmodels.discrete.discrete_model.Probit.predict "statsmodels.discrete.discrete_model.Probit.predict")(params[, exog, linear]) \| Predict response variable of a model given exogenous variables. \| \| [`score`](statsmodels.discrete.discrete_model.probit.score#statsmodels.discrete.discrete_model.Probit.score "statsmodels.discrete.discrete_model.Probit.score")(params) \| Probit model score (gradient) vector \| \| [`score_obs`](statsmodels.discrete.discrete_model.probit.score_obs#statsmodels.discrete.discrete_model.Probit.score_obs "statsmodels.discrete.discrete_model.Probit.score_obs")(params) \| Probit model Jacobian for each observation \| #### Attributes \| \| \| \| --- \| --- \| \| `endog_names` \| Names of endogenous variables \| \| `exog_names` \| Names of exogenous variables \| statsmodels statsmodels.regression.linear_model.GLSAR.whiten statsmodels.regression.linear\_model.GLSAR.whiten ================================================= `GLSAR.whiten(X)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/regression/linear_model.html#GLSAR.whiten) Whiten a series of columns according to an AR(p) covariance structure. This drops initial p observations. \| Parameters: \| X (array-like) – The data to be whitened, \| \| Returns: \| \| \| Return type: \| whitened array \|	programming_docs
statsmodels statsmodels.tsa.vector_ar.irf.IRAnalysis.plot_cum_effects statsmodels.tsa.vector\_ar.irf.IRAnalysis.plot\_cum\_effects ============================================================ `IRAnalysis.plot_cum_effects(orth=False, impulse=None, response=None, signif=0.05, plot_params=None, subplot_params=None, plot_stderr=True, stderr_type='asym', repl=1000, seed=None)` Plot cumulative impulse response functions \| Parameters: \| * orth (bool, default False) – Compute orthogonalized impulse responses * impulse (string or int) – variable providing the impulse * response (string or int) – variable affected by the impulse * signif (float (0 < signif < 1)) – Significance level for error bars, defaults to 95% CI * subplot\_params ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)")) – To pass to subplot plotting funcions. Example: if fonts are too big, pass {‘fontsize’ : 8} or some number to your taste. * plot\_params ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)")) – * plot\_stderr (bool, default True) – Plot standard impulse response error bands * stderr\_type (string) – ‘asym’: default, computes asymptotic standard errors ‘mc’: monte carlo standard errors (use rpl) * repl (int, default 1000) – Number of replications for monte carlo standard errors * seed (int) – np.random.seed for Monte Carlo replications \| statsmodels statsmodels.sandbox.regression.gmm.IVRegressionResults.t_test statsmodels.sandbox.regression.gmm.IVRegressionResults.t\_test ============================================================== `IVRegressionResults.t_test(r_matrix, cov_p=None, scale=None, use_t=None)` Compute a t-test for a each linear hypothesis of the form Rb = q \| Parameters: \| * r\_matrix (array-like, str, tuple) – + array : If an array is given, a p x k 2d array or length k 1d array specifying the linear restrictions. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q). If q is given, can be either a scalar or a length p row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – An optional `scale` to use. Default is the scale specified by the model fit. * use\_t (bool, optional) – If use\_t is None, then the default of the model is used. If use\_t is True, then the p-values are based on the t distribution. If use\_t is False, then the p-values are based on the normal distribution. \| \| Returns: \| res – The results for the test are attributes of this results instance. The available results have the same elements as the parameter table in `summary()`. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> r = np.zeros_like(results.params) >>> r[5:] = [1,-1] >>> print(r) [ 0. 0. 0. 0. 0. 1. -1.] ``` r tests that the coefficients on the 5th and 6th independent variable are the same. ``` >>> T_test = results.t_test(r) >>> print(T_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 -1829.2026 455.391 -4.017 0.003 -2859.368 -799.037 ============================================================================== >>> T_test.effect -1829.2025687192481 >>> T_test.sd 455.39079425193762 >>> T_test.tvalue -4.0167754636411717 >>> T_test.pvalue 0.0015163772380899498 ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.formula.api import ols >>> dta = sm.datasets.longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = 'GNPDEFL = GNP, UNEMP = 2, YEAR/1829 = 1' >>> t_test = results.t_test(hypotheses) >>> print(t_test) Test for Constraints ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ c0 15.0977 84.937 0.178 0.863 -177.042 207.238 c1 -2.0202 0.488 -8.231 0.000 -3.125 -0.915 c2 1.0001 0.249 0.000 1.000 0.437 1.563 ============================================================================== ``` See also [`tvalues`](statsmodels.sandbox.regression.gmm.ivregressionresults.tvalues#statsmodels.sandbox.regression.gmm.IVRegressionResults.tvalues "statsmodels.sandbox.regression.gmm.IVRegressionResults.tvalues") individual t statistics [`f_test`](statsmodels.sandbox.regression.gmm.ivregressionresults.f_test#statsmodels.sandbox.regression.gmm.IVRegressionResults.f_test "statsmodels.sandbox.regression.gmm.IVRegressionResults.f_test") for F tests [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") statsmodels statsmodels.sandbox.regression.gmm.IVRegressionResults.cov_params statsmodels.sandbox.regression.gmm.IVRegressionResults.cov\_params ================================================================== `IVRegressionResults.cov_params(r_matrix=None, column=None, scale=None, cov_p=None, other=None)` Returns the variance/covariance matrix. The variance/covariance matrix can be of a linear contrast of the estimates of params or all params multiplied by scale which will usually be an estimate of sigma^2. Scale is assumed to be a scalar. \| Parameters: \| * r\_matrix (array-like) – Can be 1d, or 2d. Can be used alone or with other. * column (array-like, optional) – Must be used on its own. Can be 0d or 1d see below. * scale (float, optional) – Can be specified or not. Default is None, which means that the scale argument is taken from the model. * other (array-like, optional) – Can be used when r\_matrix is specified. \| \| Returns: \| cov – covariance matrix of the parameter estimates or of linear combination of parameter estimates. See Notes. \| \| Return type: \| ndarray \| #### Notes (The below are assumed to be in matrix notation.) If no argument is specified returns the covariance matrix of a model `(scale)(X.T X)^(-1)` If contrast is specified it pre and post-multiplies as follows `(scale) r_matrix (X.T X)^(-1) r_matrix.T` If contrast and other are specified returns `(scale) * r_matrix (X.T X)^(-1) other.T` If column is specified returns `(scale) * (X.T X)^(-1)[column,column]` if column is 0d OR `(scale) * (X.T X)^(-1)[column][:,column]` if column is 1d statsmodels statsmodels.tsa.arima_model.ARIMAResults.save statsmodels.tsa.arima\_model.ARIMAResults.save ============================================== `ARIMAResults.save(fname, remove_data=False)` save a pickle of this instance \| Parameters: \| * fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. * remove\_data (bool) – If False (default), then the instance is pickled without changes. If True, then all arrays with length nobs are set to None before pickling. See the remove\_data method. In some cases not all arrays will be set to None. \| #### Notes If remove\_data is true and the model result does not implement a remove\_data method then this will raise an exception. statsmodels statsmodels.tsa.vector_ar.vecm.VECMResults.resid statsmodels.tsa.vector\_ar.vecm.VECMResults.resid ================================================= `VECMResults.resid()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/vecm.html#VECMResults.resid) Return the difference between observed and fitted values. \| Returns: \| resid – The residuals. \| \| Return type: \| array (nobs x neqs) \| statsmodels statsmodels.discrete.discrete_model.GeneralizedPoissonResults.llf statsmodels.discrete.discrete\_model.GeneralizedPoissonResults.llf ================================================================== `GeneralizedPoissonResults.llf()` statsmodels statsmodels.tsa.holtwinters.SimpleExpSmoothing.loglike statsmodels.tsa.holtwinters.SimpleExpSmoothing.loglike ====================================================== `SimpleExpSmoothing.loglike(params)` Log-likelihood of model. statsmodels statsmodels.genmod.generalized_linear_model.GLM.score statsmodels.genmod.generalized\_linear\_model.GLM.score ======================================================= `GLM.score(params, scale=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_linear_model.html#GLM.score) score, first derivative of the loglikelihood function \| Parameters: \| * params (ndarray) – parameter at which score is evaluated * scale (None or float) – If scale is None, then the default scale will be calculated. Default scale is defined by `self.scaletype` and set in fit. If scale is not None, then it is used as a fixed scale. \| \| Returns: \| score – The first derivative of the loglikelihood function calculated as the sum of `score_obs` \| \| Return type: \| ndarray\_1d \| statsmodels statsmodels.regression.quantile_regression.QuantRegResults.t_test_pairwise statsmodels.regression.quantile\_regression.QuantRegResults.t\_test\_pairwise ============================================================================= `QuantRegResults.t_test_pairwise(term_name, method='hs', alpha=0.05, factor_labels=None)` perform pairwise t\_test with multiple testing corrected p-values This uses the formula design\_info encoding contrast matrix and should work for all encodings of a main effect. \| Parameters: \| * result (result instance) – The results of an estimated model with a categorical main effect. * term\_name (str) – name of the term for which pairwise comparisons are computed. Term names for categorical effects are created by patsy and correspond to the main part of the exog names. * method (str or list of strings) – multiple testing p-value correction, default is ‘hs’, see stats.multipletesting * alpha (float) – significance level for multiple testing reject decision. * factor\_labels (None, list of str) – Labels for the factor levels used for pairwise labels. If not provided, then the labels from the formula design\_info are used. \| \| Returns: \| results – The results are stored as attributes, the main attributes are the following two. Other attributes are added for debugging purposes or as background information.* result\_frame : pandas DataFrame with t\_test results and multiple testing corrected p-values. * contrasts : matrix of constraints of the null hypothesis in the t\_test. \| \| Return type: \| instance of a simple Results class \| #### Notes Status: experimental. Currently only checked for treatment coding with and without specified reference level. Currently there are no multiple testing corrected confidence intervals available. #### Examples ``` >>> res = ols("np.log(Days+1) ~ C(Weight) + C(Duration)", data).fit() >>> pw = res.t_test_pairwise("C(Weight)") >>> pw.result_frame coef std err t P>\|t\| Conf. Int. Low 2-1 0.632315 0.230003 2.749157 8.028083e-03 0.171563 3-1 1.302555 0.230003 5.663201 5.331513e-07 0.841803 3-2 0.670240 0.230003 2.914044 5.119126e-03 0.209488 Conf. Int. Upp. pvalue-hs reject-hs 2-1 1.093067 0.010212 True 3-1 1.763307 0.000002 True 3-2 1.130992 0.010212 True ``` statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.sigma_u_mle statsmodels.tsa.vector\_ar.var\_model.VARResults.sigma\_u\_mle ============================================================== `VARResults.sigma_u_mle()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARResults.sigma_u_mle) (Biased) maximum likelihood estimate of noise process covariance statsmodels statsmodels.nonparametric.kde.KDEUnivariate statsmodels.nonparametric.kde.KDEUnivariate =========================================== `class statsmodels.nonparametric.kde.KDEUnivariate(endog)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/nonparametric/kde.html#KDEUnivariate) Univariate Kernel Density Estimator. \| Parameters: \| endog (array-like) – The variable for which the density estimate is desired. \| #### Notes If cdf, sf, cumhazard, or entropy are computed, they are computed based on the definition of the kernel rather than the FFT approximation, even if the density is fit with FFT = True. `KDEUnivariate` is much faster than `KDEMultivariate`, due to its FFT-based implementation. It should be preferred for univariate, continuous data. `KDEMultivariate` also supports mixed data. See also `KDEMultivariate`, `kdensity`, `kdensityfft` #### Examples ``` >>> import statsmodels.api as sm >>> import matplotlib.pyplot as plt ``` ``` >>> nobs = 300 >>> np.random.seed(1234) # Seed random generator >>> dens = sm.nonparametric.KDEUnivariate(np.random.normal(size=nobs)) >>> dens.fit() >>> plt.plot(dens.cdf) >>> plt.show() ``` #### Methods \| \| \| \| --- \| --- \| \| [`cdf`](statsmodels.nonparametric.kde.kdeunivariate.cdf#statsmodels.nonparametric.kde.KDEUnivariate.cdf "statsmodels.nonparametric.kde.KDEUnivariate.cdf")() \| Returns the cumulative distribution function evaluated at the support. \| \| [`cumhazard`](statsmodels.nonparametric.kde.kdeunivariate.cumhazard#statsmodels.nonparametric.kde.KDEUnivariate.cumhazard "statsmodels.nonparametric.kde.KDEUnivariate.cumhazard")() \| Returns the hazard function evaluated at the support. \| \| [`entropy`](statsmodels.nonparametric.kde.kdeunivariate.entropy#statsmodels.nonparametric.kde.KDEUnivariate.entropy "statsmodels.nonparametric.kde.KDEUnivariate.entropy")() \| Returns the differential entropy evaluated at the support \| \| [`evaluate`](statsmodels.nonparametric.kde.kdeunivariate.evaluate#statsmodels.nonparametric.kde.KDEUnivariate.evaluate "statsmodels.nonparametric.kde.KDEUnivariate.evaluate")(point) \| Evaluate density at a single point. \| \| [`fit`](statsmodels.nonparametric.kde.kdeunivariate.fit#statsmodels.nonparametric.kde.KDEUnivariate.fit "statsmodels.nonparametric.kde.KDEUnivariate.fit")([kernel, bw, fft, weights, gridsize, …]) \| Attach the density estimate to the KDEUnivariate class. \| \| [`icdf`](statsmodels.nonparametric.kde.kdeunivariate.icdf#statsmodels.nonparametric.kde.KDEUnivariate.icdf "statsmodels.nonparametric.kde.KDEUnivariate.icdf")() \| Inverse Cumulative Distribution (Quantile) Function \| \| [`sf`](statsmodels.nonparametric.kde.kdeunivariate.sf#statsmodels.nonparametric.kde.KDEUnivariate.sf "statsmodels.nonparametric.kde.KDEUnivariate.sf")() \| Returns the survival function evaluated at the support. \| statsmodels statsmodels.genmod.families.links.CLogLog.inverse statsmodels.genmod.families.links.CLogLog.inverse ================================================= `CLogLog.inverse(z)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#CLogLog.inverse) Inverse of C-Log-Log transform link function \| Parameters: \| z (array-like) – The value of the inverse of the CLogLog link function at `p` \| \| Returns: \| p – Mean parameters \| \| Return type: \| array \| #### Notes g^(-1)(`z`) = 1-exp(-exp(`z`)) statsmodels statsmodels.tsa.vector_ar.vecm.VECM.fit statsmodels.tsa.vector\_ar.vecm.VECM.fit ======================================== `VECM.fit(method='ml')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/vecm.html#VECM.fit) Estimates the parameters of a VECM. The estimation procedure is described on pp. 269-304 in [[1]](#id2). \| Parameters: \| method (str {"ml"}, default: "ml") – Estimation method to use. “ml” stands for Maximum Likelihood. \| \| Returns: \| est \| \| Return type: \| [`VECMResults`](statsmodels.tsa.vector_ar.vecm.vecmresults#statsmodels.tsa.vector_ar.vecm.VECMResults "statsmodels.tsa.vector_ar.vecm.VECMResults") \| #### References \| \| \| \| --- \| --- \| \| [[1]](#id1) \| Lütkepohl, H. 2005. New Introduction to Multiple Time Series Analysis. Springer. \| statsmodels statsmodels.discrete.discrete_model.NegativeBinomialResults.aic statsmodels.discrete.discrete\_model.NegativeBinomialResults.aic ================================================================ `NegativeBinomialResults.aic()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/discrete/discrete_model.html#NegativeBinomialResults.aic) statsmodels statsmodels.stats.mediation.Mediation statsmodels.stats.mediation.Mediation ===================================== `class statsmodels.stats.mediation.Mediation(outcome_model, mediator_model, exposure, mediator=None, moderators=None, outcome_fit_kwargs=None, mediator_fit_kwargs=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/mediation.html#Mediation) Conduct a mediation analysis. \| Parameters: \| * outcome\_model (statsmodels model) – Regression model for the outcome. Predictor variables include the treatment/exposure, the mediator, and any other variables of interest. * mediator\_model (statsmodels model) – Regression model for the mediator variable. Predictor variables include the treatment/exposure and any other variables of interest. * exposure (string or (int, int) tuple) – The name or column position of the treatment/exposure variable. If positions are given, the first integer is the column position of the exposure variable in the outcome model and the second integer is the position of the exposure variable in the mediator model. If a string is given, it must be the name of the exposure variable in both regression models. * mediator (string or int) – The name or column position of the mediator variable in the outcome regression model. If None, infer the name from the mediator model formula (if present). * moderators ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)")) – Map from variable names or index positions to values of moderator variables that are held fixed when calculating mediation effects. If the keys are index position they must be tuples `(i, j)` where `i` is the index in the outcome model and `j` is the index in the mediator model. Otherwise the keys must be variable names. * outcome\_fit\_kwargs (dict-like) – Keyword arguments to use when fitting the outcome model. * mediator\_fit\_kwargs (dict-like) – Keyword arguments to use when fitting the mediator model. * a MediationResults object. (Returns) – \| #### Notes The mediator model class must implement `get_distribution`. #### Examples A basic mediation analysis using formulas: ``` >>> import statsmodels.api as sm >>> import statsmodels.genmod.families.links as links >>> probit = links.probit >>> outcome_model = sm.GLM.from_formula("cong_mesg ~ emo + treat + age + educ + gender + income", ... data, family=sm.families.Binomial(link=probit())) >>> mediator_model = sm.OLS.from_formula("emo ~ treat + age + educ + gender + income", data) >>> med = Mediation(outcome_model, mediator_model, "treat", "emo").fit() >>> med.summary() ``` A basic mediation analysis without formulas. This may be slightly faster than the approach using formulas. If there are any interactions involving the treatment or mediator variables this approach will not work, you must use formulas. ``` >>> import patsy >>> outcome = np.asarray(data["cong_mesg"]) >>> outcome_exog = patsy.dmatrix("emo + treat + age + educ + gender + income", data, ... return_type='dataframe') >>> probit = sm.families.links.probit >>> outcome_model = sm.GLM(outcome, outcome_exog, family=sm.families.Binomial(link=probit())) >>> mediator = np.asarray(data["emo"]) >>> mediator_exog = patsy.dmatrix("treat + age + educ + gender + income", data, ... return_type='dataframe') >>> mediator_model = sm.OLS(mediator, mediator_exog) >>> tx_pos = [outcome_exog.columns.tolist().index("treat"), ... mediator_exog.columns.tolist().index("treat")] >>> med_pos = outcome_exog.columns.tolist().index("emo") >>> med = Mediation(outcome_model, mediator_model, tx_pos, med_pos).fit() >>> med.summary() ``` A moderated mediation analysis. The mediation effect is computed for people of age 20. ``` >>> fml = "cong_mesg ~ emo + treatage + emoage + educ + gender + income", >>> outcome_model = sm.GLM.from_formula(fml, data, ... family=sm.families.Binomial()) >>> mediator_model = sm.OLS.from_formula("emo ~ treat*age + educ + gender + income", data) >>> moderators = {"age" : 20} >>> med = Mediation(outcome_model, mediator_model, "treat", "emo", ... moderators=moderators).fit() ``` #### References Imai, Keele, Tingley (2010). A general approach to causal mediation analysis. Psychological Methods 15:4, 309-334. <http://imai.princeton.edu/research/files/BaronKenny.pdf> Tingley, Yamamoto, Hirose, Keele, Imai (2014). mediation : R package for causal mediation analysis. Journal of Statistical Software 59:5. <http://www.jstatsoft.org/v59/i05/paper> #### Methods \| \| \| \| --- \| --- \| \| [`fit`](statsmodels.stats.mediation.mediation.fit#statsmodels.stats.mediation.Mediation.fit "statsmodels.stats.mediation.Mediation.fit")([method, n\_rep]) \| Fit a regression model to assess mediation. \|	programming_docs
statsmodels statsmodels.discrete.discrete_model.DiscreteResults.f_test statsmodels.discrete.discrete\_model.DiscreteResults.f\_test ============================================================ `DiscreteResults.f_test(r_matrix, cov_p=None, scale=1.0, invcov=None)` Compute the F-test for a joint linear hypothesis. This is a special case of `wald_test` that always uses the F distribution. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length k row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> A = np.identity(len(results.params)) >>> A = A[1:,:] ``` This tests that each coefficient is jointly statistically significantly different from zero. ``` >>> print(results.f_test(A)) <F test: F=array([[ 330.28533923]]), p=4.984030528700946e-10, df_denom=9, df_num=6> ``` Compare this to ``` >>> results.fvalue 330.2853392346658 >>> results.f_pvalue 4.98403096572e-10 ``` ``` >>> B = np.array(([0,0,1,-1,0,0,0],[0,0,0,0,0,1,-1])) ``` This tests that the coefficient on the 2nd and 3rd regressors are equal and jointly that the coefficient on the 5th and 6th regressors are equal. ``` >>> print(results.f_test(B)) <F test: F=array([[ 9.74046187]]), p=0.005605288531708235, df_denom=9, df_num=2> ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.datasets import longley >>> from statsmodels.formula.api import ols >>> dta = longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = '(GNPDEFL = GNP), (UNEMP = 2), (YEAR/1829 = 1)' >>> f_test = results.f_test(hypotheses) >>> print(f_test) <F test: F=array([[ 144.17976065]]), p=6.322026217355609e-08, df_denom=9, df_num=3> ``` See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`wald_test`](statsmodels.discrete.discrete_model.discreteresults.wald_test#statsmodels.discrete.discrete_model.DiscreteResults.wald_test "statsmodels.discrete.discrete_model.DiscreteResults.wald_test"), [`t_test`](statsmodels.discrete.discrete_model.discreteresults.t_test#statsmodels.discrete.discrete_model.DiscreteResults.t_test "statsmodels.discrete.discrete_model.DiscreteResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.stats.outliers_influence.OLSInfluence.resid_press statsmodels.stats.outliers\_influence.OLSInfluence.resid\_press =============================================================== `OLSInfluence.resid_press()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/outliers_influence.html#OLSInfluence.resid_press) (cached attribute) PRESS residuals statsmodels statsmodels.sandbox.regression.gmm.LinearIVGMM.set_param_names statsmodels.sandbox.regression.gmm.LinearIVGMM.set\_param\_names ================================================================ `LinearIVGMM.set_param_names(param_names, k_params=None)` set the parameter names in the model \| Parameters: \| * param\_names (list of strings) – param\_names should have the same length as the number of params * k\_params (None or int) – If k\_params is None, then the k\_params attribute is used, unless it is None. If k\_params is not None, then it will also set the k\_params attribute. \| statsmodels statsmodels.sandbox.distributions.transformed.LogTransf_gen.logcdf statsmodels.sandbox.distributions.transformed.LogTransf\_gen.logcdf =================================================================== `LogTransf_gen.logcdf(x, args, kwds)` Log of the cumulative distribution function at x of the given RV. \| Parameters: \| x (array\_like) – quantiles * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| logcdf – Log of the cumulative distribution function evaluated at x \| \| Return type: \| array\_like \| statsmodels statsmodels.tsa.regime_switching.markov_autoregression.MarkovAutoregression.untransform_params statsmodels.tsa.regime\_switching.markov\_autoregression.MarkovAutoregression.untransform\_params ================================================================================================= `MarkovAutoregression.untransform_params(constrained)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/regime_switching/markov_autoregression.html#MarkovAutoregression.untransform_params) Transform constrained parameters used in likelihood evaluation to unconstrained parameters used by the optimizer \| Parameters: \| constrained (array\_like) – Array of constrained parameters used in likelihood evalution, to be transformed. \| \| Returns: \| unconstrained – Array of unconstrained parameters used by the optimizer. \| \| Return type: \| array\_like \| statsmodels statsmodels.discrete.discrete_model.CountResults.wald_test_terms statsmodels.discrete.discrete\_model.CountResults.wald\_test\_terms =================================================================== `CountResults.wald_test_terms(skip_single=False, extra_constraints=None, combine_terms=None)` Compute a sequence of Wald tests for terms over multiple columns This computes joined Wald tests for the hypothesis that all coefficients corresponding to a `term` are zero. `Terms` are defined by the underlying formula or by string matching. \| Parameters: \| * skip\_single (boolean) – If true, then terms that consist only of a single column and, therefore, refers only to a single parameter is skipped. If false, then all terms are included. * extra\_constraints (ndarray) – not tested yet * combine\_terms (None or list of strings) – Each string in this list is matched to the name of the terms or the name of the exogenous variables. All columns whose name includes that string are combined in one joint test. \| \| Returns: \| test\_result – The result instance contains `table` which is a pandas DataFrame with the test results: test statistic, degrees of freedom and pvalues. \| \| Return type: \| result instance \| #### Examples ``` >>> res_ols = ols("np.log(Days+1) ~ C(Duration, Sum)C(Weight, Sum)", data).fit() >>> res_ols.wald_test_terms() <class 'statsmodels.stats.contrast.WaldTestResults'> F P>F df constraint df denom Intercept 279.754525 2.37985521351e-22 1 51 C(Duration, Sum) 5.367071 0.0245738436636 1 51 C(Weight, Sum) 12.432445 3.99943118767e-05 2 51 C(Duration, Sum):C(Weight, Sum) 0.176002 0.83912310946 2 51 ``` ``` >>> res_poi = Poisson.from_formula("Days ~ C(Weight) C(Duration)", data).fit(cov_type='HC0') >>> wt = res_poi.wald_test_terms(skip_single=False, combine_terms=['Duration', 'Weight']) >>> print(wt) chi2 P>chi2 df constraint Intercept 15.695625 7.43960374424e-05 1 C(Weight) 16.132616 0.000313940174705 2 C(Duration) 1.009147 0.315107378931 1 C(Weight):C(Duration) 0.216694 0.897315972824 2 Duration 11.187849 0.010752286833 3 Weight 30.263368 4.32586407145e-06 4 ``` statsmodels statsmodels.genmod.generalized_estimating_equations.GEEResults.cov_params statsmodels.genmod.generalized\_estimating\_equations.GEEResults.cov\_params ============================================================================ `GEEResults.cov_params(r_matrix=None, column=None, scale=None, cov_p=None, other=None)` Returns the variance/covariance matrix. The variance/covariance matrix can be of a linear contrast of the estimates of params or all params multiplied by scale which will usually be an estimate of sigma^2. Scale is assumed to be a scalar. \| Parameters: \| * r\_matrix (array-like) – Can be 1d, or 2d. Can be used alone or with other. * column (array-like, optional) – Must be used on its own. Can be 0d or 1d see below. * scale (float, optional) – Can be specified or not. Default is None, which means that the scale argument is taken from the model. * other (array-like, optional) – Can be used when r\_matrix is specified. \| \| Returns: \| cov – covariance matrix of the parameter estimates or of linear combination of parameter estimates. See Notes. \| \| Return type: \| ndarray \| #### Notes (The below are assumed to be in matrix notation.) If no argument is specified returns the covariance matrix of a model `(scale)(X.T X)^(-1)` If contrast is specified it pre and post-multiplies as follows `(scale) r_matrix (X.T X)^(-1) r_matrix.T` If contrast and other are specified returns `(scale) * r_matrix (X.T X)^(-1) other.T` If column is specified returns `(scale) * (X.T X)^(-1)[column,column]` if column is 0d OR `(scale) * (X.T X)^(-1)[column][:,column]` if column is 1d statsmodels statsmodels.tools.eval_measures.bic statsmodels.tools.eval\_measures.bic ==================================== `statsmodels.tools.eval_measures.bic(llf, nobs, df_modelwc)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tools/eval_measures.html#bic) Bayesian information criterion (BIC) or Schwarz criterion \| Parameters: \| * llf (float) – value of the loglikelihood * nobs (int) – number of observations * df\_modelwc (int) – number of parameters including constant \| \| Returns: \| bic – information criterion \| \| Return type: \| float \| #### References <http://en.wikipedia.org/wiki/Bayesian_information_criterion> statsmodels statsmodels.discrete.count_model.ZeroInflatedGeneralizedPoissonResults.conf_int statsmodels.discrete.count\_model.ZeroInflatedGeneralizedPoissonResults.conf\_int ================================================================================= `ZeroInflatedGeneralizedPoissonResults.conf_int(alpha=0.05, cols=None, method='default')` Returns the confidence interval of the fitted parameters. \| Parameters: \| * alpha (float, optional) – The significance level for the confidence interval. ie., The default `alpha` = .05 returns a 95% confidence interval. * cols (array-like, optional) – `cols` specifies which confidence intervals to return * method (string) – Not Implemented Yet Method to estimate the confidence\_interval. “Default” : uses self.bse which is based on inverse Hessian for MLE “hjjh” : “jac” : “boot-bse” “boot\_quant” “profile” \| \| Returns: \| conf\_int – Each row contains [lower, upper] limits of the confidence interval for the corresponding parameter. The first column contains all lower, the second column contains all upper limits. \| \| Return type: \| array \| #### Examples ``` >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> results.conf_int() array([[-5496529.48322745, -1467987.78596704], [ -177.02903529, 207.15277984], [ -0.1115811 , 0.03994274], [ -3.12506664, -0.91539297], [ -1.5179487 , -0.54850503], [ -0.56251721, 0.460309 ], [ 798.7875153 , 2859.51541392]]) ``` ``` >>> results.conf_int(cols=(2,3)) array([[-0.1115811 , 0.03994274], [-3.12506664, -0.91539297]]) ``` #### Notes The confidence interval is based on the standard normal distribution. Models wish to use a different distribution should overwrite this method. statsmodels statsmodels.discrete.count_model.GenericZeroInflated.information statsmodels.discrete.count\_model.GenericZeroInflated.information ================================================================= `GenericZeroInflated.information(params)` Fisher information matrix of model Returns -Hessian of loglike evaluated at params. statsmodels statsmodels.discrete.discrete_model.BinaryResults.predict statsmodels.discrete.discrete\_model.BinaryResults.predict ========================================================== `BinaryResults.predict(exog=None, transform=True, args, kwargs)` Call self.model.predict with self.params as the first argument. \| Parameters: \| exog (array-like, optional) – The values for which you want to predict. see Notes below. * transform (bool, optional) – If the model was fit via a formula, do you want to pass exog through the formula. Default is True. E.g., if you fit a model y ~ log(x1) + log(x2), and transform is True, then you can pass a data structure that contains x1 and x2 in their original form. Otherwise, you’d need to log the data first. * kwargs (args,) – Some models can take additional arguments or keywords, see the predict method of the model for the details. \| \| Returns: \| prediction – See self.model.predict \| \| Return type: \| ndarray, [pandas.Series](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.html#pandas.Series "(in pandas v0.22.0)") or [pandas.DataFrame](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html#pandas.DataFrame "(in pandas v0.22.0)") \| #### Notes The types of exog that are supported depends on whether a formula was used in the specification of the model. If a formula was used, then exog is processed in the same way as the original data. This transformation needs to have key access to the same variable names, and can be a pandas DataFrame or a dict like object. If no formula was used, then the provided exog needs to have the same number of columns as the original exog in the model. No transformation of the data is performed except converting it to a numpy array. Row indices as in pandas data frames are supported, and added to the returned prediction. statsmodels statsmodels.sandbox.distributions.extras.ACSkewT_gen.interval statsmodels.sandbox.distributions.extras.ACSkewT\_gen.interval ============================================================== `ACSkewT_gen.interval(alpha, args, kwds)` Confidence interval with equal areas around the median. \| Parameters: \| alpha (array\_like of float) – Probability that an rv will be drawn from the returned range. Each value should be in the range [0, 1]. * arg2, .. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information). * loc (array\_like, optional) – location parameter, Default is 0. * scale (array\_like, optional) – scale parameter, Default is 1. \| \| Returns: \| a, b – end-points of range that contain `100 * alpha %` of the rv’s possible values. \| \| Return type: \| ndarray of float \| statsmodels statsmodels.regression.mixed_linear_model.MixedLMResults.conf_int statsmodels.regression.mixed\_linear\_model.MixedLMResults.conf\_int ==================================================================== `MixedLMResults.conf_int(alpha=0.05, cols=None, method='default')` Returns the confidence interval of the fitted parameters. \| Parameters: \| * alpha (float, optional) – The significance level for the confidence interval. ie., The default `alpha` = .05 returns a 95% confidence interval. * cols (array-like, optional) – `cols` specifies which confidence intervals to return * method (string) – Not Implemented Yet Method to estimate the confidence\_interval. “Default” : uses self.bse which is based on inverse Hessian for MLE “hjjh” : “jac” : “boot-bse” “boot\_quant” “profile” \| \| Returns: \| conf\_int – Each row contains [lower, upper] limits of the confidence interval for the corresponding parameter. The first column contains all lower, the second column contains all upper limits. \| \| Return type: \| array \| #### Examples ``` >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> results.conf_int() array([[-5496529.48322745, -1467987.78596704], [ -177.02903529, 207.15277984], [ -0.1115811 , 0.03994274], [ -3.12506664, -0.91539297], [ -1.5179487 , -0.54850503], [ -0.56251721, 0.460309 ], [ 798.7875153 , 2859.51541392]]) ``` ``` >>> results.conf_int(cols=(2,3)) array([[-0.1115811 , 0.03994274], [-3.12506664, -0.91539297]]) ``` #### Notes The confidence interval is based on the standard normal distribution. Models wish to use a different distribution should overwrite this method. statsmodels statsmodels.sandbox.stats.multicomp.tiecorrect statsmodels.sandbox.stats.multicomp.tiecorrect ============================================== `statsmodels.sandbox.stats.multicomp.tiecorrect(xranks)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/stats/multicomp.html#tiecorrect) should be equivalent of scipy.stats.tiecorrect statsmodels statsmodels.tsa.statespace.varmax.VARMAXResults.tvalues statsmodels.tsa.statespace.varmax.VARMAXResults.tvalues ======================================================= `VARMAXResults.tvalues()` Return the t-statistic for a given parameter estimate. statsmodels statsmodels.discrete.discrete_model.CountModel.score statsmodels.discrete.discrete\_model.CountModel.score ===================================================== `CountModel.score(params)` Score vector of model. The gradient of logL with respect to each parameter. statsmodels statsmodels.tsa.arima_model.ARMAResults.wald_test_terms statsmodels.tsa.arima\_model.ARMAResults.wald\_test\_terms ========================================================== `ARMAResults.wald_test_terms(skip_single=False, extra_constraints=None, combine_terms=None)` Compute a sequence of Wald tests for terms over multiple columns This computes joined Wald tests for the hypothesis that all coefficients corresponding to a `term` are zero. `Terms` are defined by the underlying formula or by string matching. \| Parameters: \| * skip\_single (boolean) – If true, then terms that consist only of a single column and, therefore, refers only to a single parameter is skipped. If false, then all terms are included. * extra\_constraints (ndarray) – not tested yet * combine\_terms (None or list of strings) – Each string in this list is matched to the name of the terms or the name of the exogenous variables. All columns whose name includes that string are combined in one joint test. \| \| Returns: \| test\_result – The result instance contains `table` which is a pandas DataFrame with the test results: test statistic, degrees of freedom and pvalues. \| \| Return type: \| result instance \| #### Examples ``` >>> res_ols = ols("np.log(Days+1) ~ C(Duration, Sum)C(Weight, Sum)", data).fit() >>> res_ols.wald_test_terms() <class 'statsmodels.stats.contrast.WaldTestResults'> F P>F df constraint df denom Intercept 279.754525 2.37985521351e-22 1 51 C(Duration, Sum) 5.367071 0.0245738436636 1 51 C(Weight, Sum) 12.432445 3.99943118767e-05 2 51 C(Duration, Sum):C(Weight, Sum) 0.176002 0.83912310946 2 51 ``` ``` >>> res_poi = Poisson.from_formula("Days ~ C(Weight) C(Duration)", data).fit(cov_type='HC0') >>> wt = res_poi.wald_test_terms(skip_single=False, combine_terms=['Duration', 'Weight']) >>> print(wt) chi2 P>chi2 df constraint Intercept 15.695625 7.43960374424e-05 1 C(Weight) 16.132616 0.000313940174705 2 C(Duration) 1.009147 0.315107378931 1 C(Weight):C(Duration) 0.216694 0.897315972824 2 Duration 11.187849 0.010752286833 3 Weight 30.263368 4.32586407145e-06 4 ```	programming_docs
statsmodels statsmodels.genmod.cov_struct.Independence statsmodels.genmod.cov\_struct.Independence =========================================== `class statsmodels.genmod.cov_struct.Independence(cov_nearest_method='clipped')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/cov_struct.html#Independence) An independence working dependence structure. #### Methods \| \| \| \| --- \| --- \| \| [`covariance_matrix`](statsmodels.genmod.cov_struct.independence.covariance_matrix#statsmodels.genmod.cov_struct.Independence.covariance_matrix "statsmodels.genmod.cov_struct.Independence.covariance_matrix")(expval, index) \| Returns the working covariance or correlation matrix for a given cluster of data. \| \| [`covariance_matrix_solve`](statsmodels.genmod.cov_struct.independence.covariance_matrix_solve#statsmodels.genmod.cov_struct.Independence.covariance_matrix_solve "statsmodels.genmod.cov_struct.Independence.covariance_matrix_solve")(expval, index, …) \| Solves matrix equations of the form `covmat * soln = rhs` and returns the values of `soln`, where `covmat` is the covariance matrix represented by this class. \| \| [`initialize`](statsmodels.genmod.cov_struct.independence.initialize#statsmodels.genmod.cov_struct.Independence.initialize "statsmodels.genmod.cov_struct.Independence.initialize")(model) \| Called by GEE, used by implementations that need additional setup prior to running `fit`. \| \| [`summary`](statsmodels.genmod.cov_struct.independence.summary#statsmodels.genmod.cov_struct.Independence.summary "statsmodels.genmod.cov_struct.Independence.summary")() \| Returns a text summary of the current estimate of the dependence structure. \| \| [`update`](statsmodels.genmod.cov_struct.independence.update#statsmodels.genmod.cov_struct.Independence.update "statsmodels.genmod.cov_struct.Independence.update")(params) \| Updates the association parameter values based on the current regression coefficients. \| statsmodels statsmodels.tsa.statespace.varmax.VARMAX.opg_information_matrix statsmodels.tsa.statespace.varmax.VARMAX.opg\_information\_matrix ================================================================= `VARMAX.opg_information_matrix(params, transformed=True, approx_complex_step=None, *kwargs)` Outer product of gradients information matrix \| Parameters: \| params (array\_like, optional) – Array of parameters at which to evaluate the loglikelihood function. * *\\kwargs* – Additional arguments to the `loglikeobs` method. \| #### References Berndt, Ernst R., Bronwyn Hall, Robert Hall, and Jerry Hausman. 1974. Estimation and Inference in Nonlinear Structural Models. NBER Chapters. National Bureau of Economic Research, Inc. statsmodels statsmodels.emplike.descriptive.DescStatUV.ci_mean statsmodels.emplike.descriptive.DescStatUV.ci\_mean =================================================== `DescStatUV.ci_mean(sig=0.05, method='gamma', epsilon=1e-08, gamma_low=-10000000000, gamma_high=10000000000)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/emplike/descriptive.html#DescStatUV.ci_mean) Returns the confidence interval for the mean. \| Parameters: \| * sig (float) – significance level. Default is .05 * method (str) – Root finding method, Can be ‘nested-brent’ or ‘gamma’. Default is ‘gamma’ ’gamma’ Tries to solve for the gamma parameter in the Lagrange (see Owen pg 22) and then determine the weights. ’nested brent’ uses brents method to find the confidence intervals but must maximize the likelihhod ratio on every iteration. gamma is generally much faster. If the optimizations does not converge, try expanding the gamma\_high and gamma\_low variable. * gamma\_low (float) – Lower bound for gamma when finding lower limit. If function returns f(a) and f(b) must have different signs, consider lowering gamma\_low. * gamma\_high (float) – Upper bound for gamma when finding upper limit. If function returns f(a) and f(b) must have different signs, consider raising gamma\_high. * epsilon (float) – When using ‘nested-brent’, amount to decrease (increase) from the maximum (minimum) of the data when starting the search. This is to protect against the likelihood ratio being zero at the maximum (minimum) value of the data. If data is very small in absolute value (<10 `` -6) consider shrinking epsilon When using ‘gamma’, amount to decrease (increase) the minimum (maximum) by to start the search for gamma. If fucntion returns f(a) and f(b) must have differnt signs, consider lowering epsilon. \| \| Returns: \| Interval** – Confidence interval for the mean \| \| Return type: \| tuple \| statsmodels statsmodels.tsa.statespace.mlemodel.MLEResults.cov_params statsmodels.tsa.statespace.mlemodel.MLEResults.cov\_params ========================================================== `MLEResults.cov_params(r_matrix=None, column=None, scale=None, cov_p=None, other=None)` Returns the variance/covariance matrix. The variance/covariance matrix can be of a linear contrast of the estimates of params or all params multiplied by scale which will usually be an estimate of sigma^2. Scale is assumed to be a scalar. \| Parameters: \| * r\_matrix (array-like) – Can be 1d, or 2d. Can be used alone or with other. * column (array-like, optional) – Must be used on its own. Can be 0d or 1d see below. * scale (float, optional) – Can be specified or not. Default is None, which means that the scale argument is taken from the model. * other (array-like, optional) – Can be used when r\_matrix is specified. \| \| Returns: \| cov – covariance matrix of the parameter estimates or of linear combination of parameter estimates. See Notes. \| \| Return type: \| ndarray \| #### Notes (The below are assumed to be in matrix notation.) If no argument is specified returns the covariance matrix of a model `(scale)(X.T X)^(-1)` If contrast is specified it pre and post-multiplies as follows `(scale) r_matrix (X.T X)^(-1) r_matrix.T` If contrast and other are specified returns `(scale) * r_matrix (X.T X)^(-1) other.T` If column is specified returns `(scale) * (X.T X)^(-1)[column,column]` if column is 0d OR `(scale) * (X.T X)^(-1)[column][:,column]` if column is 1d statsmodels statsmodels.iolib.table.SimpleTable.copy statsmodels.iolib.table.SimpleTable.copy ======================================== `SimpleTable.copy() → list -- a shallow copy of L` statsmodels statsmodels.discrete.count_model.ZeroInflatedGeneralizedPoisson.hessian statsmodels.discrete.count\_model.ZeroInflatedGeneralizedPoisson.hessian ======================================================================== `ZeroInflatedGeneralizedPoisson.hessian(params)` Generic Zero Inflated model Hessian matrix of the loglikelihood \| Parameters: \| params (array-like) – The parameters of the model \| \| Returns: \| hess – The Hessian, second derivative of loglikelihood function, evaluated at `params` \| \| Return type: \| ndarray, (k\_vars, k\_vars) \| #### Notes statsmodels statsmodels.discrete.count_model.ZeroInflatedGeneralizedPoissonResults.llf statsmodels.discrete.count\_model.ZeroInflatedGeneralizedPoissonResults.llf =========================================================================== `ZeroInflatedGeneralizedPoissonResults.llf()` statsmodels statsmodels.robust.robust_linear_model.RLMResults.resid statsmodels.robust.robust\_linear\_model.RLMResults.resid ========================================================= `RLMResults.resid()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/robust/robust_linear_model.html#RLMResults.resid) statsmodels statsmodels.genmod.families.links.inverse_squared.inverse_deriv statsmodels.genmod.families.links.inverse\_squared.inverse\_deriv ================================================================= `inverse_squared.inverse_deriv(z)` Derivative of the inverse of the power transform \| Parameters: \| z (array-like) – `z` is usually the linear predictor for a GLM or GEE model. \| \| Returns: \| * g^(-1)’(z) (array) – The value of the derivative of the inverse of the power transform * function \| statsmodels statsmodels.discrete.count_model.ZeroInflatedPoissonResults.initialize statsmodels.discrete.count\_model.ZeroInflatedPoissonResults.initialize ======================================================================= `ZeroInflatedPoissonResults.initialize(model, params, *kwd)` statsmodels statsmodels.discrete.discrete_model.NegativeBinomialResults.save statsmodels.discrete.discrete\_model.NegativeBinomialResults.save ================================================================= `NegativeBinomialResults.save(fname, remove_data=False)` save a pickle of this instance \| Parameters: \| fname (string or filehandle) – fname can be a string to a file path or filename, or a filehandle. * remove\_data (bool) – If False (default), then the instance is pickled without changes. If True, then all arrays with length nobs are set to None before pickling. See the remove\_data method. In some cases not all arrays will be set to None. \| #### Notes If remove\_data is true and the model result does not implement a remove\_data method then this will raise an exception. statsmodels statsmodels.genmod.generalized_estimating_equations.GEEResults.predict statsmodels.genmod.generalized\_estimating\_equations.GEEResults.predict ======================================================================== `GEEResults.predict(exog=None, transform=True, args, kwargs)` Call self.model.predict with self.params as the first argument. \| Parameters: \| exog (array-like, optional) – The values for which you want to predict. see Notes below. * transform (bool, optional) – If the model was fit via a formula, do you want to pass exog through the formula. Default is True. E.g., if you fit a model y ~ log(x1) + log(x2), and transform is True, then you can pass a data structure that contains x1 and x2 in their original form. Otherwise, you’d need to log the data first. * kwargs (args,) – Some models can take additional arguments or keywords, see the predict method of the model for the details. \| \| Returns: \| prediction – See self.model.predict \| \| Return type: \| ndarray, [pandas.Series](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.Series.html#pandas.Series "(in pandas v0.22.0)") or [pandas.DataFrame](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html#pandas.DataFrame "(in pandas v0.22.0)") \| #### Notes The types of exog that are supported depends on whether a formula was used in the specification of the model. If a formula was used, then exog is processed in the same way as the original data. This transformation needs to have key access to the same variable names, and can be a pandas DataFrame or a dict like object. If no formula was used, then the provided exog needs to have the same number of columns as the original exog in the model. No transformation of the data is performed except converting it to a numpy array. Row indices as in pandas data frames are supported, and added to the returned prediction. statsmodels statsmodels.tsa.stattools.q_stat statsmodels.tsa.stattools.q\_stat ================================= `statsmodels.tsa.stattools.q_stat(x, nobs, type='ljungbox')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/stattools.html#q_stat) Return’s Ljung-Box Q Statistic `x : array-like` Array of autocorrelation coefficients. Can be obtained from acf. `nobs : int` Number of observations in the entire sample (ie., not just the length of the autocorrelation function results. \| Returns: \| * q-stat (array) – Ljung-Box Q-statistic for autocorrelation parameters * p-value (array) – P-value of the Q statistic \| #### Notes Written to be used with acf. statsmodels statsmodels.stats.power.FTestPower.solve_power statsmodels.stats.power.FTestPower.solve\_power =============================================== `FTestPower.solve_power(effect_size=None, df_num=None, df_denom=None, nobs=None, alpha=None, power=None, ncc=1)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/power.html#FTestPower.solve_power) solve for any one parameter of the power of a F-test for the one sample F-test the keywords are: effect\_size, df\_num, df\_denom, alpha, power Exactly one needs to be `None`, all others need numeric values. \| Parameters: \| * effect\_size (float) – standardized effect size, mean divided by the standard deviation. effect size has to be positive. * nobs (int or float) – sample size, number of observations. * alpha (float in interval (0,1)) – significance level, e.g. 0.05, is the probability of a type I error, that is wrong rejections if the Null Hypothesis is true. * power (float in interval (0,1)) – power of the test, e.g. 0.8, is one minus the probability of a type II error. Power is the probability that the test correctly rejects the Null Hypothesis if the Alternative Hypothesis is true. * alternative (string, 'two-sided' (default) or 'one-sided') – extra argument to choose whether the power is calculated for a two-sided (default) or one sided test. ‘one-sided’ assumes we are in the relevant tail. \| \| Returns: \| value – The value of the parameter that was set to None in the call. The value solves the power equation given the remainding parameters. \| \| Return type: \| float \| #### Notes The function uses scipy.optimize for finding the value that satisfies the power equation. It first uses `brentq` with a prior search for bounds. If this fails to find a root, `fsolve` is used. If `fsolve` also fails, then, for `alpha`, `power` and `effect_size`, `brentq` with fixed bounds is used. However, there can still be cases where this fails. statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.resid statsmodels.tsa.statespace.dynamic\_factor.DynamicFactorResults.resid ===================================================================== `DynamicFactorResults.resid()` (array) The model residuals. An (nobs x k\_endog) array. statsmodels statsmodels.nonparametric.kernel_density.KDEMultivariateConditional.imse statsmodels.nonparametric.kernel\_density.KDEMultivariateConditional.imse ========================================================================= `KDEMultivariateConditional.imse(bw)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/nonparametric/kernel_density.html#KDEMultivariateConditional.imse) The integrated mean square error for the conditional KDE. \| Parameters: \| bw (array\_like) – The bandwidth parameter(s). \| \| Returns: \| CV – The cross-validation objective function. \| \| Return type: \| float \| #### Notes For more details see pp. 156-166 in [[1]](#id3). For details on how to handle the mixed variable types see [[2]](#id4). The formula for the cross-validation objective function for mixed variable types is: \[CV(h,\lambda)=\frac{1}{n}\sum\_{l=1}^{n} \frac{G\_{-l}(X\_{l})}{\left[\mu\_{-l}(X\_{l})\right]^{2}}- \frac{2}{n}\sum\_{l=1}^{n}\frac{f\_{-l}(X\_{l},Y\_{l})}{\mu\_{-l}(X\_{l})}\] where \[G\_{-l}(X\_{l}) = n^{-2}\sum\_{i\neq l}\sum\_{j\neq l} K\_{X\_{i},X\_{l}} K\_{X\_{j},X\_{l}}K\_{Y\_{i},Y\_{j}}^{(2)}\] where $K\_{X\_{i},X\_{l}}$ is the multivariate product kernel and $\mu\_{-l}(X\_{l})$ is the leave-one-out estimator of the pdf. $K\_{Y\_{i},Y\_{j}}^{(2)}$ is the convolution kernel. The value of the function is minimized by the `_cv_ls` method of the `GenericKDE` class to return the bw estimates that minimize the distance between the estimated and “true” probability density. #### References \| \| \| \| --- \| --- \| \| [[1]](#id1) \| Racine, J., Li, Q. Nonparametric econometrics: theory and practice. Princeton University Press. (2007) \| \| \| \| \| --- \| --- \| \| [[2]](#id2) \| Racine, J., Li, Q. “Nonparametric Estimation of Distributions with Categorical and Continuous Data.” Working Paper. (2000) \| statsmodels statsmodels.discrete.discrete_model.NegativeBinomialResults.get_margeff statsmodels.discrete.discrete\_model.NegativeBinomialResults.get\_margeff ========================================================================= `NegativeBinomialResults.get_margeff(at='overall', method='dydx', atexog=None, dummy=False, count=False)` Get marginal effects of the fitted model. \| Parameters: \| * at (str, optional) – Options are: + ’overall’, The average of the marginal effects at each observation. + ’mean’, The marginal effects at the mean of each regressor. + ’median’, The marginal effects at the median of each regressor. + ’zero’, The marginal effects at zero for each regressor. + ’all’, The marginal effects at each observation. If `at` is all only margeff will be available from the returned object.Note that if `exog` is specified, then marginal effects for all variables not specified by `exog` are calculated using the `at` option. * method (str, optional) – Options are: + ’dydx’ - dy/dx - No transformation is made and marginal effects are returned. This is the default. + ’eyex’ - estimate elasticities of variables in `exog` – d(lny)/d(lnx) + ’dyex’ - estimate semielasticity – dy/d(lnx) + ’eydx’ - estimate semeilasticity – d(lny)/dxNote that tranformations are done after each observation is calculated. Semi-elasticities for binary variables are computed using the midpoint method. ‘dyex’ and ‘eyex’ do not make sense for discrete variables. * atexog (array-like, optional) – Optionally, you can provide the exogenous variables over which to get the marginal effects. This should be a dictionary with the key as the zero-indexed column number and the value of the dictionary. Default is None for all independent variables less the constant. * dummy (bool, optional) – If False, treats binary variables (if present) as continuous. This is the default. Else if True, treats binary variables as changing from 0 to 1. Note that any variable that is either 0 or 1 is treated as binary. Each binary variable is treated separately for now. * count (bool, optional) – If False, treats count variables (if present) as continuous. This is the default. Else if True, the marginal effect is the change in probabilities when each observation is increased by one. \| \| Returns: \| DiscreteMargins – Returns an object that holds the marginal effects, standard errors, confidence intervals, etc. See `statsmodels.discrete.discrete_margins.DiscreteMargins` for more information. \| \| Return type: \| marginal effects instance \| #### Notes When using after Poisson, returns the expected number of events per period, assuming that the model is loglinear. statsmodels statsmodels.sandbox.distributions.transformed.TransfTwo_gen.isf statsmodels.sandbox.distributions.transformed.TransfTwo\_gen.isf ================================================================ `TransfTwo_gen.isf(q, args, kwds)` Inverse survival function (inverse of `sf`) at q of the given RV. \| Parameters: \| q (array\_like) – upper tail probability * arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional) – scale parameter (default=1) \| \| Returns: \| x – Quantile corresponding to the upper tail probability q. \| \| Return type: \| ndarray or scalar \| statsmodels statsmodels.stats.weightstats.ttost_ind statsmodels.stats.weightstats.ttost\_ind ======================================== `statsmodels.stats.weightstats.ttost_ind(x1, x2, low, upp, usevar='pooled', weights=(None, None), transform=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/stats/weightstats.html#ttost_ind) test of (non-)equivalence for two independent samples TOST: two one-sided t tests null hypothesis: m1 - m2 < low or m1 - m2 > upp alternative hypothesis: low < m1 - m2 < upp where m1, m2 are the means, expected values of the two samples. If the pvalue is smaller than a threshold, say 0.05, then we reject the hypothesis that the difference between the two samples is larger than the the thresholds given by low and upp. \| Parameters: \| * x2 (x1,) – two independent samples, see notes for 2-D case * upp (low,) – equivalence interval low < m1 - m2 < upp * usevar (string, 'pooled' or 'unequal') – If `pooled`, then the standard deviation of the samples is assumed to be the same. If `unequal`, then Welsh ttest with Satterthwait degrees of freedom is used * weights (tuple of None or ndarrays) – Case weights for the two samples. For details on weights see `DescrStatsW` * transform (None or function) – If None (default), then the data is not transformed. Given a function, sample data and thresholds are transformed. If transform is log, then the equivalence interval is in ratio: low < m1 / m2 < upp \| \| Returns: \| * pvalue (float) – pvalue of the non-equivalence test * t1, pv1 (tuple of floats) – test statistic and pvalue for lower threshold test * t2, pv2 (tuple of floats) – test statistic and pvalue for upper threshold test \| #### Notes The test rejects if the 2\*alpha confidence interval for the difference is contained in the `(low, upp)` interval. This test works also for multi-endpoint comparisons: If d1 and d2 have the same number of columns, then each column of the data in d1 is compared with the corresponding column in d2. This is the same as comparing each of the corresponding columns separately. Currently no multi-comparison correction is used. The raw p-values reported here can be correction with the functions in `multitest`.	programming_docs
statsmodels statsmodels.discrete.discrete_model.CountResults.llnull statsmodels.discrete.discrete\_model.CountResults.llnull ======================================================== `CountResults.llnull()` statsmodels statsmodels.sandbox.stats.runs.cochrans_q statsmodels.sandbox.stats.runs.cochrans\_q ========================================== `statsmodels.sandbox.stats.runs.cochrans_q(x)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/stats/runs.html#cochrans_q) Cochran’s Q test for identical effect of k treatments Cochran’s Q is a k-sample extension of the McNemar test. If there are only two treatments, then Cochran’s Q test and McNemar test are equivalent. Test that the probability of success is the same for each treatment. The alternative is that at least two treatments have a different probability of success. \| Parameters: \| x (array\_like, 2d (N,k)) – data with N cases and k variables \| \| Returns: \| * q\_stat (float) – test statistic * pvalue (float) – pvalue from the chisquare distribution \| #### Notes In Wikipedia terminology, rows are blocks and columns are treatments. The number of rows N, should be large for the chisquare distribution to be a good approximation. The Null hypothesis of the test is that all treatments have the same effect. #### References <http://en.wikipedia.org/wiki/Cochran_test> SAS Manual for NPAR TESTS statsmodels statsmodels.regression.recursive_ls.RecursiveLSResults.cov_params_opg statsmodels.regression.recursive\_ls.RecursiveLSResults.cov\_params\_opg ======================================================================== `RecursiveLSResults.cov_params_opg()` (array) The variance / covariance matrix. Computed using the outer product of gradients method. statsmodels statsmodels.tsa.vector_ar.var_model.VARResults.forecast_cov statsmodels.tsa.vector\_ar.var\_model.VARResults.forecast\_cov ============================================================== `VARResults.forecast_cov(steps=1, method='mse')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARResults.forecast_cov) Compute forecast covariance matrices for desired number of steps \| Parameters: \| steps (int) – \| #### Notes \[\Sigma\_{\hat y}(h) = \Sigma\_y(h) + \Omega(h) / T\] Ref: Lütkepohl pp. 96-97 \| Returns: \| covs \| \| Return type: \| ndarray (steps x k x k) \| statsmodels statsmodels.tsa.regime_switching.markov_regression.MarkovRegression.fit statsmodels.tsa.regime\_switching.markov\_regression.MarkovRegression.fit ========================================================================= `MarkovRegression.fit(start_params=None, transformed=True, cov_type='approx', cov_kwds=None, method='bfgs', maxiter=100, full_output=1, disp=0, callback=None, return_params=False, em_iter=5, search_reps=0, search_iter=5, search_scale=1.0, *kwargs)` Fits the model by maximum likelihood via Hamilton filter. \| Parameters: \| start\_params (array\_like, optional) – Initial guess of the solution for the loglikelihood maximization. If None, the default is given by Model.start\_params. * transformed (boolean, optional) – Whether or not `start_params` is already transformed. Default is True. * cov\_type (str, optional) – The type of covariance matrix estimator to use. Can be one of ‘approx’, ‘opg’, ‘robust’, or ‘none’. Default is ‘approx’. * cov\_kwds ([dict](https://docs.python.org/3.2/library/stdtypes.html#dict "(in Python v3.2)") or None, optional) – Keywords for alternative covariance estimators * method (str, optional) – The `method` determines which solver from `scipy.optimize` is used, and it can be chosen from among the following strings: + ’newton’ for Newton-Raphson, ‘nm’ for Nelder-Mead + ’bfgs’ for Broyden-Fletcher-Goldfarb-Shanno (BFGS) + ’lbfgs’ for limited-memory BFGS with optional box constraints + ’powell’ for modified Powell’s method + ’cg’ for conjugate gradient + ’ncg’ for Newton-conjugate gradient + ’basinhopping’ for global basin-hopping solverThe explicit arguments in `fit` are passed to the solver, with the exception of the basin-hopping solver. Each solver has several optional arguments that are not the same across solvers. See the notes section below (or scipy.optimize) for the available arguments and for the list of explicit arguments that the basin-hopping solver supports. * maxiter (int, optional) – The maximum number of iterations to perform. * full\_output (boolean, optional) – Set to True to have all available output in the Results object’s mle\_retvals attribute. The output is dependent on the solver. See LikelihoodModelResults notes section for more information. * disp (boolean, optional) – Set to True to print convergence messages. * callback (callable callback(xk), optional) – Called after each iteration, as callback(xk), where xk is the current parameter vector. * return\_params (boolean, optional) – Whether or not to return only the array of maximizing parameters. Default is False. * em\_iter (int, optional) – Number of initial EM iteration steps used to improve starting parameters. * search\_reps (int, optional) – Number of randomly drawn search parameters that are drawn around `start_params` to try and improve starting parameters. Default is 0. * search\_iter (int, optional) – Number of initial EM iteration steps used to improve each of the search parameter repetitions. * search\_scale (float or array, optional.) – Scale of variates for random start parameter search. * *\\kwargs* – Additional keyword arguments to pass to the optimizer. \| \| Returns: \| \| \| Return type: \| MarkovSwitchingResults \| statsmodels statsmodels.miscmodels.tmodel.TLinearModel.score statsmodels.miscmodels.tmodel.TLinearModel.score ================================================ `TLinearModel.score(params)` Gradient of log-likelihood evaluated at params statsmodels statsmodels.sandbox.distributions.transformed.TransfTwo_gen.median statsmodels.sandbox.distributions.transformed.TransfTwo\_gen.median =================================================================== `TransfTwo_gen.median(args, kwds)` Median of the distribution. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – Location parameter, Default is 0. * scale (array\_like, optional) – Scale parameter, Default is 1. \| \| Returns: \| median – The median of the distribution. \| \| Return type: \| float \| See also `stats.distributions.rv_discrete.ppf` Inverse of the CDF statsmodels statsmodels.discrete.discrete_model.GeneralizedPoissonResults.tvalues statsmodels.discrete.discrete\_model.GeneralizedPoissonResults.tvalues ====================================================================== `GeneralizedPoissonResults.tvalues()` Return the t-statistic for a given parameter estimate. statsmodels statsmodels.duration.hazard_regression.PHRegResults.baseline_cumulative_hazard_function statsmodels.duration.hazard\_regression.PHRegResults.baseline\_cumulative\_hazard\_function =========================================================================================== `PHRegResults.baseline_cumulative_hazard_function()` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/duration/hazard_regression.html#PHRegResults.baseline_cumulative_hazard_function) A list (corresponding to the strata) containing function objects that calculate the cumulative hazard function. statsmodels statsmodels.regression.linear_model.RegressionResults.f_test statsmodels.regression.linear\_model.RegressionResults.f\_test ============================================================== `RegressionResults.f_test(r_matrix, cov_p=None, scale=1.0, invcov=None)` Compute the F-test for a joint linear hypothesis. This is a special case of `wald_test` that always uses the F distribution. \| Parameters: \| * r\_matrix (array-like, str, or tuple) – + array : An r x k array where r is the number of restrictions to test and k is the number of regressors. It is assumed that the linear combination is equal to zero. + str : The full hypotheses to test can be given as a string. See the examples. + tuple : A tuple of arrays in the form (R, q), `q` can be either a scalar or a length k row vector. * cov\_p (array-like, optional) – An alternative estimate for the parameter covariance matrix. If None is given, self.normalized\_cov\_params is used. * scale (float, optional) – Default is 1.0 for no scaling. * invcov (array-like, optional) – A q x q array to specify an inverse covariance matrix based on a restrictions matrix. \| \| Returns: \| res – The results for the test are attributes of this results instance. \| \| Return type: \| ContrastResults instance \| #### Examples ``` >>> import numpy as np >>> import statsmodels.api as sm >>> data = sm.datasets.longley.load() >>> data.exog = sm.add_constant(data.exog) >>> results = sm.OLS(data.endog, data.exog).fit() >>> A = np.identity(len(results.params)) >>> A = A[1:,:] ``` This tests that each coefficient is jointly statistically significantly different from zero. ``` >>> print(results.f_test(A)) <F test: F=array([[ 330.28533923]]), p=4.984030528700946e-10, df_denom=9, df_num=6> ``` Compare this to ``` >>> results.fvalue 330.2853392346658 >>> results.f_pvalue 4.98403096572e-10 ``` ``` >>> B = np.array(([0,0,1,-1,0,0,0],[0,0,0,0,0,1,-1])) ``` This tests that the coefficient on the 2nd and 3rd regressors are equal and jointly that the coefficient on the 5th and 6th regressors are equal. ``` >>> print(results.f_test(B)) <F test: F=array([[ 9.74046187]]), p=0.005605288531708235, df_denom=9, df_num=2> ``` Alternatively, you can specify the hypothesis tests using a string ``` >>> from statsmodels.datasets import longley >>> from statsmodels.formula.api import ols >>> dta = longley.load_pandas().data >>> formula = 'TOTEMP ~ GNPDEFL + GNP + UNEMP + ARMED + POP + YEAR' >>> results = ols(formula, dta).fit() >>> hypotheses = '(GNPDEFL = GNP), (UNEMP = 2), (YEAR/1829 = 1)' >>> f_test = results.f_test(hypotheses) >>> print(f_test) <F test: F=array([[ 144.17976065]]), p=6.322026217355609e-08, df_denom=9, df_num=3> ``` See also [`statsmodels.stats.contrast.ContrastResults`](http://www.statsmodels.org/stable/dev/generated/statsmodels.stats.contrast.ContrastResults.html#statsmodels.stats.contrast.ContrastResults "statsmodels.stats.contrast.ContrastResults"), [`wald_test`](statsmodels.regression.linear_model.regressionresults.wald_test#statsmodels.regression.linear_model.RegressionResults.wald_test "statsmodels.regression.linear_model.RegressionResults.wald_test"), [`t_test`](statsmodels.regression.linear_model.regressionresults.t_test#statsmodels.regression.linear_model.RegressionResults.t_test "statsmodels.regression.linear_model.RegressionResults.t_test"), [`patsy.DesignInfo.linear_constraint`](http://patsy.readthedocs.io/en/latest/API-reference.html#patsy.DesignInfo.linear_constraint "(in patsy v0.5.0+dev)") #### Notes The matrix `r_matrix` is assumed to be non-singular. More precisely, r\_matrix (pX pX.T) r\_matrix.T is assumed invertible. Here, pX is the generalized inverse of the design matrix of the model. There can be problems in non-OLS models where the rank of the covariance of the noise is not full. statsmodels statsmodels.genmod.generalized_estimating_equations.GEEResults.standard_errors statsmodels.genmod.generalized\_estimating\_equations.GEEResults.standard\_errors ================================================================================= `GEEResults.standard_errors(cov_type='robust')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/generalized_estimating_equations.html#GEEResults.standard_errors) This is a convenience function that returns the standard errors for any covariance type. The value of `bse` is the standard errors for whichever covariance type is specified as an argument to `fit` (defaults to “robust”). \| Parameters: \| cov\_type (string) – One of “robust”, “naive”, or “bias\_reduced”. Determines the covariance used to compute standard errors. Defaults to “robust”. \| statsmodels statsmodels.genmod.families.links.cauchy.deriv2 statsmodels.genmod.families.links.cauchy.deriv2 =============================================== `cauchy.deriv2(p)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/genmod/families/links.html#cauchy.deriv2) Second derivative of the Cauchy link function. \| Parameters: \| p (array-like) – Probabilities \| \| Returns: \| g’‘(p) – Value of the second derivative of Cauchy link function at `p` \| \| Return type: \| array \| statsmodels statsmodels.tools.tools.recipr statsmodels.tools.tools.recipr ============================== `statsmodels.tools.tools.recipr(x)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tools/tools.html#recipr) Return the reciprocal of an array, setting all entries less than or equal to 0 to 0. Therefore, it presumes that X should be positive in general. statsmodels statsmodels.graphics.correlation.plot_corr_grid statsmodels.graphics.correlation.plot\_corr\_grid ================================================= `statsmodels.graphics.correlation.plot_corr_grid(dcorrs, titles=None, ncols=None, normcolor=False, xnames=None, ynames=None, fig=None, cmap='RdYlBu_r')` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/graphics/correlation.html#plot_corr_grid) Create a grid of correlation plots. The individual correlation plots are assumed to all have the same variables, axis labels can be specified only once. \| Parameters: \| * dcorrs (list or iterable of ndarrays) – List of correlation matrices. * titles (list of str, optional) – List of titles for the subplots. By default no title are shown. * ncols (int, optional) – Number of columns in the subplot grid. If not given, the number of columns is determined automatically. * normcolor (bool or tuple, optional) – If False (default), then the color coding range corresponds to the range of `dcorr`. If True, then the color range is normalized to (-1, 1). If this is a tuple of two numbers, then they define the range for the color bar. * xnames (list of str, optional) – Labels for the horizontal axis. If not given (None), then the matplotlib defaults (integers) are used. If it is an empty list, [], then no ticks and labels are added. * ynames (list of str, optional) – Labels for the vertical axis. Works the same way as `xnames`. If not given, the same names as for `xnames` are re-used. * fig (Matplotlib figure instance, optional) – If given, this figure is simply returned. Otherwise a new figure is created. * cmap (str or Matplotlib Colormap instance, optional) – The colormap for the plot. Can be any valid Matplotlib Colormap instance or name. \| \| Returns: \| fig – If `ax` is None, the created figure. Otherwise the figure to which `ax` is connected. \| \| Return type: \| Matplotlib figure instance \| #### Examples ``` >>> import numpy as np >>> import matplotlib.pyplot as plt >>> import statsmodels.api as sm ``` In this example we just reuse the same correlation matrix several times. Of course in reality one would show a different correlation (measuring a another type of correlation, for example Pearson (linear) and Spearman, Kendall (nonlinear) correlations) for the same variables. ``` >>> hie_data = sm.datasets.randhie.load_pandas() >>> corr_matrix = np.corrcoef(hie_data.data.T) >>> sm.graphics.plot_corr_grid([corr_matrix] * 8, xnames=hie_data.names) >>> plt.show() ``` statsmodels statsmodels.tsa.statespace.sarimax.SARIMAXResults.test_normality statsmodels.tsa.statespace.sarimax.SARIMAXResults.test\_normality ================================================================= `SARIMAXResults.test_normality(method)` Test for normality of standardized residuals. Null hypothesis is normality. \| Parameters: \| method (string {'jarquebera'} or None) – The statistical test for normality. Must be ‘jarquebera’ for Jarque-Bera normality test. If None, an attempt is made to select an appropriate test. \| #### Notes If the first `d` loglikelihood values were burned (i.e. in the specified model, `loglikelihood_burn=d`), then this test is calculated ignoring the first `d` residuals. In the case of missing data, the maintained hypothesis is that the data are missing completely at random. This test is then run on the standardized residuals excluding those corresponding to missing observations. See also [`statsmodels.stats.stattools.jarque_bera`](statsmodels.stats.stattools.jarque_bera#statsmodels.stats.stattools.jarque_bera "statsmodels.stats.stattools.jarque_bera") statsmodels statsmodels.discrete.discrete_model.MultinomialResults.set_null_options statsmodels.discrete.discrete\_model.MultinomialResults.set\_null\_options ========================================================================== `MultinomialResults.set_null_options(llnull=None, attach_results=True, *kwds)` set fit options for Null (constant-only) model This resets the cache for related attributes which is potentially fragile. This only sets the option, the null model is estimated when llnull is accessed, if llnull is not yet in cache. \| Parameters: \| llnull (None or float) – If llnull is not None, then the value will be directly assigned to the cached attribute “llnull”. * attach\_results (bool) – Sets an internal flag whether the results instance of the null model should be attached. By default without calling this method, thenull model results are not attached and only the loglikelihood value llnull is stored. * kwds (keyword arguments) – `kwds` are directly used as fit keyword arguments for the null model, overriding any provided defaults. \| \| Returns: \| \| \| Return type: \| no returns, modifies attributes of this instance \| statsmodels statsmodels.tsa.statespace.sarimax.SARIMAXResults.cov_params_robust_approx statsmodels.tsa.statespace.sarimax.SARIMAXResults.cov\_params\_robust\_approx ============================================================================= `SARIMAXResults.cov_params_robust_approx()` (array) The QMLE variance / covariance matrix. Computed using the numerical Hessian as the evaluated hessian. statsmodels statsmodels.tsa.statespace.dynamic_factor.DynamicFactorResults.llf statsmodels.tsa.statespace.dynamic\_factor.DynamicFactorResults.llf =================================================================== `DynamicFactorResults.llf()` (float) The value of the log-likelihood function evaluated at `params`. statsmodels statsmodels.sandbox.sysreg.SUR statsmodels.sandbox.sysreg.SUR ============================== `class statsmodels.sandbox.sysreg.SUR(sys, sigma=None, dfk=None)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/sandbox/sysreg.html#SUR) Seemingly Unrelated Regression \| Parameters: \| * sys (list) – [endog1, exog1, endog2, exog2,…] It will be of length 2 x M, where M is the number of equations endog = exog. * sigma (array-like) – M x M array where sigma[i,j] is the covariance between equation i and j * dfk (None, 'dfk1', or 'dfk2') – Default is None. Correction for the degrees of freedom should be specified for small samples. See the notes for more information. \| `cholsigmainv` array – The transpose of the Cholesky decomposition of `pinv_wexog` `df_model` array – Model degrees of freedom of each equation. p\_{m} - 1 where p is the number of regressors for each equation m and one is subtracted for the constant. `df_resid` array – Residual degrees of freedom of each equation. Number of observations less the number of parameters. `endog` array – The LHS variables for each equation in the system. It is a M x nobs array where M is the number of equations. `exog` array – The RHS variable for each equation in the system. It is a nobs x sum(p\_{m}) array. Which is just each RHS array stacked next to each other in columns. `history` dict – Contains the history of fitting the model. Probably not of interest if the model is fit with `igls` = False. `iterations` int – The number of iterations until convergence if the model is fit iteratively. `nobs` float – The number of observations of the equations. `normalized_cov_params` array – sum(p\_{m}) x sum(p\_{m}) array $\left[X^{T}\left(\Sigma^{-1}\otimes\boldsymbol{I}\right)X\right]^{-1}$ `pinv_wexog` array – The pseudo-inverse of the `wexog` `sigma` array – M x M covariance matrix of the cross-equation disturbances. See notes. `sp_exog` CSR sparse matrix – Contains a block diagonal sparse matrix of the design so that exog1 … exogM are on the diagonal. `wendog` array – M \* nobs x 1 array of the endogenous variables whitened by `cholsigmainv` and stacked into a single column. `wexog` array – M\*nobs x sum(p\_{m}) array of the whitened exogenous variables. #### Notes All individual equations are assumed to be well-behaved, homoeskedastic iid errors. This is basically an extension of GLS, using sparse matrices. \[\begin{split}\Sigma=\left[\begin{array}{cccc} \sigma\_{11} & \sigma\_{12} & \cdots & \sigma\_{1M}\\ \sigma\_{21} & \sigma\_{22} & \cdots & \sigma\_{2M}\\ \vdots & \vdots & \ddots & \vdots\\ \sigma\_{M1} & \sigma\_{M2} & \cdots & \sigma\_{MM}\end{array}\right]\end{split}\] #### References Zellner (1962), Greene (2003) #### Methods \| \| \| \| --- \| --- \| \| [`fit`](statsmodels.sandbox.sysreg.sur.fit#statsmodels.sandbox.sysreg.SUR.fit "statsmodels.sandbox.sysreg.SUR.fit")([igls, tol, maxiter]) \| igls : bool Iterate until estimates converge if sigma is None instead of two-step GLS, which is the default is sigma is None. \| \| [`initialize`](statsmodels.sandbox.sysreg.sur.initialize#statsmodels.sandbox.sysreg.SUR.initialize "statsmodels.sandbox.sysreg.SUR.initialize")() \| \| \| [`predict`](statsmodels.sandbox.sysreg.sur.predict#statsmodels.sandbox.sysreg.SUR.predict "statsmodels.sandbox.sysreg.SUR.predict")(design) \| \| \| [`whiten`](statsmodels.sandbox.sysreg.sur.whiten#statsmodels.sandbox.sysreg.SUR.whiten "statsmodels.sandbox.sysreg.SUR.whiten")(X) \| SUR whiten method. \|	programming_docs
statsmodels statsmodels.genmod.families.family.Tweedie.loglike statsmodels.genmod.families.family.Tweedie.loglike ================================================== `Tweedie.loglike(endog, mu, var_weights=1.0, freq_weights=1.0, scale=1.0)` The log-likelihood function in terms of the fitted mean response. \| Parameters: \| * endog (array) – Usually the endogenous response variable. * mu (array) – Usually but not always the fitted mean response variable. * var\_weights (array-like) – 1d array of variance (analytic) weights. The default is 1. * freq\_weights (array-like) – 1d array of frequency weights. The default is 1. * scale (float) – The scale parameter. The default is 1. \| \| Returns: \| ll – The value of the loglikelihood evaluated at (endog, mu, var\_weights, freq\_weights, scale) as defined below. \| \| Return type: \| float \| #### Notes Where $ll\_i$ is the by-observation log-likelihood: \[ll = \sum(ll\_i \* freq\\_weights\_i)\] `ll_i` is defined for each family. endog and mu are not restricted to `endog` and `mu` respectively. For instance, you could call both `loglike(endog, endog)` and `loglike(endog, mu)` to get the log-likelihood ratio. statsmodels statsmodels.tsa.vector_ar.var_model.VARProcess.get_eq_index statsmodels.tsa.vector\_ar.var\_model.VARProcess.get\_eq\_index =============================================================== `VARProcess.get_eq_index(name)` [[source]](http://www.statsmodels.org/stable/_modules/statsmodels/tsa/vector_ar/var_model.html#VARProcess.get_eq_index) Return integer position of requested equation name statsmodels statsmodels.sandbox.distributions.transformed.Transf_gen.stats statsmodels.sandbox.distributions.transformed.Transf\_gen.stats =============================================================== `Transf_gen.stats(args, kwds)` Some statistics of the given RV. \| Parameters: \| arg2, arg3,.. (arg1,) – The shape parameter(s) for the distribution (see docstring of the instance object for more information) * loc (array\_like, optional) – location parameter (default=0) * scale (array\_like, optional (continuous RVs only)) – scale parameter (default=1) * moments (str, optional) – composed of letters [‘mvsk’] defining which moments to compute: ‘m’ = mean, ‘v’ = variance, ‘s’ = (Fisher’s) skew, ‘k’ = (Fisher’s) kurtosis. (default is ‘mv’) \| \| Returns: \| stats – of requested moments. \| \| Return type: \| sequence \| statsmodels Statsmodels Examples Statsmodels Examples ==================== This page provides a series of examples, tutorials and recipes to help you get started with statsmodels. Each of the examples shown here is made available as an IPython Notebook and as a plain python script on the [statsmodels github repository](https://github.com/statsmodels/statsmodels/tree/master/examples). If you are not comfortable with git, we also encourage users to submit their own examples, tutorials or cool statsmodels tricks to the [Examples wiki page](https://github.com/statsmodels/statsmodels/wiki/Examples). Topics ------ * [Linear Regression Models](#regression) * [Plotting](#plotting) * [Discrete Choice Models](#discrete) * [Nonparametric Statistics](#nonparametric) * [Generalized Linear Models](#glm) * [Robust Regression](#robust) * [Statistics](#stats) * [Time Series Analysis](#stats) * [State space models](#statespace) * [User Notes](#user) Linear Regression Models ------------------------ * Ordinary Least Squares * Generalized Least Squares * Quantile Regression * Recursive Least Squares * Regression Diagnostics * Weighted Least Squares * Linear Mixed-Effects Plotting -------- * Regression Plots * Categorical Interactions Discrete Choice Models ---------------------- * Getting Started * Fair's Affairs Data Nonparametric Statistics ------------------------ * Univariate Kernel Density Estimator Generalized Linear Models ------------------------- * Generalized Linear Models Overview * Using Formulas with GLMs Robust Regression ----------------- * M-estimators for Robust Regression * Comparing OLS and RLM Statistics ---------- * ANOVA Time Series Analysis -------------------- * ARMA: Sunspots Data * ARMA: Artificial Data * Time Series Filters * Markov switching dynamic regression * Markov switching autoregression State space models ------------------ * SARIMAX: Introduction * SARIMAX: Model selection, missing data * VARMAX: introduction * Dynamic Factor Models: Application * Unobserved Components: Application * Trends and cycles in unemployment * State space modeling: Local Linear Trends * ARMA: Sunspots Data User Notes ---------- * Contrasts * Formulas * Prediction * Generic Maximum Likelihood * Dates in Time-Series Models statsmodels Regression Plots Regression Plots ================ In [1]: ``` %matplotlib inline from __future__ import print_function from statsmodels.compat import lzip import numpy as np import pandas as pd import matplotlib.pyplot as plt import statsmodels.api as sm from statsmodels.formula.api import ols ``` Duncan's Prestige Dataset ------------------------- ### Load the Data We can use a utility function to load any R dataset available from the great [Rdatasets package](http://vincentarelbundock.github.com/Rdatasets/). In [2]: ``` prestige = sm.datasets.get_rdataset("Duncan", "car", cache=True).data ``` In [3]: ``` prestige.head() ``` Out[3]: \| \| type \| income \| education \| prestige \| \| --- \| --- \| --- \| --- \| --- \| \| accountant \| prof \| 62 \| 86 \| 82 \| \| pilot \| prof \| 72 \| 76 \| 83 \| \| architect \| prof \| 75 \| 92 \| 90 \| \| author \| prof \| 55 \| 90 \| 76 \| \| chemist \| prof \| 64 \| 86 \| 90 \| In [4]: ``` prestige_model = ols("prestige ~ income + education", data=prestige).fit() ``` In [5]: ``` print(prestige_model.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: prestige R-squared: 0.828 Model: OLS Adj. R-squared: 0.820 Method: Least Squares F-statistic: 101.2 Date: Mon, 14 May 2018 Prob (F-statistic): 8.65e-17 Time: 21:45:30 Log-Likelihood: -178.98 No. Observations: 45 AIC: 364.0 Df Residuals: 42 BIC: 369.4 Df Model: 2 Covariance Type: nonrobust ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ Intercept -6.0647 4.272 -1.420 0.163 -14.686 2.556 income 0.5987 0.120 5.003 0.000 0.357 0.840 education 0.5458 0.098 5.555 0.000 0.348 0.744 ============================================================================== Omnibus: 1.279 Durbin-Watson: 1.458 Prob(Omnibus): 0.528 Jarque-Bera (JB): 0.520 Skew: 0.155 Prob(JB): 0.771 Kurtosis: 3.426 Cond. No. 163. ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` ### Influence plots Influence plots show the (externally) studentized residuals vs. the leverage of each observation as measured by the hat matrix. Externally studentized residuals are residuals that are scaled by their standard deviation where $$var(\hat{\epsilon}\_i)=\hat{\sigma}^2\_i(1-h\_{ii})$$ with $$\hat{\sigma}^2\_i=\frac{1}{n - p - 1 \;\;}\sum\_{j}^{n}\;\;\;\forall \;\;\; j \neq i$$ $n$ is the number of observations and $p$ is the number of regressors. $h\_{ii}$ is the $i$-th diagonal element of the hat matrix $$H=X(X^{\;\prime}X)^{-1}X^{\;\prime}$$ The influence of each point can be visualized by the criterion keyword argument. Options are Cook's distance and DFFITS, two measures of influence. In [6]: ``` fig, ax = plt.subplots(figsize=(12,8)) fig = sm.graphics.influence_plot(prestige_model, ax=ax, criterion="cooks") ``` As you can see there are a few worrisome observations. Both contractor and reporter have low leverage but a large residual. RR.engineer has small residual and large leverage. Conductor and minister have both high leverage and large residuals, and, therefore, large influence. ### Partial Regression Plots Since we are doing multivariate regressions, we cannot just look at individual bivariate plots to discern relationships. Instead, we want to look at the relationship of the dependent variable and independent variables conditional on the other independent variables. We can do this through using partial regression plots, otherwise known as added variable plots. In a partial regression plot, to discern the relationship between the response variable and the $k$-th variabe, we compute the residuals by regressing the response variable versus the independent variables excluding $X\_k$. We can denote this by $X\_{\sim k}$. We then compute the residuals by regressing $X\_k$ on $X\_{\sim k}$. The partial regression plot is the plot of the former versus the latter residuals. The notable points of this plot are that the fitted line has slope $\beta\_k$ and intercept zero. The residuals of this plot are the same as those of the least squares fit of the original model with full $X$. You can discern the effects of the individual data values on the estimation of a coefficient easily. If obs\_labels is True, then these points are annotated with their observation label. You can also see the violation of underlying assumptions such as homooskedasticity and linearity. In [7]: ``` fig, ax = plt.subplots(figsize=(12,8)) fig = sm.graphics.plot_partregress("prestige", "income", ["income", "education"], data=prestige, ax=ax) ``` In [8]: ``` fix, ax = plt.subplots(figsize=(12,14)) fig = sm.graphics.plot_partregress("prestige", "income", ["education"], data=prestige, ax=ax) ``` As you can see the partial regression plot confirms the influence of conductor, minister, and RR.engineer on the partial relationship between income and prestige. The cases greatly decrease the effect of income on prestige. Dropping these cases confirms this. In [9]: ``` subset = ~prestige.index.isin(["conductor", "RR.engineer", "minister"]) prestige_model2 = ols("prestige ~ income + education", data=prestige, subset=subset).fit() print(prestige_model2.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: prestige R-squared: 0.876 Model: OLS Adj. R-squared: 0.870 Method: Least Squares F-statistic: 138.1 Date: Mon, 14 May 2018 Prob (F-statistic): 2.02e-18 Time: 21:45:33 Log-Likelihood: -160.59 No. Observations: 42 AIC: 327.2 Df Residuals: 39 BIC: 332.4 Df Model: 2 Covariance Type: nonrobust ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ Intercept -6.3174 3.680 -1.717 0.094 -13.760 1.125 income 0.9307 0.154 6.053 0.000 0.620 1.242 education 0.2846 0.121 2.345 0.024 0.039 0.530 ============================================================================== Omnibus: 3.811 Durbin-Watson: 1.468 Prob(Omnibus): 0.149 Jarque-Bera (JB): 2.802 Skew: -0.614 Prob(JB): 0.246 Kurtosis: 3.303 Cond. No. 158. ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` For a quick check of all the regressors, you can use plot\_partregress\_grid. These plots will not label the points, but you can use them to identify problems and then use plot\_partregress to get more information. In [10]: ``` fig = plt.figure(figsize=(12,8)) fig = sm.graphics.plot_partregress_grid(prestige_model, fig=fig) ``` ### Component-Component plus Residual (CCPR) Plots The CCPR plot provides a way to judge the effect of one regressor on the response variable by taking into account the effects of the other independent variables. The partial residuals plot is defined as $\text{Residuals} + B\_iX\_i \text{ }\text{ }$ versus $X\_i$. The component adds $B\_iX\_i$ versus $X\_i$ to show where the fitted line would lie. Care should be taken if $X\_i$ is highly correlated with any of the other independent variables. If this is the case, the variance evident in the plot will be an underestimate of the true variance. In [11]: ``` fig, ax = plt.subplots(figsize=(12, 8)) fig = sm.graphics.plot_ccpr(prestige_model, "education", ax=ax) ``` As you can see the relationship between the variation in prestige explained by education conditional on income seems to be linear, though you can see there are some observations that are exerting considerable influence on the relationship. We can quickly look at more than one variable by using plot\_ccpr\_grid. In [12]: ``` fig = plt.figure(figsize=(12, 8)) fig = sm.graphics.plot_ccpr_grid(prestige_model, fig=fig) ``` ### Regression Plots The plot\_regress\_exog function is a convenience function that gives a 2x2 plot containing the dependent variable and fitted values with confidence intervals vs. the independent variable chosen, the residuals of the model vs. the chosen independent variable, a partial regression plot, and a CCPR plot. This function can be used for quickly checking modeling assumptions with respect to a single regressor. In [13]: ``` fig = plt.figure(figsize=(12,8)) fig = sm.graphics.plot_regress_exog(prestige_model, "education", fig=fig) ``` ### Fit Plot The plot\_fit function plots the fitted values versus a chosen independent variable. It includes prediction confidence intervals and optionally plots the true dependent variable. In [14]: ``` fig, ax = plt.subplots(figsize=(12, 8)) fig = sm.graphics.plot_fit(prestige_model, "education", ax=ax) ``` Statewide Crime 2009 Dataset ---------------------------- Compare the following to <http://www.ats.ucla.edu/stat/stata/webbooks/reg/chapter4/statareg_self_assessment_answers4.htm> Though the data here is not the same as in that example. You could run that example by uncommenting the necessary cells below. In [15]: ``` #dta = pd.read_csv("http://www.stat.ufl.edu/~aa/social/csv_files/statewide-crime-2.csv") #dta = dta.set_index("State", inplace=True).dropna() #dta.rename(columns={"VR" : "crime", # "MR" : "murder", # "M" : "pctmetro", # "W" : "pctwhite", # "H" : "pcths", # "P" : "poverty", # "S" : "single" # }, inplace=True) # #crime_model = ols("murder ~ pctmetro + poverty + pcths + single", data=dta).fit() ``` In [16]: ``` dta = sm.datasets.statecrime.load_pandas().data ``` In [17]: ``` crime_model = ols("murder ~ urban + poverty + hs_grad + single", data=dta).fit() print(crime_model.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: murder R-squared: 0.813 Model: OLS Adj. R-squared: 0.797 Method: Least Squares F-statistic: 50.08 Date: Mon, 14 May 2018 Prob (F-statistic): 3.42e-16 Time: 21:45:37 Log-Likelihood: -95.050 No. Observations: 51 AIC: 200.1 Df Residuals: 46 BIC: 209.8 Df Model: 4 Covariance Type: nonrobust ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ Intercept -44.1024 12.086 -3.649 0.001 -68.430 -19.774 urban 0.0109 0.015 0.707 0.483 -0.020 0.042 poverty 0.4121 0.140 2.939 0.005 0.130 0.694 hs_grad 0.3059 0.117 2.611 0.012 0.070 0.542 single 0.6374 0.070 9.065 0.000 0.496 0.779 ============================================================================== Omnibus: 1.618 Durbin-Watson: 2.507 Prob(Omnibus): 0.445 Jarque-Bera (JB): 0.831 Skew: -0.220 Prob(JB): 0.660 Kurtosis: 3.445 Cond. No. 5.80e+03 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. [2] The condition number is large, 5.8e+03. This might indicate that there are strong multicollinearity or other numerical problems. ``` ### Partial Regression Plots In [18]: ``` fig = plt.figure(figsize=(12,8)) fig = sm.graphics.plot_partregress_grid(crime_model, fig=fig) ``` In [19]: ``` fig, ax = plt.subplots(figsize=(12,8)) fig = sm.graphics.plot_partregress("murder", "hs_grad", ["urban", "poverty", "single"], ax=ax, data=dta) ``` ### Leverage-Resid2 Plot Closely related to the influence\_plot is the leverage-resid2 plot. In [20]: ``` fig, ax = plt.subplots(figsize=(8,6)) fig = sm.graphics.plot_leverage_resid2(crime_model, ax=ax) ``` ### Influence Plot In [21]: ``` fig, ax = plt.subplots(figsize=(8,6)) fig = sm.graphics.influence_plot(crime_model, ax=ax) ``` ### Using robust regression to correct for outliers. Part of the problem here in recreating the Stata results is that M-estimators are not robust to leverage points. MM-estimators should do better with this examples. In [22]: ``` from statsmodels.formula.api import rlm ``` In [23]: ``` rob_crime_model = rlm("murder ~ urban + poverty + hs_grad + single", data=dta, M=sm.robust.norms.TukeyBiweight(3)).fit(conv="weights") print(rob_crime_model.summary()) ``` ``` Robust linear Model Regression Results ============================================================================== Dep. Variable: murder No. Observations: 51 Model: RLM Df Residuals: 46 Method: IRLS Df Model: 4 Norm: TukeyBiweight Scale Est.: mad Cov Type: H1 Date: Mon, 14 May 2018 Time: 21:45:40 No. Iterations: 50 ============================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ Intercept -4.2986 9.494 -0.453 0.651 -22.907 14.310 urban 0.0029 0.012 0.241 0.809 -0.021 0.027 poverty 0.2753 0.110 2.499 0.012 0.059 0.491 hs_grad -0.0302 0.092 -0.328 0.743 -0.211 0.150 single 0.2902 0.055 5.253 0.000 0.182 0.398 ============================================================================== If the model instance has been used for another fit with different fit parameters, then the fit options might not be the correct ones anymore . ``` In [24]: ``` #rob_crime_model = rlm("murder ~ pctmetro + poverty + pcths + single", data=dta, M=sm.robust.norms.TukeyBiweight()).fit(conv="weights") #print(rob_crime_model.summary()) ``` There isn't yet an influence diagnostics method as part of RLM, but we can recreate them. (This depends on the status of [issue #888](https://github.com/statsmodels/statsmodels/issues/808)) In [25]: ``` weights = rob_crime_model.weights idx = weights > 0 X = rob_crime_model.model.exog[idx.values] ww = weights[idx] / weights[idx].mean() hat_matrix_diag = ww(Xnp.linalg.pinv(X).T).sum(1) resid = rob_crime_model.resid resid2 = resid*2 resid2 /= resid2.sum() nobs = int(idx.sum()) hm = hat_matrix_diag.mean() rm = resid2.mean() ``` In [26]: ``` from statsmodels.graphics import utils fig, ax = plt.subplots(figsize=(12,8)) ax.plot(resid2[idx], hat_matrix_diag, 'o') ax = utils.annotate_axes(range(nobs), labels=rob_crime_model.model.data.row_labels[idx], points=lzip(resid2[idx], hat_matrix_diag), offset_points=[(-5,5)]nobs, size="large", ax=ax) ax.set_xlabel("resid2") ax.set_ylabel("leverage") ylim = ax.get_ylim() ax.vlines(rm, ylim) xlim = ax.get_xlim() ax.hlines(hm, xlim) ax.margins(0,0) ```	programming_docs
statsmodels Time Series Filters Time Series Filters =================== In [1]: ``` %matplotlib inline from __future__ import print_function import pandas as pd import matplotlib.pyplot as plt import statsmodels.api as sm ``` In [2]: ``` dta = sm.datasets.macrodata.load_pandas().data ``` In [3]: ``` index = pd.Index(sm.tsa.datetools.dates_from_range('1959Q1', '2009Q3')) print(index) ``` ``` DatetimeIndex(['1959-03-31', '1959-06-30', '1959-09-30', '1959-12-31', '1960-03-31', '1960-06-30', '1960-09-30', '1960-12-31', '1961-03-31', '1961-06-30', ... '2007-06-30', '2007-09-30', '2007-12-31', '2008-03-31', '2008-06-30', '2008-09-30', '2008-12-31', '2009-03-31', '2009-06-30', '2009-09-30'], dtype='datetime64[ns]', length=203, freq=None) ``` In [4]: ``` dta.index = index del dta['year'] del dta['quarter'] ``` In [5]: ``` print(sm.datasets.macrodata.NOTE) ``` ``` :: Number of Observations - 203 Number of Variables - 14 Variable name definitions:: year - 1959q1 - 2009q3 quarter - 1-4 realgdp - Real gross domestic product (Bil. of chained 2005 US$, seasonally adjusted annual rate) realcons - Real personal consumption expenditures (Bil. of chained 2005 US$, seasonally adjusted annual rate) realinv - Real gross private domestic investment (Bil. of chained 2005 US$, seasonally adjusted annual rate) realgovt - Real federal consumption expenditures & gross investment (Bil. of chained 2005 US$, seasonally adjusted annual rate) realdpi - Real private disposable income (Bil. of chained 2005 US$, seasonally adjusted annual rate) cpi - End of the quarter consumer price index for all urban consumers: all items (1982-84 = 100, seasonally adjusted). m1 - End of the quarter M1 nominal money stock (Seasonally adjusted) tbilrate - Quarterly monthly average of the monthly 3-month treasury bill: secondary market rate unemp - Seasonally adjusted unemployment rate (%) pop - End of the quarter total population: all ages incl. armed forces over seas infl - Inflation rate (ln(cpi_{t}/cpi_{t-1}) * 400) realint - Real interest rate (tbilrate - infl) ``` In [6]: ``` print(dta.head(10)) ``` ``` realgdp realcons realinv realgovt realdpi cpi m1 \ 1959-03-31 2710.349 1707.4 286.898 470.045 1886.9 28.98 139.7 1959-06-30 2778.801 1733.7 310.859 481.301 1919.7 29.15 141.7 1959-09-30 2775.488 1751.8 289.226 491.260 1916.4 29.35 140.5 1959-12-31 2785.204 1753.7 299.356 484.052 1931.3 29.37 140.0 1960-03-31 2847.699 1770.5 331.722 462.199 1955.5 29.54 139.6 1960-06-30 2834.390 1792.9 298.152 460.400 1966.1 29.55 140.2 1960-09-30 2839.022 1785.8 296.375 474.676 1967.8 29.75 140.9 1960-12-31 2802.616 1788.2 259.764 476.434 1966.6 29.84 141.1 1961-03-31 2819.264 1787.7 266.405 475.854 1984.5 29.81 142.1 1961-06-30 2872.005 1814.3 286.246 480.328 2014.4 29.92 142.9 tbilrate unemp pop infl realint 1959-03-31 2.82 5.8 177.146 0.00 0.00 1959-06-30 3.08 5.1 177.830 2.34 0.74 1959-09-30 3.82 5.3 178.657 2.74 1.09 1959-12-31 4.33 5.6 179.386 0.27 4.06 1960-03-31 3.50 5.2 180.007 2.31 1.19 1960-06-30 2.68 5.2 180.671 0.14 2.55 1960-09-30 2.36 5.6 181.528 2.70 -0.34 1960-12-31 2.29 6.3 182.287 1.21 1.08 1961-03-31 2.37 6.8 182.992 -0.40 2.77 1961-06-30 2.29 7.0 183.691 1.47 0.81 ``` In [7]: ``` fig = plt.figure(figsize=(12,8)) ax = fig.add_subplot(111) dta.realgdp.plot(ax=ax); legend = ax.legend(loc = 'upper left'); legend.prop.set_size(20); ``` ### Hodrick-Prescott Filter The Hodrick-Prescott filter separates a time-series $y\_t$ into a trend $\tau\_t$ and a cyclical component $\zeta\_t$ $$y\_t = \tau\_t + \zeta\_t$$ The components are determined by minimizing the following quadratic loss function $$\min\_{\\{ \tau\_{t}\\} }\sum\_{t}^{T}\zeta\_{t}^{2}+\lambda\sum\_{t=1}^{T}\left[\left(\tau\_{t}-\tau\_{t-1}\right)-\left(\tau\_{t-1}-\tau\_{t-2}\right)\right]^{2}$$ In [8]: ``` gdp_cycle, gdp_trend = sm.tsa.filters.hpfilter(dta.realgdp) ``` In [9]: ``` gdp_decomp = dta[['realgdp']].copy() gdp_decomp["cycle"] = gdp_cycle gdp_decomp["trend"] = gdp_trend ``` In [10]: ``` fig = plt.figure(figsize=(12,8)) ax = fig.add_subplot(111) gdp_decomp[["realgdp", "trend"]]["2000-03-31":].plot(ax=ax, fontsize=16); legend = ax.get_legend() legend.prop.set_size(20); ``` ### Baxter-King approximate band-pass filter: Inflation and Unemployment #### Explore the hypothesis that inflation and unemployment are counter-cyclical. The Baxter-King filter is intended to explictly deal with the periodicty of the business cycle. By applying their band-pass filter to a series, they produce a new series that does not contain fluctuations at higher or lower than those of the business cycle. Specifically, the BK filter takes the form of a symmetric moving average $$y\_{t}^{\}=\sum\_{k=-K}^{k=K}a\_ky\_{t-k}$$ where $a\_{-k}=a\_k$ and $\sum\_{k=-k}^{K}a\_k=0$ to eliminate any trend in the series and render it stationary if the series is I(1) or I(2). For completeness, the filter weights are determined as follows $$a\_{j} = B\_{j}+\theta\text{ for }j=0,\pm1,\pm2,\dots,\pm K$$ $$B\_{0} = \frac{\left(\omega\_{2}-\omega\_{1}\right)}{\pi}$$ $$B\_{j} = \frac{1}{\pi j}\left(\sin\left(\omega\_{2}j\right)-\sin\left(\omega\_{1}j\right)\right)\text{ for }j=0,\pm1,\pm2,\dots,\pm K$$ where $\theta$ is a normalizing constant such that the weights sum to zero. $$\theta=\frac{-\sum\_{j=-K^{K}b\_{j}}}{2K+1}$$ $$\omega\_{1}=\frac{2\pi}{P\_{H}}$$ $$\omega\_{2}=\frac{2\pi}{P\_{L}}$$ $P\_L$ and $P\_H$ are the periodicity of the low and high cut-off frequencies. Following Burns and Mitchell's work on US business cycles which suggests cycles last from 1.5 to 8 years, we use $P\_L=6$ and $P\_H=32$ by default. In [11]: ``` bk_cycles = sm.tsa.filters.bkfilter(dta[["infl","unemp"]]) ``` We lose K observations on both ends. It is suggested to use K=12 for quarterly data. In [12]: ``` fig = plt.figure(figsize=(12,10)) ax = fig.add_subplot(111) bk_cycles.plot(ax=ax, style=['r--', 'b-']); ``` ### Christiano-Fitzgerald approximate band-pass filter: Inflation and Unemployment The Christiano-Fitzgerald filter is a generalization of BK and can thus also be seen as weighted moving average. However, the CF filter is asymmetric about $t$ as well as using the entire series. The implementation of their filter involves the calculations of the weights in $$y\_{t}^{\}=B\_{0}y\_{t}+B\_{1}y\_{t+1}+\dots+B\_{T-1-t}y\_{T-1}+\tilde B\_{T-t}y\_{T}+B\_{1}y\_{t-1}+\dots+B\_{t-2}y\_{2}+\tilde B\_{t-1}y\_{1}$$ for $t=3,4,...,T-2$, where $$B\_{j} = \frac{\sin(jb)-\sin(ja)}{\pi j},j\geq1$$ $$B\_{0} = \frac{b-a}{\pi},a=\frac{2\pi}{P\_{u}},b=\frac{2\pi}{P\_{L}}$$ $\tilde B\_{T-t}$ and $\tilde B\_{t-1}$ are linear functions of the $B\_{j}$'s, and the values for $t=1,2,T-1,$ and $T$ are also calculated in much the same way. $P\_{U}$ and $P\_{L}$ are as described above with the same interpretation. The CF filter is appropriate for series that may follow a random walk. In [13]: ``` print(sm.tsa.stattools.adfuller(dta['unemp'])[:3]) ``` ``` (-2.536458467334637, 0.10685366457233464, 9) ``` In [14]: ``` print(sm.tsa.stattools.adfuller(dta['infl'])[:3]) ``` ``` (-3.0545144962572373, 0.030107620863485774, 2) ``` In [15]: ``` cf_cycles, cf_trend = sm.tsa.filters.cffilter(dta[["infl","unemp"]]) print(cf_cycles.head(10)) ``` ``` infl unemp 1959-03-31 0.237927 -0.216867 1959-06-30 0.770007 -0.343779 1959-09-30 1.177736 -0.511024 1959-12-31 1.256754 -0.686967 1960-03-31 0.972128 -0.770793 1960-06-30 0.491889 -0.640601 1960-09-30 0.070189 -0.249741 1960-12-31 -0.130432 0.301545 1961-03-31 -0.134155 0.788992 1961-06-30 -0.092073 0.985356 ``` In [16]: ``` fig = plt.figure(figsize=(14,10)) ax = fig.add_subplot(111) cf_cycles.plot(ax=ax, style=['r--','b-']); ``` Filtering assumes a priori* that business cycles exist. Due to this assumption, many macroeconomic models seek to create models that match the shape of impulse response functions rather than replicating properties of filtered series. See VAR notebook. statsmodels Contrasts Overview Contrasts Overview ================== In [1]: ``` from __future__ import print_function import numpy as np import statsmodels.api as sm ``` This document is based heavily on this excellent resource from UCLA <http://www.ats.ucla.edu/stat/r/library/contrast_coding.htm> A categorical variable of K categories, or levels, usually enters a regression as a sequence of K-1 dummy variables. This amounts to a linear hypothesis on the level means. That is, each test statistic for these variables amounts to testing whether the mean for that level is statistically significantly different from the mean of the base category. This dummy coding is called Treatment coding in R parlance, and we will follow this convention. There are, however, different coding methods that amount to different sets of linear hypotheses. In fact, the dummy coding is not technically a contrast coding. This is because the dummy variables add to one and are not functionally independent of the model's intercept. On the other hand, a set of contrasts for a categorical variable with `k` levels is a set of `k-1` functionally independent linear combinations of the factor level means that are also independent of the sum of the dummy variables. The dummy coding isn't wrong per se. It captures all of the coefficients, but it complicates matters when the model assumes independence of the coefficients such as in ANOVA. Linear regression models do not assume independence of the coefficients and thus dummy coding is often the only coding that is taught in this context. To have a look at the contrast matrices in Patsy, we will use data from UCLA ATS. First let's load the data. #### Example Data In [2]: ``` import pandas as pd url = 'https://stats.idre.ucla.edu/stat/data/hsb2.csv' hsb2 = pd.read_table(url, delimiter=",") ``` In [3]: ``` hsb2.head(10) ``` Out[3]: \| \| id \| female \| race \| ses \| schtyp \| prog \| read \| write \| math \| science \| socst \| \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| \| 0 \| 70 \| 0 \| 4 \| 1 \| 1 \| 1 \| 57 \| 52 \| 41 \| 47 \| 57 \| \| 1 \| 121 \| 1 \| 4 \| 2 \| 1 \| 3 \| 68 \| 59 \| 53 \| 63 \| 61 \| \| 2 \| 86 \| 0 \| 4 \| 3 \| 1 \| 1 \| 44 \| 33 \| 54 \| 58 \| 31 \| \| 3 \| 141 \| 0 \| 4 \| 3 \| 1 \| 3 \| 63 \| 44 \| 47 \| 53 \| 56 \| \| 4 \| 172 \| 0 \| 4 \| 2 \| 1 \| 2 \| 47 \| 52 \| 57 \| 53 \| 61 \| \| 5 \| 113 \| 0 \| 4 \| 2 \| 1 \| 2 \| 44 \| 52 \| 51 \| 63 \| 61 \| \| 6 \| 50 \| 0 \| 3 \| 2 \| 1 \| 1 \| 50 \| 59 \| 42 \| 53 \| 61 \| \| 7 \| 11 \| 0 \| 1 \| 2 \| 1 \| 2 \| 34 \| 46 \| 45 \| 39 \| 36 \| \| 8 \| 84 \| 0 \| 4 \| 2 \| 1 \| 1 \| 63 \| 57 \| 54 \| 58 \| 51 \| \| 9 \| 48 \| 0 \| 3 \| 2 \| 1 \| 2 \| 57 \| 55 \| 52 \| 50 \| 51 \| It will be instructive to look at the mean of the dependent variable, write, for each level of race ((1 = Hispanic, 2 = Asian, 3 = African American and 4 = Caucasian)). In [4]: ``` hsb2.groupby('race')['write'].mean() ``` Out[4]: ``` race 1 46.458333 2 58.000000 3 48.200000 4 54.055172 Name: write, dtype: float64 ``` #### Treatment (Dummy) Coding Dummy coding is likely the most well known coding scheme. It compares each level of the categorical variable to a base reference level. The base reference level is the value of the intercept. It is the default contrast in Patsy for unordered categorical factors. The Treatment contrast matrix for race would be In [5]: ``` from patsy.contrasts import Treatment levels = [1,2,3,4] contrast = Treatment(reference=0).code_without_intercept(levels) print(contrast.matrix) ``` ``` [[0. 0. 0.] [1. 0. 0.] [0. 1. 0.] [0. 0. 1.]] ``` Here we used `reference=0`, which implies that the first level, Hispanic, is the reference category against which the other level effects are measured. As mentioned above, the columns do not sum to zero and are thus not independent of the intercept. To be explicit, let's look at how this would encode the `race` variable. In [6]: ``` hsb2.race.head(10) ``` Out[6]: ``` 0 4 1 4 2 4 3 4 4 4 5 4 6 3 7 1 8 4 9 3 Name: race, dtype: int64 ``` In [7]: ``` print(contrast.matrix[hsb2.race-1, :][:20]) ``` ``` [[0. 0. 1.] [0. 0. 1.] [0. 0. 1.] [0. 0. 1.] [0. 0. 1.] [0. 0. 1.] [0. 1. 0.] [0. 0. 0.] [0. 0. 1.] [0. 1. 0.] [0. 0. 1.] [0. 0. 1.] [0. 0. 1.] [0. 0. 1.] [0. 1. 0.] [0. 0. 1.] [0. 0. 1.] [0. 0. 1.] [0. 0. 1.] [0. 0. 1.]] ``` In [8]: ``` sm.categorical(hsb2.race.values) ``` Out[8]: ``` array([[4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [3., 0., 0., 1., 0.], [1., 1., 0., 0., 0.], [4., 0., 0., 0., 1.], [3., 0., 0., 1., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [3., 0., 0., 1., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [3., 0., 0., 1., 0.], [1., 1., 0., 0., 0.], [1., 1., 0., 0., 0.], [3., 0., 0., 1., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [2., 0., 1., 0., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [1., 1., 0., 0., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [3., 0., 0., 1., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [3., 0., 0., 1., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [1., 1., 0., 0., 0.], [2., 0., 1., 0., 0.], [4., 0., 0., 0., 1.], [1., 1., 0., 0., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [1., 1., 0., 0., 0.], [4., 0., 0., 0., 1.], [1., 1., 0., 0., 0.], [4., 0., 0., 0., 1.], [1., 1., 0., 0., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [1., 1., 0., 0., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [1., 1., 0., 0., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [1., 1., 0., 0., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [1., 1., 0., 0., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [2., 0., 1., 0., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [1., 1., 0., 0., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [1., 1., 0., 0., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [3., 0., 0., 1., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [3., 0., 0., 1., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [1., 1., 0., 0., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [1., 1., 0., 0., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [3., 0., 0., 1., 0.], [1., 1., 0., 0., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [3., 0., 0., 1., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [2., 0., 1., 0., 0.], [4., 0., 0., 0., 1.], [3., 0., 0., 1., 0.], [4., 0., 0., 0., 1.], [2., 0., 1., 0., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [3., 0., 0., 1., 0.], [1., 1., 0., 0., 0.], [3., 0., 0., 1., 0.], [1., 1., 0., 0., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [1., 1., 0., 0., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [1., 1., 0., 0., 0.], [3., 0., 0., 1., 0.], [3., 0., 0., 1., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [1., 1., 0., 0., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [3., 0., 0., 1., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [1., 1., 0., 0., 0.], [3., 0., 0., 1., 0.], [2., 0., 1., 0., 0.], [3., 0., 0., 1., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [2., 0., 1., 0., 0.], [2., 0., 1., 0., 0.], [4., 0., 0., 0., 1.], [2., 0., 1., 0., 0.], [4., 0., 0., 0., 1.], [3., 0., 0., 1., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [2., 0., 1., 0., 0.], [4., 0., 0., 0., 1.], [2., 0., 1., 0., 0.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.], [4., 0., 0., 0., 1.]]) ``` This is a bit of a trick, as the `race` category conveniently maps to zero-based indices. If it does not, this conversion happens under the hood, so this won't work in general but nonetheless is a useful exercise to fix ideas. The below illustrates the output using the three contrasts above In [9]: ``` from statsmodels.formula.api import ols mod = ols("write ~ C(race, Treatment)", data=hsb2) res = mod.fit() print(res.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: write R-squared: 0.107 Model: OLS Adj. R-squared: 0.093 Method: Least Squares F-statistic: 7.833 Date: Mon, 14 May 2018 Prob (F-statistic): 5.78e-05 Time: 21:45:07 Log-Likelihood: -721.77 No. Observations: 200 AIC: 1452. Df Residuals: 196 BIC: 1465. Df Model: 3 Covariance Type: nonrobust =========================================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------------------- Intercept 46.4583 1.842 25.218 0.000 42.825 50.091 C(race, Treatment)[T.2] 11.5417 3.286 3.512 0.001 5.061 18.022 C(race, Treatment)[T.3] 1.7417 2.732 0.637 0.525 -3.647 7.131 C(race, Treatment)[T.4] 7.5968 1.989 3.820 0.000 3.675 11.519 ============================================================================== Omnibus: 10.487 Durbin-Watson: 1.779 Prob(Omnibus): 0.005 Jarque-Bera (JB): 11.031 Skew: -0.551 Prob(JB): 0.00402 Kurtosis: 2.670 Cond. No. 8.25 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` We explicitly gave the contrast for race; however, since Treatment is the default, we could have omitted this. ### Simple Coding Like Treatment Coding, Simple Coding compares each level to a fixed reference level. However, with simple coding, the intercept is the grand mean of all the levels of the factors. Patsy doesn't have the Simple contrast included, but you can easily define your own contrasts. To do so, write a class that contains a code\_with\_intercept and a code\_without\_intercept method that returns a patsy.contrast.ContrastMatrix instance In [10]: ``` from patsy.contrasts import ContrastMatrix def _name_levels(prefix, levels): return ["[%s%s]" % (prefix, level) for level in levels] class Simple(object): def _simple_contrast(self, levels): nlevels = len(levels) contr = -1./nlevels * np.ones((nlevels, nlevels-1)) contr[1:][np.diag_indices(nlevels-1)] = (nlevels-1.)/nlevels return contr def code_with_intercept(self, levels): contrast = np.column_stack((np.ones(len(levels)), self._simple_contrast(levels))) return ContrastMatrix(contrast, _name_levels("Simp.", levels)) def code_without_intercept(self, levels): contrast = self._simple_contrast(levels) return ContrastMatrix(contrast, _name_levels("Simp.", levels[:-1])) ``` In [11]: ``` hsb2.groupby('race')['write'].mean().mean() ``` Out[11]: ``` 51.67837643678162 ``` In [12]: ``` contrast = Simple().code_without_intercept(levels) print(contrast.matrix) ``` ``` [[-0.25 -0.25 -0.25] [ 0.75 -0.25 -0.25] [-0.25 0.75 -0.25] [-0.25 -0.25 0.75]] ``` In [13]: ``` mod = ols("write ~ C(race, Simple)", data=hsb2) res = mod.fit() print(res.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: write R-squared: 0.107 Model: OLS Adj. R-squared: 0.093 Method: Least Squares F-statistic: 7.833 Date: Mon, 14 May 2018 Prob (F-statistic): 5.78e-05 Time: 21:45:07 Log-Likelihood: -721.77 No. Observations: 200 AIC: 1452. Df Residuals: 196 BIC: 1465. Df Model: 3 Covariance Type: nonrobust =========================================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------------------- Intercept 51.6784 0.982 52.619 0.000 49.741 53.615 C(race, Simple)[Simp.1] 11.5417 3.286 3.512 0.001 5.061 18.022 C(race, Simple)[Simp.2] 1.7417 2.732 0.637 0.525 -3.647 7.131 C(race, Simple)[Simp.3] 7.5968 1.989 3.820 0.000 3.675 11.519 ============================================================================== Omnibus: 10.487 Durbin-Watson: 1.779 Prob(Omnibus): 0.005 Jarque-Bera (JB): 11.031 Skew: -0.551 Prob(JB): 0.00402 Kurtosis: 2.670 Cond. No. 7.03 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` ### Sum (Deviation) Coding Sum coding compares the mean of the dependent variable for a given level to the overall mean of the dependent variable over all the levels. That is, it uses contrasts between each of the first k-1 levels and level k In this example, level 1 is compared to all the others, level 2 to all the others, and level 3 to all the others. In [14]: ``` from patsy.contrasts import Sum contrast = Sum().code_without_intercept(levels) print(contrast.matrix) ``` ``` [[ 1. 0. 0.] [ 0. 1. 0.] [ 0. 0. 1.] [-1. -1. -1.]] ``` In [15]: ``` mod = ols("write ~ C(race, Sum)", data=hsb2) res = mod.fit() print(res.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: write R-squared: 0.107 Model: OLS Adj. R-squared: 0.093 Method: Least Squares F-statistic: 7.833 Date: Mon, 14 May 2018 Prob (F-statistic): 5.78e-05 Time: 21:45:08 Log-Likelihood: -721.77 No. Observations: 200 AIC: 1452. Df Residuals: 196 BIC: 1465. Df Model: 3 Covariance Type: nonrobust ===================================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------------- Intercept 51.6784 0.982 52.619 0.000 49.741 53.615 C(race, Sum)[S.1] -5.2200 1.631 -3.200 0.002 -8.437 -2.003 C(race, Sum)[S.2] 6.3216 2.160 2.926 0.004 2.061 10.582 C(race, Sum)[S.3] -3.4784 1.732 -2.008 0.046 -6.895 -0.062 ============================================================================== Omnibus: 10.487 Durbin-Watson: 1.779 Prob(Omnibus): 0.005 Jarque-Bera (JB): 11.031 Skew: -0.551 Prob(JB): 0.00402 Kurtosis: 2.670 Cond. No. 6.72 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` This corresponds to a parameterization that forces all the coefficients to sum to zero. Notice that the intercept here is the grand mean where the grand mean is the mean of means of the dependent variable by each level. In [16]: ``` hsb2.groupby('race')['write'].mean().mean() ``` Out[16]: ``` 51.67837643678162 ``` ### Backward Difference Coding In backward difference coding, the mean of the dependent variable for a level is compared with the mean of the dependent variable for the prior level. This type of coding may be useful for a nominal or an ordinal variable. In [17]: ``` from patsy.contrasts import Diff contrast = Diff().code_without_intercept(levels) print(contrast.matrix) ``` ``` [[-0.75 -0.5 -0.25] [ 0.25 -0.5 -0.25] [ 0.25 0.5 -0.25] [ 0.25 0.5 0.75]] ``` In [18]: ``` mod = ols("write ~ C(race, Diff)", data=hsb2) res = mod.fit() print(res.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: write R-squared: 0.107 Model: OLS Adj. R-squared: 0.093 Method: Least Squares F-statistic: 7.833 Date: Mon, 14 May 2018 Prob (F-statistic): 5.78e-05 Time: 21:45:08 Log-Likelihood: -721.77 No. Observations: 200 AIC: 1452. Df Residuals: 196 BIC: 1465. Df Model: 3 Covariance Type: nonrobust ====================================================================================== coef std err t P>\|t\| [0.025 0.975] -------------------------------------------------------------------------------------- Intercept 51.6784 0.982 52.619 0.000 49.741 53.615 C(race, Diff)[D.1] 11.5417 3.286 3.512 0.001 5.061 18.022 C(race, Diff)[D.2] -9.8000 3.388 -2.893 0.004 -16.481 -3.119 C(race, Diff)[D.3] 5.8552 2.153 2.720 0.007 1.610 10.101 ============================================================================== Omnibus: 10.487 Durbin-Watson: 1.779 Prob(Omnibus): 0.005 Jarque-Bera (JB): 11.031 Skew: -0.551 Prob(JB): 0.00402 Kurtosis: 2.670 Cond. No. 8.30 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` For example, here the coefficient on level 1 is the mean of `write` at level 2 compared with the mean at level 1. Ie., In [19]: ``` res.params["C(race, Diff)[D.1]"] hsb2.groupby('race').mean()["write"][2] - \ hsb2.groupby('race').mean()["write"][1] ``` Out[19]: ``` 11.541666666666664 ``` ### Helmert Coding Our version of Helmert coding is sometimes referred to as Reverse Helmert Coding. The mean of the dependent variable for a level is compared to the mean of the dependent variable over all previous levels. Hence, the name 'reverse' being sometimes applied to differentiate from forward Helmert coding. This comparison does not make much sense for a nominal variable such as race, but we would use the Helmert contrast like so: In [20]: ``` from patsy.contrasts import Helmert contrast = Helmert().code_without_intercept(levels) print(contrast.matrix) ``` ``` [[-1. -1. -1.] [ 1. -1. -1.] [ 0. 2. -1.] [ 0. 0. 3.]] ``` In [21]: ``` mod = ols("write ~ C(race, Helmert)", data=hsb2) res = mod.fit() print(res.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: write R-squared: 0.107 Model: OLS Adj. R-squared: 0.093 Method: Least Squares F-statistic: 7.833 Date: Mon, 14 May 2018 Prob (F-statistic): 5.78e-05 Time: 21:45:08 Log-Likelihood: -721.77 No. Observations: 200 AIC: 1452. Df Residuals: 196 BIC: 1465. Df Model: 3 Covariance Type: nonrobust ========================================================================================= coef std err t P>\|t\| [0.025 0.975] ----------------------------------------------------------------------------------------- Intercept 51.6784 0.982 52.619 0.000 49.741 53.615 C(race, Helmert)[H.2] 5.7708 1.643 3.512 0.001 2.530 9.011 C(race, Helmert)[H.3] -1.3431 0.867 -1.548 0.123 -3.054 0.368 C(race, Helmert)[H.4] 0.7923 0.372 2.130 0.034 0.059 1.526 ============================================================================== Omnibus: 10.487 Durbin-Watson: 1.779 Prob(Omnibus): 0.005 Jarque-Bera (JB): 11.031 Skew: -0.551 Prob(JB): 0.00402 Kurtosis: 2.670 Cond. No. 7.26 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` To illustrate, the comparison on level 4 is the mean of the dependent variable at the previous three levels taken from the mean at level 4 In [22]: ``` grouped = hsb2.groupby('race') grouped.mean()["write"][4] - grouped.mean()["write"][:3].mean() ``` Out[22]: ``` 3.169061302681982 ``` As you can see, these are only equal up to a constant. Other versions of the Helmert contrast give the actual difference in means. Regardless, the hypothesis tests are the same. In [23]: ``` k = 4 1./k * (grouped.mean()["write"][k] - grouped.mean()["write"][:k-1].mean()) k = 3 1./k * (grouped.mean()["write"][k] - grouped.mean()["write"][:k-1].mean()) ``` Out[23]: ``` -1.3430555555555561 ``` ### Orthogonal Polynomial Coding The coefficients taken on by polynomial coding for `k=4` levels are the linear, quadratic, and cubic trends in the categorical variable. The categorical variable here is assumed to be represented by an underlying, equally spaced numeric variable. Therefore, this type of encoding is used only for ordered categorical variables with equal spacing. In general, the polynomial contrast produces polynomials of order `k-1`. Since `race` is not an ordered factor variable let's use `read` as an example. First we need to create an ordered categorical from `read`. In [24]: ``` hsb2['readcat'] = np.asarray(pd.cut(hsb2.read, bins=3)) hsb2.groupby('readcat').mean()['write'] ``` Out[24]: ``` readcat (27.952, 44.0] 45.000000 (44.0, 60.0] 53.356436 (60.0, 76.0] 60.127660 Name: write, dtype: float64 ``` In [25]: ``` from patsy.contrasts import Poly levels = hsb2.readcat.unique().tolist() contrast = Poly().code_without_intercept(levels) print(contrast.matrix) ``` ``` [[-7.07106781e-01 4.08248290e-01] [-4.43378006e-17 -8.16496581e-01] [ 7.07106781e-01 4.08248290e-01]] ``` In [26]: ``` mod = ols("write ~ C(readcat, Poly)", data=hsb2) res = mod.fit() print(res.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: write R-squared: 0.320 Model: OLS Adj. R-squared: 0.313 Method: Least Squares F-statistic: 46.32 Date: Mon, 14 May 2018 Prob (F-statistic): 3.25e-17 Time: 21:45:08 Log-Likelihood: -694.55 No. Observations: 200 AIC: 1395. Df Residuals: 197 BIC: 1405. Df Model: 2 Covariance Type: nonrobust ============================================================================================== coef std err t P>\|t\| [0.025 0.975] ---------------------------------------------------------------------------------------------- Intercept 52.8280 0.588 89.845 0.000 51.668 53.988 C(readcat, Poly).Linear 10.6969 1.118 9.567 0.000 8.492 12.902 C(readcat, Poly).Quadratic -0.6472 0.908 -0.713 0.477 -2.438 1.143 ============================================================================== Omnibus: 9.800 Durbin-Watson: 1.698 Prob(Omnibus): 0.007 Jarque-Bera (JB): 10.330 Skew: -0.536 Prob(JB): 0.00571 Kurtosis: 2.702 Cond. No. 2.08 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` As you can see, readcat has a significant linear effect on the dependent variable `write` but not a significant quadratic or cubic effect.	programming_docs
statsmodels Autoregressive Moving Average (ARMA): Sunspots data Autoregressive Moving Average (ARMA): Sunspots data =================================================== In [1]: ``` %matplotlib inline from __future__ import print_function import numpy as np from scipy import stats import pandas as pd import matplotlib.pyplot as plt import statsmodels.api as sm ``` In [2]: ``` from statsmodels.graphics.api import qqplot ``` Sunpots Data ------------ In [3]: ``` print(sm.datasets.sunspots.NOTE) ``` ``` :: Number of Observations - 309 (Annual 1700 - 2008) Number of Variables - 1 Variable name definitions:: SUNACTIVITY - Number of sunspots for each year The data file contains a 'YEAR' variable that is not returned by load. ``` In [4]: ``` dta = sm.datasets.sunspots.load_pandas().data ``` In [5]: ``` dta.index = pd.Index(sm.tsa.datetools.dates_from_range('1700', '2008')) del dta["YEAR"] ``` In [6]: ``` dta.plot(figsize=(12,8)); ``` In [7]: ``` fig = plt.figure(figsize=(12,8)) ax1 = fig.add_subplot(211) fig = sm.graphics.tsa.plot_acf(dta.values.squeeze(), lags=40, ax=ax1) ax2 = fig.add_subplot(212) fig = sm.graphics.tsa.plot_pacf(dta, lags=40, ax=ax2) ``` In [8]: ``` arma_mod20 = sm.tsa.ARMA(dta, (2,0)).fit(disp=False) print(arma_mod20.params) ``` ``` const 49.659542 ar.L1.SUNACTIVITY 1.390656 ar.L2.SUNACTIVITY -0.688571 dtype: float64 ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/tsa/base/tsa_model.py:171: ValueWarning: No frequency information was provided, so inferred frequency A-DEC will be used. % freq, ValueWarning) ``` In [9]: ``` arma_mod30 = sm.tsa.ARMA(dta, (3,0)).fit(disp=False) ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/tsa/base/tsa_model.py:171: ValueWarning: No frequency information was provided, so inferred frequency A-DEC will be used. % freq, ValueWarning) ``` In [10]: ``` print(arma_mod20.aic, arma_mod20.bic, arma_mod20.hqic) ``` ``` 2622.636338065809 2637.5697031734 2628.606725911055 ``` In [11]: ``` print(arma_mod30.params) ``` ``` const 49.749936 ar.L1.SUNACTIVITY 1.300810 ar.L2.SUNACTIVITY -0.508093 ar.L3.SUNACTIVITY -0.129650 dtype: float64 ``` In [12]: ``` print(arma_mod30.aic, arma_mod30.bic, arma_mod30.hqic) ``` ``` 2619.4036286964474 2638.0703350809363 2626.866613503005 ``` * Does our model obey the theory? In [13]: ``` sm.stats.durbin_watson(arma_mod30.resid.values) ``` Out[13]: ``` 1.9564807635787604 ``` In [14]: ``` fig = plt.figure(figsize=(12,8)) ax = fig.add_subplot(111) ax = arma_mod30.resid.plot(ax=ax); ``` In [15]: ``` resid = arma_mod30.resid ``` In [16]: ``` stats.normaltest(resid) ``` Out[16]: ``` NormaltestResult(statistic=49.845019661107585, pvalue=1.5006917858823576e-11) ``` In [17]: ``` fig = plt.figure(figsize=(12,8)) ax = fig.add_subplot(111) fig = qqplot(resid, line='q', ax=ax, fit=True) ``` In [18]: ``` fig = plt.figure(figsize=(12,8)) ax1 = fig.add_subplot(211) fig = sm.graphics.tsa.plot_acf(resid.values.squeeze(), lags=40, ax=ax1) ax2 = fig.add_subplot(212) fig = sm.graphics.tsa.plot_pacf(resid, lags=40, ax=ax2) ``` In [19]: ``` r,q,p = sm.tsa.acf(resid.values.squeeze(), qstat=True) data = np.c_[range(1,41), r[1:], q, p] table = pd.DataFrame(data, columns=['lag', "AC", "Q", "Prob(>Q)"]) print(table.set_index('lag')) ``` ``` AC Q Prob(>Q) lag 1.0 0.009179 0.026287 8.712023e-01 2.0 0.041793 0.573041 7.508717e-01 3.0 -0.001335 0.573600 9.024484e-01 4.0 0.136089 6.408927 1.706199e-01 5.0 0.092468 9.111841 1.046855e-01 6.0 0.091948 11.793261 6.674304e-02 7.0 0.068748 13.297220 6.518940e-02 8.0 -0.015020 13.369248 9.976074e-02 9.0 0.187592 24.641927 3.393887e-03 10.0 0.213718 39.322013 2.229457e-05 11.0 0.201082 52.361156 2.344931e-07 12.0 0.117182 56.804207 8.574192e-08 13.0 -0.014055 56.868344 1.893888e-07 14.0 0.015398 56.945583 3.997628e-07 15.0 -0.024967 57.149337 7.741415e-07 16.0 0.080916 59.296791 6.872107e-07 17.0 0.041138 59.853761 1.110934e-06 18.0 -0.052021 60.747450 1.548419e-06 19.0 0.062496 62.041713 1.831628e-06 20.0 -0.010301 62.077000 3.381216e-06 21.0 0.074453 63.926674 3.193563e-06 22.0 0.124955 69.154790 8.978292e-07 23.0 0.093162 72.071053 5.799744e-07 24.0 -0.082152 74.346705 4.712985e-07 25.0 0.015695 74.430061 8.288987e-07 26.0 -0.025037 74.642919 1.367275e-06 27.0 -0.125861 80.041162 3.722546e-07 28.0 0.053225 81.009996 4.716253e-07 29.0 -0.038693 81.523822 6.916596e-07 30.0 -0.016904 81.622241 1.151655e-06 31.0 -0.019296 81.750954 1.868756e-06 32.0 0.104990 85.575078 8.927916e-07 33.0 0.040086 86.134579 1.247503e-06 34.0 0.008829 86.161822 2.047816e-06 35.0 0.014588 86.236459 3.263793e-06 36.0 -0.119329 91.248909 1.084450e-06 37.0 -0.036665 91.723876 1.521917e-06 38.0 -0.046193 92.480525 1.938728e-06 39.0 -0.017768 92.592893 2.990669e-06 40.0 -0.006220 92.606716 4.696967e-06 ``` * This indicates a lack of fit. * In-sample dynamic prediction. How good does our model do? In [20]: ``` predict_sunspots = arma_mod30.predict('1990', '2012', dynamic=True) print(predict_sunspots) ``` ``` 1990-12-31 167.047417 1991-12-31 140.993002 1992-12-31 94.859112 1993-12-31 46.860896 1994-12-31 11.242577 1995-12-31 -4.721303 1996-12-31 -1.166920 1997-12-31 16.185687 1998-12-31 39.021884 1999-12-31 59.449878 2000-12-31 72.170152 2001-12-31 75.376793 2002-12-31 70.436464 2003-12-31 60.731586 2004-12-31 50.201791 2005-12-31 42.076018 2006-12-31 38.114277 2007-12-31 38.454635 2008-12-31 41.963810 2009-12-31 46.869285 2010-12-31 51.423261 2011-12-31 54.399720 2012-12-31 55.321692 Freq: A-DEC, dtype: float64 ``` In [21]: ``` fig, ax = plt.subplots(figsize=(12, 8)) ax = dta.loc['1950':].plot(ax=ax) fig = arma_mod30.plot_predict('1990', '2012', dynamic=True, ax=ax, plot_insample=False) ``` In [22]: ``` def mean_forecast_err(y, yhat): return y.sub(yhat).mean() ``` In [23]: ``` mean_forecast_err(dta.SUNACTIVITY, predict_sunspots) ``` Out[23]: ``` 5.636960215843405 ``` ### Exercise: Can you obtain a better fit for the Sunspots model? (Hint: sm.tsa.AR has a method select\_order) ### Simulated ARMA(4,1): Model Identification is Difficult In [24]: ``` from statsmodels.tsa.arima_process import arma_generate_sample, ArmaProcess ``` In [25]: ``` np.random.seed(1234) # include zero-th lag arparams = np.array([1, .75, -.65, -.55, .9]) maparams = np.array([1, .65]) ``` Let's make sure this model is estimable. In [26]: ``` arma_t = ArmaProcess(arparams, maparams) ``` In [27]: ``` arma_t.isinvertible ``` Out[27]: ``` True ``` In [28]: ``` arma_t.isstationary ``` Out[28]: ``` False ``` * What does this mean? In [29]: ``` fig = plt.figure(figsize=(12,8)) ax = fig.add_subplot(111) ax.plot(arma_t.generate_sample(nsample=50)); ``` In [30]: ``` arparams = np.array([1, .35, -.15, .55, .1]) maparams = np.array([1, .65]) arma_t = ArmaProcess(arparams, maparams) arma_t.isstationary ``` Out[30]: ``` True ``` In [31]: ``` arma_rvs = arma_t.generate_sample(nsample=500, burnin=250, scale=2.5) ``` In [32]: ``` fig = plt.figure(figsize=(12,8)) ax1 = fig.add_subplot(211) fig = sm.graphics.tsa.plot_acf(arma_rvs, lags=40, ax=ax1) ax2 = fig.add_subplot(212) fig = sm.graphics.tsa.plot_pacf(arma_rvs, lags=40, ax=ax2) ``` * For mixed ARMA processes the Autocorrelation function is a mixture of exponentials and damped sine waves after (q-p) lags. * The partial autocorrelation function is a mixture of exponentials and dampened sine waves after (p-q) lags. In [33]: ``` arma11 = sm.tsa.ARMA(arma_rvs, (1,1)).fit(disp=False) resid = arma11.resid r,q,p = sm.tsa.acf(resid, qstat=True) data = np.c_[range(1,41), r[1:], q, p] table = pd.DataFrame(data, columns=['lag', "AC", "Q", "Prob(>Q)"]) print(table.set_index('lag')) ``` ``` AC Q Prob(>Q) lag 1.0 0.254921 32.687669 1.082216e-08 2.0 -0.172416 47.670733 4.450737e-11 3.0 -0.420945 137.159383 1.548473e-29 4.0 -0.046875 138.271291 6.617736e-29 5.0 0.103240 143.675896 2.958739e-29 6.0 0.214864 167.132989 1.823728e-33 7.0 -0.000889 167.133391 1.009211e-32 8.0 -0.045418 168.185742 3.094851e-32 9.0 -0.061445 170.115792 5.837244e-32 10.0 0.034623 170.729845 1.958746e-31 11.0 0.006351 170.750546 8.267093e-31 12.0 -0.012882 170.835899 3.220248e-30 13.0 -0.053959 172.336537 6.181225e-30 14.0 -0.016606 172.478955 2.160225e-29 15.0 0.051742 173.864477 4.089565e-29 16.0 0.078917 177.094270 3.217951e-29 17.0 -0.001834 177.096018 1.093173e-28 18.0 -0.101604 182.471927 3.103838e-29 19.0 -0.057342 184.187761 4.624089e-29 20.0 0.026975 184.568275 1.235677e-28 21.0 0.062359 186.605952 1.530266e-28 22.0 -0.009400 186.652354 4.548216e-28 23.0 -0.068037 189.088173 4.562034e-28 24.0 -0.035566 189.755190 9.901143e-28 25.0 0.095679 194.592612 3.354304e-28 26.0 0.065650 196.874866 3.487639e-28 27.0 -0.018404 197.054602 9.008792e-28 28.0 -0.079244 200.393998 5.773739e-28 29.0 0.008499 200.432491 1.541393e-27 30.0 0.053372 201.953764 2.133202e-27 31.0 0.074816 204.949384 1.550168e-27 32.0 -0.071187 207.667232 1.262293e-27 33.0 -0.088145 211.843145 5.480841e-28 34.0 -0.025283 212.187439 1.215233e-27 35.0 0.125690 220.714889 8.231642e-29 36.0 0.142724 231.734107 1.923091e-30 37.0 0.095768 236.706149 5.937808e-31 38.0 -0.084744 240.607793 2.890898e-31 39.0 -0.150126 252.878971 3.963021e-33 40.0 -0.083767 256.707729 1.996181e-33 ``` In [34]: ``` arma41 = sm.tsa.ARMA(arma_rvs, (4,1)).fit(disp=False) resid = arma41.resid r,q,p = sm.tsa.acf(resid, qstat=True) data = np.c_[range(1,41), r[1:], q, p] table = pd.DataFrame(data, columns=['lag', "AC", "Q", "Prob(>Q)"]) print(table.set_index('lag')) ``` ``` AC Q Prob(>Q) lag 1.0 -0.007889 0.031302 0.859569 2.0 0.004132 0.039906 0.980245 3.0 0.018103 0.205415 0.976710 4.0 -0.006760 0.228538 0.993948 5.0 0.018120 0.395024 0.995466 6.0 0.050688 1.700447 0.945087 7.0 0.010252 1.753954 0.972197 8.0 -0.011206 1.818017 0.986092 9.0 0.020292 2.028518 0.991009 10.0 0.001029 2.029060 0.996113 11.0 -0.014035 2.130167 0.997984 12.0 -0.023858 2.422925 0.998427 13.0 -0.002108 2.425216 0.999339 14.0 -0.018783 2.607429 0.999590 15.0 0.011316 2.673698 0.999805 16.0 0.042159 3.595419 0.999443 17.0 0.007943 3.628205 0.999734 18.0 -0.074311 6.503855 0.993686 19.0 -0.023379 6.789067 0.995256 20.0 0.002398 6.792073 0.997313 21.0 0.000487 6.792198 0.998516 22.0 0.017952 6.961435 0.999024 23.0 -0.038576 7.744466 0.998744 24.0 -0.029816 8.213249 0.998859 25.0 0.077850 11.415824 0.990675 26.0 0.040408 12.280448 0.989479 27.0 -0.018612 12.464275 0.992262 28.0 -0.014764 12.580187 0.994586 29.0 0.017650 12.746191 0.996111 30.0 -0.005486 12.762264 0.997504 31.0 0.058256 14.578546 0.994614 32.0 -0.040840 15.473085 0.993887 33.0 -0.019493 15.677311 0.995393 34.0 0.037269 16.425466 0.995214 35.0 0.086212 20.437449 0.976296 36.0 0.041271 21.358847 0.974774 37.0 0.078704 24.716879 0.938948 38.0 -0.029729 25.197056 0.944895 39.0 -0.078397 28.543388 0.891179 40.0 -0.014466 28.657578 0.909268 ``` ### Exercise: How good of in-sample prediction can you do for another series, say, CPI In [35]: ``` macrodta = sm.datasets.macrodata.load_pandas().data macrodta.index = pd.Index(sm.tsa.datetools.dates_from_range('1959Q1', '2009Q3')) cpi = macrodta["cpi"] ``` #### Hint: In [36]: ``` fig = plt.figure(figsize=(12,8)) ax = fig.add_subplot(111) ax = cpi.plot(ax=ax); ax.legend(); ``` P-value of the unit-root test, resoundly rejects the null of no unit-root. In [37]: ``` print(sm.tsa.adfuller(cpi)[1]) ``` ``` 0.990432818833742 ``` statsmodels Generalized Least Squares Generalized Least Squares ========================= In [1]: ``` from __future__ import print_function import statsmodels.api as sm import numpy as np from statsmodels.iolib.table import (SimpleTable, default_txt_fmt) ``` The Longley dataset is a time series dataset: In [2]: ``` data = sm.datasets.longley.load() data.exog = sm.add_constant(data.exog) print(data.exog[:5]) ``` ``` [[1.00000e+00 8.30000e+01 2.34289e+05 2.35600e+03 1.59000e+03 1.07608e+05 1.94700e+03] [1.00000e+00 8.85000e+01 2.59426e+05 2.32500e+03 1.45600e+03 1.08632e+05 1.94800e+03] [1.00000e+00 8.82000e+01 2.58054e+05 3.68200e+03 1.61600e+03 1.09773e+05 1.94900e+03] [1.00000e+00 8.95000e+01 2.84599e+05 3.35100e+03 1.65000e+03 1.10929e+05 1.95000e+03] [1.00000e+00 9.62000e+01 3.28975e+05 2.09900e+03 3.09900e+03 1.12075e+05 1.95100e+03]] ``` Let's assume that the data is heteroskedastic and that we know the nature of the heteroskedasticity. We can then define `sigma` and use it to give us a GLS model First we will obtain the residuals from an OLS fit In [3]: ``` ols_resid = sm.OLS(data.endog, data.exog).fit().resid ``` Assume that the error terms follow an AR(1) process with a trend: $\epsilon\_i = \beta\_0 + \rho\epsilon\_{i-1} + \eta\_i$ where $\eta \sim N(0,\Sigma^2)$ and that $\rho$ is simply the correlation of the residual a consistent estimator for rho is to regress the residuals on the lagged residuals In [4]: ``` resid_fit = sm.OLS(ols_resid[1:], sm.add_constant(ols_resid[:-1])).fit() print(resid_fit.tvalues[1]) print(resid_fit.pvalues[1]) ``` ``` -1.4390229839744777 0.17378444788789812 ``` While we don't have strong evidence that the errors follow an AR(1) process we continue In [5]: ``` rho = resid_fit.params[1] ``` As we know, an AR(1) process means that near-neighbors have a stronger relation so we can give this structure by using a toeplitz matrix In [6]: ``` from scipy.linalg import toeplitz toeplitz(range(5)) ``` Out[6]: ``` array([[0, 1, 2, 3, 4], [1, 0, 1, 2, 3], [2, 1, 0, 1, 2], [3, 2, 1, 0, 1], [4, 3, 2, 1, 0]]) ``` In [7]: ``` order = toeplitz(range(len(ols_resid))) ``` so that our error covariance structure is actually rho\\order which defines an autocorrelation structure In [8]: ``` sigma = rho*order gls_model = sm.GLS(data.endog, data.exog, sigma=sigma) gls_results = gls_model.fit() ``` Of course, the exact rho in this instance is not known so it it might make more sense to use feasible gls, which currently only has experimental support. We can use the GLSAR model with one lag, to get to a similar result: In [9]: ``` glsar_model = sm.GLSAR(data.endog, data.exog, 1) glsar_results = glsar_model.iterative_fit(1) print(glsar_results.summary()) ``` ``` GLSAR Regression Results ============================================================================== Dep. Variable: y R-squared: 0.996 Model: GLSAR Adj. R-squared: 0.992 Method: Least Squares F-statistic: 295.2 Date: Mon, 14 May 2018 Prob (F-statistic): 6.09e-09 Time: 21:45:02 Log-Likelihood: -102.04 No. Observations: 15 AIC: 218.1 Df Residuals: 8 BIC: 223.0 Df Model: 6 Covariance Type: nonrobust ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ const -3.468e+06 8.72e+05 -3.979 0.004 -5.48e+06 -1.46e+06 x1 34.5568 84.734 0.408 0.694 -160.840 229.953 x2 -0.0343 0.033 -1.047 0.326 -0.110 0.041 x3 -1.9621 0.481 -4.083 0.004 -3.070 -0.854 x4 -1.0020 0.211 -4.740 0.001 -1.489 -0.515 x5 -0.0978 0.225 -0.435 0.675 -0.616 0.421 x6 1823.1829 445.829 4.089 0.003 795.100 2851.266 ============================================================================== Omnibus: 1.960 Durbin-Watson: 2.554 Prob(Omnibus): 0.375 Jarque-Bera (JB): 1.423 Skew: 0.713 Prob(JB): 0.491 Kurtosis: 2.508 Cond. No. 4.80e+09 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. [2] The condition number is large, 4.8e+09. This might indicate that there are strong multicollinearity or other numerical problems. ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/stats.py:1394: UserWarning: kurtosistest only valid for n>=20 ... continuing anyway, n=15 "anyway, n=%i" % int(n)) ``` Comparing gls and glsar results, we see that there are some small differences in the parameter estimates and the resulting standard errors of the parameter estimate. This might be do to the numerical differences in the algorithm, e.g. the treatment of initial conditions, because of the small number of observations in the longley dataset. In [10]: ``` print(gls_results.params) print(glsar_results.params) print(gls_results.bse) print(glsar_results.bse) ``` ``` [-3.79785490e+06 -1.27656454e+01 -3.80013250e-02 -2.18694871e+00 -1.15177649e+00 -6.80535580e-02 1.99395293e+03] [-3.46796063e+06 3.45567846e+01 -3.43410090e-02 -1.96214395e+00 -1.00197296e+00 -9.78045986e-02 1.82318289e+03] [6.70688699e+05 6.94308073e+01 2.62476822e-02 3.82393151e-01 1.65252692e-01 1.76428334e-01 3.42634628e+02] [8.71584052e+05 8.47337145e+01 3.28032450e-02 4.80544865e-01 2.11383871e-01 2.24774369e-01 4.45828748e+02] ``` statsmodels Maximum Likelihood Estimation (Generic models) Maximum Likelihood Estimation (Generic models) ============================================== This tutorial explains how to quickly implement new maximum likelihood models in `statsmodels`. We give two examples: 1. Probit model for binary dependent variables 2. Negative binomial model for count data The `GenericLikelihoodModel` class eases the process by providing tools such as automatic numeric differentiation and a unified interface to `scipy` optimization functions. Using `statsmodels`, users can fit new MLE models simply by "plugging-in" a log-likelihood function. Example 1: Probit model ----------------------- In [1]: ``` from __future__ import print_function import numpy as np from scipy import stats import statsmodels.api as sm from statsmodels.base.model import GenericLikelihoodModel ``` The `Spector` dataset is distributed with `statsmodels`. You can access a vector of values for the dependent variable (`endog`) and a matrix of regressors (`exog`) like this: In [2]: ``` data = sm.datasets.spector.load_pandas() exog = data.exog endog = data.endog print(sm.datasets.spector.NOTE) print(data.exog.head()) ``` ``` :: Number of Observations - 32 Number of Variables - 4 Variable name definitions:: Grade - binary variable indicating whether or not a student's grade improved. 1 indicates an improvement. TUCE - Test score on economics test PSI - participation in program GPA - Student's grade point average GPA TUCE PSI 0 2.66 20.0 0.0 1 2.89 22.0 0.0 2 3.28 24.0 0.0 3 2.92 12.0 0.0 4 4.00 21.0 0.0 ``` Them, we add a constant to the matrix of regressors: In [3]: ``` exog = sm.add_constant(exog, prepend=True) ``` To create your own Likelihood Model, you simply need to overwrite the loglike method. In [4]: ``` class MyProbit(GenericLikelihoodModel): def loglike(self, params): exog = self.exog endog = self.endog q = 2 endog - 1 return stats.norm.logcdf(qnp.dot(exog, params)).sum() ``` Estimate the model and print a summary: In [5]: ``` sm_probit_manual = MyProbit(endog, exog).fit() print(sm_probit_manual.summary()) ``` ``` Optimization terminated successfully. Current function value: 0.400588 Iterations: 292 Function evaluations: 494 MyProbit Results ============================================================================== Dep. Variable: GRADE Log-Likelihood: -12.819 Model: MyProbit AIC: 33.64 Method: Maximum Likelihood BIC: 39.50 Date: Mon, 14 May 2018 Time: 21:44:55 No. Observations: 32 Df Residuals: 28 Df Model: 3 ============================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ const -7.4523 2.542 -2.931 0.003 -12.435 -2.469 GPA 1.6258 0.694 2.343 0.019 0.266 2.986 TUCE 0.0517 0.084 0.617 0.537 -0.113 0.216 PSI 1.4263 0.595 2.397 0.017 0.260 2.593 ============================================================================== ``` Compare your Probit implementation to `statsmodels`' "canned" implementation: In [6]: ``` sm_probit_canned = sm.Probit(endog, exog).fit() ``` ``` Optimization terminated successfully. Current function value: 0.400588 Iterations 6 ``` In [7]: ``` print(sm_probit_canned.params) print(sm_probit_manual.params) ``` ``` const -7.452320 GPA 1.625810 TUCE 0.051729 PSI 1.426332 dtype: float64 [-7.45233176 1.62580888 0.05172971 1.42631954] ``` In [8]: ``` print(sm_probit_canned.cov_params()) print(sm_probit_manual.cov_params()) ``` ``` const GPA TUCE PSI const 6.464166 -1.169668 -0.101173 -0.594792 GPA -1.169668 0.481473 -0.018914 0.105439 TUCE -0.101173 -0.018914 0.007038 0.002472 PSI -0.594792 0.105439 0.002472 0.354070 [[ 6.46416770e+00 -1.16966617e+00 -1.01173181e-01 -5.94789009e-01] [-1.16966617e+00 4.81472117e-01 -1.89134591e-02 1.05438228e-01] [-1.01173181e-01 -1.89134591e-02 7.03758403e-03 2.47189233e-03] [-5.94789009e-01 1.05438228e-01 2.47189233e-03 3.54069514e-01]] ``` Notice that the `GenericMaximumLikelihood` class provides automatic differentiation, so we didn't have to provide Hessian or Score functions in order to calculate the covariance estimates. Example 2: Negative Binomial Regression for Count Data ------------------------------------------------------ Consider a negative binomial regression model for count data with log-likelihood (type NB-2) function expressed as: $$ \mathcal{L}(\beta\_j; y, \alpha) = \sum\_{i=1}^n y\_i ln \left ( \frac{\alpha exp(X\_i'\beta)}{1+\alpha exp(X\_i'\beta)} \right ) - \frac{1}{\alpha} ln(1+\alpha exp(X\_i'\beta)) + ln \Gamma (y\_i + 1/\alpha) - ln \Gamma (y\_i+1) - ln \Gamma (1/\alpha) $$ with a matrix of regressors $X$, a vector of coefficients $\beta$, and the negative binomial heterogeneity parameter $\alpha$. Using the `nbinom` distribution from `scipy`, we can write this likelihood simply as: In [9]: ``` import numpy as np from scipy.stats import nbinom ``` In [10]: ``` def _ll_nb2(y, X, beta, alph): mu = np.exp(np.dot(X, beta)) size = 1/alph prob = size/(size+mu) ll = nbinom.logpmf(y, size, prob) return ll ``` ### New Model Class We create a new model class which inherits from `GenericLikelihoodModel`: In [11]: ``` from statsmodels.base.model import GenericLikelihoodModel ``` In [12]: ``` class NBin(GenericLikelihoodModel): def __init__(self, endog, exog, kwds): super(NBin, self).__init__(endog, exog, kwds) def nloglikeobs(self, params): alph = params[-1] beta = params[:-1] ll = _ll_nb2(self.endog, self.exog, beta, alph) return -ll def fit(self, start_params=None, maxiter=10000, maxfun=5000, kwds): # we have one additional parameter and we need to add it for summary self.exog_names.append('alpha') if start_params == None: # Reasonable starting values start_params = np.append(np.zeros(self.exog.shape[1]), .5) # intercept start_params[-2] = np.log(self.endog.mean()) return super(NBin, self).fit(start_params=start_params, maxiter=maxiter, maxfun=maxfun, kwds) ``` Two important things to notice: `nloglikeobs`: This function should return one evaluation of the negative log-likelihood function per observation in your dataset (i.e. rows of the endog/X matrix). * `start_params`: A one-dimensional array of starting values needs to be provided. The size of this array determines the number of parameters that will be used in optimization. That's it! You're done! ### Usage Example The [Medpar](http://vincentarelbundock.github.com/Rdatasets/doc/COUNT/medpar.html) dataset is hosted in CSV format at the [Rdatasets repository](http://vincentarelbundock.github.com/Rdatasets). We use the `read_csv` function from the [Pandas library](http://pandas.pydata.org) to load the data in memory. We then print the first few columns: In [13]: ``` import statsmodels.api as sm ``` In [14]: ``` medpar = sm.datasets.get_rdataset("medpar", "COUNT", cache=True).data medpar.head() ``` Out[14]: \| \| los \| hmo \| white \| died \| age80 \| type \| type1 \| type2 \| type3 \| provnum \| \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| \| 0 \| 4 \| 0 \| 1 \| 0 \| 0 \| 1 \| 1 \| 0 \| 0 \| 30001 \| \| 1 \| 9 \| 1 \| 1 \| 0 \| 0 \| 1 \| 1 \| 0 \| 0 \| 30001 \| \| 2 \| 3 \| 1 \| 1 \| 1 \| 1 \| 1 \| 1 \| 0 \| 0 \| 30001 \| \| 3 \| 9 \| 0 \| 1 \| 0 \| 0 \| 1 \| 1 \| 0 \| 0 \| 30001 \| \| 4 \| 1 \| 0 \| 1 \| 1 \| 1 \| 1 \| 1 \| 0 \| 0 \| 30001 \| The model we are interested in has a vector of non-negative integers as dependent variable (`los`), and 5 regressors: `Intercept`, `type2`, `type3`, `hmo`, `white`. For estimation, we need to create two variables to hold our regressors and the outcome variable. These can be ndarrays or pandas objects. In [15]: ``` y = medpar.los X = medpar[["type2", "type3", "hmo", "white"]].copy() X["constant"] = 1 ``` Then, we fit the model and extract some information: In [16]: ``` mod = NBin(y, X) res = mod.fit() ``` ``` Optimization terminated successfully. Current function value: 3.209014 Iterations: 805 Function evaluations: 1238 ``` Extract parameter estimates, standard errors, p-values, AIC, etc.: In [17]: ``` print('Parameters: ', res.params) print('Standard errors: ', res.bse) print('P-values: ', res.pvalues) print('AIC: ', res.aic) ``` ``` Parameters: [ 0.2212642 0.70613942 -0.06798155 -0.12903932 2.31026565 0.44575147] Standard errors: [0.05059259 0.07613047 0.05326097 0.06854141 0.06794692 0.01981542] P-values: [1.22297920e-005 1.76978024e-020 2.01819161e-001 5.97481600e-002 2.15079626e-253 4.62688439e-112] AIC: 9604.95320583016 ``` As usual, you can obtain a full list of available information by typing `dir(res)`. We can also look at the summary of the estimation results. In [18]: ``` print(res.summary()) ``` ``` NBin Results ============================================================================== Dep. Variable: los Log-Likelihood: -4797.5 Model: NBin AIC: 9605. Method: Maximum Likelihood BIC: 9632. Date: Mon, 14 May 2018 Time: 21:44:58 No. Observations: 1495 Df Residuals: 1490 Df Model: 4 ============================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ type2 0.2213 0.051 4.373 0.000 0.122 0.320 type3 0.7061 0.076 9.275 0.000 0.557 0.855 hmo -0.0680 0.053 -1.276 0.202 -0.172 0.036 white -0.1290 0.069 -1.883 0.060 -0.263 0.005 constant 2.3103 0.068 34.001 0.000 2.177 2.443 alpha 0.4458 0.020 22.495 0.000 0.407 0.485 ============================================================================== ``` ### Testing We can check the results by using the statsmodels implementation of the Negative Binomial model, which uses the analytic score function and Hessian. In [19]: ``` res_nbin = sm.NegativeBinomial(y, X).fit(disp=0) print(res_nbin.summary()) ``` ``` NegativeBinomial Regression Results ============================================================================== Dep. Variable: los No. Observations: 1495 Model: NegativeBinomial Df Residuals: 1490 Method: MLE Df Model: 4 Date: Mon, 14 May 2018 Pseudo R-squ.: 0.01215 Time: 21:44:58 Log-Likelihood: -4797.5 converged: True LL-Null: -4856.5 LLR p-value: 1.404e-24 ============================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ type2 0.2212 0.051 4.373 0.000 0.122 0.320 type3 0.7062 0.076 9.276 0.000 0.557 0.855 hmo -0.0680 0.053 -1.276 0.202 -0.172 0.036 white -0.1291 0.069 -1.883 0.060 -0.263 0.005 constant 2.3103 0.068 34.001 0.000 2.177 2.443 alpha 0.4457 0.020 22.495 0.000 0.407 0.485 ============================================================================== ``` In [20]: ``` print(res_nbin.params) ``` ``` type2 0.221218 type3 0.706173 hmo -0.067987 white -0.129053 constant 2.310279 alpha 0.445748 dtype: float64 ``` In [21]: ``` print(res_nbin.bse) ``` ``` type2 0.050592 type3 0.076131 hmo 0.053261 white 0.068541 constant 0.067947 alpha 0.019815 dtype: float64 ``` Or we could compare them to results obtained using the MASS implementation for R: ``` url = 'http://vincentarelbundock.github.com/Rdatasets/csv/COUNT/medpar.csv' medpar = read.csv(url) f = los~factor(type)+hmo+white library(MASS) mod = glm.nb(f, medpar) coef(summary(mod)) Estimate Std. Error z value Pr(>\|z\|) (Intercept) 2.31027893 0.06744676 34.253370 3.885556e-257 factor(type)2 0.22124898 0.05045746 4.384861 1.160597e-05 factor(type)3 0.70615882 0.07599849 9.291748 1.517751e-20 hmo -0.06795522 0.05321375 -1.277024 2.015939e-01 white -0.12906544 0.06836272 -1.887951 5.903257e-02 ``` ### Numerical precision The `statsmodels` generic MLE and `R` parameter estimates agree up to the fourth decimal. The standard errors, however, agree only up to the second decimal. This discrepancy is the result of imprecision in our Hessian numerical estimates. In the current context, the difference between `MASS` and `statsmodels` standard error estimates is substantively irrelevant, but it highlights the fact that users who need very precise estimates may not always want to rely on default settings when using numerical derivatives. In such cases, it is better to use analytical derivatives with the `LikelihoodModel` class.	programming_docs
statsmodels SARIMAX: Introduction SARIMAX: Introduction ===================== This notebook replicates examples from the Stata ARIMA time series estimation and postestimation documentation. First, we replicate the four estimation examples <http://www.stata.com/manuals13/tsarima.pdf>: 1. ARIMA(1,1,1) model on the U.S. Wholesale Price Index (WPI) dataset. 2. Variation of example 1 which adds an MA(4) term to the ARIMA(1,1,1) specification to allow for an additive seasonal effect. 3. ARIMA(2,1,0) x (1,1,0,12) model of monthly airline data. This example allows a multiplicative seasonal effect. 4. ARMA(1,1) model with exogenous regressors; describes consumption as an autoregressive process on which also the money supply is assumed to be an explanatory variable. Second, we demonstrate postestimation capabilitites to replicate <http://www.stata.com/manuals13/tsarimapostestimation.pdf>. The model from example 4 is used to demonstrate: 1. One-step-ahead in-sample prediction 2. n-step-ahead out-of-sample forecasting 3. n-step-ahead in-sample dynamic prediction In [1]: ``` %matplotlib inline ``` In [2]: ``` import numpy as np import pandas as pd from scipy.stats import norm import statsmodels.api as sm import matplotlib.pyplot as plt from datetime import datetime import requests from io import BytesIO ``` ### ARIMA Example 1: Arima As can be seen in the graphs from Example 2, the Wholesale price index (WPI) is growing over time (i.e. is not stationary). Therefore an ARMA model is not a good specification. In this first example, we consider a model where the original time series is assumed to be integrated of order 1, so that the difference is assumed to be stationary, and fit a model with one autoregressive lag and one moving average lag, as well as an intercept term. The postulated data process is then: $$ \Delta y\_t = c + \phi\_1 \Delta y\_{t-1} + \theta\_1 \epsilon\_{t-1} + \epsilon\_{t} $$ where $c$ is the intercept of the ARMA model, $\Delta$ is the first-difference operator, and we assume $\epsilon\_{t} \sim N(0, \sigma^2)$. This can be rewritten to emphasize lag polynomials as (this will be useful in example 2, below): $$ (1 - \phi\_1 L ) \Delta y\_t = c + (1 + \theta\_1 L) \epsilon\_{t} $$ where $L$ is the lag operator. Notice that one difference between the Stata output and the output below is that Stata estimates the following model: $$ (\Delta y\_t - \beta\_0) = \phi\_1 ( \Delta y\_{t-1} - \beta\_0) + \theta\_1 \epsilon\_{t-1} + \epsilon\_{t} $$ where $\beta\_0$ is the mean of the process $y\_t$. This model is equivalent to the one estimated in the Statsmodels SARIMAX class, but the interpretation is different. To see the equivalence, note that: $$ (\Delta y\_t - \beta\_0) = \phi\_1 ( \Delta y\_{t-1} - \beta\_0) + \theta\_1 \epsilon\_{t-1} + \epsilon\_{t} \\ \Delta y\_t = (1 - \phi\_1) \beta\_0 + \phi\_1 \Delta y\_{t-1} + \theta\_1 \epsilon\_{t-1} + \epsilon\_{t} $$ so that $c = (1 - \phi\_1) \beta\_0$. In [3]: ``` # Dataset wpi1 = requests.get('http://www.stata-press.com/data/r12/wpi1.dta').content data = pd.read_stata(BytesIO(wpi1)) data.index = data.t # Fit the model mod = sm.tsa.statespace.SARIMAX(data['wpi'], trend='c', order=(1,1,1)) res = mod.fit(disp=False) print(res.summary()) ``` ``` Statespace Model Results ============================================================================== Dep. Variable: wpi No. Observations: 124 Model: SARIMAX(1, 1, 1) Log Likelihood -135.351 Date: Mon, 14 May 2018 AIC 278.703 Time: 21:44:47 BIC 289.951 Sample: 01-01-1960 HQIC 283.272 - 10-01-1990 Covariance Type: opg ============================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ intercept 0.0943 0.068 1.389 0.165 -0.039 0.227 ar.L1 0.8742 0.055 16.028 0.000 0.767 0.981 ma.L1 -0.4120 0.100 -4.119 0.000 -0.608 -0.216 sigma2 0.5257 0.053 9.849 0.000 0.421 0.630 =================================================================================== Ljung-Box (Q): 37.12 Jarque-Bera (JB): 9.78 Prob(Q): 0.60 Prob(JB): 0.01 Heteroskedasticity (H): 15.93 Skew: 0.28 Prob(H) (two-sided): 0.00 Kurtosis: 4.26 =================================================================================== Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step). ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/tsa/base/tsa_model.py:171: ValueWarning: No frequency information was provided, so inferred frequency QS-OCT will be used. % freq, ValueWarning) ``` Thus the maximum likelihood estimates imply that for the process above, we have: $$ \Delta y\_t = 0.1050 + 0.8740 \Delta y\_{t-1} - 0.4206 \epsilon\_{t-1} + \epsilon\_{t} $$ where $\epsilon\_{t} \sim N(0, 0.5226)$. Finally, recall that $c = (1 - \phi\_1) \beta\_0$, and here $c = 0.1050$ and $\phi\_1 = 0.8740$. To compare with the output from Stata, we could calculate the mean: $$\beta\_0 = \frac{c}{1 - \phi\_1} = \frac{0.1050}{1 - 0.8740} = 0.83$$ Note: these values are slightly different from the values in the Stata documentation because the optimizer in Statsmodels has found parameters here that yield a higher likelihood. Nonetheless, they are very close. ### ARIMA Example 2: Arima with additive seasonal effects This model is an extension of that from example 1. Here the data is assumed to follow the process: $$ \Delta y\_t = c + \phi\_1 \Delta y\_{t-1} + \theta\_1 \epsilon\_{t-1} + \theta\_4 \epsilon\_{t-4} + \epsilon\_{t} $$ The new part of this model is that there is allowed to be a annual seasonal effect (it is annual even though the periodicity is 4 because the dataset is quarterly). The second difference is that this model uses the log of the data rather than the level. Before estimating the dataset, graphs showing: 1. The time series (in logs) 2. The first difference of the time series (in logs) 3. The autocorrelation function 4. The partial autocorrelation function. From the first two graphs, we note that the original time series does not appear to be stationary, whereas the first-difference does. This supports either estimating an ARMA model on the first-difference of the data, or estimating an ARIMA model with 1 order of integration (recall that we are taking the latter approach). The last two graphs support the use of an ARMA(1,1,1) model. In [4]: ``` # Dataset data = pd.read_stata(BytesIO(wpi1)) data.index = data.t data['ln_wpi'] = np.log(data['wpi']) data['D.ln_wpi'] = data['ln_wpi'].diff() ``` In [5]: ``` # Graph data fig, axes = plt.subplots(1, 2, figsize=(15,4)) # Levels axes[0].plot(data.index._mpl_repr(), data['wpi'], '-') axes[0].set(title='US Wholesale Price Index') # Log difference axes[1].plot(data.index._mpl_repr(), data['D.ln_wpi'], '-') axes[1].hlines(0, data.index[0], data.index[-1], 'r') axes[1].set(title='US Wholesale Price Index - difference of logs'); ``` In [6]: ``` # Graph data fig, axes = plt.subplots(1, 2, figsize=(15,4)) fig = sm.graphics.tsa.plot_acf(data.iloc[1:]['D.ln_wpi'], lags=40, ax=axes[0]) fig = sm.graphics.tsa.plot_pacf(data.iloc[1:]['D.ln_wpi'], lags=40, ax=axes[1]) ``` To understand how to specify this model in Statsmodels, first recall that from example 1 we used the following code to specify the ARIMA(1,1,1) model: ``` mod = sm.tsa.statespace.SARIMAX(data['wpi'], trend='c', order=(1,1,1)) ``` The `order` argument is a tuple of the form `(AR specification, Integration order, MA specification)`. The integration order must be an integer (for example, here we assumed one order of integration, so it was specified as 1. In a pure ARMA model where the underlying data is already stationary, it would be 0). For the AR specification and MA specification components, there are two possiblities. The first is to specify the maximum degree of the corresponding lag polynomial, in which case the component is an integer. For example, if we wanted to specify an ARIMA(1,1,4) process, we would use: ``` mod = sm.tsa.statespace.SARIMAX(data['wpi'], trend='c', order=(1,1,4)) ``` and the corresponding data process would be: $$ y\_t = c + \phi\_1 y\_{t-1} + \theta\_1 \epsilon\_{t-1} + \theta\_2 \epsilon\_{t-2} + \theta\_3 \epsilon\_{t-3} + \theta\_4 \epsilon\_{t-4} + \epsilon\_{t} $$ or $$ (1 - \phi\_1 L)\Delta y\_t = c + (1 + \theta\_1 L + \theta\_2 L^2 + \theta\_3 L^3 + \theta\_4 L^4) \epsilon\_{t} $$ When the specification parameter is given as a maximum degree of the lag polynomial, it implies that all polynomial terms up to that degree are included. Notice that this is not the model we want to use, because it would include terms for $\epsilon\_{t-2}$ and $\epsilon\_{t-3}$, which we don't want here. What we want is a polynomial that has terms for the 1st and 4th degrees, but leaves out the 2nd and 3rd terms. To do that, we need to provide a tuple for the specifiation parameter, where the tuple describes the lag polynomial itself. In particular, here we would want to use: ``` ar = 1 # this is the maximum degree specification ma = (1,0,0,1) # this is the lag polynomial specification mod = sm.tsa.statespace.SARIMAX(data['wpi'], trend='c', order=(ar,1,ma))) ``` This gives the following form for the process of the data: $$ \Delta y\_t = c + \phi\_1 \Delta y\_{t-1} + \theta\_1 \epsilon\_{t-1} + \theta\_4 \epsilon\_{t-4} + \epsilon\_{t} \\ (1 - \phi\_1 L)\Delta y\_t = c + (1 + \theta\_1 L + \theta\_4 L^4) \epsilon\_{t} $$ which is what we want. In [7]: ``` # Fit the model mod = sm.tsa.statespace.SARIMAX(data['ln_wpi'], trend='c', order=(1,1,1)) res = mod.fit(disp=False) print(res.summary()) ``` ``` Statespace Model Results ============================================================================== Dep. Variable: ln_wpi No. Observations: 124 Model: SARIMAX(1, 1, 1) Log Likelihood 381.892 Date: Mon, 14 May 2018 AIC -755.785 Time: 21:44:49 BIC -744.536 Sample: 01-01-1960 HQIC -751.216 - 10-01-1990 Covariance Type: opg ============================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ intercept 0.0019 0.001 1.660 0.097 -0.000 0.004 ar.L1 0.8209 0.052 15.924 0.000 0.720 0.922 ma.L1 -0.3646 0.097 -3.771 0.000 -0.554 -0.175 sigma2 0.0001 1.01e-05 11.532 0.000 9.71e-05 0.000 =================================================================================== Ljung-Box (Q): 40.31 Jarque-Bera (JB): 87.61 Prob(Q): 0.46 Prob(JB): 0.00 Heteroskedasticity (H): 2.33 Skew: 0.91 Prob(H) (two-sided): 0.01 Kurtosis: 6.71 =================================================================================== Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step). ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/tsa/base/tsa_model.py:171: ValueWarning: No frequency information was provided, so inferred frequency QS-OCT will be used. % freq, ValueWarning) ``` ### ARIMA Example 3: Airline Model In the previous example, we included a seasonal effect in an additive way, meaning that we added a term allowing the process to depend on the 4th MA lag. It may be instead that we want to model a seasonal effect in a multiplicative way. We often write the model then as an ARIMA $(p,d,q) \times (P,D,Q)\_s$, where the lowercast letters indicate the specification for the non-seasonal component, and the uppercase letters indicate the specification for the seasonal component; $s$ is the periodicity of the seasons (e.g. it is often 4 for quarterly data or 12 for monthly data). The data process can be written generically as: $$ \phi\_p (L) \tilde \phi\_P (L^s) \Delta^d \Delta\_s^D y\_t = A(t) + \theta\_q (L) \tilde \theta\_Q (L^s) \epsilon\_t $$ where: * $\phi\_p (L)$ is the non-seasonal autoregressive lag polynomial * $\tilde \phi\_P (L^s)$ is the seasonal autoregressive lag polynomial * $\Delta^d \Delta\_s^D y\_t$ is the time series, differenced $d$ times, and seasonally differenced $D$ times. * $A(t)$ is the trend polynomial (including the intercept) * $\theta\_q (L)$ is the non-seasonal moving average lag polynomial * $\tilde \theta\_Q (L^s)$ is the seasonal moving average lag polynomial sometimes we rewrite this as: $$ \phi\_p (L) \tilde \phi\_P (L^s) y\_t^\* = A(t) + \theta\_q (L) \tilde \theta\_Q (L^s) \epsilon\_t $$ where $y\_t^\* = \Delta^d \Delta\_s^D y\_t$. This emphasizes that just as in the simple case, after we take differences (here both non-seasonal and seasonal) to make the data stationary, the resulting model is just an ARMA model. As an example, consider the airline model ARIMA $(2,1,0) \times (1,1,0)\_{12}$, with an intercept. The data process can be written in the form above as: $$ (1 - \phi\_1 L - \phi\_2 L^2) (1 - \tilde \phi\_1 L^{12}) \Delta \Delta\_{12} y\_t = c + \epsilon\_t $$ Here, we have: * $\phi\_p (L) = (1 - \phi\_1 L - \phi\_2 L^2)$ * $\tilde \phi\_P (L^s) = (1 - \phi\_1 L^12)$ * $d = 1, D = 1, s=12$ indicating that $y\_t^\$ is derived from $y\_t$ by taking first-differences and then taking 12-th differences. $A(t) = c$ is the constant trend polynomial (i.e. just an intercept) * $\theta\_q (L) = \tilde \theta\_Q (L^s) = 1$ (i.e. there is no moving average effect) It may still be confusing to see the two lag polynomials in front of the time-series variable, but notice that we can multiply the lag polynomials together to get the following model: $$ (1 - \phi\_1 L - \phi\_2 L^2 - \tilde \phi\_1 L^{12} + \phi\_1 \tilde \phi\_1 L^{13} + \phi\_2 \tilde \phi\_1 L^{14} ) y\_t^\* = c + \epsilon\_t $$ which can be rewritten as: $$ y\_t^\* = c + \phi\_1 y\_{t-1}^\* + \phi\_2 y\_{t-2}^\* + \tilde \phi\_1 y\_{t-12}^\* - \phi\_1 \tilde \phi\_1 y\_{t-13}^\* - \phi\_2 \tilde \phi\_1 y\_{t-14}^\* + \epsilon\_t $$ This is similar to the additively seasonal model from example 2, but the coefficients in front of the autoregressive lags are actually combinations of the underlying seasonal and non-seasonal parameters. Specifying the model in Statsmodels is done simply by adding the `seasonal_order` argument, which accepts a tuple of the form `(Seasonal AR specification, Seasonal Integration order, Seasonal MA, Seasonal periodicity)`. The seasonal AR and MA specifications, as before, can be expressed as a maximum polynomial degree or as the lag polynomial itself. Seasonal periodicity is an integer. For the airline model ARIMA $(2,1,0) \times (1,1,0)\_{12}$ with an intercept, the command is: ``` mod = sm.tsa.statespace.SARIMAX(data['lnair'], order=(2,1,0), seasonal\_order=(1,1,0,12)) ``` In [8]: ``` # Dataset air2 = requests.get('http://www.stata-press.com/data/r12/air2.dta').content data = pd.read_stata(BytesIO(air2)) data.index = pd.date_range(start=datetime(data.time[0], 1, 1), periods=len(data), freq='MS') data['lnair'] = np.log(data['air']) # Fit the model mod = sm.tsa.statespace.SARIMAX(data['lnair'], order=(2,1,0), seasonal_order=(1,1,0,12), simple_differencing=True) res = mod.fit(disp=False) print(res.summary()) ``` ``` Statespace Model Results ========================================================================================== Dep. Variable: D.DS12.lnair No. Observations: 131 Model: SARIMAX(2, 0, 0)x(1, 0, 0, 12) Log Likelihood 240.821 Date: Mon, 14 May 2018 AIC -473.643 Time: 21:44:49 BIC -462.142 Sample: 02-01-1950 HQIC -468.970 - 12-01-1960 Covariance Type: opg ============================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ ar.L1 -0.4057 0.080 -5.045 0.000 -0.563 -0.248 ar.L2 -0.0799 0.099 -0.809 0.419 -0.274 0.114 ar.S.L12 -0.4723 0.072 -6.592 0.000 -0.613 -0.332 sigma2 0.0014 0.000 8.403 0.000 0.001 0.002 =================================================================================== Ljung-Box (Q): 49.89 Jarque-Bera (JB): 0.72 Prob(Q): 0.14 Prob(JB): 0.70 Heteroskedasticity (H): 0.54 Skew: 0.14 Prob(H) (two-sided): 0.04 Kurtosis: 3.23 =================================================================================== Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step). ``` Notice that here we used an additional argument `simple_differencing=True`. This controls how the order of integration is handled in ARIMA models. If `simple_differencing=True`, then the time series provided as `endog` is literatlly differenced and an ARMA model is fit to the resulting new time series. This implies that a number of initial periods are lost to the differencing process, however it may be necessary either to compare results to other packages (e.g. Stata's `arima` always uses simple differencing) or if the seasonal periodicity is large. The default is `simple_differencing=False`, in which case the integration component is implemented as part of the state space formulation, and all of the original data can be used in estimation. ### ARIMA Example 4: ARMAX (Friedman) This model demonstrates the use of explanatory variables (the X part of ARMAX). When exogenous regressors are included, the SARIMAX module uses the concept of "regression with SARIMA errors" (see <http://robjhyndman.com/hyndsight/arimax/> for details of regression with ARIMA errors versus alternative specifications), so that the model is specified as: $$ y\_t = \beta\_t x\_t + u\_t \\ \phi\_p (L) \tilde \phi\_P (L^s) \Delta^d \Delta\_s^D u\_t = A(t) + \theta\_q (L) \tilde \theta\_Q (L^s) \epsilon\_t $$ Notice that the first equation is just a linear regression, and the second equation just describes the process followed by the error component as SARIMA (as was described in example 3). One reason for this specification is that the estimated parameters have their natural interpretations. This specification nests many simpler specifications. For example, regression with AR(2) errors is: $$ y\_t = \beta\_t x\_t + u\_t \\ (1 - \phi\_1 L - \phi\_2 L^2) u\_t = A(t) + \epsilon\_t $$ The model considered in this example is regression with ARMA(1,1) errors. The process is then written: $$ \text{consump}\_t = \beta\_0 + \beta\_1 \text{m2}\_t + u\_t \\ (1 - \phi\_1 L) u\_t = (1 - \theta\_1 L) \epsilon\_t $$ Notice that $\beta\_0$ is, as described in example 1 above, not the same thing as an intercept specified by `trend='c'`. Whereas in the examples above we estimated the intercept of the model via the trend polynomial, here, we demonstrate how to estimate $\beta\_0$ itself by adding a constant to the exogenous dataset. In the output, the $beta\_0$ is called `const`, whereas above the intercept $c$ was called `intercept` in the output. In [9]: ``` # Dataset friedman2 = requests.get('http://www.stata-press.com/data/r12/friedman2.dta').content data = pd.read_stata(BytesIO(friedman2)) data.index = data.time # Variables endog = data.loc['1959':'1981', 'consump'] exog = sm.add_constant(data.loc['1959':'1981', 'm2']) # Fit the model mod = sm.tsa.statespace.SARIMAX(endog, exog, order=(1,0,1)) res = mod.fit(disp=False) print(res.summary()) ``` ``` Statespace Model Results ============================================================================== Dep. Variable: consump No. Observations: 92 Model: SARIMAX(1, 0, 1) Log Likelihood -340.508 Date: Mon, 14 May 2018 AIC 691.015 Time: 21:44:50 BIC 703.624 Sample: 01-01-1959 HQIC 696.105 - 10-01-1981 Covariance Type: opg ============================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ const -36.0710 56.619 -0.637 0.524 -147.043 74.901 m2 1.1220 0.036 30.835 0.000 1.051 1.193 ar.L1 0.9348 0.041 22.718 0.000 0.854 1.015 ma.L1 0.3091 0.089 3.488 0.000 0.135 0.483 sigma2 93.2562 10.889 8.564 0.000 71.915 114.598 =================================================================================== Ljung-Box (Q): 38.72 Jarque-Bera (JB): 23.49 Prob(Q): 0.53 Prob(JB): 0.00 Heteroskedasticity (H): 22.51 Skew: 0.17 Prob(H) (two-sided): 0.00 Kurtosis: 5.45 =================================================================================== Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step). ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/tsa/base/tsa_model.py:171: ValueWarning: No frequency information was provided, so inferred frequency QS-OCT will be used. % freq, ValueWarning) ``` ### ARIMA Postestimation: Example 1 - Dynamic Forecasting Here we describe some of the post-estimation capabilities of Statsmodels' SARIMAX. First, using the model from example, we estimate the parameters using data that excludes the last few observations (this is a little artificial as an example, but it allows considering performance of out-of-sample forecasting and facilitates comparison to Stata's documentation). In [10]: ``` # Dataset raw = pd.read_stata(BytesIO(friedman2)) raw.index = raw.time data = raw.loc[:'1981'] # Variables endog = data.loc['1959':, 'consump'] exog = sm.add_constant(data.loc['1959':, 'm2']) nobs = endog.shape[0] # Fit the model mod = sm.tsa.statespace.SARIMAX(endog.loc[:'1978-01-01'], exog=exog.loc[:'1978-01-01'], order=(1,0,1)) fit_res = mod.fit(disp=False) print(fit_res.summary()) ``` ``` Statespace Model Results ============================================================================== Dep. Variable: consump No. Observations: 77 Model: SARIMAX(1, 0, 1) Log Likelihood -243.316 Date: Mon, 14 May 2018 AIC 496.633 Time: 21:44:50 BIC 508.352 Sample: 01-01-1959 HQIC 501.320 - 01-01-1978 Covariance Type: opg ============================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ const 0.6786 18.492 0.037 0.971 -35.565 36.922 m2 1.0379 0.021 50.328 0.000 0.997 1.078 ar.L1 0.8775 0.059 14.859 0.000 0.762 0.993 ma.L1 0.2771 0.108 2.571 0.010 0.066 0.488 sigma2 31.6982 4.683 6.769 0.000 22.520 40.877 =================================================================================== Ljung-Box (Q): 46.78 Jarque-Bera (JB): 6.05 Prob(Q): 0.21 Prob(JB): 0.05 Heteroskedasticity (H): 6.09 Skew: 0.57 Prob(H) (two-sided): 0.00 Kurtosis: 3.76 =================================================================================== Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step). ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/tsa/base/tsa_model.py:171: ValueWarning: No frequency information was provided, so inferred frequency QS-OCT will be used. % freq, ValueWarning) ``` Next, we want to get results for the full dataset but using the estimated parameters (on a subset of the data). In [11]: ``` mod = sm.tsa.statespace.SARIMAX(endog, exog=exog, order=(1,0,1)) res = mod.filter(fit_res.params) ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/tsa/base/tsa_model.py:171: ValueWarning: No frequency information was provided, so inferred frequency QS-OCT will be used. % freq, ValueWarning) ``` The `predict` command is first applied here to get in-sample predictions. We use the `full_results=True` argument to allow us to calculate confidence intervals (the default output of `predict` is just the predicted values). With no other arguments, `predict` returns the one-step-ahead in-sample predictions for the entire sample. In [12]: ``` # In-sample one-step-ahead predictions predict = res.get_prediction() predict_ci = predict.conf_int() ``` We can also get dynamic predictions. One-step-ahead prediction uses the true values of the endogenous values at each step to predict the next in-sample value. Dynamic predictions use one-step-ahead prediction up to some point in the dataset (specified by the `dynamic` argument); after that, the previous predicted endogenous values are used in place of the true endogenous values for each new predicted element. The `dynamic` argument is specified to be an offset relative to the `start` argument. If `start` is not specified, it is assumed to be `0`. Here we perform dynamic prediction starting in the first quarter of 1978. In [13]: ``` # Dynamic predictions predict_dy = res.get_prediction(dynamic='1978-01-01') predict_dy_ci = predict_dy.conf_int() ``` We can graph the one-step-ahead and dynamic predictions (and the corresponding confidence intervals) to see their relative performance. Notice that up to the point where dynamic prediction begins (1978:Q1), the two are the same. In [14]: ``` # Graph fig, ax = plt.subplots(figsize=(9,4)) npre = 4 ax.set(title='Personal consumption', xlabel='Date', ylabel='Billions of dollars') # Plot data points data.loc['1977-07-01':, 'consump'].plot(ax=ax, style='o', label='Observed') # Plot predictions predict.predicted_mean.loc['1977-07-01':].plot(ax=ax, style='r--', label='One-step-ahead forecast') ci = predict_ci.loc['1977-07-01':] ax.fill_between(ci.index, ci.iloc[:,0], ci.iloc[:,1], color='r', alpha=0.1) predict_dy.predicted_mean.loc['1977-07-01':].plot(ax=ax, style='g', label='Dynamic forecast (1978)') ci = predict_dy_ci.loc['1977-07-01':] ax.fill_between(ci.index, ci.iloc[:,0], ci.iloc[:,1], color='g', alpha=0.1) legend = ax.legend(loc='lower right') ``` Finally, graph the prediction error. It is obvious that, as one would suspect, one-step-ahead prediction is considerably better. In [15]: ``` # Prediction error # Graph fig, ax = plt.subplots(figsize=(9,4)) npre = 4 ax.set(title='Forecast error', xlabel='Date', ylabel='Forecast - Actual') # In-sample one-step-ahead predictions and 95% confidence intervals predict_error = predict.predicted_mean - endog predict_error.loc['1977-10-01':].plot(ax=ax, label='One-step-ahead forecast') ci = predict_ci.loc['1977-10-01':].copy() ci.iloc[:,0] -= endog.loc['1977-10-01':] ci.iloc[:,1] -= endog.loc['1977-10-01':] ax.fill_between(ci.index, ci.iloc[:,0], ci.iloc[:,1], alpha=0.1) # Dynamic predictions and 95% confidence intervals predict_dy_error = predict_dy.predicted_mean - endog predict_dy_error.loc['1977-10-01':].plot(ax=ax, style='r', label='Dynamic forecast (1978)') ci = predict_dy_ci.loc['1977-10-01':].copy() ci.iloc[:,0] -= endog.loc['1977-10-01':] ci.iloc[:,1] -= endog.loc['1977-10-01':] ax.fill_between(ci.index, ci.iloc[:,0], ci.iloc[:,1], color='r', alpha=0.1) legend = ax.legend(loc='lower left'); legend.get_frame().set_facecolor('w') ```	programming_docs
statsmodels Plot Interaction of Categorical Factors Plot Interaction of Categorical Factors ======================================= In this example, we will vizualize the interaction between categorical factors. First, we will create some categorical data are initialized. Then plotted using the interaction\_plot function which internally recodes the x-factor categories to ingegers. In [1]: ``` %matplotlib inline import numpy as np import matplotlib.pyplot as plt import pandas as pd from statsmodels.graphics.factorplots import interaction_plot ``` In [2]: ``` np.random.seed(12345) weight = pd.Series(np.repeat(['low', 'hi', 'low', 'hi'], 15), name='weight') nutrition = pd.Series(np.repeat(['lo_carb', 'hi_carb'], 30), name='nutrition') days = np.log(np.random.randint(1, 30, size=60)) ``` In [3]: ``` fig, ax = plt.subplots(figsize=(6, 6)) fig = interaction_plot(x=weight, trace=nutrition, response=days, colors=['red', 'blue'], markers=['D', '^'], ms=10, ax=ax) ``` statsmodels Autoregressive Moving Average (ARMA): Artificial data Autoregressive Moving Average (ARMA): Artificial data ===================================================== In [1]: ``` %matplotlib inline from __future__ import print_function import numpy as np import statsmodels.api as sm import pandas as pd from statsmodels.tsa.arima_process import arma_generate_sample np.random.seed(12345) ``` Generate some data from an ARMA process: In [2]: ``` arparams = np.array([.75, -.25]) maparams = np.array([.65, .35]) ``` The conventions of the arma\_generate function require that we specify a 1 for the zero-lag of the AR and MA parameters and that the AR parameters be negated. In [3]: ``` arparams = np.r_[1, -arparams] maparams = np.r_[1, maparams] nobs = 250 y = arma_generate_sample(arparams, maparams, nobs) ``` Now, optionally, we can add some dates information. For this example, we'll use a pandas time series. In [4]: ``` dates = sm.tsa.datetools.dates_from_range('1980m1', length=nobs) y = pd.Series(y, index=dates) arma_mod = sm.tsa.ARMA(y, order=(2,2)) arma_res = arma_mod.fit(trend='nc', disp=-1) ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/tsa/base/tsa_model.py:171: ValueWarning: No frequency information was provided, so inferred frequency M will be used. % freq, ValueWarning) ``` In [5]: ``` print(arma_res.summary()) ``` ``` ARMA Model Results ============================================================================== Dep. Variable: y No. Observations: 250 Model: ARMA(2, 2) Log Likelihood -353.445 Method: css-mle S.D. of innovations 0.990 Date: Mon, 14 May 2018 AIC 716.891 Time: 21:45:03 BIC 734.498 Sample: 01-31-1980 HQIC 723.977 - 10-31-2000 ============================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ ar.L1.y 0.7904 0.134 5.878 0.000 0.527 1.054 ar.L2.y -0.2314 0.113 -2.044 0.042 -0.453 -0.009 ma.L1.y 0.7007 0.127 5.525 0.000 0.452 0.949 ma.L2.y 0.4061 0.095 4.291 0.000 0.221 0.592 Roots ============================================================================= Real Imaginary Modulus Frequency ----------------------------------------------------------------------------- AR.1 1.7079 -1.1851j 2.0788 -0.0965 AR.2 1.7079 +1.1851j 2.0788 0.0965 MA.1 -0.8628 -1.3108j 1.5693 -0.3427 MA.2 -0.8628 +1.3108j 1.5693 0.3427 ----------------------------------------------------------------------------- ``` In [6]: ``` y.tail() ``` Out[6]: ``` 2000-06-30 0.173211 2000-07-31 -0.048325 2000-08-31 -0.415804 2000-09-30 0.338725 2000-10-31 0.360838 dtype: float64 ``` In [7]: ``` import matplotlib.pyplot as plt fig, ax = plt.subplots(figsize=(10,8)) fig = arma_res.plot_predict(start='1999-06-30', end='2001-05-31', ax=ax) legend = ax.legend(loc='upper left') ``` statsmodels State space modeling: Local Linear Trends State space modeling: Local Linear Trends ========================================= This notebook describes how to extend the Statsmodels statespace classes to create and estimate a custom model. Here we develop a local linear trend model. The Local Linear Trend model has the form (see Durbin and Koopman 2012, Chapter 3.2 for all notation and details): $$ \begin{align} y\_t & = \mu\_t + \varepsilon\_t \qquad & \varepsilon\_t \sim N(0, \sigma\_\varepsilon^2) \\ \mu\_{t+1} & = \mu\_t + \nu\_t + \xi\_t & \xi\_t \sim N(0, \sigma\_\xi^2) \\ \nu\_{t+1} & = \nu\_t + \zeta\_t & \zeta\_t \sim N(0, \sigma\_\zeta^2) \end{align} $$ It is easy to see that this can be cast into state space form as: $$ \begin{align} y\_t & = \begin{pmatrix} 1 & 0 \end{pmatrix} \begin{pmatrix} \mu\_t \\ \nu\_t \end{pmatrix} + \varepsilon\_t \\ \begin{pmatrix} \mu\_{t+1} \\ \nu\_{t+1} \end{pmatrix} & = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \begin{pmatrix} \mu\_t \\ \nu\_t \end{pmatrix} + \begin{pmatrix} \xi\_t \\ \zeta\_t \end{pmatrix} \end{align} $$ Notice that much of the state space representation is composed of known values; in fact the only parts in which parameters to be estimated appear are in the variance / covariance matrices: $$ \begin{align} H\_t & = \begin{bmatrix} \sigma\_\varepsilon^2 \end{bmatrix} \\ Q\_t & = \begin{bmatrix} \sigma\_\xi^2 & 0 \\ 0 & \sigma\_\zeta^2 \end{bmatrix} \end{align} $$ In [1]: ``` %matplotlib inline import numpy as np import pandas as pd from scipy.stats import norm import statsmodels.api as sm import matplotlib.pyplot as plt ``` To take advantage of the existing infrastructure, including Kalman filtering and maximum likelihood estimation, we create a new class which extends from `statsmodels.tsa.statespace.MLEModel`. There are a number of things that must be specified: 1. k\_states, k\_posdef: These two parameters must be provided to the base classes in initialization. The inform the statespace model about the size of, respectively, the state vector, above $\begin{pmatrix} \mu\_t & \nu\_t \end{pmatrix}'$, and the state error vector, above $\begin{pmatrix} \xi\_t & \zeta\_t \end{pmatrix}'$. Note that the dimension of the endogenous vector does not have to be specified, since it can be inferred from the `endog` array. 2. update: The method `update`, with argument `params`, must be specified (it is used when `fit()` is called to calculate the MLE). It takes the parameters and fills them into the appropriate state space matrices. For example, below, the `params` vector contains variance parameters $\begin{pmatrix} \sigma\_\varepsilon^2 & \sigma\_\xi^2 & \sigma\_\zeta^2\end{pmatrix}$, and the `update` method must place them in the observation and state covariance matrices. More generally, the parameter vector might be mapped into many different places in all of the statespace matrices. 3. statespace matrices: by default, all state space matrices (`obs_intercept, design, obs_cov, state_intercept, transition, selection, state_cov`) are set to zeros. Values that are fixed (like the ones in the design and transition matrices here) can be set in initialization, whereas values that vary with the parameters should be set in the `update` method. Note that it is easy to forget to set the selection matrix, which is often just the identity matrix (as it is here), but not setting it will lead to a very different model (one where there is not a stochastic component to the transition equation). 4. start params: start parameters must be set, even if it is just a vector of zeros, although often good start parameters can be found from the data. Maximum likelihood estimation by gradient methods (as employed here) can be sensitive to the starting parameters, so it is important to select good ones if possible. Here it does not matter too much (although as variances, they should't be set zero). 5. initialization: in addition to defined state space matrices, all state space models must be initialized with the mean and variance for the initial distribution of the state vector. If the distribution is known, `initialize_known(initial_state, initial_state_cov)` can be called, or if the model is stationary (e.g. an ARMA model), `initialize_stationary` can be used. Otherwise, `initialize_approximate_diffuse` is a reasonable generic initialization (exact diffuse initialization is not yet available). Since the local linear trend model is not stationary (it is composed of random walks) and since the distribution is not generally known, we use `initialize_approximate_diffuse` below. The above are the minimum necessary for a successful model. There are also a number of things that do not have to be set, but which may be helpful or important for some applications: 1. transform / untransform: when `fit` is called, the optimizer in the background will use gradient methods to select the parameters that maximize the likelihood function. By default it uses unbounded optimization, which means that it may select any parameter value. In many cases, that is not the desired behavior; variances, for example, cannot be negative. To get around this, the `transform` method takes the unconstrained vector of parameters provided by the optimizer and returns a constrained vector of parameters used in likelihood evaluation. `untransform` provides the reverse operation. 2. param\_names: this internal method can be used to set names for the estimated parameters so that e.g. the summary provides meaningful names. If not present, parameters are named `param0`, `param1`, etc. In [2]: ``` """ Univariate Local Linear Trend Model """ class LocalLinearTrend(sm.tsa.statespace.MLEModel): def __init__(self, endog): # Model order k_states = k_posdef = 2 # Initialize the statespace super(LocalLinearTrend, self).__init__( endog, k_states=k_states, k_posdef=k_posdef, initialization='approximate_diffuse', loglikelihood_burn=k_states ) # Initialize the matrices self.ssm['design'] = np.array([1, 0]) self.ssm['transition'] = np.array([[1, 1], [0, 1]]) self.ssm['selection'] = np.eye(k_states) # Cache some indices self._state_cov_idx = ('state_cov',) + np.diag_indices(k_posdef) @property def param_names(self): return ['sigma2.measurement', 'sigma2.level', 'sigma2.trend'] @property def start_params(self): return [np.std(self.endog)]3 def transform_params(self, unconstrained): return unconstrained2 def untransform_params(self, constrained): return constrained0.5 def update(self, params, args, *kwargs): params = super(LocalLinearTrend, self).update(params, args, *kwargs) # Observation covariance self.ssm['obs_cov',0,0] = params[0] # State covariance self.ssm[self._state_cov_idx] = params[1:] ``` Using this simple model, we can estimate the parameters from a local linear trend model. The following example is from Commandeur and Koopman (2007), section 3.4., modeling motor vehicle fatalities in Finland. In [3]: ``` import requests from io import BytesIO from zipfile import ZipFile # Download the dataset ck = requests.get('http://staff.feweb.vu.nl/koopman/projects/ckbook/OxCodeAll.zip').content zipped = ZipFile(BytesIO(ck)) df = pd.read_table( BytesIO(zipped.read('OxCodeIntroStateSpaceBook/Chapter_2/NorwayFinland.txt')), skiprows=1, header=None, sep='\s+', engine='python', names=['date','nf', 'ff'] ) ``` Since we defined the local linear trend model as extending from `MLEModel`, the `fit()` method is immediately available, just as in other Statsmodels maximum likelihood classes. Similarly, the returned results class supports many of the same post-estimation results, like the `summary` method. In [4]: ``` # Load Dataset df.index = pd.date_range(start='%d-01-01' % df.date[0], end='%d-01-01' % df.iloc[-1, 0], freq='AS') # Log transform df['lff'] = np.log(df['ff']) # Setup the model mod = LocalLinearTrend(df['lff']) # Fit it using MLE (recall that we are fitting the three variance parameters) res = mod.fit(disp=False) print(res.summary()) ``` ``` Statespace Model Results ============================================================================== Dep. Variable: lff No. Observations: 34 Model: LocalLinearTrend Log Likelihood 27.510 Date: Mon, 14 May 2018 AIC -49.020 Time: 21:44:44 BIC -44.623 Sample: 01-01-1970 HQIC -47.563 - 01-01-2003 Covariance Type: opg ====================================================================================== coef std err z P>\|z\| [0.025 0.975] -------------------------------------------------------------------------------------- sigma2.measurement 0.0010 0.003 0.346 0.730 -0.005 0.007 sigma2.level 0.0074 0.005 1.564 0.118 -0.002 0.017 sigma2.trend 2.442e-11 0.000 1.63e-07 1.000 -0.000 0.000 =================================================================================== Ljung-Box (Q): 24.37 Jarque-Bera (JB): 0.68 Prob(Q): 0.80 Prob(JB): 0.71 Heteroskedasticity (H): 0.75 Skew: -0.02 Prob(H) (two-sided): 0.64 Kurtosis: 2.29 =================================================================================== Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step). ``` Finally, we can do post-estimation prediction and forecasting. Notice that the end period can be specified as a date. In [5]: ``` # Perform prediction and forecasting predict = res.get_prediction() forecast = res.get_forecast('2014') ``` In [6]: ``` fig, ax = plt.subplots(figsize=(10,4)) # Plot the results df['lff'].plot(ax=ax, style='k.', label='Observations') predict.predicted_mean.plot(ax=ax, label='One-step-ahead Prediction') predict_ci = predict.conf_int(alpha=0.05) predict_index = np.arange(len(predict_ci)) ax.fill_between(predict_index[2:], predict_ci.iloc[2:, 0], predict_ci.iloc[2:, 1], alpha=0.1) forecast.predicted_mean.plot(ax=ax, style='r', label='Forecast') forecast_ci = forecast.conf_int() forecast_index = np.arange(len(predict_ci), len(predict_ci) + len(forecast_ci)) ax.fill_between(forecast_index, forecast_ci.iloc[:, 0], forecast_ci.iloc[:, 1], alpha=0.1) # Cleanup the image ax.set_ylim((4, 8)); legend = ax.legend(loc='lower left'); ``` ### References ``` Commandeur, Jacques J. F., and Siem Jan Koopman. 2007. An Introduction to State Space Time Series Analysis. Oxford ; New York: Oxford University Press. Durbin, James, and Siem Jan Koopman. 2012. Time Series Analysis by State Space Methods: Second Edition. Oxford University Press. ``` statsmodels None Markov switching autoregression models -------------------------------------- This notebook provides an example of the use of Markov switching models in Statsmodels to replicate a number of results presented in Kim and Nelson (1999). It applies the Hamilton (1989) filter the Kim (1994) smoother. This is tested against the Markov-switching models from E-views 8, which can be found at <http://www.eviews.com/EViews8/ev8ecswitch_n.html#MarkovAR> or the Markov-switching models of Stata 14 which can be found at <http://www.stata.com/manuals14/tsmswitch.pdf>. In [1]: ``` %matplotlib inline import numpy as np import pandas as pd import statsmodels.api as sm import matplotlib.pyplot as plt import requests from io import BytesIO # NBER recessions from pandas_datareader.data import DataReader from datetime import datetime usrec = DataReader('USREC', 'fred', start=datetime(1947, 1, 1), end=datetime(2013, 4, 1)) ``` ### Hamilton (1989) switching model of GNP This replicates Hamilton's (1989) seminal paper introducing Markov-switching models. The model is an autoregressive model of order 4 in which the mean of the process switches between two regimes. It can be written: $$ y\_t = \mu\_{S\_t} + \phi\_1 (y\_{t-1} - \mu\_{S\_{t-1}}) + \phi\_2 (y\_{t-2} - \mu\_{S\_{t-2}}) + \phi\_3 (y\_{t-3} - \mu\_{S\_{t-3}}) + \phi\_4 (y\_{t-4} - \mu\_{S\_{t-4}}) + \varepsilon\_t $$ Each period, the regime transitions according to the following matrix of transition probabilities: $$ P(S\_t = s\_t \| S\_{t-1} = s\_{t-1}) = \begin{bmatrix} p\_{00} & p\_{10} \\ p\_{01} & p\_{11} \end{bmatrix} $$ where $p\_{ij}$ is the probability of transitioning from* regime $i$, to regime $j$. The model class is `MarkovAutoregression` in the time-series part of `Statsmodels`. In order to create the model, we must specify the number of regimes with `k_regimes=2`, and the order of the autoregression with `order=4`. The default model also includes switching autoregressive coefficients, so here we also need to specify `switching_ar=False` to avoid that. After creation, the model is `fit` via maximum likelihood estimation. Under the hood, good starting parameters are found using a number of steps of the expectation maximization (EM) algorithm, and a quasi-Newton (BFGS) algorithm is applied to quickly find the maximum. In [2]: ``` # Get the RGNP data to replicate Hamilton dta = pd.read_stata('http://www.stata-press.com/data/r14/rgnp.dta').iloc[1:] dta.index = pd.DatetimeIndex(dta.date, freq='QS') dta_hamilton = dta.rgnp # Plot the data dta_hamilton.plot(title='Growth rate of Real GNP', figsize=(12,3)) # Fit the model mod_hamilton = sm.tsa.MarkovAutoregression(dta_hamilton, k_regimes=2, order=4, switching_ar=False) res_hamilton = mod_hamilton.fit() ``` In [3]: ``` res_hamilton.summary() ``` Out[3]: Markov Switching Model Results\| Dep. Variable: \| rgnp \| No. Observations: \| 131 \| \| Model: \| MarkovAutoregression \| Log Likelihood \| -181.263 \| \| Date: \| Mon, 14 May 2018 \| AIC \| 380.527 \| \| Time: \| 21:45:28 \| BIC \| 406.404 \| \| Sample: \| 04-01-1951 \| HQIC \| 391.042 \| \| \| - 10-01-1984 \| \| \| \| Covariance Type: \| approx \| \| \| Regime 0 parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| const \| -0.3588 \| 0.265 \| -1.356 \| 0.175 \| -0.877 \| 0.160 \| Regime 1 parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| const \| 1.1635 \| 0.075 \| 15.614 \| 0.000 \| 1.017 \| 1.310 \| Non-switching parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| sigma2 \| 0.5914 \| 0.103 \| 5.761 \| 0.000 \| 0.390 \| 0.793 \| \| ar.L1 \| 0.0135 \| 0.120 \| 0.112 \| 0.911 \| -0.222 \| 0.249 \| \| ar.L2 \| -0.0575 \| 0.138 \| -0.418 \| 0.676 \| -0.327 \| 0.212 \| \| ar.L3 \| -0.2470 \| 0.107 \| -2.310 \| 0.021 \| -0.457 \| -0.037 \| \| ar.L4 \| -0.2129 \| 0.111 \| -1.926 \| 0.054 \| -0.430 \| 0.004 \| Regime transition parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| p[0->0] \| 0.7547 \| 0.097 \| 7.819 \| 0.000 \| 0.565 \| 0.944 \| \| p[1->0] \| 0.0959 \| 0.038 \| 2.542 \| 0.011 \| 0.022 \| 0.170 \| Warnings: [1] Covariance matrix calculated using numerical (complex-step) differentiation. We plot the filtered and smoothed probabilities of a recession. Filtered refers to an estimate of the probability at time $t$ based on data up to and including time $t$ (but excluding time $t+1, ..., T$). Smoothed refers to an estimate of the probability at time $t$ using all the data in the sample. For reference, the shaded periods represent the NBER recessions. In [4]: ``` fig, axes = plt.subplots(2, figsize=(7,7)) ax = axes[0] ax.plot(res_hamilton.filtered_marginal_probabilities[0]) ax.fill_between(usrec.index, 0, 1, where=usrec['USREC'].values, color='k', alpha=0.1) ax.set_xlim(dta_hamilton.index[4], dta_hamilton.index[-1]) ax.set(title='Filtered probability of recession') ax = axes[1] ax.plot(res_hamilton.smoothed_marginal_probabilities[0]) ax.fill_between(usrec.index, 0, 1, where=usrec['USREC'].values, color='k', alpha=0.1) ax.set_xlim(dta_hamilton.index[4], dta_hamilton.index[-1]) ax.set(title='Smoothed probability of recession') fig.tight_layout() ``` From the estimated transition matrix we can calculate the expected duration of a recession versus an expansion. In [5]: ``` print(res_hamilton.expected_durations) ``` ``` [ 4.07604744 10.42589389] ``` In this case, it is expected that a recession will last about one year (4 quarters) and an expansion about two and a half years. ### Kim, Nelson, and Startz (1998) Three-state Variance Switching This model demonstrates estimation with regime heteroskedasticity (switching of variances) and no mean effect. The dataset can be reached at <http://econ.korea.ac.kr/~cjkim/MARKOV/data/ew_excs.prn>. The model in question is: $$ \begin{align} y\_t & = \varepsilon\_t \\ \varepsilon\_t & \sim N(0, \sigma\_{S\_t}^2) \end{align} $$ Since there is no autoregressive component, this model can be fit using the `MarkovRegression` class. Since there is no mean effect, we specify `trend='nc'`. There are hypotheized to be three regimes for the switching variances, so we specify `k_regimes=3` and `switching_variance=True` (by default, the variance is assumed to be the same across regimes). In [6]: ``` # Get the dataset ew_excs = requests.get('http://econ.korea.ac.kr/~cjkim/MARKOV/data/ew_excs.prn').content raw = pd.read_table(BytesIO(ew_excs), header=None, skipfooter=1, engine='python') raw.index = pd.date_range('1926-01-01', '1995-12-01', freq='MS') dta_kns = raw.loc[:'1986'] - raw.loc[:'1986'].mean() # Plot the dataset dta_kns[0].plot(title='Excess returns', figsize=(12, 3)) # Fit the model mod_kns = sm.tsa.MarkovRegression(dta_kns, k_regimes=3, trend='nc', switching_variance=True) res_kns = mod_kns.fit() ``` In [7]: ``` res_kns.summary() ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/base/model.py:1092: RuntimeWarning: invalid value encountered in sqrt bse_ = np.sqrt(np.diag(self.cov_params())) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:879: RuntimeWarning: invalid value encountered in greater return (self.a < x) & (x < self.b) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:879: RuntimeWarning: invalid value encountered in less return (self.a < x) & (x < self.b) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:1821: RuntimeWarning: invalid value encountered in less_equal cond2 = cond0 & (x <= self.a) ``` Out[7]: Markov Switching Model Results\| Dep. Variable: \| 0 \| No. Observations: \| 732 \| \| Model: \| MarkovRegression \| Log Likelihood \| 1001.895 \| \| Date: \| Mon, 14 May 2018 \| AIC \| -1985.790 \| \| Time: \| 21:45:33 \| BIC \| -1944.428 \| \| Sample: \| 01-01-1926 \| HQIC \| -1969.834 \| \| \| - 12-01-1986 \| \| \| \| Covariance Type: \| approx \| \| \| Regime 0 parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| sigma2 \| 0.0012 \| 0.000 \| 6.675 \| 0.000 \| 0.001 \| 0.002 \| Regime 1 parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| sigma2 \| 0.0040 \| 0.000 \| 8.477 \| 0.000 \| 0.003 \| 0.005 \| Regime 2 parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| sigma2 \| 0.0311 \| 0.006 \| 5.539 \| 0.000 \| 0.020 \| 0.042 \| Regime transition parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| p[0->0] \| 0.9747 \| nan \| nan \| nan \| nan \| nan \| \| p[1->0] \| 0.0195 \| 0.012 \| 1.681 \| 0.093 \| -0.003 \| 0.042 \| \| p[2->0] \| 2.354e-08 \| 0.004 \| 5.61e-06 \| 1.000 \| -0.008 \| 0.008 \| \| p[0->1] \| 0.0253 \| 0.018 \| 1.408 \| 0.159 \| -0.010 \| 0.061 \| \| p[1->1] \| 0.9688 \| 0.014 \| 68.322 \| 0.000 \| 0.941 \| 0.997 \| \| p[2->1] \| 0.0493 \| 0.040 \| 1.223 \| 0.221 \| -0.030 \| 0.128 \| Warnings: [1] Covariance matrix calculated using numerical (complex-step) differentiation. Below we plot the probabilities of being in each of the regimes; only in a few periods is a high-variance regime probable. In [8]: ``` fig, axes = plt.subplots(3, figsize=(10,7)) ax = axes[0] ax.plot(res_kns.smoothed_marginal_probabilities[0]) ax.set(title='Smoothed probability of a low-variance regime for stock returns') ax = axes[1] ax.plot(res_kns.smoothed_marginal_probabilities[1]) ax.set(title='Smoothed probability of a medium-variance regime for stock returns') ax = axes[2] ax.plot(res_kns.smoothed_marginal_probabilities[2]) ax.set(title='Smoothed probability of a high-variance regime for stock returns') fig.tight_layout() ``` ### Filardo (1994) Time-Varying Transition Probabilities This model demonstrates estimation with time-varying transition probabilities. The dataset can be reached at <http://econ.korea.ac.kr/~cjkim/MARKOV/data/filardo.prn>. In the above models we have assumed that the transition probabilities are constant across time. Here we allow the probabilities to change with the state of the economy. Otherwise, the model is the same Markov autoregression of Hamilton (1989). Each period, the regime now transitions according to the following matrix of time-varying transition probabilities: $$ P(S\_t = s\_t \| S\_{t-1} = s\_{t-1}) = \begin{bmatrix} p\_{00,t} & p\_{10,t} \\ p\_{01,t} & p\_{11,t} \end{bmatrix} $$ where $p\_{ij,t}$ is the probability of transitioning from regime $i$, to regime $j$ in period $t$, and is defined to be: $$ p\_{ij,t} = \frac{\exp\{ x\_{t-1}' \beta\_{ij} \}}{1 + \exp\{ x\_{t-1}' \beta\_{ij} \}} $$ Instead of estimating the transition probabilities as part of maximum likelihood, the regression coefficients $\beta\_{ij}$ are estimated. These coefficients relate the transition probabilities to a vector of pre-determined or exogenous regressors $x\_{t-1}$. In [9]: ``` # Get the dataset filardo = requests.get('http://econ.korea.ac.kr/~cjkim/MARKOV/data/filardo.prn').content dta_filardo = pd.read_table(BytesIO(filardo), sep=' +', header=None, skipfooter=1, engine='python') dta_filardo.columns = ['month', 'ip', 'leading'] dta_filardo.index = pd.date_range('1948-01-01', '1991-04-01', freq='MS') dta_filardo['dlip'] = np.log(dta_filardo['ip']).diff()100 # Deflated pre-1960 observations by ratio of std. devs. # See hmt_tvp.opt or Filardo (1994) p. 302 std_ratio = dta_filardo['dlip']['1960-01-01':].std() / dta_filardo['dlip'][:'1959-12-01'].std() dta_filardo['dlip'][:'1959-12-01'] = dta_filardo['dlip'][:'1959-12-01'] std_ratio dta_filardo['dlleading'] = np.log(dta_filardo['leading']).diff()*100 dta_filardo['dmdlleading'] = dta_filardo['dlleading'] - dta_filardo['dlleading'].mean() # Plot the data dta_filardo['dlip'].plot(title='Standardized growth rate of industrial production', figsize=(13,3)) plt.figure() dta_filardo['dmdlleading'].plot(title='Leading indicator', figsize=(13,3)); ``` The time-varying transition probabilities are specified by the `exog_tvtp` parameter. Here we demonstrate another feature of model fitting - the use of a random search for MLE starting parameters. Because Markov switching models are often characterized by many local maxima of the likelihood function, performing an initial optimization step can be helpful to find the best parameters. Below, we specify that 20 random perturbations from the starting parameter vector are examined and the best one used as the actual starting parameters. Because of the random nature of the search, we seed the random number generator beforehand to allow replication of the result. In [10]: ``` mod_filardo = sm.tsa.MarkovAutoregression( dta_filardo.iloc[2:]['dlip'], k_regimes=2, order=4, switching_ar=False, exog_tvtp=sm.add_constant(dta_filardo.iloc[1:-1]['dmdlleading'])) np.random.seed(12345) res_filardo = mod_filardo.fit(search_reps=20) ``` In [11]: ``` res_filardo.summary() ``` Out[11]: Markov Switching Model Results\| Dep. Variable: \| dlip \| No. Observations: \| 514 \| \| Model: \| MarkovAutoregression \| Log Likelihood \| -586.572 \| \| Date: \| Mon, 14 May 2018 \| AIC \| 1195.144 \| \| Time: \| 21:45:43 \| BIC \| 1241.808 \| \| Sample: \| 03-01-1948 \| HQIC \| 1213.433 \| \| \| - 04-01-1991 \| \| \| \| Covariance Type: \| approx \| \| \| Regime 0 parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| const \| -0.8659 \| 0.153 \| -5.658 \| 0.000 \| -1.166 \| -0.566 \| Regime 1 parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| const \| 0.5173 \| 0.077 \| 6.706 \| 0.000 \| 0.366 \| 0.668 \| Non-switching parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| sigma2 \| 0.4844 \| 0.037 \| 13.172 \| 0.000 \| 0.412 \| 0.556 \| \| ar.L1 \| 0.1895 \| 0.050 \| 3.761 \| 0.000 \| 0.091 \| 0.288 \| \| ar.L2 \| 0.0793 \| 0.051 \| 1.552 \| 0.121 \| -0.021 \| 0.180 \| \| ar.L3 \| 0.1109 \| 0.052 \| 2.136 \| 0.033 \| 0.009 \| 0.213 \| \| ar.L4 \| 0.1223 \| 0.051 \| 2.418 \| 0.016 \| 0.023 \| 0.221 \| Regime transition parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| p[0->0].tvtp0 \| 1.6494 \| 0.446 \| 3.702 \| 0.000 \| 0.776 \| 2.523 \| \| p[1->0].tvtp0 \| -4.3595 \| 0.747 \| -5.833 \| 0.000 \| -5.824 \| -2.895 \| \| p[0->0].tvtp1 \| -0.9945 \| 0.566 \| -1.758 \| 0.079 \| -2.103 \| 0.114 \| \| p[1->0].tvtp1 \| -1.7702 \| 0.508 \| -3.484 \| 0.000 \| -2.766 \| -0.775 \| Warnings: [1] Covariance matrix calculated using numerical (complex-step) differentiation. Below we plot the smoothed probability of the economy operating in a low-production state, and again include the NBER recessions for comparison. In [12]: ``` fig, ax = plt.subplots(figsize=(12,3)) ax.plot(res_filardo.smoothed_marginal_probabilities[0]) ax.fill_between(usrec.index, 0, 1, where=usrec['USREC'].values, color='gray', alpha=0.2) ax.set_xlim(dta_filardo.index[6], dta_filardo.index[-1]) ax.set(title='Smoothed probability of a low-production state'); ``` Using the time-varying transition probabilities, we can see how the expected duration of a low-production state changes over time: In [13]: ``` res_filardo.expected_durations[0].plot( title='Expected duration of a low-production state', figsize=(12,3)); ``` During recessions, the expected duration of a low-production state is much higher than in an expansion.	programming_docs
statsmodels Discrete Choice Models Discrete Choice Models ====================== Fair's Affair data ------------------ A survey of women only was conducted in 1974 by Redbook asking about extramarital affairs. In [1]: ``` %matplotlib inline from __future__ import print_function import numpy as np import pandas as pd from scipy import stats import matplotlib.pyplot as plt import statsmodels.api as sm from statsmodels.formula.api import logit, probit, poisson, ols ``` In [2]: ``` print(sm.datasets.fair.SOURCE) ``` ``` Fair, Ray. 1978. "A Theory of Extramarital Affairs," `Journal of Political Economy`, February, 45-61. The data is available at http://fairmodel.econ.yale.edu/rayfair/pdf/2011b.htm ``` In [3]: ``` print( sm.datasets.fair.NOTE) ``` ``` :: Number of observations: 6366 Number of variables: 9 Variable name definitions: rate_marriage : How rate marriage, 1 = very poor, 2 = poor, 3 = fair, 4 = good, 5 = very good age : Age yrs_married : No. years married. Interval approximations. See original paper for detailed explanation. children : No. children religious : How relgious, 1 = not, 2 = mildly, 3 = fairly, 4 = strongly educ : Level of education, 9 = grade school, 12 = high school, 14 = some college, 16 = college graduate, 17 = some graduate school, 20 = advanced degree occupation : 1 = student, 2 = farming, agriculture; semi-skilled, or unskilled worker; 3 = white-colloar; 4 = teacher counselor social worker, nurse; artist, writers; technician, skilled worker, 5 = managerial, administrative, business, 6 = professional with advanced degree occupation_husb : Husband's occupation. Same as occupation. affairs : measure of time spent in extramarital affairs See the original paper for more details. ``` In [4]: ``` dta = sm.datasets.fair.load_pandas().data ``` In [5]: ``` dta['affair'] = (dta['affairs'] > 0).astype(float) print(dta.head(10)) ``` ``` rate_marriage age yrs_married children religious educ occupation \ 0 3.0 32.0 9.0 3.0 3.0 17.0 2.0 1 3.0 27.0 13.0 3.0 1.0 14.0 3.0 2 4.0 22.0 2.5 0.0 1.0 16.0 3.0 3 4.0 37.0 16.5 4.0 3.0 16.0 5.0 4 5.0 27.0 9.0 1.0 1.0 14.0 3.0 5 4.0 27.0 9.0 0.0 2.0 14.0 3.0 6 5.0 37.0 23.0 5.5 2.0 12.0 5.0 7 5.0 37.0 23.0 5.5 2.0 12.0 2.0 8 3.0 22.0 2.5 0.0 2.0 12.0 3.0 9 3.0 27.0 6.0 0.0 1.0 16.0 3.0 occupation_husb affairs affair 0 5.0 0.111111 1.0 1 4.0 3.230769 1.0 2 5.0 1.400000 1.0 3 5.0 0.727273 1.0 4 4.0 4.666666 1.0 5 4.0 4.666666 1.0 6 4.0 0.852174 1.0 7 3.0 1.826086 1.0 8 3.0 4.799999 1.0 9 5.0 1.333333 1.0 ``` In [6]: ``` print(dta.describe()) ``` ``` rate_marriage age yrs_married children religious \ count 6366.000000 6366.000000 6366.000000 6366.000000 6366.000000 mean 4.109645 29.082862 9.009425 1.396874 2.426170 std 0.961430 6.847882 7.280120 1.433471 0.878369 min 1.000000 17.500000 0.500000 0.000000 1.000000 25% 4.000000 22.000000 2.500000 0.000000 2.000000 50% 4.000000 27.000000 6.000000 1.000000 2.000000 75% 5.000000 32.000000 16.500000 2.000000 3.000000 max 5.000000 42.000000 23.000000 5.500000 4.000000 educ occupation occupation_husb affairs affair count 6366.000000 6366.000000 6366.000000 6366.000000 6366.000000 mean 14.209865 3.424128 3.850141 0.705374 0.322495 std 2.178003 0.942399 1.346435 2.203374 0.467468 min 9.000000 1.000000 1.000000 0.000000 0.000000 25% 12.000000 3.000000 3.000000 0.000000 0.000000 50% 14.000000 3.000000 4.000000 0.000000 0.000000 75% 16.000000 4.000000 5.000000 0.484848 1.000000 max 20.000000 6.000000 6.000000 57.599991 1.000000 ``` In [7]: ``` affair_mod = logit("affair ~ occupation + educ + occupation_husb" "+ rate_marriage + age + yrs_married + children" " + religious", dta).fit() ``` ``` Optimization terminated successfully. Current function value: 0.545314 Iterations 6 ``` In [8]: ``` print(affair_mod.summary()) ``` ``` Logit Regression Results ============================================================================== Dep. Variable: affair No. Observations: 6366 Model: Logit Df Residuals: 6357 Method: MLE Df Model: 8 Date: Mon, 14 May 2018 Pseudo R-squ.: 0.1327 Time: 21:44:43 Log-Likelihood: -3471.5 converged: True LL-Null: -4002.5 LLR p-value: 5.807e-224 =================================================================================== coef std err z P>\|z\| [0.025 0.975] ----------------------------------------------------------------------------------- Intercept 3.7257 0.299 12.470 0.000 3.140 4.311 occupation 0.1602 0.034 4.717 0.000 0.094 0.227 educ -0.0392 0.015 -2.533 0.011 -0.070 -0.009 occupation_husb 0.0124 0.023 0.541 0.589 -0.033 0.057 rate_marriage -0.7161 0.031 -22.784 0.000 -0.778 -0.655 age -0.0605 0.010 -5.885 0.000 -0.081 -0.040 yrs_married 0.1100 0.011 10.054 0.000 0.089 0.131 children -0.0042 0.032 -0.134 0.893 -0.066 0.058 religious -0.3752 0.035 -10.792 0.000 -0.443 -0.307 =================================================================================== ``` How well are we predicting? In [9]: ``` affair_mod.pred_table() ``` Out[9]: ``` array([[3882., 431.], [1326., 727.]]) ``` The coefficients of the discrete choice model do not tell us much. What we're after is marginal effects. In [10]: ``` mfx = affair_mod.get_margeff() print(mfx.summary()) ``` ``` Logit Marginal Effects ===================================== Dep. Variable: affair Method: dydx At: overall =================================================================================== dy/dx std err z P>\|z\| [0.025 0.975] ----------------------------------------------------------------------------------- occupation 0.0293 0.006 4.744 0.000 0.017 0.041 educ -0.0072 0.003 -2.538 0.011 -0.013 -0.002 occupation_husb 0.0023 0.004 0.541 0.589 -0.006 0.010 rate_marriage -0.1308 0.005 -26.891 0.000 -0.140 -0.121 age -0.0110 0.002 -5.937 0.000 -0.015 -0.007 yrs_married 0.0201 0.002 10.327 0.000 0.016 0.024 children -0.0008 0.006 -0.134 0.893 -0.012 0.011 religious -0.0685 0.006 -11.119 0.000 -0.081 -0.056 =================================================================================== ``` In [11]: ``` respondent1000 = dta.iloc[1000] print(respondent1000) ``` ``` rate_marriage 4.000000 age 37.000000 yrs_married 23.000000 children 3.000000 religious 3.000000 educ 12.000000 occupation 3.000000 occupation_husb 4.000000 affairs 0.521739 affair 1.000000 Name: 1000, dtype: float64 ``` In [12]: ``` resp = dict(zip(range(1,9), respondent1000[["occupation", "educ", "occupation_husb", "rate_marriage", "age", "yrs_married", "children", "religious"]].tolist())) resp.update({0 : 1}) print(resp) ``` ``` {1: 3.0, 2: 12.0, 3: 4.0, 4: 4.0, 5: 37.0, 6: 23.0, 7: 3.0, 8: 3.0, 0: 1} ``` In [13]: ``` mfx = affair_mod.get_margeff(atexog=resp) print(mfx.summary()) ``` ``` Logit Marginal Effects ===================================== Dep. Variable: affair Method: dydx At: overall =================================================================================== dy/dx std err z P>\|z\| [0.025 0.975] ----------------------------------------------------------------------------------- occupation 0.0400 0.008 4.711 0.000 0.023 0.057 educ -0.0098 0.004 -2.537 0.011 -0.017 -0.002 occupation_husb 0.0031 0.006 0.541 0.589 -0.008 0.014 rate_marriage -0.1788 0.008 -22.743 0.000 -0.194 -0.163 age -0.0151 0.003 -5.928 0.000 -0.020 -0.010 yrs_married 0.0275 0.003 10.256 0.000 0.022 0.033 children -0.0011 0.008 -0.134 0.893 -0.017 0.014 religious -0.0937 0.009 -10.722 0.000 -0.111 -0.077 =================================================================================== ``` `predict` expects a `DataFrame` since `patsy` is used to select columns. In [14]: ``` respondent1000 = dta.iloc[[1000]] affair_mod.predict(respondent1000) ``` Out[14]: ``` 1000 0.518782 dtype: float64 ``` In [15]: ``` affair_mod.fittedvalues[1000] ``` Out[15]: ``` 0.07516159285056234 ``` In [16]: ``` affair_mod.model.cdf(affair_mod.fittedvalues[1000]) ``` Out[16]: ``` 0.5187815572121469 ``` The "correct" model here is likely the Tobit model. We have an work in progress branch "tobit-model" on github, if anyone is interested in censored regression models. ### Exercise: Logit vs Probit In [17]: ``` fig = plt.figure(figsize=(12,8)) ax = fig.add_subplot(111) support = np.linspace(-6, 6, 1000) ax.plot(support, stats.logistic.cdf(support), 'r-', label='Logistic') ax.plot(support, stats.norm.cdf(support), label='Probit') ax.legend(); ``` In [18]: ``` fig = plt.figure(figsize=(12,8)) ax = fig.add_subplot(111) support = np.linspace(-6, 6, 1000) ax.plot(support, stats.logistic.pdf(support), 'r-', label='Logistic') ax.plot(support, stats.norm.pdf(support), label='Probit') ax.legend(); ``` Compare the estimates of the Logit Fair model above to a Probit model. Does the prediction table look better? Much difference in marginal effects? ### Genarlized Linear Model Example In [19]: ``` print(sm.datasets.star98.SOURCE) ``` ``` Jeff Gill's `Generalized Linear Models: A Unified Approach` http://jgill.wustl.edu/research/books.html ``` In [20]: ``` print(sm.datasets.star98.DESCRLONG) ``` ``` This data is on the California education policy and outcomes (STAR program results for 1998. The data measured standardized testing by the California Department of Education that required evaluation of 2nd - 11th grade students by the the Stanford 9 test on a variety of subjects. This dataset is at the level of the unified school district and consists of 303 cases. The binary response variable represents the number of 9th graders scoring over the national median value on the mathematics exam. The data used in this example is only a subset of the original source. ``` In [21]: ``` print(sm.datasets.star98.NOTE) ``` ``` :: Number of Observations - 303 (counties in California). Number of Variables - 13 and 8 interaction terms. Definition of variables names:: NABOVE - Total number of students above the national median for the math section. NBELOW - Total number of students below the national median for the math section. LOWINC - Percentage of low income students PERASIAN - Percentage of Asian student PERBLACK - Percentage of black students PERHISP - Percentage of Hispanic students PERMINTE - Percentage of minority teachers AVYRSEXP - Sum of teachers' years in educational service divided by the number of teachers. AVSALK - Total salary budget including benefits divided by the number of full-time teachers (in thousands) PERSPENK - Per-pupil spending (in thousands) PTRATIO - Pupil-teacher ratio. PCTAF - Percentage of students taking UC/CSU prep courses PCTCHRT - Percentage of charter schools PCTYRRND - Percentage of year-round schools The below variables are interaction terms of the variables defined above. PERMINTE_AVYRSEXP PEMINTE_AVSAL AVYRSEXP_AVSAL PERSPEN_PTRATIO PERSPEN_PCTAF PTRATIO_PCTAF PERMINTE_AVTRSEXP_AVSAL PERSPEN_PTRATIO_PCTAF ``` In [22]: ``` dta = sm.datasets.star98.load_pandas().data print(dta.columns) ``` ``` Index(['NABOVE', 'NBELOW', 'LOWINC', 'PERASIAN', 'PERBLACK', 'PERHISP', 'PERMINTE', 'AVYRSEXP', 'AVSALK', 'PERSPENK', 'PTRATIO', 'PCTAF', 'PCTCHRT', 'PCTYRRND', 'PERMINTE_AVYRSEXP', 'PERMINTE_AVSAL', 'AVYRSEXP_AVSAL', 'PERSPEN_PTRATIO', 'PERSPEN_PCTAF', 'PTRATIO_PCTAF', 'PERMINTE_AVYRSEXP_AVSAL', 'PERSPEN_PTRATIO_PCTAF'], dtype='object') ``` In [23]: ``` print(dta[['NABOVE', 'NBELOW', 'LOWINC', 'PERASIAN', 'PERBLACK', 'PERHISP', 'PERMINTE']].head(10)) ``` ``` NABOVE NBELOW LOWINC PERASIAN PERBLACK PERHISP PERMINTE 0 452.0 355.0 34.39730 23.299300 14.235280 11.411120 15.918370 1 144.0 40.0 17.36507 29.328380 8.234897 9.314884 13.636360 2 337.0 234.0 32.64324 9.226386 42.406310 13.543720 28.834360 3 395.0 178.0 11.90953 13.883090 3.796973 11.443110 11.111110 4 8.0 57.0 36.88889 12.187500 76.875000 7.604167 43.589740 5 1348.0 899.0 20.93149 28.023510 4.643221 13.808160 15.378490 6 477.0 887.0 53.26898 8.447858 19.374830 37.905330 25.525530 7 565.0 347.0 15.19009 3.665781 2.649680 13.092070 6.203008 8 205.0 320.0 28.21582 10.430420 6.786374 32.334300 13.461540 9 469.0 598.0 32.77897 17.178310 12.484930 28.323290 27.259890 ``` In [24]: ``` print(dta[['AVYRSEXP', 'AVSALK', 'PERSPENK', 'PTRATIO', 'PCTAF', 'PCTCHRT', 'PCTYRRND']].head(10)) ``` ``` AVYRSEXP AVSALK PERSPENK PTRATIO PCTAF PCTCHRT PCTYRRND 0 14.70646 59.15732 4.445207 21.71025 57.03276 0.0 22.222220 1 16.08324 59.50397 5.267598 20.44278 64.62264 0.0 0.000000 2 14.59559 60.56992 5.482922 18.95419 53.94191 0.0 0.000000 3 14.38939 58.33411 4.165093 21.63539 49.06103 0.0 7.142857 4 13.90568 63.15364 4.324902 18.77984 52.38095 0.0 0.000000 5 14.97755 66.97055 3.916104 24.51914 44.91578 0.0 2.380952 6 14.67829 57.62195 4.270903 22.21278 32.28916 0.0 12.121210 7 13.66197 63.44740 4.309734 24.59026 30.45267 0.0 0.000000 8 16.41760 57.84564 4.527603 21.74138 22.64574 0.0 0.000000 9 12.51864 57.80141 4.648917 20.26010 26.07099 0.0 0.000000 ``` In [25]: ``` formula = 'NABOVE + NBELOW ~ LOWINC + PERASIAN + PERBLACK + PERHISP + PCTCHRT ' formula += '+ PCTYRRND + PERMINTEAVYRSEXPAVSALK + PERSPENKPTRATIOPCTAF' ``` #### Aside: Binomial distribution Toss a six-sided die 5 times, what's the probability of exactly 2 fours? In [26]: ``` stats.binom(5, 1./6).pmf(2) ``` Out[26]: ``` 0.16075102880658435 ``` In [27]: ``` from scipy.misc import comb comb(5,2) * (1/6.)*2 (5/6.)*3 ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/ipykernel_launcher.py:2: DeprecationWarning: `comb` is deprecated! Importing `comb` from scipy.misc is deprecated in scipy 1.0.0. Use `scipy.special.comb` instead. ``` Out[27]: ``` 0.1607510288065844 ``` In [28]: ``` from statsmodels.formula.api import glm glm_mod = glm(formula, dta, family=sm.families.Binomial()).fit() ``` In [29]: ``` print(glm_mod.summary()) ``` ``` Generalized Linear Model Regression Results ================================================================================ Dep. Variable: ['NABOVE', 'NBELOW'] No. Observations: 303 Model: GLM Df Residuals: 282 Model Family: Binomial Df Model: 20 Link Function: logit Scale: 1.0000 Method: IRLS Log-Likelihood: -2998.6 Date: Mon, 14 May 2018 Deviance: 4078.8 Time: 21:44:44 Pearson chi2: 4.05e+03 No. Iterations: 5 Covariance Type: nonrobust ============================================================================================ coef std err z P>\|z\| [0.025 0.975] -------------------------------------------------------------------------------------------- Intercept 2.9589 1.547 1.913 0.056 -0.073 5.990 LOWINC -0.0168 0.000 -38.749 0.000 -0.018 -0.016 PERASIAN 0.0099 0.001 16.505 0.000 0.009 0.011 PERBLACK -0.0187 0.001 -25.182 0.000 -0.020 -0.017 PERHISP -0.0142 0.000 -32.818 0.000 -0.015 -0.013 PCTCHRT 0.0049 0.001 3.921 0.000 0.002 0.007 PCTYRRND -0.0036 0.000 -15.878 0.000 -0.004 -0.003 PERMINTE 0.2545 0.030 8.498 0.000 0.196 0.313 AVYRSEXP 0.2407 0.057 4.212 0.000 0.129 0.353 PERMINTE:AVYRSEXP -0.0141 0.002 -7.391 0.000 -0.018 -0.010 AVSALK 0.0804 0.014 5.775 0.000 0.053 0.108 PERMINTE:AVSALK -0.0040 0.000 -8.450 0.000 -0.005 -0.003 AVYRSEXP:AVSALK -0.0039 0.001 -4.059 0.000 -0.006 -0.002 PERMINTE:AVYRSEXP:AVSALK 0.0002 2.99e-05 7.428 0.000 0.000 0.000 PERSPENK -1.9522 0.317 -6.162 0.000 -2.573 -1.331 PTRATIO -0.3341 0.061 -5.453 0.000 -0.454 -0.214 PERSPENK:PTRATIO 0.0917 0.015 6.321 0.000 0.063 0.120 PCTAF -0.1690 0.033 -5.169 0.000 -0.233 -0.105 PERSPENK:PCTAF 0.0490 0.007 6.574 0.000 0.034 0.064 PTRATIO:PCTAF 0.0080 0.001 5.362 0.000 0.005 0.011 PERSPENK:PTRATIO:PCTAF -0.0022 0.000 -6.445 0.000 -0.003 -0.002 ============================================================================================ ``` The number of trials In [30]: ``` glm_mod.model.data.orig_endog.sum(1) ``` Out[30]: ``` 0 807.0 1 184.0 2 571.0 3 573.0 4 65.0 5 2247.0 6 1364.0 7 912.0 8 525.0 9 1067.0 10 3016.0 11 235.0 12 556.0 13 688.0 14 252.0 15 925.0 16 377.0 17 69.0 18 1092.0 19 115.0 20 139.0 21 449.0 22 309.0 23 116.0 24 81.0 25 66.0 26 1259.0 27 190.0 28 322.0 29 2394.0 ... 273 120.0 274 224.0 275 733.0 276 120.0 277 135.0 278 776.0 279 207.0 280 41.0 281 43.0 282 259.0 283 342.0 284 250.0 285 1750.0 286 150.0 287 134.0 288 53.0 289 266.0 290 304.0 291 1338.0 292 1170.0 293 1431.0 294 248.0 295 516.0 296 591.0 297 59.0 298 342.0 299 154.0 300 595.0 301 709.0 302 156.0 Length: 303, dtype: float64 ``` In [31]: ``` glm_mod.fittedvalues glm_mod.model.data.orig_endog.sum(1) ``` Out[31]: ``` 0 470.732584 1 138.266178 2 285.832629 3 392.702917 4 20.963146 5 1543.545102 6 454.209651 7 598.497867 8 261.720305 9 540.687237 10 722.479333 11 203.583934 12 258.167040 13 303.902616 14 168.330747 15 684.393625 16 195.911948 17 29.285268 18 616.911004 19 68.139395 20 48.369683 21 253.303415 22 154.420779 23 41.360255 24 16.809362 25 12.057599 26 565.702043 27 91.247771 28 193.088229 29 1408.837645 ... 273 47.775769 274 63.404739 275 297.019427 276 36.144700 277 35.640558 278 343.034529 279 83.929791 280 16.140299 281 23.773918 282 36.529829 283 60.021489 284 48.727397 285 704.464980 286 31.525238 287 13.014093 288 33.470295 289 68.855461 290 174.264199 291 827.377548 292 506.242734 293 958.896993 294 187.988967 295 259.823500 296 379.553974 297 17.656181 298 111.464708 299 61.037884 300 235.517446 301 290.952508 302 53.312851 Length: 303, dtype: float64 ``` First differences: We hold all explanatory variables constant at their means and manipulate the percentage of low income households to assess its impact on the response variables: In [32]: ``` exog = glm_mod.model.data.orig_exog # get the dataframe ``` In [33]: ``` means25 = exog.mean() print(means25) ``` ``` Intercept 1.000000 LOWINC 41.409877 PERASIAN 5.896335 PERBLACK 5.636808 PERHISP 34.398080 PCTCHRT 1.175909 PCTYRRND 11.611905 PERMINTE 14.694747 AVYRSEXP 14.253875 PERMINTE:AVYRSEXP 209.018700 AVSALK 58.640258 PERMINTE:AVSALK 879.979883 AVYRSEXP:AVSALK 839.718173 PERMINTE:AVYRSEXP:AVSALK 12585.266464 PERSPENK 4.320310 PTRATIO 22.464250 PERSPENK:PTRATIO 96.295756 PCTAF 33.630593 PERSPENK:PCTAF 147.235740 PTRATIO:PCTAF 747.445536 PERSPENK:PTRATIO:PCTAF 3243.607568 dtype: float64 ``` In [34]: ``` means25['LOWINC'] = exog['LOWINC'].quantile(.25) print(means25) ``` ``` Intercept 1.000000 LOWINC 26.683040 PERASIAN 5.896335 PERBLACK 5.636808 PERHISP 34.398080 PCTCHRT 1.175909 PCTYRRND 11.611905 PERMINTE 14.694747 AVYRSEXP 14.253875 PERMINTE:AVYRSEXP 209.018700 AVSALK 58.640258 PERMINTE:AVSALK 879.979883 AVYRSEXP:AVSALK 839.718173 PERMINTE:AVYRSEXP:AVSALK 12585.266464 PERSPENK 4.320310 PTRATIO 22.464250 PERSPENK:PTRATIO 96.295756 PCTAF 33.630593 PERSPENK:PCTAF 147.235740 PTRATIO:PCTAF 747.445536 PERSPENK:PTRATIO:PCTAF 3243.607568 dtype: float64 ``` In [35]: ``` means75 = exog.mean() means75['LOWINC'] = exog['LOWINC'].quantile(.75) print(means75) ``` ``` Intercept 1.000000 LOWINC 55.460075 PERASIAN 5.896335 PERBLACK 5.636808 PERHISP 34.398080 PCTCHRT 1.175909 PCTYRRND 11.611905 PERMINTE 14.694747 AVYRSEXP 14.253875 PERMINTE:AVYRSEXP 209.018700 AVSALK 58.640258 PERMINTE:AVSALK 879.979883 AVYRSEXP:AVSALK 839.718173 PERMINTE:AVYRSEXP:AVSALK 12585.266464 PERSPENK 4.320310 PTRATIO 22.464250 PERSPENK:PTRATIO 96.295756 PCTAF 33.630593 PERSPENK:PCTAF 147.235740 PTRATIO:PCTAF 747.445536 PERSPENK:PTRATIO:PCTAF 3243.607568 dtype: float64 ``` Again, `predict` expects a `DataFrame` since `patsy` is used to select columns. In [36]: ``` resp25 = glm_mod.predict(pd.DataFrame(means25).T) resp75 = glm_mod.predict(pd.DataFrame(means75).T) diff = resp75 - resp25 ``` The interquartile first difference for the percentage of low income households in a school district is: In [37]: ``` print("%2.4f%%" % (diff[0]100)) ``` ``` -11.8863% ``` In [38]: ``` nobs = glm_mod.nobs y = glm_mod.model.endog yhat = glm_mod.mu ``` In [39]: ``` from statsmodels.graphics.api import abline_plot fig = plt.figure(figsize=(12,8)) ax = fig.add_subplot(111, ylabel='Observed Values', xlabel='Fitted Values') ax.scatter(yhat, y) y_vs_yhat = sm.OLS(y, sm.add_constant(yhat, prepend=True)).fit() fig = abline_plot(model_results=y_vs_yhat, ax=ax) ``` #### Plot fitted values vs Pearson residuals Pearson residuals are defined to be $$\frac{(y - \mu)}{\sqrt{(var(\mu))}}$$ where var is typically determined by the family. E.g., binomial variance is $np(1 - p)$ In [40]: ``` fig = plt.figure(figsize=(12,8)) ax = fig.add_subplot(111, title='Residual Dependence Plot', xlabel='Fitted Values', ylabel='Pearson Residuals') ax.scatter(yhat, stats.zscore(glm_mod.resid_pearson)) ax.axis('tight') ax.plot([0.0, 1.0],[0.0, 0.0], 'k-'); ``` #### Histogram of standardized deviance residuals with Kernel Density Estimate overlayed The definition of the deviance residuals depends on the family. For the Binomial distribution this is $$r\_{dev} = sign\left(Y-\mu\right)\\sqrt{2n(Y\log\frac{Y}{\mu}+(1-Y)\log\frac{(1-Y)}{(1-\mu)}}$$ They can be used to detect ill-fitting covariates In [41]: ``` resid = glm_mod.resid_deviance resid_std = stats.zscore(resid) kde_resid = sm.nonparametric.KDEUnivariate(resid_std) kde_resid.fit() ``` In [42]: ``` fig = plt.figure(figsize=(12,8)) ax = fig.add_subplot(111, title="Standardized Deviance Residuals") ax.hist(resid_std, bins=25, normed=True); ax.plot(kde_resid.support, kde_resid.density, 'r'); ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/matplotlib/axes/_axes.py:6462: UserWarning: The 'normed' kwarg is deprecated, and has been replaced by the 'density' kwarg. warnings.warn("The 'normed' kwarg is deprecated, and has been " ``` #### QQ-plot of deviance residuals In [43]: ``` fig = plt.figure(figsize=(12,8)) ax = fig.add_subplot(111) fig = sm.graphics.qqplot(resid, line='r', ax=ax) ```	programming_docs
statsmodels Generalized Linear Models (Formula) Generalized Linear Models (Formula) =================================== This notebook illustrates how you can use R-style formulas to fit Generalized Linear Models. To begin, we load the `Star98` dataset and we construct a formula and pre-process the data: In [1]: ``` from __future__ import print_function import statsmodels.api as sm import statsmodels.formula.api as smf star98 = sm.datasets.star98.load_pandas().data formula = 'SUCCESS ~ LOWINC + PERASIAN + PERBLACK + PERHISP + PCTCHRT + \ PCTYRRND + PERMINTEAVYRSEXPAVSALK + PERSPENKPTRATIOPCTAF' dta = star98[['NABOVE', 'NBELOW', 'LOWINC', 'PERASIAN', 'PERBLACK', 'PERHISP', 'PCTCHRT', 'PCTYRRND', 'PERMINTE', 'AVYRSEXP', 'AVSALK', 'PERSPENK', 'PTRATIO', 'PCTAF']].copy() endog = dta['NABOVE'] / (dta['NABOVE'] + dta.pop('NBELOW')) del dta['NABOVE'] dta['SUCCESS'] = endog ``` Then, we fit the GLM model: In [2]: ``` mod1 = smf.glm(formula=formula, data=dta, family=sm.families.Binomial()).fit() mod1.summary() ``` Out[2]: Generalized Linear Model Regression Results\| Dep. Variable: \| SUCCESS \| No. Observations: \| 303 \| \| Model: \| GLM \| Df Residuals: \| 282 \| \| Model Family: \| Binomial \| Df Model: \| 20 \| \| Link Function: \| logit \| Scale: \| 1.0000 \| \| Method: \| IRLS \| Log-Likelihood: \| -127.33 \| \| Date: \| Mon, 14 May 2018 \| Deviance: \| 8.5477 \| \| Time: \| 21:44:55 \| Pearson chi2: \| 8.48 \| \| No. Iterations: \| 4 \| Covariance Type: \| nonrobust \| \| \| \| \| \| \| \| \| \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| \| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| Intercept \| 0.4037 \| 25.036 \| 0.016 \| 0.987 \| -48.665 \| 49.472 \| \| LOWINC \| -0.0204 \| 0.010 \| -1.982 \| 0.048 \| -0.041 \| -0.000 \| \| PERASIAN \| 0.0159 \| 0.017 \| 0.910 \| 0.363 \| -0.018 \| 0.050 \| \| PERBLACK \| -0.0198 \| 0.020 \| -1.004 \| 0.316 \| -0.058 \| 0.019 \| \| PERHISP \| -0.0096 \| 0.010 \| -0.951 \| 0.341 \| -0.029 \| 0.010 \| \| PCTCHRT \| -0.0022 \| 0.022 \| -0.103 \| 0.918 \| -0.045 \| 0.040 \| \| PCTYRRND \| -0.0022 \| 0.006 \| -0.348 \| 0.728 \| -0.014 \| 0.010 \| \| PERMINTE \| 0.1068 \| 0.787 \| 0.136 \| 0.892 \| -1.436 \| 1.650 \| \| AVYRSEXP \| -0.0411 \| 1.176 \| -0.035 \| 0.972 \| -2.346 \| 2.264 \| \| PERMINTE:AVYRSEXP \| -0.0031 \| 0.054 \| -0.057 \| 0.954 \| -0.108 \| 0.102 \| \| AVSALK \| 0.0131 \| 0.295 \| 0.044 \| 0.965 \| -0.566 \| 0.592 \| \| PERMINTE:AVSALK \| -0.0019 \| 0.013 \| -0.145 \| 0.885 \| -0.028 \| 0.024 \| \| AVYRSEXP:AVSALK \| 0.0008 \| 0.020 \| 0.038 \| 0.970 \| -0.039 \| 0.041 \| \| PERMINTE:AVYRSEXP:AVSALK \| 5.978e-05 \| 0.001 \| 0.068 \| 0.946 \| -0.002 \| 0.002 \| \| PERSPENK \| -0.3097 \| 4.233 \| -0.073 \| 0.942 \| -8.606 \| 7.987 \| \| PTRATIO \| 0.0096 \| 0.919 \| 0.010 \| 0.992 \| -1.792 \| 1.811 \| \| PERSPENK:PTRATIO \| 0.0066 \| 0.206 \| 0.032 \| 0.974 \| -0.397 \| 0.410 \| \| PCTAF \| -0.0143 \| 0.474 \| -0.030 \| 0.976 \| -0.944 \| 0.916 \| \| PERSPENK:PCTAF \| 0.0105 \| 0.098 \| 0.107 \| 0.915 \| -0.182 \| 0.203 \| \| PTRATIO:PCTAF \| -0.0001 \| 0.022 \| -0.005 \| 0.996 \| -0.044 \| 0.044 \| \| PERSPENK:PTRATIO:PCTAF \| -0.0002 \| 0.005 \| -0.051 \| 0.959 \| -0.010 \| 0.009 \| Finally, we define a function to operate customized data transformation using the formula framework: In [3]: ``` def double_it(x): return 2 * x formula = 'SUCCESS ~ double_it(LOWINC) + PERASIAN + PERBLACK + PERHISP + PCTCHRT + \ PCTYRRND + PERMINTEAVYRSEXPAVSALK + PERSPENKPTRATIOPCTAF' mod2 = smf.glm(formula=formula, data=dta, family=sm.families.Binomial()).fit() mod2.summary() ``` Out[3]: Generalized Linear Model Regression Results\| Dep. Variable: \| SUCCESS \| No. Observations: \| 303 \| \| Model: \| GLM \| Df Residuals: \| 282 \| \| Model Family: \| Binomial \| Df Model: \| 20 \| \| Link Function: \| logit \| Scale: \| 1.0000 \| \| Method: \| IRLS \| Log-Likelihood: \| -127.33 \| \| Date: \| Mon, 14 May 2018 \| Deviance: \| 8.5477 \| \| Time: \| 21:44:55 \| Pearson chi2: \| 8.48 \| \| No. Iterations: \| 4 \| Covariance Type: \| nonrobust \| \| \| \| \| \| \| \| \| \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| \| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| Intercept \| 0.4037 \| 25.036 \| 0.016 \| 0.987 \| -48.665 \| 49.472 \| \| double\_it(LOWINC) \| -0.0102 \| 0.005 \| -1.982 \| 0.048 \| -0.020 \| -0.000 \| \| PERASIAN \| 0.0159 \| 0.017 \| 0.910 \| 0.363 \| -0.018 \| 0.050 \| \| PERBLACK \| -0.0198 \| 0.020 \| -1.004 \| 0.316 \| -0.058 \| 0.019 \| \| PERHISP \| -0.0096 \| 0.010 \| -0.951 \| 0.341 \| -0.029 \| 0.010 \| \| PCTCHRT \| -0.0022 \| 0.022 \| -0.103 \| 0.918 \| -0.045 \| 0.040 \| \| PCTYRRND \| -0.0022 \| 0.006 \| -0.348 \| 0.728 \| -0.014 \| 0.010 \| \| PERMINTE \| 0.1068 \| 0.787 \| 0.136 \| 0.892 \| -1.436 \| 1.650 \| \| AVYRSEXP \| -0.0411 \| 1.176 \| -0.035 \| 0.972 \| -2.346 \| 2.264 \| \| PERMINTE:AVYRSEXP \| -0.0031 \| 0.054 \| -0.057 \| 0.954 \| -0.108 \| 0.102 \| \| AVSALK \| 0.0131 \| 0.295 \| 0.044 \| 0.965 \| -0.566 \| 0.592 \| \| PERMINTE:AVSALK \| -0.0019 \| 0.013 \| -0.145 \| 0.885 \| -0.028 \| 0.024 \| \| AVYRSEXP:AVSALK \| 0.0008 \| 0.020 \| 0.038 \| 0.970 \| -0.039 \| 0.041 \| \| PERMINTE:AVYRSEXP:AVSALK \| 5.978e-05 \| 0.001 \| 0.068 \| 0.946 \| -0.002 \| 0.002 \| \| PERSPENK \| -0.3097 \| 4.233 \| -0.073 \| 0.942 \| -8.606 \| 7.987 \| \| PTRATIO \| 0.0096 \| 0.919 \| 0.010 \| 0.992 \| -1.792 \| 1.811 \| \| PERSPENK:PTRATIO \| 0.0066 \| 0.206 \| 0.032 \| 0.974 \| -0.397 \| 0.410 \| \| PCTAF \| -0.0143 \| 0.474 \| -0.030 \| 0.976 \| -0.944 \| 0.916 \| \| PERSPENK:PCTAF \| 0.0105 \| 0.098 \| 0.107 \| 0.915 \| -0.182 \| 0.203 \| \| PTRATIO:PCTAF \| -0.0001 \| 0.022 \| -0.005 \| 0.996 \| -0.044 \| 0.044 \| \| PERSPENK:PTRATIO:PCTAF \| -0.0002 \| 0.005 \| -0.051 \| 0.959 \| -0.010 \| 0.009 \| As expected, the coefficient for `double_it(LOWINC)` in the second model is half the size of the `LOWINC` coefficient from the first model: In [4]: ``` print(mod1.params[1]) print(mod2.params[1] * 2) ``` ``` -0.020395987154757125 -0.020395987154757402 ``` statsmodels Regression diagnostics Regression diagnostics ====================== This example file shows how to use a few of the `statsmodels` regression diagnostic tests in a real-life context. You can learn about more tests and find out more information abou the tests here on the [Regression Diagnostics page.](../../../diagnostic) Note that most of the tests described here only return a tuple of numbers, without any annotation. A full description of outputs is always included in the docstring and in the online `statsmodels` documentation. For presentation purposes, we use the `zip(name,test)` construct to pretty-print short descriptions in the examples below. Estimate a regression model --------------------------- In [1]: ``` %matplotlib inline from __future__ import print_function from statsmodels.compat import lzip import statsmodels import numpy as np import pandas as pd import statsmodels.formula.api as smf import statsmodels.stats.api as sms import matplotlib.pyplot as plt # Load data url = 'http://vincentarelbundock.github.io/Rdatasets/csv/HistData/Guerry.csv' dat = pd.read_csv(url) # Fit regression model (using the natural log of one of the regressors) results = smf.ols('Lottery ~ Literacy + np.log(Pop1831)', data=dat).fit() # Inspect the results print(results.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: Lottery R-squared: 0.348 Model: OLS Adj. R-squared: 0.333 Method: Least Squares F-statistic: 22.20 Date: Mon, 14 May 2018 Prob (F-statistic): 1.90e-08 Time: 21:44:58 Log-Likelihood: -379.82 No. Observations: 86 AIC: 765.6 Df Residuals: 83 BIC: 773.0 Df Model: 2 Covariance Type: nonrobust =================================================================================== coef std err t P>\|t\| [0.025 0.975] ----------------------------------------------------------------------------------- Intercept 246.4341 35.233 6.995 0.000 176.358 316.510 Literacy -0.4889 0.128 -3.832 0.000 -0.743 -0.235 np.log(Pop1831) -31.3114 5.977 -5.239 0.000 -43.199 -19.424 ============================================================================== Omnibus: 3.713 Durbin-Watson: 2.019 Prob(Omnibus): 0.156 Jarque-Bera (JB): 3.394 Skew: -0.487 Prob(JB): 0.183 Kurtosis: 3.003 Cond. No. 702. ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` Normality of the residuals -------------------------- Jarque-Bera test: In [2]: ``` name = ['Jarque-Bera', 'Chi^2 two-tail prob.', 'Skew', 'Kurtosis'] test = sms.jarque_bera(results.resid) lzip(name, test) ``` Out[2]: ``` [('Jarque-Bera', 3.3936080248431706), ('Chi^2 two-tail prob.', 0.18326831231663335), ('Skew', -0.486580343112234), ('Kurtosis', 3.003417757881633)] ``` Omni test: In [3]: ``` name = ['Chi^2', 'Two-tail probability'] test = sms.omni_normtest(results.resid) lzip(name, test) ``` Out[3]: ``` [('Chi^2', 3.713437811597183), ('Two-tail probability', 0.15618424580304813)] ``` Influence tests --------------- Once created, an object of class `OLSInfluence` holds attributes and methods that allow users to assess the influence of each observation. For example, we can compute and extract the first few rows of DFbetas by: In [4]: ``` from statsmodels.stats.outliers_influence import OLSInfluence test_class = OLSInfluence(results) test_class.dfbetas[:5,:] ``` Out[4]: ``` array([[-0.00301154, 0.00290872, 0.00118179], [-0.06425662, 0.04043093, 0.06281609], [ 0.01554894, -0.03556038, -0.00905336], [ 0.17899858, 0.04098207, -0.18062352], [ 0.29679073, 0.21249207, -0.3213655 ]]) ``` Explore other options by typing `dir(influence_test)` Useful information on leverage can also be plotted: In [5]: ``` from statsmodels.graphics.regressionplots import plot_leverage_resid2 fig, ax = plt.subplots(figsize=(8,6)) fig = plot_leverage_resid2(results, ax = ax) ``` Other plotting options can be found on the [Graphics page.](../../../graphics) Multicollinearity ----------------- Condition number: In [6]: ``` np.linalg.cond(results.model.exog) ``` Out[6]: ``` 702.1792145490066 ``` Heteroskedasticity tests ------------------------ Breush-Pagan test: In [7]: ``` name = ['Lagrange multiplier statistic', 'p-value', 'f-value', 'f p-value'] test = sms.het_breushpagan(results.resid, results.model.exog) lzip(name, test) ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/ipykernel_launcher.py:3: DeprecationWarning: `het_breushpagan` is deprecated, use `het_breuschpagan` instead! Use het_breuschpagan, het_breushpagan will be removed in 0.9 (Note: misspelling missing 'c') This is separate from the ipykernel package so we can avoid doing imports until ``` Out[7]: ``` [('Lagrange multiplier statistic', 4.893213374094033), ('p-value', 0.0865869050235188), ('f-value', 2.5037159462564778), ('f p-value', 0.08794028782672685)] ``` Goldfeld-Quandt test In [8]: ``` name = ['F statistic', 'p-value'] test = sms.het_goldfeldquandt(results.resid, results.model.exog) lzip(name, test) ``` Out[8]: ``` [('F statistic', 1.1002422436378143), ('p-value', 0.38202950686925324)] ``` Linearity --------- Harvey-Collier multiplier test for Null hypothesis that the linear specification is correct: In [9]: ``` name = ['t value', 'p value'] test = sms.linear_harvey_collier(results) lzip(name, test) ``` Out[9]: ``` [('t value', -1.0796490077784473), ('p value', 0.2834639247558297)] ``` statsmodels Autoregressive Moving Average (ARMA): Sunspots data Autoregressive Moving Average (ARMA): Sunspots data =================================================== This notebook replicates the existing ARMA notebook using the `statsmodels.tsa.statespace.SARIMAX` class rather than the `statsmodels.tsa.ARMA` class. In [1]: ``` %matplotlib inline ``` In [2]: ``` from __future__ import print_function import numpy as np from scipy import stats import pandas as pd import matplotlib.pyplot as plt import statsmodels.api as sm ``` In [3]: ``` from statsmodels.graphics.api import qqplot ``` Sunpots Data ------------ In [4]: ``` print(sm.datasets.sunspots.NOTE) ``` ``` :: Number of Observations - 309 (Annual 1700 - 2008) Number of Variables - 1 Variable name definitions:: SUNACTIVITY - Number of sunspots for each year The data file contains a 'YEAR' variable that is not returned by load. ``` In [5]: ``` dta = sm.datasets.sunspots.load_pandas().data ``` In [6]: ``` dta.index = pd.Index(sm.tsa.datetools.dates_from_range('1700', '2008')) del dta["YEAR"] ``` In [7]: ``` dta.plot(figsize=(12,4)); ``` In [8]: ``` fig = plt.figure(figsize=(12,8)) ax1 = fig.add_subplot(211) fig = sm.graphics.tsa.plot_acf(dta.values.squeeze(), lags=40, ax=ax1) ax2 = fig.add_subplot(212) fig = sm.graphics.tsa.plot_pacf(dta, lags=40, ax=ax2) ``` In [9]: ``` arma_mod20 = sm.tsa.statespace.SARIMAX(dta, order=(2,0,0), trend='c').fit(disp=False) print(arma_mod20.params) ``` ``` intercept 14.793947 ar.L1 1.390659 ar.L2 -0.688568 sigma2 274.761105 dtype: float64 ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/tsa/base/tsa_model.py:171: ValueWarning: No frequency information was provided, so inferred frequency A-DEC will be used. % freq, ValueWarning) ``` In [10]: ``` arma_mod30 = sm.tsa.statespace.SARIMAX(dta, order=(3,0,0), trend='c').fit(disp=False) ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/tsa/base/tsa_model.py:171: ValueWarning: No frequency information was provided, so inferred frequency A-DEC will be used. % freq, ValueWarning) ``` In [11]: ``` print(arma_mod20.aic, arma_mod20.bic, arma_mod20.hqic) ``` ``` 2622.6363381415795 2637.5697032491703 2628.6067259868255 ``` In [12]: ``` print(arma_mod30.params) ``` ``` intercept 16.762205 ar.L1 1.300810 ar.L2 -0.508122 ar.L3 -0.129612 sigma2 270.102651 dtype: float64 ``` In [13]: ``` print(arma_mod30.aic, arma_mod30.bic, arma_mod30.hqic) ``` ``` 2619.4036296632785 2638.0703360477673 2626.866614469836 ``` * Does our model obey the theory? In [14]: ``` sm.stats.durbin_watson(arma_mod30.resid) ``` Out[14]: ``` 1.9564844876123837 ``` In [15]: ``` fig = plt.figure(figsize=(12,4)) ax = fig.add_subplot(111) ax = plt.plot(arma_mod30.resid) ``` In [16]: ``` resid = arma_mod30.resid ``` In [17]: ``` stats.normaltest(resid) ``` Out[17]: ``` NormaltestResult(statistic=49.84700589340767, pvalue=1.4992021644395493e-11) ``` In [18]: ``` fig = plt.figure(figsize=(12,4)) ax = fig.add_subplot(111) fig = qqplot(resid, line='q', ax=ax, fit=True) ``` In [19]: ``` fig = plt.figure(figsize=(12,8)) ax1 = fig.add_subplot(211) fig = sm.graphics.tsa.plot_acf(resid, lags=40, ax=ax1) ax2 = fig.add_subplot(212) fig = sm.graphics.tsa.plot_pacf(resid, lags=40, ax=ax2) ``` In [20]: ``` r,q,p = sm.tsa.acf(resid, qstat=True) data = np.c_[range(1,41), r[1:], q, p] table = pd.DataFrame(data, columns=['lag', "AC", "Q", "Prob(>Q)"]) print(table.set_index('lag')) ``` ``` AC Q Prob(>Q) lag 1.0 0.009176 0.026273 8.712350e-01 2.0 0.041820 0.573727 7.506142e-01 3.0 -0.001342 0.574292 9.022915e-01 4.0 0.136064 6.407488 1.707135e-01 5.0 0.092433 9.108334 1.048203e-01 6.0 0.091919 11.788018 6.686842e-02 7.0 0.068735 13.291375 6.531940e-02 8.0 -0.015021 13.363411 9.994248e-02 9.0 0.187599 24.636916 3.400197e-03 10.0 0.213724 39.317881 2.233182e-05 11.0 0.201092 52.358270 2.347759e-07 12.0 0.117192 56.802109 8.581667e-08 13.0 -0.014051 56.866210 1.895534e-07 14.0 0.015394 56.943403 4.001106e-07 15.0 -0.024986 57.147464 7.747085e-07 16.0 0.080892 59.293626 6.880520e-07 17.0 0.041120 59.850085 1.112486e-06 18.0 -0.052030 60.744064 1.550379e-06 19.0 0.062500 62.038494 1.833802e-06 20.0 -0.010292 62.073718 3.385224e-06 21.0 0.074467 63.924062 3.196544e-06 22.0 0.124962 69.152771 8.984834e-07 23.0 0.093170 72.069532 5.802915e-07 24.0 -0.082149 74.345041 4.715787e-07 25.0 0.015689 74.428332 8.294019e-07 26.0 -0.025049 74.641400 1.367992e-06 27.0 -0.125875 80.040873 3.722922e-07 28.0 0.053215 81.009318 4.717357e-07 29.0 -0.038699 81.523324 6.917767e-07 30.0 -0.016896 81.621648 1.151883e-06 31.0 -0.019286 81.750227 1.869202e-06 32.0 0.105001 85.575148 8.927710e-07 33.0 0.040094 86.134872 1.247384e-06 34.0 0.008834 86.162142 2.047607e-06 35.0 0.014588 86.236784 3.263460e-06 36.0 -0.119334 91.249666 1.084187e-06 37.0 -0.036673 91.724837 1.521456e-06 38.0 -0.046204 92.481861 1.937920e-06 39.0 -0.017775 92.594310 2.989370e-06 40.0 -0.006219 92.608125 4.694972e-06 ``` * This indicates a lack of fit. * In-sample dynamic prediction. How good does our model do? In [21]: ``` predict_sunspots = arma_mod30.predict(start='1990', end='2012', dynamic=True) ``` In [22]: ``` fig, ax = plt.subplots(figsize=(12, 8)) dta.loc['1950':].plot(ax=ax) predict_sunspots.plot(ax=ax, style='r'); ``` In [23]: ``` def mean_forecast_err(y, yhat): return y.sub(yhat).mean() ``` In [24]: ``` mean_forecast_err(dta.SUNACTIVITY, predict_sunspots) ``` Out[24]: ``` 5.63555011045144 ``` statsmodels Robust Linear Models Robust Linear Models ==================== In [1]: ``` %matplotlib inline from __future__ import print_function import numpy as np import statsmodels.api as sm import matplotlib.pyplot as plt from statsmodels.sandbox.regression.predstd import wls_prediction_std ``` Estimation ---------- Load data: In [2]: ``` data = sm.datasets.stackloss.load() data.exog = sm.add_constant(data.exog) ``` Huber's T norm with the (default) median absolute deviation scaling In [3]: ``` huber_t = sm.RLM(data.endog, data.exog, M=sm.robust.norms.HuberT()) hub_results = huber_t.fit() print(hub_results.params) print(hub_results.bse) print(hub_results.summary(yname='y', xname=['var_%d' % i for i in range(len(hub_results.params))])) ``` ``` [-41.02649835 0.82938433 0.92606597 -0.12784672] [9.79189854 0.11100521 0.30293016 0.12864961] Robust linear Model Regression Results ============================================================================== Dep. Variable: y No. Observations: 21 Model: RLM Df Residuals: 17 Method: IRLS Df Model: 3 Norm: HuberT Scale Est.: mad Cov Type: H1 Date: Mon, 14 May 2018 Time: 21:44:56 No. Iterations: 19 ============================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ var_0 -41.0265 9.792 -4.190 0.000 -60.218 -21.835 var_1 0.8294 0.111 7.472 0.000 0.612 1.047 var_2 0.9261 0.303 3.057 0.002 0.332 1.520 var_3 -0.1278 0.129 -0.994 0.320 -0.380 0.124 ============================================================================== If the model instance has been used for another fit with different fit parameters, then the fit options might not be the correct ones anymore . ``` Huber's T norm with 'H2' covariance matrix In [4]: ``` hub_results2 = huber_t.fit(cov="H2") print(hub_results2.params) print(hub_results2.bse) ``` ``` [-41.02649835 0.82938433 0.92606597 -0.12784672] [9.08950419 0.11945975 0.32235497 0.11796313] ``` Andrew's Wave norm with Huber's Proposal 2 scaling and 'H3' covariance matrix In [5]: ``` andrew_mod = sm.RLM(data.endog, data.exog, M=sm.robust.norms.AndrewWave()) andrew_results = andrew_mod.fit(scale_est=sm.robust.scale.HuberScale(), cov="H3") print('Parameters: ', andrew_results.params) ``` ``` Parameters: [-40.8817957 0.79276138 1.04857556 -0.13360865] ``` See `help(sm.RLM.fit)` for more options and `module sm.robust.scale` for scale options Comparing OLS and RLM --------------------- Artificial data with outliers: In [6]: ``` nsample = 50 x1 = np.linspace(0, 20, nsample) X = np.column_stack((x1, (x1-5)*2)) X = sm.add_constant(X) sig = 0.3 # smaller error variance makes OLS<->RLM contrast bigger beta = [5, 0.5, -0.0] y_true2 = np.dot(X, beta) y2 = y_true2 + sig1. * np.random.normal(size=nsample) y2[[39,41,43,45,48]] -= 5 # add some outliers (10% of nsample) ``` ### Example 1: quadratic function with linear truth Note that the quadratic term in OLS regression will capture outlier effects. In [7]: ``` res = sm.OLS(y2, X).fit() print(res.params) print(res.bse) print(res.predict()) ``` ``` [ 5.14089837 0.51512862 -0.01220956] [0.4527239 0.06989446 0.00618458] [ 4.83565943 5.09371686 5.34770613 5.59762725 5.84348021 6.08526501 6.32298165 6.55663014 6.78621047 7.01172264 7.23316665 7.45054251 7.6638502 7.87308974 8.07826113 8.27936435 8.47639942 8.66936633 8.85826509 9.04309568 9.22385812 9.4005524 9.57317853 9.74173649 9.9062263 10.06664795 10.22300144 10.37528678 10.52350396 10.66765298 10.80773384 10.94374655 11.0756911 11.20356749 11.32737572 11.4471158 11.56278772 11.67439148 11.78192708 11.88539453 11.98479381 12.08012495 12.17138792 12.25858274 12.34170939 12.4207679 12.49575824 12.56668042 12.63353445 12.69632032] ``` Estimate RLM: In [8]: ``` resrlm = sm.RLM(y2, X).fit() print(resrlm.params) print(resrlm.bse) ``` ``` [ 5.08557977e+00 4.99250913e-01 -2.31002828e-03] [0.14231557 0.0219716 0.00194415] ``` Draw a plot to compare OLS estimates to the robust estimates: In [9]: ``` fig = plt.figure(figsize=(12,8)) ax = fig.add_subplot(111) ax.plot(x1, y2, 'o',label="data") ax.plot(x1, y_true2, 'b-', label="True") prstd, iv_l, iv_u = wls_prediction_std(res) ax.plot(x1, res.fittedvalues, 'r-', label="OLS") ax.plot(x1, iv_u, 'r--') ax.plot(x1, iv_l, 'r--') ax.plot(x1, resrlm.fittedvalues, 'g.-', label="RLM") ax.legend(loc="best") ``` Out[9]: ``` <matplotlib.legend.Legend at 0x115cbae48> ``` ### Example 2: linear function with linear truth Fit a new OLS model using only the linear term and the constant: In [10]: ``` X2 = X[:,[0,1]] res2 = sm.OLS(y2, X2).fit() print(res2.params) print(res2.bse) ``` ``` [5.6330183 0.39303304] [0.38915455 0.03353113] ``` Estimate RLM: In [11]: ``` resrlm2 = sm.RLM(y2, X2).fit() print(resrlm2.params) print(resrlm2.bse) ``` ``` [5.14977947 0.48062536] [0.11092148 0.00955744] ``` Draw a plot to compare OLS estimates to the robust estimates: In [12]: ``` prstd, iv_l, iv_u = wls_prediction_std(res2) fig, ax = plt.subplots(figsize=(8,6)) ax.plot(x1, y2, 'o', label="data") ax.plot(x1, y_true2, 'b-', label="True") ax.plot(x1, res2.fittedvalues, 'r-', label="OLS") ax.plot(x1, iv_u, 'r--') ax.plot(x1, iv_l, 'r--') ax.plot(x1, resrlm2.fittedvalues, 'g.-', label="RLM") legend = ax.legend(loc="best") ```	programming_docs
statsmodels Prediction (out of sample) Prediction (out of sample) ========================== In [1]: ``` %matplotlib inline from __future__ import print_function import numpy as np import statsmodels.api as sm ``` Artificial data --------------- In [2]: ``` nsample = 50 sig = 0.25 x1 = np.linspace(0, 20, nsample) X = np.column_stack((x1, np.sin(x1), (x1-5)*2)) X = sm.add_constant(X) beta = [5., 0.5, 0.5, -0.02] y_true = np.dot(X, beta) y = y_true + sig np.random.normal(size=nsample) ``` Estimation ---------- In [3]: ``` olsmod = sm.OLS(y, X) olsres = olsmod.fit() print(olsres.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: y R-squared: 0.979 Model: OLS Adj. R-squared: 0.978 Method: Least Squares F-statistic: 730.4 Date: Mon, 14 May 2018 Prob (F-statistic): 8.64e-39 Time: 21:44:43 Log-Likelihood: -4.2900 No. Observations: 50 AIC: 16.58 Df Residuals: 46 BIC: 24.23 Df Model: 3 Covariance Type: nonrobust ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ const 4.9950 0.094 53.315 0.000 4.806 5.184 x1 0.4908 0.014 33.965 0.000 0.462 0.520 x2 0.4860 0.057 8.557 0.000 0.372 0.600 x3 -0.0194 0.001 -15.303 0.000 -0.022 -0.017 ============================================================================== Omnibus: 0.621 Durbin-Watson: 1.956 Prob(Omnibus): 0.733 Jarque-Bera (JB): 0.681 Skew: -0.244 Prob(JB): 0.711 Kurtosis: 2.701 Cond. No. 221. ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` In-sample prediction -------------------- In [4]: ``` ypred = olsres.predict(X) print(ypred) ``` ``` [ 4.50966384 4.97889316 5.40995859 5.77637232 6.06120589 6.2598714 6.38087536 6.44442107 6.47908926 6.51714238 6.58922395 6.71932393 6.92083724 7.19436301 7.52760613 7.89739732 8.27349977 8.62357697 8.91850548 9.13715987 9.26988354 9.32007527 9.30363083 9.24633134 9.1796075 9.13537562 9.14079386 9.21380021 9.36016536 9.57254456 9.83168435 10.10958587 10.37410495 10.59423335 10.74519331 10.81250845 10.79438222 10.70199306 10.55765783 10.39116516 10.23488133 10.11843255 10.06383744 10.08188948 10.17038361 10.31447858 10.48913528 10.66323061 10.80467092 10.88566489] ``` Create a new sample of explanatory variables Xnew, predict and plot ------------------------------------------------------------------- In [5]: ``` x1n = np.linspace(20.5,25, 10) Xnew = np.column_stack((x1n, np.sin(x1n), (x1n-5)2)) Xnew = sm.add_constant(Xnew) ynewpred = olsres.predict(Xnew) # predict out of sample print(ynewpred) ``` ``` [10.87574726 10.73750459 10.48999684 10.17665926 9.85466789 9.58094089 9.39820303 9.32452509 9.3488996 9.43393577] ``` Plot comparison --------------- In [6]: ``` import matplotlib.pyplot as plt fig, ax = plt.subplots() ax.plot(x1, y, 'o', label="Data") ax.plot(x1, y_true, 'b-', label="True") ax.plot(np.hstack((x1, x1n)), np.hstack((ypred, ynewpred)), 'r', label="OLS prediction") ax.legend(loc="best"); ``` Predicting with Formulas ------------------------ Using formulas can make both estimation and prediction a lot easier In [7]: ``` from statsmodels.formula.api import ols data = {"x1" : x1, "y" : y} res = ols("y ~ x1 + np.sin(x1) + I((x1-5)2)", data=data).fit() ``` We use the `I` to indicate use of the Identity transform. Ie., we don't want any expansion magic from using `2` In [8]: ``` res.params ``` Out[8]: ``` Intercept 4.995017 x1 0.490756 np.sin(x1) 0.486022 I((x1 - 5) 2) -0.019414 dtype: float64 ``` Now we only have to pass the single variable and we get the transformed right-hand side variables automatically In [9]: ``` res.predict(exog=dict(x1=x1n)) ``` Out[9]: ``` 0 10.875747 1 10.737505 2 10.489997 3 10.176659 4 9.854668 5 9.580941 6 9.398203 7 9.324525 8 9.348900 9 9.433936 dtype: float64 ``` statsmodels Detrending, Stylized Facts and the Business Cycle Detrending, Stylized Facts and the Business Cycle ================================================= In an influential article, Harvey and Jaeger (1993) described the use of unobserved components models (also known as "structural time series models") to derive stylized facts of the business cycle. Their paper begins: ``` "Establishing the 'stylized facts' associated with a set of time series is widely considered a crucial step in macroeconomic research ... For such facts to be useful they should (1) be consistent with the stochastic properties of the data and (2) present meaningful information." ``` In particular, they make the argument that these goals are often better met using the unobserved components approach rather than the popular Hodrick-Prescott filter or Box-Jenkins ARIMA modeling techniques. Statsmodels has the ability to perform all three types of analysis, and below we follow the steps of their paper, using a slightly updated dataset. In [1]: ``` %matplotlib inline import numpy as np import pandas as pd import statsmodels.api as sm import matplotlib.pyplot as plt from IPython.display import display, Latex ``` Unobserved Components --------------------- The unobserved components model available in Statsmodels can be written as: $$ y\_t = \underbrace{\mu\_{t}}\_{\text{trend}} + \underbrace{\gamma\_{t}}\_{\text{seasonal}} + \underbrace{c\_{t}}\_{\text{cycle}} + \sum\_{j=1}^k \underbrace{\beta\_j x\_{jt}}\_{\text{explanatory}} + \underbrace{\varepsilon\_t}\_{\text{irregular}} $$ see Durbin and Koopman 2012, Chapter 3 for notation and additional details. Notice that different specifications for the different individual components can support a wide range of models. The specific models considered in the paper and below are specializations of this general equation. ### Trend The trend component is a dynamic extension of a regression model that includes an intercept and linear time-trend. $$ \begin{align} \underbrace{\mu\_{t+1}}\_{\text{level}} & = \mu\_t + \nu\_t + \eta\_{t+1} \qquad & \eta\_{t+1} \sim N(0, \sigma\_\eta^2) \\\\ \underbrace{\nu\_{t+1}}\_{\text{trend}} & = \nu\_t + \zeta\_{t+1} & \zeta\_{t+1} \sim N(0, \sigma\_\zeta^2) \\ \end{align} $$ where the level is a generalization of the intercept term that can dynamically vary across time, and the trend is a generalization of the time-trend such that the slope can dynamically vary across time. For both elements (level and trend), we can consider models in which: * The element is included vs excluded (if the trend is included, there must also be a level included). * The element is deterministic vs stochastic (i.e. whether or not the variance on the error term is confined to be zero or not) The only additional parameters to be estimated via MLE are the variances of any included stochastic components. This leads to the following specifications: \| \| Level \| Trend \| Stochastic Level \| Stochastic Trend \| \| --- \| --- \| --- \| --- \| --- \| \| Constant \| ✓ \| \| \| \| \| Local Level (random walk) \| ✓ \| \| ✓ \| \| \| Deterministic trend \| ✓ \| ✓ \| \| \| \| Local level with deterministic trend (random walk with drift) \| ✓ \| ✓ \| ✓ \| \| \| Local linear trend \| ✓ \| ✓ \| ✓ \| ✓ \| \| Smooth trend (integrated random walk) \| ✓ \| ✓ \| \| ✓ \| ### Seasonal The seasonal component is written as: $$ \gamma\_t = - \sum\_{j=1}^{s-1} \gamma\_{t+1-j} + \omega\_t \qquad \omega\_t \sim N(0, \sigma\_\omega^2) $$ The periodicity (number of seasons) is `s`, and the defining character is that (without the error term), the seasonal components sum to zero across one complete cycle. The inclusion of an error term allows the seasonal effects to vary over time. The variants of this model are: * The periodicity `s` * Whether or not to make the seasonal effects stochastic. If the seasonal effect is stochastic, then there is one additional parameter to estimate via MLE (the variance of the error term). ### Cycle The cyclical component is intended to capture cyclical effects at time frames much longer than captured by the seasonal component. For example, in economics the cyclical term is often intended to capture the business cycle, and is then expected to have a period between "1.5 and 12 years" (see Durbin and Koopman). The cycle is written as: $$ \begin{align} c\_{t+1} & = c\_t \cos \lambda\_c + c\_t^\* \sin \lambda\_c + \tilde \omega\_t \qquad & \tilde \omega\_t \sim N(0, \sigma\_{\tilde \omega}^2) \\\\ c\_{t+1}^\* & = -c\_t \sin \lambda\_c + c\_t^\* \cos \lambda\_c + \tilde \omega\_t^\* & \tilde \omega\_t^\* \sim N(0, \sigma\_{\tilde \omega}^2) \end{align} $$ The parameter $\lambda\_c$ (the frequency of the cycle) is an additional parameter to be estimated by MLE. If the seasonal effect is stochastic, then there is one another parameter to estimate (the variance of the error term - note that both of the error terms here share the same variance, but are assumed to have independent draws). ### Irregular The irregular component is assumed to be a white noise error term. Its variance is a parameter to be estimated by MLE; i.e. $$ \varepsilon\_t \sim N(0, \sigma\_\varepsilon^2) $$ In some cases, we may want to generalize the irregular component to allow for autoregressive effects: $$ \varepsilon\_t = \rho(L) \varepsilon\_{t-1} + \epsilon\_t, \qquad \epsilon\_t \sim N(0, \sigma\_\epsilon^2) $$ In this case, the autoregressive parameters would also be estimated via MLE. ### Regression effects We may want to allow for explanatory variables by including additional terms $$ \sum\_{j=1}^k \beta\_j x\_{jt} $$ or for intervention effects by including $$ \begin{align} \delta w\_t \qquad \text{where} \qquad w\_t & = 0, \qquad t < \tau, \\\\ & = 1, \qquad t \ge \tau \end{align} $$ These additional parameters could be estimated via MLE or by including them as components of the state space formulation. Data ---- Following Harvey and Jaeger, we will consider the following time series: * US real GNP, "output", ([GNPC96](https://research.stlouisfed.org/fred2/series/GNPC96)) * US GNP implicit price deflator, "prices", ([GNPDEF](https://research.stlouisfed.org/fred2/series/GNPDEF)) * US monetary base, "money", ([AMBSL](https://research.stlouisfed.org/fred2/series/AMBSL)) The time frame in the original paper varied across series, but was broadly 1954-1989. Below we use data from the period 1948-2008 for all series. Although the unobserved components approach allows isolating a seasonal component within the model, the series considered in the paper, and here, are already seasonally adjusted. All data series considered here are taken from [Federal Reserve Economic Data (FRED)](https://research.stlouisfed.org/fred2/). Conveniently, the Python library [Pandas](http://pandas.pydata.org/) has the ability to download data from FRED directly. In [2]: ``` # Datasets from pandas_datareader.data import DataReader # Get the raw data start = '1948-01' end = '2008-01' us_gnp = DataReader('GNPC96', 'fred', start=start, end=end) us_gnp_deflator = DataReader('GNPDEF', 'fred', start=start, end=end) us_monetary_base = DataReader('AMBSL', 'fred', start=start, end=end).resample('QS').mean() recessions = DataReader('USRECQ', 'fred', start=start, end=end).resample('QS').last().values[:,0] # Construct the dataframe dta = pd.concat(map(np.log, (us_gnp, us_gnp_deflator, us_monetary_base)), axis=1) dta.columns = ['US GNP','US Prices','US monetary base'] dates = dta.index._mpl_repr() ``` To get a sense of these three variables over the timeframe, we can plot them: In [3]: ``` # Plot the data ax = dta.plot(figsize=(13,3)) ylim = ax.get_ylim() ax.xaxis.grid() ax.fill_between(dates, ylim[0]+1e-5, ylim[1]-1e-5, recessions, facecolor='k', alpha=0.1); ``` Model ----- Since the data is already seasonally adjusted and there are no obvious explanatory variables, the generic model considered is: $$ y\_t = \underbrace{\mu\_{t}}\_{\text{trend}} + \underbrace{c\_{t}}\_{\text{cycle}} + \underbrace{\varepsilon\_t}\_{\text{irregular}} $$ The irregular will be assumed to be white noise, and the cycle will be stochastic and damped. The final modeling choice is the specification to use for the trend component. Harvey and Jaeger consider two models: 1. Local linear trend (the "unrestricted" model) 2. Smooth trend (the "restricted" model, since we are forcing $\sigma\_\eta = 0$) Below, we construct `kwargs` dictionaries for each of these model types. Notice that rather that there are two ways to specify the models. One way is to specify components directly, as in the table above. The other way is to use string names which map to various specifications. In [4]: ``` # Model specifications # Unrestricted model, using string specification unrestricted_model = { 'level': 'local linear trend', 'cycle': True, 'damped_cycle': True, 'stochastic_cycle': True } # Unrestricted model, setting components directly # This is an equivalent, but less convenient, way to specify a # local linear trend model with a stochastic damped cycle: # unrestricted_model = { # 'irregular': True, 'level': True, 'stochastic_level': True, 'trend': True, 'stochastic_trend': True, # 'cycle': True, 'damped_cycle': True, 'stochastic_cycle': True # } # The restricted model forces a smooth trend restricted_model = { 'level': 'smooth trend', 'cycle': True, 'damped_cycle': True, 'stochastic_cycle': True } # Restricted model, setting components directly # This is an equivalent, but less convenient, way to specify a # smooth trend model with a stochastic damped cycle. Notice # that the difference from the local linear trend model is that # `stochastic_level=False` here. # unrestricted_model = { # 'irregular': True, 'level': True, 'stochastic_level': False, 'trend': True, 'stochastic_trend': True, # 'cycle': True, 'damped_cycle': True, 'stochastic_cycle': True # } ``` We now fit the following models: 1. Output, unrestricted model 2. Prices, unrestricted model 3. Prices, restricted model 4. Money, unrestricted model 5. Money, restricted model In [5]: ``` # Output output_mod = sm.tsa.UnobservedComponents(dta['US GNP'], unrestricted_model) output_res = output_mod.fit(method='powell', disp=False) # Prices prices_mod = sm.tsa.UnobservedComponents(dta['US Prices'], unrestricted_model) prices_res = prices_mod.fit(method='powell', disp=False) prices_restricted_mod = sm.tsa.UnobservedComponents(dta['US Prices'], restricted_model) prices_restricted_res = prices_restricted_mod.fit(method='powell', disp=False) # Money money_mod = sm.tsa.UnobservedComponents(dta['US monetary base'], unrestricted_model) money_res = money_mod.fit(method='powell', disp=False) money_restricted_mod = sm.tsa.UnobservedComponents(dta['US monetary base'], *restricted_model) money_restricted_res = money_restricted_mod.fit(method='powell', disp=False) ``` Once we have fit these models, there are a variety of ways to display the information. Looking at the model of US GNP, we can summarize the fit of the model using the `summary` method on the fit object. In [6]: ``` print(output_res.summary()) ``` ``` Unobserved Components Results ===================================================================================== Dep. Variable: US GNP No. Observations: 241 Model: local linear trend Log Likelihood 770.200 + damped stochastic cycle AIC -1528.400 Date: Mon, 14 May 2018 BIC -1507.592 Time: 21:45:14 HQIC -1520.013 Sample: 01-01-1948 - 01-01-2008 Covariance Type: opg ==================================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------------ sigma2.irregular 4.87e-08 7.26e-06 0.007 0.995 -1.42e-05 1.43e-05 sigma2.level 7.311e-06 4.94e-05 0.148 0.882 -8.95e-05 0.000 sigma2.trend 3.006e-06 1.43e-06 2.101 0.036 2.02e-07 5.81e-06 sigma2.cycle 3.838e-05 2.55e-05 1.503 0.133 -1.17e-05 8.84e-05 frequency.cycle 0.4544 0.049 9.280 0.000 0.358 0.550 damping.cycle 0.8639 0.043 20.232 0.000 0.780 0.948 =================================================================================== Ljung-Box (Q): 40.32 Jarque-Bera (JB): 9.85 Prob(Q): 0.46 Prob(JB): 0.01 Heteroskedasticity (H): 0.27 Skew: -0.04 Prob(H) (two-sided): 0.00 Kurtosis: 4.00 =================================================================================== Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step). ``` For unobserved components models, and in particular when exploring stylized facts in line with point (2) from the introduction, it is often more instructive to plot the estimated unobserved components (e.g. the level, trend, and cycle) themselves to see if they provide a meaningful description of the data. The `plot_components` method of the fit object can be used to show plots and confidence intervals of each of the estimated states, as well as a plot of the observed data versus the one-step-ahead predictions of the model to assess fit. In [7]: ``` fig = output_res.plot_components(legend_loc='lower right', figsize=(15, 9)); ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/tsa/statespace/structural.py:1676: RuntimeWarning: invalid value encountered in sqrt std_errors = np.sqrt(component_bunch['%s_cov' % which]) ``` Finally, Harvey and Jaeger summarize the models in another way to highlight the relative importances of the trend and cyclical components; below we replicate their Table I. The values we find are broadly consistent with, but different in the particulars from, the values from their table. In [8]: ``` # Create Table I table_i = np.zeros((5,6)) start = dta.index[0] end = dta.index[-1] time_range = '%d:%d-%d:%d' % (start.year, start.quarter, end.year, end.quarter) models = [ ('US GNP', time_range, 'None'), ('US Prices', time_range, 'None'), ('US Prices', time_range, r'$\sigma_\eta^2 = 0$'), ('US monetary base', time_range, 'None'), ('US monetary base', time_range, r'$\sigma_\eta^2 = 0$'), ] index = pd.MultiIndex.from_tuples(models, names=['Series', 'Time range', 'Restrictions']) parameter_symbols = [ r'$\sigma_\zeta^2$', r'$\sigma_\eta^2$', r'$\sigma_\kappa^2$', r'$\rho$', r'$2 \pi / \lambda_c$', r'$\sigma_\varepsilon^2$', ] i = 0 for res in (output_res, prices_res, prices_restricted_res, money_res, money_restricted_res): if res.model.stochastic_level: (sigma_irregular, sigma_level, sigma_trend, sigma_cycle, frequency_cycle, damping_cycle) = res.params else: (sigma_irregular, sigma_level, sigma_cycle, frequency_cycle, damping_cycle) = res.params sigma_trend = np.nan period_cycle = 2 np.pi / frequency_cycle table_i[i, :] = [ sigma_level1e7, sigma_trend1e7, sigma_cycle1e7, damping_cycle, period_cycle, sigma_irregular1e7 ] i += 1 pd.set_option('float_format', lambda x: '%.4g' % np.round(x, 2) if not np.isnan(x) else '-') table_i = pd.DataFrame(table_i, index=index, columns=parameter_symbols) table_i ``` Out[8]: \| \| \| \| $\sigma\_\zeta^2$ \| $\sigma\_\eta^2$ \| $\sigma\_\kappa^2$ \| $\rho$ \| $2 \pi / \lambda\_c$ \| $\sigma\_\varepsilon^2$ \| \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| \| Series \| Time range \| Restrictions \| \| \| \| \| \| \| \| US GNP \| 1948:1-2008:1 \| None \| 73.11 \| 30.06 \| 383.8 \| 0.86 \| 13.83 \| 0.49 \| \| US Prices \| 1948:1-2008:1 \| None \| 36.89 \| 31.99 \| 0.04 \| 0.93 \| 10.1 \| 12.15 \| \| $\sigma\_\eta^2 = 0$ \| 40.84 \| - \| 0.03 \| 0.92 \| 9.98 \| 24.07 \| \| US monetary base \| 1948:1-2008:1 \| None \| 64.13 \| 19.46 \| 195.3 \| 0.89 \| 23.12 \| 0 \| \| $\sigma\_\eta^2 = 0$ \| 18.84 \| - \| 247.3 \| 0.89 \| 23.84 \| 0 \|	programming_docs
statsmodels Generalized Linear Models Generalized Linear Models ========================= In [1]: ``` %matplotlib inline from __future__ import print_function import numpy as np import statsmodels.api as sm from scipy import stats from matplotlib import pyplot as plt ``` GLM: Binomial response data --------------------------- ### Load data In this example, we use the Star98 dataset which was taken with permission from Jeff Gill (2000) Generalized linear models: A unified approach. Codebook information can be obtained by typing: In [2]: ``` print(sm.datasets.star98.NOTE) ``` ``` :: Number of Observations - 303 (counties in California). Number of Variables - 13 and 8 interaction terms. Definition of variables names:: NABOVE - Total number of students above the national median for the math section. NBELOW - Total number of students below the national median for the math section. LOWINC - Percentage of low income students PERASIAN - Percentage of Asian student PERBLACK - Percentage of black students PERHISP - Percentage of Hispanic students PERMINTE - Percentage of minority teachers AVYRSEXP - Sum of teachers' years in educational service divided by the number of teachers. AVSALK - Total salary budget including benefits divided by the number of full-time teachers (in thousands) PERSPENK - Per-pupil spending (in thousands) PTRATIO - Pupil-teacher ratio. PCTAF - Percentage of students taking UC/CSU prep courses PCTCHRT - Percentage of charter schools PCTYRRND - Percentage of year-round schools The below variables are interaction terms of the variables defined above. PERMINTE_AVYRSEXP PEMINTE_AVSAL AVYRSEXP_AVSAL PERSPEN_PTRATIO PERSPEN_PCTAF PTRATIO_PCTAF PERMINTE_AVTRSEXP_AVSAL PERSPEN_PTRATIO_PCTAF ``` Load the data and add a constant to the exogenous (independent) variables: In [3]: ``` data = sm.datasets.star98.load() data.exog = sm.add_constant(data.exog, prepend=False) ``` The dependent variable is N by 2 (Success: NABOVE, Failure: NBELOW): In [4]: ``` print(data.endog[:5,:]) ``` ``` [[452. 355.] [144. 40.] [337. 234.] [395. 178.] [ 8. 57.]] ``` The independent variables include all the other variables described above, as well as the interaction terms: In [5]: ``` print(data.exog[:2,:]) ``` ``` [[3.43973000e+01 2.32993000e+01 1.42352800e+01 1.14111200e+01 1.59183700e+01 1.47064600e+01 5.91573200e+01 4.44520700e+00 2.17102500e+01 5.70327600e+01 0.00000000e+00 2.22222200e+01 2.34102872e+02 9.41688110e+02 8.69994800e+02 9.65065600e+01 2.53522420e+02 1.23819550e+03 1.38488985e+04 5.50403520e+03 1.00000000e+00] [1.73650700e+01 2.93283800e+01 8.23489700e+00 9.31488400e+00 1.36363600e+01 1.60832400e+01 5.95039700e+01 5.26759800e+00 2.04427800e+01 6.46226400e+01 0.00000000e+00 0.00000000e+00 2.19316851e+02 8.11417560e+02 9.57016600e+02 1.07684350e+02 3.40406090e+02 1.32106640e+03 1.30502233e+04 6.95884680e+03 1.00000000e+00]] ``` ### Fit and summary In [6]: ``` glm_binom = sm.GLM(data.endog, data.exog, family=sm.families.Binomial()) res = glm_binom.fit() print(res.summary()) ``` ``` Generalized Linear Model Regression Results ============================================================================== Dep. Variable: ['y1', 'y2'] No. Observations: 303 Model: GLM Df Residuals: 282 Model Family: Binomial Df Model: 20 Link Function: logit Scale: 1.0000 Method: IRLS Log-Likelihood: -2998.6 Date: Mon, 14 May 2018 Deviance: 4078.8 Time: 21:45:26 Pearson chi2: 4.05e+03 No. Iterations: 5 Covariance Type: nonrobust ============================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ x1 -0.0168 0.000 -38.749 0.000 -0.018 -0.016 x2 0.0099 0.001 16.505 0.000 0.009 0.011 x3 -0.0187 0.001 -25.182 0.000 -0.020 -0.017 x4 -0.0142 0.000 -32.818 0.000 -0.015 -0.013 x5 0.2545 0.030 8.498 0.000 0.196 0.313 x6 0.2407 0.057 4.212 0.000 0.129 0.353 x7 0.0804 0.014 5.775 0.000 0.053 0.108 x8 -1.9522 0.317 -6.162 0.000 -2.573 -1.331 x9 -0.3341 0.061 -5.453 0.000 -0.454 -0.214 x10 -0.1690 0.033 -5.169 0.000 -0.233 -0.105 x11 0.0049 0.001 3.921 0.000 0.002 0.007 x12 -0.0036 0.000 -15.878 0.000 -0.004 -0.003 x13 -0.0141 0.002 -7.391 0.000 -0.018 -0.010 x14 -0.0040 0.000 -8.450 0.000 -0.005 -0.003 x15 -0.0039 0.001 -4.059 0.000 -0.006 -0.002 x16 0.0917 0.015 6.321 0.000 0.063 0.120 x17 0.0490 0.007 6.574 0.000 0.034 0.064 x18 0.0080 0.001 5.362 0.000 0.005 0.011 x19 0.0002 2.99e-05 7.428 0.000 0.000 0.000 x20 -0.0022 0.000 -6.445 0.000 -0.003 -0.002 const 2.9589 1.547 1.913 0.056 -0.073 5.990 ============================================================================== ``` ### Quantities of interest In [7]: ``` print('Total number of trials:', data.endog[0].sum()) print('Parameters: ', res.params) print('T-values: ', res.tvalues) ``` ``` Total number of trials: 807.0 Parameters: [-1.68150366e-02 9.92547661e-03 -1.87242148e-02 -1.42385609e-02 2.54487173e-01 2.40693664e-01 8.04086739e-02 -1.95216050e+00 -3.34086475e-01 -1.69022168e-01 4.91670212e-03 -3.57996435e-03 -1.40765648e-02 -4.00499176e-03 -3.90639579e-03 9.17143006e-02 4.89898381e-02 8.04073890e-03 2.22009503e-04 -2.24924861e-03 2.95887793e+00] T-values: [-38.74908321 16.50473627 -25.1821894 -32.81791308 8.49827113 4.21247925 5.7749976 -6.16191078 -5.45321673 -5.16865445 3.92119964 -15.87825999 -7.39093058 -8.44963886 -4.05916246 6.3210987 6.57434662 5.36229044 7.42806363 -6.44513698 1.91301155] ``` First differences: We hold all explanatory variables constant at their means and manipulate the percentage of low income households to assess its impact on the response variables: In [8]: ``` means = data.exog.mean(axis=0) means25 = means.copy() means25[0] = stats.scoreatpercentile(data.exog[:,0], 25) means75 = means.copy() means75[0] = lowinc_75per = stats.scoreatpercentile(data.exog[:,0], 75) resp_25 = res.predict(means25) resp_75 = res.predict(means75) diff = resp_75 - resp_25 ``` The interquartile first difference for the percentage of low income households in a school district is: In [9]: ``` print("%2.4f%%" % (diff100)) ``` ``` -11.8753% ``` ### Plots We extract information that will be used to draw some interesting plots: In [10]: ``` nobs = res.nobs y = data.endog[:,0]/data.endog.sum(1) yhat = res.mu ``` Plot yhat vs y: In [11]: ``` from statsmodels.graphics.api import abline_plot ``` In [12]: ``` fig, ax = plt.subplots() ax.scatter(yhat, y) line_fit = sm.OLS(y, sm.add_constant(yhat, prepend=True)).fit() abline_plot(model_results=line_fit, ax=ax) ax.set_title('Model Fit Plot') ax.set_ylabel('Observed values') ax.set_xlabel('Fitted values'); ``` Plot yhat vs. Pearson residuals: In [13]: ``` fig, ax = plt.subplots() ax.scatter(yhat, res.resid_pearson) ax.hlines(0, 0, 1) ax.set_xlim(0, 1) ax.set_title('Residual Dependence Plot') ax.set_ylabel('Pearson Residuals') ax.set_xlabel('Fitted values') ``` Out[13]: ``` Text(0.5,0,'Fitted values') ``` Histogram of standardized deviance residuals: In [14]: ``` from scipy import stats fig, ax = plt.subplots() resid = res.resid_deviance.copy() resid_std = stats.zscore(resid) ax.hist(resid_std, bins=25) ax.set_title('Histogram of standardized deviance residuals'); ``` QQ Plot of Deviance Residuals: In [15]: ``` from statsmodels import graphics graphics.gofplots.qqplot(resid, line='r') ``` Out[15]: GLM: Gamma for proportional count response ------------------------------------------ ### Load data In the example above, we printed the `NOTE` attribute to learn about the Star98 dataset. Statsmodels datasets ships with other useful information. For example: In [16]: ``` print(sm.datasets.scotland.DESCRLONG) ``` ``` This data is based on the example in Gill and describes the proportion of voters who voted Yes to grant the Scottish Parliament taxation powers. The data are divided into 32 council districts. This example's explanatory variables include the amount of council tax collected in pounds sterling as of April 1997 per two adults before adjustments, the female percentage of total claims for unemployment benefits as of January, 1998, the standardized mortality rate (UK is 100), the percentage of labor force participation, regional GDP, the percentage of children aged 5 to 15, and an interaction term between female unemployment and the council tax. The original source files and variable information are included in /scotland/src/ ``` Load the data and add a constant to the exogenous variables: In [17]: ``` data2 = sm.datasets.scotland.load() data2.exog = sm.add_constant(data2.exog, prepend=False) print(data2.exog[:5,:]) print(data2.endog[:5]) ``` ``` [[7.12000e+02 2.10000e+01 1.05000e+02 8.24000e+01 1.35660e+04 1.23000e+01 1.49520e+04 1.00000e+00] [6.43000e+02 2.65000e+01 9.70000e+01 8.02000e+01 1.35660e+04 1.53000e+01 1.70395e+04 1.00000e+00] [6.79000e+02 2.83000e+01 1.13000e+02 8.63000e+01 9.61100e+03 1.39000e+01 1.92157e+04 1.00000e+00] [8.01000e+02 2.71000e+01 1.09000e+02 8.04000e+01 9.48300e+03 1.36000e+01 2.17071e+04 1.00000e+00] [7.53000e+02 2.20000e+01 1.15000e+02 6.47000e+01 9.26500e+03 1.46000e+01 1.65660e+04 1.00000e+00]] [60.3 52.3 53.4 57. 68.7] ``` ### Fit and summary In [18]: ``` glm_gamma = sm.GLM(data2.endog, data2.exog, family=sm.families.Gamma()) glm_results = glm_gamma.fit() print(glm_results.summary()) ``` ``` Generalized Linear Model Regression Results ============================================================================== Dep. Variable: y No. Observations: 32 Model: GLM Df Residuals: 24 Model Family: Gamma Df Model: 7 Link Function: inverse_power Scale: 0.0035843 Method: IRLS Log-Likelihood: -83.017 Date: Mon, 14 May 2018 Deviance: 0.087389 Time: 21:45:29 Pearson chi2: 0.0860 No. Iterations: 6 Covariance Type: nonrobust ============================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ x1 4.962e-05 1.62e-05 3.060 0.002 1.78e-05 8.14e-05 x2 0.0020 0.001 3.824 0.000 0.001 0.003 x3 -7.181e-05 2.71e-05 -2.648 0.008 -0.000 -1.87e-05 x4 0.0001 4.06e-05 2.757 0.006 3.23e-05 0.000 x5 -1.468e-07 1.24e-07 -1.187 0.235 -3.89e-07 9.56e-08 x6 -0.0005 0.000 -2.159 0.031 -0.001 -4.78e-05 x7 -2.427e-06 7.46e-07 -3.253 0.001 -3.89e-06 -9.65e-07 const -0.0178 0.011 -1.548 0.122 -0.040 0.005 ============================================================================== ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/genmod/generalized_linear_model.py:302: DomainWarning: The inverse_power link function does not respect the domain of the Gamma family. DomainWarning) ``` GLM: Gaussian distribution with a noncanonical link --------------------------------------------------- ### Artificial data In [19]: ``` nobs2 = 100 x = np.arange(nobs2) np.random.seed(54321) X = np.column_stack((x,x2)) X = sm.add_constant(X, prepend=False) lny = np.exp(-(.03x + .0001x2 - 1.0)) + .001 np.random.rand(nobs2) ``` ### Fit and summary In [20]: ``` gauss_log = sm.GLM(lny, X, family=sm.families.Gaussian(sm.families.links.log)) gauss_log_results = gauss_log.fit() print(gauss_log_results.summary()) ``` ``` Generalized Linear Model Regression Results ============================================================================== Dep. Variable: y No. Observations: 100 Model: GLM Df Residuals: 97 Model Family: Gaussian Df Model: 2 Link Function: log Scale: 1.0531e-07 Method: IRLS Log-Likelihood: 662.92 Date: Mon, 14 May 2018 Deviance: 1.0215e-05 Time: 21:45:29 Pearson chi2: 1.02e-05 No. Iterations: 7 Covariance Type: nonrobust ============================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ x1 -0.0300 5.6e-06 -5361.316 0.000 -0.030 -0.030 x2 -9.939e-05 1.05e-07 -951.091 0.000 -9.96e-05 -9.92e-05 const 1.0003 5.39e-05 1.86e+04 0.000 1.000 1.000 ============================================================================== ``` statsmodels M-Estimators for Robust Linear Modeling M-Estimators for Robust Linear Modeling ======================================= In [ ]: ``` %matplotlib inline from __future__ import print_function from statsmodels.compat import lmap import numpy as np from scipy import stats import matplotlib.pyplot as plt import statsmodels.api as sm ``` * An M-estimator minimizes the function $$Q(e\_i, \rho) = \sum\_i~\rho \left (\frac{e\_i}{s}\right )$$ where $\rho$ is a symmetric function of the residuals * The effect of $\rho$ is to reduce the influence of outliers * $s$ is an estimate of scale. * The robust estimates $\hat{\beta}$ are computed by the iteratively re-weighted least squares algorithm * We have several choices available for the weighting functions to be used In [ ]: ``` norms = sm.robust.norms ``` In [ ]: ``` def plot_weights(support, weights_func, xlabels, xticks): fig = plt.figure(figsize=(12,8)) ax = fig.add_subplot(111) ax.plot(support, weights_func(support)) ax.set_xticks(xticks) ax.set_xticklabels(xlabels, fontsize=16) ax.set_ylim(-.1, 1.1) return ax ``` ### Andrew's Wave In [ ]: ``` help(norms.AndrewWave.weights) ``` In [ ]: ``` a = 1.339 support = np.linspace(-np.pia, np.pia, 100) andrew = norms.AndrewWave(a=a) plot_weights(support, andrew.weights, ['$-\pia$', '0', '$\pia$'], [-np.pia, 0, np.pia]); ``` ### Hampel's 17A In [ ]: ``` help(norms.Hampel.weights) ``` In [ ]: ``` c = 8 support = np.linspace(-3c, 3c, 1000) hampel = norms.Hampel(a=2., b=4., c=c) plot_weights(support, hampel.weights, ['3c', '0', '3c'], [-3c, 0, 3c]); ``` ### Huber's t In [ ]: ``` help(norms.HuberT.weights) ``` In [ ]: ``` t = 1.345 support = np.linspace(-3t, 3t, 1000) huber = norms.HuberT(t=t) plot_weights(support, huber.weights, ['-3t', '0', '3t'], [-3t, 0, 3t]); ``` ### Least Squares In [ ]: ``` help(norms.LeastSquares.weights) ``` In [ ]: ``` support = np.linspace(-3, 3, 1000) lst_sq = norms.LeastSquares() plot_weights(support, lst_sq.weights, ['-3', '0', '3'], [-3, 0, 3]); ``` ### Ramsay's Ea In [ ]: ``` help(norms.RamsayE.weights) ``` In [ ]: ``` a = .3 support = np.linspace(-3a, 3a, 1000) ramsay = norms.RamsayE(a=a) plot_weights(support, ramsay.weights, ['-3a', '0', '3a'], [-3a, 0, 3a]); ``` ### Trimmed Mean In [ ]: ``` help(norms.TrimmedMean.weights) ``` In [ ]: ``` c = 2 support = np.linspace(-3c, 3c, 1000) trimmed = norms.TrimmedMean(c=c) plot_weights(support, trimmed.weights, ['-3c', '0', '3c'], [-3c, 0, 3c]); ``` ### Tukey's Biweight In [ ]: ``` help(norms.TukeyBiweight.weights) ``` In [ ]: ``` c = 4.685 support = np.linspace(-3c, 3c, 1000) tukey = norms.TukeyBiweight(c=c) plot_weights(support, tukey.weights, ['-3c', '0', '3c'], [-3c, 0, 3c]); ``` ### Scale Estimators * Robust estimates of the location In [ ]: ``` x = np.array([1, 2, 3, 4, 500]) ``` * The mean is not a robust estimator of location In [ ]: ``` x.mean() ``` * The median, on the other hand, is a robust estimator with a breakdown point of 50% In [ ]: ``` np.median(x) ``` * Analagously for the scale * The standard deviation is not robust In [ ]: ``` x.std() ``` Median Absolute Deviation $$ median\_i \|X\_i - median\_j(X\_j)\|) $$ Standardized Median Absolute Deviation is a consistent estimator for $\hat{\sigma}$ $$\hat{\sigma}=K \cdot MAD$$ where $K$ depends on the distribution. For the normal distribution for example, $$K = \Phi^{-1}(.75)$$ In [ ]: ``` stats.norm.ppf(.75) ``` In [ ]: ``` print(x) ``` In [ ]: ``` sm.robust.scale.mad(x) ``` In [ ]: ``` np.array([1,2,3,4,5.]).std() ``` * The default for Robust Linear Models is MAD * another popular choice is Huber's proposal 2 In [ ]: ``` np.random.seed(12345) fat_tails = stats.t(6).rvs(40) ``` In [ ]: ``` kde = sm.nonparametric.KDEUnivariate(fat_tails) kde.fit() fig = plt.figure(figsize=(12,8)) ax = fig.add_subplot(111) ax.plot(kde.support, kde.density); ``` In [ ]: ``` print(fat_tails.mean(), fat_tails.std()) ``` In [ ]: ``` print(stats.norm.fit(fat_tails)) ``` In [ ]: ``` print(stats.t.fit(fat_tails, f0=6)) ``` In [ ]: ``` huber = sm.robust.scale.Huber() loc, scale = huber(fat_tails) print(loc, scale) ``` In [ ]: ``` sm.robust.mad(fat_tails) ``` In [ ]: ``` sm.robust.mad(fat_tails, c=stats.t(6).ppf(.75)) ``` In [ ]: ``` sm.robust.scale.mad(fat_tails) ``` ### Duncan's Occupational Prestige data - M-estimation for outliers In [ ]: ``` from statsmodels.graphics.api import abline_plot from statsmodels.formula.api import ols, rlm ``` In [ ]: ``` prestige = sm.datasets.get_rdataset("Duncan", "car", cache=True).data ``` In [ ]: ``` print(prestige.head(10)) ``` In [ ]: ``` fig = plt.figure(figsize=(12,12)) ax1 = fig.add_subplot(211, xlabel='Income', ylabel='Prestige') ax1.scatter(prestige.income, prestige.prestige) xy_outlier = prestige.loc['minister', ['income','prestige']] ax1.annotate('Minister', xy_outlier, xy_outlier+1, fontsize=16) ax2 = fig.add_subplot(212, xlabel='Education', ylabel='Prestige') ax2.scatter(prestige.education, prestige.prestige); ``` In [ ]: ``` ols_model = ols('prestige ~ income + education', prestige).fit() print(ols_model.summary()) ``` In [ ]: ``` infl = ols_model.get_influence() student = infl.summary_frame()['student_resid'] print(student) ``` In [ ]: ``` print(student.loc[np.abs(student) > 2]) ``` In [ ]: ``` print(infl.summary_frame().loc['minister']) ``` In [ ]: ``` sidak = ols_model.outlier_test('sidak') sidak.sort_values('unadj_p', inplace=True) print(sidak) ``` In [ ]: ``` fdr = ols_model.outlier_test('fdr_bh') fdr.sort_values('unadj_p', inplace=True) print(fdr) ``` In [ ]: ``` rlm_model = rlm('prestige ~ income + education', prestige).fit() print(rlm_model.summary()) ``` In [ ]: ``` print(rlm_model.weights) ``` ### Hertzprung Russell data for Star Cluster CYG 0B1 - Leverage Points * Data is on the luminosity and temperature of 47 stars in the direction of Cygnus. In [ ]: ``` dta = sm.datasets.get_rdataset("starsCYG", "robustbase", cache=True).data ``` In [ ]: ``` from matplotlib.patches import Ellipse fig = plt.figure(figsize=(12,8)) ax = fig.add_subplot(111, xlabel='log(Temp)', ylabel='log(Light)', title='Hertzsprung-Russell Diagram of Star Cluster CYG OB1') ax.scatter(dta.values.T) # highlight outliers e = Ellipse((3.5, 6), .2, 1, alpha=.25, color='r') ax.add_patch(e); ax.annotate('Red giants', xy=(3.6, 6), xytext=(3.8, 6), arrowprops=dict(facecolor='black', shrink=0.05, width=2), horizontalalignment='left', verticalalignment='bottom', clip_on=True, # clip to the axes bounding box fontsize=16, ) # annotate these with their index for i,row in dta.loc[dta['log.Te'] < 3.8].iterrows(): ax.annotate(i, row, row + .01, fontsize=14) xlim, ylim = ax.get_xlim(), ax.get_ylim() ``` In [ ]: ``` from IPython.display import Image Image(filename='star_diagram.png') ``` In [ ]: ``` y = dta['log.light'] X = sm.add_constant(dta['log.Te'], prepend=True) ols_model = sm.OLS(y, X).fit() abline_plot(model_results=ols_model, ax=ax) ``` In [ ]: ``` rlm_mod = sm.RLM(y, X, sm.robust.norms.TrimmedMean(.5)).fit() abline_plot(model_results=rlm_mod, ax=ax, color='red') ``` Why? Because M-estimators are not robust to leverage points. In [ ]: ``` infl = ols_model.get_influence() ``` In [ ]: ``` h_bar = 2(ols_model.df_model + 1 )/ols_model.nobs hat_diag = infl.summary_frame()['hat_diag'] hat_diag.loc[hat_diag > h_bar] ``` In [ ]: ``` sidak2 = ols_model.outlier_test('sidak') sidak2.sort_values('unadj_p', inplace=True) print(sidak2) ``` In [ ]: ``` fdr2 = ols_model.outlier_test('fdr_bh') fdr2.sort_values('unadj_p', inplace=True) print(fdr2) ``` Let's delete that line In [ ]: ``` l = ax.lines[-1] l.remove() del l ``` In [ ]: ``` weights = np.ones(len(X)) weights[X[X['log.Te'] < 3.8].index.values - 1] = 0 wls_model = sm.WLS(y, X, weights=weights).fit() abline_plot(model_results=wls_model, ax=ax, color='green') ``` * MM estimators are good for this type of problem, unfortunately, we don't yet have these yet. * It's being worked on, but it gives a good excuse to look at the R cell magics in the notebook. In [ ]: ``` yy = y.values[:,None] xx = X['log.Te'].values[:,None] ``` In [ ]: ``` %load_ext rpy2.ipython ``` In [ ]: ``` %R library(robustbase) %Rpush yy xx %R mod <- lmrob(yy ~ xx); %R params <- mod$coefficients; %Rpull params ``` In [ ]: ``` %R print(mod) ``` In [ ]: ``` print(params) ``` In [ ]: ``` abline_plot(intercept=params[0], slope=params[1], ax=ax, color='red') ``` ### Exercise: Breakdown points of M-estimator In [ ]: ``` np.random.seed(12345) nobs = 200 beta_true = np.array([3, 1, 2.5, 3, -4]) X = np.random.uniform(-20,20, size=(nobs, len(beta_true)-1)) # stack a constant in front X = sm.add_constant(X, prepend=True) # np.c_[np.ones(nobs), X] mc_iter = 500 contaminate = .25 # percentage of response variables to contaminate ``` In [ ]: ``` all_betas = [] for i in range(mc_iter): y = np.dot(X, beta_true) + np.random.normal(size=200) random_idx = np.random.randint(0, nobs, size=int(contaminate * nobs)) y[random_idx] = np.random.uniform(-750, 750) beta_hat = sm.RLM(y, X).fit().params all_betas.append(beta_hat) ``` In [ ]: ``` all_betas = np.asarray(all_betas) se_loss = lambda x : np.linalg.norm(x, ord=2)**2 se_beta = lmap(se_loss, all_betas - beta_true) ``` #### Squared error loss In [ ]: ``` np.array(se_beta).mean() ``` In [ ]: ``` all_betas.mean(0) ``` In [ ]: ``` beta_true ``` In [ ]: ``` se_loss(all_betas.mean(0) - beta_true) ```	programming_docs
statsmodels Kernel Density Estimation Kernel Density Estimation ========================= Kernel density estimation is the process of estimating an unknown probability density function using a kernel function $K(u)$. While a histogram counts the number of data points in somewhat arbitrary regions, a kernel density estimate is a function defined as the sum of a kernel function on every data point. The kernel function typically exhibits the following properties: 1. Symmetry such that $K(u) = K(-u)$. 2. Normalization such that $\int\_{-\infty}^{\infty} K(u) \ du = 1$ . 3. Monotonically decreasing such that $K'(u) < 0$ when $u > 0$. 4. Expected value equal to zero such that $\mathrm{E}[K] = 0$. For more information about kernel density estimation, see for instance [Wikipedia - Kernel density estimation](https://en.wikipedia.org/wiki/Kernel_density_estimation). A univariate kernel density estimator is implemented in `sm.nonparametric.KDEUnivariate`. In this example we will show the following: * Basic usage, how to fit the estimator. * The effect of varying the bandwidth of the kernel using the `bw` argument. * The various kernel functions available using the `kernel` argument. In [1]: ``` %matplotlib inline import numpy as np from scipy import stats import statsmodels.api as sm import matplotlib.pyplot as plt from statsmodels.distributions.mixture_rvs import mixture_rvs ``` A univariate example -------------------- In [2]: ``` np.random.seed(12345) # Seed the random number generator for reproducible results ``` We create a bimodal distribution: a mixture of two normal distributions with locations at `-1` and `1`. In [3]: ``` # Location, scale and weight for the two distributions dist1_loc, dist1_scale, weight1 = -1 , .5, .25 dist2_loc, dist2_scale, weight2 = 1 , .5, .75 # Sample from a mixture of distributions obs_dist = mixture_rvs(prob=[weight1, weight2], size=250, dist=[stats.norm, stats.norm], kwargs = (dict(loc=dist1_loc, scale=dist1_scale), dict(loc=dist2_loc, scale=dist2_scale))) ``` The simplest non-parametric technique for density estimation is the histogram. In [4]: ``` fig = plt.figure(figsize=(12, 5)) ax = fig.add_subplot(111) # Scatter plot of data samples and histogram ax.scatter(obs_dist, np.abs(np.random.randn(obs_dist.size)), zorder=15, color='red', marker='x', alpha=0.5, label='Samples') lines = ax.hist(obs_dist, bins=20, edgecolor='k', label='Histogram') ax.legend(loc='best') ax.grid(True, zorder=-5) ``` Fitting with the default arguments ---------------------------------- The histogram above is discontinuous. To compute a continuous probability density function, we can use kernel density estimation. We initialize a univariate kernel density estimator using `KDEUnivariate`. In [5]: ``` kde = sm.nonparametric.KDEUnivariate(obs_dist) kde.fit() # Estimate the densities ``` We present a figure of the fit, as well as the true distribution. In [6]: ``` fig = plt.figure(figsize=(12, 5)) ax = fig.add_subplot(111) # Plot the histrogram ax.hist(obs_dist, bins=20, normed=True, label='Histogram from samples', zorder=5, edgecolor='k', alpha=0.5) # Plot the KDE as fitted using the default arguments ax.plot(kde.support, kde.density, lw=3, label='KDE from samples', zorder=10) # Plot the true distribution true_values = (stats.norm.pdf(loc=dist1_loc, scale=dist1_scale, x=kde.support)weight1 + stats.norm.pdf(loc=dist2_loc, scale=dist2_scale, x=kde.support)weight2) ax.plot(kde.support, true_values, lw=3, label='True distribution', zorder=15) # Plot the samples ax.scatter(obs_dist, np.abs(np.random.randn(obs_dist.size))/40, marker='x', color='red', zorder=20, label='Samples', alpha=0.5) ax.legend(loc='best') ax.grid(True, zorder=-5) ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/matplotlib/axes/_axes.py:6462: UserWarning: The 'normed' kwarg is deprecated, and has been replaced by the 'density' kwarg. warnings.warn("The 'normed' kwarg is deprecated, and has been " ``` In the code above, default arguments were used. We can also vary the bandwidth of the kernel, as we will now see. Varying the bandwidth using the `bw` argument --------------------------------------------- The bandwidth of the kernel can be adjusted using the `bw` argument. In the following example, a bandwidth of `bw=0.2` seems to fit the data well. In [7]: ``` fig = plt.figure(figsize=(12, 5)) ax = fig.add_subplot(111) # Plot the histrogram ax.hist(obs_dist, bins=25, label='Histogram from samples', zorder=5, edgecolor='k', normed=True, alpha=0.5) # Plot the KDE for various bandwidths for bandwidth in [0.1, 0.2, 0.4]: kde.fit(bw=bandwidth) # Estimate the densities ax.plot(kde.support, kde.density, '--', lw=2, color='k', zorder=10, label='KDE from samples, bw = {}'.format(round(bandwidth, 2))) # Plot the true distribution ax.plot(kde.support, true_values, lw=3, label='True distribution', zorder=15) # Plot the samples ax.scatter(obs_dist, np.abs(np.random.randn(obs_dist.size))/50, marker='x', color='red', zorder=20, label='Data samples', alpha=0.5) ax.legend(loc='best') ax.set_xlim([-3, 3]) ax.grid(True, zorder=-5) ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/matplotlib/axes/_axes.py:6462: UserWarning: The 'normed' kwarg is deprecated, and has been replaced by the 'density' kwarg. warnings.warn("The 'normed' kwarg is deprecated, and has been " ``` Comparing kernel functions -------------------------- In the example above, a Gaussian kernel was used. Several other kernels are also available. In [8]: ``` from statsmodels.nonparametric.kde import kernel_switch list(kernel_switch.keys()) ``` Out[8]: ``` ['gau', 'epa', 'uni', 'tri', 'biw', 'triw', 'cos', 'cos2'] ``` ### The available kernel functions In [9]: ``` # Create a figure fig = plt.figure(figsize=(12, 5)) # Enumerate every option for the kernel for i, (ker_name, ker_class) in enumerate(kernel_switch.items()): # Initialize the kernel object kernel = ker_class() # Sample from the domain domain = kernel.domain or [-3, 3] x_vals = np.linspace(domain, num=210) y_vals = kernel(x_vals) # Create a subplot, set the title ax = fig.add_subplot(2, 4, i + 1) ax.set_title('Kernel function "{}"'.format(ker_name)) ax.plot(x_vals, y_vals, lw=3, label='{}'.format(ker_name)) ax.scatter([0], [0], marker='x', color='red') plt.grid(True, zorder=-5) ax.set_xlim(domain) plt.tight_layout() ``` ### The available kernel functions on three data points We now examine how the kernel density estimate will fit to three equally spaced data points. In [10]: ``` # Create three equidistant points data = np.linspace(-1, 1, 3) kde = sm.nonparametric.KDEUnivariate(data) # Create a figure fig = plt.figure(figsize=(12, 5)) # Enumerate every option for the kernel for i, kernel in enumerate(kernel_switch.keys()): # Create a subplot, set the title ax = fig.add_subplot(2, 4, i + 1) ax.set_title('Kernel function "{}"'.format(kernel)) # Fit the model (estimate densities) kde.fit(kernel=kernel, fft=False, gridsize=210) # Create the plot ax.plot(kde.support, kde.density, lw=3, label='KDE from samples', zorder=10) ax.scatter(data, np.zeros_like(data), marker='x', color='red') plt.grid(True, zorder=-5) ax.set_xlim([-3, 3]) plt.tight_layout() ``` A more difficult case --------------------- The fit is not always perfect. See the example below for a harder case. In [11]: ``` obs_dist = mixture_rvs([.25, .75], size=250, dist=[stats.norm, stats.beta], kwargs = (dict(loc=-1, scale=.5), dict(loc=1, scale=1, args=(1, .5)))) ``` In [12]: ``` kde = sm.nonparametric.KDEUnivariate(obs_dist) kde.fit() ``` In [13]: ``` fig = plt.figure(figsize=(12, 5)) ax = fig.add_subplot(111) ax.hist(obs_dist, bins=20, normed=True, edgecolor='k', zorder=4, alpha=0.5) ax.plot(kde.support, kde.density, lw=3, zorder=7) # Plot the samples ax.scatter(obs_dist, np.abs(np.random.randn(obs_dist.size))/50, marker='x', color='red', zorder=20, label='Data samples', alpha=0.5) ax.grid(True, zorder=-5) ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/matplotlib/axes/_axes.py:6462: UserWarning: The 'normed' kwarg is deprecated, and has been replaced by the 'density' kwarg. warnings.warn("The 'normed' kwarg is deprecated, and has been " ``` The KDE is a distribution ------------------------- Since the KDE is a distribution, we can access attributes and methods such as: `entropy` * `evaluate` * `cdf` * `icdf` * `sf` * `cumhazard` In [14]: ``` obs_dist = mixture_rvs([.25, .75], size=1000, dist=[stats.norm, stats.norm], kwargs = (dict(loc=-1, scale=.5), dict(loc=1, scale=.5))) kde = sm.nonparametric.KDEUnivariate(obs_dist) kde.fit(gridsize=2*10) ``` In [15]: ``` kde.entropy ``` Out[15]: ``` 1.314324140492138 ``` In [16]: ``` kde.evaluate(-1) ``` Out[16]: ``` array([0.18085886]) ``` ### Cumulative distribution, it's inverse, and the survival function In [17]: ``` fig = plt.figure(figsize=(12, 5)) ax = fig.add_subplot(111) ax.plot(kde.support, kde.cdf, lw=3, label='CDF') ax.plot(np.linspace(0, 1, num = kde.icdf.size), kde.icdf, lw=3, label='Inverse CDF') ax.plot(kde.support, kde.sf, lw=3, label='Survival function') ax.legend(loc = 'best') ax.grid(True, zorder=-5) ``` ### The Cumulative Hazard Function In [18]: ``` fig = plt.figure(figsize=(12, 5)) ax = fig.add_subplot(111) ax.plot(kde.support, kde.cumhazard, lw=3, label='Cumulative Hazard Function') ax.legend(loc = 'best') ax.grid(True, zorder=-5) ``` statsmodels Weighted Least Squares Weighted Least Squares ====================== In [1]: ``` %matplotlib inline from __future__ import print_function import numpy as np from scipy import stats import statsmodels.api as sm import matplotlib.pyplot as plt from statsmodels.sandbox.regression.predstd import wls_prediction_std from statsmodels.iolib.table import (SimpleTable, default_txt_fmt) np.random.seed(1024) ``` WLS Estimation -------------- ### Artificial data: Heteroscedasticity 2 groups Model assumptions: Misspecification: true model is quadratic, estimate only linear * Independent noise/error term * Two groups for error variance, low and high variance groups In [2]: ``` nsample = 50 x = np.linspace(0, 20, nsample) X = np.column_stack((x, (x - 5)*2)) X = sm.add_constant(X) beta = [5., 0.5, -0.01] sig = 0.5 w = np.ones(nsample) w[nsample 6//10:] = 3 y_true = np.dot(X, beta) e = np.random.normal(size=nsample) y = y_true + sig * w * e X = X[:,[0,1]] ``` ### WLS knowing the true variance ratio of heteroscedasticity In this example, `w` is the standard deviation of the error. `WLS` requires that the weights are proportional to the inverse of the error variance. In [3]: ``` mod_wls = sm.WLS(y, X, weights=1./(w ** 2)) res_wls = mod_wls.fit() print(res_wls.summary()) ``` ``` WLS Regression Results ============================================================================== Dep. Variable: y R-squared: 0.927 Model: WLS Adj. R-squared: 0.926 Method: Least Squares F-statistic: 613.2 Date: Mon, 14 May 2018 Prob (F-statistic): 5.44e-29 Time: 21:44:50 Log-Likelihood: -51.136 No. Observations: 50 AIC: 106.3 Df Residuals: 48 BIC: 110.1 Df Model: 1 Covariance Type: nonrobust ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ const 5.2469 0.143 36.790 0.000 4.960 5.534 x1 0.4466 0.018 24.764 0.000 0.410 0.483 ============================================================================== Omnibus: 0.407 Durbin-Watson: 2.317 Prob(Omnibus): 0.816 Jarque-Bera (JB): 0.103 Skew: -0.104 Prob(JB): 0.950 Kurtosis: 3.075 Cond. No. 14.6 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` OLS vs. WLS ----------- Estimate an OLS model for comparison: In [4]: ``` res_ols = sm.OLS(y, X).fit() print(res_ols.params) print(res_wls.params) ``` ``` [5.24256099 0.43486879] [5.24685499 0.44658241] ``` Compare the WLS standard errors to heteroscedasticity corrected OLS standard errors: In [5]: ``` se = np.vstack([[res_wls.bse], [res_ols.bse], [res_ols.HC0_se], [res_ols.HC1_se], [res_ols.HC2_se], [res_ols.HC3_se]]) se = np.round(se,4) colnames = ['x1', 'const'] rownames = ['WLS', 'OLS', 'OLS_HC0', 'OLS_HC1', 'OLS_HC3', 'OLS_HC3'] tabl = SimpleTable(se, colnames, rownames, txt_fmt=default_txt_fmt) print(tabl) ``` ``` ===================== x1 const --------------------- WLS 0.1426 0.018 OLS 0.2707 0.0233 OLS_HC0 0.194 0.0281 OLS_HC1 0.198 0.0287 OLS_HC3 0.2003 0.029 OLS_HC3 0.207 0.03 --------------------- ``` Calculate OLS prediction interval: In [6]: ``` covb = res_ols.cov_params() prediction_var = res_ols.mse_resid + (X * np.dot(covb,X.T).T).sum(1) prediction_std = np.sqrt(prediction_var) tppf = stats.t.ppf(0.975, res_ols.df_resid) ``` In [7]: ``` prstd_ols, iv_l_ols, iv_u_ols = wls_prediction_std(res_ols) ``` Draw a plot to compare predicted values in WLS and OLS: In [8]: ``` prstd, iv_l, iv_u = wls_prediction_std(res_wls) fig, ax = plt.subplots(figsize=(8,6)) ax.plot(x, y, 'o', label="Data") ax.plot(x, y_true, 'b-', label="True") # OLS ax.plot(x, res_ols.fittedvalues, 'r--') ax.plot(x, iv_u_ols, 'r--', label="OLS") ax.plot(x, iv_l_ols, 'r--') # WLS ax.plot(x, res_wls.fittedvalues, 'g--.') ax.plot(x, iv_u, 'g--', label="WLS") ax.plot(x, iv_l, 'g--') ax.legend(loc="best"); ``` Feasible Weighted Least Squares (2-stage FWLS) ---------------------------------------------- Like ,`w`, `w_est` is proportional to the standard deviation, and so must be squared. In [9]: ``` resid1 = res_ols.resid[w==1.] var1 = resid1.var(ddof=int(res_ols.df_model)+1) resid2 = res_ols.resid[w!=1.] var2 = resid2.var(ddof=int(res_ols.df_model)+1) w_est = w.copy() w_est[w!=1.] = np.sqrt(var2) / np.sqrt(var1) res_fwls = sm.WLS(y, X, 1./((w_est 2))).fit() print(res_fwls.summary()) ``` ``` WLS Regression Results ============================================================================== Dep. Variable: y R-squared: 0.931 Model: WLS Adj. R-squared: 0.929 Method: Least Squares F-statistic: 646.7 Date: Mon, 14 May 2018 Prob (F-statistic): 1.66e-29 Time: 21:44:51 Log-Likelihood: -50.716 No. Observations: 50 AIC: 105.4 Df Residuals: 48 BIC: 109.3 Df Model: 1 Covariance Type: nonrobust ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ const 5.2363 0.135 38.720 0.000 4.964 5.508 x1 0.4492 0.018 25.431 0.000 0.414 0.485 ============================================================================== Omnibus: 0.247 Durbin-Watson: 2.343 Prob(Omnibus): 0.884 Jarque-Bera (JB): 0.179 Skew: -0.136 Prob(JB): 0.915 Kurtosis: 2.893 Cond. No. 14.3 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` statsmodels Ordinary Least Squares Ordinary Least Squares ====================== In [1]: ``` %matplotlib inline from __future__ import print_function import numpy as np import statsmodels.api as sm import matplotlib.pyplot as plt from statsmodels.sandbox.regression.predstd import wls_prediction_std np.random.seed(9876789) ``` OLS estimation -------------- Artificial data: In [2]: ``` nsample = 100 x = np.linspace(0, 10, 100) X = np.column_stack((x, x2)) beta = np.array([1, 0.1, 10]) e = np.random.normal(size=nsample) ``` Our model needs an intercept so we add a column of 1s: In [3]: ``` X = sm.add_constant(X) y = np.dot(X, beta) + e ``` Fit and summary: In [4]: ``` model = sm.OLS(y, X) results = model.fit() print(results.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: y R-squared: 1.000 Model: OLS Adj. R-squared: 1.000 Method: Least Squares F-statistic: 4.020e+06 Date: Mon, 14 May 2018 Prob (F-statistic): 2.83e-239 Time: 21:45:09 Log-Likelihood: -146.51 No. Observations: 100 AIC: 299.0 Df Residuals: 97 BIC: 306.8 Df Model: 2 Covariance Type: nonrobust ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ const 1.3423 0.313 4.292 0.000 0.722 1.963 x1 -0.0402 0.145 -0.278 0.781 -0.327 0.247 x2 10.0103 0.014 715.745 0.000 9.982 10.038 ============================================================================== Omnibus: 2.042 Durbin-Watson: 2.274 Prob(Omnibus): 0.360 Jarque-Bera (JB): 1.875 Skew: 0.234 Prob(JB): 0.392 Kurtosis: 2.519 Cond. No. 144. ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` Quantities of interest can be extracted directly from the fitted model. Type `dir(results)` for a full list. Here are some examples: In [5]: ``` print('Parameters: ', results.params) print('R2: ', results.rsquared) ``` ``` Parameters: [ 1.34233516 -0.04024948 10.01025357] R2: 0.9999879365025871 ``` OLS non-linear curve but linear in parameters --------------------------------------------- We simulate artificial data with a non-linear relationship between x and y: In [6]: ``` nsample = 50 sig = 0.5 x = np.linspace(0, 20, nsample) X = np.column_stack((x, np.sin(x), (x-5)*2, np.ones(nsample))) beta = [0.5, 0.5, -0.02, 5.] y_true = np.dot(X, beta) y = y_true + sig np.random.normal(size=nsample) ``` Fit and summary: In [7]: ``` res = sm.OLS(y, X).fit() print(res.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: y R-squared: 0.933 Model: OLS Adj. R-squared: 0.928 Method: Least Squares F-statistic: 211.8 Date: Mon, 14 May 2018 Prob (F-statistic): 6.30e-27 Time: 21:45:09 Log-Likelihood: -34.438 No. Observations: 50 AIC: 76.88 Df Residuals: 46 BIC: 84.52 Df Model: 3 Covariance Type: nonrobust ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ x1 0.4687 0.026 17.751 0.000 0.416 0.522 x2 0.4836 0.104 4.659 0.000 0.275 0.693 x3 -0.0174 0.002 -7.507 0.000 -0.022 -0.013 const 5.2058 0.171 30.405 0.000 4.861 5.550 ============================================================================== Omnibus: 0.655 Durbin-Watson: 2.896 Prob(Omnibus): 0.721 Jarque-Bera (JB): 0.360 Skew: 0.207 Prob(JB): 0.835 Kurtosis: 3.026 Cond. No. 221. ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` Extract other quantities of interest: In [8]: ``` print('Parameters: ', res.params) print('Standard errors: ', res.bse) print('Predicted values: ', res.predict()) ``` ``` Parameters: [ 0.46872448 0.48360119 -0.01740479 5.20584496] Standard errors: [0.02640602 0.10380518 0.00231847 0.17121765] Predicted values: [ 4.77072516 5.22213464 5.63620761 5.98658823 6.25643234 6.44117491 6.54928009 6.60085051 6.62432454 6.6518039 6.71377946 6.83412169 7.02615877 7.29048685 7.61487206 7.97626054 8.34456611 8.68761335 8.97642389 9.18997755 9.31866582 9.36587056 9.34740836 9.28893189 9.22171529 9.17751587 9.1833565 9.25708583 9.40444579 9.61812821 9.87897556 10.15912843 10.42660281 10.65054491 10.8063004 10.87946503 10.86825119 10.78378163 10.64826203 10.49133265 10.34519853 10.23933827 10.19566084 10.22490593 10.32487947 10.48081414 10.66779556 10.85485568 11.01006072 11.10575781] ``` Draw a plot to compare the true relationship to OLS predictions. Confidence intervals around the predictions are built using the `wls_prediction_std` command. In [9]: ``` prstd, iv_l, iv_u = wls_prediction_std(res) fig, ax = plt.subplots(figsize=(8,6)) ax.plot(x, y, 'o', label="data") ax.plot(x, y_true, 'b-', label="True") ax.plot(x, res.fittedvalues, 'r--.', label="OLS") ax.plot(x, iv_u, 'r--') ax.plot(x, iv_l, 'r--') ax.legend(loc='best'); ``` OLS with dummy variables ------------------------ We generate some artificial data. There are 3 groups which will be modelled using dummy variables. Group 0 is the omitted/benchmark category. In [10]: ``` nsample = 50 groups = np.zeros(nsample, int) groups[20:40] = 1 groups[40:] = 2 #dummy = (groups[:,None] == np.unique(groups)).astype(float) dummy = sm.categorical(groups, drop=True) x = np.linspace(0, 20, nsample) # drop reference category X = np.column_stack((x, dummy[:,1:])) X = sm.add_constant(X, prepend=False) beta = [1., 3, -3, 10] y_true = np.dot(X, beta) e = np.random.normal(size=nsample) y = y_true + e ``` Inspect the data: In [11]: ``` print(X[:5,:]) print(y[:5]) print(groups) print(dummy[:5,:]) ``` ``` [[0. 0. 0. 1. ] [0.40816327 0. 0. 1. ] [0.81632653 0. 0. 1. ] [1.2244898 0. 0. 1. ] [1.63265306 0. 0. 1. ]] [ 9.28223335 10.50481865 11.84389206 10.38508408 12.37941998] [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2] [[1. 0. 0.] [1. 0. 0.] [1. 0. 0.] [1. 0. 0.] [1. 0. 0.]] ``` Fit and summary: In [12]: ``` res2 = sm.OLS(y, X).fit() print(res2.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: y R-squared: 0.978 Model: OLS Adj. R-squared: 0.976 Method: Least Squares F-statistic: 671.7 Date: Mon, 14 May 2018 Prob (F-statistic): 5.69e-38 Time: 21:45:09 Log-Likelihood: -64.643 No. Observations: 50 AIC: 137.3 Df Residuals: 46 BIC: 144.9 Df Model: 3 Covariance Type: nonrobust ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ x1 0.9999 0.060 16.689 0.000 0.879 1.121 x2 2.8909 0.569 5.081 0.000 1.746 4.036 x3 -3.2232 0.927 -3.477 0.001 -5.089 -1.357 const 10.1031 0.310 32.573 0.000 9.479 10.727 ============================================================================== Omnibus: 2.831 Durbin-Watson: 1.998 Prob(Omnibus): 0.243 Jarque-Bera (JB): 1.927 Skew: -0.279 Prob(JB): 0.382 Kurtosis: 2.217 Cond. No. 96.3 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` Draw a plot to compare the true relationship to OLS predictions: In [13]: ``` prstd, iv_l, iv_u = wls_prediction_std(res2) fig, ax = plt.subplots(figsize=(8,6)) ax.plot(x, y, 'o', label="Data") ax.plot(x, y_true, 'b-', label="True") ax.plot(x, res2.fittedvalues, 'r--.', label="Predicted") ax.plot(x, iv_u, 'r--') ax.plot(x, iv_l, 'r--') legend = ax.legend(loc="best") ``` Joint hypothesis test --------------------- ### F test We want to test the hypothesis that both coefficients on the dummy variables are equal to zero, that is, $R \times \beta = 0$. An F test leads us to strongly reject the null hypothesis of identical constant in the 3 groups: In [14]: ``` R = [[0, 1, 0, 0], [0, 0, 1, 0]] print(np.array(R)) print(res2.f_test(R)) ``` ``` [[0 1 0 0] [0 0 1 0]] <F test: F=array([[145.49268198]]), p=1.2834419617287236e-20, df_denom=46, df_num=2> ``` You can also use formula-like syntax to test hypotheses In [15]: ``` print(res2.f_test("x2 = x3 = 0")) ``` ``` <F test: F=array([[145.49268198]]), p=1.2834419617287776e-20, df_denom=46, df_num=2> ``` ### Small group effects If we generate artificial data with smaller group effects, the T test can no longer reject the Null hypothesis: In [16]: ``` beta = [1., 0.3, -0.0, 10] y_true = np.dot(X, beta) y = y_true + np.random.normal(size=nsample) res3 = sm.OLS(y, X).fit() ``` In [17]: ``` print(res3.f_test(R)) ``` ``` <F test: F=array([[1.22491119]]), p=0.3031864410631761, df_denom=46, df_num=2> ``` In [18]: ``` print(res3.f_test("x2 = x3 = 0")) ``` ``` <F test: F=array([[1.22491119]]), p=0.3031864410631761, df_denom=46, df_num=2> ``` ### Multicollinearity The Longley dataset is well known to have high multicollinearity. That is, the exogenous predictors are highly correlated. This is problematic because it can affect the stability of our coefficient estimates as we make minor changes to model specification. In [19]: ``` from statsmodels.datasets.longley import load_pandas y = load_pandas().endog X = load_pandas().exog X = sm.add_constant(X) ``` Fit and summary: In [20]: ``` ols_model = sm.OLS(y, X) ols_results = ols_model.fit() print(ols_results.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: TOTEMP R-squared: 0.995 Model: OLS Adj. R-squared: 0.992 Method: Least Squares F-statistic: 330.3 Date: Mon, 14 May 2018 Prob (F-statistic): 4.98e-10 Time: 21:45:10 Log-Likelihood: -109.62 No. Observations: 16 AIC: 233.2 Df Residuals: 9 BIC: 238.6 Df Model: 6 Covariance Type: nonrobust ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ const -3.482e+06 8.9e+05 -3.911 0.004 -5.5e+06 -1.47e+06 GNPDEFL 15.0619 84.915 0.177 0.863 -177.029 207.153 GNP -0.0358 0.033 -1.070 0.313 -0.112 0.040 UNEMP -2.0202 0.488 -4.136 0.003 -3.125 -0.915 ARMED -1.0332 0.214 -4.822 0.001 -1.518 -0.549 POP -0.0511 0.226 -0.226 0.826 -0.563 0.460 YEAR 1829.1515 455.478 4.016 0.003 798.788 2859.515 ============================================================================== Omnibus: 0.749 Durbin-Watson: 2.559 Prob(Omnibus): 0.688 Jarque-Bera (JB): 0.684 Skew: 0.420 Prob(JB): 0.710 Kurtosis: 2.434 Cond. No. 4.86e+09 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. [2] The condition number is large, 4.86e+09. This might indicate that there are strong multicollinearity or other numerical problems. ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/stats.py:1394: UserWarning: kurtosistest only valid for n>=20 ... continuing anyway, n=16 "anyway, n=%i" % int(n)) ``` #### Condition number One way to assess multicollinearity is to compute the condition number. Values over 20 are worrisome (see Greene 4.9). The first step is to normalize the independent variables to have unit length: In [21]: ``` norm_x = X.values for i, name in enumerate(X): if name == "const": continue norm_x[:,i] = X[name]/np.linalg.norm(X[name]) norm_xtx = np.dot(norm_x.T,norm_x) ``` Then, we take the square root of the ratio of the biggest to the smallest eigen values. In [22]: ``` eigs = np.linalg.eigvals(norm_xtx) condition_number = np.sqrt(eigs.max() / eigs.min()) print(condition_number) ``` ``` 56240.8714071224 ``` #### Dropping an observation Greene also points out that dropping a single observation can have a dramatic effect on the coefficient estimates: In [23]: ``` ols_results2 = sm.OLS(y.iloc[:14], X.iloc[:14]).fit() print("Percentage change %4.2f%%\n"7 % tuple([i for i in (ols_results2.params - ols_results.params)/ols_results.params100])) ``` ``` Percentage change 4.55% Percentage change -2228.01% Percentage change 154304695.31% Percentage change 1366329.02% Percentage change 1112549.36% Percentage change 92708715.91% Percentage change 817944.26% ``` We can also look at formal statistics for this such as the DFBETAS -- a standardized measure of how much each coefficient changes when that observation is left out. In [24]: ``` infl = ols_results.get_influence() ``` In general we may consider DBETAS in absolute value greater than $2/\sqrt{N}$ to be influential observations In [25]: ``` 2./len(X)*.5 ``` Out[25]: ``` 0.5 ``` In [26]: ``` print(infl.summary_frame().filter(regex="dfb")) ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/stats/outliers_influence.py:323: RuntimeWarning: invalid value encountered in sqrt return self.results.resid / sigma / np.sqrt(1 - hii) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:879: RuntimeWarning: invalid value encountered in greater return (self.a < x) & (x < self.b) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:879: RuntimeWarning: invalid value encountered in less return (self.a < x) & (x < self.b) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:1821: RuntimeWarning: invalid value encountered in less_equal cond2 = cond0 & (x <= self.a) /Users/taugspurger/sandbox/statsmodels/statsmodels/stats/outliers_influence.py:337: RuntimeWarning: invalid value encountered in sqrt dffits_ = self.resid_studentized_internal np.sqrt(hii / (1 - hii)) /Users/taugspurger/sandbox/statsmodels/statsmodels/stats/outliers_influence.py:366: RuntimeWarning: invalid value encountered in sqrt dffits_ = self.resid_studentized_external * np.sqrt(hii / (1 - hii)) ``` ``` dfb_const dfb_GNPDEFL dfb_GNP dfb_UNEMP dfb_ARMED \ 0 -0.016406 -169.822675 1.673981e+06 54490.318088 51447.824036 1 -0.020608 -187.251727 1.829990e+06 54495.312977 52659.808664 2 -0.008382 -65.417834 1.587601e+06 52002.330476 49078.352379 3 0.018093 288.503914 1.155359e+06 56211.331922 60350.723082 4 1.871260 -171.109595 4.498197e+06 82532.785818 71034.429294 5 -0.321373 -104.123822 1.398891e+06 52559.760056 47486.527649 6 0.315945 -169.413317 2.364827e+06 59754.651394 50371.817827 7 0.015816 -69.343793 1.641243e+06 51849.056936 48628.749338 8 -0.004019 -86.903523 1.649443e+06 52023.265116 49114.178265 9 -1.018242 -201.315802 1.371257e+06 56432.027292 53997.742487 10 0.030947 -78.359439 1.658753e+06 52254.848135 49341.055289 11 0.005987 -100.926843 1.662425e+06 51744.606934 48968.560299 12 -0.135883 -32.093127 1.245487e+06 50203.467593 51148.376274 13 0.032736 -78.513866 1.648417e+06 52509.194459 50212.844641 14 0.305868 -16.833121 1.829996e+06 60975.868083 58263.878679 15 -0.538323 102.027105 1.344844e+06 54721.897640 49660.474568 dfb_POP dfb_YEAR 0 207954.113588 -31969.158503 1 25343.938289 -29760.155888 2 107465.770565 -29593.195253 3 456190.215133 -36213.129569 4 -389122.401699 -49905.782854 5 144354.586054 -28985.057609 6 -107413.074918 -32984.462465 7 92843.959345 -29724.975873 8 83931.635336 -29563.619222 9 18392.575057 -29203.217108 10 93617.648517 -29846.022426 11 95414.217290 -29690.904188 12 258559.048569 -29296.334617 13 104434.061226 -30025.564763 14 275103.677859 -36060.612522 15 -110176.960671 -28053.834556 ```	programming_docs
statsmodels Linear Mixed Effects Models Linear Mixed Effects Models =========================== In [1]: ``` %matplotlib inline import numpy as np import statsmodels.api as sm import statsmodels.formula.api as smf ``` In [2]: ``` %load_ext rpy2.ipython ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/rpy2/ipython/rmagic.py:73: UserWarning: The Python package 'pandas' is stronglyrecommended when using `rpy2.ipython`. Unfortunately it could not be loaded, but at least we found 'numpy'. "but at least we found 'numpy'."))) ``` In [3]: ``` %R library(lme4) ``` ``` Error in library(lme4) : there is no package called ‘lme4’ ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/rpy2/rinterface/__init__.py:145: RRuntimeWarning: Error in library(lme4) : there is no package called ‘lme4’ warnings.warn(x, RRuntimeWarning) ``` Comparing R lmer to Statsmodels MixedLM ======================================= The Statsmodels imputation of linear mixed models (MixedLM) closely follows the approach outlined in Lindstrom and Bates (JASA 1988). This is also the approach followed in the R package LME4. Other packages such as Stata, SAS, etc. should also be consistent with this approach, as the basic techniques in this area are mostly mature. Here we show how linear mixed models can be fit using the MixedLM procedure in Statsmodels. Results from R (LME4) are included for comparison. Here are our import statements: Growth curves of pigs --------------------- These are longitudinal data from a factorial experiment. The outcome variable is the weight of each pig, and the only predictor variable we will use here is "time". First we fit a model that expresses the mean weight as a linear function of time, with a random intercept for each pig. The model is specified using formulas. Since the random effects structure is not specified, the default random effects structure (a random intercept for each group) is automatically used. In [4]: ``` data = sm.datasets.get_rdataset('dietox', 'geepack').data md = smf.mixedlm("Weight ~ Time", data, groups=data["Pig"]) mdf = md.fit() print(mdf.summary()) ``` ``` Mixed Linear Model Regression Results ======================================================== Model: MixedLM Dependent Variable: Weight No. Observations: 861 Method: REML No. Groups: 72 Scale: 11.3669 Min. group size: 11 Likelihood: -2404.7753 Max. group size: 12 Converged: Yes Mean group size: 12.0 -------------------------------------------------------- Coef. Std.Err. z P>\|z\| [0.025 0.975] -------------------------------------------------------- Intercept 15.724 0.788 19.952 0.000 14.179 17.268 Time 6.943 0.033 207.939 0.000 6.877 7.008 Group Var 40.394 2.149 ======================================================== ``` Here is the same model fit in R using LMER: In [5]: ``` %%R data(dietox, package='geepack') ``` ``` Error in find.package(package, lib.loc, verbose = verbose) : there is no package called ‘geepack’ ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/rpy2/rinterface/__init__.py:145: RRuntimeWarning: Error in find.package(package, lib.loc, verbose = verbose) : there is no package called ‘geepack’ warnings.warn(x, RRuntimeWarning) ``` In [6]: ``` %R print(summary(lmer('Weight ~ Time + (1\|Pig)', data=dietox))) ``` ``` Error in lmer("Weight ~ Time + (1\|Pig)", data = dietox) : could not find function "lmer" ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/rpy2/rinterface/__init__.py:145: RRuntimeWarning: Error in lmer("Weight ~ Time + (1\|Pig)", data = dietox) : could not find function "lmer" warnings.warn(x, RRuntimeWarning) ``` Note that in the Statsmodels summary of results, the fixed effects and random effects parameter estimates are shown in a single table. The random effect for animal is labeled "Intercept RE" in the Statmodels output above. In the LME4 output, this effect is the pig intercept under the random effects section. There has been a lot of debate about whether the standard errors for random effect variance and covariance parameters are useful. In LME4, these standard errors are not displayed, because the authors of the package believe they are not very informative. While there is good reason to question their utility, we elected to include the standard errors in the summary table, but do not show the corresponding Wald confidence intervals. Next we fit a model with two random effects for each animal: a random intercept, and a random slope (with respect to time). This means that each pig may have a different baseline weight, as well as growing at a different rate. The formula specifies that "Time" is a covariate with a random coefficient. By default, formulas always include an intercept (which could be suppressed here using "0 + Time" as the formula). In [7]: ``` md = smf.mixedlm("Weight ~ Time", data, groups=data["Pig"], re_formula="~Time") mdf = md.fit() print(mdf.summary()) ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/base/model.py:508: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals "Check mle_retvals", ConvergenceWarning) /Users/taugspurger/sandbox/statsmodels/statsmodels/base/model.py:508: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals "Check mle_retvals", ConvergenceWarning) /Users/taugspurger/sandbox/statsmodels/statsmodels/base/model.py:508: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals "Check mle_retvals", ConvergenceWarning) /Users/taugspurger/sandbox/statsmodels/statsmodels/base/model.py:508: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals "Check mle_retvals", ConvergenceWarning) ``` ``` Mixed Linear Model Regression Results =========================================================== Model: MixedLM Dependent Variable: Weight No. Observations: 861 Method: REML No. Groups: 72 Scale: 5.7891 Min. group size: 11 Likelihood: -2220.3890 Max. group size: 12 Converged: No Mean group size: 12.0 ----------------------------------------------------------- Coef. Std.Err. z P>\|z\| [0.025 0.975] ----------------------------------------------------------- Intercept 15.739 0.672 23.438 0.000 14.423 17.055 Time 6.939 0.085 81.326 0.000 6.772 7.106 Group Var 30.266 4.271 Group x Time Cov 0.746 0.304 Time Var 0.483 0.046 =========================================================== ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/base/model.py:508: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals "Check mle_retvals", ConvergenceWarning) /Users/taugspurger/sandbox/statsmodels/statsmodels/regression/mixed_linear_model.py:2026: ConvergenceWarning: Gradient optimization failed. warnings.warn(msg, ConvergenceWarning) ``` Here is the same model fit using LMER in R: In [8]: ``` %R print(summary(lmer("Weight ~ Time + (1 + Time \| Pig)", data=dietox))) ``` ``` Error in lmer("Weight ~ Time + (1 + Time \| Pig)", data = dietox) : could not find function "lmer" ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/rpy2/rinterface/__init__.py:145: RRuntimeWarning: Error in lmer("Weight ~ Time + (1 + Time \| Pig)", data = dietox) : could not find function "lmer" warnings.warn(x, RRuntimeWarning) ``` The random intercept and random slope are only weakly correlated $(0.294 / \sqrt{19.493 \* 0.416} \approx 0.1)$. So next we fit a model in which the two random effects are constrained to be uncorrelated: In [9]: ``` .294 / (19.493 * .416)*.5 ``` Out[9]: ``` 0.10324316832591753 ``` In [10]: ``` md = smf.mixedlm("Weight ~ Time", data, groups=data["Pig"], re_formula="~Time") free = sm.regression.mixed_linear_model.MixedLMParams.from_components(np.ones(2), np.eye(2)) mdf = md.fit(free=free) print(mdf.summary()) ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/base/model.py:508: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals "Check mle_retvals", ConvergenceWarning) /Users/taugspurger/sandbox/statsmodels/statsmodels/base/model.py:508: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals "Check mle_retvals", ConvergenceWarning) /Users/taugspurger/sandbox/statsmodels/statsmodels/base/model.py:508: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals "Check mle_retvals", ConvergenceWarning) /Users/taugspurger/sandbox/statsmodels/statsmodels/base/model.py:508: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals "Check mle_retvals", ConvergenceWarning) ``` ``` Mixed Linear Model Regression Results =========================================================== Model: MixedLM Dependent Variable: Weight No. Observations: 861 Method: REML No. Groups: 72 Scale: 5.8015 Min. group size: 11 Likelihood: -2220.0996 Max. group size: 12 Converged: No Mean group size: 12.0 ----------------------------------------------------------- Coef. Std.Err. z P>\|z\| [0.025 0.975] ----------------------------------------------------------- Intercept 15.739 0.672 23.416 0.000 14.421 17.056 Time 6.939 0.084 83.012 0.000 6.775 7.103 Group Var 30.322 4.025 Group x Time Cov 0.000 0.000 Time Var 0.462 0.040 =========================================================== ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/base/model.py:508: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals "Check mle_retvals", ConvergenceWarning) /Users/taugspurger/sandbox/statsmodels/statsmodels/regression/mixed_linear_model.py:2026: ConvergenceWarning: Gradient optimization failed. warnings.warn(msg, ConvergenceWarning) ``` The likelihood drops by 0.3 when we fix the correlation parameter to 0. Comparing 2 x 0.3 = 0.6 to the chi^2 1 df reference distribution suggests that the data are very consistent with a model in which this parameter is equal to 0. Here is the same model fit using LMER in R (note that here R is reporting the REML criterion instead of the likelihood, where the REML criterion is twice the log likeihood): In [11]: ``` %R print(summary(lmer("Weight ~ Time + (1 \| Pig) + (0 + Time \| Pig)", data=dietox))) ``` ``` Error in lmer("Weight ~ Time + (1 \| Pig) + (0 + Time \| Pig)", data = dietox) : could not find function "lmer" ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/rpy2/rinterface/__init__.py:145: RRuntimeWarning: Error in lmer("Weight ~ Time + (1 \| Pig) + (0 + Time \| Pig)", data = dietox) : could not find function "lmer" warnings.warn(x, RRuntimeWarning) ``` Sitka growth data ----------------- This is one of the example data sets provided in the LMER R library. The outcome variable is the size of the tree, and the covariate used here is a time value. The data are grouped by tree. In [12]: ``` data = sm.datasets.get_rdataset("Sitka", "MASS").data endog = data["size"] data["Intercept"] = 1 exog = data[["Intercept", "Time"]] ``` Here is the statsmodels LME fit for a basic model with a random intercept. We are passing the endog and exog data directly to the LME init function as arrays. Also note that endog\_re is specified explicitly in argument 4 as a random intercept (although this would also be the default if it were not specified). In [13]: ``` md = sm.MixedLM(endog, exog, groups=data["tree"], exog_re=exog["Intercept"]) mdf = md.fit() print(mdf.summary()) ``` ``` Mixed Linear Model Regression Results ======================================================= Model: MixedLM Dependent Variable: size No. Observations: 395 Method: REML No. Groups: 79 Scale: 0.0392 Min. group size: 5 Likelihood: -82.3884 Max. group size: 5 Converged: Yes Mean group size: 5.0 ------------------------------------------------------- Coef. Std.Err. z P>\|z\| [0.025 0.975] ------------------------------------------------------- Intercept 2.273 0.088 25.864 0.000 2.101 2.446 Time 0.013 0.000 47.796 0.000 0.012 0.013 Intercept Var 0.374 0.345 ======================================================= ``` Here is the same model fit in R using LMER: In [14]: ``` %%R data(Sitka, package="MASS") print(summary(lmer("size ~ Time + (1 \| tree)", data=Sitka))) ``` ``` Error in lmer("size ~ Time + (1 \| tree)", data = Sitka) : could not find function "lmer" ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/rpy2/rinterface/__init__.py:145: RRuntimeWarning: Error in lmer("size ~ Time + (1 \| tree)", data = Sitka) : could not find function "lmer" warnings.warn(x, RRuntimeWarning) ``` We can now try to add a random slope. We start with R this time. From the code and output below we see that the REML estimate of the variance of the random slope is nearly zero. In [15]: ``` %R print(summary(lmer("size ~ Time + (1 + Time \| tree)", data=Sitka))) ``` ``` Error in lmer("size ~ Time + (1 + Time \| tree)", data = Sitka) : could not find function "lmer" ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/rpy2/rinterface/__init__.py:145: RRuntimeWarning: Error in lmer("size ~ Time + (1 + Time \| tree)", data = Sitka) : could not find function "lmer" warnings.warn(x, RRuntimeWarning) ``` If we run this in statsmodels LME with defaults, we see that the variance estimate is indeed very small, which leads to a warning about the solution being on the boundary of the parameter space. The regression slopes agree very well with R, but the likelihood value is much higher than that returned by R. In [16]: ``` exog_re = exog.copy() md = sm.MixedLM(endog, exog, data["tree"], exog_re) mdf = md.fit() print(mdf.summary()) ``` ``` Mixed Linear Model Regression Results =============================================================== Model: MixedLM Dependent Variable: size No. Observations: 395 Method: REML No. Groups: 79 Scale: 0.0264 Min. group size: 5 Likelihood: -62.4834 Max. group size: 5 Converged: Yes Mean group size: 5.0 --------------------------------------------------------------- Coef. Std.Err. z P>\|z\| [0.025 0.975] --------------------------------------------------------------- Intercept 2.273 0.101 22.513 0.000 2.075 2.471 Time 0.013 0.000 33.888 0.000 0.012 0.013 Intercept Var 0.646 0.914 Intercept x Time Cov -0.001 0.003 Time Var 0.000 0.000 =============================================================== ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/regression/mixed_linear_model.py:2045: ConvergenceWarning: The MLE may be on the boundary of the parameter space. warnings.warn(msg, ConvergenceWarning) ``` We can further explore the random effects struture by constructing plots of the profile likelihoods. We start with the random intercept, generating a plot of the profile likelihood from 0.1 units below to 0.1 units above the MLE. Since each optimization inside the profile likelihood generates a warning (due to the random slope variance being close to zero), we turn off the warnings here. In [17]: ``` import warnings with warnings.catch_warnings(): warnings.filterwarnings("ignore") likev = mdf.profile_re(0, 're', dist_low=0.1, dist_high=0.1) ``` Here is a plot of the profile likelihood function. We multiply the log-likelihood difference by 2 to obtain the usual $\chi^2$ reference distribution with 1 degree of freedom. In [18]: ``` import matplotlib.pyplot as plt ``` In [19]: ``` plt.figure(figsize=(10,8)) plt.plot(likev[:,0], 2likev[:,1]) plt.xlabel("Variance of random slope", size=17) plt.ylabel("-2 times profile log likelihood", size=17) ``` Out[19]: ``` Text(0,0.5,'-2 times profile log likelihood') ``` Here is a plot of the profile likelihood function. The profile likelihood plot shows that the MLE of the random slope variance parameter is a very small positive number, and that there is low uncertainty in this estimate. In [20]: ``` re = mdf.cov_re.iloc[1, 1] likev = mdf.profile_re(1, 're', dist_low=.5re, dist_high=0.8re) plt.figure(figsize=(10, 8)) plt.plot(likev[:,0], 2*likev[:,1]) plt.xlabel("Variance of random slope", size=17) plt.ylabel("-2 times profile log likelihood", size=17) ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/regression/mixed_linear_model.py:2045: ConvergenceWarning: The MLE may be on the boundary of the parameter space. warnings.warn(msg, ConvergenceWarning) /Users/taugspurger/sandbox/statsmodels/statsmodels/regression/mixed_linear_model.py:2045: ConvergenceWarning: The MLE may be on the boundary of the parameter space. warnings.warn(msg, ConvergenceWarning) /Users/taugspurger/sandbox/statsmodels/statsmodels/regression/mixed_linear_model.py:2045: ConvergenceWarning: The MLE may be on the boundary of the parameter space. warnings.warn(msg, ConvergenceWarning) /Users/taugspurger/sandbox/statsmodels/statsmodels/regression/mixed_linear_model.py:2045: ConvergenceWarning: The MLE may be on the boundary of the parameter space. warnings.warn(msg, ConvergenceWarning) /Users/taugspurger/sandbox/statsmodels/statsmodels/regression/mixed_linear_model.py:2045: ConvergenceWarning: The MLE may be on the boundary of the parameter space. warnings.warn(msg, ConvergenceWarning) /Users/taugspurger/sandbox/statsmodels/statsmodels/regression/mixed_linear_model.py:2045: ConvergenceWarning: The MLE may be on the boundary of the parameter space. warnings.warn(msg, ConvergenceWarning) /Users/taugspurger/sandbox/statsmodels/statsmodels/regression/mixed_linear_model.py:2045: ConvergenceWarning: The MLE may be on the boundary of the parameter space. warnings.warn(msg, ConvergenceWarning) /Users/taugspurger/sandbox/statsmodels/statsmodels/regression/mixed_linear_model.py:2045: ConvergenceWarning: The MLE may be on the boundary of the parameter space. warnings.warn(msg, ConvergenceWarning) /Users/taugspurger/sandbox/statsmodels/statsmodels/regression/mixed_linear_model.py:2045: ConvergenceWarning: The MLE may be on the boundary of the parameter space. warnings.warn(msg, ConvergenceWarning) /Users/taugspurger/sandbox/statsmodels/statsmodels/regression/mixed_linear_model.py:2045: ConvergenceWarning: The MLE may be on the boundary of the parameter space. warnings.warn(msg, ConvergenceWarning) /Users/taugspurger/sandbox/statsmodels/statsmodels/regression/mixed_linear_model.py:2045: ConvergenceWarning: The MLE may be on the boundary of the parameter space. warnings.warn(msg, ConvergenceWarning) ``` Out[20]: ``` Text(0,0.5,'-2 times profile log likelihood') ```	programming_docs
statsmodels Recursive least squares Recursive least squares ======================= Recursive least squares is an expanding window version of ordinary least squares. In addition to availability of regression coefficients computed recursively, the recursively computed residuals the construction of statistics to investigate parameter instability. The `RLS` class allows computation of recursive residuals and computes CUSUM and CUSUM of squares statistics. Plotting these statistics along with reference lines denoting statistically significant deviations from the null hypothesis of stable parameters allows an easy visual indication of parameter stability. In [1]: ``` %matplotlib inline import numpy as np import pandas as pd import statsmodels.api as sm import matplotlib.pyplot as plt from pandas_datareader.data import DataReader np.set_printoptions(suppress=True) ``` Example 1: Copper ----------------- We first consider parameter stability in the copper dataset (description below). In [2]: ``` print(sm.datasets.copper.DESCRLONG) dta = sm.datasets.copper.load_pandas().data dta.index = pd.date_range('1951-01-01', '1975-01-01', freq='AS') endog = dta['WORLDCONSUMPTION'] # To the regressors in the dataset, we add a column of ones for an intercept exog = sm.add_constant(dta[['COPPERPRICE', 'INCOMEINDEX', 'ALUMPRICE', 'INVENTORYINDEX']]) ``` ``` This data describes the world copper market from 1951 through 1975. In an example, in Gill, the outcome variable (of a 2 stage estimation) is the world consumption of copper for the 25 years. The explanatory variables are the world consumption of copper in 1000 metric tons, the constant dollar adjusted price of copper, the price of a substitute, aluminum, an index of real per capita income base 1970, an annual measure of manufacturer inventory change, and a time trend. ``` First, construct and fir the model, and print a summary. Although the `RLS` model computes the regression parameters recursively, so there are as many estimates as there are datapoints, the summary table only presents the regression parameters estimated on the entire sample; except for small effects from initialization of the recursiions, these estimates are equivalent to OLS estimates. In [3]: ``` mod = sm.RecursiveLS(endog, exog) res = mod.fit() print(res.summary()) ``` ``` Statespace Model Results ============================================================================== Dep. Variable: WORLDCONSUMPTION No. Observations: 25 Model: RecursiveLS Log Likelihood -153.737 Date: Mon, 14 May 2018 AIC 317.474 Time: 21:45:18 BIC 322.453 Sample: 01-01-1951 HQIC 318.446 - 01-01-1975 Covariance Type: nonrobust ================================================================================== coef std err z P>\|z\| [0.025 0.975] ---------------------------------------------------------------------------------- const -6513.9922 2367.666 -2.751 0.006 -1.12e+04 -1873.452 COPPERPRICE -13.6553 15.035 -0.908 0.364 -43.123 15.812 INCOMEINDEX 1.209e+04 762.595 15.853 0.000 1.06e+04 1.36e+04 ALUMPRICE 70.1441 32.667 2.147 0.032 6.117 134.171 INVENTORYINDEX 275.2805 2120.286 0.130 0.897 -3880.403 4430.964 =================================================================================== Ljung-Box (Q): 14.53 Jarque-Bera (JB): 1.91 Prob(Q): 0.75 Prob(JB): 0.39 Heteroskedasticity (H): 3.48 Skew: -0.74 Prob(H) (two-sided): 0.12 Kurtosis: 2.65 =================================================================================== Warnings: [1] Parameters and covariance matrix estimates are RLS estimates conditional on the entire sample. ``` The recursive coefficients are available in the `recursive_coefficients` attribute. Alternatively, plots can generated using the `plot_recursive_coefficient` method. In [4]: ``` print(res.recursive_coefficients.filtered[0]) res.plot_recursive_coefficient(range(mod.k_exog), alpha=None, figsize=(10,6)); ``` ``` [ 2.88890056 4.94425552 1505.27013958 1856.55145415 1597.98710024 2171.9827817 -889.38268842 122.17365406 -4184.26788419 -6242.7260132 -7111.4525403 -6400.38238234 -6090.45417093 -7154.9661487 -6290.92444686 -5805.25744629 -6219.31774195 -6684.49621649 -6430.13809589 -5957.57738675 -6407.05966649 -5983.49282153 -5224.71693423 -5286.62151094 -6513.99218247] ``` The CUSUM statistic is available in the `cusum` attribute, but usually it is more convenient to visually check for parameter stability using the `plot_cusum` method. In the plot below, the CUSUM statistic does not move outside of the 5% significance bands, so we fail to reject the null hypothesis of stable parameters at the 5% level. In [5]: ``` print(res.cusum) fig = res.plot_cusum(); ``` ``` [ 0.27819036 0.51898777 1.05399613 1.94931229 2.44814579 3.37264501 3.04780124 2.47333616 2.96189072 2.58229248 1.49434496 -0.50007844 -2.01111974 -1.75502595 -0.90603272 -1.41035323 -0.80382506 0.71254655 1.19152452 -0.93369337] ``` Another related statistic is the CUSUM of squares. It is available in the `cusum_squares` attribute, but it is similarly more convenient to check it visually, using the `plot_cusum_squares` method. In the plot below, the CUSUM of squares statistic does not move outside of the 5% significance bands, so we fail to reject the null hypothesis of stable parameters at the 5% level. In [6]: ``` res.plot_cusum_squares(); ``` Quantity theory of money ======================== The quantity theory of money suggests that "a given change in the rate of change in the quantity of money induces ... an equal change in the rate of price inflation" (Lucas, 1980). Following Lucas, we examine the relationship between double-sided exponentially weighted moving averages of money growth and CPI inflation. Although Lucas found the relationship between these variables to be stable, more recently it appears that the relationship is unstable; see e.g. Sargent and Surico (2010). In [7]: ``` start = '1959-12-01' end = '2015-01-01' m2 = DataReader('M2SL', 'fred', start=start, end=end) cpi = DataReader('CPIAUCSL', 'fred', start=start, end=end) ``` In [8]: ``` def ewma(series, beta, n_window): nobs = len(series) scalar = (1 - beta) / (1 + beta) ma = [] k = np.arange(n_window, 0, -1) weights = np.r_[betak, 1, betak[::-1]] for t in range(n_window, nobs - n_window): window = series.iloc[t - n_window:t + n_window+1].values ma.append(scalar * np.sum(weights * window)) return pd.Series(ma, name=series.name, index=series.iloc[n_window:-n_window].index) m2_ewma = ewma(np.log(m2['M2SL'].resample('QS').mean()).diff().iloc[1:], 0.95, 104) cpi_ewma = ewma(np.log(cpi['CPIAUCSL'].resample('QS').mean()).diff().iloc[1:], 0.95, 104) ``` After constructing the moving averages using the $\beta = 0.95$ filter of Lucas (with a window of 10 years on either side), we plot each of the series below. Although they appear to move together prior for part of the sample, after 1990 they appear to diverge. In [9]: ``` fig, ax = plt.subplots(figsize=(13,3)) ax.plot(m2_ewma, label='M2 Growth (EWMA)') ax.plot(cpi_ewma, label='CPI Inflation (EWMA)') ax.legend(); ``` In [10]: ``` endog = cpi_ewma exog = sm.add_constant(m2_ewma) exog.columns = ['const', 'M2'] mod = sm.RecursiveLS(endog, exog) res = mod.fit() print(res.summary()) ``` ``` Statespace Model Results ============================================================================== Dep. Variable: CPIAUCSL No. Observations: 141 Model: RecursiveLS Log Likelihood 686.267 Date: Mon, 14 May 2018 AIC -1368.535 Time: 21:45:23 BIC -1362.666 Sample: 01-01-1970 HQIC -1366.150 - 01-01-2005 Covariance Type: nonrobust ============================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ const -0.0033 0.001 -5.935 0.000 -0.004 -0.002 M2 0.9098 0.037 24.597 0.000 0.837 0.982 =================================================================================== Ljung-Box (Q): 1857.42 Jarque-Bera (JB): 18.30 Prob(Q): 0.00 Prob(JB): 0.00 Heteroskedasticity (H): 5.30 Skew: -0.81 Prob(H) (two-sided): 0.00 Kurtosis: 2.29 =================================================================================== Warnings: [1] Parameters and covariance matrix estimates are RLS estimates conditional on the entire sample. ``` In [11]: ``` res.plot_recursive_coefficient(1, alpha=None); ``` The CUSUM plot now shows subtantial deviation at the 5% level, suggesting a rejection of the null hypothesis of parameter stability. In [12]: ``` res.plot_cusum(); ``` Similarly, the CUSUM of squares shows subtantial deviation at the 5% level, also suggesting a rejection of the null hypothesis of parameter stability. In [13]: ``` res.plot_cusum_squares(); ``` statsmodels SARIMAX: Model selection, missing data SARIMAX: Model selection, missing data ====================================== The example mirrors Durbin and Koopman (2012), Chapter 8.4 in application of Box-Jenkins methodology to fit ARMA models. The novel feature is the ability of the model to work on datasets with missing values. In [1]: ``` %matplotlib inline ``` In [2]: ``` import numpy as np import pandas as pd from scipy.stats import norm import statsmodels.api as sm import matplotlib.pyplot as plt ``` In [3]: ``` import requests from io import BytesIO from zipfile import ZipFile # Download the dataset dk = requests.get('http://www.ssfpack.com/files/DK-data.zip').content f = BytesIO(dk) zipped = ZipFile(f) df = pd.read_table( BytesIO(zipped.read('internet.dat')), skiprows=1, header=None, sep='\s+', engine='python', names=['internet','dinternet'] ) ``` ### Model Selection As in Durbin and Koopman, we force a number of the values to be missing. In [4]: ``` # Get the basic series dta_full = df.dinternet[1:].values dta_miss = dta_full.copy() # Remove datapoints missing = np.r_[6,16,26,36,46,56,66,72,73,74,75,76,86,96]-1 dta_miss[missing] = np.nan ``` Then we can consider model selection using the Akaike information criteria (AIC), but running the model for each variant and selecting the model with the lowest AIC value. There are a couple of things to note here: * When running such a large batch of models, particularly when the autoregressive and moving average orders become large, there is the possibility of poor maximum likelihood convergence. Below we ignore the warnings since this example is illustrative. * We use the option `enforce_invertibility=False`, which allows the moving average polynomial to be non-invertible, so that more of the models are estimable. * Several of the models do not produce good results, and their AIC value is set to NaN. This is not surprising, as Durbin and Koopman note numerical problems with the high order models. In [5]: ``` import warnings aic_full = pd.DataFrame(np.zeros((6,6), dtype=float)) aic_miss = pd.DataFrame(np.zeros((6,6), dtype=float)) warnings.simplefilter('ignore') # Iterate over all ARMA(p,q) models with p,q in [0,6] for p in range(6): for q in range(6): if p == 0 and q == 0: continue # Estimate the model with no missing datapoints mod = sm.tsa.statespace.SARIMAX(dta_full, order=(p,0,q), enforce_invertibility=False) try: res = mod.fit(disp=False) aic_full.iloc[p,q] = res.aic except: aic_full.iloc[p,q] = np.nan # Estimate the model with missing datapoints mod = sm.tsa.statespace.SARIMAX(dta_miss, order=(p,0,q), enforce_invertibility=False) try: res = mod.fit(disp=False) aic_miss.iloc[p,q] = res.aic except: aic_miss.iloc[p,q] = np.nan ``` For the models estimated over the full (non-missing) dataset, the AIC chooses ARMA(1,1) or ARMA(3,0). Durbin and Koopman suggest the ARMA(1,1) specification is better due to parsimony. $$ \text{Replication of:}\\ \textbf{Table 8.1} ~~ \text{AIC for different ARMA models.}\\ \newcommand{\r}[1]{{\color{red}{#1}}} \begin{array}{lrrrrrr} \hline q & 0 & 1 & 2 & 3 & 4 & 5 \\ \hline p & {} & {} & {} & {} & {} & {} \\ 0 & 0.00 & 549.81 & 519.87 & 520.27 & 519.38 & 518.86 \\ 1 & 529.24 & \r{514.30} & 516.25 & 514.58 & 515.10 & 516.28 \\ 2 & 522.18 & 516.29 & 517.16 & 515.77 & 513.24 & 514.73 \\ 3 & \r{511.99} & 513.94 & 515.92 & 512.06 & 513.72 & 514.50 \\ 4 & 513.93 & 512.89 & nan & nan & 514.81 & 516.08 \\ 5 & 515.86 & 517.64 & nan & nan & nan & nan \\ \hline \end{array} $$ For the models estimated over missing dataset, the AIC chooses ARMA(1,1) $$ \text{Replication of:}\\ \textbf{Table 8.2} ~~ \text{AIC for different ARMA models with missing observations.}\\ \begin{array}{lrrrrrr} \hline q & 0 & 1 & 2 & 3 & 4 & 5 \\ \hline p & {} & {} & {} & {} & {} & {} \\ 0 & 0.00 & 488.93 & 464.01 & 463.86 & 462.63 & 463.62 \\ 1 & 468.01 & \r{457.54} & 459.35 & 458.66 & 459.15 & 461.01 \\ 2 & 469.68 & nan & 460.48 & 459.43 & 459.23 & 460.47 \\ 3 & 467.10 & 458.44 & 459.64 & 456.66 & 459.54 & 460.05 \\ 4 & 469.00 & 459.52 & nan & 463.04 & 459.35 & 460.96 \\ 5 & 471.32 & 461.26 & nan & nan & 461.00 & 462.97 \\ \hline \end{array} $$ Note: the AIC values are calculated differently than in Durbin and Koopman, but show overall similar trends. ### Postestimation Using the ARMA(1,1) specification selected above, we perform in-sample prediction and out-of-sample forecasting. In [6]: ``` # Statespace mod = sm.tsa.statespace.SARIMAX(dta_miss, order=(1,0,1)) res = mod.fit(disp=False) print(res.summary()) ``` ``` Statespace Model Results ============================================================================== Dep. Variable: y No. Observations: 99 Model: SARIMAX(1, 0, 1) Log Likelihood -225.770 Date: Mon, 14 May 2018 AIC 457.541 Time: 21:44:54 BIC 465.326 Sample: 0 HQIC 460.691 - 99 Covariance Type: opg ============================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ ar.L1 0.6562 0.092 7.125 0.000 0.476 0.837 ma.L1 0.4878 0.111 4.390 0.000 0.270 0.706 sigma2 10.3402 1.569 6.591 0.000 7.265 13.415 =================================================================================== Ljung-Box (Q): 36.52 Jarque-Bera (JB): 1.87 Prob(Q): 0.63 Prob(JB): 0.39 Heteroskedasticity (H): 0.59 Skew: -0.10 Prob(H) (two-sided): 0.13 Kurtosis: 3.64 =================================================================================== Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step). ``` In [7]: ``` # In-sample one-step-ahead predictions, and out-of-sample forecasts nforecast = 20 predict = res.get_prediction(end=mod.nobs + nforecast) idx = np.arange(len(predict.predicted_mean)) predict_ci = predict.conf_int(alpha=0.5) # Graph fig, ax = plt.subplots(figsize=(12,6)) ax.xaxis.grid() ax.plot(dta_miss, 'k.') # Plot ax.plot(idx[:-nforecast], predict.predicted_mean[:-nforecast], 'gray') ax.plot(idx[-nforecast:], predict.predicted_mean[-nforecast:], 'k--', linestyle='--', linewidth=2) ax.fill_between(idx, predict_ci[:, 0], predict_ci[:, 1], alpha=0.15) ax.set(title='Figure 8.9 - Internet series'); ``` statsmodels Quantile regression Quantile regression =================== This example page shows how to use `statsmodels`' `QuantReg` class to replicate parts of the analysis published in * Koenker, Roger and Kevin F. Hallock. "Quantile Regressioin". Journal of Economic Perspectives, Volume 15, Number 4, Fall 2001, Pages 143–156 We are interested in the relationship between income and expenditures on food for a sample of working class Belgian households in 1857 (the Engel data). Setup ----- We first need to load some modules and to retrieve the data. Conveniently, the Engel dataset is shipped with `statsmodels`. In [1]: ``` %matplotlib inline from __future__ import print_function import patsy import numpy as np import pandas as pd import statsmodels.api as sm import statsmodels.formula.api as smf import matplotlib.pyplot as plt from statsmodels.regression.quantile_regression import QuantReg data = sm.datasets.engel.load_pandas().data data.head() ``` Out[1]: \| \| income \| foodexp \| \| --- \| --- \| --- \| \| 0 \| 420.157651 \| 255.839425 \| \| 1 \| 541.411707 \| 310.958667 \| \| 2 \| 901.157457 \| 485.680014 \| \| 3 \| 639.080229 \| 402.997356 \| \| 4 \| 750.875606 \| 495.560775 \| Least Absolute Deviation ------------------------ The LAD model is a special case of quantile regression where q=0.5 In [2]: ``` mod = smf.quantreg('foodexp ~ income', data) res = mod.fit(q=.5) print(res.summary()) ``` ``` QuantReg Regression Results ============================================================================== Dep. Variable: foodexp Pseudo R-squared: 0.6206 Model: QuantReg Bandwidth: 64.51 Method: Least Squares Sparsity: 209.3 Date: Mon, 14 May 2018 No. Observations: 235 Time: 21:45:02 Df Residuals: 233 Df Model: 1 ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ Intercept 81.4823 14.634 5.568 0.000 52.649 110.315 income 0.5602 0.013 42.516 0.000 0.534 0.586 ============================================================================== The condition number is large, 2.38e+03. This might indicate that there are strong multicollinearity or other numerical problems. ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/linalg/basic.py:1321: RuntimeWarning: internal gelsd driver lwork query error, required iwork dimension not returned. This is likely the result of LAPACK bug 0038, fixed in LAPACK 3.2.2 (released July 21, 2010). Falling back to 'gelss' driver. x, resids, rank, s = lstsq(a, b, cond=cond, check_finite=False) ``` Visualizing the results ----------------------- We estimate the quantile regression model for many quantiles between .05 and .95, and compare best fit line from each of these models to Ordinary Least Squares results. ### Prepare data for plotting For convenience, we place the quantile regression results in a Pandas DataFrame, and the OLS results in a dictionary. In [3]: ``` quantiles = np.arange(.05, .96, .1) def fit_model(q): res = mod.fit(q=q) return [q, res.params['Intercept'], res.params['income']] + \ res.conf_int().loc['income'].tolist() models = [fit_model(x) for x in quantiles] models = pd.DataFrame(models, columns=['q', 'a', 'b','lb','ub']) ols = smf.ols('foodexp ~ income', data).fit() ols_ci = ols.conf_int().loc['income'].tolist() ols = dict(a = ols.params['Intercept'], b = ols.params['income'], lb = ols_ci[0], ub = ols_ci[1]) print(models) print(ols) ``` ``` q a b lb ub 0 0.05 124.880099 0.343361 0.268632 0.418090 1 0.15 111.693660 0.423708 0.382780 0.464636 2 0.25 95.483539 0.474103 0.439900 0.508306 3 0.35 105.841294 0.488901 0.457759 0.520043 4 0.45 81.083647 0.552428 0.525021 0.579835 5 0.55 89.661370 0.565601 0.540955 0.590247 6 0.65 74.033435 0.604576 0.582169 0.626982 7 0.75 62.396584 0.644014 0.622411 0.665617 8 0.85 52.272216 0.677603 0.657383 0.697823 9 0.95 64.103964 0.709069 0.687831 0.730306 {'a': 147.47538852370576, 'b': 0.4851784236769236, 'lb': 0.45687381301842334, 'ub': 0.5134830343354239} ``` ### First plot This plot compares best fit lines for 10 quantile regression models to the least squares fit. As Koenker and Hallock (2001) point out, we see that: 1. Food expenditure increases with income 2. The dispersion of food expenditure increases with income 3. The least squares estimates fit low income observations quite poorly (i.e. the OLS line passes over most low income households) In [4]: ``` x = np.arange(data.income.min(), data.income.max(), 50) get_y = lambda a, b: a + b * x fig, ax = plt.subplots(figsize=(8, 6)) for i in range(models.shape[0]): y = get_y(models.a[i], models.b[i]) ax.plot(x, y, linestyle='dotted', color='grey') y = get_y(ols['a'], ols['b']) ax.plot(x, y, color='red', label='OLS') ax.scatter(data.income, data.foodexp, alpha=.2) ax.set_xlim((240, 3000)) ax.set_ylim((240, 2000)) legend = ax.legend() ax.set_xlabel('Income', fontsize=16) ax.set_ylabel('Food expenditure', fontsize=16); ``` ### Second plot The dotted black lines form 95% point-wise confidence band around 10 quantile regression estimates (solid black line). The red lines represent OLS regression results along with their 95% confindence interval. In most cases, the quantile regression point estimates lie outside the OLS confidence interval, which suggests that the effect of income on food expenditure may not be constant across the distribution. In [5]: ``` n = models.shape[0] p1 = plt.plot(models.q, models.b, color='black', label='Quantile Reg.') p2 = plt.plot(models.q, models.ub, linestyle='dotted', color='black') p3 = plt.plot(models.q, models.lb, linestyle='dotted', color='black') p4 = plt.plot(models.q, [ols['b']] * n, color='red', label='OLS') p5 = plt.plot(models.q, [ols['lb']] * n, linestyle='dotted', color='red') p6 = plt.plot(models.q, [ols['ub']] * n, linestyle='dotted', color='red') plt.ylabel(r'$\beta_{income}$') plt.xlabel('Quantiles of the conditional food expenditure distribution') plt.legend() plt.show() ```	programming_docs
statsmodels Formulas: Fitting models using R-style formulas Formulas: Fitting models using R-style formulas =============================================== Since version 0.5.0, `statsmodels` allows users to fit statistical models using R-style formulas. Internally, `statsmodels` uses the [patsy](http://patsy.readthedocs.org/) package to convert formulas and data to the matrices that are used in model fitting. The formula framework is quite powerful; this tutorial only scratches the surface. A full description of the formula language can be found in the `patsy` docs: * [Patsy formula language description](http://patsy.readthedocs.org/) Loading modules and functions ----------------------------- In [1]: ``` from __future__ import print_function import numpy as np import statsmodels.api as sm ``` #### Import convention You can import explicitly from statsmodels.formula.api In [2]: ``` from statsmodels.formula.api import ols ``` Alternatively, you can just use the `formula` namespace of the main `statsmodels.api`. In [3]: ``` sm.formula.ols ``` Out[3]: ``` <bound method Model.from_formula of <class 'statsmodels.regression.linear_model.OLS'>> ``` Or you can use the following conventioin In [4]: ``` import statsmodels.formula.api as smf ``` These names are just a convenient way to get access to each model's `from_formula` classmethod. See, for instance In [5]: ``` sm.OLS.from_formula ``` Out[5]: ``` <bound method Model.from_formula of <class 'statsmodels.regression.linear_model.OLS'>> ``` All of the lower case models accept `formula` and `data` arguments, whereas upper case ones take `endog` and `exog` design matrices. `formula` accepts a string which describes the model in terms of a `patsy` formula. `data` takes a [pandas](http://pandas.pydata.org/) data frame or any other data structure that defines a `__getitem__` for variable names like a structured array or a dictionary of variables. `dir(sm.formula)` will print a list of available models. Formula-compatible models have the following generic call signature: `(formula, data, subset=None, args, kwargs)` OLS regression using formulas ----------------------------- To begin, we fit the linear model described on the [Getting Started](gettingstarted) page. Download the data, subset columns, and list-wise delete to remove missing observations: In [6]: ``` dta = sm.datasets.get_rdataset("Guerry", "HistData", cache=True) ``` In [7]: ``` df = dta.data[['Lottery', 'Literacy', 'Wealth', 'Region']].dropna() df.head() ``` Out[7]: \| \| Lottery \| Literacy \| Wealth \| Region \| \| --- \| --- \| --- \| --- \| --- \| \| 0 \| 41 \| 37 \| 73 \| E \| \| 1 \| 38 \| 51 \| 22 \| N \| \| 2 \| 66 \| 13 \| 61 \| C \| \| 3 \| 80 \| 46 \| 76 \| E \| \| 4 \| 79 \| 69 \| 83 \| E \| Fit the model: In [8]: ``` mod = ols(formula='Lottery ~ Literacy + Wealth + Region', data=df) res = mod.fit() print(res.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: Lottery R-squared: 0.338 Model: OLS Adj. R-squared: 0.287 Method: Least Squares F-statistic: 6.636 Date: Mon, 14 May 2018 Prob (F-statistic): 1.07e-05 Time: 21:44:51 Log-Likelihood: -375.30 No. Observations: 85 AIC: 764.6 Df Residuals: 78 BIC: 781.7 Df Model: 6 Covariance Type: nonrobust =============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------- Intercept 38.6517 9.456 4.087 0.000 19.826 57.478 Region[T.E] -15.4278 9.727 -1.586 0.117 -34.793 3.938 Region[T.N] -10.0170 9.260 -1.082 0.283 -28.453 8.419 Region[T.S] -4.5483 7.279 -0.625 0.534 -19.039 9.943 Region[T.W] -10.0913 7.196 -1.402 0.165 -24.418 4.235 Literacy -0.1858 0.210 -0.886 0.378 -0.603 0.232 Wealth 0.4515 0.103 4.390 0.000 0.247 0.656 ============================================================================== Omnibus: 3.049 Durbin-Watson: 1.785 Prob(Omnibus): 0.218 Jarque-Bera (JB): 2.694 Skew: -0.340 Prob(JB): 0.260 Kurtosis: 2.454 Cond. No. 371. ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` Categorical variables --------------------- Looking at the summary printed above, notice that `patsy` determined that elements of Region* were text strings, so it treated Region as a categorical variable. `patsy`'s default is also to include an intercept, so we automatically dropped one of the Region categories. If Region had been an integer variable that we wanted to treat explicitly as categorical, we could have done so by using the `C()` operator: In [9]: ``` res = ols(formula='Lottery ~ Literacy + Wealth + C(Region)', data=df).fit() print(res.params) ``` ``` Intercept 38.651655 C(Region)[T.E] -15.427785 C(Region)[T.N] -10.016961 C(Region)[T.S] -4.548257 C(Region)[T.W] -10.091276 Literacy -0.185819 Wealth 0.451475 dtype: float64 ``` Patsy's mode advanced features for categorical variables are discussed in: [Patsy: Contrast Coding Systems for categorical variables](contrasts) Operators --------- We have already seen that "~" separates the left-hand side of the model from the right-hand side, and that "+" adds new columns to the design matrix. ### Removing variables The "-" sign can be used to remove columns/variables. For instance, we can remove the intercept from a model by: In [10]: ``` res = ols(formula='Lottery ~ Literacy + Wealth + C(Region) -1 ', data=df).fit() print(res.params) ``` ``` C(Region)[C] 38.651655 C(Region)[E] 23.223870 C(Region)[N] 28.634694 C(Region)[S] 34.103399 C(Region)[W] 28.560379 Literacy -0.185819 Wealth 0.451475 dtype: float64 ``` ### Multiplicative interactions ":" adds a new column to the design matrix with the interaction of the other two columns. "\" will also include the individual columns that were multiplied together: In [11]: ``` res1 = ols(formula='Lottery ~ Literacy : Wealth - 1', data=df).fit() res2 = ols(formula='Lottery ~ Literacy Wealth - 1', data=df).fit() print(res1.params, '\n') print(res2.params) ``` ``` Literacy:Wealth 0.018176 dtype: float64 Literacy 0.427386 Wealth 1.080987 Literacy:Wealth -0.013609 dtype: float64 ``` Many other things are possible with operators. Please consult the [patsy docs](https://patsy.readthedocs.org/en/latest/formulas.html) to learn more. Functions --------- You can apply vectorized functions to the variables in your model: In [12]: ``` res = smf.ols(formula='Lottery ~ np.log(Literacy)', data=df).fit() print(res.params) ``` ``` Intercept 115.609119 np.log(Literacy) -20.393959 dtype: float64 ``` Define a custom function: In [13]: ``` def log_plus_1(x): return np.log(x) + 1. res = smf.ols(formula='Lottery ~ log_plus_1(Literacy)', data=df).fit() print(res.params) ``` ``` Intercept 136.003079 log_plus_1(Literacy) -20.393959 dtype: float64 ``` Any function that is in the calling namespace is available to the formula. Using formulas with models that do not (yet) support them --------------------------------------------------------- Even if a given `statsmodels` function does not support formulas, you can still use `patsy`'s formula language to produce design matrices. Those matrices can then be fed to the fitting function as `endog` and `exog` arguments. To generate `numpy` arrays: In [14]: ``` import patsy f = 'Lottery ~ Literacy * Wealth' y,X = patsy.dmatrices(f, df, return_type='matrix') print(y[:5]) print(X[:5]) ``` ``` [[41.] [38.] [66.] [80.] [79.]] [[1.000e+00 3.700e+01 7.300e+01 2.701e+03] [1.000e+00 5.100e+01 2.200e+01 1.122e+03] [1.000e+00 1.300e+01 6.100e+01 7.930e+02] [1.000e+00 4.600e+01 7.600e+01 3.496e+03] [1.000e+00 6.900e+01 8.300e+01 5.727e+03]] ``` To generate pandas data frames: In [15]: ``` f = 'Lottery ~ Literacy * Wealth' y,X = patsy.dmatrices(f, df, return_type='dataframe') print(y[:5]) print(X[:5]) ``` ``` Lottery 0 41.0 1 38.0 2 66.0 3 80.0 4 79.0 Intercept Literacy Wealth Literacy:Wealth 0 1.0 37.0 73.0 2701.0 1 1.0 51.0 22.0 1122.0 2 1.0 13.0 61.0 793.0 3 1.0 46.0 76.0 3496.0 4 1.0 69.0 83.0 5727.0 ``` In [16]: ``` print(sm.OLS(y, X).fit().summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: Lottery R-squared: 0.309 Model: OLS Adj. R-squared: 0.283 Method: Least Squares F-statistic: 12.06 Date: Mon, 14 May 2018 Prob (F-statistic): 1.32e-06 Time: 21:44:51 Log-Likelihood: -377.13 No. Observations: 85 AIC: 762.3 Df Residuals: 81 BIC: 772.0 Df Model: 3 Covariance Type: nonrobust =================================================================================== coef std err t P>\|t\| [0.025 0.975] ----------------------------------------------------------------------------------- Intercept 38.6348 15.825 2.441 0.017 7.149 70.121 Literacy -0.3522 0.334 -1.056 0.294 -1.016 0.312 Wealth 0.4364 0.283 1.544 0.126 -0.126 0.999 Literacy:Wealth -0.0005 0.006 -0.085 0.933 -0.013 0.012 ============================================================================== Omnibus: 4.447 Durbin-Watson: 1.953 Prob(Omnibus): 0.108 Jarque-Bera (JB): 3.228 Skew: -0.332 Prob(JB): 0.199 Kurtosis: 2.314 Cond. No. 1.40e+04 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. [2] The condition number is large, 1.4e+04. This might indicate that there are strong multicollinearity or other numerical problems. ``` statsmodels Trends and cycles in unemployment Trends and cycles in unemployment ================================= Here we consider three methods for separating a trend and cycle in economic data. Supposing we have a time series $y\_t$, the basic idea is to decompose it into these two components: $$ y\_t = \mu\_t + \eta\_t $$ where $\mu\_t$ represents the trend or level and $\eta\_t$ represents the cyclical component. In this case, we consider a stochastic trend, so that $\mu\_t$ is a random variable and not a deterministic function of time. Two of methods fall under the heading of "unobserved components" models, and the third is the popular Hodrick-Prescott (HP) filter. Consistent with e.g. Harvey and Jaeger (1993), we find that these models all produce similar decompositions. This notebook demonstrates applying these models to separate trend from cycle in the U.S. unemployment rate. In [1]: ``` %matplotlib inline ``` In [2]: ``` import numpy as np import pandas as pd import statsmodels.api as sm import matplotlib.pyplot as plt ``` In [3]: ``` from pandas_datareader.data import DataReader endog = DataReader('UNRATE', 'fred', start='1954-01-01') ``` ### Hodrick-Prescott (HP) filter The first method is the Hodrick-Prescott filter, which can be applied to a data series in a very straightforward method. Here we specify the parameter $\lambda=129600$ because the unemployment rate is observed monthly. In [4]: ``` hp_cycle, hp_trend = sm.tsa.filters.hpfilter(endog, lamb=129600) ``` ### Unobserved components and ARIMA model (UC-ARIMA) The next method is an unobserved components model, where the trend is modeled as a random walk and the cycle is modeled with an ARIMA model - in particular, here we use an AR(4) model. The process for the time series can be written as: $$ \begin{align} y\_t & = \mu\_t + \eta\_t \\ \mu\_{t+1} & = \mu\_t + \epsilon\_{t+1} \\ \phi(L) \eta\_t & = \nu\_t \end{align} $$ where $\phi(L)$ is the AR(4) lag polynomial and $\epsilon\_t$ and $\nu\_t$ are white noise. In [5]: ``` mod_ucarima = sm.tsa.UnobservedComponents(endog, 'rwalk', autoregressive=4) # Here the powell method is used, since it achieves a # higher loglikelihood than the default L-BFGS method res_ucarima = mod_ucarima.fit(method='powell', disp=False) print(res_ucarima.summary()) ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/tsa/base/tsa_model.py:171: ValueWarning: No frequency information was provided, so inferred frequency MS will be used. % freq, ValueWarning) ``` ``` Unobserved Components Results ============================================================================== Dep. Variable: UNRATE No. Observations: 772 Model: random walk Log Likelihood 245.883 + AR(4) AIC -479.767 Date: Mon, 14 May 2018 BIC -451.881 Time: 21:44:52 HQIC -469.036 Sample: 01-01-1954 - 04-01-2018 Covariance Type: opg ================================================================================ coef std err z P>\|z\| [0.025 0.975] -------------------------------------------------------------------------------- sigma2.level 0.0178 0.003 6.399 0.000 0.012 0.023 sigma2.ar 0.0107 0.003 3.473 0.001 0.005 0.017 ar.L1 1.0491 0.068 15.431 0.000 0.916 1.182 ar.L2 0.4590 0.106 4.330 0.000 0.251 0.667 ar.L3 -0.3368 0.130 -2.583 0.010 -0.592 -0.081 ar.L4 -0.1826 0.079 -2.303 0.021 -0.338 -0.027 =================================================================================== Ljung-Box (Q): 76.31 Jarque-Bera (JB): 41.45 Prob(Q): 0.00 Prob(JB): 0.00 Heteroskedasticity (H): 0.48 Skew: 0.25 Prob(H) (two-sided): 0.00 Kurtosis: 4.02 =================================================================================== Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step). ``` ### Unobserved components with stochastic cycle (UC) The final method is also an unobserved components model, but where the cycle is modeled explicitly. $$ \begin{align} y\_t & = \mu\_t + \eta\_t \\ \mu\_{t+1} & = \mu\_t + \epsilon\_{t+1} \\ \eta\_{t+1} & = \eta\_t \cos \lambda\_\eta + \eta\_t^\* \sin \lambda\_\eta + \tilde \omega\_t \qquad & \tilde \omega\_t \sim N(0, \sigma\_{\tilde \omega}^2) \\ \eta\_{t+1}^\* & = -\eta\_t \sin \lambda\_\eta + \eta\_t^\* \cos \lambda\_\eta + \tilde \omega\_t^\* & \tilde \omega\_t^\* \sim N(0, \sigma\_{\tilde \omega}^2) \end{align} $$ In [6]: ``` mod_uc = sm.tsa.UnobservedComponents( endog, 'rwalk', cycle=True, stochastic_cycle=True, damped_cycle=True, ) # Here the powell method gets close to the optimum res_uc = mod_uc.fit(method='powell', disp=False) # but to get to the highest loglikelihood we do a # second round using the L-BFGS method. res_uc = mod_uc.fit(res_uc.params, disp=False) print(res_uc.summary()) ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/tsa/base/tsa_model.py:171: ValueWarning: No frequency information was provided, so inferred frequency MS will be used. % freq, ValueWarning) ``` ``` Unobserved Components Results ===================================================================================== Dep. Variable: UNRATE No. Observations: 772 Model: random walk Log Likelihood 211.379 + damped stochastic cycle AIC -414.757 Date: Mon, 14 May 2018 BIC -396.177 Time: 21:44:53 HQIC -407.606 Sample: 01-01-1954 - 04-01-2018 Covariance Type: opg =================================================================================== coef std err z P>\|z\| [0.025 0.975] ----------------------------------------------------------------------------------- sigma2.level 0.0106 0.005 2.286 0.022 0.002 0.020 sigma2.cycle 0.0209 0.005 4.531 0.000 0.012 0.030 frequency.cycle 0.0636 0.005 12.503 0.000 0.054 0.074 damping.cycle 0.9910 0.004 268.108 0.000 0.984 0.998 =================================================================================== Ljung-Box (Q): 158.59 Jarque-Bera (JB): 87.54 Prob(Q): 0.00 Prob(JB): 0.00 Heteroskedasticity (H): 0.46 Skew: 0.48 Prob(H) (two-sided): 0.00 Kurtosis: 4.35 =================================================================================== Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step). ``` ### Graphical comparison The output of each of these models is an estimate of the trend component $\mu\_t$ and an estimate of the cyclical component $\eta\_t$. Qualitatively the estimates of trend and cycle are very similar, although the trend component from the HP filter is somewhat more variable than those from the unobserved components models. This means that relatively mode of the movement in the unemployment rate is attributed to changes in the underlying trend rather than to temporary cyclical movements. In [7]: ``` fig, axes = plt.subplots(2, figsize=(13,5)); axes[0].set(title='Level/trend component') axes[0].plot(endog.index, res_uc.level.smoothed, label='UC') axes[0].plot(endog.index, res_ucarima.level.smoothed, label='UC-ARIMA(2,0)') axes[0].plot(hp_trend, label='HP Filter') axes[0].legend(loc='upper left') axes[0].grid() axes[1].set(title='Cycle component') axes[1].plot(endog.index, res_uc.cycle.smoothed, label='UC') axes[1].plot(endog.index, res_ucarima.autoregressive.smoothed, label='UC-ARIMA(2,0)') axes[1].plot(hp_cycle, label='HP Filter') axes[1].legend(loc='upper left') axes[1].grid() fig.tight_layout(); ```	programming_docs
statsmodels Interactions and ANOVA Interactions and ANOVA ====================== Note: This script is based heavily on Jonathan Taylor's class notes <http://www.stanford.edu/class/stats191/interactions.html> Download and format data: In [1]: ``` %matplotlib inline from __future__ import print_function from statsmodels.compat import urlopen import numpy as np np.set_printoptions(precision=4, suppress=True) import statsmodels.api as sm import pandas as pd pd.set_option("display.width", 100) import matplotlib.pyplot as plt from statsmodels.formula.api import ols from statsmodels.graphics.api import interaction_plot, abline_plot from statsmodels.stats.anova import anova_lm try: salary_table = pd.read_csv('salary.table') except: # recent pandas can read URL without urlopen url = 'http://stats191.stanford.edu/data/salary.table' fh = urlopen(url) salary_table = pd.read_table(fh) salary_table.to_csv('salary.table') E = salary_table.E M = salary_table.M X = salary_table.X S = salary_table.S ``` Take a look at the data: In [2]: ``` plt.figure(figsize=(6,6)) symbols = ['D', '^'] colors = ['r', 'g', 'blue'] factor_groups = salary_table.groupby(['E','M']) for values, group in factor_groups: i,j = values plt.scatter(group['X'], group['S'], marker=symbols[j], color=colors[i-1], s=144) plt.xlabel('Experience'); plt.ylabel('Salary'); ``` Fit a linear model: In [3]: ``` formula = 'S ~ C(E) + C(M) + X' lm = ols(formula, salary_table).fit() print(lm.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: S R-squared: 0.957 Model: OLS Adj. R-squared: 0.953 Method: Least Squares F-statistic: 226.8 Date: Mon, 14 May 2018 Prob (F-statistic): 2.23e-27 Time: 21:44:50 Log-Likelihood: -381.63 No. Observations: 46 AIC: 773.3 Df Residuals: 41 BIC: 782.4 Df Model: 4 Covariance Type: nonrobust ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ Intercept 8035.5976 386.689 20.781 0.000 7254.663 8816.532 C(E)[T.2] 3144.0352 361.968 8.686 0.000 2413.025 3875.045 C(E)[T.3] 2996.2103 411.753 7.277 0.000 2164.659 3827.762 C(M)[T.1] 6883.5310 313.919 21.928 0.000 6249.559 7517.503 X 546.1840 30.519 17.896 0.000 484.549 607.819 ============================================================================== Omnibus: 2.293 Durbin-Watson: 2.237 Prob(Omnibus): 0.318 Jarque-Bera (JB): 1.362 Skew: -0.077 Prob(JB): 0.506 Kurtosis: 2.171 Cond. No. 33.5 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` Have a look at the created design matrix: In [4]: ``` lm.model.exog[:5] ``` Out[4]: ``` array([[1., 0., 0., 1., 1.], [1., 0., 1., 0., 1.], [1., 0., 1., 1., 1.], [1., 1., 0., 0., 1.], [1., 0., 1., 0., 1.]]) ``` Or since we initially passed in a DataFrame, we have a DataFrame available in In [5]: ``` lm.model.data.orig_exog[:5] ``` Out[5]: \| \| Intercept \| C(E)[T.2] \| C(E)[T.3] \| C(M)[T.1] \| X \| \| --- \| --- \| --- \| --- \| --- \| --- \| \| 0 \| 1.0 \| 0.0 \| 0.0 \| 1.0 \| 1.0 \| \| 1 \| 1.0 \| 0.0 \| 1.0 \| 0.0 \| 1.0 \| \| 2 \| 1.0 \| 0.0 \| 1.0 \| 1.0 \| 1.0 \| \| 3 \| 1.0 \| 1.0 \| 0.0 \| 0.0 \| 1.0 \| \| 4 \| 1.0 \| 0.0 \| 1.0 \| 0.0 \| 1.0 \| We keep a reference to the original untouched data in In [6]: ``` lm.model.data.frame[:5] ``` Out[6]: \| \| S \| X \| E \| M \| \| --- \| --- \| --- \| --- \| --- \| \| 0 \| 13876 \| 1 \| 1 \| 1 \| \| 1 \| 11608 \| 1 \| 3 \| 0 \| \| 2 \| 18701 \| 1 \| 3 \| 1 \| \| 3 \| 11283 \| 1 \| 2 \| 0 \| \| 4 \| 11767 \| 1 \| 3 \| 0 \| Influence statistics In [7]: ``` infl = lm.get_influence() print(infl.summary_table()) ``` ``` ================================================================================================== obs endog fitted Cook's student. hat diag dffits ext.stud. dffits value d residual internal residual -------------------------------------------------------------------------------------------------- 0 13876.000 15465.313 0.104 -1.683 0.155 -0.722 -1.723 -0.739 1 11608.000 11577.992 0.000 0.031 0.130 0.012 0.031 0.012 2 18701.000 18461.523 0.001 0.247 0.109 0.086 0.244 0.085 3 11283.000 11725.817 0.005 -0.458 0.113 -0.163 -0.453 -0.162 4 11767.000 11577.992 0.001 0.197 0.130 0.076 0.195 0.075 5 20872.000 19155.532 0.092 1.787 0.126 0.678 1.838 0.698 6 11772.000 12272.001 0.006 -0.513 0.101 -0.172 -0.509 -0.170 7 10535.000 9127.966 0.056 1.457 0.116 0.529 1.478 0.537 8 12195.000 12124.176 0.000 0.074 0.123 0.028 0.073 0.027 9 12313.000 12818.185 0.005 -0.516 0.091 -0.163 -0.511 -0.161 10 14975.000 16557.681 0.084 -1.655 0.134 -0.650 -1.692 -0.664 11 21371.000 19701.716 0.078 1.728 0.116 0.624 1.772 0.640 12 19800.000 19553.891 0.001 0.252 0.096 0.082 0.249 0.081 13 11417.000 10220.334 0.033 1.227 0.098 0.405 1.234 0.408 14 20263.000 20100.075 0.001 0.166 0.093 0.053 0.165 0.053 15 13231.000 13216.544 0.000 0.015 0.114 0.005 0.015 0.005 16 12884.000 13364.369 0.004 -0.488 0.082 -0.146 -0.483 -0.145 17 13245.000 13910.553 0.007 -0.674 0.075 -0.192 -0.669 -0.191 18 13677.000 13762.728 0.000 -0.089 0.113 -0.032 -0.087 -0.031 19 15965.000 17650.049 0.082 -1.747 0.119 -0.642 -1.794 -0.659 20 12336.000 11312.702 0.021 1.043 0.087 0.323 1.044 0.323 21 21352.000 21192.443 0.001 0.163 0.091 0.052 0.161 0.051 22 13839.000 14456.737 0.006 -0.624 0.070 -0.171 -0.619 -0.170 23 22884.000 21340.268 0.052 1.579 0.095 0.511 1.610 0.521 24 16978.000 18742.417 0.083 -1.822 0.111 -0.644 -1.877 -0.664 25 14803.000 15549.105 0.008 -0.751 0.065 -0.199 -0.747 -0.198 26 17404.000 19288.601 0.093 -1.944 0.110 -0.684 -2.016 -0.709 27 22184.000 22284.811 0.000 -0.103 0.096 -0.034 -0.102 -0.033 28 13548.000 12405.070 0.025 1.162 0.083 0.350 1.167 0.352 29 14467.000 13497.438 0.018 0.987 0.086 0.304 0.987 0.304 30 15942.000 16641.473 0.007 -0.705 0.068 -0.190 -0.701 -0.189 31 23174.000 23377.179 0.001 -0.209 0.108 -0.073 -0.207 -0.072 32 23780.000 23525.004 0.001 0.260 0.092 0.083 0.257 0.082 33 25410.000 24071.188 0.040 1.370 0.096 0.446 1.386 0.451 34 14861.000 14043.622 0.014 0.834 0.091 0.263 0.831 0.262 35 16882.000 17733.841 0.012 -0.863 0.077 -0.249 -0.860 -0.249 36 24170.000 24469.547 0.003 -0.312 0.127 -0.119 -0.309 -0.118 37 15990.000 15135.990 0.018 0.878 0.104 0.300 0.876 0.299 38 26330.000 25163.556 0.035 1.202 0.109 0.420 1.209 0.422 39 17949.000 18826.209 0.017 -0.897 0.093 -0.288 -0.895 -0.287 40 25685.000 26108.099 0.008 -0.452 0.169 -0.204 -0.447 -0.202 41 27837.000 26802.108 0.039 1.087 0.141 0.440 1.089 0.441 42 18838.000 19918.577 0.033 -1.119 0.117 -0.407 -1.123 -0.408 43 17483.000 16774.542 0.018 0.743 0.138 0.297 0.739 0.295 44 19207.000 20464.761 0.052 -1.313 0.131 -0.511 -1.325 -0.515 45 19346.000 18959.278 0.009 0.423 0.208 0.216 0.419 0.214 ================================================================================================== ``` or get a dataframe In [8]: ``` df_infl = infl.summary_frame() ``` In [9]: ``` df_infl[:5] ``` Out[9]: \| \| dfb\_Intercept \| dfb\_C(E)[T.2] \| dfb\_C(E)[T.3] \| dfb\_C(M)[T.1] \| dfb\_X \| cooks\_d \| dffits \| dffits\_internal \| hat\_diag \| standard\_resid \| student\_resid \| \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| \| 0 \| -0.505123 \| 0.376134 \| 0.483977 \| -0.369677 \| 0.399111 \| 0.104186 \| -0.738880 \| -0.721753 \| 0.155327 \| -1.683099 \| -1.723037 \| \| 1 \| 0.004663 \| 0.000145 \| 0.006733 \| -0.006220 \| -0.004449 \| 0.000029 \| 0.011972 \| 0.012120 \| 0.130266 \| 0.031318 \| 0.030934 \| \| 2 \| 0.013627 \| 0.000367 \| 0.036876 \| 0.030514 \| -0.034970 \| 0.001492 \| 0.085380 \| 0.086377 \| 0.109021 \| 0.246931 \| 0.244082 \| \| 3 \| -0.083152 \| -0.074411 \| 0.009704 \| 0.053783 \| 0.105122 \| 0.005338 \| -0.161773 \| -0.163364 \| 0.113030 \| -0.457630 \| -0.453173 \| \| 4 \| 0.029382 \| 0.000917 \| 0.042425 \| -0.039198 \| -0.028036 \| 0.001166 \| 0.075439 \| 0.076340 \| 0.130266 \| 0.197257 \| 0.194929 \| Now plot the reiduals within the groups separately: In [10]: ``` resid = lm.resid plt.figure(figsize=(6,6)); for values, group in factor_groups: i,j = values group_num = i2 + j - 1 # for plotting purposes x = [group_num] len(group) plt.scatter(x, resid[group.index], marker=symbols[j], color=colors[i-1], s=144, edgecolors='black') plt.xlabel('Group'); plt.ylabel('Residuals'); ``` Now we will test some interactions using anova or f\_test In [11]: ``` interX_lm = ols("S ~ C(E) * X + C(M)", salary_table).fit() print(interX_lm.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: S R-squared: 0.961 Model: OLS Adj. R-squared: 0.955 Method: Least Squares F-statistic: 158.6 Date: Mon, 14 May 2018 Prob (F-statistic): 8.23e-26 Time: 21:44:50 Log-Likelihood: -379.47 No. Observations: 46 AIC: 772.9 Df Residuals: 39 BIC: 785.7 Df Model: 6 Covariance Type: nonrobust =============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------- Intercept 7256.2800 549.494 13.205 0.000 6144.824 8367.736 C(E)[T.2] 4172.5045 674.966 6.182 0.000 2807.256 5537.753 C(E)[T.3] 3946.3649 686.693 5.747 0.000 2557.396 5335.333 C(M)[T.1] 7102.4539 333.442 21.300 0.000 6428.005 7776.903 X 632.2878 53.185 11.888 0.000 524.710 739.865 C(E)[T.2]:X -125.5147 69.863 -1.797 0.080 -266.826 15.796 C(E)[T.3]:X -141.2741 89.281 -1.582 0.122 -321.861 39.313 ============================================================================== Omnibus: 0.432 Durbin-Watson: 2.179 Prob(Omnibus): 0.806 Jarque-Bera (JB): 0.590 Skew: 0.144 Prob(JB): 0.744 Kurtosis: 2.526 Cond. No. 69.7 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` Do an ANOVA check In [12]: ``` from statsmodels.stats.api import anova_lm table1 = anova_lm(lm, interX_lm) print(table1) interM_lm = ols("S ~ X + C(E)C(M)", data=salary_table).fit() print(interM_lm.summary()) table2 = anova_lm(lm, interM_lm) print(table2) ``` ``` df_resid ssr df_diff ss_diff F Pr(>F) 0 41.0 4.328072e+07 0.0 NaN NaN NaN 1 39.0 3.941068e+07 2.0 3.870040e+06 1.914856 0.160964 OLS Regression Results ============================================================================== Dep. Variable: S R-squared: 0.999 Model: OLS Adj. R-squared: 0.999 Method: Least Squares F-statistic: 5517. Date: Mon, 14 May 2018 Prob (F-statistic): 1.67e-55 Time: 21:44:50 Log-Likelihood: -298.74 No. Observations: 46 AIC: 611.5 Df Residuals: 39 BIC: 624.3 Df Model: 6 Covariance Type: nonrobust ======================================================================================= coef std err t P>\|t\| [0.025 0.975] --------------------------------------------------------------------------------------- Intercept 9472.6854 80.344 117.902 0.000 9310.175 9635.196 C(E)[T.2] 1381.6706 77.319 17.870 0.000 1225.279 1538.063 C(E)[T.3] 1730.7483 105.334 16.431 0.000 1517.690 1943.806 C(M)[T.1] 3981.3769 101.175 39.351 0.000 3776.732 4186.022 C(E)[T.2]:C(M)[T.1] 4902.5231 131.359 37.322 0.000 4636.825 5168.222 C(E)[T.3]:C(M)[T.1] 3066.0351 149.330 20.532 0.000 2763.986 3368.084 X 496.9870 5.566 89.283 0.000 485.728 508.246 ============================================================================== Omnibus: 74.761 Durbin-Watson: 2.244 Prob(Omnibus): 0.000 Jarque-Bera (JB): 1037.873 Skew: -4.103 Prob(JB): 4.25e-226 Kurtosis: 24.776 Cond. No. 79.0 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. df_resid ssr df_diff ss_diff F Pr(>F) 0 41.0 4.328072e+07 0.0 NaN NaN NaN 1 39.0 1.178168e+06 2.0 4.210255e+07 696.844466 3.025504e-31 ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:879: RuntimeWarning: invalid value encountered in greater return (self.a < x) & (x < self.b) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:879: RuntimeWarning: invalid value encountered in less return (self.a < x) & (x < self.b) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:1821: RuntimeWarning: invalid value encountered in less_equal cond2 = cond0 & (x <= self.a) ``` The design matrix as a DataFrame In [13]: ``` interM_lm.model.data.orig_exog[:5] ``` Out[13]: \| \| Intercept \| C(E)[T.2] \| C(E)[T.3] \| C(M)[T.1] \| C(E)[T.2]:C(M)[T.1] \| C(E)[T.3]:C(M)[T.1] \| X \| \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| --- \| \| 0 \| 1.0 \| 0.0 \| 0.0 \| 1.0 \| 0.0 \| 0.0 \| 1.0 \| \| 1 \| 1.0 \| 0.0 \| 1.0 \| 0.0 \| 0.0 \| 0.0 \| 1.0 \| \| 2 \| 1.0 \| 0.0 \| 1.0 \| 1.0 \| 0.0 \| 1.0 \| 1.0 \| \| 3 \| 1.0 \| 1.0 \| 0.0 \| 0.0 \| 0.0 \| 0.0 \| 1.0 \| \| 4 \| 1.0 \| 0.0 \| 1.0 \| 0.0 \| 0.0 \| 0.0 \| 1.0 \| The design matrix as an ndarray In [14]: ``` interM_lm.model.exog interM_lm.model.exog_names ``` Out[14]: ``` ['Intercept', 'C(E)[T.2]', 'C(E)[T.3]', 'C(M)[T.1]', 'C(E)[T.2]:C(M)[T.1]', 'C(E)[T.3]:C(M)[T.1]', 'X'] ``` In [15]: ``` infl = interM_lm.get_influence() resid = infl.resid_studentized_internal plt.figure(figsize=(6,6)) for values, group in factor_groups: i,j = values idx = group.index plt.scatter(X[idx], resid[idx], marker=symbols[j], color=colors[i-1], s=144, edgecolors='black') plt.xlabel('X'); plt.ylabel('standardized resids'); ``` Looks like one observation is an outlier. In [16]: ``` drop_idx = abs(resid).argmax() print(drop_idx) # zero-based index idx = salary_table.index.drop(drop_idx) lm32 = ols('S ~ C(E) + X + C(M)', data=salary_table, subset=idx).fit() print(lm32.summary()) print('\n') interX_lm32 = ols('S ~ C(E) X + C(M)', data=salary_table, subset=idx).fit() print(interX_lm32.summary()) print('\n') table3 = anova_lm(lm32, interX_lm32) print(table3) print('\n') interM_lm32 = ols('S ~ X + C(E) * C(M)', data=salary_table, subset=idx).fit() table4 = anova_lm(lm32, interM_lm32) print(table4) print('\n') ``` ``` 32 OLS Regression Results ============================================================================== Dep. Variable: S R-squared: 0.955 Model: OLS Adj. R-squared: 0.950 Method: Least Squares F-statistic: 211.7 Date: Mon, 14 May 2018 Prob (F-statistic): 2.45e-26 Time: 21:44:51 Log-Likelihood: -373.79 No. Observations: 45 AIC: 757.6 Df Residuals: 40 BIC: 766.6 Df Model: 4 Covariance Type: nonrobust ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ Intercept 8044.7518 392.781 20.482 0.000 7250.911 8838.592 C(E)[T.2] 3129.5286 370.470 8.447 0.000 2380.780 3878.277 C(E)[T.3] 2999.4451 416.712 7.198 0.000 2157.238 3841.652 C(M)[T.1] 6866.9856 323.991 21.195 0.000 6212.175 7521.796 X 545.7855 30.912 17.656 0.000 483.311 608.260 ============================================================================== Omnibus: 2.511 Durbin-Watson: 2.265 Prob(Omnibus): 0.285 Jarque-Bera (JB): 1.400 Skew: -0.044 Prob(JB): 0.496 Kurtosis: 2.140 Cond. No. 33.1 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. OLS Regression Results ============================================================================== Dep. Variable: S R-squared: 0.959 Model: OLS Adj. R-squared: 0.952 Method: Least Squares F-statistic: 147.7 Date: Mon, 14 May 2018 Prob (F-statistic): 8.97e-25 Time: 21:44:51 Log-Likelihood: -371.70 No. Observations: 45 AIC: 757.4 Df Residuals: 38 BIC: 770.0 Df Model: 6 Covariance Type: nonrobust =============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------- Intercept 7266.0887 558.872 13.001 0.000 6134.711 8397.466 C(E)[T.2] 4162.0846 685.728 6.070 0.000 2773.900 5550.269 C(E)[T.3] 3940.4359 696.067 5.661 0.000 2531.322 5349.549 C(M)[T.1] 7088.6387 345.587 20.512 0.000 6389.035 7788.243 X 631.6892 53.950 11.709 0.000 522.473 740.905 C(E)[T.2]:X -125.5009 70.744 -1.774 0.084 -268.714 17.712 C(E)[T.3]:X -139.8410 90.728 -1.541 0.132 -323.511 43.829 ============================================================================== Omnibus: 0.617 Durbin-Watson: 2.194 Prob(Omnibus): 0.734 Jarque-Bera (JB): 0.728 Skew: 0.162 Prob(JB): 0.695 Kurtosis: 2.468 Cond. No. 68.7 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. df_resid ssr df_diff ss_diff F Pr(>F) 0 40.0 4.320910e+07 0.0 NaN NaN NaN 1 38.0 3.937424e+07 2.0 3.834859e+06 1.850508 0.171042 df_resid ssr df_diff ss_diff F Pr(>F) 0 40.0 4.320910e+07 0.0 NaN NaN NaN 1 38.0 1.711881e+05 2.0 4.303791e+07 4776.734853 2.291239e-46 ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:879: RuntimeWarning: invalid value encountered in greater return (self.a < x) & (x < self.b) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:879: RuntimeWarning: invalid value encountered in less return (self.a < x) & (x < self.b) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:1821: RuntimeWarning: invalid value encountered in less_equal cond2 = cond0 & (x <= self.a) ``` Replot the residuals In [17]: ``` try: resid = interM_lm32.get_influence().summary_frame()['standard_resid'] except: resid = interM_lm32.get_influence().summary_frame()['standard_resid'] plt.figure(figsize=(6,6)) for values, group in factor_groups: i,j = values idx = group.index plt.scatter(X[idx], resid[idx], marker=symbols[j], color=colors[i-1], s=144, edgecolors='black') plt.xlabel('X[~[32]]'); plt.ylabel('standardized resids'); ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/pandas/core/series.py:696: FutureWarning: Passing list-likes to .loc or [] with any missing label will raise KeyError in the future, you can use .reindex() as an alternative. See the documentation here: http://pandas.pydata.org/pandas-docs/stable/indexing.html#deprecate-loc-reindex-listlike return self.loc[key] ``` Plot the fitted values In [18]: ``` lm_final = ols('S ~ X + C(E)C(M)', data = salary_table.drop([drop_idx])).fit() mf = lm_final.model.data.orig_exog lstyle = ['-','--'] plt.figure(figsize=(6,6)) for values, group in factor_groups: i,j = values idx = group.index plt.scatter(X[idx], S[idx], marker=symbols[j], color=colors[i-1], s=144, edgecolors='black') # drop NA because there is no idx 32 in the final model plt.plot(mf.X[idx].dropna(), lm_final.fittedvalues[idx].dropna(), ls=lstyle[j], color=colors[i-1]) plt.xlabel('Experience'); plt.ylabel('Salary'); ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/pandas/core/series.py:696: FutureWarning: Passing list-likes to .loc or [] with any missing label will raise KeyError in the future, you can use .reindex() as an alternative. See the documentation here: http://pandas.pydata.org/pandas-docs/stable/indexing.html#deprecate-loc-reindex-listlike return self.loc[key] ``` From our first look at the data, the difference between Master's and PhD in the management group is different than in the non-management group. This is an interaction between the two qualitative variables management,M and education,E. We can visualize this by first removing the effect of experience, then plotting the means within each of the 6 groups using interaction.plot. In [19]: ``` U = S - X interX_lm32.params['X'] plt.figure(figsize=(6,6)) interaction_plot(E, M, U, colors=['red','blue'], markers=['^','D'], markersize=10, ax=plt.gca()) ``` Out[19]: Minority Employment Data ------------------------ In [20]: ``` try: jobtest_table = pd.read_table('jobtest.table') except: # don't have data already url = 'http://stats191.stanford.edu/data/jobtest.table' jobtest_table = pd.read_table(url) factor_group = jobtest_table.groupby(['MINORITY']) fig, ax = plt.subplots(figsize=(6,6)) colors = ['purple', 'green'] markers = ['o', 'v'] for factor, group in factor_group: ax.scatter(group['TEST'], group['JPERF'], color=colors[factor], marker=markers[factor], s=122) ax.set_xlabel('TEST'); ax.set_ylabel('JPERF'); ``` In [21]: ``` min_lm = ols('JPERF ~ TEST', data=jobtest_table).fit() print(min_lm.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: JPERF R-squared: 0.517 Model: OLS Adj. R-squared: 0.490 Method: Least Squares F-statistic: 19.25 Date: Mon, 14 May 2018 Prob (F-statistic): 0.000356 Time: 21:44:53 Log-Likelihood: -36.614 No. Observations: 20 AIC: 77.23 Df Residuals: 18 BIC: 79.22 Df Model: 1 Covariance Type: nonrobust ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ Intercept 1.0350 0.868 1.192 0.249 -0.789 2.859 TEST 2.3605 0.538 4.387 0.000 1.230 3.491 ============================================================================== Omnibus: 0.324 Durbin-Watson: 2.896 Prob(Omnibus): 0.850 Jarque-Bera (JB): 0.483 Skew: -0.186 Prob(JB): 0.785 Kurtosis: 2.336 Cond. No. 5.26 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` In [22]: ``` fig, ax = plt.subplots(figsize=(6,6)); for factor, group in factor_group: ax.scatter(group['TEST'], group['JPERF'], color=colors[factor], marker=markers[factor], s=122) ax.set_xlabel('TEST') ax.set_ylabel('JPERF') fig = abline_plot(model_results = min_lm, ax=ax) ``` In [23]: ``` min_lm2 = ols('JPERF ~ TEST + TEST:MINORITY', data=jobtest_table).fit() print(min_lm2.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: JPERF R-squared: 0.632 Model: OLS Adj. R-squared: 0.589 Method: Least Squares F-statistic: 14.59 Date: Mon, 14 May 2018 Prob (F-statistic): 0.000204 Time: 21:44:53 Log-Likelihood: -33.891 No. Observations: 20 AIC: 73.78 Df Residuals: 17 BIC: 76.77 Df Model: 2 Covariance Type: nonrobust ================================================================================= coef std err t P>\|t\| [0.025 0.975] --------------------------------------------------------------------------------- Intercept 1.1211 0.780 1.437 0.169 -0.525 2.768 TEST 1.8276 0.536 3.412 0.003 0.698 2.958 TEST:MINORITY 0.9161 0.397 2.306 0.034 0.078 1.754 ============================================================================== Omnibus: 0.388 Durbin-Watson: 3.008 Prob(Omnibus): 0.823 Jarque-Bera (JB): 0.514 Skew: 0.050 Prob(JB): 0.773 Kurtosis: 2.221 Cond. No. 5.96 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` In [24]: ``` fig, ax = plt.subplots(figsize=(6,6)); for factor, group in factor_group: ax.scatter(group['TEST'], group['JPERF'], color=colors[factor], marker=markers[factor], s=122) fig = abline_plot(intercept = min_lm2.params['Intercept'], slope = min_lm2.params['TEST'], ax=ax, color='purple'); fig = abline_plot(intercept = min_lm2.params['Intercept'], slope = min_lm2.params['TEST'] + min_lm2.params['TEST:MINORITY'], ax=ax, color='green'); ``` In [25]: ``` min_lm3 = ols('JPERF ~ TEST + MINORITY', data = jobtest_table).fit() print(min_lm3.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: JPERF R-squared: 0.572 Model: OLS Adj. R-squared: 0.522 Method: Least Squares F-statistic: 11.38 Date: Mon, 14 May 2018 Prob (F-statistic): 0.000731 Time: 21:44:54 Log-Likelihood: -35.390 No. Observations: 20 AIC: 76.78 Df Residuals: 17 BIC: 79.77 Df Model: 2 Covariance Type: nonrobust ============================================================================== coef std err t P>\|t\| [0.025 0.975] ------------------------------------------------------------------------------ Intercept 0.6120 0.887 0.690 0.500 -1.260 2.483 TEST 2.2988 0.522 4.400 0.000 1.197 3.401 MINORITY 1.0276 0.691 1.487 0.155 -0.430 2.485 ============================================================================== Omnibus: 0.251 Durbin-Watson: 3.028 Prob(Omnibus): 0.882 Jarque-Bera (JB): 0.437 Skew: -0.059 Prob(JB): 0.804 Kurtosis: 2.286 Cond. No. 5.72 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` In [26]: ``` fig, ax = plt.subplots(figsize=(6,6)); for factor, group in factor_group: ax.scatter(group['TEST'], group['JPERF'], color=colors[factor], marker=markers[factor], s=122) fig = abline_plot(intercept = min_lm3.params['Intercept'], slope = min_lm3.params['TEST'], ax=ax, color='purple'); fig = abline_plot(intercept = min_lm3.params['Intercept'] + min_lm3.params['MINORITY'], slope = min_lm3.params['TEST'], ax=ax, color='green'); ``` In [27]: ``` min_lm4 = ols('JPERF ~ TEST * MINORITY', data = jobtest_table).fit() print(min_lm4.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: JPERF R-squared: 0.664 Model: OLS Adj. R-squared: 0.601 Method: Least Squares F-statistic: 10.55 Date: Mon, 14 May 2018 Prob (F-statistic): 0.000451 Time: 21:44:54 Log-Likelihood: -32.971 No. Observations: 20 AIC: 73.94 Df Residuals: 16 BIC: 77.92 Df Model: 3 Covariance Type: nonrobust ================================================================================= coef std err t P>\|t\| [0.025 0.975] --------------------------------------------------------------------------------- Intercept 2.0103 1.050 1.914 0.074 -0.216 4.236 TEST 1.3134 0.670 1.959 0.068 -0.108 2.735 MINORITY -1.9132 1.540 -1.242 0.232 -5.179 1.352 TEST:MINORITY 1.9975 0.954 2.093 0.053 -0.026 4.021 ============================================================================== Omnibus: 3.377 Durbin-Watson: 3.015 Prob(Omnibus): 0.185 Jarque-Bera (JB): 1.330 Skew: 0.120 Prob(JB): 0.514 Kurtosis: 1.760 Cond. No. 13.8 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` In [28]: ``` fig, ax = plt.subplots(figsize=(8,6)); for factor, group in factor_group: ax.scatter(group['TEST'], group['JPERF'], color=colors[factor], marker=markers[factor], s=12*2) fig = abline_plot(intercept = min_lm4.params['Intercept'], slope = min_lm4.params['TEST'], ax=ax, color='purple'); fig = abline_plot(intercept = min_lm4.params['Intercept'] + min_lm4.params['MINORITY'], slope = min_lm4.params['TEST'] + min_lm4.params['TEST:MINORITY'], ax=ax, color='green'); ``` In [29]: ``` # is there any effect of MINORITY on slope or intercept? table5 = anova_lm(min_lm, min_lm4) print(table5) ``` ``` df_resid ssr df_diff ss_diff F Pr(>F) 0 18.0 45.568297 0.0 NaN NaN NaN 1 16.0 31.655473 2.0 13.912824 3.516061 0.054236 ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:879: RuntimeWarning: invalid value encountered in greater return (self.a < x) & (x < self.b) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:879: RuntimeWarning: invalid value encountered in less return (self.a < x) & (x < self.b) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:1821: RuntimeWarning: invalid value encountered in less_equal cond2 = cond0 & (x <= self.a) ``` In [30]: ``` # is there any effect of MINORITY on intercept table6 = anova_lm(min_lm, min_lm3) print(table6) ``` ``` df_resid ssr df_diff ss_diff F Pr(>F) 0 18.0 45.568297 0.0 NaN NaN NaN 1 17.0 40.321546 1.0 5.246751 2.212087 0.155246 ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:879: RuntimeWarning: invalid value encountered in greater return (self.a < x) & (x < self.b) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:879: RuntimeWarning: invalid value encountered in less return (self.a < x) & (x < self.b) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:1821: RuntimeWarning: invalid value encountered in less_equal cond2 = cond0 & (x <= self.a) ``` In [31]: ``` # is there any effect of MINORITY on slope table7 = anova_lm(min_lm, min_lm2) print(table7) ``` ``` df_resid ssr df_diff ss_diff F Pr(>F) 0 18.0 45.568297 0.0 NaN NaN NaN 1 17.0 34.707653 1.0 10.860644 5.319603 0.033949 ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:879: RuntimeWarning: invalid value encountered in greater return (self.a < x) & (x < self.b) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:879: RuntimeWarning: invalid value encountered in less return (self.a < x) & (x < self.b) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:1821: RuntimeWarning: invalid value encountered in less_equal cond2 = cond0 & (x <= self.a) ``` In [32]: ``` # is it just the slope or both? table8 = anova_lm(min_lm2, min_lm4) print(table8) ``` ``` df_resid ssr df_diff ss_diff F Pr(>F) 0 17.0 34.707653 0.0 NaN NaN NaN 1 16.0 31.655473 1.0 3.05218 1.542699 0.232115 ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:879: RuntimeWarning: invalid value encountered in greater return (self.a < x) & (x < self.b) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:879: RuntimeWarning: invalid value encountered in less return (self.a < x) & (x < self.b) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:1821: RuntimeWarning: invalid value encountered in less_equal cond2 = cond0 & (x <= self.a) ``` One-way ANOVA ------------- In [33]: ``` try: rehab_table = pd.read_csv('rehab.table') except: url = 'http://stats191.stanford.edu/data/rehab.csv' rehab_table = pd.read_table(url, delimiter=",") rehab_table.to_csv('rehab.table') fig, ax = plt.subplots(figsize=(8,6)) fig = rehab_table.boxplot('Time', 'Fitness', ax=ax, grid=False) ``` In [34]: ``` rehab_lm = ols('Time ~ C(Fitness)', data=rehab_table).fit() table9 = anova_lm(rehab_lm) print(table9) print(rehab_lm.model.data.orig_exog) ``` ``` df sum_sq mean_sq F PR(>F) C(Fitness) 2.0 672.0 336.000000 16.961538 0.000041 Residual 21.0 416.0 19.809524 NaN NaN Intercept C(Fitness)[T.2] C(Fitness)[T.3] 0 1.0 0.0 0.0 1 1.0 0.0 0.0 2 1.0 0.0 0.0 3 1.0 0.0 0.0 4 1.0 0.0 0.0 5 1.0 0.0 0.0 6 1.0 0.0 0.0 7 1.0 0.0 0.0 8 1.0 1.0 0.0 9 1.0 1.0 0.0 10 1.0 1.0 0.0 11 1.0 1.0 0.0 12 1.0 1.0 0.0 13 1.0 1.0 0.0 14 1.0 1.0 0.0 15 1.0 1.0 0.0 16 1.0 1.0 0.0 17 1.0 1.0 0.0 18 1.0 0.0 1.0 19 1.0 0.0 1.0 20 1.0 0.0 1.0 21 1.0 0.0 1.0 22 1.0 0.0 1.0 23 1.0 0.0 1.0 ``` In [35]: ``` print(rehab_lm.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: Time R-squared: 0.618 Model: OLS Adj. R-squared: 0.581 Method: Least Squares F-statistic: 16.96 Date: Mon, 14 May 2018 Prob (F-statistic): 4.13e-05 Time: 21:44:56 Log-Likelihood: -68.286 No. Observations: 24 AIC: 142.6 Df Residuals: 21 BIC: 146.1 Df Model: 2 Covariance Type: nonrobust =================================================================================== coef std err t P>\|t\| [0.025 0.975] ----------------------------------------------------------------------------------- Intercept 38.0000 1.574 24.149 0.000 34.728 41.272 C(Fitness)[T.2] -6.0000 2.111 -2.842 0.010 -10.390 -1.610 C(Fitness)[T.3] -14.0000 2.404 -5.824 0.000 -18.999 -9.001 ============================================================================== Omnibus: 0.163 Durbin-Watson: 2.209 Prob(Omnibus): 0.922 Jarque-Bera (JB): 0.211 Skew: -0.163 Prob(JB): 0.900 Kurtosis: 2.675 Cond. No. 3.80 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` Two-way ANOVA ------------- In [36]: ``` try: kidney_table = pd.read_table('./kidney.table') except: url = 'http://stats191.stanford.edu/data/kidney.table' kidney_table = pd.read_csv(url, delim_whitespace=True) ``` Explore the dataset In [37]: ``` kidney_table.head(10) ``` Out[37]: \| \| Days \| Duration \| Weight \| ID \| \| --- \| --- \| --- \| --- \| --- \| \| 0 \| 0.0 \| 1 \| 1 \| 1 \| \| 1 \| 2.0 \| 1 \| 1 \| 2 \| \| 2 \| 1.0 \| 1 \| 1 \| 3 \| \| 3 \| 3.0 \| 1 \| 1 \| 4 \| \| 4 \| 0.0 \| 1 \| 1 \| 5 \| \| 5 \| 2.0 \| 1 \| 1 \| 6 \| \| 6 \| 0.0 \| 1 \| 1 \| 7 \| \| 7 \| 5.0 \| 1 \| 1 \| 8 \| \| 8 \| 6.0 \| 1 \| 1 \| 9 \| \| 9 \| 8.0 \| 1 \| 1 \| 10 \| Balanced panel In [38]: ``` kt = kidney_table plt.figure(figsize=(8,6)) fig = interaction_plot(kt['Weight'], kt['Duration'], np.log(kt['Days']+1), colors=['red', 'blue'], markers=['D','^'], ms=10, ax=plt.gca()) ``` You have things available in the calling namespace available in the formula evaluation namespace In [39]: ``` kidney_lm = ols('np.log(Days+1) ~ C(Duration) C(Weight)', data=kt).fit() table10 = anova_lm(kidney_lm) print(anova_lm(ols('np.log(Days+1) ~ C(Duration) + C(Weight)', data=kt).fit(), kidney_lm)) print(anova_lm(ols('np.log(Days+1) ~ C(Duration)', data=kt).fit(), ols('np.log(Days+1) ~ C(Duration) + C(Weight, Sum)', data=kt).fit())) print(anova_lm(ols('np.log(Days+1) ~ C(Weight)', data=kt).fit(), ols('np.log(Days+1) ~ C(Duration) + C(Weight, Sum)', data=kt).fit())) ``` ``` df_resid ssr df_diff ss_diff F Pr(>F) 0 56.0 29.624856 0.0 NaN NaN NaN 1 54.0 28.989198 2.0 0.635658 0.59204 0.556748 df_resid ssr df_diff ss_diff F Pr(>F) 0 58.0 46.596147 0.0 NaN NaN NaN 1 56.0 29.624856 2.0 16.971291 16.040454 0.000003 df_resid ssr df_diff ss_diff F Pr(>F) 0 57.0 31.964549 0.0 NaN NaN NaN 1 56.0 29.624856 1.0 2.339693 4.422732 0.03997 ``` ``` /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:879: RuntimeWarning: invalid value encountered in greater return (self.a < x) & (x < self.b) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:879: RuntimeWarning: invalid value encountered in less return (self.a < x) & (x < self.b) /Users/taugspurger/Envs/statsmodels-dev/lib/python3.6/site-packages/scipy/stats/_distn_infrastructure.py:1821: RuntimeWarning: invalid value encountered in less_equal cond2 = cond0 & (x <= self.a) ``` Sum of squares -------------- Illustrates the use of different types of sums of squares (I,II,II) and how the Sum contrast can be used to produce the same output between the 3. Types I and II are equivalent under a balanced design. Don't use Type III with non-orthogonal contrast - ie., Treatment In [40]: ``` sum_lm = ols('np.log(Days+1) ~ C(Duration, Sum) * C(Weight, Sum)', data=kt).fit() print(anova_lm(sum_lm)) print(anova_lm(sum_lm, typ=2)) print(anova_lm(sum_lm, typ=3)) ``` ``` df sum_sq mean_sq F PR(>F) C(Duration, Sum) 1.0 2.339693 2.339693 4.358293 0.041562 C(Weight, Sum) 2.0 16.971291 8.485645 15.806745 0.000004 C(Duration, Sum):C(Weight, Sum) 2.0 0.635658 0.317829 0.592040 0.556748 Residual 54.0 28.989198 0.536837 NaN NaN sum_sq df F PR(>F) C(Duration, Sum) 2.339693 1.0 4.358293 0.041562 C(Weight, Sum) 16.971291 2.0 15.806745 0.000004 C(Duration, Sum):C(Weight, Sum) 0.635658 2.0 0.592040 0.556748 Residual 28.989198 54.0 NaN NaN sum_sq df F PR(>F) Intercept 156.301830 1.0 291.153237 2.077589e-23 C(Duration, Sum) 2.339693 1.0 4.358293 4.156170e-02 C(Weight, Sum) 16.971291 2.0 15.806745 3.944502e-06 C(Duration, Sum):C(Weight, Sum) 0.635658 2.0 0.592040 5.567479e-01 Residual 28.989198 54.0 NaN NaN ``` In [41]: ``` nosum_lm = ols('np.log(Days+1) ~ C(Duration, Treatment) * C(Weight, Treatment)', data=kt).fit() print(anova_lm(nosum_lm)) print(anova_lm(nosum_lm, typ=2)) print(anova_lm(nosum_lm, typ=3)) ``` ``` df sum_sq mean_sq F PR(>F) C(Duration, Treatment) 1.0 2.339693 2.339693 4.358293 0.041562 C(Weight, Treatment) 2.0 16.971291 8.485645 15.806745 0.000004 C(Duration, Treatment):C(Weight, Treatment) 2.0 0.635658 0.317829 0.592040 0.556748 Residual 54.0 28.989198 0.536837 NaN NaN sum_sq df F PR(>F) C(Duration, Treatment) 2.339693 1.0 4.358293 0.041562 C(Weight, Treatment) 16.971291 2.0 15.806745 0.000004 C(Duration, Treatment):C(Weight, Treatment) 0.635658 2.0 0.592040 0.556748 Residual 28.989198 54.0 NaN NaN sum_sq df F PR(>F) Intercept 10.427596 1.0 19.424139 0.000050 C(Duration, Treatment) 0.054293 1.0 0.101134 0.751699 C(Weight, Treatment) 11.703387 2.0 10.900317 0.000106 C(Duration, Treatment):C(Weight, Treatment) 0.635658 2.0 0.592040 0.556748 Residual 28.989198 54.0 NaN NaN ```	programming_docs
statsmodels Dynamic factors and coincident indices Dynamic factors and coincident indices ====================================== Factor models generally try to find a small number of unobserved "factors" that influence a subtantial portion of the variation in a larger number of observed variables, and they are related to dimension-reduction techniques such as principal components analysis. Dynamic factor models explicitly model the transition dynamics of the unobserved factors, and so are often applied to time-series data. Macroeconomic coincident indices are designed to capture the common component of the "business cycle"; such a component is assumed to simultaneously affect many macroeconomic variables. Although the estimation and use of coincident indices (for example the [Index of Coincident Economic Indicators](http://www.newyorkfed.org/research/regional_economy/coincident_summary.html)) pre-dates dynamic factor models, in several influential papers Stock and Watson (1989, 1991) used a dynamic factor model to provide a theoretical foundation for them. Below, we follow the treatment found in Kim and Nelson (1999), of the Stock and Watson (1991) model, to formulate a dynamic factor model, estimate its parameters via maximum likelihood, and create a coincident index. Macroeconomic data ------------------ The coincident index is created by considering the comovements in four macroeconomic variables (versions of thse variables are available on [FRED](https://research.stlouisfed.org/fred2/); the ID of the series used below is given in parentheses): * Industrial production (IPMAN) * Real aggregate income (excluding transfer payments) (W875RX1) * Manufacturing and trade sales (CMRMTSPL) * Employees on non-farm payrolls (PAYEMS) In all cases, the data is at the monthly frequency and has been seasonally adjusted; the time-frame considered is 1972 - 2005. In [1]: ``` %matplotlib inline import numpy as np import pandas as pd import statsmodels.api as sm import matplotlib.pyplot as plt np.set_printoptions(precision=4, suppress=True, linewidth=120) ``` In [2]: ``` from pandas_datareader.data import DataReader # Get the datasets from FRED start = '1979-01-01' end = '2014-12-01' indprod = DataReader('IPMAN', 'fred', start=start, end=end) income = DataReader('W875RX1', 'fred', start=start, end=end) sales = DataReader('CMRMTSPL', 'fred', start=start, end=end) emp = DataReader('PAYEMS', 'fred', start=start, end=end) # dta = pd.concat((indprod, income, sales, emp), axis=1) # dta.columns = ['indprod', 'income', 'sales', 'emp'] ``` Note: in a recent update on FRED (8/12/15) the time series CMRMTSPL was truncated to begin in 1997; this is probably a mistake due to the fact that CMRMTSPL is a spliced series, so the earlier period is from the series HMRMT and the latter period is defined by CMRMT. This has since (02/11/16) been corrected, however the series could also be constructed by hand from HMRMT and CMRMT, as shown below (process taken from the notes in the Alfred xls file). In [3]: ``` # HMRMT = DataReader('HMRMT', 'fred', start='1967-01-01', end=end) # CMRMT = DataReader('CMRMT', 'fred', start='1997-01-01', end=end) ``` In [4]: ``` # HMRMT_growth = HMRMT.diff() / HMRMT.shift() # sales = pd.Series(np.zeros(emp.shape[0]), index=emp.index) # # Fill in the recent entries (1997 onwards) # sales[CMRMT.index] = CMRMT # # Backfill the previous entries (pre 1997) # idx = sales.loc[:'1997-01-01'].index # for t in range(len(idx)-1, 0, -1): # month = idx[t] # prev_month = idx[t-1] # sales.loc[prev_month] = sales.loc[month] / (1 + HMRMT_growth.loc[prev_month].values) ``` In [5]: ``` dta = pd.concat((indprod, income, sales, emp), axis=1) dta.columns = ['indprod', 'income', 'sales', 'emp'] ``` In [6]: ``` dta.loc[:, 'indprod':'emp'].plot(subplots=True, layout=(2, 2), figsize=(15, 6)); ``` Stock and Watson (1991) report that for their datasets, they could not reject the null hypothesis of a unit root in each series (so the series are integrated), but they did not find strong evidence that the series were co-integrated. As a result, they suggest estimating the model using the first differences (of the logs) of the variables, demeaned and standardized. In [7]: ``` # Create log-differenced series dta['dln_indprod'] = (np.log(dta.indprod)).diff() * 100 dta['dln_income'] = (np.log(dta.income)).diff() * 100 dta['dln_sales'] = (np.log(dta.sales)).diff() * 100 dta['dln_emp'] = (np.log(dta.emp)).diff() * 100 # De-mean and standardize dta['std_indprod'] = (dta['dln_indprod'] - dta['dln_indprod'].mean()) / dta['dln_indprod'].std() dta['std_income'] = (dta['dln_income'] - dta['dln_income'].mean()) / dta['dln_income'].std() dta['std_sales'] = (dta['dln_sales'] - dta['dln_sales'].mean()) / dta['dln_sales'].std() dta['std_emp'] = (dta['dln_emp'] - dta['dln_emp'].mean()) / dta['dln_emp'].std() ``` Dynamic factors --------------- A general dynamic factor model is written as: $$ \begin{align} y\_t & = \Lambda f\_t + B x\_t + u\_t \\ f\_t & = A\_1 f\_{t-1} + \dots + A\_p f\_{t-p} + \eta\_t \qquad \eta\_t \sim N(0, I)\\ u\_t & = C\_1 u\_{t-1} + \dots + C\_q u\_{t-q} + \varepsilon\_t \qquad \varepsilon\_t \sim N(0, \Sigma) \end{align} $$ where $y\_t$ are observed data, $f\_t$ are the unobserved factors (evolving as a vector autoregression), $x\_t$ are (optional) exogenous variables, and $u\_t$ is the error, or "idiosyncratic", process ($u\_t$ is also optionally allowed to be autocorrelated). The $\Lambda$ matrix is often referred to as the matrix of "factor loadings". The variance of the factor error term is set to the identity matrix to ensure identification of the unobserved factors. This model can be cast into state space form, and the unobserved factor estimated via the Kalman filter. The likelihood can be evaluated as a byproduct of the filtering recursions, and maximum likelihood estimation used to estimate the parameters. Model specification ------------------- The specific dynamic factor model in this application has 1 unobserved factor which is assumed to follow an AR(2) proces. The innovations $\varepsilon\_t$ are assumed to be independent (so that $\Sigma$ is a diagonal matrix) and the error term associated with each equation, $u\_{i,t}$ is assumed to follow an independent AR(2) process. Thus the specification considered here is: $$ \begin{align} y\_{i,t} & = \lambda\_i f\_t + u\_{i,t} \\ u\_{i,t} & = c\_{i,1} u\_{1,t-1} + c\_{i,2} u\_{i,t-2} + \varepsilon\_{i,t} \qquad & \varepsilon\_{i,t} \sim N(0, \sigma\_i^2) \\ f\_t & = a\_1 f\_{t-1} + a\_2 f\_{t-2} + \eta\_t \qquad & \eta\_t \sim N(0, I)\\ \end{align} $$ where $i$ is one of: `[indprod, income, sales, emp ]`. This model can be formulated using the `DynamicFactor` model built-in to Statsmodels. In particular, we have the following specification: * `k_factors = 1` - (there is 1 unobserved factor) * `factor_order = 2` - (it follows an AR(2) process) * `error_var = False` - (the errors evolve as independent AR processes rather than jointly as a VAR - note that this is the default option, so it is not specified below) * `error_order = 2` - (the errors are autocorrelated of order 2: i.e. AR(2) processes) * `error_cov_type = 'diagonal'` - (the innovations are uncorrelated; this is again the default) Once the model is created, the parameters can be estimated via maximum likelihood; this is done using the `fit()` method. Note: recall that we have de-meaned and standardized the data; this will be important in interpreting the results that follow. Aside: in their empirical example, Kim and Nelson (1999) actually consider a slightly different model in which the employment variable is allowed to also depend on lagged values of the factor - this model does not fit into the built-in `DynamicFactor` class, but can be accomodated by using a subclass to implement the required new parameters and restrictions - see Appendix A, below. Parameter estimation -------------------- Multivariate models can have a relatively large number of parameters, and it may be difficult to escape from local minima to find the maximized likelihood. In an attempt to mitigate this problem, I perform an initial maximization step (from the model-defined starting paramters) using the modified Powell method available in Scipy (see the minimize documentation for more information). The resulting parameters are then used as starting parameters in the standard LBFGS optimization method. In [8]: ``` # Get the endogenous data endog = dta.loc['1979-02-01':, 'std_indprod':'std_emp'] # Create the model mod = sm.tsa.DynamicFactor(endog, k_factors=1, factor_order=2, error_order=2) initial_res = mod.fit(method='powell', disp=False) res = mod.fit(initial_res.params, disp=False) ``` Estimates --------- Once the model has been estimated, there are two components that we can use for analysis or inference: * The estimated parameters * The estimated factor ### Parameters The estimated parameters can be helpful in understanding the implications of the model, although in models with a larger number of observed variables and / or unobserved factors they can be difficult to interpret. One reason for this difficulty is due to identification issues between the factor loadings and the unobserved factors. One easy-to-see identification issue is the sign of the loadings and the factors: an equivalent model to the one displayed below would result from reversing the signs of all factor loadings and the unobserved factor. Here, one of the easy-to-interpret implications in this model is the persistence of the unobserved factor: we find that exhibits substantial persistence. In [9]: ``` print(res.summary(separate_params=False)) ``` ``` Statespace Model Results ================================================================================================================= Dep. Variable: ['std_indprod', 'std_income', 'std_sales', 'std_emp'] No. Observations: 431 Model: DynamicFactor(factors=1, order=2) Log Likelihood -2046.117 + AR(2) errors AIC 4128.235 Date: Mon, 14 May 2018 BIC 4201.425 Time: 21:44:54 HQIC 4157.133 Sample: 02-01-1979 - 12-01-2014 Covariance Type: opg ==================================================================================================== coef std err z P>\|z\| [0.025 0.975] ---------------------------------------------------------------------------------------------------- loading.f1.std_indprod -0.8758 0.022 -39.851 0.000 -0.919 -0.833 loading.f1.std_income -0.2645 0.046 -5.805 0.000 -0.354 -0.175 loading.f1.std_sales -0.4965 0.026 -19.374 0.000 -0.547 -0.446 loading.f1.std_emp -0.2931 0.030 -9.679 0.000 -0.352 -0.234 sigma2.std_indprod 0.0007 0.001 0.938 0.348 -0.001 0.002 sigma2.std_income 0.8962 0.029 30.849 0.000 0.839 0.953 sigma2.std_sales 0.5870 0.034 17.344 0.000 0.521 0.653 sigma2.std_emp 0.3682 0.015 24.904 0.000 0.339 0.397 L1.f1.f1 0.2414 0.038 6.427 0.000 0.168 0.315 L2.f1.f1 0.2941 0.042 6.970 0.000 0.211 0.377 L1.e(std_indprod).e(std_indprod) -1.1552 0.012 -96.765 0.000 -1.179 -1.132 L2.e(std_indprod).e(std_indprod) -0.9889 0.012 -83.604 0.000 -1.012 -0.966 L1.e(std_income).e(std_income) -0.1824 0.023 -8.037 0.000 -0.227 -0.138 L2.e(std_income).e(std_income) -0.0808 0.047 -1.705 0.088 -0.174 0.012 L1.e(std_sales).e(std_sales) -0.4131 0.042 -9.737 0.000 -0.496 -0.330 L2.e(std_sales).e(std_sales) -0.1725 0.049 -3.517 0.000 -0.269 -0.076 L1.e(std_emp).e(std_emp) 0.2950 0.032 9.091 0.000 0.231 0.359 L2.e(std_emp).e(std_emp) 0.4880 0.028 17.343 0.000 0.433 0.543 ========================================================================================================= Ljung-Box (Q): 54.52, 26.18, 59.07, 71.14 Jarque-Bera (JB): 211.93, 12692.16, 18.88, 3720.12 Prob(Q): 0.06, 0.95, 0.03, 0.00 Prob(JB): 0.00, 0.00, 0.00, 0.00 Heteroskedasticity (H): 0.75, 4.52, 0.52, 0.42 Skew: 0.08, -1.20, 0.20, 0.74 Prob(H) (two-sided): 0.09, 0.00, 0.00, 0.00 Kurtosis: 6.43, 29.48, 3.95, 17.32 ========================================================================================================= Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step). ``` ### Estimated factors While it can be useful to plot the unobserved factors, it is less useful here than one might think for two reasons: 1. The sign-related identification issue described above. 2. Since the data was differenced, the estimated factor explains the variation in the differenced data, not the original data. It is for these reasons that the coincident index is created (see below). With these reservations, the unobserved factor is plotted below, along with the NBER indicators for US recessions. It appears that the factor is successful at picking up some degree of business cycle activity. In [10]: ``` fig, ax = plt.subplots(figsize=(13,3)) # Plot the factor dates = endog.index._mpl_repr() ax.plot(dates, res.factors.filtered[0], label='Factor') ax.legend() # Retrieve and also plot the NBER recession indicators rec = DataReader('USREC', 'fred', start=start, end=end) ylim = ax.get_ylim() ax.fill_between(dates[:-3], ylim[0], ylim[1], rec.values[:-4,0], facecolor='k', alpha=0.1); ``` Post-estimation --------------- Although here we will be able to interpret the results of the model by constructing the coincident index, there is a useful and generic approach for getting a sense for what is being captured by the estimated factor. By taking the estimated factors as given, regressing them (and a constant) each (one at a time) on each of the observed variables, and recording the coefficients of determination ($R^2$ values), we can get a sense of the variables for which each factor explains a substantial portion of the variance and the variables for which it does not. In models with more variables and more factors, this can sometimes lend interpretation to the factors (for example sometimes one factor will load primarily on real variables and another on nominal variables). In this model, with only four endogenous variables and one factor, it is easy to digest a simple table of the $R^2$ values, but in larger models it is not. For this reason, a bar plot is often employed; from the plot we can easily see that the factor explains most of the variation in industrial production index and a large portion of the variation in sales and employment, it is less helpful in explaining income. In [11]: ``` res.plot_coefficients_of_determination(figsize=(8,2)); ``` Coincident Index ---------------- As described above, the goal of this model was to create an interpretable series which could be used to understand the current status of the macroeconomy. This is what the coincident index is designed to do. It is constructed below. For readers interested in an explanation of the construction, see Kim and Nelson (1999) or Stock and Watson (1991). In essense, what is done is to reconstruct the mean of the (differenced) factor. We will compare it to the coincident index on published by the Federal Reserve Bank of Philadelphia (USPHCI on FRED). In [12]: ``` usphci = DataReader('USPHCI', 'fred', start='1979-01-01', end='2014-12-01')['USPHCI'] usphci.plot(figsize=(13,3)); ``` In [13]: ``` dusphci = usphci.diff()[1:].values def compute_coincident_index(mod, res): # Estimate W(1) spec = res.specification design = mod.ssm['design'] transition = mod.ssm['transition'] ss_kalman_gain = res.filter_results.kalman_gain[:,:,-1] k_states = ss_kalman_gain.shape[0] W1 = np.linalg.inv(np.eye(k_states) - np.dot( np.eye(k_states) - np.dot(ss_kalman_gain, design), transition )).dot(ss_kalman_gain)[0] # Compute the factor mean vector factor_mean = np.dot(W1, dta.loc['1972-02-01':, 'dln_indprod':'dln_emp'].mean()) # Normalize the factors factor = res.factors.filtered[0] factor = np.std(usphci.diff()[1:]) / np.std(factor) # Compute the coincident index coincident_index = np.zeros(mod.nobs+1) # The initial value is arbitrary; here it is set to # facilitate comparison coincident_index[0] = usphci.iloc[0] factor_mean / dusphci.mean() for t in range(0, mod.nobs): coincident_index[t+1] = coincident_index[t] + factor[t] + factor_mean # Attach dates coincident_index = pd.Series(coincident_index, index=dta.index).iloc[1:] # Normalize to use the same base year as USPHCI coincident_index = (usphci.loc['1992-07-01'] / coincident_index.loc['1992-07-01']) return coincident_index ``` Below we plot the calculated coincident index along with the US recessions and the comparison coincident index USPHCI. In [14]: ``` fig, ax = plt.subplots(figsize=(13,3)) # Compute the index coincident_index = compute_coincident_index(mod, res) # Plot the factor dates = endog.index._mpl_repr() ax.plot(dates, coincident_index, label='Coincident index') ax.plot(usphci.index._mpl_repr(), usphci, label='USPHCI') ax.legend(loc='lower right') # Retrieve and also plot the NBER recession indicators ylim = ax.get_ylim() ax.fill_between(dates[:-3], ylim[0], ylim[1], rec.values[:-4,0], facecolor='k', alpha=0.1); ``` Appendix 1: Extending the dynamic factor model ---------------------------------------------- Recall that the previous specification was described by: $$ \begin{align} y\_{i,t} & = \lambda\_i f\_t + u\_{i,t} \\ u\_{i,t} & = c\_{i,1} u\_{1,t-1} + c\_{i,2} u\_{i,t-2} + \varepsilon\_{i,t} \qquad & \varepsilon\_{i,t} \sim N(0, \sigma\_i^2) \\ f\_t & = a\_1 f\_{t-1} + a\_2 f\_{t-2} + \eta\_t \qquad & \eta\_t \sim N(0, I)\\ \end{align} $$ Written in state space form, the previous specification of the model had the following observation equation: $$ \begin{bmatrix} y\_{\text{indprod}, t} \\ y\_{\text{income}, t} \\ y\_{\text{sales}, t} \\ y\_{\text{emp}, t} \\ \end{bmatrix} = \begin{bmatrix} \lambda\_\text{indprod} & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \lambda\_\text{income} & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ \lambda\_\text{sales} & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ \lambda\_\text{emp} & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} f\_t \\ f\_{t-1} \\ u\_{\text{indprod}, t} \\ u\_{\text{income}, t} \\ u\_{\text{sales}, t} \\ u\_{\text{emp}, t} \\ u\_{\text{indprod}, t-1} \\ u\_{\text{income}, t-1} \\ u\_{\text{sales}, t-1} \\ u\_{\text{emp}, t-1} \\ \end{bmatrix} $$ and transition equation: $$ \begin{bmatrix} f\_t \\ f\_{t-1} \\ u\_{\text{indprod}, t} \\ u\_{\text{income}, t} \\ u\_{\text{sales}, t} \\ u\_{\text{emp}, t} \\ u\_{\text{indprod}, t-1} \\ u\_{\text{income}, t-1} \\ u\_{\text{sales}, t-1} \\ u\_{\text{emp}, t-1} \\ \end{bmatrix} = \begin{bmatrix} a\_1 & a\_2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & c\_{\text{indprod}, 1} & 0 & 0 & 0 & c\_{\text{indprod}, 2} & 0 & 0 & 0 \\ 0 & 0 & 0 & c\_{\text{income}, 1} & 0 & 0 & 0 & c\_{\text{income}, 2} & 0 & 0 \\ 0 & 0 & 0 & 0 & c\_{\text{sales}, 1} & 0 & 0 & 0 & c\_{\text{sales}, 2} & 0 \\ 0 & 0 & 0 & 0 & 0 & c\_{\text{emp}, 1} & 0 & 0 & 0 & c\_{\text{emp}, 2} \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} f\_{t-1} \\ f\_{t-2} \\ u\_{\text{indprod}, t-1} \\ u\_{\text{income}, t-1} \\ u\_{\text{sales}, t-1} \\ u\_{\text{emp}, t-1} \\ u\_{\text{indprod}, t-2} \\ u\_{\text{income}, t-2} \\ u\_{\text{sales}, t-2} \\ u\_{\text{emp}, t-2} \\ \end{bmatrix} R \begin{bmatrix} \eta\_t \\ \varepsilon\_{t} \end{bmatrix} $$ the `DynamicFactor` model handles setting up the state space representation and, in the `DynamicFactor.update` method, it fills in the fitted parameter values into the appropriate locations. The extended specification is the same as in the previous example, except that we also want to allow employment to depend on lagged values of the factor. This creates a change to the $y\_{\text{emp},t}$ equation. Now we have: $$ \begin{align} y\_{i,t} & = \lambda\_i f\_t + u\_{i,t} \qquad & i \in \{\text{indprod}, \text{income}, \text{sales} \}\\ y\_{i,t} & = \lambda\_{i,0} f\_t + \lambda\_{i,1} f\_{t-1} + \lambda\_{i,2} f\_{t-2} + \lambda\_{i,2} f\_{t-3} + u\_{i,t} \qquad & i = \text{emp} \\ u\_{i,t} & = c\_{i,1} u\_{i,t-1} + c\_{i,2} u\_{i,t-2} + \varepsilon\_{i,t} \qquad & \varepsilon\_{i,t} \sim N(0, \sigma\_i^2) \\ f\_t & = a\_1 f\_{t-1} + a\_2 f\_{t-2} + \eta\_t \qquad & \eta\_t \sim N(0, I)\\ \end{align} $$ Now, the corresponding observation equation should look like the following: $$ \begin{bmatrix} y\_{\text{indprod}, t} \\ y\_{\text{income}, t} \\ y\_{\text{sales}, t} \\ y\_{\text{emp}, t} \\ \end{bmatrix} = \begin{bmatrix} \lambda\_\text{indprod} & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \lambda\_\text{income} & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ \lambda\_\text{sales} & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ \lambda\_\text{emp,1} & \lambda\_\text{emp,2} & \lambda\_\text{emp,3} & \lambda\_\text{emp,4} & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} f\_t \\ f\_{t-1} \\ f\_{t-2} \\ f\_{t-3} \\ u\_{\text{indprod}, t} \\ u\_{\text{income}, t} \\ u\_{\text{sales}, t} \\ u\_{\text{emp}, t} \\ u\_{\text{indprod}, t-1} \\ u\_{\text{income}, t-1} \\ u\_{\text{sales}, t-1} \\ u\_{\text{emp}, t-1} \\ \end{bmatrix} $$ Notice that we have introduced two new state variables, $f\_{t-2}$ and $f\_{t-3}$, which means we need to update the transition equation: $$ \begin{bmatrix} f\_t \\ f\_{t-1} \\ f\_{t-2} \\ f\_{t-3} \\ u\_{\text{indprod}, t} \\ u\_{\text{income}, t} \\ u\_{\text{sales}, t} \\ u\_{\text{emp}, t} \\ u\_{\text{indprod}, t-1} \\ u\_{\text{income}, t-1} \\ u\_{\text{sales}, t-1} \\ u\_{\text{emp}, t-1} \\ \end{bmatrix} = \begin{bmatrix} a\_1 & a\_2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & c\_{\text{indprod}, 1} & 0 & 0 & 0 & c\_{\text{indprod}, 2} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & c\_{\text{income}, 1} & 0 & 0 & 0 & c\_{\text{income}, 2} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & c\_{\text{sales}, 1} & 0 & 0 & 0 & c\_{\text{sales}, 2} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & c\_{\text{emp}, 1} & 0 & 0 & 0 & c\_{\text{emp}, 2} \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} f\_{t-1} \\ f\_{t-2} \\ f\_{t-3} \\ f\_{t-4} \\ u\_{\text{indprod}, t-1} \\ u\_{\text{income}, t-1} \\ u\_{\text{sales}, t-1} \\ u\_{\text{emp}, t-1} \\ u\_{\text{indprod}, t-2} \\ u\_{\text{income}, t-2} \\ u\_{\text{sales}, t-2} \\ u\_{\text{emp}, t-2} \\ \end{bmatrix} * R \begin{bmatrix} \eta\_t \\ \varepsilon\_{t} \end{bmatrix} $$ This model cannot be handled out-of-the-box by the `DynamicFactor` class, but it can be handled by creating a subclass when alters the state space representation in the appropriate way. First, notice that if we had set `factor_order = 4`, we would almost have what we wanted. In that case, the last line of the observation equation would be: $$ \begin{bmatrix} \vdots \\ y\_{\text{emp}, t} \\ \end{bmatrix} = \begin{bmatrix} \vdots & & & & & & & & & & & \vdots \\ \lambda\_\text{emp,1} & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ \end{bmatrix} \begin{bmatrix} f\_t \\ f\_{t-1} \\ f\_{t-2} \\ f\_{t-3} \\ \vdots \end{bmatrix} $$ and the first line of the transition equation would be: $$ \begin{bmatrix} f\_t \\ \vdots \end{bmatrix} = \begin{bmatrix} a\_1 & a\_2 & a\_3 & a\_4 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \vdots & & & & & & & & & & & \vdots \\ \end{bmatrix} \begin{bmatrix} f\_{t-1} \\ f\_{t-2} \\ f\_{t-3} \\ f\_{t-4} \\ \vdots \end{bmatrix} * R \begin{bmatrix} \eta\_t \\ \varepsilon\_{t} \end{bmatrix} $$ Relative to what we want, we have the following differences: 1. In the above situation, the $\lambda\_{\text{emp}, j}$ are forced to be zero for $j > 0$, and we want them to be estimated as parameters. 2. We only want the factor to transition according to an AR(2), but under the above situation it is an AR(4). Our strategy will be to subclass `DynamicFactor`, and let it do most of the work (setting up the state space representation, etc.) where it assumes that `factor_order = 4`. The only things we will actually do in the subclass will be to fix those two issues. First, here is the full code of the subclass; it is discussed below. It is important to note at the outset that none of the methods defined below could have been omitted. In fact, the methods `__init__`, `start_params`, `param_names`, `transform_params`, `untransform_params`, and `update` form the core of all state space models in Statsmodels, not just the `DynamicFactor` class. In [15]: ``` from statsmodels.tsa.statespace import tools class ExtendedDFM(sm.tsa.DynamicFactor): def __init__(self, endog, kwargs): # Setup the model as if we had a factor order of 4 super(ExtendedDFM, self).__init__( endog, k_factors=1, factor_order=4, error_order=2, kwargs) # Note: `self.parameters` is an ordered dict with the # keys corresponding to parameter types, and the values # the number of parameters of that type. # Add the new parameters self.parameters['new_loadings'] = 3 # Cache a slice for the location of the 4 factor AR # parameters (a_1, ..., a_4) in the full parameter vector offset = (self.parameters['factor_loadings'] + self.parameters['exog'] + self.parameters['error_cov']) self._params_factor_ar = np.s_[offset:offset+2] self._params_factor_zero = np.s_[offset+2:offset+4] @property def start_params(self): # Add three new loading parameters to the end of the parameter # vector, initialized to zeros (for simplicity; they could # be initialized any way you like) return np.r_[super(ExtendedDFM, self).start_params, 0, 0, 0] @property def param_names(self): # Add the corresponding names for the new loading parameters # (the name can be anything you like) return super(ExtendedDFM, self).param_names + [ 'loading.L%d.f1.%s' % (i, self.endog_names[3]) for i in range(1,4)] def transform_params(self, unconstrained): # Perform the typical DFM transformation (w/o the new parameters) constrained = super(ExtendedDFM, self).transform_params( unconstrained[:-3]) # Redo the factor AR constraint, since we only want an AR(2), # and the previous constraint was for an AR(4) ar_params = unconstrained[self._params_factor_ar] constrained[self._params_factor_ar] = ( tools.constrain_stationary_univariate(ar_params)) # Return all the parameters return np.r_[constrained, unconstrained[-3:]] def untransform_params(self, constrained): # Perform the typical DFM untransformation (w/o the new parameters) unconstrained = super(ExtendedDFM, self).untransform_params( constrained[:-3]) # Redo the factor AR unconstraint, since we only want an AR(2), # and the previous unconstraint was for an AR(4) ar_params = constrained[self._params_factor_ar] unconstrained[self._params_factor_ar] = ( tools.unconstrain_stationary_univariate(ar_params)) # Return all the parameters return np.r_[unconstrained, constrained[-3:]] def update(self, params, transformed=True, complex_step=False): # Peform the transformation, if required if not transformed: params = self.transform_params(params) params[self._params_factor_zero] = 0 # Now perform the usual DFM update, but exclude our new parameters super(ExtendedDFM, self).update(params[:-3], transformed=True, complex_step=complex_step) # Finally, set our new parameters in the design matrix self.ssm['design', 3, 1:4] = params[-3:] ``` So what did we just do? #### `__init__` The important step here was specifying the base dynamic factor model which we were operating with. In particular, as described above, we initialize with `factor_order=4`, even though we will only end up with an AR(2) model for the factor. We also performed some general setup-related tasks. #### `start_params` `start_params` are used as initial values in the optimizer. Since we are adding three new parameters, we need to pass those in. If we hadn't done this, the optimizer would use the default starting values, which would be three elements short. #### `param_names` `param_names` are used in a variety of places, but especially in the results class. Below we get a full result summary, which is only possible when all the parameters have associated names. #### `transform_params` and `untransform_params` The optimizer selects possibly parameter values in an unconstrained way. That's not usually desired (since variances can't be negative, for example), and `transform_params` is used to transform the unconstrained values used by the optimizer to constrained values appropriate to the model. Variances terms are typically squared (to force them to be positive), and AR lag coefficients are often constrained to lead to a stationary model. `untransform_params` is used for the reverse operation (and is important because starting parameters are usually specified in terms of values appropriate to the model, and we need to convert them to parameters appropriate to the optimizer before we can begin the optimization routine). Even though we don't need to transform or untransform our new parameters (the loadings can in theory take on any values), we still need to modify this function for two reasons: 1. The version in the `DynamicFactor` class is expecting 3 fewer parameters than we have now. At a minimum, we need to handle the three new parameters. 2. The version in the `DynamicFactor` class constrains the factor lag coefficients to be stationary as though it was an AR(4) model. Since we actually have an AR(2) model, we need to re-do the constraint. We also set the last two autoregressive coefficients to be zero here. #### `update` The most important reason we need to specify a new `update` method is because we have three new parameters that we need to place into the state space formulation. In particular we let the parent `DynamicFactor.update` class handle placing all the parameters except the three new ones in to the state space representation, and then we put the last three in manually. In [16]: ``` # Create the model extended_mod = ExtendedDFM(endog) initial_extended_res = extended_mod.fit(maxiter=1000, disp=False) extended_res = extended_mod.fit(initial_extended_res.params, method='nm', maxiter=1000) print(extended_res.summary(separate_params=False)) ``` ``` Optimization terminated successfully. Current function value: 4.692103 Iterations: 280 Function evaluations: 475 Statespace Model Results ================================================================================================================= Dep. Variable: ['std_indprod', 'std_income', 'std_sales', 'std_emp'] No. Observations: 431 Model: DynamicFactor(factors=1, order=4) Log Likelihood -2022.296 + AR(2) errors AIC 4090.593 Date: Mon, 14 May 2018 BIC 4184.113 Time: 21:45:04 HQIC 4127.518 Sample: 02-01-1979 - 12-01-2014 Covariance Type: opg ==================================================================================================== coef std err z P>\|z\| [0.025 0.975] ---------------------------------------------------------------------------------------------------- loading.f1.std_indprod -0.6853 0.036 -19.220 0.000 -0.755 -0.615 loading.f1.std_income -0.2631 0.039 -6.749 0.000 -0.340 -0.187 loading.f1.std_sales -0.4367 0.023 -18.832 0.000 -0.482 -0.391 loading.f1.std_emp -0.4183 0.038 -11.109 0.000 -0.492 -0.345 sigma2.std_indprod 0.2483 0.045 5.479 0.000 0.159 0.337 sigma2.std_income 0.8628 0.029 29.269 0.000 0.805 0.921 sigma2.std_sales 0.5389 0.035 15.381 0.000 0.470 0.608 sigma2.std_emp 0.2480 0.023 10.597 0.000 0.202 0.294 L1.f1.f1 0.3093 0.060 5.186 0.000 0.192 0.426 L2.f1.f1 0.3750 0.062 6.032 0.000 0.253 0.497 L3.f1.f1 0 1.45e-10 0 1.000 -2.84e-10 2.84e-10 L4.f1.f1 0 1.45e-10 0 1.000 -2.84e-10 2.84e-10 L1.e(std_indprod).e(std_indprod) -0.3248 0.112 -2.903 0.004 -0.544 -0.106 L2.e(std_indprod).e(std_indprod) -0.2303 0.088 -2.631 0.009 -0.402 -0.059 L1.e(std_income).e(std_income) -0.2002 0.024 -8.449 0.000 -0.247 -0.154 L2.e(std_income).e(std_income) -0.0914 0.047 -1.927 0.054 -0.184 0.002 L1.e(std_sales).e(std_sales) -0.4827 0.047 -10.365 0.000 -0.574 -0.391 L2.e(std_sales).e(std_sales) -0.2222 0.050 -4.449 0.000 -0.320 -0.124 L1.e(std_emp).e(std_emp) 0.2335 0.042 5.588 0.000 0.152 0.315 L2.e(std_emp).e(std_emp) 0.5002 0.050 9.928 0.000 0.401 0.599 loading.L1.f1.std_emp -0.0703 0.038 -1.836 0.066 -0.145 0.005 loading.L2.f1.std_emp 0.0059 0.036 0.165 0.869 -0.064 0.076 loading.L3.f1.std_emp -0.1777 0.028 -6.323 0.000 -0.233 -0.123 ========================================================================================================= Ljung-Box (Q): 59.44, 25.11, 69.96, 60.63 Jarque-Bera (JB): 227.10, 13369.46, 22.74, 3355.06 Prob(Q): 0.02, 0.97, 0.00, 0.02 Prob(JB): 0.00, 0.00, 0.00, 0.00 Heteroskedasticity (H): 0.76, 4.75, 0.49, 0.45 Skew: 0.24, -1.19, 0.26, 0.73 Prob(H) (two-sided): 0.10, 0.00, 0.00, 0.00 Kurtosis: 6.52, 30.18, 4.00, 16.59 ========================================================================================================= Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step). [2] Covariance matrix is singular or near-singular, with condition number 1.79e+17. Standard errors may be unstable. ``` Although this model increases the likelihood, it is not preferred by the AIC and BIC mesaures which penalize the additional three parameters. Furthermore, the qualitative results are unchanged, as we can see from the updated $R^2$ chart and the new coincident index, both of which are practically identical to the previous results. In [17]: ``` extended_res.plot_coefficients_of_determination(figsize=(8,2)); ``` In [18]: ``` fig, ax = plt.subplots(figsize=(13,3)) # Compute the index extended_coincident_index = compute_coincident_index(extended_mod, extended_res) # Plot the factor dates = endog.index._mpl_repr() ax.plot(dates, coincident_index, '-', linewidth=1, label='Basic model') ax.plot(dates, extended_coincident_index, '--', linewidth=3, label='Extended model') ax.plot(usphci.index._mpl_repr(), usphci, label='USPHCI') ax.legend(loc='lower right') ax.set(title='Coincident indices, comparison') # Retrieve and also plot the NBER recession indicators ylim = ax.get_ylim() ax.fill_between(dates[:-3], ylim[0], ylim[1], rec.values[:-4,0], facecolor='k', alpha=0.1); ```	programming_docs
statsmodels Dates in timeseries models Dates in timeseries models ========================== In [1]: ``` from __future__ import print_function import statsmodels.api as sm import numpy as np import pandas as pd ``` Getting started --------------- In [2]: ``` data = sm.datasets.sunspots.load() ``` Right now an annual date series must be datetimes at the end of the year. In [3]: ``` from datetime import datetime dates = sm.tsa.datetools.dates_from_range('1700', length=len(data.endog)) ``` Using Pandas ------------ Make a pandas TimeSeries or DataFrame In [4]: ``` endog = pd.Series(data.endog, index=dates) ``` Instantiate the model In [5]: ``` ar_model = sm.tsa.AR(endog, freq='A') pandas_ar_res = ar_model.fit(maxlag=9, method='mle', disp=-1) ``` Out-of-sample prediction In [6]: ``` pred = pandas_ar_res.predict(start='2005', end='2015') print(pred) ``` ``` 2005-12-31 20.003298 2006-12-31 24.703996 2007-12-31 20.026133 2008-12-31 23.473641 2009-12-31 30.858566 2010-12-31 61.335414 2011-12-31 87.024635 2012-12-31 91.321196 2013-12-31 79.921585 2014-12-31 60.799495 2015-12-31 40.374852 Freq: A-DEC, dtype: float64 ``` Using explicit dates -------------------- In [7]: ``` ar_model = sm.tsa.AR(data.endog, dates=dates, freq='A') ar_res = ar_model.fit(maxlag=9, method='mle', disp=-1) pred = ar_res.predict(start='2005', end='2015') print(pred) ``` ``` [20.00329845 24.70399631 20.02613267 23.47364059 30.8585664 61.33541408 87.02463499 91.32119576 79.92158511 60.79949541 40.37485169] ``` This just returns a regular array, but since the model has date information attached, you can get the prediction dates in a roundabout way. In [8]: ``` print(ar_res.data.predict_dates) ``` ``` DatetimeIndex(['2005-12-31', '2006-12-31', '2007-12-31', '2008-12-31', '2009-12-31', '2010-12-31', '2011-12-31', '2012-12-31', '2013-12-31', '2014-12-31', '2015-12-31'], dtype='datetime64[ns]', freq='A-DEC') ``` Note: This attribute only exists if predict has been called. It holds the dates associated with the last call to predict. statsmodels None Markov switching dynamic regression models ------------------------------------------ This notebook provides an example of the use of Markov switching models in Statsmodels to estimate dynamic regression models with changes in regime. It follows the examples in the Stata Markov switching documentation, which can be found at <http://www.stata.com/manuals14/tsmswitch.pdf>. In [1]: ``` %matplotlib inline import numpy as np import pandas as pd import statsmodels.api as sm import matplotlib.pyplot as plt # NBER recessions from pandas_datareader.data import DataReader from datetime import datetime usrec = DataReader('USREC', 'fred', start=datetime(1947, 1, 1), end=datetime(2013, 4, 1)) ``` ### Federal funds rate with switching intercept The first example models the federal funds rate as noise around a constant intercept, but where the intercept changes during different regimes. The model is simply: $$r\_t = \mu\_{S\_t} + \varepsilon\_t \qquad \varepsilon\_t \sim N(0, \sigma^2)$$ where $S\_t \in \{0, 1\}$, and the regime transitions according to $$ P(S\_t = s\_t \| S\_{t-1} = s\_{t-1}) = \begin{bmatrix} p\_{00} & p\_{10} \\ 1 - p\_{00} & 1 - p\_{10} \end{bmatrix} $$ We will estimate the parameters of this model by maximum likelihood: $p\_{00}, p\_{10}, \mu\_0, \mu\_1, \sigma^2$. The data used in this example can be found at <http://www.stata-press.com/data/r14/usmacro>. In [2]: ``` # Get the federal funds rate data from statsmodels.tsa.regime_switching.tests.test_markov_regression import fedfunds dta_fedfunds = pd.Series(fedfunds, index=pd.date_range('1954-07-01', '2010-10-01', freq='QS')) # Plot the data dta_fedfunds.plot(title='Federal funds rate', figsize=(12,3)) # Fit the model # (a switching mean is the default of the MarkovRegession model) mod_fedfunds = sm.tsa.MarkovRegression(dta_fedfunds, k_regimes=2) res_fedfunds = mod_fedfunds.fit() ``` In [3]: ``` res_fedfunds.summary() ``` Out[3]: Markov Switching Model Results\| Dep. Variable: \| y \| No. Observations: \| 226 \| \| Model: \| MarkovRegression \| Log Likelihood \| -508.636 \| \| Date: \| Mon, 14 May 2018 \| AIC \| 1027.272 \| \| Time: \| 21:44:44 \| BIC \| 1044.375 \| \| Sample: \| 07-01-1954 \| HQIC \| 1034.174 \| \| \| - 10-01-2010 \| \| \| \| Covariance Type: \| approx \| \| \| Regime 0 parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| const \| 3.7088 \| 0.177 \| 20.988 \| 0.000 \| 3.362 \| 4.055 \| Regime 1 parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| const \| 9.5568 \| 0.300 \| 31.857 \| 0.000 \| 8.969 \| 10.145 \| Non-switching parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| sigma2 \| 4.4418 \| 0.425 \| 10.447 \| 0.000 \| 3.608 \| 5.275 \| Regime transition parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| p[0->0] \| 0.9821 \| 0.010 \| 94.443 \| 0.000 \| 0.962 \| 1.002 \| \| p[1->0] \| 0.0504 \| 0.027 \| 1.876 \| 0.061 \| -0.002 \| 0.103 \| Warnings: [1] Covariance matrix calculated using numerical (complex-step) differentiation. From the summary output, the mean federal funds rate in the first regime (the "low regime") is estimated to be $3.7$ whereas in the "high regime" it is $9.6$. Below we plot the smoothed probabilities of being in the high regime. The model suggests that the 1980's was a time-period in which a high federal funds rate existed. In [4]: ``` res_fedfunds.smoothed_marginal_probabilities[1].plot( title='Probability of being in the high regime', figsize=(12,3)); ``` From the estimated transition matrix we can calculate the expected duration of a low regime versus a high regime. In [5]: ``` print(res_fedfunds.expected_durations) ``` ``` [55.85400626 19.85506546] ``` A low regime is expected to persist for about fourteen years, whereas the high regime is expected to persist for only about five years. ### Federal funds rate with switching intercept and lagged dependent variable The second example augments the previous model to include the lagged value of the federal funds rate. $$r\_t = \mu\_{S\_t} + r\_{t-1} \beta\_{S\_t} + \varepsilon\_t \qquad \varepsilon\_t \sim N(0, \sigma^2)$$ where $S\_t \in \{0, 1\}$, and the regime transitions according to $$ P(S\_t = s\_t \| S\_{t-1} = s\_{t-1}) = \begin{bmatrix} p\_{00} & p\_{10} \\ 1 - p\_{00} & 1 - p\_{10} \end{bmatrix} $$ We will estimate the parameters of this model by maximum likelihood: $p\_{00}, p\_{10}, \mu\_0, \mu\_1, \beta\_0, \beta\_1, \sigma^2$. In [6]: ``` # Fit the model mod_fedfunds2 = sm.tsa.MarkovRegression( dta_fedfunds.iloc[1:], k_regimes=2, exog=dta_fedfunds.iloc[:-1]) res_fedfunds2 = mod_fedfunds2.fit() ``` In [7]: ``` res_fedfunds2.summary() ``` Out[7]: Markov Switching Model Results\| Dep. Variable: \| y \| No. Observations: \| 225 \| \| Model: \| MarkovRegression \| Log Likelihood \| -264.711 \| \| Date: \| Mon, 14 May 2018 \| AIC \| 543.421 \| \| Time: \| 21:44:45 \| BIC \| 567.334 \| \| Sample: \| 10-01-1954 \| HQIC \| 553.073 \| \| \| - 10-01-2010 \| \| \| \| Covariance Type: \| approx \| \| \| Regime 0 parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| const \| 0.7245 \| 0.289 \| 2.510 \| 0.012 \| 0.159 \| 1.290 \| \| x1 \| 0.7631 \| 0.034 \| 22.629 \| 0.000 \| 0.697 \| 0.829 \| Regime 1 parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| const \| -0.0989 \| 0.118 \| -0.835 \| 0.404 \| -0.331 \| 0.133 \| \| x1 \| 1.0612 \| 0.019 \| 57.351 \| 0.000 \| 1.025 \| 1.097 \| Non-switching parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| sigma2 \| 0.4783 \| 0.050 \| 9.642 \| 0.000 \| 0.381 \| 0.576 \| Regime transition parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| p[0->0] \| 0.6378 \| 0.120 \| 5.304 \| 0.000 \| 0.402 \| 0.874 \| \| p[1->0] \| 0.1306 \| 0.050 \| 2.634 \| 0.008 \| 0.033 \| 0.228 \| Warnings: [1] Covariance matrix calculated using numerical (complex-step) differentiation. There are several things to notice from the summary output: 1. The information criteria have decreased substantially, indicating that this model has a better fit than the previous model. 2. The interpretation of the regimes, in terms of the intercept, have switched. Now the first regime has the higher intercept and the second regime has a lower intercept. Examining the smoothed probabilities of the high regime state, we now see quite a bit more variability. In [8]: ``` res_fedfunds2.smoothed_marginal_probabilities[0].plot( title='Probability of being in the high regime', figsize=(12,3)); ``` Finally, the expected durations of each regime have decreased quite a bit. In [9]: ``` print(res_fedfunds2.expected_durations) ``` ``` [2.76105188 7.65529154] ``` ### Taylor rule with 2 or 3 regimes We now include two additional exogenous variables - a measure of the output gap and a measure of inflation - to estimate a switching Taylor-type rule with both 2 and 3 regimes to see which fits the data better. Because the models can be often difficult to estimate, for the 3-regime model we employ a search over starting parameters to improve results, specifying 20 random search repetitions. In [10]: ``` # Get the additional data from statsmodels.tsa.regime_switching.tests.test_markov_regression import ogap, inf dta_ogap = pd.Series(ogap, index=pd.date_range('1954-07-01', '2010-10-01', freq='QS')) dta_inf = pd.Series(inf, index=pd.date_range('1954-07-01', '2010-10-01', freq='QS')) exog = pd.concat((dta_fedfunds.shift(), dta_ogap, dta_inf), axis=1).iloc[4:] # Fit the 2-regime model mod_fedfunds3 = sm.tsa.MarkovRegression( dta_fedfunds.iloc[4:], k_regimes=2, exog=exog) res_fedfunds3 = mod_fedfunds3.fit() # Fit the 3-regime model np.random.seed(12345) mod_fedfunds4 = sm.tsa.MarkovRegression( dta_fedfunds.iloc[4:], k_regimes=3, exog=exog) res_fedfunds4 = mod_fedfunds4.fit(search_reps=20) ``` In [11]: ``` res_fedfunds3.summary() ``` Out[11]: Markov Switching Model Results\| Dep. Variable: \| y \| No. Observations: \| 222 \| \| Model: \| MarkovRegression \| Log Likelihood \| -229.256 \| \| Date: \| Mon, 14 May 2018 \| AIC \| 480.512 \| \| Time: \| 21:44:50 \| BIC \| 517.942 \| \| Sample: \| 07-01-1955 \| HQIC \| 495.624 \| \| \| - 10-01-2010 \| \| \| \| Covariance Type: \| approx \| \| \| Regime 0 parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| const \| 0.6555 \| 0.137 \| 4.771 \| 0.000 \| 0.386 \| 0.925 \| \| x1 \| 0.8314 \| 0.033 \| 24.951 \| 0.000 \| 0.766 \| 0.897 \| \| x2 \| 0.1355 \| 0.029 \| 4.609 \| 0.000 \| 0.078 \| 0.193 \| \| x3 \| -0.0274 \| 0.041 \| -0.671 \| 0.502 \| -0.107 \| 0.053 \| Regime 1 parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| const \| -0.0945 \| 0.128 \| -0.739 \| 0.460 \| -0.345 \| 0.156 \| \| x1 \| 0.9293 \| 0.027 \| 34.309 \| 0.000 \| 0.876 \| 0.982 \| \| x2 \| 0.0343 \| 0.024 \| 1.429 \| 0.153 \| -0.013 \| 0.081 \| \| x3 \| 0.2125 \| 0.030 \| 7.147 \| 0.000 \| 0.154 \| 0.271 \| Non-switching parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| sigma2 \| 0.3323 \| 0.035 \| 9.526 \| 0.000 \| 0.264 \| 0.401 \| Regime transition parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| p[0->0] \| 0.7279 \| 0.093 \| 7.828 \| 0.000 \| 0.546 \| 0.910 \| \| p[1->0] \| 0.2115 \| 0.064 \| 3.298 \| 0.001 \| 0.086 \| 0.337 \| Warnings: [1] Covariance matrix calculated using numerical (complex-step) differentiation. In [12]: ``` res_fedfunds4.summary() ``` Out[12]: Markov Switching Model Results\| Dep. Variable: \| y \| No. Observations: \| 222 \| \| Model: \| MarkovRegression \| Log Likelihood \| -180.806 \| \| Date: \| Mon, 14 May 2018 \| AIC \| 399.611 \| \| Time: \| 21:44:50 \| BIC \| 464.262 \| \| Sample: \| 07-01-1955 \| HQIC \| 425.713 \| \| \| - 10-01-2010 \| \| \| \| Covariance Type: \| approx \| \| \| Regime 0 parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| const \| -1.0250 \| 0.292 \| -3.514 \| 0.000 \| -1.597 \| -0.453 \| \| x1 \| 0.3277 \| 0.086 \| 3.809 \| 0.000 \| 0.159 \| 0.496 \| \| x2 \| 0.2036 \| 0.050 \| 4.086 \| 0.000 \| 0.106 \| 0.301 \| \| x3 \| 1.1381 \| 0.081 \| 13.972 \| 0.000 \| 0.978 \| 1.298 \| Regime 1 parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| const \| -0.0259 \| 0.087 \| -0.298 \| 0.766 \| -0.196 \| 0.145 \| \| x1 \| 0.9737 \| 0.019 \| 50.206 \| 0.000 \| 0.936 \| 1.012 \| \| x2 \| 0.0341 \| 0.017 \| 1.973 \| 0.049 \| 0.000 \| 0.068 \| \| x3 \| 0.1215 \| 0.022 \| 5.605 \| 0.000 \| 0.079 \| 0.164 \| Regime 2 parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| const \| 0.7346 \| 0.136 \| 5.419 \| 0.000 \| 0.469 \| 1.000 \| \| x1 \| 0.8436 \| 0.024 \| 34.798 \| 0.000 \| 0.796 \| 0.891 \| \| x2 \| 0.1633 \| 0.032 \| 5.067 \| 0.000 \| 0.100 \| 0.226 \| \| x3 \| -0.0499 \| 0.027 \| -1.829 \| 0.067 \| -0.103 \| 0.004 \| Non-switching parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| sigma2 \| 0.1660 \| 0.018 \| 9.138 \| 0.000 \| 0.130 \| 0.202 \| Regime transition parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| p[0->0] \| 0.7214 \| 0.117 \| 6.147 \| 0.000 \| 0.491 \| 0.951 \| \| p[1->0] \| 4.001e-08 \| 0.035 \| 1.13e-06 \| 1.000 \| -0.069 \| 0.069 \| \| p[2->0] \| 0.0783 \| 0.057 \| 1.372 \| 0.170 \| -0.034 \| 0.190 \| \| p[0->1] \| 0.1044 \| 0.095 \| 1.103 \| 0.270 \| -0.081 \| 0.290 \| \| p[1->1] \| 0.8259 \| 0.054 \| 15.201 \| 0.000 \| 0.719 \| 0.932 \| \| p[2->1] \| 0.2288 \| 0.073 \| 3.126 \| 0.002 \| 0.085 \| 0.372 \| Warnings: [1] Covariance matrix calculated using numerical (complex-step) differentiation. Due to lower information criteria, we might prefer the 3-state model, with an interpretation of low-, medium-, and high-interest rate regimes. The smoothed probabilities of each regime are plotted below. In [13]: ``` fig, axes = plt.subplots(3, figsize=(10,7)) ax = axes[0] ax.plot(res_fedfunds4.smoothed_marginal_probabilities[0]) ax.set(title='Smoothed probability of a low-interest rate regime') ax = axes[1] ax.plot(res_fedfunds4.smoothed_marginal_probabilities[1]) ax.set(title='Smoothed probability of a medium-interest rate regime') ax = axes[2] ax.plot(res_fedfunds4.smoothed_marginal_probabilities[2]) ax.set(title='Smoothed probability of a high-interest rate regime') fig.tight_layout() ``` ### Switching variances We can also accomodate switching variances. In particular, we consider the model $$ y\_t = \mu\_{S\_t} + y\_{t-1} \beta\_{S\_t} + \varepsilon\_t \quad \varepsilon\_t \sim N(0, \sigma\_{S\_t}^2) $$ We use maximum likelihood to estimate the parameters of this model: $p\_{00}, p\_{10}, \mu\_0, \mu\_1, \beta\_0, \beta\_1, \sigma\_0^2, \sigma\_1^2$. The application is to absolute returns on stocks, where the data can be found at <http://www.stata-press.com/data/r14/snp500>. In [14]: ``` # Get the federal funds rate data from statsmodels.tsa.regime_switching.tests.test_markov_regression import areturns dta_areturns = pd.Series(areturns, index=pd.date_range('2004-05-04', '2014-5-03', freq='W')) # Plot the data dta_areturns.plot(title='Absolute returns, S&P500', figsize=(12,3)) # Fit the model mod_areturns = sm.tsa.MarkovRegression( dta_areturns.iloc[1:], k_regimes=2, exog=dta_areturns.iloc[:-1], switching_variance=True) res_areturns = mod_areturns.fit() ``` In [15]: ``` res_areturns.summary() ``` Out[15]: Markov Switching Model Results\| Dep. Variable: \| y \| No. Observations: \| 520 \| \| Model: \| MarkovRegression \| Log Likelihood \| -745.798 \| \| Date: \| Mon, 14 May 2018 \| AIC \| 1507.595 \| \| Time: \| 21:44:52 \| BIC \| 1541.626 \| \| Sample: \| 05-16-2004 \| HQIC \| 1520.926 \| \| \| - 04-27-2014 \| \| \| \| Covariance Type: \| approx \| \| \| Regime 0 parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| const \| 0.7641 \| 0.078 \| 9.761 \| 0.000 \| 0.611 \| 0.918 \| \| x1 \| 0.0791 \| 0.030 \| 2.620 \| 0.009 \| 0.020 \| 0.138 \| \| sigma2 \| 0.3476 \| 0.061 \| 5.694 \| 0.000 \| 0.228 \| 0.467 \| Regime 1 parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| const \| 1.9728 \| 0.278 \| 7.086 \| 0.000 \| 1.427 \| 2.518 \| \| x1 \| 0.5280 \| 0.086 \| 6.155 \| 0.000 \| 0.360 \| 0.696 \| \| sigma2 \| 2.5771 \| 0.405 \| 6.357 \| 0.000 \| 1.783 \| 3.372 \| Regime transition parameters\| \| coef \| std err \| z \| P>\|z\| \| [0.025 \| 0.975] \| \| p[0->0] \| 0.7531 \| 0.063 \| 11.871 \| 0.000 \| 0.629 \| 0.877 \| \| p[1->0] \| 0.6825 \| 0.066 \| 10.301 \| 0.000 \| 0.553 \| 0.812 \| Warnings: [1] Covariance matrix calculated using numerical (complex-step) differentiation. The first regime is a low-variance regime and the second regime is a high-variance regime. Below we plot the probabilities of being in the low-variance regime. Between 2008 and 2012 there does not appear to be a clear indication of one regime guiding the economy. In [16]: ``` res_areturns.smoothed_marginal_probabilities[0].plot( title='Probability of being in a low-variance regime', figsize=(12,3)); ``` statsmodels VARMAX models VARMAX models ============= This is a brief introduction notebook to VARMAX models in Statsmodels. The VARMAX model is generically specified as: $$ y\_t = \nu + A\_1 y\_{t-1} + \dots + A\_p y\_{t-p} + B x\_t + \epsilon\_t + M\_1 \epsilon\_{t-1} + \dots M\_q \epsilon\_{t-q} $$ where $y\_t$ is a $\text{k\_endog} \times 1$ vector. In [1]: ``` %matplotlib inline ``` In [2]: ``` import numpy as np import pandas as pd import statsmodels.api as sm import matplotlib.pyplot as plt ``` In [3]: ``` dta = sm.datasets.webuse('lutkepohl2', 'http://www.stata-press.com/data/r12/') dta.index = dta.qtr endog = dta.loc['1960-04-01':'1978-10-01', ['dln_inv', 'dln_inc', 'dln_consump']] ``` Model specification ------------------- The `VARMAX` class in Statsmodels allows estimation of VAR, VMA, and VARMA models (through the `order` argument), optionally with a constant term (via the `trend` argument). Exogenous regressors may also be included (as usual in Statsmodels, by the `exog` argument), and in this way a time trend may be added. Finally, the class allows measurement error (via the `measurement_error` argument) and allows specifying either a diagonal or unstructured innovation covariance matrix (via the `error_cov_type` argument). Example 1: VAR -------------- Below is a simple VARX(2) model in two endogenous variables and an exogenous series, but no constant term. Notice that we needed to allow for more iterations than the default (which is `maxiter=50`) in order for the likelihood estimation to converge. This is not unusual in VAR models which have to estimate a large number of parameters, often on a relatively small number of time series: this model, for example, estimates 27 parameters off of 75 observations of 3 variables. In [4]: ``` exog = endog['dln_consump'] mod = sm.tsa.VARMAX(endog[['dln_inv', 'dln_inc']], order=(2,0), trend='nc', exog=exog) res = mod.fit(maxiter=1000, disp=False) print(res.summary()) ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/tsa/base/tsa_model.py:171: ValueWarning: No frequency information was provided, so inferred frequency QS-OCT will be used. % freq, ValueWarning) ``` ``` Statespace Model Results ================================================================================== Dep. Variable: ['dln_inv', 'dln_inc'] No. Observations: 75 Model: VARX(2) Log Likelihood 348.270 Date: Mon, 14 May 2018 AIC -670.540 Time: 21:45:05 BIC -640.413 Sample: 04-01-1960 HQIC -658.511 - 10-01-1978 Covariance Type: opg =================================================================================== Ljung-Box (Q): 58.29, 41.41 Jarque-Bera (JB): 17.34, 10.35 Prob(Q): 0.03, 0.41 Prob(JB): 0.00, 0.01 Heteroskedasticity (H): 0.45, 1.13 Skew: 0.07, -0.55 Prob(H) (two-sided): 0.05, 0.77 Kurtosis: 5.35, 4.45 Results for equation dln_inv ==================================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------------ L1.dln_inv -0.2766 0.088 -3.141 0.002 -0.449 -0.104 L1.dln_inc 0.3241 0.621 0.522 0.601 -0.892 1.540 L2.dln_inv -0.1158 0.157 -0.738 0.461 -0.423 0.192 L2.dln_inc 0.4004 0.387 1.034 0.301 -0.359 1.159 beta.dln_consump 0.5566 0.753 0.739 0.460 -0.919 2.032 Results for equation dln_inc ==================================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------------ L1.dln_inv 0.0339 0.042 0.805 0.421 -0.049 0.117 L1.dln_inc 0.0928 0.132 0.700 0.484 -0.167 0.352 L2.dln_inv 0.0517 0.051 1.018 0.309 -0.048 0.151 L2.dln_inc 0.2731 0.169 1.617 0.106 -0.058 0.604 beta.dln_consump 0.4837 0.199 2.430 0.015 0.094 0.874 Error covariance matrix ============================================================================================ coef std err z P>\|z\| [0.025 0.975] -------------------------------------------------------------------------------------------- sqrt.var.dln_inv 0.0441 0.003 14.176 0.000 0.038 0.050 sqrt.cov.dln_inv.dln_inc 0.0013 0.002 0.553 0.581 -0.003 0.006 sqrt.var.dln_inc -0.0127 0.001 -12.409 0.000 -0.015 -0.011 ============================================================================================ Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step). ``` From the estimated VAR model, we can plot the impulse response functions of the endogenous variables. In [5]: ``` ax = res.impulse_responses(10, orthogonalized=True).plot(figsize=(13,3)) ax.set(xlabel='t', title='Responses to a shock to `dln_inv`'); ``` Example 2: VMA -------------- A vector moving average model can also be formulated. Below we show a VMA(2) on the same data, but where the innovations to the process are uncorrelated. In this example we leave out the exogenous regressor but now include the constant term. In [6]: ``` mod = sm.tsa.VARMAX(endog[['dln_inv', 'dln_inc']], order=(0,2), error_cov_type='diagonal') res = mod.fit(maxiter=1000, disp=False) print(res.summary()) ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/tsa/base/tsa_model.py:171: ValueWarning: No frequency information was provided, so inferred frequency QS-OCT will be used. % freq, ValueWarning) ``` ``` Statespace Model Results ================================================================================== Dep. Variable: ['dln_inv', 'dln_inc'] No. Observations: 75 Model: VMA(2) Log Likelihood 353.887 + intercept AIC -683.775 Date: Mon, 14 May 2018 BIC -655.965 Time: 21:45:10 HQIC -672.670 Sample: 04-01-1960 - 10-01-1978 Covariance Type: opg =================================================================================== Ljung-Box (Q): 68.73, 39.27 Jarque-Bera (JB): 12.41, 13.31 Prob(Q): 0.00, 0.50 Prob(JB): 0.00, 0.00 Heteroskedasticity (H): 0.44, 0.81 Skew: 0.05, -0.48 Prob(H) (two-sided): 0.04, 0.60 Kurtosis: 4.99, 4.83 Results for equation dln_inv ================================================================================= coef std err z P>\|z\| [0.025 0.975] --------------------------------------------------------------------------------- const 0.0182 0.005 3.794 0.000 0.009 0.028 L1.e(dln_inv) -0.2621 0.106 -2.482 0.013 -0.469 -0.055 L1.e(dln_inc) 0.5296 0.632 0.839 0.402 -0.708 1.768 L2.e(dln_inv) 0.0343 0.149 0.231 0.818 -0.257 0.326 L2.e(dln_inc) 0.1744 0.478 0.365 0.715 -0.762 1.111 Results for equation dln_inc ================================================================================= coef std err z P>\|z\| [0.025 0.975] --------------------------------------------------------------------------------- const 0.0207 0.002 13.120 0.000 0.018 0.024 L1.e(dln_inv) 0.0482 0.042 1.158 0.247 -0.033 0.130 L1.e(dln_inc) -0.0780 0.139 -0.560 0.576 -0.351 0.195 L2.e(dln_inv) 0.0175 0.042 0.412 0.680 -0.066 0.101 L2.e(dln_inc) 0.1247 0.152 0.820 0.412 -0.173 0.423 Error covariance matrix ================================================================================== coef std err z P>\|z\| [0.025 0.975] ---------------------------------------------------------------------------------- sigma2.dln_inv 0.0020 0.000 7.353 0.000 0.001 0.003 sigma2.dln_inc 0.0001 2.33e-05 5.833 0.000 9.01e-05 0.000 ================================================================================== Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step). ``` Caution: VARMA(p,q) specifications ---------------------------------- Although the model allows estimating VARMA(p,q) specifications, these models are not identified without additional restrictions on the representation matrices, which are not built-in. For this reason, it is recommended that the user proceed with error (and indeed a warning is issued when these models are specified). Nonetheless, they may in some circumstances provide useful information. In [7]: ``` mod = sm.tsa.VARMAX(endog[['dln_inv', 'dln_inc']], order=(1,1)) res = mod.fit(maxiter=1000, disp=False) print(res.summary()) ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/tsa/statespace/varmax.py:152: EstimationWarning: Estimation of VARMA(p,q) models is not generically robust, due especially to identification issues. EstimationWarning) /Users/taugspurger/sandbox/statsmodels/statsmodels/tsa/base/tsa_model.py:171: ValueWarning: No frequency information was provided, so inferred frequency QS-OCT will be used. % freq, ValueWarning) ``` ``` Statespace Model Results ================================================================================== Dep. Variable: ['dln_inv', 'dln_inc'] No. Observations: 75 Model: VARMA(1,1) Log Likelihood 354.283 + intercept AIC -682.567 Date: Mon, 14 May 2018 BIC -652.439 Time: 21:45:12 HQIC -670.537 Sample: 04-01-1960 - 10-01-1978 Covariance Type: opg =================================================================================== Ljung-Box (Q): 68.76, 39.00 Jarque-Bera (JB): 10.81, 14.04 Prob(Q): 0.00, 0.52 Prob(JB): 0.00, 0.00 Heteroskedasticity (H): 0.43, 0.91 Skew: 0.00, -0.45 Prob(H) (two-sided): 0.04, 0.81 Kurtosis: 4.86, 4.91 Results for equation dln_inv ================================================================================= coef std err z P>\|z\| [0.025 0.975] --------------------------------------------------------------------------------- const 0.0110 0.067 0.164 0.870 -0.120 0.142 L1.dln_inv -0.0055 0.722 -0.008 0.994 -1.421 1.410 L1.dln_inc 0.3587 2.788 0.129 0.898 -5.105 5.822 L1.e(dln_inv) -0.2537 0.734 -0.346 0.729 -1.691 1.184 L1.e(dln_inc) 0.1262 3.028 0.042 0.967 -5.809 6.061 Results for equation dln_inc ================================================================================= coef std err z P>\|z\| [0.025 0.975] --------------------------------------------------------------------------------- const 0.0165 0.028 0.584 0.559 -0.039 0.072 L1.dln_inv -0.0344 0.288 -0.119 0.905 -0.599 0.530 L1.dln_inc 0.2348 1.144 0.205 0.837 -2.008 2.478 L1.e(dln_inv) 0.0904 0.295 0.307 0.759 -0.487 0.668 L1.e(dln_inc) -0.2390 1.177 -0.203 0.839 -2.545 2.067 Error covariance matrix ============================================================================================ coef std err z P>\|z\| [0.025 0.975] -------------------------------------------------------------------------------------------- sqrt.var.dln_inv 0.0449 0.003 14.529 0.000 0.039 0.051 sqrt.cov.dln_inv.dln_inc 0.0017 0.003 0.641 0.522 -0.003 0.007 sqrt.var.dln_inc 0.0116 0.001 11.648 0.000 0.010 0.013 ============================================================================================ Warnings: [1] Covariance matrix calculated using the outer product of gradients (complex-step). ```	programming_docs
statsmodels Discrete Choice Models Overview Discrete Choice Models Overview =============================== In [1]: ``` from __future__ import print_function import numpy as np import statsmodels.api as sm ``` Data ---- Load data from Spector and Mazzeo (1980). Examples follow Greene's Econometric Analysis Ch. 21 (5th Edition). In [2]: ``` spector_data = sm.datasets.spector.load() spector_data.exog = sm.add_constant(spector_data.exog, prepend=False) ``` Inspect the data: In [3]: ``` print(spector_data.exog[:5,:]) print(spector_data.endog[:5]) ``` ``` [[ 2.66 20. 0. 1. ] [ 2.89 22. 0. 1. ] [ 3.28 24. 0. 1. ] [ 2.92 12. 0. 1. ] [ 4. 21. 0. 1. ]] [0. 0. 0. 0. 1.] ``` Linear Probability Model (OLS) ------------------------------ In [4]: ``` lpm_mod = sm.OLS(spector_data.endog, spector_data.exog) lpm_res = lpm_mod.fit() print('Parameters: ', lpm_res.params[:-1]) ``` ``` Parameters: [0.46385168 0.01049512 0.37855479] ``` Logit Model ----------- In [5]: ``` logit_mod = sm.Logit(spector_data.endog, spector_data.exog) logit_res = logit_mod.fit(disp=0) print('Parameters: ', logit_res.params) ``` ``` Parameters: [ 2.82611259 0.09515766 2.37868766 -13.02134686] ``` Marginal Effects In [6]: ``` margeff = logit_res.get_margeff() print(margeff.summary()) ``` ``` Logit Marginal Effects ===================================== Dep. Variable: y Method: dydx At: overall ============================================================================== dy/dx std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ x1 0.3626 0.109 3.313 0.001 0.148 0.577 x2 0.0122 0.018 0.686 0.493 -0.023 0.047 x3 0.3052 0.092 3.304 0.001 0.124 0.486 ============================================================================== ``` As in all the discrete data models presented below, we can print a nice summary of results: In [7]: ``` print(logit_res.summary()) ``` ``` Logit Regression Results ============================================================================== Dep. Variable: y No. Observations: 32 Model: Logit Df Residuals: 28 Method: MLE Df Model: 3 Date: Mon, 14 May 2018 Pseudo R-squ.: 0.3740 Time: 21:45:07 Log-Likelihood: -12.890 converged: True LL-Null: -20.592 LLR p-value: 0.001502 ============================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ x1 2.8261 1.263 2.238 0.025 0.351 5.301 x2 0.0952 0.142 0.672 0.501 -0.182 0.373 x3 2.3787 1.065 2.234 0.025 0.292 4.465 const -13.0213 4.931 -2.641 0.008 -22.687 -3.356 ============================================================================== ``` Probit Model ------------ In [8]: ``` probit_mod = sm.Probit(spector_data.endog, spector_data.exog) probit_res = probit_mod.fit() probit_margeff = probit_res.get_margeff() print('Parameters: ', probit_res.params) print('Marginal effects: ') print(probit_margeff.summary()) ``` ``` Optimization terminated successfully. Current function value: 0.400588 Iterations 6 Parameters: [ 1.62581004 0.05172895 1.42633234 -7.45231965] Marginal effects: Probit Marginal Effects ===================================== Dep. Variable: y Method: dydx At: overall ============================================================================== dy/dx std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ x1 0.3608 0.113 3.182 0.001 0.139 0.583 x2 0.0115 0.018 0.624 0.533 -0.025 0.048 x3 0.3165 0.090 3.508 0.000 0.140 0.493 ============================================================================== ``` Multinomial Logit ----------------- Load data from the American National Election Studies: In [9]: ``` anes_data = sm.datasets.anes96.load() anes_exog = anes_data.exog anes_exog = sm.add_constant(anes_exog, prepend=False) ``` Inspect the data: In [10]: ``` print(anes_data.exog[:5,:]) print(anes_data.endog[:5]) ``` ``` [[-2.30258509 7. 36. 3. 1. ] [ 5.24755025 3. 20. 4. 1. ] [ 3.43720782 2. 24. 6. 1. ] [ 4.4200447 3. 28. 6. 1. ] [ 6.46162441 5. 68. 6. 1. ]] [6. 1. 1. 1. 0.] ``` Fit MNL model: In [11]: ``` mlogit_mod = sm.MNLogit(anes_data.endog, anes_exog) mlogit_res = mlogit_mod.fit() print(mlogit_res.params) ``` ``` Optimization terminated successfully. Current function value: 1.548647 Iterations 7 [[-1.15359746e-02 -8.87506530e-02 -1.05966699e-01 -9.15567017e-02 -9.32846040e-02 -1.40880692e-01] [ 2.97714352e-01 3.91668642e-01 5.73450508e-01 1.27877179e+00 1.34696165e+00 2.07008014e+00] [-2.49449954e-02 -2.28978371e-02 -1.48512069e-02 -8.68134503e-03 -1.79040689e-02 -9.43264870e-03] [ 8.24914421e-02 1.81042758e-01 -7.15241904e-03 1.99827955e-01 2.16938850e-01 3.21925702e-01] [ 5.19655317e-03 4.78739761e-02 5.75751595e-02 8.44983753e-02 8.09584122e-02 1.08894083e-01] [-3.73401677e-01 -2.25091318e+00 -3.66558353e+00 -7.61384309e+00 -7.06047825e+00 -1.21057509e+01]] ``` Poisson ------- Load the Rand data. Note that this example is similar to Cameron and Trivedi's `Microeconometrics` Table 20.5, but it is slightly different because of minor changes in the data. In [12]: ``` rand_data = sm.datasets.randhie.load() rand_exog = rand_data.exog.view(float).reshape(len(rand_data.exog), -1) rand_exog = sm.add_constant(rand_exog, prepend=False) ``` Fit Poisson model: In [13]: ``` poisson_mod = sm.Poisson(rand_data.endog, rand_exog) poisson_res = poisson_mod.fit(method="newton") print(poisson_res.summary()) ``` ``` Optimization terminated successfully. Current function value: 3.091609 Iterations 6 Poisson Regression Results ============================================================================== Dep. Variable: y No. Observations: 20190 Model: Poisson Df Residuals: 20180 Method: MLE Df Model: 9 Date: Mon, 14 May 2018 Pseudo R-squ.: 0.06343 Time: 21:45:08 Log-Likelihood: -62420. converged: True LL-Null: -66647. LLR p-value: 0.000 ============================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ x1 -0.0525 0.003 -18.216 0.000 -0.058 -0.047 x2 -0.2471 0.011 -23.272 0.000 -0.268 -0.226 x3 0.0353 0.002 19.302 0.000 0.032 0.039 x4 -0.0346 0.002 -21.439 0.000 -0.038 -0.031 x5 0.2717 0.012 22.200 0.000 0.248 0.296 x6 0.0339 0.001 60.098 0.000 0.033 0.035 x7 -0.0126 0.009 -1.366 0.172 -0.031 0.005 x8 0.0541 0.015 3.531 0.000 0.024 0.084 x9 0.2061 0.026 7.843 0.000 0.155 0.258 const 0.7004 0.011 62.741 0.000 0.678 0.722 ============================================================================== ``` Negative Binomial ----------------- The negative binomial model gives slightly different results. In [14]: ``` mod_nbin = sm.NegativeBinomial(rand_data.endog, rand_exog) res_nbin = mod_nbin.fit(disp=False) print(res_nbin.summary()) ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/base/model.py:508: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals "Check mle_retvals", ConvergenceWarning) ``` ``` NegativeBinomial Regression Results ============================================================================== Dep. Variable: y No. Observations: 20190 Model: NegativeBinomial Df Residuals: 20180 Method: MLE Df Model: 9 Date: Mon, 14 May 2018 Pseudo R-squ.: 0.01845 Time: 21:45:08 Log-Likelihood: -43384. converged: False LL-Null: -44199. LLR p-value: 0.000 ============================================================================== coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ x1 -0.0579 0.006 -9.515 0.000 -0.070 -0.046 x2 -0.2678 0.023 -11.802 0.000 -0.312 -0.223 x3 0.0412 0.004 9.938 0.000 0.033 0.049 x4 -0.0381 0.003 -11.216 0.000 -0.045 -0.031 x5 0.2691 0.030 8.985 0.000 0.210 0.328 x6 0.0382 0.001 26.080 0.000 0.035 0.041 x7 -0.0441 0.020 -2.201 0.028 -0.083 -0.005 x8 0.0173 0.036 0.478 0.632 -0.054 0.088 x9 0.1782 0.074 2.399 0.016 0.033 0.324 const 0.6635 0.025 26.786 0.000 0.615 0.712 alpha 1.2930 0.019 69.477 0.000 1.256 1.329 ============================================================================== ``` Alternative solvers ------------------- The default method for fitting discrete data MLE models is Newton-Raphson. You can use other solvers by using the `method` argument: In [15]: ``` mlogit_res = mlogit_mod.fit(method='bfgs', maxiter=100) print(mlogit_res.summary()) ``` ``` Warning: Maximum number of iterations has been exceeded. Current function value: 1.548650 Iterations: 100 Function evaluations: 106 Gradient evaluations: 106 ``` ``` /Users/taugspurger/sandbox/statsmodels/statsmodels/base/model.py:508: ConvergenceWarning: Maximum Likelihood optimization failed to converge. Check mle_retvals "Check mle_retvals", ConvergenceWarning) ``` ``` MNLogit Regression Results ============================================================================== Dep. Variable: y No. Observations: 944 Model: MNLogit Df Residuals: 908 Method: MLE Df Model: 30 Date: Mon, 14 May 2018 Pseudo R-squ.: 0.1648 Time: 21:45:09 Log-Likelihood: -1461.9 converged: False LL-Null: -1750.3 LLR p-value: 1.827e-102 ============================================================================== y=1 coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ x1 -0.0116 0.034 -0.338 0.735 -0.079 0.056 x2 0.2973 0.094 3.175 0.001 0.114 0.481 x3 -0.0250 0.007 -3.825 0.000 -0.038 -0.012 x4 0.0821 0.074 1.116 0.264 -0.062 0.226 x5 0.0052 0.018 0.294 0.769 -0.029 0.040 const -0.3689 0.630 -0.586 0.558 -1.603 0.866 ------------------------------------------------------------------------------ y=2 coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ x1 -0.0888 0.039 -2.269 0.023 -0.166 -0.012 x2 0.3913 0.108 3.615 0.000 0.179 0.603 x3 -0.0229 0.008 -2.897 0.004 -0.038 -0.007 x4 0.1808 0.085 2.120 0.034 0.014 0.348 x5 0.0478 0.022 2.145 0.032 0.004 0.091 const -2.2451 0.763 -2.942 0.003 -3.741 -0.749 ------------------------------------------------------------------------------ y=3 coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ x1 -0.1062 0.057 -1.861 0.063 -0.218 0.006 x2 0.5730 0.159 3.614 0.000 0.262 0.884 x3 -0.0149 0.011 -1.313 0.189 -0.037 0.007 x4 -0.0075 0.126 -0.060 0.952 -0.255 0.240 x5 0.0575 0.034 1.711 0.087 -0.008 0.123 const -3.6592 1.156 -3.164 0.002 -5.926 -1.393 ------------------------------------------------------------------------------ y=4 coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ x1 -0.0914 0.044 -2.085 0.037 -0.177 -0.005 x2 1.2826 0.129 9.937 0.000 1.030 1.536 x3 -0.0085 0.008 -1.008 0.314 -0.025 0.008 x4 0.2012 0.094 2.136 0.033 0.017 0.386 x5 0.0850 0.026 3.240 0.001 0.034 0.136 const -7.6589 0.960 -7.982 0.000 -9.540 -5.778 ------------------------------------------------------------------------------ y=5 coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ x1 -0.0934 0.039 -2.374 0.018 -0.170 -0.016 x2 1.3451 0.117 11.485 0.000 1.116 1.575 x3 -0.0180 0.008 -2.362 0.018 -0.033 -0.003 x4 0.2161 0.085 2.542 0.011 0.049 0.383 x5 0.0808 0.023 3.517 0.000 0.036 0.126 const -7.0401 0.844 -8.344 0.000 -8.694 -5.387 ------------------------------------------------------------------------------ y=6 coef std err z P>\|z\| [0.025 0.975] ------------------------------------------------------------------------------ x1 -0.1409 0.042 -3.345 0.001 -0.224 -0.058 x2 2.0686 0.143 14.433 0.000 1.788 2.349 x3 -0.0095 0.008 -1.164 0.244 -0.025 0.006 x4 0.3216 0.091 3.532 0.000 0.143 0.500 x5 0.1087 0.025 4.299 0.000 0.059 0.158 const -12.0913 1.059 -11.415 0.000 -14.167 -10.015 ============================================================================== ``` falcon The Falcon Web Framework The Falcon Web Framework ======================== Release v2.0 ([Installation](user/install#install)) Falcon is a minimalist WSGI library for building speedy web APIs and app backends. We like to think of Falcon as the `Dieter Rams` of web frameworks. When it comes to building HTTP APIs, other frameworks weigh you down with tons of dependencies and unnecessary abstractions. Falcon cuts to the chase with a clean design that embraces HTTP and the REST architectural style. ``` class QuoteResource: def on_get(self, req, resp): """Handles GET requests""" quote = { 'quote': ( "I've always been more interested in " "the future than in the past." ), 'author': 'Grace Hopper' } resp.media = quote api = falcon.API() api.add_route('/quote', QuoteResource()) ``` What People are Saying ---------------------- “We have been using Falcon as a replacement for [framework] and we simply love the performance (three times faster) and code base size (easily half of our original [framework] code).” “Falcon looks great so far. I hacked together a quick test for a tiny server of mine and was ~40% faster with only 20 minutes of work.” “Falcon is rock solid and it’s fast.” “I’m loving #falconframework! Super clean and simple, I finally have the speed and flexibility I need!” “I feel like I’m just talking HTTP at last, with nothing in the middle. Falcon seems like the requests of backend.” “The source code for Falcon is so good, I almost prefer it to documentation. It basically can’t be wrong.” “What other framework has integrated support for 786 TRY IT NOW ?” Quick Links ----------- * [Read the docs](https://falcon.readthedocs.io/en/stable) * [Falcon add-ons and complementary packages](https://github.com/falconry/falcon/wiki) * [Falcon talks, podcasts, and blog posts](https://github.com/falconry/falcon/wiki/Talks-and-Podcasts) * [falconry/user for Falcon users](https://gitter.im/falconry/user) @ Gitter * [falconry/dev for Falcon contributors](https://gitter.im/falconry/dev) @ Gitter Features -------- Falcon tries to do as little as possible while remaining highly effective. * Routes based on URI templates RFC * REST-inspired mapping of URIs to resources * Global, resource, and method hooks * Idiomatic HTTP error responses * Full Unicode support * Intuitive request and response objects * Works great with async libraries like gevent * Minimal attack surface for writing secure APIs * 100% code coverage with a comprehensive test suite * No dependencies on other Python packages * Supports Python 2.7, 3.5+ * Compatible with PyPy Who’s Using Falcon? ------------------- Falcon is used around the world by a growing number of organizations, including: * 7ideas * Cronitor * EMC * Hurricane Electric * Leadpages * OpenStack * Rackspace * Shiftgig * tempfil.es * Opera Software If you are using the Falcon framework for a community or commercial project, please consider adding your information to our wiki under [Who’s Using Falcon?](https://github.com/falconry/falcon/wiki/Who's-using-Falcon%3F) You might also like to view our [Add-on Catalog](https://github.com/falconry/falcon/wiki/Add-on-Catalog), where you can find a list of add-ons maintained by the community. Documentation ------------- * [User Guide](https://falcon.readthedocs.io/en/2.0.0/user/index.html) + [Introduction](user/intro) + [Installation](user/install) + [Quickstart](user/quickstart) + [Tutorial](user/tutorial) + [FAQ](user/faq) * [Classes and Functions](https://falcon.readthedocs.io/en/2.0.0/api/index.html) + [The API Class](api/api) + [Request & Response](api/request_and_response) + [Cookies](api/cookies) + [Status Codes](api/status) + [Error Handling](api/errors) + [Media](api/media) + [Redirection](api/redirects) + [Middleware](api/middleware) + [Hooks](api/hooks) + [Routing](api/routing) + [Utilities](api/util) + [Testing](api/testing) * [Deployment Guide](https://falcon.readthedocs.io/en/2.0.0/deploy/index.html) + [Preamble & Disclaimer](deploy/intro) + [Deploying Falcon on Linux with NGINX and uWSGI](deploy/nginx-uwsgi) * [Community Guide](https://falcon.readthedocs.io/en/2.0.0/community/index.html) + [Get Help](https://falcon.readthedocs.io/en/2.0.0/community/help.html) + [Contribute to Falcon](https://falcon.readthedocs.io/en/2.0.0/community/contribute.html) + [FAQ](user/faq) * [Changelogs](https://falcon.readthedocs.io/en/2.0.0/changes/index.html) + [2.0.0](https://falcon.readthedocs.io/en/2.0.0/changes/2.0.0.html) + [1.4.1](https://falcon.readthedocs.io/en/2.0.0/changes/1.4.1.html) + [1.4.0](https://falcon.readthedocs.io/en/2.0.0/changes/1.4.0.html) + [1.3.0](https://falcon.readthedocs.io/en/2.0.0/changes/1.3.0.html) + [1.2.0](https://falcon.readthedocs.io/en/2.0.0/changes/1.2.0.html) + [1.1.0](https://falcon.readthedocs.io/en/2.0.0/changes/1.1.0.html) + [1.0.0](https://falcon.readthedocs.io/en/2.0.0/changes/1.0.0.html) + [0.3.0](https://falcon.readthedocs.io/en/2.0.0/changes/0.3.0.html) + [0.2.0](https://falcon.readthedocs.io/en/2.0.0/changes/0.2.0.html)	programming_docs
falcon Preamble & Disclaimer Preamble & Disclaimer ===================== Falcon conforms to the standard [WSGI protocol](https://www.python.org/dev/peps/pep-0333/) that most Python web applications have been using since 2003. If you have deployed Python applications like Django, Flask, or others, you will find yourself quite at home with Falcon and your standard Apache/mod\_wsgi, gunicorn, or other WSGI servers should suffice. There are many ways to deploy a Python application. The aim of these quickstarts is to simply get you up and running, not to give you a perfectly tuned or secure environment. You will almost certainly need to customize these configurations for any serious production deployment. falcon Deploying Falcon on Linux with NGINX and uWSGI Deploying Falcon on Linux with NGINX and uWSGI ============================================== NGINX is a powerful web server and reverse proxy and uWSGI is a fast and highly-configurable WSGI application server. Together, NGINX and uWSGI create a one-two punch of speed and functionality which will suffice for most applications. In addition, this stack provides the building blocks for a horizontally-scalable and highly-available (HA) production environment and the configuration below is just a starting point. This guide provides instructions for deploying to a Linux environment only. However, with a bit of effort you should be able to adapt this configuration to other operating systems, such as OpenBSD. Running your Application as a Different User -------------------------------------------- It is best to execute the application as a different OS user than the one who owns the source code for your application. The application user should NOT have write access to your source. This mitigates the chance that someone could write a malicious Python file to your source directory through an upload endpoint you might define; when your application restarts, the malicious file is loaded and proceeds to cause any number of BadThings:sup:(tm) to happen. ``` $ useradd myproject --create-home $ useradd myproject-runner --no-create-home ``` It is helpful to switch to the project user (myproject) and use the home directory as the application environment. If you are working on a remote server, switch to the myproject user and pull down the source code for your application. ``` $ git clone [email protected]/myorg/myproject.git /home/myproject/src ``` Note You could use a tarball, zip file, scp or any other means to get your source onto a server. Next, create a virtual environment which can be used to install your dependencies. ``` # For Python 3 $ python3 -m venv /home/myproject/venv # For Python 2 $ virtualenv /home/myproject/venv ``` Then install your dependencies. ``` $ /home/myproject/venv/bin/pip install -r /home/myproject/src/requirements.txt $ /home/myproject/venv/bin/pip install -e /home/myproject/src $ /home/myproject/venv/bin/pip install uwsgi ``` Note The exact commands for creating a virtual environment might differ based on the Python version you are using and your operating system. At the end of the day the application needs a virtualenv in /home/myproject/venv with the project dependencies installed. Use the `pip` binary within the virtual environment by `source venv/bin/activate` or using the full path. Preparing your Application for Service -------------------------------------- For the purposes of this tutorial, we’ll assume that you have implemented a way to configure your application, such as with a `create_api()` function or a module-level script. This role of this function or script is to supply an instance of [`falcon.API`](../api/api#falcon.API "falcon.API"), which implements the standard WSGI callable interface. You will need to expose the [`falcon.API`](../api/api#falcon.API "falcon.API") instance in some way so that uWSGI can find it. For this tutorial we recommend creating a `wsgi.py` file. Modify the logic of the following example file to properly configure your application. Ensure that you expose a variable called `application` which is assigned to your [`falcon.API`](../api/api#falcon.API "falcon.API") instance. /home/myproject/src/wsgi.py ``` import os import myproject # Replace with your app's method of configuration config = myproject.get_config(os.environ['MYPROJECT_CONFIG']) # uWSGI will look for this variable application = myproject.create_api(config) ``` Note that in the above example, the WSGI callable is simple assigned to a variable, `application`, rather than being passed to a self-hosting WSGI server such as `wsgiref.simple_server.make_server`. Starting an independent WSGI server in your `wsgi.py` file will render unexpected results. Deploying Falcon behind uWSGI ----------------------------- With your `wsgi.py` file in place, it is time to configure uWSGI. Start by creating a simple `uwsgi.ini` file. In general, you shouldn’t commit this file to source control; it should be generated from a template by your deployment toolchain according to the target environment (number of CPUs, etc.). This configuration, when executed, will create a new uWSGI server backed by your `wsgi.py` file and listening at `12.0.0.1:8080`. /home/myproject/src/uwsgi.ini ``` [uwsgi] master = 1 vacuum = true socket = 127.0.0.1:8080 enable-threads = true thunder-lock = true threads = 2 processes = 2 virtualenv = /home/myproject/venv wsgi-file = /home/myproject/src/wsgi.py chdir = /home/myproject/src uid = myproject-runner gid = myproject-runner ``` Note Threads vs. Processes There are many questions to consider when deciding how to manage the processes that actually run your Python code. Are you generally CPU bound or IO bound? Is your application thread-safe? How many CPU’s do you have? What system are you on? Do you need an in-process cache? The configuration presented here enables both threads and processes. However, you will have to experiment and do some research to understand your application’s unique requirements, and then tailor your uWSGI configuration accordingly. Generally speaking, uWSGI is flexible enough to support most types of applications. Note TCP vs. UNIX Sockets NGINX and uWSGI can communicate via normal TCP (using an IP address) or UNIX sockets (using a socket file). TCP sockets are easier to set up and generally work for simple deployments. If you want to have finer control over which processes, users, or groups may access the uWSGI application, or you are looking for a bit of a speed boost, consider using UNIX sockets. uWSGI can automatically drop privileges with `chmod-socket` and switch users with `chown-socket`. The `uid` and `gid` settings, as shown above, are critical to securing your deployment. These values control the OS-level user and group the server will use to execute the application. The specified OS user and group should not have write permissions to the source directory. In this case, we use the `myproject-runner` user that was created earlier for this purpose. You can now start uWSGI like this: ``` $ /home/myproject/venv/bin/uwsgi -c uwsgi.ini ``` If everything goes well, you should see something like this: ``` * Operational MODE: preforking+threaded * ... * uWSGI is running in multiple interpreter mode * ... spawned uWSGI master process (pid: 91828) spawned uWSGI worker 1 (pid: 91866, cores: 2) spawned uWSGI worker 2 (pid: 91867, cores: 2) ``` Note It is always a good idea to keep an eye on the uWSGI logs, as they will contain exceptions and other information from your application that can help shed some light on unexpected behaviors. Connecting NGINX and uWSGI -------------------------- Although uWSGI may serve HTTP requests directly, it can be helpful to use a reverse proxy, such as NGINX, to offload TLS negotiation, static file serving, etc. NGINX natively supports [the uwsgi protocol](https://uwsgi-docs.readthedocs.io/en/latest/Protocol.html), for efficiently proxying requests to uWSGI. In NGINX parlance, we will create an “upstream” and direct that upstream (via a TCP socket) to our now-running uWSGI application. Before proceeding, install NGINX according to [the instructions for your platform](https://docs.nginx.com/nginx/admin-guide/installing-nginx/installing-nginx-open-source/). Then, create an NGINX conf file that looks something like this: /etc/nginx/sites-avaiable/myproject.conf ``` server { listen 80; server_name myproject.com; access_log /var/log/nginx/myproject-access.log; error_log /var/log/nginx/myproject-error.log warn; location / { uwsgi_pass 127.0.0.1:8080 include uwsgi_params; } } ``` Finally, start (or restart) NGINX: ``` $ sudo service start nginx ``` You should now have a working application. Check your uWSGI and NGINX logs for errors if the application does not start. Further Considerations ---------------------- We did not explain how to configure TLS (HTTPS) for NGINX, leaving that as an exercise for the reader. However, we do recommend using Let’s Encrypt, which offers free, short-term certificates with auto-renewal. Visit the [Let’s Encrypt site](https://certbot.eff.org/) to learn how to integrate their service directly with NGINX. In addition to setting up NGINX and uWSGI to run your application, you will of course need to deploy a database server or any other services required by your application. Due to the wide variety of options and considerations in this space, we have chosen not to include ancillary services in this guide. However, the Falcon community is always happy to help with deployment questions, so [please don’t hesitate to ask](https://falcon.readthedocs.io/en/stable/community/help.html#chat). falcon Quickstart Quickstart ========== If you haven’t done so already, please take a moment to [install](install#install) the Falcon web framework before continuing. Learning by Example ------------------- Here is a simple example from Falcon’s README, showing how to get started writing an API: ``` # things.py # Let's get this party started! import falcon # Falcon follows the REST architectural style, meaning (among # other things) that you think in terms of resources and state # transitions, which map to HTTP verbs. class ThingsResource(object): def on_get(self, req, resp): """Handles GET requests""" resp.status = falcon.HTTP_200 # This is the default status resp.body = ('\nTwo things awe me most, the starry sky ' 'above me and the moral law within me.\n' '\n' ' ~ Immanuel Kant\n\n') # falcon.API instances are callable WSGI apps app = falcon.API() # Resources are represented by long-lived class instances things = ThingsResource() # things will handle all requests to the '/things' URL path app.add_route('/things', things) ``` You can run the above example using any WSGI server, such as uWSGI or Gunicorn. For example: ``` $ pip install gunicorn $ gunicorn things:app ``` On Windows where Gunicorn and uWSGI don’t work yet you can use Waitress server ``` $ pip install waitress $ waitress-serve --port=8000 things:app ``` Then, in another terminal: ``` $ curl localhost:8000/things ``` Curl is a bit of a pain to use, so let’s install [HTTPie](https://github.com/jkbr/httpie) and use it from now on. ``` $ pip install --upgrade httpie $ http localhost:8000/things ``` More Features ------------- Here is a more involved example that demonstrates reading headers and query parameters, handling errors, and working with request and response bodies. ``` import json import logging import uuid from wsgiref import simple_server import falcon import requests class StorageEngine(object): def get_things(self, marker, limit): return [{'id': str(uuid.uuid4()), 'color': 'green'}] def add_thing(self, thing): thing['id'] = str(uuid.uuid4()) return thing class StorageError(Exception): @staticmethod def handle(ex, req, resp, params): description = ('Sorry, couldn\'t write your thing to the ' 'database. It worked on my box.') raise falcon.HTTPError(falcon.HTTP_725, 'Database Error', description) class SinkAdapter(object): engines = { 'ddg': 'https://duckduckgo.com', 'y': 'https://search.yahoo.com/search', } def __call__(self, req, resp, engine): url = self.engines[engine] params = {'q': req.get_param('q', True)} result = requests.get(url, params=params) resp.status = str(result.status_code) + ' ' + result.reason resp.content_type = result.headers['content-type'] resp.body = result.text class AuthMiddleware(object): def process_request(self, req, resp): token = req.get_header('Authorization') account_id = req.get_header('Account-ID') challenges = ['Token type="Fernet"'] if token is None: description = ('Please provide an auth token ' 'as part of the request.') raise falcon.HTTPUnauthorized('Auth token required', description, challenges, href='http://docs.example.com/auth') if not self._token_is_valid(token, account_id): description = ('The provided auth token is not valid. ' 'Please request a new token and try again.') raise falcon.HTTPUnauthorized('Authentication required', description, challenges, href='http://docs.example.com/auth') def _token_is_valid(self, token, account_id): return True # Suuuuuure it's valid... class RequireJSON(object): def process_request(self, req, resp): if not req.client_accepts_json: raise falcon.HTTPNotAcceptable( 'This API only supports responses encoded as JSON.', href='http://docs.examples.com/api/json') if req.method in ('POST', 'PUT'): if 'application/json' not in req.content_type: raise falcon.HTTPUnsupportedMediaType( 'This API only supports requests encoded as JSON.', href='http://docs.examples.com/api/json') class JSONTranslator(object): # NOTE: Starting with Falcon 1.3, you can simply # use req.media and resp.media for this instead. def process_request(self, req, resp): # req.stream corresponds to the WSGI wsgi.input environ variable, # and allows you to read bytes from the request body. # # See also: PEP 3333 if req.content_length in (None, 0): # Nothing to do return body = req.stream.read() if not body: raise falcon.HTTPBadRequest('Empty request body', 'A valid JSON document is required.') try: req.context.doc = json.loads(body.decode('utf-8')) except (ValueError, UnicodeDecodeError): raise falcon.HTTPError(falcon.HTTP_753, 'Malformed JSON', 'Could not decode the request body. The ' 'JSON was incorrect or not encoded as ' 'UTF-8.') def process_response(self, req, resp, resource): if not hasattr(resp.context, 'result'): return resp.body = json.dumps(resp.context.result) def max_body(limit): def hook(req, resp, resource, params): length = req.content_length if length is not None and length > limit: msg = ('The size of the request is too large. The body must not ' 'exceed ' + str(limit) + ' bytes in length.') raise falcon.HTTPPayloadTooLarge( 'Request body is too large', msg) return hook class ThingsResource(object): def __init__(self, db): self.db = db self.logger = logging.getLogger('thingsapp.' + __name__) def on_get(self, req, resp, user_id): marker = req.get_param('marker') or '' limit = req.get_param_as_int('limit') or 50 try: result = self.db.get_things(marker, limit) except Exception as ex: self.logger.error(ex) description = ('Aliens have attacked our base! We will ' 'be back as soon as we fight them off. ' 'We appreciate your patience.') raise falcon.HTTPServiceUnavailable( 'Service Outage', description, 30) # An alternative way of doing DRY serialization would be to # create a custom class that inherits from falcon.Request. This # class could, for example, have an additional 'doc' property # that would serialize to JSON under the covers. # # NOTE: Starting with Falcon 1.3, you can simply # use resp.media for this instead. resp.context.result = result resp.set_header('Powered-By', 'Falcon') resp.status = falcon.HTTP_200 @falcon.before(max_body(64 * 1024)) def on_post(self, req, resp, user_id): try: doc = req.context.doc except AttributeError: raise falcon.HTTPBadRequest( 'Missing thing', 'A thing must be submitted in the request body.') proper_thing = self.db.add_thing(doc) resp.status = falcon.HTTP_201 resp.location = '/%s/things/%s' % (user_id, proper_thing['id']) # Configure your WSGI server to load "things.app" (app is a WSGI callable) app = falcon.API(middleware=[ AuthMiddleware(), RequireJSON(), JSONTranslator(), ]) db = StorageEngine() things = ThingsResource(db) app.add_route('/{user_id}/things', things) # If a responder ever raised an instance of StorageError, pass control to # the given handler. app.add_error_handler(StorageError, StorageError.handle) # Proxy some things to another service; this example shows how you might # send parts of an API off to a legacy system that hasn't been upgraded # yet, or perhaps is a single cluster that all data centers have to share. sink = SinkAdapter() app.add_sink(sink, r'/search/(?P<engine>ddg\|y)\Z') # Useful for debugging problems in your API; works with pdb.set_trace(). You # can also use Gunicorn to host your app. Gunicorn can be configured to # auto-restart workers when it detects a code change, and it also works # with pdb. if __name__ == '__main__': httpd = simple_server.make_server('127.0.0.1', 8000, app) httpd.serve_forever() ``` To test this example go to the another terminal and run: ``` $ http localhost:8000/1/things authorization:custom-token ``` falcon Installation Installation ============ PyPy ---- [PyPy](http://pypy.org/) is the fastest way to run your Falcon app. Both PyPy2.7 and PyPy3.5 are supported as of PyPy v5.10. ``` $ pip install falcon ``` Or, to install the latest beta or release candidate, if any: ``` $ pip install --pre falcon ``` CPython ------- Falcon also fully supports [CPython](https://www.python.org/downloads/) 2.7 and 3.5+. Universal and manylinux wheels are available on PyPI for the Falcon framework. Installation is as simple as: ``` $ pip install falcon ``` Installing one of the pre-built Falcon wheels is a great way to get up and running quickly. However, when deploying your application in production, you may wish to compile Falcon via Cython yourself, using the target system’s native toolchain. The following commands tell pip to install Cython, and then to invoke Falcon’s `setup.py`, which will in turn detect the presence of Cython and then compile (AKA cythonize) the Falcon framework with the system’s default C compiler. ``` $ pip install cython $ pip install --no-binary :all: falcon ``` If you want to verify that Cython is being invoked, simply pass `-v` to pip in order to echo the compilation commands: ``` $ pip install -v --no-binary :all: falcon ``` Installing on OS X Xcode Command Line Tools are required to compile Cython. Install them with this command: ``` $ xcode-select --install ``` The Clang compiler treats unrecognized command-line options as errors, for example: ``` clang: error: unknown argument: '-mno-fused-madd' [-Wunused-command-line-argument-hard-error-in-future] ``` You might also see warnings about unused functions. You can work around these issues by setting additional Clang C compiler flags as follows: ``` $ export CFLAGS="-Qunused-arguments -Wno-unused-function" ``` Dependencies ------------ Falcon does not require the installation of any other packages, although if Cython has been installed into the environment, it will be used to optimize the framework as explained above. WSGI Server ----------- Falcon speaks WSGI, and so in order to serve a Falcon app, you will need a WSGI server. Gunicorn and uWSGI are some of the more popular ones out there, but anything that can load a WSGI app will do. All Windows developers can use Waitress production-quality pure-Python WSGI server with very acceptable performance. Unfortunately Gunicorn is still not working on Windows and uWSGI need to have Cygwin on Windows installed. Waitress can be good alternative for Windows users if they want quick start using Falcon on it. ``` $ pip install [gunicorn\|uwsgi\|waitress] ``` Source Code ----------- Falcon [lives on GitHub](https://github.com/falconry/falcon), making the code easy to browse, download, fork, etc. Pull requests are always welcome! Also, please remember to star the project if it makes you happy. :) Once you have cloned the repo or downloaded a tarball from GitHub, you can install Falcon like this: ``` $ cd falcon $ pip install . ``` Or, if you want to edit the code, first fork the main repo, clone the fork to your desktop, and then run the following to install it using symbolic linking, so that when you change your code, the changes will be automagically available to your app without having to reinstall the package: ``` $ cd falcon $ pip install -e . ``` You can manually test changes to the Falcon framework by switching to the directory of the cloned repo and then running pytest: ``` $ cd falcon $ pip install -r requirements/tests $ pytest tests ``` Or, to run the default set of tests: ``` $ pip install tox && tox ``` Tip See also the [tox.ini](https://github.com/falconry/falcon/blob/master/tox.ini) file for a full list of available environments. Finally, to build Falcon’s docs from source, simply run: ``` $ pip install tox && tox -e docs ``` Once the docs have been built, you can view them by opening the following index page in your browser. On OS X it’s as simple as: ``` $ open docs/_build/html/index.html ``` Or on Linux: ``` $ xdg-open docs/_build/html/index.html ```	programming_docs
falcon Tutorial Tutorial ======== In this tutorial we’ll walk through building an API for a simple image sharing service. Along the way, we’ll discuss Falcon’s major features and introduce the terminology used by the framework. First Steps ----------- The first thing we’ll do is [install](install#install) Falcon inside a fresh [virtualenv](http://docs.python-guide.org/en/latest/dev/virtualenvs/). To that end, let’s create a new project folder called “look”, and set up a virtual environment within it that we can use for the tutorial: ``` $ mkdir look $ cd look $ virtualenv .venv $ source .venv/bin/activate $ pip install falcon ``` It’s customary for the project’s top-level module to be called the same as the project, so let’s create another “look” folder inside the first one and mark it as a python module by creating an empty `__init__.py` file in it: ``` $ mkdir look $ touch look/__init__.py ``` Next, let’s create a new file that will be the entry point into your app: ``` $ touch look/app.py ``` The file hierarchy should now look like this: ``` look ├── .venv └── look ├── __init__.py └── app.py ``` Now, open `app.py` in your favorite text editor and add the following lines: ``` import falcon api = application = falcon.API() ``` This code creates your WSGI application and aliases it as `api`. You can use any variable names you like, but we’ll use `application` since that is what Gunicorn, by default, expects it to be called (we’ll see how this works in the next section of the tutorial). Note A WSGI application is just a callable with a well-defined signature so that you can host the application with any web server that understands the [WSGI protocol](http://legacy.python.org/dev/peps/pep-3333/). Next let’s take a look at the [`falcon.API`](../api/api#falcon.API "falcon.API") class. Install [IPython](http://ipython.org/) and fire it up: ``` $ pip install ipython $ ipython ``` Now, type the following to introspect the [`falcon.API`](../api/api#falcon.API "falcon.API") callable: ``` In [1]: import falcon In [2]: falcon.API.__call__? ``` Alternatively, you can use the standard Python `help()` function: ``` In [3]: help(falcon.API.__call__) ``` Note the method signature. `env` and `start_response` are standard WSGI params. Falcon adds a thin abstraction on top of these params so you don’t have to interact with them directly. The Falcon framework contains extensive inline documentation that you can query using the above technique. Tip In addition to [IPython](http://ipython.org/), the Python community maintains several other super-powered REPLs that you may wish to try, including [bpython](http://bpython-interpreter.org/) and [ptpython](https://github.com/jonathanslenders/ptpython). Hosting Your App ---------------- Now that you have a simple Falcon app, you can take it for a spin with a WSGI server. Python includes a reference server for self-hosting, but let’s use something more robust that you might use in production. Open a new terminal and run the following: ``` $ source .venv/bin/activate $ pip install gunicorn $ gunicorn --reload look.app ``` (Note the use of the `--reload` option to tell Gunicorn to reload the app whenever its code changes.) If you are a Windows user, Waitress can be used in lieu of Gunicorn, since the latter doesn’t work under Windows: ``` $ pip install waitress $ waitress-serve --port=8000 look.app:api ``` Now, in a different terminal, try querying the running app with curl: ``` $ curl -v localhost:8000 ``` You should get a 404. That’s actually OK, because we haven’t specified any routes yet. Falcon includes a default 404 response handler that will fire for any requested path for which a route does not exist. While curl certainly gets the job done, it can be a bit crufty to use. [HTTPie](https://github.com/jkbr/httpie) is a modern, user-friendly alternative. Let’s install HTTPie and use it from now on: ``` $ source .venv/bin/activate $ pip install httpie $ http localhost:8000 ``` Creating Resources ------------------ Falcon’s design borrows several key concepts from the REST architectural style. Central to both REST and the Falcon framework is the concept of a “resource”. Resources are simply all the things in your API or application that can be accessed by a URL. For example, an event booking application may have resources such as “ticket” and “venue”, while a video game backend may have resources such as “achievements” and “player”. URLs provide a way for the client to uniquely identify resources. For example, `/players` might identify the “list of all players” resource, while `/players/45301f54` might identify the “individual player with ID 45301f54”, and `/players/45301f54/achievements` the “list of all achievements for the player resource with ID 45301f54”. ``` POST /players/45301f54/achievements └──────┘ └────────────────────────────────┘ Action Resource Identifier ``` In the REST architectural style, the URL only identifies the resource; it does not specify what action to take on that resource. Instead, users choose from a set of standard methods. For HTTP, these are the familiar GET, POST, HEAD, etc. Clients can query a resource to discover which methods it supports. Note This is one of the key differences between the REST and RPC architectural styles. REST applies a standard set of verbs across any number of resources, as opposed to having each application define its own unique set of methods. Depending on the requested action, the server may or may not return a representation to the client. Representations may be encoded in any one of a number of Internet media types, such as JSON and HTML. Falcon uses Python classes to represent resources. In practice, these classes act as controllers in your application. They convert an incoming request into one or more internal actions, and then compose a response back to the client based on the results of those actions. ``` ┌────────────┐ request → │ │ │ Resource │ ↻ Orchestrate the requested action │ Controller │ ↻ Compose the result response ← │ │ └────────────┘ ``` A resource in Falcon is just a regular Python class that includes one or more methods representing the standard HTTP verbs supported by that resource. Each requested URL is mapped to a specific resource. Since we are building an image-sharing API, let’s start by creating an “images” resource. Create a new module, `images.py` next to `app.py`, and add the following code to it: ``` import json import falcon class Resource(object): def on_get(self, req, resp): doc = { 'images': [ { 'href': '/images/1eaf6ef1-7f2d-4ecc-a8d5-6e8adba7cc0e.png' } ] } # Create a JSON representation of the resource resp.body = json.dumps(doc, ensure_ascii=False) # The following line can be omitted because 200 is the default # status returned by the framework, but it is included here to # illustrate how this may be overridden as needed. resp.status = falcon.HTTP_200 ``` As you can see, `Resource` is just a regular class. You can name the class anything you like. Falcon uses duck-typing, so you don’t need to inherit from any sort of special base class. The image resource above defines a single method, `on_get()`. For any HTTP method you want your resource to support, simply add an `on_()` method to the class, where `` is any one of the standard HTTP methods, lowercased (e.g., `on_get()`, `on_put()`, `on_head()`, etc.). Note Supported HTTP methods are those specified in [RFC 7231](https://tools.ietf.org/html/rfc7231) and [RFC 5789](https://tools.ietf.org/html/rfc5789). This includes GET, HEAD, POST, PUT, DELETE, CONNECT, OPTIONS, TRACE, and PATCH. We call these well-known methods “responders”. Each responder takes (at least) two params, one representing the HTTP request, and one representing the HTTP response to that request. By convention, these are called `req` and `resp`, respectively. Route templates and hooks can inject extra params, as we shall see later on. Right now, the image resource responds to GET requests with a simple `200 OK` and a JSON body. Falcon’s Internet media type defaults to `application/json` but you can set it to whatever you like. Noteworthy JSON alternatives include [YAML](http://yaml.org/) and [MessagePack](http://msgpack.org/). Next let’s wire up this resource and see it in action. Go back to `app.py` and modify it so that it looks something like this: ``` import falcon from .images import Resource api = application = falcon.API() images = Resource() api.add_route('/images', images) ``` Now, when a request comes in for `/images`, Falcon will call the responder on the images resource that corresponds to the requested HTTP method. Let’s try it. Restart Gunicorn (unless you’re using `--reload`), and send a GET request to the resource: ``` $ http localhost:8000/images ``` You should receive a `200 OK` response, including a JSON-encoded representation of the “images” resource. Note `add_route()` expects an instance of the resource class, not the class itself. The same instance is used for all requests. This strategy improves performance and reduces memory usage, but this also means that if you host your application with a threaded web server, resources and their dependencies must be thread-safe. So far we have only implemented a responder for GET. Let’s see what happens when a different method is requested: ``` $ http PUT localhost:8000/images ``` This time you should get back `405 Method Not Allowed`, since the resource does not support the `PUT` method. Note the value of the Allow header: ``` allow: GET, OPTIONS ``` This is generated automatically by Falcon based on the set of methods implemented by the target resource. If a resource does not include its own OPTIONS responder, the framework provides a default implementation. Therefore, OPTIONS is always included in the list of allowable methods. Note If you have a lot of experience with other Python web frameworks, you may be used to using decorators to set up your routes. Falcon’s particular approach provides the following benefits: * The URL structure of the application is centralized. This makes it easier to reason about and maintain the API over time. * The use of resource classes maps somewhat naturally to the REST architectural style, in which a URL is used to identify a resource only, not the action to perform on that resource. * Resource class methods provide a uniform interface that does not have to be reinvented (and maintained) from class to class and application to application. Next, just for fun, let’s modify our resource to use [MessagePack](http://msgpack.org/) instead of JSON. Start by installing the relevant package: ``` $ pip install msgpack-python ``` Then, update the responder to use the new media type: ``` import falcon import msgpack class Resource(object): def on_get(self, req, resp): doc = { 'images': [ { 'href': '/images/1eaf6ef1-7f2d-4ecc-a8d5-6e8adba7cc0e.png' } ] } resp.data = msgpack.packb(doc, use_bin_type=True) resp.content_type = falcon.MEDIA_MSGPACK resp.status = falcon.HTTP_200 ``` Note the use of `resp.data` in lieu of `resp.body`. If you assign a bytestring to the latter, Falcon will figure it out, but you can realize a small performance gain by assigning directly to `resp.data`. Also note the use of `falcon.MEDIA_MSGPACK`. The `falcon` module provides a number of constants for common media types, including `falcon.MEDIA_JSON`, `falcon.MEDIA_MSGPACK`, `falcon.MEDIA_YAML`, `falcon.MEDIA_XML`, `falcon.MEDIA_HTML`, `falcon.MEDIA_JS`, `falcon.MEDIA_TEXT`, `falcon.MEDIA_JPEG`, `falcon.MEDIA_PNG`, and `falcon.MEDIA_GIF`. Restart Gunicorn (unless you’re using `--reload`), and then try sending a GET request to the revised resource: ``` $ http localhost:8000/images ``` Testing your application ------------------------ Fully exercising your code is critical to creating a robust application. Let’s take a moment to write a test for what’s been implemented so far. First, create a `tests` directory with `__init__.py` and a test module (`test_app.py`) inside it. The project’s structure should now look like this: ``` look ├── .venv ├── look │ ├── __init__.py │ ├── app.py │ └── images.py └── tests ├── __init__.py └── test_app.py ``` Falcon supports [testing](../api/testing#testing) its [`API`](../api/api#falcon.API "falcon.API") object by simulating HTTP requests. Tests can either be written using Python’s standard [`unittest`](https://docs.python.org/3/library/unittest.html#module-unittest "(in Python v3.7)") module, or with any of a number of third-party testing frameworks, such as [pytest](http://docs.pytest.org/en/latest/). For this tutorial we’ll use [pytest](http://docs.pytest.org/en/latest/) since it allows for more pythonic test code as compared to the JUnit-inspired [`unittest`](https://docs.python.org/3/library/unittest.html#module-unittest "(in Python v3.7)") module. Let’s start by installing the [pytest](http://docs.pytest.org/en/latest/) package: ``` $ pip install pytest ``` Next, edit `test_app.py` to look like this: ``` import falcon from falcon import testing import msgpack import pytest from look.app import api @pytest.fixture def client(): return testing.TestClient(api) # pytest will inject the object returned by the "client" function # as an additional parameter. def test_list_images(client): doc = { 'images': [ { 'href': '/images/1eaf6ef1-7f2d-4ecc-a8d5-6e8adba7cc0e.png' } ] } response = client.simulate_get('/images') result_doc = msgpack.unpackb(response.content, raw=False) assert result_doc == doc assert response.status == falcon.HTTP_OK ``` From the main project directory, exercise your new test by running pytest against the `tests` directory: ``` $ pytest tests ``` If pytest reports any errors, take a moment to fix them up before proceeding to the next section of the tutorial. Request and Response Objects ---------------------------- Each responder in a resource receives a `Request` object that can be used to read the headers, query parameters, and body of the request. You can use the standard `help()` function or IPython’s magic `?` function to list the attributes and methods of Falcon’s `Request` class: ``` In [1]: import falcon In [2]: falcon.Request? ``` Each responder also receives a `Response` object that can be used for setting the status code, headers, and body of the response: ``` In [3]: falcon.Response? ``` This will be useful when creating a POST endpoint in the application that can add new image resources to our collection. We’ll tackle this functionality next. We’ll use TDD this time around, to demonstrate how to apply this particular testing strategy when developing a Falcon application. Via tests, we’ll first define precisely what we want the application to do, and then code until the tests tell us that we’re done. Note To learn more about TDD, you may wish to check out one of the many books on the topic, such as [Test Driven Development with Python](http://www.obeythetestinggoat.com/pages/book.html). The examples in this particular book use the Django framework and even JavaScript, but the author covers a number of testing principles that are widely applicable. Let’s start by adding an additional import statement to `test_app.py`. We need to import two modules from `unittest.mock` if you are using Python 3, or from `mock` if you are using Python 2. ``` # Python 3 from unittest.mock import mock_open, call # Python 2 from mock import mock_open, call ``` For Python 2, you will also need to install the `mock` package: ``` $ pip install mock ``` Now add the following test: ``` # "monkeypatch" is a special built-in pytest fixture that can be # used to install mocks. def test_posted_image_gets_saved(client, monkeypatch): mock_file_open = mock_open() monkeypatch.setattr('io.open', mock_file_open) fake_uuid = '123e4567-e89b-12d3-a456-426655440000' monkeypatch.setattr('uuid.uuid4', lambda: fake_uuid) # When the service receives an image through POST... fake_image_bytes = b'fake-image-bytes' response = client.simulate_post( '/images', body=fake_image_bytes, headers={'content-type': 'image/png'} ) # ...it must return a 201 code, save the file, and return the # image's resource location. assert response.status == falcon.HTTP_CREATED assert call().write(fake_image_bytes) in mock_file_open.mock_calls assert response.headers['location'] == '/images/{}.png'.format(fake_uuid) ``` As you can see, this test relies heavily on mocking, making it somewhat fragile in the face of implementation changes. We’ll revisit this later. For now, run the tests again and watch to make sure they fail. A key step in the TDD workflow is verifying that your tests do not pass before moving on to the implementation: ``` $ pytest tests ``` To make the new test pass, we need to add a new method for handling POSTs. Open `images.py` and add a POST responder to the `Resource` class as follows: ``` import io import os import uuid import mimetypes import falcon import msgpack class Resource(object): _CHUNK_SIZE_BYTES = 4096 # The resource object must now be initialized with a path used during POST def __init__(self, storage_path): self._storage_path = storage_path # This is the method we implemented before def on_get(self, req, resp): doc = { 'images': [ { 'href': '/images/1eaf6ef1-7f2d-4ecc-a8d5-6e8adba7cc0e.png' } ] } resp.data = msgpack.packb(doc, use_bin_type=True) resp.content_type = falcon.MEDIA_MSGPACK resp.status = falcon.HTTP_200 def on_post(self, req, resp): ext = mimetypes.guess_extension(req.content_type) name = '{uuid}{ext}'.format(uuid=uuid.uuid4(), ext=ext) image_path = os.path.join(self._storage_path, name) with io.open(image_path, 'wb') as image_file: while True: chunk = req.stream.read(self._CHUNK_SIZE_BYTES) if not chunk: break image_file.write(chunk) resp.status = falcon.HTTP_201 resp.location = '/images/' + name ``` As you can see, we generate a unique name for the image, and then write it out by reading from `req.stream`. It’s called `stream` instead of `body` to emphasize the fact that you are really reading from an input stream; by default Falcon does not spool or decode request data, instead giving you direct access to the incoming binary stream provided by the WSGI server. Note the use of `falcon.HTTP_201` for setting the response status to “201 Created”. We could have also used the `falcon.HTTP_CREATED` alias. For a full list of predefined status strings, simply call `help()` on `falcon.status_codes`: ``` In [4]: help(falcon.status_codes) ``` The last line in the `on_post()` responder sets the Location header for the newly created resource. (We will create a route for that path in just a minute.) The [`Request`](../api/request_and_response#falcon.Request "falcon.Request") and [`Response`](../api/request_and_response#falcon.Response "falcon.Response") classes contain convenient attributes for reading and setting common headers, but you can always access any header by name with the `req.get_header()` and `resp.set_header()` methods. Take a moment to run pytest again to check your progress: ``` $ pytest tests ``` You should see a `TypeError` as a consequence of adding the `storage_path` parameter to `Resource.__init__()`. To fix this, simply edit `app.py` and pass in a path to the initializer. For now, just use the working directory from which you started the service: ``` images = Resource(storage_path='.') ``` Try running the tests again. This time, they should pass with flying colors! ``` $ pytest tests ``` Finally, restart Gunicorn and then try sending a POST request to the resource from the command line (substituting `test.png` for a path to any PNG you like.) ``` $ http POST localhost:8000/images Content-Type:image/png < test.png ``` Now, if you check your storage directory, it should contain a copy of the image you just POSTed. Upward and onward! Refactoring for testability --------------------------- Earlier we pointed out that our POST test relied heavily on mocking, relying on assumptions that may or may not hold true as the code evolves. To mitigate this problem, we’ll not only have to refactor the tests, but also the application itself. We’ll start by factoring out the business logic from the resource’s POST responder in `images.py` so that it can be tested independently. In this case, the resource’s “business logic” is simply the image-saving operation: ``` import io import mimetypes import os import uuid import falcon import msgpack class Resource(object): def __init__(self, image_store): self._image_store = image_store def on_get(self, req, resp): doc = { 'images': [ { 'href': '/images/1eaf6ef1-7f2d-4ecc-a8d5-6e8adba7cc0e.png' } ] } resp.data = msgpack.packb(doc, use_bin_type=True) resp.content_type = falcon.MEDIA_MSGPACK resp.status = falcon.HTTP_200 def on_post(self, req, resp): name = self._image_store.save(req.stream, req.content_type) resp.status = falcon.HTTP_201 resp.location = '/images/' + name class ImageStore(object): _CHUNK_SIZE_BYTES = 4096 # Note the use of dependency injection for standard library # methods. We'll use these later to avoid monkey-patching. def __init__(self, storage_path, uuidgen=uuid.uuid4, fopen=io.open): self._storage_path = storage_path self._uuidgen = uuidgen self._fopen = fopen def save(self, image_stream, image_content_type): ext = mimetypes.guess_extension(image_content_type) name = '{uuid}{ext}'.format(uuid=self._uuidgen(), ext=ext) image_path = os.path.join(self._storage_path, name) with self._fopen(image_path, 'wb') as image_file: while True: chunk = image_stream.read(self._CHUNK_SIZE_BYTES) if not chunk: break image_file.write(chunk) return name ``` Let’s check to see if we broke anything with the changes above: ``` $ pytest tests ``` Hmm, it looks like we forgot to update `app.py`. Let’s do that now: ``` import falcon from .images import ImageStore, Resource api = application = falcon.API() image_store = ImageStore('.') images = Resource(image_store) api.add_route('/images', images) ``` Let’s try again: ``` $ pytest tests ``` Now you should see a failed test assertion regarding `mock_file_open`. To fix this, we need to switch our strategy from monkey-patching to dependency injection. Return to `app.py` and modify it to look similar to the following: ``` import falcon from .images import ImageStore, Resource def create_app(image_store): image_resource = Resource(image_store) api = falcon.API() api.add_route('/images', image_resource) return api def get_app(): image_store = ImageStore('.') return create_app(image_store) ``` As you can see, the bulk of the setup logic has been moved to `create_app()`, which can be used to obtain an API object either for testing or for hosting in production. `get_app()` takes care of instantiating additional resources and configuring the application for hosting. The command to run the application is now: ``` $ gunicorn --reload 'look.app:get_app()' ``` Finally, we need to update the test code. Modify `test_app.py` to look similar to this: ``` import io # Python 3 from unittest.mock import call, MagicMock, mock_open # Python 2 # from mock import call, MagicMock, mock_open import falcon from falcon import testing import msgpack import pytest import look.app import look.images @pytest.fixture def mock_store(): return MagicMock() @pytest.fixture def client(mock_store): api = look.app.create_app(mock_store) return testing.TestClient(api) def test_list_images(client): doc = { 'images': [ { 'href': '/images/1eaf6ef1-7f2d-4ecc-a8d5-6e8adba7cc0e.png' } ] } response = client.simulate_get('/images') result_doc = msgpack.unpackb(response.content, raw=False) assert result_doc == doc assert response.status == falcon.HTTP_OK # With clever composition of fixtures, we can observe what happens with # the mock injected into the image resource. def test_post_image(client, mock_store): file_name = 'fake-image-name.xyz' # We need to know what ImageStore method will be used mock_store.save.return_value = file_name image_content_type = 'image/xyz' response = client.simulate_post( '/images', body=b'some-fake-bytes', headers={'content-type': image_content_type} ) assert response.status == falcon.HTTP_CREATED assert response.headers['location'] == '/images/{}'.format(file_name) saver_call = mock_store.save.call_args # saver_call is a unittest.mock.call tuple. It's first element is a # tuple of positional arguments supplied when calling the mock. assert isinstance(saver_call[0][0], falcon.request_helpers.BoundedStream) assert saver_call[0][1] == image_content_type ``` As you can see, we’ve redone the POST. While there are fewer mocks, the assertions have gotten more elaborate to properly check interactions at the interface boundaries. Let’s check our progress: ``` $ pytest tests ``` All green! But since we used a mock, we’re no longer covering the actual saving of the image. Let’s add a test for that: ``` def test_saving_image(monkeypatch): # This still has some mocks, but they are more localized and do not # have to be monkey-patched into standard library modules (always a # risky business). mock_file_open = mock_open() fake_uuid = '123e4567-e89b-12d3-a456-426655440000' def mock_uuidgen(): return fake_uuid fake_image_bytes = b'fake-image-bytes' fake_request_stream = io.BytesIO(fake_image_bytes) storage_path = 'fake-storage-path' store = look.images.ImageStore( storage_path, uuidgen=mock_uuidgen, fopen=mock_file_open ) assert store.save(fake_request_stream, 'image/png') == fake_uuid + '.png' assert call().write(fake_image_bytes) in mock_file_open.mock_calls ``` Now give it a try: ``` $ pytest tests -k test_saving_image ``` Like the former test, this one still uses mocks. But the structure of the code has been improved through the techniques of componentization and dependency inversion, making the application more flexible and testable. Tip Checking code [coverage](https://coverage.readthedocs.io/) would have helped us detect the missing test above; it’s always a good idea to include coverage testing in your workflow to ensure you don’t have any bugs hiding off somewhere in an unexercised code path. Functional tests ---------------- Functional tests define the application’s behavior from the outside. When using TDD, this can be a more natural place to start as opposed to lower-level unit testing, since it is difficult to anticipate what internal interfaces and components are needed in advance of defining the application’s user-facing functionality. In the case of the refactoring work from the last section, we could have inadvertently introduced a functional bug into the application that our unit tests would not have caught. This can happen when a bug is a result of an unexpected interaction between multiple units, between the application and the web server, or between the application and any external services it depends on. With test helpers such as `simulate_get()` and `simulate_post()`, we can create tests that span multiple units. But we can also go one step further and run the application as a normal, separate process (e.g. with Gunicorn). We can then write tests that interact with the running process through HTTP, behaving like a normal client. Let’s see this in action. Create a new test module, `tests/test_integration.py` with the following contents: ``` import os import requests def test_posted_image_gets_saved(): file_save_prefix = '/tmp/' location_prefix = '/images/' fake_image_bytes = b'fake-image-bytes' response = requests.post( 'http://localhost:8000/images', data=fake_image_bytes, headers={'content-type': 'image/png'} ) assert response.status_code == 201 location = response.headers['location'] assert location.startswith(location_prefix) image_name = location.replace(location_prefix, '') file_path = file_save_prefix + image_name with open(file_path, 'rb') as image_file: assert image_file.read() == fake_image_bytes os.remove(file_path) ``` Next, install the `requests` package (as required by the new test) and make sure Gunicorn is up and running: ``` $ pip install requests $ gunicorn 'look.app:get_app()' ``` Then, in another terminal, try running the new test: ``` $ pytest tests -k test_posted_image_gets_saved ``` The test will fail since it expects the image file to reside under `/tmp`. To fix this, modify `app.py` to add the ability to configure the image storage directory with an environment variable: ``` import os import falcon from .images import ImageStore, Resource def create_app(image_store): image_resource = Resource(image_store) api = falcon.API() api.add_route('/images', image_resource) return api def get_app(): storage_path = os.environ.get('LOOK_STORAGE_PATH', '.') image_store = ImageStore(storage_path) return create_app(image_store) ``` Now you can re-run the app against the desired storage directory: ``` $ LOOK_STORAGE_PATH=/tmp gunicorn --reload 'look.app:get_app()' ``` You should now be able to re-run the test and see it succeed: ``` $ pytest tests -k test_posted_image_gets_saved ``` Note The above process of starting, testing, stopping, and cleaning up after each test run can (and really should be) automated. Depending on your needs, you can develop your own automation fixtures, or use a library such as [mountepy](https://github.com/butla/mountepy). Many developers choose to write tests like the above to sanity-check their application’s primary functionality, while leaving the bulk of testing to simulated requests and unit tests. These latter types of tests generally execute much faster and facilitate more fine-grained test assertions as compared to higher-level functional and system tests. That being said, testing strategies vary widely and you should choose the one that best suits your needs. At this point, you should have a good grip on how to apply common testing strategies to your Falcon application. For the sake of brevity we’ll omit further testing instructions from the following sections, focusing instead on showcasing more of Falcon’s features. Serving Images -------------- Now that we have a way of getting images into the service, we of course need a way to get them back out. What we want to do is return an image when it is requested, using the path that came back in the Location header. Try executing the following: ``` $ http localhost:8000/images/db79e518-c8d3-4a87-93fe-38b620f9d410.png ``` In response, you should get a `404 Not Found`. This is the default response given by Falcon when it can not find a resource that matches the requested URL path. Let’s address this by creating a separate class to represent a single image resource. We will then add an `on_get()` method to respond to the path above. Go ahead and edit your `images.py` file to look something like this: ``` import io import os import re import uuid import mimetypes import falcon import msgpack class Collection(object): def __init__(self, image_store): self._image_store = image_store def on_get(self, req, resp): # TODO: Modify this to return a list of href's based on # what images are actually available. doc = { 'images': [ { 'href': '/images/1eaf6ef1-7f2d-4ecc-a8d5-6e8adba7cc0e.png' } ] } resp.data = msgpack.packb(doc, use_bin_type=True) resp.content_type = falcon.MEDIA_MSGPACK resp.status = falcon.HTTP_200 def on_post(self, req, resp): name = self._image_store.save(req.stream, req.content_type) resp.status = falcon.HTTP_201 resp.location = '/images/' + name class Item(object): def __init__(self, image_store): self._image_store = image_store def on_get(self, req, resp, name): resp.content_type = mimetypes.guess_type(name)[0] resp.stream, resp.content_length = self._image_store.open(name) class ImageStore(object): _CHUNK_SIZE_BYTES = 4096 _IMAGE_NAME_PATTERN = re.compile( '[0-9a-f]{8}-[0-9a-f]{4}-[0-9a-f]{4}-[0-9a-f]{4}-[0-9a-f]{12}\.[a-z]{2,4}$' ) def __init__(self, storage_path, uuidgen=uuid.uuid4, fopen=io.open): self._storage_path = storage_path self._uuidgen = uuidgen self._fopen = fopen def save(self, image_stream, image_content_type): ext = mimetypes.guess_extension(image_content_type) name = '{uuid}{ext}'.format(uuid=self._uuidgen(), ext=ext) image_path = os.path.join(self._storage_path, name) with self._fopen(image_path, 'wb') as image_file: while True: chunk = image_stream.read(self._CHUNK_SIZE_BYTES) if not chunk: break image_file.write(chunk) return name def open(self, name): # Always validate untrusted input! if not self._IMAGE_NAME_PATTERN.match(name): raise IOError('File not found') image_path = os.path.join(self._storage_path, name) stream = self._fopen(image_path, 'rb') content_length = os.path.getsize(image_path) return stream, content_length ``` As you can see, we renamed `Resource` to `Collection` and added a new `Item` class to represent a single image resource. Alternatively, these two classes could be consolidated into one by using suffixed responders. (See also: [`add_route()`](../api/api#falcon.API.add_route "falcon.API.add_route")) Also, note the `name` parameter for the `on_get()` responder. Any URI parameters that you specify in your routes will be turned into corresponding kwargs and passed into the target responder as such. We’ll see how to specify URI parameters in a moment. Inside the `on_get()` responder, we set the Content-Type header based on the filename extension, and then stream out the image directly from an open file handle. Note the use of `resp.content_length`. Whenever using `resp.stream` instead of `resp.body` or `resp.data`, you typically also specify the expected length of the stream using the Content-Length header, so that the web client knows how much data to read from the response. Note If you do not know the size of the stream in advance, you can work around that by using chunked encoding, but that’s beyond the scope of this tutorial. If `resp.status` is not set explicitly, it defaults to `200 OK`, which is exactly what we want `on_get()` to do. Now let’s wire everything up and give it a try. Edit `app.py` to look similar to the following: ``` import os import falcon import images def create_app(image_store): api = falcon.API() api.add_route('/images', images.Collection(image_store)) api.add_route('/images/{name}', images.Item(image_store)) return api def get_app(): storage_path = os.environ.get('LOOK_STORAGE_PATH', '.') image_store = images.ImageStore(storage_path) return create_app(image_store) ``` As you can see, we specified a new route, `/images/{name}`. This causes Falcon to expect all associated responders to accept a `name` argument. Note Falcon also supports more complex parameterized path segments that contain multiple values. For example, a version control API might use the following route template for diffing two code branches: ``` /repos/{org}/{repo}/compare/{usr0}:{branch0}...{usr1}:{branch1} ``` Now re-run your app and try to POST another picture: ``` $ http POST localhost:8000/images Content-Type:image/png < test.png ``` Make a note of the path returned in the Location header, and use it to GET the image: ``` $ http localhost:8000/images/dddff30e-d2a6-4b57-be6a-b985ee67fa87.png ``` HTTPie won’t display the image, but you can see that the response headers were set correctly. Just for fun, go ahead and paste the above URI into your browser. The image should display correctly. Introducing Hooks ----------------- At this point you should have a pretty good understanding of the basic parts that make up a Falcon-based API. Before we finish up, let’s just take a few minutes to clean up the code and add some error handling. First, let’s check the incoming media type when something is posted to make sure it is a common image type. We’ll implement this with a `before` hook. Start by defining a list of media types the service will accept. Place this constant near the top, just after the import statements in `images.py`: ``` ALLOWED_IMAGE_TYPES = ( 'image/gif', 'image/jpeg', 'image/png', ) ``` The idea here is to only accept GIF, JPEG, and PNG images. You can add others to the list if you like. Next, let’s create a hook that will run before each request to post a message. Add this method below the definition of `ALLOWED_IMAGE_TYPES`: ``` def validate_image_type(req, resp, resource, params): if req.content_type not in ALLOWED_IMAGE_TYPES: msg = 'Image type not allowed. Must be PNG, JPEG, or GIF' raise falcon.HTTPBadRequest('Bad request', msg) ``` And then attach the hook to the `on_post()` responder: ``` @falcon.before(validate_image_type) def on_post(self, req, resp): # ... ``` Now, before every call to that responder, Falcon will first invoke `validate_image_type()`. There isn’t anything special about this function, other than it must accept four arguments. Every hook takes, as its first two arguments, a reference to the same `req` and `resp` objects that are passed into responders. The `resource` argument is a Resource instance associated with the request. The fourth argument, named `params` by convention, is a reference to the kwarg dictionary Falcon creates for each request. `params` will contain the route’s URI template params and their values, if any. As you can see in the example above, you can use `req` to get information about the incoming request. However, you can also use `resp` to play with the HTTP response as needed, and you can even use hooks to inject extra kwargs: ``` def extract_project_id(req, resp, resource, params): """Adds `project_id` to the list of params for all responders. Meant to be used as a `before` hook. """ params['project_id'] = req.get_header('X-PROJECT-ID') ``` Now, you might imagine that such a hook should apply to all responders for a resource. In fact, hooks can be applied to an entire resource by simply decorating the class: ``` @falcon.before(extract_project_id) class Message(object): # ... ``` Similar logic can be applied globally with middleware. (See also: [falcon.middleware](../api/middleware#middleware)) Now that you’ve added a hook to validate the media type, you can see it in action by attempting to POST something nefarious: ``` $ http POST localhost:8000/images Content-Type:image/jpx ``` You should get back a `400 Bad Request` status and a nicely structured error body. Tip When something goes wrong, you usually want to give your users some info to help them resolve the issue. The exception to this rule is when an error occurs because the user is requested something they are not authorized to access. In that case, you may wish to simply return `404 Not Found` with an empty body, in case a malicious user is fishing for information that will help them crack your app. Check out the [hooks reference](../api/hooks#hooks) to learn more. Error Handling -------------- Generally speaking, Falcon assumes that resource responders (`on_get()`, `on_post()`, etc.) will, for the most part, do the right thing. In other words, Falcon doesn’t try very hard to protect responder code from itself. This approach reduces the number of (often) extraneous checks that Falcon would otherwise have to perform, making the framework more efficient. With that in mind, writing a high-quality API based on Falcon requires that: 1. Resource responders set response variables to sane values. 2. Untrusted input (i.e., input from an external client or service) is validated. 3. Your code is well-tested, with high code coverage. 4. Errors are anticipated, detected, logged, and handled appropriately within each responder or by global error handling hooks. When it comes to error handling, you can always directly set the error status, appropriate response headers, and error body using the `resp` object. However, Falcon tries to make things a little easier by providing a [set of error classes](../api/errors#predefined-errors) you can raise when something goes wrong. Falcon will convert any instance or subclass of [`falcon.HTTPError`](../api/errors#falcon.HTTPError "falcon.HTTPError") raised by a responder, hook, or middleware component into an appropriate HTTP response. You may raise an instance of [`falcon.HTTPError`](../api/errors#falcon.HTTPError "falcon.HTTPError") directly, or use any one of a number of [predefined errors](../api/errors#predefined-errors) that are designed to set the response headers and body appropriately for each error type. Tip Falcon will re-raise errors that do not inherit from [`falcon.HTTPError`](../api/errors#falcon.HTTPError "falcon.HTTPError") unless you have registered a custom error handler for that type. Error handlers may be registered for any type, including [`HTTPError`](../api/errors#falcon.HTTPError "falcon.HTTPError"). This feature provides a central location for logging and otherwise handling exceptions raised by responders, hooks, and middleware components. See also: [`add_error_handler()`](../api/api#falcon.API.add_error_handler "falcon.API.add_error_handler"). Let’s see a quick example of how this works. Try requesting an invalid image name from your application: ``` $ http localhost:8000/images/voltron.png ``` As you can see, the result isn’t exactly graceful. To fix this, we’ll need to add some exception handling. Modify your `Item` class as follows: ``` class Item(object): def __init__(self, image_store): self._image_store = image_store def on_get(self, req, resp, name): resp.content_type = mimetypes.guess_type(name)[0] try: resp.stream, resp.content_length = self._image_store.open(name) except IOError: # Normally you would also log the error. raise falcon.HTTPNotFound() ``` Now let’s try that request again: ``` $ http localhost:8000/images/voltron.png ``` Additional information about error handling is available in the [error handling reference](../api/errors#errors). What Now? --------- Our friendly community is available to answer your questions and help you work through sticky problems. See also: [Getting Help](https://falcon.readthedocs.io/en/2.0.0/community/help.html#help). As mentioned previously, Falcon’s docstrings are quite extensive, and so you can learn a lot just by poking around Falcon’s modules from a Python REPL, such as [IPython](http://ipython.org/) or [bpython](http://bpython-interpreter.org/). Also, don’t be shy about pulling up Falcon’s source code on GitHub or in your favorite text editor. The team has tried to make the code as straightforward and readable as possible; where other documentation may fall short, the code basically can’t be wrong. A number of Falcon add-ons, templates, and complementary packages are available for use in your projects. We’ve listed several of these on the [Falcon wiki](https://github.com/falconry/falcon/wiki) as a starting point, but you may also wish to search PyPI for additional resources.	programming_docs
falcon Introduction Introduction ============ Perfection is finally attained not when there is no longer anything to add, but when there is no longer anything to take away. - Antoine de Saint-Exupéry [Falcon](https://falconframework.org) is a reliable, high-performance Python web framework for building large-scale app backends and microservices. It encourages the REST architectural style, and tries to do as little as possible while remaining highly effective. Falcon apps work with any WSGI server, and run like a champ under CPython 2.7/3.5+ and PyPy. How is Falcon different? ------------------------ We designed Falcon to support the demanding needs of large-scale microservices and responsive app backends. Falcon complements more general Python web frameworks by providing bare-metal performance, reliability, and flexibility wherever you need it. Fast. Same hardware, more requests. Falcon turns around requests several times faster than most other Python frameworks. For an extra speed boost, Falcon compiles itself with Cython when available, and also works well with [PyPy](https://pypy.org). Considering a move to another programming language? Benchmark with Falcon + PyPy first. Reliable. We go to great lengths to avoid introducing breaking changes, and when we do they are fully documented and only introduced (in the spirit of [SemVer](http://semver.org/)) with a major version increment. The code is rigorously tested with numerous inputs and we require 100% coverage at all times. Falcon does not depend on any external Python packages. Flexible. Falcon leaves a lot of decisions and implementation details to you, the API developer. This gives you a lot of freedom to customize and tune your implementation. Due to Falcon’s minimalist design, Python community members are free to independently innovate on [Falcon add-ons and complementary packages](https://github.com/falconry/falcon/wiki). Debuggable. Falcon eschews magic. It’s easy to tell which inputs lead to which outputs. Unhandled exceptions are never encapsulated or masked. Potentially surprising behaviors, such as automatic request body parsing, are well-documented and disabled by default. Finally, when it comes to the framework itself, we take care to keep logic paths simple and understandable. All this makes it easier to reason about the code and to debug edge cases in large-scale deployments. Features -------- * Highly-optimized, extensible code base * Intuitive routing via URI templates and REST-inspired resource classes * Easy access to headers and bodies through request and response classes * DRY request processing via middleware components and hooks * Idiomatic HTTP error responses * Straightforward exception handling * Snappy unit testing through WSGI helpers and mocks * Supports Python 2.7, 3.5+ * Compatible with PyPy About Apache 2.0 ---------------- Falcon is released under the terms of the [Apache 2.0 License](http://opensource.org/licenses/Apache-2.0). This means that you can use it in your commercial applications without having to also open-source your own code. It also means that if someone happens to contribute code that is associated with a patent, you are granted a free license to use said patent. That’s a pretty sweet deal. Now, if you do make changes to Falcon itself, please consider contributing your awesome work back to the community. Falcon License -------------- Copyright 2012-2017 by Rackspace Hosting, Inc. and other contributors, as noted in the individual source code files. Licensed under the Apache License, Version 2.0 (the “License”); you may not use this file except in compliance with the License. You may obtain a copy of the License at <http://www.apache.org/licenses/LICENSE-2.0> Unless required by applicable law or agreed to in writing, software distributed under the License is distributed on an “AS IS” BASIS, WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied. See the License for the specific language governing permissions and limitations under the License. By contributing to this project, you agree to also license your source code under the terms of the Apache License, Version 2.0, as described above. falcon FAQ FAQ === * [Design Philosophy](#design-philosophy) + [Why doesn’t Falcon come with batteries included?](#why-doesn-t-falcon-come-with-batteries-included) + [Why doesn’t Falcon create a new Resource instance for every request?](#why-doesn-t-falcon-create-a-new-resource-instance-for-every-request) + [Why does raising an error inside a resource crash my app?](#why-does-raising-an-error-inside-a-resource-crash-my-app) + [How do I generate API documentation for my Falcon API?](#how-do-i-generate-api-documentation-for-my-falcon-api) * [Performance](#performance) + [Does Falcon work with HTTP/2?](#does-falcon-work-with-http-2) + [Is Falcon thread-safe?](#is-falcon-thread-safe) + [Does Falcon support asyncio?](#does-falcon-support-asyncio) + [Does Falcon support WebSocket?](#does-falcon-support-websocket) * [Routing](#routing) + [How do I implement CORS with Falcon?](#how-do-i-implement-cors-with-falcon) + [How do I implement redirects within Falcon?](#how-do-i-implement-redirects-within-falcon) + [How do I split requests between my original app and the part I migrated to Falcon?](#how-do-i-split-requests-between-my-original-app-and-the-part-i-migrated-to-falcon) + [How do I implement both POSTing and GETing items for the same resource?](#how-do-i-implement-both-posting-and-geting-items-for-the-same-resource) + [What is the recommended way to map related routes to resource classes?](#what-is-the-recommended-way-to-map-related-routes-to-resource-classes) * [Extensibility](#extensibility) + [How do I use WSGI middleware with Falcon?](#how-do-i-use-wsgi-middleware-with-falcon) + [How can I pass data from a hook to a responder, and between hooks?](#how-can-i-pass-data-from-a-hook-to-a-responder-and-between-hooks) + [How can I write a custom handler for 404 and 500 pages in falcon?](#how-can-i-write-a-custom-handler-for-404-and-500-pages-in-falcon) * [Request Handling](#request-handling) + [How do I authenticate requests?](#how-do-i-authenticate-requests) + [Why does req.stream.read() hang for certain requests?](#why-does-req-stream-read-hang-for-certain-requests) + [How does Falcon handle a trailing slash in the request path?](#how-does-falcon-handle-a-trailing-slash-in-the-request-path) + [Why is my query parameter missing from the req object?](#why-is-my-query-parameter-missing-from-the-req-object) + [Why are ‘+’ characters in my params being converted to spaces?](#why-are-characters-in-my-params-being-converted-to-spaces) + [How can I access POSTed form params?](#how-can-i-access-posted-form-params) + [How can I access POSTed files?](#how-can-i-access-posted-files) + [How do I consume a query string that has a JSON value?](#how-do-i-consume-a-query-string-that-has-a-json-value) + [How can I handle forward slashes within a route template field?](#how-can-i-handle-forward-slashes-within-a-route-template-field) + [How do I adapt my code to default context type changes in Falcon 2.0?](#how-do-i-adapt-my-code-to-default-context-type-changes-in-falcon-2-0) * [Response Handling](#response-handling) + [How can I use resp.media with types like datetime?](#how-can-i-use-resp-media-with-types-like-datetime) + [Does Falcon set Content-Length or do I need to do that explicitly?](#does-falcon-set-content-length-or-do-i-need-to-do-that-explicitly) + [Why is an empty response body returned when I raise an instance of HTTPError?](#why-is-an-empty-response-body-returned-when-i-raise-an-instance-of-httperror) + [I’m setting a response body, but it isn’t getting returned. What’s going on?](#i-m-setting-a-response-body-but-it-isn-t-getting-returned-what-s-going-on) + [I’m setting a cookie, but it isn’t being returned in subsequent requests.](#i-m-setting-a-cookie-but-it-isn-t-being-returned-in-subsequent-requests) + [How can I serve a downloadable file with falcon?](#how-can-i-serve-a-downloadable-file-with-falcon) + [Can Falcon serve static files?](#can-falcon-serve-static-files) * [Misc.](#misc) + [How do I manage my database connections?](#how-do-i-manage-my-database-connections) + [What is the recommended approach for making configuration variables available to multiple resource classes?](#what-is-the-recommended-approach-for-making-configuration-variables-available-to-multiple-resource-classes) + [How do I test my Falcon app? Can I use pytest?](#how-do-i-test-my-falcon-app-can-i-use-pytest) Design Philosophy ----------------- ### Why doesn’t Falcon come with batteries included? Falcon is designed for applications that require a high level of customization or performance tuning. The framework’s minimalist design frees the developer to select the best strategies and 3rd-party packages for the task at hand. The Python ecosystem offers a number of great packages that you can use from within your responders, hooks, and middleware components. As a starting point, the community maintains a list of [Falcon add-ons and complementary packages](https://github.com/falconry/falcon/wiki). ### Why doesn’t Falcon create a new Resource instance for every request? Falcon generally tries to minimize the number of objects that it instantiates. It does this for two reasons: first, to avoid the expense of creating the object, and second to reduce memory usage by reducing the total number of objects required under highly concurrent workloads. Therefore, when adding a route, Falcon requires an instance of your resource class, rather than the class type. That same instance will be used to serve all requests coming in on that route. ### Why does raising an error inside a resource crash my app? Generally speaking, Falcon assumes that resource responders (such as `on_get()`, `on_post()`, etc.) will, for the most part, do the right thing. In other words, Falcon doesn’t try very hard to protect responder code from itself. This approach reduces the number of checks that Falcon would otherwise have to perform, making the framework more efficient. With that in mind, writing a high-quality API based on Falcon requires that: 1. Resource responders set response variables to sane values. 2. Your code is well-tested, with high code coverage. 3. Errors are anticipated, detected, and handled appropriately within each responder and with the aid of custom error handlers. Tip Falcon will re-raise errors that do not inherit from [`HTTPError`](../api/errors#falcon.HTTPError "falcon.HTTPError") unless you have registered a custom error handler for that type (see also: [falcon.API](../api/api#api)). ### How do I generate API documentation for my Falcon API? When it comes to API documentation, some developers prefer to use the API implementation as the user contract or source of truth (taking an implementation-first approach), while other developers prefer to use the API spec itself as the contract, implementing and testing the API against that spec (taking a design-first approach). At the risk of erring on the side of flexibility, Falcon does not provide API spec support out of the box. However, there are several community projects available in this vein. Our [Add on Catalog](https://github.com/falconry/falcon/wiki/Add-on-Catalog) lists a couple of these projects, but you may also wish to search [PyPI](https://pypi.python.org/pypi) for additional packages. If you are interested in the design-first approach mentioned above, you may also want to check out API design and gateway services such as Tyk, Apiary, Amazon API Gateway, or Google Cloud Endpoints. Performance ----------- ### Does Falcon work with HTTP/2? Falcon is a WSGI framework and as such does not serve HTTP requests directly. However, you can get most of the benefits of HTTP/2 by simply deploying any HTTP/2-compliant web server or load balancer in front of your app to translate between HTTP/2 and HTTP/1.1. Eventually we expect that Python web servers (such as uWSGI) will support HTTP/2 natively, eliminating the need for a translation layer. ### Is Falcon thread-safe? The Falcon framework is, itself, thread-safe. For example, new [`Request`](../api/request_and_response#falcon.Request "falcon.Request") and [`Response`](../api/request_and_response#falcon.Response "falcon.Response") objects are created for each incoming HTTP request. However, a single instance of each resource class attached to a route is shared among all requests. Middleware objects and other types of hooks, such as custom error handlers, are likewise shared. Therefore, as long as you implement these classes and callables in a thread-safe manner, and ensure that any third-party libraries used by your app are also thread-safe, your WSGI app as a whole will be thread-safe. That being said, IO-bound Falcon APIs are usually scaled via multiple processes and green threads (courtesy of the [gevent](http://www.gevent.org/) library or similar) which aren’t truly running concurrently, so there may be some edge cases where Falcon is not thread-safe that we aren’t aware of. If you run into any issues, please let us know. ### Does Falcon support asyncio? Due to the limitations of WSGI, Falcon is unable to support `asyncio` at this time. However, we are exploring alternatives to WSGI (such as [ASGI](https://github.com/django/asgiref/blob/master/specs/asgi.rst)) that will allow us to support asyncio natively in the future. In the meantime, we recommend using the battle-tested [gevent](http://www.gevent.org/) library via Gunicorn or uWSGI to scale IO-bound services. [meinheld](https://pypi.org/project/meinheld/) has also been used successfully by the community to power high-throughput, low-latency services. Note that if you use Gunicorn, you can combine gevent and PyPy to achieve an impressive level of performance. (Unfortunately, uWSGI does not yet support using gevent and PyPy together.) ### Does Falcon support WebSocket? Due to the limitations of WSGI, Falcon is unable to support the WebSocket protocol as stated above. In the meantime, you might try leveraging [uWSGI’s native WebSocket support](http://uwsgi.readthedocs.io/en/latest/WebSockets.html), or implementing a standalone service via Aymeric Augustin’s handy [websockets](https://pypi.python.org/pypi/websockets/4.0.1) library. Routing ------- ### How do I implement CORS with Falcon? In order for a website or SPA to access an API hosted under a different domain name, that API must implement [Cross-Origin Resource Sharing (CORS)](https://developer.mozilla.org/en-US/docs/Web/HTTP/CORS). For a public API, implementing CORS in Falcon can be as simple as implementing a middleware component similar to the following: ``` class CORSComponent(object): def process_response(self, req, resp, resource, req_succeeded): resp.set_header('Access-Control-Allow-Origin', '') if (req_succeeded and req.method == 'OPTIONS' and req.get_header('Access-Control-Request-Method') ): # NOTE(kgriffs): This is a CORS preflight request. Patch the # response accordingly. allow = resp.get_header('Allow') resp.delete_header('Allow') allow_headers = req.get_header( 'Access-Control-Request-Headers', default='' ) resp.set_headers(( ('Access-Control-Allow-Methods', allow), ('Access-Control-Allow-Headers', allow_headers), ('Access-Control-Max-Age', '86400'), # 24 hours )) ``` When using the above approach, OPTIONS requests must also be special-cased in any other middleware or hooks you use for auth, content-negotiation, etc. For example, you will typically skip auth for preflight requests because it is simply unnecessary; note that such request do not include the Authorization header in any case. For more sophisticated use cases, have a look at Falcon add-ons from the community, such as [falcon-cors](https://github.com/lwcolton/falcon-cors), or try one of the generic [WSGI CORS libraries available on PyPI](https://pypi.python.org/pypi?%3Aaction=search&term=cors&submit=search). If you use an API gateway, you might also look into what CORS functionality it provides at that level. ### How do I implement redirects within Falcon? Falcon provides a number of exception classes that can be raised to redirect the client to a different location (see also [Redirection](../api/redirects#redirects)). Note, however, that it is more efficient to handle permanent redirects directly with your web server, if possible, rather than placing additional load on your app for such requests. ### How do I split requests between my original app and the part I migrated to Falcon? It is common to carve out a portion of an app and reimplement it in Falcon to boost performance where it is most needed. If you have access to your load balancer or reverse proxy configuration, we recommend setting up path or subdomain-based rules to split requests between your original implementation and the parts that have been migrated to Falcon (e.g., by adding an additional `location` directive to your NGINX config). If the above approach isn’t an option for your deployment, you can implement a simple WSGI wrapper that does the same thing: ``` def application(environ, start_response): try: # NOTE(kgriffs): Prefer the host header; the web server # isn't supposed to mess with it, so it should be what # the client actually sent. host = environ['HTTP_HOST'] except KeyError: # NOTE(kgriffs): According to PEP-3333, this header # will always be present. host = environ['SERVER_NAME'] if host.startswith('api.'): return falcon_app(environ, start_response) elif: return webapp2_app(environ, start_response) ``` See also [PEP 3333](https://www.python.org/dev/peps/pep-3333/#environ-variables) for a complete list of the variables that are provided via `environ`. ### How do I implement both POSTing and GETing items for the same resource? Suppose you have the following routes: ``` # Resource Collection GET /resources{?marker, limit} POST /resources # Resource Item GET /resources/{id} PATCH /resources/{id} DELETE /resources/{id} ``` You can implement this sort of API by simply using two Python classes, one to represent a single resource, and another to represent the collection of said resources. It is common to place both classes in the same module (see also [this section of the tutorial](tutorial#tutorial-serving-images).) Alternatively, you can use suffixed responders to map both routes to the same resource class: ``` class MyResource(object): def on_get(self, req, resp, id): pass def on_patch(self, req, resp, id): pass def on_delete(self, req, resp, id): pass def on_get_collection(self, req, resp): pass def on_post_collection(self, req, resp): pass # ... resource = MyResource() api.add_route('/resources/{id}', resource) api.add_route('/resources', resource, suffix='collection') ``` ### What is the recommended way to map related routes to resource classes? Let’s say we have the following URL schema: ``` GET /game/ping GET /game/{game_id} POST /game/{game_id} GET /game/{game_id}/state POST /game/{game_id}/state ``` We can break this down into three resources: ``` Ping: GET /game/ping Game: GET /game/{game_id} POST /game/{game_id} GameState: GET /game/{game_id}/state POST /game/{game_id}/state ``` GameState may be thought of as a sub-resource of Game. It is a distinct logical entity encapsulated within a more general Game concept. In Falcon, these resources would be implemented with standard classes: ``` class Ping(object): def on_get(self, req, resp): resp.body = '{"message": "pong"}' class Game(object): def __init__(self, dao): self._dao = dao def on_get(self, req, resp, game_id): pass def on_post(self, req, resp, game_id): pass class GameState(object): def __init__(self, dao): self._dao = dao def on_get(self, req, resp, game_id): pass def on_post(self, req, resp, game_id): pass api = falcon.API() # Game and GameState are closely related, and so it # probably makes sense for them to share an object # in the Data Access Layer. This could just as # easily use a DB object or ORM layer. # # Note how the resources classes provide a layer # of abstraction or indirection which makes your # app more flexible since the data layer can # evolve somewhat independently from the presentation # layer. game_dao = myapp.DAL.Game(myconfig) api.add_route('/game/ping', Ping()) api.add_route('/game/{game_id}', Game(game_dao)) api.add_route('/game/{game_id}/state', GameState(game_dao)) ``` Alternatively, a single resource class could implement suffixed responders in order to handle all three routes: ``` class Game(object): def __init__(self, dao): self._dao = dao def on_get(self, req, resp, game_id): pass def on_post(self, req, resp, game_id): pass def on_get_state(self, req, resp, game_id): pass def on_post_state(self, req, resp, game_id): pass def on_get_ping(self, req, resp): resp.data = b'{"message": "pong"}' # ... api = falcon.API() game = Game(myapp.DAL.Game(myconfig)) api.add_route('/game/{game_id}', game) api.add_route('/game/{game_id}/state', game, suffix='state') api.add_route('/game/ping', game, suffix='ping') ``` Extensibility ------------- ### How do I use WSGI middleware with Falcon? Instances of [`falcon.API`](../api/api#falcon.API "falcon.API") are first-class WSGI apps, so you can use the standard pattern outlined in PEP-3333. In your main “app” file, you would simply wrap your api instance with a middleware app. For example: ``` import my_restful_service import some_middleware app = some_middleware.DoSomethingFancy(my_restful_service.api) ``` See also the [WSGI middleware example](https://www.python.org/dev/peps/pep-3333/#middleware-components-that-play-both-sides) given in PEP-3333. ### How can I pass data from a hook to a responder, and between hooks? You can inject extra responder kwargs from a hook by adding them to the params dict passed into the hook. You can also set custom attributes on the `req.context` object, as a way of passing contextual information around: ``` def authorize(req, resp, resource, params): # Check authentication/authorization # ... req.context.role = 'root' req.context.scopes = ('storage', 'things') req.context.uid = 0 # ... @falcon.before(authorize) def on_post(self, req, resp): pass ``` ### How can I write a custom handler for 404 and 500 pages in falcon? When a route can not be found for an incoming request, Falcon uses a default responder that simply raises an instance of [`falcon.HTTPNotFound`](../api/errors#falcon.HTTPNotFound "falcon.HTTPNotFound"). You can use [`falcon.API.add_error_handler()`](../api/api#falcon.API.add_error_handler "falcon.API.add_error_handler") to register a custom error handler for this exception type. Alternatively, you may be able to configure your web server to transform the response for you (e.g., using Nginx’s `error_page` directive). 500 errors are typically the result of an unhandled exception making its way up to the web server. To handle these errors more gracefully, you can add a custom error handler for Python’s base [`Exception`](https://docs.python.org/3/library/exceptions.html#Exception "(in Python v3.7)") type. Request Handling ---------------- ### How do I authenticate requests? Hooks and middleware components can be used together to authenticate and authorize requests. For example, a middleware component could be used to parse incoming credentials and place the results in `req.context`. Downstream components or hooks could then use this information to authorize the request, taking into account the user’s role and the requested resource. ### Why does req.stream.read() hang for certain requests? This behavior is an unfortunate artifact of the request body mechanics not being fully defined by the WSGI spec (PEP-3333). This is discussed in the reference documentation for [`stream`](../api/request_and_response#falcon.Request.stream "falcon.Request.stream"), and a workaround is provided in the form of [`bounded_stream`](../api/request_and_response#falcon.Request.bounded_stream "falcon.Request.bounded_stream"). ### How does Falcon handle a trailing slash in the request path? If your app sets [`strip_url_path_trailing_slash`](../api/api#falcon.RequestOptions.strip_url_path_trailing_slash "falcon.RequestOptions.strip_url_path_trailing_slash") to `True`, Falcon will normalize incoming URI paths to simplify later processing and improve the predictability of application logic. This can be helpful when implementing a REST API schema that does not interpret a trailing slash character as referring to the name of an implicit sub-resource, as traditionally used by websites to reference index pages. For example, with this option enabled, adding a route for `'/foo/bar'` implicitly adds a route for `'/foo/bar/'`. In other words, requests coming in for either path will be sent to the same resource. Note Starting with version 2.0, the default for the [`strip_url_path_trailing_slash`](../api/api#falcon.RequestOptions.strip_url_path_trailing_slash "falcon.RequestOptions.strip_url_path_trailing_slash") request option changed from `True` to `False`. ### Why is my query parameter missing from the req object? If a query param does not have a value, Falcon will by default ignore that parameter. For example, passing `'foo'` or `'foo='` will result in the parameter being ignored. If you would like to recognize such parameters, you must set the `keep_blank_qs_values` request option to `True`. Request options are set globally for each instance of [`falcon.API`](../api/api#falcon.API "falcon.API") via the [`req_options`](../api/api#falcon.API.req_options "falcon.API.req_options") property. For example: ``` api.req_options.keep_blank_qs_values = True ``` ### Why are ‘+’ characters in my params being converted to spaces? The `+` character is often used instead of `%20` to represent spaces in query string params, due to the historical conflation of form parameter encoding (`application/x-www-form-urlencoded`) and URI percent-encoding. Therefore, Falcon, converts `+` to a space when decoding strings. To work around this, RFC 3986 specifies `+` as a reserved character, and recommends percent-encoding any such characters when their literal value is desired (`%2B` in the case of `+`). ### How can I access POSTed form params? By default, Falcon does not consume request bodies. However, setting the `auto_parse_form_urlencoded` to `True` on an instance of `falcon.API` will cause the framework to consume the request body when the content type is `application/x-www-form-urlencoded`, making the form parameters accessible via [`params`](../api/request_and_response#falcon.Request.params "falcon.Request.params"), [`get_param()`](../api/request_and_response#falcon.Request.get_param "falcon.Request.get_param"), etc. ``` api.req_options.auto_parse_form_urlencoded = True ``` Alternatively, POSTed form parameters may be read directly from [`stream`](../api/request_and_response#falcon.Request.stream "falcon.Request.stream") and parsed via [`falcon.uri.parse_query_string()`](../api/util#falcon.uri.parse_query_string "falcon.uri.parse_query_string") or [urllib.parse.parse\_qs()](https://docs.python.org/3.6/library/urllib.parse.html#urllib.parse.parse_qs). ### How can I access POSTed files? Falcon does not currently support parsing files submitted by an HTTP form (`multipart/form-data`), although we do plan to add this feature in a future version. In the meantime, you can use the standard `cgi.FieldStorage` class to parse the request: ``` # TODO: Either validate that content type is multipart/form-data # here, or in another hook before allowing execution to proceed. # This must be done to avoid a bug in cgi.FieldStorage env = req.env env.setdefault('QUERY_STRING', '') # TODO: Add error handling, when the request is not formatted # correctly or does not contain the desired field... # TODO: Consider overriding make_file, so that you can # stream directly to the destination rather than # buffering using TemporaryFile (see http://goo.gl/Yo8h3P) form = cgi.FieldStorage(fp=req.stream, environ=env) file_item = form[name] if file_item.file: # TODO: It's an uploaded file... read it in else: # TODO: Raise an error ``` You might also try this [streaming\_form\_data](https://streaming-form-data.readthedocs.io/en/latest/) package by Siddhant Goel, or searching PyPI for additional options from the community. ### How do I consume a query string that has a JSON value? Falcon defaults to treating commas in a query string as literal characters delimiting a comma separated list. For example, given the query string `?c=1,2,3`, Falcon defaults to adding this to your `request.params` dictionary as `{'c': ['1', '2', '3']}`. If you attempt to use JSON in the value of the query string, for example `?c={'a':1,'b':2}`, the value will get added to your `request.params` in a way that you probably don’t expect: `{'c': ["{'a':1", "'b':2}"]}`. Commas are a reserved character that can be escaped according to [RFC 3986 - 2.2. Reserved Characters](https://tools.ietf.org/html/rfc3986#section-2.2), so one possible solution is to percent encode any commas that appear in your JSON query string. The other option is to switch the way Falcon handles commas in a query string by setting the [`auto_parse_qs_csv`](../api/api#falcon.RequestOptions.auto_parse_qs_csv "falcon.RequestOptions.auto_parse_qs_csv") to `False` on an instance of [`falcon.API`](../api/api#falcon.API "falcon.API"): ``` api.req_options.auto_parse_qs_csv = False ``` When [`auto_parse_qs_csv`](../api/api#falcon.RequestOptions.auto_parse_qs_csv "falcon.RequestOptions.auto_parse_qs_csv") is set to `False`, the value of the query string `?c={'a':1,'b':2}` will be added to the `req.params` dictionary as `{'c': "{'a':1,'b':2}"}`. This lets you consume JSON whether or not the client chooses to escape commas in the request. ### How can I handle forward slashes within a route template field? In Falcon 1.3 we shipped initial support for [field converters](http://falcon.readthedocs.io/en/stable/api/routing.html#field-converters). We’ve discussed building on this feature to support consuming multiple path segments ala Flask. This work is currently planned for 2.0. In the meantime, the workaround is to percent-encode the forward slash. If you don’t control the clients and can’t enforce this, you can implement a Falcon middleware component to rewrite the path before it is routed. ### How do I adapt my code to default context type changes in Falcon 2.0? The default request/response context type has been changed from dict to a bare class in Falcon 2.0. Instead of setting dictionary items, you can now simply set attributes on the object: ``` # Before Falcon 2.0 req.context['cache_backend'] = MyUltraFastCache.connect() # Falcon 2.0 req.context.cache_backend = MyUltraFastCache.connect() ``` The new default context type emulates a dict-like mapping interface in a way that context attributes are linked to dict items, i.e. setting an object attribute also sets the corresponding dict item, and vice versa. As a result, existing code will largely work unmodified with Falcon 2.0. Nevertheless, it is recommended to migrate to the new interface as outlined above since the dict-like mapping interface may be removed from the context type in a future release. Warning If you need to mix-and-match both approaches under migration, beware that setting attributes such as items or values would obviously shadow the corresponding mapping interface functions. If an existing project is making extensive use of dictionary contexts, the type can be explicitly overridden back to dict by employing custom request/response types: ``` class RequestWithDictContext(falcon.Request): context_type = dict class ResponseWithDictContext(falcon.Response): context_type = dict # ... api = falcon.API(request_type=RequestWithDictContext, response_type=ResponseWithDictContext) ``` Response Handling ----------------- ### How can I use resp.media with types like datetime? The default JSON handler for `resp.media` only supports the objects and types listed in the table documented under [json.JSONEncoder](https://docs.python.org/3.6/library/json.html#json.JSONEncoder). To handle additional types, you can either serialize them beforehand, or create a custom JSON media handler that sets the `default` param for `json.dumps()`. When deserializing an incoming request body, you may also wish to implement `object_hook` for `json.loads()`. Note, however, that setting the `default` or `object_hook` params can negatively impact the performance of (de)serialization. ### Does Falcon set Content-Length or do I need to do that explicitly? Falcon will try to do this for you, based on the value of `resp.body`, `resp.data`, or `resp.stream_len` (whichever is set in the response, checked in that order.) For dynamically-generated content, you can choose to not set `stream_len`, in which case Falcon will then leave off the Content-Length header, and hopefully your WSGI server will do the Right Thing™ (assuming you’ve told it to enable keep-alive). Note PEP-3333 prohibits apps from setting hop-by-hop headers itself, such as Transfer-Encoding. ### Why is an empty response body returned when I raise an instance of HTTPError? Falcon attempts to serialize the [`HTTPError`](../api/errors#falcon.HTTPError "falcon.HTTPError") instance using its [`to_json()`](../api/errors#falcon.HTTPError.to_json "falcon.HTTPError.to_json") or [`to_xml()`](../api/errors#falcon.HTTPError.to_xml "falcon.HTTPError.to_xml") methods, according to the Accept header in the request. If neither JSON nor XML is acceptable, no response body will be generated. You can override this behavior if needed via [`set_error_serializer()`](../api/api#falcon.API.set_error_serializer "falcon.API.set_error_serializer"). ### I’m setting a response body, but it isn’t getting returned. What’s going on? Falcon skips processing the response body when, according to the HTTP spec, no body should be returned. If the client sends a HEAD request, the framework will always return an empty body. Falcon will also return an empty body whenever the response status is any of the following: ``` falcon.HTTP_100 falcon.HTTP_204 falcon.HTTP_416 falcon.HTTP_304 ``` If you have another case where the body isn’t being returned, it’s probably a bug! [Let us know](https://falcon.readthedocs.io/en/2.0.0/community/help.html#help) so we can help. ### I’m setting a cookie, but it isn’t being returned in subsequent requests. By default, Falcon enables the `secure` cookie attribute. Therefore, if you are testing your app over HTTP (instead of HTTPS), the client will not send the cookie in subsequent requests. (See also the [cookie documentation](../api/cookies#cookie-secure-attribute).) ### How can I serve a downloadable file with falcon? In the `on_get()` responder method for the resource, you can tell the user agent to download the file by setting the Content-Disposition header. Falcon includes the `downloadable_as` property to make this easy: ``` resp.downloadable_as = 'report.pdf' ``` ### Can Falcon serve static files? Falcon makes it easy to efficiently serve static files by simply assigning an open file to `resp.stream` [as demonstrated in the tutorial](tutorial#tutorial-serving-images). You can also serve an entire directory of files via [`falcon.API.add_static_route()`](../api/api#falcon.API.add_static_route "falcon.API.add_static_route"). However, if possible, it is best to serve static files directly from a web server like Nginx, or from a CDN. Misc. ----- ### How do I manage my database connections? Assuming your database library manages its own connection pool, all you need to do is initialize the client and pass an instance of it into your resource classes. For example, using SQLAlchemy Core: ``` engine = create_engine('sqlite:///:memory:') resource = SomeResource(engine) ``` Then, within `SomeResource`: ``` # Read from the DB result = self._engine.execute(some_table.select()) for row in result: # .... result.close() # ... # Write to the DB within a transaction with self._engine.begin() as connection: r1 = connection.execute(some_table.select()) # ... connection.execute( some_table.insert(), col1=7, col2='this is some data' ) ``` When using a data access layer, simply pass the engine into your data access objects instead. See also [this sample Falcon project](https://github.com/jmvrbanac/falcon-example) that demonstrates using an ORM with Falcon. You can also create a middleware component to automatically check out database connections for each request, but this can make it harder to track down errors, or to tune for the needs of individual requests. If you need to transparently handle reconnecting after an error, or for other use cases that may not be supported by your client library, simply encapsulate the client library within a management class that handles all the tricky bits, and pass that around instead. ### What is the recommended approach for making configuration variables available to multiple resource classes? People usually fall into two camps when it comes to this question. The first camp likes to instantiate a config object and pass that around to the initializers of the resource classes so the data sharing is explicit. The second camp likes to create a config module and import that wherever it’s needed. With the latter approach, to control when the config is actually loaded, it’s best not to instantiate it at the top level of the config module’s namespace. This avoids any problematic side-effects that may be caused by loading the config whenever Python happens to process the first import of the config module. Instead, consider implementing a function in the module that returns a new or cached config object on demand. Other than that, it’s pretty much up to you if you want to use the standard library config library or something like `aumbry` as demonstrated by this [falcon example app](https://github.com/jmvrbanac/falcon-example/tree/master/example) (See also the Configuration section of our [Complementary Packages wiki page](https://github.com/falconry/falcon/wiki/Complementary-Packages). You may also wish to search PyPI for other options). ### How do I test my Falcon app? Can I use pytest? Falcon’s testing framework supports both `unittest` and `pytest`. In fact, the tutorial in the docs provides an excellent introduction to [testing Falcon apps with pytest](http://falcon.readthedocs.io/en/stable/user/tutorial.html#testing-your-application). (See also: [Testing](http://falcon.readthedocs.io/en/stable/api/testing.html))	programming_docs
falcon Request & Response Request & Response ================== Instances of the Request and Response classes are passed into responders as the second and third arguments, respectively. ``` import falcon class Resource(object): def on_get(self, req, resp): resp.body = '{"message": "Hello world!"}' resp.status = falcon.HTTP_200 ``` Request ------- `class falcon.Request(env, options=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/request.html#Request) Represents a client’s HTTP request. Note `Request` is not meant to be instantiated directly by responders. \| Parameters: \| env ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)")) – A WSGI environment dict passed in from the server. See also PEP-3333. \| \| Keyword Arguments: \| \| \| options ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)")) – Set of global options passed from the API handler. \| `env` Reference to the WSGI environ `dict` passed in from the server. (See also PEP-3333.) \| Type: \| [dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") \| `context` Empty object to hold any data (in its attributes) about the request which is specific to your app (e.g. session object). Falcon itself will not interact with this attribute after it has been initialized. Note New in 2.0: the default `context_type` (see below) was changed from dict to a bare class, and the preferred way to pass request-specific data is now to set attributes directly on the `context` object, for example: ``` req.context.role = 'trial' req.context.user = 'guest' ``` \| Type: \| [object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)") \| `context_type` Class variable that determines the factory or type to use for initializing the `context` attribute. By default, the framework will instantiate bare objects (instances of the bare [`falcon.Context`](util#falcon.Context "falcon.Context") class). However, you may override this behavior by creating a custom child class of `falcon.Request`, and then passing that new class to `falcon.API()` by way of the latter’s `request_type` parameter. Note When overriding `context_type` with a factory function (as opposed to a class), the function is called like a method of the current Request instance. Therefore the first argument is the Request instance itself (self). \| Type: \| class \| `scheme` URL scheme used for the request. Either ‘http’ or ‘https’. Note If the request was proxied, the scheme may not match what was originally requested by the client. [`forwarded_scheme`](#falcon.Request.forwarded_scheme "falcon.Request.forwarded_scheme") can be used, instead, to handle such cases. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `forwarded_scheme` Original URL scheme requested by the user agent, if the request was proxied. Typical values are ‘http’ or ‘https’. The following request headers are checked, in order of preference, to determine the forwarded scheme: * `Forwarded` * `X-Forwarded-For` If none of these headers are available, or if the Forwarded header is available but does not contain a “proto” parameter in the first hop, the value of [`scheme`](#falcon.Request.scheme "falcon.Request.scheme") is returned instead. (See also: [RFC 7239, Section 1](https://tools.ietf.org/html/rfc7239#section-1)) \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `method` HTTP method requested (e.g., ‘GET’, ‘POST’, etc.) \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `host` Host request header field \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `forwarded_host` Original host request header as received by the first proxy in front of the application server. The following request headers are checked, in order of preference, to determine the forwarded scheme: * `Forwarded` * `X-Forwarded-Host` If none of the above headers are available, or if the Forwarded header is available but the “host” parameter is not included in the first hop, the value of [`host`](#falcon.Request.host "falcon.Request.host") is returned instead. Note Reverse proxies are often configured to set the Host header directly to the one that was originally requested by the user agent; in that case, using [`host`](#falcon.Request.host "falcon.Request.host") is sufficient. (See also: [RFC 7239, Section 4](https://tools.ietf.org/html/rfc7239#section-4)) \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `port` Port used for the request. If the request URI does not specify a port, the default one for the given schema is returned (80 for HTTP and 443 for HTTPS). \| Type: \| [int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)") \| `netloc` Returns the ‘host:port’ portion of the request URL. The port may be ommitted if it is the default one for the URL’s schema (80 for HTTP and 443 for HTTPS). \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `subdomain` Leftmost (i.e., most specific) subdomain from the hostname. If only a single domain name is given, `subdomain` will be `None`. Note If the hostname in the request is an IP address, the value for `subdomain` is undefined. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `app` The initial portion of the request URI’s path that corresponds to the application object, so that the application knows its virtual “location”. This may be an empty string, if the application corresponds to the “root” of the server. (Corresponds to the “SCRIPT\_NAME” environ variable defined by PEP-3333.) \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `uri` The fully-qualified URI for the request. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `url` Alias for `uri`. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `forwarded_uri` Original URI for proxied requests. Uses [`forwarded_scheme`](#falcon.Request.forwarded_scheme "falcon.Request.forwarded_scheme") and [`forwarded_host`](#falcon.Request.forwarded_host "falcon.Request.forwarded_host") in order to reconstruct the original URI requested by the user agent. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `relative_uri` The path and query string portion of the request URI, omitting the scheme and host. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `prefix` The prefix of the request URI, including scheme, host, and WSGI app (if any). \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `forwarded_prefix` The prefix of the original URI for proxied requests. Uses [`forwarded_scheme`](#falcon.Request.forwarded_scheme "falcon.Request.forwarded_scheme") and [`forwarded_host`](#falcon.Request.forwarded_host "falcon.Request.forwarded_host") in order to reconstruct the original URI. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `path` Path portion of the request URI (not including query string). Note `req.path` may be set to a new value by a `process_request()` middleware method in order to influence routing. If the original request path was URL encoded, it will be decoded before being returned by this attribute. If this attribute is to be used by the app for any upstream requests, any non URL-safe characters in the path must be URL encoded back before making the request. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `query_string` Query string portion of the request URI, without the preceding ‘?’ character. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `uri_template` The template for the route that was matched for this request. May be `None` if the request has not yet been routed, as would be the case for `process_request()` middleware methods. May also be `None` if your app uses a custom routing engine and the engine does not provide the URI template when resolving a route. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `remote_addr` IP address of the closest client or proxy to the WSGI server. This property is determined by the value of `REMOTE_ADDR` in the WSGI environment dict. Since this address is not derived from an HTTP header, clients and proxies can not forge it. Note If your application is behind one or more reverse proxies, you can use [`access_route`](#falcon.Request.access_route "falcon.Request.access_route") to retrieve the real IP address of the client. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `access_route` IP address of the original client, as well as any known addresses of proxies fronting the WSGI server. The following request headers are checked, in order of preference, to determine the addresses: * `Forwarded` * `X-Forwarded-For` * `X-Real-IP` If none of these headers are available, the value of [`remote_addr`](#falcon.Request.remote_addr "falcon.Request.remote_addr") is used instead. Note Per [RFC 7239](https://tools.ietf.org/html/rfc7239), the access route may contain “unknown” and obfuscated identifiers, in addition to IPv4 and IPv6 addresses Warning Headers can be forged by any client or proxy. Use this property with caution and validate all values before using them. Do not rely on the access route to authorize requests. \| Type: \| [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)") \| `forwarded` Value of the Forwarded header, as a parsed list of [`falcon.Forwarded`](#falcon.Forwarded "falcon.Forwarded") objects, or `None` if the header is missing. If the header value is malformed, Falcon will make a best effort to parse what it can. (See also: [RFC 7239, Section 4](https://tools.ietf.org/html/rfc7239#section-4)) \| Type: \| [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)") \| `date` Value of the Date header, converted to a `datetime` instance. The header value is assumed to conform to RFC 1123. \| Type: \| datetime \| `auth` Value of the Authorization header, or `None` if the header is missing. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `user_agent` Value of the User-Agent header, or `None` if the header is missing. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `referer` Value of the Referer header, or `None` if the header is missing. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `accept` Value of the Accept header, or ‘/’ if the header is missing. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `client_accepts_json` `True` if the Accept header indicates that the client is willing to receive JSON, otherwise `False`. \| Type: \| [bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)") \| `client_accepts_msgpack` `True` if the Accept header indicates that the client is willing to receive MessagePack, otherwise `False`. \| Type: \| [bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)") \| `client_accepts_xml` `True` if the Accept header indicates that the client is willing to receive XML, otherwise `False`. \| Type: \| [bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)") \| `cookies` A dict of name/value cookie pairs. The returned object should be treated as read-only to avoid unintended side-effects. If a cookie appears more than once in the request, only the first value encountered will be made available here. See also: [`get_cookie_values()`](#falcon.Request.get_cookie_values "falcon.Request.get_cookie_values") \| Type: \| [dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") \| `content_type` Value of the Content-Type header, or `None` if the header is missing. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `content_length` Value of the Content-Length header converted to an `int`, or `None` if the header is missing. \| Type: \| [int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)") \| `stream` File-like input object for reading the body of the request, if any. This object provides direct access to the server’s data stream and is non-seekable. In order to avoid unintended side effects, and to provide maximum flexibility to the application, Falcon itself does not buffer or spool the data in any way. Since this object is provided by the WSGI server itself, rather than by Falcon, it may behave differently depending on how you host your app. For example, attempting to read more bytes than are expected (as determined by the Content-Length header) may or may not block indefinitely. It’s a good idea to test your WSGI server to find out how it behaves. This can be particulary problematic when a request body is expected, but none is given. In this case, the following call blocks under certain WSGI servers: ``` # Blocks if Content-Length is 0 data = req.stream.read() ``` The workaround is fairly straightforward, if verbose: ``` # If Content-Length happens to be 0, or the header is # missing altogether, this will not block. data = req.stream.read(req.content_length or 0) ``` Alternatively, when passing the stream directly to a consumer, it may be necessary to branch off the value of the Content-Length header: ``` if req.content_length: doc = json.load(req.stream) ``` For a slight performance cost, you may instead wish to use [`bounded_stream`](#falcon.Request.bounded_stream "falcon.Request.bounded_stream"), which wraps the native WSGI input object to normalize its behavior. Note If an HTML form is POSTed to the API using the application/x-www-form-urlencoded media type, and the [`auto_parse_form_urlencoded`](api#falcon.RequestOptions.auto_parse_form_urlencoded "falcon.RequestOptions.auto_parse_form_urlencoded") option is set, the framework will consume `stream` in order to parse the parameters and merge them into the query string parameters. In this case, the stream will be left at EOF. `bounded_stream` File-like wrapper around `stream` to normalize certain differences between the native input objects employed by different WSGI servers. In particular, `bounded_stream` is aware of the expected Content-Length of the body, and will never block on out-of-bounds reads, assuming the client does not stall while transmitting the data to the server. For example, the following will not block when Content-Length is 0 or the header is missing altogether: ``` data = req.bounded_stream.read() ``` This is also safe: ``` doc = json.load(req.bounded_stream) ``` `expect` Value of the Expect header, or `None` if the header is missing. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `media` Returns a deserialized form of the request stream. When called, it will attempt to deserialize the request stream using the Content-Type header as well as the media-type handlers configured via [`falcon.RequestOptions`](api#falcon.RequestOptions "falcon.RequestOptions"). See [Media](media#media) for more information regarding media handling. Warning This operation will consume the request stream the first time it’s called and cache the results. Follow-up calls will just retrieve a cached version of the object. \| Type: \| [object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)") \| `range` A 2-member `tuple` parsed from the value of the Range header. The two members correspond to the first and last byte positions of the requested resource, inclusive. Negative indices indicate offset from the end of the resource, where -1 is the last byte, -2 is the second-to-last byte, and so forth. Only continous ranges are supported (e.g., “bytes=0-0,-1” would result in an HTTPBadRequest exception when the attribute is accessed.) \| Type: \| tuple of int \| `range_unit` Unit of the range parsed from the value of the Range header, or `None` if the header is missing \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `if_match` Value of the If-Match header, as a parsed list of [`falcon.ETag`](util#falcon.ETag "falcon.ETag") objects or `None` if the header is missing or its value is blank. This property provides a list of all `entity-tags` in the header, both strong and weak, in the same order as listed in the header. (See also: [RFC 7232, Section 3.1](https://tools.ietf.org/html/rfc7232#section-3.1)) \| Type: \| [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)") \| `if_none_match` Value of the If-None-Match header, as a parsed list of [`falcon.ETag`](util#falcon.ETag "falcon.ETag") objects or `None` if the header is missing or its value is blank. This property provides a list of all `entity-tags` in the header, both strong and weak, in the same order as listed in the header. (See also: [RFC 7232, Section 3.2](https://tools.ietf.org/html/rfc7232#section-3.2)) \| Type: \| [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)") \| `if_modified_since` Value of the If-Modified-Since header, or `None` if the header is missing. \| Type: \| datetime \| `if_unmodified_since` Value of the If-Unmodified-Since header, or `None` if the header is missing. \| Type: \| datetime \| `if_range` Value of the If-Range header, or `None` if the header is missing. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `headers` Raw HTTP headers from the request with canonical dash-separated names. Parsing all the headers to create this dict is done the first time this attribute is accessed, and the returned object should be treated as read-only. Note that this parsing can be costly, so unless you need all the headers in this format, you should instead use the `get_header()` method or one of the convenience attributes to get a value for a specific header. \| Type: \| [dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") \| `params` The mapping of request query parameter names to their values. Where the parameter appears multiple times in the query string, the value mapped to that parameter key will be a list of all the values in the order seen. \| Type: \| [dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") \| `options` Set of global options passed from the API handler. \| Type: \| [dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") \| `client_accepts(media_type)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/request.html#Request.client_accepts) Determine whether or not the client accepts a given media type. \| Parameters: \| media\_type ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – An Internet media type to check. \| \| Returns: \| `True` if the client has indicated in the Accept header that it accepts the specified media type. Otherwise, returns `False`. \| \| Return type: \| [bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)") \| `client_prefers(media_types)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/request.html#Request.client_prefers) Return the client’s preferred media type, given several choices. \| Parameters: \| media\_types (iterable of str) – One or more Internet media types from which to choose the client’s preferred type. This value must be an iterable collection of strings. \| \| Returns: \| The client’s preferred media type, based on the Accept header. Returns `None` if the client does not accept any of the given types. \| \| Return type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `context_type` alias of `falcon.util.structures.Context` `get_cookie_values(name)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/request.html#Request.get_cookie_values) Return all values provided in the Cookie header for the named cookie. (See also: [Getting Cookies](cookies#getting-cookies)) \| Parameters: \| name ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Cookie name, case-sensitive. \| \| Returns: \| Ordered list of all values specified in the Cookie header for the named cookie, or `None` if the cookie was not included in the request. If the cookie is specified more than once in the header, the returned list of values will preserve the ordering of the individual `cookie-pair`’s in the header. \| \| Return type: \| [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)") \| `get_header(name, required=False, default=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/request.html#Request.get_header) Retrieve the raw string value for the given header. \| Parameters: \| name ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Header name, case-insensitive (e.g., ‘Content-Type’) \| \| Keyword Arguments: \| \| \| * required ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Set to `True` to raise `HTTPBadRequest` instead of returning gracefully when the header is not found (default `False`). * default ([any](https://docs.python.org/3/library/functions.html#any "(in Python v3.7)")) – Value to return if the header is not found (default `None`). \| \| Returns: \| The value of the specified header if it exists, or the default value if the header is not found and is not required. \| \| Return type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| \| Raises: \| [`HTTPBadRequest`](errors#falcon.HTTPBadRequest "falcon.HTTPBadRequest") – The header was not found in the request, but it was required. \| `get_header_as_datetime(header, required=False, obs_date=False)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/request.html#Request.get_header_as_datetime) Return an HTTP header with HTTP-Date values as a datetime. \| Parameters: \| name ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Header name, case-insensitive (e.g., ‘Date’) \| \| Keyword Arguments: \| \| \| * required ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Set to `True` to raise `HTTPBadRequest` instead of returning gracefully when the header is not found (default `False`). * obs\_date ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Support obs-date formats according to RFC 7231, e.g.: “Sunday, 06-Nov-94 08:49:37 GMT” (default `False`). \| \| Returns: \| The value of the specified header if it exists, or `None` if the header is not found and is not required. \| \| Return type: \| datetime \| \| Raises: \| * [`HTTPBadRequest`](errors#falcon.HTTPBadRequest "falcon.HTTPBadRequest") – The header was not found in the request, but it was required. * `HttpInvalidHeader` – The header contained a malformed/invalid value. \| `get_param(name, required=False, store=None, default=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/request.html#Request.get_param) Return the raw value of a query string parameter as a string. Note If an HTML form is POSTed to the API using the application/x-www-form-urlencoded media type, Falcon can automatically parse the parameters from the request body and merge them into the query string parameters. To enable this functionality, set [`auto_parse_form_urlencoded`](api#falcon.RequestOptions.auto_parse_form_urlencoded "falcon.RequestOptions.auto_parse_form_urlencoded") to `True` via [`API.req_options`](api#falcon.API.req_options "falcon.API.req_options"). Note Similar to the way multiple keys in form data is handled, if a query parameter is assigned a comma-separated list of values (e.g., `foo=a,b,c`), only one of those values will be returned, and it is undefined which one. Use [`get_param_as_list()`](#falcon.Request.get_param_as_list "falcon.Request.get_param_as_list") to retrieve all the values. \| Parameters: \| name ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Parameter name, case-sensitive (e.g., ‘sort’). \| \| Keyword Arguments: \| \| \| * required ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Set to `True` to raise `HTTPBadRequest` instead of returning `None` when the parameter is not found (default `False`). * store ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)")) – A `dict`-like object in which to place the value of the param, but only if the param is present. * default ([any](https://docs.python.org/3/library/functions.html#any "(in Python v3.7)")) – If the param is not found returns the given value instead of `None` \| \| Returns: \| The value of the param as a string, or `None` if param is not found and is not required. \| \| Return type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| \| Raises: \| [`HTTPBadRequest`](errors#falcon.HTTPBadRequest "falcon.HTTPBadRequest") – A required param is missing from the request. \| `get_param_as_bool(name, required=False, store=None, blank_as_true=True, default=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/request.html#Request.get_param_as_bool) Return the value of a query string parameter as a boolean. This method treats valueless parameters as flags. By default, if no value is provided for the parameter in the query string, `True` is assumed and returned. If the parameter is missing altogether, `None` is returned as with other `get_param_()` methods, which can be easily treated as falsy by the caller as needed. The following boolean strings are supported: ``` TRUE_STRINGS = ('true', 'True', 'yes', '1', 'on') FALSE_STRINGS = ('false', 'False', 'no', '0', 'off') ``` \| Parameters: \| name* ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Parameter name, case-sensitive (e.g., ‘detailed’). \| \| Keyword Arguments: \| \| \| * required ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Set to `True` to raise `HTTPBadRequest` instead of returning `None` when the parameter is not found or is not a recognized boolean string (default `False`). * store ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)")) – A `dict`-like object in which to place the value of the param, but only if the param is found (default `None`). * blank\_as\_true ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Valueless query string parameters are treated as flags, resulting in `True` being returned when such a parameter is present, and `False` otherwise. To require the client to explicitly opt-in to a truthy value, pass `blank_as_true=False` to return `False` when a value is not specified in the query string. * default ([any](https://docs.python.org/3/library/functions.html#any "(in Python v3.7)")) – If the param is not found, return this value instead of `None`. \| \| Returns: \| The value of the param if it is found and can be converted to a `bool`. If the param is not found, returns `None` unless `required` is `True`. \| \| Return type: \| [bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)") \| \| Raises: \| [`HTTPBadRequest`](errors#falcon.HTTPBadRequest "falcon.HTTPBadRequest") – A required param is missing from the request, or can not be converted to a `bool`. \| `get_param_as_date(name, format_string='%Y-%m-%d', required=False, store=None, default=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/request.html#Request.get_param_as_date) Return the value of a query string parameter as a date. \| Parameters: \| name ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Parameter name, case-sensitive (e.g., ‘ids’). \| \| Keyword Arguments: \| \| \| * format\_string ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – String used to parse the param value into a date. Any format recognized by strptime() is supported (default `"%Y-%m-%d"`). * required ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Set to `True` to raise `HTTPBadRequest` instead of returning `None` when the parameter is not found (default `False`). * store ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)")) – A `dict`-like object in which to place the value of the param, but only if the param is found (default `None`). * default ([any](https://docs.python.org/3/library/functions.html#any "(in Python v3.7)")) – If the param is not found returns the given value instead of `None` \| \| Returns: \| The value of the param if it is found and can be converted to a `date` according to the supplied format string. If the param is not found, returns `None` unless required is `True`. \| \| Return type: \| [datetime.date](https://docs.python.org/3/library/datetime.html#datetime.date "(in Python v3.7)") \| \| Raises: \| [`HTTPBadRequest`](errors#falcon.HTTPBadRequest "falcon.HTTPBadRequest") – A required param is missing from the request, or the value could not be converted to a `date`. \| `get_param_as_datetime(name, format_string='%Y-%m-%dT%H:%M:%SZ', required=False, store=None, default=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/request.html#Request.get_param_as_datetime) Return the value of a query string parameter as a datetime. \| Parameters: \| name ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Parameter name, case-sensitive (e.g., ‘ids’). \| \| Keyword Arguments: \| \| \| * format\_string ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – String used to parse the param value into a `datetime`. Any format recognized by strptime() is supported (default `'%Y-%m-%dT%H:%M:%SZ'`). * required ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Set to `True` to raise `HTTPBadRequest` instead of returning `None` when the parameter is not found (default `False`). * store ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)")) – A `dict`-like object in which to place the value of the param, but only if the param is found (default `None`). * default ([any](https://docs.python.org/3/library/functions.html#any "(in Python v3.7)")) – If the param is not found returns the given value instead of `None` \| \| Returns: \| The value of the param if it is found and can be converted to a `datetime` according to the supplied format string. If the param is not found, returns `None` unless required is `True`. \| \| Return type: \| [datetime.datetime](https://docs.python.org/3/library/datetime.html#datetime.datetime "(in Python v3.7)") \| \| Raises: \| [`HTTPBadRequest`](errors#falcon.HTTPBadRequest "falcon.HTTPBadRequest") – A required param is missing from the request, or the value could not be converted to a `datetime`. \| `get_param_as_float(name, required=False, min_value=None, max_value=None, store=None, default=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/request.html#Request.get_param_as_float) Return the value of a query string parameter as an float. \| Parameters: \| name ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Parameter name, case-sensitive (e.g., ‘limit’). \| \| Keyword Arguments: \| \| \| * required ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Set to `True` to raise `HTTPBadRequest` instead of returning `None` when the parameter is not found or is not an float (default `False`). * min\_value ([float](https://docs.python.org/3/library/functions.html#float "(in Python v3.7)")) – Set to the minimum value allowed for this param. If the param is found and it is less than min\_value, an `HTTPError` is raised. * max\_value ([float](https://docs.python.org/3/library/functions.html#float "(in Python v3.7)")) – Set to the maximum value allowed for this param. If the param is found and its value is greater than max\_value, an `HTTPError` is raised. * store ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)")) – A `dict`-like object in which to place the value of the param, but only if the param is found (default `None`). * default ([any](https://docs.python.org/3/library/functions.html#any "(in Python v3.7)")) – If the param is not found returns the given value instead of `None` \| \| Returns: \| The value of the param if it is found and can be converted to an `float`. If the param is not found, returns `None`, unless `required` is `True`. \| \| Return type: \| [float](https://docs.python.org/3/library/functions.html#float "(in Python v3.7)") \| Raises HTTPBadRequest: The param was not found in the request, even though it was required to be there, or it was found but could not be converted to an `float`. Also raised if the param’s value falls outside the given interval, i.e., the value must be in the interval: min\_value <= value <= max\_value to avoid triggering an error. `get_param_as_int(name, required=False, min_value=None, max_value=None, store=None, default=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/request.html#Request.get_param_as_int) Return the value of a query string parameter as an int. \| Parameters: \| name ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Parameter name, case-sensitive (e.g., ‘limit’). \| \| Keyword Arguments: \| \| \| * required ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Set to `True` to raise `HTTPBadRequest` instead of returning `None` when the parameter is not found or is not an integer (default `False`). * min\_value ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – Set to the minimum value allowed for this param. If the param is found and it is less than min\_value, an `HTTPError` is raised. * max\_value ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – Set to the maximum value allowed for this param. If the param is found and its value is greater than max\_value, an `HTTPError` is raised. * store ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)")) – A `dict`-like object in which to place the value of the param, but only if the param is found (default `None`). * default ([any](https://docs.python.org/3/library/functions.html#any "(in Python v3.7)")) – If the param is not found returns the given value instead of `None` \| \| Returns: \| The value of the param if it is found and can be converted to an `int`. If the param is not found, returns `None`, unless `required` is `True`. \| \| Return type: \| [int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)") \| Raises HTTPBadRequest: The param was not found in the request, even though it was required to be there, or it was found but could not be converted to an `int`. Also raised if the param’s value falls outside the given interval, i.e., the value must be in the interval: min\_value <= value <= max\_value to avoid triggering an error. `get_param_as_json(name, required=False, store=None, default=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/request.html#Request.get_param_as_json) Return the decoded JSON value of a query string parameter. Given a JSON value, decode it to an appropriate Python type, (e.g., `dict`, `list`, `str`, `int`, `bool`, etc.) \| Parameters: \| name ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Parameter name, case-sensitive (e.g., ‘payload’). \| \| Keyword Arguments: \| \| \| * required ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Set to `True` to raise `HTTPBadRequest` instead of returning `None` when the parameter is not found (default `False`). * store ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)")) – A `dict`-like object in which to place the value of the param, but only if the param is found (default `None`). * default ([any](https://docs.python.org/3/library/functions.html#any "(in Python v3.7)")) – If the param is not found returns the given value instead of `None` \| \| Returns: \| The value of the param if it is found. Otherwise, returns `None` unless required is `True`. \| \| Return type: \| [dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") \| \| Raises: \| [`HTTPBadRequest`](errors#falcon.HTTPBadRequest "falcon.HTTPBadRequest") – A required param is missing from the request, or the value could not be parsed as JSON. \| `get_param_as_list(name, transform=None, required=False, store=None, default=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/request.html#Request.get_param_as_list) Return the value of a query string parameter as a list. List items must be comma-separated or must be provided as multiple instances of the same param in the query string ala application/x-www-form-urlencoded. \| Parameters: \| name ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Parameter name, case-sensitive (e.g., ‘ids’). \| \| Keyword Arguments: \| \| \| * transform ([callable](https://docs.python.org/3/library/functions.html#callable "(in Python v3.7)")) – An optional transform function that takes as input each element in the list as a `str` and outputs a transformed element for inclusion in the list that will be returned. For example, passing `int` will transform list items into numbers. * required ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Set to `True` to raise `HTTPBadRequest` instead of returning `None` when the parameter is not found (default `False`). * store ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)")) – A `dict`-like object in which to place the value of the param, but only if the param is found (default `None`). * default ([any](https://docs.python.org/3/library/functions.html#any "(in Python v3.7)")) – If the param is not found returns the given value instead of `None` \| \| Returns: \| The value of the param if it is found. Otherwise, returns `None` unless required is True. Empty list elements will be discarded. For example, the following query strings would both result in `[‘1’, ‘3’]`: ``` things=1,,3 things=1&things=&things=3 ``` \| \| Return type: \| [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)") \| \| Raises: \| [`HTTPBadRequest`](errors#falcon.HTTPBadRequest "falcon.HTTPBadRequest") – A required param is missing from the request, or a transform function raised an instance of `ValueError`. \| `get_param_as_uuid(name, required=False, store=None, default=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/request.html#Request.get_param_as_uuid) Return the value of a query string parameter as an UUID. The value to convert must conform to the standard UUID string representation per RFC 4122. For example, the following strings are all valid: ``` # Lowercase '64be949b-3433-4d36-a4a8-9f19d352fee8' # Uppercase 'BE71ECAA-F719-4D42-87FD-32613C2EEB60' # Mixed '81c8155C-D6de-443B-9495-39Fa8FB239b5' ``` \| Parameters: \| name ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Parameter name, case-sensitive (e.g., ‘id’). \| \| Keyword Arguments: \| \| \| * required ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Set to `True` to raise `HTTPBadRequest` instead of returning `None` when the parameter is not found or is not a UUID (default `False`). * store ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)")) – A `dict`-like object in which to place the value of the param, but only if the param is found (default `None`). * default ([any](https://docs.python.org/3/library/functions.html#any "(in Python v3.7)")) – If the param is not found returns the given value instead of `None` \| \| Returns: \| The value of the param if it is found and can be converted to a `UUID`. If the param is not found, returns `default` (default `None`), unless `required` is `True`. \| \| Return type: \| UUID \| Raises HTTPBadRequest: The param was not found in the request, even though it was required to be there, or it was found but could not be converted to a `UUID`. `has_param(name)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/request.html#Request.has_param) Determine whether or not the query string parameter already exists. \| Parameters: \| name ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Parameter name, case-sensitive (e.g., ‘sort’). \| \| Returns: \| `True` if param is found, or `False` if param is not found. \| \| Return type: \| [bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)") \| `log_error(message)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/request.html#Request.log_error) Write an error message to the server’s log. Prepends timestamp and request info to message, and writes the result out to the WSGI server’s error stream (`wsgi.error`). \| Parameters: \| message ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") or unicode) – Description of the problem. On Python 2, instances of `unicode` will be converted to UTF-8. \| `class falcon.Forwarded` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/forwarded.html#Forwarded) Represents a parsed Forwarded header. (See also: [RFC 7239, Section 4](https://tools.ietf.org/html/rfc7239#section-4)) `src` The value of the “for” parameter, or `None` if the parameter is absent. Identifies the node making the request to the proxy. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `dest` The value of the “by” parameter, or `None` if the parameter is absent. Identifies the client-facing interface of the proxy. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `host` The value of the “host” parameter, or `None` if the parameter is absent. Provides the host request header field as received by the proxy. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `scheme` The value of the “proto” parameter, or `None` if the parameter is absent. Indicates the protocol that was used to make the request to the proxy. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| Response -------- `class falcon.Response(options=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/response.html#Response) Represents an HTTP response to a client request. Note `Response` is not meant to be instantiated directly by responders. \| Keyword Arguments: \| \| \| options ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)")) – Set of global options passed from the API handler. \| `status` HTTP status line (e.g., ‘200 OK’). Falcon requires the full status line, not just the code (e.g., 200). This design makes the framework more efficient because it does not have to do any kind of conversion or lookup when composing the WSGI response. If not set explicitly, the status defaults to ‘200 OK’. Note Falcon provides a number of constants for common status codes. They all start with the `HTTP_` prefix, as in: `falcon.HTTP_204`. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `media` A serializable object supported by the media handlers configured via [`falcon.RequestOptions`](api#falcon.RequestOptions "falcon.RequestOptions"). See [Media](media#media) for more information regarding media handling. \| Type: \| [object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)") \| `body` String representing response content. If set to a Unicode type (`unicode` in Python 2, or `str` in Python 3), Falcon will encode the text as UTF-8 in the response. If the content is already a byte string, use the [`data`](#falcon.Response.data "falcon.Response.data") attribute instead (it’s faster). \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") or unicode \| `data` Byte string representing response content. Use this attribute in lieu of `body` when your content is already a byte string (`str` or `bytes` in Python 2, or simply `bytes` in Python 3). See also the note below. Note Under Python 2.x, if your content is of type `str`, using the `data` attribute instead of `body` is the most efficient approach. However, if your text is of type `unicode`, you will need to use the `body` attribute instead. Under Python 3.x, on the other hand, the 2.x `str` type can be thought of as having been replaced by what was once the `unicode` type, and so you will need to always use the `body` attribute for strings to ensure Unicode characters are properly encoded in the HTTP response. \| Type: \| [bytes](https://docs.python.org/3/library/stdtypes.html#bytes "(in Python v3.7)") \| `stream` Either a file-like object with a `read()` method that takes an optional size argument and returns a block of bytes, or an iterable object, representing response content, and yielding blocks as byte strings. Falcon will use wsgi.file\_wrapper, if provided by the WSGI server, in order to efficiently serve file-like objects. Note If the stream is set to an iterable object that requires resource cleanup, it can implement a close() method to do so. The close() method will be called upon completion of the request. `stream_len` Deprecated alias for [`content_length`](#falcon.Response.content_length "falcon.Response.content_length"). \| Type: \| [int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)") \| `context` Dictionary to hold any data about the response which is specific to your app. Falcon itself will not interact with this attribute after it has been initialized. \| Type: \| [dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") \| `context` Empty object to hold any data (in its attributes) about the response which is specific to your app (e.g. session object). Falcon itself will not interact with this attribute after it has been initialized. Note New in 2.0: the default `context_type` (see below) was changed from dict to a bare class, and the preferred way to pass response-specific data is now to set attributes directly on the `context` object, for example: ``` resp.context.cache_strategy = 'lru' ``` \| Type: \| [object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)") \| `context_type` Class variable that determines the factory or type to use for initializing the `context` attribute. By default, the framework will instantiate bare objects (instances of the bare [`falcon.Context`](util#falcon.Context "falcon.Context") class). However, you may override this behavior by creating a custom child class of `falcon.Response`, and then passing that new class to `falcon.API()` by way of the latter’s `response_type` parameter. Note When overriding `context_type` with a factory function (as opposed to a class), the function is called like a method of the current Response instance. Therefore the first argument is the Response instance itself (self). \| Type: \| class \| `options` Set of global options passed from the API handler. \| Type: \| [dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") \| `headers` Copy of all headers set for the response, sans cookies. Note that a new copy is created and returned each time this property is referenced. \| Type: \| [dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") \| `complete` Set to `True` from within a middleware method to signal to the framework that request processing should be short-circuited (see also [Middleware](middleware#middleware)). \| Type: \| [bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)") \| `accept_ranges` Set the Accept-Ranges header. The Accept-Ranges header field indicates to the client which range units are supported (e.g. “bytes”) for the target resource. If range requests are not supported for the target resource, the header may be set to “none” to advise the client not to attempt any such requests. Note “none” is the literal string, not Python’s built-in `None` type. `add_link(target, rel, title=None, title_star=None, anchor=None, hreflang=None, type_hint=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/response.html#Response.add_link) Add a link header to the response. (See also: [RFC 5988, Section 1](https://tools.ietf.org/html/rfc5988#section-1)) Note Calling this method repeatedly will cause each link to be appended to the Link header value, separated by commas. Note So-called “link-extension” elements, as defined by RFC 5988, are not yet supported. See also Issue #288. \| Parameters: \| * target ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Target IRI for the resource identified by the link. Will be converted to a URI, if necessary, per [RFC 3987, Section 3.1.](https://tools.ietf.org/html/rfc3987#section-3.1.) * rel ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Relation type of the link, such as “next” or “bookmark”. (See also: <http://www.iana.org/assignments/link-relations/link-relations.xhtml>) \| \| Keyword Arguments: \| \| \| * title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-readable label for the destination of the link (default `None`). If the title includes non-ASCII characters, you will need to use `title_star` instead, or provide both a US-ASCII version using `title` and a Unicode version using `title_star`. * title\_star (tuple of str) – Localized title describing the destination of the link (default `None`). The value must be a two-member tuple in the form of (language-tag, text), where language-tag is a standard language identifier as defined in [RFC 5646, Section 2.1](https://tools.ietf.org/html/rfc5646#section-2.1), and text is a Unicode string. Note language-tag may be an empty string, in which case the client will assume the language from the general context of the current request. Note text will always be encoded as UTF-8. If the string contains non-ASCII characters, it should be passed as a `unicode` type string (requires the ‘u’ prefix in Python 2). * anchor ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Override the context IRI with a different URI (default None). By default, the context IRI for the link is simply the IRI of the requested resource. The value provided may be a relative URI. * hreflang ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") or iterable) – Either a single language-tag, or a `list` or `tuple` of such tags to provide a hint to the client as to the language of the result of following the link. A list of tags may be given in order to indicate to the client that the target resource is available in multiple languages. * type\_hint ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Provides a hint as to the media type of the result of dereferencing the link (default `None`). As noted in RFC 5988, this is only a hint and does not override the Content-Type header returned when the link is followed. \| `append_header(name, value)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/response.html#Response.append_header) Set or append a header for this response. If the header already exists, the new value will normally be appended to it, delimited by a comma. The notable exception to this rule is Set-Cookie, in which case a separate header line for each value will be included in the response. Note While this method can be used to efficiently append raw Set-Cookie headers to the response, you may find [`set_cookie()`](#falcon.Response.set_cookie "falcon.Response.set_cookie") to be more convenient. \| Parameters: \| * name ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Header name (case-insensitive). The restrictions noted below for the header’s value also apply here. * value ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Value for the header. Must be convertable to `str` or be of type `str` or `StringType`. Strings must contain only US-ASCII characters. Under Python 2.x, the `unicode` type is also accepted, although such strings are also limited to US-ASCII. \| `cache_control` Set the Cache-Control header. Used to set a list of cache directives to use as the value of the Cache-Control header. The list will be joined with “, ” to produce the value for the header. `content_length` Set the Content-Length header. This property can be used for responding to HEAD requests when you aren’t actually providing the response body, or when streaming the response. If either the `body` property or the `data` property is set on the response, the framework will force Content-Length to be the length of the given body bytes. Therefore, it is only necessary to manually set the content length when those properties are not used. Note In cases where the response content is a stream (readable file-like object), Falcon will not supply a Content-Length header to the WSGI server unless `content_length` is explicitly set. Consequently, the server may choose to use chunked encoding or one of the other strategies suggested by PEP-3333. `content_location` Set the Content-Location header. This value will be URI encoded per RFC 3986. If the value that is being set is already URI encoded it should be decoded first or the header should be set manually using the set\_header method. `content_range` A tuple to use in constructing a value for the Content-Range header. The tuple has the form (start, end, length, [unit]), where start and end designate the range (inclusive), and length is the total length, or ‘\’ if unknown. You may pass `int`’s for these numbers (no need to convert to `str` beforehand). The optional value unit* describes the range unit and defaults to ‘bytes’ Note You only need to use the alternate form, ‘bytes \/1234’, for responses that use the status ‘416 Range Not Satisfiable’. In this case, raising `falcon.HTTPRangeNotSatisfiable` will do the right thing. (See also: [RFC 7233, Section 4.2](https://tools.ietf.org/html/rfc7233#section-4.2)) `content_type` Sets the Content-Type header. The `falcon` module provides a number of constants for common media types, including `falcon.MEDIA_JSON`, `falcon.MEDIA_MSGPACK`, `falcon.MEDIA_YAML`, `falcon.MEDIA_XML`, `falcon.MEDIA_HTML`, `falcon.MEDIA_JS`, `falcon.MEDIA_TEXT`, `falcon.MEDIA_JPEG`, `falcon.MEDIA_PNG`, and `falcon.MEDIA_GIF`. `context_type` alias of `falcon.util.structures.Context` `delete_header(name)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/response.html#Response.delete_header) Delete a header that was previously set for this response. If the header was not previously set, nothing is done (no error is raised). Otherwise, all values set for the header will be removed from the response. Note that calling this method is equivalent to setting the corresponding header property (when said property is available) to `None`. For example: ``` resp.etag = None ``` Warning This method cannot be used with the Set-Cookie header. Instead, use [`unset_cookie()`](#falcon.Response.unset_cookie "falcon.Response.unset_cookie") to remove a cookie and ensure that the user agent expires its own copy of the data as well. \| Parameters: \| name* ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Header name (case-insensitive). Must be of type `str` or `StringType` and contain only US-ASCII characters. Under Python 2.x, the `unicode` type is also accepted, although such strings are also limited to US-ASCII. \| \| Raises: \| [`ValueError`](https://docs.python.org/3/library/exceptions.html#ValueError "(in Python v3.7)") – `name` cannot be `'Set-Cookie'`. \| `downloadable_as` Set the Content-Disposition header using the given filename. The value will be used for the filename directive. For example, given `'report.pdf'`, the Content-Disposition header would be set to: `'attachment; filename="report.pdf"'`. `etag` Set the ETag header. The ETag header will be wrapped with double quotes `"value"` in case the user didn’t pass it. `expires` Set the Expires header. Set to a `datetime` (UTC) instance. Note Falcon will format the `datetime` as an HTTP date string. `get_header(name, default=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/response.html#Response.get_header) Retrieve the raw string value for the given header. Normally, when a header has multiple values, they will be returned as a single, comma-delimited string. However, the Set-Cookie header does not support this format, and so attempting to retrieve it will raise an error. \| Parameters: \| name ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Header name, case-insensitive. Must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. \| \| Keyword Arguments: \| \| \| default – Value to return if the header is not found (default `None`). \| \| Raises: \| [`ValueError`](https://docs.python.org/3/library/exceptions.html#ValueError "(in Python v3.7)") – The value of the ‘Set-Cookie’ header(s) was requested. \| \| Returns: \| The value of the specified header if set, or the default value if not set. \| \| Return type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `last_modified` Set the Last-Modified header. Set to a `datetime` (UTC) instance. Note Falcon will format the `datetime` as an HTTP date string. `location` Set the Location header. This value will be URI encoded per RFC 3986. If the value that is being set is already URI encoded it should be decoded first or the header should be set manually using the set\_header method. `retry_after` Set the Retry-After header. The expected value is an integral number of seconds to use as the value for the header. The HTTP-date syntax is not supported. `set_cookie(name, value, expires=None, max_age=None, domain=None, path=None, secure=None, http_only=True)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/response.html#Response.set_cookie) Set a response cookie. Note This method can be called multiple times to add one or more cookies to the response. See also To learn more about setting cookies, see [Setting Cookies](cookies#setting-cookies). The parameters listed below correspond to those defined in [RFC 6265](http://tools.ietf.org/html/rfc6265). \| Parameters: \| * name ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Cookie name * value ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Cookie value \| \| Keyword Arguments: \| \| \| * expires ([datetime](https://docs.python.org/3/library/datetime.html#module-datetime "(in Python v3.7)")) – Specifies when the cookie should expire. By default, cookies expire when the user agent exits. (See also: [RFC 6265, Section 4.1.2.1](https://tools.ietf.org/html/rfc6265#section-4.1.2.1)) * max\_age ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – Defines the lifetime of the cookie in seconds. By default, cookies expire when the user agent exits. If both `max_age` and `expires` are set, the latter is ignored by the user agent. Note Coercion to `int` is attempted if provided with `float` or `str`. (See also: [RFC 6265, Section 4.1.2.2](https://tools.ietf.org/html/rfc6265#section-4.1.2.2)) * domain ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Restricts the cookie to a specific domain and any subdomains of that domain. By default, the user agent will return the cookie only to the origin server. When overriding this default behavior, the specified domain must include the origin server. Otherwise, the user agent will reject the cookie. (See also: [RFC 6265, Section 4.1.2.3](https://tools.ietf.org/html/rfc6265#section-4.1.2.3)) * path ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Scopes the cookie to the given path plus any subdirectories under that path (the “/” character is interpreted as a directory separator). If the cookie does not specify a path, the user agent defaults to the path component of the requested URI. Warning User agent interfaces do not always isolate cookies by path, and so this should not be considered an effective security measure. (See also: [RFC 6265, Section 4.1.2.4](https://tools.ietf.org/html/rfc6265#section-4.1.2.4)) * secure ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Direct the client to only return the cookie in subsequent requests if they are made over HTTPS (default: `True`). This prevents attackers from reading sensitive cookie data. Note The default value for this argument is normally `True`, but can be modified by setting [`secure_cookies_by_default`](api#falcon.ResponseOptions.secure_cookies_by_default "falcon.ResponseOptions.secure_cookies_by_default") via [`API.resp_options`](api#falcon.API.resp_options "falcon.API.resp_options"). Warning For the `secure` cookie attribute to be effective, your application will need to enforce HTTPS. (See also: [RFC 6265, Section 4.1.2.5](https://tools.ietf.org/html/rfc6265#section-4.1.2.5)) * http\_only ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Direct the client to only transfer the cookie with unscripted HTTP requests (default: `True`). This is intended to mitigate some forms of cross-site scripting. (See also: [RFC 6265, Section 4.1.2.6](https://tools.ietf.org/html/rfc6265#section-4.1.2.6)) \| \| Raises: \| * [`KeyError`](https://docs.python.org/3/library/exceptions.html#KeyError "(in Python v3.7)") – `name` is not a valid cookie name. * [`ValueError`](https://docs.python.org/3/library/exceptions.html#ValueError "(in Python v3.7)") – `value` is not a valid cookie value. \| `set_header(name, value)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/response.html#Response.set_header) Set a header for this response to a given value. Warning Calling this method overwrites any values already set for this header. To append an additional value for this header, use [`append_header()`](#falcon.Response.append_header "falcon.Response.append_header") instead. Warning This method cannot be used to set cookies; instead, use [`append_header()`](#falcon.Response.append_header "falcon.Response.append_header") or [`set_cookie()`](#falcon.Response.set_cookie "falcon.Response.set_cookie"). \| Parameters: \| * name ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Header name (case-insensitive). The restrictions noted below for the header’s value also apply here. * value ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Value for the header. Must be convertable to `str` or be of type `str` or `StringType`. Strings must contain only US-ASCII characters. Under Python 2.x, the `unicode` type is also accepted, although such strings are also limited to US-ASCII. \| \| Raises: \| [`ValueError`](https://docs.python.org/3/library/exceptions.html#ValueError "(in Python v3.7)") – `name` cannot be `'Set-Cookie'`. \| `set_headers(headers)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/response.html#Response.set_headers) Set several headers at once. This method can be used to set a collection of raw header names and values all at once. Warning Calling this method overwrites any existing values for the given header. If a list containing multiple instances of the same header is provided, only the last value will be used. To add multiple values to the response for a given header, see [`append_header()`](#falcon.Response.append_header "falcon.Response.append_header"). Warning This method cannot be used to set cookies; instead, use [`append_header()`](#falcon.Response.append_header "falcon.Response.append_header") or [`set_cookie()`](#falcon.Response.set_cookie "falcon.Response.set_cookie"). \| Parameters: \| headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A dictionary of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType` and contain only US-ASCII characters. Under Python 2.x, the `unicode` type is also accepted, although such strings are also limited to US-ASCII. Note Falcon can process a list of tuples slightly faster than a dict. \| \| Raises: \| [`ValueError`](https://docs.python.org/3/library/exceptions.html#ValueError "(in Python v3.7)") – `headers` was not a `dict` or `list` of `tuple`. \| `set_stream(stream, content_length)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/response.html#Response.set_stream) Convenience method for setting both `stream` and `content_length`. Although the `stream` and `content_length` properties may be set directly, using this method ensures `content_length` is not accidentally neglected when the length of the stream is known in advance. Using this method is also slightly more performant as compared to setting the properties individually. Note If the stream length is unknown, you can set `stream` directly, and ignore `content_length`. In this case, the WSGI server may choose to use chunked encoding or one of the other strategies suggested by PEP-3333. \| Parameters: \| * stream – A readable file-like object. * content\_length ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – Length of the stream, used for the Content-Length header in the response. \| `stream_len` Set the Content-Length header. This property can be used for responding to HEAD requests when you aren’t actually providing the response body, or when streaming the response. If either the `body` property or the `data` property is set on the response, the framework will force Content-Length to be the length of the given body bytes. Therefore, it is only necessary to manually set the content length when those properties are not used. Note In cases where the response content is a stream (readable file-like object), Falcon will not supply a Content-Length header to the WSGI server unless `content_length` is explicitly set. Consequently, the server may choose to use chunked encoding or one of the other strategies suggested by PEP-3333. `unset_cookie(name)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/response.html#Response.unset_cookie) Unset a cookie in the response Clears the contents of the cookie, and instructs the user agent to immediately expire its own copy of the cookie. Warning In order to successfully remove a cookie, both the path and the domain must match the values that were used when the cookie was created. `vary` Value to use for the Vary header. Set this property to an iterable of header names. For a single asterisk or field value, simply pass a single-element `list` or `tuple`. The “Vary” header field in a response describes what parts of a request message, aside from the method, Host header field, and request target, might influence the origin server’s process for selecting and representing this response. The value consists of either a single asterisk (“\*”) or a list of header field names (case-insensitive). (See also: [RFC 7231, Section 7.1.4](https://tools.ietf.org/html/rfc7231#section-7.1.4))	programming_docs
falcon Routing Routing ======= Falcon routes incoming requests to resources based on a set of URI templates. If the path requested by the client matches the template for a given route, the request is then passed on to the associated resource for processing. If no route matches the request, control then passes to a default responder that simply raises an instance of [`HTTPNotFound`](errors#falcon.HTTPNotFound "falcon.HTTPNotFound"). Normally this will result in sending a 404 response back to the client. Here’s a quick example to show how all the pieces fit together: ``` import json import falcon class ImagesResource(object): def on_get(self, req, resp): doc = { 'images': [ { 'href': '/images/1eaf6ef1-7f2d-4ecc-a8d5-6e8adba7cc0e.png' } ] } # Create a JSON representation of the resource resp.body = json.dumps(doc, ensure_ascii=False) # The following line can be omitted because 200 is the default # status returned by the framework, but it is included here to # illustrate how this may be overridden as needed. resp.status = falcon.HTTP_200 api = application = falcon.API() images = ImagesResource() api.add_route('/images', images) ``` Default Router -------------- Falcon’s default routing engine is based on a decision tree that is first compiled into Python code, and then evaluated by the runtime. The [`add_route()`](api#falcon.API.add_route "falcon.API.add_route") method is used to associate a URI template with a resource. Falcon then maps incoming requests to resources based on these templates. Falcon’s default router uses Python classes to represent resources. In practice, these classes act as controllers in your application. They convert an incoming request into one or more internal actions, and then compose a response back to the client based on the results of those actions. (See also: [Tutorial: Creating Resources](../user/tutorial#tutorial-resources)) ``` ┌────────────┐ request → │ │ │ Resource │ ↻ Orchestrate the requested action │ Controller │ ↻ Compose the result response ← │ │ └────────────┘ ``` Each resource class defines various “responder” methods, one for each HTTP method the resource allows. Responder names start with `on_` and are named according to which HTTP method they handle, as in `on_get()`, `on_post()`, `on_put()`, etc. Note If your resource does not support a particular HTTP method, simply omit the corresponding responder and Falcon will use a default responder that raises an instance of [`HTTPMethodNotAllowed`](errors#falcon.HTTPMethodNotAllowed "falcon.HTTPMethodNotAllowed") when that method is requested. Normally this results in sending a 405 response back to the client. Responders must always define at least two arguments to receive [`Request`](request_and_response#falcon.Request "falcon.Request") and [`Response`](request_and_response#falcon.Response "falcon.Response") objects, respectively: ``` def on_post(self, req, resp): pass ``` The [`Request`](request_and_response#falcon.Request "falcon.Request") object represents the incoming HTTP request. It exposes properties and methods for examining headers, query string parameters, and other metadata associated with the request. A file-like stream object is also provided for reading any data that was included in the body of the request. The [`Response`](request_and_response#falcon.Response "falcon.Response") object represents the application’s HTTP response to the above request. It provides properties and methods for setting status, header and body data. The [`Response`](request_and_response#falcon.Response "falcon.Response") object also exposes a dict-like [`context`](request_and_response#falcon.Response.context "falcon.Response.context") property for passing arbitrary data to hooks and middleware methods. Note Rather than directly manipulate the [`Response`](request_and_response#falcon.Response "falcon.Response") object, a responder may raise an instance of either [`HTTPError`](errors#falcon.HTTPError "falcon.HTTPError") or [`HTTPStatus`](status#falcon.HTTPStatus "falcon.HTTPStatus"). Falcon will convert these exceptions to appropriate HTTP responses. Alternatively, you can handle them youself via [`add_error_handler()`](api#falcon.API.add_error_handler "falcon.API.add_error_handler"). In addition to the standard `req` and `resp` parameters, if the route’s template contains field expressions, any responder that desires to receive requests for that route must accept arguments named after the respective field names defined in the template. A field expression consists of a bracketed field name. For example, given the following template: ``` /user/{name} ``` A PUT request to “/user/kgriffs” would be routed to: ``` def on_put(self, req, resp, name): pass ``` Because field names correspond to argument names in responder methods, they must be valid Python identifiers. Individual path segments may contain one or more field expressions, and fields need not span the entire path segment. For example: ``` /repos/{org}/{repo}/compare/{usr0}:{branch0}...{usr1}:{branch1} /serviceRoot/People('{name}') ``` (See also the [Falcon tutorial](../user/tutorial#tutorial) for additional examples and a walkthough of setting up routes within the context of a sample application.) Field Converters ---------------- Falcon’s default router supports the use of field converters to transform a URI template field value. Field converters may also perform simple input validation. For example, the following URI template uses the `int` converter to convert the value of `tid` to a Python `int`, but only if it has exactly eight digits: ``` /teams/{tid:int(8)} ``` If the value is malformed and can not be converted, Falcon will reject the request with a 404 response to the client. Converters are instantiated with the argument specification given in the field expression. These specifications follow the standard Python syntax for passing arguments. For example, the comments in the following code show how a converter would be instantiated given different argument specifications in the URI template: ``` # IntConverter() api.add_route( '/a/{some_field:int}', some_resource ) # IntConverter(8) api.add_route( '/b/{some_field:int(8)}', some_resource ) # IntConverter(8, min=10000000) api.add_route( '/c/{some_field:int(8, min=10000000)}', some_resource ) ``` Built-in Converters ------------------- \| Identifier \| Class \| Example \| \| --- \| --- \| --- \| \| `int` \| [`IntConverter`](#falcon.routing.IntConverter "falcon.routing.IntConverter") \| `/teams/{tid:int(8)}` \| \| `uuid` \| [`UUIDConverter`](#falcon.routing.UUIDConverter "falcon.routing.UUIDConverter") \| `/diff/{left:uuid}...{right:uuid}` \| \| `dt` \| [`DateTimeConverter`](#falcon.routing.DateTimeConverter "falcon.routing.DateTimeConverter") \| `/logs/{day:dt("%Y-%m-%d")}` \| `class falcon.routing.IntConverter(num_digits=None, min=None, max=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/routing/converters.html#IntConverter) Converts a field value to an int. Identifier: `int` \| Keyword Arguments: \| \| \| * num\_digits ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – Require the value to have the given number of digits. * min ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – Reject the value if it is less than this number. * max ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – Reject the value if it is greater than this number. \| `convert(value)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/routing/converters.html#IntConverter.convert) Convert a URI template field value to another format or type. \| Parameters: \| value ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Original string to convert. \| \| Returns: \| `Converted field value, or None if the field` can not be converted. \| \| Return type: \| [object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)") \| `class falcon.routing.UUIDConverter` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/routing/converters.html#UUIDConverter) Converts a field value to a uuid.UUID. Identifier: `uuid` In order to be converted, the field value must consist of a string of 32 hexadecimal digits, as defined in [RFC 4122, Section 3.](https://tools.ietf.org/html/rfc4122#section-3.) Note, however, that hyphens and the URN prefix are optional. `convert(value)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/routing/converters.html#UUIDConverter.convert) Convert a URI template field value to another format or type. \| Parameters: \| value ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Original string to convert. \| \| Returns: \| `Converted field value, or None if the field` can not be converted. \| \| Return type: \| [object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)") \| `class falcon.routing.DateTimeConverter(format_string='%Y-%m-%dT%H:%M:%SZ')` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/routing/converters.html#DateTimeConverter) Converts a field value to a datetime. Identifier: `dt` \| Keyword Arguments: \| \| \| format\_string ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – String used to parse the field value into a datetime. Any format recognized by strptime() is supported (default `'%Y-%m-%dT%H:%M:%SZ'`). \| `convert(value)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/routing/converters.html#DateTimeConverter.convert) Convert a URI template field value to another format or type. \| Parameters: \| value ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Original string to convert. \| \| Returns: \| `Converted field value, or None if the field` can not be converted. \| \| Return type: \| [object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)") \| Custom Converters ----------------- Custom converters can be registered via the [`converters`](api#falcon.routing.CompiledRouterOptions.converters "falcon.routing.CompiledRouterOptions.converters") router option. A converter is simply a class that implements the `BaseConverter` interface: `class falcon.routing.BaseConverter` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/routing/converters.html#BaseConverter) Abstract base class for URI template field converters. `convert(value)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/routing/converters.html#BaseConverter.convert) Convert a URI template field value to another format or type. \| Parameters: \| value ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Original string to convert. \| \| Returns: \| `Converted field value, or None if the field` can not be converted. \| \| Return type: \| [object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)") \| Custom Routers -------------- A custom routing engine may be specified when instantiating [`falcon.API()`](api#falcon.API "falcon.API"). For example: ``` router = MyRouter() api = API(router=router) ``` Custom routers may derive from the default [`CompiledRouter`](#falcon.routing.CompiledRouter "falcon.routing.CompiledRouter") engine, or implement a completely different routing strategy (such as object-based routing). A custom router is any class that implements the following interface: ``` class MyRouter(object): def add_route(self, uri_template, resource, kwargs): """Adds a route between URI path template and resource. Args: uri_template (str): A URI template to use for the route resource (object): The resource instance to associate with the URI template. Keyword Args: suffix (str): Optional responder name suffix for this route. If a suffix is provided, Falcon will map GET requests to ``on_get_{suffix}()``, POST requests to ``on_post_{suffix}()``, etc. In this way, multiple closely-related routes can be mapped to the same resource. For example, a single resource class can use suffixed responders to distinguish requests for a single item vs. a collection of those same items. Another class might use a suffixed responder to handle a shortlink route in addition to the regular route for the resource. kwargs (dict): Accepts any additional keyword arguments that were originally passed to the falcon.API.add_route() method. These arguments MUST be accepted via the double-star variadic pattern (kwargs), and ignore any unrecognized or unsupported arguments. """ def find(self, uri, req=None): """Search for a route that matches the given partial URI. Args: uri(str): The requested path to route. Keyword Args: req(Request): The Request object that will be passed to the routed responder. The router may use `req` to further differentiate the requested route. For example, a header may be used to determine the desired API version and route the request accordingly. Note: The `req` keyword argument was added in version 1.2. To ensure backwards-compatibility, routers that do not implement this argument are still supported. Returns: tuple: A 4-member tuple composed of (resource, method_map, params, uri_template), or ``None`` if no route matches the requested path. """ ``` Default Router -------------- `class falcon.routing.CompiledRouter` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/routing/compiled.html#CompiledRouter) Fast URI router which compiles its routing logic to Python code. Generally you do not need to use this router class directly, as an instance is created by default when the falcon.API class is initialized. The router treats URI paths as a tree of URI segments and searches by checking the URI one segment at a time. Instead of interpreting the route tree for each look-up, it generates inlined, bespoke Python code to perform the search, then compiles that code. This makes the route processing quite fast. `add_route(uri_template, resource, kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/routing/compiled.html#CompiledRouter.add_route) Adds a route between a URI path template and a resource. This method may be overridden to customize how a route is added. \| Parameters: \| * uri\_template ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URI template to use for the route * resource ([object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)")) – The resource instance to associate with the URI template. \| \| Keyword Arguments: \| \| \| suffix ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Optional responder name suffix for this route. If a suffix is provided, Falcon will map GET requests to `on_get_{suffix}()`, POST requests to `on_post_{suffix}()`, etc. In this way, multiple closely-related routes can be mapped to the same resource. For example, a single resource class can use suffixed responders to distinguish requests for a single item vs. a collection of those same items. Another class might use a suffixed responder to handle a shortlink route in addition to the regular route for the resource. \| `find(uri, req=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/routing/compiled.html#CompiledRouter.find) Search for a route that matches the given partial URI. \| Parameters: \| uri ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – The requested path to route. \| \| Keyword Arguments: \| \| \| req ([Request](request_and_response#falcon.Request "falcon.Request")) – The Request object that will be passed to the routed responder. Currently the value of this argument is ignored by [`CompiledRouter`](#falcon.routing.CompiledRouter "falcon.routing.CompiledRouter"). Routing is based solely on the path. \| \| Returns: \| A 4-member tuple composed of (resource, method\_map, params, uri\_template), or `None` if no route matches the requested path. \| \| Return type: \| [tuple](https://docs.python.org/3/library/stdtypes.html#tuple "(in Python v3.7)") \| `map_http_methods(resource, kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/routing/compiled.html#CompiledRouter.map_http_methods) Map HTTP methods (e.g., GET, POST) to methods of a resource object. This method is called from [`add_route()`](#falcon.routing.CompiledRouter.add_route "falcon.routing.CompiledRouter.add_route") and may be overridden to provide a custom mapping strategy. \| Parameters: \| resource** (instance) – Object which represents a REST resource. The default maps the HTTP method `GET` to `on_get()`, `POST` to `on_post()`, etc. If any HTTP methods are not supported by your resource, simply don’t define the corresponding request handlers, and Falcon will do the right thing. \| \| Keyword Arguments: \| \| \| suffix ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Optional responder name suffix for this route. If a suffix is provided, Falcon will map GET requests to `on_get_{suffix}()`, POST requests to `on_post_{suffix}()`, etc. In this way, multiple closely-related routes can be mapped to the same resource. For example, a single resource class can use suffixed responders to distinguish requests for a single item vs. a collection of those same items. Another class might use a suffixed responder to handle a shortlink route in addition to the regular route for the resource. \| Routing Utilities ----------------- The falcon.routing module contains the following utilities that may be used by custom routing engines. `falcon.routing.map_http_methods(resource, suffix=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/routing/util.html#map_http_methods) Maps HTTP methods (e.g., GET, POST) to methods of a resource object. \| Parameters: \| resource – An object with responder methods, following the naming convention on\_\, that correspond to each method the resource supports. For example, if a resource supports GET and POST, it should define `on_get(self, req, resp)` and `on_post(self, req, resp)`. \| \| Keyword Arguments: \| \| \| suffix* ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Optional responder name suffix for this route. If a suffix is provided, Falcon will map GET requests to `on_get_{suffix}()`, POST requests to `on_post_{suffix}()`, etc. \| \| Returns: \| A mapping of HTTP methods to explicitly defined resource responders. \| \| Return type: \| [dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") \| `falcon.routing.set_default_responders(method_map)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/routing/util.html#set_default_responders) Maps HTTP methods not explicitly defined on a resource to default responders. \| Parameters: \| method\_map – A dict with HTTP methods mapped to responders explicitly defined in a resource. \| `falcon.routing.compile_uri_template(template)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/routing/util.html#compile_uri_template) Compile the given URI template string into a pattern matcher. This function can be used to construct custom routing engines that iterate through a list of possible routes, attempting to match an incoming request against each route’s compiled regular expression. Each field is converted to a named group, so that when a match is found, the fields can be easily extracted using `re.MatchObject.groupdict()`. This function does not support the more flexible templating syntax used in the default router. Only simple paths with bracketed field expressions are recognized. For example: ``` / /books /books/{isbn} /books/{isbn}/characters /books/{isbn}/characters/{name} ``` Also, note that if the template contains a trailing slash character, it will be stripped in order to normalize the routing logic. \| Parameters: \| template ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – The template to compile. Note that field names are restricted to ASCII a-z, A-Z, and the underscore character. \| \| Returns: \| (template\_field\_names, template\_regex) \| \| Return type: \| [tuple](https://docs.python.org/3/library/stdtypes.html#tuple "(in Python v3.7)") \|	programming_docs
falcon Status Codes Status Codes ============ Falcon provides a list of constants for common [HTTP response status codes](http://httpstatus.es). For example: ``` # Override the default "200 OK" response status resp.status = falcon.HTTP_409 ``` Or, using the more verbose name: ``` resp.status = falcon.HTTP_CONFLICT ``` Using these constants helps avoid typos and cuts down on the number of string objects that must be created when preparing responses. Falcon also provides a generic `HTTPStatus` class. Raise this class from a hook, middleware, or a responder to stop handling the request and skip to the response handling. It takes status, additional headers and body as input arguments. HTTPStatus ---------- `class falcon.HTTPStatus(status, headers=None, body=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/http_status.html#HTTPStatus) Represents a generic HTTP status. Raise an instance of this class from a hook, middleware, or responder to short-circuit request processing in a manner similar to `falcon.HTTPError`, but for non-error status codes. `status` HTTP status line, e.g. ‘748 Confounded by Ponies’. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `headers` Extra headers to add to the response. \| Type: \| [dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") \| `body` String representing response content. If Unicode, Falcon will encode as UTF-8 in the response. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") or unicode \| \| Parameters: \| * status ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – HTTP status code and text, such as ‘748 Confounded by Ponies’. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)")) – Extra headers to add to the response. * body ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") or unicode) – String representing response content. If Unicode, Falcon will encode as UTF-8 in the response. \| 1xx Informational ----------------- ``` HTTP_CONTINUE = HTTP_100 HTTP_SWITCHING_PROTOCOLS = HTTP_101 HTTP_PROCESSING = HTTP_102 HTTP_100 = '100 Continue' HTTP_101 = '101 Switching Protocols' HTTP_102 = '102 Processing' ``` 2xx Success ----------- ``` HTTP_OK = HTTP_200 HTTP_CREATED = HTTP_201 HTTP_ACCEPTED = HTTP_202 HTTP_NON_AUTHORITATIVE_INFORMATION = HTTP_203 HTTP_NO_CONTENT = HTTP_204 HTTP_RESET_CONTENT = HTTP_205 HTTP_PARTIAL_CONTENT = HTTP_206 HTTP_MULTI_STATUS = HTTP_207 HTTP_ALREADY_REPORTED = HTTP_208 HTTP_IM_USED = HTTP_226 HTTP_200 = '200 OK' HTTP_201 = '201 Created' HTTP_202 = '202 Accepted' HTTP_203 = '203 Non-Authoritative Information' HTTP_204 = '204 No Content' HTTP_205 = '205 Reset Content' HTTP_206 = '206 Partial Content' HTTP_207 = '207 Multi-Status' HTTP_208 = '208 Already Reported' HTTP_226 = '226 IM Used' ``` 3xx Redirection --------------- ``` HTTP_MULTIPLE_CHOICES = HTTP_300 HTTP_MOVED_PERMANENTLY = HTTP_301 HTTP_FOUND = HTTP_302 HTTP_SEE_OTHER = HTTP_303 HTTP_NOT_MODIFIED = HTTP_304 HTTP_USE_PROXY = HTTP_305 HTTP_TEMPORARY_REDIRECT = HTTP_307 HTTP_PERMANENT_REDIRECT = HTTP_308 HTTP_300 = '300 Multiple Choices' HTTP_301 = '301 Moved Permanently' HTTP_302 = '302 Found' HTTP_303 = '303 See Other' HTTP_304 = '304 Not Modified' HTTP_305 = '305 Use Proxy' HTTP_307 = '307 Temporary Redirect' HTTP_308 = '308 Permanent Redirect' ``` 4xx Client Error ---------------- ``` HTTP_BAD_REQUEST = HTTP_400 HTTP_UNAUTHORIZED = HTTP_401 # <-- Really means "unauthenticated" HTTP_PAYMENT_REQUIRED = HTTP_402 HTTP_FORBIDDEN = HTTP_403 # <-- Really means "unauthorized" HTTP_NOT_FOUND = HTTP_404 HTTP_METHOD_NOT_ALLOWED = HTTP_405 HTTP_NOT_ACCEPTABLE = HTTP_406 HTTP_PROXY_AUTHENTICATION_REQUIRED = HTTP_407 HTTP_REQUEST_TIMEOUT = HTTP_408 HTTP_CONFLICT = HTTP_409 HTTP_GONE = HTTP_410 HTTP_LENGTH_REQUIRED = HTTP_411 HTTP_PRECONDITION_FAILED = HTTP_412 HTTP_REQUEST_ENTITY_TOO_LARGE = HTTP_413 HTTP_REQUEST_URI_TOO_LONG = HTTP_414 HTTP_UNSUPPORTED_MEDIA_TYPE = HTTP_415 HTTP_REQUESTED_RANGE_NOT_SATISFIABLE = HTTP_416 HTTP_EXPECTATION_FAILED = HTTP_417 HTTP_IM_A_TEAPOT = HTTP_418 HTTP_UNPROCESSABLE_ENTITY = HTTP_422 HTTP_LOCKED = HTTP_423 HTTP_FAILED_DEPENDENCY = HTTP_424 HTTP_UPGRADE_REQUIRED = HTTP_426 HTTP_PRECONDITION_REQUIRED = HTTP_428 HTTP_TOO_MANY_REQUESTS = HTTP_429 HTTP_REQUEST_HEADER_FIELDS_TOO_LARGE = HTTP_431 HTTP_UNAVAILABLE_FOR_LEGAL_REASONS = HTTP_451 HTTP_400 = '400 Bad Request' HTTP_401 = '401 Unauthorized' # <-- Really means "unauthenticated" HTTP_402 = '402 Payment Required' HTTP_403 = '403 Forbidden' # <-- Really means "unauthorized" HTTP_404 = '404 Not Found' HTTP_405 = '405 Method Not Allowed' HTTP_406 = '406 Not Acceptable' HTTP_407 = '407 Proxy Authentication Required' HTTP_408 = '408 Request Time-out' HTTP_409 = '409 Conflict' HTTP_410 = '410 Gone' HTTP_411 = '411 Length Required' HTTP_412 = '412 Precondition Failed' HTTP_413 = '413 Payload Too Large' HTTP_414 = '414 URI Too Long' HTTP_415 = '415 Unsupported Media Type' HTTP_416 = '416 Range Not Satisfiable' HTTP_417 = '417 Expectation Failed' HTTP_418 = "418 I'm a teapot" HTTP_422 = "422 Unprocessable Entity" HTTP_423 = '423 Locked' HTTP_424 = '424 Failed Dependency' HTTP_426 = '426 Upgrade Required' HTTP_428 = '428 Precondition Required' HTTP_429 = '429 Too Many Requests' HTTP_431 = '431 Request Header Fields Too Large' HTTP_451 = '451 Unavailable For Legal Reasons' ``` 5xx Server Error ---------------- ``` HTTP_INTERNAL_SERVER_ERROR = HTTP_500 HTTP_NOT_IMPLEMENTED = HTTP_501 HTTP_BAD_GATEWAY = HTTP_502 HTTP_SERVICE_UNAVAILABLE = HTTP_503 HTTP_GATEWAY_TIMEOUT = HTTP_504 HTTP_HTTP_VERSION_NOT_SUPPORTED = HTTP_505 HTTP_INSUFFICIENT_STORAGE = HTTP_507 HTTP_LOOP_DETECTED = HTTP_508 HTTP_NETWORK_AUTHENTICATION_REQUIRED = HTTP_511 HTTP_500 = '500 Internal Server Error' HTTP_501 = '501 Not Implemented' HTTP_502 = '502 Bad Gateway' HTTP_503 = '503 Service Unavailable' HTTP_504 = '504 Gateway Time-out' HTTP_505 = '505 HTTP Version not supported' HTTP_507 = '507 Insufficient Storage' HTTP_508 = '508 Loop Detected' HTTP_511 = '511 Network Authentication Required' ``` falcon Utilities Utilities ========= URI Functions ------------- URI utilities. This module provides utility functions to parse, encode, decode, and otherwise manipulate a URI. These functions are not available directly in the `falcon` module, and so must be explicitly imported: ``` from falcon import uri name, port = uri.parse_host('example.org:8080') ``` `falcon.uri.encode(uri)` Encodes a full or relative URI according to RFC 3986. RFC 3986 defines a set of “unreserved” characters as well as a set of “reserved” characters used as delimiters. This function escapes all other “disallowed” characters by percent-encoding them. Note This utility is faster in the average case than the similar `quote` function found in `urlib`. It also strives to be easier to use by assuming a sensible default of allowed characters. \| Parameters: \| uri ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – URI or part of a URI to encode. If this is a wide string (i.e., `compat.text_type`), it will be encoded to a UTF-8 byte array and any multibyte sequences will be percent-encoded as-is. \| \| Returns: \| An escaped version of `uri`, where all disallowed characters have been percent-encoded. \| \| Return type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `falcon.uri.encode_value(uri)` Encodes a value string according to RFC 3986. Disallowed characters are percent-encoded in a way that models `urllib.parse.quote(safe="~")`. However, the Falcon function is faster in the average case than the similar `quote` function found in urlib. It also strives to be easier to use by assuming a sensible default of allowed characters. All reserved characters are lumped together into a single set of “delimiters”, and everything in that set is escaped. Note RFC 3986 defines a set of “unreserved” characters as well as a set of “reserved” characters used as delimiters. \| Parameters: \| uri ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – URI fragment to encode. It is assumed not to cross delimiter boundaries, and so any reserved URI delimiter characters included in it will be escaped. If `value` is a wide string (i.e., `compat.text_type`), it will be encoded to a UTF-8 byte array and any multibyte sequences will be percent-encoded as-is. \| \| Returns: \| An escaped version of `uri`, where all disallowed characters have been percent-encoded. \| \| Return type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `falcon.uri.decode(encoded_uri, unquote_plus=True)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/uri.html#decode) Decodes percent-encoded characters in a URI or query string. This function models the behavior of `urllib.parse.unquote_plus`, albeit in a faster, more straightforward manner. \| Parameters: \| encoded\_uri ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – An encoded URI (full or partial). \| \| Keyword Arguments: \| \| \| unquote\_plus ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Set to `False` to retain any plus (‘+’) characters in the given string, rather than converting them to spaces (default `True`). Typically you should set this to `False` when decoding any part of a URI other than the query string. \| \| Returns: \| A decoded URL. If the URL contains escaped non-ASCII characters, UTF-8 is assumed per RFC 3986. \| \| Return type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `falcon.uri.parse_host(host, default_port=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/uri.html#parse_host) Parse a canonical ‘host:port’ string into parts. Parse a host string (which may or may not contain a port) into parts, taking into account that the string may contain either a domain name or an IP address. In the latter case, both IPv4 and IPv6 addresses are supported. \| Parameters: \| host ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Host string to parse, optionally containing a port number. \| \| Keyword Arguments: \| \| \| default\_port ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – Port number to return when the host string does not contain one (default `None`). \| \| Returns: \| A parsed (host, port) tuple from the given host string, with the port converted to an `int`. If the host string does not specify a port, `default_port` is used instead. \| \| Return type: \| [tuple](https://docs.python.org/3/library/stdtypes.html#tuple "(in Python v3.7)") \| `falcon.uri.parse_query_string(query_string, keep_blank=False, csv=True)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/uri.html#parse_query_string) Parse a query string into a dict. Query string parameters are assumed to use standard form-encoding. Only parameters with values are returned. For example, given ‘foo=bar&flag’, this function would ignore ‘flag’ unless the `keep_blank_qs_values` option is set. Note In addition to the standard HTML form-based method for specifying lists by repeating a given param multiple times, Falcon supports a more compact form in which the param may be given a single time but set to a `list` of comma-separated elements (e.g., ‘foo=a,b,c’). When using this format, all commas uri-encoded will not be treated by Falcon as a delimiter. If the client wants to send a value as a list, it must not encode the commas with the values. The two different ways of specifying lists may not be mixed in a single query string for the same parameter. \| Parameters: \| * query\_string ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – The query string to parse. * keep\_blank ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Set to `True` to return fields even if they do not have a value (default `False`). For comma-separated values, this option also determines whether or not empty elements in the parsed list are retained. * csv – Set to `False` in order to disable splitting query parameters on `,` (default `True`). Depending on the user agent, encoding lists as multiple occurrences of the same parameter might be preferable. In this case, setting `parse_qs_csv` to `False` will cause the framework to treat commas as literal characters in each occurring parameter value. \| \| Returns: \| A dictionary of (name, value) pairs, one per query parameter. Note that value may be a single `str`, or a `list` of `str`. \| \| Return type: \| [dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") \| \| Raises: \| [`TypeError`](https://docs.python.org/3/library/exceptions.html#TypeError "(in Python v3.7)") – `query_string` was not a `str`. \| `falcon.uri.unquote_string(quoted)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/uri.html#unquote_string) Unquote an RFC 7320 “quoted-string”. \| Parameters: \| quoted ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Original quoted string \| \| Returns: \| unquoted string \| \| Return type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| \| Raises: \| [`TypeError`](https://docs.python.org/3/library/exceptions.html#TypeError "(in Python v3.7)") – `quoted` was not a `str`. \| Miscellaneous ------------- `falcon.deprecated(instructions)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/misc.html#deprecated) Flags a method as deprecated. This function returns a decorator which can be used to mark deprecated functions. Applying this decorator will result in a warning being emitted when the function is used. \| Parameters: \| instructions ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Specific guidance for the developer, e.g.: ‘Please migrate to add\_proxy(…)’‘ \| `falcon.http_now()` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/misc.html#http_now) Returns the current UTC time as an IMF-fixdate. \| Returns: \| The current UTC time as an IMF-fixdate, e.g., ‘Tue, 15 Nov 1994 12:45:26 GMT’. \| \| Return type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `falcon.dt_to_http(dt)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/misc.html#dt_to_http) Converts a `datetime` instance to an HTTP date string. \| Parameters: \| dt (datetime) – A `datetime` instance to convert, assumed to be UTC. \| \| Returns: \| An RFC 1123 date string, e.g.: “Tue, 15 Nov 1994 12:45:26 GMT”. \| \| Return type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `falcon.http_date_to_dt(http_date, obs_date=False)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/misc.html#http_date_to_dt) Converts an HTTP date string to a datetime instance. \| Parameters: \| http\_date ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – An RFC 1123 date string, e.g.: “Tue, 15 Nov 1994 12:45:26 GMT”. \| \| Keyword Arguments: \| \| \| obs\_date ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Support obs-date formats according to RFC 7231, e.g.: “Sunday, 06-Nov-94 08:49:37 GMT” (default `False`). \| \| Returns: \| A UTC datetime instance corresponding to the given HTTP date. \| \| Return type: \| datetime \| \| Raises: \| [`ValueError`](https://docs.python.org/3/library/exceptions.html#ValueError "(in Python v3.7)") – http\_date doesn’t match any of the available time formats \| `falcon.to_query_str(params, comma_delimited_lists=True, prefix=True)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/misc.html#to_query_str) Converts a dictionary of parameters to a query string. \| Parameters: \| * params ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)")) – A dictionary of parameters, where each key is a parameter name, and each value is either a `str` or something that can be converted into a `str`, or a list of such values. If a `list`, the value will be converted to a comma-delimited string of values (e.g., ‘thing=1,2,3’). * comma\_delimited\_lists ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Set to `False` to encode list values by specifying multiple instances of the parameter (e.g., ‘thing=1&thing=2&thing=3’). Otherwise, parameters will be encoded as comma-separated values (e.g., ‘thing=1,2,3’). Defaults to `True`. * prefix ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Set to `False` to exclude the ‘?’ prefix in the result string (default `True`). \| \| Returns: \| A URI query string, including the ‘?’ prefix (unless `prefix` is `False`), or an empty string if no params are given (the `dict` is empty). \| \| Return type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `falcon.get_http_status(status_code, default_reason='Unknown')` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/misc.html#get_http_status) Gets both the http status code and description from just a code \| Parameters: \| * status\_code – integer or string that can be converted to an integer * default\_reason – default text to be appended to the status\_code if the lookup does not find a result \| \| Returns: \| status code e.g. “404 Not Found” \| \| Return type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| \| Raises: \| [`ValueError`](https://docs.python.org/3/library/exceptions.html#ValueError "(in Python v3.7)") – the value entered could not be converted to an integer \| `falcon.get_bound_method(obj, method_name)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/misc.html#get_bound_method) Get a bound method of the given object by name. \| Parameters: \| * obj – Object on which to look up the method. * method\_name – Name of the method to retrieve. \| \| Returns: \| Bound method, or `None` if the method does not exist on the object. \| \| Raises: \| [`AttributeError`](https://docs.python.org/3/library/exceptions.html#AttributeError "(in Python v3.7)") – The method exists, but it isn’t bound (most likely a class was passed, rather than an instance of that class). \| `class falcon.TimezoneGMT` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/time.html#TimezoneGMT) GMT timezone class implementing the [`datetime.tzinfo`](https://docs.python.org/3/library/datetime.html#datetime.tzinfo "(in Python v3.7)") interface. `dst(dt)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/time.html#TimezoneGMT.dst) Return the daylight saving time (DST) adjustment. \| Parameters: \| dt ([datetime.datetime](https://docs.python.org/3/library/datetime.html#datetime.datetime "(in Python v3.7)")) – Ignored \| \| Returns: \| DST adjustment for GMT, which is always 0. \| \| Return type: \| [datetime.timedelta](https://docs.python.org/3/library/datetime.html#datetime.timedelta "(in Python v3.7)") \| `tzname(dt)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/time.html#TimezoneGMT.tzname) Get the name of this timezone. \| Parameters: \| dt ([datetime.datetime](https://docs.python.org/3/library/datetime.html#datetime.datetime "(in Python v3.7)")) – Ignored \| \| Returns: \| “GMT” \| \| Return type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `utcoffset(dt)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/time.html#TimezoneGMT.utcoffset) Get the offset from UTC. \| Parameters: \| dt ([datetime.datetime](https://docs.python.org/3/library/datetime.html#datetime.datetime "(in Python v3.7)")) – Ignored \| \| Returns: \| GMT offset, which is equivalent to UTC and so is aways 0. \| \| Return type: \| [datetime.timedelta](https://docs.python.org/3/library/datetime.html#datetime.timedelta "(in Python v3.7)") \| `class falcon.Context` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/structures.html#Context) Convenience class to hold contextual information in its attributes. This class is used as the default [`Request`](request_and_response#falcon.Request "falcon.Request") and [`Response`](request_and_response#falcon.Response "falcon.Response") context type (see [`Request.context_type`](request_and_response#falcon.Request.context_type "falcon.Request.context_type") and [`Response.context_type`](request_and_response#falcon.Response.context_type "falcon.Response.context_type"), respectively). In Falcon versions prior to 2.0, the default context type was `dict`. To ease the migration to attribute-based context object approach, this class also implements the mapping interface; that is, object attributes are linked to dictionary items, and vice versa. For instance: ``` >>> context = falcon.Context() >>> context.cache_strategy = 'lru' >>> context.get('cache_strategy') 'lru' >>> 'cache_strategy' in context True ``` Note Python 2 specific `dict` methods are exposed regardless of the Python language version, however, as they are delegated to the underlying `__dict__`, a similar error would be raised as if attempting to use these methods for a usual Python 3 dict. `class falcon.ETag` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/structures.html#ETag) Convenience class to represent a parsed HTTP entity-tag. This class is simply a subclass of `str` with a few helper methods and an extra attribute to indicate whether the entity-tag is weak or strong. The value of the string is equivalent to what RFC 7232 calls an “opaque-tag”, i.e. an entity-tag sans quotes and the weakness indicator. Note Given that a weak entity-tag comparison can be performed by using the `==` operator (per the example below), only a [`strong_compare()`](#falcon.ETag.strong_compare "falcon.ETag.strong_compare") method is provided. Here is an example `on_get()` method that demonstrates how to use instances of this class: ``` def on_get(self, req, resp): content_etag = self._get_content_etag() for etag in (req.if_none_match or []): if etag == '' or etag == content_etag: resp.status = falcon.HTTP_304 return # ... resp.etag = content_etag resp.status = falcon.HTTP_200 ``` (See also: RFC 7232) `is_weak` `True` if the entity-tag is weak, otherwise `False`. \| Type: \| [bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)") \| `dumps()` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/structures.html#ETag.dumps) Serialize the ETag to a string suitable for use in a precondition header. (See also: [RFC 7232, Section 2.3](https://tools.ietf.org/html/rfc7232#section-2.3)) \| Returns: \| An opaque quoted string, possibly prefixed by a weakness indicator `W/`. \| \| Return type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `classmethod loads(etag_str)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/structures.html#ETag.loads) Class method that deserializes a single entity-tag string from a precondition header. Note This method is meant to be used only for parsing a single entity-tag. It can not be used to parse a comma-separated list of values. (See also: [RFC 7232, Section 2.3](https://tools.ietf.org/html/rfc7232#section-2.3)) \| Parameters: \| etag\_str* ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – An ASCII string representing a single entity-tag, as defined by RFC 7232. \| \| Returns: \| An instance of `~.ETag` representing the parsed entity-tag. \| \| Return type: \| [ETag](#falcon.ETag "falcon.ETag") \| `strong_compare(other)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/util/structures.html#ETag.strong_compare) Performs a strong entity-tag comparison. Two entity-tags are equivalent if both are not weak and their opaque-tags match character-by-character. (See also: [RFC 7232, Section 2.3.2](https://tools.ietf.org/html/rfc7232#section-2.3.2)) \| Parameters: \| * other ([ETag](#falcon.ETag "falcon.ETag")) – The other [`ETag`](#falcon.ETag "falcon.ETag") to which you are comparing * one. (this) – \| \| Returns: \| `True` if the two entity-tags match, otherwise `False`. \| \| Return type: \| [bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)") \|	programming_docs
falcon Hooks Hooks ===== Falcon supports before and after hooks. You install a hook simply by applying one of the decorators below, either to an individual responder or to an entire resource. For example, consider this hook that validates a POST request for an image resource: ``` def validate_image_type(req, resp, resource, params): if req.content_type not in ALLOWED_IMAGE_TYPES: msg = 'Image type not allowed. Must be PNG, JPEG, or GIF' raise falcon.HTTPBadRequest('Bad request', msg) ``` You would attach this hook to an `on_post` responder like so: ``` @falcon.before(validate_image_type) def on_post(self, req, resp): pass ``` Or, suppose you had a hook that you would like to apply to all responders for a given resource. In that case, you would simply decorate the resource class: ``` @falcon.before(extract_project_id) class Message(object): def on_post(self, req, resp, project_id): pass def on_get(self, req, resp, project_id): pass ``` Note When decorating an entire resource class, all method names that resemble responders, including suffixed (see also [`add_route()`](api#falcon.API.add_route "falcon.API.add_route")) ones, are decorated. If, for instance, a method is called `on_get_items`, but it is not meant for handling `GET` requests under a route with the suffix `items`, the easiest workaround for preventing the hook function from being applied to the method is renaming it not to clash with the responder pattern. Note also that you can pass additional arguments to your hook function as needed: ``` def validate_image_type(req, resp, resource, params, allowed_types): if req.content_type not in allowed_types: msg = 'Image type not allowed.' raise falcon.HTTPBadRequest('Bad request', msg) @falcon.before(validate_image_type, ['image/png']) def on_post(self, req, resp): pass ``` Falcon supports using any callable as a hook. This allows for using a class instead of a function: ``` class Authorize(object): def __init__(self, roles): self._roles = roles def __call__(self, req, resp, resource, params): pass @falcon.before(Authorize(['admin'])) def on_post(self, req, resp): pass ``` Falcon [middleware components](middleware#middleware) can also be used to insert logic before and after requests. However, unlike hooks, [middleware components](middleware#middleware) are triggered globally for all requests. Tip In order to pass data from a hook function to a resource function use the `req.context` and `resp.context` objects. These context objects are intended to hold request and response data specific to your app as it passes through the framework. `falcon.before(action, args, kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/hooks.html#before) Decorator to execute the given action function before* the responder. \| Parameters: \| * action (callable) – A function of the form `func(req, resp, resource, params)`, where `resource` is a reference to the resource class instance associated with the request, and `params` is a dict of URI Template field names, if any, that will be passed into the resource responder as kwargs. Note Hooks may inject extra params as needed. For example: ``` def do_something(req, resp, resource, params): try: params['id'] = int(params['id']) except ValueError: raise falcon.HTTPBadRequest('Invalid ID', 'ID was not valid.') params['answer'] = 42 ``` * *\args** – Any additional arguments will be passed to action in the order given, immediately following the req, resp, resource, and params arguments. * *\\kwargs* – Any additional keyword arguments will be passed through to action. \| `falcon.after(action, args, kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/hooks.html#after) Decorator to execute the given action function after* the responder. \| Parameters: \| * action (callable) – A function of the form `func(req, resp, resource)`, where `resource` is a reference to the resource class instance associated with the request * *\args** – Any additional arguments will be passed to action in the order given, immediately following the req, resp, resource, and params arguments. * *\\kwargs* – Any additional keyword arguments will be passed through to action. \| falcon Middleware Middleware ========== Middleware components provide a way to execute logic before the framework routes each request, after each request is routed but before the target responder is called, or just before the response is returned for each request. Components are registered with the `middleware` kwarg when instantiating Falcon’s [API class](api#api). Note Unlike hooks, middleware methods apply globally to the entire API. Falcon’s middleware interface is defined as follows: ``` class ExampleComponent(object): def process_request(self, req, resp): """Process the request before routing it. Note: Because Falcon routes each request based on req.path, a request can be effectively re-routed by setting that attribute to a new value from within process_request(). Args: req: Request object that will eventually be routed to an on_* responder method. resp: Response object that will be routed to the on_* responder. """ def process_resource(self, req, resp, resource, params): """Process the request after routing. Note: This method is only called when the request matches a route to a resource. Args: req: Request object that will be passed to the routed responder. resp: Response object that will be passed to the responder. resource: Resource object to which the request was routed. params: A dict-like object representing any additional params derived from the route's URI template fields, that will be passed to the resource's responder method as keyword arguments. """ def process_response(self, req, resp, resource, req_succeeded): """Post-processing of the response (after routing). Args: req: Request object. resp: Response object. resource: Resource object to which the request was routed. May be None if no route was found for the request. req_succeeded: True if no exceptions were raised while the framework processed and routed the request; otherwise False. """ ``` Tip Because process\_request executes before routing has occurred, if a component modifies `req.path` in its process\_request method, the framework will use the modified value to route the request. For example: ``` # Route requests based on the host header. req.path = '/' + req.host + req.path ``` Tip The process\_resource method is only called when the request matches a route to a resource. To take action when a route is not found, a [`sink`](api#falcon.API.add_sink "falcon.API.add_sink") may be used instead. Tip In order to pass data from a middleware function to a resource function use the `req.context` and `resp.context` objects. These context objects are intended to hold request and response data specific to your app as it passes through the framework. Each component’s process\_request, process\_resource, and process\_response methods are executed hierarchically, as a stack, following the ordering of the list passed via the `middleware` kwarg of [falcon.API](api#api). For example, if a list of middleware objects are passed as `[mob1, mob2, mob3]`, the order of execution is as follows: ``` mob1.process_request mob2.process_request mob3.process_request mob1.process_resource mob2.process_resource mob3.process_resource <route to resource responder method> mob3.process_response mob2.process_response mob1.process_response ``` Note that each component need not implement all `process_` methods; in the case that one of the three methods is missing, it is treated as a noop in the stack. For example, if `mob2` did not implement process\_request* and `mob3` did not implement process\_response, the execution order would look like this: ``` mob1.process_request _ mob3.process_request mob1.process_resource mob2.process_resource mob3.process_resource <route to responder method> _ mob2.process_response mob1.process_response ``` Short-circuiting ---------------- A process\_request middleware method may short-circuit further request processing by setting [`complete`](request_and_response#falcon.Response.complete "falcon.Response.complete") to `True`, e.g.: ``` resp.complete = True ``` After the method returns, setting this flag will cause the framework to skip any remaining process\_request and process\_resource methods, as well as the responder method that the request would have been routed to. However, any process\_response middleware methods will still be called. In a similar manner, setting [`complete`](request_and_response#falcon.Response.complete "falcon.Response.complete") to `True` from within a process\_resource method will short-circuit further request processing at that point. This feature affords use cases in which the response may be pre-constructed, such as in the case of caching. Exception Handling ------------------ If one of the process\_request middleware methods raises an exception, it will be processed according to the exception type. If the type matches a registered error handler, that handler will be invoked and then the framework will begin to unwind the stack, skipping any lower layers. The error handler may itself raise an instance of [`HTTPError`](errors#falcon.HTTPError "falcon.HTTPError") or [`HTTPStatus`](status#falcon.HTTPStatus "falcon.HTTPStatus"), in which case the framework will use the latter exception to update the resp object. Note By default, the framework installs two handlers, one for [`HTTPError`](errors#falcon.HTTPError "falcon.HTTPError") and one for [`HTTPStatus`](status#falcon.HTTPStatus "falcon.HTTPStatus"). These can be overridden via [`add_error_handler()`](api#falcon.API.add_error_handler "falcon.API.add_error_handler"). Regardless, the framework will continue unwinding the middleware stack. For example, if mob2.process\_request were to raise an error, the framework would execute the stack as follows: ``` mob1.process_request mob2.process_request <skip mob1/mob2 process_resource> <skip mob3.process_request> <skip mob3.process_resource> <skip route to resource responder method> mob3.process_response mob2.process_response mob1.process_response ``` As illustrated above, by default, all process\_response methods will be executed, even when a process\_request, process\_resource, or resource responder raises an error. This behavior is controlled by the [API class’s](api#api) `independent_middleware` keyword argument. Finally, if one of the process\_response methods raises an error, or the routed `on_` responder method itself raises an error, the exception will be handled in a similar manner as above. Then, the framework will execute any remaining middleware on the stack. falcon Cookies Cookies ======= Getting Cookies --------------- Cookies can be read from a request either via the [`get_cookie_values()`](request_and_response#falcon.Request.get_cookie_values "falcon.Request.get_cookie_values") method or the [`cookies`](request_and_response#falcon.Request.cookies "falcon.Request.cookies") attribute on the [`Request`](request_and_response#falcon.Request "falcon.Request") object. Generally speaking, the [`get_cookie_values()`](request_and_response#falcon.Request.get_cookie_values "falcon.Request.get_cookie_values") method should be used unless you need a collection of all the cookies in the request. ``` class Resource(object): def on_get(self, req, resp): cookies = req.cookies my_cookie_values = req.get_cookie_values('my_cookie') if my_cookie_values: # NOTE: If there are multiple values set for the cookie, you # will need to choose how to handle the additional values. v = my_cookie_values[0] # ... ``` Setting Cookies --------------- Setting cookies on a response may be done either via [`set_cookie()`](request_and_response#falcon.Response.set_cookie "falcon.Response.set_cookie") or [`append_header()`](request_and_response#falcon.Response.append_header "falcon.Response.append_header"). One of these methods should be used instead of [`set_header()`](request_and_response#falcon.Response.set_header "falcon.Response.set_header"). With [`set_header()`](request_and_response#falcon.Response.set_header "falcon.Response.set_header") you cannot set multiple headers with the same name (which is how multiple cookies are sent to the client). Simple example: ``` class Resource(object): def on_get(self, req, resp): # Set the cookie 'my_cookie' to the value 'my cookie value' resp.set_cookie('my_cookie', 'my cookie value') ``` You can of course also set the domain, path and lifetime of the cookie. ``` class Resource(object): def on_get(self, req, resp): # Set the maximum age of the cookie to 10 minutes (600 seconds) # and the cookie's domain to 'example.com' resp.set_cookie('my_cookie', 'my cookie value', max_age=600, domain='example.com') ``` You can also instruct the client to remove a cookie with the [`unset_cookie()`](request_and_response#falcon.Response.unset_cookie "falcon.Response.unset_cookie") method: ``` class Resource(object): def on_get(self, req, resp): resp.set_cookie('bad_cookie', ':(') # Clear the bad cookie resp.unset_cookie('bad_cookie') ``` The Secure Attribute -------------------- By default, Falcon sets the `secure` attribute for cookies. This instructs the client to never transmit the cookie in the clear over HTTP, in order to protect any sensitive data that cookie might contain. If a cookie is set, and a subsequent request is made over HTTP (rather than HTTPS), the client will not include that cookie in the request. Warning For this attribute to be effective, your web server or load balancer will need to enforce HTTPS when setting the cookie, as well as in all subsequent requests that require the cookie to be sent back from the client. When running your application in a development environment, you can disable this default behavior by setting [`secure_cookies_by_default`](api#falcon.ResponseOptions.secure_cookies_by_default "falcon.ResponseOptions.secure_cookies_by_default") to `False` via [`API.resp_options`](api#falcon.API.resp_options "falcon.API.resp_options"). This lets you test your app locally without having to set up TLS. You can make this option configurable to easily switch between development and production environments. See also: [RFC 6265, Section 4.1.2.5](https://tools.ietf.org/html/rfc6265#section-4.1.2.5) falcon Media Media ===== Falcon allows for easy and customizable internet media type handling. By default Falcon only enables a single JSON handler. However, additional handlers can be configured through the [`falcon.RequestOptions`](api#falcon.RequestOptions "falcon.RequestOptions") and [`falcon.ResponseOptions`](api#falcon.ResponseOptions "falcon.ResponseOptions") objects specified on your [`falcon.API`](api#falcon.API "falcon.API"). Note To avoid unnecessary overhead, Falcon will only process request media the first time the media property is referenced. Once it has been referenced, it’ll use the cached result for subsequent interactions. Usage ----- Zero configuration is needed if you’re creating a JSON API. Just access or set the `media` attribute as appropriate and let Falcon do the heavy lifting for you. ``` import falcon class EchoResource(object): def on_post(self, req, resp): message = req.media.get('message') resp.media = {'message': message} resp.status = falcon.HTTP_200 ``` Warning Once `media` is called on a request, it’ll consume the request’s stream. Validating Media ---------------- Falcon currently only provides a JSON Schema media validator; however, JSON Schema is very versatile and can be used to validate any deserialized media type that JSON also supports (i.e. dicts, lists, etc). `falcon.media.validators.jsonschema.validate(req_schema=None, resp_schema=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/media/validators/jsonschema.html#validate) Decorator for validating `req.media` using JSON Schema. This decorator provides standard JSON Schema validation via the `jsonschema` package available from PyPI. Semantic validation via the format* keyword is enabled for the default checkers implemented by `jsonschema.FormatChecker`. Note The `jsonschema`` package must be installed separately in order to use this decorator, as Falcon does not install it by default. See [json-schema.org](http://json-schema.org/) for more information on defining a compatible dictionary. \| Parameters: \| * req\_schema ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)"), optional) – A dictionary that follows the JSON Schema specification. The request will be validated against this schema. * resp\_schema ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)"), optional) – A dictionary that follows the JSON Schema specification. The response will be validated against this schema. \| #### Example ``` from falcon.media.validators import jsonschema # -- snip -- @jsonschema.validate(my_post_schema) def on_post(self, req, resp): # -- snip -- ``` If JSON Schema does not meet your needs, a custom validator may be implemented in a similar manner to the one above. Content-Type Negotiation ------------------------ Falcon currently only supports partial negotiation out of the box. By default, when the `media` attribute is used it attempts to de/serialize based on the `Content-Type` header value. The missing link that Falcon doesn’t provide is the connection between the [`falcon.Request`](request_and_response#falcon.Request "falcon.Request") `Accept` header provided by a user and the [`falcon.Response`](request_and_response#falcon.Response "falcon.Response") `Content-Type` header. If you do need full negotiation, it is very easy to bridge the gap using middleware. Here is an example of how this can be done: ``` class NegotiationMiddleware(object): def process_request(self, req, resp): resp.content_type = req.accept ``` Replacing the Default Handlers ------------------------------ When creating your API object you can either add or completely replace all of the handlers. For example, lets say you want to write an API that sends and receives MessagePack. We can easily do this by telling our Falcon API that we want a default media-type of `application/msgpack` and then create a new [`Handlers`](#falcon.media.Handlers "falcon.media.Handlers") object specifying the desired media type and a handler that can process that data. ``` import falcon from falcon import media handlers = media.Handlers({ 'application/msgpack': media.MessagePackHandler(), }) api = falcon.API(media_type='application/msgpack') api.req_options.media_handlers = handlers api.resp_options.media_handlers = handlers ``` Alternatively, if you would like to add an additional handler such as MessagePack, this can be easily done in the following manner: ``` import falcon from falcon import media extra_handlers = { 'application/msgpack': media.MessagePackHandler(), } api = falcon.API() api.req_options.media_handlers.update(extra_handlers) api.resp_options.media_handlers.update(extra_handlers) ``` Supported Handler Types ----------------------- `class falcon.media.JSONHandler(dumps=None, loads=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/media/json.html#JSONHandler) JSON media handler. This handler uses Python’s standard [`json`](https://docs.python.org/3/library/json.html#module-json "(in Python v3.7)") library by default, but can be easily configured to use any of a number of third-party JSON libraries, depending on your needs. For example, you can often realize a significant performance boost under CPython by using an alternative library. Good options in this respect include `orjson`, `python-rapidjson`, and `mujson`. Note If you are deploying to PyPy, we recommend sticking with the standard library’s JSON implementation, since it will be faster in most cases as compared to a third-party library. Overriding the default JSON implementation is simply a matter of specifying the desired `dumps` and `loads` functions: ``` import falcon from falcon import media import rapidjson json_handler = media.JSONHandler( dumps=rapidjson.dumps, loads=rapidjson.loads, ) extra_handlers = { 'application/json': json_handler, } api = falcon.API() api.req_options.media_handlers.update(extra_handlers) api.resp_options.media_handlers.update(extra_handlers) ``` By default, `ensure_ascii` is passed to the `json.dumps` function. If you override the `dumps` function, you will need to explicitly set `ensure_ascii` to `False` in order to enable the serialization of Unicode characters to UTF-8. This is easily done by using `functools.partial` to apply the desired keyword argument. In fact, you can use this same technique to customize any option supported by the `dumps` and `loads` functions: ``` from functools import partial from falcon import media import rapidjson json_handler = media.JSONHandler( dumps=partial( rapidjson.dumps, ensure_ascii=False, sort_keys=True ), ) ``` \| Keyword Arguments: \| \| \| * dumps (func) – Function to use when serializing JSON responses. * loads (func) – Function to use when deserializing JSON requests. \| `deserialize(stream, content_type, content_length)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/media/json.html#JSONHandler.deserialize) Deserialize the [`falcon.Request`](request_and_response#falcon.Request "falcon.Request") body. \| Parameters: \| * stream ([object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)")) – Input data to deserialize. * content\_type ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Type of request content. * content\_length ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – Length of request content. \| \| Returns: \| A deserialized object. \| \| Return type: \| [object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)") \| `serialize(media, content_type)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/media/json.html#JSONHandler.serialize) Serialize the media object on a [`falcon.Response`](request_and_response#falcon.Response "falcon.Response") \| Parameters: \| * media ([object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)")) – A serializable object. * content\_type ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Type of response content. \| \| Returns: \| The resulting serialized bytes from the input object. \| \| Return type: \| [bytes](https://docs.python.org/3/library/stdtypes.html#bytes "(in Python v3.7)") \| `class falcon.media.MessagePackHandler` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/media/msgpack.html#MessagePackHandler) Handler built using the `msgpack` module. This handler uses `msgpack.unpackb()` and `msgpack.packb()`. The MessagePack `bin` type is used to distinguish between Unicode strings (`str` on Python 3, `unicode` on Python 2) and byte strings (`bytes` on Python 2/3, or `str` on Python 2). Note This handler requires the extra `msgpack` package (version 0.5.2 or higher), which must be installed in addition to `falcon` from PyPI: ``` $ pip install msgpack ``` `deserialize(stream, content_type, content_length)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/media/msgpack.html#MessagePackHandler.deserialize) Deserialize the [`falcon.Request`](request_and_response#falcon.Request "falcon.Request") body. \| Parameters: \| * stream ([object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)")) – Input data to deserialize. * content\_type ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Type of request content. * content\_length ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – Length of request content. \| \| Returns: \| A deserialized object. \| \| Return type: \| [object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)") \| `serialize(media, content_type)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/media/msgpack.html#MessagePackHandler.serialize) Serialize the media object on a [`falcon.Response`](request_and_response#falcon.Response "falcon.Response") \| Parameters: \| * media ([object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)")) – A serializable object. * content\_type ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Type of response content. \| \| Returns: \| The resulting serialized bytes from the input object. \| \| Return type: \| [bytes](https://docs.python.org/3/library/stdtypes.html#bytes "(in Python v3.7)") \| Custom Handler Type ------------------- If Falcon doesn’t have an internet media type handler that supports your use case, you can easily implement your own using the abstract base class provided by Falcon: `class falcon.media.BaseHandler` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/media/base.html#BaseHandler) Abstract Base Class for an internet media type handler `serialize(media, content_type)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/media/base.html#BaseHandler.serialize) Serialize the media object on a [`falcon.Response`](request_and_response#falcon.Response "falcon.Response") \| Parameters: \| * media ([object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)")) – A serializable object. * content\_type ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Type of response content. \| \| Returns: \| The resulting serialized bytes from the input object. \| \| Return type: \| [bytes](https://docs.python.org/3/library/stdtypes.html#bytes "(in Python v3.7)") \| `deserialize(stream, content_type, content_length)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/media/base.html#BaseHandler.deserialize) Deserialize the [`falcon.Request`](request_and_response#falcon.Request "falcon.Request") body. \| Parameters: \| * stream ([object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)")) – Input data to deserialize. * content\_type ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Type of request content. * content\_length ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – Length of request content. \| \| Returns: \| A deserialized object. \| \| Return type: \| [object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)") \| Handlers -------- `class falcon.media.Handlers(initial=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/media/handlers.html#Handlers) A dictionary like object that manages internet media type handlers. Media Type Constants -------------------- The `falcon` module provides a number of constants for common media types, including the following: ``` falcon.MEDIA_JSON falcon.MEDIA_MSGPACK falcon.MEDIA_YAML falcon.MEDIA_XML falcon.MEDIA_HTML falcon.MEDIA_JS falcon.MEDIA_TEXT falcon.MEDIA_JPEG falcon.MEDIA_PNG falcon.MEDIA_GIF ```	programming_docs
falcon Error Handling Error Handling ============== When it comes to error handling, you can always directly set the error status, appropriate response headers, and error body using the `resp` object. However, Falcon tries to make things a little easier by providing a set of error classes you can raise when something goes wrong. All of these classes inherit from [`HTTPError`](#falcon.HTTPError "falcon.HTTPError"). Falcon will convert any instance or subclass of [`HTTPError`](#falcon.HTTPError "falcon.HTTPError") raised by a responder, hook, or middleware component into an appropriate HTTP response. The default error serializer supports both JSON and XML. If the client indicates acceptance of both JSON and XML with equal weight, JSON will be chosen. Other media types may be supported by overriding the default serializer via [`set_error_serializer()`](api#falcon.API.set_error_serializer "falcon.API.set_error_serializer"). Note If a custom media type is used and the type includes a “+json” or “+xml” suffix, the default serializer will convert the error to JSON or XML, respectively. To customize what data is passed to the serializer, subclass [`HTTPError`](#falcon.HTTPError "falcon.HTTPError") or any of its child classes, and override the [`to_dict()`](#falcon.HTTPError.to_dict "falcon.HTTPError.to_dict") method. To also support XML, override the [`to_xml()`](#falcon.HTTPError.to_xml "falcon.HTTPError.to_xml") method. For example: ``` class HTTPNotAcceptable(falcon.HTTPNotAcceptable): def __init__(self, acceptable): description = ( 'Please see "acceptable" for a list of media types ' 'and profiles that are currently supported.' ) super().__init__(description=description) self._acceptable = acceptable def to_dict(self, obj_type=dict): result = super().to_dict(obj_type) result['acceptable'] = self._acceptable return result ``` All classes are available directly in the `falcon` package namespace: ``` import falcon class MessageResource(object): def on_get(self, req, resp): # ... raise falcon.HTTPBadRequest( "TTL Out of Range", "The message's TTL must be between 60 and 300 seconds, inclusive." ) # ... ``` Note also that any exception (not just instances of [`HTTPError`](#falcon.HTTPError "falcon.HTTPError")) can be caught, logged, and otherwise handled at the global level by registering one or more custom error handlers. See also [`add_error_handler()`](api#falcon.API.add_error_handler "falcon.API.add_error_handler") to learn more about this feature. Base Class ---------- `class falcon.HTTPError(status, title=None, description=None, headers=None, href=None, href_text=None, code=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/http_error.html#HTTPError) Represents a generic HTTP error. Raise an instance or subclass of `HTTPError` to have Falcon return a formatted error response and an appropriate HTTP status code to the client when something goes wrong. JSON and XML media types are supported by default. To customize the error presentation, implement a custom error serializer and set it on the [`API`](api#falcon.API "falcon.API") instance via [`set_error_serializer()`](api#falcon.API.set_error_serializer "falcon.API.set_error_serializer"). To customize what data is passed to the serializer, subclass `HTTPError` and override the `to_dict()` method (`to_json()` is implemented via `to_dict()`). To also support XML, override the `to_xml()` method. `status` HTTP status line, e.g. ‘748 Confounded by Ponies’. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `has_representation` Read-only property that determines whether error details will be serialized when composing the HTTP response. In `HTTPError` this property always returns `True`, but child classes may override it in order to return `False` when an empty HTTP body is desired. (See also: [`falcon.http_error.NoRepresentation`](#falcon.http_error.NoRepresentation "falcon.http_error.NoRepresentation")) Note A custom error serializer (see [`set_error_serializer()`](api#falcon.API.set_error_serializer "falcon.API.set_error_serializer")) may choose to set a response body regardless of the value of this property. \| Type: \| [bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)") \| `title` Error title to send to the client. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `description` Description of the error to send to the client. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `headers` Extra headers to add to the response. \| Type: \| [dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") \| `link` An href that the client can provide to the user for getting help. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `code` An internal application code that a user can reference when requesting support for the error. \| Type: \| [int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)") \| \| Parameters: \| status ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – HTTP status code and text, such as “400 Bad Request” \| \| Keyword Arguments: \| \| \| * title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly error title. If not provided, defaults to the HTTP status line as determined by the `status` argument. * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two (default `None`). * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `to_dict(obj_type=<class 'dict'>)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/http_error.html#HTTPError.to_dict) Return a basic dictionary representing the error. This method can be useful when serializing the error to hash-like media types, such as YAML, JSON, and MessagePack. \| Parameters: \| obj\_type – A dict-like type that will be used to store the error information (default `dict`). \| \| Returns: \| A dictionary populated with the error’s title, description, etc. \| \| Return type: \| [dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") \| `to_json()` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/http_error.html#HTTPError.to_json) Return a pretty-printed JSON representation of the error. \| Returns: \| A JSON document for the error. \| \| Return type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `to_xml()` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/http_error.html#HTTPError.to_xml) Return an XML-encoded representation of the error. \| Returns: \| An XML document for the error. \| \| Return type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| Mixins ------ `class falcon.http_error.NoRepresentation` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/http_error.html#NoRepresentation) Mixin for `HTTPError` child classes that have no representation. This class can be mixed in when inheriting from `HTTPError`, in order to override the `has_representation` property such that it always returns `False`. This, in turn, will cause Falcon to return an empty response body to the client. You can use this mixin when defining errors that either should not have a body (as dictated by HTTP standards or common practice), or in the case that a detailed error response may leak information to an attacker. Note This mixin class must appear before `HTTPError` in the base class list when defining the child; otherwise, it will not override the `has_representation` property as expected. Predefined Errors ----------------- `exception falcon.HTTPBadRequest(title=None, description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPBadRequest) 400 Bad Request. The server cannot or will not process the request due to something that is perceived to be a client error (e.g., malformed request syntax, invalid request message framing, or deceptive request routing). (See also: [RFC 7231, Section 6.5.1](https://tools.ietf.org/html/rfc7231#section-6.5.1)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘400 Bad Request’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPInvalidHeader(msg, header_name, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPInvalidHeader) 400 Bad Request. One of the headers in the request is invalid. \| Parameters: \| msg ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A description of why the value is invalid. * header\_name ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – The name of the invalid header. \| \| Keyword Arguments: \| \| \| * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPMissingHeader(header_name, headers=None, kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPMissingHeader) 400 Bad Request A header is missing from the request. \| Parameters: \| header\_name** ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – The name of the missing header. \| \| Keyword Arguments: \| \| \| * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPInvalidParam(msg, param_name, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPInvalidParam) 400 Bad Request A parameter in the request is invalid. This error may refer to a parameter in a query string, form, or document that was submitted with the request. \| Parameters: \| msg ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A description of the invalid parameter. * param\_name ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – The name of the parameter. \| \| Keyword Arguments: \| \| \| * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPMissingParam(param_name, headers=None, kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPMissingParam) 400 Bad Request A parameter is missing from the request. This error may refer to a parameter in a query string, form, or document that was submitted with the request. \| Parameters: \| param\_name** ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – The name of the missing parameter. \| \| Keyword Arguments: \| \| \| * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPUnauthorized(title=None, description=None, challenges=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPUnauthorized) 401 Unauthorized. The request has not been applied because it lacks valid authentication credentials for the target resource. The server generating a 401 response MUST send a WWW-Authenticate header field containing at least one challenge applicable to the target resource. If the request included authentication credentials, then the 401 response indicates that authorization has been refused for those credentials. The user agent MAY repeat the request with a new or replaced Authorization header field. If the 401 response contains the same challenge as the prior response, and the user agent has already attempted authentication at least once, then the user agent SHOULD present the enclosed representation to the user, since it usually contains relevant diagnostic information. (See also: [RFC 7235, Section 3.1](https://tools.ietf.org/html/rfc7235#section-3.1)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘401 Unauthorized’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * challenges (iterable of str) – One or more authentication challenges to use as the value of the WWW-Authenticate header in the response. (See also: [RFC 7235, Section 2.1](https://tools.ietf.org/html/rfc7235#section-2.1)) * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPForbidden(title=None, description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPForbidden) 403 Forbidden. The server understood the request but refuses to authorize it. A server that wishes to make public why the request has been forbidden can describe that reason in the response payload (if any). If authentication credentials were provided in the request, the server considers them insufficient to grant access. The client SHOULD NOT automatically repeat the request with the same credentials. The client MAY repeat the request with new or different credentials. However, a request might be forbidden for reasons unrelated to the credentials. An origin server that wishes to “hide” the current existence of a forbidden target resource MAY instead respond with a status code of 404 Not Found. (See also: [RFC 7231, Section 6.5.4](https://tools.ietf.org/html/rfc7231#section-6.5.4)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘403 Forbidden’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPNotFound(headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPNotFound) 404 Not Found. The origin server did not find a current representation for the target resource or is not willing to disclose that one exists. A 404 status code does not indicate whether this lack of representation is temporary or permanent; the 410 Gone status code is preferred over 404 if the origin server knows, presumably through some configurable means, that the condition is likely to be permanent. A 404 response is cacheable by default; i.e., unless otherwise indicated by the method definition or explicit cache controls. (See also: [RFC 7231, Section 6.5.3](https://tools.ietf.org/html/rfc7231#section-6.5.3)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly error title. If not provided, and `description` is also not provided, no body will be included in the response. * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two (default `None`). * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPMethodNotAllowed(allowed_methods, headers=None, kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPMethodNotAllowed) 405 Method Not Allowed. The method received in the request-line is known by the origin server but not supported by the target resource. The origin server MUST generate an Allow header field in a 405 response containing a list of the target resource’s currently supported methods. A 405 response is cacheable by default; i.e., unless otherwise indicated by the method definition or explicit cache controls. (See also: [RFC 7231, Section 6.5.5](https://tools.ietf.org/html/rfc7231#section-6.5.5)) \| Parameters: \| allowed\_methods** (list of str) – Allowed HTTP methods for this resource (e.g., `['GET', 'POST', 'HEAD']`). \| \| Keyword Arguments: \| \| \| * title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly error title. If not provided, and `description` is also not provided, no body will be included in the response. * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two (default `None`). * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPNotAcceptable(description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPNotAcceptable) 406 Not Acceptable. The target resource does not have a current representation that would be acceptable to the user agent, according to the proactive negotiation header fields received in the request, and the server is unwilling to supply a default representation. The server SHOULD generate a payload containing a list of available representation characteristics and corresponding resource identifiers from which the user or user agent can choose the one most appropriate. A user agent MAY automatically select the most appropriate choice from that list. However, this specification does not define any standard for such automatic selection, as described in [RFC 7231, Section 6.4.1](https://tools.ietf.org/html/rfc7231#section-6.4.1) (See also: [RFC 7231, Section 6.5.6](https://tools.ietf.org/html/rfc7231#section-6.5.6)) \| Keyword Arguments: \| \| \| description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPConflict(title=None, description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPConflict) 409 Conflict. The request could not be completed due to a conflict with the current state of the target resource. This code is used in situations where the user might be able to resolve the conflict and resubmit the request. The server SHOULD generate a payload that includes enough information for a user to recognize the source of the conflict. Conflicts are most likely to occur in response to a PUT request. For example, if versioning were being used and the representation being PUT included changes to a resource that conflict with those made by an earlier (third-party) request, the origin server might use a 409 response to indicate that it can’t complete the request. In this case, the response representation would likely contain information useful for merging the differences based on the revision history. (See also: [RFC 7231, Section 6.5.8](https://tools.ietf.org/html/rfc7231#section-6.5.8)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘409 Conflict’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPGone(headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPGone) 410 Gone. The target resource is no longer available at the origin server and this condition is likely to be permanent. If the origin server does not know, or has no facility to determine, whether or not the condition is permanent, the status code 404 Not Found ought to be used instead. The 410 response is primarily intended to assist the task of web maintenance by notifying the recipient that the resource is intentionally unavailable and that the server owners desire that remote links to that resource be removed. Such an event is common for limited-time, promotional services and for resources belonging to individuals no longer associated with the origin server’s site. It is not necessary to mark all permanently unavailable resources as “gone” or to keep the mark for any length of time – that is left to the discretion of the server owner. A 410 response is cacheable by default; i.e., unless otherwise indicated by the method definition or explicit cache controls. (See also: [RFC 7231, Section 6.5.9](https://tools.ietf.org/html/rfc7231#section-6.5.9)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly error title. If not provided, and `description` is also not provided, no body will be included in the response. * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two (default `None`). * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPLengthRequired(title=None, description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPLengthRequired) 411 Length Required. The server refuses to accept the request without a defined Content- Length. The client MAY repeat the request if it adds a valid Content-Length header field containing the length of the message body in the request message. (See also: [RFC 7231, Section 6.5.10](https://tools.ietf.org/html/rfc7231#section-6.5.10)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘411 Length Required’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPPreconditionFailed(title=None, description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPPreconditionFailed) 412 Precondition Failed. One or more conditions given in the request header fields evaluated to false when tested on the server. This response code allows the client to place preconditions on the current resource state (its current representations and metadata) and, thus, prevent the request method from being applied if the target resource is in an unexpected state. (See also: [RFC 7232, Section 4.2](https://tools.ietf.org/html/rfc7232#section-4.2)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘412 Precondition Failed’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPPayloadTooLarge(title=None, description=None, retry_after=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPPayloadTooLarge) 413 Payload Too Large. The server is refusing to process a request because the request payload is larger than the server is willing or able to process. The server MAY close the connection to prevent the client from continuing the request. If the condition is temporary, the server SHOULD generate a Retry- After header field to indicate that it is temporary and after what time the client MAY try again. (See also: [RFC 7231, Section 6.5.11](https://tools.ietf.org/html/rfc7231#section-6.5.11)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘413 Payload Too Large’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * retry\_after ([datetime](https://docs.python.org/3/library/datetime.html#module-datetime "(in Python v3.7)") or [int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – Value for the Retry-After header. If a `datetime` object, will serialize as an HTTP date. Otherwise, a non-negative `int` is expected, representing the number of seconds to wait. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPUriTooLong(title=None, description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPUriTooLong) 414 URI Too Long. The server is refusing to service the request because the request- target is longer than the server is willing to interpret. This rare condition is only likely to occur when a client has improperly converted a POST request to a GET request with long query information, when the client has descended into a “black hole” of redirection (e.g., a redirected URI prefix that points to a suffix of itself) or when the server is under attack by a client attempting to exploit potential security holes. A 414 response is cacheable by default; i.e., unless otherwise indicated by the method definition or explicit cache controls. (See also: [RFC 7231, Section 6.5.12](https://tools.ietf.org/html/rfc7231#section-6.5.12)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘414 URI Too Long’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two (default `None`). * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPUnsupportedMediaType(description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPUnsupportedMediaType) 415 Unsupported Media Type. The origin server is refusing to service the request because the payload is in a format not supported by this method on the target resource. The format problem might be due to the request’s indicated Content- Type or Content-Encoding, or as a result of inspecting the data directly. (See also: [RFC 7231, Section 6.5.13](https://tools.ietf.org/html/rfc7231#section-6.5.13)) \| Keyword Arguments: \| \| \| description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPRangeNotSatisfiable(resource_length, headers=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPRangeNotSatisfiable) 416 Range Not Satisfiable. None of the ranges in the request’s Range header field overlap the current extent of the selected resource or that the set of ranges requested has been rejected due to invalid ranges or an excessive request of small or overlapping ranges. For byte ranges, failing to overlap the current extent means that the first-byte-pos of all of the byte-range-spec values were greater than the current length of the selected representation. When this status code is generated in response to a byte-range request, the sender SHOULD generate a Content-Range header field specifying the current length of the selected representation. (See also: [RFC 7233, Section 4.4](https://tools.ietf.org/html/rfc7233#section-4.4)) \| Parameters: \| resource\_length – The maximum value for the last-byte-pos of a range request. Used to set the Content-Range header. \| `exception falcon.HTTPUnprocessableEntity(title=None, description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPUnprocessableEntity) 422 Unprocessable Entity. The server understands the content type of the request entity (hence a 415 Unsupported Media Type status code is inappropriate), and the syntax of the request entity is correct (thus a 400 Bad Request status code is inappropriate) but was unable to process the contained instructions. For example, this error condition may occur if an XML request body contains well-formed (i.e., syntactically correct), but semantically erroneous, XML instructions. (See also: [RFC 4918, Section 11.2](https://tools.ietf.org/html/rfc4918#section-11.2)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘422 Unprocessable Entity’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPLocked(title=None, description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPLocked) 423 Locked. The 423 (Locked) status code means the source or destination resource of a method is locked. This response SHOULD contain an appropriate precondition or postcondition code, such as ‘lock-token-submitted’ or ‘no-conflicting-lock’. (See also: [RFC 4918, Section 11.3](https://tools.ietf.org/html/rfc4918#section-11.3)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘423 Locked’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPFailedDependency(title=None, description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPFailedDependency) 424 Failed Dependency. The 424 (Failed Dependency) status code means that the method could not be performed on the resource because the requested action depended on another action and that action failed. (See also: [RFC 4918, Section 11.4](https://tools.ietf.org/html/rfc4918#section-11.4)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘424 Failed Dependency’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPPreconditionRequired(title=None, description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPPreconditionRequired) 428 Precondition Required. The 428 status code indicates that the origin server requires the request to be conditional. Its typical use is to avoid the “lost update” problem, where a client GETs a resource’s state, modifies it, and PUTs it back to the server, when meanwhile a third party has modified the state on the server, leading to a conflict. By requiring requests to be conditional, the server can assure that clients are working with the correct copies. Responses using this status code SHOULD explain how to resubmit the request successfully. (See also: [RFC 6585, Section 3](https://tools.ietf.org/html/rfc6585#section-3)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘428 Precondition Required’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPTooManyRequests(title=None, description=None, retry_after=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPTooManyRequests) 429 Too Many Requests. The user has sent too many requests in a given amount of time (“rate limiting”). The response representations SHOULD include details explaining the condition, and MAY include a Retry-After header indicating how long to wait before making a new request. Responses with the 429 status code MUST NOT be stored by a cache. (See also: [RFC 6585, Section 4](https://tools.ietf.org/html/rfc6585#section-4)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘429 Too Many Requests’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the rate limit that was exceeded. * retry\_after ([datetime](https://docs.python.org/3/library/datetime.html#module-datetime "(in Python v3.7)") or [int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – Value for the Retry-After header. If a `datetime` object, will serialize as an HTTP date. Otherwise, a non-negative `int` is expected, representing the number of seconds to wait. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPRequestHeaderFieldsTooLarge(title=None, description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPRequestHeaderFieldsTooLarge) 431 Request Header Fields Too Large. The 431 status code indicates that the server is unwilling to process the request because its header fields are too large. The request MAY be resubmitted after reducing the size of the request header fields. It can be used both when the set of request header fields in total is too large, and when a single header field is at fault. In the latter case, the response representation SHOULD specify which header field was too large. Responses with the 431 status code MUST NOT be stored by a cache. (See also: [RFC 6585, Section 5](https://tools.ietf.org/html/rfc6585#section-5)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘431 Request Header Fields Too Large’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the rate limit that was exceeded. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPUnavailableForLegalReasons(title=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPUnavailableForLegalReasons) 451 Unavailable For Legal Reasons. The server is denying access to the resource as a consequence of a legal demand. The server in question might not be an origin server. This type of legal demand typically most directly affects the operations of ISPs and search engines. Responses using this status code SHOULD include an explanation, in the response body, of the details of the legal demand: the party making it, the applicable legislation or regulation, and what classes of person and resource it applies to. Note that in many cases clients can still access the denied resource by using technical countermeasures such as a VPN or the Tor network. A 451 response is cacheable by default; i.e., unless otherwise indicated by the method definition or explicit cache controls. (See also: [RFC 7725, Section 3](https://tools.ietf.org/html/rfc7725#section-3)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘451 Unavailable For Legal Reasons’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two (default `None`). * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPInternalServerError(title=None, description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPInternalServerError) 500 Internal Server Error. The server encountered an unexpected condition that prevented it from fulfilling the request. (See also: [RFC 7231, Section 6.6.1](https://tools.ietf.org/html/rfc7231#section-6.6.1)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘500 Internal Server Error’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPNotImplemented(title=None, description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPNotImplemented) 501 Not Implemented. The 501 (Not Implemented) status code indicates that the server does not support the functionality required to fulfill the request. This is the appropriate response when the server does not recognize the request method and is not capable of supporting it for any resource. A 501 response is cacheable by default; i.e., unless otherwise indicated by the method definition or explicit cache controls as described in [RFC 7234, Section 4.2.2.](https://tools.ietf.org/html/rfc7234#section-4.2.2.) (See also: [RFC 7231, Section 6.6.2](https://tools.ietf.org/html/rfc7231#section-6.6.2)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘500 Internal Server Error’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPBadGateway(title=None, description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPBadGateway) 502 Bad Gateway. The server, while acting as a gateway or proxy, received an invalid response from an inbound server it accessed while attempting to fulfill the request. (See also: [RFC 7231, Section 6.6.3](https://tools.ietf.org/html/rfc7231#section-6.6.3)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘502 Bad Gateway’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPServiceUnavailable(title=None, description=None, retry_after=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPServiceUnavailable) 503 Service Unavailable. The server is currently unable to handle the request due to a temporary overload or scheduled maintenance, which will likely be alleviated after some delay. The server MAY send a Retry-After header field to suggest an appropriate amount of time for the client to wait before retrying the request. Note: The existence of the 503 status code does not imply that a server has to use it when becoming overloaded. Some servers might simply refuse the connection. (See also: [RFC 7231, Section 6.6.4](https://tools.ietf.org/html/rfc7231#section-6.6.4)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘503 Service Unavailable’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * retry\_after ([datetime](https://docs.python.org/3/library/datetime.html#module-datetime "(in Python v3.7)") or [int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – Value for the Retry-After header. If a `datetime` object, will serialize as an HTTP date. Otherwise, a non-negative `int` is expected, representing the number of seconds to wait. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPGatewayTimeout(title=None, description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPGatewayTimeout) 504 Gateway Timeout. The 504 (Gateway Timeout) status code indicates that the server, while acting as a gateway or proxy, did not receive a timely response from an upstream server it needed to access in order to complete the request. (See also: [RFC 7231, Section 6.6.5](https://tools.ietf.org/html/rfc7231#section-6.6.5)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘503 Service Unavailable’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPVersionNotSupported(title=None, description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPVersionNotSupported) 505 HTTP Version Not Supported The 505 (HTTP Version Not Supported) status code indicates that the server does not support, or refuses to support, the major version of HTTP that was used in the request message. The server is indicating that it is unable or unwilling to complete the request using the same major version as the client (as described in [RFC 7230, Section 2.6](https://tools.ietf.org/html/rfc7230#section-2.6)), other than with this error message. The server SHOULD generate a representation for the 505 response that describes why that version is not supported and what other protocols are supported by that server. (See also: [RFC 7231, Section 6.6.6](https://tools.ietf.org/html/rfc7231#section-6.6.6)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘503 Service Unavailable’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPInsufficientStorage(title=None, description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPInsufficientStorage) 507 Insufficient Storage. The 507 (Insufficient Storage) status code means the method could not be performed on the resource because the server is unable to store the representation needed to successfully complete the request. This condition is considered to be temporary. If the request that received this status code was the result of a user action, the request MUST NOT be repeated until it is requested by a separate user action. (See also: [RFC 4918, Section 11.5](https://tools.ietf.org/html/rfc4918#section-11.5)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘507 Insufficient Storage’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPLoopDetected(title=None, description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPLoopDetected) 508 Loop Detected. The 508 (Loop Detected) status code indicates that the server terminated an operation because it encountered an infinite loop while processing a request with “Depth: infinity”. This status indicates that the entire operation failed. (See also: [RFC 5842, Section 7.2](https://tools.ietf.org/html/rfc5842#section-7.2)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘508 Loop Detected’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \| `exception falcon.HTTPNetworkAuthenticationRequired(title=None, description=None, headers=None, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/errors.html#HTTPNetworkAuthenticationRequired) 511 Network Authentication Required. The 511 status code indicates that the client needs to authenticate to gain network access. The response representation SHOULD contain a link to a resource that allows the user to submit credentials. Note that the 511 response SHOULD NOT contain a challenge or the authentication interface itself, because clients would show the interface as being associated with the originally requested URL, which may cause confusion. The 511 status SHOULD NOT be generated by origin servers; it is intended for use by intercepting proxies that are interposed as a means of controlling access to the network. Responses with the 511 status code MUST NOT be stored by a cache. (See also: [RFC 6585, Section 6](https://tools.ietf.org/html/rfc6585#section-6)) \| Keyword Arguments: \| \| \| title ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Error title (default ‘511 Network Authentication Required’). * description ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Human-friendly description of the error, along with a helpful suggestion or two. * headers ([dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – A `dict` of header names and values to set, or a `list` of (name, value) tuples. Both name and value must be of type `str` or `StringType`, and only character values 0x00 through 0xFF may be used on platforms that use wide characters. Note The Content-Type header, if present, will be overridden. If you wish to return custom error messages, you can create your own HTTP error class, and install an error handler to convert it into an appropriate HTTP response for the client Note Falcon can process a list of `tuple` slightly faster than a `dict`. * href ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A URL someone can visit to find out more information (default `None`). Unicode characters are percent-encoded. * href\_text ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – If href is given, use this as the friendly title/description for the link (default ‘API documentation for this error’). * code ([int](https://docs.python.org/3/library/functions.html#int "(in Python v3.7)")) – An internal code that customers can reference in their support request or to help them when searching for knowledge base articles related to this error (default `None`). \|	programming_docs
falcon The API Class The API Class ============= Falcon’s API class is a WSGI “application” that you can host with any standard-compliant WSGI server. ``` import falcon app = falcon.API() ``` `class falcon.API(media_type='application/json', request_type=<class 'falcon.request.Request'>, response_type=<class 'falcon.response.Response'>, middleware=None, router=None, independent_middleware=True)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/api.html#API) This class is the main entry point into a Falcon-based app. Each API instance provides a callable WSGI interface and a routing engine. \| Keyword Arguments: \| \| \| * media\_type ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Default media type to use as the value for the Content-Type header on responses (default ‘application/json’). The `falcon` module provides a number of constants for common media types, such as `falcon.MEDIA_MSGPACK`, `falcon.MEDIA_YAML`, `falcon.MEDIA_XML`, etc. * middleware ([object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)") or [list](https://docs.python.org/3/library/stdtypes.html#list "(in Python v3.7)")) – Either a single object or a list of objects (instantiated classes) that implement the following middleware component interface: ``` class ExampleComponent(object): def process_request(self, req, resp): """Process the request before routing it. Note: Because Falcon routes each request based on req.path, a request can be effectively re-routed by setting that attribute to a new value from within process_request(). Args: req: Request object that will eventually be routed to an on_* responder method. resp: Response object that will be routed to the on_* responder. """ def process_resource(self, req, resp, resource, params): """Process the request and resource after routing. Note: This method is only called when the request matches a route to a resource. Args: req: Request object that will be passed to the routed responder. resp: Response object that will be passed to the responder. resource: Resource object to which the request was routed. May be None if no route was found for the request. params: A dict-like object representing any additional params derived from the route's URI template fields, that will be passed to the resource's responder method as keyword arguments. """ def process_response(self, req, resp, resource, req_succeeded) """Post-processing of the response (after routing). Args: req: Request object. resp: Response object. resource: Resource object to which the request was routed. May be None if no route was found for the request. req_succeeded: True if no exceptions were raised while the framework processed and routed the request; otherwise False. """ ``` (See also: [Middleware](middleware#middleware)) * request\_type ([Request](request_and_response#falcon.Request "falcon.Request")) – `Request`-like class to use instead of Falcon’s default class. Among other things, this feature affords inheriting from `falcon.request.Request` in order to override the `context_type` class variable. (default `falcon.request.Request`) * response\_type ([Response](request_and_response#falcon.Response "falcon.Response")) – `Response`-like class to use instead of Falcon’s default class. (default `falcon.response.Response`) * router ([object](https://docs.python.org/3/library/functions.html#object "(in Python v3.7)")) – An instance of a custom router to use in lieu of the default engine. (See also: [Custom Routers](routing#routing-custom)) * independent\_middleware ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Set to `False` if response middleware should not be executed independently of whether or not request middleware raises an exception (default `True`). When this option is set to `False`, a middleware component’s `process_response()` method will NOT be called when that same component’s `process_request()` (or that of a component higher up in the stack) raises an exception. \| `req_options` A set of behavioral options related to incoming requests. (See also: [`RequestOptions`](#falcon.RequestOptions "falcon.RequestOptions")) `resp_options` A set of behavioral options related to outgoing responses. (See also: [`ResponseOptions`](#falcon.ResponseOptions "falcon.ResponseOptions")) `router_options` Configuration options for the router. If a custom router is in use, and it does not expose any configurable options, referencing this attribute will raise an instance of `AttributeError`. (See also: [CompiledRouterOptions](#compiled-router-options)) `add_error_handler(exception, handler=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/api.html#API.add_error_handler) Register a handler for one or more exception types. Error handlers may be registered for any exception type, including [`HTTPError`](errors#falcon.HTTPError "falcon.HTTPError") or [`HTTPStatus`](status#falcon.HTTPStatus "falcon.HTTPStatus"). This feature provides a central location for logging and otherwise handling exceptions raised by responders, hooks, and middleware components. A handler can raise an instance of [`HTTPError`](errors#falcon.HTTPError "falcon.HTTPError") or [`HTTPStatus`](status#falcon.HTTPStatus "falcon.HTTPStatus") to communicate information about the issue to the client. Alternatively, a handler may modify `resp` directly. Error handlers are matched in LIFO order. In other words, when searching for an error handler to match a raised exception, and more than one handler matches the exception type, the framework will choose the one that was most recently registered. Therefore, more general error handlers (e.g., for the standard `Exception` type) should be added first, to avoid masking more specific handlers for subclassed types. Note By default, the framework installs two handlers, one for [`HTTPError`](errors#falcon.HTTPError "falcon.HTTPError") and one for [`HTTPStatus`](status#falcon.HTTPStatus "falcon.HTTPStatus"). These can be overridden by adding a custom error handler method for the exception type in question. \| Parameters: \| * exception ([type](https://docs.python.org/3/library/functions.html#type "(in Python v3.7)") or iterable of types) – When handling a request, whenever an error occurs that is an instance of the specified type(s), the associated handler will be called. Either a single type or an iterable of types may be specified. * handler (callable) – A function or callable object taking the form `func(req, resp, ex, params)`. If not specified explicitly, the handler will default to `exception.handle`, where `exception` is the error type specified above, and `handle` is a static method (i.e., decorated with @staticmethod) that accepts the same params just described. For example: ``` class CustomException(CustomBaseException): @staticmethod def handle(req, resp, ex, params): # TODO: Log the error # Convert to an instance of falcon.HTTPError raise falcon.HTTPError(falcon.HTTP_792) ``` If an iterable of exception types is specified instead of a single type, the handler must be explicitly specified. \| `add_route(uri_template, resource, *kwargs)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/api.html#API.add_route) Associate a templatized URI path with a resource. Falcon routes incoming requests to resources based on a set of URI templates. If the path requested by the client matches the template for a given route, the request is then passed on to the associated resource for processing. If no route matches the request, control then passes to a default responder that simply raises an instance of [`HTTPNotFound`](errors#falcon.HTTPNotFound "falcon.HTTPNotFound"). This method delegates to the configured router’s `add_route()` method. To override the default behavior, pass a custom router object to the [`API`](#falcon.API "falcon.API") initializer. (See also: [Routing](routing#routing)) \| Parameters: \| uri\_template ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A templatized URI. Care must be taken to ensure the template does not mask any sink patterns, if any are registered. (See also: [`add_sink()`](#falcon.API.add_sink "falcon.API.add_sink")) * resource (instance) – Object which represents a REST resource. Falcon will pass GET requests to `on_get()`, PUT requests to `on_put()`, etc. If any HTTP methods are not supported by your resource, simply don’t define the corresponding request handlers, and Falcon will do the right thing. \| \| Keyword Arguments: \| \| \| suffix ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Optional responder name suffix for this route. If a suffix is provided, Falcon will map GET requests to `on_get_{suffix}()`, POST requests to `on_post_{suffix}()`, etc. In this way, multiple closely-related routes can be mapped to the same resource. For example, a single resource class can use suffixed responders to distinguish requests for a single item vs. a collection of those same items. Another class might use a suffixed responder to handle a shortlink route in addition to the regular route for the resource. \| Note Any additional keyword arguments not defined above are passed through to the underlying router’s `add_route()` method. The default router ignores any additional keyword arguments, but custom routers may take advantage of this feature to receive additional options when setting up routes. Custom routers MUST accept such arguments using the variadic pattern (`*kwargs`), and ignore any keyword arguments that they don’t support. `add_sink(sink, prefix='/')` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/api.html#API.add_sink) Register a sink method for the API. If no route matches a request, but the path in the requested URI matches a sink prefix, Falcon will pass control to the associated sink, regardless of the HTTP method requested. Using sinks, you can drain and dynamically handle a large number of routes, when creating static resources and responders would be impractical. For example, you might use a sink to create a smart proxy that forwards requests to one or more backend services. \| Parameters: \| sink (callable) – A callable taking the form `func(req, resp)`. * prefix ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – A regex string, typically starting with ‘/’, which will trigger the sink if it matches the path portion of the request’s URI. Both strings and precompiled regex objects may be specified. Characters are matched starting at the beginning of the URI path. Note Named groups are converted to kwargs and passed to the sink as such. Warning If the prefix overlaps a registered route template, the route will take precedence and mask the sink. (See also: [`add_route()`](#falcon.API.add_route "falcon.API.add_route")) \| `add_static_route(prefix, directory, downloadable=False, fallback_filename=None)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/api.html#API.add_static_route) Add a route to a directory of static files. Static routes provide a way to serve files directly. This feature provides an alternative to serving files at the web server level when you don’t have that option, when authorization is required, or for testing purposes. Warning Serving files directly from the web server, rather than through the Python app, will always be more efficient, and therefore should be preferred in production deployments. For security reasons, the directory and the fallback\_filename (if provided) should be read only for the account running the application. Static routes are matched in LIFO order. Therefore, if the same prefix is used for two routes, the second one will override the first. This also means that more specific routes should be added after less specific ones. For example, the following sequence would result in `'/foo/bar/thing.js'` being mapped to the `'/foo/bar'` route, and `'/foo/xyz/thing.js'` being mapped to the `'/foo'` route: ``` api.add_static_route('/foo', foo_path) api.add_static_route('/foo/bar', foobar_path) ``` \| Parameters: \| * prefix ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – The path prefix to match for this route. If the path in the requested URI starts with this string, the remainder of the path will be appended to the source directory to determine the file to serve. This is done in a secure manner to prevent an attacker from requesting a file outside the specified directory. Note that static routes are matched in LIFO order, and are only attempted after checking dynamic routes and sinks. * directory ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – The source directory from which to serve files. * downloadable ([bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)")) – Set to `True` to include a Content-Disposition header in the response. The “filename” directive is simply set to the name of the requested file. * fallback\_filename ([str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)")) – Fallback filename used when the requested file is not found. Can be a relative path inside the prefix folder or any valid absolute path. \| `set_error_serializer(serializer)` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/api.html#API.set_error_serializer) Override the default serializer for instances of [`HTTPError`](errors#falcon.HTTPError "falcon.HTTPError"). When a responder raises an instance of [`HTTPError`](errors#falcon.HTTPError "falcon.HTTPError"), Falcon converts it to an HTTP response automatically. The default serializer supports JSON and XML, but may be overridden by this method to use a custom serializer in order to support other media types. Note If a custom media type is used and the type includes a “+json” or “+xml” suffix, the default serializer will convert the error to JSON or XML, respectively. Note The default serializer will not render any response body for [`HTTPError`](errors#falcon.HTTPError "falcon.HTTPError") instances where the `has_representation` property evaluates to `False` (such as in the case of types that subclass [`falcon.http_error.NoRepresentation`](errors#falcon.http_error.NoRepresentation "falcon.http_error.NoRepresentation")). However a custom serializer will be called regardless of the property value, and it may choose to override the representation logic. The [`HTTPError`](errors#falcon.HTTPError "falcon.HTTPError") class contains helper methods, such as `to_json()` and `to_dict()`, that can be used from within custom serializers. For example: ``` def my_serializer(req, resp, exception): representation = None preferred = req.client_prefers(('application/x-yaml', 'application/json')) if exception.has_representation and preferred is not None: if preferred == 'application/json': representation = exception.to_json() else: representation = yaml.dump(exception.to_dict(), encoding=None) resp.body = representation resp.content_type = preferred resp.append_header('Vary', 'Accept') ``` \| Parameters: \| serializer (callable) – A function taking the form `func(req, resp, exception)`, where `req` is the request object that was passed to the responder method, `resp` is the response object, and `exception` is an instance of `falcon.HTTPError`. \| `class falcon.RequestOptions` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/request.html#RequestOptions) Defines a set of configurable request options. An instance of this class is exposed via [`API.req_options`](#falcon.API.req_options "falcon.API.req_options") for configuring certain [`Request`](request_and_response#falcon.Request "falcon.Request") behaviors. `keep_blank_qs_values` Set to `False` to ignore query string params that have missing or blank values (default `True`). For comma-separated values, this option also determines whether or not empty elements in the parsed list are retained. \| Type: \| [bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)") \| `auto_parse_form_urlencoded` Set to `True` in order to automatically consume the request stream and merge the results into the request’s query string params when the request’s content type is application/x-www-form-urlencoded (default `False`). Enabling this option makes the form parameters accessible via [`params`](request_and_response#falcon.Request.params "falcon.Request.params"), [`get_param()`](request_and_response#falcon.Request.get_param "falcon.Request.get_param"), etc. Warning When this option is enabled, the request’s body stream will be left at EOF. The original data is not retained by the framework. Note The character encoding for fields, before percent-encoding non-ASCII bytes, is assumed to be UTF-8. The special `_charset_` field is ignored if present. Falcon expects form-encoded request bodies to be encoded according to the standard W3C algorithm (see also <http://goo.gl/6rlcux>). `auto_parse_qs_csv` Set to `True` to split query string values on any non-percent-encoded commas (default `False`). When `False`, values containing commas are left as-is. In this mode, list items are taken only from multiples of the same parameter name within the query string (i.e. `/?t=1,2,3&t=4` becomes `['1,2,3', '4']`). When `auto_parse_qs_csv` is set to `True`, the query string value is also split on non-percent-encoded commas and these items are added to the final list (i.e. `/?t=1,2,3&t=4` becomes `['1', '2', '3', '4']`). `strip_url_path_trailing_slash` Set to `True` in order to strip the trailing slash, if present, at the end of the URL path (default `False`). When this option is enabled, the URL path is normalized by stripping the trailing slash character. This lets the application define a single route to a resource for a path that may or may not end in a forward slash. However, this behavior can be problematic in certain cases, such as when working with authentication schemes that employ URL-based signatures. `default_media_type` The default media-type to use when deserializing a response. This value is normally set to the media type provided when a [`falcon.API`](#falcon.API "falcon.API") is initialized; however, if created independently, this will default to the `DEFAULT_MEDIA_TYPE` specified by Falcon. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `media_handlers` A dict-like object that allows you to configure the media-types that you would like to handle. By default, a handler is provided for the `application/json` media type. \| Type: \| [Handlers](media#falcon.media.Handlers "falcon.media.Handlers") \| `class falcon.ResponseOptions` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/response.html#ResponseOptions) Defines a set of configurable response options. An instance of this class is exposed via [`API.resp_options`](#falcon.API.resp_options "falcon.API.resp_options") for configuring certain [`Response`](request_and_response#falcon.Response "falcon.Response") behaviors. `secure_cookies_by_default` Set to `False` in development environments to make the `secure` attribute for all cookies default to `False`. This can make testing easier by not requiring HTTPS. Note, however, that this setting can be overridden via `set_cookie()`’s `secure` kwarg. \| Type: \| [bool](https://docs.python.org/3/library/functions.html#bool "(in Python v3.7)") \| `default_media_type` The default Internet media type (RFC 2046) to use when deserializing a response. This value is normally set to the media type provided when a [`falcon.API`](#falcon.API "falcon.API") is initialized; however, if created independently, this will default to the `DEFAULT_MEDIA_TYPE` specified by Falcon. \| Type: \| [str](https://docs.python.org/3/library/stdtypes.html#str "(in Python v3.7)") \| `media_handlers` A dict-like object that allows you to configure the media-types that you would like to handle. By default, a handler is provided for the `application/json` media type. \| Type: \| [Handlers](media#falcon.media.Handlers "falcon.media.Handlers") \| `static_media_types` A mapping of dot-prefixed file extensions to Internet media types (RFC 2046). Defaults to `mimetypes.types_map` after calling `mimetypes.init()`. \| Type: \| [dict](https://docs.python.org/3/library/stdtypes.html#dict "(in Python v3.7)") \| `class falcon.routing.CompiledRouterOptions` [[source]](https://falcon.readthedocs.io/en/2.0.0/_modules/falcon/routing/compiled.html#CompiledRouterOptions) Defines a set of configurable router options. An instance of this class is exposed via [`API.router_options`](#falcon.API.router_options "falcon.API.router_options") for configuring certain [`CompiledRouter`](routing#falcon.routing.CompiledRouter "falcon.routing.CompiledRouter") behaviors. `converters` Represents the collection of named converters that may be referenced in URI template field expressions. Adding additional converters is simply a matter of mapping an identifier to a converter class: ``` api.router_options.converters['mc'] = MyConverter ``` The identifier can then be used to employ the converter within a URI template: ``` api.add_route('/{some_field:mc}', some_resource) ``` Converter names may only contain ASCII letters, digits, and underscores, and must start with either a letter or an underscore. Warning Converter instances are shared between requests. Therefore, in threaded deployments, care must be taken to implement custom converters in a thread-safe manner. (See also: [Field Converters](routing#routing-field-converters))	programming_docs

Subsets and Splits